《结构力学》作业答案
结构力学作业答案

一、对下列结构分析几何组成,写出分析过程。
(说明:①代表二元体规则,②代表两刚片规则,③代表三刚片规则)1.AC DBE2.【地基刚片AB③刚片CE】结论:结论:无多余约束几何不变体系3.【【刚片ADE ③刚片EFB 杆KC】②地基】结论:无多余约束的几何不变体系4.【【杆56①点4 点7 点8 点3 点2 点1】②地基】结论:无多余约束几何不变体系5.【【地基,刚片ABC , ③刚片CDE】点F,点G,①点H,点I】结论:无多余约束几何不变体系6.【【杆AB ②地基】杆CD③杆DE】少一约束结论:可变体系二、判定图示桁架中的零杆。
图中画线的是0杆三、图示桁架,哪些杆件是零杆(不包括支座链杆)。
图中画线的是0杆四、作图示结构的弯矩图qh五、计算图示多跨静定梁,画弯矩图、剪力图.q解:qq0.5q 0.5q 0.5q q / 8M六、计算图示多跨静定梁,画弯矩图、剪力图.七、计算图示静定刚架的内力,并作内力图。
八、 作图示结构的弯矩图解:支座反力: )(42↑=KN Y B )(22↓=KN Y A )(48←=KN X A九、作图示结构的弯矩图北京交通大学现代远程教育昌平学习中心 作业二答案课程名称:结构力学 专业:土木工程本科年级:2011级 学期:2012-2013学年第一学期 学号: 姓名:一、 计算图示桁架a 、b 、c 三杆的轴力。
1)计算此结构的支座反力。
)(40↑=KN Y B )(40↑=KN Y A0=A X 2)计算指定杆内力。
0=Nb FKN F Na 60-=KN F Nc 60=二、求 图 示 桁 架 中 a 和b 杆 的 轴 力。
kn Na 210= kn N b 10-=三、求图示桁架中 a 和b 杆的轴力。
1)计算此结构的支座反力。
)(43↑=P Y A 0=A X2) 计算指定杆内力。
p F a 543= 0=b F四、解:1)设单位力2)画两个状态的弯矩图3)计算位移五、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
结构力学作业1

结构力学课程——作业一1. 荷载类型有哪些?答:荷载按作用时间的久暂可分为恒载和活载;按荷载的作用位置是否变化分为固定荷载和移动荷载;根据荷载对结构所产生的动力效应大小分为静力荷载和动力荷载。
2. 简述支座和结点类型,并画出相应的计算简图。
答:支座分为:活动铰支座、固定铰支座、固定支座、滑动支座。
计算简图如下:结点主要分为:铰结点、刚结点、组合结点。
计算简图如下:3. 名词解释:1)自由度;2)计算自由度;3)联系;4)瞬变体系;5)常变体系;6)刚片;7)几何不变体系;8)几何可变体系;9)拱轴线;10)高跨比自由度:是指体系远动时所具有的独立运动方式数目,也就是体系运动时可以独立变化的几何参数数目,或者说确定体系位置所需的独立坐标数目。
计算自由度:在分析体系是否几何不变时,可以根据体系的自由度W首先判断联系的数目是否足够。
为此,把W称为体系的计算自由度。
联系:限制运动的装置称为联系(或约束),体系的自由度可因加入联系而减少,能减少一个自由度的装置称为一个联系。
原为几何可变,经微小位移后即转化为几何不变的体系,称为瞬变体系。
经微小位移后仍能继续发生刚体运动的几何可变体系称为常变体系。
在机动分析中,由于不考虑材料的变形,因此可以把一根杆件或已知是几何不变的部分看作是一个刚体,在平面体系中又将刚体称为刚片。
由两根杆件与地基组成的胶结三角形,受到任意荷载作用时,若不考虑材料的变形,则其几何形状与位置均能保持不变,这样的体系称为几何不变体系。
胶结四边形,即使不考虑材料的变形,在很小的荷载作用下,也会发生机械运动而不能保持原有的几何形状和位置,这样的体系称为几何可变体系。
拱身各横截面形心的连线称为拱轴线。
拱高与跨度之比f/l称为高跨比。
4. 试述几何不变体系的三个基本组成规则,为什么说它们是同一规则。
答:几何不变体系的三个基本组成规则为:1、三刚片规则:三个刚片用不在同一直线上的三个单铰两两铰联,组成的体系是几何不变的,而且没有多余的联系。
结构力学-参考答案

模块1参考答案1.结构有哪几种分类?答:结构主要有:杆件结构,薄壁结构和实体结构三类。
2.结构力学的研究对象和研究任务是什么?答:结构力学的研究对象:结构力学的研究对象是杆件结构,薄壁结构和实体结构的受力分析将在弹性力学中进行研究。
严格地说,一般的杆件结构是空间结构,但它们中的大多数均可简化为平面结构。
所以,本门课程主要研究平面杆件结构,即组成结构的所有杆件及结构所承受的外荷载都在同一平面内的结构。
结构力学是研究结构的合理形式以及结构在受力状态下内力、变形、动力反应和稳定性等方面的规律性的科学。
研究的目的是使结构满足安全性、适用性和经济方面的要求。
建筑物、构筑物、结构物在各类工程中大量存在:(1)住宅、厂房等工业民用建筑物;(2)涵洞、隧道、堤坝、挡水墙等构造物;(3)桥梁、轮船、潜水艇、飞行器等结构物。
结构力学的任务:结构力学与材料力学、弹性力学有着密切的联系,他们的任务都是讨论变形体系的强度、刚度和稳定性,但在研究对象上有所区别。
材料力学基本上是研究单个杆件的计算,结构力学主要是研究杆件的结构,而弹性力学则研究各种薄壁结构和实体结构,同时对杆件也作更精确的分析。
结构力学研究杆件结构的强度、刚度和稳定性问题,其具体任务包括以下几个方面:(1)杆件结构的组成规律和合理的组成方式。
(2)杆件结构内力和变形的计算方法,以便进行结构强度和刚度的验算。
(3)杆件结构的稳定性以及在动力荷载作用下的反应。
结构力学是土木工程专业的一门重要的专业基础课,在各门课程的学习中起着承上启下的作用。
结构力学的计算方法很多,但所有方法都必须满足以下几个三个基本条件:(1)力系的平衡条件。
在一组力系作用下,结构的整体及其中任何一部分都应满足力系的平衡条件。
(2)变形的连续条件,即几何条件。
连续的结构发生变形后,仍是连续的,材料没有重叠和缝隙;同使结构的变形和位移应该满足支座和结点的约束条件。
(3)物理条件。
把结构的应力和变形联系起来的条件,即物理方程或本构方程。
结构力学(一)平时作业参考答案

1.叙述结构力学在实际工程领域中的作用。
答:该题涉及甚广,无标准答案,答题要求能联系教学内容列举一二,且叙述过程做到有理有据即可。
2.简单列举平面体系机动分析的基本方法,并举例说明其中一种方法的使用方法。
答:大体分为两刚片法和三刚片法,其中无多余约束的几何不变体系具有下述特征:1.一个刚片与两根链杆通过3个铰相连,且3个铰不在一直线上。
2.两个刚片用一个铰和一根链杆相联结,且3个铰不在同一直线上。
3.三个刚片用3个铰相连,且3个铰不在同一直线上。
4.两个刚片用3根链杆相连,且链杆不交于同一点。
此外,对于桁架也可尝试从计算自由度,零载法等进行分析,举例只需与其中一种方法相适应,且无原则性错误即可。
3.举例说明截面法和结点法计算静定桁架内力的基本方法。
答:结点法:以桁架结点为分析对象,利用平面汇交力系的基本平衡条件,首先计算支座力,再依次计算各杆内力。
截面法:用截面切断拟求内力的杆件,从桁架中截出一部分为隔离体,利用平面任意力系的基本平衡条件,计算各杆中的未知轴力。
如未知轴力只有三个,既不相交也不平行,则截面法可直接求出未知轴力。
举例要求能正确辨别分析对象,并建立相应的平衡方程。
4.举例说明对称性对简化结构力学分析的作用。
答:对称性通常对于结构形式和加载形式而言。
通常对于对称荷载下的对称结构、反对称荷载下的对称结构、任意荷载下的对称结构的几种典型的情况,均可在很大程度上简化问题,可降低结构的复杂性、减少计算的维数、使问题更加便于求解。
举例无标准答案,要求说明上述1种情况,并指出对称性的效用即可。
5.叙述何为三铰拱的合理轴线。
答:当三铰拱的轴线与压力线重合,各截面的弯矩和剪力都为零,此时轴线即为三铰拱的合理轴线。
6.简述梁、刚架结构在受力与变形方面的区别。
答:在外力作用下,梁承受弯矩和剪力的作用,其变形受制于弯矩和剪力,但通常以弯曲变形为主;刚架结构除了承受弯矩和剪力,可能还抵抗轴力的作用,其变形受制于弯矩、剪力以及轴力,同样地,通常也以弯曲变形为主,但还需要考虑刚架结构的几何形式,因此刚架结构的变形较梁复杂得多。
结构力学试题及参考答案
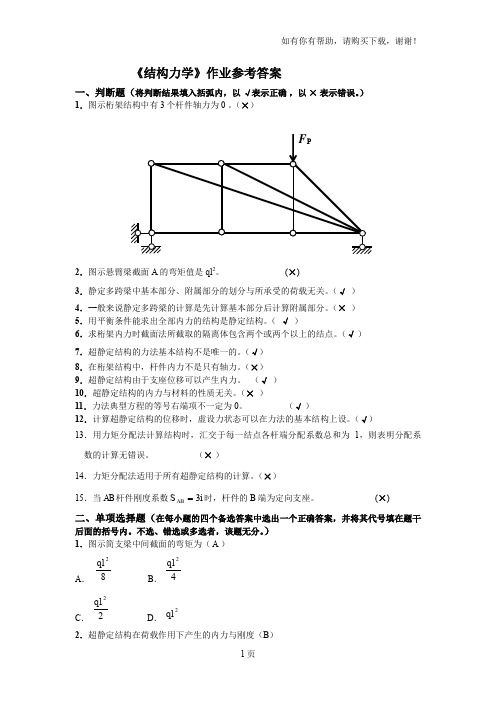
《结构力学》作业参考答案一、判断题(将判断结果填入括弧内,以 √表示正确 ,以 × 表示错误。
)1.图示桁架结构中有3个杆件轴力为0 。
(×)2.图示悬臂梁截面A 的弯矩值是ql 2。
(×)3.静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。
(√ )4.一般来说静定多跨梁的计算是先计算基本部分后计算附属部分。
(× )5.用平衡条件能求出全部内力的结构是静定结构。
( √ )6.求桁架内力时截面法所截取的隔离体包含两个或两个以上的结点。
(√ )7.超静定结构的力法基本结构不是唯一的。
(√)8.在桁架结构中,杆件内力不是只有轴力。
(×)9.超静定结构由于支座位移可以产生内力。
(√ )10.超静定结构的内力与材料的性质无关。
(× )11.力法典型方程的等号右端项不一定为0。
(√ )12.计算超静定结构的位移时,虚设力状态可以在力法的基本结构上设。
(√)13.用力矩分配法计算结构时,汇交于每一结点各杆端分配系数总和为1,则表明分配系数的计算无错误。
(× )14.力矩分配法适用于所有超静定结构的计算。
(×)15.当AB 杆件刚度系数i S AB 3 时,杆件的B 端为定向支座。
(×)二、单项选择题(在每小题的四个备选答案中选出一个正确答案,并将其代号填在题干后面的括号内。
不选、错选或多选者,该题无分。
)1.图示简支梁中间截面的弯矩为( A )A . 82qlB . 42qlC . 22ql D . 2ql2.超静定结构在荷载作用下产生的内力与刚度(B )A.无关 B.相对值有关C.绝对值有关 D.相对值绝对值都有关3.超静定结构的超静定次数等于结构中(B )A.约束的数目 B.多余约束的数目C.结点数 D.杆件数4.力法典型方程是根据以下哪个条件得到的(C)。
A.结构的平衡条件B.结构的物理条件C.多余约束处的位移协调条件D.同时满足A、B两个条件5.图示对称结构作用反对称荷载,杆件EI为常量,利用对称性简化后的一半结构为(A )。
结构力学习题及答案

构造力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系,那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕,kN F RQB 60=,kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕,m kN M B ⋅=40〔上侧受拉〕,kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c)4Fl M C =〔下侧受拉〕,θcos 2F F L QC =3-2 (a)0=E M ,m kN M F ⋅-=40〔上侧受拉〕,m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕,m kN M DF ⋅=8〔上侧受拉〕,m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕,m kN M DC ⋅=160〔上侧受拉〕,m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕,m kN M BD ⋅=45〔上侧受拉〕,kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕,m kN M DE ⋅=150〔上侧受拉〕,m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕,m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕,m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学答案(1)

结构力学答案《结构力学》第01章在线测试第一题、单项选择题(每题1分,5道题共5分)1、结构力学的研究对象是 BA、单根杆件B、杆件结构C、板壳结构D、实体结构2、对结构进行强度计算目的是为了保证结构AA、既经济又安全B、不致发生过大的变形C、美观实用D、不发生刚体运动3、对结构进行刚度计算,是为了保证结构 CA、不发生刚体运动B、美观实用C、不致发生过大的变形D、既经济又安全4、固定铰支座有几个约束反力分量? BA、一个B、两个C、三个D、四个5、可动铰支座有几个约束反力分量AA、一个B、两个C、三个D、四个第二题、多项选择题(每题2分,5道题共10分)1、结构的稳定性是指DEA、结构抵抗破坏的能力B、不发生刚体运动的能力C、结构抵抗变形的能力D、结构抵抗失稳的能力E、结构保持原有平衡形式的能力2、下列哪种情况不是平面结构BCDEA、所有杆件的轴线都位于同一平面内,荷载也作用在该平面内B、所有杆件的轴线都位于同一平面内,荷载与该平面垂直C、所有杆件的轴线都位于同一平面内,荷载与该平面平行D、所有杆件的轴线都不位于同一平面内E、荷载不作用在结构的平面内3、下列哪种情况应按空间结构处理ABDEA、所有杆件的轴线都位于同一平面内,荷载与该平面垂直B、所有杆件的轴线都不位于同一平面内C、所有杆件的轴线都位于同一平面内,荷载也作用在该平面内D、所有杆件的轴线都位于同一平面内,荷载与该平面平行E、荷载不作用在结构的平面内4、为了保证结构既经济又安全,要计算结构BA、强度B、刚度C、稳定性D、内力E、位移5、刚结点的约束特点是ABA、约束各杆端不能相对移动B、约束各杆端不能相对转动C、约束的各杆端可沿一个方向相对移动D、约束各杆端可相对转动E、约束各杆端可相对移动第三题、判断题(每题1分,5道题共5分)1、板壳结构的厚度远远小于其它两个尺度。
正确2、实体结构的厚度与其它两个尺度是同一量级。
正确3、为了保证结构既经济又安全,要对结构进行刚度计算。
中国农大网院《结构力学》作业答案第一套

对以下图示体系作几何组成分析。
如有多余的约束的几何不变体系,指出其多余约束的数目。
1、2、3、4、5、6、7、8、对以下图示静定结构进行内力分析,并作出内力图。
9、10、11、12、13、14、15、抛物线三铰拱轴线方程求:(1)支座反力(2)截面E内力(3)截面D点左右两侧的剪力和轴力。
16、抛物线三铰拱,铰C位于抛物线的顶点和最高点求:(1)铰C到支座A的水平距离(2)求支座反力(3)求D点处截面弯矩。
17、求指定杆件内力。
18、求指定杆件内力。
19、求指定杆件内力。
20、求指定杆件内力。
21、求B处的转角和C处的竖向位移(EI=常数)。
22、已知E=210Gpa,A=12×10-4m2,I=36×10-6m2,求A点的竖向位移。
23、求C点的竖向位移。
24、求D点的水平位移。
(1)设支座A向左移动1cm(2)设支座A下沉1cm(3)设支座B下沉1cm。
25、求C点的水平位移,设桁架各杆EA相等。
26、求C点的水平位移。
27、设三铰刚架内部升温30℃,外部温度不变,各杆截面为矩形,截面高度h相同,求C点竖向位移。
28、设柱AB由于材料收缩产生应变ε1,求B点的水平位移。
第一套作业答案1.没有多余约束的几何不变体系2.瞬变体系,没有多余约束3.没有多余约束的几何不变体系4.一个多余约束的几何不变体系5.没有多余约束的几何不变体系6.瞬变体系,没有多余约束7.没有多余约束的几何不变体系8.一个多余约束的几何不变体系。
结构力学-习题集(含答案)

结构⼒学-习题集(含答案)《结构⼒学》课程习题集⼀、单选题1.弯矩图肯定发⽣突变的截⾯是(D )。
A.有集中⼒作⽤的截⾯;B.剪⼒为零的截⾯;C.荷载为零的截⾯;D.有集中⼒偶作⽤的截⾯。
2.图⽰梁中C截⾯的弯矩是( D )。
4m2m4mA.12kN.m(下拉);B.3kN.m(上拉);C.8kN.m(下拉);D.11kN.m(下拉)。
3.静定结构有变温时,(C)。
A.⽆变形,⽆位移,⽆内⼒;B.有变形,有位移,有内⼒;C.有变形,有位移,⽆内⼒;D.⽆变形,有位移,⽆内⼒。
4.图⽰桁架a杆的内⼒是(D)。
A.2P;B.-2P;C.3P;D.-3P。
5.图⽰桁架,各杆EA为常数,除⽀座链杆外,零杆数为(A)。
A.四根;l= a66.图⽰梁A点的竖向位移为(向下为正)(C)。
A.)24/(3EIPl; B.)16/(3EIPl; C.)96/(53EIPl; D.)48/(53EIPl。
PEIEI A l/l/2227. 静定结构的内⼒计算与( A )。
A.EI ⽆关;B.EI 相对值有关;C.EI 绝对值有关;D.E ⽆关,I 有关。
8. 图⽰桁架,零杆的数⽬为:( C )。
A.5;9. 图⽰结构的零杆数⽬为( C )。
A.5;B.6;C.7;D.8。
10. 图⽰两结构及其受⼒状态,它们的内⼒符合( B )。
A.弯矩相同,剪⼒不同;B.弯矩相同,轴⼒不同;C.弯矩不同,剪⼒相同;D.弯矩不同,轴⼒不同。
PP2EI EI EIEI 2EI EIllhl l11. 刚结点在结构发⽣变形时的主要特征是( D )。
A.各杆可以绕结点结⼼⾃由转动; B.不变形; C.各杆之间的夹⾓可任意改变; D.各杆之间的夹⾓保持不变。
12. 若荷载作⽤在静定多跨梁的基本部分上,附属部分上⽆荷载作⽤,则( B )。
A.基本部分和附属部分均有内⼒;B.基本部分有内⼒,附属部分没有内⼒;C.基本部分⽆内⼒,附属部分有内⼒;D.不经过计算,⽆法判断。
《结构力学习题》(含答案解析)

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
中南大学《结构力学》课程作业一及参考答案(可编辑)

中南大学《结构力学》课程作业一及参考答案一单选题1图示桁架结点A处水平位移不等于零的有()。
AabBacCbcDabc参考答案:A2图示体系的几何组成是()。
A 无多余约束的几何不变体系B 几何可变体系C 有多余约束的几何不变体系D 瞬变体系参考答案:A3图示体系的几何组成是()。
A 无多余约束的几何不变体系B 几何可变体系C 有多余约束的几何不变体系D 瞬变体系参考答案:D4对于图示结构,下面结论是正确的是()。
A 该结构为桁架结构。
B 该结构是组合结构,其中只有杆57是受拉或受压杆(桁杆)。
C 杆123的内力只有轴力。
D 除杆34外,其余各杆均为桁杆。
参考答案:B5图示线弹性梁上先加F1,A、B两点挠度分别为、,再加F2,A、B两点挠度分别增加、,则F1做的总功为()。
ABCD参考答案:D6已知图a中A端转角,则图b中中梁的B端弯矩及A端转角为()。
ABCD参考答案:D7图示体系的几何组成是()。
A 无多余约束的几何不变体系B 几何可变体系C 有多余约束的几何不变体系D 瞬变体系参考答案:D8图示刚架,BC杆的B端弯矩为()。
A 25kN.m上拉B 25kN.m下拉C 10kN.m上拉D 10kN.m下拉参考答案:B9图示各体系中,几何不变且无多余约束的体系是()。
A 图aB 图bC 图cD 图d参考答案:D10图示有一切口的圆,外侧降温,内侧升温,切口处水平相对位移、铅直相对位移和相对转角的符号为(设虚力状态分别为图a、图b和图c)()。
A 大于0、小于0,等于0B 大于0、等于0,小于0C 等于0、小于0,大于0参考答案:C11对图示结构,结论正确的是()。
AB ,C ,D ,参考答案:B12图示结构A截面转角为(顺时针转为正)()。
ABCD参考答案:C13图示结构,B截面转角方向是()。
A 顺时针B 逆时针C 等于0参考答案:B14图示结构杆1的轴力以拉为正为()。
A 0BCD 2F参考答案:B15对比图(a)、(b)所示同一结构两种外因作用情况下C点的挠度和弯矩,下面结论成立的是()。
结构力学课后习题答案

结构力学课后习题答案(总23页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lf y )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
《结构力学》习题解答(内含解答图)

习题2-13试对图示体系进行几何组成分析。
习题2-13图习题2-13解答图
解:将原图结点进行编号,并将支座6换为单铰,如图(b)。取基础为刚片Ⅰ,△134为刚片Ⅱ,△235为刚片Ⅲ,由规则一知,三刚片用三个不共线的铰联结组成几何不变体。在此基础上增加二元体674、785,而杆38看作多余约束。杆910由铰联结着链杆10,可看作二元体,则整个体系为有一个多余约束的几何不变体系。
习题2-7试对图示体系进行几何组成分析。
习题2-7图习题2-7解答图
解:将题中的折杆用直杆代替,如图(b)所示。杆CD和链杆1由铰D联结构成二元体可以去掉;同理,去掉二元体杆CE和链杆2,去掉二元体ACB,则只剩下基础,故整个体系为几何不变体系,且无多余约束。
另外也可用基础与杆AC、杆BC是由不共线的三个铰联结,组成几何不变体,在此几何不变体上增加二元体杆CD和链杆1、杆CE和链杆2的方法分析。,
习题2-8试对图示体系进行几何组成分析。
习题2-8图习题2-8解答图
解:为了便于分析,对图中的链杆和刚片进行编号,分析过程见图2-21(b)。首先去掉二元体NMI、JNI,然后分析剩余部分。杆AD由固定支撑与基础联结形成一体,构成几何不变体,在此基础上增加二元体DEB、EFC、EHF形成刚片Ⅰ(注意固定铰支座与铰相同);铰结△GIJ为刚片Ⅱ;刚片I与刚片Ⅱ之间用不交于一点的杆DI、杆GI、杆HJ相连,组成几何不变体。
习题2-18试对图示体系进行几何组成分析。
解:将原图结点进行编号,并将固定铰支座换为单铰,如图(b)。折杆AD上联结杆EF,从几何组成来说是多余约束;同理,折杆CD上联结杆EF也是多余约束。取基础为刚片Ⅰ,折杆AD为刚片Ⅱ,折杆CD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由链杆A和杆BD相连,刚片Ⅰ与刚片Ⅲ是由链杆C相连,注意,杆BD只能使用一次。由规则二知,体系为几何可变体系。
结构力学练习册答案

第一章机动分析一、判断题1.( X ) 2.( X ) 3.( X ) 4.( O )二、选择题5.(B) 6.(D) 7.(C) 8.(A) 9.(A) 10.(A) 11.(C) 12.(B) 13.(A)三、填空题14.几何瞬变15. 或不定值16.两刚片用不完全相交及平行的三根链杆连接而的体系。
17.几何不变且无多余约束。
四、分析与计算题18.分析:1、2、3符合三刚片法则,几何不变;它与4、5又符合三刚片法则,几何不变;内部整体与地基符合二刚片三链杆法则。
结论:几何不变且无多余约束。
19.用两刚片法则,三链杆交于一点,几何瞬变。
20.用两刚片三链杆法则,几何不变无多余约束。
21.用两刚片三链杆法则,几何不变无多余约束。
22.用两刚片三链杆法则,几何瞬变。
23.用两刚片三链杆法则(或增加二元件),几何不变无多余约束。
24.W = 1,几何可变。
125.用两刚片三链杆法则,几何不变无多余约束。
26.用三刚片、六链杆法则,几何不变无多余约束。
27.几何不变,有两个多余约束。
28.几何不变无多余约束。
29.用三刚片、六链杆法则,几何不变无多余约束。
30.用三刚片、六链杆法则,几何不变无多余约束。
2第二章静定梁与静定刚架一、判断题1.(O)2.(O)3.(X)4.(X)5.(X)6.( X ) 7.( O ) 8.( O ) 9.( X ) 10.( O ) 11.( O )二、选择题12.(C)13.(D)14.(A)15.( C )16.( D )17.( C ) 18.( C )19.(C)20.(B)21.(C )三、填空题22.不变,零23.无关24.位移,变形,内力25.在任意荷载作用下,所有反力和内力都可由静力平衡条件求得确定的、有限的、唯一的解答。
26.0 ,027.20kN·m ,下28.75kN·m ,右29.2Pa,右30.0.5pa ,上31.Pa, 左四、分析与计算题32.33.20.5q lq l28M图PaM图3434. 35.m 16R A ql H 0M B B ql 0.5( )图M Bql 0.522______A36. 37.1050203050().图 M kN m DC BE Aql 20.5ql 2ql20.5图M DC B A38. 39.图M m CAB().图 M kN m 2020AB 5DC40. 41.BC D40120图 M ()kN .m A 408040图M PlPl2Pl ABC D542. 43.().图 M kN m 4441535图M ql 28ql 223ABDC44. 45.()图 M kN .m AB 151515151515C DE F 1515Pa 2/3图Pa 2/3Pa 2/3Pa 2/3M AB46. 47.Pa 2/3Pa /34AB图MPaPa0.5P a0.5P a 图M48. 49.PaPaPaPa图M图M650. 51.ql20.5ql20.5ql20.5ql20.5图M图M mm52. 53.P aPa0.5P a0.5P a0.5M 图m0.5m54. 55.q56. 57.1k N 1k N3k N1k N Q 图 (3.5)N 图 (3.5)758.PPPQ 图N 图59.qaqa qa /2qaqa qa/2qa /232Q 图 N 图60.61.图M图M qa 22qa 2262.ABC ED F Pa Pa 1328第三章 静 定 拱一、判断题1.(X ) 2.(O )3. ( O )二、选择题4.(C )5.(B ) 6.(D ) 7.(B ) 8.( B ) 9.( D )三、填空题10. 0 , 011. 7.5kN ·m , 下四、分析与计算题12. M K =0Q K =0N qr K =-13. M =-⋅2013()kN m Q =-531()kNN =-+531()kN14. M M Hy k K=-=-⋅010kN m Q Q H K K=-=00c o s s i n ϕϕN Q H K K=--=-010sin cos ϕϕkNs i n ,c o s ϕϕ= = N Q H KK 00201020=⋅==kN m kN kN ,,9第四章 静定桁架一、判断题1.(O ) 2.(O ) 3.(X ) 4.(X ) 5.(X ) 6.(X )二、选择题7. ( D ) 8.( D ) 9.( D ) 10.(D ) 11.(D )三、填空题12. 0 , 013. BC , FG , ED , DB , DF 14. 1.414P , -2P 15. 0.5P ( 拉 ) 16. P四、分析与计算题17. 18.图M 2Pa2Pa 2Pa Pa6Pa 6ABC D E FG图M 2qa 22qa 22qa 22qa 2qa219.ABDC806020M ()kN .m 图1020.N P ED =2取 隔 离 体 如 下 图 ,N N P P P C ∑==-⋅=0243431 ,()//21.取 截 面 I - I ,得 N 10= 由 结 点 A 平 衡 得 N P 22=22.由 I-I 截 面 ,M A =∑0, 得 N 1=P 由 II-II 截 面 ,M B ∑=0, 得N P 22=-23.由 截 面 I-I ,得 N 310kN = 由NA=∑0,得 N 2=44kN11由 截 面 II-II ,N A =∑0 ,得N 125kN =-24.N 10= N P 2233=/25.由 结 点 A 平 衡 求 1 杆 内 力 ,N 10= 由 结 点 B 平 衡 求 2 杆 内 力 ,N P 2= 由 结 点 C 平 衡 求 3 杆 内 力 ,N P 322=/26.N P 12=,N P 22=-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[0729]《结构力学》1、桁架计算的结点法所选分离体包含几个结点A. 单个2、固定铰支座有几个约束反力分量B. 2个3、从一个无多余约束的几何不变体系上去除二元体后得到的新体系是A. 无多余约束的几何不变体系4、两刚片用三根延长线交于一点的链杆相连组成A. 瞬变体系5、定向滑动支座有几个约束反力分量B. 2个6、结构的刚度是指C. 结构抵抗变形的能力7、桁架计算的截面法所选分离体包含几个结点B. 最少两个8、对结构进行强度计算的目的,是为了保证结构A. 既经济又安全9、可动铰支座有几个约束反力分量A. 1个10、固定支座(固定端)有几个约束反力分量C. 3个11、改变荷载值的大小,三铰拱的合理拱轴线不变。
A.√12、多余约束是体系中不需要的约束。
B.×13、复铰是连接三个或三个以上刚片的铰A.√14、结构发生了变形必然会引起位移,结构有位移必然有变形发生。
B.×15、如果梁的截面刚度是截面位置的函数,则它的位移不能用图乘法计算。
A.√16、一根连杆相当于一个约束。
A.√17、单铰是联接两个刚片的铰。
A.√18、连接四个刚片的复铰相当于四个约束。
B.×19、虚功原理中的力状态和位移状态都是虚设的。
B.×20、带拉杆三铰拱中拉杆的拉力等于无拉杆三铰拱的水平推力。
A.√21、瞬变体系在很小的荷载作用下会产生很大的内力,所以不能作为结构使用。
A.√22、一个无铰封闭框有三个多余约束。
A.√23、三铰拱的水平推力不仅与三铰的位置有关,还与拱轴线的形状有关。
B.×24、三铰拱的主要受力特点是:在竖向荷载作用下产生水平反力。
A.√25、两根链杆的约束作用相当于一个单铰。
B.×26、不能用图乘法求三铰拱的位移。
A.√27、零杆不受力,所以它是桁架中不需要的杆,可以撤除。
B.×28、用图乘法可以求等刚度直杆体系的位移。
A.√29、连接四个刚片的复铰相当于四个约束。
30.答:31.几何组成分析答:依次去掉二元体剩下如图所示的并排简支梁,故原体系为无多余约束的几何不变体系。
32.几何组成分析答:依次去掉基础、二元体,剩下图示部分为两刚片用两个铰相联,有一个多余约束,故原体系为有一个多余约束的几何不变系。
33、简述刚架内力计算步骤。
答:(1)求支座反力。
简单刚架可由三个整体平衡方程求出支座反力,三铰刚架及主从刚架等,一般要利用整体平衡和局部平衡求支座反力。
(2)求控制截面的内力。
控制截面一般选在支承点、结点、集中荷载作用点、分布荷载不连续点。
控制截面把刚架划分成受力简单的区段。
运用截面法或直接由截面一边的外力求出控制截面的内力值。
(3)根据每区段内的荷载情况,利用“零平斜弯”及叠加法作出弯矩图。
作刚架Q、N图有两种方法,一是通过求控制截面的内力作出;另一种方法是首先作出M图;然后取杆件为分离体,建立矩平衡方程,由杆端弯矩求杆端剪力;最后取结点为分离体,利用投影平衡由杆端剪力求杆端轴力。
当刚架构造较复杂(如有斜杆),计算内力较麻烦事,采用第二种方法。
(4)结点处有不同的杆端截面。
各截面上的内力用该杆两端字母作为下标来表示,并把该端字母列在前面。
(5)注意结点的平衡条件。
34、1、结构力学的主要研究内容。
2、几何组成分析目的。
3、如何确定独立角位移数目。
4、简述刚架内力计算步骤。
5、简述计算结构位移的目的。
6、在位移法中须解决哪些问题。
答:1、结构力学的主要研究内容。
答:结构由荷载、支座移动、温度变化、制造误差引起的内力计算——称为强度计算;结构由荷载、支座移动、温度变化、制造误差引起的变形及位移计算——称为刚度计算;结构的稳定计算;结构的组成规律及计算简图的选择。
“结构力学”就是研究结构在荷载作用下的内力和变形的计算问题。
2、几何组成分析目的。
答:(1)判别某一体系是否为几何不变,从而决定它能否作为结构。
(2)区别静定结构、超静定结构,从而选定相应计算方法。
(3)搞清结构各部分间的相互关系,以决定合理的计算顺序。
3、如何确定独立角位移数目。
答:由于在同一结点处,各杆端的转角都是相等的,因此每一个刚结点只有一个独立的角位移未知量。
在固定支座处,其转角等于零为已知量。
至于铰结点或铰支座处各杆端的转角,它们不是独立的,可不作为基本未知量。
这样,结构独立角位移数目就等于结构刚结点的数目。
4、简述刚架内力计算步骤。
答:(1)求支座反力。
简单刚架可由三个整体平衡方程求出支座反力,三铰刚架及主从刚架等,一般要利用整体平衡和局部平衡求支座反力。
(2)求控制截面的内力。
控制截面一般选在支承点、结点、集中荷载作用点、分布荷载不连续点。
控制截面把刚架划分成受力简单的区段。
运用截面法或直接由截面一边的外力求出控制截面的内力值。
(3)根据每区段内的荷载情况,利用“零平斜弯”及叠加法作出弯矩图。
作刚架Q、N图有两种方法,一是通过求控制截面的内力作出;另一种方法是首先作出M图;然后取杆件为分离体,建立矩平衡方程,由杆端弯矩求杆端剪力;最后取结点为分离体,利用投影平衡由杆端剪力求杆端轴力。
当刚架构造较复杂(如有斜杆),计算内力较麻烦事,采用第二种方法。
(4)结点处有不同的杆端截面。
各截面上的内力用该杆两端字母作为下标来表示,并把该端字母列在前面。
(5)注意结点的平衡条件。
5、简述计算结构位移的目的。
答:(1) 验算结构的刚度。
校核结构的位移是否超过允许限值,以防止构件和结构产生过大的变形而影响结构的正常使用。
(2) 为超静定结构的内力分析打基础。
超静定结构的计算要同时满足平衡条件和变形连续条件。
(3) 结构制作、施工过程中也常需先知道结构的位移。
6、在位移法中须解决哪些问题。
答:(1)单跨超静定梁在杆端发生各种位移、荷载、温度等因素作用下的内力。
(2)哪些结点位移作为基本未知量。
(3)如何确定基本未知量(求出位移)。
35、结构力学的主要研究内容。
答:结构由荷载、支座移动、温度变化、制造误差引起的内力计算——称为强度计算;结构由荷载、支座移动、温度变化、制造误差引起的变形及位移计算——称为刚度计算;结构的稳定计算;结构的组成规律及计算简图的选择。
“结构力学”就是研究结构在荷载作用下的内力和变形的计算问题。
36、1、简述弯矩图叠加的注意事项。
2、简述变形体的虚功原理。
3、简述力法的基本思路。
答:1、简述弯矩图叠加的注意事项。
答:(1)弯矩图叠加是竖标相加,不是图形的拼合;(2)要熟练地掌握简支梁在跨中荷载作用下的弯矩图;(3)利用叠加法可以少求或不求反力,就可绘制弯矩图;(4)利用叠加法可以少求控制截面的弯矩;(5)对于任意直杆段,不论其内力是静定的还是超静定的;不论是等截面杆或是变截面杆;不论该杆段内各相邻截面间是连续的还是定向联结还是铰联结弯矩叠加法均适用2、简述变形体的虚功原理。
答:变形体的虚功原理是力学中的一个基本原理,结构力学中计算位移的方法是以虚功原理为基础的。
刚体体系的虚功原理是变形体虚功原理的特殊形式。
变形体的虚功原理可表述为:设变形体在力系作用下处于平衡状态,又设变形体由于其它原因产生符合约束条件的微小连续变形,则外力在位移上所作外虚功恒等于各个微段的应力合力在变形上所作的内虚功。
3、简述力法的基本思路。
答:力法的基本思路:将超静定结构的计算转化为静定结构的计算,首先选择基本结构和基本体系,然后利用基本体系与原结构之间在多余约束方向的位移一致性和变形叠加列出力法典型方程,最后求出多余未知力和原结构的内力。
第一步:去掉原结构的多余约束,代之以多余未知力,得到静定的基本体系。
第二步:基本体系和原结构的变形相同,特别是基本体系上与多余未知力相应的位移与原超静定结构上多余约束处的位移条件一致,这是确定多余未知力大小的依据。
一般情况下,当原结构上在多余约束处没有支座位移时,则基本体系应满足的变形条件是:与多余未知力相应的位移为零。
37、简述计算结构位移的目的。
答:(1) 验算结构的刚度。
校核结构的位移是否超过允许限值,以防止构件和结构产生过大的变形而影响结构的正常使用。
(2) 为超静定结构的内力分析打基础。
超静定结构的计算要同时满足平衡条件和变形连续条件。
(3) 结构制作、施工过程中也常需先知道结构的位移。
38、在位移法中须解决哪些问题。
答:(1)单跨超静定梁在杆端发生各种位移、荷载、温度等因素作用下的内力。
(2)哪些结点位移作为基本未知量。
(3)如何确定基本未知量(求出位移)。
39、几何组成分析目的。
答:(1)判别某一体系是否为几何不变,从而决定它能否作为结构。
(2)区别静定结构、超静定结构,从而选定相应计算方法。
(3)搞清结构各部分间的相互关系,以决定合理的计算顺序。
40、如何确定独立角位移数目。
答:由于在同一结点处,各杆端的转角都是相等的,因此每一个刚结点只有一个独立的角位移未知量。
在固定支座处,其转角等于零为已知量。
至于铰结点或铰支座处各杆端的转角,它们不是独立的,可不作为基本未知量。
这样,结构独立角位移数目就等于结构刚结点的数目。
41.答:42、用力法计算图示刚架,取图示基本结构,建立力法基本方程,求出方程中的系数和自由项,不必解方程和作弯矩图。
各杆EI=常数答:43、求图示刚架A,B两截面的相对转角。
各杆EI为常数答:44、求图5所示刚架A,B两截面的相对转角。
各杆EI为常数。
答:45、试用力法计算图示刚架,并作出弯矩M图。
EI=常数。
答:46. 答:47. 答:48.答:49、用位移法作图7所示梁的弯矩图。
各杆相同,。
,。
答:无50、试用位移法计算图所示刚架,并作出弯矩M图。
各杆线刚度均为i。
答:51. 答:52、用位移法作图4所示结构M图,各杆线刚度均为i,各杆长为l 。
答:53、试用位移法计算图示刚架,并作出弯矩M图。
各杆线刚度均为i。
答:54、试用力法计算图所示刚架,并作出弯矩M图。
EI=常数。
答:55、试计算如图所示简支梁中点的竖向位移。
EI为常数。
答:56、试求如图4所示外伸梁C点的竖向位移。
梁的EI为常数。
答:57、试计算如图所示简支梁中点的竖向位移。
EI为常数。
答:58.答:59、用力法计算图所示刚架,取图示基本结构,建立力法基本方程,求出方程中的系数和自由项,不必解方程和作弯矩图。
各杆EI=常数。
答:60、1、作图示结构的弯矩图答:61、3作图示结构的弯矩图答:62、2、作图示结构的弯矩图答:63、7、作图示结构的弯矩图答:64、6、作图示结构的弯矩图答:65、4、作图示结构的弯矩图答:66、5、作图示结构的弯矩图答:。
