高二第3章导学案
第3章体液调节导学案高二上学期生物人教版选择性必修1

第三章体液调节复习案考情分析知识回扣案(知识再现、知识再认)一、忆:学法指导:对照知识清单细目表,回忆并背诵植物激素的相关知识.学法指导:根据知识清单细目表梳理思维导图,梳理并形成本章的知识网格,基础知识查漏补缺。
体液调节根据思维导图默写检测1激素的发现(1)沃泰默的观点:胰腺分泌胰液只受调节。
(2)斯他林和贝利斯的实验结论: 是由小肠黏膜分泌,经血液循环运送到胰腺,促进胰腺分泌胰液的一种。
调节:由内分泌器官或细胞分泌的化学物质—激素进行调节的方式。
2内分泌系统的组成和功能内分泌腺与外分泌腺(1)分泌腺:无导管,其分泌物(统称激素)直接进入腺体的毛细血管,再通过血液循环运送到靶器官或靶细胞发挥作用。
(2)分泌腺:有导管,其分泌物通过导管排出去(消化道、体外)。
常见的有各种消化腺、汗腺、皮脂腺、乳腺。
3、激素的种类(1)固醇类激素,如性激素。
(2)氨基酸衍生物类激素,如甲状腺激素、肾上腺素。
(3)多肽和蛋白质类激素,如胰岛素和胰高血糖素。
4、高等动物主要激素的分泌器官、功能及相互关系5、血糖平衡的调节血糖的平衡血糖平衡的调节模型(1)血糖平衡既受调节,也受调节,但激素调节起主导作用。
(2)是目前所知唯一能降低血糖浓度的激素,但使血糖浓度升高的激素并不仅有胰高血糖素,还有等。
糖尿病(1)症状:“三多一少”是指:(2)发病机理:1型糖尿病:2型糖尿病:温馨提示:出现“三多一少”症状的机理6、甲状腺激素分泌的分级调节分级调节过程(1)三级腺体:a. 、b. 、c(2)三种激素:甲;乙;甲状腺激素。
(3)两种效果:“+”“-”分别表示促进、抑制。
调节机制(1)分级调节:下丘脑控制垂体,垂体控制相应腺体,这种分层控制的方式称为分级调节。
分级调节系统也称为下丘脑一垂体一靶腺体轴,靶腺体还有肾上腺皮质、性腺。
(2)负反馈调节:(3)下丘脑是机体调节内分泌活动的枢纽。
7、激素调节的特点(1)通过体液进行运输: (2)作用于靶器官、靶细胞:(3)作为传递信息: (4):注意:(1)激素并不提供能量,也不组成细胞结构、不起催化作用,更不直接参与细胞的代谢过程,只是作为调节生命活动的信息分子。
高二必修5第三章导学案
高二上学期数学导学案一、课前准备复习:用不等式表示,某地规定本地最低生活保障金x不低于400元_______________二、新课导学※学习探究探究2:1.限速40km/h的路标,指示司机在前方路段行驶时,应使汽车的速度v不超过40km/h,写成不等式就是_______________2. 某品牌酸奶的质量检查规定,酸奶中脂肪的含量p应不少于2.5%,蛋白质的含量q应不少于2.3%,写成不等式组就是_________________※典型例题:例1 设点A与平面α的距离为d,B为平面α上的任意一点,则其中不等关系有________例2 某种杂志原以每本2.5元的价格销售,可以售出8万本. 据市场调查,若单价每提高0.1元,销售量就可能相应减少2000本. 若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元呢?例3某钢铁厂要把长度为4000mm的钢管截成500mm和600mm两种.按照生产的要求,600mm的数量不能超过500mm钢管的3倍.怎样写出满足所有上述不等关系的不等式呢?※ 动手试试:练1. 用不等式表示下面的不等关系:(1)a 与b 的和是非负数_________________(2)某公路立交桥对通过车辆的高度h “限高4m ”_______________(3) 如图(见课本74页),在一个面积为350的矩形地基上建造一个仓库,四周是绿地,仓库的长L 大于宽W 的4倍练2. 有一个两位数大于50而小于60,其个位数字比十位数大2.试用不等式表示上述关系,并求出这个两位数(用a 和b 分别表示这个两位数的十位数字和个位数字).三、总结提升 ※ 学习小结1.会用不等式(组)表示实际问题的不等关系; 2.会用不等式(组)研究含有不等关系的问题.※ 当堂检测(时间:5分钟 满分:10分)计分: 1. 下列不等式中不成立的是( ).A .12-≤B .12-<C .11-≤-D .12-≥ 2. 用不等式表示,某厂最低月生活费a 不低于300元 ( ).A .300a ≤B .300a ≥C .300a >D .300a < 3. 已知0a b +>,0b <,那么,,,a b a b --的大小关系是( ).A .a b b a >>->-B .a b a b >->->C .a b b a >->>-D .a b a b >>->- 4. 用不等式表示:a 与b 的积是非正数___________ 5. 用不等式表示:某学校规定学生离校时间t 在16点到18点之间_______________________课后作业:1. 某夏令营有48人,出发前要从A 、B 两种型号的帐篷中选择一种.A 型号的帐篷比B 型号的少5顶.若只选A 型号的,每顶帐篷住4人,则帐篷不够;每顶帐篷住5人,则有一顶帐篷没有住满.若只选B 型号的,每顶帐篷住3人,则帐篷不够;每顶帐篷住4人,则有帐篷多余.设A 型号的帐篷有x 顶,用不等式将题目中的不等关系表示出来.2. 某正版光碟,若售价20元/本,可以发行10张,售价每体高2元,发行量就减少5000张,如何定价可使销售总收入不低于224万元?高二上学期 数学导学案学习过程一、课前准备 1.在初中,我们已经学习过不等式的一些基本性质. 请同学们回忆初中不等式的的基本性质.(1),___a b b c a c >>⇒(2)____a b a c b c >⇒++(3),0____a b c ac bc >>⇒ (4),0____a b c ac bc ><⇒ 二、新课导学 ※ 学习探究问题1:如何比较两个实数的大小.问题2:同学们能证明以上的不等式的基本性质吗?并利用以上基本性质,证明不等式的下列性质:(1),;(2)0,0;(3)0,,1n n a b c d a c b d a b c d ac bd a b n N n a b>>⇒+>+>>>>⇒>>>∈>⇒>>※典型例题 例1 比较大小:(1)2 6+(2)2 21); (3; (4)当0a b >>时,12log a _______12log b .变式:比较(3)(5)a a +-与(2)(4)a a +-的大小.例2 已知0,0,a b c >><求证c ca b>.变式: 已知0a b >>,0c d >>.例3已知1260,1536,aa b a b b<<<<-求及的取值范围.变式:已知41,145a b a b -≤-≤--≤-≤,求9a b -的取值范围.※ 动手试试:练1. 用不等号“>”或“<”填空:(1),____a b c d a c b d ><⇒--; (2)0,0____a b c d ac bd >><<⇒;(3)0a b >>; (4)22110___a b a b>>⇒.练2. 已知x >012x+.三、总结提升 ※ 学习小结本节课学习了不等式的性质,并用不等式的性质证明了一些简单的不等式,还研究了 如何比较两个实数(代数式)的大小——作差法,其具体解题步骤可归纳为: 第一步:作差并化简,其目标应是n 个因式之积或完全平方式或常数的形式; 第二步:判断差值与零的大小关系,必要时须进行讨论; 第三步:得出结论. ※ 知识拓展 “作差法”、“作商法”比较两个实数的大小 (1)作差法的一般步骤:作差——变形——判号——定论 (2)作商法的一般步骤:作商——变形——与1比较大小——定论※ 当堂检测(时量:5分钟 满分:10分)计分:1. 若2()31f x x x =-+,2()21g x x x =+-,则()f x 与()g x 的大小关系为( ).A .()()f x g x >B .()()f x g x =C .()()f x g x <D .随x 值变化而变化 2. 已知0x a <<,则一定成立的不等式是( ).A .220x a <<B .22x ax a >>C .20x ax <<D .22x a ax >>3. 已知22ππαβ-≤<≤,则2αβ-的范围是( ).A .(,0)2π-B .[,0]2π-C .(,0]2π-D .[,0)2π-4. 如果a b >,有下列不等式:①22a b >,②11a b<,③33a b >,④lg lg a b >,其中成立的是 .5. 设0a <,10b -<<,则2,,a ab ab 三者的大小关系为 .课后作业 :1. .2. 某市环保局为增加城市的绿地面积,提出两个投资方案:方案A 为一次性投资500万元;方案B 为第一年投资5万元,以后每年都比前一年增加10万元.列出不等式表示“经n 年之后,方案B 的投入不少于方案A 的投入”.高二上学期数学导学案一、课前准备(预习教材P76~ P78,找出疑惑之处)复习1:解下列不等式:①112x>-;②112x->;③1102x-+>.复习2:写出一个以前所学的一元二次不等式_____________,一元二次函数________________,一元二次方程___________________二、新课导学※学习探究探究一:某同学要上网,有两家公司可供选择,公司A每小时收费1.5元(不足1小时按1小时收费);公司B的收费原则为:在第1小时内(含恰好1小时,下同)收费1.7元,第2小时内收费1.6元,以后每小时减少0.1元(若一次上网时间超过17小时按17小时计算). 如何选择?归纳:这是一个关于x的一元二次不等式,最终归结为如何解一元二次不等式.新知:只含有____个未知数,并且未知数的最高次数是_______的不等式,称为____________. 探究二:如何解一元二次不等式?能否与一元二次方程与其图象结合起来解决问题呢?(如果)解不等式时应先将二次项系数化为正,再根据图象写出其解集.※ 典型例题例1 求不等式2230x x -+->的解集.变式:求下列不等式的解集.(1)2230x x +->; (2)2230x x -+-≤.例2 求不等式24410x x -+>的解集.※ 动手试试练1. 求不等式24415x x ->的解集.练2. 求不等式21340x ->的解集.三、总结提升 ※ 学习小结解一元二次不等式的步骤:(1)将原不等式化为一般式(0a >).(2)判断∆的符号.(3)求方程的根.(4)根据图象写解集.※ 知识拓展(1)20ax bx c ++>对一切x R ∈都成立的条件为00a >⎧⎨∆<⎩(2)20ax bx c ++<对一切x R ∈都成立的条件为00a <⎧⎨∆<⎩学习评价※ 当堂检测(时量:5分钟 满分:10分)计分:1. 已知方程20ax bx c ++=的两根为12,x x ,且12x x <,若0a <,则不等式20ax bx c ++<的 解为( ).A .RB .12x x x <<C .1x x <或2x x >D .无解2. 关于x 的不等式20x x c ++>的解集是全体实数的条件是( ).A .14c <B .14c ≤C .14c >D .14c ≥3. 在下列不等式中,解集是∅的是( ).A .22320x x -+>B .2440x x ++≤C .2440x x --<D .22320x x -+-> 4. 不等式230x x -<的解集是 .5. y =的定义域为 .课后作业:1. 求下列不等式的解集(1)23100x x -->; (2)2450x x -+<.2. 若关于x 的一元二次方程2(1)0x m x m -+-=有两个不相等的实数根,求m 的取值范围.高二上学期数学导学案一、课前准备复习1:一元二次不等式的解法步骤是1.____________________ 2.________________ 3.____________________ 4._______________复习2: 解不等式.(1)23710x x -≤; (2)2250x x -+-<.二、新课导学※ 典型例题:例1 某种牌号的汽车在水泥路面上的刹车距离s m 和汽车的速度 x km/h有如下的关系:21120180s x x =+. 在一次交通事故中,测得这种车的刹车距离大于39.5m ,那么这辆汽车刹车前的速度是多少?(精确到0.01km/h )例2 一个汽车制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x (辆)与创造的价值y (元)之间有如下的关系:22220y x x =-+ 若这家工厂希望在一个星期内利用这条流水线创收6000元以上,那么它在一个星期内大约应该生产多少辆摩托车?例3 产品的总成本y (万元)与产量x 之间的函数关系式是23000200.1y x x =+-,(0,240).x ∈ 若每台产品的售价为25万元,求生产者不亏本时的最低产量.※ 动手试试练1. 在一次体育课上,某同学以初速度012/v m s =竖直上抛一排球,该排球能够在抛出点2 m 以上的位置最多停留多长时间?(注:若不计空气阻力,则竖直上抛的物体距离抛出点的高度h 与时间x 满足关系2012h v t gt =-,其中29.8/g m s =)练2.某文具店购进一批新型台灯,若按每盏台灯15元的价格销售,每天能卖出30盏;若售价每提高1元,日销售量将减少2盏. 为了使这批台灯每天获得400元以上的销售收入,应怎样制定这批台灯的销售价格?三、总结提升: ※ 学习小结进一步熟练掌握一元二次不等式的解法、一元二次不等式与一元二次方程以及一元二次函数的关系.※ 知识拓展(1)连结三个“二次”的纽带是:坐标思想:函数值y 是否大于零等价于为P (,)x y 是否在 x 轴的上方.(2)三个“二次”关系的实质是数形结合思想:20a x b x c ++=的解2y a x b x c ⇔=++图象上的点(,0)x ;20a x b x c ++>的解2y a x b x c ⇔=++图象上的点(,)x y 在x 轴的上方的x 的取值范围.学习评价:※ 当堂检测(时量:5分钟 满分:10分)计分:1. 函数y =的定义域是( ).A .{|4x x <-或3}x >B .{|43}x x -<<C .{|4x x ≤-或3}x ≥D .{|43}x x -≤≤2. 不等式2223931711()()33x x x x --+-≤的解集是( ). A .[2,4] B .(,2][4,)-∞+∞ C .R D .(,2][4,)-∞-+∞ 3. 集合A ={2|540}x x x -+≤,B =2{|560}x x x -+≥,则A B =( ). A .{|12x x ≤≤或34}x ≤≤ B .{|12x x ≤≤且34}x ≤≤C .{1,2,3,4}D .{|41x x -≤≤-或23}x ≤≤ 4. 不等式(5)(2)0x x --<的解集为 .5. 已知两个圆的半径分别为1和5,圆心距满足210240d d -+<,则两圆的位置关系为 .课后作业:1. 求下列不等式的解集:(1)23100x x --+>; (2)(9)0x x ->.2. 据气象部门预报,在距离某码头O 南偏东45︒方向600km 处的热带风暴中心A 在以20km/h 的速度向正北方向移动,距风暴中心450km 以内的地区都将受影响. 从现在起多长时间后,该码头将受到热带风暴影响,影响时间为多长?高二上学期数学导学案一、课前准备复习1:实数比较大小的方法_____________ 复习2:不等式20ax bx c ++>(0)a ≠的解集.二、新课导学 ※ 学习探究探究任务:含参数的一元二次不等式的解法问题:解关于x 的不等式: 22(21)0x m x m m -+++<分析:在上述不等式中含有参数,因此需要先判断参数对的解的影响. 先将不等式化为方程22(21)0x m x m m -+++=此方程是否有解,若有,分别为__________,其大小关系为________________ 试试:能否根据图象写出其解集为_____________ ※ 典型例题例1设关于x 的不等式210ax bx ++>的解集为1{|1}3x x -<<,求a , b.小结:二次不等式给出解集,既可以确定对应的二次函数图象开口方向(即a 的符号),又可以确定对应的二次方程的两个根,由此可根据根与系数关系建立系数字母关系式,或通过代入法求解不等式.变式:已知二次不等式20ax bx c ++<的解集为1{|3x x <或1}2x >,求关于x 的不等式20cx bx a -+>的解集.例2 2{|430}A x x x =-+<,2{|280}B x x x a =-+-≤,且A B ⊆,求a 的取值范围.小结:(1)解一元二次不等式含有字母系数时,要讨论根的大小从而确定解集. (2)集合间的关系可以借助数轴来分析,从而确定端点处值的大小关系.例3 若关于m 的不等式2(21)10mx m x m -++-≥的解集为空集,求m 的取值范围.变式1:解集为非空. 变式2:解集为一切实数.小结:m 的不同实数取值对不等式的次数有影响,当不等式为一元二次不等式时,m 的取值还会影响二次函数图象的开口方向,以及和x 轴的位置关系. 因此求解中,必须对实数m 的取值分类讨论. ※ 动手试试练1. 设2280x x a -+-≤对于一切(1,3)x ∈都成立,求a 的范围.练2. 若方程2280x x a -+-=有两个实根12,x x ,且13x ≥,21x ≤,求a 的范围.三、总结提升※ 学习小结:对含有字母系数的一元二次不等式,在求解过程中应对字母的取值范围进行讨论,其讨论的原则性一般分为四类: (1) 按二次项系数是否为零进行分类;(2) 若二次项系数不为零,再按其符号分类; (3) 按判别式∆的符号分类; (4) 按两根的大小分类. ※ 知识拓展解高次不等式时,用根轴法:就是先把不等式化为一端为零,再对另一端分解因式,并求出它的零点,把这些零点标在数轴上,再用一条光滑的曲线,从x 轴的右端上方起,依次穿过这些零点,则大于零的不等式的解对应着曲线在x 轴上方的实数x 的取值集合;小于零的不等式的解对应着曲线在x 轴下方的实数x 的取值集合. 学习评价 :※ 当堂检测(时量:5分钟 满分:8分)计分:1. 若方程20ax bx c ++=(0a <)的两根为2,3,那么20ax bx c ++>的解集为( ). A .{|3x x >或2}x <- B .{|2x x >或3}x <- C .{|23}x x -<< D .{|32}x x -<<2. 不等式220ax bx ++>的解集是11{|}23x x -<<,则a b +等于( ).A .-14B .14C .-10D .103. 关于x 的不等式2(1)10x a x ---<的解集为∅,则实数a 的取值范围是( ).A .3(,1]5-B .(1,1)-C .(1,1]-D .3(,1)5-4. 若不等式220ax bx +->的解集为1{|1}4x x -<<-,则,a b 的值分别是 .课后作业:1. m 是什么实数时,关于x 的一元二次方程2(1)0mx m x m --+=没有实数根.2. 解关于x 的不等式2(2)20x a x a +--<(a ∈R ).高二上学期数学导学案一、课前准备:复习:解下列不等式:210x-+>;二、新课导学※学习探究探究1:一元一次不等式(组)的解集可以表示为数轴上的区间,例如,3040xx+>⎧⎨-<⎩的解集为. 那么,在直角坐标系内,二元一次不等式(组)的解集表示什么图形呢?探究2:你能研究:二元一次不等式6x y-<的解集所表示的图形吗?(怎样分析和定边界?)(请认真阅读课本83页-----84页)结论:1. 二元一次不等式0Ax By c++>在平面直角坐标系中表示直线0Ax By c++=某一侧所有点组成的平面区域.(虚线表示区域不包括边界直线)2. 不等式中仅>或<不包括;但含“≤”“≥”包括;同侧同号,异侧异号. ※典型例题例1画出不等式44x y+<表示的平面区域.分析:先画___________(用线表示),再取_______判断区域,即可画出..例2用平面区域表示变式1:画不等式(21)(4)0x y x y++-+<表示不等式组3122y xx y<-+⎧⎨<⎩的解集的平面区域归纳:1.画二元一次不等式表示的平面区域常采用“直线定界,特殊点定域”的方法.特殊地,当0C≠时,常把原点作为此特殊点.2. 不等式组表示的平面区域是各个不等式所表示的平面点集的交集,因而是各个不等式所表示的平面区域的公共部分.变式2:由直线20x y ++=,210x y ++=和210x y ++=围成的三角形区域(包括边界)用不等式可表示为.※ 动手试试练1. 不等式260x y -+>表示的区域在直线260x y -+=的 __三、总结提升 ※ 学习小结由于对在直线0Ax By C ++=同一侧的所有点(,x y ),把它的坐标(,x y )代入Ax By C ++,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点00(,)x y ,从00Ax By C ++的正负即可判断0Ax By C ++>表示直线哪一侧的平面区域.(特殊地,当C ≠0时,常把原点作为此特殊点) ※ 知识拓展含绝对值不等式表示的平面区域的作法:(1)去绝对值符号,从而把含绝对值的不等式转化为普通的二元一次不等式. (2)一般采用分象限讨论去绝对值符号. (3)采用对称性可避免绝对值的讨论. (4)在方程()0f x y = 或不等式()0f x y > 中,若将x y 换成()()x y -- ,方程或不等式不变,则这个方程或不等式所表示的图形就关于()y x 轴对称.学习评价:※ 当堂检测(时量:5分钟 满分:8分)计分:1. 不等式260x y -+>表示的区域在直线260x y -+=的( ). A .右上方 B .右下方 C .左上方 D .左下方2. 不等式3260x y +-≤表示的区域是( ).3.不等式组36020x y x y -+≥⎧⎨-+<⎩表示的平面区域是( ).4. 已知点(3,1)--和(4,6)-在直线320x y a -++=的两侧,则a 的取值范围是 .课后作业:1. 用平面区域表示不等式组32326x y x x y <⎧⎪≥⎨⎪+≥⎩的解集.2. 求不等式组6003x y x y x -+≥⎧⎪+≥⎨⎪≤⎩表示平面区域的面积.高二上学期数学导学案复习:画出不等式组2312236x yx yx+≤⎧⎪+>-⎨⎪≥⎩所示平面区域.二、新课导学※典型例题例1 要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如表所示:今需要三种规格的成品分别为12块、15块、27块,用数学关系式和图形表示上述要求.例2 一个化肥厂生产甲乙两种混合肥料,生产1车皮甲肥料的主要原料是磷酸盐4t,硝酸盐18t;生产1车皮乙种肥料的主要原料是磷酸盐1t,硝酸盐15t. 现库存磷酸盐10t,硝酸盐66t,在此基础上生产这两种混合肥料. 列出满足生产条件的数学关系式,并画出相应的平面区域.※动手试试练1. 不等式组(5)()003x y x yx-++≥⎧⎨≤≤⎩所表示的平面区域是什么图形?练 2. 某人准备投资 1 200万兴办一所完全中学,对教育市场进行调查后,他得到了下面的数据表格(以班级为单位):分别用数学关系式和图形表示上述限制条件.三、总结提升 ※ 学习小结根据实际问题的条件列出约束不等式组与目标函数. 反复的读题,读懂已知条件和问题,边读边摘要,读懂之后可以列出一个表格表达题意. 然后根据题中的已知条件,找出约束条件和目标函数,完成实际问题向数学模型的转化.※ 知识拓展求不等式的整数解即求区域内的整点是教学中的难点,它为线性规划中求最优整数解作铺垫. 常有两种处理方法:一种是通过打出网络求整点;另一种是先确定区域内点的横坐标的范围,确定x 的所有整数值,再代回原不等式组,得出y 的一元一次不等式组,再确定y 的所有整数值,即先固定x ,再用x 制约y .学习评价※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 不在326x y +<表示的平面区域内的点是( ). A .(0,0) B .(1,1) C .(0,2) D.(2,0)2. 不等式组5003x y x -+≥⎧⎨≤≤⎩表示的平面区域是一个( ).A .三角形 B.直角梯形 C.梯形 D.矩形3. 不等式组13y x x y y <⎧⎪+≤⎨⎪≥⎩表示的区域为D,点1(0,2)P -,点2(0,0)P ,则( ).A .12,P D P D ∉∉B .12,P D P D ∉∈C .12,PD P D ∈∉ D .12,P D P D ∈∈ 4. 由直线20,210x y x y ++=++=和210x y ++=的平围成的三角形区域(不包括边界)用 不等式可表示为 .5. 不等式组438000x y x y ++>⎧⎪<⎨⎪<⎩表示的平面区域内的整点坐标是 .课后作业 :1. 一个小型家具厂计划生产两种类型的桌子A 和B . 每类桌子都要经过打磨、着色、上漆三道工序.桌子A 需要10min 打磨,6min 着色,6min 上漆;桌子B 需要5min 打磨,12min 着色,9min 上漆.如果一个工人每天打磨和上漆分别至多工作450min ,着色每天至多480min ,请你列出满足生产条件的数学关系式,并在直角坐标系中画出相应的平面区域.高二上学期数学导学案一、课前准备认真阅读课本P87至P88的探究,理解体会探究中的实际问题。
高二化学选择性必修3导学案 第三章 第一节

第三章烃的衍生物第一节卤代烃[明确学习目标] 1.掌握卤代烃发生取代反应和消去反应的条件及有关反应方程式。
2.掌握卤代烃中确定卤素原子种类的方法。
卤代烃1.定义烃分子中的氢原子被□01卤素原子取代后生成的化合物,官能团是□02碳卤键。
2.分类3.物理性质状态常温下,大多数卤代烃为□07液体或□08固体溶解性所有卤代烃都□09不溶于水,可溶于大多数有机溶剂溴乙烷1.分子结构2.物理性质溴乙烷为密度比水大的无色液体,沸点为38.4 ℃,□05难溶于水,可溶于多种有机溶剂。
3.化学性质(1)取代反应(水解反应)①条件:□06NaOH 水溶液、□07加热。
②反应方程式:CH 3CH 2Br +NaOH ――→水△CH 3CH 2OH +NaBr 。
(2)消去反应①概念:有机化合物在一定条件下,从一个分子中□08脱去一个或几个小分子(如H 2O 、HX 等),而生成含□09不饱和键化合物的反应。
②卤代烃的消去反应a .条件:□10强碱的醇溶液、加热。
b .反应方程式:CH 3CH 2Br +NaOH ――→乙醇△□11CH 2===CH 2↑+NaBr +H 2O 。
1.判断正误,正确的画“√”,错误的画“×”。
(1)CH 3CH 2Cl 的沸点比CH 3CH 3的沸点高。
( ) (2)溴乙烷与NaOH 水溶液共热生成乙烯。
( )(3)卤代烃属于烃。
()(4)溴乙烷通常用乙烯与溴化氢反应来制取。
()(5)氯乙烯能加成聚合生成聚氯乙烯。
()答案(1)√(2)×(3)×(4)√(5)√2.运动员的腿部肌肉不小心挫伤,队医马上对准该运动员的受伤部位喷射一种名叫氯乙烷的药剂(沸点约为12 ℃)进行冷冻麻醉处理。
关于氯乙烷的说法不正确的是()A.在一定条件下能发生水解反应B.一定条件下反应可以制备乙烯C.该物质易溶于水D.该物质官能团的名称是碳氯键答案 C解析卤代烃都不溶于水,C错误。
高二英语M5U3Grammar导学案

U 3 M5 Grammar导学案(过去分词)【学008】主备人:潘恩玉审核人:陈新来2013.10.8一、构成和用法1. 过去分词是动词非谓语形式的一种(v-ed),在句中作状语、定语、表语、宾语补足语。
(1) 作状语:1) Interested in the stories(=as they were interested in her stories), they gave Tracy Wong $15,000 inadvance.因为对她的小说感兴趣,他们预付了Tracy Wong一万五千美元。
2) The boy sat at the table buried in his lessons (=and (he) was buried in his lessons).那位男孩坐在桌前,埋头做功课。
(2) 作定语:1) The first mammal cloned from an adult cell(=that was / had been cloned from an adult cell)was Dolly thesheep.第一个用成年细胞克隆的哺乳动物是克隆羊多莉。
2) The name mentioned in the letter(=which was mentioned in the letter)was unknown to me. 信里提到的名字我不熟。
(3) 作表语:We were surprised to find that the window was broken. 窗子破了。
(4)作宾语补足语:He found it hard to make himself understood. 他发现很难使自己被理解。
问题:由上例(斜体部分)你能看出过去分词有什么特点?结论:a)过去分词(常常)表示“被动..”含义。
b)作状语和定语时,多数是由相应的从句转化而来。
2. 下面的例子中过去分词不表示被动:1) The ground is covered with fallen leaves. 地上铺满了落叶。
高二物理教案 第三章 磁场复习导学案

课后作业:
1 必做题:1、如图,相距 20cm 的两根光滑平行铜导轨,导轨
平面倾角为θ=370, 上面放着质量为 80g 的金属杆 ab, 整个装 置放在 B=0.2T 的匀强磁场中. (1)若磁场方向竖直向下,要使金属杆静止在导轨上,必须通以多大的电流. (2)若磁场方向垂直斜面向下,要使金属杆静止在导轨上,必须通以多大的电流。
态度决定高度,落实产生差距 1
选修 3-1 科目◆物理
编制人:
复核人:
授课时间:
月
号
编号:
部的磁感线方向。 5、磁感应强度:描述磁场的强弱与方向的物理量 ⑴定义: 在磁场中 磁场方向的通电导线,受到的安培力跟电流和导线长 度的乘积的比值。 ⑵表达式: 单位:特斯拉(T) ⑶ :方向为该点的磁场方向,即通过该点的磁感线的切线方向 二.安培力(1)方向: 定则 (2)安培力的大小: 三、洛仑兹力 (1)洛仑兹力提供 : (2)轨道半径: (3)周期: (4)圆心、半径、运动时间的确定 (5)洛仑洛伦兹力的方向:左手定则 圆心的确定 a、 两个速度方向 的交点。 (常用在有界磁场的入射与出射方向已知的情况下) b、有几何关系和轨道半径公式结合,来求物理题目中的所求 C、由转过的圆心角和周期公式来计算时间。 2 典例精析 1、下列说法中正确的是( ) A.磁感线可以表示磁场的方向和强弱 B.磁感线从磁体的 N 极出发,终止于磁体的 S 极 C.磁铁能产生磁场,电流也能产生磁场 D.放入通电螺线管内的小磁针,根据异名磁极相吸的原则,小磁针的 N 极一定指向 通电螺线管的 S 极 2、在地球赤道上空有一小磁针处于水平静止状态,突然发现小磁针 N 极向东偏转, 由此可知( ) A.一定是小磁针正东方向上有一条形磁铁的 N 极靠近小磁针 B.一定是小磁针正东方向上有一条形磁铁的 S 极靠近小磁针 C.可能是小磁针正上方有电子流自南向北水平通过 D.可能是小磁针正上方有电子流自北向南水平通过 3、一束电子流沿 x 轴正方向高速运动,如图所示,则电子流 产生的磁场在 z 轴上的点 P 处的方向是( ) A.沿 y 轴正方向 B.沿 y 轴负方向 C.沿 z 轴正方向 D.沿 z 轴负方向 4、关于磁感强度,正确的说法是: ( ) A、根据定义式,磁场中某点的磁感强度 B 与 F 成正比,与 IL 成反比; B、磁感强度 B 是矢量,方向与 F 的方向相同; C、B 是矢量,方向与通过该点的磁感线的切线方向相同;
直线与圆锥曲线(第5课时弦长问题)导学案高二上学期数学选择性

第3章 圆锥曲线与方程3.5 直线与圆锥曲线(第5课时 弦长问题)【学习目标】1.会求直线被椭圆所截的弦长;(重点)2.掌握有关椭圆的最值问题.(难点)【研讨·拓展】一、弦长问题问题 当直线与椭圆相交时,如何求被截的弦长?【例1】已知斜率为2的直线l 经过椭圆x 25+y 24=1的右焦点F 1,与椭圆相交于A ,B 两点,求弦AB 的长.【变式11】已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的一个顶点为A (2,0),离心率为22,直线y =k (x -1)与椭圆C 交于不同的两点M ,N .(1)求椭圆C 的方程; (2)当△AMN 的面积为103时,求k 的值.二、与弦长有关的最值、范围问题【例2】在平面直角坐标系Oxy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率e =22,且点P (2,1)在椭圆C 上.(1)求椭圆C 的方程;(2)斜率为-1的直线与椭圆C 相交于A ,B 两点,求△AOB 面积的最大值.【变式21】已知椭圆C :x 23+y 2=1的左、右顶点分别为A 1,A 2,下、上顶点分别为B 1,B 2.记四边形A 1B 1A 2B 2的内切圆为E .(1)求E 的方程;(2)过点M (m ,0)(m >0)作E 的切线l 交C 于A ,B 两点,求|AB |的最大值.【总结提炼】1.知识清单:(1)弦长问题;(2)与弦长有关的最值、范围问题.2.方法归纳:数形结合.3.常见误区:容易忽略直线斜率不存在的情况.【拓展强化】1.过椭圆x 2a 2+y 2b 2=1(a >b >0)的焦点F (c ,0)的弦中最短弦长是( )A .2b 2aB .2a 2bC .2c 2aD .2c 2b2.过椭圆x 2+2y 2=4的左焦点作倾斜角为π3的弦AB ,则弦AB 的长为( )A .67B .167C .716D .763.已知直线y =2x 与椭圆C :x 2a 2+y 2b 2=1(a >b >0)交于A ,B 两点,点F 是椭圆C 的左焦点,若|F A →|+|FB →|=22,|F A →+FB→|=2,则|AB |等于( ) A .2 B .423 C .2103 D .44.已知椭圆C 的焦点为F 1(-1,0),F 2(1,0),过F 2的直线与椭圆C 交于A ,B 两点.若|AF 2|=2|F 2B |,|AB |=|BF 1|,则椭圆C 的方程为( )A .x 22+y 2=1B .x 23+y 22=1C .x 24+y 23=1D .x 25+y 24=15.已知F 1,F 2是椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,过点F 2的直线与椭圆交于P ,Q 两点,PQ ⊥PF 1,且QF 1=2PF 1,则△PF 1F 2与△QF 1F 2的面积之比为( )A .2- 3B .2+1C .2-1D .2+36.已知椭圆两顶点A (-1,0),B (1,0),过焦点F (0,1)的直线l 与椭圆交于C ,D 两点,当|CD |=322时,直线l 的方程为________________.7.椭圆C :x 24+y 2=1,过A (0,2)作直线l 与椭圆C 交于M ,N 两点,O 为坐标原点,若△AOM 与△AON 的面积之比为5∶3,则直线l 的斜率为________.8.如图,某市有相交于点O 的一条东西走向的公路l 与一条南北走向的公路m ,有一商城A 的部分边界是椭圆的四分之一,这两条公路为椭圆的对称轴,椭圆的长半轴长为2,短半轴长为1(单位:千米).根据市民建议,欲新建一条公路PQ ,点P ,Q 分别在公路l ,m 上,且要求PQ 与椭圆形商城A 相切,当公路PQ 最短时,OQ 的长为________千米.9.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为12,点A ⎝ ⎛⎭⎪⎫-1,32在椭圆C 上,点P 是y 轴正半轴上的一点,过椭圆C 的右焦点F 和点P 的直线l 与椭圆C 交于M ,N 两点.(1)求椭圆C 的标准方程;(2)求||PM +||PN ||PF 的取值范围.。
人教版高二化学 选修4 第三章 第一节 《弱电解质的电离》导学案设计

化学选修4第三章第一节弱电解质的电离导学案(1)强弱电解质【教学目标】1、会从电离的角度认识强弱电解质的不同并能准确判断强电解质和弱电解质。
2、会正确书写电离方程式【预习案】1、复习初中化学pH值与溶液酸碱性的关系, 复习必修1课本30页有关电解质的概念2、阅读选修4课本46-47页有关C(H+)与PH的相互换算内容。
3、阅读选修4课本40页至42页相关内容,完成《百年学典》知识点1的学习和填空。
【探究案】1、从电离的角度如何认识强弱电解质的不同?2、如何书写电离方程式?【教学过程】【温故1】酸性溶液:pH 7 中性溶液:pH 7 碱性溶液:pH 7故pH越小,溶液的越强【温故2】电解质和非电解质常见的电解质是、、和【温故3】酸、碱、盐溶液是怎样导电的?酸、碱、盐溶液的导电性强弱与什么因素有关?【新课学习】【思考1】课本40页学与问酸碱盐都是电解质,在水中都能电离出离子,不同电解质的电离程度是否有区别?【探究1】观察选修4课本40页实验3-1,完成表格填空实验结果说明:等体积、等浓度的醋酸和盐酸与等量镁条反应的剧烈程度不同,而且两种酸的pH也不一样。
这是为什么呢?pH的计算方法:PH=从pH与C(H+)的换算来看,pH不同,则反映出溶液中C(H+)也。
【探究2】同样是一元酸,相同浓度的HCl和CH3COOH溶液中C(H+)为何不同呢?请注意观察课本40页图3-1、3-2,你有何发现?HCl溶液中只有离子和离子,没有分子,说明HCl 电离。
电离方程式为该过程。
CH3COOH溶液中既有离子和离子,还有分子,说明CH3COOH只有发生电离,电离方程式为该过程。
一、强电解质和弱电解质1、概念:强电解质弱电解质★2、常见的强电解质①强酸:HCl、HBr、HI、H2SO4、HNO3、HClO3、HClO4等。
②强碱:NaOH、KOH、Ba(OH)2、Ca(OH)2等。
③绝大多数盐:如NaCl、(NH4)2SO4、BaSO4等。
高二数案:第三章 3.2 复数代数形式的四则运算 3 (新人教A选修1-2)[ 高考]
![高二数案:第三章 3.2 复数代数形式的四则运算 3 (新人教A选修1-2)[ 高考]](https://img.taocdn.com/s3/m/8a4bc862e45c3b3567ec8b49.png)
3.2.1复数的加法和减法【使用说明】1、课前完成导学案,牢记基础知识,掌握基本题型;2、认真限时完成,规范书写;课上小组合作探究,答疑解惑。
【重点难点】加减法运算法则加减法的几何意义【学习目标】1、 知识与技能:掌握复数加法、减法的运算法则,能够熟练地进行加减运算;理解复数(1)通过实例分析,加减法的几何意义,能用平行四边形和三角形法则解决一些简单的问题2、过程与方法:小组合作探究;3、情感态度与价值观:以极度的热情,自动自发,如痴如醉,投入到学习中,充分享受学习的乐趣。
一,自主学习引例:已知m=3x+4y ,n=5x-6y ,求m+n ,m-n 。
1. 复数的加法运算:①.复数的加法法则:12z a bi a b R z c di c d R =+∈=+∈设(,)与(,),则二合作探究,展示,点评例1.计算(1)(14)(72)i i +-+ (2)(72)(14)i i -++(3)[(32)(43)](5)i i i --++++(4)(32)(43)(5)]i i i --++++[观察上述计算,复数的加法运算是否满足交换、结合律相反数2. 复数的减法运算:类比实数,规定复数的减法运算是加法运算的逆运算,从相反数角度转化减为加。
③:()()()()()()a bi c di a bi c di a c b d i +-+=++--=-+-,显然,两个复数的差仍为复数。
例2.计算(1)(14)(72)i i +-- (2)(52)(14)(23)i i i --+--+ (3)(32)(43)(5)]i i i --+-+-[从几何意义出发,再看复数的加减运算:1.当复数的对应向量共线时,可直接运算。
2.当复数的对应向量不共线时,加法运算可类比与向量加法的平行四边形法则;减法运算可类比与向量减法的三角形法则。
3.将所得和向量或差向量一直起点坐标原点时,该向量终点坐标就对应复数所求的坐标。
高二化学选择性必修3导学案 第三章 第二节 第二课时

第二课时酚[明确学习目标] 1.了解苯酚的组成和结构特点。
2.掌握苯酚的重要性质及其检验方法。
3.了解醇和酚结构的差别,能举例说明有机物分子中基团之间存在相互影响。
酚苯酚1.分子组成与结构2.物理性质(1)纯净的苯酚是□06无色晶体,有特殊气味,易被空气氧化,呈粉红色。
(2)苯酚室温下在水中的溶解度为9.2 g,当温度高于65 ℃时,能与水□07混溶,苯酚易溶于□08有机溶剂。
(3)苯酚有毒,对皮肤有腐蚀性,如不慎沾到皮肤上,应立即用□09酒精洗涤。
3.重要的化学性质(1)苯酚的弱酸性现象:①液体浑浊,②液体变澄清,③④液体变浑浊。
对应化学方程式为:(2)取代反应化学方程式为此反应可用于苯酚的定性检验和定量测定。
(3)显色反应遇Fe3+呈□15紫色,可用于□16检验苯酚的存在。
4.苯酚的用途苯酚是重要的化工原料,广泛用于制造□17酚醛树脂、染料、医药、农药等。
1.判断正误,正确的画“√”,错误的画“×”。
(1)常温下苯酚为粉红色晶体。
()(2)实验时手指上不小心沾上苯酚,立即用70 ℃以上的热水清洗。
()(3)含有的官能团相同,化学性质相似。
()(4)乙醇和苯酚都能与Na、NaOH反应。
()(5)苯酚有毒,但其水溶液可用作消毒剂。
()答案(1)×(2)×(3)×(4)×(5)√2.下列物质属于酚类的是()答案 B解析无苯环,属于醇类;属于酚类;属于芳香醇;属于醚,酚类是—OH直接与苯环相连的一类有机物。
3.下列物质中,分别加入金属钠,不能产生氢气的是()A.蒸馏水B.无水乙醇C.煤油D.苯酚溶液答案 C解析钠不与煤油反应,故少量的钠可保存在煤油中。
4.A、B的结构简式如下:(1)A分子中含有的官能团的名称是____________________;B分子中含有的官能团的名称是___________________________。
(2)A能否与氢氧化钠溶液反应?______________________________;B能否与氢氧化钠溶液反应?____________________________________。
第3章第1节卤代烃导学案2021-2022学年下学期高二化学人教版(2019)选择性必修2

卤代烃【学习目标】1、掌握溴乙烷的物理性质和化学性质2、掌握卤代烃的组成和结构的特点,熟悉卤代烃的水解反应和消去反应【重点知识梳理】一、烃的衍生物的相关概念1、烃的衍生物:烃分子里的氢原子被其它原子或原子团取代而生成的化合物,称之为烃的衍生物2、常见烃的衍生物有:卤代烃、醇、酚、醛、羧酸、酯3、官能团:决定化合物特殊性质的原子或原子团4、常见的官能团:碳碳双键(C=C)、碳碳三键(C≡C)、卤素原子(—X)、羟基(—OH)、醚键(C —O —C)、醛基(—CHO)、羰基(C=O)、 羧基(—COOH)、酯基(—COOC)、氨基(—NH 2)、硝基(—NO 2)常见有机物类别及官能团有机物类别 官能团 典型代表物 有机物类别 官能团 典型代表物烷烃 ——甲烷 酚 羟基(—OH) 苯酚 烯烃 碳碳双键(C=C) 乙烯 醚 醚键(C —O —C) 乙醚炔烃 碳碳三键(C≡C) 乙炔 醛 醛基(—CHO) 乙醛芳香烃 ——苯 酮 羰基(C=O) 丙酮 卤代烃 卤素原子(—X) 溴乙烷 羧酸 羧基(—COOH) 乙酸醇 羟基(—OH) 乙醇 酯 酯基(—COOC) 乙酸乙酯二、溴乙烷的分子组成和结构分子式 电子式 结构式 结构简式 球棍模型 比例模型 官能团C 2H 5Br CH 3CH 2Br 或C 2H 5Br—Br 三、溴乙烷的物理性质:纯净的溴乙烷是无色的液体,沸点比乙烷的高(38.4℃),密度比水大,不溶于水,易溶于多种有机溶剂对比:乙烷无色气体,沸点—88.6 ℃,不溶于水四、溴乙烷的化学性质:在溴乙烷分子中,由于Br 的吸引电子的能力大于C ,则C —Br 键中的共用电子对就偏向于Br 原子一端, 使Br 带有部分负电荷,C 原子带部分正电荷。
当遇到—OH 、—NH 2等试剂(带负电或富电子基团)时,该基团就会进攻带正电荷 的C 原子,—Br 则带一个单位负电荷离去(1)溴乙烷的水解反应:反应原理:CH 3CH 2Br+H 2O CH 3CH 2OH+HBr或:CH 3CH 2Br +NaOH −−→−O H 2CH 3CH 2OH +NaBr实验装置:实验步骤:取一支试管,滴入10~15滴溴乙烷,再加入5%的NaOH 溶液,充分振荡、静置,待液体分层后,用胶头滴管小心吸 取10滴上层水溶液,移入另一支盛有10ml 稀硝酸溶液的试管中,然后加入2~3滴2%的AgNO 3溶液,观察反应现象 实验现象:有淡黄色沉淀生成【注意问题】①溴乙烷水解的实质:溴乙烷分子里的溴原子被水分子里的羟基所取代生成乙醇②断裂键的位置:C —Br 键③反应类型:取代反应④溴乙烷水解的条件:NaOH 的水溶液、加热。
黑龙江省绥化市第九中学高二理科新人教A版选修2-1第三章空间向量与立体几何导学案

⿊龙江省绥化市第九中学⾼⼆理科新⼈教A版选修2-1第三章空间向量与⽴体⼏何导学案1. 理解空间向量的概念,掌握其表⽰⽅法;2. 会⽤图形说明空间向量加法、减法、数乘向量及它们的运算律;3. 能⽤空间向量的运算意义及运算律解决简单的⽴体⼏何中的问题.8486 复习1:平⾯向量基本概念:具有和的量叫向量,叫向量的模(或长度);叫零向量,记着;叫单位向量.叫相反向量, a的相反向量记着 .叫相等向量. 向量的表⽰⽅法有,,和共三种⽅法.复习2:平⾯向量有加减以及数乘向量运算:1. 向量的加法和减法的运算法则有法则和法则.2. 实数与向量的积:实数λ与向量a 的积是⼀个量,记作,其长度和⽅向规定如下: (1)|λa |= .(2)当λ>0时,λa 与A. ;当λ<0时,λa 与A. ;当λ=0时,λa = .3. 向量加法和数乘向量,以下运算律成⽴吗?加法交换律:a +b =b +a加法结合律:(a +b )+c =a +(b +c )数乘分配律:λ(a +b )=λa +λb⼆、新课导学※学习探究探究任务⼀:空间向量的相关概念问题:什么叫空间向量?空间向量中有零向量,单位向量,相等向量吗?空间向量如何表⽰?新知:空间向量的加法和减法运算:空间任意两个向量都可以平移到同⼀平⾯内,变为OB =, AB = ,试试:1. 分别⽤平⾏四边形法则和三⾓形法则求,.a b a b +-.2. 点C 在线段AB 上,且52AC CB =,则AC = AB , BC = AB . 反思:空间向量加法与数乘向量有如下运算律吗?⑴加法交换律:A. + B. = B. + a ;⑵加法结合律:(A. + b ) + C. =A. + (B. + c );⑶数乘分配律:λ(A. + b ) =λA. +λb .※典型例题例 1 已知平⾏六⾯体''''ABCD A B C D -(如图),化简下列向量表达式,并标出化简结果的向量:AB BC + ⑴;'AB AD AA ++⑵;1'2AB AD CC ++ ⑶1(')2AB AD AA ++ ⑷.变式:在上图中,⽤',,AB AD AA 表⽰'',AC BD 和'DB.⼩结:空间向量加法的运算要注意:⾸尾相接的若⼲向量之和,等于由起始向量的起点指向末尾向量的终点的向量,求空间若⼲向量之和时,可通过平移使它们转化为⾸尾相接的向量.. b1. 掌握空间向量的数乘运算律,能进⾏简单的代数式化简;2. 理解共线向量定理和共⾯向量定理及它们的推论;3. 能⽤空间向量的运算意义及运算律解决简单的⽴体⼏何中的问题.⼀、课前准备(预习教材P 86~ P 87,找出疑惑之处)复习1:化简:⑴ 5(32a b - )+4(23b a -);⑵ ()()63a b c a b c -+--+- .复习2:在平⾯上,什么叫做两个向量平⾏?在平⾯上有两个向量,a b ,若b 是⾮零向量,则a与b平⾏的充要条件是⼆、新课导学※学习探究探究任务⼀:空间向量的共线问题:空间任意两个向量有⼏种位置关系?如何判定它们的位置关系?新知:空间向量的共线:1. 如果表⽰空间向量的所在的直线互相或,则这些向量叫共线向量,也叫平⾏向量.2. 空间向量共线:定理:对空间任意两个向量,a b (0b ≠ ), //a b的充要条件是存在唯⼀实数λ,使得推论:如图,l 为经过已知点A 且平⾏于已知⾮零向量的直线,对空间的任意⼀点O ,点P 在直线l 上的充要条件是试试:已知5,28,AB a b BC a b =+=-+()3CD a b =-,求证: A,B,C 三点共线.反思:充分理解两个向量,a b共线向量的充要条件中的0b ≠,注意零向量与任何向量共线.※典型例题例 1 已知直线AB ,点O 是直线AB 外⼀点,若OP xOA yOB =+,且x +y =1,试判断A,B,P 三点是否共线?变式:已知A,B,P 三点共线,点O 是直线AB 外⼀点,若12OP OA tOB =+,那么t =例2 已知平⾏六⾯体''''ABCD A B C D -,点M 是棱AA '的中点,点G 在对⾓线A 'C 上,且CG:GA '=2:1,设CD =a ,',CB b CC c ==,试⽤向量,,a b c 表⽰向量',,,CA CA CM CG .变式1:已知长⽅体''''ABCD A B C D -,M 是对⾓线AC '中点,化简下列表达式:⑴ 'AA CB - ;⑵ '''''AB B C C D ++⑶ '111222AD AB A A +-D试试:若空间任意⼀点O 和不共线的三点A,B,C 满⾜关系式111236OP OA OB OC =++,则点P 与 A,B,C共⾯吗?反思:若空间任意⼀点O 和不共线的三点A,B,C 满⾜关系式OP xOA yOB zOC =++,且点P 与 A,B,C 共⾯,则x y z ++= .※典型例题例1 下列等式中,使M ,A ,B ,C 四点共⾯的个数是()①;OM OA OB OC =--②111;532OM OA OB OC =++③0;MA MB MC ++=④0OM OA OB OC +++= . A. 1 B. 2 C. 3 D. 4变式:已知A,B,C 三点不共线,O 为平⾯ABC 外⼀点,若向量()17,53OP OA OB OC R λλ=++∈则P ,A,B,C 四点共⾯的条件是λ=例2 如图,已知平⾏四边形ABCD,过平⾯AC 外⼀点O 作射线OA,OB,OC,OD,在四条射线上分别取点E,,F ,G ,H,并且使,OE OF OG OHk OA OB OC OD==== 求证:E,F ,G ,H 四点共⾯.变式:已知空间四边形ABCD 的四个顶点A,B,C,D 不共⾯,E,F ,G ,H 分别是AB,BC,CD,AD 的中点,求证:E,F ,G ,H 四点共⾯.⼩结:空间向量的化简与平⾯向量的化简⼀样,加法注意向量的⾸尾相接,减法注意向量要共起点,并且要注意向量的⽅向.※动⼿试试练1. 已知,,A B C 三点不共线,对平⾯外任⼀点,满⾜条件122555OP OA OB OC =++,试判断:点P 与,,A B C 是否⼀定共⾯?练 2. 已知32,(1)8a m n b x m n =-=++ ,0a ≠,若//a b ,求实数.x三、总结提升※学习⼩结 1. 空间向量的数乘运算法则及它们的运算律; 2. 空间两个向量共线的充要条件及推论. ※知识拓展平⾯向量仅限于研究平⾯图形在它所在的平⾯内的平移,⽽空间向量研究的是空间的平移,它们的共同点都是指“将图形上所有点沿相同的⽅向移动相.※⾃我评价你完成本节导学案的情况为(). A. 很好 B. 较好 C. ⼀般 D. 较差※当堂检测(时量:5分钟满分:10分)计分:1. 在平⾏六⾯体ABCD -A 1B 1C 1D 1中,向量1D A、1D C 、11AC是() A. 有相同起点的向量 B .等长向量 C .共⾯向量 D .不共⾯向量.2. 正⽅体''''ABCD A B C D -中,点E 是上底⾯''''A B C D 的中⼼,若''BB xAD yAB zAA =++, 则x =,y =,z = .3. 若点P 是线段AB 的中点,点O 在直线AB 外,则OP OA + OB .4. 平⾏六⾯体''''ABCD A B C D -, O 为A 1C 与B 1D的交点,则'1()3AB AD AA ++=AO .5. 在下列命题中:①若a 、b 共线,则a 、b 所在的直线平⾏;②若a 、b 所在的直线是异⾯直线,则a 、b ⼀定不共⾯;③若a 、b 、c 三向量两两共⾯,则a 、b 、c 三向量⼀定也共⾯;④已知三向量a 、b 、c ,则空间任意⼀个向量p 总可以唯⼀表⽰为p =x a +y b +z c .其中正确命题的个数为().A .0 B.1 C. 2D. 3 1. 若324,(1)82a m n p b x m n yp =--=+++, 0a ≠ ,若//a b ,求实数,x y .2.已知两个⾮零向量21,e e不共线,12,AB e e =+ 121228,33AC e e AD e e =+=-. 求证:,,,A B C D 共⾯.A B C D F E G H§3.1.3.空间向量的数量积(1)1. 掌握空间向量夹⾓和模的概念及表⽰⽅法;2.复习1:什么是平⾯向量a 与b的数量积?复习2:在边长为1的正三⾓形⊿ABC 中,求AB BC ?⼆、新课导学※学习探究探究任务⼀:空间向量的数量积定义和性质问题夹⾓和空间线段的长度问题?新知:1) 两个向量的夹⾓的定义:已知两⾮零向量,a b在空间⼀点O ,作,OA a OB b ==,则AOB ∠做向量a 与b 的夹⾓,记作 .试试:⑴范围: ,a b ≤<>≤,a b ?? =0时,a b 与 ;,a b ?? =π时,a b 与⑵ ,,a b b a <>=<>成⽴吗?⑶,a b <>=,则称a 与b 互相垂直,记作 .2) 向量的数量积:已知向量,a b ,则叫做,a b作a b ? ,即a b ?=.规定:零向量与任意向量的数量积等于零.反思:⑴两个向量的数量积是数量还是向量?⑵ 0a ?= (选0还是0 )⑶你能说出a b ?的⼏何意义吗? 3) 空间向量数量积的性质:(1)设单位向量e ,则||cos ,a e a a e ?=<>.(2)a b a b ⊥??=.= .4) 空间向量数量积运算律:(1)()()()a b a b a b λλλ?=?=?.(2)a b b a ?=?(交换律).(3)()a b c a b a c ?+=?+?(分配律反思:⑴ )()a b c a b c ??=??(吗?举例说明.⑵若a b a c ?=? ,则b c =吗?举例说明.⑶若0a b ?= ,则00a b ==或吗?为什么?※典型例题例1 ⽤向量⽅法证明:在平⾯上的⼀条直线,如果和这个平⾯的⼀条斜线的射影垂直,那么它也和这条斜线垂直.变式1:⽤向量⽅法证明:已知:,m n 是平⾯α内的两条相交直线,直线l 与平⾯α的交点为B ,且,l m l n ⊥⊥. 求证:l α⊥.例2 如图,在空间四边形ABCD 中,2AB =,3BC =,BD =,3CD =,30ABD ∠= ,60ABC ∠= ,求AB 与CD 的夹⾓的余弦值变式:如图,在正三棱柱ABC-A 1B 1C 1中,若AB =2BB 1,则AB 1与C 1B 所成的⾓为()A. 60°B. 90°C. 105°D. 75°例3 如图,在平⾏四边形ABCD-A 1B 1C 1D 1中,4,3AB AD ==,'5AA =,90BAD ∠=?,'BAA ∠='DAA ∠=60°,求'AC 的长.※动⼿试试练1. 已知向量,a b满⾜1a = ,2b = ,3a b +=,则a b -= ____.练 2. 222,,22a b a b ==?=-已知, 则a b 与的夹⾓⼤⼩为_____. 三、总结提升※学习⼩结1..向量的数量积的定义和⼏何意义.2. 向量的数量积的性质和运算律的运⽤.※知识拓展向量给出了⼀种解决⽴体⼏何中证明垂直问题,求两条直线的夹⾓和线段长度的新⽅法.学习评价※⾃我评价你完成本节导学案的情况为().A. 很好B. 较好C. ⼀般D. 较差※当堂检测(时量:5分钟满分:10分)计分: 1. 下列命题中:①若0a b ?= ,则a ,b 中⾄少⼀个为0②若a 0≠ 且a b a c ?=? ,则b c =③()()a b c a b c ??=??④22(32)(32)94a b a b a b +?-=-正确有个数为()A. 0个B. 1个C. 2个D. 3个2. 已知1e 和2e 是两个单位向量,夹⾓为3π,则下⾯向量中与212e e -垂直的是()A. 12e e +B. 12e e -C. 1eD. 2e 3.已知ABC ?中,,,A B C ∠∠∠所对的边为,,a b c ,且3,1a b ==,30C ∠=?,则BC CA ?=4. 已知4a = ,2b =,且a 和b 不共线,当 a b λ+ 与a b λ-的夹⾓是锐⾓时,λ的取值范围是 .5. 已知向量,a b满⾜4a = ,2b = ,3a b -= ,则a b +=____课后作业:1. 已知空间四边形ABCD 中,AB CD ⊥,AC BD ⊥,求证:AD BC ⊥.2. 已知线段AB 、BD 在平⾯α内,BD ⊥AB , 线段AC α⊥,如果AB =a ,BD =b ,AC =c ,求C 、D 间的距离.D B C§3.1.4 空间向量的正交分解及其坐标表⽰1. 掌握空间向量的正交分解及空间向量基本定理和坐标表⽰;2. 掌握空间向量的坐标运算的规律;⼀、课前准备(预习教材P 92-96找出疑惑之处)复习1:平⾯向量基本定理:对平⾯上的任意⼀个向量P ,,a b 是平⾯上两个向量,总是存在实数对(),x y ,使得向量P 可以⽤,a b 来表⽰,表达式为,其中,a b 叫做 . 若a b ⊥,则称向量P 正交分解.复习2:平⾯向量的坐标表⽰:平⾯直⾓坐标系中,分别取x 轴和y 轴上的向量,i j 作为基底,对平⾯上任意向量a ,有且只有⼀对实数x ,y ,使得a xi y j =+,,则称有序对(),x y 为向量a 的,即a = .⼆、新课导学※学习探究探究任务⼀:空间向量的正交分解问题:对空间的任意向量a ,能否⽤空间的⼏个向量唯⼀表⽰?如果能,那需要⼏个向量?这⼏个向量有何位置关系?新知:⑴空间向量的正交分解:空间的任意向量a,均可分解为不共⾯的三个向量11a λ、22a λ、33a λ,使112233a a a a λλλ=++ . 如果123,,a a a两两,这种分解就是空间向量的正交分解.(2)空间向量基本定理:如果三个向量,,a b c ,对空间任⼀向量p ,存在有序实数组{,,}x y z ,使得p xa yb zc =++. 把的⼀个基底,,,a b c 都叫做基向量.反思:空间任意⼀个向量的基底有个.⑶单位正交分解:如果空间⼀个基底的三个基向量互相,长度都为,则这个基底叫做单位正交基⑷空间向量的坐标表⽰:给定⼀个空间直⾓坐标系O -xyz 和向量a ,且设i 、j 、k 为 x 轴、y 轴、z 轴正⽅向的单位向量,则存在有序实数组{,,}x y z ,使得a xi y j zk =++,则称有序实数组{,,}x y z 为向量a的坐标,记着p =.⑸设A 111(,,)x y z ,B 222(,,)x y z ,则AB= .⑹向量的直⾓坐标运算:设a =123(,,)a a a ,b =123(,,)b b b ,则⑴a +b =112233(,,)a b a b a b +++;⑵a -b =112233(,,)a b a b a b ---;⑶λa =123(,,)a a a λλλ()R λ∈;⑷a ·b =112233a b a b a b ++.试试: 1. 设23a i j k =-+,则向量a 的坐标为 .2. 若A (1,0,2),B (3,1,1)-,则AB= . 3. 已知a =(2,3,5)-,b =(3,1,4)--,求a +b ,a -b ,8a ,a ·b※典型例题例1 已知向量,,a b c 是空间的⼀个基底,从向量,,a b c 中选哪⼀个向量,⼀定可以与向量,p a b =+q a b =-构成空间的另⼀个基底?变式:已知O,A,B,C 为空间四点,且向量,,OA OB OC不构成空间的⼀个基底,那么点O,A,B,C 是否共⾯?⼩结:判定空间三个向量是否构成空间的⼀个基底的⽅法是:这三个向量⼀定不共⾯. 例2 如图,M,N 分别是四⾯体QABC 的边OA,BC 的中点,P ,Q 是MN 的三等分点,⽤,,OA OB OC表⽰OP 和OQ .变式:已知平⾏六⾯体''''ABCD A B C D -,点G是侧⾯''BB C C 的中⼼,且OA a =,',OC b OO c == ,试⽤向量,,a b c 表⽰下列向量: ⑴''',,;OB BA CA ⑵ OG .※动⼿试试练1. 已知()()()2,3,1,2,0,3,0,0,2a b c =-==,求:⑴()a b c ?+ ;⑵68a b c +- .练2. 正⽅体''''ABCD A B C D -的棱长为2,以A 为坐标原点,以'AB,AD,AA 为x 轴、y 轴、z 轴正⽅向建⽴空间直⾓坐标系,则点1D ,',AC AC 的坐标分别是,, .三、总结提升※学习⼩结1. 空间向量的正交分解及空间向量基本定理;2. 空间向量坐标表⽰及其运算※知识拓展建⽴空间直⾓坐标系前,⼀定要验证三条轴的垂直关系,若图中没有建系的环境,则根据已知条件,.※⾃我评价你完成本节导学案的情况为(). A. 很好 B. 较好 C. ⼀般 D. 较差※当堂检测(时量:5分钟满分:10分)计分:1. 若{}a,,b c为空间向量的⼀组基底,则下列各项中,能构成基底的是()A.,,a a b a b +-B. ,,b a b a b +-C. ,,c a b a b +-D. 2,,a b a b a b ++-2. 设i 、j 、k 为空间直⾓坐标系O -xyz 中x 轴、y 轴、z 轴正⽅向的单位向量,且AB i j k =-+-,则点B 的坐标是 3. 在三棱锥OABC 中,G 是ABC ?的重⼼(三条中线的交点),选取,,OA OB OC 为基底,试⽤基底表⽰OG =4. 正⽅体''''ABCD A B C D -的棱长为2,以A 为坐标原点,以'AB,AD,AA为x 轴、y 轴、z 轴正⽅向建⽴空间直⾓坐标系,E 为BB 1中点,则E 的坐标是 .5. 已知关于x 的⽅程()222350x t x t t --+++=有两个实根,c a tb =+ ,且()()1,1,3,1,0,2a b =-=-,当t =时,c的模取得最⼤值. 1. 已知()()3,5,7,2,4,3A B =-=-,求,,AB BA线段AB的中点坐标及线段AB 的长度.2. 已知,,a b c 是空间的⼀个正交基底,向量,,a b a b c +- 是另⼀组基底,若p 在,,a b c 的坐标是()1,2,3,求p 在,,a b a b c +-的坐标.§3.1.5空间向量运算的坐标表⽰1. 掌握空间向量的长度公式、夹⾓公式、两点间距离公式、中点坐标公式;※典型例题例1. 如图,在正⽅体1111ABCD A B C D -中,点11,E F 分别是1111,A B C D 的⼀个四等分点,求1BE 与1DF 所成的⾓的余弦值.变式:如上图,在正⽅体1111A B C D A B C D -中,1111113A BB E D F ==,求1BE 与1DF 所成⾓的余弦值.例2. 如图,正⽅体1111ABCD A B C D -中,点E,F 分别是111,BB D B 的中点,求证:1EF DA ⊥.变式:如图,正⽅体1111ABCD A B C D -中,点M 是AB 的中点,求1DB 与CM 所成⾓的余弦值.1. 若a =123(,,)a a a ,b =123(,,)b b b ,则312123a a ab b b ==是//a b的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分⼜不不要条件2. 已知()()2,1,3,4,2,a b x =-=-,且a b ⊥,则x = .3. 已知()()1,0,0,0,1,1A B -,OA OB λ+ 与OB 的夹⾓为120°,则λ的值为()A. B. C. D. 4. 若()()2,2,0,3,2,a x b x x ==-,且,a b 的夹⾓为钝⾓,则x 的取值范围是()A. 4x <-B. 40x -<<C. 04x <<D. 4x >5. 已知 ()()1,2,,,1,2a y b x =-=,且(2)//(2)a b a b +-,则()A. 1,13x y ==B. 1,42x y ==-C. 12,4x y ==- D. 1,1x y ==-1. 如图,正⽅体''''ABCD ABC D -棱长为a ,⑴求'',A B B C 的夹⾓;⑵求证:''A B AC ⊥.2. 如图,正⽅体1111ABCD A B C D -中,点M,N 分别为棱11,A A B B 的中点,求CM 和1D N 所成⾓的余弦值.§3.1 空间向量及其运算(练习)1. 熟练掌握空间向量的加法,减法,向量的数乘运算,向量的数量积运算及其坐标表⽰;a xi y j zk =++,则称有序实数组{,,}x y z 为向量a的坐标,记着p =.10. 设A 111(,,)x y z ,B 222(,,)x y z ,则AB = .11. 向量的直⾓坐标运算:设a =123(,,)a a a ,b =123(,,)b b b ,则⑴a +b =;⑵a -b =;⑶λa =;⑷a ·b =※动⼿试试 1.在下列命题中:①若a 、b 共线,则a 、b 所在的直线平⾏;②若a 、b 所在的直线是异⾯直线,则a 、b ⼀定不共⾯;③若a 、b 、c 三向量两两共⾯,则a 、b 、c 三向量⼀定也共⾯;④已知三向量a 、b 、c ,则空间任意⼀个向量p 总可以唯⼀表⽰为p =x a +y b +z c .其中正确命题的个数为()A .0 B. 1 C. 2 D. 3 2.在平⾏六⾯体ABCD -A 1B 1C 1D 1中,向量1D A、1D C 、11AC 是() A .有相同起点的向量 B .等长向量C .共⾯向量D .不共⾯向量3.已知a =(2,-1,3),b =(-1,4,-2), c =(7,5,λ),若a 、b 、c 三向量共⾯,则实数λ=() A. 627 B. 637 C. 647 D. 657 4.若a 、b 均为⾮零向量,则||||?=a b a b 是a 与b 共线的() A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分⼜不必要条件5.已知△ABC 的三个顶点为A (3,3,2),B (4,-3,7),C (0,5,1),则BC 边上的中线长为() A .2 B .3C .4D .56. 32,2,a i j k b i j k =+-=-+ 则53a b ?= ()A .-15B .-5C .-3D .-1※典型例题例1 如图,空间四边形OABC 中,,OA a OB b == , OC c =,点M 在OA 上,且OM =2MA ,点N 为BC 的中点,则MN = .变式:如图,平⾏六⾯体''''ABCD A B C D -中,,AB a AD b ==,'AA c = ,点,,P M N 分别是'''',,CA CD C D 的中点,点Q 在'CA 上,且'41CQ QA =,⽤基底,,a b c表⽰下列向量:⑴ AP ; ⑵ AM ; ⑶ AN ; ⑷ AQ .例2 如图,在直三棱柱ABC —A 1B 1C 1中,190,1,2,6ABC CB CA ∠=?==,点M 是1CC 的中点,求证:1AM BA ⊥.变式:正三棱柱ABC —A 1B 1C 1的侧棱长为2,底⾯边长为1,点M 是BC 的中点,在直线1CC 上求⼀点N ,使得1MN AB ⊥※⾃我评价你完成本节导学案的情况为(). A. 很好 B. 较好 C. ⼀般 D. 较差※当堂检测(时量:5分钟满分:10分)计分:1.直三棱柱ABC —A 1B 1C 1中,若CA = a ,CB =b ,1CC = c ,则1A B =() A. +-a b c B. -+a b c C. -++a b c D.-+-a b c 2.,,m a m b ⊥⊥ (,n a b R λµλµλ=+∈向量且、0)µ≠则()A .//m nB . m 与n不平⾏也不垂直C. m n ⊥, D .以上情况都可能.3. 已知a +b +c =0 ,|a |=2,|b |=3,|c|则向量a 与b之间的夹⾓,a b <> 为()A .30°B .45°C .60°D .以上都不对4.已知()()1,1,0,1,0,2,a b==-且ka b + 与2a b - 互相垂直,则k 的值是()A. .1B. 15C. 35D. 755. 若A (m +1,n -1,3), B. (2m ,n ,m -2n ),C (m +3,n -3,9)三点共线,则m +n =如图,在棱长为1的正⽅体1111ABCD A B C D -中,点,,E F G 分别是11,,DD BD BB 的中点. ⑴求证:EF CF ⊥;⑵求EF 与CG 所成⾓的余弦;⑶求CE 的长.§3.2⽴体⼏何中的向量⽅法(1)1. 掌握直线的⽅向向量及平⾯的法向量的概念;⾏、垂直、夹⾓等⽴体⼏何问题.⼀、课前准备(预习教材P 102~ P 104,找出疑惑之处)复习1:可以确定⼀条直线;确定⼀个平⾯的⽅法有哪些?复习2:如何判定空间A ,B ,C 三点在⼀条直线上?复习3:设a =123(,,)a a a ,b =123(,,)b b b ,a ·b =⼆、新课导学※学习探究探究任务⼀:向量表⽰空间的点、直线、平⾯问题:怎样⽤向量来表⽰点、直线、平⾯在空间中的位置?新知:⑴点:在空间中,我们取⼀定点O 作为基点,那么空间中任意⼀点P 的位置就可以⽤向量OP来表⽰,我们把向量OP称为点P 的位置向量. ⑵直线:①直线的⽅向向量:和这条直线平⾏或共线的⾮零向量.②对于直线l 上的任⼀点P ,存在实数t ,使得AP t AB =,此⽅程称为直线的向量参数⽅程. ⑶平⾯:①空间中平⾯α的位置可以由α内两个不共线向量确定.对于平⾯α上的任⼀点P ,,a b是平⾯α内两个不共线向量,则存在有序实数对(,)x y ,使得OP x a y b =+ .②空间中平⾯α的位置还可以⽤垂直于平⾯的直线的⽅向向量表⽰空间中平⾯的位置.⑷平⾯的法向量:如果表⽰向量n的有向线段所在直线垂直于平⾯α,则称这个向量n垂直于平⾯α,记作n ⊥α,那么向量n叫做平⾯α的法向量.试试: .1.如果,a b 都是平⾯α的法向量,则,a b的关系 .2.向量n是平⾯α的法向量,向量a 是与平⾯α平⾏或在平⾯内,则n 与a的关系是 .反思:1. ⼀个平⾯的法向量是唯⼀的吗?2. 平⾯的法向量可以是零向量吗?⑸向量表⽰平⾏、垂直关系:设直线,l m 的⽅向向量分别为,a b,平⾯,αβ的法向量分别为,u v,则① l ∥m ?a ∥b a kb ?=② l ∥α?a u ⊥ 0a u ??=③α∥β?u ∥v .u kv ?=※典型例题例1 已知两点()()1,2,3,2,1,3A B --,求直线AB与坐标平⾯YOZ 的交点.变式:已知三点()()1,2,3,2,1,2,A B ()1,1,2P ,点Q 在OP 上运动(O 为坐标原点),求当QA QB ?取得最⼩值时,点Q 的坐标.⼩结:解决有关三点共线问题直接利⽤直线的参数⽅程即可.例2 ⽤向量⽅法证明两个平⾯平⾏的判定定理:⼀个平⾯内的两条相交直线与另⼀个平⾯平⾏,则这两个平⾯平⾏.变式:在空间直⾓坐标系中,已知()()()3,0,0,0,4,0,0,0,2A B C ,试求平⾯ABC 的⼀个法向量.⼩结:平⾯的法向量与平⾯内的任意向量都垂直.※动⼿试试练1. 设,a b分别是直线12,l l 的⽅向向量,判断直线12,l l 的位置关系:⑴ ()()1,2,2,2,3,2a b =-=-;⑵ ()()0,0,1,0,0,3a b ==.练2. 设,u v分别是平⾯,αβ的法向量,判断平⾯,αβ的位置关系:⑴ ()()1,2,2,2,4,4u v =-=--;⑵ ()()2,3,5,3,1,4u v =-=--.三、总结提升※学习⼩结1. 空间点,直线和平⾯的向量表⽰⽅法2. 平⾯的法向量求法和性质.※知识拓展:求平⾯的法向量步骤:⑴设平⾯的法向量为(,,)n x y z =;⑵找出(求出)平⾯内的两个不共线的向量的坐标;⑶根据法向量的定义建⽴关于,,x y z 的⽅程组;,即得法向量.※⾃我评价你完成本节导学案的情况为(). A. 很好 B. 较好 C. ⼀般 D. 较差※当堂检测(时量:5分钟满分:10分)计分:1. 设()()2,1,2,6,3,6a b =--=--分别是直线12,l l 的⽅向向量,则直线12,l l 的位置关系是 .2. 设()()2,2,5,6,4,4u v =-=-分别是平⾯,αβ的法向量,则平⾯,αβ的位置关系是 .3. 已知n α⊥,下列说法错误的是()A. 若a α?,则n a ⊥B.若//a α,则n a ⊥C.若,m α⊥,则//n mD.若,m α⊥,则n m = 4.下列说法正确的是()A.平⾯的法向量是唯⼀确定的B.⼀条直线的⽅向向量是唯⼀确定的C.平⾯法向量和直线的⽅向向量⼀定不是零向量D.若m 是直线l 的⽅向向量,//l α,则//m α5. 已知()()1,0,1,0,3,1AB AC =-=-,能做平⾯ABC 的法向量的是()A. ()1,2,1B.11,,13??C.()1,0,0D. ()2,1,31. 在正⽅体1111ABCD A B C D -中,求证:1DB是平⾯1ACD 的⼀个法向量.2.已知()()2,2,1,4,5,3AB AC ==,求平⾯ABC 的⼀个法向量.§3.2⽴体⼏何中的向量⽅法(2)的⽴体⼏何问题;2. 掌握向量运算在⼏何中求两点间距离和求空间图形中的⾓度的计算⽅法.⼀、课前准备(预习教材P 105~ P 107,找出疑惑之处.复习1:已知1a b ?= ,1,2a b ==,且2m a b =+ ,求m .复习2:什么叫⼆⾯⾓?⼆⾯⾓的⼤⼩如何度量?⼆⾯⾓的范围是什么?⼆、新课导学※学习探究探究任务⼀:⽤向量求空间线段的长度问题:如何⽤向量⽅法求空间线段的长度?新知:⽤空间向量表⽰空间线段,然后利⽤公式a = 求出线段长度.试试:在长⽅体''''A B C DA B C D -中,已知'1,2,1AB BC CC ===,求'AC 的长.反思:⽤向量⽅法求线段的长度,关键在于把未知量⽤已知条件中的向量表⽰.※典型例题例1 如图,⼀个结晶体的形状为平⾏六⾯体,其中,以顶点A 为端点的三条棱长都相等,且它们彼此的夹⾓都是60°,那么以这个顶点为端点的晶体的对⾓线的长与棱长有什么关系?变式1:上题中平⾏六⾯体的对⾓线1BD 的长与棱长有什么关系?变式2:如果⼀个平⾏六⾯体的各条棱长都相等,并且以某⼀顶点为端点的各棱间的夹⾓都等于α, 那么由这个平⾏六⾯体的对⾓线的长可以确定棱长吗?探究任务⼆:⽤向量求空间图形中的⾓度例2 如图,甲站在⽔库底⾯上的点A 处,⼄站在⽔坝斜⾯上的点B 处.从A ,B 到直线l (库底与⽔坝的交线)的距离,AC BD 分别为,a b ,CD 的长为c ,AB 的长为d .求库底与⽔坝所成⼆⾯⾓的余弦值.变式:如图,60?的⼆⾯⾓的棱上有,A B 两点,直线,AC BD 分别在这个⼆⾯⾓的两个半平⾯内,且都垂直于,AB 已知4,6,8AB AC BD ===,求CD 的长.※动⼿试试练1. 如图,已知线段AB 在平⾯α内,线段AC α⊥,线段BD ⊥AB ,线段'DD α⊥,'30DBD∠= ,如果AB =a ,AC =BD =b ,求C 、D 间的距离.练2. 如图,M 、N 分别是棱长为1的正⽅体''''ABCD A B C D -的棱'BB 、''B C 的中点.求异⾯直线MN 与'CD 所成的⾓.三、总结提升※学习⼩结 1. 求出空间线段的长度:⽤空间向量表⽰空间线段,然后利⽤公式a ; 2. 空间的⼆⾯⾓或异⾯直线的夹⾓,都可以转化为利⽤公式cos ,a ba b a b= 求解.※知识拓展解空间图形问题时,可以分为三步完成:(1)建⽴⽴体图形与空间向量的联系,⽤空间向量表⽰问题中涉及的点、直线、平⾯,把⽴体⼏何问题转化为向量问题(还常建⽴坐标系来辅助);(2)通过向量运算,研究点、直线、平⾯之间的位置关系以及它们之间距离和夹⾓等问题;“翻译”成相应的⼏何意义.※⾃我评价你完成本节导学案的情况为().A. 很好B. 较好C. ⼀般D. 较差※当堂检测(时量:5分钟满分:10分)计分: 1. 已知()()1,02,1,1,3A B -,则AB = .2. 已知1cos ,2a b =- ,则,a b 的夹⾓为 .3. 若M 、N 分别是棱长为1的正⽅体''''ABCD A B C D-的棱''',A B BB 的中点,那么直线,AM CN 所成的⾓的余弦为()C.35D.25 4.将锐⾓为60?边长为a 的菱形ABCD 沿较短的对⾓线折成60?的⼆⾯⾓,则,AC BD 间的距离是()A.32a C.34a 5.正⽅体'''A B C D AB C D -中棱长为a ,'13AM AC=,N 是'BB 的中点,则MN 为()1. 如图,正⽅体''''ABCD A B C D -的棱长为1, ,M N 分别是''',BB B C 的中点,求:⑴ ',MN CD 所成⾓的⼤⼩;⑵ ,MN AD 所成⾓的⼤⼩;⑶ AN 的长度.§3.2⽴体⼏何中的向量⽅法(3)C。
郑2012-13高二数学必修三导学案3.3.2

2 将[0,1]内的均匀随机数转化为[-2,6]内的均匀随机数, 需要实施 则 fn(A)=___________即为概率 P(A)的近似值. 法三:几何概型公式求: P(A)= ★3 某人对某台的电视节目作了长期的统计后得出结论: 他任意 9 时间打开电视看该台节目, 看不到广告的概率约为10, 那么该台每 ★★2、假设你家订了一份报纸,送报人可能在早上 6:30~7:30 之 间把报纸送到你家,你父亲离开家去工作的时间在早上 7:00~8:00 之间,问你父亲在离开家前能得到报纸(称为事件 A)的概率的多 ★4.半径为 1 的圆上固定一点, 然后再随机地取另一点作弦, 则 弦长超过圆内接等边三角形的边长的概率为________. 小时约有________分钟插播广告. 的变换为____________
(2)、算器上产生[0,1]的均匀随机数的函数是_____________函数. (3)、 Excel 软件产生[0,1]区间上均匀随机数的函数为_____________ (4)、由计算器不能直接产生【a,b】区间上的均匀随机数,只能通 过 线 性 变 换 得 到 , 如 果 X 是 [0,1] 区 间 上 的 均 匀 随 机 数 , 则 (a+(b-a)X)就是区间[a,b]区间上的均匀随机数,你能理解这个 问题吗?
课前完成导学案,掌握基本题型,时间不超过 20 分钟,A 层次完成所有会做的题目;B 层次完成除★★所有会做的题目; 2 C 层次完成不带★所有会做的题目,坚决杜绝抄袭现象
: 1、用模拟法估计与长度、角度有关的几何概率 取一根长度为 5 m 的绳子, 拉直后在任意位置剪断, 用均匀随机模 拟方法估计剪得两段的长都不小于 2 m 的概率有多大? 【解】 设剪得两段的长都不小于 2 m 为事件 A. 法一: 步骤是: (1)利用计算器或计算机产生 n 个 0~1 之间的均匀随机数, x=___________
高二英语选择性必修第一册(2020版)_Unit3_Using_language1_导学案

Unit3 Using language1 导学案【核心素养】1. To enhance the reading and writing skills;2. To learn about several theme parks around the world;3. To learn how to write an introduction to a theme park;【情境导入】1. Have you ever been to Beijing Olympic Forest Park?2. What do you normally do when visiting theme park?【阅读深思】Read the text and answer the following questions:(1) How many theme parks are introduced in the passage? What and where are they?______________________________________________________________________________ (2) What can you do in Chimelong Ocean Kingdom?______________________________________________________________________________【自学反馈】Activity 1: Read the text and then fill in the table.Activity 2: Study the language features1. The above table shows the introductions to each theme park. What headers would you give for Columns A to D?A Name and Location B.C. D.【自主探究】自主探究1:Find the following items in the text, and then discuss in groups how they are used and what they add to the text.A. adjectivesB. if-clausesC. imperatives自主探究2:Choose a park and make a mind map about the park from the following aspects.ShowsFood Rides(Name of park) in (place)Attractions Other【成果展示】Please show your answers based on the above discussion.【点评精讲】1. Language features of the passage;2. How to write an introduction to a park.3. Complicated sentence analysis【随堂检测】Fill the blanks with correct wordsWhichever and whatever you like, there is an incredible theme park _________ will appeal to you. Disneyland, probably most familiar _________ us, will bring you into a _________ (magic) world and make your childhood dreams come true. Here, you can travel through space, visit a pirate ship, or meet an _______ (adore) fairytale or cartoon. It also has many exciting rides _________ (amuse) you, from enormous swinging ships to scary freefall drops, In Dollywood, you can enjoy ________ (performance) put on by famous country music groups, see wood, glass and iron ________ (make) in the old-fashioned way _________ ride on the on steam engine and a superb old wooden roller coaster, Thunderhead. In Chimelong Ocean Kingdom, _________ (walk) under the Whale Shark Aquarium, you can see up to 20, 000 fish as well as all kinds of interesting animals. You can join a water fight against pirates, get ________ (turn) upside down by an exciting roller coaster and enjoy tasty food for every appetite.【巩固应用】Exercise 1 and exercise 2 of P.34参考答案Unit 3 FASCINATING PARKS ---Using LanguageTHEME PARKSFUN AND MORE THAN FUN【阅读深思】Read the text and answer the following questions:(1) How many theme parks are introduced in the passage? What and where are they?Three. They are Disneyland in several parts of the world, Dollywood in the Smoky Mountains in the southeastern USA and Chimelong Ocean Kingdom in Zhuhai, China.(2) What can you do in Chimelong Ocean Kingdom?Get turned upside down by an exciting roller coaster, see various dishes and animals, including whale sharks and polar bears, and join a water fight again pirates【自学反馈】Activity 1: Read the text and then fill in the table.Activity 2: Study the language features1. The above table shows the introductions to each theme park. What headers would you give forColumns A to D?A Name and Location B. The wonderful ridesC. What to enjoyD. Where to eat【随堂检测】Fill the blanks with correct wordsWhichever and whatever you like, there is an incredible theme park that will appeal to you. Disneyland, probably most familiar with us, will bring you into a magical (magic) world and make your childhood dreams come true. Here, you can travel through space, visit a pirate ship, or meet an adorable (adore) fairytale or cartoon. It also has many exciting rides to amuse(amuse) you, from enormous swinging ships to scary freefall drops, In Dollywood, you can enjoy performances (performance) put on by famous country music groups, see wood, glass and iron made (make) in the old-fashioned way and ride on the on steam engine and a superb old wooden roller coaster, Thunderhead. In Chimelong Ocean Kingdom, walking (walk) under the Whale Shark Aquarium, you can see up to 20, 000 fish as well as all kinds of interesting animals. You can join a water fight against pirates, get turned (turn) upside down by an exciting roller coaster and enjoy tasty food for every appetite.。
高二地理(必修三)导学案汇编

高二地理(必修三)导学案汇编目录第一章地理环境与区域发展第一节地理环境对区域发展的影响…………………………………………………………………………1~4 第二节地理信息技术在区域地理环境研究中的应用…………………………………………………………………………5~8第二章区域生态环境建设第一节荒漠化的防治——以我国西北地区为例…………………………………………………………………………9~12 第二节森林的开发和保护——以亚马孙热带雨林为例第一课时…………………………………………………………………13~16 第二课时…………………………………………………………………17~20第三章区域自然资源综合开发利用第一节能源资源的开发——以我国山西省为例第一课时…………………………………………………………………21~24 第二课时…………………………………………………………………25~28 第二节流域的综合开发———以美国田纳西河为例第一课时…………………………………………………………………29~32 第二课时…………………………………………………………………33~36第四章区域经济发展第一节区域农业发展————以我国东北平原为例第一课时…………………………………………………………………37~40 第二课时…………………………………………………………………41~44 第二节区域工业化和城市化————以我国珠江三角洲地区为例第一课时…………………………………………………………………45~48 第二课时…………………………………………………………………49~52第五章区域联系与区域协调发展第一节资源的跨区域调配————以我国西气东输为例…………………………………………………………………53~56 第二节产业转移————以东亚为例…………………………………………………………………57~60第一章地理环境与区域发展导学案第一节地理环境对区域发展的影响审定:高二地理备课组班级:组别:姓名:【学习目标】1.举例说出区域的特征2.以长江三角洲和松嫩平原为例,比较地理位置、气候、土地、矿产等条件的差异以及这些差异对区域发展带来的影响,学会区域比较的一般方法。
高二数学选修2-1人教A全册导学案第3章空间向量与立体几何§3.2《立体几何中的向量方法》

§3.2 立体几何中的向量方法知识点一用向量方法判定线面位置关系(1)设a、b分别是l1、l2的方向向量,判断l1、l2的位置关系:①a=(2,3,-1),b=(-6,-9,3).②a=(5,0,2),b=(0,4,0).(2)设u、v分别是平面α、β的法向量,判断α、β的位置关系:①u=(1,-1,2),v=(3,2,).②u=(0,3,0),v=(0,-5,0).(3)设u是平面α的法向量,a是直线l的方向向量,判断直线l与α的位置关系.①u=(2,2,-1),a=(-3,4,2).②u=(0,2,-3),a=(0,-8,12).解(1)①∵a=(2,3,-1),b=(-6,-9,3),∴a=-b,∴a∥b,∴l1∥l2.②∵a=(5,0,2),b=(0,4,0),∴a·b=0,∴a⊥b,∴l1⊥l2.(2)①∵u=(1,-1,2),v=(3,2,),∴u·v=3-2-1=0,∴u⊥v,∴α⊥β.②∵u=(0,3,0),v=(0,-5,0),∴u=-v,∴u∥v,∴α∥β.(3)①∵u=(2,2,-1),a=(-3,4,2),∴u·a=-6+8-2=0,∴u⊥a,∴l⊂α或l∥α.②∵u=(0,2,-3),a=(0,-8,12),∴u=-a,∴u∥a,∴l⊥α.知识点二利用向量方法证明平行问题如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是C1C、B1C1的中点.求证:MN∥平面A1BD.证明方法一如图所示,以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z 轴建立空间直角坐标系,设正方体的棱长为1,则可求得M (0,1,),N (,1,1),D(0,0,0),A1(1,0,1),B(1,1,0),于是=(,0,),设平面A1BD的法向量是n=(x,y,z).n=(x,y,z).则n·=0,得取x=1,得y=-1,z=-1.∴n=(1,-1,-1).又·n=(,0,)·(1,-1,-1)=0,方法二∵ =∴∥,又∵MN⊄平面A1BD.∴MN∥平面A1BD.知识点三利用向量方法证明垂直问题在正棱锥P—ABC中,三条侧棱两两互相垂直,G是△PAB的重心,E、F分别为BC、PB上的点,且BE∶EC=PF∶FB=1∶2.(1)求证:平面GEF⊥平面PBC;(2)求证:EG是PG与BC的公垂线段.证明(1)方法一如图所示,以三棱锥的顶点P为原点,以PA、PB、PC所在直线分别为x轴、y轴、z轴建立空间直角坐标系.令PA=PB=PC=3,则A(3,0,0)、B(0,3,0)、C(0,0,3)、E(0,2,1)、F(0,1,0)、G(1,1,0)、P(0,0,0).于是=(3,0,0),=(3,0,0),故=3,∴PA∥FG.而PA⊥平面PBC,∴FG⊥平面PBC,又FG⊂平面EFG,∴平面EFG⊥平面PBC.方法二同方法一,建立空间直角坐标系,则E(0,2,1)、F(0,1,0)、G(1,1,0).=(0,-1,-1),=(0,-1,-1),设平面EFG的法向量是n=(x,y,z),则有n⊥,n⊥,∴令y=1,得z=-1,x=0,即n=(0,1,-1).而显然=(3,0,0)是平面PBC的一个法向量.这样n·= 0,∴n⊥即平面PBC的法向量与平面EFG的法向量互相垂直,∴平面EFG⊥平面PBC.(2)∵=(1,1,1),=(1,1,0),=(0,3,3),∴·=11= 0,·=33 = 0,∴EG⊥PG,EG⊥BC,∴EG是PG与BC的公垂线段.知识点四利用向量方法求角四棱锥P—ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠D=∠DAB=90°,AB=4,CD=1,AD=2.(1)建立适当的坐标系,并写出点B,P的坐标;(2)求异面直线PA与BC所成角的余弦值.解(1)如图所示,以D为原点,射线DA,DC,DP分别为x轴,y轴,z轴的正方向,建立空间直角坐标系D—xyz,∵∠D=∠DAB=90°,AB=4,CD=1,AD=2,∴A(2,0,0),C(0,1,0),B(2,4,0).由PD⊥面ABCD得∠PAD为PA与平面ABCD所成的角.∴∠PAD=60°.在Rt△PAD中,由AD=2,得PD=2.∴P(0,0,2).(2)∵=(2,0,-2),=(2,3,0)∴cos〈,〉=∴PA与BC所成角的余弦值为.正方体ABEF-DCE′F′中,M、N分别为AC、BF的中点(如图所示),求平面MNA 与平面MNB所成二面角的余弦值.解取MN的中点G,连结BG,设正方体棱长为1.方法一∵△AMN,△BMN为等腰三角形,∴AG⊥MN,BG⊥MN.∴∠AGB为二面角的平面角或其补角.∵AG=BG=,,设〈,〉=θ,2=2+2·+2,∴1=()2+2××cosθ+()2.∴cosθ=,故所求二面角的余弦值为.方法二以B为坐标原点,BA,BE,BC所在的直线分别为x轴、y轴、z轴建立空间直角坐标系B-xyz则M(,0,),N (,,0),中点G(,,),A(1,0,0),B(0,0,0),由方法一知∠AGB为二面角的平面角或其补角.∴=(,-,-),=(,-,-),∴ cos<, >==,故所求二面角的余弦值为.方法三建立如方法二的坐标系,∴即取n1=(1,1,1).同理可求得平面BMN的法向量n2=(1,-1,-1).∴cos〈n1,n2〉=,故所求二面角的余弦值为知识点五用向量方法求空间的距离已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.解如图所示,以C为原点,CB、CD、CG所在直线分别为x、y、z轴建立空间直角坐标系C-xyz.由题意知C(0,0,0),A(4,4,0),B(4,0,0),D(0,4,0),E(4,2,0),F(2,4,0),G(0,0,2).=(0,2,0),=(-2,4,0),设向量⊥平面GEF,垂足为M,则M、G、E、F四点共面,故存在实数x,y,z,使= x+ y+ z,即= x(0,2,0)+y(2,4,0)+z(4,0,2)=(2y4z,2x+4y,2z).由BM⊥平面GEF,得⊥,⊥,于是·=0,·=0,即即,解得∴=(-2y-4z,2x+4y,2z)=∴||=即点B到平面GEF的距离为.考题赏析(安徽高考)如图所示,在四棱锥O—ABCD中,底面ABCD是边长为1的菱形,∠ABC=,OA⊥底面ABCD,OA=2,M为OA的中点.(1)求异面直线AB与MD所成角的大小;(2)求点B到平面OCD的距离.解作AP⊥CD于点P.如图,分别以AB、AP、AO所在直线为x、y、z轴建立平面直角坐标系.A(0,0,0),B(1,0,0),P (0,,0),D (-,,0),O(0,0,2),M(0,0,1).(1)设AB与MD所成角为θ,∵=(1,0,0),=(-,,-1),∴cos =.∴θ=.∴AB与MD所成角的大小为.(2)∵=(0,,),=(,,),∴设平面OCD的法向量为n = ( x, y , z ),则n·=0,n·= 0.得取z=,解得n = (0,4,).设点B到平面OCD的距离为d,则d为在向量n上的投影的绝对值.∵=(1,0,2),∴d=,∴点B到平面OCD的距离为,1.已知A(1,0,0)、B(0,1,0)、C(0,0,1),则平面ABC的一个单位法向量是( )A.(,,-) B.(,-,)C.(-,,) D.(-,-,-)答案 D=(-1,1,0),是平面OAC的一个法向量.=(-1,0,1),=(0,-1,1)设平面ABC的一个法向量为n=(x,y,z)∴令x=1,则y=1,z=1∴n=(1,1,1)单位法向量为:=± (,,).2.已知正方体ABCD—A1B1C1D1,E、F分别是正方形A1B1C1D1和ADD1A1的中心,则EF和CD所成的角是( )A.60°B.45°C.30°D.90°答案 B3.设l1的方向向量a=(1,2,-2),l2的方向向量b=(-2,3,m),若l1⊥l2,则m=( ) A.1 B.2 C.D.3答案 B解析因l1⊥l2,所以a·b=0,则有1×(-2)+2×3+(-2)×m=0,∴2m=6-2=4,即m=2.4.若两个不同平面α,β的法向量分别为u=(1,2,-1),v=(-3,-6,3),则( )A.α∥βB.α⊥βC.α,β相交但不垂直D.以上均不正确答案 A解析因v=-3u,∴v∥u.故α∥β.5.已知a、b是异面直线,A、B∈a,C、D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a与b所成的角是( )A.30°B.45°C.60°D.90°答案 C解析设〈,〉=θ,·=(++·= ||2= 1,cosθ=,所以θ=606.若异面直线l1、l2的方向向量分别是a=(0,-2,-1),b=(2,0,4),则异面直线l1与l2的夹角的余弦值等于( )A.B.C.-D.答案 B解析设异面直线l1与l2的夹角为θ,则cosθ=7.已知向量n=(6,3,4)和直线l垂直,点A(2,0,2)在直线l上,则点P(-4,0,2)到直线l的距离为________.答案,解析=(6,0,0),因为点A在直线l上,n与l垂直,所以点P到直线l的距离为8.平面α的法向量为(1,0,-1),平面β的法向量为(0,-1,1),则平面α与平面β所成二面角的大小为________.答案或,解析设n1=(1,0,-1),n2=(0,-1,1)则cos〈n1,n2〉=〈n1,n2〉=.因平面α与平面β所成的角与〈n1,n2〉相等或互补,所以α与β所成的角为或.9.已知四面体顶点A(2,3,1)、B(4,1,-2)、C(6,3,7)和D(-5,-4,8),则顶点D到平面ABC的距离为________.答案11解析设平面ABC的一个法向量为n =(x,y,z)则令x=1,则n = (1,2,),=(7,7,7)故所求距离为,10.如图所示,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于F.(1)证明:PA∥平面BDE;(2)证明:PB⊥平面DEF.证明(1)如图建立空间直角坐标系,设DC=a,AC∩BD=G,连结EG,则A(a,0,0),P(0,0,a),C(0,a,0),E (0,,),G (,,0).于是=(a,0,a),=(,0,),∴= 2,∴PA∥EG.又EG平面DEB.PA平面DEB.∴PA∥平面DEB.(2)由B(a,a,0),得=(a, a, a),又=(0, ,),∵·=∴PB⊥DE.又EF⊥PB,EF∩DE=E,∴PB⊥平面EFD.11.如图所示,已知点P在正方体ABCD—A′B′C′D′的对角线BD′上,∠PDA=60°.(1)求DP与CC′所成角的大小;(2)求DP与平面AA′D′D所成角的大小.解如图所示,以D为原点,DA为单位长度建立空间直角坐标系D—xyz.则=(1,0,0),= (0,0,1).连结BD,B′D′.在平面BB′D′D中,延长DP交B′D′于H.设= (m,m,1) (m>0),由已知〈,〉= 60,由·= ||||cos〈,〉,可得2m =解得m =,所以=(,,1),(1)因为cos〈,〉=(2)所以〈,〉= 45,即DP与CC′所成的角为45.(2)平面AA′D′D的一个法向量是= (0,1,0).因为cos〈,〉=所以〈,〉= 60°,可得DP与平面AA′D′D所成的角为30.12. 如图,四边形ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.平面PBD⊥平面PAC,(1)求点A到平面PBD的距离;(2)求异面直线AB与PC的距离.(1)解以AC、BD的交点为坐标原点,以AC、BD所在直线为x轴、y轴建立如图所示的空间直角坐标系,则A(3,0,0),B(0,1,0),C(,0,0),D(0,1,0),P(3,0,2).设平面PBD的一个法向量为n1=(1,y1,z1).由n1⊥,n1⊥,可得n1=(1,0,).(1)=(,0,0),点A到平面PBD的距离,,13.如图所示,直三棱柱ABC—A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC = 2a,BB1 = 3a,D为A1C1的中点,在线段AA1上是否存在点F,使CF⊥平面B1DF?若存在,求出||;若不存在,请说明理由.解以B为坐标原点,建立如图所示的空间直角坐标系B-xyz.假设存在点F,使CF⊥平面B1DF,并设=λ=λ(0,0,3a)=(0,0,3λa)(0<λ<1),∵D为A1C1的中点,∴D(,,3a)=(,,3a)-(0,0,3a)=(,,0),=∵CF⊥平面B1DF,∴CF⊥, ⊥,即解得λ=或λ=∴存在点F使CF⊥面B1DF,且当λ=时,||=,|| = a当λ=,|| =,|| = 2a.14.如图(1)所示,已知四边形ABCD是上、下底边长分别为2和6,高为eq \r(3)的等腰梯形.将它沿对称轴OO1折成直二面角,如图(2).(1)证明:AC⊥BO1;(2)求二面角O—AC—O1的余弦值.(1)证明由题设知OA⊥OO1,OB⊥OO1.所以∠AOB是所折成的直二面角的平面角,即OA⊥OB.故以O为原点,OA、OB、OO1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示,则相关各点的坐标是A(3,0,0)、B(0,3,0)、C(0,1, )、O1(0,0, ).·=-3+·=0.所以AC⊥BO1.(2)解因为·=+ ·=0.所以BO1⊥OC.由(1)AC⊥BO1,所以BO1⊥平面OAC,是平面OAC的一个法向量.设n=(x,y,z)是平面O1AC的一个法向量,由取z= ,得n=(1,0,).设二面角O-AC-O1的大小为θ,由n 、的方向可知θ=〈n,〉,所以cosθ= cos〈n ,〉=即二面角O—AC—O1的余弦值是.。
高二数学人教A版选修1-1第三章3.3.2函数的极值与导数导学案(含答案)
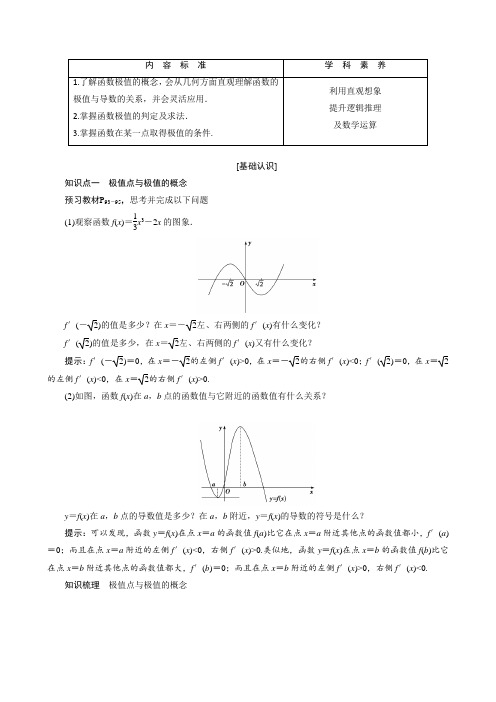
内 容 标 准学 科素 养 1.了解函数极值的概念,会从几何方面直观理解函数的极值与导数的关系,并会灵活应用. 2.掌握函数极值的判定及求法. 3.掌握函数在某一点取得极值的条件.利用直观想象 提升逻辑推理 及数学运算[基础认识]知识点一 极值点与极值的概念 预习教材P 93-95,思考并完成以下问题 (1)观察函数f (x )=13x 3-2x 的图象.f ′(-2)的值是多少?在x =-2左、右两侧的f ′(x )有什么变化? f ′(2)的值是多少,在x =2左、右两侧的f ′(x )又有什么变化?提示:f ′(-2)=0,在x =-2的左侧f ′(x )>0,在x =-2的右侧f ′(x )<0;f ′(2)=0,在x =2的左侧f ′(x )<0,在x =2的右侧f ′(x )>0.(2)如图,函数f (x )在a ,b 点的函数值与它附近的函数值有什么关系?y =f (x )在a ,b 点的导数值是多少?在a ,b 附近,y =f (x )的导数的符号是什么?提示:可以发现,函数y =f (x )在点x =a 的函数值f (a )比它在点x =a 附近其他点的函数值都小,f ′(a )=0;而且在点x =a 附近的左侧f ′(x )<0,右侧f ′(x )>0.类似地,函数y =f (x )在点x =b 的函数值f (b )比它在点x =b 附近其他点的函数值都大,f ′(b )=0;而且在点x =b 附近的左侧f ′(x )>0,右侧f ′(x )<0.知识梳理 极值点与极值的概念(1)极小值点与极小值如图,函数y =f (x )在点x =a 的函数值f (a )比它在点x =a 附近其他点的函数值都小,f ′(a )=0;而且在点x =a 附近的左侧f ′(x )<0,右侧f ′(x )>0,则把点a 叫做函数y =f (x )的极小值点,f (a )叫做函数y =f (x )的极小值.(2)极大值点与极大值如(1)中图,函数y =f (x )在点x =b 的函数值f (b )比它在点x =b 附近其他点的函数值都大,f ′(b )=0;而且在点x =b 的左侧f ′(x )>0,右侧f ′(x )<0,则把点b 叫做函数y =f (x )的极大值点,f (b )叫做函数y =f (x )的极大值.极大值点、极小值点统称为极值点,极大值和极小值统称为极值.知识点二 求函数y =f (x )的极值的方法 知识梳理 解方程f ′(x )=0,当f ′(x 0)=0时:(1)如果在x 0附近的左侧f ′(x )>0,右侧f ′(x )<0,那么f (x 0)是________. (2)如果在x 0附近的左侧f ′(x )<0,右侧f ′(x )>0,那么f (x 0)是________. 提示:(1)极大值 (2)极小值[自我检测]1.函数f (x )的定义域为R ,导函数f ′(x )的图象如图所示,则函数f (x )( )A .无极大值点,有四个极小值点B .有三个极大值点,两个极小值点C .有两个极大值点,两个极小值点D .有四个极大值点,无极小值点 答案:C2.已知函数f (x )=x +1x ,则f (x )( )A .有极大值2,极小值-2B .有极大值-2,极小值2C .无极大值,但有极小值-2D .有极大值2,无极小值 答案:B探究一极值与极值点的判断与求解[教材P98习题3.3A组4题]如图是导函数y=f′(x)的图象,在标记的点中,在哪一点处:(1)导函数y=f′(x)有极大值?(2)导函数y=f′(x)有极小值?(3)函数y=f(x)有极大值?(4)函数y=f(x)有极小值?解析:(1)点x2处f′(x)有极大值.(2)点x1、x4处f′(x)有极小值.(3)点x3处f(x)有极大值.(4)点x5处f(x)有极小值.[例1](1)已知函数y=f(x),其导函数y=f′(x)的图象如图所示,则y=f(x)()A.在(-∞,0)上为减函数B.在x=0处取极小值C.在(4,+∞)上为减函数D.在x=2处取极大值[解析]由导函数的图象可知:当x∈(-∞,0)∪(2,4)时,f′(x)>0,当x∈(0,2)∪(4,+∞)时,f′(x)<0,因此f(x)在(-∞,0),(2,4)上为增函数,在(0,2),(4,+∞)上为减函数,所以在x=0处取得极大值,在x =2处取得极小值,在x=4处取得极大值,故选C.[答案] C(2)求下列函数的极值:①f(x)=2x3+3x2-12x+1;②f(x)=x2-2ln x.[解析]①函数f(x)=2x3+3x2-12x+1的定义域为R,f′(x)=6x2+6x-12=6(x+2)(x-1),解方程6(x+2)(x-1)=0,得x1=-2,x2=1.当x变化时,f′(x)与f(x)的变化情况如下表:x (-∞,-2)-2 (-2,1) 1 (1,+∞)f ′(x ) +0 - 0 + f (x )极大值21极小值-6所以当x 当x =1时,f (x )取极小值-6.②函数f (x )=x 2-2ln x 的定义域为(0,+∞), f ′(x )=2x -2x =2(x +1)(x -1)x ,解方程2(x +1)(x -1)x =0,得x 1=1,x 2=-1(舍去).当x 变化时,f ′(x )与f (x )的变化情况如下表:x (0,1) 1 (1,+∞)f ′(x ) -0 + f (x )极小值1因此当x =1时,f (方法技巧 1.通过导函数值的正负确定函数单调性,然后进一步明确导函数图象与x 轴交点的横坐标是极大值点还是极小值点.2.求可导函数f (x )的极值的步骤 (1)确定函数的定义域,求导数f ′(x ). (2)求f (x )的拐点,即求方程f ′(x )=0的根.(3)利用f ′(x )与f (x )随x 的变化情况表,根据极值点左右两侧单调性的变化情况求极值.特别提醒:在判断f ′(x )的符号时,借助图象也可判断f ′(x )各因式的符号,还可用特殊值法判断. 跟踪探究 1.如图为y =f (x )的导函数的图象,则下列判断正确的是( )①f (x )在(-3,-1)上为增函数;②x =-1是f (x )的极小值点;③f (x )在(2,4)上为减函数,在(-1,2)上为增函数;④x =2是f (x )的极小值点.A .①②③B .②③C .③④D .①③④解析:由f ′(x )的图象知,-3<x <-1时,f ′(x )<0;f ′(-1)=0; -1<x <2时,f ′(x )>0;f ′(2)=0;2<x <4时,f ′(x )<0故f (x )在(-3,-1)和(2,4)上是减函数,在(-1,2)上是增函数,f (-1)是极小值,f (2)是极大值,所以②③正确,故选B.答案:B2.判断下列函数有无极值,如果有极值,请求出极值;如果没有极值,请说明理由. (1)y =13x 3+4;(2)y =e xx (x >0).解析:(1)f ′(x )=x 2. 令f ′(x )=0,解得x =0.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (-∞,0)0 (0,+∞)f ′(x ) + 0 + f (x )单调递增无极值单调递增(2)y ′=e x ·x -e x x 2=e x (x -1)x 2,令y ′=0,得x =1.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (0,1) 1 (1,+∞)f ′(x ) - 0 + f (x )单调递减极小值单调递增探究二 利用函数极值确定参数的值[教材P 110复习参考题A 组7题]已知函数f (x )=x (x -c )2在x =2处有极大值,求c 的值.解析:∵f (x )=x 3-2cx 2+c 2x , ∴f ′(x )=3x 2-4cx +c 2.∴f ′(2)=0,即3×4-8c +c 2=0,得c =2,或c =6. 但c =2时,f (2)是极小值,不合题意,舍去,所以c =6.[例2] (1)已知函数f (x )=x 3+3ax 2+bx +a 2在x =-1处有极值0,则a =________,b =________. (2)若函数f (x )=13x 3-x 2+ax -1有极值点,则a 的取值范围为________.[解析] (1)∵f ′(x )=3x 2+6ax +b ,且函数f (x )在x =-1处有极值0,∴⎩⎪⎨⎪⎧f ′(-1)=0,f (-1)=0, 即⎩⎪⎨⎪⎧3-6a +b =0,-1+3a -b +a 2=0,解得⎩⎪⎨⎪⎧ a =1,b =3或⎩⎪⎨⎪⎧a =2,b =9.当a =1,b =3时,f ′(x )=3x 2+6x +3=3(x +1)2≥0,此时函数f (x )在R 上为增函数,无极值,故舍去.当a =2,b =9时,f ′(x )=3x 2+12x +9=3(x +1)(x +3). 当x ∈(-∞,-3)时,f ′(x )>0, 此时f (x )为增函数;当x ∈(-3,-1)时,f ′(x )<0, 此时f (x )为减函数;当x ∈(-1,+∞)时,f ′(x )>0, 此时f (x )为增函数.故f (x )在x =-1处取得极小值, ∴a =2,b =9.(2)∵f ′(x )=x 2-2x +a ,由题意得方程x 2-2x +a =0有两个不同的实数根, ∴Δ=4-4a >0,解得a <1. [答案] (1)2 9 (2)(-∞,1)方法技巧 已知函数极值的情况,逆向应用确定函数的解析式时,应注意以下两点: (1)根据极值点处导数为0和极值两个条件列方程组,利用待定系数法求解.(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.跟踪探究 3.已知函数f (x )=ax 3+bx 2+cx (a ≠0)在x =±1处取得极值,且f (1)=-1. (1)求常数a ,b ,c 的值;(2)判断x =±1是函数的极大值点还是极小值点,试说明理由,并求出极值. 解析:(1)f ′(x )=3ax 2+2bx +c , ∵x =±1是函数f (x )的极值点,∴x =±1是方程f ′(x )=3ax 2+2bx +c =0的两根, 由根与系数的关系,得⎩⎨⎧-2b3a=0, ①c3a =-1, ②又f (1)=-1,∴a +b +c =-1.③ 由①②③解得a =12,b =0,c =-32.(2)由(1)知f (x )=12x 3-32x ,∴f ′(x )=32x 2-32=32(x -1)(x +1),当x <-1或x >1时,f ′(x )>0, 当-1<x <1时,f ′(x )<0,∴函数f (x )在(-∞,-1)和(1,+∞)上是增函数, 在(-1,1)上是减函数,∴当x =-1时,函数取得极大值f (-1)=1, 当x =1时,函数取得极小值f (1)=-1. 探究三 函数极值的综合应用[例3] 已知函数f (x )=x 3-3ax -1(a ≠0).若函数f (x )在x =-1处取得极值,直线y =m 与y =f (x )的图象有三个不同的交点,求m 的取值范围.[解析] 因为f (x )在x =-1处取得极值且f ′(x )=3x 2-3a , 所以f ′(-1)=3×(-1)2-3a =0, 所以a =1,所以f (x )=x 3-3x -1,f ′(x )=3x 2-3, 由f ′(x )=0,解得x 1=-1,x 2=1. 当x <-1时,f ′(x )>0; 当-1<x <1时,f ′(x )<0; 当x >1时,f ′(x )>0.所以f (x )的单调增区间为(-∞,-1),(1,+∞);单调减区间为(-1,1), f (x )在x =-1处取得极大值f (-1)=1, 在x =1处取得极小值f (1)=-3. 作出f (x )的大致图象如图所示.因为直线y =m 与函数y =f (x )的图象有三个不同的交点,结合f (x )的图象可知,m 的取值范围是(-3,1). 方法技巧 利用导数可以判断函数的单调性,研究函数的极值情况,并能在此基础上画出函数的大致图象,从直观上判断函数图象与x 轴的交点或两个函数图象的交点的个数,从而为研究方程根的个数问题提供了方便.延伸探究 若本例“三个不同的交点”改为“两个不同的交点”,结果如何?改为“一个交点”呢? 解析:由本例解析可知当m =-3或m =1时,直线y =m 与y =f (x )的图象有两个不同的交点;当m <-3或m >1时,直线y =m 与y =f (x )的图象只有一个交点.跟踪探究 4.已知函数f (x )=x 3-6x 2+9x +3,若函数y =f (x )的图象与y =13f ′(x )+5x +m 的图象有三个不同的交点,求实数m 的取值范围.解析:由f (x )=x 3-6x 2+9x +3, 可得f ′(x )=3x 2-12x +9,∴13f ′(x )+5x +m =13(3x 2-12x +9)+5x +m =x 2+x +3+m ,则由题意可得x 3-6x 2+9x +3=x 2+x +3+m 有三个不相等的实根,即g (x )=x 3-7x 2+8x -m 的图象与x 轴有三个不同的交点.∵g ′(x )=3x 2-14x +8 =(3x -2)(x -4),∴令g ′(x )=0,得x =23或x =4.当x 变化时,g (x ),g ′(x )的变化情况如下表:则函数g (x )的极大值为g ⎝⎛⎭⎫23=6827-m ,极小值为g (4)=-16-m . ∵由y =f (x )的图象与y =13f ′(x )+5x +m 的图象有三个不同交点,得⎩⎪⎨⎪⎧g ⎝⎛⎭⎫23=6827-m >0,g (4)=-16-m <0, 解得-16<m <6827.即m 的取值范围为⎝⎛⎭⎫-16,6827.[课后小结](1)在极值的定义中,取得极值的点称为极值点,极值点指的是自变量的值,极值指的是函数值. (2)函数的极值是函数的局部性质.可导函数f (x )在点x =x 0处取得极值的充要条件是f ′(x 0)=0且在x =x 0两侧f ′(x )符号相反.(3)利用函数的极值可以确定参数的值,解决一些方程的解和图象的交点问题.[素养培优]1.误把导函数的零点当作函数的极值点求函数f (x )=x 4-x 3的极值,并说明是极小值还是极大值.易错分析 本题易错将导数为零的点都认为是极值点,其实不然,导数为零仅是零点是极值点的必要不充分条件,错解中还有一个误区就是认为极大值一定大于极小值.事实上,极值仅描述函数在该点附近的局部特征,极大值未必一定大于极小值.考查逻辑推理及数学运算.自我纠正 f ′(x )=4x 3-3x 2,令f ′(x )=0, 即4x 3-3x 2=0时,得x 1=0,x 2=34.当x 变化时,f (x ),f ′(x )的变化情况如下表:由上表可知函数f (x )在区间(-∞,0)上是减函数,在区间⎝⎛⎭⎫0,34上还是减函数,所以x =0不是函数的极值点,而函数f (x )在区间⎝⎛⎭⎫0,34上是减函数,在区间⎝⎛⎭⎫34,+∞上是增函数,所以函数f (x )在x =34处取得极小值,极小值为-27256.2.误把切点当作函数的极值点已知函数f (x )=ax 4+bx 2+c 的图象经过点(0,1),且在x =1处的切线方程是y =x -2,求f (x )的解析式. 易错分析 本题错在将切点当做极值点,得到f ′(1)=0的错误结论.其实,虽然切点和极值点都与导数有关,但它们却是两个完全不同的概念,不能混为一谈.考查逻辑推理及数学运算的学科素养.自我纠正 f ′(1)表示函数f (x )的图象在点(1,-1)处的切线斜率,应有f ′(1)=1,再联立f (0)=1,f (1)=-1便可得到正确答案:a =52,b =-92,c =1,因此f (x )=52x 4-92x 2+1.。
高二英语M5U3Project导学案

Unit 3 M5 Project导学案【学009】主备人:潘恩玉审核人:陈新来2013.10.10 Language points:1. We will some day destroy the planet we live on if we continue in this way.(p58 L5--6)① cf: destroy & damage② live on = feed on以.......为生计,以.......为食eg .a.The earthquake ________( damage,destroy) our houses and we have to set up new onesb.My bike ____ seriously ________(damage,destroy)by a bad boy and I had to send for arepairman.c.中国人的主食是大米。
____________________________________________________.③cf.live,alive,lively,livinga.The old lady was still ______ after over 150 hours buried in the ruins.b.I like watching _____ news on TV.c.________ people should value every single day above the ground.d.Mr. Wang's lessons are ____________ and interesting.More expressions:live up to ___________ live one's dream_____________live through__________________2.Not everything that is best for nature is good for people. (p58 L7--8)not everything=everything not 不是每件事情/ 东西①(不是所有学生都)like playing computer games.②(他们俩不都是南方人)③(不是每个人都买了那本小说)3.Would anyone say that development should be stopped in favour of nature?(p58 L8-9)in favour of 有利于,赞同,赞成① do sb a favour ②ask a favour of of sbsimilar expressions:a.为了纪念①②b.代替c.就........而言d.负责,主管4.From the point of view of some people,we are only doing what humans have alwaysdone ,using nature to meet our own needs.(p58 L9--11)a. from the point of view of some people 就一些人而言,有些人的观点Similar expressions:就我个人而言(1) (2)(3) (4)b.meet one's needsc.收支平衡5.------------many developed nations are now concerned about saving nature rather thandeveloping or destroying it(p58L14--16)a.rather thanb.other thanc.more thand.more---------than-------e.no more than翻译:1.与其说他是校长还不如说他是老师。
江阴山观高级中学高二化学学业水平测试导学案03编制钱刚审核

课时3 铁、铜及其化合物①③⑥Fe 3O Fe FeCl Fe(OH)3⑩, , , , , 一、铁及其重要化合物 1.铁单质(1)铁元素在周期表中位置:铁位于周期表中________周期第________族,属黑色金属。
(2)物理性质:纯铁________色,密度7.86 g·cm -3,熔点1530 ℃、沸点3000 ℃,较好的________性、导电性、导热性,能被_______吸引。
(3)化学性质:①铁与非金属单质反应:在纯净的氧气中燃烧:________________________在氯气中燃烧:______________________________②铁与酸反应: 铁和盐酸反应:____________________ 离子方程式:___________________③铁与盐溶液反应:铁和硫酸铜溶液反应:____________ 离子方程式:___________________④铁和水反应:铁不和冷、热水反应,但在高温下能和水蒸气反应:_______________________2.铁的化合物※铝盐和铁盐有净水作用要点:1、除杂FeCl2(FeCl3) FeCl3(FeCl2)Fe(Al) Al(Fe)二、铜及其重要化合物1.铜单质(1)物理性质:铜单质呈______色,密度8.926 g·cm-3,熔点1083 ℃、沸点2582 ℃,有良好的导电、导热、延展性,导电性仅次于银。
(2)化学性质:a.与非金属单质反应: Cu+O2 =__________ Cu+Cl2 =______b.与酸反应:与银相似,铜不能与盐酸、稀硫酸反应,但却能溶解在硝酸等强氧化性酸中:Cu+ H2SO4(浓)= ________________Cu+ HNO3(浓)=______________。
Cu+ HNO3(稀)=______________。
c.与盐溶液反应:Cu+ FeCl3=______________________d.铜的锈蚀:铜在干燥空气中性质稳定,但在潮湿空气中会被腐蚀,在其表面逐渐形成一层绿色的铜锈:2Cu+O2+H2O+CO2=Cu2(OH)2CO32.铜的化合物(1)CuO:_____色粉末,不溶于水,溶于酸(CuO与盐酸反应的方程式:_______________________),具有氧化性(CuO在________条件下能被H2、C、CO等还原为铜单质),在高温分解为暗________色Cu2O。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:《3.1 电磁感应现象》导学案教学目标:1.知识与技能:启发学生观察实验现象,从中分析归纳通过磁场产生电流的条确件,理解电磁感应现象本质。
2.过程与方法:培养学生运用所学知识,独立分析问题的能力。
3.情感、态度与价值观:启发学生观察实验现象从中分析感应电流的方向与磁场方向和导线运动方向有关;掌握右手定则教学重点:感应电流的产生条件的得出。
教学难点:正确理解感应电流的产生条件。
教学仪器:电池组,电键,导线,大磁针,矩形线圈,碲形磁铁,条形磁铁,原副线圈,演示用电流表等。
教学过程:课前学习:以非常学案中的新知导学为指导,自学本节相关知识课中学习:[学习目标]:一、通过演示实验知道电磁感应现象;1、磁通量:穿过闭合回路的磁感线的条数φ。
φ= B S——不要求掌握2、闭合电路的一部分导体在磁场中做切割磁感线,或穿过闭合电路的磁通量发生变化,产生感应电流的现象。
3、电磁感应产生的电流叫做感应电流。
二、通过实验和探究产生感应电流条件:穿过闭合电路的磁通量发生变化。
“Φ变”;“Φ变”的原因:可能是B变、S变、B与S间的夹角自主学习:根据学习目标,依据课本自己学习相关内容,教师指导合作探究:奥斯特实验实验现象是什么?实验结论是什么?猜想:1、既然电能生磁,那么,磁是否能生电呢?2、如果磁能生电,那么,怎样才能实现呢?一、划时代的发现奥斯特在1820年发现的电流磁效应,使整个科学界受到了极大的震动,它证实电现象与磁现象是有联系的。
英国科学家法拉第,他做了多次尝试,经历了一次次失败,经十年努力,终于发现:磁能生电! ——这是一个划时代的发现.二、电磁感应现象1、电磁感应:回想初中研究的结论:在磁场中做切割磁感线运动时,导体中就产生电流。
物理学中把这种现象叫做电磁感应.由电磁感应产生的电流叫做感应电流.三、电磁感应的产生条件1 回顾:在磁场中做切割磁感线运动时,导体中就产生感应电流。
2 探究1:感应电流产生的条件实验过程及现象如下:3 归纳:在这个实验中,什么情况下能够产生感应电流?四、磁通量引入:为了说清楚产生电磁感应的条件,要用到一个物理量——磁通量φ。
1、定义:穿过闭合回路的的条数。
2、理解:两个闭合回路的面积相同但穿过他们的磁通量并不同。
3 思考与讨论:利用磁通量的知识,我们是否可以把前面的探究中归纳的结论引申一步,想一想:“产生感应电流的条件”于“磁通量”之间有什么联系?与同学、老师交流,并最后的观点写在下面的空栏中。
闭合回路中产生感应电流的条件是:思考:由于其他原因引起磁通量的变化是否会产长生感应电流?4 探究2:进一步探究感应电流与磁通量变化的关系5 【结论】只有当线圈A中电流发生变化,线圈B中才有感应电流只要穿过闭合电路的磁通量发生变化,闭合电路中就有感应电流【分析论证】课堂小结一、电磁感应;1、磁通量:穿过闭合回路的磁感线的条数φ。
φ= B S——不要求掌握2、闭合电路的一部分导体在磁场中做切割磁感线,或穿过闭合电路的磁通量发生变化,产生感应电流的现象。
3、电磁感应产生的电流叫做感应电流。
二、产生感应电流条件:穿过闭合电路的磁通量发生变化。
“Φ变”“Φ变”的原因:可能是B变、S变、B与S间的夹角变【课堂练习】课本50页 1 2 3 4【课后练习】非常学案本节练习题,复习本节内容,预习下节内容【课后反思】:一、什么是电磁感应现象?1、何为磁通量?2、怎样的电流叫做感应电流?二、通过实验和探究产明确生感应电流条件是什么?教后反思:课题:《3.2法拉第电磁感应定律》导学案教学目标:1、知识与技能:理解感应电动势的概念,明确感应电动势的作用。
知道磁通量的变化率是表示磁通量变化快慢的物理量,并能与磁通量的变化相区别。
理解感应电动势的大小与磁通变化率的关系,掌握法拉第电磁感应定律及应用。
2、过程与方法:通过实验探究学习法拉第电磁感应定律。
3、情感、态度与价值观:通过法拉第电磁感应定律的建立,进一步揭示电与磁的关系,培养学生空间思维能力和通过观察、实验寻找物理规律的能力。
教学重点:理解感应电动势的大小与磁通变化率的关系,掌握法拉第电磁感应定律及应用教学难点:培养学生空间思维能力和通过观察、实验寻找物理规律的能力教学仪器:投影仪、演示电流计、线圈、磁铁、导线等。
课前学习:以非常学案中的新知导学为指导,自学本节相关知识教学过程:课中学习:学习目标:1、感应电动势及感应电动势和感应电流之间存在什么关系?2、感应电动势大小(影响感应电动势大小的因素):实验探究3、法拉第电磁感应定律电磁感应现象中,闭合电路中出现了感应电流,那么有电动势存在么?自主学习:根据学习目标,依据课本自己学习相关内容,教师指导合作探究:一、感应电动势:1、感应电动势:产生的电动势叫感应电动势。
产生感应电动势的那部分导体就是电源。
(如图中的导线ab)问题1:感应电动势和感应电流之间存在什么关系?2、感应电动势和感应电流关系:感应电动势是感应电流存在的必要条件,有感应电动势不一定有感应电流(要看电路是否闭合),有感应电流一定有感应电动势。
几点说明:⑴不论电路是否闭合,只要穿过电路的磁通量发生变化,电路中就产生感应电动势,产生感应电动势是电磁感应现象的本质。
⑵磁通量是否变化是电磁感应的根本原因。
若磁通量变化了,电路中就会产生感应电动势,再若电路又是闭合的,电路中将会有感应电流。
⑶产生感应电流只不过是一个现象,它表示电路中在输送着电能;而产生感应电动势才是电磁感应现象的本质,它表示电路已经具备了随时输出电能的能力。
二、感应电动势大小(影响感应电动势大小的因素)⒈在电磁感应现象中产生的电动势叫做感应电动势。
说明:①电路闭合时有感应电动势,感应电流。
②电路断开时有感应电动势,但无感应电流。
观察实验一:在电磁感应现象中产生的感应电流的大小是不同的。
说明感应电动势有大小的不同。
感应电动势的大小跟那些因素有关呢?观察实验二:导线切割磁感线运动速度大时,产生的感应电动势大;导线切割磁感线运动速度小时,产生的感应电动势小。
观察实验三:螺线管和电流表组成闭合电路,当磁铁穿进(或抽出)的速度大时,电流表指针偏转大;当磁铁穿进(或抽出)的速度小时,电流表指针偏转小。
三、法拉第电磁感应定律定量实验表明:问题2:影响感应电动势大小的因素?实验结论:问题3:磁通量大,磁通量变化一定大吗?磁通量变化大,磁通量的变化率一定大吗?磁通量的变化率和磁通量、磁通量的变化不同。
磁通量为零,磁通量的变化率不一定为零;磁通量的变化大,磁通量的变化率也不一定大。
课堂展示:二、法拉第电磁感应定律:1、内容:电路中感应电动势的大小,跟穿过这一电路的磁通量变化率△Φ/ △t成正比.2、数学表达式拓展提升:注意:公式中Δφ应取绝对值,不涉及正负,感应电流的方向另行判断。
说明:(1)所求E为t时间内的平均感应电动势(2)Δt→0时,E为瞬时感应电动势课堂练习:1、有一个50匝的线圈,如果穿过它的磁通量的变化率为0.5Wb/s,求感应电动势。
2、一个100匝的线圈,在0. 5s内穿过它的磁通量从0.01Wb增加到0.09Wb。
求线圈中的感应电动势。
3、关于电磁感应,下列说法正确的是()A、穿过线圈的磁通量越大,感应电动势越大;B、某时刻穿过线圈的磁通量为零,感应电动势一定为零;C、穿过线圈的磁通量变化越快,感应电动势越大;D、穿过线圈的磁通量变化越大,感应电动势越大。
4.关于感应电动势的大小,下列说法正确的是A、穿过闭合回路的磁通量最大时,其感应电动势一定最大;B、穿过闭合回路的磁通量为零时,其感应电动势一定为零;C、穿过闭合回路的磁通量由不为零变为零时,其感应电动势一定为零;D、穿过闭合回路的磁通量由不为零变为零时,其感应电动势一定不为零;5.下列几种说法中正确的是()A、闭合线圈中磁通量的变化越大,线圈中产生的感应电动势一定越大B、闭合线圈中磁通量越大,线圈中产生的感应电动势一定越大C、闭合线圈放在磁场越强的地方,线圈产生的感应电动势一定越大D、闭合线圈中磁通量的变化越快,线圈中产生的感应电动势一定越大课堂小结:课后演练:6、关于感应电动势的大小,下列说法正确的是A、跟穿过闭合电路的磁通量有关B、跟穿过闭合电路的磁通量的变化大小有关C、跟穿过闭合电路的磁通量的变化快慢有关D、跟电路中电阻大小有关7、把一条形磁铁插入同一个闭合线圈中,第一次快插,第二次慢插,两次的初末位置相同,则两次中()A、磁通量的变化率相同B、磁通量的变化量相同C、产生的感应电流相同D、产生的感应电动势相同8、穿过一个闭合线圈的磁通量始终是每秒钟均匀减小0.2韦伯,则下列说法中正确的是()A、线圈中感应电动势一定是每秒钟减小0.2伏特B、线圈中感应电动势一定是0.2伏特C、线圈中感应电动势可能是0.2伏特D、条件不足,无法判断。
9、一个匝数为100、面积为10m2的线圈垂直磁场放置,在0. 5s内穿过它的磁场从1T增加到9T。
求线圈中的感应电动势。
【课后反思】1、感应电动势及感应电动势和感应电流之间存在什么关系?2、感应电动势大小(影响感应电动势大小的因素):实验探究3、法拉第电磁感应定律内容公式等教后反思:课题:3.3交变电流教学目标:1、知识与技能:交变电流的产生即变化规律。
会用公式和图像表示交变电流。
2、过程与方法:通过实验探究学习交变电流的规律。
3、情感、态度与价值观:培养学生观察实验能力和思维能力,寻找物理规律的能力。
教学重点:知道交变电流及交变电流的变化规律教学难点:识别交变电流图像教学仪器:交流发电机模型、演示电流表。
课前学习:以非常学案中的新知导学为指导,自学本节相关知识教学过程:课中学习:学习目标1.了解交变电流是怎样产生的。
2.定性了解交流的变化规律及图像表示和主要特征物理量。
3.初步了解发电机、交变电流的发明和利用对促进人类社会进步的作用,进一步体验科学、技术与社会生活之间的密切关系。
【自主学习】一、交流发电机——将机械能转化为电能1.发电机的基本构造:定子------磁体或线圈转子------线圈或磁体2.种类:(1)旋转电枢式(2)旋转磁极式3、工作原理图I m - I m4、交变电流:都随时间做周期性变化的电流叫交变电流,简称交流(AC)5.直流:只沿流动的电流叫直流电流,简称直流(DC)合作探究:二、交流的变化规律1、交流的变化规律——图像(1)图象形状:(2)物理意义:2、正弦式电流:(1)定义:电流、电压随时间按正弦函数的规律变化,叫做正弦式电流(2)正弦式电流的表达式:各量含义:u表示瞬时值;Im、Um分别是电流和电压的最大值,叫做交流的峰值;ω是线圈转动的角速度三、描述交流的周期和频率1.周期:交变电流完成一次周期性变化所需的时间,用T表示,单位是s.2.频率:1s内交变电流完成周期性变化的次数,用f表示,单位赫兹,简称赫,符号是Hz.3、频率和周期有如下关系:4、我国使用的交变电流,频率是50 Hz。
