【配套K12】2018年秋九年级数学下册 第1章 解直角三角形 1.3 解直角三角形(1)练习 (新
[推荐学习]2018年秋九年级数学下册 第1章 解直角三角形 1.3 解直角三角形(2)练习 (新版
![[推荐学习]2018年秋九年级数学下册 第1章 解直角三角形 1.3 解直角三角形(2)练习 (新版](https://img.taocdn.com/s3/m/728d0104915f804d2b16c179.png)
1.3解直角三角形(2)(见B 本55页)A 练就好基础 基础达标1.小明沿着坡比为1∶2的山坡向上走了1000 m ,则他升高了( A )A .200 5 mB .500 mC .5003mD .1000 m 2.如图所示,某游乐场一山顶滑梯的高为h ,滑梯的坡角为α,那么滑梯的长l 为( A ) A.hsin αB.htan αC.hcos αD .h ·sin α2题图3题图3.如图是以△ABC 的边为直径的半圆O ,点C 恰在半圆上,过C 作CD⊥AB 交AB 于点D.已知cos ∠ACD =35,BC =4,则AC 的长为( D )A .1B.203C .3 D.1634.人民币一角硬币的正面图案中有一个正九边形,如果这个正九边形的半径是R ,那么它的边长是( C )A .Rsin 20°B .Rsin 40°C .2Rsin 20°D .2Rsin 40°5.如图是某水库大坝横截面示意图,其中AB ,CD 分别表示水库上、下底面的水平线,∠ABC =120°,BC 的长是50 m ,则水库大坝的高度h 是( A )第5题图A .25 3 mB .25 mC .25 2 m D.2533m 6.有一拦水坝的横截面是等腰梯形,它的上底为6 m ,下底为12 m ,高为 3 m ,那么拦水坝斜坡的坡度和坡角分别是( D )A.33,60° B.3,30° C.3,60° D.33,30° 7.如图所示是一长为50 m 的游泳池的纵切面示意图,该游泳池的最浅处为1.2 m ,最深处为2.2 m ,底面为斜坡,则底面的坡度为( B )A .50∶1B .1∶50C .3∶125D .11∶250第7题图第8题图8.如图所示,小明爬一土坡,他从点A 处爬到点B 处所走的直线距离AB =4 m ,此时,他离地面的高度h =2 m ,则这个土坡的坡角A 等于__30°__.9.某校为了解决学生停车难的问题,打算新建一个自行车车棚,图1是车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图2是车棚顶部的截面示意图,弧AB 所在圆的圆心为O ,半径OA 为3米.(1)求∠AOB 的度数(结果精确到1°); (2)学校准备用某种材料制作车棚顶部,请你算一算,需该种材料多少平方米?(不考虑接缝等因素,结果精确到1平方米,参考数据:sin 53.1°≈0.80,cos 53.1°≈0.60,π取3.14)第9题图第9题答图解:(1) 作OC⊥AB 于点C, 则AC =2.4. 而OA =3, ∴sin ∠AOC =2.43=0.8,∴∠AOC ≈53.1°, ∴∠AOB =2∠AOC≈106°. (2)∵l AB ︵=106π×3180≈5.5, ∴lAB ︵×15≈83 m 2.10.2017·海南中考为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD =2米),背水坡DE 的坡度i =1∶1(即DB∶EB=1∶1),如图所示.已知AE =4米,∠EAC =130°,求水坝原来的高度BC.(参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.2)第10题图解:设BC =x 米,在Rt △ABC 中,∠CAB =180°-∠EAC=50°,AB =BC tan 50°≈BC 1.2=56x ,在Rt △EBD 中,∵i =DB∶EB=1∶1,∴BD =BE , ∴CD +BC =AE +AB ,即2+x =4+56x ,解得x =12,即BC =12,即水坝原来的高度为12米. B 更上一层楼 能力提升11.2017·六盘水中考三角形的两边a ,b 的夹角为60°且满足方程x 2-32x +4=0,则第三边的长是( A )A. 6 B .2 2 C .2 3 D .3 212.济南中考如图所示,等边三角形AOB 的顶点A 的坐标为(-4,0),顶点B 在反比例函数y =kx(x <0)的图象上,则k 的值为( C )A .-4B .4 3D .412题图13题图13.济宁中考如图所示,斜面AC 的坡度(CD 与AD 的比)为1∶2,AC =3 5 m ,坡顶有一旗杆BC ,旗杆顶端B 点与A 点用一条彩带相连.若AB =10 m ,则旗杆BC 的高度为__5__ m.14.临夏州中考如图所示,图1是小红在健身器材上进行仰卧起坐锻炼时的情景,图2是小红锻炼时上半身由ON 位置运动到与地面垂直的OM 位置时的示意图.已知AC =0.66 m ,BD =0.26 m ,α=20°.(参考数据:sin 20°≈0.342,cos 20°≈0.940,tan 20°≈0.364)(1)求AB 的长(精确到0.01 m);(2)若测得ON =0.8 m ,试计算小红头顶由N 点运动到M 点的路径MN ︵的长度(结果保留π).第14题图第14题答图 解:(1)如图,过B 作BE⊥AC 于点E ,则AE =AC -BD =0.66-0.26=0.4(m),∠AEB =90°, AB =AE sin ∠ABE =0.4sin 20°≈1.17(m).(2)∠MON=90°+20°=110°,所以MN ︵的长度是110π×0.8180=2245π(m).C 开拓新思路 拓展创新15.2017·绵阳中考如图所示,过锐角△ABC 的顶点A 作DE∥BC,AB 恰好平分∠DAC,AF 平分∠EAC 交BC 的延长线于点F.在AF 上取点M ,使得AM =13AF ,连结CM 并延长交直线DE 于点H.若AC =2,△AMH 的面积是112,则1tan ∠ACH的值是.第16题图。
浙教版数学九下第一章1.3《解直角三角形》(第3课时)ppt课件
练一练
1.如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、 C,使得∠ABC=60°, ∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高).
A
2.王同学分别在点C、点D处将旗杆上绳子 分别拉成仰角为60°、30°,如图量出 CD=8米,你能求出旗杆AB的长吗?
1. 请问1号救生员的做法是否合理?
合理
B
易 B 知 A C 3 C : ( m 0 ) 0 A , 3 B0 2 (m ) 0
从A处下水B到 时间3: 002
2
45°
=150221(2 秒)
A
C
从 A 跑C 下 到水 B 时到 3 间 03 0 : 0 = 2 0( 10秒 )BE=DE×tan a
tan BE
DE
=AC×tan a
∴AB=BE+AE = AC×tan a +CD
2 4 ta3n 00 1.2
8 31.2
≈15.1(米)
答: 电线杆的高度约为15.1米.
例2.某海防哨所O发现在它的北偏西30 ° ,距离哨所500m的A处有一艘船向正东方向 航行,经过3分时间后到达哨所东北方向的B处。问船从A处到B处的航速是每时多少km (精确到1km/h)
60 B°
DD
100米
45 °C
30°
60°
1.如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、 C,使得∠ABC=60°,
∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高AD).
解A 设D x米
在 R A t中 B A D , D 90 , 0 B B 600
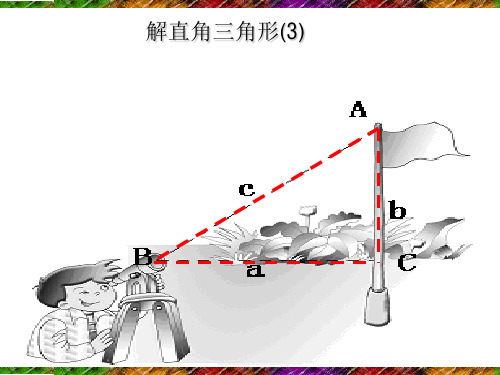
解直角三角形(3)
九年级数学下册第1章解直角三角形1.3解直角三角形第1课时解直角三角形同步练习新版浙教版201808112121

第1章 解直角三角形1.3 解直角三角形 第1课时 解直角三角形知识点 已知一边一角或两边解直角三角形1.在Rt △ABC 中,∠C =90°,sin A =35,BC =6,则AB 的长为( )A .4B .6C .8D .102.如图1-3-1,在Rt △ABC 中,∠C =90°,∠B =30°,AB =8,则BC 的长是( ) A.4 33B .4C .8 3D .4 31-3-11-3-23.图1-3-2是教学用的直角三角板,边AC =30 cm ,∠C =90°,tan ∠BAC =33,则边BC 的长为( ) A .30 3 cm B .20 3 cm C .10 3 cm D .5 3 cm4.2017·慈溪模拟在Rt △ABC 中,∠C =90°,sin A =34,AB =5,则边AC 的长是( )A .3B .4 C.154 D.5 745.在Rt △ABC 中,∠C =90°,a ,b ,c 分别为∠A ,∠B ,∠C 所对的边,c =10,∠A =45°,则a =________,b =________,∠B =________°.6. 在Rt △ABC 中,∠C =90°,a ,b ,c 分别为∠A ,∠B ,∠C 的对边,a =6,b =2 3,则∠B 的度数为________.图1-3-37.如图1-3-3,在Rt △ABC 中,∠C =90°,∠B =37°,BC =32,则AC =________.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)图1-3-48.如图1-3-4,在△ABC 中,已知∠C =90°,BC =4 cm ,tan B =32,则△ABC 的面积是________cm 2.9.如图1-3-5,在Rt △ABC 中,∠C =90°,a ,b ,c 分别为∠A ,∠B ,∠C 的对边,由下列条件解直角三角形.图1-3-5(1)∠A =60°,b =4; (2)a =13,c =23;(3)c =2 2,∠B =30°; (4)a =8,sin B =22.10.如图1-3-6,在△ABC中,∠ABC=90°,∠A=30°,D是边AB上一点,∠BDC=45°,AD=4,求BC的长.(结果保留根号)图1-3-611.等腰三角形的腰长为2 3,底边长为6,则底角等于( )A.30°B.45° C.60°D.120°12.如图1-3-7,已知在Rt△ABC中,∠ABC=90°,点D沿BC边从点B向点C运动(点D与点B,C 不重合),作BE⊥AD于点E,CF⊥AD于点F,则BE+CF的值( )A.不变 B.逐渐增大C.逐渐减小 D.先增大后减小1-3-71-3-813.如图1-3-8,在矩形ABCD中,E是CD的中点,F是BC上一点,且FC=2BF,连结AE,EF.若AB =2,AD=3,则cos∠AEF的值是________.图1-3-914.如图1-3-9,折叠矩形ABCD 的一边AD ,使点D 落在BC 边上的点F 处,已知折痕AE =5 5 cm ,且tan ∠EFC =34,那么矩形ABCD 的周长为________cm.15.如图1-3-10,∠ACB =90°,AB =13,AC =12,∠BCM =∠BAC ,求sin ∠BAC 的值和点B 到直线MC 的距离.图1-3-1016.已知:等腰三角形ABC 中,AB =AC .(1)若cos B =13,且△ABC 的周长为24,求AB 的长;(2)若tan A =52,且BC =2 3,求AB 的长.17.为了解决停车难问题,交通部门准备沿宽12米、长60米的道路边规划停车位,按每辆车长5米、宽2.4米设计停车后,道路仍有不少于7米的路宽,以保证两车可以双向通过,如图1-3-11设计方案一:车位长边与路边夹角为45°;方案二:车位长边与路边夹角为30°.(1)请计算说明,两种方案是否都能保证通行要求?(2)计算符合通行要求的方案中最多可以停多少辆车.图1-3-11。
2018年秋九年级数学下册-第一章-解直角三角形-1

果作比较.
图1-3
BC 0.766 AB
AC 0.643 AB
BC 1.192 AC
3.如图1- 4,B,B1是α一边的任意两点,作 BC AC于点C,B1C1 AC1于点C1.判断比值 BC 与 B1C1 ,AC 与 AC1 ,BC 与 B1C1 是否相等, AB AB1 AB AB1 AC AC1 并说明理由.
的值,并将所得的结果与你的同伴所得的结果 作比较.
BC 1 AB 2
AC 3 AB 2
BC 3 AC 3
2.作一个50的A(图1- 3),在角的边上任意
取一点B,作BC AC于点C.量出AB,AC,BC
(精确到1mm),计算 BC , AC , BC 的值(精确 AB AB AC
到0.01),并将所得的结果与你的同伴所得的结
• 从图1-1我们可以看到,在倾斜 角(∠α,∠β)不同的两个斜面上, 物体移动的距离都是l,而它在水平
和铅垂两个方向上运动的距离却各不 相同.物体在斜面上运动时,在斜面、
水平方向、铅垂方向所经过的距离, 以及斜面的倾斜角之间有什么关系?
1.作一个30的A(图1- 2),在角的边上任意
取一点B,作BC AC于点C.计算 BC , AC , BC AB AB AC
●锐角三角函数是将与锐角有关的比值作定义, 课本介绍了正弦、 余 弦和正切三类, 无论从函数的意义还是表示锐角三角函数符号, 以及 函数中以角为自变量, 都有别于已学过的一次函数和二次函数,其概 念比较抽象,是本节教学的难点.
两个物体在倾斜角不同的斜面上向上运动相同 的距离,它们上升的高度相同吗?
通过上面两个实践操作,你发现了什么?
图1-4
因为△A B C ∽△A B1C1,所以 BC B1C1 ,AC AC1 ,BC B1C1 . AB AB1 AB AB1 AC AC1
九年级数学下1.3解直角三角形(新浙教版)【DOC范文整理】

九年级数学下1.3解直角三角形(新浙教版)3解直角三角形教学目标:使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.渗透数形结合的数学思想,培养学生良好的学习习惯.教学重点和难点:重点:直角三角形的解法.难点:三角函数在解直角三角形中的灵活运用.教学过程:一、引入已知平顶屋面的宽度L和坡顶的设计高度h。
你能求出斜面钢条的长度和倾角a吗?变:已知平顶屋面的宽度L和坡顶的设计倾角α。
你能求出斜面钢条的长度和设计高度h吗?如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?在例题中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角.二、新像这样,在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.问:在三角形中共有几个元素?问:直角三角形ABc中,∠c=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?三边之间关系:a2+b2=c2锐角之间关系∠A+∠B=90°.边角之间关系例1:如图1—16,在Rt△ABc中,∠c=90°,∠A=50°,AB=3。
求∠B和a,b练习1:P161、2例2:已知平顶屋面的宽度L为10,坡顶的设计高度h 为3.5,。
你能求出斜面钢条的长度和倾角a。
练: 如图东西两炮台A、B相距XX米,同时发现入侵敌舰c,炮台A测得敌舰c在它的南偏东40゜的方向,炮台B测得敌舰c在它的正南方,试求敌舰与两炮台的距离.说明:本题是已知一边,一锐角.温馨提示:▲在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外,边长保留四个有效数字,角度精确到1′.▲解直角三角形,只有下面两种情况:已知两条边;已知一条边和一个锐角你会求吗?课本P17作业题三、小结:在直角三角形中,除直角外还有五个元素,知道两个元素,就可以求出另三个元素.四、布置作业:课课通。
北师版九年级下册数学第1章 解直角三角形

(3)边角之间的关系 锐角三角函数
课时导入
一个直角三角形中,若已知五个元素
A
中的两个元素(其中必须有一个元素是
边),则这样的直角三角形可解.
b
c
解直角三角形: Ca B
在直角三角形中,由已知元素求未知元素的过程,叫做 解直角三角形.
感悟新知
知识点 1 解直角三角形
导引需:要由边的比值,运用三角函数求得.
感悟新知
知1-练
解:由勾股定理得 c a2 b2 12 22 5 2.24. 由tanA==0a.5, 1得∠A≈26°34′, ∴∠B=90°b-∠2A≈63°26′.
感悟新知
知1-练
1. 在Rt△ABC中,∠C=90°,AB=2,A5 C=, 15
感悟新知
类型2已知一边及一锐角解直角三角形
知1-练
已知直角三角形的一边和一锐角,解直角三角
形时,若已知一直角边a和一锐角A:①∠B=90°-
∠A;②c=
若已知斜边c和a一个;③锐b角 A:a ①.∠B=90°-∠A; ②a=c·sinA; s③inbA=c·cosA.tan A
感悟新知
知1-练
例4在Rt△ABC,∠C=90°,∠A,∠B,∠C所对的边分 别为a,b,c,且b=30, ∠B=25°求这个三角形的其他 元素(边长精确到1).
应用勾股定理求斜边, 应用角的正切值求出 一锐角,再利用直角 三角形的两锐角互余,求 出另一锐角.一般不用正 弦或余弦值求锐角,因为 斜边是一个中间量,如果 是近似值,会影响结果的 精确度.
知1-讲
已知斜边和直角边:
已知斜边和直角边:先利 用勾股定理求出另一直角 边,再求一锐角的正弦和 余弦值,即可求出一锐角, 再利用直角三角形的两锐 角互余,求出另一锐角.
九年级下册数学知识点:第一章第3节解直角三角形

九年级下册数学知识点:第一章第3节解直角三
角形
学习是一个循序渐进的过程,也是一个不断积累不断创新的过程。
下面小编为大家整理了九年级下册数学知识点:第一章第3节解直角三角形,欢迎大家参考阅读!
一、三角函数
1.定义:在Rt△ABC中,∠C=Rt∠,则
sinA= ;cosA= ;tgA= ;ctgA= .
2. 特殊角的三角函数值:
0° 30° 45° 60° 90°
sinα
cosα
tgα /
ctgα /
3. 互余两角的三角函数关系:sin(90°-α)=cosα;…
4. 三角函数值随角度变化的关系
5.查三角函数表
二、解直角三角形
1. 定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
2. 依据:①边的关系:
②角的关系:A+B=90°
③边角关系:三角函数的定义。
注意:尽量避免使用中间数据和除法。
三、对实际问题的处理
1. 俯、仰角:
2.方位角、象限角:
3.坡度:
4.在两个直角三角形中,都缺解直角三角形的条件时,可用列方程的办法解决。
四、应用举例(略)
通过对九年级下册数学知识点:第一章第3节解直角三角形的学习,是否已经掌握了本文知识点,更多参考资料尽在查字典数学网!。
2018年秋九年级数学下册 第一章 解直角三角形 1.3 解直角三角形③课件 (新版)浙教版

CC = AD - AD 100 3(m).
(2)在Rt△BCD中,
BD = CD 50(3 + 3 3)
tan60°
3
=50(1 + 3)(m).
BD = BD + DD =(50 +150 3)(m).
在Rt△BCD中,
tanCBD = CD BD
4. 如图,从点A看一山坡上的电线杆PQ,观测杆顶端点P的仰角是 45°,向前走 6m 到达B点,测得杆顶端点P和杆底端点Q的仰角分别是 60°和 30°.求该电线杆PQ的 高度(精确到 0.1m).
解:延长PQ与AB的延长线,交于点H,可得
PH =
6 1-1
tan45° tan60°
PQ PH QH
=9 + 3 3
又在Rt△PBH中,
BH = PH 9 + 3 3 tan60° 3
=(9 + 3 3)-(3 + 3) = 6 + 2 3 9.5(m)
=3 + 3 3
在Rt△HQB中,QH BH tan30 答:电线杆PQ的高约为9. 5m.
=(3 + 3 3) 3 3
=3 + 3.
1.3 解直角三角形③
教学目标: 1. 继续经历将实际问题化归为解直角三角形问题的过程,探索 解直角三角形在解决实际问题中的一些应用. 2. 会运用三角函数解决与直角三角形有关的简单实际问题. 3. 进一步体会数形结合和函数思想的运用. 重难点: ●本节教学的重点是解直角三角形的运用. ●例5,例6均需化归为解两个直角三角形问题.但例6涉及的 两个直角三角形交叠在一起,图形和计算都较例5复杂,是本 节教学的难点.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3
解直角三角形(1)
(见A 本55页) A 练就好基础 基础达标
1.在Rt △ABC 中,已知∠C=90°,∠A =40°,AB =5,则BC =( B )
A .5sin 50°
B .5sin 40°
C .3tan 40°
D .3tan 50°
2.在Rt △ABC 中,∠C =90°,a ,b ,c 分别是∠A,∠B ,∠C 的对边,下列关系式中错误的是( A )
A .b =c·cos
B B .b =a·tan B
C .a =c·sin A
D .b =a tan A
3.两条宽度都是1的纸带,按如图交叉叠放,它们的交角为α,则它们公共部分(阴影部分)的面积为( A )
A.1sin α
B.1cos α C .sin α D .1
第3题图
第4题图
4.衢州中考如图所示,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第
二个踩档与第三个踩档的正中间处有一条60 cm 长的绑绳EF ,tan α=52
,则“人字梯”的顶端离地面的高度AD 是( B )
A .144 cm
B .180 cm
C .240 cm
D .360 cm
5.如图所示,秋千链子的长度为4 m ,当秋千向两边摆动时,两边的最大摆动角度均为30°.则它摆动至最高位置与最低位置的高度之差为( C )
A .2 m
B .(4-23) m D .(4-22) m
第5题图
第6题图
6.如图所示,菱形ABCD 的面积为24, tan ∠BAC =34
,则菱形边长为( C ) A .6 B .8 C .5 D .15
7.在△ABC 中,∠C =90°,a =35,c =352,则∠A=__45°__,b =__35__.
8.怀化中考在Rt △ABC 中,∠C =90°,sin A =45
,AC =6 cm ,则BC 的长度为__8__cm. 9.如图所示,在等腰Rt △ABC 中,∠C =90°,AC =6,点D 是AC 上一点,若tan ∠DBA =15
,则AD 的长为__2__.
第9题图
10.在△ABC 中,∠C =90°.
(1)已知c =83,∠A =60°,求∠B,a ,b ;
(2)已知a =36, ∠A =45°,求∠B,b ,c.
解:(1)∠B=30°,a =12,b =4 3.
(2)∠B=45°,b =36,c =6 3.
B 更上一层楼 能力提升
11.已知锐角A 满足关系式2sin 2A -7sin A +3=0,则sin A 的值为( A )
A.12 B .3 C.12或3 D .4
12.如图所示,钓鱼竿AC 长6 m ,露出水面的鱼线BC 长3 2 m ,某钓者想看看鱼钩上的情况,把鱼竿AC 转动到AC′的位置,此时露出水面的鱼线B′C′长3 3 m .则鱼竿转过的角度是( C )
A .60°
B .45°
C .15°
D .90°
12题图
13题图
13.如图所示,在半径为1的⊙O 中,AC 是直径,∠AOB =45°,则sin C 的值为( B ) A.22 B.2-22 C.2+22 D.24
14.在Rt △ABC 中,斜边AB =2,且sin A +cos A =52,则△ABC 的面积为__14
__. 15.台州中考如图所示,保护视力要求人写字时眼睛和笔端的距离超过30 cm ,图(a)是一位同学的坐姿,把她的眼睛B 、肘关节C 和笔端A 的位置关系抽象成图(b)的△ABC.已知BC =30 cm ,AC =22 cm ,∠ACB =53°,她的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin 53°≈0.8,cos 53°≈0.6,tan 53°≈1.3)
第15题图
第15题答图
解:她的这种坐姿不符合保护视力的要求.
理由如下:如图,过点B 作BD⊥AC 于点D ,
∵BC =30 cm, ∠ACB =53°,
∴sin 53°=BD BC =BD 30
≈0.8, ∴BD =24,又∵cos 53°=DC BC
≈0.6, ∴CD =18,
∴AB =AD 2+BD 2=42+242
=592<900,
∴她的这种坐姿不符合保护视力的要求.
第16题图
16.2017·上海中考如图所示,一座钢结构桥梁的框架是△ABC,水平横梁BC 长18米,中柱AD 高6米,其中D 是BC 的中点,且AD ⊥BC.
(1)求sin B 的值;
(2)现需要加装支架DE ,EF ,其中点E 在AB 上,BE =2AE ,且EF⊥BC,垂足为点F ,求支架DE 的长.
解:(1)在Rt △ABD 中,∵BD =DC =9,AD =6,
∴AB =BD 2+AD 2=92+62
=313,
∴sin B =AD AB =6313=21313
. (2)∵EF∥AD,BE =2AE ,∴EF AD =BF BD =BE BA =23,∴EF 6=BF 9=23
,∴EF =4,BF =6, ∴DF =3,
在Rt △DEF 中,DE =EF 2+DF 2=42+32=5(米).
C 开拓新思路 拓展创新
17.菏泽中考如图所示,△ABC 与△A′B′C′都是等腰三角形,且AB =AC =5,A ′B ′=A′C′=3.若∠B+∠B′=90°,则△ABC 与△A′B′C′的面积比为( A )
第17题图
A .25∶9
B .5∶3 C.5∶ 3 D .55∶3 3
18.如图所示,在Rt △ABC 中,∠C =90°,把∠A 的邻边与对边的比叫做∠A 的余切,
记作cot A =b a
.则下列关系式中不成立的是( D )
第18题图 A .tan A ·cot A =1
B .sin A =tan A ·cos A
C .cos A =cot A ·sin A
D .tan 2A +cot 2A =1。
