二调答案
2024武汉二调数学试题(含答案)

武汉市2024届高中毕业生二月调研考试数学试卷本试题卷共4页,19题,全卷满分150分。
考试用时120分钟。
⋆祝考试顺利⋆注意事项:1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试卷和答题卡一并上交。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A =x |2x 2+x -1<0 ,B =y y =lg x 2+1 ,则A ∩B =A.-1,0B.0,12C.-12,0D.0,12.复数z 满足2z +3z=5-2i ,则|z |=A.3B.2C.5D.63.已知ab ≠1,log a m =2,log b m =3,则log ab m =A.16B.15C.56D.654.将3个相同的红球和3个相同的黑球装人三个不同的袋中,每袋均装2个球,则不同的装法种数为A.7B.8C.9D.105.设抛物线y 2=2x 的焦点为F ,过抛物线上点P 作其准线的垂线,设垂足为Q ,若∠PQF =30°,则|PQ |=A.23B.33C.34D.326.法布里-贝罗研究多光束干涉在薄膜理论中的应用时,用光波依次透过n 层薄膜,记光波的初始功率为P 0,记P k 为光波经过第k 层薄膜后的功率,假设在经过第k 层薄膜时光波的透过率T k =P k P k -1=12k ,其中k =1,2,3⋯n ,为使得P n P 0≥2-2024,则n 的最大值为A.31B.32C.63D.647.如图,在函数f (x )=sin (ωx +φ)的部分图象中,若TA =AB,则点A 的纵坐标为A.2-22 B.3-12C.3-2D.2-38.在三棱棱P -ABC 中,AB =22,PC =1,P A +PB =4,CA -CB =2,且PC ⊥AB ,则二面角P -AB -C 的余弦值的最小值为A.23B.34C.12D.105二、选择题:本题共3小题,每小题6分,共18分。
2023年盐城二调烹饪专业答案
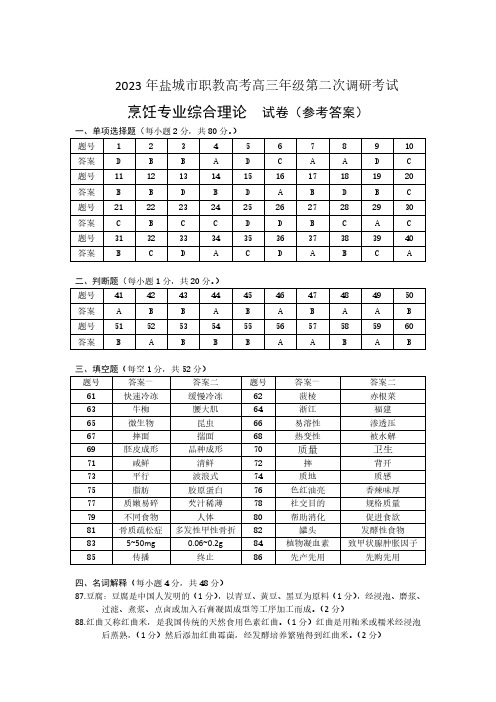
2023年盐城市职教高考高三年级第二次调研考试烹饪专业综合理论试卷(参考答案)一、单项选择题(每小题2分,共80分。
)题号12345678910答案D B B A D C A A D C题号11121314151617181920答案B B D B D A B D B C题号21222324252627282930答案C B C C D D B C A C题号31323334353637383940答案B C D A C D A B C A二、判断题(每小题1分,共20分。
)题号41424344454647484950答案A B B A B A B A A B题号51525354555657585960答案B A B B B A A B A B三、填空题(每空1分,共52分)题号答案一答案二题号答案一答案二61快速冷冻缓慢冷冻62菠棱赤根菜63牛柳腰大肌64浙江福建65微生物昆虫66易溶性渗透压67摔面揣面68热变性被水解69胚皮成形品种成形70质量卫生71咸鲜清鲜72摔背开73平行波浪式74质地质感75脂肪胶原蛋白76色红油亮香辣味厚77质嫩易碎芡汁稀薄78社交目的规格质量79不同食物人体80帮助消化促进食欲81骨质疏松症多发性甲性骨折82罐头发酵性食物835~50mg0.06~0.2g84植物凝血素致甲状腺肿胀因子85传播终止86先产先用先购先用四、名词解释(每小题4分,共48分)87.豆腐:豆腐是中国人发明的(1分),以青豆、黄豆、黑豆为原料(1分),经浸泡、磨浆、过滤、煮浆、点卤或加入石膏凝固成型等工序加工而成。
(2分)88.红曲又称红曲米,是我国传统的天然食用色素红曲。
(1分)红曲是用籼米或糯米经浸泡后蒸熟,(1分)然后添加红曲霉菌,经发酵培养繁殖得到红曲米。
(2分)89.湿磨粉是先将米淘洗,浸泡涨发,控干水分后磨制成粉。
湿磨粉的优点是较干磨粉质感细腻,富有光泽,缺点是磨出的粉需要干燥才能保藏。
高二二调年级联考试卷【含答案】

高二二调年级联考试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪种现象属于光的折射?A. 镜子中的倒影B. 水中的鱼看起来更浅C. 阳光直射时形成的影子D. 月亮在云层中的穿行2. 在化学反应中,哪种物质被称为催化剂?A. 反应物B. 物C. 中间产物D. 参与反应但不改变自身状态的物质3. 下列哪种动物属于哺乳动物?A. 鸟类B. 鱼类C. 昆虫D. 猫科动物4. 下列哪种现象属于声波的反射?A. 回声B. 声音的传播速度变化C. 声音的频率变化D. 声音的强度变化5. 下列哪种元素属于金属元素?A. 氧B. 氢C. 钠D. 硅二、判断题(每题1分,共5分)1. 地球是太阳系中最大的行星。
()2. 分子是保持物质化学性质的最小粒子。
()3. 声音在真空中无法传播。
()4. 动物细胞和植物细胞都有细胞壁。
()5. 光的传播速度在真空中是最快的。
()三、填空题(每题1分,共5分)1. 地球上的生物多样性包括_______多样性、遗传多样性和生态系统多样性。
2. 在化学反应中,反应物与物的总质量_______。
3. 光的波长越长,其在水中的折射率_______。
4. 声音的频率越高,其音调_______。
5. 人类遗传信息的载体是_______。
四、简答题(每题2分,共10分)1. 简述牛顿的三大运动定律。
2. 简述光合作用的基本过程。
3. 简述DNA的双螺旋结构模型。
4. 简述相对论的基本原理。
5. 简述地球自转和公转的周期。
五、应用题(每题2分,共10分)1. 一辆汽车以20m/s的速度行驶,突然刹车,加速度为-5m/s²,求汽车停止所需的时间。
2. 一个化学反应的平衡常数Kc=100,求反应物和物的浓度比。
3. 一束光从空气进入水中,入射角为45°,求折射角。
4. 一个音叉发出频率为440Hz的音波,求其波长。
5. 一个正方形的边长为10cm,求其面积。
2024届湖北省武汉市高中毕业生二月调研考试英语试题(含答案)

武汉市2024 届高中毕业生二月调研考试英语试卷养成良好的答题习惯,是决定高考英语成败的决定性因素之一。
做题前,要认真阅读题目要求、题干和选项,并对答案内容作出合理预测;答题时,切忌跟着感觉走,最好按照题目序号来做,不会的或存在疑问的,要做好标记,要善于发现,找到题目的题眼所在,规范答题,书写工整;答题完毕时,要认真检查,查漏补缺,纠正错误。
命题&审题:武汉市教育科学研究院第一部分听力 ( 共两节,满分 3 0 分 )做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A 、B 、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What are the speakers probably doing?A.Discussing at work.B.Talking on phoneC.Driving on the way2.What will the man do next?A.Have a dessert.B.Pay the check.C.Ask for a beer.3.What do we know about the hamburger?A.It might go bad.B.It's good-lookingC.It looked funny4.What are the speakers mainly talking about?A.The sceneryB.The transport.C.The weather.5.How does the woman sound in the end?A.Glad.B.Surprised.C.Impatient.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
2024年深圳市二调数学试题参考答案

2024年深圳市高三年级第二次调研考试数学试题参考答案及评分标准本试卷共4页,19小题,满分150分。
考试用时120分钟。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
二、选择题:本题共3小题,每小题6分,共18分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得6分,部分选对的得部分分,有选错的得0分。
三、填空题:本题共3小题,每小题5分,共15分。
12. 5 13. 8π 14.π3;,)+∞(注:第一空2分,第二空3分)四、解答题:本题共5小题,共77分。
解答应写出文字说明、证明过程或演算步骤。
15.(13分)如图,三棱柱111ABC A B C -中,侧面11BB C C ⊥底面ABC ,且AB AC =,11A B A C =.(1)证明:1AA ⊥平面ABC ;(2)若12AA BC ==,90BAC ∠=︒,求平面1A BC 与平面11A BC 夹角的余弦值.证明:(1)取BC 的中点M ,连结MA 、1MA .因为AB AC =,11A B A C =,所以BC AM ⊥,1BC A M ⊥.由于AM ,1A M ⊂平面1A MA ,且1AMA M M =,因此BC ⊥平面1A MA .…………………………………………………2分因为1A A ⊂平面1A MA ,所以BC ⊥1A A .又因为1//A A 1B B ,所以1B B BC ⊥,因为平面11BB C C ⊥平面ABC ,平面11BB C C 平面ABC BC =,且1B B ⊂平面11BB C C ,所以1BB ⊥平面ABC .因为1//A A 1B B ,所以1AA ⊥平面ABC .…………………………………………………………6分解:(2)(法一)因为90BAC ∠=︒,且2BC =,所以AB AC ==A BC1A 1B 1C M以AB ,AC ,1AA 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系, 则1(0,0,2)A,B,(0,C,1(0,2,2)C .所以1(2,0,2)A B =-,1(0,2)A C =-,11(0,A C =. ………………………………………8分设平面1A BC 的法向量为111(,,)x y z =m ,则110A B A C ⎧⋅=⎪⎨⋅=⎪⎩m m ,可得111100x y ⎧-=⎪⎨-=⎪⎩,令11z =,则=m , 设平面11A BC 的法向量为222(,,)x y z =n ,则11100A B A C ⎧⋅=⎪⎨⋅=⎪⎩n n ,可得22200x y ⎧-=⎪⎨=⎪⎩,令21z =,则=n ,……12分 设平面1A BC 与平面11A BC 夹角为θ,则||cos ||||θ⋅===m n m n ,所以平面1A BC 与平面11A BC . …………………………………………13分 (法二)将直三棱柱111ABC A B C -补成长方体1111ABDC A B D C -.连接1C D ,过点C 作1CP C D ⊥,垂足为P ,再过P 作1PQ A B ⊥,垂足为Q ,连接CQ .因为BD ⊥平面11CDD C ,且CP ⊂平面11CDD C , 所以BD CP ⊥.又因为1CP C D ⊥,由于BD ,1C D ⊂平面11A BDC ,且1BD C D D =,所以CP ⊥平面11A BDC .由于1A B ⊂平面11A BDC ,所以1A B CP ⊥. 因为CQ ,PQ ⊂平面CPQ ,且CQ PQ Q =,所以1A B ⊥平面CPQ .因为CQ ⊂平面CPQ , 所以1CQ A B ⊥.则CQP ∠为平面1A BC 与平面11A BC 的夹角或补角,………………………………………………11分 在1A BC △中,由等面积法可得CQ =. 因为11PQ A C ==cos PQ CQP CQ ∠== 因此平面1A BC 与平面11A BC . ………………………………………………13分16.(15分)已知函数()(1)e x f x ax =+,()f x '是()f x 的导函数,且()()2e x f x f x '-=. (1)若曲线()y f x =在0x =处的切线为y kx b =+,求k ,b 的值; (2)在(1)的条件下,证明:()f x kx b +.C 1ABB 1C A 1y MC 1ABB 1C A 1PQ DD 1解:(1)因为()(1)e x f x ax =+,所以()(1)e x f x ax a '=++, …………………………………………2分 则()()e x f x f x a '-=.因为()()2e x f x f x '-=,所以2a =. …………………………………………4分 则曲线()y f x =在点0x =处的切线斜率为(0)3f '=.又因为(0)1f =,所以曲线()y f x =在点0x =处的切线方程为31y x =+,即得3k =,1b =. ………………………………………………………………………………………6分 (2)证:设函数()(21)e 31x g x x x =+--,x ∈R ,则()(23)e 3x g x x '=+-. ………………………………………………………………………………8分设()()g x h x '=,则()e (25)x h x x '=+, ………………………………………………………10分 所以,当52x >-时,()0h x '>,()g x '单调递增.又因为(0)0g '=,所以,0x >时,()0g x '>,()g x 单调递增;502x -<<时,()0g x '<,()g x 单调递减. 又当52x -时,()(23)e 30x g x x '=+-<,综上()g x 在(,0)-∞上单调递减,在(0,)+∞上单调递增, ……………………………………13分 所以当0x =时,()g x 取得最小值(0)0g =, 即(21)e 310x x x +--,所以,当x ∈R 时,()31f x x +. ……………………………………………………………15分17.(15分)某大型企业准备把某一型号的零件交给甲工厂或乙工厂生产.经过调研和试生产,质检人员抽样发现:甲工厂试生产的一批零件的合格品率为94%;乙工厂试生产的另一批零件的合格品率为98%;若将这两批零件混合放在一起,则合格品率为97%.(1)从混合放在一起的零件中随机抽取3个,用频率估计概率,记这3个零件中来自甲工厂的个数为X ,求X 的分布列和数学期望;(2)为了争取获得该零件的生产订单,甲工厂提高了生产该零件的质量指标.已知在甲工厂提高质量指标的条件下,该大型企业把零件交给甲工厂生产的概率,大于在甲工厂不提高质量指标的条件下,该大型企业把零件交给甲工厂生产的概率.设事件A =“甲工厂提高了生产该零件的质量指标”,事件B =“该大型企业把零件交给甲工厂生产”.已知0()1P B <<,证明:(|)(|)P A B P A B >.解:(1)设甲工厂试生产的这批零件有m 件,乙工厂试生产的这批零件有n 件,事件M =“混合放在一起零件来自甲工厂”, 事件N =“混合放在一起零件来自乙工厂”,事件C =“混合放在一起的某一零件是合格品”, 则()m P M m n =+,()nP N m n=+, ()(|)()(|)(94%98%97%)m nP C P C M P M P C N P N m n m n=+=+=+⨯⨯+, ………………………2分 计算得3m n =. 所以1()4m P M m n ==+.…………………………………………………………………………………3分 X 的可能取值为0,1,2,3,1(3,)4X B , …………………………………………………5分13()344E X =⨯=, …………………………………………………6分00331327(0)()()4464P X C ===,11231327(1)()()4464P X C ===,2213139(2)()()4464P X C ===,3303131(3)()()4464P X C ===.所以,X 的分布列为:………………………………………………8分证明:(2)因为在甲工厂提高质量指标的条件下,该大型企业把零件交给甲工厂生产的概率,大于在甲工厂不提高质量指标的条件下,该大型企业把零件交给甲工厂生产的概率,所以(|)(|)P B A P B A >.………………………………………………………………………………10分 即()()()()P AB P AB P A P A >. 因为()0P A >,()0P A >, 所以()()()()P AB P A P AB P A >.因为()1()P A P A =-,()()()P AB P B P AB =-, 所以()1())(()())()P AB P A P B P AB P A ->-(.即得()()()P AB P A P B >, ……………………………………………………………………12分 所以()()()()()()()P AB P AB P B P A P B P AB P B ->-.即()(1())()(()())P AB P B P B P A P AB ->-. 又因为1()()P B P B -=,()()()P A P AB P AB -=, 所以()()()()P AB P B P B P AB >.因为0()1P B <<,0()1P B <<, 所以()()()()P AB P AB P B P B >. 即得证(|)(|)P A B P A B >. …………………………………………………………………………15分18.(17分)设抛物线2:2C x py =(0p >),直线:2l y kx =+交C 于A ,B 两点.过原点O 作l 的垂线,交直线2y =-于点M .对任意k ∈R ,直线AM ,AB ,BM 的斜率成等差数列.(1)求C 的方程;(2)若直线//l l ',且l '与C 相切于点N ,证明:AMN △的面积不小于.解:(1)设点11(,)A x y ,22(,)B x y ,由题可知,当0k =时,显然有0AM BM k k +=; 当0k ≠时,直线OM 的方程为1y x k=-,点(2,2)M k -. 联立直线AB 与C 的方程得2240x pkx p --=, 224160p k p ∆=+>,所以122x x pk +=,124x x p =-, ………………………………………………………………………3分因为直线AM ,AB ,BM 的斜率成等差数列,所以121222222y y k x k x k +++=--. 即121244222kx kx k x k x k +++=--,122112(4)(2)(4)(2)2(2)(2)kx x k kx x k k x k x k +-++-=--, 化简得2122(2)(4)0k x x k ++-=. …………………………………………………5分将122x x pk +=代入上式得22(2)(24)0k pk k +-=, 则2p =,所以曲线C 的方程为24x y =. …………………………………………………………………………8分 (2)(法一)设直线:l y kx n '=+,联立C 的方程,得2440x kx n --=.由0∆=,得2n k =-,点2(2,)N k k , …………………………………………10分 设AB 的中点为E , 因为1222x x k +=,21212()42222y y k x x k +++==+,则点2(2,22)E k k +. ……………12分 因为222222k k +-=,所以点M ,N ,E 三点共线,且点N 为ME 的中点, 所以AMN △面积为ABM △面积的14. ……………………………………………………………14分 记AMN △的面积为S ,点(2,2)M k -到直线AB :20kx y -+=的距离2d =,所以32221||(2)228S AB d k =⨯==+,当0k =时,等号成立.所以命题得证. ………………………………………………………………………………………17分(法二)设直线:l y kx n '=+,联立C 的方程,得2440x kx n --=.由0∆=,得2n k =-,则点2(2,)N k k .所以直线MN 与x 轴垂直. ……………………………………………………12分记AMN △的面积为S ,所以121||||22x x S MN -=⨯⨯1||4MN =⨯ …………………………………14分21|2|2k =⨯+322(2)22k =+.当0k =时,等号成立.所以命题得证. ……………………………………………………………………………………17分19.(17分)无穷数列1a ,2a ,…,n a ,…的定义如下:如果n 是偶数,就对n 尽可能多次地除以2,直到得出一个奇数,这个奇数就是n a ;如果n 是奇数,就对31n +尽可能多次地除以2,直到得出一个奇数,这个奇数就是n a .(1)写出这个数列的前7项;(2)如果n a m =且m a n =,求m ,n 的值; (3)记()n a f n =,*n ∈N ,求一个正整数n ,满足()(())n f n f f n <<<…2024(((())))ff f f n <个…….解:(1)11a =,21a =,35a =,41a =,51a =,63a =,711a =. ……………………………3分 (2)由已知,m ,n 均为奇数,不妨设nm .当1n =时,因为11a =,所以1m =,故1m n ==; ……………………………5分 当1n >时,因为314n n m +<,而n 为奇数,n a m =,所以312n m +=. ………………6分 又m 为奇数,m a n =,所以存在*k ∈N ,使得312km n +=为奇数. 所以3(31)95231122kn n n m ++=+=+=. 而95462n n n +<<,所以426k n n n <<,即426k <<,*k ∈N ,无解. …………………………7分 所以1m n ==. ……………………………………………………………………………8分 (3)显然,n 不能为偶数,否则()2nf n n <,不满足()n f n <. 所以,n 为正奇数.又1(1)1f a ==,所以3n. …………………………………………………………………10分设41n k =+或41n k =-,*k ∈N .当41n k =+时,3(41)1()31414k f n k k n ++==+<+=,不满足()n f n <; ……………12分 当41n k =-时,3(41)1()61412k f n k k n -+==->-=,即()n f n <. ……………14分 所以,取202521n k =-,*k ∈N 时,202520242024220233(21)13(321)1()321(())32122k k n f n k f f n k -+⨯-+<==⨯-<==⨯-202232023220233(321)1(((())))3212k f f f n k ⨯-+<<==⨯-………20232202420243(321)1(((())))3212k f f f n k ⨯-+<==⨯-……即()(())n f n f f n <<<…2024(((())))ff f f n <个……. ……………………………………………………17分注:只要给出21m n k =-,并满足条件*,m k ∈N ,2025m 中的其一组,m k 的值,就认为是正确的.。
2025届惠州二调物理试题+答案

惠州市2025届高三第二次调研考试试题本卷共6页,15小题考试时间:75分钟满分100分一、单项选择题:本题共7小题,每小题4分,共28分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.氡气在自然界中含量相对较高,是人类受到天然电离辐射的最主要来源,对人类的放射性剂量占所有天然放射性剂量的40%,是继吸烟以外导致肺癌的第二大危险因素.氡()22286Rn 的半衰期为3.8天,其衰变反应方程式为222218486842Rn Po He.→+下列关于氨的说法正确的是A.氨的衰变属于β衰变B.在高温高压下,氨的半衰期会变长C.该衰变产生的射线有很强的穿透能力D.10g 的氨经过7.6天后,氨还剩余2.5g2.甲、乙两车在同一平直公路的并排车道上同向运动,甲做匀加速直线运动,乙做匀速直线运动,甲、乙两车的位置x 随时间t 的变化如图所示,下列说法正确的是A.在2t 时刻两车速度相等B.从0到2t 时间内,两车走过的路程相等C.从1t 到2t 时间内,甲、乙两车的距离先变大后变小D.从1t 到2t 时间内,甲、乙两车速度不可能相等3.我国某企业正在全力研发浸没式”光刻机.原理是一种通过在光刻胶和投影物镜之间加入浸没液体,从而减小曝光波长,提高分辨率的技术,如图所示.若浸没液体的折射率为1.5,则加上液体后,该曝光光波A.在浸没液体中的传播时频率变大B.在浸没液体中的传播速度变为原来的1.5倍C.在浸没液体中的曝光波长变为原来的23D.传播相等的距离,在浸没液体中所需的时间变为原来的234.科技赋能奥运,在2024年巴黎奥运会田径比赛场,跑道外侧安装有高速轨道摄像机系统,如图所示,当运动员加速通过弯道时,摄像机与运动员保持同步运动以获得高清视频,关于摄像机下列说法正确的是A.摄像机所受合外力的大致方向可能为1FB.摄像机在弯道上运动的速度不变C.摄像机角速度比运动员的更大D.摄像机向心加速度与运动员的相等5.在中国京剧中的水袖舞表演中,水袖的波浪可视为简谐横波.图为该简谐横波0t =时刻的波形图,已知该简谐横波沿x 轴正方向传播,波速为1m /s .则 1.0s t =时,1m x =处的质点相对平衡位置的位移为A.0B.0.1mC.0.1m −D.0.2m6.2023年7月12日,中国载人航天工程办公室披露,中国计划在2030年前实现载人登月.假设将来我国宇航员登陆月球成功后,在月球表面做单摆实验,测得摆长为L 的单摆振动周期为T ,已知月球的半径为R ,万有引力常量为G .下列表达正确的是 A.若增加摆长,则振动周期变小B.若增加摆锤质量,则振动周期变大C.D.月球的质量为2324LR GTπ 7.如图所示,如果热水瓶中的热水未灌满就盖紧瓶塞,而瓶塞与瓶口的密封程度很好,经过一段时间后,要拔出瓶塞会变得很吃力.假设开始时瓶内水温为87C ,经过一段时间,温度降到47C ,热水瓶口的截面积为210cm ,手指与瓶塞的动摩擦因数为0.15.已知瓶内气体可视为理想气体,大气压强51.010Pa p =×,不考虑瓶塞的重力及瓶塞与瓶口间的摩擦力,则两手指至少要用多大的压力作用在瓶塞上才能拔出瓶塞A.74NB.37NC.3.7ND.7.4N二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,选对但不全的得3分,有选错的得0分.8.如图6(a)所示,太极球”是近年来在广大市民中较流行的一种健身器材.某熟练的太极球健身者用球拍托住太极球,在竖直平面内做匀速圆周运动,轨迹截面图如图6(b)所示,图中的A点为圆周运动最高点,、点与圆心等高.已知太极球运动的速度大小为v,半径为R,太极球的质量B点为圆周运动最低点,C D为m,重力加速度为g,不考虑空气阻力,则A.太极球在运动过程中机械能不守恒B.太极球在B点受到向心力、重力和弹力的作用C.从A点运动到点过程中,球拍对太极球做了正功D.在C点,球拍对太极球的作用力大小为9.如图所示,一轻质弹簧一端连接在固定的挡板上,另一端连接一小物块,O点为弹簧在原长时物块的位置.物块压缩弹簧后由A点静止释放,沿粗糙的水平面向右运动,最远能到达B点.在从A到B的过程中,则物块A.做简谐运动B.加速度先减小后增大C.经过O点时的速度最大D.所受弹簧弹力做的功等于其克服摩擦力做的功10.长度为2L的轻杆左端连接光滑水平转轴O,中点和右端分别固定质量均为m的小球A和B,小球可视为质点,重力加速度为g ,如图所示,当轻杆从水平位置由静止释放,在轻杆摆至竖直位置的过程中,下列结论正确的是A.A B 、两小球组成的系统机械能守恒B.A B 、两小球的速度始终相等C.在最低点,小球BD.轻杆对小球B 做的功三、非选择题:本题共5小题,共54分考生根据要求作答。
河北省衡水市2024-2025学年高三上学期9月第二次调研考试语文试题含答案

2024~2025学年高三年级学科素养检测(二调)语文(答案在最后)(时间150分钟,满分150分)注意事项:1.答题前,考生务必将自己的姓名、班级和考号填写在答题卡上2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、文言文阅读(66分)(一)文言文阅读Ⅰ(本题共5小题,20分)阅读下面的文字,完成下面小题。
材料一:初,帝好文学,自造《皇羲篇》五十章,因引诸生能为文赋者并待制鸿都门①下。
后诸为尺牍及工书鸟篆者,皆加引召,遂至数十人。
侍中祭酒乐松、贾护多引无行趣.势之徒置其间,喜陈闾里小事;帝甚悦之,待以不次之位;又久不亲行郊庙之礼②。
会诏群臣各陈政要,蔡邕上封事曰:“夫迎气五郊,清庙祭祀,养老辟雍③,皆帝者之大业也。
而有司数以种种废阙不行,忘礼敬之大,拘信小故,以亏大典。
自今斋制宜如故典,庶答风霆、灾妖之异。
又,古者取士必使诸侯岁.贡,孝武之世,郡举孝廉,又有贤良、文学之选,于是名臣辈出,文武并兴。
汉之得人,数路而已。
夫书画辞赋,才之小者;匡国治政,未有其能。
陛下即位之初,先涉经术,听政余日,观省篇章,聊以游意当代博弈,非以为教化取士之本。
而诸生竞利作者鼎沸其高者颇引经训风喻之言下则连偶俗语而有类俳优,或窃成文,虚冒名氏。
臣每受诏于盛化门,差次录第,其未及者,亦复随辈皆见拜擢。
既加之恩,难复收改,但守奉禄,于义已弘,不可复使治民及在州郡。
昔孝宣会诸儒于石渠,章帝集学士于白虎,通经释义,其事优大,文武之道,所宜从之。
若乃小能小善,虽有可观,孔子以为致远则泥.,君子固当志其大者。
”书奏,帝乃亲迎气北郊及行辟雍之礼。
(节选自《资治通鉴》卷第五十七,汉纪四十九)材料二:呜呼!世愈移而士趋日异,亦恶知其所归哉!灵帝好文学之士,能为文赋者,待制鸿都门下,乐松等以显,而蔡邕露章④谓其“游意篇章,聊代博弈”。
2023-2024学年河北省邯郸市高三上学期第二次调研监测数学试题(邯郸二调)+答案解析

2023-2024学年河北省邯郸市高三上学期第二次调研监测数学试题(邯郸二调)❖一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则()A. B.C.D.2.若角为第二象限角,,则()A. B. C.D.3.设,为两个不同的平面,a ,b ,c 为三条不同的直线,则下列命题正确的是()A.若,,则B.若,,,则C.若,,,,则D.若,,,则4.已知复数z 满足,则()A. B. C.1D.25.直线被圆截得的弦长的最小值为()A.4B.C. D.6.在的二项展开式中,各二项式系数之和为,各项系数之和为,若,则() A.4 B.5C.6D.77.已知函数,若,则实数a 的取值范围是()A.B. C.D.8.在棱长为4的正方体中,P ,Q 分别为AB ,的中点,则平面截此正方体所得的截面周长为()A. B.C.D.二、多选题:本题共4小题,共20分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知函数,则下列描述正确的是()A.函数的最小正周期为B.是函数图象的一个对称轴C.是函数图象的一个对称中心D.若函数的图象向左平移个单位长度可得函数的图象,则为奇函数10.已知实数a ,b ,m 满足,则以下大小关系正确的是()A. B.C.D.11.已知等差数列的前n 项和为,且满足,,现将数列与数列的公共项从小到大排列得到新数列,则下列叙述正确的是()A. B.C.D.数列的前10项和为12.已知椭圆的上顶点为B ,左、右焦点分别为,,则下列叙述正确的是()A.若椭圆C 的离心率为,则B.若直线与椭圆C 的另一个交点为A ,且,则C.当时,过点B 的直线被椭圆C 所截得的弦长的最大值为D.当时,椭圆C 上存在异于B 的两点P ,Q ,满足,则直线PQ 过定点三、填空题:本题共4小题,每小题5分,共20分。
惠州市2024届10月高三第二次调研考试数学试题答案

惠州市2024届高三第二次调研考试数学试题参考答案与评分细则一、单项选择题:本题共8小题,每小题满分5分,共40分.题号12345678答案ADBBCCBA1.【解析】(){}|ln 2B x y x ==- ,∴{}2B x x =<,则A B = [)1,2,故选:A .2.【解析】由题设i iz +=2,∴i ii i i i i z 21121)2(22-=-+-=+=+=,5)2(122=-+=∴z .故选D .3.【解析】320m -⨯-=,解得6m =-.故选:B .4.【解析】因为1ln ln 202a ==-<,3182b -⎛⎫== ⎪⎝⎭,6630tan 2115tan 115tan 22115tan 115tan 22==-⋅=-=c ,所以10<<c ,所以b c a >>.故选:B .5.【解析】首先将原始数据32,42,40,37,25,38,30,29从小到大排序为:42,40,383732,30,2925,,,.因为758⨯%6=,所以这组数据的第75百分位数为:3924038=+,故选:C .6.【解析】由已知ln(1)0.4ln(3)0.8m a m a +=⎧⎨+=⎩,两式相除得ln(3)2ln(1)a a +=+,所以ln(3)2ln(1)a a +=+,则2(1)3a a +=+,因为0a >,故解得1a =,设t 天后开始失去全部新鲜度,则ln(1)1m t +=,又ln(11)0.4m +=,所以ln(1)1ln 20.4t +=,则2ln(1)5ln 2ln 32t +==,所以2(1)32t +=,解得141.414 5.656t +=⨯=,所以 4.656 4.7t =≈.故选:C .7.【解析】如图所示:延长2F A ,交P F 1的延长线于点Q ,∵P A 是12F PF ∠的外角平分线,2||AQ AF ∴=,2||PQ PF =,又O 是12F F 的中点,1QF AO ∴∥,且12||QF OA ==.又1112||2QF PF PQ PF PF a =+=+=,2a ∴=,222233()a b a c ∴==-,∴离心率为ca=故选:B .8.【解析】设()t f x =,因为||||11()2()2x x f e x e f x --=--==,所以()t f x =为偶函数,且当0x >时,1()2x f x e =-为增函数,所以当0x ≤时,()t f x =为减函数,所以0min 11(0)22t f e ==-=,即12t ≥.当0x >时,()()1ln g x x x =-,则()11()ln 1ln 1g x x x x x x'=+-=-+,且)('x g 在),0(+∞上单调递增.令()0g x '=,解得1x =,所以当(0,1)x ∈时,()0g x '<,()g x 为减函数;当(1,)x ∈+∞时,()0g x '>,()g x 为增函数,又111ln 2ln 2222g ⎛⎫=-= ⎪⎝⎭.作出0x >时()g x 的图象,如图所示:所以当ln 20,2m ⎛⎫∈ ⎪⎝⎭时,1(),2y g t t =≥的图象与y m =图象有2个交点,且设为12,t t ,作出()t f x =图象,如下图所示:此时1y t =与2y t =分别与()y f x =有2个交点,即()()0g f x m -=有四个不同的解,满足题意.综上,实数m 的取值范围为ln 20,2⎛⎫⎪⎝⎭.故选:A二、多项选择题:本题共4小题,每小题满分5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得2分,有选错的得0分.题号9101112全部正确选项BCDBCDABABD9.【解析】因为22111211124n S n n n ⎛⎫=-=--+ ⎪⎝⎭,所以数列{}n S 的最大项为5S 和6S ,故C 正确;因为211n S n n =-,所以81018122=-=-=S S a ,故B 正确;当1n =时,101=a ,当2n ≥时,由211n S n n =-,得()()211111n S n n -=---,两式相减得:122+-=n a n ,又101=a ,适合上式,所以122+-=n a n ,因为21-=-+n n a a ,所以{}n a 是递减数列,故A 错误;或者,由101=a ,82=a 得{}n a 不是递增数列,故A 错误;由0112>-=n n S n 解得:110<<n ,所以满足0>n S 的最大的正整数n 为10,故D 正确;故选:BCD .10.【解析】如图作BE CD ⊥交CD 于E ,则12CD ABCE -==,3122=-=BE ,则圆台的高为3cm ,A 错误;圆台的轴截面面积为()2133c 4m 232⨯+⨯=,B 正确;圆台的侧面积为262)21(cm ππ=⨯+,C 正确;圆台的体积为()3173cm 33443πππππ⨯⨯++⋅=,D 正确;故选:BCD .11.【解析】由题意可得A 正确;,故B 正确;由于,C 错误;,所以D 错误.故选:AB .12.【解析】设()f x 的最小正周期为T ,则由函数()f x 在,36ππ⎡⎤-⎢⎥⎣⎦上单调,可得263T ππ⎛⎫≥-- ⎪⎝⎭,即T π≥.因为2T ππω=≥,所以02ω<≤.由()f x 在,36ππ⎡⎤-⎢⎥⎣⎦上单调,且63f f ππ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭,得()f x 的一个零点为36212πππ-+=-,即,012π⎛⎫- ⎪⎝⎭为()f x 的一个对称中心.因为463f f ππ⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭,432346πππ=+,所以有以下三种情况:①当47366T πππ=-=时,则2127T πω==,符合题意;②当33544126T πππ⎛⎫=--= ⎪⎝⎭时,则295T πω==,符合题意;③当3544126T πππ⎛⎫=--= ⎪⎝⎭时,则235T πω==,符合题意.因为T π≥,其他情况不满足题意.故ω的取值为712,59或53.故选:ABD .三、填空题:本题共4小题,每小题5分,共20分.13、1014、415、316、3336+13.【解析】5)2(x x +的展开式的通项公式为)5,4,3,2,1,0(2)2(255551===--+r x C xx C T r r r r r r r ,令325=-r ,得1r =,所以3x 的系数为102115=C ,故答案为:10.14.【解析】由抛物线的定义可知:AB AF =,又AF BF =,所以AF BF AB ==,则ABF 为等边三角形,设准线l 与x 轴交于点H ,则2=FH ,︒=∠=∠=∠60AFx BF A BFH ,所以42===FH BF AB .故答案为:4.16.【解析】取CE 中点O ,连接,DO OP ,由正四面体可知,DE AB CE AB⊥⊥,又DE CE E ⋂=,AB ∴⊥面CDE ,又OP AB ∥,OP ∴⊥面CDE ,当MN AM +最小时,MN ⊥面CDE ,故N 在线段DO 上.由OP ⊥面CDE可得OP OD ⊥,又111242OP AE AB ===,DP ==2OD ==,将PDO △沿PD 翻折到平面APD 上,如图所示:易知30ADP ∠= ,sin ,cos ,OP OD ODP ODP DP DP∠=∠=则()3sin sin 30sin cos30cos sin 3012ODA ODP ODP ODP ∠=∠+=∠+∠=,故MN AM +的最小值即A 到OD 的距离,即33sin 2126AD ADO ++⋅∠=⨯.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.【说明:有其他的解法,请酌情给分.】17.(本小题满分10分,其中第一小问5分,第二小问5分。
武汉市 2023 届高中毕业生二月调研考试数学参考答案

武汉市2023届高中毕业生二月调研考试数学试卷参考答案1.【答案】C 【解析】由已知可得2{|8120}{|26}B =x x x x x -+<=<<R ;所以(){3,4,5}A B =R . 2.【答案】A 【解析】由已知可设i(,,0)z a b a b b =+∈≠R ,则2222i z a ab b =+-, 所以22222222i i 2i i (21)i z z a ab b a b a b a ab b a b a a b +=+-++=-+++=-+++ 又因为2z z +是实数,所以(21)0a b +=,又因为0b ≠,所以12a =-.所以复数z 的实部是12-. 3.【答案】B 【解析】由a b ⊥ 可知,0a b ⋅= ,所以(2)240k -⨯+=.即1k =,所以(2,1)(2,4)(4,3)a b -=--=--.则5a b -== .4.【答案】C【解析】由已知得,设该二阶等差数列为数列{}n a ,则12a =,23a =,36a =,411a =.211a a -=,323a a -=,435a a -=,所以*121()n n a a n n +-=-∈N ,所以1121321()()()n n n a a a a a a a a ++=+-+-++-2*(121)213(21)22()2n n n n n +-=+++⋯⋯+-=+=+∈N ,所以2(1)2(2)n a n n =-+≥,又因为时,12a =也满足上式, 即2*(1)2()n a n n =-+∈N ,所以215(151)21962198a =-+=+=. 5.【答案】B【解析】由已知函数1,()2,x xx x af x a +⎧=⎨>⎩≤可以画出函数图象,如图,因为()f x 的值域是R ,数形结合可知,当1a >时,()f x 的值域是(,1](2,)aa -∞++∞ 不满足题意.当01a ≤≤时,()f x 的值域是R .当10a -<<时,()f x 的值域是(,1](2,)aa -∞++∞ ,不满足题意.当1a -≤时,()f x 的值域是(,1](0,)a -∞++∞ .不满足题意.6.【答案】D【解析】由已知图形可知,该圆柱形工件的表面积为原来圆柱的外侧表面积、上下底面圆的面积减去圆柱形通孔的面积、内侧表面积之和,即22215102(15)210S r r ππππ⨯⨯⨯+⨯-+⨯⨯=表222407502(5)900(015)r r r r πππππ=-++=--+<<,所以5r =时,圆柱形工件的表面积最大,为900π.故选D .7.【答案】B 【解析】由已知图形可知,函数()sin(x )f x A ωϕ=+由sin y x =进行相应变换得到,所以10x ωϕ+=,2x ωϕπ+=.所以2211x x x x ωπϕωϕ-==.在已知21xx 的条件下,可以进行确定的值是ϕ. 8.【答案】D 【解析】由空间中动点P 满足2PA PB =的点的集合为阿氏球面(即将下图的阿氏圆S 以AB为轴旋转一周得到的球面,其中圆S 以线段12PP 为直径,11BP=,2 3BP =),则所求轨迹为阿氏球面与球面O 的交线圆,从而以O 为圆心,3为半径的圆与以S 为圆心,2为半径的圆的公共弦长的一半即为所求交线圆的半径,圆心距OS ===,所以公共弦长一半为r =,所求轨迹长度为2π=.综上所述:选项D 正确.29.【答案】BCD 【解析】由椭圆22221(0)2x y m m m+=>+(如右图)的某两个顶点间的距离为4可知,①124A A =,即4=,所以m =. ②124B B =,24m =,所以2m =,③124A B =4=,所以m =.故选BCD10.【答案】ABD 【解析】选项A ,B 显然正确.对于C 选项,设甲校理科生达标人数为x ,则乙校理科生达标人数也为x ; 则理科生总人数为560%3x x ÷=,文科生总人数为1070%7x x ÷=, 所以甲校总达标率为2100%64.6%65%51037xx x ⨯≈≠+,故选项C 不正确.对于D 选项,由于甲乙两校理科生和文科生人数未知,所以假设甲校理科生为x ,假设甲校文科生为10x ,假设乙校理科生为10x ,假设乙校文科生为x .则此时甲校的总达标率为0.67100%69.1%10x xx x+⨯≈+; 则此时乙校的总达标率为为6.50.75100%65.9%10x xx x+⨯≈+.此时69.1%65.9%>.所以甲校的总达标率可能高干乙校的总达标率,故选项D 正确.故选ABD .11.【答案】ABC 【解析】对于A 选项,由概率的基本性质可知,1a b +=,故选项A 正确.对于B 选项,由12p =时,离散型随机变量x 服从二项分布1,2B n ⎛⎫ ⎪⎝⎭则111()C C ,(0,1,2,3,)222kn knk k n n P X k k n -⎛⎫⎛⎫⎛⎫===⋯⋯ ⎪ ⎪⎪⎝⎭⎝⎝⎭=⎭,所以1351(111C C C 222)2nnn n n n a -⎛⎫⎛⎫=+++== ⎪ ⎝⎭⨯⎪⎭⎝ ; 0241(111C C C 222)2nnn n n n b -⎛⎫⎛⎫=+++=⨯= ⎪ ⎪⎝⎭⎝⎭.所以a b =;B 正确. 对于C ,D 选项,[(1)]C (1)nniin ini a b p p p p -=+=+-=-∑,0[(1)]C ()(1)nni in ini a b p p p p -=-+=-+-=--∑[(1)][(1)]1(12)22n n np p p p p a -+-----∴==, 当102p <<时,1(12)2np a --=为正项为单调递增的正项等比数列,故a 随着n 的增大而增大,故选项C 正确.当112p <<时,(12)n p -为正负交替的交错数列,故选项D 不正确. 12.【答案】AC【解析】对()f x 进行分析可知,定义域为(0,)+∞,求导1()cos (0)f x x x x'=+>; 考虑cos y x =和1y x=-在0x >时的图象交点问题,如图所示,由图可知(1)n n x n ππ-<<.故选项A 正确.由图可知1n n x x π+->,故选项B 不正确.对于C 选项,(21)22n n n x x n πππ-⎛⎫-=-- ⎪⎝⎭的意义是n x 与2n ππ-两个数字之间的差,根据图象,y cos x =和1y x =-在0x >时的图象交点的横坐标n x 与2n ππ-之间的差越来越小,所以(21)2n n x π⎧⎫--⎨⎬⎩⎭为递减数列.故选项C 正确.对于D 选项,由图可知2(41)(21)2n n n x ππ--<<,且在(41)(21)2n n x ππ--<<时,1cos x x>-,即()0f x '>,所以2(41)(41)()1ln 22n n n f x f ππ--⎛⎫<=-+⎪⎝⎭.故选项D 不正确.故选AC . 13.【解析】由已知可得0,2πα⎛⎫∈ ⎪⎝⎭,,444πππα⎛⎫-∈- ⎪⎝⎭,co 4s πα⎛⎫-==⎪⎭∴⎝1cos 2sin 22sin cos 22443πππαααα⎛⎫⎛⎫⎛⎫=-=--=⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭14.【答案】8【解析】由直线1l 与直线2l 到圆心的距离相等,即直线32m n y x +=+经过圆心31,22⎛⎫-- ⎪⎝⎭,得8m n +=. 15.【答案】4 【解析】1()e exxf x a -'=+-可得()0f x '=,即1e e 0x x a -+-=,等式两边乘以e x ,可得2e e )e 0(x xa -+=,由韦达定理可得1212e ee e xx x x +==.所以121x x +=.1122122111121212()()e e e e e e (e e )x x x x x x x x f x f x ax ax a x x a --+=--+--=--++-=-.所以4a -=-.即4a =. 16.【答案】54【解析】由题意做出下图,由双曲线的第三定义可知, 2221AP PBb k k e a=-=⋅;又1PA FQ k k =-⋅,所以22PB FQ k b t ck a t a-=-=-. 所以22222514t ac c a a a a c c c +-==-++≤. 17.【解析】(1)由2n n S na =,则112(1)n n S n a ++=+,两式相减得:112(1)n n n a n a na ++=+-.(1分) 整理得:1(1)n n n a na +-=,即2n ≥时,11n n a na n +=-.···················································2分 所以2n ≥时,132122122·33(1)231n n n n n a a a n n a a n a a a n n -----=⋅⋅⋅=⋅⋅⋅⋅=--- ,·······················4分 又1n =时,112a a =,得10a =,也满足上式.故*3(1)()n a n n =-∈N .···························5分 (2)由40117a =,所以674022a <<.ABQPx t又634992a =>,所以{}n b 前40项中有34项来自{}n a ,··················································7分 故12612401234()(222)b b b a a a +++=+++++++ ··············································9分613434()2(21)16831261809221a a +-=+=+=-.·····························································10分18.(12分)【解析】(1)延长1D E 和DC 交于点M ,连MA 交BC 于点N ,连1D N .··········2分 由112C E CE =,故1112C D CM =,所以4CM AB ==,即N 为BC 中点.··································3分 此时1111 A D B C ,故四边形11A BND 为平行四边形.所以11//A B D N ,······················5分 又1D N ⊂平面1AD E ,1A B ⊂/平面1AD E .所以1//A B 平面1AD E .··································6分 (2)以C 为原点,1,,CD CB CC 所在直线分别为x 轴、y 轴、z 轴, 建立如图所示的空间直角坐标系.(7分)则11(0,4,0),(0,2,3),(4,4,0),(2,0,3),(0,0,2)B B A D E所以11(0,2,3),(2,4,3),(4,BB AD AE =-=--=--设平面1AD E 的法向量(,,)n x y z =,由100n AD n AE ⎧⋅=⎪⎨⋅=⎪⎩ ,得24304420x y z x y z --+=⎧⎨--+=⎩. 取(1,2,2)n =--,·····································································································10分故所求角的正弦值为11n BB n BB ⋅==⋅ ·························································11分 所以直线1BB 与平面1AD E ······················································12分 19.(12分)【解析】(1)在BDC △中,222cos 2BD CD BC BDC BD CD +-∠==⋅················2分cos cos ADC BDC ∠=-∠=.············································································4分 在ADC △中,2222cos 4AC AD CD AD CD ADC =+-⋅⋅∠=,所以2AC =.··················6分 (2)设AC x =,BC y =.由正弦定理,在ADC △和BDC △sin ADCx ∠=,sin sin 1BCD BDCy∠∠=.又sin sin ADC BDC ∠=∠,得sin sin BAC BCD ∠=∠.··················8分 在BDC △中,由余弦定理,2cos BCD ∠=.由2BAC BCD ∠=∠,有sin 2sin cos BAC BCD BCD ∠=∠∠.·······································9分22=,整理得:222(1)y x y =+.① 又由cos cos ADC BDC ∠=-∠22=226x y +=.②···········10分联立①②得:3227120x x x --+=.即2(3)(4)0x x x -+-=.·······································11分11x -<<,故x =.所以AC =.······································12分 20.【解析】(1)X 可能取值为4,5,6,7.3347C 1(4)C 35P X ===,3447C 4(5)C 35P X ===,3547C 10(6)C 35P X ===,3647C 20(7)C 35P X ===,(4分) 14102032()4567353535355E X =⨯+⨯+⨯+⨯=.·····························································5分 (2)Y 可能取值为4,5,6,7,设甲袋和乙袋抽取次数分别为1Y 和2Y .·····························6分1111124223C C 1(4)(2)(2)C C 18P Y P Y P Y =====⋅=,·····························································7分11111221121222223434C C C C 4(5)(2)(3)(3)(2)C C C C 18P Y P Y P Y P Y P Y ====+===⋅+⋅=,···················8分11113122121222223434C C C C 7(6)(2)(4)(3)(3)+C C C C 18P Y P Y P Y P Y P Y ====+===⋅⋅=,···················9分1476()4567618181818E Y =⨯+⨯+⨯+⨯=.·································································11分 甲袋中的球取完后直接取乙袋,若此时甲袋中还有其他球,则该球的干扰作用已经消失,所以同样是要取出4个黑球,调整后的方案总抽取次数的期望更低.·························································12分 21.【解析】(1)设直线PQ 与x 轴交于0,02p P ⎛⎫-⎪⎝⎭,······················································1分 由几何性质:20CP CP CO =⋅.即:3222p ⎛⎫=-+⋅ ⎪⎝⎭,解得:1p =,····························3分 故抛物线E 的标准方程为:22y x =.···········································································4分(2)设00(,)T x y ,11(,)A x y ,22(,)B x y .(i)由题意,TA 中点M 在抛物线E 上,即20101222y y x x ++⎛⎫=⋅ ⎪⎝⎭,又2112y x =,将2112y x =代入, 得:2210100240y y y x y -+-=.··················································································6分 同理:2220200240y y y x y -+-=. 有1202120024y y y y y x y +=⎧⎨=-⎩.此时D 点的纵坐标为1202y y y +=.所以直线TD 的斜率为0.··············8分 (ii)222200121212123422442()y x x x y y y y y y -+++-===,故点200034,2y x D y ⎛⎫- ⎪⎝⎭. 此时1212S TD y y =⋅-,2200000343222y x TD x y x -=-=-.12y y -==,S =.·························9分 又点T 在圆C 上,有2200()23x y ++=,即2200041y x x =---,代入上式可得:S ==,·················································11分由022x --+≤03x =-时,S48=. 所以S 的最大值为48.·······························································································12分22.【解析】(1)由()ln 0f x ax x =-=,得ln x a x =.设ln ()xF x x=,则()f x 的零点为函数()F x 图象与直线y a =交点的横坐标.21ln ()xF x x -'=,·······························································1分令()0F x '=,解得e x =.当0e x <<时.()0F x '>,()F x 单调递增;e x >时.()0F x '<,()F x 单调递减.···········2分 又因为0x →时,()F x →-∞;x →+∞时,()0F x →;函数()F x 图象与直线y a =有两个交点时,0(e)a F <<.所以a 的取值范围是10,e ⎛⎫⎪⎝⎭.··································································4分(2)因为(1)0F =,由(1)得:121e x x <<<.1212ln ln x x a x x ==,2211ln ln x x x x =,设21(1)x t t x =>,则11ln ln ln t x t x +=. 即1ln ln 1t x t =-,2ln ln 1t tx t =-.····················································································6分 由12k x x 有最小值ee ,即12()ln ln ln 1k t t k x x t ++=-有最小值e .设()ln ()(1)1k t tg t t t +=>-,2(1)ln 1()(1)kk t t k t g t t -++-+-'=-.········································7分记()(1)ln 1k G t k t t k t =-++-+-,221(1)()()1k k t t k G t t t t+--'=-++=, 由1t >,若1k ≤,则()0G t '>,()G t 递增,此时()(1)0G t G >=,故()0g t '>,()g t 递增, 此时()g t 在(1,)+∞没有最小值,不符合题意.································································8分 若1k >,则()G t 在(1,)k 递减,在(,)k +∞递增.又(1)0G =,且t →+∞时,()G t →+∞,故存在唯一0(,)t k ∈+∞,此时01t t <<时,()0G t <,()0g t '<,()g t 递减;0t t >时,()0G t >,()0g t '>,()g t 递增.·····················································································································9分 所以1k >时,()g t 有最小值0()g t .由000(1)ln 10kk t t k t -++-+-=,整理得:0000ln 11ln 1t t k t t -+-=+-.此时20000000()ln ln ()11l 1()n k t t t g t t t t +==-+-,由题意:0()e g t =.··········································10分 设2()(0)e 1x x h x x x -=>+-,2[(2)e 2](())e 1x x x x x h x x --++-'=+-. 设()(2)e 2x H x x x -=++-,()(1)e 1x H x x -'=-++.设()()u x H x '=,()e 0x u x x -'=>,故()H x '递增,()(0)0H x H ''>=.此时()H x 递增,有()(0)0H x H >=,此时()0h x '>. 又易证,当0x >时,e10xx -+-≠,故()h x 在(0,)+∞递增.由(1)e h =知,()e h x =的唯一解是1x =.····································································11分 故0()e g t =的唯一解是0ln 1t =,即0e t =. 综上所述:20000ln 1e 2e 1ln 1t t k t t -+-==-+-.·······································································12分。
22-23-9下-武汉市二调-简答+视频讲解

2022-2023学年度武汉市部分学校九年级调研考试数学试卷一、选择题(共10小题,每小题3分,共30分)1.“守株待兔”这个事件是()A.随机事件B.确定性事件C.必然事件D.不可能事件答案:A2.下列图形是中心对称图形的是()答案:B3.解一元二次方程x2-2x-4=0,配方后正确的是()A.(x-1)2=3B.(x-1)2=4C.(x-1)2=5D.(x-2)2=8答案:C4.已知一元二次方程x2+4x-1=0的两根分别为m,n,则mn-m-n的值是()A.5B.3C.-3D.-5答案:B5.如图,已知⊙O的半径为5,直线AB经过⊙O上一点P,下列条件不能判定直线AB与⊙O相切的是()A.OP=5B.∠APO=∠BPO C.点O到直线AB的距离是5D.OP⊥AB答案:A6.某品牌手机原来每部售价为1999元,经过连续两次降价后,该手机每部售价为1360元,设平均每次降价的百分率为x,根据题意,所列方程正确的是()A.1999x2=1360B.1999(1-x2)=1360C.1999(1-x)2=1360D.1999(1-2x)=1360答案:C7.如图,在平面直角坐标系中,矩形ABCO的两边与坐标轴重合,OA=2,O C=1.将矩形ABCO绕点O 逆时针旋转,每次旋转90°,则第2023次旋转结束时,点B的坐标是()A.(-2,-1)B.(-1,2)C.(-2,1)D.(1,-2)答案:D8.在二次函数y=-x2+2x中,若函数值大于0,则结合函数图象判断x的取值范围是()A.x<0或x>2B.x>0或x<-2C.-2<x<0D.0<x<2答案:D9.如图,在圆内接四边形ABCD 中,AB =AD ,∠BAD =90°.若四边形ABCD 的面积是S ,AC 的长是x ,则S 与x 之间的数关系式是( )A .S =x 2B .S =12x 2 C .S x 2D .S =23x 2答案:B 解析:10.根据频率估计概率原理,可以用随机摸拟的方法对圆周率π进行估计.用计算机随机产生m 个有序数对(x ,y )(0≤x ≤1,0≤y ≤1),它们对应的点金部在平面直角坐标系中某一个正方形的边界及其内部.若统计出这些点中到原点的距离小于或等于1的点有n 个,则可估计π的值是( )A .m nB .n mC .2n mD .4nm答案:D 解析:二、填空题(共6小题,每小题3分,共18分)11.在平面直角坐标系中,点P (-3,4)关于原点对称的点的坐标是________. 答案:(3,-4)12.若一个长方形的长比宽多2,且面积为80,则宽是_________. 答案:813.如图,⊙O 是△ABC 的内切圆,∠C =40°,则∠AOB 的大小是____________.答案:110°14.甲、乙、丙三位同学把自己的数学课本故在一起,每人从中随机抽取一本(不放回),三位同学抽到的课本都是自己课本的概率是_______. 答案:1615.已知抛物线y=ax2+bx+c(a,b,c是常数,0<a<c)经过点(-1,0),下列结论:①b>0:②关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根;③当x<-1时,y随x的增大而减小;④m为任意实数,若c=3a,则代数式am2+bm+c的最小值是-a.其中正确的是________(填写序号).答案:①②④解析:16.如图,D是△ABC内一点,∠BDC=90°,BD=CD,AB=20,AC=21,AD,则BC的长是_____________.解析:三、解答题(共8小题,共72分)17.(本小题满分8分)关于x的一元二次方程x2+bx+8=0有一个根是x=2,求b的值及方程的另一个根.答案:b=-6,另一个根为4如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BD,BE.(1)判断△ABD的形状;(2)求证:BE平分∠AB D.答案:(1)△ABD为等边三角形(2)证△BEA≌△BED(SSS)19.(本小题满分8分)一个不透明的布袋中装有1个红球,1个黑球和若干个白球,它们除颜色外其余都相同.从中任意摸出1个球,是白球的概率为12.(1)直接写出布袋中白球的个数;(2)从布袋中先摸出一个球后放回,再摸出一个球,请用列表或画树状图法求两次摸到的球都是白球的概率.答案:(1)2(2)1 420.(本小题满分8分)如图,AB,CD是⊙O的两条弦,∠AOB+∠COD=180°.(1)在图(1)中,∠AOB=120°,CD=6,直接写出图中阴影部分的面积;(2)在图(2)中,E是AB的中点,判断OE与CD的数量关系,并证明你的结论.答案:(1)12π-(2)CD=2OE解析:如图是由小正方形组成的7×6网格,每个小正方形的顶点叫做格点.仅用无刻度的直尺在给定网格中完成画图.(1)在图(1)中,A,B,C三点是格点,画经过这三点的圆的圆心O,并在该圆上画点D,使AD=BC;(2)在图(2)中,A,E,F三点是格点,⊙I经过点A.先过点F画AE的平行线交⊙I于M,N两点,再画弦MN的中点G.答案:解析:22.(本小题满分10分))燃放烟花是一种常见的喜庆活动.如图,武汉数学小杰燃放一种手持烟花,这种烟花每隔2 s发射一枚花弹,每枚花弹的飞行路径视为同一条抛物线,飞行相同时间后发生爆炸,小杰发射出的第一枚花弹的飞行高度h(单位:m)随飞行时间(单位:s)变化的规律如下表:(1)求第一枚花弹的飞行高度h与飞行时间t的两数解析式(不要求写出自变量的取值范围);(2)当第一枚花弹到达最高点时,求第二枚花弹到达的高度;(3)为了安全,要求花弹爆炸时的高度不低于30m.小杰发现在第一枚花弹爆炸的同时,第二枚花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求.答案:(1)h=-2t²+16t+2;(2)26m;(3)符合要求解析:操作与思考如图(1),在△ABC中,AB=AC,∠BAC=α,D是异于A,B的一点,且∠ADB=90°.武汉数学将线段AD绕点A逆时针旋转α,画出对应线段AE,连接DE交BC于点F,猜想BF与CF的数量关系,并证明你的猜想:迁移与运用如图(2),在△ABC和△CDE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,ACCD,ED的延长线交AB于点F,且∠BDC=90°,直接写出EF的长.答案:(1)BF=CF;(2)EF=3解析:如图,抛物线y =x 2-2x -6与x 轴分别相交于A ,B 两点(点A 在点B 的左侧),C 是AB 的中点,平行四边形CDEF 的顶点D ,E 均在抛物线上. (1)直接写出点C 的坐标; (2)如图(1),若点D 的横坐标是-2,点E 在第三象限,平行四边形CDEF 的面积是13,求点F 的坐标;(3)如图(2),若点F 在抛物线上,连接DF ,求证:直线DF 过一定点.答案:(1)C(1,0);(2)F(2,-5);(3)(1,-72) 解析:。
2023年江苏省宿迁市中考数学二调试卷+答案

2023年江苏省宿迁市中考数学二调试卷学校:___________姓名:___________班级:___________考号:___________第I 卷(选择题)一、选择题(本大题共8小题,共24.0分。
在每小题列出的选项中,选出符合题目的一项)1. 2023的相反数是( ) A. 12023B. −12023C. 2023D. −20232. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A.B.C.D.3. 下列计算正确的是( ) A. (2a −1)2=4a 2−1 B. 3a 6÷3a 3=a 2 C. (−ab 2)4=−a 4b 6D. −2a +(2a −1)=−14. 为调查某班学生每天使用零花钱的情况,张华随机调查了20名同学,结果如下表:则这20名同学每天使用的零花钱的众数和中位数分别是( )A. 3,3B. 3,3.5C. 3.5,3.5D. 3.5,35. 如图▱ABCD ,F 为BC 中点,延长AD 至E ,使DEAD =13,连结EF交DC 于点G ,则S△DEGS△CFG=( )A. 2:3B. 3:2C. 9:4D. 4:96. 下列命题中:(1)两组对边分别相等的四边形是平行四边形;(2)对角线相等的平行四边形是矩形;(3)一组邻边相等的平行四边形是菱形;(4)对角线相等且互相垂直的四边形是正方形,正确的命题个数为( )A. 1B. 2C. 3D. 47.如图,AB为⊙O的直径,CD切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠A的度数为( )A. 45°B. 30°C. 22.5°D. 37.5°8. 如图,在平面直角坐标系中,直线l与函数y=k(k>0,x>0)的图x象交于A、B两点,与x轴交于C点,若OA=AB,且∠OAB=90°,则tan∠AOC的值为( )A. √ 5−12B. √ 33C. √ 3−13D. 1+√ 24第II卷(非选择题)二、填空题(本大题共10小题,共30.0分)9. √ 16的平方根是______.10. 因式分解:a3−a=.11. 已知圆锥的底面半径为3,母线长为6,则此圆锥侧面展开图的圆心角是______.12. 习近平总书记指出“善于学习,就是善于进步”.“国家中小学智慧云平台”上线的某天,全国大约有5450000人在平台上学习,将这个数据用科学记数法表示为.13. 若2m+n=4,则代数式6−2m−n的值为______.14. 二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:则当−3<x<3时,y满足的范围是______ .15. 如图,在正方形ABCD中,E,F分别是BA,BC的中点.若BD=2,则EF的长是.16. 在Rt△ABC中,∠C=90°,AC=3,BC=4.若以C点为圆心,r为半径所作的圆与斜边AB只有一个公共点,则r的取值范围是______.17. 小淇利用绘图软件画出函数y=−1x(x−1)(x+1)(−2≤x≤2)的图象,下列关于该函2数性质的四种说法:①图象与x轴有两个交点;②图象关于原点中心对称;③最大值是3,最小值是−3;④当x>1时,y随x的增大而减小.其中,所有正确说法的序号是.18.如图,矩形ABCD,AB=4,BC=8,E为AB中点,F为直线BC上动点,B、G关于EF对称,连接AG,点P为平面上的动点,满足,则DP的最小值______ .三、计算题(本大题共1小题,共8.0分)19. 解分式方程:x−2x−1+2=21−x.四、解答题(本大题共9小题,共88.0分。
2022届武汉市高三二调英语答案

2022届武汉市高三二调英语答案1、Tom’s mother will let him _______ traveling if he comes back?in five days. [单选题] *A. to goB. goesC. wentD. go(正确答案)2、Tony is a quiet student, _______ he is active in class. [单选题] *A. soB. andC. but(正确答案)D. or3、--How is your friend coming?--I’m not sure. He _______ drive here. [单选题] *A. may(正确答案)B. canC. mustD. will4、This is the news _______ you want to know. [单选题] *A. that(正确答案)B. whatC. whenD. who5、72.I really don’t know how to thank you , but for your help, I ()my lost necklace.[单选题] *A.couldn’t have found(正确答案)B.mustn’t have foundC.couldn’t findD.wouldn’t find6、While they were in discussion, their manager came in by chance. [单选题] *A. 抓住时机B. 不时地C. 碰巧(正确答案)D. 及时7、If the trousers are too long, ask the clerk to bring you a shorter _____. [单选题] *A. suitB.setC.oneD.pair(正确答案)8、24.Kitty’s father ______ a policeman since 2 He loves helping people. [单选题] * A.isB.wasC.has been (正确答案)D.have been9、63.There will be? ? ? ? ??? water on the road after the heavy rain. [单选题] * A.too much(正确答案)B.much tooC.too manyD.many too10、The beautiful sweater _______ me 30 dollars. [单选题] *A. spentB. paidC. cost(正确答案)D. took11、--Whose _______ are these?? ? ? --I think they are John·s. [单选题] *A. keyB. keyesC. keys(正确答案)D. keies12、There _______ no water or milk in the fridge. [单选题] *A. is(正确答案)B. areC. hasD. have13、Tom’s sister is a nurse. I met _______ in the street yesterday . [单选题] *A. sheB. hersC. himD. her(正确答案)14、38.—Do you have ________else to say for your mistake?—________but sorry. [单选题] *A.anything; SomethingB.something; EverythingC.anything; Nothing(正确答案)D.something; Anything15、We have made a _______ tour plan to Sydney. [单选题] *A. two dayB. two daysC. two-day(正确答案)D. two-days16、She has no idea of what the book is about. She_______ have read it carefully. [单选题]*A. Can’t(正确答案)B. mustn’tC. shouldn’tD. needn’t17、The scenery is so beautiful. Let’s _______. [单选题] *A. take photos(正确答案)B. take mapsC. take busD. take exams18、( ) Do you have any difficulty _____ these flowers?I’d like to help you if you need.[单选题] *A in planting(正确答案)B for plantingC with plantingD to plant19、--Do you have a _______?--Yes, I _______ at a clothes store. [单选题] *A. work; workB. work; jobC. job; jobD. job; work(正确答案)20、A healthy life is generally thought to be()with fresh air, clean water, and homegrown food. [单选题] *A. joinedB. boundC. lackingD. associated(正确答案)21、Online shopping _______ very popular now. [单选题] *A. is(正确答案)B. areC. wasD. were22、How _______ it rained yesterday! We had to cancel(取消) our football match. [单选题] *A. heavily(正确答案)B. lightC. lightlyD. heavy23、We can’t go out ______ school nights. ()[单选题] *A. inB. on(正确答案)C. atD. by24、______this story, and you will realize that not everything can be bought with money. [单选题] *A. ReadingB. ReadC. To readD.Being read(正确答案)25、19.Students will have computers on their desks ________ . [单选题] *A.in the future(正确答案)B.on the futureC.at the momentD.in the past26、33.Will Mary's mother ______ this afternoon? [单选题] *A.goes to see a filmB.go to the filmC.see a film(正确答案)D.goes to the film27、If people _____ overanxious about remembering something, they will forget it. [单选题] *A. will beB. would beC. wereD. are(正确答案)28、Though the _____ drama is wonderful, I guess most audiences will be tired as it is too long. [单选题] *A. four-hour(正确答案)B. four hoursC. four-hoursD. four-hour's29、The man lost his camera and he ______ it now.()[单选题] *A. foundB. is findingC. is looking forD. looks for(正确答案)30、What’s your _______ for the coming new year? [单选题] *A. playB. plantC. plan(正确答案)D. plans。
2022年重庆市高考数学二调试卷+答案解析(附后)

2022年重庆市高考数学二调试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数z满足,其中i为虚数单位,则( )A. 10B. 5C.D.2.已知集合,,若有且只有2个元素,则a的取值范围是( )A. B. C. D.3.若非零实数a,b满足,则下列不等式一定成立的是( )A. B. C. D.4.《巴黎协定》是2016年4月22日签署的气候变化协定,该协定为2020年后全球应对气候变化的行动作出了统一安排,中国政府一直致力于积极推动《巴黎协定》的全面有效落实.某工厂产生的废气经过过滤后排放,排放时污染物的数量不得超过已知该工厂产生的废气在过滤过程中污染物的数量单位:毫克与过滤时间单位:小时之间的函数关系式为均为正常数,e为自然对数的底数如果在前3小时的过滤过程中污染物被排除了,那么排放前至少还需要过滤的时间是( )A. 小时B. 3小时C. 5小时D. 6小时5.若,表示两个不同的平面,m为平面内的一条直线,则下列说法正确的是( )A. “”是“”的充要条件B. “”是“”的必要不充分条件C. “”是“”的必要不充分条件D. “”是“”的充分不必要条件6.已知王大爷养了5只鸡和3只兔子,晚上关在同一间房子里,清晨打开房门,这些鸡和兔子随机逐一向外走,则恰有2只兔子相邻走出房子的概率为( )A. B. C. D.7.已知,若对任意恒成立,则实数m的最大值为( )A. 2B. 4C.D.8.已知点O,A,B是同一平面内不同的三个点,且,若的最小值为,则( )A. B. C. D.二、多选题:本题共4小题,共20分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知直线l:,圆C:,则下列结论正确的是( )A. 直线l恒过定点B. 直线l与圆C恒有两个公共点C. 直线l与圆C的相交弦长的最大值为D. 当时,圆C与圆关于直线l对称10.设数列的前n项和为,已知,且,则下列结论正确的是( )A. 是等比数列B. 是等比数列C. D.11.已知双曲线C:的左、右顶点分别为A,B,左、右焦点分别为,,点P 是双曲线C的右支上一点,且三角形为正三角形为坐标原点,记PA,PB的斜率分别为,,设I为的内心,记,,的面积分别为,,,则下列说法正确的是( )A. B. 双曲线C的离心率为C. D.12.半正多面体亦称“阿基米德多面体”,是由边数不全相同的体现了数学的对称美.传统的足球,就是根据这一发现而制正多边形围成的多面体,成,最早用于1970年的世界杯比赛.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形构成如图所示,若这个二十四等边体的棱长都为2,则下列结论正确的是( )A. 平面AEMHB. 异面直线BC和EA所成角为C. 该二十四等边体的体积为D. 该二十四等边体外接球的表面积为三、填空题:本题共4小题,每小题5分,共20分。
2023年湖北省武汉市高考物理二调试卷+答案解析(附后)

2023年湖北省武汉市高考物理二调试卷1. 一束单色光从空气射入水中,下列说法错误的是( )A. 光的速度改变B. 光的频率改变C. 光的波长改变D. 光的能量改变2. 血氧仪是一种测量人体血氧饱和度的医疗设备,血氧饱和度是人体血液中的氧合血红蛋白容量占全部可结合的血红蛋白脱氧血红蛋白与氧合血红蛋白之和容量的百分比,正常人的血氧饱和度一般在以上,如果血氧饱和度低于,就应尽快就医。
某种指夹式血氧仪是根据脱氧血红蛋白和氧合血红蛋白在红光和红外线区域的吸收光谱特性不同为依据制成的。
下列说法正确的是( )A. 红外线可以用来加热理疗B. 红光和红外线都是可见光C. 红光的波长大于红外线的波长D. 吸收光谱的特点是在连续光谱的背景上出现若干条明线3. 如图所示,A、B为两个等量负点电荷连线上的两点,B为连线的中点,C为连线中垂线上的一点,。
一个负点电荷在A、B、C点的电势能分别为、、,则( )A. B.C. D.4. 长方体A、B置于粗糙水平地面上,A和B质量相同、与地面的动摩擦因数相同。
图甲中,对A施加水平向右、大小为F的推力时,A、B间的弹力大小为;图乙中,对A施加与水平方向成斜向下、大小为2F的推力时,A、B间的弹力大小为。
两图中的A、B均做匀加速直线运动,则( )A. B. C. D.5. 2022年11月12日,天舟五号成功对接于中国空间站天和核心舱后向端口,中国航天员首次在太空迎接“天舟快递”,这次任务首次实观2小时自主快速交会对接,创造了世界纪录。
对接后中国空间站绕地球做椭圆运动,如图所示,设中国空间站在近地点、远地点的速度分别为、,近地点、远地点到地心的距离分别为、,地球质量为M,引力常量为G,则( )A. ,B. ,C. ,D. ,6. 中国高铁屡创奇迹,实现了从“追赶”到“引领”的重大跨越,正在改变中国,影响世界。
某旅客乘坐“复兴号”动车组进站时,观察车厢内的显示屏,利用手机中的秒表记录5组动车组速度变化与所用时间的关系如下:记录序号速度变化运动时间12345由此他预测:若动车组继续按上述运动规律进站,则动车组停下来还需要行驶的路程大约是( )A. 190mB. 680mC. 2450mD. 8800m7. 在光滑水平面上有一表面光滑的斜面,质量为M、高度为h、倾角为,一质量为m的物块视为质点从斜面底端以一定的初速度沿斜面向上运动,如图所示。
2024武汉二调物理答案

武汉市2024届高中毕业生二月调研考试物理试题参考答案及评分参考一、选择题:本题共10小题,每小题4分,共40分。
全部选对的得4分,选对但不全的得2分,有选错的得0分。
1.D2.D 6.A 7.C3.B8.AC4.A9.BD5.C10.BD二、非选择题:本题共5小题,共60分。
11.(8分)(1)19 .95(3分)(2)1.33 (2分)(4)9.5(3分,9.4~9.7均得分) 12. (9分)(1)不需要(2分)(2)D(2 分)(3)197(3分,195~199均得分)(4)大于(2分)13. (10分)(1)注水后储水腔内空气的体积为Vi=V-Vo由玻意耳定律poV=p₁V₁解得pi=1.4atm(2)喷水后储水腔内空气的体积为V2=V-V′由玻意耳定律poV=p₂V₂由题意,水喷射的速度v 满足p2=po+hv²解得v=5m/s ①②③④⑤⑥评分参考:本题共10分。
第(1)问5分,①式1分,②③式各2分;第(2)问5分,④式各1分,⑤⑥式2分。
其他解法正确的同样给分。
物理试题参考答案及评分参考第1页(共4页)14. (15分)(1)a 、b 一起匀速运动,对a 、b 整体有 2mg sinθ=μ·2mg cosθ 解得 μ=tanθ(2)a 、b 一起下滑距离L, 对 a 、b 整体有 2mg sinθ-μmg cosθ=2ma ₁ 由位移公式此时 a 、b 的速度为v ₁=at1b 从M 运动至N, 因绳子松弛,故对b 有 mg sinθ=ma ₂ 由位移公式而 t=t ₁+t ₂ 解得(3)b 运动至N 点后匀速运动,此时速度为 V ₂=v ₁+a ₂t ₂①②③④⑤⑥⑦⑧⑨⑩之后,a 、b 碰撞并交换速度,直至轻绳绷紧,二者以相同的速度v 匀速运动。
该过程 系统动量守恒mv ₁+mv ₂=2mv 解得⑪ ⑫评分参考:本题共15分。
第(1)问4分,①②式各2分;第(2)问7分,③④⑤⑥ ⑦⑧⑨式各1分;第(3)问4分,⑩⑫式各1分, ⑪式2分。
2024武汉二调语文试卷

选择题
下列哪部作品是鲁迅的散文集?
A. 《呐喊》
B. 《朝花夕拾》(正确答案)
C. 《彷徨》
D. 《故事新编》
“白日依山尽,黄河入海流”这句诗的作者是?
A. 李白
B. 王之涣(正确答案)
C. 杜甫
D. 王维
下列哪个成语与古代科举考试相关?
A. 画蛇添足
B. 金榜题名(正确答案)
C. 刻舟求剑
D. 滥竽充数
《红楼梦》中,贾宝玉佩戴的通灵宝玉上刻着什么字?
A. 莫失莫忘
B. 不离不弃
C. 仙寿恒昌(正确答案)
D. 吉祥如意
下列哪项不属于中国古代四大发明?
A. 造纸术
B. 火药
C. 印刷术
D. 地动仪(正确答案)
“采得百花成蜜后,为谁辛苦为谁甜”这句诗描绘了哪种昆虫?
A. 蝴蝶
B. 蜜蜂(正确答案)
C. 蜻蜓
D. 蚂蚁
下列哪部作品是巴金的代表作之一?
A. 《骆驼祥子》
B. 《家》(正确答案)
C. 《子夜》
D. 《边城》
“山不在高,有仙则名;水不在深,有龙则灵”出自哪篇古文?
A. 《岳阳楼记》
B. 《醉翁亭记》
C. 《陋室铭》(正确答案)
D. 《爱莲说》
下列哪个节日与屈原相关?
A. 春节
B. 端午节(正确答案)
C. 中秋节
D. 重阳节。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课内翻译
• ②问今是何世,乃不知有汉,无论魏晋。 (3分)
• 翻译:(渔人)问现在是什么世代,他 们竟然不知道有过汉代,更不用说魏晋 朝代了。
• 22.
• ① 横批:扬善惩恶 • 上联:从善若流,得饶人处且饶人 • 下联:嫉恶如仇,该出手时就出手 • ②第 60 回 • 忠义堂
课外翻译
• ①待诏何所乐,但美酝三升,殊可恋耳!士的肚子里。
• 21. • ① A.今天、马路上、人行道上 • B.大卡车装满了钢材 • C.撞飞1人,轻伤2人,重伤1人 •② D • ③卡车连撞数人,司机安然无恙
我每天喝酒,不超过五合(半升),天下不能饮酒的人中,没有在我之下的。然而, 喜欢看别人饮酒,看见客人举杯开怀畅饮,我的心中为他们感到痛快淋漓, 坦荡豁达,酣畅惬意的滋味,甚至超过客人。我闲居在家没有一天没客人, 而每次客人来了没有一次不置酒,天下所有喜好饮酒的人,也没有在我之上 的了。经常对人说:人生最大的快乐,莫过于身体没病而心中没有忧愁,我 就是没有这两种烦恼的人。但是,常因这两种烦恼困扰的人接踵来到我的面 前,我怎能也让他们享尽人生的快乐呢?所以,他们来了我经常准备良药, 凡是遇到有求的人就送给他们,而这其中尤其喜欢酿酒让客人来饮。(古诗 百科)有人问我:“你没病却储存好多的药,不善喝酒却酿造好多的酒,辛 劳自己而为别人,你为的什么?”我笑着说:“得病的人如果得到了药,我就 为他们感到身体轻松;饮酒的人酣饮在酒中,我就为他们感到酣畅而舒服, 这大概就是专门为自己满足的。”
• 16.
• 答:人工智能领域的国际竞争日益激烈; (2分)
• 观点1:麻省理工学院在全球大学人工智能 影响力上排名第一;(1分)
• 观点2,人工智能是法日俄三国强国强军的 战略手段。(1分)
• 17.作者缅怀巴金,侧重评价巴金是一个独立 思考者的理由是什么?(3分)
• 答:
• ①大多数人纪念巴金忽略了他思考者的角色; • ②思考者的角色在巴金的后半生愈加明晰; • ③作为思考者的巴金是我们时代大写的人。
• 18.一句众人皆知的常识“讲真话”,为 什么说是巴金留给我们的最宝贵财富?(3 分)
• 答: ①巴金说出了关于我们的历史和时代
的真话;
• ②巴金说出了对真话的思考(讲真话的艰
辛);
• ③很多情况下,说话的人,一些所谓的思
考者都不会讲真话。
• 19.结尾第⑦段,从全文看有什么作用? (3分)
• 答:以相同的句式照应开头,使文章结构 清晰;运用反复,进一步表达了对巴金的 沉痛悼念;总结全文,再次点题,强调了 巴金思考者的角色。(一点1分)
2019峨眉二调
• 基础选择题 • 1.C 2.C 3.D 4.B 5.C
文言文6.D 7.B 8.A
• 诗歌10.D
• 社科文13.B 14.B 15.D
• ①影入平羌江水流。 • ②落花时节又逢君。 • ③独坐幽篁里, • ④百般红紫斗芳菲。 • ⑤不问苍生问鬼神。 • ⑥而今识尽愁滋味, • ⑦沉醉不知归路。 • ⑧至今遗恨迷烟树。 • ⑨ 以顺为正者,妾妇之道也。
东皋子为官在门下省任职,以待皇帝召唤,每天给他酒三升,他的弟弟 东静问他:“每天等待皇帝诏谕你快乐吗?”东皋子回答说:“等待诏谕有什 么快乐,不过每天三升美酒,是非常令人留恋的。”现在,在岭南地区没有 实行禁酒法令,我就可以自己酿酒,每月用米大概五斗,酿出酒六斗。而加 上南雄、广州、惠州、循州、梅州五个州的知州陆续送给我的酒,粗略计算 大概已经超过了东皋子。但是东皋子自称是“五斗先生”,实际每天只给三 升,应付自己喝都不够,哪能够顾及到给客人饮用呢?像我这样的人,每天
• 翻译:待命没什么高兴的,只是美酒三 升,还可以留恋罢了!
诗歌鉴赏
• 11.这首诗是诗人未曾得志时,还是失意 遭贬后写的?为什么?(3分)
• 答:是诗人未曾得志时写的;(判断1 分)从第三句得知,诗人还没有被委 以过重任。(理由2分)
• 或者:是诗人失意遭贬时写的;从标 题得知,水井被荒弃野外就暗示了诗 人被贬斥的遭遇。
