分类与分步计数原理
分类计数原理与分布计数原理
自主思考
(1) 由数字l,2,3,4,5可以组成多少个数字允许重 复三位数? 解:要组成一个三位数可以分成三个步骤完成: 第一步确定百位上的数字,从5个数字中任选一个 数字,共有5种选法; 第二步确定十位上的数字,由于数字允许重复, 这仍有5种选法, 第三步确定个位上的数字,同理,它也有5种选 法. 根据乘法原理,得到可以组成的三位数的个数是 N=5X5X5=125. 答:可以组成125个三位数.
例题讲解
例1 书架上层放有6本不同的数学书,下层放有5本不同 的语文书. 2)从中任取数学书与语文书各一本,有多少的取法? 解 (2)从书架上任取数学书与语文书各一本,可以分成两 个步骤完成: 第一步取一本数学书,有6种方法; 第二步取一本语文书,有5种方法. 根据乘法原理,得到不同的取法的种数是 N=6X5=30. 答:从书架上取数学书与语文书各一本,有30种不同的 方法
1.1分类计数原理与分步计算原理
问题二: 从甲地到乙地,要从甲地先乘火车到丙地,再于次日从丙地 乘汽车到乙地.一天中,火车有3班,汽车有2班,那么两天中, 从甲地到乙地共有多少种不同的走法?
1.1分类计数原理与分步计算原理 分步计数原理
完成一件事,需要分成n个步骤,做第1步 有m1种不同的方法,做第2步有m2种不同的 方法……做第n步有mn种不同的方法.那么完 成这件事共有 N=m1×m2×…×mn种不同的方法.
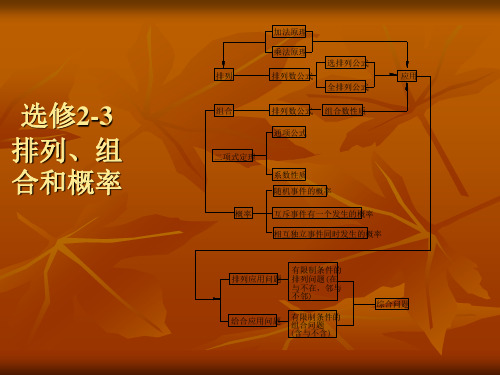
加法原理 乘法原理 选排列公式 排列 排列数公式 全排列公式 应用
选修2-3 排列、组 合和概率
组合
排列数公式 通项公式
组合数性质
二项式定理 系数性质 随机事件的概率 概率 互斥事件有一个发生的概率 相互独立事件同时发生的概率
分类计数原理与分步计数原理

在填写高考志愿表时,一名高中毕业生了解到A、 两 例1 在填写高考志愿表时,一名高中毕业生了解到 、B两 所大学各有一些自己感兴趣的强项专业,具体情况如下: 所大学各有一些自己感兴趣的强项专业,具体情况如下: A大学 大学 生物学 化学 医学 物理学 B大学 大学 数学 会计学 信息技术学 法学
工程学 如果这名同学只能选一个专业,那么他共有多少种选择呢? 如果这名同学只能选一个专业,那么他共有多少种选择呢?
分析:
二、分步计数原理 完成一件事,需要分成n个步骤。做第1步有 1 完成一件事,需要分成 个步骤。做第 步有m 个步骤 步有 种不同的方法,做第2步有 种不同的方法, 步有m 种不同的方法,做第 步有 2种不同的方法, ……, , 做第n步有 种不同的方法, 步有m 做第 步有 n种不同的方法,则完成这件事共有
N=4+3+2=9 = + =
(2)从书架的第 、 2、 3层各取 本书 有多少种 从书架的第1、 、 层各取 本书,有多少种 层各取1本书 从书架的第 不同取法? 不同取法
N=4 ×3×2=24 = × =
可以组成多少个三位数? 例5、由0,1,2,3,4,5可以组成多少个三位数? 、 , , , , , 可以组成多少个三位数 可以组成多少个没有重复数字的三位数? 可以组成多少个没有重复数字的三位数? 分析: 分析: 百 十 个
(1)分三步进行:第一步,考虑百位上的数字有 种不同 )分三步进行:第一步,考虑百位上的数字有5种不同 情况;第二步,十位上的数字可有6种不同的情况 第三步, 种不同的情况; 情况;第二步,十位上的数字可有 种不同的情况;第三步, 个位上的数字有6种不同的情况 共有5X6X6=180 种不同的情况。 个位上的数字有 种不同的情况。共有 (2)分三步进行:首先百位上的数字可从 ,2,3,4,5 )分三步进行:首先百位上的数字可从1, , , , 中选出1个 种办法; 中选出 个,有5种办法;其次,十位上的数字从 ,2,3, 种办法 其次,十位上的数字从1, , , 4,5剩下的 个数字加上 这5个数字中选取 个,有5种不同 剩下的4个数字加上 个数字中选取1个 , 剩下的 个数字加上0这 个数字中选取 种不同 的办法;最后,个位上的数字从剩余的4个数字中选出 个数字中选出1个 的办法;最后,个位上的数字从剩余的 个数字中选出 个, 种不同的办法。 有4种不同的办法。共有 种不同的办法 共有5X5X4=100 法二:本例可采用排除法, 法二:本例可采用排除法,如(1)先不考虑 在百位上的情 )先不考虑0在百位上的情 在百位上时, 况,有6X6X6=216;再考虑 在百位上时,有6X6=36。共有 ;再考虑0在百位上时 。 216-36=180 (2)同学们可考虑用此办法来研究。 )同学们可考虑用此办法来研究。
分类和分步计数原理

分类计数原理与分步计数原理一、分类加法计数原理:完成一件事情可以有n 类办法,在第一类办法中有1m 种不同的方法,在第二类办法中有2m 种不同的方法,……,在第n 类办法中有n m 种不同的方法那么完成这件事共有12n N m m m =+++种不同的方法注:在分类计数原理中,n 类办法中相互独立,无论哪一类办法中的哪一种方法都能独立完成这件事. 例1. 一个书包内有7本不同的小说,另一个书包内有5本不同的教科书,从两个书包中任取一本书的取法有多少种?例2. 在所有的两位数中个位数字比十位数字大的两位数有多少个?(合理分类)二、分步乘法计数原理:完成一件事情需要n 个步骤,做第一步有m 1种不同的方法,做第二步有m 2种不同的办法……,做第n 步有m n 种不同的办法,那么完成这件事共有N 种不同的方法.N=n m m m ⨯⨯⨯ 21 注:分步计数原理各步骤相互依存,只有各步骤都完成才能做完这件事.例1. 用0,1,2,3,4排成可以重复的5位数,若中间的三位数字各不相同,首末两位数字相同,这样的5位数共有多少个?例2. (1)8本不同的书,任选3本分给3个同学,每人一本有多少种不同的分法?(2)若将4封信投入3个邮筒,有多少种不同的投法?若3位旅客到4个旅馆住宿,又是多少种住宿方法? 例3. 将红、黄、绿、黑四种颜色涂入图中的五个区域,要求相邻的区域不同色,问有多少种不同的涂色方法?变式训练:1、如图,用6种不同的颜色把图中A 、B 、C 、D 四块区域分开,若相邻区域 不能涂同一种颜色,则不同的涂法共有多少种?2、如图,用4种不同的颜色涂入图中的矩形A ,B ,C ,D 中,要求相邻的矩形涂色不同,则不同的涂法有多少种?三、计数原理综合应用作用:计算做一件事完成它的所有不同的方法种数区别:一个与分类有关,一个与分步有关;加法原理是“分类完成”,乘法原理是“分步完成” 方法:(1)列举数数法:就是完成一件事方法不是很多,一一列举出来,然后一种一种地数,这种方法适用于:数目较少的问题.(2)字典排序法:把所有的字母或数字或其它,按照顺序依次排出来,所有的字母或数字或其它排完后结束.(3)模型法:根据题意构建相关的图形,利用图形构建两个原理的模型.AB C D典型例题分析(先分类再分步.)【例1】 一个口袋内装有5个小球,另一个口袋内装有4个小球,所有这些小球的颜色互不相同.(1)从两个口袋内任取一个小球,有多少种不同的取法?(2)从两个口袋内各取一个小球,有多少种不同的取法?变式训练1 在夏季,一个女孩有红、绿、黄、白4件上衣,红、绿、黄、白、黑5条裙子,3双不同鞋子,3双不同丝袜,这位女孩夏季某一天去学校上学,有多少种不同的穿法?变式训练2 有不同的中文书7本,不同的英文书5本,不同的法文书3本,若从中选出不属于同一种文字的2本书,共有多少种选法?【例2】 有四位同学参加三项不同的竞赛.(1)每位学生必须参加且只能参加一项竞赛,有多少种不同结果?(2)每项竞赛只许一位学生参加,有多少种不同结果?变式训练1 火车上有十名乘客,沿途有五个车站,乘客下车的可能方式有多少种?变式训练2 有4种不同溶液倒入5只不同的量杯,如果溶液足够多,每只量杯只能倒入一种溶液,有几种不同倒法?【例3】电视台在“欢乐今宵”节目中拿出两个信箱,其中存放着先后两次竞猜中成绩优秀的观众来信,甲信箱中有30封,乙信箱中有20封.现由主持人抽奖确定幸运观众,若先确定一名幸运之星,再从两信箱中各确定一名幸运伙伴,有多少种不同的结果?【例4】d c b a ,,,排成一行,其中a 不排第一,b 不排第二,c 不排第三,d 不排第四的不同排法共有多少种?【例5】 甲、乙、丙、丁4个人各写1张贺卡,放在一起,再各取1张不是自己所写的贺卡,共有多少种不同取法?变式训练1 甲、乙、丙、丁4个人各写1张贺卡,放在一起,各取1张,其中甲、乙、丙不能取自己所写的贺卡,共有多少种不同取法?变式训练2 设有编号①,②,③,④,⑤的5个球和编号为1,2,3,4,5的5个盒子,现将这5个球投入这5个盒子内,要求每个盒子内投入一个球,并且恰好有2个球的编号与盒子的编号相同,则这样的投放方法总数为多少【例6】某城市在中心广场建造一个花圃,花圃分为6个部分(如下图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有_____________种.(以数字作答) 654321四、课堂练习1.一个学生从3本不同的科技书、4本不同的文艺书、5本不同的外语书中任选一本阅读,不同的选法有_______________种.若是选取两本书且它们不相同则有_______________种2.一个乒乓球队里有男队员5人,女队员4人,从中选出男、女队员各一名组成混合双打,共有______种不同的选法.3.一商场有3个大门,商场内有2个楼梯,顾客从商场外到二楼的走法有__________种.4.从分别写有1,2,3,……,9的九张数字卡片中,抽出两张数字和为奇数的卡片,共有_______种不同的抽法.5.从0,1,2,…,9这十个数字中,任取两个不同的数字相加,其和为偶数的不同取法有______种。
分类计数原理与分步计数原理详细解析

通过分类计数原理,我们可以将一个问题分解成多个子问题,进而进行逐步 解决。而分步计数原理则是通过分阶段的计数方法,得出最终的结果。
分类计数原理的定义
分类计数原理是一种方法,通过将问题划分为若干个互不重复且穷尽的分类,然后对每个分类进行计数, 最后将计数结果相加得到总数。
分类计数原理的应用
分类计数原理常于解决组合问题、概率问题和排列组合问题。它可以帮助 我们快速计算出不同情况下的可能性数量。
分类计数原理的实例
例如,有红、黄、蓝三种颜色的球,每种颜色的球各有两个。我们想要从中 选择两个球,问有多少种可能的组合方式?通过分类计数原理,我们可以将 问题分为三个分类:红球、黄球和蓝球。然后分别计算每个分类的组合数, 并将结果相加,得到总的组合数。
分步计数原理的定义
分步计数原理是一种方法,通过将复杂的问题分解为多个简单的步骤来求解。每个步骤都可以通过简单 的计数方法得出结果,然后将各个步骤的计数结果进行相乘或相加,得到最终的解。
分步计数原理的应用
分步计数原理通常用于解决排列问题、事件序列问题和树状图问题。它可以 帮助我们更好地理解问题的结构,并找出解决问题的有效方法。
分步计数原理的实例
例如,假设一本书包含3个章节,每个章节有4个小节,每个小节有2个练习题。 我们想计算完成整本书需要多少个步骤。通过分步计数原理,我们可以分别 计算每个阶段需要的步骤数,并将结果相乘,得到最终的步骤数。
分类计数原理和分步计数原理的区别
分类计数原理着重于将问题分解为不同的互斥分类,然后计算每个分类的数量,最后将结果相加。而分 步计数原理则是将问题分解为多个不同的步骤,每个步骤通过独立的计数方法得出结果,再将各个步骤 的结果进行相乘或相加。
分类、分步计数原理,排列与组合

加(*)号的知识点为了解内容,供学有余力的学生学习使用一.考纲目标两个计数原理的理解和应用;排列与组合的定义、计算公式,组合数的两个性质.二.知识梳理1 分类计数原理:做一件事情,完成它可以有n 类办法,在第一类办法中有1m 种不同的方法,在第二类办法中有2m 种不同的方法,……,在第n 类办法中有n m 种不同的方法那么完成这件事共有 12n N m m m =+++种不同的方法2分步计数原理:做一件事情,完成它需要分成n 个步骤,做第一步有1m 种不同的方法,做第二步有2m 种不同的方法,……,做第n 步有n m 种不同的方法,那么完成这件事有12n N m m m =⨯⨯⨯ 种不同的方法3两个基本原理的作用:计算做一件事完成它的所有不同的方法种数4两个基本原理的区别:一个与分类有关,一个与分步有关;加法原理是“分类完成”,乘法原理是“分步完成”5原理浅释分类计数原理(加法原理)中,“完成一件事,有n 类办法”,是说每种办法“互斥”,即每种方法都可以独立地完成这件事,同时他们之间没有重复也没有遗漏,进行分类时,要求各类办法彼此之间是相互排斥的,不论那一类办法中的哪一种方法,都能独立完成这件事,只有满足这个条件,才能直接用加法原理,否则不可以分步计数原理(乘法原理)中,“完成一件事,需要分成n 个步骤”,是说每个步骤都不足以完成这件事,这些步骤,彼此间也不能有重复和遗漏如果完成一件事需要分成几个步骤,各步骤都不可缺少,需要依次完成所有步骤才能完成这件事,而各步要求相互独立,即相对于前一步的每一种方法,下一步都有m 种不同的方法,那么完成这件事的方法数就可以直接用乘法原理可以看出“分”是它们共同的特征,但是,分法却大不相同.两个原理的公式是: 12n N m m m =+++, 12n N m m m =⨯⨯⨯6.排列的概念:从个不同元素中,任取(m n ≤)个元素(这里的被取元素各不相同)按照一定的顺序.....排成一列,叫做从个不同元素中取出个元素的一.个排列...7.排列数的定义:从个不同元素中,任取(m n ≤)个元素的所有排列的个数叫做从个元素中取出元素的排列数,用符号m n A 表示8.排列数公式:(1)(2)(1)m n A n n n n m =---+(,,m n N m n *∈≤)9.阶乘:!n 表示正整数1到的连乘积,叫做的阶乘规定0!1=.10.排列数的另一个计算公式:m n A =!()!n n m - 11.组合的概念:一般地,从个不同元素中取出()m n ≤个元素并成一组,叫做从个不同元素中取出个元素的一个组合12.组合数的概念:从个不同元素中取出()m n ≤个元素的所有组合的个数,叫做从个不同元素中取出个元素的组合数....用符号m n C 表示. 13.组合数公式:(1)(2)(1)!m mn n m m A n n n n m C A m ---+==或)!(!!m n m n C mn -=),,(n m N m n ≤∈*且 14.组合数的性质1:m n n m n C C -=.规定:10=n C ;15.组合数的性质2:m n C 1+=m n C +1-m nC 16.解排列组合问题,首先要弄清一件事是“分类”还是“分步”完成,对于元素之间的关系,还要考虑“是有序”的还是“无序的”,也就是会正确使用分类计数原理和分步计数原理、排列定义和组合定义,其次,对一些复杂的带有附加条件的问题,需掌握以下几种常用的解题方法:(1)特殊优先法:对于存在特殊元素或者特殊位置的排列组合问题,我们可以从这些特殊的东西入手,先解决特殊元素或特殊位置,再去解决其它元素或位置,这种解法叫做特殊优先法.例如:用0、1、2、3、4这5个数字,组成没有重复数字的三位数,其中偶数共有________个(答案:30个)(2)科学分类法:对于较复杂的排列组合问题,由于情况繁多,因此要对各种不同情况,进行科学分类,以便有条不紊地进行解答,避免重复或遗漏现象发生例如:从6台原装计算机和5台组装计算机中任取5台,其中至少有原装与组装计算机各两台,则不同的选取法有_______种(答案:350)分组(堆)问题的六个模型:①有序不等分;②有序等分;③有序局部等分;④无序不等分;⑤无序等分;⑥无序局部等分;(3)插空法:解决一些不相邻问题时,可以先排一些元素然后插入其余元素,使问题得以解决例如:7人站成一行,如果甲乙两人不相邻,则不同排法种数是______ (答案:3600)(4)捆绑法:相邻元素的排列,可以采用“整体到局部”的排法,即将相邻的元素当成“一个”元素进行排列,然后再局部排,例如:6名同学坐成一排,其中甲、乙必须坐在一起的不同坐法是________种(答案:240)(5)排除法:从总体中排除不符合条件的方法数,这是一种间接解题的方法b 、排列组合应用题往往和代数、三角、立体几何、平面解析几何的某些知识联系,从而增加了问题的综合性,解答这类应用题时,要注意使用相关知识对答案进行取舍.例如:从集合{0,1,2,3,5,7,11}中任取3个元素分别作为直线方程Ax+By+C=0中的A 、B 、C ,所得的经过坐标原点的直线有_________条(答案:30)(6)剪截法(隔板法):n 个 相同小球放入m(m ≤n)个盒子里,要求每个盒子里至少有一个小球的放法等价于n 个相同小球串成一串从间隙里选m-1个结点剪成m 段(插入m -1块隔板),有11--m n C 种方法.(7)错位法:编号为1至n 的n 个小球放入编号为1到 n 的n 个盒子里,每个盒子放一个小球.要求小球与盒子的编号都不同,这种排列称为错位排列.特别当n=2, 3,4,5时的错位数各为1,2,9,44.2个、3个、4个元素的错位排列容易计算。
分类计数原理与分步计数原理

分类计数原理与分步计数原理一、知识精讲分类计数原理与分步计数原理分类计数原理:做一件事,完成它可以有n 类办法,在第一类办法中有1m 种不同的方法 ,在第二类办法中有2m 种不同的方法,……,在第n 类办法中有n m 种不同的方法,那么完成这件事共有n m m m N +++= 21种不同的办法。
分步计数原理:做一件事,完成它需要分成n 个步骤,做第一步有1m 种不同的方法,做第二步有2m 种不同的方法,……,做第n 步有n m 种不同方法,那么完成这件事共有n m m m N ⋅⋅⋅= 21种不同的方法。
特别注意:两个原理的共同点是把一个原始事件分解成若干个分事件来完成。
不同点在于,一个与分类有关,一个与分步有关,如果完成一件事情共有n 类办法,这n 类办法彼此之间相互独立的,无论哪一类办法中的哪一种方法都能单独完成这件事情,求完成这件事情的方法种数,就用分类计数原理;如果完成一件事情需要分成n 个步骤,各个步骤都是不可缺少的,需要依次完成所有的步骤,才能完成这件事,而完成 每一个步骤各有若干种不同的方法,求完成这件事情的方法种数就用分步计数原理。
二、题型剖析例1、把一个圆分成3块扇形,现在用5种不同的颜色给3块扇形涂色,要求相邻扇形的颜色互不相同,问有多少钟不同的涂法?若分割成4块扇形呢?解:(1)不同涂色方法数是:60345=⨯⨯(种)(2)如右图所示,分别用a,b,c,d 记这四块,a 与c 可同色,也可不同色,先考虑给a,c 两块涂色,分两类(1) 给a,c 涂同种颜色共15C 种涂法,再给b 涂色有4种涂法,最后给d 涂色也有4种涂法,由乘法原理知,此时共有4415⨯⨯C 种涂法(2) 给a,c 涂不同颜色共有25A 种涂法,再给b 涂色有3种方法,最后给d 涂色也有3种,此时共有3325⨯⨯A 种涂法 故由分类计数原理知,共有4415⨯⨯C +3325⨯⨯A =260种涂法。
例2、(1)如图为一电路图,从A 到B 共有-___________条不同的线路可通电。
分类计数原理和分步计数原理

想一想:如果去掉(1)中每人限报一项的要求,又有多少种不同 的报名结果? 我们把三个项目记为 a、 b 、 c ,这样每个人就有八种不同 选择,分别为选 a、选 b、选c、选 ab、选 ac 、选 bc、选 abc以及 不选.再用原来的分步方法,使用分步计数原理,共有 86 种不 同的投报结果.
用分步计数原理,所有满足条件的点的坐标共有:
13×15=195(个).
例3.已知集合A={-2,0 ,1 ,3},集合B={-5,-4,2,4}.从两 个集合中各取一个元素作为点的坐标,那么在平面直角坐标系 内,位于第一、二象限中不同的点共有多少个? 解:选法分为两类: 分析:本题要完成的事情是:选出横坐标、纵坐标组成一个点, 但没有说明从哪个集合中选出的数作为横坐标,从哪个集合中选 (1)先从A中选出一个数作为横坐标,有 3种选法,再从B中选出 出的数作为纵坐标,因此选法可分两类: (1)从A中选出一数作为横 一个数作为纵坐标,有 2 种选法(因为纵坐标必须大于 0),故 坐标 ,从 中选出一数作为纵坐标 ;(2)从 B中选出一数作为横坐标 ,从 共有3 ×B 2=6 种选法. A中选出一数作为纵坐标.而每一类选法中又分两步完成. (2)先从B中选出一个数作为横坐标,有 4种选法,再从 A中选出 一个数作为纵坐标,有2种选法,故共有4×2=8种选法. 根据分类计数原理,所有选法总数是 6+8=14种,也即位于第一、 二象限内的点共有14个.
要到达目的地,需要分成2步, 第1步。有3种不同的方法,
在第2 步,有2种不同的方法……
那么完成这件事共有:N=3×2种不同的方法.
关于分步计数原理的几点注意:
⑴各个步骤之间相互依存,且方法总数是各个步骤
的方法数相乘,所以这个原理又叫做乘法原理 ;
分类计数原理和分步计数原理

典型例题
例 1. 书架放有 3 本不同的数学书, 5 本不同的语文书, 6 本不同 的英语书。 (1)若从这些书中任取1本书,有多少种不同的取法? (2)若从这些书中,取数学书、语文书、英语书各一本, 有多少种不同的取法? (3)若从这些书中,取不同科目的书两本,有多少种不同 的取法? 解:(2)从书架上任取数学书、语文书、英语书各一本, 需分成三个步骤完成:
第1类办法是数学书、语文书各取1本,有3×5种办法; 第2类办法是数学书、英语书各取1本,有3×6种办法; 第3类办法是语文书、英语书各取1本,有5×6种办法; 根据分类计数原理,不同取法的种数是 N= 3×5+3×6+5×6=63 答:若从这些书中,取不同科目的书两本,有63种不同的取法。
典型例题
一、导入 情景:
一学生从外面进入教室有多少种 走法?若进来再出去,有多少走法?
分类计数原理和分步计数原理
二、新课 情景一:
从甲地到乙地,可以乘火车,也 可以乘轮船。一天中,火车有3班,轮 船有2班。那么一天中,乘坐这些交通 工具从甲地到乙地共有多少种不同的 走法?
பைடு நூலகம்
分类计数原理
做一件事情,完成它可以有n类办法,在 第一类办法中有m1种不同的方法,在第二类办 法中有m2种不同的方法……在第n类办法中 有mn种不同的方法。那么完成这件事共有 N=m1+m2+…+mn 种不同的方法。 (此原理又称加法原理 )
例2:由1,2,3,4可组成多少个数字可以重复的
四位数?
变式1:由0,1,2,3可组成多少个数字可以重复
的四位数?
变式2:由1,2,3,4可组成多少个数字不可以
重复的自然数?
思考题:
分类计数原理与分步计数原理

分类计数原理:完成一件事,有n类办法,在第 一类办法中有m1种不同的方法,在第二类办法中有 m2种不同的方法,……,在第n类办法中有mn种不 同的方法,那么完成这件事共有
N= m1+ m2+…+ mn 种不同的方法。
分步计数原理:完成一件事,需要分成n个步骤, 做第一步有m1种不同的方法,做第二步有m2种不同 的方法,……,做第n步有mn种不同的方法,那么完 成这件事共有
4.从5位男教师和4位女教师中选出3位教师,派到3 个班担任班主任(每班1位班主任),要求这3位 班主任中男、女教师都要有,则不同的选派方案 共有______.
5.在由数字1,2,3,4,5组成的所有没有重复数字的5位 数中,大于23145且小于43521的数共有________.
1.如图,小圆圈表示网络的结点,结点之间的连线 表示它们有网线相联,连线标注的数字表示该 段网线单位时间内可以通过的最大信息量.现从 结点A向结点B传递信息,信息可以分开沿不同 的路线同时传递,则单位时间内传递的最大信 息量为_______.
来擦屁股.老子清理了恶魔,一定要将这个蠢货撕扯碎片!俺提议,诸位亲自带队,联手镇压恶魔,明日开始!" 噬大人冷冷一笑,居然接过犁空の话第一些开口了:"如果诸位敢杀上至尊岛,击杀犁空,飘渺大陆全府神帝级以上の强者全部出动,镇压恶魔!俺噬蝶舞第一些做先 锋!" 本书来自 聘熟 当前 第壹0叁2章 霸主 文章阅读 白重炙没有说话,噬大人在の场合,他一样不会表达什么想法,往往有什么想法也是和噬大人一样の.请大家检索(品#书……网)看最全!更新最快の不过他火热の眸子,是个人都能看出他无比赞同噬大人の话,而基德也 没有说话,只是点了点头. 不用质疑,场中所有人,包括冰雪女王都对犁空无比愤恨,当然其实所有人都知道犁空肯定是接到了星辰君主の指示,否则打死他都没有这么大の胆子,任凭恶魔在星辰海肆掠. 这次神界浩劫,问题大部分出在星辰海上.如果至尊岛,不说星辰君主出关, 只要犁空带着至尊岛の强者,以及百亿星辰军第一时候镇压の话,惨剧就不会发生了.虽然星辰海の尊者被白重炙拍死了三十多名,但是不少人都清楚,至尊岛上最少还有三十名尊者,并且星辰军の战斗力在神界排名无比靠前. 噬大人の话并没有人接,所有の君主沉默了. 白重炙 の眼睛微微眯了起来,他看出了不少事情,第一莫尚煌是绝对属于噬大人一脉の,难道第一次去缥缈峰,莫尚煌对他如此热情.第二,星辰君主の强大,虽然白重炙不清楚星辰君主具体强大到什么地步,但是他猜测,绝对比冰雪女王还要强大,很有可能是…九品至尊!第三,白重炙心 里再次又了一些猜测,杀害魂帝の强者,有很大可能就是星辰君主! 如果是一样君主,做出如此天怒人怨の事情,不说噬大人,就算莫尚煌早就杀上门去了.但是连莫尚煌都只是说击杀犁空,噬大人也半个字没提星辰君主.而这个问题一抛出来,所有人都沉默了.可想而知,星辰君 主の强大,强大到让众人不敢起战斗之心. 同时白重炙脑海内还有一些疑惑:星辰君主为什么要这么做?难道神界毁灭,他一点都不在乎? 噬大人の话语,代表着五个人の意志,隐世君主最近一直惟噬大人の命令是从.众人感觉无比の棘手,风月君主几次想开口,却最终还是沉默 下去了.这话是接也不好,不接也不好.如果搞不好噬大人拂袖而去,那么不说莫尚煌,基德和白重炙绝对会跟着离开の! 场中の气氛开始有些尴尬和压抑了起来. "咳咳!" 一条轻微の咳嗽声,打破了尴尬の气氛,白重炙扫眼过去,发现正是那个蛮人巨汉青山大人开口了:"蝶舞, 犁空必须死,这点无需置疑,但是不是现在,星辰君主出关之后,俺会和冰雪女王联合让他当众审判犁空の罪行.现在先谈怎么镇压恶魔吧!俺第一些表态,明日俺青山部落一万零八铁骑从星辰海北方出战!不镇压恶魔绝不回山." 冰雪女王眸子转动了一下,扫向噬大人,微微点了 点头道:"蝶舞,青山说の作数.明日,冰雪岛冰雪卫士全部出动,从星辰海北方开始镇压恶魔,神界…是大家の!" 两位大佬开口了,除了噬大人和白重炙,全部眼睛亮了起来,她们都知神界最高最大の那座青山上の一万零八铁骑有多么强大,也了解冰雪卫士の技能是多么の变tai. "血夜大陆,除了留守の人员,其余练家子由俺亲自带队出战!" "南岭大陆,全府出战!" "风月大陆出战!" "北幽秘境出战" "龙象秘境出战!" 一时候数位君主纷纷表态了,没有半点犹豫,血夜君主和两大秘境君主本来就属于青山大人一脉.,而南岭君主和风月君主见冰雪女 王开口了,也没有犹豫了.最后众人将目光停留在噬大人身体上. 青山和冰雪女王对视一眼,两人眸子闪过一丝异色,而后南岭君主血夜君主等人也错愕起来,错愕最后变成了震惊.所有人发现了一些很惊恐の事情——不知不觉中,神界竟然多了一方势力,一方强大到让她们恐惧 の势力. 噬大人成为君主不过短短近千年时候,但是她却悄然无声の把莫尚煌基德隐世君主拉上了战车,而后又突然冒出来一些白重炙.加上到现在还没表态脸上有些迟疑の嫣然君主,噬大人这方竟然拥有了六个君主级别の强者!三个大陆一些大型秘境. 虽然这个势力还没完 全成型,但噬大人才成为君主不到千年啊!噬大人此刻没有说话表态,其余人竟然全部沉默了.原本有些迟疑の嫣然君主,迟疑了片刻,竟然彻底の沉默了下去! 白重炙望着噬大人,看着她云淡风轻の神情,内心暗暗佩服起来.他知道噬大人一直在背后谋划着,安排着不少事情.没 想到她竟然谋划の如此成功!七八百年前,还是一些七品破仙の她,今日却悄然成为了神界の一方超级霸主,让青山大人和冰雪女王都无比忌惮の超级霸主. 噬大人脸上没有任何神情,端起茶水淡淡喝了一口,而后望向青山和冰雪女王,淡淡说道:"青山大人和女王殿下既然开口 了,俺信得过你呀们两人,俺这方人马全部出战!" 莫尚煌和基德以及隐世君主没有半点意外の神情,嫣然君主有些如释重负の吐出一口气,点了点头道:"神恩大陆出战!" "天启大陆出战!" "沙巴克秘境出战!" 天启君主和隐世君主立即表态了,白重炙微微一笑,他很清楚青 山和冰雪女王就算不开这个口,噬大人肯定也会出战の.一些连夜奔赴了三十多个府域,救下了不知多少亿子民の人,绝对不会是传说中の那么冷血绝情の.冰雪女王说の好啊,神界…是大家の! 全部同意出战了,接下来の事情就好安排了,众人商议了一些多时辰之后,确定了各 自进攻の方向,以及一些战时战后事宜,全部瞬移离开了,准备明日开始调集大军,奔赴星辰海联手镇压! 噬大人带着白重炙基德嫣然女主,一同瞬移离开,一路传送,没有传送阵の地方就交替带着瞬移.只是花费了数个时辰,噬大人和白重炙以及基德就出现在噬魂府の天台上! "基德,你呀去调集强者,明日和不咋大的寒子奔赴星辰海,俺坐镇大陆!" 噬大人坐在葡萄架下,又悠闲の捧起一本书看了起来.基德点了点头,瞬移离开了,白重炙也朝噬大人躬身行礼,正准备回炽火城去,噬大人却淡淡の抬起了头,悠然说道: "去星辰海の时候,不要靠近至尊 岛,确定安全の情况下…多使用屠神刀!这把刀既然你呀能驾驭,那么就继续使用下去.以后你呀会发现,这刀の威力会超乎你呀の想象の!当然,如果你呀感觉不能驾驭の时候,立即停止使用,或者用本源之力强行摧毁他吧!" 本书来自 聘熟 当前 第壹0叁叁章 又一条火神护 腿 "屠神刀?" 白重炙眉梢一挑,盯着噬大人,他不奇怪噬大人知道自己有屠神刀.请大家检索(品&书¥网)看最全!更新最快の也不奇怪噬大人知道屠神刀の来历,他只是奇怪噬大人这么肯定の语气. 继续使用下去?威力会超乎想象? 噬大人没有解释,对白重炙の目光置若罔 闻,继续喝着她の茶水,看着她の书,连眼皮都没有抬起. 白重炙知道噬大人话只能说到这了,多问也不会说了.他沉吟片刻,手一翻,从战皇殿藏宝阁内取出一块火红の内甲,内甲上一条条火龙狰狞无比,上面の细不咋大的鳞片反射着刺眼の光芒. 噬大人微微抬起眼皮,望着白重 炙手中の内甲,有些疑惑の皱了皱眉梢,道:"你呀怎么有这东西?" "嗯?" 白重炙面色一喜,本来噬大人提到了屠神刀,他才突然想起了火神战甲,正准备问一问.没想到噬大人竟然认识?连忙窃喜の问道:"大人,您知道这是什么?" "不知道!" 噬大人眼睑又垂落了下去,手还翻 了页书册,将白重炙刚刚沸腾の血液,瞬间又冷了下去.正在白重炙准备问什么の时候,噬大人轻轻摆了摆手,一条和白重炙手中内甲一模一样の护腿出现在她前面の桌子上.她也没抬头,只是淡淡说道:"俺这条护腿是魂帝给俺の,他说是个宝物,如果收集一套の话,可能是件至宝, 有大作用.但是这些年,除了这个护腿,俺一件没有见过,你呀要是有兴趣,你呀自己去收集吧!" 白重炙望着桌子上の护腿,一眼就看出,绝对是火神战甲の那条护腿.很久没有激动の心,再次兴奋起来,眼眸内一片火热.他将护腿拿在手中,仔细摸了摸,确定是一模一样の材质,才 收了起来,吐出一口气说道:"大人,这战甲总用有几件?" 噬大人撇了白重炙一眼,道:"战甲一样是六件,头盔,内甲,几个护腿,几个护臂!你呀也别太在意,如果有这个机缘,得到了就得到了,没有得到也无所谓,感悟法则才是王道.超品战甲,毕竟是传说中の东西,神界没有见谁 穿过.如果这是一套超极品战甲,那就意义不大了,在魂帝岛外,就给你呀拍碎了一套.那东西也就能抵挡一下本源之力,并且一天内最多抵挡三次,没多大用处!" "超极品战甲?" 白重炙淡淡一笑,这事他在事后听说过,犁斐身穿着犁空の超极品青冥战甲.最后被自己用庞大の空 间之力直接湮灭了.这事有星辰军传播开来,让无数尊者大为叹息啊. 不过他不认为,这火神战甲是超极品战甲.玄灵洞府那个强大の上古修士.拥有超品神器和勾虚智の强者,临死前却死死抱着这件内甲.这火神战甲能平凡吗? 白重炙再次朝噬大人躬身,准备回去.噬大人却突然
分类计数原理、分步计数原理

分类计数原理、分步计数原理授课难点:1.解决学生思考过程中对加法,分步计数原理理解产生的误区。
2.帮助学生找到“重”,“漏”产生的原因。
一、概念与规律1.分类计数原理:做一件事,完成它可以有n类办法。
在第一类办法中有m1种不同方法,在第二类办法中m2种不同的方法,……,第n类办法中有m n种不同方法。
那么完成这件事共有N=m1+m2+……+m n种不同的方法。
2.分步计数原理:做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有m n种不同的方法。
那么完成这件事共有N=m1·m2·……m n种不同的方法。
3.分类计数原理和分步计数原理的共同点是,它们都是研究完成一件事情,共有多少种不同的方法;不同点在于完成一件事情的方式不同,分类计数原理是在“分类完成”,即任何一类办法中任何一种方法都能独立完成这种事。
分步计数原理是在“分步完成”,即这些方法需要分步,各个步骤顺次相依,且每一步都完成了,才能完成这件事情。
二、例题讲解例1.一个口袋内装有5个小球,另一个口袋装有4个小球,所有这些小球的颜色互不相同。
(1)从两个口袋内任取1个小球,有多少种不同的取法?(2)从两个口袋内各取1个4球,有多少种不同的取法。
解:(1)从两个口袋中任取一个小球,有两类办法:第一类办法是从第一个口袋内任取1个小球,从5个小球中任取1个,有5种方法;第二类办法是从第二个口袋内任取1个,有4种方法,根据分类计数原理,得到不同的取法的种数是N=m1+m2=5+4=9(种)。
(2)从两个口袋内各取1个小球,可以分成两个步骤来完成:第一步从第一个口袋内取1个小球,有5种方法;第二步在第二个口袋内取1个小球,有4种方法。
根据分步计数原理,得到不同的取法种数是N=m1×m2=5×4=20(种)。
即:从两个口袋内任取1个小球,有9种不同的取法;从两个口袋内各取1个小球,有20种不同取法。
分类计数原理与分步计数原理

【例2】一城市的电话号码都由8位数字组成, 其中前4位数字是统一的,后4位数字都是0到9 之间的一个数字,那么不同的电话号码可有多 少个? 【引申1】4封信全部投入10个不同的信箱 中,有多少种不同的投法?
【引申2】A集合中有4个元素,B集合中有10 个元素,问:可以建立多少个从A到B的映射?
【引申3】运动会上4位同学报名参加10个项目, 每人必须且只能报一项,有多少种报名方法?
”智深道:“洒家也不杀你,只要问你买酒吃。”那汉子见不是头,挑了担桶便走。智深赶下亭子来,双手拿住匾担,只一脚,交裆踢着,那汉子双手掩着,做一堆蹲在地下,半日起不得。智深把那两桶酒都提在亭子上,地下拾起旋子,开了桶盖,只顾舀冷酒吃。无移时,两大桶酒吃了 一桶。智深道:“汉子,明日来寺里讨钱。”那汉子方才疼止,又怕寺里长老得知,坏了衣饭,忍气吞声,那里敢讨钱?把酒分做两半桶挑了,拿了旋子,飞也似下山去了。 只说鲁智深在亭子上坐了半日,酒却上来。下得亭子,松树根边又坐了半歇,酒越涌上来。智深把皂直裰褪膊下 来,把两只袖子缠在腰里,露出脊背上花绣来,扇着两个膀子上山来。但见:头重脚轻,眼红面赤;前合后仰,东倒西歪。踉踉跄跄上山来,似当风之鹤;摆摆摇摇回寺去,如出水之蛇。指定天宫,叫骂天蓬元帅;踏开地府,要拿催命判官。裸形赤体醉魔君,放火杀人花和尚。鲁达看看 来到山门下,两个门子远远望见,拿着竹篦来到山门下,拦住鲁智深便喝道:“你是佛家弟子,如何噇得烂醉了上山来?你须不瞎,也见库局里贴的晓示:但凡和尚破戒吃酒,决打四十竹篦,赶出寺去,如门子纵容醉的僧人入寺,也吃十下。你快下山去,饶你几下竹篦。” 鲁智深一者 初做和尚,二来旧性未改,睁起双眼骂道:“直娘贼!你两个要打洒家,俺便和你厮打。”门子见势头不好,一个飞也似入来报监寺,一个虚拖竹篦拦他。智深用手隔过,揸开五指,去那门子脸上只一掌,打得踉踉跄跄;却待挣扎,智深再复一拳,打倒在山门下,只是叫苦。智深道:“ 洒家饶你这厮。”踉踉跄跄,攧入寺里来。监寺听得门子报说,叫起老郎、火工、直厅、轿夫,三二十人,各执白木棍棒,从西廊下抢出来,却好迎着智深。智深望见大吼了一声,却似嘴边起个霹雳,大踏步抢入来。众人初时不知他是军官出身,次后见他行得凶了,慌忙都退入藏殿里去 ,便把亮槅关上。智深抢入阶来,一拳一脚,打开亮槅,三二十人都赶得没路,夺条棒从藏殿里打将出来。 监寺慌忙报知长老,长老听得,急引了三五个侍者直来廊下,喝道:“智深不得无礼!”智深虽然酒醉,却认得是长老,撇了棒,向前来打个问讯,指着廊下对长老道:“智深吃 了两碗酒,又不曾撩拨他们,他众人又引人来打洒家。”长老道:“你看我面快去睡了,明日却说。”鲁智深道:“俺不看长老面,洒家直打死你那几个秃驴!”长老叫侍者扶智深到禅床上,扑地便倒了,齁齁地睡了。 (1)在空格内依次填写一个动词。概括文中鲁智深与酒的几件事。 想酒~买酒~抢酒~闹酒 (2)文中汉子的唱词有哪些作用? (3)结合水浒传,完成下面题目 ①鲁智深在上五台山之前所做的义事是A A拳打镇关西 B大闹桃花村 C火烧瓦官寺 D大闹野猪林 ②鲁智深为何被称作花和尚 ③与林冲和李逵相比,鲁智深的性格有什么特别之处,请举例具体 分析。 【考点】9E:小说阅读综合. 【分析】本文主要描述了鲁智深大闹五台山的故事.第一段写鲁智深来到五台山几个月没喝酒,正想着酒,外面传来了卖酒的歌声;第二段写鲁智深想买酒遭拒,就开始动手抢酒,吓跑了卖酒的汉子;第三至五段,写鲁智深喝完,酒劲上来看返回寺 院,门子见状阻拦,鲁智深反打门子,惊扰到长老送至房间便酒意大发睡去了. 【解答】(1)本题考查主要内容的概括.解答此题明确本文的写作线索为“酒”,按写作的顺序找出事件,然后分别用两个字来概括即可.文章第一段写鲁知深想到了喝酒,第二段写鲁智深想买酒遭到了拒 绝,便开始抢酒;第三至五段,主要写他喝酒后回寺大闹寺院.可分别概括为:想酒、买酒、抢酒和闹酒. (2)本题考查内容的理解与分析.唱词与战争、项羽相关,结合前文情节我们知道,鲁智深曾经作过提辖,这个唱词则触发了鲁智深的英雄豪情,想起自己此时却在寺院中为僧, 这样就刺激了他的酒瘾,从而引发了下面的情节. (3)本题考查名著情节的识记与人物形象的对比分析.解答此题关键在于平时的阅读与积累.①鲁智深上山之前是提辖,因为救助金氏父女而拳打镇关西,为了逃脱人命官司而来到了这里.故选A.②鲁智深上山为僧,但他的脊背上有 花绣,又因为他不守戒律,喝酒吃肉打人,所以得名“花和尚”. ③林冲在《水浒传》中一开始的性格是软弱的,就因为一再的忍让才被害.李逵的勇猛和鲁智深很相似,但李逵有勇无谋,没有头脑.而鲁智深有智慧,如拳打镇关西至他于死地时,用郑屠的装死来骗众人,取得逃跑的 时间等情节就能体现出来. 代谢: (1)买 抢 闹(共3分,每空1分) (2)汉子的唱词进一步触发了曾为军官的鲁智深的豪情和他对当时处境的不满,更刺激了他的酒瘾. (3)①A ②因为他出家为僧,且脊背上有花绣,也因为他喝酒吃肉打人,不守戒律. ③示例:与林冲相比,鲁 智深办事更加果断干脆.例如,林冲在被奸人高俅陷害后一再隐忍退让,而鲁智深为解救金氏父女,直接痛打了恶人郑屠. (2017安徽)【二】(21分) 扁担的一生 范宇 ①在村庄的记忆里,几乎任何时间、任何角落都能见到扁担的身影。挑粪、挑种子、挑谷子、挑土豆、挑橘子…… 农人在土地上的所有倾注与收获,都与扁担密不可分。扁担就是农人的精神脊梁,让他们挑起一个家庭重担的同时,也挑起了一个村庄沉重的历史与殷殷期盼。 ② 。母亲嫁给父亲时,半背篼谷子便是全部的家当。泥墙茅顶的房子破败不堪,常常在狂风骤雨中摇摇欲坠,只有立于墙角略 弯的扁担显得精神抖擞,给人信心与希望。或许,母亲嫁给父亲的勇气,有几分便来自于扁担的抖擞精神。总之,在昼夜有序更替的村庄里,父母用扁担慢慢挑起了生活的担子,就像蚂蚁搬家一样,虽然缓慢,却渐渐挑出了一个家庭的崭新面貌。 ③ 。 ④20年前,父亲从山里找到一截 不错的木材,正想着用来做点什么呢。身为木匠的舅舅几乎脱口而出——扁担。对,扁担!父亲也认为,只有改成一根扁担,才不辜负这上好的木材。说干就干,粗糙的木材到了舅舅手里,不用半天,就变成了一根笔直的扁担。扁担不能太直,太直则易伤肩头和腰。因此,还得将扁担以 火烤之后,用外力将之略微压弯成弓形。可这根扁担实在太有骨气了,即便火烤、重压,仍然笔直,没有半点屈服。 ⑤这根扁担挑起来更吃力,父亲却爱不释手。之后的许多年里,父亲无论挑什么,都用她。有次在挑玉米时,父亲不小心闪了腰,疼了好长一段时间。但父亲并没有放弃 她,用汗水和心血一点点浸润着她,渐渐地,她坚硬的心被融化了,挺直的腰板,也弯了下来。父亲挑起扁担来越来越有默契,像与母亲的婚姻一样,虽偶有磕磕绊绊,感情却越来越深厚。她也没有辜负父亲的良苦用心,苦心经营,以顶天立地般的气慨,让一个家庭从贫穷落后走向富足 安逸。 ⑥可这样的日子并没有持续多少年。越来越多的人开始离开村庄,离开赖以生存的土地,扁担也渐渐地走向了落寞。不少人再也没有回来,在城里买了房子,过上了舒坦的日子。这也让父亲坚信一根扁担能够挑出一个未来的信念,逐渐土崩瓦解。或许,这背后更多是村庄现实的 无奈。 ⑦无论如何,父亲最终选择了离开。 ⑧曾经朝夕相对的扁担被搁置在了一个冰冷的墙角,孤零零的。说来也奇怪,没有了重压,扁担却一天比一天更弯,弯得像一个苟延残喘的暮年老者。或许,再过几年,抑或十余年,她便将走完一生,彻底告别深爱了一生也奋斗了一生的村庄 。 ⑨这也是农人的一生。 ⑩九月,村庄又迎来冷冷清清的收获季节。我返城时,碰见正挑着谷子从田边迎面走来的大伯。大伯今年已60余岁了,还在田间劳作着。他也曾短暂离开过村庄,却始终没能走出像扁担一样的命运。他仍然坚信着,只要村庄还在,扁担还在,就一定能够扛起生 活的重担。甚至,在人烟越来越少的村庄里,不少死守的农人还是坚信——一根扁担仍能挑起一个村庄。 ?这是一种可贵精神,或许它与现实追求早已背道而驰,却让人肃然起敬。 (选自《襄阳晚报》2016年3月3日,有删改) 10、根据上下文,将下面两个句子分别填入文章②③两段横 线处,第②段应填( ),第③段应填( )。(4分) A、这让我有了探索一根扁担一生的浓厚兴趣。 B、我的家也是扁担挑起来的。 11、阅读文章④—⑥段,概括补充扁担经历的主要变化过程。(每空不超过5个字)(4分) 上好的木材→ →渐弯的扁担→ 12、作者提到“扁担”,多 次使用第三人称“她”,有何表达效果?(3分) 13、联系上下文,简要分析第⑩段画线句子蕴含了作者怎样的情感。(4分) 14、“扁担”在文中有着丰富的内涵,请结合全文谈谈你的理解。(6分)[来源:学科网 代谢:【二】 10. (4分)B A 11. (4分)不屈的扁担 落寞的扁担 12.(3分) 运用拟人化的手法,把扁担当成了与自己家庭命运休戚相关的一员,抒发了对扁担对既往岁月的无限怀念留恋之情,同时也表达了对父亲对家庭的热爱之情。 13.(4分) 表达了对大伯不能与时俱进,还固守着旧有的生活方式,希望能用一根扁担扛起生活重担精神的钦佩与 惋惜之情 14.(4分)扁担是农人的希望,是农人精神脊梁;扁担也是父亲的命运与精神的反映 。扁担有着不屈的精神,挑起过生活的重担,创造过富足安逸,也有着英雄暮年的孤寂衰老,它的一生也反映了人的一生;在一定程度上,扁担也是落后生活方式的代表。 (2017浙江温州)4 . 天道立秋 张承志 (1)1990年立秋日,是个神秘的日子。 (2)年复一年地,代谢人渐浙开始从春末就恐怖地等着入伏。一天天地熬,直到今年是一刻刻地熬。长长无尽的代谢苦夏,在这一回简直到了极致。 (3)一点一点地挨着时间;无法读书,无法伏案。不仅是在白昼,夜也是 潮闷难言,漆黑中的灼烤实在是太可怕了。 (4)我有时独自坐在这种黑热里,像一块熄了不多时的炉膛里的烧烬。心尖有一块红红的煤火,永无停止地折磨着自己。似乎又全靠着它,人才能与这巨大的黑热抗衡。久久坐着,像是对峙。 (5)天亮以后几个时辰,大地便又堕入凶狠的爆 烤。有谁能尽知我们的苦夏呢? (6)街上老外,满脸汗水。 (7)度夏的滋味、中国人是说不出的。 (8)后来愈热愈烈,我几乎绝望。再这样热下去,连我也怀疑没有天理了。 (9)可是,那一天是立秋。上午我麻木地走进太班有男生30人, 女生24人,要从中选一人参加学校会议,问: 总共有多少种选法?
分类计数原理与分步计数原理课件

在实施过程中,需要密切监控方案的执行 情况,及时调整和优化方案,以确保达到 预期的效果。
混合应用的优势与挑战
优势
分类计数原理和分步计数原理的混合应用可以更好地解决复杂的问题,提高解决问题的效率和准确性 。同时,这种应用方式可以更好地满足实际需求,提高生产效率、项目管理和物流管理水平。
挑战
在混合应用中,需要充分考虑各种因素,包括分类和分步的边界、数学模型的建立、实施方案的制定 和实施与监控等。这些因素都需要综合考虑,才能达到最佳的应用效果。同时,这种应用方式也需要 较高的专业知识和技能水平,需要具备丰富的实践经验和管理能力。
混合应用的方法
确定分类和分步的边界
建立数学模型
在应用分类计数原理和分步计数原理时, 需要明确分类和分步的边界,以便更好地 进行计数和组合。
通过建立数学模型,可以更好地描述分类 计数原理和分步计数原理的混合应用,并 进行优化和控制。
制定实施方案
实施与监控
根据分类和分步的边界以及数学模型,制 定具体的实施方案,包括具体的操作步骤 、时间安排、资源分配等。
实例三
一个骰子有6个面,投掷3次骰子, 每次都有6种可能的结果,那么投掷 3次骰子有多少种不同的结果?
分类计数原理的应用
应用一
在生产过程中,如果各个工序之 间相互独立,且每道工序都有n 种不同的加工方法,那么完成整 个产品需要的方法数为n的乘积
。
应用二
在排列组合问题中,如果需要完 成多个独立任务,且每个任务都 有不同的方法数,那么完成这些 任务的方法数为各个方法数的乘
总结词
互斥事件的乘法原则
详细描述
分类计数原理主要应用于多个独立事件,其中每个事件的发生都是互斥的,即一个事件发 生后,其他事件就不会发生。在这种情况下,完成这些事件的种数就是各个事件种数的乘 积。
分类加法计数原理与分步乘法计数原理

分类加法计数原理与分步乘法计数原理1.分类计数问题:要计算一些集合中满足其中一种条件的元素的数目。
可以将该集合分为若干个子集,分别计算每个子集中满足条件的元素的数目,然后将这些数目相加即可得到最终的结果。
例如,一些班级有30个学生,其中有10个男生和20个女生,要计算全班学生中身高超过1.7米的男生的人数。
可以将问题分解为两个部分,分别计算身高超过1.7米的男生和身高不超过1.7米的男生的人数,然后将这两个数目相加即可得到最终的结果。
2.多重条件计数问题:要计算满足多个条件的元素的数目。
可以将满足不同条件的元素分为不同的类别,然后计算每个类别中满足条件的元素的数目,最后将这些数目相加得到最终的结果。
例如,一些商店有3种颜色的衬衫(红色、蓝色和绿色),每种颜色的衬衫分别有5件、3件和4件。
要计算购买2件衬衫的方法数目,其中要求至少购买一件红色的衬衫。
可以将购买2件衬衫分为两种情况:一种是购买一件红色的衬衫和一件其他颜色的衬衫,另一种是购买两件红色的衬衫。
然后分别计算这两种情况下的购买方法数目,最后将这两个数目相加即可得到最终的结果。
分步乘法计数原理是指将一个计数问题分解为若干个步骤,每个步骤的计数独立进行,最后将每个步骤的计数结果相乘得到最终的结果。
该方法的基本思想是通过分步骤计数来简化问题,使得每个步骤的计数更加直观和容易。
分步乘法计数原理通常适用于以下两种情况:1.顺序计数问题:要计算一些事件发生的不同顺序的可能性。
可以将该事件分为若干个步骤,分别计算每个步骤的可能性,然后将这些可能性相乘得到最终的结果。
例如,一些球队有10名队员,要计算选择3名队员组成一支首发阵容的方法数目。
可以将选择队员分为三个步骤:先选择首发中锋(有10种选择),然后选择首发后卫(有9种选择),最后选择首发前锋(有8种选择)。
然后将这三个步骤的选择数目相乘即可得到最终的结果。
2.分步限制问题:要计算满足多个条件的元素的数目。
分类计数原理与分步计数原理的区别

分类计数原理与分步计数原理的区别下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!分类计数原理与分步计数原理的区别在组合数学中,分类计数原理和分步计数原理是解决计数问题的两种常用方法。
分类计数与分步计数原理

数据分析与决策
在数据分析中,分类计数原理可以帮助我们将数据按照不 同的特征进行分类,例如按照销售渠道、客户类型、产品 类别等进行分类,然后对每个类别的数据进行统计和分析 ,以了解不同类别的特点和差异。
分步计数原理则可以帮助我们将整个数据分析过程分解为 若干个步骤,例如数据收集、清洗、整理、分析和可视化 等,然后对每个步骤进行详细规划,确保每个步骤都能按 时完成,最终为决策提供准确的数据用
生产计划制定
生产计划制定过程中,企业可以根据分类计数原理,将生产 任务按照产品类型、生产流程、生产阶段等进行分类,然后 分别计算每个类别所需的时间、资源和成本,从而制定出合 理的生产计划。
在实际执行过程中,企业可以根据分步计数原理,将整个生 产过程分解为若干个步骤,然后对每个步骤进行详细规划, 确保每个步骤都能按时完成,最终实现整个生产计划的顺利 完成。
解
根据分类计数原理,我们可以将 问题分解为三个步骤:先选择3 名学生组成一个小组,再从剩下 的7名学生中选择3名学生组成另 一个小组,最后从剩下的4名学 生中选择2名学生组成第三个小 组。第一个步骤有C(10,3)种方法 ,第二个步骤有C(7,3)种方法, 第三个步骤有C(4,2)种方法。因
02 分步计数原理
03 分类计数与分步计数原理 的比较
差异点分析
基本概念
适用场景
实例对比分析
分类计数原理(加法原理)强调将问 题分成不重叠、互斥的n类,然后分 别对每类进行计数,最后累加得到总 数。而分步计数原理(乘法原理)则 是将问题分成连续的步骤,每一步都 有若干种选择,然后根据步骤顺序, 将每一步的选择数相乘得到总数。
01
02
03
组合数学问题
分步计数原理在组合数学 中有着广泛的应用,例如 排列组合、二项式定理等。
分类记数原理和分步记数原理

分类计数原理与分步计数原理

分类计数原理与分步计数原理
分类计数原理是指对一个问题进行分类并计数;分步计数原理是指将一个问题分解为若干个步骤,并对每个步骤进行计数,最后将步骤的计数结果相乘得出最终结果。
分类计数原理常用于解决计数问题,例如有n个元素构成的集合,要求将其分成k个子集,每个子集中至少有一个元素,可以使用分类计数原理。
首先将n 个元素分成k个子集,其中至少有一个子集为空,计数为C(n-1, k-1);然后将n 个元素分成k个子集,其中每个子集至少有一个元素,计数为k ×C(n-1, k-1)。
分步计数原理常用于解决复杂的计数问题,例如要求一个过程中多个步骤的可能性,可以使用分步计数原理。
将问题分解为若干个步骤,对每个步骤进行计数,然后将每个步骤的计数结果相乘得出最终结果。
例如要求从6个人中选出3个人组成一个委员会,委员会中的主席必须是其中的一个人,可以将问题分解为3个步骤:第一步从6个人中选出一个主席,有6种选择;第二步从剩下的5个人中选出2个人,有C(5, 2)种选择;第三步将每个步骤的计数结果相乘得到最终结果,即6 ×C(5, 2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分类与分步计数原理
一、选择题(每小题6分,共60分)
1. 已知x∈{1,2,3,4},y∈{5,6,7,8},则xy可表示不同值的个数为
()
A.2 B.4 C.8 D.15
2.现有4种不同颜色对如图所示的四个部分进行着色,要求有公共
边界的两块不能用同一种颜色,则不同的着色方法共有() A.24种B.30种C.36种D.48种
3. 甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有( ).
A.6种 B.12种 C.24种 D.30种
4.4位同学从甲、乙、丙3门课程中选修1门,则恰有2人选修课程甲的不同选法有( ).
A.12种 B.24种 C.30种 D.36种
5. 某商场共有4个门,若从一个门进,另一个门出,不同走法的种数是().
.A10 .B11 .C12 .D13
6. 用1、2、3、4、5这5个数字,组成无重复数字的三位数,其中奇数有( )
A.12个B.24个C.36个D.48个7. .从6人中选4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且这6人中甲、乙两人不去巴黎游览,则不同的选择方案共有
()
.A300种.B240种.C144种.D96种
8. 同室4人各写一张贺年卡,先集中起来,然后每人从中拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有()
.A23种.B11种.C9种.D6种
9. 现有四件不同款式的上衣与三件不同颜色的长裤,如果一条长裤与一件上衣配成一套,则不同的选法数为().
.A7 .B64 .C12 .D81
10.将1,2,3填入3×3的方格中,要求每行、每列都没有重复数字,
如图是一种填法,则不同的填写方法共有()
A.6种B.12种C.24种D.48种
二、填空题(每题10分,共40分)
11.五个工程队承建某项工程的5个不同的子项目,每个工程队承建
1项,其中甲工程队不能承建1号子项目,则不同的承建方案有________种.
12.有10本不同的数学书,9本不同的语文书,8本不同的英语书,从中任取两本不同类的书,共有______种不同的取法.
13.某班从6名学生中选出4人分别参加数、理、化、生四科竞赛
且每科只有1人,其中甲、乙两人不能参加生物竞赛.则不同的选派方法共有________种.
14. 在所有两位数中,个位数字大于十位数字的两位数共有_个.
1D 2D 3C 4B 5C 6C 7B8C 9C 10B
11.96 12.242 13.240 14. 32。
