华东理工大学概率论答案-4,5,6

合集下载

华理概率论06-01-B-试卷答案

华东理工大学2005–2006学年第一学期《概率论与数理统计》课程期末考试试卷 B 2006.1.开课学院：理学院，考试形式：闭卷，所需时间： 120 分钟姓名：学号：班级：任课教师一、填空题（每小题4分，共20分）1．从一装有3个红球2个白球的盒子中取出两球，取得一红一白的概率为0. 6 ；若已知其中至少有一个是白球，则另一球也是白球的概率为 1 / 7 。

2．设A 、B 是两个事件，5.0)(=A P ，2.0)(=B P ，)|()|(B A P B A P =，则=)(B A P 6.0。

3．若某人射击的命中率为0.2，则他命中目标时已经射击的次数X 为k 的概率==}{k X P 1)8.0(2.0-k ，5=EX 。

4．设随机变量X 与Y 相互独立，且1)()(==Y E X E ，2)()(==Y D X D ，则8)(=XY D 。

5．已知随机变量)2(~E X ，则X e Y =的分布密度函数为=)(y Y ϕ⎩⎨⎧≤>-11,0,23y y y 。

二、选择题（每小题4分，共20分）1．设总体 X ～)(λP , ),,,(4321X X X X 是来自总体X 的样本，则下列λ的无偏估计中最有效的是（ D ）A ．72224321X X X X +++； B ．6224321X X X X +++；C ．524321X X X X +++； D ． 44321X X X X +++。

2．对于任意两事件A 和B ，则下列结论正确的是（ C ）A ．一定不独立，，则若B A AB ∅=； B ．一定独立，，则若B A AB ∅≠；C ．有可能独立，，则若B A AB ∅≠；D ．一定独立，，则若B A AB ∅=。

3．已知二维随机变量),(Y X 的边缘分布都是正态分布，则下列不正确的结论是（ A ）A ．),(Y X 一定服从二维正态分布；B ．独立时服从正态分布与Y X ；C ．),(Y X 可能服从二维正态分布；D ．以上结论不都正确。

华理概率论06-6-A答案

华东理工大学2005–2006学年第二学期《概率论与数理统计》课程考试试卷 A 2006.6开课学院：理学院，专业：大面积，考试形式：闭卷，所需时间：120分钟考生姓名：学号：班级：任课教师：一、选择题：（每小题5分）1、设随机变量ξ服从正态分布2(,)N μσ，则概率{}2P x μσ-≥（ D ）。

A 、随μ的增加而增大 B 、随μ的增加而减小C 、随σ的增加而增大D 、等于一个常数（与μ和σ的大小没有关系）。

2、设随机变量ξ和η满足条件()E E E ξηξη=⋅，则以下命题中一定正确的是（ C ）。

A 、()D D D ξηξη=⋅ B 、ξ和η一定相互独立 C 、()D D D ξηξη+=+ D 、ξ和η一定不相互独立3、设随机变量ξ密度函数为()p x ，则31ηξ=-的密度函数()p y η为（ A ）。

A 、11()33y p +B 、13()3y p +C 、1(3(1))3p y + D 、13()3y p -4、样本),,,(21n X X X 取自正态分布2(,)N μσ，1,n X S -分别为样本均值及样本标准差，则（ B ）。

A 、2~(,)X N μσB 2)~(0,)X N μσ-C 、221~()ni n χ=∑ D 、221~()ni n χ=⎛⎫∑二、填空题：（每小题5分）1、已知()0.2,()0.5P A B P A -==，则()P AB = 0.7 。

2、已知随机变量ξ的密度函数为：1/3,[0,1]()1/6,[2,6]0,[0,1][2,6]x p x x x ∈⎧⎪=∈⎨⎪∉⎩，且{}1/4P a ξ≥=，则a = 4.5 。

3、设随机变量X 服从参数为2的指数分布，则2()X E e -== 0.5 。

4、设随机变量X 与Y 分别服从正态分布(1,4)N 和(2,9)N ，且相互独立，如果有1{}2P X Y c -≥=，则c = 1- 。

华理概率论08-1-A_答案

（B） ( X
（C） ( X
（D） ( X
三、计算题：（共 6 小题，共计 60 分）待用数据（ (2.3263) 0.99 , (1.5) 0.9332 , (2) 0.9772 ,
2 2 (2.5) 0.9938, ， 0.025 (4) 0.484, 0.05 (4) 0.711, 2 2 2 2 0.95 (4) 9.488, 0.975 (4) 11.143, 0.025 (5) 0.831, 0.05 (5) 1.145, 2 2 0.95 (5) 11.070, 0.975 (5) 12.833 ）
0
x
2

e

x2 2 2
dx （2 分）
2

0
e

x2 2 2
d(
x2 2 ) 2 2
（2 分）
解方程 (2)
ˆ

E X , 得到矩法估计

ˆX
（1 分） 2
先求似然函数：
n 1 2 xi 2 e 2 n i 1 L ( xi ) i 1 0
2
根纤维，测得其纤度为，1.32，1.55，1.36，1.40，1.44，问这一天纤度的总体方差是否正常 ( 0.05) ？这 5 个数据在 Excel 做描述统计得到如下表格：
解：以 X 表示这一天生产的维尼纶纤度，则 X ~ N ( , 0.048 2 ) （1） H 0 : 2 0.0482 , H1 : 2 0.0482 ；（2）取统计量 2
1．（8 分）甲、乙两厂生产的电池放在一起，已知其中有 75％是甲厂生产的，

【VIP专享】华理概率论答案第四册

A.单调增大 B.单调减少 C.保持不变 D. 增减不定
2．若灯管的寿命ξ ~ e(λ) ，则该灯管已使用了 a(a > 0) 小时,能再使用 b 小时的概
率（ A ）。 A. 与 a 无关 B. 与 a 有关 C. 无法确定 D. 以上答案都不对
3．随机变量 X 的概率密度函数为 p(x) ，且 p(x) = p(−x) ， F (x) 是 X 的分布函
−9
−9
1 − (1 − e 2 ) e 2
3．假设测量的随机误差ξ ~ N (0, 102 ) ，试求在 100 次独立重复测量中，至少有
二次测量误差的绝对值大于 19.6 的概率α 。
解：
P(| ξ
|>
19.6)
=
P(ξ
> 19.6)
+
P(ξ
<
−19.6)
=
2[1 − Φ
19.6 ( )]
=
0.05
0.8 。
2．设随机变量 X 在区间[2，6]上服从均匀分布，现对 X 进行了 3 次独立试验，
则正好有 2 次观测值大于 4 的概率为 3
。
8
3．设每人每次打电话的时间（单位：min）服从 E(1) ，则在 808 人次的电话中有
3 次或以上超过 6 分钟的概率为 1 2
二．选择题：
1．设 X 服从正态分布 N (μ,σ 2 ) ，则随着σ 的增大，概率 P{| X − μ |< σ}（ C ）。
10
令η 为 100 次独立重复测量中，误差的绝对值大于 19.6 的次数，
则η ~ b(100, 0.05)
P(η
≥
2)
=1−

新编概率论与数理统计 (夏宁茂秦衍倪中新着) 华东理工大学出版社课后答案

hd
= P( A1 ) + P( A2 | A2 ) P( A2 )
课
P ( B) = P( A1 ) + P( A2 A2 )
aw
后答
案网
= P( A1 ) + P( A2 | A1 ) P( A1 ) + P( A3 | A1 A2 ) P( A2 | A1 ) P( A1 )
.c
om
1.22 解: 设 Ai =“第 i 次拨通”,B=“不超过三次拨通”,则
案网
.c
1.14 解: 总方法数为 43 . 3 (1)球的最大个数为 1,即每个杯子里至多只有一个球,则方法数为 C4 3!(先从 4 个杯
om
1.17 解: 利用 P ( A U B) = P( A) + P( B) − P( AB) ,得 P ( AB) = P( A) + P( B) − P( A U B) = p + q − r , P ( AB ) = P ( A ∪ B) − P( B) = r − q , P ( AB) = P( A ∪ B) − P( A) = r − p , P ( AB ) = 1 − P( A U B ) = 1 − r . 1.18 答:
1.27 解: (1)由于 A、B、C 两两独立,则满足 P ( AB) = P( A) P ( B) = x 2 ,
P ( BC ) = P ( B ) P(C ) = x 2 , P ( AC ) = P( A) P(C ) = x 2 , 又 ABC = ∅ 则 P( ABC ) = 0 , P ( A − B − C ) = P( A) − P( AB) − P( AC ) + P( ABC ) = x − 2 x 2 ≥ 0 ⇒ 0 ≤ x ≤ 0.5 ,故 x 的最大值为 0.5. (2) P ( A U B U C ) = P ( A) + P ( B ) + P (C ) − P ( AB ) − P ( BC ) − P ( AC ) + P ( ABC ) 9 ⇒ = 3P ( A) − 3[ P( A)]2 ⇒ P( A) = 0.25, 16 而另外的一个解 P ( A) = 0.75 > 0.5 舍去. 1.28 解: 设 Ai =“第 i 个零件合格”,则

华理概率论习题5答案-2012

ac cov( X , Y ) ac DX DY
XY
4. 设两个随机变量 , ， E 2, E 4, D 4, D 9, 0.5 ，求
E (3 2 2 2 3) 。
解
E (3 2 2 2 3) 3E ( 2 ) 2 E ( ) E ( 2 ) 3 ＝3 D ( E ) 2 2cov( , ) EE D ( E ) 2 3 68
＝max( , ) 的分布函数 F ( z ) 等于
A． max{F ( z ), F ( z )} B. F ( z ) F ( z )
（ B ）
1 C． [ F ( z ) F ( z )] 2 二. 填空：
已知～ N (0 ,1) ,
1 3
D. F ( z ) F ( z ) F ( z ) F ( z )
B. 独立的充分条件，但不是必要条件 D. 不相关的充分条件，但不是必要条件）
3.
对于任意两个随机变量 X 和 Y ，若 E ( XY ) E ( X ) E (Y ) ，则（B A） D( XY ) D( X ) D(Y ) C） X 和 Y 独立
B） D( X Y ) D( X ) D(Y ) D） X 和 Y 不独立0.25 0.15
0.15 0.2 0.15
1.05 E 0 .5 E 0.25 E max( , ) _______, 1.2 E ______, ____, sin ( ) _______, 2
0.36 Dmax( , ) _______ 。
三. 计算题： 1. 已知二维随机变量 ( , ) 的联合概率分布为

华东理工大学概率论答案

华东理工大学概率论答案【篇一：华东理工大学概率论答案-15,16】选择题：1. 设随机变量?密度函数为p(x)，则??3??1的密度函数p?(y)为（ a ）。

1y?1y?11y?1) b、3p() c、p(3(y?1)) d、3p() a、p(333332. 设随机变量?和?相互独立，其分布函数分别为f?(x) 与f?(y)，则 ?＝max(?,?) 的分布函数f?(z) 等于（ b ） a．max{f?(z),f?(z)}b. f?(z)f?(z)1c．[f?(z)?f?(z)] d. f?(z)?f?(z)?f?(z)f?(z)2二. 填空：已知?～n(0,1),??? 三. 计算题, 则?的概率密度为??(y)?3y22?e?y62。

1. 已知随机变量?~u[0,2]，求???2的概率密度。

?p{?y???解: f?(y)?p{??y}??0?2y}y?0?f?(y)?f?(?y)??y?0?0y?0y?0?1p(y)?p?(?y)?故p?(y)??2y??0????1y?0?＝?4yy?0??00?y?4其他2. 设随机变量x求y?sin(?2x)的概率分布。

x?4k?1x?2k k?1,2,? x?4k?3??1x??解：由于sin()??02?1?故随机变量y的可能取值为：-1，0，1。

随机变量y的p{y??1}??p{x?4k?1}?? k?1k?1??124k?1?112??； 8115?124p{y?0}??p{x?2k}??k?1?1111???； 2k143k?12?122??p{y?1}??p{x?4k?3}??k?1k?1?124k?3?118??， 2115于是随机变量y的分布律为：3．设?~u(0,1) ，求? =?解：对应于? =?ln?ln?的分布。

lnx，y?x?e(lnx)2?f(x) ，由于f(x)?e(lnx)21?2lnx? 。

xlny当x?(0,1)时，??1x?f(y)?ef(x)?0 ，lny?1?e??1??(y)=??(x)|x?f?1(y)|(f(y))|??2ylny?0?其中当y?(??,1]时，,y?(1,??),.其它y??(y)=0是由x?(0,1)时y?(1,??) 而导出的。

华理概率论06-6-B-试卷答案

华东理工大学2005–2006学年第二学期《概率论与数理统计》课程期末考试试卷 B 2006.06开课学院：理学院，专业：大面积，考试形式：闭卷，所需时间：120分钟考生：学号：班级任课教师一、填空题（每题5分，共20分）（1）设 P ( A ) = 0.5 , P ( A B ) = 0.75 , a ）若A 与B 独立，则 P(B) ＝ 0.5 ；b). 若A 与B 不相容，则 P(B) ＝ 0.25 。

（2）设n X X X ,,21为总体2~(,)N ξμσ的样本，2111,()nnii i i X X X U n μσ==-==∑∑，则它们分别服从 2(,)N n μσ 和 2()n χ 分布。

（3）设随机变量,ξη相互独立，且4D D ξη=。

记23,23X Y ξηξη=+=-，则{()()(E XY EX EY -＝ 725 。

（4）设随机变量ξ的密度函数为：01(),120ax x p x b x x ≤<⎧⎪=-≤≤⎨⎪⎩，其它且 1E ξ=，则： ,a b的值分别等于： 1 和 2 。

二、选择题（每题5分，共20分）（1）设A,B 是任意两个概率不是零的不相容事件，则下列结论中肯定正确的是（ D ）。

（A ）A 与B 互不相容；（B ）A 与B 相容；（C ）P(AB) = P(A) P(B)；（D ）()()P A B P A -=。

（2）设随机变量,ξη相互独立，且3, 2.1E D ξξ==；4, 2.4E D ηη==，则2(2)E ξη-=（ A ）。

（A ）14.8 ；（B ） 4 ；（C ）12.4 ；（D ）其它。

（3）设随机变量X ，Y 相互独立，服从相同的两点分布：111212-⎡⎤⎢⎥⎣⎦，则下列结论中肯定正确的是（ C ）：（A ）X=Y ；（B ）P(X=Y) = 0 ；（C ）P(X=Y) = 12；（D ）P(X=Y) = 1 。

东华理工大学概率论与数理统计练习册答案

第一章概率论的基本概念一、选择题1．答案：（B ） 2. 答案：（B ）解：AUB 表示A 与B 至少有一个发生,Ω-AB 表示A 与B 不能同时发生,因此(AUB)(Ω-AB)表示A 与B 恰有一个发生． 3．答案：（C ）4. 答案：（C ）注:C 成立的条件:A 与B 互不相容.5. 答案：（C ）注:C 成立的条件:A 与B 互不相容,即AB φ=.6. 答案：（D ）注:由C 得出A+B=Ω.7. 答案：（C ）8. 答案：（D ）注：选项B 由于11111()1()1()1()1(1())nnnnni i i i i i i i i i P A P A P A P A P A ======-=-==-=--∑∑∏∏9.答案：（C ）注：古典概型中事件A 发生的概率为()()()N A P A N =Ω.10.答案：（A ）解：用A 来表示事件“此r 个人中至少有某两个人生日相同”，考虑A 的对立事件A “此r 个人的生日各不相同”利用上一题的结论可知365365!()365365rr r rC r PP A ⋅==，故365()1365rrP P A =-.11.答案：（C ） 12.答案：（B ）解：“事件A 与B 同时发生时,事件C 也随之发生”，说明A B C ⊂，故()()P AB P C ≤；而()()()()1,P A B P A P B P AB ⋃=+-≤ 故()()1()()P A P B P AB P C +-≤≤.13.答案：（D ）解：由(|)()1P A B P A B +=可知2()()()1()()()1()()()(1())()(1()()())1()(1())()(1())()(1()()())()(1())()()()()()()(())()()()P A B P A B P A B P A B P B P B P B P B P A B P B P B P A P B P A B P B P B P A B P B P B P A P B P A B P B P B P A B P A B P B P B P A P B P B P B P A B P B -⋃+=+--+--+==-⇒-+--+=-⇒-+--+=2(())()()()P B P A B P A P B -⇒=故A 与B 独立. 14.答案：（A ）解：由于事件A,B 是互不相容的，故()0P AB =，因此P(A|B)=()00()()P AB P B P B ==.15.答案：（D ）解：用A 表示事件“密码最终能被译出”，由于只要至少有一人能译出密码，则密码最终能被译出，因此事件A 包含的情况有“恰有一人译出密码”，“恰有两人译出密码”，“恰有三人译出密码”，“四人都译出密码”，情况比较复杂，所以我们可以考虑A 的对立事件A “密码最终没能被译出”，事件A 只包含一种情况，即“四人都没有译出密码”，故111112()(1)(1)(1)(1)()543633P A P A =----=⇒=.16.答案：（B ）解：所求的概率为()1()1()()()()()()()11111100444161638P A B C P A B C P A P B P C P AB P BC P AC P ABC =-⋃⋃=---+++-=---+++-=注：0()()0()0ABC AB P ABC P AB P ABC ⊂⇒≤≤=⇒=. 17.答案：（A ）解：用A 表示事件“取到白球”，用i B 表示事件“取到第i 箱” 1.2.3i =，则由全概率公式知112233()()(|)()(|)()(|)11131553353638120P A P B P A B P B P A B P B P A B =++=++=.18.答案：（C ）解：用A 表示事件“取到白球”，用i B 表示事件“取到第i 类箱子” 1.2.3i =，则由全概率公式知112233()()(|)()(|)()(|)213212765636515P A P B P A B P B P A B P B P A B =++=++=.19.答案：（C ）解：即求条件概率2(|)P B A .由Bayes 公式知3263222711223315()(|)5(|)()(|)()(|)()(|)7P B P A B P B A P B P A B P B P A B P B P A B ===++.二、填空题1.{（正，正，正），（正，正，反），（正，反，反），（反，反，反），（反，正，正），（反，反，正），（反，正，反），（正，反，正）}2.;ABC ABC ABC ABC ABC 或AB BC AC 3．0.3，0.5解：若A 与B 互斥，则P （A+B ）=P （A ）+P （B ），于是 P （B ）=P （A+B ）-P （A ）=0.7-0.4=0.3；若A 与B 独立，则P （AB ）=P （A ）P （B ），于是由P （A+B ）=P （A ）+P （B ）-P （AB ）=P （A ）+P （B ）-P （A ）P （B ），得()()0.70.4()0.51()10.4P A B P A P B P A +--===--.4.0.7解：由题设P （AB ）=P （A ）P （B|A ）=0.4，于是P （AUB ）=P （A ）+P （B ）-P （AB ）=0.5+0.6-0.4=0.7.5.0.3解：因为P （AUB ）=P （A ）+P （B ）-P （AB ），又()()()P AB P AB P A +=，所以()()()0.60.30.3P AB P A B P B =-=-= .6.0.6解：由题设P （A ）=0.7，P （AB ）=0.3，利用公式AB AB A +=知()()()P AB P A P AB =-=0.7-0.3=0.4，故()1()10.40.6P AB P AB =-=-=.7.7/12解：因为P （AB ）=0，所以P （ABC ）=0，于是()()1()1[()()()()()()()]13/42/67/12P ABC P A B C P A B C P A P B P C P AB P BC P AC P ABC ==-=-++---+=-+= . 8.1/4解：因为()()()()()()()()P A B C P A P B P C P AB P BC P AC P ABC =++---+ 由题设22()()(),()()()(),()()()()P A P B P C P AC P A P C P A P AB P A P B P A ======，2()()()(),()0P BC P B P C P A P ABC ===，因此有293()3()16P A P A =-，解得P （A ）=3/4或P （A ）=1/4，又题设P （A ）<1/2,故P （A ）=1/4. 9.1/6解：本题属抽签情况，每次抽到次品的概率相等，均为1/6，另外，用全概率公式也可求解. 10.11260解：这是一个古典概型问题，将七个字母任一种可能排列作为基本事件，则全部事件数为7！，而有利的基本事件数为12121114⨯⨯⨯⨯⨯⨯=，故所求的概率为417!1260=.11.3/7 解：设事件A={抽取的产品为工厂A 生产的}，B={抽取的产品为工厂B 生产的}，C={抽取的是次品}，则P （A ）=0.6，P （B ）=0.4，P （C|A ）=0.01，P （C|B ）=0.02，故有贝叶斯公式知()()(|)0.60.013(|)()()(|)()(|)0.60.010.40.027P AC P A P C A P A C P C P A P C A P B P C B ⨯====+⨯+⨯.12.6/11解：设A={甲射击}，B={乙射击}，C={目标被击中}，则P （A ）=P （B ）=1/2，P （C|A ）=0.6，P （C|B ）=0.5，故()()(|)0.50.66(|)()()(|)()(|)0.50.60.50.511P AC P A P C A P A C P C P A P C A P B P C B ⨯====+⨯+⨯.三、设A ，B ，C 是三事件，且0)()(,41)()()(=====BC P AB P C P B P A P ，81)(=AC P .求A ，B ，C 至少有一个发生的概率。

概率论第4-6章课后习题答案

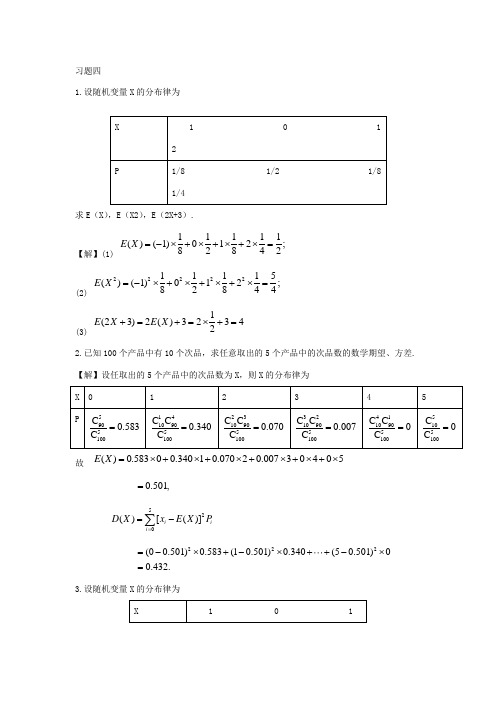
习题四1.设随机变量X的分布律为1 0 12求E（X），E（X2），E（2X+3）.【解】(1)11111 ()(1)012;82842 E X=-⨯+⨯+⨯+⨯=(2)2222211115 ()(1)012;82844 E X=-⨯+⨯+⨯+⨯=(3)1 (23)2()32342E X E X+=+=⨯+=2.已知100个产品中有10个次品，求任意取出的5个产品中的次品数的数学期望、方差.【解】设任取出的5个产品中的次品数为X，则X的分布律为故()0.58300.34010.07020.00730405E X=⨯+⨯+⨯+⨯+⨯+⨯0.501,=52()[()]i iiD X xE X P==-∑222(00.501)0.583(10.501)0.340(50.501)00.432.=-⨯+-⨯++-⨯=3.设随机变量X的分布律为1 0 1P p1 p2 p3且已知E （X ）=,E(X2)=,求P1，P2，P3. 【解】因1231P P P ++=……①,又12331()(1)010.1E X P P P P P =-++=-=……②, 222212313()(1)010.9E X P P P P P =-++=+=……③由①②③联立解得1230.4,0.1,0.5.P P P ===4.袋中有N 只球，其中的白球数X 为一随机变量，已知E （X ）=n ，问从袋中任取1球为白球的概率是多少【解】记A={从袋中任取1球为白球}，则(){|}{}Nk P A P A X k P X k ===∑全概率公式001{}{}1().NNk k k P X k kP X k NN n E X NN ========∑∑5.设随机变量X 的概率密度为f （x ）=⎪⎩⎪⎨⎧≤≤-<≤.,0,21,2,10,其他x x x x求E （X ），D （X ）. 【解】1221()()d d (2)d E X xf x x x x x x x+∞-∞==+-⎰⎰⎰21332011 1.33x x x ⎡⎤⎡⎤=+-=⎢⎥⎢⎥⎣⎦⎣⎦122232017()()d d (2)d 6E X x f x x x x x x x +∞-∞==+-=⎰⎰⎰故221()()[()].6D X E X E X =-= 6.设随机变量X ，Y ，Z 相互独立，且E （X ）=5，E （Y ）=11，E （Z ）=8，求下列随机变量的数学期望. （1） U=2X+3Y+1；（2） V=YZ4X.【解】(1) [](231)2()3()1E U E X Y E X E Y =++=++ 25311144.=⨯+⨯+= (2) [][4][]4()E V E YZ X E YZ E X =-=-,()()4()Y Z E Y E Z E X -因独立1184568.=⨯-⨯=7.设随机变量X ，Y 相互独立，且E （X ）=E （Y ）=3，D （X ）=12，D （Y ）=16，求E （3X 2Y ），D （2X3Y ）.【解】(1) (32)3()2()3323 3.E X Y E X E Y -=-=⨯-⨯=(2)22(23)2()(3)412916192.D X Y D X DY -=+-=⨯+⨯= 8.设随机变量（X ，Y ）的概率密度为f （x ，y ）=⎩⎨⎧<<<<.,0,0,10,其他x y x k试确定常数k ，并求E （XY ）.【解】因1001(,)d d d d 1,2x f x y x y x k y k +∞+∞-∞-∞===⎰⎰⎰⎰故k=210()(,)d d d 2d 0.25xE XY xyf x y x y x x y y +∞+∞-∞-∞===⎰⎰⎰⎰.9.设X ，Y 是相互独立的随机变量，其概率密度分别为fX （x ）=⎩⎨⎧≤≤;,0,10,2其他x x fY （y ）=(5)e ,5,0,.y y --⎧>⎨⎩其他求E （XY ）.【解】方法一：先求X 与Y 的均值102()2d ,3E X x x x ==⎰5(5)5()ed 5e d e d 51 6.z y y zz E Y y yz z z +∞+∞+∞=-----=+=+=⎰⎰⎰令由X 与Y 的独立性，得2()()()6 4.3E XY E X E Y ==⨯=方法二：利用随机变量函数的均值公式.因X 与Y 独立，故联合密度为(5)2e ,01,5,(,)()()0,,y X Y x x y f x y f x f y --⎧≤≤>==⎨⎩其他于是11(5)2(5)552()2e d d 2d e d 6 4.3y y E XY xy x x y x xy y +∞+∞----===⨯=⎰⎰⎰⎰10.设随机变量X ，Y 的概率密度分别为fX （x ）=⎩⎨⎧≤>-;0,0,0,22x x x e fY （y ）=⎩⎨⎧≤>-.0,0,0,44y y y e求（1） E （X+Y ）;（2） E （2X 3Y2）.【解】22-200()()d 2e d [e ]e d x x xX X xf x x x x x x+∞+∞+∞--+∞-∞==-⎰⎰⎰201e d .2x x +∞-==⎰ 401()()d 4e dy .4y Y E Y yf y y y +∞+∞--∞==⎰⎰22242021()()d 4e d .48y Y E Y y f y y y y +∞+∞--∞====⎰⎰从而(1)113()()().244E X Y E X E Y +=+=+=(2)22115(23)2()3()23288E X Y E X E Y -=-=⨯-⨯=11.设随机变量X 的概率密度为f （x ）=⎪⎩⎪⎨⎧<≥-.0,0,0,22x x cx xke求（1）系数c;（2） E （X ）;（3） D （X ）.【解】(1) 由222()d e d 12k x c f x x cx x k +∞+∞--∞===⎰⎰得22c k =.(2)2220()()d()2e d k x E X xf x x x k x x+∞+∞--∞==⎰⎰22220π2e d .2k x k x x k +∞-==⎰(3)222222201()()d()2e.k x E X x f x x x k x k +∞+∞--∞==⎰⎰故 222221π4π()()[()].4D X E X E X k k ⎛⎫-=-=-= ⎪ ⎪⎝⎭12.袋中有12个零件，其中9个合格品，3个废品.安装机器时，从袋中一个一个地取出（取出后不放回），设在取出合格品之前已取出的废品数为随机变量X ，求E （X ）和D （X ）. 【解】设随机变量X 表示在取得合格品以前已取出的废品数，则X 的可能取值为0，1，2，3.为求其分布律，下面求取这些可能值的概率，易知9{0}0.750,12P X === 39{1}0.204,1211P X ==⨯= 329{2}0.041,121110P X ==⨯⨯= 3219{3}0.005.1211109P X ==⨯⨯⨯=于是，得到X 的概率分布表如下： X 0 1 2 3 P由此可得()00.75010.20420.04130.0050.301.E X =⨯+⨯+⨯+⨯=22222222()075010.20420.04130.0050.413()()[()]0.413(0.301)0.322.E X D X E X E X =⨯+⨯+⨯+⨯==-=-=13.一工厂生产某种设备的寿命X （以年计）服从指数分布，概率密度为f （x ）=⎪⎩⎪⎨⎧≤>-.0,0,0,414x x xe为确保消费者的利益，工厂规定出售的设备若在一年内损坏可以调换.若售出一台设备，工厂获利100元，而调换一台则损失200元，试求工厂出售一台设备赢利的数学期望. 【解】厂方出售一台设备净盈利Y 只有两个值：100元和200元/41/411{100}{1}e d e 4x P Y P X x +∞--==≥==⎰1/4{200}{1}1e .P Y P X -=-=<=-故1/41/41/4()100e (200)(1e )300e 20033.64E Y ---=⨯+-⨯-=-= (元). 14.设X1，X2，…，Xn 是相互独立的随机变量，且有E （Xi ）=μ，D （Xi ）=σ2，i=1，2，…，n ，记∑==n i i S X n X 12,1，S2=∑=--n i i X X n 12)(11.（1）验证)(X E =μ，)(X D =n 2σ；（2）验证S2=)(11122∑=--ni i X n X n ；（3）验证E （S2）=σ2.【证】(1) 1111111()()().n nn i i i i i i E X E X E X E X nu u n n n n ===⎛⎫===== ⎪⎝⎭∑∑∑ 22111111()()n nni i i ii i i D X D X D X X DXn nn ===⎛⎫== ⎪⎝⎭∑∑∑之间相互独立2221.n n n σσ==(2) 因222221111()(2)2nnnniii iii i i i XX X X X X X nX X X ====-=+-=+-∑∑∑∑2222112nnii i i X nX X nX X nX===+-=-∑∑故22211()1ni i S X nX n ==--∑.(3) 因2(),()i i E X u D X σ==,故2222()()().i i i E X D X EX u σ=+=+同理因2(),()E X u D X n σ==,故222()E X u nσ=+.从而222221111()()[()()]11n ni i i i E s E X nX E X nE X n n ==⎡⎤=-=-⎢⎥--⎣⎦∑∑221222221[()()]11().1ni i E X nE X n n u n u n n σσσ==--⎡⎤⎛⎫=+-+=⎢⎥⎪-⎝⎭⎣⎦∑15.对随机变量X 和Y ，已知D （X ）=2，D （Y ）=3，Cov(X,Y)=1,计算：Cov （3X2Y+1，X+4Y3）.【解】Cov(321,43)3()10Cov(,)8()X Y X Y D X X Y D Y -++-=+- 3210(1)8328=⨯+⨯--⨯=- (因常数与任一随机变量独立，故Cov(X,3)=Cov(Y,3)=0,其余类似). 16.设二维随机变量（X ，Y ）的概率密度为f （x ，y ）=221,1,π0,.x y ⎧+≤⎪⎨⎪⎩其他试验证X 和Y 是不相关的，但X 和Y 不是相互独立的.【解】设22{(,)|1}D x y x y =+≤. 2211()(,)d d d d πx y E X xf x y x y x x y +∞+∞-∞-∞+≤==⎰⎰⎰⎰2π1001=cos d d 0.πr r r θθ=⎰⎰同理E(Y)=0. 而Cov(,)[()][()](,)d d X Y x E x y E Y f x y x y+∞+∞-∞-∞=--⎰⎰222π1200111d d sin cos d d 0ππx y xy x y r r r θθθ+≤===⎰⎰⎰⎰,由此得XY ρ=,故X 与Y 不相关.下面讨论独立性，当|x|≤1时，2212112()1.ππx X x f x y x ----当|y|≤1时，1()Yf y x.显然()()(,). X Yf x f y f x y≠故X和Y不是相互独立的.17.设随机变量（X，Y）的分布律为1 0 111验证X和Y是不相关的，但X和Y不是相互独立的.【解】联合分布表中含有零元素，X与Y显然不独立，由联合分布律易求得X，Y及XY的分布律，其分布律如下表111由期望定义易得E（X）=E（Y）=E（XY）=0.从而E(XY)=E(X)·E(Y),再由相关系数性质知ρXY=0,即X与Y的相关系数为0，从而X和Y是不相关的.又331{1}{1}{1,1}888P X P Y P X Y =-=-=⨯≠==-=-从而X 与Y 不是相互独立的.18.设二维随机变量（X ，Y ）在以（0，0），（0，1），（1，0）为顶点的三角形区域上服从均匀分布，求Cov （X ，Y ），ρXY.【解】如图，SD=12，故（X ，Y ）的概率密度为题18图2,(,),(,)0,x y D f x y ∈⎧=⎨⎩其他.()(,)d d D E X xf x y x y =⎰⎰1101d 2d 3xx x y -==⎰⎰22()(,)d d DE X x f x y x y =⎰⎰11201d 2d 6xxx y -==⎰⎰从而222111()()[()].6318D X E X E X ⎛⎫=-=-= ⎪⎝⎭ 同理11(),().318E Y D Y == 而 11001()(,)d d 2d d d 2d .12xDDE XY xyf x y x y xy x y x xy y -====⎰⎰⎰⎰⎰⎰所以1111Cov(,)()()()123336X Y E XY E X E Y =-=-⨯=-.从而11362()()111818XY D X D Y ρ-===-⨯19.设（X ，Y ）的概率密度为f （x ，y ）=1ππsin(),0,0,2220.x y x y ,⎧+≤≤≤≤⎪⎨⎪⎩其他求协方差Cov （X ，Y ）和相关系数ρXY.【解】π/2π/21π()(,)d d d sin()d .24E X xf x y x y x xx y y +∞+∞-∞-∞==+=⎰⎰⎰⎰ππ2222201ππ()d sin()d 2.282E X x x x y y =+=+-⎰⎰从而222ππ()()[()] 2.162D X E X E X =-=+-同理 2πππ(),() 2.4162E Y D Y ==+-又π/2π/2π()d sin()d d 1,2E XY x xy x y x y =+=-⎰⎰故2ππππ4Cov(,)()()()1.2444X Y E XY E X E Y -⎛⎫⎛⎫=-=--⨯=- ⎪ ⎪⎝⎭⎝⎭ 222222π4(π4)π8π164.πππ8π32π8π32()()2162XY D X D Y ρ-⎛⎫- ⎪--+⎝⎭===-=-+-+-+-20.已知二维随机变量（X ，Y ）的协方差矩阵为⎥⎦⎤⎢⎣⎡4111，试求Z1=X 2Y 和Z2=2X Y 的相关系数.【解】由已知知：D(X)=1,D(Y)=4,Cov(X,Y)=1. 从而12()(2)()4()4Cov(,)1444113,()(2)4()()4Cov(,)414414,D Z D X Y D X D Y X Y D Z D X Y D X D Y X Y =-=+-=+⨯-⨯==-=+-=⨯+-⨯=12Cov(,)Cov(2,2)Z Z X Y X Y =--2Cov(,)4Cov(,)Cov(,)2Cov(,)2()5Cov(,)2()215124 5.X X Y X X Y Y Y D X X Y D Y =--+=-+=⨯-⨯+⨯=故121212Cov(,)5513.26()()134Z Z Z Z D Z D Z ρ===⨯21.对于两个随机变量V ，W ，若E （V2），E （W2）存在，证明：［E （VW ）］2≤E（V2）E （W2）. 这一不等式称为柯西许瓦兹（CouchySchwarz ）不等式.【证】令2(){[]},.g t E V tW t R =+∈ 显然22220()[()][2]g t E V tW E V tVW t W ≤=+=++222[]2[][],.E V t E VW t E W t R =++∀∈ 可见此关于t 的二次式非负，故其判别式Δ≤0，即2220[2()]4()()E VW E W E V ≥∆=-2224{[()]()()}.E VW E V E W =- 故222[()]()()}.E VW E V E W ≤ 22.假设一设备开机后无故障工作的时间X 服从参数λ=1/5的指数分布.设备定时开机，出现故障时自动关机，而在无故障的情况下工作2小时便关机.试求该设备每次开机无故障工作的时间Y 的分布函数F （y ）.【解】设Y 表示每次开机后无故障的工作时间，由题设知设备首次发生故障的等待时间X~E(λ),E(X)=1λ=5.依题意Y=min(X,2). 对于y<0,f(y)=P{Y≤y}=0. 对于y≥2,F(y)=P(X≤y)=1.对于0≤y<2,当x≥0时，在(0,x)内无故障的概率分布为 P{X≤x}=1eλx,所以F(y)=P{Y≤y}=P{min(X,2)≤y}=P{X≤y}=1e y/5.23.已知甲、乙两箱中装有同种产品，其中甲箱中装有3件合格品和3件次品，乙箱中仅装有3件合格品.从甲箱中任取3件产品放乙箱后，求：（1）乙箱中次品件数Z 的数学期望；（2）从乙箱中任取一件产品是次品的概率.【解】（1） Z 的可能取值为0，1，2，3，Z 的概率分布为33336C C {}C k kP Z k -==, 0,1,2,3.k =Z=k 0 1 2 3Pk120 920 920 120因此，19913()0123.202020202E Z =⨯+⨯+⨯+⨯=(2) 设A 表示事件“从乙箱中任取出一件产品是次品”，根据全概率公式有3(){}{|}k P A P Z k P A Z k ====∑191921310.202062062064=⨯+⨯+⨯+⨯=24.假设由自动线加工的某种零件的内径X （毫米）服从正态分布N （μ,1），内径小于10或大于12为不合格品，其余为合格品.销售每件合格品获利，销售每件不合格品亏损，已知销售利润T （单位：元）与销售零件的内径X 有如下关系T=⎪⎩⎪⎨⎧>-≤≤<-.12,5,1210,20,10,1X X X 若若若问：平均直径μ取何值时，销售一个零件的平均利润最大【解】(){10}20{1012}5{12}E T P X P X P X =-<+≤≤->{10}20{1012}5{12}(10)20[(12)(10)]5[1(12)]25(12)21(10) 5.P X u u P u X u u P X u u u u u u u u =--<-+-≤-≤--->-=-Φ-+Φ--Φ---Φ-=Φ--Φ--故2/2d ()125(12)(1)21(10)(1)0(()e ),d 2x E T u u x u ϕϕϕπ-=-⨯---⨯-= 令这里得 22(12)/2(10)/225e 21eu u ----=两边取对数有2211ln 25(12)ln 21(10).22u u --=--解得 125111ln 11ln1.1910.91282212u =-=-≈(毫米)由此可得，当u=10.9毫米时，平均利润最大. 25.设随机变量X 的概率密度为f(x)=⎪⎩⎪⎨⎧≤≤.,0,0,2cos 21其他πx x 对X 独立地重复观察4次，用Y 表示观察值大于π/3的次数，求Y2的数学期望. （2002研考）【解】令 π1,,3(1,2,3,4)π0,3i X Y i ⎧>⎪⎪==⎨⎪≤⎪⎩X .则41~(4,)i i Y Y B p ==∑.因为ππ{}1{}33p P X P X =>=-≤及π/30π11{}cos d 3222x P X x ≤==⎰,所以111(),(),()42,242i i E Y D Y E Y ===⨯= 2211()41()()22D Y E Y EY =⨯⨯==-,从而222()()[()]12 5.E Y D Y E Y =+=+= 26.两台同样的自动记录仪，每台无故障工作的时间Ti(i=1,2)服从参数为5的指数分布，首先开动其中一台，当其发生故障时停用而另一台自动开启.试求两台记录仪无故障工作的总时间T=T1+T2的概率密度fT(t)，数学期望E （T ）及方差D （T ）. 【解】由题意知：55e ,0,()0,0t i t f t t -⎧≥=⎨<⎩. 因T1,T2独立，所以fT(t)=f1(t)*f2(t). 当t<0时，fT(t)=0; 当t≥0时，利用卷积公式得55()5120()()()d 5e 5e d 25e tx t x tT f t f x f t x x x t +∞-----∞=-==⎰⎰故得525e ,0,()0,0.t T t t f t t -⎧≥=⎨<⎩ 由于Ti ~E(5),故知E(Ti)=15,D(Ti)=125(i=1,2)因此，有E(T)=E(T1+T2)=25.又因T1,T2独立，所以D （T ）=D （T1+T2）=225.27.设两个随机变量X ，Y 相互独立，且都服从均值为0，方差为1/2的正态分布，求随机变量|XY|的方差.【解】设Z=XY ，由于22~0,,~0,,22X N Y N ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ 且X 和Y 相互独立，故Z~N （0，1）. 因22()()(||)[(||)]D X Y D Z E Z E Z -==-22()[()],E Z E Z =- 而22/21()()1,(||)||e d 2πz EZ D Z E Z z z +∞--∞===⎰2/2022e d π2πz z z +∞-==⎰，所以2(||)1πD X Y -=-.28.某流水生产线上每个产品不合格的概率为p(0<p<1)，各产品合格与否相互独立，当出现一个不合格产品时，即停机检修.设开机后第一次停机时已生产了的产品个数为X ，求E （X ）和D （X ）. 【解】记q=1p,X 的概率分布为P{X=i}=qi1p,i=1,2,…，故12111()().1(1)i ii i q p E X iq p p q p q q p ∞∞-=='⎛⎫'===== ⎪--⎝⎭∑∑ 又221211121()()i i i i i i E X i q p i i q p iq p∞∞∞---=====-+∑∑∑2232211()12112.(1)ii q pq q pq p q p pq q p q p p p ∞=''⎛⎫''=+=+⎪-⎝⎭+-=+==-∑所以22222211()()[()].p pD XE X E X p p p --=-=-=题29图29.设随机变量X 和Y 的联合分布在点（0，1），（1，0）及（1，1）为顶点的三角形区域上服从均匀分布.（如图），试求随机变量U=X+Y 的方差. 【解】D(U)=D(X+Y)=D(X)+D(Y)+2Cov(X,Y) =D(X)+D(Y)+2[E(XY)E(X)·E(Y)].由条件知X 和Y 的联合密度为2,(,),(,)0,0.x y G f x y t ∈⎧=⎨<⎩ {(,)|01,01,1}.G x y x y x y =≤≤≤≤+≥从而11()(,)d 2d 2.X xf x f x y y y x +∞-∞-===⎰⎰因此11122300031()()d 2d ,()2d ,22X E X xf x x x x E X x x =====⎰⎰⎰22141()()[()].2918D X E X E X =-=-=同理可得31(),().218E Y D Y == 11015()2d d 2d d ,12xGE XY xy x y x x y y -===⎰⎰⎰⎰541Cov(,)()()(),12936X Y E XY E X E Y =-=-=-于是 1121()().18183618D U D X Y =+=+-=30.设随机变量U 在区间[2,2]上服从均匀分布，随机变量X=1,1,1,1,U U -≤-⎧⎨>-⎩ Y=1,1,1, 1.U U -≤⎧⎨>⎩若试求（1）X 和Y 的联合概率分布；（2）D （X+Y ）.【解】（1）为求X 和Y 的联合概率分布，就要计算（X ，Y ）的4个可能取值(1,1),(1,1),(1,1)及(1,1)的概率. P{x=1,Y=1}=P{U≤1,U≤1}112d d 1{1}444x x P U ---∞-=≤-===⎰⎰ P{X=1,Y=1}=P{U≤1,U>1}=P{∅}=0, P{X=1,Y=1}=P{U>1,U≤1}11d 1{11}44x P U -=-<≤==⎰21d 1{1,1}{1,1}{1}44x P X Y P U U P U ===>->=>=⎰.故得X 与Y 的联合概率分布为(1,1)(1,1)(1,1)(1,1)(,)~1110424X Y ----⎡⎤⎢⎥⎢⎥⎣⎦.(2) 因22()[()][()]D X Y E X Y E X Y +=+-+,而X+Y 及（X+Y ）2的概率分布相应为202~111424X Y -⎡⎤⎢⎥+⎢⎥⎣⎦, 204()~1122X Y ⎡⎤⎢⎥+⎢⎥⎣⎦.从而11()(2)20,44E X Y +=-⨯+⨯=211[()]042,22E X Y +=⨯+⨯=所以22()[()][()] 2.D X Y E X Y E X Y +=+-+= 31.设随机变量X 的概率密度为f(x)=x-e 21，（∞<x<+∞）(1) 求E （X ）及D （X ）；（2）求Cov(X,|X|),并问X 与|X|是否不相关（3）问X 与|X|是否相互独立，为什么【解】(1)||1()e d 0.2x E X xx +∞--∞==⎰2||201()(0)e d 0e d 2.2x x D X x x x x +∞+∞---∞=-==⎰⎰(2) Cov(,|)(||)()(||)(||)X X E X X E X E X E X X =-=||1||e d 0,2x x x x +∞--∞==⎰所以X 与|X|互不相关.(3) 为判断|X|与X 的独立性，需依定义构造适当事件后再作出判断，为此，对定义域∞<x<+∞中的子区间（0,+∞）上给出任意点x0，则有0000{}{||}{}.x X x X x X x -<<=<⊂<所以000{||}{} 1.P X x P X x <<<<<故由00000{,||}{||}{||}{}P X x X x P X x P X x P X x <<=<><<得出X 与|X|不相互独立.32.已知随机变量X 和Y 分别服从正态分布N （1，32）和N （0，42），且X 与Y 的相关系数ρXY=1/2，设Z=23YX +. （1）求Z 的数学期望E （Z ）和方差D （Z ）；（2）求X 与Z 的相关系数ρXZ；（3）问X 与Z 是否相互独立，为什么【解】(1) 1().323X Y E Z E ⎛⎫=+= ⎪⎝⎭()2Cov ,3232XY X Y D Z D D ⎛⎫⎛⎫⎛⎫=++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭11119162Cov(,),9432X Y =⨯+⨯+⨯⨯而1Cov(,)()()3462XY X Y D X D Y ρ⎛⎫==-⨯⨯=- ⎪⎝⎭所以 1()146 3.3D Z =+-⨯=(2) 因()()11Cov(,)Cov ,Cov ,Cov ,3232X Y X Z X X X X Y ⎛⎫=+=+ ⎪⎝⎭119()(6)3=0,323D X =+⨯-=- 所以0.()()XZ D X D Z ρ==(3) 由0XZρ==，得X 与Z 不相关.又因1~,3,~(1,9)3Z N X N ⎛⎫⎪⎝⎭，所以X 与Z 也相互独立.33.将一枚硬币重复掷n 次，以X 和Y 表示正面向上和反面向上的次数.试求X 和Y 的相关系数XY ρ.【解】由条件知X+Y=n ，则有D （X+Y ）=D （n ）=0.再由X~B(n,p),Y~B(n,q)，且p=q=12,从而有 ()()4nD X npq D Y ===所以0()()()2()()XY D X Y D X D Y D X D Y ρ=+=++2,24XY n nρ=+ 故XY ρ= 1.34.设随机变量X 和Y 的联合概率分布为1 0 10 1试求X 和Y 的相关系数ρ.【解】由已知知E(X)=,E(Y)=，而XY 的概率分布为YX 10 1 P所以E （XY ）=+= Cov(X,Y)=E(XY)E(X)·E(Y)=×=0从而XY ρ=035.对于任意两事件A 和B ，0<P(A)<1，0<P(B)<1,则称Y Xρ=())()()()()()(B P A P B P A P B P A P AB P ⋅-为事件A 和B 的相关系数.试证：（1）事件A 和B 独立的充分必要条件是ρ=0；（2） |ρ|≤1.【证】（1）由ρ的定义知，ρ=0当且仅当P(AB)P(A)·P(B)=0.而这恰好是两事件A 、B 独立的定义，即ρ=0是A 和B 独立的充分必要条件. (2) 引入随机变量X 与Y 为1,,0,A X A ⎧⎪=⎨⎪⎩若发生若发生; 1,,0,B Y B ⎧⎪=⎨⎪⎩若发生若发生.由条件知，X 和Y 都服从01分布，即01~1()()X P A P A ⎧⎨-⎩ 01~1()()Y P B P B ⎧⎨-⎩从而有E(X)=P(A),E(Y)=P(B),D(X)=P(A)·P(A ),D(Y)=P(B)·P(B ), Cov(X,Y)=P(AB)P(A)·P(B)所以，事件A 和B 的相关系数就是随机变量X 和Y 的相关系数.于是由二元随机变量相关系数的基本性质可得|ρ|≤1. 36. 设随机变量X 的概率密度为fX(x)=⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<<-.,0,20,41,01,21其他x x令Y=X2，F （x,y ）为二维随机变量（X ，Y ）的分布函数，求： (1) Y 的概率密度fY(y)； (2) Cov(X,Y);(3)1(,4)2F -.解： (1) Y 的分布函数为2(){}{}Y F y P Y y P X y =≤=≤.当y≤0时， ()0Y F y =，()0Y f y =；当0＜y ＜1时，(){{0}{0Y F y P X P X P X =≤≤=≤<+≤≤=，()Y f y =；当1≤y<4时，1(){10}{02Y F y P X P X =-≤<+≤≤=()Y f y =；当y≥4时，()1Y F y =，()0Y f y =.故Y 的概率密度为1,()04,0,.Y y f y y <<=≤<⎪⎩其他(2)210111()()d d d 244+X E X =xf x x x x x x ∞∞=+=⎰⎰⎰--,2222210115()()()d d d )246+X E Y =E X =x f x x x x x x ∞∞=+=⎰⎰⎰--,2233310117()()()d d d 248+X E XY =E Y =x f x x x x x x ∞∞=+=⎰⎰⎰--, 故 Cov(X,Y) =2()()()3E XY E X E Y =⋅-.(3) 2111(,4){,4}{,4}222F P X Y P X X -=≤-≤=≤-≤11{,22}{2}22P X X P X =≤--≤≤=-≤≤-11{1}24P X =-≤≤-=. 37. 习题五1.一颗骰子连续掷4次，点数总和记为X.估计P{10<X<18}.【解】设iX 表每次掷的点数，则41ii X X ==∑22222221111117()123456,666666211111191()123456,6666666i i E X E X =⨯+⨯+⨯+⨯+⨯+⨯==⨯+⨯+⨯+⨯+⨯+⨯= 从而22291735()()[()].6212i ii D X E X E X ⎛⎫=-=-= ⎪⎝⎭ 又X1,X2,X3,X4独立同分布.从而44117()()()414,2i i i i E X E X E X =====⨯=∑∑44113535()()()4.123i i i i D X D X D X =====⨯=∑∑所以235/3{1018}{|14|4}10.271,4P X P X <<=-<≥-≈2. 假设一条生产线生产的产品合格率是.要使一批产品的合格率达到在76%与84%之间的概率不小于90%，问这批产品至少要生产多少件【解】令1,,0,i i X ⎧⎨⎩若第个产品是合格品其他情形.而至少要生产n 件，则i=1,2,…,n,且 X1，X2，…，Xn 独立同分布，p=P{Xi=1}=. 现要求n,使得1{0.760.84}0.9.nii XP n=≤≤≥∑即0.80.9niXnP -≤≤≥∑由中心极限定理得0.9,Φ-Φ≥整理得0.95,10⎛Φ≥ ⎝⎭查表 1.64,≥n≥, 故取n=269.3. 某车间有同型号机床200部，每部机床开动的概率为，假定各机床开动与否互不影响，开动时每部机床消耗电能15个单位.问至少供应多少单位电能才可以95%的概率保证不致因供电不足而影响生产.【解】要确定最低的供应的电能量，应先确定此车间同时开动的机床数目最大值m ，而m 要满足200部机床中同时开动的机床数目不超过m 的概率为95%,于是我们只要供应15m 单位电能就可满足要求.令X 表同时开动机床数目，则X~B （200，）,()140,()42,E X D X ==0.95{0}().P X m P X m =≤≤=≤=Φ 查表知1.64,= ,m=151.所以供电能151×15=2265（单位）.4. 一加法器同时收到20个噪声电压Vk （k=1，2，…，20），设它们是相互独立的随机变量，且都在区间（0，10）上服从均匀分布.记V=∑=201k kV，求P{V ＞105}的近似值.【解】易知:E(Vk)=5,D(Vk)=10012,k=1,2,…,20由中心极限定理知，随机变量201205~(0,1).10010020201212kk VZ N =-⨯==⨯⨯∑近似的于是105205{105}1010020201212P V P ⎧⎫⎪⎪-⨯⎪>=>⎨⎬⎪⎪⨯⨯⎪⎪⎩⎭ 1000.3871(0.387)0.348,102012V P ⎧⎫⎪⎪-⎪⎪=>≈-Φ=⎨⎬⎪⎪⨯⎪⎪⎩⎭即有 P{V>105}≈5. 有一批建筑房屋用的木柱，其中80%的长度不小于3m.现从这批木柱中随机地取出100根，问其中至少有30根短于3m 的概率是多少【解】设100根中有X 根短于3m ，则X~B （100，）从而{30}1{30}11000.20.8P X P X ≥=-<≈-Φ⨯⨯1(2.5)10.99380.0062.=-Φ=-=6. 某药厂断言，该厂生产的某种药品对于医治一种疑难的血液病的治愈率为.医院检验员任意抽查100个服用此药品的病人，如果其中多于75人治愈，就接受这一断言，否则就拒绝这一断言.（1）若实际上此药品对这种疾病的治愈率是，问接受这一断言的概率是多少（2）若实际上此药品对这种疾病的治愈率是，问接受这一断言的概率是多少【解】1,,1,2,,100.0,.i i X i ⎧==⎨⎩第人治愈其他令1001.i i X X ==∑(1) X~B(100,，1001{75}1{75}1i i P X P X =>=-≤≈-Φ∑1( 1.25)(1.25)0.8944.=-Φ-=Φ= (2) X~B(100,，1001{75}1{75}1i i P X P X =>=-≤≈-Φ∑11(1.09)0.1379.=-Φ=-Φ=7. 用Laplace 中心极限定理近似计算从一批废品率为的产品中，任取1000件，其中有20件废品的概率.【解】令1000件中废品数X ，则 p=,n=1000,X~B(1000,， E(X)=50，D(X)=. 故130{20} 6.895 6.895P X ϕ⎛⎫===- ⎪⎝⎭6130 4.510.6.895 6.895ϕ-⎛⎫==⨯ ⎪⎝⎭8. 设有30个电子器件.它们的使用寿命T1，…，T30服从参数λ=[单位：（小时）-1]的指数分布，其使用情况是第一个损坏第二个立即使用，以此类推.令T 为30个器件使用的总计时间，求T 超过350小时的概率.【解】11()10,0.1i E T λ=== 21()100,i D T λ==()1030300,E T =⨯= ()3000.D T = 故{350}111(0.913)0.1814.P T >≈-Φ=-Φ=-Φ=9. 上题中的电子器件若每件为a 元，那么在年计划中一年至少需多少元才能以95%的概率保证够用（假定一年有306个工作日，每个工作日为8小时）. 【解】设至少需n 件才够用.则E(Ti)=10，D(Ti)=100， E(T)=10n ，D(T)=100n.从而1{3068}0.95,ni i P T =≥⨯=∑即0.05.≈Φ 故0.95,1.64272.n =Φ=≈所以需272a 元.10. 对于一个学生而言，来参加家长会的家长人数是一个随机变量，设一个学生无家长、1 名家长、2名家长来参加会议的概率分别为,,.若学校共有400名学生，设各学生参加会议的家长数相与独立，且服从同一分布. （1）求参加会议的家长数X 超过450的概率（2）求有1名家长来参加会议的学生数不多于340的概率.【解】（1）以Xi(i=1,2,…,400)记第i 个学生来参加会议的家长数.则Xi 的分布律为易知E （Xi=）,D(Xi)=,i=1,2, (400)而400iiX X =∑,由中心极限定理得400400 1.1~(0,1).iXN -⨯=∑近似地于是{450}1{450}1P X P X >=-≤≈-Φ1(1.147)0.1357.=-Φ=(2) 以Y 记有一名家长来参加会议的学生数.则Y~B(400,由拉普拉斯中心极限定理得3404000.8{340(2.5)0.9938.4000.80.2P Y -⨯⎛⎫≤≈Φ=Φ= ⎪⨯⨯⎝⎭11. 设男孩出生率为，求在10000个新生婴儿中女孩不少于男孩的概率【解】用X 表10000个婴儿中男孩的个数，则X~B （10000，）要求女孩个数不少于男孩个数的概率，即求P{X≤5000}. 由中心极限定理有{5000}(3)1(3)0.00135.100000.5150.485P X ≤≈Φ=Φ-=-Φ= ⎪⨯⨯⎝⎭12. 设有1000个人独立行动，每个人能够按时进入掩蔽体的概率为.以95%概率估计，在一次行动中：（1）至少有多少个人能够进入（2）至多有多少人能够进入【解】用Xi 表第i 个人能够按时进入掩蔽体（i=1,2,...,1000）. 令 Sn=X 1+X2+ (X1000)(1) 设至少有m 人能够进入掩蔽体，要求P{m≤Sn≤1000}≥，事件{}.10000.90.190nn m S ≤=≤ ⎪⨯⨯⎝⎭ 由中心极限定理知：{}1{}10.95.10000.90.1n n P m S P S m ≤=-<≈-Φ≥ ⎪⨯⨯⎝⎭ 从而 0.05,90Φ≤ ⎪⎝⎭故 1.65,90=-所以 m==≈884人(2) 设至多有M 人能进入掩蔽体，要求P{0≤Sn≤M}≥.{}0.95.90n P S M ≤≈Φ= ⎪⎝⎭查表知90=,M=900+=≈916人. 13. 在一定保险公司里有10000人参加保险，每人每年付12元保险费，在一年内一个人死亡的概率为,死亡者其家属可向保险公司领得1000元赔偿费.求：（1）保险公司没有利润的概率为多大；（2）保险公司一年的利润不少于60000元的概率为多大【解】设X 为在一年中参加保险者的死亡人数，则X~B （10000，）.(1) 公司没有利润当且仅当“1000X=10000×12”即“X=120”. 于是所求概率为{120}100000.0060.994100000.0060.994P X ϕ=≈⎪⨯⨯⨯⨯⎝⎭21(60/59.64)230.1811e 59.6459.64259.640.0517eϕπ--== ⎪⎝⎭=⨯≈(2) 因为“公司利润≥60000”当且仅当“0≤X≤60”于是所求概率为{060}100000.0060.994100000.0060.994P X ≤≤≈Φ-Φ⨯⨯⨯⨯ (0)0.5.59.64⎛=Φ-Φ≈ ⎝14. 设随机变量X 和Y 的数学期望都是2，方差分别为1和4，而相关系数为试根据契比雪夫不等式给出P{|X-Y|≥6}的估计. （2001研考）【解】令Z=X-Y ，有()0,()()()()2()() 3.E Z D Z D X Y D X D Y D X D Y ρ==-=+-=所以2()31{|()|6}{||6}.63612D X Y P Z E Z P X Y --≥=-≥≤==15. 某保险公司多年统计资料表明，在索赔户中，被盗索赔户占20%，以X 表示在随机抽查的100个索赔户中，因被盗向保险公司索赔的户数. （1）写出X 的概率分布；（2）利用中心极限定理，求被盗索赔户不少于14户且不多于30户的概率近似值. （1988研考）【解】（1） X 可看作100次重复独立试验中，被盗户数出现的次数，而在每次试验中被盗户出现的概率是，因此，X~B(100,，故X 的概率分布是100100{}C 0.20.8,1,2,,100.k k k P X k k -===(2) 被盗索赔户不少于14户且不多于30户的概率即为事件{14≤X≤30}的概率.由中心极限定理，得{1430}P X ≤≤≈Φ-Φ(2.5)( 1.5)0.994[9.33]0.927.=Φ-Φ-=--=16. 一生产线生产的产品成箱包装，每箱的重量是随机的.假设每箱平均重50千克，标准差为5千克，若用最大载重量为5吨的汽车承运，试利用中心极限定理说明每辆车最多可以装多少箱，才能保障不超载的概率大于.【解】设Xi （i=1,2,…,n）是装运i 箱的重量（单位：千克），n 为所求的箱数，由条件知，可把X1，X2，…，Xn 视为独立同分布的随机变量，而n 箱的总重量Tn=X1+X2+…+Xn 是独立同分布随机变量之和，由条件知：()50,i E X =5,=()50,n E T n ==依中心极限定理，当n~(0,1)N 近似地,故箱数n 取决于条件{5000}n P T P ≤=≤0.977(2).n ≈Φ>=Φ ⎪⎝⎭因此可从2n >解出n<,即最多可装98箱. 习题六1.设总体X~N （60，152），从总体X 中抽取一个容量为100的样本，求样本均值与总体均值之差的绝对值大于3的概率. 【解】μ=60,σ2=152,n=100~(0,1)/X Z N n σ-=即60~(0,1)15/10X Z N -=(|60|3)(||30/15)1(||2)P X P Z P Z ->=>=-<2[1(2)]2(10.9772)0.0456.=-Φ=-=2.从正态总体N （，52）中抽取容量为n 的样本，若要求其样本均值位于区间（,）内的概率不小于，则样本容量n 至少取多大【解】~(0,1)5/X Z N n -=2.2 4.2 6.2 4.2(2.2 6.2)()55P X P n Z n --<<=<< 2(0.4)10.95,n =Φ-=则Φn =，故n >, 即n>，所以n 至少应取253.设某厂生产的灯泡的使用寿命X~N （1000，σ2）（单位：小时），随机抽取一容量为9的样本，并测得样本均值及样本方差.但是由于工作上的失误，事后失去了此试验的结果，只记得样本方差为S2=1002，试求P（X＞1062）.【解】μ=1000,n=9，S2=10021000~(8)100/3X Xt t-==10621000(1062)()( 1.86)0.05100/3P X P t P t->=>=>=4.从一正态总体中抽取容量为10的样本，假定有2%的样本均值与总体均值之差的绝对值在4以上，求总体的标准差.【解】~(0,1)Z N=，由P(|X-μ|>4)=得P|Z|>4(σ/n)=,故210.02σ⎡⎤⎛-Φ=⎢⎥⎢⎥⎝⎭⎣⎦,即0.99.Φ=⎝⎭查表得2.33,σ=所以5.43.σ==5.设总体X~N（μ，16），X1，X2，…，X10是来自总体X的一个容量为10的简单随机样本，S2为其样本方差，且P（S2＞a）=，求a之值.【解】2222299~(9),()0.1.1616S aP S a Pχχχ⎛⎫=>=>=⎪⎝⎭查表得914.684,16a=所以14.6841626.105.9a⨯==6.设总体X服从标准正态分布，X1，X2，…，Xn是来自总体X的一个简单随机样本，试问统计量Y=∑∑==-ni ii i X X n 62512)15(，n ＞5服从何种分布【解】2522222211~(5),~(5)inii i i X X X n χχχ====-∑∑且12χ与22χ相互独立.所以2122/5~(5,5)/5X Y F n X n =--7.求总体X~N （20，3）的容量分别为10，15的两个独立随机样本平均值差的绝对值大于的概率.【解】令X 的容量为10的样本均值，Y 为容量为15的样本均值,则X ~N(20,310),Y ~N(20,315)，且X 与Y 相互独立.则33~0,(0,0.5),1015X Y N N ⎛⎫-+= ⎪⎝⎭那么~(0,1),X YZ N =所以(||0.3)||2[1(0.424)]P X Y P Z Φ⎛->=>=- ⎝2(10.6628)0.6744.=-=8.设总体X~N （0，σ2）,X1,…,X10,…,X15为总体的一个样本.则Y=()21521221121022212X X X X X X ++++++ 服从分布,参数为 .【解】~(0,1),iX N σi=1,2, (15)那么122210152222111~(10),~(5)i i i i X X χχχχσσ==⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭∑∑且12χ与22χ相互独立,所以222110122211152/10~(10,5)2()/5X X X Y F X X X ++==++所以Y~F 分布，参数为（10,5）.9.设总体X~N （μ1,σ2）,总体Y~N(μ2,σ2),X1,X2,…,1n X 和Y1，Y2，…，2n X 分别来自总体X 和Y 的简单随机样本，则⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+-+-∑∑==2)()(21121221n n Y Y X X E n j j n i i = .【解】令 1222212111211(),(),11n n i i i j S X X S Y Y n n ===-=---∑∑则122222112211()(1),()(1),n n i j i j X X n S y y n S ==-=--=-∑∑又2222221122112222(1)(1)~(1),~(1),n S n S n n χχχχσσ--=-=-那么1222112222121212()()1()22n n i j i j X X Y Y E E n n n n σχσχ==⎡⎤-+-⎢⎥⎢⎥=+⎢⎥+-+-⎢⎥⎣⎦∑∑2221212221212[()()]2[(1)(1)]2E E n n n n n n σχχσσ=++-=-+-=+-10.设总体X~N （μ,σ2），X1，X2，…，X2n （n≥2）是总体X 的一个样本，∑==ni i X n X 2121，令Y=∑=+-+ni i n iX X X12)2(，求E(Y).【解】令Zi=Xi+Xn+i, i=1,2,…,n.则Zi~N(2μ,2σ2)(1≤i≤n),且Z1,Z2,…,Zn 相互独立.令 2211, ()/1,nni i i i Z Z S Z Z n n ====--∑∑则21111,222nn i i i i X X Z Z n n =====∑∑ 故 2Z X = 那么22211(2)()(1),n ni n i i i i Y X X X Z Z n S +===+-=-=-∑∑所以22()(1)2(1).E Y n ES n σ=-=-11. 设总体X 的概率密度为f(x)=x-e 21 (-∞<x<+∞),X1，X2，…，Xn 为总体X 的简单随机样本，其样本方差为S2，求E(S2). 解：由题意，得1e , 0,2()1e ,0,2xx x f x x -⎧<⎪⎪=⎨⎪≥⎪⎩于是 22222220()()()()1()()d e d 021()()d e d e d 2,2xx x E S D X E X E X E X xf x x x x E X x f x x x x x x +∞+∞--∞-∞+∞+∞+∞---∞-∞==-=======⎰⎰⎰⎰⎰所以2()2E S =.。

华理概率论答案第一册

2．对飞机进行两次射击，每次射一弹，设事件 A = “恰有一弹击中飞机”, 事件 B = “至少有一弹击中飞机” ，事件 C =“两弹都击中飞机”, 事件 D = “两弹都没击中飞机” ，又设随机变量 ξ 为击中飞机的次数，则下列事件中( C )不
1
表示 {ξ = 1} 。 A. 事件 A B. 事件 B − C C. 事件 B − C D. 事件 D − C
nk
放回方式摸球，则第 k 次摸球时，首次摸到 1 号球的概率为
1 。 n
二. 选择题： 1. 为了减少比赛场次，把 20 个球队任意分成两组（每组 10 队）进行比赛, 则最强的两个队被分在不同组内的概率为( B )。 1 10 5 1 A. B. C. D. 19 19 10 2 2. 从一副扑克牌(52 张)中任取 4 张,4 张牌的花色各不相同的概率( C ) A.
1 . 4
2. 同时掷五颗骰子，求下列事件的概率：（1） A=“点数各不相同” ；（2） B=“至少出现两个 6 点 ” ；（3） C=“恰有两个点数相同” ；（4） D=“某两个点数相同，另三个同是另一个点数” ；
P65 解：（1） P ( A) = 5 ； 6
（2） P ( B ) = 1 −
华东理工大学
概率论与数理统计
作业簿（第一册）
学学院号 ____________专 ____________姓业名 ____________班级 ____________ ____________任课教师____________
第一次作业
一．填空题：
⎧ 1 ⎧ 1 ⎫ 1．设 S = {x 0 ≤ x ≤ 2} ， A = ⎨ x < x ≤ 1⎬ ， B = ⎨ x ≤ x < ⎩ 2 ⎩ 4 ⎭ 3⎫ ⎬ 2 ⎭ ，具体写出下列

华理概率论答案第二册

华东理工大学
概率论与数理统计
作业簿（第二册）
学院 ____________专业 ____________班级 ____________ 学号 ____________姓名 ____________任课教师____________

第四次作业
一．填空题： 1．设事件 A,B 相互独立，且 P( A) = 0.2, P(B) = 0.5 ，则 P(B A ∪ B) ＝ 4/9
3.下列函数中，可作为某一随机变量的分布函数是（ A ）
（A）
F ( x)
=
1 2
+
1 π
arctan
x
（C）F (x)
=1+
1 x2
（B）
F
(
x)
=
⎧⎪ ⎨
1 2
(1
−
e−
x
),
x>0
⎪⎩ 0,
x≤0
∫ ∫ （D）
F(x) =
x
f (t)dt ，其中
+∞
f (t)dt = 1
−∞
−∞
4．设概率 P( X > x1 ) ≥ β ，P( X ≤ x2 ) ≥ α ，且 x1 < x2 ，则 P( x1 < X ≤ x2 ) （ C ）
D={取出一球为白球}，则
P( A) = 3 , P(B) = 1 , P(C) = 2
6
6
6
P(D | A) = 1 , P(D | B) = 2 , P(D | C) = 3
3
3
6
P(D) = 3 × 1 + 1 × 2 + 2 × 3 = 4 6363 66 9

新编概率论与数理统计(华东理工大学出版社)习题4答案

华东理工大学概率论与数理统计作业簿（第四册）学院 ____________专业 ____________班级 ____________ 学号 ____________姓名 ____________任课教师____________第十次作业一．填空题：1．若ξ在[1，6]上服从均匀分布，则方程210x x ξ++=有实根的概率 0.8 。

2．设随机变量X 在区间[2，6]上服从均匀分布，现对X 进行了3次独立试验，则正好有2次观测值大于4的概率为 38。

二．选择题：1．设X 服从正态分布2(,)N μσ，则随着σ的增大，概率{||}P X μσ-<（ C ）。

A.单调增大 B.单调减少 C.保持不变 D. 增减不定2．若灯管的寿命~()e ξλ，则该灯管已使用了(0)a a >小时,能再使用b 小时的概率（ A ）。

A. 与a 无关B. 与a 有关C. 无法确定D. 以上答案都不对三．计算题：1．某地区18岁的女青年的血压服从(110,121)N 。

在该地区任选一18岁的女青年，测量她的血压，（1）求(100),(105.5121)P X P X ≤≤≤ （2）确定最小的x ，使()0.05P X x >≤ 解：设女青年的血压为ξ，则~(110,121)N ξ，110~(0,1)11N ξ-（1）110105.5110(105.5)()(0.5)11111(0.5)10.69150.3085X P X P --<=<=Φ-=-Φ=-=12111099110(99121)()()(1)(1)11112(1)120.841310.6826P X --≤≤=Φ-Φ=Φ-Φ-=Φ-=⨯-= （3）要使()0.05P X x >≤，只须()0.95P X x ≤>(1.65)0.9Φ= 110 1.65128.1511x x -∴>⇒> 2．修理某机器所需时间（单位：小时）服从参数为12的指数分布。

大学概率论答案完全版

，
满足独立分布中心极限定理条件，所以近似服从正太分布，即近似服从
第五章数理统计的基本概念
5.1 总体样本统计量
一、选择题
1.(D)
2.(A)
3. (D)
二、应用题
1. 5，2.44
2.
3.
5.2抽样分布
一、选择题
1.(C)注：才是正确的.
2.(B)根据得到
3.(A)
解：，
由分布的定义有
（2），，，，
四、（1）；（2）；（3）“ 不都发生”就是“ 都发生”的对立事件，所以应记为；（4）；（5）“ 中最多有一事件发生”就是“ 中至少有二事件发生”的对立事件，所以应记为： .又这个事件也就是“ 中至少有二事件不发生”，即为三事件的并，所以也可以记为 .
§1.2 随机事件的概率
2.解（1）由于查t分布表得又，故得总体均值的95%的置信的区间为
（2）由于，查分布表得，，故得总体方差的90%的置信区间为
3.解查分布表得，又计算得，，故得该地年平均气温方差的90%的置信区间为
4.解造林成活率的置信区间为
6.5两个总体均值差的估计
1.解由于，查分布表得临界值又从而求得的置信概率为95%的置信区间为[7.536，20.064].即以95%的概率保证每块试验田甲稻种的平均产量比乙稻种的平均产量高7.536kg到20.064kg.
2．解：设至少要掷n次，有题设条件知应有
其中， i=1，2，…
独立同分布，且
，，
（1）用切比雪夫不等式确定
而
即要求
即
即至少应掷250次才能满足要求。
（2）用中心极限定理确定

华理概率论习题答案

华东理工大学概率论与数理统计作业簿（第一册）学院____________专业____________班级____________学号____________姓名____________任课教师____________第一次作业一．填空题：1．设{}20≤≤=x x S ，⎭⎬⎫⎩⎨⎧≤<=121x x A ，⎭⎫⎩⎨⎧<≤=2341x x B ，具体写出下列各事件：B A =1131x 422x x ⎧⎫≤≤<<⎨⎬⎩⎭或者，B A =S ，B A =B ，AB =A 。

2．设A 、B 、C 表示三个随机事件，试将下列事件用A 、B 、C 表示出来：（1）事件ABC 表示A 、B 、C 都发生；(2)事件ABC 表示A 、B 、C 都不发生；（3）事件ABC 表示A 、B 、C 不都发生；（4）事件A B C 表示A 、B 、C 中至少有一件事件发生；（5）事件AB AC BC 或AB AC BC 表示A 、B 、C 中最多有一事件发生。

二．选择题：1．设}10,,3,2,1{ =Ω，}5,3,2{=A ，}7,5,4,3{=B ，}7,4,3,1{=C ，则事件=-BC A (A )。

A.}10,9,8,6,1{B.}5,2{C.}10,9,8,6,2{D.}10,9,8,6,5,2,1{2．对飞机进行两次射击，每次射一弹，设事件=A “恰有一弹击中飞机”,事件B =“至少有一弹击中飞机”，事件C =“两弹都击中飞机”,事件=D “两弹都没击中飞机”，又设随机变量ξ为击中飞机的次数，则下列事件中(C )不表示}1{=ξ。

A.事件AB.事件C B -C.事件C B -D.事件CD -3．设A 、B 是两个事件，且∅≠A ，∅≠B ，则()()B A B A ++表示（D）。

A.必然事件B.不可能事件C.A 与B 不能同时发生D.A 与B 中恰有一个发生4．以A 表示事件“甲种产品畅销，乙种产品滞销”，则其对立事件A 表示（D）。

华东理工大学概率论6

3.线阵与面阵图像传感器

(1)电荷耦合图像传感器 - 可分（从结构）线阵 CCD

用于 - 获取线图像的

面阵 CCD

用于 - 获取面图像的
15

线阵 CCD – 主要用于

产品外部尺寸 - 非接触检测

产品表面质量 - 评定
传真和光学文字 - 识别技术

面阵 CCD – 主要用于

T 1 t 3 3f
即
1 f 3
48

CCD 器件的上限工作频率 - 主要受电荷转移快慢限制电荷在 CCD 相邻像元之间移动所需要的平均时间 - 称转移时间为使 - 电荷有效转移

对于三相 CCD - 转移时间应为
T 1 t 3 3f
即
1 f 3t
49

偏置电荷电路
输出栅和信号读出（检测）电路
18

线阵 CCD 图像传感器 - 基本形式

单沟道线阵 CCD 图像传感器双沟道线阵 CCD 图像传感器

19

有 N 个光敏单元的线阵 CCD 图像传感器结构 (图 39)
20

有 N 个光敏单元的线阵 CCD 图像传感器结构

光敏区 - 由 N 个光敏单元排成一列

不存在 - 拖影问题但这种结构 - 不适宜从光背面照射

33

4. CCD 图像传感器的特性参数

CCD 的性能参数 - 包括

灵敏度分辨率信噪比

华理概率论习题6答案

华东理工大学概率论与数理统讣作业簿(第六册)学院 _______________ 专业 _______________班级________________学号 _______________ 姓名 _______________任课教师____________第十六次作业计算题：1 一批产品的不合格率为0.02,现从中任取40只进行检查，若发现两只或两只以上不合格品就拒收这批产品，分别用以下方法拒收的概率：(1)用二项分别作精确计算；(2)用泊松分布作近似计算。

解:设不合格得产品数为(1) >2) = 1-P(g = 0)-P(g = 1) = 1 -(O.98)40-4(0.02)(0.98)39 «0.1905.⑵利用二项分布列的泊松定理近似，得2 = ^,=40x0.02 = 0.8,> 2)«1 -严-0.W "1912.2作加法时，对每个加数四舍五入取整，各个加数的取整误差可以认为是相互独立的，都服从(-0.5,0.5)上的均匀分布。

现在有1200个数相加，问取整误差总和的绝对值超过12的概率是多少？解设各个加数的取整误差为$ (心1,2,…,1200 )。

因为§〜(,=12・・・,1200)。

设取整误差的总和为帀=土刍，因为77=1200数值很大，由定理知，这时近. — 0.5 + 0.5 t/(-0.5,0.5),所以 p = E& = --------------------------- = 0(0.5 + 0.5)2 12 1 12似有〃 =£勺〜r-1 其中，/?// = 1200x0 = 0 ,na 2 = 1200x 丄= 100 o 12所以，取整误差总和的绝对值超过12的概率为卩{| 〃| > 12 } = 1 — P{-12<;/<12}^1-①(12工\ _ ①(二］二《)ylna 2 yjna-2=1-①(皇2)_①(二二。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

华东理工大学概率论与数理统计作业簿（第二册）学院 ____________专业 ____________班级 ____________ 学号 ____________姓名 ____________任课教师____________第四次作业一．填空题：1．设事件A,B 相互独立，且5.0)(,2.0)(==B P A P ，则)(B A B P ∪＝ 4/92．设A 、B 、C 两两独立，且ABC=Φ， P(A)=P(B)=P(C)<21, 169)(=∪∪C B A P 则P(C)= 0.253. 已知事件A,B 的概率()0.4,()0.6P A P B ==且()0.8P A B ∪=，则(|)P A B =13，(|)P B A =12。

4. 已知()0.3,()0.5P A P B ==，(|)0.4P A B =，则()P AB = 0.2，()P A B ∪= 0.6，(|)P B A =23。

二．选择题：1. 设袋中有a 只黑球，b 只白球，每次从中取出一球，取后不放回，从中取两次，则第二次取出黑球的概率为（ A ）；若已知第一次取到的球为黑球，那么第二次取到的球仍为黑球的概率为（ B ）A．)(b a a + B．11−+−b a a C． )1)(()1(−++−b a b a a a D．22)(b a a +2．已知()0.7,()0.6,()0.6,P A P B P B A ===则下列结论正确的为（ B ）。

A ．AB 与互不相容； B ．A B 与独立；C ．A B ⊃；D ．()0.4P B A =.3．对于任意两事件A 和B ，则下列结论正确的是（ C ）A．一定不独立，，则若B A AB ∅=； B．一定独立，，则若B A AB ∅≠； C．有可能独立，，则若B A AB ∅≠； D．一定独立，，则若B A AB ∅= 4．设事件,,,A B C D 相互独立，则下列事件对中不相互独立的是（ C ）)(A A 与BC D ∪； )(B AC D ∪与BC ； )(C BC 与A D −； )(D C A −与BD .三．计算题：1．设有2台机床加工同样的零件，第一台机床出废品的概率为0.03，第二台机床出废品的概率为0.06，加工出来的零件混放在一起，并且已知第一台机床加工的零件比第二台机床多一倍。

（1）求任取一个零件是废品的概率（2）若任取的一个零件经检查后发现是废品，则它是第二台机床加工的概率。

解：(1)设B ={取出的零件是废品}，1A ={零件是第一台机床生产的}， 2A ={零件是第二台机床生产的}，则1221(),()33P A P A ==, 由全概率公式得：112221()(|)()(|)()0.030.060.0433P B P B A P A P B A P A =+=×+×= (2)222(|)()0.02(|)0.5()0.04P B A P A P A B P B ===2．某工厂的车床、钻床、磨床、刨床的台数之比为 1:2:3:9，它们在一定时间内需要修理的概率之比为 1:3:2:1，当一台机床需要修理时，求这台机床是车床的概率。

解：设1234,,,A A A A 分别表示车床、钻床、磨床、刨床,而B 表示“机床需要修理”,利用贝叶斯公式,得11141()()179159(|)17352715372151711522(|)()iii P A B P A P A B P B A P A =×===×+×+×+×∑3．三个元件串联的电路中，每个元件发生断电的概率依次为0.1，0.2，0.5，且各元件是否断电相互独立，求电路断电的概率是多少?解：设321A A A ,,分别表示第1，2，3个元件断电，A 表示电路断电，则321A A A ,,相互独立，321A A A A ++=，4．有甲、乙、丙三个盒子，其中分别有一个白球和两个黑球、一个黑球和两个白球、三个白球和三个黑球。

掷一枚骰子，若出现1，2，3点则选甲盒，若出现4点则选乙盒，否则选丙盒。

然后从所选的中盒子中任取一球。

求：（1）取出的球是白球的概率；（2）当取出的球为白球时，此球来自甲盒的概率。

解：设A={选中的为甲盒}， B={选中的为乙盒}， C={选中的为丙盒}，D={取出一球为白球}，则 312(),(),()666P A P B P C ===123(|),(|),(|)336P D A P D B P D C ===3112234()6363669P D =×+×+×=31363(|)489P A D ×==第五次作业一．填空题：1．某班级12名女生毕业后第一年的平均月薪分别为18002000 3300185015002900 410030005000230030002500则样本均值为2770.8 ，样本中位数为2700 ，众数为3000 ，极差为 3500 ，样本方差为10392992．设随机变量ξ的分布函数为()F x ，则{}P a ξ≥=1(0)F a −−，{}P a ξ==()(0)F a F a −−640501201101111321321321.).)(.)(.()()()()()()(=−−−−=−=++−=++=A P A P A P A A A P A A A P A P20,0(),011,1x F x Ax x x ≤⎧⎪=<≤⎨⎪>⎩则常数A 的范围为 [0,1]，{0.50.8}P ξ≤≤=_0.39A ____二. 选择题：1. 描述样本数据“中心”的统计量有（A,B,C ），描述样本数据“离散程度”的统计量有（D,E ）A ．样本均值 B. 中位数 C. 众数 D. 极差 E. 样本方差 2. 下列表述为错误的有（C ）A ．分布函数一定是有界函数 B. 分布函数一定是单调函数C ．分布函数一定是连续函数 D. 不同的随机变量也可能有相同的分布函数 3.下列函数中，可作为某一随机变量的分布函数是（ A ）（A ）x x F arctan 121)(π+= （B ） 1(1),0()20,0xe x F x x −⎧−>⎪=⎨⎪≤⎩（C ）21()1F x x=+ （D ） ()()x F x f t dt −∞=∫，其中()1f t dt +∞−∞=∫4．设概率β≥>)(1x X P ，α≥≤)(2x X P ，且21x x <，则)(21x X x P ≤< （ C ）)(A 1−+≤βα； )(B )(1βα+−≤；)(C 1−+≥βα； )(D )(1βα+−≥。

三. 计算题：1. 利用EXCEL 的数据分析工具验算填空题1. 的计算结果，并把样本数据分为四组画出频率直方图（本题可选做）66331100,,,,,12131410)(≥<≤<≤<≤<⎪⎪⎪⎩⎪⎪⎪⎨⎧=x x x x x x F 试求)3(<ξP ，)3(≤ξP ，)1(>ξP ，)1(≥ξP解：由公式()()(0)P x F x F x ξ==−−,得1(3)(30)3P F ξ<=−=,1(3)(3)2P F ξ≤==,12(1)1(1)133P F ξ>=−=−=,13(1)1(10)144P F ξ≥=−−=−=3．已知随机变量ξ只能取-2，0，2，4四个值，概率依次为,,,,2643cc c c 求常数c ，并计算(1|1)P ξξ<>−解：利用规范性，有.1254643=⇒=+++c c c c c因此,)(,)(,)(,)(15245121540522=======−=ξξξξP P P P{(1)(1)}(0)4(1|1)==(1)(0)(2)(4)9P P P P P P P ξξξξξξξξξ>−<=<>−=>−=+=+=I .第六次作业一. 填空题：1. 若随机变量~[1,6]U ξ,则方程210x x ξ++=有实根的概率为0.82. 设随机变量X 的概率密度为⎩⎨⎧≤≤=其它10)(2x Ax x f , 则A =__3__3. 设离散型随机变量ξ的分布函数为⎪⎩⎪⎨⎧≥<≤−−<=0101070100x x x x F .)(则ξ的分布律为7.0)10(=−=ξP ,3.0)0(==ξP 4. 设连续型随机变量X 的概率密度函数为(0,1)()0,(0,1)x f x x ∈=⎪∉⎩则分布函数3/20,0(),011,1x F x x x x <⎧⎪=≤<⎨⎪≥⎩二. 选择题：1．在下列函数中，可以作为随机变量的概率密度函数的是（A ） A. 2,01()0,x x f x <<⎧=⎨⎩其他B ．2,01()0,x x f x ⎧<<=⎨⎩其他C ．cos ,0()0,x x f x π≤≤⎧=⎨⎩其他D ．2,0()0,0x e x f x x −⎧>=⎨≤⎩2．下列表述中不正确有（A ，D ）A ．()F x 为离散型随机变量的分布函数的充要条件是()F x 为阶梯型函数B ．连续型随机变量的分布函数一定是连续函数C ．连续型随机变量取任一单点值的概率为零D ．密度函数就是分布函数的导数三. 计算题 1. （柯西分布）设连续随机变量ξ的分布函数为x B A x F arctan )(+= +∞<<∞−x 求：（1）系数A 及B ；(2) 随机变量ξ落在区间)1,1(−内的概率；（3）随机变量ξ的概率密度。

解: (1) 按照分布函数的定义,有()lim arctan 0,2()lim arctan 1,2x x F A B x A B F A B x A B ππ→−∞→+∞−∞=+=−=+∞=+=+=得11,2A B π==.(2) 1(11)(11)(1)(1)2P P F F ξξ−<<=−<≤=−−=. (3) 2111()()arctan ,2(1)p x F x x x x ππ′⎛⎞′==+=−∞<<+∞⎜⎟+⎝⎠2．学生完成一道作业的时间Χ是一个随机变量，单位为小时，它的密度函数为其他5.000)(2≤≤⎩⎨⎧+=x xcx x p（1）确定常数c ；（2）写出Χ的分布函数；（3）试求在20min 内完成一道作业的概率；（4）试求10min 以上完成一道作业的概率。

解:(1)利用规范性,有0.52011()()21248c p x dx cx x dx c +∞−∞==+=+⇒=∫∫. (2)当0x <时,()()00xx F x p t dt dt −∞−∞===∫∫,当00.5x ≤<时,23201()()(21)72xxF x p t dt t t dt x x −∞==+=+∫∫, 当0.5x ≥时,0.520()()(21)1xF x p t dt t t dt −∞==+=∫∫,综上所述,320, 0,1()7, 00.5,21, 0.5.x F x x x x x <⎧⎪⎪=+≤<⎨⎪≥⎪⎩(3)11170()(0)3354P F F ξ⎛⎞<≤=−=⎜⎟⎝⎠. (4)12216111031031()((21)66108108P F or x x dx ξ⎛⎞>=−=+=⎜⎟⎝⎠∫3. 袋内有5个黑球3个白球,每次抽取一个不放回,直到取得黑球为至。