波的叠加之振动与波-Read
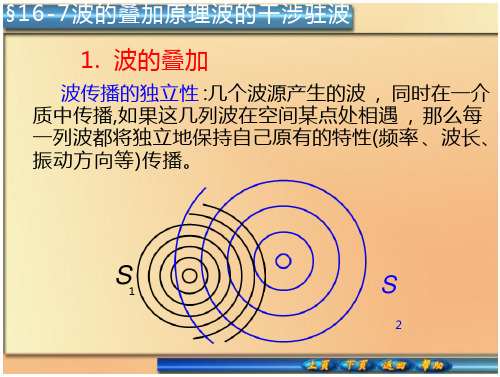
波的叠加原理-全文可读
率和波数分别为
波速
群速度
两个频率相近 、等振幅的简谐波叠加的结果是一
个振幅缓慢变化的波,它的角频率为 ,波数为 ,波
速为
。它的振幅的变化也像一个传播的波,
它的角频率为 , 波数为 ,波速为
。
上述讨论的合成波称为波包。
3. 驻波
驻波是两列振幅相同的相干波在同一条直 线上沿相反方向传播时叠加而成的。
驻 波 的 形 成
P
S1和S2单独存在时,在P点引起的振动的方程为 :
波的干涉
P点的合方程为 :
振幅A和相位
f0
对于P点
为恒量,
因此A也是恒量 ,并与P点空间位置
A=A A(合振幅最大)
.当
时,得
(合振幅最小)
当 为其他值时 ,合振幅介于
和
之间
若f 10=f 20,上述条件简化为:
(合振幅最大) (合振幅最小)
波的干涉
干涉现象的强度分布
波的干涉
例题16- 10 试计算并分析两个频率相近 、振幅相等 、 同方向振 动的简谐波的叠加。
解 波动方式: 叠加后得到
y
x
波的干涉
y
令
或。
或
变化缓慢(对应包络曲线)
x
波的干涉
把
看成是一个角频率为 、波数为
的波 ,这个波的速度为:
相速度
Am (x,t)具有沿x方向传播的简谐波的形式,它的角频
波的干涉
波程差 两列相干波源为同相位时 ,在两列波的叠加的区 域内 ,在波程差于零或等于波长的整数倍的各点 ,振 幅最大;在波程差等于半波长的奇数倍的各点 ,振幅 最小。 因
若I 1=I2,叠加后波的强度:
波的叠加原理.

返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
x l
cos
2π
t T
振幅
A´ =
2Acos2π
x l
结束 返回
振幅:
A´ =
2Acos2π
x l
波腹位置:
2π
x l
=
2k
π
2
波节位置:
2π
x l
=( 2k+1)π2
x
=2k
l 4
x =(2k+1)l4
相邻两波节(或波腹)的距离:
x k+1
x
k
=
l
2
结束 返回
驻波
波腹
波节
结束 返回
驻波
波腹
波节
结束 返回
二、波的干涉
相干波源:若有两个波源,它们的振动
方向相同、频率相同、周相差恒定,称这两
光波的叠加

合振动的大小和方向都是随时间变化的。消去参数t 合振动的大小和方向都是随时间变化的。消去参数t,得 合振动矢量末端运动轨迹方程为: 合振动矢量末端运动轨迹方程为:
Ex E y E + 2 −2 cos(α 2 − α1 ) = sin 2 (α 2 − α1 ) a a2 a1a2
其中
2 x 2 1
§11-5 11-
光波的叠加
一、波的叠加原理(振动的合成) 波的叠加原理(振动的合成) 两个或多个光波在空间某一区域相遇时,发生光波的叠加。 两个或多个光波在空间某一区域相遇时,发生光波的叠加。 频率、振幅、位相都不相同的光波叠加较复杂, 频率、振幅、位相都不相同的光波叠加较复杂,本章只讨 频率相同或频率相差很小的单色光波的叠加 的单色光波的叠加。 论频率相同或频率相差很小的单色光波的叠加。 实际光源发出的光波不能认为是余弦或正弦函数表示的单 色光波, 色光波,但可以将任何复杂的波动分解为一组由余弦函数 和正弦函数表示的单色波之和。 和正弦函数表示的单色波之和。因此讨论单色光波有实际 意义。 意义。 波的叠加原理: 波的叠加原理:几个波在相遇点产生的合振动是各个波单 独产生的振动的矢量和。 独产生的振动的矢量和。 叠加原理是波动光学的基本原理。 叠加原理是波动光学的基本原理。
2 Ex E y E x2 E y + 2 −2 cos δ = sin 2 δ a12 a2 a1a2 (1) δ = 0, ± 2π 整数倍时 E = a2 E y x a1
表示合矢量末端的运动沿着一条经过坐标原点其斜率 的直线进行,其合成光波是线偏振光。 为 a2 a1 的直线进行,其合成光波是线偏振光。 在垂直于传播方向的平面内, 在垂直于传播方向的平面内,光矢量只沿某一个固定方向 振动,则称为线偏振光,又称为平面偏振光或线偏振光。 振动,则称为线偏振光,又称为平面偏振光或线偏振光。 13
波的叠加

k 0,1,2,3,... 干涉相长
k 0,1,2,3,... 干涉相消
初位相相同的两个相干波源,在两列波叠加的 区域内,当波程差为零或波长的整数倍时,合振动 的振幅最大,干涉相长;当波程差为半波长的奇数 倍时合振幅最小,干涉相消。
r1 r2 (2k 1) , 2
相对于介质,波源不动,观察者在运动。 u vR u vR ' vs 0, vR 0 u vS u u vR ' 观察者背着波源运动, vR 0 u u vR ' 观察者向着波源运动, vR 0 u
Vs 表示波源相对于介质的运动速度。
u 声波的速度—只与介质性质有关,与波 源、观 察者运动无关。
(1)考虑波源(声源)的运动 声源以速度VS运动,在一个 周期T内由S点运动到S’点。
S
v sT
S'
uT
A
x
因为声速和声源的运动无关,S’和A两个振动状 态相同(同相)。 这相当于把声源静止时的波长,由于声源的运动 而被压缩在S’A之间了,
二、波的干涉
1.波的干涉现象 频率相同、振动方向相同、有恒定位相差的两 列波(或多列波)相遇时,在介质中某些位置的点 振幅始终最大,另一些位置振幅始终最小,而其它 位置,振动的强弱介乎二者之间,保持不变。称这 种稳定的叠加图样为干涉现象。
源满 2.相干条件 称足 为相 1.两列波振动方向相同; 相干 干条 波件 2.两列波频率相同; 源的 3.两列波有稳定的相位差。 。 波
u vs vs T v v u vs v
波长变为:
uT
S
Vs VsT
振动和波详述

第二节 波动学基础
惠更斯原理:在波的传播过程中,波阵面上的每一 点都可以看作发射次级子波的波源,在其后的任一 时刻,这些子波的包迹就成为新的波阵面.
ut
平 面 波
球 面 波
R1
O
R2
第二节 波动学基础
二、 波动方程(平面简谐波的波函数)
介质中任一质点(坐标为 x)相对其平衡位置的
位移(坐标为 y)随时间的变化关系,即 y(x,t) 称
G 切变模量
E 弹性模量
K体积模量
横波 纵波
343 m s 空气,常温
如声音的传播速度
4000 m s 左右,混凝土
第二节 波动学基础
例1 在室温下,已知空气中的声速 u1为340 m/s, 水中的声速 u2 为1450 m/s ,求频率为200 Hz和2000 Hz
的声波在空气中和水中的波长各为多少?
x/m
-1.0
t 1.0 s 时刻波形图
第二节 波动学基础
3) x 0.5m 处质点的振动规律并做图 . y (1.0m) cos[2 π( t - x ) - π] 2.0s 2.0m 2
x 0.5m 处质点的振动方程
y (1.0m) cos[(πs-1)t - π]
y
y/m
3
1.0
3*
Tλ
y(x,t) Acos(t - kx )
➢ 质点的振动速度,加速度
角波数 k 2π
v y -Asin[(t - x) ]
t
u
a
2 y t 2
-
2
A cos[ (t
-
x) u
]
第二节 波动学基础
例1 已知波动方程如下,求波长、周期和波速.
光波的叠加

π
2
的奇数倍时, 的奇数倍时, E +
a
2 x 2 1
2 Ey
a
2 2
=1
这是一个正椭圆方程,其长、短轴分量分别在X 这是一个正椭圆方程,其长、短轴分量分别在X、Y坐标 轴上,表示合成光波是椭圆偏振光。 轴上,表示合成光波是椭圆偏振光。 若
a1 = a2 = a
则
E +E =a
2 x 2 y
2Hale Waihona Puke 合矢量末端运动轨迹是一个圆, 合矢量末端运动轨迹是一个圆,此时合成光波是圆偏振 光。
I 0 = a 2 表示单个光波在P点的强度 表示单个光波在P δ = α 2 − α1 表示两光波在P点的相位差 表示两光波在P
2 I = A2 = a12 + a2 + 2a1a2 cos(α 2 − α1 )
P点合振动的光强得
I = 4 I 0 cos
2
δ
2
在P点叠加的合振动的光强I取决于两光波在叠加点的相位差。 点叠加的合振动的光强I取决于两光波在叠加点的相位差。 4
A = 2a cos(kz + ) 2
不同的Z值处有不同的振幅, 不同的Z值处有不同的振幅,但极大值和极小值的位置不 随时间而变。 随时间而变。 振幅最大值的位置称为波腹, 振幅最大值的位置称为波腹,其振幅等于两叠加光波的 波腹 振幅之和,而振幅为零的位置称为波节 波节。 振幅之和,而振幅为零的位置称为波节。 波腹的位置由下式决定 波节的位置由下式决定
11
把合矢量以角频率周期旋转, 把合矢量以角频率周期旋转,其矢量末端运动轨迹 为椭圆的光称为椭圆偏振光。 为椭圆的光称为椭圆偏振光。 椭圆偏振光 两个频率相同, 两个频率相同,振动方向互相垂直且具有一定位相差的 光波的叠加,一般可得到椭圆偏振光。 光波的叠加,一般可得到椭圆偏振光。 椭圆的形状取决于两叠加光波的振幅比 a2 a1 和相位差 光矢量在垂直于光的传播方向的平面内, 光矢量在垂直于光的传播方向的平面内,按一定频率旋 转(左旋或右旋)。如果光矢量的端点轨迹是一个椭圆, 左旋或右旋) 如果光矢量的端点轨迹是一个椭圆, 这种光叫做椭圆偏振光。 这种光叫做椭圆偏振光。
波的叠加——精选推荐

波的叠加学习目标:(1)知道波的叠加原理①知道两列机械波在传播过程中相遇,会按照各自的方向传播而互不干扰。
②知道两列机械波在相遇的区域内的介质质点同时参与两列波所引起的振动,质点的位移等于两列波所引起的位移的矢量和。
(2)知道波的干涉现象①知道什么是波的干涉现象。
②知道要得到稳定的干涉现象,叠加的两列波的波长必须相等。
③会用波的叠加原理解释干涉现象,知道到两振源的距离之差等于波长的整数倍的点是振动加强点;到两振源的距离之差等于半波长的奇数倍的点是振动减弱点。
(3)知道波的衍射现象①知道什么是波的衍射现象。
②知道能观察到明显衍射现象的条件是:障碍物或孔的大小可以与波长相比拟。
(4)知道波的干涉现象和衍射现象都是波的特有现象。
重点难点:重点:重点理论是波的叠加原理,重点知识是波的干涉和衍射,这是波的标志现象。
难点:对波的干涉和衍射的理解。
知识讲解:一、波的反射和折射波遇到障碍物返回来继续传播的现象叫做波的反射现象。
波的反射现象是很普遍的现象,如回声是声波的反射现象。
对水来说深水区与浅水区是不同的两种介质,由于水波在这两种介质中传播速度不同,当波由一种介质进入另一种介质时,在两种介质的界面上传播方向发生改变,这种现象叫做波的折射现象。
二、波的叠加原理几列波相遇时,能够保持各自原来的运动状态而互相不干扰,只是在它们重叠的区域里,介质中每个质点同时参与这几列波引起的振动,质点的位移等于这几列波分别引起的振动位移的矢量和,这就是波的叠加原理。
三、波的干涉波长相同的两列波叠加,使某些区域的振动加强,某些区域的振动减弱,并且振动加强和振动减弱的区域互相间隔并处于稳定状态,这种现象叫做波的干涉(interference),形成的图样叫干涉图样。
干涉条件:要得到稳定的干涉现象,叠加的两列波的波长必须相同(也就是频率相同)。
机械波的叠加规律适用于一切波。
所以,一切波都能发生干涉,干涉是波的特有现象之一。
关于波的干涉应注意理解以下几点:①任何两列波相遇时都可以叠加,而两列波要发生干涉必须具备一定的条件(两列波的波长必须相同),通常把符合干涉条纹的两列波的波源叫相干波源。
一波的叠加原理(superpositionprinciple).

15m
A 20m B
10 m 0.10 m 100
设 A 的相位较 B 超 前,则 A B π .
u
B A 2π
点P 合振幅
青岛科技大学
BP AP
25 15 π 2π 201 π 0.1 A A1 A2 0
1)振幅 2 A cos 2π
x
随 x 而异, 与时间无关.
cos 2 π
x
1
2π
x
0
x
k 0,1, Amax 2 A 2 1 (k ) k 0,1, Amin 0 2 2 相邻波腹(节)间距 2 相邻波腹和波节间距 4
青岛科技大学
k
1 2 π (k ) π 2
驻波的能量在相邻的波腹和波节间往复变化, 在相邻的波节间发生动能和势能间的转换,动能 主要集中在波腹,势能主要集中在波节,但无长 距离的能量传播.
青岛科技大学 大学物理讲义
七
振动的简正模式(normal mode)
最低频率 1 称为 基频
频率 n为 1的n倍, 称为n次谐频
两端固定的弦线形成驻波时,波长n 和弦线长 l 应满足 u 这些频率称为弦 n n 1 , 2 , n n 振动的本征频率 2l
2
o
2
x
x cos 2 π 0 , x , y 2 A cos 2 π x cos 2π t 4 4 x 3 x cos 2 π 0 , x , y 2 A cos 2 π cos(2 π t π ) 4 4
波之道 第三章 波的叠加与合成

第三章波的叠加与合成一、波的叠加1、几列波相遇后仍保持它们原有的特性(频率、波长、振幅、传播方向)不变,互不干扰。
好象在各自传播过程中没有遇到其它波一样。
波的独立性原理2、如果有两列以上的同类波在空间相遇,在共存的空间内,总的波是各个分波的矢量和(即相加时不仅考虑振幅,还考虑相位),而各个分波相互并不影响,分开后仍然保持各自的性质不变。
叠加性的依据是,(线性)波的方程的几个解之和仍然是这个方程的解;这个原理称叠加原理。
二、波的干涉1、波的干涉现象频率相同、振动方向相同、有恒定位相差的两列波(或多列波)相遇时,在介质中某些位置的点振幅始终最大,另一些位置振幅始终最小,而其它位置,振动的强弱介乎二者之间,保持不变。
称这种稳定的叠加图样为干涉现象。
2、相干条件1) 两列波振动方向相同;2) 两列波频率相同;3) 两列波有稳定的相位差。
满足相干条件的波源称为相干波源。
图3-1 波的干涉三、驻波有两列相干波,它们不仅频率相同、位相差恒定、振动方向相同,而且振幅也相等。
当它们在同一直线上沿相反方向传播时,在它们迭加的区域内就会形成一种特殊的波。
这种波称为驻波。
当一列波遇到障碍时产生的反射波与入射波叠加可产生驻波。
图3-2驻波驻波的特点:媒质中各质点都作稳定的振动。
波形并没有传播。
驻波的特点:媒质中各质点都作稳定的振动。
波形并没有传播。
驻波的波形、能量都不能传播,驻波不是波,是一种特殊的振动四、波的合成1)李萨如图形在实验室中,将一个正弦波信号加到示波器信号输入通道1,把另一个同样幅值正弦波信号加到示波器信号输入通道2。
这样在示波器上出现李萨如图形,如图3-3。
图3-3注意:李萨如图是一个三维运动在二维平面上的投影,但它蕴含了奇特的三维信息。
2)三相异步电动机的旋转磁场。
通常三相交流电机的定子都有对称的三相绕组。
任意一相绕组通以交流电流时产生的是脉振磁场。
但若以平衡三相电流通入三相对称绕组,就会在空间产生一个圆形旋转磁场,这可通过数学推导获的。
波的叠加原理波的干涉PPT课件

y入射波=Acos(t+2x/)
t
t
2x
反射点处的振动方程
第二步:写出入射波在反
射点的振动方程,考虑有 无半波损失,然后写出反
y MN=A cos (t - 3 / 2 +π)
射波在反射面处的振动方
在波密媒质反射有半波损失
程。
t第 数三,t步注:意x写,出u3反反射/ 4射波波的波传函播 则反射波的波动方程为
振幅皆为A=5 cm, 频率皆为100 Hz, 但当点A为波峰时,
点B适为波谷。设波速为10 m/s, (A、B两波源的振动垂
直于平面),试写出由A、B发出的两列波传到P点时干涉
的结果。
P
解:
u n
0 .1
m
15 m
设A的相位较B超前,则
A0 B0
A
20 m
B
则P点的相位差应为
201
合振幅 A A12 A22 2A1 A2 cos A 2 2A2 cos( ) 0 P点因干涉而静止。
凡是使
cos
2x
0
的各点相位为2nt。
凡是使
2x
cos
0的各点相位为-2nt。
而
cos
2x
0
的各点即波节处不振动。
因此相邻的波节之间的相位是相同的,而波节的两边
相位相反。
同一波节间的各点步调一致,相邻波节间各点的步 调正好相反。 (c) 考察驻波的能量
当各质点振动达到最大位移时,各质点动能为零,驻 波能量为势能,波节处形变最大,势能集中在波节。
一、波的叠加
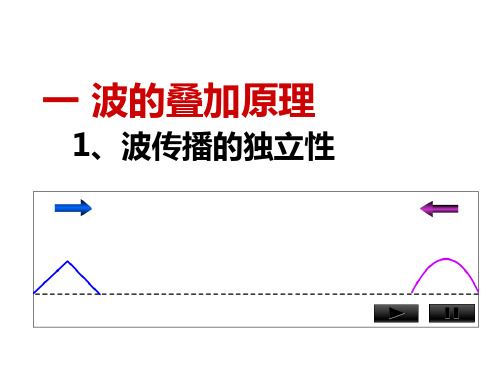
(1)几列波相遇后,仍保持它们原有的特性(频率、波长、 振幅、振动方向等)不变,并按照原耒的方向继续前进,即 各波互不干扰-----波传播的独立性。
波的叠加、干涉和衍射
实例1、在水塘里,微风激起的水 波遇到突出水面 的小石子、芦 苇, 会绕过他们继续传播,好象他 们 并不存在
实例2、听其声不见其人。 实例3、隔墙有耳
一、波的衍射
• 点击下图观看动画
现象:水波绕过小孔继续传 播.
一、衍射现象
波能绕过障碍物继续传播的 现象,叫做波的衍射。
衍——展延之意 波的衍射——波展延到“影子”区域 里的现象。
发生明显衍射现象的条件:
• 只有缝、孔的宽度或障碍物的尺寸跟波 长相差不多,或者比波长更小时,才能 观察到明显的衍射现象.
• 注意: 一切波都能发生衍射,而要发生
明显的衍射现象须满足上述条件,当不 满足上述条件时,衍射现象仍存在,只 不过是衍射现象不明显,不易被我们观 察到
小结:
1、衍射是波特有的现象,一切波都会产生衍 射现象。
波都要引起介质质 点振动,为什么有 的点的振幅很大, 而另一些点的振幅 却几乎为零呢?
二 波的干涉
加 强 减 弱
某些点振动始终加强,另一些点振 动始终减弱或完全抵消.
三.波的干涉
前言
当同一质元同时参与两个或两个以上的振动时, 该质点的振动是所有分振动的合振动。当介质中有两 列或两列以上的波动时,介质中任一质元运动情况如 何? 当介质中有两列或两列以上的波动时,介质 中任一质元也将同时参与两个或两个以上的振动。 现在讨论其规律,也就是波的合成。
一 波的叠加原理
1、波传播的独立性
几列波相遇之后, 仍然 保持它们各自原有的特征 (频率、波长、振幅、振动 方向等)不变,并按照原来 的方向继续前进,好象没有 遇到过其他波一样.
叠加
频率相同的两列波叠加
实 验 演 示
振动加强
振动减弱
波的叠加

1.加强条件
2 1
2
2 cos r2 r1 2 1 1
r2 r1 2k
( k 0,1,2) ( k 0,1,2)
当 1 2 时,波程差为 r r2 r1 k
A A1 A2 当波程差为波长的整数倍时加强。
2 A A A 2 A1 A2 cos r2 r1 2 1
2 1 2 2
2.减弱条件
2 1
2
2 cos r2 r1 2 1 1
r2
为同方向同频率振动合成。合成后振幅为
2 A A A 2 A1 A2 cos r2 r1 2 1
2 1 2 2
2 A A A 2 A1 A2 cos r2 r1 2 1
当 1 2 时,波程差为 r r2 r1 (2k 1) , 2
r2 r1 (2k 1) , ( k 0,1,2)
( k 0,1,2)
A | A1 A2 |
当波程差为半波长的奇数倍时减弱。
例:两相干波源 A、B 位置如图所示,频率 =100Hz,波速 u =10 m/s,AB=,角A为 直角。求:P 点振动情况(加强或减弱)。
2.两列波频率相同;
3.两列波有稳定的相位差。
四.加强减弱条件
两列波
t r1 y1 A1 cos 2 1 T t r2 y2 A2 cos 2 2 T
P
r1 S1 S2
解:rA 15m
波的叠加计算方法

波的叠加计算方法波的叠加呢,简单来说就是当几列波在同一个空间区域相遇的时候,它们就会叠加起来。
就像一群小伙伴凑到一块儿似的。
那怎么计算呢?如果是两列波的叠加,咱们先得知道这两列波在每个点的振动情况。
比如说波的表达式,像y1 = A1sin(ω1t + φ1)和y2 = A2sin(ω2t + φ2),这里的A就是振幅啦,表示波振动的幅度大小;ω是角频率,和波的周期、频率有关;φ呢就是初相位,就像是波出发时候的初始状态。
当这两列波叠加的时候,在某一时刻t、某一位置x处的合振动就等于这两列波单独存在时在这个位置、这个时刻的振动之和。
也就是y = y1 + y2,把表达式带进去就是y = A1sin(ω1t + φ1)+A2sin(ω2t + φ2)。
要是这两列波的频率相同,也就是ω1 = ω2的时候,那计算就会变得稍微简单一点。
咱们可以利用三角函数的一些小技巧来化简这个式子。
这时候合振动的振幅就不是简单的A1+A2了哦,它还和初相位差有关系呢。
宝子,你可别被这些公式吓着哈。
其实就像搭积木一样,每块积木(每个波的参数)都有它自己的作用,咱们只要按照规则把它们组合起来就好啦。
而且啊,在实际问题里,可能还会有一些特殊情况。
比如说有一列波很强,另一列波很弱,那叠加后的波就会更偏向于强波的样子,但弱波也还是有一丢丢影响的。
如果是多列波的叠加呢,原理也是一样的,就是把每列波在那个点的振动都加起来。
不过随着波的数量增多,计算可能会变得复杂一些,但只要咱们一步一步来,就像走小台阶一样,也没那么难啦。
总的来说,波的叠加计算就是要先搞清楚每列波自己的情况,然后按照叠加的规则把它们合到一起,就像是把不同颜色的丝线编织成漂亮的彩带一样有趣呢。
波的叠加原理与驻波现象

振动方向:在波的叠加区域,合成 振动的方向取决于各列波的振动方 向和相位。
振动速度和加速度:合成振动的速 度和加速度也是各列波单独产生的 速度和加速度的矢量和。
波的干涉现象
定义:两个或多个波在空间相遇时,产生相互加强或减弱的现象 条件:频率相同、相位差恒定 结果:形成稳定的加强区和减弱区 应用:干涉仪、双缝干涉实验等
波的叠加原理与驻波现 象
汇报人:XXX
目录
波的叠加原理
01 波动能量 04 驻波现象
02 波的传播介质 05 波动方程
03
波的叠加原理
多个波在同一直线上传播时,它们的振幅相加,产生新 的波。
波的独立传播特性:每个波独立传播,不受其他波的影响。
波的独立传播条件:各波源产生的波在同一直线上传播,且波速相同。
波动能量的计算
波动能量的定义:指在波动过程中, 介质中质点振动的动能和势能之和。
波动能量的计算公式: E=1/2mv^2+1/2Iω^2,其中E为能 量,m为质量,v为速度,I为转动 惯量,ω为角频率。
波动能量的物理意义:表示介质在 单位时间内所吸收或释放的能量。
波动能量的影响因素:波速、波长、 频率和介质的性质等。
干涉现象的应用
电子显微镜: 利用干涉现象 提高成像质量
光学仪器:通 过干涉现象提
高测量精度
量子力学:干 涉现象是量子 力学中的重要
概念
医学成像:干 涉现象在医学 成像技术中有
广泛应用
驻波现象
驻波的形成
两个或多个波源产生的振动波在同一直线上传播时相互作用 波源的频率相同或相近,振动方向相同 波源的初相位相同或相差整数倍的整数倍 波源振幅不同,最大振幅的波节位置不同
波的叠加原理

j
A1 sin ( j 1
合振动的初相位
A1 cos ( j 1
2pr1 ) A2 sin ( j 2 l 2pr1 ) A2 cos ( j 2 l
两相干波源的振动方程
合成振幅公式
A1
y10 y20
A1cos (w t + j 1) A2cos (w t + j 2) A1 cos w t + ( j 1 A2 cos w t + ( j 2 A1
2
A
A2
分别引起 P 点的振动
y1 y2
2pr1 ) l 2pr2 ) l
合振动
y
y1 + y2
A cos (w t + j )
j1
l y1 y2 两振 2pr2 ) 2pr1 ) j j A2 sin ( 2 A sin ( 1 动的相位差 1 l l j 2 p r 2 p r 2 ) 1 j P点给定,则 A1 cos 恒定。 故空间每一点的合成振幅 A 保持恒定 ) j A cos ( 2 ( 1 2 l l
) A cos 2π (t
波程差为零或为波长的整数倍时, 各质点的振幅最大,干涉相长。
波的干涉:
在两相干波的交叠区域内,有的 地方振动始终加强,有的地方振动始终 削弱,而其它位置的振动的强弱介乎二 者之间,形成振动强弱稳定分布的叠加 现象,称为波的干涉现象。
总结:波的干涉
(1) 相干波源的条件 ①频率相同; ②振动方向相同; ③相位差恒定。
(2)在A点左侧:
j j B j A
干涉相长。
30 x ) ( x ) 2p 14p
波的叠加、驻波

2 A12 + A2 + 2 A1 A2 cos[ϕ 2 − ϕ 1 −
2π
λ
( r2 − r1 )]
ϕ = arctg
λ λ 2π r1 2π r2 A1 cos( ϕ 1 − ) + A2 cos( ϕ 2 − ) λ λ
A1 sin( ϕ 1 −
2π r1
) + A2 sin( ϕ 2 − 2π
× × ×
√
2. 教材 教材P.509 已知: 已知:
15.3 u p S1
P.88 (13-16)
λ ⁄4
S2
u p′
λ , I 1 = I 2 = I 0 , ϕ 10 − ϕ 20 = π S1、 S 2为相干波源,相距 4
求:
2
S 1、 S 2 连线上, S 1外侧, S 2 外侧合成波强度
u入
O
3λ 4
P
解:1) t=0时 原点处 O
疏 密
u入
3λ 4
P
x
ψ 0 = 0,
v 0 > 0,
原点初相 ϕ 0 = −
取决于两波传至相遇点的波程差: ∆ϕ 取决于两波传至相遇点的波程差:δ = r2 − r1
对空间确定点
r1 o1 r2 o2
δ有确定值,I 有确定值
对空间不同点
p
δ 彼此不同, I 彼此不等
能量在空间稳定的非均匀分布 — 干涉现象
相同的点,振动强度相同, δ = r2 − r1 相同的点,振动强度相同, 其集合为双曲面 其集合为双曲面 合振动最强(干涉相长) 合振动最强(干涉相长) 的位置? 的位置 合振动最弱(干涉相消) 合振动最弱(干涉相消)
7.5波的叠加原理和波的干涉

7.5 波的叠加原理和波的干涉
所以,振动加强,合振幅
A1 2 A
I1 4I 0
I1 A12 2 4 I0 A
在S 2 外侧
3 ' 2 4
2
所以,振动减弱 所以,应该选
A2 0
I2 0
D
波传播的独立性:多列波在某区域相遇后 再分开,各自都能保持原来的特性(频率、波长、 振幅、振动方向和传播方向)不变,互不干扰 波的叠加性:在相遇区域,质点的振动为各 列波单独存在时在该点引起的振动的合成.该 相遇点的合位移等于各列波单独存在时在该 点引起的位移的矢量和
7.5 波的叠加原理和波的干涉
称为波程差波走过的路程之差如果即波源s1s2同初相位加强减弱75波的叠加原理和波的干涉将合振幅加强减弱的条件转化为干涉的波程差条件则有干涉的波程差条件振动加强振动减弱记住记住75波的叠加原理和波的干涉在两波源连线上因干涉加强振幅最大和干涉减弱振幅最小的点的位置
7.5 波的叠加原理和波的干涉 一 波的叠加原理
7.5 波的叠加原理和波的干涉
将合振幅加强、减弱的条件转化为干涉 的波程差条件,则有
干涉的波程差条件 当 r1 r2 k 时(半波长偶数倍)
Amax A1 A2 振动加强 记住 当 r r (2k 1) 时(半波长奇数倍) 1 2 2 合振幅最小 Amin A1 A2 振动减弱 记住
y2 A cos[ t
2x1
)
]
2 ( x x1 )
(3) 两列波在 P点的相位差为
2 (t ) 1 (t ) 2 2 2 x1 x x1 ( x x1 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
波的叠加之振动与波
背景: 波的叠加在生活中并不罕见,例如:水波的叠加;军事上用的电磁干扰,还有高
中所学的光的双缝干涉。
因此波的叠加也就不是一个陌生的概念。
波的叠加有其独特性:在相遇点,几列波互不影响,各自给出一份贡献,使该点做合成运动,且几列谐波合成仍为谐振动;相遇点外,各点振动由波源和距离共同确定。
下面具体分析波的叠加中的两种特殊模型——干涉和驻波,并在a 盘中给出波的干涉图象的源程序。
模型1:波的干涉.条件:(1)几列波的振动方向相同;(2)频率相同;(3)波源相位差恒定。
设同一平面上o ,p 两波源为干涉波,振幅分别为a1,a2,设t 时刻o 点相位1ϕ+wt ,p 点相位 2ϕ+wt ,同一t 时刻,对此平面任一H 点,引起的振动相位为:11kr wt -+ϕ
第二列波在p 引起振动相位为: 22kr wt -+ϕ
有 ϕ∆++=cos 2212221a a a a a p
)(1221r r k ---=∆ϕϕϕ
当
πϕn 21±= , n=0,1,2,……时, 21m a x a a a a +== 干涉加强 πϕ)12(1+±=n , n=0,1,2,……时, 21min a a a a -== 干涉减弱
21a a =时, a=0 因干涉而静止。
其它点 max min a a a <<
模型2: 驻波。
两相干波在同一直线上沿相向传播,且 21a a =
设驻波中两波方程分别为: )c o s (1ky wt a x -=
)cos(2ky wt a x +=
设021==ϕϕ,则驻波方程为:wt ky a x x x cos cos 2221==
+=λπ 从中可知,振幅极大为2a ,
此时 πn ky ky =±=,1cos
腹点坐标: λ2
n y =
向邻腹点间距: λ2
n y =∆ 节点坐标: 4)12(λ
+=n y
当然,波的干涉和叠加还有许多应用,此处不在细述。
