振动与波习题课
合集下载
第4章振动与波动习题课
A 0.5 cm
π 3
(2)
π v 4π sin(8πt ) 2 3π cm/s 3
π a 32π 2 cos(8πt ) 16π 2 cm/s2 3
(3)
k m 2 3.2 2 N/m
第四章习题解答
4-4. 已知弹簧振子的振动曲线如图。试求：（1）图中所标 ABCDE各点的相位，并画出旋转矢量图；（2）振动方程的表 达式。
2π 4π 解： T 1 π (1) cos ，v0 0 2 3
x 2.0 10 cos(4πt
2
1 4π (2) cos ，v0 0 2 3 4π 2 x 2.0 10 cos(4πt ) m 3
第四章习题解答
解： (1)
π 如图： A点相位为 0，B点相位为 ， 3
0 x/cm
10 5
A B
1.0
C点相位为
π 2π 4π ，D点相位为 ，E点相位为 2 3 3
2.2
t/s
C
-10
D
E
A 10 cm
T 1.2 2 2.4 s
2 π 5π T 6 1 π (2) cos ，v0 0 2 3 5π π x A cos( t ) 10cos( t ) cm 6 3
t/s
0 1 -0.2
t/s
2
-0.2
( b)
x=2m处质元的振动曲线
第四章习题解答
4-26. 一列沿x轴正方向传播的平面简谐波在t=0s时的波形如图所 示，设波速为 u 4 m/s 。求：（1）波长、周期、角频率；（2） 写出此波的波动方程；（3）在图上画出t等于四分之一周期时的波 形图并标出波的传播方向。 y/m u T 5s 解：(1) λ 20 m 0.05 u 2π 2 π 20 x/m 0 10 T 5 π -0.05 (2) cos 0，v0 0 2 x π 2π y 0.05cos ( t ) m 4 2 5 (3)
振动与波习题课及课后作业解答
O B N X
π
2π
λ
2OB π = 5π
2π
= 入 反 = π
λ
x (5π +
2π
λ
x) = 6π
4π
2kπ , 波腹 = (2k + 1)π , 波节
0≤x≤1.25λ ≤ ≤ λ
λ
x
3. 空气中声速为 空气中声速为340m/s, 一列车以 一列车以72km/h的速度行驶 车上旅客 的速度行驶, 的速度行驶 听到汽笛声频率为360Hz, 则目送此火车离去的站台上的旅客听到 听到汽笛声频率为 此汽笛声的频率为( 此汽笛声的频率为 B) (A) 360Hz (B) 340Hz (C) 382.5Hz (D) 405Hz 解:
t = ( / 2π )T = T / 12 6
A/2 -π/3
π
ω
x
A
2. 如图为用余弦函数表示的一质点作谐振动曲线 振动圆频率 如图为用余弦函数表示的一质点作谐振动曲线, ,从初始状态到达状态 所需时间为 2s 从初始状态到达状态a所需时间为 . 为 7π/6 π 从初始状态到达状态 分析: 分析:本题的关键是确定各时刻 X(m) 6 的位相, 的位相,在振动曲线上由位移和 3 速度方向(斜率的正负) 速度方向(斜率的正负)定 0 t=0时: -3 X0=A/2,v0<0 = π/3 t=1时: X=0,v>0 ωt+= 3π/2
u vs
s
u = 334m s 1 (3)
u v0 ( 4) λ ′ = ν′ 334 65 = = 0.190m 1418
ω
t = 0, v0 = ωA sin 0 = 10cm / s
3 ∴0 = π 2
π
2π
λ
2OB π = 5π
2π
= 入 反 = π
λ
x (5π +
2π
λ
x) = 6π
4π
2kπ , 波腹 = (2k + 1)π , 波节
0≤x≤1.25λ ≤ ≤ λ
λ
x
3. 空气中声速为 空气中声速为340m/s, 一列车以 一列车以72km/h的速度行驶 车上旅客 的速度行驶, 的速度行驶 听到汽笛声频率为360Hz, 则目送此火车离去的站台上的旅客听到 听到汽笛声频率为 此汽笛声的频率为( 此汽笛声的频率为 B) (A) 360Hz (B) 340Hz (C) 382.5Hz (D) 405Hz 解:
t = ( / 2π )T = T / 12 6
A/2 -π/3
π
ω
x
A
2. 如图为用余弦函数表示的一质点作谐振动曲线 振动圆频率 如图为用余弦函数表示的一质点作谐振动曲线, ,从初始状态到达状态 所需时间为 2s 从初始状态到达状态a所需时间为 . 为 7π/6 π 从初始状态到达状态 分析: 分析:本题的关键是确定各时刻 X(m) 6 的位相, 的位相,在振动曲线上由位移和 3 速度方向(斜率的正负) 速度方向(斜率的正负)定 0 t=0时: -3 X0=A/2,v0<0 = π/3 t=1时: X=0,v>0 ωt+= 3π/2
u vs
s
u = 334m s 1 (3)
u v0 ( 4) λ ′ = ν′ 334 65 = = 0.190m 1418
ω
t = 0, v0 = ωA sin 0 = 10cm / s
3 ∴0 = π 2
振动和波习题课(级)
Y
能量极 小
X
能量极 大
能量极大
能量极 小
16、惠更斯原理：波阵面上的每一点，都是发射 子波的新波源，其后任意时刻，这些子波的包络 面就是新的波阵面。
17、相干条件：两波源应满足：振动方向相同，
频率相同，位相差恒定。
18、波的干涉 在P点引起的合振动的振幅为：
2 1 2 2
S2 S1
r2
p
2 ( 2 1 )＋ ( r1 r2 ) A A A 2 A1 A2 cos S1 r1 若波在两种不同介质中传播
2
y a O b u x
[A]
11.一质点同时参与了三个简谐振动，它们的振动 1 5 方程分别为 x1 A cos( t π ) x2 A cos( t π)
x3 A cos( t π ) 其合成运动的运动方程为x = ___ 0 ．
3
3
12. 一简谐波沿x轴负方向传播，波速为1 m/s，在 x轴上某质点的振动频率为1 Hz、振幅为0.01 m．t =0 时该质点恰好在正向最大位移处．若以该质点 的平衡位置为x轴的原点．求此一维简谐波的表达 式． 结 果 : y 0 . 01 cos 2π ( t x ) (SI) 13. 当机械波在媒质中传播时，一媒质质元的最大 变形量发生在 : (A) 媒质质元离开其平衡位置最大 位移处． (B) 媒质质元离开其平衡位置( 2 A / 2 )处 (A是振动振幅)． (C) 媒质质元在其平衡位置处． 1 [C] (D) 媒质质元离开其平衡位置 2 A 处.
2
2
(C)
3 x2 A cos( t π ) 2
t π ) [B] (D)x2 A cos(
能量极 小
X
能量极 大
能量极大
能量极 小
16、惠更斯原理：波阵面上的每一点，都是发射 子波的新波源，其后任意时刻，这些子波的包络 面就是新的波阵面。
17、相干条件：两波源应满足：振动方向相同，
频率相同，位相差恒定。
18、波的干涉 在P点引起的合振动的振幅为：
2 1 2 2
S2 S1
r2
p
2 ( 2 1 )＋ ( r1 r2 ) A A A 2 A1 A2 cos S1 r1 若波在两种不同介质中传播
2
y a O b u x
[A]
11.一质点同时参与了三个简谐振动，它们的振动 1 5 方程分别为 x1 A cos( t π ) x2 A cos( t π)
x3 A cos( t π ) 其合成运动的运动方程为x = ___ 0 ．
3
3
12. 一简谐波沿x轴负方向传播，波速为1 m/s，在 x轴上某质点的振动频率为1 Hz、振幅为0.01 m．t =0 时该质点恰好在正向最大位移处．若以该质点 的平衡位置为x轴的原点．求此一维简谐波的表达 式． 结 果 : y 0 . 01 cos 2π ( t x ) (SI) 13. 当机械波在媒质中传播时，一媒质质元的最大 变形量发生在 : (A) 媒质质元离开其平衡位置最大 位移处． (B) 媒质质元离开其平衡位置( 2 A / 2 )处 (A是振动振幅)． (C) 媒质质元在其平衡位置处． 1 [C] (D) 媒质质元离开其平衡位置 2 A 处.
2
2
(C)
3 x2 A cos( t π ) 2
t π ) [B] (D)x2 A cos(
振动和波习题课
振动和波习题课壹内容提要一. 振动1.简谐振动的定义：恢复力F=-kx微分方程d2x/d t2+ω2x=0运动方程x=A cos(ωt+ϕ0)弹簧振子ω=(k/m)1/2，单摆ω=(g/l)1/2，复摆ω=(mgh/J)1/2；2.描述谐振动的物理量：(1)固有量：固有频率ω，周期T，频率ν其关系为ω=2π/T=2πνν=1/T(2)非固有量，振幅A A=(x02+v02/ω2)1/2位相ϕϕ=ωt+ϕ0初位相ϕ0tanϕ0=-v0/(ω x0)(再结合另一三角函数定出ϕ0)；3.旋转矢量法(略)；4.谐振动能量：E k=E sin2(ωt+ϕ0)E p=E cos2(ωt+ϕ0)E=E k+ E p5.谐振动的合成：(1)同方向同频率两谐振动的合成A=[A12+A22+2A1A2cos(ϕ20-ϕ10)]1/2tgϕ0=(A1sinϕ10+A2sinϕ20)/(A1cosϕ10+A2cosϕ20) (再结合另一三角函数定出ϕ0)拍∆ω<<ω1拍频∆ν=|ν2-ν1| (2)相互垂直振动的合成ω1与ω2成简单整数比时成李萨如图形ω1=ω2时为椭圆方程：x2/A12+y2/A22- 2(x/A1)(y/A2)cos(ϕ20-ϕ10)=sin2(ϕ20-ϕ10) 二. 波动1.机械波的产生必须有波源及媒质，机械波的传播实质是相位(或振动状态)的传播；2.描述波的物理量：波长λ，频率ν，周期T，波速u其关系为T=1/ν=λ/u u=λ/T=λν3.平面简谐波的波动方程y=A cos(ωt-x/u+ϕ0)=A cos[2π(t/T-x/λ)+ϕ0]=A cos[(2π/λ)(x-ut)-ϕ0]；4.平均能量密度w=ρA2ω2/2，能流密度(波的强度) I=w u=ρA2ω2u/25.惠更斯原理(略)；6.波的叠加原理：独立性，叠加性；7.波的干涉(1)相干条件：频率相同，振动方向相同，位相差恒定。
振动与波习题课.
B
P x
30x
C
x
解：（1） 1 = 2 ，在BC间取一P点(如图) BP = r1 = x 由题意，应有 代入数值 CP = r2 = 30 x
4 x (30 x) (2k 1) 4k 2 2
r1 r2 ( 2 k 1) 2
x = 2k +16
k = 0, 1, 2,
（Ａ）
（B） （C） 5 （D） 0
2 4
A
a
b
o
A
2
9 8
解：由驻波位相分布特点知，同一波节两侧各点的位相相反。
所以选（Ａ）
9、当一平面简谐波通过两种均匀介质时，不会变化的物理量 是 A、波长和频率； C、波长和波速； 答案：D 10、已知一平面简谐波的表达式为y=Acos（at-bx），a、b为 正值，则 A、波的频率为a； B、波的传播速度为b/a； C、波长为π /b 答案：D D、波的周期为2π/a B、波速和频率 D、频率和周期
t x t x C y2 A cos2 0 D y2 A cos2 T T
解：反射波的传播方向与入射波方向相反，反射点为波节， 说明有半波损失。 故应选 (D)
8 某时刻驻波波形图曲线如图所示，则a,b两点位相差是
11、一周期为T的横波沿x轴正向传播，若t时刻波形曲线如图 所示，则在t+T/4时刻，x轴上1、2、3三点的振动位移分别是
A、A，0，-A； B、 -A，0，A
C、 0，A，0；
D、 0，-A，0；
12、图中为t=0时刻，以余弦函数表示的沿x轴正向传播的平面 简谐波的波动方程，则O点处质点振动的初相位为 A、 π/2 B、0 C、3 π/2 D、 π 答案:C
大学物理振动和波习题课
12、一质点作简谐振动，周期为 T。质点由平衡
位置向Ｘ轴正方向运动时，由平衡位置到二分之一 最大位移这段路程所需要的时间为（ ）。
A T 4 B T 1 C 2 T 6 D T 8
解：令简谐振动为 xA si n t
则当 xA2 时， si n t0.5
Acos2(t 1) T2
Acos2T(t 13)
.
7.图中所示为两个简谐振动的振动曲线．若以余弦函数表 示这两个振动的合成结果，则合振动的方程为
xx1x2 0.04cos(t)
x (m)
0.08
O
-0.04
1
x1 t (s)
2 x2
.
8 如果在固定端 x0处反射的反射波方程式是
y2 Aco2stx
设反射波无能量损失，则入射波的方程式是（ ） 形成的驻波的表达式是（ ）。
y1OAcos2vt y2OA cos2vt
形成的驻入 波射 为波 ：方 程 y1Acos 2 t x
y y 1 y 2 A c 2 ot s2 x A c 2 ot s2 x
得：
S
wu
1 A22u
2
3.惠更斯原理和波的叠加原理
惠更斯原理:
波阵面上每一点都可以看作是发出球面子波的 新波源，这些子波的包络面就是下一时刻的波阵面。
波的叠加原理:
当几列波在介质中某点相遇时，该质点的
振动位移等于各列波单独传播时在该点引起位 移的矢量和。
.
4.波的干涉: 相干条件： 振动方向相同
频率相同
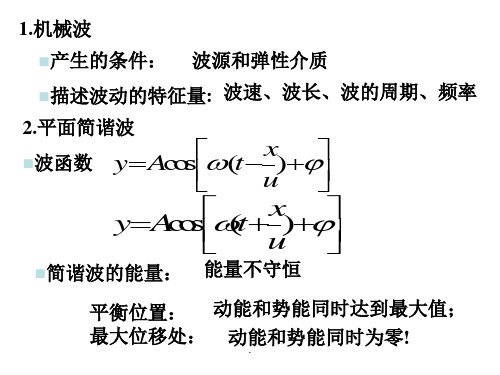
1.机械波
产生的条件： 波源和弹性介质
描述波动的特征量: 波速、波长、波的周期、频率
2.平面简谐波
波函数 yAcos(tux)
振动与波习题课
x/m
（九）波传播过程中，任一体积元的动能、 势能、总机 械能均随 t 作周期性变化，且变化是同相位的。平衡位置时， 体积元的动能、势能和总机械能均最大；位移最大时，三者 均为零。
平衡位置处 释放能量 最大位移处
Ek,Ep,E 吸收能量
0
（2）任一体积元都在不断地接收和放出能量，即不断地传 播能量。任一体积元的机械能不守恒。波动是能量传递的一 种方式。
二、基本内容
（一）简谐振动的特征
1.动力学特征 F kx
简谐振动动力学特征是物体受线性回复力作用。
简谐振动的动力学方程
d2 x 2x 0
dt2
简谐振动的特征式
2.运动学特征 x Acos(t 0 )
简谐振动的运动学方程（振动表达式或振动方程）
简谐振动的速度和加速度
v
0 )
2.时间推迟法 t x
u
y
A cos[ (t
x) u
0
]
3.波动表式的物理意义
（1）当x 一定时(x = x0)表示x0处质点的振动表式
（2）当t 一定时(t = t0)表示t0时
y/m
0.1
刻的波形曲线
o
0.05 3
（3）x、t 都变化反映了波形的传播
u 36 m/s
（2）周期 T 、频率ν和角频率ω
2π 2π
T
（3）相位 ( t 0 )和初相位 0
cos 0
x0 A
sin 0
v0
A
对给定的振动系统，频率由系统本身性质决定。
2.简谐振动的矢量图示法
M
旋转矢量表示法 3.振动曲线（x - t 图）
（九）波传播过程中，任一体积元的动能、 势能、总机 械能均随 t 作周期性变化，且变化是同相位的。平衡位置时， 体积元的动能、势能和总机械能均最大；位移最大时，三者 均为零。
平衡位置处 释放能量 最大位移处
Ek,Ep,E 吸收能量
0
（2）任一体积元都在不断地接收和放出能量，即不断地传 播能量。任一体积元的机械能不守恒。波动是能量传递的一 种方式。
二、基本内容
（一）简谐振动的特征
1.动力学特征 F kx
简谐振动动力学特征是物体受线性回复力作用。
简谐振动的动力学方程
d2 x 2x 0
dt2
简谐振动的特征式
2.运动学特征 x Acos(t 0 )
简谐振动的运动学方程（振动表达式或振动方程）
简谐振动的速度和加速度
v
0 )
2.时间推迟法 t x
u
y
A cos[ (t
x) u
0
]
3.波动表式的物理意义
（1）当x 一定时(x = x0)表示x0处质点的振动表式
（2）当t 一定时(t = t0)表示t0时
y/m
0.1
刻的波形曲线
o
0.05 3
（3）x、t 都变化反映了波形的传播
u 36 m/s
（2）周期 T 、频率ν和角频率ω
2π 2π
T
（3）相位 ( t 0 )和初相位 0
cos 0
x0 A
sin 0
v0
A
对给定的振动系统，频率由系统本身性质决定。
2.简谐振动的矢量图示法
M
旋转矢量表示法 3.振动曲线（x - t 图）
振动与波习题课
L
y2
Acos(t
2
x 2)
t
2
L 2
t
2
L 2
2
4
L
y2
Acos(t
2
x 4
L)
2
能流：单位时间内通过任一截面的能量
P wus P wus 1 A2 2us
2
波的强度： I P 1 A2 2u
3、惠更斯原理
s 2
①同一波面上各点都是发射下一级子波的波源
②下一时刻原波的波面即是各子波波面的包迹
4、干涉 条件：同方向，同频率，位相差恒定或同相 干涉：两列波在空间相遇出现的某些点振动极大，
速度： v A sin t 0 vm A
求某一时刻的速度 v A2 x2
加速度：a A 2 cos t 0 am A 2
能量：
E
Ek
Ep
1 2
kA2
A 2E k
周期性，只有振 动周期的一半
3、迭加 同方向，同频率，合成后仍是谐振动
A A12 A22 2A1 A2 cos 20 10
某些点振动极小的现象。
公式：
20
10
2
r2
r1
2k k 0,1,2 A A1 A2 强
2k 1 k 0,1,2 A A1 A2 弱
若 10 20
k k 0,1,2 强
r2 r1 2k 1 k 0,1,2 弱
2
5、驻波——干涉的特例 条件：①干涉条件，②振幅相同， ③沿同一直线相向传播 性质：①分段振动，各点振幅不同，波形、能量不向 外传播，
知在 x 2处振动方程为 y Acos。t 求（1）该
平面简谐波的波函数；（2）若在波线上 x L
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
b
c
O
a
.
b
c X t
a 0
b
2
3 c 2
10.如图（a）为t=0时的波形曲线,经0.5s后波形变为（b） 求（1）波动方程 Y (a) (b) u
（2）P点的振动方程
解：O处的振动方程为 0.1
yo A cos(t )
由图得A=0.1 =/2 =4m
( 2k 1) 2 2 1 1 2 ( 2k 1) 4 r1 [ ] 2 ( 2k 1) 2 ( 2k 1)
Y
u=0.08m/s P . 0.02
X yo A cos(t ) -0.04 0.04 P点的振动方程 2 1 T u 0.08 令x=0.02 u 2 2 3 4 y P 0.04 cos(4t ) T 2 x y 0.04 cos[4 ( t ) ] 0.08 2
A A A 2 A1 A2 cos( 2 1 ) A1 sin 1 A2 sin 2 tg A1 cos 1 A2 cos 2 2 1 B.同方向不同频率：拍 拍频为：
A. 同方向同频率：
2 1 2 2
C.两个相互垂直同频率的振动：椭圆 D.两个相互垂直不同频率的振动：李萨如图 5.平面简谐波波动方程：
u 0.84m / s 取 /3
故得波动方程为
17 / 3
O a b
u
X
x y 0.1cos[7 ( t ) ]( m ) 0.84 3
13.题中图a表示一水平轻绳，左端D为振动器，右端 固定于B点。t0时刻振动器激起的简谐波传到O点。其 波形如图b所示。已知OB＝2.4m，u=0.8m/s. 求：（1） 以为计时零点，写出O点的谐振动方程；（2）取O 点 为原点，写出向右传播的波动方程；（3）若B 处有 半波损失，写出反射波的波动方程（不计能量损失）。 2 D O 解：（1）由 B u 2 2 y(cm) 得 u 80 4 40 4
（2）P点振动方程 x= /2
y P A cos[ 2u
X
x y A cos[ ( t ) 2 ] u 2 2u x A cos[ (t 2 ) ] u 2 2u
( t 2) ] 2
8.图示为一平面简谐波在t=0时刻的波形图 求（1）波动方程 （2）P处质点的振动方程 解：设原点处质点的振动方程为
b 0
c
2
d
7.如图所示为一平面简谐波在t=2s时刻的波形图 求（1）波动方程 （已知A、u、） y u A.P O
（2）P点处质点的振动方程 解：设原点处质点的振动方程为
yo A cos(t )
t=2s时O点位相
波动方程
t 2 2 2
D O y(cm)
4
-40 -20
B
y0 4 cos(4t
x(cm)
2
)( cm )
o
x ) （SI制），传到隔 14. 有一平面波y 2 cos 600 ( t 330 板的两个小孔A、B上，A、B 两点的间距1， 若A、B
传出的子波传到C点恰好相消。求C点到A点的距离。
x ) 解： y 2 cos 600 ( t 330 x 2 cos 2 (300t ) 1.1 所以， 1.1m 相消条件：r2 r1 ( 2k 1) 2
2.描写振动的基本物理量及其关系 A.振幅： A B.圆频率、频率和周期： , , T 2 T 1 C.初相位： 由系统决定圆频率： 由初始条件确定 A和
k
：
2
2 v0
m
A
x
2 0
v0 arctg( ) x 0
！！简谐振动可以用旋转矢量表示
A
r1 r2
C
B
k=0,1,2….
（1）
2 由几何关系有： r2
r 1
2 1
A
r1
C
(r2 r1 )( r2 r1 ) 1 r2 B 1 2 r2 r1 （2） r r ( 2k 1) 2 1 r2 r1 ( 2k 1) 2
所以
由（1）、（2）式可得：
得yO A cos
2
t
6.一简谐波沿x轴正向传播，t=T/4的波形如图所示，若振动
余弦函数表示，且各点振动的初相取 —到之间，则各点 的初相为: 解：沿波线方向位相逐点落后 由旋转矢量得 Y u
Y
a b . c d X t=0
a
b
c
O
O
d O a
2
t=T/4
P
(2) 某振动振幅为A，周期为T，设t＝T/4时，质 点位移为x= A / 2 ，且向正方向运动。则振动的 3 / 4 初位相为 ________ ,质点返回原点时的最小时 时刻 t _______ 3T / 8
0
5S
T /4
2.余弦波以波速u＝0.5m/s沿x轴正向传播，在 x=1m的P点振动曲线如图a所示。现另有一沿x轴 负向传播的平面余弦波在t=1s时的波形曲线如图
由 t =0, y=0 , v＜0 知： 2 y0 4 cos(4t )( cm )
2
-40
-20
o
x(cm)
（2） 向右传播的波动方程
x y 4 cos[4 ( t ) ]( cm ) 80 2
（3）反射波的波动方程
2OB x y 4 cos[4 ( t ) ] 80 2 x 4 cos[4 ( t ) ]( cm ) 80 2
波动方程
x l y A cos[ ( t ) ] u u
（2）写出距P点为b的Q点的振动方程 Y
l b
Y P u Q O P
b
O
X
Q u
X
x l y A cos[ ( t ) ] u u
将 x l b代入
x y A cos[ ( t ) ] u
b所示，试问这两列波是否是相干波？ 4
y(cm) 1 4 a
2
3
4
t(s) b
y(cm) 1 2 3 4
x(m)
3. 沿X轴负向传播的平面谐波在t＝2秒时的波形 曲线如图所示，波速u＝0.5m/s，则原点O点的振
y0 0.5 cos( t 1) m 动表达式为＿＿＿＿＿＿＿＿＿＿＿＿＿＿ 。 2
（1）分别就图中的两种坐标写出其波动方程
（2）写出距P点为b的Q点的振动方程 Y Y
l b
b
O
P u
Q
X
O P
Q
X
l yO A cos[ ( t ) ] u
波动方程
原点的振动方程
u 原点的振动方程
yO A cos(t )
x y A cos[ ( t ) ] u
的振动规律如图 （1）求出P处质点的振动方程
（2）求此波的波动方程
（3）若图中d=/2，求O处质点的振动方程 解： Y O t=0 t=1 O
y
.
=
t=/2 = /2
1
t
y P A cos( t ) 2
d
O P X
（2）波动方程
t时刻原点的振动为 t-d/时刻P点的振动 原点的振动方程为： O
9.如图为沿x轴传播的平面余弦波在t时刻的波形图 （ 1）若沿X轴正向传播，确定各点的振动位相 （2）若沿X轴负向传播，确定各点的振动位相 u Y Y
a
a
c
b
O
a
.
b
c X t
a 0
b
2
3 c 2
（2）若沿X轴负向传播，确定各点的振动位相 u Y Y
a
a
将 x b代入
b yQ A cos[ ( t ) ] u
b yQ A cos[ ( t ) ] u
12.一平面简谐波沿x正方向传播，振幅A＝10cm，圆频 1 率 7s 当t=1.0s时，位于x=10cm处的质点a经过 平衡位置向y轴负方向运动。此时,位于x=20cm处的质 点b的位移为5cm, 且向y轴正方向运动。设该波波 长 10cm ，试求该波的波动方程。
y(m)
0.5 -
.P 1
2
t(s)
4.设波源位于坐标原点O，波
源的振动曲线如图，u＝5m/s。 沿X正方向传播。（1）画出 距波源25m处质点的振动曲 线；（2）画出t=3s时的波形 曲线。
y(cm) 2. 2 4 t(s)
y(cm)
2.P 2 4
t(s)
y(cm) 2. 10 20 x(m)
5.一平面简谐波沿X轴负向传播，波长为，P点处质点
同理 得
cos(7 1.4 / u ) 0.5
vb 0
7 1.4 / u / 3
注意a点落后于b点，故同一时刻（t=1.0s)a点的位相 取 / 2时，b点的位相只能取－ / 3（还考虑了 10cm 以及 xb xa 10cm 的条件。）
解：设该波的波动方程为：
求解的关键是求出波速u 及原点的初位相
x y A cos[ ( t ) ] u
O
a
b u
X
方法I：解析法。 由题意知t=1.0s时
x ya 0.1cos(7 7 ) 0 v a 0 u
所以
7 0.7 / u / 2