(完整版)5.1.3同位角、内错角、同旁内角PPT
5.1.3 同位角、内错角、同旁内角

3
夹在两被截直线内
,分别在截线两侧
(交错)
图中的内错角除∠3和∠5外,还有……
87 56 43 12
探究新知 ——同旁内角
观察∠3和∠6两角:
87 5
6 43 12
观察∠3和∠6两角: 各有一边在同一直线上
87 5
6
6
3
43
12
观察∠3和∠6两角: 反向
87 5
6
6
3
43
12
观察∠3和∠6两角:
F
具有对顶角关系的有:
E
A
87
56
43
C
12
B D
F
探究新知
两条直线AB和CD被第三条直线EF所截, 构成八个角,我们看那些没有公共顶点 的两个角的关系。
探究新知 ——同位角
观察∠1和∠5两角:
87 56 43 12
观察∠1和∠5两角: 各有一边在同一直线上
5
87
5
6
1
43
12
观察∠1和∠5两角: 同向
在截线同侧
(或倒置)
内错角
在两条被截直线之内, 形如字母“Z”
在截线两侧(交错)
(或反置)
同旁内角
在两条被截直线同旁, 在截线同侧
形如字母“U”
返回
请同学们分别用双手的大拇指、食指 各组成一个角, 两食指相对成一条线, 保持在同一平面内, 分别进行尝试,看可以组成哪些角。
如图,两只手的食子和拇指在同一平面内,它们 构成的一对角可以看成是什么角?类似地,你还 能用两只手的手指构成同位角和同旁内角吗?
形成些具有什么关系的角?
具 有 对
C
5.1.3同位角_内错角_同旁内角

角的名称 位置特征 基本图形 相同点 共同特征
同位角
同旁内 角
在截线的同侧, 在被截两直线
4
的同旁。
8
在截线的同侧,
在被截两直线
4
之间。
5
内错角
在截线的两侧, 在被截两直线 之间。
35
都在截 同 位 线置位的上角同有和什同么旁相内同角点在 与 侧不。同点?这这三三类角类
的角共都同特是
都在被 征没是有什么公? 截线内 位 与错 不置两之角 同上直间和 点有同 ?什。旁么共的内相顶 。角同在点点
∠1与∠2是一对同位角,
∠3与∠4是一对内错角,
D
A
∠2与∠4是一对同旁内角.
1 4
(2)如果把图看成是直线
E5
3
2
F
CD,EF被直线AB所截,
那么∠1与∠5是一对什么
B
C
角?∠4与∠5呢?
(3) 哪两条直线被哪一条直线
∠1与∠5是一对同旁内角, 所截, ∠ 2与∠ 5是同位角
∠4与∠5是一对内错角. 直线AB,CD被直线EF所截
2.如图:找出图中数字标注的角的同 位角,内错角,同旁内角。
4 13
2
5
6
l
所截
3
同位角
∠1和∠5 ∠4和∠8 ∠2和∠6 ∠3和∠7
内错角
∠3和∠5 ∠4和∠6
同旁内角
∠4和∠5 ∠3和∠6
综合思考
观察几何画板,看看谁是 谁的同位角?
特征:
角的名称 位置特征 基本图形 相同点 共同特征
同位角 在截线的同 侧,在被截
4
两直线的同 旁。
8
返回
特征:
人教版七年级数学下5.1.3-同位角、内错角、同旁内角公开课课件PPT

新课导入教学目标知识与能力1.能说出同位角、内错角和同旁内角的意义;2.会识别图形(包括变式图形和比较复杂的图形)中的同位角、内错角和同旁内角.教学目标过程与方法1.通过变式图形的识图训练,培养自己的识图能力;2.通过例题口答“为什么”,培养自己的推理能力.教学目标情感态度与价值观1.从复杂图形分解为基本图形的过程中,渗透化繁为简,化难为易的化归思想;从图形变化过程中,培养辩证唯物主义观点;2.通过“三线八角”基本图形,认识几何图形的位置美.教学重难点重点同位角、内错角、同旁内角的概念.难点在较复杂的图形中辨认同位角、内错角、同旁内角.12 348 756mn l下图所示为直线m、n被l所截,即两条直线被第三条直线所截.直线m、n叫被截线,l叫截线.两条直线被第三条直线所截,形成“三线八角”的图形.截线∠1与∠5都处于直线m 、n 的同一方从直线m 、n 来看,∠1与∠5又处于哪个位置?具有种位置关系的一对角( ∠1与∠5 )叫做同位角(F 型). 同位角l 1 4图中的同位角还有哪些?∠2与∠3、∠3与∠7、∠4与∠8.mnl12348756从直线 l 来看,∠3与∠5处于哪个位置?∠3与∠5都处于直线 l 的两侧从直线m、n来看,∠3与∠5又处于哪个位置?∠3与∠5都处于直线m、n的内部具有这种位置关系的一对角(∠3与∠5)叫做内错角(Z型).mn l12 348 75 6内错角图中的内错角还有哪些?∠2与∠8mnl12 34875 6从直线 l 来看,∠2与∠5处于哪个位置?∠2与∠5处于直线 l 的同一侧从直线m、n来看,∠2与∠5又处于哪个位置?∠2与∠5都处于直线m、n的内部具有这种位置关系的一对角(∠2与∠5)叫做同旁内角(U型).m n12 348 75 6同旁内角图中的同旁内角还有哪些?∠3与∠8mnl12348756指出下列各图中∠1与∠2的位置关系.同旁内角同位角内错角同旁内角 内错角 12 12 12 1221 21同位角练一练1.同位角、内错角、同旁内角的定义2.识别这三类角的步骤是:第一步:找截线(两角的“公用边”);第二步:将题目的图形分离出如下基本图形:课堂小结1.找出下图中∠C的同位角、∠A的内错角,并指出是哪两条直线被哪一条直线所截而成的.A QPCB∠C的同位角为∠PBQ和∠ABP;∠A的内错角为∠ABQ和∠ABP.随堂练习2.如图,下面判断中,错误的是()A.∠1和∠2是同旁内角B.∠5和∠7是同位角C.∠3和∠4是内错角D.∠4和∠6是同旁内角1234 5 67D3.如图所示,直线ABCD 补直线EF 所截,MG 是从M点引出的射线,则图中的同位角共有( )A .8对B .6对C .4对D .2对CDABGMB4.如图所示,图中与∠C 是同旁内角的角共有( )A .2个B .3个C . 4个D .5个ABE CD FC习题答案1.(2)是,(1)(3)(4)不是.2.(1)∠AOC的邻补角是∠AOD和∠BOC;∠BOE的邻补角是∠AOE和∠BOF.(2)∠DOA的对顶角是∠BOC,∠EOC的对顶角是∠DOF.(3)∠BOD=50°,∠COB=130°.3.AO⊥CO,BO⊥DO.4.过点P与l垂直的的直线只能折出一条,过点Q与直线l垂直的直线也只能折出一条,这是因为过一点有且只有一条直线与已知直线垂直.5.图略,用三角尺或量角器来画.6.图略,可以用量角器、三角尺、刻度尺.7.因为OA 平分∠EOC ,所以∠AOC = ∠EOC =35°,从而∠BOD =∠AOC =35°.218.根据“对顶角相等”,活动指针的读数,就是两直线相交成的一个角的度数.9.略.10.跳远成绩是落在沙坑中的脚印上点P 到起跳线l 的 距离,也就是垂线段PA 的长.用刻度尺量得图 中PA≈2.35(㎝),2.35×150=352.5 (㎝),因此小明同学的跳远成绩大约是3.53m .11.(1)∠1和∠2是直线AB ,CD 被直线BD 所截形 成的,它们是内错角,∠3和∠4是直线 AD ,BC 被直线BD 所截形成的,它们是内 错角;(2)∠1和∠2是直线AE ,DC 被直线BC 所截形 成的,它们是同旁内角,∠3和∠4是直线 AD ,BC 被直线AE 所截形成的,它们是同 位角.12.A ,B ,C 三点在同一直线上,这是因为如果 A ,B ,C 不在同直线上,那么过点B 就有两条 直线与直线l 垂直了,而这是不可能的.13.(1)如下图: E C BF D AG(2)由AB ,CD 相交于O ,于是∠AOC 与∠BOD ,∠AOD 与∠BOC 互为对顶角,而 OE .OF 分别是∠AOC ,∠BOD 的平分线,所以∠AOE ∠+∠AOD +∠DOF = ×360° =180°,从而射线OE ,OF 在同一条直线 上;(3)因为OG 平分∠AOD ,所以∠AOE +∠AOG= (∠AOC +∠AOD) = ×180°=90°, 所以OE ⊥OG .212121读一读视错觉视错觉就是当人或动物观察物体时,基于经验主义或不当的参照形成的错误的判断和感知.我们日常生活中,所遇到的视错觉的例子有很多:比如法国国旗红:白:兰三色的比例为35:33:37,而我们却感觉三种颜色面积相等.这是因为白色给人以扩张的感觉,而兰色则有收缩的感觉.再比如把两个有盖的桶装上沙子,一个小桶装满了沙,另一个大桶装的沙和小桶的一样多.当人们不知道里面的沙子有多少时,大多数人拎起两个桶时都会说小桶重得多.他们之所以判断错误,是看见小桶较小,想来该轻一些,谁知一拎起来竟那么重,于是过高估计了它的重量.这就是视错觉.视觉误差左下图A与B是同样大小的,右下图中间的圆圈也是同样大的,但看到的却是一大一小,这是不真的事实.法国国旗中三种色带的宽度是不相等的,蓝白红三色带宽度之比为:30:33:37 .视错觉——平行线视错觉——小正方形角上色点视错觉——直线数数看有几个黑点视错觉——在转吗这头大象一共有几条腿?画中画画中有多少个人物。
同位角、内错角、同旁内角课件

①在截线的同一侧 ②在被截线的同一方向
E 截线
3
4
B
2
1
7
8
D
6
5
F
同位角
图中除了∠1和∠5,还有同位角吗?
∠ 2和∠6、 ∠ 3和∠7、 ∠ 4和∠8
两角的公共边是截线 形如大写英文字母 F (或反置)
图中∠2和∠8的位置,它们有什么样
A
的位置ห้องสมุดไป่ตู้征?
C
∠2和∠8
在截线EF两侧
①在截线的异侧
在被截线AB、CD之间
三、同旁内角
活动3 观察∠4与∠5的位置关系:
①在直线EF的同旁
②在直线AB、CD内部
E
B
1
2
A
34
65
C
78 D
F
同旁内角
4 5
图中还有哪些同旁内角? ∠4和∠5;∠3和∠6.
变形:图中的∠1与∠2都是同旁内角.
1
1
2
2
12
12
U 特征:在形如“ ”的图形中有同旁内角.
课堂练习
3 4
6
观察下图,判断正误。
2
1
1
2
1
12
2
F 特征:在形如字母“ ”的图形中有同位角.
二、内错角
活动2 观察∠3与∠5的位置关系:
①在直线EF的两侧
内错角
②在直线AB、CD内部
A C
E
1
B
2
34
65
78 D F
3 5
图中的内错角有哪些? ∠3和∠5; ∠4和∠6
变形:图中的∠1与∠2都是内错角.
1
1
《同位角、内错角、同旁内角》PPT 图文

地理课件:/kejian/dili/
历史课件:/kej ian/lishi/
E
21
B
1
A
34
65
5
C
78 D
F
图中还有其它的同位角吗?若有,请你找出来.
⑶图中还有其它的同位角吗?若有,请你找出来.
C
2
E 1
3
4
D
65
A
7 F8
B
同位角是 F 形状
1
2
5 4
观察 问题:3、观察∠4与∠5的位置关系
同旁内角:①在直线AB、CD—之—间——
②在直线EF的—同—旁—
E
21
B
A
34
4
65
5
C
78 D
图中还有其它的同旁F内角吗?若有,请你找出来.
活动3 认识同旁内角
⑵图中还有其它的同旁内角吗?若有,请你找出来.
C
3
E 1
7
5
42
A 86
5 2
D
同旁内角是 U 形状
ba
1
2
c
(6)
同位角
1 2 (7)
1
2 (8)
内错角
1
1
2
2
(9)
(10)
同旁内角
例1:如图,直线DE截直线AB,AC,构成8个角。
指出所有的同位角、内错角和同旁内角。
A
截线
∠2和∠5
同位角 ∠3和∠6
D
21 34
58
E
67
∠4和∠7 ∠1和∠8
B
被截线
C 内错角 ∠4和∠5
∠1和∠6
同旁内角 ∠1和∠5
513同位角内错角同旁内角课件
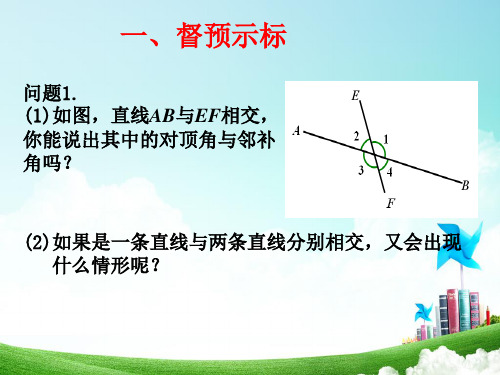
(简称三线八角)
E
A
8
5
7
B
6
C4 3
D
12
F
同位角
问题1.观察图中的∠1和∠5,它们具有怎样的位置 关系?
另一边
各有一
5
在截线 的同侧,
边在同 一直线
两角方
(截线)
1
向相同.
上
具有这种位置关系的一对角叫做同位角. 图中除∠1和∠5外,还有同位角吗?若有请指出来. 特征:两角的边组成字母F.
在截线同侧 夹在两条被截线之间
图形结构特征
形如字母 “F”
(或倒置) 形如字母 “Z” (或反置)
形如字母 “U”
四、展示评价
例1.如图,直线DE、BC被直线AB所截. (1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系 的角?
∠l与∠2是内错角,∠1与∠3是 同旁内角,∠1与∠4是同位角.
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和 ∠3互补吗?为什么?
二、自学梳理
认真看课本(P166-168); 1、结合图形分清哪条直线是截线、被 截线,理解同位角、同旁内角、内错 角的概念; 2、结合图形回答“云图”中的问题与 课后练习; 3、如有疑问,可以小组讨论或举手问 老师.五分钟后比谁能正确做出类似检 测题.
三、小组答疑
直线AB、CD与EF相交.
或说 两条直线AB、CD被第三
看图填空
A
E1 3D
B2
4
FC
(2)若ED,BF被AB所截, 则∠1与_∠__2__是同位角。
看图填空
A
E1 3D
B2
4
FC
(3)若ED,BC被AF所截,
课件1:5.1.3 同位角、内错角、同旁内角

同位角、内错角和同旁内角的结构特征:
l3
21 34
65 78
∠4与∠8是_同__位_角
l1
∠3与∠5是_内__错_角
l2
∠4与∠5是__同__旁__内__角
能力挑战: 看图填空
A
E1 3D
B2
4
F
C
(2) ∠1与∠2是_E_D_与_B_F_被_A__B_所截形成 的__同__位___角
练一练
如图:∠1和∠2是 同位 角, ∠3和∠4是 内错 角, ∠5和∠6是同旁内角,
ab
a
b
c
c
a
c b
做一做: 如图,直线DE,BC被直线 AB所截, ∠1与∠2是_内_错_角, ∠1与∠3是_同旁_内_角, ∠1与∠4是_同_位_角。
试一试:
根据图形按要求填空: (1)∠1与∠2是直线 AB 和 DE 被直线 BC 所截而得的 同位角.
北
人
游乐场
书店 学校 学
新建路
京
民
超市
(3)学校与书店的位置是什么角关系?
路
路
它们的位置是同旁内角
小结
一.同位角、内错角、同旁内角产生的条件:两条直线被第三条直线所截 而成(简称“三线八角”)。
二.找同位角、内错角、同旁内角的方法: (1)先找出截线; (2)同位角位于截线的同一侧,被截线的同一方。 (3)内错角位于截线的两旁,被截线内部。 (4)同旁内角位于截线的同旁,被截线内部。
同位角有: ∠1与∠5 ∠3与∠7
F
∠2与∠6 ∠4与∠8
辩一辩 : 如图:∠1与∠2是同位角吗?
c
(1)
A a b
同位角、内错角、同旁内角-PPT课件

截线:两侧
内错角 被截线:内部
1 2
代表 相同 字母 点
F 都在 截线 同侧
U 都在 被截
Z 线内 部
共同 特征
这三 类角 都是 没有 公共 顶点 的
随堂训练
线,即直线EF被第三条直线CD所截,构成了几个角?
B
E
4
C
1 A
3
6
2
7
5
8 F
D
简称“三线八角”.
知识讲解
一、同位角
A C
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右侧)
②在直线AB、CD的同一侧(上方)
E
21
B
34
1
同位角
65
78 D
5
F ∠2和∠6;∠3和∠7; 图中的同位角还有哪些?∠4和∠8
1
1
2
12
2 1
2
特征:在形如“Z”的图形中有内错角.
三、同旁内角
活动3 观察∠4与∠5的位置关系:
①在直线EF的同旁
②在直线AB、CD内部
E
B
1
2
A
34
65
C
78 D
F
同旁内角
4 5
图中还有哪些同旁内角? ∠3和∠6
变形:图中的∠1与∠2都是同旁内角.
1 2
1 2
12
12
特征:在形如“U”的图形中有同旁内角.
解:两条直线是AB,AC,截线是DE,
同位角:∠2与∠5,∠4与∠7,∠1与
∠8, ∠6和∠3; 内错角:∠4与∠5,∠1与∠6; 同旁内角:∠1与∠5,∠4与∠6.
D 21
3 B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新课导入
教学目标
知识与能力
1.能说出同位角、内错角和同旁内角的意义;
2.会识别图形(包括变式图形和比较复杂的图形)中的同位角、内错角和同旁内角.
教学目标
过程与方法
1.通过变式图形的识图训练,培养自己的识图能力;
2.通过例题口答“为什么”,培养自己的推理能力.
教学目标
情感态度与价值观
1.从复杂图形分解为基本图形的过程中,渗透化繁为简,化难为易的化归思想;从图形变化过程中,培养辩证唯物主义观点;
2.通过“三线八角”基本图形,认识几何图形的位置美.
教学重难点
重点
同位角、内错角、同旁内角的概念.
难点
在较复杂的图形中辨认同位角、内错角、同旁内角.
1
2 3
4
8 75
6
m
n l
下图所示为直线m、n被l所截,即两条直线被第三条直线所截.
直线m、n叫被截线,l叫截线.
两条直线被第三条直
线所截,形成“三线
八角”的图形.
截线
∠1与∠5都处于直线m 、n 的同一方
从直线m 、n 来看,∠1与∠5又处于哪个位置?
具有种位置关系的一对角(∠1与∠5 )叫做同位角(F 型).同位角
l 14
图中的同位角还有哪些?
∠2与∠3、∠3与∠7、∠4与∠8.
m
n
l
1
2
3
4
8
7
5
6
从直线m、n来看,∠3与∠5又处于哪个位置?
∠3与∠5都处于直线m、n的内部
具有这种位置关系的一对角(∠3与∠5)叫做内错角(Z型).l
1
4
内错角
图中的内错角还有哪些?
∠2与∠8
m
n
l
1
2
3
4
8
7
5
6
从直线l 来看,∠2与∠5处于哪个
位置?
∠2与∠5处于直线l 的同一侧
从直线m、n来看,∠2与∠5又处于
哪个位置?
∠2与∠5都处于直线m、n的内部
具有这种位置关系的一对角(∠2与∠5)叫做同旁内角(U型).m n
1
2 3
4
8 75 6
同旁内角
图中的同旁内角还有哪些?
∠3与∠8
m
n
l
1
2
3
4
8
7
5
6
指出下列各图中∠1与∠2的位置关系.
同旁内角
同位角
内错角
同旁内角内错角1
21
212
1
2
2
12
1
同位角
练一练
课堂小结
1.同位角、内错角、同旁内角的定义
2.识别这三类角的步骤是:
第一步:找截线(两角的“公用边”);
第二步:将题目的图形分离出如下基本图形:
1.找出下图中∠C的同位角、∠A的内错角,并指出是哪两条直线被哪一条直线所截而成的.
A
Q P
C
B
∠C的同位角为∠PBQ和∠ABP;∠A的内错角为∠ABQ和∠ABP.
随堂练习
2.如图,下面判断中,错误的是()A.∠1和∠2是同旁内角
B.∠5和∠7是同位角
C.∠3和∠4是内错角
D.∠4和∠6是同旁内角
1
2
3
45 6
7
D
3.如图所示,直线ABCD 补直线EF 所截,MG 是从M点引出的射线,则图中的同位角共有()
A .8对
B .6对
C .4对
D .2对
C
D
A
B
G
M
B
4.如图所示,图中与∠C 是同旁内角的角共有()
A .2个
B .3个
C .
4个D .5个A
B
E C
D F
C
习题答案
1.(2)是,(1)(3)(4)不是.
2.(1)∠AOC的邻补角是∠AOD和∠BOC;
∠BOE的邻补角是∠AOE和∠BOF.
(2)∠DOA的对顶角是∠BOC,∠EOC的对顶角是∠DOF.
(3)∠BOD=50°,∠COB=130°.
3.AO⊥CO,BO⊥DO.
4.过点P与l垂直的的直线只能折出一条,过点Q与直线l垂直的直线也只能折出一条,这是因为过一点有且只有一条直线与已知直线垂直.5.图略,用三角尺或量角器来画.
6.图略,可以用量角器、三角尺、刻度尺.
1
7.因为OA平分∠EOC,所以∠AOC=∠EOC =35°,从而∠BOD=∠AOC=35°.2
8.根据“对顶角相等”,活动指针的读数,就是两直
线相交成的一个角的度数.
9.略.
10.跳远成绩是落在沙坑中的脚印上点P到起跳线l的距离,也就是垂线段PA的长.用刻度尺量得图
中PA≈2.35(㎝),2.35×150=352.5
(㎝),因此小明同学的跳远成绩大约是
3.53m.
11.(1)∠1和∠2是直线AB,CD被直线BD所截形成的,它们是内错角,∠3和∠4是直线
AD,BC被直线BD所截形成的,它们是内
错角;
(2)∠1和∠2是直线AE,DC被直线BC所截形成的,它们是同旁内角,∠3和∠4是直线
AD,BC被直线AE所截形成的,它们是同
位角.
12.A,B,C三点在同一直线上,这是因为如果A,B,C不在同直线上,那么过点B就有两条
直线与直线l垂直了,而这是不可能的.13.(1)如下图:
E
C B F
D A
G
(2)由AB ,CD 相交于O ,于是∠AOC 与
∠BOD ,∠AOD 与∠BOC 互为对顶角,而OE .OF 分别是∠AOC ,∠BOD 的平分线,所以∠AOE ∠+∠AOD +∠DOF =×360°=180°,从而射线OE ,OF 在同一条直线
上;(3)因为OG 平分∠AOD ,所以∠AOE +∠AOG
=(∠AOC +∠AOD) =×180°=90°,所以OE ⊥OG .
21212
1
视错觉就是当人或动物观察物体时,基于经验主义或不当的参照形成的错误的判断和感知.我们日常生活中,所遇到的视错觉的例子有很多:
比如法国国旗红:白:兰三色的比例为35:33:37,而我们却感觉三种颜色面积相等.这是因为白色给人以扩张的感觉,而兰色则有收缩的感觉.再比如把两个有盖的桶装上沙子,一个小桶装满了沙,另一个大桶装的沙和小桶的一样多.当人们不知道里面的沙子有多少时,大多数人拎起两个桶时都会说小桶重得多.他们之所以判断错误,是看见小桶较小,想来该轻一些,谁知一拎起来竟那么重,于是过高估计了它的重量.这就是视错觉.视错觉
读一读
视觉误差
左下图A与B是同样大小的,右下图中间的圆圈也是同样大的,但看到的却是一大一小,这是不真的事实.
法国国旗中三种色带的宽度是不相等的,蓝白红三色带宽度之比为:30:33:37 .
视错觉——平行线
视错觉——小正方形角上色点
视错觉——直线
数数看有几个黑点
视错觉——在转吗
这头大象一共有几条腿?
画中画
画中有多少个人物。
