2008年广州市高二数学学业水平测试模拟题三广州44中
2008年广州市普通高中毕业班综合测试(文科)(二)

2008年广州市普通高中毕业班综合测试考试(二)数学(文科)一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的•1、函数y =sin 2x是A、周期为二的奇函数B、周期为二的偶函数C、周期为2二的奇函数D、周期为2的偶函数2、已知集合M满足M一{1, 2} ={1, 2,3},则集合M的个数是A、1B、2C、3D、43、在等差数列{a n}中,若a2 - 2a6 -印。
=120,则a3 a?等于A、30B、40C、60D、80T T T 4、在复平面内,复数1 i与1 3i分别对应向量OA和OB,其中O为坐标原点,则| AB |二A、・2B、2C、,10D、45、圆锥的母线长为2cm,过顶点和底面圆心的截面面积为2cm2,则该圆锥的侧面积为A、. 2 -cm2B、2-cm2C、2.2-cm2D、4-cm2C 、D 、0 3 2 2设 a =2 . ,b =0.3 ,c =log x (x0.3) (x ■ 1),则 a ,b , c 的大小关系是10、甲、乙两位同学玩游戏,对于给定的实数6,按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把 a 1乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把a 1除以2后再加上12,这样就可得到一个新的实数 a 2.对实数a 2仍按上述方法进行一次操作,又得到一个新的3实数a 3 •当a 3 a !时,甲获胜,否则乙获胜•甲获胜的概率为 ,则印的取值范围是4A 、(-〜12]B 、[24, ::)C 、(12 , 24)D 、,12] 一• [24 ,):■、填空题:本大题共 5小题,每小题5分,满分20分.本大题分必做题和选做题两部分 .(一)必做题:第 11、12、13题是必做题,每道试题考生都必须做答7、 A 、a :: b :: c B 、 b a :: c c 、 c b :: ab :c :: a已知命题 p : a 2 _ 0 (a • R),命题q :函数f (x)二x 2 - x 在区间[0,=)上单调递增,则下列命题中为真命题的是9、x 2如图2所示,F 为双曲线C :―9C 、(一卩)(—q)2的左焦点,双曲线点P 与F7±(i =123)关于y 轴对称,则|RF |+|F 2F|+|P 3F|—|P 4F|—RF |F 6F|的值是B 、16C 、18D 、2711、函数y =lg(x 1)的定义域是__________________ .12、某校为了了解学生的体育锻炼情况,随机调查了70名学生,得到他们在某一天各自的体育锻炼时间的数据,结果用如图3所示的条形图表示。
2008年广州普通高中毕业班综合测试

2008年广州市普通高中毕业班综合测试(二)本试卷共27小题,满分150分,考试题意120分钟可能用到的相对原子质量:N: 14 O : 16 Cl : 35.5 K : 39 Fe : 56 Cu : 64一、选择题(本题包括9小题,每小题3分,共27分。
每小题只有一个选项符合题意。
)1 .下列关于水的说法错误的是A .水是生命活动必不可少的物质B .水是含有极性共价键的共价化合物C.水的电离是放热过程D .水是极弱的电解质,在50C时水的pH小于72. 下列有关说法正确的是A .高温加热氧化镁和碳的混合物可以制单质镁B .铁的冶炼过程是通过置换反应得到单质铁C.海水提溴的过程中不发生氧化还原反应D .利用电解的方法可以从海水中获取淡水3. 下列关于铜电极的叙述正确的.是A .铜锌原电池中铜作负极B .在铁制品上电镀铜时,用铜作阴极C.电解饱和食盐水制烧碱时,用铜作阳极D .电解法精炼铜时,粗铜连接电源的正极4. 下列说法正确的是A .乙烯和聚乙烯都能使溴的四氯化碳溶液褪色B .淀粉和纤维素都可以作为工业上生产葡萄糖的原料C.油脂的水解反应,都是皂化反应D .蔗糖是高分子化合物,其水解产物能发生银镜反应5. 下列叙述正确的是A .用标准氢氧化钠溶液滴定含甲基橙的盐酸,终点时溶液由橙色变成黄色B .将SO2通人BaCb溶液中产生白色沉淀,再滴加稀硝酸沉淀不消失C.将碘盐加人淀粉溶液中,充分搅拌后溶液呈蓝色D .向葡萄糖溶液中加人新制氢氧化铜,加热至沸,静置后上层溶液显红色6. 下列反应的能量变化与其他三项不相同的是A .铝粉与氧化铁的反应B .氯化铵与消石灰的反应C.锌片与稀硫酸反应 D .钠与冷水反应7. 设N A表示阿伏加德罗常数,下列说法正确的是A .标准状况下,2.24L苯中含有的分子数为0」N AB. 0」mol/L硫酸铜溶液中含铜离子数为0」N AC. 0.lmol 188O原子中含中子数为N AD. 4.6g NO2气体中含有的原子数为0」N A&下列分离或提纯方法正确的是①用酒精萃取碘水中的碘②用Na2CO3溶液除去CaCO3固体中的少量CaSO4③用NaOH溶液除去KCl溶液中的少量MgCl2④与新制的生石灰混合后蒸馏可除去乙醇中的少量水A .①②B .②③C .③④D .②④9. 某温度下,向容积为2L的密闭反应器中充入0.10 mol SO 3,当反应器中的气体压强不再变化时测得SO3的转化率为20%,则该温度下反应2SO2(g) + O2 2SO3(g)的平衡常数为A . 3.2 x 103mol 1• LB . 1.6 x 103mol 1• LC. 8.0 x 102mol 1• LD. 4.0 x 102mol1• L二、选择题(本题包括9小题,每小题4分,共36分。
2008学年度广州市高中二年级学生学业水平测试数学试题及参考答案

2008学年度广州市高中二年级学生学业水平测试数学本试卷共4页.满分150分.考试用时120分钟1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号填写在答题卡指定的位置上. 2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3.非选择题必须髟黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应 位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.本次考试不允许使用计算器.5.考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.集合{}1,2A =的子集的个数为A .1B .2C .3D .4 2.0sin120的值为A.2 B .12 C .12- D.2-3.一支田径运动队有男运动员56人,女运动员42人,若采用分层抽样的方法在全体运动员中抽出28人进行体能测试,则抽到进行体能测试的男运动员的人数为A .12B .14C .16D .20 4.函数()sin cos ()f x x x x =+∈R 的最大值为A .2 BC. D .-25.如图所示是一个半径为1的圆及其内接等腰直角三角形.若随机向圆内丢一粒豆子,则豆子落入三角形(图中阴影部分)内的概率为A .1πB .12πC .14πD .18π6.函数()2xf x x =+的零点所在的区间为A .(-2,-1)B .(-1,0)C .(0,1) 7.如图所示,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的体积为A .4π B .2πC .πD .32π8.已知实数031log 4,5a b ⎛⎫== ⎪⎝⎭,2log 0.8c =,则,,a b c 的大小关系为A .b c a <<B .b a c <<C .c a b <<D .c b a << 9.若直线0x y a +-=被圆224x y +=截得的弦长为a 的值为A.B .2或-2C .2D .-2 10.关于x 的方程2(1)10(0,x a x a b a a +++++=≠、)b ∈R 的两实根为12,x x ,若1201x x <<<,则ba的取值范围为A .11,2⎛⎤-- ⎥⎝⎦ B .11,2⎛⎫-- ⎪⎝⎭ C .12,2⎛⎤-- ⎥⎝⎦ D .12,2⎛⎫-- ⎪⎝⎭二、填空题:本大题共4小题,每小题5分,满分20分.11.在等差数列{}n a 中,已知242,8a a ==,则公差d 的值为 . 12.过点(1,2)且与直线210x y --=平行的直线方程为 . 13.设向量(,3),(1,1)x =-=-αb ,若5-=αb ,则实数x 的值为 . 14.下图所示的得法流程图中,若3a =,则输出的T 值为 ;若输出的T =120,则a 的值为 ()a *∈N . 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 15.(本小题满分12分)已知点(,)M x y 的横坐标{}2,1,2x ∈--,纵坐标{}2,2y =-. (1)列出所有符合条件的点M 的坐标;(2)求点M 落在第二象限内的概率. 16.(本小题满分12分)已知a 、b 、c 是ABC ∆三内角A 、B 、C 的对边,且6,4,3b c A π===.(1)求a 的值;(2)求sin C 的值. 17.(本小题满分14分)如图.在正方体1111ABCD A BC D -, E 、F 分别为棱AD 、AB 的中点.(1)求证:EF ∥平面CB 1D 1;(2)求证:平面CAA 1C 1⊥平面CB 1D 1CD E 1C 1A 1B 1D18.(本小题满分14分)已知圆C 经过A (3, 2)、B (1, 6)两点,且圆心在直线2y x =上. (1)求圆C 的方程;(2)若直线l 经过点P (-1, 3)且与圆C 相切,求直线l 的方程. 19.(本小题满分14分)已知函数1()()x af x a a x+-=∈-R .(1)若(1)1f =,求实数a 的值;(2)求函数()f x 在区间[1,2]a a ++上的最小值. 20.(本小题满分14分)设数列{}n a 满足112,2,,n n n a a a n λλ*+==+∈N 为常数. (1)若20a =,求3a 的值;(2)是否存在实数λ,使得数列{}n a 为等差数列,若存在,求数列{}n a 的通项公式,若不存在,请说明理由; (3)设471,n nn b a λ-==,数列{}n b 的前n 项和为n S ,求满足0n S >的最小自然数n 的值.2008学年度上学期广州市高中二年级学生学业水平测试数学试题参考答案及评分标准一、选择题:本大题主要考查基本知识和基本运算.共10小题,每小题5分,满分50分.题号 1 2 3 4 5 6 7 8 9 10 答案 D A C B A B A D B D 二、填空题:本大题主要考查基本知识和基本运算.共4小题.每小题5分,满分20分.其中第13题写对一个给3分,第14题第一个空2分,第二个空3分. 11.3 12.20x y -= 13.2或-4 14.2;6三、解答题15.本小题主要考查古典概型等基础知识.满分12分. 解:符合条件的点M 的坐标有(-2,-2),(-2, 2),(-1,-2),(2,-2),(2, 2). ……6分 (2)落在第二象限内点M 的坐标有(-2, 2),(-1, 2). ……………………9分 所以点M 落在第二象限内的概率为2163p ==. 答:点M 落在第二象限内的概率为13. ………………………12分 16.本小题主要考查正弦定理、余弦定理等基础知识,考查运算求解能力.满分12分. 解:(1)根据余弦定理:2222cos a b c bc A =+-, ………………………3分 将6,4,3b c A π===代入可得:22264264cos283a π=+-⨯⨯⨯=.所以a = ………………………6分 (2)根据正弦定理:sin sin a cA C=, 由(1)知a =s i n 21s i n 7A C c a =⨯==. ………………………12分17.本小题主要考查空间线面位置关系,考查空间想像能力和推理论证能力.满分14分.证明:(1)连结BD .在正方体ABCD -A 1B 1C 1D 1中,对角线BD ∥B 1D 1.…………………2分 又E 、F 为棱AD 、AB 的中点,则EF ∥BD .所以EF ∥B 1D 1. …………………4分 又B 1D 1⊂平面CB 1D 1,EF ⊄平面CB 1D 1.所以EF ∥平面CB 1D 1. …………………8分 (2)在正方体ABCD -A 1B 1C 1D 1中,AA 1⊥平面A 1B 1C 1D 1,而B 1D 1⊂平面A 1B 1C 1D 1, 所以AA 1⊥B 1D 1. …………………10分 在正方形A 1B 1C 1D 1中, A 1C 1⊥B 1D 1,且AA 1∩A 1C 1=A 1,所以B 1D 1⊥平面CAA 1C 1. …………………12分又B 1D 1⊂平面CB 1D 1.所以平面CAA 1C 1⊥平面CB 1D 1. …………………14分 18.本小题主要考查直线与圆等基本知识,考查运算求解能力.满分14分.解:(1)方法1:设圆C 的方程为222()()(0)x a y b r r -+-=>, …………………1分依题意得:222222(3)(2),(1)(6),2a b r a b r b a ⎧-+-=⎪-+-=⎨⎪=⎩…………………4分解得22,4,5a b r ===. …………………7分 所以圆C 的方程为22(2)(4)5x y -+-=. …………………8分 方法2:因为A (3, 2)、B (1, 6),所以线段AB 中点D 的坐标为(2, 4),…………………1分直线AB 的斜率62213AB k -==--, …………………2分 因此直线AB 的垂直平分线l '的方程是14(2)2y x -=-,即260x y -+=.………………3分圆心C 的坐标是方程组260,2x y y x-+=⎧⎨=⎩的解. …………………4分解此方程组,得2,4.x y =⎧⎨=⎩即圆心C 的坐标为(2, 4). …………………5分圆心为C的圆的半径长||r AC === …………………7分所以圆C 的方程为22(2)(4)5x y -+-= …………………8分 方法3:因为圆心在直线2y x =上,所以可设圆心C 的坐标为(),2t t . …………………1分 因为||||AC BC =,=…………………4分解得2t =,即圆心C 的坐标为(2, 4). …………………5分 圆心为C的圆的半径长||r AC === …………………7分所以圆C 的方程为22(2)(4)5x y -+-=. …………………8分(2)方法1:由于直线l 经过点P (-1, 3),当直线l 的斜率不存在时,1x =-与圆22(2)(4)5C x y -+-=相离. …………………9分 当直线l 的斜率存在时,可设直线l 的方程为3(1)y k x -=+,即:30kx y k -++=. …………………10分 因为直线l 与圆C 相切,且圆C 的圆心为(2, 4)= …………………11分解得2k =或12k =-. …………………13分 所以直线l 的方程为32(1)y x -=+或13(1)2y x -=-+,即:250x y -+=或250x y +-=. …………………14分 方法2:由于直线l 经过点P (-1, 3),当直线l 的斜率不存在时,1x =-与圆22(2)(4)5C x y -+-=相离. …………………9分 当直线l 的斜率存在时,可设直线l 的方程为3(1)y k x -=+,联立方程组223(1),(2)(4) 5.y k x x y -=+⎧⎨-+-=⎩ …………………10分 消去y ,得2222(1)2(2)(2)0k x k k x k k ++--+-=. …………………11分 由22224(2)4(1)(2)0k k k k ∆=---+-=,解得2k =或12k =-. …………………13分 所以直线l 的方程为32(1)y x -=+或13(1)2y x -=-+,即:250x y -+=或250x y +-=. …………………14分 19.本小题主要考查函数的性质等基础知识,考查推理论证能力和运算求解能力.满分14分. 解:(1)因为1()x a f x a x +-=-,所以由(1)1f =,得211aa -=-, …………………2分 解得32a =. (2)方法1:设12,x x 是区间[]1,2a a ++上的任意两个实数,且12x x <, 则12211212121211()(1)()(1)()()()()x a x a a x x a a x x a f x f x a x a x a x a x +-+--+---+--=-=----1212()()x x a x a x -=-- …………………8分由1212a x x a +≤<≤+,得12120,21,21x x a x a x -<-≤-≤--≤-≤-,于是12()()0f x f x -<,即12()()f x f x <.所以,函数1()x af x a x +-=-在区间[]1,2a a ++上是增函数. …………………12分因此,函数1()x af x a x +-=-在区间[]1,2a a ++上的最小值为(1)2f a +=-. ………14分方法2:因为1()x af x a x+-=-,所以22()(1)1()()()a x x a f x a x a x -++-'==--. …………………8分 当[]1,2x a a ∈=++时,()0f x '>, …………………10分所以函数1()x af x a x +-=-在区间[]1,2a a ++上是增函数. …………………12分因此,函数1()x af x a x+-=-在区间[]1,2a a ++上的最小值为(1)2f a +=-.…………………14分 20.本小题主要考查数列、等差数列等基本知识,考查推理论证能力和运算求解能力.满分14分. 解:(1)由20a =得:120a λ+=,而12a =,则1λ=-. …………………1分即12n n n a a +=-+.所以23224a a =-+=. …………………2分 (2)不存在实数λ,使得数列{}n a 为等差数列,由于22132222,4(22)4224a a a a λλλλλλλ=+=+=+=++=++,若数列{}n a 为等差数列,则2132a a a =+. …………………4分 即22(22)2(224)λλλ+=+++,即210λλ-+=, …………………5分 由于140∆=-<,方程无实数根,因此,不存在实数λ,使得数列{}n a 为等差数列. …………………6分 (3)由于1λ=,即12n n n a a +=+, …………………7分 则2n ≥时,121321()()()n n n a a a a a a a a -=+-+-++-,1212(12)22222212n n n ---=++++=+=-, …………………9分而12a =,因此,n *∈N 时,2n n a =,∴472n nn b -=. …………………10分 则23315472222n nn S --=++++,2341131541147222222n n n n n S +---=+++++, 以上两式相减得:23113111474222222n n n n S +--⎛⎫=++++- ⎪⎝⎭, 即2412n n nn S --=. …………………12分 当1,2,3,4n =时,0n S <,当5n =时,0n S >, …………………13分 故满足0n S >的最小自然数n 的值为5. …………………14分。
广州2008—2009学年第一学期中段学业质量监测高三文科数学试卷

2008—2009学年第一学期中段学业质量监测高三文科数学试卷本试卷共4页,21小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再将答案填写在对应题号的横线上。
漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将答题卡一并交回. 参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么()()()P A B P A P B +=+.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知全集合{},3,2,1,0=I 集合{}2,1,0=M ,{}3,2,0=N ,则()=⋂N C M I ( ) A.{}1 B.{}3,2 C.{}2,1,0 D. φ2.复数i+12的虚部是( ) A.1 B. i - C. i D.1-3.若,0>>b a 则下列不等式不成立的是( ) A.ba 11< B.b a >C.a b +<D.ba⎪⎭⎫⎝⎛<⎪⎭⎫ ⎝⎛21214.已知几何体的三视图如图1所示,它的表面积是( ) A.24+ B. 22+ C.23+D.6主视图侧视图附视图图15.已知双曲线19222=-y ax ()0>a 的中心在原点, 右焦点与抛物线x y 162=的焦点重合,则该双曲线的离心率等于( ) A.54 B. 55558 C. 45 D. 774 6.函数()x f y =的图象如图2所示.观察图象可知 函数()x f y =的定义域、值域分别是( ) A.[][)6,20,5⋃-,[]5,0 B.[)[)+∞-,0,6,5 C.[][)6,20,5⋃-,[)+∞,0 D.[)[]5,2,,5+∞- 7.函数()0sin cos22>-=ωωωx x y 的最小正周期是π,则函数()⎪⎭⎫⎝⎛+=4sin 2πωx x f 的一个单调递增区间是( ) A. ⎥⎦⎤⎢⎣⎡-2,2ππ B. ⎥⎦⎤⎢⎣⎡49,45ππ C. ⎥⎦⎤⎢⎣⎡-43,4ππ D. ⎥⎦⎤⎢⎣⎡45,4ππ 8. 设命题p :矩形的对角线相等;命题q :()x x x f ln =的单调减区间是⎪⎭⎫ ⎝⎛∞-e 1,.则( ) A .“p 或q ”为真 B .“p 且q ”为真 C .p 假q 真 D .p ,q 均为假命题 9.为了了解高三学生的数学成绩,抽取了某 班60名学生,将所得数据整理后,画出其 频率分布直方图(如图3),已知从左到右各 长方形高的比为2:3:5:6:3:1,则该 班学生数学成绩在(80,100)之间的学生人数是( )A. 32人B. 27人C. 24人D. 33人10.若偶函数()x f ()R x ∈满足()()x f x f =+2且[]1,0∈x 时,(),x x f =则方程()x x f 3l o g =的零点个数是( )A. 2个B. 4个C. 3个D. 多于4个二、填空题:本大题共5小题,每小题5分,满分20分.本大题分为必做题和选做题两部分.图2(一)必做题:第11、12、13题是必做题,每道试题考生都必须做答. 11. 设ABC ∆是边长为1则CA CB += . 12.定义某种运算b a S ⊗=,如图4所示,则式子:31100lg ln 45tan 2-⎪⎭⎫ ⎝⎛⊗+⊗⎪⎭⎫ ⎝⎛e π的值是 .13.在区域()⎭⎬⎫⎩⎨⎧⎩⎨⎧<<<<=4020,y x y x M 内随机撒一把黄豆,落在区域()⎪⎭⎪⎬⎪⎩⎪⎨⎪⎩⎪⎨>>=0,x x y y x N 的概率是 .(二)选做题:第14、15题是选做题,考生只能选做一题,两题全答的,只计算第一题的得分. 14. (坐标系与参数方程选做题)若直线340x y m ++=与圆⎩⎨⎧+-=+=θθsin 2cos 1y x (θ为参数)相切,则实数m 的值是 .15.(几何证明选讲选做题)如图5, AB 为⊙O 的直径, AC 切⊙O 于点A ,且cm AC 22=,过C 的割线CMN 交AB 的延长线于点D ,CM=MN=ND.AD 的长等于 cm .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)将一枚骰子先后抛掷2次,观察向上面的点数 (Ⅰ)点数之和是5的概率;(Ⅱ)设b a ,分别是将一枚骰子先后抛掷2次向上面的点数,求式子12=-ba 成立的概率.图5已知:A 、B 、C 是ABC ∆的内角,c b a ,,分别是其对边长,向量()1cos ,3+=A ,()1,sin -=A ,⊥.(Ⅰ)求角A 的大小; (Ⅱ)若,33cos ,2==B a 求b 的长. 18.(本小题满分14分) 数列{}n b ()*∈Nn 是递增的等比数列,且4,53131==+b b bb .(Ⅰ)求数列{}n b 的通项公式;(Ⅱ)若3log 2+=n n b a ,求证数列{}n a 是等差数列; (Ⅲ)若+++3221a a a ……46a a m ≤+,求m 的最大值.如图6,在直角梯形ABCP 中,AP//BC ,AP ⊥AB ,AB=BC=221=AP ,D 是AP 的中点,E ,F ,G 分别为PC 、PD 、CB 的中点,将PCD ∆沿CD 折起,使得⊥PD 平面ABCD,如图7.(Ⅰ)求证:PCD AD 平面⊥; (Ⅱ)求证:AP//平面EFG ; (Ⅲ)求三棱椎PAB D -的体积.20. (本小题满分14分)已知长方形ABCD, AB=22,BC=1.以AB 的中点O 为原点建立如图8所示的平面直角坐标系xoy .(Ⅰ)求以A 、B 为焦点,且过C 、D 两点的椭圆的标准方程;(Ⅱ)过点P(0,2)的直线l 交(Ⅰ)中椭圆于M,N 两点,是否存在直线l ,使得以弦MN 为直径的圆恰好过原点?若存在,求出直线l 的方程;若不存在,ADFG CBEP图6BGCDFEAP图7图8已知()()2,ln 23+-+==x ax x x g x x x f(Ⅰ)如果函数()x g 的单调递减区间为⎪⎭⎫ ⎝⎛-1,31,求函数()x g 的解析式; (Ⅱ)在(Ⅰ)的条件下,求过点P(1,1)且与函数y=()x g 的图像相切的直线方程; (Ⅲ)对一切的()+∞∈,0x ,()()22'+≤x g x f 恒成立,求实数a 的取值范围.2008—2009学年第一学期中段学业质量监测高三文科数学参考答案和评分标准11.3 12.8 13.1214.10或0(填对一个给3分) 15. 72 三、解答题(本大题共6小题,共80分)16.(本题满分12分)解:将一枚骰子先后抛掷2次,向上的点数共有36种不同的结果.……1分(Ⅰ)将一枚骰子先后抛掷2次,向上的点数分别记为b a ,,点数之和是5的情况有以下4种不同的结果⎩⎨⎧==⎩⎨⎧==⎩⎨⎧==⎩⎨⎧==23,32,14,41b a b a b a b a ……5分 因此,点数之和是5的概率为.913641==P ……6分 (Ⅱ)由12=-ba 得022=-b a ,.,0b a b a =∴=-∴……8分而将一枚骰子先后抛掷2次向上的点数相等的情况有以下6种不同的结果:⎩⎨⎧==⎩⎨⎧==⎩⎨⎧==⎩⎨⎧==⎩⎨⎧==⎩⎨⎧==66,55,44,33,22,11b a b a b a b a b a b a ……11分 因此,式子12=-ba 成立的概率为.613662==P ……12分 17. (本题满分12分) 解:(Ⅰ) ⊥()()()()011cos sin 31,sin 1cos ,3=-⨯++=-⋅+=⋅∴A A A A1cos sin 3=-∴A A ……4分216sin =⎪⎭⎫ ⎝⎛-∴πA ……6分∵,66,6566,0ππππππ=-∴<-<-∴<<A A A ……7分BGCDFEAPO3π=∴A .……8分(Ⅱ)在ABC ∆中,3π=A ,2=a ,33cos =B 36311cos 1sin 2=-=-=∴B B ……9分 由正弦定理知:,sin sin BbA a =……10分 ∴AB a b sin sin ==32423362=⨯=. ∴=b 324……12分18. (本题满分14分) 解:(Ⅰ)由 ⎩⎨⎧=+=543131b b b b 知31,b b 是方程0452=+-x x 的两根,注意到n n b b >+1得4,131==b b .……2分∴43122==b b b 得22=b . ∴4,2,1321===b b b∴等比数列.{}n b 的公比为212=b b,1112--==∴n n n q b b ……4分(Ⅱ).23132log 3log 122+=+-=+=+=-n n b a n n n ……6分 ∵()[][]12211=+-++=-+n n a a n n ……8分∴数列{}n a 是首相为3,公差为1的等差数列. ……9分 (Ⅲ) 由(Ⅱ)知数列{}n a 是首相为3,公差为1的等差数列,有+++3221a a a ……m a +=++++32121a a a a ……1a a m -+……10分=()23631213322mm m m m m -++=-⨯-+⨯+……12分 4846=a∴482362≤-++mm m ,整理得08452≤-+m m ,解得712≤≤-m .……13分 m ∴的最大值是7. ……14分19. (本题满分14分)(Ⅰ)证明:由已知底面ABCD 是正方形∴DC AD ⊥,又∵⊥PD 面ABCDPD AD ⊥∴……2分又D CD PD =⋂……3分⊥∴AD 平面PCD . ……4分(Ⅱ)方法一)连AC,BD 交于O 点,连GO,FO,EO . ……5分∵E,F 分别为PC,PD 的中点,EF ∴//CD 21, 同理GO //12CD , EF ∴//. ∴四边形EFOG 是平行四边形,⊂∴EO 平面EFOG . ……7分又在三角形P AC 中,E,O 分别为PC,AC 的中点,∴P A//EO ……8分⊂EO 平面EFOG ,PA ⊄平面EFOG ,∴PA//平面EFOG,即PA//平面EFG . ……10分方法二) ∵E,F 分别为PC,PD 的中点, EF ∴//CD 21,同理GE //PB又//AB ,EF ∴//AB 21……6分,,B AB PB E EF EG =⋂=⋂∴平面EFG //平面P AB , ……8分又P A ⊂平面P AB ,//PA ∴平面EFG . ……10分 (Ⅲ).34222213131=⨯⨯⨯⨯=⋅==∆--PD S V V ABD DAB P PAB D ……14分20. (本题满分14分)解:(Ⅰ)由题意可得点A,B,C 的坐标分别为()()()1,2,0,2,0,2-.……1分设椭圆的标准方程是()012222>>=+b a by a x .……2分则()()()()()2,2240122012222222=∴>=-+-+-+--=+=a BC AC a ……4分224222=-=-=∴c a b .……5分 ∴椭圆的标准方程是.12422=+y x ……6分 (Ⅱ)由题意直线的斜率存在,可设直线l 的方程为()02≠+=k kx y .……7分设M,N 两点的坐标分别为()().,,,2211y x y x联立方程:⎩⎨⎧=++=42222y x kx y消去y 整理得,()0482122=+++kx xk有12122284,81212k x x x x k k +=-⋅⋅⋅⋅=++分, (9)若以MN 为直径的圆恰好过原点,则⊥,所以02121=+y y x x ,……10分 所以,()()0222121=+++kx kx x x , 即()()042121212=++++x x k x x k所以,()0421*******222=++-++k k k k 即,0214822=+-kk ……11分 得 .2,22±==k k ……12分 所以直线l 的方程为22+=x y ,或22+-=x y .……13分所以存在过P(0,2)的直线l :22+±=x y 使得以弦MN 为直径的圆恰好过原点. ……14分21. (本小题满分14分)解:(Ⅰ)()1232'-+=ax x x g ……1分 由题意01232<-+ax x 的解集是⎪⎭⎫ ⎝⎛-1,31 即01232=-+ax x 的两根分别是1,31-. 将1=x 或31-代入方程01232=-+ax x 得1-=a .……3分 ()223+--=∴x x x x g .……4分(Ⅱ)把P(1,1)代入()223+--=∴x x x x g 适合,可知P 点在()g x 的图像上……5分(ⅰ)若P(1,1)不是切点,设切点坐标是()00,y x M ()10≠x . 有1231102000--=--x x x y ……6分 将2020300+--=x x x y 代入上式整理得022020=-x x 得10=x (舍),00=x . ……7分 此时切线斜率11020321-=-⨯-⨯=k切线方程为()111-⨯-=-x y ,即02=-+y x .……8分 (ⅱ) 若P (1,1)是切点,则切线斜率01121322=-⨯-⨯=k图811 此时切线方程为1=y .……9分综上, 函数()223+--=x x x x g 的图像过点P(1,1)的切线方程为02=-+y x 或1=y .……10分(Ⅲ)由题意: 2123ln 22+-+≤ax x x x 在()0,x ∈+∞恒成立, 即123ln 22++≤ax x x x 可得xx x a 2123ln --≥……11分 设()x x x x h 2123ln --=, 则()()()22'213121231x x x x x x h +--=+-=……12分 令()0'=x h ,得31,1-==x x (舍) 当10<<x 时,()0'>x h ;当1>x 时, ()0'<x h∴当1=x 时,()x h 取得最大值, ()x h max =-2……13分2-≥∴a .a ∴的取值范围是[)+∞-,2.……14分。
2008年广州市数学调研测试、一模、二模试题分类整理

2008年广州市数学调研测试、一模、二模试题分类整理1.集合与常用逻辑用语(调研测试文1、理1)集合{}2,4,6M =的真子集的个数为A .6B .7C .8D .9(二模文2、理1)已知集合M 满足{}{}3,2,12,1= M , 则集合M 的个数是 A. 1 B. 2 C. 3 D. 4(一模文1、理1)已知全集U =R ,集合{}22A x x =-<<,{}220B x x x =-≤,则A B =A .()0,2B .(]0,2C .[]0,2D .[)0,2(一模文6、理6)已知a ∈R ,则“2a >”是“22a a >”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件(二模文8、理6)已知命题0:2≥a p (∈a R ), 命题:q 函数()x x x f -=2在区间[)∞+,0上单调递增, 则下列命题中为真命题的是A. q p ∨B. q p ∧C. ()()q p ⌝∧⌝D. ()q p ∨⌝2.函数、导数与定积分(一模文5、理3)已知函数2log ,0,()2,0.x x x f x x >⎧=⎨≤⎩若1()2f a =,则a = A .1- BC .1-D .1或(调研测试文10、理8)函数()22log 1log 1x f x x -=+,若()()1221f x f x +=(其中1x 、2x 均大于2),则()12f x x 的最小值为 A .35 B .23 C .45 D.54(二模文11)函数()1lg +=x y 的定义域是 .(二模理9)函数()21lg x y -=的定义域是 .(二模文21)(本小题满分14分)已知函数()()0122>+=x x x x f . (1)当0,021>>x x 且()()121=⋅x f x f 时, 求证: 22321+≥⋅x x ;(2)若数列{}n a 满足()n n n a f a a a =>=+11,0,1∈n (N )*, 求数列{}n a 的通项公式..3.数列(二模文3)在等差数列{}n a 中,若12021062=++a a a ,则93a a +等于 A. 30 B. 40 C. 60 D. 80(调研测试理10)已知等比数列{}n a 的前三项依次为1a -,1a +,4a +,则n a = .(调研测试文21、理21)(本小题满分14分)已知数列{}n a 中,12a =,23a =,其前n 项和n S 满足1121n n n S S S +-+=+(2n ≥,*n ∈N ). (1)求数列{}n a 的通项公式;(2)设14(1)2(n an n n b λλ-=+-⋅为非零整数,*n ∈N ),试确定λ的值,使得对任意*n ∈N ,都有n n b b >+1成立.(一模理19)(本小题满分14分)已知数列}{n a 中,51=a 且1221n n n a a -=+-(2n ≥且*n ∈N ).(1)若数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列,求实数λ的值; (2)求数列}{n a 的前n 项和n S .(二模理21)(本小题满分14分) 已知数列{}n a 满足12,1211+==+n nn a a a a ∈n (N )*. (1) 求32,a a 的值;(2) 求数列{}n a 的通项公式; (3) 求证:∑=+ni ii a a 1187<.4.不等式(调研测试文2、理2)不等式2320x x -+<的解集是A .{}21x x x <->-或B .{}12x x x <>或C .{}21x x -<<-D .{}12x x <<(二模文7、理5)设()()13.0log ,3.0,2223.0>+===x x c b a x ,则c b a ,,的大小关系是A .c b a <<B .c a b <<C .a b c <<D .a c b <<(一模文9、理7)抽气机每次抽出容器内空气的60%,要使容器内剩下的空气少于原来的0.1%,则至少要抽(参考数据:lg 20.3010=,lg30.4771=)A .14次B .13次C .9次D .8次(二模文19、理18)(本小题满分12分)某工厂生产甲、乙两种产品,每生产一吨产品所消耗的电能和煤、所需工人人数以及所得产值如下表所示:已知该工厂的工人人数最多是200人,根据限额,该工厂每天消耗电能不得超过160千度,消耗煤不得超过150吨,问怎样安排甲、乙这两种产品的生产数量, 才能使每天所得产值最大.5.平面向量与三角(调研测试文7、理5)已知向量()1,1=a ,()2,n =b ,若+= a b a b ,则n =A .3-B .1-C .1D .3(一模文10、理8)在ABC ∆所在的平面上有一点P ,满足PA PB PC AB ++=,则PBC∆与ABC ∆的面积之比是A .13B .12C .23D .34(二模文1)函数x y 2sin =是A. 周期为π的奇函数B. 周期为π的偶函数C. 周期为π2的奇函数D. 周期为π2的偶函数(二模理2)函数⎪⎭⎫⎝⎛+=2sin πx y 是 A. 周期为π2的偶函数 B. 周期为π2的奇函数 C. 周期为π的偶函数 D. 周期为π的奇函数(调研测试文3、理3)函数cos y x =的一个单调递增区间为 A .,22ππ⎛⎫-⎪⎝⎭ B .()0,π C .3,22ππ⎛⎫⎪⎝⎭D .(),2ππ(一模文2)已知3cos 5α=,则cos 2α的值为 A .2425- B .725- C .725D .2425(一模理10)已知3cos 5α=,则cos 2α= .(二模文17、理16)(本小题满分12分) 已知点()()1,0,0,1B A ,()θθcos ,sin 2C . (1)=, 求θtan 的值;(2) 若(,12=⋅+其中O 为坐标原点, 求θ2sin 的值.(一模文17、理16)(本小题满分12分)已知函数()sin cos f x a x b x =+的图象经过点,03π⎛⎫ ⎪⎝⎭和,12π⎛⎫ ⎪⎝⎭. (1)求实数a 和b 的值;(2)当x 为何值时,()f x 取得最大值.(调研测试文17、理16)(本小题满分12分)在△ABC 中,角,,A B C 所对的边分别为,,a b c ,已知2a =,3c =,1cos 4B =. (1)求b 的值;(2)求sin C 的值.6.立体几何(一模文3)一个几何体的三视图如图1所示,其中 正视图与左视图都是边长为2的正三角形,则这个几 何体的侧面积为 AB .2πC .3πD .4π(二模文5)圆锥的母线长为2 cm ,过顶点和底面圆心的截面面积为2 cm 2,则该圆锥的侧面积为A. π2cm 2B. π2cm 2C. π22cm 2D.π4cm 2图1正(主)视图 左(侧)视图俯视图(调研测试文9、理7)已知α,β是平面,m ,n 是直线,给出下列命题①若α⊥m ,β⊂m ,则βα⊥.②若α⊂m ,α⊂n ,m β ,n β ,则αβ .③如果m n m ,,αα⊄⊂、n 是异面直线,那么α与n 相交.④若m αβ= ,n ∥m ,且βα⊄⊄n n ,,则n ∥α且n ∥β. 其中正确命题的个数是A .4B .3C .2D .1(一模文12)在空间直角坐标系中O xyz -,点()1,2,3-关于坐标平面yOz 的对称点的坐标为 .(调研测试文18)(本小题满分14分)如图4所示,四棱锥P ABCD -中,底面ABCD 为正方形,PD ⊥平面ABCD ,2PD AB ==,E ,F ,G 分别为PC 、PD 、BC 的中点. (1)求证:PA 平面EFG ;(2)求三棱锥P EFG -的体积.(调研测试理18)(本小题满分14分)如图3所示,四棱锥P ABCD -中,底面ABCD 为正方形,PD ⊥平面ABCD ,2PD AB ==,E ,F ,G 分别为PC 、PD 、BC 的中点. (1)求证:PA EF ⊥;(2)求二面角D -FG -E 的余弦值.(一模文18)(本小题满分14分)如图4所示,在边长为12的正方形11AA A A''中,点,B C 在线段AA '上,且3AB =,4BC =,作1BB 1AA ,分别交11A A '、1AA '于点1B 、P ,作1CC 1AA ,分别交11A A '、1AA '于点1C 、Q ,将该正方形沿1BB 、1CC 折叠,使得1A A ''与1AA 重合,构成如图5所示的三棱柱111ABC A B C -.(1)在三棱柱111ABC A B C -中,求证:AB ⊥平面11BCC B ;(2)求平面APQ 将三棱柱111ABC A B C -分成上、下两部分几何体的体积之比.(一模理18)(本小题满分14分)如图3所示,在边长为12的正方形11AA A A''中,点,B C 在线段AA '上,且3AB =,4BC =,作1BB 1AA ,分别交11A A '、1AA '于点1B 、P ,作1CC 1AA ,分别交11A A '、1AA '于点1C 、Q ,将该正方形沿1BB 、1CC 折叠,使得1A A ''与1AA 重合,构成如图4所示的三棱柱111ABC A B C -.(1)在三棱柱111ABC A B C -中,求证:AB ⊥平面11BCC B ;(2)求平面APQ 将三棱柱111ABC A B C -分成上、下两部分几何体的体积之比; (3)在三棱柱111ABC A B C -中,求直线AP 与直线1AQ 所成角的余弦值.(二模文18)(本小题满分14分)如图5所示,在三棱锥ABC P -中,⊥PA 平面ABC ,3===CA BC AB ,M 为AB1B 1C 1A 1A '1B 1C 1A 1A '的中点,四点C M A P 、、、都在球O 的球面上. (1)证明: 平面⊥PAB 平面PCM ;(2)证明:线段PC 的中点为球O 的球心;(3)若球O 的表面积为π25, 求三棱锥ABC P -的体积.(二模理17)(本小题满分14分) 如图3所示,在三棱锥ABC P -中,⊥PA 平面ABC ,2===CA BC AB ,M 为AB 的中点,四点C M A P 、、、都在球O 的球面上. (1) 证明: 平面⊥PAB 平面PCM ;(2)证明:线段PC 的中点为球O 的球心; (3)若球O 的表面积为π20,求二面角C PB A --的平面角的余弦值.7.解析几何(二模理3)已知点()()2,,2,1m B A -,且线段AB 的垂直平分线方程是022=-+y x , 则实数m 的值是A. 2-B. 7-C. 3D. 1(一模文8、理4)直线20ax y a -+=与圆229x y +=的位置关系是A .相离B .相交C .相切D .不确定(调研测试文5)抛物线24y x =上一点M 到焦点的距离为3,则点M 的横坐标x = A .1 B .2 C .3 D .4(二模文9)如图2所示,F 为双曲线1169:22=-y x C 的左 焦点,双曲线C 上的点i P 与()3,2,17=-i P i 关于y 轴对称,则F P F P F P F P F P F P 654321---++的值是 A .9 B .16 C .18 D .27(调研测试文12)已知双曲线2214x y m-=的离心率为2,则实数m = .(调研测试理11)抛物线24y x =上一点M 到焦点的距离为3,则点M 的横坐标x = .(调研测试文19)(本小题满分14分)已知曲线Γ上任意一点P 到两个定点()1F 和)2F 的距离之和为4.(1)求曲线Γ的方程;(2)设过()0,2-的直线l 与曲线Γ交于C 、D 两点,且0OC OD ⋅=(O 为坐标原点),求直线l 的方程.(调研测试理20)(本小题满分14分)已知点,A B 的坐标分别是(0,1)-,(0,1),直线,AM BM 相交于点M ,且它们的斜率之积为12-. (1)求点M 轨迹C 的方程;(2)若过点()2,0D 的直线l 与(1)中的轨迹C 交于不同的两点E 、F (E 在D 、F 之间),试求ODE ∆与ODF ∆面积之比的取值范围(O 为坐标原点).(一模文20)(本小题满分14分)已知过点()0,1P -的直线l 与抛物线24x y =相交于11()A x y ,、22()B x y ,两点,1l 、2l 分别是抛物线24x y =在A 、B 两点处的切线,M 、N 分别是1l 、2l 与直线1y =-的交点.(1)求直线l 的斜率的取值范围;(2)试比较PM 与PN 的大小,并说明理由.(一模理21)(本小题满分14分)已知抛物线L :22x py =和点()2,2M ,若抛物线L 上存在不同两点A 、B 满足AM BM +=0.(1)求实数p 的取值范围;(2)当2p =时,抛物线L 上是否存在异于A 、B 的点C ,使得经过A 、B 、C 三点的圆和抛物线L 在点C 处有相同的切线,若存在,求出点C 的坐标,若不存在,请说明理由.8.算法、统计与概率(调研测试文8、理6)如图1所示,是关于闰年 的流程,则以下年份是闰年的为 A .1996年 B .1998年 C .2010年 D .2100年 (一模文4、理2)某赛季,甲、乙两名篮球运动员都参加了 11场比赛,他们所有比赛得分的情况用如图2所示的茎叶 图表示,则甲、乙两名运动员得分的中位数分别为 A .19、13 B .13、19 C .20、18 D .18、20(一模理5)在区间[]0,1上任取两个数,a b ,方程220x ax b ++=的两根均为实数的概率为 A .18 B .14 C .12 D .34(二模文10、理8)甲、乙两位同学玩游戏,对于给定的实数1a ,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把1a 乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把1a 除以2后再加上12,这样就可得到一个新的实数2a . 对2a 仍按上述方法进行一次操作,又得到一个新的实数3a . 当13a a >时, 甲获胜, 否则乙获胜. 若甲获胜的概率为43, 则1a 的取值范围是A. (]12,∞-B. [)∞+,24C. ()24,12D. (]12,∞- [)∞+,24图2(一模文13、理12)按如图3所示的程序框图运算. 若输入8x =,则输出k = ;若输出2k =,则输入x 的取值范围是 .(注:“1=A ”也可写成“1:=A ”或“1←A ”,均表示赋值语句)(调研测试文11、理9)某校对全校男女学生共1600名进行健康调查,选用分层抽样法抽取一个容量为200的样本.已知女生抽了95人,则该校的女生人数应是 人.(二模文12)某校为了了解学生的体育锻炼情况,随机调查了70名学生,得到他们在某一天各自的体育锻炼时间的数据,结果用如图3所示的条形图表示. 根据条形图可得这70名学生这一天平均每人的体育锻炼时间为 小时.(二模理11)在一次数学测试(满分为150分)中, 某地区10000名考生的分数X 服从正态分布()215100,N , 据统计,分数在110分以上的考生共2514人,则分数在90分以上的考生共 人.(调研测试文16)(本小题满分12分)已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.(1)求甲射击一次,命中不足8环的概率; (2)求甲射击一次,至少命中7环的概率.广州市教育局教研室 曾辛金整理 第 11 页 共 13 页 (调研测试理17)(本小题满分12分) 已知射手甲射击一次,击中目标的概率是23. (1)求甲射击5次,恰有3次击中目标的概率;(2)假设甲连续2次未击中...目标,则中止其射击,求甲恰好射击5次后,被中止射击的概率.(一模文16)(本小题满分12分)将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x ,第二次出现的点数为y .(1)求事件“3x y +≤”的概率;(2)求事件“2x y -=”的概率.(一模理17)(本小题满分12分) 某计算机程序每运行一次都随机出现一个二进制的六位数123456N n n n n n n =,其中N 的各位数中,161n n ==,k n (k =2,3,4,5)出现0的概率为23,出现1的概率为13,记123456n n n n n n ξ=+++++,当该计算机程序运行一次时,求随机变量ξ的分布列和数学期望(即均值).9.复数(调研测试文6、理4)设复数z 满足i 2i z =-,则z =A .12i --B .12i -+C .12i -D .12i +(二模文4)在复平面内, 复数1 + i 与31+i 分别对应向量和, 其中O 为坐标原点,= A.2 B.2 C.10 D. 4(一模文11、理9)若复数()()2563i z m m m =-++-是实数,则实数m = .(二模理10)在复平面内, 复数1 + i 与31+-i 分别对应向量和, 其中O 为坐标原点,= .10.计数原理(二模理7)某中学一天的课表有6节课 , 其中上午4节, 下午2节, 要排语文、数学、英语、信息技术、体育、地理6节课,要求上午第一节课不排体育,数学必须排在上午,信息技术必须排在下午,则不同排法共有A. 48种B. 108种C. 156种D. 192种(调研测试理12)已知52x ⎛- ⎝的展开式中的常数项为T ,()f x 是以T 为周期的偶共 13 页 函数,且当[0,1]x ∈时,()f x x =,若在区间[1,3]-内,函数()()g x f x kx k =--有4个零点,则实数k 的取值范围是 .11.推理与证明(二模文13、理12)已知a 为正常数, 定义运算“⊗”如下: 对任意∈n m ,N ,*若,a n m =⊗则()a n m 21=⊗+, ()11+=+⊗a n m . 当111=⊗时, 则=⊗101 , =⊗110 .(二模文20、理19)(本小题满分14分)(1) 椭圆C :22221x y a b +=()0>>b a 与x 轴交于A 、B 两点,点P 是椭圆C 上异于A 、B 的任意一点,直线PA 、PB 分别与y 轴交于点M N 、,求证:AN BM ⋅ 为定值22b a -.(2) 由(1)类比可得如下真命题: 双曲线C :()0,012222>>=-b a by a x 与x 轴交于A 、B 两点,点P 是椭圆C 上异于A 、B 的任意一点,直线PA 、PB 分别与y 轴交于点M N 、,则AN BM ⋅ 为定值.请写出这个定值(不要求给出解题过程).12.坐标系与参数方程(调研测试文14、理13)在极坐标系中,点()1,0到直线()cos sin 2ρθθ+=的距离为 .(一模文14、理13)在极坐标系中,过点4π⎛⎫ ⎪⎝⎭作圆4sin ρθ=的切线,则切线的极坐标方程是 .(二模文14、理13)已知圆C 的参数方程为⎩⎨⎧=+=θθsin ,1cos y x (θ为参数), 则点()4,4P 与圆C 上的点的最远距离是 .13.几何证明选讲(一模文15、理15)在平行四边形ABCD 中,点E 在边AB 上,且:1:2AE EB =,DE与AC 交于点F ,若AEF ∆的面积为62cm ,则ABC ∆的面积为 2cm .(调研测试文15、理15)如图3所示,AB 与CD 是O 的直径,AB ⊥CD ,P 是AB 延长线上一点,连PC 交O 于点E ,连DE 交AB 于点F ,若42==BP AB ,则=PF .图3广州市教育局教研室 曾辛金整理 第 13 页 共 13 页(二模文15、理15)如图4所示, 圆的内接ABC ∆的∠C 的平分线CD 延长后交圆于点E ,连接BE , 已知5,7,3===BC CE BD , 则线段=BE .14.不等式选讲(二模理14)不等式21<-+x x 的解集是 .(调研测试理14)不等式142x x -<-+的解集是 .(一模理14)若a 、b 、c ∈R ,且222236a b c ++=,则a b c ++的最小值是 .。
2008年广东省广州市普通高中毕业班综合测试文科数学试题广州一测及参考答案

2008年广州市普通高中毕业班综合测试(一)数 学(文科) 2008.3本试卷共4页,21小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A)填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再将答案填写在对应题号的横线上。
漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么()()()P A B P A P B +=+.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U =R ,集合{}22A x x =-<<,{}220B x x x =-≤,则AB =A.()0,2B.(]0,2C.[]0,2D.[)0,22.已知3cos 5α=,则cos 2α的值为A.2425-B.725-C.725D.24253.一个几何体的三视图如图1所示,其中正视图与左视图都是边长为2的正三角形,则这个几何体的侧面积为B.2πC.3πD.4π4.某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们所有比 赛得分的情况用如图2所示的茎叶图表示,则甲、乙两名运动员 得分的中位数分别为 A.19、13 B.13、19C.20、18D.18、20图2图1 正(主)视图 左(侧)视图俯视图5.已知函数2log ,0,()2,0.x x x f x x >⎧=⎨≤⎩若1()2f a =,则a = A.1-C.1-D.1或 6.已知a ∈R ,则“2a >”是“22a a >”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.设()f x 、()g x 是R 上的可导函数,()f x '、()g x '分别为()f x 、()g x 的导函数,且()()()()0f x g x f x g x ''+<,则当a x b <<时,有A.()()()()f x g b f b g x >B.()()()()f x g a f a g x >C.()()()()f x g x f b g b >D.()()()()f x g x f a g a > 8.直线20ax y a -+=与圆229x y +=的位置关系是A.相离B.相交C.相切D.不确定9.抽气机每次抽出容器内空气的60%,要使容器内剩下的空气少于原来的0.1%,则至少要抽(参考数据:lg 20.3010=,lg30.4771=)A.14次B.13次C.9次D.8次10.在ABC ∆所在的平面上有一点P ,满足PA PB PC AB ++=,则PBC ∆与ABC ∆的面积之比是A.13 B.12 C.23 D.34二、填空题:本大题共5小题,每小题5分,满分20分.本大题分为必做题和选做题两部分.(一)必做题:第11、12、13题是必做题,每道试题考生都必须做答. 11.若复数()()2563i z m m m =-++-是实数,则实数m = .12.在空间直角坐标系中O xyz -,点()1,2,3-关于坐标平面yOz 的对称点的坐标为 .13.按如图3所示的程序框图运算. 若输入8x =,则输出k = ;若输出2k =,则输入x 的取值范围是 . (注:“1=A ”也可写成“1:=A ”或“1←A ”,均表示 赋值语句) (二)选做题:第14、15题是选做题,考生只能选做一题,两题全答的,只计算第一题的得分. 14.(坐标系与参数方程选做题)在极坐标系中,过点4π⎛⎫⎪⎝⎭作圆4sin ρθ=的切线,则切线的极坐标方程是 .15.(几何证明选讲选做题)在平行四边形ABCD 中,点E 在边AB 上,且:1:2AE EB =,DE 与AC 交于点F ,若AEF ∆的面积为62cm ,则ABC ∆的面积为 2cm .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x ,第二次出现的点数为y .(1)求事件“3x y +≤”的概率; (2)求事件“2x y -=”的概率. 17.(本小题满分12分)已知函数()sin cos f x a x b x =+的图象经过点,03π⎛⎫⎪⎝⎭和,12π⎛⎫ ⎪⎝⎭. (1)求实数a 和b 的值;(2)当x 为何值时,()f x 取得最大值. 18.(本小题满分14分)如图4所示,在边长为12的正方形11AA A A''中,点,B C 在线段AA '上,且3AB =,4BC =,作1BB 1AA ,分别交11A A '、1AA '于点1B 、P ,作1CC 1AA ,分别交11A A '、1AA '于点1C 、Q ,将该正方形沿1BB 、1CC 折叠,使得1A A ''与1AA 重合,构成如图5所示的三棱柱111ABC A B C -.(1)在三棱柱111ABC A B C -中,求证:AB ⊥平面11BCC B ;(2)求平面APQ 将三棱柱111ABC A B C -分成上、下两部分几何体的体积之比.19.(本小题满分14分)已知数列}{n a 中,51=a 且1221nn n a a -=+-(2n ≥且*n ∈N ).(1)求2a ,3a 的值;(2)是否存在实数λ,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列,若存在,求出λ的值;若不存在,请说明理由.20.(本小题满分14分)已知过点()0,1P -的直线l 与抛物线24x y =相交于11()A x y ,、22()B x y ,两点,1l 、2l 分别是抛物线24x y =在A 、B 两点处的切线,M 、N 分别是1l 、2l 与直线1y =-的交点. (1)求直线l 的斜率的取值范围;(2)试比较PM 与PN 的大小,并说明理由.21.(本小题满分14分)已知函数()x f x e x =-(e 为自然对数的底数). (1)求函数()f x 的最小值;(2)若*n ∈N ,证明:1211n nn nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.2008年广州市普通高中毕业班综合测试(一)数学(文科)试题参考答案及评分标准一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.10.由PA PB PC AB ++=,得PA PB BA PC +++=0,即2PC AP =,所以点P 是CA 边上的第二个三等分 点,如图所示.故23PBC ABC S BC PC S BC AC ∆∆⋅==⋅. 二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,每小题5分,满分30分.其中第13题第一个空2分,第二个空3分. 11.3 12.()1,2,3-- 13.4;(]28,57 14.cos 2ρθ= 15.72三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查古典概率等基础知识,考查运算求解能力) 解:设(),x y 表示一个基本事件,则掷两次骰子包括:()1,1,()1,2,()1,3,()1,4,()1,5,()1,6,()2,1,()2,2,……,()6,5,()6,6,共36个基本事件. (1)用A 表示事件“3x y +≤”,则A 的结果有()1,1,()1,2,()2,1,共3个基本事件. ∴()313612P A ==.答:事件“3x y +≤”的概率为112. (2)用B 表示事件“2x y -=”,则B 的结果有()1,3,()2,4,()3,5,()4,6,()6,4,()5,3,()4,2,()3,1,共8个基本事件.∴()82369P B ==.答:事件“2x y -=”的概率为29. 17.(本小题满分12分)(本小题主要考查特殊角的三角函数、三角函数的性质等基础知识,考查运算求解能力) 解:(1)∵函数()sin cosf x a x b x =+的图象经过点,03π⎛⎫⎪⎝⎭和,12π⎛⎫ ⎪⎝⎭, ∴sin cos 0,33sin cos 1.22a b a b ππππ⎧+=⎪⎪⎨⎪+=⎪⎩即10,21.b a +=⎪=⎩ 解得1,a b =⎧⎪⎨=⎪⎩(2)由(1)得()sin f x x x =12sin 2x x ⎛⎫=- ⎪⎪⎝⎭2sin 3x π⎛⎫=- ⎪⎝⎭.∴当sin 13x π⎛⎫-= ⎪⎝⎭,即232x k πππ-=+,即526x k ππ=+()k ∈Z 时,()f x 取得最大值2. 18.(本小题满分14分)(本小题主要考查空间几何体中线、面的位置关系,考查空间想象能力和运算求解能力)(1)证明:在正方形11AA A A''中,∵5A C AA AB BC ''=--=, ∴三棱柱111ABC A B C -的底面三角形ABC 的边5AC =.∵3AB =,4BC =,∴222AB BC AC +=,则AB BC ⊥.∵四边形11AA A A''为正方形,11AA BB ,∴1AB BB ⊥,而1BC BB B =,∴AB ⊥平面11BCC B .(2)解:∵AB ⊥平面11BCC B ,∴AB 为四棱锥A BCQP -的高.∵四边形BCQP 为直角梯形,且3BP AB ==,7CQ AB BC =+=,∴梯形BCQP 的面积为()1202BCQP S BP CQ BC =+⨯=, ∴四棱锥A BCQP -的体积1203A BCQP BCPQ V S AB -=⨯=,由(1)知1B B AB ⊥,1B B BC ⊥,且ABBC B =,∴1B B ⊥平面ABC .∴三棱柱111ABC A B C -为直棱柱,∴三棱柱111ABC A B C -的体积为111172ABC A B C ABC V S BB -∆=⋅=. 故平面APQ 将三棱柱111ABC A B C -分成上、下两部分的体积之比为722013205-=. 19.(本小题满分14分)(本小题主要考查等比数列、递推数列等基础知识,考查综合运用知识分析问题和解决问题的能力)解:(1)∵51=a ,∴22122113a a =+-=,33222133a a =+-=.(2)方法1:假设存在实数λ,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列, 设2n n n a b λ+=, 由}{n b 为等差数列,则有3122b b b +=. ∴321232222a a a λλλ+++⨯=+.∴13533228λλλ+++=+. 解得,1λ=-. 事实上,1111122n n n n n n a a b b +++---=-()111212n n n a a ++=-+⎡⎤⎣⎦()1112112n n ++⎡⎤=-+⎣⎦1=. 综上可知,存在实数1λ=-,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. 方法2:假设存在实数λ,使得2n na λ+⎧⎫⎨⎬⎩⎭为等差数列, 设2n n na b λ+=,由}{n b 为等差数列,则有122n n n b b b ++=+(*n ∈N ). ∴12122222n n n n n n a a a λλλ+++++++⨯=+. ∴1244n n n a a a λ++=--()()121222n n n n a a a a +++=---()()12221211n n ++=---=-.综上可知,存在实数1λ=-,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. 20.(本小题满分14分)(本小题主要考查直线与圆锥曲线等基础知识,考查数形结合的数学思想方法,以及推理论证能力、运算求解能力)解:(1)依题意,直线l 的斜率存在,设直线l 的方程为1y kx =-.由方程214.y kx x y =-⎧⎨=⎩,消去y 得2440x kx -+=. ············ ①∵直线l 与抛物线24x y =相交于A ,B 两点,∴216160k ∆=->,解得1k >或1k <-.故直线l 斜率的取值范围为()(),11,-∞-+∞.(2)解法1:∵1x ,2x 是方程①的两实根,∴12124,4.x x k x x +=⎧⎨=⎩ ∴10x ≠,20x ≠. ∵214y x =,∴12y x '=.∵21114y x =,∴切线1l 的方程为211111()24y x x x x =-+.令1y =-, 得点M 的坐标为2114,12x x ⎛⎫-- ⎪⎝⎭. ∴21142x PM x -=. 同理,可得22242x PN x -=. ∵22121221222121212142444124444PMx x x x x x x PN x x x x x x x ---=⋅===---(12x x ≠).故PM PN =.解法2:可以断定PM PN =. ∵1x ,2x 是方程①的两实根, ∴12124,4.x x k x x +=⎧⎨=⎩ ∴10x ≠,20x ≠. ∵214y x =,∴12y x '=.∵21114y x =,∴切线1l 的方程为211111()24y x x x x =-+. 令1y =-,得点M 的坐标为2114,12x x ⎛⎫--⎪⎝⎭. 同理可得点N 的坐标为2224,12x x ⎛⎫-- ⎪⎝⎭. ∵()()2212121212124440222x x x x x x x x x x +---+==. ∴点P 是线段MN 的中点.故PM PN =.21.(本小题满分14分)(本小题主要考查函数的导数、最值、等比数列等基础知识,考查分析问题和解决问题的能力、以及创新意识)(1)解:∵()1x f x e '=-,令()0f x '=,得0x =.∴当0x >时,()0f x '>,当0x <时,()0f x '<.∴函数()x f x e x =-在区间(),0-∞上单调递减,在区间()0,+∞上单调递增. ∴当0x =时,()f x 有最小值1.(2)证明:由(1)知,对任意实数x 均有1xe x -≥,即1xx e +≤.令kx n=-(*,1,2,,1n k n ∈=-N ),则01k n ke n-<-≤,∴1(1,2,,1)nnkkn k e e k n n --⎛⎫⎛⎫-≤==- ⎪ ⎪⎝⎭⎝⎭. 即(1,2,,1)nkn k e k n n --⎛⎫≤=- ⎪⎝⎭. ∵1,nn n ⎛⎫= ⎪⎝⎭∴(1)(2)211211n nnnn n n n e e e e n n n n -------⎛⎫⎛⎫⎛⎫⎛⎫++++≤+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.∵(1)(2)2111111111n n n e eeee e e e e ----------+++++=<=---,∴ 1211n nnnn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.。
08广州二模

试卷类型:A2008年广州市普通高中毕业班综合测试(二)物 理2008年4月本试卷共8页,20小题,满分为150分。
考试用时120分钟。
注意事项:1.答题前,考生务必用2B 铅笔在“考生号”处填涂考生号。
用黑色字迹的钢笔或签字笔将自己所在的市县/区、学校,以及自己的姓名、考生号、试室号和座位号填写在答题 卡上。
用2B 铅笔将试卷类型(A)填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请用2B 铅笔填涂选做题的题组号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁,考试结束,将试卷和答题卡一并交回。
第I 卷(共48分)一、选择题共12小题,在每小题给出的四个选项中,有一个或一个以上选项符合题目要求, 全部选对得4分,选不全得2分,有选错或不答的得0分.1.如图所示,在竖直平面内有水平向右的匀强电场,同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球,另一端固定于0点,已知带电小球受到的电场力大于重力,小球由静止释放,到达图中竖直虚线前小球做A .平抛运动B .圆周运动C .匀加速直线运动D .匀变速曲线运动2.如图所示,物体沿着倾角不同而底边相同的光滑斜面由顶端从静止开始滑到底端A .斜面倾角越大,滑行时间越短B .斜面倾角越大,滑行时间越长C .斜面倾角越大,滑行的加速度越大D .斜面倾角越大,滑行的平均速度越大3.一交流电压的图象如图所示,将该交流电压加在一电阻两端,下列说法正确的是A .该交流电压的频率为50HzB .流过电阻的电流方向每秒钟改变50次C .并联在该电阻两端的交流电压表的示数为110VD .该交流电压的瞬时表达式为t u π100sin 2110= (V)4.正电子发射计算机断层显象(PET)的基本原理是:将放射性同位素O 158注入人体,O 158在人体内衰变放出的正电子与人体内的负电子相遇而湮灭转化为一对γ光子,被探测器探测到,经计算机处理后产生清晰的图象.根据PET 的原理,下列选项正确的是A .O 158在人体内衰变的方程式是:e N O 01157158+→B .正负电子湮灭的方程式是:γ20101→+-e eD .在PET 中,O 158的主要用途是作为示踪原子D .在PET 中,O 158的主要用途是参与人体的代谢过程5.氢原子的n=1、2、3、4各个能级的能量如图所示,一群氢原子处于n=4的激发态,当它们自发地跃迁到较低能级时A .最多激发出3种不同频率的光子B .最多激发出6种不同频率的光子C .由n=4跃迁到n=1时发出光子的频率最小D .由n=4跃迁到n=3时发出光子的频率最小6.原来静止的质量为m 1和m 2的两个物体,分别在恒力F 1和F 2的作用下开始运动,经相同的位移,动量的增加量相同,则两恒力的比值F 1/F 2为A .21m mB .12m mC .2221m m D .2122m m7.甲、乙两物体沿同一方向做直线运动,6s 末在途中相遇.它们的速度图象如图所示,可以确定A .t=0时甲在乙的前方27m 处B .t=0时乙在甲的前方27m 处C .6s 之后两物体不会再相遇D .6s 之后两物体还会再相遇8.如图所示,倾角为α的斜面静止不动,滑轮的质量和摩擦不计,质量为M 的物体A 与斜面的动摩擦因素为μ(设最大静摩擦力与滑动摩擦力大小相等),质量为m 的物体B 通过定 滑轮用细线与M 相连接.则A .当m>M(sin α+μcos α)时,m 一定有向下的加速度B .当m<M(sin α+μcos α)时,m 一定有向上的加速度C .当m>M(sin α一μcos α)时,m 一定有向下的加速度D .当m<M(sin α一μcos α)时,m 一定有向上的加速度9.用两根等长的细线各悬一个小球,并挂于同一点,已知两球质量相等,当它们带上同种电荷时,相距L 而平衡,如图所示.若使它们的带电量都减少一半,待它们重新平衡后,两球间距离A .大于L/2B .等于L/2C .小于L/2D .等于L10.小球以6m /s 的速度水平抛出,落到水平地面时的速度为10m /s ,取g=10m /s 2,小球从抛出到落地的时间及水平位移分别是A .1s 3.2mB .1s 4.8mC .0.8s 3.2mD .0.8s 4.8m11.一个面积S= 4×10-2m 2的闭合线圈,放在匀强磁场中,磁场方向垂直线圈平面,磁场的磁感应强度B 的大小随时间的变化规律如图所示A .在开始2s 内穿过线圈的磁通量变化率等于零B .在开始2s 内穿过线圈的磁通量变化率等于8×10-2Wb /sC .0~2s 和2s ~4s 内线圈中产生的感应电流大小相等D .0~1s 和1~2s 内线圈中产生的感应电流方向相反12.如图所示,带等量异种电荷的平行金属板a 、b 处于匀强磁场中,磁感应强度B 垂直纸 面向里,不计重力的带电粒子沿OO ′方向从左侧垂直于电磁场入射,从右侧射出a 、b 板间区域时动能比入射时小.要使粒子射出a 、b 板间区域时的动能比入射时大,可以A .适当增大金属板间的电压B .适当增大金属板间的距离C .适当减小金属板间的磁感应强度D .使带电粒子的电性相反第Ⅱ卷(共102分)二、非选择题13—14题为选做题,15—20题为必做题.按题目要求作答.解答题应写出必要的文字说明、方程和重要演算步骤,只写出最后答案的不能得分.有数值计算的题,答案中必须明确写出数值和单位.(一)选做题请考生从下面给出的两组选做题中选择其中的一组进行答题(不能同时选做两组,否则选做无效,不能得分),并在答题卡上将所选做题组对应的信息点涂满、涂黑。
2008年广州市普通高中毕业班综合测试(理科)(一)

秘密★启用前2008年广州市普通高中毕业班综合测试(一)数 学(理科)2008.3本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再将答案填写在对应题号的横线上。
漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么()()()P A B P A P B +=+. 如果事件A 、B 相互独立,那么()()()P A B P A P B ⋅=⋅.如果事件A 在一次试验中发生的概率是p ,那么在n 次独立重复试验中恰好发生k 次的概率()()C 1n kkkn n P k p p -=-.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知全集U =R ,集合{}22A x x =-<<,{}220B x x x =-≤,则A B =A .()0,2B .(]0,2C .[)0,2D .[]0,22.某赛季,甲、乙两名篮球运动员都参加了11赛得分的情况用如图1所示的茎叶图表示,则甲、乙两名运动员 的中位数分别为 A .19、13 B .13、19C .20、18D .18、20图13.已知函数2log ,0,()2,0.x x x f x x >⎧=⎨≤⎩若1()2f a =,则a = A .1- BC .1-D .1或 4.直线20ax y a -+=与圆229x y +=的位置关系是A .相离B .相交C .相切D .不确定 5.在区间[]0,1上任取两个数,a b ,方程220x ax b ++=的两根均为实数的概率为A .18 B .14 C .12 D .346.已知a ∈R ,则“2a >”是“22a a >”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.抽气机每次抽出容器内空气的60%,要使容器内剩下的空气少于原来的0.1%,则至少要抽(参考数据:lg 20.3010=,lg30.4771=)A .15次B .14次C .9次D .8次8.在ABC ∆所在的平面上有一点P ,满足PA PB PC AB ++=,则PBC ∆与ABC ∆的面积之比是 A .13 B .12 C .23 D .34二、填空题:本大题共7小题,每小题5分,满分30分.本大题分为必做题和选做题两部分.(一)必做题:第9、10、11、12题是必做题,每道试题考生都必须做答. 9.若复数()()2563i z m m m =-++-是实数,则实数m = . 10.已知3cos 5α=,则cos2α= . 11.根据定积分的几何意义,计算x =⎰.12.按如图2所示的程序框图运算. 若输入8x =,则输出k = ;若输出2k =,则输入x 的取值范围是 . (注:“1=A ”也可写成“1:=A ”或“1←A ”,均表示赋值 语句)(二)选做题:第13、14、15题是选做题,考生只能选做二题,三题全答的,只计算前两题的得分. 13.(坐标系与参数方程选做题)在极坐标系中,过点4π⎛⎫⎪⎝⎭作圆4sin ρθ=的切线,则切线的极坐标方程是 .14.(不等式选讲选做题)若a 、b 、c ∈R ,且222236a b c ++=,则a b c ++的最小值是 . 15.(几何证明选讲选做题)在平行四边形ABCD 中,点E 在边AB 上,且:1:2AE EB =,DE 与AC 交于点F ,若AEF ∆的面积为62cm ,则ABC ∆的面积为 2cm .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 已知函数()sin cos f x a x b x =+的图象经过点,03π⎛⎫⎪⎝⎭和,12π⎛⎫⎪⎝⎭. (1)求实数a 和b 的值;(2)当x 为何值时,()f x 取得最大值. 17.(本小题满分12分)某计算机程序每运行一次都随机出现一个二进制的六位数123456N n n n n n n =,其中N 的各位数中,161n n ==,k n (k =2,3,4,5)出现0的概率为23,出现1的概率为13,记123456n n n n n n ξ=+++++,当该计算机程序运行一次时,求随机变量ξ的分布列和数学期望(即均值). 18.(本小题满分14分)如图3所示,在边长为12的正方形11AA A A ''中,点,B C 在线段AA '上,且3AB =,4BC =,作1BB 1AA ,分别交11A A '、1AA '于点1B 、P ,作1CC 1AA ,分别交11A A '、1AA '于点1C 、Q ,将该正方形沿1BB 、1CC 折叠,使得1A A ''与1AA 重合,构成如图4所示的三棱柱111ABC A B C -.(1)在三棱柱111ABC A B C -中,求证:AB ⊥平面11BCC B ;(2)求平面APQ 将三棱柱111ABC A B C -分成上、下两部分几何体的体积之比; (3)在三棱柱111ABC A B C -中,求直线AP 与直线1A Q 所成角的余弦值.19.(本小题满分14分)已知数列}{n a 中,51=a 且1221n n n a a -=+-(2n ≥且*n ∈N ).(1)若数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列,求实数λ的值; (2)求数列}{n a 的前n 项和n S . 20.(本小题满分14分)已知函数()xf x e x =-(e 为自然对数的底数). (1)求函数()f x 的最小值;(2)若*n ∈N ,证明:1211n nn nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.21.(本小题满分14分)已知抛物线L :22x py =和点()2,2M ,若抛物线L 上存在不同两点A 、B 满足AM BM +=0.(1)求实数p 的取值范围;(2)当2p =时,抛物线L 上是否存在异于A 、B 的点C ,使得经过A 、B 、C 三点的圆和抛物线L 在点C 处有相同的切线,若存在,求出点C 的坐标,若不存在,请说明理由.2008年广州市普通高中毕业班综合测试(一)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.8.由PA PB PC AB ++=,得PA PBBA PC +++=0,即2PC AP =,所以点P 是CA 边上的第二个三等分 点,如图所示.故23PBC ABC S BC PC S BC AC ∆∆⋅==⋅.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,每小题5分,满分30分.其中第12题第一个空2分,第二个空3分.9.3 10.725-11.32π+ 12.4;(]28,5713.cos 2ρθ= 14.15.72三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查特殊角的三角函数、三角函数的性质等基础知识,考查运算求解能力) 解:(1)∵函数()sin cos f x a x bx =+的图象经过点,03π⎛⎫⎪⎝⎭和,12π⎛⎫⎪⎝⎭, ∴sin cos 0,33sin cos 1.22a b a b ππππ⎧+=⎪⎪⎨⎪+=⎪⎩即10,221.a b a +=⎪⎨⎪=⎩解得1,a b =⎧⎪⎨=⎪⎩.(2)由(1)得()sin f x x x =12sin 2x x ⎛⎫=- ⎪ ⎪⎝⎭2sin 3x π⎛⎫=- ⎪⎝⎭.∴当sin 13x π⎛⎫-= ⎪⎝⎭,即232x k πππ-=+, 即526x k ππ=+()k ∈Z 时,()f x 取得最大值2. 17.(本小题满分12分)(本小题主要考查随机变量的分布列及其数学期望等基础知识,考查运算求解能力等) 解:ξ的可能取值是2,3,4,5,6.∵161n n ==,∴()4042162C 381P ξ⎛⎫=== ⎪⎝⎭, ()31412323C 3381P ξ⎛⎫==⋅= ⎪⎝⎭,()22241284C 3327P ξ⎛⎫⎛⎫==⋅= ⎪⎪⎝⎭⎝⎭, ()3341285C 3381P ξ⎛⎫==⋅= ⎪⎝⎭, ()444116C 381P ξ⎛⎫=== ⎪⎝⎭. ∴ξ的分布列为∴ξ的数学期望为16322481102345681818181813E ξ=⨯+⨯+⨯+⨯+⨯=.18.(本小题满分14分)(本小题主要考查空间几何体中线面的位置关系,面积与体积,空间向量等基础知识,考查空间想象能力和运算求解能力)(1)证明:在正方形11AA A A ''中,∵5A C AA AB BC ''=--=, ∴三棱柱111ABC A B C -的底面三角形ABC 的边5AC =. ∵3AB =,4BC =,∴222AB BC AC +=,则AB BC ⊥.∵四边形11AA A A ''为正方形,11AA BB ,∴1AB BB ⊥,而1BCBB B =,∴AB ⊥平面11BCC B . (2)解:∵AB ⊥平面11BCC B ,∴AB 为四棱锥A BCQP -的高.∵四边形BCQP 为直角梯形,且3BP AB ==,7CQ AB BC =+=,∴梯形BCQP 的面积为()1202BCQP S BP CQ BC =+⨯=, ∴四棱锥A BCQP -的体积1203A BCQP BCPQ V S AB -=⨯=,由(1)知1B B AB ⊥,1B B BC ⊥,且AB BC B =,∴1B B ⊥平面ABC .∴三棱柱111ABC A B C -为直棱柱,∴三棱柱111ABC A B C -的体积为111172ABC A B C ABC V S BB -∆=⋅=. 故平面APQ 将三棱柱111ABC A B C -分成上、下两部分的体积之比为722013205-=. (3)解:由(1)、(2)可知,AB ,BC ,1BB 两两互相垂直.以B 为原点,建立如图所示的空间直角坐标系B xyz -,则()3,0,0A ,()13,0,12A ,()0,0,3P ,()0,4,7Q ,∴(3,0,3)AP =-,1(3,4,5)AQ =--, ∴1111cos ,5AP A QAP A Q AP A Q⋅<>==-,∵异面直线所成角的范围为0,2π⎛⎤ ⎥⎝⎦, ∴直线AP 与1A Q 所成角的余弦值为15. 19.(本小题满分14分)(本小题主要考查等比数列、递推数列等基础知识,考查综合运用知识分析问题和解决问题的能力)解:(1)方法1:∵51=a ,∴22122113a a =+-=,33222133a a =+-=.设2n n na b λ+=,由}{n b 为等差数列,则有3122b b b +=. ∴321232222a a a λλλ+++⨯=+.∴13533228λλλ+++=+. 解得 1λ=-.事实上,1111122n n n n n n a a b b +++---=-()111212n n n a a ++=-+⎡⎤⎣⎦()1112112n n ++⎡⎤=-+⎣⎦1=,综上可知,当1λ=-时,数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. 方法2:∵数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列, 设2n n na b λ+=,由}{n b 为等差数列,则有122n n n b b b ++=+(*n ∈N ). ∴12122222n n n n n n a a a λλλ+++++++⨯=+. ∴1244n n n a a a λ++=--()()121222n n n n a a a a +++=---()()12221211n n ++=---=-.综上可知,当1λ=-时,数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. (2)由(1)知,()1111122n na a n --=+-⨯, ∴()121n n a n =+⋅+. ∴()()()()12122132121121n nn S n n -⎡⎤=⋅++⋅+++⋅+++⋅+⎣⎦.即()1212232212n n n S n n n -=⋅+⋅++⋅++⋅+.令()1212232212n n n T n n -=⋅+⋅++⋅++⋅, ① 则()23122232212n n n T n n +=⋅+⋅++⋅++⋅. ②②-①,得()()12312222212n n n T n +=-⋅-+++++⋅12n n +=⋅.∴()11221n n n S n n n ++=⋅+=⋅+.20.(本小题满分14分)(本小题主要考查函数的导数、最值、等比数列等基础知识,考查分析问题和解决问题的能力、以及创新意识)(1)解:∵()xf x e x =-,∴()1xf x e '=-.令()0f x '=,得0x =.∴当0x >时,()0f x '>,当0x <时,()0f x '<.∴函数()x f x e x =-在区间(),0-∞上单调递减,在区间()0,+∞上单调递增.∴当0x =时,()f x 有最小值1.(2)证明:由(1)知,对任意实数x 均有1xe x -≥,即1xx e +≤.令k x n=-(*,1,2,,1n k n ∈=-N ),则01k n ke n-<-≤,∴1(1,2,,1)nnkkn k e e k n n --⎛⎫⎛⎫-≤==- ⎪ ⎪⎝⎭⎝⎭.即(1,2,,1)nk n k e k n n --⎛⎫≤=- ⎪⎝⎭.∵1,nn n ⎛⎫= ⎪⎝⎭∴(1)(2)211211n nn nn n n n e e e e n n n n -------⎛⎫⎛⎫⎛⎫⎛⎫++++≤+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.∵(1)(2)2111111111n n n e eeee e e e e ----------+++++=<=---,∴ 1211n nn nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.21.(本小题满分14分)(本小题主要考查直线与圆锥曲线等基础知识,考查数形结合的数学思想方法,以及推理论证能力、运算求解能力)解法1:(1)不妨设A 211,2x x p ⎛⎫ ⎪⎝⎭,B 222,2x x p ⎛⎫ ⎪⎝⎭,且12x x <,∵AM BM +=0,∴2212122,22,222x x x x p p ⎛⎫⎛⎫--+--= ⎪ ⎪⎝⎭⎝⎭0.∴124x x +=,22128x x p +=.∵()21222122x x x x ++>(12x x ≠),即88p >,∴1p >,即p 的取值范围为()1,+∞.(2)当2p =时,由(1)求得A 、B 的坐标分别为()0,0、()4,4.假设抛物线L 上存在点2,4t C t ⎛⎫⎪⎝⎭(0t ≠且4t ≠),使得经过A 、B 、C 三点的圆和抛物线L 在点C 处有相同的切线.设经过A 、B 、C 三点的圆的方程为220x y Dx Ey F ++++=,则2420,4432,1641616.F D E F tD t E F t t ⎧=⎪++=-⎨⎪++=--⎩整理得 ()()3441680t E t E ++-+=. ①∵函数24x y =的导数为2x y '=, ∴抛物线L 在点2,4t C t ⎛⎫ ⎪⎝⎭处的切线的斜率为2t , ∴经过A 、B 、C 三点的圆N 在点2,4t C t ⎛⎫ ⎪⎝⎭处的切线斜率为2t . ∵0t ≠,∴直线NC 的斜率存在.∵圆心N 的坐标为,22D E ⎛⎫-- ⎪⎝⎭, ∴242122t E t D t +⨯=-+,即()()324480t E t E ++-+=. ② ∵0t ≠,由①、②消去E ,得326320t t -+=.即()()2420t t -+=.∵4t ≠,∴2t =-.故满足题设的点C 存在,其坐标为()2,1-.解法2:(1)设A ,B 两点的坐标为1122()()A x y B x y ,,,,且12x x <。
2008年广东省广州市普通高中毕业班综合测试理科数学试题广州一测及参考答案

秘密★启用前2008年广州市普通高中毕业班综合测试(一)数 学(理科)2008.3本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A)填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再将答案填写在对应题号的横线上。
漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么()()()P A B P A P B +=+. 如果事件A 、B 相互独立,那么()()()P A B P A P B ⋅=⋅.如果事件A 在一次试验中发生的概率是p ,那么在n 次独立重复试验中恰好发生k 次的概率()()C 1n kkkn n P k pp -=-.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U =R ,集合{}22A x x =-<<,{}220B x x x =-≤,则AB =A.()0,2B.(]0,2C.[)0,2D.[]0,22.某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比 赛得分的情况用如图1所示的茎叶图表示,则甲、乙两名运动员的中位数分别为 A.19、13 B.13、19C.20、18D.18、20图13.已知函数2log ,0,()2,0.x x x f x x >⎧=⎨≤⎩若1()2f a =,则a = A.1-C.1-D.1或4.直线20ax y a -+=与圆229x y +=的位置关系是A.相离B.相交C.相切D.不确定 5.在区间[]0,1上任取两个数,a b ,方程220x ax b ++=的两根均为实数的概率为A.18 B.14 C.12 D.346.已知a ∈R ,则“2a >”是“22a a >”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.抽气机每次抽出容器内空气的60%,要使容器内剩下的空气少于原来的0.1%,则至少要抽(参考数据:lg 20.3010=,lg30.4771=)A.15次B.14次C.9次D.8次8.在ABC ∆所在的平面上有一点P ,满足PA PB PC AB ++=,则PBC ∆与ABC ∆的面积之比是 A.13 B.12 C.23 D.34二、填空题:本大题共7小题,每小题5分,满分30分.本大题分为必做题和选做题两部分.(一)必做题:第9、10、11、12题是必做题,每道试题考生都必须做答.9.若复数()()2563i z m m m =-++-是实数,则实数m = . 10.已知3cos 5α=,则cos 2α= . 11.根据定积分的几何意义,计算x =⎰.12.按如图2所示的程序框图运算. 若输入8x =,则输出k = ;若输出2k =,则输入x 的取值范围是 .(注:“1=A ”也可写成“1:=A ”或“1←A ”,均表示赋值语句)(二)选做题:第13、14、15题是选做题,考生只能选做二题,三题全答的,只计算前两题的得分.13.(坐标系与参数方程选做题)在极坐标系中,过点4π⎛⎫⎪⎝⎭作圆4sin ρθ=的切线,则切线的极坐标方程是 .14.(不等式选讲选做题)若a 、b 、c ∈R ,且222236a b c ++=,则a b c ++的最小值是 .15.(几何证明选讲选做题)在平行四边形ABCD 中,点E 在边AB 上,且:1:2AE EB =,DE 与AC 交于点F ,若AEF ∆的面积为62cm ,则ABC ∆的面积为 2cm .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数()sin cos f x a x b x =+的图象经过点,03π⎛⎫⎪⎝⎭和,12π⎛⎫ ⎪⎝⎭. (1)求实数a 和b 的值;(2)当x 为何值时,()f x 取得最大值.17.(本小题满分12分)某计算机程序每运行一次都随机出现一个二进制的六位数123456N n n n n n n =,其中N 的各位数中,161n n ==,k n (k =2,3,4,5)出现0的概率为23,出现1的概率为13,记123456n n n n n n ξ=+++++,当该计算机程序运行一次时,求随机变量ξ的分布列和数学期望(即均值).18.(本小题满分14分)如图3所示,在边长为12的正方形11AA A A ''中,点,B C 在线段AA '上,且3AB =,4BC =,作1BB 1AA ,分别交11A A '、1AA '于点1B 、P ,作1CC 1AA ,分别交11A A '、1AA '于点1C 、Q ,将该正方形沿1BB 、1CC 折叠,使得1A A ''与1AA 重合,构成如图4所示的三棱柱111ABC A B C -.(1)在三棱柱111ABC A B C -中,求证:AB ⊥平面11BCC B ;(2)求平面APQ 将三棱柱111ABC A B C -分成上、下两部分几何体的体积之比; (3)在三棱柱111ABC A B C -中,求直线AP 与直线1AQ 所成角的余弦值.19.(本小题满分14分)已知数列}{n a 中,51=a 且1221n n n a a -=+-(2n ≥且*n ∈N ). (1)若数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列,求实数λ的值; (2)求数列}{n a 的前n 项和n S .20.(本小题满分14分)已知函数()x f x e x =-(e 为自然对数的底数). (1)求函数()f x 的最小值;(2)若*n ∈N ,证明:1211n nn nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.21.(本小题满分14分)已知抛物线L :22x py =和点()2,2M ,若抛物线L 上存在不同两点A 、B 满足AM BM +=0.(1)求实数p 的取值范围;(2)当2p =时,抛物线L 上是否存在异于A 、B 的点C ,使得经过A 、B 、C 三点的圆和抛物线L 在点C 处有相同的切线,若存在,求出点C 的坐标,若不存在,请说明理由.2008年广州市普通高中毕业班综合测试(一)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.8.由PA PB PC AB ++=,得PA PB BA PC +++=0,即2PC AP=,所以点P 是CA 边上的第二个三等分 点,如图所示.故23PBC ABC S BC PC S BC AC ∆∆⋅==⋅.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,每小题5分,满分30分.其中第12题第一个空2分,第二个空3分.9.3 10.725-11.3π 12.4;(]28,57 13.cos 2ρθ= 14. 15.72三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查特殊角的三角函数、三角函数的性质等基础知识,考查运算求解能力) 解:(1)∵函数()sin cos f x ax b x =+的图象经过点,03π⎛⎫⎪⎝⎭和,12π⎛⎫ ⎪⎝⎭, ∴sin cos 0,33sin cos 1.22a b a b ππππ⎧+=⎪⎪⎨⎪+=⎪⎩即10,21.b a +=⎪=⎩解得1,a b =⎧⎪⎨=⎪⎩.(2)由(1)得()sin f x x x =12sin 2x x ⎛⎫= ⎪ ⎪⎝⎭2sin 3x π⎛⎫=- ⎪⎝⎭.∴当sin 13x π⎛⎫-= ⎪⎝⎭,即232x k πππ-=+, 即526x k ππ=+()k ∈Z 时,()f x 取得最大值2.17.(本小题满分12分)(本小题主要考查随机变量的分布列及其数学期望等基础知识,考查运算求解能力等) 解:ξ的可能取值是2,3,4,5,6.∵161n n ==,∴()4042162C 381P ξ⎛⎫===⎪⎝⎭, ()31412323C 3381P ξ⎛⎫==⋅= ⎪⎝⎭,()22241284C 3327P ξ⎛⎫⎛⎫==⋅= ⎪⎪⎝⎭⎝⎭, ()3341285C 3381P ξ⎛⎫==⋅= ⎪⎝⎭, ()444116C 381P ξ⎛⎫=== ⎪⎝⎭.∴ξ的分布列为∴ξ的数学期望为16322481102345681818181813E ξ=⨯+⨯+⨯+⨯+⨯=.18.(本小题满分14分)(本小题主要考查空间几何体中线面的位置关系,面积与体积,空间向量等基础知识,考查空间想象能力和运算求解能力)(1)证明:在正方形11AA A A''中,∵5A C AA AB BC ''=--=, ∴三棱柱111ABC A B C -的底面三角形ABC 的边5AC =.∵3AB =,4BC =,∴222AB BC AC +=,则AB BC ⊥.∵四边形11AA A A''为正方形,11AA BB ,∴1AB BB ⊥,而1BCBB B =,∴AB ⊥平面11BCC B . (2)解:∵AB ⊥平面11BCC B ,∴AB 为四棱锥A BCQP -的高.∵四边形BCQP 为直角梯形,且3BP AB ==,7CQ AB BC =+=,∴梯形BCQP 的面积为()1202BCQP S BP CQ BC =+⨯=, ∴四棱锥A BCQP -的体积1203A BCQP BCPQ V S AB -=⨯=,由(1)知1B B AB ⊥,1B B BC ⊥,且AB BC B =,∴1B B ⊥平面ABC .∴三棱柱111ABC A B C -为直棱柱,∴三棱柱111ABC A B C -的体积为111172ABC A B C ABC V S BB -∆=⋅=. 故平面APQ 将三棱柱111ABC A B C -分成上、下两部分的体积之比为722013205-=. (3)解:由(1)、(2)可知,AB ,BC ,1BB 两两互相垂直.以B 为原点,建立如图所示的空间直角坐标系B xyz -,则()3,0,0A ,()13,0,12A ,()0,0,3P ,()0,4,7Q , ∴(3,0,3)AP =-,1(3,4,5)AQ =--, ∴1111cos ,5AP AQ AP AQ AP AQ ⋅<>==-,∵异面直线所成角的范围为0,2π⎛⎤⎥⎝⎦, ∴直线AP 与1AQ 所成角的余弦值为15.19.(本小题满分14分)(本小题主要考查等比数列、递推数列等基础知识,考查综合运用知识分析问题和解决问题的能力)解:(1)方法1:∵51=a ,∴22122113a a =+-=,33222133a a =+-=. 设2n n na b λ+=,由}{n b 为等差数列,则有3122b b b +=. ∴321232222a a a λλλ+++⨯=+. ∴13533228λλλ+++=+. 解得 1λ=-.事实上,1111122n n n n nn a a b b +++---=-()111212n n n a a ++=-+⎡⎤⎣⎦()1112112n n ++⎡⎤=-+⎣⎦1=,综上可知,当1λ=-时,数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. 方法2:∵数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列, 设2n n na b λ+=,由}{n b 为等差数列,则有122n n n b b b ++=+(*n ∈N ). ∴12122222n n n n n n a a a λλλ+++++++⨯=+.∴1244n n n a a a λ++=--()()121222n n n n a a a a +++=---()()12221211n n ++=---=-.综上可知,当1λ=-时,数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. (2)由(1)知,()1111122n na a n --=+-⨯, ∴()121n n a n =+⋅+.∴()()()()12122132121121n nn S n n -⎡⎤=⋅++⋅+++⋅+++⋅+⎣⎦.即()1212232212n n n S n n n -=⋅+⋅++⋅++⋅+.令()1212232212n n n T n n -=⋅+⋅++⋅++⋅, ① 则()23122232212n n n T n n +=⋅+⋅++⋅++⋅. ②②-①,得()()12312222212n n n T n +=-⋅-+++++⋅12n n +=⋅.∴()11221n n n S n n n ++=⋅+=⋅+.20.(本小题满分14分)(本小题主要考查函数的导数、最值、等比数列等基础知识,考查分析问题和解决问题的能力、以及创新意识)(1)解:∵()x f x e x =-,∴()1xf x e '=-.令()0f x '=,得0x =.∴当0x >时,()0f x '>,当0x <时,()0f x '<.∴函数()x f x e x =-在区间(),0-∞上单调递减,在区间()0,+∞上单调递增. ∴当0x =时,()f x 有最小值1.(2)证明:由(1)知,对任意实数x 均有1xe x -≥,即1xx e +≤.令k x n=-(*,1,2,,1n k n ∈=-N ),则01k n ke n-<-≤,∴1(1,2,,1)nnkkn k e e k n n --⎛⎫⎛⎫-≤==- ⎪ ⎪⎝⎭⎝⎭.即(1,2,,1)nk n k e k n n --⎛⎫≤=- ⎪⎝⎭.∵1,nn n ⎛⎫= ⎪⎝⎭∴(1)(2)211211n nn nn n n n e e e e n n n n -------⎛⎫⎛⎫⎛⎫⎛⎫++++≤+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.∵(1)(2)2111111111n n n e eeee e e e e ----------+++++=<=---,∴ 1211n nn nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.21.(本小题满分14分)(本小题主要考查直线与圆锥曲线等基础知识,考查数形结合的数学思想方法,以及推理论证能力、运算求解能力)解法1:(1)不妨设A 211,2x x p ⎛⎫ ⎪⎝⎭,B 222,2x x p ⎛⎫ ⎪⎝⎭,且12x x <,∵AM BM +=0,∴2212122,22,222x x x x p p ⎛⎫⎛⎫--+--= ⎪ ⎪⎝⎭⎝⎭0.∴124x x +=,22128x x p +=.∵()21222122x x x x ++>(12x x ≠),即88p >,∴1p >,即p 的取值范围为()1,+∞.(2)当2p =时,由(1)求得A 、B 的坐标分别为()0,0、()4,4.假设抛物线L 上存在点2,4t C t ⎛⎫⎪⎝⎭(0t ≠且4t ≠),使得经过A 、B 、C 三点的圆和抛物线L 在点C 处有相同的切线.设经过A 、B 、C 三点的圆的方程为220x y Dx Ey F ++++=,则2420,4432,1641616.F D E F tD t E F t t ⎧=⎪++=-⎨⎪++=--⎩整理得 ()()3441680t E t E ++-+=. ①∵函数24x y =的导数为2x y '=, ∴抛物线L 在点2,4t C t ⎛⎫ ⎪⎝⎭处的切线的斜率为2t , ∴经过A 、B 、C 三点的圆N 在点2,4t C t ⎛⎫ ⎪⎝⎭处的切线斜率为2t . ∵0t ≠,∴直线NC 的斜率存在.∵圆心N 的坐标为,22D E ⎛⎫-- ⎪⎝⎭, ∴242122t E t D t +⨯=-+,即()()324480t E t E ++-+=. ② ∵0t ≠,由①、②消去E ,得326320t t -+=.即()()2420t t -+=.∵4t ≠,∴2t =-.故满足题设的点C 存在,其坐标为()2,1-.解法2:(1)设A ,B 两点的坐标为1122()()A x y B x y ,,,,且12x x <。
广州市2008年普通高中毕业班综合测试(一)(文数)
2008年广州市普通高中毕业班综合测试(一)数学(文科) 2008.3一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知全集U=R,集合{|22}A x x =-<<,2{|20}B x x x =-≤,则A B =( ) A .(0,2)B .(0,2]C .[0,2]D .[0,2)2. 已知3c o s 5α=,则co s 2α的值为( ) A .2425-B .725-C .725D .24253. 一个几何体的三视图如图所示,其中正视图与左视图都是边长为2的正三角形,则这个几何体的侧面积为 ( )A .3π3B .2πC .3πD .4π4. 某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别是 ( ) A .19、13 B .13、19C .20、18D .18、205. 已知函数2lo g (0)()2(0)x xx f x x >⎧=⎨≤⎩,若1()2f a =,则实数a= ( )A .1-B .2C .1-或2D .1或2-6. 已知a ∈R ,则“2a >”是“22a a>”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7. 设()f x 、()g x 是R 上的可导函数,()f x '、()g x '分别为()f x 、()g x 的导函数,且满足()()()()0f x g x f x g x ''+<,则当ax b<<时,有( )A .()()()()f xg b f b g x >B .()()()()f xg a f a g x > 俯视图左(侧)视图正(主)视图甲 乙 7 9 8 0 7 8 55 7 9 1 1 1 3 3 46 2 2 0 2 3 1 01 4 0C .()()()()f xg x f b g b >D .()()()()f xg x f a g a > 8. 直线20a x y a -+=与圆229x y+=的位置关系是( )A .相离B .相交C .相切D .不确定9. 抽气机每次抽出容器内空气的60%,要使容器内剩下的空气少于原来的0.1%,则至少要抽(参考数据:lg 20.3010=,lg 30.4771=)( ) A .15次B .14次C .9次D .8次 10. 在A B C ∆所在的平面上有一点P ,满足P A P B P C A B ++=,则P B C∆与A B C ∆的面积之比是( ) A .13B .12C .23D .34二、填空题:本大题共5小题,每小题5分,满分20分.本大题分为必做题和选做题两部分.(一)必做题:第1113 题为必做题,每道试题考生都必须作答. 11. 若复数2(56)(3)izmm m =-++-是实数,则实数m=.12. 在空间直角坐标系O x y z -中,点(1,2,3)-关于坐标平面yO z 的对称点的坐标为 . 13. 按如图所示的程序框图运算:若输入8x =,则输出k = ;若输出2k =,则输入x 的取值范围是 . (注:“1A =”也可写成“:1A =”或“1A ←”,均 表示赋值语句)(二)选做题:第1415 题为选做题,考生只能选做其中的一 题,两题全答的,只计算第一题的得分.14. (坐标系与参数方程选做题)在极坐标系中,过点π22,4⎛⎫ ⎪⎝⎭作圆4sin ρθ=的切线,则切线的极坐标方程是 .15. (几何证明选讲选做题)在平行四边形A B C D 中,点E 在边A B 上,且:1:2A E E B=,D E与A C 交于点F ,若AEF ∆的面积为26c m,则A B C ∆的面积为2c m.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程或演算步骤. 16. (本小题满分12分)将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次, 记第一次出现的点数为x ,第二次出现的点数为y . (Ⅰ)求事件“3x y +≤”的概率;(Ⅱ)求事件“||2x y -=”的概率. 否是开始 输入xk =21x x =+1k k =+115x >输出x 、k结束17. (本小题满分12分)已知函数()sin co s f x a x b x=+的图像经过点π,03⎛⎫⎪⎝⎭和π,12⎛⎫⎪⎝⎭.(Ⅰ)求实数a 和b 的值;(Ⅱ)当x 为何值时,()f x 取得最大值.18. (本小题满分14分)如图1所示,在边长为12的正方形11A A A A ''中,点B 、C 在线段A A '上,且3A B=,4B C =,作1B B ∥1A A ,分别交11A A '、1A A '于点1B 、P ,作1C C ∥1A A ,分别交11A A '、1A A '于点1C 、Q ,将该正方形沿1B B 、1C C 折叠,使得1A A ''与1A A 重合,构成如图2所示的三棱柱111A B C A B C -.(Ⅰ)在三棱柱111A B CA B C -中,求证:AB ⊥平面11B C C B ;(Ⅱ)求平面A P Q 将三棱柱111A B C A B C -分成上、下两部分几何体的体积之比.A 1C 1C 1B 1A'1A 1B 119. (本小题满分14分)已知数列{}n a 中,15a =,1221n n n a a -=+-(n *∈N且2n≥).(Ⅰ)求2a 、3a 的值;(Ⅱ)是否存在实数λ,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列?若存在,求出λ的值;若不存在,请说明理由.20. (本小题满分14分)已知过点(0,1)P -的直线l 与抛物线24x y =相交于11(,)A x y 、22(,)B x y 两点,1l 、2l 分别是该抛物线在A 、B 两点处的切线,M 、N 分别是1l 、2l 与直线1y =-的交点.(Ⅰ)求直线l 的斜率的取值范围;(Ⅱ)试比较||P M 与||P N 的大小,并说明理由.21. (本小题满分14分)已知函数()xf x e x=-(其中e 为自然对数的底).(Ⅰ)求函数()f x 的最小值;(Ⅱ)若n *∈N ,证明:1211n n n nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.2008年广州市普通高中毕业班综合测试(一)数学(文科)参考答案一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.题号 1 2 3 4 5 6 7 8 9 10 答案DBBACACBDC二、填空题:本大题共5小题,每小题5分,满分20分.本大题分为必做题和选做题两部分.(一)必做题:第1113 题为必做题,每道试题考生都必须作答.11.3 12.(1,2,3)-- 13.4,(28,57] (二)选做题:第1415 题为选做题,考生只能选做其中的一题,两题全答的,只计算第一题的得分.14.co s 2ρθ= 15.72 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程或演算步骤. 16. 解:将一颗质地均匀的正方体骰子先后抛掷两次的基本事件总数为6636N =⨯=个.(Ⅰ)因为事件“3x y +≤”包含(1,1)、(1,2)、(2,1)三个基本事件,所以事件“3x y +≤” 的概率为1313612P ==;(Ⅱ)因为事件“||2x y -=” 包含(1,3)、(2,4)、(3,5)、(4,6)、(3,1)、(4,2)、(5,3)、(6,4)共8个基本事件,所以事件“||2x y -=”的概率为282369P ==.17. 解:(Ⅰ)依题意,有π3103221,3π12f a b a b f a ⎧⎛⎫=+=⎪ ⎪⎪⎝⎭⇒==-⎨⎛⎫⎪== ⎪⎪⎝⎭⎩;(Ⅱ)由(Ⅰ)知:π()s in 3c o s 2s in 3f x x x x ⎛⎫=-=- ⎪⎝⎭.因此,当ππ2π32xk -=+,即5π2π6xk =+(k ∈Z )时,()f x 取得最大值2.18. 解:(Ⅰ)证明:因为3A B=,4B C=,所以5A C=,从而有 222A C AB B C=+,即A B B C⊥.又因为1A BB B ⊥,而1BC B B B= ,所以AB ⊥平面11B C C B ; (Ⅱ)因为3B PA B ==,7C QA C ==,所以()(37)42022B C Q P B P C Q B CS +⋅+⨯===,从而112032033A B C Q PB C Q P V S A B -=⋅⋅=⨯⨯=. 又因为111113412722A B C A B C A B C V S A A -=⋅=⨯⨯⨯=,所以平面A P Q 将三棱柱111A B CA B C -分成上、下两部分几何体的体积之比为7220521320205V V -===上下.19. 解:(Ⅰ)依题意,有221221104113a a =+-=+-=, 332221268133a a =+-=+-=;(Ⅱ)因为1221n n n a a -=+-(n *∈N且2n ≥),所以111221112222nn n n nnn na a a λλλλ---++-+++==+-.显然,当且仅当102nλ+=,即1λ=-时,数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列.20. 解:(Ⅰ)设直线:1l y kx =-,则2214404y k x x k y x y=-⎧⇒-+=⎨=⎩, ……①依题意,有2161601kk ∆=->⇒<-或1k>;(Ⅱ)由2211442x y y x y x'=⇒=⇒=,所以抛物线在A 处的切线1l 的方程为211111()42y x x x x -=-,即2111124yx x x =-.令1y=-,得21142Mx x x -=.同理,得22242Nx x x -=.注意到1x 、2x 是方程①的两个实根,故124x x =,即214x x =,从而有2221212114444822NMx x x x x x x x ⎛⎫- ⎪--⎝⎭====-,因此,||||P M P N =.21. 解:(Ⅰ)因为()xf x e x=-,所以()1xf x e '=-.显然,当0x<时,()0f x '<;当0x>时,()0f x '>.因此,()f x 在(,0)-∞上单调递减,在(0,)+∞上单调递增.因此,当0x =时,()f x 取得最小值(0)101f =-=;(Ⅱ)证明:由(Ⅰ)知:当0x≠时,有()1f x >,即1xx e-<,故1nnnn k k nnk n k e e n n e--⎡⎤-⎛⎫⎛⎫=-<=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦(1,2,,kn= ),从而有121nnnnn n n n n n -⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21()nne e e e<+++1(1)1111nnnne e e e e eeee e --=⋅=⋅<---.。
2008年广州市普通高中毕业班综合测试(一)数 学(文科)

2008年广州市普通高中毕业班综合测试(一)数 学(文科) 2008.3本试卷共4页,21小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再将答案填写在对应题号的横线上。
漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么()()()P A B P A P B +=+.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U =R ,集合{}22A x x =-<<,{}220B x x x =-≤,则A B =A .()0,2B .(]0,2C .[]0,2D .[)0,22.已知3cos 5α=,则cos 2α的值为A .2425-B .725-C .725D .24253.一个几何体的三视图如图1所示,其中正视图与左视图都是边长为2的正三角形,则这个几何体的侧面积为AB .2πC .3πD .4π4.某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们所有比 赛得分的情况用如图2所示的茎叶图表示,则甲、乙两名运动员 得分的中位数分别为 A .19、13 B .13、19C .20、18D .18、20图2图1 正(主)视图 左(侧)视图俯视图5.已知函数2log ,0,()2,0.x x x f x x >⎧=⎨≤⎩若1()2f a =,则a = A .1- BC .1-D .1或 6.已知a ∈R ,则“2a >”是“22a a >”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.设()f x 、()g x 是R 上的可导函数,()f x '、()g x '分别为()f x 、()g x 的导函数,且()()()()0f x g x f x g x ''+<,则当a x b <<时,有A .()()()()f x g b f b g x >B .()()()()f x g a f a g x >C .()()()()f x g x f b g b >D .()()()()f x g x f a g a > 8.直线20ax y a -+=与圆229x y +=的位置关系是A .相离B .相交C .相切D .不确定9.抽气机每次抽出容器内空气的60%,要使容器内剩下的空气少于原来的0.1%,则至少要抽(参考数据:lg 20.3010=,lg30.4771=)A .14次B .13次C .9次D .8次10.在ABC ∆所在的平面上有一点P ,满足PA PB PC AB ++=,则PBC ∆与ABC ∆的面积之比是A .13 B .12 C .23 D .34二、填空题:本大题共5小题,每小题5分,满分20分.本大题分为必做题和选做题两部分.(一)必做题:第11、12、13题是必做题,每道试题考生都必须做答.11.若复数()()2563i z m m m =-++-是实数,则实数m = .12.在空间直角坐标系中O xyz -,点()1,2,3-关于坐标平面yOz 的对称点的坐标为 .13.按如图3所示的程序框图运算. 若输入8x =,则输出k = ;若输出2k =,则输入x 的取值范围是 . (注:“1=A ”也可写成“1:=A ”或“1←A ”,均表示 赋值语句)(二)选做题:第14、15题是选做题,考生只能选做一题,两题全答的,只计算第一题的得分. 14.(坐标系与参数方程选做题)在极坐标系中,过点,4π⎛⎫⎪⎝⎭作圆4sin ρθ=的切线,则切线的极坐标方程是 .15.(几何证明选讲选做题)在平行四边形ABCD 中,点E 在边AB 上,且:1:2AE EB =,DE 与AC交于点F ,若AEF ∆的面积为62cm ,则ABC ∆的面积为 2cm .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x ,第二次出现的点数为y .(1)求事件“3x y +≤”的概率; (2)求事件“2x y -=”的概率. 17.(本小题满分12分)已知函数()sin cos f x a x b x =+的图象经过点,03π⎛⎫⎪⎝⎭和,12π⎛⎫⎪⎝⎭. (1)求实数a 和b 的值;(2)当x 为何值时,()f x 取得最大值. 18.(本小题满分14分)如图4所示,在边长为12的正方形11AA A A''中,点,B C 在线段AA '上,且3AB =,4BC =,作1BB 1AA ,分别交11A A '、1AA '于点1B 、P ,作1CC1AA ,分别交11A A '、1AA '于点1C 、Q ,将该正方形沿1BB 、1CC 折叠,使得1A A ''与1AA 重合,构成如图5所示的三棱柱111ABC A B C -.(1)在三棱柱111ABC A B C -中,求证:AB ⊥平面11BCC B ;(2)求平面APQ 将三棱柱111ABC A B C -分成上、下两部分几何体的体积之比.19.(本小题满分14分)已知数列}{n a 中,51=a 且1221nn n a a -=+-(2n ≥且*n ∈N ).(1)求2a ,3a 的值;(2)是否存在实数λ,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列,若存在,求出λ的值;若不存在,请说明理由. 20.(本小题满分14分)已知过点()0,1P -的直线l 与抛物线24x y =相交于11()A x y ,、22()B x y ,两点,1l 、2l 分别是抛物线24x y =在A 、B 两点处的切线,M 、N 分别是1l 、2l 与直线1y =-的交点. (1)求直线l 的斜率的取值范围;(2)试比较PM 与PN 的大小,并说明理由.21.(本小题满分14分)已知函数()x f x e x =-(e 为自然对数的底数). (1)求函数()f x 的最小值;(2)若*n ∈N ,证明:1211n n n nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.2008年广州市普通高中毕业班综合测试(一)数学(文科)试题参考答案及评分标准40分.10.由PA PB PC AB ++= ,得PA PB BA PC +++=0,即2PC AP =,所以点P 是CA 边上的第二个三等分点,如图所示.故23PBC ABC S BC PC S BC AC ∆∆⋅==⋅. 二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,每小题5分,满分30分.其中第13题第一个空2分,第二个空3分. 11.3 12.()1,2,3-- 13.4;(]28,57 14.cos 2ρθ= 15.72三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查古典概率等基础知识,考查运算求解能力)解:设(),x y 表示一个基本事件,则掷两次骰子包括:()1,1,()1,2,()1,3,()1,4,()1,5,()1,6,()2,1,()2,2,……,()6,5,()6,6,共36个基本事件.(1)用A 表示事件“3x y +≤”,则A 的结果有()1,1,()1,2,()2,1,共3个基本事件. ∴()313612P A ==.答:事件“3x y +≤”的概率为112. (2)用B 表示事件“2x y -=”,则B 的结果有()1,3,()2,4,()3,5,()4,6,()6,4,()5,3,()4,2,()3,1,共8个基本事件.∴()82369P B ==.答:事件“2x y -=”的概率为29. 17.(本小题满分12分)(本小题主要考查特殊角的三角函数、三角函数的性质等基础知识,考查运算求解能力) 解:(1)∵函数()sin cos f x a x b x =+的图象经过点,03π⎛⎫⎪⎝⎭和,12π⎛⎫⎪⎝⎭,∴sin cos 0,33sin cos 1.22a b a b ππππ⎧+=⎪⎪⎨⎪+=⎪⎩即10,221.b a +=⎪⎨⎪=⎩解得1,a b =⎧⎪⎨=⎪⎩ (2)由(1)得()sin f x x x =12sin 2x x ⎛⎫= ⎪ ⎪⎝⎭2sin 3x π⎛⎫=- ⎪⎝⎭. ∴当sin 13x π⎛⎫-= ⎪⎝⎭,即232x k πππ-=+,即526x k ππ=+()k ∈Z 时,()f x 取得最大值2. 18.(本小题满分14分)(本小题主要考查空间几何体中线、面的位置关系,考查空间想象能力和运算求解能力)(1)证明:在正方形11AA A A''中,∵5A C AA AB BC ''=--=, ∴三棱柱111ABC A B C -的底面三角形ABC 的边5AC =.∵3AB =,4BC =,∴222AB BC AC +=,则AB BC ⊥.∵四边形11AA A A''为正方形,11AA BB ,∴1AB BB ⊥,而1BC BB B = ,∴AB ⊥平面11BCC B .(2)解:∵AB ⊥平面11BCC B ,∴AB 为四棱锥A BCQP -的高.∵四边形BCQP 为直角梯形,且3BP AB ==,7CQ AB BC =+=,∴梯形BCQP 的面积为()1202BCQP S BP CQ BC =+⨯=, ∴四棱锥A BCQP -的体积1203A BCQP BCPQ V S AB -=⨯=,由(1)知1B B AB ⊥,1B B BC ⊥,且AB BC B = , ∴1B B ⊥平面ABC .∴三棱柱111ABC A B C -为直棱柱, ∴三棱柱111ABC A B C -的体积为111172ABC A B C ABC V S BB -∆=⋅=. 故平面APQ 将三棱柱111ABC A B C -分成上、下两部分的体积之比为722013205-=. 19.(本小题满分14分)(本小题主要考查等比数列、递推数列等基础知识,考查综合运用知识分析问题和解决问题的能力)解:(1)∵51=a ,∴22122113a a =+-=,33222133a a =+-=.(2)方法1:假设存在实数λ,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列, 设2n n n a b λ+=, 由}{n b 为等差数列,则有3122b b b +=. ∴321232222a a a λλλ+++⨯=+. ∴13533228λλλ+++=+. 解得,1λ=-. 事实上,1111122n n n n n n a a b b +++---=-()111212n n n a a ++=-+⎡⎤⎣⎦()1112112n n ++⎡⎤=-+⎣⎦1=. 综上可知,存在实数1λ=-,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. 方法2:假设存在实数λ,使得2n na λ+⎧⎫⎨⎬⎩⎭为等差数列, 设2n n na b λ+=,由}{n b 为等差数列,则有122n n n b b b ++=+(*n ∈N ). ∴12122222n n n n n n a a a λλλ+++++++⨯=+. ∴1244n n n a a a λ++=--()()121222n n n n a a a a +++=--- ()()12221211n n ++=---=-.综上可知,存在实数1λ=-,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. 20.(本小题满分14分)(本小题主要考查直线与圆锥曲线等基础知识,考查数形结合的数学思想方法,以及推理论证能力、运算求解能力)解:(1)依题意,直线l 的斜率存在,设直线l 的方程为1y kx =-.由方程214.y kx x y =-⎧⎨=⎩,消去y 得2440x kx -+=. ············· ①∵直线l 与抛物线24x y =相交于A ,B 两点,∴216160k ∆=->,解得1k >或1k <-.故直线l 斜率的取值范围为()(),11,-∞-+∞ . (2)解法1:∵1x ,2x 是方程①的两实根,∴12124,4.x x k x x +=⎧⎨=⎩ ∴10x ≠,20x ≠. ∵214y x =,∴12y x '=.∵21114y x =,∴切线1l 的方程为211111()24y x x x x =-+.令1y =-,得点M 的坐标为2114,12x x ⎛⎫-- ⎪⎝⎭. ∴21142x PM x -=. 同理,可得22242x PN x -=.∵22121221222121212142444124444PMx x x x x x x PN x x x x x x x ---=⋅===---(12x x ≠).故PM PN =. 解法2:可以断定PM PN =. ∵1x ,2x 是方程①的两实根, ∴12124,4.x x k x x +=⎧⎨=⎩ ∴10x ≠,20x ≠. ∵214y x =,∴12y x '=.∵21114y x =,∴切线1l 的方程为211111()24y x x x x =-+. 令1y =-,得点M 的坐标为2114,12x x ⎛⎫--⎪⎝⎭. 同理可得点N 的坐标为2224,12x x ⎛⎫-- ⎪⎝⎭. ∵()()2212121212124440222x x x x x x x x x x +---+==. ∴点P 是线段MN 的中点.故PM PN =.21.(本小题满分14分)(本小题主要考查函数的导数、最值、等比数列等基础知识,考查分析问题和解决问题的能力、以及创新意识) (1)解:∵()1xf x e'=-,令()0f x '=,得0x =.∴当0x >时,()0f x '>,当0x <时,()0f x '<. ∴函数()x f x e x =-在区间(),0-∞上单调递减,在区间()0,+∞上单调递增. ∴当0x =时,()f x 有最小值1.(2)证明:由(1)知,对任意实数x 均有1xe x -≥,即1xx e +≤.令k x n =-(*,1,2,,1n k n ∈=-N ),则01kn k e n-<-≤,∴1(1,2,,1)nnkk n k e e k n n --⎛⎫⎛⎫-≤==- ⎪ ⎪⎝⎭⎝⎭. 即(1,2,,1)n k n k e k n n --⎛⎫≤=- ⎪⎝⎭ . ∵1,n n n ⎛⎫= ⎪⎝⎭∴(1)(2)211211n n n nn n n n e e e e n n n n -------⎛⎫⎛⎫⎛⎫⎛⎫++++≤+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. ∵(1)(2)2111111111n n n e eeee e e e e ----------+++++=<=--- , ∴ 1211n n n nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.。
广东省实验中学2008年高三第三次模拟考试(数学理)

2008年高考热身训练题数 学(理科)本试卷共4页,21小题,满分150分,考试用时l20分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,如需改动,先划掉原来的答案,然后再写上新的答案,不准使用铅笔和涂改液,不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回。
一、选择题(每题5分 共40分) 1、下列各式中,值为0.5的是( )︒-︒︒︒+︒︒︒︒+︒︒︒︒15cos 15sin 15sin 45sin 15cos 45cos 15sin 45cos 15cos 45sin 15sin 105sin 222D C B A2、从全年级学生的数学考试成绩中,随机抽取10名学生的成绩,抄录如下:(单位:分)82 90 74 81 77 94 82 68 89 75根据样本频率分布估计总体分布的原理,该年级学生的数学考试成绩在79.5~85.5之间的概率约为( ). 9251103132D C B A 3、如图所示的韦恩图中,A ,B 是非空集合,定义集合A #B 为阴影部分表示的集合.若x,y ∈R,A={x|y=22x x -},B={y|y=3x ,x>0},则A #B=( )A {x|0<x<2}B {x|1<x ≤2}C {x|0≤x ≤1或x ≥2}D {x|0≤x ≤1或x>2}4、对某种产品市场产销量情况如图所示,其中:L 1表示产品各年年产量的变化规律;L 2表示产品各年的销售情况。
下列叙述:(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去; (2)产品已出现了供大于求的情况,价格将趋跌;(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量; (4)产品的产、销情况均以一定的年增长率递增。
2008年广州市普通高中毕业班综合测试(一)理数

秘密★启用前2008年广州市普通高中毕业班综合测试(一)数 学(理科)2008.3本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上. 3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再将答案填写在对应题号的横线上。
漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么()()()P A B P A P B +=+. 如果事件A 、B 相互独立,那么()()()P A B P A P B ⋅=⋅.如果事件A 在一次试验中发生的概率是p ,那么在n 次独立重复试验中恰好发生k 次的概率()()C 1n kk kn n P k p p -=-.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U =R ,集合{}22A x x =-<<,{}220B x x x =-≤,则A B =A .()0,2B .(]0,2C .[)0,2D .[]0,22.某赛季,甲、乙两名篮球运动员都参加了11赛得分的情况用如图1所示的茎叶图表示,则甲、乙两名运动员 的中位数分别为 A .19、13 B .13、19C .20、18D .18、203.已知函数2log ,0,()2,0.x x x f x x >⎧=⎨≤⎩若1()2f a =,则a = A .1- B C .1- D .1或 4.直线20ax y a -+=与圆229x y +=的位置关系是A .相离B .相交C .相切D .不确定 5.在区间[]0,1上任取两个数,a b ,方程220x ax b ++=的两根均为实数的概率为 A .18 B .14 C .12 D .346.已知a ∈R ,则“2a >”是“22a a >”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.抽气机每次抽出容器内空气的60%,要使容器内剩下的空气少于原来的0.1%,则至少要抽(参考数据:lg 20.3010=,lg30.4771=)A .15次B .14次C .9次D .8次8.在ABC ∆所在的平面上有一点P ,满足PA PB PC AB ++=,则PBC ∆与ABC ∆的面积之比是A .13 B .12 C .23 D .34二、填空题:本大题共7小题,每小题5分,满分30分.本大题分为必做题和选做题两部分.(一)必做题:第9、10、11、12题是必做题,每道试题考生都必须做答.9.若复数()()2563i z m m m =-++-是实数,则实数m = . 10.已知3cos 5α=,则cos 2α= . 11.根据定积分的几何意义,计算x =⎰.12.按如图2所示的程序框图运算. 若输入8x =,则输出k = ;若输出2k =,则输入x 的取值范围是 . (注:“1=A ”也可写成“1:=A ”或“1←A ”,均表示赋值 语句)(二)选做题:第13、14、15题是选做题,考生只能选做二题,三题全答的,只计算前两题的得分. 13.(坐标系与参数方程选做题)在极坐标系中,过点4π⎛⎫⎪⎝⎭作圆4sin ρθ=的切线,则切线的极坐标方程是 .14.(不等式选讲选做题)若a 、b 、c ∈R ,且222236a b c ++=,则a b c ++的最小值是 . 15.(几何证明选讲选做题)在平行四边形ABCD 中,点E 在边AB 上,且:1:2AE EB =,DE 与AC 交于点F ,若AEF ∆的面积为62cm ,则ABC ∆的面积为 2cm .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 已知函数()s i n c o s f x a xb x =+的图象经过点,03π⎛⎫ ⎪⎝⎭和,12π⎛⎫⎪⎝⎭.(1)求实数a 和b 的值;(2)当x 为何值时,()f x 取得最大值. 17.(本小题满分12分)某计算机程序每运行一次都随机出现一个二进制的六位数123456N n n n n n n =,其中N 的各位数中,161n n ==,k n (k =2,3,4,5)出现0的概率为23,出现1的概率为13,记123456n n n n n n ξ=+++++,当该计算机程序运行一次时,求随机变量ξ的分布列和数学期望(即均值).18.(本小题满分14分)如图3所示,在边长为12的正方形11AA A A''中,点,B C 在线段AA '上,且3AB =,4BC =,作1BB 1AA ,分别交11A A '、1AA '于点1B 、P ,作1CC 1AA ,分别交11A A '、1AA '于点1C 、Q ,将该正方形沿1BB 、1CC 折叠,使得1A A ''与1AA 重合,构成如图4所示的三棱柱111ABC A B C -. (1)在三棱柱111ABC A B C -中,求证:AB ⊥平面11BCC B ;(2)求平面APQ 将三棱柱111ABC A B C -分成上、下两部分几何体的体积之比; (3)在三棱柱111ABC A B C -中,求直线AP 与直线1AQ 所成角的余弦值.19.(本小题满分14分)已知数列}{n a 中,51=a 且1221n n n a a -=+-(2n ≥且*n ∈N ).(1)若数列2n n a λ+⎧⎫⎨⎬⎩⎭为等差数列,求实数λ的值;(2)求数列}{n a 的前n 项和n S . 20.(本小题满分14分)已知函数()xf x e x =-(e 为自然对数的底数). (1)求函数()f x 的最小值;(2)若*n ∈N ,证明:1211n n n nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.21.(本小题满分14分)已知抛物线L :22x py =和点()2,2M ,若抛物线L 上存在不同两点A 、B 满足AM BM +=0.(1)求实数p 的取值范围;(2)当2p =时,抛物线L 上是否存在异于A 、B 的点C ,使得经过A 、B 、C 三点的圆和抛物线L 在点C 处有相同的切线,若存在,求出点C 的坐标,若不存在,请说明理由.2008年广州市普通高中毕业班综合测试(一)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.8.由PA PB PC AB ++= ,得PA PB BA PC +++=0,即2PC AP =,所以点P 是CA 边上的第二个三等分点,如图所示.故23PBC ABC S BC PC S BC AC ∆∆⋅==⋅. 二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,每小题5分,满分30分.其中第12题第一个空2分,第二个空3分.9.3 10.725- 11.3π 12.4;(]28,5713.cos 2ρθ= 14.15.72三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)(本小题主要考查特殊角的三角函数、三角函数的性质等基础知识,考查运算求解能力)解:(1)∵函数()sin cos f x a x b x =+的图象经过点,03π⎛⎫ ⎪⎝⎭和,12π⎛⎫⎪⎝⎭,∴sin cos 0,33sin cos 1.22a b a b ππππ⎧+=⎪⎪⎨⎪+=⎪⎩即10,221.a b a +=⎪⎨⎪=⎩ 解得1,a b =⎧⎪⎨=⎪⎩.(2)由(1)得()sin f x x x =12sin 2x x ⎛⎫= ⎪ ⎪⎝⎭2sin 3x π⎛⎫=- ⎪⎝⎭.∴当sin 13x π⎛⎫-= ⎪⎝⎭,即232x k πππ-=+, 即526x k ππ=+()k ∈Z 时,()f x 取得最大值2. 17.(本小题满分12分)(本小题主要考查随机变量的分布列及其数学期望等基础知识,考查运算求解能力等) 解:ξ的可能取值是2,3,4,5,6.∵161n n ==,∴()4042162C 381P ξ⎛⎫=== ⎪⎝⎭, ()31412323C 3381P ξ⎛⎫==⋅= ⎪⎝⎭,()22241284C 3327P ξ⎛⎫⎛⎫==⋅= ⎪⎪⎝⎭⎝⎭, ()3341285C 3381P ξ⎛⎫==⋅= ⎪⎝⎭, ()444116C 381P ξ⎛⎫=== ⎪⎝⎭. ∴ξ的分布列为∴ξ的数学期望为16322481102345681818181813E ξ=⨯+⨯+⨯+⨯+⨯=.18.(本小题满分14分)(本小题主要考查空间几何体中线面的位置关系,面积与体积,空间向量等基础知识,考查空间想象能力和运算求解能力)(1)证明:在正方形11AA A A''中,∵5A C AA AB BC ''=--=, ∴三棱柱111ABC A B C -的底面三角形ABC 的边5AC =. ∵3AB =,4BC =,∴222AB BC AC +=,则AB BC ⊥.∵四边形11AA A A ''为正方形,11AA BB ,∴1AB BB ⊥,而1BC BB B = , ∴AB ⊥平面11BCC B .(2)解:∵AB ⊥平面11BCC B ,∴AB 为四棱锥A BCQP -的高.∵四边形BCQP 为直角梯形,且3BP AB ==,7CQ AB BC =+=,∴梯形BCQP 的面积为()1202BCQP S BP CQ BC =+⨯=,∴四棱锥A BCQP -的体积1203A BCQP BCPQ V S AB -=⨯=,由(1)知1B B AB ⊥,1B B BC ⊥,且AB BC B = , ∴1B B ⊥平面ABC .∴三棱柱111ABC A B C -为直棱柱,∴三棱柱111ABC A B C -的体积为111172ABC A B C ABC V S BB -∆=⋅=. 故平面APQ 将三棱柱111ABC A B C -分成上、下两部分的体积 之比为722013205-=. (3)解:由(1)、(2)可知,AB ,BC ,1BB 两两互相垂直.以B 为原点,建立如图所示的空间直角坐标系B xyz -, 则()3,0,0A ,()13,0,12A ,()0,0,3P ,()0,4,7Q ,∴(3,0,3)AP =-,1(3,4,5)AQ =-- , ∴1111cos ,5AP AQ AP AQ AP AQ ⋅<>==-, ∵异面直线所成角的范围为0,2π⎛⎤⎥⎝⎦,∴直线AP 与1AQ 所成角的余弦值为15. 19.(本小题满分14分)(本小题主要考查等比数列、递推数列等基础知识,考查综合运用知识分析问题和解决问题的能力) 解:(1)方法1:∵51=a ,∴22122113a a =+-=,33222133a a =+-=.设2n n na b λ+=,由}{n b 为等差数列,则有3122b b b +=.∴321232222a a a λλλ+++⨯=+.∴13533228λλλ+++=+. 解得 1λ=-.事实上,1111122n n n n n n a a b b +++---=-()111212n n n a a ++=-+⎡⎤⎣⎦()1112112n n ++⎡⎤=-+⎣⎦1=,综上可知,当1λ=-时,数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. 方法2:∵数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列, 设2n n na b λ+=,由}{n b 为等差数列,则有122n n n b b b ++=+(*n ∈N ). ∴12122222n n n n n n a a a λλλ+++++++⨯=+. ∴1244n n n a a a λ++=--()()121222n n n n a a a a +++=---()()12221211n n ++=---=-.综上可知,当1λ=-时,数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列.(2)由(1)知,()1111122n n a a n --=+-⨯, ∴()121nn a n =+⋅+.∴()()()()12122132121121n nn S n n -⎡⎤=⋅++⋅+++⋅+++⋅+⎣⎦ .即()1212232212n n n S n n n -=⋅+⋅++⋅++⋅+ .令()1212232212n n n T n n -=⋅+⋅++⋅++⋅ , ①则()23122232212nn n T n n +=⋅+⋅++⋅++⋅ . ②②-①,得()()12312222212n n n T n +=-⋅-+++++⋅12n n +=⋅. ∴()11221n n n S n n n ++=⋅+=⋅+.20.(本小题满分14分)(本小题主要考查函数的导数、最值、等比数列等基础知识,考查分析问题和解决问题的能力、以及创新意识)(1)解:∵()xf x e x =-,∴()1xf x e '=-.令()0f x '=,得0x =.∴当0x >时,()0f x '>,当0x <时,()0f x '<.∴函数()xf x e x =-在区间(),0-∞上单调递减,在区间()0,+∞上单调递增.∴当0x =时,()f x 有最小值1.(2)证明:由(1)知,对任意实数x 均有1xe x -≥,即1xx e +≤.令k x n =-(*,1,2,,1n k n ∈=-N ),则01kn k e n-<-≤,∴1(1,2,,1)nnkkn k e e k n n --⎛⎫⎛⎫-≤==- ⎪ ⎪⎝⎭⎝⎭. 即(1,2,,1)nk n k e k n n --⎛⎫≤=- ⎪⎝⎭. ∵1,nn n ⎛⎫= ⎪⎝⎭∴(1)(2)211211n n n nn n n n e e e e n n n n -------⎛⎫⎛⎫⎛⎫⎛⎫++++≤+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. ∵(1)(2)2111111111n n n e eeee e e e e ----------+++++=<=--- , ∴ 1211n n n nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.21.(本小题满分14分)(本小题主要考查直线与圆锥曲线等基础知识,考查数形结合的数学思想方法,以及推理论证能力、运算求解能力)解法1:(1)不妨设A 211,2x x p ⎛⎫ ⎪⎝⎭,B 222,2x x p ⎛⎫ ⎪⎝⎭,且12x x <,∵AM BM +=0 ,∴2212122,22,222x x x x p p ⎛⎫⎛⎫--+--= ⎪ ⎪⎝⎭⎝⎭0.∴124x x +=,22128x x p +=.∵()21222122x x x x ++>(12x x ≠),即88p >,∴1p >,即p 的取值范围为()1,+∞.(2)当2p =时,由(1)求得A 、B 的坐标分别为()0,0、()4,4.假设抛物线L 上存在点2,4t C t ⎛⎫⎪⎝⎭(0t ≠且4t ≠),使得经过A 、B 、C 三点的圆和抛物线L 在点C 处有相同的切线.设经过A 、B 、C 三点的圆的方程为220x y Dx Ey F ++++=, 则2420,4432,1641616.F D E F tD t E F t t ⎧=⎪++=-⎨⎪++=--⎩整理得 ()()3441680t E t E ++-+=. ①∵函数24x y =的导数为2xy '=,∴抛物线L 在点2,4t C t ⎛⎫ ⎪⎝⎭处的切线的斜率为2t,∴经过A 、B 、C 三点的圆N 在点2,4t C t ⎛⎫ ⎪⎝⎭处的切线斜率为2t .∵0t ≠,∴直线NC 的斜率存在.∵圆心N 的坐标为,22D E ⎛⎫-- ⎪⎝⎭,∴242122t E t D t +⨯=-+,即()()324480t E t E ++-+=. ②∵0t ≠,由①、②消去E ,得326320t t -+=.即()()2420t t -+=.∵4t ≠,∴2t =-.故满足题设的点C 存在,其坐标为()2,1-.解法2:(1)设A ,B 两点的坐标为1122()()A x y B x y ,,,,且12x x <。
2008年广州市高三第一次模拟考试试题答案

2008年广州市普通高中毕业班综合测试(一)数学(文科)试题参考答案及评分标准40分.10.由PA PB PC AB ++=,得PA PB BA PC +++=0,即2PC AP =,所以点P 是CA 边上的第二个三等分 点,如图所示.故23PBC ABC S BC PC S BC AC ∆∆⋅==⋅. 二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,每小题5分,满分30分.其中第13题第一个空2分,第二个空3分. 11.3 12.()1,2,3-- 13.4;(]28,57 14.cos 2ρθ= 15.72三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查古典概率等基础知识,考查运算求解能力)解:设(),x y 表示一个基本事件,则掷两次骰子包括:()1,1,()1,2,()1,3,()1,4,()1,5,()1,6,()2,1,()2,2,……,()6,5,()6,6,共36个基本事件.(1)用A 表示事件“3x y +≤”,则A 的结果有()1,1,()1,2,()2,1,共3个基本事件. ∴()313612P A ==.答:事件“3x y +≤”的概率为112. (2)用B 表示事件“2x y -=”,则B 的结果有()1,3,()2,4,()3,5,()4,6,()6,4,()5,3,()4,2,()3,1,共8个基本事件.∴()82369P B ==.答:事件“2x y -=”的概率为29.(本小题主要考查特殊角的三角函数、三角函数的性质等基础知识,考查运算求解能力) 解:(1)∵函数()sin cos f x a x b x =+的图象经过点,03π⎛⎫⎪⎝⎭和,12π⎛⎫⎪⎝⎭, ∴sin cos 0,33sin cos 1.22a b a b ππππ⎧+=⎪⎪⎨⎪+=⎪⎩即10,221.b a +=⎪⎨⎪=⎩解得1,a b =⎧⎪⎨=⎪⎩ (2)由(1)得()sin f x x x =12sin 2x x ⎛⎫= ⎪ ⎪⎝⎭2sin 3x π⎛⎫=- ⎪⎝⎭. ∴当sin 13x π⎛⎫-= ⎪⎝⎭,即232x k πππ-=+,即526x k ππ=+()k ∈Z 时,()f x 取得最大值2. 18.(本小题满分14分)(本小题主要考查空间几何体中线、面的位置关系,考查空间想象能力和运算求解能力)(1)证明:在正方形11AA A A''中,∵5A C AA AB BC ''=--=, ∴三棱柱111ABC A B C -的底面三角形ABC 的边5AC =.∵3AB =,4BC =,∴222AB BC AC +=,则AB BC ⊥.∵四边形11AA A A''为正方形,11AA BB ,∴1AB BB ⊥,而1BC BB B =,∴AB ⊥平面11BCC B .(2)解:∵AB ⊥平面11BCC B ,∴AB 为四棱锥A BCQP -的高.∵四边形BCQP 为直角梯形,且3BP AB ==,7CQ AB BC =+=,∴梯形BCQP 的面积为()1202BCQP S BP CQ BC =+⨯=, ∴四棱锥A BCQP -的体积1203A BCQP BCPQ V S AB -=⨯=,由(1)知1B B AB ⊥,1B B BC ⊥,且ABBC B =,∴1B B ⊥平面ABC .∴三棱柱111ABC A B C -为直棱柱, ∴三棱柱111ABC A B C -的体积为111172ABC A B C ABC V S BB -∆=⋅=. 故平面APQ 将三棱柱111ABC A B C -分成上、下两部分的体积之比为722013205-=.(本小题主要考查等比数列、递推数列等基础知识,考查综合运用知识分析问题和解决问题的能力) 解:(1)∵51=a ,∴22122113a a =+-=,33222133a a =+-=. (2)方法1:假设存在实数λ,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为等差数列, 设2n n n a b λ+=, 由}{n b 为等差数列,则有3122b b b +=. ∴321232222a a a λλλ+++⨯=+. ∴13533228λλλ+++=+. 解得,1λ=-. 事实上,1111122n n n n n n a a b b +++---=-()111212n n n a a ++=-+⎡⎤⎣⎦()1112112n n ++⎡⎤=-+⎣⎦1=. 综上可知,存在实数1λ=-,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. 方法2:假设存在实数λ,使得2n na λ+⎧⎫⎨⎬⎩⎭为等差数列, 设2n n na b λ+=,由}{n b 为等差数列,则有122n n n b b b ++=+(*n ∈N ). ∴12122222n n n n n n a a a λλλ+++++++⨯=+. ∴1244n n n a a a λ++=--()()121222n n n n a a a a +++=---()()12221211n n ++=---=-.综上可知,存在实数1λ=-,使得数列2n na λ+⎧⎫⎨⎬⎩⎭为首项是2、公差是1的等差数列. 20.(本小题满分14分)(本小题主要考查直线与圆锥曲线等基础知识,考查数形结合的数学思想方法,以及推理论证能力、运算求解能力)解:(1)依题意,直线l 的斜率存在,设直线l 的方程为1y kx =-.由方程214.y kx x y =-⎧⎨=⎩,消去y 得2440x kx -+=. ············· ①∵直线l 与抛物线24x y =相交于A ,B 两点,∴216160k ∆=->,解得1k >或1k <-.故直线l 斜率的取值范围为()(),11,-∞-+∞.(2)解法1:∵1x ,2x 是方程①的两实根,∴12124,4.x x k x x +=⎧⎨=⎩ ∴10x ≠,20x ≠. ∵214y x =,∴12y x '=.∵21114y x =,∴切线1l 的方程为211111()24y x x x x =-+.令1y =-, 得点M 的坐标为2114,12x x ⎛⎫-- ⎪⎝⎭. ∴21142x PM x -=. 同理,可得22242x PN x -=. ∵22121221222121212142444124444PMx x x x x x x PN x x x x x x x ---=⋅===---(12x x ≠).故PM PN =. 解法2:可以断定PM PN =. ∵1x ,2x 是方程①的两实根,∴12124,4.x x k x x +=⎧⎨=⎩ ∴10x ≠,20x ≠. ∵214y x =,∴12y x '=.∵21114y x =,∴切线1l 的方程为211111()24y x x x x =-+. 令1y =-,得点M 的坐标为2114,12x x ⎛⎫--⎪⎝⎭. 同理可得点N 的坐标为2224,12x x ⎛⎫-- ⎪⎝⎭. ∵()()2212121212124440222x x x x x x x x x x +---+==. ∴点P 是线段MN 的中点.故PM PN =.21.(本小题满分14分)(本小题主要考查函数的导数、最值、等比数列等基础知识,考查分析问题和解决问题的能力、以及创新意识) (1)解:∵()1xf x e'=-,令()0f x '=,得0x =.∴当0x >时,()0f x '>,当0x <时,()0f x '<. ∴函数()x f x e x =-在区间(),0-∞上单调递减,在区间()0,+∞上单调递增. ∴当0x =时,()f x 有最小值1.(2)证明:由(1)知,对任意实数x 均有1xe x -≥,即1xx e +≤.令kx n=-(*,1,2,,1n k n ∈=-N ),则01kn ke n-<-≤, ∴1(1,2,,1)nnkkn k e e k n n --⎛⎫⎛⎫-≤==- ⎪ ⎪⎝⎭⎝⎭. 即(1,2,,1)nkn k e k n n --⎛⎫≤=- ⎪⎝⎭. ∵1,nn n ⎛⎫= ⎪⎝⎭∴(1)(2)211211n n nnn n n n e e e e n n n n -------⎛⎫⎛⎫⎛⎫⎛⎫++++≤+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. ∵(1)(2)2111111111n n n e e e e e e e e e ----------+++++=<=---, ∴ 1211nnn nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.。
2008学年广州市高中二年级学生学业水平测试(试题+答案)-推荐下载

2008 学年度上学期广州市高中二年级学生学业水平测试
数学
本试卷共 4 页. 满分 150 分. 考试用时 120 分钟. 注意事项: 1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号填写在答题卡指定 的位置上. 2.选择题每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动, 用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上. 3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域 内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和 涂改液. 不按以上要求作答的答案无效. 4.本次考试不允许使用计算器. 5.考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回.
2,
否
1 2
n a?
是 输出
D.
T
2,
1 2
;若输出的T 120 ,则 a 的值为
解答须写出文字说明、证明过程和演算步
结束
.
.
.
16.(本小题满分 12 分) 已知 a,b, c 是 ABC 三内角 A, B,C 的对边,且 b 6, c 4, A . 3
B. 1, 0
7.如图所示,一个空间几何体的正视图和侧视图都是边
长为 1 的正方形,俯视图是一个圆,那么这个几何
体的体积为( )
A.
4
C.
8.已知实数
A. b c a
a
log3
4
B.
2
D. 3 2
,
b
B. b a c
1 5
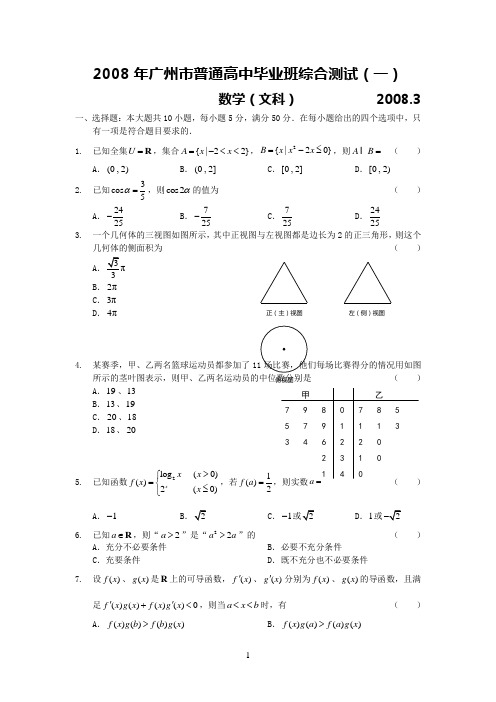
2008年广州市普通高中毕业班综合测试(一)

2008年广州市普通高中毕业班综合测试(一)数学(理科) 2008.3一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知全集U =R ,集合{|22}A x x =-<<,2{|20}B x x x =-≤,则AB = ( )A .(0,2)B .(0,2]C .[0,2)D .[0,2]2. 某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别是 ( ) A .19、13 B .13、19C .20、18D .18、203. 已知函数2log (0)()2(0)xx x f x x >⎧=⎨≤⎩,若1()2f a =,则实数a = ( )A .1-B .2C .1-或2D .1或2- 4. 直线20ax y a -+=与圆229x y +=的位置关系是( )A .相离B .相交C .相切D .不确定5. 在区间[0,1]上任取两个数a 、b ,则方程220x ax b ++=有实根的概率为( )A .18B .14 C .12D .346. 已知a ∈R ,则“2a >”是“22a a >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7. 抽气机每次抽出容器内空气的60%,要使容器内剩下的空气少于原来的0.1%,则至少要抽(参考数据:lg 20.3010=,lg30.4771=)( ) A .15次B .14次C .9次D .8次8. 在ABC ∆所在的平面上有一点P ,满足PA PB PC AB ++=,则PBC ∆与ABC ∆的面积之比是( ) A .13B .12C .23D .34二、填空题:本大题共7小题,每小题5分,满分30分.本大题分为必做题和选做题两部分.甲 乙 7 9 8 0 7 8 55 7 9 1 1 1 3 3 46 2 2 0 2 3 1 01 4 0(一)必做题:第912题为必做题,每道试题考生都必须作答. 9. 若复数2(56)(3)i z m m m =-++-是实数,则实数m = . 10. 已知3cos 5α=,则cos 2α= . 11. 根据定积分的几何意义,计算:1204d x x -=⎰.12. 按如图所示的程序框图运算:若输入8x =,则输出k = ;若输出2k =,则输入x 的取值范围是 . (注:“1A =”也可写成“:1A =”或“1A ←”,均 表示赋值语句)(二)选做题:第1315题为选做题,考生只能选做其中的两题,三题全答的,只计算前两题的得分.13. (坐标系与参数方程选做题)在极坐标系中,过点π22,4⎛⎫ ⎪⎝⎭作圆4sin ρθ=的切线,则切线的极坐标方程是 .14. (不等式选讲选做题)若a 、b 、c ∈R ,且222236a b c ++=,则a b c ++的最小值等于 .15. (几何证明选讲选做题)在平行四边形ABCD 中,点E 在边AB 上,且:1:2AE EB =,DE 与AC 交于点F ,若AEF ∆的面积为26cm ,则ABC ∆的面积为 2cm .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程或演算步骤. 16. (本小题满分12分)已知函数()sin cos f x a x b x =+的图像经过点π,03⎛⎫ ⎪⎝⎭和π,12⎛⎫⎪⎝⎭.(Ⅰ)求实数a 和b 的值;(Ⅱ)当x 为何值时,()f x 取得最大值.17. (本小题满分12分)某计算机程序每运行一次都随机出现一个二进制的六位数123456N n n n n n n =,其 中N 的各位数字中,161n n ==,k n (2,3,4,5k =)出现0的概率为23,出现1的概率为13,记123456n n n n n n ξ=+++++,当该计算机程序运行一次时,求随机变量ξ的分面列和数学期望.否是 开始 输入x 0k =21x x =+1k k =+115x >输出x 、k 结束18. (本小题满分14分)如图1所示,在边长为12的正方形11AA A A ''中,点B 、C 在线段AA '上,且3AB =, 4BC =,作1BB ∥1AA ,分别交11A A '、1AA '于点1B 、P ,作1CC ∥1AA ,分别交11A A '、1AA '于点1C 、Q ,将该正方形沿1BB 、1CC 折叠,使得1A A ''与1AA 重合,构成如图2所示的三棱柱111ABC A B C -.(Ⅰ)在三棱柱111ABC A B C -中,求证:AB ⊥平面11BCC B ;(Ⅱ)求平面APQ 将三棱柱111ABC A B C -分成上、下两部分几何体的体积之比; (Ⅲ)在三棱柱111ABC A B C -中,求直线AP 与直线1A Q 所成角的余弦值.19. (本小题满分14分)已知数列{}n a 中,15a =,1221n n n a a -=+-(n *∈N 且2n ≥).(Ⅰ)若数列2n n a λ+⎧⎫⎨⎬⎩⎭为等差数列,求实数λ的值;(Ⅱ)求数列{}n a 的前n 项和n S .图2图1P QA 1C 1Q P C 1B 1C B A'1A 1A A'BCAB 120. (本小题满分14分)已知函数()x f x e x =-(其中e 为自然对数的底). (Ⅰ)求函数()f x 的最小值;(Ⅱ)若n *∈N ,证明:1211n nn nn n e n n n n e -⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.21. (本小题满分14分)已知抛物线2:2L x py =(0p >)和点(2,2)M ,若抛物线L 上存在不同的两点A 、B 满足0AM BM +=.(Ⅰ)求实数p 的取值范围;(Ⅱ)当2p =时,抛物线L 上是否存在异于A 、B 的点C ,使得经过A 、B 、C 三点的圆和抛物线L 在点C 处有相同的切线?若存在,求出点C 的坐标;若不存在,请说明理由.2008年广州市普通高中毕业班综合测试(一)数学(理科)参考答案一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.题号 1 2 3 4 5 6 7 8 答案CACBBADC二、填空题:本大题共7小题,每小题5分,满分30分.本大题分为必做题和选做题两部分.(一)必做题:第912题为必做题,每道试题考生都必须作答.9.310.725-11.π332+ 12.4,(28,57] (二)选做题:第1315题为选做题,考生只能选做其中的两题,三题全答的,只计算前两题的得分.13.cos 2ρθ= 14.11-15.72三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程或演算步骤. 16. 解:(Ⅰ)依题意,有π3103221,3π12f a b a b f a ⎧⎛⎫=+=⎪ ⎪⎪⎝⎭⇒==-⎨⎛⎫⎪== ⎪⎪⎝⎭⎩;(Ⅱ)由(Ⅰ)知:π()sin 3cos 2sin 3f x x x x ⎛⎫=-=- ⎪⎝⎭.因此,当ππ2π32x k -=+,即5π2π6x k =+(k ∈Z )时,()f x 取得最大值2. 17. 解:依题意,知ξ的可能取值为2,3,4,5,6,其概率分别为2ξ=表示k n (2,3,4,5k =)中全为零,故404216(2)381P C ξ⎛⎫==⋅= ⎪⎝⎭;3ξ=表示k n (2,3,4,5k =)中恰有一个1,故3142132(3)3381P C ξ⎛⎫==⋅⋅= ⎪⎝⎭;4ξ=表示k n (2,3,4,5k =)中恰有两个1,故22242124(4)3381P C ξ⎛⎫⎛⎫==⋅⋅= ⎪ ⎪⎝⎭⎝⎭; 5ξ=表示k n (2,3,4,5k =)中恰有三个1,故334218(5)3381P C ξ⎛⎫⎛⎫==⋅⋅= ⎪ ⎪⎝⎭⎝⎭;6ξ=表示k n (2,3,4,5k =)中全部为1,故44411(6)381P C ξ⎛⎫==⋅=⎪⎝⎭. 因此,ξ的分布列为ξ2 3 4 5 6P1681 3281 2481 881 181ξ的数学期望为16322481102345681818181813E ξ=⨯+⨯+⨯+⨯+⨯=. 18. 解:(Ⅰ)证明:因为3AB =,4BC =,所以5AC =,从而有222AC AB BC =+,即AB BC ⊥.又因为1AB BB ⊥,而1BC BB B =,所以AB ⊥平面11BCC B ;(Ⅱ)因为3BP AB ==,7CQ AC ==,所以()(37)42022BCQP BP CQ BC S +⋅+⨯===,从而112032033A BCQP BCQP V S AB -=⋅⋅=⨯⨯=. 又因为111113412722ABC A B C ABC V S AA -=⋅=⨯⨯⨯=,所以平面APQ 将三棱柱111ABC A B C -分成上、下两部分几何体的体积之比为7220521320205V V -===上下; (Ⅲ)如图建立空简直角坐标系,则(3,0,0)A 、(0,0,3)P 、 1(3,0,12)A 、(0,4,7)Q ,所以(3,0,3)AP =-,1(3,4,5)AQ =--.设直线AP 与直线1A Q 所成角为θ,则11||61cos 5||||3252AP AQ AP AQ θ⋅===⋅⨯.19. 解:(Ⅰ)因为1221n n n a a -=+-(n *∈N 且2n ≥),所以111221112222n n n n n n n na a a λλλλ---++-+++==+-. 显然,当且仅当102nλ+=,即1λ=-时,数列2n n a λ+⎧⎫⎨⎬⎩⎭为等差数列; (Ⅱ)由(Ⅰ)的结论知:数列12n n a -⎧⎫⎨⎬⎩⎭是首项为1122a -=,公差为1的等差数列,故有12(1)112n na n n -=+-⨯=+,即 (1)21n n a n =+⋅+(n *∈N ).因此,有 23223242(1)2n n S n n =⨯+⨯+⨯+++⋅+,23412223242(1)22n n S n n +=⨯+⨯+⨯+++⋅+,两式相减,得2314(222)(1)2n n n S n n +-=++++-+⋅-,整理,得1(21)n n S n +=+(n *∈N ).20. 解:(Ⅰ)因为()x f x e x =-,所以()1x f x e '=-.显然,当0x <时,()0f x '<;当0x >时,()0f x '>.因此,()f x 在(,0)-∞上单调 递减,在(0,)+∞上单调递增.因此,当0x =时,()f x 取得最小值(0)101f =-=;(Ⅱ)证明:由(Ⅰ)知:当0x ≠时,有()1f x >,即1x x e -<,故1nn nn k kn n k n k een n e--⎡⎤-⎛⎫⎛⎫=-<=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦(1,2,,k n =),从而有121n nn nn n n n n n -⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21()n n e e e e<+++ 1(1)1111n n n n e e e e e e e e e e --=⋅=⋅<---. 21. 解:(Ⅰ)由0AM BM +=知:M 是线段AB 的中点.设直线AB :2(2)y k x -=-,则222(2)24(1)02y k x x kpy p k x py-=-⎧⇒-+-=⎨=⎩. 依题意,有222A B M x x x kp k p+===⇒=. ……①又由222416(1)0440k p p k k p k ∆=-->⇒-+>,由此及①可得4840p p-+>,即1p >; (Ⅱ)若存在满足条件的点C ,则因为M 是线段AB 的中点,所以CM AB ⊥,即CM 经过ABC ∆的外接圆圆心,故CM 与抛物线L 在点C 处的切线垂直,即直线AB 与抛物线L 在点C 处的切线平行.当2p =时,由①知:直线AB 的斜率21k p==,从而抛物线L 在点C 处的切线的斜率 为1,故由1122y x x '==⇒=,2114y x ==知:点C 的坐标为(2,1).。
2008年广州市普通高中毕业班综合测试(理科)(二)

试卷类型:A2008年广州市普通高中毕业班综合测试(二)数 学 (理科)2008.4本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再将答案填写在对应题号的横线上。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式: 0122n nn n n n C C C C =+++⋅⋅⋅+(n ∈N *)球的表面积公式为24S R π=,其中R 为球的半径.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M 满足{1,2}{1,2,3}M =,则集合M 的个数是A . 1B . 2C . 3D . 42.函数sin()2y x π=+是A .周期为2π的偶函数B .周期为2π的奇函数C .周期为π的偶函数D .周期为π的奇函数3.已知点A (1,-2), B (m ,, 2),若线段AB 的垂直平分线方程是220x y +-=,则实数m 的值是 A . -2B .-7C . 3D . 14.己知二次函数()f x 的图象如图1所示,则其导函数'()f x 的图象大致形状是A .B .图 1C .D .5.设0.3222,0.3,log (0.3)(1)x a b c x x ===+>,则a ,b ,c 的大小关系是A .a <b <cB .b <a <cC .c <b <aD .b <c <a6.已知命题p :20()a a R ≥∈,命题q :函数()f x =2x x -在区间[0,+∝)上单调递增,则下列命题中为真命题的是A .p ∨qB . p ∧qC .()()p q ⌝∧⌝D .()p q ⌝∨7.某班星期二的课表有6节课,其中上午4节,下午2节,要排语文、数学、英语、信息技术、体育、地理各1节,要求上午第一节课不排体育,数学必须排在上午,则不同排法种数共有A .600种B .480种C .408种D .384种8.甲、乙两位同学玩游戏,对于给定的实数1a ,按下列方法操作一次产生一个新的实数: 由甲、乙同时各掷一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把1a 乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把1a 除以2后再加上12,这样就可得到一个新的实数2a .对实数2a 仍按上述方法进行一次操作,又得到一个新的实数3a .当31a a >时,甲获胜,否则乙获胜.若甲获胜的概率为34,则1a 的取值范围是A .(-∝,12]B .[ 24, +∝)C .(12,24)D .(-∝,12][24,+∝)二、填空题:本大题共7小题,每小题5分,满分30分.本大题分必做题和选做题两部分.APCMB (一)必做题:第9、10、11、12题是必做题,每道试题考生都必须做答.9. 函数2lg(1)y x =-的定义域是_________.10.在复平面内,复数1+i 与-1+3i 分别对应向量OA 与OB ,其中O 为坐标原点,则||AB =_________. 11.在一次数学测试(满分为150分)中,某地区10000名考生的分数X 服从正态分布2(100,15)N ,据统计,分数在110分以上的考生共2514人,则分数在90分以上的考生共________人.12.已知a 为正常数,定义运算“○×”,如下:对任意m ,n ∈N *,若m ○×n =a ,则(m +1) ○×n =2a ,m ○×(n +1)=a +1.当1○×1=1时,则1○×10=______,5○×10=________.(二)选做题:第13、14、15题是选做题,考生只能选做二题,三题全答的,只计算前两题的得分.13.(坐标系与参数方程)已知圆C 的参数方程为cos 1sin x y θθ=+⎧⎨=⎩(θ为参数),则点P (4, 4) 与圆C 上的点的最远距离是_________.14.(不等式选讲)不等式12x x +-<的解集是__________. 15.(几何证明选讲)如图2所示,圆内接∆ABC 的∠C 的平分线CD延长后交圆于点E ,连接BE ,己知BD =3,CE =7,BC =5,则线段BE =__________.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分) 已知点(1,0)A ,(0,1)B ,(2sin ,cos )C θθ. (1)若||||AC BC =,求tan θ的值;(2)若(2)1OA OB OC +⋅=,其中O 为坐标原点,求sin 2θ的值.17.(本小题满分14分)如图3所示,在三棱锥P -AB C 中,P A ⊥平面ABC ,AB =BC =CA =2, M 为AB 的中点,四点P 、A 、M 、C 都在球O 的球面上. (1)证明:平面P AB ⊥平面PCM ; (2)证明:线段PC 的中点为球O 的球心;(3)若球O 的表面积为20π,求二面角A -PB -C 的平面角的余弦值.18.(本小题满分12分)图 2图 3:已知该工厂的工人人数最多是200人,根据限额,该工厂每天消耗电能不得超过160千度,消耗煤不得超过150吨,问怎样安排甲、乙两种产品的生产数量,才能使每天所得的产值最大. 19.〔本小题满分14分)(1)椭圆C :22221x y a b+=(a >b >0)与x 轴交于A 、B 两点,点P 是椭圆C 上异于A 、B 的任意一点,直线P A 、 PB 分别与y 轴交于点M 、N ,求证:AN BM ⋅为定值22b a -.(2)由(1)类比可得如下真命题:双曲线C :22221x y a b-=(a >0,b >0)与x 轴交于A 、B 两点,点P 是双曲线C 上异于A 、B 的任意一点,直线P A 、PB 分别与y 轴交于点M 、N ,求证:AN BM ⋅为定值.请写出这个定值(不要求给出解题过程).20.(本小题满分14分) 已知函数()f x =22ln x a x ax -+(a ∈R ). (1)当1a =时,证明函数()f x 只有一个零点;(2)若函数()f x 在区间(1,+∝)上是减函数,求实数a 的取值范围.21.(本小题满分14分) 已知数列{a n }满足a 1=1,2121n n n a a a +=+(n ∈N *).(1)求a 2 , a 3的值;(2)求数列{a n }的通项公式; (3)求证:1718ni i ia a =<+∑.。
2008届广州市高三数学调研测试试题(理科) (2)

秘密★启用前2008年广州市高三教学质量抽测试题数 学(理科)2008.1 本试卷共4页,21小题,满分150分.考试用时120分钟. 注意事项:1.答选择题前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号、考试科目填写在答题卡上,并用2B 铅笔将相应的信息点涂黑.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回.参考公式:如果事件A 、B 互斥,那么()()()P A B P A P B +=+. 如果事件A 、B 相互独立,那么()()()P A B P A P B ⋅=⋅.如果事件A 在一次试验中发生的概率是p ,那么在n 次独立重复试验中恰好发生k 次的概率()()C 1n kkkn n P k p p -=-.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.集合{}2,4,6M =的真子集的个数为A .6B .7C .8D .9 2.不等式2320x x -+<的解集是A .{}21x x x <->-或B .{}12x x x <>或 C .{}12x x << D .{}21x x -<<- 3.函数cos y x =的一个单调递增区间为A .,22ππ⎛⎫-⎪⎝⎭ B .()0,π C .3,22ππ⎛⎫⎪⎝⎭D .(),2ππ 4.设复数z 满足i 2i z =-,则z =A .12i --B .12i -C .12i +D .12i -+5.已知向量()1,1=a ,()2,n =b ,若+=a b a b ,则n = A .3- B .1- C .1 D .3 6.如图1所示,是关于判断闰年的流程图,则以 下年份是闰年的为 A .1996年 B .1998年 C .2010年 D .2100年7.已知α,β是平面,m ,n 是直线,给出下 列命题①若α⊥m ,β⊂m ,则βα⊥. ②若α⊂m ,α⊂n ,mβ,n β,则αβ.③如果m n m ,,αα⊄⊂、n 是异面直线,那么α与n 相交. ④若m αβ=,n ∥m ,且βα⊄⊄n n ,,则n ∥α且n ∥β.其中正确命题的个数是A .4B .3C .2D .1 8.函数()22log 1log 1x f x x -=+,若()()1221f x f x +=(其中1x 、2x 均大于2),则()12f x x 的最小值为 A .35 B .23 C .45D .554-二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15是选做题,考生只能选做二题,三题全答的,只计算前两题得分.9.某校对全校男女学生共1600名进行健康调查,选用分层抽样法抽取一个容量为200的样本.已知女生比男生少抽了10人,则该校的女生人数应是 人. 10.已知等比数列{}n a 的前三项依次为1a -,1a +,4a +,则n a = . 11.抛物线24y x =上一点M 到焦点的距离为3,则点M 的横坐标x = .12.已知5235x x ⎛ ⎝的展开式中的常数项为T ,()f x 是以T 为周期的偶函数,且当[0,1]x ∈时,()f x x =,若在区间[1,3]-内,函数()()g x f x kx k =--有4个零点,则实数k 的取值范围是 .13.(坐标系与参数方程选做题)在极坐标系中,点()1,0到直线()cos sin 2ρθθ+=的距离为 .14.(不等式选讲选做题)不等式142x x -<-+的解集 是 . 15.(几何证明选讲选做题)如图2所示,AB 与CD 是O 的直径,AB ⊥CD ,P 是AB 延长线上一点,连PC 交O 于点E ,连DE 交AB 于点F ,若42==BP AB ,则=PF .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)在△ABC 中,角,,A B C 所对的边分别为,,a b c ,已知2a =,3c =,1cos 4B =. (1)求b 的值; (2)求sinC 的值.17.(本小题满分12分)已知射手甲射击一次,击中目标的概率是23. (1)求甲射击5次,恰有3次击中目标的概率;(2)假设甲连续2次未击中...目标,则中止其射击,求甲恰好射击5次后,被中止射击的概率.18.(本小题满分14分)如图3所示,四棱锥P ABCD -中,底面ABCDPD ⊥平面ABCD ,2PD AB ==,E ,F ,G 分别为 PC 、PD 、BC 的中点.(1)求证:PA EF ⊥;(2)求二面角D -FG -E 的余弦值.C 图219.(本小题满分14分)设函数()()2()2ln 11f x x x =---. (1)求函数)(x f 的单调递增区间;(2)若关于x 的方程()230f x x x a +--=在区间[]2,4内恰有两个相异的实根,求实数a 的取值范围. 20.(本小题满分14分)已知点,A B 的坐标分别是(0,1)-,(0,1),直线,AM BM 相交于点M ,且它们的斜率之积为12-. (1)求点M 轨迹C 的方程;(2)若过点()2,0D 的直线l 与(1)中的轨迹C 交于不同的两点E 、F (E 在D 、F 之间),试求ODE ∆与ODF ∆面积之比的取值范围(O 为坐标原点). 21.(本小题满分14分)已知数列{}n a 中,12a =,23a =,其前n 项和n S 满足1121n n n S S S +-+=+(2n ≥,*n ∈N ).(1)求数列{}n a 的通项公式;(2)设14(1)2(n an n n b λλ-=+-⋅为非零整数,*n ∈N ),试确定λ的值,使得对任意*n ∈N ,都有n n b b >+1成立.2008年广州市高三教学质量抽测数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.8.方法1:由()()1221f x f x +=,得()()22212122log 21log 11log 1log 21x x x x --+=++,即22214log log 1x x =-.于是()212212221214log log log log 5log 1x x x x x x =+=+≥-,所以()()()()21212212212log 1221log 1log 13x x f x x x x x x -==-≥++.方法2:由()()1221f x f x +=,得()()22212122log 21log 11log 1log 21x x x x --+=++,即22214log log 1x x =-.于是()221212122122212121log log 44log log log log log 1log 1x x x x x x x x x -+=+=+=--, 则()()()2212122212log 125log 13x x t t f x x x x t --+==++(其中21log 1t x =>),再利用导数的方法求解.二、填空题:本大题主要考查基本知识和基本运算.共7小题,每小题5分,满分30分.9.760 10.1342n -⎛⎫⋅ ⎪⎝⎭11.2 12.10,4⎛⎤ ⎥⎝⎦13.2 14.53,22⎛⎫- ⎪⎝⎭15.3三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查正弦定理、余弦定理、解三角形等基础知识,考查运算求解能力) 解:(1)由余弦定理,2222cos b a c ac B =+-,………………………………………2分得222123223104b =+-⨯⨯⨯=,…………………………………………………4分∴b =6分(2)方法1:由余弦定理,得222cos 2a b c C ab+-=,………………………………8分==,………………………10分 ∵C 是ABC ∆的内角,∴sin C ==.………………………………………………………12分 方法2:∵1cos 4B =,且B 是ABC ∆的内角,∴sin B ==.………………………………………………………8分 根据正弦定理,sin sin b cB C=,……………………………………………………10分得3sin sin c BC b===. ……………………………………………12分17.(本小题满分12分)(本小题主要考查独立重复试验等基础知识,考查或然与必然的数学思想与方法,以及运算求解能力) 解:(1)设“甲射击5次,恰有3次击中目标”为事件A ,则()32352180C 33243P A ⎛⎫⎛⎫=⋅=⎪⎪⎝⎭⎝⎭. 答:甲射击5次,恰有3次击中目标的概率为24380.………………………………6分 (2)方法1:设“甲恰好射击5次后,被中止射击”为事件C ,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则()2221222212116C C 33333243P C ⎡⎤⎛⎫⎛⎫=+⋅⋅⋅=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦. 答:甲恰好射击5次后,被中止射击的概率为16243.……………………………12分 方法2:设“甲恰好射击5次后,被中止射击”为事件C ,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则()2222121161C 333243P C ⎡⎤⎛⎫⎛⎫=-⋅⋅=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦. 答:甲恰好射击5次后,被中止射击的概率为16243.……………………………12分 18.(本小题满分14分)(本小题主要考查空间中线面关系,二面角及其平面角、坐标方法的运用等基础知识,考查数形结合的数学思想和方法,以及空间想象能力、逻辑推理能力和运算求解能力) (1)证法1:∵PD ⊥平面ABCD ,CD ⊂平面ABCD ,∴CD PD ⊥.又ABCD 为正方形,∴CD AD ⊥.∵PD AD D =,∴CD ⊥平面PAD .……………………………………………3分∵PA ⊂平面PAD ,∴CD PA ⊥. ∵EFCD ,∴PA EF ⊥.…………………………………………………………6分证法2:以D 为原点,建立如图所示的空间直角坐标系D xyz -,则(0,0,1)F ,(0,1,1)E ,(0,0,2)P ,(2,0,0)A ,(2,0,2)PA =-,(0,1,0)EF =-.…………………………………………………4分∵()()2,0,20,1,00PA EF =--=,∴PA EF ⊥.………………………………………6分 (2)解法1:以D 为原点,建立如图所示的空间直角坐标系D xyz -,则(0,0,0)D ,(0,0,1)F ,(1,2,0)G ,(0,1,1)E ,(0,0,1)DF =,(0,1,0)EF =-,(1,2,1)FG =-.………………………………8分设平面DFG 的法向量为111(,,)x y z =m ,∵11110,0,20.0.z DF x y z FG ⎧=⋅=⎧⎪∴⎨⎨+-=⋅=⎩⎪⎩m m令11y =,得()2,1,0=-m 是平面DFG 的一个法向量.…………………………10分 设平面EFG 的法向量为222(,,)x y z =n ,∵22220,0,20.0.y EF x y z FG ⎧-=⋅=⎧⎪∴⎨⎨+-=⋅=⎩⎪⎩n n令21z =,得()1,0,1=n 是平面EFG 的一个法向量.……………………………12分∵cos ,||||5⋅<>====-⋅m n m n m n 设二面角D FG E --的平面角为θ,则,θ=<>m n .所以二面角D FG E --的余弦值为5-.………………………………………14分 解法2:以D 为原点,建立如图所示的空间直角坐标系D xyz -,则(0,0,0)D ,(0,0,1)F ,(1,2,0)G ,(0,1,1)E ,(0,0,1)DF =,(1,2,0)DG =,(0,1,0)EF =-,(1,1,1)EG =-,(1,2,1)FG =-.………………………………8分过D 作FG 的垂线,垂足为M ,∵,,F G M 三点共线,∴()1DM DF DG λλ=+-, ∵0DM FG =,∴()10DF FG DG FG λλ+-=,即()()1150λλ⨯-+-⨯=,解得56λ=.∴51115,,66636DM DF DG ⎛⎫=+= ⎪⎝⎭.…………10分再过E 作FG 的垂线,垂足为N ,∵,,F G N 三点共线,∴()1EN EF EG μμ=+-, ∵0EN FG =,∴()10EF FG EG FG μμ+-=,即()()2140μμ⨯-+-⨯=,解得23μ=. ∴21111,,33333EN EF EG ⎛⎫=+=-- ⎪⎝⎭.……………………………………………12分∴cos ,DM EN DM EN DM EN==-⋅. ∵DM与EN 所成的角就是二面角D FG E --的平面角, 所以二面角D FG E --的余弦值为5-.………………………………………14分 19.(本小题满分14分)(本小题主要考查函数、微积分基本定理和导数的应用,考查综合运用数学知识分析和解决问题的能力)解:(1)函数()f x 的定义域为()1,+∞,…………………………………………………1分∵()()221()2111x x f x x x x -⎡⎤'=--=-⎢⎥--⎣⎦,………………………………………2分∵1x >,则使()0f x '>的x 的取值范围为()1,2,故函数()f x 的单调递增区间为()1,2. ……………………………………………4分 (2)方法1:∵()()2()2ln 11f x x x =---,∴()2()3012ln 10f x x x a x a x +--=⇔++--=.…………………………6分令()()12ln 1g x x a x =++--, ∵23()111x g x x x -'=-=--,且1x >, 由()03()03g x x g x x ''>><<<得,得1.∴()g x 在区间[2,3]内单调递减,在区间[3,4]内单调递增,……………………9分故2()30f x x x a +--=在区间[]2,4内恰有两个相异实根(2)0,(3)0,(4)0.g g g ≥⎧⎪⇔<⎨⎪≥⎩……12分即30,42ln 20,52ln 30.a a a +≥⎧⎪+-<⎨⎪+-≥⎩解得:2ln352ln 24a -≤<-. 综上所述,a 的取值范围是[)2ln35,2ln 24--.………………………………14分 方法2:∵()()2()2ln 11f x x x =---,∴()2()3012ln 10f x x x a x a x +--=⇔++--=.…………………………6分 即()2ln 11a x x =---, 令()()2ln 11h x x x =---, ∵23()111xh x x x -'=-=--,且1x >, 由()03,()03h x x h x x ''><<<>得1得.∴()h x 在区间[2,3]内单调递增,在区间[3,4]内单调递减.……………………9分 ∵()23h =-,()32ln 24h =-,()42ln35h =-, 又()()24h h <,故2()30f x x x a +--=在区间[]2,4内恰有两个相异实根()()43h a h ⇔≤<.……………………………………12分即2ln352ln 24a -≤<-.综上所述,a 的取值范围是[)2ln35,2ln 24--. ……………………………14分 20.(本小题满分14分)(本小题主要考查椭圆的概念、椭圆的方程等基础知识,考查待定系数法、数形结合的数学思想与方法,以及运算求解能力) 解:(1)设点M 的坐标为(,)x y ,∵12AM BM k k ⋅=-………………………………………2分0x ≠),这就是动点M 的轨迹方程.……………………4分 (2)方法1:如图,由题意知直线l 的斜率存在, 设l 的方程为()2y k x =-(12k ≠±) …… ①…………………………………5分将①代入122=+y , 得0)28(8)12(2222=-+⋅-+k x k x k ,………………6分由0∆>,解得2102k <<.…………………………………………………………7分 设()11,E x y ,()22,F x y ,则⎪⎪⎩⎪⎪⎨⎧+-=+=+.1228,12822212221k k x x k k x x …… ② ……………………8分 令OBE OBF S S λ∆∆=,则||||BE BF λ=,即BE BF λ=⋅,即()1222x x λ-=-,且0 1.λ<< ……………………9分 由②得,12212121224(2)(2),2122)(2)2()4.21x x k x x x x x x k -⎧-+-=⎪⎪+⎨⎪-⋅-=-++=⎪+⎩( 即()()()22222412,2122.21x k x k λλ-⎧+-=⎪⎪+⎨⎪-=⎪+⎩ 22222141,(1)8(1)2k k λλλλ+∴==-++即.……………………………………………11分 2102k <<且214k ≠24110(1)22λλ∴<-<+且2411(1)24λλ-≠+.解得33λ-<<+13λ≠………………………………………………13分 01λ<<,1223<<-∴λ且13λ≠. ∴△OBE 与△OBF面积之比的取值范围是113,133⎛⎫⎛⎫- ⎪⎪⎝⎭⎝⎭.……………14分 方法2:如图,由题意知直线l 的斜率存在,设l 的方程为2x sy =+(2)s ≠±…… ①…………5分将①代入122=+y , 整理,得22(2)420s y sy +++=,…………6分由0∆>,解得22s >.………………………………………………………………7分 设()11,E x y ,()22,F x y ,则1221224,22.2s y y s y y s ⎧+=-⎪⎪+⎨⎪=⎪+⎩…… ② ……………………8分 令11221212OBEOBF OB y S y S y OB y λ∆∆⋅===⋅,且01λ<<.…………………………………9分 将12y y λ=代入②,得()2222241,22.2s y s y s λλ⎧+=-⎪⎪+⎨⎪=⎪+⎩∴()222182s s λλ+=+.即()2222161s λλλ+=--.……………………………………11分 ∵22s >且24s ≠,∴()2221261λλλ+>--且()2221461λλλ+≠--. 即2610λλ-+<且13λ≠.解得33λ-<<+13λ≠.……………………………………………13分 01λ<<,1223<<-∴λ且13λ≠. 故△OBE 与△OBF面积之比的取值范围是113,133⎛⎫⎛⎫- ⎪⎪⎝⎭⎝⎭.……………14分21.(本小题满分14分)(本小题主要考查等差数列、不等式及其性质等基础知识,考查分类讨论、化归与转化的数学思想方法,以及抽象概括能力、运算求解能力)解:(1)由已知,()()111n n n n S S S S +----=(2n ≥,*n ∈N ), …………………2分 即11n n a a +-=(2n ≥,*n ∈N ),且211a a -=.∴数列{}n a 是以12a =为首项,公差为1的等差数列.∴1n a n =+.……………………………………………………………………………4分(2)∵1n a n =+,∴114(1)2n n n n b λ-+=+-⋅,要使n n b b >+1恒成立,∴()()112114412120n n n n n n n n b b λλ-++++-=-+-⋅--⋅>恒成立, ∴()11343120n n n λ-+⋅-⋅->恒成立, ∴()1112n n λ---<恒成立.……………………………………………………………6分(ⅰ)当n 为奇数时,即12n λ-<恒成立,…………………………………………7分当且仅当1n =时,12n -有最小值为1,∴1λ<.………………………………………………………………………………9分 (ⅱ)当n 为偶数时,即12n λ->-恒成立,………………………………………10分 当且仅当2n =时,12n --有最大值2-,∴2λ>-.……………………………………………………………………………12分 即21λ-<<,又λ为非零整数,则1λ=-.综上所述,存在1λ=-,使得对任意*n ∈N ,都有1n n b b +>.…………………14分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州市四十四中学2007年高二数学统测练习试卷
(时间:120分钟 满分:150分)
一、选择题(每题5分,共50分)
1、下列集合中恰有两个元素的集合是 ( )
A . {x 2-x=0}
B . {y |y 2-y=0}
C . {x |y=x 2-x } D. {y |y=x 2-x }
2、函数y=(2k+1)x+b 在实数集上是增函数,则 ( )
A. k >—21
B. k <—21
C. b >0
D. b <0
3、已知两个球的表面积之比为1:9,则这两个球的半径之比为 ( ) A. 1:3 B. 1:3 C. 1:9 D. 1:81
4、一个圆锥的母线长为20㎝,母线与轴的夹角为30°,则圆锥的高为 ( ) A. 103㎝ B. 202㎝ C. 20㎝ D. 10㎝
5、垂直于梯形两腰的直线与梯形两底所在的平面的位置关系是 ( )
A. 垂直
B. 平行
C. 直线在平面内
D. 无法确定
6、三条直线y+2x-4=0, x-y+1=0与 ax-y+2=0共有两个交点,则a 的值为 ( )
A. 1
B. 2
C. 1或-2
D. -1或2
7、如果直线l: x+ay+2=0 平行于直线2x-y+3=0,则直线l 在两坐标轴上截距之和为 ( )
A. 6
B. 2
C. -1
D. -2
8、圆x 2+y 2-4x=0在点P(1, 3)处的切线方程为 ( ) A. x+3y-2=0 B. x+3y-4=0 C. x-3y-4=0 D. x-3y+2=0 ( )
9、圆(x+2)2+y 2
=5关于原点O(0,0)直线对称的圆的方程为 ( )
A. (x-2)2+y 2=5
B. x 2+(y-2)2=5
C. (x+2)2+(y+2)2=5
D. x 2+(y+2)2=5 ( )
10、若a <0,则关于x 的不等式x 2-4ax-5a 2>0的解是 ( )
A. x >5a 或x <-a
B. x >-a 或x <5a
C. 5a <x <-a
D. –a <x <5a ( )
二、填空题(每题5分,共20分)
11、若实数x,y 满足⎪⎪⎩
⎪⎪⎨⎧≤+≤+≥≥626
2,0,
0y x y x y x 则z=2x+3y 的最大值为 。
12、若连续掷两次骰子,第一次掷得的点数为m ,第二次掷得的点数为n ,则点P(m,n)落在圆x 2+y 2=16内的概率是 。
13、已知算法如下:
若输入变量n 的值为3,则输出变量s 的值为 ;若输出变量s 的值为30,则
输入变量n 的值为 。
14、已知向量−→−OA =(0,1),−→−OB =(0,3),把向量−→
−AB 绕点A 逆时针旋转90°,得到向
量−→−AC ,则向量−→
−OC = 。
三、解答题(本大题6小题,共80分。
解答应写出文字说明,证明过程或演算步骤。
)
15、已知m ∈R 时,函数f(x)=m(x 2-1)+x-a 恒有零点,求实数a 的取值范围。
(12分)
16、在△ABC 中,a, b, c 分别是∠A, ∠B, ∠C 的对边,已知a, b, c 成等比数列, a 2-c 2=ac-bc,求∠A 的大小及
c B b sin 的值。
(12分)
17、求经过两圆x 2+y 2+6x-4=0和x 2+y 2+6x-28=0的交点,且圆心在直线x-y-4=0上的圆的方
程。
(12分)
18、在正三棱柱ABC —A 1B 1C 1中,D 是BC 的中点。
(14分)
(1)求证:A 1D ⊥B 1C 1 ;
(2)判断A 1B 与平面ADC 1的位置关系,并证明你的结论。
19、已知函数y=862++-k kx kx 的定义域是R 。
(15分)
(1)求实数k 的取值范围;
(2)设k 变化时,已知函数的最小值为f(k),求f(k)的表达式及函数f(k)的值域。
20、某人开车以60km/h 的速率从A 地到150km 远处的B 地,在B 地停留1h 后,再以50km/h 的速率返回A 地,把汽车与A 地的距离xkm 表示为时间t h (从A 地出发时开始)的函数,并画出函数的图象;再把车速v km/h 表示为时间t h 的函数,并画出函数的图象。
(15分)。
