轴对称、角平分线、垂直平分线、等腰三角形
垂直平分线、等腰三角形

第1讲垂直平分线、等腰三角形【知识点】一、垂直平分线1、线段垂直平分线的定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.2、线段垂直平分线的性质:垂直平分线上的点线与这条线段两个端点的距离相等几何语言:3、线段垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 几何语言:4、线段垂直平分线的画法:二、等腰三角形1、等腰三角形的定义:有两边相等的三角形叫做等腰三角形2、等腰三角形的性质:性质1:等腰三角形的两个底角相等(简写成“等边对等角”)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高线互相重合(简写成“三线合一”)几何语言:(1)AB=AC,AD⊥BC,∠=______∠______,______=______。
(2) AB=AC;BD=DC,∠______=∠______,______⊥______。
(3) AB=AC,AD平分∠BAC______⊥______,______=______.性质3:等腰三角形是轴对称图形3、等腰三角形的判定(1)定义(2)如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)几何语言:三、等边三角形1、等边三角形的性质:(1)等边三角形的三条边相等;等边三角形的三个内角都相等,并且每一个内角都等于60°(2)等边三角形是轴对称图形,它有三条对称轴.E D C B A(3)三线合一2、等边三角形的判定(1)定义(2)三个角都相等的三角形是等边三角形.(3)有一个角是60°的等腰三角形是等边三角形.3、含30°角直角三角形的性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
【典型例题】 1、如图2,DE 是∆ABC 中AC 边的垂直平分线,若BC=8厘米, AB=10厘米,则∆EBC 的周长为( )厘米A .16B .28C .26D .18。
中考知识点梳理-角平分线的判定和性质-垂直平分线的判定
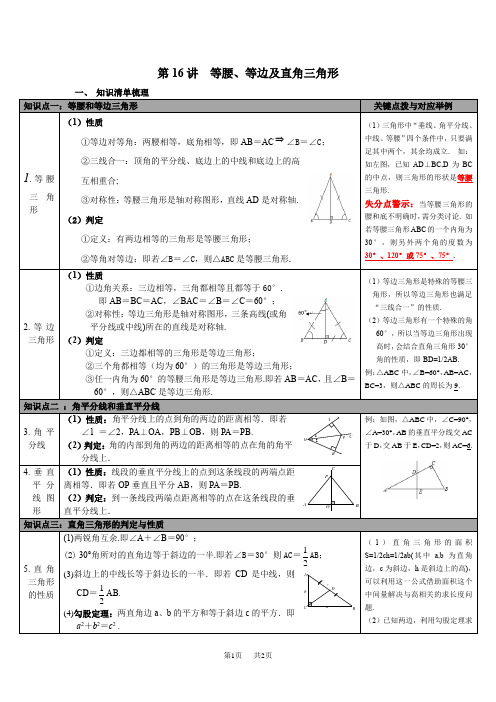
第16讲等腰、等边及直角三角形
(1)性质
①等边对等角:两腰相等,底角相等,即AB=AC ∠B=∠C;
②三线合一:顶角的平分线、底边上的中线和底边上的高
互相重合;
③对称性:等腰三角形是轴对称图形,直线AD是对称轴.
(2)判定
①定义:有两边相等的三角形是等腰三角形;
②等角对等边:即若∠B=∠C,则△ABC是等腰三角形.
(1)性质
①边角关系:三边相等,三角都相等且都等于60°.
即AB=BC=AC,∠BAC=∠B=∠C=60°;
②对称性:等边三角形是轴对称图形,三条高线(或角
平分线或中线)所在的直线是对称轴.
(2)判定
①定义:三边都相等的三角形是等边三角形;
②三个角都相等(均为60°)的三角形是等边三角形;
③任一内角为60°的等腰三角形是等边三角形.即若AB=AC,且∠B=
60°,则△ABC是等边三角形.
知识点二:角平分线和垂直平分线
例:如图,△ABC中,∠C=90°,
∠A=30°,AB的垂直平分线交AC
于D,交AB于E,CD=2,则AC=6.
B
c
D
c
D。
等腰三角形知识点总结等腰三角形知识点归纳重点

等腰三角形知识点总结等腰三角形知识点归纳重点等腰三角形是初中数学中的一种基本几何图形,具有很多特殊的性质和定理。
本文将对等腰三角形的相关知识点进行总结和归纳,帮助读者更好地理解和掌握等腰三角形的特点和应用。
以下是等腰三角形知识点总结汇总,希望对大家的学习有所帮助。
1、等腰三角形知识总结,定义(1)等腰三角形:有两条边相等的三角形叫等腰三角形,相等的两条边叫腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角。
(2)等边三角形:特殊的等腰三角形,三条边都相等的三角形叫做等边三角形。
2、等腰三角形知识总结,等腰三角形的相关概念(1)等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在的直线就是它的对称轴。
(2)等腰三角形的外心、内心、重心和垂心都在顶角平分线上,即四心共线。
(3)等边三角形的外心、内心、重心和垂心四心合一,成为等边三角形的中心。
3、等腰三角形知识总结,等腰三角形的性质定理(1)推理格式:在△ABC中,因为AB=AC,所以∠B=∠C。
(2)定理的作用:证明同—个三角形中的两个角相等。
4、等腰三角形知识总结,等腰三角形性质定理的推论(1)等腰三角形的顶角平分线平分底边并且垂直于底边。
(2)等边三角形的三个内角都相等,并且每个角都等于60°。
5、等腰三角形知识总结,等腰三角形的判定定理(1)该定理是证明两条线段相等的重要定理,是将三角形中的角的相等关系转化为边的相等关系的重要依据。
(2)注意:该定理不能叙述为“如果一个三角形中有两个底角相等,那么它的两腰也相等”。
因为在没有判定出它是等腰三角形之前,不能用“底角”、“腰”这些名词,只有等腰三角形才有“底角”、“腰”。
相等的两条边叫腰;两腰的夹角叫顶角;顶角所对的边叫底;腰与底的夹角叫底角。
(2)等边对等角;(3)底边上的高、底边上的中线、顶角平分线互相重合;(4)是轴对称图形,对称轴是顶角平分线;(5)底边小于腰长的两倍并且大于零,腰长大于底边的一半;(6)顶角等于180°减去底角的两倍;(7)顶角可以是锐角、直角、钝角,而底角只能是锐角.等边三角形性质:①具备等腰三角形的一切性质。
等腰三角形的轴对称性质

化学实验
生物学实验
在生物学实验中,等腰三角形可用于 模拟生物体的形态和结构,如细胞结 构和生物体的平衡。
在化学实验中,等腰三角形可用于表 示化学反应中的物质变化和能量转化。
04
等腰三角形与其他几何图形的关系
与直角三角形的关系
直角三角形可以是等腰的,即两个锐 角相等,两腰也相等。
等腰直角三角形是一种特殊的等腰三 角形,它的两个锐角都是45度,两腰 相等,并且斜边是两腰的平方和的平 方根。
THANK YOU
感谢聆听
角度判定
如果一个三角形有两个底角相 等,则它是等腰三角形。
综合判定
如果一个三角形同时满足边长 相等和角度相等,则它是等腰 三角形。
02
等腰三角形的轴对称性
轴对称的定义
轴对称
如果一个平面图形关于某一直线对称 ,那么这个图形叫做轴对称图形,这 条直线叫做对称轴。
轴对称的性质
轴对称图形是全等图形,对称轴两侧 的图形可以完全重合。
角度相等
等腰三角形的两个底角相等,顶角与底角也相等。
等腰三角形的性质
80%
轴对称
等腰三角形是轴对称图形,其对 称轴是穿过顶角的高线。
100%
角度恒定
等腰三角形的角度恒定,即两个 底角相等,顶角与底角也相等。
80%
面积恒定
等腰三角形的面积恒定,可以通 过底和高计算面积。
等腰三角形的判定
边长判定
如果一个三角形有两边长度相 等,则它是等腰三角形。
绘画和雕塑
等腰三角形在绘画和雕塑 中常被用来表现形式美感 和立体感,如人体结构和 自然形态。
服装设计
在服装设计中,等腰三角 形可以作为设计元素,用 于服装的款式和图案设计。
北师大版七年级下册数学[《生活中的轴对称》全章复习与巩固(提高)知识点整理及重点题型梳理]
![北师大版七年级下册数学[《生活中的轴对称》全章复习与巩固(提高)知识点整理及重点题型梳理]](https://img.taocdn.com/s3/m/fe639f3a4b7302768e9951e79b89680203d86b9a.png)
北师大版七年级下册数学[《生活中的轴对称》全章复习与巩固(提高)知识点整理及重点题型梳理]研究目标】1.增进对身边轴对称图形的认识和欣赏,提高对数学的兴趣。
2.了解轴对称的概念,探索轴对称图形的基本性质和应用。
3.探究线段垂直平分线、角平分线和等腰三角形的性质及判定方法。
4.能够按照要求画出一些轴对称图形。
要点梳理】要点一、轴对称1.轴对称图形和轴对称1)轴对称图形如果一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴。
轴对称图形的性质:轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线。
2)轴对称定义:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴。
要点诠释:成轴对称的两个图形的性质:①关于某条直线对称的两个图形形状相同,大小相等,是全等形;②如果两个图形关于某条直线对称,则对称轴是任何一对对应点所连线段的垂直平分线;③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么它们的交点在对称轴上。
3)轴对称图形与轴对称的区别和联系要点诠释:轴对称是指两个图形的位置关系,轴对称图形是指具有特殊形状的一个图形;轴对称涉及两个图形,而轴对称图形是对一个图形来说的。
联系:如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条轴对称;如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形。
2.线段的垂直平分线线段的垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等;反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
要点诠释:线段的垂直平分线的性质是证明两线段相等的常用方法之一。
同时也给出了引辅助线的方法,即遇见线段的垂直平分线,画出到线段两个端点的距离,这样就出现相等线段,直接或间接地为构造全等三角形创造条件。
三角形三边垂直平分线交于一点,该点到三角形三顶点的距离相等,这点是三角形外接圆的圆心——外心。
轴对称重点和难点

轴对称图形主要内容:轴对称与轴对称图形、轴对称的性质、设计轴对称图案、线段、角的轴对称性、等腰三角形的轴对称性、等腰梯形的轴对称性。
重点:垂直平分线、角平分线、等腰三角形(直角三角形、等边三角形)的性质、等腰梯形的常用辅助线;难点是如何灵活应用所学知识解决问题。
难点:通过具体的轴对称图形实例,让学生经历观察、比较、分析等数学活动,从而让学生认识轴对称图形,知道轴对称与轴对称图形之间的区别,而后通过线段与角、等腰三角形、等腰梯形等轴对称图形加深对轴对称图形的理解。
变换:将图形绕某点旋转一定的角度到另一个位置,这种变换叫做旋转变换。
考点三、等腰三角形1、等腰三角形的性质(1)等腰三角形的性质定理及推论:定理:等腰三角形的两个底角相等(简称:等边对等角)推论1:等腰三角形顶角平分线平分底边并且垂直于底边。
即等腰三角形的顶角平分线、底边上的中线、底边上的高重合。
推论2:等边三角形的各个角都相等,并且每个角都等于60°。
(2)等腰三角形的其他性质:①等腰直角三角形的两个底角相等且等于45°②等腰三角形的底角只能为锐角,不能为钝角(或直角),但顶角可为钝角(或直角)。
③等腰三角形的三边关系:设腰长为a ,底边长为b ,则2b <a④等腰三角形的三角关系:设顶角为顶角为∠A ,底角为∠B 、∠C ,则∠A=180°—2∠B ,∠B=∠C=2180A ∠-︒ 2、等腰三角形的判定等腰三角形的判定定理及推论:定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边)。
这个判定定理常用于证明同一个三角形中的边相等。
推论1:三个角都相等的三角形是等边三角形推论2:有一个角是60°的等腰三角形是等边三角形。
推论3:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
等腰三角形的性质与判定等腰三角形性质 等腰三角形判定 中线1、等腰三角形底边上的中线垂直底边,平分顶角;2、等腰三角形两腰上的中线相等,并且它们的交点与底边两端点距离相等。
11、轴对称与等腰三角形

轴对称与等腰三角形知识点1、等腰三角形1、等腰三角形的定义:有两边相等的三角形叫做等腰三角形。
相等的两边叫做等腰三角形的腰,另一边叫做底边;两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
注意:①等腰三角形的顶角不一定是锐角,但是底角一定是锐角;②钝角三角形也可以是等腰三角形2、等腰三角形的性质①等边对等角:等腰三角形的两底角相等;②三线合一:等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合;③等腰三角形两腰上的高、中线分别相等,两底角的平分线相等;④等腰三角形是轴对称图形,对称轴为顶角角平分线(三线合一)所在直线。
注意:①等腰三角形的性质是指在同一个等腰三角形而言的;②三线合一要注意位置,在等腰三角形中所有的中线、角平分线等并不是合一的。
3、等腰三角形的判定①有两个角相等的三角形是等腰三角形。
(等角对等边)②三线合一也能作为判定等腰三角形的依据③推论在直角三角形中,30°所对的直角边是斜边的一半1-9、如图,已知在等腰三角形ABC 中,AC AB =,BC AE //.求证:AE 平分∠DAC .例2、等腰三角形的判定2-1、如图,OC 平分∠AOB ,OB CD //,若cm OD 3=,则CD 等于.2-2、已知:如图,在△ABC 中,∠ACB =90°,CD 是AB 上的高,AE 分别交CB 、CD 于E 、F ,且CF CE =,求证:AE 平分∠BAC .2-3、如图,△ABC 中,∠ACB =90º,CD ⊥BA 于D ,AE 平分∠BAC 交CD 于F ,交BC 于E ,求证△CEF 是等腰三角形。
DC AB 02-5、如图,在△ABC中,AB知识点2、等边三角形1、等边三角形的定义三边相等的三角形叫做等边三角形,也叫正三角形2、等边三角形性质:①每个角都是60°;②轴对称图形;③有3条对称轴。
3、等边三角形的判定定理①三边相等的三角形是等边三角形;②三个角都相等的三角形是等边三角形;③有一个角是60°的等腰三角形是等边三角形。
轴对称图形知识点归纳

轴对称知识梳理一、基本概念1.轴对称图形如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就叫做对称轴.折叠后重合的点是对应点,叫做对称点.2.线段的垂直平分线经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线3.轴对称变换由一个平面图形得到它的轴对称图形叫做轴对称变换.4.等腰三角形有两条边相等的三角形,叫做等腰三角形.相等的两条边叫做腰,另一条边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.5.等边三角形三条边都相等的三角形叫做等边三角形.二、主要性质1.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.或者说轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.2.线段垂直平分钱的性质线段垂直平分线上的点与这条线段两个端点的距离相等.3.(1)点P(x,y)关于x轴对称的点的坐标为P′(x,-y).(2)点P(x,y)关于y轴对称的点的坐标为P″(-x,y).4.等腰三角形的性质(1)等腰三角形的两个底角相等(简称“等边对等角”).(2)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.(3)等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴.(4)等腰三角形两腰上的高、中线分别相等,两底角的平分线也相等.(5)等腰三角形一腰上的高与底边的夹角是顶角的一半。
(6)等腰三角形顶角的外角平分线平行于这个三角形的底边.5.等边三角形的性质(1)等边三角形的三个内角都相等,并且每一个角都等于60°.(2)等边三角形是轴对称图形,共有三条对称轴.(3)等边三角形每边上的中线、高和该边所对内角的平分线互相重合.三、有关判定1.与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.2.如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).3.三个角都相等的三角形是等边三角形.4.有一个角是60°的等腰三角形是等边三角形.。
图形的轴对称角平分线的性质

对于任何一个图形,如果它关于某条直线对称, 那么该图形在这条直线的两侧的部分是全等的。
3
应用
在几何学中,轴对称角平分线可以用于解决各种 问题,例如找到图形的重心、证明图形的相等或 全等等。
02
轴对称角平分线的性质
轴对称角平分线的性质定理
轴对称角平分线将对 应的三角形分成两个 全等三角形。
轴对称角平分线将对 应的四边形分成两个 全等梯形。
轴对称角平分线所在 的直线也是三角形的 高线。
证明轴对称角平分线的性质定理
证明方法一
利用轴对称的性质,通过作辅助 线将轴对称角平分线转化为角平 分线,再利用通 过轴对称角平分线将三角形分成 两个全等三角形,再利用全等三 角形的性质证明。
轴对称角平分线的性质的应用
等腰三角形的高线
在等腰三角形中,底边的中垂线(即角平分线)也是高线。利用这一性质,我们可以更容 易地找到等腰三角形的顶点。
三角形内角平分线定理
在三角形中,内角平分线定理指出,三条内角的平分线将三角形的边分为三段,这三段与 对应的角的两边成正比。利用这一性质,我们可以解决一些与比例有关的几何问题。
在解析几何中的应用
图形的轴对称角平分线的性 质
汇报人: 日期:
目录
• 轴对称角平分线的定义 • 轴对称角平分线的性质 • 轴对称角平分线的应用 • 轴对称角平分线的扩展知识 • 总结与展望
01
轴对称角平分线的定义
轴对称角平分线的定义
01
轴对称角平分线是指将图形划分 为两个对称部分的直线。
02
当图形关于某条直线对称时,该 直线即为轴对称角平分线。
01
在几何问题中,可以利用轴对称角平分线的性质进行证明和计 算。
2022人教版数学《精品 等腰三角形的性质2》配套教案(精选)

13.3.1 等腰三角形第1课时等腰三角形的性质教学目标(一)教学知识点1.等腰三角形的概念.2.等腰三角形的性质.3.等腰三角形的概念及性质的应用.(二)能力训练要求1.经历作(画)出等腰三角形的过程,•从轴对称的角度去体会等腰三角形的特点.2.探索并掌握等腰三角形的性质.教学重点1.等腰三角形的概念及性质.2.等腰三角形性质的应用.教学难点等腰三角形三线合一的性质的理解及其应用.教学过程提出问题,创设情境在前面的学习中,我们认识了轴对称图形,探究了轴对称的性质,•并且能够作出一个简单平面图形关于某一直线的轴对称图形,•还能够通过轴对称变换来设计一些美丽的图案.这节课我们就是从轴对称的角度来认识一些我们熟悉的几何图形.来研究:①三角形是轴对称图形吗?②什么样的三角形是轴对称图形?导入新课同学们通过自己的思考来做一个等腰三角形.AICABI作一条直线L,在L上取点A,在L外取点B,作出点B关于直线L的对称点C,连结AB、BC、CA,则可得到一个等腰三角形.提问:1.等腰三角形是轴对称图形吗?请找出它的对称轴.2.等腰三角形的两底角有什么关系?3.顶角的平分线所在的直线是等腰三角形的对称轴吗?4.底边上的中线所在的直线是等腰三角形的对称轴吗?•底边上的高所在的直线呢?等腰三角形的性质:1.等腰三角形的两个底角相等(简写成“等边对等角”).2.等腰三角形的顶角平分线,底边上的中线、•底边上的高互相重合(通常称作“三线合一”).[例1]如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求:△ABC各角的度数.分析:根据等边对等角的性质,我们可以得到∠A=∠ABD,∠ABC=∠C=∠BDC,•再由∠BDC=∠A+∠ABD,就可得到∠ABC=∠C=∠BDC=2∠A.再由三角形内角和为180°,•就可求出△ABC的三个内角.[例]因为AB=AC,BD=BC=AD,所以∠ABC=∠C=∠BDC.∠A=∠ABD(等边对等角).设∠A=x,则∠BDC=∠A+∠ABD=2x,从而∠ABC=∠C=∠BDC=2x.于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,解得x=36°.在△ABC中,∠A=35°,∠ABC=∠C=72°.[师]下面我们通过练习来巩固这节课所学的知识.随堂练习练习1.如下图,在下列等腰三角形中,分别求出它们的底角的度数.(2)120︒36︒(1)答案:(1)72° (2)30°2.如右图,△ABC 是等腰直角三角形(AB=AC ,∠BAC=90°),AD 是底边BC 上的高,标出∠B 、∠C 、∠BAD 、∠DAC 的度数,图中有哪些相等线段?D CAB答案:∠B=∠C=∠BAD=∠DAC=45°;AB=AC ,BD=DC=AD .3.如右图,在△ABC 中,AB=AD=DC ,∠BAD=26°,求∠B 和∠C 的度数.D CAB答:∠B=77°,∠°.课时小结这节课我们主要探讨了等腰三角形的性质,并对性质作了简单的应用.等腰三角形是轴对称图形,它的两个底角相等(等边对等角),等腰三角形的对称轴是它顶角的平分线,并且它的顶角平分线既是底边上的中线,又是底边上的高. 我们通过这节课的学习,首先就是要理解并掌握这些性质,并且能够灵活应用它们.活动与探究如右图,在△ABC 中,过C 作∠BAC 的平分线AD 的垂线,垂足为D ,DE ∥AB 交AC 于E .求证:AE=CE .EDCAB过程:通过分析、讨论,让学生进一步了解全等三角形的性质和判定,•等腰三角形的性质. 结果:证明:延长CD 交AB 的延长线于P ,如右图,在△ADP 和△A DC 中12,,,AD AD ADP ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADP ≌△ADC . ∴∠P=∠ACD . 又∵DE ∥AP , ∴∠4=∠P . ∴∠4=∠ACD . ∴DE=EC .同理可证:AE=DE . ∴AE=CE . 板书设计等腰三角形一、设计方案作出一个等腰三角形EDCABP二、等腰三角形性质 1.等边对等角 2.三线合一第2章 图形的轴对称复习课学习目标:1、理解轴对称与轴对称图形的概念,掌握轴对称的性质.2、掌握线段的垂直平分线、角的平分线的性质及应用.3、理解等腰三角形的性质并能够简单应用.4、理解等边三角形的性质并能够简单应用.5、能够按要求做出简单的平面图形的轴对称图形,初步体会从对称的角度欣赏设计简单的轴对称图案.重点:掌握线段的垂直平分线、角的平分线的性质、等腰三角形的性质及应用. 难点:轴对称图形以及关于某条直线成轴对称的概念,等腰三角形的性质应用 复习过程: 【课前准备】如何画一个图形关于某条直线对称的图形? 【课内探究】 知识点整理:1、如果一个图形沿着某条直线折叠..后,直线两旁的部分能够互相重合..,那么这个图形就叫做轴对称图形,这条直线叫做这个图形的对称轴. 轴对称图形是—个具有特殊性质的图形.常见的轴对称图形有:线段、角、等腰三角形、等边三角形、矩形、菱形、 正方形、等腰梯形、正n 边形、圆形.2、 把一个图形沿着某条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线就是它们的对称轴.而两个图形中的各自的相对应点叫做关于这条直线的对称点. (1) 轴对称是指两个图形之间的位置关系;(2) 关于某条直线对称的两个图形是互相重合的;如果两个图形关于某直线对称,那么对称轴是对应点所连的线段的垂直平分线.1、 什么叫轴对称图形?2、 什么叫做两个图形关于某一条直线成轴对称?3、 “轴对称图形”与“两个图形关于某一条直线成轴对称”有什么区别?4、 什么叫做线段的垂直平分线?线段的垂直平分线有什么性质?如何用尺规作出线段的垂直平分线?5、 角的平分线具有什么性质?如何做角平分线?6、 等腰三角形有哪些性质?等边三角形呢?已知哪些条件,可以用尺规做出等腰三角形?7、 如果两个图形关于某直线对称,那么这两个图形具有什么性质?E D BC A 牛刀小试:下面几种图形,一定是轴对称图形的是( )3、有两条边相等的三角形叫做等腰三角形.巩固训练:(1)已知△ABC 中,AB = AC ,其周长为18cm ,AB = 5cm ,则BC = . (2)已知等腰三角形的腰长为4cm ,底边长为6cm ,则它的周长为 . (3)已知等腰三角形的两边长分别为6cm 、3cm ,则它的周长是 . (4)已知等腰三角形一边长为3,另一边为5,则它的周长是 .4、线段垂直平分线、角平分线、等腰三角形的性质: ① 等腰三角形的两个底角相等;② 等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合;(三线合一) ③ 等腰三角形是轴对称图形,它的对称轴是顶角平分线(或底边上的高或底边上的中线)所在的直线. 巩固训练:(1) 已知△ABC 中,AB = AC ,∠C = 50°,则∠B = .(2) △ABC 中,AB = AC ,若AD ⊥BC 于D ,则∠1 ∠2,BD CD. (3) 已知等腰三角形的一个底角为45°,则它的顶角为 . (4) 已知等腰三角形的一个角是70°,则其余两个角的度数是 . (5) 已知等腰三角形的一个角是120°,则其余两个角的度数是 . 思考:本章的作图有哪几种类型? (1)作线段的垂直平分线;(2)作角的平分线; (3)作等腰三角形;(4)作对称点. 【巩固提升】1、已知A (-1,1),在y 轴上找一点P,使△AOP 是等腰三角形.这样的P 点可能有几个?2、已知Rt △ABC 中,∠C=90°,DE 垂直平分AB(1)若∠CAD=20°,则∠B=____°(2)若AC=4,BC=5,则△ACD 的周长为______. (3) 若∠B=30°,则∠CAD=____°图中共有几组相等的线段?为什么?【课堂小结】通过今天的学习,你对本章又增加了哪些新的认识? 【达标检测】1、下列图形中一定是轴对称的图形是( ). A 、梯形 B 、直角三角形 C 、角 D 、平行四边形2、等腰三角形的一个内角是50°,则另外两个角的度数分别是( ).A、65° 65°B、50°80°C、65°65°或50°80°D、50° 50°3、如果等腰三角形的两边长是6和3,那么它的周长是().A、9B、12C、12或 15D、154、到三角形的三个顶点距离相等的点是().A、三条角平分线的交点B、三条中线的交点C、三条高的交点D、三条边的垂直平分线的交点第1课时等腰三角形的性质【知识与技能】1.理解掌握等腰三角形的性质.2.运用等腰三角形性质进行证明和计算.、发展形象思维.【过程与方法】、观察、证明等腰三角形的性质,发展学生推理能力.2.通过运用等腰三角形的性质解决有关问题,提高运用知识和技能解决问题的能力.【情感态度】引导学生对图形的观察、发现,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中取得成功的体验.【教学重点】等腰三角形的性质及应用.【教学难点】等腰三角形的证明.一、情境导入,初步认识问题 1 让学生根据自己的理解,做一个等腰三角形.要求学生独立思考,动手做图后,再互相交流评价.可按下列方法做出:作一条直线l,在l上取点A,在l外取点B,作出点B关于直线l的对称点C,连接AB,AC,CB,则可得到一个等腰三角形.问题2 老师拿出事先准备好的长方形纸片,按下图方式折叠剪裁.观察并讨论:△ABC有什么特点?教师指导,并介绍等腰三角形的相关概念,及等腰三角形是轴对称图形.【教学说明】教师讲课前,先让学生完成“自主预习”.二、思考探究,获取新知教师依据学生讨论发言的情况,归纳等腰三角形的性质:①∠B=∠C→两个底角相等.②BD=CD→AD为底边BC上的中线.③∠BAD=∠CAD→AD为顶角∠BAC的平分线.∠ADB=∠ADC=90°→AD为底边BC上的高.指导学生用语言叙述上述性质.性质1等腰三角形的两个底角相等(简写成:“等边对等角”).性质2等腰三角形的顶角平分线、底边上的中线,底边上的高重合(简记为:“三线合一”).教师指导对等腰三角形性质的证明.1.证明等腰三角形底角的性质.教师要求学生根据猜想的结论画出相应的图形,写出已知和求证.在引导学生分析思路时强调:∠B=∠C,需证明以∠B,∠C为元素的两个三角形全等,需要添加辅助线构造符合证明要求的两个三角形.(2)添加辅助线的方法可以有多种方式:如作顶角平分线,或作底边上的中线,或作底边上的高等.“三线合一”的性质.【教学说明】在证明中,设计辅助线是关键,引导学生用全等的方法去处理,在不同的辅助线作法中,由辅助线带来的条件是不同的,重视这一点,要求学生板书证明过程,以体会一题多解带来的体验.例如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.解:∵AB=AC,BD=BC=AD,∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角).设∠A=x,则∠BDC=∠A+∠ABD=2x,从而∠ABC=∠C=∠BDC=2x.于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,解得x=36°于是在△ABC中,有∠A=36°,∠ABC=∠C=72°.【教学说明】等腰三角形“等边对等角”及“三线合一”性质,可以实现由边到角的转化,从而可求出相应角的度数.要在解题过程中,学会从复杂图形中分解出等腰三角形,用方程思想和数形结合思想解决几何问题.三、运用新知,深化理解第1组练习:1.如图,在下列等腰三角形中,分别求出它们的底角的度数.2.如图,△ABC是等腰直角三角形,AB=AC,∠BAC=90°,AD是底边BC上的高,标出∠B,∠C,∠BAD,∠DAC的度数,指出图中有哪些相等线段.3.如图,在△ABC,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.第2组练习:△ABC是轴对称图形,则它一定是( )°,它的顶角的度数是( )A.80°B.20°°和20°°或50°2cm,并且它的周长为16cm.求这个等腰三角形的边长.4.如图,在△ABC中,过C作∠BAC的平分线AD的垂线,垂足为D,DE∥AB 交AC于E.求证:AE=CE.【教学说明】等腰三角形解边方面的计算类型较多,引导学生见识不同类型,并适时概括归纳,帮学生形成解题能力,注意提醒学生分类讨论思想的应用.【答案】第1组练习答案:1.(1)72°;(2)30°2.∠B=∠C=∠BAD=∠DAC=45°;AB=AC,BD=DC=AD3.∠B=77°,∠°第2组练习答案:3.设三角形的底边长为xcm,则其腰长为(x+2)cm,根据题意,得2(x+2)+x=16.解得x=4.∴等腰三角形的三边长为4cm,6cm和6cm.4.延长CD交AB的延长线于P,在△ADP和△ADC中,∠PAD=∠CAD,AD=AD,∠PDA=∠CDA,∴△ADP≌△ADC.∴∠P=∠∵DE∥AP,∴∠CDE=∠P.∴∠CDE=∠ACD,∴DE=EC.同理可证:AE=DE.∴AE=CE.四、师生互动,课堂小结这节课主要探讨了等腰三角形的性质,并对性质作了简单的应用.请学生表述性质,提醒每个学生要灵活应用它们.学生间可交流体会与收获.1.布置作业:从教材“习题”中选取.2.完成练习册中本课时的练习.本课时应把重点放在逐步展示知识的形成过程上,先让学生通过剪纸认识等腰三角形;再通过折纸猜测、验证等腰三角形的性质;然后运用全等三角形的知识加以论证.由特殊到一般、由感性上升到理性,逻辑演绎,层层展开,步步深入.。
轴对称知识点总结

轴对称知识点总结轴对称是初中数学中的重要概念,在几何图形的研究和实际生活中都有广泛的应用。
下面我们来详细总结一下轴对称的相关知识点。
一、轴对称的定义如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
例如,等腰三角形是轴对称图形,底边的高所在的直线就是它的对称轴;矩形是轴对称图形,对边中点的连线所在的直线是它的对称轴。
二、轴对称图形的性质1、对称轴是任何一对对应点所连线段的垂直平分线。
2、对应线段相等,对应角相等。
3、成轴对称的两个图形全等。
三、轴对称与轴对称图形的区别与联系1、区别轴对称是指两个图形沿着某条直线对折后能够完全重合,是两个图形的位置关系。
轴对称图形是指一个图形沿着某条直线对折后直线两旁的部分能够完全重合,是一个图形自身的特性。
2、联系都有对称轴。
如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形;如果把轴对称图形沿对称轴分成两部分,那么这两部分关于这条对称轴成轴对称。
四、作轴对称图形1、作轴对称图形的对称轴如果一个图形是轴对称图形,那么连接一对对应点的线段的垂直平分线就是该图形的对称轴。
对于两个成轴对称的图形,对称轴是连接对称点的线段的垂直平分线。
2、作轴对称图形几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形。
五、用坐标表示轴对称1、点(x,y)关于 x 轴对称的点的坐标为(x,y)。
2、点(x,y)关于 y 轴对称的点的坐标为(x,y)。
例如,点(2,3)关于 x 轴对称的点的坐标为(2,-3);点(-1,4)关于 y 轴对称的点的坐标为(1,4)。
六、轴对称的实际应用轴对称在实际生活中有很多应用,比如:1、建筑设计中,许多建筑都采用了轴对称的设计,使得建筑更加美观、稳定。
2、飞机、汽车等交通工具的外形设计也常常运用轴对称,以减少空气阻力,提高性能。
几种常见的轴对称图形和中心对称图形

几种常见的轴对称图形和中心对称图形:
轴对称图形:线段、角、等腰三角形、等边三角形、菱形、矩形、正方形、等腰梯形、圆
对称轴的条数:角有一条对称轴,即该角的角平分线;等腰三角形有一条对称轴,是底边的垂直平分线;等边三角形有三条对称轴,分别是三边上的垂直平分线;菱形有两条对称轴,分别是两条对角线所在的直线,矩形有两条对称轴分别是两组对边中点的直线;
中心对称图形:线段、平行四边形、菱形、矩形、正方形、圆
对称中心:线段的对称中心是线段的中点;平行四边形、菱形、矩形、正方形的对称中心是对角线的交点,圆的对称中心是圆心。
说明:线段、菱形、矩形、正方形以及圆它们即是轴对称图形又是中心对称图形。
坐标系中的轴对称变换与中心对称变换:
点P(x,y)关于x轴对称的点P1的坐标为(x,-y),关于y轴对称的点P2的坐标为(-x,y)。
关于原点对称的点的坐标P3的坐标是(-x,-y)这个规律也可以记为:关于y轴(x轴)对称的点的纵坐标(横坐标)相同,横坐标(纵坐标)互为相反数。
关于原点成中心对称的点的,横坐标为原横坐标的相反数,纵坐标为原纵坐标的相反数,即横坐标、纵坐标同乘以-1。
证明二---等腰、直角三角形及角平分线、中垂线的典型例题

第 10 页 共 10 页
六、新课探究---<5>角平分线的应用 经典例题 ( 1 ) 如 图 , AB // CD , DE EA , CE 平 分 DCB , 求 证 : CD AB BC ;
C 60 , ABC 中, (2) 如图, 内角平分线 AD、BE 相交于点 P ,
求证: PD PE ;
举一反三 ① 如图,已知线段 AB // CD ,连接 AD、BC ,若 BP 平分 ABC , 且 AP PD ,猜想线段 AB、BC、CD 三者之间有怎样的等量关系? 请写出你的结论并予以证明
第 6 页 共 10 页
音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的 一切。 ——F.Klein
(2)如图, ABC 中, AB AC , A 36 , D 是 AC 上一点, 且 BD BC ,过点 D 分别作 DE AB 、 DF BC ,垂足分别是 E、F .给出以下四个结论:① DE DF ;②点 D 是 AC 的中点; ③ DE 垂直平分 AB ;④ AB BC CD .其中正确结论的序号是 _______________;
举一反三 ①如图, AD 是 ABC 的角平分线, EF 是 AD 的垂直平分线. 求证: (1) EAD EDA ; (2) DF // AC ; (3) EAC B .
第 7 页 共 10 页
音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的 一切。 ——F.Klein
第 4 页 共 10 页
音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的 一切。 ——F.Klein
等腰三角形、角平分线

课 题 等腰三角形、角的平分线授课时间: 2013.备课时间:教学目标1. 熟练掌握等腰三角形、角的平分线的相关知识和性质。
教学内容(包括知识点、典型例题、课后作业)等腰三角形知识梳理一、等腰三角形的边角关系 1)判定定理 等角对等边 2)性质定理 等边对等角3)特殊角之间的关系 ∠B = ∠C=90°-21∠BAC∠BAC=180°-2∠B =180°-2∠C 4)底边BC 小于2倍的腰长AB 二、等腰三角形“三线”间的关系1)顶角的角平分线、底边上的中线、底边上的高(“三线合一”)2)等腰三角形两腰上的高相等、两腰上的中线相等、两底角的平分线相等; 三、等边三角形 1)概念2)性质 等边三角形具备所有等腰三角形的性质外还有: 三边都相等;三个内角都相等,且都等于60°;等边三角形是轴对称图形,有三条对称轴。
3)判定利用定义; 三个角都相等的三角形是等边三角形; 有一个角是60°的等腰三角形是等边三角形。
四、含30°的直角三角形1)定理 在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边的斜边的一半。
2)逆定理 在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的角等于30°五、等腰三角形的对称性等腰三角形是轴对称图形,有一条对称轴(底边的垂直平分线) 等边三角形有三条对称轴,即三边的垂直平分线。
复习巩固1、(2009•山西)如图,在Rt△ABC 中,∠ACB=90°,BC=3,AC=4,AB 的垂直平分线DE 交BC 的延长2线于点E,则CE 的长为 。
2、(2004•湖州)已知如图,在△ABC 中,BC=8,AB 的中垂线交BC 于D,AC 的中垂线交BC 与E,则△ADE 的周长等于 .3、(2010•娄底)如图,在四边形ABCD 中,AD∥BC,E 为CD 的中点,连接AE、BE,BE⊥AE,延长AE 交BC 的延长线于点F.求证:(1)FC=AD; (2)AB=BC+AD .典型例题 一.选择题1、已知等腰三角形的一个角等于42°,则它的底角为 ( ).A、42 °B、69°C、69°或84°D、42°或69°2、如图,ABC △中,AB AC ,30A ,DE 垂直平分AC ,则BCD 的度数为( ) A.80 B.75C.65 D.453、等腰三角形的顶角是80°,则一腰上的高与底边的夹角是( )A.40° B.50° C.60° D.30°4. 如图,15A ∠,AB BC CD DE EF ,则DEF ∠等于( )A .90 B.75 C.70 D.60A B D EC5、如图,△MNP中, ∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是( )PQMNGA.8+2a B.8+a C.6+a D.6+2a二.选择题1. 在△ABC 中,AB=AC,若∠B=56º,则∠C=__________.2.等腰三角形底边中点与一腰的距离为6,则腰上的高为______.3.如图,在△ABC 中,AB=AC,CD 平分∠ACB 交AB 于点D,AE∥DC 交BC 的延长线于点E,已知∠E=36°,则∠B= .4.如图,在ABC △中,点D 是BC 上一点,80BAD °,AB AD DC ,则C .三.解答题1. 下午2时,一轮船从A 处出发,以每小时40海里的速度向正南方向行驶,下午4时,到达B 处,在A 处测得灯塔C 在东南方向,在B 处测得灯塔C 在正东方向,在图中画出示意图 ,并求出B、C 之间的距离.2. 如图,在四边形ABCD 中,AB=AD,CB=CD,求证:∠ABC=∠ADC.AC B D804DCAB加强巩固角的平分线DCAEB一、知识准备: 1)角的平分线的画法2)角的平分线的性质: 。
人教版八年级上册13.3.1《等腰三角形》

《等腰三角形》◆教材分析本节课是在前面学习了三角形的有关概念及性质、轴对称变换、全等三角形、垂直平分线和尺规作图的基础上,研究等腰三角形的定义及其重要性质,它既是前面所学知识的延伸,也是后面直角三角形、等边三角形的知识的重要储备,我们常常利用它证明角相等、线段相等、两直线垂直,因此本节课具有承上启下的重要作用。
◆教学目标【知识与能力目标】1、理解并掌握等腰三角形的性质。
2、会运用等腰三角形的概念和性质解决有关问题。
3、观察等腰三角形的对称性、发展形象思维。
4、探索等腰三角形的判定定理【过程与方法目标】1、通过实践、观察、证明等腰三角形的性质,培养学生的推理能力。
2、通过运用等腰三角形的性质解决有关的问题,提高运用知识和技能解决问题的能力,发展应用意识。
3、探索等腰三角形的判定定理,进一步体验轴对称的特征,发展空间观念【情感态度价值观目标】1、引导学生对图形的观察、发现,激发学生的好奇心和求知欲。
2、在运用数学知识解决问题的活动中获取成功的体验,建立学习的自信心。
3、感受图形中的动态美、和谐美、对称美,感受合作交流带来的成功感,树立自信心。
4、通过对等腰三角形的判定定理的探索,让学生体会探索学习的乐趣,并通过等腰三角形的判定定理的简单应用,加深对定理的理解.从而培养学生利用已有知识解决实际问题的能力【教学重点】1、等腰三角形的概念和性质及其应用。
2、等腰三角形的判定定理及其应用【教学难点】1、等腰三角形的性质的证明。
2、探索等腰三角形的判定定理◆教学过程一、情景导入:师:日常生活中,我们会经常看到一些美丽的图案,其中一些是平面几何图形,接下来我们观察几幅图片,说一说你们看到了什么图形?(课件向学生展示平常见到的有关等腰三角形的图片)学生观察一组图片,回答问题。
【设计意图】使学生能从实际生活中抽象出等腰三角形,初步感知等腰三角形在实际生活中的广泛应用,用美丽的画面激发学生的求知欲。
培养学生勤观察,肯思考的学习习惯。
八年级数学角平分线的性质及等腰三角形(轴对称)基础练习(含答案)

八年级数学角平分线的性质及等腰三角形(轴对称)基础练习试卷简介:全卷满分120分,测试时间60分钟,共四个大题:第一题选择,2个小题,每小题5分;第二题证明题,9个小题,每小题10分;第三题计算题,1个小题,10分;第四题探究题,一个小题,10分。
学习建议:本讲主要内容是角平分线的性质及等腰三角形,在中考中经常出现,大家需要熟练掌握这些知识,学会灵活运用。
本讲题目灵活多变,但万变不离其宗,只要掌握最基本的概念及相关性质,再多加练习,就能掌握。
一、单选题(共2道,每道5分)1.直线l1、l2、l3表示三条相互交叉的公路,现要建立一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有()A.一处B.二处C.三处D.四处答案:D解题思路:到三条相互交叉的公路距离相等的地点应是三条角平分线的交点.把三条公路的中心部位看作三角形,那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求.满足条件的有:(1)三角形两个内角平分线的交点,共一处;(2)三个外角两两平分线的交点,共三处.故选D.易错点:易漏掉外角平分线试题难度:三颗星知识点:角平分线的性质2.已知:如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A的度数是()A.30°B.36°C.45°D.54°答案:C解题思路:∵AD=DE ∴∠A=∠AED ∵DE=EB ∴∠EBD=∠EDB ∵∠AED=∠EBD+∠EDB=2∠EBD ∴∠A=2∠EBD ∵BD=BC ∵∠BDC=∠A+∠EBD=3∠EBD ∴∠C=3∠EBD ∵AB=AC ∴∠C=∠ABC ∵∠A+∠C+∠ABC=180°∴∠A+2∠C=180°2∠EBD+2×3∠EBD=8∠EBD=4∠A=180°∴∠A=45°.易错点:对等腰三角形的性质及三角形的内角和定理、三角形外角的性质掌握不牢试题难度:三颗星知识点:等腰三角形的性质二、计算题(共1道,每道10分)1.如图,AO=OC,且DO垂直AC并交AB于点D,若AB=7cm,BC=5cm,则△BDC的周长是多少?答案:12cm解题思路:∵AO=OC,且DO垂直AC并交AB于点D ∴直线OD是线段AC的垂直平分线∴AD=CD ∴△BDC的周长=BD+CD+BC= BD+AD+BC=AB+BC=12cm易错点:对垂直平分线的性质掌握不牢试题难度:三颗星知识点:线段垂直平分线的性质三、证明题(共9道,每道10分)1.已知,△ABC的角平分线BM、CN相交于点P,求证点P到三边AB、AC、BC的距离相等.答案:作PD、PE、PF分别垂直于三边AB、BC、CA,D、E、F为垂足,∵BM为△ABC的角平分线,PD⊥AB,PE⊥BC,∴PD=PE(角平分线上的点到这个角两边的距离相等).同理可证:PF=PE.∴PD=PE=PF.即点P 到三边AB、BC、CA的距离相等.解题思路:作PD、PE、PF分别垂直于三边AB、BC、CA,D、E、F为垂足,根据角平分线性质可得PD=PE,PF=PE,所以PD=PE=PF.易错点:对角平分线的性质掌握不牢试题难度:二颗星知识点:角平分线的性质2.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA交OA于点D,PE⊥OB交OB于点E,F是OC上另一点,连接DF、EF,求证DF=EF.答案:∵点P在∠AOB的角平分线OC上′,PE⊥OB,∴PD=PE,∠DOP=∠EOP,∠PDO=∠PEO=90°,∴△DPO≌△EPO,∴∠DPO=∠EPO,∴∠DPF=∠EPF,在△DPF 和△EPF中,PD=PE,∠DPF=∠EPF,PF=PF ∴△DPF≌△EPF ∴DF=EF.解题思路:根据角平分线的性质,得PD=PE,根据三角形的外角的性质,得∠DPF=∠EPF,再根据SAS证明△DPF≌△EPF,则DF=EF.易错点:对角平分线的性质掌握不牢试题难度:三颗星知识点:全等三角形的性质3.如图,AD是△ABC的角平分线,DE、DF分别是△ABD与△ACD的高,求证AD垂直EF.答案:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF.∴D在线段EF的垂直平分线上.在Rt△ADE和Rt△ADF中,AD=AD,DE=DF ∴Rt△ADE≌Rt△ADF.∴AE=AF.∴A点在EF的垂直平分线上.∵两点确定一条直线,∴AD是线段EF的垂直平分线.解题思路:找到Rt△AED和Rt△ADF,通过两个三角形全等,找到各量之间的关系,即可证明.易错点:对三角形的角平分线的性质定理和垂直平分线的性质定理掌握不牢试题难度:三颗星知识点:线段垂直平分线的性质4.已知点D、E在△ABC的边BC上,AB=AC,AD=AE,求证BD=CE.答案:∵AB=AC,AD=AE,∴∠B=∠C,∠ADE=∠AED,∵∠ADE=∠B+∠BAD,∠AED=∠C+∠EAC,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≌△ACE,∴BD=CE.解题思路:根据等腰三角形的性质可得到几组相等的角,再根据三角形外角的性质可推出∠BAD=∠CAE,从而可利用SAS判定△ABD≌△ACE,根据全等三角形的性质即可证得结论.易错点:对全等三角形的判定条件掌握不牢试题难度:二颗星知识点:全等三角形的判定与性质5.如图,AD是△ABC的角平分线,DE、DF分别是△ABD与△ACD的高,求证AD垂直平分EF.答案:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF.∴D在线段EF的垂直平分线上.在Rt△ADE和Rt△ADF中,AD=AD,DE=DF ∴Rt△ADE≌Rt△ADF.∴AE=AF.∴A点在EF的垂直平分线上.∵两点确定一条直线,∴AD是线段EF的垂直平分线.解题思路:找到Rt△AED和Rt△ADF,通过两个三角形全等,找到各量之间的关系,即可证明.易错点:对直角三角形全等的判定条件掌握不牢试题难度:三颗星知识点:角平分线的性质6.如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD.求证:BD=DE.答案:∵BD是正三角形ABC的AC边的中线,∴BD⊥AC,BD平分∠ABC,∠DBE=30°.∵CD=CE,∴∠CDE=∠E.∵∠ACE=120°,∴∠CDE+∠E=60°.∴∠CDE=∠E=30°.∴BD=DE.解题思路:欲证BD=DE,只需证∠DBE=∠E,根据等边三角形的性质及角的等量关系可证明∠DBE=∠E=30°.易错点:对等腰三角形性质掌握不牢试题难度:三颗星知识点:等边三角形的性质7.如图:在△ABC中,BA=BC,D是AC的中点.求证:BD⊥AC.答案:∵D是AC的中点∴AD=CD 在△BAD和△BCD中,BA=BC,AD=CD,BD=BD ∴△BAD≌△BCD ∴∠BDA=∠BDC 又∵A、D、C在同一条直线上∴∠BDA=∠BDC=90°∴BD⊥AC解题思路:通过BA=BC,AD=CD,BD=BD可以证明△BAD和△BCD,进而得到∠BDA=∠BDC=90°,从而得到结论。
八上数学知识点归纳

八上数学知识点归纳三角形知识概念1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2.三边关系:三角形任意两条边之和大于第三条边,任意两条边之差小于第三条边。
3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高。
4.中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线。
5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
6.三角形的稳定性:三角形的形状是固定的,三角形的这种性质叫做三角形的稳定性。
7.多边形:在平面上,由一些首尾相连的线段组成的图形称为多边形。
8.多边形的内角:多边形的两条相邻边所形成的角叫做它的内角。
9.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。
10.多边形的对角线:连接多边形两个不相邻顶点的线段称为多边形的对角线。
11.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形。
12.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面。
2一次函数一.定义1.在按某种规律变化的过程中,数值发生变化的量为变量,始终不变的是常量。
2.一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么x是自变量,y是x的函数.如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
3.一般地,形如y=kx[k是常数,k≠0]的函数,叫做正比例函数.其中k叫做比例系数.[一个数字与一个自变量的积的形式]。
4.形如y=kx+b[k,b为常数,k≠0]的函数,叫做一次函数。
二.重点1.自变量的取值范围:(1)整式型y=3x+1──全体实数;(2)分式型──使分母不为0;(3)根式型──使被开方数非负;(4)综合型。
2.作函数图象的一般步骤:(1)列表;(2)描点。
初中数学等腰三角形和垂直平分线

等腰三角形和垂直平分线模块一等腰三角形2判定到一条线段两个端点距离相等的点,在 这条线段的垂直平分线上.如图,若DA DB ,则点 D 在线段 AB 的垂直平分线上.DA C E B模块一 等腰三角形例题1(1)(2015—2016 年七育周练) 等腰三角形的一边长为 10,另一边长为 4,则这个等腰三 角形的周长是 __________ .( 2)等腰三角形的一边长为 6cm ,且周长为 16cm ,则这个三角形的底边为 ________ . (3)等腰三角形两内角的度数之比为 1:4 ,则该三角形底角的度数为 __________ . ( 4)等腰三角形一个角为 30 ,则这个三角形腰上的高与底边所夹角的度数为 ______ . (5)等腰三角形一腰上的中线将三角形的的周长分为两部分, 分别是 12与 15,则腰长为1) 24 ;(2) 4cm 或 6cm ;( 3)30 或 80 ;(4) 30 或15 ;a=5,腰长为 10;b7 a=4b a=411,腰长为 8.教师备课提示】 这道题主要考查等腰三角形的定义,腰或底角不确定.例题21)等腰三角形一腰上的高与另一腰的夹角为 45 ,则这个等腰三角形的顶角为 ________ . 解析】 a b 123a 153a 12 a b152)已知BD 是等腰△ABC 一腰上的高,且ABD 50 ,则△ABC 的底角为__________ .解析】(1)45 或135 (提示:等腰三角形可能是锐角三角形或钝角三角形)(2)20 或40 或70 ;区40 70 70 例题3B P 2P 14 解析】 AF MNB CC BD D 140 100 AD DM (2) 分别在边 ①求证: ②求证: P 1 若 △ ABC 为钝角三角形时 若 △ ABC 为钝角三角形时若 △ ABC 为锐角三角形时 教师备课提示】 年嘉祥期末) AC 上, BM P 2P 3 14—15AB 、A 为顶角时,三内角大小为 A 为底角时,三内角大小为A 为顶角,三内角大小为 这道题主要考查分在 A 1B 上取一点 C ,延长 AA 1 D ,延长 A 1A 2到 A 3,使得 n ( 1)如图 4-1,△ABC 中, BE CD , G 是 EF 的中点 A A 1 P 12 BD ;DN ,且 DM DN AAB AC ,点 D 、E 、F 分别在 BC 、AB 、AC 上,且 BD CF 求证: DG EF .20 , 20 40 , 40 如图 4-2,在 △ABC 中, AB AC , BAC 90 ,点 M 、 N AN ,点 D 是 BC 的中点,连接 AD . P 13 P 3 P 11 P 5 P 9 P7 图 3-2(1)如图 3-1,在第 1 个△ABA 1 中, B 20 ,AB A 1B 到 A 2 ,使得在第 2 个△A 1CA 2 中, A 1A 2 A 1C ;在 A 2C 上取一点 在第 3个△A 2DA 3中, A 2A 3 A 2D ;⋯⋯,按此做法进行下去,第 点的内角的度数为 _______________________ .D EP4 P 10 P 6 P8 A A 2 A 3A 4 A n 图 3-1 13P 14 P 14 A1) 160n ;( 2) 12 . 2n 教师备课提示】 这道题主要考查等腰三角形的性质结合外角倒角找规律 (2)如图 3-2的钢架中,焊上 13根钢条来加固钢架. 若AP 则 C 的度数是 _______ .图 4-1 图 4-2CFBD CB CD BE AF G B CAD B D DM AF EC C B BD D C 45AD BDAN BM笔例题5AB AC , B C , 在 △EDB 和 △ DFC 中②由①知 DAN 45在 △ ADN 和 △ BDM中 DAN DBM解析】 (1)连接 ED 、DF , 教师备课提示】 这两道小题主要考查等腰三角形三线合一的性质结合全等.△ABC 中, AD 是BC 边上的中线,又是 BC 边上的高,求证: △ABC 是等腰 ( 2)如图, 等腰△ABC 中,AD 是 BAC 的角平分线, AD 是 BC 边上的高,求证: △ABC 是( 3)如图, △ABC 中,AD是 是等腰三角形.A BAC 的角平分线, △ABC 解析】 1)AD 为 BC 中垂线,所以 AB AC ,所以 △ABC 是等腰三角形2) △ ABD 和△ACD 中,△ EDB ≌△ DFC (SAS) , DE DF , G是EF 的中点,∴ DG EF .( 2)① AB AC , BAC 90 ,点D 是BC 的中点,DN , MDB NDA ,( 1)如图, 三角AD 是 BC 边上的中线,求证: BAD 1 BAC 45 ,2 BD , △ ADN ADB ≌△BDM (SAS) , 90 , DM DN2)连接 CP ,由 S CPB S CPA SCAB ,例题6AD PE AC 于 C C C E E P B B B F D F D 区 PF 和 AC DF (3)如果 P 为等腰三角形 ABC 的底边 AB 延长线上的任意一点,请直接写出 AD 三边满足的关系. 点, PE 、PF 、PG ∴ AB 教师备课提示】 PE AD 之间存 笔 AP ABC 内任意 D AD AD ADB ADC =90 其余条件保持 PF 和 BAD CAD AG (2)如图 6-2,如果 P 为等腰三角形 ABC 的底边 BA 延长线上的任意一点, 不变,( 1)中的结论还成立吗?若成立,请说明理由;不成立,请求出 PE 边满足的关系. (1)如图 6-1,P 为等腰三角形 ABC 的底边 AB 上的任意一点, PE AC 于点 E ,PF BC 于点 F , AD BC 于点 D ,求证: PE PF AD .(4)如图 6-3,如果 △ ABC 是等边三角形,点 P 为三角形点 E , PF BC 于点 F , PG AB 于点 G , AD BC 于点 在怎样的数量关系,并说明理由. E A 作 DE AB 于点 E , AC , DE AB ,∴ DE DF △ABD ≌△ ACD ,∴ AB AC , △ABC 是等腰三角形 3)过点 D 作 DF AC 于点 F , AD 是 BAC 的角平分线, DF AD 为中线,∴ S △ ADB S △ ADC , 11 S △ ADB AB DE , S △ ADC △ 2 △ 2 AC ,∴ △ ABC 是等腰三角形.这道题主要考查三线合一的性质倒过来推等腰三角形图 6-1 图 6-2 图 6-3 解析】 ( 1)连接 CP . ∵ S APC即 1 AC2而 AC S BPC 1 EP BC PF 2 S ABC , 1 BC AD , 2 BC ,∴ PE PF AD ;教师备课提示】这道题主要考查等腰三角形的一个常见题型,面积法.例题7(1)如图7-1,AB AC, A 54 ,DE 垂直平分AB交AC于E,垂足为D,△ABC周长为28cm,BC解析】(1)18cm,9 ;(2)110 .教师备课提示】这道题主要考查垂直平分线的性质.得:1BC PF2 又∵AC1AC PE21BC AD2BC ,∴ PFPE AD ;(3)PE PFAD ;(4)连接CP、AP、BP,∴ S APC S PBC S APB1∴ AC EP2 而AC ∴ EPS PBC1BC PF2S ABC ,1AB PG21BC AD ,2BCFPAB,GPAD .模块二垂直平分线8cm,则△BCE 的周长为,EBC2)如图BAC7-2,DAE△ABC 的两边AB 和AC 的垂直平分线分别交150 ,则BAC的度数为___________ .BC 于点D、E,若C图7-2( 1)例如题图8 8-1,已知:在△ ABC 中, B 22.5 ,边 AB 的垂直平分线交 BC 于 D ,DF AC 于 F ,交 BC 边上的高于 G .求证: EG EC .(2)如图 8-2, △ ABC 中, AB AC , BAC 54 , 线交于点 O ,将 C 沿 EFCE 在 BC 上,F 在 AC 上折叠, 为 _____________ .∴ DA DB , B 22.5 ,∴ BAD B 22.5 ,∴ ADE 45 , AE BC ,∴ DAEADE 45 ,∴ AE DE , DF AC , FDC C 90 , 又∵ EAC C 90 ,∴ EAC EDG , 在△EDG 和△EAC 中EAC EDGED EAAEC DEG△ EDG ≌△ EAC (ASA) , ∴ EG EC .中, OEC 180 COE OCB 180 36 36 108 .记 笔区解析】 1)连接 AD ,∵D 为 AB 的垂直平分线上一点,BAC 的平分线与 AB 的垂直平分 点 C 与点 O 恰好重合, 则 OEC 2)如图,连接 OB 、 OC , BAC 的平分线,BAC BAO ABC 54 1 2 1 (180 2 ,AO 为 1 2 BAC 54 BAC) 27 ,又∵ AB AC 1 12(180 ∵ DO 是 AB 的垂直平分线, ∴ OAOB ,∴ ABO BAO 27∴ OBC ABC ABO 63 27∵ DO 是 AB 的垂直平分线, AO 为 ∴ OB OC ,∴ OCB OBC 36 折叠,点 C 与点 O 恰好重合,∴ OE36 , BAC 的平分线, ,∵将 C 沿 EF (E 在 BC 上,F 在 AC上) CE ,∴ COE OCB 36 ,在 △OCE ∴点O 是 △ABC 的外心, C54) 63 ,例题9证明:三角形三边的垂直平分线交于一点.【解析】如图,在△ABC 中,设AB、AC 的垂直平分线相交于点O,连接OA、OB、OC,由垂直平分线的性质可知:OA OB,OA OC ,∴ OB OC ,∴点O 在BC的垂直平分线上,∴三角形三边的垂直平分线交于一点.复习巩固模块一等腰三角形演练11)已知一个等腰三角形的两条边分别为3cm 和4cm,则这个三角形的周长为 ______ .2)等腰三角形的一个外角为100 ,则顶角为___________ .3)等腰三角形一腰上的中线将它们的周长分为 6 和12 两部分,则腰长为_______ .4)等腰三角形一腰上的高与另一腰的夹角为40 ,则这个等腰三角形的底角为______ .解析】(1)10cm或11cm;(2)20 或80 ;(3)8;(4)65 或25 .腰三角形的有()①②A.1个B.2 个AOB1)(武侯区期末)如图,在下列三角形中,若AB AC ,则能被一条直线分成两个小等C .3 个D.4个2)如图, AOB是一个钢架,且 AOB 10 ,为了使钢架更加牢固,需要在内部添加一些钢管 EF 、则 IHBFG 、GH 、HI ,且有 OE EF FG GH HI ,IAOEFHB(3)如图,AD ( )度. 是等边三角形ABC 的中线, AE AD ,则 EDCAA . 30B .20C . 25D .15【解析】 ( 1) C ;(2) 50 ;(3)D .E【解析】BD C演练3【解析】如图,在△ ABC 中,AB AC ,点 D 、E 、F 分别在 AB 、BC 、AC 边上,且 BE CF ,BD CE .1)求证: △DEF 是等腰三角形; 2)当 A 40 时,求 DEF 的度数.解析】 (1) AB AC , B C , 在△EDB 和△FEC 中:BE CF BC BD CE△EDB ≌△ FEC (SAS ) ,DE EF , △DEF 是等腰三角形. ( 2) A 40 , B C 70 , 由( 1)知 EFC DEB , DEB 演练4 (1)如图4-1:已知等边 △ABC 中,D 是AC 的中点,E 是BC 延长线上的一点, 且CE CD , DM BC ,垂足为 M ,求证: M 是 BE 的中点.2)如图 4-2,等边三角形 ABC 中,E ,D 分别在 AC ,BC 上,且 AE DC ,求 AD 与解析】 ( 1)连接 BD ,EFC FEC 110 ,FEC 110 , DEF 70BE 所夹锐角的度数.图 4-1演练5( 2)(15 年嘉祥半期)平分线 BE 交 AD 于点 E ,连接 EC ,则 AEC 的度数是∵ △ ABC 为等边三角形, 1∴ DBC ABC 302∵ CD CE ,∴ CDE 又∵等边△ABC 中 ACB 60 , ∴E 12 ∴ CBD 又∵ DM60 BE 30 ,D 为 AC 中点,E ,∴ BD ED , ∴M为 BE 中点.( 2) 60 .模块二垂直平分线( 1)(15 年育才期末) 点 E 、D ,连接 AD ,若 A . 4cm如图 5-1,在 △ABC中,△ADC 的周长为 7cm , B .5cmAB 边上的中垂线 DE 分别交 AB 、BC 于 AC 2cm ,则 BC 的长为( ). C . 3cm D .以上答案都不对 AD 垂直平分线段 BC 于点 D , ABC 的如图 5-2, ABC 50 , 解析】 ( 1) B ; 2) 115 .如图,在△ ABC 中,D 为BC 中点,DE BC 交 BAC 的平分线于点 E ,EF AB 于F , EG图 5-1CBF CG .记笔区解析】连接BE、CE.DE 垂直平分BC,BE CE ,AE平分BAC,EF AB,EG AC,EFEG ,又BFE CGE 90 ,Rt△BEF ≌Rt△CEG (HL) ,BF CG .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《轴对称、垂直平分线、角平分线、等腰三角形》 例题1:在ABC ∆中,由A 点向BC 边引高线,垂足D 落在BC 上,如果2C B ∠=∠,求证:AC CD BD +=.
A
B C D
例题2:如图所示,在ABC ∆中,AB AC >,BE 、CF 为ABC ∆的两条高,求证:AB CF AC BE +>+.
E
F
C B A
例题3:如图所示,在ABC ∆中,2ACB ABC ∠=∠,P 为三角形内一点,AP AC =,
PB PC =,求证:3BAC BAP ∠=∠.
P
C B A
例题4:如图,直线l 1,l 2,l 3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有【 】
A 、1处
B 、2处
C 、3处
D 、4处 l 2
l 1l 3
例题5:如图,△ABC 中,∠C =90°,AC =BC ,AD 平分∠CAB 交BC 于D ,DE ⊥AB 于E ,且AB =6㎝,则△DEB 的周长为【 】
A 、4㎝
B 、6㎝
C 、10㎝
D 、不能确定 D
C
E B
例题6:如图,已知BE 平分∠ABC ,CE 平分∠ACD ,且交BE 于E .求证:AE 平分∠FAC.
D
F
C A E
例题7:如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB、BC延长线于F、E
求证:(1)∠EAD=∠EDA(2)DF∥AC(3)∠EAC=∠B
例题8:如右图,△ABC中,AB=AC=16cm,AB的垂直平分线ED交AC于D点. (1)当AE=13cm时,BE= cm;
(2)当△BEC的周长为26cm时,则BC= cm;
(3)当BC=15cm,则△BEC的周长是cm.
例题9:如图,在△ABC 中,AB =AC ,∠BAD =300
,且AE =AD ,则x = 度.
x
E
D C
B A
例题10:已知:点O 到△ABC 的两边AB 、AC 所在直线的距离相等,且OB =OC 。
(1)如图1,若点O 在BC 上,求证:AB =AC ;
(2)如图2,若点O 在△ABC 的内部,求证:AB =AC ;
(3)若点O 在△ABC 的外部,AB =AC 成立吗?请画图表示。
例题11:如图,在等腰ΔABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连结AP交BC于点E,连结BP交AC于点F。
(1)证明:∠CA E=∠CBF;
(2)证明:A E=BF;
练习试题
1.坐标平面内,点A的坐标是(x+a,y-b)那么
①点A关于横轴的对称点B的坐标是()
②点A关于纵轴的对称点C的坐标是()
③点A关于原点的对称点D的坐标是()
2.坐标平面内,点M(a,-b)与点N(-a,b)是关于___的对称,点P(m-3,n)与点Q(3-m,n)是关于___的对称点
3.已知:直线m的同一侧有两个点A和B求作:在m上一点P,使PA+PB为最小
m
A B
4.已知:等边△ABC求作:点P,使△PAB,△PBC,△PAC都是等腰三角形(至少4个点P)
5.已知:AD 是△ABC 的外角平分线,点这P 在射线AD 上求证:PB+PC ≥AB+AC
E
P D
B C A
6.如图,在河湾处M 点有一个观察站,观察员要从M 点出发,先到AB 岸,再到CD 岸然后返回M
点,画出该船应该走的最短路线(先画图,再用字母表示)。
7.求代数式1062+-x x +
3462++x x 的最小值。
8.AB =AD ,CB =CD ,AC 、BD 相交于点O ,则下列结论正确的是【 】
A .OA =OC
B .点O 到AB 、CD 的距离相等
C .∠BDA =∠BDC
D .点O 到CB 、CD 的距离相等
9.如图,已知BE ⊥AC 于E ,CF ⊥AB 于F ,BE 、CF 相交于点D ,若BD =CD .求证:AD 平分∠BAC.
10.如图,∠B =∠C =90°,M 是BC 的中点,DM 平分∠ADC ,求证:AM 平分∠DAB.
11.如图,在锐角ABC △中,45AB BAC =∠=°,BAC ∠的平分线交BC 于点D M N ,、分别是AD 和AB 上的动点,则BM MN +的最小值是___________ .
12.在△ABC 中,AB 、AC 的垂直平分线相交于点P ,则PA 、PB 、PC 的大小关系是 。
13.下列说法:①若直线PE 是线段AB 的垂直平分线,则EA=EB ,PA=PB ;②若PA=PB ,
EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的直线垂直平分线段AB.其中正确的个数有【】A.1个B.2个C.3个D.4个
14.如图,NM是线段AB的中垂线,下列说法正确的有:.
①AB⊥MN,②AD=DB,③MN⊥AB,④MD=DN,⑤AB是MN的垂直平分线.
15.(1)如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;
(2)如图,ΔOAB固定不动,保持ΔOCD的形状和大小不变,将ΔOCD绕着点O旋转(ΔOAB和ΔOCD不能重叠),求∠AEB的大小.。
