引力场中的高斯定理
高斯定理在万有引力场中的应用

与静电场相似 , 任何物体的周围空间都存在引力场 , 万有引力是通过引力场来传递的 。在静电场中 , 我
们用电场强度来描述电场中某点性质 , 同样 , 在引力场中 , 我们可以把场中每点的 F / m 定义为该点的引力
※
场强度 , 用Eg 表示 , 即
※
Eg
=
F m
(1)
※
其中 m 为试探质点质量 , F 为试探质点在某点受到的引力 , Eg 即为该点的引力场强度 , 简称引力场强 。
16
(湖南人文科技学院 物理与信息工程系 , 湖南 娄底 417000)
摘 要 :通过类比万有引力场和静电场 , 给出了引力场强度的概念 , 在此基础上 , 将静电 场中的高斯 定理推广 到万有引 力场中 , 并利用它分析了两个具体问题 , 说明了利用高斯定理可以简化具有对称性的引力场的相关 计算 。
场中任一闭合面的引力场通量等于该曲面内所有物体的质量和乘以 4πG 的负值 , 即 :
可以看出 ,(6)式同静电场的高斯定理
∑ ※
※
Eg·d S =-4πG mi
S
i =1
(6)
∑ S
※
E·dቤተ መጻሕፍቲ ባይዱ
※
S
=
1 ε0
qi
i
(7)
非常相似 ,(6)式中的常数 4πG 相当于(7)式中的常数 ε10 ,(6)式中的 mi 相当于(7)式中的 qi 。 下面举例说明 :当质量分布具有某些特殊的对称性 , 从而使相应的引力场分布也具有一定的对称性
过 P 点作一半径为 r , 高为 l 的同轴闭合圆柱面 , 则通过此闭合面的引力场通量
= 侧 + 上底 + 下底 =-Eg2πrl +0 +0 =-Eg2πrl 上式不论 P 点在柱面外(r > R)或在柱面内(r < R)都适用 。
引力场中的高斯定理在计算煤矸石重量方面的应用

{ 。 = ̄ pV gd 4 Gld . s r
其中, g为 引力场 强 度 , G为, 为地球的体积元. d 上式的意义是 : 通过任一闭合曲面的引力场强
1 引力场 中的高斯定理
收稿 日期 : 0 9 1— 0 20 — 2 1
,
则
就表 示 单位 质 量 的质 点在 该 点所 受 到 的
力定律只适用于质点. 星体虽然很大 ,但满足上述
条件 , 能 直接 应用 . 球 表 面和矿 井 里 的石 块 不 故 地
引 力Ⅲ 它是 一个 与 物体 质量 无关 的物理 量 , , 叫做 该
点的引力场强度 , g 用 来表示 , 即
度通量 ,等于该曲面所包 围的所有质元质量 的代数
作者简介: 李颢 (9 3 ) 女 , 16一 , 山东临沂 人 , 助理实 验师 , 究方 向:物理实验 研
山西大 同大学学报( 自然科学 版)
和乘以 4 G 这就是引力场中的高斯定理.  ̄ , r
关系 不成立 ,而是 与质点 离地心 的距 离成 正 比,即
文章 编 号 : 6 4 07 (0 0 0 ~ 0 9 0 17 — 84 2 1 ) 10 7— 2
引力场 中的高斯定理在计 算煤矸石重量 方面的应 用
李 颢
( 山西 大 同大 学工 学 院 , 山西 大 同 0 70 ) 303
摘 要: 文章根 据引力场与静 电场的相似性 , 出了计 算地球 内质点所受引力的新方法 ,即引力场中的高斯定 提
即地心处的质点所受地球 的万有引力 的合力为零 ( 不受 力 ) 或 .
( ) 地球表 面 附近 ,rR 时 , 2在 = 有
G ,
等. 以地心为球心 , 为半径作一球面, 故 r 即高斯面. 根 据高斯 定理 有
万有引力场中高斯定理应用举例
g ∙ ds =
上底
g ∙ ds +
下底
g ∙ ds +
侧面
g ∙ ds(19)
圆柱面的上下底面由于 g 的方向与 dS 方向处处垂直,故通量为 0。在圆柱的侧面,g 的 方向与 dS 方向处处夹 180 度角,且侧面上各点的 g 大小相等。因此 Φg =
s
g ∙ ds =
侧面
g ∙ ds = −g ∙
cos θ dy r2 sin θ dy r2
=
Gm 0 ρ a
(cos θ1 − cos θ2 )
(16)
=
Gm 0 ρ a
(sin θ2 − sin θ1 )
(17)
方向沿 y 轴负向;当a ≪ L L 为细杆的长度 时,细杆可视为无限长,这时有θ1 = 0,θ2 = π。于 是有: Fy = 0,Fx =
侧面
ds = −g ∙ 2πrl
(20)
高斯面内包围的质量 mi = ρl,由引力场的高斯定理得到:
图2
−g ∙ 2πrl = −4πGρl g=
2G ρ l
(21)
方向垂直于细竿沿着径向指向细杆。于是高斯面上质量为m0 的质点受到的引力大小为: Fx =
2Gm 0 ρ a
(22)
方向垂直细杆沿着径向指向细杆。 这和方法(1)得到的结果相同。比较两种方法可知:应用引力场中的高斯定理大大简化了 繁琐的运算。
`赤峰学院本科学年论文
利用牛顿万有引力定律和微积分求解问题
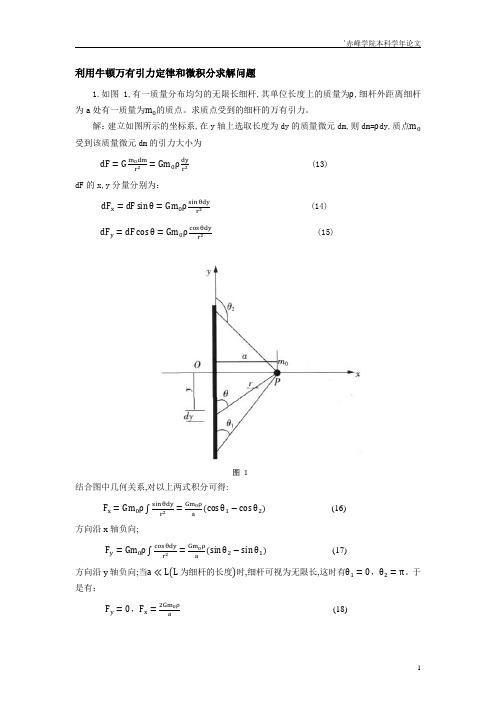
1.如图 1,有一质量分布均匀的无限长细杆,其单位长度上的质量为ρ,细杆外距离细杆 为 a 处有一质量为m0 的质点。求质点受到的细杆的万有引力。 解: 建立如图所示的坐标系,在 y 轴上选取长度为 dy 的质量微元 dm,则 dm=ρdy,质点m0 受到该质量微元 dm 的引力大小为 dF = G
高斯定理在空间对称引力场中的应用重点讲义资料

本科毕业论文题目:高斯定理在空间对称引力场的应用姓名:石宇学号:20120341006 院别:工程技术学学院专业:物理学年级:2012级1班指导教师:黄永超目录1引言 (1)2引力场建立的背景及初步认识 (2)2.1引力场建立的背景 (2)2.2引力场的初步认识 (2)3静电场中高斯定理的理解与应用 (3)3.1静电场中高斯定理的理解 (3)3.1静电场中高斯定理的应用 (4)4静电场与万有引力场的分析与类比 (5)4.1静电场与万有引力场的分析 (5)4.2静电场与万有引力场的类比 (6)5高斯定理在空间对称引力场中的应用 (8)5.1质量分布具有球对称性 (8)5.2质量分布具有轴对称性 (9)5.3质量分布具有面对称性 (10)6结束语 (11)参考文献 (12)致谢 (13)摘要在静电场中,当电荷具有某种对称性时,场强的计算可以通过应用高斯定理而简化计算。
所以,本文将通过比较静电场和引力场,从而用类比的方法把静电场中高斯定理的形式推广到万有引力场中。
在此基础上,通过万有引力场中的“高斯定理”,从而解决在空间对称引力场中的相关问题。
关键词:高斯定理;万有引力;空间对称引力场;应用AbstractIn the electrostatic field, when the charge has a certain symmetry, the field strength calculation can be calculated by applying the simplified Gauss theorem. Therefore, this article will compare the electrostatic field and the gravitational field, which by analogy method to form an electrostatic field Gauss theorem to the gravitational field. On this basis, through the gravitational field of the "Gauss theorem" to solve symmetric gravitational field in space related issues. Learn gravitational field Gauss theorem space symmetry.Key words: Gauss theorem; gravitation; space symmetric gravitational field; application1引言高斯定理也叫作高斯公式,或叫作散度定理、高斯散度定理、高斯-奥斯特罗格拉德斯基公式、奥氏定理或高-奥公式(通常情况下高斯定理都是指该定理,也有其它同名定理)。
引力场中的高斯定理

引力场中的高斯定理引力和静电力都是有势力,相应的引力势和静电势都满足三维空间里最简单的二阶(偏微分)方程——拉普拉斯方程.用ψ代表引力势或者静电势场,它在三维空间里所满足的拉普拉斯方程采取如下的形式:(∂2/∂x2+∂2/∂y2+∂2/∂z2)ψ(x,y,z)=0.由于相应的静电力和引力等于势的微分(的负值),它的大小便与半径r成反比了,即ψ(r)∝1/r,F(r)=- dψ/dr∝1/r2由于万有引力定律与Coulomb,s law本质是一样的,因此引力场中也存在高斯定理,并且与万有引力定律等价.Ⅰ、预备知识引力场场强:引力场场强是一个向量,其大小等于1千克的质点在该处所受引力的大小,方向与该质点在该处所受引力的方向一致.引力线:如果在引力场中出一些曲线,使这些曲线上每一点的切线方向和该点的引力场强方向一致,那么所有这样可以作出的曲线叫做引力线.引力线数密度:在引力场中任一点取一小面元ΔS与该点的场强方向垂直,设穿过ΔS 的引力线有ΔN根,则比值ΔN/ΔS叫做该点的引力线数密度,它的意义是通过该点单位垂直截面的引力线根数,规定引力场场强E∝ΔN/ΔS.引力线性质:引力线其自无穷远点,止与该质点,引力线在宇宙中处处存在.一个质点的任何两条引力线不会相交,不形成闭合线.引力通量:通过一面元ΔS的引力通量为该点场强的大小E与ΔS在垂直于场强方向的投影面积ΔS′=ΔScosθ的乘积.Ⅱ、通过一个任意闭合曲面S的引力通量φ=4πG∑m,与闭合曲面外的引力质量无关.证明:(1)通过包括质点m的同心球面的引力通量都等于4πGm.以质点m所在处为中心以任意半径r作一球面.根据万有引力定律,在球面上各点场强大小一样E=G m /r2,场强的方向沿半径向外呈辐射状.在球面上任意取一面元dS,其外法线向量n也是沿着半径方向向外的,即n和E间夹角θ=0,所以通过dS的引力通量为dφ=EcosθdS=EdS= G m /r2dS,通过整个闭合球面的引力通量为φ=dS= G m /r2×4πr2=4πGm.(2)通过包围质点的任意闭合曲面S的引力通量都等于4πGm在闭合面S内以质点m所在处O为中心作一任意半径的球面S′,根据(1)通过此球面的事情感兴趣,要勤奋地工作!”。
高斯定理在万有引力场中的应用

高斯定理在万有引力场中的应用
高斯定理是物理学界以及数学界较为重要的定理之一,它可以被广泛地用于万有引力场的研究中。
首先,我们需要了解高斯定理的核心部分——高斯梯度定理:它指出了引力场的数学表示和图像的梯度的空间表示之间的联系,即:万有引力场的空间表示有一个正定的悬赏函数,和任意点的梯度之间存在明确的联系,此外,这个悬赏函数的倒数是一个完全定义的单值函数,接下来,我们就可以用这个悬赏函数来求出万有引力场的强度以及各种有关物理量。
另一方面,万有引力场对空间上某点上发生的结构变化也有着重要的影响,它可以通过高斯梯度定理来计算这种变化。
高斯梯度定理中,梯度是一个十分重要的概念,它是三维空间中某点处的万有引力场变化速率。
对此,高斯定理可以让我们通过知道梯度 at 点 P 的方向和大小来推断出空间上某个点处的引力场的强度和变化情况,也就是我们可以根据某点的梯度来计算出空间上的点的引力场的强度以及计算出不同空间上的点之间的引力场是否在变化。
至此,我们可以看出,高斯定理在万有引力场的有效应用中发挥了重要作用,它提供了万有引力场变化情况的推断,可以让我们很快的分析出物体之间的引力场变化情况,这样使我们可以进一步研究万有引力场,更好的理解它。
此外,高斯定理也有许多其它的应用,例如他可以用于空气动力学,静电学以及地学等领域。
引力场中高斯定理的应用

引力场中高斯定理的应用王宁;孙彩霞;齐玉红【摘要】本文用类比的方法将静电场中的高斯定理的形式推广到万有引力场中,从而引出万有引力场中的"高斯定理".通过万有引力场中的"高斯定理",将某些质量分布具有对称性的物体引起的引力场强的计算得到简化.【期刊名称】《山东轻工业学院学报(自然科学版)》【年(卷),期】2010(024)004【总页数】3页(P78-80)【关键词】万有引力定律;万有引力场强;类比;高斯定理【作者】王宁;孙彩霞;齐玉红【作者单位】黄河科技学院实验中心,河南,郑州,450006;黄河科技学院数理部,河南,郑州,450006;郑州大学,河南,郑州,450006【正文语种】中文【中图分类】O314万有引力是自然界普遍存在的作用力,宇宙之中,小到微观粒子,任何有质量的物体与物体之间都存在着相互吸引的力,这种力就称为万有引力[1]。
假设有两个质点,质量分别为m1和m2,相隔距离为 r.那么它们之间相互作用的万有引力用矢量形式表示根据实验测定G=6.67×10-11m3·kg-1·s-2,负号表示和方向相反。
在万有引力的周围存在着引力场,那么我们可以利用万有引力定律以及微积分的知识能解决引力场场强的求解问题,但是计算却是一个相当繁琐的过程。
那么能不能够用简单的方法求解出质量分布具有对称性的物体的引力场强呢?在此我们引入万有引力场中的高斯定理求解问题。
我们知道万有引力定律和库仑定律都是平方反比定律,两者的形式非常相似,而静电场中的高斯定理是库仑定律和叠加原理的必然结论[2]。
那么利用万有引力定律和叠加原理也可以得到引力场中的高斯定理。
通过引力场中的高斯定理,来解决一些具有对称性物体的引力场强问题时,可以大大简化复杂的积分计算,非常方便。
通过对万有引力场和静电场来做类比,得到任意闭合曲面内的万有引力场的高斯定理,万有引力场强通量是否具有静电场中高斯定理的形式呢?我们来加以推导。
万有引力与高斯定理--类比在物理学中的应用

万有引力与高斯定理--类比在物理学中的应用
万有引力定律和高斯定理是两个非常重要的物理概念,它们分别描述了物体间的引力和电场的分布。
虽然它们描述的是不同的物理现象,但它们之间有着深刻的类比关系。
在物理学中,高斯定理经常用来计算电场或者磁场的分布,而万有引力定律则用来描述天体之间的引力作用。
然而,这两个定理的数学形式却非常相似,因此它们在物理学中经常被类比使用。
例如,在研究地球上的引力问题时,可以使用与高斯定理类似的方法来计算引力的分布。
具体而言,可以将地球看作是一个非常大的球体,对球心外的任意一点上的引力进行积分,从而得到该点的引力大小和方向。
这个积分过程与高斯定理类似,只不过换成了引力场的积分。
同样的方法也可以用来描述其他天体之间的引力作用。
例如,在计算行星之间的引力时,我们可以将每个行星看作是一个点电荷,然后利用高斯定理类似的方法来计算电场强度的分布。
除了在计算引力场和电场分布时,万有引力定律和高斯定理还可以在其他物理学问题中相互类比使用。
例如,在研究气体分子运动时,我们可以将分子间的相互作用看作是引力作用,然后用类似于高斯定理的方法来计算分子间的引力和方向。
这种方法被称为分子动力学模拟,在化学、材料科学、生物学等领域均有重要应
用。
总之,万有引力定律和高斯定理虽然描述的是不同的物理现象,但它们之间的数学类比关系使得它们在物理学的各个领域中都具有广泛的应用。
引力场中的高斯定理

大学物理课程作业-高斯定理
白晓宇
5130369070
类比电场中的电场强度E 的定义,
定义引力场强度E g ,引力场中一场点的引力场强度等于该点处的单位质量质点所受的引力。
类比电场中的电通量Φ的定义,定义引力通量Φg 为通过电场中任意曲面的引力场线的条数。
那么,就有引力场中的高斯定理如下:
若质量分布是连续分布,则:
Φg =∯ ∙ 4 ∭
若是一系列质点的集合,则:
Φg =∯ ∙ 4 ∑
类比高斯定理在电场中的推导过程,推导引力场中的高斯定理。
(1) 在封闭曲面内单个质点的引力场:
以该质点所在位置为球心,以R 为半径做一个球面S 0,该球面处于封闭曲面S 内。
又质点的引力场强度,根据其定义,为E g=
,关于球心对称,所以通过球面与封闭面的
引力场线相同,又球面上各处的引力场强度大小处处相同,所以:
Φg =∯ ∙ ∯
=4πGm
(2) 在封闭曲线外单个质点的引力场:
因为有一条引力线自外穿进封闭面的同时,必定有一条引力场线穿出封闭面,所以对封闭曲面外的单个质点,其引力通量
Φg =0
(3) 对于任意体系的引力场:
设有n 个质点组成的质点系,部分质点在封闭面内,部分质点在封闭线外按照场强叠加原理,可知:
Φg =∯ ∙ 4 ∑
对于质量任意连续分布的物体,可以将其看成是无限个质点的集合,此时有:
Φg =∯ ∙ 4 ∭
引力场中的高斯定理成立。
高斯定理在万有引力场的推广

。垂 一
r > R U  ̄, g g=
l
一
( 1 ) 单个质点: g
。
( 2)均匀质量球壳 :当r < R 时, g o;当 R 时, g ( 3 )均匀质量的实心球体 :当r < R 时,g
。
( 相 当于 质 量集 中在 球壳 中心 )。
r ;当
( 4 ) 无 限 长 的 棒 : g 去 ( 表 示 质 量 的 线 密 度 ) 。
( 4) 无限 长的棒 : , = ~I n ( 表示质 量的线 密度 ) 。 r
( 5) 无 限大 的平 面 : ( r t 一, : ) 。
但正方向为从内到外,与季实际方向相
对于 球状 质 点 系 ,通过 单位 表 面 积的 引 力通 量是
:
S业技 术 学 院 赵 三平
法 、定 义 、推 导 、延伸 、推广 ,在 万有 引力
场 中取 得 一 系列 重 要 的 发 现 和 应 用 。
1 问题 的 提 出
3 对 万 有 引 力 场 中 的 高 斯 定 理 的 应 用
应 用一 :求 万 有 引力场 场 强 。
47 E r
…
( 6) 两个无限大的平行平面 :两板之间
=
r ;两板
( 1 ) 万 有 引力通 量 ,
=一 f 』 g c 。 s 0 A s ( 注 意 负 号) .
s
两( 外) 边 . : =÷一 ( r 一 , : ) ( 表示质量的面密度 ) 。
现 这种 反物 质 , 为公 式 中的质 量和 是 代数 和 。
G
‘
d S =G
‘ S
4 结 语
高斯定理的三个公式

高斯定理的三个公式高斯定理在物理学中可是个相当重要的概念,它有三个关键公式,咱们一起来瞅瞅。
咱先来说说高斯定理的第一个公式。
这就好比你有一个充满电荷的球体,你想知道这个球体产生的电场强度在球体外的分布情况。
这个时候,高斯定理就派上用场啦!它能帮咱们快速算出电场的分布。
想象一下,你站在一个大大的操场上,操场上有一个透明的大球,里面装满了电荷。
你从远处观察这个球,虽然看不到里面的电荷具体是怎么分布的,但通过高斯定理,就能算出这个球在周围空间产生的电场强度。
接下来是第二个公式。
这就像是在一个封闭的房间里,电荷在房间里到处跑,但不管它们怎么跑,通过高斯定理咱们都能清楚地知道整体的情况。
比如说,你在一个房间里,灯光有点昏暗,电荷就像那些忽明忽暗的光影,而高斯定理就是能让你看清整体状况的神奇工具。
最后是第三个公式。
这个公式就更有趣啦!它就像一个超级侦探,能帮我们解决很多复杂的电场问题。
比如说,有一个形状不规则的带电体,用常规方法很难计算它产生的电场,但是用高斯定理的第三个公式,就能巧妙地找到答案。
记得我之前给学生们讲高斯定理的时候,有个小家伙一脸迷茫地问我:“老师,这高斯定理到底有啥用啊?”我笑着回答他:“这就好比你要在一堆乱麻中找到线头,高斯定理就是那根能让你快速理清头绪的神奇线头!”然后我给他举了个例子,假如我们要计算一个无限大带电平面产生的电场,按照常规思路,那得费好大的劲。
但是用高斯定理,咱们只需要做一个合适的高斯面,就能轻松得出结果。
那个小家伙听完,眼睛一下子亮了起来,好像突然明白了其中的奥妙。
其实啊,高斯定理的这三个公式就像是三把神奇的钥匙,能打开很多电学难题的大门。
只要我们认真理解、多多练习,就能熟练运用它们解决各种各样的问题。
不管是在学习中还是在实际的科学研究中,高斯定理都是我们的得力助手。
所以,同学们,可别小看了这三个公式,好好掌握它们,能让我们在电学的世界里畅游无阻!。
高斯定律 引力

高斯定律引力高斯定律是物理学中的一项重要定律,描述了电场的性质。
然而,在引力领域中也存在类似的定律,即引力的高斯定律。
本文将介绍引力的高斯定律及其应用。
引力是地球吸引物体的力量,也是宇宙中所有物体之间相互吸引的力量。
根据牛顿的万有引力定律,两个物体之间的引力与它们的质量成正比,与它们之间的距离的平方成反比。
然而,高斯定律提供了一种更一般的描述引力的方式。
引力的高斯定律表明,引力场中的引力通量与被围绕物体的质量有关。
通量是指通过一个封闭曲面的力线数量。
根据高斯定律,引力通量正比于被封闭曲面内的物体质量。
换句话说,当物体的质量增加时,引力通量也会增加。
为了更好地理解高斯定律在引力中的应用,我们可以考虑一个简单的例子。
假设有一个质量为M的球体,它的引力场在球体外部是均匀的。
我们可以选择一个球面作为封闭曲面,该球面的半径为r。
根据高斯定律,通过这个球面的引力通量只与球内的物体质量有关,与球面的半径无关。
这意味着无论球面的半径如何变化,引力通量都保持不变。
高斯定律在引力场中的应用不仅限于均匀引力场,对于非均匀引力场也同样适用。
在非均匀引力场中,引力通量的值将随着曲面的形状而变化。
通过选择不同形状的曲面,我们可以计算出在不同位置上的引力通量,从而了解引力场的分布情况。
引力的高斯定律还可以帮助我们理解引力的产生和体验引力场的强度。
通过选择不同大小和形状的曲面,我们可以计算出通过这些曲面的引力通量,并由此推导出在不同位置上引力场的强度。
这使得我们能够更好地理解引力场的分布和变化,从而更好地理解和解释引力的性质。
除了理论上的应用之外,引力的高斯定律还具有实际的应用。
在天文学中,高斯定律可以帮助科学家们研究星系和宇宙的结构,从而揭示宇宙的奥秘。
在地球物理学中,高斯定律可以帮助科学家们研究地球内部的引力场,进而了解地球的内部结构和地壳运动。
总结起来,引力的高斯定律是描述引力场性质的重要定律。
它通过引力通量的概念,描述了引力与物体质量之间的关系。
引力场中的高斯定理

μ = m / 4πa (面密度 )之一 ,它是反映电磁场的基本规律的重要定理. 高 d U = - G m ′2πa 2μsin θd θ/ r 斯定理在静电场的应用是最为普遍的 ,利用它可以 分析和解决许多复杂的电磁学问题. 本文将其推广 到同具有保守性的引力场 ,为解决引力场问题提供 新思路 ,利用它可解决较复杂的引力计算问题.所以 利用2 r 2 2= a + R - 2R a c o sθ 两边微分得 r d r = R a s i nθd θ s i nθd θ d r 即 = R a1 引力场中的球壳问题设有一只薄球壳 ,半径为 a, 质量为 m , 现求距球心 R 处一个质量为 m ′的质点所受的力.取球壳中的一个圆环 , 圆环上的所有点与点 P 距离均为 r . 这个圆环对 P 点质量为 m ′产生的引力r 所以积分得d U = - G m ′2πa μd r / R Gm ′2πa μ R +a Gm ′mR ∫- a d r = -( 1 )U = -RR如果 P 点在球内 , 则式 ( 1 ) 中积分应为 a - RG m ′d m / r. [ 1 ] 势能为 d U = - a + R , 得= -Gm ′2πa μ G m ′m·2R = -U ( 2 )Ra式 ( 1 ) 、( 2 ) 表示 :在球外 , 此球壳在 P 点的场 等价于质量全部集中在球心时的场 ; 在球内 , 引力势能为一常值 , m ′不受力作用.由势能求保守力情况 , 得d U G m ′m R ≥ aF = -= - 2 Rd R F = 0R < a式 [ 3 ].假设我们尚不知牛顿万有引力定律 , 由式 ( 3 ) 去得出万有引力定律.2 定义引力场强度为了定量地讨论引力场在空间的分布和传播 , 这里引入引力场强度的概念. 定义引力场强度 为单位质元 m ′在引力场中某点所受的引力F g以质点 M 所在点为圆心 , 作一半径为 (图 2 ) , 对于球面的引力通量为r 的球面E g<g = λE g ·ds = 4πG ME g= as对于多个质点产生的引力场 , 其引力场强度满足叠 加原理 [ 2 ]. 定义了引力场强度后 , 就可以仿照电场中定义电场强度通量 Фe , 来定义引力通量 <g , 则d <g = E g ·ds = E g d s co s e式中 e 为引力场强度 E g 与面元 ds 外法向之间的夹 角.3 高斯定理在引力场中的类比应用上面有了通量的概念后 , 就可以讨论穿过闭合 面的引力通量问题. 对球壳问题应用高斯定理 ( K为比例常数 ) :取半径为 R 的球面为高斯面 , 考虑到 对称性 , 则由图 2F i g . 2考虑对称性 , 高斯面上任一点的引力场强度的大小E g 相同 , E g 的方向与球面径向相反 , 由式 ( 3 ) 应有M2- E g ·4πr = 4πG M , 可得出 E g = - G 2 , 在高斯面λsE g·ds = K ∑mir上若有一质量为 m 的质点 , M 对 m 引力的大小则为得M m2R > a - E g ·4πR = KmF = - G, 过球心 O 向 m 引一矢径 r , 即可写出万 r2 有引力的矢量式.这一结果说明引力场的高斯定理与万有引力 定律等价.参考文献 :[ 1 ] F . S 梅里特. 工程中的现代数学方法 [ M ]. 北京 : 科学出版社 ,1981 . 8 ~11.[ 2 ] 李兴鳌. 高斯定理在力学中的推广及应用 [ J ]. 湖北民族学院学报 , 1998 , ( 6 ) : 12 ~14.[ 3 ] 刘大为. 关于 引力场 的高 斯定理 [ J ]. 甘 肃 教 育 学 院 学 报 ,1998 , ( 1 ) : 5 ~7.F gKm m m ′ GmE g = -= = - G = - 4πR 22 R m ′2R∴K = 4πG 则 λs= 4πG ∑miE g = 0E g·dsR < a此结果与牛顿力学计算一致. 由此得出λsE g ·ds = 4πG ∑mi( 3 )i ( s 内 )这就是万有引力场中的高斯定理 , 与电场中的 1高斯定理 Фe = λE g ·d s =∑q i 具有相同的形ε0 i ( s 内 )sGa u s s ′Theorem of Gra v ita t iona l F ie ldGAO Y an( X inzhou Teachers U n i versity, X inzhou 034000, S h anx i , Ch ina )A b s tra c t : I t is founded on the con s e r va t i o n law of e l ec t r o s ta t ic fie l d .B a sed on the sam e con s e r va t ion law of gravita t iona l fie l d, th i s the s is d i scu sse s the app lica t i o n of G au s s ′theo r em in the theo r y of non - re l a t ive gravita t i o na l fie l d, and e s tab l ishe s the G au s s ′theo r em of gravita t iona l fie l d . U sin g the theo r e m to ana l yze s p e c i fic m e chan i c s p r ob l em s, we can si m p lify the comp u t a t i o n fo r the gravita t iona l fie l d w i th s p a t ia l sy mm e t ry .Key word s : G au s s ′theo r em ; con s e r va t i o n law; sy mm e t ry sp a ce in t en s ity of gravita t i o na l fie l d。
论万有引力场中的高斯定理

论万有引力场中的高斯定理
高斯定理是物理学中一个重要的定理,它描述了万有引力场中物体的引力的分布情况。
高斯定理的表述方式有很多种,常见的表述方式如下:
在万有引力场中,满足高斯定理的物体的重力势能可以表示为:
$$U=\frac{1}{2}\int \rho(\vec{r}) \phi(\vec{r}) dV$$
其中,$U$是物体的重力势能,$\rho(\vec{r})$是物体的质量密度,$\phi(\vec{r})$是物体的重力势能,$dV$是在三维空间中的体积元。
在万有引力场中,满足高斯定理的物体的引力势能可以表示为:
$$\phi(\vec{r})=-\frac{Gm}{r}$$
其中,$G$是万有引力常数,$m$是物体的质量,$r$是物体到参考点的距离。
在万有引力场中,满足高斯定理的物体的引力势能可以表示为:
$$\nabla^2\phi(\vec{r})=4\pi G\rho(\vec{r})$$
其中,$\nabla^2$是二阶偏导数算子,$\phi(\vec{r})$是物体的引力势能,$\rho(\vec{r})$是物体的质量密度。
高斯定理是物理学中一个重要的定理,在研究万有引力场中物体的引力和势能等方面
有着广泛的应用。
例如,可以利用高斯定理来计算地球的重力场、月球的重力场等。
此外,高斯定理还可以用于研究物体的重力势能、引力势能等物理量的分布情况。
高斯定理表达式

高斯定理表达式
高斯定理表达式是:∮F·dS=∫(▽·F)dV。
高斯定理也称为高斯通量理论,或称作散度定理、高斯散度定理、高斯-奥斯特罗格拉德斯基公式、奥氏定理或高-奥公式(通常情况的高斯定理都是指该定理,也有其它同名定理)。
在静电学中,表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。
高斯定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中。
因为数学上的相似性,高斯定律也可以应用于其它由平方反比律决定的物理量,例如引力或者辐照度。
物理中结果为g的表达式

物理中结果为g的表达式
物理学中,“g”是重力加速度的文字符号,一般用于描述自由落体运动。
以下是一般表达式,其中t为时间:
简单表达式:
g=dv/dt
其中dv/dt 是速度变化的率,即速度的函数的导数(即加速度)。
此外,还有几种还原得更清楚的表达方式:
1. 牛顿运动定律:F=ma、g=F/m
其中F为物体受到的外力,m为物体的质量,ma为物体总加速度,g 为重力加速度。
2. 高斯定理:g=G*M/r²
其中G为万有引力常数,M为物体的质量,r为物体和引力的作用点的距离。
3. 物体受重力潜力时的加速度公式:g=G*M/(h+r)²
其中G为万有引力常数,M为物体的质量,h为物体到引力的作用点
的距离,r为物体的原点到引力的作用点的距离。
关于重力加速度g的表达式是由于它与物体质量、场强和力间的距离有关,故有多种表示方式,除此以上表达式外,也有物体受力时加速度和米勒定理表达式:a=Fnet/m和g=G*M/r^2。
总之,关于“g”的表达式可以有多种,只要表达出它与物体质量、场强和力间的距离有关就OK。
引力场与高斯定理

t;F’,总的来说当质点在赤道平面以 上或一下时受到的合外力总是指向地心的。所以小 球将做以地心为平衡位置的简谐振动。
F
m g G 2 r
r
2.当在球体内时:作半径为r(r<R)与球体同心的球面.
2 g gds gds g4r s s 2 g4r 4Gm M r3 M g G 2 r 3 G 3 r R R
Mm F m g G 2 r 1
Mm F' G 2 r2
g
r
s s
2
r
s2
在任一闭合面的引力场通量:
4 G m g
i 1
质量M均匀分布在半径为R的球体上 1.当在球外时:过P点作半径为r(r>R)与球体同心的球面。 过此面的
g ds g ds g 4 r g
s s
2
g 4r
2
4 Gm
引力场与高斯定理
库仑定律:
q0 q F 4 0 r 2
万有引力定律:
m1m2 F G 2 r
比较库仑定律和万有引力定律的表达式会发现:两者都服从平方反比定律。其 1
中
4
和万有引力定律中的G相当,都是常量,而q和m相当。
0
因此我们可以将 静电场的研究方法及有关概念引入到引力场中
引力场的高斯定理
把引力场中的F/m定义 为点的引力强度 F 所以 g m 故质量为m的质点在引 力场中某点的引力场 强
m g G 3 r r
静电场的高斯定理: 半径为r的球面s,一位于球心的点电荷q 场 强E 电荷在球面内:
m ds 可以推导在相似条件下的引力场通量: g ds G ds Gm 4 Gm
高斯引力定律

高斯重力定律也称为高斯引力通量定律, 描述的是通过一个闭曲面的引力通量与其中包含的质量之间的关系, 本质上等价于牛顿万有引力定律. 尽管它们具有等价性, 但许多时候高斯重力定律提供了一种比牛顿万有引力定律更为简便的求解引力问题的方法.
高斯重力定律在形式上与静电学的高斯定律相同(也是马克士威方程组中的一个方程). 事实上, 它们都是三维空间中力场与距离平方反比(库仑定律)的结果.
定律的定性描述
定义引力场g 为空间中每一点及每一时刻该处的假想放置的粒子受到的引力除以粒子质量. 显然g 是个向量场.
引力通量是引力场通过一个曲面的面积分. 在高斯重力定律中, 要求此曲面必须是可定向闭曲面.
高斯重力定律断言:
通过一个可定向闭曲面的引力通量正比于其中包含的质量。
万有引力场的高斯定理

万有引力场的高斯定理一 问题的提出在大一上学期学习力学,在学到简谐运动那一章时,胡老师曾举个一个例子,是摘自老版本大学物理学的一道书上例题,题目是这样的:将地球看做一个半径为R 的均匀球体,密度为ρ,假定沿直径开一条通道,若有质量为m 的质点沿通道做无摩擦运动,证明此运动为简谐运动。
(题目示意图如下)例题图当时做这道题时不知道如何列出质点的受力方程,后来老师直接讲到质点的受力大小仅与质点所在圆面内包围的质量有关,而与外部的质量无关。
列出受力大小公式,经过化简发现受到的万有引力大小是一个和质点所在面的半径r 成正比的○1,即质点在地球内部受到了一个线性回复力的作用,方向和质点相对于平衡位置(地心)的位移方向相反,即质点做的是简谐运动。
具体的解题公式和过程不再写出,这些不是本文章的重点。
场景转换到大一下学期(现在),在老师讲到电磁学中静电场的高斯定理时,惊奇的发现:∑⎰⎰==Φ)(01cos 内S iE q dS E εθ这个公式告诉我们:通过一个任意闭合曲面S 的电通量E Φ等于该面所包围的所有电荷的代数和Σq 除以ε0,与闭合面外的电荷无关。
这就是著名的电场中的高斯定理的表述。
其他有关高斯定理的证明请见《电磁学》(赵凯华、陈熙谋版)第54页至59页,这里不再抄写证明。
高斯提出了电通量的概念,并根据库仑定律推导出来,使很多电场问题步骤和思路大大简化,并提炼出了这个公式。
学到这里时我就突然想到了本文最开始的那道有关万有引力的题目,并且想到牛顿的万有引力定律公式——221r m m GF =万和库仑定律公式——221cr q q k=F 有着十分相似的形式,既然库仑定律能够推导出电场的高斯定理,那么高斯定理应该在万有引力场中同样适用。
在这里先给几个定义和公式:万有引力强度,用g表示,定义式为2rm 中万G m F g == ,但正方向为从内到外,与g实际方向相反。
对于球状质点系,通过单位表面积的引力通量是:-g r4r 4*g -S 22==Φ=Φππ万d 1, 万有引力通量,⎰⎰∆-=ΦSS gcos θ万(注意负号)2, 仿照041πε=k ,令041g G π=,这里的0g 姑且命名为真空介万常数,呵呵,根据真空介电常数改的,大小约为1.193*10^9。
引力的高斯定理

引力的高斯定理赵旋物理系201011141030 众所周知,我们学习过的电场力的高斯定理:EdS=q/ε0.对于与电场力极其相似的万有引力,也会不会有相同于高斯定理的表现其有源性的公式呢?我们知道,电场力是有源的;同样,万有引力也是有源的。
所以,我们完全可以根据电场力的高斯定理,仿造出万有引力的高斯定理。
首先,由于万有引力F=GMmR2∙e n,所以定义F=m∙E′或者E′=Fm,对于两质点间的万有引力即是定义E′=GMmR2。
为了更好地类比引力高斯定理,我们在定义q′=m.这时万有引力的公式变为:F=q′∙E′.又根据点电荷之间电场力的表达式:F=14πε0∙q1q2R2,按照F=GMmR2∙e n可得到ε0′=14πG.到此我们将万有引力公式完完全全地改为了:F=10∙q1′q2′其中,q′=m,ε0′=14πG。
这就是一个跟电场力完全相同的万有引力公式。
然后根据电场力的高斯定理:EdS=q/ε0可以得出万有引力的高斯定理:E′dS=q′/ε0′将其还原为万有引力我们通常使用的量即是:F∙dS=4πG∙M.公式的意义在于表示对于某一区域引力场强度在一封闭曲面上的面积分与封闭曲面所包围的物体质量成正比,与曲面内质量的分布情况无关,与封闭曲面外的质量亦无关。
对于引力高斯定理的证明,由于我们在之前已经把万有引力的所有重要的公式都换成了跟电场力很是相似的公式,所以对引力高斯定理进行证明的时候,只需要对照电场力高斯定理就可以了,在证明的时候只需把E、q、ε0分别换成E′、q′、ε0′就可以了。
步骤基本完全相似……于此同时,与电场力有关的所有定理几乎都可以移植到万有引力。
比如会有万有引力的环路定理:E′∙dl=0.等等……。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四. 引力场中的高斯定理
引力和静电力都是有势力,相应的引力势和静电势都满足三维空间里最简单的二阶(偏微分)方程——拉普拉斯方程。
用ψ代表引力势或者静电势场,它在三维空间里所满足的拉普拉斯方程采取如下的形式:(¶2/¶x2+¶2/¶y2+¶2/¶z2)ψ(x,y,z)=0.由于相应的静电力和引力等于势的微分(的负值),它的大小便与半径r成反比了,即ψ(r)∝1/r,F(r)=- dψ/dr∝1/r2由于万有引力定律与Coulomb,s law 本质是一样的,因此引力场中也存在Gauss, theorem,并且与万有引力定律等价。
1、预备知识
引力场场强:引力场场强是一个向量,其大小等于1千克的质点在该处所受引力的大小,方向与该质点在该处所受引力的方向一致。
引力线:如果在引力场中出一些曲线,使这些曲线上每一点的切线方向和该点的引力场强方向一致,那么所有这样可以作出的曲线叫做引力线。
引力线数密度:在引力场中任一点取一小面元ΔS与该点的场强方向垂直,设穿过ΔS的引力线有ΔN 根,则比值ΔN/ΔS叫做该点的引力线数密度,它的意义是通过该点单位垂直截面的引力线根数,规定引力场场强E∝ΔN/ΔS。
引力线性质:引力线其自无穷远点,止与该质点,引力线在宇宙中处处存在。
一个质点的任何两条引力线不会相交,不形成闭合线。
引力通量:通过一面元ΔS的引力通量为该点场强的大小E与ΔS在垂直于场强方向的投影面积
ΔS`=ΔScosθ的乘积。
2、引力场中的Gauss, theorem
通过一个任意闭合曲面S的引力通量φ=4πG∑m,与闭合曲面外的引力质量无关。
证明:(1)通过包括质点m的同心球面的引力通量都等于4πGm。
以质点m所在处为中心以任意半径r作一球面.根据万有引力定律,在球面上各点场强大小一样E=G m /r2,场强的方向沿半径向外呈辐射状。
在球面上任意取一面元dS,其外法线向量n也是沿着半径方向向外的,即n和E间夹角θ=0,所以通过dS的引力通量为dφ=EcosθdS=EdS= G m /r2dS,通过整个闭合球面的引力通量为φ=dS= G m /r2×4πr2=4πGm。
(2)通过包围质点的任意闭合曲面S的引力通量都等于4πGm
在闭合面S内以质点m所在处O为中心作一任意半径的球面S``,根据(1)通过此球面的引力通量等于4πGm。
由于引力场分布的球对称性,这引力通量均匀地分布在4π球面度的立体角内,因此在每个元立体角dΩ内的引力通量是GmdΩ。
如果把这个立体角的锥面延长,使它在闭合面S上截出一个面元dS。
设dS到质点m的距离为r,dS的法线n与场强E的夹角为θ,则通过dS的引力通量
dφ=EcosθdS=Gm/r2cosθdS, cosθdS= dS`是dS在垂直于场强方向的投影面积,所以dφ=EdS`= G m /r2dS`= GmdΩ。
所以通过面元dS的引力通量和通过球面S``上与dS对应的面元dS``的引力通量相等,所以通过整个闭合面S的引力通量都必定和通过球面S``的引力通量一样,等于4πGm。
(3)通过不包括质点的任意闭合面S的引力通量恒为0。
因为单个质点产生的引力线是辐向的直线,它们在空间连续不断。
当质点在闭合面S之外时,从某个面元dS上进入闭合面的引力线必然从另外一个面元dS`上穿出,而这一对面元dS和dS`对质点所张的立体角相等,通过dS的引力通量和通出dS`的引力通量的代数和为0,通过整个闭合面S的引力通量是通过这样一对对面元的引力通量之和,当然也是等于0的。
(4)多个质点的引力通量等于它们单独存在时的引力通量的代数和。
设物体有m1.m2.m3…mk个质点,其中第1到第n个被高斯面S所包围,第n+1到第k个在高斯面之外,则k个质点同时存在时通过S的引力通量为
φ=φ1+φ2+φ3+…+φn+φn+1+…+φk=φ1+φ2+φ3+…+φn=4πG(m1+ m2+…+ mn)= 4πG∑m.。
