6轴心受压构件PPT课件
合集下载
钢筋混凝土教学课件—第6章受压构件的截面承载力
2.受压破坏形态（如下图）
N
e0
N N
e0
e0
实际重心轴
s As
f y As
s As
f y As
f y As
s As
h0
(a )
h0
( b)
h0
(c)
10
有三种情况：
（1）如上图(a)所示：相对偏心距稍大且远侧钢筋较多；
A.N较小时，远侧受拉，近侧受压；
B.破坏时，远侧钢筋受拉但不能屈服，近侧钢筋受压屈服，
B.N较小时，全截面受压（远侧和近侧钢筋均受压）；
C.近侧受压程度小于远侧受压程度；
D.破坏时，近侧钢筋受压但不能屈服，远侧钢筋受压屈服，
远侧混凝土压碎； 综合（1）~（3）可知： （1）远侧钢筋均不能受拉且屈服；以混凝土受压破坏为标志，称 为“受压破坏”； （2）相对偏心距较小，称为“小偏心受压”；
1
3.本章重点：单向偏心受压构件（或简称偏心
受压构件） 二.工程应用 1.轴心受压构件：结构的中间柱（近似）； 2.单向偏心受压构件：结构的边柱； 3.双向偏心受压构件：结构的角柱； 如下图所示。
2
3
围范的载恒 受承柱的应相为分部影 阴，置布面平构结架框
柱边
柱角
柱间中
§6.1 受压构件一般构造要求
17
§6.5 矩形截面偏心受压构件正截面
受压承载力基本计算公式
一.区分大、小偏心受压破坏形态的界限
由下图可知：
1.受拉破坏时，远侧钢筋先受拉屈服，然后近侧钢筋受压屈服和近
侧混凝土压坏；
2.受压破坏时，近侧钢筋受压屈服和混凝土压坏时，远侧钢筋不能 受拉屈服； 3.界限破坏时，远侧钢筋受拉屈服和近侧混凝土压坏同时发生； 4.受压区太小（如 x 2a ），远侧钢筋先屈服，然后混凝土压坏， 但近侧钢筋不能受压屈服。
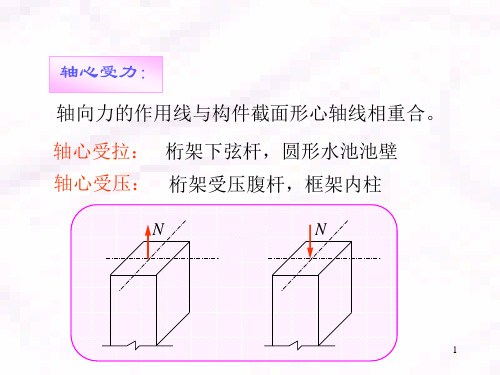
N
e0
N N
e0
e0
实际重心轴
s As
f y As
s As
f y As
f y As
s As
h0
(a )
h0
( b)
h0
(c)
10
有三种情况：
（1）如上图(a)所示：相对偏心距稍大且远侧钢筋较多；
A.N较小时，远侧受拉，近侧受压；
B.破坏时，远侧钢筋受拉但不能屈服，近侧钢筋受压屈服，
B.N较小时，全截面受压（远侧和近侧钢筋均受压）；
C.近侧受压程度小于远侧受压程度；
D.破坏时，近侧钢筋受压但不能屈服，远侧钢筋受压屈服，
远侧混凝土压碎； 综合（1）~（3）可知： （1）远侧钢筋均不能受拉且屈服；以混凝土受压破坏为标志，称 为“受压破坏”； （2）相对偏心距较小，称为“小偏心受压”；
1
3.本章重点：单向偏心受压构件（或简称偏心
受压构件） 二.工程应用 1.轴心受压构件：结构的中间柱（近似）； 2.单向偏心受压构件：结构的边柱； 3.双向偏心受压构件：结构的角柱； 如下图所示。
2
3
围范的载恒 受承柱的应相为分部影 阴，置布面平构结架框
柱边
柱角
柱间中
§6.1 受压构件一般构造要求
17
§6.5 矩形截面偏心受压构件正截面
受压承载力基本计算公式
一.区分大、小偏心受压破坏形态的界限
由下图可知：
1.受拉破坏时，远侧钢筋先受拉屈服，然后近侧钢筋受压屈服和近
侧混凝土压坏；
2.受压破坏时，近侧钢筋受压屈服和混凝土压坏时，远侧钢筋不能 受拉屈服； 3.界限破坏时，远侧钢筋受拉屈服和近侧混凝土压坏同时发生； 4.受压区太小（如 x 2a ），远侧钢筋先屈服，然后混凝土压坏， 但近侧钢筋不能受压屈服。
第 6 章 受压构件的截面承载力
第6 章受压构件的截面承载力思考题6.1 轴心受压普通钢筋短柱与长柱的破坏形态有何不同？轴心受压长柱的稳定系数? 如何确定？轴心受压普通箍筋短柱的破坏形态是随着荷载的增加，柱中开始出现微细裂缝，在临近破坏荷载时，柱四周出现明显的纵向裂缝，箍筋间的纵筋发生压屈，向外凸出，混凝土被压碎，柱子即告破坏。
而长柱破坏时，首先在凹侧出现纵向裂缝，随后混凝土被压碎，纵筋被压屈向外凸出；凸侧混凝土出现垂直于纵轴方向的横向裂缝，侧向挠度急剧增大，柱子破坏。
l s l s 《混凝土结构设计规范》采用稳定系数? 来表示长柱承载力的降低程度，即? ＝N u / N u ，N u 和N u 分别为长柱和短柱的承载力。
根据试验结果及数理统计可得? 的经验计算公式：当l0／b＝8～34 时，? ＝1.177－0.021l0／b；当l0／b＝35～50 时，? ＝0.87－0.012l0／b。
《混凝土结构设计规范》中，对于长细比l0／b 较大的构件，考虑到荷载初始偏心和长期荷载作用对构件承载力的不利影响较大，的? 取值比按经验公式所得到的? 值还要降低一些，以保证安全。
对于长细比l0／b 小于20 的构件，考虑到过去使用经验，? 的取值略微抬高一些，以使计算用钢量不致增加过多。
6.2 简述偏心受压短柱的破坏形态。
偏心受压构件如何分类？钢筋混凝土偏心受压短柱的破坏形态有受拉破坏和受压破坏两种情况。
受拉破坏形态又称大偏心受压破坏，它发生于轴向力N 的相对偏心距较大，且受拉钢筋配置得不太多时。
随着荷载的增加，首先在受拉区产生横向裂缝；荷载再增加，拉区的裂缝随之不断地开裂，在破坏前主裂缝逐渐明显，受拉钢筋的应力达到屈服强度，进入流幅阶段，受拉变形的发展大于受压变形，中和轴上升，使混凝土压区高度迅速减小，最后压区边缘混凝土达到极限压应变值，出现纵向裂缝而混凝土被压碎，构件即告破坏，破坏时压区的纵筋也能达到受压屈服强度，这种破坏属于延性破坏类型，其特点是受拉钢筋先达到屈服强度，导致压区混凝土压碎。
课件轴心受压构件的整体稳定性.
二、工字形组合截面板件的局部屈曲
对于局部屈曲问题，通常有两种考虑方法： 方法1：不允许板件屈曲先于构件整体屈曲，目前一般钢结构就是不允许局部屈曲先于整体屈曲来限制板件宽厚比。 方法2：允许板件先于整体屈曲，采用有效截面的概念来考虑局部屈曲对构件承载力的不利影响，冷弯薄壁型钢结构，轻型门式刚架结构的腹板就是这样考虑的。
残余应力对压杆临界荷载的影响
对x-x轴屈曲时: 对y-y轴屈曲时:
残余应力对弱轴的影响比对强轴严重得多!
4、杆端约束对轴心受压构件整体稳定性的影响
杆件临界力： － 计算长度系数
四、压杆曲线的确定
焊接工字形截面轴心受压柱稳定系数
12种不同截面尺寸，不同残余应力和分布以及不同钢材牌号轴心压构件曲线。
板的挠度为： 板的屈曲力为： 式中 a、b 受压方向板的长度和板的宽度； m、n 板屈曲后纵向和横向的半波数。 当n =1时，
K为板的屈曲系数：
四边简支均匀受压板的屈曲系数
当a>b时，减小板的非加载边a的长度不能提高板的临界承载力。 不同的边界约束条件取不同的屈曲系数；
4、缀板构件：
为防止单肢件失稳先于整体失稳，规范规定： 缀板构件：单肢长细比小于等于40且不大于两方向长细比较大值0.5倍；
二、杆件的截面选择
肢件：对实轴的稳定计算同实腹式压杆那样计算确定截面尺寸； 肢件距离：对实轴和虚轴的等稳定条件所决定；
缀条构件：
预先估计缀条面积A1y
缀板构件：
三、缀件计算 1、剪力计算 当格构式压杆绕虚轴弯曲时，因变形而产生剪力（由缀材承受）。假设其初始挠曲线为y0=v0sin∏x／l，则任意截面处的总挠度为： 在杆的任意截面的弯矩： 任意截面的剪力：
3.塔架
第六章受压构件
§ 6.1 轴心受压构件承载力计算
Strength of Axially Loaded Members
6.1.1 轴心受压构件的破坏特征
按照长细比（the slenderness）l０／ｂ的大小，轴心受
压柱可分为短柱和长柱两类。对方形和矩形柱，当 l０／ｂ ≤ 8 时属于短柱，否则为长柱。其中l０为柱的计算长度，
（4）验算配筋率
As ' 1677 =1.86% A 300 300 min＞ =0.6%，且＜3% ，满足最小配筋率要求，且勿
'
需重算。
纵筋选用4 如图。
25（As′=1964mm2），箍筋配置φ8@300，
Φ8@300
300
4 25
300
【习题2】某现浇底层钢筋混凝土轴心受压柱，截面尺寸
1 1 =0.869 1 0.002 (l 0 / b 8) 2 1 0.002(16.7 8) 2
（3）计算钢筋截面面积As′
N 1400 103 fc A 14.3 3002 0.9 As' 0.9 0.869 =1677mm2 fy ' 300
选用8Φ 28， As' ＝4926mm2 。 配筋率ρ= As/A =4926/125600=3.92%
6.3.3
螺旋箍筋柱简介
（ the
spiral columns）
1．螺旋箍筋柱的受力特点：螺旋箍筋柱的箍筋既是构 造钢筋又是受力钢筋。由于螺旋筋或焊接环筋的套箍作用 可约束核心混凝土（螺旋筋或焊接环筋所包围的混凝土）
若采用该柱直径为400mm，则 l0 4200 10.5, 查表得＝0.95 d 400
钢结构教学课件PPT轴心受力构件
第六章 轴心受力构件
§6.1 轴心受力构件的应用及截面形式
6.1.1 轴心受力构件的应用
a)
轴心受力构件是指承受通过截面形 心轴线的轴向力作用的构件。包括 轴心受拉构件（轴心拉杆）和轴心 受压构件（轴心压杆）。
在钢结构中应用广泛，如桁架、网 架中的杆件，工业厂房及高层钢结 构的支撑，操作平台和其它结构的 支柱等。
1、弹性弯曲屈曲
欧拉（Euler）早在1744年通过对理想轴心压杆的整体稳定问题进 行的研究，当轴心力达到临界值时，压杆处于屈曲的微弯状态。 在弹性微弯状态下，根据外力矩平衡条件，可建立平衡微分方程， 求解后得到了著名的欧拉临界力和欧拉临界应力。
钢结构设计原理 Design Principles of Steel Structure
其临界力。
钢结构设计原理 Design Principles of Steel Structure
第六章 轴心受力构件
2、弹塑性弯曲屈曲
1889年恩格塞尔，用应力－应变曲线的切线模量代替欧拉公式中 的弹性模量E，将欧拉公式推广应用于非弹性范围，即：
Ncr
2Et I
l02
2 Et
2
A
（6.3.5）
钢结构设计原理 Design Principles of Steel Structure
第六章 轴心受力构件
对于高强螺栓的摩擦型连接，可以认为连接传力所依靠的摩擦力 均匀分布于螺孔四周，故在孔前接触面已传递一半的力，因此最 外列螺栓处危险截面的净截面强度应按下式计算：
N f
An,1
其中：An,1 b n1 d0 t;
+
+
+
+
b)
++
§6.1 轴心受力构件的应用及截面形式
6.1.1 轴心受力构件的应用
a)
轴心受力构件是指承受通过截面形 心轴线的轴向力作用的构件。包括 轴心受拉构件（轴心拉杆）和轴心 受压构件（轴心压杆）。
在钢结构中应用广泛，如桁架、网 架中的杆件，工业厂房及高层钢结 构的支撑，操作平台和其它结构的 支柱等。
1、弹性弯曲屈曲
欧拉（Euler）早在1744年通过对理想轴心压杆的整体稳定问题进 行的研究，当轴心力达到临界值时，压杆处于屈曲的微弯状态。 在弹性微弯状态下，根据外力矩平衡条件，可建立平衡微分方程， 求解后得到了著名的欧拉临界力和欧拉临界应力。
钢结构设计原理 Design Principles of Steel Structure
其临界力。
钢结构设计原理 Design Principles of Steel Structure
第六章 轴心受力构件
2、弹塑性弯曲屈曲
1889年恩格塞尔，用应力－应变曲线的切线模量代替欧拉公式中 的弹性模量E，将欧拉公式推广应用于非弹性范围，即：
Ncr
2Et I
l02
2 Et
2
A
（6.3.5）
钢结构设计原理 Design Principles of Steel Structure
第六章 轴心受力构件
对于高强螺栓的摩擦型连接，可以认为连接传力所依靠的摩擦力 均匀分布于螺孔四周，故在孔前接触面已传递一半的力，因此最 外列螺栓处危险截面的净截面强度应按下式计算：
N f
An,1
其中：An,1 b n1 d0 t;
+
+
+
+
b)
++
6钢筋混凝土轴心受拉构件
E c
2Eftk
2
弹性状态时：
N A A
SS
CC
N ( A A )
ES
C
C
塑性状态时：
随着荷载的增加，混凝土受拉塑性变形开始出现。
N (A A )
Es
C
C
——钢筋弹性模量与混凝土变形模量（割线模 E 量）之比。
3
即将开裂时：
混凝土应力等于其开裂强度，并且进入了塑性 发展阶段，其变形模量降低 E'c=0.5Ec
箍 筋：
固定纵筋位置
8
§4.3 轴心受拉构件的裂缝宽度验算
裂缝宽度的计算公 式 平均裂缝间距lcr
Lcr=1.1(2.7c+0.1d/ρte)v
式中 c—最外层纵向受拉钢筋外边缘至受拉区底边的距离 （mm），当c<20时，取c=20;
d—钢筋直径（ mm）
ρte—按有效受拉混凝土截面面积计算的纵向受拉钢筋
Nu= As fy
5
§4.2 轴心受拉构件的承载力计算 一、计算公式
N Nu= As fy N ––– 轴向拉力的设计值 N u ––– 轴向受拉构件的极限承载力 As ––– 纵向受拉钢筋截面面积
6
fy ––– 钢筋抗拉设计强度值
注: 对于轴心受拉和小偏心受拉构件而言，当 fy>
300N/mm2时，仍按300N/mm2取用； 目的：为了控制受拉构件在使用荷载下的变形和 裂缝开展；
配筋率 v—纵向受拉钢筋表面特征系数
9
最大裂缝宽度ωmax
2.7
ss
(2.7c
0.1
d
)v
max
E
s
te
式中 ψ—裂缝间纵向受拉钢筋应变不均匀系数
第六章 轴心受力构件承载力分解
螺旋式箍筋柱的受力特点：
轴向压力较小时，混凝土和纵筋分别受压， 螺旋箍筋受拉但对混凝土的横向作用不明显； 接近极限状态时，螺旋箍筋对核芯混凝土产 生较大的横向约束，提高混凝土强度，从而 间接提高柱的承载能力。当螺旋箍筋达到抗 拉屈服强度时，不能有效约束混凝土的横向 变形，构件破坏。在螺旋箍筋受到较大拉应 力时其外侧的混凝土保护层开裂，计算时不 考虑此部分混凝土。
前述是短柱的破坏特征。对于长 细比较大的长柱，试验表明，由于各 种偶然因素造成的初始偏心距的影响 是不可忽略的。加载后由于有初始偏 心距将产生附加弯距，这样相互影响 的结果使长柱最终在弯矩及轴力共同 作用下发生破坏。对于长细比很大的 长柱，还有可能发生“失稳破坏”的 现象，长柱的破坏荷载低于其他条件 相同的短柱破坏荷载。
⑵箍筋
◆ 受压构件中箍筋应采用封闭式，其直径不应小于d/4，且 不小于6mm，此处d为纵筋的最大直径。 ◆ 箍筋间距不应大于400mm，也不应大于截面短边尺寸； 对绑扎钢筋骨架，箍筋间距不应大于15d；对焊接钢筋骨 架不应大于20d，此处d为纵筋的最小直径。 ◆ 当柱中全部纵筋的配筋率超过3%，箍筋直径不宜小于 8mm，且箍筋末端应应作成135°的弯钩，弯钩末端平直 段长度不应小于5 d（箍筋直径），或焊成封闭式；此时 箍筋间距不应大于10纵筋最小直径，也不应大于200mm。 ◆ 当柱截面短边大于400mm，且各边纵筋配置根数超过多 于3根时，或当柱截面短边未大于400mm，但各边纵筋配 置根数超过多于4根时，应设置复合箍筋。 ◆ 对截面形状复杂的柱，不得采用具有内折角的箍筋，以 避免箍筋受拉时使折角处混凝土破损。
试验表明，长柱的破 坏荷载低于其他条件相同 的短柱破坏荷载，《规 范》中采用稳定系数 表 示承载能力的降低程度， 即
《轴心受压构》PPT课件
cr 按稳定极限承载力理论的计算方法
轴心受压构件考虑初始缺陷后的受力属于压弯状态 ，用数值积分法求解微分方程，可以考虑影响轴 心压杆稳定极限承载力的许多因素，如截面的形 状和尺寸、材料的力学性能、残余应力的分布和 大小、构件的初弯曲和初扭曲、荷载作用点的初 偏心、构件的失稳方向等等，因此是比较精确的 方法。我国钢结构设计规范采用了这个方法。
5.3.3 轴心压杆的弯曲失稳、扭转失稳、弯扭失稳
在弹塑性阶段，当研究式（a）时，只要截面上的
残余应力对称于y轴，同时又有 u0=0 和 θ0=0，则
该式将始终与其它两式无关，可以单独研究。这样， 压杆将只发生y方向位移，整体失稳呈弯曲变形状 态，成为弯曲失稳。
同样，式（b）也是弯曲失稳，只是弯曲失稳的 方向不同而已。
m
0 1 N
N Ex
NEX ——绕x轴的欧拉临界应力
5.3.4 弯曲失稳的极限承载力
由边缘纤维屈服准则可得 N Nm 将perΔrym公m NA代式入NW上xm式，fy并解出平均A应力W xc r
fy 后，即得
crfy(1 20)E x fy(1 20)E x2fyEx
0 ——初偏心率 0 A ； W x0
5.2 轴心受压构件的强度
以净截面的平均应力强度为准则，即
σ N fy f An rR
轴心受压构件，当截面无削弱时，强度不必计算。
轴心受压实腹构件的整体稳定
5.3.1 理想轴心压杆的整体稳定
1、整体稳定的临界应力
理想轴心压杆：假定杆件完全挺直、荷载沿杆件形心轴作 用, 杆件在受荷之前无初始应力、初弯曲和初偏心, 截面沿杆 件是均匀的。
欧拉双曲线
O
lp
非弹性 弹性
阶段 阶段
轴心受压构件考虑初始缺陷后的受力属于压弯状态 ，用数值积分法求解微分方程，可以考虑影响轴 心压杆稳定极限承载力的许多因素，如截面的形 状和尺寸、材料的力学性能、残余应力的分布和 大小、构件的初弯曲和初扭曲、荷载作用点的初 偏心、构件的失稳方向等等，因此是比较精确的 方法。我国钢结构设计规范采用了这个方法。
5.3.3 轴心压杆的弯曲失稳、扭转失稳、弯扭失稳
在弹塑性阶段，当研究式（a）时，只要截面上的
残余应力对称于y轴，同时又有 u0=0 和 θ0=0，则
该式将始终与其它两式无关，可以单独研究。这样， 压杆将只发生y方向位移，整体失稳呈弯曲变形状 态，成为弯曲失稳。
同样，式（b）也是弯曲失稳，只是弯曲失稳的 方向不同而已。
m
0 1 N
N Ex
NEX ——绕x轴的欧拉临界应力
5.3.4 弯曲失稳的极限承载力
由边缘纤维屈服准则可得 N Nm 将perΔrym公m NA代式入NW上xm式，fy并解出平均A应力W xc r
fy 后，即得
crfy(1 20)E x fy(1 20)E x2fyEx
0 ——初偏心率 0 A ； W x0
5.2 轴心受压构件的强度
以净截面的平均应力强度为准则，即
σ N fy f An rR
轴心受压构件，当截面无削弱时，强度不必计算。
轴心受压实腹构件的整体稳定
5.3.1 理想轴心压杆的整体稳定
1、整体稳定的临界应力
理想轴心压杆：假定杆件完全挺直、荷载沿杆件形心轴作 用, 杆件在受荷之前无初始应力、初弯曲和初偏心, 截面沿杆 件是均匀的。
欧拉双曲线
O
lp
非弹性 弹性
阶段 阶段
【学习课件】第6章受压构件的截面承载力
第六章 受压构件的截面承载力
ppt课件
1
第六章 受压构件
第一节 概 述
ppt课件
2
第六章 受压构件
ppt课件
3
第六章 受压构件
一 、轴心受压构件
ppt课件
4
第六章 受压构件 二 、一般构造
ppt课件
5
第六章 受压构件
1.纵筋作用
ppt课件
6
第六章 受压构件
2.箍筋作用
柱受压时，混凝土产生纵向压缩变形的 同时，产生横向变形，纵筋外凸。箍筋 的作用可约束混凝土横向变形。
第七节 矩形截面偏心受压构件计算 总适用条件（不论大、小偏心）： 1. As与As’均需满足最小配筋率要求；
37
第六章 受压构件
ppt课件
38
第六章 受压构件
ppt课件
39
第六章 受压构件
ppt课件
40
第六章 受压构件
x= xn
x / h0= xn / h0
= xn / h0
若 = 则 xn / h ＝1 0 ppt课件 即 xn = h0
41
第六章 受压构件
试验资料表明，与 接近直线关系
35
第六章 受压构件
破坏从靠近N一侧压区边缘混凝土达到极限压 应变开始
同时，靠近N一侧受压钢筋达到受压屈服强度
远离N一侧钢筋可能受压也可能受拉，但达不到 屈服强度
只有当偏心距很小，N较大，远离N一侧钢筋可 能受压屈服
脆性破坏类型
ppt课件
36
第六章 受压构件
第四节 大小偏心受压破坏界限
ppt课件
受拉破坏
ppt课件
30
第六章 受压构件
ppt课件
1
第六章 受压构件
第一节 概 述
ppt课件
2
第六章 受压构件
ppt课件
3
第六章 受压构件
一 、轴心受压构件
ppt课件
4
第六章 受压构件 二 、一般构造
ppt课件
5
第六章 受压构件
1.纵筋作用
ppt课件
6
第六章 受压构件
2.箍筋作用
柱受压时，混凝土产生纵向压缩变形的 同时，产生横向变形，纵筋外凸。箍筋 的作用可约束混凝土横向变形。
第七节 矩形截面偏心受压构件计算 总适用条件（不论大、小偏心）： 1. As与As’均需满足最小配筋率要求；
37
第六章 受压构件
ppt课件
38
第六章 受压构件
ppt课件
39
第六章 受压构件
ppt课件
40
第六章 受压构件
x= xn
x / h0= xn / h0
= xn / h0
若 = 则 xn / h ＝1 0 ppt课件 即 xn = h0
41
第六章 受压构件
试验资料表明，与 接近直线关系
35
第六章 受压构件
破坏从靠近N一侧压区边缘混凝土达到极限压 应变开始
同时，靠近N一侧受压钢筋达到受压屈服强度
远离N一侧钢筋可能受压也可能受拉，但达不到 屈服强度
只有当偏心距很小，N较大，远离N一侧钢筋可 能受压屈服
脆性破坏类型
ppt课件
36
第六章 受压构件
第四节 大小偏心受压破坏界限
ppt课件
受拉破坏
ppt课件
30
第六章 受压构件
钢筋混凝土结构原理6 受压构件
第6章 钢筋混凝土轴心受力构件正截面承载力计算
当混凝土压应力达到峰值应 外荷载不再增加， 变 ， 外荷载不再增加 ， 压缩 变形继续增加， 变形继续增加 ， 出现的纵向 裂缝继续发展， 裂缝继续发展 ， 箍筋间的纵 筋发生压屈向外凸出， 筋发生压屈向外凸出 ， 混凝 土被压碎而整个构件破坏。 土被压碎而整个构件破坏。 应力峰值时的压应变一般在0.0025～0.0035之间。 《 规范》 偏于 ～ 之间。 规范》 应力峰值时的压应变一般在 之间 安 全 地 取 最 大 压 应 变 为 0.002 。 受 压 纵 筋 屈 服 强 度 约
(a)轴心受压
(b)单向偏心受压
(c)双向偏心受压
第6章 钢筋混凝土偏心受力构件承载力计算
偏心受压构件的构造要求
1. 混凝土强度等级、计算长度及截面尺寸 混凝土强度等级、 截面形状和尺寸： ⑴截面形状和尺寸：P124 采用矩形截面，单层工业厂房的预制柱常采用工字形截面。 ◆ 采用矩形截面，单层工业厂房的预制柱常采用工字形截面。 圆形截面主要用于桥墩、桩和公共建筑中的柱。 ◆ 圆形截面主要用于桥墩、桩和公共建筑中的柱。 柱的截面尺寸不宜过小，一般应控制在l ◆ 柱的截面尺寸不宜过小，一般应控制在 0/b≤30及l0/h≤25。 及 。 ◆当柱截面的边长在800mm以下时，一般以50mm为模数，边长 当柱截面的边长在 以下时，一般以 为模数， 以下时 为模数 以上时， 为模数。 在800mm以上时，以100mm为模数。 以上时 为模数 （ 2）混凝土强度等级 ： 受压构件的承载力主要取决于混凝土强 ） 混凝土强度等级： 一般应采用强度等级较高的混凝土。 度，一般应采用强度等级较高的混凝土。目前我国一般结构中柱 的混凝土强度等级常用C30~C40，在高层建筑中，C50~C60级混 的混凝土强度等级常用 ，在高层建筑中， 级混 凝土也经常使用。 凝土也经常使用。
第5章 钢结构设计原理-轴心受压构件
3. 不对称截面的弯扭失稳
三式相互联系，失稳时呈弯扭变形状态——弯扭失稳。
21/85
5.3.4 弯曲失稳的极限承载力
1. 弯曲失稳极限承载力的准则
① 边缘纤维屈服准则——截面边缘纤维最大应力达到屈服点fy。 ② 稳定极限承载力理论——压力达到极限型失稳的顶点。
2. 临界应力σcr按边缘屈服准则的计算方法
2. 单轴对称截面的弯曲失稳和弯扭失稳 剪力中心在对称轴(如x轴)上，y0=0，由式(5-8)有：
P29
(5-27a、c) 相互联立，弯曲变形ν和扭转变形θ同时产生 ——弯扭失稳。
(5-27b) 独立，对称平面内的失稳——弯曲失稳。
20/85
5.3.3 轴心压杆的弯曲失稳、扭转失稳和弯扭失稳
初选截面形式 计算λx ，λy 按附表4-3～4-6确定φx 、φy
按表5-4确定a、b、c、d类
Nx =φxAf、 Ny=φyAf
Nx =min(NX,NY)
31/85
52．【背景资料】（25分） 两端铰接轴心受压钢柱，高10m,钢材为Q235，强度设计值ƒ=215 N/mm2，采
用图示截面，焊接工字型截面，翼缘为焰切边，尺寸单位mm。 1、计算构件截面积（2分）
初始缺陷包括： 初弯曲、初扭曲、初偏心、残余应力及材质的不均匀性
实际杆件的稳定承载力不再是长细比的唯一函数。 初始缺陷导致试验结果形成一个很宽的分布带。
15/85
5.3.3 轴心压杆的弯曲失稳、扭转失稳和弯扭失稳
钢结构压杆一般都是开口薄壁杆件。
根据开口薄壁杆件理论，具有初始缺陷的轴压杆的弹性微分 方程为(x0、y0为剪力中心坐标；u0、v0、θ0为初始缺陷引起的位移)：
（5-35a） （5-35b）
三式相互联系，失稳时呈弯扭变形状态——弯扭失稳。
21/85
5.3.4 弯曲失稳的极限承载力
1. 弯曲失稳极限承载力的准则
① 边缘纤维屈服准则——截面边缘纤维最大应力达到屈服点fy。 ② 稳定极限承载力理论——压力达到极限型失稳的顶点。
2. 临界应力σcr按边缘屈服准则的计算方法
2. 单轴对称截面的弯曲失稳和弯扭失稳 剪力中心在对称轴(如x轴)上，y0=0，由式(5-8)有：
P29
(5-27a、c) 相互联立，弯曲变形ν和扭转变形θ同时产生 ——弯扭失稳。
(5-27b) 独立，对称平面内的失稳——弯曲失稳。
20/85
5.3.3 轴心压杆的弯曲失稳、扭转失稳和弯扭失稳
初选截面形式 计算λx ，λy 按附表4-3～4-6确定φx 、φy
按表5-4确定a、b、c、d类
Nx =φxAf、 Ny=φyAf
Nx =min(NX,NY)
31/85
52．【背景资料】（25分） 两端铰接轴心受压钢柱，高10m,钢材为Q235，强度设计值ƒ=215 N/mm2，采
用图示截面，焊接工字型截面，翼缘为焰切边，尺寸单位mm。 1、计算构件截面积（2分）
初始缺陷包括： 初弯曲、初扭曲、初偏心、残余应力及材质的不均匀性
实际杆件的稳定承载力不再是长细比的唯一函数。 初始缺陷导致试验结果形成一个很宽的分布带。
15/85
5.3.3 轴心压杆的弯曲失稳、扭转失稳和弯扭失稳
钢结构压杆一般都是开口薄壁杆件。
根据开口薄壁杆件理论，具有初始缺陷的轴压杆的弹性微分 方程为(x0、y0为剪力中心坐标；u0、v0、θ0为初始缺陷引起的位移)：
（5-35a） （5-35b）
同济大学课件-钢结构设计原理
钢结构基本原理及设计
6.3.3 力学缺陷对弯曲屈曲的影响
1．残余应力的产生与分布规律
（1）残余应力产生 热轧H型钢 （2）
火焰切割边钢板焊
接H型钢 （3）量测残余应力 分割法、钻孔法
钢结构基本原理及设计
热轧的宽翼缘工字钢(H型 钢)，翼缘宽度较大，热轧后冷 却过程中，翼缘两端由于其暴露 于空气中的面积较翼缘与腹板交 接部分为多而冷却较快， 腹板中间部位则因厚度较薄 而冷却较快，翼缘与腹板交接部 位冷却收缩变形受到先冷却部分 的约束而出现残余拉应力，先冷 却部分则出现残余压应力。
钢结构基本原理及设计
欧拉公式
N cr E I cr 2 A l A 2 2 2 E E E 2 2 2 i 2 l l i2
其中，
2 EI 2 EI 2 EA N cr 2 2 2 （l ) l0 2
考虑剪切影响？
i
分岔屈曲后，结构只能在比临界荷载低的荷载下才能维 持平衡位形。承受轴向荷载的圆柱壳，承受均匀外压的球壳都 呈不定分岔屈曲形式。长细比不大的圆管压杆与圆柱壳很相似， 薄壁方管压杆亦有指表现为不稳定分岔屈曲。 P
v
钢结构基本原理及设计
(3)跃越屈曲
结构以大幅度的变形从一个平衡位形跳到另一个平衡 位形。 铰接坦拱和油罐的扁球壳顶盖都属于这种失稳情形。 在发生跃越后，荷载一般还可以显著增加，但是其变形大 大超出了正常使用极限状态，显然不宜以此为承载能力的 极限状态。
钢结构基本原理及设计
第6章 轴心受力构件
§6-1 §6-2 §6-3 §6-4 §6-5 §6-6 §6-7 §6-8 构件的应用和截面形式 构件的强度和刚度 轴心受压构件的整体稳定 实际轴心受压构件整体稳定的计算 轴心受压构件的局部稳定 实腹式轴心受压构件的截面设计 格构式轴心受压构件 柱头、柱脚
钢结构基础第六章 轴心受力构件
杆长中点总挠度为：
v0 m 0 1 N NE
根据上式，可得理想无 限弹性体的压力挠度曲 线如右图所示。实际压 杆并非无限弹性体，当
具有初弯曲压杆的压力挠度曲线
N达到某值时，在N和N∙v的共同作用下，截面边缘开始屈
服，进入弹塑性阶段，其压力—挠度曲线如虚线所示。
第六章 轴心受力构件
便于和相邻的构件连接
截面开展而壁厚较薄
第六章 轴心受力构件
6.2 轴心受拉构件的受力性能和计算
承载极限： 截面平均应力达到fu ，但缺少安全储备
毛截面平均应力达fy ，结构变形过大
计算准则：
毛截面平均应力不超过fy
钢材的应力应变关系
第六章 轴心受力构件
应力集中现象
孔洞处截面应力分布
应用：主要承重结构、平台、支柱、支撑等 截面形式 热轧型钢截面
热轧型钢截面
第六章 轴心受力构件
冷弯薄壁型钢截面
冷弯薄壁型钢截面
第六章 轴心受力构件
型钢和钢板的组合截面
实腹式组合截面
格构式组合截面
第六章 轴心受力构件
对截面形式的要求 能提供强度所需要的截面积 制作比较简便
1数值积分法2有限单元法6324稳定极限承载能力第六章轴心受力构件稳定问题的相关性6325稳定问题的多样性整体性和相关性第六章轴心受力构件64理想轴心受压构件的整体稳定性不考虑构件初弯曲初偏心对轴心受压构件整体稳定性的影响不考虑焊接残余应力对轴心受压构件整体稳定性的影响第六章轴心受力构件641理想轴心受压构件的整体稳定弯曲屈曲轴心受压柱的实际承载力实际轴心受压柱不可避免地存在几何缺陷和残余应力同时柱的材料还可能不均匀
μ—计算长度系数。
轴心受力构件
只发生弯曲变形，截面只绕一个主轴旋转，杆纵轴 由直线变为曲线，是双轴对称截面常见的失稳形式；
（2）扭转失稳失稳时除杆件的支撑端外，各截面均绕 纵轴扭转，是某些双轴对称截面可能发生的失稳形式；
（3）弯扭失稳单轴对称截面绕对称轴屈曲时，杆件发 生弯曲变形的同时必然伴随着扭转。
二、理想轴心受压构件的屈曲
假定: A、达到临界力Ncr时杆件挺直; B、杆微弯时,轴心力增加△N，其产生的平均压应力 与弯曲拉应力相等。
临界力和临界应力：
Ncr
2Et I
l2 0
cr
2Et 2
初始缺陷对压杆稳定的影响
如前所述，如果将钢材视为理想的弹塑性材料， 则压杆的临界力与长细比的关系曲线(柱子曲线)应为：
初 始
轴心受压构件的承载能力大多由其稳定条件 决定,截面强度计算一般不起控制作用。若构件截 面没有孔洞削弱,可不必计算其截面强度。当有孔 洞削弱时,若孔洞压实(实孔,如螺栓孔或铆钉孔),截 面无削弱,则可仅按毛截面式(5.2.1)计算;若孔洞为 没有紧固件的虚孔,则还应对孔心所在截面按净截 面式(5.2.2)计算。
长而细的轴心受压构件主要是失去整体 稳定性而破坏。
§6.3 轴心受压构件的整体稳定
6.3.1 轴心受压构件的整体失稳现象
（1）弯曲失稳
N较小，直线平衡状态。 N渐增，有干扰力使构件微弯，当干扰力移 去后，构件仍保持微弯状态而不能恢复到原来直 线平衡状态 N再稍微增加，弯曲变形迅速增大构件丧失 承载能力，称为构件弯曲屈曲或弯曲失稳。
EIy N( y0 y) 0
2）最大弯矩
中点挠度
v v0 v1
v0
Nv0 NE N
NEv0 NE N
v0 1 N NE
第六章 轴心受压构件的扭转屈曲和弯曲屈曲
6.1 概述
6.2 开口薄壁构件截面的剪力中心
6.2.1 开口薄壁截面的剪力流
6.2.2 截面的剪力中心坐标
6.3 开口薄壁构件的扭转
6.3.1扭转的形式
6.3.2开口薄壁构件的自由扭转
6.3.3 开口薄壁构件的约束扭转
6.4 轴心受压构件的弹性扭转屈曲
6.4.1 轴心受压构件的弹性扭转屈曲荷载
6.4.2 残余应力对扭转屈曲荷载的影响
6.4.3 构件两端边界条件的影响
6.5 轴心受压构件的弹塑性扭转屈曲
6.5.1切线模量扭转屈曲荷载
6.5.2 钢材为理想弹塑性体的屈曲荷载
6.6 轴心受压构件的弹性弯扭屈曲
6.6.1单轴对称截面轴心受压构件的平衡方程
6.6.2两端简支轴心受压构件的的弯扭屈曲荷载
6.6.3 两端固定的轴心受压构件的弯扭屈曲荷载
6.6.4 不对称截面手心受压构件的弯扭屈曲荷载
6.7 轴心受压构件的弹塑性弯扭屈曲
6.7.1 切线模量弯扭屈曲荷载
6.7.2考虑残余应力的单轴对称截面轴心受压构件弹塑性弯扭屈曲荷载
6.7.3 不对称截面轴心受压构件的弹塑性弯扭屈曲荷载
6.8轴心受压构件的扭转屈曲和弯扭屈曲理论在钢结构设计中的应用
6.8.1 双轴对称截面轴心受压构件、
6.8.2 单轴对称截面轴心受压构件
6.8.3 单面连接的单角钢轴心受压构件。
《轴心受压构件计算》课件
稳定性条件：构件在受力 作用下保持稳定的条件
轴心受压构件：承受轴 向压力的构件
轴向压力：沿构件轴线 方向的压力
弯曲应力：构件在弯曲 变形时产生的应力
应力分布：构件内部应 力的分布情况
刚度条件：构件在受力 作用下不变形的条件
轴心受压构件主要承受轴向压力
轴心受压构件的受力特点与荷载大 小、分布、方向等因素有关
计算步骤：按照计算步骤进行计算，如荷载分析、应力分析、变形分 析等
结果分析：对计算结果进行分析，如应力分布、变形情况、稳定性等
结论：得出结论，如构件的承载能力、稳定性等，并提出改进措施或 建议
实例：某轴心受压构件
计算方法：采用有限元法
计算结果：构件的应力分布、 变形情况等
结论：构件的承载能力、稳定 性等满足设计要求
复合材料：采用高强度复合材料，如玻璃纤维、碳纤维等，保证构件的强度和刚度
地震作用下的构造要求：加强构件的抗震性能，提高构件的稳定性 高温环境下的构造要求：考虑构件在高温下的变形和强度降低，采取相应的措施 腐蚀环境下的构造要求：考虑构件在腐蚀环境下的耐腐蚀性能，采取相应的防腐措施 疲劳作用下的构造要求：考虑构件在疲劳作用下的疲劳寿命，采取相应的疲劳设计措施
PART SIX
强度要求：保 证构件在受压 状态下的强度 满足设计要求
刚度要求：保 证构件在受压 状态下的刚度 满足设计要求
稳定性要求： 保证构件在受 压状态下的稳 定性满足设计
要求
耐久性要求： 保证构件在受 压状态下的耐 久性满足设计
要求
钢材：采用高强度钢材，如Q235、Q345等，保证构件的强度和刚度 混凝土：采用高强度混凝土，如C30、C40等，保证构件的强度和刚度 木材：采用高强度木材，如松木、杉木等，保证构件的强度和刚度
轴心受压构件的计算长度系数PPT课件
对于均匀受压的等截面直杆，此系数取决于构件两端的约束条件。这样一 来，具有各种约束条件的轴心受压构件的屈曲荷载转化为欧拉荷载的通式是：
2EI Pcr ( l ) 2
2
讨论：
2 EI Pcr (l )2
1、Pcr与E、I、l、μ有关，即与材料及结构的形式均有关；
.
2、Pcr与EI成正比，不同的方向EI不一样，压杆要求EI 在 各方向上尽可能相差不大，且其数值尽可能大；
表中μ值还可用简便的实用计算公式确定
11.21.42 10.42
在求解轴心受压构件的弹性屈曲荷载时，均采用了平衡法，但是有许多轴心受压构 件用平衡法无法直接求解，如沿构件的轴线压力有变化和沿轴线截面尺寸有变化等10， 将遇到很难求解的变系数微分方程，这时可采用能量法或其他近似方法求解。
.
谢谢
11
3、Pcr与EI、l、μ有关，同一构件，不同的方向，I不同，
μ不同，视综合情况而定；
4、端约束越强，Pcr越大，越不易失稳；
5、为了保证不同的方向μ尽可能相同，端约束用球铰，
这样，各方向有较一致的约束； 3
6、Pcr非外力也非内力，是反映构件承载能力的力学量。
.
构件截面的平均应力称为屈曲应力：
cr
cr
pE Pcr
2EI
l2Pcr
5
项次 支承条件
1 两端铰接
2 两端固定
3
上端铰接 下端固定
4
上端平移 但不转动 下端固定
5
上端自由 下端固定
6
上端平移 但不转动 下端铰接
.
变形曲线 l0=μl
实例 应用
理论μ值
1.0
设计μ值
1.0
0.5
2EI Pcr ( l ) 2
2
讨论：
2 EI Pcr (l )2
1、Pcr与E、I、l、μ有关，即与材料及结构的形式均有关；
.
2、Pcr与EI成正比，不同的方向EI不一样，压杆要求EI 在 各方向上尽可能相差不大，且其数值尽可能大；
表中μ值还可用简便的实用计算公式确定
11.21.42 10.42
在求解轴心受压构件的弹性屈曲荷载时，均采用了平衡法，但是有许多轴心受压构 件用平衡法无法直接求解，如沿构件的轴线压力有变化和沿轴线截面尺寸有变化等10， 将遇到很难求解的变系数微分方程，这时可采用能量法或其他近似方法求解。
.
谢谢
11
3、Pcr与EI、l、μ有关，同一构件，不同的方向，I不同，
μ不同，视综合情况而定；
4、端约束越强，Pcr越大，越不易失稳；
5、为了保证不同的方向μ尽可能相同，端约束用球铰，
这样，各方向有较一致的约束； 3
6、Pcr非外力也非内力，是反映构件承载能力的力学量。
.
构件截面的平均应力称为屈曲应力：
cr
cr
pE Pcr
2EI
l2Pcr
5
项次 支承条件
1 两端铰接
2 两端固定
3
上端铰接 下端固定
4
上端平移 但不转动 下端固定
5
上端自由 下端固定
6
上端平移 但不转动 下端铰接
.
变形曲线 l0=μl
实例 应用
理论μ值
1.0
设计μ值
1.0
0.5
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
随遇（中性）平衡是从稳定平衡过渡到不稳定平衡的
临界状态
中性平衡时的轴心压力 称为临界力
相应的截面应力
称为临界应力
无缺陷的轴心受压构件发生弯曲屈曲时，构件的变形 发生了性质上的变化，即构件由直线形式改变为弯曲形式 ，且这种变化带有突然性。
大纲要求
1、了解“轴心受力构件(axially-loaded members)”的应用和 截面形式(applications and cross sections)； 2、掌握轴心受拉构件(axial tension members)设计计算； 3、了解“轴心受压构件”稳定理论的基本概念和分析方法 (basic concept and analysis method) ；
保证构件在运输(tranportation)、安装
(installation and erection)、使用(service)时不会产
生过大变形。
l0 [ ]
i
(6.2.4)
l0 构件的计算长度； i I 截面的回转半径；
A
[ ] 构件的容许长细比，其 取值详见规范或教材。
轴心受压构件受力后的破坏方式主要有 两类：
（2）扭转失稳(torsional buckling)--失稳时除杆件的支 撑端外，各截面均绕纵轴扭转，是某些双轴对称截面可 能发生的失稳形式；
（3）弯扭失稳(bending and torsional buckling)—单轴 对称截面绕对称轴屈曲时，杆件发生弯曲变形的同时必 然伴随着扭转。
1.(4)平衡状态的分枝：从直线平衡状态过渡到微弯曲平衡状态。 2.(5)临界力 临界应力
Ⅲ ⅡⅠ
N
NN
N
(a)螺栓并列排列时钢板的净面积
(b)螺栓错列排列时钢板的净面积
净截面面积的计算
B．高强度螺栓摩擦型连接
0.5
N n
孔
N
N N&传
N
力
0.5
N n
N
N
轴心力作用下的摩擦型高强度螺栓连接
N ' N (1 0.5n1 / n)
N' f
An
验算净截面强度外，还应验算毛截面强度
截面形式可分为：实腹式和格构式两大类。
12.实格腹构式截面-截面由两个或多个型钢肢件通过缀材连接而成。
轴心受力构件
§6.2 轴心受力构件的强度和刚度
(Strength and Stiffness of Axially-Loaded Members)
强度 （承载能力极限状态） 轴心受拉构件 刚度 （正常使用极限状态）
强度 （承载能力极限状态） 轴心受压构件 稳定
刚度 （正常使用极限状态）
6.2.1 强度计算(calculation of strength)（承载能力极 限状态）
A．有孔洞构件
1）应力集中现象 孔洞处截面上应力分布不均匀 2）在弹性阶段，孔壁边缘的最大应力可能达到构件 毛截面平均应力的3倍 3）极限状态时，净截面上的应力为均匀屈服应力。 净截面强度计算：
短而粗的受压构件主要是强度破坏。当 其某一截面上的平均应力到达某控制应力如屈 服点，就认为构件已到达承载能力极限状态。 计算方法与轴心受拉构件相同。
长而细的轴心受压构件主要是失去整体 稳定性而破坏。
§6.3 轴心受压构件的整体稳定(overall stability)
6.3.1 轴心受压构件的整体失稳(overall buckling)现象
C．单面连接的单角钢
1）偏心受力。 2）单面连接的单角钢按轴心受力计算强度。 3）强度设计值乘以折减系数0.85。 4）验算轴心受力构件强度时，不必考虑残余应力的影响。
节点板 N
ey y x
N O y
e xx
O点为节点板传来N的作用点
单面连接的单角钢轴心受压构件
6.2.2 刚度计算(Calculation of Stiffness) （正常使 用极限状态）
塔架(tower)
网架(grid structures)
桁架(truss)
轴心受压柱 (axially-loaded compression column)
实腹式(solid web)轴压柱与格构式(built-up section) 轴压柱
二、轴心受压构件(axially-loaded compression members)的截面形式(cross-sections)
第 六 章
第六章 轴心受力构件 (Axially-Loaded Members)
§6-1 轴心受力构件的应用和截面形式 (application and sectional types) §6-2 轴心受力构件的强度和刚度(strength and stiffness) §6-3 轴心受压构件的整体稳定(overall stability) §6-4 实际轴心受压构件整体稳定的计算 §6-5 轴心受压构件的局部稳定(local stability) §6-6 实腹式轴心受压构件的截面设计(sectional design) §6-7 格构式轴心受压构件(axially-loaded members with buitup cross-section) §6-8 柱头、柱脚
4、掌握现行规范关于“轴心受压构件”设计计算方法，重点 及难点是构件的整体稳定(overall stability)和局部稳定(local stability)；
5、掌握格构式(buit-up section)轴心受压构件设计方法。
§6.1 轴心受力构件的应用和截面形式
一、轴心受力构件的应用 (application of axially-loaded members)
1.（1）弯曲失稳(bending buckling)
P
2. P 较小，直线平衡状态。
P 渐增，有干扰力使构件微弯，当干扰力移
去后，构件仍保持微弯状态而不能恢复到原来直
线平衡状态
P再稍微增加，弯曲变形迅速增大构件丧失
承载能力，称为构件弯曲屈曲或弯曲失稳。
v
只发生弯曲变形，截面只绕一个主轴旋转，杆纵轴 由直线变为曲线，是双轴对称截面常见的失稳形式；
N f
An
(6.2.2)
N—轴心拉力或压力设计值；
An—构件的净截面面积； f—钢材的抗拉强度设计值。
截面削弱处的应力分布
普通螺栓连接
并列布置, 按(I—I截面)计算。
错列布置，沿正交截面I—I破坏，也可能沿齿状截面
Ⅱ—Ⅱ或Ⅲ-Ⅲ破坏
应取I—I、Ⅱ—Ⅱ或Ⅲ-Ⅲ的较小面积计算
Ⅰ
Ⅲ ⅡⅠ
N
NN
Ⅱ
N
Ⅰ