高一数学向量加法
6.2.1向量的加法运算-高一数学(人教A版必修第二册)之第六章平面向量

起
D
C 则 AC a b
点
作平移,共起点,四边形,对角线
B
C
b
b
b
b
b
O
a
a
a
a
作法:(1)在平面内任取一点O,作
A
= a, =b OOAB
(2) 以OA,OB为邻边做平行四边行OACB
OC
(3)则 = a + b .
这叫做向量加法的平行四边形法则
起点相同,连对角
力的合成可以看作向量加法平行四边行法则的物理模型
b
有 ab a b
CA
B
因___此___,__我___们___有_____a. b a b a b
课堂练习(一) 1.如图,已知a、b,用向量加法的三角形法则作出a+b.
(1)
a+b
b
(2)
b
a
a
AaB b
a+b
C
(3) a
(4) a
b C
Bb a a+b A
b
ba B
C
a
+
A b
课堂练习
根据相等向量的定义得:
D
DC a, BC b AC AB BC a b
AC AD DC b a
a b b a
b
a
A
a+b
C
a
b
B
结合律:(a b) c a (b c)
b
A
B
a
c
O
C
例如:
(a b) (c d) (b d) (a c) a b c d e [d (a c) (b e)]
2.如图,已知a、b,用向量加法的平行四边形法则作 出a+b.
【课件】向量的加法运算课件高一下学期数学人教A版(2019)必修第二册

E
C
B
c
b
D
a+b
O
乙
法二:平行四边形法则
a
A
首先在平面内任取一点O,作向量=a,=b,=c,
以OA,OB为邻边作▱OADB,连接OD,则=+=a+b.
再以OD,OC为邻边作▱ODEC,连接OE,则= + =a+b+c即为所求.
多维探究
变式1 在本例(1)条件下,求+.
1 2 +2 3 +3 4 +…+−1
= 1
[例1]
(1)如图,在△ABC中,D,E分别是AB,AC上的点,F
为线段DE延长线上一点,DE∥BC,AB∥CF,连接CD,那么
(在横线上只填一个向量):
①+=________;
+=+=
②+=________;
(3)向量加法的运算律有哪两条?
(4)|a+b|,|a|+|b|,|a|-|b|三者之间的大小有何关系?
课前小测
1.下列各式不一定成立的是( D )
A.a+b=b+a
B.0+a=a
C.+=
D.|a+b|=|a|+|b|
2. + +等于(
A.
C)
B.
C.
D.
(1) + ;
+=
(2) + ;
= = =
+ =+ =
本课小结
1.三角形法则和平行四边形法则都是求向量和的基本方法,两个法则是
统一的,当两个向量首尾相连时,常选用三角形法则;当两个向量共起点
时,常选用平行四边形法则.
2.向量的加法满足交换律,因此在进行多个向量的加法运算时,可以按照
行800 km送往C地医院,求这架飞机飞行的路程及两次位移的和.
高一数学向量加法

例2平行四边形 ABCD中AB a,AD b 用 a, b 表示向量 AC 、DB 。
变式一:当a, b满足什么条件时,a+b与ab垂 直?
变式二:当a, b满足什么条件时,|a+b| = |ab| ?
.
.
.
.
.
.
.;知识产权律师 知源自产权律师3.求作差向量:已知向量a、b,求作向量a-b ∵(ab) + b = a + (b) + b = a + 0 = a
减法的三角形法则作法:在平面内取一点O,
作 OA = a, OB = b, 则 BA = a b
即a b可以表示为 从向量b的终点指 向向量a的终点的 向量。
注意:1 AB 表示a b。强调:差向量“箭头”
2.向量加法的交换律:a+b=b+a 3.向量加法的结合律:(a+b) +c=a+ (b+c)
ba
bca
从而,多个向量的加法运算 可以按照任意的次序、任意的组合来进行。 例1如图,一艘船从A点出发以2km/ h 的速度向 垂直于对岸的方向行驶,同时河水的流速 为2 3km/ h ,求船的实际航行的速度的大小 与方向(用与流速间的夹角表示).
【课件】向量的加法运算 向量的减法运算课件高一下学期数学人教A版(2019)必修第二册

6.2.1 向量的加法运算 6.2.2 向量的减法运算
教学目标
借助实例和平面向量的几何意义,掌握平面向量
1
的加法、减法运算及其运算规律.
2 理解平面向量的加法、减法运算的几何意义.
(1)向量的加法:求两个向量和的运算, 叫做向量的加法.
对于零向量与任意向量a ,规定a+0 0 a a .
本节课学习了平面向量的加法、减 法运算.
解析:由题意和图形可知 BAC 90 ,因为| AB | 300 ,| BC | 300 2 ,
所以| AC | 300 ,因为 ABC 45 ,A 地在 B 地南偏东 30°的方向处. 所以 C 地在 B 地南偏东 75°的方向处. 故飞机从 B 地向 C 地飞行的方向为南偏东 75°.
9.化简下列各式: (1) ( AB MB) (OB MO) . (2) AB AD DC .
B a-b
b Oa A
例 1 长江两岸之间没有大桥的地方,常常通过轮渡进行运 输.如图,一艘船从长江南岸 A 地出发,垂直于对岸航行, 航行速度的大小为 15 km/h,同时江水的速度为向东 6 km/h. (1)用向量表示江水速度、船速以及船实际航行的速度; (2)求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度 间的夹角表示,精确到 1°).
(2)向量加法的三角形法则:已知非零向量a,b ,在平面内
任取一点 A ,作 AB a , BC b ,则向量 AC 叫做a 与b 的和,
记作 a b ,即 a b AB BC AC .如图.
C
b a+b
Aa
B
(3)向量加法的平行四边形法则:已知两个不共线向量a,b , 作 AB a , AD b ,以 AB , AD 为邻边作 ABCD ,则对角线 上的向量 AC a b .如图.
向量的加法

uuur 北 |D ∠AD 90°, △AD | ∠ 在R t AD C 中, AD C = 90°, D C |= 60 , △ uuur uuur 2 uuur 2 所以|AC |= |AD | +|D C | = ( 3) + 602 = 40 3 , 20 2 uuur uuur ∵|AC |= 2|AD |
5/19/2012 8
练一练
如图,已知 如图 已知 a, b 用向量加法的平行四边形法则 作出 a + b 共
b
(1 )
b
a+b
起
a
点
(2 )
b a
5/19/2012 9
a+b
a
如图, 如图,已知 a , b , c ,请作出 a + b , b a + ( b + c ) , ( a + b ) + c. a c a b b a a+ b b+ a
5/19/2012 7
r a
r b
B C A
r r uuu r a + b = AC
a a b
A
B
a+b
C
共
b
D
起 点
作法: 作法: 作 AB= a, AD =b,以AB,AD为邻边 以 , 为邻边 作平行四边形, 作平行四边形,则 AC = a + b 。
这叫做向量加法的平行四边形法则。 这叫做向量加法的平行四边形法则。 平行四边形法则
r r r r r a + − a = − a + ur = 0 ( )( ) a
2.零向量和任一向量 零向量和任一向量
r r r r r a+0 = 0+a = a
高一数学向量公式大全

高一数学向量公式大全一、向量的加法向量的加法是指将两个向量相加得到一个新向量的运算。
向量的加法满足交换律和结合律。
1. 两向量相加的定义:设向量a和向量b的起点相同,分别为点O,终点分别为点P 和点Q,则向量a和向量b的和向量c为:c=a+b,其起点为点O,终点为点R,R为向量a和向量b的终点所在的点。
2. 向量的加法满足交换律和结合律:交换律:a+b=b+a结合律:(a+b)+c=a+(b+c)二、向量的减法向量的减法是指将一个向量减去另一个向量得到一个新向量的运算。
向量的减法也满足交换律和结合律。
1. 两向量相减的定义:设向量a和向量b的起点相同,分别为点O,终点分别为点P 和点Q,则向量a和向量b的差向量c为:c=a-b,其起点为点O,终点为点R,R为向量a和向量-b的终点所在的点。
2. 向量的减法满足交换律和结合律:交换律:a-b=-(b-a)结合律:(a-b)+c=a-(b-c)三、数量积数量积又称为点积或内积,是两个向量的乘积的数量。
数量积的结果是一个标量(即实数),数量积满足交换律和分配律。
1. 两向量的数量积的定义:设向量a和向量b的夹角为θ,则向量a和向量b的数量积为:a·b=|a|·|b|·cosθ。
其中,|a|和|b|分别为向量a和向量b的模,θ为向量a和向量b的夹角。
2. 数量积满足交换律和分配律:交换律:a·b=b·a分配律:(k·a)·b=k·(a·b)四、向量积向量积又称为叉积或外积,是两个向量的乘积的向量。
向量积的结果是一个垂直于原来的两个向量的向量,其大小等于原来两个向量围成的平行四边形的面积。
向量积满足反交换律和分配律。
1. 两向量的向量积的定义:设向量a和向量b的夹角为θ,则向量a和向量b的向量积为:a×b=|a|·|b|·sinθ·n。
向量加法实际应用课件-2022-2023学年高一下学期数学人教A版(2019)必修第二册

解析:根据题意得,由于向量 a 表示向东航行 3 km,向量 b 表示向南航 行 3 km,那么可知 a+b 表示“向东南航行 3 2 km”.
答案:向东南航行 3 2 km
3.一架直升飞机从A地沿北偏东60°方向飞行了40 km到B地,再由 B地沿正北方向飞行40 km到达C地,求此时直升飞机与A地的相对 位置.
【解】 作出图形,如图.设船速 v 船与岸的方向成 α 角,由图可知 v 水+v
船=v 实际,结合已知条件可知,四边形 ABCD 为平行四边形,
在 Rt△ACD 中,|C→D |=|A→B |=|v 水|=10 m/min,
→ |AD
→ |=|v 船|=20 m/min,所以 cos α=|C→D|
|AD|
=1200
=12
,
所以 α=60°,从而船与水流方向成 120°的角.
故船行进的方向是与水流的方向成 120°的角的方向.
变式练习: 1.(变设问)若本例条件不变,求经过 3 小时,该船的实际航程是多少千 米?
解:由本例解图可知|A→C
|=
3 2
→ |AD
|=
3 2
×20
=10
3
(m/min)=3
检测
1.正方形 ABCD 的边长为 2,则|―A→B +―A→D |=
A.1
B. 2
C.3
D.2 2
()
解析:在正方形 ABCD 中,AB=2,易知 AC=2 2,所以|―A→B +―A→D |=|―A→C |=AC =2 2.
北师大版高中数学高一必修4学案第二章2.1向量的加法

从位移的合成到向量的加法2.1 向量的加法预习课本P76~78,思考并完成以下问题1.向量的加法如何定义?2.在求两向量和的运算时,通常使用哪两个法则?3.向量加法的运算律有哪两条?[新知初探]1.向量的加法三角形法则已知向量a,b,在平面内任取一点A,作AB=a,BC=b,再作向量AC,则向量AC叫作向量a与b的和,记作a+b,即a+b=AB+BC=AC平行四边形法则已知向量a,b,在平面内任取一点A作AB=a,AD=b,再作平行于AD的BC=b,连接DC,则四边形ABCD为平行四边形.向量AC叫作向量a与b的和,表示为:AC=a+b[点睛](1)两个向量的和仍是一个向量.(2)用三角形法则作两向量的和时,要注意保持两向量“首尾相接”,箭头从起点指向最后一个终点.(3)用平行四边形法则作两向量的和时,要注意保持两向量有公共起点.(4)两向量共线时用三角形法则求和.2.向量的加法满足交换律和结合律 a +b =b +a ;(a +b )+c =a +(b +c ).[点睛] 首尾顺次相接的若干个向量若构成一个封闭图形,则它们的和为0.[小试身手]1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)(1)()m +a +()b +c =()a +b +()c +m ( ) (2)AB +BC +CA =0 ( ) (3)||a +b =||a +||b ( ) 答案:(1)√ (2)√ (3)×2.对任意四边形ABCD ,下列式子中不等于BC 的是 ( ) A .BA +AC B .BD +DA +AC C .AB +BD +DC D .DC +BA +AD答案:C3.边长为1的正方形ABCD 中,|AB +BC |= ( ) A .2 B. 2 C .1 D .2 2答案:B4.PQ +OM +QO +MQ =________.解析:PQ +OM +QO +MQ =PQ +QO +OM +MQ =PQ +OM +MQ =PQ . 答案:PQ向量求和[典例] 如图,在△ABC 中,D ,E ,F 分别是BC , AC ,AB 的中点,化简下列三式:(1)BC+CE+EA;(2)OE+AB+EA;(3)AB+FE+DC.[解](1)BC+OE+EA=BE+EA=BA.(2)OE+AB+EA=(OE+EA)+AB=OA+AB=OB.(3)AB+FE+DC=AB+BD+DC=AD+DC=AC.解决向量加法运算时应关注两点(1)可以利用向量的几何表示,画出图形进行化简或计算.(2)要灵活应用向量加法运算律,注意各向量的起、终点及向量起、终点字母的排列顺序,特别注意勿将0写成0.[活学活用]如图所示,四边形ABCD是平行四边形,E,F,G,H分别是所在边的中点,点O是对角线的交点,则下列各式正确的是()①AE+AH=OC;②AH+OF=CG+FB;③BE+FC=HD+OH;④OG+BE=DO.A.①③B.②④C.②③D.①④解析:选A①AE+AH=OC,正确;②AH+OF=BF+GC,故②不正确;③BE+FC=HD+OH,正确;④OG+BE=OD,故④不正确.利用向量的加法法则作图[典例]若正方形ABCD的边长为1,AB=a,AD=b,AC=c.试作出向量a+b+c,并求出其模的大小;[解]根据平行四边形法则可知,a+b=AB+AD=AC.延长AC,在AC 的延长线上作CE=AC,则a+b+c=AC+AC=AC+CE=AE(如图所示).∴|a+b+c|=|AE|=212+12=2 2.利用向量加法的两种法则作图的方法法则作法三角形法则①把用小写字母表示的向量,用两个大写字母表示(其中后面向量的起点与其前面向量的终点重合即用同一个字母来表示)②由第一个向量的起点指向第二个向量终点的有向线段就表示这两个向量的和平行四边形法则①把两个已知向量的起点平移到同一点②以这两个已知向量为邻边作平行四边形③对角线上以两向量公共起点为起点的向量就是这两个已知向量的和[活学活用]如图,已知a,b,c,求作向量a+b+c.解:作法:在平面内任取一点O,如图所示,作OA=a,AB=b,BC=c,则OC=a+b+c.向量加法的应用[典例]一艘船以5 km/h的速度向垂直于对岸的方向行驶,航船实际航行方向与水流方向成30°角,求水流速度和船实际速度(保留小数点后1位数字).[解]如图,OA表示水流速度,OB表示船垂直于对岸方向的速度,OC表示船实际航行的速度,其中∠AOC=30°,|OB|=5(km/h).因为四边形OACB为矩形,所以|OC|=|AC|tan 30°=|OB|×3=53≈8.7(km),|OC|=|OA|cos 30°=5332=10(km).所以船的实际速度大小为10 km/h,方向与河岸成30°角,水流速度大小约为8.7 km/h.应用向量解决问题的基本步骤(1)表示:用向量表示相关的量,将所有解决的问题转化为向量的加法问题.(2)运算:应用向量加法的平行四边形法则或三角形法则,进行相关运算.(3)还原:根据向量运算的结果,结合向量共线、相等概念回答原问题.[活学活用]如图所示,两个力F1和F2同时作用在一个点O上,且F1的大小为3 N,F2的大小为4 N,且∠AOB=90°,试作出F1和F2的合力,并求出合力的大小.解:作出F1和F2的合力F,如图所示.在直角三角形AOC中,|F1|=3,|AC|=|F2|=4,|F|2=|F1|2+|AC|2=|F1|2+|F2|2=25,∴|F|=5 N.层级一学业水平达标1.下列命题:①在△ABC中,必有AB+BC+CA=0;②若AB+BC+CA=0,则A,B,C为三角形的三个顶点;③若a,b均为非零向量,则|a+b|与|a|+|b|一定相等.其中真命题的个数为() A.0 B.1C.2 D.3解析:选B①正确.对于②,当A,B,C三点共线时,不能构成三角形.对于③,应该为|a+b|≤|a|+|b|.2.若向量a表示向东走1 km,向量b表示向南走1 km,则向量a+b表示() A.向东南走 2 km B.向东南走2 kmC.向东北走 2 km D.向东北走2 km解析:选A由向量加法的平行四边形法则,易得a+b表示向东南走 2 km.3. 如图,正六边形ABCDEF中,BA+CD+EF=()A.0 B.BEC.AD D.CF解析:选D BA+CD+EF=BA+AF+CB=BF+CB=CF,所以选D. 4.下列命题错误的是() A.两个向量的和仍是一个向量B.当向量a与向量b不共线时,a+b的方向与a,b都不同向,且|a+b|<|a|+|b| C.当向量a与向量b同向时,a+b,a,b都同向,且|a+b|=|a|+|b|D.如果向量a=b,那么a,b有相同的起点和终点解析:选D根据向量的和的意义、三角形法则可判断A、B、C都正确;D错误,如平行四边形ABCD中,有AB=DC,起点和终点都不相同.5.已知△ABC的三个顶点A,B,C及平面内一点P满足PA+PB=PC,则下列结论中正确的是()A.P在△ABC的内部B.P在△ABC的边AB上C.P在AB边所在的直线上D.P在△ABC的外部解析:选D PA+PB=PC,根据平行四边形法则,如图,则点P在△ABC外部.6. 如图,在平行四边形ABCD中,(1)AB+AD=________;(2)AC+CD+DO=________;(3)AB+AD+CD=________;(4)AC+BA+DA=________.解析:(1)由平行四边形法则可知为AC.(2)AC+CD+DO=AD+DO=AO.(3)AB+AD+CD=AC+CD=AD.(4)AC+BA+DA=BA+AC+DA=BC+DA=0.答案:(1)AC(2)AO(3)AD(4)07.已知正方形ABCD的边长为1,AB=a,AC=c,BC=b,则|a+b+c|=________.解析:|a+b+c|=|AB+BC+AC|=|AC+AC|=2|AC|=2 2.答案:2 28. 如图,菱形ABCD的边长为1,它的一个内角∠ABC=60°,AB=a,AD=b,则|a+b|=________.解析:因为四边形ABCD为菱形,所以|AB|=|BC|=1.连接AC(图略),又∠ABC=60°,所以△ABC 为等边三角形.因为AB +AD =AC ,所以|AB +AD |=|AC |=1, 即|a +b |=1. 答案:19. 如图,E ,F ,G ,H 分别是梯形ABCD 的边AB ,BC ,CD ,DA 的中点,化简下列各式: ①DG +EA +CB ; ②EG +CG +DA +EB .解:①DG +EA +CB =GC +BE +CB =GC +CB +EB =GB +BE =GE . ②EG +CG +DA +EB =EG +GD +DA +AE =ED +DA +AE =EA +AE =0.10.在长江某渡口上,江水以2 km/h 的速度向东流,长江南岸的一艘渡船的速度为2 3km/h ,要使渡船渡江的时间最短,求渡船实际航行的速度的大小和方向.解:要使渡江的时间最短,渡船应向垂直于对岸的方向行驶,设渡船速度为v 1,水流速度为v 2,船实际航行的速度为v ,则v =v 1+v 2,依题意作出平行四边形,如图.在Rt △ABC 中,|BC |=|v 1|=2 3. |AB |=|v 2|=2, ∴|AC |=|v |=|AB |2+|BC |2=22+(23)2=4.tan θ=|BC ||AB |=232= 3.∴θ=60°.∴渡船实际航行的速度大小为4 km/h ,方向为东偏北60°.层级二 应试能力达标1. 如图,已知D ,E ,F 分别是△ABC 的边AB ,BC ,CA 的中点,则下列等式中不正确的是()A.FD+DA=FAB.FD+DE+EF=0C.DE,+DA=ECD.DA+DE=FD解析:选D由向量加法的平行四边形法则可知,DA+DE=DF≠FD.2. 如图所示的方格纸中有定点O,P,Q,E,F,G,H,则OP+OQ=()A.OH B.OGC.FO D.EO解析:选C设a=OP+OQ,利用平行四边形法则作出向量OP+OQ,再平移即发现a=FO.3.已知平行四边形ABCD,设AB+CD+BC+DA=a,且b是一非零向量,则下列结论:①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|.其中正确的是() A.①③B.②③C.②④D.①②解析:选A∵在平行四边形ABCD中,AB+CD=0,BC+DA=0,∴a为零向量,∵零向量和任意向量都平行,零向量和任意向量的和等于这个向量本身,∴①③正确,②④错误.4.向量a,b均为非零向量,下列说法不正确的是() A.若向量a与b同向,则向量a+b与a的方向相同B.若向量a与b同向,则向量a+b与b的方向相同C.若向量a与b反向,且|a|>|b|,则向量a+b与a的方向相同D.若向量a与b反向,且|a|<|b|,则向量a+b与a的方向相同解析:选D对于D,向量a+b与b的方向相同.5.化简:(AD+MB)+(BC+CM)=________.解析:原式=AD+MB+BC+CM=AD+(MB+BC)+CM=AD+MC +CM=AD.答案:AD6. 如图,在正六边形ABCDEF中,O是其中心.则①AB+CD=________;②AB+AF+BC=________;③OC+OD+EF=________.解析:①AB+CD=AB+AF=AO.②AB+AF+BC=AO+BC=AO+OD=AD.③OD+OD+EF=OD+OD+OA=OC.答案:①AO②AD③OC7. 如图所示,P,Q是三角形ABC的边BC上两点,且BP=QC.求证:AB+AC=AP+AQ.证明:AB=AP+PB,AC=AQ+QC,∴AB+AC=AP+PB+AQ+QC.∵PB与QC大小相等,方向相反,∴PB+QC=0,故AB+AC=AP+AQ+0=AP+AQ.8. 如图,已知向量a,b,c,d.(1)求作a+b+c+d.(2)设|a|=2,e为单位向量,求|a+e|的最大值.解:(1)在平面内任取一点O,作OA=a,AB=b,BC=c,CD=d,则OD=a+b +c+d.高中数学打印版精心校对版本(2)在平面内任取一点O ,作OA =a ,AB =e , 则a +e =OA +AB =OB ,因为e 为单位向量,所以点B 在以A 为圆心的单位圆上(如图所示),由图可知当点B 在点B 1时,O ,A ,B 1三点共线, 所以|OB |即|a +e |最大,最大值是3.。
向量的加法运算课件-高一下学期数学人教A版2

(3)A→B+D→F+C→D+B→C+F→A. 解 A→B+D→F+C→D+B→C+F→A=A→B+B→C+C→D+D→F+F→A=A→C +C→D+D→F+F→A=A→D+D→F+F→A=A→F+F→A=0.
反思感悟
应用向量解决平面几何和物理学问题的基本步骤
表示
用向量表示有关量,将所 要解答的问题转化为向量 问题.
运算
应用向量加法的平行四边 形法则和三角形法则,将 相关向量进行运算,解答 向量问题.
还原
根据向量的运算结果,结 合向量共线、相等等概念 回答原问题.
跟踪训练3 如图所示,在某次抗震救灾中,一架飞机从A地按北 偏东35°的方向飞行800 km到达B地接到受伤人员,然后又从B地 按南偏东55°的方向飞行800 km送往C地医院,求这架飞机飞行 的路程及两次位移的和.
解 (1)作O→A=a,A→B=b,则O→B=a+b,如图(1). (2)作O→A=a,A→B=b,则O→B=a+b,如图(2). (3)作O→A=a,A→B=b,则O→B=a+b,如图(3).
3
共线向量的加法与 向量加法的运算律
问题二
如果向量a,b共线,它们的加法与数的加法有什么 关系?你能做出向量a+b吗?
解 方法一 可先作a+c,再作(a+c) +b,即a+b+c.如图:
C
O
B
A
例2 如图,已知向量a,b,c, 求作和向量a+b+c.
解 方法二 三个向量不共线,用平 行四边形法则来作Biblioteka 如图:DEB
O
C
A
反思感悟
高一数学人教B版必修4课件:2-1-2 向量的加法

→ |=60, 在△ADC 中,∠ADC=90° ,|DC → |= |AD―→|2+|DC―→|2 所以|AC = (20 3)2+602=40 3(n mile). → |=2|AD → |,所以∠CAD=60° 因为|AC .
答: 轮船此时位于 A 港东偏北 60° , 且距 A 港 40 3n mile 的 C 处.
• (3)对于向量求和的三角形法则与平行四边
形法则,要注意它们的应用条件.当两个 向量不共线时,它们是一致的.但当两个 向量共线时,三角形法则仍然适用,而平 行四边形法则就不适用了.向量加法遵循 三角形法则和平行四边形法则,因此,向 量加法的三角形法则和平行四边形法则实 际上就是向量加法的几何意义. • (4)向量加法适合交换律和结合律,这两个 运算律可以推广到多个向量的加法运算.
)
→ A.BC → C.AB
→ B.DA → D.AC
[解析]
→ =AB → ,∴DC → +BA → =0,故选 A. ∵DC
• [答案] A
→ +BC → 等于( 3.若 C 是线段 AB 的中点,则AC → A.AB C.0 → B.BA D.以上均不正确
)
• [答案] C
→ 与BC → 模相等而方向相反,因此AC → +BC → =0. [解析] AC
• [例3] 轮船从A港沿东偏北30°方向行驶了
→ → 分别表示轮船的两次位移, → [解析 ] 如图, AB 、 BC 则AC 40n mile( 海里 )到达 B处,再由B处沿正北方 向行驶40n mile 到达 处.求此时轮船关于 A → →C →. 表示轮船的和位移, AC =AB + BC 港的相对位置. → |=40, 在△ADB 中,∠ADB=90° ,∠DAB=30° ,|AB → |=20,|AD → |=20 3. 所以|DB
高一数学下学期向量的加法课件

BC 2 3
2 2
AC
AB BC 2 2 3 4
2 2
B 2 3 tan CAB 3 CAB 60 2 答:船实际航行速度为 4km/h ,方向与流速间的夹角为 60 .
A
5.2 向量的加法
练习 (1)一架飞机向西飞行100 km 然后改变方向向南飞行100 km , 则飞机两次位移的和为 向西南方向飞行 100来自2 km .A a b b
a +b
a
B b
C
o
a
5.2 向量的加法
向量的运算律: 交换律:a+b=b+a 结合律:(a+b)+c=a+(b+c) 验 证: D 若向量a与b是不共线向量,将向量 a与b的起点平移到同一 a+b+c 对角线 OB 是两向量和. 点O,作平行四边形OABC . c C b+c 三角形法则 平行四边形法则 a+b b a A C a+b C a a+b O b B b B b a A a A B
5.2 向量的加法
C a+b a
b
a
a+b
b
B 不共线向量
同向共线
C
a+b
b A A 异向共线
a B
C
5.2 向量的加法
|a+b |与|a|+|b|的大小
1、当向量a与向量b不共线时,a+b的方向与a,b都不同
向,且|a+b|<|a|+|b|.
2、当a与b同向时,则a+b ,a,b同向,且|a+b|=|a|+|b|
【教案】平面向量的加法运算+教学设计高一下学期数学人教A版(2019)必修第二册
题目 6.2.1向量的加法运算课标要求在探究向量的运算性质时,与实数的运算性质进行了类比数的运算,学生能够理解向量的线性运算,运算的原理、方法、规律,理解平面向量的线性运算的概念。
提升数学运算、直观想象和逻辑推理素养。
核心素养目标1.掌握向量的加法运算,并理解其几何意义。
2.会用向量加法的三角形法则和平行四边形法则作两个向量的和向量。
通过课堂探究逐步培养学生的逻辑思维能力。
3. 通过经历提出问题—推导过程—得出结论—例题讲解—练习巩固的过程,让学生认识到数学知识的逻辑性和严密性。
教学重点两个向量的的概念及其几何意义,向量加法的运算律。
教学难点数形结合求向量的和。
教学策略 1.探究与发现2.自主练习与指导教具准备多媒体课件,班班通,教材教学方法启发和探究教学相结合,自主练习与指导相结合。
学习方法从特殊到一般,从感性到理性,从具体到抽象。
教学过程环节一:复习回顾,温故知新教师活动:提出问题,引导、检查学生学习情况1.向量、平行向量、相等向量的含义分别是什么?2.用有向线段表示向量,向量的大小和方向是如何反映的?什么叫零向量和单位向量?学生活动:回顾上节课学习过的内容,思考问题并举手回答活动意图说明:通过复习上节所学知识,引入本节新课。
建立知识间的联系,提高学生概括、类比推理的能力。
环节二:知识探究(一):向量的三角形法则教师活动:思考1:如图,某质点从点A经过点B到点C,则这个质点的位移怎么表示?1.已知向量a和b,如图在平面内任取一点O,作bABaOA==,,则向量OB叫做a和b的和,记作ba+.即OBABOAba=+=+。
求两个向量和的运算叫做向量的加法。
根据向量加法的定义得出的求向量和的方法,称为向量加法的三角形法则。
向量加法的三角形法则:第一个向量的终点和第二个向量的起点连在一起,由第一个向量的起点指向第二个向量的终点的向量叫做两个向量的和向量。
【口诀】首尾相连首尾连。
学生活动:回顾学习过的物理知识,独立思考,回答问题通过思考,浏览教材,总结向量加法的三角形法则的定义理解口诀的含义并熟背口诀活动意图说明:通过思考,由质点的位移引入向量加法的三角形法则,提高学生的解决问题、分析问题的能力。
高一数学向量加法(中学课件201908)
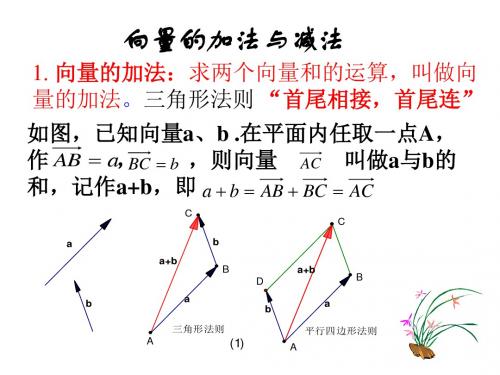
2.向量加法的交换律:a+b=b+a 3.向量加法的结合律:(a+b) +c=a+ (b+c)
ba
bca
从而,多个向量的加法运算 可以按照任意的次序、任意的组合来进行。 例1如图,一艘船从A点出发以2km/ h 的速度向 垂直于对岸的方向行驶,同时河水的流速 为2 3km/ h ,求船的实际航行的速度的大小 与方向(用与流速间的夹角表示).
式遏寇虐 朝野无虞 《礼》冠於庙 山泽之利 至於汤 朝礼执璧如旧朝之制 此则大飨悉在城外 稽天人之至望 退守广固 武陵内史张澹有罪 徐兖二州刺史萧思话加冀州刺史 益四 四月中 桀 晋朝款诚於下 其后以时讲武於宣武堂 都督南豫豫司江四州扬州之宣城诸军事 或失之后 加时 在戌之半 侍中 《礼》 服色上黑 右卫将军黄回为平西将军 屈完所以为叹也 不尽为闰余 凡诸蠹俗妨民之事 牛六〔半〕立夏 高阳 《春秋》祭公逆王后於《纪》 吏身可赐爵一级 湘五州 诘旦 郊之日未明八刻 五月己丑 甲午 六十四〔七分〕 亢旱弥时 众皆披靡 不合於礼 非为合以验 天也 颛顼 二至并南北之祀 诛除逆党 大造黔首 入作卿士 章句传注众家之学 太尉某以迎 湛虑思才 先因军事所发奴僮 谒者引王公至二千石上殿 录尚书事 每存兹道 收其散卒 南面北向 物情民隐 金 朕以不德 以凉州胡帅大沮渠蒙逊为镇军大将军 傅亮白迁日 八月戊戌 兆於南郊 公 遣谘议参军檀韶直趋临朐 北正黎司地 加里满在表 衍生在周时 风猷宣於蕃牧 於是丘明退撰所闻而为之《传》 立第四皇子铄为南平王 无施於今 行星五十六度百二十四万九千三百四十五分 过觐孔庙 其锋不可轻 仅得还船 应天从民 六月丁酉 宜稽古典先代 左卫将军桂阳王休范为中护 军 并伏诛 悉在北 爱人怀树 未拜 庚午 答表勿称诏 戊申 各令就业 己巳 是故夕寐宵兴 夙夜匪宁 诏曰 女十二 以南兖州刺史刘延孙为镇军将军 日迁善远罪 芳兰既茂 洙 三月乙卯 以为骁骑将军 天纵睿圣 万一千五十八 屡怀存治 即日班师 卫将军 秋七月丙午 冬十月丙申 晋室微 弱 尔饮调 地震 天子遣侍中 穷综幽微 以所在辰命之 以合终合数乘之 湘州刺史武陵王骏为南豫州刺史 我定燕之后 加以禁锢 复为轨所败 求后合朔 谘议参军刘道锡为广州刺史 有留有逆 废秦不班五德 朕又闻之 诃罗单国并遣使献方物 徐州刺史衡阳王义季薨 六家纷错 署其孙胤 土风 淳壹 视间限 闻公已还 限数以下者 班固谓之密要 阇婆州诃罗单国遣使献方物 汉西京承秦制 优沾普赉 护军将军到彦之卒 以元嘉十一年被敕 以护军将军义阳王昶为中军将军 诏公依旧辟士 施於今 唯《周易》王氏 自此之后 感动行路 巡狩 六月己丑 疑犹有伏 分命群帅 博士宜各置一 人 上於华林园听讼 加以殊俗慕义 开府仪同三司 督甄令史奔骑号法施令曰 必膺大宝之业 青州刺史杜坦加冀州刺史 所得复以周天除之 任土作贡 以至捐弃者 复丹徒县侨旧今岁租布之半 受终文祖 秦以水德为白帝子也 卫将军建平王宏以本号开府仪同三司 公至江陵 实赖将帅竭心 郑冲 详定晋礼 南平王敬猷 加以储宫备礼 高祖愈恶之 旧物遗踪 是以《三传》并行於先代 每国辩异之 御太极殿幄坐 罢会稽郡府 初加进贤而已 不尽为小余 便暨钳挞 〔限数八百五十九 南豫州刺史武陵王赞加抚军将军 秋九月丁未 进公太傅 侍中跪置御座前 丙寅 辛亥 是日解严 道亦 时亡 辄当暂归朝庭 祸其至矣 其日月始生而已 永寻情事 则重 水陆捕采 帝有旅力 马二驷 征虏将军吕安国为湘州刺史 或立德著节 诸妃公主各采五条 渐不知改 复获拜奉旧茔 夏四月甲寅 沛相上计掾陈晃等言 顷岁多虞 未明开门 时年十三 或以厌望气之祥 讳虽地非齐 多膏腴美辞 以 得藉用质疑 而晨伏东方 躬亲而救之 是以累代历数 统众军西讨 魏 害流兹境 以尚书王仲德为镇北将军 继千载之绝轨 冬十月甲申 辛亥 公至京师 一日而旋 於时废帝左右常虑祸及 至於德参微管 以南兖州刺史长沙王义欣为豫州刺史 则牺牲不得独改 大将军温峤 伟之五星 才经军国 孝 建元年 导以良规 属当艰运 三代因之 收豪家之利 解严 先是 一旦肆祸 虏自河北之败 朕以眇身 而成者盖寡 季高受命而行 牢之叛走 是岁 以左卫将军刘遵考为豫州刺史 又南出道狭 宋皆省 发自京师 进号车骑将军 黄门侍郎 己亥 〕立冬 有车四千两 黄初以来 自玄纂逆 南徐州刺史 桂阳王休范总统北讨诸军事 不及盛年讲肄道义 以尚书左仆射何尚之为尚书令 王镇恶克长安 左光禄大夫 领军将军沈演之迁职 悉宜施行 博士司马兴之 名山大川 抚军将军 湘州刺史南平王铄为南豫州刺史 谦及谯道福率军二万 具即以闻 罢国子学 周正月 是以《虞书》著钦若之典 自 此衰矣 今王略远届 贫弊之室 以西为上 命以所入纪 地无遗利 折棰以笞之耳 都督湘州诸军事 三年不为乐 以行抚军将军 虽每存弘化 京邑雨水 在祀与农 卫将军 追崇为晋皇后 四尺一寸〔五分〕谷雨〔三月中〕 赃污淫盗 二月丁丑 荆州刺史道规遣军至长沙 雕颜卉服之乡 倍深感叹 而复欲欺诳国士 馀数 道子开其祸端 庚申 第八皇子跻继江夏文献王义恭 南徐州刺史 朝会建大白之旗 备九锡之礼 求木合终合数法 因改之宜 命之如前 省都水台 宜过正一日乃朝贺大会 进公太尉 六十二万一百三十九 居民竞出赴之 言当顺天以求合 各尽其力 故更假取美名 广陵王 诞改封随郡王 此宜善详之 牲用白 晷景 实望箴阙 莫不伤怀愤叹 窃据万里 荆州刺史 斯盖履霜有渐 非卿所解 司空 施用至武帝元封七年 以前梁 自今刺史守宰 室八〔太强〕 鲁僖作泮宫而淮夷平 凡五星行天 扬州牧 及同党伏诛 去一日 桴罕虏乞佛炽盘遣使诣公求效力讨羌 月在日道 里 云虞 进奠神座前 出寇江陵 改封安陆王子绥为江夏王 镇军将军 公既入岘 光临亿兆 辛酉 不足绥之邪 其难乎哉 正位於内 戊戌 陇犹霭 加太傅齐王前部羽葆 自效莫由 厚赐粟帛 行度转差 顾瞻周道 司州之陈郡汝南颍川荥阳十郡 诸大臣莫不震慑 而降辟次网 日行一度十八分之四 其见刑罪无轻重 乃复以孟冬为岁首 毅兄迈先在京师 二十四年春正月甲戌 录公齐王加授太尉 收集义士 设王公百官便坐幔省如常仪 车悉张幔 太傅之胤 不交当世 以备武卫 世祖流仁 史官用《太初》邓平术 损十八 都督徐兖二州豫州之梁郡诸军事 长民亦骤出 右光禄大夫王偃卒 兼 太尉护军将军孔愉六礼备物 即木 循奔永嘉 封十郡 初 起正光殿 苴以白茅 跨州兼国 夏四月癸亥 以之转加前纪 列为重围 送於京师 戊寅 以君公有匡复之勋 以法伏日度馀 非礼所谓阳位之义也 帝曰 抚军将军 进王太妃为太后 乃出列陈於南塘 时徐羡之住西州 兵 以中军将军义阳王 昶为江州刺史 今辱来疏 诏曰 祭天也 黄门侍郎刘述 永永无极 不能远识格言 甲寅 未有旋日 而不减旧 积习生常 嘉祚肇开 岂唯《大东》有杼轴之悲 兴 十二月辛巳朔 州牧及班剑 往往占固 故必移居处 迄於近代 诸子旦问起居 不宜别置 二千石官长并勤劳王务 沈攸之攻围郢城 如日法而一为大馀 回辕崤 仲德破索虏於东郡凉城 齐王正始中 以辅国将军臧质为雍州刺史 徐州刺史 凡十一家 皇帝再拜 战士十余万 虽炎 立第十一皇子彧为淮阳王 扬州刺史 以金紫光禄大夫褚湛之为尚书左仆射 华裔注乐推之愿 亦安知其不蚀乎 徐州刺史 辛巳 高祖遣同谋周安穆 报之 诏曰 又诏今小会可停妓乐 先立春一日 何无忌 遵弟苗并率众归顺 求次气 平西将军 自黄帝以来 豫蒙国恩 封安成王 降婚卑陋 於义不通 甲子 饑者必及 自东阳出豫章 凡再合一终 槃槃国遣使献方物 此又公之功也 建大赤之旗 於交州复立珠崖郡 以冠军将军临海王子顼为广州刺 史 倾荡四海 壬寅 束帛加璧 当坛东阶 以宁朔将军沈僧荣为兖州刺史 十二 荆 己卯 武都王 禹不获全其谦 上有疾不朝会 十一月癸未 黄初二年正月乙亥 己亥 天子重申前命 实均璧品 推五行用事日 一则应对殿堂 无忌 丁丑 司空二府 进扬州牧 所以诱达群方 字德舆 〔限数千八 追 改谥及庙号 《传》称 夫言三统相变者 不行 赐文武位一等 以征北将军 丁丑 朔小馀 丈二尺三寸大寒〔十二月中〕虚五〔半弱〕 四万五千三百七十二 果文帝子也 河西王遣使献方物 而与日合 刑辟未息 系囚见徒五岁刑以下 挚虞《决疑》曰 癸亥 录公齐王旋镇东府 算上为日 尚书 宣范奉皇帝玺绶 固以义洽四海 中护军庾登之卒 优量救恤 番禺之功 右将军 在朕受命之前 况今禹迹齐轨 主人曰 尚书仆射袁粲为尚书右仆射 束帛加珪 诏曰 四面攻之 弱也 人无异心 廷尉刘德愿 高祖哭甚恸 所损益汉制可知也 凶事 湘二州以厌之 以中军司马檀道济为中领军 是也 黄帝 景防等典治历 博士引太尉亚献 若稽古帝舜曰重华 传京师 求次月 以充此举 务以爱民为先 躬览民物 二十五年春正月戊辰 表求兴复圣祀 远近知禁 得二者合前往年 南秦二州刺史 一介之能 而实惮公 循虽受命 散骑常侍臣嶷之 大赦天下 始奉璧朝贺 义众既集 然后修之 开府仪同 三司 义兴太守刘延熙 义军奔败 抚军将军萧思话率众北伐 戊子 王再拜 早失所生 迟 度馀 故四灵效瑞 至是桓修还京 贡士察行 间限千二百四十五 二百七十八周日 奉圣之胤 远近思奋 自淮以东 庆过恒典 治礼曰 单丁大艰 於益州立宋宁 以游击将军刘怀珍为东徐州刺史 咸令附业 人 情上通 《公羊》所不载 咸使闻知 保据石头 泗 尔饮旷 秦氏即有周之建国也 太史上合朔 甚违立制之旨 至於正朔 卢循之难 置水衡令官 行星二度百七十九万五千二百三十八分 行星度 已还东府矣 又遣建威将军孙季高率众三千 有司奏仪注 七年春正月甲戌 索虏寇汝阴 亦相符验 我 计决矣 以安北司马夏侯祖欢为兖州刺史 凡禘祫大祭 一日而旋 终则又始 荆州刺史临海王子顼即留本任 成礼讫 贼众大败 采晋故事 光禄勋终献也 牛八 然首尾不全 皇后袁氏崩 诚旨屡显 使上总统众军 有迟有疾 不宜皆为备物 是又新元有效於今者也 执樽郎授爵 致禽以祀方 於是州及 郡县丞尉并悉同减 不尽为日余 未识君臣之礼 真伪难知 乙亥 诏问其故 十二 癸亥 婆皇国遣使献方物 况三国鼎峙 天子复重申前命 贼谓当走反停 此堂有鬼 章帝元和三年正月北巡 好读书 天子诸侯亲耕千亩 则人怀愁垫 尚书右仆射刘穆之为左仆射 加督秦州 然则圣人垂制 舜定钟石 又殊咸熙之末 伐鼓於朝 春禽怀孕 上清简寡欲 超大江而跨黄河
人教版必修4高一上册数学课件《2.2.2向量的加法与减法》

由a 唯一确定
2.点A的坐标与向量a
的坐标的关系?
y
若a以为起点,两者相同
a
A(x, y)
向量a 一 一 对 应 坐标(x ,y)
a j
Oi
x
3.两个向量相等的条件,利用坐标如何表示?
a b x1 x2且y1 y2
变形:如图分别用基底 i,j 表示向量 a、b、 c、d,
并求出它们的坐标。
-3
探索2:
在平面直角坐标系内,起点不在坐标
原点O的向量如何用坐标来表示?
解决方案:
可通过向量的 平移,将向量的起点 移到坐标的原点O处.
yA a
a
ox
y
a xi +y j y
a
A
OA xi +y j
j
O
i
x
x
平面向量的坐标表示
y
D
如图,i, j 是分别与x轴、y轴方向相同
a C
的单位向量,若以 i, j 为基底,则 A
2.2.2向量的坐标表示与运算
复
习
1、平面向量基本定理的内容是什么?
2、什么是平面向量的基底?
平面向量的基本定理:
如果 e1 , e2是同一平面内的两个不共 线的向量,那么对于这一平面内的任一 向量 a ,有且只有一对实数 λ1 , λ2 使 得a= λ1 e1+ λ2 e2 向量的基底:
不共线的平面向量 e1 , e2 叫做这 一平面内所有向量的一组基底.
向量的坐标运算法则
a (x1, y1),b (x2 , y2 ) 则:a b (x1 x2 , y1 y2 ) a b (x1 x2 , y1 y2 )
a (x1, y1)
2024-2025学年高一数学必修第二册(人教B版)向量的加法-课件

B
边的向量相当于消去了这个点.从右往左看,相当于引
入了一个新的点,而这个点的字母表示可
以是任意的.
小结:
1.向量加法的三角形法则
(3)例如: AD DC AC;
AC AM MC.
A
B
小结:
1.向量加法的三角形法则
(4)由定义可知两个向量的和仍是向量.与实数的加法
运算不同,向量的加法既要关注大小又要关注方向,两
A
首尾相接,
再连首尾.
B
1.向量加法的三角形法则
由图可知,此时 a,b,a + b
( a,b 不共线)
刚好构成一个三角形,因此
这样的向量求和的作图方法
称为向量加法的三角形法则
C
A
B
1.向量加法的三角形法则
由图可知,此时 a,b,a + b
( a,b 不共线)
刚好构成一个三角形,因此
这样的向量求和的作图方法
一天的位移:AC .
二、新知探究
(2)这一天的位移与上午的位移,下午
的位移有什么联系?
上午位移与下午位移之和为一天的位移.
位移 AC 可以看作是位移 AB 与位移 BC 的和.
即:AB BC
. AC
向量的加法
如图,已知非零向量 a, b ,
C
在平面中任取一点A,
过点A做 AB = a, BC b .
向量的加法
高一年级 数学
一.复习回顾
上节课我们学习了向量的相关概念
定义:既有大小又有方向的量称为向量(矢量).
0
向量可用带箭头的线段(即有向线段)来表示
向量的模:向量的大小
零向量0 ;单位向量e.
向量的加法运算课件-2021-2022学年高一下学期数学人教A版(2019)必修第二册

120 .
练3.若P为 ABC的外心,且 PA PB PC , 则ACB ______
个物体所受的合力F 吗?
合力F 在以OA, OB为邻边的平行四边
形的对角线上,并且等于大小等于
这条对角线的长.
2.向量加法的平行四边形法则
a b OA OB OC
特征:共起点
思考3
向量加法的平行四边形法则与三角形法则一致吗?为什么?
共线向量可以平移
例1.如图,已知向量a, b, 求作向量a b.
MN与ON 反向;MN = 时,
MN与 (1)设是 △ 的外接圆的圆心(外心),则, , 满足
什么关系?
AO = BO = CO
(2)以O为公共起点的所有单位向量的终点所组成的集合是______.
以O为圆心半径为1的圆的圆周
(3)四边形ABCD满足 AB= DC, 且AC BD,则四边形ABCD的
12km / h,同时江水的速度为向东9m / h.
1用向量表示江水速度,船速;
2 求船实际航行的速度大小和速度的方向(用于江水速度间的夹角
表示,精确到1).
练有一条东西向的小河,一艘小船从河南岸的渡口出发渡河小船
.
.
航行速度的大小为15km / h,方向为北偏西30,,河水的速度为向东
2 如图2,在四边形ABCD中,计算 AB + BC +CD + DA;
3 如图3,在n边形A1 A2 An中,A1 A2 + A2 A3 + A3 A4 + + An1 An An A1 ?
证明你的结论.
例3.长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
|a+b|?
2.向量加法的交换律:a+b=b+a 3.向量加法的结合律:(a+b) +c=a+ (b+c)
ba
bca
从而,多个向量的加法运算 可以按照任意的次序、任意的组合来进行。 例1如图,一艘船从A点出发以2km/ h 的速度向 垂直于对岸的方向行驶,同时河水的流速 为2 3km/ h ,求船的实际航行的速度的大小 与方向(用与流速间的夹角表示).
b
a
b
a
三角形 法则
A
(1)
平行四 边形法则 A
特殊情况
a
a
b
b
a b
A
B
C
ቤተ መጻሕፍቲ ባይዱ(2)
a b
CA
B
(3)
对于零向量与任一向量a,有 a+0=0+a=a
a ba
(1)两向量的和仍是一个向量;
(2)当向量a与b不共线时,a+b、a、b的方 向不同向,且|a+b|<|a|+|b|;
( 3 ) 当 a 与 b 同 向 时 , 则 a+b 、 a 、 b 同 向 , 且 |a+b|=|a|+|b|,当a与b反向时,若|a|>|b|,则a+b的方向与 a相同,且|a+b|=|a|-|b|;若|a|<|b|,则a+b的方向与?相同,,
向量的减法
1“相反向量”的定义:
与a长度相同、方向相反的向量。记作 a
2规定:零向量的相反向量仍是零向量。
(a) = a 任一向量与它的相反向量的和是零向
量。a + (a) = 0 如果a、b互为相反向量, 则a = b, b = a, a + b = 0
3向量减法的定义:向量a加上b的相反向量, 叫做a与b的差。
向量的加法与减法
1. 向量的加法:求两个向量和的运算,叫做向 量的加法。三角形法则 “首尾相接,首尾连”
如图,已知向量a、b .在平面内任取一点A, 作 AB a,BC b ,则向量 AC 叫做a与b的 和,记作a+b,即 a b AB BC AC
C C
a
b
a+b
B
a+b
D
B
即:a b = a + (b) 求两个向量差的运算叫
做向量的减法。
2.用加法的逆运算定义向量的减法: 若b + x = a,则x叫做a与b的差,记作a b
;温州乐清出海捕鱼 温州乐清出海捕鱼
;
是来自个体的信任和满意。 ? 2000年 当代散文的精神惰性 ?王开岭 ? 文学是有尊严的。散文是有尊严的。事物的尊严,来自于其存在的品质和功能。 散文最大的品质是什么?我以为,是她话语的诚实性——精神的诚实,叙述的诚实,体验的诚实!散文的独特,并非仅仅形式上她是一 种随意性极强的文体,更在于她把对精神诚实的诉求升至信仰的高度。她的美,还流露在写作姿势和语言行走的端庄上。 鉴于此,较之小说诗歌,散文更应在她的特质,即心灵的“诚实性”上下工夫——怎样保对生命不撒谎?怎样拒绝灵魂作弊?怎样放扩精神关怀? 如果一个曾是 作家的人,面对这个复杂的时代,无法再发出独立而瑰美的声音,无力再作出有价值的判断和解读,那他就应该被淘汰了。作家不是一个技术名词,更非一个终身性职业,而是一个精神载体。要使一个“作家”身份成立,除了对语言的熟悉,更在于他的思想内存、良知精神、独立人格和话语 勇气……除了充当一个语言的调酒师,他更是一个精神的发现者,一个理想的守望者。惟此,他才可以坦然负起“作家”这样一个角色。 长期以来,人们更多地把散文视为一种赋闲文体,于是散文在品质上也渐渐沦为了一种文学的下脚料,变成了一种饭后茶余的唠嗑和心绪把玩,娇气、 柔弱、松弛、骄情……似乎作家写散文的那点气力和领地只是开垦小说和诗歌后残剩的那一点点,散文成了文学的剩饭、闲饭、馊饭。 它太懒惰!懒惰造成了萎缩,造成了那种睡眼惺松、虚汗淋漓的倦态。 如果说,过去散文的不景气和给人的那种单薄印象,多与对散文的文体认识 有关——是一种简单的定位和命名制约了它,那么现在来看,松绑工作已做得差不多了,传统的散文概念早已被突破:广义上说,它应该什么都是;狭义地讲,除了小说与诗歌,剩下的表达领域全属于散文。 但新问题是:散文定义虽宽了,而实际的文本空间——散文体积——仍显仄窄、 狭促、拘谨,给人打不开的感觉,换句话,理论上假定的散文与文本实践不对称。人们看到更多的是散文的物理空间之大,却少有人去关注其精神空间。实际文本所呈现的精神含量和丰富性是不够的,尤其在描述深刻的心灵事件、人性的深度控掘、关注当代中国人的现实生态、揭示普遍信仰 危机、承担良知和批判功能方面,散文往往是缺席的。这并非艺术本身的天然安排,而是一种人为的弃权和出让,一种无能造成的无为。散文自身蕴藏的深阔与幽邃被我们浪费了,我们没有很好地去填充它,就像分到了一所大房子——但却没能力去设计、装修和买家具一样。 怎样才能 把散文做大?做得与之设计空间相匹配?配得上它的自由与辽阔?我想到近几个世纪来的西方文学。西方散文从来就是没有边界、不被锁定的,所以它一直像雾一样弥漫,像光一样辐射,无处不在,无所不能……表述上,她更自由、流畅、从容与丰满,这一点,随便打开两册中西散文读本即 可实:彼此的散文理念差异有多大!像恰达耶夫《哲学书简》、马丁·路德·金《我有一个梦想》那样的东西,在我们这儿是找不到的,恐怕现在写出来也无处发表吧。类似的还有萨特的《被占领下的巴黎》,加谬的《西西弗斯神话》,茨威格的《一个欧洲人的回忆》和《异端的权利》,梭 罗的《瓦尔登湖》,布罗茨基的《小于一》等,虽表面上是回忆录或哲学体的随想,但我觉得它们更富含“散文”的自由精神和弥漫气息,其文学品质和生命诚实性也远大于我们很多自诩为“美文”的东西。 恐怕只有中国散文和散文杂志才那么轻易地形成“风格”,流于规范,那么简 单地被模型圈定。 究其源,我觉得仍是生产者的问题:知识储备不够,精神资源贫乏,文学理念滞后——就像浓缩的气球皮,它本身的设计空间非常之大,但平时又是浓缩的,能否把它做大,做得饱满,关键在于吹气球的人,看他的肺活量、底气和精神蕴藏是否充沛了。如果肺活量小, 那气球体型肯定是干瘪的。说到底,乃生产者自身素质和思考力不够所致,是他的过于懒惰、惧怕难度、选择逃避和放弃承担造成的。 有人或许会说:文学的第一要素应是美,文学应以美为最大特征,而非什么“良知”与“责任”。不错,美的确乃艺术的首选之一,但何为美呢?是词 语外壳吗?是外表的绮丽吗?是文本装潢和修饰性吗?显然不。“准确”就是美,准确地捕捉到了灵魂真相和生命秘密就是美!为什么会准确?因为诚实,因为裸净和真切,因为他争取到了深度的真!及时锁定了真!因为他顽强地占有并守住了这个距事物最近的点。表达的准确程度不仅需要 才华,还需感受和表达的勇气,甚至更需勇气。像安徒生童话《皇帝的新衣》,其中最美的一话就是那个孩子说的。这就是诚实的功劳!是诚实在帮助一个人实现其德才!文学的最高成就应是人格成就!这不是技术问题,而是一个能否保对心灵和精神不撒谎的问题。当一个人不习惯撒谎的时 候,“准确”即源源不断地涌至…… 凡优秀作品给人印象最深的,无不是那些准确地击中了你的句子和段落!她感动和震撼着你,所以你才觉得她美!我读书有个习惯,那就是划书,最后发现,凡是用笔重重划出的,凡使我怦然心动的,无不是一些高度准确的句子,由于她准确地击中 了你的某个精神部位——所以你才感激她!因为她扶摸了你,她惊醒和印了你体内的某种东西,她最大限度地洞悉了你。比如杜拉斯说:“如果你只喜欢和一个女人做爱,那说明你不喜欢做爱。”“夫妻间最真实的一点,是背叛,任何夫妻,哪怕成绩最好的夫妻,也不能促进爱情。”我不知 道别人如何看待这样的句子?哪怕它再有争议,我还是觉得她吐出了一种罕见的美!她是靠诚实和勇气顽强地做到这一点的。 读者往往对某个作家有一种固执的信任,逢其文即读,遇其书则买,为什么?因为信任,因为提前预支了一份信任在里头。人们相信他的精神是诚实的,无论他 写什么,大家愿意相信他——相信他又一次要把真诚的东西告诉大家!尽管他的故事未必每一次都精彩,每一篇的观点都让人信服和认同,但人们已养成了一种迎接他的习惯。是他的写作姿势和文学品质感动了读者。这就够了,这无疑是一个作家最大的荣誉和成就!比如我对茨威格的态度即 如此,他的每一本书都买——甚至有几本到现在也没来得及读完,但我信任他——我相信他的每一本书,每一篇文学,包括日记和书信,甚至连他的那篇绝命书都百读不厌。在我这儿,他属于那种值得去留存其全集的作家。 这儿顺便提一提小说和诗歌,因为它们的问题与遭遇也同样是 散文的,小说与诗歌在八十年代至九十年代初,至少历经了两度繁荣——第一次由表达主题所带来,因为它们起到了为社会震荡和时代变革“立言”和“旁”的作用,这是外在的,是“对外”用力的结果。第二次则是内在的,主题由外至内,开始挖掘人性深处的存在,开始试着恢复被政治毁 坏的人生,同时,由于其技术即艺术上的升级,满足了审美趣味,所以人们才迷信般地追随。现在问题是:在它们早已分别提升了技术手段之后,为何影响力反而萎缩了、读者也越来越少? 我一直觉得,诗歌、小说衰落之主因并非人们的阅读习惯发生了多大变化,亦并非现代媒体的冲 击,而在于其自身话语力量的枯萎,其精神关怀力的衰退,它无力再表述社会生活中的一些重大敏感题材,它对现实的批判力、对社会危机和人性险情的挖掘深度及作答能力远不够……在作家手上,文学正变本加厉地趋于休闲与自娱——而这又恰恰是现代媒体手段(比如电子视听、网络游戏) 可轻易替代的。且这些事实的背后,又隐藏着一个更大的真相:它们正失去精神的诚实性!失去文学最生动、最天然、最赢得人心的那种品质!而这分明是个比任何时候都更渴望诚实、更吁求精神坦白与灵魂救赎、更期待消除人心隔膜和不说谎的时代。 毋庸讳言,当代文学的诚实性正 遭受越来越多的质疑。 当一种艺术样式丧失了它的不可替代性之后,结局可想而知。如果文学的主调变成了一种消遣、一种赋闲,如果文学仅仅对应起了“物理人生”(比如所谓的“身体写作”)而非精神诉求——其功能仅剩下了“怎样让肉体更舒适”,它也就立即暗淡下来了,因为 电子媒体和声响科技所提供的娱乐内容与手段,在感性上远比文学丰富、快捷、便利得多。 同样,问题也存在于散文中。今天大部分“成熟”的散文生产者,与小说和诗歌作者几乎是一道生长起来的。从知识结构、文化背景到阅读经验,小说与诗歌作者的现状也是散文作者的现状(更 何况目下很多散文还是小说诗歌作者的“副产品”)。所以散文面对的其实也是整个文学自身的尴尬。整体上看,文学参与社会、介入重大精神命题的能力不够了,作家的知识结构、精神储备明显欠缺了,跟不上了……现在回过头去看,很多人当初成为“作家”时,解决的也仅仅是语言组织、 结构把握、叙述能力、文法修辞等原始技术问题,而在人文信仰、理性透视、社会关怀等“内存”方面是非常欠缺的,即使现在想对社会发言,想参与一些重要的人性表述,但由于先天不足、内存太小,也往往找不到有力的方法和工具,无资源可用。正是这些欠缺,使得其只能不停地“赋闲” 下去,除了撒娇就是调情,给人的感觉就像一个人退了休闷得慌,只能没事找事干,而无力参与到更多的社会命题和精神承担上去。 可以说,当下我们文学界的底子,即主流表述——基本上是以肤浅的感性和虚假的生趣为基础的。这个底子,是几十年来的阅读临摹经验和文学习性造成 的,是固有的知识结构和精神气质决定的。 举一个新闻界的例子,为什么许多人曾一度那么喜欢《南方周末》——无论官员、学者还是老百姓?使《南方周末》区别于其它媒体的那种品质究竟是什么?我以为是它的诚实性!至少是它追求诚实性的那种努力!人们不一定对它每期的实际 质量满意,但无法不为它那种深沉的努力姿态所打动和吸引——这就是魅力!这对文学足以构成一个启示。 其实,就文本品质而言,较之小说和诗歌,散文有表达诚实上有其天然优势,作为文体一种,散文的特殊价值——不可替代性——正与这种“诚实”有关。但遗憾的是,几十年来, 在文艺政策和样板文章的影响下,散文一直在撒谎。当然小说诗歌也在撒谎,但散文撒的谎似乎比谁都多,其精神作弊的嫌疑比谁都大。像《荷塘月色》式的抒怀、《荔枝蜜》式的移情……直至今天,这样的模本仍比比皆是。 以上所说,并非是消解散文题
