初一几何难题练习题集(含答案解析)
初中数学几何题(超难)及答案分析-七年级几何题超难

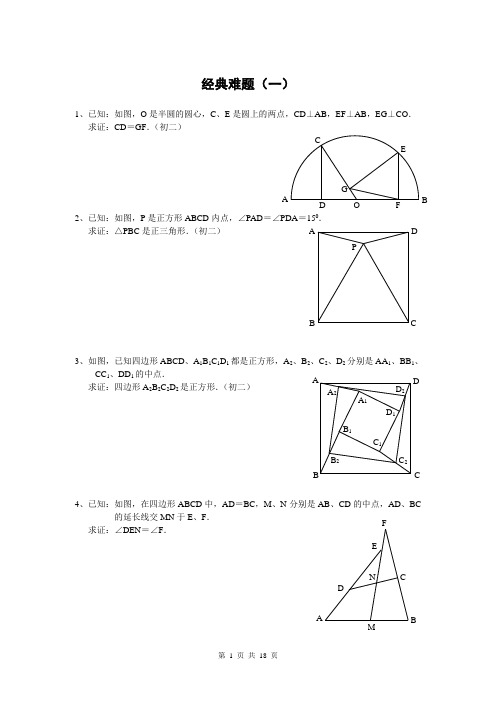
几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点)(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .C D17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.CCD20、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA =200,求∠BED的度数.解答1.如下图做GH⊥AB,连接EO。
七年级数学几何图形初步难题精选(含解析答案)

第1页 共16页七年级数学几何图形初步难题精选(含解析答案)1. 美术课上,老师要求同学们将如图所示的白纸只沿虚线剪开,用裁开的纸片和白纸上的阴影部分围成一个立体模型,然后放在桌面上,下面四个示意图中,只有一个符合上述要求,那么这个示意图是A. B. C. D2. 《几何原本》的诞生,标志着几何学已成为一个有着严密理论系统和科学方法的学科,它奠定了现代数学的基础.它是下列哪位数学家的著作( )A. 欧几里得B. 杨辉C. 费马D. 刘徽3.如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,BD ⊥DC ,BD =DC ,CE 平分∠BCD ,交AB 于点E ,交BD 于点H ,EN ∥DC 交BD 于点N ,下列结论:①BH =DH ;②CH =(√2+1)EH ;③S △ENH S △EBH =EHEC.其中正确的是( )A. ①②③B. 只有②③C. 只有②D. 只有③4. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,下列图形中,是该几何体的表面展开图的是( )A. B. C. D.5. 如图,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展开后的图形是( )A. AB. BC. CD. D6. 图1所示的正方体木块棱长为6 cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图2的几何体,一只蚂蚁沿着图2的几何体表面从顶点A爬行到顶点B的最短距离为cm.7. 如图1,图2,图3,用一种大小相等的正多边形密铺成一个“环”,我们称之为环形密铺,但图4,图5不是我们所说的环形密铺.请你再写出一种可以进行环形密铺的正多边形:.8. 如图,n+1个上底、两腰长皆为1,下底长为2的等腰梯形的下底均在同一直线上,设四边形P1M1N1N2面积为S1,四边形P2M2N2N3的面积为S2,…,四边形PnMnNnNn+1的面积记为Sn,通过逐一计算S1,S2,…,可得Sn=________.9. 有一张矩形纸片ABCD,按下面步骤进行折叠:第一步:如图①,将矩形纸片ABCD折叠,使点B,D重合,点C落在点C′处,得折痕EF;第二步:如图②,将五边形AEFC′D折叠,使AE,C′F重合,得折痕DG,再打开;第三步:如图③,进一步折叠,使AE,C′F均落在DG上,点A,C′落在点A′处,点E,F落在点E′处,得折痕MN,QP.第3页 共16页这样,就可以折出一个五边形DMNPQ .(1)请写出图①中一组相等的线段__________(写出一组即可);(2)若这样折出的五边形DMNPQ (如图③)恰好是一个正五边形,当AB =a ,AD =b ,DM =m 时,有下列结论:①a 2-b 2=2ab tan 18°; ②m =√a 2+b 2tan 18°;③b =m +a tan 18°; ④b =32m +m tan 18°其中,正确结论的序号是______(把你认为正确结论的序号都.填上). 10. 一个圆柱形的蛋糕,将它截三刀,能截出六块、七块或八块吗?若能,画出示意图;若不能,请说明理由.11. 图①的正方体切去一块,得到图②~⑤的几何体.(1)所得几何体各有多少个面?多少条棱?多少个顶点?(2)举例说明其他形状的几何体也切去一块,所得到的几何体的面数、棱数和顶点数各是多少? (3)若面数记为f ,棱数记为e ,顶点数记为v ,则f , v , e 应满足什么关系?12. 有一副直角三角板,其中一个三角板的内角是45°,45°,90°,另一个三角板的内角是30°,60°,90°.(1)将该副三角板按如图①所示方式放置,AB ⊥AD ,则∠CAE =________,BC 与AD 的位置关系是________;(2)在第1问的基础上,再拿一个内角为30°,60°,90°的直角三角板,按如图②所示方式放置,AC'边和AD 边部分重合,则AE 平分∠CAB′吗?请说明理由;(3)根据第1问和第2问的计算,请解决下列问题:如图③,∠BAG =90°,∠BAC =∠FAG =20°,将一个内角为45°,45°,90°的直角三角板的一直角边与AG 部分重合,锐角顶点与∠BAG 的顶点重合,AE 平分∠CAF 吗?请说明理由;(4)如果图③中的∠BAC =∠FAG =∠α(∠α是锐角),其他条件不变,那么第3问中的结论还成立吗?只需回答成立或者不成立,不需要说明理由.13. 如图给出的正多边形的边长都是20 cm.请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线表示,在图中标注出必要的符号和数据,并作简要说明)(1)将图①中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;(2)将图②中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;(3)将图③中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.14. 十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察如图所示的几种简单多面体模型,解答下列问题.四面体长方体正八面体正十二面体(1)根据上面的多面体模型,补全表格:顶点数(V)、面数(F)、棱数(E)之间存在的关系式是________;(2)一个多面体的顶点数比面数大8,且有30条棱,则这个多面体的面数是________;(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成的,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面的三角形的个数为x,八边形的个数为y,求x+y 的值.15. 在图中,对于四个平面图形①②③④,我们规定:如图形③,它的顶点为共5个,区域为△AED,△ABE,△BEC,△CED,共4个,边为AE,EC,DE,EB,AB,BC,CD,DA,共8条.①②③④(1)按此规定将图形①②④的顶点数、边数、区域数填入下列表格:第5页 共16页(2)观察上表,请你归纳上述平面图形的顶点数、边数、区域数之间的数量关系;(3)如果有一个平面图形满足第2问中归纳所得的数量关系,它共有9个区域,且从每一个顶点出发都有3条边,那么这个平面图形共有多少条边?16. 在多边形中,三角形是最基本的图形,而研究多边形一般是将多边形分割成三角形,那么一个八边形至少可以分割成多少个三角形?n 边形呢?17. 如图,P 是定长线段AB 上一点,C ,D 两点同时从P ,B 出发分别以1cm s ⁄和2 cm/s 的速度沿线段向左运动(C 在线段AP 处上,D 在线段BP 上).已知C ,D 运动到任一时刻时,总有PD =2AC .(1)线段AP 与线段AB 的数量关系是________;(2)若Q 是线段AB 上一点,且AQ -BQ =PQ ,求证:AP =PQ .(3)若C ,D 运动5秒,恰好有CD =12AB ,此时C 点停止运动,D 点在线段BP 上继续运动, M ,N 分别是CD , PD 的中点,问MN AB 的值是否发生变化?若变化,请说明理由;若不变,请求出MNAB的值. 18. 已知在同一平面内,∠AOB =90°,∠AOC =60°. (1)∠COB = ;(2)如果OD 平分∠BOC ,OE 平分∠AOC ,那么∠DOE 的度数为 ;(3)试问在第2问的条件下,如果将题目中∠AOC =60°改成∠AOC =2α(α<45°),其他条件不变,你能求出∠DOE 的度数吗?若能,请写出求解过程;若不能,请说明理由.19. 先阅读下面的材料,然后解答问题:在一条直线上有依次排列的n (n >1)台机床在工作,我们要设置一个零件供应站P ,使这n 台机床到供应站P 的距离总和最小,要解决这个问题,先“退”到比较简单的情形:如图所示,如果直线上有2台机床甲、乙,很明显供应站P 设在A 1和A 2之间的任何地方都行,因为甲和乙到P 的距离之和等于A 1到A 2的距离.如图所示,如果直线上有3台机床甲、乙、丙,不难判断,供应站P 设在中间A 2处最合适,因为如果P设在A 2处,甲和丙到P 的距离之和恰好为A 1到A 3的距离,而如果把P 设在别处,例如D 处,那么甲和丙到P 的距离之和仍是A 1到A 3的距离,可是乙到P 的距离是从A 2到D 的这一段的长,这是多出来的,因此P 放在A 2处最合适.不难知道,如果直线上有4台机床,P 应设在第2台与第3台之间的任何地方;有5台机床,P 应设在第3台处.(1)有n (n >1)台机床时,P 应设在何处?(2)根据第1问的结论,求|x-1|+|x-2|+|x-3|+…+|x-617|的最小值.(3)变式:某公司员工分别住在离公路较近的A,B,C三个住宅区,其中A区有75人,B区有45人,C区有30人,A,B,C三区与公路的连接点分别为D,E,F,如图,且DE=100米,EF=200米,该公司的接送车打算在公路上只设一个停靠点,为使所有员工在公路上步行到停靠点的路程之和最小,那么停靠点的位置应设在.20. 如图,两个形状、大小完全相同的含有30°,60°角的三角尺如图①放置,PA,PB与直线MN重合,且三角尺PAC,三角尺PBD均可以绕点P逆时针旋转.(1)试说明:∠DPC=90°;(2)如图②,若三角尺PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;(3)如图③,若三角尺PAC的边PA从PN处开始绕点P逆时针旋转,转速为3°/秒,同时三角尺PBD的边PB从PM处开始绕点P逆时针旋转,转速为2°/秒,在两个三角尺旋转过程中(PC转到与PM重合时,两三角尺都停止转动),以下两个结论:①∠CPD∠BPN为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.21. 已知线段AB=12,CD=6,线段CD在直线AB上运动(如图,A在B的左侧,C在D的左侧,且运动中D在B的右侧).(1)M,N分别是线段AC,BD的中点,若BC=4,求MN的长;(2)当线段CD运动到D点与B点重合时,P是线段AB的延长线上一点,下列两个结论:①PA+PBPC 是定值,②PA-PBPC是定值.其中有一个正确,请你选出正确的结论,并求出这个定值.22. 墙角处有由若干大小相同的小正方体堆成的如图所示的立体图形,如果你打算搬走其中部分小正方体(不考虑操作技术的限制),但希望搬完后从正面、上面、右面用平行光线照射时,在墙面及地面上的影子不变,那么你最多可以搬走多少个小正方体?23. 已知C为直线AB上任意一点,M,N分别为AC,BC的中点,试探究MN与AB之间的关系,并说明理由.24. 已知直线AB上有点O,OD,OC是从点O出发的两条射线,∠AOD=42°,∠BOC=34°,求∠AOD 与∠BOC的角平分线的夹角的度数.25. 如图,射线OM,ON分别是∠AOC和∠BOC的平分线,且∠AOB=90°.(1)求∠MON的度数;(2)当OC在∠AOB内转动时,∠MON的度数是否会发生变化?简单说明理由.26. 比较两个角的大小,有以下两种方法(规则):①用量角器度量两个角的大小,用度数表示,则角度大的角大;②构造图形,如果一个角包含(或覆盖)另一个角,则这个角大.对于如图给定的∠ABC与∠DEF,用以上两种方法分别比较它们的大小.27. 如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.(1)求∠MON的度数;(2)若将题干中的∠AOB=90°改为∠AOB=α,其余条件不变,求∠MON的度数;(3)若将题干中的∠BOC=30°改为∠BOC=β(β为锐角),其余条件不变,求∠MON的度数;(4)从前面的结果中,你能得出什么结论?28. 根据所给图形解答问题.第7页共16页(1)如图1,已知∠AOB=80°,OC是∠AOB的平分线,OD,OE分别平分∠COB,∠AOC,求∠DOE的度数;(2)如图2,在第1问中把“OC是∠AOB的平分线”改为“OC是∠AOB内任意一条射线”,其他任何条件都不变,试求∠DOE的度数;(3)如图3,在第1问中把“OC是∠AOB的平分线”改为“OC是∠AOB外任意一条射线”,其他任何条件都不变,你能求出∠DOE的度数吗?说明理由.29. 一只蜘蛛在一个正方体的顶点A处,一只蚊子在正方体的顶点B处,如图所示,现在蜘蛛想尽快地捉到这只蚊子,那么它所走的最短路线是怎样的?在图上画出来,这样的最短路线有几条?参考答案1. 【答案】B【解析】由图的特征可知B选项符合题意2. 【答案】A【解析】由常识可知选A.3. 【答案】B【解析】过点H作HM⊥BC于M.∵CE平分∠BCD.∴DH=HM.在Rt△BMH中BH>HM∴BH>DH.故①不正确②③正确故选B.4. 【答案】B【解析】实际动手做一下,就可知几何体表面展开图是B.5. 【答案】D【解析】相反操作顺序展开,再利用对称性作图,可得D正确.6. 【答案】3√2+3√6【解析】本题考查平面展开图及最短路径问题,难度较大.将图②的几何体表面展开,根据“两点之间线段最短”得出结果.如图所示,蚂蚁爬行的最短距离即线段AB的长度,∵BC=BD,AC=AD,∴AB垂直平分线段CD,设垂足为点E,∵△BCD是等腰直角三角形,∴CD=√BC2+BD2=第9页 共16页√62+62=6√2(cm),∴BE =12CD =3√2(cm),∵AD ,AC ,CD 均为正方形的对角线,∴AD =AC =CD =6√2,即△ACD 是等边三角形,∴AE =AD sin 60°=6√2×√32=3√6, ∴AB =BE +AE =3√2+3√6(cm),∴蚂蚁爬行的最短距离为(3√2+3√6)cm.7. 【答案】正十二边形(答案不唯一)【解析】本题考查平面图形的镶嵌问题,属于较难题.由题意知,符合环形密铺的条件是各正多边形的重心到所围成的图形的重心距离要相等,即正多边形的重心在一个圆上,图中的④,⑤明显的不符合,正六边形符合,则正十二边形也符合.8. 【答案】3√34-12n+1√34【解析】当上底为1,腰为1,下底为2时,高为√1−14=√32,上底与下底的比为1∶2,∴S △1=14S △AN 1M 1=2×√32×23×14×12=√312, S 1=12(1+2)√32-√312=3√34-√312=2√33,S 1=3√34-12×1+1√34,同理,由相似,S 2=3√34-12×2+1√34,…,以此类推,S n =3√34-12n+1√34. 9.(1) 【答案】AD =C ′D (答案不唯一,也可以是AE =C ′F 等)【解析】图①中,AD =C ′D ,AE =C ′F ,DE =BE ,C ′F =CF 等 (2) 【答案】①②③【解析】延长MN ,则M 、N 、B 在一条直线上,∴∠MBA =18°, ∴AM AB =AMa=tan 18°,∴AM =a tan 18°,又AD =AM +MD ,∴b =m +a tan 18°,延长线BM 至M ′,使DM =DM ′,∠DM ′M =∠DMM ′=72°, ∴∠M ′DB =90° ∴DM =DM ′=BD tan18°=√a 2+b 2tan18°=m .∴AE =b tan 18°,DE =BE =a -b tan 18°,AD =b .∴b 2+b 2tan 2 18°=a 2-2ab tan 18°+b 2tan 18°,∴2ab tan 18°=a2-b2.故①②③正确10. 【答案】垂直、平行于底面各截一刀,第三刀刚好过前两个截面的交线,如图1,可以截出六块(方法不唯一);垂直、平行于底面各截一刀,第三刀不过前两个截面的交线,如图2,可以截出七块;垂直于底面交叉截两刀,再平行于底面横截一刀,如图3,可以截出八块.11.(1) 【答案】题图②有7个面、15条棱、10个顶点,题图③有7个面、14条棱、9个顶点,题图④有7个面、13条棱、8个顶点,题图⑤有7个面、12条棱、7个顶点.(2) 【答案】例如:三棱锥被切去一块,如图所示,所得到的几何体有5个面、9条棱、6个顶点.(3) 【答案】由前两问可得到规律,f+v-e=2,所以f,v,e应满足的关系是f+v-e=2.12.(1) 【答案】15°;BC∥AD.(2) 【答案】AE平分∠CAB′,理由:易知∠EAB′=15°,由第1问知,∠CAE=15°,所以∠CAE=∠EAB′,所以AE平分∠CAB′.(3) 【答案】AE平分∠CAF,理由:因为∠GAE=45°,∠BAG=90°,所以∠BAE=45°,因为∠BAC=∠FAG=20°,所以∠CAE=25°,∠EAF=25°,即∠CAE=∠EAF,则AE平分∠CAF. (4) 【答案】成立.13.(1) 【答案】将图①中四个角上的4个小正方形剪下,拼成一个正方形,作为直四棱柱的一个底面.(2) 【答案】将图②中三个角上的3个四边形剪下,拼成一个正三角形,作为直三棱柱的一个底面.第11页 共16页(3) 【答案】将图③中五个角上的5个四边形剪下,拼成一个正五边形,作为直五棱柱的一个底面.14.(1) 【答案】6;6;V +F −E =2.(2) 【答案】12.(3) 【答案】这个多面体的面数为x +y ,棱数为24×32=36,根据V +F −E =2可得24+(x +y)−36=2,所以x +y =14. 15.(1) 【答案】①栏依次填入:4;6;3;②栏依次填入:6;9;4;④栏依次填入:10;15;6.(2) 【答案】顶点数+区域数-边数=1.(3) 【答案】设这个平面图形有n 个顶点.因为从每一个顶点出发都有3条边,所以它3n2有条边.根据上述数量关系,有n +9−3n 2=1,可得n =16.所以3n2=24,所以这个平面图形共有24条边.16. 【答案】(1)将八边形内一点与各个顶点相连,可把八边形分割成8个三角形(如图(1)),用同样方法分割,可知n 边形可以分割成n 个三角形;(2)从八边形边上一点出发,连接各个顶点,能分成7个三角形(如图(2)),用同样方法分割,可知n 边形可以分割成(n −1)个三角形;(3)将八边形的一个顶点与同它不相邻的各顶点相连可以分割成6个三角形(如图(3)),用同样方法分割,可知n 边形可以分割成(n −2)个三角形.综上所述,八边形至少可以分割成6个三角形,n 边形至少可以分割成(n −2)个三角形.17.(1) 【答案】 AB =3AP .(提示:因为PD =2AC,DB =2PC ,所以PB =PD +DB =2(AC +PC )=2AP ,AB = AP +PB ,所以AB =3AP )(2) 【答案】证明:如图,由题意得AQ>BQ,∴AQ=AP+PQ,又∵AQ−BQ=PQ,∴AQ=BQ+PQ,∴AP=BQ.由第1问得,AP=13AB,∴PQ=AB−AP−BQ=13AB.∴AP=PQ.(3) 【答案】MNAB的值不变.当C点恰好停止运动时,有CD=12AB,∴AC+BD=12AB,∴AP−PC+BD=12AB,又∵AP=13AB,当C点恰好停止运动时,PC=1×5=5cm,BD=2×5=10cm,∴13AB−5+10=12AB,∴AB=30cm.∵M是CD的中点,N是PD的中点,∴MN=CD−MC−ND=CD−12CD−12PD=12(CD−PD)=12CP=52(cm),∴MNAB =112.18.(1) 【答案】150°或30°(2) 【答案】45°(3) 【答案】能求出∠DOE的度数.当OC在∠AOB内部时,如图①,因为∠AOB=90°,∠AOC=2α,所以∠BOC=90°-2α,因为OD,OE分别平分∠BOC,∠AOC,所以∠DOC=12∠BOC=45°-α,∠COE=12∠AOC=α,所以∠DOE=∠DOC+∠COE=(45°-α)+α=45°;当OC在∠AOB外部时,如图②,因为∠AOB=90°,∠AOC=2α,所以∠BOC=90°+2α,因为OD,OE分别平分∠BOC,∠AOC,所以∠DOC=12∠BOC=45°+α,∠COE=12∠AOC=α,所以∠DOE=∠DOC-∠COE=(45°+α)-α=45°.综上所述,∠DOE=45°.第13页 共16页19.(1) 【答案】当n 为奇数时,P 应设在第n+12台处;当n 为偶数时,P 应设在第n 2台和第(n 2+1)台之间的任何地方.(2) 【答案】根据绝对值的几何意义,求|x -1|+|x -2|+|x -3|+…+|x -617|的最小值就是在数轴上找出表示x 的点,使它到表示1,2,…,617各点的距离之和最小,根据问题(1)的结论知,当x =309时,原式的值最小.最小值是:|309-1|+|309-2|+|309-3|+…+|309-308|+0+|309-310|+|309-311|+…+|309-617|=308+307+306+…+1+1+2+…+308=308×309=95172. (3) 【答案】D 与E 两点之间(包括点D ,E )20.(1) 【答案】因为∠DPB =30°, ∠CPA =60°,所以∠DPC =180°-30°-60°=90°.(2) 【答案】设∠CPE =∠DPE =x ,∠CPF =y ,则∠APF =∠DPF =2x +y ,因为∠CPA =60°,所以y +2x +y =60°,所以x +y =30°,所以∠EPF =x +y =30°.(3) 【答案】①正确,②不正确.理由:设旋转时间为t 秒,则∠BPM =(2t )°,∠APN =(3t )°.所以∠BPN =180°-∠BPM =(180-2t )°,∠DPM =30°-∠BPM =(30-2t )°.所以∠CPD =180°-∠DPM -∠CPA -∠APN =(90-t )°,所以∠CPD ∠BPN =90-t 180-2t =12.21.(1) 【答案】如图①,因为M ,N 分别为线段AC ,BD 的中点,所以AM=12AC =12(AB +BC)=8,DN =12BD =12(CD +BC )=5,所以MN =AD -AM -DN =9;如图②,困为M ,N 分别为线段AC ,BD 的中点,所以AM =12AC =12(AB -BC )=4,DN =12BD =12(CD -BC )=1,所以MN =AD -AM -DN =9. (2) 【答案】①正确.因为PA+PB PC =(PC+AC)+(PC -CB)PC =2PC PC =2,所以PA+PBPC是定值2.22. 【答案】第1列最多可以搬走9个小正方体; 第2列最多可以搬走8个小正方体;第3列最多可以搬走3个小正方体;第4列最多可以搬走5个小正方体;第5列最多可以搬走2个小正方体,因为9+8+3+5+2=27(个),所以最多可以搬走27个小正方体.23. 【答案】因为M是线段AC的中点,所以CM=12AC.因为点N是线段BC的中点,所以CN=12BC.分以下三种情况:①当点C在线段AB上时,如图1,则有MN=CM+CN=12AC+12BC=12(AC+BC)=12AB;②当点C在线段AB的延长线上时,如图2,则有MN=CM−CN=12AC−12BC=12(AC−BC)=12AB;③当点C在线段BA的延长线上时,如图3,则有MN=CN−CM=12BC−12AC=12(BC−AC)=12AB.综上所述,MN=12AB.24. 【答案】设∠AOD,∠BOC的角平分线分别为OE,OF.分两种情况讨论.①当射线OD和射线OC在直线AB的同侧时,由题意,得∠BOF=12∠BOC=17°,∠AOE=12∠AOD=21°,故∠EOF=180°−∠BOF−∠AOE=180°−17°−21°=142°;②当射线OD和射线OC在直线AB的异侧时,∠EOF=180°−∠AOE+∠BOF=180°−21°+17°=176°.综上所述,∠AOD与∠BOC的角平分线的夹角为142°或176°.25.(1) 【答案】因为∠NOC=12∠BOC,∠MOC=12∠AOC,所以∠MON=∠NOC+∠MOC=12∠AOC+12∠BOC=12(∠AOC+∠BOC)=12∠AOB=45°.(2) 【答案】由第1问知,∠NOC+∠MOC是个定值,所以当OC在∠AOB内转动时,∠MON的度数不会发生改变,恒为45°.26. 【答案】①测量∠ABC=45°,∠DEF=65°,所以∠ABC<∠DEF.②如图,使∠ABC的一边BC与∠DEF的一边EF、顶点B与E分别重合,BA落在∠DEF的内部,所以∠ABC<∠DEF.27.(1) 【答案】因为OM平分∠AOC,ON平分∠BOC,所以∠MOC=12∠AOC,∠NOC=12∠BOC,又因为∠AOB=90°,∠BOC=30°所以∠MON=∠MOC−∠NOC=12∠AOC−12∠BOC=12(∠AOC−∠BOC)=12∠AOB=12×90°=45°.(2) 【答案】当∠AOB=α,其他条件不变时,∠MON=12∠AOB=12α.(3) 【答案】当∠BOC=β,其他条件不变时,∠MON=12∠AOB=12×90°=45°.(4) 【答案】∠MON总等于∠AOB的一半,而与∠BOC的大小无关.28.(1) 【答案】因为∠AOB=80°,OC是∠AOB的平分线,所以∠AOC=∠BOC=12∠AOB=40°. 因为OD,OE分别平分∠BOC,∠AOC,所以∠COD=12∠BOC=20°,∠COE=12∠AOC=20°,所以∠DOE=∠COD+∠COE=40°.第15页共16页(2) 【答案】因为OD,OE分别平分∠BOC,∠AOC,所以∠COD=12∠BOC,∠COE=12∠AOC,所以∠DOE=∠COD+∠COE=12(∠BOC+∠AOC)=12∠AOB=12×80°=40°.(3) 【答案】能.∠DOE=∠DOC−∠COE=12∠BOC−12∠AOC=12(∠BOC−∠AOC)=12∠AOB=12×80°=40°.29. 【答案】欲求从A点到B点的最短路线,在立体图形中难以解决,可以考虑把正方体展开成平面图形.如图所示.在两点之间,走线段最短,因而沿着从A到B的虚线(如上图)走路程最短.在正方体中,像这样的最短路线一共有六条,如图所示.。
七年级经典几何难题20道题

七年级经典几何难题20道题以下是七年级经典几何难题20道题:1. 已知等边三角形的一边长为a,求面积。
答案:面积为√3/4 * a²。
2. 如果一个矩形的长比宽大2cm,它的面积是24cm²,求矩形的长和宽。
答案:长为6cm,宽为4cm。
3. 已知一个正方形的边长为4cm,求周长和面积。
答案:周长为4*4=16cm,面积为4*4=16cm²。
4. 求一个直径为10cm的圆的面积。
答案:面积为π*(10/2)²=25πcm²。
5. 求一个等腰三角形底为6cm,高为8cm的面积。
答案:面积为1/2 * 6 * 8 = 24cm²。
6. 已知一个长方形的长为10cm,宽为5cm,求面积。
答案:面积为10*5=50cm²。
7. 求一个正方形的对角线长度为13cm的面积。
答案:面积为(13/2)²=169/4=42.25cm²。
8. 已知一个等边三角形的边长为8cm,求面积。
答案:面积为√3/4 * 8²=16√3 cm²。
9. 求一个半径为5cm的圆的周长。
答案:周长为2π*5=10πcm。
10. 已知一个矩形的长为12cm,宽为3cm,求面积。
答案:面积为12*3=36cm²。
11. 求一个边长为6cm的正方形的对角线长度。
答案:对角线长度为6√2 cm。
12. 已知一个等腰三角形底为10cm,高为12cm,求面积。
答案:面积为1/2 * 10 * 12 = 60cm²。
13. 求一个半径为7cm的圆的面积。
答案:面积为π*7²=49πcm²。
14. 已知一个长方形的长为15cm,宽为2cm,求面积。
答案:面积为15*2=30cm²。
15. 求一个正方形的边长为9cm的面积。
答案:面积为9*9=81cm²。
16. 求一个等边三角形的一边长为6cm的面积。
(完整版)初中数学几何题(超难)及答案分析

(完整版)初中数学⼏何题(超难)及答案分析⼏何经典难题1、已知:如图,O 是半圆的圆⼼,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初三)2、已知:如图,P 是正⽅形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三⾓形.(初⼆)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正⽅形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正⽅形.(初⼆)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂⼼(各边⾼线的交点)(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外⼀直线,过O 作OA ⊥MN 于A ,⾃A,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移⾄圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初三)8、如图,分别以△ABC 的AC 和BC 为⼀边,在△ABC 的外侧作正⽅形ACDE 和正⽅形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的⼀半.N9、如图,四边形ABCD 为正⽅形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初⼆)10、如图,四边形ABCD 为正⽅形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正⽅形ABCD ⼀边BC求证:PA =PF .(初⼆)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三⾓形,P 是三⾓形内⼀点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初⼆)14、设P 是平⾏四边形ABCD 内部的⼀点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初⼆)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平⾏四边形ABCD 中,设E 、F 分别是BC 、AB 上的⼀点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .17、设P 是边长为1的正△ABC 内任⼀点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正⽅形ABCD 内的⼀点,求PA +PB +PC 的最⼩值.19、P 为正⽅形ABCD 内的⼀点,并且PA =a ,PB =2a ,PC =3a ,求正⽅形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH ⊥AB,连接EO 。
可打印初中数学几何题(超难)及的答案分析完整版
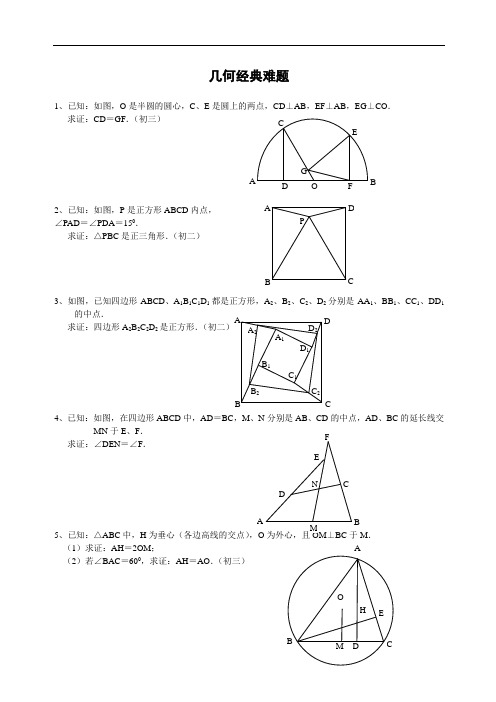
几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 A N FE CD MB· A DHE M CBOPCGFBQADE6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· G A O DB E CQ P NM ·O QP B DE C NM · A9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)11、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)A F D E CB E DA CB F DF E P C B AO D BFAECP13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCBAACBPD解答1.如下图做GH ⊥AB,连接EO 。
七年级数学几何图形初步难题精选(含解析答案)

七年级数学几何图形初步难题精选(含解析答案)1.美术课上,老师要求同学们将如图所示的白纸只沿虚线剪开,用裁开的纸片和白纸上的阴影部分困成一个立体模型,然后放在桌而上,下面四个示意图中,只有一个符合上述要求,那么这个示意图是D2.《几何原本》的诞生,标志着几何学已成为一个有着严密理论系统和科学方法的学科,它奠左了现代数学的基础•它是下列哪位数学家的著作()A.欧几里得B.杨辉C.费马D.刘徽 3•如图,在直角梯形ABCD中,AD//BC, ZABC=90。
,丄DC, BD=DC, CE 平分/BCD,交 AB 于点E,交BD于点H, EN//DC交BD于点、N,下列结论:①BH=DH;②CH=(A/2+1)EH:③护廻=学.其中正确的是()S QH ECA __________ DA.①②③B.只有②(③C.只有②D.只有③4•如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个而涂有颜色,下列图形中,是该几何体的表而展开图的是()6•图1所示的正方体木块棱长为6 cm 船其相邻三个而的对角线(图中虚线)剪掉一角,得到如图2的几何 体,一只蚂蚁沿着图2的几何体表而从顶点A 爬行到顶点B 的最短距离为 _________ c m.&如图,n+1个上底、两腰长皆为1, P 阿“凡而积为» 四边形PN 斟汕的而积为亠,…,四边形屮的面积记为» 通过逐一计9•有一张矩形纸片ABCD.按下而步骤进行折叠:第一步:如图①,将矩形纸片ABCD 折叠,使点B, D 重合,点C 落在点C ,处,得折痕EF :第二步:如图②,将五边形AEFCD 折叠,使CF 重合,得折痕DG,再打开:第三步:如图③,进一步折叠,使AE, CF 均落在DG 上,点A, U 落在点/V 处,点E, F 落在点E 处, 得折痕MN, QP.n> 下底长为2的等腰梯形的下底均在同一直线上,设四边形A. B. D.A. AB. BC.CD. D图1图3图2 7•如图1罔2,图3,用一种大小相等的正多边形密铺成一个“环二我们称之为环形密铺,但图4,图5不是我(1) 请写出图①中一组相等的线段 _________ (写出一组即可);(2) 若这样折岀的五边形DMNPQ(如图③)恰好是一个正五边形,当AB=a, AD=b, DM=m 时,有下列 结论: (X)a 2—b 2=2cih tan 18°; (2)w=-/a 2 + b 2 tan 18°;③b=m+a tan 18°: ④b=^n+m tan 18°其中,正确结论的序号是 _____ (把你认为正确结论的序号都填上).■10.—个圆柱形的蛋糕,将它截三刀,能截出六块、七块或八块吗?若能,画出示意图:若不能,请说 明理由.11•图①的正方体切去一块,得到图②迴的几何体.① ② ③ ④ ⑤(1)所得几何体各有多少个而?多少条棱?多少个顶点? (2)举例说明其他形状的几何体也切去一块,所得到的几何体的而数、棱数和顶点数各是多少? (3) 若而数记为「棱数记为e,顶点数记为-则f f v f e 应满足什么关系?12.有一副直角三角板,其中一个三角板的内角是45。
初中数学几何题超难及答案分析-七年级几何题超难
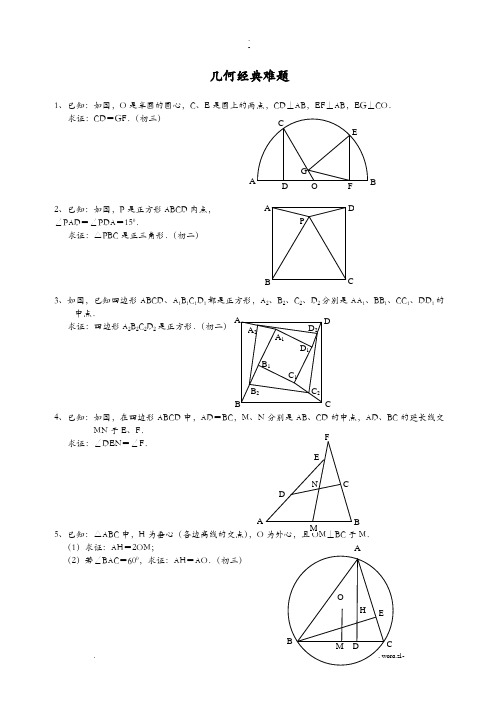
几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点) (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FGCE B O D D 2 C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E EP13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB C B D AFPDECBA. -18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH⊥AB,连接EO。
初一几何难题例题_练习题(含答案)(优选.)

最新文件---------------- 仅供参考--------------------已改成-----------word文本 --------------------- 方便更改1、证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。
很多其它问题最后都可化归为此类问题来证。
证明两条线段或两角相等最常用的方法是利用全等三角形的性质,其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。
例 1. 已知:如图1所示,∆ABC中,90,,,。
∠=︒===C AC BC AD DB AE CFAC BCA BACB AD DBCD BD AD DCB B AAE CF A DCB AD CD =∴∠=∠∠=︒=∴==∠=∠=∠=∠=∠=90,,,,∴≅∴=∆∆ADE CDF DE DF例2. 已知:如图2所示,AB =CD ,AD =BC ,AE =CF 。
在∆ABC 和∆CDA 中,AB CD BC AD AC CAABC CDA SSS B D AB CD AE CFBE DF===∴≅∴∠=∠==∴=,,,∆∆()在∆BCE 和∆DAF 中,BE DF B DBC DA BCE DAF SAS E F=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∆∆()例3. 如图3所示,设BP 、CQ 是∆ABC 的内角平分线,AH 、AK 分别为A 到BP 、CQ 的垂线。
交BC 于M∵BH 平分∠ABC∴=∠∠ABH NBH又BH ⊥AH∴==︒∠∠AHB NHB 90BH =BH∴≅∴==∆∆ABH NBH ASA BA BN AH HN (),同理,CA =CM ,AK =KM∴KH 是∆AMN 的中位线∴KH MN //即KH//BC例 4. 已知:如图4所示,AB =AC ,∠,,A AE BF BD DC =︒==90。
求证:FDAB AC BD DCDAE DABBAC BD DC BD ADB DAB DAE==∴+=︒==︒=∴=∴==,∠∠,∠∠∠,∠∠∠129090在∆ADE 和∆BDF 中,AE BF B DAE AD BDADE BDFFD ED===∴≅∴∠=∠∴∠+∠=︒∴⊥,∠∠,∆∆313290证明二:如图5所示,延长ED 到M ,使DM =ED ,连结FE ,BDM CDE DM DEBDM CDECE BM C CBMBM ACA ABM AAB AC BF AEAF CE BM ∠=∠=∴≅∴=∠=∠∴∠=︒∴∠=︒=∠==∴==,,,∆∆//9090∴≅∴==∴⊥∆∆AEF BFMFE FMDM DEFD ED3、证明一线段和的问题(一)在较长线段上截取一线段等一较短线段,证明其余部分等于另一较短线段。
最新初中数学几何图形初步难题汇编含答案
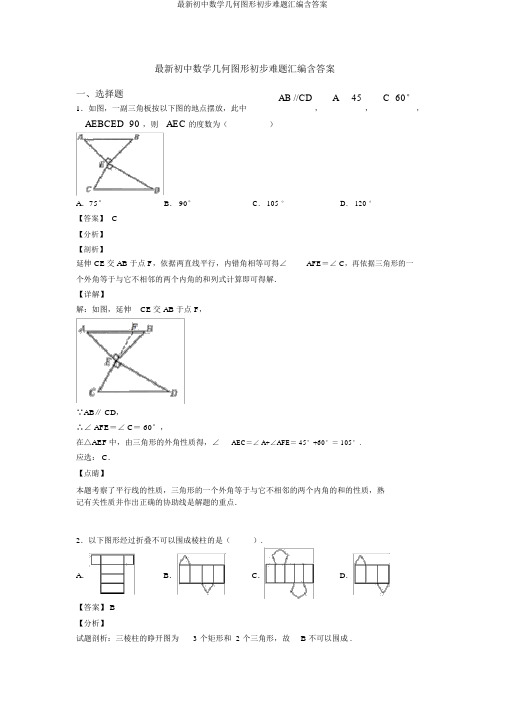
最新初中数学几何图形初步难题汇编含答案一、选择题AB //CD A45 C 60°1.如图,一副三角板按以下图的地点摆放,此中,,,AEBCED 90 ,则 AEC 的度数为()A.75°B. 90°C. 105 °D. 120 °【答案】C【分析】【剖析】AFE=∠ C,再依据三角形的一延伸 CE交 AB 于点 F,依据两直线平行,内错角相等可得∠个外角等于与它不相邻的两个内角的和列式计算即可得解.【详解】解:如图,延伸CE交 AB 于点 F,∵AB∥ CD,∴∠ AFE=∠ C= 60°,在△AEF中,由三角形的外角性质得,∠AEC=∠ A+∠AFE= 45°+60°= 105°.应选: C.【点睛】本题考察了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记有关性质并作出正确的协助线是解题的重点.2.以下图形经过折叠不可以围成棱柱的是().A.B.C.D.【答案】 B【分析】试题剖析:三棱柱的睁开图为 3 个矩形和 2 个三角形,故 B 不可以围成 .考点:棱柱的侧面睁开图.3.将一副三角板以以下图搁置,使点A 落在DE上,若BC P DE,则AFC 的度数为()A.90°B. 75°C. 105 °D. 120 °【答案】 B【分析】【剖析】依据平行线的性质可得∠E∠BCE30 ,再依据三角形外角的性质即可求解AFC 的度数.【详解】∵BC //DE∴∠E∠BCE30∴∠AFC∠B∠BCE45 3075故答案为: B.【点睛】本题考察了三角板的角度问题,掌握平行线的性质、三角形外角的性质是解题的重点.4.如图,直线a∥b,点 B 在直线 b 上,且 AB⊥ BC,∠ 1=55 °,那么∠ 2 的度数是()A.20°B. 30°C. 35°D. 50°【答案】 C【分析】【剖析】由垂线的性质可得∠ABC=90°,因此∠ 3=180°﹣ 90°﹣∠ 1=35°,再由平行线的性质可获得∠2的度数.【详解】解:由垂线的性质可得∠ABC=90°,因此∠ 3=180°﹣ 90°﹣∠ 1=35°,又∵ a∥b ,因此∠ 2=∠3=35°.应选 C.【点睛】本题主要考察了平行线的性质.5.如图,在直角坐标系中,点 A、 B 的坐标分别为( 1, 4)和( 3, 0),点 C 是 y 轴上的一个动点,且 A、 B、 C 三点不在同一条直线上,当△ABC 的周长最小时,点 C 的坐标是A.( 0, 0)B.( 0, 1)C.( 0, 2)D.( 0, 3)【答案】 D【分析】【详解】解:作 B 点对于 y 轴对称点 B′点,连结 AB′,交 y 轴于点 C′,此时△ABC 的周长最小,∵点 A、 B 的坐标分别为(1, 4)和( 3, 0),∴B′点坐标为:(-3,0 ),则 OB′=3过点 A 作 AE 垂直 x 轴,则 AE=4, OE=1则 B′E=4,即 B′E=AE,∴∠ EB′A=∠B′AE,∵C′O∥ AE,∴∠ B′C′O=∠ B′AE,∴∠ B′C′O=∠ EB′A∴B′O=C′O=3,∴点 C′的坐标是( 0, 3),此时△ABC的周长最小.应选 D.6.以下图是一个正方体睁开图,图中六个正方形内分别标有“新”、“时”、“代”、“去”、“奋”、“斗”、六个字,将其围成一个正方体后,则与“奋”相对的字是()A.斗B.新C.时D.代【答案】 C【分析】剖析:正方体的表面睁开图,相对的面之间必定相隔一个正方形,依据这一特色作答.详解:正方体的表面睁开图,相对的面之间必定相隔一个正方形,“时”相对的字是“奋”;“代”相对的字是“新”;“去”相对的字是“斗”.应选 C.点睛:本题主要考察了正方体的平面睁开图,解题的重点是掌握立方体的 11 种睁开图的特色.7.某包装盒以以下图所示,则在以下四种样式的纸片中,能够是该包装盒的睁开图的是()A.B.C.D.【答案】 A【分析】【剖析】将睁开图折叠复原成包装盒,即可判断正确选项.【详解】解: A、睁开图折叠后以以下图,与本题中包装盒同样,故本选项正确;B、睁开图折叠后以以下图,与本题中包装盒不一样,故本选项错误;C、睁开图折叠后以以下图,与本题中包装盒不一样,故本选项错误;D、睁开图折叠后以以下图,与本题中包装盒不一样,故本选项错误;应选: A.【点睛】本题主要考察了含图案的正方体的睁开图,学生要经历必定的实验操作过程,自然学生也能够将操作活动转变为思想活动,在脑筋中模拟(想象)折纸、翻转活动,较好地考察了学生空间观点.8.如图,假如用剪刀沿直线将一个正方形图片剪掉一部分,发现剩下部分的周长比原正方形图片的周长要小,能正确解说这一现象的数学知识是()A.线段比曲线短B.经过一点有无数条直线C.经过两点,有且仅有一条直线D.两点之间,线段最短【答案】 D【分析】【剖析】以以下图,只要要剖析AB+BC< AC 即可【详解】∵线段 AC 是点 A 和点 C 之间的连线,AB+BC是点 A 和点 C 经过弯折后的路径又∵两点之间线段最短∴AC<AB+BC应选: D本题考察两点之间线段最短,在应用的过程中,要弄清楚线段长度表示的是哪两个点之间的距离9.如图,在周长为12 的菱形 ABCD中, AE=1,AF=2,若 P 为对角线BD 上一动点,则EP+FP 的最小值为()A.1B.2C.3D.4【答案】 C【分析】试题剖析:作 F 点对于 BD 的对称点F′,则 PF=PF′,连结 EF′交 BD 于点 P.∴E P+FP=EP+F′.由两点之间线段最短可知:当E、 P、 F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′ P=EF.′∵四边形ABCD为菱形,周长为12,∴A B=BC=CD=DA=3,AB∥CD,∵AF=2,AE=1,∴D F=AE=1,∴四边形AEF′D是平行四边形,∴E F′=AD=3.∴E P+FP的最小值为 3.应选 C.考点:菱形的性质;轴对称-最短路线问题10.如图是由若干个大小同样的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是()A.主视图B.俯视图C.左视图D.同样大【分析】如图,该几何体主视图是由 5 个小正方形构成,左视图是由 3 个小正方形构成,俯视图是由 5 个小正方形构成,故三种视图面积最小的是左视图,应选 C.11.如图,快艇从P 处向正北航行到 A 处时,向左转50°航行到 B 处,再向右转80°持续航行,此时的航行方向为()A.北偏东30°B.北偏东80°C.北偏西 30°D.北偏西50°【答案】 A【分析】【剖析】依据平行线的性质,可得∠2,依据角的和差,可得答案.【详解】如图,AP∥ BC,∴∠ 2=∠ 1=50°,∵∠ EBF=80°=∠2+∠ 3,∴∠ 3=∠ EBF﹣∠ 2=80°﹣ 50°=30°,∴此时的航行方向为北偏东30°,应选 A.【点睛】本题考察了方向角,利用平行线的性质得出∠ 2 是解题重点.12.如图,ABC为等边三角形,点P从 A 出发,沿A B C A 作匀速运动,则线段 AP 的长度y与运动时间x之间的函数关系大概是()A.B.C.D.【答案】 B【分析】【剖析】依据题意可知点P 从点 A 运动到点 B 时以及从点 C 运动到点 A 时是一条线段,故可清除选C 时, y 是 x 的二次函数,而且有最小值,应选项 B 切合项 C与 D;点 P从点 B运动到点题意,选项 A 不合题意.【详解】依据题意得,点 P 从点A运动到点 B 时以及从点C运动到点A时是一条线段,应选项C与选项D 不合题意;点P从点B运动到点 C 时, y 是x的二次函数,而且有最小值,∴选项 B 切合题意,选项 A 不合题意.应选 B.【点睛】y 与x 的函数本题考察了动点问题的函数图象:经过分类议论,利用三角形面积公式获得关系,而后依据二次函数和一次函数图象与性质解决问题.13.如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm 的点 C 处有一滴蜂蜜,此时一只蚂蚁正幸亏杯外壁,离杯上沿4cm 与蜂蜜相对的 A 处,则蚂蚁抵达蜂蜜的最短距离() cm.A.14B. 15C. 16D. 17【答案】 B【分析】【剖析】在侧面睁开图中,过 C 作 CQ⊥ EF于 Q,作 A 对于 EH的对称点A′,连结 A′C交 EH于 P,连结 AP,则 AP+PC就是蚂蚁抵达蜂蜜的最短距离,求出A′Q, CQ,依据勾股定理求出A′C 即可.【详解】解:沿过 A 的圆柱的高剪开,得出矩形EFGH,过 C 作 CQ⊥ EF于 Q,作 A 对于 EH 的对称点A′,连结 A′C 交 EH 于 P,连结 AP,则AP+PC就是蚂蚁抵达蜂蜜的最短距离,∵AE= A′E, A′P=AP,∴A P+PC= A′P+PC=A′C,∵CQ=1× 18cm= 9cm, A′Q= 12cm﹣ 4cm+4cm= 12cm,2在 Rt△A′QC 中,由勾股定理得: A′C=12292= 15cm,应选: B.【点睛】本题考察了圆柱的最短路径问题,掌握圆柱的侧面睁开图、勾股定理是解题的重点.14.以下图形中,是圆锥的侧面睁开图的为()A.B.C.D.【答案】 B【分析】【剖析】依据圆锥的侧面睁开图的特色作答.【详解】圆锥的侧面睁开图是圆滑的曲面,没有棱,不过扇形.应选 B.【点睛】考察了几何体的睁开图,圆锥的侧面睁开图是扇形.15.假如和互余,以下表的补角的式子中:① 180 °-,② 90°+,③2+,④2+,正确的有()A.①②B.①②③C.①②④D.①②③④【答案】 B【分析】【剖析】90°,进行判断即可.依据互余的两角之和为【详解】∠β的补角 =180°﹣∠ β,故①正确;∵∠ α和∠β互余,∴∠β=90°-∠ α,∴∠β的补角 =180°﹣∠ β=180°﹣( 90°-∠ α) =90°+,故② 正确;∵∠ α和∠β互余,∠α+∠ β=90°,∴∠β的补角 =180°﹣∠ β=2(∠α+∠ β)﹣∠β=2∠ α+∠β,故③ 正确;∵∠ α+∠ β=90°,∴ 2∠ β+∠α=90°+∠ β,不是∠β的补角,故④错误.故正确的有①②③.应选 B.【点睛】本题考察了余角和补角的知识,解答本题的重点是掌握互余的两角之和为 90°,互补的两角之和为 180°.16.以下说法中,正确的个数为 ( )①过同一平面内 5 点,最多能够确立9条直线;②连结两点的线段叫做两点的距离;③若 AB BC ,则点B是线段 AC 的中点;④三条直线两两订交,必定有3个交点.A.3个B.2个C.1个D.0个【答案】 D【分析】【剖析】.依据直线交点、两点间距离、线段中点定义分别判断即可获得答案【详解】①过同一平面内 5 点,最多能够确立10 条直线,故错误;② 连结两点的线段的长度叫做两点的距离,故错误;③若 AB BC ,则点B不必定是线段AC 的中点,故错误;④ 三条直线两两订交,能够都交于同一点,故错误;应选: D.【点睛】本题考察直线交点、两点间距离定义、线段中点定义,正确理解定义是解题的重点.17.一个角的补角比这个角的余角 3 倍还多 10°,则这个角的度数为()A.140 ° B.130 ° C. 50° D. 40°【答案】 C【分析】【剖析】依据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°,列出方程,而后解方程即可.【详解】设这个角为α,则它的余角为90°-α,补角为180°-α,依据题意得, 180°-α=3( 90°-α) +10°,180 °-α =270-3°α +10,°解得α=50°.应选 C.【点睛】本题考察了互为余角与补角的性质,表示出这个角的余角与补角而后列出方程是解题的重点.18.小张同学的座右铭是“态度决定全部”,他将这几个字写在一个正方体纸盒的每个面上,其平面睁开图以下图,那么在该正方体中,和“一”相对的字是()A.态B.度C.决D.切【答案】 A 【分析】【剖析】正方体的平面睁开图中,相对面的特色是之间必定相隔一个正方形,据此可得和“ ”一相对的字.【详解】正方体的平面睁开图中,相对面的特色是之间必定相隔一个正方形,因此和“一”相对的字是:态.应选 A.【点睛】注意正方体的空间图形,从相对面下手,剖析及解答问题.19.如图,小强从 A 处出发沿北偏东70°方向行走,走至 B 处,又沿着北偏西30°方向行走至 C 处,此时需把方向调整到与出发时一致,则方向的调整应是()A.左转 80 °B.右转 80°C.右转 100 °D.左转 100 °【答案】 C【分析】【剖析】过 C 点作 CE∥ AB,延伸 CB与点 D,依据平行线的性质得出∠A+∠ ABH=180°,∠ ECB=∠ABC,求出∠ ABH=110°,∠ ABC=80°,即可求出∠ECB=80°,得出答案即可.【详解】过 C 点作 CE∥ AB,延伸 CB与点 D,如图∵依据题意可知:AF∥ BH,AB∥ CE,∴∠ A+∠ ABH=180°,∠ ECB=∠ ABC,∵依据题意可知:∠FAB=70°,∠ HBC=30°,∴∠ ABH=180°-70°=110°,∠ ABC=110°30-°=80°,∴∠ ECB=80°,∴∠ DCE=180°80-°=100°,即方向的调整应是右转100°.故答案选 C.【点睛】本题考察了平行线的判断与性质,解题的重点是娴熟的掌握平行线的判断与性质.20.如图,已知直线AB和CD订交于G 点,CG EG,GF均分AGE,CGF34,则BGD 大小为()A.22B.34C.56D.90【答案】 A【分析】【剖析】先依据垂直的定义求出∠EGF的度数,而后依据GF 均分∠ ABE 可得出∠ AGF的度数,再由∠AGC=∠ AGF-∠ CGF求出∠ AGC的度数,最后依据对顶角相等可得出∠BGD的度数.【详解】解:∵ CG⊥ EG,∴∠ EGF=90°-∠ CGF=90°-34 °=56°,又 GF 均分∠ AGE,∴∠ AGF=∠ EGF=56°,∴∠ AGC=∠ AGF-∠ CGF=56°-34 °=22°,∴∠ BGD=∠ AGC=22°.应选:A.【点睛】本题考察了对顶角的性质,垂直的定义以及角均分线的定义,掌握基本观点和性质是解题的重点.。
初中数学经典几何难题与答案解析
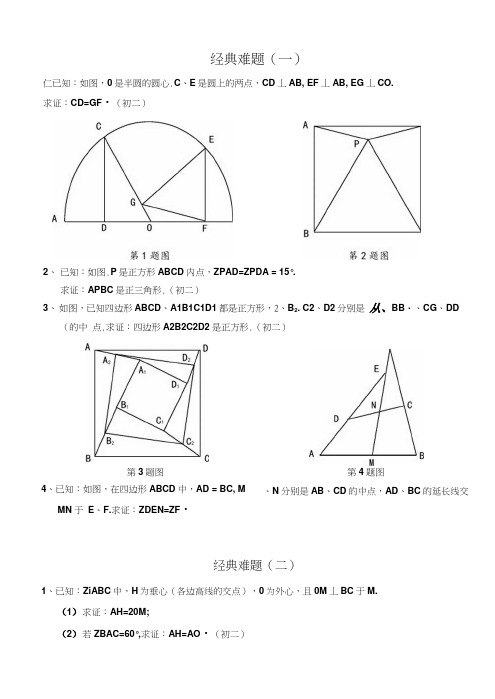
经典难题(一)仁已知:如图,0是半圆的圆心.C 、E 是圆上的两点,CD 丄AB, EF 丄AB, EG 丄CO. 求证:CD=GF ・(初二)求证:APBC 是正三角形.(初二)3、 如图,已知四边形ABCD 、A1B1C1D1都是正方形,2、B 2. C2、D2分别是 从、BB ・、CG 、DD(的中 点.求证:四边形A2B2C2D2是正方形.(初二)第3题图4、已知:如图,在四边形ABCD 中,AD = BC, MMN 于 E 、F.求证:ZDEN=ZF ・经典难题(二)1、已知:ZiABC 中,H 为垂心(各边高线的交点),0为外心,且0M 丄BC 于M.(1) 求证:AH=20M;(2) 若ZBAC=60°,求证:AH=AO ・(初二)第4题图、N 分别是AB 、CD 的中点,AD 、BC 的延长线交2、 已知:如图.P 是正方形ABCD 内点,ZPAD=ZPDA = 15°.2、设MN 是圆0外一直线.过0作0A 丄MN 于A,自A 引圆的两条直线,交圆于B 、C 及D 、E,直线EB 及CD 分别交MN 于P 、Q.求证:AP=AQ ・(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆0的弦,过MN 的中点A 任作两弦BC. DE,设CD 、EB 分别交MN 于P 、Q. 求证:AP=AQ ・(初二)求证:点P 到边AB 的距离等于AB 的一半・(初二)经典难题(三)1、如图,四边形ABCD 为正方形,DE/7AC, AE=AC, AE 与CD 相交于F. 求证:CE=CF ・(初二)第4题图在AABC 的外侧作正方形ACDE 和正方形CBFG,点PAGA第2题图是EF 的中点.3、设P 是正方形ABCD-边BC 上的任一点,PF 丄AP, CF 平分ZDCE. 求证:PA=PF ・(初二)第3题图 第4题图4、如图,PC 切圆0于C, AC 为圆的直径,PEF 为國的割线,AE 、AF 与直线P0相交于B 、D.求证:AB=DC, BC=AD ・(初三)经典难题(四)1.已知:ZiABC 是正三角形,P 是三角形内一点,PA=3, PB=4, PC=5.求:ZAPB 的慶数.(初二)求证:AE=AF ・(初二)2、 设P 是平行四边形ABCD 内部的一点,且ZPBA=ZPDA ・求证:ZPAB=ZPCB.(初二)3、 设ABCD 为圆内接凸四边形,求证:AB • CD+AD • BC=AC • BD.(初三)2、P 是边长为1的正方形ABCD 内的一点,求PA + PB+PC 的最小值. A4、平行四边形ABCD 中,设E 、F 分别是BC.AE = CF ・ 求证:ZDPA=ZDPC ・(初二)经典难题(五)1 >设 P 是边长为1的正△ ABC 内任一点,L = PA + PB + PC ,求证:WLV2.3、P为正方形ABCD内的一点,并且PA=a, PB = 2a, PC = 3a,求正方形的边长.经典难题(一)1、已知:如图,0是半圆的圆心,C、E是圆上的两点,CD丄AB, EF丄AB, EG丄CO.求证:CD=GFo (初二)证一:连接0E。
(word完整版)初中数学经典几何题(难)及答案分析
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC , AE 与CD 相交于F . 求证:CE =CF .(初二) 延长CD 至G ,使CD=DG ,连结AG 、EG 。
则AG=AC易证得△AED ≌△GED ,得AE=GE ,则AE=AG=GE ,得∠AEG=60°2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)GE B经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC0,∠EBA =200,求∠BED 的度数.经典难题(一)1.如下图做GH ⊥AB,连接EO 。
初中数学几何题(超难)及答案分析-七年级几何题超难

几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠P AD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初三)A P C D B A F G C E B O D D 2 C 2 B 2 A2 D 1 C 1 B 1 C B D A A 1 A N F E C D M B ·A H E C B O P C G F B Q A D E 6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初三(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P是EF 的中点.的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)(初二)· G A O D B E C Q P N M · O O Q P B D E C N M ·A 9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)(初二)11、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:P A =PF.(初二)(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)(初三)A F D E C B E D A C B F D F E P C B A O D B F A E C P 13、已知:△ABC 是正三角形,P 是三角形内一点,P A =3,PB =4,PC =5. 求:∠APB 的度数.(初二)(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠P AB =∠PCB .(初二)(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)(初三)16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且,且 AE =CF .求证:∠DP A =∠DPC.(初二)(初二)17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.A P C B P A D C B C B D A F P D E C B A 18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且P A =a ,PB =2a ,PC =3a ,求正方形的边长.,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA=200,求∠BED 的度数.的度数.A PCBACBPDEDAACBPD解答1.如下图做GH ⊥AB,连接EO 。
初一几何难题练习题集(含答案解析)

1.证明线段相等或角相等两条线段或两个角相等就是平面几何证明中最基本也就是最重要得一种相等关系。
很多其它问题最后都可化归为此类问题来证。
证明两条线段或两角相等最常用得方法就是利用全等三角形得性质,其它如线段中垂线得性质、角平分线得性质、等腰三角形得判定与性质等也经常用到。
例1. 已知:如图1求证:DE =DF分析:由∆ABC 连结CD,易得CD = 证明:连结CDAC BC A BACB AD DBCD BD AD DCB B A AE CF A DCB AD CD=∴∠=∠∠=︒=∴==∠=∠=∠=∠=∠=90,,,,∴≅∴=∆∆ADE CDFDE DF说明:在直角三角形中,作斜边上得中线就是常用得辅助线;在等腰三角形中,作顶角得平分线或底边上得中线或高就是常用得辅助线。
显然,在等腰直角三角形中,更应该连结CD,因为CD 既就是斜边上得中线,又就是底边上得中线。
本题亦可延长ED 到G,使DG =DE,连结BG,证∆EFG 就是等腰直角三角形。
有兴趣得同学不妨一试。
例2. 已知:如图2所示,AB =CD,AD =BC,AE =CF 。
求证:∠E =∠FAB CD BC AD AC CA ABC CDA SSS B DAB CD AE CF BE DF===∴≅∴∠=∠==∴=,,,∆∆()在∆BCE 与∆DAF 中,BE DF B D BC DA BCE DAF SAS E F=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∆∆()说明:利用三角形全等证明线段求角相等。
常须添辅助线,制造全等三角形,这时应注意: (1)制造得全等三角形应分别包括求证中一量; (2)添辅助线能够直接得到得两个全等三角形。
2.证明直线平行或垂直在两条直线得位置关系中,平行与垂直就是两种特殊得位置。
证两直线平行,可用同位角、内错角或同旁内角得关系来证,也可通过边对应成比例、三角形中位线定理证明。
证两条直线垂直,可转化为证一个角等于90°,或利用两个锐角互余,或等腰三角形“三线合一”来证。
初中几何经典难题合集(附答案)

初中几何经典难题合集(附答案)1.已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO。
求证:CD=GF。
(初二)证明:如图,作GH⊥AB,连接EO。
因为GOFE四点共圆,所以∠GFH=∠OEG。
又因为∠GHF=∠OGE =90°,所以△GHF∽△OGE。
可得GF/GE=GH/OE。
因为CO=EO,所以GF/GE=GH/CO,即GF=GH·GE/CO。
又因为∠CDO=∠EGO=90°,∠COD=∠EOG,所以△CDO∽△EGO。
可得CD/GE=CO/OE,即CD=CO·GE/OE。
因为CO=EO,所以CD=GF,得证。
已知:如图,在△ABC中,AB = AC,∠BAC = 80°,P为△ABC内一点,∠PBC = 10°,∠PCB = 30°,求∠PAB的度数。
(初二)证明:作∠BAC的平分线AD,交BC于点D。
因为AB = AC,∠BAC = 80°,所以∠ABC = ∠ACB = (180°- ∠BAC) / 2 = (180° - 80°) / 2 = 50°。
因为∠PBC = 10°,∠PCB = 30°,所以∠ABP = ∠ABC - ∠PBC = 50°- 10° = 40°,∠ACP = ∠ACB - ∠PCB = 50° - 30° = 20°。
在△ABC中,根据三角形内角和定理,∠BAC + ∠ABC + ∠ACB = 180°,所以∠BAC = 180° - ∠ABC - ∠ACB = 180° - 50° - 50° = 80°。
因为AD是∠BAC的平分线,所以∠BAD = ∠CAD = ∠BAC / 2 = 80° / 2 = 40°。
初中数学几何题超难及答案分析-七年级几何题超难

几何经典难题1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初三)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂心(各边高线的交点) (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FGCE B O D D 2 C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初三 )8、如图,分别以△ABC 的AC 和BC 为一边,在△,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.N9、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)10、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E EP13、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)14、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +16、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)17、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB C B D AFPDECBA. -18、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.19、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH⊥AB,连接EO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、证明线段相等或角相等
两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。
很多其它问题最后都可化归为此类问题来证。
证明两条线段或两角相等最常用的方法是利用全等三角形的性质,其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。
例1. 已知:如图1
求证:DE =DF 分析:由∆ABC 连结CD ,易得CD = 证明:连结CD
ΘΘΘAC BC A B
ACB AD DB
CD BD AD DCB B A AE CF A DCB AD CD
=∴∠=∠∠=︒=∴==∠=∠=∠=∠=∠=90,,,,
∴≅∴=∆∆ADE CDF
DE DF
说明:在直角三角形中,作斜边上的中线是常用的辅助线;在等腰三角形中,作顶角的平分线或底边上的中线或高是常用的辅助线。
显然,在等腰直角三角形中,更应该连结CD ,因为CD 既是斜边上的中线,又是底边上的中线。
本题亦可延长ED 到G ,使DG =DE ,连结BG ,证∆EFG 是等腰直角三角形。
有兴趣的同学不妨一试。
ΘΘAB CD BC AD AC CA ABC CDA SSS B D
AB CD AE CF BE DF
===∴≅∴∠=∠==∴=,,,∆∆()
在∆BCE 和∆DAF 中,
ΘBE DF B D BC DA BCE DAF SAS E F
=∠=∠=⎧⎨⎪
⎩
⎪∴≅∴∠=∠∆∆()
说明:利用三角形全等证明线段求角相等。
常须添辅助线,制造全等三角形,这时应注意:
(1)制造的全等三角形应分别包括求证中一量; (2)添辅助线能够直接得到的两个全等三角形。
2、证明直线平行或垂直
在两条直线的位置关系中,平行与垂直是两种特殊的位置。
证两直线平行,可用同位角、内错角或同旁内角的关系来证,也可通过边对应成比例、三角形中位线定理证明。
证两条直线垂直,可转化为证一个角等于90°,或利用两个锐角互余,或等腰三角形“三线合一”
来证。
例3. 如图3所示,设BP 、CQ 是∆ABC 的内角平分线,AH 、AK 分别为A 到BP 、CQ 的垂
证明:延长AH 交BC 于N ,延长AK 交BC 于M ∵BH 平分∠ABC ∴=∠∠ABH NBH 又BH ⊥AH
∴==︒∠∠AHB NHB 90 BH =BH
∴≅∴==∆∆ABH NBH ASA BA BN AH HN
(),
同理,CA =CM ,AK =KM ∴KH 是∆AMN 的中位线 ∴KH MN //
即KH 已知:如图4所示,AB =AC ,∠,,A AE BF BD DC =︒==90。
求证:FD ⊥ED
证明一:连结AD
ΘΘAB AC BD BAC BD DC
BD AD
B DAB DAE
=∴+==︒=∴=∴==,∠∠∠,∠∠∠129090
在∆ADE 和∆BDF 中,
ΘAE BF B DAE AD BD ADE BDF
FD ED
===∴≅∴∠=∠∴∠+∠=︒∴⊥,∠∠,∆∆31
3290
说明:有等腰三角形条件时,作底边上的高,或作底边上中线,或作顶角平分线是常用辅助线。
证明二:如图5
ΘΘΘBD DC
BDM CDE DM DE BDM CDE CE BM C CBM BM AC
A ABM A A
B A
C BF AE AF CE BM
=∠=∠=∴≅∴=∠=∠∴∠=︒
∴∠=︒=∠==∴==,,,∆∆//9090
∴≅∴==∴⊥∆∆AEF BFM
FE FM DM DE FD ED
Θ
说明:证明两直线垂直的方法如下:
(1)首先分析条件,观察能否用提供垂直的定理得到,包括添常用辅助线,见本题证二。
(2)找到待证三直线所组成的三角形,证明其中两个锐角互余。
(3)证明二直线的夹角等于90°。
3、证明一线段和的问题
(一)在较长线段上截取一线段等一较短线段,证明其余部分等于另一较短线段。
(截长法)
例5. 已知:如图6所示在∆ABC 中,∠=︒B 60,∠BAC 、∠BCA 的角平分线AD 、CE 相交于O 。
分析:在AC 上截取AF =AE 。
易知∆∆AEO AFO ≅,∴∠=∠12。
由∠=︒B 60,知
∠+∠=︒∠=︒∠+∠=︒566016023120,,。
∴∠=∠=∠=∠=︒123460,得:∆∆FOC DOC FC DC ≅∴=,
证明:在AC 上截取AF =AE
()
Θ∠=∠=∴≅∴∠=∠BAD CAD AO AO
AEO AFO SAS ,∆∆42
又∠=︒B 60
∴∠+∠=︒∴∠=︒
∴∠+∠=︒
∴∠=∠=∠=∠=︒∴≅∴=566016023120123460∆∆FOC DOC AAS FC DC
()
即AC AE CD =+
(二)延长一较短线段,使延长部分等于另一较短线段,则两较短线段成为一条线段,证明该线段等于较长线段。
(补短法)
例6. 已知:如图7所示,正方形ABCD 中,F 在DC 上,E 在BC 上,∠=︒EAF 45。
求证:EF =BE +DF
分析:使BG =DF 。
证明:延长CB 至G
在正方形ABCD 中,∠=∠=︒=ABG D AB AD 90,
∴≅∴=∠=∠∆∆ABG ADF SAS AG AF (),13
又∠=︒EAF 45
∴∠+∠=︒∴∠+∠=︒23452145
即∠GAE =∠FAE ∴=∴=+GE EF
EF BE DF
4、中考题:
如图8所示,已知∆ABC 为等边三角形,延长BC 到D ,延长BA 到E ,并且使AE =BD ,连结CE 、DE 。
作
∴==BA AF EF EAC DFE SAS EC ED
()
∴≅∴=∆∆>AB AC
2. 已知:如图12所示,在∆ABC 中,∠=∠A B 2,CD 是∠C 的平分线。
求证:BC =AC +AD
3. 已知:如图13所示,过 ABC的顶点A,在∠A内任引一射线,过B、C作此射线的垂线BP和CQ。
设M为BC的中点。
求证:MP=MQ
4. ∆ABC 中,∠=︒⊥BAC AD BC 90,于D ,求证:()AD AB AC BC <++1
4
【试题答案】
1. 证明:取
ΘAC AD
AF CD AFC =∴⊥∴∠= 又∠+∠=︒∠+∠=︒14901390,
∴∠=∠=∴≅∴=∴=43
12
ΘAC CE
ACF CED ASA CF ED
DE CD ∆∆
()
2. 分析:本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法。
“截长”即将长的线段截
ΘΘCB CE BCD ECD
CD CD CBD CED
B E BA
C B
BAC E
=∠=∠=⎧⎨⎪⎩
⎪∴≅∴∠=∠∠=∠∴∠=∠∆∆22
又∠=∠+∠BAC ADE E
∴∠=∠∴=∴==
ADE E AD AE BC CE , 3. 证明:延长PM ΘCQ AP BP BP CQ PBM ⊥∴∴∠=∠,// 又BM CM =, ∴≅∴=∆∆BPM CRM PM RM
∴QM 是Rt QPR ∆斜边上的中线 ∴=MP MQ。
