正方体展开图相关题型
正方体的展开与折叠(通用版)(含答案)

正方体的展开与折叠(小学五、六年级)单选题(共12道,每道8分)1.如图是一个正方体的表面展开图,把它折叠成一个正方体时,与点M重合的点是( )A.点A和点HB.点K和点HC.点B和点HD.点B和点L2.如图是一个正方体的表面展开图,把它再折回成正方体后,则下列说法:①点H与点C重合;②点D与点M、点R重合;③点B与点Q重合;④点A与点S重合.其中正确说法的序号是( )A.②④B.①④C.②③D.①③3.如图是一个正方体的表面展开图,如果将它折叠成原来的正方体,那么与边LK重合的边是( )A.ABB.FJC.IJD.NM4.如图,有一个无盖的正方体纸盒,下底面标有字母“M”,沿图中粗线将其剪开展成平面图形,这个平面图形是( )A. B.C. D.5.如图,有一个无盖的正方体纸盒,下底面挖去了一个小洞,沿图中粗线将其剪开展成平面图形,这个平面图形是( )A. B.C. D.6.如图是正方体的表面展开图,折叠成正方体后,其中哪两个完全相同( )A.(1)(2)B.(2)(3)C.(3)(4)D.(2)(4)7.明明用如图所示的硬纸片折成了一个正方体的盒子,里面装了一瓶墨水,只凭观察,选出墨水在哪个盒子中( )A. B.C. D.8.将下图正方体的相邻两面各划分成九个相同的小正方形,并分别标上“○”、“×”两符号.若下列有一图形为此正方体的展开图,则此图为( )A. B.C. D.9.如图是一个正方体的表面展开图,这个正方体是( )A. B.C. D.10.如图是一个正方体的表面展开图,这个正方体是( )A. B.C. D.11.如图是一个正方体的表面展开图,这个正方体是( )A. B. C. D.12.有一个正方体和四个展开的正方体表面图形,其中可以折叠成如图正方体的是( )A. B.C. D.正方体的展开与折叠答案与解析1答案:C解题思路:一条棱被剪开,变成了两条边,折叠以后这两条边是重合的.该图EC与EN重合,CB和NM重合,GH和GM重合,因此M与H重合,C与N重合,B与M重合,故与点M重合的点是点B和点H,故选C.试题难度:三颗星知识点:几何体的展开与折叠找重合的点2答案:A解题思路:1.解题思路:本题主要考查正方体的展开与折叠找重合的点,一条棱被剪开,变成了两条边,折叠以后这两条边是重合的;一个顶点连着三条棱,当一条棱被剪开时,该顶点还是一个点,当两条棱被剪开时,该顶点变成两个点,当三条棱都被剪开时,该顶点变成了三个点.2.解题过程:根据正方体展开图的特征,ED与EM重合,NM与NR重合,故点D,M,R重合,②正确;FG与FC重合,GH与CB重合,故点C与点G重合,点H与点B重合,①、③错误;DA与RS重合,点D与点R重合,点A与点S重合,故④正确.综上,正确的为②④,故选A.3.易错点:由正方体的表面展开图不会判断哪些棱重合,哪些点重合.4.方案:如果此题有问题,建议观看:初中数学图形的展开与折叠拔高课.视频链接:/course/1127.html试题难度:三颗星知识点:几何体的展开与折叠找重合的点3答案:C解题思路:一条棱被剪开,变成了两条边,折叠以后这两条边是重合的,AB与IH重合,FK与FJ重合,KL和JI重合,故与边LK重合的边是IJ,故选C.试题难度:三颗星知识点:几何体的展开与折叠找重合的边4答案:B解题思路:面M的相对面是空的,即展开之后面M没有相对面,排除选项A,D;根据图中的粗线将其剪开之后,与M相连的面是展开的四个面中的第二个或第三个,故选B.试题难度:三颗星知识点:无盖模型的展开与折叠5答案:D解题思路:根据无盖的位置及展开后的平面图形,面“○”展开之后没有相对面,排除选项B;按图中的粗线将其剪开之后与面“○”相连的四条棱均没有被剪开,排除选项A和C,故选D.试题难度:三颗星知识点:无盖模型的展开与折叠6答案:D解题思路:既然折叠成正方体后两个图形完全相同,那么它们对应的平面图形的相对面必须完全一样.根据正方体11种展开图的相对面:(1)中面“△”与面“#”相对,(2)中面“△”与面“+”相对,排除选项A;(2)中面“#”与面“○”相对,(3)中面“#”与面“×”相对,排除选项B;(3)中面“#”与面“×”相对,(4)中面“#”与面“○”相对,排除选项C;故选D.我们也可以看一下(2)和(4)中的相对面确实是一样的:(2)中面“△”与面“+”相对,面“#”与面“○”相对,面“☆”与面“×”相对;(4)中面“△”与面“+”相对,面“#”与面“○”相对,面“☆”与面“×”相对.试题难度:三颗星知识点:正方体的展开与折叠7答案:B解题思路:此题可以通过棱来判断.如下图,折叠之后AB与EF重合,因此可以判断面“ABCD”与面“EFGH”折起来之后阴影部分相连,因此排除选项A和D;DA与DI重合,JI与HE重合,因此两个阴影的面与面“○”相连的部分都是空白三角形,排除选项C,故选B.试题难度:三颗星知识点:正方体的展开与折叠8答案:C解题思路:此题可以通过棱来判断.如下图,面“ABCD”和面“ABEF”有一条重合的棱AB,并且“×”与棱AB的距离是1个网格,“○”与棱AB的距离是2个网格,可以排除选项B和D;并且“×”和“○”距离上下底面的高度不同,排除选项A,故选C.试题难度:三颗星知识点:正方体的展开与折叠9答案:A解题思路:根据图中正方体的三个带图案的面是相邻的,可以排除选项C和D,正方体中两个带阴影三角形的面的相邻部分是空白的,可以排除选项B,故选A.试题难度:三颗星知识点:正方体的展开与折叠10答案:C解题思路:根据示正方体的展开图,三个带竖线的面有两个是相对的,因此三个面不可能同时出现,也不可能都不出现,排除选项A和D;三个带竖线的面与面“○”相邻,竖线与“○”垂直,排除选项B,故选C.试题难度:三颗星知识点:正方体的展开与折叠11答案:B解题思路:1.解题思路:本题主要考查正方体的展开与折叠,先根据相对面、相邻面排除,然后再根据一条棱剪开变成两条边,两相邻面与公共棱的关系进一步排除.2.解题过程:观察正方体的展开图,三个带竖线的面有两个是相对的,因此三个面不可能同时出现,也不可能都不出现,排除选项D;三个带竖线的面与面“△”相邻,竖线与“△”垂直,排除选项A;如下图,带竖线的面“ABCD”与“CEFG”相邻,面“CEFG”与面“GHIJ”相邻,并且竖线都与重合的棱平行,排除选项C,故选B.3.易错点:①相对面、相邻面判断错误;②一条棱剪开变成两条边,不知道哪两条边折叠之后重合成一条棱;③不会根据两相邻面与公共棱的关系判断.4.方案:如果此题有问题,建议观看:初中数学图形的展开与折叠拔高课.视频链接:/course/1127.html试题难度:三颗星知识点:正方体的展开与折叠12答案:C解题思路:正方体的三个带阴影的直角三角形有公共边,并且有一个公共的直角顶点,所以选项中图形折叠之后应该满足这两条特征。
(完整版)正方体的展开图练习题
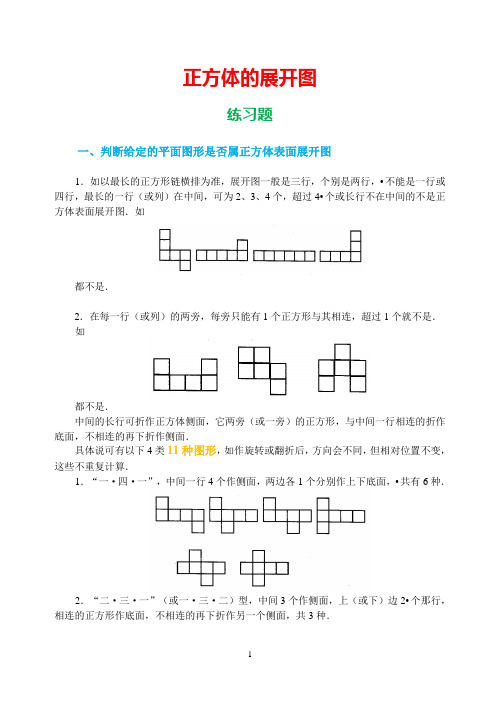
正方体的展开图练习题一、判断给定的平面图形是否属正方体表面展开图1.如以最长的正方形链横排为准,展开图一般是三行,个别是两行,•不能是一行或四行,最长的一行(或列)在中间,可为2、3、4个,超过4•个或长行不在中间的不是正方体表面展开图.如都不是.2.在每一行(或列)的两旁,每旁只能有1个正方形与其相连,超过1个就不是.如都不是.中间的长行可折作正方体侧面,它两旁(或一旁)的正方形,与中间一行相连的折作底面,不相连的再下折作侧面.具体说可有以下4类11种图形,如作旋转或翻折后,方向会不同,但相对位置不变,这些不重复计算.1.“一·四·一”,中间一行4个作侧面,两边各1个分别作上下底面,•共有6种.2.“二·三·一”(或一·三·二)型,中间3个作侧面,上(或下)边2•个那行,相连的正方形作底面,不相连的再下折作另一个侧面,共3种.3.“二·二·二”型,成阶梯状.4.“三·三”型,两行只能有1个正方形相连.二、找正方体相邻或相对的面1.从展开图找.(1)正方体中相邻的面,在展开图中有公共边或公共顶点.如,•或在正方形长链中相隔两个正方形.如中A与D.(2)在正方体中相对的面,在展开图中同行(或列)中,中间隔一个正方形.如ABCD中,A与C,B与D,或和中间一行(或列)•均相连的两正方形亦相对.例1 右图中哪两个字所在的正方形,在正方体中是相对的面.解“祝”与“似”,“你”和“程”,“前”和“锦”相对.例2在A、B、C内分别填上适当的数.使得它们折成正方体后,对面上的数互为倒数,则填入正方形A、B、C•的三数依次是:(A)12,13,1 (B)13,12,1 (C)1,12,13(D)12,1,13分析A与2,B与3中间都隔一个正方形,C与1分处正方形链两边且与其相连,选(A).例3 在A、B、C内分别填上适当的数,使它们折成正方体后,对面上的数互为相反数.分析A与0,B与2,C和-1都分处正方形链两侧且与其相连,∴A─0,B─-2,C ─1.例4 代出折成正方体后相对的面.解A和C,D和F,B和E是相对的面.2.从立体图找.例5 正方体有三种不同放置方式,问下底面各是几?分析先找相邻的面,余下就是相对的面.上图出现最多的是3,和3相连的有2、4、5、6,余下的1就和3相对.再看6,•和6相邻的有2、3、4,和3相对的是1,必和6相邻,故6和5相对,余下是4和2相对,•下底面依次是2、5、1.例6由下图找出三组相对的面.分析和2相连的是1、3、5、6,相对的是4,和3相连的是2、4、5、6,相对的是1,和6相连的是1、2、3、4,相对的是5.三、由带标志的正方体图去判断是否属于它的展开图例7 如下图,正方体三个侧面分别画有不同图案,它的展开图可以是().分析基本方法是先看上下,后定左右,图A图B都是□和+两个面相对,不合题意,图C“□”和“○”之上,从立体图看“+”在右,符合要求.图D•“□”和“+”之上,“○”在右,而立体图“○”应在左,不合要求,故选(C).例8 下面各图都是正方体的表面展开图,若将它们折成正方体,•则其中两个正方体各面图案完全一样,它们是().分析首先找出上下两底,(1)是+和*,(2)是+和*,(3)(4)都是□和×,排除(1)(2),再检查侧面,(3)(4)顺序相同,所以选(3)(4).。
正方体的展开与折叠练习题(答案)

①一个正方体的六个面分别写着不同的数字(忽略数字本身的方向),请根据下面三个图形,
判断7对面的数字是多少。
答案:1
解析:图一中2,3都与7相邻,图二中5,8都与7相邻,
所以2,3,5,8是相邻面,只能图三中的1是7的相对面。
②如图桌子上放着一个上方无盖的正方体纸盒,已知它的底面被剪了一个圆洞,
那么它的正确展开图是( )。
答案:D
解析:A,B,C的圆洞都有相对面
所以只有D正确。
③如图一个正方体,如果把它展开,可能是哪一个展开图,选( )。
答案:D
解析:A,C有两个图形是相对面
B三个图形的时针方向不对
或者根据斜线的方向不对
所以只有D正确。
④如图左边是立方体的展开图,那么折叠后可能是( )。
答案:C
解析:把三角形的面的四边编上号1,2,3,4
A中边2的相邻面是错误的。
B中边1的相邻面是错误的,直线的方向不对。
D中边1的相邻面是错误的。
所以答案是C
⑤下图是一个正方体的展开图,该正方体的相对两个面的代数式的值相等,那么求m的值。
答案:-72
解析:给的条件是相对面值相等,所以先找相对面。
2a与-12相对,所以2a=-12,a=-6
3b与36相对,所以3b=36,b=12
m与ab相对,所以m=ab=-72
⑥如图,左边是立方体纸盒的外表展开图,右面4个立体图形中( )可以由展开图折叠而成。
答案:B
解析:C中1,2不相对,排除
A中1,6,4的时针方向不对。
D中2,4,5的时针方向不对。
只有B可以,所以答案是B。
(完整版)长方体和正方体的展开图练习题

长方体和正方体展开图1、画图操作。
根据给出的长、宽、高想象并画出长方体的六个面。
2、带有两个正方形面的特殊长方体。
一个长方体最多有()条棱长相等,最多有( )个面是正方形。
3、观察长方体和正方体。
从同一个角度观察长方体或正方体,最少能看到()个面,最多能看到()面。
4、根据棱长总和求问题。
(1)一个长方体的棱长总和是80厘米,长10厘米,宽是7厘米。
高是( ?)厘米。
(2)一根长96厘米的铁丝围成一个正方体,这个正方体的棱长是(?? )厘米。
(3)用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是()厘米。
5、长方体和正方体外面的彩带的长度。
(1)一种长方体的礼品盒,长0.9米,宽0.4米,高0.25米,如果用包装带把它捆扎(如图)起来,打结处的包装带长0.2米,一共要多少米的包装带?(2)有一个长5分米、宽和高都是3分米的长方体硬纸箱,如果用绳子将箱子横着捆两道,长着捆一道,打结处共用2分米(如图)。
一共要用绳子多长?6、拼成正方体。
至少要用()块同样的小正方体才能拼成一个稍大的正方体,还可以用()块,()块、()块……也能拼成更大的正方体。
7、会正确判断给定的平面图形能否围成长方体或正方体(如下图)。
8、相对的面。
下图中与5号相对的面是()号,与()号与6号是相对的面。
9、会把展5 61 2 34开图补充完整(如下图)。
10. 下图是一个正方体纸盒展开图,请根据图中数据计算它的棱长总和以及底面积。
仅供个人用于学习、研究;不得用于商业用途。
For personal use only in study and research; not for commercial use.Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.以下无正文。
正方体的展开图 小学数学 随堂练习
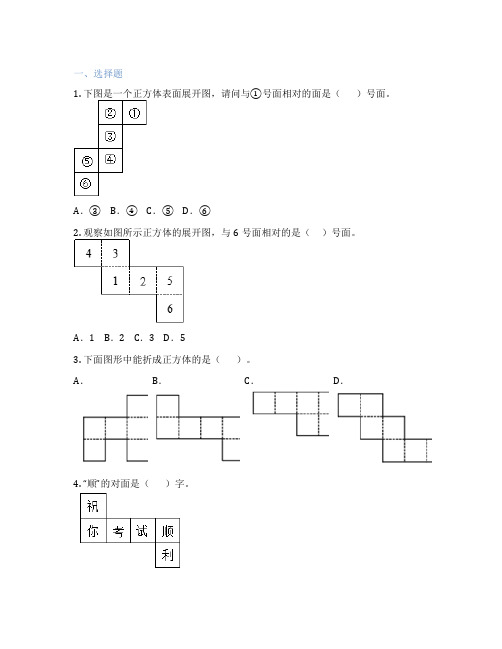
一、选择题1. 下图是一个正方体表面展开图,请问与①号面相对的面是()号面。
A.③B.④C.⑤D.⑥2. 观察如图所示正方体的展开图,与6号面相对的是()号面。
A.1 B.2 C.3 D.53. 下面图形中能折成正方体的是()。
A.B.C.D.4. “顺”的对面是()字。
A.“考”B.“你”C.“祝”D.“利”5. 下图是一个正方体的展开图,和3号面相对的面是()。
A.3号B.4号C.6号D.5号二、填空题6. 观察图形,填空.折一折,能折成________体;其中②号面与________面相对;③号面与________面相对;⑤号面与________面相对.7. 折一折,用做一个,“3”的对面是( ),“1”的对面是( )。
8. 将下面这个展开图围成一个正方体后,与红色的面相对的面是( )色.9. 如图,26个英文字母排成S形,一个正方体木块的六个面上分别写着数字1到6,数字1和6相对,2和5相对,3和4相对.开始时,木块放在字母A上,木块朝上的面上的数字是1.现将木块沿着图中的方格滚动,当木块滚动到字母Z上时,木块朝上的面上的数字是________.10. 下面是一个正方体的展开图。
(1)①号面相对的是( )号面;⑤号面相对的是( )号面。
(2)如果这个正方体的棱长是2cm,那么它的表面积是( )。
三、解答题11. 将1、2、3、4、5、6分别填在如图中的每个方格内,使折成的正方体中相对的2个面的数之和相等。
12. 把一个棱长为的正方体的6个面展开(如图)。
(1)在展开图中标出剩下三个面的名称。
(2)这个正方体的棱长总和是(),表面积是(),体积是()。
13. 如图,这是一个正方体的展开图,如果将它组成原来的正方体,哪些点与点P重合。
14. (1)如图中涂色的四个正方形是个正方体展开图中的4个面(每个小方格1平方分米),请你画出展开图的另外的两个面并涂上阴影。
(2)如果要把12个上面这样的正方体装进一个长方体包装盒,这个长方体的长、宽、高分别是()分米、()分米,()分米时,所用的包装纸最少,是()平方分米。
展开图形练习题

展开图形练习题在几何学里,展开图形是指将一个三维的图形展开成二维的形式。
展开图形练习题主要用于训练学生在二维空间中观察和理解三维图形的能力。
下面,我们将通过几个展开图形练习题来帮助你更好地理解展开图形的概念。
题目一: 立方体将一个立方体展开成二维图形。
解析:首先,让我们来观察立方体的形状。
一个立方体有六个面,每个面都是一个正方形。
我们将每个面的边长标记为a。
根据立方体的性质,我们可以发现,如果我们将立方体打开成平面图形,会得到一个由六个相邻正方形组成的形状。
我们可以根据这个规律开始绘制展开图形。
1. 首先,选择一个正方形作为展开图形的底部。
标记这个正方形为A。
2. 在A的上方,绘制另外一个正方形B。
确保B的底边与A的顶边对齐。
3. 在B的右侧,绘制正方形C。
与A、B的顶边对齐。
4. 在A、B、C的上方,绘制正方形D。
与B、C的顶边对齐。
5. 在D的右侧,绘制正方形E。
与A、B、C的顶边对齐。
6. 最后,在E的上方,绘制正方形F。
与B、C、D、E的顶边对齐。
现在,我们得到了一个由六个相邻正方形组成的展开图形。
这个图形就是立方体的展开形式。
你可以根据需要对图形进行标记,用来表示立方体的各个面。
题目二: 正四面体将一个正四面体展开成二维图形。
解析:正四面体是一个具有四个面的多面体,每个面都是一个等边三角形。
正四面体没有对称性,所以展开图形需要仔细观察每个面之间的关系。
1. 首先,选择一个等边三角形作为展开图形的底部。
标记这个三角形为A。
2. 在A的上方,绘制另外一个等边三角形B。
确保B的底边与A的顶边对齐。
3. 在A和B的中间,绘制一个等边三角形C。
与A、B的底边对齐。
4. 在C的上方,绘制另外一个等边三角形D。
与C的底边对齐。
现在,我们得到了一个由四个相邻等边三角形组成的展开图形。
这个图形就是正四面体的展开形式。
你可以根据需要对图形进行标记,用来表示正四面体的各个面。
通过以上两个展开图形练习题,我们可以看出,展开图形是一种将三维图形转化成二维的方法。
正方体展开图训练题

正方体展开图的训练题1.如图,是正方体的一种平面展开图,各面都标有数字,则数字为-4的面与它对面的数字之积是。
1题2题2.如图是一个正方体的侧面展开图,如果将它折叠成一个正方体后相对的面上的数相等,则图中x的值为。
3题4题3.如图是一个正方体纸盒的展开图,如果其中一面标上A,那么与标有A的面相对的一面上所标的数字是4.如图,是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是。
5.下列四个图形中,每个小正方形都标上了颜色.若要求一个正方体两个相对面上的颜色都一样,那么不可能是这一个正方体的展开图的是()A、B、C、D、6.如图是3个完全相同的正方体的三种不同放置方式,下底面依次是______。
7.小丽制作了一个如下左图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是()8.下面各图都是正方体的表面展开图,若将它们折成正方体,则其中两个正方体各面图案完全一样,它们是_______。
9.判断题(1)如图中,①是②的表面展开图.()(2)长方体的表面展开图只有一种.()(3)由于圆锥体可以由直角三角形旋转得到,所以圆锥体的侧面展开图也可以是三角形.()(4)圆锥体的侧面展开图只有一种.()10.圆锥的侧面展开图是________________.11.三棱柱的侧面展开图是__________________.12.如图是一个正方体的展开图,每个面都标注了字母.(1)如果面A在多面体的底部,上面是哪一个面?(2)如果F在前面,从左看是面B,上面是哪一面?(3)从右面看到面C,面D在后面,上面是哪一面?BA CD。
正方体找对面的题型一年级

正方体找对面的题型一年级一、基础题型(1 - 10题)题1:- 题目:一个正方体展开图如下(简单的1 - 4 - 1型展开图,例如上面一行中间一个正方形,下面一行四个正方形),已知写着数字1的面朝上,数字3的面朝前,问数字1的对面是哪个数字?- 解析:对于正方体的展开图,相对的面是间隔出现的。
在这种1 - 4 - 1型展开图中,1和3中间隔了一个正方形,所以1的对面是3后面的那个面,也就是数字5。
题2:- 题目:正方体展开图(2 - 3 - 1型,上面一行两个正方形,中间一行三个正方形,下面一行一个正方形),数字2的面在左边,数字4的面在上面,问数字2的对面是哪个数字?- 解析:在2 - 3 - 1型展开图中,先看数字2所在的位置。
2的对面是与它不相邻且间隔的面。
数字2与数字4不相邻且间隔,所以2的对面是数字4对面的数字,也就是数字6。
题3:- 题目:正方体展开图(3 - 3型,上下两行各三个正方形),数字1的面在前面,数字3的面在上面,问数字1的对面是哪个数字?- 解析:在3 - 3型展开图里,数字1和数字3是相邻面。
从整体看,1的对面是与1间隔的面,所以1的对面是数字5。
题4:- 题目:有一个正方体,它的六个面上分别标有字母A、B、C、D、E、F。
正方体展开图如下(1 - 4 - 1型),字母A的面在前面,字母C的面在上面,问字母A的对面是哪个字母?- 解析:根据正方体展开图相对面间隔出现的规律,A与C相邻,A的对面应该是与A间隔的面,所以A的对面是字母F。
题5:- 题目:正方体展开图(2 - 3 - 1型),标有红色的面在右边,标有蓝色的面在上面,问红色面的对面是什么颜色的面?- 解析:在2 - 3 - 1型展开图中,红色面在右边,它的对面是与它间隔的面。
蓝色面在上面,红色面的对面就是蓝色面下面的面,假设为绿色面(题目未明确其他颜色的关系,这里假设一种颜色)。
题6:- 题目:一个正方体六个面分别画着苹果、香蕉、橘子、梨、桃、西瓜。
正方体展开图的练习题

五 年 级 数 学 家 作(3.18)
姓名( )
同学们:今天的课堂上我们学习了正方体的展开图,知道了正方体的展开图可以分成以下四大类,已
知确定了其中的一个面,请分别标出“前、后、左、右、上、下”的其中五个面。
二、简便计算:(这三道题有点难度的噢,如果你真想不出来就明天课堂上好好听讲解噢!) 1÷112 ÷113 ÷114 ÷115 、、、、÷1119 2.009×43+20.09×2.9+200.9×0.28 2324 ×19
三、解决问题:
1、光明小学数学兴趣小组有男生32人,比女生多13
,数学兴趣小级共有多少人
2、有一群羊正在山坡吃草。
其中白羊占总数的920 ,这时又来16只黑羊后,白羊只数就占总数的14
,问:这群羊中白羊有多少只? 第4类:两排各有3个,有1种。
正方体的展开图 小学数学 练习题

一、选择题1. 一个正方体相对两个面上标的数互为倒数,下图是它的展开图,则a=()。
C.1 D.3A.B.2. 如图是一个正方体展开图,正方体的六个面分别写上“祝你学习进步”六个字,其中“学”字相对的面上的字是()。
A.习B.进C.步3. 将下图沿虚线折起来,可折成一个正方体.这时正方体的5号面所对的面是( )号面.A.2 B.3 C.4 D.64. 下列图形可以折叠围成长方体的有(),可以折叠成正方体的有()。
应选择()。
A.④②B.⑥③C.⑤①D.④③5. 把左图折成,数字“2”的对面是()。
A.“1”B.“5”C.“6”二、填空题6. 下图是一个正方体的展开图。
2号的对面是( )号,4号的对面是( )号。
7. 将下面这个展开图围成一个正方体后,与红色的面相对的面是( )色.8. 用围成一个正方体,“5”的对面是“()”,“3”的对面是“()”。
9. 如图是一个正方体的展开图,这个正方体的①号的对面是________,⑤号的对面是________。
10. 在下图中添上一个正方形、使它能围成一个正方体,共有()种添加方法。
三、解答题11. 下面哪一个图形折叠起来能做成一只开口的盒子?请在图形下面对应的字母打上“√”。
12. 如果将如图的图形折叠成一个正方体,那么与∠A的两条边相邻的两个面上所写的数的和是多少?13. 如果将如图的展开图折叠起来成为一个正方体,则箭头所指的A点相邻的两个面的数字和是多少?14. 下图是一个正方体展开图,正方体的六个面分别写上“祝你学习进步”六个字,请你说出每个字相对的面上的字是哪个字?。
七年级上册数学正方体题型

七年级上册数学正方体题型一、正方体的展开图相关(8题)1. 下列图形中,是正方体展开图的是()- 选项A:“田”字形。
- 选项B:“凹”字形。
- 选项C:1 - 4 - 1型的展开图(符合正方体展开图的一种常见类型)。
- 选项D:五个正方形连成一排。
解析:正方体展开图有11种基本情况,常见的有1 - 4 - 1型、2 - 3 - 1型、2 - 2 - 2型、3 - 3型。
“田”字形和“凹”字形不能折成正方体,五个正方形连成一排也不能折成正方体,而1 - 4 - 1型可以折成正方体,所以答案是C。
2. 一个正方体的展开图如图所示,相对面上的数字互为相反数,则x + y的值为()- 展开图中,数字3与x所在面相对,数字 - 2与y所在面相对。
解析:因为相对面上的数字互为相反数,所以x=-3,y = 2,则x + y=-3+2=-1。
3. 将一个正方体沿某些棱剪开,展成一个平面图形,至少需要剪几条棱?解析:正方体有12条棱,要将正方体展开成平面图形,需要将7条棱剪开,因为展开图中相邻的面之间有一条棱是剪开的,而正方体有6个面,展开后有5条棱是相连的,所以12 - 5=7条棱。
4. 如图是一个正方体纸盒的展开图,在其中的四个正方形内标有数字1、2、3和- 3,要在其余正方形内分别填上 - 1、 - 2,使得按虚线折成正方体后,相对面上的两数互为相反数,则A处应填()- 从展开图可以看出,与标有数字1的面相对的面是A所在面。
解析:因为相对面上的两数互为相反数,1的相反数是 - 1,所以A处应填 - 1。
5. 一个正方体的展开图中,有四个正方形连成一排,那么另外两个正方形的位置可能有几种情况?解析:另外两个正方形的位置可能有以下三种情况:- 在这一排正方形的同侧(上下位置),形成2 - 4型展开图。
- 在这一排正方形的两侧(一上一下),形成3 - 3型展开图。
- 其中一个与这一排中的一个正方形相连,另一个在其相对位置,形成2 - 3 - 1型展开图。
正方体平面展开图练习(含答案)

inh ei r 正方体平面展开图练习正方体的平面展开图中相对的两个面的特点是:相对的两个面中间一定隔着一个小正方形,且没有公共的顶点,且相距最近。
【同类题】如图是正方体的一种展开图,其中每个面上都标有一个数字,那么在原正方体中,与数字“2”相对的面上的数字是______.解:这是一个正方体的平面展开图,共有六个面,其中面“2”与面“4”相对,面“3”与面“5”相对,“1”与面“6”相对.故答案为:4.【同类题】一个无盖的立方体纸盒,将它展开成平面图,有几种可能的图形?分析 与例10不同的是立方体少一个面,而且其平面展开图不唯一.因此要按五个面,运用分类的数学思想,应用简单枚举法,将平面图形的可能情况一一列举出来. 答案 将可能的情况分为三类:(1)四个正方形连成一排的有两种情况,如图.(2)三个正方形连成一排的有五种情况,如图.(3)两个正方形连成一排的有一种情况,如图.综上所述,一共有八种展开图h ingsf odA l lt h i ng si nh ei r be i ng ar eg oo dABC解:D= 3x 2-7xy +4y 2,F= 9x 2-11xy +2y 27.有一个正方体,A ,B ,C 的对面分别是x ,y ,z 三个字母,如图所示,将这个正方体从现有位置依此翻到第1,2,3,4,5,6格,当正方体翻到第6格时正方体向上一面的字母是( )A 、xB 、AC 、BD 、C解:翻到1时,C 与1重合,翻到2时,B 与2重合,翻到3时,A 与3重合,C 与4重合,x 与5重合,y 与6重合,∵B 的对面是y ,∴正方体向上一面的字母是B .故答案为:C .8.下列四个图形中,每个小正方形都标上了颜色.若要求一个正方体两个相对面上的颜色都一样,那么不可能是这一个正方体的展开图的是( )9.如图,是一个正方体纸盒的两个表面展开图,请把-8,5,8,-2,-5,2分别填入六个正方形中,使得折成正方体后,相对面上的两数互为相反数.10.如图是一个正方体纸盒的平面展开图,每一个正方形内部都有一个单项式.当折成正方体后,“?”所表示的单项式与对面正方形上的单项式是同类项,则“?”所表示的单项式是( )A、bB、cC、dD、e。
立体图形的展开 小学数学 习题集

一、填空题
1. 如图是一个正方形纸盒的展开图,当折叠成正方体纸盒时,D点与( )点重合。
2. 仔细观察,上面的图形是下面哪个图形的展开图?
________
________
________
A. B. C.
3. 图11中的正方体A点有一只蚂蚁要沿着棱爬到B点,那么,取最短路线的走法有______种.
4. 用做成一个,□的对面是( )。
二、解答题
5. 用不同的颜色把下面的图形分成大小和形状完全相同的两部分.
6. 棱长是厘米(为整数)的正方体的若干面涂上红色,然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为,此时的最小值是多少?
7. 图为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为毫米,问:这卷纸展开后大约有多长?
8. 如下图,剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折,沿实线粘),这个多面体的面数、顶点数和棱数的总和是多少?。
数学七年级上册《正方体的展开与折叠》专题复习

解:(1)由正方体表面展开图可知“x”与“M”是相对的面, “-2”与“-3”是相对的面, “4x”与“2x+3”是相对的面, 又因为标注了字母 M 的是正方体的前面,标注了-2 的是正方体的底面, 所以标注了字母 x 的是正方体的后面,标注了-3 的是正方体的上面, 因此标注“2x+3”与“4x”是左面和右面, 又因为正方体的左面与右面标注的式子的和为 21, 所以 2x+3+4x=21,解得 x=3.
( C)
类型 2:找正方体的相对面 在通过正方体展开图形找相对面时,首先在同层中隔一面寻找,再在异 层中隔两面寻找,剩下的两面自然相对.
5.(大庆中考)将正方体的表面沿某些棱剪开,展成如图所示的平面图形,
则原正方体中与数字 5 所在的面相对的面上标的数字为
( B)
A.1 B.2 C.3 D.4
6.(达州中考)下列正方体的展开图上每个面上都有一个汉字.其中,
“手”的对面是“口”的是
( B)
7.(历下区期末)如图是一个正方体的展开图,把展开图折叠成正方体后, 与“山”字相对面上的字是__绣__.
8.(合阳县期末)如图是一个正方体的平面展开图,标注了字母 M 的是正 方体的前面,标注了-2 的是正方体的底面,正方体的左面与右面标注的 式子的和为 21. (1)求 x 的值; (2)求正方体的上面和后面的数字的积.
知能素养小专题(五) 正方体的展开与 折叠
类型 1:判断正方体的展开图 正方体的展开图有以下几种类型:141 型(分 3 行,中间 4 个,上下各 1 个,共 6 种情况),132 型(分 3 行,中间 3 个,上行 1 个,下行 2 个连在 一起,共 3 种情况),222 型(每行 2 个,首尾相连,1 种情况),33 型(每 行 3 个,下一行跟末尾一个相连,1 种情况).
正方体展开图经典测试题及解题技巧

正方体展开图经典测试题及解题技巧1、下列图形中可能是正方体展开图的是()A.B.C.D.解题思路:判断正方体的侧面展开图正确与否,可以从三个角度进行破解。
一看阵型进行对号入座(包括141阵型6种、231阵型3种、222阵型1种、33阵型1种类),找到符合的阵型即可;也可以采用排除特殊的阵型。
如“田”、“凹”“七”字阵型和“一字长蛇阵”均不能构成正方体。
二看是否“隔河相望”,一般分三层,中间一层相当于一条河,第一层和第三层形成隔河相望的状态(11种类除过333阵型,只有两层;三看正方形的相对面。
正方形的相对面,如果正方形的相对面出现两个,不符合常规,即排除。
A项.属于222阵型,成阶梯状,属于11中类型中的其中一种,属于“隔河相望”,相对面在“Z”的两端,正确。
B项属于“一字长蛇阵”排除,且只有一层,不能构成“隔河相望”,且第三个面分别与第一个面和第五个面相对,第四个面分别与第二个面和第六个面相对,不符合逻辑,故排除。
C项,属于“田”字型,只有两层,不能构成“隔河相望”排除;D项属于“七”字型,且只有两层,不能构成“隔河相望”,第二层3号面分别与第一个面和第5个面相对,不符合逻辑,故排除。
所以正确答案为A。
2.下面图形中是正方体平面展开图的是()A. B. C. D.解题思路:观察正方体平面展开图要把握动态的思维,有时需要对图像进行翻转和旋转来观察,如C项,需要把图像旋转90度,可以发现它就是222阵型。
直接采用排除法,排除特殊的阵型,即可得到正确答案。
A项属于“田”字型;B 项把图像逆时针旋转90度,得到“凹”字型,D项是明显的“凹”字形,故选C3.如图是一个小正方形的展开图,把展开图折叠成小正方体后,有“您”字的一面相对面上的字是() A.学 B.习C.进 D.步解题思路:要找出正方体“您”字的一面相对面上的字,有两种方法;一是看您字和哪一个字构成“Z”结构;“您”和“进”在“Z”的两端;二是看您字与“进”没有交点和公共边。
正方体展开图相关题型

第一帖丰富多彩的图形世界----正方体展开图相关题型常考题型1---正方体的展开图分类型记忆:1-4-1型共有6种;2-3-1型共有3种,3-3型共有1种,2-2-2型共有1种;同学们除了展开图形的形状外还需记忆:图中相同颜色部分表示相对的面(前面-后面、左面-右面、上面-下面)关于哪个面与哪个面相对,我们一定要记牢了,因为在考察正方体的展开图的时候会经常考到。
如果实在记不得哪个面与哪个面相对,我们可以采用标六面的方法:①先找小正方形比较密集部位的中心位置处的小正方形将其标记为下面,②在此基础上,将展开图形还原成立体图形并将上、前、后、左、右给标到其他的小正方形上.如此,我们就能轻而易举的知道相对的两个面是哪两个面。
如下图所示左前上右后下 将正方体按照标六面的方法正确标出六个面之后,下面的解题过程对我们来说就是小菜一碟了。
同学们可以试着用这个方法去做一下下面这写题一、选择题1、右图中是正方体的展开图的有( )个A 、2个B 、3个 C 、4个D 、5个 2、下列哪个正方体的展开图不可能如图所示图形()A. B. C. D.3、下列选项中是如图所示正方体的展开图的是( )A. B. C. D.4、一个正方体的表面展开图如图所示,则原正方体中的“★”所在面的对面所标的字是( )A. 实B. 验C. 欢D. 迎5、将左边的正方体展开能得到的图形是 ( )6C面的对面是______面.7、如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是 .8、如图都是正方体的表面展开图,还原成正方体后,其中两个完全一样的是 .9、如图是一个正方体纸盒的展开图,当折叠成正方体纸盒时,A 点与 点重合.10、如图是一个正方体的侧面展开图,如果将它折叠成一个正方体后相对的面上的数相等,则图中x 的值为 .11、如图是一个正方体纸盒的展开图,要使得它折成正方体后,相对面上的两个数都互为相反数,则A ,B .12、当下面这个图案被折起来组成一个正方体,数字_______会在与数字2所在的平面相对的平面上13、已知一不透明的正方体的六个面上分别写着1至6六个数字,如图是我们能看到的三种情况,那么1和5的对面数字分别是____和_____。
小学奥数必刷的13个经典问题

小学奥数必刷的13个经典问题一、正方体展开图正方体有6个面,12条棱,当沿着某棱将正方体剪开,可以得到正方体的展开图形,很显然,正方体的展开图形不是唯一的,但也不是无限的,事实上,正方体的展开图形有且只有11种,11种展开图形又可以分为4种类型:1、141型中间一行4个作侧面,上下两个各作为上下底面,共有6种基本图形。
2、231型中间一行3个作侧面,共3种基本图形。
3、222型中间两个面,只有1种基本图形。
4、33型中间没有面,两行只能有一个正方形相连,只有1种基本图形。
二、和差问题已知两数的和与差,求这两个数。
【口诀】:和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
例:已知两数和是10,差是2,求这两个数。
按口诀,则大数=(10 2)/2=6,小数=(10-2)/2=4。
三、鸡兔同笼问题【口诀】:假设全是鸡,假设全是兔。
多了几只脚,少了几只足?除以脚的差,便是鸡兔数。
例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36X2)/(4-2)=24求鸡时,假设全是兔,则鸡数 =(4X36-120)/(4-2)=12四、浓度问题(1)加水稀释【口诀】:加水先求糖,糖完求糖水。
糖水减糖水,便是加糖量。
例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20X15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3/10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)(2)加糖浓化【口诀】:加糖先求水,水完求糖水。
糖水减糖水,求出便解题。
例:有20千克浓度为15%的糖水,加糖多少千克后,浓度变为20%?加糖先求水,原来含水为:20X(1-15%)=17(千克)水完求糖水,含17千克水在20%浓度下应有多少糖水,17/(1-20%)=21.25(千克)糖水减糖水,后的糖水量减去原来的糖水量,21.25-20=1.25(千克)五、路程问题(1)相遇问题【口诀】:相遇那一刻,路程全走过。
正方体展开图练习题

正方体展开图练习题一、选择题1. 正方体展开图共有多少种不同的展开方式?A. 8种B. 11种C. 12种D. 15种2. 以下哪种展开方式不是正方体的展开图?A. 1-4-1型B. 2-2-2型C. 3-3型D. 2-3-1型3. 在正方体展开图中,相邻的两个面在展开后的位置关系是什么?A. 相邻B. 对角C. 相对D. 相隔二、填空题4. 正方体的六个面在展开图中,每个面至少与________个面相邻。
5. 1-4-1型展开图中,共有________个正方形是相邻的。
三、判断题6. 正方体的每个顶点在展开图中都连接着三个面。
()7. 正方体的任意两个相对面在展开图中不可能相邻。
()四、简答题8. 请列举出正方体展开图的四种基本类型,并简要说明每种类型的展开特点。
五、作图题9. 根据题目所给的正方体展开图,请在答题纸上画出其对应的立体图。
六、计算题10. 假设有一个正方体,其每个面的面积为a²。
如果将其展开成一个平面图形,求展开图的总面积。
七、推理题11. 给定一个正方体展开图,其中有两个相邻的面被涂成了不同的颜色。
如果将这个展开图重新折叠成正方体,那么这两个面在立体图中的位置关系是什么?八、综合应用题12. 某工厂需要制作一个正方体的包装盒,包装盒的每个面都需要贴上不同的图案。
请根据正方体展开图的特点,设计一种展开图,使得每个面都能被均匀地贴上图案,并且相邻的两个面图案不重复。
九、创新题13. 假设你是一名设计师,需要设计一款以正方体为原型的拼图玩具。
请根据正方体展开图的特性,设计出一款至少有两种不同展开方式的拼图,并简要说明每种展开方式的特点。
十、论述题14. 论述正方体展开图在实际生活中的应用,以及它在解决空间问题时的优势。
通过这些练习题,学生可以更深入地理解正方体展开图的特点和应用,提高空间想象能力和逻辑推理能力。
正方体11种平面展开图分类及练习
“二二二” 型
“一四一”型
“二三一”型
课后作业
1.请你设计制作一款正方 体形状的产品包装盒。 2.教科书87页6题、88页11 题
共有四种不同的选法
挑战自我 1.在A、B、C内分别填上适当的图 案,使它们折成正方体后,相对的面上的图 案相同 ( C ) A A B C B
A
B C
CDຫໍສະໝຸດ 2.在A、B、C内分别填上适当的 数,使它们折成正方体后,相对的 面上的数互为相反数 ( ) B
A 2 B2 -1 — 0 1 C 0
A —2,0,1 B B 0 0, ,— —2 2, ,1 1 C 1,0,—2 D 0,1,—2
正 方 体 展 开 图
1 7
2 8
3 9
4 10
5
6 11
1、观察上面的11种正方体的展开图有什么特点? 2、小组讨论这些正方体展开图可以分为几类?为 什么?
我们的探索
“一四一”型
一三二”型
“二二二”型
“三三”型
“一四一”
“一三二”
“三个二”小楼梯
“二个三”大楼梯
我们的探索
“一四一”型
我们的探索
“一四一”型
“一四一”
记忆口诀:中间四个面,上下各一面
“一三二”
记忆口诀:中间三个面,一二隔河见
“三个二”小楼梯
记忆口诀:中间两个面,楼梯天天见
“二个三”大楼梯
记忆口诀:中间没有面,三三连一线
(三)知识再现 1.根据口诀快速说出下列图形是 不是正方体的平面展开图?
1
“一三二”
2
2个“三”日字 连
3、如果“你”在前面,那么哪个字在后面?
了 太 棒
!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方体展开图相关题型 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】
第一帖 丰富多彩的图形世界----正方体展开图相关题型 常考题型1---正方体的展开图
分类型记忆:
1-4-1型共有6种;2-3-1型共有3种,3-3型共有1种,2-2-2型共有1种;
同学们除了展开图形的形状外还需记忆:
图中相同颜色部分表示相对的面(前面-后面、左面-右面、上面-下面) 关于哪个面与哪个面相对,我们一定要记牢了,因为在考察正方体的展开图的时候会经常考到。
如果实在记不得哪个面与哪个面相对,我们可以采用标六面的方法:
① 先找小正方形比较密集部位的中心位置处的小正方形将其标记为下面, ②在此基础上,将展开图形还原成立体图形并将上、前、后、左、右给标到其他的小正方形上.
如此,我们就能轻而易举的知道相对的两个面是哪两个面。
如下图所示
将正方体按照标六面的方法正确标出六个面之后,下面的解题过程对我们来说就是小菜一碟了。
同学们可以试着用这个方法去做一下下面这写题
一、选择题
1 A 、2个 B 、3个 C 、4个 D 、5个
2、下列哪个正方体的展开图不可能如图所示图形( )
A. B. C. D.
3、下列选项中是如图所示正方体的展开图的是( )
A. B. C. D.
1
2 5 4
3 6
4、一个正方体的表面展开图如图所示,则原正方体中的“★”所
在面的对
面所标的字是()
A. 实
B. 验
C. 欢
D. 迎
5、将左边的正方体展开能得到的图形是()
6、如图是一个正方体的展开图,和C面的对面是______面.
7、如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值
是 .
8、如图都是正方体的表面展开图,还原成正方体后,其中两个完全一样的
是 .
9、如图是一个正方体纸盒的展开图,当折叠成正方体纸盒时,A点与点重合.
10、如图是一个正方体的侧面展开图,如果将它折叠成一个正方体后相对
的面上的数相等,则图中x的值为 .
11、如图是一个正方体纸盒的展开图,要使得它折成正
方体后,
相对面上的两个数都互为相反数,则A ,
B .
12、当下面这个图案被折起来组成一个正方体,数字_______会在
与数字2所在的平面相对的平面上
13、已知一不透明的正方体的六个面上分别写着1至6六个数字,如图是我
们能看到的三种情况,那么1和5的对面数字分别是____和_____。
14、正方体是由六个平面图形围成的立体图形,设想沿着正方体的一些棱将它剪开,就可
以把正方体剪成一个平面图形,但同一个正方体,按不同的方式展开所得的平面展开图是不一样的,下面的图形是由6个大小一样的正方形,拼接而成的,请问这些图形中哪些可以折成正方体并分别写出它们所属的类型。
(8分)。
