人教版初中数学《内接多边形》教学课件
合集下载
人教版初中数学多边形及其内角和_实用课件1

注意:正多边形必须同时具备两个条件.①各个 角都相等;②各条边都相等.
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
探究新知
下列图形是正四边形吗?
矩形
矩形各个内角都相 等,但各边不相等, 不是正四边形.
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
课堂练习
1.画出下列多边形的全部对角线.
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
探究新知
四边形 五边形 六边形
…… n边形
过一个顶点画对 角线的条数
1 2
3 …… n-3
把多边形分成几 个三角形
2 3 4 …… n-2
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
探究新知
以十边形为例:在这里n= 10 ,就可套
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
探究新知
多边形的概念
在平面内,由一些线段首尾顺次相接 组成的封闭图形叫做多边形.
注意:①在同一平面内;②若干条线段; ③首尾顺次相接;④封闭图形.
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
第十一章 三角形 11.3 多边形及其内角和
11.3.1 多边形
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
情境导入
观察下面的图片,其中的房屋结构、蜂巢结构、 足球的外皮,其中都有由一些线段围成的图形的形象, 你能从下图中抽象出几个由一些线段围成的图形吗?
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
探究新知
下列图形是正四边形吗?
矩形
矩形各个内角都相 等,但各边不相等, 不是正四边形.
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
课堂练习
1.画出下列多边形的全部对角线.
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
探究新知
四边形 五边形 六边形
…… n边形
过一个顶点画对 角线的条数
1 2
3 …… n-3
把多边形分成几 个三角形
2 3 4 …… n-2
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
探究新知
以十边形为例:在这里n= 10 ,就可套
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
探究新知
多边形的概念
在平面内,由一些线段首尾顺次相接 组成的封闭图形叫做多边形.
注意:①在同一平面内;②若干条线段; ③首尾顺次相接;④封闭图形.
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
第十一章 三角形 11.3 多边形及其内角和
11.3.1 多边形
人 教 版 初 中 数学多 边形及 其内角 和_实用 课件1
情境导入
观察下面的图片,其中的房屋结构、蜂巢结构、 足球的外皮,其中都有由一些线段围成的图形的形象, 你能从下图中抽象出几个由一些线段围成的图形吗?
初中数学九年级下册《3.8圆内接正多边形》PPT课件 (1)

8 圆内接正多边形(2) (第2课时)
实际生活中,经常会遇到画平面正多边形的问题,比如画一个六角 螺帽的平面图,画一个五角形等,这些问题都与等分圆周有关,要 制造如图以这样来画一个边长为2cm的正六边形.
3第60一 种方60法,如图,以2cm为半径作一个⊙O,用量角器画一个等于
O·
探究
参照图,按照一定比例,画一 个停车让行的交通标志的外缘.
练习
用等分圆周的方法画出下列图案:
6
的圆心角,它对着一段弧,然后在圆上依次截取与这
条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出
正六边形.
O·
60°
利用这种 方法可以 画出任意 的正n边 形.
第二种方法,如图,以2cm为半径作一个⊙O,由于正六边形的半径等 于边长,所以在圆上依次截取等于2cm的弦,就可以将圆六等分,顺 次连接各分点即可.
实际生活中,经常会遇到画平面正多边形的问题,比如画一个六角 螺帽的平面图,画一个五角形等,这些问题都与等分圆周有关,要 制造如图以这样来画一个边长为2cm的正六边形.
3第60一 种方60法,如图,以2cm为半径作一个⊙O,用量角器画一个等于
O·
探究
参照图,按照一定比例,画一 个停车让行的交通标志的外缘.
练习
用等分圆周的方法画出下列图案:
6
的圆心角,它对着一段弧,然后在圆上依次截取与这
条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出
正六边形.
O·
60°
利用这种 方法可以 画出任意 的正n边 形.
第二种方法,如图,以2cm为半径作一个⊙O,由于正六边形的半径等 于边长,所以在圆上依次截取等于2cm的弦,就可以将圆六等分,顺 次连接各分点即可.
人教版初中数学《多边形及其内角和》精品课件1

人教版初中数学《多边形及其内角和 》精品 课件1
人教版初中数学《多边形及其内角和 》精品 课件1
二、填空题(每小题6分,共6分) 14.若过n边形的一个顶点有2m条对角线,m边形没有对角线,k边 形有k条对角线,则(n-k)m=_1_2_.
人教版初中数学《多边形及其内角和 》精品 课件1
人教版初中数学《多边形及其内角和 》精品 课件1
第十一章 三角形
11.3 多边形及其内角和
第1课时 多边形
人教版初中数学《多边形及其内角和 》精品 课件1 人教版初中数学《多边形及其内角和 》精品 课件1
人教版初中数学《多边形及其内角和 》精品 课件1
1.在平面内,由一些线段首尾顺次相接组成的封闭图形叫做 __多__边__形___. 2.多边形的边与它的邻边的延长线组成的角叫做多边形的_外__角_. 3.连接多边形不相邻的两个顶点的线段叫做多边形的_对__角__线__. 4.各个角都相等,各条边都相等的多边形叫做正__多__边__形__.
人教版初中数学《多边形及其内角和 》精品 课件1
人教版初中数学《多边形及其内角和 》精品 课件1 人教版初中数学《多边形及其内角和 》精品 课件1
人教版初中数学《多边形及其内角和 》精品 课件1
一、选择题(每小题6分,共12分) 12.下列说法正确的是( C ) A.由一些线段首尾顺次相接组成的图形叫做多边形 B.多边形的两边所在直线组成的角是这个多边形的内角或外角 C.各个角都相等,各条边都相等的多边形是正多边形 D.连接多边形两个顶点的线段,叫做多边形的对角线 13.要使一个六边形的木架稳定,至少要钉木条的根数为( A ) A.3根 角和 》精品 课件1
解:从表中可以看出对角线随多边形边数增加的规律:四边形 的对角线 2 条;五边形的对角线 5 条,即 5=2+3;六边形的对 角线 9 条,即 9=2+3+4;七边形的对角线 14 条,即 14=2+ 3+4+5;八边形的对角线 20 条,即 20=2+3+4+5+6;n 边 形 的 对 角 线 条 数 : 2 + 3 + 4 + 5 + … + (n - 2) = n(n2-3) 条 (n≥3),所以十边形有10×(120-3)=35(条)
人教版初中数学《多边形及其内角和 》精品 课件1
二、填空题(每小题6分,共6分) 14.若过n边形的一个顶点有2m条对角线,m边形没有对角线,k边 形有k条对角线,则(n-k)m=_1_2_.
人教版初中数学《多边形及其内角和 》精品 课件1
人教版初中数学《多边形及其内角和 》精品 课件1
第十一章 三角形
11.3 多边形及其内角和
第1课时 多边形
人教版初中数学《多边形及其内角和 》精品 课件1 人教版初中数学《多边形及其内角和 》精品 课件1
人教版初中数学《多边形及其内角和 》精品 课件1
1.在平面内,由一些线段首尾顺次相接组成的封闭图形叫做 __多__边__形___. 2.多边形的边与它的邻边的延长线组成的角叫做多边形的_外__角_. 3.连接多边形不相邻的两个顶点的线段叫做多边形的_对__角__线__. 4.各个角都相等,各条边都相等的多边形叫做正__多__边__形__.
人教版初中数学《多边形及其内角和 》精品 课件1
人教版初中数学《多边形及其内角和 》精品 课件1 人教版初中数学《多边形及其内角和 》精品 课件1
人教版初中数学《多边形及其内角和 》精品 课件1
一、选择题(每小题6分,共12分) 12.下列说法正确的是( C ) A.由一些线段首尾顺次相接组成的图形叫做多边形 B.多边形的两边所在直线组成的角是这个多边形的内角或外角 C.各个角都相等,各条边都相等的多边形是正多边形 D.连接多边形两个顶点的线段,叫做多边形的对角线 13.要使一个六边形的木架稳定,至少要钉木条的根数为( A ) A.3根 角和 》精品 课件1
解:从表中可以看出对角线随多边形边数增加的规律:四边形 的对角线 2 条;五边形的对角线 5 条,即 5=2+3;六边形的对 角线 9 条,即 9=2+3+4;七边形的对角线 14 条,即 14=2+ 3+4+5;八边形的对角线 20 条,即 20=2+3+4+5+6;n 边 形 的 对 角 线 条 数 : 2 + 3 + 4 + 5 + … + (n - 2) = n(n2-3) 条 (n≥3),所以十边形有10×(120-3)=35(条)
《圆内接正多边形》圆PPT课件

这个圆就是这个正多边形的外接圆.
正方形
正五边形
正六边形
核心知识点二
正多边形与圆的关系
探究归纳
问题3:把圆五等分,顺次连接各等分点能得到正五边形吗?
将一个圆n(n≥3)等分,
依次连接各等分点可
得到一个正n多边形
(1)各边相等
(2)各角相等
圆的内接正多边形
正多边形的外接圆
正多边形的有关概念及性质
核心知识点三
(精确到0.1 m2).
F
抽象成
E
O
A
B
D
C
解:连接OB、OC,过点O作OM⊥BC于M.
BC 4
在Rt△OMB中,OB=4,MB= 2,
2
2
利用勾股定理,可得边心距
r 42 22 2 3.
亭子地基的周长l=6×4=24(m)
亭子地基的面积
1
1
S l r 24 2 3 41.6(m2 ).
形都是轴对称图形吗?都是中心对称图形吗?
问题1
注意
正n边形都是轴对称图形,都有n条对称轴;
只有边数为偶数的正多边形才是中心对称图形
观察发现
观察下图中图形的构成,试着发现它们的规律.
发现展示
正多边形与圆的关系
正多边形和圆的关系十分密切,只要把一个圆分
成相等的一些弧,就可以作出这个圆的内接正多边形,
A
A
类比学习
R
+
圆心角
圆心
B
O
弦心距r
弦a
C
M
B
中心角
圆内接正多边形
D
F
中心
O半径R
边心距r
正方形
正五边形
正六边形
核心知识点二
正多边形与圆的关系
探究归纳
问题3:把圆五等分,顺次连接各等分点能得到正五边形吗?
将一个圆n(n≥3)等分,
依次连接各等分点可
得到一个正n多边形
(1)各边相等
(2)各角相等
圆的内接正多边形
正多边形的外接圆
正多边形的有关概念及性质
核心知识点三
(精确到0.1 m2).
F
抽象成
E
O
A
B
D
C
解:连接OB、OC,过点O作OM⊥BC于M.
BC 4
在Rt△OMB中,OB=4,MB= 2,
2
2
利用勾股定理,可得边心距
r 42 22 2 3.
亭子地基的周长l=6×4=24(m)
亭子地基的面积
1
1
S l r 24 2 3 41.6(m2 ).
形都是轴对称图形吗?都是中心对称图形吗?
问题1
注意
正n边形都是轴对称图形,都有n条对称轴;
只有边数为偶数的正多边形才是中心对称图形
观察发现
观察下图中图形的构成,试着发现它们的规律.
发现展示
正多边形与圆的关系
正多边形和圆的关系十分密切,只要把一个圆分
成相等的一些弧,就可以作出这个圆的内接正多边形,
A
A
类比学习
R
+
圆心角
圆心
B
O
弦心距r
弦a
C
M
B
中心角
圆内接正多边形
D
F
中心
O半径R
边心距r
最新3.8圆内接正多边形教学讲义ppt课件

A. ①②③ B. ①③④ C. ②③④ D. 【①答②案】④B
正多边形的外角和是__3_6_0__°______; 360 °
一个内角是______n______;
一、阅读课本97页说出并以下概念
1.圆内接正多边形; 2.圆内接正多边形的中心; 3.圆内接正多边形的半径; 4.圆内接正多边形的中心角; 5.圆内接正多边形的边心距。
二、正多边形有关的概念
正多边形的中心:
依又次∵顶连点结A各、分B、点C所、得D、的E多都边在形⊙是O上这个圆
的内∴接五边正形多A边BC形D.E是⊙O的 内接正五边形.
例 有一个亭子它的地基是半径为4m的正六边形,求
地基的周长和面积(精确到0.1平方米).
解:
由于ABCDEF是正六边形,所以
F
E
它的中心角等于360 60,
6 OBC是等边三角形,从而正
归纳
(1)用量角器等分圆周作正n边形; (2)用尺规作正方形及由此扩展作正八 边形, 用尺规作正六边形及由此扩展作正 12边形、正三角形.
小结
360
正n边形的中心角是_____n______;
正多边形的中心角与外角的 大小关系是__相__等____.
1、正多边形和圆有什么关系?你能举例说明吗? 2、什么是正多边形的中心、半径、中心角、
边心距?你能举例说明吗? 3、如何计算正多边形的半径、边心距及边长? 4、说说作正多边形的方法有哪些?
还有哪些疑问?
抢答题:
1、O是正△ABC的中心,它是△ABC的 外接
圆与 内切 圆的圆心。
A
2、OB叫正△ABC的半径,它是正
△ABC的
外接 圆的半径。 3、OD叫作正△ABC的 边心距 ,.O 它是正△ABC的 内切 圆的半径。
正多边形的外角和是__3_6_0__°______; 360 °
一个内角是______n______;
一、阅读课本97页说出并以下概念
1.圆内接正多边形; 2.圆内接正多边形的中心; 3.圆内接正多边形的半径; 4.圆内接正多边形的中心角; 5.圆内接正多边形的边心距。
二、正多边形有关的概念
正多边形的中心:
依又次∵顶连点结A各、分B、点C所、得D、的E多都边在形⊙是O上这个圆
的内∴接五边正形多A边BC形D.E是⊙O的 内接正五边形.
例 有一个亭子它的地基是半径为4m的正六边形,求
地基的周长和面积(精确到0.1平方米).
解:
由于ABCDEF是正六边形,所以
F
E
它的中心角等于360 60,
6 OBC是等边三角形,从而正
归纳
(1)用量角器等分圆周作正n边形; (2)用尺规作正方形及由此扩展作正八 边形, 用尺规作正六边形及由此扩展作正 12边形、正三角形.
小结
360
正n边形的中心角是_____n______;
正多边形的中心角与外角的 大小关系是__相__等____.
1、正多边形和圆有什么关系?你能举例说明吗? 2、什么是正多边形的中心、半径、中心角、
边心距?你能举例说明吗? 3、如何计算正多边形的半径、边心距及边长? 4、说说作正多边形的方法有哪些?
还有哪些疑问?
抢答题:
1、O是正△ABC的中心,它是△ABC的 外接
圆与 内切 圆的圆心。
A
2、OB叫正△ABC的半径,它是正
△ABC的
外接 圆的半径。 3、OD叫作正△ABC的 边心距 ,.O 它是正△ABC的 内切 圆的半径。
人教版数学九年级上册《圆内接多边形》课件

点E,连接EO并延长交⊙O于点F,连接BFE2 +BE2的值为(
A.8
)
B.12
C.16
解:∵四边形BCDE内接于⊙O,且∠EDC=135°,
∴∠EFC=∠ABC=180°-∠EDC=45°,
∵∠ACB=90°,∴△ABC是等腰直角三角形,
∴AC=BC,
∠B+ ∠D=180º.
如何证明你的猜想呢?
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
圆的内接四边形的对角互补.
图中∠A与∠DCE的大小有何关系?
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
D
∴∠A+∠C=180°,
同理∠B+∠D=180°,
由圆周角定理得,∠BOD=2∠A=120°.
D.90°
课堂练习
1.如图,四边形ABCD为⊙O的内接四边形.AB与DC的延长线交于点G,
AO⊥CD,垂足为E,连接BD,∠GBC=50° ,则∠DBC的度数为( C
A.50°
B.60°
C.80°
)
D.90°
解:延长AE交⊙O于点F,
= ,
∵AE⊥CD,∴
则∠ADB= 70 °.
,∠CAD=30°,
解:∵ =
∴∠CAB=∠CAD=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ACB=∠ADB=180°-∠CAB-∠ABC=180°-30°-50°-30°=70°.
2.如图,四边形ABCD内接于⊙O,四边形ABCO是平行
又∵EF是⊙O的直径,
A.8
)
B.12
C.16
解:∵四边形BCDE内接于⊙O,且∠EDC=135°,
∴∠EFC=∠ABC=180°-∠EDC=45°,
∵∠ACB=90°,∴△ABC是等腰直角三角形,
∴AC=BC,
∠B+ ∠D=180º.
如何证明你的猜想呢?
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
圆的内接四边形的对角互补.
图中∠A与∠DCE的大小有何关系?
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
D
∴∠A+∠C=180°,
同理∠B+∠D=180°,
由圆周角定理得,∠BOD=2∠A=120°.
D.90°
课堂练习
1.如图,四边形ABCD为⊙O的内接四边形.AB与DC的延长线交于点G,
AO⊥CD,垂足为E,连接BD,∠GBC=50° ,则∠DBC的度数为( C
A.50°
B.60°
C.80°
)
D.90°
解:延长AE交⊙O于点F,
= ,
∵AE⊥CD,∴
则∠ADB= 70 °.
,∠CAD=30°,
解:∵ =
∴∠CAB=∠CAD=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ACB=∠ADB=180°-∠CAB-∠ABC=180°-30°-50°-30°=70°.
2.如图,四边形ABCD内接于⊙O,四边形ABCO是平行
又∵EF是⊙O的直径,
人教版数学八年级上册:多边形的内角和ppt演讲教学
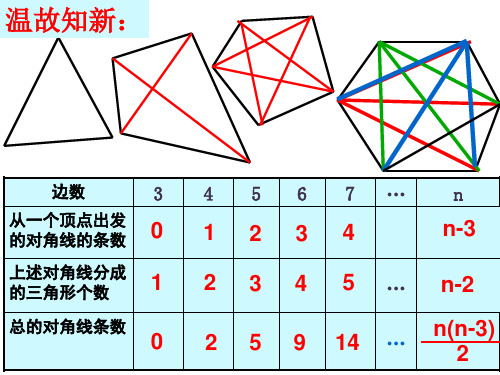
分成 三角形,n边形的内角和等于
。
结论:n边形的内角和等于(__n_一_2_)_·_1_80_°____.
2、n边形的外角和等于___3_60_°__。
人教版数学八年级上册:多边形的内 角和ppt 演讲教 学
人教版数学八年级上册:多边形的内 角和ppt 演讲教 学
你能算它的内 角和吗?
人教版数学八年级上册:多边形的内 角和ppt 演讲教 学
六边形
七边形
人教版数学八年级上册:多边形的内 角和ppt 演讲教 学
4× 180°
=7200
5× 180°
=9000
人教版数学八年级上册:多边形的内 角和ppt 演讲教 学
学一学
四边形的内角和 (4-2)× 180° = 360° 五边形的内角和 (5-2)× 180°=540° 六边形的内角和(6-2)× 180°=720° 七边形的内角(7-2)×180°=900°
人教版数学八年级上册:多边形的内 角和ppt 演讲教 学
探索过程一掠:
三角形 A
B
1800
人教版数学八年级上册:多边形的内 角和ppt 演讲教 学
四边形
A D
B
CB
C
2× 180°
= 3600
五边形 A
E
C
D
3× 180°
=5400
人教版数学八年级上册:多边形的内 角和ppt 演讲教 学
那么六边形、七边形的内角和呢?
最终结论
n边形内角和等于 (n-2)·180°
人教版数学八年级上册:多边形的内 角和ppt 演讲教 学
人教版数学八年级上册:多边形的内 角和ppt 演讲教 学
做一做 1.求下列图形中x的值:
《圆内接正多边形》课件

pos t r e a di ng r e f l e c ti ons , e s s a y e nc yc l ope di a s , l e s s on
pl a n m a t e r i a l s, ot he r s a m pl e e s s a ys , e t c . I f you w a nt t o
6
A. 2
3
B.4
6
C. 3
4
D.3
【变式拓展】以半径为1的圆内接正三角形、正方形、正六边形的边长为三边作三角
形,则 ( B )
A.这个三角形是等腰三角形
B.这个三角形是直角三角形
C.这个三角形是锐角三角形
D.不能构成三角形
第三章
3.8 圆内接正多边形
知识要点基础练
综合能力提升练
拓展探究突破练
-5-
.
第三章
3.8 圆内究突破练
-6-
知识点2 正多边形的画法
7.图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图
2,AE是☉O的直径,用直尺和圆规作☉O的内接正八边形ABCDEFGH.(不写作法,保留作
图痕迹)
解:如图所示,正八边形ABCDEFGH即为所求.
learn about different formats and writing methods of
s a m pl e e s s a ys , pl e a s e s t a y t une d!
第三章
3.8 圆内接正多边形
知识要点基础练
综合能力提升练
拓展探究突破练
-3-
知识点1 正多边形的有关概念及计算
∠CPD的度数为 ( B )
pl a n m a t e r i a l s, ot he r s a m pl e e s s a ys , e t c . I f you w a nt t o
6
A. 2
3
B.4
6
C. 3
4
D.3
【变式拓展】以半径为1的圆内接正三角形、正方形、正六边形的边长为三边作三角
形,则 ( B )
A.这个三角形是等腰三角形
B.这个三角形是直角三角形
C.这个三角形是锐角三角形
D.不能构成三角形
第三章
3.8 圆内接正多边形
知识要点基础练
综合能力提升练
拓展探究突破练
-5-
.
第三章
3.8 圆内究突破练
-6-
知识点2 正多边形的画法
7.图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图
2,AE是☉O的直径,用直尺和圆规作☉O的内接正八边形ABCDEFGH.(不写作法,保留作
图痕迹)
解:如图所示,正八边形ABCDEFGH即为所求.
learn about different formats and writing methods of
s a m pl e e s s a ys , pl e a s e s t a y t une d!
第三章
3.8 圆内接正多边形
知识要点基础练
综合能力提升练
拓展探究突破练
-3-
知识点1 正多边形的有关概念及计算
∠CPD的度数为 ( B )
七年级数学下册 第9章 多边形 9.2 多边形的内角和与外角和课件

在每个顶点处取这个多边形的一个外角,它们(tā men)
的和叫做这个多边形的外角和.
一般地,在多边形的任一顶点(dǐngdiǎn)
处按顺(逆)时针方向可作外角,n边形 有n个外角.
12/12/2021
第八页,共二十页。
探究在n边形的每个顶点(dǐngdiǎn)处各取一个
外角,这些外角的和叫做n边形的外角
……
……
n-2
(n-2)×180º
第六页,共二十页。
n 边形的内角(nèi 和公式: jiǎo)
(n2)180
n是大于或等于(děngyú)3的自然数
12/12/2021
第七页,共二十页。
多边形内角(nèi jiǎo)的一边与另一边的反向延长线所
组成的角叫做这个多边形的外角(exterior angle)
是几边形?它的内角和是多少?
解: 依题意(tíyì), 这个多边形是七边形, 它的内角和是(7-2) ×180°=900°
例2. 如果一个多边形的内角(nèi jiǎo)和是1440°,
那么这是 十 边形.
方法小结:
解:由n边形的内角和公式可得
求多边形的边数、
(n -2)·180 = 1440
角度的常用方法:
n -2 = 8
利用公式列方程.
12/12/2021
n = 10
∴这是十边形.
第十页,共二十页。
例3
若正n边形的一个内角(nèi jiǎo)是144°,那么n= 10 .
解:由n边形的内角(nèi jiǎo)和公式可得:
(n -2) ·180 = 144n 180n – 360 = 144n 180n -144n=360 36n = 360 n = 10
的和叫做这个多边形的外角和.
一般地,在多边形的任一顶点(dǐngdiǎn)
处按顺(逆)时针方向可作外角,n边形 有n个外角.
12/12/2021
第八页,共二十页。
探究在n边形的每个顶点(dǐngdiǎn)处各取一个
外角,这些外角的和叫做n边形的外角
……
……
n-2
(n-2)×180º
第六页,共二十页。
n 边形的内角(nèi 和公式: jiǎo)
(n2)180
n是大于或等于(děngyú)3的自然数
12/12/2021
第七页,共二十页。
多边形内角(nèi jiǎo)的一边与另一边的反向延长线所
组成的角叫做这个多边形的外角(exterior angle)
是几边形?它的内角和是多少?
解: 依题意(tíyì), 这个多边形是七边形, 它的内角和是(7-2) ×180°=900°
例2. 如果一个多边形的内角(nèi jiǎo)和是1440°,
那么这是 十 边形.
方法小结:
解:由n边形的内角和公式可得
求多边形的边数、
(n -2)·180 = 1440
角度的常用方法:
n -2 = 8
利用公式列方程.
12/12/2021
n = 10
∴这是十边形.
第十页,共二十页。
例3
若正n边形的一个内角(nèi jiǎo)是144°,那么n= 10 .
解:由n边形的内角(nèi jiǎo)和公式可得:
(n -2) ·180 = 144n 180n – 360 = 144n 180n -144n=360 36n = 360 n = 10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求证:∠CBE =∠ABD.
D C
A
O
B
A
O
B
D
CE l
3.利用性质解决问题
已知:△ABC 中,AB=AC,D 是△ABC 外接圆 AC 上的点(不与 A,C 重合),延长 BD 到 E.
求证:AD 的延长线平分∠CDE.
A DE
O
F
B
C
3.利用性质解决问题
拓展:如图,AD、BE 是△ABC 的两条高. 求证:∠CED=∠ABC.
C D
E
A
B
课堂小结
圆内接多边形
如果一个多边形的所有顶点都在同__一__个__圆__上, 这个多边形 叫 __外做__接圆__圆内__接.多边形,这个圆叫做这个多边形的
2.性质探究
观察圆内接四边形对角之间有什么关系.
如何验证你的猜想呢?
A
A
O
D
O
DE F
B
B
C
C 圆内接四边形的对角互补,并且任何一角的外角都
等于它的内对角.
相等,都等于这条弧所对的___圆__心_的角一半. 1:在同圆或等圆中,如果两个_圆__周__角___相等,它们
所对的弧一定相等. 2:半圆(或直径)所对的圆周角是__直__角____,90°的圆
周角所对的弦是直径. 3:同弧所对的圆周角—相—等
1.提出问题
什么叫圆内接三角形? 什么叫圆内接四边形?
(1)本节课主要学习了哪些内容? (2)本节课学到了哪些思想方法?
1)如下图左,四边形 ABCD 内接于⊙O,AB 是 直径,∠ABD =30°,则∠BCD 的度数为多少?
(2)如下图右,在⊙O 中,AB 为直径,直线 l 与 ⊙O 交于点 C、D,BE⊥l 于点 E,连接 BD、BC.
四边形 ABCD 是圆内接四边形,点 E 是 BC 延长线上一点,若∠BAD=105°,则∠DCE 的大小是 B
A.115° B.105° C.100° D.95°
如图 ,在⊙O 的内接四边形 ABCD 中,∠BCD =130°,则∠BOD 的度数是_1_0_0_°______.
如图,已知四边形 ABCD 内接于⊙O, ∠BOD =80°,求∠BAD 和∠BCD 的度数.
人教版初中数学
弧、弦、圆心角和圆周角
1.圆心角的定义 (1)定义:我们把__顶__点____在__圆__心____的角叫做圆心角. (2)特征:顶点在圆心.
2.弧、弦、圆心角之间的相等关系 (1)在同圆或等圆中,相等的圆心角所对的弧__相 等_____,所
对的弦_相__等_____. (2)在同圆或等圆中,如果两条弧相等,那么它们所对的圆
心角__相__等____,所对的弦也_相__等_____. (3)在同圆或等圆中,如果两条弦相等,那么它们所对的圆
心角__相__等____,所对的弧也__相__等____.
3.圆周角的定义 顶点在_____圆__周_上,并且两边都_____和__圆__相__交___的角叫做 圆周角.
4.圆周角定理及推论 定理:在同圆或等圆中,______同__弧__或__等__弧__ 所对的圆周角
D C
A
O
B
A
O
B
D
CE l
3.利用性质解决问题
已知:△ABC 中,AB=AC,D 是△ABC 外接圆 AC 上的点(不与 A,C 重合),延长 BD 到 E.
求证:AD 的延长线平分∠CDE.
A DE
O
F
B
C
3.利用性质解决问题
拓展:如图,AD、BE 是△ABC 的两条高. 求证:∠CED=∠ABC.
C D
E
A
B
课堂小结
圆内接多边形
如果一个多边形的所有顶点都在同__一__个__圆__上, 这个多边形 叫 __外做__接圆__圆内__接.多边形,这个圆叫做这个多边形的
2.性质探究
观察圆内接四边形对角之间有什么关系.
如何验证你的猜想呢?
A
A
O
D
O
DE F
B
B
C
C 圆内接四边形的对角互补,并且任何一角的外角都
等于它的内对角.
相等,都等于这条弧所对的___圆__心_的角一半. 1:在同圆或等圆中,如果两个_圆__周__角___相等,它们
所对的弧一定相等. 2:半圆(或直径)所对的圆周角是__直__角____,90°的圆
周角所对的弦是直径. 3:同弧所对的圆周角—相—等
1.提出问题
什么叫圆内接三角形? 什么叫圆内接四边形?
(1)本节课主要学习了哪些内容? (2)本节课学到了哪些思想方法?
1)如下图左,四边形 ABCD 内接于⊙O,AB 是 直径,∠ABD =30°,则∠BCD 的度数为多少?
(2)如下图右,在⊙O 中,AB 为直径,直线 l 与 ⊙O 交于点 C、D,BE⊥l 于点 E,连接 BD、BC.
四边形 ABCD 是圆内接四边形,点 E 是 BC 延长线上一点,若∠BAD=105°,则∠DCE 的大小是 B
A.115° B.105° C.100° D.95°
如图 ,在⊙O 的内接四边形 ABCD 中,∠BCD =130°,则∠BOD 的度数是_1_0_0_°______.
如图,已知四边形 ABCD 内接于⊙O, ∠BOD =80°,求∠BAD 和∠BCD 的度数.
人教版初中数学
弧、弦、圆心角和圆周角
1.圆心角的定义 (1)定义:我们把__顶__点____在__圆__心____的角叫做圆心角. (2)特征:顶点在圆心.
2.弧、弦、圆心角之间的相等关系 (1)在同圆或等圆中,相等的圆心角所对的弧__相 等_____,所
对的弦_相__等_____. (2)在同圆或等圆中,如果两条弧相等,那么它们所对的圆
心角__相__等____,所对的弦也_相__等_____. (3)在同圆或等圆中,如果两条弦相等,那么它们所对的圆
心角__相__等____,所对的弧也__相__等____.
3.圆周角的定义 顶点在_____圆__周_上,并且两边都_____和__圆__相__交___的角叫做 圆周角.
4.圆周角定理及推论 定理:在同圆或等圆中,______同__弧__或__等__弧__ 所对的圆周角
