挡土墙后粘性填土的主动土压力计算
挡土墙主动土压力计算公式
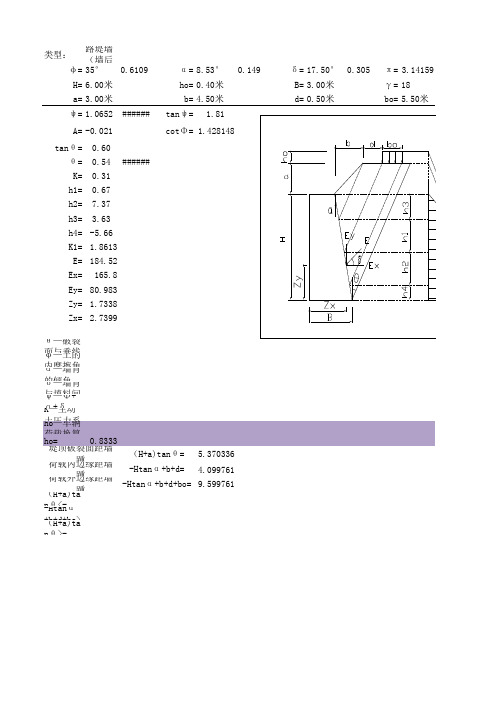
类型:路堤墙(墙后填土表面为折面,破裂面交于荷载外)φ=35°0.6109α=8.53°0.149δ=17.50°0.305π=3.14159H=6.00米ho=0.40米B=3.00米γ=18a=3.00米b=4.50米d=0.50米bo=5.50米ψ=1.0652######tan ψ= 1.81A=-0.021cot Φ= 1.428148tan θ=0.60θ=0.54######K=0.31h1=0.67h2=7.37h3= 3.63h4=-5.66K1= 1.8613E=184.52Ex=165.8Ey=80.983Zy= 1.7338Zx= 2.7399θ—破裂面与垂线的夹角 ,破裂角φ—土的内摩擦角α—墙背的倾角(仰斜α取负值,俯斜取正值)δ—墙背与填料间的摩擦角ψ—Φ+α+δK—主动土压力系数ho—车辆荷载换算土层厚度,ho=p/γ,p—车辆荷载(H<2m,p=20kN/m2;H>10m,p=10kN/m2,其余高度取差值)ho=0.83335.3703364.0997619.599761(H+a)tan θ<-Htan α+b+d,破裂面交于荷载外(内缘)-Htan α+b+d+bo>(H+a)tan θ>-Htan α+b+d,破裂面交于荷载内(H+a)tan θ>-Htan α+b+d+bo,破裂面交于荷载外(外缘)堤顶破裂面距墙踵荷载内边缘距墙踵荷载外边缘距墙踵(H +a)tan θ=-Htan α+b+d=-Htan α+b+d+bo=kN/m3/m2,其余高度取差值)。
土体主动被动土压力概念及计算公式习题

土体主动、被动土压力概念及计算公式习题主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力Pa。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力Pp。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知Pp>Po>Pa。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直;(2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,ζz仍保持不变,但ζx将不断增大并超过ζz值,当土墙挤压土体使ζx增大到使土体达到被动极限平衡状态时,如图6-4的应力园O3,ζz变为小主应力,ζx变为大主应力,即为朗肯被动土压力(pp)。
土体中产生的两组破裂面与水平面的夹角为45???。
2朗肯主动土压力的计算根据土的极限平衡条件方程式ζ1=ζ3tg(45°+2?2?)+2c·tg(45°+?2?) ζ3=ζ1tg(45°-2)-2c·tg(45°-)当z=H时pa=γHKa-2cKa在图中,压力为零的深度z0,可由pa=0的条件代入式(6-3)求得z0?2c?Ka (6-4)在z0深度范围内pa为负值,但土与墙之间不可能产生拉应力,说明在z0深度范围内,填土对挡土墙不产生土压力。
土体主动、主动土压力概念及计算公式

[ 指南] 土体主动、主动土压力概念及计算公式主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P。
a被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P。
上述三种土压力的移动情况和它们在相同条件下的数值比较,p可用图6-2 来表示。
由图可知P,P,P。
poa朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857 年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中, 首先作出以下基本假定。
(1) 挡土墙是刚性的墙背垂直;(2) 挡土墙的墙后填土表面水平;(3) 挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,Z仍保持不变,但Z将不断增大并超过Z值,ZXZ当土墙挤压土体使z增大到使土体达到被动极限平衡状态时,如图6-4的应力园O, Z x3z变为小主应力,Z变为大主应力,即为朗肯被动土压力(p) 。
土体中产生的两组破裂面与xp,45:, 水平面的夹角为。
2 朗肯主动土压力的计算根据土的极限平衡条件方程式,,2 Z =Z tg(45?+)+2c?tg(45?+) 1322,,2 Z =Z tg(45?-)-2c?tg(45?-) 3122土体处于主动极限平衡状态时,Z = Z =Y z, Z = Z =p,代入上式得1z3xa1) 填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为,,2,ap= 丫ztg(45?-)-2c?tg(45?-)= 丫zK-2c (6-3) aa22由公式(6-3) ,可知,主动土压力p 沿深度Z 呈直线分布,如图6-5 所示。
【doc】粘性土主动土压力的计算

粘性土主动土压力的计算竹高古洲0流,此时几乎所有顾粒的浓度都接近其S值,虽然承流速度已高达7.sTY/.,仍没有发生冲刷.图5是洪水前后河床地形.可见洪水过后河床虽有较犬变化,但没有发生冲刷.五,结论试验爱现,不同粒径的沙都有一个极限悬浮浓度s,在任何条件下悬沙浓度不可能超过其S值.一种沙的S值不受粒径小得多的颗粒存在的影响.悃此混合沙的悬浮浓度可以超过均匀抄的悬浮浓度.在同样水流条件下,粗细混合沙比均匀沙更容易达到较高的含沙量.高含沙水流常引起河床严重冲刷,但含沙量极高时反而不会冲刷,就是由于极限悬浮浓度的限制的缘故.参考文献[1]钱宁,万兆惠,掘沙运动力学.科学出版社,1984年.[2]WangZha0yinandQianN缸LamfmedLoad—nsDevelopmentand MechsmismofMo'~ion,TmemJ.ofsedimeResarch,[I~TCES,Nov.i987,PP.102—124.f3]王兆印,钱宁,高浓度混抄悬浮液物理特性的实验研究.亦利,1984年第4期.粘性土主动土压力的计算顾慰慈(北京水利电力经挤管理学院)提要粘性土对刚性挡土墙的压力,目前研究得还很少,也缺乏实用的计算公式.本文根据墙后填±为均匀的軎向同性介质,墙体和壤土均属平面变形问题和楫裂面为平面的假定,导出粘性土主动土压力的库仑精确解和近似解,并以算例与实援l资料作了比较.一,引言粘性土对刚性挡土墙的压力,前多采用库仑理论米计算,并曾提出过一些计算方法'".但对滑裂面的形状,建筑物与粘土之间的粘着力,墙后裂缝出现的可能性等. 仍未能从理论上得到解决.在土压力计算中,由目前的试验资料表明,滑裂面的形状不仅与填土的性质有关, 特别是和挡土墙的位移方式和土与墙面之面的摩撼角有关.当墙体产生水平位移时,滑裂面通常为一平面,当墙体绕顶端和底端转动时,滑裂面为一曲面'",但是滑裂面的上部均接近平面.试验也表明,随着填土与墙面之间摩擦角的减小,滑裂面的下}车文于1988年9月lD日收瓢帮也趋向予平面.田此,目前在尚未取得足够蟹料和获得滑裂面的合理和实席盼簸学楼塑之前,在壤土与墙面阃的摩擦角不大的情况下,采用滑裂面隽平面的假定也是可行的.在建筑物与粘土产生相对位移时,两者的接触面之间将存在一定的牯着力,这已为一些工程的拔桩试验所证实.根据 A.且.莫热菲季诺失的研究,认为填土与挡土墙面之嗥的粘着力K可以采用填土凝聚力c的l/4一l/2,或者采甩K/C=tgO/Ig~(其中8为"填土与墙面问的摩攘角,妒为填土的内摩攘角).粘着力置对土压力的影响可由图I(b>鸯l(c)中看出,当<(p呻)时(为挡土墙面与垂直线的夹角,口为裂面与水平线的夹角),考虑墙面粘着力的结果将使土压力减小,反之使土压力增大.圈J不考虑填土表面裂麓时土压力的计算图¨~lj_一}在计算粘土的土压力时,墙后填土出现裂缝的可能性与填土的性质,特荆是和墙体的变形有极太关系.根据H.n.普罗科菲也夫的试验",当墙体绕墙顶转动时,墙后表层部分填土不会产生水平位移,填土的变形主要表现为下沉,所以填土的上部不可能产生拉裂,而主要是剪切破坏.因此在计算粘性士的土压力时,应考虑墙体实际变形的可能.对于墙体可船产生水平位移和绕墙底转动时,可按填土表面出现裂缝的情况计算;而当墙休绕墙顶转动时,则可按不考虑填土表面出现裂缝的情况计算.本文根据上述考虑,假定墙后填土为均质的各向同性介质,墙体和填土均为平面变形问题,且滑裂面为平面的情况下,导出粘性土主动土压力的库仑精确解.二,不考虑填土表面出现裂缝的情况挡土墙如图l(d)所示,填土表面作用有均布超载g,滑裂土体为ABC'重量为w. ABN~@用土压力E和粘着力K,土压力E与墙面法线成8角.滑NBC~作用有反力和凝聚力C.包括超载在内,滑裂土体的垂直重力:56G=w+Q一.o目(一)面+q-.毗(1)式中,Q为作用在Ac面上的均布超载的台力;H为挡土墙的高度;为填土的容重; 为挡土墙面与垂直线的夹角;为填土表面与水平线的夹角;AC'~9AC面的长度.粘着力K和凝聚力C为:K=kC=c-BC,(2)式中k为填土与墙面问的粘着力强度;c为填土的凝聚力强度:BC为Bc面的长度. 根据图1(口)中作用力的平衡条件,可绘制成如图l(b)的力闭台多边形,其中,dE是由于凝聚力C和粘着力的作用而减小的土压力,G是由于凝聚力c和粘着力的作用而减轻的滑裂土体的垂直重量.为了计算方便,将图l(b)中的多边形与三角形绘制在一起,如图l(c).由图l(C)W见,3G=一ae+一dc+一gf.根据图l(c)和图l(d)中的几何关系可得:=C0St;~0S譬,(4)【"十oJ五[H等一Adsin(],(5)=[_一(.一HsinkH(抖sina圳]砑,(6】式中为c面长度,丽为BE面长度如令L-二再百,L:=C耳=蛋叵则G可写成:G一+面詈[H{鲁~Lsin(+a]+[百巧(L..s一H目ina)一丽蔬k∞Hsi(na+a)J]1}.(7)根据图l(d)中的几何关系可得:二t—A+-B,.(8)L=D—F-B,.(9)式中A,=一器等A=.os(珂a+a而):Hoos("一)D万'F=,))))(;式中为填土的内摩擦角.由图l(b)中三角形j与图l(d)中三.角形BCE相似的条件可得. =(G一4G)告.(14>将式(1)和(7)代入式(14),得土压力E的表达式为:E={[{H-_L+qL,oosB]一萄石kH..酉s~一T导干×[H--L~sln(州H(L,cos.8一蹦nkHsinaJ]B}告=H+口0邢】L】+黑L,}告一LJ+(c+o-0一,2.——石F一山,f——一干百了L-+c+ 土压力也可以写成下形式:E=(告H+h)H式中h为填土表面超载的折算高度,即口co8∞目卢h前,(15>(16'(17'为土压力系数其值为:=鲁+{?挚一-+×58(c+击))丽0十—i,,根据投值条件dE/dB=0,可得B值为B=Hoes(a-丽B)(18)l;(-+普)a,'.H,.H…oOS(a+a+一芦)—了耳一sin(q~--B)oos(a--f1)oosa"(1+普2h\j2cOOSH'.H,.…r根据式(19)计算得B以后,即可按式(15)或式(16)flgg~/~2E根据圈1(d)中的几何关系可得填土的滑裂角为::arctLFH面+L,丽sinB](19>(20)三,考虑填土出现裂缝的情况在计算粘性土的士压力时r作用在墙面上的土压力是从法向接触应力为零的点开始的.因此,根据填土表面上均布超载的大小,可分两种情况来计算土压力:均布超载的折算高度h大于从超载折算表面到法向接触应力为零的点的深度h.(即h>h)和h<h.的隋况.(一)当>.时此时作用在墙上的土压力如图2所示,由于h>h.,故填土表面实际上并未出现裂缝.因此,作用在挡土墙上的土压力仍可用式(15)表示.根据圈2上的土压力作用图形,土压力也可用下式来表示:故圈2n>时土压力的计算图圈3h<.时土压力的计算罔F—(H+h—h.)H一(21)比较式(i5)和(2i)可得:一[L1一]专一¨(c+),(22)了+』,【Jh.一一二2.点L一HcosB'C0g干-{c;n(]去+一(c+击)sn}.根据极Yt%ICdE/aB=0,可得:(导H+h)苦一一..由式(22)和(23)可得:d(.)Drcoos(一B)oos@一—=l干再百干=丽(24)(25).c0sll十面丽J百一A,coos(d+d)COS了'面丽干=,(26)一卜一一1.(27dB)~一——再—I一一『-一一:J-LJ将式(26)和(27)代人式(25),经整理后B的计算式与式(15)相同.根据式(15)计算得B值以后,即可根据式(23)和(24)计算和h.,并按式(21)计算土59压办.此时作用在挡土墙上,距墙顶以下深度为的任意点处的土压力强度为: e=Y(y+h-h.)^.(28)填土的滑裂角仍可按公式(20)计算.《=)当h<h时此时填土的裂缝深度为一,作用在挡土墙上的土压力如图3新示.由于填土面产生了裂缝,裂缝处填土不再具有凝聚力,也不存在切力和法向接触应力,因此相当于填土表面由Ac移至Ac,滑裂楔体变成了ABc,而4c面以上的填土则相当于超载作用在新的填土表面Ac'上.冉图2中的几何关系可知,Ac面的长度且c为一堕等此时滑裂楔体的重量w__}(H+h—):coHs(o0a-8Z)r.,(29)(30)且c面以上超载的重量Q=L旦.(31)根据滑裂楔体上作用力的平衡条体,仍可绘制图l)所示的用合力多边形.根据图l),(c)和(d)中的几何关系,可得土压力E的表达式为:Ely(H+h,—cos(a—-/3).,00S55(±二!占HB.rcsin(a+8一)L(H+h-h)(+c)c0目81十【—可厂——]一一oosaoos(a+~J,,L2coosflL(H+h-h.).sina?(H+h--h)一面丽————一十—丽广×(c+告).同样,由图3可知,此耐作用在挡土墙上的土压力E也可写成下列形式; E—1(H+一)¨.比较式(32)和(33)可知:.=[一(k+c)oos町~]×生B一—7cos(c+OOS,/,,,(+)\a'.cOOSaoosflBOOge—yoos(a-~)oos(a+8)1=_一了而×r~.血cos((a++88)一(c+k)Hc0日8C0S~XO08(+d)一"*cos(a-3)coms(a+0)c+一)一£,一0十—一厂£r,.COS(一芦)L.L:一HOOSO~B(32)-(33)(34)(35:(36)式中(H+m.)一由式(34)和(36)得::A.+[鲁a+簪8—淀厂=ⅢI?十L予Hoo8() ×(F)+(k+c)oos8号],:畿(一一AlFo面——豇i—一一—瓦一一; 将式(35),(38)和(39)代入式(37),整理后得, N.+N.B+NB=+N.,B+NB=0,N.=一{[斋sin(+8+(1+鲁)一(蚪a)]A+(00S—z,/}A'\—l…一'n(蚪a+(?+叠)..巾]x(A.D—AF)A+毕..8×[+一F)]+掣}AlD_{+一s[+]壬}×A.AtD;N产{-[斋sn(+(?+鲁)一()]x(,D—F)+半{器F+(+c)sin一.声×(竿)N5=f[击sin(蚪8一声)+(1+蛊)一(卅8)]F+昔oos口}AF.(37)(38)(39)(4O)(4I)解方程式(4O),即可求得B值,然后根据式(3s)和(36)计算h.和^值,并按式(33)计算土压力E.此时墙上任一点处的土压强度为e一(y+h-h.)^,(42)6式中兰,为墙顶以下至计算点的深度.根据墙面上接触应力不应为负值的条件,在深度<(h-h)的一段墙高范围内,土压力强度应令其为零.此时,填土的滑裂角口仍按式(20)计算.在填土表面水平,且不考虑填土与墙面之间的牯着力和摩擦角的情况下,h.值和系数可直接按下列公式求得.当k==0时:h一f!±2『一!一'TOOS6~Lc0sⅡ一si./~coa(d+)sinaoos(+)oosa(o0目d--sin~)=.(44)面而一【,当=8=卢:d=0时:等tg(45.+÷);(45)g(45.一詈).(46)由式(45)和(48)可见,当填土表面水平.墙面垂直和光滑,且不考虑填土与墙面之间的粘着力时,按库仑理论求得的h和的计算式与按朗肯理论求得的计算式完全相同.所以,朗肯理论的土压力计算式实际上只是库仑土压力计算式中的一个特例.四,土压力计算的简化在填土表面为水平的情况下,如若近似地取k=c-tg8/tg仍则可使式(37)的求解大大简化,从而使土压力的计算较为简便.当卢=0,k=c-tg/tg时{n蚪.).eosasin(+6)十丽面丽F.cog础indc0g(d+8+)(%g~oos~+tg8)Fl[oo目"c08(+8)+sinin(+艿)]一2sin(=丽[oo咖一][古一sin],式中√磊.当=卢嚣时[na],62(50)式中=[一一J[奇n~/.(51)(52)当r8=8=—O和d=卢=6=k=0的情况下,h.和值可分别按式(43)一(46)进行计算.d(61留牯土主萄±压力的图辫方j骞'五,图解方法上列计算公式仅适用在填土表面作用均布超载目的情况,如若填土表面作用集中超载P,或既作用均布超载q,又作用集中超载P时,作用在挡土墙上的土压力可按图4 所示的图解方法来确定.在考虑填土表面裂缝的情况下,必须根据前面所述的计算公式,分剐不同情况,预先确定7;值,定出裂缝末端平面AC(围44).然后假定一系列滑裂面卫,I,BE',..?,分别计算各滑裂体AABCC.,AABC:c,,AA'Be;c.…的重量w.,W,w.…,以及作用在滑裂体上的超载0.,0,0,…和P.,P,,P.…,作用在墙面AB上的粘着力K和作用在滑裂面BC:,BC;,BC,..-上的凝聚力C.,C.,C.….对于其中的每一个滑裂体,根据作用力平衡的原则均可绘制出图4(b)所示的力闭合多边形abceda.将各滑裂体相应的力闭合多边形叠合绘制在一起,则可得图4(c)所示的圈形.将各滑裂体相应的力闭合多边形中的e点(即e,e,e.…)连接成光滑的曲线.e{ele.e,…e.eB..一,然后作dd线的平行线m与上述曲线相交于g点,通过g点作如线的平行线与口d线交于,点,则,g线的长度即为所要求的主动土压力E.6"3六,计算实例刚性挡土墙高H=4.dm,墙后回填粘性土,一l9.3kN/m.,c—10kPa,=l5.,8=10.,;0.,填土表面作用均布超载口10kPa,墙面垂直,"=0.(一)按不考虑出现裂缝情况计算经计算得作用在挡土墙上的总土压力为E一68.896kN,实测土压力为79.6kN,两者相比,计算值较实测值/J~,l3.32.(=)按出现裂缝情况计算(1)按式(35),(36)和(40)计算得h=1.3559m,:0.5307,E=72.480kN,较实测土压力小8.9.裂缝深度h=0.8378m.为了简便起见,在计算B值时可先按式(19)作初步估算.在本例情况下,按式(i9)算得的B值与按式(40)算得的B值十分接近.(2)略去幻自对h的影响,按式(45)和(46)计算得h=1.3505m,^一0.5888,根据式(33)计算得主动土压力E一80.6538kN,较实测土压力太1.32.由上述计算可见,当=舟==0时,可直接根据式(45)和(46)计算h.和^值.七,结语在计算粘性土对刚性挡土墙的土压力时,滑动面为平面的库仑理论仍具有一定的可靠性.计算中是否考虑墙后填土裂缝的问题,应根据墙体在土压力作用下的变形情况来决定,在一般情况应考虑填土出现裂缝,否则计算结果较实际土压力偏小较多.在填土表面规则变化,填土上作用均布超载时,土压力应按式(35),(36)和(40)计算,但从实用角度考虑,B值可按式(19)计算,而在计算h.时,可略去6角的影响.当填土表面不规则,上面作用非均布超载时,粘性土的土压力宜按图解方法计算. 参考文献顾慰慈,挡土墙的土压力.工程建设,1957年第12期.朱裥措,.刘渣瑞.粘性土主动土压力计算.中国土木工程学会第三届4-力学及基础工程学术会议论支选集,中国建筑工业出版社,1981年.C髓e硒H蝴B.BJ9KcⅡepⅡMe眦舶mOeHayq衄He06pO啦H皿H咖矗~OHb- ~eHzHBcMⅡyq晡cpe~eTpyO~卅H.r,B啪131JM.,TpaⅡc】l【郫ⅡOp血撇, 1961Ⅱape直立3.B.J8cⅡep直姗虹TaH0ecⅡeⅡ0BaⅡl【e栅姐gcmnyq曲印M Hano~nopnmec're2i~cB田阻n啪0茸3a~eiirI覃b卫.HrOpE3佣TabⅡ0茸HO- 拧印XH0CTI~t03aCM~IEH.0加阳"J《时0枷州"M#xam~ar胛0l965,№4.KaeitaFK.JCTp0ⅡT㈣姐MexaH~xac咖yⅡⅡxTeJICrp0酋Ⅱ3珏aTJ1977? IlpoKo~eaH.Ⅱ.,皿aB丑咖ecMⅡyer0T鲫aHL~ZcqCrno~nopiinxCTelIOK? M,Crp0H3矾rJ1947.1)据据四』fl省建筑科学研究所实捌贽科肯]]]]?Jl23456}[[[。
挡土墙计算

一、土压力计算简图:
二、土压力计算:
取土楔ABC为脱离体,土楔在下述三个力的作用下达到静力平衡。其一是墙壁对土楔的反 力P,其作用方向与墙壁背面的法线成δ 角(它是墙壁与土之间的外摩擦角,称为墙背摩擦 角);其二是滑动面BC上的反力R,其方向与BC面的法线成φ 角(φ 是土的内摩擦角);其 三是土楔ABC的重力W,它的大小和方向均为已知。因为土的重度γ 及墙壁背倾角ε ,填土表 面与水平面夹角β 都已给出,所以,只要假设滑动面与水平面的夹角为α ,便可以根据W、P、 R三力构成力的平衡三角形。利用正弦定理,可得出: 土压力:Pa= γ (kN/m ) H 21
3
1 H 2 Ka 2
Ka 1.8 0.323862
cos2 ( )
Ka的计算:Ka= φ 28 ε 0
cos2 cos( )[ 1
δ 16 β 0
sin( ) sin( ) 2 ] cos( ) cos( )
Pa(kN) 11.01779207
( ) 2 ] s( )
Ka 0.323862201 0.6 0.8 1.95 2.15 4.5 4.5 V 152.6625
0.5
50.37
顺时针力矩 20
kc 2.448 b 0.5 b 2.5 h 4 v 138
Σ G(kN) 515
Σ PY(kN) 3.036915073
25 25 25 25 25 25
124.9875 渠堤 428.05 渠堤 65.45 挡墙 162 挡墙 67.5 挡墙 1.63125 板自重
1
2
21
73.08
0.15
10.962
土体主动、主动土压力概念及计算公式

[指南]土体主动、主动土压力概念及计算公式主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P。
a被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P。
上述三种土压力的移动情况和它们在相同条件下的数值比较,p可用图6-2来表示。
由图可知P,P,P。
poa朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直;(2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,ζ仍保持不变,但ζ将不断增大并超过ζ值,zxz当土墙挤压土体使ζ增大到使土体达到被动极限平衡状态时,如图6-4的应力园O,ζx3z变为小主应力,ζ变为大主应力,即为朗肯被动土压力(p)。
土体中产生的两组破裂面与xp,45:,水平面的夹角为。
2朗肯主动土压力的计算根据土的极限平衡条件方程式,,2ζ=ζtg(45?+)+2c?tg(45?+) 1322,,2ζ=ζtg(45?-)-2c?tg(45?-) 3122土体处于主动极限平衡状态时,ζ=ζ=γz,ζ=ζ=p,代入上式得 1z3xa1)填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为,,2,ap=γztg(45?-)-2c?tg(45?-)=γzK-2c (6-3) aa22由公式(6-3),可知,主动土压力p沿深度Z呈直线分布,如图6-5所示。
土主动被动土压力概念及计算公式

主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P a 。
被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P p 。
上述三种土压力的移动情况和它们在相同条件下的数值比较,可用图6-2来表示。
由图可知P p >P o >P a 。
朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin )1857年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中,首先作出以下基本假定。
(1)挡土墙是刚性的墙背垂直; (2)挡土墙的墙后填土表面水平;(3)挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,σz 仍保持不变,但σx 将不断增大并超过σz 值,当土墙挤压土体使σx 增大到使土体达到被动极限平衡状态时,如图6-4的应力园O 3,σz 变为小主应力,σx 变为大主应力,即为朗肯被动土压力(p p )。
土体中产生的两组破裂面与水平面的夹角为245ϕ-︒。
朗肯主动土压力的计算根据土的极限平衡条件方程式σ1=σ3tg 2(45°+2ϕ)+2c ·tg(45°+2ϕ) σ3=σ1tg 2(45°-ϕ)-2c ·tg(45°-ϕ)a0K c 2z γ=(6-4)在z 0深度范围内p a 为负值,但土与墙之间不可能产生拉应力,说明在z 0深度范围内,填土对挡土墙不产生土压力。
墙背所受总主动土压力为P a ,其值为土压力分布图中的阴影部分面积,即γ+-γ=--γ=22c 2K cH 2K H 21)z H )(K c 2HK (21P a a 0a a a (6-5)2)填土为无粘性土(砂土)时根据极限平衡条件关系方程式,主动土压力为a a zK )245(ztg p 2γ=ϕ-︒γ= (6-6)上式说明主动土压力P a 沿墙高呈直线分布,即土压力为三角形分布,如图6-6所示。
土体主动、主动土压力概念及计算公式

[ 指南] 土体主动、主动土压力概念及计算公式主动土压力挡土墙向前移离填土,随着墙的位移量的逐渐增大,土体作用于墙上的土压力逐渐减小,当墙后土体达到主动极限平衡状态并出现滑动面时,这时作用于墙上的土压力减至最小,称为主动土压力P。
a被动土压力挡土墙在外力作用下移向填土,随着墙位移量的逐渐增大,土体作用于墙上的土压力逐渐增大,当墙后土体达到被动极限平衡状态并出现滑动面时,这时作用于墙上的土压力增至最大,称为被动土压力P。
上述三种土压力的移动情况和它们在相同条件下的数值比较,p可用图6-2 来表示。
由图可知P,P,P。
poa朗肯基本理论朗肯土压力理论是英国学者朗肯(Rankin)1857 年根据均质的半无限土体的应力状态和土处于极限平衡状态的应力条件提出的。
在其理论推导中, 首先作出以下基本假定。
(1) 挡土墙是刚性的墙背垂直;(2) 挡土墙的墙后填土表面水平;(3) 挡土墙的墙背光滑,不考虑墙背与填土之间的摩擦力。
把土体当作半无限空间的弹性体,而墙背可假想为半无限土体内部的铅直平面,根据土体处于极限平衡状态的条件,求出挡土墙上的土压力。
如果挡土墙向填土方向移动压缩土体,ζ仍保持不变,但ζ将不断增大并超过Z 值,ZXZ当土墙挤压土体使Z增大到使土体达到被动极限平衡状态时,如图6-4的应力园O, Z x3z变为小主应力,Z变为大主应力,即为朗肯被动土压力(p) 。
土体中产生的两组破裂面与xp,45:, 水平面的夹角为。
2 朗肯主动土压力的计算根据土的极限平衡条件方程式,,2 Z =Z tg(45?+)+2c?tg(45?+) 1322,,2 Z =Z tg(45?-)-2c?tg(45?-) 3122土体处于主动极限平衡状态时,Z = Z = Y Z, Z = Z =p,代入上式得1z3xa1) 填土为粘性土时填土为粘性土时的朗肯主动土压力计算公式为,,2,ap= γztg(45?-)-2c?tg(45?-)= γzK-2c (6-3) aa22由公式(6-3) ,可知,主动土压力p 沿深度Z 呈直线分布,如图6-5 所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
η
cos ρ
B = qd (1 − η tan ϕ tan ρ ) (1 + tan 2 ϕ ) 。
( cy + E tan ϕ )
。
(4)
根据土体的受力状况,x、y 向诸分力的平衡方程 为
因系主动土压力,故根号前应取负号。 当墙背为直立(即 ρ = 0 ) ,且 d = 0 时,
tan θ =
(1 + η ) tan ϕ − sec ϕ
─────── 收稿日期: 2005–03–07
第5期
李巨文,等. 挡土墙后粘性填土的主动土压力计算
651
各种因素(如墙背倾斜程度、粗糙程度) ,本文取 [1] tan δ = η tan ϕ ,c′ = η c , 由此, η 为介于 0~1 的系数。 墙背阻力 F=
⎛1 ⎞ 式中, A = ⎜ γ y 2 + qy ⎟ tan ϕ + cy , ⎝2 ⎠
η tan ϕ − 1
2
1+η
;
(10)
∑ y = Q + W − F cos ρ − T cosθ − N sin θ − E tan ρ
=0 , ∑ x = T sin θ − N cosθ + E − F sin ρ = 0
。 (5) (6) 式中,Q 为作用于楔形土体表面的均载总和,即 Q = qy ( tan θ + tan ρ ) − qd 。 (7) 将式(1) 、 ( 3) 、 (4 ) 、 (7)代入平衡方程(5) 、 (6)联立求解,消去 N,得 1 qy ( tan θ + tan ρ ) − qd + ry 2 ( tan θ + tan ρ ) 2 → E − η ( cy + E tan ϕ ) tan ρ
AB[(η tan 2 ϕ − 1) + (1 + η ) tan ϕ tan ρ ]}2 ← , (1 + η ) tan ϕ tan ρ ]
1
(9)
当 y ′ = 0 时, ω q′ = ψ c ,当 y ′ ≠ 0 时,式(17)中的第 2、 4 项总是等量增加, 从而互相抵消。 故式 (17) 、 (18) 又可简化为 1 1 2 E = ωγ y ′2 − ζ qd = ωγ ( y − y0 ) − ζ qd , (19) 2 2
第 28 卷 2006 年
第5期 5月
岩
土
工
程
学
报
Chinese Journal of Geotechnical Engineering
Vol.28 No.5 May, 2006
挡土墙后粘性填土的主动土压力计算
李巨文,王 翀,梁永朵,冯 震
(防灾技术高等专科学校,河北 三河 065201)
摘
要:根据库伦土压力的计算原理,从滑动楔体处于极限平衡状态时力的静力平衡条件出发,推导出了计算粘性土
2
填土表面倾斜时的土压力
对填土表面与水平面相交成 β 角的倾斜面时(见 如图 3) ,仍选填土表面为 x 轴,以与 x 轴相垂直、并 通过墙背某一计算深度的点为 y 轴,按作用于土体上 的诸力,分别列出 x、y 向的极限平衡方程,即 ∑ y = ( Q + W ) cos β − F cos ρ − T cosθ −
652
岩
土
工
程
学
报
2006 年
σ 3 = ωγ ( y − y0 ) 。
(20)
←
η tan ρ ( tan ϕ + tan θ ) 。 (1 + η )( tan ϕ − tan ϕ tan θ tan ρ )
若 β = 0 ,式(23)变为式(8) 。令 ∂E / ∂θ = 0 ,则可 求得产生最大主动土压力时的滑裂角
Abstract: According to the Coulomb’s earth pressure theory, from the condition of the static equilibrium of the force when the slide wedge was in limit equilibrium, a formula was derivated for the calculation of active earth pressure of cohesive or non-cohesive backfill soils. This formula could be used in the calculation of earth pressure with superimposed load uniformly distributed on any location of ground surface behind retaining wall. Some suggestions were proposed to the calculation of earth pressure in gravity retaining wall design. Key words: Coulomb’s theory; retaining wall; active earth pressure; uniformly distributed load
式中, γ 为土的重度。当楔体处于极限平衡时,挡土 墙和静止土体对楔体的阻力分别为 1 (2) F= ( c′y + E tan δ ) , cos ρ T = cl + N tan ϕ 。 (3) 式中 δ 、 ϕ 分别为墙背对土体的摩擦角和土体的内 摩擦角; c′ 、 c 分别为背与土体间的粘结力和土体内 的粘聚力; l 为滑裂面 BC 的长度。 墙背阻力F由粘结阻力、摩擦阻力组成。考虑到
当 y = 0 时,求得其最大拉力强度为 σ 3 = ω q −ψ c , (15) 于是求得拉力区的总拉力 y0 1 2 E ′ = ∫ σ 3 dy = − (ω q − ψ c ) 。 (16) 0 2ωγ
{ A2 (1 + η )sec 2 ϕ sec 2 ρ (1 − η tan ϕ tan ρ ) − → ⋅[(η tan 2 ϕ − 1) +
= [(η tan 2 ϕ − 1)(tan θ + tan ρ ) − (1 + η )(tan ϕ − tan ϕ tan θ tan ρ )]E ,从而求得极限平衡时,挡土墙上 的正压力在 x 方向的分量为 1 E = ωγ y 2 + ω qy − ζ qd − ψ cy 。 (8) 2 式中 ( tanθ + tan ρ )(1 − tanϕ tanθ ) ω= , 2 (1 −η tan ϕ ) ( tanθ + tan ρ ) + (1+ η )( tanϕ − tanϕ tanθ tan ρ )
tan θ =
式中
图 2 均载置换后土体的受力情况 Fig. 2 Forces acting on the soil with uniform load substi) D 。 −F
(24)
A = (1 + η ) tan ϕ + (1 − η tan 2 ϕ ) tan ρ,
Computation of earth pressure of cohesive backfill on retaining wall
LI Ju-wen, WANG Chong, LIANG Yong-duo, FENG Zhen
(College of Disaster Prevention Techniques, Sanhe 065201, China)
← −cy − E tan ρ − η ( cy + E tan ϕ ) +cy tan θ = tan ϕ + tan θ , 1 − tan ϕ tan θ
当墙背为直立且光滑 (即 η = 0 , ρ = 0) , 且 d = 0 时, ϕ tan θ = tan(45o − ) ,此时
1 ϕ ϕ E = ( γ y 2 + qy ) tan 2 (45o − ) − 2cy tan(45o − ) 。(11) 2 2 2 式(11)就是朗肯公式。 将式(8)对 S 微分(S 为 AB 长度,y=S cos ρ ) , 得土体对挡土墙背的正压力强度在 x 方向的分量为 e = (ωγ y + ω q − ψ c ) cos ρ 。 (12) 将式(12)除以 cos ρ ,则求得沿 y 轴分布的正压力强 度在 x 方向的分量,即 σ 3 = ωγ y + ω q − ψ c 。 (13) 当 σ 3 = 0 时,由式(13)得正压力强度零点的高度 ψc q − ; (14) y0 =
2
整理得 ⎛1 2 ⎞ ⎛1 2 ⎞ ⎜ γ y + qy ⎟ ( tanθ + tan ρ ) tan ϕ tanθ − ⎜ γ y + qy ⎟ ⋅ ⎝2 ⎠ ⎝2 ⎠
ωγ
γ
( tanθ + tan ρ ) + qd (1 − tanϕ tanθ ) +
2 cy ⎡ ⎣1 + η + tan θ − η tanϕ tanθ − η tan ρ ( tan ϕ + tanθ ) ⎤ ⎦
0
前
言
重力式挡土墙的主动土压力计算方法虽多,但都 有缺陷。对无粘性土采用库仑公式误差不大,但对于 粘性土的主动土压力,尤其是均布荷载距墙顶有一定 距离的情况(如图 1) ,目前还没有比较精确、简单的 计算方法。文献[1-2]仅适用于均布荷载从挡墙顶开始 作用的情况。本文在文献[1]的基础上,给出了地面连 续均布荷载 q 从墙后某一距离 d 开始作用的主动土压 力计算公式,对文献[1]的作了必要的扩充。
