挡土墙及土压力计算
挡土墙土压力计算
(3)Ea
r ( A0tg
cos(25031' 350 ) B0 ) sin(25031' 690 )
17 (22.8 tg25031'
5.6847)
cos(25031'350 ) sin(25031' 690 )
139.05KN
/
m
Ex Ea cos( ) 139 .05 cos(20 0 14 0 ) 115 .28KN / n Eg Ea sin( ) 77.76KN / m
a)ctg1
Htg ]2
* cos sin 1 cos( 1)
其中: AB (b L) (H a)ctg1 Htg
在ABC
中,由正弦定理:CD
BC
sin
1
AB
cos sin 1 cos( 1)
BC
sin(90
)
AB
sin(90
1)
BC
AB
sin(900 ) sin(900 1)
b
d ]H 0
1 2
(a
H
2h0
)(a
H )tg
1 2
ab
(b
d )h0
1 2
H
(H
2a
2h0
)tg
令: A0
1(a 2
H
2h0
)(a
H
)
B0
1 2
ab
(b
d )h0
1 2
H(H
2a
2h0 )tg
则: S A0tg B0
破裂棱体的重:G rs r( A0tg B0 )
Ea
r ( A0tg
S Somnp SpnB SQmp SOQA SABC Sklij
各个挡土墙详细计算和计算图形

目录1.重力式挡土墙 (2)1.1土压力计算 (2)1.2挡土墙检算 (4)2.2设计计算 (6)3.扶壁式挡土墙 (9)3.1土压力计算 (9)5.2锚杆设计计算 (16)5.3锚杆长度计算 (17)6.锚定板挡土墙 (17)6.1土压力计算 (17)6.3抗拔力计算 (18)7.土钉墙 (18)7.1土压力计算 (18)7.2土钉长度计算和强度检算 (18)7.3土钉墙内部整体稳定性检算 (19)7.4土钉墙外部整体稳定性检算 (19)1.重力式挡土墙 1.1土压力计算⑴第一破裂面ψϕδα=++tan tan θψ=-±土压力系数:()()()cos tan tan sin θϕλθαθψ+=-+土压力:()()()00cos tan sin a E A B θϕγθθψ+=-+()cos ax a E E δα=- ()sin ay a E E δα=-① 破裂面在荷载分布内侧()2012A A a H =+ ()012tan 22H B ab H a α=-+ a a σγλ= H H σγλ=1tan tan tan b a h θθα-=+ 21h H h =-()()32211223332x H a H h H h Z H a H h +-+=⎡⎤+-⎣⎦tan y x Z B Z α=-②破裂面在荷载分布范围中()()00122A a H h a H =+++ ()()000122tan 22HB ab b d h H a h α=++-++00h σγλ= a a σγλ= H H σγλ=1tan tan tan b a h θθα-=+ 2tan tan dh θα=+ 312h H h h =--()()322211032103333322x H a H h H h h h Z H aH ah h h +-++=+-+ tan y x Z B Z α=-③破裂面在荷载分布外侧()2012A a H =+ ()00012tan 22HB ab l h H a α=--+00h σγλ= a a σγλ= H H σγλ=1tan tan tan b a h θθα-=+ 2tan tan dh θα=+ 03tan tan l h θα=+ 4123h H h h h =---()()()322211033421033332322x H a H h H h h h h h Z H aH ah h h +-+++=+-+tan y x Z B Z α=-⑵第二破裂面 查有关的计算手册。
砌体挡土墙计算实例

砌体挡土墙计算实例在土木工程中,砌体挡土墙是一种常见的结构,用于支撑土体,防止其坍塌或滑移。
为了确保挡土墙的稳定性和安全性,需要进行精确的计算。
下面,我们将通过一个具体的实例来详细介绍砌体挡土墙的计算过程。
假设我们要设计一个高度为 5 米的砌体挡土墙,墙背填土为砂土,填土表面水平,墙后地下水位在墙底以下 1 米处。
挡土墙采用 MU30 毛石、M75 水泥砂浆砌筑,墙身重度为 22kN/m³。
一、土压力计算首先,我们需要计算作用在挡土墙上的土压力。
根据库仑土压力理论,主动土压力系数可以通过以下公式计算:Ka =tan²(45° φ/2)其中,φ 为填土的内摩擦角。
假设填土的内摩擦角为 30°,则主动土压力系数 Ka 为:Ka = tan²(45° 30°/2) = 033土压力的分布呈三角形,顶部为零,底部最大。
土压力强度可以通过以下公式计算:σa =γhKa其中,γ 为填土的重度,h 为计算点距离填土表面的高度。
假设填土重度为 18kN/m³,则墙顶处土压力强度为零,墙底处土压力强度为:σa = 18×5×033 = 297kN/m²土压力的合力可以通过三角形面积计算:Ea = 05×297×5 = 7425kN/m合力作用点距离墙底的高度为:h = 5/3 = 167m二、抗滑移稳定性验算为了保证挡土墙不会沿基底滑移,需要进行抗滑移稳定性验算。
抗滑移稳定系数 Ks 可以通过以下公式计算:Ks =(μ∑Gn + Ep) / Ea其中,μ 为基底摩擦系数,∑Gn 为垂直于基底的重力之和,Ep 为墙前被动土压力。
由于本例中不考虑墙前被动土压力,Ep 为零。
假设基底摩擦系数为 04,重力之和为:∑Gn = G + Ey其中,G 为挡土墙自重,Ey 为墙后土压力的水平分力。
挡土墙自重 G 可以通过墙身体积乘以重度计算:G = 05×5×22 = 55kN/m墙后土压力的水平分力 Ey 为:Ey =Ea×cos(δ)其中,δ 为墙背与填土之间的摩擦角,假设为 15°。
土压力计算及挡土墙设计最终版

Ka
tan2(45 φ) 2
④单位墙长度上的土压力合
力Ea
Ea
1 2
γh2Ka
无粘性土主动土压力
2.朗肯主动土压力计算——粘性土
①②沿粘深性度土方的向极主限动平土衡压条力件的:分σ3 布σ 1ta 2(4 n 5φ 2)2cta4n 5φ 2 ()
p a γ z ta 2 (4 n 5 φ 2 ) 2 c ta 4 n 5 φ 2 ) ( γ za K 2 cK a
③土压力分布特点:墙背受到的土压力一般呈三角形分布,最大
压力强度发生在底部,类似于静水压力的分布。
刚性挡土墙背上的图压力分布
二、挡土墙类型
(按刚度及位移方式分为刚性挡土墙和柔性挡土墙)
2.柔性挡土墙
①定义:一般指用钢筋混凝土桩或地下连续墙所筑成的断面较小而长
度较大的挡土结构
锚杆
板桩 基坑
基坑
板桩变形
②根据土的极限平衡条件:
粘性土: pa (qγz)Ka2c Ka
砂土: pa (qγz)Ka
2c q
③填土为粘性土时,临界深度:
z0 γ
Ka γ
④若超载q较大,计算的z0为负值,
墙顶处土压力
paqK a2c Ka
2.分层填土:按各层的土质情况,分
别确定每层土作用于墙背的土压力。 ①第一层土按指标γ1、φ1和c1计算土压
在相同的墙高和填土条件下:Ea<E0<Ep
3.静止土压力计算
①按半空间弹性变形体在土的自重作用 下无侧向变形时的水平侧压力:
p =K0γz ②若土体为均质土,则K0与γ均为常数
K0=μ/(1-μ) 由计于算土。的μ很难确定,K0常用经验公式
挡土墙工程土压力计算、边坡整体稳定性计算方法

附录A 土压力计算A.0.1侧向岩土压力可采用库伦土压力或郎肯土压力公式计算,侧向岩土压力分布应根据支护类型确定。
A.0.2当墙后土体倾斜时,墙后主动土压力合力用公式(A.0.2-1)计算,侧向土压力分布形式为三角形,合力作用点位置距墙底1/3H 处,计算简图见图A.0.2。
2ak a12E H K γ=(A.0.2-1){[22sin()sin()sin()sin sin ()a q K K αβαβαδααβϕδ+=+-+--]sin()sin()2sin cos cos()ϕδϕβηαϕαβϕδ++-++---(A.0.2-2)2sin cos 1sin()q q K H αβγαβ=++(A.0.2-3)2c Hηγ=(A.0.2-4)式中:ak E —主动土压力合力标准值(kN/m );a K —主动土压力系数;H —挡土墙高度(m );γ—土体重度(kN/m 3)。
;c —土的黏聚力(kPa );ϕ—土的内摩擦角(°);q —地表均布荷载标准值(kN/m 2);δ—土对挡土墙墙背的摩擦角(°),可按表A.0.2取值;β—填土表面与水平面的夹角(°);α—挡土墙墙背的倾角(°);θ—滑裂面与水平面的夹角(°)。
图A.0.2库伦土压力计算表A.0.2土对挡土墙墙背的摩擦角δ挡土墙情况摩擦角δ墙背平滑,排水不良(0~0.33)ϕ墙背粗糙,排水良好(0.33~0.50)ϕ墙背很粗糙,排水良好(0.50~0.67)ϕ墙背与填土间不可能滑动(0.67~1.00)ϕA.0.3当墙后土体水平,墙后主动土压力标准值可按公式(A.0.3)计算。
aikj j ai 12i j e h q K c γ=⎛⎫=+- ⎪⎝⎭∑(A.0.3)式中:aik e —计算点处的主动土压力标准值(kN/m 2),当aik e <0时取aik e =0;ai K —计算点处的主动土压力系数,取2o aii tan (452)K ϕ=-;i c —计算点处土的黏聚力(kN/m 2);i ϕ—计算点处土的内摩擦角(°)。
挡土墙计算
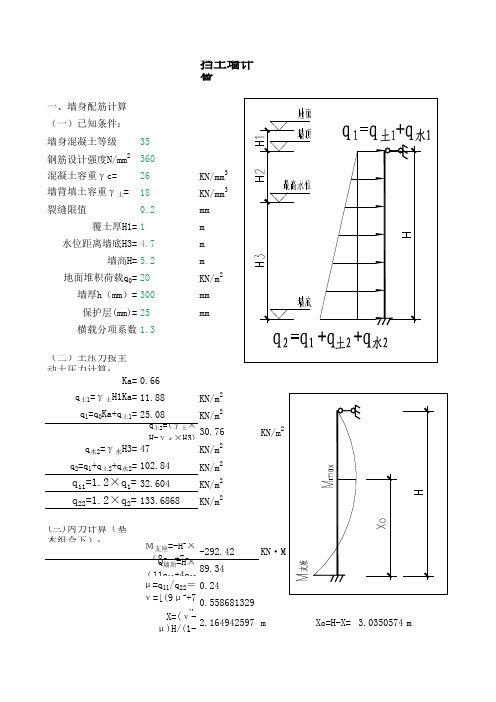
挡土墙计算一、墙身配筋计算(一)已知条件:墙身混凝土等级35钢筋设计强度N/mm 2360混凝土容重γc=26KN/mm 3墙背填土容重γ土=18KN/mm 3裂缝限值0.2mm 覆土厚H1=1m 水位距离墙底H3=4.7m 墙高H=5.2m 地面堆积荷载q 0=20KN/m 2墙厚h(mm)=300mm 保护层(mm)=25mm 横载分项系数1.3(二)土压力按主动土压力计算:Ka=0.66q土1=γ土H1Ka=11.88KN/m 2q 1=q 0Ka+q 土1=25.08KN/m 2q 土2=(γ土×H-γ水×H3)30.76KN/m 2q 水2=γ水H3=47KN/m 2q 2=q 1+q 土2+q 水2=102.84KN/m 2q 11=1.2×q 1=32.604KN/m 2q 22=1.2×q 2=133.6868KN/m 2(三)内力计算(基本组合下):M支座=-H 2×(8q 22+7q 11-292.42KN·M Q 墙顶=H×(11q 11+4q 2289.34μ=q 11/q 22=0.24ν=[(9μ2+7μ0.558681329X=(ν-μ)H/(1-2.164942597m Xo=H-X= 3.0350574mMmax =Q 墙顶X-q 11X 2/2+84.13227KN·M (四)配筋计算混凝土抗压强度fcd=16.7N/mm 2ho=265mm 钢筋设计强度fy=360N/mm 2计算宽度b=1000mm M支座 =f cd bx(h 0-x/2)292420114.00 =16700x(265-x/2)x =77.371 m ≤ξb h 0 =0.53×265.00 =140.5mm 解得A s = M支座/(ho-3691mm 2Mmax =f cd bx(h 0-x/2)84000000.00 =16700x(265-x/2)x =19.714 mm ≤ξb h 0 =0.53×265.00 =140.5mm 解得跨中A s = Mmax/(ho-940mm 2(五)裂缝计算钢筋直径d=22mm 钢筋间距75mm 每延米实配钢筋A s =5068.44mm 2标准组合下Mk 支座=-H 2×-224.94KN·M σsk=Mk支座192.4974N/mm2αcr=2.1ρte=0.033789574ftk=2.2ψ=0.880148956< 1 且>0.2所以ψ取0.880148956Es=200000c=25deq=22裂缝宽度W fk =0.177163082mm 裂缝满足要求。
挡土墙及土压力计算

RD 一定位于 R 的下方,即 RD 与 N 之间的夹角φD 一定大于 R 与 N 之间的夹角φ ,鉴于
挡土墙:为G防止12土体 坍H 塌2 而sin修(9建0第o的s六i挡n章(土:结挡)构土)s。inc墙土(o9及s压02 o土力压:墙力后计 )土算体对墙背的作用力称为土压力。
一、三种土压力——根据墙、土间可能的位移方向的不同,土压力可以分为三种类型:
1.主动土压力 Ea——在土压力作用下,挡土墙发生离开土体方向的位移,墙后填土达到极
2.被动土压力 压力系数,应用时,查表。
其中
库仑被动土
Ep 沿深度呈三角形分布,其作用点距墙底 H/3,位于墙背法线下方,与墙背法线成δ角。 库仑理论应用中的几个问题 1. 关于δ的取值: δ值与墙后填土的性质、填土含水量及墙背的粗糙程度变化于 0~φ之间,实用中常取δ =1/2~1/3φ。 2. 当墙后填土为粘性土时——为了得到确切的解析解,库仑理论假设墙后填土为无粘性土,
二、三种土压力在数量上的关系
墙、土间无位移,墙后填土处于弹性平衡状态,与天然状态相同,此时的土压力为静止土压
力;在此基础上,墙发生离开土体方向的位移,墙、土间的接触作用减弱,墙、土间的接触
压力减小,因此主动土压力在数值上将比静止土压力小;而被动土压力是在静止土压力的基
础上墙挤向土体,随着墙、土间挤压位移量的增加,这种挤压作用越来越强,挤压应力越来
此,实用中,可考虑将粘性土的φ值适当增大,用增大后的Δφ来近似考虑 c 值对土压力的
精品课件- 土压力计算与挡土墙设计
1. 作用在土楔体ABC上的力 • 假设滑动面AC与水平面夹角为α,取滑动土楔体ABC为脱离体,则作用在土楔体ABC上
的力有:
(1)土楔体自重 • 在三角形ABC中,利用正弦定理可得:
(2)滑动面 上B的C反力R
应力分别为:
• (因为已假设墙背是光滑的、直立的,所以在单元上不存在剪应力。) • 该应力状态仅由填土的自重产生,故此时土体处于弹性状态,其相应的莫尔园如下
图所示的园Ⅰ,一定处于填土抗剪强度曲线之下。
• 当挡土墙离开填土向前发生微小的转动或位移时, σ1 =σz =yz不变, σ3 =σx而却不断减 少,相应的莫尔园也在逐步扩大。当位移量达到一定值时, σ3减少到σ3f ,由σ3f与 σ1 =yz构成的应力园与抗剪强度曲线相切,如图Ⅱ所示,称为主动极限应力园。此时, 土中各点均处于极限平衡状态,达到最低什的小主应力σ3f称为朗肯主动土压力pa(即 pa = σ3f )。与此同时,土体中存在过墙踵的滑动面(剪切破坏面),滑动面与大主 应力作用平面(水平面)的夹角为450+φ/2。
•
q——填土面上的均布荷载,kPa。
四、墙后有地下水时
• 若墙后有地下水时,水下应取浮重度,同时应考虑静水压力,如下图所示。
• 五、墙背倾斜时 • 式中:W0——楔体ABB‘的自重。
§3 朗肯土压力理论
一、基本概念
1.假设 (1)墙背直立、光滑; (2)墙后填土面水平; (3)土体为均质各向
同性体。 2.主动朗肯状态 • 如上图所示,在墙后土体中深度Z处任取一单元体,当挡土墙静止不动时,则两个主
•
h=q/r
挡土墙上土压力的计算

郎 肯 土 压
γz(σ3)
移,竖向应力保持不变, 水平应力逐渐增大,位移
增大到△p,墙后土体处
h
z
力
σp(σ1)于朗肯被动状态时,墙后
的
土体出现一组滑裂面,它
计 算
45o-ϕ/2
与小主应力面夹角45o-
ϕ/2,水平应力增大到最
大值
极限平衡条件
朗肯被动土压力强度
σ1
=
σ
3
tan2
⎜⎛ ⎝
45o+ϕ
2
⎟⎞+2c ⎠
哪种情况下墙后土体更密实,挡土墙上的土压力更大?
挡土结构与基坑工程
挡土墙上土压力的计算
1.主动土压力(Ea)
土 当墙在土压力作用下
压 力 的
向前移动或转动时, 达到一定位移量时,
类 墙后土体达到极限平
型 衡状态,此时的土压
力叫主动土压力
2.被动土压力(Ep) 3.静止土压力(Eo)
挡土墙在外力作用 下向后移动,压缩 填土达到极限平衡 状态,此时作用于
Kp
挡土结构与基坑工程
挡土墙上土压力的计算
滑动面
450 + ϕ / 2
σ3
σ1 = γ z
γz K0γ z
主动土压力
静止土压力
滑动面
450 −ϕ / 2
σ3
=
σ γ
1
z
被动土压力
挡土结构与基坑工程
挡土墙上土压力的计算
库
理论假设
仑
土 压
1. 墙背倾斜,具有倾角α;
力
2. 墙后填土为砂土,表面倾角为角β;
H
2
Ea
H 3
γ HKa
1.无粘性土主动土压力强度与z成正比,沿墙高呈三角形分布
各种挡土墙计算公式

各种挡土墙计算公式在土木工程中,挡土墙是一种常见的结构,用于支撑填土或山坡土体,防止其坍塌或滑坡。
为了确保挡土墙的稳定性和安全性,需要进行精确的设计和计算。
下面我们将介绍一些常见的挡土墙计算公式。
一、重力式挡土墙重力式挡土墙主要依靠自身的重量来抵抗土压力,其稳定性取决于墙体的自重、墙底摩擦力和墙背与填土之间的摩擦力。
1、土压力计算静止土压力:$P_0 = K_0 \gamma z$,其中$K_0$为静止土压力系数,$\gamma$为填土的重度,$z$为计算点距离墙顶的深度。
主动土压力:$P_a =\frac{1}{2} \gamma z^2 K_a$,$K_a$为主动土压力系数,可通过库仑土压力理论或朗肯土压力理论计算得出。
2、稳定性验算抗滑移稳定性:$K_s =\frac{(W + E_{px})\mu}{E_{py}}$,$W$为挡土墙自重,$E_{px}$和$E_{py}$分别为主动土压力的水平和垂直分量,$\mu$为墙底与地基之间的摩擦系数。
要求$K_s \geq 13$。
抗倾覆稳定性:$K_t =\frac{M_R}{M_O}$,$M_R$为抗倾覆力矩,$M_O$为倾覆力矩。
要求$K_t \geq 15$。
3、基底应力验算偏心距:$e =\frac{B}{2} \frac{M_R}{W}$,$B$为基底宽度。
基底最大应力:$\sigma_{max} =\frac{W}{B}(1 +\frac{6e}{B})$基底最小应力:$\sigma_{min} =\frac{W}{B}(1 \frac{6e}{B})$二、悬臂式挡土墙悬臂式挡土墙由立壁、趾板和踵板组成,其稳定性主要依靠墙身的抗弯能力和踵板上的土重。
1、土压力计算同重力式挡土墙。
2、内力计算立壁弯矩:根据墙后土压力分布,计算立壁在不同高度处的弯矩。
踵板弯矩:考虑踵板上的土重和作用在踵板上的土压力,计算踵板的弯矩。
3、截面设计根据内力计算结果,确定立壁和踵板的截面尺寸和配筋。
第六章:挡土墙及土压力计算

RD 一定位于 R 的下方,即 RD 与 N 之间的夹角φD 一定大于 R 与 N 之间的夹角φ ,鉴于
库仑主动土压力系数,应用时,查表。
Ea 沿深度呈三角形分布,其作用点距墙底 H/3,位于墙背法线上方,与墙背法线成δ角。
E
1 2
H
2
s具in(90o sin(
) sin(90o体 ) cos2
)
sin(如 ) sin(90o
)
图
:
Ea
Em a x
1 2
H
2
Ka
Ka f (,, , )
越大,因此被动土压力最大。即:Ea<Eo<Ep 三、静止土压力 Eo 的计算
E
sin( ) sin(90o
)
G
Eo =Ko *γ*H2/2,(kN/m)
式中: γ为填土的容重(kN/m3) ,Ko 为静止土压力系数,可近似取 Ko =1-sinφ',φ'为土
的有效内摩擦角。
H 为挡土墙高度,m。
2.被动土压力 压力系数,应用时,查表。
其中
库仑被动土
Ep 沿深度呈三角形分布,其作用点距墙底 H/3,位于墙背法线下方,与墙背法线成δ角。 库仑理论应用中的几个问题 1. 关于δ的取值: δ值与墙后填土的性质、填土含水量及墙背的粗糙程度变化于 0~φ之间,实用中常取δ =1/2~1/3φ。 2. 当墙后填土为粘性土时——为了得到确切的解析解,库仑理论假设墙后填土为无粘性土,
挡土墙设计主动土压力计算

土压力的水平 和垂直为:
E x E a cos( ) E y E a sin( )
1 2 cos( ) sin( ) 2 G H sec 2 cos( )
1.破裂面交于内边坡
sin(90 ) cos( ) Ea G G sin( ) sin( )
1 2 cos( ) sin( ) 2 G H sec 2 cos( )
8、一般条件下库伦主动土压力计算
挡土墙库仑土压力理论
挡土墙土压力计算时应用了库仑(Coulomb)土压 力理论,通过对墙背后破坏棱体的受力分析,得到土 压力的反力E是破裂角的函数,即 E f (),再求E的极 值可以得到主动土压力和被动土压力。 库仑法的假定为:破裂面为平面且通过墙踵、填 料为砂性土(c=0)、墙背存在摩擦、挡墙和破坏土体为 刚体。
南京工业大学交通学院
挡土墙土压力考虑
1、主动土压力与被动土压力的区分:
假定挡土墙处于极限移动状态,土体有沿墙及假 想破裂面移动的趋势,则土推墙即为主动土压力, 墙推土即为被动土压力。
2、路基挡土墙的土压力考虑:
路基挡土墙一般都有可能有向外的位移或倾覆, 因此,在设计中按墙背土体达到主动极限平衡状态 考虑,且取一定的安全系数以保证墙背土体的稳定。 墙趾前土体的被动土压力一般不计。
南京工业大学交通学院
用土压应力分布图计算主动土压力
土力学土压力与挡土墙计算

墙体位移和土压力性质
拱桥桥台
岩石
2.主动土压力
Active earth pressure
1.静止土压力
Earth pressure at rest
3.被动土压力
Passive earth pressure
§6.3 朗肯(Rankine)土压力理论 一.半无限土体中极限平衡应力状态和朗肯土压力
半无限土体内各点的应力从弹性平 衡状态发展为极限平衡状态的条件
半无限土体
v z
h
45o+/2 90o-
主动极限平衡状态
Pa
K0v
v
朗肯土压力理论基本条件和假定 条件 墙背光滑 墙背垂直 填土表面水平
假设 墙后各点均处于极限平衡状态
(一) 填土为砂土
1.主动土压力
v
pa=h=tg2(45- /2 )gz (kN/m2) Pa K0v
土压力 pa = Kaz
水压力 pu=u (静水压力、 渗流压力、超静孔压)
土工织物反滤
砂砾石料
排水管
排水孔
墙基不透水 A
gf
H1
B
gf
H2
C 不透水层
土压力
Ka gH1
水压力
Ka (gH1+gH2) gwH2
§6.4 库仑土压力理论
假设条件:
平面滑裂面假设:滑裂面为平面 刚体滑动假设:破坏土楔为刚体 滑动楔体在两个平面上处于极限平衡状态
主动土压力系数 Ka= tg2(45-f/2 )
土压力直线分布
合力 Ea=1/2 Ka gH2 (kN/m)
H
作用点:底部以上1/3H处
H/3
土压力计算和挡土墙设计最终版

柔性挡土墙上的土压力分布
2
土压力的分类与相互作用
1.分类:按位移方向和墙后土体的应力状态分为:
静止土压力、主动土压力、被动土压力
挡土墙的三种土压力
2.土压力性质和大小:是由挡土墙位移方向和位移量决定。
3
静止土压力计算
弹性平衡状态。
1.静止土压力定义:墙无移动、土无变形,土体处于 2.墙身位移与静止土压力E0的关系:
φ φ p p γz tan2 (45 ) 2c tan(45 ) γz Kp 2c K p 2 2 1 Ep γh 2 K p 2ch K p 2
φ
φ
粘性土被动土压力分布
三、几种常见情况下的土压力计算
常在工程中遇到的一些特殊的情况,如何利用朗肯土压 力的基本公式计算这些情况下的主动土压力? 1. 填土面上有均布荷载(超载) 2. 分层填土 3. 填土中有地下水
1. 填土面上有均布荷载q (超载)
①在墙后距填土面为z深度处: 大主应力(竖向) σ1=q+γz, 小主应力(水平向) σ3=pa ②根据土的极限平衡条件: pa (q γz )K a 2c K a 粘性土: 砂土: pa (q γz )K a ③填土为粘性土时,临界深度: z 0 ④若超载 q 较大,计算的 z0 为负值, 墙顶处土压力
建筑边坡工程技术规范6.2.6:土中有地下水但未形成渗流
时,作用在支护结构上的侧压力按下列规定计算: 1 对砂土和粉土按水土分算原则计算 2对粘性土宜根据工程经验按水土分算或水土合算原则计算 3 按水土分算原则计算时,作用在支护结构的侧压力等于土 压力和静止水压力之和,地下水位以下的土压力采用浮重度 γ’和有效抗剪强度指标(C’ 、φ’)计算 4 按照水土合算原则计算时,地下水位以下的土压力采用饱 和重度γsat和总应力强度指标(C,φ)计算 6.2.7土中有地下水形成渗流时,作用在支护结构上的侧压力除 按6.2.6计算外,尚应计算动水压力。
土压力计算及挡土墙设计 最终版

土压力计算及挡土墙设计最终版在土木工程领域中,土压力的计算和挡土墙的设计是至关重要的环节。
这不仅关系到工程的稳定性和安全性,还直接影响到工程造价和施工难度。
接下来,让我们深入探讨一下土压力计算及挡土墙设计的相关内容。
一、土压力的基本概念土压力是指挡土墙后的填土因自重或外荷载作用对墙背产生的侧向压力。
根据挡土墙的位移情况和墙后土体的应力状态,土压力可分为静止土压力、主动土压力和被动土压力三种类型。
静止土压力是指挡土墙在土压力作用下不发生任何位移或转动时,墙后土体处于弹性平衡状态时的土压力。
主动土压力是指挡土墙在墙后土体的推力作用下,向前发生位移或转动,墙后土体达到主动极限平衡状态时的土压力。
被动土压力则是指挡土墙在外力作用下向后发生位移或转动,墙后土体达到被动极限平衡状态时的土压力。
二、土压力的计算方法1、静止土压力计算静止土压力的计算通常采用弹性理论,其计算公式为:$E_0 =\frac{1}{2}K_0\gamma H^2$ ,其中$K_0$ 为静止土压力系数,可通过试验或经验公式确定;$\gamma$ 为填土的重度;$H$ 为挡土墙的高度。
2、主动土压力计算库仑理论和朗肯理论是计算主动土压力常用的方法。
库仑理论假定墙后填土为无粘性土,破坏面为一平面,通过分析墙后土体的静力平衡条件,得到主动土压力的计算公式。
朗肯理论则基于土的极限平衡条件,假定填土表面水平且无限延伸,墙背垂直光滑,从而推导出主动土压力的计算公式。
3、被动土压力计算被动土压力的计算方法与主动土压力类似,也可以采用库仑理论和朗肯理论,但计算过程相对复杂。
三、影响土压力的因素土压力的大小和分布受到多种因素的影响,主要包括填土的性质(如填土的重度、内摩擦角、粘聚力等)、挡土墙的形状和尺寸、墙背的粗糙度、填土表面的荷载以及挡土墙的位移方向和位移量等。
例如,填土的重度越大,土压力就越大;内摩擦角和粘聚力越大,土压力则越小。
墙背越粗糙,土压力越大;墙背越光滑,土压力越小。
挡土墙主动土压力计算公式

挡土墙主动土压力计算公式
1.土壤的重力是均匀分布的;
2.土壤的内摩擦角和墙与土壤的摩擦角没有明显差异;
3.挡土墙和土壤之间的界面摩擦是充分发展的。
根据这些假设,挡土墙主动土压力可以通过卡诺定理进行计算。
卡诺定理的基本原理是,土壤对挡土墙产生的压力可以分解为水平分量和垂直分量,其中水平分量对应于土壤壁面的水平压力,垂直分量对应于土壤壁面的垂直压力。
Pa=1/2*γ*H^2*Ka,
其中
Pa为挡土墙的主动土压力(单位为kN/m);
γ为土壤的干容重(单位为kN/m^3);
H为挡土墙的高度(单位为m);
Ka为活动土压力系数,其大小取决于土壤的内摩擦角和挡土墙的后坡角度。
活动土压力系数Ka的取值通常根据实际情况进行确定,可以通过查表或进行现场试验得到。
常见的Ka值范围在0.15到0.45之间,取决于土壤的类型和挡土墙的几何形状。
需要注意的是,挡土墙的主动土压力只是整个挡土墙稳定性计算中的一个因素,还需要考虑其他因素,如墙体的抗滑稳定性、抗倾覆稳定性和
抗底部推力等。
因此,在实际工程中,对挡土墙的设计和计算需要综合考虑各种因素的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章:挡土墙及土压力计算 挡土墙:为防止土体坍塌而修建的挡土结构。
土压力:墙后土体对墙背的作用力称为土压力。
一、三种土压力——根据墙、土间可能的位移方向的不同,土压力可以分为三种类型:1.主动土压力Ea ——在土压力作用下,挡土墙发生离开土体方向的位移,墙后填土达到极限平衡状态,此时墙背上的土压力称为主动土压力,记为Ea 。
2.被动土压力Ep ——在外力作用下,挡土墙发生挤向土体方向的位移,墙后填土达到极限平衡状态,此时墙背上的土压力称为被动土压力,记为Ep 。
3.静止土压力Eo ——墙土间无位移,墙后填土处于弹性平衡状态,此时墙背上的土压力称为静止土压力,记为Eo 。
二、三种土压力在数量上的关系墙、土间无位移,墙后填土处于弹性平衡状态,与天然状态相同,此时的土压力为静止土压力;在此基础上,墙发生离开土体方向的位移,墙、土间的接触作用减弱,墙、土间的接触压力减小,因此主动土压力在数值上将比静止土压力小;而被动土压力是在静止土压力的基础上墙挤向土体,随着墙、土间挤压位移量的增加,这种挤压作用越来越强,挤压应力越来越大,因此被动土压力最大。
即:Ea<Eo<Ep 三、静止土压力Eo 的计算Eo =Ko *γ*H 2/2,式中: γ为填土的容重(kN/m3) ,Ko 为静止土压力系数,可近似取 Ko =1-sin φ',φ'为土的有效内摩擦角。
H 为挡土墙高度,m 。
朗肯土压力理论——1857年,朗肯根据半空间应力状态下的极限平衡条件导出了土压力的计算公式;称为朗肯土压力理论。
1.主动土压力Ea m ——朗肯主动土压力系数;c ——填土的内聚力,(kPa );挡土墙墙高为H ,墙后填土的容重为γ ,内摩擦角为φ。
(对于砂土c=0)2.被动土压力Ep1/m ——朗肯被动土压力系数;库仑土压力理论——墙离开或挤向土体时的极限状态下,墙后形成一具有滑动趋势的土楔体,根据该土楔体的静力平衡条件求解。
假设:墙后填土是理想的无粘性土,滑裂面为过墙踵的平面。
1.主动土压力(1)土楔体自重G(2)滑动面BC 上的作用力R ——主动状态,墙向前移动,土楔体下滑,摩擦力向上,BC 面上总的摩擦力与法向力之和为R ,按物理学:f =μ.Nμ—为摩擦系数,BC 面上,两种介质相同,均为土,按库仑定律律,土与土之间的摩擦系数为tan φ,所以, f /N = tan φ,据此知:R 位于N 的下方,与N 的作用线成φ角,与G 的作用线成:θ- φ。
(3)墙背AB 面上的作用力E ——与BC 面一样,墙背上作用有法向力和摩擦力,该面上总的摩擦力与法向力之和为E ,则E 和墙背法线之间的夹角为δ ,与G 作用线间的夹角为:γγ2222221cm H c m H E a ⋅+⋅⋅⋅-⋅⋅⋅=)245tan(ϕ-=o m mH c m H E p /2/2122⋅⋅⋅+⋅⋅⋅=γ)245tan(1ϕ+=o m εβθεθβεγ22cos )sin()90sin()90sin(21⋅-+-⋅+-⋅⋅⋅=o o H G G E o⋅+-++-=)90sin()sin(ϕθεδϕθ90° - δ-ε土楔体在这三个力作用下处于静力平衡,所以力的作用线应交于一点,力三角形应封闭,作力三角形:E 为墙背对土楔体的作用力,其极限状下的最大反作用力就是土压力,解三角形得:将前面G 的表达式代入得:由于θ角代表的BC 面是假设的滑动面,真正的滑动面是所有可能的θ值中最容易使土体滑动的那个,由于墙体是向前移动,所以最容易滑动的是E 值最大的那个面。
求E 的最大值:库仑主动土压力系数,应用时,查表。
Ea 沿深度呈三角形分布,其作用点距墙底H/3,位于墙背法线上方,与墙背法线成δ角。
具体如图:2.被动土压力 其中 库仑被动土压力系数,应用时,查表。
Ep 沿深度呈三角形分布,其作用点距墙底H/3,位于墙背法线下方,与墙背法线成δ角。
库仑理论应用中的几个问题 1. 关于δ的取值:δ值与墙后填土的性质、填土含水量及墙背的粗糙程度变化于0~φ之间,实用中常取δ=1/2~1/3φ。
库仑理论假设墙后填土为无粘性土,当用粘性土回填时,在BC 面上各力合成时,将出现粘聚力之和 C = c.BC 弧长,由于BC 弧长度是变量,故无法得其确切解析解;C 参与合成后,C 、N 和f 三者之和设为R D ,由图知:RD 一定位于R 的下方,即RD 与N 之间的夹角φD 一定大于R 与N 之间的夹角φ ,鉴于εβθεθβεγ22cos )sin()90sin()90sin(21⋅-+-⋅+-⋅⋅⋅=o o H E ⋅+-++-⋅)90sin()sin(ϕθεδϕθo a a K H E E ⋅⋅⋅==2max 21γ),,,(βδϕεf K a =pp K H E E ⋅⋅⋅==2min 21γ),,,(βδϕεf K p =此,实用中,可考虑将粘性土的φ值适当增大,用增大后的Δφ来近似考虑c值对土压力的影响。
3. 库仑理论和朗肯理论间的差异——库仑理论是利用土楔体在极限状态的静力平衡条件求解,朗肯理论应用的是半空间应力状态下的极限平衡关系式。
两者的出发点不同;在库仑公式中,若δ=0(墙背光滑)、ε=0(墙背垂直、β=0(填土面水平),则库仑理论的Ka=tan2(45- φ/2),即朗肯理论可以看成是库仑理论当δ=0、ε=0、β=0时的特例。
4. 关于滑动面的形状——理论推导时,假设滑动面BC是平面,而实际上是一曲面;主动状态墙向前移,真正的滑动面接近于圆弧(筒)面,当半径较大时,基本上可以看成是平面,因而,按平面计算,其误差相对较小,约为2~10%,尚可以满足工程要求;故工程上,主动土压力一般可以按库仑土理论计算;而在被动状态,墙挤向土体,土中滑动面接近于对数螺线面,根本就不是平面,此时,再按平面计算,无疑会产生很大的误差;其误差随着φ值的增大而增大,甚至达到2~3倍,以致工程上无法直接应用。
*几种常见情况下土压力的计算一、填土面有均布荷载1.墙背光滑、填土面水平时此时的临界深度Zo仍可按相似比进行计算,也可按公式:2. 填土面倾斜时然后,以CD为墙背,按H+h为墙高进行计算,但这种计算仅在墙高范围内有效。
3.局部均布荷载作用墙背垂直、光滑时θ=45+ φ/2在a点以上,不考虑地面超载,c点以全考虑地面超载,ac点之间,按直线处理。
第1种第2种第3种二、墙后填土为成层土时在中γ.z项仍取计算点处的自重应力,其计算点处的c、φ按所在土层取用;即计算点位置哪层土中,c、φ值就按哪层土取用,在两层土界面时,分别计算。
分别求面积后、叠加,即得所求土压力。
mcmqzpa⋅⋅-⋅+⋅=2)(2γ22mqmczo⋅-⋅⋅=γγγβεβεqh⋅-⋅=)cos(coscosmcmzpa⋅⋅-⋅⋅=22γ2222221132)(mcmhhpa⋅⋅-⋅⋅+⋅=γγ在 中γ.z 项仍取计算点处的自重应力,地下水位以下当土颗粒受到水浮力时取用有效容重,其它按成层土考虑,即地下水位面上、下按成层土处理。
例题:图示挡土墙,墙背光滑、垂直,填土面水平,其它指标见图,求作用在墙背上的主动土压力和被子动土压力的值。
解:主动土压力根据三角形相似比:被动土压力本题中:Ep/Ea=2072.01/157.63=13.14可见:被动土压力大大大于主动土压力。
mc m z p a ⋅⋅-⋅⋅=22γ577.012233.0)205.3180.419(⨯⨯-⨯+⨯+⨯=2222221132)(m c m q h h p a ⋅⋅-⋅+⋅⋅+⋅=γγ)(89.17kPa =577.012233.0)200.419(⨯⨯-⨯+⨯=22221122)(m c m q h p a ⋅⋅-⋅+⋅=γ下)(20.4kPa -=70.010249.020⨯⨯-⨯=112112)0(m c m q p a ⋅⋅-⋅+=)(04.33kPa =70.010249.0)200.419(⨯⨯-⨯+⨯=11211122)(m c m q h p a ⋅⋅-⋅+⋅=γ上577.0)23045tan(=-=oo )245tan(22ϕ-=om 70.0)22045tan(=-=o o )245tan(11ϕ-=o m )(68.38kPa =)/(63.15700.9963.58m kN =+=五、车辆荷载土压力Lo=H*(tg ε+ctg α),设桥台计算宽度为B ,则在B*Lo 范围内,当量土厚度ho , Lo ——破坏棱柱长度,m ;γ——土的容重,kN/m 3;ΣG ——破坏棱体内,所有各车轮压之和,kN ;B ——桥台计算宽度,按下列几种情况之一取值: 1.桥台横向全宽;2.挡土墙的计算长度 a.汽车15级作用时,取挡土墙分段长度,但不大于15mb.汽车20级作用时,取重车扩散长度,挡土墙分段长度在10m 以下时,扩散长度不超过10m ,当挡土墙分段长度在10m 以上时,扩散长度不超过15m ,重车扩散长度: l ——汽车重车或平板挂车的前后轴距,(履带车为零)m ;a ——车轮或履带着地长度,m ;H ——挡土墙高度,m ;c.——汽车超20级作用时,取重车的扩散长度,但不超过20m 。
d.——平板挂车或履带车作用时,取挡土墙分段长度和重车扩散长度两者较大者,但不大于15m 。
车轮重力ΣG 的取值: 在B*Lo 内可能布置的车轮重力,挡土墙计算时,汽车车轮荷载布置规定:纵向:当取用挡土墙分段长度时,为分段长度内可能布置的车轮重力之和;当取用1辆重车的扩散长度时,为1辆重车所有轮压之和;横向:破坏棱体长度Lo 范围内可能布置的车轮轮压之和,车辆外侧车轮中线距路面、安全带边缘的距离为0.5m ;平板挂车或履带车荷载纵向只考虑1辆;横向为破坏棱体Lo 长度范围内可能布置的车轮或履带。
车辆外侧车轮或履带中线距路面、安全带边缘的距离为1.0m 。
破坏面与水平面的夹角余切:——确定破坏棱体长度Lo)/(00.995.3)68.3889.17(212m kN E a =⨯+⨯=)/(63.58)451.04(04.33211m kN E a =-⨯⨯=451.02.404.332.40.4=⨯+=o z 21a a a EE E +=577.0122577.0)200.419(2÷⨯+÷+⨯=2222112/2/)(m c m q h p p ⋅++⋅=γ下)(49.224kPa =70.010270.0)200.419(2÷⨯+÷+⨯=1121112/2/)(m c m q h p p ⋅++⋅=γ上)(39.69kPa =70.010270.0202÷⨯+÷=11211/2/)0(m c m q p p ⋅++=)(57.329kPa =222222113/2/)(m c m q h h p p ⋅++⋅+⋅=γγ577.0122577.0)205.3180.419(2÷⨯+÷+⨯+⨯=)(57.518kPa =)/(76.587)49.22439.69(0.4211m kN E p =+⨯⨯=5.3)57.51857.329(212⨯+⨯=p E 25.148476.58721+=+=p p p E E E )/(25.1484m kN =γ**o e L B Gh ∑=boH a l B 30tan *++==0墙背仰斜ε<0,Ea 值最小;墙背垂直ε=0,Ea 值居中;墙背俯斜ε>0,Ea 值最大。
