【精品PPT】挡土墙土压力计算
合集下载
挡土结构物上的土压力PPT课件
1.1 概述
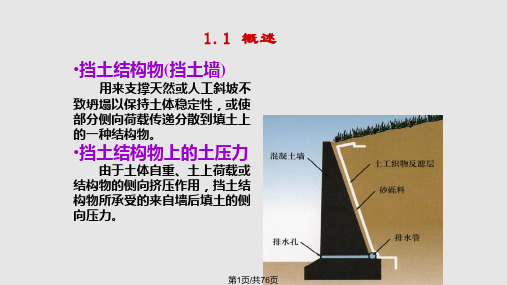
•挡土结构物(挡土墙)
用来支撑天然或人工斜坡不 致坍塌以保持土体稳定性,或使 部分侧向荷载传递分散到填土上 的一种结构物。
•挡土结构物上的土压力
由于土体自重、土上荷载或 结构物的侧向挤压作用,挡土结 构物所承受的来自墙后填土的侧 向压力。
第1页/共76页
1.1 概述
E
地下室
填土
E
桥面
E
1.2 静止土压力计 算
静止土压力计算
z
p0 K0z
H
E0
1H 3
K0H
总静止土压力
E0
1 2
K 0H
2
第14页/共76页
1.3 朗肯土压力理论
1 朗肯极限平衡应力状态
自重应力作用下,半无限土体内各点的应力从 弹性平衡状态发展为极限平衡状态的情况。
s1
s3
45+/2
主动极限平衡应力状态
s3f K0sv sv=z s
实际0
Ep'
Ea
R
主动土压力 偏大
Ea' W
Ep
R
被动土压力
W
偏小
第43页/共76页
1.5 两种土压力理论的比较 3 计算误差 ——库仑土压力理论
滑动面
滑动面
实际滑裂面不一定是平面
主动土压力搜索得到 的不一定是最大值
被动土压力搜索得到 的不一定是最小值
主动土压力 偏小
被动土压力 偏大
第44页/共76页
于是:主动土压力强度
pa sh s3 z tg2(45 - / 2) - 2c tg(45 - / 2)
第20页/共76页
1.3 朗肯土压力理论 •朗肯主动土压力计算-填土为粘性土
•挡土结构物(挡土墙)
用来支撑天然或人工斜坡不 致坍塌以保持土体稳定性,或使 部分侧向荷载传递分散到填土上 的一种结构物。
•挡土结构物上的土压力
由于土体自重、土上荷载或 结构物的侧向挤压作用,挡土结 构物所承受的来自墙后填土的侧 向压力。
第1页/共76页
1.1 概述
E
地下室
填土
E
桥面
E
1.2 静止土压力计 算
静止土压力计算
z
p0 K0z
H
E0
1H 3
K0H
总静止土压力
E0
1 2
K 0H
2
第14页/共76页
1.3 朗肯土压力理论
1 朗肯极限平衡应力状态
自重应力作用下,半无限土体内各点的应力从 弹性平衡状态发展为极限平衡状态的情况。
s1
s3
45+/2
主动极限平衡应力状态
s3f K0sv sv=z s
实际0
Ep'
Ea
R
主动土压力 偏大
Ea' W
Ep
R
被动土压力
W
偏小
第43页/共76页
1.5 两种土压力理论的比较 3 计算误差 ——库仑土压力理论
滑动面
滑动面
实际滑裂面不一定是平面
主动土压力搜索得到 的不一定是最大值
被动土压力搜索得到 的不一定是最小值
主动土压力 偏小
被动土压力 偏大
第44页/共76页
于是:主动土压力强度
pa sh s3 z tg2(45 - / 2) - 2c tg(45 - / 2)
第20页/共76页
1.3 朗肯土压力理论 •朗肯主动土压力计算-填土为粘性土
《挡土墙上的土压力》课件

土压力的分布
墙背的粗糙度与形状、填土的物理性质、地下水的影响、地震作用等都会对土压力的分布和大小产生影响。
影响因素
通过改变墙背的形状,使其更符合土的应力分布,或者采用轻质、高强度的新型材料,可以有效地减小土压力。
改变墙背形状和材料
通过在墙后设置排水系统,改善填土的排水条件,或者采取预压等固结措施,减小填土中的孔隙水压力,从而减小有效应力,降低土压力。
《挡土墙上的土压力》PPT课件
目录
挡土墙概述土压力理论挡土墙上的土压力分析挡土墙的稳定性分析工程实例分析
01
CHAPTER
挡土墙概述
一种建筑物,用于防止土体滑坡、崩塌或移动,保持土体的稳定。
挡土墙
保护坡脚、岸坡、填方等免受侵蚀和破坏,防止水土流失,美化环境。
作用
类型
重力式、悬臂式、扶壁式、加筋土等。
排水和固结措施
在挡土墙中加入加筋材料,或者设置锚杆或锚索,通过提高墙体的整体性和抗剪强度,减小土压力。
加筋和锚固措施
04
CHAPTER
挡土墙的稳定性分析
01
02
挡土墙的稳定性与其设计、施工、材料、环境等因素密切相关,是评价挡土墙性能的重要指标之一。
挡土墙是一种用于防止土体滑移或坍塌的建筑物,其稳定性是指在各种外力作用下,保持其整体稳定不发生破坏的能力。
计算公式
Ea为主动土压力;Ka为主动土压力系数,与填土的摩擦角和粘聚力有关。
公式中
计算公式
Ep=1/2γH2Kp
公式中
Ep为被动土压力;Kp为被动土压力系数,与填土的摩擦角和粘聚力有关。
03
CHAPTER
挡土墙上的土压力分析
土压力在挡土墙上的分布情况受到多种因素的影响,包括土的性质、挡土墙的几何形状和尺寸、以及墙后填土的密实度和排水条件等。
墙背的粗糙度与形状、填土的物理性质、地下水的影响、地震作用等都会对土压力的分布和大小产生影响。
影响因素
通过改变墙背的形状,使其更符合土的应力分布,或者采用轻质、高强度的新型材料,可以有效地减小土压力。
改变墙背形状和材料
通过在墙后设置排水系统,改善填土的排水条件,或者采取预压等固结措施,减小填土中的孔隙水压力,从而减小有效应力,降低土压力。
《挡土墙上的土压力》PPT课件
目录
挡土墙概述土压力理论挡土墙上的土压力分析挡土墙的稳定性分析工程实例分析
01
CHAPTER
挡土墙概述
一种建筑物,用于防止土体滑坡、崩塌或移动,保持土体的稳定。
挡土墙
保护坡脚、岸坡、填方等免受侵蚀和破坏,防止水土流失,美化环境。
作用
类型
重力式、悬臂式、扶壁式、加筋土等。
排水和固结措施
在挡土墙中加入加筋材料,或者设置锚杆或锚索,通过提高墙体的整体性和抗剪强度,减小土压力。
加筋和锚固措施
04
CHAPTER
挡土墙的稳定性分析
01
02
挡土墙的稳定性与其设计、施工、材料、环境等因素密切相关,是评价挡土墙性能的重要指标之一。
挡土墙是一种用于防止土体滑移或坍塌的建筑物,其稳定性是指在各种外力作用下,保持其整体稳定不发生破坏的能力。
计算公式
Ea为主动土压力;Ka为主动土压力系数,与填土的摩擦角和粘聚力有关。
公式中
计算公式
Ep=1/2γH2Kp
公式中
Ep为被动土压力;Kp为被动土压力系数,与填土的摩擦角和粘聚力有关。
03
CHAPTER
挡土墙上的土压力分析
土压力在挡土墙上的分布情况受到多种因素的影响,包括土的性质、挡土墙的几何形状和尺寸、以及墙后填土的密实度和排水条件等。
土压力计算介绍

土压力计算介绍 (PPT 77页)
❖ 在土木工程实践中,经常要计算作用在各种挡土结 构上的侧压力,其中最常见的是土压力。土压力的 准确计算是相当困难的问题。因为它与墙的位移方 向与大小、墙后填土的种类和性质、墙背的倾斜方 向与粗糙程度等多种因素有关。本章介绍的计算方 法是目前在工程实践中最常用的方法。
(3)理论假设条件 (4)理论公式直接适用于粘性土和无粘性土 (5)由于忽略了墙背与填土之间的摩擦,主动土压 力偏大,被动土压力偏小。
❖
P0= K0 r Z (6-1)
❖
❖ 式中
❖
P0= K0 r Z (6-1) K0— 静止土压力系数; r—土体重度,kN/m3。
❖ 静止土压力系数的确定方法:
通过侧限条件下 测的 定 —试 —验 较可靠
采用经验公 K0式 =1- : sin——较适合于砂
采用经验值
rZ K0r Z
H E0
H 3
为K0rZ,即为主动 土压力强度。
0
a K0 z
z
主动朗肯状态时的莫尔圆
2.土体在水平方向压缩
单元体在水平截面上的法向应力z不变而竖直截面上的 法向应力x却逐渐增大,直至满足极限平衡条件(称为被
动朗肯状态)。
f ctg
0
K0 z
z
p
被动朗肯状态时的莫尔圆
f ctg
0
a K0 z
z
p
三种状态时的莫尔圆
作用对墙背产生的侧压力。 ❖ 作用于挡土墙背上的土压力是设计挡土墙要考虑的
主要荷载。
土压力的类型
❖ 试验表明,土压力的大小主要与挡土墙的位移、挡 土墙的形状、墙后填土的性质等因素有关,但起决 定因素的是墙的位移。根据墙身位移的情况,作用 在墙背上的土压力可分为静止土压力、主动土压力 和被动土压力。
❖ 在土木工程实践中,经常要计算作用在各种挡土结 构上的侧压力,其中最常见的是土压力。土压力的 准确计算是相当困难的问题。因为它与墙的位移方 向与大小、墙后填土的种类和性质、墙背的倾斜方 向与粗糙程度等多种因素有关。本章介绍的计算方 法是目前在工程实践中最常用的方法。
(3)理论假设条件 (4)理论公式直接适用于粘性土和无粘性土 (5)由于忽略了墙背与填土之间的摩擦,主动土压 力偏大,被动土压力偏小。
❖
P0= K0 r Z (6-1)
❖
❖ 式中
❖
P0= K0 r Z (6-1) K0— 静止土压力系数; r—土体重度,kN/m3。
❖ 静止土压力系数的确定方法:
通过侧限条件下 测的 定 —试 —验 较可靠
采用经验公 K0式 =1- : sin——较适合于砂
采用经验值
rZ K0r Z
H E0
H 3
为K0rZ,即为主动 土压力强度。
0
a K0 z
z
主动朗肯状态时的莫尔圆
2.土体在水平方向压缩
单元体在水平截面上的法向应力z不变而竖直截面上的 法向应力x却逐渐增大,直至满足极限平衡条件(称为被
动朗肯状态)。
f ctg
0
K0 z
z
p
被动朗肯状态时的莫尔圆
f ctg
0
a K0 z
z
p
三种状态时的莫尔圆
作用对墙背产生的侧压力。 ❖ 作用于挡土墙背上的土压力是设计挡土墙要考虑的
主要荷载。
土压力的类型
❖ 试验表明,土压力的大小主要与挡土墙的位移、挡 土墙的形状、墙后填土的性质等因素有关,但起决 定因素的是墙的位移。根据墙身位移的情况,作用 在墙背上的土压力可分为静止土压力、主动土压力 和被动土压力。
土力学系列土压力计算PPT教案

2
)
zK
p
2c
Kp
pp
z tan2 (45
2
)
zK
p
土压力系数
Kp
tan2 (45
)
2
被动土压力沿深度呈直线分布。
第24页/共56页
7.3.4 典型情况下的朗肯土压力
填土表面有超载:
❖ 相当于在深度z处增加q值的作用。 ❖ 将 z 用(q+z)代替:
粘性土 pa ( z q)Ka 2c Ka 砂性土 pa ( z q)Ka
❖ 作用点位于形心处
对于砂性土有:
Ea
1
2
KaH 2
合力Ea作用在距挡土墙底面H/3处。
第21页/共56页
对于粘性土:
当z=0时,知 pa=-2c Ka
令pa=0,可得
h0
2c Ka
但,填土与墙背之间不可能承受拉应力,出现裂缝 。
合力:Ea
1 2
(H
h0 )(
HKa
2c
Ka )
合力Ea作用于距挡土墙底面 (H-h0) /3 处。
[解] 主动土压力系数
Ka
tan2 (45
) tan2 (45
2
30 2
) 0.333
第31页/共56页
各点主动土压力:
a点: b点: c点:
pal=1zKa=0 pa2=1h1Ka=1860.333=36 kPa pa3=(1h1+ h2)Ka =(186+94) 0.333=48 kPa
BC AB 2
H
cos( )
sin( )
cos sin( )
于是
G
1 2
H
土压力计算ppt课件

zta2n452cta4n5
2
2
2.土体在水平方向压缩
单元体在水平截面上的法向应力z不变而竖 直截面上的法向应力x却逐渐增大,直至满足极
限平衡条件(称为被动朗肯状态)。
被动朗肯状态 f ctg
时的莫尔圆
0 K0 z z
p
1
3ta2n4
52c
2
ta4n5
2
zta2n452cta4n5
2
2
• 若为无粘性土,上式中的第二项为零。
例题5-5 挡土墙高5m,墙背直立,光滑, 墙后填土水平,共分两层,各土层的物理 力学指标如图所示,试求主动土压力并绘 出土压力分布图。
例题5-5 挡土墙高5m,墙背直立,光滑,墙后填土
水平,共分两层,各土层的物理力学指标如图5-12所
示,试求主动土压力并绘出土压力分布图。
2c
Ka )
12H2Ka 2cH
Ka
2c2
பைடு நூலகம்
z0
2c Ka
粘性土的主动土压力强度分布图
de
z0
2c
H
a
z0 ka
Ea
b
c
HK a 2c Ka
H z0 3
Ea
1(H 2
z0)(HKa
2c
Ka )
12H2Ka 2cH
Ka
c2 2
例5-2 有一挡土墙高5m,墙背垂直光滑, 墙后填土面水平。填土的物理力学性能指标为: c=10.0kPa,φ =300, γ =18.0kN/m3。试计算 主动土压力大小及作用点位置,并绘出主动土 压力强度沿墙高的分布图。
用均布荷载q=18.0kPa。计算作用在挡土墙上的 主动土压力。
精品课件- 土压力计算与挡土墙设计
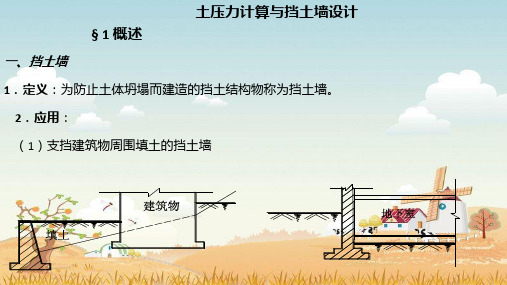
能滑动,二者之间的相互作用力即为主动土压力。所以,主动土压力的大小可由土 楔体的静力平衡条件来确定。
1. 作用在土楔体ABC上的力 • 假设滑动面AC与水平面夹角为α,取滑动土楔体ABC为脱离体,则作用在土楔体ABC上
的力有:
(1)土楔体自重 • 在三角形ABC中,利用正弦定理可得:
(2)滑动面 上B的C反力R
应力分别为:
• (因为已假设墙背是光滑的、直立的,所以在单元上不存在剪应力。) • 该应力状态仅由填土的自重产生,故此时土体处于弹性状态,其相应的莫尔园如下
图所示的园Ⅰ,一定处于填土抗剪强度曲线之下。
• 当挡土墙离开填土向前发生微小的转动或位移时, σ1 =σz =yz不变, σ3 =σx而却不断减 少,相应的莫尔园也在逐步扩大。当位移量达到一定值时, σ3减少到σ3f ,由σ3f与 σ1 =yz构成的应力园与抗剪强度曲线相切,如图Ⅱ所示,称为主动极限应力园。此时, 土中各点均处于极限平衡状态,达到最低什的小主应力σ3f称为朗肯主动土压力pa(即 pa = σ3f )。与此同时,土体中存在过墙踵的滑动面(剪切破坏面),滑动面与大主 应力作用平面(水平面)的夹角为450+φ/2。
•
q——填土面上的均布荷载,kPa。
四、墙后有地下水时
• 若墙后有地下水时,水下应取浮重度,同时应考虑静水压力,如下图所示。
• 五、墙背倾斜时 • 式中:W0——楔体ABB‘的自重。
§3 朗肯土压力理论
一、基本概念
1.假设 (1)墙背直立、光滑; (2)墙后填土面水平; (3)土体为均质各向
同性体。 2.主动朗肯状态 • 如上图所示,在墙后土体中深度Z处任取一单元体,当挡土墙静止不动时,则两个主
•
h=q/r
1. 作用在土楔体ABC上的力 • 假设滑动面AC与水平面夹角为α,取滑动土楔体ABC为脱离体,则作用在土楔体ABC上
的力有:
(1)土楔体自重 • 在三角形ABC中,利用正弦定理可得:
(2)滑动面 上B的C反力R
应力分别为:
• (因为已假设墙背是光滑的、直立的,所以在单元上不存在剪应力。) • 该应力状态仅由填土的自重产生,故此时土体处于弹性状态,其相应的莫尔园如下
图所示的园Ⅰ,一定处于填土抗剪强度曲线之下。
• 当挡土墙离开填土向前发生微小的转动或位移时, σ1 =σz =yz不变, σ3 =σx而却不断减 少,相应的莫尔园也在逐步扩大。当位移量达到一定值时, σ3减少到σ3f ,由σ3f与 σ1 =yz构成的应力园与抗剪强度曲线相切,如图Ⅱ所示,称为主动极限应力园。此时, 土中各点均处于极限平衡状态,达到最低什的小主应力σ3f称为朗肯主动土压力pa(即 pa = σ3f )。与此同时,土体中存在过墙踵的滑动面(剪切破坏面),滑动面与大主 应力作用平面(水平面)的夹角为450+φ/2。
•
q——填土面上的均布荷载,kPa。
四、墙后有地下水时
• 若墙后有地下水时,水下应取浮重度,同时应考虑静水压力,如下图所示。
• 五、墙背倾斜时 • 式中:W0——楔体ABB‘的自重。
§3 朗肯土压力理论
一、基本概念
1.假设 (1)墙背直立、光滑; (2)墙后填土面水平; (3)土体为均质各向
同性体。 2.主动朗肯状态 • 如上图所示,在墙后土体中深度Z处任取一单元体,当挡土墙静止不动时,则两个主
•
h=q/r
6 挡土墙及土压力-PPT文档资料

总静止土压力作用点,位于墙底以上H/3=2m处。
土力学与地基基础
抗剪强度和土坡稳定分析
§6.2 朗肯土压力理论
一、基本原理 自重应力作用下,半无限土体内各点的应力从弹性平衡状态发展 为极限平衡状态。 1、假设条件 挡土墙背垂直
A
虚 构 挡 土 墙
墙后填土表面水平
挡墙背面光滑,即不考虑墙与 土之间的摩擦力。
pa 3
z 1
极限平衡条件
2
H
z(σ1)
z
o o tan 45 2 c tan 45 3 1 2 2
朗肯主动土压力强度
pa(σ3) 45o+/2 处于主动朗肯状态,σ1方向竖直,
p zK 2 cK a a a
的方向和位移量决定着所产生的土压力性质和土压力大小。 根据墙的位移情况和墙后土体所处的应力状态,土压力可分为以下三种 1、静止土压力(E0) 墙受侧向土压力后,墙身变形或位移 很小,可认为墙不发生转动或位移,墙后 土体没有破坏,处于弹性平衡状态,墙上 承受土压力称为静止土压力E0 。
E0
土力学与地基基础
(a)支撑土坡的挡土墙 (b)堤岸挡土墙 (c)地下室侧墙 (d)拱桥桥台
土力学与地基基础
抗剪强度和土坡稳定分析
一、挡土墙的位移与土体的状态
挡土墙土压力的大小及其分布规律受到墙体可能的移动方向、墙 后填土的种类、填土面的形式、墙的截面刚度和地基的变形等一系列
因素的影响。墙体位移是影响土压力诸多因素中最主要的。墙体位移
抗剪强度和土坡稳定分析
【例】设计一堵岩基上的挡土墙,墙高H=6.0m,墙后填土
为中砂,重度r=18.5kN/m3,内摩擦角φ= 30o。计算作用
土力学与地基基础
抗剪强度和土坡稳定分析
§6.2 朗肯土压力理论
一、基本原理 自重应力作用下,半无限土体内各点的应力从弹性平衡状态发展 为极限平衡状态。 1、假设条件 挡土墙背垂直
A
虚 构 挡 土 墙
墙后填土表面水平
挡墙背面光滑,即不考虑墙与 土之间的摩擦力。
pa 3
z 1
极限平衡条件
2
H
z(σ1)
z
o o tan 45 2 c tan 45 3 1 2 2
朗肯主动土压力强度
pa(σ3) 45o+/2 处于主动朗肯状态,σ1方向竖直,
p zK 2 cK a a a
的方向和位移量决定着所产生的土压力性质和土压力大小。 根据墙的位移情况和墙后土体所处的应力状态,土压力可分为以下三种 1、静止土压力(E0) 墙受侧向土压力后,墙身变形或位移 很小,可认为墙不发生转动或位移,墙后 土体没有破坏,处于弹性平衡状态,墙上 承受土压力称为静止土压力E0 。
E0
土力学与地基基础
(a)支撑土坡的挡土墙 (b)堤岸挡土墙 (c)地下室侧墙 (d)拱桥桥台
土力学与地基基础
抗剪强度和土坡稳定分析
一、挡土墙的位移与土体的状态
挡土墙土压力的大小及其分布规律受到墙体可能的移动方向、墙 后填土的种类、填土面的形式、墙的截面刚度和地基的变形等一系列
因素的影响。墙体位移是影响土压力诸多因素中最主要的。墙体位移
抗剪强度和土坡稳定分析
【例】设计一堵岩基上的挡土墙,墙高H=6.0m,墙后填土
为中砂,重度r=18.5kN/m3,内摩擦角φ= 30o。计算作用
《挡土墙上的土压力 》课件

土压力的计算
1 应力原理
土压力的计算基于土体的应力分布原理,考虑土体的力学性质和挡土墙的几何形状。
2 克尔森公式
克尔森公式是一种常用的计算土压力的公式,结合土体参数和挡土墙几何形状。
3 土压力系数
土压力系数是用于简化土压力计算的参数,根据土体类型和墙体形状进行选择。
挡土墙的设计
挡土墙的类型
挡土墙可以根据材料和结构形 式的不同分为多种类型,如重 力式挡土墙、悬臂式挡土墙等。
结语
总结
挡土墙上的土压力是挡土墙工程设计中需要重点考虑的因素,通过合理的计算和设计,可以 确保工程的安全和可靠性。
展望未来
随着科技的进步和工程需求的变化,挡土墙设计领域仍有许多创新和发展的机会。
墙体结构的设计
挡土墙的墙体结构设计需考虑 力学性能、稳定性和使用寿命 等因素,确保工程安全可靠。
挡土墙的基础设计
挡土墙的基础设计是保证挡土 墙稳定性的关键,需考虑基础 类型和土体力学参数。源自挡土墙的稳定性分析1
滑动稳定性分析
滑动稳定性分析考虑挡土墙的平面内滑动,以确保墙体不会产生水平位移。
2
翻倒稳定性分析
挡土墙上的土压力
土压力是指挡土墙所承受的来自土体的压力,本课件将介绍挡土墙的基本概 念、计算方法、设计原则、稳定性分析以及加固方法。让我们一起探索挡土 墙工程中土压力所扮演的重要角色。
简介
什么是挡土墙
挡土墙是一种结构,用于抵抗土体的侧向压力,常用于土地开发和道路建设等工程中。
土压力的概念
土压力是指土体对挡土墙施加的垂直于墙面方向的力,是挡土墙设计中的关键参数。
翻倒稳定性分析考虑挡土墙的翻倒问题,以确保墙体不会倒塌。
3
坍塌稳定性分析
挡土结构物上的土压力计算.ppt

Ea (h z0 )(hKa 2c Ka ) / 2
1.粘性土主动土压力强度存在负侧 压力区(计算中不考虑)
2.合力大小为分布图形的面积(不 计负侧压力部分)
3.合力作用点在三角形形心,即作 用在离墙底(h-z0)/3处
• 三、被动土压力
挡土墙在外力作用下,
挤压墙背后土体,产生
h
z
z(σ3)
土体处于朗肯主动状态时,
pa(σ3) 墙后土体出现一组滑裂面,
45o+/2
它与大主应力面夹角45o+/2, 水平应力降低到最低极限值
极限平衡条件
3
1
tan2 45o
2
2c tan 45o
2
朗肯主动土 压力强度
朗肯主动土压 力系数
pa zK a 2c K a
• 讨论: 朗肯主动土 压力强度
第6章 挡土结构物上的土压力计算
填土面
第一节 概 述
EE
E
E
码头
隧道侧墙
桥台
土压力通常是指挡土墙后的填土因自重或外荷载作用 对墙背产生的侧压力
土压力
静止土压力
主动土压力
1.静止土压力
挡土墙在压力作用下不 发生任何变形和位移, 墙后填土处于弹性平衡 状态时,作用在挡土墙 背的土压力
被动土压力
Eo
-△ +△
E
Ep
Eo
Ea
o
-△ △a
△p
+△
对同一挡土墙,在填土 的物理力学性质相同的
1. Ea <Eo <<Ep
条件下有以下规律: 2. △p >>△a
第2节 静止土压力计算
作用在挡土结构背面的静止土压力可视为天然土层自重
7挡土墙与土压力 共59页PPT资料

2006.03
E p
7.3 朗肯土压力理论
应用
板桩
2006.03
H L
7.4 库仑土压力理论 墙背倾斜、粗糙、填土倾斜时? 库仑土压力理论
库仑
C. A. Coulomb (1736-1806)
2006.03
7.4 库仑土压力理论
出发点:
墙背倾斜,具有倾角
墙背粗糙,与填土摩擦角为
填土表面有倾角
静止土压力系数 K01-sin KaK01Kp
土压力 E Ep
H
2006.03
E0
H
_ H
Ea
+
H
1~5%
1~5% 0
7.3 朗肯土压力理论
几个概念
– 总土压力:
每延米
• 单位长度挡土墙上土压力
• 单位:kN/m,大小、方向、作用点
– 土压力强度: • 单位面积上的土压力 • 单位:kN/m2
静止土压力 E0 主动土压力 Ea
被动土压力 Ep
_ H
2006.03
土压力 E Ep
H
1~5%
E0 Ea
1~5% 0
H
+
H
7.1 概述
土压力的类型
挡土墙所受土压力 的大小并不是一个 常数,而是随位移 量的变化而变化。
桥面
E
静止土压力 E0:坚硬地基上,断面较大
主动土压力 Ea:一般挡土墙
2006.0-填土为粘性土
主动土压力强度 负号
pazKa-2c Ka
Katg 2(45 -/2)
-朗肯主动土压力系数
z0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
>0.1H
绕墙顶转动
0.05H
平移 粘土 主动
绕墙趾转动
0.004H 0.004H
第六章
第8页/共43页
•挡土墙在土压力作用下,不向任何方向发生位移和转动时, 墙后土体处于弹性平衡状态,作用在墙背上的土压力称为 静止土压力。
•当挡土墙沿墙趾向离开填土方向转动或平行移动,且位移 达到一定量时,墙后土体达到主动极限平衡状态,填土中 开始出现滑动面 ,这时在挡土墙上的土压力称为主动土压 力。
下图表示半无限土体中深度为z处土单元的应力 状态:
v
z
h h
v
z
z
h=p0
H
(a) 第六章
(b) 第10页/共43页
设想用一挡土墙代替单元体左侧的土体,挡土 墙墙背光滑,则墙后土体的应力状态并没有变化, 仍处于侧限应力状态。
竖向应力为自重应力: z=z
水平向应力为原来土体内部应力变成土对墙的 应力,即为静止土压力强度p0:
p0=h=K0z
第六章
第11页/共43页
z z
h=p0 H
H
P0
3
p z
(b)
K0H
(d)
静止土压力沿墙高呈三角(形c) 分布,作用于墙背面单位
长度上的总静止土压力(P0):
H
P0 p0dz 12K0H2 0
P0的作用点位于墙底面往上1/3H处,单位[kN/m]。 (d)图是处在静止土压力状态下的土单元的应力摩尔
第六章 挡土墙土压力计算
第一节 概述 第二节 静止土压力计算 第三节 朗肯土压力理论 第四节 库伦土压力理论 第五节 若干问题的讨论
第六章
第1页/共43页
按刚度及位移方式分:
刚性挡土墙、柔性挡土墙 、 临时支撑
第六章
第4页/共43页
二、墙体位移与土压力类型
墙体位移的方向和位移量决定着所产生的土
P0 B
Pa 墙向后移 墙向前移 位移
极限平衡状态 被动土压力对应于图中C点
墙位移与土压力
墙向填土的方向位移,墙后土体处于被动极限平衡
状态第六章ຫໍສະໝຸດ Pa<P0<Pp
第6页/共43页
试验表明:
(1) 挡土墙所受到的土压力类型,首先取决于墙体 是否发生位移以及位移方向;
(2) 挡土墙所受土压力的大小随位移量而变化, 并不是一个常数;
第六章
第13页/共43页
表面水平的均质弹性半空间体的极限平衡状态图
第六章
第14页/共43页
v
z
h h
v (a)
土体内每一竖直面都是对称面,地 面下深度z处的M点在自重作用下,垂直 截面和水平截面上的剪应力均为零,该 点处于弹性平衡状态(静止土压力状 态),其大小为:
1 v z 3 h K0z
p z
(d)
用1、、3作摩尔应力圆,如左 图所示。其中 3 ( h)既为静止土 压力强度。
第六章
第15页/共43页
二、主动土压力的计算
用1,3作摩尔应力圆,如图中应力圆I所示。 使挡土墙向左方移动,则右半部分土体有伸张 的趋势,此时竖向应力v不变,墙面的法向应力h 减小。v 、h仍为大小主应力。当挡土墙的位移使 得h减小到土体已达到极限平衡状态时,则h减小 到最低限值pa ,即为所求的朗肯主动土压力强度。
第六章
第16页/共43页
对于无粘性土
主动土压力强度p为 a : 3 ztg( 2 45O 2)zKa
总的土压力为 Pa : 12H2tg( 2 45O
)
2
12H2Ka
作用点位置在墙 1 H高 处。 3
第六章
第17页/共43页
对于粘性土:
主动土压力强p度 a 为 3: ztg( 2 45O2) 2ctg(45O2)zKa 2c Ka
第六章
第19页/共43页
对于无粘性土
被动土压力强度p为 p : 1 ztg( 2 45O 2)zKp
总的土压力为 Pp
: 1H2tg( 2 45O
2
)
2
12H2Kp
作用点位置在墙 1 H高 处。 3
第六章
第20页/共43页
对于粘性土:
被动土压力强度为:
pp
1z
t( g2 4
5O) 2ctg(4
压力性质和土压力大小。
太
C
沙
土
基 的
压 力
模
Pp A
型 试
P0
B
Pa
验
墙向后移 墙向前移 位移
结 果
墙位移与土压力
第六章
第5页/共43页
三种土压力的关系:
C 土
压
静止土压力对应于图中A点
力
墙位移为0,墙后土体 处于弹性平衡状态
Pp A
主动土压力对应于图中B点 墙向离开填土的方向位 移,墙后土体处于主动
令pa 0
得临界深 z 度 Z0
2c Ka
总的土压力为:
Pa 12(HZ0)(HKa 2c Ka)12H2Ka 2cH Ka 2c
作用点位置在墙H底 Z往 0 处 上。 3
第六章
第18页/共43页
三、被动土压力的计算
同计算主动土压力一样用1、3作摩尔应力圆,如下图。 使挡土墙向右方移动,则右半部分土体有压缩的趋势,墙 面的法向应力h增大 。h、 v为大小主应力。当挡土墙的位 移使得h增大到使土体达到极限平衡状态时,则h达到最高限 值pp ,即为所求的朗肯被动土压力强度。
2
5O)z
2
Kp2c
Kp
总的土压P力 p 为 12H: 2Kp2cHKp
作用点位置通心 过。 梯形形
• 当挡土墙在外力作用下向墙背填土方向转动或平行移动 时,土压力逐渐增大,当位移达到一定量时,潜在滑动面 上的剪应力等于土的抗剪强度,墙后土体达到被动极限平 衡状态,填土内开始出现滑动面 ,这时作用在挡土墙上的 土压力增加至最大,称为被动土压力。
第六章
第9页/共43页
第二节 静止土压力计算
静止土压力强度(p0)可按半空间直线变形体 在土的自重作用下无侧向变形时的水平侧向应力h 来计算。
圆,可以看出,这种应力状态离破坏包线很远,属于弹性
平衡应力状态。
第六章
第12页/共43页
第三节 朗肯土压力理论
1857年英国学者朗肯(Rankine)从研究弹性半 空间体内的应力状态,根据土的极限平衡理论,得出 计算土压力的方法,又称极限应力法。
一、基本原理
朗肯理论的基本假设:
1.墙本身是刚性的,不考虑墙身的变形; 2.墙后填土延伸到无限远处,填土表面水平 (=0); 3.墙背垂直光滑(墙与垂向夹角 =0,墙与土的 摩擦角=0)。
(3) 主动和被动土压力是特定条件下的土压力, 仅当墙有足够大位移或转动时才能产生。
第六章
第7页/共43页
表6-1 产生主动和被动土压力所需墙的位移量
土类 应力状态 墙运动形式 可能需要的位移量
平移
0.0001H
主动 绕墙趾转动
0.001H
砂土
绕墙顶转动 平移
0.02H 0.05H
被动 绕墙趾转动
