初中数学反比例函数随堂练习20
人教版苏科版初中数学—反比例函数(经典例题 )

班级小组姓名成绩(满分120)一、反比例函数(一)反比例函数的定义(共4小题,每题3分,题组共计12分)例1.下列函数中,是反比例函数的是()A.()11x y -=B.11y x =+C.21y x =D.13y x=例1.变式1.若函数()22351mm y m x +-=-为反比例函数,求的m 值.例1.变式2.当k 为时,反比例函数.例1.变式3.下列函数关系是反比例函数关系的是()A.三角形的底边为一常数,则三角形的面积y 与三角形的高x 间的函数关系B.力F 为一常数,则力所做的功W 与物体在力的方向上移动的距离S 间的函数关系C.矩形的面积为一常数,则矩形的长y 与宽x 间的函数关系D.当圆锥的底面积为一常数,圆锥的体积V 与圆锥的高h 间的函数关系(二)根据描述列出反比例函数的表达式(共4小题,每题3分,题组共计12分)例2.已知y 是x 的反比例函数,下表给出了x 与y 的一些值,由表知函数表达式为.根据函数表达式完成下表.x -1368y3-32例2.变式1.若y 与21x +成反比例,且1x =时,2y =,则此函数表达式为.例2.变式2.已知12y y y =+,1y 与x 成正比例,2y 与x 成反比例,且当2x =时,4y =-;当1x =-时,5y =,则y 与x 之间的函数表达式为.()223kk y k k x--=+例2.变式3.已知12y y y =+,1y 与x 成正比例,2y 与x 成反比例,且当1x =时,4y =;当3x =时,5y =,求1x =-时y 的值.(三)确定实际问题中函数表达式(共4小题,每题3分,题组共计12分)例3.一块长方形花圃,长为a 米,宽为b 米,面积为8平方米,那么a 与b 成函数关系,列出a 关于b 的函数关系式为.例3.变式1.已知一个长方体的体积是100m³,它的长是y m ,宽是5m ,高为x m ,试写出,x y之间的函数关系式,并注明x 的取值范围.例3.变式2.有一水池装水12m³,如果从水管中1h 流出x m³的水,则经过y h 可以把水放完,写出y与x 的函数关系式及自变量x 的取值范围.例3.变式3.一定质量的氧气,它的密度()3/kg m ρ是它的体积()3V m 的反比例函数,当310V m =时,31.43/kg m ρ=.(1)求ρ与V 的函数关系式;(2)求当32V m =时,氧气的密度ρ.二、反比例函数的图像和性质(一)反比例函数的图象(共4小题,每题3分,题组共计12分)例4.关于反比例函数4y x=的图象,下列说法正确的是()A.必经过点(1,1)B.两个分支位于第二、四象限内C.两个分支关于x 轴成轴对称D.两个分支关于原点成中心对称例4.变式1.已知点(1,1)在反比例函数ky x=(k 是常数,0k ≠)的图象上,则这个反比例函数的大致图象是()A. B. C. D.例4.变式2.函数2y x =与函数1y x-=在同一坐标系中的大致图象是()A. B. C. D.例4.变式3.反比例函数1m y x-=的图象在第一、三象限内,则m 的取值范围是.(二)反比例函数的性质(共4小题,每题3分,题组共计12分)例5.如图,反比例函数ky x=的图象经过点A(-1,-2),则当1x >时,函数值y 的取值范围是()A.1y >B.01y << C.2y > D.02y <<例5.变式1.若点1P (1,m),2P (2,n)在反比例函数ky x=(0k <)的图象上,则m n(填“>”“<”或“=”).例5.变式2.在函数21a y x--=(a 为常数)的图像上有三点()11,x y 、()22,x y 、()33,x y ,且1230x x x <<<,则123,,y y y 的大小关系是()A.231y y y <<B.321y y y <<C.123y y y << D.312y y y <<例5.变式3.已知函数1y x-=,当自变量的取值为10x -<<或2x ≥,函数值y 的取值范围为.(三)反比例函数比例系数k 的几何意义(共4小题,每题3分,题组共计12分)例6.如图,已知A 是反比例函数ky x=(k 是常数,0k ≠)的图像上一点,AB⊥x 轴于点B,且△ABO 的面积是3,则k 的值是()A.3B.3-C.6D.6-例6.变式1.如图,正方形ABOC 的边长为2,反比例函数ky x=的图象过点A,则k 的值是()A.2B.2-C.4D.4-例6.变式2.如图,点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB∥x 轴,C,D 在x 轴上,若四边形ABCD 为矩形,则它的面积为.例6.变式3.如图,矩形AOBC 的面积为4,反比例函数ky x=的图象的一支经过矩形对角线的交点P,则该反比例函数的表达式是()A.4y x=B.2y x=C.1y x=D.12y x=三、反比例函数的应用(一)反比例函数解析式和图象问题(共4小题,每题3分,题组共计12分)例7.某段公路全长200km,一辆汽车要行驶完这段路程,则所行驶速度v (km/h)和时间t (h)间的关系式为,若限定汽车行驶速度不超过80km/h,则所用时间最少要.例7.变式1.一个三角形的面积为10,则底边长a 与这条边上的高h 间的关系式为,自变量的取值范围为.例7.变式2.某变阻器两端的电压为220V,则通过变阻器的电流I(A)与它的电阻R(Ω)之间的函数关系的图象大致为下图中的()例7.变式3.学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边长y (m)与相邻的另一边长x (m)之间的关系如图所示.(1)绿化带面积是多少?你能写出这一函数的表达式吗?(2)完成下表,并回答问题:如果该绿化带的长不得超过40m,那么它的宽应控制在什么范围内?(二)函数图象交点问题(共4小题,每题3分,题组共计12分)例8.双曲线8y x=与直线2y x =的交点坐标为.例8.变式1.同一坐标系中,正比例函数2y x =的图象与反比例函数()22k y k x-=≠的图象有公共点,则k 的取值范围为.例8.变式2.函数1y x =(x ≥0),29y x=(x >0)的图象如图所示,则有如下结论:①两函数图象的交点A 的坐标为(3,3);②当x >3时,21y y >;③当1x =时,BC=8;④当x 逐渐增大时,1y 随着x 的增大而增大,2y 随着x 的增大而减小.其中正确结论的序号是.x(m)10203040y(m)例8.变式3.右图中曲线是反比例函数7nyx+=的图象的一支.(1)这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?(2)若一次函数2433y x=-+的图象与反比例函数7nyx+=的图象交于点A,与x轴交于点B,△AOB的面积为2,求n的值.(三)反比例函数的综合应用(共4小题,每题3分,题组共计12分)例9.(1)已知反比例函数kyx=(0k≠),当13x=-,6y=-时,求这个函数的表达式.(2)若一次函数4y mx=-的图象与(1)中的反比例函数kyx=的图象有交点,求m的取值范围.例9.变式1.今年两会提出:随着城镇化水平的提高,为了房产去库存,国家鼓励农民进城买房,可享受政府担保免收利息的惠民政策,小王家购买了一套学区房,首付15万元后,剩余部分贷款,贷款金额按月分期还款,每月还款数相同,计划每月还款y万元,x个月还清贷款,已知y是x的反比例函数,其图象如图所示.(1)求y与x的函数关系式,并求小王家购买学区房的总价是多少万元?(2)若计划80个月还清贷款,则每月应还款多少万元?例9.变式2.如图,函数11y k x b =+的图象与函数()220k y x x=>的图象相交于A,B 两点,与y 轴交于点C,已知,A 点坐标为(2,1),C 点坐标为(0,3).(1)求这两个函数表达式和点B 的坐标;(2)观察图像,比较0x >时,1y 与2y 大小.例9.变式3.如图,在直角坐标系中,O 为坐标原点.已知反比例函数ky x=(k >0)的图象经过点A(2,m),过点A 作AB⊥x 轴于点B,且△AOB 的面积为12.(1)求k 和m 的值;(2)点C(x ,y )在反比例函数ky x=的图象上,求当1≤x ≤3时函数值y 的取值范围;(四)反比例函数的跨学科应用(共4小题,每题3分,题组共计12分)例10.某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例.右图表示的是该电路中电流I 与电阻R 之间的函数关系的图象,则用电阻R 表示电流I 的函数表达式为()A.()60I R R =>B.()60I R R =->C.()30I R R=>D.()20I R R=>例10.变式1.某一电路中,电源电压()U V 保持不变,电流()I A 与电阻()R Ω之间的函数图像如图所示.(1)I 与R 的函数关系式为;(2)结合图象回答,当电路中的电流不超过12A 时,电路中电阻R 的取值范围是.例10.变式2.一定质量的二氧化碳,当它的体积35V m =时,它的密度31.98/kg m r =,则r 关于V 的函数图象大致是()例10.变式3.某小组到野外考察,路过一段临时铺设的木板路,木板对地面的压强()p Pa 是木板面积()2S m 的反比例函数,其图象如图所示.(1)请写出函数的表达式和变量的取值范围;(2)当木板的面积为20.2m 时,压强是多少;(3)如果要求压强不超过6000Pa ,木板的面积至少要多大?。
初中数学反比例函数精华练习题

初中数学反比例函数精华练习题1.反比例函数y=m/x的图象两支分布在第二、四象限,则点(m,m-2)在x=k的图象经过点(-2,-1),那么当x>0时,图象所在象限是()A。
第一象限 B。
第二象限 C。
第三象限 D。
第四象限2.如果反比例函数y=k/x的图象经过点(1,-3),则k的值为()3.下列函数中,当x>0时,y随x的增大而减小的是()A。
y=3x+4 B。
y=141/(x-2) C。
y=-3x/2 D。
y=4x/(3x-2)4.如图,某个反比例函数的图象经过点P,则它的解析式为()5.如图是三个反比例函数y=1/(kx),y=-1/(kx),y=2/(x<0),y=-3/(x<0)的图象,由此观察得到k1、k2、k3的大小关系为()A。
k1>k2>k3 B。
k3>k2>k1 C。
k2>k3>k1 D。
k3>k1>k26.如图,正比例函数y=x和y=mx(m>0)的图象与反比例函数y=k/x(k>0)的图象分别交于第一象限内的A、C两点,过A、C两点分别向x轴作垂线,垂足分别为B、D,若△AOB与△COD的面积分别为S1和S2,则S1与S2的关系为()A。
S1>S2 B。
S1<S2 C。
S1=S2 D。
与m、k值有关7.如果点(a,-2a)在双曲线y=2x-1的图象上,则a所在的象限是第_______象限.8.当x>0时,反比例函数y=mx随x的减小而增大,则双曲线y=(3m-1)/(2x+1)在第_______象限.9.如果一次函数y=mx+n与反比例函数y=k/x的图象都经过点(1,2),那么双曲线y=(3n-m)/(x-1)在第_______象限.求此一次函数的解析式.10.已知一次函数y=kx+b的图象与双曲线y=-3/(x-2)的图象相交于点(1,2),那么该直线与双曲线的另一个交点的坐标为()11.关于x的一次函数y=-2x+m和反比例函数y=(n+1)/x的图象都经过点A(-2,1).求:(1)m、n的值;(2)这两个函数的解析式.12.如图,点A、B在反比例函数 $y=\frac{k}{x}$ 的图象上,且点A、B的横坐标分别为 $a$、$2a$($a>0$),$AC$ 垂直 $x$ 轴于 $C$,且 $\triangle AOC$ 的面积为 $2$。
数学(冀教版)九年级上册30.1 反比例函数 同步练习(含答案)

30.1 反比例函数习题精选1.下列是反比例函数的是( )A .x y 5-=B .xy 51-= C .2)7(-=x y D .24x y = 2.若524-=n x y 是反比例函数,则n= ,图像在 象限。
3.如果521-=n x y 是反比例函数,则n= 。
4.已知y 与(2x+1)成反比,x=1时,y=4,则y 与x 之间的函数关系式 。
5.一个长方形的面积为10,则这个长方形的长与宽之间的函数关系是( )A .正比例函数关系B .反比例函数关系C .一次函数关系D .不能确定6.甲、乙两地相距100km ,一辆汽车从甲地开往乙地,把汽车到达乙地所用的时间t (h )表示为汽车速度v (km/h )的函数,并说明t 是v 的什么函数。
7.已知一个面积为60的平行四边形,设它的其中一边长为x ,这边上的高为y ,试写出y 与x 的函数关系式,并判断它是什么函数。
8.近视镜的度数y (度)与镜片焦距为0.5米,则眼镜度数y 与镜片焦距x 之间的函数关系式为 。
9.购买x 斤水果需24元,购买一斤水果的单价y 与x 的关系式是( )A .)0(24>=x x yB .)(24为自然数x xy = C .)(24为整数x x y = D .)(24为正整数x xy = 10.水池内装有12立方米的水,如果从排水管中每小时流出x 立方米的水,则经过y 小时就可以把水放完,求y 与x 的函数关系,并说明y 是x 的什么函数。
11.已知道21y y y +=,y 1与x 2成正比例,y 2与x+3成反比例。
并且x=0时,y=2,x=1时,y=0。
试求函数y 的解析式,并指出自变量的取值范围。
12.水池内有水40m 3,经过排水管的时间y (h )与每小时流出的水量xm 3之间的关系是反比例函数吗?13.计划修建铁路1200km ,试写出铺轨天数y (d )与每天铺轨量x (km/d )之间的函数关系式,并判断该函数是否是反比例函数。
初中数学分段函数反比例函数专练

初中数学分段函数反比例函数练习一.解答题(共13小题)1.荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:(1)求日销售量y与时间t的函数关系式?(2)哪一天的日销售利润最大?最大利润是多少?(3)该养殖户有多少天日销售利润不低于2400元?(4)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m (m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.2.宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=.(1)工人甲第几天生产的产品数量为70件?(2)设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x 天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?3.今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队既是联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=﹣x+m(m为常数).(1)求该企业月生产量y(千件)与出厂价x(元)之间的函数关系式,并写出自变量x的取值范围.(2)当该企业生产出的产品出厂价定为多少元时,月利润W(元)最大?最大利润是多少?[月利润=(出厂价﹣成本)×月生产量﹣工人月最低工资].4.铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀,小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:6<x≤15第x天1≤x≤610x+6每天的销售量y/盒(1)求p与x的函数关系式;(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.5.如图,已知反比例函数y=的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.(1)求k和m的值;(2)若点C(x,y)也在反比例函数y=的图象上,当﹣3≤x≤﹣1时,求函数值y的取值范围.6.如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=.(1)若OA=4,求k的值;(2)连接OC,若BD=BC,求OC的长.7.如图,在平面直角坐标系xOy中,双曲线y=经过▱ABCD的顶点B,D.点D 的坐标为(2,1),点A在y轴上,且AD∥x轴,S▱ABCD=5.(1)填空:点A的坐标为;(2)求双曲线和AB所在直线的解析式.8.已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).(1)求这两个函数的表达式;(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.9.如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2,点A的纵坐标为4.(1)求该反比例函数和一次函数的解析式;(2)连接MC,求四边形MBOC的面积.10.如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB 的面积为3.(1)求一次函数与反比例函数的解析式;(2)直接写出当x>0时,kx+b﹣<0的解集.11.如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=(x <0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.(1)求m的值;(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.12.如图,直线y=3x与双曲线y=(k≠0,且x>0)交于点A,点A的横坐标是1.(1)求点A的坐标及双曲线的解析式;(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.13.将直线y=3x+1向下平移1个单位长度,得到直线y=3x+m,若反比例函数y=的图象与直线y=3x+m相交于点A,且点A的纵坐标是3.(1)求m和k的值;(2)结合图象求不等式3x+m>的解集.参考答案与试题解析一.解答题(共13小题)1.荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:(1)求日销售量y与时间t的函数关系式?(2)哪一天的日销售利润最大?最大利润是多少?(3)该养殖户有多少天日销售利润不低于2400元?(4)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m (m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.【解答】解:(1)设解析式为y=kt+b,将(1,198)、(80,40)代入,得:,解得:,∴y=﹣2t+200(1≤x≤80,t为整数);(2)设日销售利润为w,则w=(p﹣6)y,①当1≤t≤40时,w=(t+16﹣6)(﹣2t+200)=﹣(t﹣30)2+2450,=2450;∴当t=30时,w最大②当41≤t≤80时,w=(﹣t+46﹣6)(﹣2t+200)=(t﹣90)2﹣100,∴当t=41时,w=2301,最大∵2450>2301,∴第30天的日销售利润最大,最大利润为2450元.(3)由(2)得:当1≤t≤40时,w=﹣(t﹣30)2+2450,令w=2400,即﹣(t﹣30)2+2450=2400,解得:t1=20、t2=40,由函数w=﹣(t﹣30)2+2450图象可知,当20≤t≤40时,日销售利润不低于2400元,而当41≤t≤80时,w最大=2301<2400,∴t的取值范围是20≤t≤40,∴共有21天符合条件.(4)设日销售利润为w,根据题意,得:w=(t+16﹣6﹣m)(﹣2t+200)=﹣t2+(30+2m)t+2000﹣200m,其函数图象的对称轴为t=2m+30,∵w随t的增大而增大,且1≤t≤40,∴由二次函数的图象及其性质可知2m+30≥40,解得:m≥5,又m<7,∴5≤m<7.2.宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=.(1)工人甲第几天生产的产品数量为70件?(2)设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x 天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?【解答】解:(1)根据题意,得:∵若7.5x=70,得:x=>4,不符合题意;∴5x+10=70,解得:x=12,答:工人甲第12天生产的产品数量为70件;(2)由函数图象知,当0≤x≤4时,P=40,当4<x≤14时,设P=kx+b,将(4,40)、(14,50)代入,得:,解得:,∴P=x+36;①当0≤x≤4时,W=(60﹣40)•7.5x=150x,∵W随x的增大而增大,=600元;∴当x=4时,W最大②当4<x≤14时,W=(60﹣x﹣36)(5x+10)=﹣5x2+110x+240=﹣5(x﹣11)2+845,=845,∴当x=11时,W最大∵845>600,∴当x=11时,W取得最大值,845元,答:第11天时,利润最大,最大利润是845元.3.今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队既是联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=﹣x+m(m为常数).(1)求该企业月生产量y(千件)与出厂价x(元)之间的函数关系式,并写出自变量x的取值范围.(2)当该企业生产出的产品出厂价定为多少元时,月利润W(元)最大?最大利润是多少?[月利润=(出厂价﹣成本)×月生产量﹣工人月最低工资].【解答】解:(1)把(40,3)代入y=﹣x+m得,3=﹣×40+m,∴m=5,∴y=﹣x+5,(25≤x≤40),设BC的解析式为:y=kx+b,把(40,3),(50,2)代入y=kx+b 得,,解得,∴y=﹣x+7,(40<x≤50),综上所述:y=;(2)设该企业生产出的产品出厂价定为x元时,月利润W(元)最大,根据题意得,W=(﹣x+5)(x﹣20)﹣32000=﹣x2+6x﹣32100=﹣(x﹣60)2+33900,∵25≤x≤40,=30299元,∴当x=40时,W最大W=(﹣x+7)(x﹣20)﹣32000=﹣x2+9x﹣32140=﹣(x﹣45)2+32342.5,∵40<x≤50,∴当x=45时,W=32342.5元,最大∵30299<32342.5,∴当该企业生产出的产品出厂价定为45元时,月利润W(元)最大,最大利润是45元.4.铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀,小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:第x天1≤x≤6<x≤15610x+6每天的销售量y/盒(1)求p与x的函数关系式;(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.【解答】解:(1)设p=kx+b(k≠0),∵第3天时,每盒成本为21元;第7天时,每盒成本为25元,∴,解得,所以,p=x+18;(2)1≤x≤6时,w=10[50﹣(x+18)]=﹣10x+320,6<x≤15时,w=[50﹣(x+18)](x+6)=﹣x2+26x+192,所以,w与x的函数关系式为w=,1≤x≤6时,∵﹣10<0,∴w随x的增大而减小,∴当x=1时,w最大为﹣10+320=310,6<x≤15时,w=﹣x2+26x+192=﹣(x﹣13)2+361,∴当x=13时,w最大为361,综上所述,第几天时当天的销售利润最大,最大销售利润是361元;(3)w=325时,﹣x2+26x+192=325,x2﹣26x+133=0,解得x1=7,x2=13,所以,7≤x≤13时,即第7、8、9、10、11、12、13天共7天销售利润不低于325元.5.如图,已知反比例函数y=的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.(1)求k和m的值;(2)若点C(x,y)也在反比例函数y=的图象上,当﹣3≤x≤﹣1时,求函数值y的取值范围.【解答】解:(1)∵△AOB的面积为2,∴k=4,∴反比例函数解析式为y=,∵A(4,m),∴m==1;(2)∵当x=﹣3时,y=﹣;当x=﹣1时,y=﹣4,又∵反比例函数y=在x<0时,y随x的增大而减小,∴当﹣3≤x≤﹣1时,y的取值范围为﹣4≤y≤﹣.6.如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=.(1)若OA=4,求k的值;(2)连接OC,若BD=BC,求OC的长.【解答】解:(1)作CE⊥AB,垂足为E,∵AC=BC,AB=4,∴AE=BE=2.在Rt△BCE中,BC=,BE=2,∴CE=,∴CE=,∵OA=4,∴C点的坐标为:(,2),∵点C在的图象上,∴k=5,(2)设A点的坐标为(m,0),∵BD=BC=,∴AD=,∴D,C两点的坐标分别为:(m,),(m﹣,2).∵点C,D都在的图象上,∴m=2(m﹣),∴m=6,∴C点的坐标为:(,2),作CF⊥x轴,垂足为F,∴OF=,CF=2,在Rt△OFC中,OC2=OF2+CF2,∴OC=.7.如图,在平面直角坐标系xOy中,双曲线y=经过▱ABCD的顶点B,D.点D 的坐标为(2,1),点A在y轴上,且AD∥x轴,S▱ABCD=5.(1)填空:点A的坐标为(0,1);(2)求双曲线和AB所在直线的解析式.【解答】解:(1)∵点D的坐标为(2,1),点A在y轴上,且AD∥x轴,∴A(0,1);故答案为(0,1);(2)∵双曲线y=经过点D(2,1),∴k=2×1=2,∴双曲线为y=,∵D(2,1),AD∥x轴,∴AD=2,∵S▱ABCD=5,∴AE=,∴OE=,∴B点纵坐标为﹣,把y=﹣代入y=得,﹣=,解得x=﹣,∴B(﹣,﹣),设直线AB得解析式为y=ax+b,代入A(0,1),B(﹣,﹣)得:,解得,∴AB所在直线的解析式为y=x+1.8.已知反比例函数y1=的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).(1)求这两个函数的表达式;(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.【解答】解:(1)∵A(1,4)在反比例函数图象上,∴把A(1,4)代入反比例函数y1=得:4=,解得k1=4,∴反比例函数解析式为y1=的,又B(m,﹣2)在反比例函数图象上,∴把B(m,﹣2)代入反比例函数解析式,解得m=﹣2,即B(﹣2,﹣2),把A(1,4)和B坐标(﹣2,﹣2)代入一次函数解析式y2=ax+b得:,解得:,∴一次函数解析式为y2=2x+2;(2)根据图象得:﹣2<x<0或x>1.9.如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2,点A的纵坐标为4.(1)求该反比例函数和一次函数的解析式;(2)连接MC,求四边形MBOC的面积.【解答】解:(1)由题意可得,BM=OM,OB=2,∴BM=OM=2,∴点B的坐标为(﹣2,﹣2),设反比例函数的解析式为y=,则﹣2=,得k=4,∴反比例函数的解析式为y=,∵点A的纵坐标是4,∴4=,得x=1,∴点A的坐标为(1,4),∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(﹣2,﹣2),∴,得,即一次函数的解析式为y=2x+2;(2)∵y=2x+2与y轴交与点C,∴点C的坐标为(0,2),∵点B(﹣2,﹣2),点M(﹣2,0),点O(0,0),∴OM=2,OC=2,MB=2,∴四边形MBOC的面积是:==4.10.如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB 的面积为3.(1)求一次函数与反比例函数的解析式;(2)直接写出当x>0时,kx+b﹣<0的解集.【解答】解:(1)∵S=3,OB=3,△AOB∴OA=2,∴B(3,0),A(0,﹣2),代入y=kx+b得:,解得:k=,b=﹣2,∴一次函数y=x﹣2,∵OD=6,∴D(6,0),CD⊥x轴,当x=6时,y=×6﹣2=2∴C(6,2),∴n=6×2=12,∴反比例函数的解析式是y=;(2)当x>0时,kx+b﹣<0的解集是0<x<6.11.如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=(x <0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.(1)求m的值;(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.【解答】解:(1)∵点B(﹣2,n)、D(3﹣3n,1)在反比例函数y=(x<0)的图象上,∴,解得:.(2)由(1)知反比例函数解析式为y=﹣,∵n=3,∴点B(﹣2,3)、D(﹣6,1),如图,过点D作DE⊥BC于点E,延长DE交AB于点F,在△DBE和△FBE中,∵,∴△DBE≌△FBE(ASA),∴DE=FE=4,∴点F(2,1),将点B(﹣2,3)、F(2,1)代入y=kx+b,∴,解得:,∴y=﹣x+2.12.如图,直线y=3x与双曲线y=(k≠0,且x>0)交于点A,点A的横坐标是1.(1)求点A 的坐标及双曲线的解析式;(2)点B 是双曲线上一点,且点B 的纵坐标是1,连接OB ,AB ,求△AOB 的面积.【解答】解:(1)将x=1代入y=3x ,得:y=3,∴点A 的坐标为(1,3),将A (1,3)代入y=,得:k=3,∴反比例函数的解析式为y=;(2)在y=中y=1时,x=3,∴点B (3,1),如图,S △AOB =S 矩形OCED ﹣S △AOC ﹣S △BOD ﹣S △ABE=3×3﹣×1×3﹣×1×3﹣×2×2=4.13.将直线y=3x +1向下平移1个单位长度,得到直线y=3x +m ,若反比例函数y=的图象与直线y=3x +m 相交于点A ,且点A 的纵坐标是3.(1)求m 和k 的值;(2)结合图象求不等式3x+m>的解集.【解答】解:(1)由平移得:y=3x+1﹣1=3x,∴m=0,当y=3时,3x=3,x=1,∴A(1,3),∴k=1×3=3;(2)画出直线y=3x和反比例函数y=的图象:如图所示,由图象得:不等式3x+m>的解集为:﹣1<x<0或x>1.。
中考数学《反比例函数》专项练习题(附带答案)
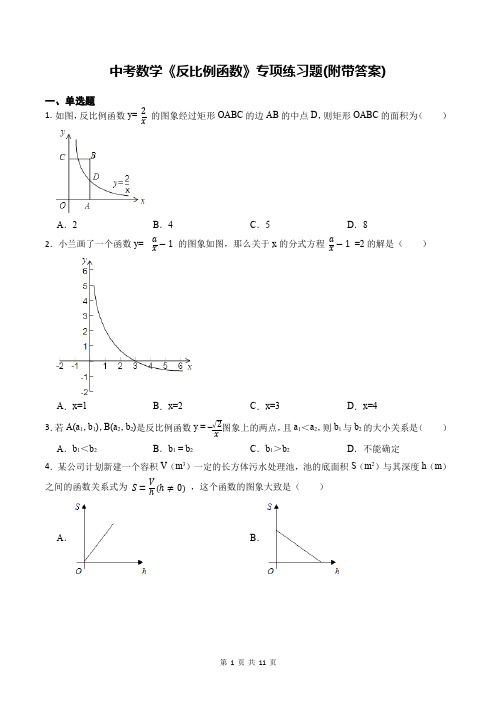
中考数学《反比例函数》专项练习题(附带答案)一、单选题1.如图,反比例函数y= 2x的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为()A.2B.4C.5D.82.小兰画了一个函数y= ax−1的图象如图,那么关于x的分式方程ax−1=2的解是()A.x=1B.x=2C.x=3D.x=43.若A(a1,b1),B(a2,b2)是反比例函数y = –√2x图象上的两点,且a1<a2,则b1与b2的大小关系是()A.b1<b2B.b1 = b2C.b1>b2D.不能确定4.某公司计划新建一个容积V(m3)一定的长方体污水处理池,池的底面积S(m2)与其深度h(m)之间的函数关系式为S=Vℎ(ℎ≠0),这个函数的图象大致是()A.B.C.D.5.若反比例函数y=k x(k为常数,且k≠0)的图象过点(3,-4),则下列各点在该图象上的是()A.(6,-8)B.(-6,8)C.(-3,4)D.(-3,-4)6.已知反比例函数y=k x(k>0)的图象与直线y=﹣x+6相交于第一象限A、B的两点.如图所示,过A、B两点分别作x、y轴的垂线,线段AC、BD相交与P,给出以下结论:①OA=OB;②四边形OCPD 是正方形;③若k=5.则△ABP的面积是8;④P点一定在直线y=x上,其中正确命题的个数是几个()A.4B.3C.2D.17.已知点P(3,2)在反比例函数y=k x(k≠0)图象上,则下列各点中在此反比例函数图象上的是()A.(−3,−2)B.(3,−2)C.(−2,3)D.(2,−3)8.下列函数:①y=−x;②y=−1x;③y=√2x;④y=120x2+240x+3(x<0)中,y随x的增大而减小的函数有()A.1个B.2个C.3个D.4个9.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,顶点B在函数y=k x(x >0)的图象上,若△C=60°,AB=2,则k的值为()A.√2B.√3C.1D.2 10.对于反比例函数y=﹣1x,下列说法正确的是()A.图象经过点(1,1)B.图象位于第一、三象限C.图象是中心对称图形D.当x<0时,y随x的增大而减小11.一次函数y=ax+a与反比例函数y=−ax(a≠0)在同一平面直角坐标系中的图象可能是()A.B.C.D.12.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是() A.B.C.D.二、填空题13.如图,在平面直角坐标系中,菱形ABCD的顶点A与D在函数y=k x(x>0)的图象上,AC⊥x轴,垂足为C,∠BCO=30°,点B的坐标为(0,1),则k的值为.14.如图,反比例函数y=6x在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB 的面积是.15.反比例函数y=7x图象与正比例函数y=kx图象交于A(x1,y1),B(x2,y2),则x1y2+x2y1的值为.16.如图,正比例函数y1=ax(a≠0)与反比例函数y2=k x(k≠0)的图象相交于A,B两点,其中点A的坐标为(1,3).当y1<y2时,x的取值范围是.17.如图,在平面直角坐标系中,O为坐标原点,平行四边形ABCD的边AB在x轴上、顶点D在y 轴的正半轴上,点C在第二象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处、点B恰好为OE的中点.DE与BC交于点F.若y=kx(k≠0)图象经过点C,且S△BEF=12,则k的值为.18.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点M,N,与反比例函数y=kx的图象在第一象限内交于点B,过点B作BA△x轴,BC△y轴.垂足分别为点A,C.当矩形OABC与△OMN 的面积相等时,点B的坐标为.三、综合题19.如图,双曲线y1=k x(k为常数,且k≠0)与直线y2=﹣13x+b交于点A(﹣2,a)和B(3c,2﹣c).(1)求k,b的值;(2)求直线与x轴的交点坐标.20.如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y= k1x的图象的一个交点为A(1,m).过点B作AB的垂线BD,与反比例函数y= k2x(x>0)的图象交于点D(n,﹣2).(1)求k1和k2的值;(2)若直线AB、BD分别交x轴于点C、E,试问在y轴上是否存在一个点F,使得△BDF△△ACE?若存在,求出点F的坐标;若不存在,请说明理由.21.如图,直线y=2x+1与双曲线相交于点A(m,32)与x轴交于点B.(1)求双曲线的函数表达式:(2)点P在x轴上,如果△ABP的面积为6,求点P坐标.22.在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,观察分析函数特征,概括函数性质的过程,已知函数y=﹣2|x−2|x−1上,结合已有的学习经验,完成下列各小题.(1)请在表格中空白处填入恰当的数据:x…﹣3﹣2﹣101243322345…y (5)2834﹣40﹣1﹣43…(2)根据表中的数据,在所给的平面直角坐标系中画出函数y=﹣2|x−2|x−1的图象;(3)根据函数图象,写出该函数的一条性质:;(4)结合所画函数图象,直接写出不等式﹣2|x−2|x−1<﹣53x+5的解集为:.(保留1位小数,误差不超过0.2)23.在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在抛物线y=−x2+2ax−a2−a+2(a 是常数)上.(1)若该二次函数图象的顶点在第二象限时,求a的取值范围;(2)若抛物线的顶点在反比例函数y=−8x(x<0)的图象上,且y1=y2,求x1+x2的值;(3)若当1<x1<x2时,都有y2<y1<1,求a的取值范围.24.如图,点A(m,m+1),B(m+3,m﹣1)是反比例函数y=k x(x>0)与一次函数y=ax+b的交点.求:(1)反比例函数与一次函数的解析式;(2)根据图象直接写出当反比例函数的函数值大于一次函数的函数值时x的取值范围.参考答案1.【答案】B2.【答案】A3.【答案】D4.【答案】C5.【答案】C6.【答案】A7.【答案】A8.【答案】A9.【答案】B10.【答案】C11.【答案】A12.【答案】B13.【答案】2√314.【答案】815.【答案】-1416.【答案】x<-1或0<x<117.【答案】-1218.【答案】(−1+√3,1+√3)19.【答案】(1)解:∵点B(3c,2﹣c)在直线y2=﹣13x+b的图象上∴−13×3c+b=2−c解得:b=2∴直线解析式为y2=﹣13x+2∵点A(﹣2,a)在直线y2=﹣13x+2的图象上∴a=−13×(−2)+2=83∴点A坐标为(-2,8 3)∵点A(-2,83)在y1=kx图象上∴83=k−2解得:k=−16 3 .(2)解:∵直线解析式为y2=﹣13x+2∴当y2=0时,x=6∴直线与x轴的交点坐标为(6,0).20.【答案】(1)解:将A(1,m)代入一次函数y=2x+2中,得:m=2+2=4,即A(1,4)将A(1,4)代入反比例解析式y= k1x得:k1=4;过A作AM△y轴,过D作DN△y轴∴△AMB=△DNB=90°∴△BAM+△ABM=90°∵AC△BD,即△ABD=90°∴△ABM+△DBN=90°∴△BAM=△DBN∴△ABM△△BDN∴AMBN=BMDN,即14=2DN∴DN=8∴D(8,﹣2)将D坐标代入y= k2x得:k2=﹣16(2)解:符合条件的F坐标为(0,﹣8),理由为:由y=2x+2,求出C坐标为(﹣1,0)∵OB=ON=2,DN=8∴OE=4可得AE=5,CE=5,AC=2 √5,BD=4 √5,△EBO=△ACE=△EAC若△BDF△△ACE,则BDAC=BFAE,即√52√5=BF5解得:BF=10则F(0,﹣8).综上所述:F点坐标为(0,﹣8)时,△BDF△△ACE.21.【答案】(1)解:把A(m,32)代入直线y=2x+1得:32=2m+1,即m=14∴A(14,32)∵点A(14,32)为直线与反比例函数y=kx的交点把A点坐标代入y=k x,得k=14× 32=38则双曲线解析式为y=38x;(2)解:对于直线y=2x+1,令y=0,得到x=−12,即B(−12,0)设P(x,0),可得PB=|x+1 2|∵△ABP面积为6∴12×|x+12|×32=6,即|x+12|=8解得:x=7.5或x=﹣8.5则P坐标为(7.5,0)或(﹣8.5,0). 22.【答案】(1)解:如下表所示:x…﹣3﹣2﹣101243322345…y (5)283346﹣4-20﹣1﹣43-32…(3)当x<1时,y随x的增大而增大(4)x<0.3或1<x<3.723.【答案】(1)解:∵y=−x2+2ax−a2−a+2=−(x−a)2−a+2第 11 页 共 11 页 ∴ 抛物线 y =−x 2+2ax −a 2−a +2 的顶点为 (a ,−a +2) ∵ 抛物线的顶点在第二象限∴{a <0−a +2>0解得 2<a <0 ;(2)解: ∵ 抛物线 y =−x 2+2ax −a 2−a +2 的顶点在反比例函数 y =−8x(x <0) 的图象上 ∴a(−a +2)=−8解得 a =4 或 a =−2∵a <0∴a =−2∴ 顶点为 (−2,4)∵y 1=y 2∴ 点 A(x 1,y 1) , B(x 2,y 2) 关于直线 x =−2 对称∴x 1+x22=−2∴x 1+x 2=−4 ;(3)解: ∵ 当 1<x 1<x 2 时,都有 y 2<y 1<1∴ 抛物线的对称轴 x =a <1 ,经过点为 (1,1)∴{a <1−1+2a −a 2−a +2=1解得 a =0 或 a =−3故 a 的取为0或-3.24.【答案】(1)解:由题意可知,m (m+1)=(m+3)(m ﹣1). 解得m=3.∴A (3,4),B (6,2); ∴k=4×3=12, ∴y =12x∵A 点坐标为(3,4),B 点坐标为(6,2), ∴{3a +b =46a +b =2 , ∴{a =−23b =6 ,∴y=﹣ 23 x+6 (2)解:根据图象得x 的取值范围:0<x <3或x >6.。
专题20反比例函数(3个知识点4种题型1种中考考法)(原卷版)-初中数学北师大版9年级上册

专题20反比例函数(3个知识点4种题型1种中考考法)【目录】倍速学习四种方法【方法一】脉络梳理法知识点1.反比例函数的概念及表达式(重点)知识点2.反比例函数表达式的确定(重点)知识点3.根据实际问题列反比例函数的表达式(重点)【方法二】实例探索法题型1.根据反比例函数的概念求未知字母的值题型2.反比例关系的应用题型3.反比例函数关系的判断及应用题型4.应用几何图形中的数量关系建立反比例函数关系【方法三】仿真实战法考法.反比例函数的概念【方法四】成果评定法【学习目标】1.理解反比例函数的概念,会判断一个函数是不是反比例函数。
2.能结合具体问题确定反比例函数的表达式,并会确定实际问题中自变量的取值范围,求出函数值。
【知识导图】【倍速学习四种方法】【方法一】脉络梳理法知识点1.反比例函数的概念及表达式(重点)如果两个变量的每一组对应值的乘积是一个不等于零的常数,那么就说这两个变量成反比例.即xy k=,或表示为kyx=,其中k是不等于零的常数.一般地,形如kyx=(k为常数,0k≠)的函数称为反比例函数,其中x是自变量,y是函数,自变量x的取值范围是不等于0的一切实数.注意:(1)在kyx=中,自变量x是分式kx的分母,当0x=时,分式kx无意义,所以自变量x的取值范围是,函数y的取值范围是0y≠.故函数图象与x轴、y轴无交点.(2)kyx=()可以写成()的形式,自变量x的指数是-1,在解决有关自变量指数问题时应特别注意系数这一条件.(3)kyx=()也可以写成的形式,用它可以迅速地求出反比例函数的比例系数k,从而得到反比例函数的解析式.【例1】(2023春•邗江区期末)下列式子中,表示y是x的反比例函数的是()A.xy=1B.y=C.y=D.y=【变式】(2022秋•怀化期末)下列函数不是反比例函数的是()A.y=3x﹣1B.y=﹣C.xy=5D.y=知识点2.反比例函数表达式的确定(重点)待定系数法求反比例函数解析式一般步骤:【例2】(2022秋·九年级单元测试)已知y=y1-y2,y1与x成反比例,y=5;当x=1时,y=-1;求当x=-1时,y的值.知识点3.根据实际问题列反比例函数的表达式(重点)【方法二】实例探索法题型1.根据反比例函数的概念求未知字母的值一、单选题2.(2022秋•岳阳县期末)若函数y=(m+4)x|m|﹣5是反比例函数,则m的值为()A.4B.﹣4C.4或﹣4D.03.(2022秋•惠来县期末)函数y=x k﹣1是反比例函数,则k=()A.3B.2C.1D.0题型2.反比例关系的应用k15.(2023春·上海浦东新·九年级校考阶段练习)在平面直角坐标系中,如果一个点的横坐标与纵坐标相等,16.(2022秋·河北保定·九年级校联考阶段练习)写出下列函数关系式,指出其中的正比例函数和反比例函题型4.应用几何图形中的数量关系建立反比例函数关系19.(2022春·九年级课时练习)如图,某养鸡场利用一面长为11m 的墙,其他三面用栅栏围成矩形,面积为260m ,设与墙垂直的边长为x m ,与墙平行的边长为y m .(1)直接写出y 与x 的函数关系式为______;(2)现有两种方案5x =或6x =,试选择合理的设计方案,并求此栅栏总长.20.如图,在矩形ABCD 中,点P 是BC 边上一动点,连接AP ,过点D 作DE AP ⊥于点E.设AP x =,DE y =,若6AB =,8BC =,试求y 与x 之间的函数关系式.【方法三】仿真实战法考法.反比例函数的概念1.(2023•临沂)正在建设中的临滕高速是我省“十四五”重点建设项目.一段工程施工需要运送土石方总量为105m3,设土石方日平均运送量为V(单位:m3/天),完成运送任务所需要的时间为t(单位:天),则V与t满足()A.反比例函数关系B.正比例函数关系C.一次函数关系D.二次函数关系2.(2018•柳州)已知反比例函数的解析式为y=,则a的取值范围是()A.a≠2B.a≠﹣2C.a≠±2D.a=±2【方法四】成果评定法一、单选题A.①②B.9.(2022春·九年级课时练习)下列选项中,能写成反比例函数的是(A.人的体重和身高B.正三角形的边长和面积二、填空题18.(2021春·全国·九年级专题练习)已知反比例函数的解析式为三、解答题19.(2023秋·九年级课时练习)下列例系数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学反比例函数随堂练习20
一、选择题(共5小题;共25分)
1. 点在反比例函数的图象上,则的值是
D.
2. 当路程一定时,速度是时间的
A. 正比例函数
B. 反比例函数
C. 一次函数
D. 无法确定
3. 已知抛物线与反比例函数的图象在第一象限有一个公共点,其横坐
标为,则一次函数的图象可能是
A. B.
C. D.
4. 如图,点在反比例函数的图象上,且横坐标为.若将点先向右平移两个
单位,再向上平移一个单位后得到点.则在第一象限内,经过点的反比例函数图象的解析
式是
A. B.
C. D.
5. 如图,矩形的边在轴的负半轴上,顶点在反比例函数的图象上,
直线交轴点,且,则的值为
A.
二、填空题(共4小题;共20分)
6. 如图所示,点是反比例函数上一点,,垂足为点,则
.
7. 在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度
也会随之改变,密度(单位:)是体积(单位:)的反比例函数,它的图象如图所示.当时,气体的密度是.
8. 如图,直线与坐标轴交于,两点,点是曲线上一点,若
是以的等腰三角形,则.
9. 已知反比例函数,当时,函数的图象在第二、四象限.
三、解答题(共4小题;共52分)
10. 在同一直角坐标平面内,画出函数,的图象,说出这两个函数图象各自所在的
象限,并指出的值随的值变化而变化的情况.
11. 如图,,两点的坐标分别为.求的面积.
12. 如图,一次函数与反比例函数的图象交于,两点.
(1)求一次函数与反比例函数的解析式.
(2)过点作轴,垂足为,连接,求的面积.
13. 已知与成反比例,且时,,当时,求的值.
答案
第一部分
1. A
2. B
3. B 【解析】抛物线与反比例函数的图象在第一象限有一个公共点,
,
交点横坐标为,
,
,
,
一次函数的图象经过第一、三、四象限.
4. D 【解析】点在反比例函数的图象上,且横坐标为,
点的坐标为,
将点先向右平移两个单位,再向上平移一个单位后得到点.
点的坐标为,
经过点的反比例函数图象的解析式为.
5. B
第二部分
6.
8.
9.
【解析】函数的图象在第二、四象限,
,解得.
第三部分
10. 略.
11. .
答:的面积为.
12. (1)点在的图象上,
,
反比例函数的解析式为:,
,
点,在的图象上,
解得:
一次函数的解析式为.
(2)以为底,则边上的高为,
.
答:的面积是.
13. 由与成反比例,
可设解析式为: .
时,,
,即 .
.
当时,.。
