数数有多少个正方形
正方形个数的题

正方形个数的题
以下是一道正方形个数的题:
有若干个正方形,它们的边长为1。
现在要从这些正方形中取出一些正方形,使得这些正方形的面积之和等于25个单位面积。
请问,最多可以取出多少个正方形?
答案是:最多可以取出5个正方形。
解释:
首先,我们需要知道正方形面积的计算公式为:边长^2。
因此,如果要将正方形面积之和等于25个单位面积,那么我们只需要将25分解成正方形面积之和。
而边长为1的正方形的面积是1,因此只有一种组合方式:正方形个数为 25/1 = 5 个。
因此,答案为:最多可以取出5个正方形。
一年级数正方形个数的方法

一年级数正方形个数的方法
一、计算一年级数正方形个数的方法
1、考虑个别班级情况:
班级内学生数*正方形一边的长度=正方形总数
例如:班级学生数为20个,一边假设为2厘米,那么2*20=40,就是该班级学生一共可以拼出的正方形的个数是40个。
2、全班的计算:
全班学生数*(正方形一边的长度)的平方=正方形总数
例如:全班学生数为126,正方形一边的长度为2厘米,那么
(2*2)*126=504,就是当前的学生可以拼出的正方形的个数是504个。
3、家长参与计算
家长可以把正方形一边的长度按照自己的喜好改变,例如:家长可以让孩子们以3厘米,5厘米等不同的长度拼出正方形,由于一边不同,那么也就拼出的正方形个数也不一样,例子:全班学生数为126,正方形一边的长度为5厘米,那么(5*5)*126=3,150,就是当前的学生可以拼出的正方形总数是3150个。
4、全校计算
全校学生数*(正方形一边的长度)的四次方=正方形总数
例如:全校学生数为3000,正方形一边的长度为2厘米,那么
(2*2*2*2)*3000=96,000,就是该学校学生可以拼出的正方形总数是96000个。
5、总结
计算正方形个数关键在于学生人数和正方形一边的长度,一边的长度越长,正方形个数就越多。
在去计算的时候,也要考虑一下当前的学生的实际情况,看有多少学生会参加拼图活动,以及所使用的正方形一边的长度,在考虑所有的情况后,就可以按照不同的学生情况、数量和正方形一边的长度来计算出相应班级、全校等学生可以拼出的正方形的个数了。
数正方形个数的简便方法

数正方形个数的简便方法数正方形的问题在数学中有着广泛的应用,包括计算几何、组合数学、算法等领域。
本文将介绍数正方形的简便方法,同时讨论该问题在不同领域中的应用。
一、基本概念在介绍数正方形的方法之前,我们先来回顾一下数正方形的基本概念和问题描述。
问题描述:给定一个网格图,其中有若干个正方形格子,要求计算正方形的数量。
例如下图所示的网格图中,红色方框所圈出的格子就是一个正方形。
[Image]基本概念:我们定义一个正方形的边长为k,如果这个正方形的面积为k*k,则称它为一个大小为k的正方形。
根据定义,大小为k的正方形的个数可以表示为:(n-k+1)^2,其中,n表示网格图的大小。
我们可以用一个二元组(i,j)表示一个正方形的左上角,其中,i表示该正方形在竖直方向上的位置,j表示该正方形在水平方向上的位置。
则一个大小为k的正方形就可以用左上角的坐标来表示,即左上角的坐标为(i,j)时,对应的正方形大小为k的正方形。
因此,我们可以枚举所有可能的左上角坐标,然后判断以该坐标为左上角时,能否构成一个大小为k的正方形。
假设网格图的大小为n*n,则总共有\binom{n}{2}个左上角坐标可以枚举。
二、暴力方法我们可以枚举所有可能的左上角坐标(i,j),然后检查以该坐标为左上角时,能否构成一个正方形。
如果可以,则计数器cnt+1。
最终的答案即为cnt的值。
下面是暴力枚举左上角坐标的代码实现:pythondef countSquare(n, mat):cnt = 0for i in range(n):for j in range(n):# 如果该坐标所在的格子是1if mat[i][j] == 1:# 枚举正方形边长for k in range(1, n):# 如果以该坐标为左上角的正方形大小为kif i + k < n and j + k < n and mat[i][j+k] == 1 and mat[i+k][j] == 1 and mat[i+k][j+k] == 1:# 计数器加1cnt += 1return cnt# 测试mat = [[1, 1, 1], [1, 1, 1], [1, 1, 1]]print(countSquare(3, mat))该方法的时间复杂度为O(n^5),显然随着n的大小增加,计算时间会非常长,并且难以应用到大规模数据中。
2022四年级数学下册第2单元认识三角形和四边形第10招用图形计数法解决数图形个数问题课件北师大

三个组合的三角形有2个,
四个三角形组合的三角形有1个
4+3+2+1=10(个)
(2)
4+3+2+1=10(个)
4+3+2+1=10(个)
(4+3+2+1)×2=20(个)
类 型 2 数长方形中长方形的个数
2. 数一数,下图中共有多少个长方形? 长边上线段的总数:2+1
宽边上线段的总数:4+3+2+1
32+22+12=9+4+1=14(个)
5. 数一数,下图中共有多少个正方形?
1个小正方形组成的正方形有4×6=24(个) 4个小正方形组成的正方形有3×5=15(个) 9个小正方形组成的正方形有4×5=8(个) 16个小正方形组成的正方形有3×1=3(个) 24+15+8+3=50(个)
类 型 4 数平行四边形中平行四边形的个数
长方形的总数=长边上线段的总数×宽边上线段的总数 (2+1)×(4+3+2+1)=30(个)
3. 数一数,下图中共有多少个长方形? 长边上线段的总数:4+3+2+1 宽边上线段的总数:4+3+2+1
(4+3+2+1)×(4+3+2+1)= 100(个)
类 型 3 数正方形或长方形中正方形的个数
4. 数一数,下图中共有多少个正方形? 1个小正方形组成的正方形有3×3=9(个) 4个小正方形组成的正方形有2×2=4(个) 9个小正方形组成的正方形有1个
BS 四年级下册
第10招 用“图形计数法”解决数图形个 数问题
经典例题
数出下图中正方形的个数。 分别数出边长为1,2,3,4 的正方形的个数
把1个正方形的各边平均分成n份 图中所有正方形的个数为1×1+2×2+3×3+…+n×n
规范解答:
边长为1的正方形:4×4=16(个) 边长为2的正方形:3×3=9(个) 边长为3的正方形:2×2=4(个) 边长为4的正方形:1×1=1(个) 正方形总数:1+4+9+16=30(个)
数正方体个数的题目

数正方体个数的题目
数正方体个数的题目可以是一道数学题或者几何题,其主要考察对几何形体的理解和计数能力。
在一个正方体中,每个面都有一个正方形,共有六个面。
如果我们只考虑正方体的表面,那么它就有六个面,每个面上都有一个正方形,一共有六个正方形。
如果将正方体切成若干个小立方体,那么每个小立方体都有一个表面,每个表面上都有一个正方形,所以它的表面上就有n个正方形,其中n表示正方体每条边上的小立方体数目。
因此,我们可以通过计算正方体每条边上的小立方体数目,来确定它的表面上有多少个正方形。
如果正方体的每条边上都有m个小立方体,那么它的表面上就有6m个正方形。
除了计算表面上的正方形个数,还可以考虑正方体内部的小立方体个数。
如果正方体的每条边上都有m个小立方体,那么正方体内部就有m个小立方体。
每个小立方体都可以看做一个点,那么这些点组成的集合就是正方体的内部。
我们可以使用组合数学的知识来计算正方体内部点的个数,例如可以使用二项式系数计算C(m,3)。
- 1 -。
数数有多少个正方形

结论一:每个人看同样一件事物的深度是不同的,人需要认识到自己的局限性;(许多人说到26时正确的看法/知识/等,才能从他人处学习到有用的知识。(有人在别人的答案出来之后,经过思考,决定放弃自己的答案,相信他人的答案;学会放弃自己的不正确看法,就是一种进步
数数有多少个正方形
问:下面由八条相等线段组成图形总共有多少个正方形?
要求:迅速做答,越快越好,可以补答;
讲师:将学员所答答案全部依次记下,反复询问是否还有新的答案。
学员一般反应:从20个到30个均有答案,
正确答案:设定最小正方型边为1的话,则:
边长为1的有16
边长为2的有9
边长为3的有4
边长为4的有1
摘自/《企业COACH世界》
四年级奥数之数数图形一

数数图形
1 .数一数下图中有多少个长方形?
2 .数一数,下面各图中分别有几个长方形?
3 .数一数,下图中有多少个正方形?(每个小方格是边长为1的正方形)
4 .数一数下列各图中分别有多少个正方形?(每个小方格为边长是1的小正方形)
5 .数一数下图中有多少个正方形?(其中每个小方格都是边长为1个长度单位的正方形)
6.数一数下列各图中分别有多少个正方形。
7 .下图中有多少个长方形,其中有多少个是正方形?
8 .从广州到北京的某次快车中途要停靠8个大站,铁路局
要为这次快车准备多少种不同车的车票?这些车票中有多少种不同的票价?
9 .从上海到武汉的航运线上,有9个停靠码头,航运公司要为这段航运线准备多少种不同的船票?
10 .从上海至青岛的某次直快列车,中途要停靠6个大站,这次列车有几种不同票价?
11 .从成都到南京的快车,中途要停靠9个站,有几种不
同的票价?
12 .求下列图中线段长度的总和。
(单位:厘米)
13 .一条线段上有21个点(包括两个端点),相邻两点的距离都是4厘米,所有线段长度的总和是多少?
14 .求下图中所有线段的总和。
(单位:米)
15 .求下图中所有线段的总和。
(单位:厘米)。
小学数学 图形专题 数数(线段、三角形、长方形和正方形)
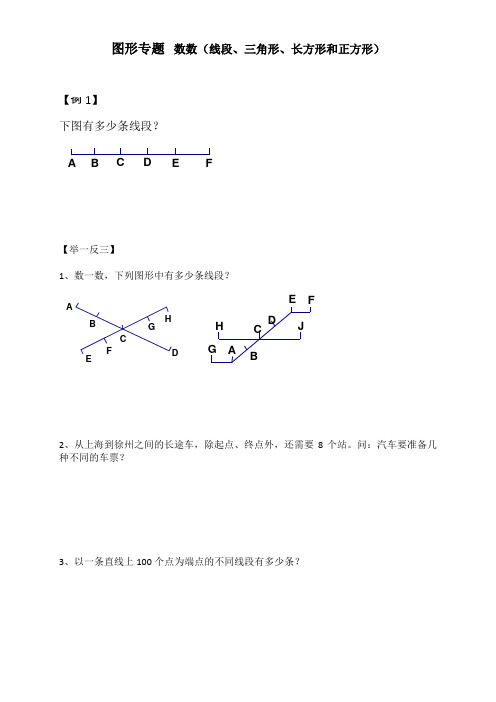
图形专题 数数(线段、三角形、长方形和正方形)
【例1】
下图有多少条线段?
【举一反三】
1、数一数,下列图形中有多少条线段?
2、从上海到徐州之间的长途车,除起点、终点外,还需要8个站。
问:汽车要准备几种不同的车票?
3、以一条直线上100个点为端点的不同线段有多少条?
F
E D C B A
H
F
E
D
G
C
B
A
J
H
F E
D
G C B
A
【例2】数出图中共有多少个三角形。
【举一反三】
1、数一数、下图中各有多少个角?
2、数一数、下图共有多少个三角形?
3、数一数、下图中有几个三角形?
F
E
D C B
A
050
49
【例3】数一数、右图中有多少个长方形?
【举一反三】
1、数一数,图中有多少个正方形?
2、数一数,图中有多少个正方形?
3、数一数,图中有多少个正方形?
答案
例1、15
举一反三:1、16,15;2、90;3、4950;
例2、10;
及一反三:1、10, 1275;2、20,45;3、27,15;
例3、30;
举一反三:1、17,10;2、22,11;3、10,16;。
数正方形题目

数正方形题目在一个由小正方形组成的网格中,如果要数出其中正方形的总数,以下哪种方法不是必要的?A. 分别数出不同大小的正方形B. 注意正方形的重叠情况C. 计算网格中的小正方形总数D. 标记并分类不同大小的正方形以避免重复计数在一个8x8的网格中,最小正方形的边长是1个单位,最大正方形的边长是8个单位。
那么,边长为2个单位的正方形有多少个?A. 64B. 56C. 49D. 36在数网格中的正方形时,如果一个较大的正方形由多个小正方形组成,那么在计数时应该如何处理?A. 只计算大正方形,不计算小正方形B. 只计算小正方形,不计算大正方形C. 大正方形和小正方形都要计算D. 根据题目要求决定是否计算重叠的正方形在一个由100个小正方形组成的10x10网格中,如果要数出所有正方形的总数,以下哪个数值是不可能的?A. 100B. 289C. 385D. 5050在数网格中的正方形时,以下哪种策略有助于减少计数错误?A. 随意数,不记录过程B. 按照正方形的大小顺序依次计数C. 只数一次,不检查重复D. 不分类,直接数出所有正方形的总数在一个由小正方形组成的网格中,边长为1的正方形有16个,边长为2的正方形有9个。
那么,边长为3的正方形最多可能有多少个?A. 4B. 5C. 6D. 7在数网格中的正方形时,如果一个正方形由其他正方形组成(如2x2由4个1x1组成),在计数时应该如何处理这种情况?A. 只计算最大的正方形B. 只计算最小的正方形C. 每个正方形都独立计算D. 根据题目要求决定是否计算内部的正方形在一个由小正方形组成的网格中,要数出所有正方形的总数。
以下哪种方法是最有效的?A. 直接用眼睛数,不记录B. 分别数出每种大小的正方形,然后相加C. 只数出最大的正方形和最小的正方形D. 随机选择正方形进行计数,然后估算总数。
毕达哥拉斯正方形数

毕达哥拉斯正方形数
毕达哥拉斯正方形数,也称为平方数,是指能够表示为某个整数
的平方的数。
它们的特点是,其平方根是一个整数。
一个常见的例子是3²=9,所以9是一个毕达哥拉斯正方形数。
同样地,我们还有4²=16、5²=25等等。
这些数是非常有趣的,因为
它们有很多有趣的性质和关系。
毕达哥拉斯正方形数在数学中有广泛的应用,尤其在几何学和代
数学中。
在几何学中,它们与正方形的边长和对角线的关系密切相关。
在代数学中,它们与平方根和开方的运算有关。
毕达哥拉斯正方形数除了在数学中有应用外,还在实际生活中有
很多应用。
例如,在建筑和设计中,我们经常需要计算正方形的边长
或对角线的长度。
这时,毕达哥拉斯正方形数就能派上用场了。
总之,毕达哥拉斯正方形数是一类具有特殊性质的数,它们在数
学和实际生活中都有重要的应用价值。
巧数正方形

正方形 个数总
=
行数×列数+(行数-1)×(列数-1)+(行数-2)×(列数-2)+
和
······+ ×1
下列图形各有多少个正方形?
2019/7/11
人有了知识,就会具备各种分析能力, 明辨是非的能力。 所以我们要勤恳读书,广泛阅读, 古人说“书中自有黄金屋。 ”通过阅读科技书籍,我们能丰富知识, 培养逻辑思维能力; 通过阅读文学作品,我们能提高文学鉴赏水平, 培养文学情趣; 通过阅读报刊,我们能增长见识,扩大自己的知识面。 有许多书籍还能培养我们的道德情操, 给我们巨大的精神力量, 鼓舞我们前进。
2、统计思想:本题解题时需把不同类别的正方 形不重复也不遗漏地数出来并记录下来,最后 将记录的结果加起来,体现了统计的思想方法。
3、有序思维的思想:解题过程中渗 透由简单到复杂、由特殊到一般的有 序思维的数学思想。
问题的变式与思考
如果将原有图形加 上一列,得到如右图形, 正方形的个数是多少呢? 我们能否类比得出数此 类正方形个数的一般方 法呢?
思路分析
形如
边长为1个单位的正方形有:
4×4=16个
题目分析
形如
边长为
2个单位的正方形有 3×3=9个
题目分析
形如
边长为3个单位
的正方形有2×2=4个
题目分析
形如 边长为4个单位的 正方形有1×1=1个
题目解答过程
本题采用分类数图形方法,我们可以将图中的正方形分成
、
、
、
四种类型,然后分类统计它们的 个数。
将 图形
按照分类数图形,将图中的正方形分成
、
、
、
四种类型,然后分类统计它们的个
巧数正方形

正方形 个数总
=
行数×列数+(行数-1)×(列数-1)+(行数-2)×(列数-2)+
和
······+ ×1
下列图形各有多少个正方形?
2020/2/29
形如
形如 形如
边长为1个单位的正方形有4×4=16个;
边长为2个单位的正方形有3×3=9个; 边长为3个单位的正方形有2×2=4个;
形如
边长为4个单位的正方形有1×1=1个。
所以正方形的个数总共有: 4×4+3×3+2×2+1×1=30个。
题目中蕴含的基本数学思想方法:
1、分类思想:本题的解题过程当中,我们将正方 形分成了边长分别为1个单位、2个单位、3个单位、 4个单位的不同大小的正方形。而且这样的分类是 解决该问题的关键。
巧数正方形
题目:
如图,图中有多少个正方形?
题目分析
本题是四年级 《数图形中的学问》 的引申,题目给出了 一个四行四列的正方 形网格状图形,要求 数出这个图形当中所 有的正方形个数,对 于学生来说难度以将图中的正方形分成
、
、
、
四种类型,然后分类统计它们的 个数。
思路分析
形如
边长为1个单位的正方形有:
4×4=16个
题目分析
形如
边长为
2个单位的正方形有 3×3=9个
题目分析
形如
边长为3个单位
的正方形有2×2=4个
题目分析
形如 边长为4个单位的 正方形有1×1=1个
题目解答过程
本题采用分类数图形方法,我们可以将图中的正方形分成
、
、
、
四种类型,然后分类统计它们的 个数。
奥数二年级图形的个数

正方形有( )个,长方形有( )个,三角形 有( )个,圆有( )个
例2 数一数,右图有多少个三角形?
例3 数一数,下图中共有多少 个长方形?
例4 数一数,下图中有多少个正方形?
例5 仔细观察, 在( )个长方形 中。
1.下图中有( )个三角形?
2.下图中有( )个正方形?
3.数一数,再填空:
有 ( )个 有 ( )个
4.下图中一共有( )个圆
5.下图中有( )个长方形?
6.下图是由哪些图形组成的?各有 几个?
7.下图中 在( )个正方形中
8.数一数,下图中共有几个正方形? 几个三角形?
正方形有( )个 三角形有( )个
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问:下面由八条相等线段组成图形总共有多少个正方形?
要求:迅速做答,越快越好,可以补答;
讲师:将学员所答答案全部依次记下,反复询问是否还有新的答案。
学员一般反应:从20个到30个均有答案,
正确答案:设定最小正方型边为1的话,则:
边长为1的有16
边长为2的有9
边长为3的有4
Hale Waihona Puke 边长为4的有1总数则为30个
结论一:每个人看同样一件事物的深度是不同的,人需要认识到自己的局限性;(许多人说到26时,不能相信别人30的答案是正确的,认为不可能)
结论二:人需要放弃自己不正确的看法/知识/等,才能从他人处学习到有用的知识。(有人在别人的答案出来之后,经过思考,决定放弃自己的答案,相信他人的答案;学会放弃自己的不正确看法,就是一种进步
摘自/《企业COACH世界》
