圆中考试题集锦
圆初三试题及答案

圆初三试题及答案一、选择题(每题3分,共30分)1. 圆的周长公式是()。
A. C=2πrB. C=πr²C. C=2πdD. C=πd答案:A2. 圆的面积公式是()。
A. S=πrB. S=2πr²C. S=πr²D. S=πd²答案:C3. 如果一个圆的半径是5cm,那么它的直径是()。
A. 10cmB. 15cmC. 5cmD. 25cm答案:A4. 圆的直径是半径的()倍。
A. 2B. 4C. 8D. 16答案:A5. 一个圆的半径增加一倍,它的面积增加()倍。
A. 2B. 4C. 8D. 16答案:B6. 圆的周长与直径的比值称为()。
A. 圆周率B. 直径率C. 周长率D. 半径率答案:A7. 圆的周长与半径的比值是()。
A. 2πB. πC. 1/2πD. 2答案:A8. 一个圆的半径是3cm,那么它的周长是()。
A. 6πcmB. 9πcmC. 18πcmD. 27πcm答案:B9. 圆的面积与半径的平方成正比,比例系数是()。
A. πB. 2πC. 4πD. 8π答案:A10. 如果一个圆的面积是25πcm²,那么它的半径是()。
A. 5cmB. 10cmC. 2.5cmD. 1cm答案:A二、填空题(每题3分,共30分)1. 一个圆的半径是4cm,它的周长是_______cm。
答案:8π2. 圆的直径是8cm,那么它的半径是_______cm。
答案:43. 圆的周长是31.4cm,那么它的直径是_______cm。
答案:104. 圆的面积是28.26cm²,那么它的半径是_______cm。
答案:35. 圆的周长是62.8cm,那么它的半径是_______cm。
答案:106. 圆的面积是50.24cm²,那么它的直径是_______cm。
答案:47. 圆的直径是12cm,那么它的周长是_______cm。
初中初三数学圆试题及答案

初中初三数学圆试题及答案一、选择题(每题2分,共10分)1. 圆的半径是10,那么圆的直径是()A. 5B. 20C. 15D. 252. 已知圆心为O,点A在圆上,OA的长度是半径的2倍,那么点A()A. 在圆内B. 在圆上C. 在圆外D. 不存在3. 圆的周长公式是()A. C = πdB. C = 2πrC. C = πrD. C = 4r4. 圆的面积公式是()A. S = πr²B. S = πd²C. S = 2πrD. S = πd5. 如果一个圆的半径增加1cm,那么它的面积将增加多少平方厘米?(π取3.14)A. 3.14B. 6.28C. 2πD. π二、填空题(每题2分,共10分)1. 半径为r的圆的周长是______。
2. 半径为r的圆的面积是______。
3. 如果一个扇形的圆心角为30°,半径为5cm,那么它的弧长是______。
4. 一个圆的直径是20cm,那么它的半径是______。
5. 圆周角定理指出,圆周上一点到圆心的两条半径所夹的角是圆心角的______。
三、解答题(每题5分,共30分)1. 已知圆O的半径为5cm,点P在圆O上,求OP的长度。
答案:OP的长度为5cm。
2. 一个圆的周长是44cm,求这个圆的半径。
答案:设半径为r,根据周长公式C = 2πr,44 = 2 × 3.14 × r,解得r = 7cm。
3. 一个圆的面积是78.5平方厘米,求这个圆的半径。
答案:设半径为r,根据面积公式S = πr²,78.5 = 3.14 × r²,解得r = √(78.5 / 3.14) ≈ 5cm。
4. 已知圆心角为60°,半径为10cm的扇形,求这个扇形的弧长。
答案:弧长= (60/360) × 2π × 10 = π × 10 = 31.4cm。
中考圆练习题及答案

中考圆练习题及答案一、选择题1. 已知圆的半径为5,圆心到直线的距离为3,那么直线与圆的位置关系是什么?A. 直线与圆相交B. 直线与圆相切B. 直线与圆相离D. 无法确定答案:A2. 圆的圆心在点A(-3, -4),半径为6,求点B(1, 2)到圆心的距离。
A. 5B. 10C. 15D. 20答案:B3. 圆的方程为(x-3)² + (y-4)² = 16,点P(1, 5)是否在圆内?A. 是B. 否答案:A4. 已知两圆的半径分别为2和3,圆心距为2,两圆的位置关系是什么?A. 两圆外切B. 两圆内切C. 两圆相交D. 两圆相离答案:B5. 已知圆的方程为x² + y² = 25,求圆的圆心坐标。
A. (0, 0)B. (5, 0)C. (0, 5)D. (5, 5)答案:A二、填空题6. 圆的半径为7,圆心坐标为(1, 1),圆上一点P的坐标为(a, b),则a² + b² = _______。
答案:507. 已知圆的方程为(x-2)² + (y-3)² = 9,求圆的直径。
答案:68. 若圆的半径为4,圆心到直线3x + 4y - 5 = 0的距离为2,则直线与圆的位置关系是________。
答案:相离9. 圆的方程为x² + y² - 6x - 8y + 9 = 0,求圆心坐标。
答案:(3, 4)10. 已知点A(-2, 3)和点B(4, -1),求以线段AB为直径的圆的圆心坐标。
答案:(1, 1)三、解答题11. 已知圆的方程为x² + y² - 10x - 6y + 25 = 0,求圆的圆心和半径。
解答:首先将圆的方程化为标准形式,即(x-5)² + (y-3)² = 4。
由此可知,圆心坐标为(5, 3),半径为2。
12. 已知点P(2, -1)在圆x² + y² = 9上,求过点P的最短弦所在直线的方程。
中考数学《圆》专项复习综合练习题-附带答案
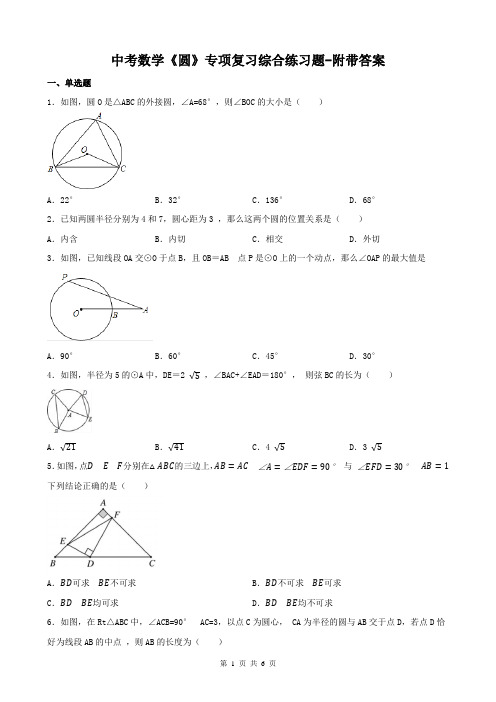
中考数学《圆》专项复习综合练习题-附带答案一、单选题1.如图,圆O是△ABC的外接圆,∠A=68°,则∠BOC的大小是()A.22°B.32°C.136°D.68°2.已知两圆半径分别为4和7,圆心距为3 ,那么这两个圆的位置关系是()A.内含B.内切C.相交D.外切3.如图,已知线段OA交⊙O于点B,且OB=AB 点P是⊙O上的一个动点,那么∠OAP的最大值是A.90°B.60°C.45°D.30°4.如图,半径为5的⊙A中,DE=2 √5,∠BAC+∠EAD=180°,则弦BC的长为()A.√21B.√41C.4 √5D.3 √55.如图,点D E F分别在△ABC的三边上,AB=AC∠A=∠EDF=90°与∠EFD=30°AB=1下列结论正确的是()A.BD可求BE不可求B.BD不可求BE可求C.BD BE均可求D.BD BE均不可求6.如图,在Rt△ABC中,∠ACB=90° AC=3,以点C为圆心, CA为半径的圆与AB交于点D,若点D恰好为线段AB的中点,则AB的长度为()B.3 C.9 D.6A.327.如图,⊙O是△ABC的外接圆,弦BD交AC于点E,AE=DE, BC=CE,过点O作OF⊥AC于点F,延长FO 交BE于点G ,若DE=6,EG=4,则AB的长为()A.4√5B.8√3C.13 D.148.如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形…,重复上述过程,经过2018次后所得到的正六边形边长是原正六边形边长的()A.(√2)2016倍B.(√3)2017倍C.(√3)2018倍D.(√2)2019倍二、填空题9.如图,PA、PB切⊙O于点A、B ,已知⊙O半径为2 且∠APB=60°,则AB= .10.如图,矩形ABCD中,BC=4 CD=2 以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为.(结果保留π)11.如图,两边平行的刻度尺在圆上移动当刻度尺的一边与直径为6.5cm的圆相切时另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则刻度尺的宽为 cm.12.如图,两圆相交于A、B两点小圆经过大圆的圆心O 点C D分别在两圆上若∠ADB=100°则∠ACB的度数为。
圆中考试题集锦(附答案)

圆中考试题一、选择题1.(北京市西城区)如图,BC 是⊙O 的直径,P 是CB 延长线上一点,PA 切⊙O 于点A ,如果PA =3,PB =1,那么∠APC 等于 ()(A )15 (B )30 (C )45 (D )602.(北京市西城区)如果圆柱的高为20厘米,底面半径是高的41,那么这个圆柱的侧面积是 ()(A )100π平方厘米 (B )200π平方厘米(C )500π平方厘米 (D )200平方厘米3.(北京市西城区)“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题,“今在圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为E ,CE =1寸,AB =10寸,求直径CD 的长”.依题意,CD 长为 ( )(A )225寸 (B )13寸 (C )25寸 (D )26寸4.(北京市朝阳区)已知:如图,⊙O 半径为5,PC 切⊙O 于点C ,PO 交⊙O 于点A ,PA =4,那么PC 的长等于 ( )(A )6 (B )25 (C )210 (D )2145.(北京市朝阳区)如果圆锥的侧面积为20π平方厘米,它的母线长为5厘米,那么此圆锥的底面半径的长等于 ( )(A )2厘米 (B )22厘米 (C )4厘米 (D )8厘米6.(天津市)相交两圆的公共弦长为16厘米,若两圆的半径长分别为10厘米和17厘米,则这两圆的圆心距为 ( )(A )7厘米 (B )16厘米 (C )21厘米 (D )27厘米7.(重庆市)如图,⊙O 为△ABC 的内切圆,∠C =90,AO 的延长线交BC 于点D ,AC =4,DC =1,,则⊙O 的半径等于 ( )(A )54 (B )45 (C )43 (D )658.(重庆市)一居民小区有一正多边形的活动场.为迎接“AAPP ”会议在重庆市的召开,小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台,花台都以多边形的顶点为圆心,比多边形的内角为圆心角,花台占地面积共为12π平方米.若每个花台的造价为400元,则建造这些花台共需资金 ( )(A )2400元 (B )2800元 (C )3200元 (D )3600元9.(河北省)如图,AB 是⊙O 直径,CD 是弦.若AB =10厘米,CD =8厘米,那么A 、B 两点到直线CD 的距离之和为 ( )(A )12厘米 (B )10厘米 (C )8厘米 (D )6厘米10.(河北省)某工件形状如图所示,圆弧BC 的度数为60,AB =6厘米,点B 到点C 的距离等于AB ,∠BAC = 30,则工件的面积等于 ( )(A )4π (B )6π (C )8π (D )10π11.(沈阳市)如图,PA 切⊙O 于点A ,PBC 是⊙O 的割线且过圆心,PA =4,PB =2,则⊙O 的半径等于 ( )(A )3 (B )4 (C )6 (D )812.(哈尔滨市)已知⊙O 的半径为35厘米,⊙O '的半径为5厘米.⊙O 与⊙O '相交于点D 、E .若两圆的公共弦DE 的长是6厘米(圆心O 、O '在公共弦DE 的两侧),则两圆的圆心距O O '的长为 ( )(A )2厘米 (B )10厘米 (C )2厘米或10厘米 (D )4厘米13.(陕西省)如图,两个等圆⊙O 和⊙O '的两条切线OA 、OB ,A 、B 是切点,则∠AOB 等于 ( )(A )30 (B )45 (C )60 (D )9014.(甘肃省)如图,AB 是⊙O 的直径,∠C =30,则∠ABD = ( )(A ) 30 (B ) 40 (C ) 50 (D )6015.(甘肃省)弧长为6π的弧所对的圆心角为60,则弧所在的圆的半径为( )(A )6 (B )62 (C )12 (D )1816.(甘肃省)如图,在△ABC 中,∠BAC =90,AB =AC =2,以AB 为直径的圆交BC 于D ,则图中阴影部分的面积为 ( )(A )1 (B )2 (C )1+4π (D )2-4π17.(宁夏回族自治区)已知圆的内接正六边形的周长为18,那么圆的面积为 ( )(A )18π (B )9π (C )6π (D )3π18.(山东省)如图,点P 是半径为5的⊙O 内一点,且OP =3,在过点P的所有弦中,长度为整数的弦一共有 ( )(A )2条 (B )3条 (C )4条 (D )5条19.(南京市)如图,正六边形ABCDEF 的边长的上a ,分别以C 、F 为圆心,a 为半径画弧,则图中阴影部分的面积是 ( )(A )261a π (B )231a π (C )232a π (D )234aπ20.(杭州市)过⊙O 内一点M 的最长的弦长为6厘米,最短的弦长为4厘米,则OM 的长为 ( )(A )3厘米 (B )5厘米 (C )2厘米 (D )5厘米21.(安徽省)已知圆锥的底面半径是3,高是4,则这个圆锥侧面展开图的面积是 ( )(A )12π (B )15π (C )30π (D )24π22.(安微省)已知⊙O 的直径AB 与弦AC 的夹角为30,过C 点的切线PC 与AB 延长线交P .PC =5,则⊙O 的半径为 ( )(A )335 (B )635 (C )10 (D )523.(福州市)如图:PA 切⊙O 于点A ,PBC 是⊙O 的一条割线,有PA=32,PB =BC ,那么BC 的长是 ( )(A )3 (B )32 (C )3 (D )3224.(河南省)如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是 ( )(A )π (B )1.5π (C )2π (D )2.5π25.(四川省)正六边形的半径为2厘米,那么它的周长为 ( )(A )6厘米 (B )12厘米 (C )24厘米 (D )122厘米26.(四川省)一个圆柱形油桶的底面直径为0.6米,高为1米,那么这个油桶的侧面积为 ( )(A )0.09π平方米 (B )0.3π平方米 (C )0.6平方米 (D )0.6π平方米27.(贵阳市)一个形如圆锥的冰淇淋纸筒,其底面直径为6厘米,母线长为5厘米,围成这样的冰淇淋纸筒所需纸片的面积是 ( )(A )66π平方厘米 (B )30π平方厘米 (C )28π平方厘米 (D )15π平方厘米28.(新疆乌鲁木齐)在半径为2的⊙O 中,圆心O 到弦AB 的距离为1,则弦AB 所对的圆心角的度数可以是 ( )(A )60 (B )90 (C )120 (D )15029.(新疆乌鲁木齐)将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面,(接口损耗不计),则桶底的面积为 ( )(A )π1600平方厘米 (B )1600π平方厘米(C )π6400平方厘米 (D )6400π平方厘米30.(成都市)如图,已知AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD =10厘米,AP ∶PB =1∶5,那么⊙O 的半径是 ( )(A )6厘米 (B )53厘米 (C )8厘米 (D )35厘米31.(成都市)在Rt △ABC 中,已知AB =6,AC =8,∠A =90.如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥,其表面积为S 1;把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥,其表面积为S 2,那么S 1∶S 2等于 ( )(A )2∶3 (B )3∶4 (C )4∶9 (D )5∶1232.(苏州市)如图,⊙O 的弦AB =8厘米,弦CD 平分AB 于点E .若CE =2厘米.ED 长为 ( )(A )8厘米 (B )6厘米 (C )4厘米 (D )2厘米33.(苏州市)如图,四边形ABCD 内接于⊙O ,若∠BOD =160,则∠BCD = ( )(A )160 (B ) 100 (C ) 80 (D )2034.(镇江市)如图,正方形ABCD 内接于⊙O ,E 为DC 的中点,直线BE交⊙O 于点F .若⊙O 的半径为2,则BF 的长为 ( )(A )23 (B )22(C )556 (D )55435.(扬州市)如图,AB 是⊙O 的直径,∠ACD =15,则∠BAD 的度数为 ( )(A ) 75 (B ) 72 (C ) 70 (D )6536.(扬州市)已知:点P 直线l 的距离为3,以点P 为圆心,r 为半径画圆,如果圆上有且只有两点到直线l 的距离均为2,则半径r 的取值范围是 ( )(A )r >1 (B )r >2 (C )2<r <3 (D )1<r <537.(绍兴市)边长为a 的正方边形的边心距为 ( )(A )a (B )23a (C )3a (D )2a38.(绍兴市)如图,以圆柱的下底面为底面,上底面圆心为顶点的圆锥的母线长为4,高线长为3,则圆柱的侧面积为 ( )(A )30π (B )76π (C )20π (D )74π39.(昆明市)如图,扇形的半径OA =20厘米,∠AOB =135,用它做成一个圆锥的侧面,则此圆锥底面的半径为 ( )(A )3.75厘米 (B )7.5厘米 (C )15厘米 (D )30厘米40.(昆明市)如图,正六边形ABCDEF 中.阴影部分面积为123平方厘米,则此正六边形的边长为 ( )(A )2厘米 (B )4厘米 (C )6厘米 (D )8厘米41.(温州市)已知扇形的弧长是2π厘米,半径为12厘米,则这个扇形的圆心角是 ( )(A )60 (B )45 (C )30 (D )2042.(温州市)圆锥的高线长是厘米,底面直径为12厘米,则这个圆锥的侧面积是 ( )(A )48π厘米 (B )24π13平方厘米(C )48π13平方厘米 (D )60π平方厘米43.(温州市)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PC是⊙O 的切线,C 为切点,PC =26,PA =4,则⊙O 的半径等于 ( )(A )1 (B )2 (C )23(D )2644.(常州市)已知圆柱的母线长为5厘米,表面积为28π平方厘米,则这个圆柱的底面半径是 ( )(A )5厘米 (B )4厘米 (C )2厘米 (D )3厘米45.(常州市)半径相等的圆内接正三角形、正方形、正六边形的边长之比为 ( )(A )1∶2∶3 (B )3∶2∶1(C )3∶2∶1 (D )1∶2∶346.(广东省)如图,若四边形ABCD 是半径为1和⊙O 的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为 ( )(A )(2π-2)厘米 (B )(2π-1)厘米(C )(π-2)厘米 (D )(π-1)厘米47.(武汉市)如图,已知圆心角∠BOC =100,则圆周角∠BAC 的度数是( )(A ) 50 (B )100 (C )130 (D )20048.(武汉市)半径为5厘米的圆中,有一条长为6厘米的弦,则圆心到此弦的距离为 ( )(A )3厘米 (B )4厘米 (C )5厘米 (D )6厘米49.已知:Rt △ABC 中,∠C =90,O 为斜边AB 上的一点,以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ,若AC =1,BC =3,则⊙O 的半径为 ( )(A )21(B )32 (C )43 (D )5450.(武汉市)已知:如图,E 是相交两圆⊙M 和⊙O 的一个交点,且ME ⊥NE ,AB 为外公切线,切点分别为A 、B ,连结AE 、BE .则∠AEB 的度数为 ( )(A )145° (B )140° (C )135° (D )130°二、填空题1.(北京市东城区)如图,AB 、AC 是⊙O 的两条切线,切点分别为B 、C ,D是优弧上的一点,已知∠BAC =80,那么∠BDC =__________度.2.(北京市东城区)在Rt △ABC 中,∠C =90,A B=3,BC =1,以AC 所在直线为轴旋转一周,所得圆锥的侧面展开图的面积是__________.3.(北京市海淀区)如果圆锥母线长为6厘米,那么这个圆锥的侧面积是_______平方厘米4.(北京市海淀区)一种圆状包装的保鲜膜,如图所示,其规格为“20厘米×60米”,经测量这筒保鲜膜的内径1ϕ、外径2ϕ的长分别为3.2厘米、4.0厘米,则该种保鲜膜的厚度约为_________厘米(π取3.14,结果保留两位有效数字).5.(上海市)两个点O 为圆心的同心圆中,大圆的弦AB 与小圆相切,如果AB 的长为24,大圆的半径OA 为13,那么小圆的半径为___________.6.(天津市)已知⊙O 中,两弦AB 与CD 相交于点E ,若E 为AB 的中点,CE ∶ED =1∶4,AB =4,则CD 的长等于___________.7.(重庆市)如图,AB 是⊙O 的直径,四边形ABCD 内接于⊙O ,,,的度数比为3∶2∶4,MN 是⊙O 的切线,C 是切点,则∠BCM 的度数为___________.8.(重庆市)如图,P 是⊙O 的直径AB 延长线上一点,PC 切⊙O 于点C ,PC =6,BC ∶AC =1∶2,则AB 的长为___________.9.(重庆市)如图,四边形ABCD 内接于⊙O ,AD ∥BC ,=,若AD =4,BC =6,则四边形ABCD 的面积为__________.10.(山西省)若一个圆柱的侧面积等于两底面积的和,则它的高h 与底面半径r 的大小关系是__________.11.(沈阳市)要用圆形铁片截出边长为4厘米的正方形铁片,则选用的圆形铁片的直径最小要___________厘米.12.(沈阳市)圆内两条弦AB 和CD 相交于P 点,AB 长为7,AB 把CD 分成两部分的线段长分别为2和6,那么=__________.13.(沈阳市)△ABC 是半径为2厘米的圆内接三角形,若BC =23厘米,则∠A 的度数为________.14.(沈阳市)如图,已知OA 、OB 是⊙O 的半径,且OA =5,∠AOB =15,AC ⊥OB 于C ,则图中阴影部分的面积(结果保留π)S =_________.15.(哈尔滨市)如图,圆内接正六边形ABCDEF 中,AC 、BF 交于点M .则ABM S △∶AFM S △=_________.16.(哈尔滨市)两圆外离,圆心距为25厘米,两圆周长分别为15π厘米和10π厘米.则其内公切线和连心线所夹的锐角等于__________度.17.(哈尔滨市)将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周,所得圆柱体的表面积为_________平方厘米.18.(陕西省)如图,在⊙O 的内接四边形ABCD 中,∠BCD =130,则∠BOD 的度数是________.19.(陕西省)已知⊙O 的半径为4厘米,以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积,则这个小圆的半径是______厘米.20.(陕西省)如图,⊙O 1的半径O 1A 是⊙O 2的直径,C 是⊙O 1上的一点,O 1C 交⊙O 2于点B .若⊙O 1的半径等于5厘米,的长等于⊙O 1周长的101,则的长是_________.21.(甘肃省)正三角形的内切圆与外接圆面积之比为_________.22.(甘肃省)如图,AB =8,AC =6,以AC 和BC 为直径作半圆,两圆的公切线MN 与AB 的延长线交于D ,则BD 的长为_________.23.(宁夏回族自治区)圆锥的母线长为5厘米,高为3厘米,在它的侧面展开图中,扇形的圆心角是_________度.24.(南京市)如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足是G ,F 是CG 的中点,延长AF 交⊙O 于E ,CF =2,AF =3,则EF 的长是_________.25.(福州市)在⊙O 中,直径AB =4厘米,弦CD ⊥AB 于E ,OE =3,则弦CD 的长为__________厘米.26.(福州市)若圆锥底面的直径为厘米,线线长为5厘米,则它的侧面积为__________平方厘米(结果保留π).27.(河南省)如图,AB 为⊙O 的直径,P 点在AB 的延长线上,PM 切⊙O 于M 点.若OA =a ,PM =3a ,那么△PMB 的周长的__________.28.(长沙市)在半径9厘米的圆中,60的圆心角所对的弧长为__________厘米.29.(四川省)扇形的圆心角为120,弧长为6π厘米,那么这个扇形的面积为_________.30.(贵阳市)如果圆O 的直径为10厘米,弦AB 的长为6厘米,那么弦AB 的弦心距等于________厘米.31.(贵阳市)某种商品的商标图案如图所求(阴影部分),已知菱形ABCD 的边长为4,∠A =60,是以A 为圆心,AB 长为半径的弧,是以B 为圆心,BC 长为半径的弧,则该商标图案的面积为_________.32.(云南省)已知,一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周,所得圆锥的表面积是__________.33.(新疆乌鲁木齐)正六边形的边心距与半径的比值为_________.34.(新疆乌鲁木齐)如图,已知扇形AOB 的半径为12,OA ⊥OB ,C 为OA 上一点,以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切,则半圆1O 的半径为__________.35.(成都市)如图,PA 、PB 与⊙O 分别相切于点A 、点B ,AC 是⊙O 的直径,PC 交⊙O 于点D .已知∠APB =60,AC =2,那么CD 的长为________.36.(苏州市)底面半径为2厘米,高为3厘米的圆柱的体积为_________立方厘米(结果保留π).37.(扬州市)边长为2厘米的正六边形的外接圆半径是________厘米,内切圆半径是________厘米(结果保留根号).38.(绍兴市)如图,PT 是⊙O 的切线,T 为切点,PB 是⊙O 的割线交⊙O 于A 、B 两点,交弦CD 于点M ,已知:CM =10,MD =2,PA =MB =4,则PT 的长等于__________.39.(温州市)如图,扇形OAB 中,∠AOB =90,半径OA =1,C 是线段AB的中点,CD ∥OA ,交于点D ,则CD =________.40.(常州市)已知扇形的圆心角为150 ,它所对的弧长为20π厘米,则扇形的半径是________厘米,扇形的面积是__________平方厘米.41.(常州市)如图,AB 是⊙O 直径,CE 切⊙O 于点C ,CD ⊥AB ,D 为垂足,AB =12厘米,∠B =30 ,则∠ECB =__________ ;CD =_________厘米.42.(常州市)如图,DE 是⊙O 直径,弦AB ⊥DE ,垂足为C ,若AB =6,CE =1,则CD =________,OC =_________.43.(常州市)如果把人的头顶和脚底分别看作一个点,把地球赤道作一个圆,那么身高压2米的汤姆沿着地球赤道环道环行一周,他的头顶比脚底多行________米.44.(海南省)已知:⊙O 的半径为1,M 为⊙O 外的一点,MA 切⊙O 于点A ,MA =1.若AB 是⊙O 的弦,且AB =2,则MB 的长度为_________.45.(武汉市)如果圆的半径为4厘米,那么它的周长为__________厘米.三、解答题:1.(苏州市)已知:如图,△ABC 内接于⊙O ,过点B 作⊙O 的切线,交CA 的延长线于点E ,∠EBC=2∠C .①求证:AB =AC ;②若tan ∠ABE =21,(ⅰ)求BCAB的值;(ⅱ)求当AC =2时,AE 的长.2.(广州市)如图,PA 为⊙O 的切线,A 为切点,⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ,PA =8cm ,PB =4cm ,求⊙O 的半径.3.(河北省)已知:如图,BC 是⊙O 的直径,AC 切⊙O 于点C ,AB 交⊙O 于点D ,若AD ︰DB =2︰3,AC=10,求sin B 的值.4.(北京市海淀区)如图,PC 为⊙O 的切线,C 为切点,PAB 是过O 的割线,CD ⊥AB 于点D ,若tan B =21,PC =10cm ,求三角形BCD 的面积.5.(宁夏回族自治区)如图,在两个半圆中,大圆的弦MN 与小圆相切,D 为切点,且MN ∥AB ,MN =a ,ON 、CD 分别为两圆的半径,求阴影部分的面积.6.(四川省)已知,如图,以△ABC 的边AB 作直径的⊙O ,分别并AC 、BC 于点D 、E ,弦FG ∥AB ,S △CDE ︰S △ABC =1︰4,DE =5cm ,FG =8cm ,求梯形AFGB 的面积.7.(贵阳市)如图所示:PA 为⊙O 的切线,A 为切点,PBC 是过点O 的割线,PA =10,PB =5,求:(1)⊙O 的面积(注:用含π的式子表示);(2)cos ∠BAP 的值.参考答案一、选择题1.B 2.B 3.D 4.D 5.C 6.C 7.A 8.C 9.D 10.B 11.A 12.B 13.C 14.D 15.D 16.A 17.B 18.C 19.C 20.B 21.C 22.A 23.A 24.B 25.B 26.D 27.D 28.C 29.A 30.B 31.A 32.A 33.B 34.C 35.A 36.D 37.B 38.B 39.B 40.B 41.C 42.D 43.A 44.C 45.B 46.C 47.A 48.B 49.C 50.C二、填空题1.50 2.2π 3.18π 4.4105.7-⨯ 5.5 6.5 7.30° 8.9 9.25 10.h =r 11.4212.3或4 13.60°或120° 14.8252425-π 15.1:2 16.30 17.80π或120π 18.100° 19.22 20.π 21.1:4 22.1 23.288 24.4 25.2 26.15π 27.()a 23+ 28.3π 29.27π平方厘米 30.4 31.34 32.24π平方厘米或36π平方厘米 33.2334.4 35.774 36.12π 37.2,3 38.132 39.213- 40.24,240π 41.60°,33 42.9,4 43.4π 44.1或5 45.8π三、解答题:1.(1)∵ BE 切⊙O 于点B ,∴ ∠ABE =∠C .∵ ∠EBC =2∠C ,即 ∠ABE +∠ABC =2∠C ,∴ ∠C +∠ABC =2∠C ,∴ ∠ABC =∠C ,∴ AB =AC . (2)①连结AO ,交BC 于点F ,∵ AB =AC ,∴=,∴ AO ⊥BC 且BF =FC .在Rt △ABF 中,BFAF=tan ∠ABF ,又 tan ∠ABF =tan C =tan ∠ABE =21,∴ BF AF =21,∴ AF =21BF .∴ AB =22BF AF +=2221BF BF +⎪⎭⎫ ⎝⎛=25BF .∴452==BF AB BC AB .②在△EBA 与△ECB 中,∵ ∠E =∠E ,∠EBA =∠ECB ,∴ △EBA ∽△ECB .∴ ⎪⎩⎪⎨⎧⋅==ECEA BE BC ABEB EA 2,解之,得516EA 2=EA ·(EA +AC ),又EA ≠0,∴511EA =AC ,EA =115×2=1110.2.设⊙的半径为r ,由切割线定理,得PA 2=PB ·PC ,∴ 82=4(4+2r ),解得r =6(cm ).即⊙O 的半径为6cm .3.由已知AD ︰DB =2︰3,可设AD =2k ,DB =3k (k >0).∵ AC 切⊙O 于点C ,线段ADB 为⊙O 的割线,∴ AC 2=AD ·AB ,∵ AB =AD +DB =2k +3k =5k ,∴ 102=2k ×5k ,∴ k 2=10,∵ k >0,∴ k =10.∴ AB =5k =510.∵ AC 切⊙O 于C ,BC 为⊙O 的直径,∴ AC ⊥BC .在Rt △ACB 中,sin B =51010510==AB AC .4.解法一:连结AC .∵ AB 是⊙O 的直径,点C 在⊙O 上,∴ ∠ACB =90°.CD ⊥AB 于点D ,∴ ∠ADC =∠BDC =90°,∠2=90°-∠BAC =∠B .∵ tan B =21, ∴ tan ∠2=21.∴ CBACDB CD CD AD ===21.设AD =x (x >0),CD =2x ,DB =4x ,AB =5x .∵ PC 切⊙O 于点C ,点B 在⊙O 上,∴ ∠1=∠B .∵ ∠P =∠P ,∴ △PAC ∽△PCB ,∴21==CB AC PC PA . ∵ PC =10,∴ PA =5,∵ PC 切⊙O 于点C ,PAB 是⊙O 的割线,∵ PC 2=PA ·PB ,∴ 102=5(5+5 x ).解得x =3.∴ AD =3,CD =6,DB =12.∴ S △BCD =21CD ·DB =21×6×12=36.即三角形BCD 的面积36cm 2.解法二:同解法一,由△PAC ∽△PCB ,得21==CB AC PC PA .∵ PA =10,∴ PB =20.由切割线定理,得PC 2=PA ·PB .∴ PA =201022-PB PC =5,∴ AB =PB -PA =15,∵ AD +DB =x +4x =15,解得x =3,∴ CD =2x =6,DB =4x =12.∴ S △BCD =21CD ·DB =21×6×12=36.即三角形BCD 的面积36cm 2.5.解:如图取MN 的中点E ,连结OE ,∴ OE ⊥MN ,EN =21MN =21a .在四边形EOCD 中,∵ CO ⊥DE ,OE ⊥DE ,DE ∥CO ,∴ 四边形EOCD 为矩形.∴ OE =CD ,在Rt △NOE 中,NO 2-OE 2=EN 2=22⎪⎭⎫⎝⎛a .∴ S 阴影=21π(NO 2-OE 2)=21π·22⎪⎭⎫⎝⎛a =28πa .6.解:∵ ∠CDE =∠CBA ,∠DCE =∠BCA ,∴ △CDE ∽△ABC .∴ 2⎪⎭⎫⎝⎛=∆∆AB DE S S ABC CDE∴AB DE =ABCCDE S S ∆∆=41=21,即215=AB ,解得 AB =10(cm ),作OM ⊥FG ,垂足为M ,则FM =21FG =21×8=4(cm ),连结OF ,∵ OA =21AB =21×10=5(cm ).∴ OF =OA =5(cm ).在Rt △OMF 中,由勾股定理,得OM =22FM OF -=2245-=3(cm ).∴ 梯形AFGB 的面积=2FG AB +·OM =2810⨯×3=27(cm 2).7.⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(⇒PA 2=PB ·PC ⇒PC =20⇒半径为7.5⇒圆面积为π4225(或56.25π)(平方单位).⎭⎬⎫∠=∠∠=∠P P B A P C )2(⇒△ACP ∽△BAP ⇒PB PA AB AC =⇒12=AB AC .解法一:设AB =x ,AC =2x ,BC 为⊙O 的直径∠CAB =90°,则 BC =5x .∵ ∠BAP =∠C ,∴ cos ∠BAP =cos ∠C =55252==xx BC AC解法二:设AB =x ,在Rt △ABC 中,AC 2+AB 2=BC 2,即 x 2+(2x )2=152,解之得 x =35,∴ AC =65,∵ ∠BAP =∠C ,∴ ∴ cos ∠BAP =cos ∠C =5521556==BC AC。
中考数学复习《圆》专题训练-附带有答案

中考数学复习《圆》专题训练-附带有答案一、选择题1.下列有关圆的一些结论:①平分弧的直径垂直于弧所对的弦;②平分弦的直径垂直于弦;③在同圆或等圆中,相等的弦所对的圆周角相等;④同弧或等弧所对的弦相等,其中正确的有()A.①④B.②③C.①③D.②④2.在同一平面内,已知⊙O的半径为3cm,OP=4cm,则点P与⊙O的位置关系是()A.点P在⊙O圆外B.点P在⊙O上C.点P在⊙O内D.无法确定3.如图,AB是⊙O的直径,C是⊙O上一点.若∠BOC=66°()A.66°B.33°C.24°D.30°4.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠CDA=118°,则∠C的度数为()A.32°B.33°C.34°D.44°5.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=26°,则∠D等于()A.26°B.48°C.38°D.52°6.如图,四边形ABCD内接于⊙O,∠C=100°,那么∠A是()A.60°B.50°C.80°D.100°7.如图,AB为⊙O的直径,C是⊙O上的一点,若∠BCO=35°,AO=2,则AC⌢的长度为()A.29πB.59πC.πD.79π8.如图,点A、B、C、D、E都是⊙O上的点AC⌢=AE⌢,∠D=130°则∠B的度数为()A.130°B.128°C.115°D.116°二、填空题9.半径为6的圆上,一段圆弧的长度为3π,则该弧的度数为°.10.如图,在△ABC中,∠ACB= 130°,∠BAC=20°,BC=2.以C为圆心,CB为半径的圆交AB于点D,则BD的长为.11.如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC.∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE= √2,则BD的长为.12.如图,四边形ABCD为⊙O的内接四边形,若∠ADC=85°,则∠B=.13.如图,在△ABC中∠ACB=90°,O为BC边上一点CO=2.以O为圆心,OC为半径作半圆与AB边交π,则阴影部分的面积为.于E,且OE⊥AB.若弧CE的长为43三、解答题14.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,OD∥BC(1)求证:AD=CD;(2)若AC=8,DE=2,求BC的长.15.如图,AB是⊙O的直径,F为⊙O上一点,AC平分∠FAB交⊙O于点C.过点C作CD⊥AF交AF的延长线于点D.(1)求证:CD是⊙O的切线.(2)若DC=3,AD=9,求⊙O半径.⌢上一点,AG与DC的延长线交于点F.16.已知,如图,AB是⊙O的直径,弦CD⊥AB于点E,G是AC(1)如CD=8,BE=2,求⊙O的半径长;(2)求证:∠FGC=∠AGD.17.如图,在△ABC中AB=AC,以底边BC为直径的⊙O交两腰于点D,E .(1)求证:BD=CE;⌢的长.(2)当△ABC是等边三角形,且BC=4时,求DE18.如图,在△ABC中,经过A,B两点的⊙O与边BC交于点E,圆心O在BC上,过点O作OD⊥BC交⊙O 于点D,连接AD交BC于点F,且AC=FC.(1)试判断AC与⊙O的位置关系,并说明理由;(2)若FC=√3,CE=1.求图中阴影部分的面积(结果保留π).参考答案1.A2.A3.B4.C5.C6.C7.D8.C9.9010.2√311.2√212.95°π13.4√3−4314.(1)证明:∵AB是⊙O的直径∴∠ACB=90°∵OD∥BC∴∠AEO=∠ACB=90°⌢=CD⌢∴AD∴AD=CD;(2)解:∵OD⊥AC,AC=8AC=4∴AE=12设⊙O的半径为r∵DE=2∴OE=OD﹣DE=r﹣2在Rt△AEO中,AE2+OE2=AO2∴16+(r﹣2)2=r2解得:r=5∴AB=2r=10在Rt△ACB中,BC=√AB2−AC2=√102−82=6∴BC的长为6.15.(1)证明:连接OC∵AC平分∠FAB∴∠FAC=∠CAO∵AO=CO∴∠ACO=∠CAO∴∠FAC=∠ACO∴AD∥OC∵CD⊥AF∴CD⊥OC∵OC为半径∴CD是⊙O的切线;(2)解:过点O作OE⊥AF于EAF,∠OED=∠EDC=∠OCD=90°∴AE=EF=12∴四边形OEDC为矩形∴CD=OE=3,DE=OC设⊙O的半径为r,则OA=OC=DE=r∴AE=9﹣r∵OA2﹣AE2=OE2∴r2﹣(9﹣r)2=32解得r=5.∴⊙O半径为5.16.(1)解:连接OC.设⊙O的半径为R.∵CD⊥AB∴DE=EC=4在Rt △OEC中,∵OC2=OE2+EC2∴R2=(R−2)2+42解得R=5.(2)解:连接AD∵弦CD⊥AB̂ = AĈ∴AD∴∠ADC=∠AGD∵四边形ADCG是圆内接四边形∴∠ADC=∠FGC∴∠FGC=∠AGD.17.(1)证明:∵AB=AC∴∠B=∠C⌢=BE⌢∴CD⌢=CE⌢∴BD∴BD=CE;(2)解:连接OD、OE∵△ABC 是等边三角形∴∠B =∠C =60°∴∠COD =120°∴∠COD +∠BOE =∠COE +∠DOE +∠BOD +∠DOE =240° ∴∠DOE =240°−180°=60°∵BC =4∴⊙O 的半径为 2∴DE ⌢ 的长 =60π×2180=2π3 .18.(1)解:AC 与⊙O 的相切,理由如下∵AO =DO∴∠D =∠OAD∵CF =CA∴∠CAF =∠CFA又∵∠CFA =∠OFD∴∠CAF =∠OFD∵OD ⊥BC∴∠OFD +∠ODF =90°∴∠CAF +∠OAF =90°∴OA ⊥AC∵OA 是半径∴AC 是⊙O 的切线∴ AC 与⊙O 的相切;(2)解:过A 作AM ⊥BC 于M ,如图设OA=OE=r∵FC=√3,CE=1在Rt△CAO中AO=r,AC=FC=√3,OC=OE+EC=r+1AO2+AC2=OC2∴r2+(√3)2=(r+1)2解得r=1∴OC=OE+EC=2∴AO=12 OC∴∠C=30°∴∠AOC=60°∴∠AOB=180−∠AOC=120°在Rt△CAM中AM=12AC=12FC=√32∴S△AOB=12⋅OB⋅AM=12×1×√32=√34∴S扇形AOB=120360π×1=π3∴S阴影部分=S△AOB−S扇形AOB=π3−√34.。
数学初三圆的试题及答案

数学初三圆的试题及答案# 数学初三圆的试题及答案一、选择题1. 已知圆的半径为5,圆心到直线的距离为3,那么直线与圆的位置关系是:- A. 直线与圆相离- B. 直线与圆相切- C. 直线与圆相交- D. 直线在圆内答案:C2. 圆的周长为44cm,求圆的直径:- A. 14cm- B. 22cm- C. 7cm- D. 无法确定答案:B3. 点P在圆O的内部,PA和PB是点P到圆O的两条半径,如果PA=6,PB=8,那么OP的长度是:- A. 2√7- B. 10- C. 4√2- D. 2√13答案:A二、填空题4. 已知圆的半径为r,圆心角为α,那么弧长l的计算公式是:______。
答案:l = rα5. 圆的面积公式是:______。
答案:A = πr²6. 如果一个扇形的半径为5,圆心角为60°,那么扇形的面积是:______。
答案:(25π/6)平方单位三、解答题7. 已知圆的方程为 \((x-3)^2 + (y-4)^2 = 25\),求圆心坐标和半径。
答案:圆心坐标为 (3, 4),半径为5。
8. 点A(2,3)在圆O上,圆O的半径为6,求圆O的方程。
答案:根据圆的标准方程,圆心O的坐标为 (2, 3),半径为6,所以圆O的方程为 \((x-2)^2 + (y-3)^2 = 36\)。
9. 已知圆C的圆心在x轴上,且圆C经过点P(2,1)和点Q(-2,5),求圆C的方程。
答案:首先求出PQ的中点M,M的坐标为(0,3)。
接着求出PQ的斜率k_PQ = (5-1)/(-2-2) = -1,因此PQ的中垂线斜率为1,中垂线方程为 y = x + 3。
解方程组:\[\begin{cases}y = x + 3 \\y = 0\end{cases}\]得到圆心C的坐标为 (-3, 0)。
接着求半径r,使用点P到圆心C 的距离公式:\[r = \sqrt{(-3-2)^2 + (0-1)^2} = \sqrt{25} = 5\]因此,圆C的方程为 \((x+3)^2 + y^2 = 25\)。
最新经典必考圆中考试题集锦(附答案)

圆中考试题集锦一、选择题1.如图,BC 是⊙O 的直径,P 是CB 延长线上一点,PA 切⊙O 于点A ,如果PA =3,PB =1,那么∠APC 等于()(A )15(B )30(C )45(D )602.如果圆柱的高为20厘米,底面半径是高的41,那么这个圆柱的侧面积是()(A )100π平方厘米(B )200π平方厘米(C )500π平方厘米(D )200平方厘米3.“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题,“今在圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为E ,CE =1寸,AB =10寸,求直径CD 的长”.依题意,CD 长为()(A )225寸(B )13寸(C )25寸(D )26寸4.已知:如图,⊙O 半径为5,PC 切⊙O 于点C ,PO 交⊙O 于点A ,PA =4,那么PC 的长等于()(A )6(B )25(C )210(D )2145.如果圆锥的侧面积为20π平方厘米,它的母线长为5厘米,那么此圆锥的底面半径的长等于()(A )2厘米(B )22厘米(C )4厘米(D )8厘米6.相交两圆的公共弦长为16厘米,若两圆的半径长分别为10厘米和17厘米,则这两圆的圆心距为()(A )7厘米(B )16厘米(C )21厘米(D )27厘米7.如图,⊙O 为△ABC 的内切圆,∠C =90,AO 的延长线交BC 于点D ,AC=4,DC =1,,则⊙O 的半径等于()(A )54(B )45(C )43(D )658.一居民小区有一正多边形的活动场.小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台,花台都以多边形的顶点为圆心,以多边形的内角为圆心角,花台占地面积共为12π平方米.若每个花台的造价为400元,则建造这些花台共需资金()(A )2400元(B )2800元(C )3200元(D )3600元9.如图,AB是⊙O直径,CD是弦.若AB=10厘米,CD=8厘米,那么A、B两点到直线CD的距离之和为()(A)12厘米(B)10厘米(C)8厘米(D)6厘米10.某工件形状如图所示,圆弧BC的度数为60,AB=6厘米,点B到点C的距离等于AB,∠BAC=30,则工件的面积等于()(A)4π(B)6π(C)8π(D)10π11.如图,PA切⊙O于点A,PBC是⊙O的割线且过圆心,PA=4,PB=2,则⊙O的半径等于()(A)3 (B)4 (C)6 (D)812.已知⊙O的半径为35厘米,⊙O的半径为5厘米.⊙O与⊙O相交于点D、E.若两圆的公共弦DE的长是6厘米(圆心O、O在公共弦DE的两侧),则两圆的圆心距O O的长为()(A)2厘米(B)10厘米(C)2厘米或10厘米(D)4厘米13.如图,两个等圆⊙O和⊙O的两条切线OA、OB,A、B是切点,则∠AOB等于()(A)30(B)45(C)60(D)9014.如图,AB是⊙O的直径,∠C=30,则∠ABD=()(A)30(B)40(C)50(D)6015.弧长为6π的弧所对的圆心角为60,则弧所在的圆的半径为()(A)6 (B)62(C)12 (D)1816.如图,在△ABC中,∠BAC=90,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分的面积为()(A)1 (B)2 (C)1+4(D)2-417.已知圆的内接正六边形的周长为18,那么圆的面积为()(A)18π(B)9π(C)6π(D)3π18.如图,点P 是半径为5的⊙O 内一点,且OP =3,在过点P 的所有弦中,长度为整数的弦一共有()(A )2条(B )3条(C )4条(D )5条19.如图,正六边形ABCDEF 的边长为a ,分别以C 、F 为圆心,a 为半径画弧,则图中阴影部分的面积是()(A )261a(B )231a(C )232a(D )234a20.过⊙O 内一点M 的最长的弦长为6厘米,最短的弦长为4厘米,则OM 的长为()(A )3厘米(B )5厘米(C )2厘米(D )5厘米21.已知圆锥的底面半径是3,高是4,则这个圆锥侧面展开图的面积是()(A )12π(B )15π(C )30π(D )24π22.已知⊙O 的直径AB 与弦AC 的夹角为30,过C 点的切线PC 与AB 延长线交P .PC =5,则⊙O 的半径为()(A )335(B )635(C )10 (D )523.如图:PA 切⊙O 于点A ,PBC 是⊙O 的一条割线,有PA =32,PB =BC ,那么BC 的长是()(A )3 (B )32(C )3(D )3224.如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是()(A )π(B )1.5π(C )2π(D )2.5π25.正六边形的半径为2厘米,那么它的周长为()(A )6厘米(B )12厘米(C )24厘米(D )122厘米26.一个圆柱形油桶的底面直径为0.6米,高为1米,那么这个油桶的侧面积为()(A )0.09π平方米(B )0.3π平方米(C )0.6平方米(D )0.6π平方米27.一个形如圆锥的冰淇淋纸筒,其底面直径为6厘米,母线长为5厘米,围成这样的冰淇淋纸筒所需纸片的面积是()(A )66π平方厘米(B )30π平方厘米(C )28π平方厘米(D )15π平方厘米28.在半径为2的⊙O 中,圆心O 到弦AB 的距离为1,则弦AB 所对的圆心角的度数可以是()(A )60(B )90(C )120(D )15029.将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面,(接口损耗不计),则桶底的面积为()(A )1600平方厘米(B )1600π平方厘米(C )6400平方厘米(D )6400π平方厘米30.如图,已知AB 是⊙O 的直径,弦CD⊥AB 于点P ,CD =10厘米,AP ∶PB =1∶5,那么⊙O 的半径是()(A )6厘米(B )53厘米(C )8厘米(D )35厘米31.在Rt △ABC 中,已知AB =6,AC =8,∠A =90.如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥,其表面积为S 1;把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥,其表面积为S 2,那么S 1∶S 2等于()(A )2∶3(B )3∶4(C )4∶9(D )5∶1232.如图,⊙O 的弦AB =8厘米,弦CD 平分AB 于点E .若CE =2厘米.ED 长为()(A )8厘米(B )6厘米(C )4厘米(D )2厘米33.如图,四边形ABCD 内接于⊙O ,若∠BOD =160,则∠BCD =()(A )160(B )100(C )80(D )2034.如图,正方形ABCD 内接于⊙O ,E 为DC 的中点,直线BE 交⊙O 于点F .若⊙O 的半径为2,则BF 的长为()(A )23(B )22(C )556(D )55435.如图,AB 是⊙O 的直径,∠ACD =15,则∠BAD 的度数为()(A )75(B )72(C )70(D )6536.已知:点P 直线l 的距离为3,以点P 为圆心,r 为半径画圆,如果圆上有且只有两点到直线l 的距离均为2,则半径r 的取值范围是()(A )r >1(B )r >2(C )2<r <3 (D )1<r <537.边长为a 的正方边形的边心距为()(A )a (B )23a (C )3a(D )2a38.如图,以圆柱的下底面为底面,上底面圆心为顶点的圆锥的母线长为4,高线长为3,则圆柱的侧面积为()(A )30π(B )76π(C )20π(D )74π39.如图,扇形的半径OA =20厘米,∠AOB =135,用它做成一个圆锥的侧面,则此圆锥底面的半径为()(A )3.75厘米(B )7.5厘米(C )15厘米(D )30厘米40.如图,正六边形ABCDEF 中.阴影部分面积为123平方厘米,则此正六边形的边长为()(A )2厘米(B )4厘米(C )6厘米(D )8厘米41.已知扇形的弧长是2π厘米,半径为12厘米,则这个扇形的圆心角是()(A )60(B )45(C )30(D )2042.圆锥的高线长是厘米,底面直径为12厘米,则这个圆锥的侧面积是()(A )48π厘米(B )2413平方厘米(C )4813平方厘米(D )60π平方厘米43.如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PC 是⊙O 的切线,C 为切点,PC =26,PA=4,则⊙O 的半径等于()(A )1 (B )2 (C )23(D )2644.已知圆柱的母线长为5厘米,表面积为28π平方厘米,则这个圆柱的底面半径是()(A )5厘米(B )4厘米(C )2厘米(D )3厘米45.半径相等的圆内接正三角形、正方形、正六边形的边长之比为()(A )1∶2∶3(B )3∶2∶1(C )3∶2∶1(D )1∶2∶346.如图,若四边形ABCD 是半径为1和⊙O 的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为()(A )(2π-2)厘米(B )(2π-1)厘米(C )(π-2)厘米(D )(π-1)厘米47.如图,已知圆心角∠BOC=100,则圆周角∠BAC 的度数是()(A )50(B )100(C )130(D )20048.半径为5厘米的圆中,有一条长为6厘米的弦,则圆心到此弦的距离为()(A )3厘米(B )4厘米(C )5厘米(D )6厘米49.已知:Rt △ABC 中,∠C =90,O 为斜边AB 上的一点,以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ,若AC =1,BC =3,则⊙O 的半径为()(A )21(B )32(C )43(D )5450.已知:如图,E 是相交两圆⊙M 和⊙O 的一个交点,且ME ⊥NE ,AB 为外公切线,切点分别为A 、B ,连结AE 、BE .则∠AEB 的度数为()(A )145°(B )140°(C )135°(D )130°二、填空题1.如图,AB、AC是⊙O的两条切线,切点分别为B、C,D是优弧上的一点,已知∠BAC=80,那么∠BDC=__________度.2.在Rt△ABC中,∠C=90,AB=3,BC=1,以AC所在直线为轴旋转一周,所得圆锥的侧面展开图的面积是__________.3.如果圆锥母线长为6厘米,那么这个圆锥的侧面积是_______平方厘米4.一种圆状包装的保鲜膜,如图所示,其规格为“20厘米×60米”,经测量这筒保鲜膜的内径、外径2的长分别为 3.2厘米、4.0厘米,1则该种保鲜膜的厚度约为_________厘米(π取3.14,结果保留两位有效数字).5.两个点O为圆心的同心圆中,大圆的弦AB与小圆相切,如果AB的长为24,大圆的半径OA为13,那么小圆的半径为___________.6.已知⊙O中,两弦AB与CD相交于点E,若E为AB的中点,CE∶ED=1∶4,AB=4,则CD的长等于___________.7.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,,,的度数比为3∶2∶4,MN是⊙O的切线,C是切点,则∠BCM的度数为___________.8.如图,P是⊙O的直径AB延长线上一点,PC切⊙O于点C,PC=6,BC∶AC=1∶2,则AB的长为___________.9.如图,四边形ABCD内接于⊙O,AD∥BC,=,若AD=4,BC=6,则四边形ABCD的面积为__________.10.若一个圆柱的侧面积等于两底面积的和,则它的高h与底面半径r的大小关系是__________.11.要用圆形铁片截出边长为4厘米的正方形铁片,则选用的圆形铁片的直径最小要___________厘米.12.圆内两条弦AB和CD相交于P点,AB长为7,AB把CD分成两部分的线段长分别为2和6,那么=__________.13.△ABC 是半径为2厘米的圆内接三角形,若BC =23厘米,则∠A 的度数为________.14.如图,已知OA 、OB 是⊙O 的半径,且OA =5,∠AOB =15,AC ⊥OB 于C ,则图中阴影部分的面积(结果保留π)S =_________.15.如图,圆内接正六边形ABCDEF 中,AC 、BF 交于点M .则ABM S △∶AFM S △=_________.16.两圆外离,圆心距为25厘米,两圆周长分别为15π厘米和10π厘米.则其内公切线和连心线所夹的锐角等于__________度.17.将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周,所得圆柱体的表面积为_________平方厘米.18.如图,在⊙O 的内接四边形ABCD中,∠BCD =130,则∠BOD 的度数是________.19.已知⊙O 的半径为4厘米,以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积,则这个小圆的半径是______厘米.20.如图,⊙O 1的半径O 1A 是⊙O 2的直径,C 是⊙O 1上的一点,O 1C 交⊙O 2于点B .若⊙O 1的半径等于5厘米,的长等于⊙O 1周长的101,则的长是_________.21.正三角形的内切圆与外接圆面积之比为_________.22.如图,AB =8,AC =6,以AC 和BC 为直径作半圆,两圆的公切线MN 与AB 的延长线交于D ,则BD 的长为_________.23.圆锥的母线长为5厘米,高为3厘米,在它的侧面展开图中,扇形的圆心角是_________度.24.如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足是G ,F 是CG 的中点,延长AF 交⊙O 于E ,CF =2,AF =3,则EF 的长是_________.25.在⊙O 中,直径AB =4厘米,弦CD ⊥AB 于E ,OE =3,则弦CD 的长为__________厘米.26.若圆锥底面的直径为厘米,线线长为5厘米,则它的侧面积为__________平方厘米(结果保留π).27.如图,AB 为⊙O 的直径,P 点在AB 的延长线上,PM 切⊙O 于M 点.若OA =a ,PM =3a ,那么△PMB 的周长的__________.28.在半径9厘米的圆中,60的圆心角所对的弧长为__________厘米.29.扇形的圆心角为120,弧长为6π厘米,那么这个扇形的面积为_________.30.如果圆O 的直径为10厘米,弦AB 的长为6厘米,那么弦AB 的弦心距等于________厘米.31.某种商品的商标图案如图所求(阴影部分),已知菱形ABCD 的边长为4,∠A =60,是以A 为圆心,AB 长为半径的弧,是以B 为圆心,BC 长为半径的弧,则该商标图案的面积为_________.32.已知,一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周,所得圆锥的表面积是__________.33.正六边形的边心距与半径的比值为_________.34.如图,已知扇形AOB 的半径为12,OA ⊥OB ,C 为OA 上一点,以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切,则半圆1O 的半径为__________.35.如图,PA 、PB 与⊙O 分别相切于点A 、点B ,AC 是⊙O 的直径,PC 交⊙O 于点D .已知∠APB =60,AC =2,那么CD 的长为________.36.底面半径为2厘米,高为3厘米的圆柱的体积为_________立方厘米(结果保留π).37.边长为2厘米的正六边形的外接圆半径是________厘米,内切圆半径是________厘米(结果保留根号).38.如图,PT 是⊙O 的切线,T 为切点,PB 是⊙O 的割线交⊙O 于A 、B 两点,交弦CD 于点M,已知:CM =10,MD =2,PA =MB =4,则PT 的长等于__________.39.如图,扇形OAB 中,∠AOB =90,半径OA =1,C 是线段AB 的中点,CD ∥OA ,交于点D ,则CD =________.40.已知扇形的圆心角为150,它所对的弧长为20π厘米,则扇形的半径是________厘米,扇形的面积是__________平方厘米.41.如图,AB 是⊙O 直径,CE 切⊙O 于点C ,CD ⊥AB ,D 为垂足,AB =12厘米,∠B =30,则∠ECB =__________;CD=_________厘米.42.如图,DE 是⊙O 直径,弦AB ⊥DE ,垂足为C ,若AB =6,CE =1,则CD =________,OC =_________.43.如果把人的头顶和脚底分别看作一个点,把地球赤道作一个圆,那么身高压2米的汤姆沿着地球赤道环道环行一周,他的头顶比脚底多行________米.44.已知:⊙O 的半径为1,M 为⊙O 外的一点,MA 切⊙O 于点A ,MA =1.若AB 是⊙O 的弦,且AB =2,则MB的长度为_________.45.如果圆的半径为4厘米,那么它的周长为__________厘米.三、解答题:1.已知:如图,△ABC 内接于⊙O ,过点B 作⊙O 的切线,交CA 的延长线于点E ,∠EBC =2∠C .①求证:AB =AC ;②若tan ∠ABE =21,(ⅰ)求BCAB的值;(ⅱ)求当AC =2时,AE 的长.2.如图,PA 为⊙O 的切线,A 为切点,⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ,PA =8cm ,PB =4cm ,求⊙O 的半径.3.已知:如图,BC 是⊙O 的直径,AC 切⊙O 于点C ,AB 交⊙O 于点D ,若AD ︰DB =2︰3,AC =10,求AC ︰A B 的值.4.如图,PC 为⊙O 的切线,C 为切点,PAB 是过O 的割线,CD ⊥AB 于点D ,若CD ︰DB =21,PC =10cm ,求三角形BCD 的面积.5.如图,在两个半圆中,大圆的弦MN 与小圆相切,D 为切点,且MN ∥AB ,MN =a ,ON 、CD 分别为两圆的半径,求阴影部分的面积.6.已知,如图,以△ABC 的边AB 作直径的⊙O ,分别并AC 、BC 于点D 、E ,弦FG ∥AB ,S △CDE ︰S △ABC =1︰4,DE =5cm ,FG =8cm ,求梯形AFGB 的面积.7.如图所示:PA 为⊙O 的切线,A 为切点,PBC 是过点O 的割线,PA =10,PB =5,求:(1)⊙O 的面积(注:用含π的式子表示);(2)cos ∠BAP 的值.参考答案一、选择题1.B 2.B 3.D 4.D 5.C 6.C 7.A 8.C 9.D 10.B 11.A 12.B 13.C 14.D 15.D 16.A 17.B 18.C 19.C 20.B 21.B 22.A 23.A 24.B 25.B 26.D 27.D 28.C 29.A 30.B 31.A 32.A 33.B 34.C 35.A 36.D 37.B 38.B 39.B 40.B 41.C 42.D 43.A 44.C 45.B 46.C 47.A 48.B 49.C 50.C 二、填空题1.50 2.2π3.18π4.4105.75.56.5 7.30°8.9 9.25 10.h =r11.4212.3或4 13.60°或120°14.825242515.1:2 16.30 17.80π或120π18.100°19.2220.π21.1:4 22.1 23.288 24.4 25.2 26.15π27.a2328.3π29.27π平方厘米30.431.3432.24π平方厘米或36π平方厘米33.2334.4 35.77436.12π37.2,338.13239.21340.24,240π41.60°,3342.9,4 43.4π44.1或545.8π三、解答题:1.(1)∵BE 切⊙O 于点B ,∴∠ABE =∠C .∵∠EBC =2∠C ,即∠ABE +∠ABC =2∠C ,∴∠C +∠ABC =2∠C ,∴∠ABC =∠C ,∴AB =AC .(2)①连结AO ,交BC 于点F ,∵AB =AC ,∴=,∴AO ⊥BC 且BF =FC .在Rt △ABF 中,BFAF=tan ∠ABF ,又tan ∠ABF =tan C =tan ∠ABE =21,∴BFAF =21,∴AF =21BF .∴AB =22BFAF=2221BFBF =25BF .∴452BFAB BCAB .②在△EBA 与△ECB 中,∵∠E =∠E ,∠EBA =∠ECB ,∴△EBA ∽△ECB .∴ECEA BEBC AB EB EA 2,解之,得516EA 2=EA ·(EA +AC ),又EA ≠0,∴511EA =AC ,EA =115×2=1110.2.设⊙的半径为r ,由切割线定理,得PA 2=PB ·PC ,∴82=4(4+2r ),解得r =6(cm ).即⊙O 的半径为6cm .3.由已知AD ︰DB =2︰3,可设AD =2k ,DB =3k (k >0).∵AC 切⊙O 于点C ,线段ADB 为⊙O 的割线,∴AC 2=AD ·AB ,∵AB =AD +DB =2k +3k =5k ,∴102=2k ×5k ,∴k 2=10,∵k >0,∴k =10.∴AB =5k =510.∵AC 切⊙O 于C ,BC 为⊙O 的直径,∴AC⊥BC .在Rt △ACB 中,sin B =51010510ABAC .4.解法一:连结AC .∵AB 是⊙O 的直径,点C 在⊙O 上,∴∠ACB =90°.CD ⊥AB 于点D ,∴∠ADC =∠BDC =90°,∠2=90°-∠BAC =∠B .∵tan B =21,∴tan ∠2=21.∴CBAC DBCD CDAD 21.设AD =x (x >0),CD =2x ,DB =4x ,AB =5x .∵PC 切⊙O 于点C ,点B 在⊙O 上,∴∠1=∠B .∵∠P =∠P ,∴△PAC ∽△PCB ,∴21CB AC PC PA.∵PC =10,∴PA =5,∵PC 切⊙O 于点C ,PAB 是⊙O 的割线,∵PC 2=PA ·PB ,∴102=5(5+5 x ).解得x =3.∴AD=3,CD =6,DB =12.∴S △BCD =21CD ·DB =21×6×12=36.即三角形BCD 的面积36cm 2.解法二:同解法一,由△PAC∽△PCB ,得21CBAC PCPA .∵PA =10,∴PB =20.由切割线定理,得PC 2=PA ·PB .∴PA=201022PB PC=5,∴AB=PB -PA =15,∵AD +DB =x +4x =15,解得x =3,∴CD =2x =6,DB =4x =12.∴S △BCD=21CD·DB =21×6×12=36.即三角形BCD 的面积36cm 2.5.解:如图取MN 的中点E ,连结OE ,∴OE⊥MN ,EN =21MN=21a .在四边形EOCD 中,∵CO ⊥DE ,OE ⊥DE ,DE ∥CO ,∴四边形EOCD 为矩形.∴OE =CD ,在Rt △NOE 中,NO 2-OE 2=EN 2=22a.∴S 阴影=21π(NO 2-OE 2)=21π·22a =28πa .6.解:∵∠CDE =∠CBA ,∠DCE =∠BCA ,∴△CDE ∽△ABC .∴2AB DE S SABCCDE∴ABDE =ABCCDE SS =41=21,即215AB,解得AB =10(cm ),作OM ⊥FG ,垂足为M ,则FM =21FG =21×8=4(cm ),连结OF ,∵OA =21AB =21×10=5(cm ).∴OF =OA =5(cm ).在Rt △OMF 中,由勾股定理,得OM =22FMOF=2245=3(cm ).∴梯形AFGB 的面积=2FG AB ·OM =2810×3=27(cm 2).7.的割线⊙是的切线⊙是O PBC O PA )1(PA 2=PB·PC PC =20半径为7.5圆面积为π4225(或56.25π)(平方单位).PPB A P C)2(△ACP ∽△BAPPBPA ABAC 12ABAC .解法一:设AB =x ,AC =2x ,BC 为⊙O 的直径∠CAB =90°,则BC=5x .∵∠BAP =∠C ,∴cos ∠BAP =cos ∠C =55252xx BCAC 解法二:设AB =x ,在Rt △ABC 中,AC 2+AB 2=BC 2,即x 2+(2x )2=152,解之得x =35,∴AC =65,∵∠BAP =∠C ,∴∴cos ∠BAP =cos ∠C =5521556BCAC 6.解:∵∠CDE =∠CBA ,∠DCE =∠BCA ,∴△CDE ∽△ABC .∴2AB DES SABCCDE∴ABDE =ABCCDE SS =41=21,即215AB,解得AB =10(cm ),作OM ⊥FG ,垂足为M ,则FM =21FG =21×8=4(cm ),连结OF ,∵OA=21AB=21×10=5(cm ).∴OF =OA =5(cm ).在Rt △OMF 中,由勾股定理,得OM =22FMOF=2245=3(cm ).∴梯形AFGB 的面积=2FG AB ·OM =2810×3=27(cm 2).7.的割线⊙是的切线⊙是O PBC O PA )1(PA 2=PB·PC PC =20半径为7.5圆面积为π4225(或56.25π)(平方单位).PPB A P C)2(△ACP ∽△BAPPBPA ABAC 12ABAC .解法一:设AB =x ,AC =2x ,BC 为⊙O 的直径∠CAB =90°,则BC =5x .∵∠BAP =∠C ,∴cos ∠BAP =cos ∠C =55252xx BCAC 解法二:设AB =x ,在Rt △ABC 中,AC 2+AB 2=BC 2,即x 2+(2x )2=152,解之得x =35,∴AC =65,∵∠BAP =∠C ,∴∴cos ∠BAP =cos ∠C =5521556BCAC6.解:∵∠CDE =∠CBA ,∠DCE =∠BCA ,∴△CDE ∽△ABC .∴2AB DE S S ABCCDE∴ABDE =ABCCDE SS =41=21,即215AB,解得AB =10(cm ),作OM ⊥FG ,垂足为M ,则FM =21FG=21×8=4(cm ),连结OF ,∵OA =21AB =21×10=5(cm ).∴OF =OA =5(cm ).在Rt △OMF 中,由勾股定理,得OM =22FMOF=2245=3(cm ).∴梯形AFGB 的面积=2FGAB ·OM =2810×3=27(cm 2).7.的割线⊙是的切线⊙是O PBC O PA )1(PA 2=PB ·PC PC =20半径为7.5圆面积为π4225(或56.25π)(平方单位).PPB A P C)2(△ACP ∽△BAPPBPA ABAC 12ABAC .解法一:设AB =x ,AC =2x ,BC 为⊙O 的直径∠CAB =90°,则BC =5x .∵∠BAP =∠C ,∴cos ∠BAP =cos ∠C =55252xx BCAC 解法二:设AB =x ,在Rt △ABC 中,AC 2+AB 2=BC 2,即x 2+(2x )2=152,解之得x =35,∴AC =65,∵∠BAP =∠C ,∴∴cos ∠BAP =cos ∠C =5521556BCAC 圆是中考中的必考内容,大约占整个分数的百分之30左右,希望大家能够加深练习,提到自己的做题能力。
初三中考圆的试题及答案

初三中考圆的试题及答案一、选择题(每题3分,共30分)1. 若圆的半径为5,圆心为坐标原点,则圆的方程为()A. (x-0)^2 + (y-0)^2 = 25B. (x-5)^2 + (y-5)^2 = 25C. (x+5)^2 + (y+5)^2 = 25D. (x-5)^2 + (y+5)^2 = 25答案:A2. 圆与直线相切的条件是()A. 圆心到直线的距离等于半径B. 圆心到直线的距离小于半径C. 圆心到直线的距离大于半径D. 圆心到直线的距离等于直径答案:A3. 已知圆的半径为3,圆心坐标为(-2, 3),求圆上的点(1, 4)与圆心的距离为()A. 2B. 3C. 4D. 5答案:D4. 圆的直径是()A. 圆上任意两点间最长的线段B. 圆上任意两点间最短的线段C. 圆上任意两点间距离的两倍D. 圆上任意两点间距离的一半答案:A5. 圆的周长公式为()A. C = 2πrB. C = πrC. C = 4πrD. C = πr^2答案:A6. 圆的面积公式为()A. S = πr^2B. S = 2πrC. S = πrD. S = 4πr^2答案:A7. 圆内接四边形的对角线()A. 相等B. 不相等C. 垂直D. 平行答案:A8. 圆的切线与半径的关系是()A. 切线与半径垂直B. 切线与半径平行C. 切线与半径相交D. 切线与半径重合答案:A9. 圆的内切圆与外切圆的半径之和等于()A. 圆的直径B. 圆的半径C. 圆的周长D. 圆的面积答案:A10. 圆的内接三角形的面积公式为()A. S = 1/2 * a * b * sin(C)B. S = 1/2 * a * b * cos(C)C. S = 1/2 * r * (a + b + c)D. S = 1/2 * r * (a - b + c)答案:C二、填空题(每题3分,共30分)1. 圆的方程为(x-2)^2 + (y+3)^2 = 16,则圆心坐标为______。
中考数学复习《圆》专题训练--含有参考答案

中考数学复习《圆》专题训练--含有参考答案一、选择题1.已知⊙O 的半径是3cm ,则⊙O 中最长的弦长是( )A .3cmB .6cmC .1.5cmD .√3cm2.如图,AB 是⊙O 的直径,C 、D 在⊙O 上∠CAB =20°,则∠ADC 等于( )A .70°B .110°C .140°D .160°3.如图,AB 是⊙O 的直径,过点A 作⊙O 的切线AC ,连接BC ,与⊙O 交于点D ,E 是⊙O 上一点,连接AE ,DE 若∠C =48°,则∠AED 的度数为( )A .42°B .48°C .32°D .38°4.如图,线段AB 经过⊙O 的圆心,AC ,BD 分别与⊙O 相切于点C ,D .若AC =BD =2√3,∠A =30°,则CD⌢的长度为( )A .πB .23πC .√23πD .2π5.如图,PA ,PB 是⊙O 的切线,AC 是⊙O 的直径,若∠BAC =25°,则∠P 的度数为( )A .50°B .70°C .110°D .40°6.如图,四边形ABCD 是半圆O 的内接四边形,AB 是直径,C 是BD⌢的中点.若∠C=110°,则∠ABC 的度数为()A.55°B.60°C.65°D.75°7.如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为()A.55°B.65°C.60°D.75°8.如图,半径为10的扇形OAB中∠AOB=90°,C为弧AB上一,CD⊥OA,CE⊥OB垂足分别为D,E.若∠CDE=40°则图中阴影部分的面积为()A.403πB.1109πC.1009πD.10π二、填空题9.如图,在⊙O中,弦AB的长为4,圆心到弦AB的距离为2,则∠AOC的度数为.10.如图,四边形ABCD内接于圆O,若∠D=100°,则∠B的度数是.11.如图,PA、PB是⊙O的切线,切点分别为A、B,若∠P=40°,则弦AB所对的圆周角的度数为度.12.如图,PA,PB分别与半径为3的⊙O相切于点A,B,直线CD分别交PA,PB于点C,D,并切⊙O于点E,当PO=6时,△PCD的周长为.13.如图,在Rt△ABC中AB=AC,以AB为直径的⊙O交BC于点D,若BC=4√2cm,则图中阴影部分的面积为cm2.三、解答题14.如图,是直径,足的弦.(1)求的度数.(2)若的半径,求的长.15.如图,AB是的直径,点C,M为上两点,且C点为的中点,过C点的切线交射线BM、BA于点EF.(1)求证:;(2)若, MB=2 ,求的长度.⌢的中点,过D作DE∥AC,交OC的延16.如图,AB为半圆O的直径,C为半圆上一点,连接AC,点D为AC长线于点E.(1)求证:DE是半圆O的切线.(2)若OC=3,CE=2,求AC的长.⌢=AD⌢.17.已知:△ABD内接于⊙O,AB(1)如图①,点C在⊙O上,若∠BCD=60°,求∠ABD和∠ADB的大小;(2)如图②,点C在⊙O外,BD是⊙O的直径,BC与⊙O相切于点B,若∠BCD=50°,求∠CDA的大小.18.如图,AB是的弦,C是外一点,CO交AB于点P,交于点D,且CP=CB.(1)判断直线与的位置关系,并说明理由;(2)若,OP=2,求图中阴影部分的面积.参考答案1.B2.B3.A4.B5.A6.A7.B8.C9.45°10.80°11.70°或110°12.6√313.(π+2)14.(1)解:是的直径∴∴∵∴;(2)解:∵∵的半径,AB是直径∴∴.15.(1)证明:如图连接.∵是的切线∴∵点C是的中点∴∵OB=OC∴∴∴∴∴(2)解:如图,连接∵∴∵OM=OB∴为等边三角形∴OB=MB=2∴的长度16.(1)证明:如图,连接OD交AC于点F.⌢的中点∵D是AC⌢=CD⌢∴AD∴∠AOD=∠COD∵OC=OA∴OD⊥AC∵DE∥AC∴OD⊥DE∴DE是半圆O的切线. (2)解:∵OC=3∴OE=5∴在Rt△ODE中∴cosE=DEOE =45∵AC∥DE∴∠FCO=∠E∴cos∠FCO=45∴FC=OC⋅cos∠FCO=3×45=125∵OD⊥AC∴AC=2FC=245.17.(1)解:∵四边形ABCD内接于⊙O∴∠BAD=180°−∠BCD=120°∵AB⌢=AD⌢∴AB=AD∴∠ABD=∠ADB=12(180°−∠BAD)=30°;(2)解:∵BC与⊙O相切于点B∴BD⊥BC,∴∠CBD=90°∵在RtΔBCD中∴∠BDC=90°−∠BCD=40°∵BD是⊙O的直径∴∠BAD=90°∵AB⌢=AD⌢∴AB=AD∴∠ABD=∠ADB=12×90°=45°∴∠CDA=∠ADB+∠BDC=45°+40°=85°.18.(1)解:直线BC与⊙O相切理由:连接OB∵OA=OB∴∠OAB=∠OBA∵CP=CB∴∠CPB=∠CBP∵∠CPB=∠APO∴∠CBP=∠APO∵∴∠AOC=90°在Rt△AOP中∵∠OAB +∠APO=90°∴∠OBA+∠CBP=90°∴∠OBC=90°∴OB⊥CB又∵OB是半径∴CB与⊙O相切;(2)解:∵∠A=30°,∠AOP=90°,OP=2 ∴∠APO=60°,AP=2OP=4∴AO=BO∵OA=OB∴∠OBA=∠A=30°∴∠BOP=∠APO﹣∠OBA=30°=∠OBP∴OP=PB=2∵∠BPD=∠APO=60°,PC=CB∴△PBC是等边三角形∴∠PCB=∠CBP=60°∴BC=PB=2∴图中阴影部分的面积=S△OBC﹣S扇形OBD2×2π∵OA=√22∴AC=√3OA=√62∴S Rt△OAC=12OA·AC=12×√22×√62=√34∴S阴影=S Rt△OAC−S扇形OAE=√34−π12.。
经典必考圆中考试卷集锦(附答案)

圆中考试题集锦一、选择题1.如图,BC 是⊙O 的直径,P 是CB 延长线上一点,PA 切⊙O 于点A ,如果PA =3,PB =1,那么∠APC 等于 ( )(A ) 15 (B ) 30 (C ) 45 (D ) 602.如果圆柱的高为20厘米,底面半径是高的41,那么这个圆柱的侧面积是 ( ) (A )100π平方厘米 (B )200π平方厘米(C )500π平方厘米 (D )200平方厘米3.“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题,“今在圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为E ,CE =1寸,AB =寸,求直径CD 的长”.依题意,CD 长为 ( )(A )225寸 (B )13寸 (C )25寸 (D )26寸 4.已知:如图,⊙O 半径为5,PC 切⊙O 于点C ,PO 交⊙O 于点A ,PA =4,那么PC 的长等于 ( )(A )6 (B )25 (C )210 (D )2145.如果圆锥的侧面积为20π平方厘米,它的母线长为5厘米,那么此圆锥的底面半径的长等于 ( )(A )2厘米 (B )22厘米 (C )4厘米 (D )8厘米6.相交两圆的公共弦长为16厘米,若两圆的半径长分别为10厘米和17厘米,则这两圆的圆心距为 ( )(A )7厘米 (B )16厘米 (C )21厘米 (D )27厘米7.如图,⊙O 为△ABC 的内切圆,∠C =90,AO 的延长线交BC 于点D ,AC =4,DC =1,,则⊙O 的半径等于 ( )(A )54 (B )45 (C )43 (D )65 8.(重庆市)一居民小区有一正多边形的活动场.为迎接“AAPP ”会议在重庆市的召开,小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台,花台都以多边形的顶点为圆心,比多边形的内角为圆心角,花台占地面积共为12π平方米.若每个花台的造价为400元,则建造这些花台共需资金 ( )(A )2400元 (B )2800元 (C )3200元 (D )3600元9.(河北省)如图,AB 是⊙O 直径,CD 是弦.若AB =10厘米,CD =8厘米,那么A 、B 两点到直线CD 的距离之和为 ( )(A )12厘米 (B )10厘米 (C )8厘米 (D )6厘米10.(河北省)某工件形状如图所示,圆弧BC 的度数为60,AB =6厘米,点B 到点C 的距离等于AB ,∠BAC = 30,则工件的面积等于 ( )(A )4π (B )6π (C )8π (D )10π11.(沈阳市)如图,PA 切⊙O 于点A ,PBC 是⊙O 的割线且过圆心,PA =4,PB =2,则⊙O 的半径等于 ( )(A )3 (B )4 (C )6 (D )812.(哈尔滨市)已知⊙O 的半径为35厘米,⊙O '的半径为5厘米.⊙O 与⊙O '相交于点D 、E .若两圆的公共弦DE 的长是6厘米(圆心O 、O '在公共弦DE 的两侧),则两圆的圆心距O O '的长为 ( )(A )2厘米 (B )10厘米 (C )2厘米或10厘米 (D )4厘米13.(陕西省)如图,两个等圆⊙O 和⊙O '的两条切线OA 、OB ,A 、B 是切点,则∠AOB 等于 ( )(A ) 30 (B ) 45 (C ) 60 (D )9014.(甘肃省)如图,AB 是⊙O 的直径,∠C = 30,则∠ABD = ( )(A ) 30 (B ) 40 (C ) 50 (D ) 6015.(甘肃省)弧长为6π的弧所对的圆心角为 60,则弧所在的圆的半径为( )(A )6 (B )62 (C )12 (D )1816.(甘肃省)如图,在△ABC 中,∠BAC = 90,AB =AC =2,以AB 为直径的圆交BC 于D ,则图中阴影部分的面积为 ( )(A )1 (B )2 (C )1+4π (D )2-4π 17.(宁夏回族自治区)已知圆的内接正六边形的周长为18,那么圆的面积为 ( )(A )18π (B )9π (C )6π (D )3π18.(山东省)如图,点P 是半径为5的⊙O 内一点,且OP =3,在过点P的所有弦中,长度为整数的弦一共有 ( )(A )2条 (B )3条 (C )4条 (D )5条19.(南京市)如图,正六边形ABCDEF 的边长的上a ,分别以C 、F 为圆心,a 为半径画弧,则图中阴影部分的面积是 ( )(A )261a π (B )231a π (C )232a π (D )234a π20.(杭州市)过⊙O 内一点M 的最长的弦长为6厘米,最短的弦长为4厘米,则OM 的长为 ( )(A )3厘米 (B )5厘米 (C )2厘米 (D )5厘米21.(安徽省)已知圆锥的底面半径是3,高是4,则这个圆锥侧面展开图的面积是 ( )(A )12π (B )15π (C )30π (D )24π22.(安微省)已知⊙O 的直径AB 与弦AC 的夹角为 30,过C 点的切线PC 与AB 延长线交P .PC =5,则⊙O 的半径为 ( )(A )335 (B )635 (C )10 (D )5 23.(福州市)如图:PA 切⊙O 于点A ,PBC 是⊙O 的一条割线,有PA=32,PB =BC ,那么BC 的长是 ( )(A )3 (B )32 (C )3 (D )3224.(河南省)如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是 ( )(A )π (B )1.5π (C )2π (D )2.5π25.(四川省)正六边形的半径为2厘米,那么它的周长为 ( )(A )6厘米 (B )12厘米 (C )24厘米 (D )122厘米26.(四川省)一个圆柱形油桶的底面直径为0.6米,高为1米,那么这个油桶的侧面积为 ( )(A )0.09π平方米 (B )0.3π平方米 (C )0.6平方米 (D )0.6π平方米27.(贵阳市)一个形如圆锥的冰淇淋纸筒,其底面直径为6厘米,母线长为5厘米,围成这样的冰淇淋纸筒所需纸片的面积是 ( )(A )66π平方厘米 (B )30π平方厘米 (C )28π平方厘米 (D )15π平方厘米28.(新疆乌鲁木齐)在半径为2的⊙O 中,圆心O 到弦AB 的距离为1,则弦AB 所对的圆心角的度数可以是 ( )(A ) 60 (B ) 90 (C ) 120 (D ) 15029.(新疆乌鲁木齐)将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面,(接口损耗不计),则桶底的面积为 ( )(A )π1600平方厘米 (B )1600π平方厘米(C )π6400平方厘米 (D )6400π平方厘米 30.(成都市)如图,已知AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD =10厘米,AP ∶PB =1∶5,那么⊙O 的半径是 ( )(A )6厘米 (B )53厘米 (C )8厘米 (D )35厘米31.(成都市)在Rt △ABC 中,已知AB =6,AC =8,∠A =90.如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥,其表面积为S 1;把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥,其表面积为S 2,那么S 1∶S 2等于 ( )(A )2∶3 (B )3∶4 (C )4∶9 (D )5∶1232.(苏州市)如图,⊙O 的弦AB =8厘米,弦CD 平分AB 于点E .若CE =2厘米.ED 长为 ( )(A )8厘米 (B )6厘米 (C )4厘米 (D )2厘米33.(苏州市)如图,四边形ABCD 内接于⊙O ,若∠BOD =160,则∠BCD = ( )(A ) 160 (B ) 100 (C ) 80 (D ) 2034.(镇江市)如图,正方形ABCD 内接于⊙O ,E 为DC 的中点,直线BE交⊙O 于点F .若⊙O 的半径为2,则BF 的长为 ( )(A )23 (B )22 (C )556 (D )554 35.(扬州市)如图,AB 是⊙O 的直径,∠ACD = 15,则∠BAD 的度数为 ( )(A ) 75 (B ) 72 (C ) 70 (D )6536.(扬州市)已知:点P 直线l 的距离为3,以点P 为圆心,r 为半径画圆,如果圆上有且只有两点到直线l 的距离均为2,则半径r 的取值范围是 ( )(A )r >1 (B )r >2 (C )2<r <3 (D )1<r <537.(绍兴市)边长为a 的正方边形的边心距为 ( )(A )a (B )23a (C )3a (D )2a 38.(绍兴市)如图,以圆柱的下底面为底面,上底面圆心为顶点的圆锥的母线长为4,高线长为3,则圆柱的侧面积为 ( )(A )30π (B )76π (C )20π (D )74π39.(昆明市)如图,扇形的半径OA =20厘米,∠AOB = 135,用它做成一个圆锥的侧面,则此圆锥底面的半径为 ( )(A )3.75厘米 (B )7.5厘米 (C )15厘米 (D )30厘米40.(昆明市)如图,正六边形ABCDEF 中.阴影部分面积为123平方厘米,则此正六边形的边长为 ( )(A )2厘米 (B )4厘米 (C )6厘米 (D )8厘米41.(温州市)已知扇形的弧长是2π厘米,半径为12厘米,则这个扇形的圆心角是 ( )(A ) 60 (B ) 45 (C ) 30 (D ) 2042.(温州市)圆锥的高线长是厘米,底面直径为12厘米,则这个圆锥的侧面积是 ( )(A )48π厘米 (B )24π13平方厘米(C )48π13平方厘米 (D )60π平方厘米43.(温州市)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PC是⊙O 的切线,C 为切点,PC =26,PA =4,则⊙O 的半径等于 ( )(A )1 (B )2 (C )23 (D )26 44.(常州市)已知圆柱的母线长为5厘米,表面积为28π平方厘米,则这个圆柱的底面半径是( )(A )5厘米 (B )4厘米 (C )2厘米 (D )3厘米45.(常州市)半径相等的圆内接正三角形、正方形、正六边形的边长之比为 ( )(A )1∶2∶3 (B )3∶2∶1(C )3∶2∶1 (D )1∶2∶346.(广东省)如图,若四边形ABCD 是半径为1和⊙O 的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为 ( )(A )(2π-2)厘米 (B )(2π-1)厘米(C )(π-2)厘米 (D )(π-1)厘米47.(武汉市)如图,已知圆心角∠BOC = 100,则圆周角∠BAC 的度数是( )(A ) 50 (B ) 100 (C ) 130 (D ) 20048.(武汉市)半径为5厘米的圆中,有一条长为6厘米的弦,则圆心到此弦的距离为 ( )(A )3厘米 (B )4厘米 (C )5厘米 (D )6厘米49.已知:Rt △ABC 中,∠C = 90,O 为斜边AB 上的一点,以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ,若AC =1,BC =3,则⊙O 的半径为 ( )(A )21 (B )32 (C )43 (D )54 50.(武汉市)已知:如图,E 是相交两圆⊙M 和⊙O 的一个交点,且ME ⊥NE ,AB 为外公切线,切点分别为A 、B ,连结AE 、BE .则∠AEB 的度数为 ( )(A )145° (B )140° (C )135° (D )130°二、填空题1.(北京市东城区)如图,AB 、AC 是⊙O 的两条切线,切点分别为B 、C ,D 是优弧上的一点,已知∠BAC =80,那么∠BDC =__________度.2.(北京市东城区)在Rt △ABC 中,∠C =90,A B=3,BC =1,以AC 所在直线为轴旋转一周,所得圆锥的侧面展开图的面积是__________.3.(北京市海淀区)如果圆锥母线长为6厘米,那么这个圆锥的侧面积是_______平方厘米4.(北京市海淀区)一种圆状包装的保鲜膜,如图所示,其规格为“20厘米×60米”,经测量这筒保鲜膜的内径1ϕ、外径2ϕ的长分别为3.2厘米、4.0厘米,则该种保鲜膜的厚度约为_________厘米(π取3.14,结果保留两位有效数字).5.(上海市)两个点O 为圆心的同心圆中,大圆的弦AB 与小圆相切,如果AB 的长为24,大圆的半径OA 为13,那么小圆的半径为___________.6.(天津市)已知⊙O 中,两弦AB 与CD 相交于点E ,若E 为AB 的中点,CE ∶ED =1∶4,AB =4,则CD 的长等于___________.7.(重庆市)如图,AB 是⊙O 的直径,四边形ABCD 内接于⊙O ,,,的度数比为3∶2∶4,MN 是⊙O 的切线,C 是切点,则∠BCM 的度数为___________.8.(重庆市)如图,P 是⊙O 的直径AB 延长线上一点,PC 切⊙O于点C ,PC =6,BC ∶AC =1∶2,则AB 的长为___________.9.(重庆市)如图,四边形ABCD 内接于⊙O ,AD ∥BC ,=,若AD =4,BC =6,则四边形ABCD 的面积为__________.10.(山西省)若一个圆柱的侧面积等于两底面积的和,则它的高h 与底面半径r 的大小关系是__________.11.(沈阳市)要用圆形铁片截出边长为4厘米的正方形铁片,则选用的圆形铁片的直径最小要___________厘米.12.(沈阳市)圆内两条弦AB 和CD 相交于P 点,AB 长为7,AB 把CD 分成两部分的线段长分别为2和6,那么=__________.13.(沈阳市)△ABC 是半径为2厘米的圆内接三角形,若BC =23厘米,则∠A 的度数为________.14.(沈阳市)如图,已知OA 、OB 是⊙O 的半径,且OA =5,∠AOB =15 ,AC⊥OB 于C ,则图中阴影部分的面积(结果保留π)S =_________.15.(哈尔滨市)如图,圆内接正六边形ABCDEF 中,AC 、BF 交于点M .则ABM S △∶AFM S △=_________.16.(哈尔滨市)两圆外离,圆心距为25厘米,两圆周长分别为15π厘米和10π厘米.则其内公切线和连心线所夹的锐角等于__________度.17.(哈尔滨市)将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周,所得圆柱体的表面积为_________平方厘米.18.(陕西省)如图,在⊙O 的内接四边形ABCD 中,∠BCD =130,则∠BOD的度数是________.19.(陕西省)已知⊙O 的半径为4厘米,以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积,则这个小圆的半径是______厘米.20.(陕西省)如图,⊙O 1的半径O 1A 是⊙O 2的直径,C 是⊙O 1上的一点,O 1C 交⊙O 2于点B .若⊙O 1的半径等于5厘米,的长等于⊙O 1周长的101,则的长是_________.21.(甘肃省)正三角形的内切圆与外接圆面积之比为_________.22.(甘肃省)如图,AB =8,AC =6,以AC 和BC 为直径作半圆,两圆的公切线MN 与AB 的延长线交于D ,则BD 的长为_________.23.(宁夏回族自治区)圆锥的母线长为5厘米,高为3厘米,在它的侧面展开图中,扇形的圆心角是_________度.24.(南京市)如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足是G ,F 是CG 的中点,延长AF 交⊙O 于E ,CF =2,AF =3,则EF 的长是_________.25.(福州市)在⊙O 中,直径AB =4厘米,弦CD ⊥AB 于E ,OE =3,则弦CD 的长为__________厘米.26.(福州市)若圆锥底面的直径为厘米,线线长为5厘米,则它的侧面积为__________平方厘米(结果保留π).27.(河南省)如图,AB 为⊙O 的直径,P 点在AB 的延长线上,PM 切⊙O 于M 点.若OA =a ,PM =3a ,那么△PMB 的周长的__________.28.(长沙市)在半径9厘米的圆中, 60的圆心角所对的弧长为__________厘米.29.(四川省)扇形的圆心角为120 ,弧长为6π厘米,那么这个扇形的面积为_________.30.(贵阳市)如果圆O 的直径为10厘米,弦AB 的长为6厘米,那么弦AB 的弦心距等于________厘米.31.(贵阳市)某种商品的商标图案如图所求(阴影部分),已知菱形ABCD的边长为4,∠A = 60,是以A 为圆心,AB 长为半径的弧,是以B 为圆心,BC 长为半径的弧,则该商标图案的面积为_________.32.(云南省)已知,一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周,所得圆锥的表面积是__________.33.(新疆乌鲁木齐)正六边形的边心距与半径的比值为_________.34.(新疆乌鲁木齐)如图,已知扇形AOB 的半径为12,OA ⊥OB ,C 为OA 上一点,以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切,则半圆1O 的半径为__________.35.(成都市)如图,PA 、PB 与⊙O 分别相切于点A 、点B ,AC 是⊙O 的直径,PC 交⊙O 于点D .已知∠APB =60,AC =2,那么CD 的长为________.36.(苏州市)底面半径为2厘米,高为3厘米的圆柱的体积为_________立方厘米(结果保留π).37.(扬州市)边长为2厘米的正六边形的外接圆半径是________厘米,内切圆半径是________厘米(结果保留根号).38.(绍兴市)如图,PT 是⊙O 的切线,T 为切点,PB 是⊙O 的割线交⊙O 于A 、B 两点,交弦CD 于点M ,已知:CM =10,MD =2,PA =MB =4,则PT 的长等于__________.39.(温州市)如图,扇形OAB 中,∠AOB = 90,半径OA =1,C 是线段AB的中点,CD ∥OA ,交于点D ,则CD =________.40.(常州市)已知扇形的圆心角为150 ,它所对的弧长为20π厘米,则扇形的半径是________厘米,扇形的面积是__________平方厘米.41.(常州市)如图,AB 是⊙O 直径,CE 切⊙O 于点C ,CD ⊥AB ,D 为垂足,AB =12厘米,∠B =30,则∠ECB =__________ ;CD =_________厘米.42.(常州市)如图,DE 是⊙O 直径,弦AB ⊥DE ,垂足为C ,若AB =6,CE =1,则CD =________,OC =_________.43.(常州市)如果把人的头顶和脚底分别看作一个点,把地球赤道作一个圆,那么身高压2米的汤姆沿着地球赤道环道环行一周,他的头顶比脚底多行________米.44.(海南省)已知:⊙O 的半径为1,M 为⊙O 外的一点,MA 切⊙O 于点A ,MA =1.若AB 是⊙O 的弦,且AB =2,则MB 的长度为_________.45.(武汉市)如果圆的半径为4厘米,那么它的周长为__________厘米.三、解答题:1.(苏州市)已知:如图,△ABC 内接于⊙O ,过点B 作⊙O 的切线,交CA的延长线于点E ,∠EBC =2∠C .①求证:AB =AC ;②若tan ∠ABE =21,(ⅰ)求BCAB 的值;(ⅱ)求当AC =2时,AE 的长.2.(广州市)如图,PA 为⊙O 的切线,A 为切点,⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ,PA =8cm ,PB =4cm ,求⊙O 的半径.3.(河北省)已知:如图,BC 是⊙O 的直径,AC 切⊙O 于点C ,AB 交⊙O 于点D ,若AD ︰DB =2︰3,AC =10,求sin B 的值.4.(北京市海淀区)如图,PC 为⊙O 的切线,C 为切点,PAB 是过O 的割线,CD ⊥AB 于点D ,若tan B =21,PC =10cm ,求三角形BCD 的面积.5.(宁夏回族自治区)如图,在两个半圆中,大圆的弦MN 与小圆相切,D 为切点,且MN ∥AB ,MN =a ,ON 、CD 分别为两圆的半径,求阴影部分的面积.6.(四川省)已知,如图,以△ABC 的边AB 作直径的⊙O ,分别并AC 、BC 于点D 、E ,弦FG ∥AB ,S △CDE ︰S △ABC =1︰4,DE =5cm ,FG =8cm ,求梯形AFGB 的面积.7.(贵阳市)如图所示:PA 为⊙O 的切线,A 为切点,PBC 是过点O 的割线,PA =10,PB =5,求:(1)⊙O 的面积(注:用含π的式子表示);(2)cos ∠BAP 的值.参考答案一、选择题1.B 2.B 3.D 4.D 5.C6.C 7.A 8.C 9.D 10.B 11.A 12.B 13.C 14.D 15.D 16.A 17.B 18.C 19.C20.B 21.C 22.A 23.A 24.B 25.B 26.D 27.D 28.C 29.A 30.B 31.A 32.A33.B 34.C 35.A 36.D 37.B 38.B 39.B 40.B 41.C 42.D 43.A 44.C 45.B46.C 47.A 48.B 49.C 50.C二、填空题1.50 2.2π 3.18π 4.4105.7-⨯ 5.5 6.5 7.30° 8.9 9.25 10.h =r 11.4212.3或4 13.60°或120° 14.8252425-π 15.1:2 16.30 17.80π或120π 18.100° 19.22 20.π 21.1:4 22.1 23.288 24.4 25.2 26.15π 27.()a 23+ 28.3π 29.27π平方厘米 30.4 31.34 32.24π平方厘米或36π平方厘米 33.23 34.4 35.774 36.12π 37.2,3 38.132 39.213- 40.24,240π 41.60°,33 42.9,4 43.4π 44.1或5 45.8π三、解答题:1.(1)∵ BE 切⊙O 于点B ,∴ ∠ABE =∠C .∵ ∠EBC =2∠C ,即 ∠ABE +∠ABC =2∠C ,∴ ∠C +∠ABC =2∠C ,∴ ∠ABC =∠C ,∴ AB =AC .(2)①连结AO ,交BC 于点F ,∵ AB =AC ,∴=,∴ AO ⊥BC 且BF =FC .在Rt △ABF 中,BFAF =tan ∠ABF , 又 tan ∠ABF =tan C =tan ∠ABE =21,∴ BF AF =21, ∴ AF =21BF . ∴ AB =22BF AF +=2221BF BF +⎪⎭⎫ ⎝⎛=25BF . ∴ 452==BF AB BC AB . ②在△EBA 与△ECB 中,∵ ∠E =∠E ,∠EBA =∠ECB ,∴ △EBA ∽△ECB .∴ ⎪⎩⎪⎨⎧⋅==EC EA BE BC AB EB EA 2,解之,得516EA 2=EA ·(EA +AC ),又EA ≠0,∴ 511EA =AC ,EA =115×2=1110. 2.设⊙的半径为r ,由切割线定理,得PA 2=PB ·PC ,∴ 82=4(4+2r ),解得r =6(cm ).即⊙O 的半径为6cm .3.由已知AD ︰DB =2︰3,可设AD =2k ,DB =3k (k >0). ∵ AC 切⊙O 于点C ,线段ADB 为⊙O 的割线,∴ AC 2=AD ·AB ,∵ AB =AD +DB =2k +3k =5k ,∴ 102=2k ×5k ,∴ k 2=10,∵ k >0,∴ k =10.∴ AB =5k =510.∵ AC 切⊙O 于C ,BC 为⊙O 的直径,∴ AC ⊥BC .在Rt △ACB 中,sin B =51010510==AB AC .4.解法一:连结AC .∵ AB 是⊙O 的直径,点C 在⊙O 上,∴ ∠ACB =90°.CD ⊥AB 于点D ,∴ ∠ADC =∠BDC =90°,∠2=90°-∠BAC =∠B . ∵ tan B =21,∴ tan ∠2=21.∴ CB ACDB CDCD AD ===21.设AD =x (x >0),CD =2x ,DB =4x ,AB =5x .∵ PC 切⊙O 于点C ,点B 在⊙O 上,∴ ∠1=∠B . ∵ ∠P =∠P ,∴ △PAC ∽△PCB ,∴ 21==CB AC PC PA.∵ PC =10,∴ PA =5,∵ PC 切⊙O 于点C ,PAB 是⊙O 的割线,∵ PC 2=PA ·PB ,∴ 102=5(5+5 x ).解得x =3.∴ AD =3,CD =6,DB =12.∴ S △BCD =21CD ·DB =21×6×12=36.即三角形BCD 的面积36cm 2.解法二:同解法一,由△PAC ∽△PCB ,得21==CB AC PC PA.∵ PA =10,∴ PB =20.由切割线定理,得PC 2=PA ·PB .∴ PA =201022-PB PC =5,∴ AB =PB -PA =15,∵ AD +DB =x +4x =15,解得x =3,∴ CD =2x =6,DB =4x =12.∴ S △BCD =21CD ·DB =21×6×12=36.即三角形BCD 的面积36cm 2.5.解:如图取MN 的中点E ,连结OE ,∴ OE ⊥MN ,EN =21MN =21a .在四边形EOCD 中,∵ CO ⊥DE ,OE ⊥DE ,DE ∥CO ,∴ 四边形EOCD 为矩形.∴ OE =CD ,在Rt △NOE 中,NO 2-OE 2=EN 2=22⎪⎭⎫⎝⎛a .∴ S 阴影=21π(NO 2-OE 2)=21π·22⎪⎭⎫ ⎝⎛a =28πa .6.解:∵ ∠CDE =∠CBA ,∠DCE =∠BCA ,∴ △CDE ∽△ABC .∴ 2⎪⎭⎫ ⎝⎛=∆∆ABDE S S ABC CDE∴ AB DE =ABC CDES S ∆∆=41=21,即215=AB ,解得 AB =10(cm ),作OM ⊥FG ,垂足为M ,则FM =21FG =21×8=4(cm ),连结OF ,∵ OA =21AB =21×10=5(cm ).∴ OF =OA =5(cm ).在Rt △OMF 中,由勾股定理,得OM =22FM OF -=2245-=3(cm ).∴ 梯形AFGB 的面积=2FGAB +·OM =2810⨯×3=27(cm 2).7.⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(⇒PA 2=PB ·PC ⇒PC =20⇒半径为7.5⇒圆面积为π4225(或56.25π)(平方单位).⎭⎬⎫∠=∠∠=∠P P B A PC )2(⇒△ACP ∽△BAP ⇒PB PAAB AC=⇒12=AB AC.解法一:设AB =x ,AC =2x ,BC 为⊙O 的直径⇒∠CAB =90°,则 BC =5x .∵ ∠BAP =∠C ,∴ cos ∠BAP =cos ∠C =55252==xx BC AC 解法二:设AB =x ,在Rt △ABC 中,AC 2+AB 2=BC 2,即 x 2+(2x )2=152,解之得 x =35,∴ AC =65, ∵ ∠BAP =∠C ,∴∴ cos ∠BAP =cos ∠C =5521556==BC AC。
初三圆试题及答案数学

初三圆试题及答案数学
一、选择题
1. 已知圆的半径为5,圆心到直线的距离为3,则直线与圆的位置关系是()
A. 相离
B. 相切
C. 相交
D. 圆内
答案:C
2. 圆的周长为62.8,则圆的半径是()
A. 10
B. 5
C. 3
D. 2
答案:A
二、填空题
1. 圆的直径为10,则圆的周长是______。
答案:31.4
2. 一个圆的面积为28.26平方厘米,那么它的半径是______。
答案:3厘米
三、解答题
1. 已知圆的半径为7,求圆的面积。
答案:圆的面积公式为S=πr²,所以面积S=3.14×7²=153.86平方
厘米。
2. 一个圆的直径增加2厘米,求圆的面积增加多少。
答案:设原圆的半径为r,则增加后的半径为r+1。
原圆面积为πr²,增加后的圆面积为π(r+1)²。
面积增加量为π(r+1)²-
πr²=π(2r+1)。
中考数学复习《圆》专题训练-附带参考答案

中考数学复习《圆》专题训练-附带参考答案一、选择题1.下列语句:①长度相等的弧是等弧;②过平面内三点可以作一个圆;③平分弦的直径垂直于弦;④90°的圆周角所对的弦是直径;⑤等弦对等弧.其中正确的个数是( )A .1个B .2个C .3个D .4个2.如图,点A ,B ,C 在⊙O 上,∠C =44°,则∠AOB 的大小为( )A .22°B .88°C .66°D .70°3.已知扇形的圆心角为120°,半径为3cm ,则弧长为( )A .2π3cmB .2πcmC .4cmD .π3cm 4.如图,⊙O 中,弦AB ⊥CD 于E ,若∠A =30°,⊙O 的半径等于6,则弧AC 的长为( )A .6πB .5πC .4πD .3π5.如图,⊙O 的半径为9,PA 、PB 分别切⊙O 于点A ,B.若P =60∘,则AB⌢的长为( )A .133πB .136πC .6πD .52π 6.如图,四边形ABCD 是⊙O 的内接四边形,点D 是AC ⌢的中点,点E 是BC ⌢上的一点,若∠ADC =110°,则∠DEC的度数是( )A .35°B .45°C .50°D .55°7.如图,正六边形ABCDEF内接于00,若0 O的周长等于6π,则正六边形的边长为()A.√3B.3 C.2√3D.√68.如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为()A.2πB.2√2C.2π−4D.2π−2√2二、填空题9.如图,AB,CD是⊙O的弦,连结AD,延长AB,CD相交于点P,已知∠P=30°,∠ADC=40°,则BD 的度数是.10.如图,AB为⊙O的切线点A为切点,OB交⊙O于点C,点D在⊙O上,连接AD、CD、OA,若∠ADC=25°,则∠ABO的度数为.11.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若⊙O半径是4,∠B=22.5°,那么BC的长是.12.如图,正六边形ABCDEF内接于⊙O,连接OC、OD,若OC长为2cm,则正六形ABCDEF的周长为cm.13.如图,在矩形ABCD中AB=2√3,以点A为圆心,AD长为半径画弧交BC于点E,连接AE,∠BAE=30°则阴影部分的面积为.三、解答题14.如图,在⊙O中AB=CD,弦AB与CD相交于点M.⌢=BD⌢.(1)求证:AC(2)连接AC,AD,若AD是⊙O的直径.求证:∠BAC+2∠BAD=90∘.15.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上∠PBC=∠C.(1)求证:CB∥PD;(2)若CD=8,BE=2,求⊙O的半径.⌢的中点,过D作DE∥AC,交OC的延16.如图,AB为半圆O的直径,C为半圆上一点,连接AC,点D为AC长线于点E.(1)求证:DE是半圆O的切线.(2)若OC=3,CE=2求AC的长.17.如图,△ABC内接于⊙O,AB=AC=10,BC=12,点E为上一点,点F为的中点,连结BF并延长与AE交于点G,连结AF,CF.(1)求证:∠AFC=∠AFG.(2)当BG经过圆心O时,求FG的长.18.如图,在中AB=AC以为直径的分别与、相交于点D、E,连接过点D 作,垂足为点(1)求证:是的切线;(2)若的半径为4,求图中阴影部分的面积.参考答案1.A2.B3.B4.B5.C6.A7.B8.C9.20°10.40°11.4+4√212.12π13.6√3−8314.(1)解:证明:∵AB=CD⌢=CD⌢∴AB⌢+BC⌢=BD⌢+BC⌢∴AC⌢=BD⌢.∴AC⌢=BD⌢(2)证明:∵AC∴∠ADC=∠BAD∴∠AMC=∠MAD+∠MDA=2∠BAD∵AD是⊙O的直径∴∠ACD=90°∴∠BAC+∠AMC=90°∴∠BAC+2∠BAD=90°.15.(1)证明:∵∠P=∠C,∠PBC=∠C ∴∠P=∠PBC∴CB∥PD;(2)解:连接CO设CO=x,则BO=x∵弦CD⊥AB于点E CD=8∴CE=4∵BE=2∴EO=x−2在Rt△COE中:CO2=CE2+OE2∴x2=42+(x−2)2解得:x=5∴⊙O的半径为5.16.(1)证明:如图,连接OD交AC于点F.⌢的中点∵D是AC⌢=CD⌢∴AD∴∠AOD=∠COD∵OC=OA∴OD⊥AC∵DE∥AC∴OD⊥DE∴DE是半圆O的切线.(2)解:∵OC=3,CE=2∴OE=5,OD=OC=3∴在Rt△ODE中DE=√OE2−OD2=√52−32=4∴cosE=DEOE =45∵AC∥DE∴∠FCO=∠E∴cos∠FCO=45∴FC=OC⋅cos∠FCO=3×45=125∵OD⊥AC∴AC=2FC=245.17.(1)证明:∵AB=AC∴∠ABC=∠ACB∵∠ACB=∠AFB∴∠ABC=∠AFB∵∠ABC+∠AFC=180°,∠AFG+∠AFB=180°∴∠AFC=∠AFG;(2)解:连结AO并延长AO交于点H,如图∵AB=AC∴∴AH⊥BC,BH=CH=6∴AH8设OH=x,则OA=OB=8﹣x在Rt△OBH中,x2+62=(8﹣x)2解得x∵OB=OF,BH=CH∴OH是Rt△BCF的中位线∴CF=2OH∵点F为的中点∴∠EAF=∠CAF在△AFG和△AFC中∴△AFG≌△AFC(ASA)∴FG=FC.18.(1)证明:连接.是的直径.又AB=AC,∴D是BC的中点.连接;由中位线定理,知又.是的切线;(2)解:连接的半径为。
(完整版)圆中考试题集锦(附答案)

圆中考试题一、选择题1.(北京市西城区)如图,BC 是⊙O 的直径,P 是CB 延长线上一点,PA 切⊙O于点A ,如果PA =3,PB =1,那么∠APC 等于 ()(A )ο15 (B )ο30 (C )ο45 (D )ο602.(北京市西城区)如果圆柱的高为20厘米,底面半径是高的41,那么这个圆柱的侧面积是 ()(A )100π平方厘米 (B )200π平方厘米(C )500π平方厘米 (D )200平方厘米3.(北京市西城区)“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题,“今在圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为E ,CE =1寸,AB =10寸,求直径CD 的长”.依题意,CD 长为 ( )(A )225寸 (B )13寸 (C )25寸 (D )26寸 4.(北京市朝阳区)已知:如图,⊙O 半径为5,PC 切⊙O 于点C ,PO 交⊙O 于点A ,PA =4,那么PC 的长等于 ( )(A )6 (B )25 (C )210 (D )2145.(北京市朝阳区)如果圆锥的侧面积为20π平方厘米,它的母线长为5厘米,那么此圆锥的底面半径的长等于 ( )(A )2厘米 (B )22厘米 (C )4厘米 (D )8厘米6.(天津市)相交两圆的公共弦长为16厘米,若两圆的半径长分别为10厘米和17厘米,则这两圆的圆心距为 ( )(A )7厘米 (B )16厘米 (C )21厘米 (D )27厘米7.(重庆市)如图,⊙O 为△ABC 的内切圆,∠C =ο90,AO 的延长线交BC 于点D ,AC =4,DC =1,,则⊙O 的半径等于 ( )(A )54 (B )45 (C )43 (D )65 8.(重庆市)一居民小区有一正多边形的活动场.为迎接“AAPP ”会议在重庆市的召开,小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台,花台都以多边形的顶点为圆心,比多边形的内角为圆心角,花台占地面积共为12π平方米.若每个花台的造价为400元,则建造这些花台共需资金 ( )(A )2400元 (B )2800元 (C )3200元 (D )3600元9.(河北省)如图,AB 是⊙O 直径,CD 是弦.若AB =10厘米,CD =8厘米,那么A 、B 两点到直线CD 的距离之和为 ( )(A )12厘米 (B )10厘米 (C )8厘米 (D )6厘米10.(河北省)某工件形状如图所示,圆弧BC 的度数为ο60,AB =6厘米,点B 到点C 的距离等于AB ,∠BAC =ο30,则工件的面积等于 ( )(A )4π (B )6π (C )8π (D )10π11.(沈阳市)如图,PA 切⊙O 于点A ,PBC 是⊙O 的割线且过圆心,PA =4,PB =2,则⊙O 的半径等于 ( )(A )3 (B )4 (C )6 (D )812.(哈尔滨市)已知⊙O 的半径为35厘米,⊙O '的半径为5厘米.⊙O 与⊙O '相交于点D 、E .若两圆的公共弦DE 的长是6厘米(圆心O 、O '在公共弦DE 的两侧),则两圆的圆心距O O '的长为 ( )(A )2厘米 (B )10厘米 (C )2厘米或10厘米 (D )4厘米13.(陕西省)如图,两个等圆⊙O 和⊙O '的两条切线OA 、OB ,A 、B 是切点,则∠AOB 等于 ( )(A )ο30 (B )ο45 (C )ο60 (D )ο9014.(甘肃省)如图,AB 是⊙O 的直径,∠C =ο30,则∠ABD = ( )(A )ο30 (B )ο40 (C )ο50 (D )ο6015.(甘肃省)弧长为6π的弧所对的圆心角为ο60,则弧所在的圆的半径为( )(A )6 (B )62 (C )12 (D )1816.(甘肃省)如图,在△ABC 中,∠BAC =ο90,AB =AC =2,以AB 为直径的圆交BC 于D ,则图中阴影部分的面积为 ( )(A )1 (B )2 (C )1+4π (D )2-4π 17.(宁夏回族自治区)已知圆的内接正六边形的周长为18,那么圆的面积为 ( )(A )18π (B )9π (C )6π (D )3π18.(山东省)如图,点P 是半径为5的⊙O 内一点,且OP =3,在过点P的所有弦中,长度为整数的弦一共有 ( )(A )2条 (B )3条 (C )4条 (D )5条19.(南京市)如图,正六边形ABCDEF 的边长的上a ,分别以C 、F 为圆心,a 为半径画弧,则图中阴影部分的面积是 ( )(A )261a π (B )231a π (C )232a π (D )234a π20.(杭州市)过⊙O 内一点M 的最长的弦长为6厘米,最短的弦长为4厘米,则OM 的长为 ( )(A )3厘米 (B )5厘米 (C )2厘米 (D )5厘米21.(安徽省)已知圆锥的底面半径是3,高是4,则这个圆锥侧面展开图的面积是 ( )(A )12π (B )15π (C )30π (D )24π22.(安微省)已知⊙O 的直径AB 与弦AC 的夹角为ο30,过C 点的切线PC 与AB 延长线交P .PC =5,则⊙O 的半径为 ( )(A )335 (B )635 (C )10 (D )5 23.(福州市)如图:PA 切⊙O 于点A ,PBC 是⊙O 的一条割线,有PA=32,PB =BC ,那么BC 的长是 ( )(A )3 (B )32 (C )3 (D )3224.(河南省)如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是 ( )(A )π (B )1.5π (C )2π (D )2.5π25.(四川省)正六边形的半径为2厘米,那么它的周长为 ( )(A )6厘米 (B )12厘米 (C )24厘米 (D )122厘米26.(四川省)一个圆柱形油桶的底面直径为0.6米,高为1米,那么这个油桶的侧面积为 ( )(A )0.09π平方米 (B )0.3π平方米 (C )0.6平方米 (D )0.6π平方米27.(贵阳市)一个形如圆锥的冰淇淋纸筒,其底面直径为6厘米,母线长为5厘米,围成这样的冰淇淋纸筒所需纸片的面积是 ( )(A )66π平方厘米 (B )30π平方厘米 (C )28π平方厘米 (D )15π平方厘米28.(新疆乌鲁木齐)在半径为2的⊙O 中,圆心O 到弦AB 的距离为1,则弦AB 所对的圆心角的度数可以是 ( )(A )ο60 (B )ο90 (C )ο120 (D )ο15029.(新疆乌鲁木齐)将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面,(接口损耗不计),则桶底的面积为 ( )(A )π1600平方厘米 (B )1600π平方厘米(C )π6400平方厘米 (D )6400π平方厘米 30.(成都市)如图,已知AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD =10厘米,AP ∶PB =1∶5,那么⊙O 的半径是 ( )(A )6厘米 (B )53厘米 (C )8厘米 (D )35厘米31.(成都市)在Rt △ABC 中,已知AB =6,AC =8,∠A =ο90.如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥,其表面积为S 1;把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥,其表面积为S 2,那么S 1∶S 2等于 ( )(A )2∶3 (B )3∶4 (C )4∶9 (D )5∶1232.(苏州市)如图,⊙O 的弦AB =8厘米,弦CD 平分AB 于点E .若CE =2厘米.ED 长为 ( )(A )8厘米 (B )6厘米 (C )4厘米 (D )2厘米 33.(苏州市)如图,四边形ABCD 内接于⊙O ,若∠BOD =ο160,则∠BCD = ( )(A )ο160 (B )ο100 (C )ο80 (D )ο2034.(镇江市)如图,正方形ABCD 内接于⊙O ,E 为DC 的中点,直线BE交⊙O 于点F .若⊙O 的半径为2,则BF 的长为 ( )(A )23 (B )22 (C )556 (D )554 35.(扬州市)如图,AB 是⊙O 的直径,∠ACD =ο15,则∠BAD 的度数为 ( )(A )ο75 (B )ο72 (C )ο70 (D )ο6536.(扬州市)已知:点P 直线l 的距离为3,以点P 为圆心,r 为半径画圆,如果圆上有且只有两点到直线l 的距离均为2,则半径r 的取值范围是 ( )(A )r >1 (B )r >2 (C )2<r <3 (D )1<r <537.(绍兴市)边长为a 的正方边形的边心距为 ( )(A )a (B )23a (C )3a (D )2a 38.(绍兴市)如图,以圆柱的下底面为底面,上底面圆心为顶点的圆锥的母线长为4,高线长为3,则圆柱的侧面积为 ( )(A )30π (B )76π (C )20π (D )74π39.(昆明市)如图,扇形的半径OA =20厘米,∠AOB =ο135,用它做成一个圆锥的侧面,则此圆锥底面的半径为 ( )(A )3.75厘米 (B )7.5厘米 (C )15厘米 (D )30厘米40.(昆明市)如图,正六边形ABCDEF 中.阴影部分面积为123平方厘米,则此正六边形的边长为 ( )(A )2厘米 (B )4厘米 (C )6厘米 (D )8厘米41.(温州市)已知扇形的弧长是2π厘米,半径为12厘米,则这个扇形的圆心角是 ( )(A )ο60 (B )ο45 (C )ο30 (D )ο2042.(温州市)圆锥的高线长是厘米,底面直径为12厘米,则这个圆锥的侧面积是 ( )(A )48π厘米 (B )24π13平方厘米(C )48π13平方厘米 (D )60π平方厘米43.(温州市)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PC是⊙O 的切线,C 为切点,PC =26,PA =4,则⊙O 的半径等于 ( )(A )1 (B )2 (C )23 (D )26 44.(常州市)已知圆柱的母线长为5厘米,表面积为28π平方厘米,则这个圆柱的底面半径是( )(A )5厘米 (B )4厘米 (C )2厘米 (D )3厘米45.(常州市)半径相等的圆内接正三角形、正方形、正六边形的边长之比为 ( )(A )1∶2∶3 (B )3∶2∶1(C )3∶2∶1 (D )1∶2∶346.(广东省)如图,若四边形ABCD 是半径为1和⊙O 的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为 ( )(A )(2π-2)厘米 (B )(2π-1)厘米(C )(π-2)厘米 (D )(π-1)厘米47.(武汉市)如图,已知圆心角∠BOC =ο100,则圆周角∠BAC 的度数是( )(A )ο50 (B )ο100 (C )ο130 (D )ο20048.(武汉市)半径为5厘米的圆中,有一条长为6厘米的弦,则圆心到此弦的距离为 ( )(A )3厘米 (B )4厘米 (C )5厘米 (D )6厘米49.已知:Rt △ABC 中,∠C =ο90,O 为斜边AB 上的一点,以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ,若AC =1,BC =3,则⊙O 的半径为 ( )(A )21 (B )32 (C )43 (D )54 50.(武汉市)已知:如图,E 是相交两圆⊙M 和⊙O 的一个交点,且ME ⊥NE ,AB 为外公切线,切点分别为A 、B ,连结AE 、BE .则∠AEB 的度数为 ( )(A )145° (B )140° (C )135° (D )130°二、填空题1.(北京市东城区)如图,AB 、AC 是⊙O 的两条切线,切点分别为B 、C ,D 是优弧上的一点,已知∠BAC =ο80,那么∠BDC =__________度.2.(北京市东城区)在Rt △ABC 中,∠C =ο90,A B=3,BC =1,以AC 所在直线为轴旋转一周,所得圆锥的侧面展开图的面积是__________.3.(北京市海淀区)如果圆锥母线长为6厘米,那么这个圆锥的侧面积是_______平方厘米4.(北京市海淀区)一种圆状包装的保鲜膜,如图所示,其规格为“20厘米×60米”,经测量这筒保鲜膜的内径1ϕ、外径2ϕ的长分别为3.2厘米、4.0厘米,则该种保鲜膜的厚度约为_________厘米(π取3.14,结果保留两位有效数字).5.(上海市)两个点O 为圆心的同心圆中,大圆的弦AB 与小圆相切,如果AB 的长为24,大圆的半径OA 为13,那么小圆的半径为___________.6.(天津市)已知⊙O 中,两弦AB 与CD 相交于点E ,若E 为AB 的中点,CE ∶ED =1∶4,AB =4,则CD 的长等于___________.7.(重庆市)如图,AB 是⊙O 的直径,四边形ABCD 内接于⊙O ,,,的度数比为3∶2∶4,MN 是⊙O 的切线,C 是切点,则∠BCM 的度数为___________.8.(重庆市)如图,P 是⊙O 的直径AB 延长线上一点,PC 切⊙O 于点C ,PC =6,BC ∶AC =1∶2,则AB 的长为___________.9.(重庆市)如图,四边形ABCD 内接于⊙O ,AD ∥BC ,=,若AD =4,BC =6,则四边形ABCD 的面积为__________.10.(山西省)若一个圆柱的侧面积等于两底面积的和,则它的高h 与底面半径r 的大小关系是__________. 11.(沈阳市)要用圆形铁片截出边长为4厘米的正方形铁片,则选用的圆形铁片的直径最小要___________厘米.12.(沈阳市)圆内两条弦AB 和CD 相交于P 点,AB 长为7,AB 把CD 分成两部分的线段长分别为2和6,那么=__________.13.(沈阳市)△ABC 是半径为2厘米的圆内接三角形,若BC =23厘米,则∠A 的度数为________.14.(沈阳市)如图,已知OA 、OB 是⊙O 的半径,且OA =5,∠AOB =15ο,AC⊥OB 于C ,则图中阴影部分的面积(结果保留π)S =_________.15.(哈尔滨市)如图,圆内接正六边形ABCDEF 中,AC 、BF 交于点M .则ABM S △∶AFM S △=_________.16.(哈尔滨市)两圆外离,圆心距为25厘米,两圆周长分别为15π厘米和10π厘米.则其内公切线和连心线所夹的锐角等于__________度.17.(哈尔滨市)将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周,所得圆柱体的表面积为_________平方厘米.18.(陕西省)如图,在⊙O 的内接四边形ABCD 中,∠BCD =130ο,则∠BOD的度数是________.19.(陕西省)已知⊙O 的半径为4厘米,以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积,则这个小圆的半径是______厘米.20.(陕西省)如图,⊙O 1的半径O 1A 是⊙O 2的直径,C 是⊙O 1上的一点,O 1C 交⊙O 2于点B .若⊙O 1的半径等于5厘米,的长等于⊙O 1周长的101,则的长是_________. 21.(甘肃省)正三角形的内切圆与外接圆面积之比为_________.22.(甘肃省)如图,AB =8,AC =6,以AC 和BC 为直径作半圆,两圆的公切线MN 与AB 的延长线交于D ,则BD 的长为_________.23.(宁夏回族自治区)圆锥的母线长为5厘米,高为3厘米,在它的侧面展开图中,扇形的圆心角是_________度.24.(南京市)如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足是G ,F 是CG 的中点,延长AF 交⊙O 于E ,CF =2,AF =3,则EF 的长是_________.25.(福州市)在⊙O 中,直径AB =4厘米,弦CD ⊥AB 于E ,OE =3,则弦CD 的长为__________厘米.26.(福州市)若圆锥底面的直径为厘米,线线长为5厘米,则它的侧面积为__________平方厘米(结果保留π).27.(河南省)如图,AB 为⊙O 的直径,P 点在AB 的延长线上,PM 切⊙O 于M 点.若OA =a ,PM =3a ,那么△PMB 的周长的__________.28.(长沙市)在半径9厘米的圆中,ο60的圆心角所对的弧长为__________厘米.29.(四川省)扇形的圆心角为120ο,弧长为6π厘米,那么这个扇形的面积为_________.30.(贵阳市)如果圆O 的直径为10厘米,弦AB 的长为6厘米,那么弦AB 的弦心距等于________厘米.31.(贵阳市)某种商品的商标图案如图所求(阴影部分),已知菱形ABCD的边长为4,∠A =ο60,是以A 为圆心,AB 长为半径的弧,是以B 为圆心,BC 长为半径的弧,则该商标图案的面积为_________.32.(云南省)已知,一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周,所得圆锥的表面积是__________.33.(新疆乌鲁木齐)正六边形的边心距与半径的比值为_________.34.(新疆乌鲁木齐)如图,已知扇形AOB 的半径为12,OA ⊥OB ,C 为OA 上一点,以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切,则半圆1O 的半径为__________.35.(成都市)如图,PA、PB与⊙O分别相切于点A、点B,AC是⊙O60,AC=2,那么CD的长为的直径,PC交⊙O于点D.已知∠APB=ο________.36.(苏州市)底面半径为2厘米,高为3厘米的圆柱的体积为_________立方厘米(结果保留π).37.(扬州市)边长为2厘米的正六边形的外接圆半径是________厘米,内切圆半径是________厘米(结果保留根号).38.(绍兴市)如图,PT是⊙O的切线,T为切点,PB是⊙O的割线交⊙O于A、B两点,交弦CD于点M,已知:CM=10,MD=2,PA=MB=4,则PT的长等于__________.90,半径OA=1,C是线段AB39.(温州市)如图,扇形OAB中,∠AOB=ο的中点,CD∥OA,交于点D,则CD=________.40.(常州市)已知扇形的圆心角为150ο,它所对的弧长为20π厘米,则扇形的半径是________厘米,扇形的面积是__________平方厘米.41.(常州市)如图,AB是⊙O直径,CE切⊙O于点C,CD⊥AB,D为垂足,AB=12厘米,∠B=30ο,则∠ECB=__________ο;CD=_________厘米.42.(常州市)如图,DE是⊙O直径,弦AB⊥DE,垂足为C,若AB=6,CE=1,则CD=________,OC=_________.43.(常州市)如果把人的头顶和脚底分别看作一个点,把地球赤道作一个圆,那么身高压2米的汤姆沿着地球赤道环道环行一周,他的头顶比脚底多行________米.44.(海南省)已知:⊙O的半径为1,M为⊙O外的一点,MA切⊙O于点A,MA=1.若AB是⊙O 的弦,且AB=2,则MB的长度为_________.45.(武汉市)如果圆的半径为4厘米,那么它的周长为__________厘米.三、解答题:1.(苏州市)已知:如图,△ABC 内接于⊙O ,过点B 作⊙O 的切线,交CA 的延长线于点E ,∠EBC =2∠C .①求证:AB =AC ;②若tan ∠ABE =21,(ⅰ)求BC AB 的值;(ⅱ)求当AC =2时,AE 的长.2.(广州市)如图,PA 为⊙O 的切线,A 为切点,⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ,PA =8cm ,PB =4cm ,求⊙O 的半径.3.(河北省)已知:如图,BC 是⊙O 的直径,AC 切⊙O 于点C ,AB 交⊙O 于点D ,若AD ︰DB =2︰3,AC =10,求sin B 的值.4.(北京市海淀区)如图,PC 为⊙O 的切线,C 为切点,PAB 是过O 的割线,CD ⊥AB 于点D ,若tan B =21,PC =10cm ,求三角形BCD 的面积.5.(宁夏回族自治区)如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积.6.(四川省)已知,如图,以△ABC的边AB作直径的⊙O,分别并AC、BC于点D、E,弦FG∥AB,S△CDE︰S△ABC=1︰4,DE=5cm,FG=8cm,求梯形AFGB的面积.7.(贵阳市)如图所示:PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,求:(1)⊙O的面积(注:用含π的式子表示);(2)cos∠BAP的值.参考答案 一、选择题 1.B 2.B 3.D 4.D 5.C6.C 7.A 8.C 9.D 10.B 11.A 12.B 13.C 14.D 15.D 16.A 17.B 18.C 19.C20.B 21.C 22.A 23.A 24.B 25.B 26.D 27.D 28.C 29.A 30.B 31.A 32.A33.B 34.C 35.A 36.D 37.B 38.B 39.B 40.B 41.C 42.D 43.A 44.C 45.B46.C 47.A 48.B 49.C 50.C二、填空题1.50 2.2π 3.18π 4.4105.7-⨯ 5.5 6.5 7.30° 8.9 9.25 10.h =r 11.42 12.3或4 13.60°或120° 14.8252425-π 15.1:2 16.30 17.80π或120π 18.100° 19.22 20.π 21.1:4 22.1 23.288 24.4 25.2 26.15π 27.()a 23+ 28.3π 29.27π平方厘米 30.4 31.34 32.24π平方厘米或36π平方厘米 33.23 34.4 35.774 36.12π 37.2,3 38.132 39.213- 40.24,240π 41.60°,33 42.9,4 43.4π 44.1或5 45.8π三、解答题:1.(1)∵ BE 切⊙O 于点B ,∴ ∠ABE =∠C .∵ ∠EBC =2∠C ,即 ∠ABE +∠ABC =2∠C ,∴ ∠C +∠ABC =2∠C ,∴ ∠ABC =∠C ,∴ AB =AC .(2)①连结AO ,交BC 于点F ,∵ AB =AC ,∴ =,∴ AO ⊥BC 且BF =FC .在Rt △ABF 中,BFAF =tan ∠ABF , 又 tan ∠ABF =tan C =tan ∠ABE =21,∴ BF AF =21, ∴ AF =21BF .∴ AB =22BF AF +=2221BF BF +⎪⎭⎫ ⎝⎛=25BF . ∴ 452==BF AB BC AB . ②在△EBA 与△ECB 中,∵ ∠E =∠E ,∠EBA =∠ECB ,∴ △EBA ∽△ECB .∴ ⎪⎩⎪⎨⎧⋅==EC EA BE BC AB EB EA 2,解之,得516EA 2=EA ·(EA +AC ),又EA ≠0, ∴ 511EA =AC ,EA =115×2=1110. 2.设⊙的半径为r ,由切割线定理,得PA 2=PB ·PC ,∴ 82=4(4+2r ),解得r =6(cm ).即⊙O 的半径为6cm .3.由已知AD ︰DB =2︰3,可设AD =2k ,DB =3k (k >0).∵ AC 切⊙O 于点C ,线段ADB 为⊙O 的割线,∴ AC 2=AD ·AB ,∵ AB =AD +DB =2k +3k =5k ,∴ 102=2k ×5k ,∴ k 2=10,∵ k >0,∴ k =10.∴ AB =5k =510.∵ AC 切⊙O 于C ,BC 为⊙O 的直径,∴ AC ⊥BC .在Rt △ACB 中,sin B =51010510==AB AC . 4.解法一:连结AC .∵ AB 是⊙O 的直径,点C 在⊙O 上,∴ ∠ACB =90°.CD ⊥AB 于点D ,∴ ∠ADC =∠BDC =90°,∠2=90°-∠BAC =∠B .∵ tan B =21, ∴ tan ∠2=21. ∴ CB AC DB CD CD AD ===21. 设AD =x (x >0),CD =2x ,DB =4x ,AB =5x .∵ PC 切⊙O 于点C ,点B 在⊙O 上,∴ ∠1=∠B .∵ ∠P =∠P ,∴ △PAC ∽△PCB ,∴ 21==CB AC PC PA . ∵ PC =10,∴ PA =5,∵ PC 切⊙O 于点C ,PAB 是⊙O 的割线,∵ PC 2=PA ·PB ,∴ 102=5(5+5 x ).解得x =3.∴ AD =3,CD =6,DB =12.∴ S △BCD =21CD ·DB =21×6×12=36. 即三角形BCD 的面积36cm 2.解法二:同解法一,由△PAC ∽△PCB ,得21==CB AC PC PA . ∵ PA =10,∴ PB =20.由切割线定理,得PC 2=PA ·PB . ∴ PA =201022-PB PC =5,∴ AB =PB -PA =15, ∵ AD +DB =x +4x =15,解得x =3,∴ CD =2x =6,DB =4x =12.∴ S △BCD =21CD ·DB =21×6×12=36.即三角形BCD 的面积36cm 2.5.解:如图取MN 的中点E ,连结OE ,∴ OE ⊥MN ,EN =21MN =21a .在四边形EOCD 中,∵ CO ⊥DE ,OE ⊥DE ,DE ∥CO ,∴ 四边形EOCD 为矩形.∴ OE =CD ,在Rt △NOE 中,NO 2-OE 2=EN 2=22⎪⎭⎫⎝⎛a .∴ S 阴影=21π(NO 2-OE 2)=21π·22⎪⎭⎫ ⎝⎛a =28πa .6.解:∵ ∠CDE =∠CBA ,∠DCE =∠BCA ,∴ △CDE ∽△ABC .∴ 2⎪⎭⎫⎝⎛=∆∆AB DE S S ABC CDE∴ AB DE =ABC CDE S S∆∆=41=21,即215=AB ,解得 AB =10(cm ),作OM ⊥FG ,垂足为M ,则FM =21FG =21×8=4(cm ),连结OF ,∵ OA =21AB =21×10=5(cm ).∴ OF =OA =5(cm ).在Rt △OMF 中,由勾股定理,得OM =22FM OF -=2245-=3(cm ).∴ 梯形AFGB 的面积=2FG AB +·OM =2810⨯×3=27(cm 2). 7. ⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(⇒PA 2=PB ·PC ⇒PC =20⇒半径为7.5⇒圆面积为π4225(或56.25π)(平方单位).⎭⎬⎫∠=∠∠=∠P P BAP C )2(⇒△ACP ∽△BAP ⇒PB PA AB AC =⇒12=AB AC . 解法一:设AB =x ,AC =2x ,BC 为⊙O 的直径⇒∠CAB =90°,则 BC =5x .∵ ∠BAP =∠C ,∴ cos ∠BAP =cos ∠C =55252==xx BC AC 解法二:设AB =x ,在Rt △ABC 中,AC 2+AB 2=BC 2,即 x 2+(2x )2=152,解之得 x =35,∴ AC =65, ∵ ∠BAP =∠C ,∴ ∴ cos ∠BAP =cos ∠C =5521556==BC AC。
经典必考圆中考试题集锦(附答案)
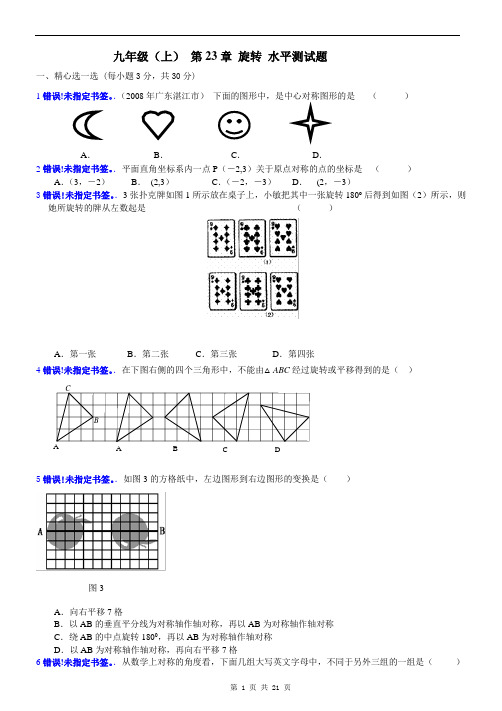
九年级(上) 第23章 旋转 水平测试题一、精心选一选 (每小题3分,共30分)1错误!未指定书签。
.(2008年广东湛江市) 下面的图形中,是中心对称图形的是 ( )A.B .C .D . 2错误!未指定书签。
.平面直角坐标系内一点P (-2,3)关于原点对称的点的坐标是 ( )A .(3,-2)B . (2,3)C .(-2,-3)D . (2,-3) 3错误!未指定书签。
.3张扑克牌如图1所示放在桌子上,小敏把其中一张旋转180º后得到如图(2)所示,则她所旋转的牌从左数起是 ( )A .第一张B .第二张C .第三张D .第四张4错误!未指定书签。
.在下图右侧的四个三角形中,不能由△ABC 经过旋转或平移得到的是( )5错误!未指定书签。
.如图3的方格纸中,左边图形到右边图形的变换是( )A .向右平移7格B .以AB 的垂直平分线为对称轴作轴对称,再以AB 为对称轴作轴对称C .绕AB 的中点旋转1800,再以AB 为对称轴作轴对称D .以AB 为对称轴作轴对称,再向右平移7格 6错误!未指定书签。
.从数学上对称的角度看,下面几组大写英文字母中,不同于另外三组的一组是( )A BC A B C DA .A N E GB .K B X NC .X I H OD .Z D W H 7错误!未指定书签。
.如图4,C 是线段BD 上一点,分别以BC 、CD 为边在BD 同侧作等边△ABC 和等边△CDE,AD 交CE 于F ,BE 交AC 于G ,则图中可通过旋转而相互得到的三角形对数有( ).A .1对B .2对C .3对D .4对 8错误!未指定书签。
.下列这些复杂的图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们中每一个图案都可以由一个“基本图案”通过连续旋转得来,旋转的角度是( )A ︒30B ︒45C ︒60D ︒90 9错误!未指定书签。
.如图5所示,图中的一个矩形是另一个矩形顺时针方向旋转90°后形成的个数是( )A .l 个B .2个C .3个D .4个 10错误!未指定书签。
人教版圆中考试题集锦(附答案)

圆中考经典试题 一、选择题1.(北京市西城区)如图,BC 是⊙O 的直径,P 是CB 延长线上一点,PA 切⊙O于点A ,如果PA =3,PB =1,那么∠APC 等于 ()(A ) 15 (B ) 30 (C ) 45 (D ) 602.(北京市西城区)如果圆柱的高为20厘米,底面半径是高的41,那么这个圆柱的侧面积是 ()(A )100π平方厘米 (B )200π平方厘米(C )500π平方厘米 (D )200平方厘米3.(北京市西城区)“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题,“今在圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为E ,CE =1寸,AB =10寸,求直径CD 的长”.依题意,CD 长为 ( )(A )225寸 (B )13寸 (C )25寸 (D )26寸 4.(北京市朝阳区)已知:如图,⊙O 半径为5,PC 切⊙O 于点C ,PO 交⊙O 于点A ,PA =4,那么PC 的长等于 ( )(A )6 (B )25 (C )210 (D )2145.(北京市朝阳区)如果圆锥的侧面积为20π平方厘米,它的母线长为5厘米,那么此圆锥的底面半径的长等于 ( )(A )2厘米 (B )22厘米 (C )4厘米 (D )8厘米6.(天津市)相交两圆的公共弦长为16厘米,若两圆的半径长分别为10厘米和17厘米,则这两圆的圆心距为 ( )(A )7厘米 (B )16厘米 (C )21厘米 (D )27厘米7.(重庆市)如图,⊙O 为△ABC 的内切圆,∠C =90,AO 的延长线交BC 于点D ,AC =4,DC =1,,则⊙O 的半径等于 ( )(A )54 (B )45 (C )43 (D )65 8.(重庆市)一居民小区有一正多边形的活动场.为迎接“AAPP ”会议在重庆市的召开,小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台,花台都以多边形的顶点为圆心,比多边形的内角为圆心角,花台占地面积共为12π平方米.若每个花台的造价为400元,则建造这些花台共需资金 ( )(A )2400元 (B )2800元 (C )3200元 (D )3600元9.(河北省)如图,AB 是⊙O 直径,CD 是弦.若AB =10厘米,CD=8厘米,那么A 、B 两点到直线CD 的距离之和为 ( )(A )12厘米 (B )10厘米 (C )8厘米 (D )6厘米10.(河北省)某工件形状如图所示,圆弧BC 的度数为60,AB =6厘米,点B 到点C 的距离等于AB ,∠BAC = 30,则工件的面积等于 ( )(A )4π (B )6π (C )8π (D )10π11.(沈阳市)如图,PA 切⊙O 于点A ,PBC 是⊙O 的割线且过圆心,PA =4,PB =2,则⊙O 的半径等于 ( )(A )3 (B )4 (C )6 (D )812.(哈尔滨市)已知⊙O 的半径为35厘米,⊙O '的半径为5厘米.⊙O 与⊙O '相交于点D 、E .若两圆的公共弦DE 的长是6厘米(圆心O 、O '在公共弦DE 的两侧),则两圆的圆心距O O '的长为 ( )(A )2厘米 (B )10厘米 (C )2厘米或10厘米 (D )4厘米13.(陕西省)如图,两个等圆⊙O 和⊙O '的两条切线OA 、OB ,A 、B 是切点,则∠AOB 等于 ( )(A ) 30 (B ) 45 (C ) 60 (D )9014.(甘肃省)如图,AB 是⊙O 的直径,∠C = 30,则∠ABD = ( )(A ) 30 (B ) 40 (C ) 50 (D ) 6015.(甘肃省)弧长为6π的弧所对的圆心角为 60,则弧所在的圆的半径为( )(A )6 (B )62 (C )12 (D )1816.(甘肃省)如图,在△ABC 中,∠BAC = 90,AB =AC =2,以AB 为直径的圆交BC 于D ,则图中阴影部分的面积为 ( )(A )1 (B )2 (C )1+4π (D )2-4π 17.(宁夏回族自治区)已知圆的内接正六边形的周长为18,那么圆的面积为 ( )(A )18π (B )9π (C )6π (D )3π18.(山东省)如图,点P 是半径为5的⊙O 内一点,且OP =3,在过点P的所有弦中,长度为整数的弦一共有 ( )(A )2条 (B )3条 (C )4条 (D )5条19.(南京市)如图,正六边形ABCDEF 的边长的上a ,分别以C 、F 为圆心,a 为半径画弧,则图中阴影部分的面积是 ( )(A )261a π (B )231a π (C )232a π (D )234a π20.(杭州市)过⊙O 内一点M 的最长的弦长为6厘米,最短的弦长为4厘米,则OM 的长为 ( )(A )3厘米 (B )5厘米 (C )2厘米 (D )5厘米21.(安徽省)已知圆锥的底面半径是3,高是4,则这个圆锥侧面展开图的面积是 ( )(A )12π (B )15π (C )30π (D )24π22.(安微省)已知⊙O 的直径AB 与弦AC 的夹角为 30,过C 点的切线PC 与AB 延长线交P .PC =5,则⊙O 的半径为 ( )(A )335 (B )635 (C )10 (D )5 23.(福州市)如图:PA 切⊙O 于点A ,PBC 是⊙O 的一条割线,有PA =32,PB =BC ,那么BC 的长是 ( )(A )3 (B )32 (C )3 (D )3224.(河南省)如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是 ( )(A )π (B )1.5π (C )2π (D )2.5π25.(四川省)正六边形的半径为2厘米,那么它的周长为 ( )(A )6厘米 (B )12厘米 (C )24厘米 (D )122厘米26.(四川省)一个圆柱形油桶的底面直径为0.6米,高为1米,那么这个油桶的侧面积为 ( )(A )0.09π平方米 (B )0.3π平方米 (C )0.6平方米 (D )0.6π平方米27.(贵阳市)一个形如圆锥的冰淇淋纸筒,其底面直径为6厘米,母线长为5厘米,围成这样的冰淇淋纸筒所需纸片的面积是 ( )(A )66π平方厘米 (B )30π平方厘米 (C )28π平方厘米 (D )15π平方厘米28.(新疆乌鲁木齐)在半径为2的⊙O 中,圆心O 到弦AB 的距离为1,则弦AB 所对的圆心角的度数可以是 ( )(A ) 60 (B ) 90 (C ) 120 (D ) 15029.(新疆乌鲁木齐)将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面,(接口损耗不计),则桶底的面积为 ( )(A )π1600平方厘米 (B )1600π平方厘米(C )π6400平方厘米 (D )6400π平方厘米 30.(成都市)如图,已知AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD =10厘米,AP ∶PB =1∶5,那么⊙O 的半径是 ( )(A )6厘米 (B )53厘米 (C )8厘米 (D )35厘米31.(成都市)在Rt △ABC 中,已知AB =6,AC =8,∠A =90.如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥,其表面积为S 1;把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥,其表面积为S 2,那么S 1∶S 2等于 ( )(A )2∶3 (B )3∶4 (C )4∶9 (D )5∶1232.(苏州市)如图,⊙O 的弦AB =8厘米,弦CD 平分AB 于点E .若CE=2厘米.ED 长为 ( )(A )8厘米 (B )6厘米 (C )4厘米 (D )2厘米 33.(苏州市)如图,四边形ABCD 内接于⊙O ,若∠BOD =160,则∠BCD = ( )(A ) 160 (B ) 100 (C ) 80 (D ) 2034.(镇江市)如图,正方形ABCD 内接于⊙O ,E 为DC 的中点,直线BE交⊙O 于点F .若⊙O 的半径为2,则BF 的长为 ( )(A )23 (B )22 (C )556 (D )554 35.(扬州市)如图,AB 是⊙O 的直径,∠ACD = 15,则∠BAD 的度数为 ( )(A ) 75 (B ) 72 (C ) 70 (D )6536.(扬州市)已知:点P 直线l 的距离为3,以点P 为圆心,r 为半径画圆,如果圆上有且只有两点到直线l 的距离均为2,则半径r 的取值范围是 ( )(A )r >1 (B )r >2 (C )2<r <3 (D )1<r <537.(绍兴市)边长为a 的正方边形的边心距为 ( )(A )a (B )23a (C )3a (D )2a 38.(绍兴市)如图,以圆柱的下底面为底面,上底面圆心为顶点的圆锥的母线长为4,高线长为3,则圆柱的侧面积为 ( )(A )30π (B )76π (C )20π (D )74π39.(昆明市)如图,扇形的半径OA =20厘米,∠AOB = 135,用它做成一个圆锥的侧面,则此圆锥底面的半径为 ( )(A )3.75厘米 (B )7.5厘米 (C )15厘米 (D )30厘米40.(昆明市)如图,正六边形ABCDEF 中.阴影部分面积为123平方厘米,则此正六边形的边长为 ( )(A )2厘米 (B )4厘米 (C )6厘米 (D )8厘米41.(温州市)已知扇形的弧长是2π厘米,半径为12厘米,则这个扇形的圆心角是 ( )(A ) 60 (B ) 45 (C ) 30 (D ) 2042.(温州市)圆锥的高线长是厘米,底面直径为12厘米,则这个圆锥的侧面积是 ( )(A )48π厘米 (B )24π13平方厘米(C )48π13平方厘米 (D )60π平方厘米43.(温州市)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PC是⊙O 的切线,C 为切点,PC =26,PA =4,则⊙O 的半径等于 ( )(A )1 (B )2 (C )23 (D )26 44.(常州市)已知圆柱的母线长为5厘米,表面积为28π平方厘米,则这个圆柱的底面半径是( )(A )5厘米 (B )4厘米 (C )2厘米 (D )3厘米45.(常州市)半径相等的圆内接正三角形、正方形、正六边形的边长之比为 ( )(A )1∶2∶3 (B )3∶2∶1(C )3∶2∶1 (D )1∶2∶346.(广东省)如图,若四边形ABCD 是半径为1和⊙O 的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为 ( )(A )(2π-2)厘米 (B )(2π-1)厘米(C )(π-2)厘米 (D )(π-1)厘米47.(武汉市)如图,已知圆心角∠BOC = 100,则圆周角∠BAC 的度数是( )(A ) 50 (B ) 100 (C ) 130 (D ) 20048.(武汉市)半径为5厘米的圆中,有一条长为6厘米的弦,则圆心到此弦的距离为 ( )(A )3厘米 (B )4厘米 (C )5厘米 (D )6厘米49.已知:Rt △ABC 中,∠C = 90,O 为斜边AB 上的一点,以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ,若AC =1,BC =3,则⊙O 的半径为 ( )(A )21 (B )32 (C )43 (D )54二、填空题1.(北京市东城区)如图,AB 、AC 是⊙O 的两条切线,切点分别为B 、C ,D是优弧上的一点,已知∠BAC = 80,那么∠BDC =__________度.2.(北京市东城区)在Rt △ABC 中,∠C = 90,A B=3,BC =1,以AC 所在直线为轴旋转一周,所得圆锥的侧面展开图的面积是__________.3.(北京市海淀区)如果圆锥母线长为6厘米,那么这个圆锥的侧面积是_______平方厘米5.(上海市)两个点O为圆心的同心圆中,大圆的弦AB与小圆相切,如果AB的长为24,大圆的半径OA为13,那么小圆的半径为___________.6.(天津市)已知⊙O中,两弦AB与CD相交于点E,若E为AB的中点,CE∶ED=1∶4,AB=4,则CD的长等于___________.7.(重庆市)如图,AB是⊙O的直径,四边形ABCD内接于⊙O,,,的度数比为3∶2∶4,MN是⊙O的切线,C是切点,则∠BCM的度数为___________.8.(重庆市)如图,P是⊙O的直径AB延长线上一点,PC切⊙O于点C,PC=6,BC∶AC=1∶2,则AB的长为___________.9.(重庆市)如图,四边形ABCD内接于⊙O,AD∥BC,=,若AD=4,BC=6,则四边形ABCD的面积为__________.10.(山西省)若一个圆柱的侧面积等于两底面积的和,则它的高h与底面半径r的大小关系是__________.11.(沈阳市)要用圆形铁片截出边长为4厘米的正方形铁片,则选用的圆形铁片的直径最小要___________厘米.12.(沈阳市)圆内两条弦AB和CD相交于P点,AB长为7,AB把CD分成两部分的线段长分别为2和6,那么=__________.13.(沈阳市)△ABC是半径为2厘米的圆内接三角形,若BC=23厘米,则∠A的度数为________.14.(沈阳市)如图,已知OA、OB是⊙O的半径,且OA=5,∠AOB=15 ,AC⊥OB于C,则图中阴影部分的面积(结果保留π)S=_________.18.(陕西省)如图,在⊙O的内接四边形ABCD中,∠BCD=130 ,则∠BOD的度数是________.19.(陕西省)已知⊙O的半径为4厘米,以O为圆心的小圆与⊙O组成的圆环的面积等于小圆的面积,则这个小圆的半径是______厘米.21.(甘肃省)正三角形的内切圆与外接圆面积之比为_________.2 23.(宁夏回族自治区)圆锥的母线长为5厘米,高为3厘米,在它的侧面展开图中,扇形的圆心角是_________度.24.(南京市)如图,AB是⊙O的直径,弦CD⊥AB,垂足是G,F是CG的中点,延长AF交⊙O于E,CF=2,AF=3,则EF的长是_________.2 26.(福州市)若圆锥底面的直径为厘米,线线长为5厘米,则它的侧面积为__________平方厘米(结果保留π).27.(河南省)如图,AB为⊙O的直径,P点在AB的延长线上,PM切⊙O于M点.若OA=a,PM=3a,那么△PMB的周长的__________.60的圆心角所对的弧长为__________厘米.28.(长沙市)在半径9厘米的圆中,29.(四川省)扇形的圆心角为120 ,弧长为6π厘米,那么这个扇形的面积为_____ 37.(扬州市)边长为2厘米的正六边形的外接圆半径是________厘米,内切圆半径是________厘米(结果保留根号).38.(绍兴市)如图,PT是⊙O的切线,T为切点,PB是⊙O的割线交⊙O于A、B两点,交弦CD于点M,已知:CM=10,MD=2,PA=MB=4,则PT的长等于__________.90,半径OA=1,C是线段AB39.(温州市)如图,扇形OAB中,∠AOB=的中点,CD∥OA,交于点D,则CD=________.三、解答题:1.(苏州市)已知:如图,△ABC 内接于⊙O ,过点B 作⊙O 的切线,交CA的延长线于点E ,∠EBC =2∠C .①求证:AB =AC ;②若tan ∠ABE =21,(ⅰ)求BC AB 的值;(ⅱ)求当AC =2时,AE 的长.4.(北京市海淀区)如图,PC 为⊙O 的切线,C 为切点,PAB 是过O 的割线,CD ⊥AB 于点D ,若tan B =21,PC =10cm ,求三角形BCD 的面积.7.(贵阳市)如图所示:PA 为⊙O 的切线,A 为切点,PBC 是过点O 的割线,PA =10,PB =5,求:(1)⊙O 的面积(注:用含π的式子表示);(2)cos ∠BAP 的值.。
最新经典必考圆中考试题集锦(附答案)

圆中考试题集锦之巴公井开创作时间:二O二一年七月二十九日一、选择题1.如图,BC是⊙O的直径,P是CB延长线上一点,PA切⊙O 于点A,如果PA=,PB=1,那么∠APC即是()(A)(B)(C)(D)2.如果圆柱的高为20厘米,底面半径是高的,那么这个圆柱的正面积是()(A)100π平方厘米(B)200π平方厘米(C)500π平方厘米(D)200平方厘米3.“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题,“今在圆材,埋在壁中,不知年夜小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,求直径CD的长”.依题意,CD长为()(A)寸(B)13寸(C)25寸(D)26寸4.已知:如图,⊙O半径为5,PC切⊙O于点C,PO交⊙O于点A,PA=4,那么PC的长即是()(A)6(B)2(C)2(D)25.如果圆锥的正面积为20π平方厘米,它的母线长为5厘米,那么此圆锥的底面半径的长即是()(A)2厘米(B)2厘米(C)4厘米(D)8厘米6.相交两圆的公共弦长为16厘米,若两圆的半径长分别为10厘米和17厘米,则这两圆的圆心距为()(A)7厘米(B)16厘米(C)21厘米(D)27厘米7.如图,⊙O为△ABC的内切圆,∠C=,AO的延长线交BC于点D,AC=4,DC=1,,则⊙O的半径即是()(A)(B)(C)(D)8.一居民小区有一正多边形的活动场.小区管委会决定在这个多边形的每个极点处修建一个半径为2米的扇形花台,花台都以多边形的极点为圆心,以多边形的内角为圆心角,花台占空中积共为12π平方米.若每个花台的造价为400元,则建造这些花台共需资金()(A)2400元(B)2800元(C)3200元(D)3600元9.如图,AB是⊙O直径,CD是弦.若AB=10厘米,CD=8厘米,那么A、B两点到直线CD的距离之和为()(A)12厘米(B)10厘米(C)8厘米(D)6厘米10.某工件形状如图所示,圆弧BC的度数为,AB=6厘米,点B到点C的距离即是AB,∠BAC=,则工件的面积即是()(A)4π(B)6π(C)8π(D)10π11.如图,PA切⊙O于点A,PBC是⊙O的割线且过圆心,PA=4,PB=2,则⊙O的半径即是()(A)3(B)4(C)6(D)812.已知⊙O的半径为3厘米,⊙的半径为5厘米.⊙O与⊙相交于点D、E.若两圆的公共弦DE的长是6厘米(圆心O、在公共弦DE的两侧),则两圆的圆心距O的长为()(A)2厘米(B)10厘米(C)2厘米或10厘米(D)4厘米13.如图,两个等圆⊙O和⊙的两条切线OA、OB,A、B是切点,则∠AOB即是()(A)(B)(C)(D)14.如图,AB是⊙O的直径,∠C=,则∠ABD=()(A)(B)(C)(D)15.弧长为6π的弧所对的圆心角为,则弧所在的圆的半径为()(A)6(B)6(C)12(D)1816.如图,在△ABC中,∠BAC=,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部份的面积为()(A)1(B)2(C)1+(D)2-17.已知圆的内接正六边形的周长为18,那么圆的面积为()(A)18π(B)9π(C)6π(D)3π18.如图,点P是半径为5的⊙O内一点,且OP=3,在过点P的所有弦中,长度为整数的弦一共有()(A)2条(B)3条(C)4条(D)5条19.如图,正六边形ABCDEF的边长为a,分别以C、F为圆心,a 为半径画弧,则图中阴影部份的面积是()(A)(B)(C)(D)20.过⊙O内一点M的最长的弦长为6厘米,最短的弦长为4厘米,则OM的长为()(A)厘米(B)厘米(C)2厘米(D)5厘米21.已知圆锥的底面半径是3,高是4,则这个圆锥正面展开图的面积是()(A)12π(B)15π(C)30π(D)24π22.已知⊙O的直径AB与弦AC的夹角为,过C点的切线PC与AB延长线交P.PC=5,则⊙O的半径为()(A)(B)(C)10(D)523.如图:PA切⊙O于点A,PBC是⊙O的一条割线,有PA=3,PB=BC,那么BC的长是()(A)3(B)3(C)(D)24.如图,⊙A、⊙B、⊙C、⊙D、⊙E相互外离,它们的半径都是1,顺次连结五个圆心获得五边形ABCDE,则图中五个扇形(阴影部份)的面积之和是()(A)π(C)2π25.正六边形的半径为2厘米,那么它的周长为()(A)6厘米(B)12厘米(C)24厘米(D)12厘米26.一个圆柱形油桶的底面直径为0.6米,高为1米,那么这个油桶的正面积为()27.一个形如圆锥的冰淇淋纸筒,其底面直径为6厘米,母线长为5厘米,围成这样的冰淇淋纸筒所需纸片的面积是()(A)66π平方厘米(B)30π平方厘米(C)28π平方厘米(D)15π平方厘米28.在半径为2的⊙O中,圆心O到弦AB的距离为1,则弦AB 所对的圆心角的度数可以是()(A)(B)(C)(D)29.将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的正面,(接口损耗不计),则桶底的面积为()(A)平方厘米(B)1600π平方厘米(C)平方厘米(D)6400π平方厘米30.如图,已知AB是⊙O的直径,弦CD⊥AB于点P,CD=10厘米,AP∶PB=1∶5,那么⊙O的半径是()(A)6厘米(B)厘米(C)8厘米(D)厘米31.在Rt△ABC中,已知AB=6,AC=8,∠A=.如果把Rt△ABC绕直线AC旋转一周获得一个圆锥,其概况积为S;把Rt△ABC绕直线AB旋转一周获得另一个圆锥,其概况积为S,那么S∶S即是()(A)2∶3(B)3∶4(C)4∶9(D)5∶1232.如图,⊙O的弦AB=8厘米,弦CD平分AB于点E.若CE=2厘米.ED长为()(A)8厘米(B)6厘米(C)4厘米(D)2厘米33.如图,四边形ABCD内接于⊙O,若∠BOD=,则∠BCD=()(A)(B)(C)(D)34.如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O 于点F.若⊙O的半径为,则BF的长为()(A)(B)(C)(D)35.如图,AB是⊙O的直径,∠ACD=,则∠BAD的度数为()(A)(B)(C)(D)36.已知:点P直线l的距离为3,以点P为圆心,r为半径画圆,如果圆上有且只有两点到直线l的距离均为2,则半径r的取值范围是()(A)r>1(B)r>2(C)2<r<3(D)1<r<537.边长为a的正方边形的边心距为()(A)a(B)a(C)a(D)2a38.如图,以圆柱的下底面为底面,上底面圆心为极点的圆锥的母线长为4,高线长为3,则圆柱的正面积为()(A)30π(B)π(C)20π(D)π39.如图,扇形的半径OA=20厘米,∠AOB=,用它做成一个圆锥的正面,则此圆锥底面的半径为()(C)15厘米(D)30厘米40.如图,正六边形ABCDEF中.阴影部份面积为12平方厘米,则此正六边形的边长为()(A)2厘米(B)4厘米(C)6厘米(D)8厘米41.已知扇形的弧长是2π厘米,半径为12厘米,则这个扇形的圆心角是()(A)(B)(C)(D)42.圆锥的高线长是厘米,底面直径为12厘米,则这个圆锥的正面积是()(A)48π厘米(B)24平方厘米(C)48平方厘米(D)60π平方厘米43.如图,AB是⊙O的直径,点P在BA的延长线上,PC是⊙O的切线,C为切点,PC=2,PA=4,则⊙O的半径即是()(A)1(B)2(C)(D)44.已知圆柱的母线长为5厘米,概况积为28π平方厘米,则这个圆柱的底面半径是()(A)5厘米(B)4厘米(C)2厘米(D)3厘米45.半径相等的圆内接正三角形、正方形、正六边形的边长之比为()(A)1∶∶(B)∶∶1(C)3∶2∶1(D)1∶2∶346.如图,若四边形ABCD是半径为1和⊙O的内接正方形,则图中四个弓形(即四个阴影部份)的面积和为()(A)(2π-2)厘米(B)(2π-1)厘米(C)(π-2)厘米(D)(π-1)厘米47.如图,已知圆心角∠BOC=,则圆周角∠BAC的度数是()(A)(B)(C)(D)48.半径为5厘米的圆中,有一条长为6厘米的弦,则圆心到此弦的距离为()(A)3厘米(B)4厘米(C)5厘米(D)6厘米49.已知:Rt△ABC中,∠C=,O为斜边AB上的一点,以O 为圆心的圆与边AC、BC分别相切于点E、F,若AC=1,BC=3,则⊙O的半径为()(A)(B)(C)(D)50.已知:如图,E是相交两圆⊙M和⊙O的一个交点,且ME⊥NE,AB为外公切线,切点分别为A、B,连结AE、BE.则∠AEB的度数为()(A)145°(B)140°(C)135°(D)130°二、填空题1.如图,AB、AC是⊙O的两条切线,切点分别为B、C,D是优弧上的一点,已知∠BAC=,那么∠BDC=__________度.2.在Rt△ABC中,∠C=,AB=3,BC=1,以AC所在直线为轴旋转一周,所得圆锥的正面展开图的面积是__________.3.如果圆锥母线长为6厘米,那么这个圆锥的正面积是_______平方厘米4.一种圆状包装的保鲜膜,如图所示,其规格为“20厘米×60米”,经丈量这筒保鲜膜的内径、外径的长分别为3.2厘米、4.0厘米,则该种保鲜膜的厚度约为_________厘米(π取3.14,结果保管两位有效数字).5.两个点O为圆心的同心圆中,年夜圆的弦AB与小圆相切,如果AB的长为24,年夜圆的半径OA为13,那么小圆的半径为___________.6.已知⊙O中,两弦AB与CD相交于点E,若E为AB的中点,CE∶ED=1∶4,AB=4,则CD的长即是___________.7.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,,,的度数比为3∶2∶4,MN是⊙O的切线,C是切点,则∠BCM的度数为___________.8.如图,P是⊙O的直径AB延长线上一点,PC切⊙O于点C,PC=6,BC∶AC=1∶2,则AB的长为___________.9.如图,四边形ABCD内接于⊙O,AD∥BC,=,若AD=4,BC=6,则四边形ABCD的面积为__________.10.若一个圆柱的正面积即是两底面积的和,则它的高h与底面半径r的年夜小关系是__________.11.要用圆形铁片截出边长为4厘米的正方形铁片,则选用的圆形铁片的直径最小要___________厘米.12.圆内两条弦AB和CD相交于P点,AB长为7,AB把CD分成两部份的线段长分别为2和6,那么=__________.13.△ABC是半径为2厘米的圆内接三角形,若BC=2厘米,则∠A的度数为________.14.如图,已知OA、OB是⊙O的半径,且OA=5,∠AOB=15,AC⊥OB于C,则图中阴影部份的面积(结果保管π)S=_________.15.如图,圆内接正六边形ABCDEF中,AC、BF交于点M.则∶=_________.16.两圆外离,圆心距为25厘米,两圆周长分别为15π厘米和10π厘米.则其内公切线和连心线所夹的锐角即是__________度.17.将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周,所得圆柱体的概况积为_________平方厘米.18.如图,在⊙O的内接四边形ABCD中,∠BCD=130,则∠BOD的度数是________.19.已知⊙O的半径为4厘米,以O为圆心的小圆与⊙O组成的圆环的面积即是小圆的面积,则这个小圆的半径是______厘米.20.如图,⊙O的半径O A是⊙O的直径,C是⊙O上的一点,O C交⊙O于点B.若⊙O的半径即是5厘米,的长即是⊙O周长的,则的长是_________.21.正三角形的内切圆与外接圆面积之比为_________.22.如图,AB=8,AC=6,以AC和BC为直径作半圆,两圆的公切线MN与AB的延长线交于D,则BD的长为_________.23.圆锥的母线长为5厘米,高为3厘米,在它的正面展开图中,扇形的圆心角是_________度.24.如图,AB是⊙O的直径,弦CD⊥AB,垂足是G,F是CG的中点,延长AF交⊙O于E,CF=2,AF=3,则EF的长是_________.25.在⊙O中,直径AB=4厘米,弦CD⊥AB于E,OE=,则弦CD的长为__________厘米.26.若圆锥底面的直径为厘米,线线长为5厘米,则它的正面积为__________平方厘米(结果保管π).27.如图,AB为⊙O的直径,P点在AB的延长线上,PM切⊙O于M 点.若OA=a,PM=a,那么△PMB的周长的__________.28.在半径9厘米的圆中,的圆心角所对的弧长为__________厘米.29.扇形的圆心角为120,弧长为6π厘米,那么这个扇形的面积为_________.30.如果圆O的直径为10厘米,弦AB的长为6厘米,那么弦AB的弦心距即是________厘米.31.某种商品的商标图案如图所求(阴影部份),已知菱形ABCD的边长为4,∠A=,是以A为圆心,AB长为半径的弧,是以B为圆心,BC长为半径的弧,则该商标图案的面积为_________.32.已知,一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周,所得圆锥的概况积是__________.33.正六边形的边心距与半径的比值为_________.34.如图,已知扇形AOB的半径为12,OA⊥OB,C为OA上一点,以AC为直径的半圆和以OB为直径的半圆相切,则半圆的半径为__________.35.如图,PA、PB与⊙O分别相切于点A、点B,AC是⊙O的直径,PC交⊙O于点D.已知∠APB=,AC=2,那么CD的长为________.36.底面半径为2厘米,高为3厘米的圆柱的体积为_________立方厘米(结果保管π).37.边长为2厘米的正六边形的外接圆半径是________厘米,内切圆半径是________厘米(结果保管根号).38.如图,PT是⊙O的切线,T为切点,PB是⊙O的割线交⊙O于A、B两点,交弦CD于点M,已知:CM=10,MD=2,PA=MB=4,则PT 的长即是__________.39.如图,扇形OAB中,∠AOB=,半径OA=1,C是线段AB的中点,CD∥O A,交于点D,则CD=________.40.已知扇形的圆心角为150,它所对的弧长为20π厘米,则扇形的半径是________厘米,扇形的面积是__________平方厘米.41.如图,AB是⊙O直径,CE切⊙O于点C,CD⊥AB,D为垂足,AB=12厘米,∠B=30,则∠ECB=__________;CD=_________厘米.42.如图,DE是⊙O直径,弦AB⊥DE,垂足为C,若AB=6,CE=1,则CD=________,OC=_________.43.如果把人的头顶和脚底分别看作一个点,把地球赤道作一个圆,那么身高压2米的汤姆沿着地球赤道环道环行一周,他的头顶比脚底多行________米.44.已知:⊙O的半径为1,M为⊙O外的一点,MA切⊙O于点A,MA =1.若AB是⊙O的弦,且AB=,则MB的长度为_________.45.如果圆的半径为4厘米,那么它的周长为__________厘米.三、解答题:1.已知:如图,△ABC内接于⊙O,过点B作⊙O的切线,交CA的延长线于点E,∠EBC=2∠C.①求证:AB=AC;②若tan∠ABE=,(ⅰ)求的值;(ⅱ)求当AC=2时,AE的长.2.如图,PA为⊙O的切线,A为切点,⊙O的割线PBC过点O与⊙O分别交于B、C,PA=8cm,PB=4cm,求⊙O的半径.3.已知:如图,BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,若AD︰DB=2︰3,AC=10,求AC︰AB的值.4.如图,PC为⊙O的切线,C为切点,PAB是过O的割线,CD⊥AB于点D,若CD︰DB=,PC=10cm,求三角形BCD的面积.5.如图,在两个半圆中,年夜圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部份的面积.6.已知,如图,以△ABC的边AB作直径的⊙O,分别并AC、BC于点D、E,弦FG∥AB,S△CDE︰S△ABC=1︰4,DE=5cm,FG=8cm,求梯形AFGB的面积.7.如图所示:PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,求:(1)⊙O的面积(注:用含π的式子暗示);(2)cos∠BAP的值.参考谜底一、选择题1.B 2.B 3.D 4.D 5.C 6.C 7.A 8.C 9.D 10.B 11.A 12.B 13.C 14.D 15.D 16.A 17.B 18.C 19.C 20.B 21.B 22.A 23.A 24.B 25.B 26.D 27.D 28.C 29.A 30.B 31.A 32.A 33.B 34.C 35.A 36.D 37.B 38.B 39.B 40.B 41.C 42.D 43.A 44.C 45.B 46.C 47.A 48.B 49.C 50.C二、填空题1.50 2.2π3.18π4.5.5 6.5 7.30°8.9 9.25 10.h=r 11.412.3或 4 13.60°或120°14.15.1:2 16.30 17.80π或120π18.100°19.20.π21.1:4 22.1 23.288 24.4 25.2 26.15π27.28.3π29.27π平方厘米30.4 31.32.24π平方厘米或36π平方厘米33.34.4 35.36.12π37.2,38.39.40.24,240π41.60°,42.9,4 43.4π44.1或45.8π三、解答题:1.(1)∵BE切⊙O于点B,∴∠ABE=∠C.∵∠EBC=2∠C,即∠ABE+∠ABC=2∠C,∴∠C+∠ABC=2∠C,∴∠ABC=∠C,∴AB=AC.(2)①连结AO,交BC于点F,∵AB=AC,∴=,∴AO⊥BC且BF=FC.在Rt△ABF中,=tan∠ABF,又tan∠ABF=tanC=tan∠ABE=,∴=,∴AF=BF.∴AB===BF.∴.②在△EBA与△ECB中,∵∠E=∠E,∠EBA=∠ECB,∴△EBA∽△ECB.∴,解之,得EA2=EA·(EA+AC),又EA≠0,∴EA=AC,EA=×2=.2.设⊙的半径为r,由切割线定理,得PA2=PB·PC,∴82=4(4+2r),解得r=6(cm).即⊙O的半径为6cm.3.由已知AD︰DB=2︰3,可设AD=2k,DB=3k(k>0).∵AC切⊙O于点C,线段ADB为⊙O的割线,∴AC2=AD·AB,∵AB=AD+DB=2k+3k=5k,∴102=2k×5k,∴k2=10,∵k>0,∴k=.∴AB=5k=5.∵AC切⊙O于C,BC为⊙O的直径,∴AC⊥BC.在Rt△ACB中,sinB=.4.解法一:连结AC.∵AB是⊙O的直径,点C在⊙O上,∴∠ACB=90°.CD⊥AB于点D,∴∠ADC=∠BDC=90°,∠2=90°-∠BAC=∠B.∵tanB=,∴tan∠2=.∴.设AD=x(x>0),CD=2x,DB=4x,AB=5x.∵PC切⊙O于点C,点B在⊙O上,∴∠1=∠B.∵∠P=∠P,∴△PAC∽△PCB,∴.∵PC=10,∴PA=5,∵PC切⊙O于点C,PAB是⊙O的割线,∵PC2=PA·PB,∴102=5(5+5 x).解得x=3.∴AD=3,CD=6,DB=12.∴S△BCD=CD·DB=×6×12=36.即三角形BCD的面积36cm2.解法二:同解法一,由△PAC∽△PCB,得.∵PA=10,∴PB=20.由切割线定理,得PC2=PA·PB.∴PA==5,∴AB=PB-PA=15,∵AD+DB=x+4x=15,解得x=3,∴CD=2x=6,DB=4x=12.∴S△BCD=CD·DB=×6×12=36.即三角形BCD的面积36cm2.5.解:如图取MN的中点E,连结OE,∴OE⊥MN,EN=MN=a.在四边形EOCD中,∵CO⊥DE,OE⊥DE,DE∥CO,∴四边形EOCD为矩形.∴OE=CD,在Rt△NOE中,NO2-OE2=EN2=.∴S阴影=π(NO2-OE2)=π·=.6.解:∵∠CDE=∠CBA,∠DCE=∠BCA,∴△CDE∽△ABC.∴∴===,即,解得AB=10(cm),作OM⊥FG,垂足为M,则FM=FG=×8=4(cm),连结OF,∵OA=AB=×10=5(cm).∴OF=OA=5(cm).在Rt△OMF中,由勾股定理,得OM===3(cm).∴梯形AFGB的面积=·OM=×3=27(cm2).7.PA2=PB·PC(或56.25π)(平方单元).Þ△ACP∽△BAPÞÞ.解法一:设AB=x,AC=2x,BC为⊙O的直径∠CAB=90°,则BC=x.∵∠BAP=∠C,∴cos∠BAP=cos∠C=解法二:设AB=x,在Rt△ABC中,AC2+AB2=BC2,即x2+(2x)2=152,解之得x=3,∴AC=6,∵∠BAP=∠C,∴∴cos∠BAP=cos∠C=6.解:∵∠CDE=∠CBA,∠DCE=∠BCA,∴△CDE∽△ABC.∴∴===,即,解得AB=10(cm),作OM⊥FG,垂足为M,则FM=FG=×8=4(cm),连结OF,∵OA=AB=×10=5(cm).∴OF=OA=5(cm).在Rt△OMF中,由勾股定理,得OM===3(cm).∴梯形AFGB的面积=·OM=×3=27(cm2).7.PA2=PB·PC(或56.25π)(平方单元).Þ△ACP∽△BAPÞÞ.解法一:设AB=x,AC=2x,BC为⊙O的直径∠CAB=90°,则BC=x.∵∠BAP=∠C,∴cos∠BAP=cos∠C=解法二:设AB=x,在Rt△ABC中,AC2+AB2=BC2,即x2+(2x)2=152,解之得x=3,∴AC=6,∵∠BAP=∠C,∴∴cos∠BAP=cos∠C=6.解:∵∠CDE=∠CBA,∠DCE=∠BCA,∴△CDE∽△ABC.∴∴===,即,解得AB=10(cm),作OM⊥FG,垂足为M,则FM=FG=×8=4(cm),连结OF,∵OA=AB=×10=5(cm).∴OF=OA=5(cm).在Rt△OMF中,由勾股定理,得OM===3(cm).∴梯形AFGB的面积=·OM=×3=27(cm2).7.PA2=PB·PC(或56.25π)(平方单元).Þ△ACP∽△BAPÞÞ.解法一:设AB=x,AC=2x,BC为⊙O的直径∠CAB=90°,则BC=x.∵∠BAP=∠C,∴cos∠BAP=cos∠C=解法二:设AB=x,在Rt△ABC中,AC2+AB2=BC2,即x2+(2x)2=152,解之得x=3,∴AC=6,∵∠BAP=∠C,∴∴cos∠BAP=cos∠C=圆是中考中的必考内容,年夜约占整个分数的百分之30左右,希望年夜家能够加深练习,提到自己的做题能力.时间:二O二一年七月二十九日。
中考数学试题圆及答案

中考数学试题圆及答案中考数学试题:圆一、选择题(每题3分,共15分)1. 已知圆的半径为5,圆心到直线的距离为3,则直线与圆的位置关系是:A. 相离B. 相切C. 相交D. 内切2. 若圆的方程为 \( (x-3)^2 + (y-4)^2 = 16 \),圆心坐标为:A. (3, 4)B. (-3, 4)C. (3, -4)D. (-3, -4)3. 圆心在原点,半径为4的圆的方程是:A. \( x^2 + y^2 = 8 \)B. \( x^2 + y^2 = 16 \)C. \( (x-2)^2 + y^2 = 4 \)D. \( x^2 + y^2 = 4 \)4. 已知点A(2,3)在圆 \( x^2 + y^2 = 25 \) 上,点B(-2,-3)与圆的位置关系是:A. 在圆上B. 在圆内C. 在圆外D. 不确定5. 若圆经过点(2,1)且圆心在x轴上,半径为2,则圆的方程是:A. \( (x-2)^2 + y^2 = 4 \)B. \( (x-1)^2 + y^2 = 4 \)C. \( x^2 + (y-1)^2 = 4 \)D. \( x^2 + y^2 = 4 \)二、填空题(每题3分,共12分)6. 已知圆的半径为7,圆心到直线 \( 3x + 4y - 15 = 0 \) 的距离为4,则直线与圆_________。
7. 若圆的方程为 \( x^2 + y^2 + 2gx + 2fy + c = 0 \),且圆心坐标为(-g, -f),则圆的半径 \( r \) 为 \( \sqrt{g^2 + f^2 - c} \)。
8. 已知圆 \( x^2 + y^2 - 6x - 8y + 16 = 0 \) 与x轴相交于A、B 两点,则线段AB的长度为_________。
9. 若圆 \( (x-a)^2 + (y-b)^2 = r^2 \) 经过点P(1,1),则a+b的值为_________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆中考试题集锦一、选择题1.(北京市西城区)如图,BC 是⊙O 的直径,P 是CB 延长线上一点,PA 切⊙O 于点A ,如果PA =3,PB =1,那么∠APC 等于 ( )(A ) 15 (B ) 30 (C ) 45 (D ) 602.(北京市西城区)如果圆柱的高为20厘米,底面半径是高的41,那么这个圆柱的侧面积是 ( )(A )100π平方厘米 (B )200π平方厘米(C )500π平方厘米 (D )200平方厘米4.(北京市朝阳区)已知:如图,⊙O 半径为5,PC 切⊙O 于点C ,PO交⊙O 于点A ,PA =4,那么PC 的长等于 ( )(A )6 (B )25 (C )210 (D )2145.(北京市朝阳区)如果圆锥的侧面积为20π平方厘米,它的母线长为5厘米,那么此圆锥的底面半径的长等于 ( )(A )2厘米 (B )22厘米 (C )4厘米 (D )8厘米6.(天津市)相交两圆的公共弦长为16厘米,若两圆的半径长分别为10厘米和17厘米,则这两圆的圆心距为 ( )(A )7厘米 (B )16厘米 (C )21厘米 (D )27厘米7.(重庆市)如图,⊙O 为△ABC 的内切圆,∠C = 90,AO 的延长线交BC 于点D ,AC =4,DC =1,,则⊙O 的半径等于 ( )(A )54 (B )45 (C )43 (D )65 8.(重庆市)一居民小区有一正多边形的活动场.为迎接“AAPP ”会议在重庆市的召开,小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台,花台都以多边形的顶点为圆心,比多边形的内角为圆心角,花台占地面积共为12π平方米.若每个花台的造价为400元,则建造这些花台共需资金 ( )(A )2400元 (B )2800元 (C )3200元 (D )3600元9.(河北省)如图,AB是⊙O直径,CD是弦.若AB=10厘米,CD=8厘米,那么A 、B 两点到直线CD 的距离之和为 ( )(A )12厘米 (B )10厘米 (C )8厘米 (D )6厘米10.(河北省)某工件形状如图所示,圆弧BC 的度数为60,AB =6厘米,点B 到点C 的距离等于AB ,∠BAC = 30,则工件的面积等于 ( )(A )4π (B )6π (C )8π (D )10π11.(沈阳市)如图,PA 切⊙O 于点A ,PBC 是⊙O 的割线且过圆心,PA =4,PB =2,则⊙O 的半径等于 ( )(A )3 (B )4 (C )6 (D )812.(哈尔滨市)已知⊙O 的半径为35厘米,⊙O '的半径为5厘米.⊙O 与⊙O '相交于点D 、E .若两圆的公共弦DE 的长是6厘米(圆心O 、O '在公共弦DE 的两侧),则两圆的圆心距O O '的长为 ( )(A )2厘米 (B )10厘米 (C )2厘米或10厘米 (D )4厘米13.(陕西省)如图,两个等圆⊙O 和⊙O '的两条切线OA 、OB ,A 、B是切点,则∠AOB 等于 ( )(A ) 30 (B ) 45 (C ) 60 (D ) 9014.(甘肃省)如图,AB 是⊙O 的直径,∠C = 30,则∠ABD = ( )(A ) 30 (B ) 40 (C ) 50 (D ) 6015.(甘肃省)弧长为6π的弧所对的圆心角为 60,则弧所在的圆的半径为( )(A )6 (B )62 (C )12 (D )1816.(甘肃省)如图,在△ABC 中,∠BAC = 90,AB =AC =2,以AB 为直径的圆交BC 于D ,则图中阴影部分的面积为 ( )(A )1 (B )2 (C )1+4π (D )2-4π17.(宁夏回族自治区)已知圆的内接正六边形的周长为18,那么圆的面积为 ( )(A )18π (B )9π (C )6π (D )3π18.(山东省)如图,点P 是半径为5的⊙O 内一点,且OP =3,在过点P的所有弦中,长度为整数的弦一共有 ( )(A )2条 (B )3条 (C )4条 (D )5条19.(南京市)如图,正六边形ABCDEF 的边长的上a ,分别以C 、F 为圆心,a 为半径画弧,则图中阴影部分的面积是 ( )(A )261a π (B )231a π (C )232a π (D )234a π20.(杭州市)过⊙O 内一点M 的最长的弦长为6厘米,最短的弦长为4厘米,则OM 的长为 ( )(A )3厘米 (B )5厘米 (C )2厘米 (D )5厘米21.(安徽省)已知圆锥的底面半径是3,高是4,则这个圆锥侧面展开图的面积是 ( )(A )12π (B )15π (C )30π (D )24π22.(安微省)已知⊙O 的直径AB 与弦AC 的夹角为 30,过C 点的切线PC 与AB 延长线交P .PC =5,则⊙O 的半径为 ( )(A )335 (B )635 (C )10 (D )523.(福州市)如图:PA 切⊙O 于点A ,PBC 是⊙O 的一条割线,有PA=32,PB =BC ,那么BC 的长是 ( )(A )3 (B )32 (C )3 (D )3224.(河南省)如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是 ( )(A )π (B )1.5π (C )2π (D )2.5π25.(四川省)正六边形的半径为2厘米,那么它的周长为 ( )(A )6厘米 (B )12厘米 (C )24厘米 (D )122厘米 26.(四川省)一个圆柱形油桶的底面直径为0.6米,高为1米,那么这个油桶的侧面积为 ( )(A )0.09π平方米 (B )0.3π平方米 (C )0.6平方米 (D )0.6π平方米27.(贵阳市)一个形如圆锥的冰淇淋纸筒,其底面直径为6厘米,母线长为5厘米,围成这样的冰淇淋纸筒所需纸片的面积是 ( )(A )66π平方厘米 (B )30π平方厘米 (C )28π平方厘米 (D )15π平方厘米28.(新疆乌鲁木齐)在半径为2的⊙O 中,圆心O 到弦AB 的距离为1,则弦AB 所对的圆心角的度数可以是 ( )(A ) 60 (B ) 90 (C ) 120 (D ) 15029.(新疆乌鲁木齐)将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面,(接口损耗不计),则桶底的面积为 ( )(A )π1600平方厘米 (B )1600π平方厘米(C )π6400平方厘米 (D )6400π平方厘米 30.(成都市)如图,已知AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD =10厘米,AP ∶PB =1∶5,那么⊙O 的半径是 ( )(A )6厘米 (B )53厘米 (C )8厘米 (D )35厘米31.(成都市)在Rt △ABC 中,已知AB =6,AC =8,∠A = 90.如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥,其表面积为S 1;把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥,其表面积为S 2,那么S 1∶S 2等于 ( )(A )2∶3 (B )3∶4 (C )4∶9 (D )5∶1232.(苏州市)如图,⊙O 的弦AB =8厘米,弦CD 平分AB 于点E .若CE =2厘米.ED 长为 ( )(A )8厘米 (B )6厘米 (C )4厘米 (D )2厘米33.(苏州市)如图,四边形ABCD 内接于⊙O ,若∠BOD =160,则∠BCD = ( )(A ) 160 (B ) 100 (C ) 80 (D ) 2034.(镇江市)如图,正方形ABCD 内接于⊙O ,E 为DC 的中点,直线BE交⊙O 于点F .若⊙O 的半径为2,则BF 的长为 ( ) (A )23 (B )22 (C )556 (D )554 35.(扬州市)如图,AB 是⊙O 的直径,∠ACD = 15,则∠BAD 的度数为 ( )(A ) 75 (B ) 72 (C ) 70 (D ) 6536.(扬州市)已知:点P 直线l 的距离为3,以点P 为圆心,r 为半径画圆,如果圆上有且只有两点到直线l 的距离均为2,则半径r 的取值范围是 ( )(A )r >1 (B )r >2 (C )2<r <3 (D )1<r <537.(绍兴市)边长为a 的正方边形的边心距为 ( )(A )a (B )23a (C )3a (D )2a 38.(绍兴市)如图,以圆柱的下底面为底面,上底面圆心为顶点的圆锥的母线长为4,高线长为3,则圆柱的侧面积为 ( )(A )30π (B )76π (C )20π (D )74π39.(昆明市)如图,扇形的半径OA =20厘米,∠AOB =135,用它做成一个圆锥的侧面,则此圆锥底面的半径为 ( )(A )3.75厘米 (B )7.5厘米 (C )15厘米 (D )30厘米40.(昆明市)如图,正六边形ABCDEF 中.阴影部分面积为123平方厘米,则此正六边形的边长为 ( )(A )2厘米 (B )4厘米 (C )6厘米 (D )8厘米41.(温州市)已知扇形的弧长是2π厘米,半径为12厘米,则这个扇形的圆心角是 ( )(A ) 60 (B ) 45 (C ) 30 (D ) 2042.(温州市)圆锥的高线长是厘米,底面直径为12厘米,则这个圆锥的侧面积是 ( )(A )48π厘米 (B )24π13平方厘米(C )48π13平方厘米 (D )60π平方厘米43.(温州市)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PC 是⊙O 的切线,C 为切点,PC =26,PA =4,则⊙O 的半径等于( )(A )1 (B )2 (C )23 (D )26 44.(常州市)已知圆柱的母线长为5厘米,表面积为28π平方厘米,则这个圆柱的底面半径是 ( )(A )5厘米 (B )4厘米 (C )2厘米 (D )3厘米45.(常州市)半径相等的圆内接正三角形、正方形、正六边形的边长之比为 ( )(A )1∶2∶3 (B )3∶2∶1(C )3∶2∶1 (D )1∶2∶346.(广东省)如图,若四边形ABCD 是半径为1和⊙O 的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为 ( )(A )(2π-2)厘米 (B )(2π-1)厘米(C )(π-2)厘米 (D )(π-1)厘米47.(武汉市)如图,已知圆心角∠BOC =100,则圆周角∠BAC 的度数是 ( )(A ) 50 (B ) 100 (C ) 130 (D ) 20048.(武汉市)半径为5厘米的圆中,有一条长为6厘米的弦,则圆心到此弦的距离为 ( )(A )3厘米 (B )4厘米 (C )5厘米 (D )6厘米49.已知:Rt △ABC 中,∠C = 90,O 为斜边AB 上的一点,以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ,若AC =1,BC =3,则⊙O 的半径为 ( )(A )21 (B )32 (C )43 (D )54 50.(武汉市)已知:如图,E 是相交两圆⊙M 和⊙O 的一个交点,且ME ⊥NE ,AB 为外公切线,切点分别为A 、B ,连结AE 、BE .则∠AEB的度数为 ( )(A )145° (B )140° (C )135° (D )130°二、填空题1.(北京市东城区)如图,AB 、AC 是⊙O 的两条切线,切点分别为B 、C ,D 是优弧上的一点,已知∠BAC =80,那么∠BDC =__________度.2.(北京市东城区)在Rt △ABC 中,∠C =90,A B=3,BC =1,以AC 所在直线为轴旋转一周,所得圆锥的侧面展开图的面积是__________.3.(北京市海淀区)如果圆锥母线长为6厘米,那么这个圆锥的侧面积是_______平方厘米4.(北京市海淀区)一种圆状包装的保鲜膜,如图所示,其规格为“20厘米×60米”,经测量这筒保鲜膜的内径1ϕ、外径2ϕ的长分别为3.2厘米、4.0厘米,则该种保鲜膜的厚度约为_________厘米(π取3.14,结果保留两位有效数字).5.(上海市)两个点O 为圆心的同心圆中,大圆的弦AB 与小圆相切,如果AB 的长为24,大圆的半径OA 为13,那么小圆的半径为___________.6.(天津市)已知⊙O 中,两弦AB 与CD 相交于点E ,若E 为AB 的中点,CE ∶ED =1∶4,AB =4,则CD 的长等于___________.7.(重庆市)如图,AB 是⊙O 的直径,四边形ABCD 内接于⊙O ,,,的度数比为3∶2∶4,MN 是⊙O 的切线,C 是切点,则∠BCM 的度数为___________.8.(重庆市)如图,P 是⊙O 的直径AB 延长线上一点,PC 切⊙O 于点C ,PC =6,BC ∶AC =1∶2,则AB 的长为___________.9.(重庆市)如图,四边形ABCD 内接于⊙O ,AD ∥BC ,=,若AD =4,BC =6,则四边形ABCD 的面积为__________.10.(山西省)若一个圆柱的侧面积等于两底面积的和,则它的高h 与底面半径r 的大小关系是__________.11.(沈阳市)要用圆形铁片截出边长为4厘米的正方形铁片,则选用的圆形铁片的直径最小要___________厘米.12.(沈阳市)圆内两条弦AB 和CD 相交于P 点,AB 长为7,AB 把CD 分成两部分的线段长分别为2和6,那么=__________.13.(沈阳市)△ABC 是半径为2厘米的圆内接三角形,若BC =23厘米,则∠A 的度数为________.14.(沈阳市)如图,已知OA 、OB 是⊙O 的半径,且OA =5,∠AOB =15 ,AC ⊥OB 于C ,则图中阴影部分的面积(结果保留π)S =_________.15.(哈尔滨市)如图,圆内接正六边形ABCDEF 中,AC 、BF 交于点M .则ABM S △∶AFM S △=_________.16.(哈尔滨市)两圆外离,圆心距为25厘米,两圆周长分别为15π厘米和10π厘米.则其内公切线和连心线所夹的锐角等于__________度.17.(哈尔滨市)将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周,所得圆柱体的表面积为_________平方厘米.18.(陕西省)如图,在⊙O 的内接四边形ABCD 中,∠BCD =130 ,则∠BOD 的度数是________.19.(陕西省)已知⊙O 的半径为4厘米,以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积,则这个小圆的半径是______厘米. 20.(陕西省)如图,⊙O 1的半径O 1A 是⊙O 2的直径,C 是⊙O 1上的一点,O 1C 交⊙O 2于点B .若⊙O 1的半径等于5厘米,的长等于⊙O 1周长的101,则的长是_________.21.(甘肃省)正三角形的内切圆与外接圆面积之比为_________. 22.(甘肃省)如图,AB =8,AC =6,以AC 和BC 为直径作半圆,两圆的公切线MN 与AB 的延长线交于D ,则BD 的长为_________.23.(宁夏回族自治区)圆锥的母线长为5厘米,高为3厘米,在它的侧面展开图中,扇形的圆心角是_________度.24.(南京市)如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足是G ,F 是CG 的中点,延长AF 交⊙O 于E ,CF =2,AF =3,则EF 的长是_________.25.(福州市)在⊙O 中,直径AB =4厘米,弦CD ⊥AB 于E ,OE =3,则弦CD 的长为__________厘米.26.(福州市)若圆锥底面的直径为厘米,线线长为5厘米,则它的侧面积为__________平方厘米(结果保留π).27.(河南省)如图,AB 为⊙O 的直径,P 点在AB 的延长线上,PM 切⊙O 于M 点.若OA =a ,PM =3a ,那么△PMB 的周长的__________.28.(长沙市)在半径9厘米的圆中,60的圆心角所对的弧长为__________厘米. 29.(四川省)扇形的圆心角为120 ,弧长为6π厘米,那么这个扇形的面积为_________. 30.(贵阳市)如果圆O 的直径为10厘米,弦AB 的长为6厘米,那么弦AB 的弦心距等于________厘米.31.(贵阳市)某种商品的商标图案如图所求(阴影部分),已知菱形ABCD 的边长为4,∠A =60,是以A 为圆心,AB 长为半径的弧,是以B 为圆心,BC 长为半径的弧,则该商标图案的面积为_________.32.(云南省)已知,一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周,所得圆锥的表面积是__________.33.(新疆乌鲁木齐)正六边形的边心距与半径的比值为_________.34.(新疆乌鲁木齐)如图,已知扇形AOB 的半径为12,OA ⊥OB ,C 为OA 上一点,以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切,则半圆1O 的半径为__________.35.(成都市)如图,PA 、PB 与⊙O 分别相切于点A 、点B ,AC 是⊙O 的直径,PC 交⊙O 于点D .已知∠APB =60,AC =2,那么CD 的长为________.36.(苏州市)底面半径为2厘米,高为3厘米的圆柱的体积为_________立方厘米(结果保留π).37.(扬州市)边长为2厘米的正六边形的外接圆半径是________厘米,内切圆半径是________厘米(结果保留根号).38.(绍兴市)如图,PT 是⊙O 的切线,T 为切点,PB 是⊙O 的割线交⊙O 于A 、B 两点,交弦CD 于点M ,已知:CM =10,MD =2,PA =MB =4,则PT 的长等于__________.39.(温州市)如图,扇形OAB 中,∠AOB =90,半径OA =1,C 是线段AB 的中点,CD ∥OA ,交于点D ,则CD =________.40.(常州市)已知扇形的圆心角为150 ,它所对的弧长为20π厘米,则扇形的半径是________厘米,扇形的面积是__________平方厘米. 41.(常州市)如图,AB 是⊙O 直径,CE 切⊙O 于点C ,CD ⊥AB ,D 为垂足,AB =12厘米,∠B =30 ,则∠ECB =__________ ;CD =_________厘米.42.(常州市)如图,DE 是⊙O 直径,弦AB ⊥DE ,垂足为C ,若AB =6,CE =1,则CD =________,OC =_________.43.(常州市)如果把人的头顶和脚底分别看作一个点,把地球赤道作一个圆,那么身高压2米的汤姆沿着地球赤道环道环行一周,他的头顶比脚底多行________米.44.(海南省)已知:⊙O 的半径为1,M 为⊙O 外的一点,MA 切⊙O 于点A ,MA =1.若AB 是⊙O 的弦,且AB =2,则MB 的长度为_________.三、解答题:1.(苏州市)已知:如图,△ABC 内接于⊙O ,过点B 作⊙O 的切线,交CA 的延长线于点E ,∠EBC =2∠C . ①求证:AB =AC ; ②若tan ∠ABE =21,(ⅰ)求BCAB的值;(ⅱ)求当AC =2时,AE 的长.2.(广州市)如图,PA 为⊙O 的切线,A 为切点,⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ,PA =8cm ,PB =4cm ,求⊙O 的半径.3.(河北省)已知:如图,BC 是⊙O 的直径,AC 切⊙O 于点C ,AB 交⊙O 于点D ,若AD ︰DB =2︰3,AC =10,求sin B 的值.4.(北京市海淀区)如图,PC 为⊙O 的切线,C 为切点,PAB 是过O 的割线,CD ⊥AB 于点D ,若tan B =21,PC =10cm ,求三角形BCD 的面积.5.(宁夏回族自治区)如图,在两个半圆中,大圆的弦MN 与小圆相切,D 为切点,且MN ∥AB ,MN =a ,ON 、CD 分别为两圆的半径,求阴影部分的面积.6.(四川省)已知,如图,以△ABC 的边AB 作直径的⊙O ,分别并AC 、BC 于点D 、E ,弦FG ∥AB ,S △CDE ︰S △ABC =1︰4,DE =5cm ,FG =8cm ,求梯形AFGB 的面积.7.(贵阳市)如图所示:PA 为⊙O 的切线,A 为切点,PBC 是过点O 的割线,PA =10,PB =5,求:(1)⊙O 的面积(注:用含π的式子表示); (2)cos ∠BAP 的值.二次函数与其他函数的综合测试题一、选择题:(每小题3分,共45分)1.已知h 关于t 的函数关系式为221gt h ,(g 为正常数,t 为时间),则函数图象为( )(A ) (B ) (C ) (D )2.在地表以下不太深的地方,温度y (℃)与所处的深度x (k m )之间的关系可以近似用关系式y =35x +20表示,这个关系式符合的数学模型是( ) (A )正比例函数 (B )反比例函数. (C )二次函数 (D )一次函数3.若正比例函数y =(1-2m )x 的图像经过点A (1x ,1y )和点B (2x ,2y ),当1x <2x 时1y >2y ,则m 的取值范围是( ) (A )m <0 (B )m >0 (C )m<21 (D )m >214.函数y = k x + 1与函数xy k =在同一坐标系中的大致图象是( )OxyOxyOxyOxy(A ) (B ) (C ) (D )5.下列各图是在同一直角坐标系内,二次函数c x c a ax y +++=)(2与一次函数y =a x +c的大致图像,有且只有一个是正确的,正确的是( )(A ) (B ) (C ) (D ) 6.抛物线1)1(22+-=x y 的顶点坐标是( )A .(1,1)B .(1,-1)C .(-1,1)D .(-1,-1)7.函数y =a x +b 与y =a x 2+bx +c 的图象如右图所示,则下列选项中正确的是( ) A . a b >0, c>0 B . a b <0, c>0 C . a b >0, c<0 D . a b <0, c<0 8.已知a ,b ,c 均为正数,且k=ba cc a b c b a +=+=+,在下列四个点中,正比例函数kx y = 的图像一定经过的点的坐标是( ) A .(l ,21) B .(l ,2) C .(l ,-21) D .(1,-1) 9.如图,在平行四边形ABCD 中,AC=4,B D=6,P 是BD 上的任一点,过P 作EF ∥AC ,与平行四边形的两条边分别交于点E ,F .设BP =x ,EF =y ,则能反映y 与x 之间关系的图象为……………( )A BCDEFP10.如图4,函数图象①、②、③的表达式应为( )(A )x y 25-=,2+=x y ,x y 4-= (B )x y 25=, 2+-=x y ,x y 4=(C )x y 25-=,2-=x y ,x y 4=(D )x y 25-=,2-=x y ,xy 4-=11.张大伯出去散步,从家走了20分钟,到一个离家900米的阅报亭,看了10分钟报纸后,用了15分钟返回到家,下面哪个图形表示张大伯离家时间与距离之间的关系( )12.二次函数y =x 2-2x +2有 ( ) A . 最大值是1 B .最大值是2 C .最小值是1 D .最小值是213.设A (x 1,y 1)、B (x 2,y 2)是反比例函数y =x2-图象上的两点,若x 1<x 2<0,则y 1与y 2之间的关系是( )A . y 2< y 1<0B . y 1< y 2<0C . y 2> y 1>0D . y 1> y 2>0 14.若抛物线y =x 2-6x +c 的顶点在x 轴上,则c 的值是 ( )A . 9B . 3C .-9D . 0 15.二次函数2332+-=x x y 的图象与x 轴交点的个数是( ) A .0个 B .1个 C .2个 D .不能确定二、填空题:(每小题3分,共30分)1.完成下列配方过程:122++px x =()[]()________________22+++px x=()()____________2++x ;2.写出一个反比例函数的解析式,使它的图像不经过第一、第三象限:_________. 3.如图,点P 是反比例函数2y x=-上的一点,P D ⊥x 轴于点D ,则△P OD 的面积为 ;x第3题图yPD O4、已知实数m 满足022=--m m ,当m =___________时,函数()11++++=m x m x y m的图象与x 轴无交点.5.二次函数)1()12(22-+++=m x m x y 有最小值,则m =_________;6.抛物线322--=x x y 向左平移5各单位,再向下平移2个单位,所得抛物线的解析式为___________; 7.某商场销售一批名牌衬衫,平均每天可售出20件,每件可 盈利40元.为了扩大销售量,增加盈利,采取了降价措施,经调查发现如果每件计划降价1元,那么商场平均每天可多售出2件.若商场平均每天要赢利1200元,则每件衬衫应降价__________;8.某学生在体育测试时推铅球,千秋所经过的路线是二次函数图像的一部分,如果这名学生出手处为A (0,2),铅球路线最高处为B (6,5),则该学生将铅球推出的距离是________; 9.二次函数)0(2≠++=a c bx ax y 的图像与x 轴交点横坐标为-2,b ,图像与y 轴交点到圆点距离为3,则该二次函数的解析式为___________; 10.如图,直线)0(2〉-=k kx y 与双曲线xky =在第一象限内的交点R ,与x 轴、y 轴的交点分别为P 、Q .过R 作RM ⊥x 轴,M 为垂足,若△OPQ 与△PRM 的面积相等,则k 的值等于 .三、解答题:(1-3题,每题7分,计21分;4-6题每题8分,计24分;本题共45分)1已知二次函数c bx x y ++=2的图像经过A (0,1),B (2,-1)两点.(1)求b 和c 的值;(2)试判断点P (-1,2)是否在此函数图像上?2.已知一次函数y kx k =+的图象与反比例函数8y x=的图象交于点P (4,n ). (1)求n 的值.(2)求一次函数的解析式.3.看图,解答下列问题.(1)求经过A 、B 、C 三点的抛物线解析式;(2)通过配方,求该抛物线的顶点坐标和对称轴;(3)用平滑曲线连结各点,画出该函数图象.4.已知函数y=x2+bx-1的图象经过点(3,2)(1)求这个函数的解析式;(2)画出它的图象,并指出图象的顶点坐标;(3)当x>0时,求使y≥2的x的取值范围.5.某工厂设门市部专卖某产品,该产品每件成本40元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:每件销售价(元)506070758085…每天售出件数30024018015012090…假设当天定的售价是不变的,且每天销售情况均服从这种规律.(1)观察这些统计数据,找出每天售出件数y与每件售价x(元)之间的函数关系,并写出该函数关系式.(2)门市部原设有两名营业员,但当销售量较大时,在每天售出量超过168件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为40元.求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)6.如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状.(1) (2)(1)一身高0.7米的小孩站在离立柱0.4米处,其头部刚好触上绳子,求绳子最低点到地面的距离;(2)为供孩子们打秋千,把绳子剪断后,中间系一块长为0.4米的木板,除掉系木板用去的绳子后,两边的绳长正好各为2米,木板与地面平行.求这时木板到地面的距离(供选用数据:36.3≈1.8,64.3≈1.9,36.4≈2.1)7.已知抛物线y =-x 2+mx -m +2.(Ⅰ)若抛物线与x 轴的两个交点A 、B 分别在原点的两侧,并且AB 5,试求m 的值;(Ⅱ)设C 为抛物线与y 轴的交点,若抛物线上存在关于原点对称的两点M 、N ,并且 △MNC 的面积等于27,试求m 的值.参考答案:一、选择题: 1.A 2.D 3.D 4.B 5.D 6.A 7.D 8.A 9.A 10.C 11.D 12.C 13.C 14.A 15.C 二、填空题:1.2p ,21p -,p ,21p - . 2 y =x 2-3. 1 4.2或-1 5. 45- 6.1082++=x x y 7.10元或20元8.6+52 9. 3412--=x x y 或 3412+=-=x x y 10.22三、解答题:1.2.解:(1)由题意得:84n =, 2.n ∴= (2)由点P (4,2)在y kx k =+上,24,k k ∴=+ 25k ∴=. ∴一次函数的解析式为2255y x =+. 3.解:(1)由图可知A (-1,-1),B (0,-2),C (1,1) 设所求抛物线的解析式为y =ax 2+bx +c依题意,得121a b c c a b c -+=-⎧⎪=-⎨⎪++=⎩,, 解得212a b c =⎧⎪=⎨⎪=-⎩,, ∴ y =2x 2+x -2.(2)y =2x 2+x -2=2(x +41)2-817∴ 顶点坐标为(-41,817),对称轴为x =-41(3)图象略,画出正确图象4.解:(1)函数y =x 2+bx -1的图象经过点(3,2)∴9+3b -1=2,解得b =-2 . ∴函数解析式为y =x 2-2x -1(2)y =x 2-2x -1=(x -1)2-2 ,图象略, 图象的顶点坐标为(1,-2) (3)当x =3 时,y =2, 根据图象知,当x ≥3时,y ≥2 ∴当x >0时,使y ≥2的x 的取值范围是x ≥3.5.解:(1)由统计数据知,该函数关系为一次函数关系,每天售出件数y 与每件售价x 之间的函数关系为: x y 6600-=.(2)当168=y 时, 6006168+-=x , 解得:72=x ; 设门市部每天纯利润为z ①当72<x 时,168>y()()()52807063406600402+--=⨯---=x x x z当70=x 时,5280max =z②当72≥x 时,168≤y()()()53207062406600402+--=⨯---=x x x z70≥x 时,y 随x 的增大而减少72=∴x 时,52965320262max =+⨯-=z52805296> 72=∴x 当时,纯利润最大为5296元.6.(1) (2)解:(1)如图,建立直角坐标系, 设二次函数解析式为 y =ax 2+c ∵ D (-0.4,0.7),B (0.8,2.2), ∴ ⎩⎨⎧.=+,=+2.264.07.016.0c a c a∴ ⎪⎩⎪⎨⎧.=,=2.0528c a ∴绳子最低点到地面的距离为0.2米.(2)分别作EG ⊥AB 于G ,FH ⊥AB 于H , AG =21(AB -EF )=21(1.6-0.4)=0.6. 在Rt △AGE 中,AE =2,EG =22AG AE -=226.02-=64.3≈1.9.∴ 2.2-1.9=0.3(米). ∴ 木板到地面的距离约为0.3米.7.解: (I)设点A(x 1,0),B (x 2,0) , 则x 1 ,x 2是方程 x 2-mx +m -2=0的两根.∵x 1 + x 2 =m , x 1·x 2 =m -2 <0 即m <2;又AB =∣x 1 x 2121245x x x x -=2(+)m 2-4m +3=0 .解得:m =1或m =3(舍去) ,∴m 的值为1 . (II )设M (a ,b ),则N (-a ,-b ) .∵M 、N 是抛物线上的两点,∴222,2.a ma m b a ma m b ⎧-+-+=⎪⎨---+=-⎪⎩①②①+②得:-2a 2-2m +4=0 . ∴a 2=-m +2.∴当m <2时,才存在满足条件中的两点M 、N . ∴2a m=±-.这时M 、N 到y 轴的距离均为2m -, 又点C 坐标为(0,2-m ),而S △M N C = 27 , ∴2×12×(2-m )×2m -=27 . ∴解得m =-7 . 。
