第四章(1)--弯曲内力--20141124
合集下载
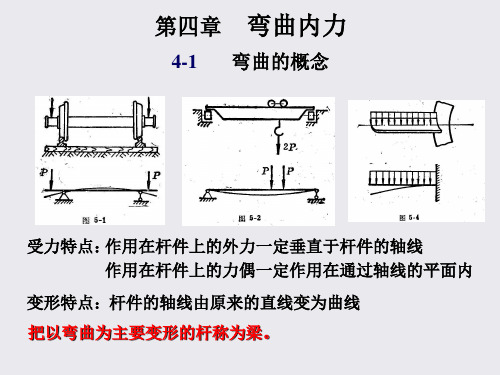
4-1弯曲内力

FS <0
或者:左上右下为正、 右上左下为负
、弯矩 M: 上凹下凸形的为正
下凹上凸形的为负
M ≥0
M ≤0
15
弯曲内力
例 2 。求下图示梁1--1、2--2截面处的内力。 qL 1 1 a qL A x1 FS1
图(b)
2
q
解:截面法求内力∶
1--1截面处剪力、弯矩如图(b)
2
b 图(a) M1
M
弯曲内力
简 易 作 图 法 : 1 ,计算特殊点的内力值确定图的起点或中间点或终点; 2,利用内力和外力的微分关系判定线形; 3,计算特殊点的内力值判定图的正确性,是否封闭;
33
弯曲内力
特殊点:
1,梁的端点∶自由端、固定端、外伸端、中间铰,等等; 2,载荷的端点∶分布力的起终端、集中力(力矩)点,等等; 3,梁的支座∶固定端、固定铰,滚动铰、中间铰,等等; 4,内力的特殊点∶ FS =0的M有极值点,等等; 计算法∶
20
弯曲内力
q( x )
A
RA
qo
M ( x)
FS ( x )
x RB B
q0 x 2 1 1 2 M x RA x q( x ) x x (L x ) 6L 2 3
21
弯曲内力
§4-3 剪力方程、弯矩方程、剪力图和弯矩图 1、内力方程:内力与截
面位置坐标(x)间的函
FS ( Pi ) ( Pj )
弯曲内力
例 3 。求下图示梁 AB 、 BC 、 CD 段的的内力。
q
qa2
D C
A
B a qa a
a
FS 2 RA 2 qa q( x2 a )
材料力学第四章 弯曲内力

§4-4 剪力、弯矩和荷载集度之间的关系 二、内力图特征
外力 情况
FQ
q(x)=0
q(x)=C<0 C
FQ FQ
②
F
m C
FQ图
特征
① ②
x
①
③
x
F
③
⑤ ④ ① ② ③
FQ
x x x x x
C ①
③
②
x
水平直线
③1 ③3 ③2
向下斜直线
C 处有突变 与F 方向一致
①
C 处无变化
② ③ ①
M图
特征
M
x
x2
x 72 8 x 88
x 3.6m
x1
dM ( x) FQ ( x)dx
x1
M 2 M1 FQ ( x)dx
x1
M1 0 M 2 72 2 144kN m CB段 F 72kN Q3 FQ4 72 20 8 88kN M3 72 2 160 16kN m M 4 20 2 20 2 1 80kN m
第4章 弯曲内力
例题5
q0 A
1 2 q0l
试作图示悬臂梁的剪力图和弯矩图
q (x) 一次直线
x
解: 1、求x截面荷载集度
B
l
q0 q ( x ) (l x ) l
2、列内力方程
二次曲线
FQ
1 2 6 q0l
三次曲线
M
1 1 q0 FQ ( x) q ( x)(l x) (l x) 2 2 2 l 1 1 M ( x) q( x)(l x) (l x) 2 3 q0 (l x)3 6l
第四章弯曲内力精品文档

(Shear- force and bending- moment in beams)
一、内力计算(Calculating internal force)
[举例] 已知 如图,F,a,l.
a
求距A端x处截面上内力.
解: 求支座反力
Fx 0 , FRAx 0
A l
Fa M A 0 , FRB l
上的剪力和弯矩.
F1=F
FRA
FRB F2=F
C
A
D
B
b
a c
解:(1)求支座反力
2019/10/F 26R A F R B F 6k 0N
27
(Internal forces in beams)
(2)计算C 横截面上的剪力FSC和弯矩 MC
看左侧
F S C F 1 6k 0N M C F 1 b 6 . 0 k m N
解得 FSEFRA MFc 2019/10/26 E R A
FRA
FSE
ME
A
E
c
20
(Internal forces in beams)
FRA
A
FSE ME
E
c
取右段为研究对象
FSE
F1
ME
EC
F2
FRB
D
B
a-c b-c l-c
Fy 0 F S E F R B F 1 F 2 0
(3)计算D横截面上的剪力FSD 和弯矩 MD
看左侧
F S D F R A F 1 6 6 0 0 0
M D F R A ( c a ) F 1 c F 1 . 8 k a 3 m
第四章弯曲内力课件

例3 求图示梁1-1,2-2截面的内力。 P=3kN A 2m
m2=6kNm m1=2kNm 1 2 q=1kN/m 1
B 2 1m RB=4kN 2m 2m
1m RA=5kN 2m
解:(1) 求反力
RA 5kN
RB 4kN
P=3kN
m2=6kNm m1=2kNm 1 2 q=1kN/m
依方程画出剪力图和弯矩图。
FS ( x ) F M ( x ) Fx
(0 x l ) (0 x l )
F
A x l B
FS
x
M
F
x
q
x q x
FS l
例题6 悬臂梁受均布载荷作用。 试写出剪力和弯矩方程,并画出 剪力图和弯矩图。
M x
解 : 任选一截面 x ,写出剪力
和弯矩 方程
FS x
M =0, M =0
B
M
M x1 =Fbx1 / l 0 x1 a FS x2 = Fa / l a x2 l M x2 =Fal x2 / l a x2 l
依方程画出剪力图和弯矩图。
3.
a
M
b
A
FAY
x1
M /l
C
l
x2
B
x
O
O
例题5 如图所示的悬臂梁在自由端受集中荷载 F 作用, 试作此
梁的剪力图和弯矩图. 解 (1) 将坐标原点取在梁的左端,
列出梁的剪力方程 和弯矩方程
F
B x l
A
FS ( x ) F M ( x ) Fx
(0 x l ) (0 x l )
F SA左 0
第4章 弯曲内力

§4.3 剪力、弯矩方程及剪力图和弯矩图
一、剪力方程和弯矩方程
在一般情况下,梁横截面上的剪力和弯矩随截
面的位置而变化。
M0 8KN.m
q=2KN/m
P=2KN
A
E
C
F
B
D
1m 1m
2m
1m 1m
因此,剪力和弯矩均可表示为截面位置x的函数,即
FQ FQ (x), M M (x)
称为剪力方程和弯矩方程
x
AB段:
a
B a
Cx
FQ (x) 0 (0 x a)M (x) m a (0 x a)BC段:
m=Pa P
FQ (x) P (a x 2a) M (x) m P(x a)
A
xB a
a
2Pa Px (a x 2a)
2、作梁的剪力图和弯矩图
3、求
FQ
和M
max
max
第四章 弯曲内力
目录
§4-1 平面弯曲的概念和梁的计算简图
§4.1.1 平面 弯曲的概念
起重机大梁
q
P
A
B
工程实际中的弯曲问题
P
P
P
以弯曲变形为主的杆件通常称为梁
受力特点:在构件的纵向对称平面内,受 到垂直于梁的轴线的力或力偶作用,使构 件的轴线在此平面内弯曲为曲线,这样的 弯曲称为平面弯曲。
内力偶M是与横截面垂直的内力系的合
力偶矩,有使梁产生弯曲的趋势,故称 力偶矩M弯矩。
4.2.3 剪力与弯矩正负号规定
同一位置处左、右侧截面上内力分量必须具有相同的正负号。
剪力Q :截面上的剪力对所选梁段上任意一点的矩为 顺时针转向时,剪力为正;反之为负。 概括 为“左段下右段上,剪力为正”。
第四章 弯曲内力

(3)画剪力图和弯矩图
(a x l )
Pb l
M max Pab l
x
FS max
例5
画出图示梁的FS图和M图。
y
A
RA
(1)先求出约束反力: 解:
a
x
C x
M
b
(2)剪力方程和弯矩方程:
M RA l
M RB l
B
x
l
RB
M l Ma l
AC段: FS M FS1 ( x) RA (0 x a ) l Mx M 1 ( x) R A x (0 x a ) l CB段: M (a x l ) M FS 2 ( x) RA l M M 2 ( x) R A x M xM l (a x l )
0 x3
x
M ( x) P(4 x) 3(4 x) 3 x 4
(3)作剪力和弯矩图;
x
3kN m
dM ( x) 2 2x 0 dx
当 x 1m 时
M | x1m 1kN m
—— 极值点
§4. 5 载荷集度、剪力和弯矩间的关系
图示简支梁,建立如图坐标系。 约定: 分布力q向上为正,向下为负。
M | x 0 0
—— 斜直线 1 2 M | x l ql 2 —— 二次抛物线
x
ql 2 2
FS
max
ql
M
max
ql 2 2
例4
画出图示梁的FS图和M图。
y
(1)先求出约束反力: 解:
a
A
P
C x l
Pb l Pa l
Pab l
《材料力学》第4章弯曲内力 课后答案

0 ; FS−C
= b F, a+b
M
− C
=
ba a+b
F
FS+C
=
−a a+b
F
,
M
+ C
=
ba a+b
F ; FSB
=
−A a+b
F
,MB
=
0
d解
图(d1), ∑ Fy
=
0,F
=
1 2
ql
,
∑
M
A
= 0,M A
=
− 3 ql 2 8
仿题 a 截面法得
FSA
=
1 2
ql
,MA
=
−
3 8
ql
2
;
FS−C
FS (x) = −F
⎜⎛ 0 < x < l ⎟⎞
⎝
2⎠
M (x) = −Fx ⎜⎛0 ≤ x ≤ l ⎟⎞
⎝
2⎠
FS (x) = F
⎜⎛ l < x < l ⎟⎞
⎝2
⎠
45
M (x) =
FA x +
FB
⎜⎛ ⎝
x
−
l 2
⎟⎞ ⎠
,
FB
= 2F
M (x) = Fx − Fl ⎜⎛ l ≤ x ≤ l ⎟⎞
( ) 解
∑MB
=
0 , FA
⋅l
+
ql 2
×
3l 4
− ql 2
=
0
, FA
=
5 ql 8
↑
( ) ∑ Fy
= 0 , FB
材料力学考研复习资料第4章弯曲内力

M eb l
发生在C截面右侧
思考:对称性与反对称性
FA
F
FB
A
B C
l/2
l/2
Fs
F/2
x
F/2
x
M
Fl/4
FA
Me
FB
A
B C
l/2
l/2
Fs
Me l
x
Me/2
M
Me/2
x
结论:
• 结构对称、外力对称时,弯矩图为正对称, 剪力图为反对称
• 结构对称、外力反对称时,弯矩图为反对称, 剪力图为正对称
34
A1 2
34
Bx
内力
FS M
1—1 -P -Pa
2—2 2P -Pa
3—3 2P Pa
4—4 2P -2Pa
3、在集中力作用处,剪力值发生突变,突变值= 集中力大小;
在集中力偶作用处,弯矩值发生突变,突变值= 集中力偶矩大小。
例 图示简支梁受到三角形分布荷载的作用,最大荷
载集度为q0,试求截面C上的内力。
1 FS1
M1 Fa ( 顺 )
截面2—2
Fy 0 FS2 FA F 0
F
C2 2 M2
FA 2 FS2
FS2 FA F 2F MC2 0 M2 F a 0
M 2 Fa ( 顺 )
y
Me =3Fa
F
1A2 3 4
B
1 2 34
x
a
a
FA
2a
FB
截面3—3 F
C33 M3
1 8
ql
FSB左
1 ql 8
剪力方程为常数,剪力图为
水平线。
M图:
四章弯曲内力

§4-4 剪力图和弯矩图
例题5-2
q
悬臂梁受均布载荷作用。
x
l
q
试写出剪力和弯矩方程,并
画出剪力图和弯矩图。
解:任选一截面x ,写出
x
FS
M x
剪力和弯矩 方程
FS x=qx
0 x l
FS x
ql
M x=qx2 / 2 0 x l
依方程画出剪力图和弯矩图
Ma / l
FAy=M / l FBy= -M / l
2.写出剪力和弯矩方程
AC FS x1=M / l 0 x1 a
M x1=Mx1 / l 0 x1 a
Mb / l
CB FS x2 =M / l 0 x2 b
M x2 = Mx2 / l 0 x2 b
d
2M (x) dx2
dFs (x) dx
q(x)
5
目录
26
§4-5 载荷集度、剪力和弯矩间的关系
载荷集度、剪力和弯矩关系:
d 2M (x) dx2
dFs (x) dx
q(x)
1. q=0,Fs=常数, 剪力图为直线; M(x) 为 x 的一次函数,弯矩图为斜直线。
2.q=常数,Fs(x) 为 x 的一次函数,剪力图为斜直线; M(x) 为 x 的二次函数,弯矩图为抛物线。
FSE
FBy
F 3
FAy
5F 3
O
ME
分析右段得到:
FAy
FBy
ME
O
FSE
Fy 0 FSE FBy 0
F
FBy
第四章 弯曲内力

§4–1 工程实际中的弯曲问题
2.梁的计算简图 2.梁的计算简图
(3) 载荷简化 ②分布力 q — 均布力 均布力 q(x) — 分布力
③集中力偶、分布力偶 集中力偶、 M — 集中力偶 m — 分布力偶
§4–1 工程实际中的弯曲问题
2.梁的计算简图 2.梁的计算简图
(4) 支座简化
A
① 固定铰支座 2个约束,1个自由度. 个约束, 个自由度. 如:桥梁下的固定支座,止 桥梁下的固定支座, 推滚珠轴承等. 推滚珠轴承等.
第四章 弯曲内力
第四章 弯曲内力
§4–1 工程实际中的弯曲问题 §4–2 剪力和弯矩 §4–3 剪力图和弯矩图 剪力、 §4–4 剪力、弯矩和分布载荷集度间的关系
第四章 弯曲内力
【本章学习目的】
1. 了解平面弯曲的概念 2. 能够列出剪力方程和弯矩方程 掌握剪力、 3. 掌握剪力、弯矩和分布载荷集度间的关系 4. 熟练绘制剪力图和弯矩图
F FA = FB = 2
(2)列内力方程 )
F FS1 = FA = 2 F M1 = FA x1 = x1 2
内力图对称中垂线. 内力图对称中垂线
( 0 < x1 < a ) ( 0 ≤ x1 ≤ a )
M max Fl = 4
FS max
F = 2
§4–3 剪力图和弯矩图 简支梁,受集中力偶M 作用,作内力图. 例4-5 简支梁,受集中力偶 e作用,作内力图 解: (1)求支座反力 )
( 0 < x1 < a ) ( 0 ≤ x1 ≤ a ) ( 0 < x2 < b ) ( 0 ≤ x2 ≤ b )
Fa Fab = M max = l l
(3)根据方程作内力图 FS max )
材料力学4材力弯曲内力

m A i0 m A 3 1 1 .5 5 1 0 9.5 k 6N m
§4-2 梁的剪力和弯矩
同样应S联he系ar变F形or来ce定a义nd剪B力enQd和in弯g 矩MMom的e正nt负in。B如ea图m,规定:
为了正计剪算力梁使的微应梁力段和产位生左移上,右首下先的应相该对确错定动梁时在(外Q力≥作0)用。下任一
m
Ai
0 : RBl
q0l 2
2l 3
0
RB
q0l 3 m Bi来自0 : R Al
q0l 2
l 3
0
RA
q0l 6
显然,所得到的RA和 RB与梁上荷载的合力一 起能满足 SY=0 这一平 衡方程,故计算结果是
正确的。
§4-2 梁的剪力和弯矩
Yi例0 4:- 5a 2 S 如hq e0 l图a ar aQ F所C o 示rc0e, andQ C B e nq d2 0a li2 n g M2 2o 0 m2 1 2e n 5 tk inN Beam 一性 根 分m C 在布 c整荷0:个载M C 长作度用q 2 0a l上的2 受悬a 3 线臂0M Cq 6 0a l32 6 0 2 1 3 1.66 kN m
§4-1对称弯曲的概念及梁的计算简图
Ⅱ.梁的计算简图
例题4-1计算图a所示悬臂梁的支反力。
解:在竖直荷载作用下,梁固定端的支反力有两个,即矩为mA的支反力偶和铅垂
支反力RA。设mA和RA的转向和指向如图b所示。 将梁上的均布荷载以其合力ql/2
代替,合力的作用线通过均布荷载图形面积的形心,即到固定端的距离为3l/4。
称为平面弯曲Plane bending,或更确切地称为对称 弯曲。若梁不具有纵对称面,或者,梁虽具有纵 对称面但外力并不作用在纵对称面内,这种弯曲 则统称为非对称弯曲。对称弯曲是弯曲问题中最简单
§4-2 梁的剪力和弯矩
同样应S联he系ar变F形or来ce定a义nd剪B力enQd和in弯g 矩MMom的e正nt负in。B如ea图m,规定:
为了正计剪算力梁使的微应梁力段和产位生左移上,右首下先的应相该对确错定动梁时在(外Q力≥作0)用。下任一
m
Ai
0 : RBl
q0l 2
2l 3
0
RB
q0l 3 m Bi来自0 : R Al
q0l 2
l 3
0
RA
q0l 6
显然,所得到的RA和 RB与梁上荷载的合力一 起能满足 SY=0 这一平 衡方程,故计算结果是
正确的。
§4-2 梁的剪力和弯矩
Yi例0 4:- 5a 2 S 如hq e0 l图a ar aQ F所C o 示rc0e, andQ C B e nq d2 0a li2 n g M2 2o 0 m2 1 2e n 5 tk inN Beam 一性 根 分m C 在布 c整荷0:个载M C 长作度用q 2 0a l上的2 受悬a 3 线臂0M Cq 6 0a l32 6 0 2 1 3 1.66 kN m
§4-1对称弯曲的概念及梁的计算简图
Ⅱ.梁的计算简图
例题4-1计算图a所示悬臂梁的支反力。
解:在竖直荷载作用下,梁固定端的支反力有两个,即矩为mA的支反力偶和铅垂
支反力RA。设mA和RA的转向和指向如图b所示。 将梁上的均布荷载以其合力ql/2
代替,合力的作用线通过均布荷载图形面积的形心,即到固定端的距离为3l/4。
称为平面弯曲Plane bending,或更确切地称为对称 弯曲。若梁不具有纵对称面,或者,梁虽具有纵 对称面但外力并不作用在纵对称面内,这种弯曲 则统称为非对称弯曲。对称弯曲是弯曲问题中最简单
材料力学-第4章-1

9 FAy= qa , 4 3 FBy= qa 4
2.确定控制面 由于AB段上作用有连续分布载荷,故A、B两个截 面为控制面,约束力 FBy 右侧的截面,以及集中力 qa 左侧的截面,也都是控制面。
§4-5
载荷集度、剪力和弯矩间的关系
q
C
D
A
B
9 4
qa FAy
4a
FS 9qa / 4
(+)
O
ME FAy 2F
M
E
2F
a 2
3 2
Fa
ME
§4.3
剪力和弯矩
(1)求支反力RA、RB
M 0, RB 4 2 2 3 8 1 0
A
例题:简支梁,求1-1,2-2截面上的内力
P 8kN q 2kN m
1 A
1m 1m 2m
2
B
RA
1.5m
1
3m
RB ∑Y=0,
强调:外力符号取法:以左段为研究对象,求剪力时
外力向上取正,向下去负;求弯矩时外力对截面形心的 矩顺正逆负。右段反之。
§4.4 剪力方程和弯矩方程 剪力图和弯矩图
q
x q x
FS l
悬臂梁受均布载荷作用。 试写出剪力和弯矩方程,并画出 剪力图和弯矩图。
M x
解:任选一截面x ,写出剪力 和弯矩 方程
材料力学
第四章 弯曲内力
目 录
§4.1 弯曲的概念和实例
§4.2 受弯杆件的简化
§4.3 剪力和弯矩
§4.4 剪力方程和弯矩方程 剪力图和弯矩图
§4.5 载荷集度、剪力和弯矩之间的关系
§4.6 平面曲杆的弯曲内力 §4.7 用叠加法作内力图
2.确定控制面 由于AB段上作用有连续分布载荷,故A、B两个截 面为控制面,约束力 FBy 右侧的截面,以及集中力 qa 左侧的截面,也都是控制面。
§4-5
载荷集度、剪力和弯矩间的关系
q
C
D
A
B
9 4
qa FAy
4a
FS 9qa / 4
(+)
O
ME FAy 2F
M
E
2F
a 2
3 2
Fa
ME
§4.3
剪力和弯矩
(1)求支反力RA、RB
M 0, RB 4 2 2 3 8 1 0
A
例题:简支梁,求1-1,2-2截面上的内力
P 8kN q 2kN m
1 A
1m 1m 2m
2
B
RA
1.5m
1
3m
RB ∑Y=0,
强调:外力符号取法:以左段为研究对象,求剪力时
外力向上取正,向下去负;求弯矩时外力对截面形心的 矩顺正逆负。右段反之。
§4.4 剪力方程和弯矩方程 剪力图和弯矩图
q
x q x
FS l
悬臂梁受均布载荷作用。 试写出剪力和弯矩方程,并画出 剪力图和弯矩图。
M x
解:任选一截面x ,写出剪力 和弯矩 方程
材料力学
第四章 弯曲内力
目 录
§4.1 弯曲的概念和实例
§4.2 受弯杆件的简化
§4.3 剪力和弯矩
§4.4 剪力方程和弯矩方程 剪力图和弯矩图
§4.5 载荷集度、剪力和弯矩之间的关系
§4.6 平面曲杆的弯曲内力 §4.7 用叠加法作内力图
工程力学4第四章弯曲内力

FS=-FB+F2 =ΣFi右
B
M
m
C
F2 FB
FS m
M=FB(l-x)-F2(l-x-b)
=ΣM(Fi)右
•规律: 剪力:某一截面的剪力在数值上等于截面一侧 (左或右)梁段上所有外力的代数和。
FS=±ΣFi左或右
•弯矩:某一截面的弯矩在数值上等于截面一侧 (左或右)梁段上所有外力对该截面形心的力矩 的代数和。
例2 图示简支梁及其上所受荷载。求 1-1、2-2 、3-3、4-4及5-5截面上的内力。
解 (1) 求支座反力。
由
M
FA
B
0
A FA
Me=4Fa B 1 2 3 4 5 a a a FB
F
2 Fa 4Fa 2F 3a
由
MA 0
4Fa Fa FB F 3a
(2) 求各指定截面上的内力。
x
q(x) M x
d 2 M ( x) q( x) 0 2 dx
q(x)
d 2 M ( x) q( x) 0 2 dx
M
qx
1. 梁段上q(x)=0
FS x FS x c
FS图水平线
M x
M x Cx D
M图斜直线
2. 梁段上q(x)=c
MA
q0
A
q(x)
B
( 2)
画剪力图和弯矩图
FA
x
l
q0 1 FS ( x) q( x)(l x) (l x)2 2 2l
q0l/2 Fs q0l2/6 +
1 1 q0 M ( x) q( x)(l x) (l x) (l x)3 2 3 6l
B
M
m
C
F2 FB
FS m
M=FB(l-x)-F2(l-x-b)
=ΣM(Fi)右
•规律: 剪力:某一截面的剪力在数值上等于截面一侧 (左或右)梁段上所有外力的代数和。
FS=±ΣFi左或右
•弯矩:某一截面的弯矩在数值上等于截面一侧 (左或右)梁段上所有外力对该截面形心的力矩 的代数和。
例2 图示简支梁及其上所受荷载。求 1-1、2-2 、3-3、4-4及5-5截面上的内力。
解 (1) 求支座反力。
由
M
FA
B
0
A FA
Me=4Fa B 1 2 3 4 5 a a a FB
F
2 Fa 4Fa 2F 3a
由
MA 0
4Fa Fa FB F 3a
(2) 求各指定截面上的内力。
x
q(x) M x
d 2 M ( x) q( x) 0 2 dx
q(x)
d 2 M ( x) q( x) 0 2 dx
M
qx
1. 梁段上q(x)=0
FS x FS x c
FS图水平线
M x
M x Cx D
M图斜直线
2. 梁段上q(x)=c
MA
q0
A
q(x)
B
( 2)
画剪力图和弯矩图
FA
x
l
q0 1 FS ( x) q( x)(l x) (l x)2 2 2l
q0l/2 Fs q0l2/6 +
1 1 q0 M ( x) q( x)(l x) (l x) (l x)3 2 3 6l
第四章弯曲内力

§4.3 剪力和弯矩
材料力学
一.弯曲内力的含义
设有一简支梁AB,受集中力F作用。现 分析距A端为x处的横截面m-m上的内力。
a mF b
A
B
xm L
材料力学
a mF b
A
F Ay
A F Ay
xm L
m
oM
x
Fs
m
材料力学
1.根据平衡条件求支座反力
Fb
Fa
B
FAy L
FBy L
FBy 2.求m-m截面上的内力
材料力学
M 2Pa - Px (a x 2a)
弯曲内力/剪力方程和弯矩方程 剪力图和弯矩图
2.作梁的剪力图和弯矩图
AB段:
FS ( x) 0 M Pa
m=Pa
P
A
(0 x a)
(0 x a)
B
C
a
a
BC段:
FS ( x) P M 2Pa - Px
(a x 2a)
剪力图: Fs
x
弯矩图: M
x
材料力学
绘制剪力图和弯矩图的注意事项:
1.横坐标要与杆件长度相对应; 2.纵坐标要标明数值大小及正负; 3.纵坐标大小要成比例; 4.是一条连续的图线,不能间断; 5.在图上要画出阴影线.
材料力学
练习一:悬臂梁受力如图所示,列出梁的剪力 方程和弯矩方程, 作出梁的剪力图和弯矩图, 并求出梁的FSmax和Mmax 及其所在截面位置。
材料力学
弯曲内力/剪力和弯矩
如以右侧梁作为研究对象,则:
Fy 0
q
M
Fs q 2a FBy 0
C
Fs
材料力学
一.弯曲内力的含义
设有一简支梁AB,受集中力F作用。现 分析距A端为x处的横截面m-m上的内力。
a mF b
A
B
xm L
材料力学
a mF b
A
F Ay
A F Ay
xm L
m
oM
x
Fs
m
材料力学
1.根据平衡条件求支座反力
Fb
Fa
B
FAy L
FBy L
FBy 2.求m-m截面上的内力
材料力学
M 2Pa - Px (a x 2a)
弯曲内力/剪力方程和弯矩方程 剪力图和弯矩图
2.作梁的剪力图和弯矩图
AB段:
FS ( x) 0 M Pa
m=Pa
P
A
(0 x a)
(0 x a)
B
C
a
a
BC段:
FS ( x) P M 2Pa - Px
(a x 2a)
剪力图: Fs
x
弯矩图: M
x
材料力学
绘制剪力图和弯矩图的注意事项:
1.横坐标要与杆件长度相对应; 2.纵坐标要标明数值大小及正负; 3.纵坐标大小要成比例; 4.是一条连续的图线,不能间断; 5.在图上要画出阴影线.
材料力学
练习一:悬臂梁受力如图所示,列出梁的剪力 方程和弯矩方程, 作出梁的剪力图和弯矩图, 并求出梁的FSmax和Mmax 及其所在截面位置。
材料力学
弯曲内力/剪力和弯矩
如以右侧梁作为研究对象,则:
Fy 0
q
M
Fs q 2a FBy 0
C
Fs
材料力学 第四章 弯曲内力

M 2 10kN.m
3-3截面
Fy 0; FA Fs 3 P 0
Fs3 7kN
M3 0; M 3 FA 2 0
M 3 10kN.m
F=12kN
1 A1
23 2D 3
2m
2m
q=2kN/m 4
B C4 2m
2
A FA
2 Fs2 M2
P=12kN
A
3 3
M3
FA
Fs3
F=12kN
建立剪力与弯矩方程,画剪力与弯矩图
解:1. 支反力计算
FCy qa,
MC
qa2 2
2. 建立剪力与弯矩方程
AB 段
BC 段
FS1 qx1
M1
qx12 2
(0 x1 a) (0 x1 a)
FS2 qa (0 x2 a)
M2
qax2
qa2 2
(0 x2 a)
§4–4 剪力、弯矩与分布荷载集度间的关系
AB 段
BC 段
FS1 qx1
M1
qx12 2
(0 x1 a) (0 x1 a)
FS2 qa (0 x2 a)
M2
qax2
qa2 2
(0 x2 a)
3. 画剪力与弯矩图
剪力图:
FS1 qx1
FS2 qa
弯矩图:
M1
qx12 2
M2
qax2
qa2 2
剪力弯矩最大值:
FS max qa
简单静定梁:
悬臂梁
简支梁
外伸梁
§4-2 剪力和弯矩
FS-剪力
M-弯矩
剪力-作用线位于所切横截面的内力。 弯矩-矢量位于所切横截面的内力偶矩。
3-3截面
Fy 0; FA Fs 3 P 0
Fs3 7kN
M3 0; M 3 FA 2 0
M 3 10kN.m
F=12kN
1 A1
23 2D 3
2m
2m
q=2kN/m 4
B C4 2m
2
A FA
2 Fs2 M2
P=12kN
A
3 3
M3
FA
Fs3
F=12kN
建立剪力与弯矩方程,画剪力与弯矩图
解:1. 支反力计算
FCy qa,
MC
qa2 2
2. 建立剪力与弯矩方程
AB 段
BC 段
FS1 qx1
M1
qx12 2
(0 x1 a) (0 x1 a)
FS2 qa (0 x2 a)
M2
qax2
qa2 2
(0 x2 a)
§4–4 剪力、弯矩与分布荷载集度间的关系
AB 段
BC 段
FS1 qx1
M1
qx12 2
(0 x1 a) (0 x1 a)
FS2 qa (0 x2 a)
M2
qax2
qa2 2
(0 x2 a)
3. 画剪力与弯矩图
剪力图:
FS1 qx1
FS2 qa
弯矩图:
M1
qx12 2
M2
qax2
qa2 2
剪力弯矩最大值:
FS max qa
简单静定梁:
悬臂梁
简支梁
外伸梁
§4-2 剪力和弯矩
FS-剪力
M-弯矩
剪力-作用线位于所切横截面的内力。 弯矩-矢量位于所切横截面的内力偶矩。
材料力学B第4章弯曲内力

第四章 弯曲内力
弯曲内力的符号约定: 弯矩的符号约定:
M
剪力的符号约定:
FQ FQ
材料力学
M
第四章 弯曲内力
例 4-1
qL M 1
2
1a
2
y x
qL M 1 M1
x1FQ1
q b FR
材料力学
悬臂梁受力如图所示,计算1 截面和2截面上的剪力和弯 矩. 解: 1 求支反力
MR
2
FR qL qb
梁:以弯曲变形为主要变形的杆件.
第四章 弯曲内力
材料力学
对称面
c) 平面弯曲: 如果作用于杆件上的所有外力都在纵向对称面内,
弯曲变形后的轴线也将位于这个平面内,这类弯曲称 为平面弯曲。
第四章 弯曲内力
弯曲的一些实例
材料力学
第四章 弯曲内力
材料力学
第四章 弯曲内力
材料力学
第四章 弯曲内力
§4-2 受弯杆件的简化
剪力方程: FQ FQ (x) 弯矩方程: M M (x)
内力方程
材料力学
以坐标(x,FQ) 和(x,M)表示剪力和弯矩沿轴线变化 的图线称为剪力图和弯矩图。
x 表示梁截面的位置 。 FQ 和M 分别表示剪力和弯矩的大小。
第四章 弯曲内力
例 4-2 写出梁的内力方程,并画内力图。
材料力学
MO
x
M(
x
)
1 2
qx2
– qL ②根据方程画内力图.
qL2 2
第四章 弯曲内力
材料力学
例 4-4 图示简支梁受一集中力F作用,试作此梁的内力图。
a
b
A
B
04章弯曲内力-M,Q方程(54学时)(1)
(3)作Q、M图
规律:结构、载荷均对称, Q图反对称,M 图对称。
x l 4 : M 3ql2 32; ql
Q max 2
x l 2 :M ql2 8;
ql 2
M
max
8
q
RA
RA x Q ql / 2
l
RB
M(x)
n
Q(x)
l2
M ql 2/8
ql / 2
叠加法作弯矩图、剪力图
P
q
A x
轴力: 背离截面为正; 指向截面为负; 剪力: 对研究对象任一点取矩,顺时针转向为正,反之为负; 弯矩: 使曲杆曲率增大的弯矩为正;反之 为负;
习题
《材料力学》
4-1-(a),(f),4-2-(c),(e),(i)
梁发生弯曲变形时,任一横截面上同时有两种内力:
1、与截面相切: 剪力 2、内力偶:弯矩
内力符号规定:
•剪力符号:
+Q
•弯矩符号:
-Q +M -M
l 3
P
I
l 2
RA
2)取 左侧:
I
l
l
P
3
o
l 2
Q1
RA
M1
3)取 o
右侧:
Q1
l 2
解、1)求约束反力:
M A(F) 0
RB
P 3
RB
Y 0
RA
结构对称,载荷反对称,Q图对称,M图反对称。
例4-3 求梁的剪力弯矩方程并作Q、M 图。
解:(1)列Q、M方程
q
Q(x) qx
(2)作Q、M图
M (x) q x2 2
x l 4 : M ql 2 32; x l 2 : M ql 2 8;
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fs F 2
l M F ( x) FB (l x) 0 2
M Fx 2
F m
A
m m m m
B
m
FS FS
m
dx
FS FS
m
M
M M
dx
dx
m
m
M
dx
左端向上 右端向下
正剪力 顺时针
左端向下 右端向上
负剪力 逆时针
向下凹 下部受拉
正弯矩 箭头向上
向上凸 上部受拉
A
Mx Fx Mx
Fab l
+ x
x –
Fa l
对于右段(a x l)
FA
M ( x ) Fa (l x )
l
F ( x) FB
Fa l
D
B
Fx
M(x)
x l-x
③ 根据方程画内力图
FB
[例4] 作出下图梁的剪力图和弯矩图。
解:① 求支反力
FA Me M , FB e l l
对称弯曲:
纵向对称面
F1 对称轴
q
M
对称轴
对称弯曲:梁的横截面具有对称轴,且梁的所有外力都作用在
纵向对称面内。则梁变形后的轴线一定是一条在该 纵向对称面内的平面曲线。 非对称弯曲:梁不具有纵向对称面,或虽有纵向对称面但外力 没有作用在纵向对称面内。
二、梁的计算简图
实际工程当中,梁的支承条件与载荷情况一般都比较复杂,
F2
M2
F
Y
F F2 q( x2 a) 0
F2 q(x2 a) F
1 2 M B (F ) Fx2 M 2 2 q(x2 a ) 0
1 M 2 q(x2 a ) 2 Fx2 2
二、剪力方程和弯矩方程 · 剪力图和弯矩图
1. 内力方程:内力与截面位置坐标(x)间的函数关系式。
第四章
弯曲内力
§4–1 对称弯曲的概念及梁的计算简图
一、弯曲的概念
从一根筷子说起……
F3
A
F4
B
要把这根筷子折断,你会怎么做?
F1 F2
F A B
F A
F B
F A
F
F
F B
q
A
q
B
F
F
F
F
F
F
F F
A
F
q
F
F
B
A
q
B
弯曲: 杆件承受垂直于轴线方向外力的作用,称为弯曲。
弯曲作用下杆件的轴线将变为曲线。 梁: 以弯曲为主要变形的杆件,通称为梁。
F ( x)
dx
F ( x ) dF ( x )
q( x )
M ( x)
A
M ( x ) dM ( x )
F ( x)
dx
F ( x ) dF ( x )
M
A
0
1 F ( x )dx M ( x ) q( x )( dx ) 2 M ( x ) dM ( x ) 0 2
为了便于分析计算,应进行必要的简化,抽象出计算简图。
1. 构件本身的简化 通常取梁的轴线来代替梁。 2. 载荷简化 作用于梁上的载荷(包括支座反力)可简化为三种类型:
集中力、集中力偶和分布载荷。
F
q
M
3. 支座简化
① 固定铰链支座 2个约束分量,1个自由度。
A
FAy
FAx
② 可动铰链支座
1个约束分量,2个自由度。
0.2m
B C
1m
E
1.6m
D
0.2m
FA
F ( x)
80 KN
FB
解: ① 利用对称性求支反力
x
80 KN
0
FA FB 80KN
x
16 KN m 48KN m
② 分段画出剪力图
16 KN m
③ 分段画出弯矩图
M ( x)
dM ( x ) Fs ( x ) dx
几何意义?
b
a
dM ( x) Fs ( x)dx
a
b
M B M A Fs ( x)dx
a
b
B 截面的弯矩和A 截面的弯矩差等于两截面间剪力图的面积。
[例9] 利用荷载集度、剪力和弯矩的微分关系作出梁的剪力图和弯矩图。
q=100KN/m A
ql 2 8
x
③ 根据方程画内力图 弯矩方程
[例3] 作出下图梁的剪力图和弯矩图。 a 解:① 求支反力
FA Fb Fa , FB l l
F
b
B
A
l
② 列平衡方程求内力
对于左段 (0 x a)
Fb F ( x ) FA l
Fb x l
FA
F(x)
FB
Fb l C
M ( x)
每个轮子对梁的作用力为F。试求梁内的最大弯矩为极大值时 小车的位置,以及此时的极大弯矩值。
F
A C
d
F
B D
解:① 设左轮C最大弯矩为极大值时
FA F (l x) F (l x d ) l F (2l 2 x d ) l
x
FA
l
此时 M C FA x
F (2l 2 x d ) x l
F FA 2
A
FS F FB 2 m M
剪力
x
FA F 2
m
弯矩
F
y
0
M
m
0
FA FS 0
Fs FA F 2
FA x M 0
M FA x Fx 2
F
m A m B
F
m B l-x
M
FS
m
FB
F 2
F
y
0
M
m
0
FS F FB 0
F ( x)dx dM ( x)
dM ( x ) F ( x) dx
弯矩图上某点处的切线斜率 等于该点处剪力的大小。 几何意义?
综上亦可得出:
d 2 M ( x) q( x ) 2 dx
几种常见荷载作用下 剪力图和弯矩图的几何特征
无外力 均布载荷 集中力 集中力偶
外 力
q=0
水平直线
q 解: 先找出关键点的剪力和弯矩:
A
a
F(x)
B
a
C
A点: F qa ; M 0 x B点: F qa;
M qa 2
3 M qa 2 2
qa
qa
3 qa 2 2
C点: F 0;
qa 2
x
M(x)
2、 剪力、弯矩与分布荷载间微分关系的进一步研究
① 若梁在 x=a 和 x=b 处两个横截面A、B之间无集中力作用
FA qx Fx 0 ql qx Fx FA qx 2
x FA x qx Mx 0 剪力方程 2 x qlx qx 2 M x FA x qx 2 2 2
ql A2
FA
F ( x)
FB
q
Mx
x
C
x
ql 2
Fx
FA
+
M ( x)
a
A
Me
b
B
② 列平衡方程求内力
对于左段 (0 x a)
M F ( x) e l
l
l
FA
A F(x)
CM e
l
FB Mx
x
D B
M ( x) M e x
对于右段(a x l)
Me l
x
Fx
M eb Ml
x
FA
M ( x ) M e (l x )
Fs Fs (x)
M M (x)
2. 剪力图和弯矩图: 剪力图
剪力方程 弯矩方程
Fs Fs (x) 的图形表示
正值画在x轴上侧
弯矩图
M M (x) 的图形表示
正值画在x轴下侧
[例2] 作出下图梁的剪力图和弯矩图。
解:① 求支反力
ql FA FB 2
q B
A
l
② 列平衡方程求内力
③ 根据方程画内力图
x
M(x)
[例6] 作出下图梁的剪力图和弯矩图。
q A 解:① 不用求支座反力
l
F(x)
B
x
q
② 列平衡方程求内力
F ( x) qx
Mx
ql
1 2 ql 2
A
x
C
1 M ( x ) qx2 2
③ 根据方程画内力图
Fx
x
M(x)
[例7] 桥式起重机的大梁AB,其跨度为l。梁上小车轮子的轮距为d。
负弯矩 箭头向下
[例1] 求下图所示梁的1截面和2截面处的内力。 x1 x2 1
q
F
2
a
b
解:1截面处截取的隔离体如图:
F
Y
F F1 0
F
A
M1 F1
F1 F
ቤተ መጻሕፍቲ ባይዱM
A
(F ) Fx1 M1 0
x1
M1 Fx1
2截面处截取的隔离体如图:
F
a
B x2
q
dFs ( x ) q( x ) dx
几何意义?
b
l M F ( x) FB (l x) 0 2
M Fx 2
F m
A
m m m m
B
m
FS FS
m
dx
FS FS
m
M
M M
dx
dx
m
m
M
dx
左端向上 右端向下
正剪力 顺时针
左端向下 右端向上
负剪力 逆时针
向下凹 下部受拉
正弯矩 箭头向上
向上凸 上部受拉
A
Mx Fx Mx
Fab l
+ x
x –
Fa l
对于右段(a x l)
FA
M ( x ) Fa (l x )
l
F ( x) FB
Fa l
D
B
Fx
M(x)
x l-x
③ 根据方程画内力图
FB
[例4] 作出下图梁的剪力图和弯矩图。
解:① 求支反力
FA Me M , FB e l l
对称弯曲:
纵向对称面
F1 对称轴
q
M
对称轴
对称弯曲:梁的横截面具有对称轴,且梁的所有外力都作用在
纵向对称面内。则梁变形后的轴线一定是一条在该 纵向对称面内的平面曲线。 非对称弯曲:梁不具有纵向对称面,或虽有纵向对称面但外力 没有作用在纵向对称面内。
二、梁的计算简图
实际工程当中,梁的支承条件与载荷情况一般都比较复杂,
F2
M2
F
Y
F F2 q( x2 a) 0
F2 q(x2 a) F
1 2 M B (F ) Fx2 M 2 2 q(x2 a ) 0
1 M 2 q(x2 a ) 2 Fx2 2
二、剪力方程和弯矩方程 · 剪力图和弯矩图
1. 内力方程:内力与截面位置坐标(x)间的函数关系式。
第四章
弯曲内力
§4–1 对称弯曲的概念及梁的计算简图
一、弯曲的概念
从一根筷子说起……
F3
A
F4
B
要把这根筷子折断,你会怎么做?
F1 F2
F A B
F A
F B
F A
F
F
F B
q
A
q
B
F
F
F
F
F
F
F F
A
F
q
F
F
B
A
q
B
弯曲: 杆件承受垂直于轴线方向外力的作用,称为弯曲。
弯曲作用下杆件的轴线将变为曲线。 梁: 以弯曲为主要变形的杆件,通称为梁。
F ( x)
dx
F ( x ) dF ( x )
q( x )
M ( x)
A
M ( x ) dM ( x )
F ( x)
dx
F ( x ) dF ( x )
M
A
0
1 F ( x )dx M ( x ) q( x )( dx ) 2 M ( x ) dM ( x ) 0 2
为了便于分析计算,应进行必要的简化,抽象出计算简图。
1. 构件本身的简化 通常取梁的轴线来代替梁。 2. 载荷简化 作用于梁上的载荷(包括支座反力)可简化为三种类型:
集中力、集中力偶和分布载荷。
F
q
M
3. 支座简化
① 固定铰链支座 2个约束分量,1个自由度。
A
FAy
FAx
② 可动铰链支座
1个约束分量,2个自由度。
0.2m
B C
1m
E
1.6m
D
0.2m
FA
F ( x)
80 KN
FB
解: ① 利用对称性求支反力
x
80 KN
0
FA FB 80KN
x
16 KN m 48KN m
② 分段画出剪力图
16 KN m
③ 分段画出弯矩图
M ( x)
dM ( x ) Fs ( x ) dx
几何意义?
b
a
dM ( x) Fs ( x)dx
a
b
M B M A Fs ( x)dx
a
b
B 截面的弯矩和A 截面的弯矩差等于两截面间剪力图的面积。
[例9] 利用荷载集度、剪力和弯矩的微分关系作出梁的剪力图和弯矩图。
q=100KN/m A
ql 2 8
x
③ 根据方程画内力图 弯矩方程
[例3] 作出下图梁的剪力图和弯矩图。 a 解:① 求支反力
FA Fb Fa , FB l l
F
b
B
A
l
② 列平衡方程求内力
对于左段 (0 x a)
Fb F ( x ) FA l
Fb x l
FA
F(x)
FB
Fb l C
M ( x)
每个轮子对梁的作用力为F。试求梁内的最大弯矩为极大值时 小车的位置,以及此时的极大弯矩值。
F
A C
d
F
B D
解:① 设左轮C最大弯矩为极大值时
FA F (l x) F (l x d ) l F (2l 2 x d ) l
x
FA
l
此时 M C FA x
F (2l 2 x d ) x l
F FA 2
A
FS F FB 2 m M
剪力
x
FA F 2
m
弯矩
F
y
0
M
m
0
FA FS 0
Fs FA F 2
FA x M 0
M FA x Fx 2
F
m A m B
F
m B l-x
M
FS
m
FB
F 2
F
y
0
M
m
0
FS F FB 0
F ( x)dx dM ( x)
dM ( x ) F ( x) dx
弯矩图上某点处的切线斜率 等于该点处剪力的大小。 几何意义?
综上亦可得出:
d 2 M ( x) q( x ) 2 dx
几种常见荷载作用下 剪力图和弯矩图的几何特征
无外力 均布载荷 集中力 集中力偶
外 力
q=0
水平直线
q 解: 先找出关键点的剪力和弯矩:
A
a
F(x)
B
a
C
A点: F qa ; M 0 x B点: F qa;
M qa 2
3 M qa 2 2
qa
qa
3 qa 2 2
C点: F 0;
qa 2
x
M(x)
2、 剪力、弯矩与分布荷载间微分关系的进一步研究
① 若梁在 x=a 和 x=b 处两个横截面A、B之间无集中力作用
FA qx Fx 0 ql qx Fx FA qx 2
x FA x qx Mx 0 剪力方程 2 x qlx qx 2 M x FA x qx 2 2 2
ql A2
FA
F ( x)
FB
q
Mx
x
C
x
ql 2
Fx
FA
+
M ( x)
a
A
Me
b
B
② 列平衡方程求内力
对于左段 (0 x a)
M F ( x) e l
l
l
FA
A F(x)
CM e
l
FB Mx
x
D B
M ( x) M e x
对于右段(a x l)
Me l
x
Fx
M eb Ml
x
FA
M ( x ) M e (l x )
Fs Fs (x)
M M (x)
2. 剪力图和弯矩图: 剪力图
剪力方程 弯矩方程
Fs Fs (x) 的图形表示
正值画在x轴上侧
弯矩图
M M (x) 的图形表示
正值画在x轴下侧
[例2] 作出下图梁的剪力图和弯矩图。
解:① 求支反力
ql FA FB 2
q B
A
l
② 列平衡方程求内力
③ 根据方程画内力图
x
M(x)
[例6] 作出下图梁的剪力图和弯矩图。
q A 解:① 不用求支座反力
l
F(x)
B
x
q
② 列平衡方程求内力
F ( x) qx
Mx
ql
1 2 ql 2
A
x
C
1 M ( x ) qx2 2
③ 根据方程画内力图
Fx
x
M(x)
[例7] 桥式起重机的大梁AB,其跨度为l。梁上小车轮子的轮距为d。
负弯矩 箭头向下
[例1] 求下图所示梁的1截面和2截面处的内力。 x1 x2 1
q
F
2
a
b
解:1截面处截取的隔离体如图:
F
Y
F F1 0
F
A
M1 F1
F1 F
ቤተ መጻሕፍቲ ባይዱM
A
(F ) Fx1 M1 0
x1
M1 Fx1
2截面处截取的隔离体如图:
F
a
B x2
q
dFs ( x ) q( x ) dx
几何意义?
b
