第4章-振动wzj
大学物理——第4章-振动和波

合成初相 与计时起始时刻有关.
v A 2
ω
v A
2
O
x2
1
v A 1
x1
xx
分振动初相差2 1与计时起始时刻无关,但它对合成振幅 是相长还是相消合成起决定作用.
20
讨 论
2 A = A2 + A2 + 2A A2 cos(2 1) 1 1
F = kx
3
l0
k
m
A
F = kx = ma
k 令ω = m
2
A x = Acos(ωt +)
o
x
积分常数,根据初始条件确定
a = ω2 x
dx = ω2 x dt 2
2
dx υ = = Aω sin( ωt +) dt
dx 2 a = 2 = Aω cos(ωt +) dt
4
2
x = Acos(ωt +)
15
π
例 4-3 有两个完全相同的弹簧振子 A 和 B,并排的放在光滑 的水平面上,测得它们的周期都是 2s ,现将两个物体从平衡 位置向右拉开 5cm,然后先释放 A 振子,经过 0.5s 后,再释 放 B 振子,如图所示,如以 B 释放的瞬时作为时间的起点, (1)分别写出两个物体的振动方程; (2)它们的相位差是多少?分别画出它们的 x—t 图.
5cm
O
x
16
解: (1)振动方程←初始条件
x0 = 0.05m, υ0 = 0 , T = 2s
2π ω= = π rad/s T
2 υ0 2 A = x0 + 2 = 0.05m ω υ0 对B振子: tan B = = 0 B = 0 x0ω
第4章 机械振动 湘潭大学 大学物理 期末复习

v0 0 arctg ( ) 0, x0
(2)按题意
t=0 时 x0=0,v0>0 m O
x0=Acos0=0 , cos0=0 0=/2 ,3/2 v0=-Asin>0 , sin 0 <0, 取0=3/2
x=9.810-2cos(10t+3/2) m
3、位相、初位相、位相差(Phase, Initial phase, Phase difference) 从简谐振动的运动学方程,可以看到,对于振幅和圆频率都已知的谐振 动中,任意时刻的振动状态完全取决于物理量 . t 0 位相:确定振动系统任意时刻运动状态的物理量。
v0 初位相:T=0 时刻的位相。 tan 0 x0
如位移,电流,电场,磁场,温度等
如:机械波:机械振动在连续介质中的传播; 电磁波:电磁振动在真空或介质中的传播; 物质波:和实物粒子相联系的波。
2、从物理学角度看,振动和波动是唯一一个横跨物理学所有学科,既 与经典物理紧密联系,又与现代物理融为一体的概念。
3、振动和波动在各分支学科中,具体内容不同、本质不同,但描述形 式却具有相似性,,并且都具有干涉、衍射等波动特征。
x A cos( t 0 )
v vm cos(t 0
2
)
a am cos( t 0 )
例1:如图m=2×10-2kg,弹簧的静止形变为l=9.8cm t=0时, x0=-9.8cm,v0=0,1)取开始振动时为计时零点, 写出振动方程;2)若取x0=0,v0>0为计时零点,写 出振动方程,并计算振动频率。 ⑴ 确定平衡位置取为原点:k=mg/ l 令向下有位移x, 则:f=mg-k(l +x)=-kx 作谐振动 设振动方程为:
汽车振动基础第4章-多自由度(定稿)

k11 k1 x1 k2 x1 k1 k2
k21 k12 k2 x1 k2
k22 k2 x2 k3 x2 k2 k3
j2
k31 k13 0
k32 k23 k3 x2 k3
0 k1 k 2 k 2 K k 2 k 2 k3 k3 0 k3 k3
– 拉格朗日法
• 方程的形式
广义坐标
qi (i 1, 2,3,, n)
T:系统的总动能
d T T ( ) Qi 0 dt qi qi
i 1, 2,3, , n
对应于第i个广义 坐标的广义力
– 保守系统
» 系统作用的主动力仅为势力 Qi
d T T U ( ) 0 dt qi qi qi
m2 m22 m3 4
④柔度矩阵的影响系数法
F ij
柔度影响系数 ij 的意义是在第j个坐标上施加单位力作用时,在第i个坐 标上引起的位移。 例题4-8 用影响系数法求图示系统的柔度矩阵
11 F 21 31
12 22 32
13 23 33
也可写成 其中
或
或
MX KX 0
力方程 位移方程
K 1MX X 0
m x 0 或 x
称为柔度,而
FMX X 0
1 称为柔度矩阵
1 k
FK
②刚度矩阵的影响系数法
K kij
刚度影响系数 k 的意义是使系统的第j个坐标产生单位位移,而其它的 ij 坐标位移为零时,在第i个坐标上所施加的作用力的大小。
仅代表外部激励 广义力
大学物理教案-第4章 机械振动 机械波

动的时刻)。
反映 t=0 时刻的振动状态(x0、v0)。
x0 Acos0
v0 Asin0 x
m
A
0=0
o
A
X0 = A
o x
-A x
t T
0 = /2
m
A
o X0 = 0
m
-A
o
X0 = -A
o x
-A x
A
o x
-A
t T
0 = Tt
4、振幅和初位相由初始条件决定
由
x0 Acos0
v0 Asin 0
A A12 A22 2 A1A2 cos2 1 ,
tan A1 sin 1 A2 sin 2 。 A1 cos1 A2 cos2
3. 两种特殊情况
(1)若两分振动同相 2 1 2k ,则 A A1 A2 , 两分振动相互加强, 如 A1=
A2 ,则 A = 2A1
(2)若两分振动反相,2 1 2k 1 , 则 A | A1 A2 | ,两分振动相互减弱,
波动是振动的传播过程。 机械波----机械振动的传播 波动 电磁波----电磁场的传播 粒子波----与微观粒子对应的波动 虽然各种波的本质不同,但都具有一些相似的规律。
一、 弹簧振子的振动 m
o X0 = 0
§4.1
m
简谐振动的动力学特征
二、谐振动方程 f=-kx
a f k x
x
mm
令 k 2 则有 m
教学内容
备注
1
大学物理学
大学物理简明教程教案
第 4 章 机械振动 机械波
前言 1. 振动是一种重要的运动形式 2. 振动有各种不同的形式 机械振动:位移 x 随 t 变化;电磁振动;微观振动 广义振动:任一物理量(如位移、电流等)在某一数值附近反复变化。 3. 振动分类
大物习题答案第4章机械振动

第4章 机械振动4.1基本要求1.掌握描述简谐振动的振幅、周期、频率、相位和初相位的物理意义及之间的相互关系2.掌握描述简谐振动的解析法、旋转矢量法和图线表示法,并会用于简谐振动规律的讨论和分析3.掌握简谐振动的基本特征,能建立一维简谐振动的微分方程,能根据给定的初始条件写出一维简谐振动的运动方程,并理解其物理意义4.理解同方向、同频率简谐振动的合成规律,了解拍和相互垂直简谐振动合成的特点4.2基本概念1.简谐振动 离开平衡位置的位移按余弦函数(或正弦函数)规律随时间变化的运动称为简谐振动。
简谐振动的运动方程 cos()x A t ωϕ=+2.振幅A 作简谐振动的物体的最大位置坐标的绝对值。
3.周期T 作简谐振动的物体完成一次全振动所需的时间。
4.频率ν 单位时间内完成的振动次数,周期与频率互为倒数,即1T ν=5.圆频率ω 作简谐振动的物体在2π秒内完成振动的次数,它与频率的关系为22Tπωπν== 6.相位和初相位 简谐振动的运动方程中t ωϕ+项称为相位,它决定着作简谐振动的物体状态;t=0时的相位称为初相位ϕ7.简谐振动的能量 作简谐振动的系统具有动能和势能。
弹性势能222p 11cos ()22E kx kA t ωϕ==+ 动能[]22222k 111sin()sin ()222E m m A t m A t ωωϕωωϕ==-+=+v弹簧振子系统的机械能为222k p 1122E E E m A kA ω=+== 8.阻尼振动 振动系统因受阻尼力作用,振幅不断减小。
9.受迫振动 系统在周期性外力作用下的振动。
周期性外力称为驱动力。
10.共振 驱动力的角频率为某一值时,受迫振动的振幅达到极大值的现象。
4.3基本规律1.一个孤立的简谐振动系统的能量是守恒的物体做简谐振动时,其动能和势能都随时间做周期性变化,位移最大时,势能达到最大值,动能为零;物体通过平衡位置时,势能为零,动能达到最大值,但其总机械能却保持不变,且机械能与振幅的平方成正比。
第4章《振动》选择题解答与分析

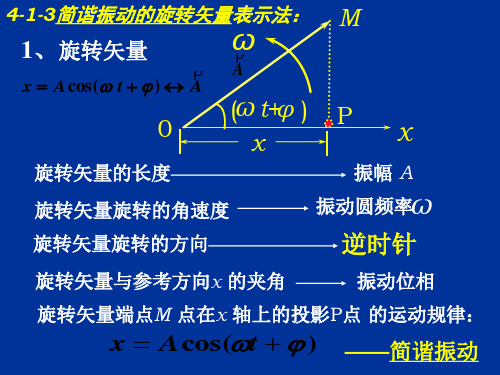
4振动4.1旋转矢量1. 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为答案:(B)参考解答:简谐振动可以用一个旋转矢量的投影来表示。
这一描述简谐振动的几何方法称为旋转矢量法。
以坐标原点o 为始端作一矢量A,该矢量以角速度ω绕o 点逆时针匀速转动。
0=t 时,旋转矢量与x 轴正向的夹角等于ϕ,则在转动过程中的任意时刻t ,矢量A与x 轴正向的夹角为)(ϕω+t ,其端点M 在坐标轴上的投影P 的坐标为)cos(ϕω+=t A x ,P 所代表的运动正是简谐振动。
本题(B)图中,旋转矢量端点在坐标轴上投影点的坐标与运动方向符合题设的要求,即为答案。
对所有选择,均给出参考解答,直接进入下一题。
2. 一质点作简谐振动,周期为T .当它由平衡位置向x 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的时间为 (A) T /12. (B) T /8. (C) T /6. (D) T /4. 答案:(C) 参考解答:根据旋转矢量法,以坐标原点o 为始端作一矢量A,该矢量以角速度ω绕o 点逆时针匀速转动。
0=t 时,旋转矢量与x 轴正向的夹角等于ϕ,则在转动过程中的任意时刻t ,矢量A与x 轴正向的夹角为)(ϕω+t ,其端点在坐标轴上的投影的坐标为)cos(ϕω+=t A x 所代表的运动正是简谐振动。
本题按题意画旋转矢量图,由,3πωθ==t πω2=T 两式联立,解出.6Tt =对所有选择,均给出参考解答,直接进入下一题。
4.2振动曲线、初相1. 一质点作简谐振动.其运动速度与时间的曲线如图所示.若质点的振动规律用余弦函数描述,则其初相应为(A) π/6. (B) 5π/6. (C) -5π/6.(D) -π/6. (E) -2π/3.答案:(C)参考解答:令简谐振动的表达式:)cos(ϕω+=t A x ,)(ϕω+t 称为振动系统在t 时刻的位相。
《机械振动》张义民—第4章第1、2节ppt

◆当振动系统需要两个独立坐标描述其运动时, 那么这个系统就是两个自由度系统。
◆两自由度系统是最简单的多自由度系统。 ◆两自由度系统的振动微分方程一般由两个联立 的微分方程组成。 ◆两自由度系统有两个固有频率及固有振型。
◆在任意初始条件下的自由振动一般由这两个固 有振型叠加,只有在特殊的初始条件下系统才按某 一个固有频率作固有振动。
大象体积庞大,走起路来 更是别具一格,四只脚移动 时分别各自相差90度的位移 差。没有一只脚做的是相同 位移的移动。
◆四只脚动物可以看作是“四个振动体耦合在一起的 系统”吗?事实上,四个振动体组成的系统的基本运动 模式,确实与所提到的那四种走路方式一模一样。
◆可是动物们为什么会按照耦合振动体的方式来行走 呢?虽说现在关于这个问题还没有定论。生物学家们认 为,掌管运动的脑神经网(由数突连接起来的神经细胞) 看起来更接近“耦合振动体”一些。有推测认为,正是 脑神经网的动力学特性,使得动物走起路来才会表现出 振动体的特点。
1998年匈牙利的物理学家塔 马斯·维塞克在布达佩斯音乐学 院举行的一场音乐会上意外地发 现了同步化的现象。
演出相当成功,落幕后观众们热烈的掌声长达 3分钟之久,而维塞克博士便在这里发现了有趣 的东西。音乐会刚一结束,观众们雷鸣暴雨般的 掌声响起,然而过了一段时间之后,观众们的热 烈的掌声显然同步化了,变成了同一种节奏的拍 手。为了答谢观众们的热情,演奏者重新走上台 来谢幕,这时的掌声又突然之间失去了刚才的节 奏,雨点般疯狂地响起。在最后长达3分钟的鼓 掌声中,狂热的掌声和同步的掌声依次交替出现。
◆强迫简谐振动发生在激励频率,而这两个坐标 的振幅将在这两个固有频率下趋向最大值。共振时 的振型就是与固有频率相应的固有振型。
第四章振动下
结论: 结论:
振子在振动过程中, (1) 振子在振动过程中,动能和势能分别随时间 变化,但任一时刻总机械能保持不变。 变化,但任一时刻总机械能保持不变。 (2) 动能和势能的变化频率是弹簧振子振动频 率的两倍。 频率一定时, (3)频率一定时,谐振动的总能量与振幅的平方 成正比。(适合于任何谐振系统) 。(适合于任何谐振系统 成正比。(适合于任何谐振系统) 弹性势能
小结:
描述简谐振动的三种方法: 描述简谐振动的三种方法: 运动方程,振动曲线,旋转矢量。 运动方程,振动曲线,旋转矢量。
的简谐振动, 例1:一物体沿 轴作振 幅为 A 的简谐振动,若初始时该球的 :一物体沿x轴作振 状态为( ) ;(2)在平衡位置且向X轴正方向运动 轴正方向运动; 状态为(1)X0= -A;( )在平衡位置且向 轴正方向运动; ;( 处向X轴负方向运动;(4) 轴负方向运动;( (3)在 X0=1/2 A 处向 轴负方向运动;( )在 ) / 方向运动。试用旋转矢量法确定相应的初相位。 处向正 方向运动。试用旋转矢量法确定相应的初相位。 3π r ϕ = ϕ =π
k = m
得
X
g b
mg
b, v 0 = 0
g t+π) b
A =b, φ = π
[ 例2] 一谐振动的振动曲线如图所示。 一谐振动的振动曲线如图所示。
ω 以及振动方程。 求: ϕ 0 以及振动方程。
−
π
x
x
A 2
3r
A
1.0
0
解:
t
r A
A
π
2
x
π
3
t=
A x0 = = A cos ϕ 0 2 0时 v 0 = − ω A sin ϕ 0 > 0
《振动与声基础》第四章第三节

第三节 球形声源的声辐射
第三节
球形声源的声辐射
第三节 球形声源的声辐射 1、均匀脉动球面的声辐射
Z
a
0 Y
X
第四章 声波的辐射
第三节
球形声源的声辐射
(一)方程和边条件及其解:
2 p(r ) k 2 p(r ) 0; 其中, k / c; un (r ) r a v0 p(r ) r 满足无穷远辐射条件 e jt 略
(2)
c(ka)2
1 (ka) 2
ka 1
4 a 2 c; 0
ka 1
2
c(ka)
1 (ka)
2
a ,小球辐射时(ka 1)低频) (
2
辐射阻 : Rs 4 a
c(ka) 2
1 (ka)
2 ka 1
cS 2
2
;
4 3 辐射抗 : X s 4 a 3( a ) 3M 0 2 1 (ka) ka 1 3
2
c( ka )
1 ( ka )2
第四章
声波的辐射
第三节
球形声源的声辐射
均匀脉动球面声源的辐射阻和辐射抗随 ka 的变化曲线
第四章 声波的辐射
第三节
球形声源的声辐射
(1)
a ,大球辐射时(ka 1 (高频) )
辐射阻 : Rs 4 a 2 辐射抗 : X s 4 a
(二)声源强度和点声源的概念 定义:谐合律振动声源,排开介质的体积速度的幅值为 声源强度,记Q。 均匀脉动球源 : 球面振速, v0e jt ; Q 4 a 2v0 均匀脉动球源的辐射声压场可表示为 : ckQ j ( ka 0 ) 1 j ( t kr ) p(r , t ) e e ; r 4 1 ( ka ) 2 振动面面积,4 a 2 ;
普通物理A(1) 课程指导 第4章《振动》

N
2
cost
N 1
2
2
14
7. 分别敲击某待测音叉和标准音叉,使它们同时发音,听到时强时弱 的拍音.若测得在20 s内拍的次数为180次,标准音叉的频率为300 Hz, 则待测音叉的频率为______________.
拍频: 单位时间内强弱变化的次数 2 1 ( 2 1)
设1 300 Hz 则有: 2 1 9,或者1 2 9 2 309 Hz,或者 2 291Hz
0.08
O
-0.04
1
x1 t (s)
2 x2
x1
0.08 c os (t
2
),
x2
0.04 c os (t
) 2
A2
0
x
A
A1
10
6. N个同方向、同频率的简谐振动,它们的振幅相等,初相分别为0, , 2, ..., 依次差一个恒量 ,求合振动的振幅。
x1 Acost x2 Acos(t ) x3 Acos(t 2)
4
1. 一质点作简谐振动,周期为T.当它由平衡位置向x轴正方向运 动时,从二分之一最大位移处到最大位移处这段路程所需要的时 间为
(A) T /12. (B) T /8. (C) T /6. (D) T /4.
旋转矢量法
[C ]
首先画出二分之一最大位移处旋转矢量图,
然后,再画最大位移处旋转矢量图。
设所求的时间为t,则有
(1) 质点的振动方程; (2) 质点在A点处的速率.
AB
x
解: 3
4
4
t = 0时, x 5cm Acos
A 5 5 2 cm
cos(3 / 4)
∴ 振动方程
x 5 2 102 cos(t 3) (SI) 44
大物习题答案第4章 机械振动

第4章 机械振动基本要求1.掌握描述简谐振动的振幅、周期、频率、相位和初相位的物理意义及之间的相互关系2.掌握描述简谐振动的解析法、旋转矢量法和图线表示法,并会用于简谐振动规律的讨论和分析3.掌握简谐振动的基本特征,能建立一维简谐振动的微分方程,能根据给定的初始条件写出一维简谐振动的运动方程,并理解其物理意义4.理解同方向、同频率简谐振动的合成规律,了解拍和相互垂直简谐振动合成的特点基本概念1.简谐振动 离开平衡位置的位移按余弦函数(或正弦函数)规律随时间变化的运动称为简谐振动。
简谐振动的运动方程 cos()x A t ωϕ=+2.振幅A 作简谐振动的物体的最大位置坐标的绝对值。
3.周期T 作简谐振动的物体完成一次全振动所需的时间。
4.频率ν 单位时间内完成的振动次数,周期与频率互为倒数,即1T ν=5.圆频率ω 作简谐振动的物体在2π秒内完成振动的次数,它与频率的关系为22Tπωπν== 6.相位和初相位 简谐振动的运动方程中t ωϕ+项称为相位,它决定着作简谐振动的物体状态;t=0时的相位称为初相位ϕ7.简谐振动的能量 作简谐振动的系统具有动能和势能。
弹性势能222p 11cos ()22E kx kA t ωϕ==+ 动能[]22222k 111sin()sin ()222E m m A t m A t ωωϕωωϕ==-+=+v弹簧振子系统的机械能为222k p 1122E E E m A kA ω=+== 8.阻尼振动 振动系统因受阻尼力作用,振幅不断减小。
9.受迫振动 系统在周期性外力作用下的振动。
周期性外力称为驱动力。
10.共振 驱动力的角频率为某一值时,受迫振动的振幅达到极大值的现象。
基本规律1.一个孤立的简谐振动系统的能量是守恒的物体做简谐振动时,其动能和势能都随时间做周期性变化,位移最大时,势能达到最大值,动能为零;物体通过平衡位置时,势能为零,动能达到最大值,但其总机械能却保持不变,且机械能与振幅的平方成正比。
大学物理课后习题答案第四章

第四章机械振动4.1一物体沿x 轴做简谐振动,振幅A = 0.12m ,周期T = 2s .当t = 0时,物体的位移x = 0.06m ,且向x 轴正向运动.求:(1)此简谐振动的表达式;(2)t = T /4时物体的位置、速度和加速度;(3)物体从x = -0.06m ,向x 轴负方向运动第一次回到平衡位置所需的时间. [解答](1)设物体的简谐振动方程为x = A cos(ωt + φ),其中A = 0.12m ,角频率ω = 2π/T = π.当t = 0时,x = 0.06m ,所以cos φ = 0.5,因此φ = ±π/3. 物体的速度为v = d x /d t = -ωA sin(ωt + φ).当t = 0时,v = -ωA sin φ,由于v > 0,所以sin φ< 0,因此:φ = -π/3.简谐振动的表达式为:x = 0.12cos(πt – π/3).(2)当t = T /4时物体的位置为;x = 0.12cos(π/2 – π/3) = 0.12cosπ/6 = 0.104(m). 速度为;v = -πA sin(π/2 – π/3) = -0.12πsinπ/6 = -0.188(m·s -1).加速度为:a = d v /d t = -ω2A cos(ωt + φ)= -π2A cos(πt - π/3)= -0.12π2cosπ/6 = -1.03(m·s -2). (3)方法一:求时间差.当x = -0.06m 时,可得cos(πt 1 - π/3) = -0.5, 因此πt 1 - π/3 = ±2π/3.由于物体向x 轴负方向运动,即v < 0,所以sin(πt 1 - π/3) > 0,因此πt 1 - π/3 = 2π/3,得t 1 = 1s .当物体从x = -0.06m 处第一次回到平衡位置时,x = 0,v > 0,因此cos(πt 2 - π/3) = 0, 可得 πt 2 - π/3 = -π/2或3π/2等.由于t 2> 0,所以πt 2 - π/3 = 3π/2, 可得t 2 = 11/6 = 1.83(s).所需要的时间为:Δt = t 2 - t 1 = 0.83(s).方法二:反向运动.物体从x = -0.06m ,向x 轴负方向运动第一次回到平衡位置所需的时间就是它从x = 0.06m ,即从起点向x 轴正方向运动第一次回到平衡位置所需的时间.在平衡位置时,x = 0,v < 0,因此cos(πt - π/3) = 0,可得 πt - π/3 = π/2,解得t = 5/6 = 0.83(s).[注意]根据振动方程x = A cos(ωt + φ),当t = 0时,可得φ = ±arccos(x 0/A ),(-π<φ<= π), 初位相的取值由速度决定.由于v = d x /d t = -ωA sin(ωt + φ),当t = 0时,v = -ωA sin φ,当v > 0时,sin φ< 0,因此 φ = -arccos(x 0/A );当v < 0时,sin φ> 0,因此φ = arccos(x 0/A )π/3.可见:当速度大于零时,初位相取负值;当速度小于零时,初位相取正值.如果速度等于零,当初位置x 0 = A 时,φ = 0;当初位置x 0 = -A 时,φ = π.4.2已知一简谐振子的振动曲线如图所示,试由图求:(1)a ,b ,c ,d ,e 各点的位相,及到达这些状态的时刻t 各是多少?已知周期为T ; (2)振动表达式; (3)画出旋转矢量图. [解答]方法一:由位相求时间.(1)设曲线方程为x = A cos Φ,其中A 表示振幅,Φ = ωt + φ表示相位. 由于x a = A ,所以cos Φa = 1,因此Φa = 0.由于x b = A /2,所以cos Φb = 0.5,因此Φb = ±π/3;由于位相Φ随时间t 增加,b 点位相就应该大于a 点的位相,因此Φb = π/3.由于x c = 0,所以cos Φc = 0,又由于c 点位相大于b 位相,因此Φc = π/2.同理可得其他两点位相为:Φd = 2π/3,Φe = π.c 点和a 点的相位之差为π/2,时间之差为T /4,而b 点和a 点的相位之差为π/3,时间之差应该为T /6.因为b 点的位移值与O 时刻的位移值相同,所以到达a 点的时刻为t a = T /6. 到达b 点的时刻为t b = 2t a = T /3.图4.2到达c 点的时刻为t c = t a + T /4 = 5T /12. 到达d 点的时刻为t d = t c + T /12 = T /2. 到达e 点的时刻为t e = t a + T /2 = 2T /3.(2)设振动表达式为:x = A cos(ωt + φ),当t = 0时,x = A /2时,所以cos φ = 0.5,因此φ =±π/3; 由于零时刻的位相小于a 点的位相,所以φ = -π/3, 因此振动表达式为. 另外,在O 时刻的曲线上作一切线,由于速度是位置对时间的变化率,所以切线代表速度的方向;由于其斜率大于零,所以速度大于零,因此初位相取负值,从而可得运动方程.(3)如图旋转矢量图所示.方法二:由时间求位相.将曲线反方向延长与t 轴 相交于f 点,由于x f = 0,根据运动方程,可得所以:.显然f 点的速度大于零,所以取负值,解得t f = -T /12.从f 点到达a 点经过的时间为T /4,所以到达a 点的时刻为:t a = T /4 + t f = T /6, 其位相为:. 由图可以确定其他点的时刻,同理可得各点的位相.4.3 有一弹簧,当其下端挂一质量为M 的物体时,伸长量为9.8×10-2m .若使物体上下振动,且规定向下为正方向.(1)t = 0时,物体在平衡位置上方8.0×10-2m 处,由静止开始向下运动,求运动方程;(2)t = 0时,物体在平衡位置并以0.60m·s -1速度向上运动,求运动方程. [解答]当物体平衡时,有:Mg – kx 0 = 0, 所以弹簧的倔强系数为:k = Mg/x 0, 物体振动的圆频率为:s -1). 设物体的运动方程为:x = A cos(ωt + φ).(1)当t = 0时,x 0 = -8.0×10-2m ,v 0 = 0,因此振幅为:=8.0×10-2(m);由于初位移为x 0 = -A ,所以cos φ = -1,初位相为:φ = π. 运动方程为:x = 8.0×10-2cos(10t + π).(2)当t = 0时,x 0 = 0,v 0 = -0.60(m·s -1),因此振幅为:v 0/ω|=6.0×10-2(m);由于cos φ = 0,所以φ = π/2;运动方程为:x = 6.0×10-2cos(10t +π/2).4.4 质量为10×10-3kg 的小球与轻弹簧组成的系统,按的规律作振动,式中t 以秒(s)计,x 以米(m)计.求: (1)振动的圆频率、周期、振幅、初位相; (2)振动的速度、加速度的最大值;(3)最大回复力、振动能量、平均动能和平均势能;cos(2)3t x A T ππ=-cos(2)03t T ππ-=232f t Tπππ-=±203a a t T πΦπ=-=ω==0||A x ==A =20.1cos(8)3x t ππ=+(4)画出这振动的旋转矢量图,并在图上指明t 为1,2,10s 等各时刻的矢量位置. [解答](1)比较简谐振动的标准方程:x = A cos(ωt + φ),可知圆频率为:ω =8π,周期T = 2π/ω = 1/4 = 0.25(s),振幅A = 0.1(m),初位相φ = 2π/3.(2)速度的最大值为:v m = ωA = 0.8π = 2.51(m·s -1); 加速度的最大值为:a m = ω2A = 6.4π2 = 63.2(m·s -2). (3)弹簧的倔强系数为:k = mω2,最大回复力为:f = kA = mω2A = 0.632(N); 振动能量为:E = kA 2/2 = mω2A 2/2 = 3.16×10-2(J), 平均动能和平均势能为:= kA 2/4 = mω2A 2/4 = 1.58×10-2(J). (4)如图所示,当t 为1,2,10s 等时刻时,旋转矢量的位置是相同的.4.5 两个质点平行于同一直线并排作同频率、同振幅的简谐振动.在振动过程中,每当它们经过振幅一半的地方时相遇,而运动方向相反.求它们的位相差,并作旋转矢量图表示.[解答]设它们的振动方程为:x = A cos(ωt + φ), 当x = A /2时,可得位相为:ωt + φ = ±π/3.由于它们在相遇时反相,可取Φ1 = (ωt + φ)1 = -π/3,Φ2 = (ωt + φ)2 = π/3,它们的相差为:ΔΦ = Φ2 – Φ1 = 2π/3,或者:ΔΦ` = 2π –ΔΦ = 4π/3.矢量图如图所示.4.6一氢原子在分子中的振动可视为简谐振动.已知氢原子质量m = 1.68×10-27kg ,振动频率v = 1.0×1014Hz ,振幅A = 1.0×10-11m .试计算:(1)此氢原子的最大速度; (2)与此振动相联系的能量.[解答](1)氢原子的圆频率为:ω = 2πv = 6.28×1014(rad·s -1), 最大速度为:v m = ωA = 6.28×103(m·s -1).(2)氢原子的能量为:= 3.32×10-20(J).4.7 如图所示,在一平板下装有弹簧,平板上放一质量为1.0kg 的重物,若使平板在竖直方向上作上下简谐振动,周期为0.50s ,振幅为2.0×10-2m ,求:(1)平板到最低点时,重物对平板的作用力;(2)若频率不变,则平板以多大的振幅振动时,重物跳离平板? (3)若振幅不变,则平板以多大的频率振动时,重物跳离平板? [解答](1)重物的圆频率为:ω = 2π/T = 4π,其最大加速度为:a m = ω2A ,合力为:F = ma m ,方向向上.重物受到板的向上支持力N 和向下的重力G ,所以F = N – G . 重物对平板的作用力方向向下,大小等于板的支持力: N = G + F = m (g +a m ) = m (g +ω2A ) = 12.96(N).(2)当物体的最大加速度向下时,板的支持为:N = m (g - ω2A ). 当重物跳离平板时,N = 0,频率不变时,振幅为:A = g/ω2 = 3.2×10-2(m).(3)振幅不变时,频率为:3.52(Hz).4.8 两轻弹簧与小球串连在一直线上,将两弹簧拉长后系在固定点A 和B 之间,整个系统放在光滑水平面上.设两弹簧的原长分别为l 1和l 2,倔强系统分别为k 1和k 2,A和B 间距为L ,小球的质量为m .(1)试确定小球的平衡位置;k pE E =212m E mv=2ωνπ==(2)使小球沿弹簧长度方向作一微小位移后放手,小球将作振动,这一振动是否为简谐振动?振动周期为多少?[解答](1)这里不计小球的大小,不妨设L > l 1 + l 2,当小球平衡时,两弹簧分别拉长x 1和x 2,因此得方程:L = l 1 + x 1 + l 2 + x 2;小球受左右两边的弹簧的弹力分别向左和向右,大小相等,即k 1x 1 = k 2x 2. 将x 2 = x 1k 1/k 2代入第一个公式解得:.小球离A 点的距离为:.(2)以平衡位置为原点,取向右的方向为x 轴正方向,当小球向右移动一个微小距离x 时,左边弹簧拉长为x 1 + x ,弹力大小为:f 1 = k 1(x 1 + x ), 方向向左;右边弹簧拉长为x 1 - x ,弹力大小为:f 2 = k 2(x 2 - x ), 方向向右.根据牛顿第二定律得:k 2(x 2 - x ) - k 1(x 1 + x ) = ma ,利用平衡条件得:,即小球做简谐振动.小球振动的圆频率为:.4.9如图所示,质量为10g 的子弹以速度v = 103m·s -1水平射入木块,并陷入木块中,使弹簧压缩而作简谐振动.设弹簧的倔强系数k = 8×103N·m -1,木块的质量为4.99kg ,不计桌面摩擦,试求:(1)振动的振幅;(2)振动方程.[解答](1)子弹射入木块时,由于时间很短,木块还来不及运动,弹簧没有被压缩,它们的动量守恒,即:mv = (m + M)v 0.解得子弹射入后的速度为:v 0 = mv/(m + M) = 2(m·s -1),这也是它们振动的初速度.子弹和木块压缩弹簧的过程机械能守恒,可得:(m + M ) v02/2 = kA 2/2, 所以振幅为:10-2(m). (2)振动的圆频率为:= 40(rad·s -1).取木块静止的位置为原点、向右的方向为位移x 的正方向,振动方程可设为:x = A cos(ωt + φ).当t = 0时,x = 0,可得:φ = ±π/2;由于速度为正,所以取负的初位相,因此振动方程为:x = 5×10-2cos(40t - π/2).4.10如图所示,在倔强系数为k 的弹簧下,挂一质量为M 的托盘.质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞,而使其作简谐振动,设两物体碰后瞬时为t = 0时刻,求振动方程.[解答]物体落下后、碰撞前的速度为:物体与托盘做完全非弹簧碰撞后,根据动量守恒定律可得它们的共同速度为,这也是它们振动的初速度.设振动方程为:x = A cos(ωt + φ),211212()k x L l l k k =--+211111212()k L l x l L l l k k =+=+--+2122d ()0d xm kk x t++=ω=22T πω==A v =ω=v =0m v v m M ==+图4.9 图4.10其中圆频率为:物体没有落下之前,托盘平衡时弹簧伸长为x 1,则:x 1 = Mg/k .物体与托盘磁盘之后,在新的平衡位置,弹簧伸长为x 2,则:x 2= (M + m )g/k . 取新的平衡位置为原点,取向下的方向为正,则它们振动的初位移为x 0 = x 1 - x 2 = -mg/k .因此振幅为:初位相为:4.11 装置如图所示,轻弹簧一端固定,另一端与物体m 间用细绳相连,细绳跨于桌边定滑轮M 上,m 悬于细绳下端.已知弹簧的倔强系数为k = 50N·m -1,滑轮的转动惯量J = 0.02kg·m 2,半径R = 0.2m ,物体质量为m = 1.5kg ,取g = 10m·s -2.(1)试求这一系统静止时弹簧的伸长量和绳的张力;(2)将物体m 用手托起0.15m ,再突然放手,任物体m 下落而整个系统进入振动状态.设绳子长度一定,绳子与滑轮间不打滑,滑轮轴承无摩擦,试证物体m 是做简谐振动; (3)确定物体m 的振动周期;(4)取物体m 的平衡位置为原点,OX 轴竖直向下,设振物体m 相对于平衡位置的位移为x ,写出振动方程.[解答](1)在平衡时,绳子的张力等于物体的重力T = G = mg = 15(N).这也是对弹簧的拉力,所以弹簧的伸长为:x 0 = mg/k = 0.3(m).(2)以物体平衡位置为原点,取向下的方向为正,当物体下落x 时,弹簧拉长为x 0 + x ,因此水平绳子的张力为:T 1 = k (x 0+ x ).设竖直绳子的张力为T 2,对定滑轮可列转动方程:T 2R – T 1R = Jβ, 其中β是角加速度,与线加速度的关系是:β = a/R .对于物体也可列方程:mg - T 2 = ma . 转动方程化为:T 2 – k (x 0 + x ) = aJ/R 2,与物体平动方程相加并利用平衡条件得:a (m + J/R 2) = –kx ,可得微分方程:,故物体做简谐振动. (3)简谐振动的圆频率为:s -1). 周期为:T 2 = 2π/ω = 1.26(s).(4)设物体振动方程为:x = A cos(ωt + φ),其中振幅为:A = 0.15(m). 当t = 0时,x = -0.15m ,v 0 = 0,可得:cos φ = -1,因此φ = π或-π, 所以振动方程为:x = 0.15cos(5t + π),或x = 0.15cos(5t - π).4.12一匀质细圆环质量为m ,半径为R ,绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动,求摆动的周期.[解答]通过质心垂直环面有一个轴,环绕此轴的转动惯量为:I c = mR 2.根据平行轴定理,环绕过O 点的平行轴的转动惯量为I = I c + mR 2 = 2mR 2.当环偏离平衡位置时,重力的力矩为:M = mgR sin θ, 方向与角度θ增加的方向相反.ω=A ==00arctan v x ϕω-==222d 0d /x kx t m J R +=+ω=根据转动定理得:Iβ = -M ,即,由于环做小幅度摆动,所以sin θ≈θ,可得微分方程:. 摆动的圆频率为:周期为:4.13 重量为P 的物体用两根弹簧竖直悬挂,如图所示,各弹簧的倔强系数标明在图上.试求在图示两种情况下,系统沿竖直方向振动的固有频率.[解答](1)前面已经证明:当两根弹簧串联时,总倔强系数为k = k1k 2/(k 1 + k 2),因此固有频率为(2)前面还证明:当两根弹簧并联时,总倔强系数等于两个弹簧的倔强系数之和,因此固有频率为.4.14质量为0.25kg 的物体,在弹性力作用下作简谐振动,倔强系数k = 25N·m -1,如果开始振动时具有势能0.6J ,和动能0.2J ,求:(1)振幅;(2)位移多大时,动能恰等于势能?(3)经过平衡位置时的速度.[解答]物体的总能量为:E = E k + E p = 0.8(J).(1)根据能量公式E = kA2/2,得振幅为:.(2)当动能等于势能时,即E k = E p ,由于E = E k + E p ,可得:E = 2E p ,即,解得:= ±0.179(m). (3)再根据能量公式E = mv m2/2,得物体经过平衡位置的速度为: 2.53(m·s -1).4.15 两个频率和振幅都相同的简谐振动的x-t 曲线如图所示,求: (1)两个简谐振动的位相差;(2)两个简谐振动的合成振动的振动方程. [解答](1)两个简谐振动的振幅为:A = 5(cm), 周期为:T = 4(s),圆频率为:ω =2π/T = π/2,它们的振动方程分别为:x 1 = A cos ωt =5cosπt /2, x 2 = A sin ωt =5sinπt /2 =5cos(π/2 - πt /2)即x 2=5cos(πt /2 - π/2).位相差为:Δφ = φ2 - φ1 = -π/2. (2)由于x = x 1 + x 2 = 5cosπt /2 +5sinπt /2 = 5(cosπt /2·cosπ/4 +5sinπt /2·sinπ/4)/sinπ/4 合振动方程为:(cm).22d sin 0d I mgR tθθ+=22d 0d mgRt Iθθ+=ω=222T πω===2ωνπ===2ωνπ===A =2211222kA kx =⨯/2x =m v =cos()24x t ππ=- (b)图4.134.16 已知两个同方向简谐振动如下:,.(1)求它们的合成振动的振幅和初位相; (2)另有一同方向简谐振动x 3 = 0.07cos(10t +φ),问φ为何值时,x 1 + x 3的振幅为最大?φ为何值时,x 2 + x 3的振幅为最小?(3)用旋转矢量图示法表示(1)和(2)两种情况下的结果.x 以米计,t 以秒计.[解答](1)根据公式,合振动的振幅为:=8.92×10-2(m). 初位相为:= 68.22°.(2)要使x 1 + x 3的振幅最大,则:cos(φ– φ1) = 1,因此φ– φ1 = 0,所以:φ = φ1 = 0.6π. 要使x 2 + x 3的振幅最小,则 cos(φ– φ2) = -1,因此φ– φ2 = π,所以φ = π + φ2 = 1.2π.(3)如图所示.4.17质量为0.4kg 的质点同时参与互相垂直的两个振动:, .式中x 和y 以米(m)计,t 以秒(s)计.(1)求运动的轨道方程;(2)画出合成振动的轨迹;(3)求质点在任一位置所受的力.[解答](1)根据公式:,其中位相差为:Δφ = φ2 – φ1 = -π/2,130.05cos(10)5x t π=+210.06cos(10)5x t π=+A =11221122sin sin arctancos cos A A A A ϕϕϕϕϕ+=+0.08cos()36x t ππ=+0.06cos()33y t ππ=-2222212122cos sin x y xyA A A A ϕϕ+-∆=∆所以质点运动的轨道方程为:. (2)合振动的轨迹是椭圆.(3)两个振动的圆频率是相同的ω = π/3,质点在x 方向所受的力为,即F x = 0.035cos(πt /3 + π/6)(N).在y 方向所受的力为,即F y = 0.026cos(πt /3 - π/3)(N).用矢量表示就是,其大小为,与x 轴的夹角为θ = arctan(F y /F x ).4.18 将频率为384Hz 的标准音叉振动和一待测频率的音叉振动合成,测得拍频为3.0Hz ,在待测音叉的一端加上一小块物体,则拍频将减小,求待测音叉的固有频率.[解答]标准音叉的频率为v 0 = 384(Hz), 拍频为Δv = 3.0(Hz), 待测音叉的固有频率可能是v 1 = v 0 - Δv = 381(Hz), 也可能是v 2 = v 0 + Δv = 387(Hz).在待测音叉上加一小块物体时,相当于弹簧振子增加了质量,由于ω2 = k/m ,可知其频率将减小.如果待测音叉的固有频率v 1,加一小块物体后,其频率v`1将更低,与标准音叉的拍频将增加;实际上拍频是减小的,所以待测音叉的固有频率v 2,即387Hz .4.19示波器的电子束受到两个互相垂直的电场作用.电子在两个方向上的位移分别为x = A cos ωt 和y = A cos(ωt +φ).求在φ = 0,φ = 30º,及φ = 90º这三种情况下,电子在荧光屏上的轨迹方程.[解答]根据公式,其中Δφ = φ2 – φ1 = -π/2,而φ1 = 0,φ2 = φ.(1)当Δφ = φ = 0时,可得,质点运动的轨道方程为y = x ,轨迹是一条直线.(2)当Δφ = φ = 30º时,可得质点的轨道方程, 即,轨迹是倾斜的椭圆.(3)当Δφ = φ = 90º时,可得, 即x 2 + y 2 = A 2,质点运动的轨迹为圆.4.20三个同方向、同频率的简谐振动为,,.222210.080.06x y +=22d d x x x F ma m t==20.08cos()6m t πωω=-+22d d y y y F ma m t==20.06cos()3m t ωω=--πi+j x y F F F =F =2222212122cos sin x y xyA A A A ϕϕ+-∆=∆2222220x y xyA A A+-=222214x y A+=222/4x y A +=22221x y A A +=10.08cos(314)6x t π=+20.08cos(314)2x t π=+350.08cos(314)6x t π=+求:(1)合振动的圆频率、振幅、初相及振动表达式; (2)合振动由初始位置运动到所需最短时间(A 为合振动振幅). [解答]合振动的圆频率为:ω = 314 = 100π(rad·s -1). 设A 0 = 0.08,根据公式得:A x = A 1cos φ1 + A 2cos φ2 + A 3cos φ3 = 0,A y = A 1sin φ1 + A 2sin φ2 + A 3sin φ3 = 2A 0 = 0.16(m), 振幅为:,初位相为:φ = arctan(A y /A x ) = π/2.合振动的方程为:x = 0.16cos(100πt + π/2).(2)当时,可得:,解得:100πt + π/2 = π/4或7π/4.由于t > 0,所以只能取第二个解,可得所需最短时间为t = 0.0125s .x A =A =/2x =cos(100/2)2t ππ+。
第四章-机械振动
x(m)
t
A
曲线2曲线1
-A
t
t
t2
t1
1
2
当:t t2 t1 0, 2 1 0
振动2比振动1超前
t(s)
§4.1 简谐振动
例1.如图的谐振动x-t 曲线,试求其谐振方程
解:由图知
x(m)
A 2m T 2s 2
可得: 2 T O
振动表达式为
1
2t (s)
x Acos( t )
dt 2 l
谐振方程为:
设 2 2T
ml
x Acos(t )
§4.2 简谐振动的实例分析
(5)U形管中液体无粘滞振荡
x x
l
为管内液体密度,
l为液体在管内的长度。
动力学方程为:
l
d2 dt
x
2
2gx
0
谐振方程为:
2 2g
l
x Acos(t )
§4.2 简谐振动的实例分析
(6)LC谐振电路
P sin m dv
dt
v l
P
sin 1 3 (小角度时)
6
g 0
l
令 2 g
l
2 0
结论: 小角度摆动时,单摆的运动是谐振动.
周期和角频率为:T 2 l
g
g
l
§4.2 简谐振动的实例分析
(2) 复摆(物理摆)
以物体为研究对象
设 角沿逆时针方向为正
mghsin JZ
10
即: Asin( ) 0 sin( ) 0
6
2
x
1
cos(
t 2 )(m)
10 6 3
§4.1 简谐振动
机械振动基础--第四章--多自由度系统PPT课件

.
5
例 4.1 求图示的简化的汽车4自由度模型的刚度矩阵。
解:取yA,yB,y1,y2为描述系统运动的广义坐标,即 {x}={yA,yB,y1,y2}T
各个自由度原点均取静平衡位置,向上为正。
.
6
(1) 求[K]的第一列:设yA沿坐标正方向有一个单位位 移,其余广义坐标位移为零,则只有k2被伸长,此时: 外力{f}=???
x2 ) c3 x2
[M ]{x} [C]{x} [K]{x} {F(t)}
.
1
本章内容:
1) 多自由度系统振动的基本理论,多自由度系统的固有 频率和振型的理论;
2) 分析多自由度系统动力响应常用的振型迭加方法; 3) 用变换方法求多自由度系统动力(态)响应的问题。
.
2
§4.1 运动微分方程
kij
2U xix j
2U x jxi
k ji
质量矩阵、阻尼矩阵和刚度. 矩阵均是对称矩阵。 9
针对本例:系统的动能为杆的平动 动能和转动动能与两个质量的动能 之和,设杆的质心在杆的中点,质 量为M。系统的动能为:
ET
M 2
y A
2
yB
2
I 2
yB
L
y A
2
1 2
m1 y12
1 2
在静力学中,各自由度的位移{x}、系统的刚度矩阵[K]、 各自由度上所受到的外力关系为:
{ f } [K]{x}
——如系统第j个自由度沿其坐标正方向有一个单位位移, 其余各个自由度的位移保持为零,为保持系统这种变形状 态需要在各个自由度施加外力,其中在第i个自由度上施 加的外力就是kij。
.
4
系统第j个自由度有一个正向单位位移,其余自由度位移 为零这种变形状态可以由向量{x}={ej}描述。
第4章 多自由度系统的振动题解

62 / 2962习 题4-1 在题3-10中,设m 1=m 2=m ,l 1=l 2=l ,k 1=k 2=0,求系统的固有频率和主振型。
解:由题3-10的结果22121111)(l g m l g m m k k +++=,2221l gm k -=,2212l g m k -=,22222l gm k k += 代入m m m ==21,021==k k ,l l l ==21可求出刚度矩阵K 和质量矩阵M⎥⎦⎤⎢⎣⎡=m m M 00;⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=l mg lmg l mg l mg K 3 由频率方程02=-M p K ,得0322=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=mp l mg l mg lmgmp l mg B 0242222242=+-∴l g m p l g m p ml g p )22(1-=∴ ,lgp )22(2+= 为求系统主振型,先求出adjB 的第一列⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=l mg mp lmg adjB 2分别将频率值21p p 和代入,得系统的主振型矩阵为题4-1图63 / 2963⎥⎦⎤⎢⎣⎡-=112)1(A ⎥⎦⎤⎢⎣⎡+=112)2(A4-2 题4-2图所示的均匀刚性杆质量为m 1,求系统的频率方程。
解:设杆的转角θ和物块位移x 为广义坐标。
利用刚度影响系数法求刚度矩阵k 。
设0,1==x θ,画出受力图,并施加物体力偶与力2111,k k ,由平衡条件得到,222111a k b k k +=, a k k 221-=设1,0==x θ,画出受力图,并施加物体力偶与力2212,k k ,由平衡条件得到,12k a k 2-=, a k k 222=得作用力方程为⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡--++⎭⎬⎫⎩⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡0000312222221221x a k a k a k a k b k x m a m θθ由频率方程02=-M K p ,得031222222212221=----+p m a k ak a k p a m a k b k4-3 题4-3图所示的系统中,两根长度题4-3图题4-2图64 / 2964为l 的均匀刚性杆的质量为m 1及m 2,求系统的刚度矩阵和柔度矩阵,并求出当m 1=m 2=m 和k 1=k 2=k 时系统的固有频率。
机械振动第四章

第四章两自由度系统的振动当振动系统需要两个独立坐标描述其运动时,称为两自由度振动系统。
两自由度系统是最简单的多自由度系统,因此研究两自由度系统是分析和掌握多自由度系统的基础。
两自由度系统具有两个固有频率,两自由度系统以固有频率进行的振动与单自由度系统不同,它以固有频率进行的振动是指整个系统在运动过程中莫一位移形状,称为固有振型,因此两自由度具有两个与固有频率对应的两个固有振型。
在任意初始条件下的自由振动响应一般由两个固有振型的叠加得到。
受迫简谐振动的频率与激励频率相同。
两自由度系统的振动微分方程一般由两个联立的微分方程组成。
如果恰当地选取坐标,可使两个微分方程解除耦合,这种坐标称为主坐标或固有坐标。
用固有坐标建立的系统振动微分方程为两个独立的单自由度系统的微分方程。
4.1系统的自由振动如图所示的无阻尼两质量-弹簧系统,可沿光滑水平面滑动的两个质量与分别用弹簧与连至定点,并用弹簧相互连接。
三个弹簧的轴线沿同一水平线,质量与只限于沿着该直线进行往复运动。
这样与的任一瞬时的位置只需用坐标与就可以完全确定,因此该系统具有两个自由度。
图两自由度系统的振动取与的静平衡位置为坐标原点。
在振动过程中任一瞬时t,与的位置分别为与,作用于与的重力于光滑水平面的法向反力相平衡,在质量的水平方向作用有弹性恢复力和,质量的水平方向则受到和作用,方向如图所示。
取加速度和力的正方向与坐标正方向一致,根据牛顿运动定律有移项得方程()就是图所示的两自由度系统自由振动的微分方程,为二阶常系数线性齐次常微分方程组。
方程()可以使用矩阵形式来表示,写成由系数矩阵组成的常数矩阵m和k分别称为质量矩阵和刚度矩阵,向量x 称为位移向量。
因此设分别为刚度矩阵k中的元素,因而方程()可以写成方程()为系统自由振动的微分方程。
方程()是齐次的,如果和位方程()的一个解,那么与其相差一个因子的和也将是一个解。
通常感兴趣的是一种特殊形式的解,也就是和同步运动的解。
振动理论讲义第4章 单自由度系统受迫振动

(4.6)
前面两项是无阻尼自由振动,第三项是无阻尼受迫振动。 方程(4.6)的前两项是具有固有频率 的正弦波,而第三项受迫振动的正弦波的频率 是外来激励的频率 。显然,这两个频率是相互完全独立的。(4.6)是由两个正弦波叠加 而成,合成之后的波不再是简谐运动。 进一步分析(4.5)式表示的含义。显然, 波,该振幅取决于频率比 。 是一个具有振幅为 的正弦
第4章 单自由 由度系统 统受迫振动 4.1 前 前言
前面 面讨论的是 是在外界初始 始干扰下依 依靠系统本身 身的弹性恢 恢复力维持的 的振动。下 下面将讨 论系统由外界持续 续激振引起的振动。 强迫振动从外 强 外界不断获 获取能量来补 补偿阻尼所 所消耗的 能量,使系统得以 以维持持续的等幅振动 动。 响应:外界激振引 引起的系统 统的振动状态 态。对于不 不同的外界激 激励,系统 统具有不同的 的响应, 一般以位 位移形式表 表达,有时也以速度或 或加速度的形式来表达 达。
4.2 无 无阻尼受迫 迫振动
首先 先研究简单 单的情况,使 使单自由度 度振动方程的 的阻尼项为 为零,得到如 如下方程 kx P0 sin mx n t 观察可知函数 x x0 sin t 可以满足这个方程 程,代入上式,有
2
(4.1)
(4.2)
振动理论
x0 k m 2 P0
北京大学力学系 陈永强
或者
x0 P0 P0 / k P0 / k 2 2 k m 1 m / k 1 2 / n2
代回(4.2),有
x P0 / k sin t 1 2 / n2
(4.3)
即为所求的位移响应。上面方程中的 P0 / k 具有简单的物理意义:荷载 P0 作用下的弹簧 的静变形。如果记
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拍这种现象在声学、光学、无线电技术等方面均 有广泛的应用.
例如
两分振动的频率
1 9 Hz 2
1秒
8 Hz
合振动频率
合振动振幅 (包络线) 变化的频率称为 “ 拍频 ”
1 2
8.5 Hz
1 2
1 Hz
1 2
385 Hz 383 Hz 拍的演示
听到的音频 384 Hz 强度节拍性变化 2 Hz
二、同方向、不同频率简谐振动的合成
两个或两个以上同方向、不同频率的简谐振动的 合成, 其合振动不再是简谐振动, 但仍然是周期性运 动, 一般可用图示法解释:
拍(beat): 两个同方向、振幅和初位 相相同;频率不 同, 但频率非常接近的振动合成所产生的合振动做周 期性的加强和减弱的现象. x1=Acos(1t+) x2=Acos(2t+)
1. 振幅(amplitude) A: t+ =0时 , x=A 2. 周期(period) T : 频率(frequency) : 角频率(angular frequency) :
2 2 T
求: 弹簧振子的角频率、频率、周期?
k , m
2
k 1 , m 2
T
2 2 02(1) < 0时, 欠阻尼状态(underdamping); (2) = 0时, 临界阻尼状态(critical damping); (3) > 0时, 过阻尼状态(overdamping).
二、受迫振动(Forced Vibration) 如果振动系统除了本身的弹性力和阻力外, 同时是在 周期性外力(驱动力)的持续作用下, 按照外力的周期作 振 动, 称为受迫振动. 稳定受迫振动是一个与简谐驱动力同 频率的简谐振动. 三、共振(Resonance) 当外力的频率接近或等于系统的 固有频率, 受迫振动的振幅急剧增 较小 大, 这种现象称为共振. 共振应用举例。 较大
第二节 阻尼振动、受迫振动和共振
(Damped Vibration,Force Vibration and Resonance)
一、阻尼振动 (Damped Vibration) 由于振动系统不是在真空中, 而是在某一媒质中进行, 故在振 动时必然受到媒质的摩擦阻力, 使振动能量(振幅等)逐渐减小, 这种振动称之为阻尼振动. 阻尼振动的周期
x x1 x2 A cos(1t ) A cos(2t )
(1 2 )t (1 2 )t x x1 x2 2 A cos cos 2 2
作周期性慢变的振幅 频率相对较高的简谐振动
拍率(振幅变化的频率): 2 1
(2) x0 0, v0 0 , 即 x0 A cos 0
又 v0 A sin 0 2 2 A 1 ( 3) x0 , v0 0 , 即 cos 2 2 又 v0 A sin 0 3 3 A 1 (4) x0 , v0 0, 即 cos 2 2 又 v0 A sin 0 3 3
一、同方向、同频率简谐振动的合成(combinations of SHM of the same frequency along the same line) 设两个频率、振动方向相同,A、不同
x1=A1cos(t+1) x2=A2cos(t+2)
旋转矢量法求合振动:
x=x1+x2=Acos(t+)
解(1) x
由旋转矢量 得 3 2 x 0.1 cos t 3 (2)先求 t 由旋转矢量法
A cos(t ) 2 1 (rad s ) T 2
t0
A/ 2
A 2
o
t
x
t 1s(半个周期)
v A sin(t ) 0.1 sin( 2 3) 0.27m s a A 2 cos(t )
第四章 振动(Vibration)
第一节 简谐振动 (simple harmonic motion, SHM) 第二节 阻尼振动、受迫振动和共振 (damped vibration, force vibration and resonance) 第三节 简谐振动的合成 (combination of SHM) 问题:
2x,
2
5. 简谐振动质点的速度、加速度 dx v A sin(t ) A cos(t ) dt 2 2 dv d x 2 2 A cos(t ) a 2 A cos(t ) dt dt
二、简谐振动的特征量 (the characteristic parameter of SHM)
E
E Ep Ek
E
E Ep
A
+A
x
Ek
t
例题4-1 单摆(simple pendulum)
d ml 2 mg sin mg dt d 2 g 2 2 0,其中 2 dt l 单摆的振动方程:
2
单摆
0 cos(t )
1 1 2 )2 1 m 2 l 2 2 sin2 (t ) 动能: Ek mv m( l 0 2 2 2 1 1 2 势能: E p mgh mgl (1 cos ) mgl mgl 02 cos 2 (t ) 2 2 1 1 2 2 2 总能: E Ek E p mgl 0 [sin (t ) cos (t )] mgl 02 2 2
解: 设向上运动为正方向,且质点的振动服从 x =Acos(t+) 则其速度服从 v = Asin(t+) 依题意, 四种情况的解如下:
(1) x0 0, v0 0 , 即 x0 A cos 0 又 v0 A sin 0 2 2
速度超前位移 /2 但落后加速度 /2 位移与加速度反相
结论:
简谐振动的基本特征是具有周期性,特征量参数 是振幅、角频率(周期、频率)和相位。
4. A和 可以由初始条件决定
设
x A cos(t )
x0 A cos
v0 A sin
2 v0
利用初始条件
A
2 x0
A 0.2 m T 4 s
x/m
2 1
1
2
3
4
5
6
t /s
3 x1 0.2 cos t 2 2 5 2 或
3
3
5 x2 0.2 cos t 3 2
5 3 2 1 3 2 6
0.1 cos( 2 3)
2
t0
t'
1
A 2
x
t
0.49m s
由旋转矢量法
2
5 ' 2 3 6 ' 5 6 5 t s 6
例3 已知 x-t 曲线, 写出振动方程, 并求它们的位相差? 解
2 (rad s -1 ) 0.2 T 2 0 .1 3 1 或2 o 2
三、简谐振动的矢量图示法
如图, 长度为A、起始位置极角为 的矢量 A以角速度 绕O旋转. 用 t 时刻矢量A(t)在极轴 X上的投影 x =Acos(t+)
表示简谐振动.
振幅 A=|A(t)|
旋转矢量
角频率
旋转矢量
初始极角
例2 已知简谐振动A=10 cm,T=2s,当t=0时位移为 5 cm,且向 x 轴负向运动。 求:(1)振动方程。 (2) x =5 cm且向x轴正向运动时的速度、加速度 及从这一位置回到平衡位置的最小时间。
三、谐振分析(Spectral Analysis) 1. 付里叶理论(Fourier Theory): 任何一个复杂的周期 性振动, 都可以分解为一系列的SHM, 每个分振动的 频率都是合振动频率的整数倍. 基频(fundamental frequency): 分=合 倍频或n次谐频(harmonic frequency): 分=n合 2. 振动的分解(合成的逆过程): 任一角频率为的振动都 可以分解为一系列简谐振动,这些振动的角频率分别 为(基频)、 2(二倍频)、3(三倍频)…即: x(t)=b0+b1cost+c1sin t+b2cos2 t+c2sin2 t+ … 叫做复杂振动的傅里叶级数. 式中b0、b1、c1、 b2、 c2、…均为常数, 表示相应简谐振动在合振动所占的 相对大小.
m k , T 2 k m
3. 相位和初相位(phase and initial phase): t+ : 决定 t 时刻的振动状态( x, v, a) Example: t+ = /2 3 /2 0 x=0 0 A A v = A A 0 0 a=0 0 2A 2A (1) t=0的 叫初相(initial phase); (2) 两振动相位之差叫相差(phase difference); 相差是的偶数倍叫同相(in-phase) ; 相差是的奇数倍叫反相(anti-phase); (3) 位移速度加速度位相比较
r 02 2 2
Ar h 2 02 2
大桥共振 360º 秋千
阻尼振动
受迫振动
共振( 外 )
如何设计一防振台?
要使 大理石板 充气轮胎
外 !
m大
k小
k 小 m
还有多级隔振!
乘客 座椅弹簧 车身 底座弹簧 轮轴 轮胎
汽车的减振系统
