2014高考数学(理)一轮复习学案课件第11编基本算法语句

合集下载

高考数学一轮复习必考部分第十一篇复数算法推理与证明第4节综合法分析法反证法课件文北师大版

解析:至少有一个”的反面应是“一个都没有”.故应选B.
4.设a,b是两个实数,给出下列条件: ①a+b>1;②a+b=2;③a+b>2;④a2+b2>2;⑤ab>1. 其中能推出:“a,b中至少有一个大于1”的条件是
(填序号).
解析:当 a= 2 ,b= 2 时,a+b= 4 >1,排除①;
33
3
证明:法一因为 a+b+c=1,
所以(a+b+c)2=a2+b2+c2+2ab+2ac+2bc≤
a2+b2+c2+a2+b2+a2+c2+b2+c2=3(a2+b2+c2),所以 a2+b2+c2≥ 1 . 3
法二设 a= 1 +α,b= 1 +β,c= 1 +γ.则由 a+b+c=1 可知α+β+γ=0,
(2)试用反证法证明 1 >c. a
证明:(2)假设 1 <c,又 1 >0,
a
a
由 0<x<c 时,f(x)>0,
知 f( 1 )>0,与 f( 1 )=0 矛盾,
a
a
所以 1 ≥c, a
又因为 1 ≠c, a
所以 1 >c. a
备选例题
【例题】 (2014 高考北京卷)对于数对序列 P:(a1,b1),(a2,b2),…,(an,bn), 记 T1(P)=a1+b1,Tk(P)=bk+max{Tk-1(P),a1+a2+…+ak}(2≤k≤n),其中 max{Tk-1(P),a1+a2+…+ak}表示 Tk-1(P)和 a1+a2+…+ak 两个数中最大的数, (1)对于数对序列 P:(2,5),(4,1),求 T1(P),T2(P)的值;

高考数学理一轮总复习教师课件11.2基本算法语句

2
x≥0 x<0
的函数值；③求面积为
6 的正方形的周长，其中不需要用条件语句来描述其算法的有( A． 0 个 C． 2 个 ) B． 1 个 D． 3 个
答案：B
3．120与2010的最大公约数是________．答案：30
4．(2011· 高考福建卷)运行如图所示的程序，输出的结果是________． a＝ 1 b＝ 2 a＝ a＋ b print a end
2x x<3 【答案】 (1)3 (2)①15 ②y＝2 x＝3 x2－1 x>3
【名师点评】
解答或编写有条件语句的程序时注
意条件满足与不满足所对应的不同结果，另外还要
注意if—else—end或if—end的配对，尤其在嵌套结构时，一层配对就是一个完整的条件结构，明确了配对关系，也就说明了嵌套关系．
课前热身 1．关于赋值语句下列说法不正确的是( )
A．赋值语句就是将表达式所代表的值赋给变量 B．赋值号左右不能互换
C．赋值号与数学中的符号有着完全相同的意义
D．执行赋值语句时，先计算“＝”右边表达式的值答案：C
2．给出以下四个问题， ①输入一个数 x，输出它的绝对值；
x －1， ②求函数 f(x)＝ 2 x ＋2x，
假，则执行else后面的语句序列1；如果表达式结果为______ 面的语句序列2. 真，则执行表达式后 ②最简单格式：如果表达式结果为 ____ 跳过语句序列1 面的语句序列1，否则__________________.
3．循环语句 (1)概念：用来处理算法中的循环结构的语句． (2)一般格式
解析：a＝1，b＝2，a＝a＋b＝1＋2＝3，所以输出
的结果为3. 答案：3

高考高考数学一轮总复习第11章算法初步课件理

知识点二基本算法语句
1.输入语句、输出语句、赋值语句的格式与功能
语句
一般格式
功能
输入语句
INPUT“提示内容”；变量
输入信息
输出语句
PRINT“提示内容”；表达式
输出常量、变量的值和系统信息
赋值语句
变量＝表达式
将表达式所代表的值赋给变量
2.条件语句 ①IF－THEN格式
②IF－THEN－ELSE格式
【例2】阅读下面两个算法语句：图1
图2
执行图1中语句的结果是输出________；执行图2中语句的结果是输出________.
解析执行语句1，得到(i，i·(i＋1))结果依次为(1，2)，(2， 6)，(3，12)，(4，20)，故输出i＝4. 执行语句2的情况如下： i＝1，i＝i＋1＝2，i·(i＋1)＝6<20(是)，结束循环，输出i＝2. 答案 i＝4 i＝2 [点评] 解决算法语句有三个步骤：首先通读全部语句，把它翻译成数学问题；其次领悟该语句的功能；最后根据语句的功能运行程序，解决问题.
2019/7/14
最新中小学教学课件
30
① 根据课堂提问抓住老师的思路。老师在讲课过程中往往会提出一些问题，有的要求回答，有的则是自问自答。一般来说，老师在课堂上提出的问题都是学习中的关键，若能抓住老师提出的问题深入思考，就可以抓住老师的思路。
② 根据自己预习时理解过的逻辑结构抓住老师的思路。老师讲课在多数情况下是根据教材本身的知识结构展开的，若把自己预习时所理解过的知识逻辑结构与老师的讲解过程进行比较，便可以抓住老师的思路。
A.k≥6?
B.k≥7?
C.k≥8? D.k≥9?
解析第一次运行结；第三次运行结果为S＝720，k＝7.这个程序满足判断框的条件时执行循环，故判断条件是k≥8？. 故选C. 答案 C

高三理科数学一轮总复习第十一章算法初步

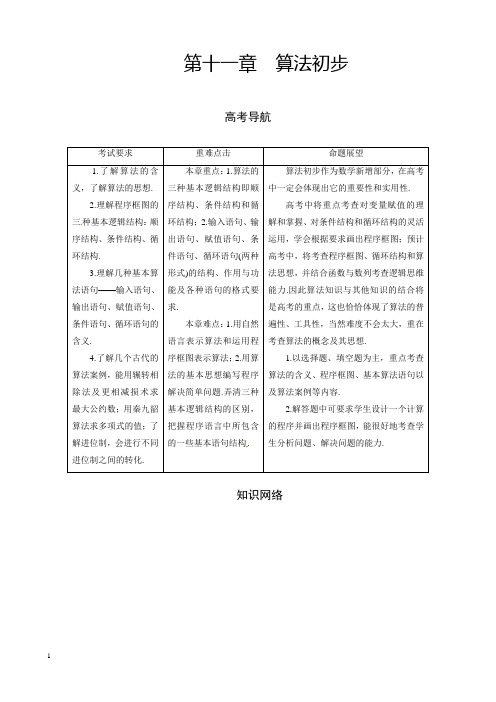
第十一章算法初步高考导航种基本逻辑结构：的一些基本语句结构.知识网络11.1 算法的含义与程序框图典例精析题型一算法的含义【例1】已知球的表面积是16π，要求球的体积，写出解决该问题的一个算法. 【解析】算法如下：第一步，s ＝16π. 第二步，计算R ＝s 4π. 第三步，计算V ＝4πR 33.第四步，输出V .【点拨】给出一个问题，设计算法应该注意：(1)认真分析问题，联系解决此问题的一般数学方法，此问题涉及到的各种情况； (2)将此问题分成若干个步骤； (3)用简练的语句将各步表述出来.【变式训练1】设计一个计算1×3×5×7×9×11×13的算法.图中给出程序的一部分，则在横线①上不能填入的数是( )A.13B.13.5C.14D.14.5【解析】当I ＜13成立时，只能运算 1×3×5×7×9×11.故选A.题型二程序框图【例2】图一是某县参加2010年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A 1，A 2，…，A 10(如A 2表示身高(单位：cm)在[150,155)内的学生人数).图二是统计图一中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160～180 cm(含160 cm ，不含180 cm)的学生人数，那么在流程图中的判断框内应填写的条件是( )A.i ＜6？B.i ＜7？C.i ＜8？D.i ＜9？图一【解析】根据题意可知，i 的初始值为4，输出结果应该是A 4＋A 5＋A 6＋A 7，因此判断框中应填写i ＜8？，选C.【点拨】本题的命题角度较为新颖，信息量较大，以条形统计图为知识点进行铺垫，介绍了算法流程图中各个数据的引入来源，其考查点集中于循环结构的终止条件的判断，考查了学生合理地进行推理与迅速作出判断的解题能力，解本题的过程中不少考生误选A ，实质上本题中的数据并不大，考生完全可以直接从头开始限次按流程图循环观察，依次写出每次循环后的变量的赋值，即可得解.【变式训练2】(2009辽宁)某店一个月的收入和支出，总共记录了N 个数据a 1，a 2，…，a N .其中收入记为正数，支出记为负数，该店用如图所示的程序框图计算月总收入S 和月净盈利V ，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的( )A.A ＞0？，V ＝S －TB.A ＜0？，V ＝S －TC.A ＞0？，V ＝S ＋TD.A ＜0？，V ＝S ＋T 【解析】选C.题型三算法的条件结构【例3】某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算： f ＝⎩⎨⎧⨯-+⨯).50＞(85.0)50(53.050),50≤＜0(53.0ωωωω其中f (单位：元)为托运费，ω为托运物品的重量(单位：千克)，试写出一个计算费用f 的算法，并画出相应的程序框图.【解析】算法如下：第一步，输入物品重量ω.第二步，如果ω≤50，那么f＝0.53ω，否则，f＝50×0.53＋(ω－50)×0.85.第三步，输出托运费f.程序框图如图所示.【点拨】求分段函数值的算法应用到条件结构，因此在程序框图的画法中需要引入判断框，要根据题目的要求引入判断框的个数，而判断框内的条件不同，对应的框图中的内容或操作就相应地进行变化.【变式训练3】(2010天津)阅读如图的程序框图，若输出s的值为－7，则判断框内可填写()A.i＜3？B.i＜4？C.i＜5？D.i＜6？【解析】i＝1，s＝2－1＝1；i＝3，s＝1－3＝－2；i＝5，s＝－2－5＝－7.所以选D.题型四算法的循环结构【例4】设计一个计算10个数的平均数的算法，并画出程序框图.【解析】算法步骤如下：第一步，令S＝0.第二步，令I＝1.第三步，输入一个数G.第四步，令S＝S＋G.第五步，令I＝I＋1.第六步，若I＞10，转到第七步，若I≤10，转到第三步.第七步，令A＝S/10.第八步，输出A.据上述算法步骤，程序框图如图.【点拨】(1)引入变量S作为累加变量，引入I为计数变量，对于这种多个数据的处理问题，可通过循环结构来达到；(2)计数变量用于记录循环次数，同时它的取值还用于判断循环是否终止，累加变量用于输出结果.【变式训练4】设计一个求1×2×3×…×10的程序框图.【解析】程序框图如下面的图一或图二.图一图二总结提高1.给出一个问题，设计算法时应注意：(1)认真分析问题，联系解决此问题的一般数学方法；(2)综合考虑此类问题中可能涉及的各种情况；(3)借助有关的变量或参数对算法加以表述；(4)将解决问题的过程划分为若干个步骤；(5)用简练的语言将各个步骤表示出来.2.循环结构有两种形式，即当型和直到型，这两种形式的循环结构在执行流程上有所不同，当型循环是当条件满足时执行循环体，不满足时退出循环体；而直到型循环则是当条件不满足时执行循环体，满足时退出循环体.所以判断框内的条件，是由两种循环语句确定的，不得随便更改.3.条件结构主要用在一些需要依据条件进行判断的算法中.如分段函数的求值，数据的大小关系等问题的算法设计.11.2 基本算法语句典例精析题型一输入、输出与赋值语句的应用【例1】阅读程序框图(如下图)，若输入m ＝4，n ＝6，则输出a ＝，i ＝ .【解析】a ＝12，i ＝3.【点拨】赋值语句是一种重要的基本语句，也是程序必不可少的重要组成部分，使用赋值语句，要注意其格式要求.【变式训练1】(2010陕西)如图是求样本x 1，x 2，…，x 10的平均数x 的程序框图，则图中空白框中应填入的内容为( )A.S ＝S ＋x nB.S ＝S ＋x nnC.S ＝S ＋nD.S ＝S ＋1n【解析】因为此步为求和，显然为S ＝S ＋x n ，故选A. 题型二循环语句的应用【例2】设计算法求11×2＋12×3＋13×4＋…＋199×100的值.要求画出程序框图，写出用基本语句编写的程序.【解析】这是一个累加求和问题，共99项相加，可设计一个计数变量，一个累加变量，用循环结构实现这一算法.程序框图如下图所示：程序如下：语句编写程序解决问题时，一定要注意格式和条件的表述方法，WHILE语句是当条件满足时执行循环体，UNTIL语句是当条件不满足时执行循环体.(2)在解决一些需要反复执行的运算任务，如累加求和、累乘求积等问题中应注意考虑利用循环语句来实现.(3)在循环语句中，也可以嵌套条件语句，甚至是循环语句，此时需要注意嵌套的这些语句，保证语句的完整性，否则就会造成程序无法执行.【变式训练2】下图是输出某个有限数列各项的程序框图，则该框图所输出的最后一个数据是 .【解析】由程序框图可知，当N ＝1时，A ＝1；N ＝2时，A ＝13；N ＝3时，A ＝15，…，即输出各个A值的分母是以1为首项以2为公差的等差数列，故当N ＝50时，A ＝11＋(50－1)×2＝199，即为框图最后输出的一个数据.故填199.题型三算法语句的实际应用【例3】某电信部门规定：拨打市内电话时，如果通话时间3分钟以内，收取通话费0.2元，如果通话时间超过3分钟，则超过部分以每分钟0.1元收取通话费(通话不足1分钟时按1分钟计算).试设计一个计算通话费用的算法，要求写出算法，编写程序.【解析】我们用c (单位：元)表示通话费，t (单位：分钟)表示通话时间，则依题意有⎩⎨⎧⨯+=,3＞2],[0.10.23,≤＜0,2.0t t-t c算法步骤如下：第一步，输入通话时间t .第二步，如果t ≤3，那么c ＝0.2；否则c ＝0.2＋0.1×[t －2]. 第三步，输出通话费用c . 程序如下：IF 【点拨】法步骤，画出程序框图，最后准确地编写出程序，同时要注意结合题意加深对算法的理解.【变式训练3】(2010江苏)下图是一个算法流程图，则输出S 的值是 .【解析】n＝1时，S＝3；n＝2时，S＝3＋4＝7；n＝3时，S＝7＋8＝15；n＝4时，S＝15＋24＝31；n ＝5时，S＝31＋25＝63.因为63≥33，所以输出的S值为63.总结提高1.输入、输出语句可以设计提示信息，加引号表示出来，与变量之间用分号隔开.2.赋值语句的赋值号左边只能是变量而不能是表达式；赋值号左右两边不能对换，不能利用赋值语句进行代数式计算，利用赋值语句可以实现两个变量值的互换，方法是引进第三个变量，用三个赋值语句完成.3.在某些算法中，根据需要，在条件语句的THEN分支或ELSE分支中又可以包含条件语句.遇到这样的问题，要分清内外条件结构，保证结构的完整性.4.分清WHILE语句和UNTIL语句的格式，在解决一些需要反复执行的运算任务，如累加求和，累乘求积等问题中应主要考虑利用循环语句来实现，但也要结合其他语句如条件语句.5.编程的一般步骤：(1)算法分析；(2)画出程序框图；(3)写出程序.11.3 算法案例典例精析题型一求最大公约数【例1】(1)用辗转相除法求840与1 764的最大公约数；(2)用更相减损术求440与556的最大公约数.【解析】(1)用辗转相除法求840与1 764的最大公约数：1 764＝840×2＋84，840＝84×10＋0.所以840与1 764的最大公约数是84.(2)用更相减损术求440与556的最大公约数：556－440＝116，440－116＝324，324－116＝208，208－116＝92，116－92＝24，92－24＝68，68－24＝44，44－24＝20，24－20＝4，20－4＝16，16－4＝12，12－4＝8，8－4＝4.所以440与556的最大公约数是4.【点拨】(1)辗转相除法与更相减损术是求两个正整数的最大公约数的方法，辗转相除法用较大的数除以较小的数，直到大数被小数除尽结束运算，较小的数就是最大公约数；更相减损术是用两数中较大的数减去较小的数，直到所得的差和较小数相等为止，这个较小数就是这两个数的最大公约数.一般情况下，辗转相除法步骤较少，而更相减损术步骤较多，但运算简易，解题时要灵活运用.(2)两个以上的数求最大公约数，先求其中两个数的最大公约数，再用所得的公约数与其他各数求最大公约数即可.【变式训练1】求147,343,133的最大公约数.【解析】先求147与343的最大公约数.343－147＝196，196－147＝49，147－49＝98，98－49＝49，所以147与343的最大公约数为49.再求49与133的最大公约数.133－49＝84，84－49＝35，49－35＝14，35－14＝21，21－14＝7，14－7＝7.所以147,343,133的最大公约数为7.题型二秦九韶算法的应用【例2】用秦九韶算法写出求多项式f(x)＝1＋x＋0.5x2＋0.016 67x3＋0.041 67x4＋0.008 33x5在x＝－0.2时的值的过程.【解析】先把函数整理成f(x)＝((((0.008 33x＋0.041 67)x＋0.166 67)x＋0.5)x＋1)x＋1，按照从内向外的顺序依次进行.x＝－0.2，a5＝0.008 33，v0＝a5＝0.008 33；a4＝0.041 67，v1＝v0x＋a4＝0.04；a3＝0.016 67，v2＝v1x＋a3＝0.008 67；a2＝0.5，v3＝v2x＋a2＝0.498 27；a1＝1，v4＝v3x＋a1＝0.900 35；a0＝1，v5＝v4x＋a0＝0.819 93；所以f(－0.2)＝0.819 93.【点拨】秦九韶算法是多项式求值的最优算法，特点是：(1)将高次多项式的求值化为一次多项式求值；(2)减少运算次数，提高效率；(3)步骤重复实施，能用计算机操作.【变式训练2】用秦九韶算法求多项式f(x)＝8x7＋5x6＋3x4＋2x＋1当x＝2时的值为.【解析】1 397.题型三进位制之间的转换【例3】(1)将101 111 011(2)转化为十进制的数；(2)将53(8)转化为二进制的数.【解析】(1)101 111 011(2)＝1×28＋0×27＋1×26＋1×25＋1×24＋1×23＋0×22＋1×21＋1＝379.(2)53(8)＝5×81＋3＝43.所以53(8)＝101 011(2).【点拨】将k进制数转换为十进制数，关键是先写成幂的积的形式再求和，将十进制数转换为k进制数，用“除k取余法”，余数的书写是由下往上，顺序不能颠倒，k进制化为m进制(k，m≠10)，可以用十进制过渡.【变式训练3】把十进制数89化为三进制数.【解析】具体的计算方法如下：89＝3×29＋2，29＝3×9＋2，9＝3×3＋0，3＝3×1＋0，1＝3×0＋1，所以89(10)＝10 022(3).总结提高1.辗转相除法和更相减损术都是用来求两个数的最大公约数的方法.其算法不同，但二者的原理却是相似的，主要区别是一个是除法运算，一个是减法运算，实质都是一个递推的过程.用秦九韶算法计算多项式的值，关键是正确的将多项式改写，然后由内向外，依次计算求解.2.将k进制数转化为十进制数的算法和将十进制数转化为k进制数的算法操作性很强，要掌握算法步骤，并熟练转化；要熟练应用“除基数，倒取余，一直除到商为0”.。

2014届高考数学一轮复习第十一章《算法框图及推理与证明》精编配套试题(含解析)理新人教A版

2014届高考数学（理）一轮复习单元测试第十一章算法框图s 及推理与证明一、选择题(本大题共12小题，每小题5分，共60分．) 1、, 当输入x 为60时, 输出y 的值为（）A ．25B ．30C ．31D ．612．（2013年高考某某卷（理））阅读如下程序框图,如果输出5i =,那么在空白矩形框中应填入的语句为（）A ．2*2S i =-B ．2*1S i =-C ．2*S i =D ．2*4S i =+3．下列推理正确的是( )A ．把a (b ＋c )与log a (x ＋y )类比，则有log a (x ＋y )＝log a x ＋log a yB ．把a (b ＋c )与sin(x ＋y )类比，则有sin(x ＋y )＝sin x ＋sin yC ．把(ab )n 与(x ＋y )n 类比，则有(x ＋y )n ＝x n ＋y nD ．把(a ＋b )＋c 与(xy )z 类比，则有(xy )z ＝x (yz ) 4、（2013高考某某理）设整数4n ≥,集合{}1,2,3,,X n =.令集合(){},,|,,,,,S x y z x y z X x y z y z x z x y =∈<<<<<<且三条件恰有一个成立若(),,x y z 和(),,z w x 都在S 中,则下列选项正确的是( )A .(),,y z w S ∈,(),,x y w S ∉B ．(),,y z w S ∈,(),,x y w S ∈C ．(),,y z w S ∉,(),,x y w S ∈D ．(),,y z w S ∉,(),,x y w S ∈5、古希腊人常用小石子在沙滩上摆成各种形状来研究数。

比如:输入xIf x ≤50 Then y =0.5 * x Elsey =25+0.6*(x -50) End If 输出y他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1，4，9，16，…这样的数为正方形数。

(人教A版浙江专用)2014年高考数学(理)一轮复习方案--第11单元-算法初步、复数、推理与证明

定义
程序框图
返回目录
第62讲
双向固基础
算法初步

四、框图 1．流程图图形符号文字说明 (1)定义：由一些________和________构成的图示称为流程图．动态过程 (2)表示：流程图常常用来表示一些________，通常会一个或多个一个有________“起点”，_______________“终点”． 2．工序流程图工业生产用于描述____________________的流程图称为工序流程图． 3．结构图系统结构 (1)定义：描述______________的图示称为结构图． (2)构成：结构图一般由构成系统的若干要素和表达各箭头要素之间关系的________(或________)构成．连线方向
)
返回目录
第62讲
算法初步
[思考流程] 分析：依据判断语句需要条件语句；推理： ①③都需要逻辑判断；结论：可得①③都需要条件语句．
点面讲考点
返回目录
第62讲
算法初步
[答案] B [解析] 算法中需要逻辑判断的都要用到条件语句；从直到型循环结构和当型循环结构入手，分析它们各自的特点，容易得出正确结论．①③都需要进行逻辑判断，故都要用到条件语句，②只需用顺序结构就能描述其算法．
返回目录
3．课时安排本单元包含4讲和1个45分钟滚动基础训练卷，1个单元能力检测卷，建议每讲1课时，45分钟滚动基础训练卷1课时，单元能力检测卷2课时，本单元共需7课时．
返回目录
双向固基础点面讲考向多元提能力教师备用题
第62讲算法初步
返回目录
考试说明
[答案] (1)√ (2)× (3)× (4)× (5)× (6)√

(新课标)高考数学一轮复习 11.2算法初步名师课件

3 12 4
4 20 5
出
循环,故选B.
3.执行如图所示的程序框图,如果输入a=2,b=2,那么输出的a值为 ( ) A.4 B.16 C.256 D.log316
答案 C log32>4不成立,执行第一次循环,a=22=4; log34>4不成立,执行第二次循环,a=42=16; log316>4不成立,执行第三次循环,a=162=256; log3256>4=log381成立,跳出循环,输出a的值为256,故选C.
n 3, k 7, S 1, m n 1 5;
S 7, k 6, m n 1

5;
S 42, k 5, m n
1

5;
S k
输2出10,S=210.故选C.
4 m n 1.
1.当需要对研究的对象进行逻辑判断时,要使用条件结构,它是根据指定条件选择执行不同指令的控制结构. 2.注意直到型循环和当型循环的本质区别:直到型循环是先执行再判断,直到满足条件才结束循环;当型循环是先判断再执行,若满足条件,则进入循环体,否则结束循环. 3.循环结构主要用在一些有规律的重复计算的算法中,如累加求和、累乘求积等.
8 10
10
1-2 (2014山东,11,5分)执行如图所示的程序框图,若输入的x的值为1,则输
出的n的值为
.
答案 3 解析 x=1,n=0→1-4+3=0→x=2,n=1→22-4×2+3=-1<0→x=3,n=2→32-4×3+ 3=0→x=4,n=3→42-4×4+3>0→输出n=3.
基本算法语句典例2 (2013陕西,4,5分)根据下列算法语句,当输入x为60时,输出y的值为

高三数学第一轮复习第11编 2基本算法语句课件新人教B版

end
print(%io(2),x) 返回目录
编写实际问题中的条件语句时，应先分析实际问题，将实际问题转化为数学问题，理清算法步骤，然后用条件语句编程.
返回目录
某玩具厂1996年生产总值为200万元，如果年生产增长率为5%,计算最早在哪一年生产总值超过300万元.画出程序框图,写出程序.
1+ 1 1 1 + +…+ 3 5 2n - 1
（3）本题的算法设计具有灵活性和通用性，如果将 S=S+1/i变为S=S+i，则变为1+2+3+…+n的值;将 S=S+1/i不变，而i=i+1变为i=i+2，则变为求的值；若将i=i+1不变，而S=S+1/i变为 S=S*i，则变为1×2×3×…×n的值.

(2)利用赋值语句可以实现两个变量值的互换,方法是引进第三个变量,用三个赋值语句完成.
返回目录
P(P - a)(P - b)(P - c)
若三角形的三边长分别为a,b,c，借助三角形面积公式 S= 三角形面积的程序.
a+b+c (P= )，编写一个求 2
返回目录
该问题的算法程序框图如图，则程序如下 a=input(“a=”) b=input(“b=”) c=input(“c=”) P=(a+b+c)/2 S=SQRT(P*(P-a)*(P-b)*(P-c); disp(“S”) S 返回目录
x=
{
0.25×w 0.25×50+0.35×(w-50)
(w≤50) (50<w≤100)
0.25×50+0.35×50+0.45×(w-100) (w>100) 返回目录

2014届高考数学一轮复习第12章《基本算法语句》名师首选学案新人教A版

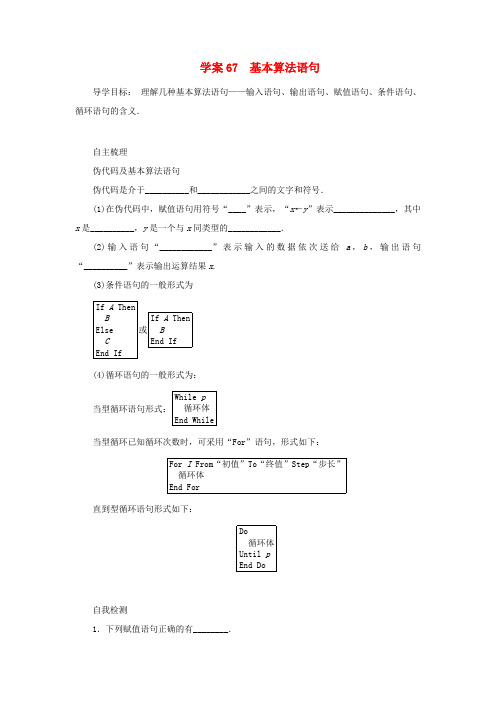
学案67 基本算法语句导学目标：理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义．自主梳理伪代码及基本算法语句伪代码是介于__________和____________之间的文字和符号．(1)在伪代码中，赋值语句用符号“____”表示，“x←y”表示______________，其中x是__________，y是一个与x同类型的____________．(2)输入语句“____________”表示输入的数据依次送给a，b，输出语句“__________”表示输出运算结果x.(3)条件语句的一般形式为If A ThenBElseC End If 或If A ThenBEnd If(4)循环语句的一般形式为：当型循环语句形式：While p循环体End While当型循环已知循环次数时，可采用“For”语句，形式如下：For I From“初值”To“终值”Step“步长”循环体End For直到型循环语句形式如下：Do循环体Until pEnd Do自我检测1．下列赋值语句正确的有________．①a←3，b←4，c←5；②6←x＋y；③3.2←a；④x←y←7；⑤a2－b2←(a＋b)(a－b)；⑥m←m＋2.2．当a＝1，b＝3时，执行完如下的一段伪代码后x的值为________．If a<b Thenx←a＋bElsex←a－bEnd If3．当x＝2时，下面的伪代码运行结果为________．i ←1s←0While i≤4s←s×x＋1i←i＋1End WhilePrint s4．下列伪代码执行后输出的结果为________．i←11s←1Dos←s×ii←i－1Until i<9Print sEnd Do探究点一输入、输出和赋值语句的应用例1 写出下列语句描述的算法的输出结果：(1)a←5b←3c←a＋b/2d←c×cPrint d(2)a←1b←2c←a＋bb←a＋c－bPrint a，b，c 变式迁移1 阅读下面伪代码，回答问题：①x←3y←4x←y②x←3y←4y←x(1)求上述两种伪代码输出的x和y值；(2)上述两种伪代码中的第三行有什么区别．探究点二条件语句例2 已知某商店对顾客购买货款数满500元，减价3%，不足500元不予优惠，输入一顾客购物的货款数，计算出这个顾客实交的货款，画出流程图，写出伪代码．变式迁移2 求过两点P1(x1，y1)，P2(x2，y2)的直线的斜率，画出流程图并写出相应的伪代码．探究点三循环语句例3 设计求满足条件1＋2＋3＋…＋n>106的最小自然数的算法．并画出流程图，写出伪代码．变式迁移3 已知S＝5＋10＋15＋…＋1 500，请用流程图描述求S的算法并用伪代码表示．1．赋值语句是最重要的一种基本语句，也是一个程序必不可少的重要组成部分，使用赋值语句，一定要注意其格式要求，如：赋值号左边只能是变量而不能是表达式；赋值号左右两边不能对换；不能利用赋值语句进行代数式计算等．利用赋值语句可以实现两个变量值的互换，方法是引进第三个变量，用三个赋值语句完成．2．要实现循环结构就要用到循环语句．循环语句有“While语句”，“Do语句”，“For 语句”．“While”语句是前测试，即先判断，后执行；“Do”语句是后测试，即先执行，再判断．“For”语句选用于循环次数确定的情况．课后练习(满分：90分)一、填空题(每小题6分，共48分)1．下列语句中：①m←x3－x2；②T←T×1；③32←A；④A←2×(B＋1)＝2×B＋2；⑤A←A＋2；⑥p←((7x ＋3)x－5)x＋1，其中是赋值语句的个数为________．2．根据如图所示的伪代码，当输入a，b分别为2,3时，最后输出的m的值为________．Read a，bIf a>b Thenm←aElsem←bEnd IfPrint m3．下面所示的伪代码执行后，a，b的值分别为___________________________________．a←15b←20a←a＋bb←a－ba←a－b4．下面的流程图与伪代码是同一个程序的设计方案，请根据联系填空．流程图如图所示：伪代码：i←2S←0DoS←S＋i__②__Until i>100End Do输出③______上述①应填__________；②应填______；③输出结果为________．5．某算法的伪代码如图所示，如果输出的y值是4，那么输入的x的所有可能的值是______________．Read xIf x< 0 Theny←x－2Elsey←x2－3xEnd IfPrint y6．伪代码如下：t ←1i ←2While i ≤4t ←t ×i i ←i ＋1End While Print t以上伪代码输出的结果t 为________． 7．如图伪代码输出的结果为________．P ←1For K From 1 To 9 Step 2 P ←P ＋2×K －1End For Print P8．以下伪代码：Read xIf x ≤2 Then y ←2x －3Else y ←log 2x End If Print y表示的函数表达式是________．二、解答题(共42分)9．(12分)编写函数y ＝⎩⎪⎨⎪⎧x 2＋1，x ≤2.5x 2－1，x >2.5的算法并写出对应的伪代码，根据输入的x的值，计算y 的值．10．(14分)根据下面的算法伪代码，绘制流程图，指出该算法的功能是什么？并将伪代码改为“For”语句的形式．伪代码S←0I←3While I≤99S←S＋I3I←I＋2End WhilePrint S11．(16分)用循环语句来书写1＋122＋132＋…＋1n2>100的最小自然数n的算法，画出算法流程图，并写出相应的伪代码．学案67 基本算法语句答案自主梳理自然语言计算机语言(1)←将y的值赋给x一个变量变量或表达式(2)Read a，b Print x自我检测1．①⑥解析依据赋值语句的格式与作用可知①和⑥正确，②③④⑤是错误的．2．4解析 ∵1<3，∴x ＝1＋3＝4. 3．15解析当x ＝2时，i ＝1≤4，s ＝0×2＋1＝1；i ＝1＋1＝2≤4，s ＝1×2＋1＝3； i ＝2＋1＝3≤4，s ＝3×2＋1＝7； i ＝3＋1＝4≤4，s ＝7×2＋1＝15； i ＝4＋1＝5>4，输出s ＝15.4．990解析由题意s ＝11×10×9＝990. 课堂活动区例 1 解题导引 (1)赋值语句左边只能是变量名字，而不是表达式，右边可以是一个常量、变量或含变量的运算式．如：2←x 是错误的．(2)赋值号的左右两边不能对换．赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量．如“A ←B ”和“B ←A ”的运行结果是不同的．解 (1)∵a ＝5，b ＝3，c ＝a ＋b2＝4，∴d ＝c 2＝16，即输出16.(2)∵a ＝1，b ＝2，c ＝a ＋b ，∴c ＝3，又∵b ＝a ＋c －b ， ∴b ＝1＋3－2＝2，∴a ＝1，b ＝2，c ＝3，即输出1,2,3.变式迁移1 解 (1)①x ，y 的值分别为4,4； ②x ，y 的值分别为3,3.(2)伪代码①中的x ←y 是将y 的值赋给x ，赋值后的x 变为4，②中y ←x 是将x 的值赋给y ，赋值后y 的值变为3.例2 解设购买货款数为x 元，则顾客实际应交的货款y 元为y ＝⎩⎪⎨⎪⎧x 1－3%x ≥500，x 0≤x <500，即y ＝⎩⎪⎨⎪⎧0.97x x ≥500，x 0≤x <500.流程图如图所示：伪代码为：Read xIf x ≥500 Then y ←0.97x Else y ←x End If Print y变式迁移2 解算法的流程图如图所示：伪代码为：例3 解题导引由于n 的值事先不知道，又没有公式可套用，我们可借助于变量引入循环，累积变量S初始值设定为0，计数变量i 初始值设定为1，步长为1，累加的数值为i .应该用“While”Read x 1，x 2，y 1，y 2 If x 1＝x 2 ThenPrint 直线的斜率不存在 Else k ←2121y y x x --Print k End If即当型循环来实现．相应的伪代码的书写也应该用“While”语句．解算法如下：S1 S←0；S2 i←1；S3 S←S＋i；S4 如果S≤106，使i←i＋1，返回S3重复执行S3、S4，否则输出i－1.相应的伪代码如下：S←0i←1While S≤106S←S＋ii←i＋1End WhilePrint i－1对应的流程图如图所示：变式迁移3 解流程图如图所示：从流程图可以看出是一个循环结构，我们可以运用循环语句来实现．伪代码为： S ←0For I From 5 To 1 500 Step 5S ←S ＋I End ForPrint S课后练习区1．4解析正确的是①②⑤⑥，赋值语句只能将表达式或数值赋给一个变量．2．3解析 ∵a ＝2，b ＝3，∴a <b ，应把b 值赋给m ，∴m 的值为3.3．20,154．①i >100； ②i ←i ＋2； ③2 550解析程序的功能是计算100以内的偶数和．5．－12或4 解析依据伪代码可得，当x <0时，1x 2＝4， ∴x ＝－12或x ＝12. 又∵x <0，∴x ＝－12. 当x ≥0时，x 2－3x ＝4，∴x ＝4或x ＝－1，又∵x ≥0，∴x ＝4.综上所述，x ＝－12或x ＝4. 6．24解析依据伪代码可得，当i ＝2时，t ＝1×2＝2；当i ＝3时，t ＝2×3＝6；当i ＝4时，t ＝6×4＝24.伪代码输出的结果是24.7．468．y ＝⎩⎪⎨⎪⎧ 2x －3 x ≤2log 2x x >29．解其算法步骤如下：S1 输入x ；S2 若x ≤2.5，则y ←x 2＋1，否则y ←x 2－1；S3 输出y . (6分) 用伪代码可表示如下：Read xIf x ≤2.5 Theny ←x 2＋1Else y ←x 2－1End IfPrint y(12分)10．解伪代码对应的流程图如图所示，它用的是“While”语句，功能是求33＋53＋…＋993. (4分)(10分)利用“For”语句伪代码可以改为：S ←0For I From 3 To 99 Step 2S←S＋I3End ForPrint S(14分) 11．解算法如下：S1 S←0；S2 n←1；S3 S←S＋1n2；S4 如果S≤100，使n←n＋1，并返回S3，否则输出n－1. (4分) 相应流程图如图所示．(10分)相应的伪代码S←0n←1While S≤100S←S＋\f(1,n2)n←n＋1End WhilePrint n－1(16分)。

2014高考数学(理)一轮复习学案课件 第11编 基本算法语句

高考数学一轮复习 必考部分 第十一篇 复数 算法 推理与证明 第4节 综合法 分析法 反证法课件 文 北师大版