10年(2010-2019)高考数学真题分类练习与讲解---第二十二讲 空间几何体的三视图、表面积和体积
理科数学十年高考真题(2010-2019)专项训练-专题八 立体几何 第二十二讲 空间几何体的三视图、表面积体积
2020高考冲刺 提分必备 2010-2019十年高考真题专项训练专题八 立体几何初步第二十二讲 空间几何体的三视图、表面积和体积一、选择题1.(2018北京)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为俯视图侧(左)视图正(主)视图A .1B .2C .3D .42.(2018全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为BAA .172B .52C .3D .23.(2018全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4.(2018全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC ∆为等边三角形且其面积为3,则三棱锥D ABC -体积的最大值为 A .3B .3C .3D .35.(2018上海)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设1AA 是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点,以1AA 为底面矩形的一边,则这样的阳马的个数是( )A 1AA .4B .8C .12D .166.(2018浙江)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是俯视图正视图2211A .2B .4C .6D .87.(2017新课标Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A.10 B.12 C.14 D.168.(2017新课标Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为A.90πB.63πC.42πD.36π9.(2017新课标Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A.πB.34πC.2πD.4π10.(2017浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:3cm)是俯视图11311A.12π+B.32π+C.312π+D.332π+11.(2017北京)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为A.2B.3C.2D.212.(2016山东)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为A .1233+π B .1233+π C .1236+π D .216+π 13.(2016全国I )如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,若该几何体的体积是28π3,则它的表面积是A .17πB .18πC .20πD .28π 14.(2016全国II )如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为A .20πB .24πC .28πD .32π15.(2016年全国III )如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为A .185+B .54185+C .90D .8116.(2015浙江)某几何体的三视图如图所示(单位:cm ),则该几何体的体积是A .38cm B .312cm C .3323cm D .3403cm 17.(2015陕西)一个几何体的三视图如图所示,则该几何体的表面积为A .3πB .4πC .24π+D .34π+ 18.(2015重庆)某几何体的三视图如图所示,则该几何体的体积为A .13π+ B .23π+ C .123π+ D .223π+ 19.(2015新课标)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为A .81 B .71 C .61 D .51 20.(2015安徽)一个四面体的三视图如图所示,则该四面体的表面积是A .13+B .23+C .122+D .2221.(2015湖南)某工件的三视图如图3所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积原工件的体积)A .89πB .169πC .34(21)πD .312(21)π22.(2015新课标Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π,则r =A.1 B.2 C.4 D.823.(2014新课标Ⅰ)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A.62B.6 C.42D.424.(2014新课标Ⅱ)如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为A.1727B.59C.1027D.1325.(2014安徽)一个多面体的三视图如图所示,则该多面体的表面积为A.213+B.183+C.21D.1826.(2014福建)某空间几何体的正视图是三角形,则该几何体不可能是A.圆柱B.圆锥C.四面体D.三棱柱27.(2014浙江)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是俯视图侧视图正视图3333344A.902cm B.1292cm C.1322cm D.1382cm28.(2014新课标Ⅱ)正三棱柱111ABC A B C-的底面边长为23D为BC中点,则三棱锥11A B DC-的体积为A.3 B.32C.1 D329.(2014福建)以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于A.2πB.πC.2 D.130.(2014辽宁)某几何体三视图如图所示,则该几何体的体积为主(正)视左(侧)视俯视俯视图左视图主视图122122211A .82π-B .8π-C .82π-D .84π-31.(2014陕西)将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积为A .4πB .3πC .2πD .π32.(2014江西)一几何体的直观图如右图,下列给出的四个俯视图中正确的是ABCD33.(2013新课标Ⅰ)某几何体的三视图如图所示,则该几何体的体积为A .168π+B .88π+C .1616π+D .816π+ 34.(2013江西)一几何体的三视图如右所示,则该几何体的体积为俯视图侧视图正视图A .200+9πB .200+18πC .140+9πD .140+18π 35.(2012广东)某几何体的三视图如图所示,它的体积为A .12πB .45πC .57πD .81π36.(2012湖北)已知某几何体的三视图如图所示,则该几何体的体积为俯视图正视图A .8π3 B .3π C .10π3D .6π 37.(2011新课标)在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为俯视图正视图DCB A38.(2011安徽)一个空间几何体的三视图如图所示,则该几何体的表面积为侧视图A .48B .C .D .8039.(2011辽宁)如图,四棱锥S —ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确...的是 BCASDA .AC ⊥SB B .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D .AB 与SC 所成的角等于DC 与SA 所成的角40.(2010安徽)一个几何体的三视图如图,该几何体的表面积为A.280 B.292 C.360 D.372 41.(2010浙江)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是侧视图正视图A.3523cm3B.3203cm3 C.2243cm3D.1603cm3二、填空题42.(2018天津)已知正方体1111ABCD A B C D-的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M EFGH-的体积为.1ACA43.(2018江苏)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .44.(2017新课标Ⅰ)如图,圆形纸片的圆心为O ,半径为5 cm ,该纸片上的等边三角形ABC的中心为O .D 、E 、F 为圆O 上的点,DBC ∆,ECA ∆,FAB ∆分别是以BC ,CA ,AB 为底边的等腰三角形。
(2010-2019)十年高考数学真题分类汇编:空间向量(含解析)

(2010-2019)十年高考数学真题分类汇编:空间向量(含解析)1.(2014·全国2·理T11)直三棱柱ABC-A 1B 1C 1中,∠BCA=90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC=CA=CC 1,则BM 与AN 所成角的余弦值为( ) A.110B.25C.√3010D.√22【答案】C【解析】如图,以点C 1为坐标原点,C 1B 1,C 1A 1,C 1C 所在的直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系,不妨设BC=CA=CC 1=1,可知点A (0,1,1),N (0,12,0),B (1,0,1),M (12,12,0). ∴AN ⃗⃗⃗⃗⃗⃗ =(0,-12,-1),BM ⃗⃗⃗⃗⃗⃗ =(-12,12,-1).∴cos <AN ⃗⃗⃗⃗⃗⃗ ,BM ⃗⃗⃗⃗⃗⃗ >=AN ⃗⃗⃗⃗⃗⃗ ·BM⃗⃗⃗⃗⃗⃗⃗ |AN ⃗⃗⃗⃗⃗⃗ ||BM⃗⃗⃗⃗⃗⃗⃗ |=√3010. 根据AN ⃗⃗⃗⃗⃗⃗ 与BM ⃗⃗⃗⃗⃗⃗ 的夹角及AN 与BM 所成角的关系可知,BM 与AN 所成角的余弦值为√3010.2.(2013·北京·文T8)如图,在正方体ABCD-A 1B 1C 1D 1中,P 为对角线BD 1的三等分点,P 到各顶点的距离的不同取值有( ) A.3个B.4个C.5个D.6个【答案】B【解析】设正方体的棱长为a.建立空间直角坐标系,如图所示.则D (0,0,0),D 1(0,0,a ),C 1(0,a ,a ),C (0,a ,0),B (a ,a ,0),B 1(a ,a ,a ),A (a ,0,0),A 1(a ,0,a ),P (23a ,23a ,13a), 则|PB⃗⃗⃗⃗⃗ |=√19a 2+19a 2+19a 2=√33a , |PD⃗⃗⃗⃗⃗ |=√49a 2+49a 2+19a 2=a , |PD 1⃗⃗⃗⃗⃗⃗⃗ |=√49a 2+49a 2+49a 2=2√33a , |PC 1⃗⃗⃗⃗⃗⃗⃗ |=|PA 1⃗⃗⃗⃗⃗⃗⃗ |=√49a 2+19a 2+49a 2=a ,|PC⃗⃗⃗⃗⃗ |=|PA ⃗⃗⃗⃗⃗ |=√49a 2+19a 2+19a 2=√63a , |PB 1⃗⃗⃗⃗⃗⃗⃗ |=√19a 2+19a 2+49a 2=√63a , 3.(2012·陕西·理T5)如图,在空间直角坐标系中有直三棱柱ABC -A 1B 1C 1,CA=CC 1=2CB ,则直线BC 1与直线AB 1夹角的余弦值为( ) A.√55B.√53C.2√55D.35【答案】A【解析】不妨设CB=1,则CA=CC 1=2.由题图知,A 点的坐标为(2,0,0),B 点的坐标为(0,0,1),B 1点的坐标为(0,2,1),C 1点的坐标为(0,2,0). 所以BC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,-1),AB 1⃗⃗⃗⃗⃗⃗⃗ =(-2,2,1).所以cos <BC 1⃗⃗⃗⃗⃗⃗⃗ ,AB 1⃗⃗⃗⃗⃗⃗⃗ >=3√5=√55.4.(2010·大纲全国·文T6)直三棱柱ABC-A 1B 1C 1中,若∠BAC=90°,AB=AC=AA 1,则异面直线BA 1与AC 1所成的角等于( ) A.30° B.45° C.60° D.90° 【答案】C【解析】不妨设AB=AC=AA 1=1,建立空间直角坐标系如图所示,则B(0,-1,0),A 1(0,0,1),A(0,0,0),C 1(-1,0,1), ∴BA 1⃗⃗⃗⃗⃗⃗⃗⃗ =(0,1,1),AC 1⃗⃗⃗⃗⃗⃗⃗ =(-1,0,1). ∴cos <BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗⃗ >=BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ·AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ||AA 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=√2×√2=12.∴<BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗⃗ >=60°.∴异面直线BA 1与AC 1所成的角为60°.5.(2019·天津·理T17)如图,AE ⊥平面ABCD ,CF ∥AE ,AD ∥BC ,AD ⊥AB ,AB=AD=1,AE=BC=2. (1)求证:BF ∥平面ADE;(2)求直线CE 与平面BDE 所成角的正弦值; (3)若二面角E-BD-F 的余弦值为13,求线段CF 的长.【解析】(1)证明依题意,可以建立以A 为原点,分别以AB ⃗⃗⃗⃗⃗ ,AD ⃗⃗⃗⃗⃗ ,AE ⃗⃗⃗⃗⃗ 的方向为x 轴,y 轴,z 轴正方向的空间直角坐标系(如图),可得A(0,0,0),B(1,0,0),C(1,2,0),D(0,1,0),E(0,0,2).设CF=h(h>0),则F(1,2,h).依题意,AB ⃗⃗⃗⃗⃗ =(1,0,0)是平面ADE 的法向量,又BF ⃗⃗⃗⃗⃗ =(0,2,h ),可得BF ⃗⃗⃗⃗⃗ ·AB ⃗⃗⃗⃗⃗ =0,又因为直线BF ⊄平面ADE ,所以BF ∥平面ADE. (2)解依题意,BD ⃗⃗⃗⃗⃗⃗ =(-1,1,0),BE ⃗⃗⃗⃗⃗ =(-1,0,2),CE ⃗⃗⃗⃗⃗ =(-1,-2,2). 设n =(x ,y ,z )为平面BDE 的法向量,则{n ·BD ⃗⃗⃗⃗⃗⃗ =0,n ·BE ⃗⃗⃗⃗⃗ =0,即{-x +y =0,-x +2z =0,不妨令z=1,可得n =(2,2,1).因此有cos <CE ⃗⃗⃗⃗⃗ ,n >=CE ⃗⃗⃗⃗⃗·n |CE⃗⃗⃗⃗⃗ ||n |=-49. 所以,直线CE 与平面BDE 所成角的正弦值为49. (3)解设m =(x ,y ,z )为平面BDF 的法向量, 则{m ·BD ⃗⃗⃗⃗⃗⃗ =0,m ·BF ⃗⃗⃗⃗⃗ =0,即{-x +y =0,2y +ℎz =0,不妨令y=1,可得m =1,1,-2ℎ. 由题意,有|cos <m ,n >|=|m ·n ||m ||n |=|4-2ℎ|3√2+ℎ2=13,解得h=87,经检验,符合题意. 所以,线段CF 的长为87.6.(2019·浙江·T 19)如图,已知三棱柱ABC-A 1B 1C 1,平面A 1ACC 1⊥平面ABC ,∠ABC=90°,∠BAC=30°,A 1A=A 1C=AC ,E ,F 分别是AC ,A 1B 1的中点. (1)证明:EF ⊥BC ;(2)求直线EF 与平面A 1BC 所成角的余弦值.【解析】方法一:(1)连接A 1E ,因为A 1A=A 1C ,E 是AC 的中点, 所以A 1E ⊥AC.。
十年高考真题分类汇编(2010-2019) 数学 专题10 立体几何

十年高考真题分类汇编(2010—2019)数学专题10立体几何1.(2019·浙江·T4)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V 柱体=Sh,其中S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm 3)是( )A.158B.162C.182D.324【答案】B【解析】由三视图得该棱柱的高为6,底面五边形可以看作是由两个直角梯形组合而成,其中一个上底为4,下底为6,高为3,另一个的上底为2,下底为6,高为3,则该棱柱的体积为2+62×3+4+62×3×6=162.2.(2019·全国1·理T12)已知三棱锥P-ABC 的四个顶点在球O 的球面上,PA=PB=PC,△ABC 是边长为2的正三角形,E,F 分别是PA,AB 的中点,∠CEF=90°,则球O 的体积为( ) A.8√6π B.4√6π C.2√6π D.√6π【答案】D【解析】设PA=PB=PC=2x. ∵E,F 分别为PA,AB 的中点, ∴EF ∥PB,且EF=12PB=x.∵△ABC 为边长为2的等边三角形, ∴CF=√3.又∠CEF=90°,∴CE=√3-x 2,AE=12PA=x. 在△AEC 中,由余弦定理可知cos ∠EAC=x 2+4-(3-x 2)2×2·x .作PD ⊥AC 于点D,∵PA=PC,∴D 为AC 的中点,cos ∠EAC=AD PA =12x . ∴x 2+4-3+x 24x=12x. ∴2x 2+1=2.∴x 2=12,即x=√22. ∴PA=PB=PC=√2. 又AB=BC=AC=2, ∴PA ⊥PB ⊥PC. ∴2R=√2+2+2=√6. ∴R=√62. ∴V=43πR 3=43π×6√68=√6π.故选D.3.(2019·全国2·理T7文T7)设α,β为两个平面,则α∥β的充要条件是( ) A.α内有无数条直线与β平行 B.α内有两条相交直线与β平行 C.α,β平行于同一条直线 D.α,β垂直于同一平面 【答案】B【解析】由面面平行的判定定理知,“α内有两条相交直线与β平行”是“α∥β”的充分条件.由面面平行的性质知,“α内有两条相交直线与β平行”是“α∥β”的必要条件,故选B.4.(2019·全国3·理T8文T8)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD,M 是线段ED 的中点,则( ) A.BM=EN,且直线BM,EN 是相交直线B.BM ≠EN,且直线BM,EN 是相交直线C.BM=EN,且直线BM,EN 是异面直线D.BM ≠EN,且直线BM,EN 是异面直线 【答案】B【解析】如图,连接BD,BE.在△BDE 中,N 为BD 的中点,M 为DE 的中点, ∴BM,EN 是相交直线,排除选项C 、D. 作EO ⊥CD 于点O,连接ON. 作MF ⊥OD 于点F,连接BF.∵平面CDE ⊥平面ABCD,平面CDE ∩平面ABCD=CD,EO ⊥ CD,EO ⊂平面CDE,∴EO ⊥平面ABCD. 同理,MF ⊥平面ABCD.∴△MFB 与△EON 均为直角三角形. 设正方形ABCD 的边长为2,易知 EO=√3,ON=1,MF=√32,BF=√22+94=52, 则EN=√3+1=2,BM=√34+254=√7,∴BM ≠EN.故选B.5.(2019·浙江·T8)设三棱锥V-ABC 的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点).记直线PB 与直线AC 所成的角为α,直线PB 与平面ABC 所成的角为β,二面角P-AC-B 的平面角为γ,则( ) A.β<γ,α<γ B.β<α,β<γ C.β<α,γ<α D.α<β,γ<β 【答案】B【解析】如图G 为AC 中点,点V 在底面ABC 上的投影为点O,则点P 在底面ABC 上的投影点D 在线段AO 上,过点D 作DE 垂直AE,易得PE ∥VG,过点P 作PF ∥AC 交VG 于点F,过点D 作DH ∥AC,交BG 于点H,则α=∠BPF,β=∠PBD,γ=∠PED,所以cos α=PFPB=EG PB=DH PB<BDPB=cos β,所以α>β,因为tan γ=PDED>PDBD=tan β,所以γ>β.故选B.6.(2018·全国3·理T10文T12)设A,B,C,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为9√3,则三棱锥D-ABC 体积的最大值为( ) A.12√3 B.18√3C.24√3D.54√3【答案】B【解析】由△ABC 为等边三角形且面积为9√3,设△ABC 边长为a,则S=12a ·√32a=9√3.∴a=6,则△ABC 的外接圆半径r=√32×23a=2√3<4. 设球的半径为R,如图,OO 1=√R 2-r 2=√42-(2√3)2=2.当D 在O 的正上方时,V D-ABC =1S △ABC ·(R+|OO 1|)=1×9√3×6=18√3,最大.故选B.7.(2018·全国1·理T7文T9)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A,圆柱表面上的点N 在左视图上的对应点为B,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( ) A.2√17 B.2√5 C.3 D.2【答案】B【解析】如图所示,易知N 为CD⏜的中点,将圆柱的侧面沿母线MC 剪开,展平为矩形MCC'M',易知CN=14CC'=4,MC=2,从M 到N 的路程中最短路径为MN.在Rt△MCN中,MN=√MC2+NC2=2√5.8.(2018·全国3·理T3文T3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )【答案】A【解析】由题意可知带卯眼的木构件的直观图如图所示,由直观图可知其俯视图应为A中图形.9.(2018·北京·理T5文T6)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )A.1B.2C.3D.4【答案】C【解析】由该四棱锥的三视图,得其直观图如图.由正视图和侧视图都是等腰直角三角形,知PD⊥平面ABCD,所以侧面PAD和PDC都是直角三角形.由俯视图为直角梯形,易知DC⊥平面PAD.又AB∥DC,所以AB⊥平面PAD,所以AB⊥PA,所以侧面PAB也是直角三角形.易知PC=2√2,BC=√5,PB=3,从而△PBC不是直角三角形.故选C.10.(2018·上海·T15)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA1是正六棱柱的一条侧棱,如图.若阳马以该正六棱柱的顶点为顶点,以AA1为底面矩形的一边,则这样的阳马的个数是( )A.4B.8C.12D.16【答案】D【解析】设正六棱柱为ABCDEF-A1B1C1D1E1F1,以侧面AA1B1B,AA1F1F为底面矩形的阳马有E-AA 1B 1B,E 1-AA 1B 1B,D-AA 1B 1B,D 1-AA 1B 1B,C-AA 1F 1F,C 1-AA 1F 1F,D-AA 1F 1F,D 1-AA 1F 1F,共8个,以对角面AA 1C 1C,AA 1E 1E 为底面矩形的阳马有F-AA 1C 1C,F 1-AA 1C 1C,D-AA 1C 1C,D 1-AA 1C 1C,B-AA 1E 1E,B 1-AA 1E 1E,D-AA 1E 1E,D 1-AA 1E 1E,共8个,所以共有8+8=16(个),故选D.11.(2018·全国1·文T10)在长方体ABCD-A 1B 1C 1D 1中,AB=BC=2,AC 1与平面BB 1C 1C 所成的角为30°,则该长方体的体积为( ) A.8 B.6√2 C.8√2 D.8√3【答案】C【解析】在长方体ABCD-A 1B 1C 1D 1中,AB ⊥平面BCC 1B 1,连接BC 1,则∠AC 1B 为AC 1与平面BB 1C 1C 所成的角,∠AC 1B=30°,所以在Rt △ABC 1中,BC 1=AB tan∠AC 1B =2√3,又BC=2,所以在Rt △BCC 1中,CC 1=√(2√3)2-22=2√2, 所以该长方体体积V=BC ×CC 1×AB=8√2.12.(2018·全国2·理T9)在长方体ABCD-A 1B 1C 1D 1中,AB=BC=1,AA 1=√3,则异面直线AD 1与DB 1所成角的余弦值为( ) A.15B.√56C.√55D.√22【答案】C【解析】以DA,DC,DD 1所在直线为坐标轴建立空间直角坐标系如图, 则D 1(0,0,√3),A(1,0,0),D(0,0,0),B 1(1,1,√3).∴AD 1⃗⃗⃗⃗⃗⃗⃗ =(-1,0,√3),DB 1⃗⃗⃗⃗⃗⃗⃗⃗ =(1,1,√3).设异面直线AD 1与DB 1所成的角为θ. ∴cos θ=|AD 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·DB1⃗⃗⃗⃗⃗⃗⃗⃗⃗ |AD 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ||DB 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ||=|2×√5|=√55.∴异面直线AD 1与DB 1所成角的余弦值为√55.13.(2018·全国2·文T9)在正方体ABCD-A 1B 1C 1D 1中,E 为棱CC 1的中点,则异面直线AE 与CD 所成角的正切值为( ) A.√22 B.√32C.√52D.√72【答案】C【解析】如图,因为AB∥CD,所以AE与CD所成的角为∠EAB. 在Rt△ABE中,设AB=2,则BE=√5,则tan∠EAB=BEAB =√52,所以异面直线AE与CD所成角的正切值为√52.14.(2018·全国1·文T5)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )A.12√2πB.12πC.8√2πD.10π【答案】B【解析】过直线O1O2的平面截该圆柱所得的截面为圆柱的轴截面,设底面半径为r,母线长为l,因为轴截面是面积为8的正方形,所以2r=l=2√2,r=√2,所以圆柱的表面积为2πrl+2πr2=8π+4π=12π.15.(2018·浙江·T3)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )A.2B.4C.6D.8【答案】C【解析】由三视图可知该几何体为直四棱柱.∵S底=12×(1+2)×2=3,h=2,∴V=Sh=3×2=6.16.(2017·全国2·理T4文T6)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A.90πB.63πC.42πD.36π【答案】B【解析】由三视图知,该几何体是一个圆柱截去一部分所得,如图所示.其体积等于下部分圆柱的体积加上上部分圆柱体积的12,所以该几何体的体积V=π×32×4+π×32×6×12=63π.17.(2017·全国1·理T7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( ) A.10B.12C.14D.16【答案】B【解析】由三视图可还原出几何体的直观图如图所示.该五面体中有两个侧面是全等的直角梯形,且该直角梯形的上底长为2,下底长为4,高为2,则S 梯=(2+4)×2÷2=6,所以这些梯形的面积之和为12.18.(2017·全国2·理T10)已知直三棱柱ABC-A 1B 1C 1中,∠ABC=120°,AB=2,BC=CC 1=1,则异面直线AB 1与BC 1所成角的余弦值为( ) A.√32 B.√155C.√105D.√33【答案】C【解析】方法一:把三棱柱ABC-A 1B 1C 1补成四棱柱ABCD-A 1B 1C 1D 1,如图, 连接C 1D,BD,则AB 1与BC 1所成的角为∠BC 1D. 由题意可知BC 1=√2,BD=√22+12-2×2×1×cos60°=√3,C 1D=AB 1=√5.可知B C 12+BD 2=C 1D 2,所以cos ∠BC 1D=√2√5=√105,故选C.方法二:以B 1为坐标原点,B 1C 1所在的直线为x 轴,垂直于B 1C 1的直线为y 轴,BB 1所在的直线为z 轴建立空间直角坐标系,如图所示. 由已知条件知B 1(0,0,0),B(0,0,1),C 1(1,0,0),A(-1,√3,1),则BC 1⃗⃗⃗⃗⃗⃗⃗ =(1,0,-1),AB 1⃗⃗⃗⃗⃗⃗⃗ =(1,-√3,-1).所以cos<AB 1⃗⃗⃗⃗⃗⃗⃗ ,BC 1⃗⃗⃗⃗⃗⃗⃗ >=AB 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·BC 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ |AB 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ |·|BC 1⃗⃗⃗⃗⃗⃗⃗⃗⃗|=√5×√2=√105.所以异面直线AB 1与BC 1所成角的余弦值为√105.19.(2017·北京·理T7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )A.3√2B.2√3C.2√2D.2【答案】B【解析】由题意可知,直观图为四棱锥A-BCDE(如图所示),最长的棱为正方体的体对角线AE=√22+22+22=2√3.故选B.20.(2017·全国3·理T8文T9)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( ) A .π B.3π4C.π2D.π4【答案】B【解析】由题意可知球心即为圆柱体的中心,画出圆柱的轴截面如图所示,则AC=1,AB=12,底面圆的半径r=BC=√32,所以圆柱的体积是V=πr 2h=π×(√32)2×1=3π4,故选B.21.(2017·全国1·文T6)如图,在下列四个正方体中,A,B 为正方体的两个顶点,M,N,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( )【答案】A【解析】易知选项B 中,AB ∥MQ,且MQ ⊂平面MNQ,AB ⊄平面MNQ,则AB ∥平面MNQ;选项C 中,AB ∥MQ,且MQ ⊂平面MNQ,AB ⊄平面MNQ,则AB ∥平面MNQ;选项D 中,AB ∥NQ,且NQ ⊂平面MNQ,AB ⊄平面MNQ,则AB ∥平面MNQ,故排除选项B,C,D;故选A.4.(2016·浙江·理T2文T2)已知互相垂直的平面α,β交于直线l,若直线m,n 满足m ∥α,n ⊥β,则( ) A.m ∥l B.m ∥nC.n ⊥lD.m ⊥n 【答案】C【解析】对于选项A,∵α∩β=l ,∴l ⊂α,∵m ∥α,∴m 与l 可能平行,也可能异面,故选项A 不正确; 对于选项B,D,∵α⊥β,m ∥α,n ⊥β,∴m 与n 可能平行,可能相交,也可能异面,故选项B,D 不正确. 对于选项C,∵α∩β=l ,∴l ⊂β. ∵n ⊥β,∴n ⊥l.故选C.22.(2016·天津·文T3)将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为( )【答案】B【解析】由题意得该长方体沿相邻三个面的对角线截去一个棱锥,如下图所示.易知其左视图为B 项中图.故选B.23.(2016·全国3·理T10文T11)在封闭的直三棱柱ABC-A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC,AB=6,BC=8,AA 1=3,则V 的最大值是( ) A.4π B.9π2C.6πD.32π3【答案】B【解析】先计算球与直三棱柱三个侧面相切的球的半径,再和与直三棱柱两底面相切的球的半径相比较,半径较小的球即为所求.设球的半径为R,∵AB ⊥BC,AB=6,BC=8,∴AC=10.当球与直三棱柱的三个侧面相切时,有12(6+8+10)×R=12×6×8,此时R=2;当球与直三棱柱两底面相切时,有2R=3,此时R=32.所以在封闭的直三棱柱中,球的最大半径只能为32,故最大体积V=4π(3)3=9π.24.(2016·全国1·文T4)体积为8的正方体的顶点都在同一球面上,则该球的表面积为( )A.12πB. πC.8πD.4π【答案】A【解析】设正方体的棱长为a,由a3=8,得a=2.由题意可知,正方体的体对角线为球的直径,故2r=2则r=√3.所以该球的表面积为4π×(√3)2=12π,故选A.25.(2016·全国1·理T11文T11)平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )A.√32B.√22C.√33D.13【答案】A【解析】∵α∥平面CB1D1,平面ABCD∥平面A1B1C1D1,α∩平面ABCD=m,平面CB1D1∩平面A1B1C1D1=B1D1,∴m∥B1D1.∵α∥平面CB1D1,平面ABB1A1∥平面DCC1D1,α∩平面ABB1A1=n,平面CB1D1∩平面DCC1D1=CD1,∴n∥CD1.∴B1D1,CD1所成的角等于m,n所成的角,即∠B1D1C等于m,n所成的角.∵△B1D1C为正三角形,∴∠B1D1C=60°,∴m,n所成的角的正弦值为√32.26.(2016·全国1·理T6文T7)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是( )A.17πB.18πC.20πD.28π【答案】A【解析】由三视图可知该几何体是球截去18后所得几何体,则78×4π3×R 3=28π3,解得R=2,故其表面积为78×4πR 2+34×πR 2=14π+3π=17π. 27.(2016·全国2·理T6文T7)下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为 ( )A.20πB.24πC.28πD.32π 【答案】C【解析】因为原几何体由同底面的一个圆柱和一个圆锥构成,所以其表面积为S=π×(42)2+4π×4+12×4π×√(2√3)2+22=28π,故选C.28.(2016·全国3·理T9文T10)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( ) A.18+36√5 B.54+18√5 C.90D.81【答案】B【解析】由题意知该几何体为四棱柱,且四棱柱的底面是边长为3的正方形,侧棱长为3√5,所以所求表面积为(3×3+3×6+3×3√5)×2=54+18√5,故选B.29.(2016·山东·理T5)一个由半球和四棱锥组成的几何体,其三视图如下图所示.则该几何体的体积为( ) A.1+2πB.1+√2πC.1+√2πD.1+√2π【答案】C【解析】由三视图可知,上面是半径为√22的半球,体积为V 1=12×43π×(√22)3=√2π6,下面是底面积为1,高为1的四棱锥,体积V 2=13×1×1=13,故选C.30.(2016·北京·理T6)某三棱锥的三视图如图所示,则该三棱锥的体积为( )A.16B.13C.12D.1【答案】A【解析】由三视图可得,三棱锥的直观图如图,则该三棱锥的体积V=13×12×1×1×1=16,故选A.31.(2015·全国1·理T6文T6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A.14斛B.22斛C.36斛D.66斛 【答案】B【解析】设底面圆弧半径为R,∵米堆底部弧长为8尺,∴14·2πR=8,∴R=16π. ∴体积V=14×13π×(16π)2×5.∵π≈3,∴V ≈3209(尺3).∴堆放的米约为3209×1.62≈22(斛). 32.(2015·全国2·理T6文T6)一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.15【答案】D【解析】由题意知该正方体截去了一个三棱锥,如图所示,设正方体棱长为a,则V 正方体=a 3,V 截去部分=16a 3,故截去部分体积与剩余部分体积的比值为16a 3∶56a 3=1∶5.33.(2015·重庆·理T5)某几何体的三视图如图所示,则该几何体的体积为( )A.13+π B.23+π C.13+2πD.23+2π【答案】A【解析】由题中三视图可知,该几何体是一个组合体,其左边是一个三棱锥,底面是等腰直角三角形(斜边长等于2),高为1,所以体积V 1=13×12×2×1×1=13;其右边是一个半圆柱,底面半径为1,高为2,所以体积V 2=π·12·2·12=π,所以该几何体的体积V=V 1+V 2=13+π.34.(2015·浙江·理T2)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( ) A.8 cm 3 B.12 cm 3C.323 cm 3D.403 cm 3【答案】C【解析】由题中三视图知该几何体是一个正方体与正四棱锥的组合体,其中正方体与正四棱锥的底面边长为2 cm,正四棱锥的高为2 cm,则该几何体的体积V=2×2×2+13×2×2×2=323(cm 3),故选C.35.(2015·山东·理T7)在梯形ABCD 中,∠ABC=π2,AD ∥BC,BC=2AD=2AB=2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.2π3 B.4π3 C.5π3 D.2π【答案】C【解析】由题意可得旋转体为一个圆柱挖掉一个圆锥,如图所示. V 圆柱=π×12×2=2π,V 圆锥=13×π×12×1=π3. ∴V 几何体=V 圆柱-V 圆锥=2π-π3=5π3.36.(2015·湖南·文T10)某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积原工件的体积)( )A.89πB.827πC.24(√2-1)3πD.8(√2-1)3π【答案】A【解析】由三视图可知该几何体是一个圆锥,其底面半径r=1,母线长l=3,所以其高h=√l 2-r 2=2√2.故该圆锥的体积V=π3×12×2√2=2√2π3.由题意可知,加工后的正方体是该圆锥的一个内接正方体,如图所示.正方体ABCD-EFGH 的底面在圆锥的底面内,下底面中心与圆锥底面的圆心重合,上底面中心在圆锥的高线上,设正方体的棱长为x.在轴截面SMN 中,由O 1G ∥ON可得,O 1GON=SO 1SO ,即√22x 1=√2-2√2,解得x=2√23.所以正方体的体积为V 1=(2√23)3=16√227.所以该工件的利用率为V1V =16√22722π3=89π.故选A.37.(2015·全国1·理T11文T11)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=( ) A.1 B.2 C.4D.8【答案】B【解析】由条件及几何体的三视图可知该几何体是由一个圆柱被过圆柱底面直径的平面所截剩下的半个圆柱及一个半球拼接而成的.其表面积由一个矩形的面积、两个半圆的面积、圆柱的侧面积的一半及一个球的表面积的一半组成.∴S 表=2r ×2r+2×12πr 2+πr ×2r+12×4πr 2=5πr 2+4r 2=16+20π, 解得r=2.38.(2015·北京·理T5)某三棱锥的三视图如图所示,则该三棱锥的表面积是( ) A.2+√5B.4+√5C.2+2√5D.5【答案】C【解析】作出三棱锥的直观图如图,在△ABC 中,作AB 边上的高CD,连接SD.在三棱锥S-ABC 中,SC ⊥底面ABC,SC=1,底面三角形ABC 是等腰三角形,AC=BC=√5,AB 边上的高CD=2,AD=BD=1,斜高SD=√5.所以S 表=S △ABC +S △SAC +S △SBC +S △SAB =12×2×2+12×1×√5+12×1×√5+12×2×√5=2+2√5. 39.(2015·陕西·理T5文T5)一个几何体的三视图如图所示,则该几何体的表面积为( ) A.3π B.4π C.2π+4 D.3π+4【答案】D【解析】由三视图可知,该几何体是一个半圆柱,圆柱的底面半径r=1,高h=2.所以几何体的侧面积S 1=C底·h=(π×1+2)×2=2π+4.几何体的底面积S 2=12π×12=12π.故该几何体的表面积为S=S 1+2S 2=2π+4+2×π2=3π+4.故选D.40.(2015·浙江·理T8)如图,已知△ABC,D 是AB 的中点,沿直线CD 将△ACD 翻折成△A'CD,所成二面角A'-CD-B 的平面角为α,则( ) A.∠A'DB ≤α B.∠A'DB ≥α C.∠A'CB ≤α D.∠A'CB ≥α【答案】B【解析】设∠ADC=θ,设AB=2,则由题意AD=BD=1. 在空间图形中,设A'B=t.在△A'BD 中, cos ∠A'DB=A 'D 2+DB 2-AB 22A 'D×DB =12+12-t 22×1×1=2-t 22. 在空间图形中,过A'作A'N ⊥DC,过B 作BM ⊥DC,垂足分别为N,M.过N 作NP MB,连接A'P,所以NP ⊥DC. 则∠A'NP 就是二面角A'-CD-B 的平面角, 所以∠A'NP=α.在Rt △A'ND 中,DN=A'Dcos ∠A'DC=cos θ,A'N=A'Dsin ∠A'DC=sin θ. 同理,BM=PN=sin θ,DM=cos θ.故BP=MN=2cos θ. 显然BP ⊥面A'NP,故BP ⊥A'P.在Rt △A'BP 中,A'P 2=A'B 2-BP 2=t 2-(2cos θ)2=t 2-4cos 2θ.在△A'NP 中,cos α=cos ∠A'NP=A 'N 2+NP 2-A 'P 22A 'N×NP=sin 2θ+sin 2θ-(t 2-4cos 2θ)=2+2cos 2θ-t 22=2-t 22+cos 2θ2=12cos ∠A'DB+cos 2θ2. 因为1sin 2θ≥1,cos 2θsin 2θ≥0,所以cos α≥cos∠A'DB (当θ=π2时取等号),因为α,∠A'DB ∈[0,π],而y=cos x 在[0,π]上为递减函数,所以α≤∠A'DB.故选B.41.(2015·全国2·理T9文T10)已知A,B 是球O 的球面上两点,∠AOB=90°,C 为该球面上的动点.若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为 ( ) A.36π B.64π C.144π D.256π 【答案】C【解析】因为∠AOB=90°,所以S △AOB =12R 2. 因为V O-ABC =V C-AOB ,而△AOB 面积为定值,所以三棱锥底面OAB 上的高最大时,其体积最大.因为高最大为半径R,所以V C-AOB =13×12R 2×R=36,解得R=6,故S 球=4πR 2=144π.42.(2015·安徽·理T5)已知m,n 是两条不同直线,α,β是两个不同平面,则下列命题正确的是( ) A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行...与β平行的直线...,则在α内不存在D.若m,n不平行...垂直于同一平面...,则m与n不可能【答案】D【解析】A选项α,β可能相交;B选项m,n可能相交,也可能异面;C选项若α与β相交,则在α内平行于它们交线的直线一定平行于β;由垂直于同一个平面的两条直线一定平行,可知D选项正确.43.(2015·浙江·文T4)设α,β是两个不同的平面,l,m是两条不同的直线,且l⊂α,m⊂β.( )A.若l⊥β,则α⊥βB.若α⊥β,则l⊥mC.若l∥β,则α∥βD.若α∥β,则l∥m【答案】A【解析】若l⊥β,又l⊂α,由面面垂直的判定定理,得α⊥β,故选项A正确;选项B,l⊥m或l∥m或l与m 相交或异面都有可能;选项C,α∥β或α与β相交都有可能;选项D,l∥m或l与m异面都有可能.44.(2015·广东·文T6)若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交【答案】D【解析】l1与l在平面α内,l2与l在平面β内,若l1,l2与l都不相交,则l1∥l,l2∥l,根据直线平行的传递性,则l1∥l2,与已知矛盾,故l至少与l1,l2中的一条相交.45.(2014·浙江·理T3)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )A.90 cm2B.129 cm2C.132 cm2D.138 cm2【答案】D【解析】由题干中的三视图可得原几何体如图所示.故该几何体的表面积S=2×4×6+2×3×4+3×6+3×3+3×4+3×5+2××3×4=138(cm2).故选D.46.(2014·陕西·文T5)将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )A.4πB.3πC.2πD.π【答案】C【解析】依题意,知所得几何体是一个圆柱,且其底面半径为1,母线长也为1,因此其侧面积为2π×1×1=2π,故选C.47.(2014·辽宁·理T4文T4)已知m,n表示两条不同直线,α表示平面.下列说法正确的是( )A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α【答案】B【解析】对A:m,n还可能异面、相交,故A不正确.对C:n还可能在平面α内,故C不正确.对D:n还可能在α内,故D不正确.对B:由线面垂直的定义可知正确.48.(2014·广东·理T7)在空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是( )A.l1⊥l4B.l1∥l4C.l1与l4既不垂直也不平行D.l1与l4的位置关系不确定【答案】D【解析】如图,在正方体ABCD-A1B1C1D1中,取l1为BC,l2为CC1,l3为C1D1.满足l1⊥l2,l2⊥l3.若取l4为A1D1,则有l1∥l4;若取l4为DD1,则有l1⊥l4.因此l1与l4的位置关系不确定,故选D.49.(2014·浙江·文T6)设m,n是两条不同的直线,α,β是两个不同的平面.( )A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α【答案】C【解析】当m⊥n,n∥α时,可能有m⊥α,但也有可能m∥α或m⊂α,故A选项错误;当m∥β,β⊥α时,可能有m⊥α,但也有可能m∥α或m⊂α,故选项B错误;当m⊥β,n⊥β,n⊥α时,必有α∥β,从而m⊥α,故选项C正确;在如图所示的正方体ABCD-A1B1C1D1中,取m为B1C1,n为CC1,β为平面ABCD,α为平面ADD1A1,这时满足m⊥n,n ⊥β,β⊥α,但m⊥α不成立,故选项D错误.50.(2014·陕西·理T5)已知底面边长为1,侧棱长为√2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )A.32π3B.4π C.2π D.4π3【答案】D【解析】依题意可知正四棱柱体对角线的长度等于球的直径,可设球半径R,则2R=√12+12+(√2)2=2,解得R=1,所以V=4π3R 3=4π3.51.(2014·大纲全国·理T8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A.81π4B.16πC.9πD.27π4【答案】A【解析】由图知,R 2=(4-R)2+2, ∴R 2=16-8R+R 2+2,∴R=94, ∴S 表=4πR 2=4π×8116=814π,选A.52.(2014·湖南·理T7文T8)一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( ) A.1 B.2 C.3 D.4【答案】B【解析】由三视图可得原石材为如右图所示的直三棱柱A 1B 1C 1-ABC,且AB=8,BC=6,BB 1=12.若要得到半径最大的球,则此球与平面A 1B 1BA,BCC 1B 1,ACC 1A 1相切,故此时球的半径与△ABC 内切圆的半径相等,故半径r=6+8-102=2.故选B. 53.(2014·全国1·理T12)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )A.6√2B.6C.4√2D.4【答案】B【解析】如图所示的正方体ABCD-A1B1C1D1的棱长为4.取B1B的中点G,即三棱锥G-CC1D1为满足要求的几何体,其中最长棱为D1G,D1G=√(4√2)2+22=6.54.(2014·全国1·文T8)如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )A.三棱锥B.三棱柱C.四棱锥D.四棱柱【答案】B【解析】由所给三视图可知该几何体是一个三棱柱(如图).55.(2014·北京·理T7)在空间直角坐标系O-xyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1, √2).若S1,S2,S3分别是三棱锥D-ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( )A.S1=S2=S3B.S2=S1且S2≠S3C.S3=S1且S3≠S2D.S3=S2且S3≠S1【答案】D【解析】三棱锥的各顶点在xOy 坐标平面上的正投影分别为A 1(2,0,0),B 1(2,2,0),C 1(0,2,0),D 1(1,1,0).显然D 1点为A 1C 1的中点,如图(1),正投影为Rt △A 1B 1C 1,其面积S 1=12×2×2=2.三棱锥的各顶点在yOz 坐标平面上的正投影分别为A 2(0,0,0),B 2(0,2,0),C 2(0,2,0),D 2(0,1,√2).显然B 2,C 2重合,如图(2),正投影为△A 2B 2D 2,其面积S 2=12×2×√2=√2.三棱锥的各顶点在zOx 坐标平面上的正投影分别为A 3(2,0,0),B 3(2,0,0),C 3(0,0,0),D 3(1,0,√2),由图(3)可知,正投影为△A 3D 3C 3,其面积S 3=12×2×√2=√2. 综上,S 2=S 3,S 3≠S 1.故选D.56.(2014·大纲全国·理T11)已知二面角α-l-β为60°,AB ⊂α,AB ⊥l,A 为垂足,CD ⊂β,C ∈l,∠ACD=135°,则异面直线AB 与CD 所成角的余弦值为( ) A.14B.√24C.√34D.12【答案】B【解析】如图,在平面α内过C 作CE ∥AB,则∠ECD 为异面直线AB 与CD 所成的角或其补角,不妨取CE=1,过E 作EO ⊥β于O. 在平面β内过O 作OH ⊥CD 于H, 连EH,则EH ⊥CD.因为AB ∥CE,AB ⊥l,所以CE ⊥l. 又因为EO ⊥平面β,所以CO ⊥l.故∠ECO 为二面角α-l-β的平面角,所以∠ECO=60°. 而∠ACD=135°,CO ⊥l,所以∠OCH=45°.在Rt △ECO 中,CO=CE ·cos ∠ECO=1·cos 60°=12.在Rt △COH 中,CH=CO ·cos ∠OCH=12·sin 45°=√24. 在Rt △ECH 中,cos ∠ECH=CHCE=√241=√24.所以异面直线AB 与CD 所成角的余弦值为√24.故选B.57.(2014·大纲全国·文T4)已知正四面体ABCD 中,E 是AB 的中点,则异面直线CE 与BD 所成角的余弦值为( ) A.16B.√36C.13D.√33【答案】B【解析】如图所示,取AD 的中点F,连EF,CF,则EF ∥BD,∴异面直线CE 与BD 所成的角即为CE 与EF 所成的角∠CEF.由题知,△ABC,△ADC 为正三角形,设AB=2,则 CE=CF=√3,EF=12BD=1.∴在△CEF 中,由余弦定理, 得cos ∠CEF=CE 2+EF 2-CF 22CE ·EF=√3)22√3)22×√3×1=√36.故选B.58.(2014·全国2·理T6文T6)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727 B.59C.1027D.13【答案】C【解析】由零件的三视图可知,该几何体为两个圆柱组合而成,如图所示. 切削掉部分的体积V 1=π×32×6-π×22×4-π×32×2=20π(cm 3), 原来毛坯体积V 2=π×32×6=54π(cm 3). 故所求比值为V1V 2=20π54π=1027.59.(2014·全国2·文T7)正三棱柱ABC-A 1B 1C 1的底面边长为2,侧棱长为√3,D 为BC 中点,则三棱锥A-B 1DC 1的体积为( )A.3B.32C.1D.√32【答案】C【解析】∵D 是等边△ABC 的边BC 的中点,∴AD ⊥BC. 又ABC-A 1B 1C 1为正三棱柱, ∴AD ⊥平面BB 1C 1C. 又四边形BB 1C 1C 为矩形,∴S △DB 1C 1=12S 四边形BB 1C 1C =12×2×√3=√3. 又AD=2×√32=√3,∴V A -B 1DC 1=13S △B 1DC 1·AD=13×√3×√3=1.60.(2013·全国1·理T8文T11)某几何体的三视图如图所示,则该几何体的体积为( )A.16+8πB.8+8πC.16+16πD.8+16π【答案】A【解析】该几何体为一个半圆柱与一个长方体组成的一个组合体. V 半圆柱= π×22×4=8π,V 长方体=4×2×2=16. 所以所求体积为16+8π.故选A.61.(2013·浙江·文T5)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( ) A.108 cm 3B.100 cm 3C.92 cm 3D.84 cm 3【答案】B【解析】由三视图可知,该几何体是如图所示长方体去掉一个三棱锥,故几何体的体积是6×3×6-13×12×3×42=100(cm 3).故选B.62.(2013·山东·理T4)已知三棱柱ABC-A 1B 1C 1的侧棱与底面垂直,体积为9,底面是边长为√3的正三角形.若P 为底面A 1B 1C 1的中心,则PA 与平面ABC 所成角的大小为( ) A.5π12B.π3C.π4D.π6【答案】B【解析】如图所示,由棱柱体积为94,底面正三角形的边长为√3,可求得棱柱的高为√3.设P 在平面ABC 上射影为O,则可求得AO 长为1,故AP 长为√12+(√3)2=2.故∠PAO=π3,即PA 与平面ABC 所成的角为π3.63.(2013·全国2·理T7文T9)一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为 ( )【答案】A【解析】该四面体在空间直角坐标系O-xyz 中的图象如图所示.则它在平面zOx 上的投影,即正视图为.64.(2013·湖南·理T7)已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于( ) A.1 B.√2 C.√2-12 D.√2+12【答案】C【解析】当俯视图是面积为1的正方形时,其正视图的最小面积等于一个面的面积1,最大面积等于对角面的面积√2.故正视图面积S 的取值范围为1≤S≤√2. 因为√2-12<1,故选C.65.(2013·全国1·理T6)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为( ) A.500π3 cm 3B.866π3 cm 3C.1372π3 cm 3D.2048π3cm 3【答案】A【解析】设球半径为R,由题可知R,R-2,正方体棱长的一半可构成直角三角形,即△OBA 为直角三角形,如图. BC=2,BA=4,OB=R-2,OA=R, 由R 2=(R-2)2+42,得R=5,所以球的体积为4π3×53=5003π(cm 3),故选A.66.(2013·辽宁·理T10)已知直三棱柱ABC-A 1B 1C 1的6个顶点都在球O 的球面上.若AB=3,AC=4,AB ⊥AC,AA 1=12,则球O 的半径为( ) A.3√172 B.2√10C.132D.3√10【答案】C。
(北京卷)十年真题(2010_2019)高考数学真题分类汇编专题01集合文(含解析)

专题01集合历年考题细目表历年高考真题汇编1.【2019年北京文科01】已知集合A={x|﹣1<x<2},B={x|x>1},则A∪B=()A.(﹣1,1)B.(1,2)C.(﹣1,+∞)D.(1,+∞)【解答】解:∵A={x|﹣1<x<2},B={x|x>1},∴A∪B={x|﹣1<x<2}∪{x|x>1}=(﹣1,+∞).故选:C.2.【2018年北京文科01】已知集合A={x||x|<2},B={﹣2,0,1,2},则A∩B=()A.{0,1} B.{﹣1,0,1} C.{﹣2,0,1,2} D.{﹣1,0,1,2}【解答】解:A={x||x|<2}={x|﹣2<x<2},B={﹣2,0,1,2},则A∩B={0,1},故选:A.3.【2018年北京文科08】设集合A={(x,y)|x﹣y≥1,ax+y>4,x﹣ay≤2},则()A.对任意实数a,(2,1)∈AB.对任意实数a,(2,1)∉AC.当且仅当a<0时,(2,1)∉AD.当且仅当a时,(2,1)∉A【解答】解:当a=﹣1时,集合A={(x,y)|x﹣y≥1,ax+y>4,x﹣ay≤2}={(x,y)|x﹣y≥1,﹣x+y>4,x+y≤2},显然(2,1)不满足,﹣x+y>4,x+y≤2,所以A不正确;当a=4,集合A={(x,y)|x﹣y≥1,ax+y>4,x﹣ay≤2}={(x,y)|x﹣y≥1,4x+y>4,x﹣4y≤2},显然(2,1)在可行域内,满足不等式,所以B不正确;当a=1,集合A={(x,y)|x﹣y≥1,ax+y>4,x﹣ay≤2}={(x,y)|x﹣y≥1,x+y>4,x﹣y≤2},显然(2,1)∉A,所以当且仅当a<0错误,所以C不正确;故选:D.4.【2017年北京文科01】已知全集U=R,集合A={x|x<﹣2或x>2},则∁U A=()A.(﹣2,2)B.(﹣∞,﹣2)∪(2,+∞)C.[﹣2,2] D.(﹣∞,﹣2]∪[2,+∞)【解答】解:∵集合A={x|x<﹣2或x>2}=(﹣∞,﹣2)∪(2,+∞),全集U=R,∴∁U A=[﹣2,2],故选:C.5.【2016年北京文科01】已知集合A={x|2<x<4},B={x|x<3或x>5},则A∩B=()A.{x|2<x<5} B.{x|x<4或x>5} C.{x|2<x<3} D.{x|x<2或x>5}【解答】解:∵集合A={x|2<x<4},B={x|x<3或x>5},∴A∩B={x|2<x<3}.故选:C.6.【2015年北京文科01】若集合A={x|﹣5<x<2},B={x|﹣3<x<3},则A∩B=()A.{x|﹣3<x<2} B.{x|﹣5<x<2} C.{x|﹣3<x<3} D.{x|﹣5<x<3}【解答】解:集合A={x|﹣5<x<2},B={x|﹣3<x<3},则A∩B={x|﹣3<x<2}.故选:A.7.【2014年北京文科01】若集合A={0,1,2,4},B={1,2,3},则A∩B=()A.{0,1,2,3,4} B.{0,4} C.{1,2} D.{3}【解答】解:∵A={0,1,2,4},B={1,2,3},∴A∩B={0,1,2,4}∩{1,2,3}={1,2}.故选:C.8.【2013年北京文科01】已知集合A={﹣1,0,1},B={x|﹣1≤x<1},则A∩B=()A.{0} B.{﹣1,0} C.{0,1} D.{﹣1,0,1}【解答】解:∵A={﹣1,0,1},B={x|﹣1≤x<1},∴A∩B={﹣1,0}.故选:B.9.【2012年北京文科01】已知集合A={x∈R|3x+2>0},B={x∈R|(x+1)(x﹣3)>0},则A∩B=()A.(﹣∞,﹣1)B.(﹣1,)C.(,3)D.(3,+∞)【解答】解:因为B={x∈R|(x+1)(x﹣3)>0}={x|x<﹣1或x>3},又集合A={x∈R|3x+2>0}={x|x},所以A∩B={x|x}∩{x|x<﹣1或x>3}={x|x>3},故选:D.10.【2011年北京文科01】已知全集U=R,集合P={x|x2≤1},那么∁U P=()A.(﹣∞,﹣1] B.[1,+∞)C.[﹣1,1] D.(﹣∞,﹣1)∪(1,+∞)【解答】解:由集合P中的不等式x2≤1,解得﹣1≤x≤1,所以集合P=[﹣1,1],由全集U=R,得到∁U P=(﹣∞,1)∪(1,+∞).故选:D.11.【2010年北京文科01】集合P={x∈Z|0≤x<3},M={x∈Z|x2<9},则P∩M=()A.{1,2} B.{0,1,2} C.{x|0≤x<3} D.{x|0≤x≤3}【解答】解:∵集合P={x∈Z|0≤x<3},∴P={0,1,2},∵M={x∈Z|x2<9},。
十年真题(2010_2019)高考数学真题分类汇编专题02复数理(含解析)

专题02复数历年考题细目表题型年份考点试题位置单选题2019 数系的扩充与复数的定义2019年新课标1理科02单选题2018 复数的四则运算2018年新课标1理科01单选题2017 数系的扩充与复数的定义2017年新课标1理科03单选题2016 复数的四则运算2016年新课标1理科02单选题2015 复数的四则运算2015年新课标1理科01单选题2014 复数的四则运算2014年新课标1理科02单选题2013 复数的四则运算2013年新课标1理科02单选题2012 数系的扩充与复数的定义2012年新课标1理科03单选题2011 复数的四则运算2011年新课标1理科01单选题2010 复数的四则运算2010年新课标1理科02历年高考真题汇编1.【2019年新课标1理科02】设复数z满足|z﹣i|=1,z在复平面内对应的点为(x,y),则()A.(x+1)2+y2=1 B.(x﹣1)2+y2=1C.x2+(y﹣1)2=1 D.x2+(y+1)2=1【解答】解:∵z在复平面内对应的点为(x,y),∴z=x+yi,∴z﹣i=x+(y﹣1)i,∴|z﹣i|,∴x2+(y﹣1)2=1,故选:C.2.【2018年新课标1理科01】设z2i,则|z|=()A.0 B.C.1 D.【解答】解:z2i2i=﹣i+2i=i,则|z|=1.3.【2017年新课标1理科03】设有下面四个命题p1:若复数z满足∈R,则z∈R;p2:若复数z满足z2∈R,则z∈R;p 3:若复数z1,z2满足z1z2∈R,则z1;p 4:若复数z∈R,则∈R.其中的真命题为()A.p1,p3B.p1,p4C.p2,p3D.p2,p4【解答】解:若复数z满足∈R,则z∈R,故命题p1为真命题;p2:复数z=i满足z2=﹣1∈R,则z∉R,故命题p2为假命题;p3:若复数z1=i,z2=2i满足z1z2∈R,但z1,故命题p3为假命题;p 4:若复数z∈R,则z∈R,故命题p4为真命题.故选:B.4.【2016年新课标1理科02】设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=()A.1 B.C.D.2【解答】解:∵(1+i)x=1+yi,∴x+xi=1+yi,即,解得,即|x+yi|=|1+i|,故选:B.5.【2015年新课标1理科01】设复数z满足i,则|z|=()A.1 B.C.D.2【解答】解:∵复数z满足i,∴1+z=i﹣zi,∴z(1+i)=i﹣1,∴z i,∴|z|=1,6.【2014年新课标1理科02】()A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i【解答】解:(1+i)=﹣1﹣i,故选:D.7.【2013年新课标1理科02】若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为()A.﹣4 B.C.4 D.【解答】解:∵复数z满足(3﹣4i)z=|4+3i|,∴z i,故z的虚部等于,故选:D.8.【2012年新课标1理科03】下面是关于复数z的四个命题:其中的真命题为(),p1:|z|=2,p2:z2=2i,p3:z的共轭复数为1+i,p4:z的虚部为﹣1.A.p2,p3B.p1,p2C.p2,p4D.p3,p4【解答】解:∵z1﹣i,∴,,p3:z的共轭复数为﹣1+i,p4:z的虚部为﹣1,故选:C.9.【2011年新课标1理科01】复数的共轭复数是()A.B.C.﹣i D.i【解答】解:复数i,它的共轭复数为:﹣i.故选:C.10.【2010年新课标1理科02】已知复数,是z的共轭复数,则()A.B.C.1 D.2【解答】解:由可得.另解:故选:A.考题分析与复习建议本专题考查的知识点为:复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算,与向量结合考查复数及其加法、减法的几何意义等,历年考题主要以选择题题型出现,重点考查的知识点为复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算,重点考查复数的除法运算等,预测明年本考点题目会比较稳定,备考方向以知识点复数的基本概念(复数的实部、虚部、共轭复数、复数的模等),复数相等的充要条件,考查复数的代数形式的四则运算为重点较佳.最新高考模拟试题1.复数52iz=-在复平面上的对应点位于()A.第一象限B.第二象限C.第三象限D.第四象限【答案】A【解析】()()()52i 52i 2i 2i 2i z +===+--+,在复平面上的对应点为()2,1,位于第一象限. 故选A. 2.设i z a b =+(a ,b ∈R ,i 是虚数单位),且22i z =-,则有( ) A .1a b +=- B .1a b -=- C .0a b -= D .0a b +=【答案】D 【解析】因为2222()()22z a bi a b abi i =+=-+=-,所以220a b -=,22ab =-,解得11a b =⎧⎨=-⎩或11a b =-⎧⎨=⎩,所以0a b +=,故选D.3.若复数1i1ia z +=+为纯虚数,则实数a 的值为( ) A .1 B .1-C .0D .2【答案】B 【解析】()()()()()11111i 1i 112ai i a a ia z i i +-++-+===++- 故10,10a a +=-≠ ,解1a =- 故选:B4.复数i (1+i )的虚部为( )A B .1C .0D .1-【答案】B 【解析】∵i (1+i )=-1+i , ∴i (1+i )的虚部为1. 故选:B .5.已知复数11z i =-+,复数2z 满足122z z =-,则2z = ( )A .2BCD .10【答案】B 【解析】 由题得222(1)2(1)11(1)(1)2i i z i i i i -------====+-+-+--,所以2z 故选:B6.已知复数312i z i=+,则复数z 的实部为( )A .25-B .25i -C .15-D .15i -【答案】A 【解析】解:∵3(12)2112(12)(12)55i i i z i i i i --===--++-, ∴复数z 的实部为25-. 故选A . 7.复数122ii-=+( ) A .1i - B .i -C .iD .1i +【答案】B 【解析】12(12)(2)2422(2)(2)5i i i i i i i i i ------===-++-. 故选B8.已知i 为虚数单位,复数z 满足:()z 12i i +=-,则在复平面上复数z 对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】D 【解析】 因为2(2)(1)131312222i i i i z i i ----====-+,所以复平面上复数z 对应的点为13(,)22-,位于第四象限, 故选D .9.设复数z a i =+,z 是其共轭复数,若3455z i z =+,则实数a =( ) A .4 B .3C .2D .1【答案】C 【解析】 解: z a i =+Qz a i ∴=-343443++2555555z a a i a i i a z ⎛⎫∴=+⇒+=-⇒= ⎪⎝⎭10.已知i 是虚数单位,复数z 满足2(1)1i i z-=+,则z =( )A B .2 C .1D 【答案】A 【解析】22(1)(1)22(1)1(1)111(1)(1)i i i i i i z i i i z i i i i ----⋅-=+⇒====--=--+++⋅-,所以1z i =--==A.11.复数()()21z i i =+-,其中i 为虚数单位,则z 的实部是( ) A .-1 B .1 C .2 D .3【答案】D 【解析】解:∴()()212213z i i i i i =+-=-++=-, ∴z 的实部是3 故选:D .12.已知复数(1)1z i i -=+,则复数z =( ) A .2i +B .2i -C .iD .i -【解析】由题意,复数(1)1z i i -=+,则()()()()11121112i i i iz i i i i +++====--+,故选C. 13.已知i 为虚数单位,若1(,)1a bi a b R i=+∈-,则b a =( ) A .1 BC2D .2【答案】C 【解析】 i 为虚数单位,若1(,)1a bi a b R i =+∈-,1112i a bi i +==+- 根据复数相等得到1212a b ⎧=⎪⎪⎨⎪=⎪⎩.121()22b a ==故答案为:C.14.已知复数z 满足2(1i)(3i)z +=+,则||z =( ) ABC.D .8【答案】C 【解析】∵2(1)(3)z i i +=+,∴2(3)86(86)(1)(43)(1)711(1)(1)i i i i z i i i i i i i +++-====+-=-+++-,∴||z === 故选C .15.已知i 是虚数单位,则复数11i i -+在复平面上所对应的点的坐标为( ) A .()0,1B .()1,0-C .()1,0D .()0,1-【解析】 ∵()()()()111111i i i i i i i ---==++-,∴该复数在复平面上对应的点的坐标为()0,1. 故选A.16.若复数z 满足(1i)|1|z +=+,则在复平面内z 的共轭复数对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】A 【解析】 由题得22(1)1(1)(1)(1i)i z i i i -===-++-, 所以1z i =+,所以在复平面内z 的共轭复数对应的点为(1,1),在第一象限. 故选:A17.已知复数z 满足12iz i =+,则z 的虚部是( ) A .1- B .i -C .2D .2i【答案】A 【解析】 因为12iz i =+所以221222i i i z i i i++===-所以虚部为1- 所以选A 18.已知31iz i-=-(其中i 为虚数单位),则z 的虚部为( ) A .i - B .1-C .1D .2【答案】B 【解析】因为3(3)(1)4221(1)(1)2i i i iz i i i i --++====+--+, 所以2z i =-,故z 的虚部为1-,故选B.19.复数2(1)41i z i -+=+的虚部为( )A .1-B .3-C .1D .2【答案】B 【解析】()()2421(1)44213112i i i i z i i i ---+-====-++ 所以z 的虚部为3- 故选B 项.20.已知复数()11z ai a R =+∈,212z i =+(i 为虚数单位),若12z z 为纯虚数,则a =( ) A .2- B .2C .12-D .12【答案】C 【解析】∵()12112z ai a R z i =+∈=+,,∴121(1)(12)12212(12)(12)55z ai ai i a a i z i i i ++-+-===+++-, ∵12z z 为纯虚数, ∴12020a a +=⎧⎨-≠⎩,解得12a =-.故选:C . 21.设复数z 满足2ii z+=,则z =( ) A .1BC .3D .5【答案】B【解析】2ii z +=Q ,221iz i i +∴==+22112ii i =+=-,z ∴== B.22.已知复数1iz i =-,则z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限【答案】A【解析】∵ ()()()11111122i i iz i i i i +===-+--+,∴ 12z i =+,∴z 在复平面内对应的点的坐标为12⎫⎪⎪⎝⎭,位于第一象限. 故选:A .23.复数z 满足(1)2z i i -=,则复数z =( )A .1i -B .12i +C .1i +D .1i --【答案】D【解析】 由题意得:()()()2121111i i iz i i i i +===-+--+ 1z i ∴=--本题正确选项:D24.若复数2(1)z m m m i =+++是纯虚数,其中m 是实数,则1z =( )A .iB .i -C .2iD .2i -【答案】B【解析】复数z =m (m +1)+(m +1)i 是纯虚数,故m (m +1)=0且(m +1)≠0,解得m =0,故z =i ,故111iz i i i ⋅===-⋅i .故选:B .25.设i 为虚数单位,则复数22iz i -=+的共扼复数z =( )A .3455i + B .3455i -C .3455i -+ D .3455i --【答案】A【解析】 解:22i(2i)34i 2i (2i)(2i)55z --===-++-Q ,3455z i ∴=+故选:A .26.已知复数1z 、2z在复平面内对应的点关于虚轴对称,11z =,则12z z =( )A .2 BCD .1【答案】D【解析】由题意,复数1z 、2z在复平面内对应的点关于虚轴对称,11z =,则21z =-,所以12212z z ====,故选D.27.已知复数z 1=1+2i ,z 2=l ﹣i ,则12z z =( )A .13i 22--B .13i 22-+ C .13i 22- D .13i 22+【答案】B【解析】∵1212,1z i z i =+=-, ∴1212(12)(1)131(1)(1)22z i i i i z i i i +++===-+--+.故选:B .28.在复平面内,复数(2i)z -对应的点位于第二象限,则复数z 可取( )A .2B .-1C .iD .2i + 【答案】B【解析】不妨设(),z a bi a b R =+∈,则()()()()()2222i z i a bi a b b a i -=-+=++-,结合题意可知:20,20a b b a +<->,逐一考查所给的选项:对于选项A :24,22a b b a +=-=-,不合题意;对于选项B :22,21a b b a +=--=,符合题意;对于选项C :21,22a b b a +=-=,不合题意;对于选项D :25,20a b b a +=-=,不合题意;故选:B .29.已知i 为虚数单位,则复数3(1)i z i i +=-的虚部为( ) A .1B .2C .1-D .2- 【答案】C【解析】 因为3(3)(1)122(1)2i i i i i i i i i++++===--,所以z 的虚部为1-. 30.已知复数(i)(1i)z a =+-(i 为虚数单位)在复平面内对应的点在直线2y x =上,则实数a 的值为( )A .0B .1-C .1D .13- 【答案】D【解析】因为(i)(1i)1(1)z a a a i =+-=++-,对应的点为(1,1)a a +-,因为点在直线2y x =上,所以12(1)a a -=+,解得13a =-. 故选D.。
高考数学(理)十年真题(2010-2019)专题10 立体几何与空间向量解答题(新课标Ⅰ卷)(解析版)

专题10立体几何与空间向量解答题历年考题细目表历年高考真题汇编1.【2019年新课标1理科18】如图,直四棱柱ABCD﹣A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求二面角A﹣MA1﹣N的正弦值.【解答】(1)证明:如图,过N作NH⊥AD,则NH∥AA1,且,又MB∥AA1,MB,∴四边形NMBH为平行四边形,则NM∥BH,由NH∥AA1,N为A1D中点,得H为AD中点,而E为BC中点,∴BE∥DH,BE=DH,则四边形BEDH为平行四边形,则BH∥DE,∴NM∥DE,∵NM⊄平面C1DE,DE⊂平面C1DE,∴MN∥平面C1DE;(2)解:以D为坐标原点,以垂直于DC得直线为x轴,以DC所在直线为y轴,以DD1所在直线为z轴建立空间直角坐标系,则N(,,2),M(,1,2),A1(,﹣1,4),,,设平面A1MN的一个法向量为,由,取x,得,又平面MAA1的一个法向量为,∴cos.∴二面角A﹣MA1﹣N的正弦值为.2.【2018年新课标1理科18】如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.【解答】(1)证明:由题意,点E、F分别是AD、BC的中点,则,,由于四边形ABCD为正方形,所以EF⊥BC.由于PF⊥BF,EF∩PF=F,则BF⊥平面PEF.又因为BF⊂平面ABFD,所以:平面PEF⊥平面ABFD.(2)在平面PEF中,过P作PH⊥EF于点H,连接DH,由于EF为面ABCD和面PEF的交线,PH⊥EF,则PH⊥面ABFD,故PH⊥DH.在三棱锥P﹣DEF中,可以利用等体积法求PH,因为DE∥BF且PF⊥BF,所以PF⊥DE,又因为△PDF≌△CDF,所以∠FPD=∠FCD=90°,所以PF⊥PD,由于DE∩PD=D,则PF⊥平面PDE,故V F﹣PDE,因为BF∥DA且BF⊥面PEF,所以DA⊥面PEF,所以DE⊥EP.设正方形边长为2a,则PD=2a,DE=a在△PDE中,,所以,故V F﹣PDE,又因为,所以PH,所以在△PHD中,sin∠PDH,即∠PDH为DP与平面ABFD所成角的正弦值为:.3.【2017年新课标1理科18】如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP =90°.(1)证明:平面P AB⊥平面P AD;(2)若P A=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.【解答】(1)证明:∵∠BAP=∠CDP=90°,∴P A⊥AB,PD⊥CD,∵AB∥CD,∴AB⊥PD,又∵P A∩PD=P,且P A⊂平面P AD,PD⊂平面P AD,∴AB⊥平面P AD,又AB⊂平面P AB,∴平面P AB⊥平面P AD;(2)解:∵AB∥CD,AB=CD,∴四边形ABCD为平行四边形,由(1)知AB⊥平面P AD,∴AB⊥AD,则四边形ABCD为矩形,在△APD中,由P A=PD,∠APD=90°,可得△P AD为等腰直角三角形,设P A=AB=2a,则AD.取AD中点O,BC中点E,连接PO、OE,以O为坐标原点,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系,则:D(),B(),P(0,0,),C().,,.设平面PBC的一个法向量为,由,得,取y=1,得.∵AB⊥平面P AD,AD⊂平面P AD,∴AB⊥PD,又PD⊥P A,P A∩AB=A,∴PD⊥平面P AB,则为平面P AB的一个法向量,.∴cos.由图可知,二面角A﹣PB﹣C为钝角,∴二面角A﹣PB﹣C的余弦值为.4.【2016年新课标1理科18】如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF 为正方形,AF=2FD,∠AFD=90°,且二面角D﹣AF﹣E与二面角C﹣BE﹣F都是60°.(Ⅰ)证明平面ABEF⊥平面EFDC;(Ⅱ)求二面角E﹣BC﹣A的余弦值.【解答】(Ⅰ)证明:∵ABEF为正方形,∴AF⊥EF.∵∠AFD=90°,∴AF⊥DF,∵DF∩EF=F,∴AF⊥平面EFDC,∵AF⊂平面ABEF,∴平面ABEF⊥平面EFDC;(Ⅱ)解:由AF⊥DF,AF⊥EF,可得∠DFE为二面角D﹣AF﹣E的平面角;由ABEF为正方形,AF⊥平面EFDC,∵BE⊥EF,∴BE⊥平面EFDC即有CE⊥BE,可得∠CEF为二面角C﹣BE﹣F的平面角.可得∠DFE=∠CEF=60°.∵AB∥EF,AB⊄平面EFDC,EF⊂平面EFDC,∴AB∥平面EFDC,∵平面EFDC∩平面ABCD=CD,AB⊂平面ABCD,∴AB∥CD,∴CD∥EF,∴四边形EFDC为等腰梯形.以E为原点,建立如图所示的坐标系,设FD=a,则E(0,0,0),B(0,2a,0),C(,0,a),A(2a,2a,0),∴(0,2a,0),(,﹣2a,a),(﹣2a,0,0)设平面BEC的法向量为(x1,y1,z1),则,则,取(,0,﹣1).设平面ABC的法向量为(x2,y2,z2),则,则,取(0,,4).设二面角E﹣BC﹣A的大小为θ,则cosθ,则二面角E﹣BC﹣A的余弦值为.5.【2015年新课标1理科18】如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.(Ⅰ)证明:平面AEC⊥平面AFC(Ⅱ)求直线AE与直线CF所成角的余弦值.【解答】解:(Ⅰ)连接BD,设BD∩AC=G,连接EG、EF、FG,在菱形ABCD中,不妨设BG=1,由∠ABC=120°,可得AG=GC,BE⊥平面ABCD,AB=BC=2,可知AE=EC,又AE⊥EC,所以EG,且EG⊥AC,在直角△EBG中,可得BE,故DF,在直角三角形FDG中,可得FG,在直角梯形BDFE中,由BD=2,BE,FD,可得EF,从而EG2+FG2=EF2,则EG⊥FG,(或由tan∠EGB•tan∠FGD••1,可得∠EGB+∠FGD=90°,则EG⊥FG)AC∩FG=G,可得EG⊥平面AFC,由EG⊂平面AEC,所以平面AEC⊥平面AFC;(Ⅱ)如图,以G为坐标原点,分别以GB,GC为x轴,y轴,|GB|为单位长度,建立空间直角坐标系G﹣xyz,由(Ⅰ)可得A(0,,0),E(1,0,),F(﹣1,0,),C(0,,0),即有(1,,),(﹣1,,),故cos,.则有直线AE与直线CF所成角的余弦值为.6.【2014年新课标1理科19】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB ⊥B1C.(Ⅰ)证明:AC=AB1;(Ⅱ)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值.【解答】解:(1)连结BC1,交B1C于点O,连结AO,∵侧面BB1C1C为菱形,∴BC1⊥B1C,且O为BC1和B1C的中点,又∵AB⊥B1C,∴B1C⊥平面ABO,∵AO⊂平面ABO,∴B1C⊥AO,又B10=CO,∴AC=AB1,(2)∵AC⊥AB1,且O为B1C的中点,∴AO=CO,又∵AB=BC,∴△BOA≌△BOC,∴OA⊥OB,∴OA,OB,OB1两两垂直,以O为坐标原点,的方向为x轴的正方向,||为单位长度,的方向为y轴的正方向,的方向为z轴的正方向建立空间直角坐标系,∵∠CBB1=60°,∴△CBB1为正三角形,又AB=BC,∴A(0,0,),B(1,0,0,),B1(0,,0),C(0,,0)∴(0,,),(1,0,),(﹣1,,0),设向量(x,y,z)是平面AA1B1的法向量,则,可取(1,,),同理可得平面A1B1C1的一个法向量(1,,),∴cos,,∴二面角A﹣A1B1﹣C1的余弦值为7.【2013年新课标1理科18】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(Ⅰ)证明AB⊥A1C;(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C与平面BB1C1C所成角的正弦值.【解答】解:(Ⅰ)取AB的中点O,连接OC,OA1,A1B,因为CA=CB,所以OC⊥AB,由于AB=AA1,∠BAA1=60°,所以△AA1B为等边三角形,所以OA1⊥AB,又因为OC∩OA1=O,所以AB⊥平面OA1C,又A1C⊂平面OA1C,故AB⊥A1C;(Ⅱ)由(Ⅰ)知OC⊥AB,OA1⊥AB,又平面ABC⊥平面AA1B1B,交线为AB,所以OC⊥平面AA1B1B,故OA,OA1,OC两两垂直.以O为坐标原点,的方向为x轴的正向,||为单位长,建立如图所示的坐标系,可得A(1,0,0),A1(0,,0),C(0,0,),B(﹣1,0,0),则(1,0,),(﹣1,,0),(0,,),设(x,y,z)为平面BB1C1C的法向量,则,即,可取y=1,可得(,1,﹣1),故cos,,又因为直线与法向量的余弦值的绝对值等于直线与平面的正弦值,故直线A1C与平面BB1C1C所成角的正弦值为:.8.【2012年新课标1理科19】如图,直三棱柱ABC﹣A1B1C1中,AC=BC AA1,D是棱AA1的中点,DC1⊥BD(1)证明:DC1⊥BC;(2)求二面角A1﹣BD﹣C1的大小.【解答】(1)证明:在Rt△DAC中,AD=AC,∴∠ADC=45°同理:∠A1DC1=45°,∴∠CDC1=90°∴DC1⊥DC,DC1⊥BD∵DC∩BD=D∴DC1⊥面BCD∵BC⊂面BCD∴DC1⊥BC(2)解:∵DC1⊥BC,CC1⊥BC,DC1∩CC1=C1,∴BC⊥面ACC1A1,∵AC⊂面ACC1A1,∴BC⊥AC取A1B1的中点O,过点O作OH⊥BD于点H,连接C1O,OH∵A1C1=B1C1,∴C1O⊥A1B1,∵面A1B1C1⊥面A1BD,面A1B1C1∩面A1BD=A1B1,∴C1O⊥面A1BD而BD⊂面A1BD∴BD⊥C1O,∵OH⊥BD,C1O∩OH=O,∴BD⊥面C1OH∴C1H⊥BD,∴点H与点D重合且∠C1DO是二面角A1﹣BD﹣C1的平面角设AC=a,则,,∴sin∠C1DO∴∠C1DO=30°即二面角A1﹣BD﹣C1的大小为30°9.【2011年新课标1理科18】如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.(Ⅰ)证明:P A⊥BD;(Ⅱ)若PD=AD,求二面角A﹣PB﹣C的余弦值.【解答】(Ⅰ)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD,从而BD2+AD2=AB2,故BD⊥AD又PD⊥底面ABCD,可得BD⊥PD所以BD⊥平面P AD.故P A⊥BD(Ⅱ)如图,以D为坐标原点,AD的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz,则A(1,0,0),B(0,,0),C(﹣1,,0),P(0,0,1).(﹣1,,0),(0,,﹣1),(﹣1,0,0),设平面P AB的法向量为(x,y,z),则即,因此可取(,1,)设平面PBC的法向量为(x,y,z),则,即:可取(0,1,),cos故二面角A﹣PB﹣C的余弦值为:.10.【2010年新课标1理科18】如图,已知四棱锥P﹣ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD中点(Ⅰ)证明:PE⊥BC(Ⅱ)若∠APB=∠ADB=60°,求直线P A与平面PEH所成角的正弦值.【解答】解:以H为原点,HA,HB,HP分别为x,y,z轴,线段HA的长为单位长,建立空间直角坐标系如图,则A(1,0,0),B(0,1,0)(Ⅰ)设C(m,0,0),P(0,0,n)(m<0,n>0)则.可得.因为所以PE⊥BC.(Ⅱ)由已知条件可得m ,n =1,故C (),设(x ,y ,z )为平面PEH 的法向量则即因此可以取,由,可得所以直线P A 与平面PEH 所成角的正弦值为.考题分析与复习建议本专题考查的知识点为:直线、平面平行、垂直的判定与性质,空间向量及其运算,立体几何中的向量方法(证明平行与垂直、求空间角和距离)等.历年考题主要以解答题题型出现,重点考查的知识点为:直线、平面平行、垂直的判定与性质,空间向量及其运算,立体几何中的向量方法(证明平行与垂直、求空间角和距离)等.预测明年本考点题目会比较稳定,备考方向以知识点直线、平面平行、垂直的判定与性质,空间向量及其运算,立体几何中的向量方法(证明平行与垂直、求空间角和距离)等为重点较佳.最新高考模拟试题1.如图,在三棱柱111ABC A B C -中,侧面11ABB A 是菱形,160BAA ∠=︒,E 是棱1BB 的中点,CA CB =,F 在线段AC 上,且2AF FC =.(1)证明:1//CB 面1A EF ;(2)若CA CB ⊥,面CAB ⊥面11ABB A ,求二面角1F A E A --的余弦值. 【答案】(1)详见解析;(2. 【解析】解:(1)连接1AB 交1A E 于点G ,连接FG . 因为11AGA B GE ∆∆,所以1112AA AG GB EB ==,又因为2AF FC=,所以1AF AG FC GB =,所以1//FG CB ,又1CB ⊄面1A EF ,FG ⊂面1A EF ,所以1//CB 面1A EF .(2)过C 作CO AB ⊥于O ,因为CA CB =,所以O 是线段AB 的中点. 因为面CAB ⊥面11ABB A ,面CAB面11ABB A AB =,所以CO ⊥面1ABA .连接1OA ,因为1ABA ∆是等边三角形,O 是线段AB 的中点,所以1OA AB ⊥.如图以O 为原点,OA ,1OA ,OC 分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标,不妨设2AB =,则(1,0,0)A,1A ,(0,0,1)C ,(1,0,0)B -,12(,0,)33F ,由11AA BB =,得(B -,1BB的中点3(2E -,13(,2A E =-,112(,)33A F =-.设面1A FE 的一个法向量为1111(,,)n x y z =,则111100A E n A F n ⎧⋅=⎪⎨⋅=⎪⎩,即11112033302x z x y ⎧-+=⎪⎪⎨⎪-=⎪⎩,得方程的一组解为11115x y z =-⎧⎪=⎨⎪=⎩1(1n =-.面1ABA 的一个法向量为2(0,0,1)n =,则121212529cos ,n n n n n n⋅<>==, 所以二面角1F A E A --的余弦值为29.2.如图,菱形ABCD 与正三角形BCE 的边长均为2,它们所在平面互相垂直,FD ⊥平面ABCD ,EF 平面ABCD .(1)求证:平面ACF ⊥平面BDF ;(2)若60CBA ∠=︒,求二面角A BC F --的大小. 【答案】(1)见证明;(2) 4π 【解析】(1)∵菱形ABCD ,∴AC BD ⊥, ∵FD ⊥平面ABCD ,∴FD AC ⊥, ∵BD FD D ⋂=,∴AC ⊥平面BDF , ∵AC ⊂平面ACF ,∴平面ACF ⊥平面BDF . (2)设ACBD O =,以O 为原点,OB 为x 轴,OA 为y 轴,过O 作平面ABCD 的垂线为z 轴,建立空间直角坐标系,则B ,()0,1,0C -,(F ,(1,0)BC =-,(BF =-,设平面BCF 的法向量(,,)n x y z =,则3020n BC y n BF ⎧⋅=--=⎪⎨⋅=-+=⎪⎩,取1x =,得(1,3,2)n =-, 平面ABC 的法向量(0,0,1)m =, 设二面角A BC F --的大小为θ, 则||cos ||||28m n m n θ⋅===⋅ ∴4πθ=.∴二面角A BC F --的大小为4π. 3.如图,在几何体1111ACD A B C D -中,四边形1111ADD A CDD C ,为矩形,平面11ADD A ⊥平面11CDD C ,11B A ⊥平面11ADD A ,1111,2AD CD AA A B ====,E 为棱1AA 的中点.(Ⅰ)证明:11B C ⊥平面1CC E ;(Ⅱ)求直线11B C 与平面1B CE 所成角的正弦值.【答案】(Ⅰ)证明见解析;. 【解析】(Ⅰ)因为11B A ⊥平面11ADD A , 所以111B A DD ⊥,又11111111DD D A B A D A A ⊥⋂=,, 所以1DD ⊥平面1111D C B A , 又因为11//DD CC ,所以1CC ⊥平面1111D C B A ,11B C ⊂平面1111D C B A ,所以111CC B C ⊥,因为平面11ADD A ⊥平面11CDD C , 平面11ADD A ⋂平面111CDD C DD =,111C D DD ⊥,所以11C D ⊥平面11ADD A ,经计算可得1111B E BC EC 从而2221111B E B C EC =+,所以在11B EC 中,111B C C E ⊥,又11CC C E ⊂,平面1111CC E CC C E C ⋂=,,所以11B C ⊥平面1CC E .(Ⅱ)如图,以点A 为原点建立空间直角坐标系,依题意得()()()10001,0,00,2,2A C B ,,,,,()()11,2,10,1,0C E ,.∵1(1,1,1)(1,2,1)CE B C =--=--,,设平面1B CE 的一个法向量(,,)m x y z =则100m B C m CE ⎧⋅=⎨⋅=⎩,, 即200x y z x y z --=⎧⎨-+-=⎩,,消去x 得20y z +=, 不妨设1z =,可得()3,2,1m =--,又()111,0,1B C =-, 设直线11B C 与平面1B CE 所成角为θ,于是111111sin cos ,14||m B C m B C m B C θ⋅====⋅,故直线11B C 与平面1B CE . 4.如图,在四凌锥P ABCD -中,PC ABCD ⊥底面,底面ABCD 是直角梯形,AB AD ⊥,AB CD ∥,222AB AD CD ===,4PC =,E 为线段PB 上一点(1)求证:EAC PBC ⊥平面平面;(2)若二面角P AC E --,求BE BP 的值【答案】(1)见解析(2)13BE BP = 【解析】(1)如图,由题意,得AC BC ==2AB =,∴BC AC ⊥∵ABCD PC ⊥底面,∴PC AC ⊥又∵PC BC C ⋂=,∴AC ⊥底面PBC∵AC ⊂平面EAC ,∴平面EAC ⊥平面PBC(2)如图,以C 为原点,取AB 中点M ,以CM ,CD ,CP 所在直线为,,x y z 轴建立空间直角坐标系则()1,1,0B -,()0,0,4P ,()1,1,0A ,设(),,E x y z ,且()01BE BP λλ=<<,得 ()()1,1,1,1,4x y z λ-+=-,即()1,1,4E λλλ--()()1,1,0,1,1,4CA CE λλλ==--,设平面EAC 的法向量为(),,n x y z =,由00CE n CA n ⎧⋅=⎪⎨⋅=⎪⎩即()()11400x y z x y λλλ⎧-+-+=⎨+=⎩,令1x =,得11,1,2n λλ-⎛⎫=- ⎪⎝⎭ 又BC AC ⊥,且BC PC ⊥,所以BC ⊥平面PAC故平面PAC 的法向量为()1,1,0m BC ==-,由二面角P AC E --cos ,m n m n m n⋅===⋅,解得1λ=-或13,由01λ<<得13λ=,即13BE BP = 5.如图,在三棱锥P ABC -中,20{ 28x x ->-≥,2AB BC =,D 为线段AB 上一点,且3AD DB =,PD ⊥平面ABC ,PA 与平面ABC 所成的角为45.(1)求证:平面PAB ⊥平面PCD ;(2)求二面角P AC D --的平面角的余弦值。
十年(2010-2019)高考数学真题分类汇编(试卷版+解析版):常用逻辑用

A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
28.(2014•陕西•理 T8)原命题为“若 z1,z2 互为共轭复数,则|z1|=|z2|”,关于其逆命题,否命题,逆否命题真
假性的判断依次如下,正确的是( )
A.真,假,真 B.假,假,真
C.真,真,假 D.假,假,假
的( )
A.充要条件
B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
3
18.(2016•山东•理 T6)已知直线 a,b 分别在两个不同的平面 α,β 内.则“直线 a 和直线 b 相交”是“平面
α 和平面 β 相交”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
13.(2017•天津•理 T4)设 θ∈R,则“
π
- 12
<
π
12”是“sin
1
θ<2”的(
)
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
14.(2017•浙江•理 T6)已知等差数列{an}的公差为 d,前 n 项和为 Sn,则“d>0”是“S4+S6>2S5”的 ( )
+ ≥ 6, 1.(2019•全国 3•文 T11)记不等式组 2 - ≥ 0 表示的平面区域为 D.命题 p:∃(x,y)∈D,2x+y≥9;命题 q:∀(x,y)∈D,2x+y≤12.下面给出了四个命题 ①p∨q ②¬p∨q ③p∧¬q ④¬p∧¬q 这四个命题中,所有真命题的编号是( ) A.①③ B.①② C.②③ D.③④
十年高考真题分类汇编(2010-2019) 数学 专题10 立体几何 Word版含解析

十年高考真题分类汇编(2010—2019)数学专题10立体几何1.(2019·浙江·T4)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=Sh,其中S是柱体的底面积,h是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm3)是( )A.158B.162C.182D.324【答案】B【解析】由三视图得该棱柱的高为6,底面五边形可以看作是由两个直角梯形组合而成,其中一个上底为4,下底为6,高为3,另一个的上底为2,下底为6,高为3,则该棱柱的体积为2+62×3+4+62×3×6=162.2.(2019·全国1·理T12)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )A.8√6πB.4√6πC.2√6πD.√6π【答案】D【解析】设PA=PB=PC=2x.∵E,F 分别为PA,AB 的中点,∴EF ∥PB,且EF=12PB=x.∵△ABC 为边长为2的等边三角形, ∴CF=√3.又∠CEF=90°,∴CE=√3-x 2,AE=12PA=x.在△AEC 中,由余弦定理可知cos ∠EAC=x 2+4-(3-x 2)2×2·x .作PD ⊥AC 于点D,∵PA=PC,∴D 为AC 的中点,cos ∠EAC=AD PA =12x . ∴x 2+4-3+x 24x =12x.∴2x 2+1=2.∴x 2=12,即x=√22.∴PA=PB=PC=√2. 又AB=BC=AC=2, ∴PA ⊥PB ⊥PC. ∴2R=√2+2+2=√6.∴R=√62.∴V=43πR 3=43π×6√68=√6π.故选D.3.(2019·全国2·理T7文T7)设α,β为两个平面,则α∥β的充要条件是( ) A.α内有无数条直线与β平行 B.α内有两条相交直线与β平行 C.α,β平行于同一条直线 D.α,β垂直于同一平面 【答案】B【解析】由面面平行的判定定理知,“α内有两条相交直线与β平行”是“α∥β”的充分条件.由面面平行的性质知,“α内有两条相交直线与β平行”是“α∥β”的必要条件,故选B.4.(2019·全国3·理T8文T8)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD,M 是线段ED 的中点,则( ) A.BM=EN,且直线BM,EN 是相交直线 B.BM ≠EN,且直线BM,EN 是相交直线 C.BM=EN,且直线BM,EN 是异面直线 D.BM ≠EN,且直线BM,EN 是异面直线 【答案】B【解析】如图,连接BD,BE.在△BDE 中,N 为BD 的中点,M 为DE 的中点, ∴BM,EN 是相交直线,排除选项C 、D. 作EO ⊥CD 于点O,连接ON. 作MF ⊥OD 于点F,连接BF.∵平面CDE ⊥平面ABCD,平面CDE ∩平面ABCD=CD,EO ⊥ CD,EO ⊂平面CDE,∴EO ⊥平面ABCD. 同理,MF ⊥平面ABCD.∴△MFB 与△EON 均为直角三角形. 设正方形ABCD 的边长为2,易知EO=√3,ON=1,MF=√32,BF=√22+94=52,则EN=√3+1=2,BM=√34+254=√7,∴BM ≠EN.故选B.5.(2019·浙江·T8)设三棱锥V-ABC 的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点).记直线PB 与直线AC 所成的角为α,直线PB 与平面ABC 所成的角为β,二面角P-AC-B 的平面角为γ,则( ) A.β<γ,α<γ B.β<α,β<γ C.β<α,γ<α D.α<β,γ<β 【答案】B【解析】如图G 为AC 中点,点V 在底面ABC 上的投影为点O,则点P 在底面ABC 上的投影点D 在线段AO 上,过点D 作DE 垂直AE,易得PE ∥VG,过点P 作PF ∥AC 交VG 于点F,过点D 作DH ∥AC,交BG于点H,则α=∠BPF,β=∠PBD,γ=∠PED,所以cos α=PFPB=EGPB=DHPB<BDPB=cos β,所以α>β,因为tan γ=PDED>PDBD=tan β,所以γ>β.故选B.6.(2018·全国3·理T10文T12)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9√3,则三棱锥D-ABC体积的最大值为( )A.12√3B.18√3C.24√3D.54√3【答案】B【解析】由△ABC为等边三角形且面积为9√3,设△ABC边长为a,则S=12a·√32a=9√3.∴a=6,则△ABC的外接圆半径r=√32×23a=2√3<4.设球的半径为R,如图,OO1=√R2-r2=√42-(2√3)2=2.当D在O的正上方时,VD-ABC =13S△ABC·(R+|OO1|)=13×9√3×6=18√3,最大.故选B.7.(2018·全国1·理T7文T9)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )A.2√17B.2√5C.3D.2【答案】B【解析】如图所示,易知N为CD⏜的中点,将圆柱的侧面沿母线MC剪开,展平为矩形MCC'M',易知CN=14CC'=4,MC=2,从M到N的路程中最短路径为MN.在Rt△MCN中,MN=√MC2+NC2=2√5.8.(2018·全国3·理T3文T3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )【答案】A【解析】由题意可知带卯眼的木构件的直观图如图所示,由直观图可知其俯视图应为A中图形.9.(2018·北京·理T5文T6)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为 ( )A.1B.2C.3D.4【答案】C【解析】由该四棱锥的三视图,得其直观图如图.由正视图和侧视图都是等腰直角三角形,知PD ⊥平面ABCD,所以侧面PAD和PDC都是直角三角形.由俯视图为直角梯形,易知DC⊥平面PAD.又AB∥DC,所以AB⊥平面PAD,所以AB⊥PA,所以侧面PAB也是直角三角形.易知PC=2√2,BC=√5,PB=3,从而△PBC不是直角三角形.故选C.10.(2018·上海·T15)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA1是正六棱柱的一条侧棱,如图.若阳马以该正六棱柱的顶点为顶点,以AA1为底面矩形的一边,则这样的阳马的个数是( )A.4B.8C.12D.16【答案】D【解析】设正六棱柱为ABCDEF-A1B1C1D1E1F1,以侧面AA1B1B,AA1F1F为底面矩形的阳马有E-AA 1B 1B,E 1-AA 1B 1B,D-AA 1B 1B,D 1-AA 1B 1B,C-AA 1F 1F,C 1-AA 1F 1F,D-AA 1F 1F,D 1-AA 1F 1F,共8个,以对角面AA 1C 1C,AA 1E 1E 为底面矩形的阳马有F-AA 1C 1C,F 1-AA 1C 1C,D-AA 1C 1C,D 1-AA 1C 1C,B-AA 1E 1E,B 1-AA 1E 1E,D-AA 1E 1E,D 1-AA 1E 1E,共8个,所以共有8+8=16(个),故选D.11.(2018·全国1·文T10)在长方体ABCD-A 1B 1C 1D 1中,AB=BC=2,AC 1与平面BB 1C 1C 所成的角为30°,则该长方体的体积为( ) A.8 B.6√2 C.8√2 D.8√3【答案】C【解析】在长方体ABCD-A 1B 1C 1D 1中,AB ⊥平面BCC 1B 1,连接BC 1,则∠AC 1B 为AC 1与平面BB 1C 1C 所成的角,∠AC 1B=30°,所以在Rt △ABC 1中,BC 1=ABtan∠AC 1B =2√3,又BC=2,所以在Rt △BCC 1中,CC 1=√(2√3)2-22=2√2, 所以该长方体体积V=BC ×CC 1×AB=8√2.12.(2018·全国2·理T9)在长方体ABCD-A 1B 1C 1D 1中,AB=BC=1,AA 1=√3,则异面直线AD 1与DB 1所成角的余弦值为( )A.15B.√56C.√55D.√22【答案】C【解析】以DA,DC,DD 1所在直线为坐标轴建立空间直角坐标系如图, 则D 1(0,0,√3),A(1,0,0),D(0,0,0),B 1(1,1,√3).∴AD 1⃗⃗⃗⃗⃗⃗⃗ =(-1,0,√3),DB 1⃗⃗⃗⃗⃗⃗⃗⃗ =(1,1,√3).设异面直线AD 1与DB 1所成的角为θ. ∴cos θ=|AD 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·DB1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ |AD 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ||DB 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ||=|22×√5|=√55.∴异面直线AD 1与DB 1所成角的余弦值为√55.13.(2018·全国2·文T9)在正方体ABCD-A 1B 1C 1D 1中,E 为棱CC 1的中点,则异面直线AE 与CD 所成角的正切值为( )A.√22 B.√32 C.√52 D.√72【答案】C【解析】如图,因为AB∥CD,所以AE与CD所成的角为∠EAB. 在Rt△ABE中,设AB=2,则BE=√5,则tan∠EAB=BEAB=√52,所以异面直线AE与CD所成角的正切值为√5 2.14.(2018·全国1·文T5)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ) A.12√2π B.12πC.8√2πD.10π【答案】B【解析】过直线O1O2的平面截该圆柱所得的截面为圆柱的轴截面,设底面半径为r,母线长为l,因为轴截面是面积为8的正方形,所以2r=l=2√2,r=√2,所以圆柱的表面积为2πrl+2πr2=8π+4π=12π.15.(2018·浙江·T3)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )A.2B.4C.6D.8【答案】C【解析】由三视图可知该几何体为直四棱柱.∵S底=12×(1+2)×2=3,h=2,∴V=Sh=3×2=6.16.(2017·全国2·理T4文T6)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A.90πB.63πC.42πD.36π【答案】B【解析】由三视图知,该几何体是一个圆柱截去一部分所得,如图所示.其体积等于下部分圆柱的体积加上上部分圆柱体积的12,所以该几何体的体积V=π×32×4+π×32×6×12=63π.17.(2017·全国1·理T7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )A.10B.12C.14D.16【答案】B【解析】由三视图可还原出几何体的直观图如图所示.该五面体中有两个侧面是全等的直角梯形,且该直角梯形的上底长为2,下底长为4,高为2,则S梯=(2+4)×2÷2=6,所以这些梯形的面积之和为12.18.(2017·全国2·理T10)已知直三棱柱ABC-A 1B 1C 1中,∠ABC=120°,AB=2,BC=CC 1=1,则异面直线AB 1与BC 1所成角的余弦值为( ) A.√32 B.√155C.√105D.√33【答案】C【解析】方法一:把三棱柱ABC-A 1B 1C 1补成四棱柱ABCD-A 1B 1C 1D 1,如图,连接C 1D,BD,则AB 1与BC 1所成的角为∠BC 1D. 由题意可知BC 1=√2,BD=√22+12-2×2×1×cos60°=√3,C 1D=AB 1=√5.可知B C 12+BD 2=C 1D 2, 所以cos ∠BC 1D=√2√5=√105,故选C. 方法二:以B 1为坐标原点,B 1C 1所在的直线为x 轴,垂直于B 1C 1的直线为y 轴,BB 1所在的直线为z 轴建立空间直角坐标系,如图所示.由已知条件知B 1(0,0,0),B(0,0,1),C 1(1,0,0),A(-1,√3,1),则BC 1⃗⃗⃗⃗⃗⃗⃗ =(1,0,-1),AB 1⃗⃗⃗⃗⃗⃗⃗ =(1,-√3,-1). 所以cos<AB 1⃗⃗⃗⃗⃗⃗⃗ ,BC 1⃗⃗⃗⃗⃗⃗⃗ >=AB 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ·BC 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ |AB 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ |·|BC 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=2√5×√2=√105.所以异面直线AB 1与BC 1所成角的余弦值为√105.19.(2017·北京·理T7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )A.3√2B.2√3C.2√2D.2【答案】B【解析】由题意可知,直观图为四棱锥A-BCDE(如图所示),最长的棱为正方体的体对角线AE=√22+22+22=2√3.故选B.20.(2017·全国3·理T8文T9)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( ) A .π B.3π4C.π2D.π4【答案】B【解析】由题意可知球心即为圆柱体的中心,画出圆柱的轴截面如图所示,则AC=1,AB=12,底面圆的半径r=BC=√32,所以圆柱的体积是V=πr 2h=π×(√32)2×1=3π4,故选B.21.(2017·全国1·文T6)如图,在下列四个正方体中,A,B 为正方体的两个顶点,M,N,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( )【答案】A【解析】易知选项B中,AB∥MQ,且MQ⊂平面MNQ,AB⊄平面MNQ,则AB∥平面MNQ;选项C中,AB ∥MQ,且MQ⊂平面MNQ,AB⊄平面MNQ,则AB∥平面MNQ;选项D中,AB∥NQ,且NQ⊂平面MNQ,AB⊄平面MNQ,则AB∥平面MNQ,故排除选项B,C,D;故选A.4.(2016·浙江·理T2文T2)已知互相垂直的平面α,β交于直线l,若直线m,n满足m∥α,n ⊥β,则( )A.m∥lB.m∥nC.n⊥lD.m⊥n【答案】C【解析】对于选项A,∵α∩β=l,∴l⊂α,∵m∥α,∴m与l可能平行,也可能异面,故选项A不正确; 对于选项B,D,∵α⊥β,m∥α,n⊥β,∴m与n可能平行,可能相交,也可能异面,故选项B,D不正确. 对于选项C,∵α∩β=l,∴l⊂β.∵n⊥β,∴n⊥l.故选C.22.(2016·天津·文T3)将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为( )【答案】B【解析】由题意得该长方体沿相邻三个面的对角线截去一个棱锥,如下图所示.易知其左视图为B项中图.故选B.23.(2016·全国3·理T10文T11)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )A.4πB.9π2 C.6π D.32π3【答案】B【解析】先计算球与直三棱柱三个侧面相切的球的半径,再和与直三棱柱两底面相切的球的半径相比较,半径较小的球即为所求.设球的半径为R,∵AB⊥BC,AB=6,BC=8,∴AC=10.当球与直三棱柱的三个侧面相切时,有12(6+8+10)×R=12×6×8,此时R=2;当球与直三棱柱两底面相切时,有2R=3,此时R=32.所以在封闭的直三棱柱中,球的最大半径只能为32,故最大体积V=43π(32)3=9π2.24.(2016·全国1·文T4)体积为8的正方体的顶点都在同一球面上,则该球的表面积为( )A.12πB. πC.8πD.4π【答案】A【解析】设正方体的棱长为a,由a3=8,得a=2.由题意可知,正方体的体对角线为球的直径,故2r=√3a2,则r=√3.所以该球的表面积为4π×(√3)2=12π,故选A.25.(2016·全国1·理T11文T11)平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )A.√32 B.√22 C.√33 D.13【答案】A【解析】∵α∥平面CB1D1,平面ABCD∥平面A1B1C1D1,α∩平面ABCD=m,平面CB1D1∩平面A 1B1C1D1=B1D1,∴m∥B1D1.∵α∥平面CB1D1,平面ABB1A1∥平面DCC1D1,α∩平面ABB1A1=n,平面CB1D1∩平面DCC1D1=CD1,∴n∥CD1.∴B1D1,CD1所成的角等于m,n所成的角,即∠B1D1C等于m,n所成的角.∵△B1D1C为正三角形,∴∠B1D1C=60°,∴m,n所成的角的正弦值为√3 2.26.(2016·全国1·理T6文T7)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是( )A.17πB.18πC.20πD.28π【答案】A【解析】由三视图可知该几何体是球截去18后所得几何体,则78×4π3×R3=28π3,解得R=2,故其表面积为78×4πR2+34×πR2=14π+3π=17π.27.(2016·全国2·理T6文T7)下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为 ( )A.20πB.24πC.28πD.32π【答案】C【解析】因为原几何体由同底面的一个圆柱和一个圆锥构成,所以其表面积为S=π×(42)2+4π×4+12×4π×√(2√3)2+22=28π,故选C.28.(2016·全国3·理T9文T10)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A.18+36√5B.54+18√5C.90D.81【答案】B【解析】由题意知该几何体为四棱柱,且四棱柱的底面是边长为3的正方形,侧棱长为3√5,所以所求表面积为(3×3+3×6+3×3√5)×2=54+18√5,故选B.29.(2016·山东·理T5)一个由半球和四棱锥组成的几何体,其三视图如下图所示.则该几何体的体积为( )A.13+23π B.13+√23πC.13+√26πD.1+√26π【答案】C【解析】由三视图可知,上面是半径为√22的半球,体积为V1=12×43π×(√22)3=√2π6,下面是底面积为1,高为1的四棱锥,体积V2=13×1×1=13,故选C.30.(2016·北京·理T6)某三棱锥的三视图如图所示,则该三棱锥的体积为( )A.16B.13C.12D.1【答案】A【解析】由三视图可得,三棱锥的直观图如图,则该三棱锥的体积V=13×12×1×1×1=16,故选A.31.(2015·全国1·理T6文T6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A.14斛B.22斛C.36斛D.66斛 【答案】B【解析】设底面圆弧半径为R,∵米堆底部弧长为8尺,∴14·2πR=8,∴R=16π.∴体积V=14×13π×(16π)2×5.∵π≈3,∴V ≈3209(尺3).∴堆放的米约为3209×1.62≈22(斛).32.(2015·全国2·理T6文T6)一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )A.18 B.17 C.16 D.15【答案】D【解析】由题意知该正方体截去了一个三棱锥,如图所示,设正方体棱长为a,则V正方体=a3,V截去部分=16a3,故截去部分体积与剩余部分体积的比值为16a3∶56a3=1∶5.33.(2015·重庆·理T5)某几何体的三视图如图所示,则该几何体的体积为( )A.13+π B.23+π C.13+2π D.23+2π【答案】A【解析】由题中三视图可知,该几何体是一个组合体,其左边是一个三棱锥,底面是等腰直角三角形(斜边长等于2),高为1,所以体积V1=13×12×2×1×1=13;其右边是一个半圆柱,底面半径为1,高为2,所以体积V2=π·12·2·12=π,所以该几何体的体积V=V1+V2=13+π.34.(2015·浙江·理T2)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )A.8 cm3B.12 cm3C.323 cm3 D.403 cm3【答案】C【解析】由题中三视图知该几何体是一个正方体与正四棱锥的组合体,其中正方体与正四棱锥的底面边长为2 cm,正四棱锥的高为2 cm,则该几何体的体积V=2×2×2+13×2×2×2=323(cm3),故选C.35.(2015·山东·理T7)在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3 B.4π3C.5π3 D.2π【答案】C【解析】由题意可得旋转体为一个圆柱挖掉一个圆锥,如图所示.V圆柱=π×12×2=2π,V圆锥=13×π×12×1=π3.∴V几何体=V圆柱-V圆锥=2π-π3=5π3.36.(2015·湖南·文T10)某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积原工件的体积)()A.89π B.827πC.24(√2-1)3π D.8(√2-1)3π【答案】A【解析】由三视图可知该几何体是一个圆锥,其底面半径r=1,母线长l=3,所以其高h=√l2-r2=2√2.故该圆锥的体积V=π3×12×2√2=2√2π3.由题意可知,加工后的正方体是该圆锥的一个内接正方体,如图所示.正方体ABCD-EFGH的底面在圆锥的底面内,下底面中心与圆锥底面的圆心重合,上底面中心在圆锥的高线上,设正方体的棱长为x.在轴截面SMN中,由O1G∥ON可得,O1GON=SO1SO,即√22x1=√2-2√2,解得x=2√23.所以正方体的体积为V1=(2√23)3=16√227.所以该工件的利用率为V1V=16√2272√2π3=89π.故选A.37.(2015·全国1·理T11文T11)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=( )A.1B.2C.4D.8【答案】B【解析】由条件及几何体的三视图可知该几何体是由一个圆柱被过圆柱底面直径的平面所截剩下的半个圆柱及一个半球拼接而成的.其表面积由一个矩形的面积、两个半圆的面积、圆柱的侧面积的一半及一个球的表面积的一半组成.∴S表=2r×2r+2×12πr2+πr×2r+12×4πr2=5πr2+4r2=16+20π,解得r=2.38.(2015·北京·理T5)某三棱锥的三视图如图所示,则该三棱锥的表面积是( )A.2+√5B.4+√5C.2+2√5D.5【答案】C【解析】作出三棱锥的直观图如图,在△ABC中,作AB边上的高CD,连接SD.在三棱锥S-ABC 中,SC ⊥底面ABC,SC=1,底面三角形ABC 是等腰三角形,AC=BC=√5,AB 边上的高CD=2,AD=BD=1,斜高SD=√5.所以S 表=S △ABC +S △SAC +S △SBC +S △SAB =12×2×2+12×1×√5+12×1×√5+12×2×√5=2+2√5.39.(2015·陕西·理T5文T5)一个几何体的三视图如图所示,则该几何体的表面积为( ) A.3π B.4π C.2π+4D.3π+4【答案】D【解析】由三视图可知,该几何体是一个半圆柱,圆柱的底面半径r=1,高h=2.所以几何体的侧面积S 1=C 底·h=(π×1+2)×2=2π+4.几何体的底面积S 2=12π×12=12π.故该几何体的表面积为S=S 1+2S 2=2π+4+2×π2=3π+4.故选D.40.(2015·浙江·理T8)如图,已知△ABC,D 是AB 的中点,沿直线CD 将△ACD 翻折成△A'CD,所成二面角A'-CD-B 的平面角为α,则( ) A.∠A'DB ≤α B.∠A'DB ≥α C.∠A'CB ≤α D.∠A'CB ≥α 【答案】B【解析】设∠ADC=θ,设AB=2,则由题意AD=BD=1. 在空间图形中,设A'B=t.在△A'BD 中, cos ∠A'DB=A 'D 2+DB 2-AB 22A 'D×DB=12+12-t 22×1×1=2-t 22.在空间图形中,过A'作A'N ⊥DC,过B 作BM ⊥DC,垂足分别为N,M.过N 作NP MB,连接A'P,所以NP ⊥DC.则∠A'NP 就是二面角A'-CD-B 的平面角, 所以∠A'NP=α.在Rt △A'ND 中,DN=A'Dcos ∠A'DC=cos θ,A'N=A'Dsin ∠A'DC=sin θ.同理,BM=PN=sin θ,DM=cos θ.故BP=MN=2cos θ. 显然BP ⊥面A'NP,故BP ⊥A'P.在Rt △A'BP 中,A'P 2=A'B 2-BP 2=t 2-(2cos θ)2=t 2-4cos 2θ.在△A'NP 中,cos α=cos ∠A'NP=A 'N 2+NP 2-A 'P 22A 'N×NP=sin 2θ+sin 2θ-(t 2-4cos 2θ)2sinθ×sinθ=2+2cos 2θ-t 22sin 2θ=2-t 22sin 2θ+cos 2θsin 2θ=1sin 2θcos ∠A'DB+cos 2θsin 2θ.因为1sin 2θ≥1,cos 2θsin 2θ≥0,所以cos α≥cos∠A'DB (当θ=π2时取等号),因为α,∠A'DB ∈[0,π],而y=cos x 在[0,π]上为递减函数,所以α≤∠A'DB.故选B. 41.(2015·全国2·理T9文T10)已知A,B 是球O 的球面上两点,∠AOB=90°,C 为该球面上的动点.若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为 ( ) A.36π B.64π C.144π D.256π【答案】C【解析】因为∠AOB=90°,所以S △AOB =12R 2.因为V O-ABC =V C-AOB ,而△AOB 面积为定值,所以三棱锥底面OAB 上的高最大时,其体积最大.因为高最大为半径R,所以V C-AOB =13×12R 2×R=36,解得R=6,故S 球=4πR 2=144π.42.(2015·安徽·理T5)已知m,n 是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )A.若α,β垂直于同一平面,则α与β平行B.若m,n 平行于同一平面,则m 与n 平行C.若α,β不平行...,则在α内不存在...与β平行的直线D.若m,n 不平行...,则m 与n 不可能...垂直于同一平面 【答案】D【解析】A选项α,β可能相交;B选项m,n可能相交,也可能异面;C选项若α与β相交,则在α内平行于它们交线的直线一定平行于β;由垂直于同一个平面的两条直线一定平行,可知D选项正确.43.(2015·浙江·文T4)设α,β是两个不同的平面,l,m是两条不同的直线,且l⊂α,m⊂β.( )A.若l⊥β,则α⊥βB.若α⊥β,则l⊥mC.若l∥β,则α∥βD.若α∥β,则l∥m【答案】A【解析】若l⊥β,又l⊂α,由面面垂直的判定定理,得α⊥β,故选项A正确;选项B,l⊥m或l∥m或l与m相交或异面都有可能;选项C,α∥β或α与β相交都有可能;选项D,l∥m或l 与m异面都有可能.44.(2015·广东·文T6)若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交【答案】D【解析】l1与l在平面α内,l2与l在平面β内,若l1,l2与l都不相交,则l1∥l,l2∥l,根据直线平行的传递性,则l1∥l2,与已知矛盾,故l至少与l1,l2中的一条相交.45.(2014·浙江·理T3)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )A.90 cm2B.129 cm2C.132 cm2D.138 cm2【答案】D【解析】由题干中的三视图可得原几何体如图所示.故该几何体的表面积S=2×4×6+2×3×4+3×6+3×3+3×4+3×5+2××3×4=138(cm2).故选D.46.(2014·陕西·文T5)将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )A.4πB.3πC.2πD.π【答案】C【解析】依题意,知所得几何体是一个圆柱,且其底面半径为1,母线长也为1,因此其侧面积为2π×1×1=2π,故选C.47.(2014·辽宁·理T4文T4)已知m,n表示两条不同直线,α表示平面.下列说法正确的是( )A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α【答案】B【解析】对A:m,n还可能异面、相交,故A不正确.对C:n还可能在平面α内,故C不正确.对D:n还可能在α内,故D不正确.对B:由线面垂直的定义可知正确.48.(2014·广东·理T7)在空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是( )A.l1⊥l4B.l1∥l4C.l1与l4既不垂直也不平行D.l1与l4的位置关系不确定【答案】D【解析】如图,在正方体ABCD-A1B1C1D1中,取l1为BC,l2为CC1,l3为C1D1.满足l1⊥l2,l2⊥l3.若取l 4为A1D1,则有l1∥l4;若取l4为DD1,则有l1⊥l4.因此l1与l4的位置关系不确定,故选D.49.(2014·浙江·文T6)设m,n是两条不同的直线,α,β是两个不同的平面.( )A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α【答案】C【解析】当m⊥n,n∥α时,可能有m⊥α,但也有可能m∥α或m⊂α,故A选项错误; 当m∥β,β⊥α时,可能有m⊥α,但也有可能m∥α或m⊂α,故选项B错误;当m⊥β,n⊥β,n⊥α时,必有α∥β,从而m⊥α,故选项C正确;在如图所示的正方体ABCD-A1B1C1D1中,取m为B1C1,n为CC1,β为平面ABCD,α为平面ADD1A1,这时满足m⊥n,n⊥β,β⊥α,但m⊥α不成立,故选项D错误.50.(2014·陕西·理T5)已知底面边长为1,侧棱长为√2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )A.32π3 B.4π C.2π D.4π3【答案】D【解析】依题意可知正四棱柱体对角线的长度等于球的直径,可设球半径R,则2R=√12+12+(√2)2=2,解得R=1,所以V=4π3R3=4π3.51.(2014·大纲全国·理T8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )A.81π4 B.16π C.9π D.27π4【答案】A【解析】由图知,R2=(4-R)2+2,∴R2=16-8R+R2+2,∴R=9 4,∴S表=4πR2=4π×8116=814π,选A.52.(2014·湖南·理T7文T8)一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A.1B.2C.3D.4【答案】B【解析】由三视图可得原石材为如右图所示的直三棱柱A1B1C1-ABC,且AB=8,BC=6,BB1=12.若要得到半径最大的球,则此球与平面A1B1BA,BCC1B1,ACC1A1相切,故此时球的半径与△ABC内切圆的半径相等,故半径r=6+8-102=2.故选B.53.(2014·全国1·理T12)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )A.6√2B.6C.4√2D.4 【答案】B【解析】如图所示的正方体ABCD-A1B1C1D1的棱长为4.取B1B的中点G,即三棱锥G-CC1D1为满足要求的几何体,其中最长棱为D1G,D1G=√(4√2)2+22=6.54.(2014·全国1·文T8)如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )A.三棱锥B.三棱柱C.四棱锥D.四棱柱【答案】B【解析】由所给三视图可知该几何体是一个三棱柱(如图).55.(2014·北京·理T7)在空间直角坐标系O-xyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1, √2).若S1,S2,S3分别是三棱锥D-ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则( )A.S1=S2=S3B.S2=S1且S2≠S3C.S3=S1且S3≠S2D.S3=S2且S3≠S1【答案】D【解析】三棱锥的各顶点在xOy坐标平面上的正投影分别为A 1(2,0,0),B1(2,2,0),C1(0,2,0),D1(1,1,0).显然D1点为A1C1的中点,如图(1),正投影为Rt△A1B1C1,其面积S1=12×2×2=2.三棱锥的各顶点在yOz坐标平面上的正投影分别为A 2(0,0,0),B2(0,2,0),C2(0,2,0),D2(0,1,√2).显然B2,C2重合,如图(2),正投影为△A2B2D2,其面积S2=12×2×√2=√2.三棱锥的各顶点在zOx坐标平面上的正投影分别为A 3(2,0,0),B3(2,0,0),C3(0,0,0),D3(1,0,√2),由图(3)可知,正投影为△A3D3C3,其面积S 3=12×2×√2=√2.综上,S2=S3,S3≠S1.故选D.56.(2014·大纲全国·理T11)已知二面角α-l-β为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C ∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )A.14 B.√24 C.√34 D.12【答案】B【解析】如图,在平面α内过C作CE∥AB,则∠ECD为异面直线AB与CD所成的角或其补角,不妨取CE=1,过E作EO⊥β于O. 在平面β内过O作OH⊥CD于H,连EH,则EH⊥CD.因为AB∥CE,AB⊥l,所以CE⊥l.又因为EO⊥平面β,所以CO⊥l.故∠ECO为二面角α-l-β的平面角,所以∠ECO=60°.而∠ACD=135°,CO ⊥l,所以∠OCH=45°.在Rt △ECO 中,CO=CE ·cos ∠ECO=1·cos 60°=12.在Rt △COH 中,CH=CO ·cos ∠OCH=12·sin45°=√24.在Rt △ECH 中,cos ∠ECH=CH CE =√241=√24.所以异面直线AB 与CD 所成角的余弦值为√24.故选B.57.(2014·大纲全国·文T4)已知正四面体ABCD 中,E 是AB 的中点,则异面直线CE 与BD 所成角的余弦值为( )A.16B.√36C.13D.√33【答案】B【解析】如图所示,取AD 的中点F,连EF,CF,则EF ∥BD,∴异面直线CE 与BD 所成的角即为CE 与EF 所成的角∠CEF.由题知,△ABC,△ADC 为正三角形,设AB=2,则CE=CF=√3,EF=12BD=1.∴在△CEF 中,由余弦定理,得cos ∠CEF=CE 2+EF 2-CF22CE ·EF=√3)22√3)22×√3×1=√36.故选B.58.(2014·全国2·理T6文T6)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13【答案】C【解析】由零件的三视图可知,该几何体为两个圆柱组合而成,如图所示. 切削掉部分的体积V 1=π×32×6-π×22×4-π×32×2=20π(cm 3), 原来毛坯体积V 2=π×32×6=54π(cm 3).故所求比值为V 1V 2=20π54π=1027.59.(2014·全国2·文T7)正三棱柱ABC-A 1B 1C 1的底面边长为2,侧棱长为√3,D 为BC 中点,则三棱锥A-B 1DC 1的体积为( ) A.3 B.32C.1D.√32【答案】C【解析】∵D 是等边△ABC 的边BC 的中点,∴AD ⊥BC. 又ABC-A 1B 1C 1为正三棱柱, ∴AD ⊥平面BB 1C 1C. 又四边形BB 1C 1C 为矩形,∴S △DB 1C 1=12S 四边形BB 1C 1C =12×2×√3=√3.又AD=2×√32=√3,∴V A -B 1DC 1=13S △B 1DC 1·AD=13×√3×√3=1.60.(2013·全国1·理T8文T11)某几何体的三视图如图所示,则该几何体的体积为( )A.16+8πB.8+8πC.16+16πD.8+16π 【答案】A【解析】该几何体为一个半圆柱与一个长方体组成的一个组合体. V 半圆柱= π×22×4=8π,V 长方体=4×2×2=16. 所以所求体积为16+8π.故选A.61.(2013·浙江·文T5)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )A.108 cm 3B.100 cm 3C.92 cm 3D.84 cm 3【答案】B【解析】由三视图可知,该几何体是如图所示长方体去掉一个三棱锥,故几何体的体积是6×3×6-13×12×3×42=100(cm 3).故选B.62.(2013·山东·理T4)已知三棱柱ABC-A 1B 1C 1的侧棱与底面垂直,体积为94,底面是边长为√3的正三角形.若P 为底面A 1B 1C 1的中心,则PA 与平面ABC 所成角的大小为( )A.5π12B.π3C.π4D.π6【答案】B【解析】如图所示,由棱柱体积为94,底面正三角形的边长为√3,可求得棱柱的高为√3.设P 在平面ABC 上射影为O,则可求得AO 长为1,故AP 长为√12+(√3)2=2.故∠PAO=π3,即PA 与平面ABC 所成的角为π3.63.(2013·全国2·理T7文T9)一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为 ( )【答案】A【解析】该四面体在空间直角坐标系O-xyz中的图象如图所示.则它在平面zOx上的投影,即正视图为.64.(2013·湖南·理T7)已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于( )A.1B.√2C.√2-12 D.√2+12【答案】C【解析】当俯视图是面积为1的正方形时,其正视图的最小面积等于一个面的面积1,最大面积等于对角面的面积√2.故正视图面积S的取值范围为1≤S≤√2.因为√2-12<1,故选C.65.(2013·全国1·理T6)如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为( )A.500π3 cm3 B.866π3 cm3C.1372π3 cm3 D.2048π3 cm3【答案】A【解析】设球半径为R,由题可知R,R-2,正方体棱长的一半可构成直角三角形,即△OBA为直角三角形,如图.BC=2,BA=4,OB=R-2,OA=R, 由R2=(R-2)2+42,得R=5,所以球的体积为4π3×53=5003π(cm3),故选A.66.(2013·辽宁·理T10)已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上.若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为( )A.3√172 B.2√10 C.132 D.3√10【答案】C【解析】过C点作AB的平行线,过B点作AC的平行线,交点为D,同理过C1作A1B1的平行线,过B 1作A1C1的平行线,交点为D1,连接DD1,则ABCD-A1B1C1D1恰好成为球的一个内接长方体,故球的半径r=√32+42+1222=132.67.(2013·全国2·理T4)已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则( )A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l【答案】D【解析】因为m⊥α,l⊥m,l⊄α,所以l∥α.同理可得l∥β.又因为m,n为异面直线,所以α与β相交,且l平行于它们的交线.故选D.68.(2013·广东·理T6)设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是 ( )A.若α⊥β,m⊂α,n⊂β,则m⊥nB.若α∥β,m⊂α,n⊂β,则m∥nC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若m⊥α,m∥n,n∥β,则α⊥β【答案】D【解析】选项A中, m与n还可能平行或异面,故不正确;。
河北省2019-2010年十年对口招生高考(对口升学)数学试题含答案

河北省对口招生高考数学历年真题(2010-2019)目录✧..2019年河北省普通高等学校对口招生考试数学试题 (1)✧..2019年河北省对口招生考试数学参考答案 (4)✧..2018年河北省普通高等学校对口招生考试数学试题 (7)✧..2018年河北省对口招生考试数学参考答案 (12)✧..2017年河北省普通高等学校对口招生考试数学试题 (13)✧..2017年河北省对口招生考试数学参考答案 (18)✧..2016年河北省普通高等学校对口招生考试数学试题 (23)✧..2016年河北省对口招生考试数学参考答案 (28)✧..2015年河北省普通高等学校对口招生考试数学试题 (29)✧..2015年河北省对口招生考试数学参考答案 (34)✧..2014年河北省普通高等学校对口招生考试数学试题 (36)✧..2014年河北省对口招生考试数学参考答案 (41)✧..2013年河北省普通高等学校对口招生考试数学试题 (42)✧..2013年河北省对口招生考试数学参考答案 (47)✧..2012年河北省普通高等学校对口招生考试数学试题 (50)✧..2012年河北省对口招生考试数学参考答案 (54)✧..2011年河北省普通高等学校对口招生考试数学试题 (55)✧..2011年河北省对口招生考试数学参考答案 (59)✧..2010年河北省普通高等学校对口招生考试数学试题 (63)✧..2010年河北省对口招生考试数学参考答案 (67)2019年河北省普通高等学校对口招生考试数学试题一、选择题(每题3分,共45分)1.设集合A={b,c,d},则集合A 的子集共有()A.5个B.6个C.7个D.8个2.若22b a <,则下列不等式成立的是()A.ba < B.ba 22< C.0)(log 222<-a b D.||||b a <3.在ABC ∆中,“sinA=sinB ”是“A=B ”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件4.已知一次函数b kx y +=关于原点对称,则二次函数)0(2≠++=a c bx ax y 一定是()A.奇函数B.偶函数C.非奇非偶函数D.奇偶性和c 有关5.函数|cos sin |x x y =的最小正周期为()A.2π B.πC.π2D.π46.设向量b a x b a ∥且),1,(),2,4(==,则x=()A.2B.3C.4D.57二次函数b ax x y ++=2图像的顶点坐标为(-3,1),则b a ,的值为()A.10,6=-=b a B.10,6-=-=b a C.10,6==b a D.10,6-==b a 8.在等差数列}{n a 中,n S 为前n 项和,===642,8,0a S S 则若()A.5B.7C.9D.169.在等比数列}{n a 中,=+=⋅>1047498log log ,161.0a a a a a n 则若()A.-2 B.-1 C.0 D.210.下列四组函数中,图像相同的是()A.x x y x y 220cos sin +==和B.xy x y lg 10==和C.xy x y 222log 2log ==和 D.)2cos(sin x y x y -==π和11.过点A(1,2)且与直线012=-+y x 平行的直线方程为()A.042=-+y x B.052=-+y x C.02=-y x D.032=++y x 12.北京至雄安将开通高铁,共设有6个高铁站(包含北京站和雄安站),则需设计不同车票的种类有()A.12种B.15种C.20种D.30种13.二项式于的展开式中,常数项等122)12(x x -()A.84122⋅C B.84122⋅-C C.66122⋅C D.66122⋅-C 14.在正方体1111D C B A ABCD -中,棱C D D A 11与所成的角为()A.6π B.4π C.3π D.32π15.已知双曲线方程为192522=-y x ,则其渐近线方程为()A.x y 45±=B.xy 35±= C.xy 54±= D.xy 53±=二、填空题(每题2分,共30分)16.已知函数3)(3++=bx ax x f 满足=-=)1(,6)1(f f 则.17.函数|3|lg 37121)(2-++-=x x x x f 的定义域为.18.计算:=-+++|3|281log 45tan2log 31e e π.19.若不等式02<-+b ax x 的解集为(1,2),则)(log 6ab =.20.数列1,22241-3121,,-的通项公式为.21.若|b |3b a 4b a 4|a |→→→→→→==⋅=,则,,,π=.22.已知ααααα2cos 137cos sin 1317cos sin ,则,=-=+=.23.已知以21F F ,为焦点的椭圆1361622=+y x 交x 轴正半轴于点A ,则21F AF ∆的面积为.24.已知99.0log 10099.010099.0100===c b a ,,,则c b a ,,按由小到大的顺序排列为.25.在正方体1111D C B A ABCD -中,与AB 为异面直线的棱共有条.26.某学校参加2019北京世界园艺博览会志愿活动,计划从5名女生,3名男生中选出4人组成小分队,则选出的4人中2名女生2名男生的选法有种.27.已知αβαβαβαβα2sin 81)sin()cos()cos()sin(,则=-++-+=.28.设,,,,)sin 11()1cos 1(A n A m +-=+=→→其中∠A 为ABC ∆的内角.→→⊥n m 若,则∠A=.29.不等式x x 5log )6(log 222>+的解集为.30.一口袋里装有4个白球和4个红球,现在从中任意取3个球,则取到既有白球又有红球的概率为.三、解答题(7个小题,共45分)31.(5分)设集合R B A m x x B x x x A =≥+=>--= ,若,}1|{}012|{2,求m 的取值范围.32.(6分)某广告公司计划设计一块周长为16米的矩形广告牌,设计费为每平方米500元.设该矩形一条边长为x 米,面积为y 平方米.(1)写出y 与x 的函数关系式;(2)问矩形广告牌长和宽各为多少米时,设计费最多,最多费用为多少元?33.(8分)若数列}{n a 是公差为23的等差数列,且前5项和155=S .(1)求数列}{n a 的通项公式;(2)若n a n e b =,求证}{n b 为等比数列并指出公比q ;(3)求数列}{n b 的前5项之积.34.(6分)函数x x y 2sin )23sin(+-=π(1)求该函数的最小正周期;(2)当x 为何值时,函数取最小值,最小值为多少?35.(6分)过抛物线x y 42=的焦点,且斜率为2的直线l 交抛物线于A ,B 两点.(1)求直线l 的方程;(2)求线段AB 的长度.36.(7分)如图所示,底面ABCD 为矩形,PD ⊥平面ABCD ,|PD|=2,平面PBC 与底面ABCD所成角为45°,M 为PC 中点.(1)求DM 的长度;(2)求证:平面BDM ⊥平面PBC.37.(7分)一颗骰子连续抛掷3次,设出现能被3整除的点的次数为ξ,(1)求)2(=ξP ;(2)求ξ的概率分布.P DMCAB2019年河北省对口招生考试数学参考答案一、选择题题号123456789101112131415答案DDCBAACCADBDACD二、填空题16.017.),3()3,(+∞-∞ 18.019.120.21)1(n a n n +-=21.222.169119-23.5824.ba c <<25.426.3027.8128.4π29.),3()2,0(+∞ 30.76三、解答题31.解:}34|{}012|{2-<>=>--=x x x x x x A 或}1|{}1|{m x x m x x B -≥=≥+=因为R B A = 所以431≥-≤-m m 即所以m 的取值范围为),4[+∞.32.解:矩形的另一边长为)(82216米x x-=-则x x x x y 8)8(2+-=-=(0<x<8)(2)16)4(822+--=+-=x x x y 当x=4米时,矩形的面积最大,最大面积为16平方米此时广告费为)(800016500元=⨯所以当广告牌长和宽都为4米时矩形面积最大,设计费用最多,最多费用为8000元.33.解:(1)由已知23,155==d S 得1552)(53515==+=a a a S 解得33=a所以232323)3(3)3(3-=⋅-+=-+=n n d n a a n (2)由)2323(-==n a n eeb n所以n eb 231=+所以23a 111e e e ee b b d a a a n n n n n n ====-+++,又101==e b 所以}{n b 为以1为首项23e 为公比的等比数列.(3)由题意可得155)13(235354321)(e eb b b b b b ===⋅⋅⋅⋅-,所以}{n b 的前5项积为15e .34.解:x x x x x y 2sin 2sin 3cos 2cos 3sin 2sin )23sin(+-=+-=πππ=)32sin(2cos 232sin 21π+=+x x x 所以函数的最小正周期为ππ==22T (2)当1-)(125)(2232小值为时,函数有最小值,最即Z k k x Z k k x ∈-=∈-=+πππππ.35.解:(1)由抛物线方程x y 42=得焦点F(1,0),又直线l 的斜率为2,所以直线方程为022)1(2=---=y x x y 即.(2).设抛物线与直线的交点坐标为),(),,(2211y x B y x A 联立两方程得01322422=+-⎩⎨⎧-==x x x y xy 整理得由韦达定理得1,32121==+x x x x 由弦长公式得549414)(1||212212=-+=-++=x x x x k AB 36.解:(1)因为PD ⊥平面ABCD 所以PD ⊥BC又因为ABCD 为矩形,得BC ⊥CD 所以BC ⊥平面PCD 所以BC ⊥PC所以∠PCD 为平面PBC 与平面ABCD 所成角即∠PCD=45°从而△PDC 为等腰直角三角形在RT ∆PDC 中||||45sin PC PD =︒得2245sin ||||=︒=PD PC 又M 为PC 的中点,则DM ⊥PC所以在2||21||==∆PC DM DMC RT 中,(2)证明:由(1)可知BC ⊥平面PCD 所以BC ⊥DM由(1)可知DM ⊥PC ,且BC PC=C,所以DM ⊥平面PBC又DM ⊆平面BDM ,所以平面BDM ⊥平面PBC37.解:(1)能被3整除的只有3和6,则在一次抛掷中出现的概率为31,从而出现不能被3整除的点的概率为32所以9232()31(223=⨯⨯=C P (2)ξ的可能取值为0,1,2,3且278)32()31()0(3003=⨯⨯==C P ξ94)32(31()1(2113=⨯⨯==C P ξ9232()31()2(1223=⨯⨯==C P ξ271)32()31()3(0333=⨯⨯==C P ξ所以ξ的概率分布为ξ0123P27894922712018年河北省普通高等学校对口招生考试数学试题一、选择题(本大题共15小题,每小题3分,共45分)1、设集合M={0,1,2,3,4},N={xl0<x ≤3},则N M ⋂=()A{1,2}B{0,1,2}C{1,2,3}D{0,1,2,3}2、若a,b,c 为实数,且a>b,则()A a-c>b-cB a 2>b 2C ac>bcD ac 2>bc 23、2>x 是x>2的()A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件4、下列函数中,既是奇函数又是减函数的是()A xy 31=B 22x y =C 3x y -=D xy 1=5、函数42sin(π-=x y 的图像可以有函数x y 2sin =的图像如何得到()A 向左平移4π个单位B 向右平移4π个单位C 向左平移8π个单位D 向右平移8π个单位6、已知),,3(),2,1(m b a =-=b a b a -=+则m=()A -23B23C 6D -67、下列函数中,周期为π的偶函数是()A xy sin =B xy 2sin =C xy sin =D 2cosx y =8、在等差数列{a n }中,若a 1+a 2+a 3=12,a 2+a 3+a 4=18,则a 3+a 4+a 5=()A 22B 24C 26D 309、记S n 为等比数列{a n }的前n 项和,若S 2=10,S 4=40,则S 6=()A 50B 70C 90D 13010、下列各组函数中,表示同一个函数的是()A x y =与2x y =B x y =与33x y =C x y =与2x y =D 2x y =与33x y =11、过圆2522=+y x 上一点(3,4)的切线方程为()A 3x+4y-25=0B 3x+4y+25=0C 3x-4y-25=0D 3x-4y+25=012、某体育兴趣小组共有4名同学,如果随机分为两组进行对抗赛,每组两名队员,分配方案共有()A2种B3种C6种D12种13、设(2x-1)2018=a 0+a 1x+a 2x 2+……….+a 2018x 2018,则a 0+a 1+a 2+…….+a 2018=()A 0B 1C -1D 22018-114、已知平面上三点A (1,-2),B (3,0),C (4,3),则点B 关于AC 中点是对称点的坐标是()A (1,4)B (5,6)C (-1,-4)D (2,1)15、下列命题中正确的是()(1)平行于同一直线的两条直线平行(2)平行于同一平面的两条直线平行(3)平行于同一直线的两个平面平行(4)平行于同一平面的两个平面平行A(1)(2)B(1)(3)C(1)(4)D(2)(4)二、填空题(共15小题。
十年真题(2010_2019)高考数学真题分类汇编专题01集合文(含解析)

专题01集合历年考题细目表历年高考真题汇编1.【2019年新课标1文科02】已知集合U={1,2,3,4,5,6,7},A={2,3,4,5},B={2,3,6,7},则B∩∁U A=()A.{1,6} B.{1,7} C.{6,7} D.{1,6,7}【解答】解:∵U={1,2,3,4,5,6,7},A={2,3,4,5},B={2,3,6,7},∴∁U A={1,6,7},则B∩∁U A={6,7}故选:C.2.【2018年新课标1文科01】已知集合A={0,2},B={﹣2,﹣1,0,1,2},则A∩B=()A.{0,2} B.{1,2}C.{0} D.{﹣2,﹣1,0,1,2}【解答】解:集合A={0,2},B={﹣2,﹣1,0,1,2},则A∩B={0,2}.故选:A.3.【2017年新课标1文科01】已知集合A={x|x<2},B={x|3﹣2x>0},则()A.A∩B={x|x} B.A∩B=∅C.A∪B={x|x} D.A∪B=R【解答】解:∵集合A={x|x<2},B={x|3﹣2x>0}={x|x},∴A∩B={x|x},故A正确,B错误;A∪B={x||x<2},故C,D错误;故选:A.4.【2016年新课标1文科01】设集合A={1,3,5,7},B={x|2≤x≤5},则A∩B=()A.{1,3} B.{3,5} C.{5,7} D.{1,7}【解答】解:集合A={1,3,5,7},B={x|2≤x≤5},则A∩B={3,5}.故选:B.5.【2015年新课标1文科01】已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则集合A∩B中元素的个数为()A.5 B.4 C.3 D.2【解答】解:A={x|x=3n+2,n∈N}={2,5,8,11,14,17,…},则A∩B={8,14},故集合A∩B中元素的个数为2个,故选:D.6.【2014年新课标1文科01】已知集合M={x|﹣1<x<3},N={x|﹣2<x<1},则M∩N=()A.(﹣2,1)B.(﹣1,1)C.(1,3)D.(﹣2,3)【解答】解:M={x|﹣1<x<3},N={x|﹣2<x<1},则M∩N={x|﹣1<x<1},故选:B.7.【2013年新课标1文科01】已知集合A={1,2,3,4},B={x|x=n2,n∈A},则A∩B=()A.{1,4} B.{2,3} C.{9,16} D.{1,2}【解答】解:根据题意得:x=1,4,9,16,即B={1,4,9,16},∵A={1,2,3,4},∴A∩B={1,4}.故选:A.8.【2012年新课标1文科01】已知集合A={x|x2﹣x﹣2<0},B={x|﹣1<x<1},则()A.A⊊B B.B⊊A C.A=B D.A∩B=∅【解答】解:由题意可得,A={x|﹣1<x<2},∵B={x|﹣1<x<1},在集合B中的元素都属于集合A,但是在集合A中的元素不一定在集合B中,例如x∴B⊊A.故选:B.9.【2011年新课标1文科01】已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,则P的子集共有()A.2个B.4个C.6个D.8个【解答】解:∵M={0,1,2,3,4},N={1,3,5},∴P=M∩N={1,3}∴P的子集共有22=4故选:B.10.【2010年新课标1文科01】已知集合A={x||x|≤2,x∈R},B={x|4,x∈Z},则A∩B=()A.(0,2)B.[0,2] C.{0,2} D.{0,1,2}【解答】解:∵A={x||x|≤2}={x|﹣2≤x≤2}B={x|4,x∈Z}={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}则A∩B={0,1,2}故选:D.考题分析与复习建议本专题考查的知识点为:集合关系及其运算,历年考题主要以选择填空题型出现,重点考查的知识点为:交并补运算,预测明年本考点题目会比较稳定,备考方向以知识点交并补运算为重点较佳.最新高考模拟试题 1.若集合,,则AB =( )A .B .C .D .【答案】A 【解析】 解:,则,故选:A . 2.已知集合,,则AB =( )A .[2,3]B .(1,5)C .{}2,3D .{2,3,4}【答案】C 【解析】,,又,所以,故本题选C.3.已知集合,,则A B =( )A .B .{}1,0,1,2,3-C .{}3,2--D .【答案】B 【解析】因为,∴.4.已知全集U =R ,集合,则()U A B =ð( )A .(1,2)B .(]1,2 C .(1,3) D .(,2]-∞【答案】B 【解析】由24x >可得2x >,可得13x <<,所以集合,(,2]U A =-∞ð,所以()U A B =ð(]1,2,故选B.5.已知集合,集合,则集合A B ⋂的子集个数为( ) A .1 B .2C .3D .4【答案】D 【解析】由题意得,直线1y x =+与抛物线2y x =有2个交点,故A B ⋂的子集有4个. 6.已知集合,,则()R M N ⋂ð=( )A .{-1,0,1,2,3}B .{-1,0,1,2}C .{-1,0,1}D .{-1,3}【答案】D 【解析】 由题意,集合,则或3}x ≥又由,所以,故选D.7.已知集合,,则()R A B I ð=( )A .{}1,0-B .{}1,0,1-C .{}1,2,3D .{}2,3【答案】B 【解析】 因为,所以,又,所以.8.已知R 是实数集,集合,,则()AB =Rð( )A .{}1,0-B .{}1C .1,12⎡⎤⎢⎥⎣⎦D .1,2⎛⎫-∞ ⎪⎝⎭【答案】A 【解析】即故选A 。
十年(2010-2019)高考数学真题分类汇编(试卷版+解析版):函数

49.(2016•全国 1•T9)函数 y=2x -e 在[-2,2]的图象大致为( )
2
50.(2016•浙江•文 T3)函数 y=sin x 的图象是( )
x
51.(2016•浙江•文 T7)已知函数 f(x)满足:f(x)≥|x|,且 f(x)≥2 ,x∈R.( )
b
A.若 f(a)≤|b|,则 a≤b B.若 f(a)≤2 ,则 a≤b
cc
A.a <b
cc
B.ab <ba
C.alogbc<blogac
D.logac<logbc
9
46.(2016•全国 3•理 T6)已知 a=2 ,b=4:,c=25 ,则( )
A.b<a<c B.a<b<c C.b<c<a D.c<a<b
9
47.(2016•全国 3•文 T7)已知 a=2 ,b=3 ,c=25 ,则( )
!"#
35.(2017•全国 1•文 T8)函数 y= 的部分图象大致为( )
-%&!
!"#
36.(2017•全国 3•文 T7)函数 y=1+x+ 的部分图象大致为( )
5
37.(2017•山东•理
T10)已知当
x∈[0,1]时,函数
2
y=(mx-1)
的图象与
y=√x+m
的图象有且只有一个交点,则正
③f(x)在[-π,π]有 4 个零点 ④f(x)的最大值为 2
其中所有正确结论的编号是( )
A.①②④ B.②④
C.①④
D.①③
6.(2019•全国 3•理 T11 文 T12)设 f(x)是定义域为 R 的偶函数,且在(0,+∞)单调递减,则( )
十年(2010-2019)高考数学真题分类汇编(试卷版+解析版):导数与定积分

(1)f(x)存在唯一的极值点;
(2)f(x)=0 有且仅有两个实根,且两个实根互为倒数.
49.(2019·江苏,19,16 分,难度)设函数 f(x)=(x-a)(x-b)(x-c),a,b,c∈R,f'(x)为 f(x)的导函数.
(1)若 a=b=c,f(4)=8,求 a 的值;
(2)若 a≠b,b=c,且 f(x)和 f'(x)的零点均在集合{-3,1,3}中,求 f(x)的极小值;
3
38.(2015·全国 1·文 T14)已知函数 f(x)=ax +x+1 的图象在点(1,f(1))处的切线过点(2,7),则 a= .
2
39.(2015·全国 2·文 T16)已知曲线 y=x+ln x 在点(1,1)处的切线与曲线 y=ax +(a+2)x+1 相切,则 a= .
x
1
40.(2015·陕西·理 T15)设曲线 y=e 在点(0,1)处的切线与曲线 y=x (x>0)上点 P 处的切线垂直,则 P 的坐
T13) 已 知 函 数
y=f(x) 的 图 象 是 折 线 段
ABC, 其 中
A(0,0),B
1 2
,5
,C(1,0). 函 数
y=xf(x)(0≤x≤1)的图象与 x 轴围成的图形的面积为________________.
44.(2012·全国·文 T13)曲线 y=x(3ln x+1)在点(1,1)处的切线方程为 .
34.(2017·天津,文 10)已知 a∈R,设函数 f(x)=ax-ln x 的图象在点(1,f(1))处的切线为 l,则 l 在 y 轴上的
截距为 .
十年真题(2010_2019)高考数学真题分类汇编专题10平面解析几何选择填空题文(含解析)
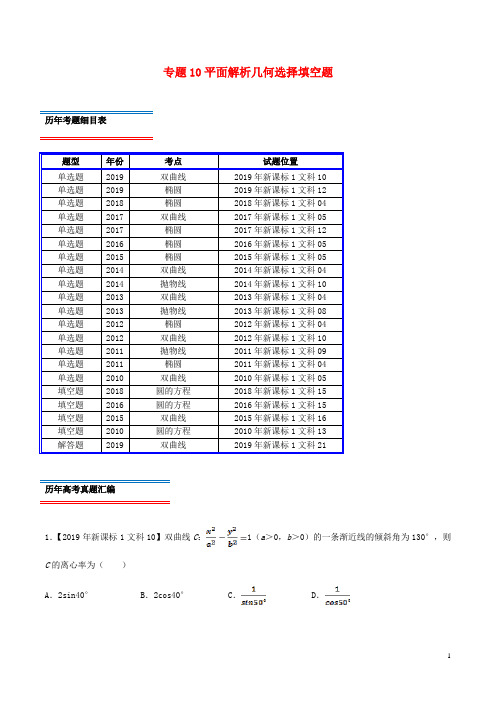
∪[4,+∞) 【解答】解:假设椭圆的焦点在 x 轴上,则 0<m<3 时,
C.(0,1]∪[4,+∞) D.(0, ]
设椭圆的方程为:
(a>b>0),设 A(﹣a,0),B(a,0),M(x,y),y>0,
则 a2﹣x2
,
∠MAB=α,∠MBA=β,∠AMB=γ,tanα
,tanβ
,
则 tanγ = tan[π ﹣ ( α+β ) ] = ﹣ tan ( α+β )
,
∴e
.
故选:D. 2.【2019 年新课标 1 文科 12】已知椭圆 C 的焦点为 F1(﹣1,0),F2(1,0),过 F2 的直线与 C 交于 A,B 两点.若|AF2|=2|F2B|,|AB|=|BF1|,则 C 的方程为( )
A. y2=1
B.
1
C.
1
D.
1
【解答】解:∵|AF2|=2|BF2|,∴|AB|=3|BF2|, 又|AB|=|BF1|,∴|BF1|=3|BF2|,
∴△APF 的面积 S 丨 AP 丨×丨 PF 丨 ,
3
同理当 y<0 时,则△APF 的面积 S , 故选:D.
5.【2017 年新课标 1 文科 12】设 A,B 是椭圆 C:
1 长轴的两个端点,若 C 上存在点 M 满足∠AMB
=120°,则 m 的取值范围是(
)
A.(0,1]∪[9,+∞) B.(0, ]∪[9,+∞)
1 的右焦点,P 是 C 上一点,且 PF 与 x 轴垂直,
点 A 的坐标是(1,3),则△APF 的面积为(
)
A.
B.
C.
D.
【解答】解:由双曲线 C:x2
十年(2010-2019)高考数学真题分类汇编(试卷版+解析版): 复数

A.1+2i
B.-1+2i
C.1-2i
D.-1-2i
1
42.(2014·全国 1·文 T3)设 z=1+ +i,则|z|=( )
1
√2
√3
A.2
B. 2
C. 2
D.2
43.(2013·全国 1·理 T2)若复数 z 满足(3-4i)z=|4+3i|,则 z 的虚部为( )
A.-4
4
B.-5
4
C.4
D.√2
1+2i
8.(2018·全国 2·理 T1) =( )
1-2i
4
A.-5
−
3
5i
4
B.-5
+
3
5i
3
C.-5
−
4
5i
3
D.-5
+
4
5i
9.(2018·全国 2·文 T1)i(2+3i)=( )
A.3-2i
B.3+2i
1
C.-3-2i
D.-3+2i
10.(2018·全国 3·理 T2 文 T2)(1+i)(2-i)=( )
A.√3
B.√5
C.3
D.5
4.(2019·全国 2·文 T2)设 z=i(2+i),则 =( )
A.1+2i
B.-1+2i
C.1-2i
D.-1-2i
5.(2019·全国 1·理 T2)设复数 z 满足|z-i|=1,z 在复平面内对应的点为(x,y),则( )
A.(x+1)2+y2=1
B.(x-1)2+y2=1
十年(2010-2019)高考数学真题分类汇编(试卷版+解析版):不等式

A.-15 B.-9
C.1 D.9
3x + 2y-6 ≤ 0,
8.(2017·全国 3·文 T5)设 x,y 满足约束条件 x ≥ 0,
则 z=x-y 的取值范围是( )
y ≥ 0,
A.[-3,0] B.[-3,2]
C.[0,2] D.[0,3] x + 3y ≤ 3,
9.(2017·全国 1·文 T7)设 x,y 满足约束条件 x-y ≥ 1, 则 z=x+y 的最大值为( ) y ≥ 0,
A.对任意实数 a,(2,1)∈A
B.对任意实数 a,(2,1)∉A
C.当且仅当 a<0 时,(2,1)∉A
D.当且仅当 a≤ 时,(2,1)∉A
1
2x + 3y-3 ≤ 0,
7.(2017·全国 2·理 T5 文 T7)设 x,y 满足约束条件 2x-3y + 3 ≥ 0,则 z=2x+y 的最小值是( ) y + 3 ≥ 0,
十年(2010—2019)数学高考真题分类汇编
不等式
1.(2019·全国 1·理 T4 文 T4)古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之
√5-1 √5-1
比是 2 ( 2 ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽
√5-1
喉的长度与咽喉至肚脐的长度之比也是 2 .若某人满足上述两个黄金分割比例,且腿长为 105 cm,头顶至脖
A.√2 B.2 C.2√2 D.4
x + y-2 ≤ 0, 19.(2015·重庆·文 T10)若不等式组 x + 2y-2 ≥ 0,表示的平面区域为三角形,且其面积等于43,则 m 的值为
十年(2010-2019)高考数学真题分类汇编(试卷版+解析版):三角函数

A.sinα>0 B.cosα>0
C.sin 2α>0 D.cos 2α>0
43.(2014·大纲全国·文 T2)已知角 α 的终边经过点(-4,3),则 cosα=( )
4
3
3
4
A.5
B.5
C.-5
D.-5
44.(2014·全国 1·理 T8)设 α∈
0,
π 2
,β∈
0,
π 2
,且 tan
1+sin2
段上,角 α 以 Ox 为始边,OP 为终边.若 tan α<cosα<sin α,则 P 所在的圆弧是( )
A.
B. C. D.
8.(2018·全国 1·文 T11)已知角 α 的顶点为坐标原点,始边与 x 轴的非负半轴重合,终边上有两点
2
A(1,a),B(2,b),且 cos 2α=3,则|a-b|=( )
A.1 B.2 C.3 D.4
1
1
37.(2015·重庆·文 T6)若 tan α=3,tan(α+β)=2,则 tan β=( )
1
1
5
5
A.7
B.6
C.7
D.6
2π
38.(2015·安徽·理 T10)已知函数 f(x)=Asin(ωx+φ)(A,ω,φ 均为正的常数)的最小正周期为 π,当 x= 3
5π
11π
18.(2017·天津·T7)设函数 f(x)=2sin(ωx+φ),x∈R,其中 ω>0,|φ|<π,若 f 8 =2,f 8 =0,且 f(x)
的最小正周期大于 2π,则( )
2
π
2
十年真题(2010-2019)高考数学(理)分类汇编专题09 立体几何与空间向量选择填空题(新课标Ⅰ卷)(解析版
专题09立体几何与空间向量选择填空题历年考题细目表填空题2010 三视图与直观图2010年新课标1理科14历年高考真题汇编1.【2019年新课标1理科12】已知三棱锥P﹣ABC的四个顶点在球O的球面上,P A=PB=PC,△ABC是边长为2的正三角形,E,F分别是P A,AB的中点,∠CEF=90°,则球O的体积为()A.8πB.4πC.2πD.π【解答】解:如图,由P A=PB=PC,△ABC是边长为2的正三角形,可知三棱锥P﹣ABC为正三棱锥,则顶点P在底面的射影O为底面三角形的中心,连接BO并延长,交AC于G,则AC⊥BG,又PO⊥AC,PO∩BG=O,可得AC⊥平面PBG,则PB⊥AC,∵E,F分别是P A,AB的中点,∴EF∥PB,又∠CEF=90°,即EF⊥CE,∴PB⊥CE,得PB⊥平面P AC,∴正三棱锥P﹣ABC的三条侧棱两两互相垂直,把三棱锥补形为正方体,则正方体外接球即为三棱锥的外接球,其直径为D.半径为,则球O的体积为.故选:D.2.【2018年新课标1理科07】某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.2B.2C.3 D.2【解答】解:由题意可知几何体是圆柱,底面周长16,高为:2,直观图以及侧面展开图如图:圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:2.故选:B.3.【2018年新课标1理科12】已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为()A.B.C.D.【解答】解:正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:所示的正六边形平行的平面,并且正六边形时,α截此正方体所得截面面积的最大,此时正六边形的边长,α截此正方体所得截面最大值为:6.故选:A.4.【2017年新课标1理科07】某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为()A.10 B.12 C.14 D.16【解答】解:由三视图可画出直观图,该立体图中只有两个相同的梯形的面,S梯形2×(2+4)=6,∴这些梯形的面积之和为6×2=12,故选:B.5.【2016年新课标1理科06】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π【解答】解:由题意可知三视图复原的几何体是一个球去掉后的几何体,如图:可得:,R=2.它的表面积是:4π•2217π.故选:A.6.【2016年新课标1理科11】平面α过正方体ABCD﹣A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD =m,α∩平面ABB1A1=n,则m、n所成角的正弦值为()A.B.C.D.【解答】解:如图:α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABA1B1=n,可知:n∥CD1,m∥B1D1,∵△CB1D1是正三角形.m、n所成角就是∠CD1B1=60°.则m、n所成角的正弦值为:.故选:A.7.【2015年新课标1理科06】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14斛B.22斛C.36斛D.66斛【解答】解:设圆锥的底面半径为r,则r=8,解得r,故米堆的体积为π×()2×5,∵1斛米的体积约为1.62立方,∴ 1.62≈22,故选:B.8.【2015年新课标1理科11】圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1 B.2 C.4 D.8【解答】解:由几何体三视图中的正视图和俯视图可知,截圆柱的平面过圆柱的轴线,该几何体是一个半球拼接半个圆柱,∴其表面积为:4πr2πr22r×2πr+2r×2rπr2=5πr2+4r2,又∵该几何体的表面积为16+20π,∴5πr2+4r2=16+20π,解得r=2,故选:B.9.【2014年新课标1理科12】如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.6B.6 C.4D.4【解答】解:几何体的直观图如图:AB=4,BD=4,C到BD的中点的距离为:4,∴.AC6,AD=4,显然AC最长.长为6.故选:B.10.【2013年新课标1理科06】如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm,如不计容器的厚度,则球的体积为()A.B.C.D.【解答】解:设正方体上底面所在平面截球得小圆M,则圆心M为正方体上底面正方形的中心.如图.设球的半径为R,根据题意得球心到上底面的距离等于(R﹣2)cm,而圆M的半径为4,由球的截面圆性质,得R2=(R﹣2)2+42,解出R=5,∴根据球的体积公式,该球的体积V.故选:A.11.【2013年新课标1理科08】某几何体的三视图如图所示,则该几何体的体积为()A.16+8πB.8+8πC.16+16πD.8+16π【解答】解:三视图复原的几何体是一个长方体与半个圆柱的组合体,如图,其中长方体长、宽、高分别是:4,2,2,半个圆柱的底面半径为2,母线长为4.∴长方体的体积=4×2×2=16,半个圆柱的体积22×π×4=8π所以这个几何体的体积是16+8π;故选:A.12.【2012年新课标1理科07】如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6 B.9 C.12 D.18【解答】解:该几何体是三棱锥,底面是俯视图,三棱锥的高为3;底面三角形斜边长为6,高为3的等腰直角三角形,此几何体的体积为V6×3×3=9.故选:B.13.【2012年新课标1理科11】已知三棱锥S﹣ABC的所有顶点都在球O的表面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此三棱锥的体积为()A.B.C.D.【解答】解:根据题意作出图形:设球心为O,过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,延长CO1交球于点D,则SD⊥平面ABC.∵CO1,∴OO1,∴高SD=2OO1,∵△ABC是边长为1的正三角形,∴S△ABC,∴V三棱锥S﹣ABC.故选:C.14.【2011年新课标1理科06】在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()A.B.C.D.【解答】解:由俯视图和正视图可以得到几何体是一个简单的组合体,是由一个三棱锥和被轴截面截开的半个圆锥组成,∴侧视图是一个中间有分界线的三角形,故选:D.15.【2010年新课标1理科10】设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点都在一个球面上,则该球的表面积为()A.πa2B.C.D.5πa2【解答】解:根据题意条件可知三棱柱是棱长都为a的正三棱柱,上下底面中心连线的中点就是球心,则其外接球的半径为,球的表面积为,故选:B.16.【2017年新课标1理科16】如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△F AB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△F AB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为.【解答】解法一:由题意,连接OD,交BC于点G,由题意得OD⊥BC,OG BC,即OG的长度与BC的长度成正比,设OG=,则BC=2,DG=5﹣,三棱锥的高h,3,则V,令f()=254﹣105,∈(0,),f′()=1003﹣504,令f′()≥0,即4﹣23≤0,解得≤2,则f()≤f(2)=80,∴V4cm3,∴体积最大值为4cm3.故答案为:4cm3.解法二:如图,设正三角形的边长为,则OG,∴FG=SG=5,SO=h,∴三棱锥的体积V,令b()=54,则,令b′()=0,则430,解得=4,∴(cm3).故答案为:4cm3.17.【2011年新课标1理科15】已知矩形ABCD的顶点都在半径为4的球O的球面上,且AB=6,BC=2,则棱锥O﹣ABCD的体积为.【解答】解:矩形的对角线的长为:,所以球心到矩形的距离为:2,所以棱锥O﹣ABCD的体积为:8.故答案为:818.【2010年新课标1理科14】正视图为一个三角形的几何体可以是(写出三种)【解答】解:正视图为一个三角形的几何体可以是三棱锥、三棱柱(放倒的情形)、圆锥、四棱锥等等.故答案为:三棱锥、圆锥、三棱柱.考题分析与复习建议本专题考查的知识点为:空间几何体的结构、三视图和直观图,空间几何体的表面积与体积,空间点、直线、平面之间的位置关系,直线、平面平行、垂直的判定与性质,空间向量及其运算,立体几何中的向量方法(证明平行与垂直、求空间角和距离)等.历年考题主要以选择填空题型出现,重点考查的知识点为:空间几何体的结构、三视图和直观图,空间几何体的表面积与体积,空间点、直线、平面之间的位置关系,直线、平面平行、垂直的判定与性质等.预测明年本考点题目会比较稳定,备考方向以知识点空间几何体的结构、三视图和直观图,空间几何体的表面积与体积,空间点、直线、平面之间的位置关系,直线、平面平行、垂直的判定与性质等为重点较佳.最新高考模拟试题1.在四棱锥P ABCD -中,所有侧棱都为42,底面是边长为26的正方形,O 是P 在平面ABCD 内的射影,M 是PC 的中点,则异面直线OP 与BM 所成角为( ) A .30o B .45oC .60oD .90o【答案】C 【解析】由题可知O 是正方形ABCD 的中心, 取N 为OC 的中点,所以OP MN P , 则BMN ∠是异面直线OP 与BM 所成的角. 因为OP ⊥平面ABCD , 所以MN ⊥平面ABCD ,因为在四棱锥P ABCD -中,所有侧棱都为42,底面是边长为26的正方形, 所以23OC =,所以321225OP =-=,因此5MN =,又在PBC ∆中,2223232245cos 22328PB PC BC BPC PB PC +-+-∠===•⨯,所以22252cos 32824222208BM PB PM PB PM BPC =+-••∠=+-⨯⨯⨯=, 即25BM =, 所以1cos 2MN BMN MB ∠==, 则异面直线OP 与BM 所成的角为60o . 故选C2.已知,m n 是两条不重合的直线,,αβ是两个不重合的平面,下列命题正确的是( )A .若m αP ,m βP ,n α∥,n β∥,则αβPB .若m n ∥,m α⊥,n β⊥,则αβPC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m n ⊥,m αP ,n β⊥,则αβ⊥ 【答案】B 【解析】A 选项,若m αP ,m βP ,n α∥,n β∥,则αβP 或α与β相交;故A 错;B 选项,若m n ∥,m α⊥,则n α⊥,又n β⊥,,αβ是两个不重合的平面,则αβP ,故B 正确;C 选项,若m n ⊥,m α⊂,则n α⊂或n α∥或n 与α相交,又n β⊂,,αβ是两个不重合的平面,则αβP 或α与β相交;故C 错;D 选项,若m n ⊥,m αP ,则n α⊂或n α∥或n 与α相交,又n β⊥,,αβ是两个不重合的平面,则αβP 或α与β相交;故D 错; 故选B3.已知正方体1111ABCD A B C D -的棱长为1,在对角线1A D 上取点M ,在1CD 上取点N ,使得线段MN平行于对角面11A ACC ,则||MN 的最小值为( ) A .1 B .2C .2D .3 【答案】D 【解析】作1MM AD ⊥,垂足为1M ,作1NN CD ⊥,垂足为1N ,如下图所示:在正方体1111ABCD A B C D -中,根据面面垂直的性质定理,可得11,MM NN ,都垂直于平面ABCD ,由线面垂直的性质,可知11MM NN P ,易知:1111//M M A N N ACC 平面,由面面平行的性质定理可知://11M N AC ,设11DM DN x ==,在直角梯形11MM N N 中,222211(2)(12)633MN x x x ⎛⎫=-+-=-+ ⎪⎝⎭,当13x =时,||MN 的最小值为33, 故本题选D.4.如图,某几何体的三视图如图所示,则此几何体的体积为( )A .3B .23C .3D .3【答案】A 【解析】解:根据几何体得三视图转换为几何体为:故:V 11321332=⨯⨯⨯=. 故选:A .5.已知正四棱锥P ABCD -的所有顶点都在球O 的球面上,2PA AB ==,则球O 的表面积为( )A .2πB .4πC .8πD .16π【答案】C 【解析】解:∵正四棱锥P ﹣ABCD 的所有顶点都在球O 的球面上,P A =AB =2, ∴连结AC ,BD ,交于点O ,连结PO , 则PO ⊥面ABCD ,OA =OB =OC =OD 221122222AC ==+=, OP 22422PB OB =-=-=,∴O 是球心,球O 的半径r 2=,∴球O 的表面积为S =4πr 2=8π. 故选:C .6.已知长方体全部棱长的和为36,表面积为52,则其体对角线的长为( ) A .4 B 29C .223D .17【答案】B 【解析】设长方体的三条棱的长分别为:,,x y z , 则2()524()36xy yz zx x y z ++=⎧⎨++=⎩,22222()2()95229x y z x y z xy yz zx ++=++-++=-=.故选:B .7.如图所示,边长为a 的空间四边形ABCD 中,∠BCD=90°,平面ABD⊥平面BCD ,则异面直线AD 与BC所成角的大小为()A.30°B.45°C.60°D.90°【答案】C【解析】由题意得BC=CD=a,∠BCD=90°,∴BD=2a,∴∠BAD=90°,取BD中点O,连结AO,CO,∵AB=BC=CD=DA=a,∴AO⊥BD,CO⊥BD,且AO=BO=OD=OC=22a,又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊥BD,∴AO⊥平面BCD,延长CO至点E,使CO=OE,连结ED,EA,EB,则四边形BCDE为正方形,即有BC∥DE,∴∠ADE(或其补角)即为异面直线AD与BC所成角,由题意得AE=a,ED=a,∴△AED为正三角形,∴∠ADE=60°,∴异面直线AD与BC所成角的大小为60°.故选:C.8.鲁班锁起于中国古代建筑中首创的榫卯结构,相传由春秋时代鲁国工匠鲁班所作. 下图是经典的六柱鲁班锁及六个构件的图片,下图是其中一个构件的三视图,则此构件的体积为A .334000mmB .333000mmC .332000mmD .330000mm【答案】C 【解析】由三视图得鲁班锁的其中一个零件是:长为100,宽为20,高为20的长方体的上面的中间部分去掉一个长为40,宽为20,高为10的小长体的一个几何体,如图,∴该零件的体积:V =100×20×20﹣40×20×10=32000(mm 3).故选:C .9.在正方体1111ABCD A B C D -中,动点E 在棱1BB 上,动点F 在线段11A C 上,O 为底面ABCD 的中心,若1,BE x A F y ==,则四面体O AEF -的体积( )A .与,x y 都有关B .与,x y 都无关C .与x 有关,与y 无关D .与y 有关,与x 无关【答案】B 【解析】因为V O -AEF =V E -OAF ,所以,考察△AOF 的面积和点E 到平面AOF 的距离的值, 因为BB 1∥平面ACC 1A 1,所以,点E 到平面AOE 的距离为定值, 又AO∥A 1C 1,所以,OA 为定值,点F 到直线AO 的距离也为定值, 即△AOF 的面积是定值,所以,四面体O AEF -的体积与,x y 都无关,选B 。
十年(2010-2019)高考数学真题分类汇编(试卷版+解析版):不等式

A.-15 B.-9
C.1 D.9
3x + 2y-6 ≤ 0,
8.(2017·全国 3·文 T5)设 x,y 满足约束条件 x ≥ 0,
则 z=x-y 的取值范围是( )
y ≥ 0,
A.[-3,0] B.[-3,2]
C.[0,2] D.[0,3] x + 3y ≤ 3,
9.(2017·全国 1·文 T7)设 x,y 满足约束条件 x-y ≥ 1, 则 z=x+y 的最大值为( ) y ≥ 0,
A.-7 B.-6
C.-5 D.-3
x ≥ 1,
x + y ≤ 3,
35.(2013·全国 2·理 T9)已知 a>0,x,y 满足约束条件
若 z=2x+y 的最小值为 1,则 a=( )
y ≥ a(x-3).
1
1
A.4
B.2
C.1
D.2
36.(2013·湖北·文 T9)某旅行社租用 A,B 两种型号的客车安排 900 名客人旅行,A,B 两种车辆的载客量分
x-3y + 3 ≥ 0,
A.8 B.7 C.2 D.1
2
2
33.(2013·重庆·文 T7)关于 x 的不等式 x -2ax-8a <0(a>0)的解集为(x1,x2),且 x2-x1=15,则 a=( )
5
7
15
15
A.2
B.2
C. 4
D. 2
x-y + 1 ≥ 0,
34.(2013·全国 2·文 T3)设 x,y 满足约束条件 x + y-1 ≥ 0,则 z=2x-3y 的最小值是( ) x ≤ 3,
十年(2010—2019)数学高考真题分类汇编
2010-2019年十年高考数学真题分类汇编.docx

A.1
B.2
C.3
D.4
31(. 2017Ⅲ理 1)已知集合 A = (x, y) x2 + y2 = 1 ,B = (x, y) y = x ,则 A I B 中元素的个数为( )
A.3
B.2
C.1
D.0
32.(2018Ⅰ文 1)已知集合 A = 0,2 , B = -2,-1,0,1,2 ,则 A I B = ( )
A.(-14,16)
B.(-14,20)
C.(-12,18)
D.(-12,20)
x-3 2.(2010Ⅱ文 2)不等式 0 的解集为( )
x+2
A.{x|-2< x<3} B.{ x|x<-2}
C.{ x|x<-2,或 x>3} D.{ x∣x>3}
x -1
3.(2010Ⅱ文
5
理
3)若变量
x,y
1.集合
1.(2010Ⅰ文理 1)已知集合 A = x | x 2,x R,B = x | x 4,x Z ,则 A I B =( )
A.(0,2)
B.[0,2]
C.{0,2}
D.{0,1,2}
2.(2010Ⅱ文 1)设全集 U= x N * | x 6 ,集合 A={1,3},B={3,5},则 CU A U B =( )
A.{-1,0}
B.{0,1}
C.{-1,0,1}
D.{0,1,2}
20.(2016Ⅰ文 1)设集合 A={1,3,5,7},B={x| 2 x 5},则 A∩B=( )
A.{1,3}
B.{3,5}
C.{5,7}
D.{1,7}
21.(2016Ⅰ理 1)设集合 A={x|x2-4x+3<0},B={x|2x-3>0},则 A I B = ( )
十年真题(2010-2019)高考数学(理)分类汇编专题12 平面解析几何解答题(新课标Ⅰ卷)(原卷版)
专题12平面解析几何解答题历年考题细目表题型年份考点试题位置解答题2019 抛物线2019年新课标1理科19解答题2018 椭圆2018年新课标1理科19解答题2017 椭圆2017年新课标1理科20解答题2016 圆的方程2016年新课标1理科20解答题2015 抛物线2015年新课标1理科20解答题2014 椭圆2014年新课标1理科20解答题2013 圆的方程2013年新课标1理科20解答题2012 抛物线2012年新课标1理科20解答题2011 抛物线2011年新课标1理科20解答题2011 圆的方程2011年新课标1理科22解答题2010 椭圆2010年新课标1理科20历年高考真题汇编1.【2019年新课标1理科19】已知抛物线C:y2=3的焦点为F,斜率为的直线l与C的交点为A,B,与轴的交点为P.(1)若|AF|+|BF|=4,求l的方程;(2)若3,求|AB|.2.【2018年新课标1理科19】设椭圆C:y2=1的右焦点为F,过F的直线l与C交于A,B两点,点M的坐标为(2,0).(1)当l与轴垂直时,求直线AM的方程;(2)设O为坐标原点,证明:∠OMA=∠OMB.3.【2017年新课标1理科20】已知椭圆C:1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1,),P4(1,)中恰有三点在椭圆C上.(1)求C的方程;(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为﹣1,证明:l 过定点.4.【2016年新课标1理科20】设圆2+y2+2﹣15=0的圆心为A,直线l过点B(1,0)且与轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.(Ⅰ)证明|EA|+|EB|为定值,并写出点E的轨迹方程;(Ⅱ)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.5.【2015年新课标1理科20】在直角坐标系Oy中,曲线C:y与直线l:y=+a(a>0)交于M,N两点.(Ⅰ)当=0时,分別求C在点M和N处的切线方程.(Ⅱ)y轴上是否存在点P,使得当变动时,总有∠OPM=∠OPN?(说明理由)6.【2014年新课标1理科20】已知点A(0,﹣2),椭圆E:1(a>b>0)的离心率为,F是椭圆的右焦点,直线AF的斜率为,O为坐标原点.(Ⅰ)求E的方程;(Ⅱ)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.7.【2013年新课标1理科20】已知圆M:(+1)2+y2=1,圆N:(﹣1)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线C.(Ⅰ)求C的方程;(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.8.【2012年新课标1理科20】设抛物线C:2=2py(p>0)的焦点为F,准线为l,A∈C,已知以F为圆心,F A为半径的圆F交l于B,D两点;(1)若∠BFD=90°,△ABD的面积为,求p的值及圆F的方程;(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.9.【2011年新课标1理科20】在平面直角坐标系Oy中,已知点A(0,﹣1),B点在直线y=﹣3上,M 点满足∥,•,M点的轨迹为曲线C.(Ⅰ)求C的方程;(Ⅱ)P为C上的动点,l为C在P点处的切线,求O点到l距离的最小值.10.【2011年新课标1理科22】如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于的方程2﹣14+mn=0的两个根.(Ⅰ)证明:C,B,D,E四点共圆;(Ⅱ)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.11.【2010年新课标1理科20】设F1,F2分别是椭圆的左、右焦点,过F1斜率为1的直线ℓ与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.(1)求E的离心率;(2)设点P(0,﹣1)满足|P A|=|PB|,求E的方程.考题分析与复习建议本专题考查的知识点为:直线方程、圆的方程,直线与圆、圆与圆的位置关系,椭圆、双曲线、抛物线及其性质,直线与圆锥曲线,曲线与方程等.历年考题主要以解答题题型出现,重点考查的知识点为:直线与圆、圆与圆的位置关系,椭圆、双曲线、抛物线及其性质,直线与圆锥曲线等,预测明年本考点题目会比较稳定,备考方向以知识点直线与圆、圆与圆的位置关系,椭圆、双曲线、抛物线及其性质,直线与圆锥曲线等为重点较佳.最新高考模拟试题1.已知椭圆22122:1(0)x y C a b a b +=>>的离心率为6,椭圆22222:1(0)33x y C a b a b +=>>经过点33,22⎛⎫ ⎪ ⎪⎝⎭. (1)求椭圆1C 的标准方程;(2)设点M 是椭圆1C 上的任意一点,射线MO 与椭圆2C 交于点N ,过点M 的直线l 与椭圆1C 有且只有一个公共点,直线l 与椭圆2C 交于,A B 两个相异点,证明:NAB △面积为定值.2.如图,在平面直角坐标系Oy 中,椭圆C :22221x y a b+=(a >b >0)经过点(0,3-),点F 是椭圆的右焦点,点F 到左顶点的距离和到右准线的距离相等.过点F 的直线l 交椭圆于M ,N 两点.(1)求椭圆C 的标准方程;(2)当MF =2FN 时,求直线l 的方程;(3)若直线l 上存在点P 满足PM·PN=PF 2,且点P 在椭圆外,证明:点P 在定直线上.3.已知抛物线C :24y x =的焦点为F ,直线l 与抛物线C 交于A ,B 两点,O 是坐标原点.(1)若直线l 过点F 且8AB =,求直线l 的方程;(2)已知点(2,0)E -,若直线l 不与坐标轴垂直,且AEO BEO ∠=∠,证明:直线l 过定点.4.已知椭圆22221(0)x y a b a b+=>>,()2,0A 是长轴的一个端点,弦BC 过椭圆的中心O ,点C 在第一象限,且0AC BC ⋅=u u u r u u u r ,||2||OC OB AB BC -=+u u u r u u u r u u u r u u u r.(1)求椭圆的标准方程;(2)设P 、Q 为椭圆上不重合的两点且异于A 、B ,若PCQ ∠的平分线总是垂直于x 轴,问是否存在实数λ,使得PQ AB =λu u u r u u u r ?若不存在,请说明理由;若存在,求λ取得最大值时的PQ 的长.5.已知抛物线216y x =,过抛物线焦点F 的直线l 分别交抛物线与圆22(4)16x y -+=于,,,A C D B (自上而下顺次)四点.(1)求证:||||AC BD ⋅为定值;(2)求||||AB AF ⋅的最小值.6.已知O 为坐标原点,点()()2,02,0A B -,,()01AC AD CB CD λλ===<<u u u r u u u r ,过点B 作AC的平行线交AD 于点E .设点E 的轨迹为τ.(Ⅰ)求曲线τ的方程;(Ⅱ)已知直线l 与圆22:1O x y +=相切于点M ,且与曲线τ相交于P ,Q 两点,PQ 的中点为N ,求三角形MON 面积的最大值.7.已知椭圆2222:1(0)x y C a b a b +=>>F 是椭圆C 的一个焦点.点(02)M ,,直线MF 的(1)求椭圆C 的方程;(2)若过点M 的直线l 与椭圆C 交于A B ,两点,线段AB 的中点为N ,且AB MN =.求l 的方程.8.已知椭圆2222:1(0)x y C a b a b +=>>过点(,右焦点F 是抛物线28y x =的焦点. (1)求椭圆C 的方程;(2)已知动直线l 过右焦点F ,且与椭圆C 分别交于M ,N 两点.试问x 轴上是否存在定点Q ,使得13516QM QN ⋅=-u u u u r u u u r 恒成立?若存在求出点Q 的坐标若不存在,说明理由.9.关于椭圆的切线由下列结论:若11(,)P x y 是椭圆22221(0)x y a b a b+=>>上的一点,则过点P 的椭圆的切线方程为11221x x y y a b +=.已知椭圆22:143x y C +=. (1)利用上述结论,求过椭圆C 上的点(1,)(0)P n n >的切线方程;(2)若M 是直线4x =上任一点,过点M 作椭圆C 的两条切线MA ,MB (A ,B 为切点),设椭圆的右焦点为F ,求证:MF AB ⊥.10.已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12F F ,,离心率为12,P 为椭圆上一动点(异于左右顶点),若12AF F △(1)求椭圆C 的方程;(2)若直线l 过点1F 交椭圆C 于,A B 两点,问在x 轴上是否存在一点Q ,使得QA QB ⋅u u u r u u u r 为定值?若存在,求点Q 的坐标;若不存在,请说明理由.11.已知点()1,0F ,直线:1l x =-,P 为平面上的动点,过点P 作直线的垂线,垂足为Q ,且QP QF FP FQ ⋅=⋅u u u r u u u r u u u r u u u r .(1)求动点P 的轨迹C 的方程;(2)设直线y kx b =+与轨迹C 交于两点,()11,A x y 、()22,B x y ,且12y y a -= (0a >,且a 为常数),过弦AB 的中点M 作平行于x 轴的直线交轨迹C 于点D ,连接AD 、BD .试判断ABD ∆的面积是否为定值,若是,求出该定值,若不是,请说明理由12.已知点P 在抛物线()220C x py p =:>上,且点P 的横坐标为2,以P 为圆心,PO 为半径的圆(O 为原点),与抛物线C 的准线交于M ,N 两点,且2MN =.(1)求抛物线C 的方程;(2)若抛物线的准线与y 轴的交点为H .过抛物线焦点F 的直线l 与抛物线C 交于A ,B ,且AB HB ⊥,求AF BF -的值.13.已知抛物线方程24y x =,F 为焦点,P 为抛物线准线上一点,Q 为线段PF 与抛物线的交点,定义()PF d P FQ=. (1)当8(1)3P --,时,求()d P ; (2)证明存在常数a ,使得2()d P PF a =+.(3)123,,P P P 为抛物线准线上三点,且1223PP P P =,判断13()()d P d P +与22()d P 的关系. 14.已知抛物线2:2(0)C x py p =>的焦点F 到准线距离为2.(1)若点(1,1)E ,且点P 在抛物线C 上,求||||PE PF +的最小值;(2)若过点(0,)N b 的直线l 与圆22:(2)4M x y +-=相切,且与抛物线C 有两个不同交点,A B ,求AOB ∆的面积.15.已知曲线C 上的任意一点到直线l :=12的距离与到点F (102,)的距离相等. (1)求曲线C 的方程;(2)若过P (1,0)的直线与曲线C 相交于A ,B 两点,Q (1,0)为定点,设直线AQ 的斜率为1,直线BQ 的斜率为2,直线AB 的斜率为,证明:22212112k k k +-为定值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
柱的体积为
.
(4. 2019 全国Ⅰ理 12)已知三棱锥 P-ABC 的四个顶点在球 O 的球面上, , PA=PB=PC △ABC
是边长为 2 的正三角形,E,F 分别是 , PA AB 的中点,∠CEF=90°,则球 O 的体积为
.A 8 6π
.B 4 6π
.C 2 6π
.D 6π
1 / 20
(5. 2019 浙江 4)祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同,则积不容异” 称为祖暅原理,利用该原理可以得到柱体体积公式 V 柱体=Sh,其中 S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示,则该柱体的体积是
.A 8cm3
. . B 12cm3 C 32 cm3
.D 40 cm3
3
3
.( 17 2015 陕西)一个几何体的三视图如图所示,则该几何体的表面积为
7 / 20
. . . . A 3π B 4π C 2π + 4 D 3π + 4 .( 18 2015 重庆)某几何体的三视图如图所示,则该几何体的体积为
10 年(2010-2019)高考数学真题分类练习与讲解
第二十二讲 空间几何体的三视图、表面积和体积
2019 年
(1. 2019 全国Ⅲ理 16)学生到工厂劳动实践,利用 3D 打印技术制作模型.如图,该模型为 长方体 ABCD − A1B1C1D1 挖去四棱锥 O—EFGH 后所得几何体,其中 O 为长方体的中心, E,F,G,H 分别为所在棱的中点, AB = BC = 6cm, AA1 = 4cm ,3D 打印所用原料密度 为 0.9 g/cm3,不考虑打印损耗,制作该模型所需原料的质量为___________.
积为
π .A 1 + 2 33
.B
1+ 2 3 3π
.C
1+ 2 3 6π
.D
1+
2 6π
.( 13 2016 全国 I)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直
的半径,若该几何体的体积是283π,则它的表面积是
.A 17π
.B 18π
.C 20π
.D 28π
.( 14 2016 全国 II)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积
(2. 2019 江苏 9)如图,长方体 ABCD − A1B1C1D1 的体积是 , 120 E 为CC1 的中点,则三棱 锥 E-BCD 的体积是 .
(3. 2019 天津理 11)已知四棱锥的底面是边长为 2 的正方形,侧棱长均为 5 .若圆柱的一
个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆
为
6 / 20
.A 20π
.B 24π
.C 28π
.D 32π
.( 15 2016 年全国 III)如图,网格纸上小正方形的边长为 1,粗实线画出的是某多面体的三
视图,则该多面体的表面积为
.A 18 + 36 5
.B 54 +18 5
.C 90
.D 81
.16 (2015 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积是
4 / 20
.A 90π
.B 63π
.C 42π
.D 36π
.(9 2017 新课标Ⅲ)已知圆柱的高为 1,它的两个底面的圆周在直径为 2 的同一个球的球面
上,则该圆柱的体积为
A.π
B. 3π
C. π
D. π
4
2
4
.( 10 2017 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3 )
直角三角形组成,正方形的边长为 2,俯视图为等腰直角三角形,该多面体的各个面中
有若干个是梯形,这些梯形的面积之和为
.A 10
.B 12
.C 14
.D 16
.(8 2017 新课标Ⅱ)如图,网格纸上小正方形的边长为 1,粗实线画出的是某几何体的三视
图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为
A B
.A 2 17
.B 2 5
.C 3
.D 2
.3 (2018 全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进
部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的
木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是
.4 (2018 全国卷Ⅲ)设 A , B ,C , D 是同一个半径为 4 的球的球面上四点,∆ABC 为等
2
正1(主)视1俯 侧(左2)视俯
俯俯俯
2 / 20
.A 1
.B 2
.C 3
.D 4
.2 (2018 全国卷Ⅰ)某圆柱的高为 2,底面周长为 16,其三视图如图.圆柱表面上的点 M 在
正视图上的对应点为 A,圆柱表面上的点 N 在左视图上的对应点为B ,则在此圆柱侧面
上,从M 到 N 的路径中,最短路径的长度为
3 / 20
A1
A
.A 4
.B 8
.C 12
.D 16
.6 (2018 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3 )
是
2
正1 侧侧1 侧侧2 侧
俯侧侧
.A 2
.B 4
.C 6
.D 8
.(7 2017 新课标Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰
.A 158
.B 162
.C 182
.D 32
(6. 2019 北京 11)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示。如果
网格纸上小正方形的边长为 1,那么该几何体的体积为________.
2010-2018 年
一、选择题 .1 (2018 北京)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为
边三角形且其面积为9 3 ,则三棱锥 D − ABC 体积的最大值为
.A 12 3
.B 18 3
.C 24 3
.D 54 3
.5 (2018 上海《) 九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设 AA1 是正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点,以 AA1为底面矩形 的一边,则这样的阳马的个数是( )
是
3
正1 俯俯1
侧1 俯俯1
俯俯俯
. . π
A +1
π B +.D 3π + 3
2
2
2
2
.( 11 2017 北京)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为
5 / 20
.A 3 2
.B 2 3
.C 2 2
.D 2
.( 12 2016 山东)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体
