求不规则物体的体积题型总结

不规则物体的体积计算公式

不规则物体的体积计算公式以下是几种常用的方法来计算不规则物体的体积：1.浸水法：这是一种最常见的方法，适用于固体物体。

首先，测量物体在空气中的质量。

然后，将物体完全浸入水中，并测量所需水的体积。

最后，用浸水后的物体所取得的质量减去空气中的质量，得到物体的净质量增量。

根据物体的质量增加以及水的密度，可以使用以下公式计算物体的体积：体积=（浸水后物体的净重量）/（水的密度）2.图像处理法：对于二维平面上的图像，可以使用图像处理软件来计算不规则物体的体积。

首先，将物体放置在一个标准背景上，并拍摄照片。

然后，使用图像处理软件将物体的轮廓与背景分离，并量化轮廓的像素值。

根据像素值和已知的标准尺寸，可以得出物体的面积。

最后，通过将物体的面积乘以物体的高度，可以计算出物体的体积。

3.位移法：这是一种适用于液体物体的方法。

将液体物体放在一个容器内并测量容器的初始体积。

然后，将物体放在容器中并测量物体和容器的组合体积。

最后，通过将组合体积减去容器的初始体积，可以得到物体的体积。

4.比例估计法：当无法直接测量不规则物体时，可以使用比例估计法来估算物体的体积。

首先，选取一个已知形状和尺寸的物体，将其放置在物体旁边。

然后，测量这个已知物体的体积和不规则物体的尺寸，以及已知和不规则物体之间的比例关系。

最后，通过将已知物体的体积与比例关系相乘，可以估算出不规则物体的体积。

需要注意的是，不规则物体的体积计算通常都是近似值，并且可能存在一定的误差。

因此，在进行具体计算时，应尽量采用精确的测量方法，并对结果进行合理的范围估计。

总结起来，计算不规则物体的体积需要根据物体的特点选择合适的方法，如浸水法、图像处理法、位移法或比例估计法。

通过这些方法，可以估算或测量不规则物体的体积，从而满足相关的工程或科学需求。

不规则物体的体积计算公式(二)

不规则物体的体积计算公式(二)不规则物体的体积计算公式1. 概述在计算物体体积时，我们通常会使用基本几何体的公式，如长方体、圆柱体等。

然而，对于不规则形状的物体，这些基本公式无法直接适用。

本文将介绍几种用于计算不规则物体体积的公式，并附带示例说明。

2. 水位法水位法是一种简单但有效的方法，通过在容器中浸入物体并测量水位的变化，来计算物体的体积。

公式如下：体积 = 水位变化× 容器截面积例如，假设有一个不规则形状的石块，我们将其放入一个容器中，并在容器内装满水，测量水位变化为10 cm，容器截面积为1000 cm^2。

那么石块的体积可以计算为：体积= 10 cm × 1000 cm^2 = 10000 cm^33. 序列法序列法是一种逐层逼近的方法，通过将不规则物体划分成多个较简单的几何形状，然后逐个计算它们的体积，并将所有体积相加得到最终结果。

例如，假设有一个复杂形状的雕塑，我们可以将它划分成一个个的长方体、球体和圆柱体。

分别计算它们的体积，然后将所有体积求和即可得到整个雕塑的体积。

4. CAD软件测量对于较为复杂的不规则物体，可以使用计算机辅助设计（CAD）软件来测量其体积。

CAD软件提供了强大的建模工具，可以对不规则物体进行精确的测量和计算。

例如，假设我们有一个复杂的机械零件，我们可以使用CAD软件绘制其三维模型，并通过软件提供的体积计算功能得到准确的体积结果。

5. 比例尺测量对于一些简单但不规则的物体，我们可以使用比例尺来进行近似测量。

首先需要制作一个比例尺模型，然后使用比例尺模型对不规则物体进行测量，并进行计算。

例如，假设我们要计算一个不规则岩石的体积，我们可以先制作一个比例尺模型，测量比例尺模型的体积，并记录比例尺值。

然后，将比例尺模型用于测量岩石的尺寸，然后根据比例计算岩石的实际体积。

6. 其他方法除了上述方法外，还有许多其他方法可以用于计算不规则物体的体积。

如激光测量、光学测量等。

不规则物体的体积计算公式(一)

不规则物体的体积计算公式(一)不规则物体的体积计算公式1. 体积计算公式的介绍对于不规则物体的体积计算，我们需要使用一些特定的公式来求解。

这些公式根据不同的物体类型和形状而有所不同。

下面列举了几个常用的不规则物体体积计算公式。

2. 立方体和长方体的体积计算公式立方体（Cube）的体积公式立方体的体积公式为：V = a^3，其中a为立方体的边长。

例如，一个边长为5厘米的立方体的体积可以通过公式计算为V = 5^3 = 125立方厘米。

长方体（Rectangular Prism）的体积公式长方体的体积公式为：V = lwh，其中l、w、h分别为长方体的长度、宽度和高度。

假设一个长方体的长度为10厘米，宽度为8厘米，高度为6厘米，可以通过公式计算其体积为V = 10 * 8 * 6 = 480立方厘米。

3. 圆柱体和圆锥体的体积计算公式圆柱体（Cylinder）的体积公式圆柱体的体积公式为：V = πr^2h，其中r为圆柱体的底面半径，h为圆柱体的高度，π取近似值。

假设一个圆柱体的底面半径为4厘米，高度为10厘米，可以通过公式计算其体积为V = * 4^2 * 10 =立方厘米。

圆锥体（Cone）的体积公式圆锥体的体积公式为：V = (1/3)πr^2h，其中r为圆锥体的底面半径，h为圆锥体的高度，π取近似值。

假设一个圆锥体的底面半径为6厘米，高度为12厘米，可以通过公式计算其体积为V = (1/3) * * 6^2 * 12 = 立方厘米。

4. 球体的体积计算公式球体的体积公式为：V = (4/3)πr^3，其中r为球体的半径，π取近似值。

假设一个球体的半径为7厘米，可以通过公式计算其体积为V = (4/3) * * 7^3 = 立方厘米。

5. 特殊形状的体积计算公式除了上述提到的常见不规则物体，还存在一些特殊形状的物体体积计算公式，如圆环、球冠等，这些公式根据物体的具体形状和属性而不同。

以上就是一些常用的不规则物体体积计算公式的介绍和示例。

不规则的物体体积计算方法

不规则的物体体积计算方法计算不规则物体体积的方法有多种，以下将介绍其中常用的几种方法。

1.几何解法：这种方法适用于能将不规则物体转化为几何图形进行计算体积的情况，比如由平面图形堆叠而成的物体。

步骤如下：(1)将不规则物体分解为几何图形组合，如长方体、圆柱体、球体等；(2)分别计算每个几何图形的体积；(3)将所有几何图形的体积相加即可得到不规则物体的体积。

2.水位法：这种方法适用于能够被水完全浸泡的物体。

步骤如下：(1)准备一个能承装住整个物体的容器，并在其旁边放置一个容器来接水；(2)将接水容器放在底部，加入适量的水，记录接水容器中的水位；(3)将不规则物体完全浸入到容器中，水会溢出并流入到接水容器中，记录此刻接水容器中的水位；(4)用接水容器中的水位减去初始水位，即可得到不规则物体的体积。

3.位移法：这种方法适用于能够依靠称重获取物体的质量信息的情况。

步骤如下：(1)将空容器放在天平上，并记录容器的质量；(2)将不规则物体放入容器中，记录新的质量；(3)用新的质量减去初始质量，即可得到物体在空容器中的质量；(4)将物体浸入水中，并记录此时的质量；(5)利用物体在空气中的质量减去物体在水中的质量，即可得到物体的体积。

4.投影法：这种方法适用于能够通过物体的截面积及其高度计算体积的情况。

步骤如下：(1)将不规则物体放置在一块平面上，使其截面正对平面；(2)使用测量仪器，如卡尺、尺子等，测量物体截面的长度及宽度，并记录下来；(3)测量物体在垂直方向上的高度，并记录下来；(4)根据测得的截面长度、宽度和高度，计算物体的截面积；(5)将所有截面积相加，乘以高度，即可得到物体的体积。

以上介绍了几种计算不规则物体体积的常用方法，具体应根据不规则物体的特点选择合适的方法进行计算。

求不规则物体体积的方法

求不规则物体体积的方法1. 嘿，用水来测量呀！就像测一块奇形怪状的石头，把它放进装满水的容器里，溢出来的水的体积不就是石头的体积嘛！你说这办法是不是超简单？例子：咱拿个不规则的小摆件，把它丢进一盆水里，看水往外溢了多少，那就是小摆件的体积咯！2. 哎呀，还可以用填补法呢！比如说有个坑坑洼洼的东西，用一些规则的小物件把它填满，然后算算这些小物件的体积总和，不就知道那个不规则物体的体积啦？这多有意思呀！例子：像那个形状怪模怪样的箱子，咱用小立方体往里填，填满了一统计小立方体的数量，不就成啦！3. 哈哈，还有称重法呢！你知道不，先称出这个不规则物体的重量，再找一个和它材质相同但形状规则的东西，称出规则物体的重量和体积，通过比例就能算出不规则物体体积啦，是不是很神奇呢？例子：那个奇奇怪怪的金属玩意儿，先称它多重，再找个同样金属的规则小块，这一对比计算不就有啦！4. 哇塞，利用投影法呀！把这个不规则物体投影到一个面上，测量投影的相关数据，通过一些计算也可以得到它的体积呢，好厉害吧！例子：那个弯弯扭扭的模型，投影到板子上，量一量算一算，体积就出来咯！5. 嘿呀，用排沙法呀！把不规则物体埋在沙子里，测量沙子被排开的多少，就是它的体积呀，这多好玩！例子：把那个模样奇特的小玩意埋进沙堆里，看看沙子鼓出来多少，嗯嗯，简单！6. 咦，还能通过标记法呢！在不规则物体上做标记，然后进行切割或者拆分，计算各部分的体积再相加，也能知道啦，这办法酷不酷？例子：那个怪里怪气的雕塑，做上标记一块块来算，加起来不就行了嘛！7. 哇哦，利用油膜法呀！让不规则物体在油膜上滚一圈，测量油膜被铺开的面积，也能间接算出体积呢，真的好特别哦！例子：像那个软趴趴的奇怪东西，在油膜上这么一滚，哈哈，就有线索算体积啦！我觉得呀，这些方法都各有各的奇妙之处，都能帮我们很好地求出不规则物体的体积呢！。

不规则物体的体积计算公式

不规则物体的体积计算公式在数学和几何学中，一个不规则物体是指没有对称性或边界不规则的三维物体。

计算这样的物体的体积可能会比较复杂，但有几种方法可以用来近似计算。

在本文中，将介绍几种常见的计算不规则物体体积的方法。

方法一：分块法分块法是一种常见的计算不规则物体体积的方法。

它的基本思想是将不规则物体划分为一系列规则的子块，然后计算每个子块的体积，并将它们相加。

这种方法适用于不规则物体可以被分解成简单形状（如长方体、球体、圆柱体等）的情况。

例如，如果要计算一个不规则四面体的体积，可以先将其划分为四个三角形和一个底面为等腰梯形的长方体。

然后，计算每个三角形和长方体的体积，最后将它们相加即可得到整个四面体的体积。

方法二：积分法积分法是一种适用于连续曲线和曲面的计算体积的方法。

它基于微积分的概念，通过对曲线或曲面的方程进行求积分来计算其面积或体积。

对于不规则物体的体积计算，可以首先找到一个能够完全包围该物体的曲面，然后使用积分法计算这个曲面的体积。

这种方法适用于不规则物体的形状比较复杂，难以被分块法处理的情况。

方法三：几何测量法几何测量法是一种基于实际测量的计算不规则物体体积的方法。

它通过使用测量工具（如尺子、量角器、测量杯等）来获得物体的尺寸，然后使用相应的几何公式来计算体积。

在测量不规则物体体积时，需要采取适当的方法来测量其尺寸。

例如，可以使用尺子或测量线来测量物体的长度、宽度和高度，然后使用相应的几何公式（如长方体的体积公式）来计算体积。

总结：不规则物体的体积计算是一个相对复杂的问题，没有统一的计算公式。

通常情况下，我们可以使用分块法、积分法或几何测量法来近似计算不规则物体的体积。

具体的计算方法取决于不规则物体的形状和复杂程度。

在实际应用中，我们可以根据具体情况选择合适的方法来计算不规则物体的体积。

求不规则物体的体积的方法

求不规则物体的体积的方法不规则物体的体积是指无法通过简单的几何公式计算得出的物体的容量。

这种类型的物体可能具有复杂的形状和表面，因此要计算它们的体积需要使用一些特殊的方法和工具。

下面将介绍一些常见的求解不规则物体体积的方法。

1.浮法（水位法）测量体积法：这种方法通常适用于液体以及可溶于液体的固体不规则物体。

首先，将一个容器内填满水；然后将不规则物体浸没于水中。

根据浸没之前和之后水位的差值，可以求出物体的体积。

这是因为，物体浸没进水中，水位上升的体积等于物体的体积。

2.几何建模计算体积法：这种方法适用于能够通过几何建模软件进行三维建模的不规则物体。

首先，使用计算机辅助设计（CAD）软件创建物体的三维模型。

然后通过计算软件对模型进行体积计算。

这种方法在工程、建筑等领域中经常使用。

3.分割求和法：对于无法通过几何建模计算的大型不规则物体，可以将其分割成若干个简化的几何形状，然后计算各个分割部分的体积，并将它们求和得到整体体积。

这种方法适用于多边形、曲面及不规则多面体等简化模型的不规则物体。

4.倾斜平台法：这种方法适用于密度均匀的不规则物体。

首先，将不规则物体放在一个平台上，该平台可倾斜。

然后测量物体在水平位置和倾斜位置时平台的倾斜角度和重量。

通过计算不规则物体在不同角度下的受力差异，可以求得物体的体积。

5.光学投影法：这种方法适用于具有清晰表面且不透明的不规则物体。

通过使用光源照射物体，观察其投影在平面上的形状，从而对物体的体积进行估算。

通过测量投影的面积和计算物体与平面之间的距离，可以得出物体的体积。

值得注意的是，以上方法都是近似求解不规则物体体积的方法，因此其准确性可能与物体的形状和性质有关。

此外，在实际应用中，还需要注意样品制备与操作的精确性，以及各种误差产生的可能性，并辅以合理的结果检验与验证。

不规则的物体体积计算方法

不规则的物体体积计算方法在我们日常生活中，我们经常会遇到一些不规则的物体，如水果、蔬菜、岩石等。

对于这些不规则的物体，我们可能会想知道它们的体积，以便更好地理解它们的特性和应用。

本文将介绍一些计算不规则物体体积的方法。

一、水位法水位法是计算不规则物体体积的一种简单有效的方法。

它的原理是利用容器的体积变化来计算物体的体积。

具体操作步骤如下：1. 准备一个容器，容器的口径要大于物体的最大尺寸；2. 在容器中加入一定量的水，记录此时的水位；3. 将物体完全浸入水中，注意确保物体表面没有气泡存在；4. 再次记录水位；5. 物体的体积等于第二次记录的水位减去第一次记录的水位。

二、位移法位移法是通过测量不规则物体在浸入液体前后所占据的空间位移来计算体积的方法。

具体操作步骤如下：1. 准备一个容器，容器的尺寸要能够容纳物体；2. 在容器中加入一定量的液体，液体的种类可以根据物体的性质选择；3. 将容器放在一个平稳的表面上，并记录液体的初始高度；4. 将物体浸入液体中，并记录液体的最终高度；5. 通过液体高度的变化来计算物体的体积。

三、分割法分割法是将不规则物体分割成几个规则的几何体，然后计算各个几何体的体积之和来得到物体的体积。

具体操作步骤如下：1. 观察物体的形状，并尝试将其分割成几个规则的几何体，如长方体、圆柱体等；2. 测量分割后每个几何体的尺寸，如底面积、高度等；3. 使用相应的体积公式计算每个几何体的体积；4. 将每个几何体的体积相加，得到物体的总体积。

四、模型法模型法是通过制作一个与不规则物体相似但尺寸可测量的模型来计算物体的体积。

具体操作步骤如下：1. 选择一种易于加工的材料，如黏土、泥土等；2. 根据物体的形状和尺寸制作一个与之相似的模型；3. 测量模型的尺寸，如长度、宽度、高度等；4. 使用相应的体积公式计算模型的体积；5. 将模型的体积与物体的相似比例关系来计算物体的体积。

通过以上四种方法，我们可以计算出不规则物体的体积。

不规则物体的体积公式

不规则物体的体积公式1. 球体（Sphere）：球体是一种常见的几何体，其体积可以通过以下公式进行计算：V球=(4/3)πr³2. 圆柱体（Cylinder）：圆柱体由一个圆形底面和一个平行于底面的侧面组成。

其体积可以通过以下公式进行计算：V柱=πr²h3. 锥体（Cone）：锥体由一个圆形底面和一个相交于底面的侧面组成。

其体积可以通过以下公式进行计算：V锥=(1/3)πr²h4. 多面体（Polyhedron）：多面体是由多个平面多边形组成的立体。

其体积可以通过不同的方法进行计算，具体取决于多面体的形状。

以下是几个常见多面体的体积计算公式：- 三棱锥（Triangular Pyramid）：V三棱锥=(1/3)Bh其中，V三棱锥表示三棱锥的体积，B是底面积，h是高度。

- 正方体（Cube）：V正方体=a³其中，V正方体表示正方体的体积，a是正方体的边长。

- 正四面体（Tetrahedron）：V正四面体=(1/3)Ö2*a³其中，V正四面体表示正四面体的体积，a是正四面体的边长。

- 正八面体（Octahedron）：V正八面体=(1/3)Ö2*a³其中，V正八面体表示正八面体的体积，a是正八面体的边长。

- 正十二面体（Dodecahedron）：V正十二面体=(15+7Ö5)/4*a³其中，V正十二面体表示正十二面体的体积，a是正十二面体的边长。

- 正二十面体（Icosahedron）：V正二十面体=(5/12)(3+Ö5)*a³其中，V正二十面体表示正二十面体的体积，a是正二十面体的边长。

这些是关于不规则物体的几个常见体积公式的介绍。

不规则物体的体积计算可能涉及许多其他形状和公式，这里只是列举了一些常见的例子。

在实际应用中，根据不同的不规则形状，可能需要使用其他特定的体积计算公式。

求不规则物体体积

1、一个长50厘米，宽40厘米，高30厘米的长方体容器，水深23厘米，放入几个土豆后，水面上升了5厘米，求这几个土豆的体积。

思路分析：土豆的体积就是上升的水的体积。

直接利用公式“不规则物体的体积＝长×宽×上升的高度”进行计算就可以。

2.一个棱长为1.2分米的正方体容器，放入一个苹果，再向里面注满水，拿出苹果后，这时测量水面高度为0.8分米，求苹果的体积。

解法一：思路分析：苹果的体积就是下降的水的体积。

直接利用公式“不规则物体的体积＝长×宽×下降的高度”进行计算。

下降的高度不知道，需要先求出来。

解法二：思路分析：苹果的体积就是下降的水的体积。

所以用“水和苹果的体积和－水的体积＝苹果的体积。

”即可。

3、一个长方体的容器里从里面量，长和宽都是2分米，容器里有水5.5升，把一块石头浸入水中，水深15厘米，求石头的体积。

思路分析：石头的体积就是上升的水的体积。

因没有告诉原水面的高度，所以先求出水和物一共的体积，再减去水的体积就求出了石头的体积。

4、在一个装满水的棱长40厘米（从里面量）的正方体水缸里，有一块被水浸没了的长方体铁块，它的长20厘米，宽16厘米，当把铁块取出来后，水面下降了2厘米，求长方体铁块的高是多少？思路分析：求长方体铁块的高，需要先求出长方体的体积。

由题意可知下降的水的体积就是长方体的体积。

5、一个长方体玻璃缸，从里面量长8分米，宽6分米，高4分米，水深3分米。

投入一棱长4分米的正方体铁块，缸里的水能溢出多少？思路分析：求缸里的水能溢出多少？就是求正方体铁块的体积比玻璃缸空余部分的体积多多少。

用正方体的体积－空余部分的体积。

求不规则物体的体积的方法完整版本

感谢亲观看此幻灯片，此课件部分内容来源于网络，如有侵权请及时联系我们删除，谢谢配合！
2分米=20厘米 h=V÷ab =20×20×20÷（50×40） =8000 ÷ 2000 =4（厘米）
答：水面会上升4厘米。
拓展应用
（24－12）÷3 =12÷3 =4(ml)
12－4 =8(ml)
答：大圆球的体积是8ml。
综合应用棱是用角钢做的
四周用玻璃做成
底面用铁板做成
小结小合设计本师单元整理的概念,说一说下列问题实际要求什么?
（（（（521侧43底水）棱）体））面这做的面做长这做积个这这积个体积这和:鱼个6个鱼个:积::×(缸鱼6鱼(6缸鱼6×:×3装缸缸6+占缸×3×了要要4多要=++4多用3用少4用3=×少多)多×空多×升少3少间少44=水平)分？=平×？方米方分2的分=米角米的钢的铁？玻皮璃？？
条件: 长：6 dm 宽：3 dm 高：4 dm 原水深：3dm 现水深：3.5dm
解决问题
1、把一个铁球沉没在长1.5分米,宽
1.2分米的长方体容器里,水面由4.5分米上升到6分米,你能求出这个铁球的体积是多少吗?
V=abh =1.5×1.2×（6－4.5） =1.8×1.5 =2.7（立方分米）
答：这个铁球的体积是2.7立方分米。
2、在一只长50厘米，宽40厘米的长方体玻璃水缸中，放入一块棱长2分米的正方体铁块后，水面会上升多少厘米？
（（（24135））））做这做做这这个这这个个鱼个个鱼鱼缸鱼鱼缸缸占缸缸能要多要要装用少用用多多空多多少少间少少升平？分平水方米方？分的分米角米的钢的铁？玻皮璃？？
底侧棱体容面长积积积和
棱是用角钢做的

求不规则物体的体积

12cm
V V 水= 正=棱长×棱长×棱长
=6×6×6 =36×6 =216（立方厘米）
答：水的体积是216立方厘米。
三，新授
把土豆块放入装有水的长方体器皿中，你发现了什么？
12cm
观察：
你有什么发现？
1cm
发现：
1.水面上升 2.水的体积不变 3.总体积变大
1cm
6厘米
6厘米
6厘米
练习：
450-200=250（ml) 250ml=250立方厘米答：梨的体积是250立方厘米。
练习：
1. 在长6厘米，宽6厘米，高12厘米的装有水的长方体器皿中有一个石块，把石块从水中取出，水面下降了2厘米，求石块的体积是多少立方厘米？
V V 石= 下降部分水的体积=长×宽×水面下降的高度
=6×6×2 =36Байду номын сангаас2 =72（立方厘米）答：石块的体积是72立方厘米。
小结：
用排水法求不规则物体的体积：
不规则物体的体积=长×宽×水面上升（下降）的高度 =底面积×水面上升（下降）的高度
一，回顾旧知
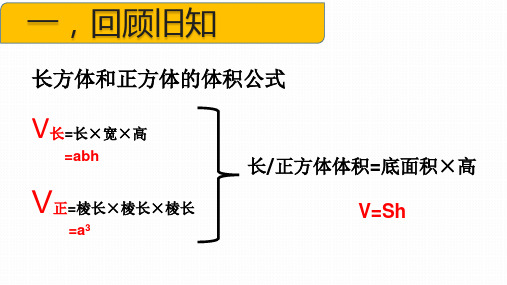
长方体和正方体的体积公式
V长=长×宽×高
=abh
V正=棱长×棱长×棱长
=a³
长/正方体体积=底面积×高 V=Sh
二，运用旧知
求下面长方体的体积
6厘米
12厘米 6厘米
V长=长×宽×高
=6×6×12 =36×12 =432（立方厘米）
在长方体器皿中倒入高为6厘米的水，求水的体积是多少立方厘米？
3. 在长6厘米，宽6厘米，高12厘米的装有高度为6厘米水的长方体中放入一个棱长3厘米的正方体，水未溢出，求现在水深多少厘米？

不规则体积粗略计算公式

不规则体积粗略计算公式一、排水法。

1. 原理。

- 对于形状不规则且不溶于水的固体，根据阿基米德原理，物体浸入液体中所排开液体的体积等于物体自身的体积。

2. 公式及操作。

- 当使用有刻度的容器（如量筒）时，若将不规则物体完全浸入水中，物体的体积V = V_2 - V_1。

其中V_1是未放入物体时水的体积，V_2是放入物体后水和物体的总体积。

- 例如，量筒中原有水的体积为50毫升，放入不规则物体后，水面上升到70毫升，那么该物体的体积V = 70 - 50=20毫升（因为1毫升= 1立方厘米，所以物体体积为20立方厘米）。

二、分割法。

1. 原理。

- 将不规则物体分割成若干个规则的部分（如长方体、正方体、圆柱体等），然后分别计算这些规则部分的体积，最后将它们相加得到不规则物体的体积。

2. 公式及操作。

- 假设将一个不规则物体分割成两部分，一部分是长方体，长、宽、高分别为a、b、c，其体积V_1 = a× b× c；另一部分是圆柱体，底面半径为r，高为h，其体积V_2=π r^2h。

那么该不规则物体的体积V = V_1+V_2=a× b× c+π r^2h。

三、填补法。

1. 原理。

- 对于一些有空洞或凹陷的不规则物体，可以通过填补的方式将其转化为规则物体。

计算出填补后的规则物体体积和填补部分的体积，两者相减就得到不规则物体的实际体积。

2. 公式及操作。

- 例如有一个内部有空腔的不规则物体，我们先把它看作一个完整的大正方体，边长为A，其体积V_大 = A^3。

内部空腔为小正方体，边长为a，其体积V_小=a^3。

那么该不规则物体的体积V = V_大 - V_小=A^3-a^3。

不规则物体体积的计算

不规则物体体积的计算一、近似计算法近似计算法是指通过将不规则物体分为一些规则几何图形的组合来估算其体积。

常见的近似计算方法有以下几种：1.离散逼近法：将不规则物体看作一系列离散点的集合，通过计算这些离散点的体积来估算整体的体积。

这种方法适用于不规则物体的形状比较复杂或不规则程度较高的情况。

2.整体逼近法：将不规则物体用一个规则几何图形（如长方体、圆柱体等）来逼近，然后计算逼近图形的体积。

这种方法适用于不规则物体的形状较简单且有明显的几何特征的情况。

3.切割逼近法：将不规则物体切割成一系列规则几何图形，并计算这些图形的体积之和来近似不规则物体的体积。

这种方法适用于不规则物体可以通过切割成几个简单几何图形来逼近的情况。

二、精确计算法精确计算法是指通过数学模型和积分等数值计算方法来精确计算不规则物体的体积。

常见的精确计算方法有以下几种：1.离散体积法：将不规则物体离散化为一系列小立方体，然后计算这些小立方体的体积之和来得到整体的体积。

这种方法适用于不规则物体的形状比较规则或可以通过离散化来近似为规则的情况。

2.曲面积分法：通过对不规则物体的曲面进行积分计算来得到物体的体积。

这种方法适用于不规则物体的曲面方程或参数方程已知的情况。

3.三维扫描法：使用三维扫描仪对不规则物体进行扫描，然后通过对扫描点云进行数学建模和计算来得到物体的体积。

这种方法适用于不规则物体的形状和曲面方程等无法用简单数学模型表示的情况。

需要注意的是，不规则物体的体积计算通常是一个复杂的过程，需要根据具体情况选择合适的方法和工具进行计算。

另外，对于一些特殊形状的不规则物体，可能还需要结合实际测量数据和计算模型进行计算。

不规则物体体积计算

不规则物体体积计算方法一：离散化法这种方法适用于不规则物体的形状比较复杂、曲线较多的情况。

它的基本原理是将不规则物体划分为多个小的规则形状，计算这些规则形状的体积之和来估算整体的体积。

具体步骤如下：1.将不规则物体进行离散化，划分为多个小的规则形状，比如立方体、圆柱体、锥体等。

可以根据物体的形状选择划分的规则形状。

2.对每个小的规则形状，分别计算其体积。

对于立方体，可以直接使用体积公式V=a^3（a为边长）；对于圆柱体，可以使用体积公式V=πr^2h（r为半径，h为高度）等。

3.将每个规则形状的体积相加，得到整体的体积。

方法二：位移法位移法又称为装水法，适用于物体的内部为空心或已知其他物质的密度分布情况的情况。

基本原理是将不规则物体浸入水中，通过测量位于水中的物体位移量来计算其体积。

具体步骤如下：1.准备一个能够容纳不规则物体的容器，并且能够装满水。

2.在容器内装满水，记录初始水位。

3.将不规则物体缓慢地放入容器中，确保其完全浸入水中，并记录此时水位的变化量。

4.根据阿基米德原理，物体浸入液体中的位移量等于物体的体积。

根据位移量和液体的密度，即可计算出物体的体积。

需要注意的是，以上两种方法都是估算体积的近似方法，无法得到完全准确的结果。

对于一些特殊的不规则物体，可能需要使用更复杂的方法来进行计算，例如有限元分析等。

另外，对于多孔状的物体，还需要考虑孔隙的体积的影响。

总结起来，不规则物体体积的计算方法因物体形状和实际情况而异。

在实际应用中，可以根据不同情况选择适合的方法来进行计算，以得到较为准确的结果。

不规则物体体积知识点全部

不规则物体体积知识点不规则物体体积是几何学中的一个重要概念，用来描述不具备规则形状的物体所占据的空间大小。

在实际生活中，我们经常会遇到不规则物体，比如石头、树木、水果等，它们的形状复杂多样，不便用传统的几何方法计算体积。

本文将介绍一些计算不规则物体体积的知识点和方法。

1.概念理解不规则物体的体积是指该物体所占据的空间大小。

在几何学中，我们通常使用立方单位（如立方米、立方厘米等）来表示体积。

计算不规则物体体积的关键是找到合适的方法来近似表示该物体的形状。

2.分割法分割法是计算不规则物体体积的一种常用方法。

它的基本思想是将不规则物体分割成一系列更简单、更规则的部分，然后计算每个部分的体积，并将它们相加得到整个物体的体积。

例如，对于一个复杂的石头，我们可以将其分割成多个立方体体积相同的小块，然后通过计算每个小块的体积并相加来得到整个石头的体积。

3.浸水法浸水法是另一种计算不规则物体体积的方法。

它的基本原理是通过将不规则物体完全浸入水中，根据位移原理计算物体的体积。

具体来说，我们首先测量物体在水中的位移，然后根据“物体体积=位移体积”来计算物体的体积。

这种方法适用于那些可以浸入水中且不溶于水的物体。

4.近似计算对于一些特殊的不规则物体，我们可能无法通过分割法或浸水法来准确计算其体积。

这时，我们可以采用近似计算的方法来估算物体的体积。

例如，对于一个复杂的树木，我们可以使用棱柱或锥体的体积公式来近似表示其形状，并计算出一个大致的体积值。

5.计算工具在计算不规则物体体积时，我们可以借助计算机辅助工具来提高计算的准确性和效率。

例如，我们可以使用CAD软件来建模不规则物体，并通过计算软件自带的体积计算功能来得到准确的体积值。

另外，一些在线体积计算器也可以帮助我们快速计算不规则物体的体积。

综上所述，不规则物体体积的计算可以通过分割法、浸水法、近似计算以及计算工具来实现。

在实际应用中，我们可以根据不同的情况选择合适的方法来计算物体的体积，从而更好地理解和应用几何学知识。

求不规则物体的体积题型总结

求不规则物体的体积题型总
结
-标准化文件发布号：（9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII
求不规则物体的体积的方法
1.一个长方体鱼缸长60厘米，宽20厘米，水深25厘米。

放入一条鱼后，水深27厘米。

这条鱼的体积是多少立方厘米？
2.一个长方体水槽长80分米，宽30分米，放入一块石头后，水面上升了3厘米。

这块石头的体积是多少立方分米？
3.一个长方体鱼缸长32厘米，宽25厘米，原来鱼缸里有水6400立方厘米，放入一条鱼后，浴缸里有水8000立方厘米，放入鱼后水面上升了多少厘米？
4.一个长方体水箱从里面量长和宽都是20厘米。

向水箱里放入一条250立方厘米的金鱼后，水面上升了多少厘米？
5.在一个长50厘米、宽40厘米的玻璃缸中，放入一块石头，这时水深20厘米。

如果把石头从缸中取出，缸中水深17厘米。

石头的体积是多少立方厘米？
7.有一个长160厘米、宽120厘米的长方体水槽，现将一块长方体浸入水中，水面比原来上升12厘米。

已知铁块的长和宽都是20厘米，铁块高是多少厘米？
2。

不规则几何体体积的求法

不规则几何体体积的求法当所给几何体形状不规则时，无法直接利用体积公式求解，可尝试用以下几种常用的方法求出原几何体的体积，下面逐一介绍，供同学们参考．一、等积转换法当所给几何体的体积不能直接套用公式或套用公式时某一量（底面积或高）不易求出时，可以转换一下几何体中有关元素的相对位置进行计算求解，该方法尤其适用于求三棱锥的体积．例1在边长为a的正方体ABCD—A1B1C1D1中，M，N，P分别是棱A1B1，A1D1，A1A上的点，且满足A1M = 12A1B1，A1N=2ND1，A1P= 34A1A（如图1），试求三棱锥A1—MNP的体积．分析：若用公式V= 13Sh直接计算三棱锥A1—MNP的体积，则需要求出△MNP的面积和该三棱锥的高，这两者显然都不易求出，但若将三棱锥A1—MNP的顶点和底面转换一下，变为求三棱锥P—A1MN的体积，便能很容易的求出其高和底面△A1MN的面积，从而代入公式求解．解：V A1-MNP =V A1—MNP = 13·S△A1MN ·h =13×12·A1M1·A1N·A1P=13×12×12a·23a·34a=124a3．评注：转换顶点和底面是求三棱锥体积的一种常用方法，也是以后学习求点到平面距离的一个理论依据．二、分割法分割法也是体积计算中的一种常用方法，在求一些不规则的几何体的体积以及求两个几何体的体积之比时经常要用到分割法．例2如图2，在三棱柱ABC—A1B1C1中，E,F分别为AB,AC的中点，平面EB1C1F 将三棱柱分成两部分，求这两部分的体积之比．分析：截面EB1C1F将三棱柱分成两部分，一部分是三棱台AEF—A1B1C1；另一部分是一个不规则几何体，其体积可以利用棱柱的体积减去棱台的体积求得．解：设棱柱的底面积为S，高为h，其体积V=Sh．则三角形AEF的面积为14S．由于V AEF -A 1B 1C 1=13 ·h ·(s 4 +S+s 2 )= 712Sh , 则剩余不规则几何体的体积为V ′=V -V AEF -A 1B 1C 1=Sh -712 Sh = 512Sh ，所以两部分的体积之比为V AEF -A 1B 1C 1：V ′=7：5.评注：在求一个几何体被分成的两部分体积之比时，若有一部分为不规则几何体，则可用整个几何体的体积减去规则几何体的体积求出其体积，再进行计算．三、补形法某些空间几何体是某一个几何体的一部分，在解题时，把这个几何体通过“补形”补成完整的几何体或置于一个更熟悉的几何体中，巧妙地破解空间几何体的体积问题，这是一种重要的解题策略——补形法．常见的补形法有对称补形、联系补形与还原补形.对于还原补形，主要涉及台体中“还台为锥”问题．例3 已知某几何体的三视图如图所示，则该几何体的体积为______.分析：由三视图画出直观图，补一个大小相同的几何体，构成一个圆柱即可求其体积. 解：由三视图可知，此几何体是底面半径为1，高为4的圆柱被从母线的中点处截去了圆柱的14，根据对称性，可补全此圆柱如图，故体积V ＝34×π×12×4＝3π. 评注：“对称”是数学中的一种重要关系，在解决空间几何体中的问题时善于发现对称关系对空间想象能力的提高很有帮助．。

求不规则物体体积思想总结

求不规则物体体积思想总结不规则物体体积是三维几何的基础内容之一。

计算不规则物体体积需要通过各种方法来求解，下面我将总结几种常用的思想。

第一种思想是“利用子体积的叠加”。

对于由不规则形状组成的物体，我们可以将其分成若干个子体积，然后将这些子体积的体积进行叠加。

这种思想的难点在于如何确定子体积以及如何计算每个子体积的体积。

常用的确定子体积的方法有切割法和分割法。

切割法是将不规则物体用刀或平面切成若干个平面几何体，然后再计算每个平面几何体的体积，最后将它们相加得到整个物体的体积。

分割法是将不规则物体分割成若干个规则几何体，然后计算每个规则几何体的体积，最后将它们相加得到整个物体的体积。

第二种思想是“利用重心法”。

这种方法适用于具有对称性的不规则物体。

其基本思想是将物体分割成若干个小的部分，然后将每个部分的重心计算出来，并计算出每个部分的体积，最后将它们相加得到整个物体的体积。

这种方法的优点是计算相对简便，但是需要对对称性有比较深入的了解。

第三种思想是“利用密度法”。

这种方法适用于材料均匀的不规则物体。

其基本思想是通过测量物体的质量和密度，然后利用公式V= m/ρ计算出体积。

这种方法的难点在于如何测量质量和密度，需要使用一些专门的测量工具和设备。

第四种思想是“利用近似法”。

这种方法适用于复杂的不规则物体，通过将其近似成规则几何体，然后根据规则几何体的体积公式计算体积。

这种方法的难点在于如何选择适当的规则几何体进行近似，以及如何准确计算近似后的体积。

总结起来，不规则物体体积的计算方法有很多种，不同的方法适用于不同的情况。

在计算不规则物体体积时，需要根据具体的情况选择合适的方法，并注意进行适当的近似。

此外，对于较为复杂的不规则物体，可能需要运用多种方法进行计算，以求得准确的结果。