人教A版高中数学必修四同步检测第3章3.2简单的三角恒等变换
人教新课标A版高中数学必修4 第三章三角恒等变换 3.2简单的三角恒等变换 同步测试(II)卷

(1) 求函数f(x)与g(x)的解析式;
(2) 当a≥1,求实数a与正整数n,使F(x)=f(x)+ag(x)在(0,nπ)恰有2019个零点.
25. (5分) 已知关于x的方程sinxsin5x=a在x∈[0,π)上有唯一解,求实数a的取值范围.
参考答案
一、 单选题 (共15题;共30分)
1-1、
3-1、
4-1、
5-1、
6-1、
7-1、
.
B .
C .
D .
12. (2分) (2017高一上·眉山期末) 已知α是第一象限角,那么 是( )
A . 第一象限角
B . 第二象限角
C . 第一或第二象限角
D . 第一或第三象限角
13. (2分) (2018高一下·平顶山期末) 已知 ,则 ( )
A .
B .
C .
D .
14. (2分) 计算cos18°cos42°﹣cos72°cos48°=( )
A . 1
B . 2
C . 3
D . 4
7. (2分) (2017高一下·简阳期末) 已知cos α= ,α∈( ) ,则cos 等于( )
A .
B . ﹣
C .
D . ﹣
8. (2分) 已知f(x)=2sinωx(cosωx+sinωx)的图象在x∈[0,1]上恰有一个对称轴和一个对称中心,则实数ω的取值范围为( )
人教新课标A版必修4数学3.2 简单的三角恒等变换式同步检测C卷

人教新课标A版必修4数学3.2 简单的三角恒等变换式同步检测C卷姓名:________ 班级:________ 成绩:________一、选择题 (共15题;共30分)1. (2分) (2018高一上·鹤岗月考) 已知,则 =()A .B .C .D .2. (2分)(2017·榆林模拟) 已知cosα=﹣,且α∈(,π),则tan(α+ )等于()A . ﹣B . ﹣7C .D . 73. (2分)函数y=sin2x的图象的一个对称中心为()A . (0,0)B . (,0)C . (,)D . (,1)4. (2分) (2017高一下·芮城期末) 若,则的值为()A .B .C .D .5. (2分)已知向量若则的值为()A .B .C .D .6. (2分) (2018高一下·大同期末) 若,且,则角是()A . 第一象限B . 第二象限C . 第四象限D . 第三象限7. (2分) (2018高三上·昭通期末) 函数f(x)=sin2x,将f(x)的图象向左平移主个单位后得到g(x)的图象,则g(x)()A . 在( ]上单调递减B . 在()上单调递增C . 在( ]上单调递减D . 在()上单调递增8. (2分) (2016高一下·延川期中) 已知两点A(2,1),B(3,3),则直线AB的斜率为()A . 2B .C .D . ﹣29. (2分)已知tan=,则的值为()A .B . -C . 7D . -710. (2分)将函数y=sin2x的图象向左平移个单位,再向上平移1个单位,所得图象的函数解析式是().A . y=cos2xB .C .D .11. (2分)已知tan(α+β) =,tan(β-)=,那么tan(α +)为()A .B .C .D .12. (2分)函数是()A . 最小正周期为的偶函数B . 最小正周期为2的偶函数C . 最小正周期为2的奇函数D . 最小正周期为的奇函数13. (2分)设向量,若t是实数,则的最小值为()A .B .C . 1D .14. (2分)若对所有实数x,均有,则k= ()A . 3B . 4C . 5D . 615. (2分)为锐角三角形,则,则a与b的大小关系为()。
人教新课标A版高中数学必修4 第三章三角恒等变换 3.2简单的三角恒等变换 同步测试C卷

B .
C .
D .
9. (2分) (2018高一下·新乡期末) 设 , , ,则 , , 的大小关系为( )
A .
B .
C .
D .
10. (2分) 函数 ( )
A . 在 单调递减
B . 在 单调递增
C . 在 单调递减
D . 在 单调递增
11. (2分) △ABC中,角A,B,C成等差数列是 成立的( )
23. (5分) (2018高一下·栖霞期末) 已知角 的顶点均为坐标原点,始边均为 轴的非负半轴,若 的终边分别于单位圆相交于 两点,且 ;
(1) 求 的值,并确定点 所在的象限;
(2) 若点 的坐标为 ,求 的值.
24. (5分) (2016高三上·呼和浩特期中) 已知函数f(x)=2sinωx,其中常数ω>0.
B . E>F>G
C . F>E>G
D . F>G>E
二、 填空题 (共5题;共5分)
16. (1分) (2018高三上·山西期末) 在平面直角坐标系 中,已知角 的顶点和点 重合,始边与 轴的非负半轴重合, 终边上一点 坐标为 ,则 ________.
17. (1分) 已知 ,且 ,则 的值为________.
14-1、
15-1、
二、 填空题 (共5题;共5分)
16-1、
17-1、
18-1、
19-1、
20-1、
三、 解答题 (共5题;共25分)
21-1、
22-1、
22-2、
23-1、
23-2、
24-1、
25-1、
人教新课标A版高中数学必修4 第三章三角恒等变换 3.2简单的三角恒等变换 同步测试C卷
贵州省人教新课标A版高中数学必修4第三章三角恒等变换3.2简单的三角恒等变换同步测试

20. (1分) 已知α、β均为锐角,且tanβ= , 则tan(α+β)=________
三、 解答题 (共5题;共25分)
21. (5分) 已知sinα= , sin(α+β)= , α与β均为锐角,求cos . (cos = )
(Ⅰ)求函数 f(x)最的小正周期;
(Ⅱ)求函数f(x)在区间[ , ]上的最小值和最大值.
25. (5分) (2018高一上·海安月考) 已知sinα+cosβ= ,cosα+sinβ= ,求:
(1) sin(α+β)的值;
(2) cosα sinβ的值.
参考答案
一、 单选题 (共15题;共30分)
1-1、
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
11-1、
12-1、
13-1、
14-1、
15、答案:略
二、 填空题 (共5题;共5分)
16-1、
17-1、
18-1、
19-1、
20-1、
三、 解答题 (共5题;共25分)
21-1、
22-1、
22-2、
23-1、
24-1、
A .
B .
C .
D .
3. (2分) (2020·丹东模拟) 已知当 时,函数 取得最小值,则 ( )
A .
B .
C .
D .
4. (2分) (2017·榆林模拟) 已知cosα=﹣ ,且α∈( ,π),则tan(α+ )等于( )
人教新课标A版高中数学必修4 第三章三角恒等变换 3.2简单的三角恒等变换 同步测试A卷

三、 解答题 (共5题;共25分)
21. (5分) 已知 , 请用m分别表示tanθ、tan2θ、 . .
22. (5分) 求sin10°sin30°sin50°sin70°的值.
23. (5分) 计算题
(1) 求值: ;
C .
D .
5. (2分) 若 , 则 的值为( )
A .
B .
C .
D .
6. (2分) 已知向量 若 则 的值为( )
A .
B .
C .
D .
7. (2分) (2018高一下·应县期末) 若 , 是第三象限的角,则 ( )
A . 3
B .
C .
D .
8. (2分) 下列函数中,最小正周期为π且图象关于原点对称的函数是( )
A . [﹣1,1]
B . [﹣ , ]
C . [- , ]
D . [- , ]
15. (2分) 已知 , 记 , 要得到函数 的图象,只需将函数y=f(x)的图象( )
A . 向左平移 个单位长度
B . 向右平移 个单位长度
C . 向左平移 个单位长度
D . 向右平移 个单位长度
二、 填空题 (共5题;共5分)
人教新课标A版高中数学必修4 第三章三角恒等变换 3.2简单的三角恒等变换 同步测试A卷
姓名:________班级:________ 成绩:________
一、 单选题 (共15题;共30分)
1. (2分) θ∈[0,π], , 则 =( )
A .
B .
C . 7
D .
2. (2分) (2018高一上·玉溪期末) 将函数 的图象向右平移 个单位长度后,所得到的图象关于坐标原点对称,则 的最小值是( )
高中数学第三章三角恒等变换3.2简单的三角恒等变换练习新人教A版必修4(2021年整理)

2017-2018学年高中数学第三章三角恒等变换3.2 简单的三角恒等变换练习新人教A版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017-2018学年高中数学第三章三角恒等变换3.2 简单的三角恒等变换练习新人教A版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017-2018学年高中数学第三章三角恒等变换3.2 简单的三角恒等变换练习新人教A版必修4的全部内容。
3.2 简单的三角恒等变换题号1234567891011得分答案一、选择题(本大题共7小题,每小题5分,共35分)1.函数y=错误!的最小正周期等于( )A.错误! B.πC.2π D.3π2。
错误!=()A.1 B.2C. 2 D。
错误!3.函数y=3sin 4x+错误!cos 4x的最大值是( )A. 3 B.2 错误!C.3 D.64.函数f(x)=(1+tan x)cos x的最小正周期为()A.2π B.错误!C.π D.错误!5.函数y=cos2错误!+sin2错误!-1是()A.最小正周期为2π的奇函数B.最小正周期为π的偶函数C.最小正周期为π的奇函数D.最小正周期为2π的偶函数6.如果函数f(x)=sin 2x+acos 2x的图像关于直线x=-错误!对称,则实数a的值为()A.2 B.-2C.1 D.-17.已知函数f(x)=错误!sin ωx+cos ωx(ω〉0),y=f(x)的图像与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是( )A.错误!,k∈ZB。
错误!,k∈ZC.错误!,k∈ZD。
错误!,k∈Z二、填空题(本大题共4小题,每小题5分,共20分)8.函数f(x)=sin x-cos x的单调递增区间是____________________.9.已知sin(α+错误!)+sin α=-错误!,-错误!<α<0,则cos α=________.10.函数y=sin 2x3+cos(错误!+错误!)的图像中相邻的两条对称轴之间的距离是________.11.已知函数f(x)=cos 2x-2 3sin xcos x,给出下列结论:①存在x1,x2,当x1-x2=π时,f(x1)=f(x2)成立;②f(x)在区间[-错误!,错误!]上单调递增;③函数f(x)的图像关于点(错误!,0)中心对称;④将函数f(x)的图像向左平移错误!个单位后所得图像与g(x)=2sin 2x的图像重合.其中正确结论的序号为________.三、解答题(本大题共2小题,共25分)得分12.(12分)已知函数f(x)=4cos xsin 错误!-1.(1)求f(x)的最小正周期;(2)求f(x)在区间错误!上的最大值和最小值.13。
数学人教A版必修4同步优化训练:3.2简单的三角恒等变
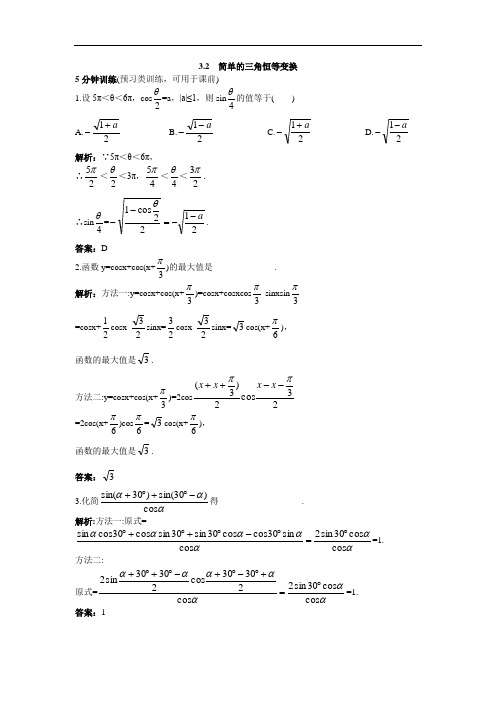
3.2 简单的三角恒等变换5分钟训练(预习类训练,可用于课前) 1.设5π<θ<6π,cos2θ=a ,|a|≤1,则sin 4θ的值等于( ) A.21a +-B.21a-- C.21a +- D.21a -- 解析:∵5π<θ<6π, ∴25π<2θ<3π,45π<4θ<23π. ∴sin4θ=2122cos1a --=--θ. 答案:D2.函数y=cosx+cos(x+3π)的最大值是______________. 解析:方法一:y=cosx+cos(x+3π)=cosx+cosxcos 3π-sinxsin 3π=cosx+21cosx-23sinx=23cosx-23sinx=3cos(x+6π),函数的最大值是3.方法二:y=cosx+cos(x+3π)=2cos 23cos 2)3(ππ--++x x x x =2cos(x+6π)cos 6π=3cos(x+6π),函数的最大值是3. 答案:3 3.化简αααcos )30sin()30sin(-︒+︒+得___________________.解析:方法一:原式=αααααααcos cos 30sin 2cos sin 30cos cos 30sin 30sin cos 30cos sin ︒=︒-︒+︒+︒=1.方法二:原式=αααααααcos cos 30sin 2cos 23030cos23030sin2︒=+︒-︒+-︒+︒+=1.答案:14.已知tan2α=2,则sinα的值为__________,cosα的值为__________,tanα的值为________. 解析:由万能代换,可得sinα=542tan 12tan22=-αα,cosα=532tan 12tan 12-=+-αα,tanα=2tan 342tan 12tan22-=-αα. 答案:54 -53 34-10分钟训练(强化类训练,可用于课中) 1.若sin(α-β)cosα-cos(α-β)sinα=54且β在第三象限,则cos 2β为( ) A.55-B.±55C.552-D.±552 解析:由题意知sin(α-β-α)=54,即sin(-β)=54,∴sinβ=54-. ∵β是第三象限角,∴cosβ=-53,且2β是二、四象限角.∴cos2β=±2cos 1β+=±2531-=±55. 答案:B2.设α、β为钝角,且sinα=55,cos β=10103-,则α+β的值为( ) A.43π B.45π C.47π D.45π或47π解析:由题意知cosα=552-,sinβ=1010, ∴cos(α+β)=552-×(10103-)-55×1010=22. ∵2π<α<π,2π<β<π,∴π<α+β<2π. ∴α+β=47π.答案:C 3.若tan(α+4π)=223+,则αα2sin 2cos 1-=_______________.解析:原式=αααcos sin 2sin 22=tanα.由tan(α+4π)=223tan 1tan 1+=-+αα,解得tanα=22.答案:22 4.已知sinα=43,且α为第二象限角,则tan 2α的值为_________.解析:∵α为第二象限角,∴cosα=4131631-=--. tan2α=33934434131sin cos 12cos2sin22sin 22cos2sin2+=+=-==ααααααα.答案:33934+5.设25sin 2x+sinx-24=0,x 是第二象限角,求cos 2x的值. 解:因为25sin 2x+sinx-24=0,所以sinx=2524或sinx=-1. 又因为x 是第二象限角,所以sinx=2524,cosx=-257.又2α是第一或第三象限角, 从而cos2x =±2cos 1x +=±22571-=±53.6.求函数y=4sinx·cosx 的最值和周期.解:∵y=4sinx·cosx=2sin2x ,∴y max =2,y min =-2,且T=π. 30分钟训练(巩固类训练,可用于课后) 1.已知π<α<2π,则cos2α的值等于( ) A.2cos 1α+-B.2cos 1α-C.2cos 1α+D.2cos 1α-- 解析:∵π<α<2π,∴2π<2α<π,cos 2α<0, cos2α=2cos 1α+-.答案:A 2.sinα+sinβ=33(cosβ-cosα),且α∈(0,π),β∈(0,π),则α-β等于( ) A.-32π B.-3π C.3π D.32π 解析:由已知得2sin2βα+cos2βα-=33·2sin 2βα+sin 2βα-.∵0<2βα+<π,-2π<2βα-<2π,∴sin 2βα+>0.∴tan 2βα-=3.∴2βα-=3π,α-β=32π.答案:D3.已知sin(α+β)sin(β-α)=m ,则cos 2α-cos 2β等于( )A.-mB.mC.-4mD.4m 解析:cos 2α-cos 2β=21(1+cos2α)21-(1+cos2β)=22cos 2cos βα-=-sin(α+β)sin(α-β)=sin(α+β)sin(β-α)=m.答案:B4.已知sinθ=53-,3π<θ<27π,则tan 2θ的值为________________. 解析:因为sinθ=-53,3π<θ<27π,∴cosθ=54-,且23π<2θ<47π.∴tan2θ=θθcos 1cos 1+--=-3. 答案:-35.若25π<α<411π,sin2α=-54,求tan 2α. 解:∵25π<α<411π,∴45π<2α<811π,5π<2α<211π,即2α、2α是第三象限角,α是第二象限角. 又sin2α=-54,∴cos2α=-53.∴cosα=253122cos 1--=+-α=-55.∴tan 2α=2155555551551cos 1cos 1+=-+=-+=+-αα. 6.求证:2sin(4π-x)·sin(4π+x)=cos2x. 证明:左边=2sin(4π-x)·sin(4π+x)=2sin(4π-x)·cos(4π-x)=sin(2π-2x)=cos2x=右边.7.在△ABC 中,已知cosA=Bb a b B a cos cos ∙--∙,求证:b a b a B A-+=2tan 2tan 22. 证明:∵cosA=B b a bB a cos cos ∙--∙,∴1-cosA=B b a B b a cos )cos 1()(∙--∙+,1+cosA=Bb a B b a cos )cos 1()(∙-+∙+.∴)cos 1()()cos 1()(cos 1cos 1B b a B b a A A +∙--∙+=+-.而2cos 22sin 2cos 1cos 122A AAA =+-=tan 22A ,B B cos 1cos 1+-=tan 22B , ∴tan 2)()(2b a b a A -+=·tan 22B ,即b a b a B A -+=2tan 2tan 22. 8.求证:4cos(60°-θ)cosθcos (60°+θ)=cos3θ. 证明:左边=2cosθ[cos120°+cos(-2θ)]=2cosθ(21-+cos2θ) =-cosθ+(cos3θ+cosθ)=cos3θ=右边. 9.已知sinα+sinβ=2,cosα+cosβ=32,求tan(α+β)的值. 解:322cos cos sin sin -++βαβα,由和差化积公式得2cos2cos 22cos2sin2βαβαβαβα-+-+=3,∴tan2βα+=3,从而tan(α+β)=4331222tan 12tan222-=-⨯=+-+βαβα. 10.已知f(x)=21-+2sin225sinx x,x ∈(0,π). (1)将f(x)表示成cosx 的多项式; (2)求f(x)的最小值.解:(1)f(x)=2sin2sin 23cos 22sin 22sin 25sinx xx x x x =-=2cos 23x cos 2x=cos2x+cosx=2cos 2x+cosx-1.(2)∵f(x)=2(cosx+41)2-89,且-1≤cosx≤1, ∴当cosx=41-时,f(x)取得最小值89-.快乐时光误人子弟督学到某学校视察,看见教室里有个地球仪,便问学童甲:“你说说看,这个地球仪为何会倾斜23.5度?”学童甲惶恐地答道:“不是我弄歪的!”督学摇摇头,转问学童乙.学童乙双手一摊,说道:“您也看见了,我是刚刚才进来的!”督学疑惑地问教师怎么回事.教师满怀歉意地说:“不能怪他们,这地球仪买回来时已经是这样的了.”校长见督学的脸色越来越难看,忙解释:“说来惭愧,因为学校经费有限,我们买的是地摊货.”。
高中数学(人教版A版必修四)配套单元检测:第3章:3.2 简单的三角恒等变换 3.2 Word版含答

§3.2 简单的三角恒等变换课时目标 1.了解半角公式及推导过程.2.能利用两角和与差的公式进行简单的三角恒等变换.3.了解三角变换在解数学问题时所起的作用,进一步体会三角变换的规律.1.半角公式(1)S α2:sin α2=____________________;(2)C α2:cos α2=____________________________;(3)T α2:tan α2=______________(无理形式)=________________=______________(有理形式).2.辅助角公式使a sin x +b cos x =a 2+b 2sin(x +φ)成立时,cos φ=__________________,sin φ=______,其中φ称为辅助角,它的终边所在象限由__________决定.一、选择题1.已知180°<α<360°,则cos α2的值等于( )A .-1-cos α2 B. 1-cos α2C .-1+cos α2 D. 1+cos α22.函数y =sin ⎝⎛⎭⎫x +π3+sin ⎝⎛⎭⎫x -π3的最大值是( ) A .2 B .1 C.12D. 33.函数f (x )=sin x -cos x ,x ∈⎣⎡⎦⎤0,π2的最小值为( ) A .-2 B .- 3 C .- 2 D .-14.使函数f (x )=sin(2x +θ)+3cos(2x +θ)为奇函数的θ的一个值是( ) A.π6 B.π3 C.π2 D.2π35.函数f (x )=sin x -3cos x (x ∈[-π,0])的单调递增区间是( )A.⎣⎡⎦⎤-π,-5π6B.⎣⎡⎦⎤-5π6,-π6 C.⎣⎡⎦⎤-π3,0 D.⎣⎡⎦⎤-π6,0 6.若cos α=-45,α是第三象限的角,则1+tanα21-tanα2等于( )A .-1 B.1C .2D .-2题 号1 2 3 4 5 6答 案7.函数f (x )=sin(2x -π4)-22sin 2x 的最小正周期是______.8.已知等腰三角形底角的余弦值为23,则顶角的正弦值是________.9.已知等腰三角形顶角的余弦值为45,则底角的正切值为________.10.2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成一个大正方形(如图所示).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos 2θ的值等于____. 三、解答题11.已知函数f (x )=3sin ⎝⎛⎭⎫2x -π6+2sin 2⎝⎛⎭⎫x -π12 (x ∈R ). (1)求函数f (x )的最小正周期;(2)求使函数f (x )取得最大值的x 的集合.12.已知向量m =(cos θ,sin θ)和n =(2-sin θ,cos θ),θ∈(π,2π),且|m +n |=825,求cos ⎝⎛⎭⎫θ2+π8的值. 能力提升13.当y =2cos x -3sin x 取得最大值时,tan x 的值是( ) A.32 B .-32C.13 D .4 14.求函数f (x )=3sin(x +20°)+5sin(x +80°)的最大值.1.学习三角恒等变换,千万不要只顾死记硬背公式,而忽视对思想方法的理解,要学会借助前面几个有限的公式来推导后继公式,立足于在公式推导过程中记忆公式和运用公式. 2.辅助角公式a sin x +b cos x =a 2+b 2sin(x +φ),其中φ满足: ①φ与点(a ,b )同象限;②tan φ=b a (或sin φ=b a 2+b 2,cos φ=aa 2+b2). 3.研究形如f (x )=a sin x +b cos x 的函数性质,都要运用辅助角公式化为一个整体角的正弦函数或余弦函数的形式.因此辅助角公式是三角函数中应用较为广泛的一个重要公式,也是高考常考的考点之一.对一些特殊的系数a 、b 应熟练掌握.例如sin x ±cos x =2sin ⎝⎛⎭⎫x ±π4;sin x ±3cos x =2sin ⎝⎛⎭⎫x ±π3等.1.(1)±1-cos α2 (2)± 1+cos α2(3)± 1-cos α1+cos α sin α1+cos α1-cos αsin α2.a a 2+b 2 b a 2+b 2 点(a ,b )作业设计 1.C2.B [y =2sin x cos π3=sin x .]3.D [f (x )=2sin ⎝⎛⎭⎫x -π4,x ∈⎣⎡⎦⎤0,π2. ∵-π4≤x -π4≤π4,∴f (x )min =2sin ⎝⎛⎭⎫-π4=-1.] 4.D [f (x )=sin(2x +θ)+3cos(2x +θ)=2sin ⎝⎛⎭⎫2x +π3+θ. 当θ=23π时,f (x )=2sin(2x +π)=-2sin 2x .]5.D [f (x )=2sin ⎝⎛⎭⎫x -π3,f (x )的单调递增区间为⎣⎡⎦⎤2k π-π6,2k π+56π (k ∈Z ), 令k =0得增区间为⎣⎡⎦⎤-π6,56π.] 6.A [∵α是第三象限角,cos α=-45,∴sin α=-35.∴1+tan α21-tan α2=1+sin α2cos α21-sin α2cos α2=cos α2+sin α2cos α2-sin α2=cos α2+sin α2cos α2-sin α2·cos α2+sin α2cos α2+sin α2=1+sin αcos α=1-35-45=-12.]7.π解析 f (x )=22sin 2x -22cos 2x -2(1-cos 2x )=22sin 2x +22cos 2x - 2=sin(2x +π4)-2,∴T =2π2=π.8.459解析 设α为该等腰三角形的一底角,则cos α=23,顶角为180°-2α.∴sin(180°-2α)=sin 2α=2sin αcos α=21-⎝⎛⎭⎫232·23=459. 9.3解析 设该等腰三角形的顶角为α,则cos α=45,底角大小为12(180°-α).∴tan ⎣⎡⎦⎤12(180°-α)=tan ⎝⎛⎭⎫90°-α2=1tan α2=1+cos αsin α=1+4535=3. 10.725解析 由题意,5cos θ-5sin θ=1,θ∈⎝⎛⎭⎫0,π4. ∴cos θ-sin θ=15.由(cos θ+sin θ)2+(cos θ-sin θ)2=2.∴cos θ+sin θ=75.∴cos 2θ=cos 2 θ-sin 2 θ=(cos θ+sin θ)(cos θ-sin θ)=725.11.解 (1)∵f (x )=3sin2⎝⎛⎭⎫x -π12+1-cos2⎝⎛⎭⎫x -π12 =2⎣⎡⎦⎤32sin2⎝⎛⎭⎫x -π12-12cos2⎝⎛⎭⎫x -π12+1=2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π12-π6+1 =2sin ⎝⎛⎭⎫2x -π3+1,∴T =2π2=π. (2)当f (x )取得最大值时,sin ⎝⎛⎭⎫2x -π3=1, 有2x -π3=2k π+π2,即x =k π+5π12(k ∈Z ),∴所求x 的集合为{x |x =k π+5π12,k ∈Z }.12.解 m +n =(cos θ-sin θ+2,cos θ+sin θ),|m +n |=(cos θ-sin θ+2)2+(cos θ+sin θ)2=4+22(cos θ-sin θ)=4+4cos ⎝⎛⎭⎫θ+π4 =21+cos ⎝⎛⎭⎫θ+π4. 由已知|m +n |=825,得cos ⎝⎛⎭⎫θ+π4=725. 又cos ⎝⎛⎭⎫θ+π4=2cos 2⎝⎛⎭⎫θ2+π8-1, 所以cos 2⎝⎛⎭⎫θ2+π8=1625. ∵π<θ<2π, ∴5π8<θ2+π8<9π8. ∴cos ⎝⎛⎭⎫θ2+π8<0.∴cos ⎝⎛⎭⎫θ2+π8=-45. 13.B [y =2cos x -3sin x =13⎝⎛⎭⎫213cos x -313sin x =13(sin φcos x -cos φsin x )=13sin(φ-x ),当sin(φ-x )=1,φ-x =2k π+π2时,y 取到最大值.∴φ=2k π+π2+x ,(k ∈Z )∴sin φ=cos x ,cos φ=-sin x ,∴cos x =sin φ=213,sin x =-cos φ=-313.∴tan x =-32.]14.解 3sin(x +20°)+5sin(x +80°)=3sin(x +20°)+5sin(x +20°)cos 60°+5cos(x +20°)sin 60°=112sin(x +20°)+532cos(x +20°)=⎝⎛⎭⎫1122+⎝⎛⎭⎫5322sin(x +20°+φ)=7sin ()x +20°+φ 其中cos φ=1114,sin φ=5314.所以f (x )max =7.。
最新人教A版高中数学必修4同步辅导与检测第三章3.2简单的三角恒等变换

最新人教A版高中数学必修4同步辅导与检测第三章3.2简单的三角恒等变换第三章三角恒等变换3.2简单的三角恒等变换甲类基础加固一、选择题1.已知sinα-cosα=54,则sin2α的值等于()a、 716b.-716c.-916d。
916解析:按sinα-cosα=54,(sinα-cosα)2=1-2sinαcosα=1-sin2α=25十六,所以sin2α=916.答案:c2.如果函数f(x)=-sin2x+1二(x∈r),则f(x)是()a、最小正周期为π2的奇函数b、最小正周期为πC的奇数函数最小正周期为2πD的偶数函数最小正周期为π的偶数函数分析:F(x)=-1-cos2x112+2=2cos2x.回答:D3.若sin(π-α)=-5? 3和α∈? 3π??π,2??πα??,则sin??2+2??等于()1a.-6666b.-c.d.3663?3?5? 分析:从标题α=α的意义上认识罪∈π,2π?,3??二所以cosα=-,三个α?π3? 因为∈? 2,4π?,2??? π α?α?? 所以sin2+2=cos=2??-1+cosα6=-.26回答:B4.若sin(α+β)cosβ-cos(α+β)sinβ=0,则sin(α+2β)+sin(α-2β)等于()a、 1b.-1c.0d.±1解析:因为sin(α+β)cosβ-cos(α+β)sinβ=sin(α+β-β)=sinα=0,所以sin(α+两β)+sin(α-两β)=2sinαcos2β=0。
回答:Cπ5.如果函数f(x)=(1+3tanx)cosx,0≤ x<F(x)的最大值2是()a、 1b.2c。
3+1d。
3+2分析:F(x)=(1+3tanx)cosx= ?sinx??1+3?Coxx?cosx=3sinx+cosx=0??π?2分钟?x+6?。
??二。
人教A版高中数学必修四3.2简单的三角恒等变换练习

高中数学学习材料(灿若寒星 精心整理制作)一.选择题1. 函数sin 3cos 22x x y =+的图像的一条对称轴方程是 ( ) A.113x π= B.53x π= C.53x π=- D .3x π=- 2.函数)cos (sin sin 2x x x y +=的最大值为( )A.21+B.12-C.2D.23.函数x x y cos sin 21++=的最大值是( ) A .122- B .122+ C .221- D .1+2 4.已知α,β是一个钝角三角形的两个锐角,下列四个不等式中不正确的是( )1tan tan .A <⋅βα2sin sin .B <+βα 1cos cos .C >+βα 2t a n )t a n (21.D βαβα+<+5.在△ABC 中,已知tan A +tan B =3tan A ·tan B -3,且sin B cos B =43,则△ABC 是( ) A.正三角形 B.直角三角形C.正三角形或直角三角形D.直角三角形或等腰三角形 6.函数22()sin ()sin ()44f x x x ππ=+--是( ) A.周期为π的偶函数 B.周期为π的奇函数C.周期为2π的偶函数D.周期为2π的奇函数7. 已知等腰三角形顶角的余弦值等于54,则这个三角形底角的正弦值为( )1010.A 1010.B - 10103.C 10103.D - 8.当04x π<<时,函数22cos ()cos sin sin x f x x x x=-的最小值是 ( ) A.4 B.12 C.2 D.14二.填空题9.已知a 是第二象限的角,4tan(2)3a π+=-,则tan a = . 10. ABC ∆的三个内角为A 、B 、C ,当A =_______时,cos 2cos2B C A ++取得最大值,且这个最大值为____________.11.函数xx y sin 12tan -=的最小正周期是___________________。
人教新课标A版高中数学必修4 第三章三角恒等变换 3.2简单的三角恒等变换 同步测试D卷

人教新课标A版高中数学必修4 第三章三角恒等变换 3.2简单的三角恒等变换同步测试D卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题;共30分)1. (2分)函数的图像与函数的图像所有交点的纵坐标之和等于()A . 2B . 4C . 6D . 82. (2分)实数x满足,则的值为()A . 8.5B . 8.5或7.5C . 7.5D . 不确定3. (2分) (2018高三上·沈阳期末) 定义行列式运算,将函数的图像向左平移个单位,所得图像关于轴对称,则的最小值为()A .B .C .D .4. (2分) (2018高一下·大同期末) 若,且,则角是()A . 第一象限B . 第二象限C . 第四象限D . 第三象限5. (2分)()A . tanxB . sinxC . cosxD . cotx6. (2分)已知和都是锐角,且,,则的值是()A .B .C .D .7. (2分)函数y=12sin+5sin的最大值为()A . 6+B . 17D . 128. (2分) (2017高三上·太原期末) 将函数f(x)= sinxcosx+sin2x的图象上各点的纵坐标不变,横坐标变为原来的2倍,再沿x轴向右平移个单位,得到函数y=g(x)的图象,则y=g(x)的一个递增区间是()A .B .C .D .9. (2分)若,且,则()A .B .C .D .10. (2分) (2018高一下·平顶山期末) 已知,则()A .B .C .11. (2分)将函数-3的图形按向量平移后得到函数g(x)的图形,满足和g(-x)+g(x)=0,则向量的一个可能值是()A .B .C .D .12. (2分)已知α为钝角,β为锐角,且sinα=,sinβ=,则的值为()A . -7B . 7C . -D .13. (2分) (2018高一下·贺州期末) 已知矩形,,点为矩形内一点,且,则的最大值为()A . 0B . 2C . 4D . 614. (2分)将函数的图像按向量平移,得到函数,那么函数可以是()A .B .C .D .15. (2分)sin54°sin18°=()A .B .C .D .二、填空题 (共5题;共5分)16. (1分)若θ∈(,),sin2θ=,则cosθ﹣sinθ的值是________17. (1分)已知,且,则的值为________.18. (1分)若=2,则sin(θ﹣5π)•sin=________19. (1分)若cosα=,且α∈(0,π),则tan=120. (1分)在△ABC中,已知tan=sinC,则△ABC的形状为________三、解答题 (共5题;共25分)21. (5分)已知sinα=, sin(α+β)=,α与β均为锐角,求cos.(cos=)22. (5分)的值为23. (5分)(2017高一下·正定期末) 在中,分别是角的对边,且.(Ⅰ)求的大小;(Ⅱ)若,求的面积24. (5分)已知函数f(x)=sin + cos ,x∈R.(1)求函数f(x)的最小正周期;(2)求函数f(x)在x∈[﹣2π,2π]上的单调递增区间.25. (5分)化简:cos•cos.参考答案一、单选题 (共15题;共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、二、填空题 (共5题;共5分) 16-1、17-1、18-1、19-1、20-1、三、解答题 (共5题;共25分) 21-1、22-1、23-1、24-1、24-2、25-1、。
人教新课标A版高中数学必修4第三章三角恒等变换3.2简单的三角恒等变换同步测试B卷

人教新课标A版高中数学必修4 第三章三角恒等变换 3.2简单的三角恒等变换同步测试B卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题;共30分)1. (2分)过与轴的交点,且倾斜角等于该直线倾斜角一半的直线方程为()A .B .C .D .2. (2分)函数的值域为()A .B .C .D .3. (2分)设则()A .B .C .D .4. (2分) (2018高一上·鹤岗月考) 已知,则 =()A .B .C .D .5. (2分)的三个内角所对的边分别为,,则()A .B .C .D .6. (2分)设,,.则它们的大小关系是()A . p<n<mB . n<p<mC . m<p<nD . m<n<p7. (2分) (2016高一下·黄石期中) 若sin74°=m,则cos8°=()A .B .C .D .8. (2分)已知为锐角,,则的值为()A .B . 3C .D .9. (2分)(2018·保定模拟) 2002年国际数学家大会在北京召开,会标是以我国古代数学家赵爽的弦图为基础设计.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的边长为2,大正方形的边长为10,直角三角形中较小的锐角为,则()A .B .C .D .10. (2分)将函数y=sin(x+)图像上各点的横坐标缩短到原来的倍(纵坐标不变),再向右平移个单位,那么所得图像的一条对称轴方程为()A . x=-B . x=-C . x=D . x=11. (2分)设向量,若t是实数,则的最小值为()A .B .C . 1D .12. (2分) (2019高三上·广州月考) ,若,则()A . 1B . 2C . 4D . 813. (2分) (2016高一下·周口期末) 若0<α<,﹣<β<0,cos(+α)= ,cos(﹣)= ,则cos(α+ )=()A .B . ﹣C .D . ﹣14. (2分)函数的值域是()A . [-1,3]B . [-1,4]C . (-6,3]D . (-2,4]15. (2分)sin54°sin18°=()A .B .C .D .二、填空题 (共5题;共5分)16. (1分)已知θ是第三象限角,且sin4θ+cos4θ=,那么sin2θ=________17. (1分)已知,且,则的值为________.18. (1分)若tanαtanβ+1=0,且,则sinα﹣cosβ=________19. (1分)若cosα=,且α∈(0,π),则tan=120. (1分) (2017高三上·辽宁期中) 已知,,则 ________.三、解答题 (共5题;共25分)21. (5分)已知,请用m分别表示tanθ、tan2θ、..22. (5分)已知A为△ABC的内角,求sinA+2sin2的取值范围.23. (5分)化简求值(1)化简;(2)证明:.24. (5分) (2015高一下·自贡开学考) 已知函数f(x)=cos2x﹣sinxcosx(1)求f(x)的最小正周期;(2)求函数f(x)的单调递增区间;(3)求f(x)在区间上的最大值和最小值.25. (5分)化简:cos•cos.参考答案一、单选题 (共15题;共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、二、填空题 (共5题;共5分) 16-1、17-1、18-1、19-1、20-1、三、解答题 (共5题;共25分) 21-1、22-1、23-1、23-2、24-1、24-2、24-3、25-1、。
人教A版数学必修四习题:第三章三角恒等变换3.2简单的三角恒等变换分层训练进阶冲关Word版含答案

分层训练·进阶冲关A组基础练(建议用时20分钟)1.(·银川高一检测)已知tan θ=2,且θ∈,则cos 2θ=( C )A. B. C.- D.-2.若-2π<α<-,则的值是( D )A.sinB.cosC.-sinD.-cos3.(2019·通化高一检测)已知函数f(x)=+asin cos的最大值为2,则常数a的值为( C )A. B.- C.± D.±4.已知sin 2α=,则cos2= ( D )A.-B.C.-D.5.已知sin=,cos 2α=,则sin α=( C )A. B.- C. D.-6.若θ∈,sin 2θ=,则sin θ等于 ( D )A. B. C. D.7.已知函数f(x)=(sin x+cos x)sin x,x∈R,则f(x)的最小值是.8.已知=,0<x<π,则tan x=-.9.设α∈,β∈,且5sin α+5cosα=8,sin β+cos β=2,则cos(α+β)的值为-.10.(2019·邢台高一检测)已知tan(3π-α)=-,tan(β-α)=-,则tan β=.11.已知函数f(x)=sin(ωx+φ)的图象关于直线x=对称,且图象上相邻两个最高点的距离为π.(1)求ω和φ的值.(2)若f=,求cos的值.【解析】(1)由已知,f(x)的最小正周期为π,所以=π,|ω|=2,又ω>0,所以ω=2.又图象关于直线x=对称,所以2×+φ=kπ+,k∈Z,又-≤φ<,所以φ=-.(2)因为f=,所以sin=,sin=.因为0<α-<,所以cos==,所以cos=sin α=sin=sin cos+cos sin=×+×=.12.(2019·合肥高一检测)已知cos·cos=-,α∈.(1)求sin 2α的值.(2)求tan α-的值.【解析】(1)因为cos cos=cos sin=sin=-,所以sin=-.因为α∈,所以2α+∈,所以cos=-,所以sin 2α=sin=sin cos -cos sin =.(2)因为α∈,所以2α∈.又由(1)知sin 2α=,所以cos 2α=-.所以tan α-=-==-=-2×=2.B组提升练(建议用时20分钟)13.已知2sin α=1+cosα,则tan= ( B )A. B.或不存在C.2D.2或不存在14.已知函数f(x)=sin ωx+cosωx(ω>0),x∈R.在曲线y=f(x)与直线y=1的交点中,若相邻交点距离的最小值为,则f(x)的最小正周期为( C )A. B. C.π D.2π15.已知tan(3π-x)=2,则= -3.16.已知函数f(x)=Acos2(ωx+φ)+1A>0,ω>0,0<φ<的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+…+f(2 016)= 4 032.17.已知cos 2θ=,<θ<π,(1)求tan θ的值.(2)求的值.【解析】(1)因为cos 2θ=,所以=,所以=,解得tan θ=±,因为<θ<π,所以tan θ=-.(2)=,因为<θ<π,tan θ=-,所以sin θ=,cos θ=-,所以===-4.18.已知函数f(x)=sin ωx+m cos ωx(ω>0,m>0)的最小值为-2,且图象上相邻两个最高点的距离为π.(1)求ω和m的值.(2)若f=,θ∈,求f的值.【解析】(1)易知f(x)=sin(ωx+φ)(φ为辅助角),所以f(x)m in=-=-2,又m>0,所以m=.由已知,函数f(x)的最小正周期为π,所以=π,所以ω=2.(2)由(1)得f(x)=sin 2x+cos 2x=2sin,所以f=2sin=,所以sin=.因为θ∈,所以θ+∈,所以cos=-=-,所以sin θ=sin=sin·cos -cos·sin =,所以f=2sin=2sin=2cos 2θ=2(1-2sin 2θ)=2=-.C组培优练(建议用时15分钟)19.已知直角三角形中两锐角为A和B,则sin Asin B ( B )A.有最大值和最小值0B.有最大值,但无最小值C.既无最大值,也无最小值D.有最大值1,但无最小值20.已知向量a=(sin B,1-cos B)与向量b=(2,0)的夹角为,其中A,B,C是△ABC的内角.(1)求B的大小.(2)求sin A+sin C的取值范围.【解析】(1)由已知, |a|==,|b|=2,a·b=2sin B.cos=,整理得1-cos B-2sin2B=0,即2cos2B-cos B-1=0.所以cos B=1(舍去)或cos B=-.又因为0<B<π,所以B=.(2)因为A+B+C=π,所以A+C=,所以-<A-C<.所以-<<.所以sin A+sin C=2sin cos=2sin cos =cos .所以sin A+sin C的取值范围是.关闭Word文档返回原板块。
人教A版高中数学必修四 3.2 简单的三角恒等变换(2)测试(教师版)

3.2 简单的三角恒等变换(2) (检测教师版)时间:40分钟 总分:60分班级: 姓名:一、 选择题(共6小题,每题5分,共30分)1.函数y =cos 2⎝⎛⎭⎫x -π12+sin 2⎝⎛⎭⎫x +π12-1是( ) A .奇函数 B .偶函数C .奇函数且是偶函数D .既不是奇函数,又不是偶函数解析:y =1+cos ⎝⎛⎭⎫2x -π62+1-cos ⎝⎛⎭⎫2x +π62-1=12⎣⎡⎦⎤cos ⎝⎛⎭⎫2x -π6-cos ⎝⎛⎭⎫2x +π6=12sin2x ,是奇函数.答案:A2.已知f (x )=sin 2⎝⎛⎭⎫x +π4,若a =f (lg5),b =f ⎝⎛⎭⎫lg 15,则( ) A .a +b =0 B .a -b =0 C .a +b =1 D .a -b =1解析:因为f (x )=sin 2⎝⎛⎭⎫x +π4=1-cos ⎝⎛⎭⎫2x +π22=1+sin2x 2,不妨令lg5=t ,则lg 15=-t , 所以a =f (lg5)=f (t )=1+sin2t 2,b =f ⎝⎛⎭⎫lg 15=f (-t )=1-sin2t2.所以a +b =1.故选C. 答案:C3.已知角α在第一象限,且cos α=35,则1+2cos ⎝⎛⎭⎫2α-π4sin ⎝⎛⎭⎫α+π2等于( )A.25B.75C.145 D .-25 解析:原式=1+2⎝⎛⎭⎫cos2αcos π4+sin2αsin π4cos α=1+cos2α+sin2αcos α=2cos 2α+2sin αcos αcos α=2×(cos α+sin α)=2×⎝⎛⎭⎫35+45=145. 答案:C4.设函数f (x )=2cos 2x +3sin2x +a (a 为实常数)在区间⎣⎡⎦⎤0,π2上的最小值为-4,那么a 的值等于( )A .4B .-6C .-4D .-3解析:f (x )=2cos 2x +3sin2x +a =1+cos2x +3sin2x +a =2sin ⎝⎛⎭⎫2x +π6+a +1.当x ∈⎣⎡⎦⎤0,π2时, 2x +π6∈⎣⎡⎦⎤π6,7π6,∴f (x )min =2·⎝⎛⎭⎫-12+a +1=-4.∴a =-4. 答案:C5.使f (x )=sin(2x +θ)+3cos(2x +θ)为奇函数,且在区间⎣⎡⎦⎤0,π4上是减函数的θ的一个值是( )A .-π3 B.π3 C.23π D.43π解析:f (x )=2sin ⎝⎛⎭⎫2x +θ+π3,当θ取-π3时,为奇函数,但在⎣⎡⎦⎤0,π4上递增;θ取π3和43π时为非奇非偶函数;当θ取2π3时,f (x )=-2sin2x 符合题意. 答案:C6.设△ABC 的三个内角为A ,B ,C ,向量m =(3sin A ,sin B ),n =(cos B ,3cos A ),若m·n =1+cos(A +B ),则C =( )A.π6B.π3C.2π3D.5π6 解析:依题意得3sin A cos B +3cos A sin B =1+cos(A +B ),3sin(A +B )=1+cos(A +B ),3sin C +cos C =1,2sin ⎝⎛⎭⎫C +π6=1,sin ⎝⎛⎭⎫C +π6=12. 又π6<C +π6<7π6,因此C +π6=5π6,C =2π3,故选C. 答案:C二、填空题(共2小题,每题5分,共10分)7.函数f (x )=sin 2x +3sin x cos x 在区间⎣⎡⎦⎤π4,π2上的最大值是解析:由已知得f (x )=1-cos2x 2+32sin2x =12+sin ⎝⎛⎭⎫2x -π6,当x ∈⎣⎡⎦⎤π4,π2时,2x -π6∈⎣⎡⎦⎤π3,5π6,sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤12,1,因此f (x )的最大值等于12+1=32. 答案:328.若函数f (x )=(1+3tan x )cos x ,0≤x <π2,则f (x )的最大值是解析: f (x )=(1+3tan x )cos x =⎝⎛⎭⎫1+3sin x cos x cos x =3sin x +cos x =2sin ⎝⎛⎭⎫x +π6. ∵0≤x <π2,∴π6≤x +π6<23π,∴当x +π6=π2时,f (x )取到最大值2.答案: 2三、解答题(共2小题,每题10分,共20分) 9.已知函数f (x )=cos 2x 2-sin x 2cos x 2-12.(1)求函数f (x )的最小正周期和值域; (2)若f (α)=3210,求sin2α的值.解析:(1)f (x )=cos 2x 2-sin x 2cos x 2-12=12(1+cos x )-12sin x -12=22cos ⎝⎛⎭⎫x +π4. 所以f (x )的最小正周期为2π,值域为⎣⎡⎦⎤-22,22. (2)由(1)知f (α)=22cos ⎝⎛⎭⎫α+π4=3210,所以cos ⎝⎛⎭⎫α+π4=35. 所以sin2α=-cos ⎝⎛⎭⎫π2+2α=-cos ⎣⎡⎦⎤2⎝⎛⎭⎫α+π4=1-2cos 2⎝⎛⎭⎫α+π4=1-1825=725. 10.已知函数f (x )=sin(π-ωx )cos ωx +cos 2ωx (ω>0)的最小正周期为π.(1)求ω的值;(2)将函数y =f (x )的图象上各点的横坐标缩短到原来的12,纵坐标不变,得到函数y =g (x )的图象,求函数g (x )在区间⎣⎡⎦⎤0,π16上的最小值. 解析:(1)因为f (x )=sin(π-ωx )cos ωx +cos 2ωx .所以f (x )=sin ωx cos ωx +1+cos2ωx 2=12sin2ωx +12cos2ωx +12=22sin ⎝⎛⎭⎫2ωx +π4+12. 由于ω>0,依题意得2π2ω=π.所以ω=1.(2)由(1)知f (x )=22sin ⎝⎛⎭⎫2x +π4+12.所以g (x )=f (2x )=22sin ⎝⎛⎭⎫4x +π4+12. 当0≤x ≤π16时,π4≤4x +π4≤π2.所以22≤sin ⎝⎛⎭⎫4x +π4≤1.因此1≤g (x )≤1+22. 故g (x )在区间⎣⎡⎦⎤0,π16上的最小值为1.。
高中数学人教A版必修四同步练测:3.2简单的三角恒等变换

高中数学学习材料 (灿若寒星 精心整理制作)3.2 简单的三角恒等变换(数学人教A 版必修4)建议用时 实际用时满分 实际得分45分钟100分一、选择题(每小题5分,共20分)1.当0<x <π4时,函数22cos ()cos sin sin x f x x x x=-的最小值是( ) A .3 B .12 C .2D .142.函数f (x )=sin x -cos x ,x ∈⎣⎡⎦⎤0,π2的最小值为( )A .-2B .- 3C .- 2D .-13. 已知向量a =(2,-2),b =(cos θ,sin θ),a∥b ,则θ的大小为( ) A .π4 B .-π4C .θ=π4+k π(k ∈Z ) D .θ=3π4+k π(k ∈Z ) 4. 已知向量a =(1,1-cos θ), b =(1+cos θ,12),且a ∥b ,则锐角θ等于( )A .30°B .45°C .60°D .75° 二、填空题(每小题5分,共10分)5.函数x x y cos 3sin +=在区间⎣⎡⎦⎤0,π2上的最小值为 .6.给出下列命题:①存在实数x ,使3s i n c o s 2x x +=;②若,αβ是第一象限角,且αβ>,则c o s c o s αβ<;③函数2πsin()32y x =+是偶函数;④函数sin 2y x =的图象向左平移π4个单位,得到函数πsin(2)4y x =+的图象.其中正确命题的序号是____________.三、解答题(共70分)7.(17分)已知函数f(x)=sin(x +θ)+cos(x -θ)的定义域为R .(1)当θ=0时,求f(x)的单调递增区间;(2)若θ∈(0,π),且sin x≠0,当θ为何值时,f(x)是偶函数?8.(17分)已知f(x)=2cos2x+3sin 2x+a,a∈R.(1)若f(x)有最大值为2,求实数a的值;(2)求函数y=f(x)的单调区间.9.(18分)已知函数f(x)=sin(θ+x)+sin(θ-x)-2sinθ,θ∈(0 ,3π2),且tan2θ=34-,若对任意x∈R,都有f(x)≥0成立,求cosθ的值.10. (18分)若函数f(x)=log2(2+x)+log2(2-x).(1)求函数f(x)的定义域,判断函数f(x)的奇偶性.(2)若关于θ(θ∈R)的方程f(sinθ)=2,求θ.3.2 简单的三角恒等变换(数学人教A版必修4)答题纸得分:一、选择题题号 1 2 3 4答案二、填空题5. 6.三、解答题7.8.9.10.3.2 简单的三角恒等变换(数学人教A 版必修4)答案一、选择题1. A 解析:min 22111(),tan ,()411tan tan 2(tan )24f x x f x x x x ====---+当时.2. D 解析:f(x)=2sin (x -π4),x ∈⎣⎡⎦⎤0,π2.∵-π4≤x -π4≤π4. ∴f(x)min =2sin(-π4)=-1.3. D 解析:∵ a ∥ b ,∴2sin θ-(-2)cos θ=0,∴sin θ=-cos θ,tan θ=-1,∴θ=34π+k π(k ∈Z ),故选D .4. B 解析:向量a =(1, 1-cos θ), b =(1+cos θ,12),且a ∥b , ∴12-(1-cos θ)(1+cos θ)=0,∴cos θ=±22.又∵ θ是锐角,∴ θ=45°.故选B.二、填空题5.1 解析:π2sin()3y x =+,min ππ5π5π,2sin 1.3366x y ≤+≤==. 6. ③ 解析: 对于①,π3sin cos 2sin()242x x x +=+≤<;对于②,反例为,虽然αβ>,但是cos cos αβ=;对于○4,ππsin 2sin 2()sin(2).42y x y x x =→=+=+三、解答题7. 解: (1)θ=0时,f(x)=sin x +cos x =2sin π()4x +. 当2k π-π2≤x +π4≤2k π+π2(k ∈Z ), 即2k π-34π≤x ≤2k π+π4(k ∈Z )时,f(x)是增函数,∴f(x)的单调递增区间是3π2ππ,2π44k k ⎡⎤-+⎢⎥⎣⎦(k ∈Z ). (2)由f(x)是偶函数,得f(-x)=f (x),∴sin(-x +θ)+cos(-x -θ)=sin(x +θ)+cos(x -θ). ∴sin(x +θ)+sin(x -θ)=cos(x +θ)-cos(x -θ). ∴2sin xcos θ=-2sin xsin θ. ∵sinx ≠0,∴cos θ=-sin θ.∴2sin (θ+π4)=0,θ+π4=k π,k ∈Z .又θ∈(0,π),令k =1,得θ=34π,∴当θ=34π时,f(x)是偶函数.8. 解:(1)f(x)=2cos 2x +3sin 2x +a =1+cos 2x +3sin 2x +a =2(32sin 2x +12cos 2x)+1+a =2sin(2x +π6)+1+a.当2x +π6=π2+2k π(k ∈Z )时,f(x)取最大值,解得x =π6+k π(k ∈Z )时,f(x)取最大值3+a.由3+a =2,解得a =-1.(2)令-π2+2k π≤2x +π6≤π2+2k π,k ∈Z ,解得k π-π3≤x ≤k π+π6,k ∈Z ,即单调递增区间是πππ,π36k k ⎡⎤-+⎢⎥⎣⎦(k ∈Z ). 同理,可求得单调递减区间是π2ππ,π63k k ⎡⎤++⎢⎥⎣⎦ (k ∈Z ). 9.解:依题意f (x )=2sin θcos x -2sin θ=2sin θ(cos x-1), 又对任意x ∈R ,都有f (x )≥0成立, ∵cosx-1≤0,∴sin θ≤0,∴π≤θ<3π2. 由tan2θ=34-得tan θ=3, ∴cos θ=-1010,即要求的三角函数值是-1010.10.解:(1)要使函数f (x )=log 2(2+x )+log 2(2-x )的解析式有意义, 自变量x 必须满足:20,20,x x +>⎧⎨->⎩解得-2<x <2.∴函数f (x )=log 2(2+x )+log 2(2-x )的定义域为(-2,2). 又∵f (-x )=log 2(2-x )+log 2(2+x )=f (x ), 故函数f (x )=log 2(2+x )+log 2(2-x )为偶函数.(2)∵f (sin θ)=log 2(2+sin θ)+log 2(2-sin θ)=log 2(4-sin2θ),∴方程f (sin θ)=2可化为4-sin 2θ=4,即sin2θ=0,即sin θ=0,解得θ=k π(k ∈Z ).。
人教A版数学必修四3.2简单的三角恒等变换基础达标(含答案解析)

高中数学学习材料 (灿若寒星 精心整理制作)1.计算cos 24°cos 36°-cos 66°cos 54°的结果为( )A .0 B.12C.32 D .-12 解析:选B.原式=cos 24°cos 36°-sin 24°sin 36°=cos(24°+36°)=cos 60°=12. 2.若α∈(π2,π),且sin α=45,则sin(α+π4)+cos(α+π4)=( ) A.425 B .-425 C.325 D .-325解析:选D.∵sin α=45,π2<α<π, ∴cos α=-35. ∴sin(α+π4)+cos(α+π4)=2sin(α+π2) =2cos α=-325. 3.(2013·山西考前适应性训练)sin 20°cos 20°cos 50°=( ) A .2 B.22 C.2 D.12解析:选D.sin 20°cos 20°cos 50°=12sin 40°cos 50°=12sin 40°sin 40°=12. 4.(2013·沈阳四校联考)若1+cos 2αsin 2α=12,则tan 2α等于( )A.54B .-54 C.43 D .-43解析:选D.1+cos 2αsin 2α=2cos 2α2sin αcos α=cos αsin α=12, ∴tan α=2,∴tan 2α=2tan α1-tan 2α=41-4=-43,故选D. 5.(2013·石家庄质检)计算tan (π4+α)·cos 2α2cos 2(π4-α)的值为( )A .-2B .2C .-1D .1 解析:选D.tan (π4+α)·cos 2α2cos 2(π4-α) =sin (π4+α)·cos 2α2sin 2(π4+α)cos (π4+α) =cos 2α2sin (π4+α)cos (π4+α)=cos 2αsin2(π4+α) =cos 2αsin (π2+2α)=cos 2αcos 2α=1,选D. 6.已知sin θ2+cos θ2=233,则cos 2θ=__________. 解析:因为sin θ2+cos θ2=233, 所以1+sin θ=43,即sin θ=13, 所以cos 2θ=1-2sin 2θ=1-29=79. 答案:797.若3sin x -3cos x =23sin(x +φ),φ∈(-π,π),则φ=________. 解析:∵3sin x -3cos x=23(32sin x -12cos x ) =23sin(x -π6),∴φ=-π6. 答案:-π68.化简:sin α+sin 2α1+cos α+cos 2α=________. 解析:原式=sin α(1+2cos α)1+cos α+2cos 2α-1=sin α(1+2cos α)cos α(1+2cos α)=tan α. 答案:tan α9.求3tan 12°-3sin 12°(4cos 212°-2)的值.解:原式=3sin 12°-3cos 12°cos 12°sin 12°·2cos 24°=3sin 12°-3cos 12°sin 24°cos 24° =43(sin 12°cos 60°-cos 12°sin 60°)2sin 24°cos 24°=43sin (-48°)sin 48°=-4 3. 10.已知α为钝角,β为锐角,且sin α=45,sin β=1213,求cos α-β2. 解:∵α为钝角,β为锐角,sin α=45,sin β=1213, ∴cos α=-35,cos β=513. cos(α-β)=cos αcos β+sin αsin β=-35×513+45×1213=3365. 又π2<α<π,0<β<π2, ∴0<α-β<π,0<α-β2<π2. ∴cos α-β2= 1+cos (α-β)2= 1+33652=76565.。
人教版高中数学必修四练习3.2简单的三角恒等变换

基础达标1.已知tan α2=3,则cos α=( ). A.45 B.-45 C.415D.-35解析 ∵tan α2=3,∴tan 2α2=1-cos α1+cos α=9,∴cos α=-45.答案 B2.化简tan α·tan 2αtan 2α-tan α的结果为( ).A .sin 2α B.cos 2α C .sin αD.cos α解析 tan α·tan 2αtan 2α-tan α=2tan 2α1-tan 2α2tan α-tan α+tan 3α1-tan 2α=2tan α1+tan 2α=2sin αcos α1+sin 2αcos 2α=2sin αcos α×cos 2α=2sin α·cos α=sin 2α, ∴选A. 答案 A3.当-π3≤x ≤π3时,函数y =sin x +3cos x 的最大值和最小值分别为( ). A .1,-1 B.1,-12 C .2, 3D.2,0解析 y =sin x +3cos x =2sin ⎝ ⎛⎭⎪⎫x +π3,而-π3≤x ≤π3,∴x +π3∈⎣⎢⎡⎦⎥⎤0,2π3,故sin ⎝ ⎛⎭⎪⎫x +π3∈[0,1],从而y ∈[0,2],因此选D. 答案 D4.函数y=sin2x的最小正周期为________.解析∵y=sin2x=1-cos 2x2=-12cos 2x+12.∴T=2π2=π.答案π5.设α为第四象限角,且sin 3αsin α=135,则tan 2α=________.解析sin 3αsin α=sin(2α+α)sin α=(1-2sin2α)sin α+2cos2αsin αsin α=2cos 2α+1=135,所以cos 2α=45,又α是第四象限角,所以sin 2α=-35,tan 2α=-3 4.答案-3 46.已知f(x)=1-x1+x,若α∈⎝⎛⎭⎪⎫π2,π,则f(cos α)+f(-cos α)可化简为________.解析f(cos α)+f(-cos α)=1-cos α1+cos α+1+cos α1-cos α=sinα2cosα2+cosα2sinα2=2 sin α.答案2 sin α7.已知tan 2θ=-22,π<2θ<2π.求:(1)tan θ;(2)2cos 2θ2-sin θ-12sin ⎝ ⎛⎭⎪⎫θ+π4.解 (1)由tan 2θ=2tan θ1-tan 2θ=-22,解得tan θ=2,或tan θ=-22. ∵π<2θ<2π,∴π2<θ<π,∴tan θ=-22. (2)原式=1+cos θ-sin θ-12sin ⎝ ⎛⎭⎪⎫θ+π4=cos θ-sin θsin θ+cos θ =1-tan θ1+tan θ=1-⎝ ⎛⎭⎪⎫-221+⎝⎛⎭⎪⎫-22=3+2 2. 能力提升8.(2012·佛山高一检测)使函数f (x )=sin(2x +θ)+3cos(2x +θ)为奇函数的θ的一个值是( ). A.π6 B.π3 C.π2D.2π3解析 f (x )=sin(2x +θ)+3cos(2x +θ) =2sin ⎝ ⎛⎭⎪⎫2x +π3+θ.当θ=23π时,f (x )=2sin(2x +π)=-2sin 2x . 答案 D9.已知向量a =(3,4),b =(sin α,cos α),且a ∥b ,则tan 2α=________. 解析 ∵a ∥b ,∴34=sin αcos α=tan α.∴tan 2α=2tan α1-tan 2α=2×341-⎝ ⎛⎭⎪⎫342=247.答案 24710.如图,将一块圆心角为120°,半径为20 cm 的扇形铁片裁成一块矩形,有两种裁法:让矩形一边在扇形的一半径OA 上(如图①)或让矩形一边与弦AB 平行(如图②),请问哪种裁法得到的矩形的最大面积大?请求出这个最大值.解 对于图①,MN =20sin θ,ON =20cos θ, ∴S 1=ON ·NM =400sin θcos θ=200sin 2θ, ∴当sin 2θ=1,即θ=45°时,(S 1)max =200 cm 2. 对于图②,MQ =40sin(60°-α),MN =4033sin α, ∴S 2=80033[cos(2α-60°)-cos60°],当cos(2α-60°)=1,即2α-60°=0,即α=30°时, (S 2)max =40033 cm 2.∵40033>200,∴用图②这种裁法得到的矩形的最大面积大,为40033cm 2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.已知 sin α-cos α=- , 则 sin 2α 的值等于( )
16
B .-
7
16
C .-
9
16
D. 9 A. 7
解析:由 sin α-cos α=- ,
(sin α-cos α)2=1-2sin αcos α=1-sin 2α= 25 所以 sin 2α=- 9
2.若函数 f (x )=-sin 2 x + (x ∈R),则 f (x )是( )
A .最小正周期为 的奇函数 解析:f (x )=- 1-cos 2x 1 1
3.若 sin(π-α)=- 5 3 且 α∈ π, 2 ⎪,则 sin 2+2⎪等于(
第三章
三角恒等变换
3.2
简单的三角恒等变换
A 级 基础巩固
一、选择题
5
4
5
4
16.
答案:C
1
2
π
2
B .最小正周期为 π 的奇函数
C .最小正周期为 2π 的偶函数
D .最小正周期为 π 的偶函数
2 +2=2cos 2x .
答案:D
⎛ 3π⎫ ⎛π α⎫
⎝ ⎭ ⎝
⎭ 16
16 ,
)
A .- 6
B .- C. D. 解析:由题意知 sin α=- ,α∈ π,2π
⎪,3
所以 cos α=- ,
因为 ∈ 2,4π
⎪,2 所以 sin 2+2⎪=cos -
1+cos α =- . 5.若函数 f (x )=(1+ 3tan x )cos x ,0≤x < ,则 f (x )的最大值 1+ 3 cos x ⎪⎭cos x = 3sin x +cos x = 2sin x + ⎪.
6 6 6
3 6 6
3
5 ⎛ 3 ⎫ ⎝
⎭
2
3
α ⎛π 3 ⎫
⎝
⎭
⎛π α⎫ α ⎝ ⎭
2
=
6
2 6
答案:B
4.若 sin(α+ β )cos
β-cos(α+ β )sin β=0,则 sin(α+2 β )
+sin(α-2 β )等于(
)
A .1
B .-1
C .0
D .±1
解析:因为 sin(α+ β )cos
β-cos(α+ β )sin β=sin(α+ β-
β )=sin α=0,
所以 sin(α+2 β )+sin (α-2 β )=2sin αcos 2 β=0.
答案:C
π
2
是(
)
A .1
B .2 C. 3+1
D. 3+2
解析:f (x )=(1+ 3tan x )cos x =
⎛
sin x ⎫ ⎝
⎛
π⎫ ⎝ 6⎭
因为 0≤x < ,所以 ≤x + < π,
所以当 x + = 时,f (x )取到最大值 2.
6.若 sin α=cos 2α,α∈ 2 ,π⎪,则 tan α=________.
解得 sin α= 或-1.
又 α∈ 2
,π⎪,所以 α= π,6 tan α=tan π=- .
答案:- 3
解析 : 因为 3sin x - 3cos x = 2 3 sin x - cos x ⎪ = 2 3
sin x -6⎪,因为 φ∈(-π,π),所以 φ=- .6
2 18 18
cos - 3sin 18 18
π π π 2
2 6 6 3
π π
6 2
答案:B
二、填空题
⎛π ⎫ ⎝
⎭
解析:由题意得 2sin 2 α+sin α-1=0,
1
2
⎛π ⎫ 5 ⎝
⎭
5 3
6 3
3
7.若 3sin x - 3cos x =2 3sin(x +φ),φ∈(-π,π),则 φ=
________.
⎛ 3
1 ⎫
⎝ 2 ⎭
⎛ π⎫ π ⎝
⎭
答案:-
π
6
8.
1 3
π - π =________.
sin cos
π π
18 18
解析:原式= =
π π
sin cos
18⎪⎭ ⎝2
2 cos - sin sin 2tan
4-α⎪)sin 2 4+α⎪
2tan 4-α⎪sin 2( +α)4
2cos 4+α⎪
2
+α⎪
·sin 4 sin 4+α⎪
= =1.
sin 2+2α⎪
10.已知 2sin 4+α⎪=sin θ +cos θ ,2sin2β =sin 2θ ,求证:
sin 2α + cos 2β =0.
证明:由 2sin 4
+α⎪=sin θ+cos θ, 即 2sin 2α+cos 2β=0,所以 sin 2α+ cos 2β=0.
⎛1 π 3 π ⎫ 18 2 1 π
2 9
=
4sin
sin
π 9 π
=4.
9
答案:4
三、解答题
2cos 2 α-1
9.化简 .
⎛π ⎫ ⎛π ⎫ ⎝
⎭ ⎝ ⎭
2cos 2α-1
解: =
⎛π ⎫ π ⎝
⎭
cos 2α
⎛π ⎫ ⎝ ⎭ ⎛π ⎫ ⎛π ⎫ ⎝ ⎭ ⎝
⎭
=
cos 2α cos 2α
⎛π ⎫ cos 2α ⎝
⎭
⎛
π ⎫ ⎝
⎭
1
2
⎛π ⎫ ⎝
⎭
得 2cos α+ 2sin α=sin θ+cos θ,
两边平方得,2(1+sin 2α)=1+sin 2θ,①
又 sin2β=sin 2θ,②
由①②两式消去 sin 2θ,得 2(1+sin 2α)=1+2sin2β,
1
2
2 2
=4 sin x + cos x ⎪ cos x - sin x ⎪
=4sin x +6⎪cos x +6⎪=2sin 2x +3⎪, 所以 T = 2π
=π.
=sin 2x + 3cos 2x =2sin 2x +3⎪,
所以 T = 2π
=π.
2.在△ABC 中,若 cos A = ,则 sin 2 +cos 2A 等于________. 解析:在△ABC 中,
= - , ⎫⎛ 3
2 2 所以 sin 2B +C 2 - +cos 2A =sin 2
2 ⎪⎭
+cos
2A =
+cos 2A =
+2cos 2 A -1=- .
B 级 能力提升
1.(2016· 山东卷)函数 f (x )=( 3sin x +cos x )( 3cos x -sin x )的最
小正周期是(
)
π A.
3π C. B .π
D .2π
解析:法一:因为 f (x )=( 3sin x +cos x )( 3cos x -sin x )
⎛ 3 1 1 ⎫ ⎝ 2 ⎭⎝ 2 ⎭
⎛ π⎫ ⎛ π⎫ ⎛ π⎫
⎝
⎭ ⎝ ⎭ ⎝ ⎭
2
法二:因为 f (x )=( 3sin x +cos x )( 3cos x -sin x )
=3sin x cos x + 3cos2x - 3sin2x -sin x cos x
⎛ π⎫
⎝
⎭
2
答案:B
1
B +
C 3 2
B +
C π A
2 2 2
⎛π 2
⎝
A ⎫
cos 2 A 1+cos A 1
2 2 9
(2)求 f (x )在区间⎢0, ⎥上的最大值和最小值.
+cos 2x = 2sin 2x + ⎪+1,
所以函数 f (x )的最小正周期为 T = =π.
(2)由(1)的计算结果知,f (x )= 2sin 2x +4⎪+1.
当 x ∈⎢0,2⎥时,2x + ∈⎢4, 4 ⎥,4 由正弦函数 y =sin x 在⎢4, 4 ⎥上的图象知,
当 2x + = ,即 x = 时,f (x )取得最大值 2+1;
当 2x + = ,即 x = 时,f (x )取得最小值 0.
综上,f (x )在⎢0,2⎥上的最大值为 2+1,最小值为 0. ⎣
答案:-
1
9
3.(2015· 安徽卷)已知函数 f (x )=(sin x +cos x )2+cos 2x .
(1)求 f (x )的最小正周期;
⎡
π⎤ ⎣
2⎦
解:(1)因为 f (x )=sin 2x +cos 2x +2sin x cos x +cos 2 x =1+sin 2 x
⎛
π⎫ ⎝
4⎭
2π
2
⎛ π⎫ ⎝
⎭
⎡ π⎤ π ⎡π 5π⎤
⎣
⎦ ⎦
⎡π 5π⎤
⎣
⎦
π π π
4 2 8
π 5π π
4 4 2
⎡ π⎤
⎣
⎦。
