26.1二次函数(2)图象与性质(4)
26.1.2二次函数图像和性质00
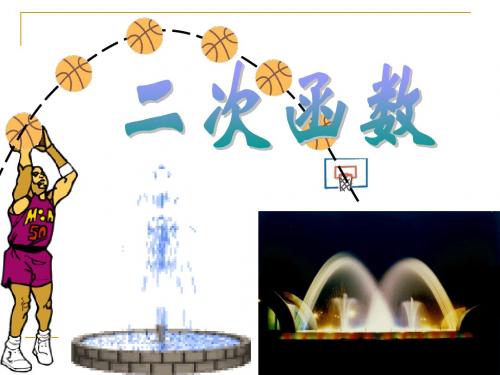
向上
顶点从(0,0)移到了 (0,–2),即x=0时, y取最大值–2
5 4 3 2 1
y
顶点从(0,0)移到了 (0, 2),即x=0时, y取最大值2
x 1 2 3 4 5
–5 –4 –3 –2 –1 O –1 –2 1 2 y x 2 –3 3 –4 –5
1 2 y x 2 3 1 2 y x 3
下 3、函数y =-2(x+1)2的图象开口向____,对称轴 (-1,0) 是____________,顶点坐标是________,当 直线x=-1
大 < -1 0 -1 x=____时,函数有最____值为____;当x_____
> -1 时,y随x的增大而增大,当x_____时, y随x的 增大而减小。 4、抛物线y=3x2-4,y=3(x-1)2与抛物线y=3x2 位置 形状 的_______相同,_______不同。抛物线y=3x2-4 是由抛物线y=3x2向____平移____单位而得到; 下 4 右 抛物线y=3(x-1)2是由抛物线y=3x2向____平移 1 ____单位而得到。
y=a(x-h)2 (a≠0) 开口方向 顶点坐标 对称轴 增 减 性
a>0
a<0
向上 (h ,0) x=h
当x<h时, y随着x的增大而减小。 当x>h时, y随着x的增大而增大。
向下 (h ,0) x=h
当x<h时, y随着x的增大而增大。 当x>h时, y随着x的增大而减小。
极值
x=h时,y最小值=0
1y 2x 3
2
向上
2
直线x=3 直线x= –1
直线x=0 (Y轴)
二次函数的全章教案

26.1二次函数(一)一、学习目标1.知识与技能目标:(1)理解并掌握二次函数的概念;(2)能判断一个给定的函数是否为二次函数,并会用待定系数法求函数解析式;(3)能根据实际问题中的条件确定二次函数的解析式。
二、学习重点难点1.重点:理解二次函数的概念,能根据已知条件写出函数解析式; 2.难点:理解二次函数的概念。
三、教学过程(一)创设情境、导入新课:回忆一下什么是正比例函数、一次函数、反比例函数?它们的一般形式是怎样的? (二)自主探究、合作交流:问题1: 正方体的六个面是全等的正方形,如果正方形的棱长为x ,表面积为y ,写出y 与x 的关系。
问题2: n 边形的对角线数d 与边数n 之间有怎样的关系?问题3: 某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比上一年的产量增加x 倍,那么两年后这种产品的数量y 将随计划所定的x 的值而定,y 与x 之间的关系怎样表示?问题4:观察以上三个问题所写出来的三个函数关系式有什么特点?小组交流、讨论得出结论:经化简后都具有 的形式。
问题5:什么是二次函数?形如 。
问题6:函数y=ax²+bx+c ,当a 、b 、c 满足什么条件时,(1)它是二次函数? (2)它是一次函数? (3)它是正比例函数?(三)尝试应用:例1. 关于x 的函数 是二次函数, 求m 的值.mm 221)x (m y --=注意:二次函数的二次项系数必须是的数。
例2.已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7。
求这个二次函数的解析式.(待定系数法)(四)巩固提高:1.下列函数中,哪些是二次函数?(1)y=3x-1 ; (2)y=3x2+2; (3)y=3x3+2x2; (4)y=2x2-2x+1; (5)y=x2-x(1+x); (6)y=x-2+x.2.一个圆柱的高等于底面半径,写出它的表面积S与半径R之间的关系式。
26.1.3二次函数的图像(2)

1 2 y ( x 1 ) 画出二次函数 2
1 y、 ( x 1) 2 2
解: 先列表
点(-1,0)且与x轴垂直的直 线,我们把它记为x=-1, 顶点是(-1,0); 1 1 2 y ( x 1 ) y ( x 1) 抛物线 呢 ? 2 2
2
x=-1
-5 -6 -7 -8 -9 -10
x
向上或向下平移|k|得到. (k>0,向上平移;k<0向下平移.)
求抛物线y=-2x2+1与x轴、y 轴的交点坐标
的 图像,并考虑它们的开口方向、对称轴和顶点.:
… -3 -2 -1 0 1 2 3 … 1 y ( x 1) 2 … -2 -0.5 0 -0.5 -2 -4.5 -8 … 2 1 y ( x 1) 2 … -8 -4.5 -2 -0.5 0 -0.5 -2 … 2 y 1 2 1 然后描点画图,得 y ( x 1) 2 1 2 -5 -4 -3 -2 -1 o 1 2 3 4 5 x 和 y 2 ( x 1) 的图象. -1 -2 1 2 可以看出,抛物线 y 1 ( x 1) 2 y ( x 1 ) -3 2 2 -4 的开口向下, 对称轴是经过 x
右 平移____ 1 物线y=3(x-1)2是由抛物线y=3x2向____
单位而得到。
5、指出抛物线抛物线y= 2x2-4x+2的开口方向, 对称轴,顶点坐标;函数有最大值还是最小值? 是多少?
6.函数 y 4 x 4 x 1 的图象与坐标 2 轴有几个交点?可以由抛物线 y 4 x 平移得到吗?应怎样平移?
顶点是(-1, -1). 平移方法1:
x
平移方法2:
华师大版数学九年级下册《26.1 二次函数》教学设计3

华师大版数学九年级下册《26.1 二次函数》教学设计3一. 教材分析华师大版数学九年级下册《26.1 二次函数》是学生在初中阶段学习二次函数的起始章节,它是在学生已经掌握了函数概念、一次函数和二次方程的基础上进行的。
本节课的主要内容是介绍二次函数的定义、性质和图像,以及二次函数的顶点公式。
教材通过生动的实例和丰富的练习,帮助学生理解和掌握二次函数的知识,为学生进一步学习高中数学打下坚实的基础。
二. 学情分析九年级的学生已经具备了一定的数学基础,对函数概念、一次函数和二次方程有一定的了解。
但二次函数相对于一次函数来说,其图像和性质更加复杂,需要学生通过实例和练习来进一步理解和掌握。
此外,学生的学习兴趣和动机对他们的学习效果有很大影响,因此教师需要设计有趣的教学活动来激发学生的学习兴趣。
三. 教学目标1.知识与技能:使学生理解和掌握二次函数的定义、性质和图像,能够运用二次函数的知识解决实际问题。
2.过程与方法:通过实例和练习,培养学生的观察能力、推理能力和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的合作意识和创新精神。
四. 教学重难点1.重点:二次函数的定义、性质和图像。
2.难点:理解二次函数的顶点公式,并能运用其解决实际问题。
五. 教学方法采用问题驱动法、案例教学法和小组合作法。
通过提出问题,引导学生思考和探索;通过分析具体案例,使学生理解和掌握二次函数的知识;通过小组合作,培养学生的合作意识和解决问题的能力。
六. 教学准备1.准备相关的教学案例和练习题。
2.准备多媒体教学设备,如投影仪和黑板。
3.准备教案和教学笔记。
七. 教学过程1.导入(5分钟)通过提出问题,引导学生思考和探索二次函数的概念。
例如:“什么是二次函数?它与一次函数有什么区别?”2.呈现(10分钟)通过分析具体案例,使学生理解和掌握二次函数的定义、性质和图像。
例如,展示一个二次函数的图像,引导学生观察其特点。
九年级数学下第26章二次函数26.1二次函数及其图象2二次函数y=ax2的图象习题新人教

•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月27日星期日2022/3/272022/3/272022/3/27 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/272022/3/272022/3/273/27/2022 •3、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之失败。 2022/3/272022/3/27March 27, 2022
x> 0时 , y随 x的 增 大 而 增 大 , x< 0时 , y随 x的 增 大 而 减 小 .
2.a<0⇔开口向下⇔有最大值⇔
x> 0时 , y随 x的 增 大 而 减 小 , x< 0时 , y随 x的 增 大 而 增 大 .
知识点 2 求二次函数y=ax2的解析式
【例2】(2013·山西中考)如图是我省某地一座抛物线形拱桥,
(1)求此抛物线的解析式. (2)过点P作CB所在直线的垂线,垂足为点R, 求证:PF=PR.
【解析】(1)由题意可得:点A的坐标为(2,-1),
∵抛物线的顶点为坐标原点O,
∴可设抛物线的解析式为:y=ax2, 将点A(2,-1)代入可得:4a=-1,解得a=- 1 ,
4
∴抛物线的解析式为y=- 1 x2.
【例1】函数 ym2xm 2m 4 是关于x的二次函数,求:
(1)满足条件的m的值. (2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何 值时,y随x的增大而增大? (3)m为何值时,抛物线的开口方向向下?这时当x为何值时,y随x 的增大而减小?
【解题探究】(1)函数是二次函数的条件是自变量的最高次数
26.1 二次函数y=ax2的图象与性质 精品作业课件(课程配套练习) 公开课一等奖课件

1 2 解:(1)y= x (2)图略 (3)抛物线;当 x>0 时,y 随 x 4 的增大而增大 (4)有最小值为 0
18. (10 分)如图所示, 某桥洞的截面是抛物线形, 在图中 建立的直角坐标系中,抛物线所对应的二次函数的关系式为 1 2 y=- x ,当桥洞中水面宽 AB 为 12 米时,求水面到桥拱顶 4 点 O 的距离.
解:水面到桥拱顶点 O 的距离为 9 米
【综合运用】 19.(12 分)已知点 A(-3,-9)是顶点在原点的抛物线上 的一点 ,点 P(x,y)是抛物线上的一个动点 ,且在第四象限 内.点 B 在 x 轴正半轴上,且 OB=4,△OPB 的面积为 S. (1)求抛物线的函数关系式; (2)分别求 S 和 y,S 和 x 之间的函数关系式,并判断它们 是什么函数,直接写出自变量的取值范围.
)
3.(4分)某课外兴趣小组为了了解所在地区老年人的健康状况,分别做了四种不 同的抽样调查,你认为抽样比较合理的是( D ) A.在某个公园调查了1 000名老年人的健康状况 B.在医院调查了1 000名老年人的健康状况 C.调查了10名老年邻居的健康状况 D.利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 4.(4分)下列调查的样本缺乏代表性的是( C ) A.在大学生中调查大学生课余时间娱乐的主要方式 B.调查学号为3的倍数的学生,以了解学生对学校某项新举措的意见和建议 C.在老年活动中心调查市民对春节联欢会的喜好程度 D.在某校九年级中调查全市九年级学生的身体发育情况
解: (1)y=-x2 (2)S=-2y, 它是一次函数, 自变量 y< 0;S=2x2,它是二次函数,自变量的取值范围为 x>0.
抽样调查时 , 所选取的样本要有 __ 代表性 __ , 样本容量要足够 __大__.仅仅增加调查人数不一定能够提高调查质量 ,开展调查 之前,要仔细检查总体中的每个个体是否都有可能成为 _调查对象 __.
26.1.2二次函数y=ax2的图象和性质

y
Q(0,b)
(-,+) o (-,-)
(+,+)
P(a,0)
x (+,-)
3. 点的位置及其坐标特征: ①.各象限内的点: ③.对称于坐标轴的两点: y
C(m,n) M(a,b)
②.各坐标轴上的点: ④.对称于原点的两点:
N(a,-b) A(x,y)
o
x
D(-m,-n) B(-x,y)
试学活动一
二次函数y=ax 二次函数y=ax2的图象和性质
y
x
平面直角坐标系: 一. 平面直角坐标系 1. 有关概念: 2. 平面内点的坐标:
你还记得有关 y 平面直角坐标 P (a,b) b 系的相关知识 吗? a o
(纵轴) 第二象限 第一象限 第三象限 第四象限
x(横轴)
3. 点的位置及其坐标特征: ①.各象限内的点: ②.各坐标轴上的点:
y=- 2 3 x
2
试学活动二
2
,
的图象。
x
y= 1 2 x y=x2 2
... ... ... ...
-4 -3 8 4.5
-2 -1 2 0.5
0 0 0 0 0 0
1 0.5 0.5 0.5 1
− 2 3
2 2 1 2 1.5 1.5
3 4.5 1.5 4.5 2
− 8 3
4 8 2 8 3 -6
y = 2x2
y = − x2
2 y = − x2 3
二次函数y=ax2的图象形如物体抛射时 所经过的路线,我们把它叫做抛物线。 抛物线。 抛物线 这条抛物线关于y轴 这条抛物线关于 轴 这条抛物线关于y轴 这条抛物线关于 轴 这条抛物线关于y轴 这条抛物线关于 轴 对称, 轴就是它的 对称,y轴就是它的 对称, y轴就是它的 对称,y轴就是它的 对称, 对称, 轴就是它的 对称轴。 对称轴。轴就是它的 对称轴。 对称轴。 对称轴。 对称轴。 对称轴与抛物线 抛物线的交点 对称轴与抛物线的交点 对称轴与抛物线的交点 叫做抛物线的顶点。 叫做抛物线的顶点
26.1二次函数y=a(x-h)2图像与性质学案4

实验中学九年级数学学案
顶点
对称轴
最值
增减性
也画上去(草图).①抛物线y =-12 (x +1)2 ,y =-12 x 2,y =-1
2 (x
.它们之间如何平移得到?
练习平台一、循序渐进:
2.对于二次函数的图象,只要|a|相等,则它们的形状_________,只是_________不同.3.抛物线y=4 (x-2)2与y轴的交点坐标是___________,与x轴的交点坐标为________.4.把抛物线y=3x2向右平移4个单位后,得到的抛物线的表达式为________________.把抛物线y=3x2向左平移6个单位后,得到的抛物线的表达式为_______________.
5.将抛物线y=-1
3(x-1)x
2向右平移2个单位后,得到的抛物线解析式为____________.
6.写出一个顶点是(5,0),形状、开口方向与抛物线y=-2x2都相同的二次函数解析式__________________.
7.抛物线y=2 (x+3)2的开口______________;顶点坐标为__________________;对称轴是_________;
当x>-3时,y______________;当x=-3时,y有_______值是_________.
8.抛物线y=m (x+n)2向左平移2个单位后,得到的函数关系式是y=-4 (x-4)2,则m=__________,n=___________.
9.若将抛物线y=2x2+1向下平移2个单位后,得到的抛物线解析式为______________.
10.若抛物线y=m (x+1)2过点(1,-4),则m=_______________.。
26.1 二次函数及其图像 课件4(数学人教版九年级下册)

y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
h,k
直线x h
向上
当x h时, 最小值为 k
h,k
直线x h
向下
当x h时,最大值为 k
练习1
说出下列抛物线的开口方向、对称轴及顶点:
( 1 )y ( 2 x 3) 5;(2)y ( 3 x 1 ) 2;
-5 -4 -3 -2 -1 o 1 2 3 4 5
x
抛物线y=x2+1:
开口向上,对称轴是y轴, 顶点为(0,1). 抛物线y=x2-1: 开口向上,对称轴是y轴, 顶点为(0, -1).
(1) 抛物线 2 2 y=x +1,y=x -1 的开口方向、对 称轴、顶点各是 什么?
10 9 8 7 6 5 4 3 2 ● 1
y
三、观察三条抛物线:
2 (2)开口大小有没有 1 变化? -3 -2 -1 0 1 2 3 x -1 -2 没有变化 -3 1 2 -4 y x -5 2 1 1 2 y ( x 1) -6 y ( x 1) 2 2 -7 2 -8
y
三、观察三条抛物线:
2 (3)对称轴是什么? 1 -3 -2 -1 0 1 2 3 x -1 -2 -3 y 轴 x=-1 x=1 1 2 -4 y x -5 2 1 1 2 y ( x 1) -6 y ( x 1) 2 2 -7 2 -8
抛物线y a ( x h) 2 k有如下特点: (1)当a 0时,开口向上 ____;当a 0,开口向下 ___; x=h ; (2)对称轴是直线____ (3)顶点坐标是 ______ 。 ( h,k)
26.1.2二次函数图像与性质
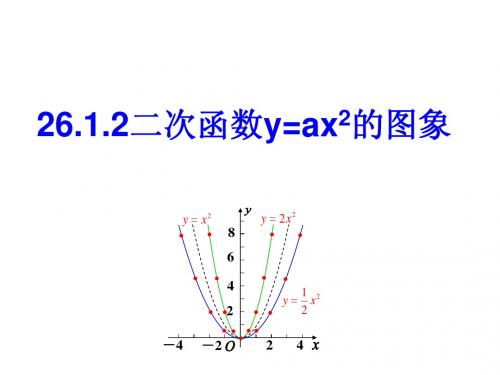
的图象,并考虑这些抛物
x
· -4 · ·
-3
-4.5 -1.5
-2
-2 -1 -2
-1 -0.5
-0.5 -0.5
0 0
1
-0.5 0 0
2
3
4
-8 2
· · · · · ·
· · 1 2· -8 y x 2
x · -2 · ·
-2 -4.5 1 1.5
0.5
· · ·
· · ·
· · ·
-8 -4.5 -0.5 -2 -4.5 -8
(2 2 , 6)
3 y x 4
练一练:
1.若抛物线 y
(2m 1) x
)
2
的开口向下,则
m的取值范围为(B
( A)m 0
1 (C )m 2
1 ( B )m 2 1 ( D )m 2
练习三、已知抛物线y ax 2 a 0 与双曲线 2 y 交点的横坐标大于零。问a是大于零 x 还是小于零?
二次函数y=ax2的性质
y=ax2 图象 a>0 a<0
O O
开口
开口向上
开口向下
对称性
顶点 增减性
|a|越大,开口越小 关于y轴对称 顶点坐标是原点(0,0) 顶点是最低点 顶点是最高点 在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减
y = x2
9
6
3 -3 3
看出: y轴是抛物线y = x 2 的对称轴,抛物抛物线y = x2 的顶点,它是抛物线y = x 2 的最低点.
实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线 的顶点.顶点是抛物线的最低点或最高点.
人教版九年级数学下册全册教案(表格式)

义务教育课程标准人教版数学教案九年级下册教师:班级:教学时间课题26.1二次函数(2)课型新授课教学目标知识和能力使学生会用描点法画出y=ax2的图象,理解抛物线的有关概念。
过程和方法使学生经历、探索二次函数y=ax2图象性质的过程情感态度价值观培养学生观察、思考、归纳的良好思维习惯教学重点使学生理解抛物线的有关概念,会用描点法画出二次函数y=ax2的图象是教学的重点。
教学难点用描点法画出二次函数y=ax2的图象以及探索二次函数性质是教学的难点。
教学准备教师多媒体课件学生“五个一”课堂教学程序设计二次复备一、提出问题1,同学们可以回想一下,一次函数的性质是如何研究的?(先画出一次函数的图象,然后观察、分析、归纳得到一次函数的性质)2.我们能否类比研究一次函数性质方法来研究二次函数的性质呢?如果可以,应先研究什么?(可以用研究一次函数性质的方法来研究二次函数的性质,应先研究二次函数的图象)3.一次函数的图象是什么?二次函数的图象是什么?二、范例例1、画二次函数y=x2的图象。
解:(1)列表:在x的取值范围内列出函数对应值表:x …-3 -2 -1 0 1 2 3 …y …9 4 1 0 1 4 9 …(2)在直角坐标系中描点:用表里各组对应值作为点的坐标,在平面直角坐标系中描点(3)连线:用光滑的曲线顺次连结各点,得到函数y=x2的图象,如图所示。
提问:观察这个函数的图象,它有什么特点?让学生观察,思考、讨论、交流,归结为:它有一条对称轴,且对称轴和图象有一点交点。
抛物线概念:像这样的曲线通常叫做抛物线。
顶点概念:抛物线与它的对称轴的交点叫做抛物线的顶点.三、做一做1.在同一直角坐标系中,画出函数y=x2与y=-x2的图象,观察并比较两个图象,你发现有什么共同点?又有什么区别?2.在同一直角坐标系中,画出函数y=2x2与y=-2x2的图象,观察并比较这两个函数的图象,你能发现什么?3.将所画的四个函数的图象作比较,你又能发现什么?在学生画函数图象的同时,教师要指导中下水平的学生,讲评时,要引导学生讨论选几个点比较合适以及如何选点。
26.1.2 二次函数的图象和性质

3、画函数图象的一般步骤及各步注意的问题。
二、探索新知:
画二次函数 的图象.
【提示:画图象的一般步骤:①列表(取几组x、y的对应值;②描点(表中x、y的数值在坐标平面中描点(x,y);③连线(用平滑曲线).】
列表:
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
…
描点,并连线
由图象可得二次函数 的性质:
东辛店中学验标题
(满分:50+20时间:10分钟成绩:)
必做题:(共5题,每题10分)
1.函数y=x2的图象开口向_______,顶点是__________,对称轴是________,
当x=___________时,有最_________值是_________.
2.二次函数y=mx 有最低点,则m=___________.
对称,开口大小_______________.
3.当a>0时,a越大,抛物线的开口越___________;
当a<0时,|a|越大,抛物线的开口越_________;
因此,|a|越大,抛物线的开口越________,反之,|a|越小,抛物线的开口越________.
六、课堂训练
1.填表:
开口方向
顶点
1、二次函数 是一条曲线,把这条曲线叫做______________.
2、二次函数 中,二次函数a=_______,抛物线 的图象开口__________.
3、自变量x的取值范围是____________.
4、观察图象,当两点的横坐标互为相反数时,函数y值相等,所描出的各对应点关于________对称,从而图象关于___________对称.
26.1二次函数(第4课时)

巩固 下列二次函数: 下列二次函数:
1 2 y= x 2
1 2 y = ( x + 2) 2
1 2 y = ( x − 2) 2
1.说明三条抛物线的相互关系,并分别指出它们的开口方 说明三条抛物线的相互关系, 说明三条抛物线的相互关系 向、对称轴及顶点. 对称轴及顶点.
1 2 2.若将函数y = (x + 2) 向左平移5个单位长度, 2 得到的是那个函数的图象?
么关系? 么关系?
你能说出函数y = a(x − h) 的图象和性质吗?
2
归纳
二次函数y 二次函数 = a﹙x-h﹚2的性质 ﹙ ﹚ 的性质:
(1)开口方向:当a>0时,开口向上 )开口方向: > 时 开口向上; 当a<0时,开口向下; < 时 开口向下; (2)对称轴: 对称轴直线 )对称轴: 对称轴直线x=h; 3)顶点坐标: 顶点坐标是(h,0) (3)顶点坐标: 顶点坐标是(h,0) (4)函数的增减性: )函数的增减性: 增大而减小, 当a>0时, 对称轴左侧 随x增大而减小, > 时 对称轴左侧y随 增大而减小 对称轴右侧y随 增大而增大 增大而增大; 对称轴右侧 随x增大而增大; 增大而增大, 当a<0时, 对称轴左侧 随x增大而增大, < 时 对称轴左侧y随 增大而增大 对称轴右侧y随 增大而减小 增大而减小。 对称轴右侧 随x增大而减小。
(1,0) 是_________________. .
1 2 1 1 2 y = − ( x − 1) 与抛物线 y = − x 2 抛物线 y = − ( x + 1) 2 2 2
有什么关系? 有什么关系?
1 2 向左平移1个单位 个单位, x 向左平移 个单位,就得到抛物 2 1 1 2 y = − x 2 向右平移 个单位,就得到抛物 向右平移1个单位 个单位, 线y = − ( x + 1);把抛物线 2 2
最全二次函数概念的图像与性质(系统归纳)完整版.doc
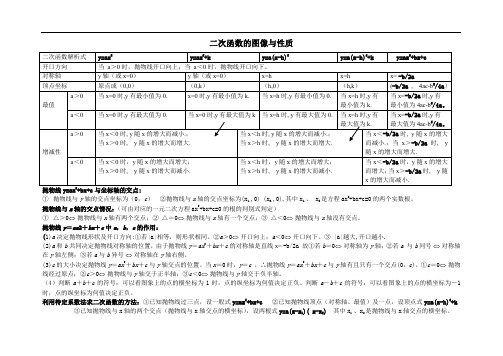
二次函数的图像与性质抛物线y=ax+bx+c与坐标轴的交点:①抛物线与y轴的交点坐标为(0,c)②抛物线与x轴的交点坐标为(x1,,0) (x2,,0),其中x1,、 x2是方程ax2+bx+c=0的两个实数根。
抛物线与x轴的交点情况:(可由对应的一元二次方程ax2+bx+c=0的根的判别式判定)①△>0⇔抛物线与x轴有两个交点;②△=0⇔抛物线与x轴有一个交点;③△<0⇔抛物线与x轴没有交点。
抛物线y=ax2+bx+c中a,b,c的作用:(1)a决定抛物线形状及开口方向:①若|a|相等,则形状相同。
②a>0⇔开口向上;a<0⇔开口向下。
③ |a|越大,开口越小.(2)a和b共同决定抛物线对称轴的位置,由于抛物线y=ax2+bx+c的对称轴是直线x= -b/2a 故①若b=0⇔对称轴为y轴;②若a与b同号⇔对称轴在y轴左侧;③若a与b异号⇔对称轴在y轴右侧。
(3)c的大小决定抛物线y=ax2+bx+c与y轴交点的位置。
当x=0时,y=c ,∴抛物线y=ax2+bx+c与y轴有且只有一个交点(0,c)。
①c=0⇔抛物线经过原点;②c>0⇔抛物线与y轴交于正半轴;③c<0⇔抛物线与y轴交于负半轴。
(4)判断a+b+c的符号:可以看图象上的点的横坐标为1时,点的纵坐标为何值决定正负。
判断a-b+c的符号:可以看图象上的点的横坐标为-1时,点的纵坐标为何值决定正负。
利用待定系数法求二次函数的方法:①已知抛物线过三点,设一般式y=ax2+bx+c ②已知抛物线顶点(对称轴、最值)及一点,设顶点式y=a(x-h)2+k③已知抛物线与x轴的两个交点(抛物线与x轴交点的横坐标),设两根式y=a(x-x1)( x-x2) 其中x1 、x2是抛物线与x轴交点的横坐标。
赠送以下资料《二次函数的应用》中考题集锦10题已知抛物线222(0)y x mx m m =+-≠.(1)求证:该抛物线与x 轴有两个不同的交点;(2)过点(0)P n ,作y 轴的垂线交该抛物线于点A 和点B (点A 在点P 的左边),是否存在实数m n ,,使得2AP PB =?若存在,则求出m n ,满足的条件;若不存在,请说明理由.答案:解:(1)证法1:22229224m y x mx m x m ⎛⎫=+-=+- ⎪⎝⎭,当0m ≠时,抛物线顶点的纵坐标为2904m -<, ∴顶点总在x 轴的下方.而该抛物线的开口向上,∴该抛物线与x 轴有两个不同的交点.(或者,当0m ≠时,抛物线与y 轴的交点2(02)m -,在x 轴下方,而该抛物线的开口向上,∴该抛物线与x 轴有两个不同的交点.)证法2 :22241(2)9m m m ∆=-⨯⨯-=,当0m ≠时,290m >,∴该抛物线与x 轴有两个不同的交点.(2)存在实数m n ,,使得2AP PB =.设点B 的坐标为()t n ,,由2AP PB =知,①当点B 在点P 的右边时,0t >,点A 的坐标为(2)t n -,, 且2t t -,是关于x 的方程222x mx m n +-=的两个实数根.2224(2)940m m n m n ∴∆=---=+>,即294n m >-.且(2)t t m +-=-(I ),2(2)t t m n -=--(II )由(I )得,t m =,即0m >.将t m =代入(II )得,0n =.∴当0m >且0n =时,有2AP PB =.②当点B 在点P 的左边时,0t <,点A 的坐标为(2)t n ,, 且2t t ,是关于x 的方程222x mx m n +-=的两个实数根.2224(2)940m m n m n ∴∆=---=+>,即 294n m >-.且2t t m +=-(I ),222t t m n =--(II )由(I )得,3mt =-,即0m >. 将3m t =-代入(II )得,2209n m =-且满足294n m >-.∴当0m >且2209n m =-时,有2AP PB =t (秒)间的关系式为210S t t =+,若滑到坡底第11题一人乘雪橇沿如图所示的斜坡笔直滑下,滑下的距离S (米)与时间的时间为2秒,则此人下滑的高度为( ) A.24米 B.12米C.D.6米答案:B第12题我市英山县某茶厂种植“春蕊牌”绿茶,由历年来市场销售行情知道,从每年的3月25日起的180天内,绿茶市场销售单价y (元)与上市时间t (天)的关系可以近似地用如图(1)中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z (元)与上市时间t (天)的关系可以近似地用如图(2)的抛物线表示.(2)求出图(2)中表示的种植成本单价z (元)与上市时间t (天)(0t >)的函数关系式; (3)认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大? (说明:市场销售单价和种植成本单价的单位:元/500克.)答案:解:(1)依题意,可建立的函数关系式为:2160(0120)380(120150)220(150180)5t t y t t t ⎧-+<<⎪⎪=<⎨⎪⎪+⎩,,. ≤ ≤≤ (2)由题目已知条件可设2(110)20z a t =-+.)图(1)图(2)天)图象过点85(60)3,,2851(60110)203300a a ∴=-+∴=.. 21(110)20300z t ∴=-+ (0)t >. (3)设纯收益单价为W 元,则W =销售单价-成本单价.故22221160(110)20(0120)3300180(110)20(120150)3002120(110)20(150180)5300t t t W t t t t t ⎧-+---<<⎪⎪⎪=---<⎨⎪⎪+---⎪⎩,,. ≤ ≤≤ 化简得2221(10)100(0120)3001(110)60(120150)3001(170)56(150180)300t t W t t t t ⎧--+<<⎪⎪⎪=-+<⎨⎪⎪--+⎪⎩,,. ≤ ≤≤①当21(10)100(0120)300W t t =--+<<时,有10t =时,W 最大,最大值为100; ②当21(110)60(120150)300W t t =--+<≤时,由图象知,有120t =时,W 最大,最大值为2593; ③当21(170)56(150180)300W t t =--+≤≤时,有170t =时,W 最大,最大值为56. 综上所述,在10t =时,纯收益单价有最大值,最大值为100元.第13题如图,足球场上守门员在O 处开出一高球,球从离地面1米的A 处飞出(A 在y 轴上),运动员乙在距O 点6米的B 处发现球在自己头的正上方达到最高点M ,距地面约4米高,球落地后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.(1)求足球开始飞出到第一次落地时,该抛物线的表达式. (2)足球第一次落地点C距守门员多少米?(取7=)(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取5=)答案:解:(1)(3分)如图,设第一次落地时, 抛物线的表达式为2(6)4y a x =-+. 由已知:当0x =时1y =. 即1136412a a =+∴=-,. ∴表达式为21(6)412y x =--+.(或21112y x x =-++) (2)(3分)令210(6)4012y x =--+=,.212(6)4861360x x x ∴-===-<.≈,(舍去). ∴足球第一次落地距守门员约13米.(3)(4分)解法一:如图,第二次足球弹出后的距离为CD根据题意:CD EF =(即相当于将抛物线AEMFC 向下平移了2个单位)212(6)412x ∴=--+解得1266x x =-=+1210CD x x ∴=-=. 1361017BD ∴=-+=(米). 解法二:令21(6)4012x --+=.解得16x =-,2613x =+.∴点C 坐标为(13,0).设抛物线CND 为21()212y x k =--+.将C 点坐标代入得:21(13)2012k --+=.解得:11313k =-<(舍去),2667518k =+++=.21(18)212y x =--+ 令210(18)212y x ==--+,0.118x =-,21823x =+. 23617BD ∴=-=(米).解法三:由解法二知,18k =, 所以2(1813)10CD =-=, 所以(136)1017BD =-+=. 答:他应再向前跑17米.第14题荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知:平均修建每公顷大棚要用支架、农膜等材料费2.7万元;购置滴灌设备,这项费用(万元)与大棚面积(公顷)的平方成正比,比例系数为0.9;另外每公顷种植蔬菜需种子、化肥、农药等开支0.3万元.每公顷蔬菜年均可卖7.5万元. (1)基地的菜农共修建大棚x (公顷),当年收益(扣除修建和种植成本后)为y (万元),写出y 关于x 的函数关系式. (2)若某菜农期望通过种植大棚蔬菜当年获得5万元收益,工作组应建议他修建多少公项大棚.(用分数表示即可)(3)除种子、化肥、农药投资只能当年受益外,其它设施3年内不需增加投资仍可继续使用.如果按3年计算,是否修建大棚面积越大收益越大?修建面积为多少时可以得到最大收益?请帮工作组为基地修建大棚提一项合理化建议.答案:(1)()227.5 2.70.90.30.9 4.5y x x x x x x =-++=-+. (2)当20.9 4.55x x -+=时,即2945500x x -+=,153x =,2103x =从投入、占地与当年收益三方面权衡,应建议修建53公顷大棚. (3)设3年内每年的平均收益为Z (万元)()()2227.50.90.30.30.3 6.30.310.533.075Z x x x x x x x =-++=-+=--+(10分)不是面积越大收益越大.当大棚面积为10.5公顷时可以得到最大收益.建议:①在大棚面积不超过10.5公顷时,可以扩大修建面积,这样会增加收益. ②大棚面积超过10.5公顷时,扩大面积会使收益下降.修建面积不宜盲目扩大.③当20.3 6.30x x -+=时,10x =,221x =.大棚面积超过21公顷时,不但不能收益,反而会亏本.(说其中一条即可)第15题一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.(1)求出月销售量y (万件)与销售单价x (元)之间的函数关系式(不必写x 的取值范围); (2)求出月销售利润z (万元)(利润=售价-成本价)与销售单价x (元)之间的函数关系式(不必写x 的取值范围); (3)请你通过(2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于480万元.答案:略.第16题一座隧道的截面由抛物线和长方形构成,长方形的长为8m ,宽为2m ,隧道最高点P 位于AB 的中央且距地面6m ,建立如图所示的坐标系(1)求抛物线的解析式;(2)一辆货车高4m ,宽2m ,能否从该隧道内通过,为什么?(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?答案:(1)由题意可知抛物线经过点()()()024682A P B ,,,,,设抛物线的方程为2y ax bx c =++ 将A P D ,,三点的坐标代入抛物线方程. 解得抛物线方程为21224y x x =-++ (2)令4y =,则有212244x x -++=解得1244x x =+=-212x x -=>∴货车可以通过.(3)由(2)可知21122x x -=>∴货车可以通过.第17题如图,在矩形ABCD 中,2AB AD =,线段10EF =.在EF 上取一点M ,分别以EM MF ,为一边作矩形EMNH 、矩形MFGN ,使矩形MFGN ∽矩形ABCD .令M N x =,当x 为何值时,矩形EMNH 的面积S 有最大值?最大值是多少?答案:解:矩形MFGN ∽矩形ABCD ,MN MFAD AB∴=. 2AB AD MN x ==,,2MF x ∴=.102EM EF MF x ∴=-=-. (102)S x x ∴=-2210x x =-+ 2525222x ⎛⎫=--+ ⎪⎝⎭.∴当52x =时,S 有最大值为252.B A D MF第18题某企业信息部进行市场调研发现:信息一:如果单独投资A 种产品,则所获利润A y (万元)与投资金额x (万元)之间存在正比例函数关系:A y kx =,并且当投资5万元时,可获利润2万元.信息二:如果单独投资B 种产品,则所获利润B y (万元)与投资金额x (万元)之间存在二次函数关系:2B y ax bx =+,并且当投资2万元时,可获利润2.4万元;当投资4万元时,可获利润3.2万元.(1)请分别求出上述的正比例函数表达式与二次函数表达式; (2)如果企业同时对A B ,两种产品共投资10万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?答案:解:(1)当5x =时,12250.4y k k ===,,, 0.4A y x ∴=,当2x =时, 2.4B y =;当4x =时, 3.2B y =.2.4423.2164a ba b=+⎧∴⎨=+⎩ 解得0.21.6a b =-⎧⎨=⎩∴20.2 1.6B y x x =-+.(2)设投资B 种商品x 万元,则投资A 种商品(10)x -万元,获得利润W 万元,根据题意可得220.2 1.60.4(10)0.2 1.24W x x x x x =-++-=-++ 20.2(3) 5.8W x ∴=--+当投资B 种商品3万元时,可以获得最大利润5.8万元,所以投资A 种商品7万元,B 种商品3万元,这样投资可以获得最大利润5.8万元.第19题如图所示,图(1)是一座抛物线型拱桥在建造过程中装模时的设计示意图,拱高为30m ,支柱3350m A B =,5根支柱1122334455A B A B A B A B A B ,,,,之间的距离均为15m ,1515B B A A ∥,将抛物线放在图(2)所示的直角坐标系中. (1)直接写出图(2)中点135B B B ,,的坐标; (2)求图(2)中抛物线的函数表达式; (3)求图(1)中支柱2244A B A B ,的长度.答案:(1)1(30)B -,0,3(030)B ,,5(300)B ,; (2)设抛物线的表达式为(30)(30)y a x x =-+,把3(030)B ,代入得(030)(030)30y a =-+=. 130a =-∴. ∵所求抛物线的表达式为:1(30)(30)30y x x =--+. (3)4B ∵点的横坐标为15, 4B ∴的纵坐标4145(1530)(1530)302y =--+=.B 图(1)图(2)l3350A B =∵,拱高为30,∴立柱44458520(m)22A B =+=. 由对称性知:224485(m)2A B A B ==。
26.1.2_二次函数图像与性质(4)(1)

想一想:下列函数是由y=2x2或y=-2x2 经过怎样的平移得到的?指出它们的开 口方向、对称轴、顶点坐标,最大值或 最小值各是什么及增减性如何? 抛物线 y=−2(x+3)2-2 y=2(x-1)2+3 x=-3
对称轴
顶点坐标
X=1 (1,3)
X=1时, y最小=3
(-3,-2)
X=-3时, y最大=-2
开口向上 对称轴:x=1
顶点坐标(1,2)
10 9 8 x=1 y=2(x-1)² +2 7 6 5 4 3 2 1 (1,2) -5 -4 -3 -2 -1 o 1 2 3 4 5 x
y
猜想:
二次函数y=2x² y=2(x-1)² , , y=2(x-1)² +2的图象的位置关系?
y
y=2(x-1)2+2
1 说出下列函数图象的开口方向,对称轴,顶点, 最值情况:
1)y=ax2Biblioteka 2)y=ax2+c
3)y=a(x-h)2
2 二次函数y=ax² +c与y=ax² 有何平移关系? 规律:上加下减 y=a(x-h)2与y=ax² 呢?
规律:左加右减
3请说出二次函数y=2x2-5与抛物线y=2x2+2如何由 y=2x2平移而来? 4抛物线y=2(x-5)2与抛物线y=2(x+2)2呢?
( 2 , -6 )
y=-5(2-x)2-6
2.请回答抛物线y = 4(x-3)2+7由抛物线y=4x2怎 样平移得到? 3.抛物线y =-4(x-3)2+7能够由抛物线y=4x2平移 得到吗?
练习:对称轴是直线x=-2的抛物线是( C )
A y=-2x2-2 C y=-1/2(x+2)2-2 B y=2x2-2 D y=-5(x-2)2-6
二次函数及其图像教案
课堂练习
1、教师巡视,指导学生解 图像,并分别指出他
题,
们的开口方向和开口
10 分钟 5 分钟
2、评讲练习,反馈矫正。 大小,顶点以及对称
轴:y=1/2x²,y=-2x²,
y=2x²,y=2(x+1)²,
精 讲 点 拨
(2)
y=2(x+1)²
3、二 次 函 数 y=a (x+h)²+k 及图像的(抛物
(抛物线)开口 不同而变化。
值不同而变化。
方向,顶点,对 2、通过图形的对折确定图 2、思考 a 的值决定
称轴。
像的对称轴的位置。
二次函数哪些性质。
2、二 次 函 数 3、提问 a 的值决定二次函 3、认真听老师总结函
y=ax²的性质。 数哪些性质。
数的性质
4、总结函数 y=ax²的性质。
画出下列二次函数的
质。
a,h 和 k 分别决定图像哪些 结果。
性质。
3、认真听老师总结
布 1、思考二次函数 y=ax²+bx+c(a>0)的图像是怎样的,并写出抛物线的方向,顶
置 点以及对称轴
作 2、课本 12 页,第 1,3,5,9 题。
业
可修改
精选文档
板书设计 26.1 二次函数及其图像
1、二次函数的定义:..................................
精选文档
学院
数学与信息科学学院
年 级 三年级 学 科
数学
讲课人
授课时间
四十分钟
教材
义务教育课程标准实验教科书 数学 九年级下册
课题
26.1 二次函数及其图像
1、认识理解二次函数的定义及其开口方向,顶点,对称轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注: y=a(x-h)2 +k (a≠0)的形式称二次函数的 顶点式
二次函数
开口方向 对称轴 顶点坐标 向上 向下 向上 向下
y=2(x+3)2+5
y = -3 (x-1)2 -2 y = 4(x-3)2 +7 y = -5(2-x)2 - 6
最值 当x=0时,最小值为k.
当x=0时,最大值为k.
2 7.二次函数y=a(x-h)
的图象和性质
抛物线
开口方向
y=a(x-h)2 (a>0)
y=a(x-h)2 (a<0)
对称轴
顶点坐标
向上 直线x=h (h,0)
向下 直线x=h (h,0)
增减性
在对称轴的左侧,y随着x的增大 在对称轴的左侧,y随着x的增大 而减小. 在对称轴的右侧, y随 而增大. 在对称轴的右侧, y随 着x的增大而增大. 着x的增大而减小.来自+k的图象和性质
抛物线
开口方向
对称轴
顶点坐标
y=ax2 +k(a>0) 向上 直线x=0 (0,k)
y=ax2 +k(a<0) 向下 直线x=0 (0,k)
增减性
在对称轴的左侧,y随着x的增大 在对称轴的左侧,y随着x的增大 而减小. 在对称轴的右侧, y随 而增大. 在对称轴的右侧, y随 着x的增大而增大. 着x的增大而减小.
y
8
7
6 6
5
4 4
3 2 2 1
-5
y 3x
1 2
2
-5
-4
-3
-2
-1
0 -1
-2 2
3
4
5
5
x
-4
-6
2+k的图像和性质 y=a(x-h)
1.填表
抛物线 开口方向 对称轴
2
顶点坐标
(0, 0)
(0, 1) (0, - 1)
y 0.5 x
2
向下
向下 向下
x=0
x=0 x=0
y 0.5 x 1
X=1
想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2 的图象和抛物线y=-3x² ,y=-3(x+1)2
二次函数y=-3(x+1)2+2与 2 y 3x 1 2 y=-3(x+1)2-2的图象和抛物 线y=-3x² ,y=-3(x+1)2有什 2 y 3x 1 么关系? 它的开口方向,对 称轴和顶点坐标分别是什么? 2
y 3x 1 2
2
顶点是(1,-2).
X=1 对称轴仍是平行于y轴的直线 (x=1);增减性与y=3x2类似. 开口向上, 当x=1时y有 最小值:且 最小值= -2.
想一想,二次函数y=-3(x-1)2+2和y=-3x² ,y=3(x-1)2的图象有什么关系?它们的开口方向,对 称轴和顶点坐标分别是什么?再作图看一看.
3.抛物线的平移: (1)把二次函数y=3x 2的图像, 先沿x轴向左平移3个单位, 再沿y轴向下平移2个单位, y=3(x+3)2-2 得到_____________的图像; y=-3(x+6)2 (2)把二次函数_____________的图像, 先沿y轴向下平移2个单位, 再沿x轴向右平移3个单位, 得到y=-3(x+3) 2-2的图像.
二次函数y=3(x-1)2+2的 图象可以看作是抛物线 y=3x2先沿着x轴向右平移 1个单位,再沿直线x=1向 上平移2个单位后得到的.
y 3x 1 2
2
y 3x 1
2
X=1 对称轴仍是平行于y轴 的直线(x=1);增减性与 y=3x2类似.
开口向上,当 X=1时有最小 值:且最小值=2.
y 0.5 x 1
2
y 2x
2
2
2
向上
向上 向上
x=0
x=1 x= - 1
(0, 0)
(1, 0) (- 1, 0)
y 2( x 1)
y 2( x 1)
2.上下 平移
1 2 如何由 y 3 x 的图象得到 1 2 1 2 y y x 3 、 x 3 的图象。 3 3
先想一想,再总结二次函数y=a(x-h)2+k的图象和性质.
二次函数y=a(x-h)² +k与y=ax² 的关系
一般地,由y=ax² 的图象便可得到二次函数y=a(xh)² +k的图象:y=a(x-h)² +k(a≠0) 的图象可以看 成y=ax² 的图象先沿x轴整体左(右)平移|h|个单 位(当h>0时,向右平移;当h<0时,向左平移),再沿 对称轴整体上(下)平移|k|个单位 (当k>0时向上 平移;当k<0时,向下平移)得到的. 因此,二次函数y=a(x-h)² +k的图象是一条抛物线, 它的开口方向、对称轴和顶点坐标与a,h,k的值 有关.
对称轴 ( -3, 5 ) 直线x=-3 顶点坐标
直线x=1 ( 1 , -2 ) 直线x=3 ( 3 , 7) 直线x=2 ( 2 , -6 )
指出下列函数图象的开口方向,对称轴和顶点坐标. 开口 对称轴 顶点坐标
2
1y 2x 3
5
2
向上 向下 向下 向上
直线x=3 直线x= –1 直线x=0 直线x=2
y 3x 1 2
顶点分别是 (-1,2)和(-1,-2)..
y 3x 2
二次函数y=-3(x+1)2+2与 y=-3(x+1)2-2的图象可 以看作是抛物线y=-3x2 先沿着x轴向左平移1个 单位,再沿直线x=-1向上 (或向下)平移2个单位后 得到的.
x=1 开口向下, 当x=-1时y有 对称轴仍是平行于y轴的直线 最大值:且 (x=-1);增减性与y= -3x2类似. 最大值= 2 (或最大值= - 2).
y
y ( x 2) 的图象。 3
5 x= - 2 4 x= 2 3 2 (-2,0) 1 (2,0) x –52 –4 –3 –2 –1O 1 2 3 4 5 1 1 2 –1 y x 2 y x 2 –2 3 3 –3 1 2 y x –4 3 –5
y 5 4(0,3) 1 2 y x 3 3 3 2 1 x –5 –4 –3 –2 –1O 1 2 3 4 5 –1 –2 (0,-3) 1 2 –3 1 2 y x –4 y x 3 3 –5 3
3.左右 平移
1 1 2 2 y x 的图象得到 y ( x 2) 如何由 3 、 3 1 2
y=ax2(a<0) 向下 直线x=0 (0,0)
增减性
在对称轴的左侧,y随着x的增大 在对称轴的左侧,y随着x的增大 而减小. 在对称轴的右侧, y随 而增大. 在对称轴的右侧, y随 着x的增大而增大. 着x的增大而减小.
最值 当x=0时,最小值为0.
当x=0时,最大值为0.
2 6.二次函数y=ax
二次函数y=a(x-h)2+k的图象和性质
抛物线
开口方向
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
对称轴
顶点坐标
向上 直线x=h (h,k)
向下 直线x=h (h,k)
增减性
在对称轴的左侧,y随着x的增大 在对称轴的左侧,y随着x的增大 而减小. 在对称轴的右侧, y随 而增大. 在对称轴的右侧, y随 着x的增大而增大. 着x的增大而减小.
(3,–5) (–1,0)
2 y 0 .5 x 1
2
3 2 3y x 1 4
(0,–1)
(2, 5) (– 4,2) (3,0)
4 y 2 x 2 5 2 5y 0.5x 4 2
向上 直线x= – 4
3 2 6 y x 3 4
最值 当x=h时,最小值为k.
当x=h时,最大值为k.
一般地,抛物线y=a(x-h)2+k与y=ax2 的 形状 相同, 位置 不同
y=ax2
上加下减 左加右减
y=a(x-h)2+k
y = a( x – h )2 + k
平左 移右 y= ax2 +k 平上 移下 y = a(x – h )2
上下平移 y = ax2 左右平移
在同一坐标系中作出二次函数 y=3x² ,y=3(x-1)2和y=3(x-1)2+2的图象.
二次函数y=3x² ,y=3(x-1)2和 y=3(x-1)2+2的图象有什么关系?它们 的开口方向,对称轴和顶点坐标分别是 什么?作图看一看.
?
二次函数y=3(x-1)2+2的
y 3x 2
图象和抛物线 y=3x² ,y=3(x-1)2有什么关 系?它的开口方向,对称轴 和顶点坐标分别是什么?
顶点是(1,2).
先猜一猜,再做一做,在同一坐标系中作 二次函数y=3(x-1)2-2,会是什么样?
二次函数y=3(x-1)2-2的
y 3x 2
y 3x 1
2
图象与抛物线y=3x2和 y=3(x-1)2有何关系?它的 开口方向、对称轴和顶点 坐标分别是什么?
二次函数y=3(x-1)2-2的 图象可以看作是抛物线 y=3x2先沿着x轴向右平移 1个单位,再沿直线x=1向 下平移2个单位后得到的.
