高三数学下期中模拟试卷带答案(8)
北京市海淀区2024届高三下学期期中练习(一模)数学试题(解析版)

海淀区2023—2024学年第二学期期中练习高三数学本试卷共6页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知全集{|22}U x x =-≤≤,集合{}12A x x =-≤<,则U A =ð()A.(2,1)--B.[2,1]--C.(2,1){2}-- D.[2,1){2}-- 【答案】D 【解析】【分析】根据给定条件,利用补集的定义求解即得.【详解】全集{|22}U x x =-≤≤,集合{}12A x x =-≤<,所以[2,1){2}U A =-- ð.故选:D2.若复数z 满足i 1i z =+,则z 的共轭复数是()A.1i --B.1i +C.1i -+D.1i-【答案】B 【解析】【分析】根据复数代数形式的除法运算求出复数z 即可求解结果.【详解】解:复数z 满足i 1i z =+,所以()21i 1i 1i1i i i i 1z ++-+====--.所以z 的共轭复数是1i +.故选:B .3.已知{}n a 为等差数列,n S 为其前n 项和.若122a a =,公差0,0m d S ≠=,则m 的值为()A.4B.5C.6D.7【答案】B 【解析】【分析】利用等差数列的通项公式求出1a 和d 的关系,代入0m S =计算可得m 的值.【详解】由已知()12122a a a d ==+,得12a d =-,又()()1112022m m m m m S ma d md d --=+=-+=,又0d ≠,所以()1202m m m --+=,解得5m =或0m =(舍去)故选:B.4.已知向量,a b 满足||2,(2,0)a b ==,且||2a b += ,则,a b 〈〉= ()A.π6B.π3C.2π3 D.5π6【答案】C 【解析】【分析】将||2a b +=两边同时平方,将条件带入计算即可.【详解】由已知||2,2a b ==,所以()22224222cos ,44a b a b a b a b +=+⋅+=+⨯⨯⨯〈〉+=r r r r r r r r,得1cos ,2a b 〈〉=- ,又[],0,πa b 〈〉∈ ,所以2π,3a b 〈〉= .故选:C.5.若双曲线22221(0,0)x y a b a b-=>>上的一点到焦点(的距离比到焦点的距离大b ,则该双曲线的方程为()A.2214x y -= B.2212x y -= C.2212y x -= D.2214y x -=【答案】D 【解析】【分析】根据题意及双曲线的定义可知2a b =,c =,再结合222+=a b c ,求出,a b ,即可求出结果.【详解】由题知c =,根据题意,由双曲线的定义知2a b =,又222+=a b c ,所以255a =,得到221,4a b ==,所以双曲线的方程为2214y x -=,故选:D.6.设,αβ是两个不同的平面,,l m 是两条直线,且,m l αα⊂⊥.则“l β⊥”是“//m β”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】A 【解析】【分析】通过面面平行的性质判断充分性,通过列举例子判断必要性.【详解】l β⊥,且l α⊥,所以//αβ,又m α⊂,所以//m β,充分性满足,如图:满足//m β,,m l αα⊂⊥,但l β⊥不成立,故必要性不满足,所以“l β⊥”是“//m β”的充分而不必要条件.故选:A .7.已知()()3,0lg 1,0x x f x x x ⎧≤⎪=⎨+>⎪⎩,函数()f x 的零点个数为m ,过点(0,2)与曲线()y f x =相切的直线的条数为n ,则,m n 的值分别为()A.1,1B.1,2C.2,1D.2,2【答案】B 【解析】【分析】借助分段函数性质计算可得m ,借助导数的几何意义及零点的存在性定理可得n .【详解】令()0f x =,即0x ≤时,30x =,解得0x =,0x >时,()lg 10x +=,无解,故1m =,设过点(0,2)与曲线()y f x =相切的直线的切点为()00,x y ,当0x <时,()23f x x '=,则有()320003y x x x x -=-,有()3200023x x x -=-,整理可得301x =-,即01x =-,即当00x <时,有一条切线,当0x >时,()lg e1f x x '=+,则有()()000lg 1e lg 1y x x x x -=-++,有()()000l 2g elg 11x x x -+=-+,整理可得()()()000221lg 10lg e x x x ++-++=,令()()()()()2l 0g 2l 1e 1g g x x x x x =++-++>,则()()2lg 1g x x '=-+,令()0g x '=,可得99x =,故当()0,99x ∈时,()0g x '>,即()g x 在()0,99上单调递增,当()99,x ∈+∞时,()0g x '<,即()g x 在()99,∞+上单调递减,由()()992lg e 99220099lg e 0g =+⨯+-=>,()02020g =-=>,故()g x 在()0,99x ∈上没有零点,又()()9992lg e 999210003999lg e 10000g =+⨯+-⨯=-<,故()g x 在()99,999上必有唯一零点,即当00x >时,亦可有一条切线符合要求,故2n =.故选:B.8.在平面直角坐标系xOy 中,角α以Ox 为始边,终边在第三象限.则()A.sin cos tan ααα-≤B.sin cos tan ααα-≥C.sin cos tan ααα⋅<D.sin cos tan ααα⋅>【答案】C 【解析】【分析】对A 、B :举出反例即可得;对C 、D :借助三角函数的商数关系及其值域计算即可得.【详解】由题意可得sin 0α<、cos 0α<,tan 0α>,对A :当sin 0α-→时,cos 1α→-,则sin cos 1αα-→,tan 0α→,此时sin cos tan ααα->,故A 错误;对B :当5π4α=时,1sin cos sinc 5π5π5π0tan 44os 4αα-=-=<=,故B 错误;对C 、D :22sin sin cos cos cos tan cos ααααααα⋅=⋅=⋅,由1cos 0α-<<,故()2cos 0,1α∈,则2cos tan tan ααα⋅<,即sin cos tan ααα⋅<,故C 正确,D 错误.故选:C.9.函数()f x 是定义在(4,4)-上的偶函数,其图象如图所示,(3)0f =.设()f x '是()f x 的导函数,则关于x 的不等式(1)()0f x f x '+⋅≥的解集是()A.[0,2]B.[3,0][3,4)-C.(5,0][2,4)-D.(4,0][2,3)- 【答案】D 【解析】【分析】借助函数图象与导数的关系计算即可得.【详解】由(3)0f =,且()f x 为偶函数,故(3)0f -=,由导数性质结合图象可得当()4,0x ∈-时,()0f x '<,当()0,4x ∈时,()0f x '>,当0x =时,即()00f '=,则由(1)()0f x f x '+⋅≥,有41444x x -<+<⎧⎨-<<⎩,解得43x -<<,亦可得()()100f x f x ⎧+>>'⎪⎨⎪⎩,或()()100f x f x ⎧+<<'⎪⎨⎪⎩,或()10f x +=,或()0f x '=,由()()100f x f x ⎧+>>'⎪⎨⎪⎩可得41304x x -<+<-⎧⎨<<⎩或31404x x <+<⎧⎨<<⎩,即23x <<,由()()100f x f x ⎧+<<'⎪⎨⎪⎩可得31340x x -<+<⎧⎨-<<⎩,即40x -<<,由()10f x +=,可得13x +=±,即2x =或4x =-(舍去,不在定义域内),由()0f x '=,可得0x =,综上所述,关于x 的不等式(1)()0f x f x '+⋅≥的解集为(4,0][2,3)- .故选:D.10.某生物兴趣小组在显微镜下拍摄到一种黏菌的繁殖轨迹,如图1.通过观察发现,该黏菌繁殖符合如下规律:①黏菌沿直线繁殖一段距离后,就会以该直线为对称轴分叉(分叉的角度约为60︒),再沿直线繁殖,…;②每次分叉后沿直线繁殖的距离约为前一段沿直线繁殖的距离的一半.于是,该组同学将整个繁殖过程抽象为如图2所示的一个数学模型:黏菌从圆形培养皿的中心O 开始,沿直线繁殖到11A ,然后分叉向21A 与22A 方向继续繁殖,其中21112260A A A ∠=︒,且1121A A 与1122A A 关于11OA 所在直线对称,112111221112A A A A OA ==….若114cm OA =,为保证黏菌在繁殖过程中不会碰到培养皿壁,则培养皿的半径r (*N r ∈,单位:cm )至少为()A.6B.7C.8D.9【答案】C 【解析】【分析】根据黏菌的繁殖规律可得每次繁殖在11OA 方向上前进的距离,结合无穷等比递缩数列的和的计算公式,即可判断答案.【详解】由题意可知,114cm OA =,只要计算出黏菌沿直线一直繁殖下去,在11OA 方向上的距离的范围,即可确定培养皿的半径的范围,依题意可知黏菌的繁殖规律,由此可得每次繁殖在11OA 方向上前进的距离依次为:1114,2,222482⨯⨯⨯ ,则31353842155722244+⨯++⨯=+>+=,黏菌无限繁殖下去,每次繁殖在11OA 方向上前进的距离和即为两个无穷等比递缩数列的和,即1311432164316841+281142282331144++⎛⎫⎛⎫++++++≈+⨯= ⎪ ⎪⎝⎭⎝⎭--,综合可得培养皿的半径r (*N r ∈,单位:cm )至少为8cm ,故选:C【点睛】关键点点睛:本题考查了数列的应用问题,背景比较新颖,解答的关键是理解题意,能明确黏菌的繁殖规律,从而求出每次繁殖在11OA 方向上前进的距离的和,结合等比数列求和即可.第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.已知ln 2ab=,则22ln ln a b -=_______.【答案】4【解析】【分析】直接利于对数的运算性质求解.【详解】因为ln2ab=,所以22222ln ln ln ln 2ln 4a a a a b b b b ⎛⎫-==== ⎪⎝⎭.故答案为:4.12.已知22:(1)3C x y -+= ,线段AB 是过点(2,1)的弦,则AB 的最小值为_______.【答案】2【解析】【分析】借助直径与弦AB 垂直时,AB 有最小,计算即可得.【详解】由22(21)123-+=<,故点(2,1)在圆的内部,且该圆圆心为()1,0设圆心到直线AB 的距离为d ,由垂径定理可得2222AB r d ⎛⎫=- ⎪⎝⎭,即AB =,故当d 取最大值时,AB 有最小值,又max d ==故2AB =≥=.故答案为:2.13.若443243210(2)x a x a x a x a x a -=++++,则0a =_______;13024a a a a a +=++_______.【答案】①.16②.4041-【解析】【分析】借助赋值法,分别令0x =、1x =、=1x -计算即可得.【详解】令0x =,可得40(02)a -=,即40216a ==,令1x =,可得443210(12)a a a a a -=++++,即()44321011a a a a a ++++=-=,令=1x -,可得443210(12)a a a a a --=-+-+,即()443210381a a a a a -+-+=-=,则()()()4321043210420218182a a a a a a a a a a a a a +++++-+-+=++=+=,即42082412a a a ++==,则()42103114140a a a a a =-++==-+-,故130244041a a a a a +=-++.故答案为:16;4041-.14.已知函数π()sin sin 24f x x x ⎛⎫=+ ⎪⎝⎭,则5π4f ⎛⎫= ⎪⎝⎭_________;函数()f x 的图象的一个对称中心的坐标为_______.【答案】①.1-②.π(,0)4-(答案不唯一)【解析】【分析】根据函数表达式,代入即可求出5π4f ⎛⎫ ⎪⎝⎭的函数值,根据条件,先求出使()0f x =的一个取值π4x =-,再证明π(,0)4-是()f x 的一个对称中心即可.【详解】因为π()sin sin 24f x x x ⎛⎫=+⎪⎝⎭,所以55ππππsin()sin(214444f ⎛⎫=+⨯=- ⎪⎝⎭,因为()f x 定义域为R ,当π4x =-时,ππππ()sin sin()04442f ⎛⎫-=-+-= ⎪⎝⎭,下证π(,0)4-是()f x 的一个对称中心,在π()sin sin 24f x x x ⎛⎫=+ ⎪⎝⎭上任取点()00,P x y ,其关于π(,0)4-对称的点为00π(,)2P x y '---,又00000000ππππππ()sin sin 2()sin()sin(π2)sin()sin(2)224244f x x x x x x x y ⎛⎫--=--+--=----=-+=- ⎪⎝⎭,所以函数()f x 的图象的一个对称中心的坐标为π(,0)4-,故答案为:1-;π(,0)4-(答案不唯一)15.已知函数()f x =①函数()f x 是奇函数;②R k ∀∈,且0k ≠,关于x 的方程0()f x kx -=恰有两个不相等的实数根;③已知P 是曲线()y f x =上任意一点,1,02A ⎛⎫-⎪⎝⎭,则12AP ≥;④设()11,M x y 为曲线()y f x =上一点,()22,N x y 为曲线()y f x =-上一点.若121x x +=,则1MN ≥.其中所有正确结论的序号是_________.【答案】②③④【解析】【分析】对①:计算定义域即可得;对②:对0k >与0k <分类讨论,结合二次函数求根公式计算即可得;对③:借助两点间的距离公式与导数求取最值计算即可得;对④:结合函数性质与③中所得结论即可得.【详解】对①:令30x x -≥,即有()()110x x x +-≥,即[][]1,01,x ∞∈-⋃+,故函数()f x 不是奇函数,故①错误;对②:0()f x kx kx -=-=kx =,当0x =00-=,故0是该方程的一个根;当0x ≠,0k >kx =,故0x >,结合定义域可得[]1,x ∞∈+,有322x x k x -=,即()2210x x k x --=,令2210x k x --=,440k ∆=+>,有242k x +=或242k x -=(负值舍去),则20122k x ++=>=,故2210x k x --=必有一个大于1的正根,即0()f x kx -=必有一个大于1的正根;当0x ≠,0k <kx =,故0x <,结合定义域有[)1,0∈-x ,有322x x k x -=,即()2210x x k x --=,令2210x k x --=,440k ∆=+>,有242k x =或242k x +=(正值舍去),令244k t +=>,即24k t =-,则22211711744242412222k t x ⎫⎛⎫---⎪ ⎪--⎝⎭⎝⎭===>=-,即212k x =>-,故2210x k x --=在定义域内亦必有一根,综上所述,R k ∀∈,且0k ≠,关于x 的方程0()f x kx -=恰有两个不相等的实数根,故②正确;对③:令(),P x y,则有y =222321124AP x x x ⎛⎫=++=++⎪⎝⎭,令()3214g x x x =++,[][]1,01,x ∞∈-⋃+,()()23232g x x x x x =='++,当()21,1,3x ∞⎛⎫∈--⋃+ ⎪⎝⎭时,()0g x '>,当2,03x ⎛⎫∈- ⎪⎝⎭时,()0g x '<,故()g x 在21,3⎛⎫--⎪⎝⎭、()1,∞+上单调递增,在2,03⎛⎫- ⎪⎝⎭上单调递减,又()1111144g -=-++=,()110044g =+=,故()14g x ≥恒成立,即214AP ≥,故12AP ≥,故③正确;对④:当12x x =时,由[][]1,01,x ∞∈-⋃+,121x x +=,故1212x x ==-,此时,124y y =-==,则12MN =≥,当12x x ≠时,由()y f x =与()y f x =-关于x 轴对称,不妨设12x x <,则有1210x x -≤<≤或121012x x -≤≤<≤≤,当121012x x -≤≤<≤≤时,由2121x x x -≥≥,有121MN x x =≥-≥,故成立;当1210x x -≤<≤时,即有211x x =-,由③知,点M 与点N 在圆2211:24A x y ⎛⎫++= ⎪⎝⎭上或圆外,设点()1,M x m '与点()2,N x n '在圆上且位于x 轴两侧,则1M N ''=,故1MN M N ''≥=;综上所述,1MN ≥恒成立,故④正确.故答案为:②③④.【点睛】关键点点睛:结论④中的关键点在于借助结论③,结合函数的对称性,从而得到当1x 、2x 都小于零时,MN 的情况.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.在ABC 中,sin cos 2b C B c =.(1)求B ∠;(2)若4a b c =+=,求ABC 的面积.【答案】(1)π6(2【解析】【分析】(1)根据条件,利用正弦定理边转角得到sin 2B B +=,再利用辅助角公式及特殊角的三角函数值,即可求出结果;(2)根据(1)中π6B =及条件,由余弦定理得到22126c b c +-=,再结合4b c +=,即可求出2c =,再利用三角形面积公式,即可求出结果.【小问1详解】因为sin cos 2b C B c =,由正弦定理可得sin sin cos 2sin B C C B C =,又(0,π)C ∈,所以sin 0C ≠,得到sin 2B B +=,即π2sin(23B +=,所以πsin()13B +=,又因为(0,π)B ∈,所以2ππ3B +=,得到π6B =.【小问2详解】由(1)知π6B =,所以2223cos 22a cb B ac +-==,又a =,得到22126c b c +-=①,又4b c +=,得到4b c =-代入①式,得到2c =,所以ABC 的面积为11πsin 2sin 226ABC S ac B ==⨯⨯= .17.如图,在四棱锥P ABCD -中,,AD BC M //为BP 的中点,//AM 平面CDP .(1)求证:2BC AD =;(2)若,1PA AB AB AP AD CD ⊥====,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使四棱锥P ABCD -存在且唯一确定.(i )求证:PA ⊥平面ABCD ;(ⅱ)设平面CDP ⋂平面BAP l =,求二面角C l B --的余弦值.条件①:BP DP =;条件②:AB PC ⊥;条件③:CBM CPM ∠=∠.注:如果选择的条件不符合要求,第(1)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.【答案】(1)证明见解析(2)(i )证明见解析;(ⅱ)77【解析】【分析】(1)借助线面平行的性质定理与中位线的性质即可得;(2)(i )借助线面垂直的判定定理即可得;(ⅱ)结合所给条件建立适当的空间直角坐标系后借助空间向量计算即可得.【小问1详解】取PC 的中点N ,连接,MN ND ,因为M 为BP 的中点,所以1,//2MN BC MN BC =,因为//AD BC ,所以//AD MN ,所以,,,M N D A 四点共面,因为//AM 平面CDP ,平面MNDA 平面CDP DN =,AM ⊂平面MNDA ,所以//AM DN ,所以四边形AMND 为平行四边形,所以MN AD =,所以2BC AD =;【小问2详解】(i )取BC 的中点E ,连接,AE AC ,由(1)知2BC AD =,所以EC AD =,因为//EC AD ,所以四边形AECD 是平行四边形,所以1,EC AD AE CD ===,因为1AB CD ==,所以112AE BC ==,所以90BAC ∠= ,即AB AC ⊥,选条件①:BP DP =,因为1,AB AD PA PA ===,所以PAB 与PAD 全等,所以PAB PAD ∠=∠,因为AB PA ⊥,所以90PAB ∠=o ,所以90PAD ∠= ,即AP AD ⊥,又因为AB AC A ⋂=,AB 、AC ⊂平面ABCD ,所以AP ⊥平面ABCD ;(ⅱ)由(i )知AP ⊥平面ABCD ,而AC ⊂平面ABCD ,所以AP AC ⊥,因为,1PA AB AP ⊥=,建立如图所示空间直角坐标系A xyz -,则()()10,0,1,0,,,22P C D ⎛⎫- ⎪ ⎪⎝⎭,所以()1313,,0,,,12222CD PD AC ⎛⎫⎛⎫=--=--= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,,设平面PDC 的法向量为(),,n x y z = ,则0n CD n PD ⎧⋅=⎪⎨⋅=⎪⎩,即102213022x y x y z ⎧--=⎪⎪⎨⎪-+-=⎪⎩,令x =,则1,y z =-=,于是1,n =-,因为AC 为平面PAB 的法向量,且7cos ,7AC n AC n AC n ⋅===-⋅,所以二面角C l B --的余弦值为77.选条件③:CBM CPM ∠=∠,(i)因为CBM CPM ∠=∠,所以CB CP =,因为1,AB AP CA CA ===,所以ABC 与APC △全等,所以90∠=∠= PAC BAC ,即PA AC ⊥,因为PA AB ⊥,又因为AB AC A ⋂=,AB 、AC ⊂平面ABCD ,所以PA ⊥平面ABCD ;(ii)同选条件①.不可选条件②,理由如下:由(i )可得AB AC ⊥,又PA AB ⊥,PA AC A = ,PA 、AC ⊂平面PAC ,所以AB ⊥平面PAC ,又因为PC ⊂平面PAC ,所以AB PC ⊥,即AB PC ⊥是由已知条件可推出的条件,故不可选条件②.18.某学校为提升学生的科学素养,要求所有学生在学年中完成规定的学习任务,并获得相应过程性积分.现从该校随机抽取100名学生,获得其科普测试成绩(百分制,且均为整数)及相应过程性积分数据,整理如下表:科普测试成绩x科普过程性积分人数90100x ≤≤4108090x ≤<3a 7080x ≤<2b 6070x ≤<123060x ≤<02(1)当35a =时,(i )从该校随机抽取一名学生,估计这名学生的科普过程性积分不少于3分的概率;(ⅱ)从该校科普测试成绩不低于80分的学生中随机抽取2名,记X 为这2名学生的科普过程性积分之和,估计X 的数学期望()E X ;(2)从该校科普过程性积分不高于1分的学生中随机抽取一名,其科普测试成绩记为1Y ,上述100名学生科普测试成绩的平均值记为2Y .若根据表中信息能推断12Y Y ≤恒成立,直接写出a 的最小值.【答案】(1)(i )0.45;(ⅱ)589;(2)7.【解析】【分析】(1)(i )求出科普过程性积分不少于3分的学生数,再求出频率,并用频率估计概率即得;(ⅱ)求出X 的所有可能值,由(i )的结论结合独立重复试验的概率问题求出各个取值的概率,再求出期望即得.(2)求出1Y 的最大值,再求出100名学生科普测试成绩的平均值2Y 的最小值,由题设信息列出不等式求解即得.【小问1详解】当35a =时,(i )由表知,科普过程性积分不少于3分的学生人数为103545+=,则从该校随机抽取一名学生,这名学生的科普过程性积分不少于3分的频率为450.45100=,所以从该校随机抽取一名学生,这名学生的科普过程性积分不少于3分的概率估计为0.45.(ⅱ)依题意,从样本中成绩不低于80分的学生中随机抽取一名,这名学生的科普过程性积分为3分的频率为35735109=+,所以从该校学生科普测试成绩不低于80分的学生中随机抽取一名,这名学生的科普过程性积分为3分的概率估计为79,同理,从该校学生科普测试成绩不低于80分的学生中随机抽取一名,这名学生的科普过程性积分为4分的概率估计为29,X 的所有可能值为6,7,8,7749(6)9981P X ==⨯=,7228(7)29981P X ==⨯⨯=,224(8)9981P X ==⨯=,所以X 的数学期望4928458()6788181819E X =⨯+⨯+⨯=.【小问2详解】由表知,10232100a b ++++=,则65b a =-,从该校科普过程性积分不高于1分的学生中随机抽取一名,其科普测试成绩记为1Y ,则1Y 的最大值为69,100名学生科普测试成绩的平均值记为2Y ,要12Y Y ≤恒成立,当且仅当2min ()69Y ≥,显然2Y 的最小值为各分数段取最小值求得的平均分,因此2min 1683()108070(65)602302]10010a Y a a +=⨯++-+⨯+⨯=,则6836910a+≥,解得7a ≥,所以根据表中信息能推断12Y Y ≤恒成立的a 的最小值是7.19.已知椭圆22:G x my m +=的离心率为12,,2A A 分别是G 的左、右顶点,F 是G 的右焦点.(1)求m 的值及点F 的坐标;(2)设P 是椭圆G 上异于顶点的动点,点Q 在直线2x =上,且PF FQ ⊥,直线PQ 与x 轴交于点M .比较2MP 与12MA MA ⋅的大小.【答案】(1)2m =,()1,0F (2)122MA A MP M <⋅【解析】【分析】(1)借助离心率计算即可得;(2)设()00,P x y ,表示出M 与Q 点坐标后,可得2MP 、12MA MA ⋅,借助作差法计算即可得.【小问1详解】由22:G x my m +=,即22:1x G y m+=,由题意可得1m >,故2=,解得2m =,故22:12x G y +=1=,故()1,0F ;【小问2详解】设()00,P x y ,00,0x y ≠,0x <<,有220012x y +=,由PF FQ ⊥,则有()()001210Q x y y -⋅-+⋅=,即01Q x y y -=,由0PQ k ≠,故有0002Q My y y x x x -=--,即有()()()2000000000200000022211M Q y x y x y x x x x x x y y x y y y ---=-=-=------()200320000022000012222422x x x x x x x x x x x ⎛⎫-- ⎪--+⎝⎭=-=---()()32320000002200000002222242222x x x x x x x x x x x x x ----+=-==---,由22:12x G y +=可得()1A、)2A ,则22222222000000022200002444441322x x MP x y x y x x x x x ⎛⎫=-+=-++=-++-=-+ ⎪⎝⎭,1220002242MA MA x x x ⎛⋅==- ⎝,则222001222004432122x x MP MA MA x x -⋅=-+-+=-,由0x <<,故20102x -<,即212MP MA MA <⋅.20.已知函数12()ea x f x x -=.(1)求()f x 的单调区间;(2)若函数2()()e ,(0,)g x f x a x -=+∈+∞存在最大值,求a 的取值范围.【答案】(1)()f x 的增区间为(),2∞-,减区间为(2,)+∞(2)1a ≥-【解析】【分析】(1)对函数求导,得到121(1))e 2(a x f x x -=-',再求出()0f x '>和()0f x '<对应的x 取值,即可求出结果;(2)令2()()e h x f x a -=+,对()h x 求导,利用导数与函数单调性间的关系,求出()h x 的单调区间,进而得出()h x 在(0,)+∞上取值范围,从而将问题转化成1222ee e a a a ---+≥成立,构造函数12()e e x m x x --=+,再利用()m x 的单调性,即可求出结果.【小问1详解】易知定义域为R ,因为12()ea x f x x -=,所以11122211(1)()e2e e 2a x a x a x x x x f ----=-'=,由()0f x '=,得到2x =,当2x <时,()0f x '>,当2x >时,()0f x '<,所以,函数()f x 的单调递增区间为(),2∞-,单调递减区间为()2,∞+.【小问2详解】令2()()e h x f x a -=+,则()()h x f x ''=,由(1)知,函数()f x 的单调递增区间为(),2∞-,单调递减区间为()2,∞+,所以()h x 在2x =时取得最大值12(2)2e e a h a --=+,所以当2x >时,1222()e e e (0)a x h x x a a h ---=+>=,当02x <<时,()(0)h x h >,即当,()0x ∈+∞时,(]()(0),(2)h x h h ∈,所以函数122()ee a x g x x a --=+在(0,)+∞存在最大值的充要条件是1222e e e a a a ---+≥,即122122e e e e +e 02a a a a a -----++=≥,令12()e e x m x x --=+,则12()e e 0x m x --'=+>恒成立,所以12()e e x m x x --=+是增函数,又因为22(1)e e 0m ---=-=,所以12()e e 0a m a a --=+≥的充要条件是1a ≥-,所以a 的取值范围为[)1,-+∞.【点睛】关键点点晴:本题的关键在于第(2)问,构造函数122()e e a x h x x a --=+,利用函数单调性得到,()0x ∈+∞时,(]()(0),(2)h x h h ∈,从而将问题转化成1222e e e a a a ---+≥,构造函数12()e e x m x x --=+,再利用()m x 的单调性来解决问题.21.已知:()2*12:,,,2,m Q a a a m m ≥∈N为有穷正整数数列,其最大项的值为m ,且当0,1,,1k m =- 时,均有(1)km i km j a a i j m ++≠≤<≤.设00b =,对于{0,1,,1}t m ∈- ,定义{}1min ,t t n b n n b a t +=>>,其中,min M 表示数集M 中最小的数.(1)若:3,1,2,2,1,3,1,2,3Q ,写出13,b b 的值;(2)若存在Q 满足:12311b b b ++=,求m 的最小值;(3)当2024m =时,证明:对所有2023,20240Q b ≤.【答案】(1)11b =,36b =(2)4(3)证明见解析【解析】【分析】(1)结合定义逐个计算出1b 、2b 、3b 即可得;(2)当3m =时,可得12310b b b ++≤,故4m ≥,找到4m =时符合要求的数列Q 即可得;(3)结合题意,分两段证明,先证10122024b ≤,定义1120251012,2k k C C C ++⎡⎤==⎢⎥⎣⎦,再证得2024k C b k ≤,即可得证,【小问1详解】由:3,1,2,2,1,3,1,2,3Q ,00b =,则{}1min 0,0n b n n a =>>,故11b =,则{}2min 1,1n b n n a =>>,故23b =,则{}3min 3,2n b n n a =>>,故36b =;【小问2详解】由题意可知,3m ≥,当3m =时,由1n a ≥,{}1min 0,0n b n n a =>>,故11b =,则{}2min 1,1n b n n a =>>,由题意可得123a a a ≠≠,故2a 、3a 总有一个大于1,即22b =或23b =,{}32min ,2n b n n b a =>>,由456a a a ≠≠,故4a 、5a 、6a 总有一个大于2,故36b ≤,故当3m =时,12310b b b ++≤,不符,故4m ≥,当4m =时,取数列:4,1,3,2,1,2,3,4,1,2,3,4,1,2,3,4Q ,有11b =,23b =,37b =,即12311b b b ++=,符合要求,故m 的最小值为4;【小问3详解】因为{}11min ,,0,1,,2023t n b nn b a t t +=>>= ∣,所以11,0,1,,2023i b b t +>= ,(i)若12024t b +≤,则当1t n b +<时,至少以下情况之一成立:①n a t ≤,这样的n 至少有t 个,②存在,i i t b n ≤=,这样的n 至多有t 个,所以小于1t b +的n 至多有2t 个,所以1121t b t t t +≤++=+,令212024t +≤,解得11012t +≤,所以10122024b ≤,(ii)对*k ∈N ,若12024t t b k b +≤<,且()1202420241t l k b k ++<≤+,因为{}1min ,t l t l n b nn b a t l +++=>>+∣,所以当()12024,t l n k b ++∈时,至少以下情况之一成立:①n a t l ≤+,这样的n 至多有t l +个;②存在,i t i i l <≤+且i b n =,这样的n 至多有l 个,所以120241202421t l b k t l l k t l ++≤++++=+++,令212024t l ++≤,解得20232t l -⎡⎤≤⎢⎥⎣⎦,即202512t t l +⎡⎤++≤⎢⎥⎣⎦,其中[]x 表示不大于x 的最大整数,所以当12024t t b k b +≤<时,()2025220241t b k +⎡⎤⎢⎥⎣⎦≤+;综上所述,定义1120251012,2k k C C C ++⎡⎤==⎢⎥⎣⎦,则2024k C b k ≤,依次可得:2345671518,1771,1898,1961,1993,2009C C C C C C ======,89102017,2021,2023C C C ===,所以202320241020240b ≤⨯=.【点睛】关键点点睛:涉及数列新定义问题,关键是正确理解所给出的定义,由给定数列结合新定义探求出数列的相关性质,进行合理的计算、分析、推理等方法综合解决.。
江西省南昌市进贤县一中2024届高三下学期期中试卷数学试题
江西省南昌市进贤县一中2024届高三下学期期中试卷数学试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
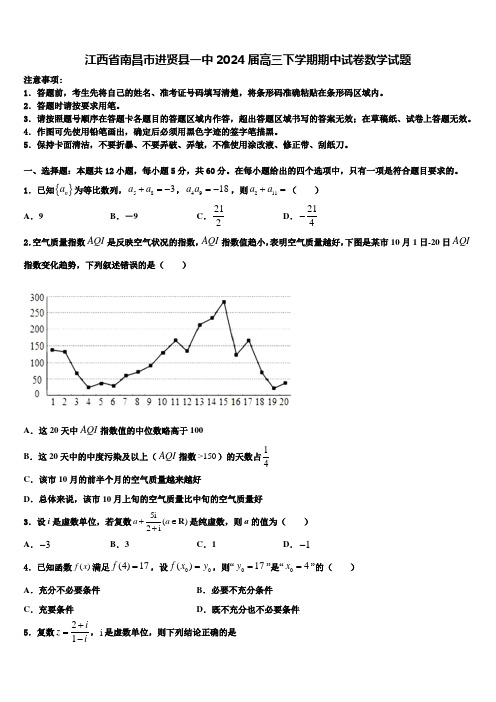
1.已知{}n a 为等比数列,583a a +=-,4918a a =-,则211a a +=( ) A .9B .-9C .212D .214-2.空气质量指数AQI 是反映空气状况的指数,AQI 指数值趋小,表明空气质量越好,下图是某市10月1日-20日AQI指数变化趋势,下列叙述错误的是( )A .这20天中AQI 指数值的中位数略高于100B .这20天中的中度污染及以上(AQI 指数>150)的天数占14C .该市10月的前半个月的空气质量越来越好D .总体来说,该市10月上旬的空气质量比中旬的空气质量好 3.设i 是虚数单位,若复数5i2i()a a +∈+R 是纯虚数,则a 的值为( ) A .3-B .3C .1D .1-4.已知函数()f x 满足(4)17f =,设00()f x y =,则“017y =”是“04x =”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件5.复数2iz +=,i 是虚数单位,则下列结论正确的是A .5z =B .z 的共轭复数为31+22i C .z 的实部与虚部之和为1D .z 在复平面内的对应点位于第一象限6.运行如图所示的程序框图,若输出的值为300,则判断框中可以填( )A .30i >?B .40i >?C .50i >?D .60i >?7.执行如图所示的程序框图,则输出S 的值为( )A .16B .48C .96D .1288.某市气象部门根据2018年各月的每天最高气温平均数据,绘制如下折线图,那么,下列叙述错误的是( )A .各月最高气温平均值与最低气温平均值总体呈正相关B .全年中,2月份的最高气温平均值与最低气温平均值的差值最大C .全年中各月最低气温平均值不高于10°C 的月份有5个D .从2018年7月至12月该市每天最高气温平均值与最低气温平均值呈下降趋势9.设过点(),P x y 的直线分别与x 轴的正半轴和y 轴的正半轴交于,A B 两点,点Q 与点P 关于y 轴对称,O 为坐标原点,若2BP PA =,且1OQ AB ⋅=,则点P 的轨迹方程是( )A .()223310,02x y x y +=>> B .()223310,02x y x y -=>> C .()223310,02x y x y -=>>D .()223310,02x y x y +=>>10.复数12z i =+,若复数12,z z 在复平面内对应的点关于虚轴对称,则12z z 等于( ) A .345i+-B .345i+ C .34i -+D .345i-+ 11.已知集合{}1,0,1,2A =-,{}|lg(1)B x y x ==-,则A B =( )A .{2}B .{1,0}-C .{}1-D .{1,0,1}-12.在正方体1111ABCD A B C D -中,点E ,F ,G 分别为棱11A D ,1D D ,11A B 的中点,给出下列命题:①1AC EG ⊥;②//GC ED ;③1B F ⊥平面1BGC ;④EF 和1BB 成角为4π.正确命题的个数是( ) A .0B .1C .2D .3二、填空题:本题共4小题,每小题5分,共20分。
山东省临沂市2022-2023学年高三期中数学试题含答案

临沂市高三教学质量检测考试数㊀学2022.11注意事项:1.答卷前,考生务必将自己的姓名㊁考生号等填写在答题卡和试卷指定位置上㊂2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑㊂如需改动,用橡皮擦干净后,再选涂其他答案标号㊂回答非选择题时,将答案写在答题卡上㊂写在本试卷上无效㊂3.考试结束后,将本试卷和答题卡一并交回㊂一㊁选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={x|3-x<2},B={1,2,4,5},则Bɘ∁RA=A.{1}㊀㊀㊀㊀㊀㊀B.{1,2}㊀㊀㊀㊀㊀㊀C.{1,2,4}㊀㊀㊀㊀㊀㊀D.{4,5}2.若z=5ii-2,则z=A.2+iB.-2+iC.1+2iD.1-2i3.若扇形的弧长与面积都是6,则这个扇形的圆心角的弧度数是A.2B.3C.4D.54.为了保护水资源,提倡节约用水,某城市对居民用水实行 阶梯水价 .计费方法如下表:每户每月用水量水价不超过12m34元/m3超过12m3但不超过18m36元/m3超过18m38元/m3若某户居民上月交纳的水费为66元,则该户居民上月用水量为A.13m3B.14m3C.15m3D.16m35.已知p:x2+x-2>0,q:x>a,若p是q的必要不充分条件,则A.aȡ1B.aɤ1C.aȡ-2D.aɤ-26.已知向量OAң=(1,7),OBң=(5,1),OMң=(2,1),若点P是直线OM上的一个动点,则PAң㊃PBң的最小值为A.-4B.-6C.-8D.-10㊀7.已知a=54ln54,b=14,c=2ln(sin18+cos18),则A.b<c<aB.a<c<bC.c<a<bD.c<b<a8.函数f(x)是定义在(0,+ɕ)上的单调函数,且对定义域内的任意x,均有f(f(x)-lnx-x)=2,则f(e)=A.e+1B.e+2C.e2+1D.e2+2二㊁选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.欧拉公式exi=cosx+isinx(其中i为虚数单位,xɪR)将指数函数的定义域扩大到复数,建立了三角函数与指数函数的关联,在复变函数论中占有非常重要的地位,被誉为数学中的天桥.依据欧拉公式,则A.eπi=1B.eπi2为纯虚数C.exi3+i=12D.复数e2i对应的点位于第三象限10.函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则A.ω+φ=π2B.f(-2)=-22C.f(x)的图象关于点(2022,0)对称D.f(2x)在[3,4]上单调递增11.南宋数学家杨辉所著的‘详解九章算法㊃商功“中出现了如图所示的形状,后人称之为 三角垛 . 三角垛 最上层有1个球,第二层有3个球,第三层有6个球, ,以此类推.设从上到下各层球数构成一个数列{an},则A.a4=9B.an+1-an=n+1C.a10=55D.ðni=11ai=2nn+112.若a>b>0,且a+b=1,则A.alnb>blnaB.2a+abȡ2+22C.(a2+1)(b2+1)<32D.a2a+2+b2b+1ȡ14三㊁填空题:本题共4小题,每小题5分,共20分.13.已知向量a在b方向上的投影向量是-2e(e是与b同方向的单位向量),|b|=3,则a㊃b=㊀㊀㊀㊀.14.已知tan(π8-α)=23,则sin(π4+2α)=㊀㊀㊀㊀.15.设函数f(x)=log12(-x)-1,x<0log2x+1,x>0{,若f(a)>f(-a),则a的取值范围是㊀㊀㊀㊀.16.摩天轮是一种大型转轮状的机械建筑设施,某摩天轮最高点距离地面高度128米,转盘直径为120米,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周需要30分钟.若游客甲坐上摩天轮的座舱,开始旋转t分钟后距离地面的高度为h米,则h关于t的函数解析式为㊀㊀㊀㊀㊀㊀;若游客甲在t1,t2时刻距离地面的高度相等,则t1+t2的最小值为㊀㊀㊀㊀.四㊁解答题:本题共6小题,共70分.解答应写出文字说明㊁证明过程或演算步骤.17.(10分)已知函数f(x)=x2+bx+c的图象过点(0,2),且满足f(-1)=f(3).(1)求f(x)的解析式;(2)解关于x的不等式f(x)<(2a-2)x.18.(12分)已知函数f(x)=cos4x+2sinxcosx-sin4x.(1)求f(x)的最小正周期;(2)将f(x)的图象向右平移π4个单位,得到函数g(x)的图象,若g(x)在[0,m]上的最小值为g(0),求m的最大值.19.(12分)已知函数f(x)=aex+bsinx-2x,曲线y=f(x)在点(0,f(0))处的切线为y=1.(1)求a,b;(2)求f(x)的最小值.㊀20.(12分)已知正项数列{an}的前n项和Sn,且an+1an=2Sn.(1)证明:数列{Sn2}为等差数列;(2)记Tn=1S1+1S2+1S3+ +1Sn,证明Tn<2n.21.(12分)әABC中,AB=4,cosA=78,AC>AB.(1)若ABң㊃BCң=12,求BC;(2)若cos(B-C)=14,求әABC的面积.22.(12分)已知函数f(x)=lnxx和g(x)=axex有相同的最大值.(1)求a,并说明函数h(x)=f(x)-g(x)在(1,e)上有且仅有一个零点;(2)证明:存在直线y=b,其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,并且从左到右的三个交点的横坐标成等比数列.临沂市高三教学质量检测考试数学试题参考答案及评分标准2022.11说明:一㊁本解答只给出了一种解法供参考,如考生的解法与本解答不同,可根据试题的主要考查内容参照评分标准酌情赋分.二㊁当考生的解答在某一步出错误时,如果后继部分的解答未改该题的内容与难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确答案应得分数一半;如果后继部分的解答有较严重的错误或又出现错误,就不再给分.三㊁解答右端所注分数,表示考生正确做到这一步应得的累加分数.四㊁只给整数分数,选择题和填空题不给中间分.一㊁选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.D㊀2.C㊀3.B㊀4.C㊀5.A㊀6.C㊀7.D㊀8.B㊀二㊁选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.BC㊀10.ABD㊀11.BCD㊀12.BD㊀三㊁填空题:本大题共4小题,每小题5分,共20分.13.-6㊀14.513㊀15.(-12,0)ɣ(12,+ɕ)㊀16.h(t)=60sin(π15t-π2)+68,tɪ[0,+ɕ)㊀30(第一空3分,第二空2分)四㊁解答题:本题共6小题,共70分.解答应写出文字说明㊁证明过程或演算步骤.17.(10分)解:(1)ȵf(x)的图象过点(0,2),即f(0)=2,ʑc=2.1分又f(-1)=f(3),ʑf(x)图象的对称轴为x=-1+32=1,2分 ʑ-b2=1,ʑb=-2.4分故f(x)=x2-2x+2.5分 (2)不等式f(x)<(2a-2)x,可化为x2-2ax+2<0.6分①当Δ=4a2-8ɤ0,即-2ɤaɤ2时,不等式x2-2ax+2ȡ0恒成立,此时不等式x2-2ax+2<0的解集为Ø.7分 ②当Δ=4a2-8>0,即a<-2或a>2时,㊀方程x2-2ax+2=0有两个根为x1=a-a2-2,x2=a+a2-2,8分此时不等式x-2ax+2<0的解集为{x|a-a2-2<x<a+a2-2}.9分综上,当-2ɤaɤ2时,不等式的解集为Ø;当a<-2或a>2时,不等式的解集为{x|a-a2-2<x<a+a2-2}.10分18.(12分)解:(1)f(x)=(cos2x+sin2x)(cos2x-sin2x)+2sinxcosx=cos2x+sin2x2分=2sin(2x+π4)4分ʑ最小正周期T=2π2=π.5分(2)g(x)=2sin[2(x-π4)+π4],7分即g(x)=2sin(2x-π4),8分ȵ0ɤxɤm,ʑ-π4ɤ2x-π4ɤ2m-π4.9分由g(x)在[0,m]上最小值为g(0),ʑ2m-π4ɤ5π4.ʑmɤ3π4.10分ʑ0<mɤ3π4.11分即m的最大值为3π4.12分19.(12分)解:(1)由已知:fᶄ(x)=aex+bcosx-2,1分ȵ曲线y=f(x)在点(0,f(0))处的切线方程为y=1,ʑf(0)=1,fᶄ(0)=0,{即a=1,a+b-2=0,{ʑa=1,b=1.{5分(2)由(1)知,fᶄ(x)=ex+cosx-2,6分当x<0时,ȵex<1,cosx<1,ʑfᶄ(x)ɤ0,ʑf(x)单调递减.8分当x>0时,令g(x)=fᶄ(x),则gᶄ(x)=ex-sinx,ȵex>1,sinxɤ1ʑgᶄ(x)>0,ʑfᶄ(x)单调递增,ʑfᶄ(x)>fᶄ(0)=0.10分ʑ当x>0时,f(x)单调递增.11分ʑf(x)min=f(0)=1.ʑf(x)的最小值为1.12分20.(12分)解:(1)证明:ȵan+1an=2Sn,ʑ当nȡ2时,Sn-Sn-1+1Sn-Sn-1=2Sn,1分ʑ1Sn-Sn-1=Sn+Sn-1),ʑSn2-Sn-12=1.3分当n=1时,a1+1a1=2a1,ʑa12=1,即S12=1,4分 故{Sn2}是首项为1,公差为1的等差数列,5分 (2)证明:由(1)知Sn2=n,Sn=n;7分 1Sn=1n=22n<2n+n-1=2(n-n-1),9分 ʑTn=1S1+1S2+1S3+ +1Sn<2(1-0+2-1+3-2+ +n-n-1)=2n.11分 即Tn<2n.12分21.(12分)解:(1)ȵABң㊃BCң=ABң㊃(ACң-ABң)=ABң㊃ACң-|ABң|21分=|ABң|㊃|ACң|㊃cosA-42=4ˑACˑ78-16=72AC-16,2分 由72AC-16=12,得AC=8.3分 ʑBC2=AB2+AC2-2AB㊃ACcosA=24,4分 ʑBC=26.5分 (2)法一:ȵcos(B-C)=14,ʑπ3<B-C<π2,2π3<2(B-C)<π,6分又cos2(B-C)=2cos2(B-C)-1=-78,又cosA=78,0<A<π3,ʑ2(B-C)=π-A,㊀ʑ2(B-C)=B+C,ʑB=3C,7分ʑA=π-4C,ʑcosA=cos(π-4C)=78,ʑcos4C=-78,ʑ2cos22C-1=-78,8分ʑcos2C=14,ʑ1-2sin2C=14,ʑsinC=64,9分由正弦定理得,ABsinC=BCsinA,又sinA=1-cos2A=158,AB=4,ʑBC=4ˑ158ˑ46=10,10分又sin2C=154,cosC=104,ʑsinB=sin3C=sin(C+2C)=sinCcos2C+cosCsin2C=64ˑ14+104ˑ154=368,11分ʑSәABC=12AB㊃BCsinB=12ˑ4ˑ10ˑ368=3152.12分法二:在AC上取点D,使得øCBD=øC,ȵcos(B-C)=14,ʑcosøABD=14,6分ʑsinøABD=1-cos2øABD=154,又sinA=1-cos2A=158,7分ʑcosøADB=cos[π-(øA+øABD)]=-cos(øA+øABD)=sinA㊃sinøABD-cosAcosøABD=158ˑ154-78ˑ14=14,8分ʑcosøADB=cosøABD,ʑøADB=øABD.ʑAD=AB=4.9分 又BD2=AB2+AD2-2AB㊃AD㊃cosA=16+16-2ˑ4ˑ4ˑ78=4,ʑBD=2,10分 ʑDC=BD=2,AC=AD+DC=6,11分 ʑSәABC=12AB㊃AC㊃sinA=12ˑ4ˑ6ˑ158=3152.12分22.(12分)解:(1)fᶄ(x)=1-lnxx2,1分 当xɪ(0,e)时,fᶄ(x)>0,f(x)单调递增;当xɪ(e,+ɕ)时,fᶄ(x)<0,f(x)单调递减,ʑx=e时,f(x)取得最大值.即f(x)max=f(e)=1e.2分 gᶄ(x)=a(1-x)ex,当a>0时,xɪ(-ɕ,1)时,gᶄ(x)>0,g(x)单调递增;xɪ(1,+ɕ)时,gᶄ(x)<0,g(x)单调递减,ʑg(x)max=g(1)=ae.3分 当a=0时,g(x)=0,不合题意;当a<0时,可知g(x)min=g(1),不合题意.故ae=1e,即a=1.4分 ʑh(x)=f(x)-g(x)=lnxx-xex.5分 ȵhᶄ(x)=1-lnxx2-1-xex,当1<x<e时,1-lnx>0,1-x<0,ʑhᶄ(x)>0,ʑh(x)在[1,e]上单调递增,又h(1)=-1e<0,h(e)=1e-eee=1e-1ee-1=ee-1-eee>0,ʑh(x)在(1,e)上有且仅有一个零点.6分(2)由(1)知,y=f(x),y=g(x)的图象大致如下图:㊀7分直线y=b与曲线y=f(x),y=g(x)三个交点的横坐标从左至右依次为x1,x2,x3,且0<x1<1<x2<e<x3,8分 ʑ0<lnx2<1<lnx3且lnx3x3=lnx2x2=x1ex1=b.9分 由x1ex1=lnx2x2=lnx2elnx2即g(x1)=g(lnx2),x1,lnx2ɪ(0,1),ʑx1=lnx2即x2=ex1.① 10分 由x2ex2=lnx3x3=lnx3elnx3即g(x2)=g(lnx3),ʑx2=lnx3.② 11分 由①,②,x22=ex1lnx3,又lnx3x3=x1ex1即ex1lnx3=x1x3,ʑx22=x1x3.12分。
高三数学下期中试题(含答案)(3)

高三数学下期中试题(含答案)(3)一、选择题1.已知数列121,,,4a a 成等差数列,1231,,,,4b b b 成等比数列,则212a ab -的值是 ( ) A .12B .12-C .12或12- D .142.已知数列{}n a 的前n 项和2n S n =,()1nn n b a =-则数列{}n b 的前n 项和n T 满足( ) A .()1nn T n =-⨯ B .n T n = C .n T n =-D .,2,.n n n T n n ⎧=⎨-⎩为偶数,为奇数3.若变量x ,y 满足约束条件1358x y x x y ≥-⎧⎪≥⎨⎪+≤⎩,,,则2yz x =-的取值范围是( ) A .113⎡⎤-⎢⎥⎣⎦,B .11115⎡⎤--⎢⎥⎣⎦,C .111153⎡⎤-⎢⎥⎣⎦, D .3153⎡⎤-⎢⎥⎣⎦,4.已知点(),P x y 是平面区域()4{04y x y x m y ≤-≤≥-内的动点, 点()1,1,A O -为坐标原点, 设()OP OA R λλ-∈u u u r u u u r的最小值为M ,若M ≤恒成立, 则实数m 的取值范围是( )A .11,35⎡⎤-⎢⎥⎣⎦B .11,,35⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭C .1,3⎡⎫-+∞⎪⎢⎣⎭D .1,2⎡⎫-+∞⎪⎢⎣⎭5.数列{}{},n n a b 为等差数列,前n 项和分别为,n n S T ,若3n 22n n S T n +=,则77a b =( ) A .4126B .2314C .117 D .1166.变量,x y 满足条件1011x y y x -+≤⎧⎪≤⎨⎪>-⎩,则22(2)x y -+的最小值为( ) A.2BC .5D .927.已知函数22()()()n n f n n n 为奇数时为偶数时⎧=⎨-⎩,若()(1)n a f n f n =++,则123100a a a a ++++=LA .0B .100C .100-D .102008.设{}n a 是首项为1a ,公差为-1的等差数列,n S 为其前n 项和,若124,,S S S 成等比数列,则1a =( ) A .2B .-2C .12D .12-9.已知等比数列{}n a 中,31174a a a =,数列{}n b 是等差数列,且77b a =,则59b b +=( ) A .2B .4C .16D .810.,x y 满足约束条件362000x y x y x y -≤⎧⎪-+≥⎪⎨≥⎪⎪≥⎩,若目标函数(0,0)z ax by a b =+>>的最大值为12,则23a b+的最小值为 ( ) A .256B .25C .253D .511.已知正数x 、y 满足1x y +=,则141x y++的最小值为( )A .2B .92C .143D .512.“中国剩余定理”又称“孙子定理”1852年英国来华传教士伟烈亚力将《孙子算经》中“物不知数问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1至2019中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列{}n a ,则此数列的项数为( ) A .134B .135C .136D .137二、填空题13.已知0a >,0b >,当()214a b ab++取得最小值时,b =__________. 14.在等差数列{}n a 中,12a =,3510a a +=,则7a = .15.已知函数()2xf x =,等差数列{}n a 的公差为2,若()2468104f a a a a a ++++=,则()()()()212310log f a f a f a f a ⋅⋅⋅⋅=⎡⎤⎣⎦L ___________.16.若正项数列{}n a 满足11n n a a +-<,则称数列{}n a 为D 型数列,以下4个正项数列{}n a 满足的递推关系分别为:①2211n naa +-=②1111n na a +-= ③121n n n a a a +=+ ④2121n n a a +-=,则D 型数列{}n a 的序号为_______.17.已知的三边长分别为3,5,7,则该三角形的外接圆半径等于_________.18.海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径A ,B 两点间的距离,现在珊瑚群岛上取两点C ,D ,测得80CD =,135ADB ∠=︒,15BDC DCA ∠∠==︒,120ACB ∠=︒,则A ,B 两点的距离为________.19.在△ABC 中,已知sinA:sinB:sinC=3:5:7,则此三角形最大内角的大小..为________.20.已知函数()3af x x x=++,*x ∈N ,在5x =时取到最小值,则实数a 的所有取值的集合为______.三、解答题21.已知数列中,,. (1)求证:是等比数列,并求的通项公式; (2)数列满足,求数列的前项和.22.ABC 的内角A 、B 、C 所对的边分别为a b c ,,,且sin sin sin 2sin a A b B c C a B +=+()1求角C ; ()2求3sin cos 4A B π⎛⎫-+ ⎪⎝⎭的最大值.23.已知角A ,B ,C 为等腰ABC ∆的内角,设向量(2sin sin ,sin )m A C B =-r ,(cos ,cos )n C B =r ,且//m n r r,7BC =(1)求角B ;(2)在ABC ∆的外接圆的劣弧»AC 上取一点D ,使得1AD =,求sin DAC ∠及四边形ABCD 的面积.24.设函数1()|(0)f x x x a a a=++- (1)证明:()2f x ≥;(2)若(3)5f <,求a 的取值范围.25.ABC V 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos cos a C c A a +=. (1)求证:A B =; (2)若6A π=,ABC V,求ABC V 的周长.26.已知数列{}n a 的前n 项和()2*,,n S pn qn p q n =+∈∈R N ,且143,24.a S ==(1)求数列{}n a 的通项公式;(2)设2n an b =,求数列{}n b 的前n 项和n T .【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【解析】由题意可知:数列1,a 1,a 2,4成等差数列,设公差为d , 则4=1+3d ,解得d =1, ∴a 1=1+2=2,a 2=1+2d =3.∵数列1,b 1,b 2,b 3,4成等比数列,设公比为q , 则4=q 4,解得q 2=2, ∴b 2=q 2=2.则21221122a ab --==. 本题选择A 选项.2.A解析:A 【解析】 【分析】先根据2n S n =,求出数列{}n a 的通项公式,然后利用错位相减法求出{}n b 的前n 项和n T .【详解】解:∵2n S n =,∴当1n =时,111a S ==;当2n ≥时,()221121n n n a S S n n n -=-=--=-, 又当1n =时,11a =符合上式,∴21n a n =-, ∴()()()1121nnn n b a n =-=--,∴()()()()()123113151121nn T n =⨯-+⨯-+⨯-+⋅⋅⋅+--①,∴()()()()()2341113151121n n T n +-=⨯-+⨯-+⨯-+⋅⋅⋅+--②,①-②,得()()()()()()23412121111211n n n T n +⎡⎤=-+⨯-+-+-+⋅⋅⋅+---⨯-⎣⎦()()()()()()211111122112111n n n n n -+⎡⎤---⎣⎦=-+⨯--⨯-=---,∴()1nn T n =-,∴数列{}n b 的前n 项和()1nn T n =-.故选:A . 【点睛】本题考查了根据数列的前n 项和求通项公式和错位相减法求数列的前n 项和,考查了计算能力,属中档题.3.A解析:A 【解析】 【分析】画出满足条件的平面区域,求出角点的坐标,结合2yz x =-的几何意义求出其范围,即可得到答案. 【详解】由题意,画出满足条件的平面区域,如图所示:由358y x x y =⎧⎨+=⎩,解得11A (,),由1x y x =-⎧⎨=⎩,解得(11)B --,, 而2yz x =-的几何意义表示过平面区域内的点与0(2)C ,的直线斜率, 结合图象,可得1AC k =-,13BC k =, 所以2y z x =-的取值范围为113⎡⎤-⎢⎥⎣⎦,, 故选:A.【点睛】本题主要考查了简单的线性规划问题,其中解答中作出约束条件所表示的平面区域,结合图象确定出目标函数的最优解是解答的关键,着重考查了数形结合思想,以及计算能力,属于基础题.4.C解析:C 【解析】试题分析:直线()4x m y =-恒过定点(0,4),当0m >时,约束条件()4{04y x y x m y ≤-≤≥-对应的可行域如图,则()OP OA R λλ-∈u u u r u u u r的最小值为0M =,满足2M ≤,当0m =时,直线()4x m y =-与y 轴重合,平面区域()4{04y x y x m y ≤-≤≥-为图中y 轴右侧的阴影区域,则()OP OA R λλ-∈u u u r u u u r的最小值为0M =,满足2M ≤,当0m <时,由约束条件()4{04y x y x m y ≤-≤≥-表示的可行域如图,点P 与点B 重合时,()OP OA R λλ-∈u u u r u u u r的最小值为M OB =u u u r ,联立{(4)y x x m y ==-,解得44(,)11m mB m m --,所以421m OB m =-u u u r ,由4221m m ≤-1135m -≤≤,所以103m -≤≤,综上所述,实数m 的取值范围是1,3⎡⎫-+∞⎪⎢⎣⎭,故选C.考点:简单的线性规划.【方法点晴】本题主要考查了二元一次不等式组所表示的平面区域、简单的线性规划求最值问题,着重考查了数形结合思想方法及分类讨论的数学思想方法的应用,关键是正确的理解题意,作出二元一次不等式组所表示的平面区域,转化为利用线性规划求解目标函数的最值,试题有一定的难度,属于难题.5.A解析:A【解析】依题意,113713113713132412226132a aa Sb bb T+⋅===+⋅.6.C解析:C【解析】由约束条件画出可行域,如下图,可知当过A(0,1)点时,目标函数取最小值5,选C.7.B解析:B 【解析】试题分析:由题意可得,当n 为奇数时,()22()(1)121;n a f n f n n n n =++=-+=--当n 为偶数时,()22()(1)121;n a f n f n n n n =++=-++=+所以()1231001399a a a a a a a ++++=+++L L ()()()2410021359999224610099100a a a ++++=-++++-++++++=L L L ,故选B.考点:数列的递推公式与数列求和.【方法点晴】本题主要考查了数列的递推公式与数列求和问题,考查了考生的数据处理与运算能力,属于中档题.本题解答的关键是根据给出的函数()22(){()n n f n n n =-当为奇数时当为偶数时及()(1)n a f n f n =++分别写出n 为奇数和偶数时数列{}n a 的通项公式,然后再通过分组求和的方法得到数列{}n a 前100项的和.8.D解析:D 【解析】 【分析】把已知2214S S S =用数列的首项1a 和公差d 表示出来后就可解得1a .,【详解】因为124S S S ,,成等比数列,所以2214S S S =,即211111(21)(46).2a a a a -=-=-,故选D. 【点睛】本题考查等差数列的前n 项和,考查等比数列的性质,解题方法是基本量法.本题属于基础题.9.D解析:D 【解析】 【分析】利用等比数列性质求出a 7,然后利用等差数列的性质求解即可. 【详解】等比数列{a n }中,a 3a 11=4a 7, 可得a 72=4a 7,解得a 7=4,且b 7=a 7, ∴b 7=4,数列{b n }是等差数列,则b 5+b 9=2b 7=8.故选D . 【点睛】本题考查等差数列以及等比数列的通项公式以及简单性质的应用,考查计算能力.10.A解析:A 【解析】 【分析】先画不等式组表示的平面区域,由图可得目标函数(0,0)z ax by a b =+>>何时取最大值,进而找到a b ,之间的关系式236,a b +=然后可得23123()(23)6a b a b a b+=++,化简变形用基本不等式即可求解。
2024届湖北省秋季鄂东南省级示范高中期中联考高三数学试卷及答案

2023年秋季鄂东南省级示范高中教育教学改革联盟学校期中联考高三数学试卷考试时间:2023年11月1日下午15:00-17:00试卷满分:150分一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)4. 已知G 为ABC ∆的重心,32π=∠A ,2-=⋅AC AB ,则||AG 的最小值为( )A .81B .94C .91D .32A .m35B .m50C .m60D .m906. 将函数()cos f x x =的图像先向右平移3π个单位长度,再把所得函数图像上的每个点的横坐标都变为原来的()10ωω>倍,纵坐标不变,得到函数()g x 的图像,若函数()g x 在()0,π-上单调递增,则ω的取值范围是( )7. 函数b x x a x x f +--+=23)1()(为R 上的奇函数,过点)1,21(-P 作曲线)(x f y =的切线,可作切线条数为( )A .B 1.C 2.D 3.不确定8. 在ABC ∆中,AC AB 2=,且ABC ∆的面积为1,则BC 的最小值为()A .2B .C .1D .2二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.10.)(x f 是定义在R 上的连续可导函数,)(x f '为其导函数,下列说法正确的有()A .若)()(x f x f =-,则)()(x f x f '-=-'B .若)(x f '为偶函数,则)(x f 为奇函数C .若)(x f '是周期为)(0≠T T 的函数,则)(x f 也是周期为T 的函数D .已知x x f x f 2)()(=--且0)1()1(=--+x f x f ,则1)1()0(='+'f f 11.已知函数⎪⎪⎩⎪⎪⎨⎧≤≤-<<=144),36cos(440log )(21x x x x x f ππ,,若方程m x f =)(有四个不等的实根1x ,2x ,3x ,4x ,且4321x x x x <<<,则下列结论正确的是( )A .20<<m B .2121=x x C .)55,48(43∈x x D .)5,1(31∈x x 12.正项数列}{n a 的前n 项和为n S ,若122+=n n n a S a ,nn n S S b 22log +=,数列的}{n b 前n 项和为n T ,下面结论正确的有( )A .n n a a >+1B .}{2n S 是等差数列C .nS n 22ln ≥+D .满足2≥n T 的最小正整数n 为5三、填空题:本题共4小题,每小题5分,共20分.13.已知向量),2(λλ=a ,),(1λ=b ,若向量a 与向量b 共线,则实数λ的值为 .14.已知函数122)193(log )(22+-++=x x x x f ,若2)2()1(-≤-+-a f a f ,则实数a 的解集为.15.已知数列}{n a 的首项531=a ,且1231+=+n n n a a a ,202411121<++na a a ,则满足条件的最大整数=n.16.已知实数0>a ,对2>∀x ,)2ln(2a ax a a e x->+恒成立,则a 的取值范围为 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.(1)求数列}{n a 的通项公式;(2)求数列|}{|n a 的前n 项和n T .20.(本题满分12分)已知函数x a e x f xsin 1)(--=.(1)若曲线)(x f y =在点))0(0(f ,处的切线方程为x y -=,求a 的值;(2)当2=a 时,)(12)(Z c c x f ∈-≥在],0[π∈x 恒成立,求c 的最大值.21.(本题满分12分)已知}{n a 为等比数列,且14432=++a a a ,432,1,a a a +成等差数列.(1)求数列}{n a 的通项公式;(2)当}{n a 为递增数列时,)12)(12()26()1(1+++-=+n n n n n a b ,数列}{n b 的前n 项和为n T ,若存在n T m N n ≥∈*,,求m 的取值范围.22.(本题满分12分)已知函数1ln )(-+=xmx x f .(1)若存在实数x ,使1)(-<x f 成立,求实数m 的取值范围;(2)若)(x f 有两个不同零点21,x x ,求证:e x x <+<212.2023年秋季鄂东南省级示范高中教育教学改革联盟学校期中联考19.解:(1)设}{n a 的公差为d ,则:⎪⎩⎪⎨⎧=⨯+==+=6427881121813d a S d a a ⎩⎨⎧-==⇒2151d a ,n a n 217-=∴;(5分)(2)n n nn S n 162)21715(2+-=-+=,当80217≤⇒>-=n n a n ,当8≤n 时,0>n a ,nn n a a a a a a T ++=++=2121||||||n n S n 162+-==,(8分)当9≥n 时,0<n a ,)(||||||982121n n n a a a a a a a a T ++-+++=++= nn S S S S S -=--=8882)(12816)16()8168(2222+-=+--⨯+-=n n n n .(11分)综上所述:⎪⎩⎪⎨⎧≥+-≤+-=9,1281681622n n n n n n T n ,.(12分)20.解:(1)x a e x f xsin 1)(--=x a e x f xcos )(-='⇒,11)0(-=-='∴a f 2=⇒a 且此时切线方程为x y -=;(4分)(2)依题意:,min )1)((21+≤x f c ,当2=a 时,x e x f xsin 21)(--=,x e x f xcos 2)(-=',且)(x f '在],0[π上单调递增,01)0(<-='f ,024(4>-='ππe f ,)4,0(0π∈∃∴x ,使得0)(0='x f ,即0cos 20x e x =,)(x f 在),0(0x 上单调递减,)(0π,x 上单调递增,1sin 2)()(00min 0--==x e x f x f x 1sin 2cos 200--=x x 1)4cos(220-+=πx ,(8分)4,0(0π∈x ,2,4(40πππ∈+∴(x ,)22,0(4cos0∈+)(πx ,)1,1()()2,0(4cos 2200-∈⇒∈+∴x f x (π,)1,0()1)((210∈+x f ,0,≤∴∈c Z c ,c 的最大值为0.(12分)21.解:(1)⎩⎨⎧+=+=++)1(214342432a a a a a a ⎪⎩⎪⎨⎧==⎩⎨⎧==⇒2142433q a q a 或12-=∴n n a 或n n a -=52;(5分)(2))12)(12(223)1(1+++⋅-=+n n n nn b 121121(11+++-=+n n n)((7分)当n 为偶数时,)121121(121121(121121(1322++++++++++++-=+n n n T 121311++-=+n 在*∈N n 上单调递减,]92,31(--∈∴n T ,(9分);当n 为奇数时,121121(121121(121121(1322+++-++++++++-=+n n n T 121311+--=+n 在*∈N n 上单调递增,31,158[--∈∴n T ,(11分)158-≥∴m.(12分)()()()()()()()()()()()()()()()()()()()()[] ()()()()()()()()()()()()()()()exxexxemxmexexxge qxqexqxxqexxxqexexxgxqmxxxgxxgxxxpxxxgxpexyBxgxyOAeBAexxxxxxxxxgxgxgxgxgxgxgxghx hx hxlxgxgxhxxgxgx hexxmggxgxgxxgxgxxxmxgxgxxxgxxxxmxxxfeexxxexxxexxxxmxxxxxmxmxxf<+<<+∴+-<∴>+-∴+-<∴=<∴∴>-='--=<<+--=<>∴>∴>-=<<-=+-==<+>+∴->∴>->-<∴=-<-<∴=<∴∴>+---=-'+'='∴<<--=<<<<<<∴=>=<'+∞∈>'∈-='==-=-=∴<∴=≤∴<'>>'<<--='<-=∞+-<<+-<2121222211121211212122111221212121max2,0)()(,1)(.0ln1)(,)ln2()()1)(()()(,)(,0ln)()10()()()(,),0,(),1,1(22,12,122,2,011011n2121,1e,011,0,1)(,01,0lng,,ln1,)ln1(,)()2(e1m1)1()()(,0)(1)(,0)(1,ln1)()(,ln)(lnln1)(1.22综上递增,在则设即则设处的切线为在的方程直线设下证又即递增,,在令不妨设,又递减时递增,当时,当又则令有两个不同实根有两个不同零点递减时,当递增时,当只需令)有解,在(即得)由(ϕϕϕϕϕϕϕϕϕ。
高三数学下期中一模试卷含答案

高三数学下期中一模试卷含答案一、选择题1.已知正数x 、y 满足1x y +=,且2211x y m y x +≥++,则m 的最大值为( ) A .163B .13C .2D .42.已知在中,,,分别为角,,的对边,为最小角,且,,,则的面积等于( ) A .B .C .D .3.在R 上定义运算:A()1B A B =-,若不等式()x a -()1x a +<对任意的实数x ∈R 恒成立,则实数a 的取值范围是( ) A .11a -<<B .02a <<C .1322a -<< D .3122a -<< 4.数列{}{},n n a b 为等差数列,前n 项和分别为,n n S T ,若3n 22n n S T n +=,则77a b =( ) A .4126B .2314C .117 D .1165.设数列{}n a 是等差数列,且26a =-,86a =,n S 是数列{}n a 的前n 项和,则( ). A .45S S <B .45S S =C .65S S <D .65S S =6.已知数列{}n a 满足112,0,2121,1,2n n n n n a a a a a +⎧≤<⎪⎪=⎨⎪-≤<⎪⎩若135a =,则数列的第2018项为 ( )A .15B .25C .35D .457.已知等比数列{}n a ,11a =,418a =,且12231n n a a a a a a k +++⋅⋅⋅+<,则k 的取值范围是( ) A .12,23⎡⎤⎢⎥⎣⎦B .1,2⎡⎫+∞⎪⎢⎣⎭C .12,23⎡⎫⎪⎢⎣⎭D .2,3⎡⎫+∞⎪⎢⎣⎭8.已知等比数列{}n a 的前n 项和为n S ,且满足122n n S λ+=+,则λ的值是( )A .4B .2C .2-D .4-9.已知等差数列{}n a 的前n 项和为n S ,19a =,95495S S -=-,则n S 取最大值时的n 为A .4B .5C .6D .4或510.已知{}n a 是等比数列,22a =,514a =,则12231n n a a a a a a +++⋅⋅⋅+=( ) A .()1614n--B .()1612n--C .()32123n -- D .()32143n -- 11.某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为和,第一排和最后一排的距离为56米(如图所示),旗杆底部与第一排在同一个水平面上.若国歌长度约为秒,要使国歌结束时国旗刚好升到旗杆顶部,升旗手升旗的速度应为()(米 /秒)A .110B .310C .12D .71012.如果等差数列{}n a 中,3a +4a +5a =12,那么1a +2a +…+7a =( ) A .14B .21C .28D .35二、填空题13.如果一个数列由有限个连续的正整数组成(数列的项数大于2),且所有项之和为N ,那么称该数列为N 型标准数列,例如,数列2,3,4,5,6为20型标准数列,则2668型标准数列的个数为______.14.在平面直角坐标系中,设点()0,0O ,(3A ,点(),P x y 的坐标满足303200x y x y -≤+≥⎨⎪≥⎪⎩,则OA u u u v 在OP uuu v 上的投影的取值范围是__________ 15.若变量,x y 满足约束条件{241y x y x y ≤+≥-≤,则3z x y =+的最小值为_____.16.数列{}n a 满足10a =,且()1*11211n nn N a a +-=∈--,则通项公式n a =_______.17.已知二次函数22()42(2)21f x x p x p p =----+,若在区间[1,1]-内至少存在一个实数x 使()0f x >,则实数p 的取值范围是__________.18.已知数列{}n a 的前n 项和为n S ,11a =,且1n n S a λ=-(λ为常数).若数列{}n b 满足2n n a b n =-920n +-,且1n n b b +<,则满足条件的n 的取值集合为________.19.已知数列是各项均不为的等差数列,为其前项和,且满足()221n n a S n *-=∈N.若不等式()()11181nn n n a nλ++-+⋅-≤对任意的n *∈N 恒成立,则实数的取值范围是 .20.我国古代数学名著《九章算术》里有问题:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢,问:__________日相逢?三、解答题21.已知在等比数列{}n a 中, 11a =,且2a 是1a 和31a -的等差中项. (1)求数列{}n a 的通项公式;(2)若数列{}n b 满足()*21n n b n a n N =-+∈,求{}nb 的前n 项和nS.22.若0,0a b >>,且11ab a b+= (1)求33+a b 的最小值;(2)是否存在,a b ,使得236a b +=?并说明理由. 23.已知在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,sin tan cos sin tan cos b B C b B a A C a A -=-. (1)求证:A B =;(2)若3c =,3cos 4C =,求ABC ∆的周长.24.在平面四边形ABCD 中,已知34ABC π∠=,AB AD ⊥,1AB =.(1)若5AC =ABC ∆的面积;(2)若5sin 5CAD ∠=,4=AD ,求CD 的长. 25.如图,游客从某旅游景区的景点A 处下上至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50/minm.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C,假设缆车匀速直线运动的速度为130/minm,山路AC长为1260m,经测量12 cos13A=,3cos5C=.(1)求索道AB的长;(2)问:乙出发多少min后,乙在缆车上与甲的距离最短?(3)为使两位游客在C处互相等待的时间不超过3min,乙步行的速度应控制在什么范围内?26.已知向量113,sin222x xa⎛⎫+⎝=⎪⎪⎭v与()1,b y=v共线,设函数()y f x=.(1)求函数()f x的最小正周期及最大值.(2)已知锐角ABC∆的三个内角分别为,,A B C,若有33f Aπ⎛⎫-=⎪⎝⎭,边217,sinBC B==,求ABC∆的面积.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】由已知条件得()()113x y+++=,对代数式2211x yy x+++变形,然后利用基本不等式求出2211x yy x+++的最小值,即可得出实数m的最大值.【详解】正数x、y满足1x y+=,则()()113x y+++=,()()()()()()222222221212111111111111y x y x y x x y y x y x y x y x +-+-⎡⎤⎡⎤----⎣⎦⎣⎦+=+=+=+++++++++444444141465111111y x x y y x x y x y =+-+++-+=+++-=+-++++++()()14441111525311311y x x y x y x y ⎛⎫⎛⎫++=++++-=++-⎡⎤ ⎪ ⎪⎣⎦++++⎝⎭⎝⎭41112253113x y y x ⎛⎫++≥⨯+⋅-= ⎪ ⎪++⎝⎭, 当且仅当12x y ==时,等号成立,即2211x y y x +++的最小值为13,则13m ≤. 因此,实数m 的最大值为13. 故选:B. 【点睛】本题考查利用基本不等式恒成立求参数,对代数式合理变形是解答的关键,考查计算能力,属于中等题.2.C解析:C 【解析】 【分析】根据同角三角函数求出;利用余弦定理构造关于的方程解出,再根据三角形面积公式求得结果. 【详解】由余弦定理得:,即解得:或为最小角本题正确选项: 【点睛】本题考查余弦定理解三角形、三角形面积公式的应用、同角三角函数关系,关键是能够利用余弦定理构造关于边角关系的方程,从而求得边长.3.C解析:C 【解析】【分析】根据新运算的定义, ()x a -()x a +22x x a a =-++-,即求221x x a a -++-<恒成立,整理后利用判别式求出a 范围即可【详解】Q A()1B A B =-∴()x a -()x a +()()()()22=11x a x a x a x a x x a a --+=--+-=-++-⎡⎤⎣⎦Q ()x a -()1x a +<对于任意的实数x ∈R 恒成立,221x x a a ∴-++-<,即2210x x a a -++--<恒成立,()()2214110a a ∴∆=-⨯-⨯--<,1322a ∴-<<故选:C 【点睛】本题考查新定义运算,考查一元二次不等式中的恒成立问题, 当x ∈R 时,利用判别式是解题关键4.A解析:A 【解析】依题意,113713113713132412226132a a a S b b b T +⋅===+⋅. 5.B解析:B 【解析】分析:由等差数列的性质,即2852a a a +=,得5=0a ,又由545S S a =+,得54S S =. 详解:Q 数列{}n a 为等差数列, 2852a a a ∴+= 又286,6a a =-=Q ,5=0a ∴由数列前n 项和的定义545S S a =+,54S S ∴= 故选B.点睛:本题考查等差数列的性质与前n 项和计算的应用,解题时要认真审题,注意灵活运用数列的基本概念与性质.6.A解析:A 【解析】 【分析】利用数列递推式求出前几项,可得数列{}n a 是以4为周期的周期数列,即可得出答案. 【详解】1112,0321521,12n n n n n a a a a a a +⎧≤<⎪⎪==⎨⎪-≤<⎪⎩Q ,211215a a =-=,32225a a ==,43425a a ==,5413215a a a =-== ∴数列{}n a 是以4为周期的周期数列,则201845042215a a a ⨯+===. 故选A . 【点睛】本题考查数列的递推公式和周期数列的应用,考查学生分析解决问题的能力,属于中档题.7.D解析:D 【解析】设等比数列{}n a 的公比为q ,则34118a q a ==,解得12q =, ∴112n n a -=, ∴1121111222n n n n n a a +--=⨯=, ∴数列1{}n n a a +是首项为12,公比为14的等比数列,∴1223111(1)21224(1)134314n n n n a a a a a a +-++⋅⋅⋅+==-<-, ∴23k ≥.故k 的取值范围是2[,)3+∞.选D .8.C解析:C 【解析】 【分析】利用n S 先求出n a ,然后计算出结果. 【详解】根据题意,当1n =时,11224S a λ==+,142a λ+∴=,故当2n ≥时,112n n n n a S S --=-=,Q 数列{}n a 是等比数列,则11a =,故412λ+=, 解得2λ=-, 故选C . 【点睛】本题主要考查了等比数列前n 项和n S 的表达形式,只要求出数列中的项即可得到结果,较为基础.9.B解析:B 【解析】由{}n a 为等差数列,所以95532495S S a a d -=-==-,即2d =-, 由19a =,所以211n a n =-+, 令2110n a n =-+<,即112n >, 所以n S 取最大值时的n 为5, 故选B .10.D解析:D 【解析】 【分析】 先求出31()2n n a -=,再求出2511()2n n n a a -+=,即得解.【详解】由题得35211,82a q q a ==∴=. 所以2232112()()22n n n n a a q---==⨯=,所以32251111()()()222n n n n n a a ---+=⋅=. 所以1114n n n n a a a a +-=,所以数列1{}n n a a +是一个等比数列. 所以12231n n a a a a a a +++⋅⋅⋅+=18[1()]4114n --=()32143n --.故选:D 【点睛】本题主要考查等比数列通项的求法和前n 项和的计算,意在考查学生对这些知识的理解掌握水平.11.B解析:B 【解析】试题分析: 如下图:由已知,在ABC ∆中,105,45,56ABC ACB BC ∠=∠==o o ,从而可得:30BAC ∠=o 由正弦定理,得:56sin 45AB =o 103AB ∴=那么在Rt ADB ∆中,60ABD o ∠=,3sin 6010315AD AB ∴===o , 即旗杆高度为15米,由3155010÷=,知:升旗手升旗的速度应为310(米 /秒). 故选B .考点:解三角形在实际问题中的应用.12.C解析:C 【解析】试题分析:等差数列{}n a 中,34544123124a a a a a ++=⇒=∴=,则()()174127477272822a a a a a a a +⨯+++====L考点:等差数列的前n 项和二、填空题13.6【解析】【分析】由题意公差d=1na1+=2668∴n (2a1+n-1)=5336=23×23×29得出满足题意的组数即可得出结论【详解】由题意公差d=1na1+=2668∴n (2a1+n-1)=解析:6 【解析】 【分析】由题意,公差d=1,na 1+()12n n -=2668,∴n (2a 1+n-1)=5336=23×23×29,得出满足题意的组数,即可得出结论. 【详解】由题意,公差d=1,na 1+()12n n -=2668,∴n (2a 1+n-1)=5336=23×23×29, ∵n <2a 1+n-1,且二者一奇一偶,∴(n ,2a 1+n-1)=(8,667),(23,232),(29,184)共三组; 同理d=-1时,也有三组. 综上所述,共6组. 故答案为6. 【点睛】本题考查组合知识的运用,考查等差数列的求和公式,属于中档题.14.【解析】【分析】根据不等式组画出可行域可知;根据向量投影公式可知所求投影为利用的范围可求得的范围代入求得所求的结果【详解】由不等式组可得可行域如下图阴影部分所示:由题意可知:在上的投影为:本题正确结 解析:[]3,3-【解析】 【分析】根据不等式组画出可行域,可知5,66AOP ππ⎡⎤∠∈⎢⎥⎣⎦;根据向量投影公式可知所求投影为cos OA AOP ∠u u u v,利用AOP ∠的范围可求得cos AOP ∠的范围,代入求得所求的结果.【详解】由不等式组可得可行域如下图阴影部分所示:由题意可知:6AOB π∠=,56AOC π∠=OA u u u v 在OP uuu v上的投影为:cos 93cos 23cos OA AOP AOP AOP ∠=+∠=∠u u u vAOB AOP AOC ∠≤∠≤∠Q 5,66AOP ππ⎡⎤∴∠∈⎢⎥⎣⎦33cos ,22AOP ⎡⎤∴∠∈-⎢⎥⎣⎦[]cos 3,3OA AOP ∴∠∈-u u u v本题正确结果:[]3,3- 【点睛】本题考查线性规划中的求解取值范围类问题,涉及到平面向量投影公式的应用;关键是能够根据可行域确定向量夹角的取值范围,从而利用三角函数知识来求解.15.8【解析】【分析】【详解】作出不等式组表示的平面区域得到如图的△A BC 及其内部其中A (22)B ()C (32)设z=F (xy )=3x+y 将直线l :z=3x+y 进行平移当l 经过点A (22)时目标函数z 达解析:8 【解析】 【分析】 【详解】作出不等式组 表示的平面区域,得到如图的△ABC 及其内部,其中A (2,2),B (53,22),C (3,2)设z =F (x ,y )=3x +y ,将直线l :z =3x +y 进行平移, 当l 经过点A (2,2)时,目标函数z 达到最小值 ∴z 最小值=F (2,2)=8 故选:C16.【解析】【分析】构造数列得到数列是首项为1公差为2的等差数列得到【详解】设则数列是首项为1公差为2的等差数列故答案为【点睛】本题考查了数列的通项公式的求法构造数列是解题的关键意在考查学生对于数列通项解析:2221n n -- 【解析】 【分析】构造数列11n nb a =-,得到数列n b 是首项为1公差为2的等差数列21n b n =-,得到2221n n a n -=-. 【详解】 设11n n b a =-,则12n n b b +-=,11111b a ==- 数列n b 是首项为1公差为2的等差数列1222121121n n n b n n a n n a -=⇒=--⇒--= 故答案为2221n n -- 【点睛】本题考查了数列的通项公式的求法,构造数列11n nb a =-是解题的关键,意在考查学生对于数列通项公式的记忆,理解和应用.17.【解析】试题分析:因为二次函数在区间内至少存在一个实数使的否定是:函数在区间内任意实数使所以即整理得解得或所以二次函数在区间内至少存在一个实数使的实数的取值范围是考点:一元二次方程的根与系数的关系【解析:3(3,)2-【解析】试题分析:因为二次函数()f x 在区间[1,1]-内至少存在一个实数x ,使()0f x >的否定是:“函数()f x 在区间[1,1]-内任意实数x ,使()0f x ≤”,所以(1)0{(1)0f f ≤-≤,即2242(2)210{42(2)210p p p p p p ----+≤+---+≤,整理得222390{210p p p p +-≥--≥,解得32p ≥或3p ≤-,所以二次函数在区间[1,1]-内至少存在一个实数x ,使()0f x >的实数p 的取值范围是3(3,)2-.考点:一元二次方程的根与系数的关系.【方法点晴】本题主要考查了一元二次方程的根的分布与系数的关系,其中解答中涉及到一元二次函数的图象与性质、不等式组的求解、命题的转化等知识点的综合考查,着重考查了学生分析问题和解答问题的能力,其中根据二次函数的图象是开口方向朝上的抛物线,得到对于区间[1,1]-内的任意一个x 都有()0f x >时,得到不等式组是解答的关键,属于中档试题.18.【解析】【分析】利用可求得;利用可证得数列为等比数列从而得到进而得到;利用可得到关于的不等式解不等式求得的取值范围根据求得结果【详解】当时解得:当且时即:数列是以为首项为公比的等比数列解得:又或满足 解析:{5,6}【解析】 【分析】利用11a S =可求得2λ=;利用1n n n a S S -=-可证得数列{}n a 为等比数列,从而得到12n n a -=,进而得到n b ;利用10n n b b +-<可得到关于n 的不等式,解不等式求得n 的取值范围,根据n *∈N 求得结果. 【详解】当1n =时,1111a S a λ==- 11λ∴-=,解得:2λ=21n n S a ∴=-当2n ≥且n *∈N 时,1121n n S a --=-1122n n n n n a S S a a --\=-=-,即:12n n a a -=∴数列{}n a 是以1为首项,2为公比的等比数列 12n n a -\=2920n n a b n n =-+-Q 219202n n n n b --+-∴= ()()222111912092011280222n n n n nn n n n n n b b +--+++--+--+∴-=-=< 20n >Q ()()21128470n n n n ∴-+=--<,解得:47n <<又n *∈N 5n ∴=或6∴满足条件的n 的取值集合为{}5,6本题正确结果:{}5,6 【点睛】本题考查数列知识的综合应用,涉及到利用n a 与n S 的关系求解通项公式、等比数列通项公式的求解、根据数列的单调性求解参数范围等知识;关键是能够得到n b 的通项公式,进而根据单调性可构造出关于n 的不等式,从而求得结果.19.【解析】试题分析:由题意则当为偶数时由不等式得即是增函数当时取得最小值所以当为奇数时函数当时取得最小值为即所以综上的取值范围是考点:数列的通项公式数列与不等式恒成立的综合问题解析:77,153⎡⎤--⎢⎥⎣⎦【解析】试题分析:由题意,则,当为偶数时由不等式()()11181nn n n a nλ++-+⋅-≤得821n n n λ-≤+,即(8)(21)n n nλ-+≤, (8)(21)8215n n y n n n-+==--是增函数,当2n =时取得最小值15-,所以15;λ≤-当为奇数时,(8)(21)8217n n n n n λ++-≤=++,函数8217y n n=++,当3n =时取得最小值为773,即77,3λ-≤所以773λ≥-,综上, 的取值范围是77,153⎡⎤--⎢⎥⎣⎦. 考点:数列的通项公式,数列与不等式恒成立的综合问题.20.9【解析】解:由题意可知:良马与驽马第天跑的路程都是等差数列设路程为由题意有:故:满足题意时数列的前n 项和为由等差数列前n 项和公式可得:解得:即二马相逢需9日相逢点睛:本题考查数列的实际应用题(1)解析:9 【解析】解:由题意可知:良马与驽马第n 天跑的路程都是等差数列,设路程为{}{},n n a b , 由题意有:()()1111031131390,97197222n n a n n b n n ⎛⎫=+-⨯=+=+-⨯-=-+ ⎪⎝⎭, 故:111871222n n n c a b n =+=+ , 满足题意时,数列{}n c 的前n 项和为112522250n S =⨯= ,由等差数列前n 项和公式可得:11111871218712222222502n n ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭⨯= ,解得:9n = .即二马相逢,需9日相逢点睛:本题考查数列的实际应用题. (1)解决数列应用题的基本步骤是:①根据实际问题的要求,识别是等差数列还是等比数列,用数列表示问题的已知; ②根据等差数列和等比数列的知识以及实际问题的要求建立数学模型; ③求出数学模型,根据求解结果对实际问题作出结论. (2)数列应用题常见模型:①等差模型:如果增加(或减少)的量是一个固定量,该模型是等差数列模型,增加(或减少)的量就是公差;②等比模型:如果后一个量与前一个量的比是一个固定的数,该模型是等比数列模型,这个固定的数就是公比;③递推数列模型:如果题目中给出的前后两项之间的关系不固定,随项的变化而变化时,应考虑是a n 与a n -1的递推关系,或前n 项和S n 与S n -1之间的递推关系.三、解答题21.(1) 12n n a -=(2) n S 221n n =+-【解析】 【分析】(1)由题意结合等差数列的性质得到关于公比的方程,解方程求得公比的值,然后结合首项求解数列的通项公式即可.(2)结合(1)的结果首先确定数列{}n b 的通项公式,然后分组求和即可求得数列{}n b 的前n 项和n S . 【详解】(1)设等比数列{}n a 的公比为q ,则2a q =,23a q =,∵2a 是1a 和31a -的等差中项, ∴()21321a a a =+-, 即()2211q q =+-, 解得2q =,∴12n n a -=.(2) 121212n n n b n a n -=-+=-+,则()()11321122n n S n -⎡⎤=+++-++++⎣⎦L L()12112212n n n ⎡⎤+--⎣⎦=+-. 221n n =+-.【点睛】数列求和的方法技巧:(1)倒序相加:用于等差数列、与二项式系数、对称性相关联的数列的求和. (2)错位相减:用于等差数列与等比数列的积数列的求和. (3)分组求和:用于若干个等差或等比数列的和或差数列的求和.22.(1);(2)不存在. 【解析】 【分析】(1)由已知11a b+=,利用基本不等式的和积转化可求2ab ≥,利用基本不等式可将33+a b 转化为ab ,由不等式的传递性,可求33+a b 的最小值;(2)由基本不等式可求23a b +的最小值为6>,故不存在.【详解】(111a b =+≥,得2ab ≥,且当a b ==故33+a b ≥≥a b ==所以33+a b 的最小值为(2)由(1)知,23a b +≥≥由于6>,从而不存在,a b ,使得236a b +=成立. 【考点定位】 基本不等式.23.(1)证明见解析;(2). 【解析】 【分析】(1)利用三角函数恒等变换的应用化简已知等式可求in 0()s A B -=,可得()A B k k Z π-=∈,结合范围A ,(0,)B π∈,即可得证A B =.(2)由(1)可得a b =,进而根据余弦定理可求a b ==ABC ∆的周长.【详解】(1)sin tan cos sin tan cos b B C b B a A C a A -=-Q ,∴sin sin sin sin cos cos cos cos b B C a A C b B a A C C-=-,sin sin cos cos sin sin cos cos b B C b B C a A C a A C ∴-=-, cos()cos()a A C b B C ∴+=+,又A B C π++=Q ,cos cos a B b A ∴-=-,sin cos sin cos A B B A ∴-=-, sin()0A B ∴-=,()A B k k Z π∴-=∈,又A Q ,(0,)B π∈,A B ∴=. (2)Q 由(1)可知A B =,可得a b =,又c =Q 3cos 4C =,∴2232342a a-==,226a b ∴==,可得a b ==ABC ∆∴的周长a b c ++=【点睛】本题考查三角函数恒等变换的应用、余弦定理在解三角形中的综合应用,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力,求解时注意三角函数求值时,要先写出角的范围.24.(1)12;(2 【解析】 【分析】(1)在ΔABC 中,由余弦定理,求得BC =进而利用三角形的面积公式,即可求解;(2)利用三角函数的诱导公式化和恒等变换的公式,求解sin BCA 10∠=,再在ΔABC 中,利用正弦定理和余弦定理,即可求解. 【详解】(1)在ΔABC 中,222AC AB BC 2AB BC COS ABC ∠=+-⋅⋅即251BC BC =++ 2BC 40⇒+-=,解得BC =.所以ΔABC 111S AB BC sin ABC 12222∠=⋅⋅=⨯=.(2)因为0BAD 90,sin CAD ∠∠==,所以cos BAC ∠=,sin BAC 5∠=, πsin BCA sin BAC 4所以∠∠⎛⎫=- ⎪⎝⎭ )cos BAC sin BAC ∠∠=-2==⎝⎭.在ΔABC 中,AC AB sin ABC sin BCA ∠∠=, AB sin ABCAC sin BCA∠∠⋅∴==222CD AC AD 2AC AD cos CAD ∠=+-⋅⋅所以 5162413=+-=所以CD = 【点睛】本题主要考查了正弦定理、余弦定理和三角形的面积公式的应用,其中在解有关三角形的题目时,要有意识地考虑用哪个定理更合适,要抓住能够利用某个定理的信息.一般地,如果式子中含有角的余弦或边的二次式时,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理,着重考查了运算与求解能力,属于基础题. 25.(1)=1040AB m (2)3537(3)1250625[,]4314(单位:m/min ) 【解析】 【分析】 【详解】(1)在ABC ∆中,因为12cos 13A =,3cos 5C =,所以5sin 13A =,4sin 5C =, 从而[]sin sin ()B A C π=-+sin()A C =+5312463sin cos sin cos 13513565A C C A =+=⨯+⨯=.由正弦定理sin sin AB AC C B=,得12604sin 104063sin 565AC AB C B =⨯=⨯=(m ). (2)假设乙出发min t 后,甲、乙两游客距离为d ,此时,甲行走了(10050)m t +,乙距离A 处130t m , 所以由余弦定理得22212(10050)(130)2130(10050)13d t t t t =++-⨯⨯+⨯2200(377050)t t =-+, 由于10400130t ≤≤,即08t ≤≤, 故当35min 37t =时,甲、乙两游客距离最短. (3)由正弦定理sin sin BC ACA B=, 得12605sin 50063sin 1365AC BC A B=⨯=⨯=(m ). 乙从B 出发时,甲已走了50(281)550⨯++=(m ),还需走710m 才能到达C . 设乙步行的速度为/min vm ,由题意得5007103350v -≤-≤,解得12506254314v ≤≤, 所以为使两位游客在C 处互相等待的时间不超过3min ,乙步行的速度应控制在1250625,4314⎡⎤⎢⎥⎣⎦(单位:/min m )范围内. 考点:正弦、余弦定理在实际问题中的应用. 【方法点睛】本题主要考查了正弦、余弦定理在实际问题中的应用,考查了考生分析问题和利用所学知识解决问题的能力,属于中档题.解答应用问题,首先要读懂题意,设出变量建立题目中的各个量与变量的关系,建立函数关系和不等关系求解.本题解得时,利用正余弦定理建立各边长的关系,通过二次函数和解不等式求解,充分体现了数学在实际问题中的应用. 26.(1) 2,T π=当2,6x k k Z ππ=+∈时,()max 2f x =(2) 2ABC S ∆= 【解析】【分析】 【详解】(1)因为a r与b r共线,所以11(sin )0222y x x -+= 则()2sin 3y f x x π⎛⎫==+ ⎪⎝⎭,所以()f x 的周期2T π= 当26x k ππ=+,k Z ∈,max 2f =(2)∵3f A π⎛⎫-= ⎪⎝⎭∴2sin 33A ππ⎛⎫-+= ⎪⎝⎭∴sin 2A = ∵02A π<<∴3A π=由正弦定理得sin sin BC ACA B=又sin B =∴sin 2sin BC B AC A ==,且sin C =∴1sin 2ABC S AC BC C ∆==。
高三数学下期中一模试卷附答案

高三数学下期中一模试卷附答案一、选择题1.若0a b <<,则下列不等式恒成立的是A .11a b> B .a b -> C .22a b > D .33a b <2.设等比数列{}n a 的前n 项和为n S ,若633S S =, 则96S S =( ) A .2B .73C .83D .33.在R 上定义运算:A()1B A B =-,若不等式()x a -()1x a +<对任意的实数x ∈R 恒成立,则实数a 的取值范围是( ) A .11a -<<B .02a <<C .1322a -<< D .3122a -<< 4.在△ABC 中,若1tan 15013A C BC ︒===,,,则△ABC 的面积S 是( ) A .338- B .334- C .338+ D 33+5.已知ABC ∆的三个内角、、A B C 所对的边为a b c 、、,面积为S ,且223tan 2S B =+,则A 等于( )A .6π B .4π C .3π D .2π 6.已知等比数列{}n a 的各项都是正数,且13213,,22a a a 成等差数列,则8967a a a a +=+ A .6B .7C .8D .97.设等差数列{a n }的前n 项和为S n ,已知(a 4-1)3+2 016(a 4-1)=1,(a 2 013-1)3+2 016·(a 2 013-1)=-1,则下列结论正确的是( ) A .S 2 016=-2 016,a 2 013>a 4 B .S 2 016=2 016,a 2 013>a 4 C .S 2 016=-2 016,a 2 013<a 4 D .S 2 016=2 016,a 2 013<a 48.若正数,x y 满足20x y xy +-=,则32x y+的最大值为( ) A .13B .38C .37D .19.已知不等式2230x x --<的解集为A ,260x x +-<的解集为B ,不等式2+0x ax b +<的解集为A B I ,则a b +=( )A.-3B.1C.-1D.310.若ln2ln3ln5 ,,235a b c===,则A.a b c<<B.c a b<<C.c b a<<D.b a c<<11.已知数列{an}的通项公式为an=2()3nn则数列{an}中的最大项为()A.89B.23C.6481D.12524312.如图,有四座城市A、B、C、D,其中B在A的正东方向,且与A相距120km,D在A的北偏东30°方向,且与A相距60km;C在B的北偏东30°方向,且与B相距6013km,一架飞机从城市D出发以360/km h的速度向城市C飞行,飞行了15min,接到命令改变航向,飞向城市B,此时飞机距离城市B有()A.120km B.606km C.605km D.3km二、填空题13.已知变数,x y满足约束条件340{210,380x yx yx y-+≥+-≥+-≤目标函数(0)z x ay a=+≥仅在点(2,2)处取得最大值,则a的取值范围为_____________.14.已知0a>,0b>,当()214a bab++取得最小值时,b=__________.15.已知向量()()1,,,2a xb x y==-r r,其中0x>,若ar与br共线,则yx的最小值为__________.16.设正项数列{}n a的前n项和是n S,若{}n a和{}n S都是等差数列,且公差相等,则1a=_______.17.已知数列{}n a、{}n b均为等差数列,且前n项和分别为n S和n T,若321nnS nT n+=+,则44ab=_____.18.已知ABC ∆的内角,,A B C 的对边分别为,,a b c .若1c =,ABC ∆的面积为2214a b +-,则ABC ∆面积的最大值为_____. 19.某公司一年购买某种货物600吨,每次购买x 吨,运费为6万元/次,一年的总存储费用为4x 万元.要使一年的总运费与总存储费用之和最小,则x 的值是__________. 20.已知数列{}n a 满足1133,2,n n a a a n +=-=则na n的最小值为__________. 三、解答题21.已知ABC ∆的内角,,A B C 所对的边分别为,,a b c ,且2a =. (1)若b =30A =︒,求角B 的值; (2)若ABC ∆的面积3ABC S ∆=,cos 45B =,求,b c 的值. 22.已知函数()11f x x x =-++. (1)解不等式()2f x ≤;(2)设函数()f x 的最小值为m ,若a ,b 均为正数,且14m a b+=,求+a b 的最小值. 23.已知{}n a 是递增数列,其前n 项和为n S ,11a >,且10(21)(2)n n n S a a =++,*n ∈N . (Ⅰ)求数列{}n a 的通项n a ;(Ⅱ)是否存在*,,m n k N ∈使得2()m n k a a a +=成立?若存在,写出一组符合条件的,,m n k 的值;若不存在,请说明理由;(Ⅲ)设32n n n b a -=-,若对于任意的*n N ∈,不等式12111(1)(1)(1)31n b b b ≤+++L m 的最大值. 24.已知数列{}n a 的前n 项和为n S ,且1,n a ,n S 成等差数列. (1)求数列{}n a 的通项公式;(2)若数列{}n b 满足12n n n a b na =+,求数列{}n b 的前n 项和n T .25.在ABC V 中,角A ,B ,C 的对边分别是a ,b ,c()cos 2cos C b A =(Ⅰ)求角A 的大小;(Ⅱ)若2a =,求ABC V 面积的最大值.26.在ABC ∆角中,角A 、B 、C 的对边分别是a 、b 、c,若asinB =. (1)求角A ;(2)若ABC ∆的面积为5a =,求ABC ∆的周长.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 ∵0a b << ∴设1,1a b =-= 代入可知,,A B C 均不正确对于D ,根据幂函数的性质即可判断正确 故选D2.B解析:B 【解析】 【分析】首先由等比数列前n 项和公式列方程,并解得3q ,然后再次利用等比数列前n 项和公式,则求得答案. 【详解】设公比为q ,则616363313(1)1113(1)11a q S q q q a q S qq---===+=---, ∴32q =,∴93962611271123S q S q --===--. 故选:B . 【点睛】本题考查等比数列前n 项和公式,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力,求解时也可以利用连续等长片断的和序列仍然成等比数列,进行求解.3.C解析:C 【解析】【分析】根据新运算的定义, ()x a -()x a +22x x a a =-++-,即求221x x a a -++-<恒成立,整理后利用判别式求出a 范围即可【详解】Q A()1B A B =-∴()x a -()x a +()()()()22=11x a x a x a x a x x a a --+=--+-=-++-⎡⎤⎣⎦Q ()x a -()1x a +<对于任意的实数x ∈R 恒成立,221x x a a ∴-++-<,即2210x x a a -++--<恒成立,()()2214110a a ∴∆=-⨯-⨯--<,1322a ∴-<<故选:C 【点睛】本题考查新定义运算,考查一元二次不等式中的恒成立问题, 当x ∈R 时,利用判别式是解题关键4.A解析:A 【解析】 【分析】由正弦定理求出c , 【详解】A 是三角形内角,1tan 3A =,∴10sin A =由正弦定理sin sin a c A C=得sin 10sin 10a C c A ===, 又2222cos c a b ab C =+-,即22512cos150132b b b b =+-︒=+, 23302b b +-=,332b -=(332b -=舍去), ∴113333sin 122ABC S ab C ∆--==⨯︒=. 故选:A . 【点睛】本题考查正弦定理、余弦定理、三角形面积公式,考查同角间的三角函数关系.解三角形中公式较多,解题时需根据已知条件确定先选用哪个公式,再选用哪个公式.要有统筹安排,不致于凌乱.5.C解析:C 【解析】 【分析】利用三角形面积公式可得2tan 1acsinB 2bc c B +=,结合正弦定理及三角恒等变换知识cosA 1-=,从而得到角A. 【详解】∵2tan bc c B S +=∴2tan 1acsinB 2bc c B +=即c tan asinB a b B +==()B sinAcosB sinB sinC sinB sin A B +=+=++ cosA 1-= ∴1sin 62A π⎛⎫-= ⎪⎝⎭, ∴5666A 或πππ-=(舍) ∴3A π=故选C 【点睛】此题考查了正弦定理、三角形面积公式,以及三角恒等变换,熟练掌握边角的转化是解本题的关键.6.D解析:D 【解析】 【分析】设各项都是正数的等比数列{a n }的公比为q ,(q >0),由题意可得关于q 的式子,解之可得q ,而所求的式子等于q 2,计算可得. 【详解】设各项都是正数的等比数列{a n }的公比为q ,(q >0)由题意可得31212322a a a ⨯=+, 即q 2-2q-3=0, 解得q=-1(舍去),或q=3,故()26728967679a a qa a q a a a a .++===++ 故选:D . 【点睛】本题考查等差数列和等比数列的通项公式,求出公比是解决问题的关键,属基础题.7.D解析:D 【解析】∵(a 4-1)3+2 016(a 4-1)=1,(a 2 013-1)3+2 016(a 2 013-1)=-1, ∴(a 4-1)3+2 016(a 4-1)+(a 2 013-1)3+2 016(a 2 013-1)=0, 设a 4-1=m ,a 2 013-1=n , 则m 3+2 016m +n 3+2 016n =0, 化为(m +n )·(m 2+n 2-mn +2 016)=0, ∵2222132?0162016024m n mn m n n ⎛⎫=-++> ⎪⎝⎭+-+,∴m +n =a 4-1+a 2 013-1=0, ∴a 4+a 2 013=2, ∴()()1201642013201620162016201622a a a a S ++===.很明显a 4-1>0,a 2 013-1<0,∴a 4>1>a 2 013, 本题选择D 选项.8.A解析:A 【解析】 【分析】根据条件可得出2x >,212y x =+-,从而33222(2)52x y x x =+-++-,再根据基本不等式可得出3123x y ≤+,则32x y +的最大值为13.【详解】0x Q >,0y >,20x y xy +-=,2122x y x x ∴==+--,0x >,333222212(2)522x y x x x x ∴==+++-++--,22(2)5592x x -++≥=-Q , 当且仅当122x x -=-,即3x =时取等号, 31232(2)52x x ∴≤-++-,即3123x y ≤+,32x y ∴+的最大值为13. 故选:A. 【点睛】本题考查了利用基本不等式求最值的方法,注意说明等号成立的条件,考查了计算和推理能力,属于中档题.9.A解析:A 【解析】 【分析】根据题意先求出集合,A B ,然后求出=1,2A B -I (),再根据三个二次之间的关系求出,a b ,可得答案.【详解】由不等式2230x x --<有13x -<<,则(1,3)A =-. 由不等式260x x +-<有,则32x -<<,则(3,2)B =-. 所以=1,2A B -I ().因为不等式2+0x ax b +<的解集为A B I , 所以方程2+=0x ax b +的两个根为1,2-.由韦达定理有:1212a b -+=-⎧⎨-⨯=⎩,即=12a b -⎧⎨=-⎩. 所以3a b +=-. 故选:A. 【点睛】本题考查二次不等式的解法和三个二次之间的关系,属于中档题.10.B解析:B 【解析】试题分析:因为ln 2ln 3ln8ln 9ln 2ln 30,23623--=<<,ln 2ln 5ln 32ln 25ln 2ln 50,251025--=>>,故选B. 考点:比较大小.11.A解析:A 【解析】解法一 a n +1-a n =(n +1)n +1-nn=·n,当n <2时,a n +1-a n >0,即a n +1>a n ; 当n =2时,a n +1-a n =0,即a n +1=a n ; 当n >2时,a n +1-a n <0,即a n +1<a n . 所以a 1<a 2=a 3,a 3>a 4>a 5>…>a n ,所以数列{a n }中的最大项为a 2或a 3,且a 2=a 3=2×2=.故选A.解法二 ==,令>1,解得n <2;令=1,解得n =2;令<1,解得n >2.又a n >0,故a 1<a 2=a 3,a 3>a 4>a 5>…>a n ,所以数列{a n }中的最大项为a 2或a 3,且a 2=a 3=2×2=.故选A.12.D解析:D 【解析】 【分析】先判断三角形DAB 为直角三角形,求出BD ,然后推出CBD ∠为直角,可得CD ,进一步可得cos BDF ∠,最后在三角形EDB 中用余弦定理可得BF . 【详解】取AB 的中点E ,连DE ,设飞机飞行了15分钟到达F 点,连BF ,如图所示:则BF 即为所求.因为E 为AB 的中点,且120AB km =,所以60AE km =, 又60DAE ∠=o ,60AD km =,所以三角形DAE 为等边三角形,所以60DE km =,60ADE ∠=o ,在等腰三角形EDB 中,120DEB ∠=o ,所以30EDB EBD ∠=∠=o , 所以90ADB ∠=o ,由勾股定理得2BD 22221206010800AB AD =-=-=, 所以603BD km =,因为9030CBE ∠=+o o 120=o ,30EBD ∠=o ,所以CBD ∠90=o , 所以222108006013240CD BD BC =+=+⨯=km ,所以6033cos BD BDC CD ∠===, 因为1360904DF km =⨯=, 所以在三角形BDF 中,2222232cos (603)902603904BF BD DF BD DF BDF =+-⋅⋅∠=+-⨯⨯⨯g 10800=,所以603BF =km .故一架飞机从城市D 出发以360/km h 的速度向城市C 飞行,飞行了15min ,接到命令改变航向,飞向城市B ,此时飞机距离城市B 有603km . 故选D . 【点睛】本题考查了利用余弦定理解斜三角形,属于中档题.二、填空题13.【解析】【分析】【详解】试题分析:由题意知满足条件的线性区域如图所示:点而目标函数仅在点处取得最大值所以考点:线性规划最值问题解析:1(,)3+∞【解析】 【分析】 【详解】试题分析:由题意知满足条件的线性区域如图所示:,点(22)A ,,而目标函数(0)z x ay a =+≥仅在点(2,2)处取得最大值,所以1133AB k a a ->=-∴> 考点:线性规划、最值问题.14.【解析】【分析】根据均值不等式知即再由即可求解注意等号成立的条件【详解】(当且仅当等号成立)(当且仅当等号成立)(当且仅当等号成立)故答案为【点睛】本题主要考查了均值不等式不等式等号成立的条件属于中 解析:14【解析】 【分析】根据均值不等式知,4a b +≥=()2416a b ab +≥,再由41684ab a b +≥=⋅即可求解,注意等号成立的条件. 【详解】4a b +≥=Q (当且仅当4a b =等号成立),()2416a b ab ∴+≥(当且仅当4a b =等号成立),()2444a b a b ∴++≥⋅8=(当且仅当4a b =等号成立), ()224281a a a∴+=⇒=. 故答案为14b =. 【点睛】本题主要考查了均值不等式,不等式等号成立的条件,属于中档题.15.【解析】【分析】根据两个向量平行的充要条件写出向量的坐标之间的关系之后得出利用基本不等式求得其最小值得到结果【详解】∵其中且与共线∴即∴当且仅当即时取等号∴的最小值为【点睛】该题考查的是有关向量共线解析:【解析】 【分析】根据两个向量平行的充要条件,写出向量的坐标之间的关系,之后得出2y x x x=+,利用基本不等式求得其最小值,得到结果. 【详解】∵()1,a x =r , (),2b x y =-r ,其中0x >,且a r 与b r共线∴()12y x x ⨯-=⋅,即22y x =+∴222y x x x x x+==+≥,当且仅当2x x =即x =时取等号∴yx的最小值为 【点睛】该题考查的是有关向量共线的条件,涉及到的知识点有向量共线坐标所满足的条件,利用基本不等式求最值,属于简单题目.16.【解析】分析:设公差为d 首项利用等差中项的性质通过两次平方运算即可求得答案详解:设公差为d 首项和都是等差数列且公差相等即两边同时平方得:两边再平方得:又两数列公差相等即解得:或为正项数列故答案为:点 解析:14【解析】分析:设公差为d ,首项1a ,利用等差中项的性质,通过两次平方运算即可求得答案. 详解:设公差为d ,首项1a ,Q {}n a 和都是等差数列,且公差相等,∴=,即=,两边同时平方得:()1114233a d a a d +=+++14a d +=两边再平方得:()221111168433a a d d a a d ++=+,∴2211440a a d d -+=,12d a =,又两数列公差相等,2112a a d a =-==,12a =, 解得:114a =或10a =, Q {}n a 为正项数列,∴114a =.故答案为:14. 点睛:本题考查等差数列的性质,考查等差中项的性质,考查化归与方程思想.17.【解析】【分析】根据等差数列中等差中项的性质将所求的再由等差数列的求和公式转化为从而得到答案【详解】因为数列均为等差数列所以【点睛】本题考查等差中项的性质等差数列的求和公式属于中档题 解析:238【解析】 【分析】根据等差数列中等差中项的性质,将所求的174417a a ab b b +=+,再由等差数列的求和公式,转化为77S T ,从而得到答案. 【详解】因为数列{}n a 、{}n b 均为等差数列 所以7474141422a a b b a a b b ==++ ()()1771777272a a S b b T +==+37223718⨯+==+ 【点睛】本题考查等差中项的性质,等差数列的求和公式,属于中档题.18.【解析】【分析】结合已知条件结合余弦定理求得然后利用基本不等式求得的最大值进而求得三角形面积的最大值【详解】由于三角形面积①由余弦定理得②由①②得由于所以故化简得故化简得所以三角形面积故答案为【点睛【解析】 【分析】结合已知条件,结合余弦定理求得π4C =,然后利用基本不等式求得ab 的最大值,进而求得三角形ABC 面积的最大值. 【详解】由于三角形面积2211sin 24a b S ab C +-==①,由余弦定理得221cos 2a b C ab +-=②,由①②得sin cos C C =,由于()0,πC ∈,所以π4C =.故221cos 22a b C ab +-==,化简221a b =+-22121a b ab =+-≥-,化简得22ab +≤所以三角形面积11sin 22S ab C =≤=.. 【点睛】本小题主要考查余弦定理解三角形,考查三角形的面积公式,考查基本不等式求最值的方法,属于中档题.19.【解析】【详解】总费用为当且仅当即时等号成立故答案为30点睛:在利用基本不等式求最值时要特别注意拆拼凑等技巧使其满足基本不等式中正(即条件要求中字母为正数)定(不等式的另一边必须为定值)等(等号取得 解析:30【解析】 【详解】总费用为600900464()4240x x x x +⨯=+≥⨯=,当且仅当900x x=,即30x =时等号成立.故答案为30.点睛:在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误.20.【解析】【分析】先利用累加法求出an =33+n2﹣n 所以设f (n )由此能导出n =5或6时f (n )有最小值借此能得到的最小值【详解】解:∵an+1﹣an =2n∴当n≥2时an =(an ﹣an ﹣1)+(a 解析:212【解析】 【分析】先利用累加法求出a n =33+n 2﹣n ,所以331n a n n n =+-,设f (n )331n n=+-,由此能导出n =5或6时f (n )有最小值.借此能得到na n的最小值. 【详解】解:∵a n +1﹣a n =2n ,∴当n ≥2时,a n =(a n ﹣a n ﹣1)+(a n ﹣1﹣a n ﹣2)+…+(a 2﹣a 1)+a 1=2[1+2+…+(n ﹣1)]+33=n 2﹣n +33 且对n =1也适合,所以a n =n 2﹣n +33. 从而331n a n n n=+-设f (n )331n n =+-,令f ′(n )23310n-=+>,则f (n )在)+∞上是单调递增,在(0上是递减的,因为n ∈N +,所以当n =5或6时f (n )有最小值. 又因为55355a =,66321662a ==, 所以n a n 的最小值为62162a = 故答案为 212【点睛】本题考查了利用递推公式求数列的通项公式,考查了累加法.还考查函数的思想,构造函数利用导数判断函数单调性.三、解答题21.(1)60B =︒或120︒. (2) b =【解析】 【分析】(1)根据正弦定理,求得sin B =,进而可求解角B 的大小; (2)根据三角函数的基本关系式,求得3sin 5B =,利用三角形的面积公式和余弦定理,即可求解。
2024届湖北省荆州市部分县市下学期高三期中模拟数学试题试卷

2024届湖北省荆州市部分县市下学期高三期中模拟数学试题试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}10A x x =+≤,{|}B x x a =≥,若A B R =,则实数a 的值可以为( )A .2B .1C .0D .2-2.总体由编号为01,02,...,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表(如表)第1行的第4列和第5列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )A .23B .21C .35D .323.已知函数()(0xf x m m m =->,且1)m ≠的图象经过第一、二、四象限,则|2)|a f =,384b f ⎛⎫= ⎪⎝⎭,|(0)|c f =的大小关系为( ) A .c b a << B .c a b << C .a b c <<D .b a c <<4.直角坐标系 xOy 中,双曲线2222 1x y a b -=(0a b ,>)与抛物线2 2?y bx =相交于 A 、B 两点,若△ OAB 是等边三角形,则该双曲线的离心率e =( ) A .43B .54C .65D .765.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积是( )A .83B .163C .43 D .8 6.已知正项等比数列{}n a 的前n 项和为2317,,927n S S S ==,则12n a a a 的最小值为( )A .24()27B .34()27C .44()27D .54()277.已知函数()2121f x ax x ax =+++-(a R ∈)的最小值为0,则a =( )A .12 B .1- C .±1D .12±8.在311(21)x x ⎛⎫++ ⎪⎝⎭展开式中的常数项为( ) A .1B .2C .3D .79.已知m ∈R ,复数113z i =+,22z m i =+,且12z z ⋅为实数,则m =( ) A .23-B .23C .3D .-310.观察下列各式:2x y ⊗=,224x y ⊗=,339x y ⊗=,4417x y ⊗=,5531x y ⊗=,6654x y ⊗=,7792x y ⊗=,,根据以上规律,则1010x y ⊗=( )A .255B .419C .414D .25311.在ABC ∆中,a ,b ,c 分别为角A ,B ,C 的对边,若ABC ∆的面为S ,且()2243S a b c =+-,则sin 4C π⎛⎫+= ⎪⎝⎭( ) A .1B .22C 62- D 62+12.已知双曲线22122:1x y C a b -=与双曲线222:14y C x -=没有公共点,则双曲线1C 的离心率的取值范围是( )A .(3⎤⎦B .)3,⎡+∞⎣C .(5D .)5,⎡+∞⎣二、填空题:本题共4小题,每小题5分,共20分。
最新高三数学下期中模拟试卷附答案

最新高三数学下期中模拟试卷附答案一、选择题1.已知数列{}n a 的前n 项和为n S ,点(,3)n n S +*()n N ∈在函数32xy =⨯的图象上,等比数列{}n b 满足1n n n b b a ++=*()n N ∈,其前n 项和为n T ,则下列结论正确的是( )A .2n n S T =B .21n n T b =+C .n n T a >D .1n n T b +<2.在R 上定义运算:A()1B A B =-,若不等式()x a -()1x a +<对任意的实数x ∈R 恒成立,则实数a 的取值范围是( ) A .11a -<<B .02a <<C .1322a -<< D .3122a -<< 3.已知实数,x y 满足0{20x y x y -≥+-≤则2y x -的最大值是( )A .-2B .-1C .1D .24.设x y ,满足约束条件10102x y x y y -+≤⎧⎪+-⎨⎪≤⎩>,则yx 的取值范围是( )A .()[),22,-∞-+∞B .(]2,2-C .(][),22,-∞-+∞D .[]22-,5.在ABC ∆中,a ,b ,c 分别是角A ,B ,C 的对边,若2b c =,6a =7cos 8A =,则ABC ∆的面积为( ) A 17B .3C 15D .1526.若直线2y x =上存在点(,)x y 满足30,230,,x y x y x m +-≤⎧⎪--≥⎨⎪≥⎩则实数m 的最大值为A .2-B .1-C .1D .37.在ABC 中,4ABC π∠=,2AB =3BC =,则sin BAC ∠=( )A .1010B .105C 310D 5 8.数列{}n a 中,()1121nn n a a n ++-=-,则数列{}n a 的前8项和等于( ) A .32B .36C .38D .409.设{}n a 是公差不为0的等差数列,12a =且136,,a a a 成等比数列,则{}n a 的前n 项和n S =( )A .27 44 n n+B.2533n n+C.2324n n+D.2n n+10.某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为和,第一排和最后一排的距离为56米(如图所示),旗杆底部与第一排在同一个水平面上.若国歌长度约为秒,要使国歌结束时国旗刚好升到旗杆顶部,升旗手升旗的速度应为()(米 /秒)A.110B.310C.12D.71011.已知数列{}n a中,3=2a,7=1a.若数列1{}na为等差数列,则9=a( )A.12B.54C.45D.45-12.“中国剩余定理”又称“孙子定理”1852年英国来华传教士伟烈亚力将《孙子算经》中“物不知数问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1至2019中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列{}n a,则此数列的项数为()A.134B.135C.136D.137二、填空题13.若变量,x y满足约束条件12,{20,20,x yx yx y+≤-≥-≤则z y x=-的最小值为_________.14.已知锐角三角形的边长分别为1,3,a,则a的取值范围是__________.15.已知n S是数列{}n a的前n项和,122n nS a+=-,若212a=,则5S=__________.16.已知0a>,0b>,且31a b+=,则43a b+的最小值是_______.17.已知实数x ,y 满足不等式组203026x y x y x y -≤⎧⎪+-≥⎨⎪+≤⎩,则2z x y =-的最小值为__________.18.已知等差数列{}n a 的前n 项和为n S ,且136S =,则91032a a -=__________. 19.正项等比数列{}n a 满足2418-=a a ,6290-=a a ,则{}n a 前5项和为________. 20.设{}n a 是等差数列,且13a =,2536a a +=,则{}n a 的通项公式为__________.三、解答题21.设数列{}n a 满足()*164n n n a a n a +-=∈-N ,其中11a =. (Ⅰ)证明:32n n a a ⎧⎫-⎨⎬-⎩⎭是等比数列; (Ⅱ)令112n n b a =--,设数列{}(21)n n b -⋅的前n 项和为n S ,求使2019n S <成立的最大自然数n 的值.22.在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,设平面向量()()sin cos ,sin ,cos sin ,sin p A B A q B A B =+=-,且2cos p q C ⋅=(Ⅰ)求C ;(Ⅱ)若c a b =+=ABC ∆中边上的高h .23.在等比数列{}n a 中,125a a +=,且2320a a +=. (1)求{}n a 的通项公式;(2)求数列{3n a +的前n 项和n S . 24.数列{}n a 中,11a =,121n n a a n +=++. (1)求{}n a 的通项公式; (2)设141n n b a =-,求出数列{}n b 的前n 项和.25.设各项均为正数的数列{a n }的前n 项和为S n ,满足:对任意的n ∈N *,都有a n +1+S n +1=1,又a 112=. (1)求数列{a n }的通项公式; (2)令b n =log 2a n ,求12231111n n b b b b b b ++++(n ∈N *) 26.已知{}n a 为等差数列,前n 项和为()*n S n N∈,{}nb 是首项为2的等比数列,且公比大于0,2312b b +=,3412b a a =-,11411S b =.(1)求{}n a 和{}n b 的通项公式; (2)求数列{}221n n a b -⋅的前n 项和.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【解析】 【分析】 【详解】由题意可得:332,323n nn n S S +=⨯=⨯- ,由等比数列前n 项和的特点可得数列{}n a 是首项为3,公比为2的等比数列,数列的通项公式:132n n a -=⨯ ,设11n nb b q -= ,则:111132n n n b q b q --+=⨯ ,解得:11,2b q == ,数列{}n b 的通项公式12n nb -= ,由等比数列求和公式有:21nn T =- ,考查所给的选项:13,21,,n n n n n n n n S T T b T a T b +==-<< .本题选择D 选项.2.C解析:C 【解析】 【分析】根据新运算的定义, ()x a -()x a +22x x a a =-++-,即求221x x a a -++-<恒成立,整理后利用判别式求出a 范围即可【详解】A()1B A B =-∴()x a -()x a +()()()()22=11x a x a x a x a x x a a --+=--+-=-++-⎡⎤⎣⎦()x a -()1x a +<对于任意的实数x ∈R 恒成立,221x x a a ∴-++-<,即2210x x a a -++--<恒成立,()()2214110a a ∴∆=-⨯-⨯--<,1322a ∴-<<故选:C 【点睛】本题考查新定义运算,考查一元二次不等式中的恒成立问题, 当x ∈R 时,利用判别式是解题关键3.C解析:C 【解析】作出可行域,如图BAC ∠内部(含两边),作直线:20l y x -=,向上平移直线l ,2z y x =-增加,当l 过点(1,1)A 时,2111z =⨯-=是最大值.故选C .4.A解析:A 【解析】 【分析】根据题意,作出可行域,分析yx的几何意义是可行域内的点(),x y 与原点O 连线的斜率,根据图象即可求解. 【详解】作出约束条件表示的可行域,如图所示,yx 的几何意义是可行域内的点(),x y 与原点O 连线的斜率,由102x y y -+=⎧⎨=⎩,得点A 的坐标为()1,2,所以2OA k =,同理,2OB k =-,所以yx 的取值范围是()[),22,-∞-+∞.故选:A 【点睛】本题考查简单的线性规划,考查斜率型目标函数问题,考查数形结合思想,属于中等题型.5.D解析:D 【解析】 【分析】三角形的面积公式为1sin 2ABC S bc A ∆=,故需要求出边b 与c ,由余弦定理可以解得b 与c . 【详解】解:在ABC ∆中,2227cos 28b c a A bc +-==将2b c =,a =22246748c c c +-=, 解得:2c =由7cos 8A =得sin A ==所以,11sin 2422ABC S bc A ∆==⨯⨯=故选D. 【点睛】三角形的面积公式常见形式有两种:一是12(底⨯高),二是1sin 2bc A .借助12(底⨯高)时,需要将斜三角形的高与相应的底求出来;借助1sin 2bc A 时,需要求出三角形两边及其夹角的正弦值.6.B解析:B 【解析】 【分析】首先画出可行域,然后结合交点坐标平移直线即可确定实数m 的最大值. 【详解】不等式组表示的平面区域如下图所示, 由2230y x x y =⎧⎨--=⎩,得:12x y =-⎧⎨=-⎩,即C 点坐标为(-1,-2),平移直线x =m ,移到C 点或C 点的左边时,直线2y x =上存在点(,)x y 在平面区域内, 所以,m ≤-1, 即实数m 的最大值为-1.【点睛】本题主要考查线性规划及其应用,属于中等题.7.C解析:C 【解析】试题分析:由余弦定理得229223cos5,54b b π=+-⋅==.由正弦定理得35sin sin 4BAC =∠310sin 10BAC ∠=. 考点:解三角形.8.B解析:B 【解析】 【分析】根据所给数列表达式,递推后可得()121121n n n a a n ++++-=+.并将原式两边同时乘以()1n-后与变形后的式子相加,即可求得2n n a a ++,即隔项和的形式.进而取n 的值,代入即可求解. 【详解】由已知()1121nn n a a n ++-=-,① 得()121121n n n a a n ++++-=+,②由()1n ⨯-+①②得()()()212121nn n a a n n ++=-⋅-++,取1,5,9n =及2,6,10n =,易得13572a a a a +=+=,248a a +=,6824a a +=,故81234836S a a a a a =++++⋅⋅⋅+=. 故选:B. 【点睛】本题考查了数列递推公式的应用,对数列表达式进行合理变形的解决此题的关键,属于中档题.9.A解析:A 【解析】 【分析】 【详解】 设公差为d 则解得,故选A.10.B解析:B 【解析】试题分析: 如下图:由已知,在ABC ∆中,105,45,56ABC ACB BC ∠=∠==,从而可得:30BAC ∠= 由正弦定理,得:56sin 45sin 30AB =, 103AB ∴=那么在Rt ADB ∆中,60ABD ∠=,3sin 6010315AD AB ∴===, 即旗杆高度为15米,由3155010÷=,知:升旗手升旗的速度应为310(米 /秒). 故选B .考点:解三角形在实际问题中的应用.11.C解析:C 【解析】 【分析】由已知条件计算出等差数列的公差,然后再求出结果 【详解】依题意得:732,1a a ==,因为数列1{}na 为等差数列,所以7311111273738--===--a a d ,所以()9711159784a a =+-⨯=,所以945=a ,故选C . 【点睛】本题考查了求等差数列基本量,只需结合题意先求出公差,然后再求出结果,较为基础12.B解析:B 【解析】 【分析】由题意得出1514n a n =-,求出15142019n a n =-≤,即可得出数列的项数. 【详解】因为能被3除余1且被5除余1的数就是能被15整除余1的数,故1514n a n =-.由15142019n a n =-≤得135n ≤,故此数列的项数为135,故答案为B.【点睛】本题主要考查阅读能力及建模能力、转化与化归思想及等差数列的通项公式及数学的转化与化归思想.属于中等题.二、填空题13.【解析】由约束条件作出可行域如图联立解得化目标函数得由图可知当直线过点时直线在y 轴上的截距最小有最小值为故答案为点睛:本题主要考查线性规划中利用可行域求目标函数的最值属简单题求目标函数最值的一般步骤 解析:4-【解析】由约束条件12,20,20,x y x y x y +≤⎧⎪-≥⎨⎪-≤⎩作出可行域如图,联立12 {20x y x y +=-=,解得()84A ,,化目标函数z y x =-,得y x z =+,由图可知,当直线y x z =+过点()84A ,时,直线在y 轴上的截距最小,z 有最小值为4-,故答案为4-. 点睛:本题主要考查线性规划中利用可行域求目标函数的最值,属简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.14.【解析】由三角形中三边关系及余弦定理可得应满足解得∴实数的取值范围是答案:点睛:根据三角形的形状判断边满足的条件时需要综合考虑边的限制条件在本题中要注意锐角三角形这一条件的运用必须要考虑到三个内角的 解析:2210a <<【解析】由三角形中三边关系及余弦定理可得a 应满足22222222224130130310a a a a <<⎧⎪+->⎪⎨+->⎪⎪+->⎩,解得2210a << ∴实数a 的取值范围是(22,10). 答案:(22,10) 点睛:根据三角形的形状判断边满足的条件时,需要综合考虑边的限制条件,在本题中要注意锐角三角形这一条件的运用,必须要考虑到三个内角的余弦值都要大于零,并由此得到不等式,进一步得到边所要满足的范围.15.【解析】【分析】由题意首先求得然后结合递推关系求解即可【详解】由题意可知:且:整理可得:由于故【点睛】本题主要考查递推关系的应用前n 项和与通项公式的关系等知识意在考查学生的转化能力和计算求解能力 解析:3116【解析】 【分析】由题意首先求得1S ,然后结合递推关系求解5S 即可. 【详解】由题意可知:12221S a =-=,且:()122n n n S S S +=--,整理可得:()11222n n S S +-=-, 由于121S -=-,故()455113121,21616S S ⎛⎫-=-⨯=-∴= ⎪⎝⎭. 【点睛】本题主要考查递推关系的应用,前n 项和与通项公式的关系等知识,意在考查学生的转化能力和计算求解能力.16.【解析】【分析】利用1的代换将求式子的最小值等价于求的最小值再利用基本不等式即可求得最小值【详解】因为等号成立当且仅当故答案为:【点睛】本题考查1的代换和基本不等式求最值考查转化与化归思想的运用求解 解析:25【解析】 【分析】利用1的代换,将求式子43a b +的最小值等价于求43()(3)a b a b++的最小值,再利用基本不等式,即可求得最小值. 【详解】因为4343123()(3)491325b a a b a b a b a b +=++=+++≥+, 等号成立当且仅当21,55a b ==. 故答案为:25. 【点睛】本题考查1的代换和基本不等式求最值,考查转化与化归思想的运用,求解时注意一正、二定、三等的运用,特别是验证等号成立这一条件.17.-6【解析】由题得不等式组对应的平面区域为如图所示的△ABC 当直线经过点A(03)时直线的纵截距最大z 最小所以故填-6解析:-6 【解析】由题得不等式组对应的平面区域为如图所示的△ABC,当直线122zy x =-经过点A(0,3)时,直线的纵截距2z-最大,z 最小.所以min 023 6.z =-⨯=-故填-6. 18.【解析】分析:根据等差数列中下标和的性质和前n 项和公式求解详解:∵等差数列中∴∴设等差数列的公差为则点睛:等差数列的项的下标和的性质即若则这个性质经常和前n 项和公式结合在一起应用利用整体代换的方法可解析:613. 【解析】分析:根据等差数列中下标和的性质和前n 项和公式求解. 详解:∵等差数列{}n a 中136S =, ∴()11371313132622a a a S +⨯===, ∴7613a =. 设等差数列{}n a 的公差为d ,则()9109109976322213a a a a a a d a -=-+=-==. 点睛:等差数列的项的下标和的性质,即若()*,,,,m n p q m n p q Z+=+∈,则m n p q a a a a +=+,这个性质经常和前n 项和公式()12n n n a a S +=结合在一起应用,利用整体代换的方法可使得运算简单.19.93【解析】【分析】运用等比数列通项公式基本量的计算先求出首项和公比然后再运用等比数列前项和公式求出前项和【详解】正项等比数列满足即则有代入有又因为则故答案为【点睛】本题考查了求等比数列前项和等比数解析:93【解析】 【分析】运用等比数列通项公式基本量的计算,先求出首项和公比,然后再运用等比数列前n 项和公式求出前5项和. 【详解】正项等比数列{}n a 满足2418-=a a ,6290-=a a ,即24222218,90a q a a q a -=-=则有()()()22222118,1190a q a q q -=-+= 代入有221=5,4q q +=又因为0q >,则212,6,3q a a =∴==()553129312S ⨯-∴==-故答案为93 【点睛】本题考查了求等比数列前n 项和等比数列通项公式的运用,需要熟记公式,并能灵活运用公式及等比数列的性质等进行解题,本题较为基础.20.【解析】【分析】先根据条件列关于公差的方程求出公差后代入等差数列通项公式即可【详解】设等差数列的公差为【点睛】在解决等差等比数列的运算问题时有两个处理思路一是利用基本量将多元问题简化为首项与公差(公 解析:63n a n =-【解析】 【分析】先根据条件列关于公差的方程,求出公差后,代入等差数列通项公式即可. 【详解】设等差数列{}n a 的公差为d ,13334366a d d d =∴+++=∴=,,,36(1)6 3.n a n n ∴=+-=-【点睛】在解决等差、等比数列的运算问题时,有两个处理思路,一是利用基本量,将多元问题简化为首项与公差(公比)问题,虽有一定量的运算,但思路简洁,目标明确:二是利用等差、等比数列的性质,性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.三、解答题21.(Ⅰ)证明见解析(Ⅱ)6 【解析】 【分析】(Ⅰ)由递推公式凑出1132n n a a ++--与32n n a a --的关系,即可得证(Ⅱ)由(Ⅰ)可得2111222n n n n n a b a a --=-==--,即可得到{}(21)n n b -⋅的通项公式,再用错位相减法求和,证明其单调性,可得得解. 【详解】 解:(Ⅰ)()*164n n n a a n a +-=∈-N 1163346224n n n n n n a a a a a a ++----∴=---- 6312628n n n n a a a a --+=--+2(3)(2)n n a a --=--322n n a a -=- 32n n a a ⎧⎫-∴⎨⎬-⎩⎭是首项为113132212a a --==--,公比为2的等比数列 (Ⅱ)由(Ⅰ)知,322n n n a a -=-, 即2111222n n n n n a b a a --=-==--, 21212n n n b n ∴-⋅=-⋅()()123S 123252...(21)2n n n =⋅+⋅+⋅++-⋅①23412S 123252...(21)2n n n +=⋅+⋅+⋅++-⋅②,①减②得11231142S 122(22...2)(21)222(21)212n n n n n n n +++--=⋅+++--⋅=+⋅--⋅-1(32)26n n +=-⋅-. 1S (23)26n n n +∴=-⋅+2111S S (21)2(23)22210n n n n n n n n ++++∴-=-⋅--⋅=+>(),S n ∴单调递增.76S 92611582019=⨯+=<,87S 112628222019=⨯+=>.故使S 2019n <成立的最大自然数6n =. 【点睛】本题考查利用递推公式证明函数是等比数列,以及错位相减法求和,属于中档题. 22.(1)3C π=;(2)32. 【解析】分析:(1)由向量的数量积的运算,得222sin sin sin sin sin A B C A B +-=, 根据正弦、余弦定理得1cos 2C =,即可得到3C π=;(2)由余弦定理和a b +=3ab =,再利用三角形的面积公式,求得32h =,即可得到结论.详解:(1)因为22cos sin sin sin p q B A A B ⋅=-+,所以222cos sin sin sin cos B A A B C -+=,即2221sin sin sin sin 1sin B A A B C --+=-, 即222sin sin sin sin sin A B C A B +-=,根据正弦定理得222a b c ab +-=,所以2221cos 222a b c ab C ab ab +-===,所以3C π=;(2)由余弦定理()22232cos33a b ab a b ab π=+-=+-,又a b +=3ab =,根据ABC ∆△的面积11sin 22S ab C ch ==,即113222⨯⨯=, 解得32h =, 所以ABC ∆中AB 边上的高32h =. 点睛:本题主要考查了利用正弦定理、余弦定理和三角形的面积公式的应用,对于解三角形问题,通常利用正弦定理进行“边转角”寻求角的关系,利用“角转边”寻求边的关系,利用余弦定理借助三边关系求角,利用两角和差公式及二倍角公式求三角函数值. 利用正、余弦定理解三角形问题是高考高频考点,经常利用三角形内角和定理,三角形面积公式,结合正、余弦定理解题. 23.(1)14n n a -=;(2)n S 4121n n =-+-.【解析】 【分析】(1)由数列{}n a 是等比数列,及125a a +=,且2320a a +=,两式相除得到公比q ,再代入125a a +=可求1a ,则通项公式可求.(2)利用分组求和求出数列{3n a 的前n 项和n S . 【详解】解:(1)因为等比数列{}n a 中,125a a +=,且2320a a +=. 所以公比23124a a q a a +==+, 所以12155a a a +==, 即11a =, 故14n n a -=.(2)因为14n n a -=所以113342n n n a --=⋅+,所以141231412n nn S --=⨯+--4121n n =-+- 422n n =+-. 【点睛】本题考查等比数列的通项公式的计算与等比数列前n 项和公式的应用,属于基础题.24.(1)2n a n =;(2)21nn +. 【解析】 【分析】(1)直接根据累加法即可求得数列{}n a 的通项公式; (2)利用裂项相加即可得出数列{}n b 的前n 项和。
上海市大同中学2022届高三下学期期中数学试题(含答案解析)

上海市大同中学2022届高三下学期期中数学试题学校:___________姓名:___________班级:___________考号:___________一、填空题1.已知集合{|ln(3)}M x y x ==-,{|e }x N y y ==,则R ()M N ⋂=ð__.2.已知复数i1iz =-(其中i 为虚数单位),则z 的共轭复数z =________.3.5(2)x y -的展开式中23x y 的系数为__.4.记n S 是公差不为0的等差数列{}n a 的前n 项和,若35a S =,145a a a =,则n a =________.5.直线11031-+=-x y 的倾斜角为__.6.某校有5名大学生打算前往观看冰球,速滑,花滑三场比赛,每场比赛至多2名学生前往,则甲同学不去观看冰球比赛的方案种数有__种.7.已知点(5,2)A ,点F 为抛物线24y x =的焦点,点P 在抛物线上移动,则||||PA PF +的最小值为__.8.中国古塔多为六角形或八角形﹒已知某八角形塔的一个水平截面为正八边形ABCDEFGH ,如图所示,2AB a =,则AC AE ⋅=__.9.已知π0,2θ⎛⎫∈ ⎪⎝⎭,π2tan tan 43θθ⎛⎫+=- ⎪⎝⎭,则sin cos2sin cos θθθθ=+__.10.已知函数2log ,02()3,2x x f x x x ⎧<<=⎨-+≥⎩,若123,,x x x 均不相等,且123()()()f x f x f x ==,则123x x x ⋅⋅的取值范围是___________11.过点()1,1P 的直线与椭圆22132x y +=交于点A 和B ,且AP PB λ= .点Q 满足AQ QB λ=-,若O 为坐标原点,则线段OQ 长度的最小值为__________.12.若()*(,)2),,=+∈∈n n f x y y n x y N R ,则下列结论中正确的有_____.①若(1,,1),=n n n n n f a a b 为整数,则3321a b -=;②(1,1)(1,1)n n f f --是正整数;③21(1,1)n f --是21(1,1)n f -的小数部分;④设(1,1)-=n n n f c ,若n c 、n d 为整数,则212(1)5++-=n n n c d .二、单选题13.已知a ,b ∈R ,则“0ab ≠”的一个必要条件是()A .0a b +≠B .220a b +≠C .330a b +≠D .110a b+≠14.函数()1cos xf x x=+在(),ππ-上的图象大致是()A .B .C .D .15.已知函数()4sin(2)2(0)3f x x πωω=-->在[]0,π内有且仅有两个零点,则ω的取值范围是()A .75,62⎛⎤ ⎥⎝⎦B .75,62⎡⎫⎪⎢⎣⎭C .75,124⎛⎤ ⎥⎝⎦D .75,124⎡⎫⎪⎢⎣⎭16.若双曲线()2222:10,0x y C a b a b-=>>的左右焦点分别为1F ,2F ,点P 为C 的左支上任意一点,直线l 是双曲线的一条渐近线,PQ l ⊥,垂足为Q .当2PF PQ +的最小值为6时,1FQ 的中点在双曲线C 上,则C 的方程为()A .222x y -=B .224x y -=C .22116y x -=D .22124x y -=三、解答题17.如图,在多面体ABCDE 中,AEB △为等边三角形,AD BC ∥,BC AB ⊥,CE =,22AB BC AD ===,F 为EB 的中点.(1)证明:AF ∥平面DEC ;(2)求锐二面角A CD E --的余弦值.18.已知四边形ABCD 内接于圆O ,2AB =,30ADB ∠=︒,BAD ∠是钝角.(1)求AC 的最大值;(2)BD =ABCD 周长的最大值.19.某创业投资公司拟投资开发某种新能源产品,估计能获得25万元~1600万元的投资收益,现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,奖金不超过75万元,同时奖金不超过投资收益的20%.(即:设奖励方案函数模型为y=f (x)时,则公司对函数模型的基本要求是:当x ∈[25,1600]时,①f(x)是增函数;②f (x)≤75恒成立; ③()5xf x ≤恒成立.(1)判断函数() 1030xf x =+是否符合公司奖励方案函数模型的要求,并说明理由;(2)已知函数()()51g x a =≥符合公司奖励方案函数模型要求,求实数a 的取值范围.20.已知圆M 过点(1,0),且与直线=1x -相切.(1)求圆心M 的轨迹C 的方程;(2)S 为轨迹C 上的动点,T 为直线40x y ++=上的动点,求||ST 的最小值;(3)过点(2,0)P 作直线l 交轨迹C 于A 、B 两点,点A 关于x 轴的对称点为A '.问A B '是否经过定点,若经过定点,求出定点坐标;若不经过,请说明理由.21.已知n 行n 列()2n ≥的数表111212122212n n n n nn a a a a a a A a a a ⋅⋅⋅⎛⎫ ⎪⋅⋅⋅⎪= ⎪⎪⋅⋅⋅⎝⎭ 中,对任意的{}1,2,,i n ∈⋅⋅⋅,{}1,2,,j n ∈⋅⋅⋅,都有{}0,1ij a ∈.若当0st a =时,总有11nnit sj i j a a n ==+≥∑∑,则称数表A 为典型表,此时记11n nn ij i j S a ===∑∑.(1)若数表001100110B ⎛⎫ ⎪= ⎪ ⎪⎝⎭,1100110000110011C ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭,请直接写出B ,C 是否是典型表;(2)当6n =时,是否存在典型表A 使得617S =,若存在,请写出一个A ;若不存在,请说明理由;(3)求n S 的最小值.参考答案:1.(]0,3【分析】根据对数函数的定义域与指数函数的值域,结合交集与补集的运算求解即可.【详解】集合{}{|ln(3)}3M x y x x x ==-=,{}{|e }0xN y y y y ===,所以R {|3}M x x =≤ð,则R ()(0,3]M N ⋂=ð.故答案为:(]0,32.i 12--【分析】利用复数的除法化简可得i 12z -=,再结合共轭复数的定义,即得解【详解】由题意,i i (1i)i 11i (1i)(1i)2z ⨯+-===--+故i 12z --=故答案为:i 12--3.80-【分析】根据二项式展开式的通项公式,直接计算即可得到结果.【详解】展开式的通项公式为55155C (2)C (2)r rr rr r r r T xy x y --+=-=⋅-,令52r -=,则3r =,所以23x y 的系数为335C (2)80⋅-=-.故答案为:80-4.3n -##3n -+【分析】利用1,a d 表示出已知的等量关系,解方程组求得1,a d 后,利用等差数列通项公式求解即可.【详解】设等差数列{}n a 的公差为()0d d ≠,由35145a S a a a =⎧⎨=⎩得:()111115425234a d a d a a d a d⨯⎧+=+⎪⎨⎪+=+⎩,解得:121a d =⎧⎨=-⎩,()213n a n n ∴=--=-.故答案为:3n -.5.1πarctan3-【分析】将直线化为一般式,得到其斜率,然后根据倾斜角与斜率的关系,即可得到结果.【详解】直线方程为13(1)0-++=x y ,斜率为13-,则倾斜角为1πarctan 3-.故答案为:1πarctan 3-6.60【分析】先根据部分均匀分组,由先分组再分配解决即可.【详解】由题知,①将5名大学生分成1,2,2的三组,有22153122C C C 15P =种分组方法,②甲同学所在的组不去观看冰球比赛,有2种情况,剩下的2组任意选择,有222P 4=种情况,所以有15460⨯=种方案.故答案为:607.6【分析】作出图形,过点P 作直线=1x -的垂线,垂足为点E ,由抛物线的定义可知,当点A 、P 、E 三点共线时,即当AP 与直线=1x -垂直时,||||PA PF +取得最小值,即可求解.【详解】抛物线24y x =的焦点为(1,0)F ,准线方程为=1x -,过点P 作直线=1x -的垂线,垂足为点E ,由抛物线的定义得PF PE =,||||||||PA PF PA PE +=+,当点A 、P 、E 三点共线时,即当AP 与直线=1x -垂直时,||||PA PF +取得最小值,且最小值为516+=.故答案为:6.8.2(8a +【分析】根据投影的定义,可得212⋅= AC AE AE ,结合余弦定理即可得到AE =,从而得到结果.【详解】由投影的概念,212⋅= AC AE AE ,因为2AB a =,正八边形每个内角为135︒,则22222cos135(8AC AB BC AB BC =+-⋅⋅︒=+,易得ACE △为等腰直角三角形,则AE =,所以2221(82⋅===+ AC AE AE AC .故答案为:2(8a +9.35-##-0.6【分析】利用和差公式计算得到tan 3θ=,再化简得到原式为22tan tan tan 1θθθ-+,代入计算得到答案.【详解】π0,2θ⎛⎫∈ ⎪⎝⎭,π2tan tan 43θθ⎛⎫+=- ⎪⎝⎭,所以1tan 2tan 1tan 3θθθ+=--,所以22tan 5tan 30θθ--=,所以tan 3θ=或1tan 2θ=-(舍去),所以22sin cos 2sin (cos sin )sin (cos sin )sin cos sin cos θθθθθθθθθθθθ-==-++2222sin (cos sin )tan tan 3sin cos tan 15θθθθθθθθ--===-++.故答案为:35-10.(2,3)【分析】不妨设123x x x <<,结合函数图像可得2122log log x x =,从而得出121=x x ,即可得出答案.【详解】不妨设123x x x <<,由图可得,()21223log log 30,1x x x ==-+∈,所以2122log log ,x x =-即121=x x ,由123()()()f x f x f x ==得,3(2,3)x ∈,所以123x x x 的取值范围是(2,3)故答案为:(2,3)11【分析】利用向量数乘的坐标运算可得()22222211221323232x y x y mn λλ⎛⎫⎛⎫+-+=-+ ⎪⎝⎭⎝⎭,由此可求得Q 点轨迹为直线,将问题转化为原点到直线距离的求解即可.【详解】设()11,A x y ,()22,B x y ,(),Q m n ,()111,1AP x y ∴=-- ,()221,1PB x y =-- ,()11,AQ m x n y =-- ,()22,QB x m y n =--,由AP PB λ= ,AQ QB λ=- 得:()()121211x x m x x m λλ⎧-=-⎪⎨-=--⎪⎩,()121211x x x x m λλλλ+=+⎧∴⎨-=-⎩,两式相乘得:()2222121x x m λλ-=-,同理可得:()222121y y n λλ-=-,()22222211221323232x y x y m n λλ⎛⎫⎛⎫∴+-=-+ ⎪ ⎪⎝⎭⎝⎭,由题意知:0λ>且1λ≠,否则与AQ QB λ=- 矛盾,132m n∴+=,Q ∴点轨迹为132yx +=,即直线2360x y +-=,∴线段OQ长度的最小值即为原点到直线的距离,min OQ ∴【点睛】关键点点睛:本题解题关键是能够利用向量坐标运算求得动点Q 的轨迹方程,根据轨迹为直线可将问题转化为坐标原点到直线距离的求解.12.①③④【分析】求出33,a b 可判断①的正误;取2n =可判断②的正误;利用二项式定理可判断③的正误;分n 为偶数和n 为奇数两种情况分析讨论,结合二项式定理可判断④的正误.【详解】①因为3333(1,1)2)38==+=f a ,所以3338,17==a b ,则3321a b -=,①正确;②(1,1)(1,1)2)2)--=--n n n n f f ,因为2222(1,1)(1,1)2)2)--=-=f f③21212121(1,1)(1,1)2)2)-------=--n n n n f f 22222)2)--=-n n 2212324222222)C 2C (2n n n n n -----⎡⎤=+⋅+⋅+⎣⎦ 2212324222222)C ((2)C ((2)n n n n n -----⎡⎤-+⋅-+⋅-+⎣⎦222242224C (2)n n n ---⎡⎤+⋅-+⎣⎦= 12332532223C C 2n n n n ----⎤+++⋅⎦ ,两部分都是整数,所以21212121(1,1)(1,1)Z 2)2)n n n n f f ------=-∈-,且21210(1,1)2)1--<-=-<n n f ,所以21(1,1)n f --是21(1,1)n f -的小数部分,③正确;④(1,1)2)-==n n n n f c ,当n 为奇数时,11333C (2)C 2()n n n n n c --=-+⋅-+ ,0222C C (2)n nn n n -=+-+ ,011222C C (2)C ((2)(2)n n n n n nn n c ---=--+-+= ,所以)2))12-=+=-n n n n n n c c ,故212(1)5++-=n n n c d ,当n 为偶数时,0222444C C (2)C (2)n n n n n n n c --=⋅+⋅⋅-+⋅-+ ,11333555C (2)C ((2)C ((2)n nn n n n ---=⋅⋅-+-+⋅-+ ,2)-=-n n n c ,所以2)12))-=+=--n n n n n n c c ,所以212(1)5++-=n n n c d ,故④正确;故答案为:①③④.【点睛】关键点点睛:③中将21212121(1,1)(1,1)2)2)-------=-n n n n f f 转化为二项展开式的形式展开求解,④的讨论关键在于当n 为奇数时,11333C (2)C 2()n n n n n c --=-+⋅-+ ,0222C C (2)n nn n n -=+-+ ,n 为偶数时,0222444C C (2)C ((2)n nn n n n c --=⋅+⋅⋅-+⋅-+ ,11333555C (2)C ((2)C ((2)n nn n n n ---=⋅⋅-+-+⋅-+ .13.B【分析】利用3,3a b ==-否定ACD 选项,进而得答案.【详解】解:对于A 选项,当3,3a b ==-时,0ab ≠,此时0a b +=,故0a b +≠不是0ab ≠的必要条件,故错误;对于B 选项,当0ab ≠时,220a b +≠成立,反之,不成立,故220a b +≠是0ab ≠的必要条件,故正确;对于C 选项,当3,3a b ==-时,0ab ≠,但此时330a b +=,故330a b +≠不是0ab ≠的必要条件,故错误;对于D 选项,当3,3a b ==-时,0ab ≠,但此时110a b +=,故故110a b+≠不是0ab ≠的必要条件,故错误.故选:B 14.A【分析】利用排除法,先判断函数的奇偶性,再由函数在()0,π上的取值可判断【详解】因为()()1cos()1cos x xf x f xx x--==-=-+-+所以函数()1cos xf x x=+为奇函数,故排除选项C ,D ;因为在()0,π上,()0f x >,所以排除选项B .故选:A .15.D 【分析】根据给定条件确定23x πω-的范围,求解不等式作答.【详解】由()0f x =得1sin(232x πω-=,而当[]0,x π∈,0ω>时,22333x πππωπω-≤-≤-,又5131sin sin sin 6662πππ===,函数()f x 在[]0,π内有且仅有两个零点,于是得5132636ππππω≤-<,解得75124ω≤<,所以ω的取值范围是75[,)124.故选:D16.B【分析】由双曲线定义21||||2PF PF a -=得到21122PF PQ PF PQ a F Q a +=++≥+,再利用焦点到渐近线的距离为b 求得26b a +=,设出渐近线方程求得1FQ 的中点坐标代入双曲线方程联解求得a b 、的解.【详解】212PF PF a -= ,211||||22PF PQ PF PQ a FQ a ∴+=++≥+,又()1,0F c =- ,()2,0F c =,双曲线的渐近线方程为:b y x a=±,即0bx ay ±=,∴bc b c ==,即1FQ 的最小值为b ,即26b a +=,不妨设直线OQ 为:b y x a=,1F Q OQ ⊥ ,∴点()1,0F c -,2(,)a ab Q c c --,1FQ 的中点为22(,)22a c ab c c+--,将其代入双曲线C 的方程,得:2222222()144a c a a c c+-=,即22222221144a ca a c c ⎛⎫+ ⎪⎝⎭-=,解得:c =又26b a += ,222+=a b c ,2a b ∴==,故双曲线C 的方程为224x y -=.故选:B.17.(1)证明见解析【分析】(1)考虑所给的条件,找出相应的几何关系即可;(2)建立空间直角坐标系,写出相应点的坐标,用空间向量的方法即可.【详解】(1)取EC 中点M ,连结FM ,DM ,∵AD BC FM ∥∥,12AD BC MF ==,∴四边形AFMD 为平行四边形,∴AF DM ∥,又AF ⊄平面DEC ,DM ⊂平面DEC ,AF ∥平面DEC ;(2)∵222EB CB EC +=,∴CB BE ⊥,又∵CB AB ⊥,AB BE B = ,∴CB ⊥平面ABE ,BC ⊂平面ABCD ,∴平面ABCD ⊥平面ABE ,取AB 的中点O ,以OE 为x 轴,AB 为y 轴,过点O 做平行于BC 的直线为z 轴,建立如图所示的空间直角坐标系O xyz -,∴)E ,()0,1,2C ,()0,1,1D -,∴)1,2CE =-- ,()0,2,1CD =-- ,设平面CDE 的一个法向量为(),,n x y z = ,∴2020y z y z --=--=⎪⎩,∴()2n =- ,平面ABCD 的一个法向量为()1,0,0m = ,∴cos ,m n == ,所以平面CDE 和平面ABCD故答案为:证明见解析,4.18.(1)4(2)4+【分析】(1)利用正弦定理求出圆O 的直径即得AC 的最大值;(2)先在ABD △中根据所给条件,利用正弦定理求出BAD ∠的值和AD 的长,然后在BCD △中通过余弦定理和基本不等式求出BC 与CD 之和的最大值即可求解.【详解】(1)设圆O 的半径为R .因为ABD △内接于圆O ,且2AB =,30ADB ∠=︒,由正弦定理得2241sin 2AB R ADB ===∠.又AC 是圆O 的弦,所以4AC ≤,所以AC 的最大值为4.(2)在ABD △中,由正弦定理得sin sin BD AB BAD ADB =∠∠,即2sin sin 30BAD =∠︒,所以sin 2BAD ∠=.因为BAD ∠是钝角,所以120BAD ∠=︒,所以30ADB ABD ∠=∠=︒,即2AD AB ==.由120BAD ∠=︒得60BCD ∠=︒,设BC x =,CD y =,在BCD △中,由余弦定理得2222cos BD BC DC BC DC BCD =+-⨯⨯∠,即()()()222222123324x y x y x y xy x y xy x y ++⎛⎫=+-=+-≥+-⨯= ⎪⎝⎭,所以x y +≤仅当x y ==x y +取得最大值所以四边形ABCD 周长的最大值为4+.19.(1)函数模型()1030x f x =+,不符合公司要求,详见解析(2)[1,2]【分析】(1)依次验证题干中的条件即可;(2)根据题干得,要满足三个条件,根据三个条件分别列出式子得到a 的范围,取交集即可.【详解】(1)对于函数模型()1030x f x =+,当x ∈[25,1600]时,f (x)是单调递增函数,则f (x)≤f (1600)≤75,显然恒成立,若函数()5x f x ≤恒成立,即10305x x +≤,解得x≥60.∴()5x f x ≤不恒成立,综上所述,函数模型()1030x f x =+,满足基本要求①②,但是不满足③,故函数模型()1030x f x =+,不符合公司要求.(2)当x ∈[25,1600]时,()5(1)g x a =≥单调递增,∴最大值(1600)540575g a ==-≤∴2a ≤设()55x g x =≤恒成立,∴22(5)5x a x ≤+恒成立,即225225x a x ≤++,∵25225x x +≥,当且仅当x=25时取等号,∴a 2≤2+2=4∵a ≥1,∴1≤a ≤2,故a 的取值范围为[1,2]【点睛】这个题目考查了函数模型的应用,这类题目关键是选对函数模型,读懂题意,将实际问题转化为数学问题,利用数学知识解决问题.20.(1)24y x =;(2)2;(3)过定点(2,0)-.【分析】(1)根据抛物线的定义进行求解即可;(2)根据点到直线距离公式,结合配方法进行求解即可;(3)根据直线斜率公式,结合直线方程进行求解即可.【详解】(1)由题意得点M 到直线=1x -的距离等于到点(1,0)的距离,所以点M 是以(1,0)F 为焦点,以=1x -为准线的抛物线,焦点到准线的距离2p =,所以点M 的轨迹方程为24y x =;(2)设2(4,4)S t t ,S 到直线40x y ++=的距离22=d 2≥=,所以||ST;(3)设223434(,),(,)44y y A y B y ,4322433444AB y y k y y y y -==-+,则直线AB 的方程为34344()0x y y y y y -++=,因为AB 过点(2,0)P ,所以34800-+=y y ,所以348y y =-.因为A '与A 关于x 轴对称,故33,()'-A x y ,同理,直线A B '的方程为34344()0x y y y y y --+-=,因为348y y =-,所以A B '的方程为344()80x y y y --++=,所以直线A B '过定点(2,0)-.【点睛】关键点睛:利用抛物线的定义是解题的关键.21.(1)B 不是典型表,C 是典型表;(2)不存在;(3)n 为偶数时2min )2(n n S =,n 为奇数时2min 1)(2n n S +=.【分析】(1)由题设典型表的定义,结合给定的数表判断即可.(2)根据题设分析知:数值分配时有6min ()17S ≤即可,结合典型表的定义及数表的对称性确定6S 最小时{}0,1在数表上的分布情况,即可判断是否存在.(3)结合(2)的分析,讨论n 为偶数、奇数情况下n S 的最小值.【详解】(1)对于数表B 有120a =,而211123n ni j i j a a ==+=≥∑∑不成立,故数表B 不是典型表;对于数表C ,当0st a =时总有114n nit sj i j a a ==+≥∑∑成立,故数表C 是典型表.(2)由题设知:当6n =要存在典型表A 使得617S =,则需6min ()17S ≤.∵要使6S 最小,即典型表A 中的“1”最少,又0st a =时总有11n n it sj i j a a n ==+≥∑∑,∴让尽量多的横列和116n nit sj i j a a ==+=∑∑,故将表分成4个33⨯数表,对角的两个数表数值相同,但上下、左右对称的数表数值不同,此时可保证6S 最小.∴如典型表111000111000111000000111000111000111A ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭,有6min ()18S =.∴不存在典型表A 使得617S =.(3)要使n S 最小,需让尽量多的横列和11n nit sj i j a a n ==+=∑∑或典型表中“1”尽量少,当n 为偶数时,由(2)知:22min )2()2(2n n n S =⨯=;当n 为奇数时,在偶数n 1-的数表中间加一行一列,并在新增行列中添加n 个“1”,即可满足典型数列,此时222min 1(1)1)2()22(2n n n n S n n --+=⨯+=+=;【点睛】关键点点睛:第二问,通过6n =,结合数表的对称性确定6S 最小时的数值分布情况,即可判断存在性,第三问,由第二问6n =情况归纳n 为偶数时min ()n S ,进而推广到n 为奇数时min ()n S .。
人教版数学高三期中测试精选(含答案)8

【答案】A
9.设 a, b, c 是互不相等的整数,则下列不等式中不恒成立的是( )
A.| a b || a c | | b c |
C.
|
a
b
|
a
1
b
2
B. a2
1 a2
a
1 a
D. a 3 a 1 a 2 a
【来源】上海市上海中学 2018-2019 学年高三上学期期中数学试题
x [2, 4] ,不等式 f (x) t 2 恒成立,则 t 的取值范围为__________.
【来源】山东省菏泽一中、单县一中 2016-2017 学年高二下学期期末考试数学(文)试
题 【答案】 (,10]
2x y 1 0,
12.设关于
x
,
y
的不等式组
x m 0,
表示的平面区域为 D ,若存在点
【答案】(1)见解析;(2) 2- n 2 n n2
2n
2
7x 5y 23 0
30.已知
x,y
满足条件:
x
7
y
11
0
,求:
4x y 10 0
(1) 4x 3y 的最小值; x y 1
(2) x 5 的取值范围.
【来源】上海市上海中学 2015-2016 学年高二上学期期中数学试卷
an
2n
的前
n
项和
Sn
.
【来源】江西省抚州市临川一中 2019-2020 届高三上学期第一次联合考试数学(文科)
试题
【答案】(1) an
1 2
n
;(2)
Sn
2n1
n2
n
2
.
34.已知等差数列an 的前 n 项和为 Sn , a2 a8 82 , S41 S9 .
高三数学下期中试卷(带答案)

高三数学下期中试卷(带答案)一、选择题1.已知实数x 、y 满足约束条件00134x y x ya a⎧⎪≥⎪≥⎨⎪⎪+≤⎩,若目标函数231x y z x ++=+的最小值为32,则正实数a 的值为( ) A .4B .3C .2D .12.ABC ∆中有:①若A B >,则sin sin A>B ;②若22sin A sin B =,则ABC ∆—定为等腰三角形;③若cos acosB b A c -=,则ABC ∆—定为直角三角形.以上结论中正确的个数有( ) A .0B .1C .2D .33.已知点(),P x y 是平面区域()4{04y x y x m y ≤-≤≥-内的动点, 点()1,1,A O -为坐标原点, 设()OP OA R λλ-∈u u u r u u u r的最小值为M ,若M ≤恒成立, 则实数m 的取值范围是( )A .11,35⎡⎤-⎢⎥⎣⎦B .11,,35⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭C .1,3⎡⎫-+∞⎪⎢⎣⎭D .1,2⎡⎫-+∞⎪⎢⎣⎭4.在ABC V 中,A ,B ,C 的对边分别为a ,b ,c ,2cos 22C a ba+=,则ABC V 的形状一定是( ) A .直角三角形B .等边三角形C .等腰三角形D .等腰直角三角形5.在ABC ∆中,角,,A B C 的对边分别为a ,b ,c .若ABC ∆为锐角三角形,且满足sin (12cos )2sin cos cos sin B C A C A C +=+,则下列等式成立的是( )A .2a b =B .2b a =C .2A B =D .2B A =6.已知数列{a n }满足331log 1log ()n n a a n N +++=∈且2469a a a ++=,则15793log ()a a a ++的值是( )A .-5B .-15 C .5 D .15 7.已知{}n a 为等差数列,若20191<-a a ,且数列{}n a 的前n 项和n S 有最大值,则n S 的最小正值为( )A .1SB .19SC .20SD .37S8.已知锐角三角形的边长分别为1,3,a ,则a 的取值范围是( )A .()8,10B .()22,10C .()22,10D .()10,89.当()1,2x ∈时,不等式220x mx ++≥恒成立,则m 的取值范围是( ) A .()3,-+∞B .()22,-+∞C .[)3,-+∞D .)22,⎡-+∞⎣10.在ABC V 中,角A 、B 、C 的对边分别为a 、b 、c ,若(cos )sin (cos )sin a c B B b c A A -⋅⋅=-⋅⋅,则ABC V 的形状为()A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰三角形或直角三角形11.已知等差数列{}n a 的前n 项和为n S ,若341118a a a ++=则11S =( ) A .9B .22C .36D .6612.已知数列{}n a 中,3=2a ,7=1a .若数列1{}na 为等差数列,则9=a ( ) A .12B .54C .45D .45-二、填空题13.如果一个数列由有限个连续的正整数组成(数列的项数大于2),且所有项之和为N ,那么称该数列为N 型标准数列,例如,数列2,3,4,5,6为20型标准数列,则2668型标准数列的个数为______. 14.若为等比数列的前n 项的和,,则=___________15.计算:23lim 123n n nn→+∞-=++++L ________16.若正数,a b 满足3ab a b =++,则+a b 的取值范围_______________。
高考数学高三模拟考试试卷压轴题专题八平面向量的基本定理A卷

高考数学高三模拟考试试卷压轴题专题八平面向量的基本定理(A 卷)(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知点(0,1),(3,2)A B ,向量(4,3)AC =--,则向量BC =( ) A. (7,4)-- B.(7,4) C.(1,4)- D.(1,4) 【答案】A【解析】∵AB OB OA =-=(3,1),∴BC =AC AB -=(7,4),故选A.2.【黄石市第三中学(稳派教育)高三阶段性检测】若()1,3MA =-,()1,7MB =,则12AB = ( ) A. ()0,5 B. ()1,2 C. ()0,10 D. ()2,4 【答案】B 【解析】()()()111,3,1,7,22MA MB AB MB MA =-=∴=-()()()1111,732,41,222=+-==,故选B.3.已知向量()2,4a =,()1,1b =-,则2a b -=( ) A.()5,7 B.()5,9 C.()3,7 D.()3,9 【答案】A【解析】因为2(4,8)a =,所以2(4,8)(1,1)a b -=--=()5,7,故选A. 4.【重庆市第一中学高三上学期期中】已知直角坐标系中点,向量,,则点的坐标为( )A.B.C.D.【答案】C 【解析】∵向量,,∴,又∴∴点的坐标为故选:C.5.在ABC ∆中,D 为AB 边上一点,12AD DB = ,23CD CA CB λ=+,则λ=( ) A .13- B.13C.231-D.2 【答案】B【解析】由已知得,13AD AB =,故13CD CA AD CA AB =+=+1()3CA CB CA =+-2133CA CB =+,故13λ=.6. 已知平面向量(1,2)a =,(2,)a k =-,若a 与b 共线,则|3|a b +=( ) A .3 B .4 C .5 D .5 【答案】C.【解析】∵a 与b 共线,∴⇒=-⨯-⨯0)2(21k 4-=k ,∴3(1,2)a b +=,|3|5a b +=. 7.已知向量(,),(1,2)a x y b ==-,且(1,3)a b +=,则|2|a b -等于( ) A .1 B .3 C .4 D .5 【答案】D 【解析】因(1,3)a b +=,(1,2)b =-,故(2,1)a =,所以2(4,3)a b -=-,故22|2|435a b -=+=,故应选D.8.【襄阳市四校(襄州一中、枣阳一中、宜城一中、曾都一中)高三上期中联考】点G 为ABC ∆的重心(三边中线的交点).设,GB a GC b ==,则12AB 等于() A.3122a b - B. 12a b + C. 2a b - D. 2a b + 【答案】B 【解析】如图,∵点G 为ABC ∆的重心,∴0GA GB GC GA a b ++=++=, ∴GA a b =--, ∴()()11112222AB GB GA a a b a b ⎡⎤=-=++=+⎣⎦.选B.9.已知向量()()2,3,cos ,sin a b θθ==,且//a b ,则tan θ=( )A .32 B .32- C .23 D .23- 【答案】A 【解析】由//a b ,可知2sin 3cos 0θθ-=,解得tan θ=32,故选A. 10.向量()1,tan cos ,1,3a b αα⎛⎫== ⎪⎝⎭,且//a b ,则cos 2α⎛⎫+= ⎪⎝⎭( )A .13-B .13C .2-D .22-【答案】A11.在平行四边形ABCD 中,AC 与BD 交于点O E ,是线段OD 的中点,AE 的延长线与CD 交于点F .若AC =a ,BD =b ,则AF =( )A.1142+a b B.1124+a b C.2133+a b D. 1233+a b 【答案】C 【解析】,AC a BD b ==,11112222AD AO OD AC BD a b ∴=+=+=+ 因为E 是OD 的中点,||1||3DE EB ∴=,所以,13DF AB = ()1111133322DF AB OB OA BD AC ⎛⎫⎛⎫∴==-=⨯--- ⎪ ⎪⎝⎭⎝⎭=1166AC BD -=1166a b - ,11112266AF AD DF a b a b =+=++-=2133a b +,故选C.12. ABC ∆中,点E 为AB 边的中点,点F 为AC 边的中点,BF 交CE 于点G ,若AG x AE y AF =+,则x y +等于( )A.32B.43C.1D.23【答案】B .第II 卷(共90分)二、填空题(本大题共4小题,每小题5分,共20分。
2020-2021高三数学下期中模拟试卷附答案(8)

2020-2021高三数学下期中模拟试卷附答案(8)一、选择题1.已知正数x 、y 满足1x y +=,且2211x y m y x +≥++,则m 的最大值为( ) A .163B .13C .2D .42.等比数列{}n a 的前n 项和为n S ,若36=2S =18S ,,则105S S 等于( ) A .-3B .5C .33D .-313.已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( ) A .138B .135C .95D .234.我国的《洛书》中记载着世界上最古老的一个幻方:将1,2,...,9填入33⨯的方格内,使三行、三列、两对角线的三个数之和都等于15 (如图).一般地,将连续的正整数1,2,3,…,2n 填入n n ⨯的方格内,使得每行、每列、每条对角线上的数的和相等,这个正方形就叫做n 阶幻方.记n 阶幻方的一条对角线上数的和为n N (如:在3阶幻方中,315N =),则10N =( )A .1020B .1010C .510D .5055.“0x >”是“12x x+≥”的 A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件6.已知等比数列{}n a 的各项均为正数,且564718a a a a +=,则313233310log log log log a a a a +++⋅⋅⋅+=( )A .10B .12C .31log 5+D .32log 5+7.等差数列{}n a 满足120182019201820190,0,0a a a a a >+>⋅<,则使前n 项和0n S >成立的最大正整数n 是( ) A .2018B .2019C .4036D .40378.设{}n a 是首项为1a ,公差为-2的等差数列,n S 为其前n 项和,若1S ,2S ,4S 成等比数列,则1a = ( ) A .8B .-8C .1D .-19.若ln 2ln 3ln 5,,235a b c ===,则 A .a b c << B .c a b << C .c b a <<D .b a c <<10.如果等差数列{}n a 中,3a +4a +5a =12,那么1a +2a +…+7a =( ) A .14B .21C .28D .3511.已知x ,y 均为正实数,且111226x y +=++,则x y +的最小值为( ) A .20B .24C .28D .3212.两个等差数列{}n a 和{}n b ,其前n 项和分别为n S ,n T ,且723n n S n T n +=+,则220715a ab b +=+( )A .49B .378C .7914D .14924二、填空题13.若变量,x y 满足约束条件12,{20,20,x y x y x y +≤-≥-≤ 则z y x =-的最小值为_________.14.若为等比数列的前n 项的和,,则=___________15.已知0,0a b >>,且20a b +=,则lg lg a b +的最大值为_____.16.海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径A ,B 两点间的距离,现在珊瑚群岛上取两点C ,D ,测得80CD =,135ADB ∠=︒,15BDC DCA ∠∠==︒,120ACB ∠=︒,则A ,B 两点的距离为________.17.数列{}n b 中,121,5b b ==且*21()n n n b b b n N ++=-∈,则2016b =___________.18.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,5cos2C =,且cos cos 2a B b A +=,则ABC ∆面积的最大值为 .19.若log 41,a b =-则+a b 的最小值为_________.20.在锐角ΔABC 中,内角,,A B C 的对边分别为,,a b c ,已知24,sin 4sin 6sin sin a b a A b B a B C +=+=,则ABC n 的面积取最小值时有2c =__________.三、解答题21.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且222sin sin sin 3sin sin A C B A C +-=.(1)求角B ;(2)点D 在线段BC 上,满足DA DC =,且11a =,5cos()5A C -=,求线段DC 的长.22.已知在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,sin tan cos sin tan cos b B C b B a A C a A -=-. (1)求证:A B =;(2)若3c =,3cos 4C =,求ABC ∆的周长.23.已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,且acos C +3asin C -b -c =0.(1)求A ;(2)若AD 为BC 边上的中线,cos B =17,AD =129,求△ABC 的面积. 24.在平面四边形ABCD 中,已知34ABC π∠=,AB AD ⊥,1AB =.(1)若5AC =ABC ∆的面积;(2)若5sin 5CAD ∠=,4=AD ,求CD 的长. 25.已知数列{}n a 的前n 项和()2*,,n S pn qn p q n =+∈∈R N ,且143,24.a S ==(1)求数列{}n a 的通项公式;(2)设2n an b =,求数列{}n b 的前n 项和n T .26.已知等差数列{}n a 的前n 项和为n S ,且211a =,7161S =. (1)求数列{}n a 的通项公式;(2)若6512n n S a n >--,求n 的取值范围; (3)若11n n n b a a +=,求数列{}n b 的前n 项和n T .【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【解析】 【分析】由已知条件得()()113x y +++=,对代数式2211x y y x +++变形,然后利用基本不等式求出2211x y y x +++的最小值,即可得出实数m 的最大值. 【详解】正数x 、y 满足1x y +=,则()()113x y +++=,()()()()()()222222221212111111111111y x y x y x x y y x y x y x y x +-+-⎡⎤⎡⎤----⎣⎦⎣⎦+=+=+=+++++++++444444141465111111y x x y y x x y x y =+-+++-+=+++-=+-++++++()()14441111525311311y x x y x y x y ⎛⎫⎛⎫++=++++-=++-⎡⎤ ⎪ ⎪⎣⎦++++⎝⎭⎝⎭412533⎛≥⨯+-= ⎝, 当且仅当12x y ==时,等号成立,即2211x y y x +++的最小值为13,则13m ≤. 因此,实数m 的最大值为13.故选:B. 【点睛】本题考查利用基本不等式恒成立求参数,对代数式合理变形是解答的关键,考查计算能力,属于中等题.2.C解析:C 【解析】 【分析】由等比数列的求和公式结合条件求出公比,再利用等比数列求和公式可求出105S S . 【详解】设等比数列{}n a 的公比为q (公比显然不为1),则()()61636333111119111a q S q q q S qa q q---===+=---,得2q =, 因此,()()101105510555111111233111a q S q q q S q a qq---===+=+=---,故选C. 【点睛】本题考查等比数列基本量计算,利用等比数列求和公式求出其公比,是解本题的关键,一般在求解等比数列问题时,有如下两种方法:(1)基本量法:利用首项和公比列方程组解出这两个基本量,然后利用等比数列的通项公式或求和公式来进行计算;(2)性质法:利用等比数列下标有关的性质进行转化,能起到简化计算的作用.3.C解析:C 【解析】 试题分析:∵24354{10a a a a +=+=,∴1122{35a d a d +=+=,∴14{3a d =-=, ∴1011091040135952S a d ⨯=+⨯=-+=. 考点:等差数列的通项公式和前n 项和公式.4.D解析:D 【解析】n 阶幻方共有2n 个数,其和为()222112...,2n n n n ++++=Q 阶幻方共有n 行,∴每行的和为()()2221122n n n n n++=,即()()2210110101,50522n n n N N+⨯+=∴==,故选D.5.C解析:C 【解析】先考虑充分性,当x>0时,12x x +≥=,当且仅当x=1时取等.所以充分条件成立. 再考虑必要性,当12x x+≥时,如果x>0时,22210(1)0x x x -+≥∴-≥成立,当x=1时取等.当x<0时,不等式不成立. 所以x>0. 故选C.6.A解析:A 【解析】 【分析】利用对数运算合并,再利用等比数列{}n a 的性质求解。
新高三数学下期中模拟试题含答案

新高三数学下期中模拟试题含答案一、选择题1.等差数列{}n a 中,已知70a >,390a a +<,则{}n a 的前n 项和n S 的最小值为( ) A .4SB .5SC .6SD .7S2.若直线()100,0ax by a b ++=>>把圆()()224116x y +++=分成面积相等的两部分,则122a b+的最小值为( ) A .10B .8C .5D .43.设x y ,满足约束条件70310,350x y x y x y +-⎧⎪-+⎨⎪--⎩,,………则2z x y =-的最大值为( ).A .10B .8C .3D .24.数列{}n a 为等比数列,若11a =,748a a =,数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,则5(S = )A .3116B .158C .7D .315.已知变量x , y 满足约束条件13230x x y x y ≥⎧⎪+≤⎨⎪--≤⎩,则2z x y =+的最小值为( )A .1B .2C .3D .66.已知x ,y 均为正实数,且111226x y +=++,则x y +的最小值为( ) A .20B .24C .28D .327.在等差数列{a n }中,1233,a a a ++=282930165a a a ++=,则此数列前30项和等于( ) A .810B .840C .870D .9008.已知{}n a 为等差数列,n S 为其前n 项和,若3572a a +=,则13S =( ) A .49B .91C .98D .1829.已知等比数列{}n a 中,11a =,356a a +=,则57a a +=( ) A .12B .10C.D.10.已知,x y 满足0404x y x y x -≥⎧⎪+-≥⎨⎪≤⎩,则3x y -的最小值为( )A .4B .8C .12D .1611.已知幂函数()y f x =过点(4,2),令(1)()n a f n f n =++,n +∈N ,记数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,则10n S =时,n 的值是( ) A .10B .120C .130D .14012.若正数,x y 满足40x y xy +-=,则3x y+的最大值为 A .13B .38C .37D .1二、填空题13.已知lg lg 2x y +=,则11x y+的最小值是______. 14.在ABC ∆中,角,,A B C 所对的边为,,a b c ,若23sin c ab C =,则当b aa b+取最大值时,cos C =__________;15.已知数列{}{}n n a b 、满足ln n n b a =,*n ∈N ,其中{}n b 是等差数列,且431007e a a ⋅=,则121009b b b +++=L ________.16.若直线1(00)x ya b a b+=>,>过点(1,2),则2a+b 的最小值为______. 17.已知命题20001:,02p x R ax x ∃∈++≤,若命题p 是假命题,则实数a 的取值范围是________.18.设不等式组30,{230,1x y x y x +-<--≤≥表示的平面区域为1Ω,平面区域2Ω与1Ω关于直线20x y +=对称,对于任意的12,C D ∈Ω∈Ω,则CD 的最小值为__________.19.若a>0,b>0,a+b=2,则下列不等式对一切满足条件的a ,b 恒成立的是 (写出所有正确命题的编号).①ab≤1; ②a +b ≤2; ③a 2+b 2≥2;④a 3+b 3≥3;112a b+≥⑤. 20.已知二次函数22()42(2)21f x x p x p p =----+,若在区间[1,1]-内至少存在一个实数x 使()0f x >,则实数p 的取值范围是__________.三、解答题21.设 的内角 的对边分别为 已知.(1)求角 ;(2)若,,求的面积.22.在△ABC 中,角,,A B C 所对的边分别为,,,a b c 向量()23,3m a b c =-u r,向量s )(co ,n B cosC =r ,且//m n u r r .(1)求角C 的大小; (2)求3()3y sinA sin B π=+-的最大值.23.已知函数()11f x x x =-++. (1)解不等式()2f x ≤;(2)设函数()f x 的最小值为m ,若a ,b 均为正数,且14m a b+=,求+a b 的最小值.24.在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,已知()3cos cos 0a b C c B ++=. (1)求cos C 的值;(2)若6c =,ABC ∆的面积为324,求+a b 的值; 25.已知数列为等差数列,且12a =,12312a a a ++=. (1) 求数列的通项公式; (2) 令,求证:数列是等比数列.(3)令11n n n c a a +=,求数列{}n c 的前n 项和n S . 26.在ABC ∆角中,角A 、B 、C 的对边分别是a 、b 、c ,若3asinB bcosA =. (1)求角A ;(2)若ABC ∆的面积为235a =,,求ABC ∆的周长.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】 【分析】先通过数列性质判断60a <,再通过数列的正负判断n S 的最小值. 【详解】∵等差数列{}n a 中,390a a +<,∴39620a a a +=<,即60a <.又70a >,∴{}n a 的前n 项和n S 的最小值为6S .故答案选C 【点睛】本题考查了数列和的最小值,将n S 的最小值转化为{}n a 的正负关系是解题的关键.2.B解析:B 【解析】 【分析】由于直线将圆平分,故直线过圆的圆心,将圆心坐标代入直线方程,利用“1”的代换的方法以及基本不等式,求得所求和的最小值. 【详解】圆的圆心为()4,1--,由于直线将圆平分,故直线过圆心,即410a b --+=,即41a b +=,故()121288444282222b a b a a b a b a b a b a b⎛⎫+=++=++≥+⋅= ⎪⎝⎭,当且仅当82b aa b =,即11,82a b ==时,取得最小值为8.故选B. 【点睛】本小题主要考查直线和圆的位置关系,考查利用“1”的代换和基本不等式求解和式的最小值问题.直线能将圆平分成面积相等的两个部分,则这条直线是经过圆心的.要注意的是,圆的标准方程是()()222x a y b r -+-=,圆心是(),a b ,所以本题的圆心是()4,1--,而不是()4,1.3.B解析:B 【解析】 【分析】作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数即可求解. 【详解】 作出可行域如图:化目标函数为2y x z =-,联立70310x y x y +-=⎧⎨-+=⎩,解得5,2A(). 由图象可知,当直线过点A 时,直线在y 轴上截距最小,z 有最大值25-28⨯=. 【点睛】本题主要考查了简单的线性规划,数形结合的思想,属于中档题.4.A解析:A 【解析】 【分析】先求等比数列通项公式,再根据等比数列求和公式求结果. 【详解】Q 数列{}n a 为等比数列,11a =,748a a =,638q q ∴=,解得2q =, 1112n n n a a q --∴==, Q 数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S , 55111111131211248161612S ⎛⎫⨯- ⎪⎝⎭∴=++++==-.故选A . 【点睛】本题考查等比数列通项公式与求和公式,考查基本分析求解能力,属基础题.5.A解析:A 【解析】 【分析】画出可行域,平移基准直线20x y +=到可行域边界的点()1,1C -处,由此求得z 的最小值. 【详解】画出可行域如下图所示,平移基准直线20x y +=到可行域边界的点()1,1C -处,此时z 取得最小值为()2111⨯+-=. 故选:A.【点睛】本小题主要考查线性规划问题,考查数形结合的数学思想方法,属于基础题.6.A解析:A 【解析】分析:由已知条件构造基本不等式模型()()224x y x y +=+++-即可得出. 详解:,x y Q 均为正实数,且111226x y +=++,则116122x y ⎛⎫+= ⎪++⎝⎭(2)(2)4x y x y ∴+=+++-116()[(2)(2)]422x y x y =++++-++ 22226(2)46(22)4202222y x y x x y x y ++++=++-≥+⋅-=++++ 当且仅当10x y ==时取等号.x y ∴+的最小值为20. 故选A.点睛:本题考查了基本不等式的性质,“一正、二定、三相等”.7.B解析:B 【解析】数列前30项和可看作每三项一组,共十组的和,显然这十组依次成等差数列,因此和为10(3165)8402+= ,选B. 8.B解析:B 【解析】∵3572a a +=,∴11272(4)a d a d ++=+,即167a d +=,∴13711313(6)13791S a a d ==+=⨯=,故选B .9.A解析:A 【解析】由已知24356a a q q +=+=,∴22q =,∴25735()2612a a q a a +=+=⨯=,故选A.10.A解析:A 【解析】 【分析】作出可行域,变形目标函数并平移直线3y x =,结合图象,可得最值. 【详解】作出x 、y 满足0404x y x y x -≥⎧⎪+-≥⎨⎪≤⎩所对应的可行域(如图ABC V ),变形目标函数可得3y x z =-,平移直线3y x =可知, 当直线经过点(2,2)A 时,截距z -取得最大值, 此时目标函数z 取得最小值3224⨯-=. 故选:A.【点睛】本题考查简单线性规划,准确作图是解决问题的关键,属中档题.11.B解析:B 【解析】 【分析】根据幂函数所过点求得幂函数解析式,由此求得n a 的表达式,利用裂项求和法求得n S 的表达式,解方程10n S =求得n 的值. 【详解】设幂函数为()f x x α=,将()4,2代入得142,2αα==,所以()f x x =所以1n a n n =+11nn n a =+1121n S n n n n =+-L 11n =+,由1110n S n =+=解得120n =,故选B. 【点睛】本小题主要考查幂函数解析式的求法,考查裂项求和法,考查方程的思想,属于基础题.12.A解析:A 【解析】 【分析】 分析题意,取3x y +倒数进而求3x y+的最小值即可;结合基本不等式中“1”的代换应用即可求解。
新高三数学下期中模拟试卷(含答案)

新高三数学下期中模拟试卷(含答案)一、选择题1.等差数列{}n a 中,已知70a >,390a a +<,则{}n a 的前n 项和n S 的最小值为( ) A .4SB .5SC .6SD .7S2.在ABC ∆中,,,a b c 分别为角,,A B C 的对边,若,1,3A b π==ABC ∆则a 的值为( ) A .2BC.2D .13.程大位《算法统宗》里有诗云“九百九十六斤棉,赠分八子做盘缠.次第每人多十七,要将第八数来言.务要分明依次弟,孝和休惹外人传.”意为:996斤棉花,分别赠送给8个子女做旅费,从第一个开始,以后每人依次多17斤,直到第八个孩子为止.分配时一定要等级分明,使孝顺子女的美德外传,则第八个孩子分得斤数为( ) A .65B .184C .183D .1764.设,x y 满足约束条件330280440x y x y x y -+≥⎧⎪+-≤⎨⎪+-≥⎩,则3z x y =+的最大值是( )A .9B .8C .3D .45.设实数,x y 满足242210x y x y x -≤⎧⎪+≤⎨⎪-≥⎩,则1y x +的最大值是( )A .-1B .12C .1D .326.在等差数列{a n }中,a 1>0,a 10·a 11<0,若此数列的前10项和S 10=36,前18项的和S 18=12,则数列{|a n |}的前18项和T 18的值是 ( ) A .24B .48C .60D .847.设ABC ∆的三个内角, , A B C 成等差数列,sin A 、sin B 、sin C 成等比数列,则这个三角形的形状是 ( ) A .直角三角形B .等边三角形C .等腰直角三角形D .钝角三角形8.《周髀算经》有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸,冬至、立春、春分日影之和为三丈一尺五寸,前九个节气日影之和为八丈五尺五寸,问芒种日影长为( ) A .一尺五寸B .二尺五寸C .三尺五寸D .四尺五寸9.已知等比数列{}n a 的各项均为正数,且564718a a a a +=,则313233310log log log log a a a a +++⋅⋅⋅+=( )A .10B .12C .31log 5+D .32log 5+10.设{}n a 是首项为1a ,公差为-1的等差数列,n S 为其前n 项和,若124,,S S S 成等比数列,则1a =( ) A .2B .-2C .12D .12-11.,x y 满足约束条件362000x y x y x y -≤⎧⎪-+≥⎪⎨≥⎪⎪≥⎩,若目标函数(0,0)z ax by a b =+>>的最大值为12,则23a b+的最小值为 ( ) A .256B .25C .253D .512.已知x ,y 满足条件0{20x y xx y k ≥≤++≤(k 为常数),若目标函数z =x +3y 的最大值为8,则k =( ) A .-16B .-6C .-83D .6二、填空题13.数列{}n a 满足11,a =前n 项和为n S ,且*2(2,)n n S a n n N =≥∈,则{}n a 的通项公式n a =____;14.已知函数()2xf x =,等差数列{}n a 的公差为2,若()2468104f a a a a a ++++=,则()()()()212310log f a f a f a f a ⋅⋅⋅⋅=⎡⎤⎣⎦L ___________.15.设,x y 满足约束条件0{2321x y x y x y -≥+≤-≤,则4z x y =+的最大值为 .16.已知数列{}n a 满足51()1,62,6n n a n n a a n -⎧-+<⎪=⎨⎪≥⎩,若对任意*n N ∈都有1n n a a +>,则实数a 的取值范围是_________.17.已知120,0,2a b a b>>+=,2+a b 的最小值为_______________. 18.设等差数列{}n a ,{}n b 的前n 项和分别为,n n S T 若对任意自然数n 都有2343n n S n T n -=-,则935784a ab b b b +++的值为_______. 19.数列{}n a 满足1(1)21nn n a a n ++-=-,则{}n a 的前60项和为_____. 20.设等差数列{}na 的前n 项和为n S .若35a =,且1S ,5S ,7S 成等差数列,则数列{}n a 的通项公式n a =____.三、解答题21.已知函数()21f x x =-. (1)若不等式121(0)2f x m m ⎛⎫+≥+> ⎪⎝⎭的解集为][(),22,-∞-⋃+∞,求实数m 的值; (2)若不等式()2232y y af x x ≤+++对任意的实数,x y R ∈恒成立,求正实数a 的最小值.22.已知公比为4的等比数列{}n a 的前n 项和为n S ,且485S =. (1)求数列{}n a 的通项公式; (2)求数列{(1)}n n a -的前n 项和n T .23.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且22222230a c b ac +-+=. (1)求cos B 的值; (2)求sin 24B π⎛⎫+⎪⎝⎭的值. 24.在等比数列{}n b 中,公比为()01q q <<,13511111,,,,,,50322082b b b ∈⎧⎫⎨⎬⎩⎭. (1)求数列{}n b 的通项公式;(2)设()31n n c n b =-,求数列{}n c 的前n 项和n T .25.已知数列{}n a 是递增的等比数列,且14239,8.a a a a +== (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设n S 为数列{}n a 的前n 项和,11n n n n a b S S ++=,求数列{}n b 的前n 项和n T . 26.已知函数()sin (0)f x m x x m =+>的最大值为2. (Ⅰ)求函数()f x 在[0,]π上的单调递减区间; (Ⅱ)ABC ∆中,()()sin 44f A f B A B ππ-+-=,角,,A B C 所对的边分别是,,a b c ,且060,3C c ==,求ABC ∆的面积.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】 【分析】先通过数列性质判断60a <,再通过数列的正负判断n S 的最小值. 【详解】∵等差数列{}n a 中,390a a +<,∴39620a a a +=<,即60a <.又70a >,∴{}n a 的前n 项和n S 的最小值为6S . 故答案选C 【点睛】本题考查了数列和的最小值,将n S 的最小值转化为{}n a 的正负关系是解题的关键.2.B解析:B 【解析】试题分析:由已知条件及三角形面积计算公式得131sin ,2,23c c π⨯⨯=∴=由余弦定理得考点:考查三角形面积计算公式及余弦定理.3.B解析:B 【解析】分析:将原问题转化为等差数列的问题,然后结合等差数列相关公式整理计算即可求得最终结果.详解:由题意可得,8个孩子所得的棉花构成公差为17的等差数列,且前8项和为996, 设首项为1a ,结合等差数列前n 项和公式有:811878828179962S a d a ⨯=+=+⨯=, 解得:165a =,则81765717184a a d =+=+⨯=. 即第八个孩子分得斤数为184. 本题选择B 选项.点睛:本题主要考查等差数列前n 项和公式,等差数列的应用,等差数列的通项公式等知识,意在考查学生的转化能力和计算求解能力.4.A解析:A【解析】绘制不等式组表示的平面区域如图所示,结合目标函数的几何意义可知目标还是在点()3,2C处取得最大值,其最大值为max 33329z x y=+=+⨯=.本题选择A选项.5.D解析:D【解析】【分析】由约束条件确定可行域,由1yx+的几何意义,即可行域内的动点与定点P(0,-1)连线的斜率求得答案.【详解】由约束条件242210x yx yx-≤⎧⎪+≤⎨⎪-≥⎩,作出可行域如图,联立10220x x y -=⎧⎨+-=⎩,解得A (112,),1y x+的几何意义为可行域内的动点与定点P (0,-1)连线的斜率, 由图可知,113212PAk +==最大. 故答案为32. 【点睛】本题考查简单的线性规划,考查了数形结合的解题思想方法,属于中档题型.6.C解析:C 【解析】试题分析:∵11011101100000a a a d a a ⋅∴>,<,<,>,<, ∴18110111810181060T a a a a S S S =+⋯+--⋯-=--=(),选C . 考点:1.等差数列的求和;2.数列的性质.7.B解析:B 【解析】 【分析】先由ABC ∆的三个内角, , A B C 成等差数列,得出2,33B AC ππ=+=,又因为sin A 、sin B 、sin C 成等比数列,所以23sin sin sin 4B AC =⋅=,整理计算即可得出答案.【详解】因为ABC ∆的三个内角, , A B C 成等差数列,所以2,33B AC ππ=+=, 又因为sin A 、sin B 、sin C 成等比数列, 所以23sin sin sin 4B AC =⋅= 所以222sin sin sin sin cos sin cos333A A A A A πππ⎛⎫⎛⎫⋅-=⋅-⎪ ⎪⎝⎭⎝⎭21111132sin 2cos 2sin 2424442344A A A A A π⎛⎫=+=-+=-+= ⎪⎝⎭ 即sin 213A π⎛⎫-= ⎪⎝⎭又因为203A π<< 所以3A π=故选B 【点睛】本题考查数列与三角函数的综合,关键在于求得2,33B AC ππ=+=,再利用三角公式转化,属于中档题.8.B解析:B 【解析】 【分析】从冬至日起各节气日影长设为{}n a ,可得{}n a 为等差数列,根据已知结合前n 项和公式和等差中项关系,求出通项公式,即可求解. 【详解】由题知各节气日影长依次成等差数列,设为{}n a ,n S 是其前n 项和,则()19959985.52a a S a +===尺,所以59.5a =尺,由题知1474331.5a a a a ++==, 所以410.5a =,所以公差541d a a =-=-, 所以1257 2.5a a d =+=尺。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学下期中模拟试卷带答案(8)一、选择题1.设,x y 满足约束条件 202300x y x y x y --≤⎧⎪-+≥⎨⎪+≤⎩,则46y x ++的取值范围是A .3[3,]7- B .[3,1]- C .[4,1]-D .(,3][1,)-∞-⋃+∞2.正项等比数列中,的等比中项为,令,则( ) A .6B .16C .32D .643.若n S 是等差数列{}n a 的前n 项和,其首项10a >,991000a a +>,991000a a ⋅< ,则使0n S >成立的最大自然数n 是( ) A .198B .199C .200D .2014.在ABC ∆中,a ,b ,c 分别是角A ,B ,C 的对边,若2b c =,6a =7cos 8A =,则ABC ∆的面积为( ) A 17B .3C 15D 15 5.已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( ) A .138B .135C .95D .236.已知等比数列{}n a 的各项都是正数,且13213,,22a a a 成等差数列,则8967a a a a +=+ A .6B .7C .8D .97.《周髀算经》有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸,冬至、立春、春分日影之和为三丈一尺五寸,前九个节气日影之和为八丈五尺五寸,问芒种日影长为( ) A .一尺五寸B .二尺五寸C .三尺五寸D .四尺五寸8.已知实数x ,y 满足521802030x y x y x y +-≤⎧⎪-≥⎨⎪+-≥⎩,若直线10kx y -+=经过该可行域,则实数k的最大值是( ) A .1B .32C .2D .39.20,{0,0x y z x y x y x y y k+≥=+-≤≤≤设其中实数、满足若z 的最大值为6,z 的最小值为( )A .0B .-1C .-2D .-310.已知:0x >,0y >,且211x y+=,若222x y m m +>+恒成立,则实数m 的取值范围是( ) A .()4,2- B .(][),42,-∞-+∞U C .()2,4-D .(][),24,-∞-⋃+∞11.,x y 满足约束条件362000x y x y x y -≤⎧⎪-+≥⎪⎨≥⎪⎪≥⎩,若目标函数(0,0)z ax by a b =+>>的最大值为12,则23a b+的最小值为 ( ) A .256B .25C .253D .512.如图,有四座城市A 、B 、C 、D ,其中B 在A 的正东方向,且与A 相距120km ,D 在A 的北偏东30°方向,且与A 相距60km ;C 在B 的北偏东30°方向,且与B 相距6013km ,一架飞机从城市D 出发以360/km h 的速度向城市C 飞行,飞行了15min ,接到命令改变航向,飞向城市B ,此时飞机距离城市B 有( )A .120kmB .606kmC .605kmD .3km二、填空题13.已知变数,x y 满足约束条件340{210,380x y x y x y -+≥+-≥+-≤目标函数(0)z x ay a =+≥仅在点(2,2)处取得最大值,则a 的取值范围为_____________.14.ABC ∆内角A 、B 、C 的对边分别是a ,b ,c ,且2cos (32)cos b C a c B =-.当42b =2a c =,ABC ∆的面积为______.15.已知数列{}n a 的首项12a =,且满足()*12n n n a a n N +=∈,则20a =________.16.已知x y 、满足约束条件1{1,22x y x y x y +≥-≥--≤若目标函数()0,0z ax by a b =+>>的最大值为7,则34a b+的最小值为_______. 17.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,已知274sincos 222A B C +-=,且5,a b c +==,则ab 为 .18.已知,x y 满足条件20220220x y x y x y +-≤⎧⎪--≤⎨⎪-+≥⎩,若目标函数=+z -ax y 取得最大值的最优解不唯一,则实数a 的值为__________.19.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c,cos2C =,且cos cos 2a B b A +=,则ABC ∆面积的最大值为 .20.我国古代数学名著《九章算术》里有问题:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢,问:__________日相逢?三、解答题21.已知等差数列{}n a 的所有项和为150,且该数列前10项和为10,最后10项的和为50.(1)求数列{}n a 的项数; (2)求212230a a a ++⋅⋅⋅+的值.22.已知实数x 、y 满足6003x y x y x -+≥⎧⎪+≥⎨⎪≤⎩,若z ax y =+的最大值为39a +,最小值为33a -,求实数a 的取值范围.23.等差数列{a n }的前n 项和为S n ,且3a =9,S 6=60. (I )求数列{a n }的通项公式;(II )若数列{b n }满足b n+1﹣b n =n a (n∈N +)且b 1=3,求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和T n . 24.已知等差数列{}n a 的前n 项和为n S ,公差0d ≠,且3550S S +=,1a ,4a ,13a 成等比数列.(1)求数列{}n a 的通项公式;(2)设n n b a ⎧⎫⎨⎬⎩⎭是首项为1公比为2的等比数列,求数列{}n b 前n 项和n T .25.设数列的前项和为,且.(1)求数列的通项公式; (2)设,求数列的前项和.26.在ΔABC 中,角,,A B C 所对的边分别为,,a b c ,且222sin sin sin sin sin A C B A C +=-.(1)求B 的大小;(2)设BAC ∠的平分线AD 交BC 于,23,1D AD BD ==,求sin BAC ∠的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【解析】 【分析】 【详解】 先作可行域,而46y x ++表示两点P (x,y )与A (-6,-4)连线的斜率,所以46y x ++的取值范围是[,][3,1]AD AC k k =-,选B.点睛:线性规划问题,首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值取法、值域范围.2.D解析:D 【解析】因为,即,又,所以.本题选择D 选项.3.A解析:A 【解析】 【分析】先根据10a >,991000a a +>,991000a a ⋅<判断出991000,0a a ><;然后再根据等差数列前n 项和公式和等差中项的性质,即可求出结果. 【详解】∵991000a a ⋅<, ∴99a 和100a 异号; ∵1991000,0a a a >+>,991000,0a a ∴><, 有等差数列的性质可知,等差数列{}n a 的公差0d <, 当99,*n n N ≤∈时,0n a >;当100,*n n N ≥∈时,0n a <; 又()()119899100198198198022a a a a S +⨯+⨯==> ,()119919910019919902a a S a+⨯==<,由等差数列的前n 项和的性质可知,使前n 项和0n S >成立的最大自然数n 是198. 故选:A . 【点睛】本题主要考查了等差数列的性质.考查了学生的推理能力和运算能力.4.D解析:D 【解析】 【分析】三角形的面积公式为1sin 2ABC S bc A ∆=,故需要求出边b 与c ,由余弦定理可以解得b 与c . 【详解】解:在ABC ∆中,2227cos 28b c a A bc +-==将2b c =,a =22246748c c c +-=, 解得:2c =由7cos 8A =得sin 8A ==所以,11sin 242282ABC S bc A ∆==⨯⨯⨯=故选D. 【点睛】三角形的面积公式常见形式有两种:一是12(底⨯高),二是1sin 2bc A .借助12(底⨯高)时,需要将斜三角形的高与相应的底求出来;借助1sin 2bc A 时,需要求出三角形两边及其夹角的正弦值.5.C解析:C 【解析】 试题分析:∵24354{10a a a a +=+=,∴1122{35a d a d +=+=,∴14{3a d =-=, ∴1011091040135952S a d ⨯=+⨯=-+=. 考点:等差数列的通项公式和前n 项和公式.6.D解析:D 【解析】设各项都是正数的等比数列{a n }的公比为q ,(q >0),由题意可得关于q 的式子,解之可得q ,而所求的式子等于q 2,计算可得. 【详解】设各项都是正数的等比数列{a n }的公比为q ,(q >0)由题意可得31212322a a a ⨯=+, 即q 2-2q-3=0, 解得q=-1(舍去),或q=3,故()26728967679a a qa a q a a a a .++===++ 故选:D . 【点睛】本题考查等差数列和等比数列的通项公式,求出公比是解决问题的关键,属基础题.7.B解析:B 【解析】 【分析】从冬至日起各节气日影长设为{}n a ,可得{}n a 为等差数列,根据已知结合前n 项和公式和等差中项关系,求出通项公式,即可求解. 【详解】由题知各节气日影长依次成等差数列,设为{}n a ,n S 是其前n 项和,则()19959985.52a a S a +===尺,所以59.5a =尺,由题知1474331.5a a a a ++==, 所以410.5a =,所以公差541d a a =-=-, 所以1257 2.5a a d =+=尺。
故选:B . 【点睛】本题考查等差数列应用问题,考查等差数列的前n 项和与通项公式的基本量运算,属于中档题.8.B解析:B 【解析】 【分析】先根据约束条件画出可行域,再利用直线20kx y -+=过定点()0,1,再利用k 的几何意义,只需求出直线10kx y -+=过点()2,4B 时,k 值即可.直线20kx y -+=过定点()0,1, 作可行域如图所示,,由5218020x y x y +-=⎧⎨-=⎩,得()2,4B .当定点()0,1和B 点连接时,斜率最大,此时413202k -==-, 则k 的最大值为:32故选:B . 【点睛】本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.9.D解析:D 【解析】作出不等式对应的平面区域, 由z=x+y,得y=−x+z,平移直线y=−x+z ,由图象可知当直线y=−x+z 经过点A 时,直线y=−x+z 的截距最大, 此时z 最大为6.即x+y=6.经过点B 时,直线y=−x+z 的截距最小,此时z 最小. 由6{x y x y +=-=得A(3,3),∵直线y=k 过A , ∴k=3. 由3{20y k x y ==+=,解得B(−6,3).此时z 的最小值为z=−6+3=−3, 本题选择D 选项.点睛:求二元一次函数z =ax +by (ab ≠0)的最值,将函数z =ax +by 转化为直线的斜截式:b zy x a b =-+,通过求直线的截距z b的最值间接求出z 的最值.最优解在顶点或边界取得.10.A解析:A 【解析】 【分析】若222x y m m +>+恒成立,则2x y +的最小值大于22m m +,利用均值定理及“1”的代换求得2x y +的最小值,进而求解即可. 【详解】由题,因为211x y+=,0x >,0y >,所以()214422242448x y x yx y x y y x y x ⎛⎫++=+++≥+⋅=+=⎪⎝⎭,当且仅当4x y y x =,即4x =,2y =时等号成立,因为222x y m m +>+恒成立,则228m m +<,即2280m m +-<,解得42m -<<, 故选:A 【点睛】本题考查均值不等式中“1”的代换的应用,考查利用均值定理求最值,考查不等式恒成立问题.11.A解析:A 【解析】 【分析】先画不等式组表示的平面区域,由图可得目标函数(0,0)z ax by a b =+>>何时取最大值,进而找到a b ,之间的关系式236,a b +=然后可得23123()(23)6a b a b a b+=++,化简变形用基本不等式即可求解。
