苏教版初中数学九年级上册第一学期第2周周考试卷
苏科版九年级数学上册第2周周练试题(2A).docx

初中数学试卷 桑水出品满分值时 间 制 卷 审 核 得 分 100 45 陈宁师 陈玉丽一、选择题(本题共28分)1.方程x 2-16=0的根为 ( )A 、x=4B 、x=-4C 、x 1=4,x 2=-4D 、x 1=2,x 2=-22.用配方法解方程x 2-4x+3=0的过程中,正确的是 ( )A 、x 2-4x+(-2)2=7B 、x 2―4x+(―2)2=1C 、(x+2)2=1D 、(x -1)2=23.若4y 2-my+25是一个完全平方式,则m 的值 ( )A 、10B 、±10C 、20D 、±204.(2014•四川宜宾中考)关于x 的一元二次方程的两个根为11x =,22x =,则这个方程是A.2320x x +-=B.2320x x -+= ( )C.2230x x -+=D.2320x x ++=5.以3、4为两边长的三角形的第三边长是方程040132=+-x x 的根,则这个三角形的周长为( )A.15或12B.12C.15D.以上都不对6.如果关于x 的一元二次方程22(21)10k x k x -++=有两个不相等的实数根,那么k 的取值范围是( )A.k >14-B.k >14-且0k ≠C.k <14-D.14k ≥-且0k ≠ 7. 定义:如果一元二次方程ax 2 + bx + c =o(a ≠0)满足a -b+c=o,那么我们称这个方程为“蝴蝶”方程。
已知关于x 的方程ax 2 + bx + c =o(a ≠0)是“蝴蝶”方程,且有两个相等的实数根,则下列结论中正确的是( )A. b=cB.a=bC.a=cD.a = b =c二、填空题(每小题3分,共21分)8.方程x(x+2)=x+2的根为_____ _____。
9.写出一个以―1和―2为两根的一元二次方程(二次项系数为1)___________。
10.若一元二次方程x 2+3x+m -1=0有两个不相等实数根,则m 的取值范围______。
苏科版九年级数学上册周练2

初中数学试卷泗洪育才实验学校2014年初三(上)第二次周练试卷数学试卷(满分120分 时间100分钟 命题人:王志)一、选择题(每题3分,共24分)1.一元二次方程2230x x --=的二次项系数、一次项系数、常数项分别是( ) A. 1,2,3-- B. 1,-2,3 C. 1,2,3 D. 1,2,3- 2.下列结论正确 ( ) A .弦是直径 B .弧是半圆 C .半圆是弧 D .过圆心的线段是直径3.要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排 21场比赛,则参赛球队的个数是 ( ) A. 5个B. 6个C. 7个D. 8个4.如图,直线l 1//l 2,点A 在直线l 1上,以点A 为圆心,适当长为半径画弧,分别交直线 l 1、l 2于B 、C 两点,连结AC 、BC .若∠ABC =54°,则∠1的 大小为( )班级 姓名 考场 考号封 线 内, 请 勿 答 题A 36° B 54° C 72° D 73°5.若⊙P 的半径为13,圆心P 的坐标为(5, 12 ), 则平面直角坐标系的原点O 与 ⊙P 的位置关系是 ( ) A .在⊙P 内 B .在⊙P 内上 C .在⊙P 外 D .无法确定6.直角三角形两直角边长分别为3和l ,那么它的外接圆的直径是 ( ) A.1 B.2 C.3 D.47.设12x x 、是方程230x x +-=的两根,那么3212419x x -+的值是 ( ) A -4 (B )8 (C )6 (D )0 8.已知函数y =的图象在第一象限的一支曲线上有一点A (a ,c ),点B (b ,c +1) 在该函数图象的另外一支上,则关于一元二次方程ax 2+bx +c =0的两根x 1,x 2判断正确的是( ) A . x 1+x 2>1,x 1•x 2>0 B . x 1+x 2<0,x 1•x 2>0C 0<x 1+x 2<1,x 1•x 2>0D . x 1+x 2与x 1•x 2的符号都不确定二、填空题(每题3分,共30分)9.将一元二次方程2x(x 3)1-=化成一般形式为 . 10.若关于x 的方程220x x m -+=有一根为3,则m =___________. 11.三角形的外心是三角形的三条 的交点.12.已知⊙O的半径为5cm,过⊙O内一点P的最短的弦长为8cm,则OP=______ .13.已知关于x的方程x2+(1﹣m)x+=0有两个不相等的实数根,则m的最大整数值是.14.用锤子以均匀的力敲击铁钉入木板.随着铁钉的深入,铁钉所受的阻力会越来越大,使得每次钉入木板的钉子的长度后一次为前一次的k倍(0<k<1).已知一个钉子受击3次后恰好全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的错误!未找到引用源。
苏科版九年级数学上册周周练试题7.docx

桑水初中数学试卷桑水出品初三数学周末练习7姓名 得分 一、精心选一选(24分)1、如图,在□ ABCD 中,E 是AD 的中点,点F 在AB 上,且△CBF ∽△CDE.若AB=10,AD=6,则AF 的值为( )A. 5B. 8.2C. 6.4D. 1.82、如图,在□ ABCD 中,点E 在BC 上,DE 、AB 的延长线相交于点F,图中相似三角形共有( ) A. 4对 B. 3对 C. 2对 D. 1对3、P 是Rt △ABC 的斜边BC 上异于点B 、C 的一点,过点P 作直线截△ABC ,使截得的三角形与△ABC 相似,满足这样条件的直线共有( ) A .1条 B .2条 C .3条 D .4条4、如图,在正方形ABCD 中,E 是CD 的中点,FC=41BC .图中与△ADE 相似的三角形有( )A .0个B .1个C .2个D .3个5、下列条件能判定△ABC ∽△A ′B ′C ′的有 ( )(1)∠A =45°,AB =12,AC =15,∠A ′=450,A ′B ′=16,A ′C ′=20 (2)∠A =47°,AB =1.5,AC =2,∠B ′=47°,A ′B ′=2.8,B ′C ′=2.1 (3)∠A =47°,AB =2,AC =3,∠B ′=47°,A ′B ′=4,B ′C ′=6 A 、0个 B 、1个 C 、2个 D 、3个6、如图,在△ABC 中,P 为AB 上的一点,在下列条件中:①∠ACP =∠B ;②∠APC =∠ACB ;③AC2=AP •AB ;④AB •CP =AP •CB ,能满足△APC ∽△ACB 的条件是 ( )A 、①②④B 、①③④C 、②③④D 、①②③7. 如图,,DE BC //且1ADE DBCE S S ∆:=:8,四边形 则:AE AC = ( )A .1︰9B .1︰3C .1︰8D .1︰28. 如图是小明设计用手电来测量某古城墙高度的示意图.点P 处放一水平的平面镜, 光线从点A 出发经平B C PAACDBABC D E ABCD FEA BCD E F第7题图AC第8题图桑水面镜反射后刚好射到古城墙CD 的顶端C 处,已知 AB ⊥BD ,CD ⊥BD, 且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是 ( ) A . 6米 B . 8米 C .18米 D .24米二、细心填一填(30分)1、在一张比例尺为1: 4000的地图上,一块多边形地区的面积是250cm 2,则这个地区的实际面积是 平方公里。
苏教版九年级数学第一学期第二阶段学业质量监测试卷

九年级数学第一学期第二阶段学业质量监测试卷注意事项:1.本试卷共6页.全卷满分120分.考试时间为120分钟.2.答选择题必须用2B 铅笔将答题卷上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卷上的指定位置,在其他位置答题一律无效.3.作图必须用2B 铅笔作答,并请加黑加粗,描写清楚.一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题..卷.相应位置....上) 1.从一副完整的扑克牌中任意抽取1张,下列事件与抽到“A ”的概率相同的是A .抽到“大王”B .抽到“2”C .抽到“小王”D .抽到“红桃” 2.某选手在比赛中的成绩(单位:分)分别是90,87,92,88,93,方差是5.2(单位:分2),如果去掉一个最高分和一个最低分,那么该选手成绩的方差会A .变大B .不变C .变小D .不确定 3.x 1,x 2是一元二次方程x 2-x -1=0的两个根,32<x 1<2,对x 2的估算正确的是A .-1<x 2<-12B .-12<x 2<0C .0<x 2<12D .12<x 2<14.如图,在方格纸中,△ABC 和△EPD 的顶点均在格点上,若△ABC ∽△EPD ,则点P 所在的格点为下列各点中的A .P 1B .P 2C .P 3D .P 45.如图,AB 是半圆O 的直径,C 是OB 的中点,过点C 作CD ⊥AB ,交半圆于点D ,则BD ⌒与AD ⌒的长度的比为A .1∶2B .1∶3C .1∶4D .1∶56.若点A (0,1)在二次函数y =ax 2-2ax +b (a 、b 是常数)的图像上,则下列各点一定..在该图像上的是(第4题)(第5题)(第10题)A .(1,0)B .(2,0)C .(1,1)D .(2,1)二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题卷相应位置.......上) 7.若 a b =23,则 a +b 2b= ▲ .8.一组数据:-1,3,2,x ,5的众数是3,则这组数据的中位数是 ▲ .9.圆锥的底面半径是4 cm ,母线长为5 cm ,则这个圆锥的侧面积是 ▲ cm 2.(结果保留π)10.如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在涂色部分的概率是 ▲ .11.将二次函数y =-2x 2+1的图像绕点(0,2)顺时针旋转180°,得到的图像所对应的函数表达式为 ▲ .12.关于x 的方程ax 2+bx +2=0的两根为x 1=1,x 2=2,则方程a (x -1)2+b (x -1)+2=0的两根分别为 ▲ .13.如图,E 、F 是线段AB 的两个黄金分割点,AB =1,则线段EF 的长为 ▲ .(结果保留根号)14.将正三角形、正方形、正五边形按如图所示的位置摆放,则∠1+∠2+∠3= ▲ °. 15.如图,二次函数y =-x 2+2x +3的图像与x 轴交于两点A 、B ,它的对称轴与x 轴交于点N .过顶点M 作ME ⊥y 轴,垂足为E ,连接BE ,交MN 于点F ,则△EMF 与△BNF 的面积的比为 ▲ .16.如图,在⊙O 中,C 是弦AB 上一点,AC =2,CB =4.连接OC ,过点C 作DC ⊥OC ,与⊙O 交于点D ,DC 的长为 ▲ .OA BEF(第13题)(第14题)123 (第15题)三、解答题(本大题共11小题,共88分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.(6分)求二次函数y =x 2+4x +5的最小值,并求出对应的x 的值.18.(8分)用代入法解二元一次方程组⎩⎨⎧x +y =10,2x +y =16的过程可以用下面的框图表示:尝试按照以上思路求方程组⎩⎨⎧x -y =0,x 2+2y =4的解.19.(6分)将二次函数y =ax 2+bx +1的图像向左平移1个单位长度后,经过点(0,3)、(2,-5),求a 、b 的值.20.(8分)青山村种的水稻2015年平均每公顷产7000 kg ,2017年平均每公顷产8470 kg .求该村种的水稻每公顷产量的年平均增长率.21.(6分)某地铁站有4个出站口,分别为1号、2号、3号、4号,小华和小明先后在该地铁站下车,任意选择一个出站口出站.(1)小华从1号出站口出站的概率是 ▲ ; (2)求两人不从..同一个出站口出站的概率.22.(8分)在物理课上,我们学习过“小孔成像”——用一个带有小孔的薄板遮挡在物体与光屏之间,在光的照射下,光屏上就会形成一个倒立的实像.如图,光线分别经过物体AB 的两端A 、B 和小孔P ,投射在与AB 平行的光屏l 上形成了实像A'B'.已知AB =a ,小孔P 与AB 、l 的距离分别为m 、n .求A'B' 的长(用含a 、m 、n 的代数式表示).23.(8分)某食品商店将甲、乙、丙3种糖果的质量按5∶4∶1配置成一种什锦糖果,已知甲、乙、丙三种糖果的单价分别为16元/kg 、20元/kg 、27元/kg .若将这种什锦糖果的单价定为这三种糖果单价的算术平均数,你认为合理吗?如果合理,请说明理由;如果不合理,请求出该什锦糖果合理的单价.l(第22题)24.(8分)如图,AB 为⊙O 的直径,AB =4,C 为⊙O 上一点,且AC ⌒=BC ⌒,P 为BC ⌒上的一动点,延长AP 至Q ,使得AP •AQ =AB 2,连接BQ . (1)求证:直线BQ 是⊙O 的切线;(2)若点P 由点B 运动到点C ,则线段PQ 扫过的面积是 ▲ .(结果保留π)25.(8分)已知二次函数y =(x -1)(x -m -3)(m 为常数).(1)求证:不论m 为何值,该函数的图像与x 轴总有公共点; (2)当m 取什么值时,该函数的图像与y 轴的交点在x 轴的下方?26.(10分)如图①,P 是⊙O 外一点,过点P 做⊙O 的两条切线,切点分别为A 、B .若∠APB =60°,则点P 叫做⊙O 的切角点.(1)如图②,⊙O 的半径是1,点O 到直线l 的距离为2.若点P 是⊙O 的切角点,且点P 在直线l 上,请用尺规作出点P ;(保留作图痕迹,不写作法)(2)如图③,在Rt △ABC 中,∠ACB =90°,∠A =30°,BC =1+3,⊙O 是△ABC的内切圆.若点P 是⊙O 的切角点,且点P 在△ABC 的边上,求AP 的长.C P(第26题)①② ③lC(第24题)27.(12分) 问题情境有一堵长为a m 的墙,利用这堵墙和长为60 m 的篱笆围成一个矩形养鸡场,怎样围面积最大?最大面积是多少? 题意理解根据题意,有两种设计方案:一边靠墙(如图①)和一边“包含”墙(如图②). 特例分析(1)当a =12时,若按图①的方案设计,则该方案中养鸡场的最大面积是 ▲ m 2;若按图②的方案设计,则该方案中养鸡场的最大面积是 ▲ m 2. (2)当a =20时,解决“问题情境”中的问题.解决问题(3)直接写出“问题情境”中的问题的答案.①②(第27题)九年级数学参考答案及评分标准说明:本评分标准每题给出了一种或几种解法供参考,如果考生的解法与本解答不同,参照本评分标准的精神给分.二、填空题(每小题2分,共计20分)7.56 8.3 9.20π 10.14 11.y =2x 2+312.2,3 13 14.84 15.1∶4 16.2 2三、解答题(本大题共11小题,共计88分) 17.(本题6分)解:方法一y =x 2+4x +5=(x +2)2+1. ····························································································· 2分 所以二次函数y =x 2+4x +5的最小值是1. ························································· 4分 对应的x 的值为-2. ······················································································ 6分 方法二 二次函数y =x 2+4x +5的最小值=4ac -b 24a··························································· 1分=1, ································································ 3分x =-b2a········································································································ 4分=-2. ······································································································ 6分18.(本题8分)解: ⎩⎨⎧x -y =0, ①x 2+2y =4. ②由①,得y =x . ③ ························································································ 2分 将③代入②,得x 2+2x =4. ····························································································· 4分解这个方程,得x 1=-1x 2=-1 ····················································· 6分将x 1、x 2分别代入③,得y 1=-1y 2=-1所以,原方程组的解是⎩⎪⎨⎪⎧x 1=-1 y 1=-1x 2=-1 y 2=-1······································ 8分(说明:在正确求出x 、y 1分)19.(本题6分)解:二次函数图像向左平移1个单位长度后,经过点(0,3)、(2,-5),可得原二次函数图像经过点(1,3)、(3,-5), ····························································· 2分 得⎩⎨⎧a +b +1=3,9a +3b +1=-5.························································································· 4分 解得 a =-2,b =4.······················································································ 6分20.(本题8分)解:设该村种的水稻每公顷产量的年平均增长率为x . ······················································· 1分根据题意,得7000(1+x )2=8470. ····························································································· 5分 解这个方程,得x 1=0.1,x 2=-2.1(不合题意,舍去). ·································································· 7分答:该村种的水稻每公顷产量的年平均增长率为10%. ········································· 8分 (说明:未列方程,只写了“设……”不给分.)21.(本题6分)解:(1)14. ········································································································ 2分(2)两人任意选择一个出站口出站,所有可能出现的结果有:(1,1)、(1,2)、(1,3)、(1,4)、(2,1)、(2,2)、(2,3)、(2,4)、(3,1)、(3,2)、(3,3)、(3,4)、(4,1)、(4,2)、(4,3)、(4,4),共有16种,它们出现的可能性相同.所有的结果中,满足“两人不从同一个出站口出站”(记为事件A )的结果有12种,所以P (A )= 34. ·················································· 6分(说明:少说明“等可能性”扣1分)22.(本题8分)解:∵AB ∥A'B',∴∠A =∠A',∠B =∠B'. ··································································· 2分∴△APB ∽△A'PB',且相似比为m ∶n . ····························································· 4分∴AB A'B'=m n. ·································································································· 6分 又∵AB =a ,∴A'B'=an m. 所以A'B' 的长为anm. ······················································································ 8分23.(本题8分)解:这样定价不合理. ·································································································· 1分x —=16×510+20×410+27×110 ··················································································· 4分=18.7(元/kg ). ····························································································· 7分 答:该什锦糖果合理的单价为18.7元/kg . ································································· 8分24.(本题8分) (1)证明:连接PB .∵AB 是⊙O 的直径,∴∠APB =90°. ···································· 1分 ∵AP •AQ =AB 2,∴AP AB =ABAQ . ·················· 2分在△ABP 和△AQB 中,∠BAP =∠QAB , ∴△ABP ∽△AQB . ······························· 4分 ∴∠ABQ =∠APB =90°,即AB ⊥BQ . ······ 5分 ∵AB 是⊙O 的直径,∴直线BQ 是⊙O 的切线. ······································································ 6分(2)解:6-π.···································································································· 8分25.(本题8分) (1)证明:方法一 当y =0时,(x -1)(x -m -3)=0. ··························································· 1分解得x 1=1,x 2=m +3. ········································································ 3分 当m +3=1,即m =-2时,方程有两个相等的实数根;当m +3≠1,即 m ≠-2时,方程有两个不相等的实数根.所以,不论m 为何值,该函数的图像与x 轴总有公共点. ···························· 4分C方法二 将原表达式化为y =x 2-(m +4)x +m +3. ················································· 1分 因为一元二次方程x 2-(m +4)x +m +3=0 ················································· 2分 的根的判别式b 2-4ac =[-(m +4)] 2-4(m +3)=m 2+4m +4=(m +2)2≥0. ······················· 3分所以,不论m 为何值,该函数的图像与x 轴总有公共点. ···························· 4分 (2)解:当x =0时,y =m +3,即该函数的图像与y 轴交点的纵坐标是m +3. ················ 6分当m +3<0,即m <-3时,该函数的图像与y 轴的交点在x 轴的下方. ············· 8分26.(本题10分)解:(1)如图,点P 即为所求. ···································(说明:若点P 未在图中标出,也没有写结论扣1分;若图中标出了点P ,未写结论不扣分)(2)∵在Rt △ABC 中,∠ACB =90°,∠A =30°,BC =1+3,∴AB =2+23,AC =3+3. ···································································· 6分 ∵⊙O 是△ABC 的内切圆,设AB 、BC 、AC 分别与⊙O 相切于点M 、N 、D ,∴OD ⊥AC ,ON ⊥BC ,OM ⊥AB ,BM =BN ,CN =CD ,AM =AD . ∵∠ACB =90°,∴四边形ONCD 为矩形. ∵OD =ON ,∴矩形ONCD 为正方形. 设⊙O 的半径为r ,则CN =CD =r , BN =BM =1+3-r ,MA =AD =1+3+r . ∴AC =AD +CD =1+3+r +r . 即1+3+r +r =3+3.解得 r =1. ···························································································· 7分 ∴CD =1,BM =3.如图①,∵∠B =60°,且BA 、BC 与⊙O 分别相切于点M 、N ,∴点B 是⊙O 的切角点,即点P 与点B 重合,此时AP =AB =2+23. ·············· 8分① (P )如图②,若⊙O 的切角点P 在线段AB 上,PQ 与⊙O 相切于点Q . 由切角点的概念知∠MPQ =60°.连接MO 、QO 、PO ,有∠PMO =∠PQO =90°. ∵MO 、QO 是⊙O 的半径,∴MO =QO . ∵PO =PO ,∴△PMO ≌△PQO . ∴∠MPO =∠QPO =12∠MPQ =30°.∵r =1,∴MP =3.∴AP =BA -BM -MP =2. ····································· 9分 如图③,若⊙O 的切角点P 在线段AC 上. 与上一种情况类似计算可得PD =3. 则AP =AC -CD -PD =2.综上,AP 的长为2+23或2. ·································································· 10分27.(本题12分)解:(1)288,324. ······························································································· 2分(2)如图①,设AB =x m ,则BC =(60-2x ) m . 所以S 矩形ABCD =x (60-2x )=-2(x -15)2+450. ········································· 4分根据题意,得20≤x <30. 因为-2<0,所以当20≤x <30时,S 矩形ABCD 随x 的增大而减小.即当x =20时,S 矩形ABCD 有最大值,最大值是400(m 2).··································· 5分如图②,设AB =x m ,则BC =(40-x ) m .所以S 矩形ABCD =x (40-x )=-(x -20)2+400.································ 7分根据题意,得0<x ≤20. 因为-1<0, 所以当x =20时,S 矩形ABCD 有最大值,最大值是400(m 2). ······················································ 8分综上,当a =20时,该养鸡场围成一个边长为20 m 的正方形时面积最大,最大面积是400 m 2. ····················································································· 9分D ③②CD(3)当0<a ≤20时,围成边长为a +604m 的正方形面积最大,最大面积是a 2+120a +360016m 2.当20<a <30时,围成两邻边长分别为a m ,60-a 2m 的养鸡场面积最大,最大面积为-a 2+60a 2m 2.当a ≥30时,当矩形的长为30 m ,宽为15 m 时,养鸡场最大面积为450 m 2.····························································································································· 12分。
苏科版九年级数学上册第2周周练试题(2B)

初中数学试卷满分值 时 间 制 卷 审 核 得 分 100分45分钟丁银东孙孝红一、选择题(本题包括4小题,每小题4分,共16分,每小题只有一个选项符合题意) 1.用配方法解方程2250x x --=时,原方程应变形为( )A .()216x +=B .()216x -=C .()229x +=D .()229x -=2.已知方程20x bx a ++=有一个根是(0)a a -≠,则下列代数式的值恒为常数的是( )A .abB .abC .a b +D .a b - 3.如果关于x 的一元二次方程22(21)10k x k x -++=有两个不相等的实数根,那么k 的取值范围是( ) A.k >14-B.k >14-且0k ≠ C .k <14- D.14k ≥-且0k ≠ 4.已知a 、b 、c 分别是三角形的三边,则方程(a + b )x 2+ 2cx + (a + b )=0的根的情况是( )A .没有实数根 B .可能有且只有一个实数根C .有两个相等的实数根D .有两个不相等的实数根二、细心填一填(6×4=24分) 5.方程042=-x x 的解是_____________6.某种商品原价是120元,经两次降价后的价格是100元,求平均每次降价的百分率.设 平均每次降价的百分率为x ,可列方程为7.已知关于x 的一元二次方程m 2x 2+(2m -1)x+1=0有两个不相等的实数根,则m 的取值范围 是8.若(a 2+b 2)(a 2+b 2-2)=8,则a 2+b 2=9.m 是方程21x x +-=0的根,则式子2010223++m m 的值为10.设x 1、x 2 是一元二次方程x 2+4x -3=0的两个根,2x 1(x 22+5x 2-3)+a =2,则a = 三、用心做一做(60分) 11.解方程(5×3)(1)01522=--x x (2)23(3)(3)0x x x -+-= (3))1(322+=x x12.(15分)在等腰△ABC 中,三边分别为a 、b 、c ,其中5a =,若关于x 的方程()2260x b x b +++-=有两个相等的实数根,求△ABC 的周长.13.(15分)(2014•毕节地区)某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.(1)若生产第x 档次的产品一天的总利润为y 元(其中x 为正整数,且1≤x ≤10),求出y 关于x 的函数关系式;(2)若生产第x 档次的产品一天的总利润为1120元,求该产品的质量档次.14.(15分)在Rt△ABC中,AB=BC=12cm,点D从点A开始沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC。
苏科版九年级数学上册第一周初三周周练.docx

初中数学试卷桑水出品翠岗中学第一周初三数学周周练班级姓名一.选择题1.(2014•历下区二模)下列关于x的方程中,一定是一元二次方程的为()A.ax2+bx+c=0 B.x2﹣2=(x+3)2C.D.x2﹣1=02.(2014•湖里区模拟)若关于x的一元二次方程ax2+bx﹣3=0满足4a﹣2b=3,则该方程一定有的根是()A.1 B .2C.﹣1 D.﹣23.(2014•本溪一模)已知关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为()A.1 B.﹣1 C.1或﹣1 D.4.(2013•牡丹江)若关于x的一元二次方程为ax2+bx+5=0(a≠0)的解是x=1,则2013﹣a﹣b的值是()A.2018 B.2008 C.2014 D.20125.关于x的方程(a ﹣1)x2+x+1=0是一元二次方程,则a的取值范围是()A.a≠1 B.a>﹣1且a≠1 C.a≥﹣1且a≠1 D.a为任意实数6.(2013•民勤县一模)若x2﹣3x﹣1=0,则x﹣的值为()A.3 B.0C.6D.﹣67.(2013•广东模拟)下列说法中,正确的说法有()①反比例函数的图象位于第二、四象限;②一元二次方程x2﹣3x=0的常数项不存在;③对角线互相平分且相等的四边形是矩形;④随机掷两枚硬币,落地后全部正面朝上的概率是.A.1个B.2个C.3个D.4个8.(2012•鄂尔多斯)若a是方程2x2﹣x﹣3=0的一个解,则6a2﹣3a的值为()A.3 B.﹣3 C.9D.﹣99.关于x的方程是一元二次方程,则()A.m=2 B.m=3 C.m=5 D.m=3或m=210.关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,则实数a的值为()A.﹣1 B.0C.1D.﹣1或111.已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是()A.m≥﹣B.m≥0 C.m≥1 D.m≥212.若一元二次方程式a(x﹣b)2=7的两根为±,其中a、b为两数,则a+b之值为何?()A.B.C.3D.513.(2013•鄞州区模拟)已知一元二次方程(x﹣3)2=1的两个解恰好分别是等腰△ABC的底边长和腰长,则△ABC的周长为()A.10 B.10或8 C.9D.814.(2014•衡阳三模)用配方法解一元二次方程x2+4x﹣5=0,此方程可变形为()A.(x+2)2=9 B.(x﹣2)2=9 C.(x+2)2=1 D.(x﹣2)2=115.已知一元二次方程x2+mx+3=0配方后为(x+n)2=22,那么一元二次方程x2﹣mx﹣3=0配方后为()A.(x+5)2=28 B.(x+5)2=19或(x﹣5)2=19C.(x﹣5)2=19 D.(x+5)2=28或(x﹣5)2=2816.(2014•海南)某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是()A.100(1+x)2=81 B.100(1﹣x)2=81 C.100(1﹣x%)2=81 D. 100x2=81 17.(2014•白银)用10米长的铝材制成一个矩形窗框,使它的面积为6平方米.若设它的一条边长为x 米,则根据题意可列出关于x的方程为()A.x(5+x)=6 B.x(5﹣x)=6 C.x(10﹣x)=6 D.x(10﹣2x)=6 18.(2014•天津)要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为()A.x(x+1)=28 B.x(x﹣1)=28 C.x(x+1)=28 D. x(x﹣1)=2819.(2014•含山县一模)某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八九月份平均每月的增长率为x,那么满足的方程是()A.50(1+x)2=196 B.50+50(1+x2)=196C.50+50(1+x)+50(1+2x)=196 D.50+50(1+x)+50(1+x)2=19620.(2013•昆明)如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2,则道路的宽应为多少米?设道路的宽为x米,则可列方程为()A.100×80﹣100x﹣80x=7644 B.(100﹣x)(80﹣x)+x2=7644C.(100﹣x)(80﹣x)=7644 D.100x+80x=356二.填空题1.(2010•南昌模拟)方程x2+1=﹣2(1﹣3x)化为一元二次方程的一般形式后,二次项系数为_________,一次项系数是_________.2.(2014•徐州模拟)已知实数m是关于x的方程x2﹣3x+2=0的一根,则代数式2m2﹣6m+2值为_________.3.(2013•上城区二模)关于x的方程a(x+m)2+b=0的解是x1=﹣3,x2=5(a,m,b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是_________.4.已知关于x的一元二次方程x2+bx+c=0有一个根为c(c≠0),则b+c的值为_________.5.若关于x 的一元二次方程(m ﹣1)x 2+5x+m 2﹣3m+2=0的常数项为0,则m 的值等于 ___. 6.(2012•荆州模拟)关于x 的一元二次方程(m ﹣1)x 2+x+m 2﹣1=0有一根为0,则m= _________ .7.当m =_______时,代数式x 2-8x +m 为完全平方式;当k =_______时,代数式x 2-kx +3为完全平方式.当m = 时,4x 2+2(m -1)x +9=0是一个完全平方式.8.已知x 2+y 2+4x -6y +13=0,x 、y 为实数,则x y =_______.9.已知a ,b 是方程x 2﹣x ﹣3=0的两个根,则代数式2a 3+b 2+3a 2﹣11a ﹣b +5的值为10.已知(a 2+b 2+1)2=16,则a 2+b 2的值为 .11.在实数范围内定义一种运算“*”,其规则为a*b=ab+2a ﹣2b .根据这个规则,方程(x ﹣1)*x=0的解为 _________.12.已知实数a ,b 满足条件:a 2+4b 2-a +4b +54=0,-ab 的平方根 .13.(2014•济宁)若一元二次方程ax 2=b (ab >0)的两个根分别是m+1与2m ﹣4,则= _________ .14.我们知道,一元二次方程x 2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i ”,使其满足i 2=﹣1(即方程x 2=﹣1有一个根为i ).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i 1=i ,i 2=﹣1,i 3=i 2•i=(﹣1)•i=﹣i ,i 4=(i 2)2=(﹣1)2=1,从而对于任意正整数n ,我们可以得到i 4n+1=i 4n •i=(i 4)n •i=i ,同理可得i 4n+2=﹣1,i 4n+3=﹣i ,i 4n =1.那么i+i 2+i 3+i 4+…+i 2012+i 2013的值为 _________ .三.解答题(共2小题)15.解方程:1. (x+1)2=(1﹣2x )2.2. 4(2x ﹣1)2=9(x+4)2.3. (x+)2﹣8=0.4.(x+1)(x ﹣1)=3. 5.用配方法解方程:x 2﹣2x=5. 6. y 2-3x -2=0;7.4x 2﹣6x ﹣4=0(用配方法) 8. 219322x x -+=16.已知关于x 的方程(m 2﹣9)x 2+(m+3)x ﹣5=0.①当m 为何值时,此方程是一元一次方程?并求出此时方程的解.②当m 为何值时,此方程是一元二次方程?并写出这个方程的二次項系数、一次项系数及常数项.17.已知关于x 的方程(m 2﹣8m+20)x 2+2mx+3=0,求证:无论m 为任何实数,该方程都是一元二次方程.18.用配方法求(1)3x2-4x+8的最小值;(2)-2x2+4x-1的最大值.19.请阅读下列材料:问题:已知方程x2+x-3=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.解:设所求方程的根为y,则y=2x,所以x=y2.把x=y2代入已知方程,得(y2)2+y2-3=0化简,得y2+2y-12=0故所求方程为y2+2y-12=0.这种利用方程根的代换求新方程的方法,我们称为“换根法”.(1)已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程根的3倍,则所求方程为;(2)已知关于x的一元二次方程ax2+bx+c=0有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;(3)已知关于x的方程x2-mx+n=0有两个实数根,求一个一元二次方程,使它的根分别是已知方程根的平方.20.如图,在平面直角坐标系中,矩形OABC的边OA=2,OC=6,在OC上取点D将△AOD沿AD翻折,使O点落在AB边上的E点处,将一个足够大的直角三角板的顶点P从D点出发沿线段DA→AB移动,且一直角边始终经过点D,另一直角边所在直线与直线DE,BC分别交于点M,N.(1)填空:D点坐标是(,),E点坐标是(,);(2)如图1,当点P在线段DA上移动时,是否存在这样的点M,使△CMN为等腰三角形?若存在,请求出M点坐标;若不存在,请说明理由;。
苏科版九年级上数学周练作业(2)

九年级数学周练作业02(2013年9月13日)班级 学号 姓名 自我评价一.选择题(每题3分,共24分) (同学们辛苦啦!祝同学们学习生活快乐!)1.若等腰三角形的一个底角为50°,则顶角为 ( ) A .50° B .100° C .80° D .65°2.等腰三角形的腰长5,底边长为6,则该等腰三角形的面积为 ( ) A .15 B .24 C .30 D .123.下列命题中,真命题是 ( ) A.两条对角线相等的四边形是矩形 B.两条对角线互相垂直的四边形是菱形 C.两条对角线互相垂直且相等的四边形是正方形 D.两条对角线互相平分的四边形是平行四边形4.已知菱形的两条对角线长分别为6和8,则菱形的周长为 ( ) A .20 B .30 C .40 D .105.如图,在菱形ABCD 中,不一定成立的 ( ) A .四边形ABCD 是平行四边形B .AC ⊥BDC .△ABD 是等边三角形 D .∠CAB =∠CAD6.如图,在ABC △中,点E D F ,,分别在边AB ,BC ,CA 上,且DE CA ∥,DF BA ∥.下列四个判断中,不正确...的是 ( ) A.四边形AEDF 是平行四边形 B.如果90BAC ∠=,那么四边形AEDF 是矩形C.如果AD 平分BAC ∠,那么四边形AEDF 是菱形D.如果AD BC ⊥且AB AC =,那么四边形AEDF 是正方形7.如上图,AD 是△ABC 的中线,E 是AD 的中点,BE 的延长线交AC 于点F ,若FC=12 则AF 的长为: A.4 B. 6 C. 10 D.8 ( ) 8.如上图,在矩形ABCD 中,AD=2AB ,点E 是BC 上一点,且AE=AD ,则∠CDE 等于 A .65° B .15° C .22.5° D .30° ( ) 二.填空题(每小题3分,共30分)9.已知平行四边形ABCD 中,AB=14cm,BC=16cm,则此平行四边形的周长为 _____cm. 10.矩形的两条对角线的夹角为600,较短的边长为12cm,则对角线长为 cm.11.如图,在平面四边形ABCD 中,CE AB ⊥,E 为垂足.如果125A =∠,则B C E =∠ 12.在四边形ABCD 中,已知AB ∥CD ,请补充一个条件: ,使得四EDCBAAFCDBE第6题FEDC BA第7题第8题边形ABCD 是平行四边形。
九年级数学上学期第一次双周测试试题(含解析) 苏科版-苏科版初中九年级全册数学试题

某某省某某市启东市滨海实验学校2016届九年级数学上学期第一次双周测试试题一、选择题1.下列函数中是二次函数的是()A.y=ax2+bx+c B.y=x3+2x﹣3 C.y=(x+1)2﹣x2D.y=3x2﹣12.二次函数y=ax2+bx+c图象上部分点的坐标满足下表:x …﹣3 ﹣2 ﹣1 0 1 …y …﹣3 ﹣2 ﹣3 ﹣6 ﹣11 …则该函数图象的顶点坐标为()A.(﹣3,﹣3) B.(﹣2,﹣2) C.(﹣1,﹣3) D.(0,﹣6)3.若二次函数y=(m+1)x2﹣mx+m2﹣2m﹣3的图象经过原点,则m的值必为()A.﹣1或3 B.﹣1 C.3 D.﹣3或14.抛物线y=x2﹣2x+1与坐标轴交点个数为()A.无交点B.1个C.2个D.3个5.如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0其中正确的个数为()A.1 B.2 C.3 D.46.如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是()A.2m B.3m C.4m D.5m二、填空题7.y=(k﹣3)+x﹣2是一个开口向下的二次函数,那么k=.8.在平面直角坐标系中,将抛物线y=x2﹣4先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为.9.已知抛物线y=﹣x2﹣x+c的顶点为(m,3),则m=,c=.10.二次函数y=2x2+mx+8的图象如图所示,则m的值是.11.已知y=﹣(x﹣3)2+2,若点A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,则y1y2(填<、>或=)12.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+b(k≠0)的图象相交于点A(﹣2,4),B(8,2),如图所示,则能使y1<y2成立的x的取值X围是.13.将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个;若这种商品的零售价在一定X围内每降价2元,其日销售量就增加4个,为了获得最大利润,则售价为元,最大利润为元.14.如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为.三、简答题15.已知二次函数y=﹣x2﹣2x+3.(1)求它的顶点坐标和对称轴;(2)求它与x轴、y轴的交点坐标;(3)直接写出x为何值时,y≤0?16.如图,已知二次函数y=﹣+bx+c的图象经过A(2,0)、B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.17.已知开口向上的抛物线y=ax2﹣2x+|a|﹣4经过点(0,﹣3).(1)确定此抛物线的解析式;(2)当x取何值时,y有最小值,并求出这个最小值.18.已知:抛物线的解析式为y=x2﹣(2m﹣1)x+m2﹣m,(1)求证:此抛物线与x轴必有两个不同的交点;(2)若此抛物线与直线y=x﹣3m+4的一个交点在y轴上,求m的值.19.如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,当一点到达终点时,另一点也停止运动.设运动时间为x秒,△PBQ的面积为y(cm2).(1)求y关于x的函数关系式,并写出x的取值X围;(2)求△PBQ的面积的最大值.20.如图,经过点A(0,﹣4)的抛物线y=x2+bx+c与x轴相交于B(﹣2,0),C两点,O为坐标原点.(1)求抛物线的解析式;(2)将抛物线y=x2+bx+c向上平移个单位长度,再向左平移m(m>0)个单位长度得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值X围;(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,求AM的长.2015-2016学年某某省某某市启东市滨海实验学校九年级(上)第一次双周测试数学试卷参考答案与试题解析一、选择题1.下列函数中是二次函数的是()A.y=ax2+bx+c B.y=x3+2x﹣3 C.y=(x+1)2﹣x2D.y=3x2﹣1【考点】二次函数的定义.【分析】根据二次函数的定义,即可作出判断.【解答】解:A、当a=0时不是二次函数,故选项错误;B、最高次数是3,不是二次函数,选项错误;C、化简后是y=2x+1是一次函数,选项错误;D、是二次函数,选项正确.故选D.【点评】本题考查了二次函数的定义.要特别注意二次项系数a≠0这一条件,当a=0时,若二次系数等于0就不是二次函数了,而b,c可以是0.2.二次函数y=ax2+bx+c图象上部分点的坐标满足下表:x …﹣3 ﹣2 ﹣1 0 1 …y …﹣3 ﹣2 ﹣3 ﹣6 ﹣11 …则该函数图象的顶点坐标为()A.(﹣3,﹣3) B.(﹣2,﹣2) C.(﹣1,﹣3) D.(0,﹣6)【考点】二次函数的性质.【专题】压轴题.【分析】根据二次函数的对称性确定出二次函数的对称轴,然后解答即可.【解答】解:∵x=﹣3和﹣1时的函数值都是﹣3相等,∴二次函数的对称轴为直线x=﹣2,∴顶点坐标为(﹣2,﹣2).故选:B.【点评】本题考查了二次函数的性质,主要利用了二次函数的对称性,仔细观察表格数据确定出对称轴是解题的关键.3.若二次函数y=(m+1)x2﹣mx+m2﹣2m﹣3的图象经过原点,则m的值必为()A.﹣1或3 B.﹣1 C.3 D.﹣3或1【考点】二次函数图象上点的坐标特征.【分析】将原点坐标代入二次函数y=(m+1)x2﹣mx+m2﹣2m﹣3中即可求出m的值,注意二次函数的二次项系数不为零.【解答】解:根据题意得m2﹣2m﹣3=0,所以m=﹣1或m=3,又因为二次函数的二次项系数不为零,即m+1≠0,所以m=3.故选C.【点评】本题考查了二次函数图象上点的坐标特征,解题时注意分析,注意理解题意.4.抛物线y=x2﹣2x+1与坐标轴交点个数为()A.无交点B.1个C.2个D.3个【考点】抛物线与x轴的交点.【分析】当x=0时,求出与y轴的纵坐标;当y=0时,求出关于x的一元二次方程x2﹣2x+1=0的根的判别式的符号,从而确定该方程的根的个数,即抛物线y=x2﹣2x+1与x轴的交点个数.【解答】解:当x=0时,y=1,则与y轴的交点坐标为(0,1),当y=0时,x2﹣2x+1=0,△=(﹣2)2﹣4×1×1=0,所以,该方程有两个相等的解,即抛物线y=x2﹣2x+2与x轴有1个点.综上所述,抛物线y=x2﹣2x+1与坐标轴的交点个数是2个.故选C.【点评】此题考查了抛物线与x轴的交点,以及一元二次方程的解法,其中令抛物线解析式中x=0,求出的y值即为抛物线与y轴交点的纵坐标;令y=0,求出对应的x的值,即为抛物线与x轴交点的横坐标.5.如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0其中正确的个数为()A.1 B.2 C.3 D.4【考点】二次函数图象与系数的关系.【专题】压轴题.【分析】由抛物线的开口方向判断a与0的关系,由x=1时的函数值判断a+b+c>0,然后根据对称轴推出2a+b与0的关系,根据图象判断﹣1<x<3时,y的符号.【解答】解:①图象开口向下,能得到a<0;②对称轴在y轴右侧,x==1,则有﹣=1,即2a+b=0;③当x=1时,y>0,则a+b+c>0;④由图可知,当﹣1<x<3时,y>0.故选C.【点评】本题主要考查图象与二次函数系数之间的关系,会利用对称轴的X围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.6.如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是()A.2m B.3m C.4m D.5m【考点】二次函数的应用.【分析】由题意可以知道M(1,),A(0,10)用待定系数法就可以求出抛物线的解析式,当y=0时就可以求出x的值,这样就可以求出OB的值.【解答】解:设抛物线的解析式为y=a(x﹣1)2+,由题意,得10=a+,a=﹣.∴抛物线的解析式为:y=﹣(x﹣1)2+.当y=0时,0=﹣(x﹣1)2+,解得:x1=﹣1(舍去),x2=3.OB=3m.故选:B.【点评】此题考查了利用待定系数法求函数的解析式的运用,运用抛物线的解析式解决实际问题.解答本题是时设抛物线的顶点式求解析式是关键.二、填空题7.y=(k﹣3)+x﹣2是一个开口向下的二次函数,那么k= ﹣1 .【考点】二次函数的定义.【分析】根据二次函数的定义函数的最高次数是2,然后根据函数开口向下,则二次项系数小于0,据此即可求解.【解答】解:根据题意得:k2﹣3k﹣2=2且k﹣3<0,解得:k=﹣1.故答案是:﹣1.【点评】本题考查了二次函数的定义.要特别注意二次项系数a≠0这一条件,当a=0时,若二次系数等于0就不是二次函数了,而b,c可以是0.8.在平面直角坐标系中,将抛物线y=x2﹣4先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为y=(x﹣2)2﹣2 .【考点】二次函数图象与几何变换.【分析】直接根据平移规律作答即可.【解答】解:将抛物线y=x2﹣4先向右平移2个单位,再向上平移2个单位后所得抛物线解析式为y=(x ﹣2)2﹣4+2.即y=(x﹣2)2﹣2.故答案为:y=(x﹣2)2﹣2.【点评】本题考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.9.已知抛物线y=﹣x2﹣x+c的顶点为(m,3),则m= ﹣1 ,c=.【考点】二次函数的性质.【分析】把二次函数解析式整理成顶点式形式,然后根据顶点坐标分别求解即可.【解答】解:y=﹣x2﹣x+c=﹣(x+1)2++c,∵顶点为(m,3),∴m=1, +c=3,解得c=.故答案为:﹣1,.【点评】本题考查了二次函数的性质,把二次函数解析式整理成顶点式形式求解更简便.10.二次函数y=2x2+mx+8的图象如图所示,则m的值是8 .【考点】抛物线与x轴的交点.【分析】利用抛物线与x轴交点个数与b2﹣4ac进而得出m的值,再利用a,b符号与对称轴之间的关系求出即可.【解答】解:∵二次函数图象与x轴一个交点,∴b2﹣4ac=m2﹣4×2×8=0,解得:m1=8,m2=﹣8,∵二次函数图象对称轴在y轴左侧,则a,b同号,∴m=8.故答案为:8.【点评】此题主要考查了抛物线与x轴的交点,熟练记忆有关规律是解题关键.11.已知y=﹣(x﹣3)2+2,若点A(m,y1)、B(n,y2)(m<n<3)都在该抛物线上,则y1<y2(填<、>或=)【考点】二次函数图象上点的坐标特征.【分析】先判断函数的增减性,根据A、B的坐标可得出答案.【解答】解:∵y=﹣(x﹣3)2+2,∴抛物线对称轴为x=3,开口向下,∴当x<3时,y随x增大而增大,∵m<n<3,∴y1<y2.故答案为:<.【点评】本题主要考查二次函数的增减性,根据二次函数解析式判断出增减性是解题的关键.12.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+b(k≠0)的图象相交于点A(﹣2,4),B(8,2),如图所示,则能使y1<y2成立的x的取值X围是﹣2<x<8 .【考点】二次函数与不等式(组).【专题】数形结合.【分析】根据图象,找出二次函数图象在一次函数图象下方的部分的x的取值X围即可.【解答】解:由图形可得,当﹣2<x<8时,二次函数图象在一次函数图象下方,y1<y2,所以,使y1<y2成立的x的取值X围是﹣2<x<8.故答案为:﹣2<x<8.【点评】本题考查了二次函数与不等式,根据函数图象求不等式的解,关键在于认准在上方与下方的函数图象所对应的函数解析式,数形结合是数学中的重要思想之一.13.将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个;若这种商品的零售价在一定X围内每降价2元,其日销售量就增加4个,为了获得最大利润,则售价为90 元,最大利润为800 元.【考点】二次函数的最值.【分析】设降价x元,利润为y,利用总利润等于单个的利润乘以销售量得到y=(100﹣70﹣x)(20+2x),利用配方法得到y=﹣2(x﹣10)2+800,然后根据二次函数的最值问题求解.【解答】解:设降价x元,利润为y,y=(100﹣70﹣x)(20+2x)=﹣2x2+40x+600=﹣2(x﹣10)2+800,当x=10时,y的最大值为800,即售价为90元时,最大利润为800元.故答案为90,800.【点评】本题考查了二次函数的最值:对于二次函数y=ax2+bx+c(a≠0),其顶点式为y=a(x+)2+当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=﹣时,y=;当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=﹣时,y=.14.如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为.【考点】二次函数图象与几何变换.【专题】压轴题.【分析】根据点O与点A的坐标求出平移后的抛物线的对称轴,然后求出点P的坐标,过点P作PM⊥y轴于点M,根据抛物线的对称性可知阴影部分的面积等于矩形NPMO的面积,然后求解即可.【解答】解:过点P作PM⊥y轴于点M,∵抛物线平移后经过原点O和点A(﹣6,0),∴平移后的抛物线对称轴为x=﹣3,得出二次函数解析式为:y=(x+3)2+h,将(﹣6,0)代入得出:0=(﹣6+3)2+h,解得:h=﹣,∴点P的坐标是(﹣3,﹣),根据抛物线的对称性可知,阴影部分的面积等于矩形NPMO的面积,∴S=|﹣3|×|﹣|=.故答案为:.【点评】本题考查了二次函数的问题,根据二次函数的性质求出平移后的抛物线的对称轴的解析式,并对阴影部分的面积进行转换是解题的关键.三、简答题15.已知二次函数y=﹣x2﹣2x+3.(1)求它的顶点坐标和对称轴;(2)求它与x轴、y轴的交点坐标;(3)直接写出x为何值时,y≤0?【考点】二次函数的性质.【分析】(1)将抛物线的一般式化为顶点式,就可以确定对称轴,顶点;(2)要求抛物线与x轴的交点,就要把解析式化为交点式,即可得到与坐标轴交点的坐标,令x=0求得与y轴的交点坐标;(3)利用二次函数的性质与x轴的交点坐标直接得出答案即可.【解答】解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点(1,4),对称轴x=1;(2)∵y=﹣x2+2x+3=﹣(x﹣3)(x+1)∴与x轴交点(3,0),(﹣1,0),与y轴交点(0,3);(2)当x≥3,或x≤﹣1时,y≤0.【点评】此题考查二次函数的性质,抛物线的对称轴、顶点坐标与抛物线解析式的关系,抛物线的顶点式:y=a(x﹣h)2+k,顶点坐标为(h,k),对称轴x=h.同时考查了用抛物线与x轴的交点坐标.16.如图,已知二次函数y=﹣+bx+c的图象经过A(2,0)、B(0,﹣6)两点.(1)求这个二次函数的解析式;(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.【考点】二次函数综合题.【专题】综合题.【分析】(1)二次函数图象经过A(2,0)、B(0,﹣6)两点,两点代入y=﹣+bx+c,算出b 和c,即可得解析式.(2)先求出对称轴方程,写出C点的坐标,计算出AC,然后由面积公式计算值.【解答】解:(1)把A(2,0)、B(0,﹣6)代入y=﹣+bx+c,得:解得,∴这个二次函数的解析式为y=﹣+4x﹣6.(2)∵该抛物线对称轴为直线x=﹣=4,∴点C的坐标为(4,0),∴AC=OC﹣OA=4﹣2=2,∴S△ABC=×AC×OB=×2×6=6.【点评】本题是二次函数的综合题,要会求二次函数的对称轴,会运用面积公式.17.已知开口向上的抛物线y=ax2﹣2x+|a|﹣4经过点(0,﹣3).(1)确定此抛物线的解析式;(2)当x取何值时,y有最小值,并求出这个最小值.【考点】待定系数法求二次函数解析式;二次函数的最值.【分析】(1)因为开口向上,所以a>0;把点(0,﹣3)代入抛物线y=ax2﹣2x+|a|﹣4中,得|a|﹣4=﹣3,再根据a>0求a,从而确定抛物线解析式;(2)根据二次函数的顶点坐标,求解即可.【解答】解:(1)由抛物线过(0,﹣3),得:﹣3=|a|﹣4,|a|=1,即a=±1.∵抛物线开口向上,∴a=1,故抛物线的解析式为y=x2﹣2x﹣3;(2)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴当x=1时,y有最小值﹣4.【点评】此题考查了二次函数的开口方向,顶点坐标,还考查了点与函数的关系.18.已知:抛物线的解析式为y=x2﹣(2m﹣1)x+m2﹣m,(1)求证:此抛物线与x轴必有两个不同的交点;(2)若此抛物线与直线y=x﹣3m+4的一个交点在y轴上,求m的值.【考点】二次函数综合题.【专题】代数综合题.【分析】(1)根据二次函数的交点与图象的关系,证明其方程有两个不同的根即△>0即可;(2)根据题意,令x=0,整理方程可得关于m的方程,解可得m的值.【解答】证明:(1)令y=0得:x2﹣(2m﹣1)x+m2﹣m=0①∵△=(2m﹣1)2﹣4(m2﹣m)×1>0∴方程①有两个不等的实数根,∴原抛物线与x轴有两个不同的交点;(2)令:x=0,根据题意有:m2﹣m=﹣3m+4解得m=﹣1+或﹣1﹣.(说明:少一个解扣2分)【点评】本题考查学生将二次函数的图象与解析式的关系.19.如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,当一点到达终点时,另一点也停止运动.设运动时间为x秒,△PBQ的面积为y(cm2).(1)求y关于x的函数关系式,并写出x的取值X围;(2)求△PBQ的面积的最大值.【考点】矩形的性质;二次函数的最值.【专题】动点型.【分析】(1)分别表示出PB、BQ的长,然后根据三角形的面积公式列式整理即可得解;(2)把函数关系式整理成顶点式解析式,然后根据二次函数的最值问题解答.【解答】解:(1)∵S△PBQ=PB•BQ,PB=AB﹣AP=18﹣2x,BQ=x,∴y=(18﹣2x)x,即y=﹣x2+9x(0<x≤4);(2)由(1)知:y=﹣x2+9x,∴y=﹣(x﹣)2+,∵当0<x≤时,y随x的增大而增大,而0<x≤4,∴当x=4时,y最大值=20,即△PBQ的最大面积是20cm2.【点评】本题考查了矩形的性质,二次函数的最值问题,根据题意表示出PB、BQ的长度是解题的关键.20.如图,经过点A(0,﹣4)的抛物线y=x2+bx+c与x轴相交于B(﹣2,0),C两点,O为坐标原点.(1)求抛物线的解析式;(2)将抛物线y=x2+bx+c向上平移个单位长度,再向左平移m(m>0)个单位长度得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值X围;(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,求AM的长.【考点】二次函数综合题.【专题】压轴题;分类讨论.【分析】(1)该抛物线的解析式中只有两个待定系数,只需将A、B两点坐标代入即可得解.(2)首先根据平移条件表示出移动后的函数解析式,进而用m表示出该函数的顶点坐标,将其代入直线AB、AC的解析式中,即可确定P在△ABC内时m的取值X围.(3)先在OA上取点N,使得∠ONB=∠ACB,那么只需令∠NBA=∠OMB即可,显然在y轴的正负半轴上都有一个符合条件的M点;以y轴正半轴上的点M为例,先证△ABN、△AMB相似,然后通过相关比例线段求出AM的长.【解答】解:(1)将A(0,﹣4)、B(﹣2,0)代入抛物线y=x2+bx+c中,得:,解得:故抛物线的解析式:y=x2﹣x﹣4.(2)由题意,新抛物线的解析式可表示为:y=(x+m)2﹣(x+m)﹣4+,即:y=x2+(m﹣1)x+m2﹣m﹣;它的顶点坐标P:(1﹣m,﹣1);由(1)的抛物线解析式可得:C(4,0);设直线AC的解析式为y=kx+b(k≠0),把x=4,y=0代入,∴4k+b=0,b=﹣4,∴y=x﹣4.同理直线AB:y=﹣2x﹣4;当点P在直线AB上时,﹣2(1﹣m)﹣4=﹣1,解得:m=;当点P在直线AC上时,(1﹣m)﹣4=﹣1,解得:m=﹣2;∴当点P在△ABC内时,﹣2<m<;又∵m>0,∴符合条件的m的取值X围:0<m<.(3)由A(0,﹣4)、C(4,0)得:OA=OC=4,且△OAC是等腰直角三角形;如图,在OA上取ON=OB=2,则∠ONB=∠ACB=45°;∴∠ONB=∠NBA+∠OAB=∠ACB=∠OMB+∠OAB,即∠OMB=∠NBA;如图,在△ABN、△AM1B中,∠BAN=∠M1AB,∠ABN=∠AM1B,∴△ABN∽△AM1B,得:AB2=AN•AM1;易得:AB2=(﹣2)2+42=20,AN=OA﹣ON=4﹣2=2;∴AM1=20÷2=10;而∠BM1A=∠BM2A=∠ABN,∴OM1=OM2=6,AM2=OM2﹣OA=6﹣4=2.综上,AM的长为10或2.【点评】考查了二次函数综合题,该函数综合题的难度较大,(3)题注意分类讨论,通过构建相似三角形是打开思路的关键所在.。
苏科版九年级数学上册 周练测试(2.1-2.3)(无答案)

九年级数学周练测试(2.1-2.3)一、选择题:1、有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中错误说法的个数是()A.1 B.2 C.3 D.42、⊙O的半径为4,圆心到点P的距离为d,且d是方程x2-2x-8=0的根,则点P与⊙O的位置关系是()A.点P在⊙O内部 B.点P在⊙O上 C.点P在⊙O外部 D.点P不在⊙O上3、如图,弦AB⊥OC,垂足为点C,连接OA,若OC=2,AB=4,则OA等于()A. B. C. D.4、如图,在△ABC中,∠A=70°.⊙O截△ABC的三条边所得的弦长相等,则△BOC的度数为()A.160° B.135° C.125° D.110°5、在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为()A.E、F、G B.F、G、H C.G、H、E D.H、E、F6、在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为()A.40cm B.60cm C.80cm D.100cm7、把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则 BC 的度数是()A.120° B.135° C.150° D.165°8、如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,下列各式中,正确的是()A.a>b>c B.a=b=c C.c>a>b D.b>c>a二、填空题:9、如图,AB、CD是圆O的两条弦,M、N分别为AB、CD的中点,且AMN=CNM,AB=6,则CD= .10、如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm,则直尺的宽度为。
苏科版九年级数学上册周周练试题.docx

初中数学试卷马鸣风萧萧一选择题(30分)1.用配方法解方程x 2-2x -1=0时,配方后得的方程为( ) A .(x +1)2=0B .(x -1)2=0C .(x +1)2=2D .(x -1)2=22.一元二次方程x 2+x -1=0 的根的情况为( ) A .有两个不相等的实数根 B .有两个相等的实数根 C .只有一个实数根D .没有实数根3.已知1x 、2x 是一元二次方程0142=+-x x 的两个根,则21x x ⋅等( )A .-4B .-1 C.1 D. 4 4.如图,AB 是⊙O 直径,∠AOC=130°,则∠D=( ) A.65° B .25°C .15°D .35° 5.在数轴上,点A 所表示的实数为3,点B 所表示的实数为a ,⊙A 的半径为2,下列说法中不正确的是( ) A .当a<5时,点B 在⊙A 内 B .当1<a<5时,点B 在⊙A 内 C .当a<1时,点B 在⊙A 外 D .当a>5时,点B 在⊙A 外6.如图,AB 是O ⊙的直径,点C 、D 在O ⊙上,110BOC ∠=°,AD OC ∥,则AOD ∠=( )A .70°B .60°C .50°D .40°7.下列说法正确的是( )A.经过三点可以作一个圆B.三角形的外心到这个三角形的三边距离相等C.等弧所对的圆心角相等D.相等的圆心角所对的弧相等8. 在平面直角坐标系xOy 中,以原点O 为圆心的圆过点A (13,0),直线y=kx ﹣3k+4与⊙O 交于B 、C 两点,则弦BC 的长的最小值为( )A.22B.24C.510D.3129.如图,正方形OABC 与正方形ODEF 是位似图形,O 为位似中心,相似比为1:2,点A 的坐标为(1,0),则E 点的坐标为( )OBD C AA .(2,0)B .(33,)22C.(2,2) D . (2,2)10.如图,AD 为等边△ABC 边BC 上的高,AB =4,AE =1,P 为高AD 上任意一点,则EP+BP 的最小值为( )。
苏科版九年级上周考试卷(主要是圆)

Ⅰ部初三数学周独立作业 Y(3)考试时间:90分钟 满分:120分 命题人:钱霞 审核人:王玉国 一、选择题(每题3分) 1、若式子23x x --有意义,则x 的取值范围为 ( )A x ≥2B x ≠3C x ≥2或x ≠3D x ≥2且x ≠32、为了准备体育中考,某班抽取6名同学参加30秒跳绳测试,成绩如下:90,100,85,85,90,90(单位:个).则下面关于这组成绩的说法中正确的是( )A .平均数是92B .中位数是85C .极差是15D .方差是203、下列四个命题:①垂直于弦的直径平分弦所对的两条弧;②在同圆或等圆中,相等的弦所对的圆周角相等;③三角形有且只有一个外接圆;④任意三角形是内心总是在三角形的内部。
其中真命题的个数有,⑤三角形的外心到三角形三边的距离相等( ) A .1个 B .2个 C .3个 D .4个4、矩形ABCD 中,AB =8,35BC =,点P 在边AB 上,且BP =3AP ,如果圆P 是以点P 为圆心,PD 为半径的圆,那么下列判断正确的是( ) A .点B 、C 均在圆P 外 B .点B 在圆P 外、点C 在圆P 内 C .点B 在圆P 内、点C 在圆P 外D .点B 、C 均在圆P 内5、如图,O ⊙是ABC △的外接圆,已知30ABO ∠=°, 则ACB ∠的大小为( ) A .60° B .50°C .55°D .40°6、如图,⊙O 的半径为2,点A 的坐标为(2,32),直线AB 为⊙O 的切线,B 为切点.则B 点的坐标为( )A .⎪⎪⎭⎫ ⎝⎛-5823, B .()13,- C . D .()31,- 7、定义:如果一元二次方程ax 2+bx+c=0(a ≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax 2+bx+c=0(a ≠0)满足a-b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是( )A.方程有两个相等的实数根B .方程有一根等于0C.方程两根之和等于0 D .方程两根之积等于0(第5题)第6题图 .ODE AB第8题图8、如图(图在前面),AB 是⊙O 的直径,⊙O 交BC 于中点D ,DE ⊥AC 于点E ,连接AD ,则下列结论中:①AD ⊥BC,②∠EDA=∠B,③OA=0.5AC ;④DE 是⊙O 的切线, 正确的个数有( )A. 1B.2C.3D.4 二、填空题(每题3分)9、若最简二次根式2a +与 是同类二次根式,则a = .10、已知⊙O 的半径为3cm ,圆心O 到直线l 的距离是4cm ,则直线l 与⊙O 的位置关系是 . 11、 如图,⊙O 是正方形 ABCD 的外接圆,点 P 在⊙O 上,则∠APB=______°第11题图 第12题图 第13题图 第15题图12、如图,已知以直角梯形ABCD 的腰CD 为直径的半圆O 与梯形上底AD 、下底BC 以及腰AB 均相切,切点分别是D ,C ,E .若半圆O 的半径为2,梯形的腰AB 为5,则该梯形的周长是 .13、如图,弦CD 垂直于⊙O 的直径AB ,垂足为H ,CD =4,BD =5,则AB 的长为_____.14、已知直角三角形两条边的长是3和4,则其内切圆的半径是______.15、如图:半径为2的P 的圆心在直线y=2x-1上运动,当P 与x 轴相切时圆心P 的坐标为 16、如下图,圆O 的直径AB=6,E F 为AB 的三等分点,M N 为弧AB 上两点,∠MEB= ∠NFB=60°,则EM+FN= 。
苏科版九年级数学上册周周清测试1229.docx

初中数学试卷 马鸣风萧萧数学部分 得分1.下列方程中有实数根的是( )A .022=++x xB .022=+-x xC . 012=--x xD .032=+-x x2、如图1,从圆O 外一点P 引圆O 的两条切线PA PB ,,切点分别为A B ,.如果60APB ∠=,8PA =,那么弦AB 的长是( )A .4B .8C .43D .833.在△ABC 中,∠C =90°,sinA =35,那么tanA 等于( )A .35 B.43 C.45 D.34 4.在△ABC 中,若tanA=1,sinB=22,则△ABC 的形状是( ) A .等腰直角三角形 B .等边三角形 C .直角三角形D .一般锐角三角形5.如图,抛物线的函数表达式是 ( )A .22+-=x x yB .22++-=x x yC .22++=x x yD .22+--=x x y6.若3x =是方程052=+-m x x 的一个根,则这个方程的另一个根是( )A .2-B .2C .5-D .57、计算(1)2sin30°+3cos60°-4tan45° (2)cos30°sin45°+sin30°cos45°8. 等腰△ABC 中,AB=AC=10,BC=12,求sinB 和cosC 。
P BA O 图19. (本题10分)如图,为了测量路灯(OS )的高度,把一根长1.5米的竹竿(AB )竖直立在水平地面上,测得竹竿的影子(BC )长为1米,然后拿竹竿向远离路灯方向走了4米(BB ‘),再把竹竿竖立在地面上, 测得竹竿的影长(B ‘C ‘)为1.8米,求路灯离地面的高度.h S A C B B 'O C 'A '。
苏科版九年级数学上册 周末综合培优训练卷(第2、3两章2020.10.17)
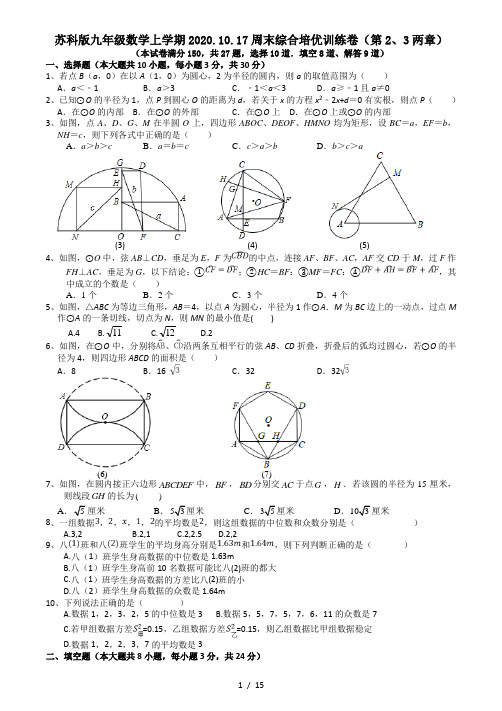
苏科版九年级数学上学期2020.10.17周末综合培优训练卷(第2、3两章)(本试卷满分150,共27题,选择10道.填空8道、解答9道)一、选择题(本大题共10小题,每小题3分,共30分)1、若点B(a,0)在以A(1,0)为圆心,2为半径的圆内,则a的取值范围为()A.a<﹣1 B.a>3 C.﹣1<a<3 D.a≥﹣1且a≠02、已知⊙O的半径为1,点P到圆心O的距离为d,若关于x的方程x2﹣2x+d=0有实根,则点P()A.在⊙O的内部B.在⊙O的外部C.在⊙O上D.在⊙O上或⊙O的内部3、如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是()A.a>b>c B.a=b=c C.c>a>b D.b>c>a(3)(4) (5)4、如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①;②HC=BF:③MF=FC:④,其中成立的个数是()A.1个B.2个C.3个D.4个5、如图,△ABC为等边三角形,AB=4,以点A为圆心,半径为1作⊙A.M为BC边上的一动点,过点M作⊙A的一条切线,切点为N,则MN的最小值是( )A.4B.11C.12D.26、如图,在⊙O中,分别将、沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是()A.8 B.16 C.32 D.32(6)(7)7、如图,在圆内接正六边形ABCDEF中,BF,BD分别交AC于点G,H.若该圆的半径为15厘米,则线段GH的长为()A.5厘米B.53厘米C.35厘米D.103厘米8、一组数据,,,,的平均数是,则这组数据的中位数和众数分别是()A.3,2B.2,1C.2,2.5D.2,29、八班和八班学生的平均身高分别是和,则下列判断正确的是()A.八(1)班学生身高数据的中位数是1.63mB.八(1)班学生身高前10名数据可能比八(2)班的都大C.八(1)班学生身高数据的方差比八(2)班的小D.八(2)班学生身高数据的众数是1.64m10、下列说法正确的是()A.数据1,2,3,2,5的中位数是3B.数据5,5,7,5,7,6,11的众数是7C.若甲组数据方差=0.15,乙组数据方差=0.15,则乙组数据比甲组数据稳定D.数据1,2,2,3,7的平均数是3二、填空题(本大题共8小题,每小题3分,共24分)11、如图,AB 是⊙O 的直径,CP 切⊙O 于点C ,交AB 的延长线于点P ,若∠P =20°,则∠A =_______(11) (12) (13)12、如图,将边长为3的正方形铁丝框ABCD ,变形为以A 为圆心,AB 为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB 的面积为________13、如图,在四边形ABCD 中,AB =CB ,AD =CD ,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形ABCD 的对角线AC ,BD 相交于点O .以点B 为圆心,BO 长为半径画弧,分别交AB ,BC 于点E ,F .若∠ABD =∠ACD =30°,AD =1,则的长为 (结果保留π).14、如图,已知点C ,D 是以AB 为直径的半圆的三等分点,弧CD 的长为31π, 则图中阴影部分的面积为( )15、小明同学参加射击训练,共射击了八发子弹,环数分别是7,10,9,8,7,9,9,8,则这组数据的中位数为 .16、学校规定学生的数学期末总评成绩由三部分组成,平时成绩占20%,期中成绩占35%,期末成绩占45%.小红的平时成绩、期中成绩、期末成绩依次为92分、86分、94分,那么小红的数学期末总评成绩为________分.17、如果一组数据、、…的方差是,那么一组新数据,、的方差是______18、植树节时,九(1)班6个小组的植树棵数分别是5,7,3,x ,6,4.已知这组数据的众数是5,则该组数据的平均数为 .三、解答题(本大题共9小题,共96分.)19、在⊙O 中,弦CD 与直径AB 相交于点P ,∠ABC =63°.(1)如图①,若∠APC =100°,求∠BAD 和∠CDB 的大小;(2)如图②,若CD ⊥AB ,过点D 作⊙O 的切线,与AB 的延长线相交于点E ,求∠E 的大小.20、如图,CD 是⊙O 的直径,AB 是⊙O 的弦,AB ⊥CD ,垂足为G ,OG :OC =3:5,AB =8.(1)求⊙O 的半径;(2)点E 为圆上一点,∠ECD =15°,将沿弦CE 翻折,交CD 于点F ,求图中阴影部分的面积.21、如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.(1)求证:点D是AB的中点;(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.22、我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:(1)将条形统计图补充完整;(2)扇形图中的“1.5 h”部分的圆心角是多少度?(3)求抽查的学生劳动时间的众数、中位数.23、在学校组织的“学习强国”阅读知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分和70分.年级组长张老师将901班和902班的成绩进行整理并绘制成如下的统计图:(1)在本次竞赛中,902班C级及以上的人数有多少?(2)请你将下面的表格补充完整:平均数(分) 中位数(分) 众数(分) B级及以上人数901班87.6 90 18902班87.6 100(3)24、如图,在四边形ABCD中,AD∥BC,AD⊥CD,AC=AB,⊙O为△ABC的外接圆.(1)如图1,求证:AD是⊙O的切线;(2)如图2,CD交⊙O于点E,过点A作AG⊥BE,垂⾜为F,交BC于点G.若AD=2,CD=3,求GF 的长.25、某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“A:文学社团、B:科技社团、C:体艺社团、D:其他社团”四项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.请你根据图中所提供的信息,完成下列问题:(1)本次调查的学生人数为;(2)在扇形统计图中,“文学社团”部分所占圆心角的度数为;(3)请将两个统计图补充完整;(4)若该校共有3000名学生,估计该校最想参加“体艺社团”的学生人数为多少人?26、要从甲、乙两名射击运动员中挑选一人参加全国比赛,在最近的5次选拔赛中、他们的成绩如下(单位:环):甲:7、8、6、8、9乙:9、7、5、8、6(1)甲运动员这5次选拔赛成绩的中位数和众数分别是多少?(3)若已知甲运动员的选拔赛成绩的方差为1.04,为了保证稳定发挥,应该选哪位运动员参加比赛?27、如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.(1)(1)求证:MH为⊙O的切线.(2)若MH=32,ACBC=34,求⊙O的半径.(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N 点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.苏科版九年级数学上学期2020.10.17周末综合培优训练卷(第2、3两章)(本试卷满分150,共27题,选择10道.填空8道、解答9道)一、选择题(本大题共10小题,每小题3分,共30分)1、若点B(a,0)在以A(1,0)为圆心,2为半径的圆内,则a的取值范围为()A.a<﹣1 B.a>3 C.﹣1<a<3 D.a≥﹣1且a≠0【解答】∵点B(a,0)在以点A(1,0)为圆心,以2为半径的圆内,∴|a﹣1|<2,∴﹣1<a<3.故选:C.2、已知⊙O的半径为1,点P到圆心O的距离为d,若关于x的方程x2﹣2x+d=0有实根,则点P()A.在⊙O的内部B.在⊙O的外部C.在⊙O上D.在⊙O上或⊙O的内部【解答】∵关于x的方程x2﹣2x+d=0有实根,∴根的判别式△=(﹣2)2﹣4×d≥0,解得d≤1,∴点在圆内或在圆上,故选:D.3、如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是()A.a>b>c B.a=b=c C.c>a>b D.b>c>a【解答】解:连接OA、OD、OM,如图所示:则OA=OD=OM,∵四边形ABOC、DEOF、HNMO均为矩形,∴OA=BC=a,OD=EF=b,OM=NH=c,∴a=b=c;故选:B.4、如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①;②HC=BF:③MF=FC:④,其中成立的个数是()A.1个B.2个C.3个D.4个【解答】解:∵F为的中点,∴,故①正确,∴∠FCM=∠F AC,∵∠FCG=∠ACM+∠GCM,∠AME=∠FMC=∠ACM+∠F AC,∴∠AME=∠FMC=∠FCG>∠FCM,∴FC>FM,故③错误,∵AB⊥CD,FH⊥AC,∴∠AEM=∠CGF=90°,∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,∴∠CFH=∠BAF,∴,∴HC=BF,故②正确,∵∠AGF=90°,∴∠CAF+∠AFH=90°,∴的度数的度数=180°,∴的度数的度数=180°,∴,故④正确,故选:C.5、如图,△ABC为等边三角形,AB=4,以点A为圆心,半径为1作⊙A.M为BC边上的一动点,过点M作⊙A的一条切线,切点为N,则MN的最小值是.A.4B.11C.12D.2【解答】作AD⊥BC于D,过D作⊙A的一条切线,切点为E,连接AE,如图所示:∵△ABC是等边三角形,AD⊥BC,∴BC=AB=4,BD=CD BC=2,∵DE是⊙A的一条切线,∴AE⊥DE,AE=1,∴DE,当点M与D重合时,N与E重合,此时MN最小,故答案为:.6、如图,在⊙O中,分别将、沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是()A.8 B.16 C.32 D.32【解答】解:过O作OH⊥AB交⊙O于E,反向延长EO交CD于G,交⊙O于F,连接OA,OB,OD,∵AB∥CD,∴EF⊥CD,∵分别将、沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,∴OH OA,∴∠HAO=30°,∴∠AOH=60°,同理∠DOG=60°,∴∠AOD=60°,∴△AOD是等边三角形,∵OA=OB,∴∠ABO=∠BAO=30°,∴∠AOB=120°,∴∠AOD+∠AOB=180°,∴D,O,B三点共线,且BD为⊙O的直径,∴∠DAB=90°,同理,∠ABC=∠ADC=90°,∴四边形ABCD是矩形,∴AD=AO=4,AB AD=4,∴四边形ABCD的面积是16,故选:B.7、如图,在圆内接正六边形ABCDEF中,BF,BD分别交AC于点G,H.若该圆的半径为15厘米,则线段GH的长为()A5厘米B.53C.35D.103厘米【解答】解:在圆内接正六边形ABCDEF中,AB AF BC CD===,120BAF ABC BCD∠=∠=∠=︒,30AFB ABF BAC ACB CBD BDC∴∠=∠=∠=∠=∠=∠=︒,AG BG∴=,BH CH=,60GBH BGH BHG∠=∠=∠=︒,AG GH BG BH CH∴====,连接OA,OB交AC于N,则OB AC⊥,60AOB∠=︒,15OA cm=,3153()AN OA cm∴==,2153()AC AN cm∴==,153()3GH AC cm∴==,故选:B.8、一组数据,,,,的平均数是,则这组数据的中位数和众数分别是(D)A.3,2B.2,1C.2,2.5D.2,29、八班和八班学生的平均身高分别是和,则下列判断正确的是(B)A.八(1)班学生身高数据的中位数是1.63mB.八(1)班学生身高前10名数据可能比八(2)班的都大C.八(1)班学生身高数据的方差比八(2)班的小D.八(2)班学生身高数据的众数是1.64m10、下列说法正确的是(D)A.数据1,2,3,2,5的中位数是3B.数据5,5,7,5,7,6,11的众数是7C.若甲组数据方差=0.15,乙组数据方差=0.15,则乙组数据比甲组数据稳定D.数据1,2,2,3,7的平均数是3二、填空题(本大题共8小题,每小题3分,共24分)11、如图,AB是⊙O的直径,CP切⊙O于点C,交AB的延长线于点P,若∠P=20°,则∠A=___35°_____.12、如图,将边长为3的正方形铁丝框ABCD,变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为____9____13、如图,在四边形ABCD中,AB=CB,AD=CD,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形ABCD的对角线AC,BD相交于点O.以点B为圆心,BO长为半径画弧,分别交AB,BC于点E,F.若∠ABD=∠ACD=30°,AD=1,则的长为(结果保留π).【答案】解:在△ABD 与△CBD 中,,∴△ABD ≌△CBD (SSS ),∴∠ABD =∠CBD =30°,∠ADB =∠CDB ,CD =AD =1,∴∠ABC =60°,∵AD =CD ,∠ADB =∠CDB ,∴BD ⊥AC ,且AO =CO ,∴∠ACB =90°﹣30°=60°,∴∠BCD =∠ACB +∠ACD =90°,在Rt △BCD 中,∵∠CBD =30°,∴BD =2CD =2,在Rt △COD 中,∵∠ACD =30°,∴OD CD ,∴OB =BD ﹣OD =2, ∴的长为:, 故答案为.14、如图,已知点C ,D 是以AB 为直径的半圆的三等分点,弧CD 的长为31π, 则图中阴影部分的面积为( )【答案】解:连接CD 、OC 、OD .∵C ,D 是以AB 为直径的半圆的三等分点,∴∠AOC =∠COD =∠DOB =60°,AC =CD ,又∵OA =OC =OD ,∴△OAC 、△OCD 是等边三角形,∴∠AOC =∠OCD ,∴CD ∥AB ,∴S △ACD =S △OCD ,∵弧CD 的长为,∴,解得:r =1,∴S 阴影=S 扇形OCD .15、小明同学参加射击训练,共射击了八发子弹,环数分别是7,10,9,8,7,9,9,8,则这组数据的中位数为 8.5 .16、学校规定学生的数学期末总评成绩由三部分组成,平时成绩占20%,期中成绩占35%,期末成绩占45%.小红的平时成绩、期中成绩、期末成绩依次为92分、86分、94分,那么小红的数学期末总评成绩为___90.8_____分.17、如果一组数据、、…的方差是,那么一组新数据,、的方差是18、植树节时,九(1)班6个小组的植树棵数分别是5,7,3,x,6,4.已知这组数据的众数是5,则该组数据的平均数为 5 .三、解答题(本大题共9小题,共96分.)19、在⊙O中,弦CD与直径AB相交于点P,∠ABC=63°.(1)如图①,若∠APC=100°,求∠BAD和∠CDB的大小;(2)如图②,若CD⊥AB,过点D作⊙O的切线,与AB的延长线相交于点E,求∠E的大小.解:(1)∵∠APC是△PBC的一个外角,∴∠C=∠APC﹣∠ABC=100°﹣63°=37°,由圆周角定理得:∠BAD=∠C=37°,∠ADC=∠ABC=63°,∵AB是⊙O的直径,∴∠ADB=90°,∴∠CDB=∠ADB﹣∠ADC=90°﹣63°=27°;(2)连接OD,如图②所示:∵CD⊥AB,∴∠CPB=90°,∴∠PCB=90°﹣∠ABC=90°﹣63°=27°,∵DE是⊙O的切线,∴DE⊥OD,∴∠ODE=90°,∵∠BOD=2∠PCB=54°,∴∠E=90°﹣∠BOD=90°﹣54°=36°.20、如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.(1)求⊙O的半径;(2)点E为圆上一点,∠ECD=15°,将沿弦CE翻折,交CD于点F,求图中阴影部分的面积.解:(1)连接AO,如右图1所示,∵CD为⊙O的直径,AB⊥CD,AB=8,∴AG==4,∵OG:OC=3:5,AB⊥CD,垂足为G,∴设⊙O的半径为5k,则OG=3k,∴(3k)2+42=(5k)2,解得,k=1或k=﹣1(舍去),∴5k=5,即⊙O的半径是5;(2)如图2所示,将阴影部分沿CE翻折,点F的对应点为M,∵∠ECD=15°,由对称性可知,∠DCM=30°,S阴影=S弓形CBM,连接OM,则∠MOD=60°,∴∠MOC=120°,过点M作MN⊥CD于点N,∴MN=MO•sin60°=5×,∴S阴影=S扇形OMC﹣S△OMC==,即图中阴影部分的面积是:.21、如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.(1)求证:点D是AB的中点;(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.【解答】证明:(1)如图1,连接CD,∵BC为⊙O的直径,∴CD⊥AB.∵AC=BC,∴AD=BD.(2)如图2,连接OD;∵AD=BD,OB=OC,∴OD是△BCA的中位线,∴OD∥AC.∵DE⊥AC,∴DF⊥OD.∵OD为半径,∴DE是⊙O的切线.22、我市开展“美丽自贡,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:(1)将条形统计图补充完整;(2)扇形图中的“1.5 h”部分的圆心角是多少度?(3)求抽查的学生劳动时间的众数、中位数.答案:(1)统计图:(2)扇形图中的“1.5 h”部分的圆心角是144°;(3)抽查的学生劳动时间的众数为1.5h、中位数为1.5h.23、在学校组织的“学习强国”阅读知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分和70分.年级组长张老师将901班和902班的成绩进行整理并绘制成如下的统计图:(1)在本次竞赛中,902班C级及以上的人数有多少?(2)请你将下面的表格补充完整:平均数(分) 中位数(分) 众数(分) B级及以上人数901班87.6 90 18902班87.6 100(3)【答案】(1)901班人数有:6+12+2+5=25(人),∵每班参加比赛的人数相同,∴902班有25人,∴C级以上(包括C级)的人数=25×(44%+4%+36%)=21(人),(2)901班成绩的众数为90分,902班A级学生=25×44%=11,B级学生=25×4%=1,C级学生=25×36%=9,D级学生=25×16%=4,902班中位数为C级学生,即80分,902班B级及以上人数为11+1=12(人),平均数(分) 中位数(分) 众数(分) B级及以上人数901班87.6 90 90 18902班87.6 80 100 12(3)②从平均数的角度看两班成绩一样,从众数的角度看902班比901班的成绩好,所以902班成绩好.(答案不唯一)24、如图,在四边形ABCD中,AD∥BC,AD⊥CD,AC=AB,⊙O为△ABC的外接圆.(1)如图1,求证:AD是⊙O的切线;(2)如图2,CD交⊙O于点E,过点A作AG⊥BE,垂⾜为F,交BC于点G.若AD=2,CD=3,求GF 的长.(1)证明:如图1,连接OA,OB,OC.在△OAC和△OAB中,,∴△OAC≌△OAB(SSS),∴∠OAC=∠OAB,∴AO平分∠BAC,∴AO⊥BC.又∵AD∥BC,∴AD⊥AO,∴AD是⊙O的切线.(2)如图2,连接AE.∵∠BCE=90°,∴∠BAE=90°.又∵AF⊥BE,∴∠AFB=90°.∵∠BAG+∠EAF=∠AEB+∠EAF=90°,∴∠BAG=∠AEB.∵∠ABC=∠ACB=∠AEB,∴∠BAG=∠ABC,∴AG=BG.在△ADC和△AFB中,,∴△ADC≌△AFB(AAS),∴AF=AD=2,BF=CD=3.设FG=x,在Rt△BFG中,FG=x,BF=3,BG=AG=x+2,∴FG2+BF2=BG2,即x2+32=(x+2)2,∴x=,∴FG=.25、某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“A:文学社团、B:科技社团、C:体艺社团、D:其他社团”四项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.请你根据图中所提供的信息,完成下列问题:(1)本次调查的学生人数为;(2)在扇形统计图中,“文学社团”部分所占圆心角的度数为;(3)请将两个统计图补充完整;(4)若该校共有3000名学生,估计该校最想参加“体艺社团”的学生人数为多少人?答案:(1)120 (2)72º(3)略(4)900人26、要从甲、乙两名射击运动员中挑选一人参加全国比赛,在最近的5次选拔赛中、他们的成绩如下(单位:环):甲:7、8、6、8、9乙:9、7、5、8、6(1)甲运动员这5次选拔赛成绩的中位数和众数分别是多少?(2)求乙运动员这5次选拔赛成绩的平均数和方差;(3)若已知甲运动员的选拔赛成绩的方差为1.04,为了保证稳定发挥,应该选哪位运动员参加比赛?解:甲运动员的成绩按照从小到大排列是:、、、、,∴甲运动员这次选拔赛成绩的中位数和众数分别是,;由题意可得,,;∵甲的方差是,乙的方差是,,∴应该选择甲运动员参加比赛.27、如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.(1)求证:MH为⊙O的切线.(2)若MH=32,ACBC=34,求⊙O的半径.(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.【解答】解:(1)连接OH、OM,∵H是AC的中点,O是BC的中点∴OH是△ABC的中位线∴OH∥AB,∴∠COH=∠ABC,∠MOH=∠OMB又∵OB=OM,∴∠OMB=∠MBO ∴∠COH=∠MOH,在△COH与△MOH中,∵OC=OM,∠COH=∠MOH,OH=OH∴△COH ≌△MOH (SAS )∴∠HCO =∠HMO =90°∴MH 是⊙O 的切线; (2)∵MH 、AC 是⊙O 的切线∴HC =MH =32∴AC =2HC =3 ∵tAC BC =34∴BC =4 ∴⊙O 的半径为2; (3)连接OA 、CN 、ON ,OA 与CN 相交于点I∵AC 与AN 都是⊙O 的切线 ∴AC =AN ,AO 平分∠CAD ∴AO ⊥CN ∵AC =3,OC =2 ∴由勾股定理可求得:A O =13∵12AC •OC =12AO •CI ,∴CI =61313 ∴由垂径定理可求得:C N =121313 设OE =x ,由勾股定理可得:2222CN CE ON OE -=- ∴22144(2)413x x -+=-,∴x =1013,∴CE =1013, 由勾股定理可求得:EN =2413,∴由垂径定理可知:NQ =2EN =4813.。
九年级数学上学期第二次周练试题无答案苏科版

江苏省东台市创新学校2017届九年级数学上学期第二次周练试题考试时间120分钟 试卷满分150一.选择题(本大题共有8小题,每小题3分,共24分.)1. 下面的一元二次方程中,常数项为5的方程是( ) A. 01352=+-x x B. 01532=++x xC. 0532=+-x xD. 532=-x x2、一元二次方程022=+x x 根的情况是 ( )A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根3、将抛物线2y x =-向右平移2个单位后,得到的抛物线的解析式是( )A .2(2)y x =-+B .22y x =-+C .2(2)y x =--D .22y x =-- 4、一元二次方程012)2(2=++-x x k 有两个不相等的实数根,则k 的取值范围是( )A. k>1B. k>1且k ≠2C. k>2D. k>-1且k ≠25、在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号大于2的概率为 A .51, B .52, C .53; D .54; 6、抛物线y=﹣5x 2﹣x+9与y 轴的交点坐标为( )A .(9,0)B .(﹣9,0)C .(0,﹣9)D .(0,9) 7、 将二次函数y=x2-2x+3化为y=(x-h )2+k 的形式,结果为 ( )A. y=(x+1)2+4B. y=(x+1)2+2C. y=(x-1)2+4D. y=(x-1)2+28、已知二次函数c bx ax y ++=2的图象如图所示,则下列结论:①042<-ac b ;②0>+-c b a ;③0>abc ;④ a b 2=中,正确结论的个数是( )A .1个B .2个C .3个D .4个第8题 第16题二、填空题(本大题共有10小题,每小题3分,共30分.)9、方程042=-x x 的解是______ __ 10、已知函数y =(m +3)x 2+2(m -1)x +m +1的图象与x 轴有交点,则m 的取值范围是______.11、将抛物线:y=x 2-2x 向上平移3个单位,再向右平移4个单位得到的抛物线是______ _;12、二次函数y=x 2+6x+5图象的顶点坐标为 .13、若关于x 的一元二次方程kx 2﹣2x ﹣1=0有两个不相等的实数根,则实数k 的取值范围是14、△ABC 为⊙O 的内接三角形,若∠AOC=160°,则∠ABC 的度数是 .15、抛掷一枚质地均匀的硬币2次,2次的结果都是正面朝上的概率是__________16、如图,是抛物线y=ax 2+bx+c 的一部分,其对称轴为直线x=1,它与x 轴的一个交点为A (3,0),根据图象,可知关于x 的一元二次方程ax 2+bx+c=0的解是 .17、若抛物线y=x 2﹣2x ﹣3与x 轴分别交于A ,B 两点,则AB 的长为 .18、已知三角形的三边分别为3、4、5,则这个三角形的内切圆半径是 ________.三、解答题(本大题共有10小题,共96分.)19、(本题满分8分)解下列方程:(1)()()2232+=+x x x ;(2)0142=+-x x (用配方法);20、(本题满分8分)已知:关于x 的方程012=-+mx x ,(1)求证:方程有两个不相等的实数根;(2)若方程的一个根是1-,求另一个根及m 值.21、(本题满分8分)盐阜人民商场经销一种商品,如果每件盈利10元,每天可以售出500件,经过市场调查发现,在进价不变的情况下,若每件涨价1元,日销售量将减少20件,现在商场要保证该商品每天盈利6000元,同时又要顾客得到实惠,那么每件应涨价多少元?22、(本题满分12分)已知函数9)2(32+--=x y .(1)当x= 时,抛物线有最大值,是 ;(2)当x 时,y 随x 的增大而增大;(3)该函数图象可由y=-3x2的图象经过怎样的平移得到?(4)求出该抛物线与x 轴的交点坐标;23、(本题满分8分)已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.(1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;(2)如图②,当直线l与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.24、(本题满分8分)如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏教版初中数学九年级上册第一学期第2周周考试卷
一、单选题(每题3分)
1. 一元二次方程(x - 2)2
= 9的两个根分别是( )
A. x 1 = 1, x 2 = -5
B. x 1 = -1, x 2 = -5
C. x 1 = 1, x 2 = 5
D. x 1 = -1, x 2 = 5 2. 用配方法解一元二次方程x 2
- 6x + 5 = 0,其中配方正确的是( )
A. (x - 3)2
= 5 , B. (x - 3)2
= -4 , C. (x - 3)2
= 4 , D. (x - 3)2
= 9 . 3.某经济技术开发区今年一月份工业产值达50亿元,且一月份、二月份、三月份的产值共为175亿元,若设平均每月的增长率为x ,根据题意可列方程( ) A .50(1+x )2=175 B .50+50(1+x )2
=175
C .50(1+x )+50(1+x )2
=175
D .50+50(1+x )+50(1+x )2
=175
4. 对于一元二次方程ax 2
+ bx + c = 0 (a ≠ 0),下列说法中错误的是( )
A. 当a > 0, c < 0时,方程一定有实数根,
B. 当c = 0时,方程至少有一个根为0,
C. 当a > 0, b = 0, c < 0时,方程的两根一定互为相反数,
D. 当abc < 0时,方程的两个根同号, 当abc > 0时,方程的两个根异号.
二、填空题 (每题3分)
5. 若x = 2是方程x 2
+ 3x - 2m = 0的一个根,则m 的值为________ . 6. 若方程(x + 3)2
+ a = 0有解,则a 的取值范围是__________. 7. 当x =__________时,代数式(3x - 4)2
与(4x - 3)2
的值相等. 8. 方程x (x + 2) = x + 2的根为_________ .
9. 写出一个以2和3为两根且二项系数为1的一元二次方程, 你写的是____________. 10. 若一元二次方程mx 2
+ 4x + 5 = 0有两个不相等实数根,则m 的取值范围__________. 11.如果二次三项式x 2﹣6x+m 2是一个完全平方式,那么m 的值__________.
三、解答题
12. 用指定方法解下列一元二次方程 (每题5分)
(1) 0152
=+-x x (用配方法) (2) ()()2232
-=-x x x
(3) 052222
=--x x (4) ()()2
2
132-=+y y
13. 选择适当的方法解下列一元二次方程 (每题5分)
(1) (3y - 2)2 = (2y - 3)2
(2) (x + 2)(x - 3) = 0
(3) -3x 2 + 4x + 1 = 0 (4) (2x -1)2
-2x + 1 = 0
(5).144(1+x )2
=169
14.己知a,b是一个直角三角形两条直角边的长,且(a2+b2)(a2+b2+1)=12,求这个直角三角形的斜边长.(本题10分)
15.已知关于x的方程是否存在正数m,使方程的两个实数根的平方和等于224?若存在,求出满足条件的m的值.(本题10分)
16.在一次同学聚会时,大家一见面就相互握手.有人统计了一下,大家一共握了45次手,参加这次聚会的同学共有多少人.(本题10分)
17.已知关于x的方程x2 -2(m+1)x+m2 -3=0.(本题10分)
(1) 当m取何值时,方程有两个不相等的实数根?
(2) 设x1、x2是方程的两个不相等的实数根,且(x1+x2)2 -(x1+x2)-12=0, 求m的值.。
