高二年级第一学期期末综合测试题及答案
高二语文上期末考试试卷及答案

一、选择题(每题2分,共20分)1. 下列词语中,字形、字音完全正确的一项是:A. 璀璨(cuǐ càn)潜移默化(qián yí mò huà)B. 腹背受敌(fù bèi shòu dí)欣喜若狂(xīn xǐ ruò kuáng)C. 莲花(lián huā)漫不经心(màn bù jīng xīn)D. 突兀(tū wù)恍若隔世(huǎng ruò gé shì)2. 下列句子中,没有语病的一项是:A. 经过这次比赛,他认识到了自己的不足,决心在今后的学习中更加努力。
B. 随着科技的飞速发展,智能手机已经成为人们生活中不可或缺的一部分。
C. 在这次活动中,他充分发挥了自己的特长,受到了大家的一致好评。
D. 由于天气原因,原定的活动被迫取消了。
3. 下列诗句中,运用比喻手法的一项是:A. 月落乌啼霜满天,江枫渔火对愁眠。
(张继《枫桥夜泊》)B. 落红不是无情物,化作春泥更护花。
(龚自珍《己亥杂诗》)C. 天门中断楚江开,碧水东流至此回。
(李白《望天门山》)D. 春风又绿江南岸,明月何时照我还?(王安石《泊船瓜洲》)4. 下列成语中,出自《诗经》的一项是:A. 青出于蓝而胜于蓝B. 己所不欲,勿施于人C. 知之者不如好之者,好之者不如乐之者D. 一日不见,如隔三秋5. 下列句子中,使用了排比修辞手法的一项是:A. 爱国之心,如日中天;报国之志,如磐石之坚。
B. 人生如梦,岁月如歌;青春似火,热情似血。
C. 读书破万卷,下笔如有神;读书百遍,其义自见。
D. 青青子衿,悠悠我心;但为君故,沉吟至今。
6. 下列词语中,属于多义词的一项是:A. 知识B. 美丽C. 高兴D. 智慧7. 下列句子中,没有使用反问修辞手法的一项是:A. 你难道没有发现,他的成绩一直在进步吗?B. 这样做,难道不是最好的选择吗?C. 难道我们不应该珍惜时间吗?D. 这样的错误,难道还会犯吗?8. 下列句子中,使用了借代修辞手法的一项是:A. 青天白日,晴空万里。
2023-2024学年第一学期高二年级期末质量检测英语试题(含答案)

邯郸市2023—2024学年第一学期高二年级期末质量检测英语注意事项:1. 答卷前, 考生务必将自己的姓名、准考证号填写在答题卡上。
2. 回答选择题时, 选出每小题答案后, 用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动, 用橡皮擦干净后, 再选涂其他答案标号。
回答非选择题时, 将答案写在答题卡上。
写在本试卷上无效。
3. 考试结束后, 将本试卷和答题卡一并交回。
第一部分听力(共两节, 满分30分)做题时, 先将答案标在试卷上。
录音内容结束后, 你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节 (共5小题;每小题1. 5分, 满分7. 5分)听下面5段对话。
每段对话后有一个小题, 从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后, 你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirtA. £19. 15.B. £9. 18.C. £9. 15.答案是C。
1. What is the weather like nowA. Cloudy,B. Rainy.C. Sunny.2. What does Sam meanA. He didn't pass the exam.B. He won't go to the library.C. He hasn't finished the paper.3. When will the conference begin this afternoonA. At 2:00.B. At 2:15.C. At 2:30.4. What are the speakers expecting John to doA. Deal with something urgent.B. Reply to their message.C. Play a game with them.5. What is the probable relationship between the speakersA. Workmates.B. Husband and wife.C. Friends.第二节 (共15小题;每小题1. 5分, 满分22. 5分)听下面5段对话或独白。
高二第一学期期末十套练习题答案

高二第一学期期末十套练习题答案本文为高二第一学期期末十套练习题的详细解答,供同学们参考。
以下是各套练习题的答案及解析:套题一:1.答案:B解析:根据题目描述,疏散标志通常会放在人们逃生的路线上,以指引人们找到离开危险区域的出口。
选项A、C和D均不符合题意。
2.答案:C解析:根据第一段最后一句话可知,学校决定每天早晨从家里接送学生上下车的决定,与交通拥堵问题相关。
选项A、B和D都没有提及交通拥堵。
3.答案:A解析:根据最后一段内容可知,关于为什么他们会使用安全帽这个问题,作者在信的开头部分就已经解释了。
其他选项中没有提及这个问题。
套题二:1.答案:B解析:根据第一段中的"And yet, this tragic event came as no surprise to me" 可知,发生这起事件并不令作者感到意外。
故选B。
2.答案:D解析:根据倒数第二段的最后一句话可知,作者认为不太可能再会发生像妈妈车祸那样的意外事件了。
故选D。
3.答案:A解析:根据文章内容可知,作者妈妈的车祸是由于她对驾驶者的不当行为而发生的。
选项B、C和D都不符合题意。
套题三:1.答案:C解析:根据第一段内容可知,宇航员在太空行走时必须佩戴太空服以便呼吸、保暖和保护自己。
选项A、B和D都没有提到这个作用。
2.答案:B解析:根据第一段最后一句话可知,太空服内有供宇航员呼吸的氧气。
选项A、C和D都没有提及这一点。
3.答案:D解析:根据第二段的最后一句话可知,太空服外层的材料可以抵挡太空的辐射和温度变化。
选项A、B和C都没有提到这一点。
套题四:1.答案:A解析:根据第二段最后一句话的描述,可以推断出Karl可能是因为自身唱功和表演吸引了评委的注意。
选项B、C和D都没有提及这一点。
2.答案:C解析:根据第三段中的"Karl's voice resonated with the audience andhis stage presence was incredible" 可知,Karl的歌声引起了观众的共鸣,并展现了令人难以置信的舞台魅力。
高二上学期 语文 期末综合测试 含答案解析

绝密★启用前2018--2019年度高一备考期末质量测评2019.1.14本试卷满分150分,考试时间150分钟。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题纸上。
2.回答选择题时,选出每小题答案后。
用铅笔把答题卡对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号;回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将答题卡上交。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1-3题。
2003年开始,玄幻小说逐渐在网络文学中崭露头角,进入2004年以后,则出现了玄幻小说的热潮,从此玄幻小说开始占据网络小说的主导地位。
玄幻小说热潮的出现不仅是一种出版领域的现象,也是一种文化现象,它是特定社会、文化土壤孕育的产物。
中国的传统文化是富于想象和奇幻色彩的。
中国的传统神话包括了从开天辟地到诸神战争等丰富的现代奇幻小说素材。
庄子的《逍遥游》、先秦的《山海经》魏晋的志怪小说、明代的《西游记》等都是中国传统文化中的浪漫主义元素在各个时代的体现,这也是现代玄幻小说得以出现的文化源泉。
此类小说多以中国特定历史时期为背景,更多地延承了传统武侠小说之风。
目前比较畅销的《搜神记》以晋代干宝的《搜神记》为题,小说在上古洪荒的背景下,展现了光怪陆离的古代神话世界。
总体上看,玄幻小说在内容上多以上古或古代社会为背景,在风格上模仿神话故事或志怪小说,在主题上则延承了中国现代武侠小说的特点,这是中国玄幻作品本土文化特征的三个主要体现。
玄幻小说的主要受众为青少年群体,其作品本身也体现了青少年文化的特征。
青少年处于人生特殊的发展阶段,通常好奇心强、想象力丰富、内在叛逆、反应敏感,而玄幻小说从风格到主题都在相当的程度上满足了青少年受众的需求。
就脉络而言,玄幻小说多是以主人公的个人奋斗经历为主线,在一定程度上留有成长小说的痕迹。
玄幻小说为青少年呈现出一个另类的奇异世界,这里表现的是一种超越世事沧桑的人生感悟,是一种看尽烟花后的自省修身之态。
2022级高二第一学期期末考试数学试卷及详解

2022级高二第一学期期末考试数学试卷(答案在最后)一、单选题(每小题五分)二、多选题(每小题五分)三、填空题(每小题5分)四、解答题(17题10分,18-22题12分)(1)证明://PC 平面ADE ;(2)若平面BDEP ⊥平面ABCD P AC 夹角的余弦值.21.已知函数()y f x =的图象经过坐标原点,且(*n ∈N ).(1)求数列{}n a 的通项公式;(2)若数列{}n b 满足3log n a +(3)令22n n a d +=,若3d n c =都有1n n c c +>成立.22.已知椭圆2222:1(x y C a b +=(1)求椭圆C 的标准方程;(2)过点()2,0T a 作直线1l (直线1的斜率不为0)与椭圆C 相交于两点,过焦点F 作与直1l 的倾斜角互补的直线2l,与椭圆C 相交于,P Q 两点,求PF QFTM TN ⋅⋅的值.参考答案:8.D【详解】 1112n n n n n n a a a a a a +-++= 112a =,418a =,∴112a =,41a 1115.99100/0.99【详解】因为2312555a a a ++所以当2n ≥时,21255a a ++将1 与2 式相减得:5nn a 1,的最小距离为d r-=则(3,0,0),(0,1,0),(0,0,3),A B P 所以(0,1,3),(3,1,0),PB CB =-= 设平面PBC 的一个法向量(n = 令3z =,则1,3x y =-=,所以联立方程()221431x y y k x ⎧+=⎪⎨⎪=-⎩,消去y 后整理为(2022级高二第一学期期末考试数学试卷一、单选题(每小题五分)二、多选题(每小题五分)三、填空题(每小题5分)表示的圆中,当圆面积最小时,此时k =.是边长为43的等边三角形,则251n a +,则{}n b 的前99项和为是该正四面体内切球球面上的动点,当PA PD ⋅取得最小值时,点四、解答题(17题10分,18-22题12分)(1)证明://PC 平面ADE ;(2)若平面BDEP ⊥平面ABCD 弦值.21.已知函数()y f x =的图象经过坐标原点,且(1)求数列{}n a 的通项公式;(2)若数列{}n b 满足3log n a +(3)令22n n a d +=,若3d n c =成立.22.已知椭圆2222:1(x y C a b +=(1)求椭圆C 的标准方程;(2)过点()2,0T a 作直线1(直线1的斜率不为0)与椭圆C 相交于,M N 两点,过焦点F 作与直1l 的倾斜角互补的直线2l ,与椭圆。
张家口市2022-2023学年度高二年级第一学期期末考试高二数学答案

张家口市2022-2023学年度高二年级第一学期期末考试数学参考答案及评分标准一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.D 【解析】由l 1⊥l 2,可得5a -6=0,所以a =65,故选D. 2.B 【解析】将点(2,4)代入y 2=2px ,则4p =16,得p =4,故准线方程为x =-2,故选B.3.A 【解析】由题意椭圆C 的长半轴长为a =50=52,短半轴长为b =30,又a 2=b 2+c 2,所以半焦距c =20=25,所以椭圆C 的离心率e =c a =105,故选A. 4.B 【解析】圆C 1的标准方程为(x -2)2+()y -32=4,所以圆心为(2,3),半径为2.圆C 2是以(-1,-1)为圆心,半径为3的圆,故||C 1C 2=()2+12+()3+12=5=2+3,所以两圆外切,故选B.公众号高中僧试题下载5.A 【解析】如图,以D 为坐标原点,建立空间直角坐标系,所以D (0,0,0),A ()3,0,0,B ()3,3,0,B 1()3,3,3.又BE →=2ED →,AF →=2FB →1,所以E ()1,1,0,F ()3,2,2,故||EF =()3-12+()2-12+()2-02=3.故选A. 6.B 【解析】设首项为第1组,接下来两项为第2组,再接下来三项为第3组,以此类推.设第k 组的项数为k ,则前k 组的项的个数之和为k (k +1)2.又13×(13+1)2=91,14×(14+1)2=105,所以第100项为第14组的第9项,所以a 100=38.故选B. 7.C 【解析】设点P (x ,y )为直线x +y =0上的动点,又x 2+y 2-2x -2y +2+(x -2)2+y 2=(x -1)2+(y -1)2+(x -2)2+y 2. 设点M (1,1),N (2,0),则点M ′(-1,-1)为点M (1,1)关于直线x +y =0的对称点,故|PM |=|PM ′|,且|M ′N |=(2+1)2+(0+1)2=10,所以|PM |+|PN |=(x -1)2+(y -1)2+(x -2)2+y 2=|PM ′|+|PN |≥|M ′N |=10, 所以x 2+y 2-2x -2y +2+(x -2)2+y 2的最小值为10.故选C.8.C 【解析】由题意,得a 5a 8=a 6a 7=-18.又a 5+a 8=-3,所以联立⎩⎨⎧a 5a 8=-18,a 5+a 8=-3,解得⎩⎪⎨⎪⎧a 5=3,a 8=-6或⎩⎪⎨⎪⎧a 5=-6,a 8=3. 当a 5=3,a 8=-6时,a 8a 5=-2=q 3,所以a 2=a 5q 3=-32,a 11=a 8q 3=12, 所以a 2+a 11=212; 当a 5=-6,a 8=3时,a 8a 5=-12=q 3,所以a 2=a 5q 3=12,a 11=a 8q 3=-32, 所以a 2+a 11=212.故选C. 二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.BCD 【解析】由x -x 0y -y 0=2可知y ≠y 0,所以x -x 0y -y 0=2不过点P ()x 0,y 0且斜率为12,所以A 错误;直线x -2y -4=0过点A ()4,0,B ()0,-2,a =12BA →,所以a =()2,1是直线x -2y -4=0的方向向量,所以B 正确;设以A ()4,1,B ()1,-2为直径的圆上的任意点为P ()x ,y ,则P A →⊥PB →,所以P A →·PB →=0,即()x -4(x -1)+()y -1()y +2=0,所以C 正确;因为()m +1×2+()2m -1×1-1-4m =0,所以D 正确.10.BC 【解析】设{a n }的公差为d .因为a 9+a 10+a 11=3a 10>0,所以a 10>0.又a 9+a 12=a 10+a 11<0,所以a 11=a 10+d <0,故d <0,所以A 错误;因为d <0,所以a 1>a 2>a 3>a 4>a 5>a 6>a 7>a 8>a 9>a 10>0>a 11>…>a n ,所以当n =10时,S n 最大,所以B 正确;因为S 19=19(a 1+a 19)2=19×2a 102>0,S 20=20(a 1+a 20)2=20(a 10+a 11)2<0, S 21=21(a 1+a 21)2=21×2a 112<0, 所以C 正确,D 错误.c a=34,△F1PF2的周长为||PF1+||PF2+||F1F211.ABD【解析】设焦距为2c,由题意,得=2a +2c =14,解得a =4,c =3.又a 2=b 2+c 2,所以b =7,故椭圆C 的方程为x 216+y 27=1,所以A 正确;因为||PF 1+||PF 2=2a =8,所以8=||PF 1+||PF 2≥2||PF 1·||PF 2,当且仅当|PF 1|=|PF 2|=4时等号成立,所以||PF 1·||PF 2≤16,所以B 正确;设△F 1PF 2内切圆的半径为r ,则S △F 1PF 2=12||F 1F 2||y p =12r ()||PF 1+||PF 2+||F 1F 2, 所以r =3||y p 7.又||y p ≤7,所以r ≤377,所以S ≤9π7,所以C 错误; 因为cos ∠F 1PF 2=||PF 12+||PF 22-||F 1F 222||PF 1·||PF 2 =()||PF 1+||PF 22-2||PF 1·||PF 2-||F 1F 222||PF 1·||PF 2=-1+14||PF 1·||PF 2. 又||PF 1·||PF 2≤16,所以-1+14||PF 1·||PF 2≥-18,所以D 正确. 12.AB 【解析】如图,以点D 为坐标原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系D -xyz .由题意可得D (0,0,0),A (2,0,0),B (2,2,0),C (0,2,0),M (0,1,0),C 1(0,2,22),D 1(0,0,22),B 1(2,2,22),所以BC →=(-2,0,0),BB 1→=(0,0,22),D 1C →=(0,2,-22),AB →=(0,2,0),D 1B →=(2,2,-22),DB 1→=(2,2,22),MC 1→=(0,1,22),所以BP →=λBC →+μBB 1→=λ(-2,0,0)+μ(0,0,22)=(-2λ,0,22μ).当λ=12,μ=12时,AP →=AB →+BP →=(0,2,0)+(-1,0,2)=(-1,2,2), 所以异面直线AP 与DB 1所成角的余弦值为||cos 〈AP →,DB 1→〉=|AP →·DB 1→||AP →|·|DB 1→|=|-2+4+4|1+4+2·4+4+8=3714,所以A 正确; 当μ=12时,BP →=(-2λ,0,2), AP →=AB →+BP →=(0,2,0)+(-2λ,0,2)=(-2λ,2,2),故AP →·D 1C →=(-2λ,2,2)·(0,2,-22)=0,所以B 正确;当λ=12时,BP →=(-1,0,22μ),AP →=AB →+BP →=(0,2,0)+(-1,0,22μ)=(-1,2,22μ),D 1P →=D 1B →+BP →=(2,2,-22)+(-1,0,22μ)=(1,2,-22+22μ),故AP →·D 1P →=(-1,2,22μ)·(1,2,-22+22μ)=0,得8μ2-8μ+3=0无解,所以C 错误;当λ=1时,BP →=(-2,0,22μ),AP →=AB →+BP →=(0,2,0)+(-2,0,22μ)=(-2,2,22μ),故MC 1→·AP →=2+8μ=0,解得μ=-14∉[0,1],所以D 错误. 三、填空题:本题共4小题,每小题5分,共20分. 13.-58 【解析】由a ∥b ,得3λ-2=2λ=λ8,所以λ=-4,故a =(3,2,-4),b =(-6,-4,8),故a ·b =3×()-6+2×()-4+()-4×8=-58.14.x 216-y 248=1 【解析】直线l 与双曲线C 有唯一交点P ,则直线l 与双曲线C 的渐近线平行,所以b a=tan 60°=3, 故b =3a ,所以c 2=a 2+b 2=4a 2.又|FP |=6,所以P (3-c ,33),所以(3-c )2a 2-(33)2b 2=(3-2a )2a 2-(33)23a 2=1,解得a =4,所以b =43,所以双曲线C 的方程为x 216-y 248=1. 15.43【解析】当n =1时,S n =S 1=1, 又当n ≥2时,a n =1n 2+3n +2=1()n +1()n +2=1n +1-1n +2, 所以S n =1+13-14+14-15+…+1n +1-1n +2=43-1n +2<43,所以λ≥43,故λ的最小值为43. 16.x -3y -1=0 【解析】圆E 的标准方程为(x -1)2+(y -2)2=6,所以E ()1,2.由题意,得P A ⊥AE ,PB ⊥BE ,所以P ,A ,E ,B 四点在以PE 为直径的圆上,且直线AB 为该圆与圆E 的交线,以PE 为直径的圆的方程为(x -1)(x -2)+(y -2)()y +1=0,化简得x 2+y 2-3x -y =0,所以直线AB 的方程为x 2+y 2-2x -4y -1-()x 2+y 2-3x -y =0,即x -3y -1=0. 另解:圆E 的标准方程为(x -1)2+(y -2)2=6,由切点弦方程可知,直线AB 的方程为()2-1(x -1)+()-1-2(y -2)=6,化简得x -3y -1=0.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)解:(1)设数列{a n }的首项为a 1,公差为d .由S 21=21a 1+21×202d =0,得a 1+10d =0.………………………………………………2分 又a 8=a 1+7d =6,所以d =-2,a 1=20,………………………………………………3分 所以a n =20+()n -1×()-2=-2n +22.…………………………………………………4分(2)由a n =-2n +22≥0,解得n ≤11,……………………………………………………5分所以数列||a n =⎩⎨⎧a n ,n ≤11,-a n ,n >11,………………………………………………………………6分 故T 50=a 1+a 2+…+a 11-a 12-a 13-…-a 50………………………………………………7分 =-()a 1+a 2+…+a 11+a 12+a 13+…+a 50+2()a 1+a 2+…+a 11=-S 50+2S 11…………………………………………………………………………………9分=-⎣⎡⎦⎤50×20+50×492×(-2)+2×⎣⎡⎦⎤11×20+11×102×(-2) =1450+220=1670.…………………………………………………………………………10分18.(本小题满分12分)(1)解:圆E 是以E (2,3)为圆心,3为半径的圆,…………………………………………1分 当直线l 过圆E 的圆心时,||AB 最大,………………………………………………………2分 所以3=2k -1,解得k =2,…………………………………………………………………3分 所以当||AB 最大时,直线l 的方程为y =2x -1. ……………………………………………4分(2)证明:设A ()x 1,y 1,B ()x 2,y 2,由题意知k 存在,联立⎩⎪⎨⎪⎧y =kx -1,(x -2)2+()y -32=9,得()k 2+1x 2-()8k +4x +11=0,………………………6分 所以x 1+x 2=8k +4k 2+1,x 1x 2=11k 2+1,且()8k +42-44()k 2+1>0.……………………………8分 因为DA →·DB →=()x 1,y 1+1·()x 2,y 2+1=x 1x 2+()y 1+1()y 2+1,…………………………10分 y 1=kx 1-1,y 2=kx 2-1,所以DA →·DB →=()k 2+1x 1x 2=11,即DA →·DB →为定值.…………………………………………12分19.(本小题满分12分)解:(1)以该桥抛物线拱形部分对应抛物线的顶点为原点,建立直角坐标系.设对应抛物线的方程为x 2=2py (p <0).………………………………………………………1分 又点(32,-32)在抛物线上,所以322=2p ×()-32,……………………………………3分 所以p =-16,即||p =16,故抛物线的焦准距为16米.……………………………………4分(2)由题意,得|OF |=8米,|FP |=16米,……………………………………………………5分所以tan ∠POF =|FP ||OF |=168=2.………………………………………………………………6分 又PO ⊥PQ ,所以tan ∠QPF =tan ∠POF =2,……………………………………………8分所以tan ∠QPF =|QF ||PF |=|QF |16=2,所以|QF |=32米.………………………………………10分 又拱形最高点与桥面距离为32米,所以桥面与水面的距离d =|OF |=8米,所以桥面与水面的距离为8米.……………………………………………………………12分20.(本小题满分12分)解:(1)由b n =a 2n -1,得b 1=a 1=2,b n +1=a 2n +1.…………………………………………1分 又a 2k =a 2k -1+2,a 2k +1=2a 2k ,k ∈N *,……………………………………………………2分故a 2k +1=2()a 2k -1+2=2a 2k -1+4,…………………………………………………………3分所以b n +1=2b n +4,故b n +1+4b n +4=2.…………………………………………………………4分 又b 1+4=6,…………………………………………………………………………………5分 所以数列{}b n +4是以6为首项,2为公比的等比数列,所以b n +4=6×2n -1=3×2n ,故b n =3×2n -4.……………………………………………6分(2)nb n =3n ·2n -4n .……………………………………………………………………………7分 设c n =n ·2n ,其前n 项和为T n ,则T n =1×2+2×22+…+n ·2n ,…………………………………………………………8分 2T n =1×22+2×23+…+n ·2n +1,所以-T n =2+22+23+…+2n -n ·2n +1=-2+2n +1-n ·2n +1,…………………………9分 所以T n =()n -12n +1+2,…………………………………………………………………10分 所以S n =3T n -4()1+2+…+n =3()n -12n +1+6-4×n ()n +12=()3n -32n +1-2n 2-2n +6. ………………………………………………………………………………………………12分21.(本小题满分12分)(1)证明:如图,以点D 为坐标原点,DA 为x 轴,DC 为y 轴,过D 垂直于平面ABCD 的直线为z 轴,建立空间直角坐标系D -xyz ,故D ()0,0,0,A ()4,0,0,B ()4,4,0,C ()0,4,0.…………………………………1分因为平面ADP ⊥平面ABCD ,设P ()a ,0,c ,所以PD =a 2+c 2=2,PB =()a -42+()0-42+c 2=27, ………………………2分 所以a 2+c 2=4,a 2+c 2-8a +32=28,所以a =1,c =±3,由图可得c >0,所以c =3,所以P ()1,0,3,………………………………………3分所以AP →=()-3,0,3,DP →=()1,0,3.又DC →=()0,4,0,所以AP →·DP →=-3+3=0,AP →·DC →=0,………………………………4分所以AP →⊥DP →,AP →⊥DC →,又CD ∩PD =D ,且CD ⊂平面CDP ,PD ⊂平面CDP ,故AP ⊥平面CDP .……………………………………………………………………………5分(2)解:设AE →=λAC →,0≤λ≤1,则E ()4-4λ,4λ,0,…………………………………6分 所以PE →=()3-4λ,4λ,-3.又直线PE 与直线DC 所成的角为π4,所以||cos 〈PE →,DC →〉=16λ4()3-4λ2+()4λ2+3=22, 解得λ=12,……………………………………………………………………………………7分 故E ()2,2,0,所以DE →=()2,2,0.设m =(x 1,y 1,z 1)为平面PDE 的法向量,则有⎩⎪⎨⎪⎧m ·DE →=0,m ·DP →=0,即⎩⎨⎧2x 1+2y 1=0,x 1+3z 1=0,可取m =(1,-1,-33).………………………………………………8分 设n =(x 2,y 2,z 2)为平面P AC 的法向量,则有⎩⎪⎨⎪⎧n ·AC →=0,n ·AP →=0,即⎩⎨⎧-4x 2+4y 2=0,-3x 2+3z 2=0,可取n =(1,1,3),………………………………………………10分 ∴|cos 〈m ,n 〉|=⎪⎪⎪⎪m ·n ||m ||n =10535,所以平面PDE 与平面P AC 夹角的余弦值为10535.………………………………………12分 22.(本小题满分12分)解:(1)设动圆的圆心为M ()x ,y ,半径为r ,则||ME =r +32,||MF =r -2,所以||ME -||MF =42<||EF =6.……………………………………………………………2分 由双曲线定义可知,M 的轨迹是以E ,F 为焦点,实轴长为42的双曲线的右支, 所以2a =42,2c =6,即a =22,c =3,所以b 2=c 2-a 2=1,所以曲线C 的方程为x 28-y 2=1,x ≥2 2.…………………………………………………4分 (2)选择①②⇒③:设直线l :y =kx +m ,A ()x 1,y 1,B ()x 2,y 2,联立⎩⎪⎨⎪⎧y =kx +m ,x 28-y 2=1,得()1-8k 2x 2-16mkx -8m 2-8=0,……………………………………5分 所以x 1+x 2=-16mk 8k 2-1,x 1x 2=8m 2+88k 2-1.………………………………………………………6分 因为P (4,1),k 1+k 2=0,所以y 2-1x 2-4+y 1-1x 1-4=0, 即()x 1-4()kx 2+m -1+()x 2-4()kx 1+m -1=0, ………………………………………7分 即2kx 1x 2+()m -1-4k ()x 1+x 2-8()m -1=0,所以2k ×8m 2+88k 2-1+()m -1-4k ⎝⎛⎭⎫-16mk 8k 2-1-8()m -1=0,………………………………8分 化简得8k 2+2k -1+m ()2k +1=0,即()2k +1()4k -1+m =0,所以k =-12或m =1-4k .…………………………………………………………………10分 当m =1-4k 时,直线l :y =kx +m =k ()x -4+1过点P ()4,1,与题意不符,舍去,故k =-12,所以③成立. ……………………………………………………………………12分 选择①③⇒②:设直线l :y =-12x +m ,A ()x 1,y 1,B ()x 2,y 2, 联立⎩⎨⎧y =-12x +m ,x 28-y 2=1,得x 2-8mx +8m 2+8=0,……………………………………………5分所以x 1+x 2=8m ,x 1x 2=8m 2+8,…………………………………………………………6分所以k 1+k 2=y 2-1x 2-4+y 1-1x 1-4……………………………………………………………………7分 =-12x 2+m -1x 2-4+-12x 1+m -1x 1-4………………………………………………………………8分 =-1+m -3x 2-4+m -3x 1-4=-1+()m -3()x 1+x 2-8x 1x 2-4()x 1+x 2+16…………………………………………………………………10分 =-1+()m -3()8m -88m 2+8-4×8m +16=0,高二数学参考答案及评分标准 第 页(共10页) 10 所以②成立.…………………………………………………………………………………12分 选择②③⇒①:设直线l :y =-12x +m ,A ()x 1,y 1,B ()x 2,y 2,P (x 0,y 0), 联立⎩⎨⎧y =-12x +m ,x 28-y 2=1,得x 2-8mx +8m 2+8=0,……………………………………………5分 所以x 1+x 2=8m ,x 1x 2=8m 2+8.……………………………………………………………6分由k 1+k 2=y 2-y 0x 2-x 0+y 1-y 0x 1-x 0=-12x 2+m -y 0x 2-x 0+-12x 1+m -y 0x 1-x 0=0,…………………………7分 得()x 1-x 0⎝⎛⎭⎫-12x 2+m -y 0+()x 2-x 0⎝⎛⎭⎫-12x 1+m -y 0=0, 即-x 1x 2+⎝⎛⎭⎫m -y 0+12x 0()x 1+x 2-2x 0()m -y 0=0,………………………………………8分 所以-8m 2-8+8m ×⎝⎛⎭⎫m -y 0+12x 0-2x 0()m -y 0=0, 故2m ()x 0-4y 0+2x 0y 0-8=0,……………………………………………………………9分 所以00002200402801.8x y x y x y ⎧⎪-=⎪⎪-=⎨⎪⎪-=⎪⎩,,………………………………………………………………………10分 又x 0>0,解得⎩⎨⎧x 0=4,y 0=1,所以P ()4,1,①成立.……………………………………………12分。
2020-2021学年高二第一学期期末试题(解析版)

2020—2021学年度第一学期期末学业水平诊断高二生物一、选择题:此题共15小题,每题2分,共30分。
每题只有一个选项符合题目要求。
1.关于内环境稳态,以下说法正确的选项是()A.稳态就是指内环境的各种理化性质处于稳定状态B.内环境是机体进行正常生命活动和细胞代谢的场所C.毛细血管处血浆和组织液之间相互转化的量总是平衡的D.血液中CO2增多引起呼吸频率加快,是由体液和神经共同调节的【答案】D【解析】A、稳态就是指内环境的各种理化性质和化学成分处于稳定状态,A错误;B、细胞质基质是机体进行正常生命活动和细胞代谢的场所,B错误;C、血浆和组织液之间不断发生组织液的生成与回流,组织液中的大分子物质需要经过淋巴回流进入血浆,血浆、组织液和淋巴三者之间保持动态平衡,C错误;D、血液中CO2增多引起位于脑干的呼吸中枢兴奋,导致呼吸频率加快,是通过体液和神经共同调节的,D 正确。
2.以下关于突触及其功能的说法,错误的选项是()A.突触前膜和突触后膜都具有选择透过性B.神经递质发挥作用后会快速降解或回收再利用C.神经递质的合成、分泌以及向突触后膜转移都需要消耗ATPD.神经递质与受体结合后,突触后膜的膜电位不一定变为外负内正【答案】C【解析】A、突触前膜和突触后膜都是生物膜,都具有选择透过性,A正确;B、神经递质发挥作用后会快速降解或回收再利用,B正确;C、神经递质的合成、分泌都需要消耗ATP,神经递质向突触后膜转移为扩散作用,不需要消耗ATP, C错误;D、神经递质分为兴奋性递质和抑制性递质,抑制性神经递质与受体结合后,突触后膜的膜电位不会变为外负内正,D正确。
3.给狗喂食会引起唾液分泌,但铃声刺激不会。
假设每次在铃声后即给狗喂食,这样屡次结合后,狗听到铃声就会分泌唾液。
以下表达正确的选项是()A.大脑皮层没有参与铃声刺激引起唾液分泌的过程B.铃声和喂食反复结合可促进相关的神经元之间形成新的联系C.食物引起味觉和铃声引起唾液分泌属于不同的反射D.铃声引起唾液分泌的反射弧和食物引起唾液分泌的反射弧相同【答案】B【解析】A、铃声刺激引起唾液分泌为条件反射,相关中枢位于大脑皮层,A错误;B、铃声和喂食反复结合会形成条件反射,是通过相关的神经元之间形成新的联系而产生的,B正确;C、味觉形成过程到神经中枢时就已经在大脑皮层完成,没有传出神经和效应器,因此不属于反射,而铃声【解析】(1)脂肪细胞膜上存在识别胰岛素的结构,叫胰岛素受体,化学本质是糖蛋白。
高二上学期语文期末统测试卷含参考答案

高二上学期语文期末统测试卷含参考答案高二上学期语文期末试卷一、默写(15分)(1)外无期功强近之亲,。
(李密《陈情表》)(2)袅袅兮秋风,。
(屈原《湘夫人》)(3) ,两朝开济老臣心。
(杜甫《蜀相》)(4)楼船夜雪瓜州渡,。
(陆游《书愤》)(5)熊咆龙吟殷岩泉,。
(李白《梦游天姥吟留别》)(6) ,渔粱渡头争渡喧。
(孟浩然《夜归鹿门歌》)(7)春水碧于天,。
(韦庄《菩萨蛮(其二)》)(8) ,乾坤日夜浮。
(杜甫《登岳阳楼》)(9)心非木石岂无感? 。
(鲍照《拟行路难·其四》)(10)引壶觞以自酌,。
(陶渊明《归去来兮辞》)(11)渔舟唱晚,。
(王勃《滕王阁序》)(12)使六国各爱其人,则足以拒秦;使秦复爱六国之人,,谁得而族灭也?(杜牧《阿房宫赋》)(13)况阳春召我以烟景,。
(李白《春夜宴从弟桃花源序》)(14) ,芙蓉泣露香兰笑。
(李贺《李凭箜篌引》)(15)小楼昨夜又东风,。
(李煜《虞美人》)二、文言文阅读(29分)阅读下面的文言文,完成2-7题。
(一)伶官传序欧阳修呜呼!盛衰之理,虽曰天命,岂非人事哉!原庄宗之所以得天下,与其所以失之者,可以知之矣。
世言晋王之将终也,以三矢赐庄宗而告之曰:“梁,吾仇也;燕王,吾所立;契丹与吾约为兄弟;而皆背晋以归梁。
此三者,吾遗恨也。
与尔三矢,尔其无忘乃父之志!”庄宗受而藏之于庙。
其后用兵,则遣从事以一少牢告庙,请其矢,盛以锦囊,负而前驱,及凯旋而纳之。
方其系燕父子以组,函梁君臣之首,入于太庙,还矢先王,而告以成功,其意气之盛,可谓壮哉!及仇雠已灭,天下已定,一夫夜呼,乱者四应,仓皇东出,未及见贼而士卒离散,君臣相顾,不知所归。
至于誓天断发,泣下沾襟,何其衰也!岂得之难而失之易欤?抑本其成败之迹,而皆自于人欤?《书》曰:“满招损,谦得益。
”忧劳可以兴国,逸豫可以亡身,自然之理也。
故方其盛也,举天下之豪杰,莫能与之争;及其衰也,数十伶人困之,而身死国灭,为天下笑。
高二上学期期末考试语文试卷(附带答案解析)

高二上学期期末考试语文试卷(附带答案解析)(考试时间:150分钟;满分:150分)一、现代文阅读(35分)(一)现代文阅读I(本题共5小题,19分)阅读下面的文字,完成1~5题。
材料一先秦儒家在考量人与动物的关系时,强调和谐、仁爱。
如何实现此种理想?路径就是“尽物之性”,即万物向荣,各尽其性。
董仲舒在总结儒家的仁爱思想时所说的“质于爱民,以下至鸟兽昆虫莫不爱。
不爱,奚足以谓仁?”实质上不过是对儒家天人合一思想下的处理人与物之关系的延伸表达而已。
不过,在先秦儒家看来,对动物的爱与对人的爱还是有区别的。
这种有区别的爱源于儒家的差等之爱理念。
这种差等之爱循着“亲亲——仁民——爱物”的路径递减。
对人的爱尚且为差等之爱,对动物的爱自然又次之。
那么,在利用乃至食用动物方面,先秦儒家如何做到与其天人合一的哲学思想相一致的呢?他们的做法是:制天命而用之,杀伐以时。
荀子认为人有气、有生、有知,亦且有义,故最为天下贵。
而动物“有父子,而无父子之亲,有牝牡而无男女之别”,其道德地位自然低人一等,因此动物可以为人所用。
不过他并不主张对动物的随便利用和过度利用,而是主张遵循自然规律而用,即“杀伐以时”。
他说:“圣王之制也:草木荣华滋硕之时,则斧斤不入山林,不夭其生,不绝其长也;鼋鼍鱼鳖鳅鳝孕别之时,罔罟毒药不入泽,不夭其生,不绝其长也;春耕、夏耘、秋收、冬藏,四者不失时,故五谷不绝,而百姓有余食也。
”从实践层面讲,这种做法至少始于禹王时代。
(摘编自王云岭《儒家视野中人与动物的关系与启示》)材料二我们之所以要坚持人与自然和谐共生,将其作为坚持与发展中国特色社会主义的基本方略和新时代生态文明建设的首要原则,乃是因为人与自然是一个生命共同体。
地球上本无人类,后来才有人类——地球形成已有45亿年,产生生命已有42亿年,出现人类不过短短的300万年,这是科学事实。
地球可以没有人类,人类却不可以没有地球,地球是至今为止被发现唯一有生命存在、适合人类生存的星球,这也是科学事实。
高二上学期期末考试语文试卷及答案

高二上学期期末考试语文试卷及答案(满分:150分;考试时间:150分钟)学校:___________班级:___________姓名:___________考号:___________一、积累运用(10分)1.按要求填空。
(5分)(1)见贤思齐焉,__________________。
(《论语·里仁》)(2)故有之以为利,__________________。
(《老子》第十一章)(3)__________________,落月摇情满江树。
(张若虚《春江花月夜》)(4)孔子在回答弟子子贡提问时,指出可以终身践行的一个字是“恕”,并指明其具体的行事准则是“__________________,__________________。
”2.按要求选择。
(5分)(1)下列各项语言表达没有逻辑错误的一项是()(2分)A.《红楼梦》后四十回历来被世人所诟病,因为它是后人续写的,B.宝玉只要与整个封建家族决裂,就能获得属于自己的真正爱情。
C.《红楼梦》是人们公认的经典,所以被高中教材选定为必读书。
D.“金陵十二钗”都以悲剧结局收场,只有李纨、巧姐得以幸免。
(2)将下列编号的语句依次填入空白处,语意连贯的一项是()(3分)在2023年新一轮榜单中,上海老字号数量依然名列全国各省份榜首。
但仍有一些耳熟能详的上海品牌被移出中华老字号名录。
由此,如何与时俱进地增强消费者的文化认同依旧是上海老字号难以回避的问题。
_________,_________,_________,_________。
这要求老字号所构建的文化认同,必须与当下的审美认知和物质需求相统一。
①然而文化认同难以维系当代消费者与品牌的情感联系②消费者对于老字号的文化认同来自民俗活动的开展和生活观念的承袭③文化认同是指个体或群体对所属文化的价值肯定和心理上的归属感④特别是年轻消费者对老字号品牌存在过时土气的刻板印象A.①④③②B.②③④①C.③①②④D.③②①④二、阅读(70分)(一)阅读下文,完成第3—7题。
第一学期高二年级期末考试试卷(数学)及答案

第一学期高二年级期末考试试卷(数学)考试时间:120分钟 总分:150分注:本巻是文理综合巻,请同学们看清题,标(文)的文科做,标(理)的理科做,多做无效。
一、选择题:(每小题5分,共60分)1.已知直线l 的方程为1y x =+,则该直线l 的倾斜角为( ).A .30 B.45 C.60 D.1352.直线1y x =+与圆221x y +=的位置关系为( )A .相切B .相交但直线不过圆心C .直线过圆心D .相离3.原点到直线052=-+y x 的距离为( ) A .1 B .3 C .2 D .54.过点(1,3)P -且垂直于直线032=+-y x 的直线方程为( )A .012=-+y xB .052=-+y xC .052=-+y xD .072=+-y x5.抛物线28y x =-的焦点坐标是( )A .(2,0)B .(- 2,0)C .(4,0)D .(- 4,0)6.(文)椭圆221168x y +=的离心率为A .13B .12CD .26.(理)若双曲线()222213x y a o a -=>的离心率为2,则a 等于( )A. 2B. 1C. 32D.7.设双曲线)0,0(12222>>=-b a by a x 的虚轴长为2,焦距为32,则双曲线的渐近线方程为( ) A.x y 2±= B .x y 2±= C .x y 22±= D.x y 21±= 8.在右图的正方体中,M 、N 分别为棱BC 和棱CC 1的中点,则异面直线AC 和MN 所成的角为( )A .30°B .45°C .90°D .60° 9.已知F 是抛物线y 2=x 的焦点,A ,B 是该抛物线上的两点,=3AF BF +,则线段AB 的中点到y 轴的距离为A .34B .1C .54D .7410.已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程是,它的一个焦点在抛物线224y x =的准线上,则双曲线的方程为 ( )(A )22136108x y -= (B ) 221927x y -= (C )22110836x y -= (D ) 221279x y -= 11、已知点P 在抛物线y 2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为( )A. (41,-1)B. (41,1)C. (1,2)D. (1,-2)12.若点O 和点F 分别为椭圆22143x y +=的中心和左焦点,点P 为椭圆上的任意一1 A点,则FP OP ∙的最大值为( )A.2B.3C.6D.8二、填空题:(每小题5分,共20分)13.己知222212:1:349O x y O x y +=+=圆与圆(-)(+),则12O O 圆与圆的位置关系为 .14.椭圆22192x y +=的焦点为12,F F ,点P 在椭圆上,若1||4PF =,则2||PF = ;12F PF ∠的大小为 .15.已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且6,AB BC ==,则棱锥O ABCD -的体积为 。
高二第一学期期末测试卷及答案(理数)

中学高二期末测试卷(理数)时量:120分钟 总分:150分一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数=++−i i i 1)21)(1(在复平面内对应的点在( ) A .第一象限,B .第二象限C .第三象限D .第四象限2.特称命题“∃实数x ,使012<+x ”的否定可以写成 A .2,10x x ∀∈+≥R B .2,10x x ∃∈+≥R C .2,10x x ∀∈+<R D .若x ∈R ,则210x +<3.下面的抽样方法是简单随机抽样的是 ( ) A .在某年明信片销售活动中,规定每100万张为一个开奖组,通过随机抽取的方式确定号码的后四位为2709的为三等奖B .某车间包装一种产品,在自动包装的传送带上,每隔30分钟抽一包产品,称其重量是否合格C .某学校分别从行政人员、教师、后勤人员中抽取2人、14人、4人了解学校机构改革的意见D .用抽签法从10件产品中选取3件进行质量检验解析:A 、B 不是简单随机抽样,因为抽取的个体间的间隔是固定的;C 不是简单随机抽样,因为总体的个体有明显的层次;D 是简单随机抽样. 答案:D4.如图所示,在一个边长为1的正方形AOBC 内,曲线2y x =和曲线y x =围成一个叶形图(阴影部分),向正方形AOBC 内随机投一点(该点落在正方形AOBC 内任何一点是等可能的),则所投的点落在叶形图内部的概率是 A .12 B .13 C .14D .165.如图,1F 和2F 分别是双曲线)0,0(12222>>=−b a by a x 的两个焦点,A 和B 是以O 为圆心,以1F O 为半径的圆与该双曲线左支的两个交点,且△AB F 2是等边三角形,则双曲线的离心率为开始A =1k =1B=2A+1A=Bk=k +1k >5?输出A结束是否甲 乙 0 8 5 2 1 3 4 6 5 4 2 3 4 6 9 7 6 6 1 1 3 3 8 9 9 4 4 8 0 5 5 8 A .31+B .5C .25 D . 36.已知下面两个程序:甲: i=1 乙:i=1000 S=0 S=0 WHILE i<=1000 DO S=S+i S=S+i i=i+l i=i -1WEND LOOP UNTIL i<1 PRINT S PRINT SEND END对甲、乙两程序和输出结果判断正确的是 ( )A .程序不同,结果不同B .程序不同,结果相同C .程序相同,结果不同D .程序相同,结果相同7.抛物线24y x =的焦点为F ,准线为l ,经过F 且斜率为3的直线与抛物线在x 轴上方的部分相交于点A ,AK l ⊥,垂足为K ,则AKF △的面积是( ) A .4B .33C .43D .88. 已知()2,0A ,()0,1B ,点()y x C ,是椭圆1422=+x y 上的点,,则使三角形ABC 的面积为21的点C 有( )个 A .4 B .3 C .2 D .1二、填空题:本大题共7小题,每小题5分,共35分.把答案填在答题卡对应题号后的横线上。
高二上学期期末考试物理试卷(附参考答案与解析)
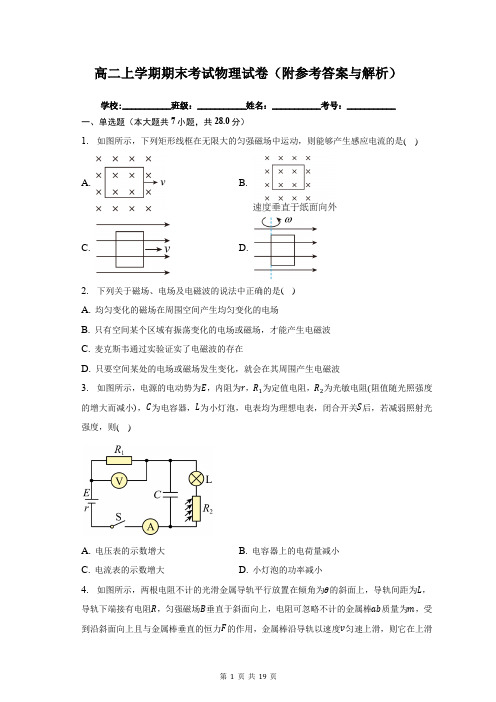
高二上学期期末考试物理试卷(附参考答案与解析)学校:___________班级:___________姓名:___________考号:___________一、单选题(本大题共7小题,共28.0分)1. 如图所示,下列矩形线框在无限大的匀强磁场中运动,则能够产生感应电流的是( )A. B.C. D.2. 下列关于磁场、电场及电磁波的说法中正确的是( )A. 均匀变化的磁场在周围空间产生均匀变化的电场B. 只有空间某个区域有振荡变化的电场或磁场,才能产生电磁波C. 麦克斯韦通过实验证实了电磁波的存在D. 只要空间某处的电场或磁场发生变化,就会在其周围产生电磁波3. 如图所示,电源的电动势为E,内阻为r,R1为定值电阻,R2为光敏电阻(阻值随光照强度的增大而减小),C为电容器,L为小灯泡,电表均为理想电表,闭合开关S后,若减弱照射光强度,则( )A. 电压表的示数增大B. 电容器上的电荷量减小C. 电流表的示数增大D. 小灯泡的功率减小4. 如图所示,两根电阻不计的光滑金属导轨平行放置在倾角为θ的斜面上,导轨间距为L,导轨下端接有电阻R,匀强磁场B垂直于斜面向上,电阻可忽略不计的金属棒ab质量为m,受到沿斜面向上且与金属棒垂直的恒力F的作用,金属棒沿导轨以速度v匀速上滑,则它在上滑ℎ高度的过程中,以下说法正确的是( )A. 安培力对金属棒所做的功为W=B2L2vℎRsinθB. 金属棒克服安培力做的功等于回路中产生的焦耳热C. 拉力F做的功等于回路中增加的焦耳热D. 重力做的功等于金属棒克服恒力F做功5. 如图所示A,B是两个完全相同的白炽灯,L是自感系数很大、电阻可忽略不计的自感线圈,下列说法正确的是( )A. 断开开关S时,A灯与B灯同时慢慢熄灭B. 断开开关S时,B灯立即熄灭而A灯慢慢熄灭C. 闭合开关S时,A,B灯同时亮,且达到正常亮度D. 闭合开关S时,A灯比B灯先亮,最后一样亮6. 在一个很小的矩形半导体薄片上制作四个电极E、F、M、N,做成了一个霍尔元件。
高二期末考试卷带答案语文上册

一、选择题(每小题2分,共20分)1. 下列词语中,字形、字音都完全正确的一项是:A. 窥视沉湎毛遂自荐B. 漫不经心贻笑大方窃窃私语C. 豁然开朗恣意妄为欣欣向荣D. 奋发图强纵情任性真心实意2. 下列句子中,没有语病的一项是:A. 通过这次参观,我对我国现代化建设的成就有了更深刻的认识。
B. 他在学术上取得了很高的成就,这与他刻苦钻研、勤奋好学是分不开的。
C. 我国人民在长期的生产斗争和科学实验中,对自然界的认识,达到了前所未有的水平。
D. 他对这个问题已经了解,但还不敢确定自己的看法。
3. 下列各句中,加点的成语使用不正确的一项是:A. 在这次比赛中,他表现出了超凡的技艺,令观众叹为观止。
B. 她的性格很内向,总是默默无闻地帮助别人。
C. 这篇文章语言流畅,内容丰富,读起来引人入胜。
D. 老师经常提醒我们,要珍惜时间,不要虚度光阴。
4. 下列各句中,标点符号使用不正确的一项是:A. “他的成绩一直很好,这次考试更是名列前茅。
”B. “我们一定要努力学习,争取早日实现我们的梦想。
”C. “我国有五千年的文明史,这是我们引以为豪的。
”D. “这本书对我帮助很大,我非常喜欢它。
”5. 下列各句中,下列句子表达效果最差的一项是:A. 他的笑容如同阳光一样温暖,让人感到无比的亲切。
B. 她的声音如同夜莺一样动听,让人陶醉其中。
C. 他的智慧如同大海一样深邃,让人敬佩不已。
D. 他的爱心如同春天一样温暖,让人感到生命的希望。
二、填空题(每空2分,共10分)6. 《背影》一文中,父亲送别儿子时,背影中蕴含了怎样的情感?答案:父爱如山,深沉而伟大。
7. 《荷塘月色》中,作者通过哪些景物描绘了荷塘月色的美丽?答案:荷叶、荷花、露珠、月光。
8. 《离骚》中,屈原表达了怎样的思想感情?答案:对祖国的热爱、对人民的关怀、对理想的追求。
9. 《赤壁赋》中,作者通过哪些手法描绘了赤壁之战的壮阔场面?答案:比喻、夸张、对比。
高二上学期期末检测物理试题含参考答案

高二物理试题第一学期期末检测注意事项:1.本试卷共6页,全卷满分100分,答题时间90分钟;2.答卷前,考生须准确填写自己的姓名、准考证号,并认真核准条形码上的姓名、准考证号;3.第Ⅰ卷选择题必须使用2B铅笔填涂,第Ⅱ卷非选择题必须使用0.5毫米黑色墨水签字笔书写,涂写要工整、清晰;4.考试结束,监考员将试题卷、答题卡一并收回。
第I卷(选择题共48分)一、选择题(本大题共12小题,每小题4分,计48分,其中1~8题为单选题,每题有一项是正确的.第9~12题为多选题,每题有几项..得0分)..得2分,错选、不选..是正确的,全部选对得4分,漏选1.下列哪项科技的应用与电磁感应原理相关()A.回旋加速器B.手机无线充电C.示波管D.电磁弹射器2.关于电场和磁场,以下说法正确的是()A.电场、磁场、电场线、磁感线都是为了研究问题方便而假想的B.电场的电场线和磁场的磁感线都是闭合的曲线C.无论是运动电荷还是静止的电荷在电场中都会受电场力的作用D.电荷在磁场中某位置受到的磁场力为零,则该位置的磁感应强度为零3.下面有关静电场的叙述正确的是()A.点电荷就是体积和带电荷量都很小的带电体B.在点电荷电场中,以点电荷为球心的同一球面上各点的场强都相同C.放在电场中某点的电荷,其电量越大,它所具有的电势能越大D.将真空中两个静止点电荷的电荷量均加倍、间距也加倍时,则库仑力大小不变4.一架悬挂于天花板上的弹簧秤下挂水平导线AB,导线中通有如图所示向右的电流1I,导线中心的正下方有与导线AB垂直的另一长直导线,当长直导线中通人向里的电流2I时,关于导线AB的运动及弹簧秤读数A.A向外、B向里转动,弹簧秤的读数增大B.A向里、B向外转动,弹簧秤的读数减小C.A向里、B向外转动,弹簧秤的读数增大D.A向外、B向里转动,弹簧秤的读数减小5.一灵敏电流计(电流表),当电流从它的正接线柱流入时,指针向正接线柱一侧偏转.现把它与开关、线圈串联,下列各图中能使灵敏电流计指针向正接线柱一侧偏转的是()A. B. C. D.6.关于电阻、电感、电容对电流作用的说法正确的是()A.电阻对直流电和交流电的阻碍作用相同B.电感线圈对交流电的阻碍作用是由于线圈自身存在电阻C.电容器两极板间是绝缘的,故电容支路上没有电流通过D.交变电流的频率增加时,电阻、电感线圈、电容器对电流的阻碍作用都增强7.关于通电直导线在匀强磁场中所受的安培力,下列说法正确的是()A.安培力的方向可以不垂直于直导线B.安培力的方向总是垂直于磁场的方向C.将通电直导线从中点折成直角,安培力的大小一定变为原来的一半D.将通电直导线从中点折成直角,安培力的大小一定变为原来的2 2倍8.甲、乙、丙三只阻值相同的电阻分别通以如图所示的三种电流,电流的最大值和周期相等,则三只电阻产A.1:2:4B.:2:2:4 D.1:1:29.下列有关说法正确的是()A.由I nqSv =可知,金属导体中自由电荷的运动速率越大,电流一定越大B.由E IR Ir =+外内内可知,电源电动势的大小与外电路电阻大小有关C.使用多用电表测电阻时,如果发现指针偏转很大,应选择倍率较小的欧姆挡重新测量D.根据Q=1PRt 可知,在电流一定时,电阻越大,相同时间内产生的热量越多10.如图所示,图中两平行板电容器、电源都完全相同,先闭合开关S ,稳定后将甲图中的开关S 断开,乙图中开关S 保持闭合,当将两图中的下极板向上移动少许,则()A.甲图中电容器的电容增大,乙图中电容器的电容不变B.甲图中电容器所带电荷量不变,乙图中电容器所带电荷量增大C.甲图中电容器两端的电势差增大,乙图中电容器两端的电势差不变D.甲图中两板间的电场强度不变,乙图中两板间的电场强度增大11.英国物理学家阿斯顿首次制成质谱仪,并用此对同位素进行了研究,若速度相同的三个带电粒子(不计重力)由左端射入质谱仪的运动轨迹如图所示,则下列相关说法中正确的是()A.三个带电粒子都带负电B.速度选择器的1P 极板带负电C.三个粒子通过狭缝0S 时速率等于1EB D.在2B 磁场中运动半径越大的粒子,比荷q m 越小12.如图所示,A 、B 、C 为匀强电场中的三个点,已知60CAB ∠= ,24cm AB AC ==,0V A ϕ=、8V B ϕ=-,将一带电量为5410C q -=⨯的正电荷从A 点移到C 点,电场力做功5810J -⨯,则下列说法正确的是()A.C 点电势为2VB.电场强度E 沿AB 方向由A B →,大小为200N/CC.该正电荷在B 点具有的电势能为43.210J--⨯D.将该正电荷从C 点移到B 点,电势能增加了42.410J-⨯第Ⅱ卷(非选择题共52分)二、实验题(本大题2小题,计16分)13.(7分)某同学用图甲所示的电路测量一节干电池的电动势和内电阻.(1)图甲中虚线框内是满偏电流为100mA 、表头电阻为9Ω的毫安表改装成量程为0.6A 的电流表,电阻1R 的电阻值为______Ω;(2)某次测量时毫安表的示数如图乙所示,则此时通过电池的电流为______A ;(3)实验得到的电压表示数U 与毫安表示数I 的关系图线如图丙所示。
高二年级第一学期期末综合测试题及答案

高二年级第一学期期末综合测试题一、选择题(本大题共25小题;每小题2分;共50分)1、 直线xcos20º+ysin20º-3=0的倾斜角是A 、200B 、1600C 、700D 、11002、 曲线f(x ;y) =0关于点(1;2)对称的曲线方程是A 、f(x-1;y-2)=0B 、 f(x-2;y-4)=0C 、f(1-x ;2-y)=0D 、f(2-x ;4-y)=03、 点(3;1)和(-4;6)在直线3x-2y+a=0的两侧;则a 的取值范围是A 、a <-7或a >24B 、-7<a <24C 、a =-7或a =24D 、a ≥-74、 给出下列命题:①所有直线都存在斜率;②截距式直线方程不能表示的直线是与两坐标轴垂直的直线;③一般式直线方程可表示任何直线。
其中正确命题的个数为A 、0B 、1C 、2D 、35、 点P(x ;y)到x 轴、y 轴和直线x+y-2=0的距离都相等;则x 的值一定是A 、2222+-或B 、22-C 、22+D 、以上结论都不对6、 直线l 过点P(3;2);与x 轴、y 轴的正半轴交于A 、B 两点;O 是坐标原点;当△AOB 面积最小时;直线l 的方程是A 、x-y-1=0B 、x+y-5=0C 、2x+y-12=0D 、3x+2y-13=07、直线ax+3y-9=0与直线x-3y+b=0关于原点对称;则a ;br 的值分别为A 、1;9B 、-1;9C 、1;-9D 、-1;-98、若直线l 过点(1;1);且与两坐标轴所围成的三角形面积为2;则直线l 的条数是A 、1B 、2C 、3D 、49、过原点的直线13422-=-y x l 与双曲线交于两点;则直线l 的斜率的取值范围是 )33()33()3333()23()23()2323(∞+--∞-∞+--∞-,,、,、,,、,、 D C B A 10、设常数m>0;椭圆x 2-2mx+m 2y 2=0的长轴是短轴的2倍;则m 等于21221222或、或、、、D C B A 11、设抛物线y=ax 2(a>0)与直线y=kx+b(k ≠0)有两个交点;其横坐标分别是1x 、2x ;而直线y=kx+b 与x 轴交点的横坐标是3x ;那么1x ;2x ;3x 的关系是A 、3x =1x +2xB 、213111x x x +=C 、231111x x x +=D 、1x =2x +3x 12、把椭圆192522=+y x 绕它的左焦点按顺时针方向旋转2π;则所得新椭圆的准线方程是 A 、44149-==y y , B 、44149-==x x , C 、44149=-=y y , D 、44149=-=x x , 13、以焦点的椭圆方程为的焦点为顶点,顶点为112422-=-y x 116414162222=+=+y x B y x A 、、 C 、1121622=+y x D 、1161222=+y x 14、点(1;2)且与曲线0683689422=-+--y x y x 只有一个公共点的直线A 、不存在B 、有两条C 、有三条D 、有四条15、若双曲线12222=-by a x 的实轴长、虚轴长、焦距成等差数列;则双曲线的离心率是 A 、2 B 、3 C 、34 D 、35 16、椭圆13422=+y x 内有一点P(-1;1);F 为右焦点;若椭圆上的点M 使得|MP|+2|MF|的值最小;则点M 为)1362()231()231()1362(-±-±-,、,、,、,、D C B A 17、双曲线14922=-y x 中;被点P(2;1)平分的弦所在的直线方程是 A 、8x-9y=7 B 、8x+9y=25 C 、4x-9y=6 D 、不存在18、抛物线2ax y =上存在关于直线x+y=0对称的两点;则a 的取值范围是 A 、43>a B 、43≥a C 、0>a D 、0≥a 19、已知直线m ;n 与平面βαγβα⊥,则,,的一个充分条件是γβγα⊥⊥,、A B 、ββα⊂⊥=n m n m ,,C 、βα////m m ,D 、βα⊥m m ,// 20、在下列命题中;真命题是A 、若直线m ;n 都平行于平面α;则m//nB 、设βα--l 是直二面角;若直线m β⊥⊥m l ,则C 、若直线m ;n 在平面α内的射影依次是一个点和一条直线;且n m ⊥;则n 在α内或n 与α平行D 、设m ;n 为异面直线;若m 与平面α平行;则n 与α相交21、等边△ABC 的边长为22;AD 是BC 边上的高;将△ABD 沿AD 折起;使之与△ACD所在平面成1200的二面角;这时A 点到BC 的距离是A 、226 B 、13 C 、3 D 、25 22、在正方体ABCD-A 1B 1C 1D 1中;M 、N 分别为棱AA 1和B 1B 的中点;若θ为直线CM 和ND 1所成的角;则cos θ等于A 、91B 、32C 、952D 、954 23、在下列命题中:①与两条异面直线都相交的两条直线是异面直线②直线上有两点到平面的距离相等;则此直线与平面平行③二面角的棱垂直于二面角的平面角所在平面④如果一个平面过另一个平面的斜线;那么这两个平面必不垂直其中错误命题的个数为A 、1B 、2C 、3D 、424、P 为正四面体ABCD 的面ABC 内的一点;则在平面ABC 内;过P 且与棱CD 所在直线成600角的直线的条数是A 、1B 、2C 、3D 、425、PA 、PB 、PC 是从P 点引出的三条射线;它们之间每两条的夹角都是600;则直线PC与平面PAB 所成的角是A 、450B 、600C 、余弦值为33的锐角D 、正切值为22的锐角 二、 填空题(本大题共6小题;每小题3分;共18分)26、等腰三角形两腰所在直线是097=--y x 和07=-+y x ;底边过点(3;-8);则底边所在的直线方程是_____________________________。
高二上期末考试题及答案

高二上期末考试题及答案一、选择题(每题2分,共20分)1. 下列关于化学反应速率的描述,正确的是()A. 温度升高,反应速率一定加快B. 反应速率与反应物的浓度无关C. 反应速率与催化剂有关D. 反应速率与反应物的接触面积无关答案:C2. 在下列物质中,属于电解质的是()A. 酒精B. 蔗糖C. 硫酸D. 醋酸答案:C3. 根据原子结构,下列元素中属于金属元素的是()A. 碳B. 氧C. 钠D. 硫答案:C4. 下列化合物中,属于共价化合物的是()A. NaClC. HClD. CaO答案:C5. 在下列反应中,属于氧化还原反应的是()A. H2 + Cl2 → 2HClB. NaOH + HCl → NaCl + H2OC. CaCO3 → CaO + CO2D. 2H2O → 2H2 + O2答案:A6. 下列物质中,能与酸反应生成气体的是()A. NaClB. Na2CO3C. NaOHD. Na2SO4答案:B7. 下列物质中,属于非金属单质的是()A. 铁B. 氧气C. 氢气D. 铜答案:C8. 下列化合物中,属于离子化合物的是()B. NaClC. CO2D. CH4答案:B9. 下列元素中,原子半径最大的是()A. 钠B. 镁C. 铝D. 硅答案:A10. 下列化合物中,属于酸性氧化物的是()A. CO2B. SO2C. NO2D. H2O答案:B二、填空题(每题2分,共20分)1. 化学反应方程式为:2H2 + O2 → 2H2O,其中反应物的摩尔比为______。
答案:2:12. 元素周期表中,第ⅠA族元素的原子最外层电子数为______。
答案:13. 根据质量守恒定律,化学反应前后______不变。
答案:元素种类4. 原子序数为17的元素是______。
答案:氯5. 化合物H2SO4中,硫元素的化合价为______。
答案:+66. 金属元素的原子结构特征是______。
答案:最外层电子数少于4个7. 氧化还原反应的特征是______的转移。
高二上 期末测试(一) 参考答案

期末测试(一)参考答案一、选择题:本题共12个小题,每小题3分,共36分.在每个小题给出的四个选项中,至少有一个是正确的.每小题全选对的得3分;选对但不全的得1分;有选错或不答的得0分.1.A 2. AD . 3.A 4 BCD 5.C 6.ABC 7.A 8.AC 9.AB 10.AC 11.AD 12.BD 二、实验填空题:本题共4个小题,满分20分,把答案直接填在题中的横线上.13.A…2分; a→b…2分14.错误!未找到引用源。
……4分;15.负…2分,S…2分16、①A2;V1;R1;E2 .②1.5欧,11.5欧,0.78(0.7-0.8均给分)③A 每空1分。
三、计算题:本题共4个小题,满分44分,解答应写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题,答案中必须明确写出数值和单位.17.(1)A点电场强度的大小E A =错误!未找到引用源。
错误!未找到引用源。
N/C =5.0×103 N/C………………4分(2)A、B两点间的电势差错误!未找到引用源。
错误!未找到引用源。
V = 20 V……………………………4分18.(1)根据闭合电路欧姆定律,通过电阻R的电流错误!未找到引用源。
………………………………4分(2)R上消耗的电功率错误!未找到引用源。
………………………………4分19.(1)带电粒子在磁场中所受洛伦兹力f =错误!未找到引用源。
(4)分(2)带电粒子在磁场中做匀速圆周运动,设其半径为R,由牛顿第二定律错误!未找到引用源。
………………………………………………4分带电粒子做匀速圆周运动的半径R=错误!未找到引用源。
…………………………………………………………2分解得m = 错误!未找到引用源。
…………………………………………………2分20.(1)由于带电微粒可以在电场、磁场和重力场共存的区域内沿竖直平面做匀速圆周运动,表明带电微粒所受的电场力和重力大小相等、方向相反。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二年级第一学期期末综合测试题一、选择题(本大题共25小题,每小题2分,共50分)1、 直线xcos20º+ysin20º-3=0的倾斜角是A 、200B 、1600C 、700D 、11002、 曲线f(x,y) =0关于点(1,2)对称的曲线方程是A 、f(x-1,y-2)=0B 、 f(x-2,y-4)=0C 、f(1-x,2-y)=0D 、f(2-x,4-y)=03、 点(3,1)和(-4,6)在直线3x-2y+a=0的两侧,则a 的取值范围是A 、a <-7或a >24B 、-7<a <24C 、a =-7或a =24D 、a ≥-74、 给出下列命题:①所有直线都存在斜率;②截距式直线方程不能表示的直线是与两坐标轴垂直的直线;③一般式直线方程可表示任何直线。
其中正确命题的个数为A 、0B 、1C 、2D 、35、 点P(x,y)到x 轴、y 轴和直线x+y-2=0的距离都相等,则x 的值一定是A 、2222+-或B 、22-C 、22+D 、以上结论都不对6、 直线l 过点P(3,2),与x 轴、y 轴的正半轴交于A 、B 两点,O 是坐标原点,当△AOB 面积最小时,直线l 的方程是A 、x-y-1=0B 、x+y-5=0C 、2x+y-12=0D 、3x+2y-13=07、直线ax+3y-9=0与直线x-3y+b=0关于原点对称,则a,br 的值分别为A 、1,9B 、-1,9C 、1,-9D 、-1,-98、若直线l 过点(1,1),且与两坐标轴所围成的三角形面积为2,则直线l 的条数是A 、1B 、2C 、3D 、49、过原点的直线13422-=-y x l 与双曲线交于两点,则直线l 的斜率的取值范围是 )33()33()3333()23()23()2323(∞+--∞-∞+--∞-,,、,、,,、,、Y Y D C B A 10、设常数m>0,椭圆x 2-2mx+m 2y 2=0的长轴是短轴的2倍,则m 等于 21221222或、或、、、D C B A 11、设抛物线y=ax 2(a>0)与直线y=kx+b(k ≠0)有两个交点,其横坐标分别是1x 、2x ,而直线y=kx+b 与x 轴交点的横坐标是3x ,那么1x ,2x ,3x 的关系是A 、3x =1x +2xB 、213111x x x +=C 、231111x x x +=D 、1x =2x +3x 12、把椭圆192522=+y x 绕它的左焦点按顺时针方向旋转2π,则所得新椭圆的准线方程是 A 、44149-==y y , B 、44149-==x x , C 、44149=-=y y , D 、44149=-=x x , 13、以焦点的椭圆方程为的焦点为顶点,顶点为112422-=-y x 116414162222=+=+y x B y x A 、、 C 、1121622=+y x D 、1161222=+y x 14、点(1,2)且与曲线0683689422=-+--y x y x 只有一个公共点的直线A 、不存在B 、有两条C 、有三条D 、有四条15、若双曲线12222=-by a x 的实轴长、虚轴长、焦距成等差数列,则双曲线的离心率是 A 、2 B 、3 C 、34 D 、35 16、椭圆13422=+y x 内有一点P(-1,1),F 为右焦点,若椭圆上的点M 使得|MP|+2|MF|的值最小,则点M 为)1362()231()231()1362(-±-±-,、,、,、,、D C B A 17、双曲线14922=-y x 中,被点P(2,1)平分的弦所在的直线方程是 A 、8x-9y=7 B 、8x+9y=25 C 、4x-9y=6 D 、不存在18、抛物线2ax y =上存在关于直线x+y=0对称的两点,则a 的取值范围是 A 、43>a B 、43≥a C 、0>a D 、0≥a 19、已知直线m ,n 与平面βαγβα⊥,则,,的一个充分条件是γβγα⊥⊥,、A B 、ββα⊂⊥=n m n m ,,IC 、βα////m m ,D 、βα⊥m m ,// 20、在下列命题中,真命题是A 、若直线m ,n 都平行于平面α,则m//nB 、设βα--l 是直二面角,若直线m β⊥⊥m l ,则C 、若直线m ,n 在平面α内的射影依次是一个点和一条直线,且n m ⊥,则n 在α内或n 与α平行D 、设m ,n 为异面直线,若m 与平面α平行,则n 与α相交21、等边△ABC 的边长为22,AD 是BC 边上的高,将△ABD 沿AD 折起,使之与△ACD所在平面成1200的二面角,这时A 点到BC 的距离是A 、226 B 、13 C 、3 D 、25 22、在正方体ABCD-A 1B 1C 1D 1中,M 、N 分别为棱AA 1和B 1B 的中点,若θ为直线CM 和ND 1所成的角,则cos θ等于A 、91B 、32 C 、952 D 、954 23、在下列命题中:①与两条异面直线都相交的两条直线是异面直线②直线上有两点到平面的距离相等,则此直线与平面平行③二面角的棱垂直于二面角的平面角所在平面④如果一个平面过另一个平面的斜线,那么这两个平面必不垂直其中错误命题的个数为A 、1B 、2C 、3D 、424、P 为正四面体ABCD 的面ABC 内的一点,则在平面ABC 内,过P 且与棱CD 所在直线成600角的直线的条数是A 、1B 、2C 、3D 、425、PA 、PB 、PC 是从P 点引出的三条射线,它们之间每两条的夹角都是600,则直线PC与平面PAB 所成的角是A 、450B 、600C 、余弦值为33的锐角D 、正切值为22的锐角 二、 填空题(本大题共6小题,每小题3分,共18分)26、等腰三角形两腰所在直线是097=--y x 和07=-+y x ,底边过点(3,-8),则底边所在的直线方程是_____________________________。
27、已知60125=+y x ,则22y x +的最小值是_____________________。
28、设平面α外两点A 和B 到平面α的距离分别为4cm 和1cm ,AB 与平面α成600角,则线段AB 的长为____________________________。
29、A 是锐二面角βα--a 的棱上一点,P 是平面β上的一点,PB ⊥α于B ,PA 与直线a成450角,PA 与平面α成300角,则二面角的大小是________________。
30、椭圆==+a y x a ,则的离心率为21198log 22_______________。
31、抛物线y 2=2px(p>0)上一点M 到它的准线距离为2,且M 到此抛物线顶点的距离等于M到它的焦点的距离,则此抛物线的焦点坐标是___________________。
三、 解答题(本大题共5小题,共32分。
解答应写出文字说明、证明过程或演算步骤。
)32、过点A (3,-1)作直线交x 轴于B ,交直线x y l 2=:于点C ,且∣BC ∣=2∣AB ∣,求直线l 的方程。
33、如图,四棱锥P-ABCD 中,侧 面PDC 是边长为2的正三角形,且与底面垂直,底面ABCD 是面积为32的菱形,∠ADC 为菱形的锐角。
(1) 求证:PA ⊥CD ;(2) 求二面角P-AB-D 的大小;AB C D P34、双曲线的中心在原点,焦点在x 轴上,且过点(3,2),又过左焦点且斜率为43-的直线交两条准线于M 、N ,以MN 为直径的圆过原点,求双曲线的方程。
35、设椭圆的中心在原点O ,一个焦点为F(0,1),长轴和短轴的长度之比为t 。
(1)求椭圆的方程;(2)设经过原点且斜率为t 的直线与椭圆在y 轴右边部分的交点为Q ,点P 在该直线上,且12-=t t OQ OP ,当t 变化时,求点P 的轨迹方程,并说明轨迹是什么图形。
36、已知椭圆C 的斜率为)321(36,,且点A 是C 上距离椭圆焦点F(1,22)最近的点。
(I)、求椭圆C 的方程;(II)、若与圆2122=+y x 相切的直线l 交椭圆于M 、N 两点,满足|OM|=|ON|(O 是坐标原点),求直线l 的方程。
高二年级第一学期期末综合测试题参考答案一、选择题:26、0130273=-+=--y x y x 或 27、1360 28、cm cm 331032或 29、450 30、9462或 31)034(,F 。
二、解答题:32、0740723=--=-+y x y x 或33、(1)略(2)a 43 (3)332 34、所求双曲线方程为:12322=-y x 。
35、(1)椭圆方程为111122222=-+-t x t ty ; (2)点P 的轨迹为抛物线y x 222=在直线x= 22右侧的部分和抛物线y x 222-=在直线22-=x 左侧的部分。
36、(I)、所求的椭圆方程为:14)1(1222=-+x y (II)所求的直线方程是22±=x。
