MCAI软件主成分分析法评价模型
机器学习技术中的主成分分析方法详解

机器学习技术中的主成分分析方法详解主成分分析(Principal Component Analysis,简称PCA)是一种在机器学习领域广泛应用的数据降维技术。
它通过将原始数据映射到新的一组低维度特征空间上,以尽可能捕获数据的最大变异性。
本文将详细介绍主成分分析方法的原理和应用。
主成分分析的核心思想是找到原始数据中的主要特征。
通常情况下,一个数据集包含多个特征,而PCA则是通过将这些特征进行线性组合,形成一组新的特征,这些新特征被称为主成分。
每个主成分都是原始特征的线性组合,并且具有不同的方差。
PCA的目标是找到这些主成分,使得用较少的主成分来表达数据时,尽可能保留原始数据的信息。
主成分分析的过程可以分为以下几个步骤:1. 数据标准化: 首先需要对原始数据进行标准化处理,以消除不同特征之间的量纲差异。
常见的方法包括Z-score标准化和归一化处理。
2. 计算数据协方差矩阵: 协方差矩阵反映了不同特征之间的线性关系。
通过计算数据的协方差矩阵,可以得到特征之间的相关程度。
3. 计算特征值和特征向量: 对协方差矩阵进行特征值分解,可以得到特征值和特征向量。
特征值表示新特征空间中每个主成分的方差,而特征向量则表示对应主成分的方向。
4. 选择主成分: 根据特征值的大小,选择前k个最大的特征值对应的特征向量作为主成分。
这些主成分对应的特征值较大,说明它们能够更好地保留原始数据的信息。
5. 数据投影: 使用所选的主成分将原始数据映射到新的低维度特征空间。
投影后的数据可以用于后续的分析和建模任务。
主成分分析的应用非常广泛,下面将介绍一些典型应用场景:1. 数据降维: 主成分分析可以将高维度的数据降低到更低的维度,减少冗余信息并提高计算效率。
例如,在图像处理中,可以使用PCA对图像进行降维,从而减少计算量并保留重要的图像特征。
2. 数据可视化: 由于PCA将数据映射到了低维度空间,可以方便地对数据进行可视化。
通过可视化分析,我们可以更好地理解数据的结构和分布。
带你认识主成分分析法

带你认识主成分分析法在研究某些问题时,需要处理带有很多变量的数据。
变量和数据虽然很多,但可能存在噪音和冗余。
然而,主成分分析法可以用少数变量来代表所有的变量,用来解释研究者所要研究的问题,化繁为简,抓住关键,也就是降维思想。
在研究某些问题时,需要处理带有很多变量的数据。
比如,研究房价的影响因素,需要考虑的变量有物价水平、土地价格、利率、就业率等。
变量和数据很多,但可能存在噪音和冗余,因为这些变量中有些是相关的,那么就可以从相关的变量中选择一个,或者将几个变量综合为一个变量,作为代表。
用少数变量来代表所有的变量,用来解释所要研究的问题,就能化繁为简,抓住关键,这也就是降维的思想。
主成分分析法(Principal Component Analysis,PCA)就是一种运用线性代数的知识来进行数据降维的方法。
它将多个变量转换出少数几个不相关的变量来,但转换后的变量能比较全面地反映整个数据集。
这是因为数据集中的原始变量之间存在一定的相关关系,可用较少的综合变量来表达各原始变量之间的信息。
具体来看,在数学变换中保持变量的总方差不变,使第一变量具有最大的方差,称为第一主成分,第二变量的方差次大且和第一变量不相关,称为第二主成分。
依次类推,i个变量就有i个主成分。
主成分分析法的核心思想是降维,而降维的基础是变量之间的相关性。
主成分分析法不要求所有变量都相关,但部分变量之间的相关性比较大才能满足降维的条件,否则强制对不相关的变量进行降维,主成分分析法就失去了实际意义。
因此,对于价格内在影响因素相关度较强的期货品种,用主成分分析法进行分析研究是比较合适的,而对于影响因素相关度较弱的期货品种不适合。
那么主成分分析法是如何降维的呢?从坐标变换的角度来获得一个感性的认识。
在短轴上,观测点数据的变化比较小,如果把这些点垂直地投影到短轴上,那么有很多点的投影会重合,这相当于很多数据点的信息没有被充分利用到。
而在长轴上,观测点的数据变化比较大。
主成分分析法的原理应用及计算步骤57270

一、概述在处理信息时,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠,例如,高校科研状况评价中的立项课题数与项目经费、经费支出等之间会存在较高的相关性;学生综合评价研究中的专业基础课成绩与专业课成绩、获奖学金次数等之间也会存在较高的相关性。
而变量之间信息的高度重叠与高度相关会给统计方法的应用带来许多障碍。
为了解决这些问题,最简单与最直接的解决方案就是削减变量的个数,但这必然又会导致信息丢失与信息不完整等问题的产生。
为此,人们希望探索一种更为有效的解决方法,它既能大大减少参与数据建模的变量个数,同时也不会造成信息的大量丢失。
主成分分析正式这样一种能够有效降低变量维数,并已得到广泛应用的分析方法。
主成分分析以最少的信息丢失为前提,将众多的原有变量综合成较少几个综合指标,通常综合指标(主成分)有以下几个特点:↓主成分个数远远少于原有变量的个数原有变量综合成少数几个因子之后,因子将可以替代原有变量参与数据建模,这将大大减少分析过程中的计算工作量。
↓主成分能够反映原有变量的绝大部分信息因子并不就是原有变量的简单取舍,而就是原有变量重组后的结果,因此不会造成原有变量信息的大量丢失,并能够代表原有变量的绝大部分信息。
↓主成分之间应该互不相关通过主成分分析得出的新的综合指标(主成分)之间互不相关,因子参与数据建模能够有效地解决变量信息重叠、多重共线性等给分析应用带来的诸多问题。
↓主成分具有命名解释性总之,主成分分析法就是研究如何以最少的信息丢失将众多原有变量浓缩成少数几个因子,如何使因子具有一定的命名解释性的多元统计分析方法。
二、基本原理主成分分析就是数学上对数据降维的一种方法。
其基本思想就是设法将原来众多的具有一定相关性的指标X1,X2,…,XP(比如p 个指标),重新组合成一组较少个数的互不相关的综合指标Fm 来代替原来指标。
那么综合指标应该如何去提取,使其既能最大程度的反映原变量Xp 所代表的信息,又能保证新指标之间保持相互无关(信息不重叠)。
《主成分分析模型》课件

主成分分析在实际生活中的应 用
主成分分析在股票价格预测、商品定价、产品优化和质量控制等领域应用广 泛。
主成分分析的局限性和应用前 景
主成分分析模型对输入变量的假定比较苛刻,且容易受到极端值和噪声干扰。 未来,随着数据科学技术的不断发展,这些限制有望得到缓解,主成分分析 模型的应用将更加广泛。
如何使用主成分分析模型?
进行调整。
3
建立回归模型
使用主成分建立回归模型,选择最优 变量。
预测结果分析
对模型预测结果进行分析,了解其背 后的原因。
主成分分析案例分析的结果解读
数据分析
通过主成分分析,我们得出该 公司的收入、成本和利润三个 主成分。
主成分解释
根据主成分系数矩阵,得出每 个主成分与原始数据的权重。
结果解读
解读主成分分析的结果,并提 出下一步优化的方向。
明确目的
确定主成分分析的目的和研 究对象。
选择变量
选择数据集中的相关变量, 并进行处理和标准化。
计算主成分
通过特征分解计算出主成分, 确定最具影响力的成分。
主成分分析的发展趋势
主成分分析在跨领域的交叉应用中将发挥越来越大的作用。未来,主成分分析模型将更加注重真实数据 的建模,有望成为精准数据科学的重要组成部分。
主成分分析的应用领域
金融
主成分分析可用于投资组合的优化、风险控制和股票价格预测。
医学
主成分分析可用于诊断和治疗疾病、分析药物疗效和评估病人风险。
工业
主成分分析可用于制造过程控制和质量管理。
主成分分析的优缺点
1 优点
降低数据维度、简化模型和提高模型准确性。
2 缺点
要求输入变量服从标准正态分布,可能会引入信息损失。
主成分分析步骤
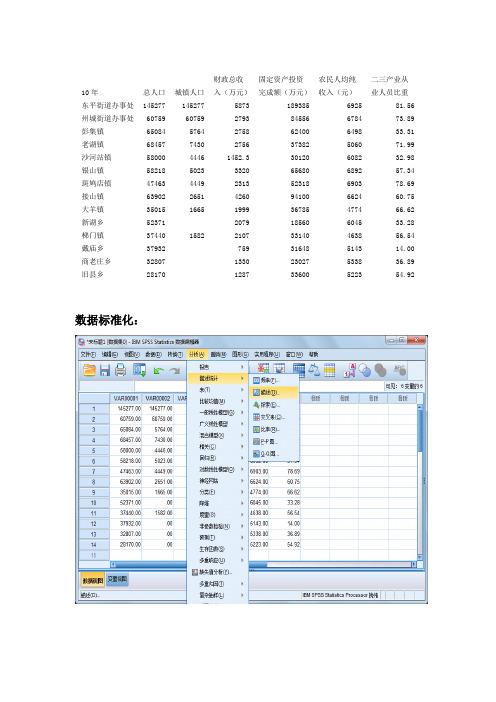
数据标准化:10年总人口 城镇人口 财政总收入(万元) 固定资产投资完成额(万元) 农民人均纯收入(元)二三产业从业人员比重东平街道办事处 145277145277 5873 189385 6925 81.56 州城街道办事处 60759 60759 2793 84556 6784 73.89 彭集镇 65084 5764 2758 62400 6498 33.31 老湖镇 68457 7430 2756 37382 5060 71.99 沙河站镇 58000 4446 1452.3 30120 6082 32.98 银山镇 58218 5023 3320 65680 6892 57.34 斑鸠店镇 47463 4449 2313 52318 6903 78.69 接山镇 63902 2651 4260 94100 6624 60.75 大羊镇 35015 16651999 36785 4774 66.62 新湖乡 52371 2079 18560 6045 33.28 梯门镇 37440 1582 2107 33140 4638 56.54 戴庙乡 37932 759 31648 5143 14.00 商老庄乡 32807 1330 23027 5338 36.89 旧县乡28170128733600522354.92在弹出对话框中把需标准化的变量选进Variable 去并在下面的提示前打钩标准化后数据,如下:10年总人口城镇人口财政总收入(万元)固定资产投资完成额(万元)农民人均纯收入(元)二三产业从业人员比重东平街道办事处 3.07912 3.19884 2.53391 2.98634 1.16159 1.35078州城街道办事处0.14797 1.089990.215870.628350.998050.97799彭集镇0.29796-0.282220.189530.129980.66633-0.99438老湖镇0.41494-0.240650.18803-0.43277-1.001530.88564沙河站镇0.05228-0.31511-0.79315-0.596120.18384-1.01041银山镇0.05984-0.300710.61250.20376 1.123310.17359斑鸠店镇-0.31315-0.31503-0.14538-0.0968 1.13607 1.21129接山镇0.25697-0.35989 1.319950.843030.812470.33933大羊镇-0.74486-0.3845-0.3817-0.4462-1.333240.62464新湖乡-0.14294-0.42604-0.32149-0.856140.14092-0.99583梯门镇-0.66076-0.38657-0.30041-0.52819-1.490980.1347戴庙乡-0.64369-0.42604-1.31493-0.56175-0.90526-1.93293商老庄乡-0.82143-0.42604-0.88519-0.75566-0.67909-0.82037旧县乡-0.98225-0.42604-0.91755-0.51784-0.812470.055962.主成分分析把标准化后的数据都选进Variables 去结果分析:表一根据计算数据可知,前二个主成分的累计贡献率已经高达85.005%,接近90%。
基于主成分分析的综合评价模型

基于主成分分析的综合评价模型在数据分析领域中,主成分分析(Principal Component Analysis,简称PCA)是一种常用的降维技术,它能够将高维的数据转化为较低维的数据,并保留数据的主要信息。
基于主成分分析的综合评价模型则是在PCA的基础上,对多个评价指标进行综合评价的模型。
本文将介绍基于主成分分析的综合评价模型的原理和应用。
一、主成分分析(PCA)简介主成分分析是一种通过线性变换将原始数据转化为低维空间的技术。
它通过找到数据中的主要方向,将数据投影到新的坐标系中,使得投影后的数据具有更好的可解释性和区分性。
主成分分析的基本步骤包括特征值分解、选择主成分和投影计算。
二、综合评价模型的构建方法基于主成分分析的综合评价模型的构建方法包括数据准备、特征值分解、主成分选择和综合评价计算。
首先,需要收集和整理待评价的指标数据,并进行归一化处理,以消除不同指标之间的量纲差异。
然后,对归一化后的指标数据进行特征值分解,得到特征值和特征向量。
接下来,选择主成分,可以根据特征值的大小顺序,选择前几个特征值对应的特征向量作为主成分。
最后,利用选定的主成分对原始指标数据进行投影,得到综合评价结果。
三、基于主成分分析的综合评价模型的应用举例以某酒店为例,我们希望对其服务质量进行综合评价。
我们收集了以下几个指标作为评价依据:员工态度、服务速度、设施条件和价格水平。
首先,对这些指标进行归一化处理,然后进行特征值分解。
假设得到的特征值分别为λ1、λ2、λ3、λ4,对应的特征向量分别为v1、v2、v3、v4。
根据特征值的大小顺序,我们选择前两个特征值对应的特征向量作为主成分。
然后,我们利用选定的主成分对原始指标数据进行投影计算,得到综合评价结果。
假设原始指标数据为X1、X2、X3、X4,对应的投影结果为Y1、Y2。
最后,通过采用某种评分方法,将投影结果转化为能够描述酒店服务质量的综合评价得分。
四、基于主成分分析的综合评价模型的优势与不足基于主成分分析的综合评价模型具有以下优势:首先,可以将多个指标融合为一个综合指标,简化评价过程;其次,可以消除不同指标之间的量纲差异,减小指标权重确定的困难。
主成分分析方法

主成分分析方法主成分分析(Principal Component Analysis, PCA)是一种常用的数据降维和特征提取方法,它可以将高维数据转换为低维数据,同时保留数据的主要特征。
在实际应用中,主成分分析方法被广泛应用于数据挖掘、模式识别、图像处理、生物信息学等领域。
本文将介绍主成分分析的基本原理、算法步骤以及应用实例。
1. 基本原理。
主成分分析的基本思想是通过线性变换将原始数据映射到一个新的坐标系中,使得在新的坐标系下,数据的方差最大化。
换句话说,主成分分析就是找到一组新的基,使得数据在这组新的基下的方差最大。
这样做的目的是为了尽可能保留原始数据的信息,同时去除数据之间的相关性,从而达到降维的效果。
2. 算法步骤。
主成分分析的算法步骤可以简单概括为以下几步:(1)数据标准化,对原始数据进行标准化处理,使得各个特征具有相同的尺度。
(2)计算协方差矩阵,对标准化后的数据计算协方差矩阵。
(3)特征值分解,对协方差矩阵进行特征值分解,得到特征值和特征向量。
(4)选择主成分,按照特征值的大小,选择最大的k个特征值对应的特征向量作为主成分。
(5)数据映射,将原始数据映射到所选的主成分上,得到降维后的数据。
3. 应用实例。
主成分分析方法在实际应用中有着广泛的应用,下面以一个简单的实例来说明主成分分析的应用过程。
假设我们有一个包含多个特征的数据集,我们希望对这些特征进行降维处理,以便更好地进行数据分析。
我们可以利用主成分分析方法对这些特征进行降维处理,得到新的特征空间。
在新的特征空间中,我们可以更好地观察数据之间的关系,找到数据的主要特征,从而更好地进行数据分析和建模。
总结。
主成分分析是一种常用的数据降维和特征提取方法,它通过线性变换将原始数据映射到一个新的坐标系中,使得数据的方差最大化。
通过对协方差矩阵进行特征值分解,我们可以得到主成分,并将原始数据映射到主成分上,实现数据的降维处理。
在实际应用中,主成分分析方法有着广泛的应用,可以帮助我们更好地理解和分析数据。
主成分综合评价模型

主成分综合评价模型引言:主成分综合评价模型是一种常用的多指标综合评价方法,可以用于评估和比较不同对象或方案的综合性能。
本文将介绍主成分综合评价模型的基本原理、应用领域以及优缺点,并结合实际案例进行说明。
一、主成分综合评价模型的基本原理主成分综合评价模型是一种基于统计学原理的多指标综合评价方法。
首先,通过对多个指标的测量或观测,计算得到各个指标的原始数据。
然后,通过主成分分析方法,将这些指标进行综合,得到一组主成分。
最后,根据主成分的贡献率,对不同对象或方案进行综合评价。
主成分分析是一种降维技术,通过线性变换将原始数据转化为一组互相无关的主成分。
主成分的选择是基于其解释方差的能力,通常选择前几个主成分,使其累计贡献率达到一定阈值。
主成分的计算和选择可以使用各种统计软件进行实现。
二、主成分综合评价模型的应用领域主成分综合评价模型在各个领域都有广泛的应用,包括经济、环境、工程、管理等方面。
以下是几个常见的应用领域:1. 经济领域:主成分综合评价模型可以用于评估不同地区或国家的经济发展水平。
通过选取合适的经济指标,如GDP、人均收入、失业率等,可以对不同地区或国家的经济综合实力进行比较和评价。
2. 环境领域:主成分综合评价模型可以用于评估环境质量。
通过选取合适的环境指标,如空气质量指数、水质指标、土壤污染程度等,可以对不同地区或场所的环境质量进行综合评价。
3. 工程领域:主成分综合评价模型可以用于评估工程项目的综合效益。
通过选取合适的评价指标,如投资回报率、工期、质量等,可以对不同工程项目进行综合评价,从而帮助决策者做出合理的决策。
4. 管理领域:主成分综合评价模型可以用于评估企业或组织的综合绩效。
通过选取合适的绩效指标,如销售额、利润率、员工满意度等,可以对不同企业或组织的综合绩效进行比较和评价,从而指导管理决策。
三、主成分综合评价模型的优缺点主成分综合评价模型具有以下优点:1. 可以综合考虑多个指标的信息,避免了单一指标评价的局限性。
数学建模之主成分分析法

主成分分析主成分分析的主要目的是希望用较少的变量去解释原来资料中的大部分变量,将我们手中许多相关性很高的变量转化成彼此相互独立或不相关的变量。
通常是选出比原始变量个数少,能解释大部分资料中的变异的几个新变量,即所谓主成分,并用以解释资料的综合性指标。
1、主成分分析的应用(1)我国各地区普通高等教育发展水平综合评价。
(2)投资效益的分析和排序等。
2、主成分分析法的步骤①对原始数据进行标准化处理用12,,,m x x x 表示主成分分析指标的m 个变量,评价对象有n 个,ij a 表示第i 个评价对象对应于第j 个指标的取值。
将每个指标值ij a 转化为标准化指标ij a ,即 ,(1,2,,;1,2,,)ij j ij j a a i n j m s μ-===式中:11n j ij i a n μ==∑,211()1nj ij j i s a n μ==--∑ 相应地,标准化指标变量为,(1,2,,)j jj j x x j m s μ-==②计算相关系数矩阵R()ij m m R r ⨯=1,(,1,2,,)1n ki kj k ij a a r i j m n =⋅==-∑ 其中:1,ii ij ji r r r ==,ij r 是第i 个指标和第j 指标之间的相关系数。
③计算相关系数矩阵的特征值与特征向量 解特征方程0=-R I λ,得到特征值(1,2,,)i i m λ=12,0m λλλ≥≥≥≥;再求出相对应的特征值i λ的特征向量(1,2,,)i u i m =,其中12(,,,)T j j j mj u u u u =,由特征向量组成的m 个新的指标变量为 11112121212122221122m m m m m m m mm my u x u x u x y u x u x u x y u x u x u x =+++⎧⎪=+++⎪⎨⎪⎪=+++⎩ 其中:1y 为第1主成分,2y 为第1主成分,⋯,m y 为第m 主成分④选择p (p ≤m )个主成分,计算综合评价值。
主成分分析与模糊综合评判方法在融资效率评价中的比较

主成分分析与模糊综合评判方法在融资效率评价中的比较提要本文分别利用模糊综合评判与主成分分析两种方法建立企业融资效率评价数学模型。
首先结合中小企业融资实际情况,考虑融资期限、融资成本、融资风险、资金使用的自由度、资金的到位率和融资主体自由度等六个因素,对于五种典型的融资方式进行单因素分析。
进而,运用这两种不同方法分别对五种不同的融资效率进行排序。
基于计算结果的比较,得出主成分方法在解决此类问题中具有更好的稳定性及操作性的结论。
关键词:中小企业;融资效率;单因素分析;模糊综合评判;主成分分析本文受安徽省高校自然科学重点项目资助(KJ2007A077)和安徽财经大学大学生科研基金项目资助中图分类号:F83文献标识码:A一、企业融资效率评价的数学模型(一)模糊综合评判模型。
总体上,中小企业融资方式分为两大类:权益性融资和债务性融资。
具体而言,权益性融资包括自我积累和股权融资,债务性融资包括银行信贷、债券融资和民间信贷(武巧珍、刘扭霞,2007)。
因此,本文将从上述的六个因素分别对这五种融资方式单项因子的融资效果优劣进行初步排序,得出表1。
(表1)表1列示了各种融资方式单因素下的初步排序,反映的是同一因素下企业的选择顺序。
结合表1中的数据,我们给各种融资方式取值,得到表2的不同融资方式的隶属度。
(表2)已经确定了权重集,计为A=(0.10,0.25,0.20,0.15,0.20,0.10),并且由表2得出了各种融资方式的单因素评价矩阵,将它们分别与权重集进行模糊变换,即得模糊综合评价模型:B=W×R,运用软件得到最终排名依次为:企业积累、股票融资、债券融资、民间信贷、银行信贷。
(二)主成分分析模型。
不同融资方式融资效率评价体系中涉及众多指标,指标间的相关关系会造成评价信息的相互重叠、相互干扰,难以有效、客观地分析各评价向量的相对地位,使层次分析法计算造成较大误差。
因此,考虑利用主成分分析法,通过对指标值进行正交变换,过滤掉指标间的重复信息,来增加综合评价的准确性。
AI技术中的预测模型构建方法解析

AI技术中的预测模型构建方法解析一、引言近年来,人工智能(Artificial Intelligence, AI)技术的快速发展给各行各业带来了巨大的变革。
在AI技术中,预测模型是重要的组成部分之一。
预测模型能够利用历史数据和算法,在未来进行预测和推测。
本文将解析AI技术中常见的预测模型构建方法,包括数据准备、选择模型、训练模型和评估模型四个关键步骤。
二、数据准备1. 数据收集:构建一个可靠和有效的预测模型首先需要收集到充足而准确的数据。
根据具体问题,可以通过调查问卷、观察研究、传感器等多种途径获得数据。
2. 数据清洗与处理:原始数据往往存在噪声、缺失值或异常值,需要进行清洗和处理。
常见的处理方法包括删除无效样本、填补缺失值或用平均值代替异常值等。
3. 特征选择与降维:对于高维度数据,选择合适的特征是非常重要的。
可以利用统计学方法或机器学习算法进行特征选择,并采用降维技术如主成分分析(Principal Component Analysis, PCA)来减少特征的数量,提高模型的计算效率。
三、选择模型选择合适的预测模型是构建预测系统中的关键一步。
常见的预测模型包括线性回归、决策树、支持向量机(Support Vector Machines, SVM)、神经网络等。
在选择模型时,需要考虑以下几个因素:1. 数据类型:根据数据的特点,选择合适的预测模型。
如果数据具有线性关系,则可以选择线性回归模型;如果数据呈现非线性关系,则可以考虑使用决策树或神经网络等非线性模型。
2. 预测目标:不同的预测目标需要不同类型的预测模型。
例如,分类问题可以使用支持向量机或决策树;而回归问题则可以采用线性回归或神经网络。
3. 数据规模:大规模数据集通常需要更复杂、更强大的模型来进行有效预测;而小规模数据集则可能只需简单的线性回归模型即可。
四、训练模型在选择了合适的预测模型后,就需要对其进行训练。
以下是一些重要的注意事项:1. 数据划分:将原始数据集划分为训练集和测试集,通常采用的比例是70%至80%的数据作为训练集,剩余的作为测试集。
主成分分析模型-精选文档

主成分分析模型与因子分析模型
一、主成分分析模型 1.什么是主成分分析 主成分概念首先是由Karl Parson 在1901年 引进的,不过当时只对非随机变量来讨论的. 1933年Hotelling将这个概念推广到随机向量.
在实际问题中,研究多指标(变量)问题是经常 遇到的,然而在多数情况下,不同指标之间是有一 定相关性.由于指标较多再加上指标之间有一定的 相关性,势必增加了分析问题的复杂性.主成分分 析就是设法将原来指标重新组合成一组新的互相 无关的几个综合指标来代替原来指标,同时根据实 际需要从中可取几个较少的综合指标尽可能多地 反映原来指标的信息.
为了有效地反映原来信息,F1已有的信息就不需要 再出现在F2中,用数学语言表达就是要求 Cov(F1,F2)=0,称F2为第二主成分,依此类推,可 以制造出第三、四……第p个主成分。不难想像这 些主成分之间不仅不相关,而且它们的方差依次递 减。因此,在实际工作中,就挑选前几个最大的主 成分(一般取信息量包含85%以上的前几个指标), 虽然这样做会损失一部分信息,但是由于它使我们 抓住了主要矛盾,并从原始数据中进一步提取了某 些新的信息,因而在某些实际问题的研究中得益比 损失大,这种既减少了变量的数目又抓住了主要矛 盾的做法有利于问题的分析和处理。
i 1
i
, 。
因此第一主成分的贡献率就是第一主成分的 方差在全部方差 中的比值。这个比值越大, 表明第一主成分综合X1,……,Xp信息的能力越 强。
2、基本思想 主成分分析就是设法将原来众多具有一定相关 性的指标(比如p个指标),重新组合成一组相互 无关的综合指标来代替原来指标。通常数学上的处 理就是将原来p个指标作线性组合,作为新的综合 指标,但是这种线性组合,如果不加限制,则可以 有很多,我们应该如何去选取呢?如果将选取的第 一个线性组合即第一个综合指标记为F1,自然希望 F1尽可能多的反映原来指标的信息,这里的“信 息”用什么来表达?最经典的方法就是用F1的方差 来表达,即Var(F1)越大,表示F1包含的信息越多。 因此在所有的线性组合中所选取的F1应该是方差最 大的,故称F1为第一主成分。如果第一主成分不足 以代表原来p个指标的信息,再考虑选取F2即选第 二个线性组合。
MCAI软件主成分分析法评价模型

0引言由于MCAI软件是用于教学的特殊软件,因此除具有一般软件的质量因素外,还有教育学、心理学因素等因素,也就是说,影响MCAI软件质量的因素比较多,那么,建立怎样的MCAI软件评价体系才能完成反映MCAI软件的质量?在对MCAI软件进行评价时,采用什么样的模型进行评价,才能对MCAI软件评价即能简化评价指标体系,又能反映原来指标体系反映的信息,这正是本文需要解决的问题——建立MCAI 软件主成分分析法评价模型。
1MCAI软件评价指标体系1.1MCAI软件评价指标体系选取的原则而影响MCAI软件的因素比较多,选取那些指标对MCAI 软件进行评价才能达到即客观又全面的评价,MCAI软件评价指标选取时要遵循的原则:(1)目的明确:对MCAI软件评价所选取的评价指标应能反映MCAI软件有关内容;(2)比较全面:MCAI软件评价指标的选取应尽可能的覆盖MCAI软件评价的内容,如果有所遗漏,评价就会片面;(3)稳定性:所选取的MCAI软件评价指标不应轻易改变,应保持其相对的稳定性。
1.2MCAI软件评价指标体系建立与一般的软件相比,MCAI软件具有特殊性:MCAI软件是用于教学活动的特殊软件,除具有一般软件的技术方面的要求外,还具有教育学、心理学及能力等多方面的要求。
因此对MCAI软件进行评价应从以下几方面考虑:(1)教学方面的要求MCAI软件与一般的计算机软件相比有其特殊性,例如MCAI软件对教学性、科学性、思想性、准确性、逻辑性、适应范围的广泛性等方面有一定的要求,因此评价时要有所反映。
(2)技术方面的要求MCAI软件与其它计算机的软件一样要考虑它的各项质量评价指标,例如它在功能性、可靠性、易使用性、可维护性、可移植性、人机交互性等方面都要达到一定的要求。
(3)学习心理方面的要求收稿日期:2010-07-11;修订日期:2010-09-15。
它是符合程序教学的基本原理,程序教学的特点是把教材内容以合乎逻辑的顺序由浅入深、循序渐进地排列起来,做到程序化的安排。
主成分分析在综合评价中的应用模型

主成分分析在综合评价中的应用张毅(长江大学信息与数学学院,湖北荆州 434023)[摘要] 应用主成分分析原理,以少数的综合变量取代原有的多维变量,使数据结构简化,把原指标综合成几个主成分,再以这几个主成分的贡献率为权数进行加权平均,构造出一个综合评价函数.文章应用该原理对23家电器企业的实力进行了综合评价,其结果是合理可信的.[关键词] 主成分分析;综合评价;排序[中图分类号] O29 [文献标识码] A [文章编号] 1008-4657(2005)06-0062-04 排序问题在我们日常生活中经常碰到,对单指标系统中的各样本点进行排序,按指标值的大小排序就可以了.而对多指标系统中的各样本点进行排序就不能按各指标值的大小这一简单原则进行了,一个常用的方法是对各指标进行总和平均后,按平均值的大小进行排序.但有时由于各指标间的量纲不一样,就不能进行加法运算了.再者,即使各指标间的量纲一致,可以作加法运算,而各指标反映系统侧面不同,对系统的作用不一样,作加法运算时,存在一个权系数的处理问题,而权系数的取定没有一个统一的标准,这样就不能得到统一的排序结果.同时,在很多情况下各指标间有一定的相关性,甚至是严重相关,从而使得这些指标所提供的信息在一定的程度上有所重叠,求和时系统信息会重叠计算,也不能得到令人信服的排序结果.本文利用主成分分析原理,对多维空间实行降维处理,在系统变异信息损失最小的情况下,得到线性无关的几个主成分,利用主成分得分,对系统中各样本点进行综合评价,这样就排除了各指标间由于量纲不同和信息重叠所造成的影响,不用人为规定权系数,排除主观因素的干扰,使得计算结果更加科学、真实可靠.1 应用实例我们对23家家电类上市公司2005年1月的财务指标作主成分分析,设定综合评价指数对23家公司进行排序,并用聚类分析验证了排序的正确性.这6项财务指标分别为:每股盈利x1(元),每股净资产x2(元),主营利润率x3(% ),净资产收益率x4(% ),负债率x5(% ),每股公积金x6(元).数据来源于武汉证券公司,数据如表1.表1 23家公司基本情况表公司名称x1x2x3x4x5x6科龙电器0. 06 2. 89 17. 95% 2. 11% 0. 75% 1. 5894康佳电器0. 03 5. 34 14. 75% 0. 64% 0. 65% 3. 0858ST华发0. 00 0. 82 -3. 91% -0. 31% 0. 44% 0. 3584TCL -0. 13 1. 98 14. 83% -5. 99% 0. 82% 0. 7662小天鹅0. 03 3. 16 22. 27% 1. 04% 0. 63% 2. 217862续表1 23家公司基本情况表公司名称x1x2x3x4x5x6美菱电器0. 02 2. 09 19. 31% 1. 08% 0. 64% 1. 3843美的电器0. 11 5. 62 17. 39% 1. 99% 0. 77% 2. 0633万家乐0. 00 1. 04 30. 98% 0. 04% 0. 81% 0. 1263ST湖山-0. 01 0. 68 11. 86% -1. 32% 0. 61% 0. 0377夏新电子0. 01 3. 07 21. 90% 0. 25% 0. 68% 0. 7019海信电器0. 05 4. 94 16. 35% 1. 05% 0. 40% 3. 0019ST博讯-0. 01 0. 08 3. 57% -1. 90% 0. 89% 0. 1052ST福日0. 21 2. 09 2. 33% 10. 11% 0. 68% 1. 1370浙江阳光0. 15 5. 26 19. 44% 2. 83% 0. 42% 2. 7996澳柯玛0. 02 3. 57 16. 50% 0. 51% 0. 70% 2. 4720广电信息0. 01 4. 47 4. 59% 0. 28% 0. 52% 2. 9576春兰股份0. 01 5. 81 10. 85% 0. 23% 0. 39% 2. 9625厦华电子0. 03 2. 20 11. 83% 1. 24% 0. 76% 2. 5512四川长虹0. 08 4. 45 14. 50% 1. 80% 0. 35% 1. 8879大显股份0. 01 2. 17 14. 51% 0. 59% 0. 39% 0. 5229宁波富达0. 01 1. 92 16. 22% 0. 59% 0. 61% 0. 2551青岛海尔0. 05 4. 83 11. 94% 1. 09% 0. 18% 2. 4520飞乐音响0. 02 1. 78 15. 84% 1. 17% 0. 53% 0. 3309首先,将数据标准化处理,然后将处理后的数据,利用SAS软件,可得指标x1,x2,x3,,,x6的相关系数矩阵为:R =1.00000.3793 1.0000-0.0627 0.1673 1.00000.9287 0.2122 -0.1150 1.0000-0.2134-0.4582 0.1825 -0.1637 1.00000.3316 0.8670 0.0329 0.2176 -0.3358 1.0000从相关系数矩阵可看出,x1与x4,x2与x6之间强相关,系统信息有重叠,计算出相关系数矩阵的特征值、特征向量及其贡献率如表2.表2 贡献率及累计贡献率主成分特征值贡献率累计贡献率1 2. 68060 0. 446767 0. 446772 1. 44684 0. 241140 0. 687913 1. 09278 0. 182130 0. 870044 0. 61751 0. 102918 0. 972955 0. 11415 0. 019024 0. 991986 0. 04813 0. 008021 1. 0000063由上表可知,当主成分个数为3时,累计贡献率已经有了87. 01%,所以主成分个数取三个即可.则其对应的主成分为:y1=0.484429x1+0.496377x2-0.025010x3+0.426082x4-0.335658x5+0.483393x6; y2=0.453670x1-0.432427x2-0.321221x3-0.209738x4+0.188846x5-0.396159x6; y3=0.196254x1+0.057543x2+0.804400x3+0.171089x4+0.530876x5+0.003727x6. 从上述公式可看出,第一主成分y1主要是由x1,x2,x4,x6的系数决定的,并且权重值相差不大,由各指标的实际意义,可知第一个主成分主要反映了企业的收益水平和资产的增利水平;第二主成分y2中,x1系数最大,x2系数最小,可知第二个主成分主要经营策划能力,即以少的资产获得较大的利润.第三主成分y2中x3的系数最大,x5的系数次之,其它系数较小,可知第三个主成分则集中反映了企业经营能力和负债偿还能力.评价系数W为:W =K1K1+K2+K3y1+K2K1+K2+K3y2+K3K1+K2+K3y3利用表2中的数据,可计算出y1,y2,y3,同时能计算出W,从而得出综合评价结果.排名如表3.表3 综合评价结果公司名称第一主成分第二主成分第三主成分综合评价结果名次科龙电器2. 21799 -1. 89662 0. 33603 0. 68362 12康佳电器4. 12284 -3. 5606 0. 44796 1. 224007 3ST华发0. 57366 -0. 48605 0. 01839 0. 163712 21TCL 1. 25058 -1. 29823 0. 2047 0. 32521 19小天鹅2. 62972 -2. 296 0. 38032 0. 793623 10美菱电器1. 70006 -1. 49789 0. 28997 0. 518531 15美的电器3. 82122 -3. 24103 0. 50011 1. 168614 4万家乐0. 56573 -0. 59752 0. 31389 0. 190604 20ST湖山0. 3399 -0. 35783 0. 13369 0. 103349 22夏新电子1. 85421 -1. 66867 0. 36146 0. 56532 14海信电器3. 89644 -3. 34864 0. 44079 1. 164996 5ST博讯0. 07269 -0. 1012 0. 03323 0. 016234 23ST福日1. 71762 -1. 20872 0. 2054 0. 589991 13浙江阳光4. 0147 -3. 36146 0. 50608 1. 235838 2澳柯玛2. 94768 -2. 56283 0. 35596 0. 877843 9广电信息3. 62206 -3. 11229 0. 31045 1. 062323 7春兰股份4. 28818 -3. 71432 0. 43716 1. 264044 1厦华电子2. 31406 -1. 97806 0. 24338 0. 690985 11四川长虹3. 14422 -2. 67179 0. 40044 0. 957878 8大显股份1. 3271 -1. 18356 0. 24859 0. 405473 16宁波富达1. 07506 -0. 97444 0. 24812 0. 333911 17青岛海尔3. 58354 -3. 06925 0. 39582 1. 072343 6飞乐音响1. 04913 -0. 93509 0. 23983 0. 329767 1864从表3中,我们可以看出,排在第一位的是春兰股份.春兰公司是我国白色家电的龙头企业,也是我国最早生产家用空调的企业之一,它现已成为中国家喻户晓的品牌,空调产品国内市场占有率始终名列前茅,洗衣机、摩托车等产品也具有较高的知名度和市场占有率,核心竞争力非常突出.排在第二位的是浙江阳光,浙江阳光股份公司主营业务是节能电光源、照明电器、仪器设备的开发、制造和销售,该公司强抓管理,降低成本,使产品的市场占有率进一步提高,经济效益稳步增长.排在最后一位的是ST博讯,由于上市当年就出现巨额亏损,引起股民哗然,被中国证监会查实有虚假上市行为,受到国务院的通报批评,并成为中国第一家被刑事起诉的上市公司.为了验证上述分析的正确性,下面我们用AVE法对上述23个公司进行聚类分析.从分类图和伪t2及伪F统计量可知, 23家上市公司可分为4类,分类情况如表4.表4 公司分类情况公司名称类别公司名称类别公司名称类别科龙电器3 ST湖山4春兰股份1康佳电器1夏新电子3厦华电子2ST华发4海信电器1四川长虹2TCL 3 ST博讯4大显股份3小天鹅2 ST福日3宁波富达3美菱电器3浙江阳光1青岛海尔1美的电器1澳柯玛2飞乐音响3万家乐4广电信息1从聚类进程图中,我们可以明显看出,公司可以分为四类(见表4):春兰股份、浙江阳光、美的电器、康佳电器、海信电器、青岛海尔为一类,是综合实力最强的公司,它们的评价系数排名也在前列.而ST华发、ST湖山、万家乐、ST博讯成一类,它们的评价系数排名排在后面,为实力较差的一类公司.2 结束语主成分分析法是一种多指标分析方法,目前已有不少研究者将它应用于社会中的很多方面.本文利用主成分分析法以及聚类分析对公司效益进行综合评价,其结果是合理的.利用主成分分析法进行综合评价可以消除评价指标之间的相关性;另外,在综合评价函数中,各主成分的权数为其贡献率,它反映了该主成分包含原始数据的信息量占全部信息量的比重,这样确定权数是客观、合理的,它克服了某些评价方法中人为确定权数的缺陷;这种方法的计算比较规范,便于在计算机上实现.[参考文献][1]范金城,梅长林.数据分析[M].北京:科学出版社, 2002.[2]何哓群.现代统计分析方法与应用[M].北京:中国人民大学出版社, 1998. 281-315.[3]王学仁,王松桂.实用多元统计分析[M].上海:上海科学技术出版社, 1990.[4]吴翎.应用数理统计[M].北京:国防科学技术大学出版社, 1995. 285-303.The Application ofPrincipalComponentAnalysis in the Comprehensive Assessment of SocietyZHANG Yi (YangtzeUniversity, Jingzhou,Hube,i 434000,China)Abstract:Ifwe apply the theory of principle component analysis, which can use less comprehensive variables to instead ofthemultivariate variables, thismethod can simplify the structure of the data and aggregate the original index into severalprincipal components. Regarding the contribution rate of this principal componentas right, countweighted average andmake up a compre-hensive function. This textapplies the theory ofprincipal componentanalysis to assess the evaluation of23 companies in real life, and the result is convincing.Key words:principle component analysis; comprehensive assessment; judge the value65。
主成分分析法的原理应用及计算步骤

一、概述在处理信息时,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠,例如,高校科研状况评价中的立项课题数与项目经费、经费支出等之间会存在较高的相关性;学生综合评价研究中的专业基础课成绩与专业课成绩、获奖学金次数等之间也会存在较高的相关性。
而变量之间信息的高度重叠和高度相关会给统计方法的应用带来许多障碍。
为了解决这些问题,最简单和最直接的解决方案是削减变量的个数,但这必然又会导致信息丢失和信息不完整等问题的产生。
为此,人们希望探索一种更为有效的解决方法,它既能大大减少参与数据建模的变量个数,同时也不会造成信息的大量丢失。
主成分分析正式这样一种能够有效降低变量维数,并已得到广泛应用的分析方法。
主成分分析以最少的信息丢失为前提,将众多的原有变量综合成较少几个综合指标,通常综合指标(主成分)有以下几个特点:主成分个数远远少于原有变量的个数原有变量综合成少数几个因子之后,因子将可以替代原有变量参与数据建模,这将大大减少分析过程中的计算工作量。
主成分能够反映原有变量的绝大部分信息因子并不是原有变量的简单取舍,而是原有变量重组后的结果,因此不会造成原有变量信息的大量丢失,并能够代表原有变量的绝大部分信息。
主成分之间应该互不相关通过主成分分析得出的新的综合指标(主成分)之间互不相关,因子参与数据建模能够有效地解决变量信息重叠、多重共线性等给分析应用带来的诸多问题。
主成分具有命名解释性总之,主成分分析法是研究如何以最少的信息丢失将众多原有变量浓缩成少数几个因子,如何使因子具有一定的命名解释性的多元统计分析方法。
二、基本原理主成分分析是数学上对数据降维的一种方法。
其基本思想是设法将原来众多的具有一定相关性的指标X1,X2,…,XP(比如p个指标),重新组合成一组较少个数的互不相关的综合指标Fm来代替原来指标。
那么综合指标应该如何去提取,使其既能最大程度的反映原变量Xp所代表的信息,又能保证新指标之间保持相互无关(信息不重叠)。
第七讲主成分分析模型

第七讲主成分分析模型PCA的基本思想是将原始的高维数据转换为一组新的低维正交特征,这些特征称为主成分。
主成分是原始特征的线性组合,它们能够最大限度地保留原始数据的方差信息。
通过这种方式,我们可以将数据的维度减少到较低的维度,而尽可能地保留原始数据中的信息。
PCA模型的步骤如下:1.数据标准化:首先,我们需要对原始数据进行标准化处理,以确保不同特征的度量单位不会影响分析结果。
标准化可以通过计算每个特征的z分数来实现。
即,对每个特征减去其均值,并除以标准差。
2.协方差矩阵的计算:接下来,我们计算标准化后的数据的协方差矩阵。
协方差矩阵显示了各个特征之间的相关性。
3.特征值和特征向量的计算:通过对协方差矩阵进行特征值分解,我们可以得到特征值和对应的特征向量。
特征值表示主成分的重要性,即占据原始数据方差的比例。
特征向量则代表了主成分的方向。
4.主成分的选择:通常,我们会选择在特征值贡献百分比累计达到一定阈值的前几个主成分。
这些主成分被称为主要成分,它们能够尽可能全面地表示原始数据的信息。
5.投影:最后,我们通过将原始数据投影到选定的主成分上,得到降维后的数据。
这样,我们就可以用较低维度的数据来代表原始数据,从而简化分析和模型构建的过程。
PCA模型有很多应用领域,包括图像处理、模式识别、金融数据分析等。
它不仅可以帮助我们发现数据中最重要的特征,还可以降低数据维度,提高计算效率。
此外,PCA还可以用于数据可视化,将高维数据映射到二维或三维空间中,以便更好地理解数据的结构和关系。
然而,PCA模型也有一些局限性。
首先,PCA假设数据是线性可分的,对于非线性关系的数据,它可能无法进行有效的降维。
此外,PCA还可能存在信息丢失的问题,因为它只保留了数据方差最大的特征。
因此,在应用PCA前,需确保对数据的理解和分析目标明确,以避免潜在问题。
总的来说,主成分分析模型是一种强大的数据分析工具,它通过降维和特征选择,可以帮助我们发现数据中的重要结构和关系。
基于主成分分析的质量安全评价模型构建

基于主成分分析的质量安全评价模型构建摘要:本文针对分析深圳市这三年各主要食品领域微生物、重金属、添加剂含量等安全情况的变化趋势的问题,首先确定评价食品安全的检测指标,建立评价指标体系,本文利用已有数据得出三年主要食品领域如蔬菜、肉制品以及水产品领域,微生物、重金属、添加剂含量以及其他影响食品安全因素检查的合格率;再利用主成分分析方法建立的数据矩阵进行求解,得出影响食品质量安全的主成分因子,以及相应的方差贡献率(又称信息贡献率)作为主成分指标变量的权重,进而定义食品安全综合指数FSCI(Food Safety Comprehensive Index ,FSCI),通过食品安全综合指数的比较,对三年来深圳市的食品安全水平进行综合评价并得出结论:在蔬菜、肉类以及水产品三个主要食品领域中,食品质量安全水平2012最优,2011在三年来相对较差,2010年居中。
关键词:主成分分析信息贡献率特征向量综合评价指数中图分类号:R155.5 文献标识码:A 文章编号:1672-5336(2014)06-0064-03针对评价深圳市这三年各主要食品领域微生物、重金属、添加剂含量等安全情况的变化趋势的问题,我们首先确立指标体系,并对相关数据进行标准化处理,建立如下基于主成分分析的综合评价模型,并利用Matlab编程进行求解。
假设进行主成分分析的指标变量有个[1],分别为,共有个评价对象,第个待评对象的第个指标值为,得到观测数据矩阵:。
将各指标值转换成标准化的指标值,有:其中:其中即和为第个指标的样本均值和样本标准差。
对应地,称为标准化的指标变量。
根据公式概率统计以及线性代数的相关知识[2]可以知道:即为标准化的指标变量和的相关系数矩阵,相关系数矩阵中的元素其中是第个指标与第个指标的相关系数,显然易见相关系数矩阵为是对称矩阵。
由上述相关系数矩阵的性质知道:相关系数矩阵为是实对称矩阵,因此相关系数矩阵进行特征分解得到[3]:,其中,是由相关系数矩阵的特征值组成的对角阵,是由的标准正交化的特征向量按列并排组成的正交矩阵,称为主成分载荷矩阵,它是用主成分指标变量表示中心标准化的原指标变量时的系数矩阵,即用矩阵可表示为:。
主成分分析模型

来刻画了。
主成分的提取
Y Y 首先讨论第一项综合性指标 1 的确定。希望 1 能尽可能多地反映原来
p 项指标所反映的信息. 在主成分分析中采用方差来度量一个随机变量所包含的信息量。 Y1 的方差 Var Y1 Var l1 X l1D X l1 l1l1
l1 Y 因此,用于决定Y1 l1 X 的向量 ,使l1 l1 越大就意味着1 所含的信 l1 息越多。但如果不对 的模 l1 l1l1 施加一定限制,随着l1 将有 VarY1 ,而无法进行比较。
Y l X l X l X l X 1p p 1 1 11 1 12 2 Y2 l 21 X 1 l 22 X 2 l 2 p X p l 2 X Y l X l X l X l X mp p m m m1 1 m 2 2
主成分的解释与命名 提取的每个主成分
YkLeabharlann 都是原p个变量X 1 , , X p 的特定的线性组合
Yk lk X lk1 X 1 lk 2 X 2 lkp X p ,
主成分Yk 可看成是对原变量 X 1 , , X p 中某一类信息的综合。 原变量 X 1 , , X p 都有明确的实际含义,那么,在对它们进行线性组合后, 得到的新综合变量 有什么含义?如何解释呢? 这只能通过观察各组合系数
l k 1 , l k 2 , , l kp
Yk
的符号、 大小, 并结合原变量
Yk
Xi
的
实际含义加以提炼、归纳、找出共性,然后对主成分 的含义做出解释。
Spss软件实现
1.心血管疾病的主成分分析:spss 数据 :13-02 关注:数据格式、结果解读 2.抑郁症测试的主成分分析:spss 数据 :抑郁症资料
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0引言由于MCAI软件是用于教学的特殊软件,因此除具有一般软件的质量因素外,还有教育学、心理学因素等因素,也就是说,影响MCAI软件质量的因素比较多,那么,建立怎样的MCAI软件评价体系才能完成反映MCAI软件的质量?在对MCAI软件进行评价时,采用什么样的模型进行评价,才能对MCAI软件评价即能简化评价指标体系,又能反映原来指标体系反映的信息,这正是本文需要解决的问题——建立MCAI 软件主成分分析法评价模型。
1MCAI软件评价指标体系1.1MCAI软件评价指标体系选取的原则而影响MCAI软件的因素比较多,选取那些指标对MCAI 软件进行评价才能达到即客观又全面的评价,MCAI软件评价指标选取时要遵循的原则:(1)目的明确:对MCAI软件评价所选取的评价指标应能反映MCAI软件有关内容;(2)比较全面:MCAI软件评价指标的选取应尽可能的覆盖MCAI软件评价的内容,如果有所遗漏,评价就会片面;(3)稳定性:所选取的MCAI软件评价指标不应轻易改变,应保持其相对的稳定性。
1.2MCAI软件评价指标体系建立与一般的软件相比,MCAI软件具有特殊性:MCAI软件是用于教学活动的特殊软件,除具有一般软件的技术方面的要求外,还具有教育学、心理学及能力等多方面的要求。
因此对MCAI软件进行评价应从以下几方面考虑:(1)教学方面的要求MCAI软件与一般的计算机软件相比有其特殊性,例如MCAI软件对教学性、科学性、思想性、准确性、逻辑性、适应范围的广泛性等方面有一定的要求,因此评价时要有所反映。
(2)技术方面的要求MCAI软件与其它计算机的软件一样要考虑它的各项质量评价指标,例如它在功能性、可靠性、易使用性、可维护性、可移植性、人机交互性等方面都要达到一定的要求。
(3)学习心理方面的要求收稿日期:2010-07-11;修订日期:2010-09-15。
它是符合程序教学的基本原理,程序教学的特点是把教材内容以合乎逻辑的顺序由浅入深、循序渐进地排列起来,做到程序化的安排。
它将教学内容按一定的序列编成许多教学单元,每前进一步都先让学生了解自己对上一教学单元的掌握情况,对学生提出问题,然后要学生做出反应,再确认其答案,以保持学生的学习积极性和取得成功的自信心。
此外,建构主义心理学的基本思想近年来也在课件开发中逐渐得到应用。
(4)能力方面的要求除了以上这些必须考虑的因素外,根据目前的发展情况,还必须要对MCAI软件是否在能力培养方面有所体现进行评价,因为注重能力培养,注重从知识到能力的转化应该是教育软件的目标之一,唯有知识转化为能力,转化为技能,才能实现MCAI软件的根本目的。
(5)用户界面的要求对一个MCAI软件,用户首先看到的是它的界面,所以界面的设计非常重要。
例如,可以考察MCAI软件的界面是否友好、操作是否通用简单,有无必要的联机帮助信息和对输入的及时反馈,输入、输出、提示、命令的格式设置是否合理,风格是否一致,有无个性化的体现,有无让人耳目一新的感觉等。
基于以上的考虑,设计MCAI软件层次评价指标体系如表1所示。
2MCAI软件主成分分析法评价模型的构建在上述评价指标体系建立之后,我们运用主成分分析法构建综合评价模型。
2.1主成分分析法基本原理主成分分析是由Hotelling于1933年提出的,该方法是一种数学变换的方法,它把给定的一组相关变量通过线性变换转成另一组不相关的变量,这些新的变量按照方差依次递减的顺序排列。
在数学变换中保持变量的总方差不变,使第一变量具有最大的方差,称为第一主成分,第二变量的方差次大,并且和第一变量不相关,称为第二主成分。
依次类推。
其主要思想是用较少指标反映的原来指标的信息。
其数学模型为:设要进行主成分分析的指标有n个:x1,x2,…,x n,共有m例样品,得到原始数据矩阵x11x12…x1nx21x22…x2nA=x31x32…x3n=(X1,X2,…,X n)…x m1x m2…x mn其中:Xj=(x1j,x2j,…x mj)T,j=1,2,…,n。
用数据矩阵A的列向量作线性组合为z1=a11X1+a21X2+…+a n1X nz2=a12X1+a22X2+…+a n2X nz3=a13X1+a23X2+…+a n3X n…z n=a1n X1+a2n X2+…+a nn X n上述方程组满足:a1i2+a2i2+…+a ni2=1,(i=1,2,3…n)。
且系数a ij由下列原则决定:()2(i=1,2,…,n;j=1,2,…,m)。
为了方便起见仍记标准化后的数据xij'为x ij,对标准化后的矩阵为X。
(2)求各指标xj的相关系数矩阵RR=(r ij)mn,r ij=s ij/(),=1(1>3>…k和前k个主成分累积方差贡献率k=(k)==1Z1+n Z n)/标准化数据如表3所示。
(2)建立变量的相关系数矩阵R如表4所示。
(3)求R的特征根、方差贡献率和累积贡献率如表5所示。
(4)从表5可以看出,前5个特征值累计贡献率已达93.462%,说明前5个主成份包括了全部指标具有的93.462%信息,我们取前5个特征值,并计算出相应的特征向量如表6所示。
(5)写出主成分和综合评价值公式Z1=0.116X1+0.096X2+0.043X3+0.009X4-0.253X5-0.122X6-0.075X7+0.105X8-0.016X9+0.051X10+0.104X11+0.036X12+ 0.008X13-0.260X14+0.227X15+0.024X16+0.069X17Z2=-0.071X1+0.050X2+0.010X3-0.093X4-0.090X5+0.096X6-0.101X7+0.166X8+0.042X9-0.161X10+0.259X11-0.080X12+0.014X13-0.102X14+0.036X15-0.219X16+0.307X17Z3=-0.053X1-0.225X2+0.214X3+0.236X4+0.019X5-0.003X6+ 0.274X7+0.023X8-0.171X9+0.171X10-0.020X11-0.022X12-0.089X13+0.075X14+0.013X15+0.043X16-0.114X17表2原始数据序号x1x2x3x4x5x6x7x8x9x10x11x12x13x14x15x16x171 2 3 4 5 6 7 80.11890.11870.11750.10720.11970.11250.11050.11820.12710.12620.12530.11560.12510.12030.11030.11510.09020.09130.09140.09070.09240.09180.09880.09090.07380.07360.07390.07320.07160.07370.07870.07980.07050.07040.07060.08060.07140.07010.06910.07150.02850.02830.03040.04040.02780.03540.03440.02950.02700.02710.02690.02760.02760.02690.02890.02700.02400.02420.02450.02520.02450.02950.02970.02550.03500.03560.03550.03520.03530.03510.03460.03530.03800.03810.03790.03760.03830.03790.03820.03870.02700.02730.02770.02740.02710.02790.02800.02730.05460.05430.05400.05430.05410.05440.05430.05420.04030.04030.04010.04040.04050.04060.04030.04040.04050.04020.04070.04500.04120.04050.04080.04150.09360.09320.09310.09010.09220.09320.09350.09380.05740.05770.05580.05530.05740.05560.05550.05770.05360.05350.05470.05420.05380.05460.05440.05361.7510.91811.0460.59791.02860.88560.74270.05160.87770.32210.53980.07710.46730.41440.5540.37951.36551.74940.37730.10290.73410.74610.32141.91420.52260.40450.69872.24330.80520.59190.59191.5411.62630.64171.28340.96250.32081.9250.3208序号x10x11x12x13x14x15x16x17123456780.57330.57330.3441.87280.44370.64850.98991.19471.46781.5010.13640.40930.4150.4150.2490.70920.06450.32240.12890.63230.30060.21770.52870.30060.54940.79820.78441.06121.1540.78440.9691.06121.1361.34290.30990.9297表4相关系数矩阵x1x2x3x4x5x6x7x8x9x10x11x12x13x14x15x16x17X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14 X15 X16 X171.000.714.127.978.594.508.556.168.652.570.851.610.235.662.171.180.287.6101.000.457.704.176.635.067.389.351.722.4571.000.416.617.341.147.042.235.2591.000.664.008.506.020.133.974.327.020.628.184.028.6641.000.330.511.618.525.144.248.719.847.575.662.902.341.008.3301.000.503.029.138.594.256.511.5031.000.008.841.175.395.602.581.508.616.416.133.715.401.183.125.419.171.176.617.618.056.207.406.610.659.588.215.525.392.841.2071.000.029.776.834.088.020.144.475.1651.000.272.290.180.147.133.248.183.105.196.022.652.192.121.406.070.1531.000.399.086.570.128.210.495.644.125.610.133.141.8911.000.417.389.020.847.602.419.659.399.4171.000.561.042.020.575.187.581.501.834.088.086.9021.000Z4=-0.064X1+0.160X2+0.071X3-0.208X4-0.059X5+0.017X6+0.139X7+0.028X8-0.347X9-0.271X10-0.139X11+0.578X12+0.030X13-0.100X14+0.019X15+0.003X16-0.134X17Z5=-0.040X1-0.155X2-0.244X3+0.121X4+0.019X5+0.125X6-0.332X7+0.280X8+0.089X9+0.229X10+0.075X11+0.071X12+0.644X13+0.028X14+0.063X15+0.068X16-0.013X17综合评价值:Z=0.39153Z1+0.25919Z2+0.12412Z3+0.9584Z4+ 0.6393Z5。
