2008年学而思杯六年级一试A卷解析

合集下载

学而思杯考试-六年级试卷

2014年“学而思杯”六年级试题考试时间：45分钟满分：150分姓名：分数：第一关：基础知识仓（26分）1.读资料，回答问题。

（每空2分，共6分）《论语》中记录了孔子及其弟子的言行，其中有两则一直以来都脍炙人口：第一则子曰：“温故而知新，可以为．师矣．。

”第二则子曰：“岁寒，然后知松柏之后diāo（）也。

”（1）为加点的字加拼音。

为（）矣（）（2）请根据拼音写汉字。

diāo（）2.请用“√”或“×”表示句子后面对于“陈”的解释的正误。

（每空2分，共8分）（1）叔叔家的客厅里陈列着很多古物。

陈：排列摆设（）（2）爸爸有一箱陈酒，准备奶奶过生日时喝。

陈：旧的，时间久（）（3）请你把事情经过陈述一遍。

陈：述说（）（4）陈阿姨是单位的先进工作者。

陈：周代诸侯国名（）3.下列数量词的搭配，符合普通话规范的是（）。

（2分）A. 一粒香烟B. 一张桌子C.一头鱼D.一头狗4.依次在下面剧中横线上填入词语，最恰当的一项是（）。

（3分）①一大把火柴发出（）的光，照的跟白天一样明亮。

②最近，国家领导人来我校进行了（）。

③他以自己（）的信念，忍受着凶猛的大鹰用无情的利爪撕裂他的肌体。

A.激烈视察坚强B.强烈考察坚定C.强烈视察坚定D.激烈考察坚强5.下面几个句子，没有语病的一项是（）。

（3分）A.夏日的清凉山，真是我们纳凉避暑、休闲娱乐的好季节。

B.蓝色，如小道上的航标，指明前进与奋斗，给人带来憧憬。

C.经过几个月紧张的学习，使我们可以从容、镇定地面对这次考试。

D.我们要学会用美的眼光去观察世界，用美的心灵去感受世界。

6.对下列句子修辞手法的判断正确的一项是（）。

（4分）①石油工人吼一吼，地球也要抖三抖。

②打了败仗的敌人，成了没头的苍蝇，到处乱撞。

③无数的小麦摇晃着脑袋，好像在嘲笑着他们。

④随着山势，溪流时而宽，时而窄，时而缓，时而急，溪流声也时时变换调子。

⑤白桦树哗哗的响，在他的头上不住地号叫。

⑥三亚的落日怎能不让人惊叹？A.夸张拟人比喻拟人拟人反问B.拟人拟人比喻排比拟人反问C.拟人比喻拟人比喻拟人反问D.夸张比喻拟人排比拟人反问7.诗词名家。

1-2-2-1分数裂项.教师版

酗雌教学目标本讲知识点属于计算大板块内容，其实分数裂项很大程度上是发现规律、利用公式的过程，可以分为观察、改造、运用公式等过程。

很多时候裂项的方式不易找到，需要进行适当的变形，或者先进行一部分运算，使其变得更加简单明了。

本讲是整个奥数知识体系中的一个精华部分，列项与通项归纳是密不可分的，所以先找通项是裂项的前提，是能力的体现，对学生要求较高。

分数裂项将算式中的项进行拆分，使拆分后的项可前后抵消，这种拆项计算称为裂项法•裂项分为分数裂项和整数裂项，常见的裂项方法是将数字分拆成两个或多个数字单位的和或差。

遇到裂项的计算题时，要仔细的观察每项的分子和分母，找出每项分子分母之间具有的相同的关系，找出共有部分，裂项的题目无需复杂的计算，一般都是中间部分消去的过程，这样的话，找到相邻两项的相似部分，让它们消去才是最根本的。

（1）对于分母可以写作两个因数乘积的分数，即丄形式的，这里我们把较小的数写在前面，即a ：：：b ，a xb（2）对于分母上为3个或4个连续自然数乘积形式的分数，即: 形式的，我们有:n (n 1) (n 2) (n 3)裂差型裂项的三大关键特征：（1）分子全部相同，最简单形式为都是1的，复杂形式可为都是 x （x 为任意自然数）的，但是只要将x提取出来即可转化为分子都是1的运算。

（2）分母上均为几个自然数的乘积形式，并且满足相邻 2个分母上的因数“首尾相接（3）分母上几个因数间的差是一个定值。

二、“裂和”型运算：常见的裂和型运算主要有以下两种形式：2丄 2 2(1)a a bJ 1 ( 2)a b a2b a bab ab ab baa b a b a b b a裂和型运算与裂差型运算的对比：裂差型运算的核心环节是“两两抵消达到简化的目的” ，裂和型运算的题目不仅有“两两抵消”型的,同时还有转化为“分数凑整”型的，以达到简化目的。

自助嵯例题精讲【例1】丄丄丄丄丄二知识点拨“裂差”型运算那么有二_______ 1 n (n 1) (n 2)12233445561b _a【考点】分数裂项【难度】2星【关键词】美国长岛，小学数学竞赛原式二k! ■ 1 U2丿€【题型】计算【解析】【答案】【巩固】【考点】【解析】【答案】【巩固】【考点】【解析】【答案】【例2】提醒学生注意要乘以(分母差)分之一，如改为: 1，计算过程就要变为:1 33 55 77 91 竹1）1- H - -4 - 4 -- = I - — — lx — .1 33 5 5 7 7 9 1 9 25 611----- + ------- + .... + ------- 10 11 11 12 59 60 分数裂项【难度】2星原式^^_1）.（!_!）.…….（丄亠丄10 11 11 12 59 6010 60丄 12 2 【题型】计算1 丄1210 99 8分数裂项原式=2： I 1_丄「9 102 2 2 - —二 ___________________ 5況4 4況3 【难度】2星1 1 . I 1 1 1 1+— — +| | \ +— — +———8 9 4 5 3 4【题型】计算1 1=23 10157_15 1 1丄 +—— + +IIIIII+丄丄小丄 1 +2+HI+100 【难度】3星【题型】计算本题为典型的“隐藏在等差数列求和公式背后的分数裂差型裂项”问题。

六年级奥数几何;第3讲;直线型面积_三_;学生版

大 7.2 平方厘米，则 △ABC 的面积是多少平方厘米？
A
NG M
B DE F C
【巩固】（2007 年四中分班考试题)如图， ΔABC 中，点 D 是边 AC 的中点，点 E 、 F 是边 BC 的三等分点，若 ΔABC 的面积为 1，那么四边形 CDMF 的面积是_________． A
9
例题 9
(第 21 届迎春杯试题)如图，已知正方形 ABCD 的边长为 4 ，F 是 BC 边的中点，E 是 DC 边上的点，且 DE : EC = 1: 3 ， AF 与 BE 相交于点 G ，求 S△ABG
A
B
G F
D E
C
1
已知长方形 ABCD 的面积为 70 厘米， E 是 AD 的中点， F 、 G 是 BC 边上的三等
2
BC 上的点，且 AE = 1 AB ， CF = 1 BC ， AF 与 CE 相交于 G ，若矩形 ABCD 的
例题 26
3
4
面积为120 ，则 ΔAEG 与 ΔCGF 的面积之和为
．
2010 年·暑假
A
D
E G
B
FC
五年级数学·第 3 讲·学生版
page 9 of 11
1
练习 1
已知 △ABC 中， DE 平行 BC ，若 AD : DB = 2 : 3 ，且 S梯形DBCE 比 S△ADE 大 8.5 cm2 ，求 S△ABC ．
D
C
F G
A
E
B
1
如图，正方形 ABCD 的面积是120 平方厘米， E 是 AB 的中点， F 是 BC 的中点，
例题 17 四边形 BGHF 的面积是_____平方厘米．

2011学而思杯六年级语文真题解析(

2011学而思杯六年级语文真题解析试卷名称：2011年六年级学而思杯语文考试试卷说明：学而思杯语文试题仅提供给学员参与，所有试题均不判定成绩。

年级：六年级科目：语文试卷满分：100分答题时间：40分钟试题形式：填空＋选择，答案随意赋值，用户答任意答案均判定为错误。

能力分值：全部为0开放时间：2011年10月6日12:20-13:00第一部分基础积累与运用（48分）一、基础单元（共17分）1．看拼音写汉字。

（每字1分，共6分）2．下面成语中有三个成语各有一个错别字，试着找出来，将正确的字写入横线。

（每改对一字得1分，共3分）原形必露走头无路再接再厉高瞻远瞩别出心裁偷粱换柱3．你能准确写出“疾”在下列词语中的含义吗？（每空1分，共2分）疾．恶如仇讳疾．忌医4．用一个成语替换句中划线的部分，使表达更简洁。

（每空1分，共2分）①任何时候，我们做事情都要从实际出发，不能不切实际地追求过高的目标（），而应该踏踏实实，一步一个脚印。

②我的家乡西安是我国多朝古都，它的历史文化非常久远。

伴随着改革的大潮，这里经济文化的发展每天每月都有新的变化（）。

5．下面一段话共有两处错误，请在文中标记出错误，并在所给横线上作相应的修改。

（每处1分，共2分）我早就期望着能去长城游览了。

今年暑假，我终于实现了自己的愿望。

登上宛如长龙似的的长城，望着虽然经历了几千年风雨，但还是那么雄伟壮丽的长城，我领会了它的气魄，难怪人们赞叹中国的长城是世界上的一大奇迹。

第一处：；第二处：16．按照例子填写符合要求的三字词语。

（每空1分，共2分）例：客人来访，拒绝客人进门叫让客人吃（闭门羹）。

①乘人不备，放箭伤人的行为叫（）。

②不怀好意的宴请或加害客人的宴会叫（）。

二、积累单元（共27分）7．争当文化百科家。

（每空1分，共3分）如图所示：含义是；含义是；含义是。

8．据提示准确填写诗句。

（每空1分，共13分，错字不得分）①高鼎的《村居》中“，”为我们展开了一幅清晰而又明丽的田园春景图；而杨万里的名句“，”则通过荷花描写了炎炎夏日里西湖的独特美景。

学而思数学六年级第2讲几何一-直线形面积练习题---答案

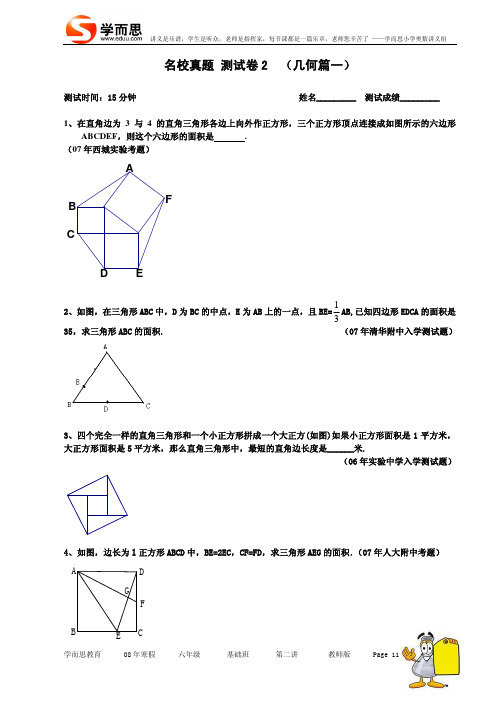
名校真题测试卷2 （几何篇一）测试时间：15分钟姓名_________ 测试成绩_________1、在直角边为3与4的直角三角形各边上向外作正方形，三个正方形顶点连接成如图所示的六边形ABCDEF ，则这个六边形的面积是 . （07年西城实验考题）FEDCB A2、如图，在三角形ABC 中，D 为BC 的中点，E 为AB 上的一点，且BE=13AB,已知四边形EDCA 的面积是35，求三角形ABC 的面积. （07年清华附中入学测试题）3、四个完全一样的直角三角形和一个小正方形拼成一个大正方(如图)如果小正方形面积是1平方米，大正方形面积是5平方米，那么直角三角形中，最短的直角边长度是______米.（06年实验中学入学测试题）4、如图，边长为l 正方形ABCD 中，BE=2EC，CF=FD，求三角形AEG 的面积．（07年人大附中考题）GFED CBA5、如图，长方形ABCD 中，AB＝8，BC＝10，E 是BA 延长线上一点，CE 交AD 于F，△AEF 比△CDF 的面积大40，求AE 的长． (07年四中分班考试题)F ED CB A附答案】图：总面积=三个正方形+中间三角形+CD 边三角形+AB 边=32+42+52【 1. 【解】如三角形+EF 边三角形+12×3×4+12×3×4+12×3×4+12×3×4=742. 【解】根据定理：ABC BED ΔΔ=3211××=61，所以四边形ACDE 的面积就是6-1=5份，这样三角形35÷5×6=42.. 【解】小正方形面积是1平方米，大正方形面积是5平方米，所以外边四个为. 【解】连接EF．因为BE=2EC，CF=FD，所以S △DEF =(C3面积和是5-1=4，所以每个三角形的面积是1，这个图形是“弦形”，所以长直角边和短直角边差就是中间正方形的边长，所以求出短边长就是1． (请注意)，先外补4个同样的小直角三角形，得到一个大正方形，其边长两直角边的和，根据两直角边的和是3(通过补完后大图的面积求得) 又根据两直角边的差是1(根据最中间的小正方形的面积求得) 所以，根据和差关系，求出长边为2, 短边为1. 421×31×21)S 正方形ABCD =121S GF ED CBA 正方形ABCD ．因为S △AED =21S 正方形ABCD ，根据燕尾定理，AG:GF=21:121=6，所以S △AGE =6S △GEF =76S △AEF ．因为S △ABE =31S 正方形ABCD ，S △ADF =41S 正方形ABCD ， S△CEF=121S 正方形ABCD ，所以S △AEF =1-31-41-121=31，所以S △AGE =76×31=72，三角形AEG 的面积是72．. 【解】（法一）△AEF 比△CDF 的面积大40，所以三角形AED 的面积比三角形DEC 大40，而两个三面积等于长方形ABCD 面积的一半，所以△CDE 的面积为40，三角形△AED 为40+40=80，5角形的高是一样的都等于10，所以三角形AED 的底比三角形DEC 的底长40×2÷10=8，即AE 的长为8+8=16（法二）△CDE 的而△AED 的高已知为10，所以△AED 的底AE 长16.第二讲小升初专项训练几何篇（一）一、小升初考试热点及命题方向随着小升初考察难度的增加，几何问题变越来越难，一方面，几何问题仍是中学考察的重点，各学校更题）．尤其重、2008年考点预测2008年的小升初考试将继续以大题形式考查几何，命题的热点在于等积变换和燕尾定理在求解三角形、主要常用数学方法运用首先我们来讨论一下和三角形面积有关的问题，大家都知道，三角形的面积喜欢几何思维好的学生，这样更有利于小学和初中的衔接；另一方面几何问题由于类型众多，很多知识点需要提前学，这就加快了学生知识的综合运用，而这恰恰是重点中学学校所期望的．几何问题是小升初考试的重要内容，分值一般在12-14分（包含1道大题和2道左右的小要的就是平面图形中的面积计算，几何从内容方面，可以简单的分为直线形面积（三角形四边形为主），圆的面积以及二者的综合．其中直线形面积近年来考的比较多，值得我们重点学习．从解题方法上来看，有割补法，代数法等，有的题目还会用到有关包含与排除的知识．二面积里的运用．同时还需要重点关注在长方形和平行四边形框架内运用边长比等于相似比的定理，请老师重点补充沙漏原理的讲解．三 1. 等积变换：在三角形中的=12×底×高，面积之比等于对应高的比和三角形面积比有关的题目中它们都能发挥巨2. 用燕尾定理，求线段比：于同一点O, 上述定理给出了一个新的转化面积比与线段比的手段，因此我们有【结论1】等底的三角形【结论2】等高的三角形面积之比等于对应底的比这2个结论看起来很显然，可大家小看它们，在许多大的作用，因为它们把三角形的面积比转化为了线段的比.运A OE DF C B 在三角形ABC 中，AD,BE,CF 相交那么S △ABO :S △ACO =BD:DC因为△ABO 和△ACO 的形状很象燕子的尾巴，所以这个定理被称为燕尾定理．该定理在许多几何题目中都有着广泛的运用．3.平行线分线段定理（即利用求面积来间接求出线段的比例关系）同学们应该对下图所示的图形非常熟悉了．相交线段AD 和AE 被平行线段BC 和DE 所截，得到的三角形ABC 和ADE 形状完全相似．所谓“形状完全相似”的含义是：两个三角形的对应角相等，对应边成比例．体现在右图中，就是AB：AD=BC：DE=AC：CE=三角形ABC 的高：三角形ADE 的高．这种关系称为“相似”，同学们上了中学将会深入学习．相似三角形对应边的比例关系在解几何问题的时候非常有用，要多加练习．EDCB ACBEDA在实际运用的时候，相似的三角形往往作为图形的一部分，有时还要经过翻转、平移等变化（如右下4. 利用“中间桥梁”联系两块图形的面积关系角形的面积，就相对比较简单了，在解题过程中5. 差不变原理的运用面积，可以给两个图形都加上一个相同的图形，化不规则为规则，然后再作比6. 其他方法类型中几何题目的考点以面积为主，但不排除出现以线段和角度为考点的题目，只、典型例题解析三角形中的运用例1】（★★）如图，四边形ABCD 中，AC 和BD 相交于O 点，三角形ADO 的面积=5，三角形DOC 的面图），往往不易看出相似关系．如（右下图）AB 平行于DE，有比例式AB：DE=AC：CE=BC：CD，三角形ABC 与三角形DEC 也是相似三角形．下图形状要牢记并且要熟练掌握比例式．比较两个四边形的面积的大小很难，但比较三将难以处理的四边形化作三角形来处理，把三角形作为“中间桥梁”建立两组图形之间的数量关系，题目处理起来就容易了. 比较不规则几何图形较，数量关系就清晰了，这种方法的实质是算术中的差不变原理. 虽然小升初考试要在解题过程中，将难以处理的量通过几何变化，化成我们熟悉的数量关系.题目即可迎刃而解.四【典型例题解析】1 等积变化在【积=4，三角形AOB 的面积=15，求三角形BOC 的面积是多少？ABCDO【解】：S △ADO =5,S △DOC =4根据结论2，△ADO 与△DOC 同高所以面积比等于底的比,即AO:OC=5:4同理S △AOB :S △BOC =AO:OC=5:4,因为S △AOB =15所以S △BOC =12．【总结】从这个题目我们可以发现，题目的条件和结论都是三角形的面积比，我们在解题过程中借助结拓展】S △AOD ×S △BOC =S △COD ×S △AOB ，也适用于任意四边形．练习】如下图，某公园的外轮廓是四边形ABCD，被对角线AC、BD 分成四个部分，△AOB 面积为1平论2，先把面积比转化成线段比，再把线段比用结论2转化成面积比，解决了问题．事实上，这2次转化的过程就相当于在条件和结论中搭了一座“桥梁”，请同学们体会一下．【【方千米，△BOC 面积为2平方千米，△COD 的面积为3平方千米，公园陆地的面积是6.92平方千米，求人工湖的面积是多少平方千米？（空白部分为陆地，阴影部分为水面．）例2】（★★★）如图，ABCD 是一长方形纸片，把它的左下角沿虚线EC 折叠过去成右图，AE 恰好AD 是的【41，三角形CDE 面积是27，三角形AHE 面积是3，三角形BCG 面积是16，问三角形DGH（阴影）的面积是多少？27EDCBA B解】S ACE =27÷3=9,S ABCE =27+9+9=45,S 阴=27-（45-3-16）=1． 2 燕尾定理在三角形中的运用例（★★★）在△ABC 中【【3】DC BD =2:1, EC AE =1:3，求OEOB=? DCE OBA【分析】题目求的是边的比值，我们可以通过分别求出每条边的值再作比值，也可以通过三角形的面积比来做桥梁，但题目没告诉我们边的长度，所以方法二是我们要首选的方法．本题的图形一看就知道是燕尾定理的基本图，但2个燕尾似乎少了一个，因此应该补全，所以第一步我们要连接OC．【解】连接OCDCAE OB因为AE:EC=1:3 (条件)，所以AOECOES S ΔΔ=1:3 若设AOE S x Δ=,则3COE S x Δ=，所以, 根据燕尾定理4AOC S x Δ=2:1AOB AOC S BD S DC ΔΔ==，所以8AOB S x Δ=，所以88:1AOB AOE S BO xOE S xΔΔ===．【例4】（★★★）三角形ABC 中，C 是直角，已知AC＝2，CD＝2,CB=3,AM=BM，那么三角形AMN（阴影部分）的面积为多少？ABD ABD C C【解】因为缺少尾巴，所以连接BN 如下，的面积为3×2÷2=3这样我们可以根据燕尾定理很容易发现ABC ΔACN Δ：ANB Δ=CD：BD=2：1；同理CBN Δ：ACN Δ=BM：AM=1：1；设面积为1份，则AMN ΔMNB Δ的面积也是1份，所以ANB Δ得面积就是1+1=2份，而：1，所以ACN Δ：ANB Δ=CD：BD=2ACN Δ得面积就是4份：；CBN ΔACN Δ=BM：AM=1：1，所以CBN 也是Δ4份，这样ABC Δ的面积总共分成4+4+1+1=103×份，所以阴影面积为1=10310．【例5】（★★★）如图，三角形A 的面积形CD BC 是16，D 是AC 的中点，E 是BD 的中点，那四边EF 的面积是多少？【解】连接DF．因为E 是BD 的中点，所以S △FBE =S △FDE ，S △ABE =S △ADE ，所以S △ABF =S △ADF ．因为D 是AC 中点，所以S △ADF =S △CDF ，所以S △ABF =S △ADF =S △CDF ．因为三角形ABC 的面积是16，所以S △CDF =316，S △ABD =8，S △AED =4，所以S △FDE =316-4=34，所以四边形CDEF 的面积是16+4=20【例6】如图，平行四边形ABCD【解】S △BCD =1+4+4+6=16,S △OCD 4和6.求：(1)求△OCF =21S 以S △OCF =8-4=4，所以，=ΔΔCEG OEG S S 所而S △OCE = S △OCB - S △OBE =8-6=2，所以，21EG CG CE ====63GF GO EB 所以S △GCE =322=×.31在三角形中的运用正方形ABCD ，M 为AD 边上的中点，求图中的阴影部分面积．3平行线分线段定理【例7】（★★★）如右图，单位【解1】（平行线分线段定理）两块阴影部分的面积相等，AM GM BC GB ==21,所以GM =32，而三角形GB ABG和三角形AMB 同底，所以S △BAG =32S △ABM =32×1×12=61×21，又因为三角形BAM 和三角形CAM 同底等高，所以阴影面积为61×2=31.【解2】(燕尾定理运用)四边形AMCB 的面积为（0.5+1）×1÷2=43，根据燕尾定理在梯形中的运用，知道：：： =A ：BC ：AM×BC：AM×BC=AMG ΔBCG ΔBAG ΔCMG ΔM 22212⎛⎞⎜⎟⎝⎠：1：221：21=1：4：2：份，所以面积为2；所以四边形AMCB 的面积分成1+4+2+2=9份，阴影面积占43×224122++++=314. 【解3】（等积变化运用）如右图，连结DG，有：S △ACM =S △BAM （同底等高）， AC 又S △AGM =S △GDM （等底同高）又S △BAG =S △ADG （△BAG 与△ADG 关于对称）因此，11AGM D S S ΔΔ==22AG ABG S Δ 2AGB ABM S S ΔΔ=3 又1111222ABM S AM AB Δ=⋅⋅=⋅⋅=14所以，2211AGB ABM S S ΔΔ==×=所以，3346123阴影AGB S S Δ=×=.是平行四边形，面积为72平方厘米，BC 的中点．则积为多少平方厘米？【例8】（★★★★）如图，ABCD E，F 分别为边AB，图形中阴影部分的面【解1】由AE:CD=1：2，CF:AD=1:2，得到对角线被DE 和DF 分为三等分. 以得到空白部分是DEBF 面积的2/3．空白部分面积为72÷2÷3×2=24平方厘米72-24=48平方厘米．理”的运用.连接BD,OE,OF 这样我们可以发现S1的面积是整个四边形的可【解2】出现梯形时可以考虑一下”燕尾定14，即14S2:S4=份×72=18（平方厘米）,在梯形AEOD 中,AD=2×OE,这样我们运用”燕尾定理”得:S5:S3:1:4:2:2,把面积分成9份,求出阴影面积占5份,同理可以求出梯形DCFO 中阴影也占5,所以阴影面积=(72-18) ×59=30,总阴影面积为30+18=48（平方厘米）.4利用“中间桥梁”联系两块图形的面积关系【例9】（★★）如图，正方形ABCD 的边长是4厘米，CG=3厘米，矩形DEFG 的长DG 为5厘米，求它DE 等于多少厘米？的宽GF EHD C BA G【解】：连结AG，自A 作FECBAH 垂直于DG 于H，在△ADG 中，AD=4，DC=4（AD 上的高）. ∴S △AGD =4×4÷2=8，又DG=5， ∴S △AGD =AH×DG÷2，∴AH=8×2÷5=3.2（厘米）， ∴DE=3.2（厘米）.5 差不变原理的运用【例10】（★★★）左下图所示的DA ABCD 的边BC 长10cm，直角三角形BCE 的直角边EC 长8cm，已知两块阴影部分的面积和比△EFG 的面积大10cm 2，求CF 的长．两块阴影部分的面积和比△EFG 的面积大10,两部分分别加上四边形BCFG，这样四边形ABCD三角形BEC 的面积大10cm2CE【解】：的面积比S △B =12底是10cm，所以高是5cm． ×10×8=40 所以四边形ABCD 的面积是50cm 2．6 其他常考题型【例11】（★★）下图中，五角星的五个顶角的度数和是多少？OEOEDCBADB AC：连接AB（见右图），AC 交BE 于点O．因为∠AOB=∠COD，所以∠OAB+∠OBA=∠OCE+∠OEC．由此角星五个顶角之和等于三角形ABD 的三个内角之和，是180度．【课外知识】春秋战国时代，一位父亲和他的儿子出征打战．父亲已做了将军，儿子还只是马前卒．又一阵号角吹响，战鼓雷鸣了，父亲庄严地托起一个箭囊，其中插着一只箭．父亲郑重对儿子说：“这是家袭宝箭，配带身边，力量无穷，但千万不可抽出来．”那是一个极其精美的箭囊，厚牛皮打制，镶着幽幽泛光的铜边儿，再看露出的箭尾．一眼便能认定用上等的孔雀羽毛制作．儿子喜上眉梢，贪婪地推想箭杆、箭头的模样，耳旁仿佛嗖嗖地箭声掠过，敌方的主帅应声折马而毙．果然，配带宝箭的儿子英勇非凡，所向披靡．当鸣金收兵的号角吹响时，儿子再也禁不住得胜的豪气，完全背弃了父亲的叮嘱，强烈的欲望驱赶着他呼一声就拔出宝箭，试图看个究竟．骤然间他惊呆了．一拂开蒙蒙的硝烟，父亲拣起那柄断箭，沉重地啐一口道：“不相信自己的意志，永远也做不成将军．”托在一只宝箭上，多么愚蠢，而当一个人把生命的核心与把柄交给别人，又多么危险！比如把在儿女身上；把幸福寄托在丈夫身上；把生活保障寄托在单位身上……己才是一只箭，若要它坚韧，若要它锋利，若要它百步穿杨，百发百中，磨砺它，拯救它的都【解】推知，五只断箭，箭囊里装着一只折断的箭．我一直刳着只断箭打仗呢！儿子吓出了一身冷汗，仿佛顷刻间失去支柱的房子，轰然意志坍塌了．结果不言自明，儿子惨死于乱军之中．把胜败寄希望寄托温馨提示：自只能是自己．练习题在三角形ABC 的各边上，分别取AD、BE、CF 各等于AB、BC、CA 长的三分之一，如果三角形DEF 的积为2平方厘米，求三角形ABC 的面积是多少？1、面答案：6平方厘米．2、在图中，四边形ABCD 的对角线AC 与BD 交F＝CE，BG＝DE，于点E，且A 当四边形ABCD 的面积为25平方厘米时，三角形EFG的面积是多少？答案：25平方厘米．如图，正方形ABCD 的面积是120平方厘米，E 是AB 的中点，F 是BC3、的中点，四边形BGHF 的面积是________平方厘米．E F GB HCD A EB C来源：02年小学数学奥林匹克试题使BK=CD．三角形EHK 与三角形DHC 成比例，DC：=2：3，所以DH：HK=2：3，由于三角形DEK 的面积=90平方厘米，所以EHK 的面积=90÷【解】：延长EB 到K，EK 3三角形5形EHK 的面积-三角形=54平方厘米，所以四边形EBFH 的面积=三角BKF 的面积=24平方厘米．同理，EB：DC=1：2，所以BG：GD=1：2，所以三角形EBG 的面积=13×三角形EBD 的面积=10平方厘米，所以，四边形BHGF 的面积是24-10=14平方厘米.4、直线CF 与平行四边形ABCD 的AB 边相交于E 点，如果三角形BEF 的面积为6平方厘米，求三角形ADE的面积是多少？答案：6平方厘米．5、（★★★）如图，正方形ABCD 的边长是4厘米，CG=3厘米，矩形DEF 宽DE 等于多少厘米？G 的长DG 为5厘米，求它的G F E HG F ED A DCB A B C【解】：连结AG，自A 作AH 垂直于DG 于H，在△ADG 中，AD=4，DC=4（AD 上的高）.∴S △AGD =4×4÷2=8（平方厘米），又DG=5（厘米）， ∴S △AGD =AH×DG÷2，米），∴DE=AH=3.2（厘米）．∴AH=8×2÷5=3.2（厘。

奥数六年级千份讲义 25 1[1].学而思杯考前辅导精编版

模块一、计算【例 1】（2008年学而思杯6年级1试第1题）计算：11111200820092010201120121854108180270++++= 。

【例 2】（2009年学而思杯6年级第6题）计算：1122426153577++++=____。

【例 3】（2008年学而思杯6年级第1题）计算：3413441344413444444441344444444412389275277527775277777777527777777775+⨯+⨯++⨯+⨯=。

【巩固】(第五届《小数报》数学竞赛初赛计算题第3题)计算：11111 123420 261220420 +++++【巩固】计算：1111111++++++学而思杯考前辅导【巩固】 111111212312100++++++++++【巩固】 234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++【巩固】 111111212312100++++++++++【巩固】 234501(12)(12)(123)(123)(1234)(12349)(12350)++++⨯++⨯++++⨯+++++++⨯++++【巩固】 (仁华学校入学测试题) 22222211111131517191111131+++++=------ .【巩固】计算：222222223571512233478++++⨯⨯⨯⨯【巩固】计算：222222222231517119931199513151711993119951++++++++++=----- ．【巩固】计算：222212350133********++++=⨯⨯⨯⨯．【巩固】11111 (......) 1200722006(2008)200622007120071111 (......) 20081200622005(2007)20061n nn n+++++-⨯⨯⨯-⨯⨯+++++⨯⨯⨯-⨯【巩固】1 2【例 4】（2009年学而思杯6年级第1题）a=10.8+10.98+10.998+10.9998+10.99998，的整数部分是。

定义新运算.汇总题库教师版

定义新运算教学目标定义新运算这类题目是在考验我们的适应能力，我们大家都习惯四则运算，定义新运算就打破了运算规则，要求我们要严格按照题目的规定做题．新定义的运算符号，常见的如△、◎、※等等，这些特殊的运算符号，表示特定的意义，是人为设定的．解答这类题目的关键是理解新定义，严格按照新定义的式子代入数值，把定义的新运算转化成我们所熟悉的四则运算。

知识点拨一定义新运算基本概念：定义一种新的运算符号，这个新的运算符号包含有多种基本（混合）运算。

基本思路：严格按照新定义的运算规则，把已知的数代入，转化为加减乘除的运算，然后按照基本运算过程、规律进行运算。

关键问题：正确理解定义的运算符号的意义。

注意事项：①新的运算不一定符合运算规律，特别注意运算顺序。

②每个新定义的运算符号只能在本题中使用。

我们学过的常用运算有：＋、－、×、÷等.如：2＋3＝5 2×3＝6都是2和3，为什么运算结果不同呢？主要是运算方式不同，实际是对应法则不同.可见一种运算实际就是两个数与一个数的一种对应方法，对应法则不同就是不同的运算.当然，这个对应法则应该是对任意两个数，通过这个法则都有一个唯一确定的数与它们对应.只要符合这个要求，不同的法则就是不同的运算.在这一讲中，我们定义了一些新的运算形式，它们与我们常用的“＋”，“－”，“×”，“÷”运算不相同.二定义新运算分类1.直接运算型2.反解未知数型3.观察规律型4.其他类型综合模块一、直接运算型【例 1】若*A B 表示()()3A B A B +⨯+，求5*7的值。

【考点】定义新运算之直接运算【难度】2星【题型】计算【解析】 A *B 是这样结果这样计算出来：先计算A ＋3B 的结果，再计算A ＋B 的结果，最后两个结果求乘积。

由A *B ＝（A ＋3B ）×（A ＋B ）可知： 5*7＝（5＋3×7）×（5＋7）＝（5＋21）×12 ＝ 26×12 ＝ 312【答案】312【巩固】定义新运算为a △b ＝（a ＋1）÷b ，求的值。

学而思杯六年级真题及详解数学

2014年六年级学而思综合能力测评（学而思杯）解析一、填空题A（本大题共10小题．每个小题5分，共50分）1.下面四个图形中，阴影面积占总面积一半的图形有个．①②③④【考点】计算，分数定义【难度】☆【答案】2【分析】图形①和④.2.杨老师按零售价买了6本相同的练习本，用了24元．如果按批发价购买，每本将便宜2元，这样可以多买．．本．【考点】应用题，基础应用题【难度】☆【答案】6【分析】零售6本24元，则每本4元，即批发价为422-=元，可以买24212÷=本，多买6本. 3.用2、0、1、4这四个数字可以组成个没有重复数字的四位数．【考点】计数，乘法原理【难度】☆【答案】18【分析】乘法原理，332118⨯⨯⨯=.4.下面的竖式中，被除数是．16□□□□□□□□□【考点】数字谜，除法数字谜【难度】☆【答案】116【分析】由第三行是10得出除数只能是2或5，又由于第五行尾数是6，那么除数只能是2，第五行是16，则商是58，被除数是116.5. 下图中，大长方形的长是40厘米，长是宽的2倍．那么阴影面积是平方厘米．（π取3.14）【考点】几何，圆与扇形，图形的分割与剪拼【难度】☆ 【答案】400【分析】图形中小正方形边长是10厘米，阴影部分正好可以拼成四个小正方形. 41010400⨯⨯=.6. 甲、乙两所小学，甲校的人数是乙校人数的25，甲校的女生人数占全校人数的40%，乙校男生人数占全校人数的60%．如果将甲、乙两校合并，女生人数占总人数的 %．【考点】应用题，分百应用题【难度】☆ 【答案】40%【分析】设甲乙两校人数分别为2份和5份，则女生共240%5(160%) 2.8⨯+⨯-=，占2.8(25)40%÷+=.另外，实际上，从甲乙两校女生都占各自的40%即可得出结论.7. 下图中，长方形ABCD 的长为16厘米，宽为10厘米，E 、F 分别是AB 、BC 的中点，那么，三角形DEF 的面积是平方厘米．E DCBA【考点】几何，三角形面积【难度】☆☆ 【答案】60【分析】用总面积减去三个白色三角形的面积，11116101658108560222⨯-⨯⨯-⨯⨯-⨯⨯=.8. 某项工程，如果甲单独做，12天完成；如果乙单独做，24天完成；如果要求10天完成任务，并且要求甲、乙两人合作的时间尽可能少，那么甲、乙合作天．【考点】应用题，工程问题【难度】☆☆ 【答案】4【分析】设工总24份，则甲每天做2份，乙每天做1份，尽量不合作的话则尽量让做得多的甲做，即全程只有两种状态：甲做、甲乙合作，则甲10天都在做，共做20份，乙需要做4份，即合作4天.9. 将8个相同的球分给甲、乙、丙、丁、戊五个小朋友，每人得到1个球或2个球，那么共有种分法．【考点】计数，排列组合【难度】☆☆ 【答案】10【分析】有2人得到1个球，3人得到2个球，25C 10=.10. 将5个自然数排成一列，从第三个数开始，每个数等于前面两个数的和，那么这5个数中，最多有个质数．【考点】数论，质数与合数，数论中的最值【难度】☆☆☆ 【答案】4【分析】注意到2、3、5、8、13中有4个质数，接下来论证不可能有5个质数.由于第三个数加第四个数等于第五个，这三个数不能都是奇数，必有一偶，这个偶数如果是2的话则它前面的数必然不能都是质数，所以这5个数不可能都是质数.二、填空题B （本大题共5小题．每个小题8分，共40分） 11. 两位数ab 比一位数a 少1个约数，那么ab 最大是．【考点】数论，数论中的最值【难度】☆☆ 【答案】97【分析】极端分析，9a =有三个因数，则ab 有两个因数，只能是个质数，97.12.将10个棱长为1厘米的立方体如下图摆放，那么，这个立体图形的表面积是平方厘米．【考点】几何，立体图形三视图【难度】☆☆【答案】36【分析】画出三视图，三个方向的面积都是1236++⨯=.++=，(666)23613.甲乙两车分别从A、B两地同时出发，相向而行．出发时，甲、乙两车的速度之比是5:4，相遇后，甲的速度增加20%，乙的速度增加50%，他们到达目的地后都立即返回，再次相遇的地点距离第一次相遇地点20千米．那么，A、B两地的距离是千米．【考点】行程，比例法解行程，多次相遇【难度】☆☆☆【答案】180【分析】相遇后两人的速度比变为[5(120%)]:[4(150%)]6:61:1⨯+⨯+==，将全程分为9份，则第一次相遇两人共走9份，其中甲走了5份，第二次相遇两人共走18份，其中甲走了9份，即第二次相遇时甲共走5914⨯=千米.+=份，两次相遇地点相距1份，所以全程距离为29018014.有一个三位数abc，满足如下性质：由a、b、c所组成的没有重复数字的三位数中，最大的三位数与最小的三位数之差恰好等于abc．那么，这个三位数abc是．【考点】数论，位值原理【难度】☆☆☆☆【答案】495【分析】如果a、b、c中没有0，设最大三位数M xyz=，99()=，则最小三位数N zyx-=-，M N x z 即99()=-是99的倍数，注意其中x是a、b、c最大的一个，而z是a、b、c中最小的一个，abc x z枚举99的倍数，有49599(94)=⨯-满足条件；如果a、b、c中有一个0，设最大三位数0=，9990N y xM xy=，则最小三位数0-=-，M N x y 即9990=-，注意其中a、b、c中有一个0，另外两个分别为x和y（x y abc x y>），通过枚举x 来算出c，发现没有符合条件的三位数；如果a、b、c中有一个0，则只能组成一个三位数，显然不满足条件.综上，只有一个三位数495满足条件.15. 将一张正方形纸片，按下图方式进行操作：将正方形的四个顶点向内折叠至正方形中心，然后将新得到的图形的四个顶点再次向内折叠至中心．最后将纸片完全展开，原正方形四条边与所有折痕所组成的新图形中，共有个正方形．．．．第二次向内折：第一次向内折：？展开【考点】计数，几何计数【难度】☆☆☆☆ 【答案】11【分析】展开后的图形如图所示：计数其中正方形的个数，共有11个.第II 卷（解答题共60分）三、解答题（本大题共5题. 解答过程请写在答题纸上、试卷作答无效） 16. 计算及解方程（每题4分、共16分）：（1）3343 4.41624815⨯+⨯+÷（2）22222222246810121416+++++++ （3）11916122030-+-（4）1291212x x+--= 【考点】计算，分数计算，公式类计算，裂项计算，分数方程【难度】☆☆ 【答案】30、816、12、5x = 【分析】（1）3341515323 4.4162(4.42)66246304815445⨯+⨯+÷=⨯++=⨯+=+=（2）2222222221246810121416289178166+++++++=⨯⨯⨯⨯=或222222222468101214164163664100144196256816 +++++++=+++++++=（3）1191111111111111111 6122030233445562443362⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+-=---++--=++-+-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭或1191191111111111 6122030122030344556362⎛⎫⎛⎫⎛⎫-+-=+-=-++--=+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭或11911052721 6122030606060602 -+-=-+-=（4）12916(1)(29)127355 212x xx x x x+--=⇒+--=⇒=⇒=17.列方程（组）解应用题（6分）小英的玩具个数是小丽的5倍，如果小英把6个玩具送给小丽，那么小丽的玩具个数就是小英的2倍了．请问：小英、小丽原来各有玩具多少个？【考点】应用题，列方程（组）解应用题【难度】☆☆【答案】10、2【分析】标准格式如下解：设小丽原有x个玩具，则小英原有5x个玩具，根据题意，得62(56)x x+=-解得2x=55210x=⨯=答：小英原有10个玩具，小丽原有2个玩具.18.如果一个数能被它前两位数字按序组成的两位数整除，则称这个数为“好数”．例如：120的前两位数字按序组成的两位数是12，120能被12整除，所以120是“好数”．请问：（1）四位数中，最小的“好数”是多少？（4分）（2）若存在连续98个自然数都不是“好数”，那么这98个数中，最小的那个数最小可能是多少？（6分）【考点】数论，数论中的最值【难度】☆☆☆【答案】1000、9901【分析】（1）极端分析，1000能被10整除.（2）注意到0xy、00xy都是好数，所以这连续98个数至少是4位数，由于连续n个自然数中必然有一个数能被n整除，所以这些数的前两位不能是10~98，所以最小的情况只可能是9901~9998.19.请回答下列问题：（1）是否能将1～8排成一个圈，使得相邻两个数字的和都是一位数？如果能，请写出一种，如果不能，请说明理由．（3分）（2）请将1～8从左到右排成一行，使得相邻两个数字的和都是一位数．写出1种即可．（3分）（3）第2问中，将1～8从左到右排成一行，相邻两数字之和都是一位数，那么共有多少种不同的排法？（6分）【考点】组合，计数，构造与论证【难度】☆☆☆【答案】不能、81634527、16【分析】（1）不能，因为8要和两个数相邻，而8只有和1相邻才能得出一位数的和.（2）所有情况如下：81634527 81635427 81453627 8154362772634518 72635418 72453618 7254361881726345 81726354 81724536 8172543663452718 63542718 45362718 54362718（3）81一定在一侧，即81（左右可颠倒，2种情况），剩余的6个格中，7一定在最左或最右，且只能与2相邻，2种情况，剩余的4个格中，6一定在最左或最右，且只能与3相邻，2种情况，最后4和5随意排，2种情况，共222216⨯⨯⨯=种.20.如图，大正方形格板是由64个1平方厘米的小正方形铺成的，A、B、C、D是其中四个格点．AD与BC相交于点E．（1）三角形ACD的面积是多少平方厘米？（4分）（2）在其它格点中标出一点F，使得三角形ABF的面积恰等于2平方厘米，这样的点F共有几个？（4分）（3）:CE EB是多少？（4分）（4）三角形ABE的面积是多少平方厘米？（4分）【考点】几何，格点，比例模型【难度】☆☆☆【答案】6、9、4:3、12 7.【分析】（1）直接套公式计算，14362⨯⨯=平方厘米.（2）如图所示，9个点分布在两条与AB平行的直线上.（3）通过数格点利用毕克公式算出593122 ABDS=+-=，或者通过整体减空白来算1119361215112222 ABDS=⨯⨯-⨯⨯-⨯⨯-⨯=.利用风筝模型，9::6:4:32ACD ABDCE EB S S===.（4）14242ABCS=⨯⨯=，3124347ABES=⨯=+.。

第一届六年级“高思杯”数学试题详解

高思杯六年级试卷评析第一试一、填空题Ⅰ1. 计算：321456123654×−×=__________．「答案」 65934．「简答」本题考验的是学生的计算能力．这道题虽然也有速算的方法，但是速算方法本身并不容易想到．如果对分配律运用不熟练，速算也就不那么“速”了．而直接计算只需要计算两次三位数的乘法，并不难做到．速算方法如下：原式()()()321123333123321333321333123333321123333=×+−×+=×−×=−×()19833320023336660066665934=×=−×=−=．2. 计算：0.10.20.30.10.20.3++=×× __________．「答案」 81．「简答」本题考验的是循环小数与分数的转化．只要知道10.19= ，20.29= ，310.393== ，解决这道题目就不成问题．3. 小明上周去百货商店用30元买了2支钢笔和4支铅笔．这周去百货商店时，他发现钢笔降价10%，铅笔加价20%．于是小明花30元买了3支钢笔和1支铅笔．现在．．买1支钢笔和1支铅笔一共需要__________元．「答案」 12．「简答」本题考验的是解应用题的能力．不管利用和差倍分问题的解法还是利用方程，都能很轻松的解决．这里推荐大家采用方程的解法．和小学不同，中学时绝大多数应用题要求必须用方程来解，直接列算式是不合要求的．4. 把2000分解为若干互不相等的自然数的乘积，这些自然数的总和最小是__________．「答案」 37．「简答」将2000分解质因数4325×，然后对不同的分解状况讨论就可以了．显然这些自然数越多越接近，总和就越小．但具体怎样分解是最好的，很难直接推理出来．不妨把最后几种情况列举出来，分别求和比较一下就可以了．2000251020=×××这种情况是最好的．5. 如图，在一个4厘米×4厘米的方格纸内画了一个格点八边形，那么这个八边形内部所有阴影部分的面积之和是________平方厘米．「答案」 2．「简答」仔细看图，容易发现这个八边形中的阴影部分是8个直角三角形，每个直角三角形的面积都是14平方厘米，故总面积为2平方厘米．6. 今年6月份的挂历如右图所示，明年__________月份的挂历恰好和它是一模一样的．「答案」 11．「简答」本题综合考察了周期问题和数表问题．依次计算2011年每月的1号是星期几，其中2月1日、3月1日和11月1日是星期二，那么排列情况就和图中所示情况相同．还应该注意到该月应该恰有30天，故答案为11月．本大题难度一般，但解题时需要仔细，不少题目很容易因为粗心导致错误．第一题错误的同学必须练习计算基本功，上了初中，基础运算题的正确率就应该做到100%．第四题和第六题都涉及多种情况讨论比较，中学非常重视思维的严谨性和过程的周密性，做题时绝对不能想当然．二、填空题Ⅱ7. 360可以分解为两个自然数m ，n 的乘积，已知m 有a 个约数，n 有b 个约数，且a b >，如果13a b +=，那么a b −=__________．「答案」 5．「简答」将360分解质因数得32360235=××，讨论m ，n 的所有情况即可．这里有一个简单一点的方法：由于13a b +=，故a ，b 中一定有一个奇数，即m ，n 中一定有一个完全平方数，故只需讨论1360×，490×，940×，3610×这四种情况．最后发现36m =，10n =，9a =，4b =，故5a b −=8. 将3个相同的红球和5个相同的绿球分给三个人（允许有人没有分到球），有___________种分法．「答案」 210．「简答」由于允许有人没有分到球，故红球和绿球可以分开考虑，再利用乘法原理即可．将3个相同的红球分给三个人，利用插板法，共有2510C =种方法（也可直接枚举出来）．将5个相同的绿球分给三个人，利用插板法，共有2721C =种方法（也可直接枚举出来）．故一共有210种方法．9. 右图中的每一块都是正方形，已知正方形A 的边长为1，那么正方形B 的边长为__________．「答案」 138125．「简答」依次考虑各块正方形的边长比．因为正方形A 的边长为1，故A 右侧正方形边长为12，再往右的大正方形边长为45．设正方形B 的边长为x ，故B 左侧大正方形边长为34x ，再往左的正方形边长为13x ．于是311414325x x x ++=++，解得138125x =．星期日星期一星期二星期三星期四星期五星期六1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 3010. 小赵是铁人三项运动的爱好者，如果他用2小时骑自行车，用3小时长跑，用4小时游泳则行进总路程为74公里；如果他用4小时骑自行车，用2小时长跑，用3小时游泳则行进总路程为91公里．又知道他进行三个项目的速度都是整数公里每小时．则他三个项目速度之和为__________公里/小时．「答案」 28．「简答」本题考察了不定方程的知识．设骑自行车每小时x 公里，长跑每小时y 公里，游泳每小时z 公里，可得2347442391x y z x y z ++=⎧⎨++=⎩，解不定方程，整数解只有1774x y z =⎧⎪=⎨⎪=⎩，故答案为28．11. 下列算式中每个字母都代表3、4、6、8、9这五个数字中的一个，不同的字母代表不同的数字，那么五位数ABCDE =________．157122A B C D E ++=××× 「答案」 43689（或43698，46389，46398，填对任意一个均可）．「简答」注意到3、6均含有一个质因子3，而9含有两个质因子3．要想最后约去3，只可能把3、6放在一起，再和9通分时约去，分别对每种情况验算即可．12. 甲从A 地，乙丙从B 地同时出发，相向而行．甲乙先相遇．甲乙相遇后，乙又行了3.2小时到达A 地，相遇后甲又行了2小时后遇见丙．甲丙相遇后，甲继续前进，3小时后到达B 地；丙12小时后到达A 地．如果乙比丙每小时多行40千米，则AB 两地相距________千米．「答案」 480．「简答」由题意，甲乙相遇后，乙又行了3.2小时到达A 地，甲又行了5小时到达B 地．这个时间比为22::v v v v v v ××=甲乙乙甲乙甲相遇时间相遇时间，故甲乙的速度比为4:5，同样可以求得甲丙的速度比为2:1，故甲乙丙的速度比为4:5:2．再根据“乙比丙每小时多行40千米”算出他们的速度，并求出AB 的距离为480千米．这道大题难度较大，要求对各种技巧能够灵活运用．第8题只要能想到乘法原理，其实不用插板法也可通过枚举得到，但大多数同学没有注意到红球和绿球可以分开考虑．第9题本身涉及到的知识并不难，但形式比较特别，不少同学无法从图中发现数量关系，导致这道题得分偏低．第12题是难度最大的一道，从时间比转化为速度比的平方，很多同学一时无法想到，或是直接把时间比当成了速度比．另外这道题目中三人的速度也均不是整数，这也进一步加深了难度．三、解答题13. L 博士乘坐飞行器要到正东方向1公里处的地方，他将飞行器交由机器人控制，自己去睡觉了．但是机器人出了故障，飞行器每行进3米，机器人就会将飞行器向左转动90°，每行进n 米就会将飞行器向右转动90°，如果里程是3和n 的公倍数，则两次操作抵消，飞行器保持航向．假设飞行器的速度是每秒1米，问：（1）当6n =时，L 博士能到达目的地吗？如果能，多少秒后才能到达目的地；如不能说明理由；（2）当7n =时，L 博士能到达目的地吗？如果能，多少秒后才能到达目的地；如不能说明理由；（3）当8n =时，L 博士能到达目的地吗？如果能，多少秒后才能到达目的地；如不能说明理由．「简答」解：（1）按题目所说过程画出飞行器前进路线（图1），发现每24秒，飞行器绕过一个正方形回到出发点，故L 博士不可能到达目的地．（2）由于[]3,721=，画出飞行器前进路线（图2），发现每21秒，飞行器向正东前进1米．故L 博士可以到达目的地．一共要前进1000米，注意到每个周期的最开始飞行器可以向正东先前进3米，故L 博士一共需要()1000321320940−×+=秒．（3）由于[]3,824=，画出飞行器前进路线（图3），发现每24秒，飞行器向前飞2米，向左飞2米．继续下去，每过96秒飞行器回到出发点，故L 博士不可能到达目的地．本题严格说来只是一个周期问题，只要能理解题意，顺利作出飞行器的路线图，这道题可以说已经解决了一大半．但是在做题时有很多地方都容易粗心犯错误．最明显的错误是对“向左转动”和“向右转动”理解不对，误以为飞行器越开越偏，实际上飞行器只是在绕圈子而已．最可惜的错误是第二问中，有些同学已经画对了图，但是发现飞行器20秒后回到出发点，就误以为飞行器一直在绕圈子了，没有按照21秒的周期进行计算．另外在这一问中，很多同学没有注意到每个周期的头3秒一直向东，只注意到每21秒向东飞行1米，于是结果算成了21000秒．本题总体得分情况并不太理想，可见对于处理这种题干很长且叙述语言较多的问题，大多数同学缺乏经验．出发点图1出发点图2出发点图3。

学而思小学六年级奥数电子版教材

．(л=3.14)
例 4 如下图所示，曲线 PRSQ 和 ROS 是两个半圆，RS 平行于 PQ.如果大半圆的半径是 1 米，那么阴影部分是多少平方米？（л取 3.14）
巩固在右图所示的正方形 ABCD 中，对角线 AC 长 2 厘米，扇形 ADC 是以 D 为圆心，以 AD 为半径的圆的一部分．求阴影部分的面积．
.
例 5 1 2+2 3+3 4+4 5+5 6+6 7+7 8+8 9+9 10=
.
巩固：2 3+3 4+4 5+…+100 101=
.
拓展计算：1 2 3+2 3 4+3 4 5+…+9 10 11=
.
例6
［2007 –（8.5 8.5-1.5 1.5）÷10］÷160-0.3=
某学校学生计划乘坐旅行社的大巴前往郊外游玩按照计划旅行社的大巴准时从车站出发后能在约定时间到达学校搭载满学生在预定时间到达目的地已知学校的位置在车站和目的地之间大巴车空载的时候的速度为60千米小时满载的时候速度为40千米小时由于某种原因大巴车晚出发了56分钟学生在约定时间没有等到大巴车的情况下步行前往目的地在途中搭载上赶上来的大巴车最后比预定时间晚了54分钟到达目的地求学生们的步行速度
13
14
巩固如图，正方形边长为 1，正方形的 4 个顶点和 4 条边分别为 4 个圆的圆心和半径，求阴影部分面积．（л取 3.14）
例 3 如图所示，在半径为 4cm 的图中有两条互相垂直的线段，阴影部分面积爿与其它部分面积 B 之差(大减小)是 cm2

2008迎春杯六年级初赛详解

b、c 得出如下方格 1
帅
2 D E 得到右图方格
列数之和，均应为 30，而这两组数只有一格不同，所以第二行第三个数为 1。设第一行前 3 个数分别为 a、
老
第 2 页
【解析】因为每行的５个数均不相等，所以每行都有 1、 2、 3、 4、 5，整个表 25 个数之和为 5× （1+2+3+4+5），
当被乘数百位为 1 时，乘数可以使 25 或 27，此时分别有 122× 25 满足题意。当被乘数百位为 4 时，乘数只能是 22，此时没有符合题意的数组。
兴趣是最好的老师
师
b=1，原九位数为 200731212。
学习有意思
快乐思维
9.
A、B 两地相距 22.4 千米。有一支游行队伍从 A 出发，向 B 匀速前进；当游行队伍队尾离开 A 时，甲、
【答案】14523
又分成的 5 块上所填数之和都相等，所以每块上的数字之和应为 1+2+3+4+5=15。考虑第二行第二个数，因为第一行空缺的 3 个应为 3、4、5，所以要使 1 所在块所有数之和为 15，则第二行第二个数必为 2;同理，第一行第一个数应与第五行第二个数相等。再考虑右边两块的数之和右边两
○位置的“马”只能走到标有× 的格中，类似于中国象棋中的“马走日”。如果“马”在 8× 8 的国际象棋棋盘中位于第一行第二列（图 2 中标有△ 的位置），要走到第八行第五列（图 2 中标有 ★的位置），最短路线有条。
【答案】12
【解析】首先找到最短路线应有哪几步组成，因为每一步最多向下移动两排，所以最少需要 4 步才能到达
老
A E F G B C D

4-2-2三角形等高模型与鸟头模型：知识例题精讲.docx

三角形等高模型与鸟头模型板块一三角形等高模型我们已经知道三角形面积的计算公式：三角形面积=底乂高一2从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积.如果三角形的底不变，高越大（小），三角形面积也就越大（小）；如果三角形的高不变，底越大（小），三角形面积也就越大（小）；这说明当三角形的面积变化吋，它的底和高之中至少有一个要发生变化.但是，当三角形的底和高同时发生变化时，三角形的面积不一定变化.比如当高变为原来的3倍，底变为原来的丄，则三角形面积与原来的一3样.这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化.同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状.在实际问题的研究中，我们还会常常用到以下结论:①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；如左图S］ : S2 = a:b③夹在一组平行线之间的等积变形，如右上图S“CD=S卫3；反之，如果Sg = S/），则可知直线AB平行于CD ・④等底等高的两个平行四边形面积相等（长方形和正方形可以看作特殊的平行四边形）；⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比.【例1］你有多少种方法将任意一个三角形分成：（1） 3个面积相等的三角形；⑵4个面积相等的三角形；⑶ 6个面积相等的三角形.【例2］如图，BD长12厘米，DC长4厘米，B、C和D在同一条直线上.（1）求三角形ABC的面积是三角形面积的多少倍？（2）求三角形ABD的面积是三角形ADC面积的多少倍?D C【例3】如右图，和CDEF都是矩形，4B的长是4厘米，BC的长是3厘米，那么图中阴影部分的面积是 _________ 平方厘米.【例4］如图，长方形ABCD的面积是56平方厘米，点E、F、G分别是长方形ABCD边上的中点，H为AD 边上的任意一点，求阴影部分的面积.【例5】长方形A3CD的面积为36伽S E、F、G为各边中点，H为4D边上任意一点，问阴影部分面积【例6】长方形ABCD的面积为36, E、F、G为各边中点，H为4D边上任意一点，问阴影部分面积是多少？【例7］如右图，E在AD上，AD垂直BC, AD=12厘米，DE = 3厘米.求三角形ABC的面积是三角形EBC 面积的几倍？【例8]如图，在平行四边形ABCD 中，EF 平行AC,连结BE 、AE. CF 、那么与BEC 等积的三角形一共有哪几个三角形？【例9]（第四届”迎春杯”试题）如图，三角形ABC 的面积为1,其中AE = 3AB f BD = 2BC ,三角形BDE 的面积是多少？【例10] （2008年四中考题）如右图，AD=DB f AE = EF = FC ,已知阴影部分面积为5平方厘米，^ABC的面积是 _______ 平方厘米.【例111 如图ABCD 是一个长方形，点E 、F 和G 分别是它们所在边的中点.如果长方形的面积是36 个平方单位，求三角形EFG 的面积是多少个平方单位.【例12] 如图，大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成.求阴影部分的面积.【例13] 如图，三角形ABC 中，DC = 2BD , CE = 3AE f 三角形ADE 的面积是20平方厘米，三角形A3C 的面积是多少？12cm2/ 48cm 2 叫/ N 48cm 2CB【例14】（2009年第七届”希望杯”二试六年级）如图，在三角形ABC中，已知三角形ADE、三角形DCE、三角形BCD的面积分别是89, 28, 26.那么三角形的面积是_______________ •【例15] （第四届《小数报》数学竞赛）如图，梯形ABCD被它的一条对角线BD分成了两部分.三角形BDC的面积比三角形ABD的面积大10平方分米.已知梯形的上底与下底的长度之和是15分米，它们的差是5分米.求梯形ABCD的面积.【例16] 图中的面积为15cm2,线段OB的长度为OD的3倍，求梯形ABCD的面积.C【解析】在AftD中，因为S/WB=15cm2, ^LOB = 3OD f所以有阿一3 = 5cn?.因为和ACD等底等高，所以有・从而SocD=15cn?,在KD中，（）CD = 45cm2,所以梯形面积：15 + 5 + 15 + 45 = 80（cm2）.【例17] 如图，把四边形ABCD改成一个等积的三角形.【例18] （第三届“华杯赛”初赛试题）一个长方形分成4个不同的三角形，绿色三角形面积占长方形面积的15%,黄色三角形面积是2\cm2.问：长方形的面积是多少平方厘米?【例19] 0是长方形ABCD内一点，已知AOBC的面积是5cm2, \OAB的面积是2cm2,求AOBD的面积是多少？【例20] 如右图，过平行四边形ABCD内的一点P作边的平行线EF、GH ,若A/迟D的面积为8平方分米，求平行四边形PHCF的面积比平行四边形PGAE的面积大多少平方分米？【例21] 如右图，正方形ABCD的面积是2(),正三角形\BPC的面积是15 ,求阴影AZ3PD的面积.【例22] 在长方形ABCD内部有一点0,形成等腰AAO3的面积为16,等腰\DOC的面积占长方形面积的18% ,那么阴影\AOC的面积是多少？【例23] (2008年“陈省身杯”国际青少年数学邀请赛六年级)如右图所示，在梯形ABCD中，E、F 分别是其两腰AB. CD的中点，G是EF上的任意一点，己知MDG的面积为15cm2,而z\BCG的面积恰好是梯形ABCD面积的Z,则梯形ABCD的面积是cm2.20 --------------------------------------------【例25] 如图，正方形ABCD 的边长为6, AE=l.5f CF =2.长方形EFGH 的面积为 ________________如图，ABCD 为平行四边形，EF 平行AC,如果ADE 的面积为4平方厘米.求三角形CDF 的面积.【例27] 图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是多少平方厘米.【例28] 如图，有三个正方形的顶点D 、G 、K 恰好在同一条直线上，其中正方形GFEB 的边长为10 厘米，求阴影部分的面积.【例26]【例请你证明它们的面积相等.F C【例29] （2008年”华杯赛”决赛）右图中，ABCD 和CGEF 是两个正方形，AG 和CF 相交于H,已知CW等于CF 的三分之一，三角形CHG 的面积等于6平方厘米，求五边形ABGEF 的面积.【例30】（第八届小数报数学竞赛决赛试题）如下图，E 、F 分别是梯形ABCD 的下底和腰CD 上的点,DF = FC ,并且甲、乙、丙3个三角形面积相等.已知梯形ABCD 的面积是32平方厘米.求图中阴影部分的面积.【例31] 如图，已知长方形 QEF 的面积16,三角形的面积是3,三角形ACF 的面积是4,那么三角形ABC 的面积是多少？【例321 如图，在平行四边形ABCD 中，BE = EC , CF = 2FD •求阴影面积与空白面积的比.【例33] （第七届”小机灵杯”数学竞赛五年级复赛）如图所示，三角形ABC 中，。

六年级学而思奥数

六年级学而思奥数11111123420261220420＋＋＋＋＋36579111357612203042++++++1111112123123100+++++++++++222222222222233333333333331121231234122611212312341226L L L +++++++++-+-+-+++++++++测试题【例1】(★★)111111357911_____.612203042+++++=计算A ．53614B ．7512C ．4121D ．1712【例2】(★★★)计算：2337911345122030+++++=( )A ．3227B ．4112C ．4121D ．2312【例3】(★★★★)11111_____12123123412310+++++=+++++++++A ．1113B ．111C ．712D ．2011【例4】(★★★★)计算：2222222222221324351820213141191++++++++=----（）A ．72019B ．15138190C ．1402D ．73620本讲学习重点： 1六年级学而思奥数2．整体约分与连锁约分技巧(2010第8届·走进美妙的数学花园·六年级初赛)211354117997⎛⎫⎛⎫+÷+ ⎪ ⎪⎝⎭⎝⎭【附加练习】2129476122323791113791113⎛⎫⎛⎫+++÷+++ ⎪ ⎪⎝⎭⎝⎭(2009·数学解题能力展示·读者评选活动小学六年级组初赛试题)89109101110111211121378910111178910++++++++-+--+-124248361210020040013926183927100300900⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯【附加练习】1246248123612181002004006001369261218391827100300600900⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯一根铁丝，第1次截去总长度的212，第2次截去剩余长度的213，第3次截去剩余长度的214…第2008次截去剩余长度的212009，此时该铁丝还剩2010厘米，那么该铁丝原长为______厘米？【附加练习】1111111113243520072009⎛⎫⎛⎫⎛⎫⎛⎫+⨯+⨯+⨯⨯+ ⎪ ⎪ ⎪ ⎪⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭已知135979924698100A ⨯⨯⨯⨯⨯＝，24696983579799B ⨯⨯⨯⨯⨯＝，110C ＝.试求A .B .C 三者大小关系.【开裆裤的课堂笔记总结】 1．整体约分：被除数.除数中的分母对应相等：要么带化假.要么假化带，考虑提取公因数后整体约分； 2．连锁约分：多分数连乘，将分子.分母都化成乘积形式，伺机约分.测试题例1 测：计算：212332213535⎛⎫⎛⎫+÷+ ⎪ ⎪⎝⎭⎝⎭A ．1118B ．118C ．118D ．518例2测：计算： 124245357478357911113579+++++++++-++-+A ．2B ．4C ．3D ．1例3 测：123246369153045234468691281216304560⨯⨯+⨯⨯+⨯⨯++⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯++⨯⨯A ．34 B ．114C ．14D ．35例4测：一条丝带，第1次剪去总长度的212，第2次剪去剩余长度的213，第3次剪去剩余长度的214…第15次剪去剩余长度的2116，此时该丝带还剩17米，那么该丝带原长为( )米？ A ．30B ．36C ．32D ．35例5测：已知13533352463436A⨯⨯⨯⨯⨯＝，24632343573335B ⨯⨯⨯⨯⨯＝，16C ＝.试求A .B .C 三者中最大的一个数是( ).A．BB ．AC ．CD ．不确定用0.1.2.3.4.5六张卡片可组成几个无重复数字的四位数？其中能被2整除的有____个.【举一反三】还是用数字0.1.2.3.4.5六个数字可组成_____个没有重复数字且能被5整除的四位数？(2010年北大附中小升初试题)一个三位数，若它的中间数字恰好为首尾数字的平均值，则称它为“好数”.则“好数”总共有______个.【举一反三】一个三位数，其反序数也是一个三位数，用这个三位数减去它的反序数得到的差大于0，且为4的倍数，满足条件的三位数有_____个.1～1999的自然数中，有______个与5678相加时，至少发生一次进位？一个七位数，其数码只能为1或3，且无两个3是相邻的.问这样的七位数共有多少个？如图所示，水通过管道从A输送到B，管道网一共有5个阀门，阀门可以是开或关，即可以让水流通过，也可以阻止水流通过.5个阀门的开或关一共有25＝32种不同的组合.问这32种不同的组合中有______种组合可以让水从A流到B.【本讲重要内容回顾】1．加乘原理16字方针：分步计数，步步相乘；分类计数，类类相加；2．排列组合问题原则：先选后排；3．乘法原理注意事项：特殊位置(元素).优先考虑.测试题1．用1 .2 .3 .4 .5 .6 六个数字，一共可以组成多少个数字不重复且能被4整除的4位数？A．84 B．72 C．60 D．962．如果一个大于9的整数，其每个数位上的数字都比他右边数位上的数字大，那么我们称它为迎春数.那么，小于2008的迎春数一共有多少个？A．225 B．205 C．185 D．1653．若自然数n使得作竖式加法n＋(n＋1)＋(n＋2)时均不产生进位现象，便称n为“连绵数”.如因为12＋13＋14不产生进位现象，所以12是“连绵数”；但13＋14＋15产生进位现象，所以13不是“连绵数”，则不超过100的“连绵数”共有()个.A．9 B．11 C．12 D．154．地图上有A，B，C，D四个国家(如下图)，现有红.黄.蓝.绿四种颜色给地图染色，使相邻国家的颜色不同，但不是每种颜色都必须要用，问有多少种染色方法？D．84C．69B．78A．80. 枪连在一起的情况的种数是3枪中恰好有4枪，命中4枪，命中8某人射击．5A ．20B ．25C ．15D ．32在1～2004的所有自然数中，既不是2的倍数，也不是3和5的倍数的数有______个.某科室有12人，其中6人会英语，5人会俄语，5人会日语，3人既会英语又会俄语，2人既会俄语又会日语，2人既会英语又会日语，1人三种语言全会.只会1种外语的人比1种外语也不会的人多______个.2006盏亮着的电灯，各有一个拉线开关控制，按顺序编号为1.2.…2006.将编号为2的倍数的灯各拉一下，再将编号为3的倍数的灯各拉一下，最后将编号为5的倍数的灯各拉一下，最后亮着的灯有______盏.在一个自助果园里，只摘山莓者两倍于只摘李子者；摘了草莓.山莓和李子的人数比只摘李子的人数多3；只摘草莓者比摘了山莓和草莓但是没有摘李子者多4人；50人没摘草莓；11人摘了山莓和李子但没有摘草莓；总共有60人摘了李子.如果参与采摘的总人数为100，你能回答下列问题吗？ ⑴有______人摘了山莓；⑵有______人同时摘了三种水果； ⑶有______人只摘了山莓；⑷有______人摘了李子和草莓，而没有摘山莓； ⑸有______人只摘了草莓.在长方形ABCD 中，AD ＝15cm ，AB ＝8cm ，四边形OEFG 的面积是9cm 2，求阴影总面积.测试题1．分母是105的最简真分数有多少个？A ．45B ．48C ．50D ．522．某自习室有15人，据调查其中6人有英语作业，5人有数学作业，7人有语文作业，3人既有英语作业又有数学作业，2人既有数学作业又有语文作业，3人既有英语作业又有语文作业，1人语.数.英三门功课都要做，问只有一门功课的人比一门功课都没有的人多多少？ A ．1 B ．2 C ．3 D ．43．2000盏亮着的电灯，各有一个拉线开关控制，按顺序编号为1.2.…2000将编号为2的倍数的灯各拉一下，再将编号为3倍数的灯各拉一下，最后将编号为5倍数的灯各拉一下，最后亮着的灯有多少盏？ A ．1000 B ．998 C ．1004 D ．10024．五年级3班有46名学生参加三项课外活动，其中24人参加了绘画小组，20人参加了合唱小组，参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的3.5倍，又是三项活动都参加人数的7倍，既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的2倍，既参加绘画小组又参加合唱小组的有10人，求参加朗诵小组的人数. A ．20 B ．21 C ．22 D ．23 5．边长为6.5.2的三个正方形，如图所示，求它们覆盖部分的面积.65A ．53B ．54C ．55D ．60经济问题几个关键词及其基本关系1．关键词：成本.预计利润(率).定价.实际利润(率)；2．基本关系：利润率＝100% 利润成本，利润率是相对于成本来说的一个百分比.(★★☆)某家商店决定将一批苹果的价格降到原价的70%卖出，这样所得利润就只有原计划的13.已知这批苹果的进价是每千克6元6角，原计划可获利润2700元，那么这批苹果共有多少千克？【举一反三】某商家决定将一批苹果的价格提高20%，这时所得的利润就是原来的两倍.已知这批苹果的进价是每千克6元，按原计划可获利润1200元，那么这批苹果共有多少千克？某商店到苹果产地去收购苹果，收购价为每千克1.2元.从产地到商店的距离是400千米，运费为每吨货物每运1千米收1.5元.如果在运输及销售过程中的损耗是10%，那么商店要想实现25%的利润率，零售价应是每千克多少元？【举一反三】果品公司购进苹果5.2万千克，每千克进价是0.98元，付运费等开支1840元，预计损耗为1%，如果希望全部进货销售后能获利17%，每千克苹果零售价应当定为多少元？甲.乙两种商品成本总共200元.甲商品按30%的利润定价，乙商品按20%的利润定价.后来两种商品都按定价的9折销售，结果仍获利27.7元.问甲商品的成本是多少元？(★★★(★★★某店原来将一批苹果按100%的利润(即利润是成本的100%)定价出售.由于定价过高，无人购买.后来不得不按38%的利润重新定价，这样出售了其中的40%.此时，因害怕剩余水果腐烂变质，不得不再次降价，售出了剩余的全部水果.结果，实际获得的总利润是原定利润的30.2%.那么第二次降价后的价格是原定价格的百分之多少？利民商店从一家日杂公司买进了一批蚊香，然后按希望获得的利润，每袋加价40%定价出售.但是，按这种定价卖出这批蚊香的90%时，夏季即将过去.为了加快资金的周转，利民商店按照定价打七折的优惠价，把剩余的蚊香全部卖出.这样，实际所得的纯利润比希望获得的纯利润少了15%.按规定，不论按什么价钱出售，卖完这批蚊香必须上缴营业税300元(税金与买蚊香用的钱一起作为成本).请问利民商店买进这批蚊香时一共用了多少元？【本讲重要内容回顾】1．经济问题中几个关键量及它们之间的关系；2．一类重要的数学思想：类比思想，比较相似条件.3．应用题重要思想：目标倒退，自问一下：要求什么？需要先求什么？注意题目中描述结果的综合性话语. 4．应用题重要方法：方程法.测试题五1．某家商店决定将一批苹果的价格降到原价的70%卖出，这样所得利润就只有原计划的13.已知这批苹果的进价是每千克3元，原计划可获利润2700元，那么这批苹果共有多少千克？ A ．1200 B ．500 C ．600 D ．11002．某商店到苹果产地去收购苹果，收购价为每千克2元.从产地到商店的距离是400千米，运费为每吨货物每运1千米收1元.如果在运输及销售过程中的损耗是10%，那么商店要想实现20%的利润率，零售价应是每千克多少元？ A ．4.5 B ．2.9 C ．3.2 D ．4.3 3．甲.乙两种商品成本共300元.商品甲按20%的利润定价，商品乙按15%的利润定价.后来两种商品都按定价的九折销售，结果仍获得利润15元.问甲种商品的成本是多少元？ A ．120 B ．150 C ．100 D ．2004．甲.乙两种商品的单价和为100元，因季节变化，甲商品降价10%.乙商品提价5%，调价后，甲.乙两种商品的单价之和比原单价之和提高了2%，求甲种商品原来的单价. A ．20 B ．80 C ．56 D ．705．某汽车工厂生产汽车，由于钢铁价格上升，汽车的成本也上升了10%，于是工厂以原售价提高5%的价格出售汽车，虽然如此，工厂每出售一辆汽车所得的利润还是减少了20%，求钢铁价格上升之前的利润率. A ．25% B ．30% C ．20% D ．28%(★★★(★★★两地相距480千米，一艘轮船在两地之间往返，顺流行驶一次需要16小时，逆流返回需要20小时.该轮船在静水中的速度是多少？水流速度是多少？A.B两个码头间的水路为90千米，其中A码头在上游，B码头在下游.第一天水速为每小时3千米，甲.乙两船分别从A.B两码头同时起航同向而行，3小时后乙船追上甲船.已知甲船的静水速为每小时18千米.乙船的静水速度是多少？第二天由于涨水，水速变为每小时5千米.甲.乙两船分别从A.B两码头同时起航相向而行，出发多长时间后相遇？在地铁入口，从站台到地面有一架向上的自动扶梯，涛涛乘坐扶梯时，如果每秒向上迈一级台阶，那么他走过20级台阶后到达地面；如果每秒向上迈两级台阶，那么走30级台阶后到达地面.从站台到地面有______级台阶.甲.乙两人在一个圆形跑道上跑步，两人从同一地点出发，甲用40分钟能跑完一圈.两人反向跑时每隔15秒相遇一次.那么两人同向跑时，乙每隔______秒追上甲一次.甲.乙两人在一条圆形跑道上锻炼.他们分别从跑道某条直径的两端同时出发，相向而行.当乙走了100米时，他们第一次相遇.相遇后两人继续前进，在甲走完一圈前60米处第二次相遇.求这条圆形跑道的周长.测试题六1．甲.乙两港间的水路长432千米，一只船从上游甲港航行到下游乙港需要18小时.从乙港返回甲港，需要24小时，求船在静水中的速度和水流速度.A．24.6B．21.6C．24.3D．21.32．甲.乙两船在静水中速度分别为每小时24千米和每小时32千米.两船从某河边相距336千米的A.B两港同时相向而行.几小时相遇？如果同向而行，几小时后，乙船追上甲船？A．6.42B．8.44C．6.44D．8.423．在某商场入口，从一楼到二楼有一架向上的自动扶梯，阳阳乘坐扶梯时，如果每向上迈一级台阶，那么他走过40级台阶后到达地面；如果每秒向上迈两级台阶，那么走60级台阶后到达地面.问从一楼到二楼有多少级台阶.A．100B．110C．120D．1304．甲，乙两人在400米的环形跑道上跑步，两人在同一地点朝相反方向跑.从第一次到第二次相遇间隔40秒，甲每秒跑6米，乙每秒跑几米？A．4B．5C．6D．85．两辆电动小汽车在周长为360米的圆形跑道上不断行驶，甲车每分行驶20米，甲乙两车同时分别从相距90米的A.B两地相背而行，相遇后乙车立即返回，甲车不改变方向，当乙车到达B地时，甲车过B地后恰好又回到A地，此时甲车立即返回(乙车过B地继续行驶)，再过多少分与乙车相遇？A．4B．3C．6D．51．按比分配——和差倍分思想2．比例法中的三个基本比例关系；3．设数法在比例关系中的应用4．比例法在行程综合分析.图解法中的应用.(★★★)一段路程分成上坡.平路.下坡三段，各段路程之比依次为1∶2∶3.小明走各段路所用时间之比依次为4∶5∶6.已知他上坡时速度为每小时3千米，路程全长10千米，问小明走完全程用______小时？(★★★★)乘火车从甲城到乙城，2008年初需要19.5小时，2008年火车第一次提速20%，2009年第二次提25%，2010年第三次提30%.经过这三次提速后，从甲城到乙城乘火车只需要多少小时？(★★★★)一条小船往返于甲.乙两港之间，已知船在静水的速度是每小时9千米，平时顺行与逆行所用时间比为1∶2.一天因为下暴雨，水流速度是原来的2倍，这条船往返共用10小时.甲.乙两港相距多少千米？(★★★★)小芳从家到学校有两条一样长的路.一条是平路，另一条是一半上坡路，一半下坡路，小芳上学走这两条所用时间一样多.已知下坡速度为平路的1.6倍，那么上坡速度为平路的______倍？(★★★★(2008年第六届小学“希望杯”全国数学邀请赛5年级第2试第11题)王叔叔开车从北京到上海，从开始出发，车速即比原计划的速度提高了19，结果提前一个半小时到达；返回时，按原计划的速度行驶280千米后，将车速提高16，于是提前1小时40分钟到达北京.北京.上海两市间的距离是______千米.(类型：变速问题)测试题七1．乘火车从甲城到乙城，1998年初需要19.5小时，1998年火车第一次提速30%，1999年第二次提速25%，2000年第三次提速20%.经过三次提速后，从甲城到乙城乘火车只需要().A．8.19小时B．10小时C．14.63小时D．15小时2．小强以２米/秒的速度从家到公园，到达后立即以3米/秒的速度返回家.求小强的平均速度是多少？A．1.2B．2.4C．3.6D．1.03．甲.乙两船在静水中速度分别为每小时24千米和每小时32千米.两船从某河边相距336千米的A.B两港同时相向而行.几小时相遇?如果同向而行，几小时后，乙船追上甲船？A．6.42B．8.44C．6.44D．8.424．一辆车从甲地开往乙地，如果把车速提高20%，可以比原定时间提前1小时到达；如果原速行驶100千米后，再将车速提高30%，也比原定时间提前1小时到达，求甲.乙两地距离.A．360B．300C．350D．4205．一段路程分为上坡.平路.下坡三段，各段路程的长度之比是1∶2∶3，某人走这三段路所用的时间之比是4∶5∶6.已知他上坡时每小时行2.5千米，路程全长为20千米.此人走完全程需多长时间？A．9B．10C．11D．8★★某校有学生465人，其中女生的23比男生45的少20人，那么男生比女生少多少人？★★★有甲.乙.丙.丁4个人，每三个人的平均年龄加上余下一人的年龄之和分别为29，23，21和17，这4人中最大年龄与最小年龄的差是多少？★★(全国小学数学奥林匹克)一个半圆形区域的周长的值等于它的面积的值，这个半圆的半径是_____. (精确到0.01，π＝3.14)★★★★(2009年迎春杯初赛)如右图，长方形ABCD 中被嵌入了6个相同的正方形.已知AB ＝22厘米，BC ＝20厘米，那么每一个正方形的面积为_____平方厘米.【拓展】★★★★小明用8个一样大的小长方形拼图，拼出了如图甲.乙的两种图案：图案甲是一个正方形，图案乙是一个大的长方形；图案甲的中间留下了边长是2cm的正方形小洞.求小长方形的长和宽？★★★(2004年南京市少年数学智力冬令营)华医生下午2时离开诊所出诊，走了一段平路后爬上一个山坡，给病人看病用了半小时，然后原路返回，下午6时回到诊所.医生走平路的速度是每小时4千米，上山的速度是每小时3千米，下山的速度是每小时6千米，华医生这次出诊一共走了______千米.★★★★(2008年清华附中考题)已知一个四位数加上它的各位数字之和后等于2008，则所有这样的四位数之和为_____ __.测试题八1．某校共有84人参加“兴趣杯”数学邀请赛，已知获奖人数的58与未获奖人数的34共57人，那么该校有多少人获奖？A．48 B．50C．36 D．402．红花.绿花和黄花共78朵，红花和绿花的总朵数比黄花多6朵，红花比绿花多6朵，红花有多少朵？A．28 B．18C．20 D．243．一个正方体的棱长和一个圆锥体的底面半径.高相等.正方体的体积是24立方米，这个圆锥体的体积是_____立方米.A．16 B．8C．8 D．204．如图，长方形中被嵌入了8个相同的正方形.已知长20厘米，宽16厘米，那么每一个正方形的面积为平方厘米.A．15 B．16C．18 D．205．一段路程分为上坡.平路.下坡三段，各段路程的长度之比是1∶2∶3，某人走这三段路所用的时间之比是4∶5∶6.已知他上坡时每小时行2.5千米，路程全长为20千米.此人走完全程需多长时间？ A ．3 B ．4 C ．5 D ．6(★★) (小数报数学竞赛)某运输队运一批大米，第一天运走总数的15多60袋，第二天运走总数的14少60袋，还剩下220袋没有运走，这批大米原来一共有多少袋？(★★★)甲乙二人欲买一件商品，按照标价，甲带的钱差40元，乙带的钱少14.经过讨价最后可以按9折购买，于是他们合买了一件，结果剩下28元.这件商品标价为多少元？(★★★★) (2008年101中学试题)北京中学生运动会男女运动员比例为19∶12，组委会决定增加女子艺术体操项目，这样男女运动员比例变为20∶13；后来又决定增加男子象棋项目，男女比例变为30∶19，已知男子象棋项目运动员比女子艺术体操运动员多15人，则现在总运动员人数为多少？(★★★★)如图所示，B与C的面积之和等于A面积的45，且A中的阴影部分面积占A面积的16，B的阴影部分面积占B面积的15，C的阴影部分面积占C面积的13.求A.B.C的面积之比.(★★★★)秀情倒满一杯纯牛奶，第一次喝了13，然后加入纯净水，将杯子斟满并搅拌均匀，第二次，又喝了13，继续用纯净水斟满并搅拌均匀，重复上述过程，那么第4次，秀情喝的纯牛奶占秀情喝的所有牛奶的几分之几？(★★★★) (2008年湖北省“创新杯”六年级二试)甲乙两种商品成本共200元.商品甲按30%的利润定价，商品乙按20%的利润定价.后来两种商品都按定价的九折销售，结果仍获得利润27.7元.问甲种商品的成本是多少元？测试题九1．孙悟空给小猴分桃子，第一天分了全部的25，第二天分了剩下的13，第二天比第一天少分20个桃子，那么孙悟空分的桃子一共有( )个. A ．50 B ．100 C ．150 D ．2002．叮叮和铛铛两个人一共有48个苹果，叮叮又买来12个苹果，铛铛又买来自己苹果的17，此时他们的苹果数相同，那么原来叮叮有( )个苹果. A ．20 B ．24 C ．28 D ．303．育英小学六年级学生分成三批去参观科技馆，第一批和第二批的的人数比是5∶4，第二批与第三批的比是3∶2，已知第一批比第二.三批人数的总和少15人，求六年级参观的有多少人？ A ．80 B ．100 C ．105 D ．1204．玲玲倒满一杯纯豆浆，第一次喝了14，然后加入牛奶，将杯子斟满并搅拌均匀，第二次玲玲又喝了14，继续用牛奶将杯子斟满并搅拌均匀，重复上述过程，那么第3次后，玲玲共喝了一杯纯豆浆的( )(用分数表示).A ．14B ．316C ．964D ．37645．图中空白部分占正方形面积的几分之几？A ．12B ．13C ．14D ．156．一批商品按50%的期望利润率定价，结果只卖了70%的商品，为了尽快卖完剩下的商品，商店决定按定价打折出售.这样所获得的全部利润是原来利润的82%.商品打了几折？ A ．七折 B ．七五折 C ．八折 D ．九折(★★)杨老师和谷老师要给小朋友们建一个小房子，两个人一起干的话6天可以建完.杨老师先做5天后，有事离开，由谷老师接着做了3天，共完成了房子的710.如果每人都单独建这个小房子，各需几天完成？(★★★)一项工程，甲单独完成需要12天，乙单独完成需要9天.若甲先做若干天后乙接着做，共用10天完成，问甲做了几天？(★★★)一池水，甲.乙两管同时开，5小时灌满；乙.丙两管同时开，4小时灌满.现在先开乙管6小时，还需甲.丙两管同时开2小时才能灌满.乙单独开几小时可以灌满？(★★★★)一项工程，甲.乙合作3125小时可以完成，若第1小时甲做，第2小时乙做，这样交替轮流做，恰好整数小时做完；若第1小时乙做，第2小时甲做，这样交替轮流做，比上次轮流做要多13小时，那么这项工作由甲单独做，要用多少小时才能完成？。

2011学而思被六年级数学真题解析(上)

2011学而思杯六年级数学真题解析(上)试卷名称：2011年六年级学而思杯数学考试年级：六年级科目：数学试卷满分：150分答题时间：90分钟试题形式：全部为填空题能力分值：全部为0开放时间：2011年10月6日9:30－11:00一、填空题(每题4分，共40分)1．2011－201.1＋20.11－2.011＋0.001＝________(4分)2．(..)÷+⨯÷254138512311854＝________(4分)3．已知N *等于N 的因数个数，比如4*＝3，则(2011*10*6*)*++＝_______(4分)4．一个非等腰三角形，一边长为6，一边长为7，还有一边长为6k ，已知k 是自然数，则三角形的周长为________(4分)5．红光大队用拖拉机耕地，2台3小时耕地75亩，照这样计算，4台5小时耕地________亩。

(4分)6．一个骗子到商店买了5元的东西，他付给店员50元钱，然后店员把剩下的钱找给了他；这时他又说自己有零钱，于是给店员5元的零钱，并且要回了开始给出的50元。

那么这个骗子一共骗了______元钱？(4分)7．已知A 、B 两数的最小公倍数是120，B 、C 两数的最小公倍数是180，A 、C 两数的最小公倍数是72，则A 、B 、C 三数的最小公倍数是_______(4分)8．2011年8月14日，伦敦羽毛球世锦赛进入最后一个比赛日。

在女单决赛中，中国选手王仪涵2比0完胜中华台北选手郑韶婕，首次夺得世锦赛冠军，中国队也实现了女单项目的八连冠。

已知二人共得到67分，其中第二局，王仪涵竟然赢了整整11分，请问，第一局郑韶婕得了_______分。

(羽毛球为21分制)(4分)9．下图为面积100的平行四边形，则阴影部分的面积和是_______(4分)10．AB 间的路被平均分成三段，王先生驾车从A 地开往B 地，已知他这三段路上的平均速度分别为30 km /h ，40 km /h 和60km /h ，则王先生在AB 间的平均速度为_______km /h 。

六年级数学试卷带答案解析

六年级数学试卷带答案解析考试范围：xxx；考试时间：xxx分钟；出题人：xxx姓名：___________班级：___________考号：___________1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1.一根绳子截去，截去的与剩余的长度比为（）A．1:3 B．1:2. C．2:3 D．3：22.2008年奥运会将在北京举行，这一年的第一季度共有（）天．A． 89 B． 90 C． 913.一条公路长 6千米，已修千米，还剩下多少千米？正确的算式是（）A．6× B．6×（1﹣） C．6﹣4.下列说法错误的一项是（）。

A．线段是轴对称图形B．等腰三角形的一个底角一定小于90°C．圆有无数条对称轴D．梯形是轴对称圆形5.小圆的直径是2厘米，大圆的半径是2厘米，小圆的面积是大圆面积的（）A． B． C． D．6.广场为观察点，学校在北偏西30°的方向上，下图中正确的是（）A． B． C． D．无答案7.一个圆柱体的底面半径是3厘米，高是18.84厘米，它的侧面展开图是（）A．正方形B．长方形C．两个圆形和一个长方形组成8.只去掉20.5%的百分号，这个数（）A．扩大到它的100倍B．缩小到它的C．大小不变D．无法确定9.有一个长方体，长是a米，宽是b米，高是h米，若把它的高增加5米，则这个长方体的体积增加（）A．abh+5 B．ab（h+5） C．5ab D．以上都不是10.下图平行四边形中（单位：厘米），长为30厘米的底边所应的高是10厘米，阴影部分面积是（）平方厘米．A．300 B．150 C．120 D．无法确定二、判断题11.所有的质数都不是2的倍数．．（判断对错）12.太白公园某一时刻的温度是0℃，表示当时没有温度．（判断对错）13.除以一个真分数，所得的商大于．．14.把一个圆经过剪拼后，成为一个近似的长方形，它的周长与面积都没有改变．．15.有公约数1的两个数叫互质数．（判断对错）三、填空题16.16米增加它的后，再增加米，一共增加米．17.a=2×3×m，b=3×5×m（m是自然数且m≠0），如果a和b的最大公因数是21，则m是________，a和b的最小公倍数是________．18.一个圆柱体削成一个与它等底等高的圆锥体，削去的部分是圆柱体的．19.5米长的铁丝，截成米长的小段，能截成段，每段是全长的．20.甲车3小时行150千米，乙车2小时行120千米，写出甲车和乙车的速度比，比值是．四、作图题21.画图。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2008年第一届“学而思杯”综合素质测评六年级1试数学试题（A卷）1.计算：11111 200820092010201120121854108180270++++= 。

2.如图，相同的汉字代表相同的数字，不同的汉字代表不同的数字，那么四位数“奥林匹克”最大是奥林匹克+奥数网20083.三个连续的自然数，从小到大依次是4、7、9的倍数，这三个自然数的和最小是。

4.在循环小数中类似于10.1428577••=，10.07692313••=等，循环节是从小数点右边的第一位（即十分位）就开始的小数，叫做纯循环小数，包括7和13在内，共有个正整数，其倒数是循环节恰好为六位的纯循环小数。

5.已知ABCD是平行四边形，:3:2BC CE=，三角形ODE的面积为6平方厘米。

则阴影部分的面积是平方厘米。

6.三位数A满足：它的所有质因数之和是26。

这样的三位数A有个。

7.电子玩具车A与B在一条轨道的两端同时出发相向而行，在轨道上往返行驶。

已知A比B的速度快50%，根据推算，第20072007次相遇点与第20082008次相遇点相距58厘米，轨道长厘米。

8.一块电子手表，显示时与分，使用12小时计时制，例如中午12点和半夜12点都显示为12:00。

如果在一天（24小时）中的随机一个时刻看手表，至少看到一个数字“1”的概率是。

9.欢欢和贝贝是同班同学，并且住在同一栋楼里。

早晨7:40，欢欢从家出发骑车去学校，7:46追上了一直匀速步行的贝贝；看到身穿校服的贝贝才想起学校的通知，欢欢立即调头，并将速度提高到原来的2倍，回家换好校服，再赶往学校；欢欢8:00赶到学校时，贝贝也恰好到学校。

如果欢欢在家换校服用去6分钟且调头时间不计，那么贝贝从家里出发时是点分。

10. 某个班的20个学生的家庭住址在城市中的分布如图（圆点是各个学生的家庭住址，线段是街道），如果这个班的学生举行一个聚会，为了尽量减少每个学生行走路程总和，那么他们应该选择十字路口附近的地点。

（横线上填十字路口的坐标，如所在的十字路口的坐标为3D ）。

11. 美国总统说：我已收到2000封来信，他们中的大多数都支持我的观点。

这些来信证明，大多数美国人都支持我的观点。

下列何者最削弱．．．总统的结论？（） (A ) 总统所谈论的事情非常容易产生分歧意见，许多人持不同观点。

(B ) 2000封来信并不能代表大多数人的观点。

(C ) 不同意总统观点的人比同意的人更加容易感情冲动。

(D ) 同意总统观点的人比不同意的人更有可能写信给总统。

(E ) 这2000封来信来自全国各地，分布可能不均匀。

12. 今年上半年，从1月至6月，大约销售了300万台录像机，这个数字仅仅是去年销售的录像机总数的35%。

所以，今年录像机的总销量肯定要低于去年。

下列何者如果为真，最严重削弱上述结论? （）（A ）去年销售的录像机总数比前年低。

(B ) 大多数对录像机感兴趣的人都已经购买了一台。

(C ) 今年的录像机比去年的便宜。

(D ) 在去年销售的录像机中，近60%是在1月销售的。

(E ) 一般地说，一年中录像机的销售量的70%是在11月和12月销售的。

第10题972113.古时候的一场大地震几乎毁灭了整个人类，只有两个部落死里逃生。

最初在这两个部落中，神帝部落所有的人都坚信人性本恶，圣地部落所有的人都坚信人性本善，并且没有既相信人性本善又相信人性本恶的人存在。

后来两个部落繁衍生息，信仰追随和部落划分也遵循着一定的规律。

部落内通婚，所生的孩子追随父母的信仰，归属原来的部落；部落间通婚，所生孩子追随母亲的信仰，归属母亲的部落。

我们发现神圣子是相信人性本善的。

在以下各项对神圣子身份的判断中，不可能为真的是：（）(A) 神圣子的父亲是神帝部落的人。

(B) 神圣子的母亲是神帝部落的人。

(D) 神圣子的母亲是圣地部落的人。

(E) 神圣子的姥姥是圣地部落的人。

14.以前的研究指出吃巧克力会增加得心脏病的危险，但是一项新的研究表明，吃巧克力不会增加心脏病的可能性。

当新的研究结果为人们知道后，巧克力的消费量无疑会大增。

上述结论根据下列何种假设？（）(A) 吃大量巧克力的大多数人不会得心脏病。

(B) 虽然知道吃巧克力会增加得心脏病可能性，但有些人仍旧照吃不误。

(D) 有些人吃很多巧克力是因为他们不知道吃巧克力会增加心脏病的可能性。

(E) 目前一些人不吃巧克力只是因为他们相信吃巧克力会增加心脏病可能性。

15.在十四世纪中叶前，除了法国和英国外，意大利北部的国家是没有大学的。

到了十五世纪末，这个地区有23所大学，其中比较著名的有德国的罗斯托克和美因兹大学，波兰的克拉科夫和捷克的布拉迪斯拉发大学。

同时，欧洲总的大学数目超过原来的两倍。

根据上述短文，下列哪一项是正确的? （）(A) 直到十五世纪大学发展时期，整个欧洲大约只有11所大学。

(B) 在十四世纪，意大利的南部有23所大学。

(D) 在十四世纪大学迅猛发展后，法国和英国不再是北欧有这种学术中心的唯一国家。

(E) 意大利是大学发展的发源地。

【参考答案】1. 【答案】51005054【考点】计算，裂项【分析】原式1111120082009201020112012366991212151518=+++++++++⨯⨯⨯⨯⨯ 1111111201059122356⎛⎫=⨯+⨯-+-++- ⎪⎝⎭51005054= 2. 【答案】1876【考点】数字谜【分析】显然“2≤奥”，所以“1=奥或2”，如果“2=奥”，则四位数与三位数的和超过2200，显然不符合条件，所以“1=奥”，所以“9≤林”，如果“9=林”那么“200819001008+=--=匹克数网”，“0=匹=数”，不符合条件，所以“林”最大只能是8，所以“20081800100108+=--=匹克数网”，为了保证不同的汉字代表不同的数字，“匹克”最大是76，所以“奥林匹克”最大是1876。

3. 【答案】483【考点】约数与倍数【分析】根据题意，设这三个数分别为71k -、7k 、71k +（k 是整数），那么71k -是4的倍数，71k + 是9的倍数，由于718(1)k k k -=-+，719(21)k k k +=--，所以1k +是4的倍数，21k -是9的倍数，由1k +是4的倍数知22k +是8的倍数，设219k n -=，那么229383k n n n +=+=++，所以3n +是8的倍数，n 最小为5，相应地k 最小为23，那么这三个自然数的和最小为7233483⨯⨯=。

4. 【答案】53【考点】计数问题、数论、循环小数化分数等知识点的综合【分析】根据容斥原理，所求的n 的个数为64(863)53-+-=（个）。

5. 【答案】21平方厘米【考点】求平面图形的面积，五大基本模型之二：蝴蝶定理【分析】连接AC 。

由于ABCD 是平行四边形，:3:2BC CE =，所以:2:3CE AD =，根据梯形蝴蝶定理，22:::2:23:23:34:6:6:9COE AOC DOE AOD SS S S =⨯⨯=，所以6AOC S =（平方厘米），9AOD S =（平方厘米），又6915ABC ACD S S ==+=（平方厘米），阴影部分面积为61521+=（平方厘米）。

6.【答案】13个【考点】分解质因数【分析】26以内的质数有2、3、5、7、11、13、17、19、23，所以这样的三位数有13个。

7.【答案】145【考点】多次相遇【分析】A，B两车速度比为(150%):13:2+=。

第20072007次相遇点的位置在：20073(220071)5(mod10)⨯⨯-≡；第20082008次相遇点的位置在：20083(220081)3(mod10)⨯⨯-≡。

所以这条轨道长58(53)5145÷-⨯=（厘米）。

8.【答案】1 2【考点】乘法原理【分析】一天中，手表显示的时刻有1260720⨯=（种），至少看到一个数字“1”的概率为3601 7202=。

9.【答案】7:25【考点】追及问题【分析】欢欢从出发到追上贝贝用了6分钟，那么她调头后速度提高到原来的2倍，回到家所用的时间为3分钟，换衣服用时6分钟，所以她再从家里出发到达学校用了206365---=（分钟），故她以原速度到达学校需要10分钟，最开始她追上贝贝用了6分钟，还剩下4分钟的路程，而这4分钟的路程贝贝走了14分钟，所以欢欢的6分钟路程贝贝要走14(64)21⨯÷=（分钟），也就是说欢欢追上贝贝时贝贝已走了21分钟，所以贝贝是7点25分出发的。

10.【答案】4C11.【答案】D12.【答案】E13.【答案】B14.【答案】E15.【答案】D。