电工电子学_03交流电路
2019年电工学-第3章-交流电路习题及答案.ppt

3.2.2 已知 A = 8 + j6 , B 8 45 。求(1)A+B ;(2) B A A-B;(3)A B ;(4) ;(5)j A+B ;(6) 。 A j B
返回主页 下一页
第 3 章
交 流 电 路
3.3.1 在图3.6(教材图3.01)所示 电路中,已知R 100 , L 31.8 mH,C 318 F, 求电源的频率和电压分别为50 Hz、100 V 和1 000 Hz,100 V两种情况下,开关S 合向 a、b、c 位置时电流表的读数,并 计算各元件中的有功功率和无功功率。 3.4.1 在图3.7(教材图3.02)所示电路中,三个照明相同 , R XC X L ,试问接于交流电源上时,照明灯的亮度有什么不 同?若该接到电压相同的直流电源上,稳定后,与接交流电 源时相比,各照明灯的亮度有什么变化? 3.4.2 求串联交流电路中下列三种情况下电路中的 R 和 X 各为多少?指出电路的性质和电压对电流的相位差
图3.15
j10 , Z 2 (40 j 30) , I
I 2 和U 。 。求:I 1 、 5 30 A
图3.17
返 回 上一页 下一页
第 3 章
交 流 电 路
Байду номын сангаас
3.5.5
在图3.18(教材图3.09)所
示电路中,已知 R X C , U 220V 总电压U 与总电流 I 相位相同。
1 1 若T 10 m s,则 f Hz 100Hz 3 T 10 10
I 7.07 180 A 7.07 180 A 7.07 A
电工电子学第三章

负半周
3
设正弦交流电流: 设正弦交流电流:
Im
Ψ
i
O π T 2π π
ωt
i = I m sin (ω t + ψ )
初相角:决定正弦量起始位置 初相角: 角频率:决定正弦量变化快慢 角频率: 幅值:决定正弦量的大小 幅值:
幅值、角频率、初相角成为正弦量的三要素。 幅值、角频率、初相角成为正弦量的三要素。
5
3.1.2 幅值与有效值 幅值: 幅值:Im、Um、Em
幅值必须大写, 幅值必须大写, 下标加 m。
有效值: 有效值:与交流热效应相等的直流定义为交流电的 有效值。 有效值。
∫0
T
2 i 2R dt = I RT
交流
直流
则有
I =
1 T
∫
T
0
i 2dt
Im 1 T 2 2 有效值必 = ∫0 Imsin ωt dt = 2 须大写 T U Em 同理: 同理: U = m E= 2 2
12
3. 正弦量的相量表示
实质:用复数表示正弦量 实质: 复数表示形式 为复数: 设A为复数 为复数 (1) 代数式 A =a + jb 式中: a = r cos ψ 式中
+j
b
A
r ψ
0
2 2
a
+1
b = r sin ψ
(2) 三角式 由欧拉公式: 由欧拉公式
r = a + b 复数的模 b ψ = arctan 复数的辐角 a
16
⑥“j”的数学意义和物理意义 因子: 旋转 90o因子:e± j90o
± j90o
e
= cos 90° ± jsin90° = ±j
电工电子学-交流电路

求:i i1 i2 。
12.7( cos 30 j sin 30 )A 11( cos 60 j sin 60 )A (16.5 - j3.18)A 16.8 10.9 A
解: (1) 相量式
+j
U 2
U 1
+1
220 20V U 1 110 45 V U 2
(2) 相量图
落后于U U 2 1
2018/7/19 2018/7/19 电工电子学B
45 20
U 2
超前 落后 U 1 ?
例2: 已知 i1 12 .7 2 sin (314 t 30 )A i2 11 2 sin(314t 60 )A
+j
b
0
2
A
2
r
a
+1
式中: a r cos ψ
b r sin ψ
(2) 三角式 由欧拉公式:
r a b 复数的模 b ψ arctan 复数的辐角 a
A r cos ψ j r sin ψ r (cos ψ j sin ψ )
cos ψ e
jψ
e 2
j ψ
e j ψ e j ψ , sin ψ 2j
2018/7/19 2018/7/19
电工电子学B
可得:
(3) (4)
cos ψ j sin ψ 指数式 A r e j ψ 极坐标式 A r ψ e
jψ
A a jb r cos j r sin re r ψ
电工学第三章三相交流电ppt课件
6
3.1.2 三相电路中负载的联结方法
1. 三相负载
分类
三相负载:需三相电源同时供电
负载
三相电动机等
单相负载:只需一相电源供电
照明负载、家用电器
对称三相负载:ZA=ZB= ZC
三相负载
如三相电动机
此时负载中性点N´即为 A, 因此负载各相电压为 N
UA 0 , UA 0
B
UB UB A, UB 380 V UC UC A , UC 380 V C
+
U A
iA
iC
– –
N´
–
iB
+ U C U B +
此情况下,B相和C相的电灯组由于承受电压上所加 的电压都超过额定电压(220V) ,这是不允许的。
(2) 相UA电B=流UBC=UIIICABCABCA=UUUUZZZClCAABB=AABBCCUP
A
+–
U AB
– U CA
B U+ BC C–
+
IB IC
ICA
ZCA
IAB
ZBC ZAB
IBC
相电流: 线电流:
IIAA、B、IIB、BC、IC ICA
线电流不等于相电流
20
(3) 线电流
IA IAB ICA
16
(2) A相断路
A
1) 中性线未断
B、C相灯仍承受220V N
电压, 正常工作。
2) 中性线断开
B
变为单相电路,如图(b) C 所示, 由图可求得
I UBC 380 12 .7 A RB RC 10 20
电工电子学第三章习题答案 (2)

第三章交流电路3-1 试写出表示u A =)120314sin(2220,314sin 22200-==t u tV u B A 和V t u C )120314sin(22200+=的,并画出相量图。
解:V U V U V U C B A 0.00120220,120220,0220∠=-∠=∠=•••3-2 如图所示的是时间t=0时电压和电流的相量图,并已知U=220V ,I 1=10A ,I 2=52A ,试分别用三角函数式和复数式表示各正弦量。
3-3已知正弦电流i 1=22sin(100πt+60°)A, i 2=32sin(100πt+30°)A,试用相量法求i=i 1+i 2。
解A tg j j j j I I I 010000210.4284.4)598.3232.3(3914.23232.3598.3)213232(23321230sin 330cos 360sin 260cos 2∠=∠=+=⨯+⨯+⨯+⨯=+++=+=-•••i= 4.842 sin (100πt+42.00) A3-4在图示电路中,已知R=100Ω,L=31.8mH ,C=318uF 。
求电源的频率和电压分别为50Hz 、100V 和1000Hz 、100V 的两种情况下,开关S 合向a 、b 、c 位置时电流表的读数,并计算各元件中的有功功率和 无功功率.解:当F=50HZ 、U=100V 时,S 接到a ,Ia=)(1100100A =;有功功率为:P=UIa=100WS 接到b ,Ib=)(1099.9100108.312501003A LV ==⨯⨯⨯=-πω 无功功率为:Q=UIb=1000Var S 接到c ,)(10100103182506A C V Ic =⨯⨯⨯⨯==-πω。
无功功率为:q=UIc=-1000Var当F=1000HZ 、U=100V 时S 接到a ,Ia=)(1100100A =;有功功率为:P=UIa=100WS 接到b ,Ib=)(5.08.199100108.31210001003A L V ==⨯⨯⨯=-πω 无功功率为:Qb=UIb=50Var S 接到c ,)(8.19910010318210006A C V Ic=⨯⨯⨯⨯==-πω。
电工学-第3章交流电路

j ( ω t u )
]
+j
Um=√2 U
Um
U
2 Im[U e
= √2 Im[U = √2 Im[U]
j u
]
O
ψ ] u
+1
第 3 章 交 流 电 路
设正弦量 u U msin( ω t ψ ) 电压的有效值相量 用相量表示: 相量的模=正弦量的有效值 jψ
O
ψ
ωt1
ωt
正弦交流电可以用 一个固定矢量表示 最大值相量 Im 有效值相量 I
O
ωt2 +j I +1 Im ψ
大连理工大学电气工程系
11
第 3 章 交 流 电 路
一、复数的基础知识 1. 复数的表示方法
+j
几何法
b
ψ
p 模 a +1 辐角
O
Op = a + j b
= c (cosψ + j sinψ ) = c e jψ
瞬时值最大值
i Im
角频 初相位 率
ψ
O
ωt
最大值 角频率 初相位
正弦交流电的三要素
3
第 3 章 交 流 电 路
正弦交流电的波形:
i ψ = 0° i 0<ψ<180°
O
ωt
O ψ
ωt
i
-180°<ψ < 0°
i
ψ = ±180°
O ψ
ωt
O
ωt
4
第 3 章 交 流 电 路
一、交流电的周期、频率、角频率
u
2 I R sin (ω1t i )
U I 。 R
(1) 频率相同。 (2)大小关系:对电阻而言,电压有效值 与电阻有效值之间符合欧姆定律。 相位差 : (3)相位关系 :
第三章交流电路优秀课件

•
U
220
45V?
42si(nωt30)A ?
2
有效值
j45
U m22e405V ?
瞬时值
4.已知:
U 10 015V
2.已知: I1060A U10V 0?负号
? i1s0i(n ω t60 )A ? 最大值
U 100ej15V
例1: 将 u1、u2 用相量表示
u 1 2 2 02sin(ω t 2 0 )V
A a j b r co jr si n r e jψ rψ
相量: 表示正弦量的复数称相量
设正弦量: uU m si(ω ntψ )
相量表示:
U Ujψ eUψ相量的模=正弦量的有效值
相量辐角=正弦量的初相角
电压的有效值相量
或:U mU m ejψU mψ相相量量辐的角模==正正弦弦量量的的初最相大角值
iIm sin(ω tψ 2)
(t 1 ) (t 2 )
ψ1 ψ2
ui u i
若 ψ1ψ20
O
电压超前电流
ωt
ψ1ψ20
电流超前电压
ui i
u
O
ωt
电压与ψ 电1 流ψ 同2相0
ui u
i
O
ωt
ψ 1ψ 290
电流超前电压90
ui u i
O
ωt
90°
ψ1ψ2180
电压与电流反相
ui u i
O
ωt
3.2 正弦量的相量表示法
1.正弦量的表示方法
u
波形图
O
ωt
瞬时值表达式 uU m si n t ()
相量 U Uψ
必须 小写
2020年电工学第3章 交流电路
量的进程。
t=0时的相位角称为初相位角或初相位
若所取计时时刻不同,则正弦量的初相位不同
相位差
ui u
i
0
2
1
i
i1
i2
0
i3
u= Umsin( t+1) 第3章 3 1
i = Imsin( t+2)
两个同频率正弦量的相位角 之差或是初相角之差,称为
相位差,用表示。
t u和i的相位差
求 i1 + i2
解:(1)用相量图法求解 (2)用复数式求解
j
•
Im2
i2 i1
0
•
Im
•
Im1
1
正弦电量 (时间函数)
变换
相量 (复数)
正弦量运算
相量运算 (复数运算)
所求正弦量 反变换 相量结果
•
Im =
•
Im1
+
•
Im2
i= I msin( t+)
交流电的瞬时值表达式: i= Imsin( t+)
P=0 Q=UI=356.4 Var 额定电压 311V
(三) 纯电感电路
第3章 3 3
i
1.电压电流关系
+
设 i = Imsin t
u
L
由
u=
L
di dt
有
–
u= L Imcos t= Umsin( t+90)
Um= Im L = Im XL
感抗 XL= L
XL
电感线圈对高频电流的阻碍作
•
I
U•
t 0
+1
电压与电流同频率、同相位
电子电工技术第3章三相交流电路

3.3 三相电功率 (任何接法的三相负载)
1、负载不对称
三相负载总的有功功率等于各相有功功率之和。即
P总 PA PB PC
2、负载对称
各相功率相等,故 P总 3PP 3U P IP cos
当对称负载Y接时 Ul= 3 Up,Il=Ip 当对称负载△接时
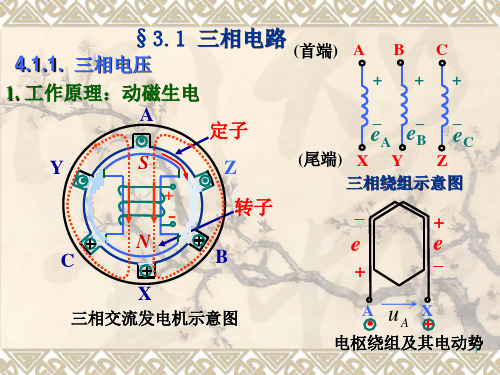
三相交流电动势是由三相交流发电机产生的。最简 单的三相交流发电机如图3.1(a)所示
eA=Emsinωt eB=Emsin(ωt-120°)
•
EA =E∠0°
•
EB =E∠-120°
eCEmsin(ωt-240°)
•
EC =E∠-240°
它们的波形图和向量图如图3.2(a)、(b)所示。
相序是A—图B3—.2C,称为正序
1.1.2、三相电源绕组的星形联接(Y接) 1、接法
2、线电压与相电压的关系 相电压,其有效值用UA、UB、UC一般用Up表示
线电压,其有效值用UAB、UBC、UCA,一般用Ul表示。
uAB=uA-uB uBC=uB-uC uCA=uC-uA
U AB U A U B U BC U B UC
UCA UC U A
1.2 负载的联接
1.2.1、负载的星形联接 1、 (负载不对称)
三相四 线制
可见
Ip=Il
流过各相负载中的电流称为相电流,用Ip表示, 流过各端线的电流称为线电流,一般用Il表示。
在三相四线制电路中,因为电源相电压对称,所以负载 的相电压也对称。
每相中电流与电压的关系
IA
UA ZA
IB
UB ZB
《电工电子技术基础教学资料》第3章 正弦交流电路ppt课件

第3章 正弦交流电路
3.3 电阻、电感或电容元件单独作用的正弦交流电路
1.电感元件上的电压与电流瞬时值的关系 如图3-11所示为一个线性电感元件的交流电路图,电 压与电流的参考方向如图3-11a所示。 为分析的方便,假设 那么电感元件上的电压电流瞬时值关系为
显然φu=φi+90°,电感元件上的电压超前电流90°,或称电流滞后电压90°。 电感上的电压与电流是同频率的正弦量,电压与电流的波形如图3-11b所示。
第3章 正弦交流电路
3.3 电阻、电感或电容元件单独作用的正弦交流电路
4.纯电阻元件的功率
.
第3章 正弦交流电路
3.3 电阻、电感或电容元件单独作用的正弦交流电路
.
第3章 正弦交流电路
3.3 电阻、电感或电容元件单独作用的正弦交流电路
3.3.2 纯电感电路
电感器是用漆包线、纱包线或塑皮线等在绝 缘骨架或磁心、铁心上绕制成的一组串联的 同轴线匝,它在电路中用字母“L〞表示。 电感元件是一个二端元件,假设电感的大小 只与线圈的构造、外形有关,与经过线圈的 电流大小无关,即L为常量,那么称为线性 电感元件,在本书中只讨论线性电感元件。
.
第3章 正弦交流电路
3.3 电阻、电感或电容元件单独作用的正弦交流电路
2.感抗 根据电感元件上的电压电流瞬时值关系得两者振幅之间的关系为
式中的XL=ωL=2πfL具有电阻的量纲,称为感抗。当L的单位为H,ω的 单位为rad/s时,XL的单位为Ω。感抗与L和ω成正比,对于一定的电感L, 当频率越高时,其所呈现的感抗越大,反之越小。换句话说,对于一 定的电感L,它对高频呈现的妨碍大,对低频呈现的妨碍小。在直流电 路中,XL=0,即电感对直流视为短路。
第 3章交流电路 电工电子技术与技能教学课件

第3章 交流电路
电感元件的功率
在电感元件组成的电路中,知道了电压和电流的变化规律和相互关系 后,便可找出瞬时功率的变化规律。
电感元件电路的平均功率为零,即电感元件的交流电路中没有能量消 耗,只有电源与电感元件间的能量互换。
22
第3章 交流电路
电容元件的功率
电容元件电路的平均功率也为零,即电容元件的交流电路中没 有能量消耗,只有电源与电容元件间的能量互换。
6
第3章 交流电路
有效值
交流电的有效值是根据电流热效应来规定的。让交流电和直流电通过相 同阻值的电阻,如果它们在相同时间内产生的热量相等,就把这一直流电 的数值叫做这一交流电的有效值。
例如某一交流电通过一段电阻丝,在一段时间内产生的热量为Q,如果 改用5安的直流电通过这段电阻丝,在相同的时间内产生的热量也为Q, 那么,这一交流电的有效值就是5安。交流电压的有效值可以用同样的方 法来确定。通常用I和U分别表示交流电的电流和电压的有效值。
10
第3章 交流电路
3.1.3交流电的常用表示方法
交流电常用表示方法有三角函数式(解析式)、波形图、相量图(矢量图)等
三角函数式
e Em sin(t e ) u Um sin(t u ) i Im sin(t i )
从表达式中可以看出交流电的变化规律,反过来只要知道了交流电的最大值、 频率、和初相位位,就可以写出它的表达式。
15
第3章 交流电路
纯电感电路
在交流电路中,如果只有电感线圈作负载,而且线圈的电阻和分布电容均 可忽略不计,这样的电路成为纯电感电路
16
第3章 交流电路
纯电感电路
1)纯电感电路中,电感两端的电压超前电流90°。
2)感抗和电压有效值之间的关系是符合欧姆定律的,
电路课件第3章交流电路

04
交流电路的功率与效率
有功功率与无功功率
有功功率
表示实际消耗的功率,用于转换和 利用电能,单位为瓦特(W)。
无功功率
表示电感或电容元件之间交换的功 率,不消耗电能,单位为乏 (var)。
视在功率与功率因数
视在功率
表示电源提供的总功率,包括有功功率和无功功率,单位为伏安(VA)。
功率因数
表示有功功率与视在功率的比值,用于衡量电路的效率,数值范围在0到1之间。
06
交流电路的实验与实践
交流电路的测量技术
交流电压和电流的测量
频率和周期的测量
使用电压表和电流表测量交流电路中 的电压和电流值,注意选择合适的量 程和测量模式。
使用频率计或周期计测量交流电的频 率和周期,了解频率与周期的关系。
功率和功率因数的测量
使用功率表测量交流电路中的有功功 率,同时通过测量电压和电流相位差 计算功率因数。
交流电路的实验设备与工具
电源
测量仪表
提供稳定的交流电源,可以选择市电或可 调电源。
电压表、电流表、功率表、频率计等。
实验线路板
连接线与线夹
用于搭建各种交流电路,包括负载、电源 、电感、电容等元件。
用于连接实验元件和线路板。
交流电路的实际应用案例
家用电器
交流电在家庭中广泛应用, 如照明、空调、洗衣机等 电器设备。
影响稳定性的因素
影响交流电路稳定性的因素有很多,如电源质量、负载特性、线路阻抗等。此外,外部环 境因素如温度、湿度、电磁干扰等也会对电路的稳定性产生影响。
稳定性分析方法
为了确保交流电路的稳定性,需要对电路进行详细的分析。常用的分析方法包括时域分析 、频域分析和暂态分析等。这些方法可以帮助工程师了解电路在不同情况下的性能表现, 从而采取相应的措施提高稳定性。
电路与电子学3交流电路

暂态的分析方法
时域分析法
通过建立电路的微分方程来求解, 得到电路中电压和电流随时间变 化的规律。
频域分析法
将电路的微分方程转化为频域表 示,通过求解频域方程得到电路 的频率响应特性。
复数分析法
利用复数表示电压和电流,简化 计算过程,方便分析交流电路的 频率特性和相位关系。
暂态的实验验证
实验设备
电源、电阻、电容、电感等电子元件,示波器、信号发生器等测量 仪器。
提高功率因数的方法
通过并联电容、使用无功补偿装置等 手段可以提高电路的功率因数,从而 提高电源的利用率和减少能源浪费。
03
交流电路的稳态分析
BIG DATA EMPOWERS TO CREATE A NEW
ERA
稳态的概念
稳态
交流电路中的电流和电压 不再随时间变化,达到稳 定状态。
产生条件
交流电源的频率与电路的 固有频率相同,相位差为0 或180度。
交流电在一个周期内的 平均值,表示交流电的
实际效果。
最大值
交流电在一个周期内的 最大值,表示交流电的
最大能量。
功率因数
表示交流电路中电压与 电流之间的相位差,影响电路的效Fra bibliotek。02
交流电路的分析
BIG DATA EMPOWERS TO CREATE A NEW
ERA
阻抗的概念
阻抗
在交流电路中,阻抗是用来表示电抗 元件对交流电的阻碍作用的物理量。 它由电阻和电抗两部分组成,包括实 部和虚部。
交流电的产生
01
02
03
发电机
利用电磁感应原理将机械 能转化为电能,产生交流 电。
变压器
通过改变一次侧和二次侧 线圈的匝数比,实现电压 的升高或降低,从而产生 不同电压等级的交流电。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
幅值、角频率、初相位反映了正弦量的大小、变化的快慢和初始值等 正弦特征,因而幅值、角频率、初相位称为正弦量的三要素。 下面讨论三要素以及相关量。 1. 瞬时值、幅值和有效值 正弦量在任一瞬间的数值称为瞬时值,用小写字母 u、i 来表示,其 中最大的瞬时值称为幅值或最大值,用带下标m的大写字母 U m 、、I m 来表示。
图3.1.3 初相不等的正弦量
6
上图两正弦量的相位差为: (t u ) (t i ) u i (3.1.9) 上式表明,两个同频率正弦量之间的相位之差并不随时间改变,它等 于两者的初相位之差。当计时起点改变时,正弦量的相位和初相位跟 着改变,但两者之间的相位差保持不变。
L
12
应当注意,感抗只是电感电压与电流的幅值或有效值之比,而不是瞬 时值之比,这与电阻电路不同。若用相量表示电感电压与电流的关系, . U Ue j 90 ; I Ie 则有
.
j 0
U I
. .
Ue j 90 Ie j 0
U j 90 e jL jX L I
U m I m sint cost
1 U m I m sin 2t 2
(3.2.10)
UI sin 2t
13
3.2.3 纯电容交流电路
图 3.2.4 电容元件的交流电路 图3.2.4(a)所示为一电容元件的交流电路。在图示的关联参考方 向下: du
iC dt
14
7
正弦量由幅值、角频率、初相位三要素来确定。而平面坐标内的一个 旋转矢量可以表示出正弦量的三要素,因此旋转矢量可以表示正弦量。 3. 2 纯电阻、纯电感、纯电容单相正弦交流电路 交流电路的分析主要有两个方面,一是确定电路中电压与电流 的关系。二是电路中能量的转换和功率的问题。 3.2.1 纯电阻交流电路
第三章
交流电路
电工电子学
1
3.1 正弦交流电的基本概念
图3.1.2 正弦交流电的波形
2
3.1 正弦交流电的基本概念
正弦电压和电流是随时间按照正弦规律变化的,称之为正弦交流电, 其波形如图3.1.2所示,正弦电压和电流等物理量都称为正弦量,其 表达式为: u U m sin(t u ) (3.1.1) (3.1.2) i I m sin(t i )
LI m sin(t 90 ) U m sin(t 90 )
(3.2.6)
可见,电压和电流是同频率的正弦量,其波形如图3.2.2(b)所示。 它们之间的关系为 相位关系 电压超前电流 大小关系 U m LI m Um U 或 (3.2.7) L
Im I
当电感电压一定时, 愈大,流过电感的电流愈小。可见 L 具有阻碍 交流电流的性质。因而称之为感抗,单位为 (欧姆),用 X 表示。 即 X L L 2fL (3.2.8)
Im I
若用相量表示,则有 U Ue j 0
.
I Ie j 0
.
U I
. .
Ue j 0 Ie j 0
.
U j 0 e R I
.
即 U RI . . 同理有 U m RIm
(3.2.3)
9
交流电路的电压和电流是随时间变化的,故电阻所消耗的功率也随时 间变化。在任一瞬间,电压瞬时值与电流瞬时值的乘积称为瞬时功率。 用小写字母 p表示。即 (3.2.4) p ui U m sint I m sint
串联交流电路如图3.3.1(a)所示,选取电流为参考正弦 量。即 i I m sint
17
同频率的正弦量相加,仍是同频率的正弦量,由KVL可得 (3.3.1) u uR uL uC U msin(t )
U U R U LU C
. . . .
T
5
3. 相位、初相位和相位差
在正弦量的表达式u U m sin(t u ) ,i I m sin(t i ) 中, (t u ) 和 (t i ) 都是随时间变化的电角度,称为正弦量的相位或相位角,它 反映了正弦量的变化进程。相位的单位是弧度,也可用度。 t 0 时的相位叫做正弦量的初相位或初相位角。初相位确定了正弦 量在 t 0 时刻的值,即初始值。初相位与计时起点的选择有关,计 时起点选的不同,正弦量的初相位就不同,正弦量的初始值也就不同。 在同一个交流电路中,电压 u和电流i 的频率是相同的,但初相 位不一定相同。两个同频率正弦量的相位之差称为相位差。用 表示。 如图3.1.3所示。
T
0
m
i
1 T1 2 I m [1 cos 2(t i )]dt T 0 2 Im 2
Um 2
同理,正弦电压和正弦电动势的有效值:
U
E
Em 2
(3.1.5) (3.1.6)
4
可见,交流电的有效值等于它的瞬时值的平方在一个周期内积分的平 均值再取平方根。所以有效值也称为方均根值。有效值用大写字母表 示。虽然与表示直流的字母相同,但物理含义不同。 2. 周期、频率和角频率 正弦量重复变化一次所需要的时间称为周期, 用T表示,单位为s (秒)。每秒内重复变化的次数称为频率,用 f表示,单位为 (赫 兹)。 周期与频率互为倒数关系,即: f 1 T (3.1.7) 我国电厂生产的交流电频率为 ,这一频率称为工业标准频率,简称 工频。 正弦量每重复变化一次,相当于变化了 弧度。为了避免与机械角度 混淆,这里称为电角度。正弦量每秒变化 次,则每秒变化的电角度 为 弧度。即每秒变化的弧度数称为正弦量的角频率或电角速度,单 位为 (弧度/秒)。 (3.1.8) 2π 2 πf
Im I
C
当电压一定时, 愈大,电流愈小。可见 具有阻碍交流电流的性 质。因而称之为容抗,单位为 (欧姆),用 X 表示,即
C
1 C
1 C
XC
1 1 C 2fC
15
若用相量表示电容电压与电流的关系,则有
U Ue
U I
. .
.
j 0
I Ie j 90
U j 90 e jX C I
.
.
Ue j 0 Ie
.
j 90
即
I I U jX C I j C jC
.
.
(3.2.16)
同理, U m jX C I m 上两式是电容电压与电流关系的相量形式。它反映了电容电压与电流 的大小及相位关系。电压和电流的相量图如图3.2.4(c)所示。 电理
U jL I jX L I
.
.
(3.2.9)
U m jL I m
.
.
上两式是电感电压和电流关系的相量形式,它反映了电感电压与电流 的大小及相位关系。电压和电流的相量图如图3.2.2(c)所示。 电感电路吸收的瞬时功率为
p ui U msin(t 90 ) I msint
2UIsin 2 t 1 U m I m (1 cos2t ) 2 UI (1 cos2t )
由瞬时功率 的表达式和波形图可知,除了过零点外,其余时间均为 正值。即 p≥0,这说明电阻元件从电源取用电能,并将电能转换为 热能,这是一种不可逆的能量转换过程。所以电阻元件是耗能元件。 瞬时功率只能说明功率的变化情况,实用意义不大。通常所说电路的 功率是指瞬时功率在一个周期内的平均值,称为平均功率,用大写字 母 P表示。即 1 1 (3.2.5) P pdt UI (1 cos 2t )dt
p ui U msint I msin(t 90 )
.
.
U m I m sint cost 1 U m I m sin 2t 2
UI sin 2t
(3.2.17)
16
3.3 简单单相正弦交流电路的计算 3.3.1 R、L、C串联交流电路
图3.3.1 、 串联交流电路
k 1
n
(3.3.12) (3.3.13)
图3.3.5 复阻抗串联 由此可见,n个复阻抗串联,其总复阻抗等于各个串联复阻抗之和。
19
图3.3.6为n个复阻抗并联的电路。由基尔霍夫电流定律得到
U U U I I 1 I 2 In Z1 Z 2 Zn . 1 .1 1 1 U( ) U Z1 Z 2 Zn Z
3
通常用有效值来表示正弦量的大小。 有效值是从电流热效应的角度规定的。设一个交流电流 和某个直流 电流 分别通过阻值相同的电阻 ,并且在相同的时间内(如一个周期 ) 产生的热量相等,则这个直流电流 的数值叫做交流电流 的有效值, T 2 2 按此定义,有: 0 Ri dt RI T 即 1 T 2 I i dt T 0 (3.1.3) 对于正弦电流 的有效值为 1 T (3.1.4) I [ I sin(t )]2 dt
图3.2.1 电阻元件的交流电路
8
设电流为参考正弦量。即 i I m sint 则有 u Ri RI m sint U m sint (3.2.1) 可见,电阻上的电流 与它两端的电压 是同频率同相位的正弦量。如图 3.2.1(b)所示,它们间的大小关系为 U m RI m 或 U m U R (3.2.2)
