初中数学四点共圆
四点共圆(知识讲解)

四点共圆(知识讲解)【学习目标】1. 理解四点共圆的定义;2. 掌握判断四点共圆的基本方法,并用于解决证明和计算问题。
【要点梳理】四点共圆常用的方法有:1、对角互补的四边形,四点共圆;2、外角等于内对角的四边形,四点共圆;3、同底同侧的顶角相等的两个三角形,四点共圆;4、到定点的距离等于定长的四个点,四点共圆。
【典型例题】类型一、四点共圆的判定1.如图,BD ,AH 分别是ABC 的高,求证:A 、B 、H 、D 四点共圆.【分析】取AB 的中点O ,连接DO 、HO ,根据BD ,AH 分别是△ABC 的高,可得△DAB和△HAB 都是直角三角形,斜边都是AB ,而点O 为斜边中点,则有DO =HO =12AB =AO =BO ,也就是说以O 为圆心、OA 为半径的圆,点D 、H 、B 也在这个圆上,即可证明A 、B 、H 、D 四点共圆.证明:如图,取AB 的中点O ,连接DO 、HO ,△BD ,AH 分别是ABC ∆的高,DAB ∴∆和HAB ∆都是直角三角形,且它们的斜边都是AB ,△点O 为斜边中点,12DO HO AB AO BO ∴====,也就是说,点D、H、B在以O为圆心、OA为半径的圆上,即点D、H、B、A都在以O为圆心、以OA为半径的圆上,故可得:A、B、H、D四点共圆.【点拨】本题考查了四点共圆,解答本题的关键是利用直角三角形斜边上的中线等于斜边的一半证得四点共圆.举一反三:【变式1】已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.【答案】点E、F、G、H四点是以AC,BD的交点O为圆心的同一个圆上,证明见分析.【分析】根据菱形的对角线互相垂直,以及直角三角形斜边中线等于斜边的一半,得出E、F、G、H到O点距离都等于定长即可.解:如图,连接AC,BD相交于点O,连接OE,OF,OG,OH,△四边形ABCD是菱形,△AB=AD=CD=BC,AC△BD,△点E是AB的中点,△OE=12AB,同理:OF=12BC,OG=12CD,OH=12AD,△OE=OF=OG=OH,△点E、F、G、H四点是以AC,BD的交点O为圆心的同一个圆上.【点拨】本题主要考查了四点共圆的条件,用到了菱形的性质及直角三角形斜边中线的性质,熟练掌握其性质是解题的关键.【变式2】如图,在Rt ABC中,△BAC=90°,△ABC=40°,将ABC绕A点顺时针旋转得到ADE,使D点落在BC边上.(1)求△BAD的度数;(2)求证:A、D、B、E四点共圆.【答案】(1)10°;(2)见分析【分析】(1)由三角形内角和定理和已知条件求得△C的度数,由旋转的性质得出AC=AD,即可得出△ADC=△C,最后由外角定理求得△BAD的度数;(2)由旋转的性质得到△ABC=△AED,由四点共圆的判定得出结论.解:(1)△在Rt ABC中,△BAC=90°,△ABC=40°,△△C=50°,△将ABC绕A点顺时针旋转得到ADE,使D点落在BC边上,△AC=AD,△△ADC=△C=50°,△△ADC=△ABC+△BAD=50°,△△BAD=50°-40°=10°证明(2)△将ABC绕A点顺时针旋转得到ADE,△△ABC=△AED,△A、D、B、E四点共圆.【点拨】本题考查了旋转的性质、等腰三角形的性质、外角定理以及四点共圆的判定,解题的关键是理解旋转后的图形与原图形对应边相等,对应角相等.【变式3】如图,在□ABCD中,△BAD为钝角,且AE△BC,A F△CD.(1) 求证:A、E、C、F四点共圆;(2) 设线段BD与(1)中的圆交于M、N.求证:BM = ND【分析】(1)只要证明A、E、C、F四点所构成的四边形的对角互补,则该四点共圆;(2)连接AC交BD于O,易得O是该圆的圆心,OM=ON,所以可得BM=ND.解:(1)△AE△BC,AF△CD,△△AEC=△AFC=90°,△△AEC+△AFC=180°,△A、E、C、F四点共圆;(2)由(1)可知,圆的直径是AC,连接AC交BD于O,△ABCD是平行四边形,△O为圆心,OB=OD,△OM=ON,△BM=ND.【点拨】本题主要考查了四点共圆的判定及平行四边形的性质,难度不大,能够灵活运用所学知识进行推理是解题关键..类型二、利用四点共圆进行证明或求解2.如图,A 、B 、C 、D 四点共圆,且△ACB =△ACD =60°.求证:△ABD 是等边三角形.【分析】先根据同弧所对的圆周角相等得出△ADB =60°=△ABD ,再用三角形的内角和定理求出△BAD ,即可得出结论.证明:△△ACB =60°,△△ADB =△ACB =60°,△△ACD =60°,△△ABD =△ACD =60°,在△ABD 中,△BAD =180°﹣△ADB ﹣△ABD =180°﹣60°﹣60°=60°,△△ABD =△ADB =△BAD =60°,△△ABD 是等边三角形.【点拨】本题考查了等边三角形的性质与判定,圆周角定理,三角形的内角和定理 ,掌握圆周角定理是解答本题的关键;举一反三:【变式】 如图所示中,60NAM ∠=︒,B ,C 分别在边AM 和AN 上,且2BC =,CP AN ⊥,BP AM ⊥垂足分别为C ,B ,求PA 的长.【答案】433PA =【分析】本题关键要建立未知线段PA 和已知线段BC 的关系,由A ,B ,P ,C 共圆,PA 和CE 为直径,于是在Rt CEB △中便可以建立CE 和BC 的关系,求出CE 的长即求出PA 的长.解:连结CD ,BD ,△,CP AN BP AM ⊥⊥,△90PCA PBA ∠=∠=︒△AD BD PD CD ===,△由圆的定义知点A ,B ,C ,P 在以D 为圆心,DA 为半径的圆上,作出辅助圆,延长CD 交圆D 于E ,连结BE ,△60BAC CEB ∠=∠=︒ 30ECB ∠=︒在Rt BCE 中,2BC =,△433EC =△433PA =【点拨】双直角三角形是典型的共圆图,解题中注意灵活应用.类型三、四点共圆综合应用3.定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.(1)如图1,△E 是△ABC 中△A 的遥望角.△若△A =40°,直接写出△E 的度数是 ;△求△E 与△A 的数量关系,并说明理由.(2)如图2,四边形ABCD 中,△ABC =△ADC =90°,点E 在BD 的延长线上,连CE ,若△BEC 是△ABC 中△BAC 的遥望角,求证:DA =DE .【答案】(1)△20°;△12∠=∠E A ,理由见分析;(2)证明见分析 【分析】 (1)△根据题目定义推出△E =12△A ,从而得出结论;△直接根据求解△过程证明即可; (2)首先根据题意推出A 、B 、C 、D 四点共圆,然后作四边形ABCD 的外接圆交CE 于点F ,连接AF ,DF ,再根据圆的内接四边形的性质等推出△AFD =△DFE ,然后根据“遥望角”的定义推出△E=△DAF,即可证△DAF△△DEF,从而得出结论.(1)解:△△△E是△ABC中△A的遥望角,△△EBC=12△ABC,△ECD=12△ACD,△△E=△ECD﹣△EBD=12(△ACD﹣△ABC)=12△A,△△A=40°,△△E=20°.故答案为:20°;△12∠=∠E A,理由如下:△△E是△ABC中△A的遥望角,△△EBC=12△ABC,△ECD=12△ACD,△△E=△ECD﹣△EBD=12(△ACD﹣△ABC)=12△A;(2)证明:△△ABC=△ADC=90°,△A、B、C、D四点共圆,作四边形ABCD的外接圆交CE于点F,连接AF,DF,△四边形FBCD内接于△O,△△DFC+△DBC=180°,△△DFC+△DFE=180°,△△DFE=△DBC,△BD平分△ABC,△△ABD=△DBC,△△ABD=△AFD,△△AFD=△DFE,△△BEC 是△ABC 中△BAC 的遥望角,由(1)得△E =12△BAC ,△△BAC =△BDC ,△△E =12△BDC ,△△E +△DCE =△BAC ,△△E =△DCE ,△△DCE =△DAF ,△△E =△DAF ,△DF =DF ,△AFD =△DFE ,△△DAF △△DEF (AAS ),△DA =DE .【点拨】本题考查新定义问题,涉及三角形角平分线的拓展运用,圆的内接四边形的性质等,理解题目定义,灵活运用“四点共圆”的证明方法是解题关键.举一反三:【变式】在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:已知:ABC ∆是等边三角形,点D 是ABC ∆内一点,连接CD ,将线段CD 绕C 逆时针旋转60︒得到线段CE ,连接BE ,DE ,AD ,并延长AD 交BE 于点F .当点D 在如图所示的位置时:(1)观察填空:△与ACD ∆全等的三角形是________;△AFB ∠的度数为(2)利用题干中的结论,证明:C ,D ,F ,E 四点共圆;(3)直接写出线段FD ,FE ,FC 之间的数量关系.____________________.【答案】(1)△BCE ∆:△60︒;(2)见分析;(3)FD FE FC +=.【分析】(1)△根据旋转的性质和等边三角形的性质可证△ACD△△BCE ;△根据已推导出的全等三角形和三角形内角和进行角度转化,可得△AFB 的大小; (2)根据△ACD△△BCE 得ADC BEC ∠∠=,推导得出四边形CDFE 中180BEC FDC ∠+∠=︒,从而证共圆;(3)先推导出△BDF 是等边三角形,可证△ABD△△CBP ,得出AD=FC ,从而得出数量关系.解:(1)△△△ABC 是等边三角形△AB=AC=BC ,△BAC=△ACB=△ABC=60°△将线段CD 绕C 逆时针旋转60︒得到线段CE△CE=CD ,△DCE=60°△△DCE 是等边三角形△△DCE=60°△△ACD+△DCB=60°,△BCE+△DCB=60°△△ACD=△BCE△△ACD△△BCE(SAS)△△△ACD△△BCE△△EBC=△DAC△△DAC+△BAD=△BAC=60°△△FBC+△BAD=60°△△AFB=180°-△ABC -△FBC -△BAF=180°-60°-60°=60°(2)△()ACD BCE SAS ∆∆≌.△ADC BEC ∠∠=,△180ADC FDC ∠+∠=︒,△180BEC FDC ∠+∠=︒.△C ,D ,F ,E 四点共圆; (证明不唯一)(3)结论:FD FE FC +=,如下图,连接BD△△ACD△△BCE△△CBE=△CAD ,AD=BE△△CAD+△BAD=60°,△BAD+△FBC=60° △△BAD+△ABD=△BDF=60° △△AFB=60°△△BDF 是等边三角形 △DF=BF,△FD+FE=BE△△ABD△△CBF(SAS)△AD=FC△FD+FE=FC【点拨】本题属于几何综合题,考查了旋转变换,全等三角形的判定与性质,等边三角形的判定与性质等知识,解题的关键是正确寻找全等三角形解决问题.。
四点共圆_精品文档

四点共圆引言在几何学中,四点共圆是一个经典的概念,它指的是四个不在一条直线上的点可以构成同一个圆。
本文将介绍四点共圆的基本概念、性质以及证明方法。
基本概念四点共圆是指当给定四个不在一条直线上的点时,存在一个圆可以通过这四个点。
为了方便讨论,我们将这四个点依次标记为A、B、C和D,并假设它们不共线。
这样,我们可以通过构造圆来证明是否四点共圆。
性质根据四点共圆的定义,我们可以得出以下性质:•任意三个点确定一个圆,即如果取三个点A、B和C,那么存在一个圆可以通过这三个点。
•如果四个点A、B、C和D共圆,那么它们的任意三个点仍然共圆,即如果A、B、C和D共圆,那么A、B和C共圆,A、B和D共圆,以及B、C和D共圆等。
证明方法下面我们将介绍两种常见的证明方法,即推论法和向量法。
推论法推论法是一种常见的证明四点共圆的方法,它基于欧氏几何的公理和定理。
以下是一个简单的推论法证明:证明:设四个点A、B、C和D不共线。
为了证明它们共圆,我们需要证明存在一个圆可以通过这四个点。
首先,选择其中三个点A、B和C。
根据性质1,存在一个圆可以通过这三个点,假设这个圆为O1。
接下来,我们选择点D。
我们希望证明点D也在圆O1上。
为此,我们需要证明点D和圆O1的半径相等。
利用欧氏几何中的定理,我们可以证明从圆心到半径上任意一点的距离相等。
因此,我们只需要证明点D到圆心O1的距离与其他三个点到圆心O1的距离相等。
通过推理,我们可以得出结论:点D也在圆O1上。
因此,四个点A、B、C和D共圆。
向量法向量法是另一种常见的证明四点共圆的方法。
它基于向量的运算和性质。
以下是一个简单的向量法证明:证明:设四个点A、B、C和D不共线。
为了证明它们共圆,我们需要证明存在一个圆可以通过这四个点。
假设圆的圆心为O,我们需要证明向量OA、OB、OC和OD共面。
根据向量运算的性质,我们可以使用向量混合积来判断向量是否共面。
根据向量混合积的定义,我们有以下公式:(OA × OB) · (OC × OD) = (OA · OC) × (OB · OD) - (OA · OD) × (OB · OC)其中,× 表示向量的叉乘,·表示向量的点乘。
专题 四点共圆模型(老师版)

专题07四点共圆模型四点共圆是初中数学的常考知识点,近年来,特别是四点共圆判定的题目出现频率较高。
相对四点共圆性质的应用,四点共圆的判定往往难度较大,往往是填空题或选择题的压轴题,而计算题或选择中四点共圆模型的应用(特别是最值问题),通常能简化运算或证明的步骤,使问题变得简单。
本文主要介绍四点共圆的四种重要模型。
四点共圆:若在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
模型1、定点定长共圆模型(圆的定义)【模型解读】若四个点到一定点的距离相等,则这四个点共圆。
这也是圆的基本定义,到定点的距离等于定长点的集合。
条件:如图,平面内有五个点O、A、B、C、D,使得OA=OB=OC=OD,结论:A、B、C、D四点共圆(其中圆心为O)。
例1、(2023•连云港期中)如图,点O为线段BC的中点,点A、C、D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是.【分析】根据题意得到四边形ABCD共圆,利用圆内接四边形对角互补即可求出所求角的度数.【详解】由题意得到OA=OB=OC=OD,作出圆O,如图所示,∴四边形ABCD为圆O的内接四边形,∴∠ABC+∠ADC=180°,∵∠ABC=40°,∴∠ADC=140°,故答案为:140°.【点睛】此题考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解本题的关键.例2.(2022·安徽合肥·校考一模)如图,O 是AB 的中点,点B ,C ,D 到点O 的距离相等,连接AC BD ,.下列结论不一定成立的是()A .12∠=∠B .3=4∠∠C .180ABC ADC ∠+∠=︒D .AC 平分BAD∠【答案】D 【分析】以点O 为圆心,OA 长为半径作圆.再根据圆内接四边形的性质,圆周角定理逐项判断即可.【详解】如图,以点O 为圆心,OA 长为半径作圆.由题意可知:OA OB OC OD ===.即点A 、B 、C 、D 都在圆O 上.A .∵AB AB =,∴12∠=∠,故A 不符合题意;B .∵BC BC =,∴3=4∠∠,故B 不符合题意;C .∵四边形ABCD 是O 的内接四边形,∴180ABC ADC ∠+∠=︒,故C 不符合题意;D .∵BC 和CD 不一定相等,∴BAC ∠和DAC ∠不一定相等,∴AC 不一定平分BAD ∠,故D 符合题意.故选:D .【点睛】本题考查圆周角定理及其推论,充分理解圆周角定理是解答本题的关键.例3.(2023·陕西·九年级期中)如图,已知AB=AC=AD ,∠CBD=2∠BDC ,∠BAC=44°,则∠CAD 的度数为()A .68°B .88°C .90°D .112°【答案】B 【详解】试题分析:本题考查了等腰三角形的性质,主要利用了等腰三角形两底角相等,熟记性质是解题的关键.根据等腰三角形两底角相等求出∠ABC=∠ACB ,再求出∠CBD ,然后根据∠ABD=∠ABC ﹣∠CBD 计算即可得解.如图,∵AB=AC=AD ,∴点B 、C 、D 在以点A 为圆心,以AB 的长为半径的圆上;∵∠CBD=2∠BDC ,∠CAD=2∠CBD ,∠BAC=2∠BDC ,∴∠CAD=2∠BAC ,而∠BAC=44°,∴∠CAD=88°,例4.(2022·绵阳市4模型2、定边对双直角共圆模型同侧型异侧型1)定边对双直角模型(同侧型)条件:若平面上A 、B 、C 、D 四个点满足90ABD ACD ∠=∠=︒,结论:A 、B 、C 、D 四点共圆,其中AD 为直径。
专题:四点共圆在中考数学及自主招生中的应用
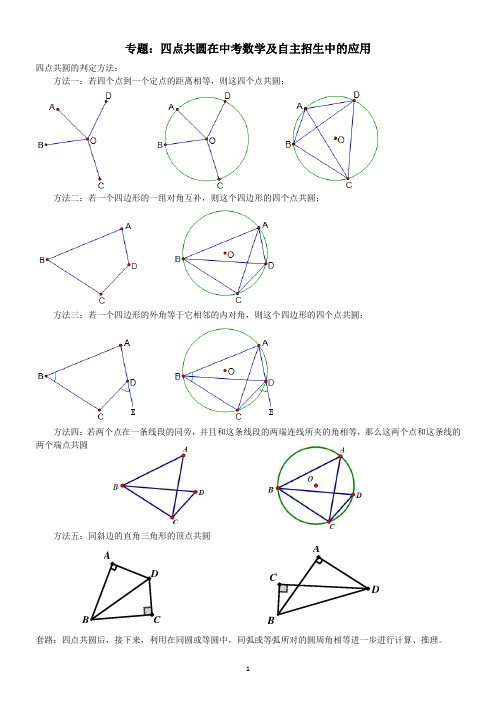
专题:四点共圆在中考数学及自主招生中的应用四点共圆的判定方法:方法一:若四个点到一个定点的距离相等,则这四个点共圆;方法二:若一个四边形的一组对角互补,则这个四边形的四个点共圆;方法三:若一个四边形的外角等于它相邻的内对角,则这个四边形的四个点共圆;方法四:若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆方法五:同斜边的直角三角形的顶点共圆C AD B C A D经典例题题型1、先证四点共圆后,然后求线段最值问题(关键是找到动点的轨迹)例1、如图1,OA=OB=4,∠OCA=135°(1)求证:AC⊥BC;(2)如图2,点P与点B关于x轴对称,试求PC的最小值。
题型2、先证四点共圆后,然后求角度、三角函数值、或线段的比值(若从一个点出发的三条线段之间的比值问题,特别注意三弦定理)例2、如图,抛物线y=ax2-4ax+b与x轴交于A、B两点,与y轴交于点C,抛物线的顶点为M,直线y=x-3经过M,B两点,交y轴于点D(1)求抛物线的解析式;(2)设P为x轴上一动点,过P作PC的垂线交直线BD于Q,连接CQ,求∠PQC的度数例3、(2013年哈尔滨)如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则sin∠BOE的值为例4、(2013•绍兴)在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD.(2)如图2,AC:AB=1:,EF⊥CE,求EF:EG的值.例5、如图1,直线y=−21x+2交x 轴、y 轴于A 、B 两点,C 为直线AB 上第二象限内一点,且S △AOC =8,双曲线 y=xk (x <0)经过点C (1)求k 的值; (2) 如图2,Q 为双曲线上另一点,连接OQ ,过C 作CM ⊥OQ 于M ,CN ⊥y 轴于N ,连接MN 。
四点共圆

相交弦定理的逆定理:对于凸四边形ABCD其对角线AC、BD交于P, 若PA·PC=PB·PD,则A、B、C、D四点共圆。
解析:对角线AC、BD交于P, 若PA·PC=PB·PD 则A,B,C,D四点共圆
知识点
四点共圆的判定六:
割线定理的逆定理:对于凸四边形ABCD两边AB、DC的延长线相交于P, 若PB·PA=PC·PD,则A、B、C、D四点共圆。
第一讲 四点共圆的性质及判定
CONTENTS
1 技巧讲解 2 例题讲解 3 对应习题 4 课程总结
初中数学知识点精讲课程
P a r t 1 四点共圆的性质及判定
知识点
一.四点共圆的判定方法:
1、若四个点到一定点的距离相等,则这四个点在同一个圆上(即这四点共圆)。 2、若一个四边形的一组对角的和等于180度,则这个四边形的四个顶点共圆。 3、若一个四边形的一个外角等于它的内对角,则这个四边形的四个顶点共圆。 4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两 个点和这条线的两个端点共圆。 5、若、两线段相交于点,且,则、、、四点共圆。 6、若、两线段延长后相交于点,且,则、、、四点共圆。 7、若四边形两组对边乘积的和等于对角线的乘积,则四边形的四个顶点共圆。
A
E
B
D
图7
F C
知识点
四点共圆的判定七:
若四边形两组对边乘积的和等于对角线的乘积,则四边形的四个顶点共圆
解析:四边形两组对边乘积的和等于对角线的乘积
ABCD AD BC AC BD
则A,B,C,D四点共圆
下次课见
A
E
B
D
图7
F C
知识点
中考数学圆中的重要模型四点共圆模型

圆中的重要模型-四点共圆模型四点共圆是初中数学的常考知识点,近年来,特别是四点共圆判定的题目出现频率较高。
相对四点共圆性质的应用,四点共圆的判定往往难度较大,往往是填空题或选择题的压轴题,而计算题或选择中四点共圆模型的应用(特别是最值问题),通常能简化运算或证明的步骤,使问题变得简单。
本文主要介绍四点共圆的四种重要模型。
四点共圆:若在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
模型1、定点定长共圆模型(圆的定义)【模型解读】若四个点到一定点的距离相等,则这四个点共圆。
这也是圆的基本定义,到定点的距离等于定长点的集合。
条件:如图,平面内有五个点O、A、B、C、D,使得OA=OB=OC=OD,结论:A、B、C、D四点共圆(其中圆心为O)。
例1、(2023•连云港期中)如图,点O为线段BC的中点,点A、C、D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是.例2.(2022秋·江西赣州·九年级校联考期中)如图,点O为线段AB的中点,点B,C,D到点O的距离相等,连接AC,BD.则下面结论不一定成立的是()A.∠ACB=90°B.∠BDC=∠BAC C.AC平分∠BAD D.∠BCD+∠BAD=180°例3.(2021·湖北随州·统考中考真题)如图,在R t A B C中,90∠A C B∠=︒,O为A B的中点,O D平分A O COF例4.(2022·北京·清华附中九年级阶段练习)如图,四边形A B C D 中,D A D B D C==,72BD C ∠=︒,则B A C∠的度数为______.模型2、定边对双直角共圆模型同侧型 异侧型 1)定边对双直角模型(同侧型)条件:若平面上A 、B 、C 、D 四个点满足90A B DA C D ∠=∠=︒,结论:A 、B 、C 、D 四点共圆,其中AD 为直径。
第16讲 四点共圆

第十五讲 四点共圆“四点共圆”问题在数学竞赛中经常出现,这类问题一般有两种形式:一是以“四点共圆”作为证题的目的,二是以“四点共圆”作为解题的手段,为解决其他问题铺平道路. 一、四点共圆如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
1、四点共圆的性质:(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等; (2)圆内接四边形的对角互补;(3)圆内接四边形的一个外角等于它的内对角。
以上性质可以根据圆周角等于它所对弧的度数的一半进行证明。
2、四点共圆的判定方法:(1)从被证共圆的四点中先选出三点作一圆,然后证另一点也在这个圆上,若能证明这一点,即可肯定这四点共圆.(2)把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆。
(可以说成:若平面上四点连成四边形的对角互补或一个外角等于其内对角,那么这四点共圆。
)(3)把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等(同弧所对的圆周角相等),从而即可肯定这四点共圆.(若能证明其两顶角为直角,即可肯定这四个点共圆,且斜边上两点连线为该圆直径。
)(4)把被证共圆的四点两两连成相交的两条线段,若能证明它们各自被交点分成的两线段之积相等,即可肯定这四点共圆(相交弦定理的逆定理);或把被证共圆的四点两两连结并延长相交的两线段,若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积,即可肯定这四点也共圆.(割线定理逆定理) (5)证被证共圆的点到某一定点的距离都相等,从而确定它们共圆.既连成的四边形三边中垂线有共同交点,即可肯定这四点共圆.(6)同斜边的两个直角三角形的四个顶点共圆,其斜边为圆的直径。
二、托勒密定理及其逆定理托勒密定理是平面几何中的一个重要定理,它揭示了圆内接四边形的对角线与边的关系。
1.托勒密定理:圆内接四边形两组对边乘积之和,等于两条对角线的乘积。
四点共圆分类知识点总结

四点共圆分类知识点总结一、四点共圆的定义四点共圆是指平面上的四个点在同一圆周上的情况。
在几何学中,这样的四点称为共圆点。
共圆的四个点可以是任意位置,且它们两两不一定成直线。
只要这四个点可以被同一个圆包含,就可以称为四点共圆。
二、四点共圆的性质1. 共圆四点的构造根据四点共圆的定义,我们可以得知构造四点共圆的方法。
在平面上,任意取三个不共线的点,依次作以这三点为圆心的圆,得到三个圆,这三个圆两两相交于三点,这三点并不共线。
因此可以构造一个圆来经过这三个点。
然后再取第四个点,若第四个点与前三个点都不共线,那么这四个点就是共圆点。
2. 共圆四点的关系共圆四点之间存在着特殊的几何关系。
在平面上,四个点共圆意味着它们之间的两两距离相等。
这是因为圆周上的任意两点到圆心的距离相等,所以当四个点共圆时,它们的两两距离相等的关系便自然而然地得到满足。
3. 共圆四点的条件共圆四点的条件是圆可经过这四点。
可以通过圆的方程来判断四个点是否共圆。
设这四个点分别为\(A(x_1, y_1), B(x_2, y_2), C(x_3, y_3), D(x_4, y_4)\),则这四个点共圆的充分必要条件是:\[ \begin{vmatrix}x^2 + y^2 & x & y & 1 \\x_1^2 + y_1^2 & x_1 & y_1 & 1 \\x_2^2 + y_2^2& x_2 & y_2 & 1 \\x_3^2 + y_3^2 & x_3 & y_3 & 1 \\x_4^2 + y_4^2 & x_4 & y_4 & 1\end{vmatrix} = 0 \]4. 共圆四点的性质四点共圆的性质包括切线性、对称性和射影性。
其中,切线性是最为重要的性质之一。
当四个点共圆时,它们之间的切线关系十分密切,这涉及到切线的性质和切线方程的应用。
四点共圆的判定与性质

四点共圆的判定与性质之巴公井开创作一、四点共圆的判定(一)判定方法1、若四个点到一个定点的距离相等,则这四个点共圆.2、若一个四边形的一组对角互补(和为180°),则这个四边形的四个点共圆.3、若一个四边形的外角即是它的内对角,则这个四边形的四个点共圆.4、若两个点在一条线段的同旁,而且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆.5、同斜边的直角三角形的极点共圆.6、若AB、CD两线段相交于P点,且PA×PB=PC×PD,则A、B、C、D四点共圆(相交弦定理的逆定理).7、若AB、CD两线段延长后相交于P.且PA×PB=PC×PD,则A、B、C、D四点共圆(割线定理).8、若四边形两组对边乘积的和即是对角线的乘积,则四边形的四个极点共圆(托勒密定理的逆定理.(二)证明1、若四个点到一个定点的距离相等,则这四个点共圆.若可以判断出OA=OB=OC=OD,则A、B、C、D四点在以O为圆心OA为半径的圆上.2、若一个四边形的一组对角互补(和为180°),则这个四边形的四个点共圆.若∠A+∠C=180°或∠B+∠D=180°,则点A、B、C、D四点共圆.3、若一个四边形的外角即是它的内对角,则这个四边形的四个点共圆.若∠B=∠CDE,则A、B、C、D四点共圆证法同上.4、若两个点在一条线段的同旁,而且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆.若∠A=∠D或∠ABD=∠ACD,则A、B、C、D四点共圆.5、同斜边的直角三角形的极点共圆.如图2,若∠A=∠C=90°,则A、B、C、D四点共圆.6、若AB、CD两线段相交于P点,且PA×PB=PC×PD,则A、B、C、D四点共圆(相交弦定理的逆定理).7、若AB、CD两线段延长后相交于P.且PA×PB=PC×PD,则A、B、C、D四点共圆(割线定理).8、若四边形两组对边乘积的和即是对角线的乘积,则四边形的四个极点共圆(托勒密定理的逆定理).已知四边形ABCD,若AB×CD+BD×AC=AD×BC,则A、B、C、D四点共圆.(三)例题123二、四点共圆的性质1、共圆的四个点所连成同侧共底的两个三角形的顶角相等.2、圆内接四边形的对角互补.3、圆内接四边形的外角即是内对角.。
圆中的重要模型之四点共圆模型(学生版)-初中数学

圆中的重要模型之四点共圆模型四点共圆是初中数学的常考知识点,近年来,特别是四点共圆判定的题目出现频率较高。
相对四点共圆性质的应用,四点共圆的判定往往难度较大,往往是填空题或选择题的压轴题,而计算题或选择中四点共圆模型的应用(特别是最值问题),通常能简化运算或证明的步骤,使问题变得简单。
本文主要介绍四点共圆的四种重要模型。
模型1.定点定长共圆模型(圆的定义)模型2.定边对双直角共圆模型模型3.定边对定角共圆模型模型4.对角互补共圆模型【知识储备】四点共圆:若在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
四点共圆模型是一种解题思想,但任何题目里都不会告诉你,亲爱的同学,请用四点共圆思想来解题吧。
那么,我们头脑里,就要快速迭代平常积累的一些模型。
四点共圆有三个性质:(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等;(2)圆内接四边形的对角互补;(3)圆内接四边形的外角等于内对角。
模型1.定点定长共圆模型(圆的定义)若四个点到一定点的距离相等,则这四个点共圆。
这也是圆的基本定义,到定点的距离等于定长点的集合。
条件:如图,平面内有五个点O 、A 、B 、C 、D ,使得OA =OB =OC =OD 。
结论:A 、B 、C 、D 四点共圆(其中圆心为O )。
证明:∵OA =OB =OC =OD∴根据圆的定义:到定点的距离等于定长点的集合为圆,确定A 、B 、C 、D 四点共圆。
1(2021·浙江嘉兴·中考真题)如图,在ΔABC 中,∠BAC =90°,AB =AC =5,点D 在AC 上,且AD =2,点E 是AB 上的动点,连结DE ,点F ,G 分别是BC ,DE 的中点,连接AG ,FG ,当AG =FG 时,线段DE 长为()A.13B.522C.412D.42(2023·安徽合肥·校考一模)如图,O 是AB 的中点,点B ,C ,D 到点O 的距离相等,连接AC ,BD .下列结论不一定成立的是()A.∠1=∠2B.∠3=∠4C.∠ABC +∠ADC =180°D.AC 平分∠BAD3(2024.九年级·湖北·专题练习)问题背景:如图1,等腰△ABC 中,AB =AC ,∠BAC =120°,作AD ⊥BC 于点D ,则D 为BC 的中点,∠BAD =12∠BAC =60°,于是BC AB =2BD AB=3;迁移应用:如图2,△ABC 和△ADE 都是等腰三角形,∠BAC =∠DAE =120°,D ,E ,C 三点在同一条直线上,连接BD .①求证:△ADB ≌△AEC ;②请直接写出线段AD ,BD ,CD 之间的等量关系式;拓展延伸:如图3,在菱形ABCD 中,∠ABC =120°,在∠ABC 内作射线BM ,作点C 关于BM 的对称点E ,连接AE 并延长交BM 于点F ,连接CE ,CF .①证明△CEF 是等边三角形;②若AE =5,CE =2,求BF 的长.模型2.定边对双直角共圆模型定边对双直角模型:一定边所对的角为两个直角,分同侧型和异侧型两种情况进行讨论。
四点共圆的9种判定方法证明

四点共圆的9种判定方法证明嘿,咱今天就来聊聊四点共圆的 9 种判定方法证明。
你可别小瞧了这四点共圆,它在数学里那可是相当重要呢!先来说说第一种方法,要是同一底边的两个同侧顶角相等,那这四个点肯定共圆。
就好像是四个小伙伴,他们有着共同的特点,自然而然就聚在一起啦。
再看看第二种,要是线段同侧的两点对线段两端点的张角相等,那它们也能共圆。
这就好比是大家有着相同的“磁场”,相互吸引着围成一个圆。
还有呢,外角等于内对角的四边形,那肯定也是四点共圆的。
你想想看,这就像是一个独特的标志,一下子就把它们联系在一起了。
若两个三角形有一条公共边,且在公共边同侧又有相等的顶角,那这四个点也能共圆。
这就好像是一个大家庭,有着亲密的关系把大家凝聚在一起。
再有就是相交弦定理的逆定理啦,如果两条线段相交,交点把每条线段分成的两条线段的积相等,那这四点不就共圆了嘛。
割线定理的逆定理也不能落下呀,如果从一点向一条线段引两条割线,这两条割线和这条线段交出的两条线段的积相等,嘿,它们也能共圆呢。
同斜边的两个直角三角形的四个顶点共圆,这不是显而易见的嘛。
四边形的一组对角互补,那它们也肯定共圆咯。
最后一种,四边形的一个外角等于它的内对角,那也能说明四点共圆呀。
你说这四点共圆的判定方法是不是很神奇?就像一把钥匙,能打开数学世界里的一扇扇奇妙之门。
在解题的时候,只要我们灵活运用这些方法,就能轻松搞定那些看似复杂的问题。
数学的世界就是这么充满魅力,四点共圆只是其中的一小部分。
我们在探索的过程中,不断发现新的规律和方法,就像是在挖掘宝藏一样。
每一个发现都让我们兴奋不已,让我们更加热爱数学这个神奇的领域。
所以呀,大家可别小看了这四点共圆的 9 种判定方法证明,它们可是我们在数学海洋中航行的重要指引呢!好好掌握它们,让我们在数学的天空中自由翱翔吧!。
初中四点共圆的6种判定方法证明

初中四点共圆的6种判定方法证明下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!一、引言初中数学中,学生经常需要证明四点共圆的问题。
四点共圆的圆的方程公式为

四点共圆的圆的方程公式为四点共圆是一个有趣且在数学中具有重要地位的概念。
咱们先来说说什么是四点共圆,简单来讲,就是平面上的四个点在同一个圆上。
要研究四点共圆,就得提到圆的方程公式。
圆的标准方程是 (x - a)²+ (y - b)² = r²,其中 (a, b) 是圆心的坐标,r 是圆的半径。
那怎么通过这四个点来确定这个圆的方程呢?这可就有点复杂啦。
咱们得先假设出圆的一般方程 x² + y² + Dx + Ey + F = 0 。
然后把这四个点的坐标分别代入这个方程,就得到了一个方程组。
接下来,就是解这个方程组,求出 D、E、F 的值,这样就能确定圆的方程啦。
给您举个例子吧。
比如说有四个点 A(1, 2)、B(3, 4)、C(5, 6)、D(7, 8) 。
把 A 点的坐标代入一般方程,就得到 1 + 4 + D + 2E + F = 0 ,也就是 5 + D + 2E + F = 0 。
同样,把 B 点坐标代入可得 9 + 16 + 3D + 4E + F = 0 ,也就是 25 + 3D + 4E + F = 0 。
再把 C 点坐标代入得到 25 + 30 + 5D + 6E + F = 0 ,即 55 + 5D + 6E + F = 0 。
最后把 D 点坐标代入得到 49 + 64 + 7D + 8E + F = 0 ,也就是 113 + 7D + 8E + F = 0 。
这样咱们就得到了一个关于 D、E、F 的方程组:\[\begin{cases}5 + D + 2E + F = 0 \\25 + 3D + 4E + F = 0 \\55 + 5D + 6E + F = 0 \\113 + 7D + 8E + F = 0\end{cases}\]解这个方程组可得 D、E、F 的值,进而确定圆的方程。
您看,这是不是挺有意思的?但说实话,解这个方程组可不容易,需要耐心和细心。
四点共圆定理及其推论

四点共圆定理及其推论《四点共圆定理及其推论,超有趣的数学发现!》我呀,最近在数学的奇妙世界里发现了一个超级酷的东西,那就是四点共圆定理及其推论。
这就像是在一个神秘的宝藏堆里发现了一颗最闪亮的宝石一样。
什么是四点共圆呢?简单来说呀,如果在一个平面内有四个点,这四个点到同一个点的距离都相等,那这四个点就在同一个圆上。
这就好比是四个小伙伴,他们都离一个特别的地方距离一样远,那他们就站在同一个神奇的圆圈里面啦。
比如说,我们在操场上玩游戏,有四个小朋友站在那里,假如他们到操场中间的一个小旗的距离都一样,那这四个小朋友就可以说是在一个以小旗为圆心的圆上。
那四点共圆定理有什么用处呢?这用处可大啦。
在做几何题的时候,要是发现有四个点可能共圆,那就像是找到了一把打开解题大门的钥匙。
我记得有一次,我做一道特别难的几何证明题,图上有四个点看起来好像有点关系,可我就是想不出来怎么证明。
后来我突然想到了四点共圆定理,就试着去证明这四个点共圆,哇塞,一旦证明出来了,后面的那些证明就像流水一样顺畅。
就好像是本来堵住的水管,一下子被打通了,水哗哗地流出来。
这四个共圆的点就像是一群团结的小战士,帮助我打败了那道难题这个大怪兽。
那它的推论呢?推论可就更有意思啦。
其中一个推论是,如果四边形的对角互补,那么这个四边形的四个顶点共圆。
这是什么意思呢?就像是有一个四边形形状的小花园,它的两个对角的度数加起来是180度,那就说明这个小花园的四个顶点都在同一个圆上。
我和我的同桌就讨论过这个推论。
我同桌当时就说:“这怎么可能呢?这四边形的角和圆有啥关系啊?”我就跟他说:“你看啊,如果把这个四边形想象成是在一个圆里面切出来的一块,那它的对角互补就很好理解啦。
就像把一个大蛋糕切成一块四边形的形状,这个四边形的对角就像是蛋糕上相对应的部分,它们加起来就是整个蛋糕的一部分,也就是180度呀。
”我同桌听了我的话,眼睛一下子就亮了,说:“哎呀,原来这么神奇啊!”还有一个推论是,如果一个四边形的一个外角等于它的内对角,那这个四边形的四个顶点共圆。
四点共圆是初中还是高中

四点共圆是初中还是高中
四点共圆是初中数学的内容。
四点共圆概念:如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
四点共圆有三个性质:1、共圆的四个点所连成同侧共底的两个三角形的顶角相等;2、圆内接四边形的对角互补;3、圆内接四边形的外角等于内对角。
四点共圆的判定方法
1、若四个点到一定点的距离相等,则这四个点在同一个圆上(即这四点共圆)。
2、若一个四边形的一组对角的和等于180度,则这个四边形的四个顶点共圆。
3、若一个四边形的一个外角等于它的内对角,则这个四边形的四个顶点共圆。
4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆。
5、若AB、CD两线段相交于P点,且PD·PC=PB·PA,则A、B、
C、D四点共圆。
6、若AB、CD两线段延长后相交于P点,且PD·PC=PB·PA,则
A、B、C、D四点共圆。
7、若四边形两组对边乘积的和等于对角线的乘积,则四边形的四个顶点共圆。
四点共圆的判定与性质

四点共圆的判定与性质之邯郸勺丸创作一、四点共圆的判定(一)判定办法1、若四个点到一个定点的距离相等,则这四个点共圆.2、若一个四边形的一组对角互补(和为180°),则这个四边形的四个点共圆.3、若一个四边形的外角等于它的内对角,则这个四边形的四个点共圆.4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆.5、同斜边的直角三角形的顶点共圆.6、若AB、CD两线段相交于P点,且PA×PB=PC×PD,则A、B、C、D四点共圆(相交弦定理的逆定理).7、若AB、CD两线段延长后相交于P.且PA×PB=PC×PD,则A、B、C、D四点共圆(割线定理).8、若四边形两组对边乘积的和等于对角线的乘积,则四边形的四个顶点共圆(托勒密定理的逆定理.(二)证明1、若四个点到一个定点的距离相等,则这四个点共圆.若可以判断出OA=OB=OC=OD,则A、B、C、D四点在以O为圆心OA为半径的圆上.2、若一个四边形的一组对角互补(和为180°),则这个四边形的四个点共圆.若∠A+∠C=180°或∠B+∠D=180°,则点A、B、C、D四点共圆.3、若一个四边形的外角等于它的内对角,则这个四边形的四个点共圆.若∠B=∠CDE,则A、B、C、D四点共圆证法同上.4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆.若∠A=∠D或∠ABD=∠ACD,则A、B、C、D四点共圆.5、同斜边的直角三角形的顶点共圆.如图2,若∠A=∠C=90°,则A、B、C、D四点共圆.6、若AB、CD两线段相交于P点,且PA×PB=PC×PD,则A、B、C、D四点共圆(相交弦定理的逆定理).7、若AB、CD两线段延长后相交于P.且PA×PB=PC×PD,则A、B、C、D四点共圆(割线定理).8、若四边形两组对边乘积的和等于对角线的乘积,则四边形的四个顶点共圆(托勒密定理的逆定理).已知四边形ABCD,若AB×CD+BD×AC=AD×BC,则A、B、C、D四点共圆.(三)例题123二、四点共圆的性质1、共圆的四个点所连成同侧共底的两个三角形的顶角相等.2、圆内接四边形的对角互补.3、圆内接四边形的外角等于内对角.。
(完整版)四点共圆

四点共圆四点共圆的性质及判断:判断定理 1:共斜边的两个直角三角形,则四个极点共圆,且直角三角形的斜边为圆的直径.判断定理 2:共底边的两个三角形顶角相等,且在底边的同侧,则四个极点共圆.判断定理 3:关于凸四边形 ABCD,对角互补四点共圆判断定理 4:订交弦定理的逆定理:关于凸四边形ABCD其对角线 AC、BD交于 P,AP PC BP PD 四点共圆判断定理 5:割线定理:关于凸四边形ABCD其边的延伸线AB、CD交于 P,PA PB PC PD四点共圆托勒密定理:圆内接四边形中,两条对角线的乘积等于两组对边乘积之和.即:若四边形ABCD 内接于圆,则有AB CD AD BC AC BD .ADBC例 1:如图,在圆内接四边形 ABCD 中,∠ A=6 0°,∠ B=90°, AB=2, CD=1,求 BC的长BCDA例 2:如图,正方形ABCD 的面积为5, E、 F 分别为 CD、 DA 的中点, BE 、 CF 订交于 P,求AP的长D EC PFA B例 3:如图,四边形 ABCD 内接于⊙ O,CB=CD=4 ,AC 与 BD 订交于 E,AE=6 ,线段 BE 和 DE 的长都是正整数,求BD 的长AEB DC例 4:如图, OQ ⊥ AB , O 为△ ABC 外接圆的圆心, F 为直线 OQ 与 AB 的交点, BC 与 OQ 交于 P 点, A 、 C、Q 三点共线,求证:OA2OP OQ.ACOF PB例 5:如图, P 是⊙ O 外一点, PA 与⊙ O 切于点 A, PBC 是⊙ O 的割线, AD ⊥ PO 于 D,求证:PB:BD PC:CD.PBDAOC例 6:如图,直线 AB 、 AC 与⊙ O 分别相切于 B、 C 两点, P 为圆上一点, P 到 AB 、 AC 的距离分别为6cm、 4cm,求 P 到 BC 的距离BMEOPANC例 7:在半⊙ O 中,AB 为直径,向来线交半圆周于C、D,交 AB 延伸线与 M( MB<MA ,AC<MD ),设 K 是△ AOC 与△ DOB 的外接圆除点 O 外的另一个交点,求证:∠ MKO=9 0°DKACO BM例 8:如图,在圆内接四边形 ABCD 中, AB=AD ,∠ BAD=6 0°, AC=a,求:四边形ABCD的面积(用a 表示)AODBC。
4点共圆的证明范文

4点共圆的证明范文4点共圆也被称为四点共线的特殊情况。
该情况下,四个点都位于同一个圆上,因此它们满足圆的性质和关系。
证明过程如下:假设有四个点A、B、C、D,我们要证明它们共圆。
1.首先,连接AB、AC和AD三条线段。
这里我们有两种情况需要讨论。
情况一:如果AB、AC和AD是相交于同一点的直线,那么它们共圆。
证明:根据直线的性质,如果三条线段相交于同一点,那么它们是共线的。
所以,根据共线的定义,这四个点也满足共圆的条件。
情况二:如果AB、AC和AD不是相交于同一点的直线,继续下面的证明。
2.接下来,将上述三条线段AB、AC和AD延长,分别与BC和CD相交于点E和F。
这样,我们得到了三个相交于同一点的直线段(BC、DE和CF)。
根据直线的性质,它们是共线的。
3.我们继续延长线段BE和CF,分别与AB和AC相交于点G和H。
这样,我们又得到了三个相交于同一点的直线段(AB、GH和AC)。
根据直线的性质,它们是共线的。
4.现在,我们要证明四个点A、B、C和D共圆。
我们令O为线段EG和FH相交的点。
通过连结线段EO和FO,我们可以得到两个直线段(EO和FO),它们相交于点O。
根据直线的性质,它们是共线的。
5.根据关于三线共点的定理,我们可以得出结论:线段BC、DE和FG 相交于同一点O。
6.既然线段BC、DE和FG相交于同一点O,根据共线的定义,我们可以断言四个点A、B、C和D共圆。
这样,我们就证明了四个点A、B、C和D共圆的问题。
总结一下,证明四点共圆的关键在于通过连接线段、找出相交的直线段,并通过共线的定义和定理得出结论。
无论是通过直接证明还是间接证明,我们都可以得出四个点共圆的结论。
2024年中考数学常见几何模型全归纳(全国通用)专题31 圆中的重要模型之四点共圆模型(解析版)

专题31圆中的重要模型之四点共圆模型四点共圆是初中数学的常考知识点,近年来,特别是四点共圆判定的题目出现频率较高。
相对四点共圆性质的应用,四点共圆的判定往往难度较大,往往是填空题或选择题的压轴题,而计算题或选择中四点共圆模型的应用(特别是最值问题),通常能简化运算或证明的步骤,使问题变得简单。
本文主要介绍四点共圆的四种重要模型。
四点共圆:若在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
模型1、定点定长共圆模型(圆的定义)【模型解读】若四个点到一定点的距离相等,则这四个点共圆。
这也是圆的基本定义,到定点的距离等于定长点的集合。
条件:如图,平面内有五个点O、A、B、C、D,使得OA=OB=OC=OD,结论:A、B、C、D四点共圆(其中圆心为O)。
【答案】2【分析】首先连接OE,由角器上对应的读数.【详解】解:连接OE,A .13B .52∵在ABC 中,90BAC【答案】30【分析】连接AC 与BD 又易知在Rt ACD △中,【详解】解:连接AC 与∵四边形形ABCD 是矩形,12OA OB OC OD AC又∵DE BF 于E ,即是直角三角形,∴12OE BD ,∴OA OC OD OE ,∴点A B 、、,由旋转的性质可知:AF AB ,【答案】122【分析】(1)根据条件,证明AOD COD△△△△,代入推断即可.(2)通过AOG ABC证明ODF CBF△△,代入推断即可.又∵∵CE CF∴CEF CFE模型2、定边对双直角共圆模型C同侧型异侧型1)定边对双直角模型(同侧型)条件:若平面上A、B、C、D四个点满足90ABD ACD,结论:A、B、C、D四点共圆,其中AD为直径。
2)定边对双直角模型(异侧型)条件:若平面上A、B、C、D四个点满足90ABC ADC,结论:A、B、C、D四点共圆,其中AC为直径。
【点睛】本题考查了圆的直径所对的圆周角为【点睛】此题主要考查圆内接四边形,直角三角形斜边上的中线等于斜边的一半和等腰三角形的性质等知识点,解答此题的关键是添加辅助线构造特殊三角形,求出线段.模型3、定边对定角共圆模型条件:如图1,平面上A 、B 、C 、D 四个点满足ADB ACB ,结论:A 、B 、C 、D 四点共圆.条件:如图2,AC 、BD 交于H ,AH CH BH DH ,结论:A B C D 、、、四点共圆.例1.(2023·江苏·九年级假期作业)如图,在Rt ABC 中,∠BAC =90°,∠ABC =40°,将 ABC 绕A 点顺时针旋转得到 ADE ,使D 点落在BC 边上.(1)求∠BAD 的度数;(2)求证:A 、D 、B 、E 四点共圆.【答案】(1)10°;(2)见解析【分析】(1)由三角形内角和定理和已知条件求得∠C 的度数,由旋转的性质得出AC =AD ,即可得出∠ADC =∠C ,最后由外角定理求得∠BAD 的度数;(2)由旋转的性质得到∠ABC =∠AED ,由四点共圆的判定得出结论.【详解】解:(1)∵在Rt ABC 中,∠BAC =90°,∠ABC =40°,∴∠C =50°,∵将 ABC 绕A 点顺时针旋转得到 ADE ,使D 点落在BC 边上,∴AC =AD ,∴∠ADC =∠C =50°,∴∠ADC =∠ABC +∠BAD =50°,∴∠BAD =50°-40°=10°证明(2)∵将 ABC 绕A 点顺时针旋转得到 ADE ,∴∠ABC =∠AED ,∴A 、D 、B 、E 四点共圆.【点睛】本题考查了旋转的性质、等腰三角形的性质、外角定理以及四点共圆的判定,解题的关键是理解旋转后的图形与原图形对应边相等,对应角相等.例3.(2022·江苏无锡·中考真题)△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=________°;现将△DCE 绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是________.【答案】804##4【分析】利用SAS 证明△BDC ≌△AEC ,得到∠DBC =∠EAC =20°,据此可求得∠BAF 的度数;利用全等三角形的性质可求得∠AFB =60°,推出A 、B 、C 、F 四个点在同一个圆上,当BF 是圆C 的切线时,即当CD ⊥BF 时,∠FBC 最大,则∠FBA 最小,此时线段AF 长度有最小值,据此求解即可.【详解】解:∵△ABC 和△DCE 都是等边三角形,∴AC =BC ,DC =EC ,∠BAC =∠ACB =∠DCE =60°,∴∠DCB +∠ACD =∠ECA +∠ACD =60°,即∠DCB =∠ECA ,在△BCD 和△ACE 中,CD CE BCD ACE BC AC,∴△ACE ≌△BCD (SAS ),∴∠EAC =∠DBC ,∵∠DBC =20°,∴∠EAC =20°,∴∠BAF =∠BAC +∠EAC =80°;设BF 与AC 相交于点H,如图:∵△ACE ≌△BCD ∴AE =BD ,∠EAC =∠DBC ,且∠AHF =∠BHC ,∴∠AFB =∠ACB =60°,∴A 、B 、C 、F 四个点在同一个圆上,∵点D 在以C 为圆心,3为半径的圆上,当BF 是圆C 的切线时,即当CD ⊥BF 时,∠FBC 最大,则∠FBA 最小,∴此时线段AF 长度有最小值,在Rt △BCD 中,BC =5,CD =3,∴BD 4,即AE =4,∴∠FDE =180°-90°-60°=30°,∵∠AFB =60°,∴∠FDE =∠FED =30°,∴FD =FE ,过点F 作FG ⊥DE 于点G ,∴DG =GE =32,∴FE =DF =cos 30DG∴AF =AE -FE 80;【点睛】本题考查了旋转的性质,等边三角形的性质,圆周角定理,切线的性质,解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件.例4.(2022·贵州遵义·统考中考真题)探究与实践:“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.提出问题:如图1,在线段AC 同侧有两点B ,D ,连接AD ,AB ,BC ,CD ,如果B D ,那么A ,B ,C ,D 四点在同一个圆上.探究展示:如图2,作经过点A ,C ,D 的O ,在劣弧AC 上取一点E (不与A ,C 重合),连接AE ,CE 则180AEC D (依据1)B D ∵180AEC B点A ,B ,C ,E 四点在同一个圆上(对角互补的四边形四个顶点共圆)点B ,D 在点A ,C ,E 所确定的O 上(依据2)点A ,B ,C ,E 四点在同一个圆上(1)反思归纳:上述探究过程中的“依据1”、“依据2”分别是指什么?依据1:__________;依据2:__________.(2)图3,在四边形ABCD 中,12 ,345 ,则4 的度数为__________.(3)拓展探究:如图4,已知ABC 是等腰三角形,AB AC ,点D 在BC 上(不与BC 的中点重合),连接AD .作点C 关于AD 的对称点E ,连接EB 并延长交AD 的延长线于F ,连接AE ,DE .①求证:A ,D ,B ,E与判定,掌握以上知识是解题的关键.模型4、对角互补共圆模型P条件:如图1,平面上A、B、C、D四个点满足ABC ADC,结论:A、B、C、D四点共圆.条件:如图2,BA、CD的延长线交于P,PA PB PD PC,结论:A、B、C、D四点共圆.A.2B.22【答案】A【分析】先根据等腰三角形的性质可得,,,A B E D四点共圆,在以BE为直径的圆上,连接【答案】43/113【分析】过点B作BH AM交F,点A,M,B,C四点共圆,得法求解,12AMBS AM DE△【详解】解析:过点B作BH 于点,如图所示:【答案】52 2【分析】连接BD并延长,利用四点共圆的判定定理得到的性质和圆周角定理得到DBF性质解答即可得出结论.(1)求证:A ,E ,B ,D 四点共圆;(2)如图2,当AD CD 时,O 是四边形AEBD O 的切线;(3)已知1206BC ,,点M 是边BC 的中点,此时P 是四边形出圆心P 与点M 距离的最小值.【答案】(1)证明见解析(2)证明见解析(3)32(3)解:如图所示,作线段AB 的垂直平分线,分别交∵120AB AC BAC ,,∴B课后专项训练1.(2023秋·河北张家口·九年级校考期末)如图①,若BC是Rt△ABC和Rt△DBC的公共斜边,则A、B、C、D在以BC为直径的圆上,则叫它们“四点共圆”.如图②,△ABC的三条高AD、BE、CF相交于点H,则图②中“四点共圆”的组数为()A.2B.3C.4D.6【答案】D【分析】根据两个直角三角形公共斜边时,四个顶点共圆,结合图形求解可得.【详解】解:如图,以AH为斜边的两个直角三角形,四个顶点共圆(A、F、H、E),以BH为斜边的两个直角三角形,四个顶点共圆(B、F、H、D),以CH为斜边的两个直角三角形,四个顶点共圆(C、D、H、E),以AB为斜边的两个直角三角形,四个顶点共圆(A、E、D、B),以BC为斜边的两个直角三角形,四个顶点共圆(B、F、E、C),以AC为斜边的两个直角三角形,四个顶点共圆(A、F、D、C),共6组.故选D.【点睛】本题考查四点共圆的判断方法.解题的关键是明确有公共斜边的两个直角三角形的四个顶点共圆.,.下2.(2023·安徽合肥·校考一模)如图,O是AB的中点,点B,C,D到点O的距离相等,连接AC BD列结论不一定成立的是()A .12B .3=4C .180ABC ADCD .AC 平分BAD【答案】D 【分析】以点O 为圆心,OA 长为半径作圆.再根据圆内接四边形的性质,圆周角定理逐项判断即可.【详解】如图,以点O 为圆心,OA 长为半径作圆.由题意可知:OA OB OC OD .即点A 、B 、C 、D 都在圆O 上.A .∵ AB AB ,∴12 ,故A 不符合题意;B .∵ BCBC ,∴3=4 ,故B 不符合题意;C .∵四边形ABCD 是O 的内接四边形,∴180ABC ADC ,故C 不符合题意;D .∵ BC 和CD不一定相等,∴BAC 和DAC 不一定相等,∴AC 不一定平分BAD ,故D 符合题意.故选:D .【点睛】本题考查圆周角定理及其推论,充分理解圆周角定理是解答本题的关键.3.(2023·江苏宿迁·九年级校考期末)如图,在Rt ABC △中,90ACB ,3BC ,4AC ,点P 为平面内一点,且CPB A ,过C 作CQ CP 交PB 的延长线于点Q ,则CQ 的最大值为()【点睛】本题考查相似三角形的判定和性质以及四点共圆,掌握同圆或等圆中,同弧所对的圆周角相等确定四点共圆,利用相似三角形性质得到线段间等量关系是解题关键.4.(2023·北京海淀·九年级校考期中)如图,点接AC,BD.请写出图中任意一组互补的角为【答案】DAB【分析】首先判断出点【答案】130【分析】根据题意得到四边形【详解】解:由题意得到∴四边形ABCD为圆∵∠ABC=50°,∴∠【点睛】此题考查了圆内接四边形的性质,熟练掌握圆内接四边形的性质是解本题的关键.6.(2023·浙江金华·A.3B.1∵PE AB 于点E ,PD AC 于点,∴90AEP ADP ,∴180AEP ADP ,∴A 、E 、D 四点共圆,PA 是直径,在Rt PDC 中,45C ,∴△是等腰直角三角形,45APD ∴APD △也是等腰直角三角形,45PAD ,∴PED PAD ∴45AED ,∴AED C ,∵EAD CAB ,∴AED ∽设2AD x ,则2PD DC x ,22x ,如图2,取AP 的中点O 则2AO OE OP x ,∵604515EAP BAC PAD ,过E 作EM AP 于M ,则EM x,cos30OM OE ,∴36222OM x x ,∴6226222AM x x x ,由勾股定理得: 222226222AE AM EM x x +【答案】3632 /323 【分析】数形结合,根据动点的运动情况判断点【详解】解:如图旋转,连接以BC 为直径作O ,以AE 为半径作在ABD △和ACE △中AB AC AD AE BAD CAEPBC PBA ACB PBC 90BAC BPC EAD ∵,122AB ∵,A 的半径为62∴又∵90BAC EAD ,CAD,∵33BC ,OP BC∵MQ,MC与圆O相切,1QOM COM COP 【答案】(1)见详解(2)证明:如下图所示由题意可知AC 逆时针旋转90得到边AE ,90E ACB ,则90ACB ∵,AE BF ∥,90 ∵,90EFC ,,F ,E 四点共圆..∵四边形ABCD是菱形,AC,且 GOC GCO90==∵, 点90DHC DOC=BDF OCH=,且BF OM ∵, 点==90AED AOD尝试应用如图2,点D 为等腰Rt ABC △外一点,AB AC ,BD CD ,过点A 的直线分别交DB 的延长线和CD 的延长线于点N ,M ,求证:12ABN ACM S S AN AM △△.问题拓展如图3,ABC 中,AB AC ,点D ,E 分别在边AC ,BC 上,60BDA BEA ,AE ,BD ,直接写出BE 的长度(用含a ,b 的式子)∵ABC 为等腰直角三角形,∴AB AC , 又∵BD CD ,即:=90BDC ,∴A 、B 在ABN 与ACE △中,AB AC ABN ACE BN CE,∴∴BAN BAE CAE BAE BAC ∴1122AME AMC S AE AM AN AM S S △△∴60AFB BAF ABF ,AB AF AC ,∵60BDA BEA ,∴A 、D 、E 、B 、F 五点共圆,则:13 ,24 ,60BEF AEB ,【答案】问题情境:见解析;问题解决:(1)102;(2)13522【分析】[问题情境]连结AC ,取AC 的中点O ,连结OB 、OD ,根据直角三角形斜边上的中线等于斜边的一半,可得OD OA OC OB ,以此即可证明;[问题解决](1)根据题意可得225AE AD DE ,由[问题情境]结论可知A 、D 、E 、据圆周角定理以及正方形的性质可得45PDE PAE ,则PAE △为等腰直角三角形,设AP 长为a ,根据勾股定理列出方程,求解即可;(2)由[问题情境]结论可知A 、D 、E 、P 四点共圆,过点O 作OG AD 于点G ,作OH 接OB 交O 于点P ,连接PB ,根据题意可得四边形MBNP 为矩形,则要求MN 的最小值,即求值,根据平行线的性质和中点的定义可得OG 为ADE V 的中位线,得1AG ,12OG ,同理可证四边形1【翻折】(1)如图1,将DEF 沿线段AB 翻折,连接CF ,下列对所得四边形ACBF 的说法正确的是平分CBF 、CAF ,②AB 、CF 互相平分,③12ACBF S AB CF 四边形,④A 、C 、B 、F 四点共圆.AB 垂直平分CF ,故②ABC ABF ACBF S S S 四边形1122AB AB FG 12AB CG 取AB 的中点O ,连接CO FO ,ABC ABF △、△均为直角三角形,∴OB OC OA OF ,∴A 、B 、F 四点共圆,故()沿线段向左平移,∴AB CF ,CF BE 的中点,∴BE BD BF特殊情况分析:(1)如图1,正方形ABCD 中,点P 为对角线时针旋转ADC 的度数,交直线BC 于点Q .小明的思考如下:连接DQ ,∵AD CQ ∥,90ADC DCQ ,∴ACQ DAC ∵90DPQ ,∴180DPQ DCQ ,∴点D P Q 、、PDQ PCQ DQP PCD∵在菱形ABCD 中BC AD ∥,180ADC DCQ ,DPQ ADC ,∵180DPQ DCQ ,∴点P C Q 、、、共圆,∴DQP ACD ,ACB PDQ ,∵AC 为菱形ABCD 的对角线,ACB ACD ,∴PDQ DQP ,∴ DP PQ ;(3)解:3PQ 或3.由于点P 为对角线AC 上一个动点,分两类情况讨论如下:所示:180302ADC ACD,。
