第十二章动量矩定理
理论力学——第12章 动量矩定理

28
maC mg sinq FS
0 mg cosq FN
JC FSR
[1] [2] [3] [4]
由[2]式得 FN mg cosq
[1] ,[3]两式中含有三个未知数aC 、FS、 ,需补充附加条件。
讨论 1.设接触面绝对光滑,即f = f´‘ =0
均为 v 。 2
17
§12-3 刚体绕定轴的转动微分方程
如图示一定轴转动刚体,由质点系对z轴动量矩定理
d
dt
(J z)
n i 1
M z (Fi )
或
d n
Jz
dt
M z (Fi )
i 1
也可为
J z M(z F )
或
d2 n
Jz
dt 2
M z (F )
i 1
以上各式称为刚体绕定轴转动微分方程
dt
rg(PA PB ) r 2PA r 2PB gJO
16
[例4] 已知:猴子A重=猴子B重,猴B以相对绳速度 v
上爬,猴A不动,问当猴B向上爬时,猴A将如何动? 动的速度多大?(轮重不计)
解:因
MO(F(e)) 0 ,
故系统的动量矩守恒。
0mAvArmB (vvA)r
vA
v 2
猴A与猴B向上的绝对速度是一样的,
R22
1 2
R11
LO
(
J1 R2 2
J2 R2 2
m2
m3 )R2v3
8
§12-2 动量矩定理
1.质点的动量矩定理
对质点动量矩求一次导数,得
d dt
MO
(mv)
d dt
第12章动量矩定理

又, a (h C 2R h A ) 0.5 7783km
c VC hC 2R hA
c a ( R h A ) 973km b a 2 c 2 7722km vB R hA v A 7.14km / s b
例二. 质量为m 的小球 悬挂在一绳索下端且以匀速率在水平面内作圆周运动. 试分析小球对O, A 两点的动量矩及其守恒问题. A
解 : 卫星在轨道运行中只受 地球的
VB b C a O′ O
B
V F VA A
引力作用, 故卫星对地心 点的 O 动量矩守恒. (R h A ) v A (R hC ) vC vC 6371 439 8.1 6.3km / s 6371 2384 ( R h A ) v A v B b
r
T
m
R O
v
mg
结论: 动量矩是否守恒, 与矩心的选择有关.
§12 – 3 刚体绕定轴转动的微分方 程
对绕定轴(不妨设为z轴)转动的刚体而言 对转轴的动量矩定理可 , 写为
n d ( J z ) M z ( F i ) dt i 1
去掉微分符号即是 J z M z ( Fi )
LO r i m i V i (r C r'i ) m i V i
Vi
r
n
n
Vi
mi
i 1 n
i 1
VC VC
C
r 'i
r C m i V i LC r C m i V i LC
i 1 i 1
n
r C MV C L C
rc
M O (m v )
12动量矩定理

图12.7 钟摆
第12章 动量矩定理
12.1 转 动 惯 量
【例12.5】 匀质圆盘与匀质杆组成的钟摆如图12.7所示。已知圆盘质量m1, 直径d,杆的质量m2,长l,试求钟摆对悬挂轴O的转动惯量J0。
解:钟摆由匀质杆和匀质盘组成,所以有 = JO JO杆 + JO
其中
JO
=J c
+
m1
l
+
d 2
平方的乘积,即
12.7
J=z J zc + md 2
(12.7)
第12章 动量矩定理
12.1 转 动 惯 量
证明:如图12.5所示,设刚体总的质量为m,轴zc通过质心C,z与zc平行且 相距为d。不失一般性,可令y与yc重合,在刚体内任取一质量为mi的质点Mi,它 至zc轴和z轴的距离分别为ric和ri。刚体对于z、zc轴的转动惯量分别为
12.9
第12章 动量矩定理
12.1 转 动 惯 量
【例12.4】 质量为m,长为l的匀质杆如图12.6所示,求杆对yc的转动惯量。
解:由例12.1知
Jy
=
1 ml2 3
,根据平行轴定理式(12.7)有
J yc
=J y
−
md 2
=1 ml2 3
−
m
l
2
2
=1 12
ml 2
12.10
图12.6 匀质杆
在工程问题上,计算刚体的转动惯量时,常应用下面公式
12.3
第12章 动量矩定理
12.1 转 动 惯 量
Jz
=
mρ
2 z
(12.2)
ρ 其中m为整个刚体的质量, z 为刚体对z轴的回转半径,它具有长
第十二章 动量矩定理

Lz=Jzω
§2 动量矩定理
一、质点的动量矩定理
设质点质量为m, 受力F, MO(mv) 动量mv,定坐标系Oxyz , 根据质点的动量定理 z
F
B
mv
r
o A y
MO(F)
d (mv ) F dt
等式两边同时与矢径r作矢量积, 即 x
d (mv ) r F r dt
MO(F)
?
d (mv ) r F 为求等式 r 左边项,先来看 dt d (r mv ) dr mv r d (mv ) dt dt dt v ( r d ( v mv∵O为定点!)mv ) dt MO(mv) =0
第十二章
动量矩定理
z
§1 动量矩的概念
一、质点的动量矩
F r
o
B A m
y
回顾: 力对点的矩 Mo(F)= r×F 若 r=xi+yj+zk F=Fxi+Fyj+Fzk
则 i M o (F ) x Fx
j y Fy k z Fz
MO(F)
x
大小:│Mo(F) │ =2S△OAB
方向:按右手螺旋规则定。
[Mo(mv)]z= M z(mv)
代数量
• 动量矩的量刚为 ML2T-1 (kg· 2/S) m
二、质点系的动量矩
质点系对固定点O的动量矩等于各质点对同 一点O的动量矩的矢量和(即质点系动量对点O 的主矩):
对定点
Lo M o (mi vi )
i 1
n
矢量
质点系对固定轴z的动量矩等于各质点对同一 轴z的动量矩的代数和,即
vC
C
Lo = M o(Mvc)
理力12(动力学)-动量矩定理

§ 12-2 动量矩定理
动量矩守恒定理
d M O (mv ) M O ( F ) dt
MO (F ) 0
M x (mv ) 恒量 M y (mv ) 恒量 M (mv ) 恒量 z
M O (mv ) 恒矢量
n d LO M O (Fi ( e ) ) dt i 1 n
29
第 十二 章 动量矩定理
§12-3 刚体绕定轴的转动微分方程
n d ( J z ) M z ( Fi ) dt i 1 n d Jz M z (Fi ) dt i 1
J z M z (Fi )
i 1
n d J z 2 M z (Fi ) dt i 1 2
θ W2
FN
例题
第十二章 动量矩定理
例 题 12-1
ω O FN W2t v M FOy
解: 取小车与鼓轮组成质点系,视小车
为质点。以顺时针为正,此质点系对O轴 的动量矩为
FOx W1
LO J m2vR
作用于质点系的外力除力偶M,重力W1 和 W2外,尚有轴承O的反力FOx和FOy ,轨道 对小车的约束力FN 。 其中W1 ,FOx ,FOy 对 O轴力矩为零。将W2 沿轨道及其垂直方向 分解为W2t和W2N, W2N与FN相抵消。
F0
r1
α
r2
LOz J O m1v1r1 m2v2 r2
考虑到 v1 = r1 , v2 = r2 ,则得 m0g
A B
LOz ( J O m1r1 m2 r2 )
2 2
( b)
v1
外力主矩仅由重力 m1g 和 m2g 产生,有
v2 m2g m1 g
理论力学第12章-动量矩定理

z
M ,底圆半径为 R ,高为 h 。
r
h z dz
解:把圆锥体分成许多厚度为 d z
的薄圆片,该薄圆片的质量为
d m r2d z
O
y
R
x
为圆锥体的密度,r为薄圆片的半径。
圆锥体的质量
M 1R2h
3
薄圆片对自身直径的转动惯量
由几何关系知: r R h z
h 薄圆片对 y 轴转动惯量 d J y 为:
x
x yi
J z mi ri2
mi
xi2
yi
d
2
mi xi2 yi2 2 yid d 2
J z mi xi2 yi2 2d mi yi mi d 2
mi xi2 yi2 JzC
mid 2 Md 2
由质心坐标公式 :
因为
yC0
mi yi M yC
速度 a 。
解:小车与鼓轮组成质点系对 O 轴的动量矩为 :
LO J O m2 v R
作用于质点系的外力除M ,G 1 和 G 2 外,尚有轴承 O 的反力 Fo x 和 Fo y ,轨道对车的约束力FN 。其中G 1 , FO x ,Fo y 对 O 轴力矩为零。将 G 2 分解为 Gτ和 G n ,
(12-10)
l 为任意轴上的单位矢量。
动量矩的单位是牛·米·秒 ( N ·m ·s )。
12.2.3 定轴转动刚体的动量矩 设刚体绕固定轴 z 转动,某瞬时刚体
的角速度。对于刚体内任一质点 M i ,
其质量为 m i ,转动半径为 r i ,动量 m i v i 。 于是质点 M i 对轴的动量矩为:
LO MO mv r mv (12-8)
质点系对各坐标轴动量矩
十二章动量矩定理

F mv
M0(F)
o
Q
y
x
由牛顿第二定律
m
dv dt
F
d dt
(mv)
F
r
d dt
(mv)
r
F
d (r mv) r d(mv) dr mv
dt
ห้องสมุดไป่ตู้
dt dt
理论力学电子教程
第十二章 动量矩定理
d (r mv) r F dt
M0(mv) m0(F)
理论力学电子教程
第十二章 动量矩定理
C
m2
IOZ M
式中
M
m1
O
IOZ
1 3
m1L2
1 2
m2
r
2
m2L2
理论力学电子教程
第十二章 动量矩定理
代入已知值得:
IOZ
1 10 0.32 3
1 40 0.152 2
40 0.32
4.35kg m2
M 20 4.6rad / s2
IOZ 4.35
理论力学电子教程
第十二章 动量矩定理
dt
M y (mv)]
my (Fe )
d [
dt
M z (mv)]
mz (Fe )
理论力学电子教程
第十二章 动量矩定理
【典型题精解】
例12-1 滑块A,B质量分别为2Kg,0.5Kg,用长1
米的绳连接,在水平光滑滑竿上滑动,绳和竿的质量不计。
竿绕铅垂轴转动,轴的摩擦也不计。当 rA 0.6m 时,滑块 A以速度0.4m/S沿竿向外运动,竿的角速度 0.5rad / s
求此时竿的角加速度。
1m
B rB
第十二章 动量矩定理

x
Z
求: J z
例题
杆质量为 m1 ,长度为 l
O
l
圆盘质量为 m2 ,直径为 d
J 求:系统的 O
§12-3 动量矩定理
一、质点的动量矩定理 二、质点系的动量矩定理 三、质点系相对于定轴的动量矩定理 四、动量矩守恒定理 五、实例
一、质点的动量矩定理
MO
mv
z
MO F
O
F
rA
mv
d
d LO
dt
M
e O
对质点系中,第i个质点
z mivi
F1
d dt
M
O
mi
vi
MO
Fii
对质点系,有
MO
Fi e
F2
m2
O ri
mi m1
n
i1
d dt
M
O
mi vi
n M O Fii
i1
n M O Fie
i1
y
n
注意到:
M O Fii 0
即:质点的动量对于固定点O 的矩称为质点对于点O的动量
x m3 mn
矩。
MO mivi ri m vi
2、质点对定轴的动量矩
M z mivi MO mivi z
二、质点系的动量矩
1、质点系对定点的动量矩
MO
z
mv
O
m2
ri
mi vi
mi m1
y
质点系中所有质点对于点O 的动量矩的矢量和,称为质 点系对点O的动量矩。
LO M O mivi
i
x m3 mn
ri mivi i
2、质点系对定轴的动量矩 Lz M z mivi
第12章-动量矩定理

旳乘积: J z m z2
细直杆 均质圆环 均质圆板
J z /m 1 / 3 l2 z 0.5774 l
J z /m R2 z R
J z /m 1 / 2 R2 z 0.7071R
z 假如把刚体旳质量全部集中在与 轴相距为ρ z 旳点
上,则此质点对 z 轴旳转动惯量与原刚体相同。
四、平行轴定理
J z J z md 2
定理:刚体对任意轴旳转动惯量,等于刚体对 于经过质心、并与该轴平行旳轴旳转动惯量, 加上刚体旳质量与两轴间距离平方旳乘积。
z
O
z
d
ri
ri
C
O
mi
zi
y( y)
C点为质心;
O z 为质心轴,O z
为与之平行旳任
xi
一轴,距离为 d 。
x d x yi J z mi ri2 mi ( xi2 yi2 )
d dt
(
J
z
)
Jz
Mz
dω dt
(Fi
)M
M z (Fi )
z
(
FN
i
)
Fi
或
Jz
d2
dt2
M z (Fi )
或 J z M z (Fi )
FNi
与 m a Fi 比较
例:已知滑轮半径为 R ,转动惯量为 J ,带动滑轮
旳皮带拉力分别为 F1 和 F2 。求滑轮旳角加速度 。
F2 解:根据定轴转动微分方程
d(ri
mivi ) dt
ri
F (e) i
ri
Fi(i)
(i 1,2,, n)
相加得
理论力学12—动量矩定理.ppt

dt v2 r2 cos 2 LCDcd qV dt v1r1 cos 1 LABab qV
应用动量矩定理
dLz (e) Mz dt
qV (v2 r2 cos 2 v1r1 cos 1 ) Mz
M z nM z qV (v2 r2 cos 2 v1r1 cos1 )
z
A
l
C
a
Lz1 Lz 2
0
a
B
l
Lz1 2(ma0 )a 2ma 0
2
D
Lz 2 2m(a l sin )2 2ma20 2m(a l sin )2 a2 0 2 (a l sin )
显然,此时的角速度< 0。
z
A
l
C
a
质点系对 某固定轴的动 量矩对时间的 导数,等于作 用于质点系的 外力对于同一 轴的矩的代数 和。
12.2.3 动量矩守恒定理
1. 质点动量矩守恒定律 如果作用在质点上的力对某定点(或定轴) 之矩恒等于零,则质点对该点(或该轴)的动量 矩保持不变。
2. 质点系动量矩守恒定律
当外力对于某定点(或某定轴)的主矩等于 零时,质点系对于该点(或该轴)的动量矩保持 不变。
(e)
FOy O FOx u
va u v LO mva r mvr 0 LO m(u v)r mvr 0 u u va v 2 2
由上可知,人与重物 A 具有相同的的速度,此速度等 于人相对绳的速度的一半。如果开始时,人与重物 A 位于同一高度,则不论人以多大的相对速度爬绳,人 与重物A将始终保持相同的高度。
O
M z (mv) mvl ml 2
合肥工业大学《理论力学》l第十二章动量矩定理

Mz
ε
ε∝ Mz
当Mz= 0 时, ε= 0,刚体作匀速转动或静止。
刚体转动惯量的大小表现了刚体转动状态改变 的难易程度转。动惯量是刚体转动时的惯性度量。
请比较 Jz = ∑Mz 与 m a = ∑F 。
§4 刚体对轴的转动惯量
一、转动惯量的概念
转动惯量是刚体转动时的惯性度量, 它 等 于 刚 体内各质点的质量与质点到轴的垂直距离平方 的乘积之和,即
z
解:分析小球受力。
r2 B
∵ ∑MZ(F(e)) = 0, ∴ LZ = const ! 初瞬时(A处),
v2 F
r1
T
LZA = mv1r1, B处, LZB = mv2r2, ∴ mv1r1 = mv2r2
A mg v1
而 r1 =2r2 得 v2 = 2v1
解毕。
二、质点系的动量矩定理
设质点系由n个质点组成,第i个质点的质量为mi, 速度为vi, 受力:外力Fi(e) 、内力Fi(i) ,则 根 据 质 点 的动量矩定理,有
d dt
Mo
(mi vi
)
Mo
( Fi ( i )
)
Mo
( Fi ( e )
)
对于n个质点,有n个这样的方程,将这些方程求和,
则
内力系主矢 = 0
n
i1
d dt
Mo (mivi )
n i1
Mo (Fi(i) )
n i1
Mo (Fi(e) )
所以得
ddtindd1tMin1o
M(moi
v(mi )i
Lz=Jzω
§2 动量矩定理
一、质点的动量矩定理
zF
B
设质点质量为m,受力F, MO(mv)
第12章 动量矩定理

§12-3 动量矩定理
例 题 5
两个鼓轮固连在一起,其总质量是 m,对水平转轴O的
转动惯量是 JO ;鼓轮的半径是 r1 和 r2 。绳端悬挂的重物 A和 B 质量分别是 m1 和 m2 ,且 m1 > m2。试求鼓轮的角 加速度(与例12-1类似)。
r1 r2
w
A
B
§12-3
动量矩定理
例 题 5
解: 1、选系统(含鼓轮,重物 A , B)为研究对象
2、运动分析 设鼓轮的角速度为w, 物 A的速度:v1= r1w 物 B的速度:v2= r2w
2
y
FO
r1 r2
w
mg
3、受力分析 重力 mg,m1g , m2g 轴O处约束力 FO
LOz ( J O m1r1 m2 r2 )w
2
v1 A m1 g v2
y
m
w
C
平面运动=随C平动+绕C转动
ri
O
rC
x
LC J C ωk , 为动量偶
第12章 动量矩定理
§12-2 刚体对轴的转动惯量
§12-2 刚体对轴的转动惯量
z
2-1 定义
J z ri mi
2
ri
vi
mi
i
均质连续体:
w
O x
y
J z M r dm
2
单位:kg· m2
3、 质点系动量矩守恒定理
若
e M O ( Fi ) 0 e M z ( Fi ) 0
dL O e MO dt
则 LO 常矢 则 Lz 常量
即:当质系所受合外力对某定点(或某定轴)的 矩为零,则质系对该点(或该轴)的动量矩保持 不变 —— 质系动量矩守恒定律。
第12章动量矩定理

n
质点系对O点的动量矩在通过O点任一轴上的投影等于 质点系对该轴的动量矩。
L L
O z
zபைடு நூலகம்
4
3.平动和转动刚体的动量矩
a 、刚体平动时可将其全部质量集中于质心,做为一个质点
计算动量矩。 L M (mv ) O O C
Lz M z (mvC )
b、刚体绕定轴转动 n n Lz M z mi vi mi vi ri
i 1
z
mi ri ri mi ri2
i 1
n
i 1
O’
ri mi
mi v i
定义:刚体对z轴转动惯量:
J z mi ri
则:
2
反映质量关于z的分布情况。
Lz J z
5
绕定轴转动刚体对其转轴的动量矩等于刚体对转轴的
转动惯量与转动角速度的乘积。
6
d [ M O ( mv )] M O ( F ) 1.质点的动量矩定理 dt 将此式在通过固定点O的三个直角坐标轴上投影,得
d [ M x ( mv )] M x ( F ) dt d [ M y ( mv )] M y ( F ) dt d [ M z ( m v )] M z ( F ) dt
0——称角振幅
周期
T 2
JO mga
——称初相位
19
例12-7:已知飞轮对O的转动惯量JO,以角速度0绕O轴转动,制动时,
闸块给轮正压力FN,已知闸块与轮之间的动滑动摩擦系数为f,轮半
径为R,轴承的摩擦忽略不计,求制动所需时间。
R O
20
例12-7:已知飞轮对O的转动惯量JO,以角速度0绕O轴转动,制动时,
第十二章 动量矩定理

2 mo mv ml l ml
O
0
mo T o
l
T
C
mo F mglsin
v
mg
注意:在计算动量矩与力矩时,符号规定应一致(在 本题中规定逆时针转向为正)。 根据动量矩定理,有
kg m 2 s
二、质点系动量矩 1、对点的动量矩:
LO M O (mi vi )
i 1
n
2、对轴的动量矩(即上式在各轴上的投影):
Lz M z (mi vi )
3、刚体的动量矩 (1)平移刚体:刚体上任意点的速度均与其质心速度 相同。故可将其看作为质量集中与质心的一个质点。 对点的:
dx 2 m glsin m l dt
即
g sin 并令 l
2 n
g sin 0 l
——(1)
则(1)式化为
0
2 n
解此微分方程,并将运动初始条件带入,即当t=0时
0
0 0
0 cosnt
质点系对固定点的动量矩定理为:
d (i) (e) M O(mi vi ) M O(Fi ) M O(Fi ) dt
其中: M O(Fi (i) ) 0
d d d LO M O(mi vi ) M O(mi vi ) dt dt dt
e d LO M O Fi dt
O
J O J O1 J O 2
l
mg
C
1 2 1 2 2 ml mR ml R 3 2
动量矩定理12章
)2
0
z
B
D
例: 均质圆盘,其绕轴O的转动惯量为J ,可绕通
过其中心的轴无摩擦地转动,另一质量为 m2
的人由 B 点按规律 s 1 at 2 沿距 O 轴半径
为 r 的圆周运动。初始2时,圆盘与人均静止。
求圆盘的角速度与角加速度。
解: 圆盘与人一起 —— 研究对象
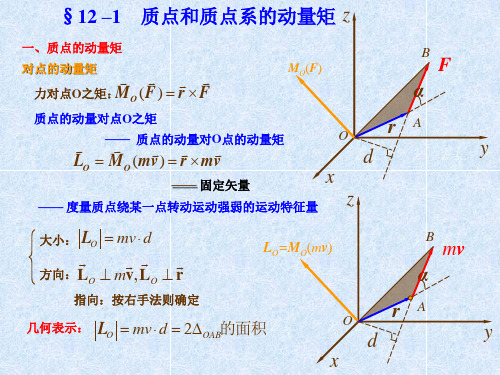
受力分析: M z (Fi ) 0
大小: LO mv d
方向:LO mv, LO r
LO=MO(mv)
B
mv α
指向:按右手法则确定
几何表示: LO mv d 2OAB的面积
O
rA
d
y
x
对轴的动量矩
类似于力对点之矩与力对轴之矩的关系: MO (F ) x M x (F ) yFz zFy
质点的动量 mv 对 x 轴之矩 :
§12 –1 质点和质点系的动量矩 z
一、质点的动量矩
对点的动量矩 力对点O之矩:MO (F ) r F
MO(F)
B
F α
质点的动量对点O之矩
—— 质点 的动量对O点的动量矩 LO MO (mv) r mv
—— 固定矢量
O
rA
d
x
y
—— 度量质点绕某一点转动运动强弱的运动特征量
z
LOz (JO m1r12 m2r22 )
(b)
外力主矩仅由重力 m1g 和 m2g 产生,有
m0g
A
B
v2 m2g
v1 m1g
MOz (m1r1 m2r2 )g
(c)
(b)
例题
dLOz dt
M Oz
(a)
LOz (JO m1r12 m2r22 )
工程力学-材料力学-第12章动量矩定理(华蕊)

maCx 0
aCy B
maCy FA mg
aA C
JC
FA
l 2
cos 60
aA
α aCtA θ
补充运动学方程
A
aC aA aCAt aCAn
在y轴方向投影
aCy
aCAt
cos
l
4
12g 7l
,
FA
4 7
mg
D B
C
Aθ
例12-9
已知:如图r,m, m1。求:1. aA;2. FAB ;3. FS2 解:分别以A、B、C为研究对象
质点对z轴的动量矩 Lz (mv ) 是质点的动量在Oxy平
面的投影(mv)xy对O点的矩。
Lz (mv ) 是代数量,从 z 轴正向看,逆时针为正,顺时 针为负。
[LO (mv )]z Lz (mv )
单位:kg·m2/s
质点系的动量矩
对点的动量矩 对轴的动量矩
n
LO LO (mivi ) i 1 n
•
作业标准记得牢,驾轻就熟除烦恼。2020年12月24日星期 四2时51分26秒 02:51:2624 December 2020
•
好的事情马上就会到来,一切都是最 好的安 排。上 午2时51分26秒 上午2时51分02:51:2620.12.24
•
专注今天,好好努力,剩下的交给时 间。20.12.2420.12.2402:5102:51:2602:51:26Dec-20
•
安全象只弓,不拉它就松,要想保安 全,常 把弓弦 绷。20.12.2402:51:2602:51Dec-2024-Dec-20
•
加强交通建设管理,确保工程建设质 量。02:51:2602:51:2602:51Thursday, December 24, 2020
第12章动量矩定理汇总

第十二章动量矩定理§12—1质点和质点系的动量矩一、质点的动量矩质点Q的动量对于点0的矩,定义为质点对于点0的动量矩M O mv = r mvM z mv 二2 0Q AM O mv [二M z mv动量矩的单位:kgm2/s、质点系的动量矩nL o 二為M o m i V ii』nL z八M z m i v iM O (mv)(r mv ) dtdtdr dtmv rmvdt绕定轴转动刚体对其转轴的动量矩等于刚体对转轴的转动惯量与转动角 速度的乘积n n n2L z 八 M z mM八 m i y 订i =mmyy ynJ z 八 m"2id :§12— 2动量矩定理、质点的动量矩定理M O mv =v mv r F dt-J—M O mv 二 M O F dt质点的动量矩定理:质点对某定点的动量矩对时间的一阶导数,等于作 用力对同一点的矩。
直角坐标投影式为d厂 一Mx(mv)= Mx(F ) dt pl 2 My(mv)=My(F ) dt plL 2M z (mv)= M z (F ) dtL z=J z :特殊情形:当质点受有心力F的作用时,如图11-4所示,力矩M°(F)=O,则质点对固定点0的动量矩M o(mv)=恒矢量,质点的动量矩守恒。
例如行星绕着恒星转,受恒星的引力作用,引力对恒星的矩M°(F)=O,行星的动量矩M o (m v )=恒矢量,此恒矢量的方向是不变的,因此行星作平面曲线运动;此恒矢量的大小是不变的,即mvh=恒量,行星的速度v与恒星到速度矢量的距离h成反比。
(1)从而由式(1)得单摆运动微分方程为护阶0(2)解式(2) 得单摆的运动规律为9 =cp o Sin( 3n t +8)其中,3-g称为单摆的角频率,单摆的周期为例1如图所示单摆,由质量为m的小球和绳索构成。
单摆悬吊于点0,绳长摆在铅垂平面内绕点0作微振幅摆动,设摆与铅垂线的夹角为「为逆时针时正,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理论力学电子教程
第十二章 动量矩定理
∑
d dt
(ri × mi vi ) = ∑ m0 ( Fie ) + ∑ m0 ( Fii )
d [∑ M 0 (mv)] = ∑ m0 ( Fie ) dt
质点系对任意固定点O的动量矩对时间的导数等于 质点系所受全部外力对该点的主矩.
理论力学电子教程
第十二章 动量矩定理
4:质点系对点之动量矩是说明在某一 瞬时质点系运动的一个量度.
理论力学电子教程
第十二章 动量矩定理
5:应用质点系动量矩定理时,可取投影式
d [∑ M x (mv)] = ∑ mx ( Fe ) dt
d [∑ M y (mv)] = ∑ m y ( Fe ) dt
d [∑ M z (mv)] = ∑ mz ( Fe ) dt
M z (mv) = ±2∆OQ′A′
质点动量对O点的矩与对Z轴之矩的关系式:
[ M 0 (mv)]z = M z (mv)
理论力学电子教程
第十二章 动量矩定理
2、质点的动量矩定理 由牛顿第二定律
z
M 0 (mv)
M 0 (F )
F
mv
dv m = ∑F dt
Q
o
x
y
d (mv) = ∑ F dt
1 2
Z1
Z2
C
b/4 b/4 b/2
理论力学电子教程
第十二章 动量矩定理
Z1 Z2
A. J Z B. J Z C. J Z D. J Z
2
2
b 2 = J Z1 + M ( ) 4 b 2 = J Z1 − M ( ) 4
b 2 b 2 3 = J Z1 − M ( ) + M ( ) = J Z1 − Mb 2 2 4 16 b 2 b 2 3 = J Z1 − M ( ) − M ( ) = J Z1 + Mb 2 2 4 16
故
LO = LOO + LOA + LOB
1 2 =( + 2 m) R ω 2M
理论力学电子教程
第十二章 动量矩定理
例12-4 如图所示,一匀质圆盘刚连于匀质细杆 OC 上, 可绕 O 轴在水平面内转动,已知杆 OC 长 L = 0.3m,质 C 量 m1 = 10kg , 圆盘半径 r = 0.15m ,质量 m2 = 40kg , 为圆盘质心。若在杆上作用一常力偶矩 M = 20 N ⋅ m ,不 计摩擦,试求杆 OC 的角加速度。
现取对 Z轴的投影式,且 则经 ∆t 时
t2 0
t2
t1
∑ m ( F ) × dt
0 i
∑ m (F ) = L
0 i
i
为常量
∫ ∑ m ( F ) × dt = L ⋅ ∆t
t1
喷嘴口的水为点的复合运动:取其为动点。动系:悬臂
∆[∑ M 0 (mi ⋅ vi )]z
水在喷嘴喷出的速度为
中的
vi
为绝对速度
r
【解】取整体为研究对象。 设角加速度为 ε ,由刚体定 轴转动微分方程,得:
C
m2
I OZ ⋅ ε = M
ε
M
O
m1
式中
I OZ
1 1 2 2 2 = m1 L + m2 r + m2 L 3 2
理论力学电子教程
第十二章 动量矩定理
代入已知值得:
I OZ
1 1 2 = ×10 × 0.3 + × 40 × 0.152 + 40 × 0.32 3 2 = 4.35 kg ⋅ m 2
例12-2 公园内的喷水器有四根旋臂,每一旋臂由两根 12水平管组成,管长分别为0.25m,0.15m,夹角为120o 每一喷 嘴喷。设喷水量为 0.01m3 / min水流相对于喷嘴的速度为12m / s 水器转动时的摩擦力矩L=0.25N.m,求喷水器喷水时的转速。
取质点系(取悬臂以及从进水口至喷嘴内所含的水) 动量矩得计算,(经∆t 后,进水口处的水流入∆m ,各喷水 1 嘴流去 ∆m 旋转臂及管内稳定流动的质量三部分引 4 起的对Z轴的动量矩变化)应用动量矩定理求得ω
故
∆m(vr ⋅ 0.25 sin 60 − ve ⋅ l ) = L ⋅ ∆t
o
l 2 = 0.1225m 2
(*)
理论力学电子教程
第十二章 动量矩定理
∆m & 当 ∆t → 0即式(*)为 →m ∆t
把已知数据代入式(*)中
& m = 4 × 0.01× 1000 = 40kg / min = 40 / 60kg / s
理论力学电子教程
第十二章 动量矩定理
【典型题精解】
例12-1 滑块A,B质量分别为2Kg,0.5Kg,用长1 12米的绳连接,在水平光滑滑竿上滑动,绳和竿的质量不计。 竿绕铅垂轴转动,轴的摩擦也不计。当 rA = 0.6m 时,滑块 A以速度0.4m/S沿竿向外运动,竿的角速度ω = 0.5rad / s 1m 求此时竿的角加速度。
O
R
ω R o
4R
A
θ
(a) )
(b) )
理论力学电子教程
第十二章 动量矩定理
【解】 (1)圆环对 O 点的转动惯量为
J O1 = 2mR
2
直杆对 O 点的转动惯量为
故
1 2 2 J O 2 = m( 4 R ) + m ( 2 R ) 12 1 2 JO = JO1 + JO2 = 2mR + ( m×16R2 + 4mR2 ) 12
mi vi
p=0
mi vi
M 0 (∑ mv) ≠ 0
理论力学电子教程
第十二章 动量矩定理
mi vi
mi vi
M
∑ mv
ε
i
= Mvc = p
a
ω
M 0 (∑ mv) ≠ 0
动量的主矩不等于零。
F
N
要解决具有转动问题还须另一定理:动量矩定理
理论力学电子教程
第十二章 动量矩定理
§12-1 质点的动量矩定理 12-
d dt
d dt
(r1 × m1v1 ) = m0 ( F1 ) + m0 ( F12 ) + m0 ( F13 )
( r2 × m2 v2 ) = m0 ( F2 ) + m0 ( F21 ) + m0 ( F23 )
d dt
( r3 × m3v3 ) = m0 ( F3 ) + m0 ( F31 ) + m0 ( F32 )
理论力学电子教程
第十二章 动量矩定理
Z
∆m / 4 0.15m
0.25m
o1
ω
120
o
A
L
∆m v1
B O
o1
120o A
vB
mvr
h
理论力学电子教程
第十二章 动量矩定理
【解】质点系 :由悬臂以及从进水口至喷嘴内所含的水 应用动量矩定理:(积分式)
[∑ M 0 (mi vi )]2 − [∑ M 0 ( mi vi )] = ∫
va = ve + vr
理论力学电子教程
第十二章 动量矩定理
ve = lω
经
∆t 后 ,对Z轴的动量矩的变化。
vr = 12m / s
悬臂及管内稳定流的这一部分水质点动量矩不变, 及动量矩之差为零
1 ∆[∑ M 0 (mi vi )] = 4 ⋅ ∆m(vr ⋅ 0.25 sin 60o − ve ⋅ l ) − ∆mv1 ⋅ 0 4
1、质点的动量矩定理 、 计算公式:
z
M 0 ( mv)
o
A
mv
M 0 (mv ) = r × mv =
Q
i
y
j
r
A′
Q′
x y & & & mx my mz
k z
(mv) xy
x
理论力学电子教程
第十二章 动量矩定理
或:
M 0 ( mv ) = mv ⋅ r sin θ = 2∆OQA
质点动量对于Z轴的矩:
M 20 ε= = 4.6rad / s 2 I OZ 4.35
理论力学电子教程
第十二章 动量矩定理
【思考题】
1.是非题 是非题 (1)质点系的内力不能改变质点系的动量与动量矩。(对) (2)若系统的动量守恒,则其对任意点的动量一定守恒, 若系统对某点的动量矩守恒,则其动量一定守恒。 (错) 2.选择题 选择题 (1)如图所示,均质矩形板质量为 M ,尺寸如图所示。已 知薄板对 Z1 轴的转动惯量 J Z 。试写出对 Z 2 轴的转动惯量 J Z 的计算公式。Z1 与 Z 2轴互相平行。( C )
1、质点系的动量矩定理 、
r2
F21
由合力矩定理知:
m2 m1v2
m1v1 F12
F1
m1 F 13
r2 F F3 32 o r1 r3 m3
F31
m3v3
F23
m0 ( F12 ) + m0 ( F21 ) = ∑ m0 ( R )
又:
R=0
理论力学电子教程
第十二章 动量矩定理
对某一质点皆可写出动量矩定理
将上式两端对t 求导,得
理论力学电子教程
第十二章 动量矩定理
故: ( m A rA 解得:
2
ε = −0.5 rad
drA + m B rB )ε + 2(m A rA − m B rB ) ω =0 dt
2
s
2
