北航10秋学期《线性代数》模拟题一
线性代数模拟试卷及答案

线性代数(文)模拟试卷(一)参考答案一。
填空题(每小题3分,共12分)1.设⎪⎪⎪⎭⎫⎝⎛=333222111c b a c b a c b a A ,⎪⎪⎪⎭⎫⎝⎛=333222111d b a d b a d b a B ,2=A ,3=B ,则B A -2=1. 解 B A -2=3332221113332221113333222211112222d b a d b a d b a c b a c b a c b a d c b a d c b a d c b a -=---=12=-B A .2。
已知向量)3,2,1(=α,)31,21,1(=β,设βαT A =,其中T α是α的转置,则n A =A n 13-.解 注意到3321)31,21,1(=⎪⎪⎪⎭⎫ ⎝⎛=T βα,故n A =βαβαβαβαT n T T T 个)())((=ββαβαβααβαTn T T T T 个)1()())((-=A n T n 1133--=βα。
注 若先写出A ,再求2A ,…,n A 将花比前更多的时间.3。
若向量组T )1,0,1(1-=α,T k )0,3,(2=α,T k ),4,1(3-=α线性相关,则k =3-.解 由1α,2α,3α线性相关,则有321,,ααα=k k 0143011--=1043011--k k k =04)1(3143=--=-k k k k 。
由此解得3-=k .4。
若4阶矩阵A 与B 相似,矩阵A 的特征值为21,31,41,51,则行列式E B --1 =24.解 因为A 与B 相似,所以A ,B 有相似的特征值,从而E B --1有特征值1,2,3,4。
故2443211=⋅⋅⋅=--E B . 注 本题解答中要用到以下结论:(1)若A 可逆,A 的特征值为λ,则1-A 的特征值为λ1。
(2)若λ是A 的特征值,则)(A f 的特征值为)(λf ,其中)(x f 为任意关于x 的多项式。
线性代数练习题(有答案)

《线性代数》 练习题一、选择题1、 设A ,B 是n 阶方阵,则必有 ……………………………………………( A )A 、|AB |=|BA | B 、2222)(B AB A B A ++=+C 、22))((B A B A B A -=-+D 、BA AB = 2、设A 是奇数阶反对称矩阵,则必有( B ) (A)、1=A (B)、0=A (C)、0≠A (D)、A 的值不确定3、向量组)0,1,1(,)9,0,3(-,)3,2,1(,)6,1,1(--的秩为____2 ________4、向量组)1,3,1,2(-,)4,5,2,4(-,)1,4,1,2(--的秩为______2__ ___.5、设A 是n m ⨯阶矩阵,r A r =)(,则齐次线性方程组O AX =的基础解系中包含解向量的个数为( C )(A)、r (B)、n (C)、r n - (D)、r m - 二、计算与证明题6、设⎪⎪⎪⎭⎫ ⎝⎛----=020212022A , ⎪⎪⎪⎭⎫⎝⎛---=221021132B 求(1)32AB A -,(2).T B A6、解(1). A AB 23-2202313212120020122--⎛⎫⎛⎫ ⎪⎪=-- ⎪⎪ ⎪⎪---⎝⎭⎝⎭2202212020-⎛⎫⎪--- ⎪ ⎪-⎝⎭2223186240-⎛⎫ ⎪=-- ⎪ ⎪--⎝⎭2202212020-⎛⎫ ⎪--- ⎪ ⎪-⎝⎭210612622680-⎛⎫ ⎪=- ⎪ ⎪--⎝⎭(2). 220231231212120120020122122T A B ---⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪=--= ⎪⎪ ⎪ ⎪⎪ ⎪-----⎝⎭⎝⎭⎝⎭222186240-⎛⎫⎪=-- ⎪ ⎪--⎝⎭7、设A ,B 是n 阶方阵满足AB B A =+,证明:E A -可逆. 7、解、1()A E B E --=-8、设方阵A 满足0332=--E A A ,证明:A 可逆,并求1-A .8、解、由2330A A E --=有A (3A E -)=3E ,于是,A [21(3A E -)]=E ,所以A 可逆,且11(3)3A A E -=-.9、计算行列式:1014300211321221---=D9、69D =-.10、计算行列式D =4232002005250230---- 10、解:D =423200200525230----0205252304--=55208---=80-=11、计算n 阶行列式abbb b a bb b a D =11、1[(1)]()n D a n b a b -=+--。
北航10秋学期线性代数模拟题一

北航10秋学期《线性代数》模拟题一本复习题页码标注所用教材为:如学员使用其他版本教材,请参考相关知识点一、 单项选择题(本大题共5小题,每小题3分,共15分)1、 设A 为2008阶可逆方阵,则()1*A -= ( )A.()*1det A AB.()1det A AC.()*1det A A D. ()11det A A --参考答案:B2、已知x 的一次多项式111111111111101-------=x D ,则式中一次项的系数为( )(A )4 (B )4- (C )1 (D )1- 参考答案:B3、 设a 为n m ⨯矩阵,则n 元齐次线性方程组0=Ax 存在非零解的充分必要条件是( )A .A 的行向量组线性无关B .A 的行向量组线性相关C .A 的列向量组线性无关D .A 的列向量组线性相关 参考答案:C4、设列向量组321,,ααα,则与三阶行列式|,,|321ααα等值的行列式是( ) (A )|,,|321311αααααα+++ (B )|3,,|31332ααααα++(C )|,,|123ααα (D )|,,|133221αααααα+++参考答案:C5、 设A 为3阶矩阵,将A 的第2行加到第1行得B ,再将B 的第1列的-1倍加到第2列得C ,记110010001P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则( )A .1.C P AP -= B .1.C PAP -= C ..T C P AP = D ..TC PAP =参考答案:B二、 判断题(本大题共5小题,每小题2分,共10分) 6、A .对B .错参考答案:A7、 两个对称矩阵一定合同。
( )A .对B .错参考答案:B8、A .对B .错参考答案:A9、 相似矩阵有相同的特征多项式。
( )A .对B .错参考答案:A10、A .对B .错参考答案:B三、填空题(本大题共10小题,每小题3分,共30分)11、设四阶行列式3214214314324321,ij A 是其()j i ,元的代数余子式,则_______3331=+A A ,_______3432=+A A 。
北航线性代数答案1

北航《线性代数》在线作业一一、单选题:1. 设方阵A与B等价,则() (满分:7)A. A与B的对称矩阵合同B. A与B相似C. r(A)=r(B)D. |A|=|B|正确答案:C2. 设A 为mxn 矩阵,非线性方程组Ax=b , r(A)=r则( ) (满分:7)A. r<m 时,方程组有无穷多解B. r=n时,方程组有唯一解C. r=m 时,方程组有解D. m=n时,方程组有唯一解正确答案:B3. n元齐次线性方程组AX=0存在非零解的充要条件是( ) (满分:7)A. A的列线性无关B. A的行线性无关C. A的行线性相关D. A的列线性相关正确答案:D4. A、B均为n阶方阵,则必有(满分:7)A. det(A)det(B)=det(B)det(A)B. det(A+B)=det(A)+det(B)C. (A+B)的转置=A+BD. (AB)的转置=A的转置乘与B的转置正确答案:A5. 题见图片(满分:7)A. AB. BC. CD. D正确答案:B6. 设A为实对称矩阵,且A的平方等于0矩阵。
那么(满分:7)A. AAA=0B. AE=EC. EA=ED. AEA=E正确答案:A7. A为n阶实对称矩阵,那么(满分:7)A. A的特征值是实数。
B. A有n个线性无关的特征向量。
C. A可能有n+1个线性无关的特征向量。
D. A最多有n个线性无关的特征向量。
正确答案:B8. 题见图片(满分:7)A. AB. BC. CD. D正确答案:D9. 题面见图片(满分:7)A.B.C.D.正确答案:D10. 题面见图片(满分:7)A.B.C.D.正确答案:A二、多选题:1. 题面见图片(满分:6)A. 错误B. 正确正确答案:B2. 若向量组是线性相关的,则必任一向量可由其余向量线性表出(满分:6)A. 错误B. 正确正确答案:A3. 若n阶矩阵A存在一个r阶子式不为零则A的秩必然大于等于r (满分:6)A. 错误B. 正确正确答案:B4. 齐次线性方程组任意两个解之和任然是原方程组的解(满分:6)A. 错误B. 正确正确答案:B5. 正交矩阵的乘积也是正交矩阵(满分:6)A. 错误B. 正确正确答案:B。
线性代数模拟考试题(4套)

线性代数模拟考试题(4套)模拟试题⼀⼀、判断题:(正确:√,错误:×)(每⼩题2分,共10分)1、若B A ,为n 阶⽅阵,则 B A B A +=+. ……………………( )2、可逆⽅阵A 的转置矩阵T A 必可逆. ……………………………( )3、n 元⾮齐次线性⽅程组b Ax =有解的充分必要条件n A R =)(.…( )4、A 为正交矩阵的充分必要条件1-=A A T .…………………………( )5、设A 是n 阶⽅阵,且0=A ,则矩阵A 中必有⼀列向量是其余列向量的线性组合.…………………………………………………………( ) ⼆、填空题:(每空2分,共20分)1、,A B 为 3 阶⽅阵,如果 ||3,||2A B ==,那么 1|2|AB -= .2、⾏列式中元素ij a 的余⼦式和代数余⼦式,ij ij M A 的关系是 .3、在5阶⾏列式中,项5541243213a a a a a 所带的正负号是 .4、已知()??-==256,102B A 则=AB .5、若?--=1225A ,则=-1A . 6、设矩阵--2100013011080101是4元⾮齐次线性⽅程组b Ax =的增⼴矩阵,则b Ax =的通解为 .7、()B A R + ()()B R A R +.8、若*A 是A 的伴随矩阵,则=*AA .9、设=A-500210111t ,则当t 时,A 的⾏向量组线性⽆关.10、⽅阵A 的特征值为λ,⽅阵E A A B 342+-=,则B 的特征值为 . 三、计算:(每⼩题8分,共16分) 1、已知4阶⾏列式1611221212112401---=D ,求4131211132A A A A +-+.2、设矩阵A 和B 满⾜B A E AB +=+2,其中=101020101A ,求矩阵B .四、(10分) 求齐次线性⽅程组=++-=-++=--+-=++-0242205230204321432143214321x x x x x x x x x x x x x x x x 的基础解系和它的通解.五、(10分) 设三元⾮齐次线性⽅程组b Ax =的增⼴矩阵为+-+----22)1)(1()2)(1(00)1(11011λλλλλλλλλλ,讨论当λ取何值时,b Ax =⽆解,有唯⼀解和有⽆穷多解,并在⽆穷多解时求出通解.六、(10分) 判断向量组---=? --=? =? -=1622,4647,3221,1123:4321a a a a A 的线性相关性,如果线性相关,求⼀个最⼤⽆关组,并⽤它表⽰其余向量. 七、综合计算:(本题14分)已知⼆次型31232221321422),,(x x x x x x x x f --+= (1)求⼆次型所对应的矩阵A ,并写出⼆次型的矩阵表⽰;(2)求A 的特征值与全部特征向量;(3)求正交变换PY X =化⼆次型为标准形, 并写出标准形;(4)判断该⼆次型的正定性。
北航考试批次《线性代数》复习题

北航1212考试批次《线性代数》复习题二客观题(总分50分)单项选择题(共10小题,每小题3分,共30分)1设向量组I : ^,二,…,〉r可由向量组II : -1, '2^' , :s线性表示,则()。
A. 当r :: S时,向量组II必线性相关B. 当r s时,向量组II必线性相关C. 当r :: s时,向量组I必线性相关D. 当r s时,向量组I必线性相关2、齐次线性方程组Ax=0与Bx=0同解的充要条件()。
A. r(A)=r(B)B. A,B为相似矩阵C. A, B的行向量组等价D. A,B的列向量组等价3、设A,B均为n阶方阵,则必有()。
A. |A||B 曰B||A|B. | A B|=|A| |B|TC A B A BT T TD. AB A T B T4、下列二次型中,秩为2的二次型是()。
A. x1x2B. x j 4xf -4x1x2C. 2x12D. x j亠x;+ 2x2x35、设入o是矩阵A的特征方程的3重根,A的属于入0的线性无关的特征向量的个数为k,则必有()。
A. k<3B. k w 3C. k=3D. k>36、设非齐次线性方程组A m b中,R A1= r,则()A. r =n时,方程组A m n^ b有唯一解 B . r =m时,方程组A m n x = b有解A.对B .错c . r :: m 时,方程组 A mn x=b 有无穷多解D . m=n 时,方程组 A mn x = b 有唯一解 7、 设A , B 是同阶正交矩阵,则下列命题错误的是(A. A 」也是正交矩阵 B .A 也是正交矩阵C. 8 A. B. AB 也是正交矩阵 设A 、B 都是 A=0 或 B=0 BA=0D. n 阶方阵,若AB=0则(A -B 也是正交矩阵)。
C. |A =0且 | B =0D. IA =o 或 =0 9、 设a 为m n 矩阵,则 n 元齐次线性方程组 Ax = 0存在非零解的充分必要条件是 () A. A 的行向量组线性无关 .A 的行向量组线性相关 C. A 的列向量组线性无关 D. A 的列向量组线性相关 10、二次型 f (X !,X 2,X 3)2X 1X 2 -2X 2X 3的秩等于( A. B. C. D. 0 1 2 3 判断题(共10小题,每小题2分,共20 分) 11、设A 为n 5矩阵,那么秩A = n 。
线性代数练习题及答案10套

1 0 1 14.设矩阵 A= 0 2 0 ,矩阵 B A E ,则矩阵 B 的秩 r(B)= __2__. 0 0 1 0 0 1 B A E = 0 1 0 ,r(B)=2. 0 0 0
15.向量空间 V={x=(x1,x2,0)|x1,x2 为实数}的维数为__2__. 16.设向量 (1,2,3) , (3,2,1) ,则向量 , 的内积 ( , ) =__10__. 17.设 A 是 4×3 矩阵,若齐次线性方程组 Ax=0 只有零解,则矩阵 A 的秩 r(A)= __3__. 18 . 已 知 某 个 3 元 非 齐 次 线 性 方 程 组 Ax=b 的 增 广 矩 阵 A 经 初 等 行 变 换 化 为 :
三、计算题(本大题共 6 小题,每小题 9 分,共 54 分)
Ibugua
交大打造不挂女神的领跑者
123 23 3 21.计算 3 阶行列式 249 49 9 . 367 67 7 123 23 3 100 20 3 解: 249 49 9 200 40 9 0 . 367 67 7 300 60 7
线代练习题及答案(一)
一、单项选择题(本大题共 10 小题,每小题 2 分,共 20 分)
1.设 A 为 3 阶方阵,且 | A | 2 ,则 | 2 A 1 | ( D A.-4 B.-1 C. 1 ) D.4
| 2 A 1 | 2 3 | A | 1 8
1 4. 2
)
1 2 3 1 2 2. 设矩阵 A= (1, 2) , B= C= 则下列矩阵运算中有意义的是 ( B 4 5 6 , 3 4 ,
行成比例值为零.
a1b2 a 2 b2 a 3 b2
线性代数模拟卷3套及答案

试卷编号 1 拟题教研室(或教师)签名 教研室主任签名课程名称(含档次) 线性代数 课程代号 0701011 一、判断题(正确答案填√,错误答案填×。
每小题2分,共10分)1.设阶方阵可逆且满足,则必有 ( )2.设是的解,则是的解 ( )3.若矩阵的列向量组线性相关,则矩阵的行向量组不一定线性相关 ( )4.设表示向量的长度,则 ( )5.设是的解,则是的解 ( ) 二、填空题:(每小题5分,共20分)1.计算行列式 = ;2.若为的解,则或必为 的解;3.设n 维向量组,当时,一定线性 ,含有零向量的向量组一定线性 ;4.设三阶方阵有3个特征值2,1,-2,则的特征值为 ; 三、计算题(每小题10分,共60分)1.;2.若线性方程组有解,问常数应满足的条件?3.设是方程组的解向量,若也是的解,则;4.求齐次线性方程组的基础解系;5.已知矩阵与矩阵相似,求的值;6.设为正定二次型,求.四、证明题(10分):设向量组线性无关,证明线性无关。
n C B A ,,E ABC =E CBA =21,ηη==x x b AX =21ηη+=x b AX =A A x x x x λλ=21,ηη==x x b AX =21ηη-=x 0=AX 231013412-βα,)0(,≠=A b b X βα-αβ-m ααα,,,:21 T n m >T A 2A 2111121111211112⎪⎪⎩⎪⎪⎨⎧=+-=+=+-=+414343232121a x x a x x a x x a x x 4321,,,a a a a s ηηη,,,21 b X =A )0(≠b s s k k k ηηη+++ 2211=+++s k k k 21⎪⎩⎪⎨⎧=++-=++-=++-020332202432143214321x x x x x x x x x x x x ⎪⎪⎭⎫ ⎝⎛=y x A 3122⎪⎪⎭⎫⎝⎛=4321B y x ,3231212322214225x x x x x ax x x x f +-+++=a 321,,ααα321211,,αααααα+++试卷编号 2 拟题教研室(或教师)签名 教研室主任签名 一、判断题:(正确填√,错误填×. 每小题2分,共10分)1.是阶矩阵,则;( )2.若均为阶矩阵,则;( )3.向量组线性相关,则至少含有一个零向量;( )4.若是齐次线性方程组的两个线性无关解向量,则不是的解; ( )5.设为阶矩阵,则与具有相同的特征向量。
线性代数第一章测试题

线性代数第一章测试题1. 向量空间的定义:- 简述向量空间的定义,并给出一个例子。
2. 向量的线性组合:- 解释什么是向量的线性组合,并给出一个具体的例子。
3. 基和维数:- 描述什么是基(Basis)和维数(Dimension),并解释它们之间的关系。
4. 线性相关与线性无关:- 给出线性相关和线性无关的定义,并用一组向量来说明它们。
5. 向量空间的子空间:- 解释什么是向量空间的子空间,并给出一个例子。
6. 线性变换:- 定义线性变换,并给出一个线性变换的例子。
7. 矩阵的秩:- 描述矩阵的秩是什么,并解释如何计算一个矩阵的秩。
8. 行列式:- 解释行列式的概念,并给出计算2x2和3x3矩阵行列式的方法。
9. 逆矩阵:- 定义什么是逆矩阵,并说明一个矩阵何时有逆矩阵。
10. 特征值和特征向量:- 描述特征值和特征向量的概念,并给出一个计算矩阵特征值和特征向量的例子。
11. 线性方程组的解:- 解释线性方程组的解集,并讨论其解的性质。
12. 矩阵的运算:- 给出矩阵加法、乘法和转置的定义,并给出相应的例子。
13. 正交性和正交基:- 解释正交性和正交基的概念,并给出一个正交基的例子。
14. 投影矩阵:- 定义投影矩阵,并说明如何使用它来投影向量。
15. 线性变换的几何解释:- 描述线性变换在几何上的解释,并给出一个具体的例子。
16. 矩阵的分解:- 简述矩阵分解的概念,并给出LU分解和QR分解的例子。
17. 范数:- 解释向量范数的概念,并给出1-范数、2-范数和无穷范数的定义。
18. 线性映射的矩阵表示:- 描述如何将一个线性映射表示为矩阵。
19. 线性代数在实际问题中的应用:- 给出一个实际问题,并展示如何使用线性代数的概念来解决它。
20. 附加题:- 给出一个矩阵,并要求学生找到它的逆矩阵,如果存在的话。
如果不存在,解释为什么。
北京大学《线性代数》六套试卷与答案
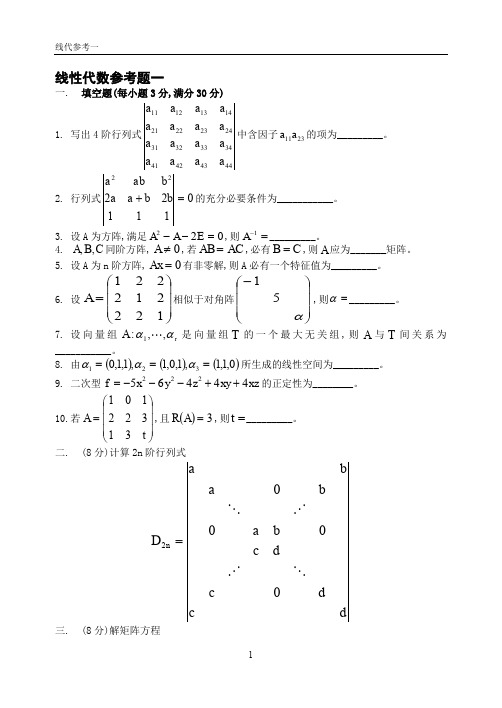
线性代数参考题一一. 填空题(每小题3分,满分30分)1. 写出4阶行列式44434241343332312423222114131211a a a a a a a a a a a a a a a a 中含因子2311a a 的项为_________。
2. 行列式01112222=+b b a a b ab a 的充分必要条件为___________。
3. 设A 为方阵,满足022=--E A A ,则=-1A _________。
4. C B A ,,同阶方阵,0≠A ,若AC AB =,必有C B =,则A 应为_______矩阵。
5. 设A 为n 阶方阵,0=Ax 有非零解,则A 必有一个特征值为_________。
6. 设⎪⎪⎪⎭⎫⎝⎛=122212221A 相似于对角阵⎪⎪⎪⎭⎫⎝⎛-α51,则=α_________。
7. 设向量组r A αα,,:1 是向量组T 的一个最大无关组,则A 与T 间关系为___________。
8. 由()()()0,1,1,1,0,1,1,1,0321===ααα所生成的线性空间为_________。
9. 二次型xz xy z y x f 44465222++---=的正定性为________。
10.若⎪⎪⎪⎭⎫⎝⎛=t A 31322101,且()3=A R ,则=t _________。
二. (8分)计算2n 阶行列式d cdc dc b a ba ba D n 0002=三. (8分)解矩阵方程⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛1302313512343122321X求?=X四. (10分)设向量组A:()()()()3,6,2,0,1,3,0,1,3,1,1,2,0,1,4,14321-=--=--==αααα求向量组A 的秩及一个最大无关组. 五. 12分)讨论方程组的解的情况⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x六. (16分)求正交变换PY X =,将二次型323121232221222222x x x x x x x x x f ---++=化为标准形,并写出其标准形.七. (8分)设n n ααβααβαβ++=+== 121211,,,且n αα,,1 线性无关, 证明:n ββ,,1 线性无关.八. (8分)A 为n 阶方阵,且A 与())1,,2,1(1-=-+n i iE A i均不可逆.则A 可否对角化?线性代数参考题二一、 填空题(每小题3分,满分30分) 1. 设B A ,都是5阶矩阵,且2,31=-=-B A ,则=A B2. 已知0222=++I A A ,则=+-1)(I A (其中I 是n 阶单位阵)3. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=12241031x A 设,已知矩阵A 的秩r(A)=2,则=x4.()814370122222632144-==⨯ija A 设,又ij A 是ij a 的代数余子式,则=+++44434241A A A A5.若一向量组只有唯一的极大无关组,则该向量组6.设3221232221321222),,(x tx x x x x x x x x f ++++=是正定二次型, 则t 的取值区间为7.设A 是n 阶正交矩阵,1-=A ,则()=*TA8.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=20002121x A 相似于对角阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--211,则=x9.设非齐次线性方程组b AX =的两个解为)(,,2121ξξξξ≠A 的秩为1-n ,则 b AX =的一般解=ξ .10.已知向量组[][][]1,4,2,1,0,,0,2,1,1,2,1321--==-=αααt 的秩为2,则=t 二.(8分)计算n 阶行列式ba a a ab a a a a b a D n n n n ---=212121三.(8分)求矩阵X 满足⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎦⎤⎢⎣⎡1041120112201117241X 四.(10分)设[][][][]10,2,1,2,4,1,5,1,3,6,3,11,5,5,10,2,3,2,1,24321-==-=-=αααα求向量组的秩及其一个极大无关组. 五. (12分)问常数b a ,各取何值时, 方程组()()⎪⎪⎩⎪⎪⎨⎧=+++++=++++=+-=+++,5853,34232,12,1432143214324321x a x x x b x x a x x x x x x x x x 无解,有唯一解,或有无穷多解,并在有无穷多解时写出其一般解. 六. (16分)求正交变换PY X =,将二次型()323121232221321222222,,x x x x x x x x x x x x f ---++=化为标准形,并写出其标准形.七. (8分)设向量432,,,1αααα线性无关,且43214432134321243211,,,ββββαββββαββββαββββα+---=-+--=--+-=---=证明向量组4321,,,ββββ线性无关.八. (8分)A 为n 阶方阵,且A 与())1,,2,1(1-=-+n i iI A i均不可逆。
《线性代数》习题集(含答案)

《线性代数》习题集(含答案)第一章【1】填空题 (1) 二阶行列式2a ab bb=___________。
(2) 二阶行列式cos sin sin cos αααα-=___________。
(3) 二阶行列式2a bi b aa bi+-=___________。
(4) 三阶行列式xy zzx y yzx =___________。
(5) 三阶行列式a bc c a b c a bbc a+++=___________。
答案:1.ab(a-b);2.1;3.()2a b -;4.3333x y z xyz ++-;5.4abc 。
【2】选择题(1)若行列式12513225x-=0,则x=()。
A -3;B -2;C 2;D 3。
(2)若行列式1111011x x x=,则x=()。
A -1, B 0, C 1, D 2,(3)三阶行列式231503201298523-=()。
A -70;B -63;C 70;D 82。
(4)行列式00000000a ba b b a ba=()。
A 44a b -;B ()222a b-;C 44b a -;D 44a b 。
(5)n 阶行列式0100002000100n n -=()。
A 0;B n !;C (-1)·n !;D ()11!n n +-•。
答案:1.D ;2.C ;3.A ;4.B ;5.D 。
【3】证明33()by az bz ax bx ay x y z bx ay by az bz ax a b zx y bz ax bx ay by azyzx++++++=++++ 答案:提示利用行列式性质将左边行列式“拆项”成八个三阶行列式之和,即得结果。
【4】计算下列9级排列的逆序数,从而确定他们的奇偶性: (1)134782695;(2)217986354;(3)987654321。
答案:(1)τ(134782695)=10,此排列为偶排列。
(完整版)线性代数习题集带答案

第一部分 专项同步练习第一章 行列式一、单项选择题1.下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)243512.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C)k n -2! (D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( )项.(A) 0 (B)2-n (C) )!2(-n (D) )!1(-n4.=0001001001001000( ).(A) 0 (B)1- (C) 1 (D) 25.=0001100000100100( ).(A) 0 (B)1- (C) 1 (D) 26.在函数1323211112)(x x xxx f ----=中3x 项的系数是( ).(A) 0 (B)1- (C) 1 (D) 27. 若21333231232221131211==a a a a a a a a a D ,则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8.若a a a a a =22211211,则=21112212ka a ka a ( ).(A)ka (B)ka - (C)a k 2 (D)a k 2-9. 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x ( ).(A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ,则D 中第一行元的代数余子式的和为( ). (A)1- (B)2- (C)3- (D)011. 若2235001011110403--=D ,则D 中第四行元的余子式的和为( ). (A)1- (B)2- (C)3- (D)012. k 等于下列选项中哪个值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x kx x kx x kx x x 有非零解.( )(A)1- (B)2- (C)3- (D)0二、填空题1. n 2阶排列)12(13)2(24-n n 的逆序数是.2.在六阶行列式中项261365415432a a a a a a 所带的符号是.3.四阶行列式中包含4322a a 且带正号的项是.4.若一个n 阶行列式中至少有12+-n n 个元素等于0, 则这个行列式的值等于.5. 行列式=100111010100111.6.行列式=-000100002000010n n .7.行列式=--001)1(2211)1(111n n n n a a a a a a .8.如果M a a a a a a a a a D ==333231232221131211,则=---=323233312222232112121311133333 3a a a a a a a a a a a a D .9.已知某5阶行列式的值为5,将其第一行与第5行交换并转置,再用2乘所有元素,则所得的新行列式的值为.10.行列式=--+---+---1111111111111111x x x x .11.n 阶行列式=+++λλλ111111111.12.已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1,则该行列式的值为.13.设行列式5678123487654321=D ,j A 4)4,3,2,1(=j 为D 中第四行元的代数余子式,则=+++44434241234A A A A .14.已知db c a cc a b b a b c a cb a D =, D 中第四列元的代数余子式的和为.15.设行列式62211765144334321-==D ,j A 4为)4,3,2,1(4=j a j 的代数余子式,则=+4241A A ,=+4443A A .16.已知行列式nn D001030102112531-=,D 中第一行元的代数余子式的和为.17.齐次线性方程组⎪⎩⎪⎨⎧=+-=+=++0020232121321x x x kx x x x kx 仅有零解的充要条件是.18.若齐次线性方程组⎪⎩⎪⎨⎧=+--=+=++0230520232132321kx x x x x x x x 有非零解,则k =.三、计算题1.cb a db a dc a dc bd c b a d c ba d cb a++++++++33332222; 2.yxyx x y x y y x y x +++;3.解方程0011011101110=x x xx ; 4.111111321321221221221----n n n n a a a a x a a a a x a a a a xa a a a x ;5. na a a a 111111111111210(n j a j ,,1,0,1 =≠); 6. bn b b----)1(1111211111311117. n a b b b a a b b a a a b 321222111111111; 8.xa a a a x a a a a x a a a a x n nn 321212121;9.2212221212121111nn n nnx x x x x x x x x x x x x x x +++; 10. 21000120000021001210001211.aa a a a a aa a D ---------=110001100011000110001.四、证明题1.设1=abcd ,证明:011111111111122222222=++++dddd c c c c b b b b a a a a .2.3332221112333332222211111)1(c b a c b a c b a x c b x a x b a c b x a x b a c b x a xb a -=++++++.3.))()()()()()((111144442222d c b a c d b d b c a d a c a b d c b a d c b adc b a +++------=.4.∏∑≤<≤=----=nj i i jni innn nn nn n nna aa a a a a a a a a a a a a 1121222212222121)(111.5.设c b a ,,两两不等,证明0111333=c b a c ba 的充要条件是0=++cb a .参考答案一.单项选择题A D A C C D ABCD B B 二.填空题1.n ;2.”“-;3.43312214a a a a ;4.0;5.0;6.!)1(1n n --;7.1)1(212)1()1(n n n n n a a a ---; 8.M 3-; 9.160-; 10.4x ; 11.1)(-+n n λλ; 12.2-;13.0; 14.0; 15.9,12-; 16.)11(!1∑=-nk k n ; 17.3,2-≠k ; 18.7=k三.计算题1.))()()()()()((c d b d b c a d a c a b d c b a ------+++-; 2. )(233y x +-; 3. 1,0,2-=x ; 4.∏-=-11)(n k kax5.)111()1(00∑∏==-+-nk k nk k a a ; 6. ))2(()1)(2(b n b b ---+- ;7. ∏=--nk k kna b1)()1(; 8. ∏∑==-+nk k nk k a x a x 11)()(;9. ∑=+nk k x 11; 10. 1+n ;11. )1)(1(42a a a ++-. 四. 证明题 (略)第二章 矩阵一、单项选择题1. A 、B 为n 阶方阵,则下列各式中成立的是( )。
线性代数模拟试卷及答案4套

线性代数模拟试卷(一)一、 填空题(每小题3分,共6小题,总分18分)1、四阶行列式44434241343332312423222114131211a a a a a a a a a a a a a a a a 展开式中,含有因子3214a a 且带正号的项为___________2、设A 为n 阶可逆方阵,将A 的第i 行和第j 行对换后得到的矩阵记为B ,则AB -1=_________3、已知向量组)2- 5, 4,- ,0( , )0 t,0, ,2( , )1 1,- 2, ,1(321'='='=ααα线性相关,则t =_________4、设三阶方阵) , ,(B ), , ,(2121γγβγγα==A ,其中 , ,,21γγβα都是三维列向量且2B 1, ==A ,则=- 2B A _________5、A 为n 阶正交矩阵, , ,,21n ααα 为A 的列向量组,当i ≠j 时,)21 ,31(j i αα=_________ 6、三阶方阵A 的特征值为1,-2,-3,则 A =_______; E+A -1的特征值为______ 二、 单项选择题(每小题2分,共6小题,总分12分) 1、 设齐次线性方程组AX=0有非零解,其中A=()nn ija ⨯,A ij 为a ij (i,j=1,2,…n) 的代数余子式,则( ) (A)0111=∑=ni i i A a(B)0111≠∑=ni i i A a(C)n A ani i i =∑=111(D)n A ani i i ≠∑=1112、若A -1+ E, E+A, A 均为可逆矩阵,E 为单位矩阵,则(A -1+ E)-1=( ) (A) A+E (B) (A+E)-1 (C) A -1+ E (D) A(A+E)-13、设A, B 为n 阶方阵 ,A*,B*分别为A, B 对应的伴随矩阵,分块矩阵⎪⎪⎭⎫ ⎝⎛=B 00 A C ,则C 的伴随矩阵C* =( )(A) ⎪⎪⎭⎫⎝⎛*A B 0 0 *B A (B) ⎪⎪⎭⎫⎝⎛*B A 0 0 *A B(C) ⎪⎪⎭⎫⎝⎛*B B 0 0 *A A (D) ⎪⎪⎭⎫⎝⎛*A A 0 0 *B B 4、若向量组 , ,,21m ααα 的秩为r ,则( )(A) 必有 r<m (B)向量组中任意小于 r 个向量的部分组线性无关 (C) 向量组中任意 r 个向量线性无关(D) 向量组中任意 r+1个向量必线性相关5、已知 ,,321ααα是四元非齐次线性方程组AX=B 的三个解,且r(A)=3, 已知)3 2, 1, ,0( , )4 3, 2, ,1(321'=+'=ααα,C 为任意常数,则AX=B 通解X=( )(A) ⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛11114321C (B)⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛32104321C(C) ⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛54324321C (D) ⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛65434321C6、设A 为三阶方阵,有特征值λ1=1,λ2= -1, λ3=2,其对应的特征向量分别为 ,,321ααα,记P=(132 ,ααα),则P -1AP=( )(A) ⎪⎪⎪⎭⎫⎝⎛1 2 1- (B)⎪⎪⎪⎭⎫⎝⎛1- 1 2(C) ⎪⎪⎪⎭⎫⎝⎛2 1- 1 (D) ⎪⎪⎪⎭⎫⎝⎛2 1 1-三、计算下列行列式 (12分)1、 D=1- 3 3- 131 1 41- 3 0 5-21- 1 3 2、D n = n1 1 1 1.....................1 1 3 1 111 12 111 1 1 1四、已知A 、B 同为3阶方阵,且满足AB=4A+2B (12分) (1)证明:矩阵A-2E 可逆(2)若B=⎪⎪⎪⎭⎫⎝⎛2 0 00 2 10 2- 1 ,求A五、求向量组 )1 1, 1,- ,1( , )3 2, 1, ,1(21'='=αα, , )6 5, 2,- ,4( , )1 3, 3, ,1( 43'='=αα)7- 4,- 1,- ,3(5'-=α的一个极大无关组,并将其余向量用该极大无关组线性表示(10分)六、已知线性方程组⎪⎪⎩⎪⎪⎨⎧=---=+++-=+-=+-+bx x x x x ax x x x x x x x x x 432143214314321 6 - 17231 4 032 ,讨论参数a 、b 为何值方程组有解,在有解时,求出通解 (12分)七、用正交变换化二次型323121232221321222333),,(x x x x x x x x x x x x f ---++=为标准形,并写出相应的正交变换 (16分)八、已知 ,,,4321αααα是AX = 0的一个基础解系,若322211,ααβααβt t +=+=,144433,ααβααβt t +=+=,讨论t 为何值, ,,,4321ββββ是AX = 0的一个基础解系 (8分)线性代数模拟试卷(二)三、 填空题(每小题3分,共5小题,总分15分)1、j i a a a a a 53544231是五阶行列式展开式中带正号的一项,则i=_____, j=_____2、设n 阶方阵A 满足A 2 =A ,则A+E 可逆且(A+E )-1=_______________(E 为n 阶单位阵)3、已知向量组)0 6, 1,- ,1( , )2k - k,- ,3 ,1( , )2- 2, 1, ,1(321'='='=ααα 若该向量组的秩为2,则k =_________4、已知四阶方阵A 相似于B ,A 的特征值为2,3,4,5,E 是单位阵,则=- E B _________5、 向量α=(4,0,5)′在基)1 ,1- ,1(,)0 ,1 ,1( ,)1 ,2 ,1(321'='='=ηηη下的坐标为_________四、 单项选择题(每小题2分,共5小题,总分10分)1、 设 A 是三阶方阵A 的行列式,A 的三个列向量以γβα ,,表示,则 A =( ) (A)αβγ (B) γβα---(C)αγγββα+++ (D) γβαβαα+++2、设A, B ,C 为n 阶方阵, 若 AB = BA, AC = CA, 则ABC=( ) (A) BCA (B) ACB (C) CBA (D) CAB3、 A, B 均为n 阶方阵, A*为A 的伴随矩阵, 3B 2, -==A ,则21-*B A = ( )(A) 32 12--n (B) 32 1--n (C) 23 12--n (D) 23 1--n4、已知向量组 , ,,4321αααα线性无关,则向量组( ) (A)14433221 , , ,αααααααα++++线性无关(B)14433221 , , ,αααααααα----线性无关(C)14433221 , , ,αααααααα-+++线性无关 (D)14433221 , , ,αααααααα--++线性无关5、若A ~ B ,则 有 ( )(A) A 、B 有相同的特征矩阵 (B) B =A(C) 对于相同的特征值λ,矩阵A 与B 有相同的特征向量 (D) A 、B 均与同一个对角矩阵相似三、计算下列行列式 (13分)2、 D=2- 3 0 112 1 - 121 0 331- 2 1 4、D n = 11 1 111 x 1 1 (1)1 1 1 x 1 1 1 1 x x ++++a)设B= ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1 0 0 01- 1 0 00 1- 1 00 0 1- 1 ,C=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2 0 0 01 2 0 03 12 043 12 ,且矩阵A 满足 E C B C E A =''--)(1, 试将关系式化简并求A (12分)b)求向量组, )4 1,- 2, ,1(1'=α )2 3, 1, ,0( 2'=α, , )14 0, 7, 3,(3'=α , )10 1, 5, 2,( 4'=α)0 2,- 2, ,1(5'=α的一个极大无关组,并将其余向量用该极大无关组线性表示 (13分)六、k 为何值时,线性方程组⎪⎪⎩⎪⎪⎨⎧=+-=++---=+++=+++kx x x x x k x x x x x x x x x x x 9 10 5 - 3)5(2 31 6 3 13 2 4321432143214321 有无穷多个解并求出通解 (14分)七、用正交变换化二次型31232221321422),,(x x x x x x x x f +-+=为标准形,并写出相应的正交变换 (16分)八、若矩阵A=⎪⎪⎪⎭⎫ ⎝⎛0y 10 1- 01 x0 有三个线性无关的特征向量,证明:x – y = 0线性代数模拟试卷(三)一、填空题(每小题3分,共18分)1、A 是三阶方阵,且|A|=6,则 |(3A)-1|= 。
线性代数模拟题及答案

模拟试题一一. 填空题 (将正确答案填在题中横线上。
每小题2分,共10分)1.n 阶行列式D 的值为c, 若将D 的所有元素改变符号, 得到的行列式值为 .2.设矩阵A = ⎪⎪⎪⎭⎫ ⎝⎛101020101 ,矩阵X 满足 E AX + = X A +2 ,则X = ⎪⎪⎪⎭⎫ ⎝⎛2010301023.设n 阶矩阵A 满足 E A A 552+- = 0 ,其中E 为n 阶单位阵,则 1)2(--E A =4.设A ,B 均为3阶方阵,A 的特征值为 1,2,3,则EA +*= .5.当 λ 满足条件 时线性方程组 ⎪⎪⎩⎪⎪⎨⎧=+--=-++-=-++-=+--00004321432143214321x x x x x x x x x x x x x x x x λλλλ 只有零解.二、单项选择题 (每小题仅有一个正确答案, 将正确答案题号填入括号内。
每小题2分,共20分)1.131211232221333231333231232221131211222333 d a a a a a a a a a a a a a a a a a a ---=则=( ).① 6d ② ―6d ③ 4d ④ ―4d 2. 向量组 s ααα,,,21 的秩为s 的充要条件是( )。
① 向量组不含零向量② 向量组没有两个向量的对应分量成比例 ③ 向量组有一个向量不能由其余向量线性表示 ④向量组线性无关3. 当t =( )时,向量组 ),4,5( , )5,2,3( , )0,1,2(321t ===ααα线性相关。
① 5 ② 10③ 15 ④ 204.已知向量组α1,α2,α3线性无关,则向量组( )线性无关。
① α1+2α2+α3, 2α1+4α2+α3, 3α1+6α2 ② α1, α1+α2, α1+α2+α3 ③ α1+α2, α2+α3, α1+2α2+α3 ④ α1-α2, α2-α3, α3-α15. 已知⎪⎪⎪⎭⎫ ⎝⎛---=63322211t A , B 为三阶非零矩阵且AB = 0, 则( ). ① 当t = 4时,B 的秩必为1 ② 当t = 4时,B 的秩必为2 ③ 当t ≠ 4时,B 的秩必为1 ④ 当t ≠ 4时,B 的秩必为26.设非齐次线性方程组A X = b 中未知量个数为n ,方程个数为m ,系数矩阵A 的秩为r ,则 .① r = m 时,方程组A X = b 有解 ② r = n 时,方程组A X = b 有唯一解 ③ m = n 时,方程组A X = b 有唯一解 ④ r < n 时,方程组A X = b 有无穷多解7. 设矩阵A 和B 等价,A 有一个k 阶子式不等于零,则B 的秩( )k.① < ② = ③ ≥ ④ ≤8. 一个向量组的极大线性无关组( ). ① 个数唯一 ② 个数不唯一③ 所含向量个数唯一 ④ 所含向量个数不唯一9. 下列关于同阶不可逆矩阵及可逆矩阵的命题正确的是( ). ① 两个不可逆矩阵之和仍是不可逆矩阵 ② 两个可逆矩阵之和仍是可逆矩阵 ③ 两个不可逆矩阵之积仍是不可逆矩阵 ④ 一个不可逆矩阵与一个可逆矩阵之积必是可逆矩阵10.已知任一n 维向量均可由n ααα,,,21 线性表示,则n ααα,,,21( )。
线性代数模拟试题及答案

班级: 姓名: 学号:131《 线性代数期末模拟试题一 》一、填空(本题20分每小题2分)1.设为四阶行列式,若表示元素的余子式,表示元素的代数余子式,则+= .2.三阶行列式中只有位于两条对角线上的元素均不为零, 则该三阶行列式的所有项中有 项不为零,这一结论对阶行列式(填成立或不成立)。
3.设均为3维列向量,记矩阵记矩阵,若,则。
4.设矩阵,则。
5.设矩阵可逆,且矩阵,所以矩阵一定可以由矩阵经过(填行或列)初等变换而得到.6.设向量组,若 则一定可以由向量唯一的线性表示。
7.非齐次线性方程组有 唯一的解是对应的齐次方程组只有零解的充分但不必要条件。
8.设3阶矩阵的行列式 ,则矩阵一定有一个特征值。
9.阶矩阵有个特征值1,2,,阶矩阵与相似,则. 10.向量组: (填是或不是)向量空间一个规范正交基。
二、单项选择(本题10分,每小题2分)得分阅卷人班级: 姓名: 学号:132注意:请务必将你的选择题的答案按要求填入下表,否则答案无效!1.设矩阵为阶方阵,则关于非齐次线性方程组的解下列说法( )不正确 (A ) 若方程组有解,则系数行列式; (B ) 若方程组无解,则系数行列式;(C ) 若方程组有解,则或者有唯一解或者有无穷多解; (D) 系数行列式是方程组有唯一解的充分必要条件.2。
设为阶可逆矩阵,下列正确的是( ) (A ) ; (B) ; (C ) ;(D ) 。
3。
奇异方阵经过( )后,矩阵的秩有可能改变。
(A ) 初等变换; (B ) 左乘初等矩阵; (C ) 左、右同乘初等矩阵; (D ) 和一个单位矩阵相加。
4.设非齐次线性方程组的系数矩阵是矩阵,且的行向量组线性无关,则有( )。
(A) 的列向量组线性无关;(B) 增广矩阵的行向量组线性无关;(C) 增广矩阵的任意4个列向量组线性无关; (D) 增广矩阵的列向量组线性无关。
5.设是非奇异矩阵的一个特征值,则矩阵有一个特征值为 ( ) (A ) 4/3; (B) 3/4;(C ) 1/2; (D) 1/4。
《线性代数》模拟试卷B及答案

《线性代数》模拟试卷B及答案一、选择题(每小题3分,共30分)(1)若A为4阶矩阵,则|3A|=()(A)4|A| (B) 34|A| (c) 4*1 (D)3|A|(2)设A, B为n阶方阵,AHO且A3 = 0,则()(A)3 = 0 (B)B4 = 0(C) (A + B¥ =A2 + B2(D)|A| = 0或网=0(3)A, B, C均为n阶方阵,则下列命题正确的是()(A) AB = BA(B) A H 0,3 H 0则A3 工0(D)若A3 = AC,贝ijB = C(4) (A + B)2=A2+2AB + B2成立的充要条件是()(A) AB = BA(B) A = E (C)B = E(D)A = B(5)线性方程组伙—l):+2y = :有唯—解,贝%为( )[2x + (k-\)y = b(A)任意实数(B)不等于(C)等于土岳(D)不等于0(6)若A为可逆阵,则⑺丁、()(A)|A|A(B)|A|A*(c)|矿A(D)|A「&(7)含有4个未知数的齐次方程组AX=09如果/?(A) = 1,则它的每个基础解系中解向量的个数(A) 0 (B) 1 (C) 2 (D) 3(8)设A为加X”矩阵,齐次方程组AX=0仅有零解的充要条件是A的()(A)列向量线性无关(B)列向量线性相关(C)行向量线性无关(D)行向量线性相关3已知矩阵A=,下列向量是A的特征向量的是(-1blb2(A)(B)(C)(D)1k°丿a11(10)二次型/(x p x2,x3) = x l2 +4可+4若+2加宀-2%宀+4心疋为正定二次型,的取值范围(A)-2<2<1 (C)-3<2<-2 (D)2>2二、计算题(第1、2小题每题5分, 第3、4小题每题10分,共30分)U计算行列式(5分)2、设A二3<3 r5 ,求A的逆A」。
(5分)3丿10、 (\3>求矩阵方程AX+B = X9其中A= -1 1 1 、B= 2o -1丿〔5 -1、0 o (10 分)一3‘4、求向量组a严(-1 I 4 3)', a2 = (2 -1 3 5)', a3=(l 0 7 8); , a4 = (5 -3 2 7)'的秩,并求出它的一个最大无关组。
线性代数网络教学阶段测试一

线性代数⽹络教学阶段测试⼀⼀、单项选择题(共20题)1.设多项式则f(x)的常数项为()A.4B.1C.-1D.-4【正确答案】A【您的答案】A【答案正确】【答案解析】f(x)=(-1)A12+xA13,故常数项为.2.设A为三阶⽅阵且()A.-108B.-12C.12D.108【正确答案】D【您的答案】A【答案解析】3.设都是三阶⽅阵,且,则下式()必成⽴.【正确答案】B【您的答案】A【答案解析】⽅阵⾏列式的性质4.当a=( )时,⾏列式的值为零。
A.0B.1C.-2C.2【正确答案】C【您的答案】A【答案解析】所以a= -2。
5.设A是n阶⽅阵,λ为实数,下列各式成⽴的是().【正确答案】C【您的答案】A【答案解析】这是⾏列式的性质.6.设⾏列式()A.-3B.-1C.1D.3【正确答案】D【您的答案】A【答案解析】7.⾏列式中第三⾏第⼆列元素的代数余⼦式的值为()A.3B.-2C.0D.1【正确答案】B【您的答案】A【答案解析】8.⾏列式中元素g的代数余⼦式的值为()。
A.bcf-bdeB.bde-bcfC.acf-adeD.ade-acf【正确答案】B【您的答案】A【答案解析】直接计算知应选B9.下列等式成⽴的是(),其中为常数.【正确答案】D【您的答案】A【答案解析】由⾏列式的性质可以判断D正确.10.设()A.k-1B.kC.1【正确答案】B【您的答案】A【答案解析】将所求⾏列的第⼆⾏的-1倍加到第⼀⾏,这样第⼀⾏可以提出⼀个k,就得到k 乘以已知的⾏列式,即为k,本题选B.11.计算四阶⾏列式=( )。
A.(x+3a)(x-a)3B.(x+3a)(x-a)2C.(x+3a)2(x-a)2D.(x+3a)3(x-a)【正确答案】A【您的答案】A【答案正确】【答案解析】12.设=()。
A.-9mB.9mC.mD.3m【正确答案】B【您的答案】A【答案解析】13.设()A.18B.-18C.-6D.6【正确答案】C【您的答案】A【答案解析】将所求⾏列的第⼀⾏的-3倍加到第⼆⾏,第⼆⾏再提出⼀个-1,就得到-1乘以已知的⾏列式,即为-6,本题选C. 14.⾏列式()【正确答案】B【您的答案】A【答案解析】为将负对⾓线上的元素换到主对⾓线上,需将第1与10列对换,2与9列对换,3与8列对换,4与7列对换,5与6列对换,共换5次.15.设某3阶⾏列式︱A︱的第⼆⾏元素分别为-1,2,3,对应的余⼦式分别为-3,-2,1,则此⾏列式︱A︱的值为().A.3B.15C.-10D.8【正确答案】C【您的答案】A【答案解析】16.已知三阶⾏列式D中的第⼆列元素依次为1,2,3,它们的余⼦式分别为-1,1,2,D的值为()A.-3B.-7C.3D.7【正确答案】A【您的答案】A【答案正确】【答案解析】根据⾏列式展开定理,得17.设A为3阶⽅阵,且已知()【正确答案】B【您的答案】A【答案解析】18.下列⾏列式的值为()。
北航线代期末考试模拟题1(含答案)

线性代数期末考试模拟题一一、单项选择题1.设A为3阶方阵, 数λ =-2, |A| =3, 则|λA| =()A.24; B.-24; C.6; D.-6.2.设A为n阶方阵, n1+n2+n3=n, 且|A|≠0, 即123AA AA⎛⎫⎪= ⎪⎪⎝⎭,则A-1=( )A.111213AA AA---⎛⎫⎪= ⎪⎪⎝⎭; B.111213AA AA---⎛⎫⎪= ⎪⎪⎝⎭;C.131211AA AA---⎛⎫⎪= ⎪⎪⎝⎭; D.131211AA AA---⎛⎫⎪= ⎪⎪⎝⎭.3.设A为n阶方阵, A的秩R(A)=r<n, 那么在A的n个列向量中()A.必有r个列向量线性无关;B.任意r个列向量线性无关;C.任意r个列向量都构成最大线性无关组;D.任何一个列向量都可以由其它r个列向量线性表出.4.若方程组AX=0有非零解, 则AX=β(≠0)()A.必有无穷多组解;B.必有唯一解;C.必定没有解;D.A、B、C都不对.5. 设A、B均为3阶方阵, 且A与B相似, A的特征值为1, 2, 3, 则(2B)-1特征值为( )A.2, 1, 32; B.12,14,16; C.1, 2, 3; D.2, 1,23.6. 设A,B为n 阶矩阵,且R(A)=R(B),则()A.AB=BA;B.存在可逆矩阵P, 使P-1AP=B;C .存在可逆矩阵C , 使C T AC =B ;D .存在可逆矩阵P 、Q ,使P AQ =B .7.实二次型()2123222132122,,x x x x x x x x f -++=是( ) A .正定二次型; B .半正定二次型; C .半负定二次型; D .不定二次型.8.设A , B 为满足AB =0的任意两个非零矩阵,则必有( )A .A 的列向量线性相关,B 的行向量线性相关; B .A 的列向量线性相关,B 的列向量线性相关;C .A 的行向量线性相关,B 的行向量线性相关;D .A 的行向量线性相关,B 的列向量线性相关.二、填空题⒈若行列式的每一行(或每一列)元素之和全为零,则行列式的值等于_______________;2.设n 阶矩阵A 满足A 2-2A +3E =O ,则A -1=_______________;3.设1230,3,1,2,1,1,2,4,3,0,7,13TT Tααα⎛⎫⎛⎫⎛⎫==-= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,则321,,ααα的一个最大线性无关组为___________________________;4. 设0γ是非齐次方程组AX =b 的一个解向量,r n -ααα,,,21 是对应的齐次方程组A X =0的一个基础解系,则 0γ,,1α,,2 αr n -α线性__________;5. 设λ1 , λ2 为n 阶方阵A 的两个互不相等的特征值,与之对应的特征向量分别为X 1,X 2,则X 1+X 2_________________________矩阵A 的特征向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北航10秋学期《线性代数》模拟题一
本复习题页码标注所用教材为:
工程数学(线性代数)
魏战线
2000年10月第2版
辽宁大学出版社
如学员使用其他版本教材,请参考相关知识点
一、 单项选择题(本大题共5小题,每小题3分,共15分)
1、 设A 为2008阶可逆方阵,则
()
1
*A -= ( )
A.
()
*1
det A A
B.
()
1
det A A
C.
()
*
1
det A A D. ()11det A A -- 参考答案:B
2、已知x 的一次多项式1
11111111
111101-------=x D ,则式中一次项的系数为( )
(A )4 (B )4- (C )1 (D )1- 参考答案:B
3、 设a 为n m ⨯矩阵,则n 元齐次线性方程组0=Ax 存在非零解的充分必要条件是( )
A .A 的行向量组线性无关
B .A 的行向量组线性相关
C .A 的列向量组线性无关
D .A 的列向量组线性相关 参考答案:C
4、设列向量组321,,ααα,则与三阶行列式|,,|321ααα等值的行列式是( ) (A )|,,|32
1311αααααα+++ (B )|3,,|31332ααααα++
(C )|,,|123ααα (D )|,,|133221αααααα+++
参考答案:C
5、 设A 为3阶矩阵,将A 的第2行加到第1行得B ,再将B 的第1列的-1倍加到第2列得C ,记110010001P ⎛⎫ ⎪
= ⎪ ⎪⎝⎭
,
则( )
A .1
.C P AP -= B .1
.C PAP -= C ..T C P AP = D ..T
C PAP =
参考答案:B
二、 判断题(本大题共5小题,每小题2分,共10分) 6、
A .对
B .错
参考答案:A
7、 两个对称矩阵一定合同。
( )
A .对
B .错
参考答案:B
8、
A .对
B .错
参考答案:A
9、 相似矩阵有相同的特征多项式。
( )
A .对
B .错
参考答案:A
10、
A .对
B .错
参考答案:B
三、填空题(本大题共10小题,每小题3分,共30分)
11、设四阶行列式
3
21421431
432
4321
,ij A 是其()j i ,元的代数余子式,则_______3331=+A A , _______
3432=+A A 。
考核知识点:行列式的概念及计算 ,参见 P35 参考答案:68, -48
12、 设实二次型
()1234,,,f x x x x 的秩为4,正惯性指数为3,则其规范形为 。
考核知识点:惯性定理与二次型的规范形 ,参见 P204
参考答案:2222
1234
z z z z ++- 13、线性方程组⎪⎩⎪
⎨⎧=+-=+-=-+
43030
23
2
1
321
321
ax x x x ax x x x ax 有非零解的充要条件是a 满足._____________ 考核知识点:齐次方程组解的结构 ,参见 P128
参考答案:01753
=--a a
14、 若矩阵20002202A β⎛⎫ ⎪
= ⎪
⎪⎝⎭
正定,则β的取值范围是 。
考核知识点:正定二次型与正定矩阵 ,参见 P205 参考答案:2β>
15、设矩阵A 与⎪⎪⎪⎭
⎫
⎝⎛-=332B 相似,则___________2=-E A , _________||*
=+E A . 考核知识点:相似矩阵 ,参见 P159 参考答案:192, 280
16、设二次型
()22212312312
,,22f x x x x x x x x =+-+的正惯性指数为
p ,负惯性指数为q ,则p q -等
于 。
考核知识点:惯性定理与二次型的规范形 ,参见 P204 参考答案:0
17、将二次型
24
232221964x x x x f +-+=化为2
4232221y y y y f -++=的可逆线性变换为___________. 考核知识点:化二次型为标准型 ,参见 P194
参考答案:⎪⎪⎪⎪
⎪⎭
⎫
⎝⎛⎪⎪⎪⎪⎪⎭⎫
⎝
⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛43
214321010
030000060
0002
x x x x y y y y 18、 设向量α、β的长度依次为2和3,则向量αβ
+与α
β-的内积(,)αβαβ+-= 。
考核知识点: 向量及其运算 ,参见 P79 参考答案:-5
19、已知3阶矩阵
A 的特征值为3,2,1,则E A A 7523+-的特征值为___________,E A A 23*-+的特征值为
___________.
考核知识点:矩阵的特征值 ,参见 P149 参考答案:3,-5,-11; 3,7,13
20、二次型
123422f x x x x =-的规范型为 。
考核知识点:二次型的规范形 ,参见 P204 参考答案:222212342222f y y y y =--+
四、计算题(本大题共5小题,每小题7分,共35分)
21、计算行列式
考核知识点:行列式的定义及计算 ,参见 P34 参考答案:
解:
22、
设3阶方阵A 的三个特征值为1231,0,1λλλ===-,A 的属于123,,λλλ的特征向量依次为1200α⎛⎫ ⎪= ⎪ ⎪⎝⎭,2012α⎛⎫ ⎪
= ⎪ ⎪⎝⎭,3025α⎛⎫
⎪
= ⎪ ⎪⎝⎭
,求方阵A 。
考核知识点: 矩阵的特征值与特征向量 ,参见 P149 参考答案:
23、设矩阵⎪⎪⎪⎭⎫ ⎝⎛--=12422421x A 与⎪⎪⎪⎭
⎫
⎝
⎛-=Λ54y 相似,求y x ,,并求一个正交矩阵P ,使得
Λ=-AP P 1.
考核知识点: 相似矩阵的概念及运算 ,参见 P159 参考答案:
解:由A 与Λ相似知)()(Λ=tr A tr ,即12-=-y x ;又4=λ也是A 的特征值,故04=-E A ,即
05
24
2424
25=---x ,计算得4-=x ,从而5-=y . 当41=λ时,解方程0)4(=-x E A 有,
⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛---=-000120101918091801415242824254E A ,从而有解⎪⎪⎪⎭
⎫ ⎝⎛=2121ξ,单位化得⎪⎪⎪
⎪⎪⎪
⎭
⎫
⎝⎛=3231
321p ;
当52-=λ时,解方程0)5(=+x E A 有
⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛=+0000002124242124245E A ,从而有两个正交解⎪⎪⎪
⎭
⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-=141,10132ξξ,单位化得
⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫
⎝⎛-=231234231,2102132p p ;因此所求得正交矩阵⎪⎪
⎪⎪⎪
⎪⎪⎭
⎫ ⎝
⎛--==2312
132234031
231
21
32
),,(321p p p P . 24、已知非齐次线性方程组
(1) 求方程组系数矩阵A 的秩()r A 。
(2) 求,a b 的值。
考核知识点:非齐次方程组解的结构 ,参见 P137 参考答案:
25、
考核知识点: 齐次方程组解的结构 ,参见 P128
参考答案:
五、证明题(本大题共1小题,每小题10分,共10分)
26、设B 为2≥n 阶矩阵, 证明:1
*
-=n B
B .
考核知识点: 矩阵及行列式的运算,参见 P13,P34 参考答案:
证明:当B 可逆时,1
11
*
---===n n B
B B B
B B ;当0=B 时,有0*
=B ,从而1
*
0-==n B
B ;当0
≠B 且B 不可逆时,有,01
*-===n B B B 否则,*B 必可逆,从而由0*==E B B B 知必有0=B ,与0≠B 矛
盾; 综上所述知结论成立。
