拉普拉斯变换及逆变换
拉普拉斯变换表

拉普拉斯变换表拉普拉斯变换是一种非常重要的数学工具,它在物理、工程、数学、经济等领域均有广泛的应用。
本文将详细介绍拉普拉斯变换的定义、性质、公式表、逆变换及其应用方面的内容。
一、拉普拉斯变换的定义拉普拉斯变换是一种数学工具,用于将一个函数f(t)在复数域上进行变换。
拉普拉斯变换L{f(t)}的定义如下:L{f(t)}=F(s)=∫_0^∞e^(-st)f(t)dt其中,s是复数域上的变量,f(t)是定义在[0,∞)上的函数。
式中的e^-st可以看作是一个因子,它起到了对f(t)作拉普拉斯变换的影响作用。
二、拉普拉斯变换的性质(1)线性性:L{af(t)+bg(t)}=aL{f(t)}+bL{g(t)}其中,a和b为任意常数。
(2)时移性:L{f(t-k)}=e^(-ks)F(s)其中,k为任意实数。
(3)尺度变换:L{f(at)}=1/aF(s/a)其中,a为任意实数,a≠0。
(4)复合性:若F(s)=L{f(t)},G(s)=L{g(t)},则L{f(g(t))}=F(G(s))。
(5)初值定理:lim_(t→0^+)f(t)=lim_(s→∞)sF(s)(6)终值定理:lim_(t→∞)f(t)=lim_(s→0^+)sF(s)三、拉普拉斯变换表以下是一些常用的函数的拉普拉斯变换表。
f(t) F(s)t^n n!/s^(n+1)e^at 1/(s-a)sin(at) a/(s^2+a^2)cos(at) s/(s^2+a^2)1 1/st 1/s^2(t^n)e^at n!/(s-a)^(n+1)u(t-a) e^(-as)/sexp(-at)u(t) 1/(s+a)1-exp(-at)u(t) 1/(s(s+a))1/(a+t) exp(-as)δ(t-a) e^(-as)t^n u(t) n!/s^(n+1)t^n exp(-at)u(t) n!/(s+a)^(n+1)(t^n sin(bt))u(t) nb^s/(s^2+b^2)^(n+1)(t^n cos(bt))u(t) s^n/(s^2+b^2)^(n+1)其中,δ(t)表示狄拉克函数,u(t)即单位阶跃函数。
拉普拉斯变换及反变换

t
重要性质
( t ) f ( t ) dt f ( 0 )
( t ) dt ( t ) dt 1
0
0
L[ ( t )]
(t ) e
st
0
dt ( t ) e
st
dt 1
第7页
黄河科技学院
(5)指数函数
f (t )
控制工程基础
f (t )
(k =const)
0 2 f ( t ) kt 1( t ) 1 2 kt t 2 2 1
0
t0
t
t0
0
t
F ( s ) L [ f ( t )]
( b)
跃函数
坡 函 kt 斜 2 数
0
1
2
e
st
dt
k s
3
F s
的原函数;L是表示进行拉氏变换的 符号。
第2页
黄河科技学院
控制工程基础
F ( s ) L [ f ( t )]
f ( t ) L [ F ( s )]
拉氏变换是这样一种变换,即在一定的 条件下,它能把一实数域中的实变函数 f t 变换为一个在复数域内与之等价的 复变函数 F s 。
控制工程基础
2)当解出s有重根时,对F(s)作因式分解:
F (s) br ( s p1 )
r
b r 1 ( s p1 )
r 1
b1 ( s p1 )
r
a r 1 ( s p r 1 )
拉普拉斯变换及其逆变换表

拉普拉斯变换及其反变换表1.表A-1 拉氏变换的基本性质2.表A-2 常用函数的拉氏变换和z变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n n n 011m 1m m m a s a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==----ΛΛ (m n >)式中系数n 1n 10a ,a ,...,a ,a -,m1m 10b ,b ,b ,b -Λ都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n 1i iin n i i 2211s s c s s c s s c s s c s s c )s (F ΛΛ 式中,Sn 2S 1S ,,,Λ是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算:或式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为 =nni i 1r 1r 111r 11r r 1r s s c s s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++--ΛΛΛ 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算: 原函数)(t f 为ts n 1r i i t s 122r 1r 1r r 1e c e c t c t )!2r (c t )!1r (c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=Λ (F-6)。
拉普拉斯变换及反变换1

——不常用解
方法二: 方法二:查拉氏变换表求解 ——对简单的象函数适用 方法三: 方法三:部分分式法——象函数为有理分式函数时适用
第21页 页
黄河科技学院
控制工程基础
应用部分分式展开式计算拉氏逆变换的 一般步骤 : 的极点; (1)计算有理分式函数F(s)的极点; (2)根据极点把F(s)的分母多项式进行因 式分解、 展开成部分分式; 式分解、并进一步把F(s)展开成部分分式; (3)对F(s)的部分分式展开式两边同时进 行拉氏逆变换。 行拉氏逆变换。
(11)卷积定理 11)
f (t ) * g (t ) = ∫
+∞
−∞
f (τ ) g (t − τ )dτ
= ∫ f (τ ) g (t − τ )dτ
0
t
L[ f (t ) * g (t )] = F ( s ) ⋅ G ( s ) = G ( s ) F ( s )
第19页 页
黄河科技学院
控制工程基础
s +1 c2 = ( s + 3) ( s + 2)( s + 3)
s = −3
(2)对F(s)的分母多项式进行因式分解、并把 (s)展开 ) ( )的分母多项式进行因式分解、并把F( ) 成部分分式
=2
第24页 页
黄河科技学院
控制工程基础
s +1 1 2 F ( s) = 2 =− + s + 5s + 6 s+2 s+3
− st
单位阶跃函数,记作 单位阶跃函数,记作1( t )
t<0 t≥0
1 L[1(t )] = s
拉普拉斯变换及逆变换

第十二章 拉普拉斯变换及逆变换拉普拉斯(Laplace)变换就是分析与求解常系数线性微分方程得一种简便得方法,而且在自动控制系统得分析与综合中也起着重要得作用。
我们经常应用拉普拉斯变换进行电路得复频域分析。
本章将扼要地介绍拉普拉斯变换(以下简称拉氏变换)得基本概念、主要性质、逆变换以及它在解常系数线性微分方程中得应用。
第一节 拉普拉斯变换在代数中,直接计算328.957812028.6⨯⨯=N 53)164.1(⨯就是很复杂得,而引用对数后,可先把上式变换为164.1lg 53)20lg 28.9lg 5781(lg 3128.6lg lg ++-+=N然后通过查常用对数表与反对数表,就可算得原来要求得数N 。
这就是一种把复杂运算转化为简单运算得做法,而拉氏变换则就是另一种化繁为简得做法。
一、拉氏变换得基本概念定义12、1 设函数()f t 当0t ≥时有定义,若广义积分()pt f t e dt +∞-⎰在P 得某一区域内收敛,则此积分就确定了一个参量为P 得函数,记作()F P ,即dte tf P F pt ⎰∞+-=)()( (12、1)称(12、1)式为函数()f t 得拉氏变换式,用记号[()]()L f t F P =表示。
函数()F P 称为()f t 得拉氏变换(Laplace) (或称为()f t 得象函数)。
函数()f t 称为()F P 得拉氏逆变换(或称为()F P 象原函数),记作)()]([1t f P F L =-,即)]([)(1P F L t f -=。
关于拉氏变换得定义,在这里做两点说明:(1)在定义中,只要求()f t 在0t ≥时有定义。
为了研究拉氏变换性质得方便,以后总假定在0t <时,()0f t =。
(2)在较为深入得讨论中,拉氏变换式中得参数P 就是在复数范围内取值。
为了方便起见,本章我们把P 作为实数来讨论,这并不影响对拉氏变换性质得研究与应用。
函数的拉普拉斯变换与逆变换

函数的拉普拉斯变换与逆变换定义函数f(t)的拉普拉斯变换定义为:F(s)=∫e−st∞f(t)dt其中s是一个复数变量。
性质拉普拉斯变换具有以下性质:1.线性性:对于任意常数a和b,以及函数f(t)和g(t),有:L[af(t)+bg(t)]=aL[f(t)]+bL[g(t)]2.时移性:对于任意常数a,有:L[f(t−a)u(t−a)]=e−as F(s)其中u(t)是单位阶跃函数。
3.微分性:对于任意可导函数f(t),有:L[f′(t)]=sF(s)−f(0)L[f″(t)]=s2F(s)−sf(0)−f′(0)4.积分性:对于任意可积函数f(t),有:L[∫ft0(τ)dτ]=F(s)s5.卷积定理:对于任意两个函数f(t)和g(t),有:L[f(t)∗g(t)]=F(s)G(s)其中∗表示卷积运算。
应用拉普拉斯变换在许多领域都有应用,包括:1.微分方程的求解:拉普拉斯变换可以将微分方程转化为代数方程,从而更容易求解。
2.信号处理:拉普拉斯变换可以用于分析和处理信号。
3. 控制理论:拉普拉斯变换可以用于分析和设计控制系统。
4. 电路分析:拉普拉斯变换可以用于分析和设计电路。
逆拉普拉斯变换拉普拉斯变换的逆变换定义为:f (t )=12πi ∫e st γ+i∞γ−i∞F (s )ds 其中 γ 是一个大于所有 F (s ) 的奇点实部的常数。
性质逆拉普拉斯变换具有以下性质:1. 线性性:对于任意常数 a 和 b ,以及函数 f (t ) 和 g (t ),有:L −1[aF (s )+bG (s )]=aL −1[F (s )]+bL −1[G (s )]2. 时移性:对于任意常数 a ,有:L −1[e as F (s )]=f (t −a )u (t −a )3. 微分性:对于任意可导函数 F (s ),有:L −1[sF (s )]=f′(t )L −1[s 2F (s )]=f″(t )4. 积分性:对于任意可积函数 F (s ),有:L −1[F (s )s ]=∫f t 0(τ)dτ 5. 卷积定理:对于任意两个函数 F (s ) 和 G (s ),有:L −1[F (s )G (s )]=f (t )∗g (t )应用逆拉普拉斯变换在许多领域都有应用,包括:1. 微分方程的求解:逆拉普拉斯变换可以将代数方程转化为微分方程,从而更容易求解。
(完整版)拉普拉斯变换及其逆变换表
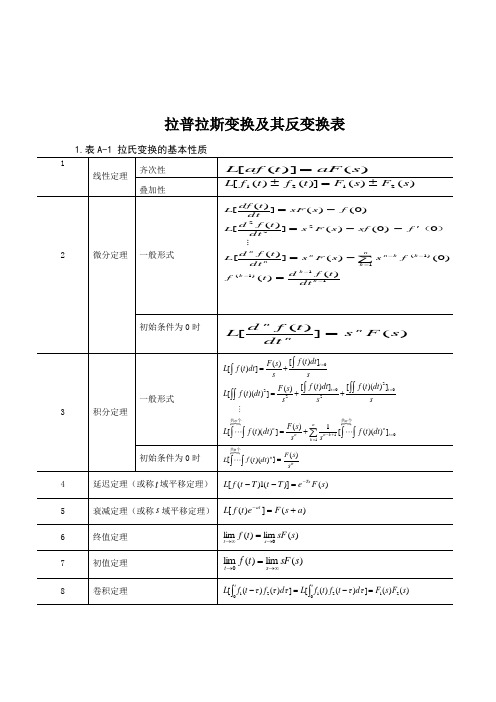
拉普拉斯变换及其反变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >)式中系数n1n 1a ,a ,...,a ,a-,m1m 1b ,b ,b ,b - 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )s (F )s s (lim c is s i-=→或is s i)s (A )s (B c='=式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数[]t s n 1i i n 1i i i 11i e c s s cL )s (F L )t (f -==--∑∑=⎥⎦⎤⎢⎣⎡-==② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为())s s ()s s ()s s ()s (B s F n1r r 1---=+=nnii1r 1r 111r 11r r 1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:)s (F )s s (lim c r1s s r-=→)]s (F )s s ([dsdlim c -=)s (F )s s (dsd lim !j 1c -=)s (F )s s (dsdlim )!1r (1c --=原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=s s cs s c s s c )s s (c )s s (c )s s (c L e c e c t c t )!2r (c t )!1r (c ∑+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)。
拉氏变换及反变换
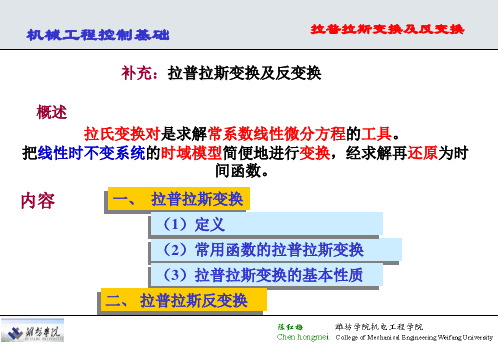
2. f (t) eatu(t) (指数函数)
f
(t)
0
(t 0)
et (t 0)
F(s)= ℒ [eat ] eatestdt 0 ℒ [ejt ] 1 s j
1
e(sa)t
sa
0
1 sa
机械工程控制基础
拉普拉斯变换及反变换
3. f (t) (t) (单位脉冲函数)
(t)
t
s0
机械工程控制基础
拉普拉斯变换及反变换
例1
u(t) t0
lim s 1 s s
1
例2 I(s) 5 2 s1 s2
i(0 ) lim s( 5 2 ) lim( 5 2 ) 3 s s 1 s 2 s 1 1/ s 1 2 / s
例3
I (s) ℒ [1 e-t ] 1 1 s s1
Ui(s) H(s) I(s)
I(s)=Ui(s)H(s)= ℒ[ui(t)] H(s)
=ℒ eat (t)
(5)作Laplace反变换得
1 R Ls
s
1
a
1 L
s
1 R
L
零状态响应电流
i(t)= ℒ-1[I(s)]
1
(e a t
Rt
e L )
(t)
L ( R a)
L
机械工程控制基础
拉普拉斯变换及反变换
的
拉
t
1/s2
普 拉
n!
tn
sn+1
1
斯
e-at
s+a
变 换
1
te-at
(s+a)2
表
tne-at
n!
(s+a)n+1
拉普拉斯变换及逆变换

第十二章拉普拉斯变换及逆变换拉普拉斯(Laplace)变换是分析和求解常系数线性微分方程的一种简便的方法,而且在自动控制系统的分析和综合中也起着重要的作用。
我们经常应用拉普拉斯变换进行电路的复频域分析。
本章将扼要地介绍拉普拉斯变换(以下简称拉氏变换)的基本概念、主要性质、逆变换以及它在解常系数线性微分方程中的应用。
第一节拉普拉斯变换(3)拉氏变换是将给定的函数通过广义积分转换成一个新的函数,它是一种积分变换。
一般来说,在科学技术中遇到的函数,它的拉氏变换总是存在的。
例12.1求斜坡函数()f t at =(0t ≥,a 为常数)的拉氏变换。
解:0000[]()[]pt ptpt pt a a a L at ate dt td e e e dt p p p +∞+∞+∞---+∞-==-=-+⎰⎰⎰二、单位脉冲函数及其拉氏变换在研究线性电路在脉冲电动势作用后所产生的电流时,要涉及到我们要介绍的脉冲函数,在原来电流为零的电路中,某一瞬时(设为0t =)进入一单位电量的脉冲,现要确定电路上的电流()i t ,以()Q t 表示上述电路中的电量,则 由于电流强度是电量对时间的变化率,即t t Q t t Q dt t dQ t i t ∆∆∆)()(lim)()(0-+==→,所以,当0t ≠时,()0i t =;当0t =时,0000→→→→εεεε,即1)]([=t L δ。
例12.3现有一单位阶跃输入0,()1,t u t t <⎧=⎨≥⎩,求其拉氏变换。
解:00011[()]()1[]pt pt pt L u t u t e dt e dt e p p+∞+∞---+∞===-=⎰⎰,(0)p >。
例12.4求指数函数()at f t e =(a 为常数)的拉氏变换。
解:()001[]atat ptp a t L e e e dt e dt p a+∞+∞---===-⎰⎰,()p a >,即类似可得22[sin ](0)L t p p ωωω=>+;22[cos ](0)pL t p p ωω=>+。
常见的拉普拉斯变换公式

常见的拉普拉斯变换公式拉普拉斯变换公式是数学中的一种重要工具,它在信号与系统、电路分析、控制理论等领域有着广泛的应用。
通过将一个函数或信号从时间域转换到复频域,拉普拉斯变换可以简化复杂的微分方程求解和系统分析问题。
以下是常见的拉普拉斯变换公式及其应用。
1. 原函数定义公式:拉普拉斯变换的第一个公式是原函数定义公式,用于将一个函数从时间域表示转换为复频域表示。
假设函数为f(t),其拉普拉斯变换为F(s),则原函数定义公式为:F(s) = L{f(t)} = ∫[0,∞] f(t)e^(-st) dt其中,s为复变量,表示函数在复频域的频率。
2. 常见的拉普拉斯变换公式:拉普拉斯变换公式包括了一系列常见函数的变换结果,以下是其中的几个常见公式及其应用:- 常数函数:L{1} = 1/s,常数函数在拉普拉斯变换后变为1除以复变量s。
- 单位阶跃函数:L{u(t)} = 1/s,单位阶跃函数在拉普拉斯变换后变为1除以复变量s。
- 指数函数:L{e^(at)} = 1/(s-a),指数函数在拉普拉斯变换后变为1除以复变量s减去常数a。
- 正弦函数:L{sin(at)} = a/(s^2 + a^2),正弦函数在拉普拉斯变换后变为常数a除以复变量s的平方加上a的平方。
- 余弦函数:L{cos(at)} = s/(s^2 + a^2),余弦函数在拉普拉斯变换后变为复变量s除以复变量s的平方加上a的平方。
3. 拉普拉斯变换的性质:拉普拉斯变换具有一系列的性质,这些性质可以方便地应用于信号处理和系统分析中。
以下是常见的拉普拉斯变换性质:- 线性性质:L{af(t) + bg(t)} = aF(s) + bG(s),其中a和b为常数,f(t)和g(t)为函数,F(s)和G(s)为它们的拉普拉斯变换。
- 平移性质:L{f(t-a)u(t-a)} = e^(-as)F(s),其中a为常数,f(t)为函数,u(t)为单位阶跃函数,F(s)为f(t)的拉普拉斯变换。
拉普拉斯变换及其逆变换表

拉普拉斯变换及其反变换表1线性定理齐次性)()]([s aF t af L =叠加性)()()]()([2121s F s F t f t f L ±=±2微分定理一般形式=-=]['- -=-=----=-∑11)1()1(1222)()()0()()(0)0()(])([)0()(])([k k k k nk kn n nndt t f d t f fss F s dt t f dL f sf s F s dtt f d L f s sF dtt df L )(初始条件为0时)(])([s F sdt t f dL nnn=3积分定理一般形式∑⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰==+-===+=++=+=nk t n n k n n nn t t t dt t f s s s F dt t f L sdt t f s dt t f s s F dt t f L sdt t f s s F dt t f L 101022022]))(([1)(])()([]))(([])([)(]))(([])([)(])([个共个共初始条件为0时n n n ss F dt t f L )(]))(([=⎰⎰个共4 延迟定理(或称t 域平移定理) )()](1)([s F e T t T t f L Ts -=--5 衰减定理(或称s 域平移定理) )(])([a s F e t f L at +=-6 终值定理 )(lim )(lim 0s sF t f s t →∞→=7 初值定理 )(lim )(lim 0s sF t f s t ∞→→=8卷积定理)()(])()([])()([21021021s F s F d t f t f L d f t f L tt =-=-⎰⎰τττττ1序号拉氏变换F(s)时间函数f(t) Z 变换F(z)1 1δ(t) 12 Tse--11∑∞=-=0)()(n T nT t t δδ1-z z 3 s1 )(1t1-z z 4 21s t2)1(-z Tz5 31s 22t32)1(2)1(-+z z z T6 11+n s!n t n)(!)1(lim 0aTn n n a e z z a n -→-∂∂- 7 as +1 at e - aTe z z-- 8 2)(1a s +atte-2)(aT aT e z Tze ---9 )(a s s a+ at e --1))(1()1(aT aT e z z z e ----- 10 ))((b s a s ab ++-btatee---bTaT e z ze z z ----- 11 22ωω+s t ωsin1cos 2sin 2+-T z z Tz ωω12 22ω+s st ωcos1cos 2)cos (2+--T z z T z z ωω 13 22)(ωω++a s t e atωsin - aTaT aT e T ze z Tze 22cos 2sin ---+-ωω 14 22)(ω+++a s a st eatωcos -aTaT aT e T ze z T ze z 222cos 2cos ---+--ωω15aT s ln )/1(1- T t a /az z -23. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
拉普拉斯变换及其逆变换表
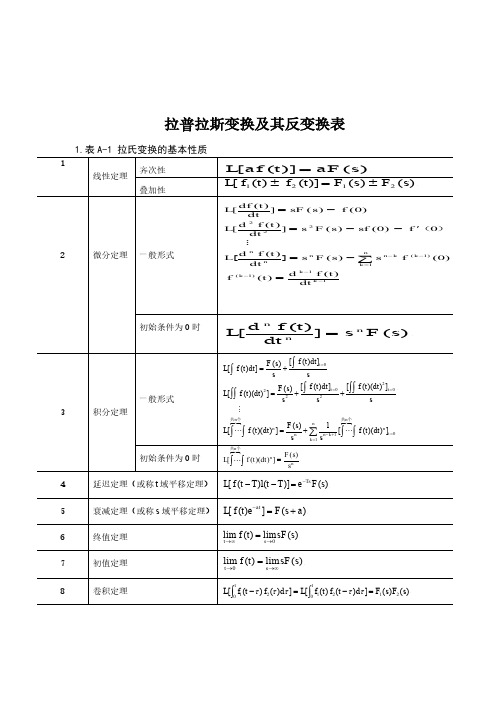
n
F ( s)
L[ f (t )dt ]
一般形式 3 积分定理
L[ f (t )(dt ) 2 ]
共n个
2 F ( s ) [ f (t )dt ]t 0 [ f (t )(dt ) ]t 0 s2 s2 s
共n个 F ( s) n 1 n L[ f (t )(dt ) ] n n k 1 [ f (t )(dt ) n ]t 0 s k 1 s
B( s ) b s b s b s b F (s ) A(s ) a s a s a s a
m m 1 m m 1 1 n n 1 n n 1 1 0
0
(n m)
式中系数 a
0
, a ,..., a , a , b , b ,b , b 都是实常数; m, n 是正整数。按
1(t )
z z 1
1 s2
1 s3
t
t2 2
Tz ( z 1) 2
T 2 z ( z 1) 2( z 1) 3
1 s n 1
1 sa
tn n!
lim
( 1) n n z ( ) n a 0 n! a z e aT
z z e aT
e at te
at
拉普拉斯变换及其反变换表表a1拉氏变换的基本性质1线性定理齐次性叠加性2微分定理一般形式初始条件为0时3积分定理一般形式初始条件为0时4延迟定理或称域平移定理5衰减定理或称域平移定理6终值定理7初值定理8卷积定理2
拉普拉斯变换及其反变换表
1.表 A-1 拉氏变换的基本性质
1 线性定理 齐次性 叠加性
c c t t c t c e c e (r 2)! (r 1)!
电路原理第九章拉普拉斯变换

利用拉普拉斯变换,通过计算系统的极点和零点,判 断系统的稳定性。
电路系统的频率响应分析
频率响应定义
电路系统在不同频率下的输入与输出关系称为频率响应。
频率响应分析方法
通过拉普拉斯变换将时域函数转换为复频域函数,进而分析频率 响应。
频率响应特性
频率响应具有幅度和相位特性,这些特性决定了电路系统在不同 频率下的性能表现。
到该函数的拉普拉斯变换。
拉普拉斯变换具有线性性和时移性等性质,使得复杂电路的分
03
析变得简单。
拉普拉斯变换的性质
1 2 3
线性性
如果函数$f(t)$和$g(t)$的拉普拉斯变换分别为 $F(s)$和$G(s)$,那么对于任意实数$k$和$l$, 有$(kf(t)+lg(t))的拉普拉斯变换=kF(s)+lG(s)$。
04
拉普拉斯变换的逆变换
逆变换的定义和性质
逆变换的定义
如果一个函数f(t)的拉普拉斯变换存在,那么就存在另一个函数g(s)的拉普拉斯 变换等于f(t),并且g(s)可以通过一定的积分运算从f(t)得到,这个过程就是逆 变换。
逆变换的性质
逆变换具有线性、时移、频移、微分、积分等性质,这些性质在求解逆变换时 非常有用。
时移性
如果函数$f(t)$的拉普拉斯变换为$F(s)$,那么 对于任意实数$a$,有$(f(t-a))的拉普拉斯变换 =e^{-as}F(s)$。
频移性
如果函数$f(t)$的拉普拉斯变换为$F(s)$,那么 对于任意实数$b$,有$(f(t)e^{bt})的拉普拉斯 变换=F(s-b)$。
拉普拉斯变换的应用
拉普拉斯变换的微分性质
微分性质
如果函数f(t)的拉普拉斯变换存在,那么对于实数a,函数f''(t)的拉普拉斯变换等于函数f(t)的拉普拉斯变换乘以 s^2。
拉普拉斯变换及反变换

初值定理 若ℒ [f(t)]=F(s),且 f(t)在t = 0处无冲激,
则 f (0 ) lim f (t) lim sF (s)
t 0
s
终值定理 f(t)及其导数f (t)可进行拉氏变换,且
lim f (t)存在时
t
f () lim f (t) lim sF(s)
t
s0
例1
u(t)t0
k2(2 ss1)52(s1)2S13 k1dds(2s5)S12
f(t)L1[F(s])2et3tet t0
例2
F(s)
s2 2s2 (s2)3
k1 (s2)
(s k22)2(s k32)3
等式两边乘 (s 2)3
F(s)(s 2)3 k1(s 2)2 k2 (s 2) k3
k3s2(s22 s)32(s2)3S22
lims11 s s
例2 I(s) 5 2 s1 s2
i( 0 ) lis ( m 52) li(m 52) 3 s s 1s 2s 1 1 /s1 2 /s
例3
I(s)ℒ [1e-t]1 1 s s1
11 i(t)t ls i0m s(ss1)1
例4:已知F(s)= 1 ,求f(0)和f(∞) sa
拉普拉斯变换的基本性质表
本讲小结: 拉普拉斯变换定义 常用函数的拉普拉斯变换
拉普拉斯变换的基本性质
(1)
利用 ℒ
• 作业
1、 写出拉普拉斯变换定义式 2、
__
1
(s-1)2
二、拉普拉斯反变换
1、由象函数求原函数 f(t)=L-1[F(s)]
(1)利用公式
f(t) 1 2πj
(S2+a1S+a0)R(S)-(S+a1)r(0-)-r/(0-)=(Sb1+b0)E(s)-b1×0
拉普拉斯变换及其逆变换表-资料类

拉普拉斯变换及其逆变换表-资料类关键信息项:1、拉普拉斯变换及其逆变换表的使用范围:____________________________2、拉普拉斯变换及其逆变换表的版权归属:____________________________3、资料的获取方式:____________________________4、资料的使用限制:____________________________5、对资料准确性的声明:____________________________6、违反协议的责任:____________________________1、协议背景11 本协议旨在规范关于拉普拉斯变换及其逆变换表(以下简称“资料”)的使用、传播和相关责任。
2、资料描述21 本协议所涉及的资料是指包含拉普拉斯变换及其逆变换相关公式、示例和解释的表格及相关文字说明。
3、使用范围31 资料仅限于学术研究、教育教学和个人学习使用。
32 禁止将资料用于商业盈利目的,包括但不限于出售、出租或以资料获取直接经济利益。
4、版权归属41 资料的版权归原作者或相关合法拥有者所有。
42 未经版权所有者明确书面许可,不得对资料进行修改、改编、翻译或创建衍生作品。
5、资料获取方式51 资料可通过合法的学术数据库、教育网站或经授权的渠道获取。
52 不得通过非法手段获取资料,如黑客攻击、网络窃取等。
6、资料使用限制61 使用者不得大量复制和分发资料,以免造成版权侵权和不正当竞争。
62 在引用资料中的内容时,应按照学术规范和版权法的要求进行正确的引用和标注。
7、对资料准确性的声明71 提供者尽力确保资料的准确性和可靠性,但不对资料中的任何错误或疏漏承担法律责任。
72 使用者在使用资料时应自行进行核实和验证,对因依赖资料而产生的任何损失或后果自行负责。
8、违反协议的责任81 若使用者违反本协议的任何条款,应承担相应的法律责任,包括但不限于停止侵权行为、赔偿损失、承担法律诉讼费用等。
拉普拉斯变换及其逆变换表
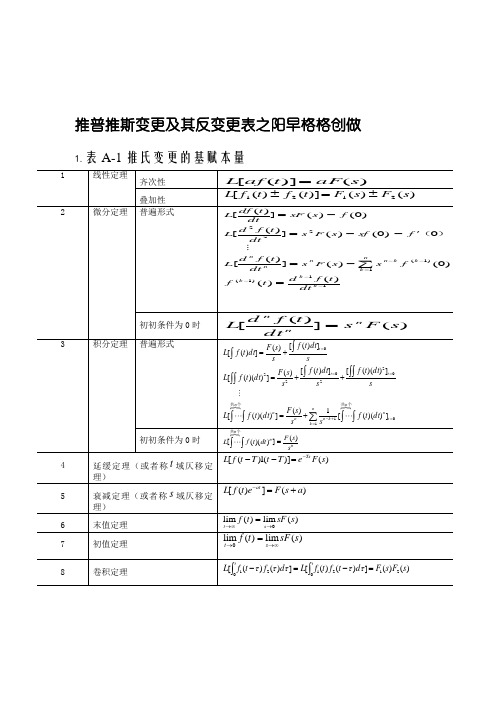
推普推斯变更及其反变更表之阳早格格创做1.表A-1 推氏变更的基赋本量2.表A-2 时常使用函数的推氏变更战z变更表3. 用查表法举止推氏反变更用查表法举止推氏反变更的闭键正在于将变更式举止部分分式展启,而后逐项查表举止反变更.设)(s F 是s 的有理真分式11n 1n nn11m 1m mma s a s a s ab s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >)式中系数n1n 1a ,a ,...,a ,a -,m1m 1b ,b ,b ,b - 皆是真常数;n m ,是正整数.按代数定理可将)(s F 展启为部分分式.分以下二种情况计划.①0)(=s A 无沉根那时,F(s)可展启为n 个简朴的部分分式之战的形式.∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,,是特性圆程A(s)=0的根.i c 为待定常数,称为F(s)正在i s 处的留数,可按下式估计:或者式中,)(s A '为)(s A 对于s 的一阶导数.根据推氏变更的本量,从式(F-1)可供得本函数 ② 0)(=s A 有沉根设0)(=s A 有r 沉根1s ,F(s)可写为=nnii1r 1r 111r 11r r1rs s cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++--式中,1s 为F(s)的r 沉根,1+r s ,…,n s 为F(s)的n-r 个单根;其中,1+r c ,…,n c 仍按式(F-2)或者(F-3)估计,r c ,1-r c ,…,1c 则按下式估计: 本函数)(t f 为ts n1r i its 122r 1r 1r r1ec e c t c t )!2r (c t )!1r (c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章 拉普拉斯变换及逆变换拉普拉斯(Laplace)变换是分析和求解常系数线性微分方程的一种简便的方法,而且在自动控制系统的分析和综合中也起着重要的作用。
我们经常应用拉普拉斯变换进行电路的复频域分析。
本章将扼要地介绍拉普拉斯变换(以下简称拉氏变换)的基本概念、主要性质、逆变换以及它在解常系数线性微分方程中的应用。
第一节 拉普拉斯变换在代数中,直接计算328.957812028.6⨯⨯=N 53)164.1(⨯是很复杂的,而引用对数后,可先把上式变换为164.1lg 53)20lg 28.9lg 5781(lg 3128.6lg lg ++-+=N然后通过查常用对数表和反对数表,就可算得原来要求的数N 。
这是一种把复杂运算转化为简单运算的做法,而拉氏变换则是另一种化繁为简的做法。
一、拉氏变换的基本概念定义12.1 设函数()f t 当0t ≥时有定义,若广义积分()pt f t e dt +∞-⎰在P 的某一区域内收敛,则此积分就确定了一个参量为P 的函数,记作()F P ,即dte tf P F pt ⎰∞+-=)()( (12.1)称(12.1)式为函数()f t 的拉氏变换式,用记号[()]()L f t F P =表示。
函数()F P 称为()f t 的拉氏变换(Laplace) (或称为()f t 的象函数)。
函数()f t 称为()F P 的拉氏逆变换(或称为()F P 象原函数),记作 )()]([1t f P F L =-,即)]([)(1P F L t f -=。
关于拉氏变换的定义,在这里做两点说明:(1)在定义中,只要求()f t 在0t ≥时有定义。
为了研究拉氏变换性质的方便,以后总假定在0t <时,()0f t =。
(2)在较为深入的讨论中,拉氏变换式中的参数P 是在复数范围内取值。
为了方便起见,本章我们把P 作为实数来讨论,这并不影响对拉氏变换性质的研究和应用。
(3)拉氏变换是将给定的函数通过广义积分转换成一个新的函数,它是一种积分变换。
一般来说,在科学技术中遇到的函数,它的拉氏变换总是存在的。
例12.1 求斜坡函数()f t at = (0t ≥,a 为常数)的拉氏变换。
解:0000[]()[]pt ptpt pt a a a L at ate dt td e e e dt p p p +∞+∞+∞---+∞-==-=-+⎰⎰⎰ 2020][0p a e p a dt e pa pt pt =-=+=∞+-∞+-⎰)0(>p二、单位脉冲函数及其拉氏变换在研究线性电路在脉冲电动势作用后所产生的电流时,要涉及到我们要介绍的脉冲函数,在原来电流为零的电路中,某一瞬时(设为0t =)进入一单位电量的脉冲,现要确定电路上的电流()i t ,以()Q t 表示上述电路中的电量,则⎩⎨⎧=≠=.0,1,0,0)(t t t Q由于电流强度是电量对时间的变化率,即t t Q t t Q dt t dQ t i t ∆∆∆)()(lim )()(0-+==→,所以,当0t ≠时,()0i t =;当0t =时,∞=-=-+=→→)1(lim )0()0(lim )0(00t t Q t Q i t t ∆∆∆∆∆。
上式说明,在通常意义下的函数类中找不到一个函数能够用来表示上述电路的电流强度.为此,引进一个新的函数,这个函数称为狄拉克函数。
定义12.2设0,01(),00,t t t t εδεεε<⎧⎪⎪=≤≤⎨⎪>⎪⎩,当0ε→时,()t εδ的极限0()lim ()t t εεδδ→=称为狄拉克(Dirac )函数,简称为δ-函数。
当0t ≠时,()t δ的值为0;当0t =时,()t δ的值为无穷大,即0,0(),0t t t δ≠⎧=⎨∞=⎩。
显然,对任何0ε>,有01()1t dt dt εεδε+∞-∞==⎰⎰,所以()1t dt δ+∞-∞=⎰。
工程技术中,常将δ-函数称为单位脉冲函数,有些工程书上,将δ-函数用一个长度等于1的有向线段来表示,这个线段的长度表示δ-函数的积分,叫做δ-函数的强度。
例12.2 求单位脉冲信号()t δ的拉氏变换。
解:根据拉氏变换的定义,有dte dt edt edt et t L pt ptptpt-→∞+-→-→∞+-⎰⎰⎰⎰=⋅+==εεεεεεεεδδ01lim0lim)1lim()()]([11lim 1)()1(lim 11lim 1][1lim 00000==''-=-=-=-→-→-→-→εεεεεεεεεεεp p p pt pe p e p e p p e ,即1)]([=t L δ。
例12.3 现有一单位阶跃输入0,0()1,t u t t <⎧=⎨≥⎩,求其拉氏变换。
解:00011[()]()1[]ptpt pt L u t u t edt e dt e p p+∞+∞---+∞===-=⎰⎰g ,(0)p >。
例12.4 求指数函数()atf t e =(a 为常数)的拉氏变换。
解:()01[]atat ptp a t L e e edt e dt p a+∞+∞---===-⎰⎰g ,()p a >,即)(1][a p a p e L at >-=类似可得22[sin ](0)L t p p ωωω=>+;22[cos ](0)pL t p p ωω=>+。
三、拉氏变换的性质拉氏变换有以下几个主要性质,利用这些性质,可以求一些较为复杂的函数的拉氏变换。
性质12.1 (线性性质) 若1a ,2a 是常数,且11[()]()L f t F p =,22[()]()L f t F p =,则)]([)]([)]()([22112211t f L a t f L a t f a t f a L +=+)()(2211p F a P F a += (12.2)证明:dte tf a dt et f a dt et f a t f a t f a t f a L pt ptpt-∞+-∞+-∞+⎰⎰⎰+=+=+)()()]()([)]()([02211221102211 )()()]([)]([22112211p F a p F a t f L a t f L a +=+=例12.5 求函数1()(1)at f t e a-=-的拉氏变换 解:)(1}11{1]}[]1[{1]1[1)]1(1[a p p a p p a e L L a e L a e a L at at at +=+-=-=-=---- 性质12.2(平移性质) 若[()][]L f t F p =,则[()]()atL e f t F p a =-(a 为常数) (12.3)证明:⎰⎰∞+--∞+--===)(0)()()()]([a p F dt e t f dt et f e t f e L t a p ptat at位移性质表明:象原函数乘以ate 等于其象函数左右平移||a 个单位。
例12.6 求[]atL te ,[sin ]atL e t ω-和[cos ]at L e t ω-。
解 因为21[]L t p =,22[sin ]L t p ωωω=+,22[cos ]pL t p ωω=+,由位移性质即得。
,,22222)(]cos [)(]sin [)(1][ωωωωω+++=++=-=--a p ap t e L a p t e L a p te L at atat性质12.3(滞后性质) 若[()][]L f t F p =,则)()]([p F e a t f L ap -=- )0(>a (12.4)证明:dtea t f a t f L pt⎰∞+--=-0)()]([=dte a tf dt ea t f apt apt⎰⎰∞+---+-)()(0,在拉氏变换的定义说明中已指出,当0t <时,()0f t =。
因此,对于函数()f t a -,当0t a -<(即t a <)时,()0f t a -=,所以上式右端的第一个积分为0,对于第二个积分,令t a τ-=,则)()()()]([0)(p F e d e f ed ef a t f L ap p apa p -∞+--∞++-===-⎰⎰ττττττ滞后性质指出:象函数乘以ape -等于其象原函数的图形沿t 轴向右平移a 个单位。
由于函数()f t a -是当t a ≥时才有非零数值。
故与()f t 相比,在时间上滞后了一个a 值,正是这个道理,我们才称它为滞后性质.在实际应用中,为了突出“滞后”这一特点,常在()f t a -这个函数上再乘()u t a -,所以滞后性质也表示为)()]()([p F e a t f a t u L ap -=--例12.7 求[()]L u t a -。
解:因为1[()]L u t p =,由滞后性质得1[()]ap L u t a e p --=。
例12.8 求()[()]a t L eu t ττ--。
解:因为1[]at L e p a =-,所以()1[()]a t p L e u t e p a τττ---=-,()p a >例12.9 已知0,0,0()2,30,3t c t a f t c a t a t a<⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩,求[()]L f t 。
解: )(t f 可用单位阶梯函数表示为)3(2)()()(a t cu a t cu t cu t f ---+=,于是 )3(2)()([)]([a t cu a t cu t cu L t f L ---+=)21(233ap ap ap ap e e p ce p c e p c p c ----+=-+=,由拉氏变换定义来验证:⎰⎰--+=a a apt ptdtce dt cet f L 032)]([)21()221(33ap ap ap ap ap e e p ce e e p c ------+=-+-=。
性质12.4(微分性质) 若[()][]L f t F p =,并设()f t 在[0,+∞)上连续,'()f t 为分段连续,则)0()()]([f p pF t f L -=' (12.5)证明:由拉氏变换定义及分部积分法,得dt et f t f L pt⎰∞+-'='0)()]([⎰∞+-∞+-+=0)(])([dte tf Pet f pt pt ,可以证明,在[()]L f t 存在的条件下,必有lim ()0ptt f t e-→+∞=。
