拉普拉斯变换及逆变换
拉普拉斯变换表

拉普拉斯变换表拉普拉斯变换是一种非常重要的数学工具,它在物理、工程、数学、经济等领域均有广泛的应用。
本文将详细介绍拉普拉斯变换的定义、性质、公式表、逆变换及其应用方面的内容。
一、拉普拉斯变换的定义拉普拉斯变换是一种数学工具,用于将一个函数f(t)在复数域上进行变换。
拉普拉斯变换L{f(t)}的定义如下:L{f(t)}=F(s)=∫_0^∞e^(-st)f(t)dt其中,s是复数域上的变量,f(t)是定义在[0,∞)上的函数。
式中的e^-st可以看作是一个因子,它起到了对f(t)作拉普拉斯变换的影响作用。
二、拉普拉斯变换的性质(1)线性性:L{af(t)+bg(t)}=aL{f(t)}+bL{g(t)}其中,a和b为任意常数。
(2)时移性:L{f(t-k)}=e^(-ks)F(s)其中,k为任意实数。
(3)尺度变换:L{f(at)}=1/aF(s/a)其中,a为任意实数,a≠0。
(4)复合性:若F(s)=L{f(t)},G(s)=L{g(t)},则L{f(g(t))}=F(G(s))。
(5)初值定理:lim_(t→0^+)f(t)=lim_(s→∞)sF(s)(6)终值定理:lim_(t→∞)f(t)=lim_(s→0^+)sF(s)三、拉普拉斯变换表以下是一些常用的函数的拉普拉斯变换表。
f(t) F(s)t^n n!/s^(n+1)e^at 1/(s-a)sin(at) a/(s^2+a^2)cos(at) s/(s^2+a^2)1 1/st 1/s^2(t^n)e^at n!/(s-a)^(n+1)u(t-a) e^(-as)/sexp(-at)u(t) 1/(s+a)1-exp(-at)u(t) 1/(s(s+a))1/(a+t) exp(-as)δ(t-a) e^(-as)t^n u(t) n!/s^(n+1)t^n exp(-at)u(t) n!/(s+a)^(n+1)(t^n sin(bt))u(t) nb^s/(s^2+b^2)^(n+1)(t^n cos(bt))u(t) s^n/(s^2+b^2)^(n+1)其中,δ(t)表示狄拉克函数,u(t)即单位阶跃函数。
laplace逆变换公式

拉普拉斯逆变换是将拉普拉斯变换的频域表达式转换回时间域的过程。
逆变换的具体形式取决于拉普拉斯变换的函数形式。
下面是一些常见的拉普拉斯逆变换公式:
常数项:L^-1 {1} = δ(t)
单位阶跃函数:L^-1 {1/s} = u(t)
指数函数:L^-1 {1/(s-a)} = e^(at) u(t)
正弦函数:L^-1 {s/(s^2 + a^2)} = (1/a)sin(at) u(t)
余弦函数:L^-1 {s/(s^2 + a^2)} = (1/a)cos(at) u(t)
指数衰减函数:L^-1 {1/(s+a)} = e^(-at) u(t)
指数增长函数:L^-1 {1/(s-a)} = e^(at) u(t)
这些是一些常见的拉普拉斯逆变换公式,用于将频域中的拉普拉斯变换表达式转换回时间域。
请注意,具体的逆变换形式还可能涉及到系数调整和时间偏移,具体取决于函数的形式和约定的定义。
在实际应用中,可以根据所给出的拉普拉斯变换函数表达式,通过查阅相关的数学表格或使用计算工具(如符号计算软件)来求取逆变换。
这样可以更准确地得到所需的逆变换结果。
拉普拉斯逆变换

即得
1 2π j
j
F
(
s)
e
st
d
j
s
n k 1
Res [
F (s)est ,
sk
].
(返回)
18
第九章 拉普拉斯变换
§9.3 Laplace 逆变换 文档仅供参考,如有不当之处,请联系改正。
附:将实系数真分式 F (s) P(s) / Q(s) 化为部分分式
1. Q(s) 含单重一阶因子旳情况 若 Q(s) 含单重一阶因子 (s a) , 即 Q(s) (s a)Q1(s) ,
第九章 拉普拉斯变换
解 措施二 利用留数法求解
(1) s1 2, s2 1 分别为 F (s) 旳一阶与二阶极点,
Res[ F (s)est,
2]
1 (s 1)2
est
s2
e2t,
Res[ F (s)est, 1] ( est ) et t et.
s 2 s1
(2) f (t ) Res[ F (s)est, 2 ] Res[ F (s)est, 1]
上面讨论了 Q(s) 含单重和多重一阶因子旳情况,假如是 在复数范围内进行分解,这两种情况已经够了。
但假如仅在实数范围内进行分解,这两种情况还不够。
因为实系数多项式旳复零点总是互为共轭地成对出现旳, 即假如复数 z a jb 为 Q(s) 旳零点,那么它旳共轭复数 z a jb 也必为 Q(s) 旳零点。 所以,Q(s)必具有(实旳) 二阶因子 (s z)(s z ) (s a)2 b2 .
(1) s1 3 , s2,3 1 2i 为 F (s) 旳一阶极点,
Res[ F (s)est, 3 ] 2e3t,
拉普拉斯变换及其逆变换表
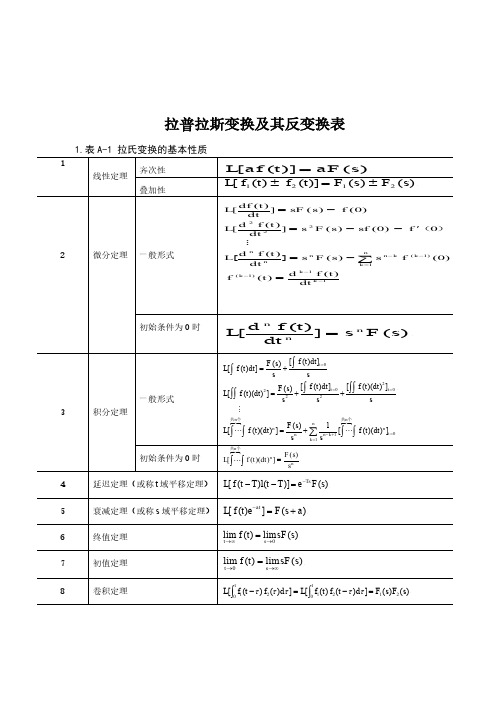
1.表 A-1 拉氏变换的基本性质
1 线性定理 齐次性 叠加性
L[ af (t )] aF ( s )
L[ f 1 (t ) f 2 (t )] F1 ( s ) F2 ( s )
df (t ) ] sF ( s ) f (0) dt d 2 f (t ) L[ ] s 2 F ( s ) sf (0) f ( 0 ) dt 2 L[
1(t )
z z 1
1 s2
1 s3
t
t2 2
Tz ( z 1) 2
T 2 z ( z 1) 2( z 1) 3
1 s n 1
1 sa
tn n!
lim
( 1) n n z ( ) n a 0 n! a z e aT
z z e aT
e at te
at
1 n 1 n 0 1 m 1 m
代数定理可将 F ( s ) 展开为部分分式。分以下两种情况讨论。 ① A( s) 0 无重根 这时,F(s)可展开为 n 个简单的部分分式之和的形式。
c c c c c F (s ) ss ss ss ss ss
1 2 i n n i i 1 1 2 i n
r 1 r 1 n r 1 1 r 1 i n r 1
c c c c c c (s s ) (s s ) (s s ) s s ss ss
r 1 1 1 r 1 i
n
式中, s1 为 F(s)的 r 重根, s r 1 ,…, sn 为 F(s)的 n-r 个单根; 其中, c r 1 ,…, cn 仍按式(F-2)或(F-3)计算, cr , cr 1 ,…, c1 则按下式计算:
函数的拉普拉斯变换与逆变换

函数的拉普拉斯变换与逆变换定义函数f(t)的拉普拉斯变换定义为:F(s)=∫e−st∞f(t)dt其中s是一个复数变量。
性质拉普拉斯变换具有以下性质:1.线性性:对于任意常数a和b,以及函数f(t)和g(t),有:L[af(t)+bg(t)]=aL[f(t)]+bL[g(t)]2.时移性:对于任意常数a,有:L[f(t−a)u(t−a)]=e−as F(s)其中u(t)是单位阶跃函数。
3.微分性:对于任意可导函数f(t),有:L[f′(t)]=sF(s)−f(0)L[f″(t)]=s2F(s)−sf(0)−f′(0)4.积分性:对于任意可积函数f(t),有:L[∫ft0(τ)dτ]=F(s)s5.卷积定理:对于任意两个函数f(t)和g(t),有:L[f(t)∗g(t)]=F(s)G(s)其中∗表示卷积运算。
应用拉普拉斯变换在许多领域都有应用,包括:1.微分方程的求解:拉普拉斯变换可以将微分方程转化为代数方程,从而更容易求解。
2.信号处理:拉普拉斯变换可以用于分析和处理信号。
3. 控制理论:拉普拉斯变换可以用于分析和设计控制系统。
4. 电路分析:拉普拉斯变换可以用于分析和设计电路。
逆拉普拉斯变换拉普拉斯变换的逆变换定义为:f (t )=12πi ∫e st γ+i∞γ−i∞F (s )ds 其中 γ 是一个大于所有 F (s ) 的奇点实部的常数。
性质逆拉普拉斯变换具有以下性质:1. 线性性:对于任意常数 a 和 b ,以及函数 f (t ) 和 g (t ),有:L −1[aF (s )+bG (s )]=aL −1[F (s )]+bL −1[G (s )]2. 时移性:对于任意常数 a ,有:L −1[e as F (s )]=f (t −a )u (t −a )3. 微分性:对于任意可导函数 F (s ),有:L −1[sF (s )]=f′(t )L −1[s 2F (s )]=f″(t )4. 积分性:对于任意可积函数 F (s ),有:L −1[F (s )s ]=∫f t 0(τ)dτ 5. 卷积定理:对于任意两个函数 F (s ) 和 G (s ),有:L −1[F (s )G (s )]=f (t )∗g (t )应用逆拉普拉斯变换在许多领域都有应用,包括:1. 微分方程的求解:逆拉普拉斯变换可以将代数方程转化为微分方程,从而更容易求解。
(完整版)拉普拉斯变换及其逆变换表
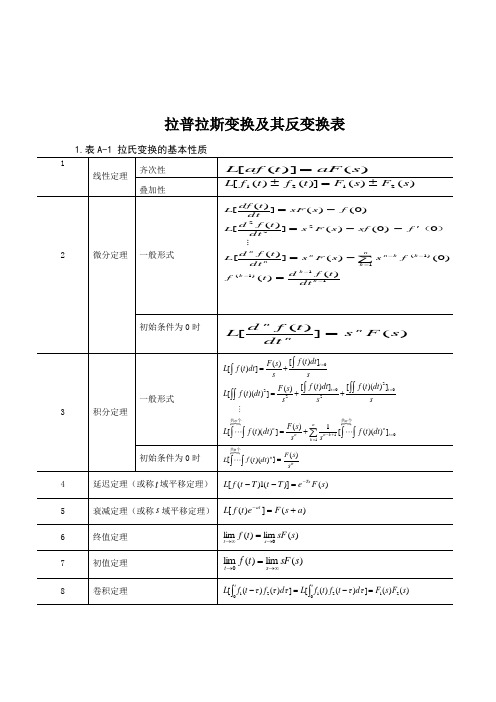
拉普拉斯变换及其反变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >)式中系数n1n 1a ,a ,...,a ,a-,m1m 1b ,b ,b ,b - 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )s (F )s s (lim c is s i-=→或is s i)s (A )s (B c='=式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数[]t s n 1i i n 1i i i 11i e c s s cL )s (F L )t (f -==--∑∑=⎥⎦⎤⎢⎣⎡-==② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为())s s ()s s ()s s ()s (B s F n1r r 1---=+=nnii1r 1r 111r 11r r 1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:)s (F )s s (lim c r1s s r-=→)]s (F )s s ([dsdlim c -=)s (F )s s (dsd lim !j 1c -=)s (F )s s (dsdlim )!1r (1c --=原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=s s cs s c s s c )s s (c )s s (c )s s (c L e c e c t c t )!2r (c t )!1r (c ∑+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)。
拉普拉斯变换及其逆变换表

拉普拉斯变换及其反变换表1. 表A-1 拉氏变换的基本性质1 L [ af ( t )] aF ( s )齐次性线性定理L [ f 1 ( t ) f 2 ( t )] F 1 ( s ) F 2 ( s ) 叠加性L [ df ( t )]sF ( s ) f ( 0 )L [ ddt2 f ( t )dt 2] s 2 F ( s ) sf ( 0 ) f (0 )L d n f ( t ) ndt ns n F ( s ) s n k f ( k 1 ) ( 0 )k 1f ( k 1 ) ( t ) d k 1 fdt( t )k 12 微分定理一般形式初始条件为0 时L [ d n f ( t )dt n] s n F ( s )L[ f (t )dt ]F ( s)s [ f (t )dt ]t 0s[ 2L[ f ( t)( dt ) ] 2 F ( s)s 2f (t) d t ]t 0s[2f (t )(dt ) ]t 0s共n个共n个L[ f (t)(dt )n ] F ( s)s nnk 1 s1n k 1[ f (t)(dt ) n ] t 0一般形式共n个3 积分定理初始条件为0 时L[ f ( t)( dt) n ]F ( s)s nTs4 延迟定理(或称t 域平移定理)L[ f (t T)1(t T )] e F ( s)精品资料精品资料5衰减定理(或称 s 域平移定理)L[ f (t )eat] F ( s a)6终值定理lim f ( t )lim tssF ( s)lim f (t ) lim sF(s)7初值定理t 0 s8卷积定理tL[ f 1( t) f 2 ( ) d ]tL[ f 1( t ) f 2 ( t) d ]F 1 (s) F 2 ( s )2. 表 A-2 常用函数的拉氏变换和 z 变换表序号拉氏变换 F(s)时间函数 f(t)Z 变 换 F(z)1 1δ(t)11 2 1 eTsT( t)(t nT )zn 0z 1 1 1(t )z sz 11 4 s2tTz ( z 1)21 t 5 s32T 2z(z 1) 2( z 1)1 t n6 n 1lim( 1) z n ( aT ) sn!a 0n!a z e17 s aeatzz e1 atTze 8 ( s a) 2tea at( z e(1 eaT )2aT) z9s(s a)1 e(z 1)( z 2 3n)3 naTaT e aT精品资料2m m 1n 1b aat btz z 10(s11a)(s b)e esin tz eaTz ebTz sin T s2 2z22 z cos T 1scos tz( z cos T )12 s2z 2 2 zcos T 1atzeaTsin T13 (s a)2 2e sin t z22 ze aTcos T e2 aTs a14 22e atcos tz2zeaTcos T( s 15s a)1 (1 / T ) ln aat / Tz22zeaTz z acos T e2 aT3.用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
常见的拉普拉斯变换公式

常见的拉普拉斯变换公式拉普拉斯变换公式是数学中的一种重要工具,它在信号与系统、电路分析、控制理论等领域有着广泛的应用。
通过将一个函数或信号从时间域转换到复频域,拉普拉斯变换可以简化复杂的微分方程求解和系统分析问题。
以下是常见的拉普拉斯变换公式及其应用。
1. 原函数定义公式:拉普拉斯变换的第一个公式是原函数定义公式,用于将一个函数从时间域表示转换为复频域表示。
假设函数为f(t),其拉普拉斯变换为F(s),则原函数定义公式为:F(s) = L{f(t)} = ∫[0,∞] f(t)e^(-st) dt其中,s为复变量,表示函数在复频域的频率。
2. 常见的拉普拉斯变换公式:拉普拉斯变换公式包括了一系列常见函数的变换结果,以下是其中的几个常见公式及其应用:- 常数函数:L{1} = 1/s,常数函数在拉普拉斯变换后变为1除以复变量s。
- 单位阶跃函数:L{u(t)} = 1/s,单位阶跃函数在拉普拉斯变换后变为1除以复变量s。
- 指数函数:L{e^(at)} = 1/(s-a),指数函数在拉普拉斯变换后变为1除以复变量s减去常数a。
- 正弦函数:L{sin(at)} = a/(s^2 + a^2),正弦函数在拉普拉斯变换后变为常数a除以复变量s的平方加上a的平方。
- 余弦函数:L{cos(at)} = s/(s^2 + a^2),余弦函数在拉普拉斯变换后变为复变量s除以复变量s的平方加上a的平方。
3. 拉普拉斯变换的性质:拉普拉斯变换具有一系列的性质,这些性质可以方便地应用于信号处理和系统分析中。
以下是常见的拉普拉斯变换性质:- 线性性质:L{af(t) + bg(t)} = aF(s) + bG(s),其中a和b为常数,f(t)和g(t)为函数,F(s)和G(s)为它们的拉普拉斯变换。
- 平移性质:L{f(t-a)u(t-a)} = e^(-as)F(s),其中a为常数,f(t)为函数,u(t)为单位阶跃函数,F(s)为f(t)的拉普拉斯变换。
拉普拉斯变换及其逆变换表

拉普拉斯变换及其逆变换表Newly compiled on November 23, 2020拉普拉斯变换及其反变换表2.表A-2 常用函数的拉氏变换和z变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n n n 011m 1m m m a s a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >) 式中系数n 1n 10a ,a ,...,a ,a -,m1m 10b ,b ,b ,b - 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n 1i iin n i i 2211s s c s s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算:或式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为 =nni i 1r 1r 111r 11r r 1r s s c s s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:原函数)(t f 为ts n 1r i it s 122r 1r 1r r 1e c e c t c t )!2r (c t )!1r (c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)。
拉普拉斯变换及其逆变换表
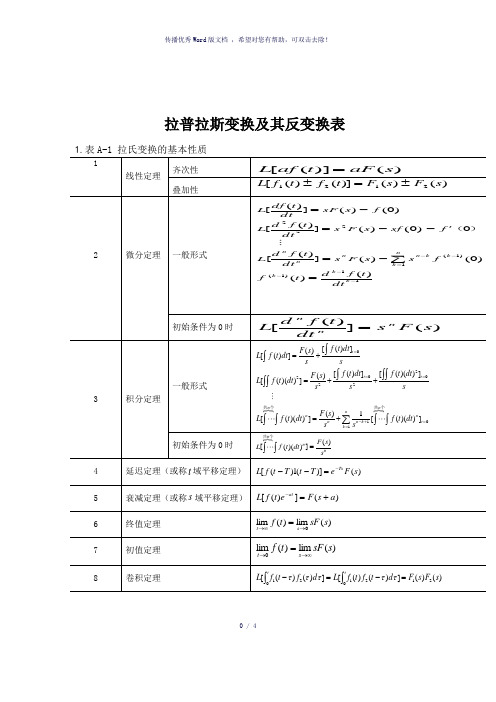
拉普拉斯变换及其反变换表0 / 43. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- (m n >)式中系数n1n 1a ,a ,...,a ,a-,m1m 1b ,b ,b ,b - 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: )s (F )s s (lim c is s ii-=→或is s i)s (A )s (B c='=式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数[]t s n 1i i n 1i i i11i e c s s c L )s (F L )t (f -==--∑∑=⎥⎦⎤⎢⎣⎡-==② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为())s s ()s s ()s s ()s (B s F n1r r 1---=+=nnii1r 1r 111r 11r r 1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算:)s (F )s s (lim c r1s s r1-=→)]s (F )s s ([dsdlim c r1s s 1r 1-=→-)s (F )s s (dsd lim !j 1c r1)j ()j (s s jr 1-=→-)s (F )s s (dsdlim )!1r (1c r1)1r ()1r (s s 11--=--→原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---nnii1r 1r 111r 11r r1r1s s cs s c s s c )s s (c )s s (c )s s (c L ts n1r i its 122r 1r 1r r1e c e c t c t )!2r (c t )!1r (c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)-----精心整理,希望对您有所帮助!。
第四章拉普拉斯变换

拉氏变换定义
如有界非周期信号 ; 有稳定幅度的周期信号 0;
随时间成正比增长的信号 0; 按指数eat 增长的信号 a。
0系统:若某些信号在0点有跳变且已知f (0 ) 则 F (s)
def
0
f (t )e st dt
2. 基本信号的单边拉氏变换 (1)阶跃函数
时间微分性质(续)
t 0 时, f t 0 ,且无原始储能, 若 f t 为有起因信号,即
即 f ( 0 ) f ( 0 ) 0 2 f ( t ) sF ( s ) f ( t ) s F ( s ), 则 ,
常用函数的拉氏变换表可查用。
3. 常用信号的拉氏变换(f(t), t>0)
1 阶跃函数 u (t ) , 0 1 s
L
L 2 冲激函数 (t )
1,
3 指数函数 e
at
1 , -a sa
L
常用信号的拉氏变换(f(t), t>0)
单边周期信号的拉氏变换(续)
(2)周期性脉冲的拉氏变换
f T ( t ) f 1 ( t ) f 1 ( t T ) f 1 ( t 2T )
FT ( s ) F1 ( s ) F1 ( s )e sT F1 ( s )e 2 sT F1 ( s )(1 e
S T 2
1 0
t
T 2
2 T
2 T sin t[u (t ) u (t )] T 2
信号加窗 第一周期
(1 e ) 2 2 S
LT
sT 2
常用拉普拉斯变换及反变换

常用拉普拉斯变换及反变换拉普拉斯变换在工程和数学中是个非常实用的工具。
它不仅能帮助我们解决微分方程,还能简化许多复杂的问题。
今天我们就来聊聊常用的拉普拉斯变换和反变换,看看它们是如何发挥作用的。
一、拉普拉斯变换的基本概念1.1 定义拉普拉斯变换是一个积分变换,它将时间域的函数转换为复频域的函数。
简单来说,它把一个函数从“时间的世界”带到了“频率的世界”。
公式上,拉普拉斯变换可以表示为:\[ \mathcal{L}\{f(t)\} = F(s) = \int_0^{\infty} e^{-st} f(t) dt \]这里的 \( s \) 是复数变量,\( f(t) \) 是我们要变换的时间域函数,\( F(s) \) 则是变换后的结果。
1.2 性质拉普拉斯变换有几个重要的性质,比如线性性、时间延迟和微分等。
这些性质使得在实际应用中,可以灵活地对待不同类型的函数。
例如,线性性让我们可以把两个函数的变换简单相加,这对于解决复杂问题很有帮助。
二、常用的拉普拉斯变换2.1 单位阶跃函数单位阶跃函数 \( u(t) \) 是拉普拉斯变换中最常用的函数之一。
它的变换结果是:\[ \mathcal{L}\{u(t)\} = \frac{1}{s} \]这个简单的公式为很多工程应用奠定了基础,因为很多信号和系统可以用阶跃函数来描述。
2.2 指数函数另一个常见的函数是指数函数 \( e^{at} \)。
它的拉普拉斯变换结果为:\[ \mathcal{L}\{e^{at}\} = \frac{1}{s - a} \]这在处理自然衰减或增长的过程时特别有用,比如在电子电路中,我们经常会遇到这种情况。
2.3 正弦和余弦函数正弦和余弦函数的拉普拉斯变换也很重要。
它们分别为:\[ \mathcal{L}\{\sin(\omega t)\} = \frac{\omega}{s^2 + \omega^2} \] \[ \mathcal{L}\{\cos(\omega t)\} = \frac{s}{s^2 + \omega^2} \]这些变换结果在振动分析和控制系统中应用广泛,帮助我们理解系统的频率响应。
拉氏变换逆变换

1 解:F ( s) s 2 s 1 f (t ) ' (t ) 2 (t ) e t (t 0)
2s 2 9s 18 (2) F ( s) 2 s 4s 8
f (t ) ILTF (s) 2 (t ) e2t cos2t u(t )
1 j st f (t ) F ( s)e ds 2j j
拉普拉斯逆变换可以按照逆变换的定义式进行求 解(留数法),实际中也可以采用其他一些简便的方 法求解。
2015-1-14 信号与系统
一、查表法
一些典型信号的逆变换可以借助于附表进行查询得到。
s 2 3s 1 (1) F ( s) s 1
K1 ( s 1 j 2) F ( s) s 2 1 j2 5
7 2 1 f (t ) e 2t 2e t cos(2t ) sin(2t ) u (t ) 5 5 5
2015-1-14 信号与系统
2 s 3 重新求解上例: F ( s ) ( s 2 2s 5)(s 2) k 2 s k3 k1 2 s 2 s 2s 5
2015-1-14 信号与系统
例:求下示函数的逆变 换 s2 3 F ( s) 2 ( s 2s 5)(s 2)
7 2t 2 t 1 f (t ) e 2e cos(2t ) sin(2t ) u (t ) 5 5 5
2015-1-14
信号与系统
201667信号与系统4444拉普拉斯逆变换拉普拉斯逆变换利用拉普拉斯变换法分析连续系统时最后都需要求象函数的逆变换得到信号的时域形式
4.4 拉普拉斯逆变换
利用拉普拉斯变换法分析连续系统时,最后都需要 求象函数的逆变换,得到信号的时域形式。因此拉普拉 斯逆变换在求解系统相应及系统分析中是非常重要的一 个环节。要求要熟练掌握。
拉普拉斯逆变换公式推导过程

拉普拉斯逆变换公式推导过程1. 介绍好啦,今天我们要聊聊拉普拉斯逆变换。
别急,听起来有点复杂,但其实挺有意思的。
想象一下,拉普拉斯变换就像是把复杂的信号变成了一个大家都能轻松看懂的公式。
而逆变换呢,就是把这个公式再变回去。
好像把一个拼图拼好之后,再拆开来重新拼一样,有点挑战,但也很有趣!在这一过程中,我们不仅能学到数学的精髓,还能体会到推导公式的乐趣。
2. 拉普拉斯变换的回顾2.1 拉普拉斯变换是啥?首先,我们得回顾一下拉普拉斯变换。
这就像是把一段信号从时域转换到频域。
换句话说,就是把一个信号从它原来的形式转化为一个更容易处理的形式。
这种转换能让很多复杂的问题变得简单明了。
比如,如果你有一个复杂的电路问题,通过拉普拉斯变换,你能把电路的动态特性转化为一个更容易解决的方程。
2.2 公式长啥样?拉普拉斯变换的公式是这样的:(mathcal{L{f(t) = F(s) = int_{0^{infty f(t)e^{st dt)。
这看起来可能像是天书,但其实挺简单的。
它的意思是:把函数 (f(t)) 乘上一个指数函数(e^{st),然后在(t) 从0到无穷大的范围内积分。
哎,数学嘛,有时候就是这么复杂,但只要掌握了方法,就会发现它也很有规律。
3. 拉普拉斯逆变换的推导3.1 逆变换的基本概念好,现在我们要做的是逆变换。
简单来说,就是把拉普拉斯变换“翻回来”。
如果拉普拉斯变换是把信号从时域转换到频域,那么逆变换就是把信号从频域转换回时域。
这就像是把刚刚做好的拼图拆掉,再按照原来的样子拼回去。
3.2 公式的推导过程咱们一步一步来,别着急。
逆变换的公式是:(mathcal{L^{1{F(s) = f(t) = frac{1{2pi i int_{ciinfty^{c+iinfty F(s)e^{st ds)。
听起来是不是很复杂?其实我们可以用一个比较直观的方法来理解。
首先,记住逆变换的核心思想就是“求解原函数”。
拉普拉斯变换及逆变换

第十二章拉普拉斯变换及逆变换拉普拉斯(Laplace)变换是分析和求解常系数线性微分方程的一种简便的方法,而且在自动控制系统的分析和综合中也起着重要的作用。
我们经常应用拉普拉斯变换进行电路的复频域分析。
本章将扼要地介绍拉普拉斯变换(以下简称拉氏变换)的基本概念、主要性质、逆变换以及它在解常系数线性微分方程中的应用。
第一节拉普拉斯变换(3)拉氏变换是将给定的函数通过广义积分转换成一个新的函数,它是一种积分变换。
一般来说,在科学技术中遇到的函数,它的拉氏变换总是存在的。
例12.1求斜坡函数()f t at =(0t ≥,a 为常数)的拉氏变换。
解:0000[]()[]pt ptpt pt a a a L at ate dt td e e e dt p p p +∞+∞+∞---+∞-==-=-+⎰⎰⎰二、单位脉冲函数及其拉氏变换在研究线性电路在脉冲电动势作用后所产生的电流时,要涉及到我们要介绍的脉冲函数,在原来电流为零的电路中,某一瞬时(设为0t =)进入一单位电量的脉冲,现要确定电路上的电流()i t ,以()Q t 表示上述电路中的电量,则 由于电流强度是电量对时间的变化率,即t t Q t t Q dt t dQ t i t ∆∆∆)()(lim)()(0-+==→,所以,当0t ≠时,()0i t =;当0t =时,0000→→→→εεεε,即1)]([=t L δ。
例12.3现有一单位阶跃输入0,()1,t u t t <⎧=⎨≥⎩,求其拉氏变换。
解:00011[()]()1[]pt pt pt L u t u t e dt e dt e p p+∞+∞---+∞===-=⎰⎰,(0)p >。
例12.4求指数函数()at f t e =(a 为常数)的拉氏变换。
解:()001[]atat ptp a t L e e e dt e dt p a+∞+∞---===-⎰⎰,()p a >,即类似可得22[sin ](0)L t p p ωωω=>+;22[cos ](0)pL t p p ωω=>+。
拉普拉斯变换和逆变换

求f(t)
K1 A jB
1
K 2 A jB K
* 1
K1 K2 f C t L s j s j
e
t
K e
1
t
K e
* t 1
2e t A cost B sint
另一种方法
求下示函数F(s) 的逆变换f(t): s F s 2 2 解: F(s)具有共轭极点,不必用部分分式展开法 t 利用 Le sin t ( s )2
s L e cos t 2 ( s )2 s F s 2 2 s s 2 2
零点 极点
z1 , z2 , z3 zm 是As 0的根, 称为F s 的零点
A( s) 0 F ( s) 0 p1 , p2 , p3 pn 是Bs 0的根, 称为F s 的极点 B( s) 0 F ( s)
按照极点之不同特点,部分分式分解方法 有以下几种情况 (1)极点为实数,无重根; (2)包含共轭复数极点 (3)有多重极点
1.第一种情况:极点为实数,无重根
A( s ) F ( s) ( s p1 )( s p2 )( s pn )
p1 , p2 , p3 pn为不同的实数根 (先考虑m n的情况) kn k1 k2 F ( s) s p1 s p2 s pn
求出k1 , k2 , k3 kn ,即可将F s 展开为部分分式
函数及其图形
拉普拉斯变换的概念 拉氏变换的运算性质 拉氏变换的逆变换 拉氏变换及其逆变换的应用
拉普拉斯变换及反变换

初值定理 若ℒ [f(t)]=F(s),且 f(t)在t = 0处无冲激,
则 f (0 ) lim f (t) lim sF (s)
t 0
s
终值定理 f(t)及其导数f (t)可进行拉氏变换,且
lim f (t)存在时
t
f () lim f (t) lim sF(s)
t
s0
例1
u(t)t0
k2(2 ss1)52(s1)2S13 k1dds(2s5)S12
f(t)L1[F(s])2et3tet t0
例2
F(s)
s2 2s2 (s2)3
k1 (s2)
(s k22)2(s k32)3
等式两边乘 (s 2)3
F(s)(s 2)3 k1(s 2)2 k2 (s 2) k3
k3s2(s22 s)32(s2)3S22
lims11 s s
例2 I(s) 5 2 s1 s2
i( 0 ) lis ( m 52) li(m 52) 3 s s 1s 2s 1 1 /s1 2 /s
例3
I(s)ℒ [1e-t]1 1 s s1
11 i(t)t ls i0m s(ss1)1
例4:已知F(s)= 1 ,求f(0)和f(∞) sa
拉普拉斯变换的基本性质表
本讲小结: 拉普拉斯变换定义 常用函数的拉普拉斯变换
拉普拉斯变换的基本性质
(1)
利用 ℒ
• 作业
1、 写出拉普拉斯变换定义式 2、
__
1
(s-1)2
二、拉普拉斯反变换
1、由象函数求原函数 f(t)=L-1[F(s)]
(1)利用公式
f(t) 1 2πj
(S2+a1S+a0)R(S)-(S+a1)r(0-)-r/(0-)=(Sb1+b0)E(s)-b1×0
拉普拉斯变换及其逆变换表

拉普拉斯变换及其反变换表2.表A-2 常用函数的拉氏变换和z变换表3. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开,然后逐项查表进行反变换。
设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a bs b s b s b )s (A )s (B )s (F ++++++++==---- (m n >)式中系数n1n 1a ,a ,...,a ,a-,m1m 1b ,b ,b ,b - 都是实常数;n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
① 0)(=s A 无重根这时,F(s)可展开为n 个简单的部分分式之和的形式。
∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中,Sn 2S 1S ,,, 是特征方程A(s)=0的根。
i c 为待定常数,称为F(s)在i s 处的留数,可按下式计算: 或式中,)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质,从式(F-1)可求得原函数② 0)(=s A 有重根设0)(=s A 有r 重根1s ,F(s)可写为 =nnii1r 1r 111r 11r r1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中,1s 为F(s)的r 重根,1+r s ,…, n s 为F(s)的n-r 个单根;其中,1+r c ,…, n c 仍按式(F-2)或(F-3)计算,r c ,1-r c ,…, 1c 则按下式计算: 原函数)(t f 为ts n1r i its 122r 1r 1r r1e c e c t c t )!2r (c t )!1r (c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-= (F-6)。
拉普拉斯变换及反变换ppt课件

一、拉氏变换及其特性 1、 拉氏变换定义
如果有一个以时间 t为自变量的实变函数 f t ,它的定义域是 t 0 ,那么 f t 的拉普
拉斯变换定义为
F
s
L
f
t
0
f
t estdt
式中,s是复变数,s j( 、
均为实数), est 称为拉普拉斯积分;F s 0
>> p=[1 -120 25 126
用num和den分别表示F(s)的分子和分母多项式, 即:num = [b0 b1 … bm]
den = [a0 a1 … an] MATLAB提供函数residue用于实现部分分式展 开,其句法为:
[r, p, k] = residue(num, den)
f (t) L1(F (s)) 1
c
j
F
(s)e
st
ds
2j c j
式中 L1 表示拉普拉斯反变换的符号
2、拉氏反变换的计算方法 由象函数求原函数的方法:
方法一:利用拉氏反变换定义求 ——不常用解
方法二:查拉氏变换表求解——对简单的象函数适用 方法三:部分分式法——象函数为有理分式函数时适用
p1)r ]}s p1
br j
1 dj
{ j!
ds
j
[F
s
(s
p1)r ]}s p1
b1
1
d r1
(r
{ 1)!
ds
r
1
[
F
s
(s
p1)r ]}s p1
例
F(s)
(s
s 1 2)3 ( s
3)
解:F (s)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章 拉普拉斯变换及逆变换拉普拉斯(Laplace)变换就是分析与求解常系数线性微分方程得一种简便得方法,而且在自动控制系统得分析与综合中也起着重要得作用。
我们经常应用拉普拉斯变换进行电路得复频域分析。
本章将扼要地介绍拉普拉斯变换(以下简称拉氏变换)得基本概念、主要性质、逆变换以及它在解常系数线性微分方程中得应用。
第一节 拉普拉斯变换在代数中,直接计算328.957812028.6⨯⨯=N 53)164.1(⨯就是很复杂得,而引用对数后,可先把上式变换为164.1lg 53)20lg 28.9lg 5781(lg 3128.6lg lg ++-+=N然后通过查常用对数表与反对数表,就可算得原来要求得数N 。
这就是一种把复杂运算转化为简单运算得做法,而拉氏变换则就是另一种化繁为简得做法。
一、拉氏变换得基本概念定义12、1 设函数()f t 当0t ≥时有定义,若广义积分()pt f t e dt +∞-⎰在P 得某一区域内收敛,则此积分就确定了一个参量为P 得函数,记作()F P ,即dte tf P F pt ⎰∞+-=)()( (12、1)称(12、1)式为函数()f t 得拉氏变换式,用记号[()]()L f t F P =表示。
函数()F P 称为()f t 得拉氏变换(Laplace) (或称为()f t 得象函数)。
函数()f t 称为()F P 得拉氏逆变换(或称为()F P 象原函数),记作)()]([1t f P F L =-,即)]([)(1P F L t f -=。
关于拉氏变换得定义,在这里做两点说明:(1)在定义中,只要求()f t 在0t ≥时有定义。
为了研究拉氏变换性质得方便,以后总假定在0t <时,()0f t =。
(2)在较为深入得讨论中,拉氏变换式中得参数P 就是在复数范围内取值。
为了方便起见,本章我们把P 作为实数来讨论,这并不影响对拉氏变换性质得研究与应用。
(3)拉氏变换就是将给定得函数通过广义积分转换成一个新得函数,它就是一种积分变换。
一般来说,在科学技术中遇到得函数,它得拉氏变换总就是存在得。
例12、1 求斜坡函数()f t at = (0t ≥,a 为常数)得拉氏变换。
解:0000[]()[]pt ptpt pt a a a L at ate dt td e e e dt p p p +∞+∞+∞---+∞-==-=-+⎰⎰⎰ 2020][0p a e p a dt e pa pt pt =-=+=∞+-∞+-⎰)0(>p二、单位脉冲函数及其拉氏变换在研究线性电路在脉冲电动势作用后所产生得电流时,要涉及到我们要介绍得脉冲函数,在原来电流为零得电路中,某一瞬时(设为0t =)进入一单位电量得脉冲,现要确定电路上得电流()i t ,以()Q t 表示上述电路中得电量,则⎩⎨⎧=≠=.0,1,0,0)(t t t Q由于电流强度就是电量对时间得变化率,即t t Q t t Q dt t dQ t i t ∆∆∆)()(lim )()(0-+==→,所以,当0t ≠时,()0i t =;当0t =时,∞=-=-+=→→)1(lim )0()0(lim)0(00t t Q t Q i t t ∆∆∆∆∆。
上式说明,在通常意义下得函数类中找不到一个函数能够用来表示上述电路得电流强度.为此,引进一个新得函数,这个函数称为狄拉克函数。
定义12、2设0,01(),00,t t t t εδεεε<⎧⎪⎪=≤≤⎨⎪>⎪⎩,当0ε→时,()t εδ得极限0()lim ()t t εεδδ→=称为狄拉克(Dirac)函数,简称为δ-函数。
当0t ≠时,()t δ得值为0;当0t =时,()t δ得值为无穷大,即0,0(),0t t t δ≠⎧=⎨∞=⎩。
显然,对任何0ε>,有01()1t dt dt εεδε+∞-∞==⎰⎰,所以()1t dt δ+∞-∞=⎰。
工程技术中,常将δ-函数称为单位脉冲函数,有些工程书上,将δ-函数用一个长度等于1得有向线段来表示,这个线段得长度表示δ-函数得积分,叫做δ-函数得强度。
例12、2 求单位脉冲信号()t δ得拉氏变换。
解:根据拉氏变换得定义,有dte dt edt edt et t L pt ptptpt-→∞+-→-→∞+-⎰⎰⎰⎰=⋅+==εεεεεεεεδδ01lim0lim)1lim()()]([11lim 1)()1(lim 11lim 1][1lim 00000==''-=-=-=-→-→-→-→εεεεεεεεεεεp p p pt pe p e p e p p e ,即1)]([=t L δ。
例12、3 现有一单位阶跃输入0,()1,0t u t t <⎧=⎨≥⎩,求其拉氏变换。
解:00011[()]()1[]pt ptpt L u t u t e dt e dt e p p+∞+∞---+∞===-=⎰⎰,(0)p >。
例12、4 求指数函数()atf t e =(a 为常数)得拉氏变换。
解:()001[]at at pt p a tL e e e dt e dt p a+∞+∞---===-⎰⎰,()p a >,即)(1][a p a p e L at >-=类似可得22[sin ](0)L t p p ωωω=>+;22[cos ](0)pL t p p ωω=>+。
三、拉氏变换得性质拉氏变换有以下几个主要性质,利用这些性质,可以求一些较为复杂得函数得拉氏变换。
性质12、1 (线性性质) 若1a ,2a 就是常数,且11[()]()L f t F p =,22[()]()L f t F p =,则)]([)]([)]()([22112211t f L a t f L a t f a t f a L +=+)()(2211p F a P F a += (12、2)证明:dte tf a dt et f a dt et f a t f a t f a t f a L pt ptpt-∞+-∞+-∞+⎰⎰⎰+=+=+)()()]()([)]()([02211221102211 )()()]([)]([22112211p F a p F a t f L a t f L a +=+=例12、5 求函数1()(1)at f t e a-=-得拉氏变换 解:)(1}11{1]}[]1[{1]1[1)]1(1[a p p a p p a e L L a e L a e a L at at at +=+-=-=-=---- 性质12、2(平移性质) 若[()][]L f t F p =,则[()]()atL e f t F p a =-(a 为常数) (12、3)证明:⎰⎰∞+--∞+--===)(0)()()()]([a p F dt e t f dt et f e t f e L t a p ptat at位移性质表明:象原函数乘以ate 等于其象函数左右平移||a 个单位。
例12、6 求[]atL te ,[sin ]atL e t ω-与[cos ]at L e t ω-。
解 因为21[]L t p =,22[sin ]L t p ωωω=+,22[cos ]p L t p ωω=+,由位移性质即得 。
,,22222)(]cos [)(]sin [)(1][ωωωωω+++=++=-=--a p ap t e L a p t e L a p te L at atat性质12、3(滞后性质) 若[()][]L f t F p =,则)()]([p F e a t f L ap -=- )0(>a (12、4)证明:dtea t f a t f L pt⎰∞+--=-0)()]([=dte a tf dt ea t f apt apt⎰⎰∞+---+-)()(0,在拉氏变换得定义说明中已指出,当0t <时,()0f t =。
因此,对于函数()f t a -,当0t a -<(即t a <)时,()0f t a -=,所以上式右端得第一个积分为0,对于第二个积分,令t a τ-=,则)()()()]([0)(p F e d e f ed ef a t f L ap p apa p -∞+--∞++-===-⎰⎰ττττττ滞后性质指出:象函数乘以ape -等于其象原函数得图形沿t 轴向右平移a 个单位。
由于函数()f t a -就是当t a ≥时才有非零数值。
故与()f t 相比,在时间上滞后了一个a 值,正就是这个道理,我们才称它为滞后性质.在实际应用中,为了突出“滞后”这一特点,常在()f t a -这个函数上再乘()u t a -,所以滞后性质也表示为)()]()([p F e a t f a t u L ap -=--例12、7 求[()]L u t a -。
解:因为1[()]L u t p =,由滞后性质得1[()]ap L u t a e p --=。
例12、8 求()[()]a t L e u t ττ--。
解:因为1[]at L e p a =-,所以()1[()]a t p L e u t e p aτττ---=-,()p a >例12、9 已知0,0,0()2,30,3t c t a f t c a t a t a<⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩,求[()]L f t 。
解: )(t f 可用单位阶梯函数表示为)3(2)()()(a t cu a t cu t cu t f ---+=,于就是 )3(2)()([)]([a t cu a t cu t cu L t f L ---+=)21(233ap ap ap ap e e p ce p c e p c p c ----+=-+=,由拉氏变换定义来验证:⎰⎰--+=a a apt ptdtce dt cet f L 032)]([)21()221(33ap ap ap ap ap e e p ce e e p c ------+=-+-=。
性质12、4(微分性质) 若[()][]L f t F p =,并设()f t 在[0,+∞)上连续,'()f t 为分段连续,则)0()()]([f p pF t f L -=' (12、5)证明:由拉氏变换定义及分部积分法,得dt et f t f L pt⎰∞+-'='0)()]([⎰∞+-∞+-+=0)(])([dte tf Pet f pt pt ,可以证明,在[()]L f t 存在得条件下,必有lim ()0ptt f t e-→+∞=。
