贝叶斯网络, 条件概率、全概率公式
全概率公式与贝叶斯公式

全概率公式与贝叶斯公式
一、全概率公式
全概率公式是概率统计学中的重要概念,它系统地表达了事件发生的
几率,它建立在一定的概率论假设和条件概率的基础上。
全概率公式由它
的发明者布朗定理提出,它以下简称为B-公式,它定义了一个事件发生
条件的概率可以由该事件发生的总概率和该事件发生条件概率之间的关系
表示出来,具体地说,就是:
P(A)=P(A,B1)P(B1)+P(A,B2)P(B2)+···+P(A,Bn)P(Bn)
其中:P(A)是A发生的概率,P(B1)~P(Bn)是相互独立的事件B1~Bn
发生的概率;P(A,B1)~P(A,Bn)是A在B1~Bn发生后发生的条件概率,
以上关系可以看作是在n个事件B1~Bn中,A发生的概率就是在所有这些
事件发生时A发生的条件概率乘以其各自发生的概率,再相加,而本质上
它是一个分母的二项式展开。
贝叶斯公式是概率统计学中的重要概念,它描述了在已知其中一种情
况的概率后,观察到其中一种事件后,该情况发生的可能性,它利用事件
的先验概率和事件发生后的后验概率进行推断,它有一下公式发挥着作用:P(A,B)P(B)=P(B,A)P(A)
其中:P(A)是事件A发生的先验概率;P(B)是事件B发生的先验概率;P(A,B)是事件B发生后A发生的条件概率;P(B,A)是事件A发生后B发
生的条件概率。
贝叶斯公式和全概率公式

贝叶斯公式和全概率公式贝叶斯公式是概率论中的重要公式,也就是所谓的贝叶斯定理。
贝叶斯定理是由十九世纪末英国数学家和统计家 Thomas Bayes 在 1763 年提出的,是概率论中最重要的原理之一,广泛应用于商业分析、医学诊断、决策分析、信息检索等多个领域中。
贝叶斯公式的公式表达形式为:<br/>P(A|B)=P(B|A)P(A)/P(B)其中,P(A|B)表示“在B条件下A的概率”,P(B|A)表示“在A条件下B的概率”,P(A)表示“A的概率”,P(B)表示“B的概率”。
从此公式中可以看到,贝叶斯公式通过将一个条件概率分解成两个条件概率的乘积,加以组合,使得概率计算变得更加简便容易。
贝叶斯公式也可以表述为一种胆怯结论,即根据已知的条件来推断未知的结果,而不是僵化地按照既定的规则来推断结果。
即可以通过已知的条件来推断未知的结果,而不是僵化地按照既定的规则来推断结果。
全概率公式是贝叶斯公式的推广,它的公式表达式如下:<br/> P(A)=ΣP(A|B_i)P(B_i)其中,P(A)表示A的概率,P(A|B_i)表示B_i条件下A的概率,P(B_i)表示B_i的概率。
从此公式中可以看到,全概率公式把一个概率分解成多个子概率的和,每个子概率都是一个条件概率,加以组合,使得概率计算更加简便容易。
全概率公式也可以表述为一种更加灵活的结论,即根据已知的概率来推断未知的结果,而不是僵化地按照既定的规则来推断结果。
即可以通过已知的概率来推断未知的结果,而不是僵化地按照既定的规则来推断结果。
因此可以看出,贝叶斯公式和全概率公式是概率论中重要的公式,它们可以帮助我们更加有效地推断出未知的结果,提高我们的决策质量,从而获得更好的结果。
全概率公式和贝叶斯公式的区别与联系

全概率公式和贝叶斯公式的区别与联系全概率公式和贝叶斯公式是两个概率论中的重要公式,用于计算条件概率。
它们之间存在一定的区别和联系。
区别:1.针对的问题不同:全概率公式用于计算一个事件的概率,在已知相应条件下,求解它的概率;而贝叶斯公式则用于反向推理,已知事件发生的条件概率,来求解与之相关的条件概率。
2.公式形式不同:全概率公式的数学形式为P(A) =∑P(A|B_i)P(B_i),其中B_i为互斥事件,且∑P(B_i) = 1;贝叶斯公式的数学形式为P(B|A) = P(A|B)P(B)/P(A)。
3.用途不同:全概率公式主要用于解决复杂事件的概率计算问题,将复杂事件分解为多个互斥事件的概率计算;贝叶斯公式则主要用于从已知的条件概率出发,反向计算待求条件概率。
联系:1.全概率公式是贝叶斯公式的基础,两者结合可以构成贝叶斯推断的完整过程。
2.贝叶斯公式可以通过全概率公式来推导得到,即根据全概率公式将条件概率表达式代入到贝叶斯公式中,可以得到贝叶斯公式的形式。
拓展:除了上述区别与联系之外,全概率公式和贝叶斯公式还能够应用于其他许多领域。
例如:1.在机器学习中,贝叶斯公式可以用于通过已知标签的数据集来计算新样本的后验概率,进而进行分类。
2.在信号处理中,贝叶斯滤波器可以通过贝叶斯公式将先验信息与测量得到的观测信息相结合,来实现对信号的滤波和估计。
3.在金融领域中,贝叶斯公式可以用于根据市场观测信息来更新关于资产价格走势的先验概率,从而进行风险度量和投资决策。
这些应用扩展了全概率公式和贝叶斯公式的应用范围,使得它们在不同领域中都能够有效地处理概率计算和推理问题。
条件概率、全概公式、贝叶斯公式

P(AB 3 36 1 ) P(A| B) = = = 。 P(B ) 6 36 2 解法2: 解法 P(A| B) = 3 = 1。 6 2
在B发生后的 发生后的 缩减样本空间 中计算
设某种动物由出生算起活到20年以上的 例2: 设某种动物由出生算起活到 年以上的 概率为0.8,活到25年以上的概率为 年以上的概率为0.4。 概率为 ,活到 年以上的概率为 。问 现年20岁的这种动物 它能活到25岁以上的 岁的这种动物, 现年 岁的这种动物,它能活到 岁以上的 概率是多少? 概率是多少? 能活20年以上 能活25年以上 解:设A={能活 年以上 B={能活 年以上 设 能活 年以上}, 能活 年以上}, 所求为P(B|A) 。 所求为 依题意, 依题意, P(A)=0.8, P(B)=0.4, ,
“先抽的人当然要比后抽的人抽到的人机会大。” 先抽的人当然要比后抽的人抽到的人机会大。 先抽的人当然要比后抽的人抽到的人机会大
我们用A 表示“ 个人抽到入场券 个人抽到入场券” 我们用 i表示“第i个人抽到入场券”, i=1,2,3,4,5。 = 。 表示“ 个人未抽到入场券 个人未抽到入场券” 则 A “第i个人未抽到入场券”, 表示 i 显然,P(A1)=1/5,P( A)=4/5, 显然, , , 1= 也就是说, 也就是说, 个人抽到入场券的概率是1/5。 第1个人抽到入场券的概率是 。 个人抽到入场券的概率是
乙两厂共同生产1000个零件,其中 个零件, 例3: 甲、乙两厂共同生产 个零件 其中300 件是乙厂生产的。而在这300个零件中,有189个 个零件中, 件是乙厂生产的。而在这 个零件中 个 是标准件,现从这1000个零件中任取一个,问这 个零件中任取一个, 是标准件,现从这 个零件中任取一个 个零件是乙厂生产的标准件的概率是多少? 个零件是乙厂生产的标准件的概率是多少? 零件是乙厂生产}, 设B={零件是乙厂生产 , 零件是乙厂生产 A={是标准件 , 是标准件}, 是标准件 所求为P(AB)。 。 所求为
全概率公式和贝叶斯公式(先验概率和后验概率)

全概率公式和贝叶斯公式(先验概率和后验概率)全概率公式(Law of Total Probability)和贝叶斯公式(Bayes' Theorem)是统计学中重要的概率公式,用于计算给定一些条件下的概率。
这两个公式是概率论和统计学中常用的工具,可以解决很多实际问题,从机器学习到社会科学中的调查研究。
P(A)=Σ[P(A,Bi)*P(Bi)]其中,P(A)表示事件A的概率,P(A,Bi)表示在给定事件Bi的条件下,事件A发生的概率,P(Bi)表示事件Bi的概率。
贝叶斯公式是在给定一些观察或证据的情况下,计算一个事件的概率的公式。
它基于条件概率的概念,将因果关系转化为条件概率的形式,并用于根据已知的先验概率更新为后验概率。
贝叶斯公式可以表示为:P(A,B)=[P(B,A)*P(A)]/P(B)其中,P(A,B)表示在观察到事件B发生的情况下,事件A发生的概率,P(B,A)表示在事件A发生的条件下,事件B发生的概率,P(A)和P(B)分别是事件A和事件B的先验概率。
全概率公式和贝叶斯公式经常一起使用,特别在机器学习和数据分析中被广泛应用。
通过使用全概率公式,可以将复杂问题分解为多个简单的条件概率问题,然后再使用贝叶斯公式根据已知的先验概率和条件概率计算后验概率。
这样可以更好地理解问题,并得到更准确的结果。
举个例子来说明这两个公式的应用:假设有两个工厂A和B,它们负责生产其中一种产品。
已知A工厂的产品次品率为20%,而B工厂的产品次品率为10%。
现在我们收到一批产品,但不知道是哪个工厂生产的。
一些产品是次品的概率是10%。
问这个产品是来自A工厂的概率是多少?首先,我们可以用全概率公式来计算得到:P(A)=0.5(因为两个工厂的概率相等)P(A,B)=[P(B,A)*P(A)]/P(B)P(B,A)是在A工厂生产的条件下产品是次品的概率P(A)已经计算得到为0.5P(B)=P(B,A)*P(A)+P(B,¬A)*P(¬A)=0.02*0.5+0.1*0.5=0.03将这些值代入贝叶斯公式,可以得到:P(A,B)=(0.02*0.5)/0.03≈0.33因此,基于给定的证据,这个产品是来自A工厂的概率约为33%。
全概率公式,贝叶斯公式的推广及其应用

全概率公式,贝叶斯公式的推广及其应用一、全概率公式全概率公式是概率论中的基本公式之一,也称作“条件概率公式”。
简单地说,它是用于计算一个事件发生的概率,而该事件可以发生在多个不同的情况下。
这个公式通常是这样表述的:P(A) = ΣP(A|B_i)*P(B_i)其中,A是要计算的事件,B_i 是 A 可以在其上发生的情况。
P(A|B_i) 是在给定的情况 B_i 下 A 发生的概率,P(B_i) 是情况B_i 发生的概率。
Σ 是对所有情况 B_i 求和。
换句话说,这个公式的含义是:要计算事件 A 发生的概率,我们需要把所有可能性下的条件发生的概率乘起来,再加起来,最终就得到了事件 A 发生的概率。
二、贝叶斯公式另一个常用的概率公式是贝叶斯公式,它与全概率公式有关。
贝叶斯公式是用于计算事件的后验概率(posterior probability),即已知某些证据的情况下再计算事件 A 发生的概率。
它经常用在统计学、机器学习等领域中。
贝叶斯公式通常表述为:P(B|A) = P(A|B)*P(B) / Σ(P(A|B_i)*P(B_i))在这个公式中,A 是已知的证据,B 是要计算的事件。
P(A|B) 是在事件 B 发生的情况下事件 A 发生的概率,P(B) 是事件 B 发生的先验概率(prior probability),即在没有任何证据的情况下事件B 发生的概率。
Σ(P(A|B_i)*P(B_i)) 是全概率公式中的求和项。
三、推广及应用全概率公式和贝叶斯公式可以相互推导,它们都是计算概率的重要工具,广泛应用于各种领域中。
例如:1、在医学诊断中,医生可以利用贝叶斯公式来计算某个病人患病的概率,而这个概率可以作为判断病人是否需要进一步检查或治疗的依据。
2、在自然语言处理中,贝叶斯公式可以用于计算文档中词汇的概率,从而实现文本分类、情感分析等任务。
3、在无人驾驶汽车中,全概率公式可以用于估计车辆在道路上的位置,贝叶斯公式可以用于预测其他车辆的行驶路线和速度,从而实现智能决策和避免碰撞。
条件概率、全概率、贝叶斯公式

杨鑫的数学课堂条件概率、全概率、贝叶斯公式、p(A|B)=P(A∩B)P(B)⇒p(A∩B)=p(A|B)×p(B)⇒p(A∩B)=P(B|A)×P(A)(1)p(A|B)=P(A∩B)P(B)=p(B|A)×P(A)p(B)(2)先举个例子,小张从家到公司上班总共有三条路可以直达(如下图),但是每条路每天拥堵的可能性不太一样,由于路的远近不同,选择每条路的概率如下:p(L1)=0.5,p(L2)=0.3,p(L3)=0.2(3)每天上述三条路不拥堵的概率分别为:p(C1)=0.2,p(C2)=0.4,p(C3)=0.7(4)其实不迟到就是对应着不拥堵,设事件C为到公司不迟到,事件Li为选择第i 条路,则:p(C)=p(L1)×p(C|L1)+p(L2)×p(C|L)+p(L3)×p(C|L3) p(C)=p(L1)×p(C1)+p(L2)×p(C2)+p(L3)×p(C3)p(C)=0.5×0.2+0.3×0.4+0.2×0.7=0.36(5)全概率计算公式p(C)=p(L1)p(C|L1)······p(L n)p(C|L n)=n∑i=1p(L i)p(C|L i)(6)三、贝叶斯公式仍旧借用上述的例子,但是问题发生了改变,问题修改为:到达公司未迟到选择第1条路的概率是多少?0.5这个概率表示的是,选择第一条路的时候并没有靠考虑是不是迟到,只是因为距离公司近才知道选择它的概率,而现在我们是知道未迟到这个结果,是在这个基础上问你选择第一条路的概率,所以并不是直接就可以得出的。
故有:p(L1|C)=p(C|L1)×p(L1)p(C)p(L1|C)=p(C|L1)×p(L1)P(L1)×p(C|L1)+P(L2)×p(C|L2)+P(L3)×p(C|L3)p(L1|C)=0.2×0.50.2×0.5+0.3×0.4+0.2×0.7=0.28(7)1。
贝叶斯网络, 条件概率、全概率公式

贝叶斯公式给出了‘结果’事件B
已发生的条件下,‘原因’事件的条 件概率.
从这个意义上讲,它是一个“执果索因”
为先验概率 (PriorProbability),而把称为后验概 率 ( Posterior Probability), 这 是
在已有附加信息(即事件B已发生)之后
§1.5 条件概率、全概率公 式和贝叶斯公式
一、条件概率
简单地说,条件概率就是在一定附加条件之 下的事件概率.
从广义上看,任何概率都是条件概率,因为 任何事件都产生于一定条件下的试验或观察, 但我们这里所说的“附加条件”是指除试验条 件之外的附加信息,这种附加信息通常表现为 “已知某某事件发生了”
这一公式最早发表于1763年,当时贝 叶斯已经去世,其结果没有受到应有 的重视. 后来,人们才逐渐认识到了 这个著名概率公式的重要性. 现在, 贝叶斯公式以及根据它发展起来的贝 叶斯统计已成为机器学习、人工智能、 知识发现等领域的重要工具.
条件概率、全概率公式、贝叶斯公式

因为 P ( A) 0.8,
P ( B ) 0.4,
P ( AB ) P ( B ),
P ( AB ) 0.4 1 . 所以 P ( B A) 0.8 2 P ( A)
第二节 全概率公式
再回忆一下条件概率的定义:
P( AB ) P( B | A) P( A) 要求 P( A) 0 .
第三章
第三章 条件概率与事件的独立性
一、条件概率 二、全概率公式 三、贝叶斯公式 四、事件的独立性 五、伯努利实验和二项概率
第一节 条件概率
前面讲的概率问题没有什么附加条件,但 实际中可能会经常遇到许多有条件的概率 问题比如: (1)已知某人爱滋病检查为阳性,求他患爱 滋病的概率; (2)在摸奖中已知第一人已经或未摸到一等 奖,求第二人摸到一等奖的概率。 (3)人寿保险中常常会考虑:已知某人已经 活了x岁,求他能再活y岁的概率。
完备事件组(样本空间的一个划分) 定义1 设事件A1,A2,…,An为样本空间 的一组事件。 … A1 如果 A2 (1) Ai Aj= (i≠j); (2)
An
A3 …
A
i 1
n
i
则称A1,A2,…,An为样本空间的一 个划分。
定理 设试验E的样本空间为Ω, 设事件A1,A2,…,An为样本空间Ω的一 个划分, 且P(Ai)>0 (i =1,2, …,n). 则对任意事件B,有
古典概型
设 A 表示任取一球,取得白球; B 表示任取一球,取得木球.
所求的概率称为在事件A 发生的条件下 事件B 发生的条件概率。记为 P B A
从而有
4 k AB P ( B | A) kA 7 k AB / n 4 /10 k A / n 7 /10
条件概率全概率公式与贝叶斯公式

(1) p 4 2 34 2 .
2 2
27
(2)
342
p
2
2
2
34
5 ? 10片中有5片安慰剂;
(1)从中任取5片,求A:? 其中至少有2片安慰剂”的概率;
解:P(A) 1 P(A) =1
(2)每次取1片,不放回地取,
[
C50C55 C150
C15C54 C150
]
求B:? 前三次都取到安慰剂”的概率;
作业 1、证明:B A AB AB
证明: AB AB ( AB)( AB) ( A U B)( AB) ( AAB) U(BAB) AB B A
2、证明: ( AB) U ( A B ) ( A B)U(B-A ) 证明: ( AB) ( AB ) AB AB
( A U B)( A U B) ( A U B) A U( A U B)B
20 定义
设 A, B 是两个事件,且 P( A) 0,称 P(B A) P( AB) P( A)
为在事件 A 发生的条件下事件B发生的条件概率.
若 P(B) 0,同样可称 P( A | B) P( AB) P(B)
为在事件 B 发生的条件下事件 A 发生的条件概率。
时间上:先后; 逻辑上:主从关系
一、条件概率
10 引入
对于古典概型问题,设试验 E 的样本空间为
S={e1,e2 , ,en },容量为 n
A容量为m,B容量为v, AB容量为k
由古典概率得
S'=A
P( A) m , P( AB) k , P(B) v ,
n
n
n
P(B | A) k ,
m
可以发现 P(B | A) P( AB) , P( A)
概率论 条件概率 全概率公式 贝叶斯公式

点的,而缩减为只包含40个样本点的 B=B. 35 P (C ) = P ( A B ) = = 0.875. 40
注 1 P ( A) = 0.85 P ( A B ).
B
A
2 P ( AB) = 0.35 P ( A B ).
P ( AB) : 以Ω为样本空间.
P ( A B ) : 以 B = B 为样本空间.
35 35 100 P ( AB ) 3 P( A B) = = = . 40 40 100 P ( B )
这是巧合吗?不是.
2. 定义1.8 (条件概率的定义)
设A,B是两个事件,且P(B) > 0, 则称 P ( AB) P( A B) = P( B) 为事件B发生的条件下,事件A发生的条件概率. 注 1 计算 P ( A B)的两种方法 :
且等于它们的总和: 出最终结果 . 义: n
i =1
P ( B ) = P ( Ai B ).
A2
B
An1
A1
An
A3
例3 甲、乙两个箱子,甲箱中装有两个白球,一 个黑球;乙箱中装有一个白球,两个黑球.现由甲 箱中任取一球放入乙箱,再从乙箱中任取一球, 问取到白球的概率是多少? 解 以A1表示事件“从甲箱中取出一个白球”, A2表示“从甲箱中取出一个黑球”这一事件, 以B表示“从乙箱中取出一个白球”这一事件, 则: A1 A2 = , A1 A2 = , 且
(1) 取出的一个为正品; A (2) 取出的一个为甲车床加工的零件; B (3) 取出的一个为甲车床加工的正品; AB
(4) 已知取出的一个为甲车床加工的零件,其为 正品. C
85 = = 0.85. (1) P ( A) 解 100 40 = 0.40. (2) P ( B) = 100 35 (3) P ( AB) = 100 = 0.35.
1-5全概率公式贝叶斯公式1-6伯努利概型
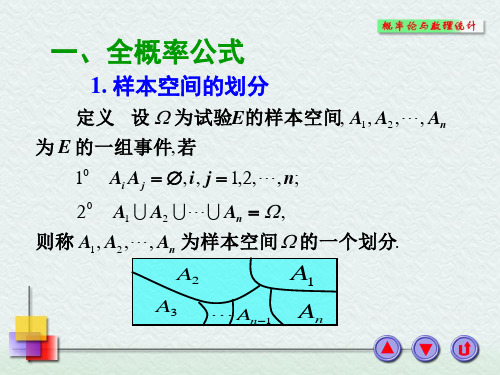
定义 如果试验E只有两个基本事件A及A, 且P(A) p, P(A) 1 p(0 p 1), 将E独立 地进行n次,则这一系列试验称为n重伯努 利试验或n重伯努利概型,简称伯努利概型.
定理 在n重伯努利试验中,设每次试验中 事件A发生的概率为p(0 p 1), 则在n次重复 试验中,事件A恰好发生k次的概率为
解 假设接待站的接待时间没有
规定,且各来访者在一周的任一天
中去接待站是等可能的.
17 27
37
47
172
周一 周二 周三 周四 周五 周六 周日
故一周内接待 12 次来访共有 712种.
12 2
32
42
122
周一 周二 周三 周四 周五 周六 周日
12 次接待都是在周二和周四进行的共有 212种.
解 设 A 为事件 "产品合格".
B 为事件 "机器调整良好". 则有
P( A B) 0.98, P( A B) 0.55,
P(B) 0.95, P(B) 0.05, 由贝叶斯公式得所求概率为
P(B A)
P( A B)P(B)
P(AB)P(B) P(AB)P(B)
0.98 0.95
0.97.
解 设X表示这一年内的死亡人数, 则 保险公司在1年的收入是2500120=300000元
保险公司这一年里付出20000X元
当20000X >300000, 即X > 15人时公司亏本
于是, P{公司亏本} =P{ X > 15} =1-P{X≤ 15}
15
P{公司亏本} 1
Ck 2500
(0.002)k
贝叶斯公式
P ( Bi
A)
经济数学课件 6.3 条件概率 全概率公式和贝叶斯公式

互斥A1 n,
A2 An
则对任一事件
B, P(B) P(A1) P(B | A1) P(A2 ) P(B | A2 ) P(An ) P(B | An )
❖
n
P( Ai ) P( B | Ai )
❖
i 1
, (3)
❖ 称此式为全概率公式.
❖
由全概率公式可知,在计算复杂事件B
的概率时,只要能找到一组适当的、互斥简
单事件 A1, A2 ,, An 使它们的和事件是必然
事件
❖ 并且P( Ai ) 和P(B | Ai ) 易于计算,那么,P(B)
i( 1, 2,, n,
)
的计算就可简化.
四、贝叶斯公式
❖
在公式(1)、(2)和(3)的条件
下,若,则立即有
❖
P( Ai
|
B)
P( Ai B) P(B)
例3 设某光学仪器厂制造的透镜, 第一次落下时 打破的概率为1/2,若第一次落下未打破, 第二次落 下打破的概率为7/10 , 若前两次落下未打破, 第三 次落下打破的概率为9/10.试求透镜落下三次而未 打破的概率.
解 以Ai (i 1,2,3)表示事件"透镜第 i 次落下打破",
以B 表示事件“透镜落下三次而未打破”.
第三节 条件概率 全概率公式和贝叶 斯公式
❖ 一、条件概率
❖
简单地说,条件概率就是在一定附加
条件之下的事件概率.
❖
从广义上看,任何概率都是条件概率,
因为任何事件都产生于一定条件下的试验或
观察,但我们这里所说的“附加条件”是指
除试验条件之外的附加信息,这种附加信息
通常表现为“已知某某事件发生了”
全概率公式和贝叶斯公式

全概率公式和贝叶斯公式一、全概率公式(法)全概率公式是概率论中一条基本的公式,用于计算一个事件的概率。
假设A1、A2、…、An是样本空间Ω的一个划分,即A1、A2、…、An是两两互斥且并起来等于Ω的一组事件。
那么对于任意一个事件B来说,全概率公式(法)可以表示为:P(B)=P(B,A1)P(A1)+P(B,A2)P(A2)+…+P(B,An)P(An)其中,P(B,Ai)表示事件B在事件Ai发生的条件下发生的概率,P(Ai)表示事件Ai的概率。
全概率公式可以用来计算一个事件的概率,即通过对所有可能的事件Ai的发生概率以及事件B在这些事件发生的条件下的概率进行加权平均。
贝叶斯公式是概率论中另一条重要的公式,用于修正一个事件的概率,当已知相关证据时。
贝叶斯公式可以表示为:P(A,B)=P(B,A)P(A)/P(B)其中,P(A,B)表示在已知事件B发生的条件下事件A发生的概率,P(B,A)表示在已知事件A发生的条件下事件B发生的概率,P(A)和P(B)分别表示事件A和事件B的概率。
贝叶斯公式的核心在于将已知的事件B对事件A发生的概率进行修正,即在已知事件B发生的情况下,重新估计事件A发生的概率。
贝叶斯公式在实际应用中具有广泛的应用,特别是在数据分析和机器学习领域。
例如,在文本分类中,可以使用贝叶斯公式计算给定一个词汇出现的情况下,文档属于一些类别的概率;在推荐系统中,可以使用贝叶斯公式计算给定用户的历史行为和其他用户的行为信息的情况下,用户对一些产品的偏好。
总结起来,全概率公式和贝叶斯公式是概率论中两个重要的计算公式。
全概率公式用于计算一个事件的概率,当已知所有可能事件的发生概率以及该事件在这些事件发生的条件下的概率。
贝叶斯公式是在已知相关证据的情况下,修正一个事件的概率。
这两个公式在实际问题中被广泛应用,对于理解和解决概率问题具有重要意义。
条件概率、全概率公式与贝叶斯公式

这里,样本空间
.易知此属于古典概型问
题.已知事件 已发生,有了这一信息,知道 不可能发生,即知试验所有可能结果所成的集合就
是 . 中共有3个元素,其中只有 属于 .于是,在 发生的条件下, 发生的概率为
对于例1,已知
容易验证在 发生的条件下, 发生的概率
对于例2,已知
容易验证 发生的条件下, 发生的概率
7/12
2014年11月26日
仅有一个发生.
条件概率、全概率公式与贝叶斯公式
[例2] 设试验 为“掷一颗骰子观察其点数”.它的样本空间 是样本空间 的一个分割.而事件组 不是样本空间 的一个分割,因为
. 的一组事件
[例3] 甲、乙、丙三人向同一飞机射击.设样本空间 ={无人命中飞机,一人命中飞机,二人命 中飞机,全命中}. 的一组事件 ={三人以下命中飞机}, ={全命中飞机}是样本空间 的一个分 割.
由此可知对上述的两个等可能性的概率模型,总有
成立.
其实,还可以验证, 这个关系式对频率也是成立的.于是,从这些共性中得到启发,引入下面的 一般定义.
二、条件概率
若
是一个概率空间, ,若
,则对于任意的 ,称
为已知事件 发生的条件下, 事件 发生的条件概率.
[例3] 一盒子中装有4只产品,其中有3只是一等品,1只是二等品.从中取产品两次,每次任取一 只,作不放回抽样,设事件 为“第二次取到的是一等品”,事件 为“第一次取到的是一等品”,试求 条件概率
4/12
2014年11月26日
条件概率、全概率公式与贝叶斯公式
只与所取出的那个球同色的球.若在袋中连续取球四次,试求第一、二次取到红球且第三、四次
取到白球的概率.
解:以 求概率为
第一章4节条件概率全概率公式与贝叶斯公式
可能结果为
返回主目录
第一章 事件与概率
§5 条 件 概 率、全概率 公式和贝叶 斯公式
(2,1) (2,2) (2,3) (2,4) 这时,事件B是在事件A已经发生的条件下的概率 ,因此这时所求的概率为
PB A 1 4
注:由例1可以看出,事件在“条件A已发生这 个附加条件的概率与不附加这个条件的概率是 不同的. 因此,有必要引入下面的定义:
即 PAn 已知
而且每一原因对结果的影响程度已知,
即 PB An 已知
则我们可用全概率公式计算结果发生的概率.
即求 PB
返回主目录
第一章 事件与概率
§5 条 件 概 率、全概率 公式和贝叶 斯公式
例6 某小组有20名射手,其中一、二、三、四级 射手分别为2、6、9、3名.又若选一、二、三、 四级射手参加比赛,则在比赛中射中目标的概 率分别为0.85、0.64、0.45、0.32,今随机选一 人参加比赛,试求该小组在比赛中射中目标的 概率.
PA1 A2 An1 0
则有
PA1 A2 An PA1P A2 A1 P A3 A1A2 P An A1A2 An1
这就是n个事件的乘法公式.
返回主目录
第一章 事件与概率
§5 条 件 概 率、全概率 公式和贝叶 斯公式
例 4 袋中有一个白球与一个黑球,现每次从中取 出一球,若取出白球,则除把白球放回外再加 进一个白球,直至取出黑球为止.求取了n次都 未取出黑球的概率.
1 2 3 n 2 3 4 n1
1 n 1
返回主目录
第一章 事件与概率
§5 条 件 概 率、全概率 公式和贝叶 斯公式
例 5 设某光学仪器厂制造的透镜,第一次落 下时打破的概率为 1/2 ,若第一次落下未打破, 第二次落下打破的概率为 7/10 ,若前两次落下 未打破,第三次落下打破的概率为 9/10 。求透 镜落下三次而未打破的概率。
第21节条件概率、全概率公式与贝叶斯公式

第二章条件概率与统计独立性•条件概率,全概率,贝叶斯公式•事件独立性•贝努利试验与直线上的随机游动•二项分布与泊松分布2.1 条件概率全概率公式与贝叶斯公式一、条件概率二、全概率公式三、贝叶斯公式一、条件概率☐问题1 一个家庭有两个孩子,问两个都是女孩的概率是多少?(假定生男生女是等可能的)☐问题2 一个家庭有两个孩子,已知其中一个是女孩,问另一个也是女孩的概率是多少?(假定生男生女是等可能的)☐问题3 一个家庭有两个孩子,已知老大是女孩,问另一个也是女孩的概率是多少?(假定生男生女是等可能的)(,,),,()0,,()(|)()(|).P B P B A P AB P A B P B P A B B A Ω∈>∈= 设是一个概率空间且则对任意的记称为在事件发生的条件下事2件发义生的条 定 2.1.件概率1ΩA B AB 说明若事件B 已发生,则为使A 也发生,试验结果必须是既在B 中又在A 中的样本点,即此点必属于AB .由于我们已经知道B 发生,故B 变成了新的样本空间.从概率的直观意义出发:若B已经发生,则要使A发生试验的结果既属于A又属于B,即属于AB。
因此,条件概率应理解为P(AB)在P(B)中的“比重”。
从几何概型的角度出发:如果在单位正方形内等可能的投点,若已知B 发生,这时A 发生的概率为:BAB S S P =BAABΩΩΩ=S S S S B AB //)()(B P AB P =“条件概率”是“概率”吗?容易验证,条件概率具有概率的公理化定义中的三个条件);()()()( )3(212121B A A P B A P B A P B A A P -+= ).(1)( )4(B A P B A P -=则有件是两两不相容的事设可加可列性, , , ,: )5(21 B B 11().i i i i P A B P A B ∞∞==⎛⎫= ⎪⎝⎭∑ 3. 性质(1) :()0;P A B ≥负非性 (|)1,(|)0P B P B Ω=∅=规同时;(2)范性2)从加入条件后改变了的情况去算4. 条件概率的计算1) 用定义计算:,)()()|(B P AB P B A P P (B )>0掷骰子例:A ={掷出2点},B ={掷出偶数点}P (A |B )=31B 发生后的改变样本空间所含样本点总数在改变样本空间中A 所含样本点个数例掷两颗均匀骰子,已知第一颗掷出6点,问“掷出点数之和不小于10”的概率是多少? 解法1: )()()|(B P AB P B A P =解法2: 2163)|(==B A P 解: 设A ={掷出点数之和不小于10}B ={第一颗掷出6点}应用定义在B 发生后的改变样本空间中计算21366363==-=⨯12121312121()()()()().n n n P A A A P A P A A P A A A P A A A A 则有且,0)(121>-n A A A P ,2,,,,21≥n n A A A n 个事件为设推广 则有且为事件设,0)(,,,>AB P C B A ()()()().P ABC P A P B A P C AB =).()()(,0)(A P A B P AB P A P =>则有设5. 乘法定理条件概率与乘法公式1996年,中国围棋大师马晓春在与韩国大师李昌镐争夺围棋世界冠军的五番棋决赛前,马晓春说了这么一句话,他说,如果前面两盘棋能够下成平手,那么他夺冠的概率就有51%.由于马晓春前一年夺得的两个世界冠军都不是从公认为世界围棋第一人的李昌镐手中赢得的,因此那一年他们两个之间的决赛非常令人期待.果然,前面两盘下成了一比一.于是,媒体根据此前马晓春的那一句话,开始了乐观的预测.例一盒子装有4 只产品,其中有3 只一等品,1只二等品.从中取产品两次,每次任取一只,作不放回抽样.设事件A 为“第一次取到的是一等品”,事件B 为“第二次取到的是一等品”,试求条件概P (B |A ).解.4;3,2,1,号为二等品为一等品将产品编号则试验的样本空间为号产品第号第二次分别取到第表示第一次以,),(j 、i 、j i )},3,4(),2,4(),1,4(,,)4,2(),3,2(),1,2(),4,1(),3,1(),2,1{( =Ω)},4,3(),2,3(),1,3(),4,2(),3,2(),1,2(),4,1(),3,1(),2,1{(=A )},2,3(),1,3(),3,2(),1,2(),3,1(),2,1{(=AB 由条件概率的公式得)()()(A P AB P A B P =129126=.32=例某种动物由出生算起活20岁以上的概率为0.8, 活到25岁以上的概率为0.4, 如果现在有一个20岁的这种动物, 问它能活到25岁以上的概率是多少?设A 表示“能活20 岁以上”的事件; B 表示“能活25 岁以上”的事件,则有,8.0)(=A P 因为.)()()(A P AB P A B P =,4.0)(=B P ),()(B P AB P =.218.04.0==)()()(A P AB P A B P =所以解例五个阄, 其中两个阄内写着“有”字, 三个阄内不写字, 五人依次抓取,问各人抓到“有”字阄的概率是否相同?解.5,4,3,2,1=i 则有,52)(1=A P )()(22Ω=A P A P ))((112A A A P =抓阄是否与次序有关?,""的事件人抓到有字阄第表示设i A i333121212()()(())P A P A P A A A A A A A =Ω= )()()(321321321A A A P A A A P A A A P ++=42534152⨯+⨯=,52=)()()()(121121A A P A P A A P A P +=)(2121A A A A P =)()(2121A A P A A P +=)()()(213121A A A P A A P A P =)()()(213121A A A P A A P A P +)()()(213121A A A P A A P A P +324253314253314352⨯⨯+⨯⨯+⨯⨯=,52=依此类推.52)()(54==A P A P 故抓阄与次序无关.波利亚罐模型=121.,,,,-b r c n n n n n 罐中有只黑球只红球每次自袋中任取一只球观察其颜色然后放回并再放入只与所取出的那只球同色的球若在袋中连续取球次试求前面次摸出黑球,后面次摸出红球的概率.例 解1(1,2,,)""i A i n i = 设为事件第次取到黑球11(1,2,,)""j A j n n n j =++ 为事件第次取到红球因此所求概率为11(1)22(1)b n c b b c b cb r b rc b r c b r n c+-++=⋅⋅⋅⋅+++++++- 此模型被波利亚用来作为描述传染病的数学模型.121211211122()()()()().n n n n n P A A A P A P A A P A A A A P A A A A ---=⨯211(1)(1)(1)r n c r r cb r nc b r n c b r n c+-+⋅⋅⋅+++++++- 当c=0时,对应有放回模型,当c=-1时,对应不放回模型,此模型是一般摸球模型1. 样本空间的分割1A 2A 3A 1-n A nA 二、全概率公式121212,,,,,(1),,,1,2,,;(2),,,,.n i j n n E A A A E A A i j i j n A A A A A A ΩΩΩ=∅≠=⋃⋃⋃⋃= 定义设为试验的样本空间为的一组事件若,则称,为样本空间的一个分割2. 全概率公式全概率公式1211221,,),,,,,,()(|)()(|)()(|)()()(|)n n n i i i P B A A A P B P B A P A P B A P A P B A P A P A P B A ΩΩ∞=∈=++++=∑ 设(为一概率空间,为的一义个分割则定i j A A =∅由()()i j BA BA ⇒=∅12()()()()n P B P BA P BA P BA ⇒=++++ 证明12.n BA BA BA = 图示B1A 2A 3A 1-n A nA 化整为零各个击破12()n B B B A A A Ω== 1122()()(|)()(|)()(|)n n P B P A P B A P A P B A P A P B A ⇒=++++说明全概率公式的主要用处在于它可以将一个复杂事件的概率计算问题,分解为若干个简单事件的概率计算问题,最后应用概率的可加性求出最终结果.B1A 2A 3A 1n A nA例有一批同一型号的产品,已知其中由一厂生产的占30% , 二厂生产的占50% , 三厂生产的占20%, 又知这三个厂的产品次品率分别为2%, 1%, 1%,问从这批产品中任取一件是次品的概率是多少?设事件A 为“任取一件为次品”,.3,2,1,""=i i B i 厂的产品任取一件为为事件123,B B B =Ω 解.3,2,1,,=∅=j i B B j i由全概率公式得,2.0)(,5.0)(,3.0)(321===B P B P B P Ω30%20%50%2%1%1%112233()()()()()()().P A P B P A B P B P A B P B P A B =++.013.02.001.05.001.03.002.0=⨯+⨯+⨯=,01.0)(,01.0)(,02.0)(321===B A P B A P B A P 112233()()()()()()()P A P B P A B P B P A B P B P A B =++故(由因求果)1A 2AnA B11()()P A P B A 22()()P A P B A ()()n n P A P B A结果原因1()()()i i i P B P A P B A ∞=∑=={}A 第1次设取到黄球,()()()())(P A P B A P A P P B B A =+20193020+504950492=5=⨯⨯20(),50P A =由题意,30()50P A =19(),49P B A =20()49P B A =利用全概率公式={}B 第2次取到黄球解:例设袋中有50只乒乓球,其中20只黄球,30只白球,现从中依次不放回地任取两个,则第二次取得黄球的概率?例设袋中有50只乒乓球,其中20只黄球,30只白球,现从中依次不放回地任取两个,则第二次取得黄球的概率?有放回抽奖和无放回抽奖一样公平!若采取有放回抽取,则第二次取得黄球的概率?2()52()5例设袋中有50只乒乓球,其中20只黄球,30只白球,现从中依次不放回地任取两个,则第二次取得黄球的概率?抽签或者抓阄都和先后顺序无关!若采取不放回抽取,则第三次取得黄球的概率?2()52()5例送检的两批灯管在运输中各打碎一支,若每批10支,而第一批中有1支次品,第二批有两支次品,现在从剩下的灯管中任取一支,问抽得次品的概率是多少?({},{}{},A AB ===解解法一)设灯管来自第一批灯管来自第二批,任取一支,抽的次品1911(|)01010910P B A =⨯+⨯=21822(|)10910910P B A =⨯+⨯=3()()(|)()(|)20P B P A P B A P A P B A =+=()918P A =()918P A =AAB考虑打碎的是次品还是正品两种情形:1234 ({},{}{}{}{},A A A AB =====解解法二)设两批打碎的都是次品两批打碎的分别是次品、正品,两批打碎的分别是正品、次品,两批打碎的都是正品,任取一支,抽的次品1234281872(),(),(),()100100100100P A P A P A P A ====123122(|),(|),(|),181818P B A P B A P B A ===413()()(|)20i i i P B P A P B A ===∑43(|),18P B A =1A 2A 3A 4A B说明由例可以看出,同一个题目,都用到了全概率公式,但方法各异。
3条件概率、全概率、贝叶斯公式

取1球
取1球
取1球 取1球
...... M 白球 M 白球
M 白球
N 红球 N 红球
N 红球
K 个盒
如上图所示, 怎么求小孩取 到红球的概率?
答案:P N M N
方法:数学归纳法。
有些问题,利用它的层次感去看问题是方便的,如前面 各例,但有些问题则适宜整个面地去看。
例如:某班有20 个同学,采取抽签的方式分配三张音乐会 门票, 求第二位同学MM抽到门票的概率.
解:设 A 表示 “A 系统有效”,B 表示“ B 系统有效”。
由题目已知:P A 0.92, P B 0.93, P B A 0.85
...... P AB 0.862
1 PC P A B P A PB P AB 0.988
设播种用的麦种由一等、二等、三等、四等的种子混合而成,
分别占 95.5 0 0 , 2 0 0 , 1.5 0 0 , 10 0 , 已知由一、二、三、
四等种子长出的麦穗含 50 粒以上麦粒的概率分别为 0.5,
0.15, 0.1, 0.05 。
在这个问题中
设 Ai 表示“此种子是第i 等的”。i 1, 2,3, 4
艾滋病病毒。设这种试验的假阴性比例为 5 0 0,假阳性比 例为10 0 。据统计人群中携带病毒者约占1 0 00,若某人的
血液检验结果呈阳性,试求该人携带艾滋病病毒的概率。
解:设 A 表示“该人携带艾滋病病毒”, B 表示“该人血液检验结果呈阳性”。
则:P A 0.001, P B A 0.95, P B A 0.01.
当PB 0时
P AB PB P A B
例2 为防止意外,矿出内设有两种报警系统,单独使用时, 系统 A 有效的概率为0.92,系统 B 有效的概率为0.93, 在系统 A 失灵的情况下,系统 B 有效的概率为0.85, 求以下事件的概率。
概率基础和贝叶斯公式

全概率公式
A AS A ( B1 B2 Bn ) AB1 AB2 ABn . 由 Bi B j ( ABi )( AB j )
证明
P ( A) P ( AB1 ) P ( AB2 ) P ( ABn )
P ( A B1 ) P ( B1 ) P ( A B2 ) P ( B2 ) P ( A Bn ) P ( Bn ).
P ( ABi ) P ( A Bi ) P ( Bi )
每一原因Bi都可能导致A发生,故 A发生的概率是各原因引起A发生概率 的总和,即全概率公式.
P ( A) P ( A Bi ) P ( Bi )
i 1 n
再看引例1 有三个罐子,1号装有 2 红 1 黑球 , 2号装有 3 红 1 黑球,3号装有 2 红 2 黑球. 某人从中随机取一罐, 再从中任意取出一球,求取得红球的概率. 解 记 Bi ={ 球取自 i 号罐 } i=1, 2, 3; A ={ 取得红球 } 1 2
3. 全概率公式与贝叶斯公式
(1) 样本空间的划分
定义 设 S 为试验E的样本空间, B1 , B2 ,, Bn 为 E 的一组事件, 若 (i ) Bi B j , i j , i , j 1, 2,, n ; (ii ) B1 B2 Bn S . 则称 B1 , B2 ,, Bn 为样本空间 S 的一个划分.
贝叶斯公式 P ( A Bi ) P ( Bi ) P ( Bi A) n , i 1, 2,, n P( A B j )P(B j )
j 1
( 2) 条件概率 P ( A B) 与积事件概率 P ( AB) 的区别.
P ( AB ) 表示在样本空间S 中, AB 发生的 概率, 而 P ( A B ) 表示在缩小的样本空间 S B B 中 , AB 发生的概率. 用古典概率公式 ,则 N ( AB ) P ( B A) , N ( SB ) N ( AB ) P ( AB ) , N (S) 一般来说, P ( B A) 比 P ( AB ) 大 .
全概率公式、贝叶斯公式推导过程

全概率公式、贝叶斯公式推导过程(1)条件概率公式设A,B是两个事件,且P(B)>0,则在事件B发生的条件下,事件A发生的条件概率(conditional probability)为:P(A|B)=P(AB)/P(B)(2)乘法公式1.由条件概率公式得:P(AB)=P(A|B)P(B)=P(B|A)P(A)上式即为乘法公式;2.乘法公式的推广:对于任何正整数n≥全概率公式、贝叶斯公式推导过程(1)条件概率公式设A,B是两个事件,且P(B)>0,则在事件B发生的条件下,事件A发生的条件概率(conditional probability)为:P(A|B)=P(AB)/P(B)(2)乘法公式1.由条件概率公式得:P(AB)=P(A|B)P(B)=P(B|A)P(A)上式即为乘法公式;2.乘法公式的推广:对于任何正整数n≥2,当P(A1A2...A n-1) > 0 时,有:P(A1A2...A n-1A n)=P(A1)P(A2|A1)P(A3|A1A2)...P(A n|A1A2...A n-1)(3)全概率公式1. 如果事件组B1,B2,.... 满足1.B1,B2....两两互斥,即B i ∩ B j = ∅,i≠j ,i,j=1,2,....,且P(B i)>0,i=1,2,....;2.B1∪B2∪....=Ω ,则称事件组B1,B2,...是样本空间Ω的一个划分设 B1,B2,...是样本空间Ω的一个划分,A为任一事件,则:上式即为全概率公式(formula of total probability)2.全概率公式的意义在于,当直接计算P(A)较为困难,而P(B i),P(A|B i) (i=1,2,...)的计算较为简单时,可以利用全概率公式计算P(A)。
思想就是,将事件A分解成几个小事件,通过求小事件的概率,然后相加从而求得事件A的概率,而将事件A进行分割的时候,不是直接对A进行分割,而是先找到样本空间Ω的一个个划分B1,B2,...B n,这样事件A就被事件AB1,AB2,...AB n分解成了n部分,即A=AB1+AB2+...+AB n, 每一B i发生都可能导致A发生相应的概率是P(A|B i),由加法公式得P(A)=P(AB1)+P(AB2)+....+P(AB n)=P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|B n)P(PB n)3.实例:某车间用甲、乙、丙三台机床进行生产,各台机床次品率分别为5%,4%,2%,它们各自的产品分别占总量的25%,35%,40%,将它们的产品混在一起,求任取一个产品是次品的概率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从这个意义上讲, 它是一个“ 执果索因” 从这个意义上讲 , 它是一个 “ 执果索因 ” 的条件概率计算公式. 的条件概率计算公式. 相对于事件B 而言 , 概 率 论 中 把 称 为 先 验 概 率 PriorProbability) (PriorProbability),而把称为后验概 Probability) 率 ( Posterior Probability), 这 是 在已有附加信息( 已发生) 在已有附加信息 ( 即事件 B 已发生 ) 之后 对事件发生的可能性做出的重新认识, 对事件发生的可能性做出的重新认识,体 现了已有信息带来的知识更新. 现了已有信息带来的知识更新.
条件概率、 §1.5 条件概率、全概率公 式和贝叶斯公式
一、条件概率 简单地说, 简单地说,条件概率就是在一定附加条件之 下的事件概率. 下的事件概率. 从广义上看,任何概率都是条件概率, 从广义上看,任何概率都是条件概率,因为 任何事件都产生于一定条件下的试验或观察, 任何事件都产生于一定条件下的试验或观察, 但我们这里所说的“附加条件” 但我们这里所说的“附加条件”是指除试验条 件之外的附加信息,这种附加信息通常表现为 件之外的附加信息, 已知某某事件发生了” “已知某某事件发生了”
这一公式最早发表于1763年 这一公式最早发表于1763年,当时贝 1763 叶斯已经去世, 叶斯已经去世,其结果没有受到应有 的重视. 后来, 的重视. 后来,人们才逐渐认识到了 这个著名概率公式的重要性. 叶斯统计已成为机器学习、人工智能、 叶斯统计已成为机器学习、人工智能、 知识发现等领域的重要工具. 知识发现等领域的重要工具. 贝叶斯公式给出了‘结果’ 贝叶斯公式给出了‘结果’事件B 已发生的条件下, 原因’ 已发生的条件下,‘原因’事件的条 件概率. 件概率.
