导数的11个专题(243页).pdf
导数公式大全

任何初等函数的导数都可以按常数和基本 初等函数的求导公式和上述复合函数的求导 法则求出.
复合函数求导的关键: 正确分解初等函数 的复合结构.
练习:求下列函数的导数(课堂练习) (1)y (-1 x2 )3; (2) y cos 3x; (3) y x2 - 3x 2;
cos x
cos x
(4) 把 tan x 当作中间变量, y ' (etan x ) ' etan x (tan x) ' sec2 xetan x
(5) 把 - x 当作中间变量, y ' (2-x ) ' 2-x ln 2(-x) ' -2-x ln 2
求导方法小结:
(3
2x2
)
'
-4x
tan(3
2x2
)
例5:求下列函数的导数
(1)y cosx2
(2)y ex2 -3x-2
(3)y ln ln ln x (4)y ln(x x2 1)
隐函数的导数
y与x的关系由方程F(x,y)=0确定,未解出因变量的 方程F(x,y)=0所确定的函数y y(x)称为隐函数
(2)
y' 1 1 x2
- 2x (1 x 2 )2
y"
-
(1 (1
x2 )' x2 )2
二阶以上的导数可利用后面的数学软件来计算
复合函数的求导法则
定理2.2 若函数u u(x)在点x可导,函数y=f (u) 在点u处可导,则复合函数y f (u(x)) 在点x可导,且 dy dy du dx du dx 或记作: dy f '(u) u '(x) dx
导数(非常典型非常全)
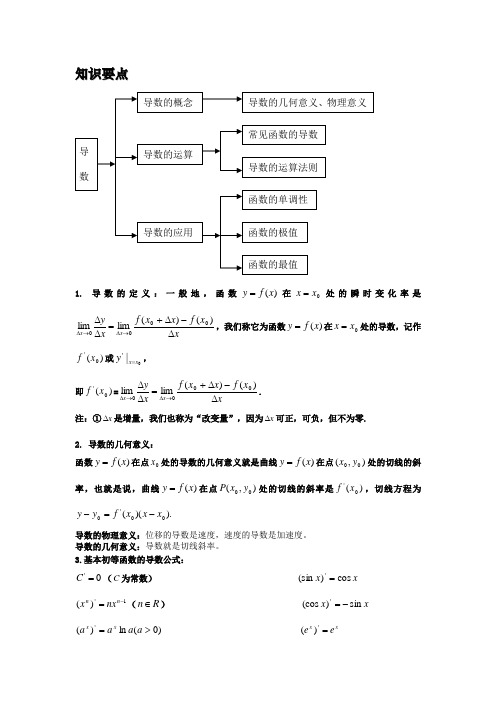
知识要点1. 导数的定义:一般地,函数)(x f y =在0x x =处的瞬时变化率是x x f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000,我们称它为函数)(x f y =在0x x =处的导数,记作)(0'x f 或0|'x x y =,即)(0'x f =xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000. 注:①x ∆是增量,我们也称为“改变量”,因为x ∆可正,可负,但不为零.2. 导数的几何意义:函数)(x f y =在点0x 处的导数的几何意义就是曲线)(x f y =在点),(00y x 处的切线的斜率,也就是说,曲线)(x f y =在点),(00y x P 处的切线的斜率是)(0'x f ,切线方程为).)((00'0x x x f y y -=-导数的物理意义:位移的导数是速度,速度的导数是加速度。
导数的几何意义:导数就是切线斜率。
3.基本初等函数的导数公式:0'=C (C 为常数) x x cos )(sin '= 1')(-=n n nx x (R n ∈) x x sin )(cos '-= )0(ln )('>=a a a a x x x x e e =')()1,0(ln 1)(log '≠>=a a ax x a x x 1)(ln '=4.导数运算法则:[])()()()('''x g x f x g x f ±=±[])()()()()()('''x g x f x g x f x g x f +=∙[])0)(()()()()()()()(2'''≠-=⎥⎦⎤⎢⎣⎡x g x g x g x f x g x f x g x f 注:)()(x g x f 、必须是可导函数.5.复合函数的求导法则:(整体代换)例如:已知2()3sin (2)3f x x π=+,求'()f x 。
导数知识点归纳及应用

导数知识点归纳及应用导数是微积分的基础知识之一,它描述了一个函数在其中一点的变化率。
导数的概念非常重要,广泛应用于科学和工程领域中的各种问题的建模和解决。
一、导数的定义及基本性质1.导数的定义:对于一个函数f(x),它的导数可以通过以下极限定义求得:f'(x) = lim ( h -> 0 ) [ f(x+h) - f(x) ] / h导数表示了函数f(x)在x点处的变化率。
如果导数存在,则称f(x)在该点可导。
2.导数的图像表示:导数可以表示为函数f(x)的图像上的斜率线,也就是切线的斜率。
3.导数的几何意义:a.函数图像在特定点的切线的斜率等于该点的导数。
b.导数为正,表示函数在该点上升;导数为负,表示函数在该点下降;导数为零,表示函数在该点取得极值。
4.基本导数公式:a.常数函数的导数为0。
b.幂函数f(x)=x^n的导数为f'(x)=n*x^(n-1)。
c. 指数函数 f(x) = a^x 的导数为 f'(x) = ln(a) * a^x。
d. 对数函数 f(x) = log_a(x) 的导数为 f'(x) = 1 / (x * ln(a))。
二、导数的计算方法1.导数的基本定义法:根据导数的定义,通过计算极限来求得导数。
2.导数的运算法则:a.和差法则:(f(x)±g(x))'=f'(x)±g'(x)。
b.乘法法则:(f(x)*g(x))'=f'(x)*g(x)+f(x)*g'(x)。
c.商法则:(f(x)/g(x))'=(f'(x)*g(x)-f(x)*g'(x))/(g(x))^2d.复合函数法则:(f(g(x)))'=f'(g(x))*g'(x)。
3.链式法则:对于复合函数f(g(x)),可以利用链式法则求导数:(f(g(x)))'=f'(g(x))*g'(x)。
导数的主要知识点总结

导数的主要知识点总结1. 导数的定义在微积分中,函数f(x)在点x=a处的导数可以用极限的概念来定义。
假设函数f(x)在x=a 处的切线斜率存在,那么这个斜率就是函数在这一点的导数。
导数可以用以下的极限式来表示:\[f'(a)=\lim_{h\to0}\frac{f(a+h)-f(a)}{h}\]其中,f'(a)表示函数在x=a处的导数。
这个式子的几何意义相当于在点(x, f(x))处做一个趋近于点(a, f(a))的切线,切线的斜率即为函数在点a处的导数。
2. 导数的计算法则导数的计算法则可以帮助我们更方便、更准确地求解函数的导数。
下面是一些常见的导数计算法则:(1) 常数法则对于常数c,它的导数为0,即\[ \frac{d}{dx}c=0 \](2) 幂函数法则对于幂函数f(x)=x^n,它的导数为\[ \frac{d}{dx}x^n=nx^{n-1} \](3) 指数函数法则对于指数函数f(x)=a^x,它的导数为\[ \frac{d}{dx}a^x=a^x\ln a \](4) 对数函数法则对于对数函数f(x)=\log_a x,它的导数为\[ \frac{d}{dx}\log_a x=\frac{1}{x\ln a} \](5) 反函数法则若y=f(x)的反函数为x=g(y),则有\[ \frac{dx}{dy}=\frac{1}{\frac{dy}{dx}} \](6) 和、差、积、商的导数法则对于两个函数u(x)和v(x),它们的和、差、积、商的导数法则分别为:\[ \frac{d}{dx}(u(x)+v(x))=\frac{du}{dx}+\frac{dv}{dx} \]\[ \frac{d}{dx}(u(x)-v(x))=\frac{du}{dx}-\frac{dv}{dx} \]\[ \frac{d}{dx}(u(x)v(x))=u(x)\frac{dv}{dx}+v(x)\frac{du}{dx} \]\[ \frac{d}{dx}\frac{u(x)}{v(x)}=\frac{u'(x)v(x)-u(x)v'(x)}{(v(x))^2} \]3. 导数的基本性质导数具有一系列的基本性质,这些性质可以帮助我们更好地理解导数的特点和应用。
导数知识点总结及答案

导数知识点总结及答案一、导数的定义在数学中,函数f(x)在某一点x=a处的导数定义为:f'(a) = lim (h→0) [f(a+h) - f(a)] / h其中,f'(a)表示函数f(x)在x=a处的导数,lim表示极限运算,h表示自变量x的增量。
导数的定义可以理解为当自变量x在x=a处发生一个很小的变化h时,函数f(x)在此点的增量f(a+h) - f(a)与自变量的增量h的比值。
当h趋向于0时,这个比值就是函数f(x)在x=a处的导数。
二、导数的性质1. 可加性:如果函数f(x)和g(x)在某一点x=a处有导数,那么它们的和、差、积、商函数在此点处也有导数,并且导数的值可以进行相应的运算。
2. 连续性:如果函数f(x)在某一点x=a处有导数,那么函数f(x)在该点处是连续的。
3. 导数与函数的关系:如果函数f(x)在某一点x=a处有导数,那么函数f(x)在该点处是可微的,反之亦然。
4. 导数与函数的图像关系:函数f'(x)在某一点x=a处的导数值,可以描述函数f(x)在该点处的切线的斜率。
5. 高阶导数:如果函数f(x)在某一点x=a处有导数,那么它的导数f'(x)也可以求导,进而得到f''(x),称为函数f(x)的二阶导数,依此类推,可以求得函数f(x)的任意阶导数。
三、常见函数的导数1. 幂函数:f(x) = x^n,其导数为f'(x) = nx^(n-1)。
2. 指数函数:f(x) = a^x,其中a为常数且a>0,a≠1,其导数为f'(x) = a^x*ln(a)。
3. 对数函数:f(x) = ln(x),其导数为f'(x) = 1/x。
4. 三角函数:f(x) = sin(x),其导数为f'(x) = cos(x);f(x) = cos(x),其导数为f'(x) = -sin(x)。
5. 反三角函数:f(x) = arcsin(x),其导数为f'(x) = 1/√(1-x^2);f(x) = arccos(x),其导数为f'(x) = -1/√(1-x^2)。
(完整版)高考导数专题(含详细解答)

导数及其应用导数的运算1. 几种常有的函数导数:①、 c( c 为常数); ②、( x n )( n R ); ③、 (sin x) = ;④、 (cos x) =;⑤、( a x ); ⑥、 ( ex); ⑦、 (log a x ) ; ⑧、 (ln x ).2. 求导数的四则运算法规:(u v)u v ; (uv) u vu'u v ' uv 'u ( v0 ) 注:① u, v 必定是可导函数 .uv ; (u)vuvvvv 223. 复合函数的求导法规:f x ( ( x))f (u) ? ( x) 或 y xy u ? u x一、求曲线的切线(导数几何意义)导数几何意义: f (x 0 ) 表示函数 y f (x) 在点 ( x 0 , f (x 0 ) )处切线 L 的斜率;函数 y f (x) 在点 ( x 0 , f (x 0 ) )处切线 L 方程为 y f (x 0 )f (x 0 )(x x 0 )1. 曲线在点 处的切线方程为( )。
A:B:C:D:答案详解 B 正确率 : 69%, 易错项 : C解析 :本题主要观察导数的几何意义、导数的计算以及直线方程的求解。
对 求导得,代入 得 即为切线的斜率, 切点为,因此切线方程为即。
故本题正确答案为B 。
2.3. 设函数f ( x) g( x) x2,曲线 y g(x) 在点 (1,g(1)) 处的切线方程为 y 2x 1,则曲线 y f ( x) 在点 (1, f (1))处切线的斜率为( )A .41C.21B . D .4 24. 已知函数 f ( x) 在R上满足 f ( x) 2 f (2 x) x28x 8,则曲线y f (x) 在点 (1, f (1)) 处的切线方程是()A . y2x 1 B. y x C. y3x 2 D. y2x 3变式二:5. 在平面直角坐标系xoy 中,点P在曲线C : y x310 x 3 上,且在第二象限内,已知曲线 C 在点 P 处的切线的斜率为 2,则点 P 的坐标为.6. 设曲线 yx n 1 (n N * ) 在点( 1,1)处的切线与 x 轴的交点的横坐标为 x n ,令 a n lg x n ,则 a 1 a 2 L a 99 的值为.7. 已知点 P 在曲线 y=4 上, 为曲线在点 P 处的切线的倾斜角,则的取值范围是e x1, 3]D 、 [ 3,A 、 [0, )B 、 [, ) C 、 ( )44 22 4 4变式三:8. 已知直线y =x+ 1 与曲线y ln( x a) 相切,则α的值为( )A . 1 B. 2 C. - 1 D. - 29. 若存在过点 (1,0)的直线与曲线 yx 3 和 y ax 2 15 x 9 都相切,则 a 等于4( )A . 1或 -25B . 1或21C . 7 或 - 25D .7或 76444 6441 110. 若曲线 yx 2 在点 a, a 2 处的切线与两个坐标围成的三角形的面积为18,则 aA 、64B 、 32C 、 16D 、811. (本小题满分 13 分) 设 f ( x)ae x 1b( a 0) . ( I )求 f ( x) 在 [0, ) 上的最小值;ae x3x ;求 a,b 的值 .( II )设曲线 yf ( x) 在点 (2, f (2)) 的切线方程为 y212. 若曲线 f x ax2Inx 存在垂直于y轴的切线,则实数 a 的取值范围是.二、求单调性或单调区间1、利用导数判断函数单调性的方法:设函数y f (x) 在某个区间 D 内可导,若是 f ( x) >0,则y f (x) 在区间D上为增函数;若是 f ( x) <0,则y f (x) 在区间 D 上为减函数;若是 f ( x) =0恒成立,则y f (x) 在区间 D 上为常数 .2、利用导数求函数单调区间的方法:不等式 f ( x) >0的解集与函数y f (x) 定义域的交集,就是y f ( x) 的增区间;不等式 f ( x) <0的解集与函数y f (x) 定义域的交集,就是y f (x) 的减区间 .1、函数f (x) ( x 3)e x的单调递加区间是( )A . ( ,2) B. (0,3) C. (1,4) D . (2, )2. 函数f (x)x315x233x 6 的单调减区间为.3. 已知函数,,谈论的单调性。
导数的11个专题PDF(243页)

目录导数专题一、单调性问题 (2)导数专题二、极值问题 (38)导数专题三、最值问题 (53)导数专题四、零点问题 (77)导数专题五、恒成立问题和存在性问题 (118)导数专题六、渐近线和间断点问题 (170)导数专题七、特殊值法判定超越函数的零点问题 (190)导数专题八、避免分类讨论的参变分离和变换主元 (201)导数专题九、公切线解决导数中零点问题 (214)导数专题十、极值点偏移问题 (219)导数专题十一、构造函数解决导数问题 (227)导数专题一、单调性问题【知识结构】【知识点】一、导函数代数意义:利用导函数的正负来判断原函数单调性;二、分类讨论求函数单调性:含参函数的单调性问题的求解,难点是如何对参数进行分类讨论,讨论的关键在于导函数的零点和定义域的位置关系.三、分类讨论的思路步骤:第一步、求函数的定义域、求导,并求导函数零点;第二步、以导函数的零点存在性进行讨论;当导函数存在多个零点的时,讨论他们的大小关系及与区间的位置关系(分类讨论);第三步、画出导函数的同号函数的草图,从而判断其导函数的符号(画导图、标正负、截定义域);第四步、(列表)根据第五步的草图列出()'f x ,()f x 随x 变化的情况表,并写出函数的单调区间;第五步、综合上述讨论的情形,完整地写出函数的单调区间,写出极值点,极值与区间端点函数值比较得到函数的最值.四、分类讨论主要讨论参数的不同取值求出单调性,主要讨论点:1.最高次项系数是否为0;2.导函数是否有极值点;3.两根的大小关系;4.根与定义域端点讨论等。
五、求解函数单调性问题的思路:(1)已知函数在区间上单调递增或单调递减,转化为()0f x '≥或()0f x '≤恒成立;(2)已知区间上不单调,转化为导函数在区间上存在变号零点,通常利用分离变量法求解参变量的范围;(3)已知函数在区间上存在单调递增或单调递减区间,转化为导函数在区间上大于零或小于零有解.六、原函数单调性转化为导函数给区间正负问题的处理方法(1)参变分离;(2)导函数的根与区间端点直接比较;(3)导函数主要部分为一元二次时,转化为二次函数根的分布问题.这里讨论的以一元二次为主。
导数知识点总结及其分类

导数知识点总结及其分类导数的定义在数学上,函数在一点处的导数定义为该点处的函数值的变化量与自变量的变化量的比值,在极限的意义下表述为:\[f'(x) = \lim_{\delta x\to 0} \frac{f(x + \delta x) - f(x)}{\delta x}\]其中,$f'(x)$表示函数$f(x)$在点$x$处的导数。
导数的性质1. 导数存在性:导数存在的条件是函数在该点处可导,即函数在该点处存在切线。
若函数在某一点可导,则该点上的导数存在。
2. 导数的连续性:若函数在某一点处可导,则函数在该点连续。
3. 导数的代数运算:导数具有代数运算的性质,即导数的和、差、积、商的运算规则。
4. 导数的复合函数:复合函数的导数可以通过链式法则进行求解。
5. 隐函数的导数:对于隐函数,可以利用导数求解其导数。
导数的计算方法1. 利用导数的定义进行求导:即利用导数的定义式进行求导数。
2. 利用基本导数法则:如常数法则、幂法则、指数函数导数、对数函数导数、三角函数导数等。
3. 利用导数的运算法则:对于复合函数的导数、和差积商的法则。
4. 利用隐函数求导:对于隐函数,可以通过求偏导数的方式进行求导数。
5. 利用参数方程求导:对于参数方程,可以通过求导数来解决相关问题。
导数的应用1. 函数的极值问题:通过导数可以求解函数的极大值和极小值。
2. 切线和法线问题:导数可以用来求曲线上某一点处的切线和法线的斜率。
3. 曲率问题:曲率是描述曲线弯曲程度的一个重要概念,利用导数可以求解曲线的曲率。
4. 函数的图像问题:通过导数可以确定函数的增减性、凹凸性,从而画出函数的图像。
5. 物理问题:在物理学中,导数可以用来描述时间、速度、加速度等物理量的关系。
导数的分类1. 基本函数的导数:即通过基本导数法则对基本函数进行求导,包括幂函数导数、指数函数导数、对数函数导数、三角函数导数等。
2. 复合函数的导数:复合函数的导数可以通过链式法则进行求解,包括外函数和内函数的导数运算。
高考文科导数考点汇总PDF.pdf

①求函数ƒ (x) 在(a,b)内的极值;
②求函数ƒ (x) 在区间端点的值ƒ(a)、ƒ(b);
2
书山有路
③将函数ƒ (x) 的各极值与ƒ(a)、ƒ(b)比较,其中最大的是最大值,其中最小的是最小值。
二、热点题型分析 题型一:利用导数研究函数的极值、最值。
而过 y = f (x)上P[1, f (1)]的切线方程为y = 3x +1.
3 + 2a + b = 3 故 a − c = −3
即2aa−+c b==−30
① ②
∵ y = f (x)在x = −2时有极值,故f (−2) = 0,−4a + b = −12 ③
由①②③得 a=2,b=-4,c=5
1. f (x) = x3 − 3x2 + 2 在区间−1,1 上的最大值是 2
2.已知函数 y = f (x) = x(x − c)2在x = 2 处有极大值,则常数 c= 6 ;
3.函数 y = 1+ 3x − x3 有极小值 -1 ,极大值 3
题型二:利用导数几何意义求切线方程
1.曲线 y = 4x − x3 在点 (−1, −3) 处的切线方程是 y = x − 2
∴ f (x) = x3 + 2x2 − 4x + 5.
(2) f (x) = 3x2 + 4x − 4 = (3x − 2)(x + 2).
− 3 x −2时, f (x) 0;当 − 2 x 2 时, f (x) 0;
当
3
当2 3
x
1时,
f
导数知识点汇总

导数1.导数的几何意义:函数()y f x =在0x x =处的导数0'()f x ,就是曲线()y f x =过点0x 的切线斜率. ∴过点00(,)x y 的切线方程为000'()()y y f x x x -=- 0'()0f x =时,切线与x 轴 . 0'()0f x >时,切线的倾斜角为 . 0'()0f x <时,切线的倾斜角为 . 0'()f x 不存在时,切线 .2.基本初等函数的导数公式:3.导数运算法则:[()()]''()'()f x g x f x g x ±=±[()()]''()()()'()f x g x f x g x f x g x ⋅=+2()'()()()g'()'()()f x f x g x f x x g x g x ⎡⎤-=⎢⎥⎣⎦4.复合函数求导:{[()]}''[()]'()f g x f g x g x =⋅:(sin 2)'2cos 2eg x x = 25242[(1)]'5(1)210(1)x x x x x +=+⋅=+5.导数与函数单调性、极值的关系. ① '()0()'()0()f x f x f x f x ⎧>⇒↑⎪⎨<⇒↓⎪⎩()'()0()'()0f x f x f x f x ⎧↑⇒≥⎪⎨↓⇒≤⎪⎩② 若0'()0,f x =且在0x 左边'()0f x >,右边'()0f x <,则0x 是()f x 的极大值点 在0x 左边'()0f x <,右边'()0f x >,则0x 是()f x 的极小值点★ 0x 为极值点 0'()0f x =题型一:导数的几何意义 【基础题】1.曲线y =(4,2)P 处的切线方程是2.已知3y x =在点P 处的切线斜率为3,则P 的坐标为 3.已知直线10x y --=与抛物线2y ax =相切,则a =4.已知曲线ln y x x =+在点(1,1)处的切线与曲线2(2)1y ax a x =+++相切,则a = 5.若曲线xy e -=上点P 处的切线平行于直线210x y ++=,则点P 的坐标为 6.若函数()f x 的导数为'()sin f x x =-,则函数图象在点(4,(4))f 处的切线倾斜角为( ).A 90︒ .0B ︒ .C 锐角 .D 钝角【提高题】 1.设点P 是曲线211ln 42y x x =+上的任意一点,P 点处切线倾斜角为α,则角α的取值范围是2.曲线21x y e -=+在点(0,2)处的切线与直线0y =和y x =围成的三角形的面积为( )1.3A 1.2B 2.3C .1D3.点P 是曲线2ln y x x =-上任意一点,则P 到直线2y x =-的距离的最小值是变式:函数2()x f x e =的图象上的点到直线240x y --=的距离的最小值是题型二:导数与函数单调性、极值、最值 【基础题】1.函数()ln (0)f x x x x =>的单调递增区间是2.函数32()39f x x ax x =++-,已知()f x 在3x =-时取得极值,则a =3.设2()ln f x a x bx x =++,在121,2x x ==处有极值,则a = ,b = . 4.已知函数32()(6)1f x x ax a x =++++有极大值和极小值,则实数a 的取值范围是 5.若函数xy e ax =+有大于0的极值点,则a 的取值范围是6.已知函数3()128f x x x =-+在区间[3,3]-上的最大值与最小值分别为,,M m 则【提高题】1.直线y a =与函数33y x x =-的图象有三个相异的交点,则a 的取值范围是 2.若函数3()26f x x x k =-+在R 上只有一个零点,求常数k 的取值范围.3.已知函数()(1)ln 1,f x x x x =+-+若'2()1xf x x ax ≤++恒成立,求a 的取值范围.4.已知函数21()2,f x ax x =-若()f x 在(0,1]上是增函数,求a 的取值范围. 变式:函数3y ax x =-在R 上是减函数,则a 的取值范围是5.已知函数2()ln (0),f x x ax x a =-->若函数()f x 是单调函数,求a 的取值范围.题型三:与函数性质有关1.若函数42()f x ax bx c =++满足'(1)2,f =则'(1)f -=2.已知函数3()f x x x =+对任意的[2,2],(2)()0m f mx f x ∈--+<恒成立,则x 的取值范围是3.已知对任意实数x ,有()(),()(),f x f xg x gx -=--=且0x >时,''()0,()0,f x g x >>则0x <时( )''.()0,()0A f x g x >> ''.()0,()0B f x g x >< ''.()0,()0C f x g x <> ''.()0,()0D f x g x <<4.若函数()f x 对定义域R 内的任意x 都有()(2)f x f x =-,且当1x ≠时其导函数'()f x 满足(1)'()0,x f x ->若12,a <<则( )2.(log )(2)(2)a A f a f f << 2.(2)(log )(2)a B f f a f << 2.(2)(2)(log )a C f f f a << 2.(log )(2)(2)a D f a f f <<5.设(),()f x g x 分别是定义在R 上的奇函数和偶函数,当0x <时,'()()()'(f x g x f x g x +>且(3)0,g -=则不等式()()0f x g x <的解集为( ).(3,0)(3,)A -+∞ .(3,0)(0,3)B - .(,3)(3,)C -∞-+∞ .(,3)(0,3)D -∞-6.已知函数()y f x =是定义在R 上的奇函数,且当(,0)x ∈-∞时,不等式()'()0f x xf x +>恒成立,0.10.122112(2),(log 2)(log 2),(log )(log )44a fb fc f ππ===,则,,a b c 的大小关系是( ).A a b c >> .B c b a >> .C b a c >> .D a c b >>题型四:图象题1.函数()f x 的定义域为开区间(,)a b ,导函数'()f x 在(,)a b 内的图象如图所示,则函数()f x 在开区间(,)a b 内有 个极小值点.2.设'()f x 是函数()f x 的导函数,将()y f x =和'()y f x =的图象画在同一个个直角坐标系中,不可能正确的是( )3.设曲线21y x =+在其上任一点(,)x y 处的切线的斜率为()g x ,则()cos y g x x =的部分图象可以为( )4.已知函数'()y xf x =的图象如右图所示,则()y f x =的图象大致是( )5.已知()y f x =在(0,1)内的一段图象是图象所示的一段圆弧,若1201,x x <<<则( )1212()().f x f x A x x < 1212()().f x f x B x x > 1212()().f x f x C x x = .D 不能确定6.若函数2()f x x bx c =++的图象顶点在第四象限,则函数'()f x 的图象是( )链接高考:1.(2015,12)设函数'()f x 是奇函数()f x 的导函数,(1)0,f -=当0x >时,'()()0x f x f x -<则使得()0f x >成立的x 的取值范围是( ).(,1)(0,1)A -∞- .(1,0)(1,)B -+∞ .(,1)(1,0)C -∞-- .(0,1)(1,)D +∞2.(2015,21)设函数2().mxf x ex mx =+-(1)证明:()f x 在(,0)-∞上单调递减,在(0,)+∞上单调递增;(2)若对于任意12,[1,1],x x ∈-都有12|()()|1,f x f x e -≤-求m 的取值范围.3.(2015,21)已知函数31(),()ln .4f x x axg x x =++=- (1)当a 为何值时,x 轴为曲线()y f x =的切线;(2)用min{,}m n 表示,m n 中的最小值,设函数()min{(),()}(0),h x f x g x x =>讨论()h x 零点的个数.4.(2014,7)设曲线ln(1)y ax x =-+在点(0,0)处的切线方程为2,y x =则a =( ).0A .1B .2C .3D5.(2014,12)设函数(),xf x mπ=若存在()f x 的极值点0x 满足22200[()],x f x m +<则m 的取值范围是 ( ).(,6)(6,)A -∞-+∞ .(,4)(4,)B -∞-+∞ .(,2)(2,)C -∞-+∞ .(,1)(1,)D -∞-+∞6.(2014,21)已知函数()2.x x f x e e x -=-- (1)讨论()f x 的单调性.(2)设()(2)4()g x f x bf x =-,当0x >时,()0,g x >求b 的最大值,(3)已知1.4142 1.4143,<估计ln 2的近似值(精确到0.001)7.(2014,11)已知函数32()31f x ax x =-+,若()f x 存在唯一零点0,x 且00x >,则a 的取值范围是8.(2014,21)设函数1()ln ,x xbe f x ae x x-=+曲线()y f x =在点(1,(1))f 处的切线方程为(1) 2.y e x =-+(1)求,.a b(2)证明:() 1.f x >9.(2013,21)设函数2(),()().xf x x ax bg x e cx d =++=+若曲线()y f x =和曲线()y g x =都过点(0,2)P ,且在点P 处有相同的切线4 2.y x =+(1)求,,,a b c d 的值.(2)若2x ≥-时,()(),f x kg x ≤求k 的取值范围.。
导数知识归纳(课件)

一、导数有关概念1.导数的概念函数y=f(x),如果自变量x 在x 0处有增量x ∆,那么函数y 相应地有增量y ∆=f (x 0+x ∆)-f (x 0),比值x y ∆∆叫做函数y=f (x )在x 0到x 0+x ∆之间的平均变化率,即x y ∆∆=xx f x x f ∆-∆+)()(00。
如果当0→∆x 时,xy ∆∆有极限,我们就说函数y=f(x)在点x 0处可导,并把这个极限叫做f (x )在点x 0处的导数,记作f ′(x 0)或y ′|0x x =。
即f ′(x 0)=0lim →∆x x y ∆∆=0lim →∆x xx f x x f ∆-∆+)()(00。
说明:(1)函数f (x )在点x 0处可导,是指0→∆x 时,x y ∆∆有极限。
如果x y ∆∆不存在极限,就说函数在点x 0处不可导,或说无导数。
(2)x ∆是自变量x 在x 0处的改变量,0≠∆x 时,而y ∆是函数值的改变量,可以是零。
2、导函数(1)定义:如果函数f(x)在开区间(a ,b )内每一点都可导,就说f(x)在区间(a ,b )内可导,这时对于区间(a ,b )内每一个确定的值x 0,都对应着一个导数f ′(x 0)。
这样在开区间(a ,b )构成一个新函数,称为f(x)在(a ,b )内导函数(简称导数)。
记f ′(x )f ′(x 0)=0lim →∆x xy ∆∆=0lim →∆x ()()f x x f x x +∆-∆ (2)在点x 0处导数、导函数关系函数在点x 0处导数就是在该点的函数改变量y ∆与自变量改变量x ∆的比的极限,是一个数值。
是导函数f ′(x )在x =x 0处的函数值3、求函数y=f (x )在点x 0处的导数的步骤: 方法一、定义法:(1)求函数的增量y ∆=f (x 0+x ∆)-f (x 0); (2)求平均变化率x y ∆∆=xx f x x f ∆-∆+)()(00; (3)取极限,得导数f’(x 0)=xy x ∆∆→∆0lim 。
导数知识点整理总结

导数知识点整理总结导数是微积分的重要概念之一,它是研究函数变化率的工具。
导数的定义是函数在某一点的变化率。
在数学中,导数可以用几何意义解释为切线的斜率,也可以用物理意义解释为速度的变化率。
导数的概念最早由牛顿和莱布尼茨独立发现,被广泛应用于数学、物理、经济等领域。
导数的研究可以追溯到十七世纪。
莱布尼茨在1684年首次提出了微分学的符号表示法,他使用了dy/dx这样的记号来表示导数。
牛顿则使用了几何表示法,他将导数解释为切线的斜率。
导数的定义如下:对于函数f(x),如果存在极限lim(x->a)(f(x)-f(a))/(x-a),则称这个极限为函数f(x)在点a的导数,记作f'(a)或者(dy/dx)(x=a)。
这个极限表示了当自变量x趋近于a时,函数f(x)在点a附近的变化率。
导数有一些基本的性质和运算规则,其中最重要的是导数的线性性质和乘法法则。
导数的线性性质指的是对于任意常数k,函数f(x)和g(x),有以下等式成立:(kf(x))' = kf'(x),(f(x)+g(x))' = f'(x) + g'(x)。
乘法法则指的是对于两个函数f(x)和g(x),它们的乘积的导数可以用它们的导数表示,即(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)。
导数的应用非常广泛,它可以用于求函数的极值、优化问题、曲线的形状分析等。
函数的极值可以通过求导数并解方程的方法求得。
导数可以帮助我们找到函数的最大值和最小值,以及函数在这些点的斜率。
导数还可以用于优化问题,例如求函数的最大值和最小值,或者找到函数的最大斜率点等。
而曲线的形状分析可以通过导数的符号和零点来完成。
导数的符号可以告诉我们函数是增加还是减少,而导数的零点则表示函数的极值点。
除了基本的导数概念和运算规则外,还有一些特殊函数的导数需要特殊的处理。
例如,对于幂函数f(x) = x^n,它的导数可以通过幂函数的求导公式f'(x) = nx^(n-1)来计算。
导数知识归纳(课件)

一、导数有关概念1.导数的概念函数y=f(x),如果自变量x 在x 0处有增量x ∆,那么函数y 相应地有增量y ∆=f (x 0+x ∆)-f (x 0),比值xy∆∆叫做函数y=f (x )在x 0到x+x ∆之间的平均变化率,即xy ∆∆=xx f x x f ∆-∆+)()(00。
如果当0→∆x 时,xy∆∆有极限,我们就说函数y=f(x)在点x 0处可导,并把这个极限叫做f (x )在点x 0处的导数,记作f ′(x 0)或y ′|0x x =。
即f ′(x 0)=0lim →∆x xy ∆∆=0lim →∆x xx f x x f ∆-∆+)()(00。
说明:(1)函数f (x )在点x 0处可导,是指0→∆x 时,x y ∆∆有极限。
如果x y∆∆不存在极限,就说函数在点x 0处不可导,或说无导数。
(2)x ∆是自变量x 在x 0处的改变量,0≠∆x 时,而y ∆是函数值的改变量,可以是零。
2、导函数(1)定义:如果函数f(x)在开区间(a ,b )内每一点都可导,就说f(x)在区间(a ,b )内可导,这时对于区间(a ,b )内每一个确定的值x 0,都对应着一个导数f ′(x 0)。
这样在开区间(a ,b )构成一个新函数,称为f(x)在(a ,b )内导函数(简称导数)。
记f ′(x )f ′(x 0)=0lim →∆x xy∆∆=0lim →∆x ()()f x x f x x+∆-∆ (2)在点x 0处导数、导函数关系函数在点x 0处导数就是在该点的函数改变量y ∆与自变量改变量x ∆的比的极限,是一个数值。
是导函数f ′(x )在x =x 0处的函数值3、求函数y=f (x )在点x 0处的导数的步骤: 方法一、定义法:(1)求函数的增量y ∆=f (x 0+x ∆)-f (x 0);(2)求平均变化率xy ∆∆=xx f x x f ∆-∆+)()(00; (3)取极限,得导数f’(x 0)=xy x ∆∆→∆0lim 。
导数的十一个小专题

比较教学法在初中生物课中的应用比较,是人类思维的基本方式,也是创造性思维的重要方法,有比较才有鉴别,通过比较,可产生强烈的刺激,促进积极思维。
那么,生物比较法教学有何作用呢?一、温故知新可使学生在已知概念的基础上,迅速而准确地去认识未知概念,获得新的知识,扩大原有知识的范围,加深原有知识的深度。
如讲细菌的营养方式——异养型,先用绿藻的自养方式作对比,引出异养的含义。
二、知识网络化可使学生牢固地建立起知识的内部联系,把一些零碎的知识组织起来,使之网络化。
生物学知识,本来有它固有的联系,但在教材编写时,不得已将它们分割开来,编入不同章节中。
我们在教学中,必须将分散了的系统的知识适时相应地集中起来,阐明复杂多样的生命现象和规律间的关系。
三、理解深入化中学生认识事物时,往往抓不住事物的本质特征,对那些相近的概念、成双成对、成列成排、前后联系的名词混淆不清,琢磨不定。
有比较才能鉴别,一切事物总是相比较而存在的。
在教学中采用比较法,突出一方,找出它们的异同,就可避免混淆和张冠李戴。
如讲穗状花序时,用总状花序作比较,找出它们之间的相同之处和不同之处,就可使学生清楚地掌握这一对概念。
四、知识直观化中学生物学主要是讲述生命现象的共性和个性,都是科学家们经过反复比较,从理论上概括总结出来的。
生命现象之间有着本质的内在联系,纵横交错,网络复杂。
生命现象的多样性决定了比较法的多样性,一般的比较法有类型或类别比较、生命各阶段的阶段比、差异比和综合比。
1.类型或类别比较根据被对比知识点的相似性和差异性,类比法又分为类型比较法和类别比较法。
前者是把同类的各个生命现象和规律进行比较,找出共同性和相似性,进行归纳教学的方法。
如学生已学过了地上茎的知识,在讲授地下茎时,将其特点分别与地上茎特点作相应比较,或者让学生把两个实物对比分析,这样可使学生在已有知识的基础上,自学似地获得新的知识,建立起同类的概念。
2.生命各阶段的阶段比即从时间上和空间上,将某一生命现象发生发展的历程分阶段进行比较的方法。
导数知识归纳(课件)

一、导数有关概念1.导数的概念函数y=f(x),如果自变量x 在x 0处有增量x ∆,那么函数y 相应地有增量y ∆=f (x 0+x ∆)-f (x 0),比值x y ∆∆叫做函数y=f (x )在x 0到x 0+x ∆之间的平均变化率,即x y ∆∆=xx f x x f ∆-∆+)()(00。
如果当0→∆x 时,xy ∆∆有极限,我们就说函数y=f(x)在点x 0处可导,并把这个极限叫做f (x )在点x 0处的导数,记作f ′(x 0)或y ′|0x x =。
即f ′(x 0)=0lim →∆x x y ∆∆=0lim →∆x xx f x x f ∆-∆+)()(00。
说明:(1)函数f (x )在点x 0处可导,是指0→∆x 时,x y ∆∆有极限。
如果x y ∆∆不存在极限,就说函数在点x 0处不可导,或说无导数。
(2)x ∆是自变量x 在x 0处的改变量,0≠∆x 时,而y ∆是函数值的改变量,可以是零。
2、导函数(1)定义:如果函数f(x)在开区间(a ,b )内每一点都可导,就说f(x)在区间(a ,b )内可导,这时对于区间(a ,b )内每一个确定的值x 0,都对应着一个导数f ′(x 0)。
这样在开区间(a ,b )构成一个新函数,称为f(x)在(a ,b )内导函数(简称导数)。
记f ′(x )f ′(x 0)=0lim →∆x xy ∆∆=0lim →∆x ()()f x x f x x +∆-∆ (2)在点x 0处导数、导函数关系函数在点x 0处导数就是在该点的函数改变量y ∆与自变量改变量x ∆的比的极限,是一个数值。
是导函数f ′(x )在x =x 0处的函数值3、求函数y=f (x )在点x 0处的导数的步骤: 方法一、定义法:(1)求函数的增量y ∆=f (x 0+x ∆)-f (x 0); (2)求平均变化率x y ∆∆=xx f x x f ∆-∆+)()(00; (3)取极限,得导数f’(x 0)=xy x ∆∆→∆0lim 。
导数基础知识点汇总及经典习题解答

导数导数基础:1. 导数(导函数的简称)的定义:设是函数定义域的一点,如果自变量在处有增量,则函数值也引起相应的增量;比值称为函数在点到之间的平均变化率;如果极限存在,则称函数在点处可导,并把这个极限叫做在处的导数,记作或,即=.②以知函数定义域为,的定义域为,则与关系为.2. 函数在点处连续与点处可导的关系:函数在点处连续是在点处可导的必要不充分条件. 常用性质:①可导的奇函数函数其导函数为偶函数. ②可导的偶函数函数其导函数为奇函数.3. 导数的几何意义:函数在点处的导数的几何意义就是曲线在点处的切线的斜率,也就是说,曲线在点P处的切线的斜率是,切线方程为4. 求导数的四则运算法则:(为常数)0x )(x f y =x 0x x ∆y )()(00x f x x f y -∆+=∆x x f x x f x y ∆-∆+=∆∆)()(00)(x f y =0x x x ∆+0x x f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000)(x f y =0x )(x f y =0x )(0'x f 0|'x x y =)(0'x f x x f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000)(x f y =A )('x f y =B A B B A ⊇)(x f y =0x 0x )(x f y =0x )(x f y =0x )(x f y =0x )(x f y =))(,(0x f x )(x f y =))(,(0x f x )(0'x f ).)((0'0x x x f y y -=-''')(v u v u ±=±)(...)()()(...)()(''2'1'21x f x f x f y x f x f x f y n n +++=⇒+++=⇒''''''')()(cv cv v c cv u v vu uv =+=⇒+=c②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.I.(为常数)()II.5. 复合函数的求导法则:或6. 函数单调性:⑴函数单调性的判定方法:设函数在某个区间内可导,如果>0,则为增函数;如果<0,则为减函数注:①是f (x )递增的充分条件,但不是必要条件,如在上并不是都有,有一个点例外即x=0时f (x ) = 0,同样是f (x )7. 极值的判别方法:(极值是在附近所有的点,都有<,则是函数的极大值,极小值同理)当函数在点处连续时, ②如果在附近的左侧<0,右侧>0,那么是极小值. ①如果在附近的左侧>0,右侧<0,那么是极大值;)0(2'''≠-=⎪⎭⎫⎝⎛v v u v vu v u 0'=C C xx cos )(sin '=2'11)(arcsin x x -=1')(-=n n nx x R n ∈x x sin )(cos '-=2'11)(arccos x x --=x x 1)(ln '=ex x a a log 1)(log '=11)(arctan 2'+=x x xx e e =')(aa a x x ln )('=11)cot (2'+-=x x arc )()())(('''x u f x f x ϕϕ=xu x u y y '''⋅=)(x f y =)('x f )(x f y =)('x f )(x f y =0)(φx f 32x y =),(+∞-∞0)(φx f 0)(πx f 0x )(x f )(0x f )(0x f )(x f )(x f 0x 0x )('x f )('x f )(0x f 0x )('x f )('x f )(0x f例1. 8.函数313y x x =+- 有 ( )A.极小值-1,极大值1B. 极小值-2,极大值3C.极小值-1,极大值3D. 极小值-2,极大值26.函数344+-=x x y 在区间[]2,3-上的最小值为( ) A .72 B .36 C .12 D .06.函数x xy ln =的最大值为( )A .1-eB .eC .2e D .3102.函数xe x xf -⋅=)(的一个单调递增区间是( )(A)[]0,1- (B) []8,2 (C) []2,1 (D) []2,03.已知对任意实数x ,有()()()()f x f x g x g x -=--=,,且0x >时,()0()0f x g x ''>>,,则0x <时( ) A .()0()0f x g x ''>>, B .()0()0f x g x ''><, C .()0()0f x g x ''<>,D .()0()0f x g x ''<<,4.若函数b bx x x f 33)(3+-=在()1,0内有极小值,则( ) (A ) 10<<b (B ) 1<b (C ) 0>b (D )21<b5.若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为( )A .430x y --=B .450x y +-=C .430x y -+=D .430x y ++=6.曲线x y e =在点2(2)e ,处的切线与坐标轴所围三角形的面积为( ) A.294eB.22eC.2eD.22e2.若'0()3f x =-,则000()(3)limh f x h f x h h →+--=( )A .3-B .6-C .9-D .12-1.(2005全国卷Ⅰ文)函数93)(23-++=x ax x x f ,已知)(x f 在3-=x 时取得极值,则a =( ) (A )2(B )3(C )4(D )52.(2008海南、宁夏文)设()ln f x x x =,若0'()2f x =,则0x =( )A. 2eB. eC. ln 22D. ln 23.(2005广东)函数13)(23+-=x x x f 是减函数的区间为( ) A .),2(+∞ B .)2,(-∞ C .)0,(-∞ D .(0,2)4.(2008安徽文)设函数1()21(0),f x x x x =+-< 则()f x ( )A .有最大值B .有最小值C .是增函数D .是减函数5.(2007福建文、理)已知对任意实数x 有f(-x)=-f(x),g(-x)=g(x),且x>0时,f’(x)>0,g’(x)>0,则x<0时( )A f’(x)>0,g’(x)>0B f’(x)>0,g’(x)<0C f’(x)<0,g’(x)>0D f’(x)<0,g’(x)<06.(2008全国Ⅱ卷文)设曲线2ax y =在点(1,a )处的切线与直线062=--y x 平行,则=a ( )A .1B .12C .12-D .1-导数答案CDA ABA ADD DBD ABA。
