重庆中考几何题分类汇编(含答案)

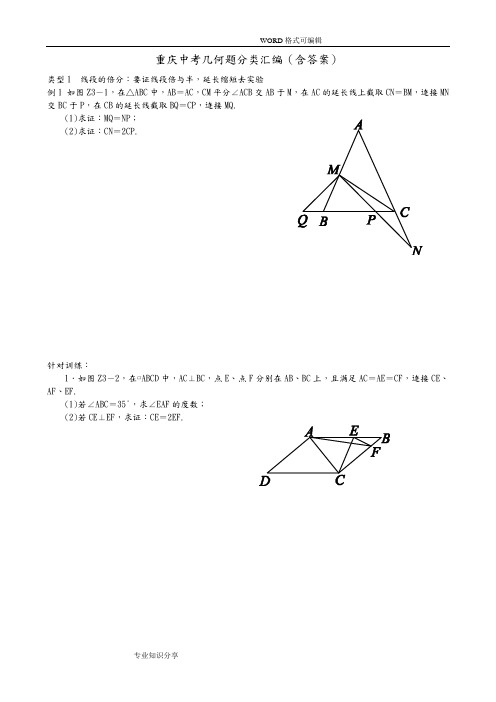
重庆中考几何题分类汇编（含答案）类型1 线段的倍分：要证线段倍与半，延长缩短去实验例1 如图Z3－1，在△ABC中，AB＝AC，CM平分∠ACB交AB于M，在AC的延长线上截取CN＝BM，连接MN 交BC于P，在CB的延长线截取BQ＝CP，连接MQ.(1)求证：MQ＝NP；(2)求证：CN＝2CP.针对训练：1．如图Z3－2，在▱ABCD中，AC⊥BC，点E、点F分别在AB、BC上，且满足AC＝AE＝CF，连接CE、AF、EF.(1)若∠ABC＝35°，求∠EAF的度数；(2)若CE⊥EF，求证：CE＝2EF.2．已知，在△ABC 中，AB ＝AC ，∠BAC ＝90°，E 为边AC 任意一点，连接BE.(1)如图①，若∠ABE＝15°，O 为BE 中点，连接AO ，且AO ＝1，求BC 的长；(2)如图②，F 也为AC 上一点，且满足AE ＝CF ，过A 作AD⊥BE 交BE 于点H ，交BC 于点D ，连接DF 交BE于点G ，连接AG.若AG 平分∠CAD，求证：AH ＝12AC.3．在△ACB 中，AB ＝AC ，∠BAC ＝90°，点D 是AC 上一点，连接BD ，过点A 作AE⊥BD 于E ，交BC 于F.(1)如图①，若AB ＝4，CD ＝1，求AE 的长；(2)如图②，点G 是AE 上一点，连接CG ，若BE ＝AE ＋AG ，求证：CG ＝2AE.4．在等腰直角三角形ABC 中，∠BAC ＝90°，AB ＝AC ，D 是斜边BC 的中点，连接AD.(1)如图①，E 是AC 的中点，连接DE ，将△CDE 沿CD 翻折到△CDE′，连接AE′，当AD ＝6时，求AE′的值．(2)如图②，在AC 上取一点E ，使得CE ＝13AC ，连接DE ，将△CDE 沿CD 翻折到△CDE′，连接AE′交BC 于点F ，求证：DF ＝CF.类型2 线段的和差：要证线段和与差，截长补短去实验例2 如图，在△ABC中，∠BAC＝90°，在BC上截取BD＝BA，连接AD，在AD左侧作∠EAD＝45°交BD于E.(1)若AC＝3，则CE＝________(直接写答案)；(2)如图①，M、N分别为AB和AC上的点，且AM＝AN，连接EM、DN，若∠AME＋∠AND＝180°，求证：DE ＝DN＋ME；(3)如图②，过E作EF⊥AE，交AD的延长线于F，在EC上选取一点H，使得EH＝BE，连接FH，在AC上选取一点G，使得AG＝AB，连接BG、FG，求证：FH＝FG.针对训练：1．如图Z3－7，在▱ABCD中，AE⊥BC于E，AE＝AD，EG⊥AB于G，延长GE、DC交于点F，连接AF.(1)若BE＝2EC，AB＝13，求AD的长；(2)求证：EG＝BG＋FC.2．如图，在正方形ABCD 中，点P 为AD 延长线上一点，连接AC 、CP ，过点C 作CF⊥CP 于点C ，交AB 于点F ，过点B 作BM⊥CF 于点N ，交AC 于点M.(1)若AP ＝78AC ，BC ＝4，求S △ACP ；(2)若CP －BM ＝2FN ，求证：BC ＝MC.3．如图，在△ABC 中，AB ＝BC ，以AB 为一边向外作菱形ABDE ，连接DC ，EB 并延长EB 交AC 于F ，且CB⊥AE 于G.(1)若∠EBG＝20°，求∠AFE；(2)试问线段AE ，AF ，CF 之间的数量关系并证明．类型3 倍长中线：三角形中有中线，延长中线等中线例3 如图Z3－10①，在Rt△ABC中，∠ABC＝90°，D、E分别为斜边AC上两点，且AD＝AB，CE＝CB，连接BD、BE.(1)求∠EBD的度数；(2)如图Z3－10②，过点D作FD⊥BD于点D，交BE的延长线于点F，在AB上选取一点H，使得BH＝BC，连接CH，在AC上选取一点G，使得GD＝CD，连接FH、FG，求证：FH＝FG.针对训练：1．如图，已知在▱ABCD中，G为BC的中点，点E在AD边上，且∠1＝∠2.(1)求证：E是AD中点；(2)若F为CD延长线上一点，连接BF，且满足∠3＝∠2，求证：CD＝BF＋DF.2．如图Z 3－12，在菱形ABCD 中，点E 、F 分别是BC 、CD 上的点，连接AE ，AF ，DE 、EF ，∠DAE ＝∠BAF.(1)求证：CE ＝CF ；(2)若∠ABC＝120°，点G 是线段AF 的中点，连接DG ，EG.求证：DG⊥GE.3．在Rt △ABC 中，∠ACB ＝90°，点D 与点B 在AC 同侧，∠ADC ＞∠BAC，且DA ＝DC ，过点B 作BE∥DA 交DC 于点E ，M 为AB 的中点，连接MD ，ME.(1)如图①，当∠ADC＝90°时，线段MD 与ME 的数量关系是________；(2)如图②，当∠ADC＝60°时，试探究线段MD 与ME 的数量关系，并证明你的结论；(3)如图③，当∠ADC＝α时，求ME MD的值．4．如图①，等边三角形ABC中，CE平分∠ACB，D为BC边上一点，且DE＝CD，连接BE.(1)若CE＝4，BC＝6 3，求线段BE的长；(2)如图②，取BE中点P，连接AP，PD，AD，求证：AP⊥P D且AP＝3PD；(3)如图③，把图Z3－14②中的△CDE绕点C顺时针旋转任意角度，然后连接BE，点P为BE中点，连接AP，PD，AD，问第(2)问中的结论还成立吗？若成立，请证明；若不成立，请说明理由．5．在△ABC中，以AB为斜边，作直角三角形ABD，使点D落在△ABC内，∠ADB＝90°.(1)如图①，若AB＝AC，∠BAD＝30°，AD＝6 3，点P、M分别为BC、AB边的中点，连接PM，求线段PM 的长；(2)如图②，若AB＝AC，把△ABD绕点A逆时针旋转一定角度，得到△ACE，连接ED并延长交BC于点P，求证：BP＝CP；(3)如图③，若AD＝BD，过点D的直线交AC于点E，交BC于点F，EF⊥AC，且AE＝EC，请直接写出线段BF、FC、AD之间的关系(不需要证明)．类型4 中位线：三角形中两中点，连接则成中位线例4 2017·河南如图①，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．(1)观察猜想：图①中，线段PM与PN的数量关系是__________，位置关系是__________；(2)探究证明：把△ADE绕点A按逆时针方向旋转到图②的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；(3)拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值．针对训练：1．如图①，在任意的三角形ABC中，分别以AB和AC为一边作等腰三角形ABE和等腰三角形ACD，AB＝AE，AC＝AD，且∠BAE＋∠CAD＝180°，连接DE，延长CA交DE于F.(1)求证：∠CAB＝∠AED＋∠ADE；(2)若∠ACB＝∠BAE＝∠CAD＝90°，如图②，求证：BC＝2AF；(3)若在△ABC中，如图③所示，作等腰三角形ABE和等腰三角形ACD，AB与DE交于点F，F为DE的中点，请问(2)中的结论还成立吗？若成立，请给出证明，若不成立，请说明理由．2．如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＋∠EAD＝180°，△ABC不动，△ADE绕点A旋转，连接BE、CD，F为BE的中点，连接AF.(1)如图①，当∠BAE＝90°时，求证：CD＝2AF；(2)当∠BAE≠90°时，(1)的结论是否成立？请结合图②说明理由．3．如图①，在等腰三角形ABC中，AB＝AC，在底边BC上取一点D，在边AC上取一点E，使AE＝AD，连接DE，在∠ABD的内部作∠ABF＝2∠EDC，交AD于点F.(1)求证：△ABF是等腰三角形；(2)如图②，BF的延长交AC于点G.若∠DAC＝∠CBG，延长AC至点M，使GM＝AB，连接BM，点N是BG的中点，连接AN，试判断线段AN、BM之间的数量关系，并证明你的结论．类型5 角的和差倍分图中有角平分线，可向两边作垂线；也可将图对折看，对称以后关系现．角平分线平行线，等腰三角形来添．角平分线加垂线，三线合一试试看．例5．如图，把△EFP放置在菱形ABCD中，使得顶点E，F，P分别在线段AB，AD，AC上，已知EP＝FP＝6，EF＝6 3，∠BAD＝60°，且AB＞6 3.(1)求∠EPF的大小；(2)若AP＝10，求AE＋AF的值．针对训练：1．已知：如图①，AD平分∠BAC，∠B＋∠C＝180°，∠B＝90°，易知：DB＝DC.探究：如图②，AD平分∠BAC，∠ABD＋∠ACD＝180°，∠ABD＜90°，求证：DB＝DC.2．在△ACB中，AB＝AC，∠BAC＝90°，点D是AC上一点，连接BD，过点A作AE⊥BD于E，交BC于F.(1)如图①，若AB＝4，CD＝1，求AE的长；(2)如图②，点P是AC上一点，连接FP，若AP＝CD，求证：∠ADB＝∠CPF.3．已知，在▱ABCD中，∠BAD＝45°，AB＝BD，E为BC上一点，连接AE交BD于F，过点D作DG⊥AE 于G，延长DG交BC于H.(1)如图①，若点E与点C重合，且AF＝5，求AD的长；(2)如图②，连接FH，求证：∠AFB＝∠HFB.4．如图，将正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点M处，点C落在点N处，MN与CD交于点P，连接EP.当点M在边AD上移动时，连接BM、BP.(1)求证：BM是∠AMP的平分线；(2)△PDM的周长是否发生变化？证明你的结论．类型6 旋转型全等问题：图中若有边相等，可用旋转做实验例6．△ABC 中，∠BAC ＝90°，AB ＝AC ，点D 为直线BC 上一动点(点D 不与B ，C 重合)，以AD 为边在AD 右侧作正方形ADEF ，连接CF.(1)观察猜想：如图①，当点D 在线段BC 上时，①BC 与CF 的位置关系为：________．②BC ，CD ，CF 之间的数量关系为：___________；(将结论直接写在横线上)(2)数学思考：如图Z 3－25②，当点D 在线段CB 的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．(3)拓展延伸：如图Z 3－25③，当点D 在线段BC 的延长线上时，延长BA 交CF 于点G ，连接GE.若已知AB＝2 2，CD ＝14BC ，请求出GE 的长．针对训练：1．在四边形ABCD 中，∠B ＋∠D＝180°，对角线AC 平分∠BAD.(1)如图①，若∠DAB＝120°，且∠B＝90°，试探究边AD 、AB 与对角线AC 的数量关系并说明理由．(2)如图②，若将(1)中的条件“∠B＝90°”去掉，(1)中的结论是否成立？请说明理由．(3)如图③，若∠DAB＝90°，探究边AD 、AB 与对角线AC 的数量关系并说明理由．2．如图①，在正方形ABCD中，点E为边BC上一点，将△ABE沿AE翻折得△AHE，延长EH交边CD于F，连接AF.(1)求证：∠EAF＝45°；(2)延长AB，AD，如图②，射线AE、AF分别交正方形两个外角的平分线于M、N，连接MN，若以BM、DN、MN为三边围成三角形，试猜想三角形的形状，并证明你的结论．3．如图①，在正方形ABCD内有一点P，PA＝5，PB＝2，PC＝1，求∠BPC的度数．【分析问题】根据已知条件比较分散的特点，我们可以通过旋转变换将分散的已知条件集中在一起，于是将△BPC绕点B逆时针旋转90°，得到了△BP′A(如图Z3－28②)，然后连接PP′.(1)请你通过计算求出图Z3－28②中∠BPC的度数；(2)如图③，若在正六边形ABCDEF内有一点P，且PA＝2 13，PB＝4，PC＝2.请求出∠BPC的度数．重庆中考几何题分类汇编答案例1. 证明：(1)∵AB＝AC ，∴∠ABC ＝∠ACB.∵∠MBQ ＋∠ABC＝180°，∠ACB ＋∠PCN＝180°，∴∠MBQ ＝∠PCN.在△QBM 和△PCN 中，⎩⎪⎨⎪⎧QB ＝PC ，∠MBQ ＝∠PCN，BM ＝CN ，∴△QBM ≌△PCN(SAS)．∴MQ＝NP.(2)过M 作MG∥AC 交BC 于G ，∵MG ∥AC ，∴∠MGB ＝∠ACB，∠MGC ＝∠PCN，∵由(1)知，∠ABC ＝∠ACB，∴∠ABC ＝∠MGB，∴MB ＝MG ，∵MB ＝CN ，∴MG ＝CN.在△MGP 和△NCP 中，⎩⎪⎨⎪⎧∠MPG＝∠CPN，∠MGC ＝∠PCN，MG ＝NC ，∴△MGP ≌△NCP(AAS)．∴PG ＝CP ，∴CG ＝CP ＋PG ，即CG ＝2CP.∵CM 平分∠ACB，∴∠BCM ＝∠MCA，∵MG ∥AC ，∴∠MCA ＝∠GMC，∴∠BCM ＝∠GMC，∴MG ＝CG ，∵MG ＝CN ，∴CN ＝CG ，∴CN ＝2CP.针对训练1. 解：(1)∵AC⊥BC，∴∠ACB ＝90°，又∵AC＝CF ，∴∠AFC ∠ABC ＝35°，∴∠EAF ＝10°；(2)证明：方法1：取CF 的中点M ，连接EM 、AM ，∵CE ⊥EF ，∴EM ＝CM ＝FM ＝12CF ， 又∵AC＝AE ，∴AM 为EC 的中垂线，∴∠CAM ＋∠ACE＝90°，又∵∠ECF＋∠ACE＝90°，∴∠CAM ＝∠FCE，又∵∠CEF＝∠ACM＝90°，∴△ACM ∽△CEF ，∴AC CM ＝CE EF， 又∵CF＝AC ＝2CM ，∴AC CM ＝CE EF ＝21，即CE ＝2EF ； 方法2：延长FE 至M ，使EF ＝EM ，连接CM ，∵CE ⊥EF ，∴△CMF 为等腰三角形，又∵AC＝AE ＝CF ，且∠ACE＝∠CFE(易证)，∴△CMF ≌△CEA ，∴FM ＝CE ＝2EF.2. 解：(1)如图①，在AB 上取一点M ，使得BM ＝ME ，连接ME.在Rt △ABE 中，∵OB ＝OE ，∴BE ＝2OA ＝2，∵MB ＝ME ，∴∠MBE ＝∠MEB＝15°，∴∠AME ＝∠MBE＋∠MEB＝30°，设AE ＝x ，则ME ＝BM ＝2x ，AM ＝3x ，∵AB 2＋AE 2＝BE 2，∴(2x ＋3x)2＋x 2＝22，∴x ＝6－22(负根舍弃)，∴AB ＝AC ＝(2＋ 3)·6－22， ∴BC ＝2AB ＝3＋1.(2)证明：如图②，作CP⊥AC，交AD 的延长线于P ，GM ⊥AC 于M.∵BE ⊥AP ，∴∠AHB ＝90°，∴∠ABH ＋∠BAH＝90°，∵∠BAH ＋∠PAC＝90°，∴∠ABE ＝∠PAC，又∵AB＝AC ，∠BAE ＝∠ACP＝90°，∴△ABE ≌△CAP ，∴AE ＝CP ＝CF ，∠AEB ＝∠P，在△DCF 和△DCP 中，⎩⎪⎨⎪⎧CD ＝CD ，∠DCF ＝∠DC P ，CF ＝CP ，∴△DCF ≌△DCP ，∴∠DFC ＝∠P，∴∠GFE ＝∠GEF，∴GE ＝GF ，∵GM ⊥EF ，∴FM ＝ME ，∵AE ＝CF ，∴AF ＝CE ，∴AM ＝CM ，在△GAH 和△GAM 中，⎩⎪⎨⎪⎧∠GAH＝∠GAM，∠AHG ＝∠AMG，AG ＝AG ，∴△AGH ≌△AGM ，∴AH ＝AM ＝CM ＝12AC.3. 解：(1)∵AB＝4，∴AC ＝AB ＝4.∵CD ＝1，∴AD ＝AC －CD ＝3.∵在Rt △ABD 中，∠BAC ＝90°，∴BD ＝AB 2＋AD 2＝5，∵S △ABD ＝12AB·AD＝12AE·BD，∴AE ＝2.4. (2)证明：如图，在线段EB 上截取EH ＝AE ，并连接AH.∵AE ⊥BD ，EH ＝AE ，∴AH ＝2AE.∵BE ＝AE ＋AG ，∴BH ＝BE －HE ＝AG.∵∠BAD ＝∠BEA＝90°，∴∠ABE ＋∠BAE＝∠CAG＋∠BAE＝90°，∴∠ABE ＝∠CAG.∵BA ＝AC ，∴△ABH ≌△CAG ，∴CG ＝AH ＝2AE.4. 解：(1)∵∠BAC＝90°，AB ＝AC ，D 是斜边BC 的中点，∴∠ADC ＝90°，∠ACD ＝45°.在Rt △ADC 中，AC ＝AD÷sin45°＝2 3.∵E 是AC 的中点，∴CE ＝12AC ＝ 3.∵将△CDE 沿CD 翻折到△CDE′，∴CE ′＝CE ＝3，∠ACE ′＝90°.由勾股定理，得AE′＝CE′2＋AC 2＝15.(2)证明：如图，过B 作AE′的垂线交AD 于点G ，交AC 于点H.∵∠ABH ＋∠BAF＝90°，∠CAF ＋∠BAF＝90°，∴∠ABH ＝∠CAF.又∵AB＝AC ，∠BAH ＝∠ACE′＝90°，∴△ABH ≌△CAE ′.∴AH ＝CE′＝CE ，∵CE ＝13AC ，∴AH ＝HE ＝CE. ∵D 是BC 中点，∴DE ∥BH ，∴G 是AD 中点．在△ABG 和△CAF 中：AB ＝AC ，∠BAD ＝∠ACD＝45°，∠ABH ＝∠CAF，∴△ABG ≌△CAF.∴AG ＝CF.∵AG ＝12AD ，∴CF ＝12AD ＝12CD.∴DF＝CF.类型2 线段的和差：要证线段和与差，截长补短去实验（2）证明：延长DN 到K ，使得NK ＝ME ，连接AK ，如图①，因为∠1＋∠3＝180°，∠1＋∠2＝180°，∴∠2＝∠3.在△AME 和△ANK 中，⎩⎪⎨⎪⎧AM ＝AN ，∠2＝∠3，ME ＝NK ，∴△AME ≌△ANK (SAS)．∴AE ＝AK ，∠4＝∠5，∴∠4＋∠EAC ＝90°，∴∠5＋∠EAC ＝90°，即∠EAK ＝90°，∵∠EAD ＝45°，∴∠KAD ＝∠EAK －∠EAD ＝90°－45°＝45°∴∠EAD ＝∠KAD .在△EAD 和△KAD 中，⎩⎪⎨⎪⎧EA ＝KA ，∠EAD ＝∠KAD ，AD ＝AD ，∴△EAD ≌△KAD (SAS)，∴ED ＝KD .∵DK ＝DN ＋KN ，∴ED ＝DN ＋KN ，又NK ＝ME ，∴ED ＝DN ＋ME .(3)证明：延长AE 到J ，使得EJ ＝AE ，连接JH ，JF.如图②，在△ABE 和△JHE 中，⎩⎪⎨⎪⎧AE ＝JE ，∠AEB ＝∠JEH，BE ＝HE ，∴△ABE ≌△JHE(SAS)，∴JH ＝AB ，∠1＝∠2，∵AB ＝AG ，∴JH ＝AG ，∵AE ＝EJ ，EF ⊥AJ ，∴AF ＝JF ，∴∠JAF ＝∠AJF＝45°，即∠2＋∠3＝45°，∵∠BAC ＝90°，∴∠1＋∠EAD＋∠4＝90°，∴∠1＋∠4＝90°－∠EAD，＝90°－45°＝45°，∵∠1＝∠2，∴∠3＝∠4，在△JHF 和△AGF 中，⎩⎪⎨⎪⎧JH ＝AG ，∠3＝∠4，JF ＝AF ，∴△JHF ≌△AGF(SAS)，∴FH ＝FG.针对训练：1. 解：(1)∵四边形ABCD 是平行四边形，∴AD ＝BC.∵BE ＝2EC ，设CE ＝x ，BE ＝2x ，∴BC ＝AD ＝AE ＝3x.又∵EG⊥AB，∴∠AEB ＝90°，∴AB 2＝AE 2＋BE 2，即13＝9x 2＋4x 2，∴x ＝1，∴AD ＝3x ＝3.(2)证明：如图，过C 作CH⊥AB 于H ，则四边形CHGF 为矩形．∴CF ＝HG ，∠CHB ＝90°，GF ＝CH.∵AE ⊥BC ，EG ⊥AB ，∴∠AEB ＝∠CHB＝90°，∠BCH ＋∠B＝90°，∠BAE ＋∠B＝90°，∴∠BCH ＝∠BA E.又∵AE＝BC ，∴△AGE ≌△CHB ，∴GE ＝BH ，AG ＝GF ，∴GE ＝BH ＝BG ＋GH ＝BG ＋CF.2. 解：(1)∵四边形ABCD 是正方形，BC ＝4，∴AB ＝AD ＝CD ＝BC ＝4，∠ADC ＝∠ABC＝90°.∵在Rt △ABC 中，AC ＝AB 2＋BC 2＝4 2，∴AP ＝78AC ＝72 2， 1(2)证明：方法一：如图①，在NC 上截取NK ＝NF ，连接BK.∵四边形ABCD 是正方形，∴AB ＝BC ＝DC ，∠ABC ＝∠BCD＝∠ADC＝90°.∵∠BCD ＝90°，CF ⊥CP ，∴∠1＋∠DCF＝∠2＋∠DCF＝90°，∴∠1＝∠2，∵在△FBC 和△PDC 中，⎩⎪⎨⎪⎧∠FBC＝∠3，BC ＝DC ，∠1＝∠2，∴△FBC ≌△PDC(ASA)，∴CF ＝CP ，∵CP －2FN ＝BM ，∴CF －FK ＝BM ，即CK ＝BM ，∵∠FBC ＝90°，BM ⊥CF ，∴∠1＋∠NBC＝∠4＋∠N BC ＝90°，∴∠1＝∠4，∵在△ABM 和△BCK 中，⎩⎪⎨⎪⎧AB ＝BC ，∠4＝∠1，BM ＝CK ，∴△ABM ≌△BCK(SAS)，∴∠7＝∠6.∵BM ⊥CF ，NK ＝NF ，∴BF ＝BK ，∵BF ＝BK ，BM ⊥CF ，∴∠4＝∠5，∴∠4＋∠7＝∠5＋∠6，∵∠8＝∠4＋∠7，∴∠8＝∠MBC，∴BC ＝MC.解：方法二：如图②，延长BM 交AD 于点G ，过A 作AE⊥BG 于E先证△AEB≌△BNC(AAS)，∴AE ＝BN ，又证△AEG≌△BNF(AAS)，∴EG ＝NF ，再证四边形BCPG 为平行四边形，∴BG ＝CP ，∵CP －BM ＝2FN ，∴BG －BM ＝2EG ，∴MG ＝2EG ，∴点E 为MG 中点，∵AE ⊥MG ，EM ＝EG ，∴AM ＝AG ，∴∠3＝∠4，∵∠2＝∠3，∠1＝∠4，∴∠1＝∠2，∴BC ＝MC.3. 解：(1)∵∠EBG＝20°，CB ⊥AE ，∴∠BEG ＝70o ，∠CBF ＝∠EBG＝20°，∵四边形ABDE 是菱形，∴∠ABE ＝∠BEG＝70°，∴∠ABG ＝50°，∵AB ＝BC ，∴∠FCB ＝25°，∴∠AFE ＝∠CBF＋∠FC B ＝45°；(2)AE ，AF ，CF 之间的数量关系是AF 2＋CF 2＝2AE 2，证明如下：连接DF ，∵四边形ABDE 是菱形，∴AB ＝DB ，∠DBE ＝∠ABE，∴∠DBF ＝∠ABF，∵BF ＝BF ，∴△DBF ≌△ABF(SAS)，∴DF ＝AF ，∠BDF ＝∠BAF，∵∠BCF ＝∠BAF，∴∠BCF ＝∠BDF，∵CB ⊥AE ，AE ∥DB ，∴DB ⊥CB ，∵CB ＝AB ＝BD ，∴△DBC 是等腰直角三角形，∴DC ＝2BD ＝2AE ，∵∠DPB ＝∠CPF，∴∠CFP ＝∠DBP＝90°，∴DF 2＋CF 2＝DC 2，即有：AF 2＋CF 2＝2AE 2.类型3 倍长中线：三角形中有中线，延长中线等中线例3解：(1)设∠BEC ＝α，∠BDA ＝β，则∠C ＝180°－2α，∠A ＝180°－2β.∵在Rt △ABC 中，∠ABC ＝90°，∴α＋β＝135°，∴∠EBD ＝45°.(2)证明：法一：如图①，延长BD 至点B′，使得DB′＝DB ，连接在△GDB′和△CDB 中，⎩⎪⎨⎪⎧GD ＝CD ，∠GDB ′＝∠CDB，B ′D ＝BD ，∴△GDB ′≌△CDB.∴GB ′＝BC ＝BH ，∠GB ′D ＝∠CBD.∵FD ⊥BD ，BD ＝DB′，∴FB ＝FB′.∵∠FB ′G ＝45°－∠GB′D，∠HBF ＝90°－45°－∠CBD＝45°－∠CBD，∴∠FB ′G ＝∠HBF.在△FHB 和△FGB′中，⎩⎪⎨⎪⎧HB ＝GB′，∠HBF ＝∠GB′F，BF ＝B′F，∴△FHB ≌△FGB ′，∴HF ＝GF.法二：如图②，延长FD 至点F ′，使得DF ′＝DF ，连接CF ′、BF ′.先证△DGF ≌△DCF ′，再证△BHF ≌△BCF ′，∴HF ＝GF .针对训练1. 证明：(1)∵四边形ABCD 是平行四边形，∴AB ＝CD ，AD ＝BC ，∠A ＝∠C .又∵∠1＝∠2，∴△ABE ≌△CDG (ASA)，∴AE ＝CG .∵G 为BC 中点，∴CG ＝12BC ， ∴AE ＝CG ＝12BC ＝12AD ，∴E 是AD 中点．(2)如图，延长BE ，CD 交于点H.∵四边形ABCD 是平行四边形，∴AB 綊CD ，∴∠A ＝∠ADH，∠1＝∠4，又∵∠1＝∠2，∠3＝∠2，∴∠1＝∠2＝∠3＝∠4，∴FH ＝FB.由(1)，E 是AD 中点，∴AE ＝DE ，∴△ABE ≌△DHE(AAS)，∴AB ＝DH ，∴CD ＝AB ＝DH ＝DF ＋FH ＝DF ＋BF ，即CD ＝BF ＋DF.2. 证明：(1)在菱形ABCD 中，AB ＝BC ＝CD ＝AD ，∠ADF ＝∠ABE，∵∠DAE ＝∠BAF，∴∠DAE －∠EAF＝∠BAF－∠EAF，即∠DAF＝∠BAE.∴△DAF ≌△BAE ，∴BE ＝DF.(2)如图，延长DG 交AB 于H ，连接EH ，∵在菱形ABCD 中，AB ∥CD ，∴∠DFA ＝∠GAH.∵G 为AF 中点，∴AG ＝GF.又∵∠DGF＝∠AGH，∴△DGF ≌△HGA.∴DG ＝GH ，AH ＝DF.又∵AB＝CD ，∴BH ＝CF.又∵AB∥CD，∠ABC ＝120°，∴∠C ＝60°.又∵CE ＝CF ，∴△CEF 为等边三角形，∴CF ＝EF ，∠CFE ＝60°，∴EF ＝BH ，∠DFE ＝∠ABC＝120°.又∵BE＝DF ，∴△EFD ≌△HBE ，∴HE ＝ED ，又∵HG＝DG ，∴DG ⊥GE.3. 解：（1）MD=ME2)MD ＝3ME.理由如下：如图①，延长EM 交DA 于点F.∵BE ∥DA ，∴∠FAM ＝∠EBM.又∵AM＝BM ，∠AMF ＝∠BME，∴△AMF ≌△BME ，∴AF ＝BE ，MF ＝ME.∵DA ＝DC ，∠ADC ＝60°，∴∠BED ＝∠ADC＝60°，∠ACD ＝60°.∵∠ACB ＝90°，∴∠ECB ＝30°，∴∠EBC ＝30°，∴CE ＝BE ，∴AF ＝EC ，∴DF ＝DE ，∴DM ⊥EF ，DM 平分∠ADC，∴∠MDE ＝30°.在Rt △MDE 中，tan ∠MDE ＝ME MD ＝33. ∴MD ＝3ME.(3)如图②，延长EM 交DA 于点F ，∵BE ∥DA ，∴∠FAM ＝∠EBM，又∵AM＝BM ，∠AMF ＝∠BME，∴△AMF ≌△BME ，∴AF ＝BE ，MF ＝ME.延长BE 交AC 于点N ，∴∠BNC ＝∠DAC.∵DA ＝DC ，∴∠DCA ＝∠DAC，∴∠BNC ＝∠DCA，∵∠ACB ＝90°，∴∠ECB ＝∠EBC，∴CE ＝BE ，∴AF ＝CE.∴DF ＝DE ，∴DM ⊥EF ，DM 平分∠ADC，∵∠ADC ＝α，∴∠MDE ＝α2. ∴在Rt △MDE 中，ME MD ＝tan ∠MDE ＝tan α2.4.解：(1)如图①，作EH ⊥BC 于点H .∵△ABC 是等边三角形，∴∠ACB ＝60°.∵CE 平分∠ACB ，∴∠ECH ＝12∠ACB ＝30°， ∵EC ＝4，∠ECH ＝30°，∴EH ＝2，HC ＝2 3.∵BC ＝6 3，∴BH ＝6 3－2 3＝4 3.在Rt △BHE 中，BE 2＝(4 3)2＋22＝52，∴BE ＝2 13.(2)如图②，延长DP 至M ，使DP ＝PM ，连接BM 、AM .在△PDE 和△PMB 中，⎩⎪⎨⎪⎧PD ＝PM ，∠EPD ＝∠BPM ，PE ＝PB ，∴△PDE ≌△PMB (SAS)．∴BM ＝DE ，∠1＝∠2.∴BM ∥DE .∴∠MBD ＋∠BDE ＝180°.∵CE 平分∠ACB ，DE ＝CD ，∴∠BDE ＝30°＋30°＝60°.∴∠MBD ＝120°.∵△ABC 是等边三角形，∴∠ABC ＝60°，∴∠3＝60°.∵BM ＝DE ，DE ＝CD ，∴BM ＝CD .在△ABM 和△ACD 中，⎩⎪⎨⎪⎧AB ＝AC ，∠3＝∠ACD ，BM ＝CD ，∴△ABM ≌△ACD (SAS)．∴AD ＝AM ，∠4＝∠5.∵PD ＝PM ，∴AP ⊥PD .∵∠4＝∠5，∠BAD ＋∠5＝60°，∴∠4＋∠BAD ＝60°，即∠MAD ＝60°.∴∠PAD ＝12∠MAD ＝30°.∵在Rt △APD 中，tan30°＝PD AP，∴AP ＝3PD .(3)第(2)问中的结论成立，理由如下：如图③，延长DP 至N ，使DP ＝PN ，连接BN 、AN ，取BE 、AC 交于点O.在△PDE 和△PNB 中，⎩⎪⎨⎪⎧PD ＝PN ，∠EPD ＝∠BPN，PE ＝PB ，∴△PDE ≌△PNB(SAS)．∴BN ＝DE ，∠1＝∠2.∵DE ＝CD ，∴BN ＝CD.∵∠AOB ＝∠EOC，∴∠1＋∠3＋∠BAO＝∠2＋∠4＋∠DEC＋∠DCE.∵∠BAO ＝60°，∠DEC ＝∠DCE ＝30°，∴∠1＋∠3＝∠2＋∠4，∴∠3＝∠4.在△ABN 和△ACD 中，⎩⎪⎨⎪⎧AB ＝AC ，∠3＝∠4，BN ＝CD ，∴△ABN ≌△ACD(SAS)．∴∠5＝∠6，AN ＝AD.∵PD ＝PN ，∴AP ⊥PD.∵∠NAC ＋∠5＝60°，∴∠NAC ＋∠6＝60°，即∠NAD＝60°.∴∠PAD ＝12∠NAD＝30°， ∵在Rt △APD 中，tan ∠PAD ＝PD AP，∴AP ＝3PD.5. 解：(1)∵∠ADB ＝90°，∠BAD ＝30°，AD ＝6 3，∴cos ∠BAD ＝AD AB ，∴32＝6 3AB，∴AB ＝12. 又∵AB ＝AC ，∴AC ＝12，∴PM 为△ABC 的中位线，∴PM ＝12AC ＝6.(2)证明：方法一：如图①，在截取ED 上截取EQ ＝PD ，∵∠ADB ＝90°，∴∠1＋∠2＝90°，又∵AD＝AE ，∴∠2＝∠3，又∵∠3＋∠4＝90°，∴∠1＝∠4.在△BD P 和△CEQ 中，PD ＝QE ，∠1＝∠4，BD ＝CE ，∴△BDP ≌△CEQ.∴BP ＝CQ ，∠DBP ＝∠QCE，又∵∠5＝∠1＋∠DBP，∠6＝∠4＋∠QCE，∴∠5＝∠6，∴PC ＝CQ ，∴BP ＝CP.方法二：如图②，过点B 作EP 的垂线交EP 的延长线于点M ，过C 点作EP EP 于点N.∵∠ADB ＝90°，∴∠1＋∠2＝90°，又∵AD＝AE ，∴∠2＝∠3，又∵∠3＋∠4＝90°，∴∠1＝∠4，在△BMD 和△CNE 中，∠1＝∠4，∠BMD ＝∠CNE＝90°，BD ＝CE ，∴△BMD ≌△CNE.∴BM ＝CN.在△BMP 和△CNP 中，∠5＝∠6，∠BMP ＝∠CNP，BM ＝CN ，∴△BMP≌△CNP，∴BP ＝CP.方法三：如图③，过点B 作BM ∥CE 交EP 的延长线于点M .略证△BMP ≌△CEP ，∴BP ＝CP .(3)BF 2＋FC 2＝2AD 2.类型4 中位线：三角形中两中点，连接则成中位线例4: 解：（1）PM=PN;PM ⊥PN(2)△PMN 为等腰直角三角形，理由如下：由题意知△ABC 和△ADE 均为等腰直角三角形，∴AB ＝AC ，AD ＝AE ，∠BAC ＝∠DA E ＝90°，∴∠BAD ＋∠DAC＝∠CAE＋∠DAC，∴∠BAD ＝∠CAE，∴△BAD ≌△CAE ，∴∠ABD ＝∠ACE，BD ＝CE.又∵M、P 、N 分别是DE 、CD 、BC 的中点，∴PM 是△CDE 的中位线，∴PM ∥CE 且PM ＝12CE ，∠MPD ＝∠ECD＝∠ACD＋∠ACE. 同理，PN ∥BD 且PN ＝12BD ，∠DBC ＝∠PNC， 又∵BD＝CE ，∠ABD ＝∠ACE，∴PM ＝PN ，∴∠MPN ＝∠MPD＋∠DPN＝∠ECD ＋∠DCN＋∠CNP＝∠ACD＋∠ACE＋∠DCN＋∠CBD＝∠ACD＋∠DCN＋∠ABD＋∠CBD＝∠ACB＋∠ABC＝90°，∴PM ⊥PN ，∴△PMN 为等腰直角三角形；(3)△PMN 面积的最大值为492.提示：在旋转的过程中，由(2)中的结论知△PMN 为等腰直角三角形，S △PMN ＝12PN 2＝18BD 2，当S △PMN 有最大值时，则BD 的值最大，由三角形三边关系可推断出当B 、A 、D 三点共线时，BD的值最大，其最大值为14，此时S △PMN ＝12PN 2＝18BD 2＝18×14×14＝492.针对训练：1. 解：(1)证明：延长DA 交BE 于G 点．∵∠BAE ＋∠CAD ＝180°，即∠EAG ＋∠GAB ＋∠CAD ＝180°，∵∠GAB ＋∠BAC ＋∠CAD ＝180°，∴∠EAG ＝∠CAB .∵∠EAG ＝∠AED ＋∠ADE ，∴∠CAB ＝∠AED ＋∠ADE .(2)证明：如图①，过E 点作DA 延长线的垂线，垂足为H .∴∠AHE ＝∠ACB ＝90°，由(1)可知，∠EAH ＝∠BAC ，又∵AE ＝AB ，∴△AHE ≌△ACB ，∴EH ＝BC ，AH ＝AC .∵AC ＝AD ，∴AH ＝AD .∵∠EHA ＝∠FAD ＝90°，∴AF ∥EH .∵A 为DH 中点，∴AF 为△DHE 中位线，∴EH ＝2AF ，∴BC ＝2AF .(3)成立．证明如下：如图②，延长DA 至M 点，使AM ＝DA ，连接EM ，∵∠BAE ＋∠CAD ＝180°，∠CAD ＋∠CAM ＝180°，∴∠BAE ＝∠CAM ，∴∠BAE ＋∠CAC ＝∠CAM ＋∠EAC ，即∠BAC ＝∠CAM .∵AM ＝AD ，AD ＝AC ，∴AM ＝AC .又∵AB ＝AE ，∠BAC ＝∠EAM ，∴△BAC ≌△EAM ，∴BC ＝EM .∵F 、A 分别为DE 、DM 中点，∴AF 为△DEM 中位线，∴EM ＝2AF ，∴BC ＝2AF .2. 解：(1)证明：∵∠BAC＋∠EAD＝180°，∠BAE ＝90°，∴∠DAC ＝90°，在△ABE 与△ACD 中，AE ＝AD ，∠BAE ＝∠CAD＝90°，AB ＝AC ，∴△ABE ≌△ACD(SAS)，∴CD ＝BE ， ∵在Rt △ABE 中，F 为BE 的中点，∴BE ＝2AF ，∴CD ＝2AF.(2)成立，证明：如图，延长EA 交BC 于G ，在AG 上截取AH ＝AD ，∵∠BAC ＋∠EAD＝180°，∴∠EAB ＋∠DAC＝180°，∵∠EAB ＋∠BAH＝180°，∴∠DAC ＝∠BAH，在△ABH 与△ACD 中，AH ＝AD ，∠BAH ＝∠CAD，AB ＝AC ，∴△ABH ≌△ACD(SAS)，∴BH ＝DC ，∵AD ＝AE ，AH ＝AD ，∴AE ＝AH ，∵EF ＝FB ，∴BH ＝2AF ，∴CD ＝2AF.3. 解：(1)证明：∵AB＝AC ，∴∠ABD ＝∠ACD，∵AE ＝AD ，∴∠ADE ＝∠AED，∵∠BAD ＋∠ABD＝∠ADE＋∠EDC，∠EDC ＋∠ACD＝∠AED ，∴∠BAD ＝2∠EDC，∵∠ABF ＝2∠EDC，∴∠BAD ＝∠ABF，∴△ABF 是等腰三角形；(2)方法一：如图①，延长CA 至点H ，使AG ＝AH ，连接BH ，∵点N 是BG 的中点，∴AN ＝12BH ， ∵∠BAD ＝∠ABF，∠DAC ＝∠CBG，∴∠CAB ＝∠CBA，∴△ABC 是等边三角形．∴AB ＝BC ＝AC ，∠BAC ＝∠BCA＝60°，∵GM ＝AB ，AB ＝AC ，∴CM ＝AG ，∴AH ＝CM ，在△BAH 和△BCM 中，⎩⎪⎨⎪⎧AB ＝BC ，∠BAH ＝∠BCM＝120°，AH ＝CM ，∴△BAH ≌△BCM(SAS)，∴BH ＝BM ，∴AN ＝12BM ， 方法二：如图②，延长AN 至K ，使NK ＝AN ，连接KB ，同方法一，先证△ABC 是等边三角形，再证△ANG ≌△KNB (SAS)，所以BK ＝AG ＝CM ，然后可以证得∠ABK ＝∠BCN ＝120°，最后证△ABK ≌△BCN (SAS)，所以BM ＝AK ＝2AN .类型5 角的和差倍分例5：解：(1)如图，过点P 作PG⊥EF 于G.∵PE ＝PF ＝6，EF ＝6 3，∴FG ＝EG ＝3 3，∠FPG ＝∠EPG＝12∠EPF. 在Rt △FPG 中，sin ∠FPG ＝FG PF ＝3 36＝32. ∴∠FPG ＝60°，∴∠EPF ＝2∠FPG＝120°.(2)如图，作PM ⊥AB 于M ，PN ⊥AD 于N .∵AC 为菱形ABCD 的对角线，∴∠DAC ＝∠BAC ，AM ＝AN ，PM ＝PN .在Rt △PME 和Rt △PNF 中，PM ＝PN ，PE ＝PF ，∴Rt △PME ≌Rt △PNF ，∴NF ＝ME .又∵AP ＝10，∠PAM ＝12∠DAB ＝30°， ∴AM ＝AN ＝AP cos30°＝10×32＝5 3. ∴AE ＋AF ＝(AM ＋ME )＋(AN －NF )＝AM ＋AN ＝10 3.针对训练：1. 证明：如图，过D 作DE ⊥AB 于E ，过D 作DF ⊥AC 于F ，∵DA 平分∠BAC ，DE ⊥AB ，DF ⊥AC ，∴DE ＝DF ，∵∠B ＋∠ACD ＝180°，∠ACD ＋∠FCD ＝180°，∴∠B ＝∠FCD ，在△DFC 和△DEB 中，⎩⎪⎨⎪⎧∠F ＝∠DEB ，∠FCD ＝∠B ，DF ＝DB ，∴△DFC ≌△DEB ，∴DC ＝DB .2. 解：(1)∵AC＝AB ＝4，且CD ＝1，∴AD ＝AC －CD ＝3.在Rt △ABD 中，∠BAD ＝90°，∴BD ＝AB 2＋AD 2＝5，∵S △ABD ＝12AB·AD＝12AE·BD， ∴AE ＝2.4.(2)证明：如图，取BC 的中点M ，连接AM 交BD 于点N .∵∠BAC ＝90°，AB ＝AC ，点M 为BC 的中点，∴AM ＝BM ＝CM ，AM ⊥BC ，∠NAD ＝∠FCP ＝45°，∴∠AMF ＝∠BMN ＝90°.∵AE ⊥BD ，∴∠MAF ＋∠ANE ＝∠MBN ＋∠BNM ＝90°，又∠ANE ＝∠BNM ，∴∠MAF ＝∠MBN ，∴△AMF ≌△BMN ，∴MF ＝MN ，∴AM －MN ＝CM －MF ，即AN ＝CF .∵AP ＝CD ，∴AC －CD ＝AC －AP ，即AD ＝CP .∴△ADN ≌△CPF ，∴∠ADB ＝∠CPF .3. 解：(1)∵AB ＝BD ，∠BAD ＝45°，∴∠BDA ＝45°，即∠ABD ＝90°.∵四边形ABCD 是平行四边形，∴当E 、C 重合时，BF ＝12BD ＝12AB . ∵在Rt △ABF 中，AB 2＋BF 2＝AF 2，∴(2BF )2＋BF 2＝(5)2，∴BF ＝1，AB ＝2.在Rt △ABD 中，AD ＝AB 2＋BD 2＝2AB 2＝2 2.(2)证明：如图，在AF 上截取AK ＝HD ，连接BK.∵∠AFD ＝∠ABF＋∠2＝∠FGD＋∠3且∠ABF＝∠FGD＝90°，∴∠2＝∠3.在△ABK 与△DBH 中，⎩⎪⎨⎪⎧AB ＝BD ，∠2＝∠3，AK ＝HD ，∴△ABK ≌△DBH ，∴BK ＝BH ，∠6＝∠5.∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠5＝∠4＝45°，∴∠6＝∠5＝45°，∴∠7＝∠ABD－∠6＝45°＝∠5.在△BFK 与△BFH 中，⎩⎪⎨⎪⎧BK ＝BH ，∠7＝∠5，BF ＝BF ，∴△BFK ≌△BFH.∴∠BFK ＝∠BFH，即∠AFB＝∠HFB.4. 解：(1)证明：由折叠知∠EMN＝∠ABC＝90°，BE ＝EM ，∴∠EMB ＝∠EBM，∴∠EMN －∠EMB＝∠ABC－∠EBM，即∠BMP＝∠MBC.∵在正方形ABCD 中，AD ∥BC ，∴∠AMB ＝∠MBC，∴∠AMB ＝∠BMP，∴BM 是∠AMP 的平分线．(2)△PDM 的周长没有发生变化．证明如下：如图，过B 作BQ ⊥MP∵∠A ＝90°，且由(1)知BM 是∠AMP 的平分线，∴BA ＝BQ ，∵∠A ＝∠MQB ＝90°，∠AMB ＝∠BMP ，MB ＝MB ，∴△AMB ≌△QMB (AAS)．∴MA ＝MQ .∵BA ＝BC ，∴BQ ＝BC ，又∵∠BQP ＝90°＝∠C ，BP ＝BP ，∴Rt △BPC ≌Rt △BPQ (HL)．∴PC ＝PQ ，∴△PDM 的周长＝MD ＋MP ＋DP ＝MD ＋MQ ＋QP ＋PD＝MD ＋MA ＋PC ＋PD ＝AD ＋DC ＝2AD .∴△PDM 的周长没有发生变化．类型6 旋转型全等问题：图中若有边相等，可用旋转做实验例6：解：(1)①∵四边形ADEF 是正方形，∴AD ＝AF ，AB ＝AC ，∵∠BAC ＝∠DAF＝90°，∴∠BAD ＝∠CAF，∴△DAB ≌△FAC ，∴∠B ＝∠ACF，∴∠ACB ＋∠ACF＝90°，即CF⊥BC；②∵△DAB ≌△FAC ，∴CF ＝BD ，∵BC ＝BD ＋CD ，∴BC ＝CF ＋CD.(2)结论①成立，结论②不成立．∵四边形ADEF 是正方形，∴AD ＝AF ，AB ＝AC.∵∠BAC ＝∠DAF＝90°，∴∠BAD ＝∠CAF，∴△DAB ≌△FAC ，∴∠ABD ＝∠ACF，CF ＝BD ，∴∠BCF ＝∠ACF－∠ACB＝∠ABD－∠ACB＝90°，即CF⊥BC；∵BC＝CD －BD ，∴BC ＝CD －CF.(3)如图，过A 作AH ⊥BC 于H ，过E 作EM ⊥BD 于M ，EN ⊥CF 于∵∠BAC ＝90°，AB ＝AC ，∴BC ＝2AB ＝4，AH ＝CH ＝12BC ＝2，∴CD ＝14BC ＝1，∴DH ＝3，同(2)证得△BAD ≌△CAF ， ∴∠ABD ＝∠ACF ＝45°，∴∠BCF ＝∠ACB ＋∠ACF ＝90°，∴BC ⊥CF ，CF ＝BD ＝5.∵四边形ADEF 是正方形，∴AD ＝DE ，∠ADE ＝90°，∵BC ⊥CF ，EM ⊥BD ，EN ⊥CF ，∴四边形CMEN 是矩形，∴NE ＝CM ，EM ＝CN ，∵∠AHD ＝∠ADE ＝∠EMD ＝90°，∴∠ADH ＋∠EDM ＝∠EDM ＋∠DEM ＝90°，∴∠ADH ＝∠DEM ，∴△ADH ≌△DEM ，∴EM ＝DH ＝3，DM ＝AH ＝2，∴CN ＝EM ＝3，EN ＝CM ＝3，∵∠ABC ＝45°，∴∠BGC ＝45°，∴△BCG 是等腰直角三角形，∴CG ＝BC ＝4，∴GN ＝1，∴EG ＝GN 2＋EN 2＝10.针对训练：1. 解：(1)AC ＝AD ＋AB .证明如下：∵∠B ＋∠D ＝180°，∠B ＝90°，∴∠D ＝90°.∵∠DAB ＝120°，AC 平分∠DAB ，∴∠DAC ＝∠BAC ＝60°，∵∠B ＝90°，∴AB ＝12AC ， 同理AD ＝12AC . ∴AC ＝AD ＋AB .(2)(1)中的结论成立，理由如下：如图①，以C 为顶点，AC 为一边作∠ACE＝60°，∠ACE 的另一边交AB 的延长线于点E ，∵∠BAC ＝60°，∴△AEC 为等边三角形，∴AC ＝AE ＝CE ，∠E ＝60°，∵∠ABC ＋∠D＝180°，∠DAB ＝120°，∴∠DCB ＝60°，∴∠DCA ＝∠ECB.在△DAC 和△BEC 中，⎩⎪⎨⎪⎧∠D AC ＝∠E，AC ＝CE ，∠DCA ＝∠BCE，∴△DAC ≌△BEC ，∴AD ＝BE ，∴AC ＝AE ＝AD ＋AB.(3)AD ＋AB ＝2AC.理由如下：如图②，过点C 作CE⊥AC 交AB 的延长线于点E∵∠ABC ＋∠D＝180°，∠DAB ＝90°，∴∠DCB ＝90°，∵∠ACE ＝90°，∴∠DCA ＝∠BCE，又∵AC 平分∠DAB，∴∠CAB ＝45°，∴∠E ＝45°，∴AC ＝CE.∴△CDA ≌△CBE ，∴AD ＝BE ，∴AD ＋AB ＝AE.∵在Rt △ACE 中，∠CAB ＝45°，∴AE ＝AC cos45°＝2AC ， ∴AD ＋AB ＝2AC.2. 解：(1)证明：∵四边形ABCD 是正方形，∴∠B ＝∠D＝∠BAD＝90°，AB ＝AD ，∵△ABE 沿AE 翻折得到△AHE，∴△ABE ≌△AHE ，∴AH ＝AB ＝AD ，BE ＝EH ，∠AHE ＝∠AHF＝∠B＝∠D＝90°.在Rt △AHF 和Rt △ADF 中，⎩⎪⎨⎪⎧AF ＝AF ，AH ＝AD ，∴Rt △AHF ≌Rt △ADF(HL)，∴∠HAF ＝∠DAF，∴∠EAF ＝∠EAH＋∠FAH＝12∠BAH＋12∠HAD＝12∠BAD＝45°，(2)以BM ，DN ，MN 为三边围成的三角形为直角三角形．证明如下：如图，过点A 作AH ⊥AN 并截取AH ＝AN ，连接BH 、HM ，∵∠1＋∠BAN ＝90°，∠3＋∠BAN ＝90°，∴∠1＝∠3，在△ABH 和△ADN 中，⎩⎪⎨⎪⎧AB ＝AD ，∠1＝∠3，AH ＝AN ，∴△ABH ≌△ADN (SAS)，∴BH ＝DN ，∠HBA ＝∠NDA ＝135°，∵∠HAN ＝90°，∠MAN ＝45°，∴∠1＋∠2＝∠HAM ＝∠MAN ＝45°，在△AHM 和△ANM 中，⎩⎪⎨⎪⎧AH ＝AN ，∠HAM ＝∠MAN ，AM ＝AM ，∴△AHM ≌△ANM (SAS)，∴HM ＝NM ，∴∠HBP ＝180°－∠HBA ＝180°－135°＝45°，∴∠HBP ＋∠PBM ＝45°＋45°＝90°，∴△HBM 是直角三角形，∵HB ＝DN ，HM ＝MN ，∴以BM ，DN ，MN 为三边围成的三角形为直角三角形．3. 解：(1)如图①，将△PBC 绕点B 逆时针旋转90°得△P ′BA ，连接PP ′，则△AP ′B ≌△CPB ， ∴P ′B ＝PB ＝2，P ′A ＝PC ＝1，∠1＝∠2，∠AP ′B ＝∠BPC .∵四边形ABCD 是正方形，∴AB ＝BC ，∠ABC ＝90°，∴∠2＋∠3＝90°，∴∠1＋∠3＝90°，即∠P ′BP ＝90°，∴∠BP ′P ＝45°.在Rt △P ′BP 中，由勾股定理，得PP ′2＝4.∵P ′A ＝1，AP ＝5∴P ′A 2＝1，AP 2＝5，∴P ′A 2＋PP ′2＝AP 2，∴△P ′AP 是直角三角形，∴∠AP ′P ＝90°，∴∠AP′B＝45°＋90°＝135°，∴∠BPC＝135°.(2)仿照【分析】中的思路，将△BPC绕点B逆时针旋转120°，得到了△BP′A，连接PP′，如图②.则△PBC≌△P′BA，∴P′B＝PB＝4，P′A＝PC＝2，∠BPC＝∠BP′A，∴△BPP′为等腰三角形，∵∠ABC ＝120°，∴∠PBP′＝120°，∴∠BP′P＝30°，过点B作BG⊥PP′于G，则∠P′GB＝90°，∴PP′＝2P′G.∵P′B＝PB＝4，∠BP′P＝30°，∴BG＝2，∴P′G＝2 3.∴PP′＝4 3，在△APP′中，∵PA＝2 13，P′A＝2，PP′＝4 3，∴P′A2＋P′P2＝PA2，∴△PP′A是直角三角形，∴∠AP′P＝90°，∴∠BPC＝∠BP′A＝∠PP′B＋∠AP′P＝30°＋90°＝120°.。