历年重庆中考几何题归类
2018届重庆中考复习_重庆中考几何题分类汇编(含答案解析)
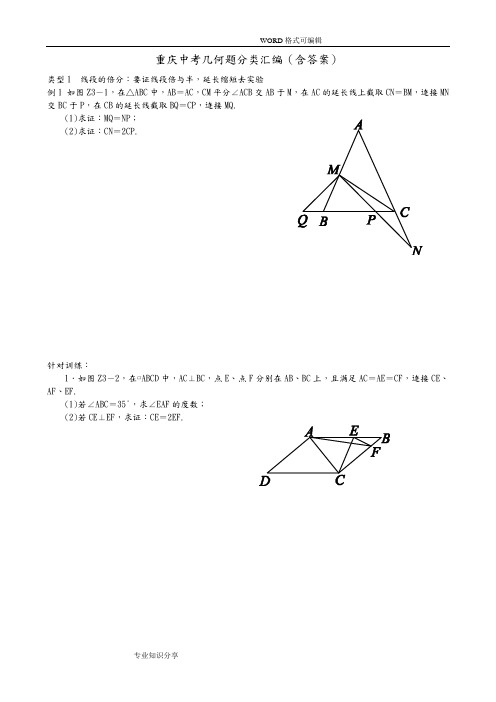
重庆中考几何题分类汇编(含答案)类型1 线段的倍分:要证线段倍与半,延长缩短去实验例1 如图Z3-1,在△ABC中,AB=AC,CM平分∠ACB交AB于M,在AC的延长线上截取CN=BM,连接MN 交BC于P,在CB的延长线截取BQ=CP,连接MQ.(1)求证:MQ=NP;(2)求证:CN=2CP.针对训练:1.如图Z3-2,在▱ABCD中,AC⊥BC,点E、点F分别在AB、BC上,且满足AC=AE=CF,连接CE、AF、EF.(1)若∠ABC=35°,求∠EAF的度数;(2)若CE⊥EF,求证:CE=2EF.2.已知,在△ABC 中,AB =AC ,∠BAC =90°,E 为边AC 任意一点,连接BE.(1)如图①,若∠ABE=15°,O 为BE 中点,连接AO ,且AO =1,求BC 的长;(2)如图②,F 也为AC 上一点,且满足AE =CF ,过A 作AD⊥BE 交BE 于点H ,交BC 于点D ,连接DF 交BE于点G ,连接AG.若AG 平分∠CAD,求证:AH =12AC.3.在△ACB 中,AB =AC ,∠BAC =90°,点D 是AC 上一点,连接BD ,过点A 作AE⊥BD 于E ,交BC 于F.(1)如图①,若AB =4,CD =1,求AE 的长;(2)如图②,点G 是AE 上一点,连接CG ,若BE =AE +AG ,求证:CG =2AE.4.在等腰直角三角形ABC 中,∠BAC =90°,AB =AC ,D 是斜边BC 的中点,连接AD.(1)如图①,E 是AC 的中点,连接DE ,将△CDE 沿CD 翻折到△CDE′,连接AE′,当AD =6时,求AE′的值.(2)如图②,在AC 上取一点E ,使得CE =13AC ,连接DE ,将△CDE 沿CD 翻折到△CDE′,连接AE′交BC 于点F ,求证:DF =CF.类型2 线段的和差:要证线段和与差,截长补短去实验例2 如图,在△ABC中,∠BAC=90°,在BC上截取BD=BA,连接AD,在AD左侧作∠EAD=45°交BD于E.(1)若AC=3,则CE=________(直接写答案);(2)如图①,M、N分别为AB和AC上的点,且AM=AN,连接EM、DN,若∠AME+∠AND=180°,求证:DE =DN+ME;(3)如图②,过E作EF⊥AE,交AD的延长线于F,在EC上选取一点H,使得EH=BE,连接FH,在AC上选取一点G,使得AG=AB,连接BG、FG,求证:FH=FG.针对训练:1.如图Z3-7,在▱ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.(1)若BE=2EC,AB=13,求AD的长;(2)求证:EG=BG+FC.2.如图,在正方形ABCD 中,点P 为AD 延长线上一点,连接AC 、CP ,过点C 作CF⊥CP 于点C ,交AB 于点F ,过点B 作BM⊥CF 于点N ,交AC 于点M.(1)若AP =78AC ,BC =4,求S △ACP ;(2)若CP -BM =2FN ,求证:BC =MC.3.如图,在△ABC 中,AB =BC ,以AB 为一边向外作菱形ABDE ,连接DC ,EB 并延长EB 交AC 于F ,且CB⊥AE 于G.(1)若∠EBG=20°,求∠AFE;(2)试问线段AE ,AF ,CF 之间的数量关系并证明.类型3 倍长中线:三角形中有中线,延长中线等中线例3 如图Z3-10①,在Rt△ABC中,∠ABC=90°,D、E分别为斜边AC上两点,且AD=AB,CE=CB,连接BD、BE.(1)求∠EBD的度数;(2)如图Z3-10②,过点D作FD⊥BD于点D,交BE的延长线于点F,在AB上选取一点H,使得BH=BC,连接CH,在AC上选取一点G,使得GD=CD,连接FH、FG,求证:FH=FG.针对训练:1.如图,已知在▱ABCD中,G为BC的中点,点E在AD边上,且∠1=∠2.(1)求证:E是AD中点;(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.2.如图Z 3-12,在菱形ABCD 中,点E 、F 分别是BC 、CD 上的点,连接AE ,AF ,DE 、EF ,∠DAE =∠BAF.(1)求证:CE =CF ;(2)若∠ABC=120°,点G 是线段AF 的中点,连接DG ,EG.求证:DG⊥GE.3.在Rt △ABC 中,∠ACB =90°,点D 与点B 在AC 同侧,∠ADC >∠BAC,且DA =DC ,过点B 作BE∥DA 交DC 于点E ,M 为AB 的中点,连接MD ,ME.(1)如图①,当∠ADC=90°时,线段MD 与ME 的数量关系是________;(2)如图②,当∠ADC=60°时,试探究线段MD 与ME 的数量关系,并证明你的结论;(3)如图③,当∠ADC=α时,求ME MD的值.(3)如图③,把图3-14②中的△CDE绕点C顺时针旋转任意角度,然后连接BE,点P为BE中点,连接AP,PD,AD,问第(2)问中的结论还成立吗?若成立,请证明;若不成立,请说明理由.5.在△ABC中,以AB为斜边,作直角三角形ABD,使点D落在△ABC内,∠ADB=90°.(1)如图①,若AB=AC,∠BAD=30°,AD=6 3,点P、M分别为BC、AB边的中点,连接PM,求线段PM 的长;(2)如图②,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP;(3)如图③,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).例4 2017·河南如图①,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.(1)观察猜想:图①中,线段PM与PN的数量关系是__________,位置关系是__________;(2)探究证明:把△ADE绕点A按逆时针方向旋转到图②的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.针对训练:1.如图①,在任意的三角形ABC中,分别以AB和AC为一边作等腰三角形ABE和等腰三角形ACD,AB=AE,AC=AD,且∠BAE+∠CAD=180°,连接DE,延长CA交DE于F.(1)求证:∠CAB=∠AED+∠ADE;(2)若∠ACB=∠BAE=∠CAD=90°,如图②,求证:BC=2AF;(3)若在△ABC中,如图③所示,作等腰三角形ABE和等腰三角形ACD,AB与DE交于点F,F为DE的中点,请问(2)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.连接BE、CD,F为BE的中点,连接AF.(1)如图①,当∠BAE=90°时,求证:CD=2AF;(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.3.如图①,在等腰三角形ABC中,AB=AC,在底边BC上取一点D,在边AC上取一点E,使AE=AD,连接DE,在∠ABD的内部作∠ABF=2∠EDC,交AD于点F.(1)求证:△ABF是等腰三角形;(2)如图②,BF的延长交AC于点G.若∠DAC=∠CBG,延长AC至点M,使GM=AB,连接BM,点N是BG的中点,连接AN,试判断线段AN、BM之间的数量关系,并证明你的结论.图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现.角平分线平行线,等腰三角形来添.角平分线加垂线,三线合一试试看.例5.如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6 3,∠BAD=60°,且AB>6 3.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值.针对训练:1.已知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.F.(1)如图①,若AB=4,CD=1,求AE的长;(2)如图②,点P是AC上一点,连接FP,若AP=CD,求证:∠ADB=∠CPF.3.已知,在▱ABCD中,∠BAD=45°,AB=BD,E为BC上一点,连接AE交BD于F,过点D作DG⊥AE 于G,延长DG交BC于H.(1)如图①,若点E与点C重合,且AF=5,求AD的长;(2)如图②,连接FH,求证:∠AFB=∠HFB.4.如图,将正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连接EP.当点M在边AD上移动时,连接BM、BP.(1)求证:BM是∠AMP的平分线;(2)△PDM的周长是否发生变化?证明你的结论.类型6 旋转型全等问题:图中若有边相等,可用旋转做实验例6.△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF.(1)观察猜想:如图①,当点D 在线段BC 上时,①BC 与CF 的位置关系为:________.②BC ,CD ,CF 之间的数量关系为:___________;(将结论直接写在横线上)(2)数学思考:如图Z 3-25②,当点D 在线段CB 的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸:如图Z 3-25③,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE.若已知AB=2 2,CD =14BC ,请求出GE 的长.针对训练:1.在四边形ABCD 中,∠B +∠D=180°,对角线AC 平分∠BAD.(1)如图①,若∠DAB=120°,且∠B=90°,试探究边AD 、AB 与对角线AC 的数量关系并说明理由.(2)如图②,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.(3)如图③,若∠DAB=90°,探究边AD 、AB 与对角线AC 的数量关系并说明理由.2.如图①,在正方形ABCD中,点E为边BC上一点,将△ABE沿AE翻折得△AHE,延长EH交边CD于F,连接AF.(1)求证:∠EAF=45°;(2)延长AB,AD,如图②,射线AE、AF分别交正方形两个外角的平分线于M、N,连接MN,若以BM、DN、MN为三边围成三角形,试猜想三角形的形状,并证明你的结论.3.如图①,在正方形ABCD内有一点P,PA=5,PB=2,PC=1,求∠BPC的度数.【分析问题】根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图Z3-28②),然后连接PP′.(1)请你通过计算求出图Z3-28②中∠BPC的度数;(2)如图③,若在正六边形ABCDEF内有一点P,且PA=2 13,PB=4,PC=2.请求出∠BPC的度数.重庆中考几何题分类汇编答案例1. 证明:(1)∵AB=AC ,∴∠ABC =∠ACB.∵∠MBQ +∠ABC=180°,∠ACB +∠PCN=180°,∴∠MBQ =∠PCN.在△QBM 和△PCN 中,⎩⎪⎨⎪⎧QB =PC ,∠MBQ =∠PCN,BM =CN ,∴△QBM ≌△PCN(SAS).∴MQ=NP.(2)过M 作MG∥AC 交BC 于G ,∵MG ∥AC ,∴∠MGB =∠ACB,∠MGC =∠PCN,∵由(1)知,∠ABC =∠ACB,∴∠ABC =∠MGB,∴MB =MG ,∵MB =CN ,∴MG =CN.在△MGP 和△NCP 中,⎩⎪⎨⎪⎧∠MPG=∠CPN,∠MGC =∠PC N ,MG =NC ,∴△MGP ≌△NCP(AAS).∴PG =CP ,∴CG =CP +PG ,即CG =2CP.∵CM 平分∠ACB,∴∠BCM =∠MCA,∵MG ∥AC ,∴∠MCA =∠GMC,∴∠BCM =∠GMC,∴MG =CG ,∵MG =CN ,∴CN =CG ,∴CN =2CP.针对训练1. 解:(1)∵AC⊥BC,∴∠ACB =90°,又∵AC=CF ,∴∠AFC ABC=35°,∴∠EAF =10°;(2)证明:方法1:取CF 的中点M ,连接EM 、AM ,∵CE ⊥EF ,∴EM =CM =FM =12CF , 又∵AC=AE ,∴AM 为EC 的中垂线,∴∠CAM +∠ACE=90°,又∵∠ECF+∠ACE=90°,∴∠CAM =∠FCE,又∵∠CEF=∠ACM=90°,∴△ACM ∽△CEF ,∴AC CM =CE EF, 又∵CF=AC =2CM ,∴AC CM =CE EF =21,即CE =2EF ; 方法2:延长FE 至M ,使EF =EM ,连接CM ,∵CE ⊥EF ,∴△CMF 为等腰三角形,又∵AC=AE =CF ,且∠ACE=∠CFE(易证),∴△CMF ≌△CEA ,∴FM =CE =2EF.2. 解:(1)如图①,在AB 上取一点M ,使得BM =ME ,连接ME.在Rt △ABE 中,∵OB =OE ,∴BE =2OA =2,∵MB =ME ,∴∠MBE =∠MEB=15°,∴∠AME =∠MBE+∠MEB=30°,设AE =x ,则ME =BM =2x ,AM =3x ,∵AB 2+AE 2=BE 2,∴(2x +3x)2+x 2=22,∴x =6-22(负根舍弃),∴AB =AC =(2+ 3)·6-22, ∴BC =2AB =3+1.(2)证明:如图②,作CP⊥AC,交AD 的延长线于P ,GM ⊥AC 于M.∵BE ⊥AP ,∴∠AHB =90°,∴∠ABH +∠BAH=90°,∵∠BAH +∠PAC=90°,∴∠ABE =∠PAC,∴△ABE ≌△CAP ,∴AE =CP =CF ,∠AEB =∠P,在△DCF 和△DCP 中,⎩⎪⎨⎪⎧CD =CD ,∠DCF =∠DCP,CF =CP ,∴△DCF ≌△DCP ,∴∠DFC =∠P,∴∠GFE =∠GEF,∴GE =GF ,∵GM ⊥EF ,∴FM =ME ,∵AE =CF ,∴AF =CE ,∴AM =CM ,在△GAH 和△GAM 中,⎩⎪⎨⎪⎧∠GAH=∠GAM,∠AHG =∠AMG,AG =AG ,∴△AGH ≌△AGM ,∴AH =AM =CM =12AC.3. 解:(1)∵AB=4,∴AC =AB =4.∵CD =1,∴AD =AC -CD =3.∵在Rt △ABD 中,∠BAC =90°,∴BD =AB 2+AD 2=5,∵S △ABD =12AB·AD=12AE·BD,∴AE =2.4. (2)证明:如图,在线段EB 上截取EH =AE ,并连接AH.∵AE ⊥BD ,EH =AE ,∴AH =2AE.∵BE =AE +AG ,∴BH =BE -HE =AG.∵∠BAD =∠BEA=90°,∴∠ABE +∠BAE=∠CAG+∠BAE=90°,∴∠ABE =∠CA G.∵BA =AC ,∴△ABH ≌△CAG ,∴CG =AH =2AE.4. 解:(1)∵∠BAC=90°,AB =AC ,D 是斜边BC 的中点,∴∠ADC =90°,∠ACD =45°.在Rt △ADC 中,AC =AD÷sin45°=2 3.∵E 是AC 的中点,∴CE =12AC = 3.∵将△CDE 沿CD 翻折到△CDE′,∴CE ′=CE =3,∠ACE ′=90°.由勾股定理,得AE′=CE′2+AC 2=15.(2)证明:如图,过B 作AE′的垂线交AD 于点G ,交AC 于点H.∵∠ABH +∠BAF=90°,∠CAF +∠BAF=90°,∴∠ABH =∠CAF.又∵AB=AC ,∠BAH =∠ACE′=90°,∴△ABH ≌△CAE ′.∴AH =CE′=CE ,∵CE =13AC ,∴AH =HE =CE. ∵D 是BC 中点,∴DE ∥BH ,∴G 是AD 中点.在△ABG 和△CAF 中:AB =AC ,∠BAD =∠ACD=45°,∠ABH =∠CAF,∴△ABG ≌△CAF.∴AG =CF.∵AG =12AD ,∴CF =12AD =12CD.∴DF=CF.类型2 线段的和差:要证线段和与差,截长补短去实验例2:解:(1)3(2)证明:延长DN 到K ,使得NK =ME ,连接AK ,如图①,因为∠1+∠3=180°,∠1+∠2=180°,∴∠2=∠3.⎩⎪⎨⎪⎧AM =AN ,∠2=∠3,ME =NK ,∴△AME ≌△ANK (SAS).∴AE =AK ,∠4=∠5,∴∠4+∠EAC =90°,∴∠5+∠EAC =90°,即∠EAK =90°,∵∠EAD =45°,∴∠KAD =∠EAK -∠EAD =90°-45°=45°.∴∠EAD =∠KAD .在△EAD 和△KAD 中,⎩⎪⎨⎪⎧EA =KA ,∠EAD =∠KAD ,AD =AD ,∴△EAD ≌△KAD (SAS),∴ED =KD .∵DK =DN +KN ,∴ED =DN +KN ,又NK =ME ,∴ED =DN +ME .(3)证明:延长AE 到J ,使得EJ =AE ,连接JH ,JF.如图②,在△ABE 和△JHE 中,⎩⎪⎨⎪⎧AE =JE ,∠AEB =∠JEH,BE =HE ,∴△ABE ≌△JHE(SAS),∴JH =AB ,∠1=∠2,∵AB =AG ,∴JH =AG ,∵AE =EJ ,EF ⊥AJ ,∴AF =JF ,∴∠JAF =∠AJF=45°,即∠2+∠3=45°,∵∠BAC =90°,∴∠1+∠EAD+∠4=90°,∴∠1+∠4=90°-∠EAD,=90°-45°=45°,∵∠1=∠2,∴∠3=∠4,在△JHF 和△AGF 中,⎩⎪⎨⎪⎧JH =AG ,∠3=∠4,JF =AF ,∴△JHF ≌△AGF(SAS),∴FH =FG.针对训练:1. 解:(1)∵四边形ABCD 是平行四边形,∴AD =BC.∵BE =2EC ,设CE =x ,BE =2x ,∴BC =AD =AE =3x.又∵EG⊥AB,∴∠AEB =90°,∴AB 2=AE 2+BE 2,即13=9x 2+4x 2,∴x =1,∴AD =3x =3.(2)证明:如图,过C 作CH⊥AB 于H ,则四边形CHGF 为矩形.∴CF =HG ,∠CHB =90°,GF =CH.∵AE ⊥BC ,EG ⊥AB ,∴∠AEB =∠CHB=90°,∠BCH +∠B=90°,∠BAE +∠B=90°,∴∠BCH =∠BAE.又∵AE=BC ,∴△AGE ≌△CHB ,∴GE =BH ,AG =GF ,∴GE =BH =BG +GH =BG +CF.2. 解:(1)∵四边形ABCD 是正方形,BC =4,∴AB =AD =CD =BC =4,∠ADC =∠ABC=90°.∵在Rt △ABC 中,AC =AB 2+BC 2=4 2,∴AP =78AC =72 2, ∴S △ACP =12AP·CD=7 2.∵四边形ABCD 是正方形,∴AB =BC =DC ,∠ABC =∠BCD=∠ADC=90°.∵∠BCD =90°,CF ⊥CP ,∴∠1+∠DCF=∠2+∠DCF=90°,∴∠1=∠2,∵在△FBC 和△PDC 中,⎩⎪⎨⎪⎧∠FBC=∠3,BC =DC ,∠1=∠2,∴△FBC ≌△PDC(ASA),∴CF =CP ,∵CP -2FN =BM ,∴CF -FK =BM ,即CK =BM ,∵∠FBC =90°,BM ⊥CF ,∴∠1+∠NBC=∠4+∠NBC=90°,∴∠1=∠4,∵在△ABM 和△BCK 中,⎩⎪⎨⎪⎧AB =BC ,∠4=∠1,BM =CK ,∴△ABM ≌△BCK(SAS),∴∠7=∠6.∵BM ⊥CF ,NK =NF ,∴BF =BK ,∵BF =BK ,BM ⊥CF ,∴∠4=∠5,∴∠4+∠7=∠5+∠6,∵∠8=∠4+∠7,∴∠8=∠MBC,∴BC =解:方法二:如图②,延长BM 交AD 于点G ,过A 作AE⊥BG 于E先证△AEB ≌△BNC(AAS),∴AE =BN ,又证△AEG ≌△BNF(AAS),∴EG =NF ,再证四边形BCPG 为平行四边形,∴BG =CP ,∵CP -BM =2FN ,∴BG -BM =2EG ,∴MG =2EG ,∴点E 为MG 中点,∵AE ⊥MG ,EM =EG ,∴AM =AG ,∴∠3=∠4,∵∠2=∠3,∠1=∠4,∴∠1=∠2,∴BC =MC.3. 解:(1)∵∠EBG=20°,CB ⊥AE ,∴∠BEG =70o ,∠CBF =∠EBG=20°,∵四边形ABDE 是菱形,∴∠ABE =∠BEG=70°,∴∠ABG =50°,∵AB =BC ,∴∠FCB =25°,∴∠AFE =∠CBF+∠FCB=45°;(2)AE ,AF ,CF 之间的数量关系是AF 2+CF 2=2AE 2,证明如下:连接DF ,∵四边形ABDE 是菱形,∴AB =DB ,∠DBE =∠ABE,∴∠DBF =∠ABF,∵BF =BF ,∴△DBF ≌△ABF(SAS),∴DF =AF ,∠BDF =∠BAF,∵∠BCF =∠BAF,∴∠BCF =∠BDF,∵CB ⊥AE ,AE ∥DB ,∴DB ⊥CB ,∵CB =AB =BD ,∴△DBC 是等腰直角三角形,∴DC =2BD =2AE ,∵∠DPB =∠CPF,∴∠CFP =∠DBP=90°,∴DF 2+CF 2=DC 2,即有:AF 2+CF 2=2AE 2.类型3 倍长中线:三角形中有中线,延长中线等中线例3解:(1)设∠BEC =α,∠BDA =β,则∠C =180°-2α,∠A =180°-2β.∵在Rt △ABC 中,∠ABC =90°,∴∠A +∠C =90°,即180°-2α+180°-2β=90°,∴α+β=135°,∴∠EBD =45°.(2)证明:法一:如图①,延长BD 至点B′,使得DB′=DB ,连接FB′、GB′.在△GDB′和△CDB 中,⎩⎪⎨⎪⎧GD =CD ,∠GDB ′=∠CDB,B ′D =BD ,∴△GDB ′≌△CDB.∴GB ′=BC =BH ,∠GB ′D =∠CBD.∵FD ⊥BD ,BD =DB′,∴FB =FB′.∵∠FB ′G =45°-∠GB′D,∠HBF =90°-45°-∠CBD=45°-∠CBD,∴∠FB ′G =∠HBF.在△FHB 和△FGB′中,⎩⎪⎨⎪⎧HB =GB′,∠HBF =∠GB′F,BF =B′F,∴△FHB ≌△FGB ′,∴HF =GF.法二:如图②,延长FD 至点F ′,使得DF ′=DF ,连接BF ′.先证△DGF ≌△DCF ′,再证△BHF ≌△BCF ′,∴HF =GF .针对训练1. 证明:(1)∵四边形ABCD 是平行四边形,∴AB =CD ,AD =BC ,∠A =∠C .又∵∠1=∠2,∴△ABE ≌△CDG (ASA),∴AE =CG .∵G 为BC 中点,∴CG =12BC , ∴AE =CG =12BC =12AD ,∴E 是AD 中点.(2)如图,延长BE ,CD 交于点H.∵四边形ABCD 是平行四边形,∴AB 綊CD ,∴∠A =∠ADH,∠1=∠4,又∵∠1=∠2,∠3=∠2,∴∠1=∠2=∠3=∠4,∴FH =FB.由(1),E 是AD 中点,∴AE =DE ,∴△ABE ≌△DHE(AAS),∴AB =DH ,∴CD =AB =DH =DF +FH =DF +BF ,即CD =BF +DF.2. 证明:(1)在菱形ABCD 中,AB =BC =CD =AD ,∠ADF =∠ABE,∵∠DAE =∠BAF,∴∠DAE -∠EAF=∠BAF-∠EAF,即∠DAF=∠BAE.∴△DAF ≌△BAE ,∴BE =DF.又∵BC=CD ,∴CE =CF∵在菱形ABCD 中,AB ∥CD ,∴∠DFA =∠GAH.∵G 为AF 中点,∴AG =GF.又∵∠DGF=∠AGH,∴△DGF ≌△HGA.∴DG =GH ,AH =DF.又∵AB=CD ,∴BH =CF.又∵AB∥CD,∠ABC =120°,∴∠C =60°.又∵CE =CF ,∴△CEF 为等边三角形,∴CF =EF ,∠CFE =60°,∴EF =BH ,∠DFE =∠ABC=120°.又∵BE=DF ,∴△EFD ≌△HBE ,∴HE =ED ,又∵HG=DG ,∴DG ⊥GE.3. 解:(1)MD=ME2)MD =3ME.理由如下:如图①,延长EM 交DA 于点F.∵BE ∥DA ,∴∠FAM =∠EBM.又∵AM=BM ,∠AMF =∠BME,∴△AMF ≌△BME ,∴AF =BE ,MF =ME.∵DA =DC ,∠ADC =60°,∴∠BED =∠ADC=60°,∠ACD =60°.∵∠ACB =90°,∴∠ECB =30°,∴∠EBC =30°,∴CE =BE ,∴AF =EC ,∴DF =DE ,∴DM ⊥EF ,DM 平分∠ADC,∴∠MDE =30°.在Rt △MDE 中,tan ∠MDE =ME MD =33. ∴MD =3ME.(3)如图②,延长EM 交DA 于点F ,∵BE ∥DA ,∴∠FAM =∠EBM,又∵AM=BM ,∠AMF =∠BME,∴△AMF ≌△BME ,∴AF =BE ,MF =ME.延长BE 交AC 于点N ,∴∠BNC =∠DAC.∵DA =DC ,∴∠DCA =∠DAC,∴∠BNC =∠DCA,∵∠ACB =90°,∴∠ECB =∠EBC,∴CE =BE ,∴AF =CE.∴DF =DE ,∴DM ⊥EF ,DM 平分∠ADC,∵∠ADC =α,∴∠MDE =α2. ∴在Rt △MDE 中,ME MD =tan ∠MDE =tan α2.4.解:(1)如图①,作EH ⊥BC 于点H .∵△ABC 是等边三角形,∴∠ACB =60°.∵CE 平分∠ACB ,∴∠ECH =12∠ACB =30°, ∵EC =4,∠ECH =30°,∴EH =2,HC =2 3.∵BC =6 3,∴BH =6 3-2 3=4 3.在Rt △BHE 中,BE 2=(4 3)2+22=52,∴BE =2 13.(2)如图②,延长DP 至M ,使DP =PM ,连接BM 、AM .在△PDE 和△PMB 中,⎩⎪⎨⎪⎧PD =PM ,∠EPD =∠BPM ,PE =PB ,∴△PDE ≌△PMB (SAS).∴BM =DE ,∠1=∠2.∴BM ∥DE .∴∠MBD +∠BDE =180°.∵CE 平分∠ACB ,DE =CD ,∴∠BDE =30°+30°=60°.∴∠MBD =120°.∵△ABC 是等边三角形,∴∠ABC =60°,∴∠3=60°.∵BM =DE ,DE =CD ,∴BM =CD .在△ABM 和△ACD 中,⎩⎪⎨⎪⎧AB =AC ,∠3=∠ACD ,BM =CD ,∴△ABM ≌△ACD (SAS).∴AD =AM ,∠4=∠5.∵PD =PM ,∴AP ⊥PD .∵∠4=∠5,∠BAD +∠5=60°,∴∠4+∠BAD =60°,即∠MAD =60°.∴∠PAD =12∠MAD =30°.∵在Rt △APD 中,tan30°=PD AP,∴AP =3PD .(3)第(2)问中的结论成立,理由如下:如图③,延长DP 至N ,使DP =PN ,连接BN 、AN ,取BE 、AC 交于点O.在△PDE 和△PNB 中,⎩⎪⎨⎪⎧PD =PN ,∠EPD =∠BPN,PE =PB ,∴△PDE ≌△PNB(SAS).∴BN =DE ,∠1=∠2.∵DE =CD ,∴BN =CD.∵∠AOB =∠EOC,∴∠1+∠3+∠BAO=∠2+∠4+∠DEC+∠DCE.∵∠BAO =60°,∠DEC =∠DCE=30°,∴∠1+∠3=∠2+∠4,∴∠3=∠4.在△ABN 和△ACD 中,⎩⎪⎨⎪⎧AB =AC ,∠3=∠4,BN =CD ,∴△ABN ≌△ACD(SAS).∴∠5=∠6,AN =AD.∵PD =PN ,∴AP ⊥PD.∵∠NAC +∠5=60°,∴∠NAC +∠6=60°,即∠NAD=60°.∴∠PAD =12∠NAD=30°, ∵在Rt △APD 中,tan ∠PAD =PD AP,∴AP =3PD.5. 解:(1)∵∠ADB =90°,∠BAD =30°,AD =6 3,∴cos ∠BAD =AD AB ,∴32=6 3AB,∴AB =12. 又∵AB =AC ,∴AC =12,∴PM 为△ABC 的中位线,∴PM =12AC =6.(2)证明:方法一:如图①,在截取ED 上截取EQ =PD ,∵∠ADB =90°,∴∠1+∠2=90°,又∵AD=AE ,∴∠2=∠3,又∵∠3+∠4=90°,∴∠1=∠4.在△BDP 和△CEQ 中,PD =QE ,∠1=∠4,BD =CE ,∴△BDP ≌△CEQ.∴BP =CQ ,∠DBP =∠QCE,又∵∠5=∠1+∠DBP,∠6=∠4+∠QCE,∴∠5=∠6,∴PC =CQ ,∴BP =CP.方法二:如图②,过点B 作EP 的垂线交EP 的延长线于点M ,过C 点作EP EP 于点N.∵∠ADB =90°,∴∠1+∠2=90°,又∵AD=AE ,∴∠2=∠3,又∵∠3+∠4=90°,∴∠1=∠4,在△BMD 和△CNE 中,∠1=∠4,∠BMD =∠CNE=90°,BD =CE ,∴△BMD ≌△CNE.∴BM =CN.在△BMP 和△CNP 中,∠5=∠6,∠BMP =∠CNP,BM =CN ,∴△BMP ≌△CNP,∴BP =CP.方法三:如图③,过点B 作BM ∥CE 交EP 的延长线于点M .略证△BMP ≌△CEP ,∴BP =CP .(3)BF 2+FC 2=2AD 2.类型4 中位线:三角形中两中点,连接则成中位线例4: 解:(1)PM=PN;PM ⊥PN(2)△PMN 为等腰直角三角形,理由如下:由题意知△ABC 和△ADE 均为等腰直角三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE=90°,∴∠BAD +∠DAC=∠CAE+∠DAC,∴∠BAD =∠CAE,∴△BAD ≌△CAE ,∴∠ABD =∠ACE,BD =CE.又∵M、P 、N 分别是DE 、CD 、BC 的中点,∴PM 是△CDE 的中位线,∴PM ∥CE 且PM =12CE ,∠MPD =∠ECD=∠ACD+∠ACE. 同理,PN ∥BD 且PN =12BD ,∠DBC =∠PNC, 又∵BD=CE ,∠ABD =∠ACE,∴PM =PN ,∴∠MPN =∠MPD+∠DPN=∠ECD +∠DCN+∠CNP=∠ACD+∠ACE+∠DCN+∠CBD=∠ACD+∠DCN+∠ABD+∠CBD=∠ACB+∠ABC=90°,∴PM ⊥PN ,∴△PMN 为等腰直角三角形;(3)△PMN 面积的最大值为492.提示:在旋转的过程中,由(2)中的结论知△PMN 为等腰直角三角形,S △PMN =12PN 2=18BD 2,当S △PMN 有最大值时,则BD 的值最大,由三角形三边关系可推断出当B 、A 、D 三点共线时,BD的值最大,其最大值为14,此时S △PMN =12PN 2=18BD 2=18×14×14=492.针对训练:1. 解:(1)证明:延长DA 交BE 于G 点.∵∠BAE +∠CAD =180°,即∠EAG +∠GAB +∠CAD =180°,∵∠GAB +∠BAC +∠CAD =180°,∴∠EAG =∠CAB .∵∠EAG =∠AED +∠ADE ,∴∠CAB =∠AED +∠ADE .(2)证明:如图①,过E 点作DA 延长线的垂线,垂足为H .∴∠AHE =∠ACB =90°,由(1)可知,∠EAH =∠BAC ,又∵AE =AB ,∴△AHE ≌△ACB ,∴EH =BC ,AH =AC .∵AC =AD ,∴AH =AD .∵∠EHA =∠FAD =90°,∴AF ∥EH .∵A 为DH 中点,∴AF 为△DHE 中位线,∴EH =2AF ,∴BC =2AF .(3)成立.证明如下:如图②,延长DA 至M 点,使AM =DA ,连接EM ,∵∠BAE +∠CAD =180°,∠CAD +∠CAM =180°,∴∠BAE =∠CAM ,∴∠BAE +∠CAC =∠CAM +∠EAC ,即∠BAC =∠CAM .∵AM =AD ,AD =AC ,∴AM =AC .又∵AB =AE ,∠BAC =∠EAM ,∴△BAC ≌△EAM ,∴BC =EM .∵F 、A 分别为DE 、DM 中点,∴AF 为△DEM 中位线,∴EM =2AF ,∴BC =2AF .2. 解:(1)证明:∵∠BAC+∠EAD=180°,∠BAE =90°,∴∠DAC =90°,在△ABE 与△ACD 中,AE =AD ,∠BAE =∠CAD=90°,AB =AC ,∴△ABE ≌△ACD(SAS),∴CD =BE , ∵在Rt △ABE 中,F 为BE 的中点,∴BE =2AF ,∴CD =2AF.(2)成立,证明:如图,延长EA 交BC 于G ,在AG 上截取AH =AD ,∵∠BAC +∠EAD=180°,∴∠EAB +∠DAC=180°,∵∠EAB +∠BAH=180°,∴∠DAC =∠BAH,在△ABH 与△ACD 中,AH =AD ,∠BAH =∠CAD,AB =AC ,∴△ABH ≌△ACD(SAS),∴BH =DC ,∵AD =AE ,AH =AD ,∴AE =AH ,∵EF =FB ,∴BH =2AF ,∴CD =2AF.3. 解:(1)证明:∵AB=AC ,∴∠ABD =∠ACD,∵AE =AD ,∴∠ADE =∠AED,∵∠BAD +∠ABD=∠ADE+∠EDC,∠EDC +∠ACD=∠AED ,∴∠BAD =2∠EDC,∵∠ABF =2∠EDC,∴∠BAD =∠ABF,∴△ABF 是等腰三角形;(2)方法一:如图①,延长CA 至点H ,使AG =AH ,连接BH ,∵点N 是BG 的中点,∴AN =12BH , ∵∠BAD =∠ABF,∠DAC =∠CBG,∴∠CAB =∠CBA,∴△ABC 是等边三角形.∴AB =BC =AC ,∠BAC =∠BCA=60°,∵GM =AB ,AB =AC ,∴CM =AG ,∴AH =CM ,在△BAH 和△BCM 中,⎩⎪⎨⎪⎧AB =BC ,∠BAH =∠BCM=120°,AH =CM ,∴△BAH ≌△BCM(SAS),∴BH =BM ,∴AN =12BM , 方法二:如图②,延长AN 至K ,使NK =AN ,连接KB ,同方法一,先证△ABC 是等边三角形,再证△ANG ≌△KNB (SAS),所以BK =AG =CM ,然后可以证得∠ABK =∠BCN =120°,最后证△ABK ≌△BCN (SAS),所以BM =AK =2AN .类型5 角的和差倍分例5:解:(1)如图,过点P 作PG⊥EF 于G.∵PE =PF =6,EF =6 3,∴FG =EG =3 3,∠FPG =∠EPG=12∠EPF. 在Rt △FPG 中,sin ∠FPG =FG PF =3 36=32. ∴∠FPG =60°,∴∠EPF =2∠FPG=120°.(2)如图,作PM ⊥AB 于M ,PN ⊥AD 于N .∵AC 为菱形ABCD 的对角线,∴∠DAC =∠BAC ,AM =AN ,PM =PN .在Rt △PME 和Rt △PNF 中,PM =PN ,PE =PF ,∴Rt △PME ≌Rt △PNF ,∴NF =ME .又∵AP =10,∠PAM =12∠DAB =30°, ∴AM =AN =AP cos30°=10×32=5 3. ∴AE +AF =(AM +ME )+(AN -NF )=AM +AN =10 3.针对训练:1. 证明:如图,过D 作DE ⊥AB 于E ,过D 作DF ⊥AC 于F ,∵DA 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,∴DE =DF ,∵∠B +∠ACD =180°,∠ACD +∠FCD =180°,∴∠B =∠FCD ,在△DFC 和△DEB 中,⎩⎪⎨⎪⎧∠F =∠DEB ,∠FCD =∠B ,DF =DB ,∴△DFC ≌△DEB ,∴DC =DB .2. 解:(1)∵AC=AB =4,且CD =1,∴AD =AC -CD =3.在Rt △ABD 中,∠BAD =90°,∴BD =AB 2+AD 2=5,∵S △ABD =12AB·AD=12AE·BD, ∴AE =2.4.(2)证明:如图,取BC 的中点M ,连接AM 交BD 于点N .∵∠BAC =90°,AB =AC ,点M 为BC 的中点,∴AM =BM =CM ,AM ⊥BC ,∠NAD =∠FCP =45°,∴∠AMF =∠BMN =90°.∵AE ⊥BD ,∴∠MAF +∠ANE =∠MBN +∠BNM =90°,又∠ANE =∠BNM ,∴∠MAF =∠MBN ,∴△AMF ≌△BMN ,∴MF =MN ,∴AM -MN =CM -MF ,即AN =CF .∵AP =CD ,∴AC -CD =AC -AP ,即AD =CP .∴△ADN ≌△CPF ,∴∠ADB =∠CPF .3. 解:(1)∵AB =BD ,∠BAD =45°,∴∠BDA =45°,即∠ABD =90°.∵四边形ABCD 是平行四边形,∴当E 、C 重合时,BF =12BD =12AB . ∵在Rt △ABF 中,AB 2+BF 2=AF 2,∴(2BF )2+BF 2=(5)2,∴BF =1,AB =2.在Rt △ABD 中,AD =AB 2+BD 2=2AB 2=2 2.(2)证明:如图,在AF 上截取AK =HD ,连接BK.∵∠AFD =∠ABF+∠2=∠FGD+∠3且∠ABF=∠FGD=90°,∴∠2=∠3.在△ABK 与△DBH 中,⎩⎪⎨⎪⎧AB =BD ,∠2=∠3,AK =HD ,∴△ABK ≌△DBH ,∴BK =BH ,∠6=∠5.∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠5=∠4=45°,∴∠6=∠5=45°,∴∠7=∠ABD-∠6=45°=∠5.在△BFK 与△BFH 中,⎩⎪⎨⎪⎧BK =BH ,∠7=∠5,BF =BF ,∴△BFK ≌△BFH.∴∠BFK =∠BFH,即∠AFB=∠HFB.4. 解:(1)证明:由折叠知∠EMN=∠ABC=90°,BE =EM ,∴∠EMB =∠EBM,∴∠EMN -∠EMB=∠ABC-∠EBM,即∠BMP=∠MBC.∵在正方形ABCD 中,AD ∥BC ,∴∠AMB =∠MBC,∴∠AMB =∠BMP,∴BM 是∠AMP 的平分线.(2)△PDM 的周长没有发生变化.证明如下:如图,过B 作BQ ⊥MP∵∠A =90°,且由(1)知BM 是∠AMP 的平分线,∴BA =BQ ,∵∠A =∠MQB =90°,∠AMB =∠BMP ,MB =MB ,∴△AMB ≌△QMB (AAS).∴MA =MQ .∵BA =BC ,∴BQ =BC ,又∵∠BQP =90°=∠C ,BP =BP ,∴Rt △BPC ≌Rt △BPQ (HL).∴PC =PQ ,∴△PDM 的周长=MD +MP +DP =MD +MQ +QP +PD=MD +MA +PC +PD =AD +DC =2AD .∴△PDM 的周长没有发生变化.类型6 旋转型全等问题:图中若有边相等,可用旋转做实验例6:解:(1)①∵四边形ADEF 是正方形,∴AD =AF ,AB =AC ,∵∠BAC =∠DAF=90°,∴∠BAD =∠CAF,∴△DAB ≌△FAC ,∴∠B =∠ACF,∴∠ACB +∠ACF=90°,即CF⊥BC;②∵△DAB ≌△FAC ,∴CF =BD ,∵BC =BD +CD ,∴BC =CF +CD.(2)结论①成立,结论②不成立.∵四边形ADEF 是正方形,∴AD =AF ,AB =AC.∵∠BAC =∠DAF=90°,∴∠BAD =∠CAF,∴△DAB ≌△FAC ,∴∠ABD =∠ACF,CF =BD ,∴∠BCF =∠ACF-∠ACB=∠ABD-∠ACB=90°,即CF⊥BC;∵BC=CD -BD ,∴BC =CD -CF.(3)如图,过A 作AH ⊥BC 于H ,过E 作EM ⊥BD 于M ,EN ⊥CF 于∵∠BAC =90°,AB =AC ,∴BC =2AB =4,AH =CH =12BC =2,∴CD =14BC =1,∴DH =3,同(2)证得△BAD ≌△CAF , ∴∠ABD =∠ACF =45°,∴∠BCF =∠ACB +∠ACF =90°,∴BC ⊥CF ,CF =BD =5.∵四边形ADEF 是正方形,∴AD =DE ,∠ADE =90°,∵BC ⊥CF ,EM ⊥BD ,EN ⊥CF ,∴四边形CMEN 是矩形,∴NE =CM ,EM =CN ,∵∠AHD =∠ADE =∠EMD =90°,∴∠ADH +∠EDM =∠EDM +∠DEM =90°,∴∠ADH =∠DEM ,∴△ADH ≌△DEM ,∴EM =DH =3,DM =AH =2,∴CN =EM =3,EN =CM =3,∵∠ABC =45°,∴∠BGC =45°,∴△BCG 是等腰直角三角形,∴CG =BC =4,∴GN =1,∴EG =GN 2+EN 2=10.针对训练:1. 解:(1)AC =AD +AB .证明如下:∵∠B +∠D =180°,∠B =90°,∴∠D =90°.∵∠DAB =120°,AC 平分∠DAB ,∴∠DAC =∠BAC =60°,∵∠B =90°,∴AB =12AC , 同理AD =12AC . ∴AC =AD +AB .(2)(1)中的结论成立,理由如下:如图①,以C 为顶点,AC 为一边作∠ACE=60°,∠ACE 的另一边交AB 的延长线于点E ,∵∠BAC =60°,∴△AEC 为等边三角形,∴AC =AE =CE ,∠E =60°,∵∠ABC +∠D=180°,∠DAB =120°,∴∠DCB =60°,∴∠DCA =∠ECB.在△DAC 和△BEC 中,⎩⎪⎨⎪⎧∠DAC=∠E,AC =CE ,∠DCA =∠BCE,∴△DAC ≌△BEC ,∴AD =BE ,∴AC =AE =AD +AB.(3)AD +AB =2AC.理由如下:如图②,过点C 作CE⊥AC 交AB 的延长线于点E∵∠ABC +∠D=180°,∠DAB =90°,∴∠DCB =90°,∵∠ACE =90°,∴∠DCA =∠BCE,又∵AC 平分∠DAB,∴∠CAB =45°,∴∠E =45°,∴AC =CE.∴△CDA ≌△CBE ,∴AD =BE ,∴AD +AB =AE.∵在Rt △ACE 中,∠CAB =45°,∴AE =AC cos45°=2AC , ∴AD +AB =2AC.2. 解:(1)证明:∵四边形ABCD 是正方形,∴∠B =∠D=∠BAD=90°,AB =AD ,∵△ABE 沿AE 翻折得到△AHE,∴△ABE ≌△AHE ,∴AH =AB =AD ,BE =EH ,∠AHE =∠AHF=∠B=∠D=90°.在Rt △AHF 和Rt △ADF 中,⎩⎪⎨⎪⎧AF =AF ,AH =AD , ∴Rt △AHF ≌Rt △ADF(HL),∴∠HAF =∠DAF,∴∠EAF =∠EAH+∠FAH=12∠BAH+12∠HAD=12∠BAD=45°,(2)以BM ,DN ,MN 为三边围成的三角形为直角三角形.证明如下:如图,过点A 作AH ⊥AN 并截取AH =AN ,连接BH 、HM ,∵∠1+∠BAN =90°,∠3+∠BAN =90°,∴∠1=∠3,在△ABH 和△ADN 中,⎩⎪⎨⎪⎧AB =AD ,∠1=∠3,AH =AN ,∴△ABH ≌△ADN (SAS),∴BH =DN ,∠HBA =∠NDA =135°,∵∠HAN =90°,∠MAN =45°,∴∠1+∠2=∠HAM =∠MAN =45°,在△AHM 和△ANM 中,⎩⎪⎨⎪⎧AH =AN ,∠HAM =∠MAN ,AM =AM ,∴△AHM ≌△ANM (SAS),∴HM =NM ,∴∠HBP =180°-∠HBA =180°-135°=45°,∴∠HBP +∠PBM =45°+45°=90°,∴△HBM 是直角三角形,∵HB =DN ,HM =MN ,∴以BM ,DN ,MN 为三边围成的三角形为直角三角形.3. 解:(1)如图①,将△PBC 绕点B 逆时针旋转90°得△P ′BA ,连接PP ′,则△AP ′B ≌△CPB , ∴P ′B =PB =2,P ′A =PC =1,∠1=∠2,∠AP ′B =∠BPC .∵四边形ABCD 是正方形,∴AB =BC ,∠ABC =90°,∴∠2+∠3=90°,∴∠1+∠3=90°,即∠P ′BP =90°,∴∠BP ′P =45°.在Rt △P ′BP 中,由勾股定理,得PP ′2=4.∵P ′A =1,AP =5∴P ′A 2=1,AP 2=5,∴P ′A 2+PP ′2=AP 2,∴△P ′AP 是直角三角形,∴∠AP ′P =90°,∴∠AP′B=45°+90°=135°,∴∠BPC=135°.(2)仿照【分析】中的思路,将△BPC绕点B逆时针旋转120°,得到了△BP′A,连接PP′,如图②.则△PBC≌△P′BA,∴P′B=PB=4,P′A=PC=2,∠BPC=∠BP′A,∴△BPP′为等腰三角形,∵∠ABC =120°,∴∠PBP′=120°,∴∠BP′P=30°,过点B作BG⊥PP′于G,则∠P′GB=90°,∴PP′=2P′G.∵P′B=PB=4,∠BP′P=30°,∴BG=2,∴P′G=2 3.∴PP′=4 3,在△APP′中,∵PA=2 13,P′A=2,PP′=4 3,∴P′A2+P′P2=PA2,∴△PP′A是直角三角形,∴∠AP′P=90°,∴∠BPC=∠BP′A=∠PP′B+∠AP′P=30°+90°=120°.。
重庆中考真题几何试卷

重庆中考真题几何试卷一、选择题(每题2分,共20分)1. 下列哪个选项不是欧几里得几何中的公理?A. 两点之间可以画一条直线B. 任意直线可以无限延伸C. 任意两点可以确定一个平面D. 所有直角都相等2. 已知三角形ABC中,AB=AC,且∠A=90°,这个三角形是:A. 锐角三角形B. 直角三角形C. 等腰三角形D. 等边三角形3. 如果一个圆的半径为5,那么它的周长是:A. 10πB. 20πC. 30πD. 40π4. 下列哪个图形不是中心对称图形?A. 正方形B. 等边三角形C. 圆D. 长方形5. 已知一个矩形的长为6cm,宽为4cm,那么它的对角线长度是:A. 2cmB. 5cmC. 10cmD. 2√13cm6. 一个正六边形的内角是:A. 60°B. 90°C. 120°D. 180°7. 一个圆柱的底面半径为2,高为4,那么它的体积是:A. 8πB. 12πC. 16πD. 20π8. 一个圆锥的底面半径为3,高为4,那么它的体积是:A. 9πB. 12πC. 15πD. 18π9. 一个球的体积公式是:A. V = 4/3πr^3B. V = πr^2hC. V = 1/3πr^2hD. V = πr^310. 已知一个正方体的棱长为a,那么它的表面积是:A. 6a^2B. 8a^2C. 10a^2D. 12a^2二、填空题(每题2分,共20分)11. 如果一个角的余角是30°,那么这个角的度数是________。
12. 一个正五边形的外接圆半径与内切圆半径之比是________。
13. 在直角三角形中,如果一个锐角是30°,那么另一个锐角的度数是________。
14. 一个长方体的长、宽、高分别是2cm、3cm、4cm,那么它的表面积是________。
15. 一个圆的直径是14cm,那么它的面积是________。
重庆中考几何题分类汇编(含答案)

重庆中考几何题分类汇编(含答案)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN重庆中考几何题分类汇编(含答案)类型1线段的倍分:要证线段倍与半,延长缩短去实验例1 如图Z3-1,在△ABC中,AB=AC,CM平分∠ACB交AB于M,在AC的延长线上截取CN=BM,连接MN交BC于P,在CB的延长线截取BQ=CP,连接MQ.(1)求证:MQ=NP;(2)求证:CN=2CP.针对训练:1.如图Z3-2,在▱ABCD中,AC⊥BC,点E、点F分别在AB、BC上,且满足AC=AE=CF,连接CE、AF、EF.(1)若∠ABC=35°,求∠EAF的度数;(2)若CE⊥EF,求证:CE=2EF.2.已知,在△ABC 中,AB =AC ,∠BAC =90°,E 为边AC 任意一点,连接BE.(1)如图①,若∠ABE=15°,O 为BE 中点,连接AO ,且AO =1,求BC 的长;(2)如图②,F 也为AC 上一点,且满足AE =CF ,过A 作AD⊥BE 交BE 于点H ,交BC 于点D ,连接DF 交BE于点G ,连接AG.若AG 平分∠CAD,求证:AH =12AC.3.在△ACB 中,AB =AC ,∠BAC =90°,点D 是AC 上一点,连接BD ,过点A 作AE⊥BD 于E ,交BC 于F.(1)如图①,若AB =4,CD =1,求AE 的长;(2)如图②,点G 是AE 上一点,连接CG ,若BE =AE +AG ,求证:CG =2AE.4.在等腰直角三角形ABC 中,∠BAC =90°,AB =AC ,D 是斜边BC 的中点,连接AD.(1)如图①,E 是AC 的中点,连接DE ,将△CDE 沿CD 翻折到△CDE′,连接AE′,当AD =6时,求AE′的值.(2)如图②,在AC 上取一点E ,使得CE =13AC ,连接DE ,将△CDE 沿CD 翻折到△CDE′,连接AE′交BC 于点F ,求证:DF =CF.类型2 线段的和差:要证线段和与差,截长补短去实验例2 如图,在△ABC中,∠BAC=90°,在BC上截取BD=BA,连接AD,在AD左侧作∠EAD=45°交BD 于E.(1)若AC=3,则CE=________(直接写答案);(2)如图①,M、N分别为AB和AC上的点,且AM=AN,连接EM、DN,若∠AME+∠AND=180°,求证:DE =DN+ME;(3)如图②,过E作EF⊥AE,交AD的延长线于F,在EC上选取一点H,使得EH=BE,连接FH,在AC上选取一点G,使得AG=AB,连接BG、FG,求证:FH=FG.针对训练:1.如图Z3-7,在▱ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.(1)若BE=2EC,AB=13,求AD的长;(2)求证:EG=BG+FC.2.如图,在正方形ABCD 中,点P 为AD 延长线上一点,连接AC 、CP ,过点C 作CF⊥CP 于点C ,交AB 于点F ,过点B 作BM⊥CF 于点N ,交AC 于点M.(1)若AP =78AC ,BC =4,求S △ACP ;(2)若CP -BM =2FN ,求证:BC =MC.3.如图,在△ABC 中,AB =BC ,以AB 为一边向外作菱形ABDE ,连接DC ,EB 并延长EB 交AC 于F ,且CB⊥AE 于G.(1)若∠EBG=20°,求∠AFE;(2)试问线段AE ,AF ,CF 之间的数量关系并证明.类型3 倍长中线:三角形中有中线,延长中线等中线例3 如图Z3-10①,在Rt△ABC中,∠ABC=90°,D、E分别为斜边AC上两点,且AD=AB,CE=CB,连接BD、BE.(1)求∠EBD的度数;(2)如图Z3-10②,过点D作FD⊥BD于点D,交BE的延长线于点F,在AB上选取一点H,使得BH=BC,连接CH,在AC上选取一点G,使得GD=CD,连接FH、FG,求证:FH=FG.针对训练:1.如图,已知在▱ABCD中,G为BC的中点,点E在AD边上,且∠1=∠2.(1)求证:E是AD中点;(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.2.如图Z 3-12,在菱形ABCD 中,点E 、F 分别是BC 、CD 上的点,连接AE ,AF ,DE 、EF ,∠DAE =∠BAF.(1)求证:CE =CF ;(2)若∠ABC=120°,点G 是线段AF 的中点,连接DG ,EG.求证:DG⊥GE.3.在Rt △ABC 中,∠ACB =90°,点D 与点B 在AC 同侧,∠ADC >∠BAC,且DA =DC ,过点B 作BE∥DA 交DC 于点E ,M 为AB 的中点,连接MD ,ME.(1)如图①,当∠ADC=90°时,线段MD 与ME 的数量关系是________;(2)如图②,当∠ADC=60°时,试探究线段MD 与ME 的数量关系,并证明你的结论;(3)如图③,当∠ADC=α时,求ME MD的值.4.如图①,等边三角形ABC中,CE平分∠ACB,D为BC边上一点,且DE=CD,连接BE.(1)若CE=4,BC=6 3,求线段BE的长;(2)如图②,取BE中点P,连接AP,PD,AD,求证:AP⊥PD且AP=3PD;(3)如图③,把图Z3-14②中的△CDE绕点C顺时针旋转任意角度,然后连接BE,点P为BE中点,连接AP,PD,AD,问第(2)问中的结论还成立吗?若成立,请证明;若不成立,请说明理由.5.在△ABC中,以AB为斜边,作直角三角形ABD,使点D落在△ABC内,∠ADB=90°.(1)如图①,若AB=AC,∠BAD=30°,AD=6 3,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;(2)如图②,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP;(3)如图③,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).类型4 中位线:三角形中两中点,连接则成中位线例4 2017·河南如图①,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.(1)观察猜想:图①中,线段PM与PN的数量关系是__________,位置关系是__________;(2)探究证明:把△ADE绕点A按逆时针方向旋转到图②的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.针对训练:1.如图①,在任意的三角形ABC中,分别以AB和AC为一边作等腰三角形ABE和等腰三角形ACD,AB=AE,AC=AD,且∠BAE+∠CAD=180°,连接DE,延长CA交DE于F.(1)求证:∠CAB=∠AED+∠ADE;(2)若∠ACB=∠BAE=∠CAD=90°,如图②,求证:BC=2AF;(3)若在△ABC中,如图③所示,作等腰三角形ABE和等腰三角形ACD,AB与DE交于点F,F为DE的中点,请问(2)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.2.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.(1)如图①,当∠BAE=90°时,求证:CD=2AF;(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.3.如图①,在等腰三角形ABC中,AB=AC,在底边BC上取一点D,在边AC上取一点E,使AE=AD,连接DE,在∠ABD的内部作∠ABF=2∠EDC,交AD于点F.(1)求证:△ABF是等腰三角形;(2)如图②,BF的延长交AC于点G.若∠DAC=∠CBG,延长AC至点M,使GM=AB,连接BM,点N是BG的中点,连接AN,试判断线段AN、BM之间的数量关系,并证明你的结论.类型5 角的和差倍分图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现.角平分线平行线,等腰三角形来添.角平分线加垂线,三线合一试试看.例5.如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6 3,∠BAD=60°,且AB>6 3.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值.针对训练:1.已知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.2.在△ACB中,AB=AC,∠BAC=90°,点D是AC上一点,连接BD,过点A作AE⊥BD于E,交BC 于F.(1)如图①,若AB=4,CD=1,求AE的长;(2)如图②,点P是AC上一点,连接FP,若AP=CD,求证:∠ADB=∠CPF.3.已知,在▱ABCD中,∠BAD=45°,AB=BD,E为BC上一点,连接AE交BD于F,过点D作DG⊥AE于G,延长DG交BC于H.(1)如图①,若点E与点C重合,且AF=5,求AD的长;(2)如图②,连接FH,求证:∠AFB=∠HFB.4.如图,将正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连接EP.当点M在边AD上移动时,连接BM、BP.(1)求证:BM是∠AMP的平分线;(2)△PDM的周长是否发生变化?证明你的结论.类型6 旋转型全等问题:图中若有边相等,可用旋转做实验例6.△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF.(1)观察猜想:如图①,当点D 在线段BC 上时,①BC 与CF 的位置关系为:________.②BC ,CD ,CF 之间的数量关系为:___________;(将结论直接写在横线上)(2)数学思考:如图Z 3-25②,当点D 在线段CB 的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸:如图Z 3-25③,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE.若已知AB =2 2,CD =14BC ,请求出GE 的长.针对训练:1.在四边形ABCD 中,∠B +∠D=180°,对角线AC 平分∠BAD.(1)如图①,若∠DAB=120°,且∠B=90°,试探究边AD 、AB 与对角线AC 的数量关系并说明理由.(2)如图②,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.(3)如图③,若∠DAB=90°,探究边AD 、AB 与对角线AC 的数量关系并说明理由.2.如图①,在正方形ABCD中,点E为边BC上一点,将△ABE沿AE翻折得△AHE,延长EH交边CD 于F,连接AF.(1)求证:∠EAF=45°;(2)延长AB,AD,如图②,射线AE、AF分别交正方形两个外角的平分线于M、N,连接MN,若以BM、DN、MN为三边围成三角形,试猜想三角形的形状,并证明你的结论.3.如图①,在正方形ABCD内有一点P,PA=5,PB=2,PC=1,求∠BPC的度数.【分析问题】根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图Z3-28②),然后连接PP′.(1)请你通过计算求出图Z3-28②中∠BPC的度数;(2)如图③,若在正六边形ABCDEF内有一点P,且PA=2 13,PB=4,PC=2.请求出∠BPC的度数.重庆中考几何题分类汇编答案例1. 证明:(1)∵AB=AC ,∴∠ABC =∠ACB.∵∠MBQ +∠ABC=180°,∠ACB +∠PCN=180°,∴∠MBQ =∠PCN.在△QBM 和△PCN 中,⎩⎪⎨⎪⎧QB =PC ,∠MBQ =∠PCN,BM =CN ,∴△QBM ≌△PCN(SAS).∴MQ=NP.(2)过M 作MG∥AC 交BC 于G ,∵MG ∥AC ,∴∠MGB =∠ACB,∠MGC =∠PCN,∵由(1)知,∠ABC =∠ACB,∴∠ABC =∠MGB,∴MB =MG ,∵MB =CN ,∴MG =CN.在△MGP 和△NCP 中,⎩⎪⎨⎪⎧∠MPG=∠CPN,∠MGC =∠PCN,MG =NC ,∴△MGP ≌△NCP(AAS).∴PG =CP ,∴CG =CP +PG ,即CG =2CP.∵CM 平分∠ACB,∴∠BCM =∠MCA,∵MG ∥AC ,∴∠MCA =∠GMC,∴∠BCM =∠GMC,∴MG =CG ,∵MG =CN ,∴CN =CG ,∴CN =2CP.针对训练1. 解:(1)∵AC⊥BC,∴∠ACB =90°,又∵AC=CF ,∴∠∵∠ABC =35°,∴∠EAF =10°;(2)证明:方法1:取CF 的中点M ,连接EM 、AM ,∵CE ⊥EF ,∴EM =CM =FM =12CF , 又∵AC=AE ,∴AM 为EC 的中垂线,∴∠CAM +∠ACE=90°,又∵∠ECF+∠ACE=90°,∴∠CAM =∠FCE,又∵∠CEF=∠ACM=90°,∴△ACM ∽△CEF ,∴AC CM =CE EF, 又∵CF=AC =2CM ,∴AC CM =CE EF =21,即CE =2EF ; 方法2:延长FE 至M ,使EF =EM ,连接CM ,∵CE ⊥EF ,∴△CMF 为等腰三角形,又∵AC=AE =CF ,且∠ACE=∠CFE(易证), ∴△CMF ≌△CEA ,∴FM =CE =2EF.2. 解:(1)如图①,在AB 上取一点M ,使得BM =ME ,连接ME.在Rt △ABE 中,∵OB =OE ,∴BE =2OA =2,∵MB =ME ,∴∠MBE =∠MEB=15°,∴∠AME =∠MBE+∠MEB=30°,设AE =x ,则ME =BM =2x ,AM =3x ,∵AB 2+AE 2=BE 2,∴(2x +3x)2+x 2=22,∴x =6-2(负根舍弃),∴AB =AC =(2+ 3)·6-22, ∴BC =2AB =3+1.(2)证明:如图②,作CP⊥AC,交AD 的延长线于P ,GM ⊥AC 于M. ∵BE ⊥AP ,∴∠AHB =90°,∴∠ABH +∠BAH=90°,∵∠BAH +∠PAC=90°,∴∠ABE =∠PAC,又∵AB=AC ,∠BAE =∠ACP=90°,∴△ABE ≌△CAP ,∴AE =CP =CF ,∠AEB =∠P,在△DCF 和△DCP 中,⎩⎪⎨⎪⎧CD =CD ,∠DCF =∠DCP,CF =CP ,∴△DCF ≌△DCP ,∴∠DFC =∠P,∴∠GFE =∠GEF,∴GE =GF , ∵GM ⊥EF ,∴FM =ME ,∵AE =CF ,∴AF =CE ,∴AM =CM ,在△GAH 和△GAM 中,⎩⎪⎨⎪⎧∠GAH=∠GAM,∠AHG =∠AMG,AG =AG ,∴△AGH ≌△AGM ,∴AH =AM =CM =12AC.3. 解:(1)∵AB=4,∴AC =AB =4.∵CD =1,∴AD =AC -CD =3.∵在Rt △ABD 中,∠BAC =90°,∴BD =AB 2+AD 2=5, ∵S △ABD =12AB·AD=12AE·BD,∴AE =2.4. (2)证明:如图,在线段EB 上截取EH =AE ,并连接AH.∵AE ⊥BD ,EH =AE ,∴AH =2AE.∵BE =AE +AG ,∴BH =BE -HE =AG.∵∠BAD =∠BEA=90°,∴∠ABE +∠B AE =∠CAG+∠BAE=90°,∴∠ABE =∠CAG.∵BA =AC ,∴△ABH ≌△CAG ,∴CG =AH =2AE.4. 解:(1)∵∠BAC=90°,AB =AC ,D 是斜边BC 的中点,∴∠ADC =90°,∠ACD =45°.在Rt △ADC 中,AC =AD÷sin45°=2 3.∵E 是AC 的中点,∴CE =12AC = 3.∵将△CDE 沿CD 翻折到△CDE′,∴CE ′=CE =3,∠ACE ′=90°.由勾股定理,得AE′=CE′2+AC 2=15.(2)证明:如图,过B 作AE′的垂线交AD 于点G ,交AC 于点H. ∵∠ABH +∠BAF=90°,∠CAF +∠BAF=90°,∴∠ABH =∠CAF.又∵AB=AC ,∠BAH =∠ACE′=90°,∴△ABH ≌△CAE ′.∴AH =CE′=CE ,∵CE =13AC ,∴AH =HE =CE. ∵D 是BC 中点,∴DE ∥BH ,∴G 是AD 中点.在△ABG 和△CAF 中:AB =AC ,∠BAD =∠ACD=45°,∠ABH =∠CAF,∴△ABG ≌△CAF.∴AG =CF.∵AG =12AD ,∴CF =12AD =12CD.∴DF=CF.类型2 线段的和差:要证线段和与差,截长补短去实验 例2:解:(1)3(2)证明:延长DN 到K ,使得NK =ME ,连接AK ,如图①, 因为∠1+∠3=180°,∠1+∠2=180°,∴∠2=∠3.在△AME 和△ANK 中,⎩⎪⎨⎪⎧AM =AN ,∠2=∠3,ME =NK ,∴△AME ≌△ANK (SAS).∴AE =AK ,∠4=∠5, ∴∠4+∠EAC =90°,∴∠5+∠EAC =90°,即∠EAK =90°,∵∠EAD =45°,∴∠KAD =∠EAK -∠EAD =90°-45°=45°∴∠EAD =∠KAD .在△EAD 和△KAD 中,⎩⎪⎨⎪⎧EA =KA ,∠EAD =∠KAD ,AD =AD ,∴△EAD ≌△KAD (SAS),∴ED =KD .∵DK =DN +KN ,∴ED =DN +KN , 又NK =ME ,∴ED =DN +ME .(3)证明:延长AE 到J ,使得EJ =AE ,连接JH ,JF.如图②,在△ABE 和△JHE 中,⎩⎪⎨⎪⎧AE =JE ,∠AEB =∠JEH,BE =HE ,∴△ABE ≌△JHE(SAS),∴JH =AB ,∠1=∠2,∵AB =AG ,∴JH =AG ,∵AE =EJ ,EF ⊥AJ ,∴AF =JF ,∴∠JAF =∠AJF=45°,即∠2+∠3=45°,∵∠BAC =90°,∴∠1+∠EAD+∠4=90°, ∴∠1+∠4=90°-∠EAD,=90°-45°=45°,∵∠1=∠2,∴∠3=∠4,在△JHF 和△AGF 中,⎩⎪⎨⎪⎧JH =AG ,∠3=∠4,JF =AF ,∴△JHF ≌△AGF(SAS),∴FH =FG.针对训练:1. 解:(1)∵四边形ABCD 是平行四边形,∴AD =BC.∵BE =2EC ,设CE =x ,BE =2x ,∴BC =AD =AE =3x.又∵EG⊥AB,∴∠AEB =90°,∴AB 2=AE 2+BE 2,即13=9x 2+4x 2,∴x =1,∴AD =3x =3.(2)证明:如图,过C 作CH⊥AB 于H ,则四边形CHGF 为矩形.∴CF =HG ,∠CHB =90°,GF =CH.∵AE ⊥BC ,EG ⊥AB ,∴∠AEB =∠CHB=90°,∠BCH +∠B=90°,∠BAE +∠B=90°,∴∠BCH =∠BAE.又∵AE=BC ,∴△AGE ≌△CHB ,∴GE =BH ,AG =GF ,∴GE =BH =BG +GH =BG +CF.2. 解:(1)∵四边形ABCD 是正方形,BC =4,∴AB =AD =CD =BC =4,∠ADC =∠ABC=90°.∵在Rt △ABC 中,AC =AB 2+BC 2=4 2,∴AP =78AC =72 2, ∴S △ACP =12AP·CD=7 2.(2)证明:方法一:如图①,在NC 上截取NK =NF ,连接BK. ∵四边形ABCD 是正方形,∴AB =BC =DC ,∠ABC =∠BCD=∠ADC=90°.∵∠BCD =90°,CF ⊥CP ,∴∠1+∠DCF=∠2+∠DCF=90°,∴∠1=∠2,∵在△FBC 和△PDC 中,⎩⎪⎨⎪⎧∠FBC=∠3,BC =DC ,∠1=∠2,∴△FBC ≌△PDC(ASA),∴CF =CP ,∵CP -2FN =BM ,∴CF -FK =BM ,即CK =BM ,∵∠FBC =90°,BM ⊥CF ,∴∠1+∠NBC=∠4+∠NBC=90°,∴∠1=∠4,∵在△ABM 和△BCK 中,⎩⎪⎨⎪⎧AB =BC ,∠4=∠1,BM =CK ,∴△ABM ≌△BCK(SAS),∴∠7=∠6.∵BM ⊥CF ,NK =NF ,∴BF =BK ,∵BF =BK ,BM ⊥CF ,∴∠4=∠5, ∴∠4+∠7=∠5+∠6,∵∠8=∠4+∠7,∴∠8=∠MBC,∴BC =MC.解:方法二:如图②,延长BM 交AD 于点G ,过A 作AE⊥BG 于E先证△AEB≌△BNC(AAS),∴AE =BN ,又证△AEG≌△BNF(AAS),∴EG =NF ,再证四边形BCPG 为平行四边形,∴BG =CP ,∵CP -BM =2FN ,∴BG -BM =2EG ,∴MG =2EG ,∴点E 为MG 中点, ∵AE ⊥MG ,EM =EG ,∴AM =AG ,∴∠3=∠4,∵∠2=∠3,∠1=∠4,∴∠1=∠2,∴BC =MC.3. 解:(1)∵∠EBG=20°,CB ⊥AE ,∴∠BEG =70o ,∠CBF =∠EBG=20°,∵四边形ABDE 是菱形,∴∠ABE =∠BEG=70°,∴∠ABG =50°,∵AB =BC ,∴∠FCB =25°,∴∠AFE =∠CBF+∠FCB=45°;(2)AE ,AF ,CF 之间的数量关系是AF 2+CF 2=2AE 2,证明如下:连接DF ,∵四边形ABDE 是菱形,∴AB =DB ,∠DBE =∠ABE,∴∠DBF =∠ABF,∵BF =BF ,∴△DBF ≌△ABF(SAS),∴DF =AF ,∠BDF =∠BAF,∵∠BCF =∠BAF,∴∠BCF =∠BDF, ∵CB ⊥AE ,AE ∥DB ,∴DB ⊥CB ,∵CB =AB =BD ,∴△DBC 是等腰直角三角形,∴DC =2BD =2AE ,∵∠DPB =∠CPF,∴∠CFP =∠DBP=90°,∴DF 2+CF 2=DC 2,即有:AF 2+CF 2=2AE 2.类型3 倍长中线:三角形中有中线,延长中线等中线例3解:(1)设∠BEC =α,∠BDA =β,则∠C =180°-2α,∠A =180°-2β.∵在Rt △ABC 中,∠ABC =90°,∴∠A +∠C =90°,即180°-2α+180°-2β=90°,∴α+β=135°,∴∠EBD =45°.(2)证明:法一:如图①,延长BD 至点B′,使得DB′=DB ,连接在△GDB′和△CDB 中,⎩⎪⎨⎪⎧GD =CD ,∠GDB ′=∠CDB,B ′D =BD ,∴△GDB ′≌△CDB.∴GB ′=BC =BH ,∠GB ′D =∠CBD.∵FD ⊥BD ,BD =DB′,∴FB =FB′.∵∠FB ′G =45°-∠GB′D,∠HBF =90°-45°-∠CBD=45°-∠CBD,∴∠FB ′G =∠HBF.在△FHB 和△FGB′中,⎩⎪⎨⎪⎧HB =GB′,∠HBF =∠GB′F,BF =B′F,∴△FHB ≌△FGB ′,∴HF =GF.法二:如图②,延长FD 至点F ′,使得DF ′=DF ,连接CF ′、BF ′.先证△DGF ≌△DCF ′,再证△BHF ≌△BCF ′,∴HF =GF .针对训练1. 证明:(1)∵四边形ABCD 是平行四边形,∴AB =CD ,AD =BC ,∠A =∠C .又∵∠1=∠2,∴△ABE ≌△CDG (ASA),∴AE =CG .∵G 为BC 中点,∴CG =12BC , ∴AE =CG =12BC =12AD ,∴E 是AD 中点.(2)如图,延长BE ,CD 交于点H.∵四边形ABCD 是平行四边形,∴AB 綊CD ,∴∠A =∠ADH,∠1=∠4,又∵∠1=∠2,∠3=∠2,∴∠1=∠2=∠3=∠4,∴FH =FB.由(1),E 是AD 中点,∴AE =DE ,∴△ABE ≌△DHE(AAS),∴AB =DH ,∴CD =AB =DH =DF +FH =DF +BF ,即CD =BF +DF.2. 证明:(1)在菱形ABCD 中,AB =BC =CD =AD ,∠ADF =∠ABE,∵∠DAE =∠BAF,∴∠DAE -∠EAF=∠BAF-∠EAF,即∠DAF=∠BAE.∴△DAF ≌△BAE ,∴BE =DF.又∵BC=CD ,∴CE =CF(2)如图,延长DG 交AB 于H ,连接EH ,∵在菱形ABCD 中,AB ∥CD ,∴∠DFA =∠GAH.∵G 为AF 中点,∴AG =GF.又∵∠DGF=∠AGH,∴△DGF ≌△HGA.∴DG =GH ,AH =DF.又∵AB=CD ,∴BH =CF.又∵AB∥CD,∠ABC =120°,∴∠C =60°.又∵CE =CF ,∴△CEF 为等边三角形,∴CF =EF ,∠CFE =60°,∴EF =BH ,∠DFE =∠ABC=120°.又∵BE=DF ,∴△EFD ≌△HBE ,∴HE =ED ,又∵HG=DG ,∴DG ⊥GE.3. 解:(1)MD=ME2)MD =3ME.理由如下:如图①,延长EM 交DA 于点F.∵BE ∥DA ,∴∠FAM =∠EBM.又∵AM=BM ,∠AMF =∠BME,∴△AMF ≌△BME ,∴AF =BE ,MF =ME.∵DA =DC ,∠ADC =60°,∴∠BED =∠ADC=60°,∠ACD =60°.∵∠ACB =90°,∴∠ECB =30°,∴∠EBC =30°,∴CE =BE ,∴AF =EC ,∴DF =DE ,∴DM ⊥EF ,DM 平分∠ADC,∴∠MDE =30°.在Rt △MDE 中,tan ∠MDE =ME MD =33. ∴MD =3ME.(3)如图②,延长EM 交DA 于点F ,∵BE ∥DA ,∴∠FAM =∠EBM,又∵AM=BM ,∠AMF =∠BME,∴△AMF ≌△BME ,∴AF =BE ,MF =ME.延长BE 交AC 于点N ,∴∠BNC =∠DAC.∵DA =DC ,∴∠DCA =∠DAC,∴∠BNC =∠DCA,∵∠ACB =90°,∴∠ECB =∠EBC,∴CE =BE ,∴AF =CE.∴DF =DE ,∴DM ⊥EF ,DM 平分∠ADC,∵∠ADC =α,∴∠MDE =α2. ∴在Rt △MDE 中,ME MD =tan ∠MDE =tan α2.4.解:(1)如图①,作EH ⊥BC 于点H .∵△ABC 是等边三角形,∴∠ACB =60°.∵CE 平分∠ACB ,∴∠ECH =12∠ACB =30°, ∵EC =4,∠ECH =30°,∴EH =2,HC =2 3.∵BC =6 3,∴BH =6 3-2 3=4 3.在Rt △BHE 中,BE 2=(4 3)2+22=52,∴BE =2 13.(2)如图②,延长DP 至M ,使DP =PM ,连接BM 、AM .在△PDE 和△PMB 中,⎩⎪⎨⎪⎧PD =PM ,∠EPD =∠BPM ,PE =PB ,∴△PDE ≌△PMB (SAS).∴BM =DE ,∠1=∠2.∴BM ∥DE .∴∠MBD +∠BDE =180°.∵CE 平分∠ACB ,DE =CD ,∴∠BDE =30°+30°=60°.∴∠MBD =120°.∵△ABC 是等边三角形,∴∠ABC =60°,∴∠3=60°.∵BM =DE ,DE =CD ,∴BM =CD .在△ABM 和△ACD 中,⎩⎪⎨⎪⎧AB =AC ,∠3=∠ACD ,BM =CD ,∴△ABM ≌△ACD (SAS).∴AD =AM ,∠4=∠5.∵PD =PM ,∴AP ⊥PD .∵∠4=∠5,∠BAD +∠5=60°,∴∠4+∠BAD =60°,即∠MAD =60°.∴∠PAD =12∠MAD =30°.∵在Rt △APD 中,tan30°=PD AP,∴AP =3PD .(3)第(2)问中的结论成立,理由如下:如图③,延长DP 至N ,使DP =PN ,连接BN 、AN ,取BE 、AC 交于点O.在△PDE 和△PNB 中,⎩⎪⎨⎪⎧PD =PN ,∠EPD =∠BPN,PE =PB ,∴△PDE ≌△PNB(SAS).∴BN =DE ,∠1=∠2.∵DE =CD ,∴BN =CD.∵∠AOB =∠EOC,∴∠1+∠3+∠BAO=∠2+∠4+∠DEC+∠DCE.∵∠BAO =60°,∠DEC =∠DCE=30°,∴∠1+∠3=∠2+∠4,∴∠3=∠4.在△ABN 和△ACD 中,⎩⎪⎨⎪⎧AB =AC ,∠3=∠4,BN =CD ,∴△ABN ≌△ACD(SAS).∴∠5=∠6,AN =AD.∵PD =PN ,∴AP ⊥PD.∵∠NAC +∠5=60°,∴∠NAC +∠6=60°,即∠NAD=60°.∴∠PAD =12∠NAD=30°, ∵在Rt △APD 中,tan ∠PAD =PD AP,∴AP =3PD.5. 解:(1)∵∠ADB =90°,∠BAD =30°,AD =6 3,∴cos ∠BAD =AD AB ,∴32=6 3AB,∴AB =12. 又∵AB =AC ,∴AC =12,∴PM 为△ABC 的中位线,∴PM =12AC =6.(2)证明:方法一:如图①,在截取ED 上截取EQ =PD ,∵∠ADB =90°,∴∠1+∠2=90°,又∵AD=AE ,∴∠2=∠3,又∵∠3+∠4=90°,∴∠1=∠4.在△BDP 和△CEQ 中,PD =QE ,∠1=∠4,BD =CE ,∴△BDP ≌△CEQ.∴BP =CQ ,∠DBP =∠QCE,又∵∠5=∠1+∠DBP,∠6=∠4+∠QCE,∴∠5=∠6,∴PC =CQ ,∴BP =CP.方法二:如图②,过点B 作EP 的垂线交EP 的延长线于点M ,过C 点作EP EP 于点N.∵∠ADB =90°,∴∠1+∠2=90°,又∵AD=AE ,∴∠2=∠3,又∵∠3+∠4=90°,∴∠1=∠4,在△BMD 和△CNE 中,∠1=∠4,∠BMD =∠CNE=90°,BD =CE ,∴△BMD ≌△CNE.∴BM =CN.在△BMP 和△CNP 中,∠5=∠6,∠BMP =∠CNP,BM =CN ,∴△BMP≌△CNP,∴BP =CP.方法三:如图③,过点B 作BM ∥CE 交EP 的延长线于点M .略证△BMP ≌△CEP ,∴BP =CP .(3)BF 2+FC 2=2AD 2.类型4 中位线:三角形中两中点,连接则成中位线例4: 解:(1)PM=PN;PM ⊥PN(2)△PMN 为等腰直角三角形,理由如下:由题意知△ABC 和△ADE 均为等腰直角三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE=90°,∴∠BAD +∠DAC=∠CAE+∠DAC,∴∠BAD =∠CAE,∴△BAD ≌△CAE ,∴∠ABD =∠ACE,BD =CE.又∵M、P 、N 分别是DE 、CD 、BC 的中点,∴PM 是△CDE 的中位线,∴PM ∥CE 且PM =12CE ,∠MPD =∠ECD=∠ACD+∠ACE. 同理,PN ∥BD 且PN =12BD ,∠DBC =∠PNC, 又∵BD=CE ,∠ABD =∠ACE,∴PM =PN ,∴∠MPN =∠MPD+∠DPN=∠ECD +∠DCN+∠CNP=∠ACD+∠ACE+∠DCN+∠CBD=∠ACD+∠DCN+∠ABD+∠CBD=∠ACB+∠ABC=90°,∴PM ⊥PN ,∴△PMN 为等腰直角三角形;(3)△PMN 面积的最大值为492.提示:在旋转的过程中,由(2)中的结论知△PMN 为等腰直角三角形,S △PMN =12PN 2=18BD 2,当S △PMN 有最大值时,则BD 的值最大,由三角形三边关系可推断出当B 、A 、D 三点共线时,BD 的值最大,其最大值为14,此时S △PMN =12PN 2=18BD 2=18×14×14=492.针对训练:1. 解:(1)证明:延长DA 交BE 于G 点.∵∠BAE +∠CAD =180°,即∠EAG +∠GAB +∠CAD =180°,∵∠GAB +∠BAC +∠CAD =180°,∴∠EAG =∠CAB .∵∠EAG =∠AED +∠ADE ,∴∠CAB =∠AED +∠ADE .(2)证明:如图①,过E 点作DA 延长线的垂线,垂足为H .∴∠AHE =∠ACB =90°,由(1)可知,∠EAH =∠BAC ,又∵AE =AB ,∴△AHE ≌△ACB ,∴EH =BC ,AH =AC .∵AC =AD ,∴AH =AD .∵∠EHA =∠FAD =90°,∴AF ∥EH .∵A 为DH 中点,∴AF 为△DHE 中位线,∴EH =2AF ,∴BC =2AF .(3)成立.证明如下:如图②,延长DA 至M 点,使AM =DA ,连接EM ,∵∠BAE +∠CAD =180°,∠CAD +∠CAM =180°,∴∠BAE =∠CAM ,∴∠BAE +∠CAC =∠CAM +∠EAC ,即∠BAC =∠CAM .∵AM =AD ,AD =AC ,∴AM =AC .又∵AB =AE ,∠BAC =∠EAM ,∴△BAC ≌△EAM ,∴BC =EM .∵F 、A 分别为DE 、DM 中点,∴AF 为△DEM 中位线,∴EM =2AF ,∴BC =2AF .2. 解:(1)证明:∵∠BAC+∠EAD=180°,∠BAE =90°,∴∠DAC =90°,在△ABE 与△ACD 中,AE =AD ,∠BAE =∠CAD=90°,AB =AC ,∴△ABE ≌△ACD(SAS),∴CD =BE , ∵在Rt △ABE 中,F 为BE 的中点,∴BE =2AF ,∴CD =2AF.(2)成立,证明:如图,延长EA 交BC 于G ,在AG 上截取AH =AD ,∵∠BAC +∠EAD=180°,∴∠EAB +∠DAC=180°,∵∠EAB +∠BAH=180°,∴∠DAC =∠BAH,在△ABH 与△ACD 中,AH =AD ,∠BAH =∠CAD,AB =AC ,∴△ABH ≌△ACD(SAS),∴BH =DC ,∵AD =AE ,AH =AD ,∴AE =AH ,∵EF =FB ,∴BH =2AF ,∴CD =2AF.3. 解:(1)证明:∵AB=AC ,∴∠ABD =∠ACD,∵AE =AD ,∴∠ADE =∠AED,∵∠BAD +∠ABD=∠ADE+∠EDC,∠EDC +∠ACD=∠AED ,∴∠BAD =2∠EDC,∵∠ABF =2∠EDC,∴∠BAD =∠ABF,∴△ABF 是等腰三角形;(2)方法一:如图①,延长CA 至点H ,使AG =AH ,连接BH ,∵点N 是BG 的中点,∴AN =12BH ,∵∠BAD =∠AB F ,∠DAC =∠CBG,∴∠CAB =∠CBA,∴△ABC 是等边三角形.∴AB =BC =AC ,∠BAC =∠BCA=60°,∵GM =AB ,AB =AC ,∴CM =AG ,∴AH =CM ,在△BAH 和△BCM 中,⎩⎪⎨⎪⎧AB =BC ,∠BAH =∠BCM=120°,AH =CM ,∴△BAH ≌△BCM(SAS),∴BH =BM ,∴AN =12BM ,方法二:如图②,延长AN 至K ,使NK =AN ,连接KB ,同方法一,先证△ABC 是等边三角形,再证△ANG ≌△KNB (SAS),所以BK =AG =CM ,然后可以证得∠ABK =∠BCN =120°,最后证△ABK ≌△BCN (SAS),所以BM =AK =2AN .类型5 角的和差倍分例5:解:(1)如图,过点P 作PG⊥EF 于G.∵PE =PF =6,EF =6 3,∴FG =EG =3 3,∠FPG =∠EPG=12∠EPF. 在Rt △FPG 中,sin ∠FPG =FG PF =3 36=32. ∴∠FPG =60°,∴∠EPF =2∠FPG=120°.(2)如图,作PM ⊥AB 于M ,PN ⊥AD 于N .∵AC 为菱形ABCD 的对角线,∴∠DAC =∠BAC ,AM =AN ,PM =PN .在Rt △PME 和Rt △PNF 中,PM =PN ,PE =PF ,∴Rt △PME ≌Rt △PNF ,∴NF =ME .又∵AP =10,∠PAM =12∠DAB =30°, ∴AM =AN =AP cos30°=10×32=5 3. ∴AE +AF =(AM +ME )+(AN -NF )=AM +AN =10 3.针对训练:1. 证明:如图,过D 作DE ⊥AB 于E ,过D 作DF ⊥AC 于F ,∵DA 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,∴DE =DF ,∵∠B +∠ACD =180°,∠ACD +∠FCD =180°,∴∠B =∠FCD ,在△DFC 和△DEB 中,⎩⎪⎨⎪⎧∠F =∠DEB ,∠FCD =∠B ,DF =DB ,∴△DFC ≌△DEB ,∴DC =DB .2. 解:(1)∵AC=AB =4,且CD =1,∴AD =AC -CD =3.在Rt △ABD 中,∠BAD =90°,∴BD =AB 2+AD 2=5,∵S △ABD =12AB·AD=12AE·BD, ∴AE =2.4.(2)证明:如图,取BC 的中点M ,连接AM 交BD 于点N .∵∠BAC =90°,AB =AC ,点M 为BC 的中点,∴AM =BM =CM ,AM ⊥BC ,∠NAD =∠FCP =45°,∴∠AMF =∠BMN =90°.∵AE ⊥BD ,∴∠MAF +∠ANE =∠MBN +∠BNM =90又∠ANE =∠BNM ,∴∠MAF =∠MBN ,∴△AMF ≌△BMN ,∴MF =MN ,∴AM -MN =CM -MF ,即AN =CF .∵AP =CD ,∴AC -CD =AC -AP ,即AD =CP .∴△ADN ≌△CPF ,∴∠ADB =∠CPF .3. 解:(1)∵AB =BD ,∠BAD =45°,∴∠BDA =45°,即∠ABD =90°.∵四边形ABCD 是平行四边形,∴当E 、C 重合时,BF =12BD =12AB . ∵在Rt △ABF 中,AB 2+BF 2=AF 2,∴(2BF )2+BF 2=(5)2,∴BF =1,AB =2.在Rt △ABD 中,AD =AB 2+BD 2=2AB 2=2 2.(2)证明:如图,在AF 上截取AK =HD ,连接BK.∵∠AFD =∠ABF+∠2=∠FGD+∠3且∠ABF=∠FGD=90°,∴∠2=∠3.在△ABK 与△DBH 中,⎩⎪⎨⎪⎧AB =BD ,∠2=∠3,AK =HD ,∴△ABK ≌△DBH ,∴BK =BH ,∠6=∠5.∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠5=∠4=45°,∴∠6=∠5=45°,∴∠7=∠ABD-∠6=45°=∠5.在△BFK 与△BFH 中,⎩⎪⎨⎪⎧BK =BH ,∠7=∠5,BF =BF ,∴△BFK ≌△BFH.∴∠BFK =∠BFH,即∠AFB=∠HFB.4. 解:(1)证明:由折叠知∠EMN=∠ABC=90°,BE =EM ,∴∠EMB =∠EBM,∴∠EMN -∠EMB=∠ABC-∠EBM,即∠BMP=∠MBC.∵在正方形ABCD 中,AD ∥BC ,∴∠AMB =∠MBC,∴∠AMB =∠BMP,∴BM 是∠AMP 的平分线.(2)△PDM 的周长没有发生变化.证明如下:如图,过B 作BQ ⊥MP∵∠A =90°,且由(1)知BM 是∠AMP 的平分线,∴BA =BQ ,∵∠A =∠MQB =90°,∠AMB =∠BMP ,MB =MB ,∴△AMB ≌△QMB (AAS).∴MA =MQ .∵BA =BC ,∴BQ =BC ,又∵∠BQP =90°=∠C ,BP =BP ,∴Rt △BPC ≌Rt △BPQ (HL).∴PC =PQ ,∴△PDM 的周长=MD +MP +DP =MD +MQ +QP +PD=MD +MA +PC +PD =AD +DC =2AD .∴△PDM 的周长没有发生变化.类型6 旋转型全等问题:图中若有边相等,可用旋转做实验例6:解:(1)①∵四边形ADEF 是正方形,∴AD =AF ,AB =AC ,∵∠BAC =∠DAF=90°,∴∠BAD =∠CAF,∴△DAB ≌△FAC ,∴∠B =∠ACF,∴∠ACB +∠ACF=90°,即CF⊥BC;②∵△DAB ≌△FAC ,∴CF =BD ,∵BC =BD +CD ,∴BC =CF +CD.(2)结论①成立,结论②不成立.∵四边形ADEF 是正方形,∴AD =AF ,AB =AC.∵∠BAC =∠DAF=90°,∴∠BAD =∠CAF,∴△DAB ≌△FAC ,∴∠ABD =∠ACF,CF =BD ,∴∠BCF =∠ACF-∠ACB=∠ABD-∠ACB=90°,即CF⊥BC;∵BC=CD -BD ,∴BC =CD -CF.(3)如图,过A 作AH ⊥BC 于H ,过E 作EM ⊥BD 于M ,EN ⊥CF 于N ,∵∠BAC =90°,AB =AC ,∴BC =2AB =4,AH =CH =12BC =2,∴CD =14BC =1,∴DH =3,同(2)证得△BAD ≌△CAF , ∴∠ABD =∠ACF =45°,∴∠BCF =∠ACB +∠ACF =90°,∴BC ⊥CF ,CF =BD =5.∵四边形ADEF 是正方形,∴AD =DE ,∠ADE =90°,∵BC ⊥CF ,EM ⊥BD ,EN ⊥CF ,∴四边形CMEN 是矩形,∴NE =CM ,EM =CN ,∵∠AHD =∠ADE =∠EMD =90°,∴∠ADH +∠EDM =∠EDM +∠DEM =90°,∴∠ADH =∠DEM ,∴△ADH ≌△DEM ,∴EM =DH =3,DM =AH =2,∴CN =EM =3,EN =CM =3,∵∠ABC =45°,∴∠BGC =45°,∴△BCG 是等腰直角三角形,∴CG =BC =4,∴GN =1,∴EG =GN 2+EN 2=10.针对训练:1. 解:(1)AC =AD +AB .证明如下:∵∠B +∠D =180°,∠B =90°,∴∠D =90°.∵∠DAB =120°,AC 平分∠DAB ,∴∠DAC =∠BAC =60°,∵∠B =90°,∴AB =12AC , 同理AD =12AC . ∴AC =AD +AB .(2)(1)中的结论成立,理由如下:如图①,以C 为顶点,AC 为一边作∠ACE=60°,∠ACE 的另一边交AB 的延长线于点E ,∵∠BAC =60°,∴△AEC 为等边三角形,∴AC =AE =CE ,∠E =60°,∵∠ABC +∠D=180°,∠DAB =120°,∴∠DCB =60°,∴∠DCA =∠ECB.在△DAC 和△BEC 中,⎩⎪⎨⎪⎧∠DAC=∠E,AC =CE ,∠DCA =∠BCE,∴△DAC ≌△BEC ,∴AD =BE ,∴AC =AE =AD +AB.(3)AD +AB =2AC.理由如下:如图②,过点C 作CE⊥AC 交AB 的延长线于点∵∠ABC +∠D=180°,∠DAB =90°,∴∠DCB =90°,∵∠ACE =90°,∴∠DCA =∠BCE,又∵AC 平分∠DAB,∴∠CAB =45°,∴∠E =45°,∴AC =CE.∴△CDA ≌△CBE ,∴AD =BE ,∴AD +AB =AE.∵在Rt △ACE 中,∠CAB =45°,∴AE =ACcos45°=2AC ,∴AD +AB =2AC.2. 解:(1)证明:∵四边形ABCD 是正方形,∴∠B =∠D=∠BAD=90°,AB =AD ,∵△ABE 沿AE 翻折得到△AHE,∴△ABE ≌△AHE ,∴AH =AB =AD ,BE =EH ,∠AHE =∠AHF=∠B=∠D=90°.在Rt △AHF 和Rt △ADF 中,⎩⎪⎨⎪⎧AF =AF ,AH =AD ,∴Rt △AHF ≌Rt △ADF(HL),∴∠HAF =∠DAF,∴∠EAF =∠EAH+∠FAH=12∠BAH+12∠HAD=12∠BAD=45°,(2)以BM ,DN ,MN 为三边围成的三角形为直角三角形.证明如下:如图,过点A 作AH ⊥AN 并截取AH =AN ,连接BH 、HM ,∵∠1+∠BAN =90°,∠3+∠BAN =90°,∴∠1=∠3,在△ABH 和△ADN 中,⎩⎪⎨⎪⎧AB =AD ,∠1=∠3,AH =AN ,∴△ABH ≌△ADN (SAS),∴BH =DN ,∠HBA =∠NDA =135°,∵∠HAN =90°,∠MAN =45°,∴∠1+∠2=∠HAM =∠MAN =45°,在△AHM 和△ANM 中,⎩⎪⎨⎪⎧AH =AN ,∠HAM =∠MAN ,AM =AM ,∴△AHM ≌△ANM (SAS),∴HM =NM ,∴∠HBP =180°-∠HBA =180°-135°=45°,31 ∴∠HBP +∠PBM =45°+45°=90°,∴△HBM 是直角三角形,∵HB =DN ,HM =MN ,∴以BM ,DN ,MN 为三边围成的三角形为直角三角形.3. 解:(1)如图①,将△PBC 绕点B 逆时针旋转90°得△P ′BA ,连接PP ′,则△AP ′B ≌△CPB , ∴P ′B =PB =2,P ′A =PC =1,∠1=∠2,∠AP ′B =∠BPC .∵四边形ABCD 是正方形,∴AB =BC ,∠ABC =90°,∴∠2+∠3=90°,∴∠1+∠3=90°,即∠P ′BP =90°,∴∠BP ′P =45°.在Rt △P ′BP 中,由勾股定理,得PP ′2=4.∵P ′A =1,AP =5∴P ′A 2=1,AP 2=5,∴P ′A 2+PP ′2=AP 2,∴△P ′AP 是直角三角形,∴∠AP ′P =90°,∴∠AP ′B =45°+90°=135°,∴∠BPC =135°.(2)仿照【分析】中的思路,将△BPC 绕点B 逆时针旋转120°,得到了△BP′A,连接PP′,如图②. 则△PBC≌△P′BA,∴P ′B =PB =4,P ′A =PC =2,∠BPC =∠BP′A,∴△BPP ′为等腰三角形,∵∠ABC =120°,∴∠PBP ′=120°,∴∠BP ′P =30°,过点B 作BG⊥PP′于G ,则∠P′GB=90°,∴PP ′=2P ′G.∵P ′B =PB =4,∠BP ′P =30°,∴BG =2,∴P ′G =2 3.∴PP ′=4 3,在△APP′中,∵PA =2 13,P ′A =2,PP ′=4 3,∴P ′A 2+P′P 2=PA 2,∴△PP ′A 是直角三角形,∴∠AP ′P =90°,∴∠BPC =∠BP′A=∠PP′B+∠AP′P=30°+90°=120°.。
届重庆中考复习重庆中考几何题分类汇编含答案

重庆中考几何题分类汇编(含答案)类型1线段的倍分:要证线段倍与半,延长缩短去实验例1如图Z3-1,在△ABC中,AB=AC,CM平分∠ACB交AB于M,在AC的延长线上截取CN=BM,连接MN交BC于P,在CB的延长线截取BQ=CP,连接MQ.(1)求证:MQ=NP;(2)求证:CN=2CP.针对训练:1.如图Z3-2,在?ABCD中,AC⊥BC,点E、点上,且满足AC=AE=CF,连接CE、AF、EF.(1)若∠ABC=35°,求∠EAF的度数;(2)若CE⊥EF,求证:CE=2EF.2.已知,在△ABC中,AB=AC,∠BAC=90°,E为AC 任意一点,连接BE.(1)如图①,若∠ABE=15°,O为BE中点,连接AO1,求BC的长;(2)如图②,F也为AC上一点,且满足AE=CF,过A作于点D,连接DF交BE于点G,连接AG.若AG平分∠CAD,求证:AH=AC.3.在△ACB中,AB=AC,∠BAC=90°,点D是AC上一点,连接BD,过点A作AE⊥BD于E,交BC于F.(1)如图①,若AB=4,CD=1,求AE的长;(2)如图②,点G是AE上一点,连接CG,若BE=AE+AG,求证:CG=AE.4.在等腰直角三角形ABC中,∠BAC=90°,AB=AC,D是斜边BC的中点,连接AD.(1)如图①,E是AC的中点,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′,当AD=时,求AE′的值.(2)如图②,在AC上取一点E,使得CE=AC,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′交BC于点F,求证:DF=CF.类型2线段的和差:要证线段和与差,截长补短去实验例2如图,在△ABC中,∠BAC=90BD=BA,连接AD,在AD左侧作∠BD于E.(1)若AC=3,则CE=________(答案);(2)如图①,M、N分别为AB和AC上的点,且AM=AN,连接EM、DN∠AME+∠AND=180°,求证:DEME;(3)如图②,过E作EF⊥AE,交AD的延长线于F,在EC上选取一点H,使得EH=BE,连接FH,在AC上选取一点G,使得AG=AB,连接BG、FG,求证:FH=FG.针对训练:1.如图Z3-7,在?ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.(1)若BE=2EC,AB=,求AD的长;(2)求证:EG=BG+FC.2.如图,在正方形ABCD中,点P为ADAC、CP,过点C作CF⊥CP于点C,交AB于点FBM⊥CF于点N,交AC于点M.(1)若AP=AC,BC=4,求S△ACP;(2)若CP-BM=2FN,求证:BC=MC.3.如图,在△ABC中,AB=BC,以AB为一外作菱形ABDE,连接DC,EB并延长EB交AC且CB⊥AE于G.(1)若∠EBG=20°,求∠AFE;(2)试问线段AE,AF,CF之间的数量关系并类型3倍长中线:三角形中有中线,延长中线等例3如图Z3-10①,在Rt△ABC中,∠ABC=90°,D、E分别为斜边AC上两点,且AD=AB,BD、BE.(1)求∠EBD的度数;(2)如图Z3-10②,过点D作FD⊥BD于点D,交延长线于点F,在AB上选取一点H,使得BH=BC连接CH,在AC上选取一点G,使得GD=CD,连接FH、FG,求证:FH=FG.针对训练:1.如图,已知在?ABCD中,G为BC的中点,点E在AD边上,且∠1=∠2.(1)求证:E是AD中点;(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.2.如图Z3-12,在菱形ABCD中,点E、F分别是BC、CD上的点,连接AE,AF,DE、EF,∠DAE=∠BAF.(1)求证:CE=CF;(2)若∠ABC=120°,点G是线段AF的中点,连接DG,EG.求证:DG⊥GE.3.在Rt△ABC中,∠ACB=90°,点D与点B同侧,∠ADC>∠BAC,且DA=DC,过点B作DA 交DC于点E,M为AB的中点,连接MD,ME.(1)如图①,当∠ADC=90°时,线段MD与是________;(2)如图②,当∠ADC=60°时,试探究线段ME的数量关系,并证明你的结论;(3)如图③,当∠ADC=α时,求的值.4.如图①,等边三角形ABC中,CE平分∠ACB,D为BC边上一点,且DE=CD,连接BE.(1)若CE=4,BC=6,求线段BE的长;(2)如图②,取BE中点P,连接AP,PD,AD,求证:AP⊥PD且AP=PD;(3)如图③,把图Z3-14②中的△CDE绕点C顺时针旋转任意角度,然后连接BE,点P为BE中点,连接AP,PD,AD,问第(2)问中的结论还成立吗?若成立,请证明;若不成立,请说明理由.5.在△ABC中,以AB为斜边,作直角三角形ABD,使点D落在△ABC内,∠ADB=90°.(1)如图①,若AB=AC,∠BAD=30°,AD=6,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;(2)如图②,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP;(3)如图③,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).类型4中位线:三角形中两中点,连接则成中位线例42017·河南如图①,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.(1)观察猜想:图①中,线段PM与PN的数量关系是__________,位置关系是__________;(2)探究证明:把△ADE绕点A按逆时针方向旋转到图②的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;(3)拓展延伸:把△ADE绕点A4,AB=10,请直接写出△PMN面积的最大值.针对训练:1.如图①,在任意的三角形分别以AB和AC为一边作等腰三角形ABE和等腰三角形ACD,AB=AE,AC=AD,且∠BAE+∠CAD=180°,连接DE,延长CA交DE于F.(1)求证:∠CAB=∠AED+∠ADE;(2)若∠ACB=∠BAE=∠CAD=90°,如图②,求证:BC=2AF;(3)若在△ABC中,如图③所示,作等腰三角形ABE和等腰三角形ACD,AB与DE交于点F,F为DE的中点,请问(2)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.2.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC 不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.(1)如图①,当∠BAE=90°时,求证:CD=2AF;(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.3.如图①,在等腰三角形ABC中,AB=AC,在底边BC上取一点D,在边AC上取一点E,使AE=AD,连接DE,在∠ABD的内部作∠ABF=2∠EDC,交AD于点F.(1)求证:△ABF是等腰三角形;(2)如图②,BF的延长交AC于点G.若∠DAC=∠CBG,延长AC至点M,使GM=AB,连接BM,点N是BG的中点,连接AN,试判断线段AN、BM之间的数量关系,并证明你的结论.类型5角的和差倍分对称以后关系现.角平分线平行线,等腰三角形来添.角平加垂线,三线合一试试看.例5.如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在段AB,AD,AC上,已知EP=FP=6,6,∠BAD=60°,且AB>6.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值.针对训练:1.已知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.2.在△ACB中,AB=AC,∠BAC=90°,点D是AC上一点,连接BD,过点A作AE⊥BD于E,交BC于F.(1)如图①,若AB=4,CD=1,求AE的长;(2)如图②,点P是AC上一点,连接FP,若AP=CD,求证:∠ADB=∠CPF.3.已知,在?ABCD中,∠BAD=45°,AB=BD,E为BC上一点,连接AE交BD 于F,过点D作DG⊥AE于G,延长DG交BC于H.(1)如图①,若点E与点C重合,且AF=,求AD的长;(2)如图②,连接FH,求证:∠AFB=∠HFB.4.如图,将正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD 边上的点M处,点C落在点N处,MN与CD交于点P,连接EP.当点M在边AD上移动时,连接BM、BP.(1)求证:BM是∠AMP的平分线;(2)△PDM的周长是否发生变化?证明你的结论.类型6旋转型全等问题:图中若有边相等,可用旋转例6.△ABC中,∠BAC=90°,AB=AC,点D为直线上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.(1)观察猜想:如图①,当点D在线段BC上时,①BC与的位置关系为:________.②BC,CD,CF之间的数量关系为:___________;论直接写在横线上)(2)数学思考:如图Z3-25②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸:如图Z3-25③,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请求出GE的长.针对训练:1.在四边形ABCD中,∠B180°,对角线AC平分∠(1)如图①,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC明理由.(2)如图②,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.(3)如图③,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.2.如图①,在正方形ABCD中,点E为边BC上一点,将△ABE沿AE翻折得△AHE,延长EH交边CD于F,连接AF.(1)求证:∠EAF=45°;(2)延长AB,AD,如图②,射线AE、AF分别交正方形两个外角的平分线于M、N,连接MN,若以BM、DN、MN为三边围成三角形,试猜想三角形的形状,并证明你的结论.3.如图①,在正方形ABCD内有一点P,PA=,PB=,PC=1,求∠BPC的度数.【分析问题】根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图Z3-28②),然后连接PP′.(1)请你通过计算求出图Z3-28②中∠BPC的度数;(2)如图③,若在正六边形ABCDEF内有一点P,且PA=2,PB=4,PC=2.请求出∠BPC的度数.重庆中考几何题分类汇编答案例1.证明:(1)∵AB=AC,∴∠ABC=∠ACB.∵∠MBQ+∠ABC=180°,∠ACB+∠PCN=180°,∴∠MBQ=∠PCN.在△QBM和△PCN中,∴△QBM≌△PCN(SAS).∴MQ=NP.(2)过M作MG∥AC交BC于G,∵MG∥AC,∴∠MGB=∠ACB,∠MGC=∠PCN,∵由(1)知,∠ABC=∠ACB,∴∠ABC=∠MGB,∴MB=MG,∵MB=CN,∴MG=CN.在△MGP和△NCP中,∴△MGP≌△NCP(AAS).∴PG=CP,∴CG=CP+PG,即CG=2CP.∵CM平分∠ACB,∴∠BCM=∠MCA,∵MG∥AC,∴∠MCA=∠GMC,∴∠BCM=∠GMC,∴MG=CG,∵MG=CN,∴CN=CG,∴CN=2CP.针对训练1.解:(1)∵AC⊥BC,∴∠ACB=90°,又∵AC=CFAFC=45°,∵∠ABC=35°,∴∠EAF=10°;(2)证明:方法1:取CF的中点M,连接EM、AM,∵CE⊥EF,∴EM=CM=FM=CF,又∵AC=AE,∴AM为EC的中垂线,∴∠CAM+90°,又∵∠ECF+∠ACE=90°,∴∠CAM=∠FCE,又∵∠CEF=∠ACM=90°,∴△ACM∽△CEF又∵CF=AC=2CM,∴==,即CE=2EF;方法2:延长FE至M,使EF=EM,连接CM,∵CE⊥EF,∴△CMF为等腰三角形,又∵AC=AE=CF,且∠ACE=∠CFE(易证),∴△CMF≌△CEA,∴FM=CE=2EF.2.解:(1)如图①,在AB上取一点M,使得BM=接ME.在Rt△ABE中,∵OB=OE,∴BE=2OA=2,∵MB=ME,∴∠MBE=∠MEB=15°,∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=x,∵AB2+AE2=BE2,∴(2x+x)2+x2=22,∴x=(负根舍弃),∴AB=AC=(2+)·,∴BC=AB=+1.(2)证明:如图②,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.∵BE⊥AP,∴∠AHB=90°,∴∠ABH+∠BAH=90°,∵∠BAH+∠PAC=90°,∴∠ABE=∠PAC,又∵AB=AC,∠BAE=∠ACP=90°,∴△ABE≌△CAP,∴AE=CP=CF,∠AEB=∠P,在△DCF和△DCP中,∴△DCF≌△DCP,∴∠DFC=∠P,∴∠GFE=∠GEF,∴GE=GF,∵GM⊥EF,∴FM=ME,∵AE=CF,∴AF=CE,∴AM=CM,在△GAH和△GAM中,∴△AGH≌△AGM,∴AH=AM=CM=AC.3.解:(1)∵AB=4,∴AC=AB=4.∵CD=1,∴AD=AC-CD=3.∵在Rt△ABD中,∠BAC=90°,∴BD==5,=AB·AD=AE·BD,∴AE=2.4.∵S△ABD(2)证明:如图,在线段EB上截取EH=AE∵AE⊥BD,EH=AE,∴AH=AE.∵BE=AE+AG,∴BH=BE-HE=AG.∵∠BAD=∠BEA=90°,∴∠ABE+∠BAE=∠CAG+∠BAE=90°,∴∠ABE=∠CAG.∵BA=AC,∴△ABH≌△CAG,∴CG=AH=AE.4.解:(1)∵∠BAC=90°,AB=AC,D是斜边BC的中点,∴∠ADC=90°,∠ACD=45°.在Rt△ADC中,AC=AD÷sin45°=2.∵E是AC的中点,∴CE=AC=.∵将△CDE沿CD翻折到△CDE′,∴CE′=CE=,∠ACE由勾股定理,得AE′==.(2)证明:如图,过B作AE′的垂线交AD于点G,交AC∵∠ABH+∠BAF=90°,∠CAF+∠BAF=90°,∴∠ABH∠CAF.又∵AB=AC,∠BAH=∠ACE′=90°,∴△ABH≌△CAE′.∴AH=CE′=CE,∵CE=AC,∴AH=HE=CE.∵D是BC中点,∴DE∥BH,∴G是AD中点.在△ABG和△CAF中:AB=AC,∠BAD=∠ACD=45°,∠ABH=∠CAF,∴△ABG≌△CAF.∴AG=CF.∵AG=AD,∴CF=AD=CD.∴DF=CF.类型2线段的和差:要证线段和与差,截长补短去实验例2:解:(1)3(2)证明:延长DN到K,使得NK=ME,连接AK,如图①,因为∠1+∠3=180°,∠1+∠2=180°,∴∠2=∠3.在△AME和△ANK中,∴△AME≌△ANK(SAS).∴AE=AK,∠4=∠5,∴∠4+∠EAC=90°,∴∠5+∠EAC=90°,即∠∵∠EAD=45°,∴∠KAD=∠EAK-∠EAD=90°-∴∠EAD=∠KAD.在△EAD和△KAD中,∴△EAD≌△KAD(SAS),∴ED=KD.∵DK=DN+KN,∴ED=DN+KN,又NK=ME,∴ED=DN+ME.(3)证明:延长AE到J,使得EJ=AE,连接JH,JF.如图②,在△ABE和△JHE中,∴△ABE≌△JHE(SAS),∴JH=AB,∠1=∠2,∵AB=AG,∴JH=AG,∵AE=EJ,EF⊥AJ,∴AF=JF,∴∠JAF=∠AJF=45°,即∠2+∠3=45°,∵∠BAC=90°,∴∠1+∠EAD+∠4=90°,∴∠1+∠4=90°-∠EAD,=90°-45°=45°,∵∠1=∠2,∴∠3=∠4,在△JHF和△AGF中,∴△JHF≌△AGF(SAS),∴FH=FG.针对训练:1.解:(1)∵四边形ABCD是平行四边形,∴AD=BC.∵BE=2EC,设CE=x,BE=2x,∴BC=AD=AE=又∵EG⊥AB,∴∠AEB=90°,∴AB2=AE2+BE2,即13=9x2+4x2,∴x=1,∴AD=3x=3.(2)证明:如图,过C作CH⊥AB于H,则四边形形.∴CF=HG,∠CHB=90°,GF=CH.∵AE⊥BC,EG⊥AB,∴∠AEB=∠CHB=90°,∠BCH+∠B=90°,∠BAE+∠B=90°,∴∠∠BAE.又∵AE=BC,∴△AGE≌△CHB,∴GE=BH,AG=GF,∴GE=BH=BG+GH=BG+CF.2.解:(1)∵四边形ABCD是正方形,BC=4,∴AB=AD=CD=BC=4,∠ADC=∠ABC=90°.∵在Rt△ABC中,AC==4,∴AP=AC=,=AP·CD=7.∴S△ACP(2)证明:方法一:如图①,在NC上截取NK=NF,连接BK.∵四边形ABCD是正方形,∴AB=BC=DC,∠ABC=∠BCD=∠ADC=90°.∵∠BCD=90°,CF⊥CP,∴∠1+∠DCF=∠2+∠DCF=90°,∴∠1=∠2,∵在△FBC和△PDC中,∴△FBC≌△PDC(ASA),∴CF=CP,∵CP-2FN=BM,∴CF-FK=BM,即CK=BM,∵∠FBC=90°,BM⊥CF,∴∠1+∠NBC=∠4+=90°,∴∠1=∠4,∵在△ABM和△BCK中,∴△ABM≌△BCK(SAS),∴∠7=∠6.∵BM⊥CF,NK=NF,∴BF=BK,∵BF=BK,BM⊥CF=∠5,∴∠4+∠7=∠5+∠6,∵∠8=∠4+∠7,∴∠8=∠MBC,∴BC=MC.解:方法二:如图②,延长BM交AD于点G,过A作AE⊥BG于E先证△AEB≌△BNC(AAS),∴AE=BN,又证△AEG≌△BNF(AAS),∴EG=NF,再证四边形BCPG为平行四边形,∴BG=CP,∵CP-BM=2FN,∴BG-BM=2EG,∴MG=2EG,∴点E为MG中点,∵AE⊥MG,EM=EG,∴AM=AG,∴∠3=∠4,∵∠2=∠3,∠1=∠4,∴∠1=∠2,∴BC=MC.3.解:(1)∵∠EBG=20°,CB⊥AE,∴∠BEG=70o,∠CBF=∠EBG=20°,∵四边形ABDE是菱形,∴∠ABE=∠BEG=70°,∴∠ABG=50°,∵AB=BC,∴∠FCB=25°,∴∠AFE=∠CBF+∠FCB=45°;(2)AE,AF,CF之间的数量关系是AF2+CF2=2AE2,证明如下:连接DF,∵四边形ABDE是菱形,∴AB=DB,∠DBE=∠ABE,∴∠DBF=∠ABF,∵BF=BF,∴△DBF≌△ABF(SAS),∴DF=AF,∠BDF=∠BAF,∵∠BCF=∠BAF,∴∠BCF=∠BDF,∵CB⊥AE,AE∥DB,∴DB⊥CB,∵CB=AB=BD,∴△DBC是等腰直角三角形,∴DC=BD=AE,∵∠DPB=∠CPF,∴∠CFP=∠DBP=90°,∴DF2+CF2=DC2,即有:AF2+CF2=2AE2.类型3倍长中线:三角形中有中线,延长中线等中线例3解:(1)设∠BEC=α,∠BDA=β,则∠C=180°-2α,∠A=180°-2β.∵在Rt△ABC中,∠ABC=90°,∴∠A+∠C=90°,即180°-2α+180°-2β=90°,∴α+β=135°,∴∠EBD=45°.(2)证明:法一:如图①,延长BD至点B′,使得DB在△GDB′和△CDB中,∴△GDB′≌△CDB.∴GB′=BC=BH,∠GB′D∵FD⊥BD,BD=DB′,∴FB=FB′.∵∠FB′G=45°-∠GB′D,∠HBF=90°-45°-∠CBD=45°-∠CBD,∴∠FB′G=∠HBF.在△FHB和△FGB′中,∴△FHB≌△FGB′,∴HF=GF.法二:如图②,延长FD至点F′,使得DF′=BF′.先证△DGF≌△DCF′,再证△BHF≌△BCF′,∴HF=GF.针对训练1.证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠A=∠C.又∵∠1=∠2,∴△ABE≌△CDG(ASA),∴AE=CG.∵G为BC中点,∴CG=BC,∴AE=CG=BC=AD,∴E是AD中点.(2)如图,延长BE,CD交于点H.∵四边形ABCD是平行四边形,∴AB綊CD,∴∠A=∠ADH,∠1=又∵∠1=∠2,∠3=∠2,∴∠1=∠2=∠3=∠4,∴FH=FB.由(1),E是AD中点,∴AE=DE,∴△ABE≌△DHE(AAS),∴AB=DH,∴CD=AB=DH=DF+FH=DF+BF,即CD=BF+DF.2.证明:(1)在菱形ABCD中,AB=BC=CD=AD,∠ADF=∠ABE,∵∠DAE=∠BAF,∴∠DAE-∠EAF=∠BAF-∠EAF,即∠DAF=∠BAE.∴△DAF≌△BAE,∴BE=DF.又∵BC=CD,∴CE=CF(2)如图,延长DG交AB于H,连接EH,∵在菱形ABCD中,AB∥CD,∴∠DFA=∠GAH.∵G为AF中点,∴AG=GF.又∵∠DGF=∠AGH,∴△DGF≌△HGA.∴DG=DF.又∵AB=CD,∴BH=CF.又∵AB∥CD,∠ABC=120°,∴∠C=60°.又∵CE=CF,∴△CEF为等边三角形,∴CF=EF,∠CFE=60°,∴EF=BH,∠DFE=∠ABC=120°.又∵BE=DF,∴△EFD≌△HBE,∴HE=ED,又∵HG=DG,∴DG⊥GE.3.解:(1)MD=ME2)MD=ME.理由如下:如图①,延长EM交DA于点F.∵BE∥DA,∴∠FAM=∠EBM.又∵AM=BM,∠AMF=∠BME,∴△AMF≌△BME,∴AF=BE,MF=ME.∵DA=DC,∠ADC=60°,∴∠BED=∠ADC=60°,∠ACD=60°.∵∠ACB=90°,∴∠ECB=30°,∴∠EBC=30°,∴CE=BE,∴AF=EC,∴DF=DE,∴DM⊥EF,DM平分∠ADC,∴∠MDE=30°.在Rt△MDE中,tan∠MDE==.∴MD=ME.(3)如图②,延长EM交DA于点F,∵BE∥DA,∴∠FAM=∠EBM,又∵AM=BM,∠AMF=∠BME,∴△AMF≌△BME,∴AF=BE,MF=ME.延长BE交AC于点N,∴∠BNC=∠DAC.∵DA=DC,∴∠DCA=∠DAC,∴∠BNC=∠DCA,∵∠ACB=90°,∴∠ECB=∠EBC,∴CE=BE,∴AF=CE.∴DF=DE,∴DM⊥EF,DM平分∠ADC,∵∠ADC=α,∴∠MDE=.∴在Rt△MDE中,=tan∠MDE=tan.4.解:(1)如图①,作EH⊥BC于点H.∵△ABC是等边三角形,∴∠ACB=60°.∵CE平分∠ACB,∴∠ECH=∠ACB=30°,∵EC=4,∠ECH=30°,∴EH=2,HC=2.∵BC=6,∴BH=6-2=4.在Rt△BHE中,BE2=(4)2+22=52,∴BE=2.(2)如图②,延长DP至M,使DP=PM,连接BM、AM.在△PDE和△PMB中,∴△PDE≌△PMB(SAS).∴BM=DE,∠1=∠2.∴BM∥DE.∴∠MBD+∠BDE=180°.∵CE平分∠ACB,DE=CD,∴∠BDE=30°+30°=∴∠MBD=120°.∵△ABC是等边三角形,∴∠ABC=60°,∴∠3=60∵BM=DE,DE=CD,∴BM=CD.在△ABM和△ACD中,∴△ABM≌△ACD(SAS).∴AD=AM,∠4=∠5.∵PD=PM,∴AP⊥PD.∵∠4=∠5,∠BAD+∠5=60°,∴∠4+∠BAD=60°,即∠MAD=60°.∴∠PAD=∠MAD=30°.∵在Rt△APD中,tan30°=,∴AP=PD.(3)第(2)问中的结论成立,理由如下:如图③,延长DP使DP=PN,连接BN、AN,取BE、AC交于点O.在△∴△PDE≌△PNB(SAS).∴BN=DE,∠1=∠2.∵DE=CD,∴BN=CD.∵∠AOB=∠EOC,∴∠1+∠3+∠BAO=∠2+∠4+∠DEC+∠DCE.∵∠BAO=60°,∠DEC=∠DCE=30°,∴∠1+∠3∠4,∴∠3=∠4.在△ABN和△ACD中,∴△ABN≌△ACD(SAS).∴∠5=∠6,AN=AD.∵PD=PN,∴AP⊥PD.∵∠NAC+∠5=60°,∴∠NAC+∠6=60°,即∠NAD=60°.∴∠PAD=∠NAD=30°,∵在Rt△APD中,tan∠PAD=,∴AP=PD.5.解:(1)∵∠ADB=90°,∠BAD=30°,AD=6,∴cos∠BAD=,∴=,∴AB=12.又∵AB=AC,∴AC=12,∴PM为△ABC的中位线,∴PM=AC=6.(2)证明:方法一:如图①,在截取ED上截取EQ=∵∠ADB=90°,∴∠1+∠2=90°,又∵AD=AE,∴∠2=∠3,又∵∠3+∠4=90°,∴∠1=∠4.在△BDP和△CEQ中,PD=QE,∠1=∠4,BD=∴△BDP≌△CEQ.∴BP=CQ,∠DBP=∠QCE,又∵∠5=∠1+∠DBP,∠6=∠4+∠QCE,∴∠5=∠6,∴PC=CQ,∴BP=CP.方法二:如图②,过点B作EP的垂线交EP的延长线于点M,过CEP的垂线交EP于点N.∵∠ADB=90°,∴∠1+∠2=90°,又∵AD=AE,∴∠2=∠3,又∵∠3+∠4=90°,∴∠1=∠4,在△BMD和△CNE中,∠1=∠4,∠BMD=∠CNE=90°,BD=CE,∴△BMD≌△CNE.∴BM=CN.在△BMP和△CNP中,∠5=∠6,∠BMP=∠CNP,BM=CN,∴△BMP≌△CNP,∴BP=CP.方法三:如图③,过点B作BM∥CE交EP M.略证△BMP≌△CEP,∴BP=CP.(3)BF2+FC2=2AD2.类型4中位线:三角形中两中点,连接则成中位线例4:解:(1)PM=PN;PM⊥PN(2)△PMN为等腰直角三角形,理由如下:由题意知△ABC和△ADE均为等腰直角三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=90°,∴∠BAD+∠DAC=∠CAE+∠DAC,∴∠BAD=∠CAE,∴△BAD≌△CAE,∴∠ABD=∠ACE,BD=CE.又∵M、P、N分别是DE、CD、BC的中点,∴PM是△CDE的中位线,∴PM∥CE且PM=CE,∠MPD=∠ECD=∠ACD+∠ACE.同理,PN∥BD且PN=BD,∠DBC=∠PNC,又∵BD=CE,∠ABD=∠ACE,∴PM=PN,∴∠MPN=∠MPD+∠DPN=∠ECD+∠DCN+∠CNP=∠ACD+∠ACE+∠DCN+∠CBD=∠ACD+∠DCN+∠ABD+∠CBD=∠ACB+∠ABC=90°,∴PM⊥PN,∴△PMN为等腰直角三角形;(3)△PMN面积的最大值为.提示:在旋转的过程中,由(2)中的结论知△PMN为等腰直角三角形,S△PMN=PN2=BD2,当S△PMN有最大值时,则BD的值最大,由三角形三边关系可推断出当B、A、D三点共线时,BD的值最大,其最大值为14,此时S=PN2=BD2=×14×14=.△PMN针对训练:1.解:(1)证明:延长DA交BE于G点.∵∠BAE+∠CAD=180°,即∠EAG+∠GAB+∠CAD=180°,∵∠GAB+∠BAC+∠CAD=180°,∴∠EAG=∠CAB.∵∠EAG=∠AED+∠ADE,∴∠CAB=∠AED+∠ADE.(2)证明:如图①,过E点作DA延长线的垂线,垂足为H.∴∠AHE=∠ACB=90°,由(1)可知,∠EAH=∠BAC,又∵AE=AB,∴△AHE≌△ACB,∴EH=BC,AH=AC.∵AC=AD,∴AH=AD.∵∠EHA=∠FAD=90°,∴AF∥EH.∵A为DH中点,∴AF为△DHE中位线,∴EH=2AF,∴BC=2AF.(3)成立.证明如下:如图②,延长DA至M点,使AM=DA,连接EM,∵∠BAE+∠CAD=180°,∠CAD+∠CAM=180∴∠BAE=∠CAM,∴∠BAE+∠CAC=∠CAM+∠EAC,即∠BAC=∠CAM.∵AM=AD,AD=AC,∴AM=AC.又∵AB=AE,∠BAC=∠EAM,∴△BAC≌△EAM,∴BC=EM.∵F、A分别为DE、DM中点,∴AF为△DEM中位线,∴EM=2AF,∴BC=2AF.2.解:(1)证明:∵∠BAC+∠EAD=180°,∠BAE=90°,∴∠DAC=90°,在△ABE与△ACD中,AE=AD,∠BAE=∠CAD=90°,AB=AC,∴△ABE≌△ACD(SAS),∴CD=BE,∵在Rt△ABE中,F为BE的中点,∴BE=2AF,∴CD=2AF.(2)成立,证明:如图,延长EA交BC于G,在AG上截取∵∠BAC+∠EAD=180°,∴∠EAB+∠DAC=180°,∵∠EAB+∠BAH=180°,∴∠DAC=∠BAH,在△ABH与△ACD中,AH=AD,∠BAH=∠CAD,AB=AC,∴△ABH≌△ACD(SAS),∴BH=DC,∵AD=AE,AH=AD,∴AE=AH,∵EF=FB,∴BH=2AF,∴CD=2AF.3.解:(1)证明:∵AB=AC,∴∠ABD=∠ACD,∵AE=AD,∴∠ADE=∠AED,∵∠BAD+∠ABD=∠ADE+∠EDC,∠EDC+∠ACD=∴∠BAD=2∠EDC,∵∠ABF=2∠EDC,∴∠BAD=∠ABF,∴△ABF是等腰三角形;(2)方法一:如图①,延长CA至点H,使AG=AH,连接BH,∵点N是BG的中点,∴AN=BH,∵∠BAD=∠ABF,∠DAC=∠CBG,∴∠CAB=∠CBA,∴△ABC是等边三角形.∴AB=BC=AC,∠BAC=∠BCA∵GM=AB,AB=AC,∴CM=AG,∴AH=CM,在△BAH和△BCM中,∴△BAH≌△BCM(SAS),∴BH=BM,∴AN=BM,方法二:如图②,延长AN至K,使NK=AN,连接KB,同方法一,先证△ABC是等边三角形,再证△ANG≌△KNB(SAS),所以BK=AG=CM,然后可以证得∠ABK=∠BCN=120°,最后证△ABK≌△BCN(SAS),所以BM=AK=2AN.类型5角的和差倍分例5:解:(1)如图,过点P作PG⊥EF于G.∵PE=PF=6,EF=6,∴FG=EG=3,∠FPG=∠EPG=∠EPF.在Rt△FPG中,sin∠FPG===.∴∠FPG=60°,∴∠EPF=2∠FPG=120°.(2)如图,作PM⊥AB于M,PN⊥AD于N.∵AC为菱形ABCD的对角线,∴∠DAC=∠BAC,AM=AN,PM=PN.在Rt△PME和Rt△PNF中,PM=PN,PE∴Rt△PME≌Rt△PNF,∴NF=ME.又∵AP=10,∠PAM=∠DAB=30°,∴AM=AN=AP cos30°=10×=5.∴AE+AF=(AM+ME)+(AN-NF)=AM+针对训练:1.证明:如图,过D作DE⊥AB于E,过D作DF⊥AC于F,∵DA平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,∵∠B+∠ACD=180°,∠ACD+∠FCD=180∴∠B=∠FCD,在△DFC和△DEB中,∴△DFC≌△DEB,∴DC=DB.2.解:(1)∵AC=AB=4,且CD=1,∴AD=AC-CD=3.在Rt△ABD中,∠BAD=90°,∴BD==5,=AB·AD=AE·BD,∵S△ABD∴AE=2.4.(2)证明:如图,取BC的中点M,连接AM交BD于点N.∵∠BAC=90°,AB=AC,点M为BC的中点,∴AM=BM=CM,AM⊥BC,∠NAD=∠FCP=45°,∴∠AMF=∠BMN=90°.∵AE⊥BD,∴∠MAF+∠ANE=∠MBN+∠BNM=90°,又∠ANE=∠BNM,∴∠MAF=∠MBN,∴△AMF≌△BMN,∴MF=MN,∴AM-MN=CM-MF,即AN=CF.∵AP=CD,∴AC-CD=AC-AP,即AD=CP.∴△ADN≌△CPF,∴∠ADB=∠CPF.3.解:(1)∵AB=BD,∠BAD=45°,∴∠BDA=45°,即∠ABD=90°.∵四边形ABCD是平行四边形,∴当E、C重合时,BF=BD=AB.∵在Rt△ABF中,AB2+BF2=AF2,∴(2BF)2+BF2=()2,∴BF=1,AB=2.在Rt△ABD中,AD===2.(2)证明:如图,在AF上截取AK=HD,连接BK.∵∠AFD=∠ABF+∠2=∠FGD+∠3且∠ABF=∠FGD=90°,∴∠2=∠3.在△ABK与△DBH中,∴△ABK≌△DBH,∴BK=BH,∠6=∠5.∵四边形ABCD是平行四边形,∴AD∥BC,∴∠5=∠4=45°,∴∠6=∠5=∴∠7=∠ABD-∠6=45°=∠5.在△BFK与△BFH中,∴△BFK≌△BFH.∴∠BFK=∠BFH,即∠AFB=∠HFB.4.解:(1)证明:由折叠知∠EMN=∠ABC=90EM,∴∠EMB=∠EBM,∴∠EMN-∠EMB=∠ABC-∠EBM,即∠BMP=∠MBC.∵在正方形ABCD中,AD∥BC,∴∠AMB=∠MBC,∴∠AMB=∠BMP,∴BM是∠AMP的平分线.(2)△PDM的周长没有发生变化.证明如下:如图,过BBQ⊥MP于Q.∵∠A=90°,且由(1)知BM是∠AMP的平分线,∴BA=BQ,∵∠A=∠MQB=90°,∠AMB=∠BMP,MB=MB,∴△AMB≌△QMB(AAS).∴MA=MQ.∵BA=BC,∴BQ=BC,又∵∠BQP=90°=∠C,BP=BP,∴Rt△BPC≌Rt△BPQ(HL).∴PC=PQ,∴△PDM的周长=MD+MP+DP=MD+MQ+QP+PD=MD+MA+PC+PD=AD+DC=2AD.∴△PDM的周长没有发生变化.类型6旋转型全等问题:图中若有边相等,可用旋转做实验例6:解:(1)①∵四边形ADEF是正方形,∴AD=AF,AB=AC,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,∴△DAB≌△FAC,∴∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BC;②∵△DAB≌△FAC,∴CF=BD,∵BC=BD+CD,∴BC=CF+CD.(2)结论①成立,结论②不成立.∵四边形ADEF是正方形,∴AD=AF,AB=AC.∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,∴△DAB≌△FAC,∴∠ABD=∠ACF,CF=BD,∴∠BCF=∠ACF-∠ACB=∠ABD-∠ACB=90°,即CF⊥BC;∵BC=CD-BD,∴BC=CD-CF.(3)如图,过A作AH⊥BC于H,过E作EM⊥BD于M∵∠BAC=90°,AB=AC,∴BC=AB=4,AH=CH∴CD=BC=1,∴DH=3,同(2)证得△BAD≌△CAF∴∠ABD=∠ACF=45°,∴∠BCF=∠ACB+∠ACF∴BC⊥CF,CF=BD=5.∵四边形ADEF是正方形,∴AD=DE,∠ADE=90∵BC⊥CF,EM⊥BD,EN⊥CF,∴四边形CMEN形,∴NE=CM,EM=CN,∵∠AHD=∠ADE=∠EMD90°,∴∠ADH+∠EDM=∠EDM+∠DEM=90°,∴∠ADH=∠DEM,∴△ADH≌△DEM,∴EM=DH=3,DM=AH=2,∴CN=EM=3,EN=CM=3,∵∠ABC=45°,∴∠BGC=45°,∴△BCG是等腰直角三角形,∴CG=BC=4,∴GN=1,∴EG==.针对训练:1.解:(1)AC=AD+AB.证明如下:∵∠B+∠D=180°,∠B=90°,∴∠D=90°.∵∠DAB=120°,AC平分∠DAB,∴∠DAC=∠BAC=60°,∵∠B=90°,∴AB=AC,同理AD=AC.∴AC=AD+AB.(2)(1)中的结论成立,理由如下:如图①,以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB的延长线于点E,∵∠BAC=60°,∴△AEC为等边三角形,∴AC=AE=CE,∠E=60°,∵∠ABC+∠D=180°,∠DAB=120°,∴∠DCB=60°,∴∠DCA=∠ECB.在△DAC和△BEC中,∴△DAC≌△BEC,∴AD=BE,∴AC=AE=AD+AB.(3)AD+AB=AC.理由如下:如图②,过点C作CE⊥AC交AB的延长于点E,∵∠ABC+∠D=180°,∠DAB=90°,∴∠DCB=90°,∵∠ACE=90°,∴∠DCA=∠BCE,又∵AC平分∠DAB,∴∠CAB=45°,∴∠E=45°,∴AC=CE.∴△CDA≌△CBE,∴AD=BE,∴AD+AB=AE.∵在Rt△ACE中,∠CAB=45°,∴AE==AC,∴AD+AB=AC.2.解:(1)证明:∵四边形ABCD是正方形,∴∠B=∠D=∠BAD=90°,AB=AD,∵△ABE沿AE翻折得到△AHE,∴△ABE≌△AHE,∴AH=AB=AD,BE=EH,∠AHE=∠AHF=∠B=∠D=90°.在Rt△AHF和Rt△ADF中,∴Rt△AHF≌Rt△ADF(HL),∴∠HAF=∠DAF,∴∠EAF=∠EAH+∠FAH=∠BAH+∠HAD=∠BAD=45 (2)以BM,DN,MN证明如下:如图,过点A作AH⊥AN并截取AH=AN BH、HM,∵∠1+∠BAN=90°,∠3+∠BAN=90°,∴∠1在△ABH和△ADN中,∴△ABH≌△ADN(SAS),∴BH=DN,∠HBA=∠NDA=135°,∵∠HAN=90°,∠MAN=45°,∴∠1+∠2=∠HAM=∠MAN=45°,在△AHM和△ANM中,∴△AHM≌△ANM(SAS),∴HM=NM,∴∠HBP=180°-∠HBA=180°-135°=45°,∴∠HBP+∠PBM=45°+45°=90°,∴△HBM是直角三角形,∵HB=DN,HM=MN,∴以BM,DN,MN为三边围成的三角形为直角三角形.3.解:(1)如图①,将△PBC绕点B逆时针旋转90°得△P′BA,连接PP′,则△AP′B≌△CPB,∴P′B=PB=,P′A=PC=1,∠1=∠2,∠AP′B=∠BPC.∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,∴∠2+∠3=90°,∴∠1+∠3=90°,即∠P′BP=90°,∴∠BP′P=45°.在Rt△P′BP中,由勾股定理,得PP′2=4.∵P′A=1,AP=∴P′A2=1,AP2=5,∴P′A2+PP′2=AP2,∴△P′AP是直角三角形,∴∠AP′P=90°,∴∠AP′B=45°+90°=135°,∴∠BPC=135°.(2)仿照【分析】中的思路,将△BPC绕点B逆时针旋转120°,得到了△BP′A,连接PP′,如图②.则△PBC≌△P′BA,∴P′B=PB=4,P′A=PC=2,∠BPC=∠BP′A,∴△BPP′为等腰三角形,∵∠ABC=120°,∴∠PBP′=120°,∴∠BP′P=30°,过点B作BG⊥PP′于G,则∠P′GB=90°,∴PP′=2P′G.∵P′B=PB=4,∠BP′P=30°,∴BG=2,∴P′G=2.∴PP′=4,在△APP′中,∵PA=2,P′A=2,PP′=4,∴P′A2+P′P2=PA2,∴△PP′A是直角三角形,∴∠AP′P=90°,∴∠BPC=∠BP′A=∠PP′B+∠AP′P=30°+90°=120°.。
重庆中考几何题分类汇编(1)

重庆中考几何题分类汇编类型1 线段的倍分:要证线段倍与半,延长缩短去实验例1 如图Z3-1,在△ABC中,AB=AC,CM平分∠ACB交AB于M,在AC的延长线上截取CN =BM,连接MN交BC于P,在CB的延长线截取BQ=CP,连接MQ.(1)求证:MQ=NP;(2)求证:CN=2CP.针对训练:1.如图Z3-2,在▱ABCD中,AC⊥BC,点E、点F分别在AB、BC上,且满足AC=AE=CF,连接CE、AF、EF.(1)若∠ABC=35°,求∠EAF的度数;(2)若CE⊥EF,求证:CE=2EF.2.已知,在△ABC 中,AB =AC ,∠BAC =90°,E 为边AC 任意一点,连接BE.(1)如图①,若∠ABE=15°,O 为BE 中点,连接AO ,且AO =1,求BC 的长;(2)如图②,F 也为AC 上一点,且满足AE =CF ,过A 作AD⊥BE 交BE 于点H ,交BC 于点D ,连接DF 交BE 于点G ,连接AG.若AG 平分∠CAD,求证:AH =12AC.3.在△ACB 中,AB =AC ,∠BAC =90°,点D 是AC 上一点,连接BD ,过点A 作AE⊥BD 于E ,交BC 于F.(1)如图①,若AB =4,CD =1,求AE 的长;(2)如图②,点G 是AE 上一点,连接CG ,若BE =AE +AG ,求证:CG =2AE.4.在等腰直角三角形ABC 中,∠BAC =90°,AB =AC ,D 是斜边BC 的中点,连接AD.(1)如图①,E 是AC 的中点,连接DE ,将△CDE 沿CD 翻折到△CDE′,连接AE′,当AD =6时,求AE′的值.(2)如图②,在AC 上取一点E ,使得CE =13AC ,连接DE ,将△CDE 沿CD 翻折到△CDE′,连接AE′交BC 于点F ,求证:DF =CF.类型2 线段的和差:要证线段和与差,截长补短去实验例2 如图,在△ABC中,∠BAC=90°,在BC上截取BD=BA,连接AD,在AD左侧作∠EAD =45°交BD于E.(1)若AC=3,则CE=________(直接写答案);(2)如图①,M、N分别为AB和AC上的点,且AM=AN,连接EM、DN,若∠AME+∠AND=180°,求证:DE=DN+ME;(3)如图②,过E作EF⊥AE,交AD的延长线于F,在EC上选取一点H,使得EH=BE,连接FH,在AC上选取一点G,使得AG=AB,连接BG、FG,求证:FH=FG.针对训练:1.如图Z3-7,在▱ABCD中,AE⊥BC于E,AE=AD,EG⊥ABDC交于点F,连接AF.(1)若BE=2EC,AB=13,求AD的长;(2)求证:EG=BG+FC.2.如图,在正方形ABCD 中,点P 为AD 延长线上一点,连接AC 、CP ,过点C 作CF⊥CP 于点C ,交AB 于点F ,过点B 作BM⊥CF 于点N ,交AC 于点M.(1)若AP =78AC ,BC =4,求S △ACP ;(2)若CP -BM =2FN ,求证:BC =MC.3.如图,在△ABC 中,AB =BC ,以AB 为一边向外作菱形ABDE ,连接DC ,EB 并延长EB 交AC 于F ,且CB⊥AE 于G.(1)若∠EBG=20°,求∠AFE;(2)试问线段AE ,AF ,CF 之间的数量关系并证明.类型3 倍长中线:三角形中有中线,延长中线等中线例3 如图Z3-10①,在Rt△ABC中,∠ABC=90°,D、E分别为斜边AC上两点,且AD=AB,CE=CB,连接BD、BE.(1)求∠EBD的度数;(2)如图Z3-10②,过点D作FD⊥BD于点D,交BE的延长线于点F,在AB上选取一点H,使得BH=BC,连接CH,在AC上选取一点G,使得GD=CD,连接FH、FG,求证:FH=FG.针对训练:1.如图,已知在▱ABCD中,G为BC的中点,点E在AD边上,且∠1=∠2.(1)求证:E是AD中点;(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.2.如图Z3-12,在菱形ABCD中,点E、F分别是BC、CD上的点,连接AE,AF,DE、EF,∠DAE=∠BAF.(1)求证:CE=CF;(2)若∠ABC=120°,点G是线段AF的中点,连接DG,EG.求证:DG⊥GE.3.在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠ADC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,M为AB的中点,连接MD,ME.(1)如图①,当∠ADC=90°时,线段MD与ME的数量关系是________;(2)如图②,当∠ADC=60°时,试探究线段MD 与ME 的数量关系,并证明你的结论;(3)如图③,当∠ADC=α时,求ME MD的值.4.如图①,等边三角形ABC 中,CE 平分∠ACB,D 为BC 边上一点,且DE =CD ,连接BE.(1)若CE =4,BC =6 3,求线段BE 的长;(2)如图②,取BE 中点P ,连接AP ,PD ,AD ,求证:AP⊥PD 且AP =3PD ;(3)如图③,把图Z 3-14②中的△CDE 绕点C 顺时针旋转任意角度,然后连接BE ,点P 为BE 中点,连接AP ,PD ,AD ,问第(2)问中的结论还成立吗?若成立,请证明;若不成立,请说明理由.5.在△ABC 中,以AB 为斜边,作直角三角形ABD ,使点D 落在△ABC 内,∠ADB =90°.(1)如图①,若AB =AC ,∠BAD =30°,AD =6 3,点P 、M 分别为BC 、AB 边的中点,连接PM ,求线段PM 的长;(2)如图②,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP;(3)如图③,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).类型4 中位线:三角形中两中点,连接则成中位线例4 2017·河南如图①,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.(1)观察猜想:图①中,线段PM与PN的数量关系是__________,位置关系是__________;(2)探究证明:把△ADE绕点A按逆时针方向旋转到图②的位置,连接MN,BD,CE,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.针对训练:1.如图①,在任意的三角形ABC中,分别以AB和AC为一边作等腰三角形ABE和等腰三角形ACD,AB=AE,AC=AD,且∠BAE+∠CAD=180°,连接DE,延长CA交DE于F.(1)求证:∠CAB=∠AED+∠ADE;(2)若∠ACB=∠BAE=∠CAD=90°,如图②,求证:BC=2AF;(3)若在△ABC中,如图③所示,作等腰三角形ABE和等腰三角形ACD,AB与DE交于点F,F 为DE的中点,请问(2)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.2.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.(1)如图①,当∠BAE=90°时,求证:CD=2AF;(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.3.如图①,在等腰三角形ABC中,AB=AC,在底边BC上取一点D,在边AC上取一点E,使AE=AD,连接DE,在∠ABD的内部作∠ABF=2∠EDC,交AD于点F.(1)求证:△ABF是等腰三角形;(2)如图②,BF的延长交AC于点G.若∠DAC=∠CBG,延长AC至点M,使GM=AB,连接BM,点N是BG的中点,连接AN,试判断线段AN、BM之间的数量关系,并证明你的结论.类型5 角的和差倍分图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现.角平分线平行线,等腰三角形来添.角平分线加垂线,三线合一试试看.例5.如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6 3,∠BAD=60°,且AB>6 3.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值.针对训练:1.已知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.2.在△ACB中,AB=AC,∠BAC=90°,点D是AC上一点,连接BD,过点A作AE⊥BD 于E,交BC于F.(1)如图①,若AB=4,CD=1,求AE的长;(2)如图②,点P是AC上一点,连接FP,若AP=CD,求证:∠ADB=∠CPF.3.已知,在▱ABCD中,∠BAD=45°,AB=BD,E为BC上一点,连接AE交BD于F,过点D作DG⊥AE于G,延长DG交BC于H.(1)如图①,若点E与点C重合,且AF=5,求AD的长;(2)如图②,连接FH,求证:∠AFB=∠HFB.4.如图,将正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连接EP.当点M在边AD上移动时,连接BM、BP.(1)求证:BM是∠AMP的平分线;(2)△PDM的周长是否发生变化?证明你的结论.类型6 旋转型全等问题:图中若有边相等,可用旋转做实验例6.△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF.(1)观察猜想:如图①,当点D 在线段BC 上时,①BC 与CF 的位置关系为:________. ②BC ,CD ,CF 之间的数量关系为:___________;(将结论直接写在横线上)(2)数学思考:如图Z 3-25②,当点D 在线段CB 的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸:如图Z 3-25③,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE.若已知AB =2 2,CD =14BC ,请求出GE的长.针对训练:1.在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.(1)如图①,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.(2)如图②,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.(3)如图③,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.2.如图①,在正方形ABCD中,点E为边BC上一点,将△ABE沿AE翻折得△AHE,延长EH交边CD于F,连接AF.(1)求证:∠EAF=45°;(2)延长AB,AD,如图②,射线AE、AF分别交正方形两个外角的平分线于M、N,连接MN,若以BM、DN、MN为三边围成三角形,试猜想三角形的形状,并证明你的结论.3.如图①,在正方形ABCD内有一点P,PA=5,PB=2,PC=1,求∠BPC的度数.【分析问题】根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图Z3-28②),然后连接PP′.(1)请你通过计算求出图Z3-28②中∠BPC的度数;(2)如图③,若在正六边形ABCDEF内有一点P,且PA=2 13,PB=4,PC=2.请求出∠BPC的度数.。
2018届重庆中考复习:重庆中考几何题分类汇编(含答案)
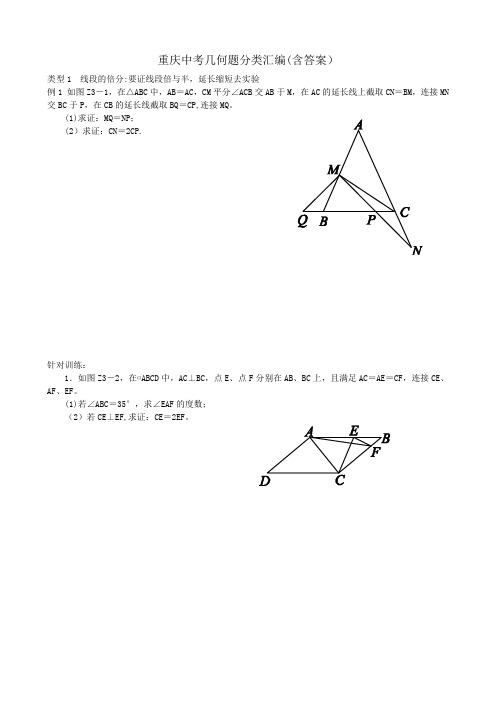
重庆中考几何题分类汇编(含答案)类型1 线段的倍分:要证线段倍与半,延长缩短去实验例1 如图Z3-1,在△ABC中,AB=AC,CM平分∠ACB交AB于M,在AC的延长线上截取CN=BM,连接MN 交BC于P,在CB的延长线截取BQ=CP,连接MQ。
(1)求证:MQ=NP;(2)求证:CN=2CP.针对训练:1.如图Z3-2,在▱ABCD中,AC⊥BC,点E、点F分别在AB、BC上,且满足AC=AE=CF,连接CE、AF、EF。
(1)若∠ABC=35°,求∠EAF的度数;(2)若CE⊥EF,求证:CE=2EF。
2.已知,在△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE。
(1)如图①,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图②,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG。
若AG平分∠CAD,求证:AH=错误!AC。
3.在△ACB中,AB=AC,∠BAC=90°,点D是AC上一点,连接BD,过点A作AE⊥BD于E,交BC于F。
(1)如图①,若AB=4,CD=1,求AE的长;(2)如图②,点G是AE上一点,连接CG,若BE=AE+AG,求证:CG=错误!AE。
4.在等腰直角三角形ABC中,∠BAC=90°,AB=AC,D是斜边BC的中点,连接AD。
(1)如图①,E是AC的中点,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′,当AD=错误!时,求AE′的值.(2)如图②,在AC上取一点E,使得CE=错误!AC,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′交BC于点F,求证:DF=CF.例2 如图,在△ABC中,∠BAC=90°,在BC上截取BD=BA,连接AD,在AD左侧作∠EAD=45°交BD于E.(1)若AC=3,则CE=________(直接写答案);(2)如图①,M、N分别为AB和AC上的点,且AM=AN,连接EM、DN,若∠AME+∠AND=180°,求证:DE =DN+ME;(3)如图②,过E作EF⊥AE,交AD的延长线于F,在EC上选取一点H,使得EH=BE,连接FH,在AC上选取一点G,使得AG=AB,连接BG、FG,求证:FH=FG.针对训练:1.如图Z3-7,在▱ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF。
重庆市2001-2019年中考数学试题分类解析专题8:平面几何基础

一、选择题1. (重庆市2002年4分)一居民小区有一正多边形的活动场。
为迎接“AAPP”会议在重庆的召开,小区管委会决定在这个多边形的每个顶点处修建一个半径为2m的扇形花台,花台都以多边形的顶点为圆心,以多边形的内角为圆心角,花台占地面积共为12 2m。
若每个花台的造价为400元,则建造这些花台共需资金【】A 2400元B 2800元C 3200元D 3600元2. (重庆市2004年4分)在如图的方格纸中,每个小方格都是边长为1的正方形,点A、B是方格纸中的两个格点(即正方形的顶点),在这个5×5的方格纸中,找出格点C使△ABC的面积为2个平方单位,则满足条件的格点C的个数是【】A、5B、4C、3D、2 【答案】A。
【考点】三角形的面积。
【分析】分别在AB的两侧找到一个使其面积是2个平方单位的点,再分别过这两点作AB 的平行线,找到所有的格点即可,即有5个。
故选A。
3. (重庆市大纲卷2005年4分)已知∠A=400,则∠A的补角等于【】A、500B、900C、1400D、18004. (重庆市课标卷2005年4分)下列图形中,既是轴对称图形,又是中心对称图形的是【】A.B.C.D5. (重庆市2007年4分)在下列各电视台的台标图案中,是轴对称图形的是【】A. B.C.D.【答案】C。
【考点】轴对称图形。
【分析】根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合。
因此,只有C 沿某条直线折叠后直线两旁的部分能够完全重合,是轴对称图形。
故选C。
6. (重庆市2007年4分)已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为【】A.20o B.120o C.20o或120o D.36o∠=°,则7. (重庆市2009年4分)如图,直线AB、CD相交于点E,DF∥AB.若AEC100∠等于【】DA.70°B.80°C.90°D.100°8. (重庆市2010年4分)如图,点B是△ADC的边AD的延长线上一点,DE∥BC,若∠C =50°,∠BDE=60°,则∠CDB的度数等于【】A.70° B.100° C.110° D.120°【答案】C。
历年重庆市中考真题分类(几何综合题)汇编(2023年整理,附答案)

历年重庆市中考真题分类(几何综合题)汇编 1.在ABC 中,AB AC =,D 是边BC 上一动点,连接AD ,将AD 绕点A 逆时针旋转至AE 的位置,使得180DAE BAC ∠+∠=︒.(1)如图1,当90BAC ∠=︒时,连接BE ,交AC 于点F .若BE 平分ABC ∠,2BD =,求AF 的长;(2)如图2,连接BE ,取BE 的中点G ,连接AG .猜想AG 与CD 存在的数量关系,并证明你的猜想;(3)如图3,在(2)的条件下,连接DG ,CE .若120BAC ∠=︒,当BD CD >,150AEC ∠=︒时,请直接写出BD DG CE-的值. 2.在等边ABC 中,6AB =,BD AC ⊥ ,垂足为D ,点E 为AB 边上一点,点F 为直线BD 上一点,连接EF .(1)将线段EF 绕点E 逆时针旋转60°得到线段EG ,连接FG .①如图1,当点E 与点B 重合,且GF 的延长线过点C 时,连接DG ,求线段DG 的长; ②如图2,点E 不与点A ,B 重合,GF 的延长线交BC 边于点H ,连接EH,求证:BE BH +;(2)如图3,当点E 为AB 中点时,点M 为BE 中点,点N 在边AC 上,且2DN NC =,点F 从BD 中点Q 沿射线QD 运动,将线段EF 绕点E 顺时针旋转60°得到线段EP ,连接FP,当12NP MP +最小时,直接写出DPN △的面积.3.如图,在Rt ABC 中,90BAC ∠=︒,AB AC =,点D 是BC 边上一动点,连接AD ,把AD 绕点A 逆时针旋转90°,得到AE ,连接CE ,DE .点F 是DE 的中点,连接CF .(1)求证:CF ; (2)如图2所示,在点D 运动的过程中,当2BD CD =时,分别延长CF ,BA ,相交于点G ,猜想AG 与BC 存在的数量关系,并证明你猜想的结论;(3)在点D 运动的过程中,在线段AD 上存在一点P ,使PA PB PC ++的值最小.当PA PB PC ++的值取得最小值时,AP 的长为m ,请直接用含m 的式子表示CE 的长.4.△ABC 为等边三角形,AB =8,AD ⊥BC 于点D ,E 为线段AD 上一点,AE =.以AE 为边在直线AD 右侧构造等边三角形AEF ,连接CE ,N 为CE 的中点.(1)如图1,EF 与AC 交于点G ,连接NG ,求线段NG 的长;(2)如图2,将△AEF 绕点A 逆时针旋转,旋转角为α,M 为线段EF 的中点,连接DN ,MN .当30°<α<120°时,猜想∠DNM 的大小是否为定值,并证明你的结论;(3)连接BN .在△AEF 绕点A 逆时针旋转过程中,当线段BN 最大时,请直接写出△ADN 的面积.5.如图,在平行四边形ABCD 中,点E 在边BC 上,连结AE ,EM ⊥AE ,垂足为E ,交CD于点M ,AF ⊥BC ,垂足为F ,BH ⊥AE ,垂足为H ,交AF 于点N ,点P 显AD 上一点,连接CP .(1)若DP =2AP =4,CPCD =5,求△ACD 的面积.(2)若AE =BN ,AN =CE ,求证:ADCM +2CE .6.在ABCD 中,BE 平分ABC ∠交AD 于点E .(1)如图1,若30D ︒∠=,AB =ABE ∆的面积;(2)如图2,过点A 作AF DC ⊥,交DC 的延长线于点F ,分别交BE ,BC 于点G ,H ,且 AB AF =.求证:ED AG FC -=.7.如图,在平行四边形ABCD 中,点O 是对角线AC 的中点,点E 是BC 上一点,且AB AE =,连接EO 并延长交AD 于点F ,过点B 作AE 的垂线,垂足为H ,交AC 于点G .(1)若3AH =,1HE =,求ABE △的面积;(2)若45ACB ︒∠=,求证:DF =.(2)求证:EB=EH .9.在△ABC 中,ABM ∠=45°,⊥AM BM ,垂足为M ,点C 是BM 延长线上一点,连接AC.(1)如图①,若AB =,BC =5,求AC 的长;(2)如图②,点D 是线段AM 上一点,MD =MC ,点E 是△ABC 外一点,EC =AC ,连接ED 并延长交BC 于点F ,且点F 是线段BC 的中点,求证:BDF ∠=CEF.∠10.如图,△ABC 中,∠ACB =90°,AC =BC ,点E 是AC 上一点,连接BE .(1)如图1,若AB =,BE =5,求AE 的长;(2)如图2,点D 是线段BE 延长线上一点,过点A 作AF ⊥BD 于点F ,连接CD 、CF ,当AF =DF 时,求证:D C =BC .最后根据等量代换可得BD DG AC AP CP CE CE CE--==,解直角三角形求出CP =即可得出答案.【答案详解】 解:(1)连接CE ,过点F 作FH BC ⊥,垂足为H .BE 平分ABC ∠,90BAC ∠=︒,FA FH ∴=.AB AC = ,45ABC ACB ∴∠=∠=︒,2FH CF ∴=, 180BAC DAE ∠∠︒+= ,90BAC DAE ∴∠=∠=︒,BAD CAE ∴∠=∠,在ABD △和ACE 中,=AB AC BAD CAE AD AE ⎧⎪∠=∠⎨⎪=⎩,()ABD ACE SAS ∴ ≌,2BD CE ∴==,45ABD ACE ∠=∠=︒,90BCE ∴∠=︒,BE 平分ABC ∠,ABF CBF ∴∠=∠.AFB BEC ∴∠=∠,AFB EFC ∠=∠ ,BEC EFC ∴∠=∠,180120DAE BAC BAC ∠+∠=︒∠=,︒ ,60DAE ∴∠=︒,由旋转的性质得:AD AE =,ADE ∴V 是等边三角形,60,AED AD DE ∴∠=︒=,150AEC ∠=︒ ,90CED AEC AED ∴∠=∠-∠=︒,120,BAC AB AC ∠=︒= ,1(1802)30ABC BA ACB C ∴∠=∠=∠=︒-︒, 180ABC AEC ∴∠+∠=︒,∴点,,,A B C E 四点共圆, 由圆周角定理得:1302AEB ACB AED ∠=∠=︒=∠, BE ∴垂直平分AD ,1302DEB AED ∠=∠=︒(等腰三角形的三线合一), ,,AG DG AP DP BD AB AC ∴====,BE ∴平分ABC ∠,1152ABE CBE ABC ∴∠=∠=∠=︒, 45CDE CBE DEB ∴∠=∠+∠=︒,Rt CDE ∴ 是等腰直角三角形,,CE DE CD ∴==,设2CE DE a ==,则2,AD a CD ==,由(2)可知,12AG CD ==,DG AG ∴==,222AG DG AD ∴+=,ADG ∴ 是等腰直角三角形,且90AGD ∠=︒,1452EGD AGD ∴∠=∠=︒(等腰三角形的三线合一), 30BDG EGD CBE ∴∠=∠-∠=︒,在BDP △和BAP 中,BD BA BP BP DP AP =⎧⎪=⎨⎪=⎩,()BDP BAP SSS ∴≅ ,120BDP BAP ∴∠=∠=︒,90GDP BDP BDG ∴∠=∠-∠=︒,18060CDP BDP ∠=︒-∠=︒,18090CPD CDP ACB ∴∠=︒-∠-∠=︒,90AGD GDP APD ∴∠=∠=∠=︒,∴四边形AGDP 是矩形,DG AP ∴=,在Rt CDP △中,cos 2CP CD PCD =⋅∠=⋅=,则22BD DG AC AP CP CE CE CE a --====. 【点睛】本题考查了图形的旋转、等边三角形的判定与性质、三角形的中位线定理、圆周角定理、解直角三角形等知识点,综合能力比较强,较难的是题(3),判断出,,,A B C E 四点共圆是解题关键.2.在等边ABC 中,6AB =,BD AC ⊥ ,垂足为D ,点E 为AB 边上一点,点F 为直线BD 上一点,连接EF .(1)将线段EF 绕点E 逆时针旋转60°得到线段EG ,连接FG .①如图1,当点E 与点B 重合,且GF 的延长线过点C 时,连接DG ,求线段DG 的长; ②如图2,点E 不与点A ,B 重合,GF 的延长线交BC 边于点H ,连接EH ,求证:BE BH +;(2)如图3,当点E 为AB 中点时,点M 为BE 中点,点N 在边AC 上,且2DN NC =,点F 从BD 中点Q 沿射线QD 运动,将线段EF 绕点E 顺时针旋转60°得到线段EP ,连接FP ,当12NP MP +最小时,直接写出DPN △的面积.【答案】(1)①②见解析;(2 【要点分析】(1)①连接AG ,根据题意得出△ABC 和△GEF 均为等边三角形,从而可证明△GBC ≌△GAC ,进一步求出AD =3,AG =BG =②以点F 为圆心,FB 的长为半径画弧,与BH 的延长线交于点K ,连接KF ,先证明出△BFK 是顶角为120°的等腰三角形,然后推出△FEB ≌△FHK ,从而得出结论即可;(2)利用“胡不归”模型构造出含有30°角的直角三角形,构造出12NP MP NP PJ +=+,当N 、P 、J 三点共线的时候满足条件,然后利用等边三角形的性质及判定、矩形的判定及性质以及解直角三角形的知识分别计算出PN 与DN 的长度,即可得出结论.【答案详解】(1)解:①如图所示,连接AG ,由题意可知,△ABC 和△GEF 均为等边三角形,∴∠GFB =60°,∵BD ⊥AC ,∴BE =KH ,∴BE +BH =KH +BH =BK ,∵FB =FK ,∠BFK =120°,∴BK ,即:BE BH +=;(2)方法一:以M 为顶点,MP 为一边,作30PML ∠=︒,ML 交BD 于G ,过P 作PH ML ⊥于H ,设MP 交BD 于K ,如图:Rt PMH ∆中,12HP MP =, 12NP MP ∴+最小即是NP HP +最小,此时N 、P 、H 共线, 将线段EF 绕点E 顺时针旋转60︒得到线段EP ,F ∴在射线QF 上运动,则P 在射线MP 上运动,根据“瓜豆原理”, F 为主动点,P 是从动点,E 为定点,60FEP ∠=︒,则F 、P 轨迹的夹角60QKP FEP ∠=∠=︒,60BKM ∴∠=︒,30ABD ∠=︒ ,90BMK ∴∠=︒,∴∠A =60°,∠BDA =90°,∠ABD =30°,∵点E 、Q 分别为AB 、BD 的中点,∴EQ 为△ABD 的中位线,∴EQ //AD ,∴∠BEQ =∠A =60°,∠BQE =∠BDA =90°,∵∠BQE =90°,∠ABD =30°,∴EQ =12BE , ∵点M 为BE 的中点,∴ME =12BE =EQ , ∵将线段EF 绕点E 顺时针旋转60°得到线段EP , ∴△EPF 为等边三角形,∠PEF =60°,PE =EF =PF ,∴∠BEQ =∠PEF ,∴∠BEQ -∠PEQ =∠PEF -∠PEQ ,即∠MEP =∠QEF ,在△MEP 与△QEF 中,ME EQ MEP QEF PE EF ⎧⎪∠∠⎨⎪⎩===,∴△MEP ≌△QEF (SAS )∴∠EMP =∠EQF =90°,∴MP ⊥BE ,∴点P 在射线MP 上运动,如图,以M 为顶点,MP 为一边,作30PML ∠=︒,ML 交BD 于G ,过P 作PH ML ⊥于H ,设MP 交BD 于K ,又2DN NC =,2DN GH ∴==,在等边ABC 中,6AB =,点E 为AB 中点时,点M 为BE 中点,32BM ∴=,sin 6sin 60BD AB A =⋅=⨯︒=∴在Rt BGM △中,1324MG BM ==,cos304BG BM =⋅︒=,114MH MG GH ∴=+=,4GD BD BG =-=,∴在Rt MHP △中,tan 30HP MH =⋅︒=PN HN HP GD HP ∴=-=-=,1122233DPN S PN DN ∴=⋅=⨯⨯=△. 【点睛】本题考查等边三角形性质及应用,涉及旋转变换、解直角三角形、三角形全等的判定及性质、矩形的判定及性质等知识,难度较大,解题的关键是构造辅助线.3.如图,在Rt ABC 中,90BAC ∠=︒,AB AC =,点D 是BC 边上一动点,连接AD ,把AD 绕点A 逆时针旋转90°,得到AE ,连接CE ,DE .点F 是DE 的中点,连接CF .(1)求证:CF ; (2)如图2所示,在点D 运动的过程中,当2BD CD =时,分别延长CF ,BA ,相交于点G ,猜想AG 与BC 存在的数量关系,并证明你猜想的结论;(3)在点D 运动的过程中,在线段AD 上存在一点P ,使PA PB PC ++的值最小.当PA PB PC ++的值取得最小值时,AP 的长为m ,请直接用含m 的式子表示CE 的长.【答案】(1)证明见解析;(2)BC =;(3)CE(1)先证△≌△BAD CAE ,可得ABD ∠=ACE ∠=45°,可求BCE ∠=90°,由直角三角形的性质和等腰直角三角形的性质可得结论;(2)连接AF ,由(1)得ABD ACE ∆≅∆,CE BD =,45ACE ABD ︒∠=∠=,推出454590DCE BCA ACE ∠=∠+∠=︒+︒=︒,然后根据现有条件说明在Rt DCE中,DE ==,点A ,D ,C ,E 四点共圆,F 为圆心,则CF AF =,在Rt AGC 中,推出AG ==,即可得出答案; (3)在△ABC 内取一点P ,连接AP 、BP 、CP ,将三角形ABP 绕点B 逆时针旋转60°得到△EBD ,证明点P 位于线段CE 上,同理得到点P 位于线段BF 上,证明BPC=120°∠,进而得到120APB BPC CPA ∠=∠=∠=︒,设PD 为a ,得出BD,AD BD =,得出a m +,解出a ,根据BD CE =即可得出答案.【答案详解】解:(1)证明如下:∵90BAC DAE ∠=∠=︒,∴BAD CAE ∠=∠, ∵AB AC =,AD AE =,∴在ABD △和ACE 中BAD CAE AB AC AD AE ∠=∠⎧⎪=⎨⎪=⎩,∴ABD ACE ∆≅∆, ∴45ABD ACE ∠=∠=︒,∴90DCE ACB ACE ∠︒=∠+∠=,在Rt ADE △中,F 为DE 中点(同时AD AE =),45ADE AED ∠=∠=︒,∴AF D E ⊥,即Rt ADF 为等腰直角三角形,∴2AF DF AD ==, ∵CF DF =,∴CF =; (2)连接AF ,由(1)得ABD ACE ∆≅∆,CE BD =,45ACE ABD ︒∠=∠=,∴454590DCE BCA ACE ∠=∠+∠=︒+︒=︒,在Rt DCE 中,DE =,∵F 为DE 中点,∴12DF EF DE ==, 在四边形ADCE 中,有90DAE DCE ∠=∠=︒,180DAE DCE ∠+∠=︒,∴点A ,D ,C ,E 四点共圆,∵F 为DE 中点,∴F 为圆心,则CF AF =,在Rt AGC 中,∵CF AF =,∴F 为CG 中点,即CG 2CF =,∴AG =, 即BC =;(3)如图1,在△ABC 内取一点P ,连接AP 、BP 、CP ,将三角形ABP 绕点B 逆时针旋转60°得到△EBD ,得到△BPD 为等边三角形,所以PD=BP ,∴AP+BP+CP=DE+DP+CP ,∴当PA PB PC ++的值取得最小值时,点P 位于线段CE 上;如图2,将三角形ACP 绕点C 顺时针旋转60°得到△FCG ,得到△PCG 为等边三角形,所以PC=GP ,∴AP+BP+CP=GF+GP+BP ,∴BD=,又AD BD==,∴a m+,m a=-1)a又BD CE∴CE.【点睛】本题是几何变换综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,旋转的性质,锐角三角函数等知识,灵活运用所学知识是解本题的关键.4.△ABC为等边三角形,AB=8,AD⊥BC于点D,E为线段AD上一点,AE=.以AE 为边在直线AD右侧构造等边三角形AEF,连接CE,N为CE的中点.(1)如图1,EF与AC交于点G,连接NG,求线段NG的长;(2)如图2,将△AEF绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接DN,MN.当30°<α<120°时,猜想∠DNM的大小是否为定值,并证明你的结论;(3)连接BN.在△AEF绕点A逆时针旋转过程中,当线段BN最大时,请直接写出△ADN 的面积.【答案】(1)NG;(2)∠DNM的为定值120°,证明见答案详解;(3)△AND的面积为【要点分析】∴AB=AC,AE=AF,60BACEAF ∠=∠=︒ ∴BAE CAF ∠=∠∴△ABE ≌△ACF .∴∠DGC =∠BHC ,∠ENM =∠ECF ,∠ABE =∠ACF又∵∠BHC =∠ABE +∠BAH =∠ABE +60°,∴∠DGC =∠ABE +60°=∠ACF +60°又∵∠DGC =∠DNC +∠GCN =∠DNC +∠ACF -∠ECF ,∴∠DNC =60°+∠ECF =60°+∠ENM , ∴∠DNE =180°-∠DNC =120°-∠ENM ,∴∠DNM =∠DNE +∠ENM =120°.(3)△AND 的面积为如图,取AC 中点P ,因为BP +PN ≥BN ,所以当B 、P 、N 在一直线上,BN 最大.∴BN =BP +PN =BP +12AE ==设BP 与AD 交于O ,NQ ⊥AD 于Q ,如图,∴BO =23BP ,ON BD =4, 由题意得△ONQ ∽△OBD ,∴NQ =72,在Rt△PGC中,GC2=CP2﹣PG2=17﹣x2,在Rt△DGC中,GC2=CD2﹣GD2=52﹣(4﹣x)2=9+8x﹣x2,∴17﹣x2=9+8x﹣x2,解得:x=1,即PG=1,∴GC=4,∵DP=2AP=4,∴AD=6,∴S△ACD=12×AD×CG=12×6×4=12;(2)证明:连接NE,如图2所示:∵AH⊥AE,AF⊥BC,AE⊥EM,∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°,∴∠NBF=∠EAF=∠MEC,在△NBF和△EAF中,NBF EAFBFN EFA AE BN∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△NBF≌△EAF(AAS),∴BF=AF,NF=EF,∴∠ABC=45°,∠ENF=45°,FC=AF=BF,∴∠ANE=∠BCD=135°,AD=BC=2AF,在△ANE和△ECM中,EAF AN ECANE ECMHEC∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ANE≌△ECM(ASA),∴CM=NE,又∵NF=2NE=2MC,∴ABE AEB ∠=∠,∴AE AB ==∴ABE ∆的面积113222AE BO =⨯==; (2)证明:作AQ BE ⊥交DF 的延长线于P ,垂足为Q ,连接PB 、PE ,如图2所示: ∵AB AE =,AQ BE ⊥,∴ABE AEB ∠=∠,BQ EQ =,∴PB PE =, ∴PBE PEB ∠=∠, ∴ABP AEP ∠=∠, ∵AB CD ∥,AF CD ⊥,∴AF AB ⊥,∴90BAF ︒∠=,∵AQ BE ⊥,∴ABG FAP ∠=∠,在ABG ∆和FAP ∆中,90ABG FAP AB AF BAG AFP ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩,∴(ASA)ABG AFP ∆≅∆,∴AG FP =,∵AB CD ∥,AD BC ∥,∴180ABP BPC ︒∠+∠=,BCP D ∠=∠,∵180AEP PED ︒∠+∠=,∴BPC PED ∠=∠,在BPC ∆和PED ∆中,BCP D BPC PED PB PE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴(AAS)BPC PED ∆≅∆,∴PC ED =,∴---ED AG PC AG PC FP FC ===.【答案详解】(1) AH 3HE 1==,,∴ AB AE AH HE 4==+=,又 在Rt ABH 中,BH ===ABE 11S AE BH 422∴==⨯= (2)过点A 作⊥AM BC 于点M ,交BG 于点K ,过点G 作⊥GN BC 于点N ,∴ AMB AME BNG ∠∠∠===90°,ACB ∠ =45°,∴ MAC ACB NGC ∠∠∠===45°AB AE = ,1BM ME BE BAM EAM 2∠∠∴===,, AE BG ⊥ 又,AHK ∠∴=90°,AHK BMK 在和中,AHK MAE AHK ∠∠∠++=180°,AMB NBG BKM ∠∠∠++=180°,MAE NBG ∠∠∴=,BAM MAE NBG α∠∠∠===设,BAG MAC BAM 45α∠∠∠∴=+=︒+,BGA ACB NBG 45α∠∠∠=+=︒+,BAG BGA ∠∠∴=,AB BG ∴=,AE BG ∴=,AME BNG 在和中,AME BNG MAE NBG AE BG ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AME BNG AAS ∴≅ ,ME NG ∴=,Rt ABE NG NC = 在等腰中,,GC BE 2∴===,BE ∴=,O AC 为的中点,OA OC ∴=,ABCD 四边形为平行四边形,AD BC AD BC ∴= ,,OAF OCE ∠∠∴=,AFO CEO ∠∠=,()AFO CEO AAS ∴≅ ,AF CE ∴=,AD AF BC CE ∴-=-,DF BE =即,DF BE ∴==.【点睛】本题考查了勾股定理、平行四边形的性质、全等三角形的判定与性质、等腰直角三角形的性质等,综合性较强,正确添加辅助线、应用数形结合思想进行解题是关键.8.如图,在▱ABCD 中,ACB=45°∠,点E 在对角线AC 上,BE=BA ,⊥BF AC 于点F ,BF 的延长线交AD 于点G .点H 在BC 的延长线上,且CH=AG ,连接EH .(1)若AB=13,求AF 的长;(2)求证:EB=EH .【答案】(1)5;(2)证明见解析.【要点分析】(1)依据⊥BF AC ,ACB=45°∠,Rt △BCF 中,BF=sin45°×BC=12,再根据勾股定理,即可得到Rt △ABF 中,; (2)连接GE ,过A 作⊥AF AG ,交BG 于P ,连接PE ,判定四边形APEG 是正方形,即可得到PF=EF ,AP=AG=CH ,进而得出△≌△APB HCE ,依据AB=EH ,AB=BE ,即可得到BE=EH .【答案详解】解:(1)如图,∵⊥BF AC ,ACB=45°∠, ∴等腰△Rt BCF 中,BF=sin45°×BC=12, 又∵AB=13,∴△Rt ABF 中,; (2)如图,连接GE ,过A 作⊥AF AG ,交BG 于P ,连接PE ,∵BE=BA ,⊥BF AC ,∴AF=FE ,∴BG 是AE 的垂直平分线, ∴AG=EG ,AP=EP ,∵∠∠GAE=ACB=45°,∴△AGE 是等腰直角三角形,即AGE=90°∠, △APE 是等腰直角三角形,即APE=90°∠,(2)延长EF 到点G ,使得FG=EF ,证ΔBMD ΔANC ≌得AC=BD ,再证ΔBFG ΔCFE ≌得BG=CE ,G=E,∠∠从而得BD=BG=CE ,即可得BDG=G= E.∠∠∠ 试题解析:(1)∵∠ABM=45°,⊥AM BM ,∴AM=BM=ABcos45°=3×=3,则CM=BC ﹣BM=5﹣2=2,∴AC=;(2)延长EF 到点G ,使得FG=EF ,连接BG .由DM=MC ,BMD=AMC ∠∠,BM=AM ,∴△≌△BMD AMC (SAS ),∴AC=BD ,又CE=AC ,因此BD=CE ,由BF=FC ,BFG=EFC ∠∠,FG=FE ,∴△≌△BFG CFE ,故BG=CE ,G=E ∠∠,所以BD=BG=CE ,因此BDG=G=E ∠∠∠.考点:1.全等三角形的判定与性质;2.勾股定理.10.如图,△ABC 中,∠ACB =90°,AC =BC ,点E 是AC 上一点,连接BE .。
重庆中考数学24题专题

重庆中考几何一、有关几何的基本量:线段、角度、全等、面积、四边形性质1、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC 交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G为CH的中点,且∠BEH=∠HEG.(1)若HE=HG,求证:△EBH≌△GFC;(2)若CD=4,BH=1,求AD的长.(1)证明:∵HE=HG,∴∠HEG=∠HGE,∵∠HGE=∠FGC,∠BEH=∠HEG,∴∠BEH=∠FGC,∵G是HC的中点,∴HG=GC,∴HE=GC,∵∠HBE=∠CFG=90°.∴△EBH≌△GFC;(2)解:过点H作HI⊥EG于I,∵G为CH的中点,∴HG=GC,∵EF⊥DC,HI⊥EF,∴∠HIG=∠GFC=90°,∠FGC=∠HGI,∴△GIH≌△GFC,∵△EBH≌△EIH(AAS),∴FC=HI=BH=1,∴AD=4-1=3.2、已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC为边,向形外作等边△ABD 和等边△ACE.(1)如图1,连接线段BE、CD.求证:BE=CD;(2)如图2,连接DE交AB于点F.求证:F为DE中点.证明:(1)∵△ABD和△ACE是等边三角形,∴AB=AD,AC=AE,∠DAB=∠EAC=60°,∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,在△DAC和△BAE中,AC=AE ∠DAC=∠BAE AD=AB ,∴△DAC≌△BAE(SAS),∴DC=BE;(2)如图,作DG∥AE,交AB于点G,由∠EAC=60°,∠CAB=30°得:∠FAE=∠EAC+∠CAB=90°,∴∠DGF=∠FAE=90°,又∵∠ACB=90°,∠CAB=30°,∴∠ABC=60°,又∵△ABD为等边三角形,∠DBG=60°,DB=AB,∴∠DBG=∠ABC=60°,在△DGB和△ACB中,∠DGB=∠ACB ∠DBG=∠ABC DB=AB ,∴△DGB≌△ACB(AAS),∴DG=AC,又∵△AEC为等边三角形,∴AE=AC,∴DG=AE,在△DGF和△EAF中,∠DGF=∠EAF ∠DFG=∠EFA DG=EA ,∴△DGF≌△EAF(AAS),∴DF=EF,即F为DE中点.3、如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E.(1)求证:CF=CG;(2)连接DE,若BE=4CE,CD=2,求DE的长.解答:(1)证明:连接AC,∵DC ∥AB ,AB=BC ,∴∠1=∠CAB ,∠CAB=∠2, ∴∠1=∠2;∵∠ADC=∠AEC=90°,AC=AC , ∴△ADC ≌△AEC , ∴CD=CE ;∵∠FDC=∠GEC=90°,∠3=∠4, ∴△FDC ≌△GEC ,∴CF=CG .(2)解:由(1)知,CE=CD=2, ∴BE=4CE=8,∴AB=BC=CE+BE=10,∴在Rt △ABE 中,AE= AB 2-BE 2 =6, ∴在Rt △ACE 中,AC= AE 2+CE 2 =102 由(1)知,△ADC ≌△AEC , ∴CD=CE ,AD=AE ,∴C 、A 分别是DE 垂直平分线上的点, ∴DE ⊥AC ,DE=2EH ;(8分) 在Rt △AEC 中,S △AEC =21 AE •CE=21AC •EH , ∴EH=AC CEAE ⋅ =10226⨯ =5103∴DE=2EH=2×5103=5106 4、如图,AC 是正方形ABCD 的对角线,点O 是AC 的中点,点Q 是AB 上一点,连接CQ ,DP ⊥CQ 于点E ,交BC 于点P ,连接OP ,OQ ;求证:(1)△BCQ ≌△CDP ; (2)OP=OQ .证明:∵四边形ABCD 是正方形, ∴∠B=∠PCD=90°,BC=CD , ∴∠2+∠3=90°,又∵DP ⊥CQ , ∴∠2+∠1=90°, ∴∠1=∠3,在△BCQ 和△CDP 中,∠B=∠PCD BC=CD ∠1=∠3 . ∴△BCQ ≌△CDP . (2)连接OB . 由(1):△BCQ ≌△CDP 可知:BQ=PC , ∵四边形ABCD 是正方形, ∴∠ABC=90°,AB=BC , 而点O 是AC 中点, ∴BO=21AC=CO ,∠4=21∠ABC=45°=∠PCO , 在△BCQ 和△CDP 中, BQ=CP ∠4=∠PCO BO=CO∴△BOQ ≌△COP , ∴OQ=OP .5、在等腰梯形ABCD 中,AD ∥BC ,AB=AD=CD,∠ABC=60°,延长AD 到E,使DE=AD,延长DC 到F ,使DC=CF,连接BE 、BF 和EF.⑴求证:△ABE ≌△CFB; ⑵如果AD=6,tan ∠EBC 的值. 解:(1)证明:连结CE , 在△BAE 与△FCB 中,∵ BA=FC ,∠A=∠BCF ,, AE=BC , ∴△BAE ≌△FCB ;(2)延长BC 交EF 于点G ,作AH ⊥BG 于H ,作AM ⊥BG ,∵△BAE ≌△FCB ,∴∠AEB=∠FBG ,BE=BF ,∴△BEF 为等腰三角形,又∵AE ∥BC , ∴∠AEB=∠EBG ,∴∠EBG=∠FBG ,∴BG ⊥EF ,∵∠AMG=∠EGM=∠AEG=90°, ∴四边形AMGE 为矩形,∴AM=EG , 在Rt △ABM 中,AM=AB •sin60°=6×23=33 ,∴EG=AM=33, BG=BM+MG=6×2+6×cos60°=15,∴tan ∠EBC=531533==BG EG 6、如图,在梯形ABCD 中,AD ∥BC ,∠C=90°,E 为CD 的中点,EF ∥AB 交BC 于点F(1)求证:BF=AD+CF ;ABDECF(2)当AD=1,BC=7,且BE平分∠ABC时,求EF的长.(1)证明:如图(1),延长AD交FE的延长线于N∵∠NDE=∠FCE=90°∠DEN=∠FEC DE=EC∴△NDE≌△FCE ∴DN=CF ∵AB∥FN,AN∥BF∴四边形ABFN是平行四边形∴BF=AD+DN=AD+FC(2)解:∵AB∥EF,∴∠ABN=∠EFC,即∠1+∠2=∠3,又∵∠2+∠BEF=∠3,∴∠1=∠BEF,∴BF=EF,∵∠1=∠2,∴∠BEF=∠2,∴EF=BF,又∵BC+AD=7+1∴BF+CF+AD=8而由(1)知CF+AD=BF∴BF+BF=8∴2BF=8,∴BF=4,∴BF=EF=47、已知:AC是矩形ABCD的对角线,延长CB至E,使CE=CA,F是AE的中点,连接DF、CF分别交AB于G、H点(1)求证:FG=FH;(2)若∠E=60°,且AE=8时,求梯形AECD 的面积.(1)证明:连接BF∵ABCD为矩形∴AB⊥BC AB⊥AD AD=BC∴△ABE为直角三角形∵F是AE的中点∴AF=BF=BE∴∠FAB=∠FBA∴∠DAF=∠CBF∵AD=BC, ∠DAF=∠CBF ,AF=BF ,∴△DAF≌△CBF∴∠ADF=∠BCF∴∠FDC=∠FCD∴∠FGH=∠FHG ∴FG=FH ;(2)解:∵AC=CE ∠E=60° ∴△ACE 为等边三角形 ∴CE=AE=8 ∵AB ⊥BC ∴BC=BE=CE 21=4 ∴根据勾股定理AB=34 ∴梯形AECD 的面积=21×(AD+CE)×CD=21×(4+8)×34=3248、如图,直角梯形ABCD 中,AD ∥BC ,∠BCD=90°,且CD=2AD ,tan ∠ABC=2,过点D作DE ∥AB ,交∠BCD 的平分线于点E ,连接BE . (1)求证:BC=CD ;(2)将△BCE 绕点C ,顺时针旋转90°得到△DCG ,连接EG .求证:CD 垂直平分EG ; (3)延长BE 交CD 于点P .求证:P 是CD 的中点. 证明:(1)延长DE 交BC 于F ,∵AD ∥BC ,AB ∥DF ,∴AD=BF ,∠ABC=∠DFC . 在Rt △DCF 中,∵tan ∠DFC=tan ∠ABC=2, ∴CFCD=2, 即CD=2CF ,∵CD=2AD=2BF , ∴BF=CF , ∴BC=BF+CF=21CD+21CD=CD . 即BC=CD .(2)∵CE 平分∠BCD ,∴∠BCE=∠DCE , 由(1)知BC=CD , ∵CE=CE ,∴△BCE ≌△DCE , ∴BE=DE ,由图形旋转的性质知CE=CG ,BE=DG , ∴DE=DG ,∴C ,D 都在EG 的垂直平分线上, ∴CD 垂直平分EG . (3)连接BD , 由(2)知BE=DE , ∴∠1=∠2. ∵AB ∥DE ,∴∠3=∠2.∴∠1=∠3.∵AD ∥BC ,∴∠4=∠DBC .由(1)知BC=CD ,∴∠DBC=∠BDC ,∴∠4=∠BDP . 又∵BD=BD ,∴△BAD ≌△BPD(ASA)∴DP=AD . ∵AD=21CD ,∴DP=21CD .∴P 是CD 的中点. 9.(2011南岸二诊)如图,已知点P 是正方形ABCD 的对角线AC 上一点,过点P 作EF ⊥DP ,交AB 于点E ,交CD 于点G ,交BC 的延长线于点F ,连接DF .(1)若23=DF ,求DP 的长; (2)求证:CF AE =.10.如图,正方形CGEF 的对角线CE 在正方形ABCD 的边BC 的延长线上(CG >BC ),M 是线段AE 的中点,DM 的延长线交CE 于N . (1)线段AD 与NE 相等吗?请说明理由; (2)探究:线段MD 、MF 的关系,并加以证明.11、如图,梯形ABCD 中,AD ∥BC ,AB=DC=10cm ,AC 交BD 于G ,且∠AGD=60°,E 、F 分别为CG 、AB 的中点.(1)求证:△AGD 为正三角形; (2)求EF 的长度.G 24题图PFEDCBA解答:(1)证明:连接BE,∵梯形ABCD中,AB=DC,∴AC=BD,可证△ABC≌△DCB,∴∠GCB=∠GBC,又∵∠BGC=∠AGD=60°∴△AGD为等边三角形,(2)解:∵BE为△BCG的中线,∴BE⊥AC,在Rt△ABE中,EF为斜边AB上的中线,∴EF=AB=5cm.12、如图,梯形ABCD中,AD∥BC,DE=EC,EF∥AB交BC于点F,EF=EC,连接DF.(1)试说明梯形ABCD是等腰梯形;(2)若AD=1,BC=3,DC=,试判断△DCF的形状;(3)在条件(2)下,射线BC上是否存在一点P,使△PCD是等腰三角形,若存在,请直接写出PB的长;若不存在,请说明理由.解答:解:(1)证明:∵EF=EC,∴∠EFC=∠ECF,∵EF∥AB,∴∠B=∠EFC,∴∠B=∠ECF,∴梯形ABCD是等腰梯形;(2)△DCF是等腰直角三角形,证明:∵DE=EC,EF=EC,∴EF=CD,∴△CDF是直角三角形(如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形),∵梯形ABCD是等腰梯形,∴CF=(BC﹣AD)=1,∵DC=,∴由勾股定理得:DF=1,∴△DCF是等腰直角三角形;(3)共四种情况:∵DF⊥BC,∴当PF=CF时,△PCD是等腰三角形,即PF=1,∴PB=1;当P与F重合时,△PCD是等腰三角形,∴PB=2;当PC=CD=(P在点C的左侧)时,△PCD是等腰三角形,∴PB=3﹣;当PC=CD=(P在点C的右侧)时,△PCD是等腰三角形,∴PB=3+.故共四种情况:PB=1,PB=2,PB=3﹣,PB=3+.(每个1分)13.在梯形ABCD中,AD∥BC,AB=CD,且DE⊥AD于D,∠EBC=∠CDE,∠ECB=45°.⑴求证:AB=BE ;⑵延长BE ,交CD 于F .若CE =2,tan ∠CD E =31,求BF 的长. 13.⑴证明:延长DE ,交BC 于G .∵DE ⊥AD 于D ,∴∠ADE =90°又AD ∥BC , ∴∠DGC =∠BGE =∠ADE =90°, 而∠ECB =45°, ∴△EGC 是等腰直角三角形, ∴EG=CG在△BEG 和△DCG 中,EBG CDG EGB CGD EG CG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BEG ≌△DCG (AAS ) ∴BE=CD=AB ⑵连结BD .∵∠EBC=∠CDE ∴∠EBC +∠BCD =∠CDE +∠BCD =90°,即∠BFC =90° ∵CE=2,∴EG=CG=1又tan ∠CDE =31,∴13CG DG =,∴DG =3 ∵△BEG ≌△DCG ,∴BG=DG=3∴2210BE BG EG =+=∴CD=BE=10法一:∵1122BCDSBC DG CD BF ==,11431022BF ⨯⨯=⨯∴6105BF = 法二:经探索得,△BEG ∽△BFC ,∴BE BCBG BF=,∴1043BF = ∴6105BF = 14.如图,直角梯形ABCD 中,,90,45,AD BC ADC ABC AB ∠=∠=∥的垂直平分线EG 交BC 于F ,交DC 的延长线于.G求证:(1)CG CF =;(2).BC DG =AB CDEF证明:(1) ,AB EF ⊥ 45B ∠=904545EFB ∴∠=-=45CFG ∴∠=//,90AD BC ADC ∠=90FCG ∴∠=45,FCG ∴∠= CG CF =∴(2)连接AF , EF 是AB 的中垂线,AF BF FE AB ∴=⊥45=∠=∠∴BFE AFE90=∠∴AFB DCB AFB ∠=∠∴BC AD CD AF //,// ∴,AF DC BF DC ∴=∴=由(1)知CG CF = ,CG DC CF BF +=+∴即:DG BC =二、有关“截长补短”题型1、在ABCD 中,对角线,BD BC G BD ⊥为延长线上一点且ABG ∆为等边三角形,BAD ∠、CBD ∠的平分线相交于点E ,连接AE BD F 交于,连接GE 。
重庆市近五年中考数学试题分析
重庆市近五年中考数学试题分析近五年重庆市中考数学试题与重庆市教科院发布的考试说明基本一致,试卷的结构稳定,考查的内容每年有少量变化,从题型到考试内容基本固定,在13年,选择题和解答题变化较大。
选择题由过去的10道增加到12道,解答题从10个减至8个。
25题减少了原来比较复杂上的计算和跟数学知识联系不紧密的背景材料,减少了相关阅读量。
由于13年的雅安地震,反比例函数解答题改为一元二次方程运用题。
总体难度逐年有所增加。
1、题型与题量:全卷均为满分150分,三种题型,26个题,其中选择题10个,填空题6个,解答题10个,解答题中第三大题4个小题,每小题6分,第四大题4个小题,每小题10分,第五大题2个小题,共22分。
三种题型的分值比是40:24:86。
占比略为26%、16%、58%。
试卷总体难度安排略为6:2:2,容易题安排在1—7、11—14、17—22小题;中档题安排在8—9、15、23—24小题;较难题为10、16、25、26小题。
2、考察知识情况:3、评析:重庆市近五年的中考数学试题体现了新课程理念的基本要求,在学生已有知识经验和与知识体系相关的现实背景中,考查了基础知识和基本技能、数学活动过程、数学思考、解决问题能力,试题突出考查了学生运用数学知识解决实际问题的能力,加大了对学生后继学习潜能的考查,对方程与不等式、函数与图象、图形变换与坐标、统计与概率等重点内容进行了重点考查,无偏题、怪题,这些数学试题还对学生的情感、态度、价值观的形成起到了积极的引导与影响作用,让学生切实感受到了现实生活中存在大量数学知识信息,数学在现实世界中有着广泛的应用。
试题引导了学生关注社会,关注生活,体现了数学的运用价值,考查了学生在生活中运用数学的意识。
重庆市2001-2012年中考数学试题分类解析专题4:图形的变换

一、选择题1. (重庆市2003年4分)在平行四边形ABCD中,AB=6,AD=8,∠B是锐角,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内的点E处.如果AE过BC的中点,则平行四边形ABCD的面积等于【】A.48 B.. D.【答案】C。
2. (重庆市2006年4分)如图,是有几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是【】A.3B.4C. 5D. 6【答案】B。
【考点】由三视图判断几何体。
【分析】从主视图看第一列两个正方体,说明俯视图中的左边一列有两个正方体,主视图右边的一列只有一行,说明俯视图中的右边一行只有一列,所以此几何体共有四个正方体。
故选B。
3. (重庆市2007年4分)将如图所示的R t A B C△绕直角边A C旋转一周,所得几何体的主视图是【】A. B.C.D.4. (重庆市2008年4分)如图是由4个大小相同的正方体搭成的几何体,其主视图是【】A、 B、 C、 D、5. (重庆市2009年4分)由四个大小相同的正方体组成的几何体如图所示,那么它的左视图是【】A.B.C.D.【答案】A。
【考点】简单组合体的三视图。
【分析】找到从左面看所得到的图形即可:从左面看可得到第一层为2个正方形,第二层左面有一个正方形。
故选A。
6. (重庆市2009年4分)观察下列图形,则第n个图形中三角形的个数是【】A.2n2-D.4n+C.4n4+B.4n47. (重庆市2009年4分)如图,在等腰R t A B C∠=,°,F是AB边上△中,8C90A C=的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①D E F△是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是【】A.①②③B.①④⑤C.①③④D.③④⑤【答案】B。
重庆中考25题几何题(含答案)57693515.docx

1.如图1,矩形ABCD中,AB=4, AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE 交CD 于点F,连接DE.(1)求证:ADEC^AEDA;(2)求DF的值;(3)如图2,若P为线段EC上一动点,过点P作AAEC的内接矩形,使其定点Q落在线段AE 上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的而积最大?并求出其最大值.2、如图1, /\ABC是等边三角形,点E在AC边上,点D是BC边上的一个动点,以DE 为边作等边N)EF,连接CF.(1)当点Q为点3重合时,如图2,求证:CE+CF=CD;(2)当点D运动到如图3的位置吋,猜想CE、CF、CD之间的等量关系,并说明理山;A 4 A(3)只将条件“点D是BC边上的一个动点”改为“点D是BC延长线上的一个动点”,如图4,猜想CE、CF、CD Z间的等量关系为 ______________________ (不必证明).C D3.已知两个全等的等腰肓角ABC. ADEF,其屮ZACB二ZDFE二90° , E为AB屮点,ADEF可绕顶点E旋转,线段DE, EF分别交线段CA, CB(或它们所在直线)于M、N.(1)如图1,当线段EF经过ABC的顶点C时,点N与点C重合,线段DE交AC 于M,求证:AM=MC;(2)如图2,当线段EF与线段BC边交于N点,线段DE与线段AC交于M点,连MN, EC,请探究AM, MN, CN之间的等量关系,并说明理由;(3)如图3,当线段EF与BC延长线交于N点,线段DE与线段AC交于M点,连MN, EC,请猜想AM, MN, CN之间的等量关系,不必说明理由。
设矩形PQMN 的而积为S则 S=PQ ・PN =・-X 2+4X = - - (x--) +3 (0Vx<3) 3 3 2x=-,即PE=」时,短形PQMN 的血积最大,最大血积为3. 2 22、(1)证明:・・・AABC 是等边三角形1. (1)证明:由矩形的性质可知△ADC9ACEA,・・・AD=CE, DC=EA, ZACD=ZCAE,在厶ADE 与厶CED 中r AD=CE< DE 二ED・*.ADEC^AEDA (SSS);DC=EA (2) 解:如图 1,・.・ZACD=ZCAE,・\AF=CF, 设DF=x,贝ijAF=CF=4 ・ x,在RTAADF 屮,AD'+DF 2二AF 2,即32+X 2= (4 - x) 2,解得;x =l f 即DF 二丄8 8(3) 解:如图2,由矩形PQMN 的性质得PQ 〃CA.PE_PQ ^CE^CA 又 VCE=3, AC=A /AB 2+BC 2=5设PE=x (0<x<3),则2县,即PQ=-X 3 53 .CP_PN*CE _EG过E 作EG 丄AC 于G,贝lJPN 〃EG, 又・・•在RtAAEC 屮,EG ・AC=AE ・CE, 解得EG =¥ 54幕即PN 」(3・x) 3 5 所以当・・・ AB = BC = AC, ZABC= ZACB = 60・・・ABEF是等边三角形・•・ BE = BF, ZEBF = 60°・•・ ZABC= ZEBF即Z1 + Z2= Z2+ Z3・・・Z1 = Z3在Z\ABE fDACBF'P,图2 AB = BCI Z1 = Z3BE = BF・・・ AABE 9 ACBF (SAS)・・・AE = CF・・• AC = CE + AE・•・ AC = CE + CF・・・CE + CF = CD(2)解:CE二CF + CD,理由女U下: .........................................................1分过点D作DG〃AB,交AC于G..............................................................................1分・•・ ZGDC= ZABC = 60° = ZACB・・・AGDC是等边三角形....・•・ GD = DC = CG, ZGDC = 60°・・・ADEF是等边三角形・•・ DE = DF, ZEDF = 60°・•・ ZEDF= ZGDC即Z1 + Z2= Z2 + Z3・・・Zl= Z3在Z\EDG 和ZXFDC 中,DE = DF图3Z1 = Z3GD = DC・•・ AEDG 幻AFDC (SAS)・・・EG = CF・・• CE = EG + CG・•・ CE = CF + CGJ CD = CG・•・ CE = CF + CD .................(3)只将条件“点D是BC边上的一个动点”改为“点D是3C延长线上的一个动点”,如图4,猜想CE、CF、CD之间的等量关系为CF二CE + CD(不必证明).(1分)3、(1) VAC=BC, E 为4B 屮点/. CEA.AB, ZACE= ZBCE =-ACB=45°2・•・ ZAEC=90°・•・ZA=ZACE=45°・・・AE=CE1分•: DF=EF, ZDFE=90°・•・ZFED=45°・•・ ZFED=丄ZAEC2又*:AE=CE・•• AM=MC ........................................................................... 3分(2) AM=MN+CN,理由如下:--------------------------------------------------------- 4分在AM截収AH,使得AH=CN,连接由(1)矢U AE=CE f ZA=ZBCE=45°AH = CN在MHE A/NCNE 'I': J ZA =ZN CE AAHE9 ACNEAE = CE•••HE=NE, ZAEH=ZCEN••• ZHEM=ZAEC— ZAEH-MEC=ZAEC- ZCEN~MEC= ZAEC-ZMEF=9(f-45<>=450••• ZHEM=ZNEM=45°AH =CN在AHEM与\NEM中:\zA = ZNCE ••- 'HEM竺\NEMAE = CE••• HM=MN••• AM二AH+HM二CN +MN即AM=MN+CN-7分(3)猜得MN = AM +CN-8分。
届重庆中考复习重庆中考几何题分类汇编含答案

重庆中考几何题分类汇编(含答案)类型1线段的倍分:要证线段倍与半,延长缩短去实验例1如图Z3-1,在△ABC中,AB=AC,CM平分∠ACB交AB于M,在AC的延长线上截取CN=BM,连接MN交BC于P,在CB的延长线截取BQ=CP,连接MQ.(1)求证:MQ=NP;(2)求证:CN=2CP.针对训练:1.如图Z3-2,在?ABCD中,AC⊥BC,点E、点上,且满足AC=AE=CF,连接CE、AF、EF.(1)若∠ABC=35°,求∠EAF的度数;(2)若CE⊥EF,求证:CE=2EF.2.已知,在△ABC中,AB=AC,∠BAC=90°,E为AC 任意一点,连接BE.(1)如图①,若∠ABE=15°,O为BE中点,连接AO1,求BC的长;(2)如图②,F也为AC上一点,且满足AE=CF,过A作于点D,连接DF交BE于点G,连接AG.若AG平分∠CAD,求证:AH=AC.3.在△ACB中,AB=AC,∠BAC=90°,点D是AC上一点,连接BD,过点A作AE⊥BD 于E,交BC于F.(1)如图①,若AB=4,CD=1,求AE的长;(2)如图②,点G是AE上一点,连接CG,若BE=AE+AG,求证:CG=AE.4.在等腰直角三角形ABC中,∠BAC=90°,AB=AC,D是斜边BC的中点,连接AD.(1)如图①,E是AC的中点,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′,当AD=时,求AE′的值.(2)如图②,在AC上取一点E,使得CE=AC,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′交BC于点F,求证:DF=CF.类型2线段的和差:要证线段和与差,截长补短去实验例2如图,在△ABC中,∠BAC=90=BA,连接AD,在AD左侧作∠E.(1)若AC=3,则CE=________(答案);(2)如图①,M、N分别为AB和AC上的点,且AM=AN,连接EM、DN∠AND=180°,求证:DE=DN+(3)如图②,过E作EF⊥AE,交AD的延长线于F,在EC 上选取一点H,使得EH=BE,连接FH,在AC上选取一点G,使得AG=AB,连接BG、FG,求证:FH=FG.针对训练:1.如图Z3-7,在?ABCD中,AE⊥BC于E,AE=AD,EG⊥AB于G,延长GE、DC交于点F,连接AF.(1)若BE=2EC,AB=,求AD的长;(2)求证:EG=BG+FC.2.如图,在正方形ABCD中,点P为ADAC、CP,过点C作CF⊥CP于点C,交AB于点FBM⊥CF于点N,交AC于点M.(1)若AP=AC,BC=4,求S△ACP;(2)若CP-BM=2FN,求证:BC=MC.3.如图,在△ABC中,AB=BC,以AB为一作菱形ABDE,连接DC,EB并延长EB交AC于CB⊥AE于G.(1)若∠EBG=20°,求∠AFE;(2)试问线段AE,AF,CF之间的数量关系并证类型3倍长中线:三角形中有中线,延长中线等中例3如图Z3-10①,在Rt△ABC中,∠ABC=90E分别为斜边AC上两点,且AD=AB,CE=CB,连接(1)求∠EBD的度数;(2)如图Z3-10②,过点D作FD⊥BD于点D,交于点F,在AB上选取一点H,使得BH=BC,连接AC上选取一点G,使得GD=CD,连接FH、FG证:FH=FG.针对训练:1.如图,已知在?ABCD中,G为BC的中点,点E在AD边上,且∠1=∠2.(1)求证:E是AD中点;(2)若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.2.如图Z3-12,在菱形ABCD中,点E、F分别是BC、CD上的点,连接AE,AF,DE、EF,∠DAE=∠BAF.(1)求证:CE=CF;(2)若∠ABC=120°,点G是线段AF的中点,连接DG,EG.求证:DG⊥GE.3.在Rt△ABC中,∠ACB=90°,点D与点B同侧,∠ADC>∠BAC,且DA=DC,过点B作BE∥DA于点E,M为AB的中点,连接MD,ME.(1)如图①,当∠ADC=90°时,线段MD与________;(2)如图②,当∠ADC=60°时,试探究线段的数量关系,并证明你的结论;(3)如图③,当∠ADC=α时,求的值.4.如图①,等边三角形ABC中,CE平分∠ACB,D为BC边上一点,且DE=CD,连接BE.(1)若CE=4,BC=6,求线段BE的长;(2)如图②,取BE中点P,连接AP,PD,AD,求证:AP⊥PD且AP=PD;(3)如图③,把图Z3-14②中的△CDE绕点C顺时针旋转任意角度,然后连接BE,点P为BE中点,连接AP,PD,AD,问第(2)问中的结论还成立吗?若成立,请证明;若不成立,请说明理由.5.在△ABC中,以AB为斜边,作直角三角形ABD,使点D落在△ABC内,∠ADB=90°.(1)如图①,若AB=AC,∠BAD=30°,AD=6,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;(2)如图②,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP;(3)如图③,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).类型4中位线:三角形中两中点,连接则成中位线例42017·河南如图①,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC 上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.(1)观察猜想:图①中,线段PM与PN的数量关系是__________,位置关系是__________;(2)探究证明:把△ADE绕点A按逆时针方向旋转到图②的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;(3)拓展延伸:把△ADE绕点A,AB=10,请直接写出△PMN面积的最大值.针对训练:1.如图①,在任意的三角形ABC以AB和AC为一边作等腰三角形ABE和等腰三角形ACD,AB=AE,AC=AD,且∠BAE+∠CAD=180°,连接DE,延长CA交DE于F.(1)求证:∠CAB=∠AED+∠ADE;(2)若∠ACB=∠BAE=∠CAD=90°,如图②,求证:BC=2AF;(3)若在△ABC中,如图③所示,作等腰三角形ABE和等腰三角形ACD,AB与DE交于点F,F为DE的中点,请问(2)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.2.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE、CD,F为BE的中点,连接AF.(1)如图①,当∠BAE=90°时,求证:CD=2AF;(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.3.如图①,在等腰三角形ABC中,AB=AC,在底边BC上取一点D,在边AC上取一点E,使AE=AD,连接DE,在∠ABD的内部作∠ABF=2∠EDC,交AD于点F.(1)求证:△ABF是等腰三角形;(2)如图②,BF的延长交AC于点G.若∠DAC=∠CBG,延长AC至点M,使GM=AB,连接BM,点N是BG的中点,连接AN,试判断线段AN、BM之间的数量关系,并证明你的结论.类型5角的和差倍分称以后关系现.垂线,三线合一试试看.例5.如图,把△EFP放置在菱形ABCD使得顶点E,F,P分别在线段AB,AD,上,已知EP=FP=6,EF=6,∠BAD=60°,且AB>6.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值.针对训练:1.已知:如图①,AD平分∠BAC,∠B+∠C==90°,易知:DB=DC.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB =DC.2.在△ACB中,AB=AC,∠BAC=90°,点D是AC上一点,连接BD,过点A作AE⊥BD于E,交BC于F.(1)如图①,若AB=4,CD=1,求AE的长;(2)如图②,点P是AC上一点,连接FP,若AP=CD,求证:∠ADB=∠CPF.3.已知,在?ABCD中,∠BAD=45°,AB=BD,E为BC上一点,连接AE交BD于F,过点D作DG⊥AE于G,延长DG交BC于H.(1)如图①,若点E与点C重合,且AF=,求AD的长;(2)如图②,连接FH,求证:∠AFB=∠HFB.4.如图,将正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD 边上的点M处,点C落在点N处,MN与CD交于点P,连接EP.当点M在边AD上移动时,连接BM、BP.(1)求证:BM是∠AMP的平分线;(2)△PDM的周长是否发生变化?证明你的结论.类型6旋转型全等问题:图中若有边相等,可用旋转例6.△ABC中,∠BAC=90°,AB=AC,点D上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.(1)观察猜想:如图①,当点D在线段BC上时,①BC的位置关系为:________.②BC,CD,CF之间的数量关系为:___________;(将接写在横线上)(2)数学思考:如图Z3-25②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸:如图Z3-25③,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请求出GE的长.针对训练:1.在四边形ABCD中,∠B180°,对角线AC平分∠(1)如图①,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC(2)如图②,若将(1)中的条件“∠B=去掉,(1)中的结论是否成立?请说明理由.(3)如图③,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.2.如图①,在正方形ABCD中,点E为边BC上一点,将△ABE沿AE翻折得△AHE,延长EH交边CD于F,连接AF.(1)求证:∠EAF=45°;(2)延长AB,AD,如图②,射线AE、AF分别交正方形两个外角的平分线于M、N,连接MN,若以BM、DN、MN为三边围成三角形,试猜想三角形的形状,并证明你的结论.3.如图①,在正方形ABCD内有一点P,PA=,PB=,PC=1,求∠BPC的度数.【分析问题】根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图Z3-28②),然后连接PP′.(1)请你通过计算求出图Z3-28②中∠BPC的度数;(2)如图③,若在正六边形ABCDEF内有一点P,且PA=2,PB=4,PC=2.请求出∠BPC 的度数.重庆中考几何题分类汇编答案例1.证明:(1)∵AB=AC,∴∠ABC=∠ACB.∵∠MBQ+∠ABC=180°,∠ACB+∠PCN=180°,∴∠MBQ=∠PCN.在△QBM和△PCN中,∴△QBM≌△PCN(SAS).∴MQ=NP.(2)过M作MG∥AC交BC于G,∵MG∥AC,∴∠MGB=∠ACB,∠MGC=∠PCN,∵由(1)知,∠ABC=∠ACB,∴∠ABC =∠MGB,∴MB=MG,∵MB=CN,∴MG=CN.在△MGP和△NCP中,∴△MGP≌△NCP(AAS).∴PG=CP,∴CG=CP+PG,即CG=2CP.∵CM平分∠ACB,∴∠BCM=∠MCA,∵MG∥AC,∴∠MCA=∠GMC,∴∠BCM=∠GMC,∴MG=CG,∵MG=CN,∴CN=CG,∴CN=2CP.针对训练1.解:(1)∵AC⊥BC,∴∠ACB=90°,又∵AC=CF=45°,∵∠ABC=35°,∴∠EAF=10°;(2)证明:方法1:取CF的中点M,连接EM、AM,∵CE⊥EF,∴EM=CM=FM=CF,又∵AC=AE,∴AM为EC的中垂线,∴∠CAM+90°,又∵∠ECF+∠ACE=90°,∴∠CAM=∠FCE,又∵∠CEF=∠ACM=90°,∴△ACM∽△CEF又∵CF=AC=2CM,∴==,即CE=2EF;方法2:延长FE至M,使EF=EM,连接CM,∵CE⊥EF,∴△CMF为等腰三角形,又∵AC=AE=CF,且∠ACE=∠CFE(易证),∴△CMF≌△CEA,∴FM=CE=2EF.2.解:(1)如图①,在AB上取一点M,使得BM=ME,在Rt△ABE中,∵OB=OE,∴BE=2OA=2,∵MB=ME,∴∠MBE=∠MEB=15°,∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=x,∵AB2+AE2=BE2,∴(2x+x)2+x2=22,∴x=(负根舍弃),∴AB=AC=(2+)·,∴BC=AB=+1.(2)证明:如图②,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.∵BE⊥AP,∴∠AHB=90°,∴∠ABH+∠BAH=90°,∵∠BAH+∠PAC=90°,∴∠ABE=∠PAC,又∵AB=AC,∠BAE=∠ACP=90°,∴△ABE≌△CAP,∴AE=CP=CF,∠AEB=∠P,在△DCF和△DCP中,∴△DCF≌△DCP,∴∠DFC=∠P,∴∠GFE=∠GEF,∴GE=GF,∵GM⊥EF,∴FM=ME,∵AE=CF,∴AF=CE,∴AM=CM,在△GAH和△GAM中,∴△AGH≌△AGM,∴AH=AM=CM=AC.3.解:(1)∵AB=4,∴AC=AB=4.∵CD=1,∴AD=AC-CD=3.∵在Rt△ABD中,∠BAC=90°,∴BD==5,∵S=AB·AD=AE·BD,∴AE=2.4.△ABD(2)证明:如图,在线段EB上截取EH=AE∵AE⊥BD,EH=AE,∴AH=AE.∵BE=AE+AG,∴BH=BE-HE=AG.∵∠BAD=∠BEA=90°,∴∠ABE+∠BAE=∠CAG+∠BAE=90°,∴∠ABE=∠CAG.∵BA=AC,∴△ABH≌△CAG,∴CG=AH=AE.4.解:(1)∵∠BAC=90°,AB=AC,D是斜边BC的中点,∴∠ADC=90°,∠ACD=45°.在Rt△ADC中,AC=AD÷sin45°=2.∵E是AC的中点,∴CE=AC=.∵将△CDE沿CD翻折到△CDE′,∴CE′=CE=,∠ACE由勾股定理,得AE′==.(2)证明:如图,过B作AE′的垂线交AD于点G,交AC∵∠ABH+∠BAF=90°,∠CAF+∠BAF=90°,∴∠ABH∠CAF.又∵AB=AC,∠BAH=∠ACE′=90°,∴△ABH≌△CAE′.∴AH=CE′=CE,∵CE=AC,∴AH=HE=CE.∵D是BC中点,∴DE∥BH,∴G是AD中点.在△ABG和△CAF中:AB=AC,∠BAD=∠ACD=45°,∠ABH=∠CAF,∴△ABG≌△CAF.∴AG=CF.∵AG=AD,∴CF=AD=CD.∴DF=CF.类型2线段的和差:要证线段和与差,截长补短去实验例2:解:(1)3(2)证明:延长DN到K,使得NK=ME,连接AK,如图①,因为∠1+∠3=180°,∠1+∠2=180°,∴∠2=∠3.在△AME和△ANK中,∴△AME≌△ANK(SAS).∴AE=AK,∠4=∠5,∴∠4+∠EAC=90°,∴∠5+∠EAC=90°,即∠EAK∵∠EAD=45°,∴∠KAD=∠EAK-∠EAD=90°-∴∠EAD=∠KAD.在△EAD和△KAD中,∴△EAD≌△KAD(SAS),∴ED=KD.∵DK=DN+KN,∴ED=DN+KN,又NK=ME,∴ED=DN+ME.(3)证明:延长AE到J,使得EJ=AE,连接JH,JF.如图②,在△ABE和△JHE中,∴△ABE≌△JHE(SAS),∴JH=AB,∠1=∠2,∵AB=AG,∴JH=AG,∵AE=EJ,EF⊥AJ,∴AF=JF,∴∠JAF=∠AJF=45°,即∠2+∠3=45°,∵∠BAC=90°,∴∠1+∠EAD+∠4=90°,∴∠1+∠4=90°-∠EAD,=90°-45°=45°,∵∠1=∠2,∴∠3=∠4,在△JHF和△AGF中,∴△JHF≌△AGF(SAS),∴FH=FG.针对训练:1.解:(1)∵四边形ABCD是平行四边形,∴AD=BC.∵BE=2EC,设CE=x,BE=2x,∴BC=AD=AE=又∵EG⊥AB,∴∠AEB=90°,∴AB2=AE2+BE2,即13=9x2+4x2,∴x=1,∴AD=3x=3.(2)证明:如图,过C作CH⊥AB于H,则四边形形.∴CF=HG,∠CHB=90°,GF=CH.∵AE⊥BC,EG⊥AB,∴∠AEB=∠CHB=90°,∠BCH+∠B=90°,∠BAE+∠B=90°,∴∠BCH又∵AE=BC,∴△AGE≌△CHB,∴GE=BH,AG=∴GE=BH=BG+GH=BG+CF.2.解:(1)∵四边形ABCD是正方形,BC=4,∴AB=AD=CD=BC=4,∠ADC=∠ABC=90°.∵在Rt△ABC中,AC==4,∴AP=AC=,=AP·CD=7.∴S△ACP(2)证明:方法一:如图①,在NC上截取NK=NF,连接BK.∵四边形ABCD是正方形,∴AB=BC=DC,∠ABC=∠BCD=∠ADC=90°.∵∠BCD=90°,CF⊥CP,∴∠1+∠DCF=∠2+∠DCF=90°,∴∠1=∠2,∵在△FBC和△PDC中,∴△FBC≌△PDC(ASA),∴CF=CP,∵CP-2FN=BM,∴CF-FK=BM,即CK=BM,∵∠FBC=90°,BM⊥CF,∴∠1+∠NBC=∠4+∠NBC∴∠1=∠4,∵在△ABM和△BCK中,∴△ABM≌△BCK(SAS),∴∠7=∠6.∵BM⊥CF,NK=NF,∴BF=BK,∵BF=BK,BM⊥CF∠5,∴∠4+∠7=∠5+∠6,∵∠8=∠4+∠7,∴∠8=∠MBC,∴BC=MC.解:方法二:如图②,延长BM交AD于点G,过A作AE⊥BGE先证△AEB≌△BNC(AAS),∴AE=BN,又证△AEG≌△BNF(AAS),∴EG=NF,再证四边形BCPG为平行四边形,∴BG=CP,∵CP-BM=2FN,∴BG-BM=2EG,∴MG=2EG,∴点E为MG中点,∵AE⊥MG,EM=EG,∴AM=AG,∴∠3=∠4,∵∠2=∠3,∠1=∠4,∴∠1=∠2,∴BC=MC.3.解:(1)∵∠EBG=20°,CB⊥AE,∴∠BEG=70o,∠CBF=∠EBG=20°,∵四边形ABDE是菱形,∴∠ABE=∠BEG=70°,∴∠ABG=50°,∵AB=BC,∴∠FCB=25°,∴∠AFE=∠CBF+∠FCB=45°;(2)AE,AF,CF之间的数量关系是AF2+CF2=2AE2,证明如下:连接DF,∵四边形ABDE是菱形,∴AB=DB,∠DBE=∠ABE,∴∠DBF=∠ABF,∵BF=BF,∴△DBF≌△ABF(SAS),∴DF=AF,∠BDF=∠BAF,∵∠BCF=∠BAF,∴∠BCF=∠BDF,∵CB⊥AE,AE∥DB,∴DB⊥CB,∵CB=AB=BD,∴△DBC是等腰直角三角形,∴DC=BD=AE,∵∠DPB=∠CPF,∴∠CFP=∠DBP=90°,∴DF2+CF2=DC2,即有:AF2+CF2=2AE2.类型3倍长中线:三角形中有中线,延长中线等中线例3解:(1)设∠BEC=α,∠BDA=β,则∠C=180°-2α,∠A=180°-2β.∵在Rt△ABC中,∠ABC=90°,∴∠A+∠C=90°,即180°-2α+180°-2β=90°,∴α+β=135°,∴∠EBD=45°.(2)证明:法一:如图①,延长BD至点B′,使得在△GDB′和△CDB中,∴△GDB′≌△CDB.∴GB′=BC=BH,∠GB′D∵FD⊥BD,BD=DB′,∴FB=FB′.∵∠FB′G=45°-∠GB′D,∠HBF=90°-45°-∠CBD=45°-∠CBD,∴∠FB′G=∠HBF.在△FHB和△FGB′中,∴△FHB≌△FGB′,∴HF=GF.法二:如图②,延长FD至点F′,使得DF′=BF′.先证△DGF≌△DCF′,再证△BHF≌△BCF′,∴HF=GF.针对训练1.证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠A=∠C.又∵∠1=∠2,∴△ABE≌△CDG(ASA),∴AE=CG.∵G为BC中点,∴CG=BC,∴AE=CG=BC=AD,∴E是AD中点.(2)如图,延长BE,CD交于点H.∵四边形ABCD是平行四边形,∴AB綊CD,∴∠A=∠ADH,∠1=∠4,又∵∠1=∠2,∠3=∠2,∴∠1=∠2=∠3=∠4,∴FH=FB.由(1),E是AD中点,∴AE=DE,∴△ABE≌△DHE(AAS),∴AB=DH,∴CD=AB=DH=DF+FH=DF+BF,即CD=BF+DF.2.证明:(1)在菱形ABCD中,AB=BC=CD=AD,∠ADF=∠ABE,∵∠DAE=∠BAF,∴∠DAE-∠EAF=∠BAF-∠EAF,即∠DAF=∠BAE.∴△DAF≌△BAE,∴BE=DF.又∵BC=CD,∴CE=CF(2)如图,延长DG交AB于H,连接EH,∵在菱形ABCD中,AB∥CD,∴∠DFA=∠GAH.∵G为AF中点,∴AG=GF.又∵∠DGF=∠AGH,∴△DGF≌△HGA.∴DG=DF.又∵AB=CD,∴BH=CF.又∵AB∥CD,∠ABC=120°,∴∠C=60°.又∵CE=CF,∴△CEF为等边三角形,∴CF=EF,∠CFE=60°,∴EF=BH,∠DFE=∠ABC=120°.又∵BE=DF,∴△EFD≌△HBE,∴HE=ED,又∵HG=DG,∴DG⊥GE.3.解:(1)MD=ME2)MD=ME.理由如下:如图①,延长EM交DA于点F.∵BE∥DA,∴∠FAM=∠EBM.又∵AM=BM,∠AMF=∠BME,∴△AMF≌△BME,∴AF=BE,MF=ME.∵DA=DC,∠ADC=60°,∴∠BED=∠ADC=60°,∠ACD=60°.∵∠ACB=90°,∴∠ECB=30°,∴∠EBC=30°,∴CE=BE,∴AF=EC,∴DF=DE,∴DM⊥EF,DM平分∠ADC,∴∠MDE=30°.在Rt△MDE中,tan∠MDE==.∴MD=ME.(3)如图②,延长EM交DA于点F,∵BE∥DA,∴∠FAM=∠EBM,又∵AM=BM,∠AMF=∠BME,∴△AMF≌△BME,∴AF=BE,MFME.延长BE交AC于点N,∴∠BNC=∠DAC.∵DA=DC,∴∠DCA=∠DAC,∴∠BNC=∠DCA,∵∠ACB=90°,∴∠ECB=∠EBC,∴CE=BE,∴AF=CE.∴DF=DE,∴DM⊥EF,DM平分∠ADC,∵∠ADC=α,∴∠MDE=.∴在Rt△MDE中,=tan∠MDE=tan.4.解:(1)如图①,作EH⊥BC于点H.∵△ABC是等边三角形,∴∠ACB=60°.∵CE平分∠ACB,∴∠ECH=∠ACB=30°,∵EC=4,∠ECH=30°,∴EH=2,HC=2.∵BC=6,∴BH=6-2=4.在Rt△BHE中,BE2=(4)2+22=52,∴BE=2.(2)如图②,延长DP至M,使DP=PM,连接BM、AM.在△PDE和△PMB中,∴△PDE≌△PMB(SAS).∴BM=DE,∠1=∠2.∴BM∥DE.∴∠MBD+∠BDE=180°.∵CE平分∠ACB,DE=CD,∴∠BDE=30°+30°=∴∠MBD=120°.∵△ABC是等边三角形,∴∠ABC=60°,∴∠3=60∵BM=DE,DE=CD,∴BM=CD.在△ABM和△ACD中,∴△ABM≌△ACD(SAS).∴AD=AM,∠4=∠5.∵PD=PM,∴AP⊥PD.∵∠4=∠5,∠BAD+∠5=60°,∴∠4+∠BAD=60°,即∠MAD=60°.∴∠PAD=∠MAD=30°.∵在Rt△APD中,tan30°=,∴AP=PD.(3)第(2)问中的结论成立,理由如下:如图③,延长DP至N,使DP=PN,连接BN、AN,取BE、AC交于点O.在△PDE∴△PDE≌△PNB(SAS).∴BN=DE,∠1=∠2.∵DE=CD,∴BN=CD.∵∠AOB=∠EOC,∴∠1+∠3+∠BAO=∠2+∠4+∠DEC+∠DCE.∵∠BAO=60°,∠DEC=∠DCE=30°,∴∠1+∠3=∠2∠4,∴∠3=∠4.在△ABN和△ACD中,∴△ABN≌△ACD(SAS).∴∠5=∠6,AN=AD.∵PD=PN,∴AP⊥PD.∵∠NAC+∠5=60°,∴∠NAC+∠6=60°,即∠NAD=60°.∴∠PAD=∠NAD=30°,∵在Rt△APD中,tan∠PAD=,∴AP=PD.5.解:(1)∵∠ADB=90°,∠BAD=30°,AD=6,∴cos∠BAD=,∴=,∴AB=12.又∵AB=AC,∴AC=12,∴PM为△ABC的中位线,∴PM=AC=6.(2)证明:方法一:如图①,在截取ED上截取EQ=∵∠ADB=90°,∴∠1+∠2=90°,又∵AD=AE,∴∠2=∠3,又∵∠3+∠4=90°,∴∠1=∠4.在△BDP和△CEQ中,PD=QE,∠1=∠4,BD=CE∴△BDP≌△CEQ.∴BP=CQ,∠DBP=∠QCE,又∵∠5=∠1+∠DBP,∠6=∠4+∠QCE,∴∠5=∠6,∴PC=CQ,∴BP=CP.方法二:如图②,过点B作EP的垂线交EP的延长线于点M,过C的垂线交EP于点N.∵∠ADB=90°,∴∠1+∠2=90°,又∵AD=AE,∴∠2=∠3,又∵∠3+∠4=90°,∴∠1=∠4,在△BMD和△CNE中,∠1=∠4,∠BMD=∠CNE=90°,BD=CE,∴△BMD≌△CNE.∴BM=CN.在△BMP和△CNP中,∠5=∠6,∠BMP=∠CNP,BM=CN,∴△BMP≌△CNP,∴BP=CP.方法三:如图③,过点B作BM∥CE交EP.略证△BMP≌△CEP,∴BP=CP.(3)BF2+FC2=2AD2.类型4中位线:三角形中两中点,连接则成中位线例4:解:(1)PM=PN;PM⊥PN(2)△PMN为等腰直角三角形,理由如下:由题意知△ABC和△ADE均为等腰直角三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=90°,∴∠BAD+∠DAC=∠CAE+∠DAC,∴∠BAD=∠CAE,∴△BAD≌△CAE,∴∠ABD=∠ACE,BD=CE.又∵M、P、N分别是DE、CD、BC的中点,∴PM是△CDE的中位线,∴PM∥CE且PM=CE,∠MPD=∠ECD=∠ACD+∠ACE.同理,PN∥BD且PN=BD,∠DBC=∠PNC,又∵BD=CE,∠ABD=∠ACE,∴PM=PN,∴∠MPN=∠MPD+∠DPN=∠ECD+∠DCN+∠CNP=∠ACD+∠ACE+∠DCN+∠CBD=∠ACD+∠DCN+∠ABD+∠CBD=∠ACB+∠ABC=90°,∴PM⊥PN,∴△PMN为等腰直角三角形;(3)△PMN面积的最大值为.提示:在旋转的过程中,由(2)中的结论知△PMN为等腰直角三角形,S△PMN=PN2=BD2,当S△PMN有最大值时,则BD的值最大,由三角形三边关系可推断出当B、A、D三点共线时,BD的值最大,其最大值为14,此时S=PN2=BD2=×14×14=.△PMN针对训练:1.解:(1)证明:延长DA交BE于G点.∵∠BAE+∠CAD=180°,即∠EAG+∠GAB+∠CAD=180°,∵∠GAB+∠BAC+∠CAD=180°,∴∠EAG=∠CAB.∵∠EAG=∠AED+∠ADE,∴∠CAB=∠AED+∠ADE.(2)证明:如图①,过E点作DA延长线的垂线,垂足为H.∴∠AHE=∠ACB=90°,由(1)可知,∠EAH=∠BAC,又∵AE=AB,∴△AHE≌△ACB,∴EH=BC,AH=AC.∵AC=AD,∴AH=AD.∵∠EHA=∠FAD=90°,∴AF∥EH.∵A为DH中点,∴AF为△DHE中位线,∴EH=2AF,∴BC=2AF.(3)成立.证明如下:如图②,延长DA至M点,使AM=DA,连接EM,∵∠BAE+∠CAD=180°,∠CAD+∠CAM=180∴∠BAE=∠CAM,∴∠BAE+∠CAC=∠CAM+∠EAC,即∠BAC=∠CAM.∵AM=AD,AD=AC,∴AM=AC.又∵AB=AE,∠BAC=∠EAM,∴△BAC≌△EAM,∴BC=EM.∵F、A分别为DE、DM中点,∴AF为△DEM中位线,∴EM=2AF,∴BC=2AF.2.解:(1)证明:∵∠BAC+∠EAD=180°,∠BAE=90°,∴∠DAC=90°,在△ABE与△ACD中,AE=AD,∠BAE=∠CAD=90°,AB=AC,∴△ABE≌△ACD(SAS),∴CD=BE,∵在Rt△ABE中,F为BE的中点,∴BE=2AF,∴CD=2AF.(2)成立,证明:如图,延长EA交BC于G,在AG上截取∵∠BAC+∠EAD=180°,∴∠EAB+∠DAC=180°,∵∠EAB+∠BAH=180°,∴∠DAC=∠BAH,在△ABH与△ACD中,AH=AD,∠BAH=∠CAD,AB=AC,∴△ABH≌△ACD(SAS),∴BH=DC,∵AD=AE,AH=AD,∴AE=AH,∵EF=FB,∴BH=2AF,∴CD=2AF.3.解:(1)证明:∵AB=AC,∴∠ABD=∠ACD,∵AE=AD,∴∠ADE=∠AED,∵∠BAD+∠ABD=∠ADE+∠EDC,∠EDC+∠ACD∴∠BAD=2∠EDC,∵∠ABF=2∠EDC,∴∠BAD=∠ABF,∴△ABF是等腰三角形;(2)方法一:如图①,延长CA至点H,使AG=AH,连接BH,∵点N是BG的中点,∴AN=BH,∵∠BAD=∠ABF,∠DAC=∠CBG,∴∠CAB=∠CBA,∴△ABC是等边三角形.∴AB=BC=AC,∠BAC=∠BCA=∵GM=AB,AB=AC,∴CM=AG,∴AH=CM,在△BAH和△BCM中,∴△BAH≌△BCM(SAS),∴BH=BM,∴AN=BM,方法二:如图②,延长AN至K,使NK=AN,连接KB,同方法一,先证△ABC是等边三角形,再证△ANG≌△KNB(SAS),所以BK=AG=CM,然后可以证得∠ABK=∠BCN=120°,最后证△ABK≌△BCN(SAS),所以BM=AK=2AN.类型5角的和差倍分例5:解:(1)如图,过点P作PG⊥EF于G.∵PE=PF=6,EF=6,∴FG=EG=3,∠FPG=∠EPG=∠EPF.在Rt△FPG中,sin∠FPG===.∴∠FPG=60°,∴∠EPF=2∠FPG=120°.(2)如图,作PM⊥AB于M,PN⊥AD于N.∵AC为菱形ABCD的对角线,∴∠DAC=∠BAC,AM=AN,PM=PN.在Rt△PME和Rt△PNF中,PM=PN,PE∴Rt△PME≌Rt△PNF,∴NF=ME.又∵AP=10,∠PAM=∠DAB=30°,∴AM=AN=AP cos30°=10×=5.∴AE+AF=(AM+ME)+(AN-NF)=AM+AN=10.针对训练:1.证明:如图,过D作DE⊥AB于E,过D作DF⊥AC于F,∵DA平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF,∵∠B+∠ACD=180°,∠ACD+∠FCD=180∴∠B=∠FCD,在△DFC和△DEB中,∴△DFC≌△DEB,∴DC=DB.2.解:(1)∵AC=AB=4,且CD=1,∴AD=AC-CD=3.在Rt△ABD中,∠BAD=90°,∴BD==5,∵S=AB·AD=AE·BD,△ABD∴AE=2.4.(2)证明:如图,取BC的中点M,连接AM交BD于点N.∵∠BAC=90°,AB=AC,点M为BC的中点,∴AM=BM=CM,AM⊥BC,∠NAD=∠FCP=45°,∴∠AMF=∠BMN=90°.∵AE⊥BD,∴∠MAF+∠ANE=∠MBN+∠BNM=90°,又∠ANE=∠BNM,∴∠MAF=∠MBN,∴△AMF≌△BMN,∴MF=MN,∴AM-MN=CM-MF,即AN=CF.∵AP=CD,∴AC-CD=AC-AP,即AD=CP.∴△ADN≌△CPF,∴∠ADB=∠CPF.3.解:(1)∵AB=BD,∠BAD=45°,∴∠BDA=45°,即∠ABD=90°.∵四边形ABCD是平行四边形,∴当E、C重合时,BF=BD=AB.∵在Rt△ABF中,AB2+BF2=AF2,∴(2BF)2+BF2=()2,∴BF=1,AB=2.在Rt△ABD中,AD===2.(2)证明:如图,在AF上截取AK=HD,连接BK.∵∠AFD=∠ABF+∠2=∠FGD+∠3且∠ABF=∠FGD=90°,∴∠2=∠3.在△ABK与△DBH中,∴△ABK≌△DBH,∴BK=BH,∠6=∠5.∵四边形ABCD是平行四边形,∴AD∥BC,∴∠5=∠4=45°,∴∠6=∠5=45°,∴∠7=∠ABD-∠6=45°=∠5.在△BFK与△BFH中,∴△BFK≌△BFH.∴∠BFK=∠BFH,即∠AFB=∠HFB.4.解:(1)证明:由折叠知∠EMN=∠ABC=90EM,∴∠EMB=∠EBM,∴∠EMN-∠EMB=∠ABC-∠EBM,即∠BMP=∠MBC.∵在正方形ABCD中,AD∥BC,∴∠AMB=∠MBC,∴∠AMB=∠BMP,∴BM是∠AMP的平分线.(2)△PDM的周长没有发生变化.证明如下:如图,过B于Q.∵∠A=90°,且由(1)知BM是∠AMP的平分线,∴BA=BQ,∵∠A=∠MQB=90°,∠AMB=∠BMP,MB=MB,∴△AMB≌△QMB(AAS).∴MA=MQ.∵BA=BC,∴BQ=BC,又∵∠BQP=90°=∠C,BP=BP,∴Rt△BPC≌Rt△BPQ(HL).∴PC=PQ,∴△PDM的周长=MD+MP+DP=MD+MQ+QP+PD=MD+MA+PC+PD=AD+DC=2AD.∴△PDM的周长没有发生变化.类型6旋转型全等问题:图中若有边相等,可用旋转做实验例6:解:(1)①∵四边形ADEF是正方形,∴AD=AF,AB=AC,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,∴△DAB≌△FAC,∴∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BC;②∵△DAB≌△FAC,∴CF=BD,∵BC=BD+CD,∴BC=CF+CD.(2)结论①成立,结论②不成立.∵四边形ADEF是正方形,∴AD=AF,AB=AC.∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,∴△DAB≌△FAC,∴∠ABD=∠ACF,CF=BD,∴∠BCF=∠ACF-∠ACB=∠ABD-∠ACB=90°,即CF⊥BC;∵BC=CD-BD,∴BC =CD-CF.(3)如图,过A作AH⊥BC于H,过E作EM⊥BD于M∵∠BAC=90°,AB=AC,∴BC=AB=4,AH=CH∴CD=BC=1,∴DH=3,同(2)证得△BAD≌△CAF∴∠ABD=∠ACF=45°,∴∠BCF=∠ACB+∠ACF∴BC⊥CF,CF=BD=5.∵四边形ADEF是正方形,∴AD=DE,∠ADE=90∵BC⊥CF,EM⊥BD,EN⊥CF,∴四边形CMEN∴NE=CM,EM=CN,∵∠AHD=∠ADE=∠EMD90°,∴∠ADH+∠EDM=∠EDM+∠DEM=90°,∴∠ADH=∠DEM,∴△ADH≌△DEM,∴EM=DH=3,DM=AH=2,∴CN=EM=3,EN=CM=3,∵∠ABC=45°,∴∠BGC=45°,∴△BCG是等腰直角三角形,∴CG=BC=4,∴GN=1,∴EG==.针对训练:1.解:(1)AC=AD+AB.证明如下:∵∠B+∠D=180°,∠B=90°,∴∠D=90°.∵∠DAB=120°,AC平分∠DAB,∴∠DAC=∠BAC=60°,∵∠B=90°,∴AB=AC,同理AD=AC.∴AC=AD+AB.(2)(1)中的结论成立,理由如下:如图①,以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB的延长线于点E,∵∠BAC=60°,∴△AEC为等边三角形,∴AC=AE=CE,∠E=60°,∵∠ABC+∠D=180°,∠DAB=120°,∴∠DCB=60°,∴∠DCA=∠ECB.在△DAC和△BEC中,∴△DAC≌△BEC,∴AD=BE,∴AC=AE=AD+AB.(3)AD+AB=AC.理由如下:如图②,过点C作CE⊥AC交AB的延长于点E,∵∠ABC+∠D=180°,∠DAB=90°,∴∠DCB=90°,∵∠ACE=90°,∴∠DCA=∠BCE,又∵AC平分∠DAB,∴∠CAB=45°,∴∠E=45°,∴AC=CE.∴△CDA≌△CBE,∴AD=BE,∴AD+AB=AE.∵在Rt△ACE中,∠CAB=45°,∴AE==AC,∴AD+AB=AC.2.解:(1)证明:∵四边形ABCD是正方形,∴∠B=∠D=∠BAD=90°,AB=AD,∵△ABE沿AE翻折得到△AHE,∴△ABE≌△AHE,∴AH=AB=AD,BE=EH,∠AHE=∠AHF=∠B=∠D=90°.在Rt△AHF和Rt△ADF中,∴Rt△AHF≌Rt△ADF(HL),∴∠HAF=∠DAF,∴∠EAF=∠EAH+∠FAH=∠BAH+∠HAD=∠BAD=45°,(2)以BM,DN,MN为三边围成的三角形为直角三角形.证明如下:如图,过点A作AH⊥AN并截取AH=AN∵∠1+∠BAN=90°,∠3+∠BAN=90°,∴∠1=在△ABH和△ADN中,∴△ABH≌△ADN(SAS),∴BH=DN,∠HBA=∠NDA=135°,∵∠HAN=90°,∠MAN=45°,∴∠1+∠2=∠HAM=∠MAN=45°,在△AHM和△ANM中,∴△AHM≌△ANM(SAS),∴HM=NM,∴∠HBP=180°-∠HBA=180°-135°=45°,∴∠HBP+∠PBM=45°+45°=90°,∴△HBM是直角三角形,∵HB=DN,HM=MN,∴以BM,DN,MN为三边围成的三角形为直角三角形.3.解:(1)如图①,将△PBC绕点B逆时针旋转90°得△P′BA,连接PP′,则△AP′B≌△CPB,∴P′B=PB=,P′A=PC=1,∠1=∠2,∠AP′B=∠BPC.∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,∴∠2+∠3=90°,∴∠1+∠3=90°,即∠P′BP=90°,∴∠BP′P=45°.在Rt△P′BP中,由勾股定理,得PP′2=4. ∵P′A=1,AP=∴P′A2=1,AP2=5,∴P′A2+PP′2=AP2,∴△P′AP是直角三角形,∴∠AP′P=90°,∴∠AP′B=45°+90°=135°,∴∠BPC=135°.(2)仿照【分析】中的思路,将△BPC绕点B逆时针旋转120°,得到了△BP′A,连接PP′,如图②.则△PBC≌△P′BA,∴P′B=PB=4,P′A=PC=2,∠BPC=∠BP′A,∴△BPP′为等腰三角形,∵∠ABC=120°,∴∠PBP′=120°,∴∠BP′P=30°,过点B作BG⊥PP′于G,则∠P′GB=90°,∴PP′=2P′G.∵P′B=PB=4,∠BP′P=30°,∴BG=2,∴P′G=2.∴PP′=4,在△APP′中,∵PA=2,P′A=2,PP′=4,∴P′A2+P′P2=PA2,∴△PP′A是直角三角形,∴∠AP′P=90°,∴∠BPC=∠BP′A=∠PP′B+∠AP′P=30°+90°=120°.。
重庆中考数学20题典型的尺规作图+简单几何证明

20题典型的尺规作图+简单几何证明(一)编辑:天道酬勤尺规作图专题复习【知识回顾】1尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
最基本,最常用的尺规作图。
通常称基本作图。
一些复杂的尺规作图都是由基本作图组成。
2、五种基本作图:①作一条线段等于已知线段;②作一个角等于已知角;③作已知线段的垂直平分线;④作已知角的角平分线;⑤过一点作已知直线的垂线;一.题目一:作一条线段等于已知线段已知:如图,线段a求作:线段AB,使AB=a作法:(1)作射线AP;(2)在射线AP上截取AB=a则线段AB就是所求作的图形。
二.题目二:作已知线段的中点。
已知:如图,线段MN求作:点O,使MO=NO(即O是MN的中点)作法:(1)分别以M、N为圆心,大于MN的相同线段为半径画弧,两弧相交于P,Q (2)连接PQ交MN于O,则点O就是所求作的MN的中点.三.题目三:作已知角的角平分线。
已知:如图,∠AOB,求作:射线OP,使∠AOP=∠BOP(即OP平分∠AOB)。
作法:(1)以O为圆心,任意长度为半径画弧,分别交OA,OB于M,N;(2)分别以M、N为圆心,大于1MN的线段长为半径画弧,两弧交∠AOB内于P;2(3)作射线OP.则射线OP就是∠AOB的角平分线。
四.题目四:作一个角等于已知角。
已知:如图,∠AOB。
求作;∠A'O'B',使∠A'O'B'=∠AOB作法:(1)作射线O'A'(2)以O为圆心,任意长度为半径画弧,交OA于M,交OB于N(3)以O'为圆心,以OM的长为半径画弧,交O'A'于M';(4)以M'为圆心,以MN的长为半径画弧,交前弧于N'(5)连接O'N'并延长到B'。
则∠A'O'B'就是所求作的角。
五.题目五:经过直线上一点做已知直线的垂线。
已知:如图,P是直线AB上一点求作:直线CD,是CD经过点P,且CD⊥AB。
作法:(1)以P为圆心,任意长为半径画弧,交AB于M、NMN的长为半径画弧,两弧交于点Q (2)分别以M、N为圆心,大于12(3)过D、Q作直线CD.则直线CD是求作的直线。
历年重庆中考几何题归类

历年重庆中考几何题归类2015A 卷6.如图,直线AB ∥CD ,直线EF 分别与直线AB,CD 相交于点G ,H 。
若1=135°,则2的度数为( )A. 65°B. 55°C. 45°D. 35°9.如图,AB 是的直径,点C 在上,AE 是的切线,A 为切点,连接BC 并延长交AE 于点D , 若AOC=80°,则ADB 的度数为( ) A. 40° B. 50° C. 60° D. 20°12.如图,在平面直角坐标系中,菱形ABCD 在第一象限内,边BC 与轴平行,A,B 两点的纵坐标分别为3,1,反比例函数的图像经过A,B 两点,则菱形对ABCD 的面积为()A. 2B. 4C.D.15.如图,在等腰直角三角形ABC 中,ACB=90°,AB=,以A 为 圆心,AC 长为半径作弧,交AB 于点D ,则阴影部分的面积是 。
18.如图,矩形ABCD 中,AB=,AD=10,连接BD ,DBC 的角平分线BE 交DC 于点E ,现把△BCE 绕点B 逆时针旋转,记旋转后的△BCE 为△,当射线和射线都与线段AD 相交时,设交点分别F,G ,若△BFD 为等腰三角形,则线段DG 长为 。
∠∠O O O ∠∠x 3y x=2242∠4246∠BC E ''BE 'BC '6题图9题图12题图18题图16题图20.如图,在△ABD 和△FEC 中,点B,C,D,E 在同一直线上,且AB=FE,BC=DE,B=E 。
求证:ADB=FCE.五、解答题:(本大题2个小题,每小题12分,共24分)解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡...中对应的位置上.25.如图1,在△ABC 中,ACB=90°,BAC=60°,点E 角平分线上一点,过点E 作AE 的垂线,过点A 作AB 的线段,两垂线交于点D ,连接DB ,点F 是BD 的中点,DH ⊥AC ,垂足为H ,连接EF ,HF 。
重庆中考几何分类
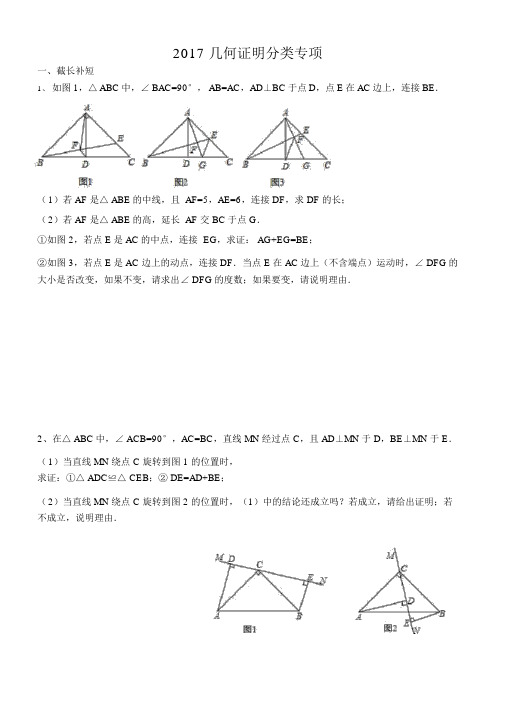
2017 几何证明分类专项一、截长补短1、如图1,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E在AC边上,连接BE.(1)若 AF 是△ ABE的中线,且 AF=5,AE=6,连接 DF,求 DF 的长;(2)若 AF 是△ ABE的高,延长 AF 交 BC于点 G.①如图 2,若点 E是 AC的中点,连接 EG,求证: AG+EG=BE;②如图 3,若点 E是 AC 边上的动点,连接 DF.当点 E 在 AC边上(不含端点)运动时,∠ DFG的大小是否改变,如果不变,请求出∠ DFG的度数;如果要变,请说明理由.2、在△ ABC中,∠ ACB=90°,AC=BC,直线 MN 经过点 C,且 AD⊥MN 于 D,BE⊥MN 于 E.(1)当直线 MN 绕点 C 旋转到图 1 的位置时,求证:①△ ADC≌△ CEB;② DE=AD+BE;(2)当直线 MN 绕点 C 旋转到图 2 的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.3、如图,已知 AD∥ BC,∠PAB的平分线与∠ CBA的平分线相交于E,CE的连线交 AP 于 D.求证:AD+BC=AB.4、如图,△ ABC中, D 是 BC的中点,过 D 点的直线 GF交 AC 于 F,交 AC的平行线 BG 于 G 点,DE⊥DF,交 AB于点 E,连结 EG、EF.(1)求证: BG=CF;(2)请你判断 BE+CF与 EF的大小关系,并说明理由.5、如图,四边形ABCD中, AD∥BC,CE⊥AB,△ BDC为等腰直角三角形,∠ BDC=90°, BD=CD;CE与 BD交于 F,连 AF, M 为 BC中点,连接 DM 交 CE于 N.请说明:(1)△ ABD≌△ NCD;(2) CF=AB+AF.6、Rt△ABC中,∠ ABC=90°,AB=BC,F 为 AB 上一点,连接 CF,过点 B 作 BH⊥ CF交 CF于G,交AC于 H.( 1)如图( 1),延长 BH 到点 E,连接 AE,当∠ EAB=90°,AE=1, F 为 AB 的三等分点,且 BF <AF时,求 BE的长;(2)如图( 2),若 F 为 AB 中点,连接 FH,求证: BH+FH=CF;(3)如图( 3),在 AB 上取点 K,使 AK=BF,连接 HK 并延长与 CF的延长线交于点 P,若 G 为CP 的中点,请直接写出 AH、BH、PG所满足的数量关系.7、如图 1,△ ABC是等边三角形,点 E 在 AC边上,点 D 是 BC边上的一个动点,以DE为边作等边△ DEF,连接 CF.(1)当点 D 与点 B 重合时,如图 2,求证: CE+CF=CD;(2)当点 D 运动到如图 3 的位置时,猜想 CE、 CF、CD之间的等量关系,并说明理由;( 3)只将条件“点 D 是 BC边上的一个动点”改为“点 D 是 BC延长线上的一个动点”,如图 4,猜想CE、CF、 CD之间的等量关系为(不必证明).8、如图( 1):在△ ABC中,∠ ACB=90°,AC=BC,过点 C 在△ ABC外作直线 MN, AM⊥ MN 于 M,BN⊥MN 于 N.(1)求证: MN=AM+BN.(2)如图( 2),若过点 C 在△ ABC内作直线 MN, AM⊥MN 于 M ,BN⊥MN 于 N,则图( 1)中的结论是否仍然成立?请说明理由.9、如图 1,△ ABC中,∠ BAC=90°,AB=AC, AD⊥ BC于点 D,点 E 在 AC边上,连接BE.( 1)若 AF 是△ ABE的中线,且 AF=5,AE=6,连结 DF,求 DF 的长;( 2)若 AF 是△ ABE的高,延长 AF 交 BC于点 G.①如图 2,若点 E是 AC边的中点,连结EG,求证: AG+EG=BE;②如图 3,若点 E是 AC 边的动点,连结 DF,当点 E 在 AC边上(不含端点)运动时,∠ DFG的大小是否改变?如果不变,请求出∠ DFG的度数;如果改变,请说明理由.10、如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点 F 是线段 AB 上一点,连接 DF,以 DF 为斜边作等腰 Rt△ DFE,连接 EA, EA满足条件 EA⊥ AB.( 1)若∠ AEF=20°,∠ ADE=50°,AC=2,求 AB 的长度;( 2)求证: AE=AF+BC;( 3)如图 2,点 F 是线段 BA 延长线上一点,探究 AE、AF、 BC之间的数量关系,并证明.11、在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.( 1)如图 1,若 D 是 BC边上的中点,∠ A=45°,DF=3,求 AC的长;(2)如图 2, D 是线段 BC上的任意一点,求证: BG=DE+DF;(3)在图 3, D 是线段 BC延长线上的点,猜想 DE、 DF与 BG 的关系,并证明.二、3 问题1、如图 1,等边△ ABC中, CE平分∠ ACB,D 为 BC边上一点,且 DE=CD,连接 BE.( 1)若 CE=4,BC=,求线段( 2)如图 2,取 BE中点 P,连接BE的长;AP, PD,AD,求证: AP⊥PD 且 AP=PD;( 3)如图3,把图2 中的△ CDE绕点C 顺时针旋转任意角度,然后连接BE,点P为BE中点,连接 AP, PD, AD,问第( 2)问中的结论还成立吗?若成立,请证明;若不成立,请说明理由.2、在△ABC中,AB=AC,点D,点E在边BC上不同的两点,且∠ADE=75°.( 1)如图 1,若∠ BAC=90°,CD=,求BC的长;( 2)如图 2,若∠ BAC=90°,∠ EAD=45°,求证: DC=BE;(3)如图 3,若∠ BAC=120°,∠ EAD=60°,请问( 2)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.三、 2 问题1、如图1,△ABC是等腰直角三角形,AC=BC,∠ACB=90°,直线l经过点C,AF⊥l于点F,BE⊥l于点 E,点 D 是 AB的中点,连接 ED.(1)求证:△ ACF≌△ CBE;(2)求证: AF=BE+ DE;(3)如图 2,将直线 l 旋转到△ ABC的外部,其他条件不变,( 2)中的结论是否仍然成立,如果成立请说明理由,如果不成立 AF、BE、DE 又满足怎样的关系?并说明理由.2、已知,在△ABC中,∠ACB=90°,CA=CD,CG⊥AD于点H,交AB于点G,E为AB上一点,连接 CE交 AD 于点 F.(1)如图 1,若 CE⊥AB 于点 E, HG=1,CH=5,求 CF的长;( 2)如图 2,若 AC=AE,∠ GEH=∠ ECH,求证: CE=HE;( 3)如图 3,若 E 为 AB 的中点,作 A 关于 CE的对称点 A′,连接 CA′, EA′, DA′,请直接写出∠ CEH,∠ A′ CD,∠ EA′D之间的等量关系.3、在△ABC中,∠ABC=2∠ACB,延长AB至点D,使BD=BC,点E是直线BC上一点,点F是直线AC上一点,连接 DE.连接 EF,且∠ DEF=∠DBC.( 1)如图 1,若∠ D=∠EFC=15°, AB=,求AC的长.( 2)如图 2,当∠ BAC=45°,点 E 为线段 BC的延长线上,点F 在线段AC的延长线上时,求证:CF= BE.(3)如图 3,当∠ BAC=90°,点 E 为线段 CB的延长线上,点 F 在线段 CA的延长线上时,猜想线段 CF与线段 BE的数量关系,并证明猜想的结论.4、如图,在等腰直角△ ABC中,∠ ACB=90°,CA=CB,CD为斜边 AB 上的中线.(1)如图 1, AE平分∠ CAB交 BC于 E,交 CD于 F,若 DF=2,求 AC 的长;(2)将图 1 中的△ ADC绕点 D 顺时针旋转一定角度得到△ ADN,如图 2, P, Q 分别为线段 AN,BC的中点,连接 AC,BN,PQ,求证: BN=PQ;(3)如图 3,将△ ADC绕点 A 顺时针旋转一定角度到△ AMN,其中 D 的对应点是 M ,C 的对应点是 N,若 B,M,N 三点在同一直线上, H 为 BN 中点,连接 CH,猜想 BM,MN,CH之间的数量关系,请直接写出结果.5、如图,在等腰 Rt△ABC中,∠ ABC=90°,AB=BC,点 D 是线段 AC 上一点,连接 BD,过点 C 作 CE⊥BD 于点 E,点 F 是 AB 垂直平分线上一点,连接 BF、EF.(1)若 AD=6 ,tan∠BCE= ,求 AB 的长;(2)如图 1,当点 F 在 AC边上时,求证: CE﹣ BE= EF;( 3)如图 2,若∠ BDC=75°,当∠ AFB=30°时,直接写出()2的值.6、如图,已知 AB=AC,AD=AE,∠ BAC=90°,∠ EAD=90°,BE的延长线交 AC于 G,交 CD于 F.( 1)求证: BF⊥CD;( 2)若 AE 平分∠ BAC,BF 平分∠ ABC,求证: EG=FG.7、如图,在等腰 Rt△ABC中,O 为斜边 AC的中点,连接 BO,以 AB 为斜边向三角内部作 Rt△ABE,且∠ AEB=90°,连接 EO.求证:(1)∠ OAE=∠OBE;(2) AE=BE+ OE.8、如图 1,在△ ACB和△ AED中,AC=BC,∠ ACB=∠ AED=90°,点 E 在 AB 上,F 是线段 BD 的中点,连接 CE、FE.(1)若 AD=6 ,BE=8,求 EF的长;(2)求证: CE= EF;(3)将图 1 中的△ AED绕点 A 顺时针旋转,使△ AED的一边 AE恰好与△ ACB的边 AC在同一条直线上(如图 2),连接 BD,取 BD 的中点 F,问( 2)中的结论是否仍然成立?并说明理由.9、等腰 Rt△ ABC中,∠ ACB=90°,AC=BC,点 G 是 BC上一点, CF⊥AG 于 E,BF⊥CF, D 为 AB中点,连接 DF.(1)求证:△ AEC≌△ CFB;(2)求证: EF= DF.10、如图,在△ ABC中,∠ ACB=45°,AD 是△ ABC的高,在 AD 上取点 E,使得 DE=DB,连接 CE 并延长,交边 AB 于点 F,连接 DF.(1)求证: AB=CE;(2)求证: BF+EF= FD.四、 2 倍关系1、已知:如图2△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点 F,H 是 BC边的中点,连结 DH 与 BE相交于点 G.(1)求证: BF=AC;(2)求证: CE= BF.2、如图,在△ ABC中, AB=AC,D 为线段 BC的延长线上一点,且 DB=DA,BE⊥ AD 于点 E,取BE 的中点 F,连接 AF.(1)若 BE=2 ,AE= ,求 AF的长;(2)若∠ BAC=∠DAF,求证: 2AF=AD;(3)请直接写出线段 AD、BE、 AE的数量关系.3、在△ ABC中, AB=AC,D 为射线 BC上一点, DB=DA,E 为射线 AD 上一点,且 AE=CD,连接BE.( 1)如图 1,若∠ ADB=120°,AC= ,求 DE的长;( 2)如图 2,若 BE=2CD,连接 CE并延长,交 AB 于点 F,求证: CE=2EF;( 3)如图 3,若 BE⊥AD,垂足为点 E,求证: AE2+.4、如图,在等腰三角形ABC中, AB=AC,D 为线段 BC中点,∠ EDF=∠ABC,AE=CD.(1)如图( 1),EF交 AD 于点 G,∠ ABC=60°,求∠ ADF的度数;(2)如图( 2),EF交 AD 于点 G,G 为 AD 中点, 2∠FDC=∠ABC,求证: AE=2EG;(3)如图( 3),若∠ ABC=45°,请直接写出线段 AE、EF之间的数量关系.5、在△ ABC中, AB=AC,AD 是 BC边上的中线,点 E 是AC边上一点,且AE= AC,连接BE.(1)如图 1,连接 DE,若∠ ABC=60°, AC=12,求 DE的长.(2)如图 2,若点 F 是 BE的中点,连接 AF 并延长交 BC于点 G,求证: DC=2BG.(3)如图 3,若∠ BAC=90°,过点 A 作 AN⊥BE交 BE于点 M ,连接 DM,请直接写出 DM 与 AB 的数量关系.6、如图,∠ BAD=∠ CAE=90°, AB=AD, AE=AC,AF⊥CF,垂足为 F.(1)若 AC=10,求四边形 ABCD的面积;(2)求证: AC平分∠ ECF;(3)求证: CE=2AF.7、如图, E、F 分别是等边三角形 ABC的边 AB、AC 上的点,且 BE=AF, CE、BF 交于点 P,且EG ⊥ BF,垂足为 G.(1)求证:∠ BCE=∠ABF;(2)求证: PE=2PG.8、如图, Rt△ ABC中,∠ BAC=90°,点 E 是 BC的中点, AD 平分∠ BAC, BD⊥AD 于点 D.(1)求证:∠ ADE=∠BDE.( 2)过点 C 作 CG⊥AD 于点 G,交 AB 于点 F,求证: DE=.9、如图,△ ABC中,∠ ACB=90°,AC=BC,点 F 在 BA 的延长线上,以 AF 为边作正方形 ADEF,连接 EB,点 M 为 EB的中点,连接 DM 并延长交 AB 于 N,连接 CM.( 1)若BN=2,AC=,求BE的长;( 2)求证: CM= DN.五、角的关系1、如图所示,△ ABC中, AB=BC,DE⊥AB 于点 E, DF⊥BC于点 D,交 AC于 F.(1)若∠ AFD=155°,求∠ EDF的度数;(2)若点 F 是 AC的中点,求证:∠ CFD= ∠ B.2、如图,在△ ABC中,AB=BC,AD⊥ BC于点 D,点 E 为 AC中点,连接 BE交 AD 于点 F,且BF=AC,过点 D 作 DG∥AB,交 AC 于点 G.求证:(1)∠ BAD=2∠DAC(2) EF=EG.3、已知矩形 ABCD中, AF为∠ DAC的角平分线, CP⊥AF 于点 F,且交 AD 的延长线于 P.连接BF交对角线 AC于点 O.(1)若 BC=4,tan∠ACB= ,求 S△DCP的值;(2)求证:∠ AOB=3∠PAF.4、如图,在等腰 Rt△ABC中,∠ ABC=90°,AB=BC,D 为斜边 AC 延长线上一点,过 D 点作 BC的垂线交其延长线于点 E,在 AB 的延长线上取一点 F,使得 BF=CE,连接 EF.(1)若 AB=2,BF=3,求 AD 的长度;(2) G 为 AC中点,连接 GF,求证:∠ AFG+∠BEF=∠GFE.5、已知在四边形 ABCD中,∠ ABC+∠ADC=180°, AB=BC.(1)如图 1,若∠ BAD=90°,AD=2,求 CD的长度;(2)如图2,点P、Q 分别在线段AD、DC上,满足PQ=AP+CQ,求证:∠PBQ=90°﹣∠ADC;(3)如图 3,若点 Q 运动到 DC的延长线上,点 P 也运动到 DA 的延长线上时,仍然满足 PQ=AP+CQ,则(2)中的结论是否成立?若成立,请给出证明过程;若不成立,请写出∠ PBQ与∠ ADC的数量关系,并给出证明过程.6、如图 1,点 D 为△ ABC边 BC的延长线上一点.(1)若∠ A:∠ ABC=3:4,∠ ACD=140°,求∠ A 的度数;(2)若∠ ABC的角平分线与∠ ACD的角平分线交于点 M ,过点 C作 CP⊥BM 于点 P.求证:∠MCP=90°﹣∠A;(3)在( 2)的条件下,将△ MBC 以直线 BC为对称轴翻折得到△ NBC,∠ NBC的角平分线与∠NCB的角平分线交于点Q(如图 2),试探究∠ BQC与∠ A 有怎样的数量关系,请写出你的猜想并证明.7、已知在四边形 ABCD中,∠ ABC+∠ADC=180°,∠ BAD+∠BCD=180°, AB=BC.(1)如图 1,连接 BD,若∠ BAD=90°,AD=7,求 DC 的长度;(2)如图 2,点 P、Q 分别在线段 AD、DC上,满足 PQ=AP+CQ,求证:∠ PBQ=∠ABP+∠QBC;(3)若点 Q 在 DC的延长线上,点 P 在 DA 的延长线上,如图 3 所示,仍然满足 PQ=AP+CQ,请写出∠ PBQ与∠ ADC的数量关系,并给出证明过程.8、如图, P 为正方形 ABCD边 BC上一点, F 在 AP 上,且 AF=AD, EF⊥AP 交 CD 于点 E,G 为 CB 延长线上一点, BG=DE.(1)求证:∠ PAG=∠BAP+ ∠DAP;(2)若 DE=2,AB=4,求 AP 的长.9、如图,已知 AD 是△ ABC的角平分线(∠ ACB>∠ B),EF⊥AD 于 P,交 BC延长线于 M,(1)如果∠ ACB=90°,求证:∠ M=∠ 1;(2)求证:∠ M= (∠ ACB﹣∠ B).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
历年重庆中考几何题归类2015A 卷6.如图,直线AB ∥CD ,直线EF 分别与直线AB,CD 相交于点G ,H 。
若1=135°,则2的度数为( )A. 65°B. 55°C. 45°D. 35°9.如图,AB 是的直径,点C 在上,AE 是的切线,A 为切点,连接BC 并延长交AE 于点D , 若AOC=80°,则ADB 的度数为( ) A. 40° B. 50° C. 60° D. 20°12.如图,在平面直角坐标系中,菱形ABCD 在第一象限内,边BC 与轴平行,A,B 两点的纵坐标分别为3,1,反比例函数的图像经过A,B 两点,则菱形对ABCD 的面积为()A. 2B. 4C.D.15.如图,在等腰直角三角形ABC 中,ACB=90°,AB=,以A 为 圆心,AC 长为半径作弧,交AB 于点D ,则阴影部分的面积是 。
18.如图,矩形ABCD 中,AB=,AD=10,连接BD ,DBC 的角平分线BE 交DC 于点E ,现把△BCE 绕点B 逆时针旋转,记旋转后的△BCE 为△,当射线和射线都与线段AD 相交时,设交点分别F,G ,若△BFD 为等腰三角形,则线段DG 长为 。
∠∠O e O e O e ∠∠x 3y x=2242∠4246∠BC E ''BE 'BC '6题图9题图12题图20.如图,在△ABD 和△FEC 中,点B,C,D,E 在同一直线上,且AB=FE,BC=DE,B=E 。
求证:ADB=FCE.五、解答题:(本大题2个小题,每小题12分,共24分)解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡...中对应的位置上.25.如图1,在△ABC 中,ACB=90°,BAC=60°,点E 角平分线上一点,过点E 作AE 的垂线,过点A 作AB 的线段,两垂线交于点D ,连接DB ,点F 是BD 的中点,DH ⊥AC ,垂足为H ,连接EF ,HF 。
(1)如图1,若点H 是AC 的中点,AC=,求AB ,BD的长。
(2)如图1,求证:HF=EF 。
(3)如图2,连接CF ,CE ,猜想:△CEF 是否是等边三角形若是,请证明;若不是,请说明理由。
∠∠∠∠∠∠2318题图16题图 20题图图1 图22015B卷9.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O与点D,连接OD,若∠BAC=55°,则∠COD的大小为A.70°B.60°C.55°D.35°12.如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,,反比例函数kyx的图像与菱形对角线AO交于D点,连接BD ,当BD ⊥x 轴时,k 的值是 A .63B .3-C .3D .123-16.如图,在边长为4的正方形ABCD 中,先以点A 为圆心,AD 的长为半径画弧,再以AB边的中点为圆心,AB 长的一半为半径画弧,则两弧之间的阴影部分面积是______ (结果保留π)18.如图,AC 是矩形ABCD 的对角线,AB=2,BC=3点E ,F 分别是线段AB ,AD 上的点,连接CE ,CF ,当∠BCE=∠ACF ,且CE=CF 时,AE+AF=___ ___.20.如图,△ABC 和△EFD 分别在线段AE 的两侧, 点C ,D 在线段AE 上, AC=DE ,AB ∥EF. 求证:BC=FD25.在△ABC 中,AB=AC ,∠A=60°,点D 是线段BC 的中点,∠EDF=120°,DE 与线段AB 相交于点E ,DF 与线段AC (或AC 的延长线)相交于点F. (1)如图1,若DF ⊥AC ,垂足为F ,AB=4,求BE 的长;(2)如图2,将(1)中的∠EDF 绕点D 顺时针旋转一定的角度,DF 扔与线段AC 相交于点F.求证:1CF 2BE AB +=; (3)如图3,将(2)中的∠EDF 继续绕点D 顺时针旋转一定的角度,使DF 与线段AC 的延长线交与点F ,作DN ⊥AC 于点N ,若DN=FN ,求证:)BE CF BE CF +=-.2014A 卷8.(4分)(2014•重庆)如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F 作FG⊥FE,交直线AB于点G,若∠1=42°,则∠2的大小是()A.56°B.48°C.46°D.40°9.(4分)(2014•重庆)如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是()A.30°B.45°C.60°D.70°12.(4分)(2014•重庆)如图,反比例函数y=﹣在第二象限的图象上有两点A、B,它们的横坐标分别为﹣1,﹣3,直线AB与x轴交于点C,则△AOC的面积为()A.8B.10C.12D.2415.(4分)(2014•重庆)如图,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的周长为_________ .16.(4分)(2014•重庆)如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,则图中阴影部分的面积为_________ .(结果保留π)18.(4分)(2014•重庆)如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为_________ .20.(7分)(2014•重庆)如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.24.(10分)(2014•重庆)如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE 平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.(1)求证:BE=CF;(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.26.(12分)(2014•重庆)已知:如图①,在矩形ABCD中,AB=5,AD=,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.(1)求AE和BE的长;(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值.(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF 为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形若存在,求出此时DQ的长;若不存在,请说明理由.2014B 卷8.如图,在矩形ABCD 中,对角线AC .BD 相交于点O ,∠ACB=30°,则∠AOB 的大小为( )A .30° B.60° C.90° D.120°11.如图,菱形ABCD 的对角线AC .BD 相交于点O ,AC =8,BD =6,以AB 为直径作一个半圆,则图中阴影部分的面积为( )A .256π-B .2562π- C .2566π- D .2568π-12.如图,正方形ABCD 的顶点B 、C 在x 轴的正半轴上,反比例函数(0)ky k x=≠在第一象限的图像经过顶点A (m ,2)和CD 边上的点E (n ,23),过点E 的直线l 交x 轴于点F ,交y 轴于点G (0,-2),则点F 的坐标是( ) A .5(,0)4 B .7(,0)4 C .9(,0)4 D .11(,0)416.如图,C 为⊙O 外点,CA 与⊙O 相切,切点为A ,AB 为⊙O 的直径,连接CB。
若⊙O的半径为2,∠ABC=60°,则BC=。
18.如图,在边长为62的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG于点H,交AD于点F,连接CE.BH。
若BH =8,则FG=。
20.如图,在△ABC中,CD⊥AB,垂足为D。
若AB=12,CD=6,3tan2A=,求sin cosB B+的值。
24.如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB 交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG。
求证:(1)AF=CG;(2)CF=2DE。
2013A卷5.如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为()A.40° B.35°C.50° D.45°8.如图,P是⊙O外一点,PA是⊙O的切线,PO=26cm,PA=24cm,则⊙O的周长为()A.18πcm B.16πcm C.20πcm D.24πcm9.如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,CD=3cm,则AF的长为()A.5cm B.6cm C.7cm D.8cm16.如图,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为_________(结果保留π)。
18.如图,菱形OABC的顶点O是坐标圆点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和C 分别落在这个坐标平面内的点B′和点C′处,且∠C′DB′=60°。
若某反比例函数的图像经过点B′,则这个反比例函数的解析式为________。
24. 如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC。
(1)求证:OE=OF;(2)若BC=23,求AB的长。
26.已知:如图①,在平行四边形ABCD中,AB=12,BC=6,AD⊥BD。
以AD为斜边在平行四边形ABCD的内部作Rt△AED,∠EAD=30°,∠AED=90°。
