专题06 结论判断问题(解析版)
专题06 规律问题(解析版)

专题06 规律问题 2021届中考数学压轴大题专项训练(解析版)1.某种球形病毒的直径约是0.01纳米,一个该种病毒每经过一分钟就能繁殖出9个与自己完全相同的病毒,假如这种病毒在人体内聚集到一定数量,按这样的数量排列成一串,长度达到1分米时,人体就会感到不适.(1米9=10纳米)(1)从感染到第一个病毒开始,经过5分钟,人体内改种病毒的总长度是多少纳米?(2)从感染到第一个病毒开始,经过多少分钟,人体会感到不适?【答案】(1)从感染到第一个病毒开始,经过5分钟,人体内改种病毒的总长度是1000纳米;(2)从感染到第一个病毒开始,经过10分钟,人体会感到不适.【解析】解:(1)由题意可知:经过5分钟,人体内改种病毒的总长度是0.01×1×105=1000(纳米) 答:从感染到第一个病毒开始,经过5分钟,人体内改种病毒的总长度是1000纳米; (2)1分米=110米8=10纳米 而810÷(0.01×1)=1010∴从感染到第一个病毒开始,经过10分钟,人体会感到不适答:从感染到第一个病毒开始,经过10分钟,人体会感到不适.2.你会求()()20182017201621?··1a a a a a a -++++++的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:()()2111a a a -+=-()()23111a a a a -++=-()()324111a a a a a -+++=-(1)由上面的规律我们可以大胆猜想,得到()()201920182017211a a a a a a -+++⋅⋅⋅+++=_____;(2)利用上面的结论求2019201820172222221++++++的值. (3)求201920182017255554+++⋅⋅⋅++的值【答案】(1)20201a -;(2)202021-;(3)()20201594-. 【解析】(1)由题可以得到()()12211n n n a a a a a a ---++++++11n a +=-()()20192018211a a a a a ∴-+++++20201a =-(2)由结论得:2019201820172222221++++++()()2019201822122221=-⋅+++++ 202021=-(3)201920182017255554+++++()()2019201820172515555+5+1-24-+++=()202015124=-- ()20201594=- 3.计算|1﹣12|+|12﹣13|+|13﹣14|+…+|199﹣1100|. 【答案】99100【解析】解:111111112233499100-+-+-++-111111=1223499100-+--++- 1=1100- 99=100. 4.观察下列等式:第1个等式:11111212a ==-⨯;第2个等式:21112323a ==-⨯; 第3个等式:31113434a ==-⨯;第4个等式:41114545a ==-⨯; ……解答下列问题:(1)按以上规律写出第5个等式:5a =—————— = ——————.(2)求1232020a a a a ++++的值.(3)求111148812121620162020++++⨯⨯⨯⨯的值. 【答案】(1)156⨯,1156-;(2)20202021;(3)631010. 【解析】解:(1)第1个等式:11111212a ==-⨯; 第2个等式:21112323a ==-⨯; 第3个等式:31113434a ==-⨯; 第4个等式:41114545a ==-⨯;…… 第5个等式:51115656a ==-⨯;故答案为:156⨯;1156-; (2)12320201111111112233420202021a a a a ++++=-+-+-++- 112021=- 20202021=; (3)111148812121620162020++++⨯⨯⨯⨯ 812111111144820162020⎛⎫=⨯-+-++- ⎪⎝⎭111442020⎛⎫=⨯- ⎪⎝⎭150442020=⨯ 631010=. 5.阅读材料:求2342015122222+++++⋯+的值.解:设234201420151222222S =+++++⋯++,将等式的两边同乘以2,得234201520162222222S =++++⋯++将下式减去上式得,2016221S S -=-即201621S =-.即2342015201612222221+++++⋯+=-请你仿照此法计算:(1)填空:231222+++= .(2)求2341012222+++++…+2的值.(3)求234111111()()()()33333n +++++⋯+的值.(其中n 为正整数) 【答案】(1)15;(2)2047;(3)311()223n -⨯. 【解析】解:(1)由题意可得,1+2+22+23=24-1=16-1=15,故答案为:15;(2)由题意可得,2341012222+++++…+2 1121=- 20481=- 2047=;(3)设234111111()()()()33333n S =+++++⋯+, 则23411111111()()()()()3333333n n S +=++++⋯++, 1111()33n S S +∴-=-, 1211()33n S +∴=-, 解得,311()223n S =-⨯, 即234111111()()()()33333n +++++⋯+的值是311()223n -⨯. 6.在日历上,我们可以发现其中某些数满足一定的规律,图是2020年1月份的日历,我们用如图所示的四边形框出五个数.2020年1月:(1)将每个四边形框中最中间位置的数去掉后,将相对的两对数分别相减,再相加,例如:(108)(162)16-+-=,(2119)(2713)16-+-=.不难发现,结果都是16.若设中间位置的数为n ,请用含n 的式子表示发现的规律,并写出验证过程.(2)用同样的四边形框再框出5个数,若其中最小数的2倍与最大数的和为56,求出这5个数中的最大数的值.(3)小明说:我用同样的四边形框也框出了5个数,其中最小数与最大数的积是120.请判断他的说法是否正确,并说明理由.【答案】(1)(1)(1)(7)(7)16n n n n +--++--=,见解析;(2)28;(3)正确,见解析【解析】(1)设中间位置的数为n ,左边数为1n -,右边数1n +,上面数7n -,下面数为7n +, 则(1)(1)(7)(7)16n n n n +--++--=(2)2(7)(7)56n n -++=,21n =,21728∴+=.(3)正确(7)(7)120n n -+=,13n ∴=- (舍去)或者13n =,可以存在.7.材料:若一个正整数,它的各个数位上的数字是左右对称的,则称这个正整数是对称数.例如:正整数22是两位对称数;正整数797是三位对称数;正整数4664是四位对称数;正整数12321是五位对称数.根据材料,完成下列问题:(1)最大的两位对称数与最小的三位对称数的和为___________(2)若将任意一个四位对称数拆分为前两位数字顺次表示的两位数和后两位数字顺次表示的两位数,则这两个两位数的差一定能被9整除吗?请说明理由.(3)如果一个四位对称数的个位数字与十位数字的和等于10,并且这个四位对称数能被7整除,请求出满足条件的四位对称数.【答案】(1)200;(2)一定可以,理由见解析;(3)3773【解析】解:(1)最大的两位对称数是99,最小的三位对称数是101,99101200+=,故答案是:200;(2)设个位和千位上的数字是a ,十位和百位上的数字是b ,则这两位数分别是10a b +、10b a +,()101099a b b a a b +-+=-, 它们的差是99a b -,这个数是9的倍数,所以这个数一定可以被9整除;(3)设这个四位数的个位数是x ,则十位数是()10x -,这个数可以表示为()()1010100101000x x x x +-+-+,化简得8911100x +,令1x =,则这个数是1991,令2x =,则这个数是2882,令3x =,则这个数是3773,……令9x =,则这个数是9119,其中只有3773能够被7整除,∴满足条件的四位数是3773.8.用棱长为2cm 的若干小正方体按如所示的规律在地面上搭建若干个几何体.图中每个几何体自上而下分别叫第一层、第二层,,第n 层(n 为正整数)(1)搭建第∴个几何体的小立方体的个数为 .(2)分别求出第∴、∴个几何体的所有露出部分(不含底面)的面积.(3)为了美观,若将几何体的露出部分都涂上油漆(不含底面),已知喷涂21cm 需要油漆0.2克,求喷涂第20个几何体,共需要多少克油漆?【答案】(1)30;(2)第∴个几何体露出部分(不含底面)面积为264cm ,第∴个几何体露出部分(不含底面)面积为2132cm ;(3)992克.【解析】(1)搭建第∴个几何体的小立方体的个数为1,搭建第∴个几何体的小立方体的个数为21412+=+,搭建第∴个几何体的小立方体的个数为22149123++=++,归纳类推得:搭建第∴个几何体的小立方体的个数为22212341491630+++=+++=, 故答案为:30;(2)第∴个几何体的三视图如下:由题意,每个小正方形的面积为2224()cm ⨯=,则第∴个几何体的所有露出部分(不含底面)面积为()232324464()cm ⨯+⨯+⨯=; 第∴个几何体的三视图如下:则第∴个几何体的所有露出部分(不含底面)面积为()2626294132()cm ⨯+⨯+⨯=; (3)第20个几何体从第1层到第20层小立方体的个数依次为221,2,,20,则第20个几何体的所有露出部分(不含底面)面积为()()2221220212202044960()cm ⎡⎤⨯++++⨯++++⨯=⎣⎦, 因此,共需要油漆的克数为49600.2992⨯=(克),答:共需要992克油漆.9. 阅读下列解题过程:=====请回答下列回题:(1)观察上面的解答过程,请写出= ; (2)请你用含n (n 为正整数)的关系式表示上述各式子的变形规律; (3)利用上面的解法,请化简:......【答案】(1)10-(21=-(3)9.【解析】(1===10=-故答案为:10-(21=-(31=- ............=......=1--1+10=9.10.先化简,再求值:(2x+y)2−(2x−y)(2x+y)−5xy,其中x=2019,y=−1.【答案】2021.【解析】原式=4x2+4xy+y2−(4x2−y2)−5xy=4x2+4xy+y2−4x2+y2−5xy,=2y2−xy,当x=2019,y=−1时,原式=2×(−1)2−2019×(−1)=202111.观察下列三行数,回答问题:-1、+3、-5、+7、-9、+11、……-3、+1、-7、+5、-11、+9、……+3、-9、+15、-21、+27、-33、……(1)第∴行第9个数是___________第∴行第9个数是___________第∴行第9个数是___________(2)在第∴行中,是否存在连续的三个数,使其和为83?若存在,求这三个数;若不存在,说明理由.(3)是否存在第m列数(每行取第m个数),这三个数的和正好为-99?若存在,求m;若不存在,说明理由.【答案】(1)-17;-19;51.(2)存在,85,-91,89;(3)第m 列数不存在,理由见解析.【解析】(1)观察到第∴行的规律是()()121n n --,第∴行的规律是将第∴行的数-2,第∴行的规律是()()1163n n +--,因此当n=9时,第∴行的数为-17∴第∴行的数为-17-2=-19,第∴行的数为()17351-⨯-=;(2)设第∴行存在连续的三个数和为83,且第一个数为x ,若0x >,即x 在第∴行中的偶数次列,满足第n 列的数为23n -(其中n 为正偶数),则()()6483x x x +--++=,得85x =,即2385,44n n -==,符合题意,x 在第∴行第44列, 此时,连续的三个数依次为85,-91,89.若0x <,即x 在第∴行中的奇数次列,满足第n 列的数为21n --(其中n 为正奇数),则()()2483x x x +--+-=,得89x =,即2189n --=,45n =-,不符合题意,故舍去,综上所述,存在这样连续的三个数使和为83,依次为85,-91,89.(3)设存在第m 列数使三个数的和为-99,且此列第∴行的数为y ,则第m 列第∴行的数为2y -,第∴行的数为3y ,()2399y y y +-+-=-,得97y ,又第∴行中奇数次列为负,偶数次列为正,()971249+÷=,即97在第∴行第49列,应为负,故假设不成立, 所以,这样的第m 列数不存在.12.回答下列问题:(1)填空:()()a b a b -+=___________________;()()22a b a ab b -++=_____________________;()()3223a b a a b ab b -+++=______________________.(2)猜想:()()1221n n n n a b a a b ab b -----++++=___________________.(其中n 为正整数,且2n ≥); (3)利用(2)猜想的结论计算:∴10987322222222+++++++; ∴10987322222222-+-+-+-.【答案】(1)22a b -;33a b -;44a b -;(2)n n a b -;(3)∴2046;∴682【解析】解:()()22a b a b a b -+=-; ()()22a b a ab b -++322223=++---a a b ab a b ab b()()3223a b a a b ab b -+++4322332234=+++----a a b a b ab a b a b ab b44a b =-;故答案为:22a b -;33a b -;44a b -;(2)根据(1)中的规律,可得猜想:()()1221-----++++=-n n n n n b a b a a b ab b a b (其中n 为正整数,且2n ≥),故答案为:n n a b -; (3)∴10987322222222+++++++1098732222222211=++++++++-10982733728910(21)(22121212121211)1=-+⨯+⨯+⨯++⨯+⨯+⨯+- 11211=--204811=--2046=;∴10987322222222-+-+-+-1098732222222211=-+-+-+-+-109827337289101[2(1)][22(1)2(1)2(1)2(1)2(1)2(1)(1)]13=⨯--+⨯-+⨯-+⨯-++⨯-+⨯-+⨯-+--11111[2(1)]13=⨯--- 1204913=⨯-=.682。
专题06 利用等腰三角形的性质求角的度数(解析版)

专题06 利用等腰三角形的性质求角的度数知识对接考点一、等腰三角形1.等腰三角形:有两条边相等的三角形叫做等腰三角形.2.性质:(1)具有三角形的一切性质.(2)两底角相等(等边对等角)(3)顶角的平分线,底边中线,底边上的高互相重合(三线合一)(4)等边三角形的各角都相等,且都等于60°.3.判定:(1)如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边);(2)三个角都相等的三角形是等边三角形;(3)有一个角为60°的等腰三角形是等边三角形.要点补充:(1)腰、底、顶角、底角是等腰三角形特有的概念;(2)等边三角形是特殊的等腰三角形.考点二、角1.对顶角(1)定义:如果两个角有一个公共顶点,而且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫对顶角.(2)性质:对顶角相等.2.邻补角(1)定义:有一条公共边,而且另一边互为反向延长线的两个角叫做邻补角.(2)性质:邻补角互补.3.同位角、内错角、同旁内角(1)基本概念:两条直线(如a、b)被第三条直线(如c)所截,构成八个角,简称三线八角,如图所示:∠1和∠8、∠2和∠7、∠3和∠6、∠4和∠5是同位角;∠1和∠6、∠2和∠5是内错角;∠1和∠5、∠2和∠6是同旁内角.(2)特点:同位角、内错角、同旁内角都是由三条直线相交构成的两个角.两个角的一条边在同一直线(截线)上,另一条边分别在两条直线(被截线)上.专项训练1一、单选题1.(2021·江苏九年级专题练习)等腰三角形的一个外角是130°,则它的底角的度数为( ) A .65° B .80°或50° C .50° D .65°或50°【答案】D 【分析】分该外角是底角的外角还是顶角的外角两种情况解答即可. 【详解】解:①当该外角是底角的外角时,底角为:180°-130°=50°; ①当该外角是顶角的外角时,则底角为:130°×12=65°所以底角为65°或50°. 故选D . 【点睛】本题主要考查了等腰三角形的定义,掌握分类讨论思想是解答本题的关键.2.(2021·湖北黄冈·九年级模拟预测)如图,有一块含有45︒角的直角三角板的两个顶点放在直尺的对边上.如果120∠=︒,那么2∠的度数是( )A .20︒B .25︒C .30D .45︒【答案】B 【分析】依题意,由直尺边是相互平行、三角形为等腰直角三角形,可得+2=45DAC ∠∠︒,即可; 【详解】由题知,如图,ABC 为等腰直角三角形,① 45BAC BCA ∠=∠=︒; 直尺边相互平行,120∠=︒① ADCE ,①120DAC ∠=∠=︒;又+245DAC ∠∠=︒,① 225∠=︒; 故选:B ;【点睛】本题考查平行线、等腰直角三角形的性质,关键在熟练应用等腰直角三角形的角的关系; 3.(2021·福建省福州咨询有限公司九年级模拟预测)如图,在①ABC 中,①B=40°,将①ABC 绕点A 逆时针旋转,得到①ADE ,点D 恰好落在直线BC 上,则旋转角的度数为( )3A .70°B .80°C .90°D .100°【答案】D 【分析】利用旋转的性质得到①ABC①①ADE ,根据全等三角形的性质可知AB=AD ,进而得到①ADB=①B=40°,再利用三角形内角和定理即可解答. 【详解】①将①ABC 绕点A 逆时针旋转,得到①ADE ①①ABC①①ADE ①AB=AD ①①ADB=①B=40° ①①ADB+①B+①BAD=180° ①①BAD=180°-40°-40°=100° 故选D 【点睛】本题考点涉及旋转的性质、全等三角形的性质、等腰三角形的性质以及三角形内角和定理,熟练掌握相关性质定理是解题关键.4.(2021·湖北黄石八中九年级三模)如图,在①ABC 中,①BAC =116°,分别以点A ,B 为圆心,大于12AB 的长为半径画弧,两弧相交于点D ,E ,作直线DE ,交BC 于点M ;分别以点A ,C 为圆心,大于12AC 的长为半径画弧,两弧相交于点P 、Q ,作直线PQ ,交BC 于点N ;连接AM 、AN .则①MAN 的度数为( )A .52°B .50°C .58°D .64°【答案】A 【分析】先根据作图可知DE 和FG 分别垂直平分AB 和AC ,再利用线段的垂直平分线的性质得到①B =①BAM ,①C =①CAN ,即可得到①MAN 的度数. 【详解】解:由作图可知,DE 和FG 分别垂直平分AB 和AC ,①MB =MA ,NA =NC ,①①B =①MAB ,①C =①NAC =116°, 在①ABC 中,BAC ∠=, ①①B +①C =180°−①BAC =64°, 即①MAB +①NAC =64°,则①MAN =①BAC −(①MAB +①NAC )=52°. 故选A . 【点睛】此题主要考查线段的垂直平分线的性质以及三角形内角和定理.解题时注意:线段的垂直平分线上的点到线段的两个端点的距离相等.5.(2021·陕西西安·交大附中分校)如图,①ABC 是①O 的内接三角形,AB =AC .BO 的延长线交AC 于点D .若①ABD =23°.则①A 的度数为( )A .23°B .32°C .46°D .60°【答案】C 【分析】延长BD 交O 于点E ,连接AE ,由圆周角定理可得90BAE ∠=︒,继而解得67AEB ∠=︒,根据等腰三角形的性质和三角形内角和定理解题即可. 【详解】解:延长BD 交O 于点E ,连接AE ,则90BAE ∠=︒23ABD ∠=︒9067AEB ABD ∴∠=︒-∠=︒67ACB AEB ∴∠=∠=︒AB AC =567ABC ACB ∴∠=∠=︒18046BAC ABC ACB ∴∠=︒-∠-∠=︒ 故选:C . 【点睛】本题考查三角形的外接圆与圆心、圆周角定理、直径所对的圆周角是90°、等腰三角形、三角形的内角和定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.6.(2021·浙江)如图,直线////a b c ,等腰直角ABC 的三个顶点分别在直线a ,b ,c 上(A 为直角顶点),若120∠=︒,则①2的度数为( )A .15°B .20°C .25°D .30°【答案】C 【分析】利用平行线的性质可以得到1320∠=∠=︒,由ABC 是等腰直角三角形可得到45ABC ∠=︒,再利用角的等量关系列式计算即可. 【详解】解:如图所示建立3∠①////a b c ①1320∠=∠=︒①ABC 是等腰直角三角形 ①45ABC ∠=︒①23452025ABC =-=︒-︒=︒∠∠∠ 故答案选:C 【点睛】本题主要考查了平行线的性质,等腰直角三角形的性质,利用平行线的性质进行角度等量代换是解题的关键.7.(2021·湖北随州·九年级一模)如图,PA、PB分别是①O的切线,A、B为切点,AC是①O的直径,已知①BAC=35°,①P的度数为()A.35°B.45°C.65°D.70°【答案】D【分析】由PA与PB都为圆的切线,根据切线的性质得到OA与AP垂直,OB与BP垂直,可得出①OAP与①OBP都为直角,又OA=OB,根据等边对等角可得①ABO与①BAC相等,由①BAC 的度数求出①ABO的度数,进而利用三角形的内角和定理求出①AOB的度数,在四边形APBO中,利用四边形的内角和定理即可求出①P的度数;【详解】①PA,PB分别是圆的切线①OA①AP,OB①BP,①①OAP=①OBP=90°,① OA=OB,①BAC=35°,① ①ABO=①BAC=35°,①①AOB=180°-35°-35°=110°,在四边形APBO中,①OAP=①OBP=90°,①AOB=110°,则① P=360°-(①OAP+①OBP+①AOB)=70°,故选:D.【点睛】此题考查了切线的性质,等腰三角形的性质,三角形及四边形的内角和定理,熟练掌握切线的性质是解本题的关键;∠=︒,则①2 8.(2021·全国)一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若120的度数是()A.15°B.20°C.25°D.40°【答案】C【分析】利用平行线的性质求得①3的度数,即可求得①2的度数.【详解】①AD①BC,①①3=①1=20︒,①①DEF是等腰直角三角形,①①EDF=45︒,①①2=45︒-①3=25︒,故选:C.【点睛】本题考查了平行线的性质,等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题.9.(2021·沙坪坝区·重庆八中九年级)如图,已知AB①CD,AD=CD,①1=40°,则①2的度数为()A.60°B.65°C.70°D.75°【答案】C【分析】由等腰三角形的性质可求①ACD=70°,由平行线的性质可求解.【详解】①AD=CD,①1=40°,①①ACD=70°,①AB①CD,①①2=①ACD=70°,故选:C.7【点睛】本题考查了等腰三角形的性质,平行线的性质,是基础题.10.(2021·河南九年级二模)如图,在①ABC中,AB=AC,AE平分①BAC,DE垂直平分AB,连接CE,①B=70°.则①BCE的度数为()A.55°B.50°C.40°D.35°【答案】B【分析】连接BE,根据等腰三角形性质求出EB=EC,根据线段垂直平分线性质求出AE=BE,根据等边对等角求出①BAE=①EBA、①BCE=①EBC,即可求出答案.【详解】解:如图,连接BE,①AB=AC,AE平分①BAC,①EB=EC,①①EBC=①ECB,①①ABC=70°,AC=AB,①①ACB=①ABC=70°,①①BAC=180°﹣①ABC﹣①ACB=40°,①AE平分①BAC,①①BAE=20°,①DE垂直平分AB,①AE=EB,①①ABE=①BAE=20°,①①BCE=①EBC=①ABC﹣①ABE=70°﹣20°=50°,故选B.【点睛】本题考查了等腰三角形的性质,线段垂直平分线的性质和三角形内角和定理等知识点,能求出①BAE=①EBA和①BCE=①EBC是解此题的关键.二、填空题11.(2021·辽宁九年级)AD是等腰三角形ABC的高,BC=2AD,则①BAC的度数是_____.【答案】90°或75°或15°【分析】可以分别从若BC是底边,即AB=AC,与若BC是腰,即BC=BA,①点D在BC边上,①若点D在CB的延长线上去分析,根据等腰三角形的性质与直角三角形的性质,即可求得答案.【详解】解:①AD是BC边上的高线,若BC是底边,即AB=AC,如图(1)所示,①BD=DC,AD①BC,①BAD=①CAD①AD=BD①①B=①BAD=45°①①BAC=2①BAD=90°若BC是腰BC=BA,①若点D在BC边上,如图(2)所示,则在Rt①BAD中,①BA=2AD,①①B=30°,①①BAC=75°;①若点D在CB的延长线上,如图(3)所示,类似地,得:①DBA=30°,则:①ABC=150°,①①BAC=15°.综上:①BAC的度数为90°,75°,15°.912.(2021·华中科技大学附属中学)如图,将Rt ABC ∆绕直角顶点C 逆时针旋转50︒,使顶点A 的对应点D 落在边AB 上,点B 的对应点E 与点D 的连线交BC 于点F ,则CFE ∠的度数为_______︒.【答案】105. 【分析】将Rt ABC ∆绕直角顶点C 逆时针旋转50︒得到Rt DEC ∆,可得旋转角=50DCA ECB ∠=∠︒,由CA =CD ,可求65A CDA ∠=∠=︒,由旋转性质①EDC =①A=65°,可求①FCD =90°-①ACD =90°-50°=40°,由外角性质=105CFE FCD CDF ∠∠+∠=︒. 【详解】解:将Rt ABC ∆绕直角顶点C 逆时针旋转50︒得到Rt DEC ∆, ①旋转角=50DCA ECB ∠=∠︒, ①CA =CD , ①()1180652A CDA DCA ∠=∠=︒-∠=︒, ①①EDC =①A=65°,①①FCD =90°-①ACD =90°-50°=40°,①=4065105CFE FCD CDF ∠∠+∠=︒+︒=︒, 故答案为:105.【点睛】本题考查旋转变换,旋转角,等腰三角形的性质,三角形内角和,互余角计算,三角形外角性质,掌握旋转变换性质,等腰三角形的性质,三角形内角和,互余角计算,三角形外角性11质,能从图中找到旋转角是解题关键.13.(2021·苏州高新区第二中学九年级二模)如图,在ABC ∆中,90,BAC ∠=︒点D 在BC 上,BD BA =,点E 在BC 的延长线上,CA CE =,连接AE ,则DAE ∠的度数为_____________.【答案】45 【分析】利用余角、等腰三角形和三角形外角的性质即可求出. 【详解】①BDA DAE AEC ∠=∠+∠,DAE DAC EAC ∠=∠+∠, ①BDA DAC EAC AEC ∠=∠+∠+∠. ①90DAC BAC BAD BAD ∠=∠-∠=︒-∠, ①90BDA BAD EAC AEC ∠=︒-∠+∠+∠. 根据题意可知=BDA BAD EAC AEC ∠=∠∠∠,. ①45BDA AEC ∠-∠=︒, ①=45DAE ∠︒. 故答案为:45. 【点睛】本题考查等腰三角形和三角形外角的性质以及余角.找出图形中角的等量关系是解答本题的关键.14.(2021·辽宁九年级)如图,在ABC 中,AB AC =,40B ∠=︒,点D 在线段BC 上运动(D 不与B 、C 重合),连接AD ,作40ADE ∠=︒,DE 交线段AC 于点E ,在点D 从B 向C 运动过程中,如果ADE 是等腰三角形,则BDA ∠的度数是____________【答案】110°或80° 【分析】根据等腰三角形的性质,先求出①BAC 的度数,然后分3种情况:①AD =AE 时,①AD=ED时,①当AE=DE时,分别求解,即可.【详解】①在①ABC中,AB=AC,①B=40°,①①B=①C=40°①①BAC=100°,①AD=AE时,①AED=①ADE=40°,①①DAE=100°,此时,点D与点B重合,不符合题意舍去,①AD=ED时,①DAE=①DEA,①①DAE=12(180°−40°)=70°,①①BAD=①BAC−①DAE=100°−70°=30°,①①BDA=180°−①B−①BAD=110°,①当AE=DE时,①DAE=①ADE=40°,①①BAD=100°−40°=60°,①①BDA=180°−40°−60°=80°,综上所述:①BDA的度数为110°或80°时,①ADE的形状是等腰三角形,故答案是:110°或80°【点睛】此题主要考查学生对等腰三角形的性质,三角形内角和定理的理解和掌握,解本题的关键是分类讨论,是一道基础题目.15.(2021·四川广安市·)规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“雅系特征值”,记作k,若2k3,则该等腰三角形的顶角为_____.【答案】45°.【分析】根据等腰三角形的性质得出①B=①C,根据三角形内角和定理和已知得出5①A=180°,求出即可.【详解】解:①①ABC中,AB=AC,①①B=①C,13①等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k ,若k=2k 3=, ①①A :①B :①C =2:3:3, 即①A=180°×22+3+3=45°, ①①A=45°. 故答案为:45°. 【点睛】本题考查三角形内角和定理和等腰三角形的性质,能根据等腰三角形性质、三角形内角和定理和已知得出①A=180°×22+3+3是解题关键. 三、解答题16.(2021·厦门市松柏中学九年级)如图,在Rt ABC △中,①BAC =90°,将Rt ABC △绕直角顶点A 逆时针旋转一定角度后得到Rt ADE △,当点D 在边BC 上时,连接CE . (1)若旋转角为60°,求①ACB 的度数; (2)若AB =3,AC =4,求sin①DAC 的值.【答案】(1)30°;(2)725【分析】(1)由旋转的性质得出AD AB =,60BAD ∠=︒,进而由等腰三角形的性质及三角形的内角和得出60B ADB ∠=∠=︒,最后再由直角三角形的两个锐角互余即可求得答案;(2)由勾股定理求出5BC =,过点A 作AF BC ⊥于点F ,由三角形的面积求出AF 的长,进而可求出CD ,DE 的长,则可得出答案. 【详解】解:(1)将Rt ABC △绕直角顶点A 旋转一定角度后得到Rt ADE △,旋转角为60°,AD AB ∴=,60BAD ∠=︒,60B ADB ∴∠=∠=︒,90BAC ∠=︒,9030ACB B ∴∠=︒-∠=︒,①①ACB 的度数为30°;(2)90BAC ∠=︒,3AB =,4AC =,5BC ∴==,如图,过点A 作AF BC ⊥于点F ,∴1122ABCSAB AC BC AF =⋅=⋅, 341255AB AC AF BC ⋅⨯∴===,95BF ∴,=AD AB ,AF BC ⊥,95DF BF ∴==, 75CD BC BD ∴=-=, 设AC 与DE 相交于点K ,①将Rt ABC △绕直角顶点A 旋转一定角度后得到Rt ADE △,AD AB ∴=,AE AC =,90BAC DAE ∠=∠=︒,B ADB ∴∠=∠,ACE AEC ∠=∠,90BAC DAE ∠=∠=︒,①90BAD DAC CAE DAC ∠+∠=∠+∠=︒,BAD CAE ∴∠=∠,又1902B BAD ∠=︒-∠,1902ECA CAE ∠=︒-∠,ECA B ∴∠=∠,又①旋转,15①B ADE ∠=∠,5DE BC ==,ECA B ADE ∠=∠=∠,AKD EKC ∠=∠,DAC CED ∴∠=∠,90ACB B ∠+∠=︒,ECA B ∠=∠,90ACB ECA ∴∠+∠=︒,775sin sin 525CD DAC CED DE ∴∠=∠===.【点睛】本题考查了旋转的性质,勾股定理,等腰三角形的性质,锐角三角函数的定义,熟练掌握旋转的性质是解题的关键.17.(2021·湖北九年级)如图,ABC 中,点D 在BC 边上,且1902ADB CAD ∠=+∠°.(1)求证:AD AC =;(2)点E 在AB 边上,连接CE 交AD 于点F ,且CFD CAB ∠=∠,AE BD =, ①求ABC ∠的度数;①若8AB =,2DF AF =,直接写出EF 的长. 【答案】(1)见解析;(2)①60°;①23EF =. 【分析】(1)根据ADB ACB CAD ∠=∠+∠,1902ADB CAD ∠=+∠°可得C ADC ∠=∠,进而可得结论;(2)①过点D 作//DG CE 交AB 于点G ,根据“AAS”证出AEC ①DGA △,进而可得BDG 为等边三角形,可得答案;①过点D 作//DH AB 交CE 于点H ,可得FAE ①ACE ,根据比例式可得答案. 【详解】解:(1)①ADB ACB CAD ∠=∠+∠,1902ADB CAD ∠=+∠°,①1902ACB ADB CAD CAD ∠=∠-∠=-∠°,①180ADB CDA ∠+∠=°,①11180180909022CDA ADB CAD CAD ⎛⎫∠=-∠=-+∠=-∠ ⎪⎝⎭°°°°,①ACB ADC ∠=∠, ①AD AC =;(2)①过点D 作//DG CE 交AB 于点G ,①CFD CAB ∠=∠,CFD CAD ACE ∠=∠+∠,CAB CAD DAB ∠=∠+∠, ①ACE DAB ∠=∠,又①ACD ADC ∠=∠,ECB ACD ACE ∠=∠-∠,B ADC DAB ∠=∠-∠, ①ECB B ∠=∠, ①CE BE =, ①//DG CE , ①ECB B ∠=∠, ①DG BG =,①AEC DGA ∠=∠,AC DA =,ACE DAG ∠=∠, ①AEC ①DGA △(AAS), ①DG AE =, 又①AE BD =, ①DG BD BG ==, ①BDG 为等边三角形, ①60ABC ∠=︒; ①23EF =. 过点D 作//DH AB 交CE 于点H ,由①知EBC 和HDC △均为等边三角形,17设AE BD x ==,则8BE BC x ==-, ①82DH CD x ==-, ①//DH AB , ①AE AF DH FD =,即182x x =-, ①2x =,①ACE DAB ∠=∠, ①FAE ①ACE , ①EF AFAE AC=, ①3AC AD AF ==, ①13EF AE =,1233EF AE ==.【点睛】本题考查等腰三角形的性质、全等三角形的判定和性质以及相似三角形的判定和性质,正确作出辅助线是解题关键,题目难度较大,综合性较强.18.(2021·江苏南通田家炳中学九年级)如图,已知点D 、E 在ABC 的边BC 上,AB AC =,AD AE =.(1)求证:BD CE =;(2)若AD BD DE CE ===,求BAE ∠的度数.【答案】(1)证明见解析;(2)90. 【分析】(1)作AF BC ⊥于点F ,利用等腰三角形三线合一的性质得到BF CF =,DF EF =,相减后即可得到正确的结论;(2)根据等边三角形的判定得到ADE 是等边三角形,根据等边三角形的性质、等腰三角形的性质以及角的和差关系即可求解. 【详解】(1)证明:如图,过点A 作AF BC ⊥于F .AB AC =,AD AE =,∴BF CF =,DF EF =, ∴BF DF CF EF -=-, ∴BD CE =.(2)AD DE AE ==,∴ADE 是等边三角形, ∴60DAE ADE ∠=∠=,AD BD =,∴DAB DBA ∠=∠, ∴1302DAB ADE ∠=∠=, ∴603090BAE DAB DAE ∠=∠+∠=+=.答:BAE ∠的度数为:90. 【点睛】本题考查了等腰三角形和等边三角形的性质,熟练掌握等腰三角形三线合一的性质是本题的关键.19.(2021·福建九年级)如图,已知等腰三角形ABC 的顶角108A ∠=︒.(1)在BC 上作一点D ,使AD CD =(要求:尺规作图,保留作图痕迹,不必写作法和证明).(2)直接写出BAD ∠的度数. 【答案】(1)见解析;(2)72° 【分析】(1)根据线段垂直平分线的性质即可在BC 上作一点D ,使AD=CD ; (2)结合(1)根据三角形内角和及等腰三角形的性质求出C ∠及DAC ∠,所以BAD BAC DAC ∠=∠-∠问题得解.【详解】19解:(1)如图,点D 即为所求;(2)连接AD ,①AB AC =,108A ∠=︒, ①36B C ∠==︒, 由(1)得:AD CD =, ①36DAC C ∠=∠=︒,1083672BAD BAC DAC ∠=∠-∠=︒-︒=︒.【点睛】本题考查了线段垂直平分线的性质,等腰三角形的性质,三角形内角和定理,根据图形正确找到角之间的关系是解题的关键.20.(2021·湖南湘西·)如图,在ABC ∆中,点D 在AB 边上,CB CD =,将边CA 绕点C 旋转到CE 的位置,使得ECA DCB ∠=∠,连接DE 与AC 交于点F ,且70B ∠=︒,10A ∠=︒. (1)求证:AB ED =; (2)求AFE ∠的度数.【答案】(1)见详解;(2)50AFE ∠=︒ 【分析】(1)由题意易得ECD ACB ∠=∠,AC EC =,则有≌ACB ECD △△,然后问题可求证; (2)由(1)可得10E A ∠=∠=︒,然后可得40ECA DCB ∠=∠=︒,进而根据三角形外角的性质可进行求解. 【详解】(1)证明:①ECA DCB ∠=∠,①ECA ACD DCB ACD ∠+∠=∠+∠,即ECD ACB ∠=∠,①AC EC =,CB CD =, ①()ACB ECD SAS ≌, ①AB ED =;(2)解:①CB CD =,70B ∠=︒, ①70CDB B ∠=∠=︒,①根据三角形内角和可得180240BCD B ∠=︒-∠=︒, ①40ECA DCB ∠=∠=︒,由(1)可得≌ACB ECD △△, ①10A ∠=︒, ①10E A ∠=∠=︒,①50AFE E ACE ∠=∠+∠=︒. 【点睛】本题主要考查等腰三角形的性质及全等三角形的性质与判定,熟练掌握等腰三角形的性质及全等三角形的性质与判定是解题的关键.21.(2021·江苏九年级)如图,在四边形ABCD 中,①B =90°,AC 平分①DAB ,DE ①AC ,垂足为E ,且AE =AB . (1)求证:BC =DE ;(2)若①DAC =40°,求①CDE 的度数.【答案】(1)见解析;(2)20° 【分析】(1)根据ASA 证明①ABC ①①AED ,由全等三角形的性质即可求证;(2)根据①ABC ①①AED 可得AC =AD ,根据等腰三角形的性质即可解决问题. 【详解】证明:①DE ①AC ,①B =90°, ①①B =①AED =90°, ①AC 平分①DAB , ①①BAC =①EAD ,21 在①ABC 和①AED 中,BAC EADAB AE B AED∠∠⎧⎪⎨⎪∠∠⎩===,①①ABC ①①AED (ASA ),①BC =DE ;(2)①①ABC ①①AED ,①AC =AD ,①①ACD =①ADC ,①①DAC =40°,DE ①AC ,①①ACD =①ADC =70°,①ADE =50°,①①CDE =20°.【点睛】本题考查了全等三角形的判定与性质,等腰三角形的判定与性质,解决本题的关键是掌握全等三角形的判定与性质,等腰三角形的判定与性质.22.(2021·浙江九年级二模)已知:如图,在五边形ABCDE 中,AB AE =,B E ∠=∠,BC ED =.(1)求证:ABC AED ≌△△.(2)当//AC DE ,40ADE ∠=︒时,求ACD ∠的度数.【答案】(1)见解析;(2)70︒【分析】(1)利用SAS 即可证明结论;(2)结合(1)可得AC =AD ,根据等腰三角形的性质即可求出①ACD 的度数.【详解】(1)证明:①AB AE =①B E ∠=∠①BC ED =①()ABC AED SAS ≌△△(2)①//AC DE ,40ADE ∠=︒①40CAD ADE ∠=∠=︒①ABC AED ≌△△①AC AD = ①()1180702ACD CAD ∠=︒-∠=︒ 【点睛】本题考查了全等三角形的判定与性质,解决本题的关键是利用边角边证明①ABC ①①AED . 23.(2021·温州市第十二中学九年级)已知:如图,点A 、B 、C 、D 在一条直线上,//FB EA 交EC 于H 点,EA FB =,AB CD =.(1)求证:ACE BDF ≌;(2)若CH BC =,50A ∠=︒,求D ∠的度数.【答案】(1)见解析;(2)80°【分析】(1)由//EA FB ,利用同位角相等可得EAC FBD ∠=∠.由AB CD =,利用等式性质可得AC BD =,可证()ACE BDF SAS ≌;(2)由//FB EA 可得=50EAC FBD ∠=∠︒,由CH BC =利用等角对等边,可求50HBC BHC ∠=∠=︒.利用三角形内角和可得80ECA ∠=︒.利用ACE BDF ≌性质,可得80ECA D ∠=∠=︒.【详解】(1)证明:①//EA FB ,①EAC FBD ∠=∠.①AB CD =,①AB BC CD BC +=+,即AC BD =,在ACE 和BDF 中,①AC BD EAC FBD EA FB =⎧⎪∠=∠⎨⎪=⎩,①()ACE BDF SAS ≌.23 (2)解://FB EA ,①=50EAC FBD ∠=∠︒,①CH BC =,①50HBC BHC ∠=∠=︒.①180505080ECA ∠=︒-︒-︒=︒.①ACE BDF ≌,①80ECA D ∠=∠=︒.【点睛】本题考查平行线性质,等腰三角形性质,三角形全等判定与性质,三角形内角和,掌握平行线性质,等腰三角形性质,三角形全等判定与性质,三角形内角和是解题关键.。
专题06 阅读理解记叙文-高考真题和模拟题英语分项汇编(解析版)

专题06阅读理解记叙文一、2022年高考真题1.(2022年全国甲卷)As Ginni Bazlinton reached Antarctica, she found herself greeted by a group of little Gentoo penguins (企鹅) longing to say hello. These gentle, lovely gatekeepers welcomed her and kick-started what was to be a trip Ginni would never forget.Ever since her childhood, Ginni, now 71, has had a deep love for travel. Throughout her career (职业) as a professional dancer, she toured in the UK, but always longed to explore further. When she retired from dancing and her sons eventually flew the nest, she decided it was time to take the plunge.After taking a degree at Chichester University in Related Arts, Ginni began to travel the world, eventually getting work teaching English in Japan and Chile. And it was in Chile she discovered she could get last-minute cheap deals on ships going to Antarctica from the islands off Tierra del Fuego, the southernmost tip of the South American mainland. “I just decided I wanted to go,” she says. “I had no idea about what I’d find there and I wasn’t nervous, I just wanted to do it. And I wanted to do it alone as I always prefer it that way.”In March 2008, Ginni boarded a ship with 48 passengers she’d never met before, to begin the journey towards Antarctica. “From seeing the wildlife to witnessing sunrises, the whole experience was amazing. Antarctica left an impression on me that no other place has,” Ginni says. “I remember the first time I saw a humpback whale; it just rose out of the water like some prehistoric creature and I thought it was smiling at us. You could still hear the operatic sounds it was making underwater.”The realization that this is a precious land, to be respected by humans, was one of the biggest things that hit home to Ginni.28. Which of the following best explains “take the plunge” underlined in paragraph 2?A. Try challenging things.B. Take a degree.C. Bring back lost memories.D. Stick to a promise.29. What made Ginni decide on the trip to Antarctica?A. Lovely penguins.B. Beautiful scenery.C. A discount fare.D. A friend’s invitation.30. What does Ginni think about Antarctica after the journey?A. It could be a home for her.B. It should be easily accessible.C. It should be well preserved.D. It needs to be fully introduced.31. What is the text mainly about?A. A childhood dream.B. An unforgettable experience.C. Sailing around the world.D. Meeting animals in Antarctica.体裁:记叙文主题:人与自我--生活-旅行【字数】300 + 98【语篇导读】文章主要介绍了71岁的Ginni Balinton从小就对旅行有着深深的热爱,渴望探险,不再跳舞和孩子们成家立业之后,她开始周游世界,并在2008年开始了前往南极洲的旅程。
2024高考物理复习专题06 机械能守恒定律 能量守恒定律(讲义)(解析版)

知积建构
机械能· 机械能是否守恒的三种判断方法
机械能与图象结合的问题, 应用机械能守恒定律解题的一般步骤
系统机械能守恒的三种表示方式· 多物体系统的机械能守恒问题
机械能及守恒的判断
机械能守恒定律
能量守恒定律
机械能守恒 定律的应用
能量守恒定律
及其应用
涉及弹簧的能量问题 摩擦力做功的能量问题
可知铅球速度变大,则动能越来越大,CD错误。 故选B。
2.(2021·全国·高考真题)如图,光滑水平地面上有一小车,一轻弹簧的一端与车厢的挡板相连,另一端 与滑块相连,滑块与车厢的水平底板间有摩擦。用力向右推动车厢使弹簧压缩,撤去推力时滑块在车厢底 板上有相对滑动。在地面参考系(可视为惯性系)中,从撤去推力开始,小车、弹簧和滑块组成的系统()
A.弹性绳刚伸直时,运动员开始减速
B.整个下落过程中,运动员的机械能保持不变 C.整个下落过程中,重力对运动员所做的功大于运动员克服弹性绳弹力所做的功
D.弹性绳从伸直到最低点的过程中,运动员的重力势能与弹性绳的弹性势能之和先减小后增大
【答案】D 【详解】A.弹性绳刚伸直时,此时运动员的重力大于弹性绳的弹力,加速度向下,运动员仍加速运动,故 A错误;B.整个下落过程中,运动员连同弹性绳的机械能总和不变,但是整个下落过程中随着弹性绳的弹 性势能增大,运动员的机械能在减小,故B错误;C.整个下落过程中,初末状态运动员的速度均为零,重
3.板块问题……………………………………20
4.传送带问题……………………………………21 题型特训·命题预测…21 考向一 能量转化及守恒定律的综合应用………21
考向二 涉及弹簧的能量问题……………………22
考向三 涉及板块、传送带的能量问题…………24
七年级数学专题06 平方根、立方根知识讲解(解析版)

专题06 平方根、立方根知识讲解知识点一:算术平方根、平方根、立方根概念【例1-1】(2020·广东东莞月考)在下列各式中正确的是( )A 3=-B .2=C 8=D 3=【答案】D.3, ∴选项A 错误;∵±2, ∴选项B 错误;4, ∴选项C 错误;3,∴选项D 正确. 故答案为:D .【例1-2】(2021·河北邯郸期末) ) A .0.2的平方根 B .0.2-的算术平方根 C .0.2的负的平方根 D .0.2-的平方根【答案】C.【解析】解:由平方根的定义可得0.2的平方根为:,其中为0.2的负的平方根 故答案为:C .【例1-3】(2020·四川通江县月考)下列说法中,正确的是( ) A .9的平方根是3 B .25-的平方根是5-C .任何一个非负数的平方根都是非负数D .一个正数的平方根有2个,它们互为相反数 【答案】D.【解析】解:A 、9的平方根是±3,错误; B 、−25的没有平方根,错误;C 、任何一个非负数的算术平方根都是非负数,错误;D 、一个正数的平方根有2个,它们互为相反数,正确. 故答案为:D .【例1-4】(2020·鹿邑县期末)若3109,b a =-且b 的算术平方根为4,则a =__________. 【答案】5.【解析】解:∵b 的算术平方根为4, ∴b=16, ∴16=a 3-109 ∴a =5. 故答案为:5.【变式1-1】(2020·福建永春月考)下列说法中,不正确的是( ) A .非负数才有平方根B .非负数的算术平方根是非负数C .任何数都有两个平方根D .负数没有平方根【答案】C.【解析】解:A. 非负数才有平方根,正确; B. 非负数的算术平方根是非负数,正确; C. 0只有1个平方根,错误; D. 负数没有平方根,正确. 故答案为:C .【变式1-2】(2020·山东济南期中)若30a ++=,则+a b 的立方根是______. 【答案】-1.【解析】解:∵30a ++=, ∴3+a=0, 2-b=0, ∴a=-3,b=2 ∴a+b=-1∴a+b 的立方根-1. 故答案为:-1.【变式1-3】(2019·河北邢台期末)有一个正方体的集装箱,原体积为364m ,现准备将其扩容以盛放更多的货物,若要使其体积达到3125m ,则它的棱长需要增加__________m . 【答案】1.【解析】解:设正方体集装箱的棱长为a , ∵体积为64m 3,∴=4m ;设体积达到125m 3的棱长为b ,则=5m , ∴b-a=5-4=1(m ). 故答案为:1.【变式1-4】对于结论:当a +b =0时,a 3+b 3=0也成立.若将a 看成a 3的立方根,b 看成是b 3的立方根,由此得出这样的结论:“如果两数的立方根互为相反数,那么这两数也互为相反数”.(1)试举一个例子来判断上述结论的猜测是否成立?(2与的值互为相反数,求1- 【答案】见解析.【解析】解:(1)答案不唯一.0=, 8与﹣8互为相反数; (2)由已知,得(3﹣2x )+(x +5)=0, 解得x =8,∴1=1﹣4=﹣3.【变式1-5】(2020·________,2________.【答案】32.,9的算术平方根为33.22,故答案为:32.【变式1-6】(2019·海南海口月考)已知a 的整数,31a b +-的平方根是4±, (1)求,a b 的值; (2)求2+a b 的平方根.【答案】(1)a=5;b=2;(2)±3.<<,且a 的整数, ∴a=5∵3a+b-1的平方根是±4, ∴3a+b-1=16 ∴b=2(2)当a=5,b=2时,a+2b=9 ∴a+2b 的平方根为:±3.知识点二:算术平方根、平方根、立方根性质【例2-1】(2020·海伦市期中)某数x 的两个不同的平方根是23a +与15a -,则x 的值是( ) A .11 B .121C .4D .11±【答案】B.【解析】解:由题意得:2a+3+a-15=0 解得:a=4当a=4时,2a+3=11 则x=112=121. 故答案为:B .【变式2-1】已知一个正数m 的平方根为2n +1和4﹣3n . (1)求m 的值;(2)|a ﹣3|(c ﹣n )2=0,a +b +c 的立方根是多少? 【答案】(1)121;(2)2.【解析】解:(1)由正数m 的平方根互为相反数,得: 2n +1+4﹣3n =0, ∴n =5, ∴2n +1=11, ∴m =112=121;(2)∵|a ﹣3|(c ﹣n )2=0, ∴a =3,b =0,c =n =5, ∴a +b +c =3+0+5=8, ∴a +b +c 的立方根是2.【变式2-2】(2021·河北唐山期末)如果一个正数a 的两个不同平方根分别是22x -和63x -,则a =______.【答案】36.【解析】解:由题意得: 2x-2+6-3x=0, 解得x=4,a=62=36 故答案为:36.【例2-2】(2020·江苏南通月考)若x ,y 为实数,且20x +=,则2021x y ⎛⎫⎪⎝⎭的值为( ) A .1 B .-1C .2D .-2【答案】B.【解析】解:由题意得: x+2=0,y-2=0 ∴x=-2,y=2∴2021202122x y ⎛⎫-⎛⎫= ⎪ ⎪⎝⎭⎝⎭=-1故答案为:B.【例2-3】﹣2x ﹣1=0,则x =_____. 【答案】0或﹣1或﹣12.﹣2x ﹣1=0,=2x+1,∴2x+1=1或2x+1=﹣1或2x+1=0, 解得x =0或x =﹣1或x =﹣12. 故答案为:0或﹣1或﹣12. 知识点三:综合题型【例3-1】(渠县月考)求下列各式中的x 的值 (1)21(1)82x +=;(2)3(21)270x -+= 【答案】(1)x=3或x=5;(2)x=-1.【解析】解:(1)两边乘以2得,(x+1)2=16, x+1=4或x+1=-4(2)(2x-1)3=-27 2x-1=-3 x=-1【变式3-1】(2020·江苏苏州月考)求下列各式中的x . (1)24120x -= (2)()216281x -= 【答案】见解析. 【解析】解:(1)4x 2=12 x 2=3(2)(x-2)2=8116 x-2=94或x-2=-94x=174或x=-14【变式3-2】(2020·剑阁县月考)(1)已知:m 3=8,n 2=9,且mn <0,求m 2-2mn+n 2的值. (2)已知a =5,b 2=9,(c-1)2=4,且ab >0,bc <0,求式子ab-bc-ca 的值. 【答案】(1)25;(2)23或39. 【解析】解:(1)由m 3=8,得m=2, 由n 2=9,得n=±3, 由mn <0,得:m=2,n=-3 当m=2,n=-3时, m 2-2mn+n 2=4+12+9=25 (2)由题意知a=±5, 由b 2=9得:b=±3, 由(c-1)2=4,得:c=3或-1 ∵ab >0,bc <0 ∴a 、b 同号,b 、c 异号当a=5,b=3,c=-1时,原式=15+3+5=23 当a=-5,b=-3,c=3时,原式=15+9+15=39. 【例4-1】(2020·浙江杭州期中)解答下列各题.(1)已知2x +3与x -18是某数的平方根,求x 的值及这个数.(2)已知20c d -+=,求d +c 的平方根. 【答案】(1)x =5,169或x=-21,1521;(2)±3. 【解析】解:(1)解:①由题意得:2x+3+x-18=0, 解得:x=5这个数是(2×5+3)2=169. ②2x+3=x-18,解得x=-21 这个数是(-21-18)2=1521; (2)由题意得:2c -d =0,d 2-36=0, 解得:d=±6,c=±3. 当d =-6,c =-3时,d +c =-9(没有平方根), 当d=6,c=3时,d+c=9,平方根为±3. 【例4-2】(2020·河南周口期中)在数学活动课上,李老师设计了一个游戏活动,四名同学分别代表一种运算,四名同学可以任意排列,每次排列代表一种运算顺序,剩余同学中,一名学生负责说一个数,其他同学负责运算,运算结果既对又快者获胜,可以得到一个奖品. 下面我们用四个卡片代表四名同学(如图):(1)列式,并计算:①﹣3经过A ,B ,C ,D 的顺序运算后,结果是多少? ②5经过B ,C ,A ,D 的顺序运算后,结果是多少?(2)探究:数a 经过D ,C ,A ,B 的顺序运算后,结果是55,a 是多少? 【答案】(1)①7;②206;(2)-1或-11. 【解析】解:(1)①()23256-⨯--+⎡⎤⎣⎦ =(-6+5)2+6=1+7 =7②()25526--⨯+⎡⎤⎣⎦, =(5+5)2×2+6 =100×2+6 =206(2)由题意得:2(a+6)2-(-5)=55, 整理得:(a+6)2=25, a+6=5或a+6=-5 ∴a=-1或a=-11.【变式4-1】已知2x +1的算术平方根是0=4,z 是﹣27的立方根,求2x +y +z 的值. 【答案】12.【解析】解:∵2x +1的算术平方根是0, ∴2x +1=0, ∴2x =﹣1,=4,∴y =16,∵z 是﹣27的立方根, ∴z =﹣3,∴2x +y +z =﹣1+16﹣3=12.【变式4-2】(2020·乐清市月考)有一个数值转换器,流程如下:当输入的x 值为64时,输出的y 值是( )A .4BC .2D 【答案】B.,是有理数,8的立方根是2,是有理数,2 故答案为:B .【例5-1】(2020·浙江期中),( ) A .287.2 B .28.72 C .13.33 D .133.3【答案】C.1.3331013.33==≈⨯=. 故答案为:C .【例5-2】(2020· 2.449≈7.746≈≈______. 【答案】0.07746.7.746=0.0774*******≈ 故答案为:0.07746.【例5-3】(2020·余干县月考)数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读其中的奥秘.你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:①31000100==,又1000593191000000<<,10100∴<,∴能确定59319的立方根是个两位数.②∵59319的个位数是9,又39729=,∴能确定59319的立方根的个位数是9.③如果划去59319后面的三位319得到数59,<34<<,可得3040<<, 由此能确定59319的立方根的十位数是3 因此59319的立方根是39.(1)现在换一个数195112,按这种方法求立方根,请完成下列填空. ①它的立方根是_______位数. ②它的立方根的个位数是_______. ③它的立方根的十位数是__________.④195112的立方根是________.(2)请直接填写....结果:=________.=________.【答案】(1)①两;②8;③5;④58;(2)①24;②56.==,1000<195112<1000000【解析】解:(1100∴<100,∴能确定195112的立方根是一个两位数,故答案为:两;②∵195112的个位数字是2,83=512,∴能确定195112的个位数字是8,故答案为:8;③如果划去195112后面三位112得到数195,<,<<,∴56<<,可得5060由此能确定195112的立方根的十位数是5,故答案为:5;④根据②③可得:195112的立方根是58,故答案为:58;(2)①13824的立方根是两位数,立方根的个位数是4,十位数是2,∴13824的立方根是24,故答案为:24;②175616的立方根是两位数,立方根的个位数是6,十位数是5,∴175616的立方根是56,故答案为:56.===,则【变式5-1】(2020·0.5325______________________.【答案】11.47【解析】解:=1.147,===⨯=1.1471011.47故答案为: 11.47.【变式5-2】(2019· 1.41421356237十三位(包括小数点),现在想知道7后面的数字是什么,可以在这个计算器中计算下面哪一个值()A.B.10)C.D【答案】B.1之后,扩大10倍即可实现,故答案为:B.【变式5-3】(2020·山西大同月考)观察下表,回答问题:(1)表格中x=_________________,y=_________________;(2)用一句话描述你发现的规律:_________________;(3)根据你发现的规律填空:≈≈≈,2.714=_________________;②58.48≈,则a=_________________.【答案】(1)0.1,10;(2)在开立方运算中,被开方数的小数点向右或向左移动3位,它的立方根的小数点就相应地向右或向左移动1位;(3)①0.2714;②200000.【解析】解:(1)根据题意,立方根的被开方数扩大1000倍,立方根扩大10倍;∴x=0.1,y=10;故答案为:0.1;10.(2)在开立方运算中,被开方数的小数点向右或向左移动3位,它的立方根的小数点就相应地向右或向左移动1位;==≈;(30.2714≈,0.5848∴1001000.584858.48≈⨯=,≈,58.48≈=100∴a=200000;故答案为:①0.2714;②200000.【例6-1】(2020·成都双流月考)定义:不超过实数x的最大整数称为x的整数部分,记作[x].例如[3.6]=3,[=﹣2,按此规定,[1﹣=_____.【答案】-4.∴4<5,∴﹣4>﹣5,∴﹣3>1﹣4,故,[1﹣=﹣4.故答案为:﹣4.【例6-2】(2020·x的所有整数x的和是_____.【答案】2.【解析】解:∵﹣21,2<3,x的所有整数有﹣1,0,1,2,∴﹣1+0+1+2=2,故答案为:2.【例6-3】(2020·太原市月考)比较大小______0.5 .(填“>”,“<”或“= ”)【答案】>.1>1故答案为:>.【例6-4】对于实数x,我们规定[]x表示不大于x的最大整数,如==-=-,现对85进行如下操作:[5]5,1,[ 3.5]4第1次第2次第3次,这样对85只需3次操作后−−−→=−−−→=−−−→=85931就变为1.类似地,按照以上操作只需进行3次操作后变为1的所有整数中,最大的正整数是________.【答案】255.=,x为正整数,则1≤,【解析】解:设1∴1≤y<4,即最大正整数是3;=,y为正整数,则3≤,设3∴9≤y<16,即最大正整数是15;=,z为正整数,则15≤,设15∴225≤z<256,即最大正整数是255.∴只需进行3次操作后变为1的所有正整数中,最大的是255.故答案为:255.【例7-1】(2020·舟山普陀区期中)我们规定,对数轴上的任意点P进行如下操作:先将点P表示的数乘以-1,再把所得数对应的点向右平移2个单位,得到点P的对应点P′,现对数轴上的点A,B进行以上操作,分别得到点A′,B′.(1)若点A 对应的数是1,则点A ′对应的数x =_________, 若点B ′对应的数是4,则点B 对应的数y =_________; (2)在(1)的条件下,求代数式x -4y 算术平方根. 【答案】(1)x=1,y=-2;(2)3.【解析】解:(1) 设P 点表示的数为x ,P′表示的数为-x+2,点A 对应的数是1,则点A ′对应的数x =-1+2=1,点B ′对应的数是4,则点B 对应的数y =4×(-1)+2=-4+2=-2, 故答案为:x=1;y=-2,(2)由(1)求出,x=1,y=-2,代数式x -4y 的值为=1-4×(-2)=9, 代数式x -4y 算术平方根为3.【例7-2】(2019·河北保定期中)先观察下列等式,再回答下列问题:111111112=+-=+;111112216=+-=+1111133112=+-=+(1) (2)请你按照上面各等式反映的规律,用含n 的等式表示(n 为正整数). 【答案】(1)1120(2)()111n n ++(n 为正整数).【解析】解:(1)14−141+=1120,=1120(2)=1+1 n−1 n 1+=1+()1n n 1+ (n 为正整数). 【变式7-1】(2019·北京昌平期中)如图,是一个无理数筛选器的工作流程图. (1)当x 为16时,y 值为_____;(2)是否存在输入有意义的x 值后,却始终输不出y 值?如果存在,写出所有满足要求的x值;如果不存在,请说明理由;(3)如果输入x值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的x值可能是什么情况;(4)当输出的y x值是否唯一,如果不唯一,请写出其中的两个.【答案】(1)(2)存在,当x=0,1时,始终输不出y值;(3)x<0;(4)x的值不唯一.x=3或x=9.【解析】解:(1)当x=16,则(2)当x=0,1时,始终输不出y值.因为0,1的算术平方根是0,1,一定是有理数;(3)当x<0时,导致开平方运算无法进行;(4)x的值不唯一.x=3或x=9.【例8-1】(2020·湖北黄冈期末)如图,一根细线上端固定,下端系一个小球,让这个小球来回自由摆动,来回摆动一次所用的时间t(单位:s)与细线的长度l(单位:m)之间满足关系2t=0.4m时,小球来回摆动一次所用的时间是多少?(结果保留小数点后一位)【答案】1.3.【解析】解:把l=0.4m代入关系式2t=得,∴12=0.45tπππ=⨯≈1.3(秒).【变式8-1】(2020·陕西宝鸡月考)自由下落的物体的高度h(m)与下落时间t(s)的关系为h=4.9t2.有一学生不慎让一个足球从19.6m高的楼上自由落下,刚好另有一学生站在与下落的足球在同一直线的地面上,在足球下落的同时,楼上的学生惊叫一声,若楼下的学生听到惊叫后开始躲.问:这时楼下的学生听到惊叫后能躲开下落的足球吗?(声音的速度为340m/s)【答案】能躲开.【解析】解:足球下落的时间:,学生的声音传播到楼下的时间:t=19.6340=0.06s由2>0.06所以楼下的学生能躲开.【变式8-2】(汉中南郑区期中)如图,每个小正方形的边长均为1,阴影部分是一个正方形.(1)阴影部分的面积是__________,边长是____________;(2)写出不大于阴影正方形边长的所有正整数;(3)a为阴影正方形边长的小数部分,b的整数部分,求+a b的值.【答案】(1)13(2)1,2,3;(3【解析】解:(1)阴影部分面积为:1554232512132⨯-⨯⨯⨯=-=,∵阴影部分是一个正方形,故答案为:13(21,2,3.(3)∵34<,∴3a =,∵34<< ∴b=3∴33+=【例9-1】(2020·四川月考)实数a ,b 在数轴上的位置如图所示,那么化简a b a ++-的结果为( )A .2a -B .22b a -C .0D .2b【答案】A.【解析】解:由图可知:a<0<b ,a+b<0, 原式=-a-b+(-a )+b =-2a故答案为:A .【变式9-1】(2020·江苏徐州月考)如图,数轴上点A ,B ,C 所对应的实数分别为a ,b ,c |-|a c【答案】2a-c.【解析】解:由数轴得a<b<0<c , ∴a-c<0,a+b<0, 原式=-b-(c-a )+(a+b) =-b-c+a+a+b =2a-c.。
高中生物 必刷经典题 专题06 期末考试(含解析)(必修2)-人教版高中必修2生物试题
期末考试1.如图为高等动物的细胞分裂示意图。
下列叙述,正确的是A.图甲一定为次级精母细胞B.图乙一定为初级卵母细胞C.图丙为次级卵母细胞或极体D.图丙中的M、m为一对同源染色体2.细胞分裂过程中一条染色体上DNA含量的变化情况如图所示。
下列叙述错误的是A.AB可表示DNA分子复制B.DE可表示减数第二次分裂全过程C.CD可表示染色体的着丝点分裂D.BC可表示有丝分裂前期和中期一条染色体上的DNA含量3.性染色体XYY的男性,患者的临床表现是举止失常,性格失调,容易冲动,部分患者生殖器官发育不完全。
下面有关说法正确的是A.父方减数第二分裂时同源染色体未分离所致B.父方减数第一次分裂时姐妹染色单体未分离所致C.其X染色体应来自祖母D.父方减数第二次分裂时出现的异常所致4.下列关于DNA分子和染色体数目的叙述,正确的是A.有丝分裂间期细胞中染色体数目因DNA复制而加倍B.有丝分裂后期细胞中DNA分子数目因染色体着丝点分裂而加倍C.减数第一次分裂完成后,染色体数目因同源染色体分别进入两个细胞而减半D.减数第二次分裂过程中细胞中染色体与DNA分子数目始终不变5.若某哺乳动物毛色由 3 对位于常染色体上的、独立分配的等位基因决定,其中 A 基因编码的酶可使黄色素转化为褐色素;B 基因编码的酶可使该褐色素转化为黑色素;D 基因的表达产物能完全抑制A 基因的表达;相应的隐性等位基因 a、b、d 的表达产物没有上述功能。
若用两个纯合黄色品种的动物作为亲本进行杂交,F1 均为黄色,F2 中毛色表现型出现了黄∶褐∶黑=52∶3∶9 的数量比,则杂交亲本的组合可以是A.AAbbDd×aaBBdd B.AABBdd×aa bbDDC.aaBBDD×AAbbdd D.AABBDD×aa bbdd6.下列关于染色体、核DNA、核基因三者之间关系的叙述,不正确的是A.三者行为具有一定的一致性B.三者都是生物细胞内的遗传物质C.每条染色体上含有1个或2个DNA分子,DNA分子上含有多个基因D.在生物的繁衍过程中,染色体的行为决定着DNA和基因的行为7.控制两对相对性状的基因自由组合,如果F2的分离比分别是9:7、9:6:1、15:1和12:3:1,那么F1与双隐性个体测交,得到的分离比分别是A.1:3、1:2:1、3:1 和2:1:1 B.1:2、1:4:1、1:3和1:2:1C.1:3、2:1:1、1:3 和1:2:1 D.3:1、1:4:1、3:1和2:1:18.假说-演绎法是现代科学研究中常用的方法,包括“提出问题、作出假设、演绎推理、检验推理、得出结论”五个基本环节。
专题06一元二次方程-备战2023年中考数学必刷真题考点分类专练(全国通用)【解析版】

备战2023年中考数学必刷真题考点分类专练(全国通用)专题06一元二次方程一.选择题(共14小题)1.(2022•天津)方程x2+4x+3=0的两个根为()A.x1=1,x2=3B.x1=﹣1,x2=3C.x1=1,x2=﹣3D.x1=﹣1,x2=﹣3【分析】根据解一元二次方程﹣因式分解法,进行计算即可解答.【解析】x2+4x+3=0,(x+3)(x+1)=0,x+3=0或x+1=0,x1=﹣3,x2=﹣1,故选:D.【点评】本题考查了解一元二次方程﹣因式分解法,熟练掌握解一元二次方程﹣因式分解法是解题的关键.2.(2022•常德)关于x的一元二次方程x2﹣4x+k=0无实数解,则k的取值范围是()A.k>4B.k<4C.k<﹣4D.k>1【分析】根据一元二次方程判别式得到Δ=(﹣4)2﹣4×1×k<0,然后求出不等式的解集即可.【解析】∵关于x的一元二次方程x2﹣4x+k=0无实数解,∴Δ=(﹣4)2﹣4×1×k<0,解得:k>4,故选:A.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2﹣4ac:当Δ>0,方程有两个不相等的实数根;当Δ=0,方程有两个相等的实数根;当Δ<0,方程没有实数根.3.(2022•新疆)若关于x的一元二次方程x2+x﹣k=0有两个实数根,则k的取值范围是()A.k>−14B.k≥−14C.k<−14D.k≤−14【分析】根据关于x的一元二次方程x2+x﹣k=0有两个实数根,可知Δ≥0,可以求得k的取值范围.【解析】∵关于x的一元二次方程x2+x﹣k=0有两个实数根,∴Δ=12﹣4×1×(﹣k)≥0,解得k≥−1 4,故选:B .【点评】本题考查根的判别式,解答本题的关键是明确一元二次方程有实数根时,Δ≥0.4.(2022•乐山)关于x 的一元二次方程3x 2﹣2x +m =0有两根,其中一根为x =1,则这两根之积为( )A .13B .23C .1D .−13 【分析】直接把x =1代入一元二次方程即可求出m 的值,根据根与系数的关系即可求得.【解析】∵方程的其中一个根是1,∴3﹣2+m =0,解得m =﹣1,∵两根的积为m 3, ∴两根的积为−13,故选:D .【点评】本题考查了一元二次方程的根已经根与系数的关系:x 1,x 2是一元二次方程ax 2+bx +c =0(a ≠0)的两根时,x 1+x 2=−b a ,x 1•x 2=c a .5.(2022•怀化)下列一元二次方程有实数解的是( )A .2x 2﹣x +1=0B .x 2﹣2x +2=0C .x 2+3x ﹣2=0D .x 2+2=0 【分析】根据各方程的系数结合根的判别式Δ=b 2﹣4ac ,可求出各方程根的判别式Δ的值,取Δ≥0的选项即可得出结论.【解析】A .∵Δ=(﹣1)2﹣4×2×1=﹣7<0,∴方程2x 2﹣x +1=0没有实数根;B .∵Δ=(﹣2)2﹣4×1×2=﹣4<0,∴方程x 2﹣2x +2=0没有实数根;C .∵Δ=32﹣4×1×(﹣2)=17>0,∴方程x 2+3x ﹣2=0有两个不相等的实数根;D .∵Δ=02﹣4×1×2=﹣8<0,∴方程x 2+2=0没有实数根.故选:C .【点评】本题考查了根的判别式,牢记“①当Δ>0时,方程有两个不相等的实数根;②当Δ=0时,方程有两个相等的实数根;③当Δ<0时,方程无实数根”是解题的关键.6.(2022•温州)若关于x 的方程x 2+6x +c =0有两个相等的实数根,则c 的值是( )A.36B.﹣36C.9D.﹣9【分析】方程x2+6x+c=0有两个相等的实数根,可知Δ=62﹣4c=0,然后即可计算出c的值.【解析】∵方程x2+6x+c=0有两个相等的实数根,∴Δ=62﹣4c=0,解得c=9,故选:C.【点评】本题考查根的判别式,解答本题的关键是明确一元二次方程有两个相等的实数根时Δ=0.7.(2022•武威)用配方法解方程x2﹣2x=2时,配方后正确的是()A.(x+1)2=3B.(x+1)2=6C.(x﹣1)2=3D.(x﹣1)2=6【分析】方程左右两边都加上1,左边化为完全平方式,右边合并即可得到结果.【解析】x2﹣2x=2,x2﹣2x+1=2+1,即(x﹣1)2=3.故选:C.【点评】本题考查了解一元二次方程﹣配方法,熟练掌握用配方法解一元二次方程的步骤是解决问题的关键.8.(2022•滨州)一元二次方程2x2﹣5x+6=0的根的情况为()A.无实数根B.有两个不等的实数根C.有两个相等的实数根D.不能判定【分析】求出判别式Δ=b2﹣4ac,判断其的符号就即可得出结论.【解析】∵Δ=(﹣5)2﹣4×2×6=25﹣48=﹣23<0,∴2x2﹣5x+6=0无实数根,故选:A.【点评】本题主要考查了一元二次方程根的判别式,掌握一元二次方程根的判别式Δ<0时,方程无实数根是解决问题的关键.9.(2022•重庆)小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为x,根据题意,下面所列方程正确的是()A.200(1+x)2=242B.200(1﹣x)2=242C.200(1+2x)=242D.200(1﹣2x)=242【分析】设该快递店揽件日平均增长率为x,关系式为:第三天揽件数=第一天揽件数×(1+揽件日平均增长率)2,把相关数值代入即可.【解析】设该快递店揽件日平均增长率为x,根据题意,可列方程:200(1+x)2=242,故选:A.【点评】本题考查了由实际问题抽象出一元二次方程,找到关键描述语,就能找到等量关系,是解决问题的关键.同时要注意增长率问题的一般规律.10.(2022•泸州)已知关于x的方程x2﹣(2m﹣1)x+m2=0的两实数根为x1,x2,若(x1+1)(x2+1)=3,则m的值为()A.﹣3B.﹣1C.﹣3或1D.﹣1或3【分析】根据方程x2﹣(2m﹣1)x+m2﹣1=0的两实数根为x1,x2,得出x1+x2与x1x2的值,再根据x12+x22=3,即可求出m的值.【解析】∵方程x2﹣(2m﹣1)x+m2=0的两实数根为x1,x2,∴x1+x2=2m﹣1,x1x2=m2,∵(x1+1)(x2+1)=x1x2+x1+x2+1=3,∴m2+2m﹣1+1=3,解得:m1=1,m2=﹣3,∵方程有两实数根,∴Δ=(2m﹣1)2﹣4m2≥0,即m≤1 4,∴m2=1(不合题意,舍去),∴m=﹣3;故选:A.【点评】本题考查了根与系数的关系及根的判别式,难度适中,关键掌握x1,x2是方程x2+px+q=0的两根时,x1+x2=﹣p,x1x2=q.11.(2022•重庆)学校连续三年组织学生参加义务植树,第一年共植树400棵,第三年共植树625棵.设该校植树棵数的年平均增长率为x,根据题意,下列方程正确的是()A.625(1﹣x)2=400B.400(1+x)2=625C.625x2=400D.400x2=625【分析】第三年的植树量=第一年的植树量×(1+年平均增长率)2,把相关数值代入即可.【解析】根据题意得:400(1+x)2=625,故选:B.【点评】考查列一元二次方程解决实际问题,读懂题意,找到等量关系列方程是解决本题的关键.12.(2022•遂宁)已知m为方程x2+3x﹣2022=0的根,那么m3+2m2﹣2025m+2022的值为()A.﹣2022B.0C.2022D.4044【分析】将方程的根代入方程,化简得m2+3m=2022,将代数式变形,整体代入求值即可.【解析】∵m为方程x2+3x﹣2022=0的根,∴m2+3m﹣2022=0,∴m2+3m=2022,∴原式=m3+3m2﹣m2﹣3m﹣2022m+2022=m(m2+3m)﹣(m2+3m)﹣2022m+2022=2022m﹣2022﹣2022m+2022=0.故选:B.【点评】本题考查了一元二次方程的解,考查整体思想,将m2+3m=2022整体代入代数式求值是解题的关键.13.(2022•新疆)临近春节的三个月,某干果店迎来了销售旺季,第一个月的销售额为8万元,第三个月的销售额为11.52万元,设这两个月销售额的月平均增长率为x,则根据题意,可列方程为()A.8(1+2x)=11.52B.2×8(1+x)=11.52C.8(1+x)2=11.52D.8(1+x2)=11.52【分析】设这两个月销售额的月平均增长率为x,先求出第二个月的销售额,再求第三个月的销售额,列出方程即可.【解析】设这两个月销售额的月平均增长率为x,第一个月的销售额为8万元,第二个月的销售额为8(1+x)万元,第三个月的销售额为8(1+x)2万元,∴8(1+x)2=11.52,故选:C.【点评】本题考查了由实际问题抽象出一元二次方程,先求出第二个月的销售额,再求第三个月的销售额是解题的关键.14.(2022•泰安)我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,遣人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是()A.3(x﹣1)x=6210B.3(x﹣1)=6210C.(3x﹣1)x=6210D.3x=6210【分析】设这批椽的数量为x株,则一株椽的价钱为3(x﹣1)文,利用总价=单价×数量,即可得出关于x的一元二次方程,此题得解.【解析】∵这批椽的数量为x株,每株椽的运费是3文,少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,∴一株椽的价钱为3(x﹣1)文.依题意得:3(x﹣1)x=6210.故选:A.【点评】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.二.填空题(共12小题)15.(2022•娄底)已知实数x1,x2是方程x2+x﹣1=0的两根,则x1x2=﹣1.【分析】根据根与系数的关系解答.【解析】∵方程x2+x﹣1=0中的a=b=1,c=﹣1,∴x1x2=ca=−1.故答案是:﹣1.【点评】此题主要考查了根与系数的关系,一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系为:x1+x2=−b a,x1•x2=c a.16.(2022•宿迁)若关于x的一元二次方程x2﹣2x+k=0有实数根,则实数k的取值范围是k≤1.【分析】先计算根的判别式,根据一元二次方程解的情况得不等式,求解即可.【解析】∵Δ=(﹣2)2﹣4×1×k=4﹣4k.又∵关于x的一元二次方程x2﹣2x+k=0有实数根,∴4﹣4k≥0.∴k≤1.故答案为:k≤1.【点评】本题考查了根的判别式,掌握“Δ=b2﹣4ac”及根的判别式与一元二次方程解的情况是解决本题的关键.17.(2022•孝感)若一元二次方程x2﹣4x+3=0的两个根是x1,x2,则x1•x2的值是3.【分析】根据根与系数的关系直接可得答案.【解析】∵x1,x2是一元二次方程x2﹣4x+3=0的两个根,∴x1•x2=3,故答案为:3.【点评】本题考查一元二次方程根与系数的关系,解题的关键是掌握一元二次方程根与系数的关系.18.(2022•眉山)设x1,x2是方程x2+2x﹣3=0的两个实数根,则x12+x22的值为10.【分析】由根与系数的关系,得到x1+x2=﹣2,x1•x2=﹣3,然后根据完全平方公式变形求值,即可得到答案.【解析】∵x1,x2是方程x2+2x﹣3=0的两个实数根,∴x1+x2=﹣2,x1•x2=﹣3,∴x12+x22=(x1+x2)2﹣2x1x2=(﹣2)2﹣2×(﹣3)=10;故答案为:10.【点评】本题考查了一元二次方程根与系数的关系,完全平方公式变形求值,解题的关键是掌握韦达定理得到x1+x2=﹣2,x1•x2=﹣3.19.(2022•扬州)请填写一个常数,使得关于x的方程x2﹣2x+0(答案不唯一)=0有两个不相等的实数根.【分析】根据方程的系数结合根的判别式Δ=b2﹣4ac>0,即可得出关于c的不等式,解之即可求出c的值.【解析】a=1,b=﹣2.∵Δ=b2﹣4ac=(﹣2)2﹣4×1×c>0,∴c<1.故答案为:0(答案不唯一).【点评】本题考查了根的判别式,牢记“当Δ>0时,方程有两个不相等的实数根”是解题的关键.20.(2022•云南)方程2x2+1=3x的解为x1=1,x2=12.【分析】方程利用因式分解法求出解即可.【解析】2x2+1=3x,2x2﹣3x+1=0,(x﹣1)(2x﹣1)=0,解得:x1=1,x2=1 2.故答案为:x1=1,x2=1 2.【点评】本题考查了解一元二次方程﹣因式分解法:掌握十字相乘法解方程是本题的关键.21.(2022•连云港)若关于x的一元二次方程mx2+nx﹣1=0(m≠0)的一个解是x=1,则m+n的值是1.【分析】把x=1代入方程mx2+nx﹣1=0得到m+n﹣1=0,然后求得m+n的值即可.【解析】把x=1代入方程mx2+nx﹣1=0得m+n﹣1=0,解得m+n=1.故答案为:1.【点评】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.22.(2022•安徽)若一元二次方程2x2﹣4x+m=0有两个相等的实数根,则m=2.【分析】根据方程的系数结合根的判别式,即可得出Δ=16﹣8m=0,解之即可得出结论.【解析】∵一元二次方程2x2﹣4x+m=0有两个相等的实数根,∴Δ=16﹣8m=0,解得:m=2.故答案为:2.【点评】本题考查了根的判别式以及解一元一次方程,牢记“当Δ=0时,方程有两个相等实数根”是解题的关键.23.(2022•成都)若一个直角三角形两条直角边的长分别是一元二次方程x2﹣6x+4=0的两个实数根,则这个直角三角形斜边的长是2√7.【分析】设直角三角形两条直角边分别为a、b,斜边为c,由一元二次方程根与系数的关系可得a+b=6,ab=4,再由勾股定理即可求出斜边长.【解析】设直角三角形两条直角边分别为a、b,斜边为c,∵直角三角形两条直角边的长分别是一元二次方程x2﹣6x+4=0的两个实数根,∴a+b=6,ab=4,∴斜边c=√a2+b2=√(a+b)2−2ab=√62−2×4=2√7,故答案为:2√7.【点评】本题考查一元二次方程根与系数的关系,涉及勾股定理、完全平方公式的应用,解题的关键是掌握一元二次方程根与系数的关系,得到a+b=6,ab=4.24.(2022•杭州)某网络学习平台2019年的新注册用户数为100万,2021年的新注册用户数为169万,设新注册用户数的年平均增长率为x(x>0),则x=30%(用百分数表示).【分析】设新注册用户数的年平均增长率为x(x>0),利用2019年的新注册用户数为100万×(1+平均增长率)2=2021年的新注册用户数为169万,即可得出关于x的一元二次方程,解之取其正值即可得出结论.【解析】新注册用户数的年平均增长率为x(x>0),依题意得:100(1+x)2=169,解得:x1=0.3,x2=﹣2.3(不合题意,舍去).0.3=30%,∴新注册用户数的年平均增长率为30%.故答案为:30%.【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.25.(2022•江西)关于x的方程x2+2x+k=0有两个相等的实数根,则k的值为1.【分析】根据根的判别式Δ=0,即可得出关于k的一元一次方程,解之即可得出k值.【解析】∵关于x的方程x2+2x+k=0有两个相等的实数根,∴Δ=22﹣4×1×k=0,解得:k=1.故答案为:1.【点评】本题考查了根的判别式,牢记“当Δ=0时,方程有两个相等的实数根”是解题的关键.26.(2022•重庆)特产专卖店销售桃片、米花糖、麻花三种特产,其中每包桃片的成本是麻花的2倍,每包桃片、米花糖、麻花的售价分别比其成本高20%、30%、20%.该店五月份销售桃片、米花糖、麻花的数量之比为1:3:2,三种特产的总利润是总成本的25%,则每包米花糖与每包麻花的成本之比为4:3.【分析】先根据比例设该店五月份销售桃片、米花糖、麻花的数量分别为x,3x,2x,每包麻花的成本为y 元,每包米花糖的成本为a元,则每包桃片的成本是2y元,由三种特产的总利润是总成本的25%列方程可得ay=43,从而解答此题.【解析】设该店五月份销售桃片、米花糖、麻花的数量分别为x,3x,2x,每包麻花的成本为y元,每包米花糖的成本为a元,则每包桃片的成本是2y元,由题意得:20%•2y•x+30%•a•3x+20%•y•2x=25%(2xy+3ax+2xy),15a=20y,∴ay=43,则每包米花糖与每包麻花的成本之比为4:3.故答案为:4:3.【点评】本题考查三元高次方程的应用,解本题要理解题意,通过找出等量关系即可求解.三.解答题(共5小题)27.(2022•随州)已知关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实数根x1,x2.(1)求k的取值范围;(2)若x1x2=5,求k的值.【分析】(1)根据判别式的意义得到Δ=(2k+1)2﹣4(k2+1)>0,然后解不等式即可;(2)根据根与系数的关系得到x1x2=k2+1,再利用x1x2=5得到k2+1=5,然后解关于k的方程,最后利用k的范围确定k的值.【解析】(1)根据题意得Δ=(2k+1)2﹣4(k2+1)>0,解得k>3 4;(2)根据题意得x1x2=k2+1,∵x1x2=5,∴k2+1=5,解得k1=﹣2,k2=2,∵k>3 4,∴k=2.【点评】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,则x1x2=c a.也考查了根的判别式.28.(2022•凉山州)解方程:x2﹣2x﹣3=0.【分析】通过观察方程形式,本题可用因式分解法进行解答.【解析】原方程可以变形为(x﹣3)(x+1)=0x﹣3=0,x+1=0∴x1=3,x2=﹣1.【点评】熟练运用因式分解法解一元二次方程.注意:常数项应分解成两个数的积,且这两个的和应等于一次项系数.29.(2022•南充)已知关于x的一元二次方程x2+3x+k﹣2=0有实数根.(1)求实数k的取值范围.(2)设方程的两个实数根分别为x1,x2,若(x1+1)(x2+1)=﹣1,求k的值.【分析】(1)根据一元二次方程x2+3x+k﹣2=0有实数根,可知Δ≥0,即可求得k的取值范围;(2)根据根与系数的关系和(x1+1)(x2+1)=﹣1,可以求得k的值.【解析】(1)∵关于x的一元二次方程x2+3x+k﹣2=0有实数根,∴Δ=32﹣4×1×(k﹣2)≥0,解得k≤17 4,即k的取值范围是k≤17 4;(2)∵方程x2+3x+k﹣2=0的两个实数根分别为x1,x2,∴x1+x1=﹣3,x1x2=k﹣2,∵(x1+1)(x2+1)=﹣1,∴x1x2+(x1+x2)+1=﹣1,∴k﹣2+(﹣3)+1=﹣1,解得k=3,即k的值是3.【点评】本题考查根与系数的关系、根的判别式,解答本题的关键是明确一元二次方有根时Δ≥0,以及根与系数的关系.30.(2022•凉山州)阅读材料:材料1:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根为x1,x2,则x1+x2=−ba,x1x2=ca.材料2:已知一元二次方程x2﹣x﹣1=0的两个实数根分别为m,n,求m2n+mn2的值.解:∵一元二次方程x2﹣x﹣1=0的两个实数根分别为m,n,∴m +n =1,mn =﹣1,则m 2n +mn 2=mn (m +n )=﹣1×1=﹣1.根据上述材料,结合你所学的知识,完成下列问题:(1)材料理解:一元二次方程2x 2﹣3x ﹣1=0的两个根为x 1,x 2,则x 1+x 2= 32.x 1x 2= −12 . (2)类比应用:已知一元二次方程2x 2﹣3x ﹣1=0的两根分别为m 、n ,求nm+m n 的值.(3)思维拓展:已知实数s 、t 满足2s 2﹣3s ﹣1=0,2t 2﹣3t ﹣1=0,且s ≠t ,求1s−1t的值. 【分析】(1)根据根与系数的关系进行求解即可;(2)根据根与系数的关系可得:m +n =32,mn =−12,再利用分式的化简求值的方法进行运算即可; (3)可把s 与t 看作是方程2x 2﹣3x ﹣1=0的两个实数根,则有s +t =32,st =−12,再利用分式的化简求值的方法进行运算即可.【解析】(1)∵一元二次方程2x 2﹣3x ﹣1=0的两个根为x 1,x 2, ∴x 1+x 2=−−32=32,x 1x 2=−12=−12, 故答案为:32,−12; (2)∵一元二次方程2x 2﹣3x ﹣1=0的两根分别为m 、n , ∴m +n =32,mn =−12, ∴n m+m n=n 2+m 2mn=(m+n)2−2mnmn=(32)2−2×(−12)−12=−132; (3)∵实数s 、t 满足2s 2﹣3s ﹣1=0,2t 2﹣3t ﹣1=0, ∴s ,与t 看作是方程2x 2﹣3x ﹣1=0的两个实数根, ∴s +t =32,st =−12, ∴(s ﹣t )2=(s +t )2﹣4st ,(s ﹣t )2=(32)2﹣4×(−12),(s ﹣t )2=174, ∴s ﹣t =±√172, ∴1s−1t=t−sst =−(s−t)st=±√172−12=±√17.【点评】本题主要考查根与系数的关系,分式的化简求值,解答的关键是把s ,t 看作是相应的方程的两个实数根.31.(2022•眉山)建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.(1)求该市改造老旧小区投入资金的年平均增长率;(2)2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?【分析】(1)设该市改造老旧小区投入资金的年平均增长率为x ,利用2021年投入资金金额=2019年投入资金金额×(1+年平均增长率)2,即可得出关于x 的一元二次方程,解之取其正值即可得出结论; (2)设该市在2022年可以改造y 个老旧小区,根据2022年改造老旧小区所需资金不多于2022年投入资金金额,即可得出关于y 的一元一次不等式,解之取其中的最大整数值即可得出结论. 【解析】(1)设该市改造老旧小区投入资金的年平均增长率为x , 依题意得:1000(1+x )2=1440,解得:x 1=0.2=20%,x 2=﹣2.2(不合题意,舍去). 答:该市改造老旧小区投入资金的年平均增长率为20%. (2)设该市在2022年可以改造y 个老旧小区, 依题意得:80×(1+15%)y ≤1440×(1+20%), 解得:y ≤43223,又∵y为整数,∴y的最大值为18.答:该市在2022年最多可以改造18个老旧小区.【点评】本题考查了一元二次方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出一元二次方程;(2)根据各数量之间的关系,正确列出一元一次不等式.。
专题06 全等三角形的性质与判定篇(解析版)

专题06 全等三角形的判定与性质1. 三角形的三边关系:三角形的任意两边之和大于第三边,任意两边之差小于第三边。
三角形的三边一旦确定,这三角形就固定了,这是三角形具有稳定性。
2. 三角形的内角和定理:三角形的三个内角之和等于180°。
3. 三角形的外角定理:三角形的一个外角等于它不相邻的两个内角之和。
大于它不相邻的任意一个内角。
4. 全等三角形的性质:若两个三角形全等,则他们的对应边相等;对应角相等;对应边上的中线相等,高线相等,角平分线也相等;且这两个三角形的周长和面积均相等。
5. 全等三角形的判定:①边边边(SSS):三条边分别对应性相等的两个三角形全等。
②边角边(SAS):两边及其这两边的夹角对应相等的两个三角形全等。
③角边角(ASA):两角及其这两角的夹边对应相等的两个三角形全等。
④角角边(AAS):两角及其其中一角的对边对应相等的两个三角形全等。
⑤直角三角形判定(HL):直角三角形中斜边与其中任意一直角边分别对应相等的两个直角三角形全等。
全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件。
在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形。
1.已知:如图,∠1=∠2,∠3=∠4.求证:AB=AD.【分析】根据邻补角的定义得出∠ACB=∠ACD,利用ASA证明△ACB≌△ACD,根据全等三角形的性质即可得解.【解答】证明:∵∠3=∠4,∴∠ACB=∠ACD,在△ACB和△ACD中,,∴△ACB≌△ACD(ASA),∴AB=AD.2.如图,△ABC是等腰三角形,点D,E分别在腰AC,AB上,且BE=CD,连接BD,CE.求证:BD=CE.【分析】根据等腰三角形的性质得出∠EBC=∠DCB,进而利用SAS证明△EBC与△DCB全等,再利用全等三角形的性质解答即可.【解答】证明:∵△ABC是等腰三角形,∴∠EBC=∠DCB,在△EBC与△DCB中,,∴△EBC≌△DCB(SAS),∴BD=CE.3.如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=50°,求∠D的大小.【分析】由∠BAD=∠EAC可得∠BAC=∠EAD,根据SAS可证△BAC≌△EAD,再根据全等三角形的性质即可求解.【解答】解:∵∠BAD=∠EAC,∴∠BAD+∠CAD=∠EAC+∠CAD,即∠BAC=∠EAD,在△BAC与△EAD中,,∴△BAC≌△EAD(SAS),∴∠D=∠C=50°.4.如图,AC平分∠BAD,CB⊥AB,CD⊥AD,垂足分别为B,D.(1)求证:△ABC≌△ADC;(2)若AB=4,CD=3,求四边形ABCD的面积.【分析】(1)由AC平分∠BAD,得∠BAC=∠DAC,根据CB⊥AB,CD⊥AD,得∠B=90°=∠D,用AAS可得△ABC≌△ADC;(2)由(1)△ABC ≌△ADC ,得BC =CD =3,S △ABC =S △ADC ,求出S △ABC =AB •BC =6,即可得四边形ABCD 的面积是12.【解答】(1)证明:∵AC 平分∠BAD ,∴∠BAC =∠DAC ,∵CB ⊥AB ,CD ⊥AD ,∴∠B =90°=∠D ,在△ABC 和△ADC 中,,∴△ABC ≌△ADC (AAS );(2)解:由(1)知:△ABC ≌△ADC ,∴BC =CD =3,S △ABC =S △ADC ,∴S △ABC =AB •BC =×4×3=6,∴S △ADC =6,∴S 四边形ABCD =S △ABC +S △ADC =12,答:四边形ABCD 的面积是12.5.如图,在△ABC 中,点D 在边BC 上,CD =AB ,DE ∥AB ,∠DCE =∠A .求证:DE =BC .【分析】利用平行线的性质得∠EDC =∠B ,再利用ASA 证明△CDE ≌△ABC ,可得结论.【解答】证明:∵DE ∥AB ,∴∠EDC =∠B ,在△CDE 和△ABC 中,,∴△CDE ≌△ABC (ASA ),∴DE =BC .6.如图,在等边三角形ABC中,点M为AB边上任意一点,延长BC至点N,使CN=AM,连接MN交AC 于点P,MH⊥AC于点H.(1)求证:MP=NP;(2)若AB=a,求线段PH的长(结果用含a的代数式表示).【分析】(1)过点M作MQ∥BC,交AC于点Q,根据等边三角形的性质以及平行线的性质可得∠AMQ =∠AQM=∠A=60°,可得△AMQ是等边三角形,易证△QMP≌△CNP(AAS),即可得证;(2)根据等边三角形的性质可知AH=HQ,根据全等三角形的性质可知QP=PC,即可表示出HP的长.【解答】(1)证明:过点M作MQ∥BC,交AC于点Q,如图所示:在等边△ABC中,∠A=∠B=∠ACB=60°,∵MQ∥BC,∴∠AMQ=∠B=60°,∠AQM=∠ACB=60°,∠QMP=∠N,∴△AMQ是等边三角形,∴AM=QM,∵AM=CN,∴QM=CN,在△QMP和△CNP中,,∴△QMP≌△CNP(AAS),∴MP=NP;(2)解:∵△AMQ是等边三角形,且MH⊥AC,∴AH=HQ,∵△QMP≌△CNP,∴QP=CP,∴PH=HQ+QP=AC,∵AB=a,AB=AC,∴PH=a.7.如图,点A,D,C,F在同一条直线上,AB=DE,BC=EF.有下列三个条件:①AC=DF,②∠ABC =∠DEF,③∠ACB=∠DFE.(1)请在上述三个条件中选取一个条件,使得△ABC≌△DEF.你选取的条件为(填写序号) (只需选一个条件,多选不得分),你判定△ABC≌△DEF的依据是 (填“SSS”或“SAS”或“ASA”或“AAS”);(2)利用(1)的结论△ABC DEF.求证:AB∥DE.【分析】(1)根据SSS即可证明△ABC≌△DEF,即可解决问题;(2)根据全等三角形的性质可得∠A=∠EDF,再根据平行线的判定即可解决问题.【解答】(1)解:在△ABC和△DEF中,,∴△ABC≌△DEF(SSS),∴在上述三个条件中选取一个条件,使得△ABC≌△DEF,选取的条件为①,判定△ABC≌△DEF的依据是SSS.故答案为:①,SSS;(答案不唯一).(2)证明:∵△ABC≌△DEF.∴∠A=∠EDF,∴AB∥DE.8.在△ABC中,∠ACB=90°,D为△ABC内一点,连接BD,DC,延长DC到点E,使得CE=DC.(1)如图1,延长BC到点F,使得CF=BC,连接AF,EF.若AF⊥EF,求证:BD⊥AF;(2)连接AE,交BD的延长线于点H,连接CH,依题意补全图2.若AB2=AE2+BD2,用等式表示线段CD与CH的数量关系,并证明.【分析】(1)证明△BCD≌△FCE(SAS),由全等三角形的性质得出∠DBC=∠EFC,证出BD∥EF,则可得出结论;(2)由题意画出图形,延长BC到F,使CF=BC,连接AF,EF,由(1)可知BD∥EF,BD=EF,证出∠AEF=90°,得出∠DHE=90°,由直角三角形的性质可得出结论.【解答】(1)证明:在△BCD和△FCE中,,∴△BCD≌△FCE(SAS),∴∠DBC=∠EFC,∴BD∥EF,∵AF⊥EF,∴BD⊥AF;(2)解:由题意补全图形如下:CD=CH.证明:延长BC到F,使CF=BC,连接AF,EF,∵AC⊥BF,BC=CF,∴AB=AF,由(1)可知BD∥EF,BD=EF,∵AB2=AE2+BD2,∴AF2=AE2+EF2,∴∠AEF=90°,∴AE⊥EF,∴BD⊥AE,∴∠DHE=90°,又∵CD=CE,∴CH=CD=CE.9.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,且点D在线段BC上,连CE.(1)求证:△ABD≌△ACE;(2)若∠EAC=60°,求∠CED的度数.【分析】(1)可利用SAS证明结论;(2)由全等三角形的性质可得∠ACE=∠ABD,利用等腰直角三角形的性质可求得∠ACE=∠ABD=∠AED=45°,再根据三角形的内角和定理可求解∠AEC的度数,进而可求可求解【解答】(1)证明:∵∠BAC=∠DAE=90°,∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);(2)解:∵△ABD≌△ACE,∴∠ACE=∠ABD,∵△ABC和△ADE都是等腰直角三角形,∴∠ACE=∠ABD=∠AED=45°,∵∠EAC=60°,∴∠AEC=180°﹣∠ACE﹣∠EAC=180°﹣45°﹣60°=75°,∴∠CED=∠AEC﹣∠AED=75°﹣45°=30°.10.如图,在△ABC中(AB<BC),过点C作CD∥AB,在CD上截取CD=CB,CB上截取CE=AB,连接DE、DB.(1)求证:△ABC≌△ECD;(2)若∠A=90°,AB=3,BD=2,求△BCD的面积.【分析】(1)由CD∥AB得∠ABC=∠ECD,而CD=CB,CE=AB,即可根据全等三角形的判定定理“SAS”证明△ABC≌△ECD;(2))由∠A=90°,根据全等三角形的对应角相等证明∠BED=∠CED=∠A=90°,设BE=x,由BD2﹣BE2=CD2﹣EC2=DE2,列方程(2)2﹣x2=(3+x)2﹣32,解方程求得符合题意的x的值为2,则BC=5,再根据勾股定理求出DE的长,即可求出△BCD的面积.【解答】(1)证明:∵CD∥AB,CD=CB,CE=AB,∴∠ABC=∠ECD,在△ABC和△ECD中,,∴△ABC≌△ECD(SAS).(2)解:∵∠A=90°,∴∠CED=∠A=90°,∴∠BED=180°﹣∠CED=90°,设BE=x,∵EC=AB=3,BD=2,∴CD=BC=3+x,∵BD2﹣BE2=CD2﹣EC2=DE2,∴(2)2﹣x2=(3+x)2﹣32,整理得x2+3x﹣10=0,解得x1=2,x2=﹣5(不符合题意,舍去),∴BE=2,BC=3+2=5,∴DE===4,=BC•DE=×5×4=10,∴S△BCD∴△BCD的面积为10.11.如图,在Rt△ABC中,∠BAC=90°,AB=AC=1,D是BC边上的一点,以AD为直角边作等腰Rt△ADE,其中∠DAE=90°,连接CE.(1)求证:△ABD≌△ACE;(2)若∠BAD=22.5°时,求BD的长.【分析】(1)由“SAS”可证△ABD≌△ACE;(2)由等腰三角形三角形的性质可得BC的长,由角度关系可求∠ADC=67.5°=∠CAD,可得AC=CD =1,即可求解.【解答】(1)证明:∵∠BAC=90°=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);(2)解:∵∠BAC=90°,AB=AC=1,∴BC=,∠B=∠ACB=45°,∵∠BAD=22.5°,∴∠ADC=67.5°=∠CAD,∴AC=CD=1,∴BD=﹣1.12.如图,已知矩形ABCD中,AB=8,BC=x(0<x<8),将△ACB沿AC对折到△ACE的位置,AE和CD交于点F.(1)求证:△CEF≌△ADF;(2)求tan∠DAF的值(用含x的式子表示).【分析】(1)根据矩形的性质得到∠B=∠D=90°,BC=AD,根据折叠的性质得到BC=CE,∠E=∠B=90°,等量代换得到∠E=∠D=90°,AD=CE,根据AAS证明三角形全等即可;(2)设DF=a,则CF=8﹣a,根据矩形的性质和折叠的性质证明AF=CF=8﹣a,在Rt△ADF中,根据勾股定理表示出DF的长,根据正切的定义即可得出答案.【解答】(1)证明:∵四边形ABCD是矩形,∴∠B=∠D=90°,BC=AD,根据折叠的性质得:BC=CE,∠E=∠B=90°,∴∠E=∠D=90°,AD=CE,在△CEF与△ADF中,,∴△CEF≌△ADF(AAS);(2)解:设DF=a,则CF=8﹣a,∵四边形ABCD是矩形,∴AB∥CD,AD=BC=x,∴∠DCA=∠BAC,根据折叠的性质得:∠EAC=∠BAC,∴∠DCA=∠EAC,∴AF=CF=8﹣a,在Rt△ADF中,∵AD2+DF2=AF2,∴x2+a2=(8﹣a)2,∴a=,∴tan∠DAF==.13.如图,△ABC和△DEF,点E,F在直线BC上,AB=DF,∠A=∠D,∠B=∠F.如图①,易证:BC+BE =BF.请解答下列问题:(1)如图②,如图③,请猜想BC,BE,BF之间的数量关系,并直接写出猜想结论;(2)请选择(1)中任意一种结论进行证明;(3)若AB=6,CE=2,∠F=60°,S=123,则BC= ,BF= .△ABC【分析】(1)根据图形分别得出答案;(2)利用AAS证明△ABC≌△DFE,得BC=EF,再根据图形可得结论;(3)首先利用含30°角的直角三角形的性质求出BH和AH的长,从而得出BC,再对点E的位置进行分类即可.【解答】解:(1)图②:BC+BE=BF,图③:BE﹣BC=BF;(2)图②:∵AB=DF,∠A=∠D,∠B=∠F,∴△ABC≌△DFE(ASA),∴BC=EF,∵BE=BC+CE,∴BC+BE=EF+BC+CE=BF;图③:∵AB=DF,∠A=∠D,∠B=∠F,∴△ABC≌△DFE(ASA),∴BC=EF,∵BE=BF+EF,∴BE﹣BC=BF+EF﹣BC=BF+BC﹣BC=BF;(3)当点E在BC上时,如图,作AH⊥BC于H,∵∠B=∠F=60°,∴∠BAH=30°,∴BH=3,∴AH=3,∵S=12,△ABC∴=12,∴BC=8,∵CE=2,∴BF=BE+EF=8﹣2+8=14;同理,当点E在BC延长线上时,如图②,BF=BC+BE=8+10=18,故答案为:8,14或18.14.△ABC和△ADE都是等边三角形.(1)将△ADE绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有PA+PB=PC(或PA+PC=PB)成立(不需证明);(2)将△ADE绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?并加以证明;(3)将△ADE绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA、PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.【分析】(2)证明△ABD≌△ACE(SAS)和△BAF≌△CAP(SAS),得AF=AP,∠BAF=∠CAP,再证明△AFP是等边三角形,最后由线段的和可得结论;(3)如图③,在PC上截取CM=PB,连接AM,同理可得结论.【解答】解:(2)PB=PA+PC,理由如下:如图②,在BP上截取BF=PC,连接AF,∵△ABC、△ADE都是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∴∠BAC+∠CAD=∠CAD+∠DAE,即∠DAB=∠EAC,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵AB=AC,BF=CP,∴△BAF≌△CAP(SAS),∴AF=AP,∠BAF=∠CAP,∴∠BAC=∠PAF=60°,∴△AFP是等边三角形,∴PF=PA,∴PB=BF+PF=PC+PA;(3)PC=PA+PB,理由如下:如图③,在PC上截取CM=PB,连接AM,同理得:△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵AB=AC,PB=CM,∴△AMC≌△APB(SAS),∴AM=AP,∠BAP=∠CAM,∴∠BAC=∠PAM=60°,∴△AMP是等边三角形,∴PM=PA,∴PC=PM+CM=PA+PB.15.【情境再现】甲、乙两个含45°角的直角三角尺如图①放置,甲的直角顶点放在乙斜边上的高的垂足O处.将甲绕点O顺时针旋转一个锐角到图②位置.小莹用作图软件Geogebra按图②作出示意图,并连接AG,BH,如图③所示,AB交HO于E,AC交OG于F,通过证明△OBE≌△OAF,可得OE=OF.请你证明:AG=BH.【迁移应用】延长GA分别交HO,HB所在直线于点P,D,如图④,猜想并证明DG与BH的位置关系.【拓展延伸】小亮将图②中的甲、乙换成含30°角的直角三角尺如图⑤,按图⑤作出示意图,并连接HB,AG,如图⑥所示,其他条件不变,请你猜想并证明AG与BH的数量关系.【分析】【情境再现】由△OBE≌△OAF,得BE=AF,OE=OF,∠BEO=∠AFO,可证明△BHE≌△AGF (SAS),得BH=AG;【迁移应用】由△BHE≌△AGF,得∠BHE=∠AGF,可得∠AGF+∠GPO=90°,从而∠BHE+∠HPD=90°,∠HDP=90°,故DG⊥BH;【拓展延伸】设AB交OH于T,交AC于K,根据△ABC,△HOG是含30°角的直角三角形,AO⊥BC,可得OB=AO,∠OBA=∠OAC=30°,∠BOT=90°﹣∠AOT=∠AOK,即得△BOT∽△AOK,有===,∠BTO=∠AKO,又OH=GO,可得==,故△BTH∽△AKG,即得==,BH=AG.【解答】【情境再现】证明:由阅读材料知△OBE≌△OAF,∴BE=AF,OE=OF,∠BEO=∠AFO,∴∠BEH=∠AFG,∵OH=OG,∴OH﹣OE=OG﹣OF,即EH=GF,在△BHE和△AGF中,,∴△BHE≌△AGF(SAS),∴BH=AG;【迁移应用】解:猜想:DG⊥BH;证明如下:由【情境再现】知:△BHE≌△AGF,∴∠BHE=∠AGF,∵∠HOG=90°,∴∠AGF+∠GPO=90°,∴∠BHE+∠GPO=90°,∵∠GPO=∠HPD,∴∠BHE+∠HPD=90°,∴∠HDP=90°,∴DG⊥BH;【拓展延伸】解:猜想:BH=AG,证明如下:设AB交OH于T,OG交AC于,如图:由已知得:△ABC,△HOG是含30°角的直角三角形,AO⊥BC,∴∠AOB=90°,∴OB=AO,∠OBA=∠OAC=30°,∠BOT=90°﹣∠AOT=∠AOK,∴△BOT∽△AOK,∴===,∠BTO=∠AKO,∴OT=OK,BT=AK,∠BTH=∠AKG,∵OH=GO,∴HT=OH﹣OT=GO﹣OK=(GO﹣OK)=KG,∴==,∴△BTH∽△AKG,∴==,∴BH=AG.。
专题06 与圆有关的问题(解析版)

专题06 与圆有关的问题【提要】与圆有关的知识包括圆的半径处处相等,垂径定理,点、直线、圆分别与圆的位置关系,等等.需要注意的是两圆相切包括内切和外切两种情况.【范例】【例1】如图,Rt△ABC中,∠ACB=90°,AC=4,BA=5,点P是AC上的动点(P不与A、C重合),设PC=x,点P到AB的距离为y.(1)求y与x的函数关系式;(2)试讨论以P为圆心,半径为x的圆与AB所在直线的位置关系,并指出相应的x的取值范围.【解】(1)过P作PQ⊥AB于Q,则PQ=y则Rt△AQP∽Rt△ACB,∴PQ∶BC=AP∶AB即y3=4-x5∴y=-35x+125(0<x<4)(2)当x<y时,x<-35x+125,∴x<32∴当0<x<32时,圆P与AB所在直线相离;当x=32时,圆P与AB所在直线相切;当32<x <4时,圆P 与AB 所在直线相交.【例2】 如图,已知△ABC 内接于圆O ,如果AB =AC ,圆O 的直径为26,且tan ∠ABC =23.求BC的长.【解】 联结OA 、OB ,OA 交BC 于点D ,则OA =OB =13. ∵AB =AC ,∴AB =AC , ∴OA ⊥BC ,BD =DC .在△ABD 中,∠ADB =90°,tan ∠ABC =AD BD =23,设AD =2k ,BD =3k ,则OD =13-2k在△BOD 中,∠BDO =90°,BD 2+OD 2=OB 2, ∴(3k )2+(13-2k )2=132, 13k 2-52k =0,k 1=0(舍去),k 2=4, ∴BD =3k =12, BC =24.【例3】 如图,P 是⊙O 的直径AB 延长线上的一点,PC 与⊙O 分别相交于点E 和点C ,过点C 作CD ⊥AB ,交⊙O 于点D ,联结PD .(1)求证:PC =PD ;(2)如果PE 的长等于⊙O 的半径OC ,求证:∠AOC =3∠APC . 【证明】 (1)设P A 与DC 交点为H ,由PH ⊥CD ,PH 经过圆心,所以CH =HD ,从而△PCH ≌△PDH ,故PC =PD .(2)联结OE ,因为PE =OE ,所以∠APC =∠EOP ,又因为OE =OC ,所以∠OCE =∠OEC ,而且∠OEC =∠OPE +∠POE =2∠OPE ,所以∠AOC =∠APC +∠OCP =2∠APC +∠APC =3∠APC . 【例4】 如图:A 是⊙O 1、⊙O 2的一个交点,点B 是O 1O 2的中点,过点A 的直线垂直于AB 交⊙O 1、⊙O 2于点M 、N ,O 2H ⊥AB 于点H .(1)求证:AM =AN ;(2)设⊙O 1、⊙O 2的半径分别为R 、r ,BH =x ,BA =y 且R 2-r 2=4,求y 与x 之间的函数关系式(不必求自变量x 的范围).(1)【证明】 作O 1P ⊥MN ,O 2Q ⊥MN 垂足分别为P 、Q ,在梯形O 1O 2QP 中,AB 是中位线,所以P A =QA ,又由垂径定理,P A =PM ,QA =QN ,所以AM =AN .(2)【解】 设O 1P =m ,O 2Q =n ,则⎩⎪⎨⎪⎧m +n =2ym -n =2x ,得m 2-n 2=4xy ;另一方面设P A =PM =QA =QN =t ,则⎩⎪⎨⎪⎧R 2-m 2=t 2r 2-n 2=t 2,得R2-r 2=m 2-n 2,所以4xy =4,即y =1x . 【例5】 已知:如图,在平面直角坐标系中,点B 在x 轴上,以3为半径的⊙B 与y 轴相切,直线l 过点A (-2,0),且和⊙B 相切,与y 轴相交于点C .(1)求直线l 的解析式;(2)若抛物线y =ax 2+bx +c (a >0)经过点O 和B ,顶点在⊙B 上,求抛物线的解析式; (3)若点H 在直线l 上,且以A 为圆心,AH 为半径的圆与⊙B 相切,求点H 的坐标.【解】 (1)过点B 作BD 垂直于l 交于点D , ∵⊙B 与l 相切,∴BD =3 在Rt △ADB 中,AB =5, AD =(5)2-(3)2=4 在Rt △ACO 中,tan ∠ACO =AO CO =AD DB =43, ∵AO =2,∴CO =1.5设l :y =kx +1.5,A (-2,0)代入得k =34,∴y =34x +1.5(2)过OB 的中点F 作EF 垂直于x 轴交⊙B 于点E ,联结BE .∵在Rt △EFB 中,BE =3,BF =1.5, EF =(3)2-(1.5)2=323, 又∵a >0 ∴E (32,-323)将O (0,0)、B (3,0)、E (32,-323)代入y =ax 2+bx +c (a >0) 得y =233x 2-23x(3)当两圆外切时,AH =2,H (-25,65)当两圆内切时,AH =8,H (225,245)【训练】1.(2019•上海)已知A e 与B e 外切,C e 与A e 、B e 都内切,且5AB =,6AC =,7BC =,那么C e 的半径长是( ) A .11B .10C .9D .8【分析】如图,设A e ,B e ,C e 的半径为x ,y ,z .构建方程组即可解决问题. 【解答】解:如图,设A e ,B e ,C e 的半径为x ,y ,z .由题意:567x y z x z y +=⎧⎪-=⎨⎪-=⎩,解得329x y z =⎧⎪=⎨⎪=⎩,故选:C .2.(2018•上海)如图,已知30POQ ∠=︒,点A 、B 在射线OQ 上(点A 在点O 、B 之间),半径长为2的A e 与直线OP 相切,半径长为3的B e 与A e 相交,那么OB 的取值范围是( )A .59OB <<B .49OB <<C .37OB <<D .27OB <<【分析】作半径AD ,根据直角三角形30度角的性质得:4OA =,再确认B e 与A e 相切时,OB 的长,可得结论.【解答】解:设A e 与直线OP 相切时切点为D ,连接AD , AD OP ∴⊥,30O ∠=︒Q ,2AD =, 4OA ∴=,当B e 与A e 相内切时,设切点为C ,如图1, 3BC =Q ,4325OB OA AB ∴=+=+-=;当A e 与B e 相外切时,设切点为E ,如图2, 4239OB OA AB ∴=+=++=,∴半径长为3的B e 与A e 相交,那么OB 的取值范围是:59OB <<,故选:A .3.(2020•金山区一模)已知在矩形ABCD 中,5AB =,对角线13AC =.C e 的半径长为12,下列说法正确的是( )A .C e 与直线AB 相交 B .C e 与直线AD 相切 C .点A 在C e 上D .点D 在C e 内【分析】根据点和圆的位置关系及直线和圆的位置关系判断即可. 【解答】解:Q 在ABC ∆中,90ACB ∠=︒,13AC =,5AB =,12BC ∴==,C Q e 的半径长为12, C ∴e 与直线AB 相切,故A 选项不正确, 512CD AB ==<Q , C ∴e 与直线AD 相交,故B 选项不正确, 1312AC =>Q ,∴点A 在C e 外,故C 选项不正确, 512CD =<Q ,∴点D 在C e 内,故D 选项正确, 故选:D .4.(2020•奉贤区一模)在ABC ∆中,9AB =,212BC AC ==,点D 、E 分别在边AB 、AC 上,且//DE BC ,2AD BD =,以AD 为半径的D e 和以CE 为半径的E e 的位置关系是( )A .外离B .外切C .相交D .内含【分析】分别计算D e 和以CE 为半径的E e 的半径,并计算DE 的长,根据外切的定义可解答. 【解答】解:如图,//DE BC Q ,∴DE ADBC AB=, 12BC =Q ,2AD BD =,∴2123DE =,8DE =,D Q e 的半径为6AD =,E e 的半径2CE =, 628AD CE DE ∴+=+==,∴以AD 为半径的D e 和以CE 为半径的E e 的位置关系是外切,故选:B .5.(2019•青浦区二模)如图,在梯形ABCD 中,//AD BC ,90B ∠=︒,2AD =,4AB =,6BC =,点O 是边BC 上一点,以O 为圆心,OC 为半径的O e ,与边AD 只有一个公共点,则OC 的取值范围是( )A .1343OC <…B .1343OC剟 C .1443OC <…D .1443OC剟 【分析】作DE BC ⊥于E ,当O e 与边AD 相切时,圆心O 与E 重合,即4OC =;当OA OC =时,O e 与AD 交于点A ,设OA OC x ==,则6OB x =-,在Rt ABO ∆中,由勾股定理得出方程,解方程得出133OC =;即可得出结论.【解答】解:作DE BC ⊥于E ,如图所示: 则4DE AB ==,2BE AD ==, 4CE DE ∴==,当O e 与边AD 相切时,切点为D ,圆心O 与E 重合,即4OC =; 当OA OC =时,O e 与AD 交于点A , 设OA OC x ==,则6OB x =-,在Rt ABO ∆中,由勾股定理得:2224(6)x x +-=, 解得:133x =; ∴以O 为圆心,OC 为半径的O e ,与边AD 只有一个公共点,则OC 的取值范围是1343x剟; 故选:B .6.(2019•虹口区二模)如图,在ABC ∆中,AB AC =,4BC =,tan 2B =,以AB 的中点D 为圆心,r 为半径作D e ,如果点B 在D e 内,点C 在D e 外,那么r 可以取( )A .2B .3C .4D .5【分析】先求出DB 和DC 的长,根据点B 在D e 内,点C 在D e 外,确定r 的取值范围,从而确定r 可以取的值.【解答】解:如图,过点A 作AF BC ⊥于点F ,连接CD 交AF 于点G , AB AC =Q ,4BC =, 2BF CF ∴==, tan 2B =Q ,∴2AFBF=,即4AF =,AB ∴==,D Q 为AB 的中点,BD ∴=,G 是ABC ∆的重心,1433GF AF ∴==,CG ∴= 32CD CG ∴=,Q 点B 在D e 内,点C 在D e 外,∴r <故选:B .7.(2020•金山区一模)已知相交两圆的半径长分别为8与15,圆心距为17,则这两圆的公共弦长为.【分析】根据相交两圆的性质,两圆的公共弦垂直于两圆心连接的直线上,又知两圆的半径,进而可以在直角三角形中解得公共弦长.【解答】解:在以两圆的一个交点和两圆圆心为顶点的三角形中,其三边分别为8,15,17,由于22217158=+,∴这个三角形是以17为斜边的直角三角形,斜边上的高8151201717⨯==,故公共弦长12024021717=⨯=,故答案为240 17.8.(2020•崇明区一模)两圆的半径之比为3:1,当它们外切时,圆心距为4,那么当它们内切时,圆心距为.【分析】只需根据两圆的半径比以及两圆外切时,圆心距等于两圆半径之和,列方程求得两圆的半径;再根据两圆内切时,圆心距等于两圆半径之差求解.【解答】解:设大圆的半径为R,小圆的半径为r,则有:1:3r R=;又4R r+=,解,得3R=,1r=,∴当它们内切时,圆心距312=-=.故答案为:2.9.(2020•闵行区一模)已知在Rt ABC∆中,90C∠=︒,3AC=,4BC=,Ce与斜边AB相切,那么Ce的半径为.【分析】r的长即为斜边AB上的高,由勾股定理易求得AB的长,根据直角三角形面积的不同表示方法,即可求出r的值.【解答】解:Rt ABC∆中,90C∠=︒,3AC=,4BC=;由勾股定理,得:2223425AB=+=,5AB∴=;又ABQ是Ce的切线,CD AB ∴⊥, CD r ∴=;1122ABC S AC BC AB r ∆==Q g g , 125r ∴=, 故答案为:125.10.(2020•嘉定区一模)如图,O e 的半径长为5cm ,ABC ∆内接于O e ,圆心O 在ABC ∆的内部.如果AB AC =,8BC cm =,那么ABC ∆的面积为 2cm .【分析】作AD BC ⊥于D ,根据等腰三角形的性质得142BD CD BC ===,即AD 垂直平分BC ,根据垂径定理得到圆心O 在AD 上;连接OB ,在Rt OBC ∆中利用勾股定理计算出3OD =,然后根据三角形面积公式进行计算.【解答】解:作AD BC ⊥于D , AB AC =Q ,142BD CD BC ∴===, AD ∴垂直平分BC ,∴圆心O 在AD 上,连接OB ,在Rt OBC ∆中,4BD =Q ,5OB =,3OD ∴===,如图,538AD OA OD =+=+=,此时188322ABC S ∆=⨯⨯=;故答案为:32.11.(2020•闵行区一模)半径分别为3cm 的1O e 与2O e 相交于A 、B 两点,如果公共弦AB =,那么圆心距12O O 的长为 cm .【分析】利用连心线垂直平分公共弦的性质,构造直角三角形利用勾股定理及有关性质解题. 【解答】解:如图,1O Q e 与2O e 相交于A 、B 两点, 12O O AB ∴⊥,且AD BD =;又AB =QAD ∴=∴在Rt △1AO D 中,根据勾股定理知11O D =厘米;在Rt △2AO D 中,根据勾股定理知23O D =厘米, 12124O O O D O D ∴=+=厘米;同理知,当小圆圆心在大圆内时,解得123O O =厘米1-厘米2=厘米. 故答案是:4或2;12.(2020•奉贤区一模)公元263年左右,我国数学家刘徽发现当正多边形的边数无限增加时,这个正多边形面积可无限接近它的外接圆的面积,因此可以用正多边形的面积来近似估计圆的面积,如图,O e 是正十二边形的外接圆,设正十二边形的半径OA 的长为1,如果用它的面积来近似估计O e 的面积,那么O e 的面积约是 .【分析】设AB 为正十二边形的边,连接OB ,过A 作AD OB ⊥于D ,由正十二边形的性质得出30AOB ∠=︒,由直角三角形的性质得出1122AD OA ==,求出AOB ∆的面积1124OB AD =⨯=,即可得出答案.【解答】解:设AB 为正十二边形的边,连接OB ,过A 作AD OB ⊥于D ,如图所示: 3603012AOB ︒∴∠==︒, AD OB ⊥Q , 1122AD OA ∴==,AOB ∴∆的面积111112224OB AD =⨯=⨯⨯=∴正十二边形的面积11234=⨯=, O ∴e 的面积≈正十二边形的面积3=,故答案为:3.13.(2019•青浦区二模)如图,在O e 中,OA 、OB 为半径,连接AB ,已知6AB =,120AOB ∠=︒,那么圆心O 到AB 的距离为 .【分析】过O 作OC AB ⊥交AB 于C 点,由垂径定理可知,OC 垂直平分AB ,再解直角三角形即可求解. 【解答】解:过O 作OC AB ⊥交AB 于C 点,如右图所示: 由垂径定理可知,OC 垂直平分AB ,则132AC AB ==, OA OB =Q ,120AOB ∠=︒,30OAB ∴∠=︒,tan tan30OCOAB AC∴∠=︒=,tan303OC AC ∴=︒==g O 到AB14.(2019•静安区二模)已知在ABC ∆中,90C ∠=︒,2AC BC ==,如果以点C 为圆心的圆与斜边AB 有且只有一个交点,那么C e 的半径是 .【分析】根据等腰直角三角形的性质和直线与圆的位置关系解答即可.【解答】解:Q 在ABC ∆中,90C ∠=︒,2AC BC ==, Q 以点C 为圆心的圆与斜边AB 有且只有一个交点,CD AB ∴⊥,1122CD AB ∴==⨯,即C e15.(2019•嘉定区二模)在Rt ACB ∆中,90C ∠=︒,3AC =,BC =A 为圆心作圆A ,要使B 、C 两点中的一点在圆A 外,另一点在圆A 内,那么圆A 的半径长r 的取值范围是 .【分析】熟记“设点到圆心的距离为d ,则当d r =时,点在圆上;当d r >时,点在圆外;当d r <时,点在圆内”即可求解,【解答】解:Rt ACB ∆Q 中,90C ∠=︒,3AC =,BC = 6AB ∴=,如果以点A 为圆心作圆,使点C 在圆A 内,则3r >, 点B 在圆A 外,则6r <,因而圆A 半径r 的取值范围为36r <<. 故答案为36r <<;16.(2019•长宁区二模)在Rt ABC ∆中,90ABC ∠=︒,6AB =,8BC =.分别以点A 、C 为圆心画圆,如果点B 在A e 上,C e 与A e 相交,且点A 在C e 外,那么C e 的半径长r 的取值范围是 . 【分析】根据勾股定理求出斜边AC ,根据点和圆的位置关系求出A e 的半径,再求出C e 的半径即可. 【解答】解:在Rt ABC ∆中,90ABC ∠=︒,6AB =,8BC =,由勾股定理得:226810AC =+=,Q 点B 在A e 上,A ∴e 的半径是6,设A e 交AC 于D ,则6AD =,1064CD =-=, Q 点A 在C e 外,C ∴e 的半径小于10,即r 的取值范围是410r <<, 故答案为:410r <<.17.(2019•闵行区二模)如图,已知在O e 中,半径OC 垂直于弦AB ,垂足为点D .如果4CD =,16AB =,那么OC = .【分析】根据垂径定理可得182AD AB ==,90ADO ∠=︒,设CO x =,则AO x =,4DO x =-,再利用勾股定理列出方程,解出x 的值即可. 【解答】解:Q 半径OC 垂直于弦AB , 182AD AB ∴==,90ADO ∠=︒, 设CO x =,则AO x =,4DO x =-,2228(4)x x =+-, 解得:10x =, 10CO ∴=,故答案为:10.18.如图,在矩形ABCD 中,过点A 的圆O 交边AB 于点E ,交边AD 于点F ,已知5AD =,2AE =,4AF =.如果以点D 为圆心,r 为半径的圆D 与圆O 有两个公共点,那么r 的取值范围是 .【分析】连接EF ,知EF 是O e 的直径,取EF 的中点O ,连接OD ,作OG AF ⊥,知点G 是AF 的中点,据此可得122GF AF ==,112OG AE ==,继而求得OF ==OD =,最后根据两圆的位置关系可得答案. 【解答】解:如图,连接EF ,Q 四边形ABCD 是矩形,90BAC ∴∠=︒,则EF 是O e 的直径,取EF 的中点O ,连接OD ,作OG AF ⊥, 则点G 是AF 的中点, 122GF AF ∴==, OG ∴是AEF ∆的中位数,112OG AE ∴==,OF ∴=OD , Q 圆D 与圆O 有两个公共点,∴r <<r <19.(2019•徐汇区二模)如图,把半径为2的O e 沿弦AB 折叠,¶AB 经过圆心O ,则阴影部分的面积为 (结果保留)π.【分析】过O 作OD AB ⊥于D ,交劣弧AB 于E ,根据勾股定理求出AD ,根据垂径定理求出AB ,分别求出扇形AOB 和三角形AOB 的面积,即可得出答案.【解答】解:过O 作OD AB ⊥于D ,交劣弧AB 于E ,如图:Q 把半径为2的O e 沿弦AB 折叠,¶AB 经过圆心O ,1OD DE ∴==,2OA =, Q 在Rt ODA ∆中,1sin 2OD A OA ==, 30A ∴∠=︒,60AOE ∴∠=︒,同理60BOE ∠=︒, 6060120AOB ∴∠=︒+︒=︒,在Rt ODA ∆中,由勾股定理得:AD = OD AB ⊥Q ,OD 过O ,2AB AD ∴==,∴阴影部分的面积2120214136023AOBAOB S S S ππ∆⨯=-=-⨯=-扇形故答案为:43π. 20.(2018•上海)已知O e 的直径2AB =,弦AC 与弦BD 交于点E .且OD AC ⊥,垂足为点F .(1)如图1,如果AC BD =,求弦AC 的长;(2)如图2,如果E 为弦BD 的中点,求ABD ∠的余切值;(3)联结BC 、CD 、DA ,如果BC 是O e 的内接正n 边形的一边,CD 是O e 的内接正(4)n +边形的一边,求ACD ∆的面积.【分析】(1)由AC BD =知¶¶¶¶AD CD CD BC +=+,得¶¶AD BC =,根据OD AC ⊥知¶¶AD CD =,从而得¶¶¶AD CDBC ==,即可知60AOD DOC BOC ∠=∠=∠=︒,利用sin AF AO AOF =∠可得答案; (2)连接BC ,设OF t =,证OF 为ABC ∆中位线及DEF BEC ∆≅∆得2BC DF t ==,由1DF t =-可得13t =,即可知23BC DF ==,继而求得143EF AC ==,由余切函数定义可得答案;(3)先求出BC 、CD 、AD 所对圆心角度数,从而求得BC AD =OF =公式计算可得.【解答】解:(1)OD AC ⊥Q , ∴¶¶AD CD=,90AFO ∠=︒, 又AC BD =Q ,∴¶¶AC BD =,即¶¶¶¶AD CD CD BC +=+, ∴¶¶AD BC=, ∴¶¶¶AD CDBC ==, 60AOD DOC BOC ∴∠=∠=∠=︒,2AB =Q ,1AO BO ∴==,sin 1AF AO AOF ∴=∠==,则2AC AF==;(2)如图1,连接BC,ABQ为直径,OD AC⊥,90AFO C∴∠=∠=︒,//OD BC∴,D EBC∴∠=∠,DE BE=Q、DEF BEC∠=∠,()DEF BEC ASA∴∆≅∆,BC DF∴=、EC EF=,又AO OB=Q,OF∴是ABC∆的中位线,设OF t=,则2BC DF t==,1DF DO OF t=-=-Q,12t t∴-=,解得:13t=,则23DF BC==、3AC=,1124EF FC AC∴==,OB OD=Q,ABD D∴∠=∠,则2cot cotDFABD DEF∠=∠==;(3)如图2,BC Q 是O e 的内接正n 边形的一边,CD 是O e 的内接正(4)n +边形的一边, 360BOC n ∴∠=、3604AOD COD n ∠=∠=+, 则36036021804n n +⨯=+, 解得:4n =,90BOC ∴∠=︒、45AOD COD ∠=∠=︒,BC AC ∴==90AFO ∠=︒Q ,cos OF AO AOF ∴=∠=,则1DF OD OF =-=111(12222ACD S AC DF ∆∴==-=g . 21.(2020•闵行区一模)如图,梯形ABCD 中,//AD BC ,90ADC ∠=︒,2AD =,4BC =,tan 3B =.以AB 为直径作O e ,交边DC 于E 、F 两点.(1)求证:DE CF =; (2)求:直径AB 的长.【分析】(1)直接利用垂径定理结合平行线分线段成比例定理得出DH HC =,进而得出答案; (2)过点A 作AG BC ⊥,垂足为点G ,再利用已知结合勾股定理得出答案. 【解答】(1)证明:过点O 作OH DC ⊥,垂足为H . //AD BC Q ,90ADC ∠=︒,OH DC ⊥,90BCN OHC ADC ∴∠=∠=∠=︒. ////AD OH BC ∴.又OA OB =Q . DH HC ∴=.OH DC ⊥Q ,OH 过圆心,EH HF ∴=,DH EH HC HF ∴-=-.即:DE CF =.(2)解:过点A 作AG BC ⊥,垂足为点G ,90AGB ∠=︒, 90AGB BCN ∠=∠=︒Q , //AG DC ∴. //AD BC Q , AD CG ∴=.2AD =Q ,4BC =,2BG BC CG ∴=-=.在Rt AGB ∆中,tan 3B =Q , tan 236AG BG B ∴==⨯=g .在Rt AGB ∆中,222AB AG BG =+AB ∴=22.(2020•嘉定区一模)如图,在O e 中,AB 、CD 是两条弦,O e 的半径长为rcm ,弧AB 的长度为1l cm ,弧CD 的长度为2l cm (温馨提醒:弧的度数相等,弧的长度相等,弧相等,有联系也有区别).当12l l =时,求证:AB CD =.【分析】根据弧长公式求得AOB COD ∠=∠,然后利用ASA 证得AOB COD ∆≅∆,即可证得结论. 【解答】解:设AOB m ∠=︒,COD n ∠=︒, 由题意,得1180mr l π=,2180nr l π=, QBG FH DG CH =,∴180180mr nr ππ=, m n ∴=,即AOB COD ∠=∠,OA Q 、OB 、OC 、OD 都是O e 的半径,OA OB OC OD ∴===,OA OC =Q ,AOB COD ∠=∠,OB OD =,()AOB COD SAS ∴∆≅∆ AB CD ∴=.23.(2019•杨浦区三模)ABC ∆中,90ACB ∠=︒,3tan 4B =,5AB =,点O 为边AB 上一动点,以O 为圆心,OB 为半径的圆交射线BC 于点E ,以A 为圆心,OB 为半径的圆交射线AC 于点G .(1)如图1,当点E 、G 分别在边BC 、AC 上,且CE CG =时,请判断圆A 与圆O 的位置关系,并证明你的结论;(2)当圆O 与圆A 存在公共弦MN 时(如图2),设OB x =,MN y =,求y 关于x 的函数解析式,并写出定义域;(3)设圆A 与边AB 的交点为F ,联结OE 、EF ,当OEF ∆为以OE 为腰的等腰三角形时,求圆O 的半径长.【分析】(1)由三角函数得出3AC =,4BC =,作OP BE ⊥于P ,则PB PE =,//OP AC ,得出OB PBAB BC=,设PB PE x ==,则42CG CE x ==-,得出54OB x =,21AG AC CG x =-=-,得出方程,得出43x =,53OB ==,求出2OA AB OB OB =-=,即可得出结论;(2)连接OM ,由相交两圆的性质得出OA 与MN 垂直平分,90ODM ∠=︒,1122DM MN y ==,1(5)2AD OD x ==-,由勾股定理得出方程,整理即可;(3)分三种情况:①当圆O 与圆A 外切,OE OF =时,圆O 与圆A 外切,圆O 的半径长53OB =; ②当OE FE =时,圆O 与圆A 相交,作EH OF ⊥于H ,则52OF OH OB ==-,证明BEH BAC ∆∆∽,得出158EH =,在Rt OEH ∆中,由勾股定理得出方程,解方程即可; ③当O 与A 重合时,OE OF =,5OE AB ==;即可得出结论. 【解答】解:(1)圆A 与圆O 外切,理由如下: 90ACB ∠=︒Q ,3tan 4B =,5AB =,3AC ∴=,4BC =, 作OP BE ⊥于P ,如图1所示: 则PB PE =,//OP AC ,∴OB PBAB BC=, 设PB PE x ==,则42CG CE x ==-, 5544x OB x ⨯∴==,21AG AC CG x =-=-, AG OB =Q , 5214x x ∴-=, 解得:43x =, 53OB ∴==, 5105233OA AB OB OB ∴=-=-==,∴圆A 与圆O 外切;(2)连接OM ,如图2所示: Q 圆O 与圆A 存在公共弦MN ,OA ∴与MN 垂直平分, 90ODM ∴∠=︒,1122DM MN y ==,1(5)2AD OD x ==-, 由勾股定理得:222DM OM OD =-,即22215()()22x y x -=-,整理得:2231025y x x =+-, 525(5)3y x ∴<<;(3)分三种情况:①当圆O 与圆A 外切,OE OF =时,圆O 与圆A 外切,圆O 的半径长53OB =; ②当OE FE =时,圆O 与圆A 相交,如图3所示: 作EH OF ⊥于H ,则52OF OH OB ==-, B B ∠=∠Q ,90EHB C ∠=︒=∠,BEH BAC ∴∆∆∽,∴EH BFAC BC=, 5315248EH ⨯∴==, 在Rt OEH ∆中,由勾股定理得:2222155()()82OB OE OB +-==,解得:12564OB =; ③当O 与A 重合时,OE OF =,F 与B 重合,5OE AB ==;综上所述,当OEF ∆为以OE 为腰的等腰三角形时,圆O 的半径长为53或12564或5.24.(2019•青浦区二模)已知:在Rt ABC∆中,90ACB∠=︒,1AC=,D是AB的中点,以CD为直径的Qe 分别交BC、BA于点F、E,点E位于点D下方,连接EF交CD于点G.(1)如图1,如果2BC=,求DE的长;(2)如图2,设BC x=,GDyGQ=,求y关于x的函数关系式及其定义域;(3)如图3,连接CE,如果CG CE=,求BC的长.【分析】(1)如图1中,连接CE.在Rt CDE∆中,求出CD,CE即可解决问题.(2)如图2中,连接CE,设AC交Qe于K,连接FK,DF,DK.想办法用x表示CD,DE,证明//FK AB,推出DG DEGQ FQ=,延长构建关系式即可解决问题.根据点E位于点D下方,确定x的取值范围即可.(3)如图3中,连接FK.证明ED EC=,由此构建方程即可解决问题.【解答】解:(1)如图1中,连接CE.在Rt ACB ∆中,90ACB ∠=︒Q ,1AC =,2BC =,AB ∴=, CD Q 是Q e 的直径, 90CED ∴∠=︒, CE AB ∴⊥,BD AD =Q ,12CD AB ∴==Q1122AB CE BC AC =g g g g ,CE ∴=,在Rt CDE ∆中,DE =(2)如图2中,连接CE ,设AC 交Q e 于K ,连接FK ,DF ,DK .90FCK ∠=︒Q ,FK ∴是Q e 的直径,∴直线FK 经过点Q ,CD Q 是Q e 的直径, 90CFD CKD ∴∠=∠=︒, DF BC ∴⊥,DK AC ⊥,DC DB DA ==Q , BF CF ∴=,CK AK =, //FK AB ∴,∴DG DEGQ FQ=, BC x =Q ,1AC =,AB ∴=DC DB DA ∴===ACE ABC ∆∆Q ∽,∴可得AE =DE AD AE ∴=-=∴2DE DECD FQ=,∴2y =, 2222(1)1x y x x -∴=>+.(3)如图3中,连接FK .CE CG =Q , CEG CGE ∴∠=∠,FKC CEG ∠=∠Q , //FK AB Q , FKC A ∴∠=∠, DC DA =Q ,A DCA ∴∠=∠,A DCA CEG CGE ∴∠=∠=∠=∠, CDA ECG ∴∠=∠, EC DE ∴=,由(2=-, 整理得:2210x x --=,1x ∴=+1,1BC ∴=.25.(2019•浦东新区二模)已知AB 是圆O 的一条弦,P 是圆O 上一点,过点O 作MN AP ⊥,垂足为点M ,并交射线AB 于点N ,圆O 的半径为5,8AB =. (1)当P 是优弧¶AB 的中点时(如图),求弦AP 的长; (2)当点N 与点B 重合时,试判断:以圆O 为圆心,32为半径的圆与直线AP 的位置关系,并说明理由; (3)当BNO BON ∠=∠,且圆N 与圆O 相切时,求圆N 半径的长.【分析】(1)连接PO 并延长交弦AB 于点H ,由垂径定理得出PH AB ⊥,AH BH =,由勾股定理得出3OH ==,在APH ∆中,90AHP ∠=︒,8PH OP OH =+=,由勾股定理求出AP 即可; (2)作OG AB ⊥于G ,先证明OBG ABM ∆∆∽,得出BM BG AB OB =,求出325BM =,得出75OM =,由7352<,即可的距离;(3)分情况讨论:①当圆N 与圆O 相外切时,作OD AB ⊥于D ,由勾股定理求出3OD ==,证出5BN OB ==,得出DN 的长,再由勾股定理求出ON ,然后由相切两圆的性质即可得出圆N 的半径; 当圆N 与圆O 相内切时,由相切两圆的性质即可得出结果.②当点N 在线段AB 上时,此时点P 在弦AB 的下方,点N 在圆O 内部,只存在圆N 与圆O 相内切,作OE AB ⊥于E ,则4AE BE ==,证出5BN OB ==,1EN BN BE ===,由勾股定理求出3OE ==,在Rt OEN ∆中,再由勾股定理得:ON == 【解答】解:(1)连接PO 并延长交弦AB 于点H ,如图1所示: P Q 是优弧¶AB 的中点,PH 经过圆心O , PH AB ∴⊥,AH BH =,在AOH ∆中,90AHO ∠=︒,142AH AB ==,5AO =,3OH ∴=,在APH ∆中,90AHP ∠=︒,538PH OP OH =+=+=,AP ∴= (2)当点N 与点B 重合时,以点O 为圆心,32为半径的圆与直线AP 相交;理由如下: 作OG AB ⊥于G ,如图2所示: OBG ABM ∠=∠Q ,OGB AMB ∠=∠, OBG ABM ∴∆∆∽,∴BM BG AB OB =,即485BM =,解得:325BM =, 327555OM ∴=-=, Q7352<, ∴当点N 与点B 重合时,以点O 为圆心,32为半径的圆与直线AP 相交; (3)①当点N 在线段AB 延长线上时,当圆N 与圆O 相外切时,作OD AB ⊥于D ,如图3所示: 5OA OB ==Q , 142AD DB AB ∴===,3OD ∴===, BNO BON ∠=∠Q , 5BN OB ∴==, 9DN DB BN ∴=+=,在Rt ODN ∆中,由勾股定理得:ON == Q 圆N 与圆O 相切,∴圆N 半径55ON =-=;当圆N 与圆O 相内切时,圆N 半径55ON =+=;②当点N 在线段AB 上时,此时点P 在弦AB 的下方,点N 在圆O 内部,只存在圆N 与圆O 相内切,如图4所示:作OE AB ⊥于E ,则4AE BE ==,3OE =, BNO BON ∠=∠Q , 5BN OB ∴==,1EN BN BE ∴===,在Rt OEN ∆中,由勾股定理得:ON =∴圆N 半径55ON =-=综上所述,当BNO BON ∠=∠,且圆N 与圆O 相切时,圆N 半径的长为5或5或5。
专题06 课内阅读理解(解析版)

专题06 课内阅读理解(解析版)学校:___________姓名:___________班级:___________考号:___________1.(2021·江苏连云港·六年级期末)课文选段。
选段①在法庭上,我们跟父亲见了面。
父亲仍旧穿着他那件灰布旧棉袍,可是没戴眼镜。
我看到了他那乱蓬蓬的长头发下面的平静而慈祥的脸。
“爹!”我忍不住喊出声来。
母亲哭了,妹妹也跟着哭起来了“不许乱喊!”法官拿起惊堂木重重地在桌子上拍了一下。
父亲瞅了瞅我们,没对我们说一句话。
他脸上的表情非常安定,非常沉着。
他的心被一种伟大的力量占据着。
这个力量就是他平日对我们讲的——他对于革命事业的信心。
选段②这段时光不好挨。
我踏着一块块方砖跳,跳房子,等母亲回来。
我看着天看着云彩走,等母亲回来,焦急又兴奋。
我蹲在院子的地上,用树枝拨弄着一个蚁穴,爬着去找更多的蚁穴。
院子里就我一个孩子,没人跟我玩,我坐在草丛里翻看一本画报,那是一本看了多少回的电影画报。
那上面有一群比我大的女孩子,一个个都非常漂亮。
我坐在草丛里看她们,想象她们的家,想象她们此刻在干什么,想象她们的兄弟姐妹和她们的父母,想象她们的声音。
去年的荒草丛里又有了绿色,院子很大,空空落落。
选段③在逃去如飞的日子里,在千门万户的世界里的我能做些什么呢?只有徘徊罢了,只有匆匆罢了;在八千多日的匆匆里,除徘徊外,又剩些什么呢?过去的日子如轻烟,被微风吹散了,如薄雾,被初阳蒸融了;我留着些什么痕迹呢?我何曾留着像游丝样的痕迹呢?我赤裸裸来到这世界,转眼间也将赤裸裸地回去吧?但不能平的,为什么偏要白白走这一遭啊?1.选段①中,父亲“没戴眼镜”“乱蓬蓬的长头发”,说明,“一种伟大的力量”指的是。
父亲的神情“非常安定,非常沉着”说明___________________________________。
2.选段②中,“我”做了四件事,用简洁的语言填写在下面的横线上①________________ ②看云彩走③________________ ④________________3.请写出你对“但不能平的,为什么偏要白白走这一遭啊?”这句话的理解:4.选段②、选段③都表达作者的真情实感,方式却截然不同:选段②中作者将焦虑的心情融于____________________进行描述,选段③则运用了____________________,把感情直接表达出来。
专题06 线段与角的画法(考点串讲)(解析版)

专题06 线段与角的画法【考点剖析】1.线段的大小比较(1)叠合法:如下图所示;用圆规截取.AB>CD AB<CD AB=CD (C )(C )D B A B A (D )(C )A D(2)度量法:用刻度尺测量每条线段的长度,再按长度的大小比较线段的大小.2.线段的性质⎧⎨⎩长度两点之间的距离:联结两点的线段的;性质线段最之间,短:两点. 3.线段的和、差、倍(1na n n a ⎧⎪⎪⎪⎨⎪>⎧⎪⎨⎪⎩⎩线段的和、差:两条线段可以相加(或相减),它们的和(或差)也是, 其长度等于这两条线段的的和(或差).倍:正整数);条线段,或线段a 的;线段的倍一条线段长度相加n 倍两条相等线段、分:中点:将一条线段分成的点. 4.角...ABC B x x x α⎧⎨⎩∠⎧⎪∠⎨⎪∠⎩︒︒︒定义:有公共的两条组成的图形;定义:定义:一条射线绕其旋转到另一个位置所成的.用表示任一角;如:表示方法:在一个顶点处时,用一个顶点的端点射线端点图形三个大写英文字母只有一个角小写的希腊字母正南大写字母表示;如:用表示.如正北方向、、正东方向、正西方向;方向角:东北方向、东南方向、、西南方向;北偏东方向西北方向、、南西偏东、北偏① ②①② ③①②③.x ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎧⎪⎪⎪⎨⎪⎪︒⎪⎩⎩南偏西 5.角的大小比较:度量法、叠合法6.画相等的角的方法:度量法、尺规法7.画角的和、差、倍⎧⎧⎪⎪⎨⎪⎪⎪⎪⎩⎨⎧⎪⎪⎪⎨⎪⎪⎪⎩⎩度量法:用量角器分别量出两个角的,根据角的和差倍画出角画法:度两个角和(或差)的角;尺规法:两角和的关键:;两角差的关键:;概念:从一个角的顶点引,把这个角分成,这角平分线: 条射线叫这个角的平分度数等于异侧同侧一条射线两个相等的角量角器直尺和圆线.画法:用画图;用作图.规①② 8.余角和补角1=60'=''901806036000909090180⎧⎧⎪⎨⎩⎪⎪⎧⎪⎨⎨⎩︒︒>︒<︒︒>︒<︒⎪⎪︒⎧⎪⎨⎪⎩⎩定义:若两个角的度数,则这两角互为余角;余角性质:同角(或等角)的相等;定义:若两个角的度数,则这两角互为补角;补角性质:同角(或等角)的相等;单位:度、分、秒, 进位; 角的度量分类:锐角:的角;直角:的角;钝和是角余角和是补角:的角且=且 【典例分析】例题1.(浦东期末5)如果一个角的补角等于它余角的4倍,那么这个角的度数是( )(A )30°;(B )45°; (C )60°; (D )90°.【答案】C ;【解析】依题可设这个角为x ,则1804(90)x x ︒-=︒-,解得60x =︒,故答案选C.例题2.(浦东四署2019期末5)利用三角板工具画角很方便,但是只能画出一些特殊的角,下列角度不能用一副三角板(不再用其他工具)画出的是( )A. 15︒;B. 20︒;C. 75︒;D. 105︒.【答案】B ;【解析】三角尺的度数有30456090︒︒︒︒、、、,这些角通过加、减、倍可以得到1575105︒︒︒、、等等,但得不出20︒,因此选B.例题3. (普陀2018期末6)如果点A 在点O 的西北方向,且点B 在点A 的正南方向,那么点B 在下列方向中,有可能在点O 的( )(A )正东方向;(B )西南方向; (C )东北方向; (D )北偏西30︒. 【答案】B ;【解析】根据题意,可画图分析,点B 在射线AP 上,故点B 可能在点O 的北偏西的方向(大于45度)或南偏西的方向或正西方向,故选B.例题4 (松江2018期末10)计算:5528'3757'︒+︒= .【答案】9325'︒;【解析】原式=5528'3757'9285'9325'︒+︒=︒=︒.例题5(黄浦2018期末13)已知线段AB 和CD ,如果将CD 移动到AB 的位置,使点C 与点A 重合,CD 与AB 叠合,点D 在线段AB 上,那么AB CD .(填“>”、“ <”或“=”)【答案】>;【解析】因为使点C 与点A 重合,CD 与AB 叠合,点D 在线段AB 上,如图所示,可知AB CD >.B (C )A D例题6(浦东2018期末12)在线段AB 延长线上截取BC =2AB ,分别取AB 、BC 的中点,分别记为点M 、N ,如果AB =2,那么MN = .【答案】3;【解析】因为BC =2AB ,AB =2,所以BC=4,又M 、N 分别是AB 、BC 的中点,故MB=1,NB =2,所以MN=MB+NB=1+2=3.例题7(松江2018期末26)如图,已知o AOP 60=∠,线段OA 与射线OP 有一公共端点O .(1)在所给图中,用直尺和圆规按所给的语句作图:①在射线OP 上截取线段BC OB 、,使OA OB =,OA BC =,(点C 与点O 不重合);②联结线段AC AB 、;③作AOP ∠的平分线OD ,与线段AC 交于D 点.(2) 用刻度尺测量AB 和OA 的长度,得出 = ,用量角器度量OAC ∠,得出=∠OAC °;(3) 写出图中与AOP ∠互余的所有角:.PO【答案与解析】(1) ①在射线OP 上截取线段OB ,BC ,使OB =OA ,BC=OA ; ②联结线段AB ,AC ;③作∠AOP 的平分线OD ,与线段AC 交于D 点. 结论:所以如图就是所求的图形。
八年级数学专题06 全等三角形的判定(知识点串讲)(解析版)

专题06 全等三角形的判定重点突破知识点一全等三角形的判定(重点)一般三角形直角三角形判定边角边(SAS)、角边角(ASA)角角边(AAS)、边边边(SSS)具备一般三角形的判定方法斜边和一条直角边对应相等(HL)性质对应边相等,对应角相等对应中线相等,对应高相等,对应角平分线相等备注:1.判定两个三角形全等必须有一组边对应相等。
2.全等三角形周长、面积相等。
知识点二证题的思路(难点)考查题型一利用SAS判断两个三角形全等典例1(2020惠州市期末)如图,点E、F分别是矩形ABCD的边AB、CD上的一点,且DF=BE. 求证:AF=CE.【答案】证明见解析【分析】由SAS证明△ADF≌△CBE,即可得出AF=CE.【详解】证明:∵四边形ABCD是矩形,∴∠D =∠B =90°,AD =BC ,在△ADF 和△CBE 中,AD BCD B DF BE⎧⎪∠∠⎨⎪⎩===,∴△ADF ≌△CBE (SAS ),∴AF =CE .变式1-1(2018·丹江口市期末)如图,点E,F 在AB 上,,,AD BC A B AE BF =∠=∠=.求证:ADF BCE ∆≅∆.【答案】详见解析【分析】 先将转化为AF =BE ,再利用证明两个三角形全等.【详解】证明:因为AE =BF ,所以,AE +EF =BF +EF ,即AF =BE ,在△ADF 和△BCE 中,AD BCA B AF BE=⎧⎪∠=∠⎨⎪=⎩所以,ADF BCE ∆≅∆变式1-2(2019·武汉市期中)已知:如图,点C 为AB 中点,CD=BE ,CD ∥BE.求证:△ACD ≌△CBE.【答案】证明见解析.【解析】证明:∵CD ∥BE ,∴∠ACD=∠B..∵点C 为AB 中点,∴AC=CB.又∵CD=BE ,∴△ACD ≌△CBE (SAS )变式1-3(2019·兰州市期末)如图,△ABC 中,AB=AC ,点E ,F 在边BC 上,BE=CF ,点D 在AF 的延长线上,AD=AC ,(1)求证:△ABE ≌△ACF ;(2)若∠BAE=30°,则∠ADC= °.【答案】(1)证明见解析;(2)75.【分析】(1)根据等边对等角可得∠B=∠ACF ,然后利用SAS 证明△ABE ≌△ACF 即可;(2)根据△ABE ≌△ACF ,可得∠CAF=∠BAE=30°,再根据AD=AC ,利用等腰三角形的性质即可求得∠ADC 的度数.【详解】(1)∵AB=AC ,∴∠B=∠ACF ,在△ABE 和△ACF 中,AB AC B ACF BE CF =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ACF (SAS );(2)∵△ABE ≌△ACF ,∠BAE=30°,∴∠CAF=∠BAE=30°, ∵AD=AC ,∴∠ADC=∠ACD ,∴∠ADC=280013︒-︒=75°, 故答案为75.考查题型二 利用ASA 判断两个三角形全等典例2(2019·玉林市期中)如图,∠A =∠B ,AE =BE ,点D 在 AC 边上,∠1=∠2,AE 和BD 相交于点O .求证:△AEC ≌△BED ;【答案】见解析【分析】根据全等三角形的判定即可判断△AEC ≌△BED ;【详解】∵AE 和BD 相交于点O ,∴∠AOD=∠BOE .在△AOD 和△BOE 中,∠A=∠B ,∴∠BEO=∠2.又∵∠1=∠2,∴∠1=∠BEO ,∴∠AEC=∠BED .在△AEC 和△BED 中,A BAE BE AEC BED∠∠⎧⎪⎨⎪∠∠⎩===∴△AEC ≌△BED (ASA ).变式2-1(2018·楚雄州期末)如图,完成下列推理过程:如图所示,点E 在△ABC 外部,点D 在BC 边上,DE 交AC 于F ,若∠1=∠3,∠E =∠C ,AE =AC ,求证:△ABC ≌△ADE.证明:∵∠E =∠C (已知),∠AFE =∠DFC ( ),∴∠2=∠3(),又∵∠1=∠3(),∴∠1=∠2(等量代换),∴__________+∠DAC=__________+∠DAC(), 即∠BAC=∠DAE,在△ABC和△ADE中∵()()()E CAE ACBAC DAE∠=∠⎧⎪=⎨⎪∠=∠⎩已知已知已证∴△ABC≌△ADE().【答案】对顶角相等;三角形内角和定理;已知;∠1;∠2;等式的性质;ASA 【详解】解:∵∠E=∠C(已知),∠AFE=∠DFC(对顶角相等),∴∠2=∠3(三角形内角和定理).又∵∠1=∠3(已知),∴∠1=∠2(等量代换),∴∠1+∠DAC=∠2+∠DAC(等式的性质),即∠BAC=∠DAE.在△ABC和△ADE中,∵E CAE ACBAC DAE∠=∠⎧⎪=⎨⎪∠=∠⎩(已知)(已知)(已证),∴△ABC≌△ADE(ASA).变式2-2(2019·德州市期末)如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE. 求证:BD=CE.【答案】见解析.【分析】先求出∠CAE=∠BAD再利用ASA证明△ABD≌△ACE,即可解答【详解】∵AB⊥AC,AD⊥AE,∴∠BAE+∠CAE=90°,∠BAE+∠BAD=90°,∴∠CAE=∠BAD.又AB=AC,∠ABD=∠ACE,∴△ABD≌△ACE(ASA).∴BD=CE.考查题型三利用AAS判断两个三角形全等典例3(2019·黄石市期中)如图,在ABCD中,经过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.(1)求证:△AED≌△CFB;(2)求证:四边形AFCE是平行四边形.【答案】(1)见解析;(2)见解析.【分析】(1)根据平行四边形的性质可得AD=BC,∠CBF=∠ADE,再根据垂线的性质可得∠CFB=∠AED=90°,再根据全等三角形的判定(角角边)来证明即可;(2)根据全等三角形的性质可得AE=CF,再由AE⊥BD,CF⊥BD可得AE∥CF,根据一组对边平行且相等的四边形为平行四边形即可证明.【详解】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠CBF=∠ADE,∵AE⊥BD,CF⊥BD,∴∠CFB=∠AED=90°,∴△AED≌△CFB(AAS).(2)证明:∵△AED≌△CFB,∴AE=CF,∵AE⊥BD,CF⊥BD,∴AE∥CF,∴四边形AFCE 是平行四边形.变式3-1(2019·兴义市期末)如图,已知在四边形ABCD 中,点E 在AD 上,∠BCE =∠ACD =90°,∠BAC =∠D ,BC =CE .(1)求证:AC =CD ;(2)若AC =AE ,求∠DEC 的度数.【答案】(1)证明见解析;(2)112.5°.【分析】()1根据同角的余角相等可得到24∠=∠,结合条件BAC D ∠=∠,再加上BC CE =, 可证得结论; ()2根据90ACD AC CD ∠=︒=,,得到145D ∠=∠=︒, 根据等腰三角形的性质得到3567.5∠=∠=︒, 由平角的定义得到1805112.5DEC ∠=︒-∠=︒.【详解】() 1证明:90BCE ACD ∠=∠=︒,2334,∴∠+∠=∠+∠ 24∴∠=∠,在△ABC 和△DEC 中,24BAC D BC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,AC CD ∴=;(2)∵∠ACD =90°,AC =CD ,∴∠1=∠D =45°, ∵AE =AC ,∴∠3=∠5=67.5°, ∴∠DEC =180°-∠5=112.5°. 变式3-2(2019·温州市期中)如图,已知A ,F ,E ,C 在同一直线上,//AB CD ,ABE CDF ∠=∠,AF CE =.试说明:ABE CDF ∆≅∆.【答案】见解析;【分析】由AB ∥CD 可得∠BAC =∠DCA ,由AF =CE 可得AE =CF ,由AAS 可得△ABE ≌△CDF .【详解】证明∵AB CD ∕∕,∴BAC ACD ∠=∠∵AF CE =,∴AF EF CE EF +=+,即AE FC =.在ABE ∆和CDF ∆中,BAC ACD ABE CDF AE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ABE CDF ∆∆≌(AAS )考查题型四 利用SSS 判断两个三角形全等典例4(2019·德州市期中)已知:如图,AB =AC ,BD =CD ,DE ⊥AB ,垂足为E ,DF ⊥AC ,垂足为F .求证:DE =DF .【答案】见解析【分析】连接AD ,利用“边边边”证明△ABD 和△ACD 全等,再根据全等三角形对应边上的高相等证明.【详解】证明:如图,连接AD ,在△ABD 和△ACD 中,AB ACBD CD AD AD=⎧⎪=⎨⎪=⎩,∴△ABD ≌△ACD (SSS ),∵DE ⊥AB ,DF ⊥AC ,∴DE =DF (全等三角形对应边上的高相等).变式4-1(2019·阳泉市期末)如图,在△ABC 中,AB =AC ,点D 是BC 的中点,点E 在AD 上,求证:∠1=∠2.【答案】证明见详解【分析】由AB=AC,AD=AD,BD=CD,可证得△ABD ≌△ACD,得到∠BAE=∠CAE,再证明△ABE ≌△ACE,即可得到结论.【详解】证明:AB=AC,AD=AD,BD=CD,在△ABD 和△ACD 中,AB ACAD AD BD CD=⎧⎪=⎨⎪=⎩∴△ABD ≌△ACD, ∠BAE=∠CAE,在△ABE 和△ACE 中, ,AB AC BAE CAE AE AE =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△ACE∴∠1=∠2.变式4-2(2019·鄂州市期中)如图,点A 、D 、C 、F 在同一条直线上,AD=CF ,AB=DE ,BC=EF.(1)求证:ΔABC ≌△DEF ;(2)若∠A=55°,∠B=88°,求∠F 的度数.【答案】(1)证明见解析;(2)37°【解析】(1)∵AC=AD+DC , DF=DC+CF ,且AD=CF∴AC=DF在△ABC 和△DEF 中,AB DE BC EF AC DF =⎧⎪=⎨⎪=⎩∴△ABC ≌△DEF (SSS )(2)由(1)可知,∠F=∠ACB∵∠A=55°,∠B=88° ∴∠ACB=180°-(∠A+∠B )=180°-(55°+88°)=37° ∴∠F=∠ACB=37°变式4-3(2020·石家庄市期末)如图,点B ,F ,C ,E 在直线l 上(F ,C 之间不能直接测量),点A ,D 在l 异侧,测得AB=DE ,AC=DF ,BF=EC .(1)求证:△ABC ≌△DEF ;(2)指出图中所有平行的线段,并说明理由.【答案】(1)详见解析;(2)∠ABC=∠DEF ,∠ACB=∠DFE,理由见解析.【解析】(1)证明:∵BF=EC ,∴BF+CF=CF+CE ,∴BC="EF"∵AB=DE ,AC="DF"∴△ABC ≌△DEF (SSS )(2)AB ∥DE,AC ∥DF,理由如下,∵△ABC ≌△DEF ,∴∠ABC=∠DEF ,∠ACB=∠DFE,∴AB ∥DE,AC ∥DF.考查题型五 利用HL 判断两个直角三角形全等典例5(2019·云龙县期中)已知:如图,AC=BD ,AD ⊥AC ,BC ⊥BD .求证:AD=BC【答案】见解析【分析】连接CD ,利用HL 定理得出Rt △ADC ≌Rt △BCD 进而得出答案.【详解】证明:如图,连接CD ,∵AD ⊥AC ,BC ⊥BD ,∴∠A=∠B=90°,在Rt △ADC 和Rt △BCD 中CD CD AC BD=⎧⎨=⎩,∴Rt △ADC ≌Rt △BCD (HL ),∴AD=BC .变式5-1(2019·开封市期中)已知:如图,AB =CD ,DE ⊥AC ,BF ⊥AC ,E ,F 是垂足,DE BF =.求证:(1)AF CE =;(2)AB CD ∥.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)根据垂直的定义得到∠DEC=∠BFA=90°,推出Rt △DCE ≌Rt △BFA (HL ),由全等三角形的性质即可得到结论.(2)根据全等三角形的性质得到∠C=∠A ,根据平行线的判定即可得到AB ∥CD.【详解】证明: ∵ DE ⊥ AC , BF ⊥ AC∴ ∠DEC=∠BFA=90°在Rt △ DEC 和Rt △ BFA 中AB=CDDE=BF∴ Rt △ DCE ≌Rt △ BFA (HL )∴ AF=CE∴ ∠C=∠A∴ AB ∥ CD变式5-2(2018·开封市期末)如图,D 、C 、F 、B 四点在一条直线上,AB DE =,AC BD ⊥,EF BD ⊥,垂足分别为点C 、点F ,CD BF =.求证:(1)ABC EDF ∆≅∆;(2)//AB DE .【答案】(1)见解析;(2)见解析.【分析】(1)由垂直的定义,结合题目已知条件可利用HL 证得结论;(2)由(1)中结论可得到∠D =∠B ,则可证得结论.【详解】证明:(1)∵AC BD ⊥,EF BD ⊥,∴ABC ∆和EDF ∆为直角三角形,∵CD BF =,∴CF BF CF CD +=+,即BC DF =,在Rt ABC ∆和Rt EDF ∆中,AB DE BC DF =⎧⎨=⎩, ∴()Rt ABC Rt EDF HL ∆≅∆;(2)由(1)可知ABC EDF ∆≅∆,∴B D ∠∠=,∴//AB DE .考查题型六 三角形全等判定的综合典例6(2019·保定市期末)下列各图中a 、b 、c 为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC 全等的是( )A .甲和乙B .乙和丙C .甲和丙D .只有丙【答案】B【解析】 乙和△ABC 全等;理由如下:在△ABC 和图乙的三角形中,满足三角形全等的判定方法:SAS ,所以乙和△ABC 全等;在△ABC 和图丙的三角形中,满足三角形全等的判定方法:AAS ,所以丙和△ABC全等;不能判定甲与△ABC全等;故选B.变式6-1(2019·武汉市期中)如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是()A.BC=EC,∠B=∠E B.BC=EC,AC=DCC.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D【答案】C【解析】试题分析:根据全等三角形的判定方法分别进行判定:A、已知AB=DE,加上条件BC=EC,∠B=∠E可利用SAS证明△ABC≌△DEC,故此选项不合题意;B、已知AB=DE,加上条件BC=EC,AC=DC可利用SSS证明△ABC≌△DEC,故此选项不合题意;C、已知AB=DE,加上条件BC=DC,∠A=∠D不能证明△ABC≌△DEC,故此选项符合题意;D、已知AB=DE,加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC≌△DEC,故此选项不合题意.故选C.变式6-2(2020·杭州市期末)如图所示,在下列条件中,不能判断△ABD≌△BAC的条件是()A.∠D=∠C,∠BAD=∠ABC B.∠BAD=∠ABC,∠ABD=∠BACC.BD=AC,∠BAD=∠ABC D.AD=BC,BD=AC【答案】C【解析】解:A、符合AAS,能判断△ABD≌△BAC;B、符合ASA,能判断△ABD≌△BAC;C、符合SSA,不能判断△ABD≌△BAC;D、符合SSS,能判断△ABD≌△BAC.所以根据全等三角形的判定方C、满足SSA不能判断两个三角形全等.故选C.变式6-3(2018·虹桥区期中)如图,在下列条件中,不能证明△ABD≌△ACD的是().A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC【答案】D【分析】两个三角形有公共边AD,可利用SSS,SAS,ASA,AAS的方法判断全等三角形.解答:【详解】分析:∵AD=AD,A、当BD=DC,AB=AC时,利用SSS证明△ABD≌△ACD,正确;B、当∠ADB=∠ADC,BD=DC时,利用SAS证明△ABD≌△ACD,正确;C、当∠B=∠C,∠BAD=∠CAD时,利用AAS证明△ABD≌△ACD,正确;D、当∠B=∠C,BD=DC时,符合SSA的位置关系,不能证明△ABD≌△ACD,错误.故选D.。
专题06 一次函数图像的五种考法(解析版)-2024年常考压轴题攻略(8年级上册北师大版)

专题06一次函数图像的五种考法类型一、图像的位置关系问题例.直线y kx k =-与直线y kx =-在同一坐标系中的大致图像可能是()A .B .C .D .【答案】A【分析】根据直线y kx k =-与直线y kx =-图像的位置确定k 的正负,若不存在矛盾则符合题意,据此即可解答.【详解】解:A 、y kx =-过第二、四象限,则0k >,所以y kx k =-过第一、三、四象限,所以A 选项符合题意;B 、y kx =-过第二、四象限,则0k >,所以y kx k =-过第一、三、四象限,所以B 选项不符合题意;C 、y kx =-过第一、三象限,则0k <,所以y kx k =-过第二、一、四象限,所以C 选项不符合题意;D 、y kx =-过第一、三象限,则0k <,所以y kx k =-过第二、一、四象限,所以D 选项不符合题意.故选A .【点睛】本题主要考查了一次函数的图像:一次函数0y kx b k =+≠()的图像为一条直线,当0k >,图像过第一、三象限;当0k <,图像过第二、四象限;直线与y 轴的交点坐标为()0b ,.【变式训练1】在同一坐标系中,直线1l :()3y k x k =-+和2l :y kx =-的位置可能是()A .B ...【答案】B【分析】根据正比例函数和一次函数的图像与性质,对平面直角坐标系中两函数图像进行讨论即可得出答案.k>,故由一次函数图像与【详解】A、由正比例函数图像可知0,即0点的上方,故选项A不符合题意;....【答案】B【分析】先根据直线1l,得出k然后再判断直线2l的k和b的符号是否与直线.B...【答案】C【分析】根据一次函数的图象性质判断即可;ab>,【详解】∵0同号,A .B .C .D .【答案】A【分析】分别分析四个选项中一次函数和正比例函数m 和n 的符号,即可进行解答.【详解】解:A 、由一次函数图象得:0,0m n <>,由正比例函数图象得:0mn <,符合题意;B 、由一次函数图象得:0,0m n <>,由正比例函数图象得:0mn >,不符合题意;C 、由一次函数图象得:0,0m n >>,由正比例函数图象得:0mn <,不符合题意;D 、由一次函数图象得:0,0m n ><,由正比例函数图象得:0mn >,不符合题意;故选:A .【点睛】本题主要考查了一次函数和正比例函数的图象,解题的关键是掌握一次函数和正比例函数图象与系数的关系.类型二、图像与系数的关系则13k≥或3k≤-,故答案为:【点睛】本题考查了一次函数的图象与性质,熟练掌握数形结合思想是解题关键.类型三、图像的平移问题例.将直线y kx b =+向左平移2个单位,再向上平移4个单位,得到直线2y x =,则()A .2k =,8b =-B .2k =-,2b =C .1k =,4b =-D .2k =,4b =【答案】A【分析】根据直线y kx b =+向左平移2个单位,变为()2y k x b =++,再向上平移4个单位,变为()24y k x b =+++,然后结合得到直线2y x =,即可解出k 和b 的值.【详解】解:直线y kx b =+向左平移2个单位,变为()2y k x b =++,再向上平移4个单位,变为()24y k x b =+++,得到直线2y x =,2k ∴=,240k b ++=,2k ∴=,8b =-,故选:A .【点睛】本题考查了一次函数图像平移变换,熟练掌握图象左加右减,上加下减的变换规律是解答本题的关键.【变式训练1】对于一次函数24y x =-+,下列结论错误的是().A .函数的图象与x 轴的交点坐标是(0,4)B .函数的图象不经过第三象限C .函数的图象向下平移4个单位长度得2y x =-的图象D .函数值随自变量的增大而减小【答案】A【分析】分别根据一次函数的性质及函数图象平移的法则进行解答即可.【详解】A 选项:当0y =时,2x =,所以函数的图象与x 轴的交点坐标是(2,0),故A 选项错误;B 选项:函数的图象经过第一、二、四象限,不经过第三象限,故B 选项正确;C 选项:函数的图象向下平移4个单位长度,得到函数244y x =-+-,即2y x =-的图象,故C 选项正确;D 选项:由于20k =-<,所以函数值随x 的增大而减小,故D 选项正确.故选:C【点睛】本题考查一次函数的图象及性质,函数图象平移的法则,熟练运用一次函数的图象及性质进行判断是解题的关键.【变式训练2】把直线3y x =-先向右平移2个单位长度,再向下平移3个单位长度,平移后的新直线与x 轴的交点为()0m ,,则m 的值为()A .3B .1C .1-D .3-【答案】B【分析】由题意知,平移后的直线解析式为()32333y x x =---=-+,将()0m ,代入得033m =-+,计算求解即可.【详解】解:由题意知,平移后的直线解析式为()32333y x x =---=-+,将()0m ,代入得033m =-+,解得1m =,故选:B .【点睛】本题考查了一次函数图象的平移,一次函数与坐标轴的交点.解题的关键在于熟练掌握图象平移:左加右减,上加下减.类型四、规律性问题例.在平面直角坐标系中,直线:1l y x =-与x 轴交于点1A ,如图所示,依次作正方形111A B C O ,正方形2221A B C C ,…,正方形1n n n n A B C C -,使得点1A ,2A ,3A ,….在直线l 上,点1C ,2C ,3C ,…,在y 轴正半轴上,则点2023B 的坐标为()A .()202220232,21-B .()202320232,2C .()202320242,21-D .()202220232,21+【答案】A【分析】根据一次函数图象上点的坐标特征结合正方形的性质可得出点11A B 、的坐标,同理可得出2A 、3A 、4A 、5A …及2B 、3B 、4B 、5B …的坐标,根据点的坐标变化可找出变化规律()12,21n n n B --(n 为正整数),依此规律即可得出结论.【详解】解:当0y =时,由10x -=,解得:1x =,∴点1A 的坐标为()1,0,111A B C O 为正方形,()11,1B ∴,同理可得:()22,1A ,()34,3A ,()48,7A ,()516,15A ,…,∴()22,3B ,()34,7B ,()48,15B ,()516,31B ,…,【答案】20222022(21,2)-【分析】先求出1A 、2A 、3A 、4A 的坐标,找出规律,即可得出答案.【详解】解: 直线1y x =+和y 轴交于1A ,1A ∴的坐标()0,1,即11OA =,四边形111C OA B 是正方形,111OC OA ∴==,【答案】()20222,0【分析】根据1A 的坐标和函数解析式,即可求出点34,A A 探究规律利用规律即可解决问题.【详解】∵直线3y x =,点1A 的坐标为∴()11,3B 在11Rt OA B △中,11131,OA A B ==,类型五、增减性问题.B...A .()15,53B .()15,63C .()17,53D 【答案】D【答案】40432【分析】根据已知先求出2OA ,3OA ,33A B ,44A B ,然后分别计算出1S ,2S 【详解】解:∵11OA =,212OA OA =,∴22OA =,∵322O A O A =,∴34OA =,∵432OA OA =,。
2024年中考数学压轴题型-专题06 与二次函数有关问题的压轴题之六大题型(解析版)6

专题06与二次函数有关问题的压轴题之六大题型目录【题型一二次函数图象和性质之选择题】 (1)【题型二二次函数的图象与系数的关系】 (4)【题型三二次函数图象和性质之解答题】 (8)【题型四二次函数与几何图形的综合问题】 (14)【题型五二次函数中的新定义型问题】 (25)【题型六实际问题与二次函数的综合问题】 (32)【题型一二次函数图象和性质之选择题】【题型二二次函数的图象与系数的关系】例题:(2023·浙江·一模)如图所示为二次函数2(0)y ax bx c a =++≠的图象,对称轴是直线1x =,下列结论:A .1B .2【答案】C 【分析】利用抛物线图像与性质进行判断,根据函数图像开口方向确定y 轴交点的确定c ,取特殊点代入函数,根据函数图像确定关于【详解】解: 抛物线与x 轴有∴2=40b ac ∆->,A.2B.3【答案】B【分析】根据图象的开口方向,对称轴,与号,判断②;根据对称性,判断x次函数图像的顶点判断⑤,进而得出结论.【详解】解:∵抛物线的开口向下,对称轴为直线【题型三二次函数图象和性质之解答题】(2)设()()1200M x N x ,,,,令0y =,则2420mx mx m -+-=,二次函数2420y mx mx m m =-+-≠(),与x 轴交于不同点∴方程2420mx mx m -+-=有两个不相等的实数根,∴()()()2Δ4424320m m m m m =---=+>,又∵0m <,∴320m +<,解得:23m <-44m x x -221m x x -【题型四二次函数与几何图形的综合问题】例题:(2023·浙江·一模)在平面直角坐标系xOy 中有三个点:()()()1,2,1,6,1,4A B C -,二次函数()230y ax bx a =++≠的图象恰好经过这三个点之中的两个点.(1)试推断二次函数23y ax bx =++的图象经过点、、A B C 之中的哪两个点?请简要说明理由;(2)求常数a 与b 的值;(3)将二次函数23y ax bx =++的图象先向下平移2个单位长度,再向右平移(0)t t >个单位长度,如果平移后所得新二次函数的图象顶点为D ,且经过点()1,4C ,连AB 、AD BD 、,请判断ABD △的形状,并证明你的判断【答案】(1)点A 、B 在抛物线上,理由见解析(2)1a =,2b =(3)等腰直角三角形,见解析【分析】(1)∥BC y 轴,故B 、C 中只有一个点在抛物线上,求得AC 的解析式,交y 轴于点()0,3,抛物线与y 轴也交于点()0,3,故C 不符要求,由此解答即可;(2)把A 、B 点的坐标代入解析式,由此解答即可;(3)由平移可得新的解析式,代入()1,4得出D 点的坐标,再判断三角形的形状.【详解】(1)∵()()1614B C ,,,,∴∥BC y 轴,故B 、C 中只有一个点在抛物线上,【点睛】本题考查了与待定系数法求二次函数解析式及判断点是否在图像上,平移变换勾股定理等知识,求解析式是解题的关键.1.(2023·浙江嘉兴·统考一模)如图,已知抛物线动点()(),004C m m <<在x 轴上,于点E .(1)求点A ,B 的坐标.(2)当2m =时,求线段PE (3)当BOE △是以BE 为腰的等腰三角形时,求【答案】(1)()(4,0,0,3A B∴92,2P⎛⎫⎪⎝⎭,22OP⎛=+⎝设直线OP的解析式为y=∴922k=,403m nn+=⎧⎨=⎩,过点E 作⊥EN OA 于点N 则EN PC P ,2,ON EN =∴tan EN PC POC ON OC ∠==∵()(),004C m m <<,过点E作EG OA⊥于点G 则EG PC OBP P,∴25 EG AE AGOB AB AO===,∴2 345 EG AG==,(1)求线段OC的长;(2)求该抛物线的函数关系式;是以BC为腰的等腰三角形?若存在,求出所有符合条(3)在抛物线的对称轴上是否存在一点P,使得BCP件的点P的坐标;若不存在,请说明理由.【答案】(1)23(1)求c 的值及顶点M 的坐标,(2)如图2,将矩形ABCD 沿x 轴正方向平移t 个单位()03t <<得到对应的矩形分别与函数24y x x c =-+的图象交于点P ,Q ,连接PQ ,过点P 作PG A B ''⊥①当2t =时,求QG 的长;②当点G 与点Q 不重合时,是否存在这样的t ,使得PGQ △的面积为1?若存在,求出此时在,请说明理由.,当点G 在点Q 的下方时,(22224QG t t t t =-+--+52(在03t <<的范围内).或52.【点睛】本题考查了二次函数图象上点的坐标特点、矩形的性质以及三角形的面积等知识,熟练掌握二次函数的图象与性质、灵活应用数形结合思想是解题的关键.【题型五二次函数中的新定义型问题】(1)判断点()1,3,()2,8,()3,7是否为函数52y x =-图象关于(2)如图1,抛物线222y x bx =++与x 轴交于A ,B 两点(A∴222x x bx c +++=,22x x bx --∴整理得:222x bx x c ++=-+或⎩(1)写出函数1y x =+关于直线1x =的“迭代函数”的解析式为(2)若函数243y x x =-++关于直线x m =的“迭代函数”图象经过(3)以如正方形ABCD 的顶点分别为:(,),(,),(,),(,)A a a B a a C a a D a a ----,其中0a >.①若函数6y x=关于直线2x =-的“迭代函数”的图象与正方形6x∴函数6yx=关于直线2x=-的“迭代函数”的图象与正方形ABCD当第一象限有两个公共点时,第三个交点在第三象限,当x=-当第三象限有两个公共点时,第三个公共点在第一象限,函数图象正好经过正方形的顶点,此时6a=,综上所述:若函数6yx=关于直线2x=-的“迭代函数”的图象与正方形6a=.②如图:若6a =,函数6y x=关于直线x n =的“迭代函数定有两个交点它们是(1,6)、(6,1);根据正方形和“迭代函数”的图象对称性,I .当1n ≥时,“迭代函数”的图象与正方形ABCD II .当01n <<时,“迭代函数”的图象与正方形III .当0n <,若第三象限由两个公共点,则第二象限无公共点,此时点(1,6)关于x n =对称点在正方形外,即:12(1--此时点(1,6)--在函数6y x=关于直线x n =的“迭代函数即:52n <-时,“迭代函数”的图象与正方形ABCD 在第三象限有两个公共点,第二象限无公共点,Ⅳ.当0n <,若第二象限有两个公共点,则第三象限无公共点,【题型六实际问题与二次函数的综合问题】①销售量不超过12万件时,利润为45②当售价为多少元时,利润最大,最大值是多少万元?(利润=销售总额-总成本)【答案】(1)y关于x的函数表达式为(1)求出启航阶段()m s 关于()s t 的函数表达式(写出自变量的取值范围)(2)已知途中阶段龙舟速度为5m /s .①当90s t =时,求出此时龙舟划行的总路程,②在距离终点125米处设置计时点,龙舟到达时,85.20s t ≤(3)冲刺阶段,加速期龙舟用时1s 将速度从5m /s 提高到5训练所需时间(精确到0.01s ).【答案】(1)21(020)8s t t =<≤(2)①龙舟划行的总路程为400m ;②该龙舟队能达标.(3)该龙舟队完成训练所需时间为109.07s4(1)请直接写出A ,B 的坐标.(2)排球第一次被垫起后,在区域内侧离边界水平距离明理由.(3)第三次垫球后,球在运动中离地面的最大高度恰好达标,求抛物线【答案】(1)311(,)28,37(,)24-(2)该女生此次垫球不达标.理由见解析(3)221y x x =--+(1)若小明投篮的初始速度为t=时,则①当0.5s②记篮球的水平方向距离为(2)在又一次投篮中,当篮球在空中飞行的水平方向距离为次投篮的篮球的初始速度(1)【种植计划】小王在调查某类水果时发现,当每平方米种植每平方米种植的株数每增加1株,单株产量减小0.25的产量?最大产量是多少?请自行设函数变量,解决问题.(2)【场地规划】小王挑选了房屋侧面的空地作为大棚场地.用来侧面加固的材料一共可以图约材料,小王打算让大棚其中一面靠房屋外墙,如图为多少?(3)【顶棚设计】在确定矩形场地规划的情况下,如图曲线满足抛物线形状,小王需要给内部两侧距离中心线标系,计算日照灯的安装高度.【答案】(1)每平方米计划种植6株时,能获得最大产量,最大产量为1350kg (2)12.5米(3)3.76米【分析】(1)设每平方米种植增加x 株,总产量为y ,根据题意可以得到()()150420.25y x x =⨯+-,将二次函数的解析式化解为顶点式即可得到答案;(2)根据矩形的面积即可求出垂直墙面一边的长度;(3)设二次函数的解析式为2y ax k =+,先根据图2得数据求出解析式,再将2x =代入即可求得答案.【详解】(1)解:设每平方米种植增加x 株,总产量为ykg ,根据题意得()()150420.25y x x =⨯+-,∴()237.521350y x =--+,∴当2x =株时,y 有最大值,且1350y =kg ,∴每平方米计划种植6株时,能获得最大产量,最大产量为1350kg ,(2)解:设与墙垂直一面的长度为多少m 米,根据题意得12150m ⨯=平方米,解方程得12.5m =米,∵12.52123740⨯+=<∴与墙垂直一面的长度为12.5米;(3)解:直角坐标系建立如下图所示,设二次函数的图像解析式为:2y ax k =+,由题意可得,抛物线过点()0,4,∵外墙长为12米,∴抛物线过点()6,1.8,t (秒)00.51 1.52 2.53 3.54H (米)19.751619.752119.75169.751(1)请解释图(2)中点A 所表示的实际意义;(2)①请将表格中的(),t h 的各组数值作为点的坐标,在图(3)的坐标系中,描出各点,连线,画出高度与时间t 的函数图象,由图象可知h 是t 的_______函数;②求h 关于t 的函数关系式;(3)当速度不足12米/秒时,求h 的取值范围.【答案】(1)点A 表示经过2秒物体的速度降为0米/秒,此时物体是上抛过程中的最高点(2)①图见解析,二次;②()25221h t =--+(3)13.821h <≤【分析】(1)根据速度与时间的关系及函数图象,即可解答;(2)①画出函数图象,即可解答;②设函数关系式为:()2221h a t =-+,再把()01,代入关系式,即可求解;(3)首先可求得1020v t =-+,把12v =代入解析式,可求得0.8t =,再代入()25221h t =--+,即可求解.【详解】(1)解:点A 表示经过2秒物体的速度降为0米/秒,此时物体是上抛过程中的最高点;(2)解:①描出各点,连线,画出高度h 与时间t 的函数图象,如下:由图象可知:h 是t 的二次函数,故答案为:二次;②解:由表可知二次函数的顶点坐标是()221,,可设函数关系式为:()2221h a t =-+,把()01,代入上式,得:()210221a =-+,解得:5a =-,∴h 关于t 的函数关系式是:25(2)21h t =--+;(3)解:设20v kt =+把点()20A ,代入上式,得:0220k =+,解得10k =-,1020v t ∴=-+,把12v =代入上式,得:121020t =-+,解得0.8t =,(1)当水柱都满足水平距离为4米时,达到最大高度为6米.t=时,求第一象限内水柱的函数表达式.①若1②用含t的代数式表示a.(2)为了美化公园,对公园及喷水设备进行升级改造,a与t之间满足4a。
高考数学(理)之立体几何与空间向量 专题06 平面与平面的平行、垂直的判定与性质(解析版)
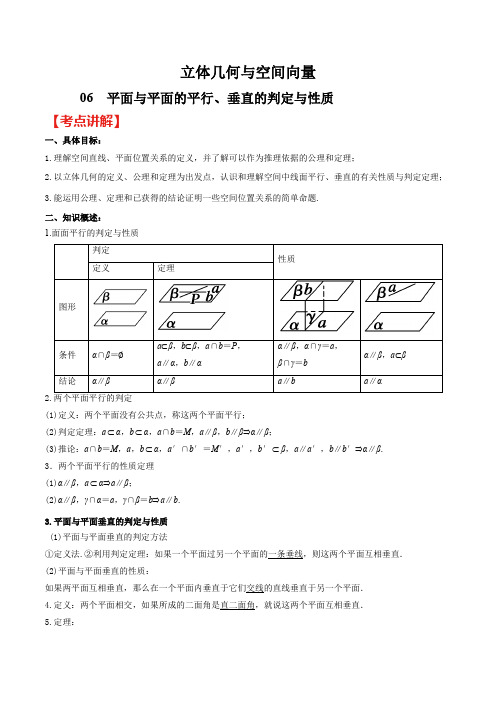
立体几何与空间向量06 平面与平面的平行、垂直的判定与性质【考点讲解】一、具体目标:1.理解空间直线、平面位置关系的定义,并了解可以作为推理依据的公理和定理;2.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定定理;3.能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题.二、知识概述:1.面面平行的判定与性质a⊂β,b⊂β,a∩b=P,α∥β,α∩γ=a,(1)定义:两个平面没有公共点,称这两个平面平行;(2)判定定理:a⊂α,b⊂α,a∩b=M,a∥β,b∥β⇒α∥β;(3)推论:a∩b=M,a,b⊂α,a′∩b′=M′,a′,b′⊂β,a∥a′,b∥b′⇒α∥β.3.两个平面平行的性质定理(1)α∥β,a⊂α⇒a∥β;(2)α∥β,γ∩α=a,γ∩β=b⇒a∥b.3.平面与平面垂直的判定与性质(1)平面与平面垂直的判定方法①定义法.②利用判定定理:如果一个平面过另一个平面的一条垂线,则这两个平面互相垂直.(2)平面与平面垂直的性质:如果两平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.4.定义:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.5.定理:⎭⎪⎬⎪⎫AB βAB ⊥α⇒β⊥α⎭⎪⎬⎪⎫α⊥βα∩β=MNAB βAB ⊥MN⇒AB ⊥α1.【2019年高考全国Ⅱ卷理数】设α,β为两个平面,则α∥β的充要条件是( ) A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线D .α,β垂直于同一平面【解析】本题考查了空间两个平面的判定与性质及充要条件.由面面平行的判定定理知:α内两条相交直线都与β平行是αβ∥的充分条件,由面面平行性质定理知,若αβ∥,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是αβ∥的必要条件,故选B . 【答案】B2.【2019年高考浙江卷】设三棱锥V –ABC 的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点).记直线PB 与直线AC 所成的角为α,直线PB 与平面ABC 所成的角为β,二面角P –AC –B 的平面角为γ,则( ) A .β<γ,α<γB .β<α,β<γC .β<α,γ<αD .α<β,γ<β【解析】本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.如图,G 为AC 中点,连接VG ,V 在底面ABC 的投影为O ,则P 在底面的投影D 在线段AO 上,过D 作DE 垂直于AC 于E ,连接PE ,BD ,易得PE VG ∥,过P 作PF AC ∥交VG 于F ,连接BF ,过D 作DH AC ∥,交BG 于H ,则,,BPF PBD PED αβγ=∠=∠=∠,结合△PFB ,△BDH ,△PDB 均为直角三角形,可得cos cos PF EG DH BDPB PB PB PBαβ===<=,即αβ>; 【真题分析】在Rt △PED 中,tan tan PD PDED BDγβ=>=,即γβ>,综上所述,答案为B.【变式1】【2018年高考浙江卷】已知四棱锥S −ABCD 的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为θ1,SE 与平面ABCD 所成的角为θ2,二面角S −AB −C 的平面角为θ3,则( )A .θ1≤θ2≤θ3B .θ3≤θ2≤θ1C .θ1≤θ3≤θ2D .θ2≤θ3≤θ1【解析】设O 为正方形ABCD 的中心,M 为AB 中点,过E 作BC 的平行线EF ,交CD 于F ,过O 作ON 垂直EF 于N ,连接SO ,SN ,SE ,SM ,OM ,OE ,则SO 垂直于底面ABCD ,OM 垂直于AB , 因此123,,,SEN SEO SMO ∠=∠=∠=θθθ从而123tan ,tan ,tan ,SN SN SO SOEN OM EO OM====θθθ 因为SN SO EO OM ≥≥,,所以132tan tan tan ,≥≥θθθ即132≥≥θθθ,故选D. 【答案】D【变式2】【2017年高考浙江卷】如图,已知正四面体–D ABC (所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP=PB ,2BQ CR QC RA==,分别记二面角D –PR –Q ,D –PQ –R ,D –QR –P 的平面角为αβγ,,,则( )A . γαβ<<B .αγβ<<C .αβγ<<D .βγα<<【解析】设O 为三角形ABC 中心,则O 到PQ 距离最小,O 到PR 距离最大,O 到RQ 距离居中,而三棱锥的高相等,因此αγβ<<,所以选B . 【答案】B3.【2018优选题】空间中,设,m n 表示不同的直线, ,,αβγ表示不同的平面,则下列命题正确的是( )A. 若,αγβγ⊥⊥,则//αβB. 若,m m αβ⊥⊥,则//αβC. 若,m βαβ⊥⊥,则//m αD. 若,n m n α⊥⊥,则//m α 【解析】本题考点是面面平行,线面平行的判定.A 项,若,αγβγ⊥⊥,过正方体同一顶点的三个平面分别为,,αβγ,则αβ⊥,故A 项不合题意;B 项,若,m m αβ⊥⊥,根据垂直于同一条直线的两个平面平行,则//αβ,故B 项符合题意;C 项,若,m βαβ⊥⊥,由同时垂直于一个平面的直线和平面的位置关系可以是直线在平面内或平行可知,直线m 在平面α内或平行,故C 项不合题意;D 项,若,n m n α⊥⊥,由同时垂直于一条直线的直线和平面的位置关系可以是直线在平面内或平行可知,直线m 在平面α内或平行,故D 项不合题意. 故选B. 【答案】B4.【2019优选题】在正四面体P -ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,则下面四个结论中不成立的是( ) A .BC ∥平面PDF B .DF ⊥平面P AE C .平面PDF ⊥平面ABCD .平面P AE ⊥平面ABC【解析】画出图形,如图所示,则BC ∥DF ,又DF ⊂平面PDF ,BC ⊄平面PDF ,∴BC ∥平面PDF ,故A 成立;由题意可得AE ⊥BC ,PE ⊥BC ,BC ∥DF ,则DF ⊥AE ,DF ⊥PE ,∴DF ⊥平面P AE ,故B 成立; 又DF ⊂平面ABC ,∴平面ABC ⊥平面P AE ,故D 成立.本题的考点是平面与平面垂直的判定.【答案】C5.【2016全国新课标2】α,β是两个平面,m ,n 是两条直线,有下列四个命题:①如果m ⊥n ,m ⊥α,n ∥β,那么α⊥β. ②如果m ⊥α,n ∥α,那么m ⊥n . ③如果α∥β,m ⊂α,那么m ∥β.④如果m ∥n ,α∥β,那么m 与α所成的角和n 与β所成的角相等. 其中正确的命题有 .(填写所有正确命题的编号)【解析】对于①,,,//m n m n αβ⊥⊥,则,αβ的位置关系无法确定,故错误;对于②,因为//n α,所以过直线n 作平面γ与平面α相交于直线c ,则//n c ,因为,,m m c m n α⊥⊥⊥所以所以,故②正确;对于③,由两个平面平行的性质可知正确;对于④,由线面所成角的定义和等角定理可知其正确,故正确的命题有②③④.本题考点是空间中的线面关系. 【答案】②③④6.【2019年高考全国Ⅰ卷理数】如图,直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ; (2)求二面角A−MA 1−N 的正弦值.【解析】(1)连结B 1C ,ME .因为M ,E 分别为BB 1,BC 的中点,所以ME ∥B 1C ,且ME =12B 1C . 又因为N 为A 1D 的中点,所以ND =12A 1D .由题设知A 1B 1=P DC ,可得B 1C =P A 1D ,故ME =P ND , 因此四边形MNDE 为平行四边形,MN ∥ED .又MN ⊄平面EDC 1,所以MN ∥平面C 1DE .(2)由已知可得DE ⊥DA .以D 为坐标原点,DA uuu r的方向为x 轴正方向,建立如图所示的空间直角坐标系D −xyz ,则(2,0,0)A ,A 1(2,0,4),2)M ,(1,0,2)N ,1(0,0,4)A A =-u u u r ,1(12)A M =--u u u u r ,1(1,0,2)A N =--u u u u r,(0,MN =u u u u r .设(,,)x y z =m 为平面A 1MA 的法向量,则1100A M A A ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u rm m ,所以2040x z z ⎧--=⎪⎨-=⎪⎩,.可取=m .设(,,)p q r =n 为平面A 1MN 的法向量,则100MN A N ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u ur ,.n n所以020p r ⎧=⎪⎨--=⎪⎩,.可取(2,0,1)=-n.于是cos ,||⋅〈〉===‖m n m n m n , 所以二面角1A MA N --的正弦值为5. 7.【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°,将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的二面角B −CG −A 的大小.【解析】(1)由已知得AD P BE ,CG P BE ,所以AD P CG ,故AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB ⊥BE ,AB ⊥BC ,故AB ⊥平面BCGE . 又因为AB ⊂平面ABC ,所以平面ABC ⊥平面BCGE .(2)作EH ⊥BC ,垂足为H .因为EH ⊂平面BCGE ,平面BCGE ⊥平面ABC ,所以EH ⊥平面ABC . 由已知,菱形BCGE 的边长为2,∠EBC =60°,可求得BH =1,EHH 为坐标原点,HC u u u r的方向为x 轴的正方向,建立如图所示的空间直角坐标系H –xyz ,则A (–1,1,0),C (1,0,0),G (2,0),CG uuu r =(1,0),AC uuu r=(2,–1,0).设平面ACGD 的法向量为n =(x ,y ,z ),则0,0,CG AC ⎧⋅=⎪⎨⋅=⎪⎩u u u ru u u r n n即0,20.x x y ⎧+=⎪⎨-=⎪⎩ 所以可取n =(3,6,.又平面BCGE 的法向量可取为m =(0,1,0),所以cos ,||||2⋅〈〉==n m n m n m . 因此二面角B –CG –A 的大小为30°.8.【2019年高考北京卷文数】如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底部ABCD 为菱形,E 为CD 的中点.(1)求证:BD ⊥平面PAC ;(2)若∠ABC =60°,求证:平面PAB ⊥平面PAE ;(3)棱PB 上是否存在点F ,使得CF ∥平面PAE ?说明理由.【解析】本题主要考查线面垂直的判定定理,面面垂直的判定.(1)因为PA ⊥平面ABCD ,所以PA BD ⊥.又因为底面ABCD 为菱形,所以BD AC ⊥. 所以BD ⊥平面PAC .(2)因为PA ⊥平面ABCD ,AE ⊂平面ABCD ,所以PA ⊥AE .因为底面ABCD 为菱形,∠ABC =60°,且E 为CD 的中点,所以AE ⊥CD .所以AB ⊥AE .所以AE ⊥平面PAB .所以平面PAB⊥平面PAE.(3)棱PB上存在点F,使得CF∥平面PAE.取F为PB的中点,取G为PA的中点,连结CF,FG,EG.则FG∥AB,且FG=12 AB.因为底面ABCD为菱形,且E为CD的中点,所以CE∥AB,且CE=12AB.所以FG∥CE,且FG=CE.所以四边形CEGF为平行四边形.所以CF∥EG.因为CF⊄平面PAE,EG⊂平面PAE,所以CF∥平面PAE.9.【2019年高考全国Ⅲ卷文数】图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的四边形ACGD的面积.【解析】本题从多面体折叠开始,考查考生在折叠过程中掌握哪些量的大小与位置关系是不变与变化的,折叠后的多面体的性质解决题中的要求.(1)由已知得AD P BE,CG P BE,所以AD P CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.又因为AB⊂平面ABC,所以平面ABC⊥平面BCGE.(2)取CG的中点M,连结EM,DM.因为AB∥DE,AB⊥平面BCGE,所以DE⊥平面BCGE,故DE⊥CG.由已知,四边形BCGE是菱形,且∠EBC=60°得EM⊥CG,故CG⊥平面DEM.因此DM⊥CG.在Rt△DEM中,DE=1,EM DM=2.所以四边形ACGD的面积为4.10.【2019年高考北京卷理数】如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC =3.E 为PD 的中点,点F 在PC 上,且13PF PC =. (1)求证:CD ⊥平面PAD ; (2)求二面角F –AE –P 的余弦值; (3)设点G 在PB 上,且23PG PB =.判断直线AG 是否在平面AEF 内,说明理由.【解析】(1)因为PA ⊥平面ABCD ,所以PA ⊥CD .又因为AD ⊥CD ,所以CD ⊥平面PAD . (2)过A 作AD 的垂线交BC 于点M .因为PA ⊥平面ABCD ,所以PA ⊥AM ,PA ⊥AD .如图建立空间直角坐标系A −xyz ,则A (0,0,0),B (2,-1,0),C (2,2,0),D (0,2,0), P (0,0,2).因为E 为PD 的中点,所以E (0,1,1).所以(0,1,1),(2,2,2),(0,0,2)AE PC AP ==-=u u u ru u u r u u u r.所以1222224,,,,,3333333PF PC AF AP PF ⎛⎫⎛⎫==-=+= ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r .设平面AEF 的法向量为n =(x ,y ,z ),则0,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n 即0,2240.333y z x y z +=⎧⎪⎨++=⎪⎩ 令z =1,则1,1y x =-=-.于是=(1,1,1)--n .又因为平面PAD 的法向量为p =(1,0,0),所以3cos ,||3⋅〈〉==-‖n p n p n p . 由题知,二面角F −AE −P .(3)直线AG 在平面AEF 内.因为点G 在PB 上,且2,(2,1,2)3PG PB PB ==--u u ur ,所以2424422,,,,,3333333PG PB AG AP PG ⎛⎫⎛⎫==--=+=- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r .由(2)知,平面AEF 的法向量=(1,1,1)--n .所以4220333AG ⋅=-++=u u u r n .所以直线AG 在平面AEF 内.11.【2019年高考天津卷文数】如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,PCD △为等边三角形,平面PAC ⊥平面PCD ,,2,3PA CD CD AD ⊥==.(1)设G ,H 分别为PB ,AC 的中点,求证:GH ∥平面PAD ; (2)求证:PA ⊥平面PCD ;(3)求直线AD 与平面PAC 所成角的正弦值.【解析】(1)连接BD ,易知AC BD H =I ,BH DH =.又由BG=PG ,故GH PD ∥. 又因为GH ⊄平面P AD ,PD ⊂平面P AD ,所以GH ∥平面P AD . (2)取棱PC 的中点N ,连接DN .依题意,得DN ⊥PC ,又因为平面PAC ⊥平面PCD ,平面PAC I 平面PCD PC =,所以DN ⊥平面P AC , 又PA ⊂平面P AC ,故DN PA ⊥.又已知PA CD ⊥,CD DN D =I ,所以PA ⊥平面PCD . (3)连接AN ,由(2)中DN ⊥平面P AC ,可知DAN ∠为直线AD 与平面P AC 所成的角, 因为PCD △为等边三角形,CD =2且N 为PC的中点,所以DN =又DN AN ⊥, 在Rt AND △中,3sinDN DAN AD ∠==.所以,直线AD 与平面P AC 所成角的正弦值为3.12.【2019年高考天津卷理数】如图,AE ⊥平面ABCD ,,CF AE AD BC ∥∥,,AD AB ⊥1,2AB AD AE BC ====.(1)求证:BF ∥平面ADE ;(2)求直线CE 与平面BDE 所成角的正弦值; (3)若二面角E BD F --的余弦值为13,求线段CF 的长.【解析】依题意,可以建立以A 为原点,分别以AB AD AE u u u r u u u r u u u r,,的方向为x 轴,y 轴,z 轴正方向的空间直角坐标系(如图),可得(0,0,0),(1,0,0),(1,2,0),(0,1,0)A B C D ,(0,0,2)E .设(0)CF h h =>>,则()1,2,F h .(1)依题意,(1,0,0)AB =u u u r 是平面ADE 的法向量,又(0,2,)BF h =u u u r ,可得0BF AB ⋅=u u u r u u u r ,又因为直线BF ⊄平面ADE ,所以BF ∥平面ADE . (2)依题意,(1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=--u u u ru u u r u u u r.设(,,)x y z =n 为平面BDE 的法向量,则0,0,BD BE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n 即0,20,x y x z -+=⎧⎨-+=⎩不妨令1z =,可得(2,2,1)=n .因此有4cos ,9||||CE CE CE ⋅==-u u u ru u u r u u u r n n n .所以,直线CE 与平面BDE 所成角的正弦值为49.(3)设(,,)x y z =m 为平面BDF 的法向量,则0,0,BD BF ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r m m 即0,20,x y y hz -+=⎧⎨+=⎩不妨令1y =,可得21,1,h ⎛⎫=- ⎪⎝⎭m.由题意,有||1cos ,||||3⋅〈〉===m n m n m n ,解得87h =.经检验,符合题意. 所以,线段CF的长为87.【模拟考场】1.设α,β是两个不同的平面,m 是直线且m α⊂.“m β∥”是“αβ∥”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件【解析】本题考点是线面平行与面面平行与充要条件的综合应用.因为α,β是两个不同的平面,m 是直线且m α⊂.若“m β∥”,则平面、αβ可能相交也可能平行,不能推出//αβ,反过来若//αβ,m α⊂,则有m β∥,则“m β∥”是“αβ∥”的必要而不充分条件,故选B. 【答案】B2.设,a b 是空间中不同的直线, ,αβ是不同的平面,则下列说法正确的是( )A. //,a b b α⊂,则//a αB. ,,//a b αβαβ⊂⊂,则//a bC. ,,//,//a b b αααββ⊂⊂,则//αβD. //,a αβα⊂,则//a β【解析】本题考点是线面平行,面面平行的判定。
专题06 菱形的性质和判定(解析版)

专题06 菱形的性质和判定姓名:___________考号:___________分数:___________(考试时间:100分钟满分:120分)一、选择题(本大题共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列命题中,正确的是().A.两邻边相等的四边形是菱形B.一条对角线平分一个内角的平行四边形是菱形C.对角线垂直且一组邻边相等的四边形是菱形D.对角线垂直的四边形是菱形【答案】B【分析】根据菱形的性质,对各个选项逐个分析,即可得到答案.【解析】两邻边相等的平行四边形是菱形,故选项A不符合题意;一条对角线平分一个内角的平行四边形是菱形,故选项B符合题意;对角线垂直且一组邻边相等的平行四边形是菱形,故选项C不符合题意;对角线垂直的平行四边形是菱形,故选项D不符合题意;故选:B.【点睛】本题考查了命题、菱形的知识;解题的关键是熟练掌握菱形的性质,从而完成求解.2.如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=8,BD=6,点E,F分别为AO,DO的中点,则线段EF的长为()A.2.5 B.3 C.4 D.5【答案】A【分析】根据菱形的对角线互相垂直平分求出AD的长,再根据中位线定理即可求出EF的长.【解析】解:因为在菱形ABCD中,对角线AC=8,BD=6,∴AC⊥BD,AO=4,DO=3,∴AD=2222435AO DO+=+=,∵点E,F分别为AO,DO的中点,∴12.52==EF AD;故选:A.【点睛】本题考查的是菱形的性质和中位线的性质,注意到菱形的对角线互相垂直平分是解决本题的关键.3.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=6,则BC的长为().A.3 B.2C.3D.32 2【答案】C【分析】根据菱形AECF,得∠FCO=∠ECO,再利用∠ECO=∠ECB,可通过折叠的性质,结合直角三角形勾股定理求解.【解析】解:∵菱形AECF,AB=6,设BE=x,则AE=CE=6-x,∵菱形AECF,∴∠FCO=∠ECO,∵∠ECO=∠ECB,∴∠ECO=∠ECB=FCO=30°,∴2BE=CE,即CE=2x,∴2x=6-x,解得:x=2,∴CE=4,又EB=2,则利用勾股定理得:23BC ,故选:C.【点睛】此题主要考查了折叠问题以及勾股定理等知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.4.如图,在菱形ABCD中,AB=6,∠ABC=60°,M为AD中点,P为对角线BD上一动点,连接PA和PM,则PA+PM的最小值是( )A.3 B.23C.33D.6【答案】C【分析】首先连接AC,交BD于点O,连接CM,则CM与BD交于点P,此时PA+PM的值最小,由在菱形ABCD中,AB=6,∠ABC=60°,易得△ACD是等边三角形,BD垂直平分AC,继而可得CM⊥AD,则可求得CM的值,继而求得PA+PM的最小值.【解析】解:连接AC,交BD于点O,连接CM,则CM与BD交于点P,此时PA+PM的值最小,∵在菱形ABCD中,AB=6,∠ABC=60°,∴∠ADC=∠ABC=60°,AD=CD=6,BD垂直平分AC,∴△ACD是等边三角形,PA=PC,∵M为AD中点,∴DM=12AD=3,CM⊥AD,∴CM=22CD DM -=33,∴PA+PM=PC+PM=CM=33.故选C .【点睛】此题考查了最短路径问题、等边三角形的判定与性质、勾股定理以及菱形的性质.注意准确找到点P 的位置是解此题的关键.5.如图在平面直角坐标系xOy 中若菱形ABCD 的顶点,A B 的坐标分别为(6,0),(4,0)-,点D 在y 轴上,则点C 的坐标是( )A .(6,8)B .(10,8)C .(10,6)D .(4,6)【答案】B【分析】 首先根据菱形的性质求出AB 的长度,再利用勾股定理求出DO 的长度,进而得到点C 的坐标.【解析】∵菱形ABCD 的顶点A 、B 的坐标分别为(-6,0)、(4,0),点D 在y 轴上,∴AB=AO+OB=6+4=10,∴AD=AB=CD=10,∴22221068DO AD AO =-=-=,∴点C 的坐标是:(10,8).故选:B .【点睛】本题主要考查了菱形的性质以及坐标与图形的性质,解题的关键是利用勾股定理求出DO 的长度. 6.如图,ABCD 中,AC 平分BAD ∠,若2,3AC AB ==ABCD 的面积为( )A .2B .22C .42D .82【答案】B【分析】 连接BD 交AC 于点O ,首先证明四边形ABCD 为菱形,然后求出BD 的长,最后根据菱形的面积公式解答.【解析】解:如图,连接BD 交AC 于点O ,在ABCD 中,//AD BC ,,DAC ACB ∴∠=∠AC 平分BAD ∠,DAC BAC ∴∠=∠,BAC BCA ∴∠=∠,AB BC ∴=,∴四边形ABCD 为菱形,11,2122AC BD OA AC ∴⊥==⨯=, 22312OB AB OA ∴=-=-222BD OB ==,ABCD ∴的面积为:112222222ABCD S AC BD =•=⨯⨯=故选B .【点睛】本题主要考查了平行四边形的性质、菱形的判定和性质以及勾股定理等知识,解题的关键是证得四边形ABCD 为菱形.7.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,过点C 作CE ⊥AD 于点E ,连接OE ,若OB =6,S 菱形ABCD =60,则OE 的长为( )A .23B .5C .5D .6【答案】C【分析】 先根据菱形的性质、面积公式可得AC 的长,再根据直角三角形斜边上的中线等于斜边的一半即可得.【解析】四边形ABCD 是菱形,6OB =,212BD OB ∴==,OA OC =,162ABCD BD AC S AC =⋅=菱形, 60ABCD S =菱形,660AC ∴=,解得10AC =,又OA OC =,CE AD ⊥,OE ∴是Rt ACE △斜边AC 上的中线,1110522OE AC ∴==⨯=, 故选:C .【点睛】本题考查了菱形的性质、直角三角形斜边上的中线等于斜边的一半,熟练掌握菱形的性质是解题关键.8.如图,在菱形ABCD 中,E F ,分别是BC CD ,的中点,设ABCD S S =四边形,1AEF S S ∆=,则( )A .112S S =B .112S S <C .112S S >D .152S S = 【答案】B【分析】利用三角形的中线得到12AECF S S =四边形,判断出A 、C 错误,B 符合题意,利用三角形中位线定理求得CEF 18S S =,通过计算得到183S S =,即可得到正确的答案. 【解析】连接BD 、AC ,∵E ,F 分别是BC ,CD 的中点, ∴ABE ABC ADF ACD 1122S S S S ==,, ∴A CD 1122AECF B S S S ==四边形菱形, ∵AEF AECF S S <四边形,即112S S <,故A 、C 错误,B 符合题意; ∵E ,F 分别是BC ,CD 的中点,∴EF=12BD ,EF ∥BD , ∴CEF CBD A CD 111488B S S S S ===菱形,∴1AEF CEF 113288AECF S S S S S S S ==-=-=四边形, 即183S S =,故D 错误,故选:B .【点睛】本题考查了菱形的性质,三角形中线有关的面积计算,三角形中位线与三角形的面积,熟练掌握菱形的性质是解决问题的关键.9.如图,在▱ABCD 中,用直尺和圆规作∠BAD 的平分线AG 交BC 于点E ,以A 为圆心,AB 为半径的弧交AD 于点F ,连接EF .若BF =6,AB =5,则四边形ABEF 面积是( )A .12B .24C .36D .48【答案】B【分析】 根据题意AB =AF ,利用角平分线和平行证明BA =BE ,用一组对边平行且相等证明四边形ABEF 为平行四边形,再用邻边相等证明它是菱形,最后用菱形面积公式计算面积.【解析】记AE 与BF 相交于O 点,如图,由作法得AB =AF =10,AE 平分∠BAD ,∴∠BAE =∠DAE ,∵四边形ABCD 为平行四边形,∴AD ∥BC ,∴∠DAE =∠BEA ,∴∠BAE =∠BEA ,∴BA =BE ,∴AF =BE ,∵AF ∥BE ,∴四边形ABEF 为平行四边形,∵AB=AF,∴四边形ABEF为菱形,∴OA=OE,OB=OF=12BF=3,AE⊥BF,在Rt△AOB中,OA22534=-=,∴AE=2AO=8,∴四边形ABEF面积116824 22AE BF=⋅=⨯⨯=.故选:B.【点睛】本题考查角平分线的性质,菱形的判定和面积求解,解题的关键是根据题目中的角平分线和平行的条件能够证明等腰三角形,再根据菱形的判定和面积公式求四边形面积.10.如图,在菱形ABCD中,AE是菱形的高,若对角线AC、BD的长分别是6、8,则AE的长是()A.174B.245C.163D.5【答案】B【分析】由菱形的性质可得AC⊥BD,BO=DO=4,CO=AO=3,由勾股定理可求CB=5,由菱形的面积公式可求AE的长.【解析】解:四边形ABCD是菱形AC BD∴⊥,4BO DO==,3CO AO==225BC BO CO ∴=+=12ABCD S AC BD BC AE =⨯⨯=⨯菱形 245AE ∴=245AE ∴= 故选B .【点睛】本题菱形的性质,熟练运用菱形的面积公式是本题的关键.11.如图,菱形ABCD 的边长为13,对角线AC 的长为24,延长AB 至E ,BF 平分CBE ∠,点G 是BF 上任意一点,则ACG 的面积为( )A .30B .60C .90D .120【答案】B【分析】 连接BD 交AC 于点O ,根据菱形的性质可得BD 与AC 互相垂直平分,再根据AC 平分∠DAB ,BF 平分∠CBE ,可以证明AC ∥FB ,根据平行线间的距离处处相等可得S △CBG =S △ABG ,进而可得S △ACG =S △ABC .【解析】解:如图,连接BD 交AC 于点O ,∵四边形ABCD 是菱形,∴BD 与AC 互相垂直平分,∴OA=OC=12,∴OB=OD=221312=5,∵DA∥CB,∴∠DAB=∠CBE,∵AC平分∠DAB,∴∠CAB=12∠DAB,∵BF平分∠CBE,∴∠FBE=12∠CBE,∴∠CAB=∠FBE,∴AC∥FB,∴S△CBG=S△ABG,∴S△ACG=S△ABC=12×AC•OB=12×24×5=60,则△ACG的面积为60.故选:B.【点睛】本题考查了菱形的性质、三角形的面积,解决本题的关键是掌握菱形的性质.12.两张全等的矩形纸片ABCD,AECF按如图方式交叉叠放在一起,AB=AF,AE=BC.若AB=1,BC=3,则图中重叠(阴影)部分的面积为().A.2 B3C.53D.43【答案】C【分析】证得四边形AGCH是平行四边形,由△ABG≌△CEG(AAS),证得四边形AGCH是菱形,设AG=CG=x,则BG=BC-CG=3-x,在Rt△ABG中,由勾股定理得出方程,解方程求得CG的长,即可求出菱形AGCH的面积.【解析】设BC 交AE 于G ,AD 交CF 于H ,如图所示:∵四边形ABCD 、四边形AECF 是全等的矩形,∴AB=CE ,∠B=∠E=90°,AD ∥BC ,AE ∥CF ,∴四边形AGCH 是平行四边形,在△ABG 和△CEG 中,AGB CGE B EAB CE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABG ≌△CEG (AAS ),∴AG=CG ,∴四边形AGCH 是菱形,设AG=CG=x ,则BG=BC-CG=3-x ,在Rt △ABG 中,由勾股定理得:12+(3-x)2=x 2,解得:x=53, ∴CG=53, ∴菱形AGCH 的面积=CG ⋅AB=55133⨯=, 即图中重叠(阴影)部分的面积为53. 故选:C . 二、填空题(本大题共6小题,每小题3分,共18分)13.菱形的周长为12cm ,一个内角等于120︒,则这个菱形的面积为_________2cm . 932【分析】作AE ⊥BC 于E ,由直角三角形的性质求出菱形的高AE ,再运用菱形面积公式=底×高计算即可.【解析】解:作AE⊥BC于E,如图所示:∵四边形ABCD是菱形,周长为12cm,∠BCD=120°,∴AB=BC=3cm,∠B=60°,∵AE⊥BC,∴∠BAE=30°,∴BE=12AB=32cm,AE=3BE=332cm,∴菱形的面积=BC•AE=3×332932cm2);932【点睛】本题考查了菱形的性质、含30°角的直角三角形的性质、菱形的面积等知识;熟练掌握菱形的性质,求出菱形的高是解决问题的关键.14.己知菱形ABCD的边长是3,点E在直线AD上,DE=1,联结BE与对角线AC相交于点M,则AMMC的值是______.【答案】23或43【分析】首先根据题意作图,注意分为E在线段AD上与E在AD的延长线上,然后由菱形的性质可得AD∥BC,则可证得△MAE∽△MCB,根据相似三角形的对应边成比例即可求得答案.【解析】解:∵菱形ABCD的边长是3,∴AD=BC=3,AD∥BC,如图①:当E在线段AD上时,∴AE=AD-DE=3-1=2,∴△MAE∽△MCB,∴23 MA AEMC BC==;如图②,当E在AD的延长线上时,∴AE=AD+DE=3+1=4,∴△MAE∽△MCB,∴43 MA AEMC BC==.∴MAMC的值是23或43.故答案为23或43.【点睛】此题考查了菱形的性质,相似三角形的判定与性质等知识.解题的关键是注意此题分为E在线段AD 上与E在AD的延长线上两种情况,小心不要漏解.15.如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF 并延长与AB的延长线相交于点G,则EG =____.【答案】10;【分析】连接菱形的另一条对角线,利用菱形性质特征和勾股定理可求BD长;利用三角形中位线定理可得EF长;在利用三角形全等可证EF GF=即可得解.【解析】连接BD 交AC 与点O ,在菱形ABCD 中 ∵111222AC BD OC OA AC OD OB BD ⊥=====,,, 在RT DOC △中 222213125OD DC OC =-=-=,∴10BD =,∵点E 、F 分别是边CD 、BC 的中点,∴152EF BD ==, ∵//AB CD ,∴BGF CEF GBF ECF ∠=∠∠=∠,,又∵CF BF =,∴BGF CEF ≅△△,∴5EF GF ==,∴10EG =.故答案为:10.【点睛】本题主要考查菱形的性质特征、三角形的中位线定理、平行线性质、勾股定理以及全等三角形等.中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.运用三角形中位线定理求线段长的方法:当题中有中点,特别是一个三角形中出现两边中点时,我们常常考虑运用三角形的中位线来解决问题,首先证明出它是三角形的中位线,然后利用中位线构造线段这间的关系,并由此建立待求线段与已知线段的联系,从而求出线段的长.16.在数学必修拓展课上,小兰利用一张直角三角形纸片折出了一个菱形AFDE ,如图所示,若∠ACB =90°,AC =3cm ,BC =4cm ,则折痕EF 的长为______.【答案】354【分析】过点D 作DH ⊥AB 于 H ,连结AD 、EF ,设CD=x ,则DH=x ,BD=4−x ,由勾股定理求得x 的值,设CF=y ,则 AF=3−y=FD ,由勾股定理求得y 的值,由菱形的性质得AD 与EF 垂直平分,进而求得EF 的长.【解析】解:如图,过点D 作DH ⊥AB 于 H ,连结AD 、EF ,∵菱形AFDE ,∴AD 平分∠BAC ,∵∠ACB=90°,∴CD=DH ,∴AH=AC=3,设CD=x ,则DH=x ,BD=4−x ,∵2222345AC BC +=+=,∴HB=5−3=2,在Rt △DBH 中,()22222242BD DH BH x x =+-=+,,∴x=1.5,即CD=1.5,设CF=y ,则AF=3−y=FD ,在Rt △CDF 中,()222222321.534CF CD FD y y y +=+=-=,,, 即CF=324,∴AF=3−324, 在Rt △ACD 中,2222363 1.5AC CD +=+=, ∴AO=136362=,由菱形的性质得AD 垂直平分EF ,OF=22223236353448AF AO ⎛⎫⎛⎫-=--= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,∴EF=2OF= 3535284⨯=, 故答案为35. 【点睛】本题考查菱形的性质,勾股定理,角平分线的性质.17.如图,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,DH AB ⊥于点H ,连接OH ,若20DHO ∠=︒,则HDB ∠的度数是______.【答案】20︒【分析】先根据菱形的性质得OD =OB ,而DH ⊥AB ,所以OH 为Rt △DHB 的斜边DB 上的中线,得到OH =OD ,利用等腰三角形的性质得∠HDB =∠DHO .【解析】∵四边形ABCD 是菱形,∴OD =OB ,∵DH ⊥AB ,∴∠DHB =90°,∴OH 为Rt △DHB 的斜边DB 上的中线,∴OH =OD ,∴∠HDB =∠DHO =20°,故填:20°.【点睛】本题考查菱形的性质,直角三角形斜边中线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.18.已知:如图,点P 是边长为2的菱形ABCD 对角线AC 上的一个动点,点M 是AB 边的中点,且60BAD ∠=︒,则MP PB +的最小值是_______.【答案】3 【分析】 找出B 点关于AC 的对称点D ,连接DM ,则DM 就是PM+PB 的最小值,求出即可.【解析】解:连接DE 交AC 于P ,连接BD ,BP ,由菱形的对角线互相垂直平分,可得B 、D 关于AC 对称,则PD=PB ,∴PE+PB=PE+PD=DE ,即DM 就是PM+PB 的最小值,∵∠BAD=60°,AD=AB ,∴△ABD 是等边三角形,∵AE=BE ,∴DE ⊥AB (等腰三角形三线合一的性质)在Rt △ADE 中,DM=22AD AM -=2221=3-.故PM+PB 的最小值为3.故答案为:3.三、解答题(本大题共6小题,共66分,解答应写出文字说明、演算步骤或推理过程) 19.如图,在矩形ABCD 中,对角线AC 与BD 相交于点O .过点B 作AC 的平行线,过点C 作BD的平行线,两线相交于点P .(1)求证:四边形OBPC 是菱形.(2)已知3AB =,5BC =,求四边形OBPC 的面积.【答案】(1)证明过程见解析;(2)152OBPC S =四边形 【分析】(1)根据平行四边形的判定证得四边形OBPC 是平行四边形,再根据矩形的性质可知OB=OC ,然后根据菱形的判定即可证得结论;(2)根据菱形的性质和三角形的中线将三角形面积平分可证得四边形OBPC 的面积等于三角形ABC 的面积,利用直角三角形的面积公式即可解答.【解析】(1)∵//BP OC ,//CP OB ,∴四边形OBPC 是平行四边形,在矩形ABCD 中,AC BD =,且AC 与BD 互相平分,∴OB OC =,∴'平行四边形OBPC 是菱形.(2)∵四边形OBPC 是菱形,∴OBC BCP S S =△△,又∵AO OC =,∴AOB BOC S S =△△,∴OBC BCP AOB S S S ==△△△,∴四边形OBPC 的面积等于三角形ABC 的面积, ∴11522ABC S AB BC =⋅=△, ∴152OBPC S =四边形. 【点睛】本题考查了矩形的性质、平行四边形的判定、菱形的判定与性质、三角形的中线与面积关系、三角形的面积公式,属于基础题型,难度适中,解答的关键是熟练掌握菱形的判定与性质的应用.20.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.(1)求证:AE=BF;(2)若点E恰好是AD的中点,AB=2,求BD的值.【答案】(1)见解析;(2)BD=2【分析】(1)根据菱形的性质和平行线的性质得到AB=BC,∠A=∠CBF,结合垂直的性质得到△AEB≌△BFC,根据三角形全等的性质即可证明;(2)首先证明BE是AD的垂直平分线,然后根据垂直平分线的性质即可求解.【解析】(1)证明:四边形ABCD是菱形∴AB=BC,AD∥BC∴∠A=∠CBF∵BE⊥AD、CF⊥AB∴∠AEB=∠BFC=90°∴△AEB≌△BFC(AAS)∴AE=BF(2)∵E是AD中点,且BE⊥AD∴直线BE为AD的垂直平分线∴BD=AB=2【点睛】本题考查了菱形的性质,三角形全等的证明,垂直平分线的性质,关键是要利用好菱形的性质求解.,连接CE.21.如图,在菱形ABCD中,E为对角线BD上一点,且AE DE(1)求证:DE CE =.(2)当EA AB ⊥于点A ,1AE ED ==时,求菱形的边长.【答案】(1)见解析;(2)3【分析】(1)根据SAS 证明△ADE ≌△CDE ,从而得到AE =CE ,再根据AE =DE ,再得出结论;(2)连接AC 交BD 于H ,由菱形的性质可得AB=AD ,AC ⊥BD ,BH=DH ,AH=CH ,由等腰三角形的性质和三角形内角和定理可求∠DAE=∠ADE=∠ABD=30°,利用直角三角形的性质可求解即可.【解析】(1)∵四边形ABCD 是菱形,∴AD =DC ,∠ADE =∠CDE ,在△ADE 和△CDE 中,AD DC ADE CDE DE DE ⎧⎪∠∠⎨⎪=⎩== ,∴△ADE ≌△CDE (SAS ),∴AE =CD ,又∵AE=DE ,∴DE CE =;(2)如图,连接AC 交BD 于H ,∵四边形ABCD 是菱形,∴AB=AD ,AC ⊥BD ,BH=DH ,AH=CH ,∴∠ABD=∠ADB ,∵AE═ED=1,∴∠DAE=∠EDA ,∴∠DAE=∠ADE=∠ABD ,∵∠DAE+∠ADE+∠BAE+∠ABD=180°,∴∠DAE=∠ADE=∠ABD=30°,∴BE=2AE=2,∴BD=BE+DE=3,∴BH=DH=32, ∵∠ABD=30°,AH ⊥BD ,∴AB=2AH ,BH=3 AH ,∴AH=3,AB=2AH=3, ∴菱形的边长为3.【点睛】考查了菱形的性质、全等三角形的判定和性质、直角三角形的性质,解题关键是灵活运用其性质. 22.如图,ABC ∆中,90BCA ∠=︒,CD 是边AB 上的中线,分别过点C ,D 作BA 和BC 的平行线,两线交于点E ,且DE 交AC 于点O ,连接AE .(1)求证:四边形ADCE 是菱形;(2)若60B ∠=︒,6BC =,求四边形ADCE 的面积.【答案】(1)证明见解析;(2)S 菱形ADCE 183=【分析】(1)先证明四边形ADCE 为平行四边形,再证明AC ⊥DE 即可证明;(2)根据勾股定理得到AC 的长度,由含30度角的直角三角形的性质求得DE 的长度,然后由菱形的面积等于对角线乘积的一半即可求.【解析】(1)证明:∵DE∥BC,EC∥AB,∴四边形DBCE是平行四边形.∴EC∥DB,且EC=DB.在Rt△ABC中,CD为AB边上的中线,∴AD=DB=CD.∴EC=AD.∴四边形ADCE是平行四边形.∴ED∥BC.∴∠AOD=∠ACB.∵∠ACB=90°,∴∠AOD=∠ACB=90°,∴AC⊥DE,∴ADCE是菱形;(2)解:Rt△ABC中,CD为AB边上的中线,∠B=60°,BC=6,∴AD=DB=CD=6.∴AB=12,由勾股定理得AC=63.∵四边形DBCE是平行四边形,∴DE=BC=6.∴S菱形ADCE6361832AC ED⋅⨯===.【点睛】本题主要考查菱形的性质和判定以及面积的计算,含30°角的直角三角形.(1)掌握菱形的判定定理并能灵活运用是解题关键;(2)中理解菱形的面积等于对角线的乘积的一半是解题关键.23.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.(1)求证:四边形OCED是菱形;(2)当AC=6时,求出四边形OCED的周长.【答案】(1)详见解析;(2)12【分析】(1)首先由CE∥BD,DE∥AC,可证得四边形OCED是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD,即可判定四边形OCED是菱形,(2)求出OC=OD=3,由菱形的性质即可得出答案.【解析】(1)∵CE∥BD,DE∥AC,∴四边形OCED为平行四边形,又∵四边形 ABCD 是矩形,∴OD=OC,∴四边形OCED为菱形;(2)∵四边形 ABCD 是矩形,∴OC=OD=12 AC,又∵AC=6,∴OC=3,由(1)知,四边形OCED为菱形,∴四边形OCED的周长为=4OC=4×3=12.【点睛】本题考查了矩形的性质、菱形的判定与性质等知识,熟练掌握菱形的判定方法是解题的关键.24.如图,四边形ABCD中,60B︒∠=,连接对角线AC,AC BC=,点E在AB上,将CE绕点C顺时针旋转60︒得到CF,且点F在AD上.(1)求证:AF BE=;(2)若AE DF=,求证:四边形ABCD是菱形.【答案】(1)证明见解析;(2)证明见解析【分析】(1)证明ABC ∆是等边三角形,由旋转的性质得出CE CF =,60ECF ︒∠=,通过证明ACF BCE ∆≅∆进行求证;(2)由已知条件可求出AD BC =,由(1)可证//AD BC ,进而可得出四边形ABCD 是平行四边形,最后根据邻边相等的平行四边形是菱形进行求证.【解析】证明:(1)∵60B ︒∠=,AC BC =,ABC ∆∴是等边三角形,60ACB ︒∴∠=,AB AC BC ==, CE 绕点C 顺时针旋转60︒得到CF ,CE CF ∴=,60ECF ︒∠=,∵ACB ACE ECB ∠=∠∠+,ECF ACE ACF ∠=∠∠+,BCE ACF ∴∠=∠,在ACF 和BCE 中AC BC ACF BCE CF CE =⎧⎪∠=∠⎨⎪=⎩,()ACF BCE SAS ∴∆≅∆,AF BE ∴=;(2)AE DF =,AF BE =,DF AF AE BE ∴+=+,即AB AD =,又AB BC =,AD BC ∴=,由(1)知BCE ACF ∆∆≌,60B CAF ︒∴∠=∠=,60ACB CAF ︒∴∠=∠=,//AD BC ∴,∴四边形ABCD 是平行四边形,又AB AD =,∴四边形ABCD 是菱形.【点睛】本题考查全等三角形的判定与性质,旋转的性质,平行四边形与菱形的判定,由已知条件证明BCE ACF ∆∆≌是解题的关键.。
专题06 立体几何中的动点及最值范围问题(解析版)

专题06 立体几何中动点及最值范围问题题型一、角度、长度最值范围问题(多选)1、设动点P 在正方体1111ABCD A B C D -的对角线1BD 上,记11D P D B λ=当APC ∠为钝角时,则实数可能的取值是( ) A .12B .23C .13D .1【答案】AB【分析】首先以D 为原点,DA ,DC ,1DD 分别为x ,y ,z 轴建立空间直角坐标系,根据题意得到0PA PC ⋅<,再解不等式即可得到答案.【解析】以D 为原点,DA ,DC ,1DD 分别为x ,y ,z 轴建立空间直角坐标系,如图所示:设正方体的边长为1,则()1,0,0A ,()1,1,0B ,()0,1,0C ,()10,0,1D ,()11,0,1D A =-,()10,1,1D C =-,()11,1,1D B =-,所以()11,,D P D B λλλλ==-. 又因为()()()11,,1,0,11,,1PA PD D A λλλλλλ=+=--+-=---,()()()11,,0,1,1,1,1PC PD DC λλλλλλ=+=--+-=---, 因为APC ∠为钝角,所以0PA PC ⋅<,即()()()()()()()2111=1310λλλλλλλ--+--+---<,解得113λ<<.故选AB【名师点睛】本题主要考查空间向量的数量积运算,属于简单题.2、如图,正方体1111ABCD A B C D -,点P 在1AB 上运动(不含端点),点E 是AC 上一点(不含端点),设EP 与平面1ACD 所成角为θ,则cosθ的最小值为( )A .13B .33C .53D .63答案: A 解析:由已知求出AC 的中点1E 与1B 的连线与平面1ACD 所成角的余弦值,在1AB 上(不含端点)任取一点P ,在平面1AB E 内过P 作11//PE B E ,则EP 与平面1ACD 所成角11OE B θ=∠,可得1cos 3θ=,结合选项即可得答案.详解:解:如图,由正方体的性质,可得1B D ⊥平面1AD C ,且1B 在平面1AD C 上的射影O 为△1AD C 的外心.设正方体的棱长为1,则△1AD C 的边长为2, 当1E 为AC 的中点时,11162326OE =-=, 1116122B E =+=,此时11616cos 362OE B ==. 在1AB 上(不含端点)任取一点P ,在平面1AB E 内过P 作11//PE B E ,则EP 与平面1ACD 所成角11OE B θ=∠,可得1cos 3θ=.结合选项可知,cos θ的最小值为13.故选:A .3、三棱柱111ABC A B C -的侧棱与底面垂直,11AA AB AC ===,AB AC ⊥,N 是BC 的中点,点P 在11A B 上,且满足111A P A B λ=,当直线PN 与平面ABC 所成的角取最大值时,λ的值为( )A .12B .22C .32D .255【答案】A【分析】建立空间直角坐标系,利用向量的夹角公式,求出直线PN 与平面ABC 所成的角,即可求得结论.【解析】如图,以AB ,AC ,1AA 分别为x ,y ,z 轴,建立空间直角坐标系A xyz -,则(,P λ0,1),11,,122PN λ⎛⎫=-- ⎪⎝⎭,平面ABC 的一个法向量为(0,n =0,1)设直线PN 与平面ABC 所成的角为θ,21sin 15()24PN nPN nθλ⋅∴==⋅-+, ∴当12λ=时,25(sin )5max θ=,此时角θ最大.故选A . 【名师点睛】本题考查了向量法求线面角的求法,考查了函数最值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.4、如图所示,在正方体1111ABCD A B C D -中,点E 为线段AB 的中点,点F 在线段AD 上移动,异面直线1B C 与EF 所成角最小时,其余弦值为( )A .0B .12C .105D .1116【答案】C【分析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,利用向量法能求出异面直线1B C 与EF 的夹角的余弦值,根据夹角最小即可求得结果.【解析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,在正方体1111ABCD A B C D -中, 点E 为线段AB 的中点,设正方体棱长为2, 则1(0,0,0),(2,1,0),(2,2,2),(0,2,0)D E B C ,1(2,0,2)B C =--,设(),0,0F m ()02m ≤≤,(2,1,0)EF m =--,设异面直线1B C 与EF 的夹角为θ,则1212|||2(2)|cos ||||122(2)1211(2)EF B C m EF B C m m θ⋅-⨯-===⋅⋅-+⋅+-, 异面直线1B C 与EF 所成角最小时,则cos θ最大,即0m =时,210cos 51102141θ===⋅+.故选C .【名师点睛】本题考查异面直线及其所成的角的余弦值,解题方法是建立空间直角坐标系,用空间向量法表示距离、求角,属于中档题.5、如图,已知正方体1111ABCD A B C D -的棱长为1,,E F 分别是棱11,AD B C 上的中点.若点P 为侧面正方形11ADD A 内(含边)动点,且存在,x y R ∈使1B P xBE yBF =+成立,则点P 的轨迹长度为A .12B .1C 5D .2π 【答案】C【分析】根据向量共面判断出1//B P 平面BEF ,由面面平行得到P 点的轨迹,在直角三角形中求出边长即可.【解析】因为1B P xBE yBF =+成立,所以1B P BE BF 、、共面,即1//B P 平面BEF , 如图,取11A D 中点Q ,连接1B Q 、1B A 、AQ , 根据正方体的性质得,1//B Q BE ,1//B A FE , 且111=B QB A B ,=FEBE E ,所以平面1//B AQ 平面BEF ,所以点P 在AQ 上运动,点P 的轨迹为线段AQ ,因为11A A =,112AQ =, 由勾股定理得151+=42QA =,故选C .题型二、动点问题(多选)1、如图,棱长为1的正方体1111ABCD A B C D -中,P 为线段1A B 上的动点(不含端点),则下列结论正确的是A .平面11D A P ⊥平面1A APB .//BC 平面11AD PC .三棱锥1D CDP -的体积为定值 D .直线1D P 与AC 所成的角可能是6π【答案】AC【解析】对于A 中,在正方体1111ABCD A B C D -中,可得1111,A D AA A D AB ⊥⊥,又由1AA AB A =,所以11A D ⊥平面1A AP ,因为11A D ⊂平面11D A P ,所以平面11D A P ⊥平面1A AP ,所以A 正确; 对于B 中,在正方体1111ABCD A B C D -中,可得11//BC A D , 所以11,,,B C A D 四点共面,所以B 不正确; 对于C 中,因为1111122CDD S=⨯⨯=,点P 到平面1CDD 的距离为1BC =, 所以三棱锥1D CDP -的体积为定值,所以C 正确;对于D 中,以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,可得1(0,0,1),(1,0,0),(0,1,0)D A C ,设(1,,)(01,01)P a b a b <<<<, 则1(1,,1),(1,1,0)D P a b AC =-=-, 则11221cos ,01(1)2D P AC D P AC D P ACa b ⋅==<⋅++-⋅,当1a =时,1,2D P AC π=;当0,1a b ==时,13,4D P AC π=, 所以直线1D P 与AC 所成的角的范围是(,)42ππ,所以D 不正确.故选AC【名师点睛】此类问题解答中熟记正方体的几何结构特征,熟练应用转化顶点,利用等体积法求解三棱锥的体积,以及合理利用空间向量的夹角公式求解异面直线所成的角是解答的关键.(多选)2、如图,在三棱柱111ABC A B C -中,侧棱1AA ⊥底面111A B C ,90BAC ︒∠=,11AB AC AA ===,D 是棱1CC 的中点,P 是AD 的延长线与11A C 的延长线的交点.若点Q 在直线1B P 上,则下列结论错误的是( ).A .当Q 为线段1B P 的中点时,DQ ⊥平面1A BD B .当Q 为线段1B P 的三等分点时,DQ ⊥平面1A BDC .在线段1B P 的延长线上,存在一点Q ,使得DQ ⊥平面1A BD D .不存在点Q ,使DQ 与平面1A BD 垂直 【答案】ABC【分析】以1A 为坐标原点,11A B ,11A C ,1A A 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,求得平面1A BD 的一个法向量(,,)n x y z =,假设DQ ⊥平面1A BD ,且11B Q B P λ=,得到11DQ DB BQ =+=11,12,2λλ⎛⎫--+- ⎪⎝⎭,则(2,1,2)n =-与11,12,2DQ λλ⎛⎫=--+- ⎪⎝⎭共线,研究1112122124λλ---+===-是否有解即可. 【解析】以1A 为坐标原点,11A B ,11A C ,1A A 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,则由1(0,0,0)A ,1(1,0,0)B ,1(0,1,0)C ,(1,0,1)B ,10,1,2D ⎛⎫ ⎪⎝⎭,(0,2,0)P ,所以1(1,0,1)A B =,110,1,2A D ⎛⎫= ⎪⎝⎭,1(1,2,0)B P =-,111,1,2DB ⎛⎫=-- ⎪⎝⎭.设平面1A BD 的一个法向量为(,,)n x y z =,则11012n A B x z n A D y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩, 取2z =-,则2x =,1y =,所以平面1A BD 的一个法向量为(2,1,2)n =-.假设DQ ⊥平面1A BD ,且11(1,2,0)(,2,0)BQ B P λλλλ==-=-, 则11DQ DB BQ =+=11,12,2λλ⎛⎫--+- ⎪⎝⎭. 因为DQ 也是平面1A BD 的法向量,所以(2,1,2)n =-与11,12,2DQ λλ⎛⎫=--+- ⎪⎝⎭共线,所以1112122124λλ---+===-成立,但此方程关于λ无解. 因此不存在点Q ,使DQ 与平面1A BD 垂直,故选ABC .(多选)3、在长方体1111ABCD A B C D -中,23AB =12AD AA ==,,,P Q R 分别是11,,AB BB AC 上的动点,下列结论正确的是 A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥ B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥ C .当1AR A C ⊥时,1AR D R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABD【分析】如图所示建立空间直角坐标系,计算142D P CQ b ⋅=-,()12222D R CQ b λλ⋅=--,134AR D R ⋅=-,10D R n ⋅=,得到答案.【解析】如图所示,建立空间直角坐标系,设()2,,0P a ,0,23a ⎡⎤∈⎣⎦,()2,23,Q b ,[]0,2b ∈,设11A R AC λ=,得到()22,23,22R λλλ--,[]0,1λ∈. ()12,,2P a D -=,()2,0,CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;()122,23,2D R λλλ=--,()12222D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确;1AR A C⊥,则()()12,23,222,23,2212440AR AC λλλλλλ⋅=--⋅--=-+-+=, 14λ=,此时11333313,,,,02222224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,C 错误; 113AC A R =,则4234,,333R ⎛⎫ ⎪ ⎪⎝⎭,14232,,333D R ⎛⎫=- ⎪ ⎪⎝⎭,设平面1BDC 的法向量为(),,n x y z =,则10n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得()3,1,3n =-,故10D R n ⋅=,故1//D R 平面1BDC ,D 正确. 故选ABD .【点睛】本题考查了空间中的线线垂直,线面平行,意在考查学生的计算能力和空间想象能力,推断能力. 题型三、确定点的位置1、如图,在三棱柱111ABC A B C -中,四边形11AAC C 是边长为3的正方形,1CC BC ⊥,1BC =,2AB =.(1)证明:平面1A BC ⊥平面1ABC ;(2)在线段1A B 上是否存在点M ,使得1CM BC ⊥,若存在,求1BMBA 的值;若不存在,请说明理由.【答案】(1)证明见解析;(2)14. 【解析】(1)在ABC 中,3AC =1BC =,2AB =,满足222AC BC AB +=,所以AC BC ⊥,又1CC BC ⊥,1CC AC C =,所以BC ⊥面11ACC A ,又1AC ⊂面11ACC A ,所以1BC A C ⊥,又四边形11AAC C 是边长为3的正方形,所以11AC AC ⊥,又1BCAC C =,所以1AC ⊥面1A CB ,又1AC ⊂平面1ABC ,所以平面1A BC ⊥平面1ABC ;(2)在线段1A B 上存在点M ,使得1CM BC ⊥,且114BM BA =, 理由如下:由(1)得,以点C 为原点,1,,CA CB CC 所在直线分别为,,x y z 轴建立空间直角坐标系,如图所示,则()3,0,0A,()0,0,0C ,()0,1,0B ,13,0,3A ,(13C ,设(),,M x y z ,1BM BA λ=,所以(),1,3,3x y z λ-=-,解得3x λ=,1y λ=-,3z λ=,所以()3,13CM λλλ=-,(10,1,3C B =-,要使1CM BC ⊥,则需10CM BC ⋅=,即130λλ--=,解得14λ=,故114BM BA =.2、如图,在多面体ABCDP 中,ABC 是边长为4的等边三角形,PA AC =,22BD CD ==,42PC PB ==,点E 为BC 的中点,平面BDC ⊥平面ABC .(1)求证://DE 平面PAC(2)线段BC 上是否存在一点T ,使得二面角T DA B --为直二面角?若存在,试指出点T 的位置;若不存在,请说明理由.【答案】(1)证明见解析;(2)存在,T 为线段BC 上靠近点C 的八等分点. 【分析】(1)根据题目条件证明DE ⊥平面ACE ,从而得到DE //PA ,得出DE //平面PAC ;(2)建立空间直角坐标系,假设存在点(),0,0T λ,计算平面TDA 和平面BDA 的法向量,使法向量数量积为零,然后求解λ,根据λ的值确定点T 的位置. 【解析】(1)因为22BD CD ==ABC 是边长为4的等边三角形, 所以((2222222216BD CD BC +=+==,所以BDC 是等腰直角三角形,90BDC ∠=︒.又点E 为BC 的中点,所以DE BC ⊥.因为平面BDC ⊥平面ABC ,平面BDC ⋂平面ABC BC =,所以DE ⊥平面ABC . 因为42PC PB ==,4PA AC AB ===,所以222224432PA AC PC +=+==,222224432PA AB PB +=+==,所以PAB △与PAC 都是直角三角形,故PA AC ⊥,PA AB ⊥. 又AC AB A ⋂=,所以PA ⊥平面ABC ,所以DE PA ∥. 因为PA ⊂平面PAC ,DE ⊄平面PAC ,所以DE 平面PAC .(2)连接AE ,以E 为原点,EC ,EA ,ED 所在直线分别为x ,y ,z 轴,建立如图所示的空间直角坐标系,则()0,23,0A ,()2,0,0B -,()2,0,0C ,()0,0,2D ,设存在(),0,0T λ,使得二面角T DA B --为直二面角,易知22λ-≤≤,且0λ≠. 设平面BAD 的法向量为()1111,,n x y z =,则由()2,0,2BD =,()0,23,2AD =-,得1111030x z y z +=⎧⎪⎨-+=⎪⎩,令11z =,得111x x =-,133y =,故131,,13n ⎛⎫=- ⎪ ⎪⎝⎭.设平面TAD 的法向量为()2222,,n x y z =,则由(),0,2DT λ=-,(),23,0AT λ=-,得222220,230x z x y λλ-=⎧⎪⎨-=⎪⎩,令21z =,得22x λ=,233y =,故223,,13n λ⎛⎫= ⎪ ⎪⎝⎭. 由122233133cos ,074433n n λλ-+⨯+==⨯+,得12103λ-+=,故32λ=. 所以当T 为线段BC 上靠近点C 的八等分点时,二面角T DA B --为直二面角.3、如图,三棱柱111ABC A B C -中,AB ⊥侧面11BB C C ,已知13BCC π∠=,1BC =,12AB C C ==,点E 是棱1C C 的中点.(1)求证:1C B ⊥平面ABC ; (2)求二面角11A EB A --的余弦值;(3)在棱CA 上是否存在一点M ,使得EM 与平面11A B E 所成角的正弦值为21111,若存在,求出CM CA 的值;若不存在,请说明理由.【答案】(1)证明见解析(225(3)存在,13CM CA =或523CM CA =.【解析】(1)由题意,因为1BC =,12CC =,13BCC π∠=,所以13BC又所以22211BC BC CC +=,所以1BC BC ⊥,因为AB ⊥侧面11BB C C ,所以1AB BC ⊥.又因为AB BC B ⋂=,AB ,BC ⊂平面ABC ,所以直线1C B ⊥平面ABC . (2)以B 为原点,分别以BC ,1BC 和BA 的方向为x ,y 和z 轴的正方向建立如图所示的空间直角坐标系,则()0,0,2A ,()13,0B -,132E ⎛⎫⎪ ⎪⎝⎭,()13,2A -,设平面1AB E 的一个法向量为()111,,n x y z =,()13,2AB =--,13,,222AE ⎛⎫=- ⎪ ⎪⎝⎭因为100n AB n AE ⎧⋅=⎨⋅=⎩,所以11111132013202x z x y z ⎧--=⎪⎨-=⎪⎩,令13y =,则11x =,所以()1,3,1n =设平面11A B E 的一个法向量为(),,m x y z =,()110,0,2A B =-,133,,222A E ⎛⎫=-- ⎪ ⎪⎝⎭, 因为11100m A B m A E ⎧⋅=⎪⎨⋅=⎪⎩,所以20332022z x y z -=⎧⎪⎨--=⎪⎩,令3y =,则1x =,所以()1,3,0m =,2m =,5n =,4m n ⋅=,所以425cos ,525m n m n m n⋅===.设二面角11A EB A --为α,则25cos cos ,5m n α==. 所以设二面角11A EB A --的余弦值为255. (3)假设存在点M ,设(),,M x y z ,因为CM CA λ=,[]0,1λ∈,所以()()1,,1,0,2x y z λ-=-,所以()1,0,2M λλ-所以13,,222EM λλ⎛⎫=-- ⎪ ⎪⎝⎭设平面11A B E 的一个法向量为()1,3,0m =,所以22132112211132424λλλ--=⎛⎫-++ ⎪⎝⎭,得2693850λλ-+=.即()()312350λλ--=,所以13λ=或523λ=,所以13CM CA =或523CM CA =.【名师点睛】本题考查了线面平行的判定与证明,以及空间角的求解问题,意在考查学生的空间想象能力和逻辑推理能力,解答中熟记线面位置关系的判定定理和性质定理,通过严密推理是线面位置关系判定的关键,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解. 强化训练(多选)1、如图所示,正方体1111ABCD A B C D -中,1AB =,点P 在侧面11BCC B 及其边界上运动,并且总是保持1AP BD ⊥,则以下四个结论正确的是A .113P AA D V -=B .点P 必在线段1BC 上 C .1AP BC ⊥D .//AP 平面11AC D【答案】BD【分析】根据三棱锥体积公式求得116P AA D V -=,知A 错误;以D 为坐标原点建立空间直角坐标系,利用空间向量法可得到1CP x B C →→=-,11AP BC →→⋅=,AP →垂直于平面11AC D 的法向量n →,由此可确定,,B C D 的正误.【解析】对于A ,P 在平面11BCC B 上,平面11//BCC B 平面1AA D ,P ∴到平面1AA D 即为C 到平面1AA D 的距离,即为正方体棱长,1111111113326P AA D AA D V S CD -∴=⋅=⨯⨯⨯⨯=△,A 错误;对于B ,以D 为坐标原点可建立如下图所示的空间直角坐标系:则()1,0,0A ,(),1,P x z ,()1,1,0B ,()10,0,1D ,()11,1,1B ,()0,1,0C()1,1,AP x z →∴=-,()11,1,1BD →=--,()11,0,1B C →=--,1AP BD ⊥,1110AP BD x z →→∴⋅=--+=,x z ∴=,即(),1,P x x ,(),0,CP x x →∴=,1CP x B C →→∴=-,即1,,B P C 三点共线,P ∴必在线段1B C 上,B 正确;对于C ,()1,1,AP x x →=-,()11,0,1BC →=-,111AP BC x x →→∴⋅=-+=,AP ∴与1BC 不垂直,C 错误;对于D ,()11,0,1A ,()10,1,1C ,()0,0,0D ,()11,0,1DA →∴=,()10,1,1DC →=, 设平面11AC D 的法向量(),,n x y z →=,1100n DA x z n DC y z ⎧⋅=+=⎪∴⎨⋅=+=⎪⎩,令1x =,则1z =-,1y =,()1,1,1n →∴=-, 110AP n x x →→∴⋅=-+-=,即AP n →→⊥,//AP ∴平面11ACD ,D 正确. 故选BD .【点睛】本题考查立体几何中动点问题相关命题的辨析,涉及到三棱锥体积公式、动点轨迹、线线垂直关系和线面平行关系等知识;解题关键是熟练应用空间向量法来验证相关结论.2、如图,在边长为2的正方体1111ABCD A B C D -中,E 为BC 的中点,点P 在底面ABCD 上移动,且满足11B P D E ⊥,则线段1B P 的长度的最大值为( )A .45B .2C .2D .3【答案】D【分析】以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系,设点(),,0P x y ,根据110B P D E ⋅=得出x 、y 满足的关系式,并求出y 的取值范围,利用二次函数的基本性质求得1B P 的最大值.【解析】如下图所示,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -,则点()12,2,2B 、()10,0,2D 、()1,2,0E ,设点()(),,002,02P x y x y ≤≤≤≤,()11,2,2D E =-,()12,2,2B P x y =---,11D E B P ⊥,()112224220B P D E x y x y ∴⋅=-+-+=+-=,得22x y =-,由0202x y ≤≤⎧⎨≤≤⎩,得022202y y ≤-≤⎧⎨≤≤⎩,得01y ≤≤, ()()2221224548B P x y y y ∴=-+-+=-+01y ≤≤,当1y =时,1B P 取得最大值3.故选D .3、在长方体1111ABCD A B C D -中,已知底面ABCD 为正方形,P 为11A D 的中点,2AD =,13AA =,点Q 为正方形ABCD 所在平面内的一个动点,且满足2QC QP =.则线段BQ 的长度的最大值是( )A .2B .4C .6D .前三个答案都不对【答案】C【分析】先以D 点为坐标原点,分别以DA ,DC ,1DD 所在方向为x 轴,y 轴,z 轴正方向,建立空间直角坐标系,由题意得到(0,2,0)C ,()1,0,3P ,(2,2,0)B ,设(,,0)Q x y ,由2QC QP =,得到22(2)(2)4-++=x y ,再由圆上的点与定点距离的问题,即可求出结果.【解析】以D 点为坐标原点,分别以DA ,DC ,1DD 所在方向为x 轴,y 轴,z 轴正方向,建立如图所示的空间直角坐标系,因为在长方体1111ABCD A B C D -中,已知底面ABCD 为正方形,P 为11A D 的中点,2AD =,13AA =(0,2,0)C ,(1,3P ,(2,2,0)B ,因为点Q 为正方形ABCD 所在平面内的一个动点,设(,,0)Q x y , 因为2QC QP =,所以()2222(2)213+-=⋅-++x y x y ,整理得:22(2)(2)4-++=x y ,即点Q 可看作圆22(2)(2)4-++=x y 上的点, 又22(2)(2)=-+-BQ x y ,所以BQ 表示圆22(2)(2)4-++=x y 上的点与定点(2,2)之间的距离, 因此22max (22)(22)426=-+--+=+=BQ r (其中r表示圆22(2)(2)4-++=x y 的半径.)故选C . 【名师点睛】本题主要考查立体几何中的轨迹问题,涉及圆上的点到定点距离的最值,灵活运用转化与化归的思想即可,属于常考题型.4、如图,已知正方体ABCD -A 1B 1C 1D 1棱长为8,点H 在棱AA 1上,且HA 1=2,在侧面BCC 1B 1内作边长为2的正方形EFGC 1,P 是侧面BCC 1B 1内一动点,且点P 到平面CDD 1C 1距离等于线段PF 的长,则当点P 在侧面BCC 1B 1运动时,2HP 的最小值是( )A .87B .88C .89D .90【答案】B【分析】建立空间直角坐标系,过点H 作1HM BB ⊥,垂足为M ,连接MP ,得出222HP HM MP =+,当MP 最小时,2HP 最小,利用空间直角坐标系求2HP 的最小值.【解析】如图,建立空间直角坐标系,过点H 作1HM BB ⊥,垂足为M ,连接MP ,则HM PM ⊥,所以222HP HM MP =+,当MP 最小时,2HP 最小, 过P 作1PN CC ⊥,垂足为N ,设(,8,)P x z ,则(2,8,6),(8,8,6),(0,8,)F M N z ,且08,08x z ≤≤≤≤,因为PN PF =,所以22(2)(6)x z x -+-=,化简得244(6)x z -=-,所以222222(8)(6)(8)441260(6)2424MP x z x x x x x =-+-=-+-=-+=-+≥, 当6x =时,2MP 取得最小值24,此时222282488HP HM MP =+=+=, 所以2HP 的最小值为88,故选B .5、如图,在棱长为2的正方体1111ABCD A B C D -中,E 为BC 的中点,点P 在底面ABCD 上(包括边界....)移动,且满足11B P D E ⊥,则线段1B P 的长度的最大值为A .55B .25C .2D .3【答案】D【分析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,利用向量法能求出线段1B P 的长度的最大值.【解析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,设P (a ,b ,0),则1D (0,0,2),E (1,2,0),1B (2,2,2),1B P =(a −2,b −2,−2),1D E =(1,2,−2), 因为1B P ⊥1D E ,()1122240B P D E a b ∴⋅=-+-+=, 所以a +2b −2=0,01b ≤≤,所以点P 的轨迹是一条线段,()()()()2222221224224548a b b B P b b b -+-+==+-+=-+, 由二次函数的性质可得当1b =时,2548b b -+可取到最大值9, 所以线段1B P 的长度的最大值为3.故选D .6、如图所示,在正方体1111ABCD A B C D -中,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则异面直线1A P 与BD 所成角的取值范围为A .3,44ππ⎡⎤⎢⎥⎣⎦B .,42ππ⎡⎤⎢⎥⎣⎦C .,32ππ⎡⎤⎢⎥⎣⎦D .2,33ππ⎡⎤⎢⎥⎣⎦【答案】C【分析】连接111,,AB AD B D ,则点P 在线段11B D 上,以D 为坐标原点建立坐标系,利用向量方法可求出范围. 【解析】过A 作平面α平面1DBC ,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则P ∈平面α,即P 在α与平面1111D C B A 的交线上,连接111,,AB AD B D ,11DD BB =,则四边形11BDD B 是平行四边形,11B D BD ∴,11B D ∴平面1DBC ,同理可证1AB ∥平面1DBC ,∴平面11AB D ∥平面1DBC ,则平面11AB D 即为α,点P 在线段11B D 上,以D 为坐标原点,1,,DA DC DD 建立如图坐标系,设正方体棱长为1,则()0,0,0D ,()1,1,0B ,()1,0,0A ,设(),,1P λλ,[]0,1λ∈,()1,1,0DB ∴=,()1,,1AP λλ=-,21DB AP λ∴⋅=-,2DB =,2222AP λλ=-+,设1A P 与BD 所成角为θ,则()22221211cos 2121DB APDB AP λλθλλλλ⋅--===-+⋅-+ 221313442121324λλλ=-=--+⎛⎫-+ ⎪⎝⎭,当12λ=时,cos θ取得最小值为0, 当0λ=或1时,cos θ取得最大值为12,10cos 2θ∴≤≤,则32ππθ≤≤.故选C .7、如图,三棱锥V ABC -的侧棱长都相等,底面ABC 与侧面VAC 都是以AC 为斜边的等腰直角三角形,E 为线段AC 的中点,F 为直线AB 上的动点,若平面VEF 与平面VBC 所成锐二面角的平面角为θ,则cos θ的最大值是A .33 B .23C 5D 6【答案】D【分析】连接BE ,以E 为原点,EB 为x 轴,EC 为y 轴,EV 为z 轴,建立空间直角坐标系,求出平面VBC 的一个法向量m ,平面VEF 的一个法向量n ,利用cos m n m nθ⋅=即可求解.【解析】底面ABC 与侧面VAC 都是以AC 为斜边的等腰直角三角形, 则Rt ABC Rt VAC ≅,所以VA VC BA BC === 设2VA VC BA BC VB =====,由E 为线段AC 的中点,则2VE BV ==, 由222VE BE VB +=,所以VE EB ⊥,以E 为原点,EB 为x 轴,EC 为y 轴,EV 为z 轴, 建立空间直角坐标系,如图所示:则()2,0C ,)2,0,0B,(2V ,设(),2,0F x x -,(0,2,2VC =-,(2,0,2VB =-,(2EV =,(,2,2VF x x =,设平面VBC 的一个法向量()111,,m x y z =,则00m VC m VB ⎧⋅=⎨⋅=⎩,即1111220220z x ⎧+=⎪⎨-=⎪⎩,令11x =,则11y =,11z =,所以()1,1,1m =. 设平面VEF 的一个法向量()222,,n x y z =,则00n EV n VF ⎧⋅=⎨⋅=⎩,即(222220220z x x x y z ⎧=⎪⋅+-⋅+=⎪⎩,解得20z =,令21y =,则221x x =-, 所以21,1,0n x ⎛⎫=- ⎪ ⎪⎝⎭, 平面VEF 与平面VBC 所成锐二面角的平面角为θ,则22cos 22232m n x m n x xθ⋅==-+,将分子、分母同除以1x,可得=令()2266632f x x x ⎛=-+=-+ ⎝⎭,当2x =时,()min 3f x =,则cos θ3=. 故选D【点睛】本题考查了空间向量法求二面角、考查了基本运算求解能力,解题的关键是建立恰当的空间直角坐标系,属于中档题.8、已知MN 是正方体内切球的一条直径,点P 在正方体表面上运动,正方体的棱长是2,则PM PN →→⋅的取值范围为 A .[]0,4 B .[]0,2C .[]1,4D .[]1,2【答案】B【分析】利用向量的线性运算和数量积运算律可将所求数量积化为21PO →-,根据正方体的特点可确定PO →的最大值和最小值,代入即可得到所求范围. 【解析】设正方体内切球的球心为O ,则1OM ON ==,2PM PN PO OM PO ON PO PO OM ON OM ON →→→→→→→→→→→→⎛⎫⎛⎫⎛⎫⋅=+⋅+=+⋅++⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,MN 为球O 的直径,0OM ON →→∴+=,1OM ON →→⋅=-,21PM PN PO →→→∴⋅=-,又P 在正方体表面上移动,∴当P 为正方体顶点时,PO →最大,最大值为;当P 为内切球与正方体的切点时,PO →最小,最小值为1,[]210,2PO →∴-∈,即PM PN →→⋅的取值范围为[]0,2.故选B .【点睛】本题考查向量数量积的取值范围的求解问题,关键是能够通过向量的线性运算将问题转化为向量模长的取值范围的求解问题.7、在正四面体D ABC -(所有棱长均相等的三棱锥)中,点E 在棱AB 上,满足2AE EB =,点F 为线段AC 上的动点.设直线DE 与平面DBF 所成的角为α,则A .存在某个位置,使得DE BF ⊥B .存在某个位置,使得4FDB π∠=C .存在某个位置,使得平面DEF ⊥平面DACD .存在某个位置,使得6πα=【答案】C【分析】设正四面体D ABC -的底面中心为点O ,连接DO ,则DO ⊥平面ABC ,以点O 为坐标原点,OB 、OD 所在直线分别为x 、z 轴建立空间直角坐标系,设正四面体D ABC -的棱长为2,然后利用空间向量法逐一分析求解可得结果. 【解析】如下图所示,设正四面体D ABC -的底面中心为点O ,连接DO ,则DO ⊥平面ABC ,以点O 为坐标原点,OB 、OD 所在直线分别为x 、z 轴建立空间直角坐标系, 设正四面体D ABC -的棱长为2,则31,0A ⎛⎫- ⎪ ⎪⎝⎭、23B ⎫⎪⎪⎝⎭、3C ⎛⎫ ⎪ ⎪⎝⎭、26D ⎛ ⎝⎭、31,03E ⎫-⎪⎪⎝⎭,设,03F λ⎛⎫- ⎪ ⎪⎝⎭,其中11λ-≤≤, 对于A 选项,若存在某个位置使得DE BF ⊥,31,333DE ⎛⎫=-- ⎪ ⎪⎝⎭,(),0BF λ=-,1103DE BF λ∴⋅=--=,解得3λ=-,不合乎题意,A 选项错误;对于B 选项,若存在某个位置使得4FDB π∠=,,33DF λ⎛=-- ⎝⎭,23DB ⎛=⎝⎭,cos ,DF DB DF DB DF DBλ⋅<>====⋅B选项错误;对于C 选项,设平面DAC 的一个法向量为()111,,m x y z =,1,DA ⎛=-- ⎝⎭,DC ⎛=-⎝⎭,由1111113033303m DA x y z m DC x y z ⎧⋅=---=⎪⎪⎨⎪⋅=-+-=⎪⎩,取11z =-,得()22,0,1m =-,设平面DEF 的一个法向量为()222,,n x y z =,31,3DE ⎛=- ⎝⎭,,DF λ⎛=- ⎝⎭, 由22222231033333n DE x y z n DF x y z λ⎧⋅=--=⎪⎪⎨⎪⋅=-+=⎪⎩,取y =,则()221n λ=+-,若存在某个位置,使得平面DEF ⊥平面DAC ,则2190m n λ⋅=+=,解得[]31,17λ=-∈-,合乎题意,C 选项正确;对于D 选项,设平面DBF 的一个法向量为()333,,u x y z =,2326,0,33DB ⎛⎫=- ⎪ ⎪⎝⎭,326,,33DF λ⎛⎫=-- ⎪ ⎪⎝⎭, 由333332326033326033u DB x z u DF x y z λ⎧⋅=-=⎪⎪⎨⎪⋅=-+-=⎪⎩,令z λ=,则()2,6,u λλ=,若存在某个位置,使得6πα=,即()()22612131sin cos ,6227272363u DE u DE u DEλλπλλ++⋅==<>===⋅⨯++⨯,整理得254120λλ-+=,162400∆=-<,该方程无解,D 选项错误. 故选C.【点评】本题考查利用空间向量法求解空间角以及利用空间向量法处理动点问题,计算量大,属于难题.10、如图,直三棱柱111ABC A B C -的底面是边长为6的等边三角形,侧棱长为2,E 是棱BC 上的动点,F 是棱11B C 上靠近1C 点的三分点,M 是棱1CC 上的动点,则二面角A FM E --的正切值不可能...是A .3155B .2155C .6D .5【答案】B【分析】建立空间直角坐标系,求得二面角A FM E --的余弦值,进而求得二面角A FM E --的正切值,求得正切值的最小值,由此判断出正确选项.【解析】取BC 的中点O ,连接OA ,根据等边三角形的性质可知OA BC ⊥,根据直三棱柱的性质,以O 为原点建立如图所示的空间直角坐标系.则()()0,33,0,1,0,2A F ,设()()3,0,02M t t ≤≤. 则()()1,33,2,2,0,2AF FM t =-=-. 设平面AMF 的一个法向量为(),,m x y z =,则()3320220m AF x z m FM x t z ⎧⋅=-+=⎪⎨⋅=+-=⎪⎩,令1y =,得633363,1,66t m t t ⎛= --⎝⎭. 平面FME 的一个法向量是()0,1,0n =,所以222cos ,28120252633363166m n m n m nt t t t t ⋅===⋅-+⎛⎫⎛⎫-++ ⎪ ⎪--⎝⎭⎝⎭,所以2sin ,1cos ,m n m n =-222710821628120252t t t t -+=-+所以二面角A FM E--的正切值为()sin ,27 cos,m nf tm n===因为02t≤≤,所以111466t-≤≤--,216125405-=-⨯结合二次函数的性质可知当1165t=--时,()f t5=;当1166t=--时,()f t=,所以()f t∈⎣,所以二面角A FM E--.故选B.【点睛】本小题主要考查二面角的求法,考查数形结合的数学思想方法,属于难题.11、直四棱柱ABCD﹣A1B1C1D1中,侧棱长为6,底面是边长为8的菱形,且∠ABC =120°,点E在边BC上,且满足BE=3EC,动点M在该四棱柱的表面上运动,并且总保持ME⊥BD1,则动点M的轨迹围成的图形的面积为_____;当MC与平面ABCD所成角最大时,异面直线MC1与AC所成角的余弦值为_____.【答案】,17【分析】由题意可知M的轨迹为过E且与直线1BD垂直的平面与直四棱柱的截面的边界,根据直棱柱的结构特征和底面棱形的性质,由线面垂直的定义可得截面与下底面的截线是与AC平行的,进而确定截面与与AB的交点F,建立空间直角坐标系,利用坐标方法求得截面与1BB的交点G,进而得到所求面积,根据线面角的定义可得M与G重合时MC与平面ABCD所成角最大,利用空间向量可求异面直线所成角的余弦值.【解析】如图,在直四棱柱1111ABCD A B C D-中,因为底面是菱形,侧棱垂直底面,所以AC ⊥平面11BDD B ,所以1BD AC ⊥.在AB 上取F ,使得3BF FA =,连接EF ,则//EF AC ,1⊥BD EF .记AC 与BD 的交点为O ,以O 为坐标原点,建立如图所示的空间直角坐标系O xyz -,则()4,0,0B ,()14,0,6D -,()1,33,0E .在1BB 上取一点G ,记为()4,0,G t ,于是()18,0,6BD =-,()3,33,EG t =-. 由12460BD EG t ⋅=-+=,得4t =,即12BG GB =, 所以EFG 的边为点M 的运动轨迹. 由题意得22213FG BF BG =+=33836344EF AC ==⨯= 动点M 的轨迹围成的图形的面积为()()22163213331532⨯-=显然当M 与G 重合时,MC 与平面ABCD 所成角最大. 因为()4,0,4M ,()10,43,6C ,所以()14,43,2MC =-. 因为AC 的一个方向向量为()0,1,0n =,所以1251cos ,17MC n =即异面直线1MC 与AC 251. 【点睛】本题考查点、线、面的位置关系,考查空间动点的轨迹,涉及线面垂直的判定与性质,异面直线所成的角,线面角,利用空间直角坐标系和空间向量确定点的位置和求异面直线所成的角,考查直观想象与数学运算的核心素养.属中档题,难度较大.12、如图,在直三棱柱111ABC A B C -中,已知90ABC ∠=︒,P 为侧棱1CC 上任意一点,Q 为棱AB 上任意一点,PQ 与AB 所成角为α,PQ 与平面ABC 所成的角为β,则α与β的大小关系为( )A .αβ=B .αβ<C .αβ>D .不能确定【答案】C【分析】建立空间直角坐标系设()()(),0,,0,,00,0,0P x z Q y x y z >≥≥,利用空间向量法分别求得cos ,cos αβ,然后根据(0,],0,22ππαβ⎡⎤∈∈⎢⎥⎣⎦,利用余弦函数的单调性求解.【解析】建立如图所示空间直角坐标系:设()()(),0,,0,,00,0,0P x z Q y x y z >≥≥,则()(),,,0,,0QP x y z QB y =-=-,所以2222,,QP QB y QP x y z QB y ⋅==++=,所以222cos QP QB y QP QBx y zα⋅==⋅++,又(0,],0,22ππαβ⎡⎤∈∈⎢⎥⎣⎦,222sin QP CP z QPx y zβ⋅==++,所以22222cos x y x y zβ+=++,所以cos cos βα>,因为cos y x = 在0,2π⎛⎫⎪⎝⎭上递减,所以αβ>,故选C 13、如图,在四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,侧棱1AA ⊥底面ABCD ,3AB =,14AA =,P 是侧面11BCC B 内的动点,且1AP BD ⊥,记AP 与平面11BCC B 所成的角为θ,则tan θ的最大值为( )A .43B .53C .2D .259【答案】B【分析】建立空间直角坐标系,利用向量法能求出线面角的正切值的最大值. 【解析】以1,,DA DC DD 所在直线分别为,,x y z 轴,建立空间直角坐标系, 设(,3,)P x z ,则1(3,3,),(3,3,4)AP x z BD =-=--,11,0AP BD AP BD ⊥∴⋅=,33(3)3340,4x z z x ∴---⨯+=∴=, 22225||(3)6916BP x z x x ∴=-+=-+225488191625255x ⎛⎫=-+ ⎪⎝⎭, ||5tan ||3AB BP θ∴=,tan θ∴的最大值为53.故选B .14、如图,在棱长都相等的正三棱柱111ABC A B C -中,D 是棱1CC 的中点,E 是棱1AA 上的动点.设AE x =,随着x 增大,平面BDE 与底面ABC 所成锐二面角的平面角是( )A .增大B .先增大再减小C .减小D .先减小再增大【答案】D【解析】设正三棱柱111ABC A B C -棱长为2,,02AE x x =≤≤, 设平面BDE 与底面ABC 所成锐二面角为α,以A 为坐标原点,过点A 在底面ABC 内与AC 垂直的直线为x 轴,1,AC AA 所在的直线分别为,y z 轴建立空间直角坐标系,则3,1,0),(0,2,1),(0,0,),(3,1,1),(0,2,1)B D E x BD ED x =-=-,设平面BDE 的法向量(,,)m s t k =,则m BDm ED⎧⊥⎨⊥⎩,即302(1)0s t k t x k ⎧-++=⎪⎨+-=⎪⎩,令3k =33,1t x s x =-=+,所以平面BDE 的一个法向量(1,33,23)m x x =+-, 底面ABC 的一个法向量为(0,0,1)n =,222233cos |cos ,|115(1)3(1)12()24m n x x x α=<>==++-+-+当1(0,)2x ∈,cos α随着x 增大而增大,则α随着x 的增大而减小,当1(,2)2x ∈,cos α随着x 增大而减小,则α随着x 的增大而增大.故选D .【点睛】本题考查空间向量法求二面角,应用函数思想讨论二面角的大小,考查直观想象、数学计算能力,素养中档题.15、如图所示,在正方体1111ABCD A B C D -中,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则异面直线1A P 与BD 所成角的取值范围为( )A .3,44ππ⎡⎤⎢⎥⎣⎦B .,42ππ⎡⎤⎢⎥⎣⎦C .,32ππ⎡⎤⎢⎥⎣⎦D .2,33ππ⎡⎤⎢⎥⎣⎦【答案】C【解析】过A 作平面α平面1DBC ,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则P ∈平面α,即P 在α与平面1111D C B A 的交线上,连接111,,AB AD B D ,11DD BB =,则四边形11BDD B 是平行四边形,11B D BD ∴,11B D ∴平面1DBC ,同理可证1AB ∥平面1DBC ,∴平面11AB D ∥平面1DBC ,则平面11AB D 即为α,点P 在线段11B D 上,以D 为坐标原点,1,,DA DC DD 建立如图坐标系,设正方体棱长为1,则()0,0,0D ,()1,1,0B ,()1,0,0A ,设(),,1P λλ,[]0,1λ∈,()1,1,0DB ∴=,()1,,1AP λλ=-,21DB AP λ∴⋅=-,2DB =,2222AP λλ=-+,设1A P 与BD 所成角为θ,则()22221211cos 2121DB APDB AP λλθλλλλ⋅--===-+⋅-+221313442121324λλλ=-=--+⎛⎫-+⎪⎝⎭12λ=时,cos θ取得最小值为0, 当0λ=或1时,cos θ取得最大值为12,10cos 2θ∴≤≤,则32ππθ≤≤.故选C .16、如图,矩形ABCD 中,222AB AD ==E 为边AB 的中点,将ADE 沿直线DE 翻折成1A DE △.在翻折过程中,直线1A C 与平面ABCD 所成角的正弦值最大为( )A .1024- B .66C .514-D .55【答案】A【解析】分别取DE ,DC 的中点O ,F ,则点A 的轨迹是以AF 为直径的圆, 以,OA OE 为,x y 轴,过O 与平面AOE 垂直的直线为z 轴建立坐标系,则()2,1,0C -,平面ABCD 的其中一个法向量为n = (0,0.1), 由11A O =,设()1cos ,0,sin A αα,则()1cos 2,1,sin CA αα=+-, 记直线1A C与平面ABCD 所成角为θ,则211|sin 1cos sin 4cos 64cos 6||CA nCA n αθαα⋅-===++⋅,设3153535102cos ,,sin 222416444t t t αθ-⎡⎤⎛⎫=+∈=-+≤-=⎪⎢⎥⎣⎦⎝⎭ 所以直线1A C 与平面ABCD 所成角的正弦值最大为1024-,故选A . (多选)17、在正方体1111ABCD A B C D -中,若棱长为1,点,E F 分别为线段11B D 、1BC 上的动点,则下列结论正确结论的是( )A .1DB ⊥面1ACD B .面11//AC B 面1ACDC .点F 到面1ACD 的距离为定值33D .直线AE 与面11BB D D 所成角的正弦值为定值13【答案】ABC【分析】以A 为坐标原点建立空间直角坐标系,利用共线向量可表示出动点,E F 的坐标,利用空间向量判断线面垂直、面面平行、求解点到面的距离和直线与平面所成角的方法依次验证各个选项即可得到结果.【解析】以A 为坐标原点可建立如下图所示的空间直角坐标系:由题意知:()0,0,0A ,()1,0,0B ,()1,1,0C ,()0,1,0D ,()10,0,1A ,()11,0,1B ,()11,1,1C ,()10,1,1D ,设(),,1E x y ,111B E B D λ→→=,即()()1,,0,,0x y λλ-=-,()1,,1E λλ∴-, 设()1,,F y z '',1BF BC μ→→=,即()()0,,0,,y z μμ''=,()1,,F μμ∴. 对于A ,()11,1,1DB →=-,()1,1,0AC →=,()10,1,1AD →=,11100DB AC DB AD ⎧⋅=⎪∴⎨⋅=⎪⎩,1DB AC ∴⊥,11DB AD ⊥, 又1,AC AD ⊂平面1ACD ,1AC AD A =,1DB ∴⊥平面1ACD ,A 正确;对于B ,1DB ⊥平面1ACD ,()11,1,1DB →∴=-为平面1ACD 的一个法向量,()111,1,0A C →=,()11,0,1A B →=-,111110DB A C DB A B ⎧⋅=⎪∴⎨⋅=⎪⎩,111DB AC ∴⊥,11DB A B ⊥, 又111,A C A B ⊂平面11A C B ,1111AC A B A =,1DB ∴⊥平面11A C B ,∴平面11//AC B平面1ACD ,B 正确;对于C ,()1,,AF μμ→=,∴点F 到面1ACD 的距离111333AF DB d DB →→→⋅===,为定值,C 正确;对于D ,几何体为正方体,AC ∴⊥平面11BB D D ,()1,1,0AC →∴=是平面11BB D D 的一个法向量,又()1,,1AE λλ→=-,设直线AE 与平面11BB D D 所成角为θ,则21sin 2222AC AEAC AEθλλ→→→→⋅==⋅-+⋅,不是定值,D 错误.故选ABC .(多选)18、如图所示,正方体1111ABCD A B C D -中,1AB =,点P 在侧面11BCC B 及其边界上运动,并且总是保持1AP BD ⊥,则以下四个结论正确的是( )A .113P AA D V -=B .点P 必在线段1BC 上 C .1AP BC ⊥D .//AP 平面11AC D【答案】BD【分析】根据三棱锥体积公式求得116P AA D V -=,知A 错误;以D 为坐标原点建立空间直角坐标系,利用空间向量法可得到1CP x B C →→=-,11AP BC →→⋅=,AP →垂直于平面11AC D 的法向量n →,由此可确定,,B C D 的正误.【解析】对于A ,P 在平面11BCC B 上,平面11//BCC B 平面1AA D ,P ∴到平面1AA D 即为C 到平面1AA D 的距离,即为正方体棱长,1111111113326P AA D AA D V S CD -∴=⋅=⨯⨯⨯⨯=△,A 错误;对于B ,以D 为坐标原点可建立如下图所示的空间直角坐标系:则()1,0,0A ,(),1,P x z ,()1,1,0B ,()10,0,1D ,()11,1,1B ,()0,1,0C()1,1,AP x z →∴=-,()11,1,1BD →=--,()11,0,1B C →=--,1AP BD ⊥,1110AP BD x z →→∴⋅=--+=,x z ∴=,即(),1,P x x ,(),0,CP x x →∴=,1CP x B C →→∴=-,即1,,B P C 三点共线,P ∴必在线段1B C 上,B 正确; 对于C ,()1,1,AP x x →=-,()11,0,1BC →=-,111AP BC x x →→∴⋅=-+=,AP ∴与1BC 不垂直,C 错误;对于D ,()11,0,1A ,()10,1,1C ,()0,0,0D ,()11,0,1DA →∴=,()10,1,1DC →=,设平面11AC D 的法向量(),,n x y z →=,1100n DA x z n DC y z ⎧⋅=+=⎪∴⎨⋅=+=⎪⎩,令1x =,则1z =-,1y =,()1,1,1n →∴=-, 110AP n x x →→∴⋅=-+-=,即AP n →→⊥,//AP ∴平面11ACD ,D 正确.故选BD . (多选)19、如图所示,棱长为1的正方体1111ABCD A B C D -中,P 为线段1A B 上的动点(不含端点),则下列结论正确的是( )。
【选填重点题型突破】专题06 结论判断问题(解析版)

【中考数学填选重点题型突破】专题六:结论判断问题【备考指南】结论判断问题是近几年来中考的一个热点问题,往往以压轴题的形式出现在填空题与选择题中.这类问题是由多选演变而来,试题中包含多个正确或错误的结论,考生对给定的已知条件通过综合分析、推理、计算等形式来论证题中所给出的结论的真伪性.试题的题境常以代数结论判断题和几何结论判断题为主,在代数结论判断题中,通常以二次函数为主的来考查函数知识,在几何结论判断题中,以考查三角形和四边形性质居多.这类试题的合性很强,难度很大,易错,不易得分,对考生综合运用知识解决问题的能力要求高.综合分析所给出的已知条件是解决此类问题的关健,同时要将已论证出来成立的结论直接应用于后继证明之中,在分析、推理过程中,要以数学思想为魂,注重灵活运用各种方法(如特殊值法、反证法、直接测量等),同时要注重计算的准确性.【典例引领】例1:已知抛物线y =ax 2+bx +c(a ≠0)的对称轴为x =−1,与x 轴的一个交点在(−3,0)和(−2,0)之间,其部分图像如图所示,则下列结论:①点(−72,y 1),(−32,y 2),(54,y 3)是该抛物线上的点,则y 1<y 2<y 3;②3b +2c <0;③t(at +b)≤a −b (t 为任意实数).其中正确结论的个数是( )A .0B .1C .2D .3【答案】C 【分析】逐一分析3条结论是否正确:①根据抛物线的对称性找出点(-134,y 3)在抛物线上,再结合抛物线对称轴左边的单调性即可得出①错误;②由x =-3时,y <0,即可得出9a -3b +c <0,根据抛物线的对称轴为x =-1,即可得出b =2a ,即可得出②正确;③∵抛物线开口向下,对称轴为x =-1,有最大值a −b +c ,再根据x =t 时的函数值为at 2+bt +c ,由此即可得出③正确.综上即可得出结论.【解答】解:①∵抛物线的对称轴为x =-1,点(54,y 3)在抛物线上,∴(-134,y 3)在抛物线上.∵-72<-134<-32,且抛物线对称轴左边图象y 值随x 的增大而增大,∴y1<y3<y2.∴①错误;②∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,∴-b2a =-1,∴2a=b,∴a=12b∵当x=-3时,y=9a-3b+c<0,∴9×12b-3b+c=32b+c<0,∴3b+2c<0,∴②正确;③∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,开口向下∴当x=-1,y最大=a−b+c∵当x=t时,y= at2+bt+c∵t为任意实数∴at2+bt+c≤a−b+c∴at2+bt≤a-b.∴③正确.故选:C.【解题指导】本题考查了二次函数图象与系数的关系、二次函数与不等式以及二次函数的最值,熟练掌握二次函数的图象和性质是解题关键,本题属于中档题,有些难度.变式训练1:如图所示的是二次函数y=ax2−bx+c(a,b,c为常数,且a≠0)的图象,其对称轴为直线x=−1,且经过点(0,1),则下列结论错误的是()A.a−b+c<0B.abc<0C.4a+2b+c<0D.c−a>1【答案】C【分析】由抛物线的开口方向判断a与0的关系,由抛物线经过点(0,1),得出c=1,然后根据对称轴判定b与0的关系;当x=1时,y=a-b+c;当x=-2时,y=4a+2b+c;然后由c=1和a<0判断c-a与1的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对称轴左边的单调性即可得出①错误;②由 x=-3 时,y<0,即可得出 9a-3b+c<0,根据抛物线的对称轴为
x=-1,即可得出 b=2a,即可得出②正确;③∵抛物线开口向下,对称轴为 x=-1,有最大值
,再根
据 x=t 时的函数值为 at2+bt+c,由此即可得出③正确.综上即可得出结论.
【解答】
b 与 0 的关系;当 x=1 时,y=a-b+c;当 x=-2 时,y=4a+2b+c;然后由 c=1 和 a<0 判断 c-a 与 1 的大小。
【解答】
解:A.∵x=1 时,y<0,∴a-b+c<0,该选项正确。
B.∵抛物线开口向下,∴a<0, ∵对称轴在 y 轴左侧,∴- <0,∴b 0,
∵抛物线经过点(0,1),∴c=1>0,∴
,
抛物线与 y 轴交于正半轴,
,
,故 错误;
,
,
,故 正确;
由图象得: 时,与抛物线有两个交点,
方程
有两个不相等的实数根,故 正确;
抛物线与 x 轴的一个交点坐标为 ,抛物线的对称轴是 ,
抛物线与 x 轴的另一个交点坐标为
,故 正确;
抛物线的对称轴是 ,
有最大值是
,
点
在该抛物线上,
,故 正确,
本题正确的结论有: 故选 B.
,该选项正确。
C. 根据抛物线的对称性可得 x=-2 时,y=1,∴4a+2b+c=1>0,该选项错误。
D.∵c=1,a<0;∴
> ,该选项正确。
故选:C.
【解题指导】本题主要考查了二次函数图象与系数的关系,关键是熟练掌握①二次项系数 a 决定抛物线的
开口方向,当 a>0 时,抛物线向上开口;当 a<0 时,抛物线向下开口;②一次项系数 b 和二次项系数 a
共同决定对称轴的位置:当 a 与 b 同号时(即 ab>0),对称轴在 y 轴左; 当 a 与 b 异号时(即 ab<0),
对称轴在 y 轴右.(简称:左同右异)③常数项 c 决定抛物线与 y 轴交点,抛物线与 y 轴交于(0,c).
变式训练 2:抛物线
的部分图象如图所示,与 x 轴的一个交点坐标为 ,抛物线
∴9 -3b+c=
<0,
∴3b+2c<0,∴②正确; ③∵抛物线 y=ax2+bx+c(a≠0)的对称轴为 x=-1,开口向下 ∴当 x=-1, 最大 ∵当 x=t 时,y= at2+bt+c
∵ 为任意实数
∴at2+bt+c≤ ∴at2+bt≤a-b.
∴③正确.
故选:C.
【解题指导】本题考查了二次函数图象与系数的关系、二次函数与不等式以及二次函数的最值,熟练掌握
解:①∵抛物线的对称轴为 x=-1,点( ,y3)在抛物线上,
∴(- ,y3)在抛物线上.
∵- <- <- ,且抛物线对称轴左边图象 y 值随 x 的增大而增大,
∴y1<y3<y2.∴①错误; ②∵抛物线 y=ax2+bx+c(a≠0)的对称轴为 x=-1,
∴- =-1,∴2a=b,∴a=
∵当 x=-3 时,y=9a-3b+c<0,
②由于∠A 不一定等于∠D,故∠AED=∠DFA 错误;
③连 AC,AD,BD,将△ACP 绕 A 点顺时针旋转 90°,使 AC 与 AD 重合(由 AB⊥CD 知 AC=AD)点 P 旋
转到 Q 点,可证得△APQ 是等腰直角三角形,CP+DP= AP,同理可得 BP+AP= DP,继而可证得结论.
【2019 年中考数学填选重点题型突破】
专题六:结论判断问题
【备考指南】
结论判断问题是近几年来中考的一个热点问题,往往以压轴题的形式出现在填空题与选择题中.这类
问题是由多选演变而来,试题中包含多个正确或错误的结论,考生对给定的已知条件通过综合分析、推理、 计算等形式来论证题中所给出的结论的真伪性.试题的题境常以代数结论判断题和几何结论判断题为主,
,4 个,
【解题指导】本题考查了二次函数图象与系数的关系:对于二次函数
,二次项系数
a 决定抛物线的开口方向和大小:当 时,抛物线向上开口;当 时,抛物线向下开口;一次项系数
b 和二次项系数 a 共同决定对称轴的位置:当 a 与 b 同号时 即
,对称轴在 y 轴左;当 a 与 b 异号时
即
,对称轴在 y 轴右;常数项 c 决定抛物线与 y 轴交点位置:抛物线与 y 轴交于 ;也考查了抛
在代数结论判断题中,通常以二次函数为主的来考查函数知识,在几何结论判断题中,以考查三角形和四
边形性质居多.这类试题的合性很强,难度很大,易错,不易得分,对考生综合运用知识解决问题的能力 要求高.
综合分析所给出的已知条件是解决此类问题的关健,同时要将已论证出来成立的结论直接应用于后继
证明之中,在分析、推理过程中,要以数学思想为魂,注重灵活运用各种方法(如特殊值法、反证法、直
接测量等),同时要注重计算的准确性.
【典例引领】
例 1:已知抛物线
的对称轴为
,与 轴的一个交点在
和
之间,
其部分图像如图所示,则下列结论:①点
,
,
是该抛物线上的点,则
;
②
;③
( 为任意实数).其中正确结论的个数是( )
A.0 【答案】C
B.1
C.2
D.3
【分析】逐一分析 3 条结论是否正确:①根据抛物线的对称性找出点(- ,y3)在抛物线上,再结合抛物线
物线与 x 轴的交点以及二次函数的性质.
例 2:如图,直径 AB、CD 相互垂直,P 为弧 BC 上任意一点,连 PC、PA、PD、PB,下列结论:①∠APC
=∠DPE;②∠AED=∠DFA;③
;其中正确的是( )
A.①③
B.只有①
C.只有②
D.①②③
【答案】A
【分析】①利用垂径定理,可得
,又由圆周角定理,即可证得∠APC=∠DPE;
二次函数的图象和性质是解题关键,本题属于中档题,有些难度.
变式训练 1:如图所示的是二次函数
( 为常数,且 )的图象,其对称轴为直线
,且经过点(0,1),则下列结论错误的是( )
A.B.Βιβλιοθήκη C.D.【答案】C
【分析】由抛物线的开口方向判断 a 与 0 的关系,由抛物线经过点(0,1),得出 c=1,然后根据对称轴判定
的对称轴是
下列结论中:
;
; 方程
有两个不相等的实数根; 抛物线与 x 轴的另一个交
点坐标为
; 若点
在该抛物线上,则
.
其中正确的有
A.5 个
B.4 个
C.3 个
D.2 个
【答案】B
【分析】结合函数图象,根据二次函数的性质及二次函数与一元二次方程、一元二次不等式间的关系逐一
判断即可.
【解答】
解: 对称轴是 y 轴的右侧,
