几何多结论选择题.

合集下载

初中数学中考复习第3关多结论的几何及二次函数问题为背景的选择填空题(原卷版)

第3关多结论的几何及二次函数问题为背景的选择填空题【考查知识点】以多结论的几何图形为背景的选择填空题题，主要考察了学生对三角形、四边形、圆知识的综合运用能力；以二次函数为背景的选择填空题，主要考察了二次函数的性质及二次函数系数与图象的关系。

【解题思路】1.以多结论的几何图形为背景的选择填空题题中，用“全等法”和“相似法”证题应该是两个基本方法，为了更好掌握这两种方法，应该熟悉一对全等或一对相似三角形的基本图形，下图中是全等三角形的基本图形。

大量积累基本图形，并在此基础上“截长补短”，“能割善补”，是学习几何图形的一个诀窍，每一个重要概念，重要定理都有一个基本图形，三线八角可以算做一个基本图形.2. 以二次函数为背景的选择填空题中，根据图象的位置确定a 、b 、c 的符号，a ＞0开口向上，a ＜0开口向下．抛物线的对称轴为x=2ba-，由图像确定对称轴的位置，由a 的符号确定出b 的符号．由x=0时,y=c ，知c 的符号取决于图像与y 轴的交点纵坐标，与y 轴交点在y 轴的正半轴时，c ＞0，与y 轴交点在y 轴的负半轴时，c ＜0．确定了a 、b 、c 的符号，易确定abc 的符号；根据对称轴确定a 与b 的关系；根据图象还可以确定△的符号，及a+b+c 和a -b+c 的符号。

【典型例题】【例1】（2019·新疆中考真题）如图，正方形ABCD 的边长为2，点E 是BC 的中点，AE 与BD 交于点P ，F 是CD 上的一点，连接AF 分别交BD ，DE 于点M ，N ，且AF ⊥DE ，连接PN ，则下列结论中:①4ABMFDM SS=；②PN =；③tan ∠EAF=34；④.PMN DPE ∽正确的是（）A ．①②③B ．①②④C ．①③④D ．②③④【名师点睛】此题考查三角函数，相似三角形的判定与性质，全等三角形的判定与性质，正方形的性质难度较大，解题关键在于综合掌握各性质【例2】（2019·湖北中考真题）抛物线2y ax bx c =++的对称轴是直线1x =-，且过点（1，0）.顶点位于第二象限，其部分图像如图所示，给出以下判断： ①0ab >且0c <； ②420a b c -+>； ③8>0+a c ； ④33c a b =-；⑤直线22y x =+与抛物线2y ax bx c =++两个交点的横坐标分别为12x x 、，则12125x x x x ++⋅=-.其中正确的个数有( )A ．5个B ．4个C ．3个D ．2个【名师点睛】本题考查了二次函数图象与系数的关系：对于二次函数y=ax 2+bx+c （a≠0），当a>0时，抛物线向上开口；当a<0时，抛物线向下开口；一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时（即ab>0），对称轴在y 轴左侧；当a 与b 异号时（即ab<0），对称轴在y 轴右侧；常数项c 决定抛物线与y 轴交点，抛物线与y 轴交于（0，c ）；抛物线与x 轴交点个数由△决定：△=b 2-4ac>0时，抛物线与x 轴有2个交点；△=b 2-4ac=0时，抛物线与x 轴有1个交点；△=b 2-4ac<0时，抛物线与x 轴没有交点．【例3】（2019·辽宁中考真题）如图，正方形ABCD 和正方形CGFE 的顶点C ，D ，E 在同一条直线上，顶点B ，C ，G 在同一条直线上．O 是EG 的中点，∠EGC 的平分线GH 过点D ，交BE 于点H ，连接FH 交EG 于点M ，连接OH ．以下四个结论：①GH ⊥BE ；②△EHM ∽△GHF；③BCCG =﹣1；④HOM HOGS S ＝2）A．①②③B．①②④C．①③④D．②③④【名师点睛】本题考查了正方形的性质，以及全等三角形的判定与性质，相似三角形的判定与性质，正确求得两个三角形的边长的比是解决本题的关键．【例4】（2018·广西中考真题）如图，抛物线y=14（x+2）（x﹣8）与x轴交于A，B两点，与y轴交于点C，顶点为M，以AB为直径作⊙D．下列结论：①抛物线的对称轴是直线x=3；②⊙D的面积为16π；③抛物线上存在点E，使四边形ACED为平行四边形；④直线CM与⊙D相切．其中正确结论的个数是（）A．1B．2C．3D．4【名师点睛】本题考查了二次函数与圆的综合题，涉及到抛物线的对称轴、圆的面积、平行四边形的判定、待定系数法、两直线垂直、切线的判定等，综合性较强，有一定的难度，运用数形结合的思想灵活应用相关知识是解题的关键.【方法归纳】1.多结论的几何选择填空题考查的知识点较多，如相似三角形的判定与性质、等腰直角三角形的性质、平行线的性质、直角三角形的性质、四边形的知识、圆的知识、等腰三角形的判定与性质以及特殊角三角函数等知识．这类题目的综合性很强，难度较大，解题的关键是注意数形结合思想的应用．2. 多结论的二次函数选择题主要考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．数形结合思想贯穿这类题目的始终，解题时应时时注意.【针对练习】1.（2018·四川中考真题）如图，在矩形ABCD 中，E 是AB 边的中点，沿EC 对折矩形ABCD ，使B 点落在点P 处，折痕为EC ，连结AP 并延长AP 交CD 于F 点，连结CP 并延长CP 交AD 于Q 点．给出以下结论：①四边形AECF 为平行四边形； ②∠PBA=∠APQ ； ③△FPC 为等腰三角形； ④△APB ≌△EPC ；其中正确结论的个数为（）A ．1B ．2C ．3D ．42.（2018·辽宁中考真题）已知抛物线y=ax 2+bx+c （0＜2a≤b ）与x 轴最多有一个交点．以下四个结论： ①abc ＞0；②该抛物线的对称轴在x=﹣1的右侧； ③关于x 的方程ax 2+bx+c+1=0无实数根； ④a b cb++≥2．其中，正确结论的个数为（） A ．1个B ．2个C ．3个D ．4个3．（2019·四川中考真题）如图，在正方形ABCD 的对角线AC 上取一点E ．使得15CDE ︒∠=，连接BE 并延长BE 到F ，使CF CB =，BF 与CD 相交于点H ，若1AB =，有下列结论：①BE DE =；②CE DE EF +=；③14DEC S ∆=-；④1DH HC =-．则其中正确的结论有（）A ．①②③B ．①②③④C ．①②④D ．①③④4．（2019·广西中考真题）如图，E 是正方形ABCD 的边AB 的中点，点H 与B 关于CE 对称，EH 的延长线与AD 交于点F ，与CD 的延长线交于点N ，点P 在AD 的延长线上，作正方形DPMN ，连接CP ，记正方形ABCD ，DPMN 的面积分别为1S ，2S ，则下列结论错误的是（）A ．212S S CP +=B ．2AF FD =C ．4CD PD = D ．3cos 5HCD ∠=5．（2019·山东中考真题）如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45°，AE 、AF 分别交BD 于M 、N ，连按EN 、EF 、有以下结论：①AN ＝EN ，②当AE ＝AF 时，BEEC＝2，③BE+DF ＝EF ，④存在点E 、F ，使得NF ＞DF ，其中正确的个数是（）A ．1B ．2C ．3D ．46．（2019·黑龙江中考真题）如图，在正方形ABCD 中，E F 、是对角线AC 上的两个动点，P 是正方形四边上的任意一点，且42AB EF ＝，＝，设AE x ＝．当PEF 是等腰三角形时，下列关于P 点个数的说法中，一定正确的是（）①当0x ＝（即E A 、两点重合）时，P 点有6个②当02x ＜＜时，P 点最多有9个③当P 点有8个时，x ＝﹣2④当PEF 是等边三角形时，P 点有4个 A ．①③B ．①④C ．②④D ．②③7．（2019·广东中考真题）如图，正方形ABCD 的边长为4，延长CB 至E 使2EB =，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K .则下列结论：①ANH GNF ∆≅∆；②AFN HFG ∠=∠；③2FN NK =；④:1:4AFN ADM S S ∆∆=.其中正确的结论有( )A ．1个B ．2个C ．3个D ．4个8．（2019·湖北中考真题）如图所示，已知二次函数2y ax bx c =++的图象与x 轴交于,A B 两点，与y 轴交于点C ，OA OC =，对称轴为直线1x =，则下列结论：①0abc <；②11024a b c ++=；③10ac b -+=；④2c +是关于x 的一元二次方程20ax bx c ++=的一个根．其中正确的有（）A ．1个B ．2个C ．3个D ．4个9．（2018·黑龙江中考真题）抛物线()2y ax bx c a 0=++≠的部分图象如图所示，与x 轴的一个交点坐标为()4,0，抛物线的对称轴是x 1.=下列结论中：abc 0>①；2a b 0+=②；③方程2ax bx c 3++=有两个不相等的实数根；④抛物线与x 轴的另一个交点坐标为()2,0-；⑤若点()A m,n 在该抛物线上，则2am bm c a b c ++≤++．其中正确的有( )A ．5个B ．4个C ．3个D ．2个10．（2018·黑龙江中考真题）如图，平行四边形ABCD 的对角线AC 、BD 相交于点O ，AE 平分∠BAD ，分别交BC 、BD 于点E 、P ，连接OE ，∠ADC=60°，AB=12BC=1，则下列结论：①∠CAD=30°②③S 平行四边形ABCD =AB•AC ④OE=14AD ⑤S △APO =12，正确的个数是（）A ．2B ．3C ．4D ．511．（2018·山东中考真题）如图，在矩形ABCD 中，∠ADC 的平分线与AB 交于E ，点F 在DE 的延长线上，∠BFE=90°，连接AF 、CF ，CF 与AB 交于G ，有以下结论： ①AE=BC ②AF=CF ③BF 2=FG•FC ④EG•AE=BG•AB其中正确的个数是（）A ．1B ．2C ．3D ．412．（2019·四川中考真题）二次函数2(0)y ax bx c a =++≠的部分图象如图所示，图象过点(1,0)-，对称轴为直线x ＝1，下列结论：①0abc ＜；②b c ＜；③30a c +=；④当0y ＞时，13x -＜＜其中正确的结论有（）A ．1个B ．2个C ．3个D ．4个13．（2019·山东中考真题）如图，正方形ABCD ，点F 在边AB 上，且:1:2AF FB =，CE DF ⊥，垂足为M ，且交AD 于点E ，AC 与DF 交于点N ，延长CB 至G ，使12BG BC =，连接CM ．有如下结论：①DE AF =；②4AN AB =；③ADF GMF ∠=∠；④:1:8ANF CNFB S S ∆=四边形．上述结论中，所有正确结论的序号是（）A ．①②B ．①③C ．①②③D ．②③④14．（2018·湖北中考真题）如图，在四边形ABCD 中，AB=AD=5，BC=CD 且BC ＞AB ，BD=8．给出以下判断：①AC 垂直平分BD ；②四边形ABCD 的面积S=AC•BD ；③顺次连接四边形ABCD 的四边中点得到的四边形可能是正方形； ④当A ，B ，C ，D 四点在同一个圆上时，该圆的半径为256； ⑤将△ABD 沿直线BD 对折，点A 落在点E 处，连接BE 并延长交CD 于点F ，当BF ⊥CD 时，点F 到直线AB 的距离为678125．其中正确的是_____．（写出所有正确判断的序号）15．（2019·广西中考真题）我们定义一种新函数：形如2y ax bx c =++（0a ≠，且240b a ->）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y=|x 2-2x -3|223y x x =--的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为()1,0-，()3,0和()0,3；②图象具有对称性，对称轴是直线1x =；③当11x -≤≤或3x ≥时，函数值y 随x 值的增大而增大；④当1x =-或3x =时，函数的最小值是0；⑤当1x =时，函数的最大值是4．其中正确结论的个数是______.16．（2018·新疆中考真题）如图，已知抛物线y 1=﹣x 2+4x 和直线y 2=2x ．我们规定：当x 取任意一个值时，x 对应的函数值分别为y 1和y 2，若y 1≠y 2，取y 1和y 2中较小值为M ；若y 1=y 2，记M=y 1=y 2．①当x ＞2时，M=y 2；②当x ＜0时，M 随x 的增大而增大；③使得M 大于4的x 的值不存在；④若M=2，则x=1．上述结论正确的是_____（填写所有正确结论的序号）．17．（2018·黑龙江中考真题）如图，抛物线y=ax 2+bx+c （a≠0）的对称轴为直线x=﹣1，下列结论中： ①abc ＜0；②9a ﹣3b+c ＜0；③b 2﹣4ac ＞0；④a ＞b ，正确的结论是_____（只填序号）18．（2019·湖南中考真题）如图，函数ky x=(k 为常数，k ＞0)的图象与过原点的O 的直线相交于A ，B 两点，点M 是第一象限内双曲线上的动点（点M 在点A 的左侧），直线AM 分别交x 轴，y 轴于C ，D 两点，连接BM 分别交x 轴，y 轴于点E ，F ．现有以下四个结论：①△ODM 与△OCA 的面积相等；②若BM ⊥AM于点M ，则∠MBA ＝30°；③若M 点的横坐标为1，△OAM 为等边三角形，则2k =④若25MF MB =，则MD ＝2MA ．其中正确的结论的序号是_______．19．（2019·辽宁中考真题）如图，点P 是正方形ABCD 的对角线BD 延长线上的一点，连接PA ，过点P 作PE ⊥PA 交BC 的延长线于点E ，过点E 作EF ⊥BP 于点F ，则下列结论中：①PA ＝PE ；②CE PD ；③BF ﹣PD ＝12BD ；④S △PEF ＝S △ADP ，正确的是___（填写所有正确结论的序号）20．（2019·内蒙古中考真题）如图，在Rt ABC ∆中，90,3,ABC BC D ︒∠==为斜边AC 的中点，连接BD ，点F 是BC 边上的动点（不与点B C 、重合），过点B 作BE BD ⊥交DF 延长线交于点E ，连接CE ，下列结论：①若BF CF =，则222CE AD DE +=；②若,4BDE BAC AB ∠=∠=，则158CE =； ③ABD ∆和CBE ∆一定相似；④若30,90A BCE ︒︒∠=∠=，则DE =其中正确的是_____．（填写所有正确结论的序号）21．（2018·湖北中考真题）如图，已知∠MON=120°，点A ，B 分别在OM ，ON 上，且OA=OB=a ，将射线OM 绕点O 逆时针旋转得到OM′，旋转角为α（0°＜α＜120°且α≠60°），作点A 关于直线OM′的对称点C ，画直线BC 交OM′于点D ，连接AC ，AD ，有下列结论：①AD=CD ；②∠ACD 的大小随着α的变化而变化；③当α=30°时，四边形OADC 为菱形；④△ACD a 2；其中正确的是_____．（把你认为正确结论的序号都填上）．。

人教版中考数学中考压轴题突破一、选填题压轴题突破重难点突破六多结论选填题

B．②④
C．③④
D．②③
3．★(2022·广元)二次函数y＝ax2＋bx＋c(a≠0)的部分图象如图所
示，图象过点(－1, 0)，对称轴为直线x＝2，下列结论：①abc<0；② 1
4a＋c>2b；③ 3b－ 2c>0；④若点A(－2，y1)，点B －2，y2 ，点 7
C 2，y3 在该函数图象上，则y1<y3<y2；⑤ 4a＋2b≥m (am＋b) (m为常数)．
2．(2022·临沂)二次函数y＝ax2＋bx＋c (a≠0)的部分图象如图所示，
1 其对称轴为直线x＝－ 2 ，且与x轴的一个交点坐标为(－2，0)．下列结
论：①abc>0；②a＝b；③2a＋c＝0；④关于x的一元二次方程ax2＋bx＋
c－1＝0有两个相等的实数根．其中正确结论的序号是
( D)
A．①③
其中正确的结论有 A．5个 B．4个 C．3个 D．2个
(C)
4．★(2021·荆门)抛物线y＝ax2＋bx＋c(a，b，c为常数)开口向下且过
点A(1，0)，B(m，0)(－2<m<－1)，下列结论：① 2b＋c>0；② 2a＋
c<0；③ a(m＋1)－b＋c>0；④若方程a(x－m)(x－1)－1＝0有两个不等
对称轴x＝－
b 2a
＝1，得b＝－2a，∴y＝ax2－
2ax－1,
确当x＝－1时，
y>0，∴aa＋＋2a2－a－1>0, 1
11 ∴a>33
，故②正正确；当m＝1时，m(am＋b)＝确
aa＋＋b，故③错错误；∵点(－2, y1)到对称轴的距离大大于点(2, y3)到

2020年中考数学点对点专题三几何多结论问题+专题七其他类课件(共20张PPT)

A．①
B．①②
C．①②③
D．①②④
图4
3．如图 5，在矩形 ABCD
中，E 是 AD 边的中点，BE⊥AC
于点 F，连接 DF，下列结论：
①△AEF∽△CAB；②CF＝2AF；
图5
③DF＝DC；④S 四边形 CDEF＝52S△ABF.其中正确的结论有
A．4 个
B．3 个( A)源自C．2 个D．1 个
A．①③
B．②③
C．①④
D．②④
图1
2．(2019 广东)如图 2，正方形
ABCD 的边长为 4，延长 CB 至 E
使 EB＝2，以 EB 为边在上方作正
方形 EFGB，延长 FG 交 DC 于 M，
连接 AM，AF，H 为 AD 的中点，
图2
连接 FH 分别与 AB，AM 交于点 N，K，则下列结论：
训练 1.如图2，AB是⊙O的弦，AB＝20，点C 是⊙O上的一个动点，且∠ACB＝45°，若点 M，N分别是AB，BC的中点，则MN的最大值是___20___.
图2
2．如图3，⊙O的半径为5 cm，弦AB的长为8 cm，P是AB延长线上一点，BP＝2 cm，则tan P1 的值是
__2____.
2020 全新版
选择题突破
专题三几何多结论问题
广东真题 1.(2017广东)如图1，已知正方形
ABCD，点E是BC边的中点，DE与AC相交于点
F，连接BF，下列结论：①S△ABF＝S△ADF；②
S△CDF＝4S△CEF；③S△ADF＝2S△CEF；④S△ADF
＝2S△CDF.其中正确的是
( C)
4．(2019攀枝花)如图6，在正方形ABCD中，E 是BC边上的一点，BE＝4，EC＝8，将正方形边AB沿AE折叠到AF，延长EF交DC于G，连接 AG，现在有如下4个结论：①∠EAG＝45°； ②FG＝FC；③FC∥AG；④S△GFC＝14.其中正确结论的个数是 ( B )

正方形选择题(中考压轴多结论)

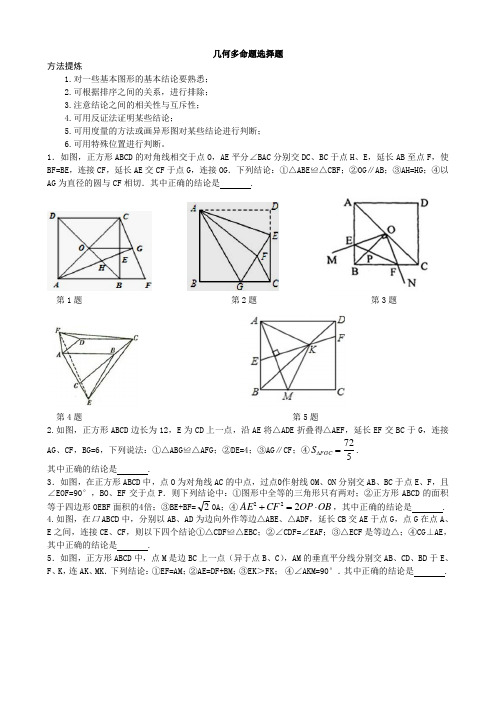
几何多命题选择题方法提炼1.对一些基本图形的基本结论要熟悉；2.可根据排序之间的关系，进行排除；3.注意结论之间的相关性与互斥性；4.可用反证法证明某些结论；5.可用度量的方法或画异形图对某些结论进行判断；6.可用特殊位置进行判断。

1．如图，正方形ABCD 的对角线相交于点O ，AE 平分∠BAC 分别交DC 、BC 于点H 、E ，延长AB 至点F ，使BF=BE ，连接CF ，延长AE 交CF 于点G ，连接OG ．下列结论：①△ABE≌△CBF；②OG∥AB；③AH=HG；④以AG 为直径的圆与CF 相切．其中正确的结论是 .第1题第2题第3题第4题第5题2.如图，正方形ABCD 边长为12，E 为CD 上一点，沿AE 将△ADE 折叠得△AEF，延长EF 交BC 于G ，连接AG 、CF ，BG=6，下列说法：①△ABG≌△AFG；②DE=4；③AG∥CF；④572=∆FGC S . 其中正确的结论是 .3．如图，在正方形ABCD 中，点O 为对角线AC 的中点，过点0作射线OM 、ON 分别交AB 、BC 于点E 、F ，且∠EOF=90°，BO 、EF 交于点P ．则下列结论中：①图形中全等的三角形只有两对；②正方形ABCD 的面积等于四边形OEBF 面积的4倍；③BE+BF=20A ；④OB OP CF AE ⋅=+222，其中正确的结论是 .4.如图，在口ABCD 中，分别以AB 、AD 为边向外作等边△ABE、△ADF，延长CB 交AE 于点G ，点G 在点A 、E 之间，连接CE 、CF ，则以下四个结论①△CDF≌△EBC；②∠CDF=∠EAF；③△ECF 是等边△；④CG⊥AE，其中正确的结论是 .5．如图，正方形ABCD 中，点M 是边BC 上一点（异于点B 、C ），AM 的垂直平分线分别交AB 、CD 、BD 于E 、F 、K ，连AK 、MK ．下列结论：①EF=AM；②AE=DF+BM；③EK＞FK ； ④∠AKM=90°．其中正确的结论是 .第6题第7题第8题6.如图，正方形ABCD 中，P 为对角线上的点，PB=AB ，连PC ，作CE⊥CP 交AP 的延长线于E ，AE 交CD 于F ，交BC 的延长线于G ，则下列结论：①E 为FG 的中点；②CD CF FG ⋅=42；③AD=DE；④CF=2DF．其中正确的结论是 .7.如图，已知四边形ABCD 是四个角都是直角，四条边都相等的正方形，点E 在BC 上，且BC CE 41=，点F 是CD 的中点，延长AF 与BC 的延长线交于点M ．以下结论：①AB=CM；②AE=AB+CE；③ABCF AEF S S 四边形41=∆；④∠AFE=90°，其中正确的结论是 .8.如图，在正方形ABCD 中，对角线AC 、BD 交于点O ，BE 平分∠DBC，交DC 于点E ，延长BC 到点F ，使CF=CE ，连接DF ，交BE 的延长线于点G ，AC 交BG 于点H ，连接OG ，下列结论：①OG∥AD；②△CHE 为等腰三角形；③BH=GH；④tan∠F=2；⑤2:1:=∆∆BDE BCE S S 其中正确的结论是 .9.如图，在边长为1的正方形ABCD 中，E 为AD 边上一点，连接BE ，将ABE 沿BE 对折，A 点恰好落在对角线BD 上的点F 处．延长AF ，与CD 边交于点G ，延长FE ，与BA 的延长线交于点H ，则下列说法：①BFH 为等腰直角三角形；②ADF FHA ≅；③60DFG ∠=︒；④22DE =-；⑤S AEF S DFG =．其中正确的结论是 .第9题第10题10.如图，正方形ABCD 中，M 为BC 上一点，且13BM BC =．△AMN 为等腰直角三角形，斜边AN 与CD 交于点F ，延长AN 与BC 的延长线交于点E ，连接MF 、CN ，作NG⊥BE，垂足为G ，下列结论：①ABM MGN ≅；②△CNG 为等腰直角三角形；③MN=EN；④S ABM S CEN =；⑤BM+DF=MF．其中正确的的结论为 .11.如图，正方形ABCD 中，点E 是对角线BD 上一点，点F 是边BC 上一点，点G 是边CD 上一点，BE=2ED ，CF=2BF ，连接AE 并延长交CD 于G ，连接AF 、EF 、FG ．给出下列五个结论：①DG=GC ；②∠FGC=∠AGF；③S△ABF=S△FCG；④2AF EF =；⑤∠AFB=∠AEB．其中正确结论结论是 . 12.如图，在正方形ABCD 中，E 为AD 的中点，DF ⊥CE 于M ，交AC 于点N ，交AB 于点F ，连接EN 、BM ．有如下结论：①△ADF ≌△DCE ；②MN=FN ；③CN=2AN ；④ADN CNFB SS 25=四边形：：⑤∠ADF=∠BMF ．其中正确的结论为 .第11题第12题第13题14.如图，把矩形纸片ABCD 沿EF 折叠，使点B 落在AD 边上的点B ′处，点A 落在点A ′处．设AE=a ，AB=b ，BF=c ，下列结论：①B ′E=BF ；②四边形B ′CFE 是平行四边形；③a 2+b 2=c 2；④△A ′B ′E ∽△B ′CD ；其中正确的是 .15.如图，在正方形ABCD 中，AB=1，E ，F 分别是边BC ，CD 上的点，连接EF 、AE 、AF ，过A 作AH⊥EF 于点H. 若EF=BE+DF ，那么下列结论：①AE 平分∠BEF；②FH=FD；③∠EAF=45°；④EAF ABE ADF S S S ∆∆∆=+；⑤△CEF 的周长为2.其中正确的结论是 .第14题第15题第16题16.如图，正方形ABCD 中，E 是AD 的中点，连接BE 、CE ，点F 是CE 的中点，连接DF 、BF ，点M 是BF 上一点且21=MF BM ，过点M 做BC MN ⊥于点N ，连接FN .下列结论中①CE BE =；②DFE BEF ∠=∠；③AB MN 61=；④61=∆EBNF FMN S S 四边形其中正确的结论是： .17.如图，正方形ABCD 中，O 为BD 中点，以BC 为边向正方形内作等边△BCE，连接并延长AE 交CD 于F ，连接BD 分别交CE 、AF 于G 、H ，下列结论：①∠CEH=45°；②GF∥DE；③2OH+DH=BD；④2BG DG =；⑤31:BEC BGC S S ∆∆+=．其中正确的结论是 .第17题第18题第19题18.如图，在正方形ABCD中，对角线AC、BD交于点O，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G，AC交BG于点H，连接OG，下列结论：①OG∥AD；②△CHE为等腰三角形；③BH=GH；④tan∠F=2；⑤2BCEBDESS∆∆=其中正确的结论有（）19.如图，将矩形ABCD的一个角翻折，使得点D恰好落在BC边上的点G处，折痕为EF，若EB为∠AEG的平分线，EF和BC的延长线交于点H．下列结论中：①∠BEF=90°；②DE=CH；③BE=EF；④△BEG和△HEG的面积相等；⑤若CD2AD=，则BG5BC6=．以上命题，正确的有的 .20.如图，在正方形ABCD中，E是BC的中点，F是CD上一点，AE⊥EF，有下列结论：①∠BAE=30°；②S△ABE=4S△ECF；③13CF CD=；④△ABE∽△AEF．正确结论的结论为 .第20题第21题21.如图，在正方形ABCD中，对角线AC、BD交于点D，CE平分∠ACD，分别交AD、BD于E、G，EF∥AC交CD于F，连接OE，下列结论：①EF AE=，②AOE AEO∠=∠，③1OG AE2=；④ACE DCES2S∆∆=；⑤AB(21)DG=．其中正确的是 .。

2019届深圳中考复习《多结论几何综合题》专题试卷含解析

2017届中考复习多结论几何综合题专题试卷一、单选题1、如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=；②S△ABC+S△CDE≥S△ACE；③BM⊥DM；④BM=DM．正确结论的个数是（）A、1个B、2个C、3个D、4个2、如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF；②=;③△ABC的面积等于四边形AFBD的面积；④BE2+DC2=DE2⑤BE+DC=DE;其中正确的是( )A、①②④B、③④⑤C、①③④D、①③⑤3、如图，将等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD ，则下列结论：①AD＝BC；②BD、AC互相平分；③四边形ACED是菱形；④BD⊥DE；其中正确的个数是（）.A、1B、2C、3D、44、如图，把一张长方形纸片ABCD沿对角线BD折叠，使C点落在E处，BE与AD相交于点F，下列结论：①BD=AD2+AB2；②△ABF≌△EDF；③＝④AD=BD•cos45°．其中正确的一组是（）A、①②B、②③C、①④D、③④5、如图，已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O．下列结论：①∠DOC=90°，②OC=OE，③tan∠OCD= ，④S△ODC=S四边形BEOF中，正确的有（）A、1个B、2个C、3个D、4个6、如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④S△BEF=．在以上4个结论中，正确的有（）A、1B、2C、3D、47、如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=BC，连接OE．下列结论：①∠CAD=30°；②S▱ABCD=AB•AC；③OB=AB；④OE=BC，成立的个数有（）A、1个B、2个C、3个D、4个8、如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下列四个结论：①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④AE+DF=AF+DE．其中正确的是（）A、②③B、②④C、①③④D、②③④9、如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：①BE=GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH，其中，正确的结论有（）A、1个B、2个C、3个D、4个10、如图，PA=PB，OE⊥PA，OF⊥PB，则以下结论：①OP是∠APB的平分线；②PE=PF③CA=BD；④CD∥AB；其中正确的有（）个．A、4B、3C、2D、111、如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE、EF．下列结论：①tan∠ADB=2；②图中有4对全等三角形；③若将△DEF沿EF折叠，则点D不一定落在AC上；④BD=BF；⑤S四边形DFOE=S△AOF，上述结论中正确的个数是（）A、1个B、2个C、3个D、4个12、如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：①AC=AD；②BD⊥AC；③四边形ACED是菱形．其中正确的个数是（）A、0B、1C、2D、313、如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQ•AC，其中正确的结论的个数是（）A 、1B 、2C 、3D 、414、如图，矩形ABCD 中，O 为AC 中点，过点O 的直线分别与AB 、CD 交于点E 、F ，连结BF 交AC 于点M ，连结DE 、BO ．若∠COB=60°，FO=FC ，则下列结论：①FB 垂直平分OC ；②△EOB ≌△CMB ；③DE=EF ；④S △AOE ：S △BCM =2：3．其中正确结论的个数是（）A 、4个B 、3个C 、2个D 、1个15、（2016•攀枝花）如图，正方形纸片ABCD 中，对角线AC 、BD 交于点O ，折叠正方形纸片ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合，展开后折痕DE 分别交AB 、AC 于点E 、G ，连结GF ，给出下列结论：①∠ADG=22.5°；②tan ∠AED=2；③S △AGD =S △OGD ；④四边形AEFG 是菱形；⑤BE=2OG ；⑥若S △OGF =1，则正方形ABCD 的面积是6+4 ，其中正确的结论个数为（）A 、2B 、3C 、4D 、516、如图，在正方形ABCD 中，E 、F 分别为BC 、CD 的中点，连接AE ，BF 交于点G ，将△BCF 沿BF 对折，得到△BPF ，延长FP 交BA 延长线于点Q ，下列结论正确的个数是（）①AE=BF ；②AE ⊥BF ；③sin ∠BQP= ；④S四边形ECFG=2S △BGE ．A 、4B 、3C 、2D 、117、如图所示，抛物线y=ax 2+bx+c （a≠0）与x 轴交于点A （﹣2，0）、B （1，0），直线x=﹣0.5与此抛物线交于点C ，与x 轴交于点M ，在直线上取点D ，使MD=MC ，连接AC 、BC 、AD 、BD ，某同学根据图象写出下列结论： ①a ﹣b=0；②当﹣2＜x ＜1时，y ＞0； ③四边形ACBD 是菱形； ④9a ﹣3b+c ＞你认为其中正确的是（）A、②③④B、①②④C、①③④D、①②③18、如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FGC=3.6．其中正确结论的个数是（）A、2B、3C、4D、519、如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足= ，连接AF并延长交⊙O于点E，连接AD，DE，若CF=2，AF=3，给出下列结论：①△ADF∽△AED；②FG=2；③tanE= ；④S△DEF=4 ，其中正确的是（）A、①②③B、②③④C、①②④D、①③④20、如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，弦CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB 于点P、Q，连接AC，给出下列结论：①∠DAC=∠ABC；②AD=CB；③点P是△ACQ的外心；④AC2=AE•AB；⑤CB∥GD，其中正确的结论是（）A、①③⑤B、②④⑤C、①②⑤D、①③④答案解析部分一、单选题1、【答案】D【考点】等腰三角形的性质，梯形中位线定理，锐角三角函数的定义【解析】【分析】①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知，；然后由直角三角形中的正切函数，得tan∠AEC=，再由等量代换求得tan∠AEC=；②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab（a=b时取等号)解答；③、④通过作辅助线MN，构建直角梯形的中位线，根据梯形的中位线定理及等腰直角三角形的判定定理解答．【解答】解：∵△ABC和△CDE均为等腰直角三角形，∴AB=BC，CD=DE，∴∠BAC=∠BCA=∠DCE=∠DEC=45°，∴∠ACE=90°；∵△ABC∽△CDE∴①∴tan∠AEC=，∴tan∠AEC=；故本选项正确；②∵S△ABC=a2，S△CDE=b2，S梯形ABDE=（a+b)2，∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab，S△ABC+S△CDE=（a2+b2)≥ab（a=b时取等号)，∴S△ABC+S△CDE≥S△ACE；故本选项正确；④过点M作MN垂直于BD，垂足为N．∵点M是AE的中点，则MN为梯形中位线，∴N为中点，∴△BMD为等腰三角形，∴BM=DM；故本选项正确；③又MN=（AB+ED)=（BC+CD)，∴∠BMD=90°，即BM⊥DM；故本选项正确．故选D．【点评】本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点．在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．2、【答案】C【考点】全等三角形的判定，勾股定理，相似三角形的判定，旋转的性质【解析】【分析】①根据旋转的性质知∠CAD=∠BAF，AD=AF，因为∠BAC=90°，∠DAE=45°，所以∠CAD+∠BAE=45°，可得∠EAF=45°=∠DAE，由此即可证明△AEF≌△AED；②当△ABE∽△ACD时，该比例式成立；③根据旋转的性质，△ADC≌△ABF，进而得出△ABC的面积等于四边形AFBD 的面积；④据①知BF=CD，EF=DE，∠FBE=90°，根据勾股定理判断．⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF；由此即可确定该说法是否正确；【解答】①根据旋转的性质知∠CAD=∠BAF，AD=AF，∵∠BAC=90°，∠DAE=45°，∴∠CAD+∠BAE=45°．∴∠EAF=45°，∴△AED≌△AEF；故本选项正确；②∵AB=AC，∴∠ABE=∠ACD；∴当∠BAE=∠CAD时，△ABE∽△ACD，∴=；当∠BAE≠∠CAD时，△ABE与△ACD不相似，即≠；∴此比例式不一定成立；故本选项错误；③根据旋转的性质知△ADC≌△AFB，∴S△ABC=S△ABD+S△ABF=S四边形AFBD，即三角形ABC的面积等于四边形AFBD的面积；故本选项正确；④∵∠FBE=45°+45°=90°，∴BE2+BF2=EF2，∵△ADC绕点A顺时针旋转90°后，得到△AFB，∴△AFB≌△ADC，∴BF=CD，又∵EF=DE，∴BE2+DC2=DE2，故本选项正确；⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF，∴BE+DC=BE+BF＞DE=EF，即BE+DC＞DE，故本选项错误；综上所述，正确的说法是①③④；故选C．【点评】此题主要考查了图形的旋转变换以及全等三角形的判定等知识，解题时注意旋转前后对应的相等关系．3、【答案】D【考点】等边三角形的性质，菱形的判定与性质，平移的性质【解析】【解答】∵△ABC、△DCE是等边三角形，∴∠ACB＝∠DCE＝60°，AC ＝CD ，∴∠ACD＝180°－∠ACB－∠DCE＝60°，∴△ACD是等边三角形，∴AD＝AC＝BC ，故①正确；由①可得AD＝BC ，∵AB＝CD ，∴四边形ABCD是平行四边形，∴BD、AC互相平分，故②正确；由①可得AD＝AC＝CE＝DE ，故四边形ACED是菱形，即③正确；∵四边形ACED是菱形，∴AC⊥BD ，∵AC∥DE ，∴∠BDE＝∠COD＝90°，∴BD⊥DE ，故④正确；综上可得①②③④正确，共4个，故选D．【分析】先求出∠ACD＝60°，继而可判断△ACD是等边三角形，从而可判断①是正确的；根据①的结论，可判断四边形ABCD是平行四边形，从而可判断②是正确的；根据①的结论，可判断③正确；根据菱形的对角线互相垂直可得AC⊥BD ，再根据平移后对应线段互相平行可得∠BDE＝∠COD＝90°，进而判断④正确．4、【答案】B【考点】勾股定理，翻折变换（折叠问题），相似三角形的判定与性质，特殊角的三角函数值【解析】【解答】①∵△ABD为直角三角形，∴BD2=AD2+AB2，不是BD=AD2+AB2，故说法错误；②根据折叠可知：DE=CD=AB，∠A=∠E，∠AFB=∠EFD，∴△ABF≌△EDF，故说法正确；③根据②可以得到△ABF∽△EDF，∴＝，故说法正确；④在Rt△ABD中，∠ADB≠45°，∴AD≠BD•cos45°，故说法错误．所以正确的是②③．故选B．【分析】①直接根据勾股定理即可判定是否正确；②利用折叠可以得到全等条件证明△ABF≌△EDF；③利用全等三角形的性质即可解决问题；④在Rt△ABD中利用三角函数的定义即可判定是否正确．此题主要考查了折叠问题，也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义，它们的综合性比较强，对于学生的综合能力要求比较高，平时加强训练．5、【答案】C【考点】全等三角形的判定与性质，勾股定理，正方形的性质，锐角三角函数的定义【解析】【解答】解：∵正方形ABCD的边长为4，∴BC=CD=4，∠B=∠DCF=90°，∵AE=BF=1，∴BE=CF=4﹣1=3，在△EBC和△FCD中，∴△EBC≌△FCD（SAS），∴∠CFD=∠BEC，∴∠BCE+∠BEC=∠BCE+∠CFD=90°，∴∠DOC=90°；故①正确；若OC=OE，∵DF⊥EC，∴CD=DE，∵CD=AD＜DE（矛盾），故②错误；∵∠OCD+∠CDF=90°，∠CDF+∠DFC=90°，∴∠OCD=∠DFC，∴tan∠OCD=tan∠DFC= = ，故③正确；∵△EBC≌△FCD，∴S△EBC=S△FCD，∴S△EBC﹣S△FOC=S△FCD﹣S△FOC，即S△ODC=S四边形BEOF．故④正确．故选C．【分析】由正方形ABCD的边长为4，AE=BF=1，利用SAS易证得△EBC≌△FCD，然后全等三角形的对应角相等，易证得①∠DOC=90°正确；②由线段垂直平分线的性质与正方形的性质，可得②错误；易证得∠OCD=∠DFC，即可求得③正确；由①易证得④正确．6、【答案】C【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】由折叠可知，DF=DC=DA，∠DFE=∠C=90°，∴∠DFG=∠A=90°，∴△ADG≌△FDG，①正确；∵正方形边长是12，∴BE=EC=EF=6，设AG=FG=x，则EG=x+6，BG=12﹣x，由勾股定理得：EG2=BE2+BG2，即：（x+6）2=62+（12﹣x）2，解得：x=4∴AG=GF=4，BG=8，BG=2AG，②正确；BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，③错误；S△GBE=×6×8=24，S△BEF=•S△GBE==，④正确．故选：C．【分析】根据正方形的性质和折叠的性质可得AD=DF，∠A=∠GFD=90°，于是根据“HL”判定△ADG≌△FDG，再由GF+GB=GA+GB=12，EB=EF，△BGE为直角三角形，可通过勾股定理列方程求出AG=4，BG=8，进而求出△BEF的面积，再抓住△BEF是等腰三角形，而△GED显然不是等腰三角形，判断③是错误的．7、【答案】C【考点】等边三角形的判定与性质，含30度角的直角三角形，平行四边形的性质【解析】【解答】∵四边形ABCD是平行四边形，∴∠ABC=∠ADC=60°，∠BAD=120°，∵AE平分∠BAD，∴∠BAE=∠EAD=60°∴△ABE是等边三角形，∴AE=AB=BE，∵AB=BC，∴AE=BC，∴∠BAC=90°，∴∠CAD=30°，故①正确；∵AC⊥AB，∴S▱ABCD=AB•AC，故②正确，∵AB=BC，OB=BD，∵BD＞BC，∴AB≠OB，故③错误；∵CE=BE，CO=OA，∴OE=AB，∴OE=BC，故④正确．故选：C．【分析】由四边形ABCD是平行四边形，得到∠ABC=∠ADC=60°，∠BAD=120°，根据AE平分∠BAD，得到∠BAE=∠EAD=60°推出△ABE是等边三角形，由于AB=BC，得到AE=BC，得到△ABC是直角三角形，于是得到∠CAD=30°，故①正确；由于AC⊥AB，得到S▱ABCD=AB•AC，故②正确，根据AB=BC，OB=BD，且BD＞BC，得到AB≠OB，故③错误；根据三角形的中位线定理得到OE=AB，于是得到OE=BC，故④正确．8、【答案】D【考点】全等三角形的判定与性质，角平分线的性质，正方形的判定【解析】【解答】如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，∴①不正确；∵AD是△ABC的角平分线，∴∠EAD∠FAD，在△AED和△AFD 中，∴△AED≌△AFD（AAS），∴AE=AF，DE=DF，∴AE+DF=AF+DE，∴④正确；在△AEO和△AFO中，，∴△AE0≌△AF0（SAS），∴EO=FO，又∵AE=AF，∴AO是EF的中垂线，∴AD⊥EF，∴②正确；∵当∠A=90°时，四边形AEDF的四个角都是直角，∴四边形AEDF是矩形，又∵DE=DF，∴四边形AEDF是正方形，∴③正确．综上，可得正确的是：②③④．故选：D．【分析】①如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，所以①不正确．②首先根据全等三角形的判定方法，判断出△AED≌△AFD，AE=AF，DE=DF；然后根据全等三角形的判定方法，判断出△AE0≌△AFO，即可判断出AD⊥EF．③首先判断出当∠A=90°时，四边形AEDF的四个角都是直角，四边形AEDF是矩形，然后根据DE=DF，判断出四边形AEDF是正方形即可．④根据△AED≌△AFD，判断出AE=AF，DE=DF，即可判断出AE+DF=AF+DE成立，据此解答即可．9、【答案】B【考点】全等三角形的判定与性质，正方形的性质，相似三角形的判定与性质【解析】【解答】∵四边形ABCD是正方形，∴∠B=∠DCB=90°，AB=BC，∵AG=CE，∴BG=BE，由勾股定理得：BE=GE，∴①错误；∵BG=BE，∠B=90°，∴∠BGE=∠BEG=45°，∴∠AGE=135°，∴∠GAE+∠AEG=45°，∵AE⊥EF，∴∠AEF=90°，∵∠BEG=45°，∴∠AEG+∠FEC=45°，∴∠GAE=∠FEC，在△GAE和△CEF中∴△GAE≌△CEF，∴②正确；∴∠AGE=∠ECF=135°，∴∠FCD=135°﹣90°=45°，∴③正确；∵∠BGE=∠BEG=45°，∠AEG+∠FEC=45°，∴∠FEC＜45°，∴△GBE和△ECH不相似，∴④错误；即正确的有2个．故选B．【分析】根据正方形的性质得出∠B=∠DCB=90°，AB=BC，求出BG=BE ，根据勾股定理得出BE=GE，即可判断①；求出∠GAE+∠AEG=45°，推出∠GAE=∠FEC，根据SAS推出△GAE≌△CEF，即可判断②；求出∠AGE=∠ECF=135°，即可判断③；求出∠FEC＜45°，根据相似三角形的判定得出△GBE和△ECH不相似，即可判断④．10、【答案】A【考点】全等三角形的判定与性质，圆心角、弧、弦的关系，相似三角形的判定与性质【解析】【解答】连接OP、OC、OA、OD、OB、CD、AB．∵PC•PA=PD•PB（相交弦定理），PA=PB（已知），∴PC=PD，∴AC=BD；在△AOC和△BOD中，∵∠AOC=∠BOD（等弦对等角），OA=OB（半径），OD=OC（半径），∴△AOC≌△BOD，∴③CA=BD；OE=OF；又∵OE⊥PA，OF⊥PB，∴①OP是∠APB的平分线；∴②PE=PF；在△PCD和△PAB中，PC：PA=PD：PB，∠DPC=∠BPA，∴△PCD∽△PAB，∴∠PDC=PBA，∴④CD∥AB；综上所述，①②③④均正确，故答案选A．【分析】①通过证明△AOC≌△BOD，再根据全等三角形的对应高相等求得OE=OF；再根据角平分线的性质证明OP是∠APB的平分线；②由角平分线的性质证明PE=PF；③通过证明△AOC≌△BOD，再根据全等三角形的对应边相等求得CA=BD；④通过证明△PCD∽△PAB，再根据相似三角形的性质对应角相等证得∠PDC=PBA；然后由平行线的判定得出结论CD∥AB．11、【答案】C【考点】全等三角形的判定与性质，翻折变换（折叠问题），锐角三角函数的定义【解析】【解答】①由折叠可得BD=DE，而DC＞DE，∴DC＞BD，∴tan∠ADB≠2，故①错误；②图中的全等三角形有△ABF≌△AEF，△ABD≌△AED，△FBD≌△FED，（由折叠可知) ∵OB⊥AC，∴∠AOB=∠COB=90°，在Rt△AOB和Rt△COB中，AB="CB" ,BO=BO ，∴Rt△AOB≌Rt△COB（HL)，则全等三角形共有4对，故②正确；③∵AB=CB，BO⊥AC，把△ABC折叠，∴∠ABO=∠CBO=45°，∠FBD=∠DEF，∴∠AEF=∠DEF=45°，∴将△DEF沿EF折叠，可得点D一定在AC上，故③错误；④∵OB⊥AC，且AB=CB，∴BO为∠ABC的平分线，即∠ABO=∠OBC=45°，由折叠可知，AD是∠BAC的平分线，即∠BAF=22.5°，又∵∠BFD为三角形ABF的外角，∴∠BFD=∠ABO+∠BAF=67.5°，易得∠BDF=180°-45°-67.5°=67.5°，∴∠BFD=∠BDF，∴BD=BF，故④正确；⑤连接CF，∵△AOF和△COF等底同高，∴S△AOF=S△COF，∵∠AEF=∠ACD=45°，∴EF∥CD，∴S△EFD=S△EFC，∴S四边形DFOE=S△COF，∴S四边形DFOE=S△AOF，故⑤正确；故正确的有3个．故选C．12、【答案】D【考点】等边三角形的性质，菱形的判定，旋转的性质【解析】【解答】解：∵将等边△ABC绕点C顺时针旋转120°得到△EDC，∴∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，∴∠ACD=120°﹣60°=60°，∴△ACD是等边三角形，∴AC=AD，AC=AD=DE=CE，∴四边形ACED是菱形，∵将等边△ABC绕点C顺时针旋转120°得到△EDC，AC=AD，∴AB=BC=CD=AD，∴四边形ABCD是菱形，∴BD⊥AC，∴①②③都正确，故选D．【分析】根据旋转和等边三角形的性质得出∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，求出△ACD是等边三角形，求出AD=AC，根据菱形的判定得出四边形ABCD和ACED都是菱形，根据菱形的判定推出AC⊥BD．本题考查了旋转的性质，菱形的性质和判定，等边三角形的性质和判定的应用，能灵活运用知识点进行推理是解此题的关键．13、【答案】D【考点】全等三角形的判定与性质，矩形的判定与性质，正方形的性质，相似三角形的判定与性质，等腰直角三角形【解析】【解答】解：∵四边形ADEF为正方形，∴∠FAD=90°，AD=AF=EF，∴∠CAD+∠FAG=90°，∵FG⊥CA，∴∠C=90°=∠ACB，∴∠CAD=∠AFG，在△FGA和△ACD中，，∴△FGA≌△ACD（AAS），∴AC=FG，①正确；∵BC=AC，∴FG=BC，∵∠ACB=90°，FG⊥CA，∴FG∥BC，∴四边形CBFG是矩形，∴∠CBF=90°，S△FAB= FB•FG= S四边形CBFG，②正确；∵CA=CB，∠C=∠CBF=90°，∴∠ABC=∠ABF=45°，③正确；∵∠FQE=∠DQB=∠ADC，∠E=∠C=90°，∴△ACD∽△FEQ，∴AC：AD=FE：FQ，∴AD•FE=AD2=FQ•AC，④正确；故选：D．【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质；熟练掌握正方形的性质，证明三角形全等和三角形相似是解决问题的关键．由正方形的性质得出∠FAD=90°，AD=AF=EF，证出∠CAD=∠AFG，由AAS证明△FGA≌△ACD，得出AC=FG，①正确；证明四边形CBFG是矩形，得出S△FAB= FB•FG= S四边形CEFG，②正确；由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°，③正确；证出△ACD∽△FEQ，得出对应边成比例，得出D•FE=AD2=FQ•AC，④正确．14、【答案】B【考点】全等三角形的判定与性质，线段垂直平分线的性质，等腰三角形的性质，矩形的性质【解析】【解答】解：①∵矩形ABCD中，O为AC中点，∴OB=OC，∵∠COB=60°，∴△OBC是等边三角形，∴OB=BC，∵FO=FC，∴FB垂直平分OC，故①正确；②∵FB垂直平分OC，∴△CMB≌△OMB，∵OA=OC，∠FOC=∠EOA，∠DCO=∠BAO，∴△FOC≌△EOA，∴FO=EO，易得OB⊥EF，∴△OMB≌△OEB，∴△EOB≌△CMB，故②正确；③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°，BF=BE，∴△BEF是等边三角形，∴BF=EF，∵DF∥BE且DF=BE，∴四边形DEBF是平行四边形，∴DE=BF，∴DE=EF，故③正确；④在直角△BOE中∵∠3=30°，∴BE=2OE，∵∠OAE=∠AOE=30°，∴AE=OE，∴BE=2AE，∴S△AOE：S△BCM=S△AOE：S△BOE=1：2，故④错误；所以其中正确结论的个数为3个；故选B【分析】①利用线段垂直平分线的性质的逆定理可得结论；②证△OMB≌△OEB得△EOB≌△CMB；③先证△BEF是等边三角形得出BF=EF，再证▱DEBF得出DE=BF，所以得DE=EF；④由②可知△BCM≌△BEO，则面积相等，△AOE和△BEO属于等高的两个三角形，其面积比就等于两底的比，即S△AOE：S△BOE=AE：BE，由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE，得出结论S△AOE：S△BOE=AE：BE=1：2．本题综合性比较强，既考查了矩形的性质、等腰三角形的性质，又考查了全等三角形的性质和判定，及线段垂直平分线的性质，内容虽多，但不复杂；看似一个选择题，其实相当于四个证明题，属于常考题型．15、【答案】B【考点】菱形的判定与性质，翻折变换（折叠问题），等腰直角三角形【解析】【解答】解：∵四边形ABCD是正方形，∴∠GAD=∠ADO=45°，由折叠的性质可得：∠ADG= ∠ADO=22.5°，故①正确．∵由折叠的性质可得：AE=EF，∠EFD=∠EAD=90°，∴AE=EF＜BE，∴AE＜AB，∴＞2，故②错误．∵∠AOB=90°，∴AG=FG＞OG，△AGD与△OGD同高，∴S△AGD＞S△OGD，故③错误．∵∠EFD=∠AOF=90°，∴EF∥AC，∴∠FEG=∠AGE，∵∠AGE=∠FGE，∴∠FEG=∠FGE，∴EF=GF，∵AE=EF，∴AE=GF，故④正确．∵AE=EF=GF，AG=GF，∴AE=EF=GF=AG，∴四边形AEFG是菱形，∴∠OGF=∠OAB=45°，∴EF=GF= OG，∴BE= EF= ×OG=2OG．故⑤正确．∵四边形AEFG是菱形，∴AB∥GF，AB=GF．∵∠BAO=45°，∠GOF=90°，∴△OGF时等腰直角三角形．∵S△OGF=1，∴OG2=1，解得OG= ，∴BE=2OG=2 ，GF= ==2，∴AE=GF=2，∴AB=BE+AE=2 +2，∴S正方形ABCD=AB2=（2 +2）2=12+8 ，故⑥错误．∴其中正确结论的序号是：①④⑤．故选B．【分析】①由四边形ABCD是正方形，可得∠GAD=∠ADO=45°，又由折叠的性质，可求得∠ADG的度数；②由AE=EF＜BE，可得AD＞2AE；③由AG=GF＞OG，可得△AGD的面积＞△OGD的面积；④由折叠的性质与平行线的性质，易得△EFG是等腰三角形，即可证得AE=GF；⑤易证得四边形AEFG是菱形，由等腰直角三角形的性质，即可得BE=2OG；⑥根据四边形AEFG是菱形可知AB∥GF，AB=GF，再由∠BAO=45°，∠GOF=90°可得出△OGF时等腰直角三角形，由S△OGF=1求出GF的长，进而可得出BE及AE的长，利用正方形的面积公式可得出结论．此题考查的是四边形综合题，涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识．此题综合性较强，难度较大，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．16、【答案】B【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】解：∵E，F分别是正方形ABCD边BC，CD的中点，∴CF=BE，在△ABE和△BCF中，，∴Rt△ABE≌Rt△BCF（SAS），∴∠BAE=∠CBF，AE=BF，故①正确；又∵∠BAE+∠BEA=90°，∴∠CBF+∠BEA=90°，∴∠BGE=90°，∴AE⊥BF，故②正确；根据题意得，FP=FC，∠PFB=∠BFC，∠FPB=90°∵CD∥AB，∴∠CFB=∠ABF，∴∠ABF=∠PFB，∴QF=QB，令PF=k（k＞0），则PB=2k在Rt△BPQ中，设QB=x，∴x2=（x﹣k）2+4k2，∴x= ，∴sin=∠BQP= = ，故③正确；∵∠BGE=∠BCF，∠GBE=∠CBF，∴△BGE∽△BCF，∵BE= BC，BF= BC，∴BE：BF=1：，∴△BGE的面积：△BCF的面积=1：5，∴S四边形ECFG=4S△BGE，故④错误．故选：B．【分析】首先证明△ABE≌△BCF，再利用角的关系求得∠BGE=90°，即可得到①AE=BF；②AE⊥BF；△BCF沿BF对折，得到△BPF，利用角的关系求出QF=QB，解出BP，QB，根据正弦的定义即可求解；根据AA可证△BGE与△BCF相似，进一步得到相似比，再根据相似三角形的性质即可求解．本题主要考查了四边形的综合题，涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点，解决的关键是明确三角形翻转后边的大小不变，找准对应边，角的关系求解．17、【答案】D【考点】二次函数的图象，二次函数的性质，菱形的判定【解析】【解答】解：①∵抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣2，0）、B（1，0），∴该抛物线的对称轴为x=﹣=﹣0.5，∴a=b，a﹣b=0，①正确；②∵抛物线开口向下，且抛物线与x轴交于点A（﹣2，0）、B（1，0），∴当﹣2＜x＜1时，y＞0，②正确；③∵点A、B关于x=0.5对称，∴AM=BM，又∵MC=MD，且CD⊥AB，∴四边形ACBD是菱形，③正确；④当x=﹣3时，y＜0，即y=9a﹣3b+c＜0，④错误．综上可知：正确的结论为①②③．故选D．【分析】①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=﹣=﹣0.5，由此即可得出a=b，①正确；②根据抛物线的开口向下以及抛物线与x轴的两交点坐标，即可得出当﹣2＜x＜1时，y＞0，②正确；③由AB关于x=0.5对称，即可得出AM=BM，再结合MC=MD以及CD⊥AB，即可得出四边形ACBD是菱形，③正确；④根据当x=﹣3时，y＜0，即可得出9a﹣3b+c＜0，④错误．综上即可得出结论．本题考查了二次函数的图象、二次函数的性质以及菱形的判定，解题的关键是逐条分析四条结论是否正确．本题属于中档题，难度不大，解决该题型题目时，根据给定的函数图象结合二次函数的性质逐条分析给定的结论是关键．18、【答案】D【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题）【解析】【解答】解：∵正方形ABCD的边长为6，CE=2DE，∴DE=2，EC=4，∵把△ADE沿AE折叠使△ADE落在△AFE的位置，∴AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，在Rt△ABG和Rt△AFG中，∴Rt△ABG≌Rt△AFG（HL），∴GB=GF，∠BAG=∠FAG，∴∠GAE=∠FAE+∠FAG= ∠BAD=45°，所以①正确；设BG=x，则GF=x，C=BC﹣BG=6﹣x，在Rt△CGE中，GE=x+2，EC=4，CG=6﹣x，∵CG2+CE2=GE2，∴（6﹣x）2+42=（x+2）2，解得x=3，∴BG=3，CG=6﹣3=3∴BG=CG，所以②正确；∵EF=ED，GB=GF，∴GE=GF+EF=BG+DE，所以③正确；∵GF=GC，∴∠GFC=∠GCF，又∵Rt△ABG≌Rt△AFG，∴∠AGB=∠AGF，而∠BGF=∠GFC+∠GCF，∴∠AGB+∠AGF=∠GFC+∠GCF，∴∠AGB=∠GCF，∴CF∥AG，所以④正确；过F作FH⊥DC∵BC⊥DH，∴FH∥GC，∴△EFH∽△EGC，∴，EF=DE=2，GF=3，∴EG=5，∴△EFH∽△EGC，∴相似比为：= ，∴S△FGC=S△GCE﹣S△FEC= ×3×4﹣×4×（×3）= =3.6，所以⑤正确．故正确的有①②③④⑤，故选：D．【分析】先计算出DE=2，EC=4，再根据折叠的性质AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，然后根据“HL”可证明Rt△ABG≌Rt△AFG，则GB=GF，∠BAG=∠FAG，所以∠GAE= ∠BAD=45°；GE=GF+EF=BG+DE；设BG=x，则GF=x，CG=BC﹣BG=6﹣x，在Rt△CGE中，根据勾股定理得（6﹣x）2+42=（x+2）2，解得x=3，则BG=CG=3，则点G为BC的中点；同时得到GF=GC，根据等腰三角形的性质得∠GFC=∠GCF，再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF，然后根据三角形外角性质得∠BGF=∠GFC+∠GCF，易得∠AGB=∠GCF，根据平行线的判定方法得到CF∥AG；过F作FH⊥DC，则△EFH∽△EGC，△EFH∽△EGC，由相似比为，可计算S△FGC．本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了三角形全等的判定与性质、勾股定理和正方形的性质．19、【答案】C【考点】垂径定理，圆周角定理，相似三角形的判定与性质，解直角三角形【解析】【解答】解：①∵AB是⊙O的直径，弦CD⊥AB，∴，DG=CG，∴∠ADF=∠AED，∵∠FAD=∠DAE（公共角），∴△ADF∽△AED；故①正确；②∵= ，CF=2，∴FD=6，∴CD=DF+CF=8，∴CG=DG=4，∴FG=CG﹣CF=2；故②正确；③∵AF=3，FG=2，∴AG= = ，∴在Rt△AGD中，tan∠ADG= = ，∴tan∠E= ；故③错误；④∵DF=DG+FG=6，AD= = ，∴S△ADF= DF•AG= ×6×=3 ，∵△ADF∽△AED，∴=（）2，∴= ，∴S△AED=7 ，∴S△DEF=S△AED﹣S△ADF=4 ；故④正确．故选C．【分析】①正确．由AB是⊙O的直径，弦CD⊥AB，根据垂径定理可得：，DG=CG，继而证得△ADF∽△AED；②正确．由= ，CF=2，可求得DF的长，继而求得CG=DG=4，则可求得FG=2；③错误．由勾股定理可求得AG的长，即可求得tan∠ADF的值，继而求得tan∠E=．④首先求得△ADF的面积，由相似三角形面积的比等于相似比的平方，即可求得△ADE的面积，继而求得S△DEF=4 ．20、【答案】D【考点】垂径定理，圆周角定理，相似三角形的判定与性质【解析】【解答】解：∵在⊙O中，点C是的中点，∴= ，∴∠CAD=∠ABC，故①正确；∵≠ ，∴≠ ，∴AD≠BC，故②错误；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB，∴∠ACE+∠CAE=∠ABC+∠CAE=90°，∴∠ACE=∠ABC，又∵C为的中点，∴= ，∴∠CAP=∠ABC，∴∠ACE=∠CAP，∴AP=CP，∵∠ACQ=90°，∴∠ACP+∠PCQ=∠CAP+∠PQC=90°，∴∠PCQ=∠PQC，∴PC=PQ，∴AP=PQ，即P为Rt△ACQ斜边AQ的中点，∴P为Rt△ACQ的外心，故③正确；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB∴根据射影定理，可得AC2=AE•AB，故④正确；如图，连接BD，则∠ADG=∠ABD，∵≠ ，∴≠ ，∴∠ABD≠∠BAC，∴∠ADG≠∠BAC，又∵∠BAC=∠BCE=∠PQC，∴∠ADG≠∠PQC，∴CB与GD不平行，故⑤错误．故答案为：D．【分析】在同圆或等圆中，同弧或等弧所对的圆周角相等，据此推理可得①正确，②错误；通过推理可得∠ACE=∠CAP，得出AP=CP，再根据∠PCQ=∠PQC，可得出PC=PQ，进而得到AP=PQ，即P为Rt△ACQ斜边AQ的中点，故P为Rt△ACQ 的外心，即可得出③正确；连接BD，则∠ADG=∠ABD，根据∠ADG≠∠BAC，∠BAC=∠BCE=∠PQC，可得出∠ADG≠∠PQC，进而得到CB与GD不平行，可得⑤错误．。

数学人教版七年级下册与三角形面积有关的多结论问题

人教版数学七年级下册第七章平面直角坐标系与三角形面积有关的多结论问题一授课人：武汉二中广雅中学陆媛教学目标：1、结合平面直角坐标系中，点坐标的含义，解决简单的面积问题。

2、在计算和画图中探寻与三角形面积有关的几何模型；提高学生分类讨论和总结归纳的能力。

3、尝试用总结的几何模型，构造满足条件的图形；提高学生实际操作的能力。

教学重点：1、提高学生数学建模的思想。

2、逐步消除学生画图中的“盲区”，增强学生画图时的分类意识。

教学难点：从特殊图形中提炼出与之有关的几何模型。

教学方法：讲练结合法。

教学过程：一、回顾旧知：1、回顾小学学习的三角形面积的计算方法。

2、说出以下三角形的面积公式：二、引入新课：例一、在平面直角坐标系中，ΔABC 的面积为2，点A （0，0）、点B （1，2）、点C 在坐标轴上。

请画出所有满足条件的ΔABC ，并求出点C 的坐标。

分析：1、点C轴、y 轴两种情况画图。

2、思考：点C 在线段AB 的哪一侧呢？3、男、女生分别就点C 在x 轴、y 轴两种情况画图计算。

（学生代表演板）4、观察分类后的两个图形，思考：（图三）当AO 与BC 满足什么位置关系时，ΔAOB 的面积等于ΔAOC 的面积？三、抽丝剥茧1、几何画板演示：在拖动点A 时，对比测量的ΔAOB 和ΔAOC 的面积。

2、利用三角形面积公式，计算两个三角形的面积。

3、探究归纳几何模型一：4、四个ΔABC 合在一个坐标系上，选取线段AB 同侧的两个三角形，连接C 2C 3，观察 C 2C 3与AB 的位置关系。

5、几何画板演示：在拖动线段AB 时，对比测量的ΔABC 和ΔABD 的面积。

6、探究归纳几何模型二：四、学以致用：例二：在平面直角坐标系中，ΔABC 的形状和位置如图所示，点C 在x 轴上，点D 在坐标轴上，并且ΔABD 的面积等于ΔABC 的面积，你能画出所有满足条件的ΔABD 吗？你能试着总结：将所有点D 找全的方法吗？依据：等底同高的两个三角形面积相等。

专题02 几何图形的多结论问题(解析版)

专题二几何图形的多结论问题【专题解读】几何类多结论判断题考查的知识点较多，主要以圆和四边形为核心开放研究型问题，所谓“开放”简单来说就是答案不唯一的，解题的方向不确定，条件或者结论不止一种情况的试题，解答此类试题时，需要对问题全方位、多层次、多角度思考审视，尽量找到解决问题的方法，根据开放性的试题的特点，主要有如下几种类型：条件开放性、结论开放性、选择开放型、综合开放型，属于中考必考题型.（2020•广东二模）如图，已知▱ABCD的对角线AC、BD交于点O，DE平分∠ADC 交BC于点E，交AC于点F，且∠BCD＝60°，BC＝2CD，连结OE．下列结论：①OE∥AB；②S平行四边形ABCD＝BD•CD；③AO＝2BO；④S△DOF＝2S△EOF．其中成立的个数有（C）A．1个B．2个C．3个D．4个【思路点拨】①证明BE＝CE，OA＝OC，根据三角形中位线定理可得结论正确；②证明BD⊥CD，可得结论正确；③设AB＝x，分别表示OA和OB的长，可以作判断；④先根据平行线分线段成比例定理可得：DF＝2EF，由同高三角形面积的比等于对应底边的比可作判断．【自主解答】①∵四边形ABCD是平行四边形，∴AD∥BC，OA＝OC，∴∠ADC+∠BCD＝180°，∵∠BCD＝60°，∴∠ADC＝120°，∵DE平分∠ADC，∴∠CDE＝60°＝∠BCD，∴△CDE是等边三角形，∴CE＝CD，∵BC＝2CD，∴BE＝CE，∵OA＝OC，∴OE∥AB；故①正确；②∵△DEC是等边三角形，∴∠DEC＝60°＝∠DBC+∠BDE，∵BE＝EC＝DE，∴∠DBC＝∠BDE＝30°，∴∠BDC＝30°+60°＝90°，∴BD⊥CD，∴S平行四边形ABCD＝BD•CD；故②正确；③设AB＝x，则AD＝2x，则BD=√3x，∴OB=√32x，由勾股定理得：AO=(√3x2)=√72x，故③不正确；④∵AD ∥EC ，∴AD EC =DF EF =21，∴DF ＝2EF ，∴S △DOF ＝2S △EOF ．故④正确；故选：C ．1．（2020•深圳模拟）在边长为2的正方形ABC D 中，P 为AB 上的一动点，E 为A D 中点，PE 交CD 延长线于Q ，过E 作EF ⊥PQ 交BC 的延长线于F ，则下列结论：①△APE ≌△DQE ；②PQ ＝EF ；③当P 为A B 中点时，CF =√2；④若H 为QC 的中点，当P 从A 移动到B 时，线段EH 扫过的面积为1，其中正确的有（）A ．1个B ．2个C ．3个D ．4个【答案】B【接卸】①∵四边形ABCD 是正方形，∴AB ＝BC ＝CD ＝AD ，∠A ＝∠B ＝∠ADC ＝90°，∴∠A ＝∠EDQ ＝90°，∵E 为A D 中点，∴AE ＝ED ，在△APE 和△DQE 中，{∠A =∠EDQAE =ED ∠AEP =∠DEQ，∴△APE ≌△DQE （ASA ），故①正确；②作PG ⊥CD 于G ，EM ⊥BC 于M ，如图1所示：∴∠PGQ ＝∠EMF ＝90°，∵EF ⊥PQ ，∴∠PEF ＝90°，∴∠PEM +∠MEF ＝90°，∵∠GPE +∠MEP ＝90°，∴∠GPE ＝∠MEF ，在△EFM 和△PQG 中，{∠EMF =∠PGQEM =PG ∠MEF =∠GPQ，∴△EFM ≌△PQG （ASA ），∴EF ＝PQ ，故②正确；③连接QF ，如图2所示：则QF ＝PF ，PB 2+BF 2＝QC 2+CF 2，设CF ＝x ，则（2+x ）2+12＝32+x 2，∴x ＝1，故③错误；④如图3所示：当P 在A 点时，Q 与D 重合，QC 的中点H 在DC 的中点S 处，当P 运动到B 时，QC 的中点H 与D 重合，故EH 扫过的面积为△ESD 的面积为12，故④错误；故选：B ．2．（2020•灌南县一模）如图，正方形ABC D 中，E 、F 分别为BC 、CD 的中点，AF 与DE 交于点G ．则下列结论中：①AF ⊥DE ；②AD ＝BG ；③GE +GF =√2GC ；④S △AGB ＝2S 四边形ECFG ．其中正确的是（）A ．1个B ．2个C ．3个D ．4个【答案】D【解析】∵正方形ABCD ，E ，F 均为中点,∴AD ＝BC ＝DC ，EC ＝DF =12BC,∵在△ADF 和△DCE 中，{AD =DC∠ADF =∠DCE DF =CE，∴△ADF ≌△DCE （SAS ），∴∠AFD ＝∠DEC ，∵∠DEC +∠CDE ＝90°，∴∠AFD +∠CDE ＝90°＝∠DGF ，∴AF ⊥DE ，故①正确；如图1，过点B 作BH ∥DE 交AD 于H ，交AF 于K ，∵AF ⊥DE ，BH ∥DE ，E 是BC 的中点，∴BH ⊥AG ，H 为AD 的中点，∴BH 是AG 的垂直平分线，∴BG ＝AB ＝AD ，故②正确，如图2，延长DE 至M ，使得EM ＝GF ，连接CM ，∵∠AFD ＝∠DEC ，∴∠CEM ＝∠CFG ，又∵E ，F 分别为BC ，DC 的中点，∴CF ＝CE ，∵在△CEM 和△CFG 中，{CE =CF∠CEM =∠CFG EM =FG，∴△CEM ≌△CFG （SAS ），∴CM ＝CG ，∠ECM ＝∠GCF ，∵∠GCF +∠BCG ＝90°，∴∠ECM +∠BCG ＝∠MCG ＝90°，∴△MCG 为等腰直角三角形，∴GM ＝GE +EM ＝GE +GF =√2GC ，故③正确；如图3，过G 点作TL ∥AD ，交AB 于T ，交DC 于L ，则GL ⊥AB ，GL ⊥DC ，设EC ＝x ，则DC ＝2x ，DF ＝x ，由勾股定理得DE =√5x ，由DE ⊥GF ，易证得△DGF ∽△DCE ， ∴DE DF =GF EC =√5x x ，∴S △DEC S △DGF =(√51)2=51， ∴S △DGF =15S △DEC ，∴S 四边形ECFG ＝S △DEC ﹣S △DGF =45S △DEC ，∵S △DEC =12⋅2x ⋅x =x 2，∴S 四边形ECFG =45x 2，S △DGF =15x 2∵DF ＝x ， ∴GL =15x 212x =25x ，∴TG ＝2x −25x =85x ，∴S △AGB =12•AB •TG =12•2x •85x =85x 2，∴S △AGB ＝2S 四边形ECFG 故④正确，故选：D ．3．（2020•东莞市一模）如图，在菱形ABC D 中，∠BAD ＝60°，AC 与BD 交于点O ，E 为CD 延长线上的一点，且CD ＝DE ，连接BE 分别交AC 、AD 于点F 、G ，连接OG ，则下列结论中一定成立的是 ①④ ．（把所有正确结论的序号都填在横线上）①OG =12AB ；②与△EGD 全等的三角形共有5个；③S 四边形ODGF ＞S △ABF ； ④由点A 、B 、D 、E 构成的四边形是菱形．【答案】①④【解析】∵四边形ABCD 是菱形，∴AB ＝BC ＝CD ＝DA ，AB ∥CD ，OA ＝OC ，OB ＝OD ，AC ⊥BD ，∴∠BAG ＝∠EDG ，△ABO ≌△BCO ≌△CDO ≌△AOD ，∵CD ＝DE ，∴AB ＝DE ，在△ABG 和△DEG 中，{∠BAG =∠EDG ∠AGB =∠DGE AB =DE，∴△ABG ≌△DEG （AAS ），∴AG ＝DG ，∴OG 是△ACD 的中位线，∴OG =12CD =12AB ，①正确；∵AB ∥CE ，AB ＝DE ，∴四边形ABDE是平行四边形，∵∠BCD＝∠BAD＝60°，∴△ABD、△BCD是等边三角形，∴AB＝BD＝AD，∠ODC＝60°，∴OD＝AG，四边形ABDE是菱形，④正确；∴AD⊥BE，由菱形的性质得：△ABG≌△BDG≌△DEG，在△ABG和△DCO中，{OD=AG∠ODC=∠BAG=60°AB=DC，∴△ABG≌△DCO（SAS），∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG，②不正确；∵OB＝OD，AG＝DG，∴OG是△ABD的中位线，∴OG∥AB，OG=12AB，∴△GOD∽△ABD，△ABF∽△OGF，∴△GOD的面积=14△ABD的面积，△ABF的面积＝△OGF的面积的4倍，AF：OF＝2：1，∴△AFG的面积＝△OGF的面积的2倍，又∵△GOD的面积＝△AOG的面积＝△BOG的面积，∴S四边形ODGF＝S△ABF；不正确；正确的是①④．故答案为：①④．4．（2020•天河区一模）如图，在正方形ABC D中，对角线AC，BD交于点O，点E，F分别在AB，BD上，且△ADE≌△FDE，DE交AC于点G，连接GF．得到下列四个结论：①∠ADG＝22.5°；②S△AGD＝S△OGD；③BE＝2OG；④四边形AEFG是菱形，其中正确的结论是①③④．（填写所有正确结论的序号）【答案】①③④．【解析】∵四边形ABCD是正方形，∴∠GAD＝∠ADO＝45°，∴由△ADE≌△FDE，可得：∠ADG=12∠ADO＝22.5°，故①正确；∵△ADE≌△FDE，∴AD＝FD，∠ADG＝∠FDG，又∵GD＝GD，∴△ADG≌△FDG（SAS），∴S△AGD＞S△OGD，故②错误；∵△ADE≌△FDE，∴EA＝EF，∵△ADG≌△FDG，∴GA＝GF，∠AGD＝∠FGD，∴∠AGE＝∠FGE．∵∠EFD＝∠AOF＝90°，∴EF∥AC，∴∠FEG＝∠AGE，∴∠FGE＝∠FEG，∴EF＝GF，∴EF＝GF＝EA＝GA，∴四边形AEFG是菱形，故④正确；∵四边形AEFG是菱形，∴AE∥FG，∴∠OGF＝∠OAB＝45°，∴△OGF为等腰直角三角形，∴FG=√2OG，∴EF=√2OG，∵△BFE为等腰直角三角形，∴BE=√2EF=√2×√2OG＝2OG，∴③正确．综上，正确的有①③④．故答案为：①③④．5．（2020•福田区一模）如图，正方形ABC D中，E是BC延长线上一点，在AB上取一点F，使点B关于直线EF的对称点G落在AD上，连接EG交CD于点H，连接BH交EF于点M，连接CM．则下列结论，①∠1＝∠2；②∠3＝∠4；③GD=√2CM；④若AG＝1，GD ＝2，则BM=√5，其中正确的是．.【答案】①②③④【解析】如图1中，过点B作BK⊥GH于K．∵B，G关于EF对称，∴EB＝EG，∴∠EBG＝∠EGB，∵四边形ABCD是正方形，∴AB＝BC，∠A＝∠ABC＝∠BCD＝90°，AD∥BC，∴∠AGB＝∠EBG，∴∠AGB＝∠BGK，∵∠A＝∠BKG＝90°，BG＝BG，∴△BAG≌△BKG（AAS），∴BK＝BA＝BC，∠ABG＝∠KBG，∵∠BKH＝∠BCH＝90°，BH＝BH，∴Rt△BHK≌Rt△BHC（HL），∴∠1＝∠2，∠HBK＝∠HBC，故①正确，∴∠GBH＝∠GBK+∠HBK=1∠ABC＝45°，2过点M作MQ⊥GH于Q，MP⊥CD于P，MR⊥BC于R．∵∠1＝∠2，∴MQ＝MP，∵∠MEQ＝∠MER，∠BCD＝45°，∴MQ＝MR，∴MP＝MR，∴∠4＝∠MCP=12∴∠GBH＝∠4，故②正确，如图2中，过点M作MW⊥AD于W，交BC于T．∵B，G关于EF对称，∴BM＝MG，∵CB＝CD，∠4＝∠MCD，CM＝CM，∴△MCB≌△MCD（SAS），∴BM＝DM，∴MG＝MD，∵MW⊥DG，∴WG＝WD，∵∠BTM＝∠MWG＝∠BMG＝90°，∴∠BMT+∠GMW＝90°，∵∠GMW+∠MGW＝90°，∴∠BMT＝∠MGW，∵MB＝MG，∴△BTM≌△MWG（AAS），∴MT＝WG，∵MC=√2TM，DG＝2WG，∴DG=√2CM，故③正确，∵AG＝1，DG＝2，∴AD＝AB＝TM＝3，EM＝WD＝TM＝1，BT＝AW＝2，∴BM=√BT2+MT2=√22+12=√5，故④正确，故答案为：①②③④．。

上八年级多结论问题

专题几何多结论问题1.如图，已知：△ABE 是等边三角形，BC 平分∠GBE, DF ∥AB. 下列结论：①△BGC 是等边三角形；②BO+OC=GO;③BO 平分∠AOG;④AF-EF=BF ，成立的是( ) A ．①②③④ B ．①②④ C ．①②③ D ．①③2.如图4，Rt△ACB 中，∠ACB=90°，△ABC 的角平分线AD 、BE 相交于点p ，过p 作PF⊥AD交BC 的延长线于点F ，交AC 于点H ，则下列结论：①∠A PB=135°；②PF=PA；③AH+BD=AB；④S 四边形ABDE =23S △ABP ，其中正确的是（） A ．①③ B ．①②④C ．①②③D ．②③3.如图，P 为等腰RT △ABC 外一点，∠BAC=90°，连PB 、PC 、PA ，PA 交BC 于E 点，且∠APC=45°。

下列结论：①∠BPA=45°；②PCPBS S ACE ABE =∆∆；③PB+PC=PA. 其中正确的是（）.A ．①B ．①②C ．②D ．①②③ 4.如图，C 为线段AE 上一动点（不与点A ，E 重合），在AE 同侧分别作正△ABC 和正△CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连结PQ ．以下五个结论：① AD =BE ；② PQ ∥AE ；③ AP =BQ ；④ DE =DP ；⑤ ∠AOB =60°．一定成立的结论有____________（把你认为正确的序号都填上）．5.如图,在⊿ABC 中,AB=AC,D 为BC 上的一点,BF=CD,CE=BD,那么∠EDF=( ) A.90°-½∠A B.90°-∠A C.180°-∠A D.45°-∠AA BF ED EB DC F C A (第11题图) (第12题图)6.如图,在⊿ABC 中,AC=BC,∠ACB=90°,AD 平分∠BAC,BE ⊥AD,交AC 的延长线于点F,且垂足为E ，则下结论：①AD=BF ， CF=CD ， AC+CD=AB ，④BE=CF ，⑤BF=2BE.其中正确的结论的D C B AE F PHPECBAABCEDO PQ个数是( )个. A.1 B.2 C.3 D.47.如图：D 、E 分别是△ABC 的边BC ，AC 上的点，若∠B=∠C ，∠ADE=∠AED ，则（） A.当∠B 为定值时，∠CDE 为定值 B.当∠α为定值时，∠CDE 为定值C.当∠β为定值时，∠CDE 为定值D.当∠γ为定值时，∠CDE 为定值8．已知，如图，△ABC 中，AB =AC ，AD 是角平分线，BE =CF ，则下列说法正确的有几个（）（1）AD 平分∠EDF ；（2）△EBD ≌△FCD ；（3）BD =CD ；（4）AD ⊥BC ．A ．1个B ．2个C ．3个D ．4个9.如图，在Rt △AEB 和Rt △AFC 中，BE 与AC 相交于点M ，与CF 相交于点D ，AB 与CF 相交于点N ，∠E =∠F=90°，∠EAC=∠FAB ，AE=AF ．给出下列结论：①∠B=∠C ；②CD=DN ；③BE =CF ；④△CAN ≌△ABM ．其中正确的结论是（）A ．①③④ B ．②③④ C ．①②③ D ．①②④10.在直角梯形ABCD 中，AD BC ∥，90ABC AB BC E ∠==°，，为AB 边上一点，15BCE ∠=°，且AE AD =．连接DE 交对角线AC 于H ，连接BH ．下列结论：①ACD ACE △≌△； ②CDE △为等边三角形； ③2EH BE =； ④EDC EHC S AHS CH=△△．其中结论正确的是（）A ．只有①②B ．只有①②④C ．只有③④D ．①②③④11.如图，在等腰Rt ABC △中，908C AC ∠==°，，F 是AB 边上的中点，点D 、E 分别在AC 、BC 边上运动，且保持AD CE =．连接DE 、DF 、EF ．在此运动变化的过程中，下列结论：①DFE △是等腰直角三角形；②四边形CDFE 不可能为正方形， ③DE 长度的最小值为4；④四边形CDFE 的面积保持不变； ⑤△CDE 面积的最大值为8．其中正确的结论是（） A ．①②③ B ．①④⑤ C ．①③④ D ．③④⑤DCBE AHa γβE A B C D AB CE MF D N第11题D FE B A C 第12题EF DC B A12．如图，∠BAC 与∠CBE 的平分线相交于点P ，BE=BC ，PB 与CE 交于点H ，PG ∥AD 交BC 于F ，交AB 于G ，下列结论：①GA=GP ；②::PAC PAB S S AC AB V V ；③BP 垂直平分CE ；④FP=FC ；其中正确的判断有（）A.只有①②B.只有③④C.只有①③④D.①②③④13.如图，将30°的直角三角尺ABC 绕直角顶点A 逆时针旋转到ADE 的位置，使B 点的对应点D 落在BC 边上，连接EB 、EC ，则下列结论：①∠DAC＝∠DCA；②ED 为AC 的垂直平分线；③EB 平分∠AED；④ED＝2AB 。

二次函数多结论压轴小题精选30道(必考点分类集训)(原卷版)—2024-2025学年九年级数学上册

二次函数多结论压轴小题精选30道1．（2024春•岳麓区校级期末）已知抛物线y ＝ax 2+bx +c 的图象如图所示，则下列结论中，正确的有（）①abc ＞0；②b 2＞4ac ；③a ﹣b +c ＜0；④2a ﹣b ＞0；⑤a +c ＜1．A ．1个B ．2个C ．3个D ．4个2．（2024•宝安区校级模拟）已知抛物线y ＝ax 2+bx +c （a ≠0）的图象如图所示，则下列结论①abc ＜0，②a +b +c ＝2，③a ＞12④0＜b ＜1中正确的有（）A ．①②B ．①②③C ．①②④D ．①②③④3．（2024•凤凰县模拟）已知二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，在下列5个结论：①abc ＜0；②b ＜a +c ；③4a +2b +c ＞0；④2c ＜3b ；⑤a +b ＜m （am +b ）（m ≠1的实数）．其中正确结论个数有（）A ．4个B ．3个C ．2个D ．1个4．（2024•汝阳县一模）图形结合法既可以由数解决形的问题，也可以由形解决数的问题．如图所示，已知二次函数y＝ax2+bx+c的图象如图所示．下列结论：①ab＞0；②4a﹣2b+c＜0；③2a﹣b＜0；④|a+c|＜|b|．其中正确的个数有（）A．1B．2C．3D．45．（2024•斗门区校级模拟）二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝1．下列结论：①abc＞0；②3a+c＞0；③（a+c）2﹣b2＜0；④a+b≤m（am+b）（m为实数）．其中结论正确的为（）A．①④B．②③④C．①②④D．①②③④6．（2024•岚山区二模）已知二次函数y＝ax2+bx+c（a≠0）与x轴的一个交点为（4，0），其对称轴为直线x＝1，其部分图象如图所示，有下列5个结论：①abc＜0；②b2﹣4ac＜0；③8a+c＝0；④若关于x 的方程ax2+bx+c＝﹣1有两个实数根x1x2，且满足x1＜x2，则x1＜﹣2，x2＞4；⑤直线y＝kx﹣4k（k≠0）经过点（0，c），则关于x的不等式ax2+（b﹣k）x+c+4k＞0的解集是0＜x＜4．其中正确结论的个数为（）A．5B．4C．3D．27．（2024•旺苍县三模）已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＞0；②b2＜4ac；③2c＜3b；④a+b＞m（am+b）（m≠1）；⑤若方程|ax2+bx+c|＝1有四个根，则这四个根的和为2．其中正确的结论有（）A．2个B．3个C．4个D．5个8．（2023秋•龙港区期中）函数y＝ax2+bx+c与y＝kx的图象如图所示，下列结论：①b2﹣4ac＞0；②a+b+c＝0；③x＝﹣2时，函数y＝﹣ax2+（k﹣b）x﹣c有最大值；④关于x的方程ax2+（b﹣k）x+c＝0的根是x1＝﹣1，x2＝﹣3，其中正确的个数是（）A．1B．2C．3D．49．（2023•石城县模拟）二次函数y＝ax2+bx+c（a≠0）的图象如图所示．下列结论：①abc＞0；②2a+b＝0；③m为任意实数，则a+b＞am2+bm；④a﹣b+c＞0；⑤若ax21+bx1=ax22+bx2且x1≠x2，则x1+x2＝2．其中正确的有（）A．①④B．③④C．②⑤D．②③⑤10．（2024•苍溪县模拟）如图，已知二次函数y＝ax2+bx+c（a，b，c是常数）的图象关于直线x＝﹣1对称，则下列五个结论：①abc＞0；②2a﹣b＝0；③9a﹣3b+c＜0；④a（m2﹣1）+b（m+1）≤0（m为任意实数）；⑤3a+c＜0．其中结论正确的个数为（）A．2个B．3个C．4个D．5个11．（2024•高青县校级一模）小明从图所示的二次函数y＝ax2+bx+c的图象中，观察得出了下面五条信息：①c＜0；②abc＞0；③a﹣b+c＞0；④2a﹣3b＝0；⑤c﹣4b＞0，你认为其中正确信息的个数有（）A．2个B．3个C．4个D．5个12．（2024•沂源县一模）已知二次函数y＝ax2+bx+c（a≠0）的图象的一部分如图所示，其中对称轴为：x ＝1，下列结论：①abc＞0；②a+c＞0；③2a+3b＞0；④a+b＞am2+bm（m≠1）；上述结论中正确结论的个数为（）A．1个B．2个C．3个D．4个13．（2024•桃江县一模）抛物线y ＝ax 2+bx +c 的顶点坐标为（2，﹣a ）（如图所示），则下列说法：①abc ＜0；②（a +b ）2≥c ；③关于x 的方程ax 2+bx ＝0有两个不相等的实数根；④﹣1≤a ≤0．则正确的结论有（）A ．1个B ．2个C ．3个D ．4个14．（2023秋•中山市校级期末）二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示．下列结论：①2a +b ＝0；②3a +c ＞0；③m 为任意实数，则a +b ＞am 2+bm ；④若A （x 1，0），B （x 2，0），则x 1+x 2＝2，其中正确的有（）A ．①②B ．①③C ．①④D ．②④15．（2023秋•西城区校级月考）已知二次函数y ＝ax 2+bx +c 的图象如图所示，则下列结论：①a ＜0；②9a +3b +c ＞0；③c ＞0；④﹣3＜―b 2a＜0其中正确的有（）A ．4个B ．3个C ．2个D ．1个16．（2023•东港区校级三模）函数y ＝x 2+bx +c 与y ＝x 的图象如图所示，有以下结论：①b 2﹣4c ＞0；②b +c ＝0；③2b +c +3＝0；④当1＜x ＜3时，x 2+（b ﹣1）x +c ＜0其中正确的有（）个．A ．4B ．3C ．2D ．117．（2023•双台子区校级一模）二次函数y ＝ax 2+bx +c 的图象如图所示，给出四个结论：①abc ＞0；②4a ﹣2b +c ＞0；③对于任意实数m ，有am 2+bm +c ＜a ﹣b +c ；④c a ＞―3，其中正确的有（）A ．①②B ．①④C ．②③D ．③④18．（2023•遂溪县模拟）如图是二次函数y ＝ax 2+bx +c 的图象，对称轴是直线l ，则以下说法：①a ﹣b +c ＝0；②4a +b ＝0；③ab c＞0；④16a +5b +2c ＞0，其中正确的个数是（）A ．1B ．2C ．3D ．419．（2023秋•义乌市期中）已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列4个结论：①abc ＞0；②b2＞4ac；③a（m2﹣1）+b（m﹣1）＜0（m≠1）；④关于x的方程|ax2+bx+c|＝1有四个根，且这四个根的和为4．其中正确的结论有（）A．①②③B．②③④C．①④D．②③20．（2023秋•铜梁区校级期中）二次函数y＝ax2+bx+c的图象如图所示，给出下列结论：①abc＞0；②2a+b＜0；③若﹣1＜m＜n＜1，则m+n＜―b a ；④3|a|+|c|＜2|b|．其中正确的结论有（）A．1个B．2个C．3个D．4个21．（2023•仁怀市模拟）如图，根据二次函数y＝ax2+bx+c的图象得到如下结论：①abc＞0 ②2a﹣b＝0 ③a+b+c＝0 ④3a+c＜0 ⑤当x＞﹣2时，y随x的增大而增大⑥一定存在实数x0，使得ax20+bx0＞a﹣b 成立．上述结论，正确的是（）A．①②⑤B．②③④C．②③⑥D．③④⑤22．（2023•广东模拟）二次函数y ＝ax 2+bx +c 的图象如图所示，有如下结论：①abc ＜0；②2a ﹣b +c ≤0；③3b ﹣2c ＜0；④对任意实数m ，都有2am 2+2bm ﹣b ≥0．其中正确的有（）A ．①②B ．②③C ．②④D ．③④23．（2023•凤凰县模拟）已知二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，下列结论①abc ＜0；②3a +b ＞―13c ；③2c ＜3b ；④（k +1）（ak +a +b ）≤a +b ，其中正确的是（）A ．①③④B ．C ．①④D ．②③④24．（2024•黄石模拟）已知抛物线y ＝ax 2+bx +c （a ＜0）与x 轴交于点（x 1，0），（2，0），其中﹣1＜x 1＜0．下列四个结论：①abc ＜0；②a ﹣b +c ＞0；③2b ﹣c ＜0；④不等式ax 2+bx +c ＞―c 2x +c 的解集为0＜x ＜2．其中正确结论的序号为（）A ．①②B ．①③C ．②③D ．①④25．（2024•殷都区模拟）如图，在平面直角坐标系中，直线y 1＝mx +n 与抛物线y 2=ax 2+bx ―3相交于点A ，B ．结合图象，判断下列结论：①当﹣3＜x ＜2时，y 1＞y 2；②x ＝﹣3是方程ax 2+bx ﹣3＝0的一个解；③若（﹣4，t 1），（1，t 2）是抛物线上的两点，则t 1＞t 2；④对于抛物线y 2=ax 2+bx ―3，当﹣3＜x ＜2时，y 2的取值范围是0＜y 2＜5．其中正确结论的个数是（）A ．4个B ．3个C ．2个D ．1个26．（2024•东港区校级一模）如图，抛物线 y ＝ax 2+bx +c （a ≠0）与x 轴交于点A （﹣1，0），顶点坐标为（1，n ），与y 轴的交点在（0，2）和（0，3）两点之间（包含端点）．下列结论中正确的是（）①不等式ax 2+c ＜﹣bx 的解集为x ＜﹣1或x ＞3；②9a 2﹣b 2＜0；③一元二次方程cx 2+bx +a ＝0的两个根分别为x 1=13，x 2＝﹣1；④6≤3n ﹣2≤10．A ．①②③B ．①②④C ．②③④D ．①③④二．填空题（共4小题）27．（2024•射洪市一模）二次函数y ＝ax 2+bx +c （a ≠0）的大致图象如图所示（1＜x ＝h ＜2，0＜x A ＜1）．下列结论：①abc ＜0；②2a +b ＞0；③若OC ＝2OA ，则2b ﹣ac ＝4；④3a ﹣c ＜0．其中正确的有．（只填写序号）28．（2023秋•太康县期末）已知二次函数y ＝ax 2+bx +c （a ≠0，a 、b 、c 为常数）的图象如图所示．下列4个结论：①b ＞0；②b ＜a +c ；③c ＜4b ；④a +b ＜k 2a +kb （k 为常数，且k ≠1）．其中正确的结论序号是．29．（2023秋•青山区期末）已知抛物线y ＝ax 2+bx +c 经过点（2，c ），且满足a ﹣b +c ＝0．下列四个结论：①抛物线的对称轴是直线x ＝1；②b 与c 同号；③若a +2b +4c ＞0，则不等式ax 2+bx +c ＜﹣2ax ﹣a ﹣b 的解集﹣2＜x ＜2；④抛物线上的两个点M （m ﹣1，y 1），N （m +2，y 2），当c ＜0，且y 1＞y 2时，m ＜12．其中一定正确的是 .（填写序号）30．（2023秋•城厢区校级月考）如图，是抛物线y 1＝ax 2+bx +c （a ≠0）图象的一部分，抛物线的顶点坐标为A （1，3），与x 轴的一个交点为B （4，0），点A 和点B 均在直线y 2＝mx +n （m ≠0）上．①2a +b ＝0；②abc ＞0；③抛物线与x 轴的另一个交点是（﹣4，0）；④方程ax 2+bx +c ＝﹣3有两个不相等的实数根；⑤a ﹣b +c ＜4m +n ；⑥不等式mx +n ＞ax 2+bx +c 的解集为1＜x ＜4．其中正确的是．。

多命题结论几何选择题(一)

多命题结论几何选择题（一）一、例题讲解：例1、如图1，已知△ABC 中，AB ＝AC ，∠BAC ＝90°，直角∠EPF 的顶点P 是BC 中点，两边PE 、PF 分别交AB 、AC 于点E 、F ，给出以下四个结论：①AE ＝CF ；②△EPF 是等腰直角三角形；③S 四边形AEPF ＝21S △ABC ；④EF ＝AP 。

当∠EPF 在△ABC 内绕顶点P 旋转时（点E 不与A 、B 重合），上述结论中始终正确的有( )A ①②③④B ①②③C ②③④D ①③④例2、如图2，AB 是⊙O 的直径，点P 在BA 的延长线上，弦CD 交AB 与E ，连结OD 、PC 、BC ，∠AOD=2∠ABC ，∠P=∠D ，过E 作弦GF ⊥BC 交圆于G 、F 两点，连结CF 、BG 。

则下列结论其中正确的是（）①CD ⊥AB ； ②PC 是⊙O 的切线；③OD ∥GF ④弦CF 的弦心距等于12BG 。

A ．①②④ B ．③④ C ．①②③ D ．①②③④例3、如图3，PA 、PB 是⊙O 的切线，A 、B 为切点，AC 为⊙O 的直径，弦BD ⊥AC.下列结论：①∠P+2∠D ＝180°； ②∠BOC ＝∠BAD ；③∠DBO ＝∠ABP ； ④∠ABP ＝∠ABD其中正确结论有（）个（A ）1；（B ）2；（C ）3；（D ）4二、课堂练习：1、如图4，⊙O 的弦AB ⊥CD 于H ，D 、E 关于AB 对称，BE 延长线交⊙O 于F ，连接FC ，作OG ⊥AB 于G ，则下列结论：①FC =CE ；②AF =AD =21CF ；④E 点关于BC 的对称点必在⊙O 上，正确的是（）A ．①②③④B ．①②③C ．②③④D ．①②④2、如图5，AB 是⊙O 的直径，弧AC=弧CE ，弦AE 交CD 于F ，交BC 于M ，下列结论：①AE=CD ；②AF=CF ；③AF=ME ；④∠EAB =∠HDO 。

圆的多结论选择题

多结论选择题1、如图，△ABC 内接于⊙O ，CD ⊥AB 于P ，交⊙O 于D ，E 为AC 的中点，EP 交BD 于F ，⊙O 的直径为d.下列结论：①EF ⊥BD ；②AC 2+BD 2＝AD 2+BC 2＝d 2；③OE ＝21BD ；④ADBC S CD AB 四边形2=⋅.其中正确的个数是（） (A)1个 (B) 2个 (C) 3个 (D) 4个2、如图，△ABC 内接于⊙O ，其外角平分线AD 交⊙O 于D ，DK ⊥AC 于K.则下列结论：①DB ＝DC ； ②AC －AB ＝2AK ；③AC+AB ＝2CK ； ④ACAB AD CD ⋅-22=1.其中正确的有（）A.只有①②B.只有①②③C.只有③④D.①②③④ 3、如图，⊙O 中，弦BC 垂直平分半径OM ，A 为优弧BC 的中点，D 是BC 上一点，且BD=2DC,DE ⊥AB 于E ，连CE 交AB 弧上一点P ，PC 交AD 于点F ，连PA,PB ，过点C 作PB 的垂线交PB的延长线于点G.下列结论：①CD=BE; ②△EAD 是等腰Rt △; ③△PAF 是等边△; ④PB+2BG=PA; ⑤PB ∥AD; 其中正确的个数有（） (A)1个 (B) 2个 (C) 3个 (D) 4个 4、如图，已知，⊙O 的直径CD ⊥弦AB ，垂足为M ，R 为BM 上任意一点，直线CR 交⊙O 于Q ，过Q 作⊙O 的切线交直线AB 于点P ，过P 作⊙O 的切线PE ，E 为切点。

连接CE 并延长交直线AB 于F ，连接CB ，RE 。

下列结论： ①PR=PQ; ②⋂⋂=QE QA ;③R,Q,F,E 四点共圆; ④CR 2+EF 2=CE 2+RF 2;其中正确的有（）A.只有①②③B.只有①②④C.只有②③④D.只有①③④5、如图，AB 为⊙O 的直径，弦CD 垂直平分半径OA ，P 是⋂BC 的中点，弦CF 平分∠DCP ，交AP 于H 点，连接PF 交AB 于G 点，以下结论： ①AB 23CD =; ②FH=FP; ③HP=BG; ④PF=CP 2; 其中正确的有（）A.①②③④B.②③④C.①②D.①③④OKE D CBAOPF ED C BAMPG B E D C F OAFPERQM BADC GH E OPFBAC D6、如右图，已知，在平面直角坐标系中，以O 为圆心，2为半径的⊙O 分别交x 轴和y 轴于A,B 和P,Q ，以A 为圆心，AP 为半径的⊙A 交x 轴于E,F ，过A 点作⊙O 的切线AC 交⊙A 于C ，CP 的延长线交⊙O 于D. （1）求证：D 为⋂BP 的中点.（2）判断△PDE 的形状，并证明你的结论.（3）如图，若M 为⋂FQ 上一动点，PM 交⊙O 于N ，S 为MN 的中点，T 为AO 的中点.下列结论： ①线段SP 为定值；②线段ST 为定值；其中只有一个是正确的，请你判断出正确的结论，给予证明并求其值.思考题：7、如图，钝角△ABC 内接于⊙O ，∠ABC 的平分线交⊙O 于D ，BE 切⊙O 于点B ，DE ⊥BE 于E ，直线OD 交BC 于F ，下列结论：①OB+OF=DE; ②BC=2BE;③∠ADO=∠CBO; ④∠EDF=∠ABC+∠ACB; 其中正确的个数有（）A.①②③④B.①②④C.②③④D.①②③8、如图，I 为⊙O 内接△ABC 的内心，AI 延长线交BC,⋂BC 分别于D,E ，作EH ⊥BC 于H,EG ⊥AB 于G ，EF ⊥过点B 的切线于F ，过E 作圆的切线交AC 延长线于N ，交BF 于M ，下列结论：①EB=EI; ②四边形ANMB 为梯形; ③EH=EF; ④222AC)(AB 41AE EG +-=; 其中正确的个数有（）(A)1个 (B) 2个 (C) 3个 (D) 4个G NM EFH D IOB C A ACBO FEDC F DQPO E B AyxTS N MF Q P O E B A yx。

部编数学七年级上册专题15选择压轴题多结论问题专题复习课堂学案及配套作业(解析版)含答案

专题15 选择压轴题多结论问题专题复习（解析版）第一部分教学案1．（2022秋•西山区期中）下列说法正确的有（）个．①如果地面向上15米记作+15米，那么地面向下6米记作﹣6米；②一个有理数不是正数就是负数；③任何一个有理数的绝对值都不可能小于零；④﹣a一定在原点左边；⑤在数轴上，一个数对应的点离原点越远，这个数越小．A．1B．2C．3D．4思路引领：根据正数和负数的定义，有理数的分类，绝对值的性质，有理数的大小比较和数轴的性质对各选项分析判断利用排除法求解．解：①如果地面向上15米记作15米，那么地面向下6米记作﹣6米，故本选项正确；②一个有理数不是正数就是零和负数，故本选项错误；③任何一个有理数的绝对值都是非负数，故本选项正确；④﹣a可以表示任意数，不一定在原点左边，故本选项错误；⑤在数轴上，原点右边的一个数对应的点离原点越远，这个数越大，故本选项错误；故选：B．总结提升：本题考查有理数，正数和负数，绝对值和数轴，解题的关键是掌握有理数的分类标准和数轴的性质．2．（2021秋•沿河县期末）现有以下四个结论：①绝对值等于其本身的有理数只有零；②相反数等于其本身的有理数只有零；③倒数等于其本身的有理数只有1；④平方等于其本身的有理数只有1．其中正确的有（）A．3个B．2个C．1个D．0个思路引领：根据绝对值的性质，相反数的定义，倒数的定义，有理数乘方的定义对各小题分析判断即可得解．解：①绝对值等于其本身的有理数是零和正数，故本小题错误；②相反数等于其本身的有理数只有零，正确；③倒数等于其本身的有理数是1和﹣1，故本小题错误；④平方等于其本身的有理数是0和1，故本小题错误；综上所述，正确的说法有②共1个．故选：C．总结提升：本题考查了有理数的乘方，相反数的定义，绝对值的性质，倒数的定义，是基础概念题，熟记概念是解题的关键．3．（2021秋•抚州）如图，数轴上点A，B，C对应的有理数分别为a，b，c，则下列结论中：①a+b+c＞0；②a•b•c＞0；③a+b﹣c＞0；④0＜ba＜1；⑤|a|＞|b|＞|c|，正确的有（）A．4个B．3个C．2个D．1个思路引领：先由数轴得出a＜﹣2＜b＜﹣1＜0＜c＜1，再根据有理数的加法法则、有理数的乘除法法则等分别分析，可得答案．解：由数轴可得：a＜﹣2＜b＜﹣1＜0＜c＜1，∴a+b+c＜0，故①错误；∵a，b，c中两负一正，∴a•b•c＞0，故②正确；∵a＜0，b＜0，c＞0，∴a+b﹣c＜0，故③错误；∵a＜﹣2＜b＜﹣1，∴0＜ba＜1，故④正确；a|＞|b|＞|c|，故⑤正确；综上可知，正确的有3个．故选：B．总结提升：本题考查了数轴在有理数加减乘除法运算中的应用，数形结合，是解题的关键．4．（2022秋•惠济区期中）有理数a，b在数轴上的对应点如图所示，则下面式子中正确的是（）①b＜0＜a；②|b|＜|a|；③b﹣a＞0；④a﹣b＞a+b．A．①②B．①④C．②③D．③④思路引领：由数轴直观得出b＜0＜a，且|b|＞|a|，然后关键有理数的有关知识解答．解：①由数轴直观得出b＜0＜a，故①正确；②由数轴直观得出|b|＞|a|，故②错；③b﹣a＝b+（﹣a）＜0；故③错；④a﹣b＝a+（﹣b）＞0，a+b＜0，故④正确．故答案为：B．总结提升：本题考查的是有理数的有关运算，解题的关键是关键数轴判断正负和绝对值的大小．5．（2022秋•金水区校级期中）已知数a，b，c在数轴上的位置如图，下列说法：①b+c＞0；②a+b−c＞0；③a|a|+b|b|+c|c|=1；④|a−b|−2|c+b|+|a−c|＝−3b+c．其中正确结论的个数是（）个．A．1B．2C．3D．4思路引领：根据数轴上的位置关系．判断出a，b，c的大小关系以及各自绝对值得大小关系，在进行判断即可．解：∵|c|＞|b|，b＜0＜c，∴b+c＞0，正确，故①正确；∵b＜0＜a，|b|＞|a|，c＞0，∴a+b−c＜0，故②错误；a|a|+b|b|+c|c|=aa+bb+cc=1﹣1+1＝1，正确，故③正确；∵a﹣b＞0，c+b＞0，a﹣c＜0∴|a−b|−2|c+b|+|a−c|，＝a﹣b﹣2（b+c）+c﹣a，＝a﹣b﹣2b﹣2c+c﹣a，＝﹣3b﹣c，故④错误，∴正确的有两个．故选：B．总结提升：本题主要考查数轴与绝对值的综合运用，解题的关键在于掌握绝对值化简的技巧．6．（2022秋•海城市校级期中）已知a、b、c在数轴上的位置如图，下列说法：①abc＜0；②c+a＞0；③c﹣b＜0；④cb＞0．正确的有（）A．1个B．2个C．3个D．4个思路引领：根据数轴上点的位置，利用有理数的加减乘除法则判断即可．解：根据数轴上点的位置得：c＜b＜0＜a，且|b|＜|a|＜|c|，∴abc＞0，c+a＜0，c﹣b＜0，cb＞0，则正确的有2个．故选：B．总结提升：此题考查了有理数的除法，数轴，有理数的加减法，以及有理数的乘法，熟练掌握运算法则是解本题的关键．7．（2022秋•行唐县校级期中）一个两位数，它的十位数字为a，个位数字为b，若把它的十位数字和个位数字对调，得到一个新的两位数，则下列判断正确的是（）甲同学：新的两位数可表示为b+a；乙同学：新的两位数与原两位数的和是11的倍数；丙同学：若b﹣a能被2整除，则新的两位数与原两位数的差能被18整除A．只有乙同学的正确B．只有乙、丙同学的正确C．只有甲、丙同学的正确D．三名同学的都不正确思路引领：根据题意表示出原数与新数即可；求出两数的差，化简后判断即可．解：由题意得：这个两位数是10a+b，新的两位数是：10b+a，故甲判断错误；新的两位数与原两位数的和是：10b+a+10a+b＝11a+11b＝11（a+b），则其和是11的倍数，故乙判断正确；新的两位数与原两位数的差是：10b+a﹣（10a+b）＝9b﹣9a＝9（b﹣a），∵b﹣a能被2整除，∴新的两位数与原两位数的差能被18整除，故丙判断正确；故判断正确的有乙、丙．故选：B．总结提升：本题主要考查整式的加减，列代数式，解答的关键是对整式的加减运算的法则的掌握．8．（2022秋•金水区校级期中）下列说法正确的有（）个．①单项式x的系数和次数都是0；②3x4﹣5x2y2﹣6y3+2的次数是11；③多项式1﹣2x+12x2是由1，﹣2x，12x2三项组成；④在13a2，x yπ，5y4x，0中整式有2个．A．1B．2C．3D．4思路引领：根据多项式、单项式、整式的相关概念解答即可．解：①单项式x的系数和次数都是1，原说法错误；②3x4﹣5x2y2﹣6y3+2的次数是4，原说法错误；③多项式1﹣2x+12x2是由1，﹣2x，12x2三项组成，原说法正确；④在13a2，x yπ，5y4x，0中整式有3个，原说法错误．说法正确的有1个．故选：A．总结提升：本题主要考查了整式的有关概念．要能准确的分清什么是整式．整式是有理式的一部分，在有理式中可以包含加，减，乘，除四种运算，但在整式中除式不能含有字母．单项式和多项式统称为整式．单项式是字母和数的乘积，只有乘法，没有加减法．多项式是若干个单项式的和，有加减法．9．（2022秋•九龙坡区校级期中）对于4个整式：A：a2，B：a+2，C：b2，D：2a，有以下几个结论：①对于a、b取任意数，都有B•D﹣2A﹣4B＝﹣8；②若b为正数，则B•C+D+A的值一定是正数；③若多项式M＝A﹣D+m•B•D（m为常数）不含a2，则m的值为―12，上述结论中，正确的有（）A．①B．①②C．②③D．①③思路引领：根据整式混合运算的顺序与运算法则分别计算即可求解．解：①：B•D﹣2A﹣4B＝（a+2）•2a﹣2a2﹣4（a+2）＝2a2+4a﹣2a2﹣4a﹣8＝﹣8，故结论①正确；②：若b为正数，则B•C+D+A＝（a+2）•b2+2a+a2＝ab2+2b2+2a+a2，∵a可取任意数，∴ab2+2a可以是负数，∴ab2+2b2+2a+a2不一定是正数，故结论②错误；③：M＝A﹣D+m•B•D＝a2﹣2a+m（a+2）•2a＝a2﹣2a+2ma2+4ma＝（1+2m）a2+（4m﹣2）a，∵多项式M＝A﹣D+m•B•D（m为常数）不含a2，∴1+2m＝0，∴m=―1 2，∴M＝9x2﹣3≥﹣3，故结论③正确．故选：D．总结提升：本题考查整式的混合运算，掌握运算法则是解题的关键．10．（2022秋•涟源市期中）规定：f（x）＝|x﹣2|，g（y）＝|y+3|．例如f（﹣4）＝|﹣4﹣2|，g（﹣4）＝|﹣4+3|．下列结论中：①若f（x）+g（y）＝0，则2x﹣3y＝13；②若x＜﹣3，则f（x）+g（x）＝﹣1﹣2x：③若x＞﹣3，则f（x）+g（x）＝2x+1；④式子f（x﹣1）+g（x+1）的最小值是7．其中正确的所有结论是（）A．①②B．①②④C．①③④D．①②③④思路引领：①根据新定义运算和非负数的性质求得x、y，再代值计算便可判断①的正误；②根据新定义运算和绝对值的性质进行计算便可；③根据新定义运算和绝对值的性质，分两种情况：﹣3＜x＜2；x≥2；分别计算便可；④根据新定义运算和绝对值的性质，进行解答便可．解：①∵f（x）+g（y）＝0，∴|x﹣2|+|y+3|＝0，∴x﹣2＝0，y+3＝0，∴x＝2，y＝﹣3，∴2x﹣3y＝13＝4+9＝13，故①正确；②∵x＜﹣3，∴f（x）+g（x）＝|x﹣2|+|x+3|＝﹣x+2﹣x﹣3＝﹣2x﹣1，故②正确：③∵x＞﹣3，f（x）+g（x）＝|x﹣2|+|x+3|∴当﹣3＜x＜2时，f（x）+g（x）＝﹣x+2+x+3＝5，当x≥2时，f（x）+g（x）＝x﹣2+x+3＝2x+1，故③错误；④f（x﹣1）+g（x+1）＝|x﹣1﹣2|+|x+1+3|＝|x﹣3|+|x+4|，当﹣4≤x≤3时，④式子f（x﹣1）+g（x+1）有最小值为：3﹣x+x+4＝7，故④正确；故选：B ．总结提升：本题考查了求代数式的值，非负数的性质，绝对值的定义，关键是应用新定义和绝对值的性质解题．11．（2022秋•庐阳区校级期中）下列各变形中：①由x ＝y ，得到x a =y a ；②由x +2＝y +2，可得到x ＝y ；③由x a =y a 可得到x ＝y ；④由x 0.3―2x 10.7=7，可得到10x 3―20x 107=70．其中一定正确的有（）A ．1个B ．2个C ．3个D ．4个思路引领：根据等式的性质对各小题进行逐一分析即可．解：①当a ＝0时，x a 与y a 无意义，故不符合题意；②由x +2＝y +2，可得到x ＝y ，符合等式的性质1，故符合题意；③由x a =y a 可得到x ＝y ，符合等式的性质2，故符合题意；④由x 0.3―2x 10.7=7，可得到10x 3―20x 107=7，故不符合题意．故选：B ．总结提升：本题考查的是等式的性质，熟知等式的两个基本性质是解题的关键．12．（2022秋•丹江口市期中）已知m ＝n ，则下列变形中正确的个数为（）①m +2＝n +2；②am ＝an ；③m n =1；④m a 21=n a 21A ．1个B ．2个C ．3个D ．4个思路引领：根据等式的性质对各小题进行解答即可．解：①∵m ＝n ，∴m +2＝n +2，故本小题符合题意；②∵m ＝n ，∴am ＝an ，故本小题符合题意；③当n ＝0时，m m 无意义，故本小题不符合题意；④∵m ＝n ，a 2+1＞0，∴m a 21=n a 21，故本小题符合题意．故选：C ．总结提升：本题考查的是等式的性质，熟知等式的性质是解题的关键．13．（2022秋•怀柔区校级月考）有m 辆客车及n 个人，若每辆客车乘40人，则还有10人不能上车，若每辆客车乘43人，则只有1人不能上车，有下列四个等式：①40m +10＝43m﹣1；②n1040=n143；③n1040=n143；④40m+10＝43m+1．其中正确的是（）A．①②B．②④C．①③D．③④思路引领：由乘车的人数不变，可得出关于m的一元一次方程；由客车辆数不变，可得出关于n的一元一次方程，再对照给定的4个等式即可得出结论．解：由人数不变，可列出方程：40m+10＝43m+1，∴等式④正确；由客车的辆数不变，可列出方程：n1040=n143，∴等式③正确．∴正确的结论是③④．故选：D．总结提升：本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．14．（2021秋•高新区校级期末）鸡兔同笼问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”图是嘉淇解题过程，需要补足横线上符号所代表的内容，则下列判断不正确的是（）解：设鸡有x只，那么兔子有□只．因为☆+兔的足数＝94，所以列方程为〇x+△（35﹣x）＝94，解这个方程，得x＝23，从而35﹣23＝12．答：鸡有23只，兔子有12只．A．□代表（35﹣x）B．☆代表鸡的足数C．〇代表2D．△代表2思路引领：设鸡有x只，则兔子有（35−x）只，根据鸡的脚的数量+兔子的脚的数量＝94可列方程，解方程即可．解：设鸡有x只，则兔子有（35−x）只，∵鸡的足数+兔的足数＝94，∴列方程为2x+4（35−x）＝94，解这个方程，得：x＝23，从而35−23＝12，∴鸡有23只，兔子有12只，∴□代表（35−x），☆代表鸡的足数，〇代表2，△代表4，故选：D．总结提升：本题主要考查一元一次方程的应用，解题的关键是理解题意，找到题目蕴含的相等关系．15．（2021秋•阳东区期末）将方程3x+6＝2x﹣8移项后，四位同学的结果分别是（1）3x+2x ＝6﹣8；（2）3x﹣2x＝﹣8+6；（3）3x﹣2x＝8﹣6；（4）3x﹣2x＝﹣6﹣8，其中正确的有（）A．0个B．1个C．2个D．3个思路引领：移项时注意改变该项的符号，据此判断即可．解：将方程3x+6＝2x﹣8移项后，可得到3x﹣2x＝﹣8﹣6，∴只有（4）是正确的，故选：B．总结提升：本题主要考查一元一次方程的知识，熟练掌握移项时改变该项的符号是解题的关键．16．（2021秋•普陀区期末）下列说法正确的是（）①若x＝1是关于x的方程a+bx+c＝0的一个解，则a+b+c＝0；②在等式3x＝3a﹣b两边都除以3，可得x＝a﹣b；③若b＝2a，则关于x的方程ax+b＝0（a≠0）的解为x=―1 2；④在等式a＝b两边都除以x2+1，可得ax21=bx21．A．①③B．②④C．①④D．②③思路引领：把x＝1代入方程a+bx+c＝0，即可判断①；根据等式的性质即可判断②④，把b＝2a代入方程ax+b＝0得出ax+2a＝0，求出x，即可判断③．解：把x＝1代入方程a+bx+c＝0得：a+b+c＝0，故①正确；等式3x＝3a﹣b两边都除以3得：x＝a―13b，故②错误；把b＝2a代入方程ax+b＝0得：ax+2a＝0，解得：x＝﹣2，故③错误；等式a＝b两边都除以x2+1得：ax21=bx21，故④正确；即正确的为①④，故选：C．总结提升：本题考查了一元一次方程的解，等式的性质和解一元一次方程，能熟记一元一次方程的解的定义和等式的性质是解此题的关键．17．（2021秋•南谯区期末）有下列说法：①若∠A+∠B+∠C＝180°，则∠A，∠B，∠C互补；②若∠1是∠2的余角，则∠2是∠1的余角；③一个锐角的补角一定比它的余角大90°；④互补的两个角中，一定是一个钝角与一个锐角．其中正确的有（）A．1个B．2个C．3个D．4个思路引领：余角和补角一定指的是两个角之间的关系，同角的补角比余角大90°．解：①补角一定指的是两个角之间的关系，错误．②若∠1是∠2的补角，则∠2是∠1的补角，正确．③同一个锐角的补角一定比它的余角大90°，正确，180﹣α﹣（90﹣α）＝90．④互补的两个角中，一定是一个钝角与一个锐角，错误，90°+90°＝180°．故选：B．总结提升：本题主要考查了余角和补角的知识，掌握余角的和等于90°，互补的两角之和为180°是关键．18．（2021秋•浦北县期末）已知∠1与∠2互为余角，∠1与∠3互为补角，下列结论：①∠3＜∠1+∠2；②∠3﹣∠2＝90°；③∠3+∠2＝270°﹣2∠1；④∠3﹣∠1＝2∠2．其中正确的有（）A．1个B．2个C．3个D．4个思路引领：根据互余的两角之和为90°，互补的两角之和为180°，即可求出有关的结论．解：由：∠1+∠2＝90°（1），∠1+∠3＝180°（2），得，∠3＝180°﹣∠1＝2∠1+2∠2﹣∠1＝∠1+2∠2，∴∠3＞∠1+∠2，∴①错误．∵∠1+∠2＝90°（1），∠1+∠3＝180°（2），∴（2）﹣（1）得，∠3﹣∠2＝90°，∴②正确．（1）+（2）得，∠3+∠2＝270°﹣2∠1，∴③正确．（2）﹣（1）×2得，∠3﹣∠1＝2∠2，∴④正确．故选：C．总结提升：本题主要考查了余角和补角的知识，掌握余角的和等于90°，互补的两角之和为180°是关键．19．（2022秋•大东区期中）下列说法正确的有（）①n棱柱有2n个顶点，2n条棱，（n+2）个面（n为不小于3的正整数）；②圆锥的侧面展开图是一个圆；③用平面去截一个正方体，截面形状可以是三角形、四边形、五边形、六边形．A．0个B．1个C．2个D．3个思路引领：根据立体图形的特征，截几何体的方法进行判定是几边形．解：①n梭柱有2n个顶点，3n条棱，（n+2）个面（n为不小于3的正整数），故说法错误；②圆锥的侧面展开图是一个扇形，故说法错误；③用平面去截一个正方体，截面的形状可以是三角形、四边形、五边形、六边形是正确的．故选：B．总结提升：本题考查了立体图形的性质，几何体的特征，截面图形的边数，解题的关键是熟练掌握几何体的定义．20．（2022秋•灞桥区校级期中）下列说法正确的个数是（）①连接两点之间的线段叫两点间的距离；②线段AB和线段BA表示同一条线段；③木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点之间，线段最短；④若AB＝2CB，则点C是AB的中点．A．1个B．2个C．3个D．4个思路引领：由直线的性质，两点的距离的概念，线段中点的概念即可判断．解：连接两点之间的线段的长叫两点间的距离，故①不符合题意；线段AB和线段BA表示同一条线段，正确，故②符合题意；木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点确定一条直线，故③不符合题意；若AB＝2CB，点C可能在AB外，则点C不一定是AB的中点，故④不符合题意．故选：A．总结提升：本题考查直线的性质，两点的距离的概念，线段中点的概念，关键是掌握：连接两点间的线段的长度叫两点间的距离；经过两点有且只有一条直线．21．（2022秋•城关区校级期中）下列说法不正确的是（）①长方体一定是柱体；②八棱柱有10个面；③六棱柱有12个顶点；④用一个平面去截几何体，若得到的图形是三角形，则这个几何体一定有一个面的形状是三角形．A．①B．④C．①④D．②③思路引领：根据棱柱的特征以及截一个几何体的方法解答即可．解：①因为长方体是棱柱，所以长方体一定是柱体，原说法正确，不符合题意；②八棱柱的侧面有8个面，有两个底面，共有10个面，原说法正确，不符合题意；③六棱柱上底面有6个顶点，下底面有6个顶点，共有12个顶点，原说法正确，不符合题意；④用一个平面去截几何体，若得到的图形是三角形，则这个几何体不一定有一个面的形状是三角形，如圆锥，原说法不正确，符合题意．说法不正确的是④．故选：B．总结提升：本题考查几何体，掌握常见几何体的概念和性质是解题的关键．22．（2022秋•山亭区校级月考）下列判断正确的有（）（1）正方体是棱柱，长方体不是棱柱；（2）正方体是棱柱，长方体也是棱柱；（3）正方体是柱体，圆柱也是柱体；（4）正方体不是柱体，圆柱是柱体．A．1个B．2个C．3个D．4个思路引领：根据棱柱和柱体的概念判断即可．解：（1）正方体是棱柱，长方体不是棱柱，故原题说法错误；（2）正方体是棱柱，长方体也是棱柱，故原题说法正确；（3）正方体是柱体，圆柱也是柱体，故原题说法正确；（4）正方体不是柱体，圆柱是柱体，故原题说法错误．故选：B．总结提升：此题主要考查了认识立体图形，关键是掌握各种立体图形的特点．23．（2022春•新泰市期中）下列语句中：①两点确定一条直线；②圆上任意两点A、B间的部分叫做圆弧；③两点之间直线最短；④三角形、四边形、五边形、六边形等都是多边形．其中正确的个数有（）A．1个B．2个C．3个D．4个思路引领：利用线段的性质、直线的性质、多边形以及圆弧的概念进行判断，即可得出结论．解：①两点确定一条直线，说法正确；②圆上任意两点A、B间的部分叫做圆弧，说法正确；③两点之间，线段最短，故原说法错误；④三角形、四边形、五边形、六边形等都是多边形，说法正确．故选：C．总结提升：本题主要考查了线段的性质、直线的性质、多边形以及圆弧的概念．两点的所有连线中，可以有无数种连法，如折线、曲线、线段等，这些所有的线中，线段最短．24．（2022•南昌模拟）如图，AB与CD相交于点O，OE是∠AOC的平分线，且OC恰好平分∠EOB，则下列结论中正确的个数有（）①∠AOE＝∠EOC②∠EOC＝∠COB③∠AOD＝∠AOE④∠DOB＝2∠AODA．1个B．2个C．3个D．4个思路引领：根据角平分线的定义得出∠AOE＝∠COE，∠COE＝∠BOC，求出∠AOE＝∠COE＝∠BOC，根据∠AOE+∠COE+∠BOC＝180°求出∠AOE＝∠COE＝∠BOC＝60°，再根据对顶角相等求出答案即可．解：∵OE是∠AOC的平分线，OC恰好平分∠EOB，∴∠AOE＝∠COE，∠COE＝∠BOC，∴∠AOE＝∠COE＝∠BOC，∵∠AOE+∠COE+∠BOC＝180°，∴∠AOE＝∠COE＝∠BOC＝60°，∴∠AOD＝∠BOC＝60°，∴∠BOD＝120°，∴①②③④都正确．故选：D．总结提升：本题考查了邻补角、对顶角，角平分线的定义等知识点，注意：①邻补角互补，②从角的顶点出发的一条射线，如果把这个角分成相等的两个角，那么这条射线叫这个角的平分线，③对顶角相等．25．（2022•定远县模拟）下列说法：①把弯曲的河道改直，能够缩短航程，这是因为两点之间，线段最短；②若线段AC＝BC，则C是线段AB的中点；③﹣a一定是负数；④非负数的任何次幂都是非负数；⑤一个角的补角大于这个角本身．其中正确的个数为（）A．1B．2C．3D．4思路引领：根据两点之间，线段最短，线段中点的定义，负数，乘方，补角的性质，逐项判断即可求解．解：①把弯曲的河道改直，能够缩短航程，这是因为两点之间，线段最短，故①正确；②当点C在线段AB上时，若线段AC＝BC，则C是线段AB的中点，故②错误；③当a＞0时，﹣a一定是负数，故③错误；④非负数的任何次幂都是非负数，故④正确；⑤一个锐角的补角大于这个角本身，故⑤错误；∴正确的有①④，共2个．故选：B．总结提升：本题主要考查两点之间，线段最短，线段中点的定义，负数，乘方，补角的性质，熟练掌握相关知识点是解题的关键．26．（2022春•香坊区期末）下列说法：①正数和负数统称为有理数；②若m+n＝0，则m、n互为相反数；③如果a＞b，则有|a|＞|b|；④几个角的和等于180°，我们就说这几个角互补；⑤23x4是7次单项式，其中正确的有（）A．1个B．2个C．3个D．4个思路引领：根据有理数的定义，相反数的定义，补角的定义，单项式的次数，非负数的性质对各项进行分析即可．解：①有理数是整数（正整数、0、负整数）和分数的统称；故①说法错误；②若m+n＝0，则m、n互为相反数；故②说法正确；③如果0＞a＞b，则有|a|＜|b|；故③说法错误；④两个角的和等于180°，我们就说这两个角互补；故④说法错误；⑤23x4是4次单项式，故⑤说法错误，正确的有②，共1个．故选：A．总结提升：本题主要考查补角，有理数，非负数性质，单项式，解答的关键是对相应的知识的掌握．27．（2022春•南岗区期末）下列四个说法：①射线AB和射线BA是同一条射线；②若点B 为线段AC的中点，则AB＝BC；③锐角和钝角互补；④一个角的补角一定大于这个角．其中正确说法的个数是（）A．0个B．1个C．2个D．3个思路引领：①根据射线的定义判断；②根据线段中点的定义判断；③根据钝角与锐角的定义判断；④根据补角的定义判断．解：①射线AB和射线BA表示的方向不同，不是同一条射线，故原说法错误；②若点B为线段AC的中点，则AB＝BC，故原说法正确；③锐角和钝角是相对于直角的大小而言，没有一定的数量关系，不一定构成互补关系，故原说法错误；④一个角的补角不一定大于这个角，如一个角是130°，它的补角是50°，即一个角的补角小于这个角，故原说法错误．故正确的说法有②，共1个．故选：B．总结提升：本题考查了射线的定义，线段中点的定义，钝角与锐角的定义，补角的定义，对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义，要善于区分不同概念之间的联系和区别．28．（2022•驿城区校级开学）下列几种说法：①两点之间线段最短；②任何数的平方都是正数；③2（2x+1）是一元一次方程；④34x3是7次单项式；⑤任何有理数的绝对值都是非负数．其中正确的语句有（）个．A．1B．2C．3D．4思路引领：根据两点之间线段最短；任何数的平方都是非负数；一元一次方程的定义；单项式中所有字母的指数的和叫做单项式的次数；绝对值的定义进行分析即可．解：①两点之间线段最短；故符合题意；②任何数的平方都是非负数；故不符合题意；③2（2x+1）不是一元一次方程；故不符合题意；④34x3是3次单项式；故不符合题意；⑤任何有理数的绝对值都是非负数，故符合题意；故选：B．总结提升：此题主要考查了线段的性质、一元一次方程定义、单项式的次数、绝对值的定义，关键是掌握课本基础知识，不能混淆．29．（2018秋•洪山区期末）如图，O为直线AB上一点，∠DOC为直角，OE平分∠BOC，OF平分∠AOD，OG平分∠AOC，下列结论：①∠BOE与∠DOF互为余角；②2∠AOE ﹣∠BOD＝90°；③∠EOD与∠COG互为补角；④∠BOE﹣∠DOF＝45°；其中正确的是（）A．①②③④B．③④C．②③D．②③④思路引领：根据余角和补角的定义以及角平分线的定义计算出各选项的结果判断即可．解：∵OE平分∠BOC，OG平分∠AOC，∴∠BOE+∠AOG＝90°，∵∠AOG≠∠DOF，∴①错误；∵∠DOC＝∠GOE＝90°，∴∠AOE＝135°―12∠AOD，∴2∠AOE＝270°﹣∠AOD，∴2∠AOE﹣∠BOD＝90°，∴②正确；∵∠DOC＝∠GOE＝90°，∴∠EOD+∠COG＝180°，∴③正确；∵OE平分∠BOC，OF平分∠AOD，∴∠DOF+∠COG＝45°，∵OE平分∠BOC，OG平分∠AOC，∴∠BOE+∠COG＝90°，∴∠BOE﹣∠DOF＝45°；∴④正确．综上所述，正确的有②③④．故选：D．总结提升：本题考查了余角和补角的定义及性质，角平分线定义，角的和差计算，准确识图是解题的关键．30．（2018秋•青山区期末）如图，货轮A在航行过程中，发现灯塔B在它北偏东60°的方向上，货轮C在它南偏东30°方向上．则下列结论：①∠NAB＝60°；②∠WAC＝120°；③图中∠NAC的补角有两个，分别是∠SAC和∠EAB；④图中有4对互余的角，其中正确的个数有（）A．1个B．2个C．3个D．4个思路引领：根据方向角以及余角与补角的定义解答即可．解：灯塔B在它北偏东60°的方向上，即∠NAB＝60°，故①正确；∠SAC＝30°，∠WAC＝90°+30°＝120°，故②正确；∠NAC＝150°，∠SAC＝∠EAB＝30°，故③正确；图中两个60°角两个30°角，一共四对互余的角，故④正确．故正确的有①②③④共4个．故选：D．总结提升：本题考查了余角与补角以及方向角的定义，正确理解方向角的定义，是解答本题的关键．第二部分配套作业1．（2022秋•巴东县期中）下列对“0”的描述：①0℃表示没有温度②0是正数③0比任何负数都大④0是自然数其中，正确的个数有（）A．1B．2C．3D．4思路引领：根据有理数的定义对各小题进行逐一分析即可．解：①0℃表示温度是0摄氏度，故本小题不符合题意；②0既不是正数，也不是负数，故本小题不符合题意；③0比任何负数都大，故本小题符合题意；④0是自然数，故本小题符合题意．故选：B．总结提升：本题考查的是有理数，熟知0既不是正数，也不是负数是解题的关键．2．（2022秋•永安市期中）下列说法正确的是（）①正有理数和负有理数统称为有理数；②一个数的相反数等于它本身，那么这个数为零；③如果一个数的绝对值等于它本身，那么这个数是正数；④﹣3.14既是负数、分数，也是有理数．A．①②③④B．①②③C．①②D．②④思路引领：分别根据有理数的分类，相反数的定义，绝对值的定义逐一判断即可．解：正有理数，0和负有理数统称为有理数，故说法①错误；一个数的相反数等于它本身，那么这个数为零，故说法②正确；如果一个数的绝对值等于它本身，那么这个数是正数或0，故说法③错误；﹣3.14既是负数，分数，也是有理数，故说法④正确．所以正确的有②④．故选：D．总结提升：本题考查了有理数的分类依据、相反数与绝对值的定义，熟记定义是解题的关键．3．（2022秋•芜湖期中）如图，A，B两点在数轴上的位置表示的数分别为a，b．有下列四个结论：①（b﹣1）（a+1）＞0；②b1|a3|＞0；③（a+b）（a﹣b）＞0；④b＞﹣a＞﹣b＞a．其中正确的结论是（）A．①④B．①②C．②③D．②④思路引领：根据数轴判断A和B所表示的数的符号，然后逐一分析即可．解：由图可知，﹣1＜a＜0，b＞1，∴b﹣1＞0，a+1＞0，∴①正确；∵|a﹣3|＞0，b﹣1＞0，∴②正确；（a+b）（a﹣b）＝a2﹣b2＜0，∴③错误；∵0＜﹣a＜1，﹣b＜﹣1，∴b＞﹣a＞a＞﹣b，∴④错误．综上①②正确，故选：B．总结提升：本题考查数轴和绝对值，能够通过数轴判断一个数的符号是解答本题的关键．4．（2022秋•桐乡市期中）数轴上点A，B，C分别表示数﹣1，m，﹣1+m，下列说法正确的是（）A．点C一定在点A的右边B．点C一定在点A的左边C．点C一定在点B的右边D．点C一定在点B的左边思路引领：由于不知道数m的数值，所以不清楚点A与点C，点A与点B的位置关系，再根据点B，C分别表示数m，﹣1+m即可判断．。

押中考数学第9-10题(多结论问题)(学生版)

押中考数学第9-10题(多结论问题)专题诠释：一直以来，函数都是中考数学的重点考察题型。

在选择题中，主要考察函数的性质、函数的图像和函数的应用，难度的跨度较大，从基础到压轴都有可能出现，满分难度较大。

多做、多想、多总结，掌握做题规律，力争不丢分！目录知识点一：函数的性质及探究1模块一〖真题回顾〗 1模块二〖押题冲关〗 5模块三〖考前预测〗 9知识点一：函数的性质及探究模块一〖真题回顾〗1.(2022·辽宁丹东·统考中考真题)如图，抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5，0)，与y轴交于点C，其对称轴为直线x=2，结合图象分析如下结论：①abc>0；②b+3a<0；③当x>0时，y随x的增大而增大；④若一次函数y=kx+b(k≠0)的图象经过点A，则点E(k，b)在第四象限；⑤点M是抛物线的顶点，若CM⊥AM，则a=66．其中正确的有()A.1个B.2个C.3个D.4个2.(2022·贵州黔西·统考中考真题)如图，在平面直角坐标系中，矩形ABCD的顶点A在第一象限，B，D分别在y轴上，AB交x轴于点E，AF⊥x轴，垂足为F．若OE=3，EF=1．以下结论正确的个数是()①OA=3AF；②AE平分∠OAF；③点C的坐标为(-4,-2)；④BD=63；⑤矩形ABCD的面积为242．A.2个B.3个C.4个D.5个3.(2022·四川宜宾·统考中考真题)如图，△ABC 和△ADE 都是等腰直角三角形，∠BAC =∠DAE =90°，点D 是BC 边上的动点(不与点B 、C 重合)，DE 与AC 交于点F ，连结CE ．下列结论：①BD =CE ；②∠DAC =∠CED ；③若BD =2CD ，则CF AF=45；④在△ABC 内存在唯一一点P ，使得PA +PB +PC 的值最小，若点D 在AP 的延长线上，且AP 的长为2，则CE =2+3．其中含所有正确结论的选项是()A.①②④B.①②③C.①③④D.①②③④4.(2022·四川眉山·中考真题)如图，四边形ABCD 为正方形，将△EDC 绕点C 逆时针旋转90°至△HBC ，点D ，B ，H 在同一直线上，HE 与AB 交于点G ，延长HE 与CD 的延长线交于点F ，HB =2，HG =3．以下结论：①∠EDC =135°；②EC 2=CD ⋅CF ；③HG =EF ；④sin ∠CED =23．其中正确结论的个数为()A.1个B.2个C.3个D.4个5.(2022·山东东营·统考中考真题)如图，已知菱形ABCD的边长为2，对角线AC、BD相交于点O，点M，N分别是边BC、CD上的动点，∠BAC=∠MAN=60°，连接MN、OM.以下四个结论正确的是()①△AMN是等边三角形；②MN的最小值是3；③当MN最小时S△CMN=18S菱形ABCD；④当OM⊥BC时，OA2=DN⋅AB.A.①②③B.①②④C.①③④D.①②③④6.(2022·黑龙江·统考中考真题)如图，正方形ABCD的对角线AC，BD相交于点O，点F是CD上一点，OE⊥OF交BC于点E，连接AE，BF交于点P，连接OP．则下列结论：①AE⊥BF；②∠OPA=45°；③AP-BP=2OP；④若BE:CE=2:3，则tan∠CAE=47；⑤四边形OECF的面积是正方形ABCD面积的14．其中正确的结论是()A.①②④⑤B.①②③⑤C.①②③④D.①③④⑤7.(2022·湖南益阳·统考中考真题)如图，已知△ABC中，∠CAB=20°，∠ABC=30°，将△ABC绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC=B′C′，②AC∥C′B′，③C′B′⊥BB′，④∠ABB′=∠ACC′，正确的有()A.①②③B.①②④C.①③④D.②③④8.(2022·黑龙江牡丹江·统考中考真题)下列图形是黄金矩形的折叠过程：第一步，如图(1)，在一张矩形纸片一端折出一个正方形，然后把纸片展平；第二步，如图(2)，把正方形折成两个相等的矩形再把纸片展平；第三步，折出内侧矩形的对角线AB ，并把AB 折到图(3)中所示的AD 处；第四步，如图(4)，展平纸片，折出矩形BCDE 就是黄金矩形．则下列线段的比中：①CD DE ，②DE AD ，③DE ND ，④AC AD，比值为5-12的是()A.①②B.①③C.②④D.②③9.(2022·黑龙江绥化·统考中考真题)如图，在矩形ABCD 中，P 是边AD 上的一个动点，连接BP ，CP ，过点B 作射线，交线段CP 的延长线于点E ，交边AD 于点M ，且使得∠ABE =∠CBP ，如果AB =2，BC =5，AP =x ，PM =y ，其中2<x ≤5．则下列结论中，正确的个数为()(1)y 与x 的关系式为y =x -4x ；(2)当AP =4时，△ABP ∽△DPC ；(3)当AP =4时，tan ∠EBP =35．A.0个B.1个C.2个D.3个10.(2022·江苏连云港·统考中考真题)如图，将矩形ABCD 沿着GE 、EC 、GF 翻折，使得点A 、B 、D 恰好都落在点O 处，且点G 、O 、C 在同一条直线上，同时点E 、O 、F 在另一条直线上．小炜同学得出以下结论：①GF ∥EC ；②AB =435AD ；③GE =6DF ；④OC =22OF ；⑤△COF ∽△CEG ．其中正确的是()A.①②③B.①③④C.①④⑤D.②③④模块二〖押题冲关〗1.(2023·江苏连云港·统考一模)如图，在边长为4的正方形ABCD中，点E是边BC的中点，连接AE、DE，分别交BD、AC于点P、Q，过点P作PF⊥AE交CB的延长线于F，下列结论：①∠AED+∠EAC+∠EDB=90°；②AP=FP；③AE=102AO；④四边形OPEQ的面积为43；⑤BF=43．其中正确的结论有()A.2个B.3个C.4个D.5个2.(2023·广东深圳·深圳市南山外国语学校校联考二模)如图，在正方形ABCD中，AD=4，E为CD中点，F为BC上的一点，且∠EAF=45°，∠ABG=∠DAE，连接EF，延长BG交AE于点M，交AD于点N，则以下结论；①DE+BF=EF②BN⊥AE③BF=83④S△BGF=1615中正确的是()A.1个B.2个C.3个D.4个3.(2023·辽宁铁岭·校联考一模)如图，正方形ABCD的对角线AC，BD相交于点O，点E是AB上一点，OF⊥OE交AD于点F，连接CF，DE交于点P，连接OP．则下列结论：①∠OPC=45°；②DE⊥CF；③CP -DP =2OP ；④若AF :FD =3:2，则tan ∠ACF =47；⑤四边形OEAF 的面积是正方形ABCD 面积的14．其中正确的结论是()A.①②④⑤B.①②③⑤C.①②③④D.①③④⑤4.(2023·江苏无锡·校考二模)如图，在正方形ABCD 中，F 是BC 边上一点，连接AF ，以AF 为斜边作等腰直角△AEF ．有下列四个结论：①∠CAF =∠DAE ；②点E 在线段BD 上；③当∠AEC =135°时，CE 平分∠ACD ；④若点F 在BC 上以一定的速度由B 向C 运动，则点F 的运动速度是点E 运动速度的2倍．其中正确的结论的个数为()A.1B.2C.3D.45.(2023·黑龙江绥化·统考一模)如图，正方形ABCD 中，BE =EF =FC ，CG =2GD ，BG 分别交AE ，AF于点M ，N ．下列结论：①AF ⊥BG ；②BN =23NF ；③BM MG=38；④S 四边形CGNF :S 四边形ANGD =18:31．其中结论正确的个数有()A.1个B.2个C.3个D.4个6.(2023·安徽滁州·校考模拟预测)如图，在边长为1的正方形ABCD 中，E 、F 是AD 边上的两个动点，且AE =FD ，连接BE 、CF 、BD ，CF 与BD 交于点G ，连接AG 交BE 于点H ，连接DH ，下列结论正确的个数是()①AG ⊥BE ；②HD 平分∠EHG ；③△ABG ∽△FDG ；④S △HDG：S △HBG =tan ∠DAG ；⑤线段DH 的最小值是5-12；⑥当E 、F 重合时，延长AG 交CD 于M ，则tan ∠EBM =34．A.5个B.4个C.3个D.2个7.(2023·黑龙江绥化·校联考一模)如图，在正方形ABCD 中，E 是线段CD 上一动点，连接AE 交BD 于点F ，过点F 作FG ⊥AE 交BC 于点G ，连接AG ，EG ，现有以下结论：①△AFG 是等腰直角三角形；②DE+BG =EG ；③点A 到EG 的距离等于正方形的边长；④当点E 运动到CD 的三等分点时，BG BC =12或BG BC=13．以上结论正确的个数有()A.1个B.2个C.3个D.4个8.(2023·山东泰安·宁阳二中校考一模)如图，在矩形ABCD 中，AC ，BD 相交于点O ，过点B 作BF ⊥AC 于点M ，交CD 于点F ，过点D 作DE ∥BF 交AC 于点N ．交AB 于点E ，连接FN ，EM ．有下列结论：①图中共有三个平行四边形；②当BD =2BC 时，四边形DEBF 是菱形；③BD ⊥ME ；④AD 2=BD ⋅CM ．其中，正确结论的序号是()A.①②③B.①②④C.①③④D.②③④9.(2023·广东深圳·模拟预测)如图，正方形ABCD 中，E 、F 分别为边AD 、DC 上的点，且AE =FC ，过F 作FH ⊥BE ，交AB 于G ，过H 作HM ⊥AB 于M ，若AB =9，AE =3，则下列结论中：①△ABE ≅△CBF ；②BE =FG ；③2DH =EH +FH ；④HM AE=35，其中结论正确有()A.1个B.2个C.3个D.4个10.(2023·浙江杭州·校联考一模)如图，在△ABC中，∠BAC=90°，AB=AC=12，点P在边AB上，D，E分别为BC，PC的中点，连接DE．过点E作BC的垂线，与BC，AC分别交于F，G两点．连接DG，交PC于点H．有以下判断：①∠EDC=45°；②DG⊥PE，且DG=PE；③当AP=6时，△APG的面积为9；④CHCE的最大值为2+12．其中正确的是()A.①③B.①③④C.①②④D.①②③④模块三〖考前预测〗11.(2023·山东东营·东营市东营区实验中学校考一模)如图，PA、PB是⊙O的切线，切点分别为A、B，BC是⊙O的直径，PO交⊙O于E点，连接AB交PO于F，连接CE交AB于D点．下列结论：①PA= PB；②OP⊥AB；③CE平分∠ACB；④OF=12AC；⑤E是△PAB的内心；⑥△CDA≌△EDF．其中一定成立的有( )个．A.5B.4C.3D.212.(2023·山东枣庄·校考模拟预测)如图，△ABC内接于⊙O，∠A所对弧的度数为120°．∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E，CE、BD相交于点F．以下四个结论：①cos∠BFE=12；②BC=BD；③EF=FD；④BF=2DF．其中结论一定正确的序号数是()A.①和②B.①和③C.②和③D.③和④13.(2023·天津·模拟预测)如图，△ABC 中，AC =BC ，点M ，N 分别在AC ，AB 上，将△AMN 沿直线MN 翻折，点A 的对应点D 恰好落在BC 边上(不含端点B ，C )，下列结论：①直线MN 垂直平分AD ；②∠CDM =∠BND ；③AD =CD ；④若M 是AC 中点，则AD ⊥BC ．其中一定正确的是()A.①②B.②③C.①②④D.①③④14.(2023·安徽芜湖·统考一模)如图，在Rt △ABC 中，∠BAC =90°，AB =AC ，D 为线段BC 上一点，以AD 为一边构造Rt △ADE ，∠DAE =90°，AD =AE ，下列说法正确的是()①∠BAD =∠EDC ；②△ADO ∼△ACD ；③BD OE =AD AO ；④2AD 2=BD 2+CD 2．A.仅有①② B.仅有①②③ C.仅有②③④ D.①②③④15.(2023·广东惠州·模拟预测)如图，已知正方形ABCD 的边长为a ，E 为CD 边上一点(不与端点重合)，将ΔADE 沿AE 翻折至△AFE ，延长EF 交边BC 于点G ，连接AG ，CF ．则下列给出的判断：①∠EAG =45°；②若DE =13a ，则tan ∠GFC =2；③若E 为CD 的中点，则△GFC 的面积为110a 2；④若CF =FG ，则DE =(2-1)a ，其中正确的是()A.①②③B.①②④C.②③④D.①②③④16.(2023·广东深圳·一模)如图，将正方形ABCD 翻折，使点C 、D 分别与点C '、D '重合，折痕为MN ，C 'D '交AD 于点E ，CC 交MN 于点F ，连接CE 、C 'M ．给出以下结论：①MN 垂直平分CC ；②DN +BC =CM ；③∠C CE =45°；④△AC 'E 的周长等于AB 的2倍．其中正确的个数有()A.1个B.2个C.3个D.4个17.(2023·山东青岛·模拟预测)如图，菱形ABCD 中，∠BAD =60°，AC 与BD 交于点O ，E 为CD 延长线上一点，且CD =DE ，连结BE ，分别交AC ，AD 于点F ，G ，连结OG ，①OG =12AB ②S 四边形ODGF =S △ABF ③由点A 、B 、D 、E 构成的四边形是菱形；④S △ACD =2S △ABG 中正确的结论是()A.①③B.②④C.①②③D.①②③④18.(2023·江苏无锡·模拟预测)如图，在平面直角坐标系中，点O 为坐标原点，矩形OABC 按如图所示摆放在第一象限，点B 的坐标为3m ,m ，将矩形OABC 绕着点O 逆时针旋转α(0<α<90°)，得到矩形OA BC ．直线OA 、B C 与直线BC 相交，交点分别为点D 、E ，有下列说法：①当m =1,α=30°时，矩形OA B C 与矩形OABC 重叠部分的面积为32；②当m =1，且B 落到y 轴的正半轴上时，DE 的长为103；③当点D 为线段BE 的中点时，点D 的横坐标为43m ；④当点D 是线段BE 的三等分点时，sin α的值为25或45．其中，说法正确的是()A.①②B.③④C.①②③D.①②④19.(2023·山东德州·统考一模)如图，在矩形ABCD中，AC，BD相交于点O，过点B作BF⊥AC于点M，交CD于点F，过点D作DE∥BF交AC于点N．交AB于点E，连接FN，EM．有下列结论：①四边形NEMF为平行四边形；②DN2=MC•NC；③△DNF为等边三角形；④当AO=AD时，四边形DEBF是菱形．其中，正确结论的序号是()A.①②④B.①②③C.①③D.②③④20.(2023·天津·一模)如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE，EF．下列结论：①AB=2BD；②图中有DFOE= 4对全等三角形；③BD=BF；④若将△DEF沿EF折叠，则点D不一定落在AC上；⑤S四边形S△AOF，上述结论中正确的个数是()A.1B.2C.3D.4。

中考数学几何多结论问题

∴正确的有4个．故选D.
3. 如图，P为正方形ABCD的对角线BD上任一
点，过点P作PE⊥BC于点E，PF⊥CD于点F，
连接EF.给出以下4个结论：
①△FPD是等腰直角三角形；②AP＝EF；③
AD＝PD；④∠PFE＝∠BAP.
其中，所有正确的结论是( )
A. ①②
B. ①④
C. ①②④
D. ①③④
∴FH≠FD， ∴S△EFH≠S△EFD， ∴S四边形EFHG＝S△HEG＋S△EFH＝S△AHG＋ S△EFH≠S△DEF＋S△AGH，故③错误，
18. 如图，点E，F分别为正方形ABCD的边BC，
CD上一点，AC，BD交于点O，且∠EAF＝
45°，AE，AF分别交对角线BD于点M，N，
则有以下结论：①△AOM∽△ADF；②EF＝
∵CG＝GF，∴∠CFG＝∠FCG， ∵∠BGF＝∠CFG＋∠FCG，又∵∠BGF＝∠AGB＋∠AGF， ∴∠CFG＋∠FCG＝∠AGB＋∠AGF， ∵∠AGB＝∠AGF，∠CFG＝∠FCG， ∴∠AGB＝∠FCG， ∴AG∥CF， ∴④正确；
8. 如图，在菱形ABCD中，AB＝6，∠DAB＝
60°，AE分别交BC，BD于点E，F，CE＝2，
连接CF，以下结论：①△ABF≌△CBF；②
点E到AB的距离是；③AF＝CF；④△ABF
的面积为 .其中一定成立的有( )个
A. 1
B. 2
C. 3 D. 4
10. 如图，在正方形ABCD中，E，F分别为BC，
CD的中点，连接AE，BF交于点G，将△BCF
11. 如图，正方形ABCD边长为6，E是BC的中
点，连接AE，以AE为边在正方形内部作
∠EAF＝45°，边AF交CD于F，连接EF.则下

2022年九年级数学中考专题十一几何多结论题

专题11 几何多结论选择题一．试题（共14小题）1．如图，矩形ABCD中，AC，BD相交于点O，过点B作BF⊥AC交CD于点F，交AC于点M，过点D作DE ∥BF交AB于点E，交AC于点N，连接FN，EM．则下列结论：①DN＝BM；②EM∥FN；③AE＝FC；④当AO＝AD时，四边形DEBF是菱形．其中，正确的结论是（）A．①③B．①②③C．①③④D．①②③④2．如图，四边形ABCD是平行四边形，点E是边CD上一点，且BC＝EC，CF⊥BE交AB于点F，P是EB延长线上一点，下列结论：①BE平分∠CBF；②CF平分∠DCB；③BC＝FB；④PF＝PC．其中正确结论的个数为（）A．1B．2C．3D．43．如图，在△AOB和△COD中，OA＝OB，OC＝OD，OA＜OC，∠AOB＝∠COD＝36°．连接AC，BD交于点M，连接OM．下列结论：①∠AMB＝36°，②AC＝BD，③OM平分∠AOD，④MO平分∠AMD．其中正确的结论个数有（）个．A．4B．3C．2D．14．如图，在△ABC中，AB＝AC，AD和CE是高，∠ACE＝45°，点F是AC的中点，AD与FE，CE分别交于点G、H，∠BCE＝∠CAD，有下列结论：①图中存在两个等腰直角三角形；②△AHE≌△CBE；③BC•AD=√2AE2；④S△ABC＝4S△ADF．其中正确的个数有（）A ．1B ．2C ．3D ．45．已知如图等腰△ABC ，AB ＝AC ，∠BAC ＝120°，AD ⊥BC 于点D ．点P 是BA 延长线上一点，O 点是线段AD 上一点，OP ＝OC ，下面的结论：①AC 平分∠P AD ；②∠APO ＝∠DCO ；③△OPC 是等边三角形；④AC ＝AO +AP ；⑤S △ABC ＝S 四边形AOCP ．其中正确的序号是．6．如图，分别以Rt △ABC 的斜边AB ，直角边AC 为边向外作等边△ABD 和等边△ACE ，F 为AB 的中点，DE ，AB 相交于点G ，若∠BAC ＝30°，下列结论：①EF ⊥AC ；②四边形ADFE 为菱形；③AD ＝4AG ；④△DBF ≌△EF A ．其中正确结论的个数有（）A ．1B ．2C ．3D ．47．如图，在矩形ABCD 中，AD =√2AB ，AE 平分∠BAD ，DF ⊥AE 于F ，BF 交DE 、CD 于O 、H ，下列结论：①∠DEA ＝∠DEC ；②BF ＝FH ；③OE ＝OD ；④BC ﹣CH ＝2EF ；⑤AB ＝HF ，其中正确结论的个数是（）A ．2个B ．3个C ．4个D ．5个 8．如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，AE 平分∠BAD ，分别交BC ，BD 于点E ，P ，连接OE ，∠ADC ＝60°，AB =12BC ＝2，下列结论：①∠CAD ＝30°；②BD ＝2√7；③S 四边形ABCD ＝AB •AC ；④OE =14AD ；⑤S △BOE =√32．其中正确的个数有（）个A．2B．3C．4D．59．如图，在等腰Rt△ABC中，AB＝AC，过A作直线交BC于G，BG＜GC，BD⊥AG于D，CE⊥AD于E，F 为BC边中点，则下列结论中：①∠BAD＝∠ACE；②BD＝CE﹣ED；③FE＝FD；④EF⊥DF，其中正确结论的个数为（）A．1个B．2个C．3个D．4个10．如图，已知△ABC和△ADE都是等腰三角形，∠BAC＝∠DAE＝90°，BD，CE交于点F，连接AF．下列结论：①BD＝CE；②BF⊥CF；③AF平分∠CAD；④∠AFE＝45°．其中正确结论的个数有（）A．1个B．2个C．3个D．4个11．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB＝60°，FO＝FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE＝EF；④S△AOE：S△BCM＝3：2．其中正确结论的个数是（）A．4个B．3个C．2个D．1个12．如图，在平行四边形ABCD中，AD＝2AB，CE⊥AB于点E，点F、G分别是AD、BC的中点，连接CF、EF、FG，下列结论：①CE⊥FG；②四边形ABGF是菱形；③EF＝CF；④∠EFC＝2∠CFD．其中正确的个数是（）A．1个B．2个C．3个D．4个13．如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②∠AOC＝∠AEC；③BC平分∠ABD；④AF＝DF；⑤BD＝2OF．其中正确结论的个数是（）A．2B．3C．4D．514．如图，△ABC中，AB＝AC，以AB为直径的⊙O交AC于E，交BC于D，DF⊥AC于F．给出以下五个结论：①BD＝DC；②CF＝EF；③弧AE＝弧DE；④∠A＝2∠FDC；⑤DF是⊙O的切线．其中正确的有（）A．5个B．4个C．3个D．2个专题11 几何多结论选择题参考答案与试题解析一．试题（共14小题）1．【解答】解：∵四边形ABCD 是矩形，∴AB ＝CD ，AB ∥CD ，∠DAE ＝∠BCF ＝90°，OD ＝OB ＝OA ＝OC ，AD ＝BC ，AD ∥BC ， ∴∠DAN ＝∠BCM ，∵BF ⊥AC ，DE ∥BF ，∴DE ⊥AC ，∴∠DNA ＝∠BMC ＝90°，在△DNA 和△BMC 中，{∠DAN =∠BCM ∠DNA =∠BMC AD =BC，∴△DNA ≌△BMC （AAS ），∴DN ＝BM ，∠ADE ＝∠CBF ，故①正确；在△ADE 和△CBF 中，{∠ADE =∠CBF AD =BC ∠DAE =∠BCF，∴△ADE ≌△CBF （ASA ），∴AE ＝FC ，DE ＝BF ，故③正确；∴DE ﹣DN ＝BF ﹣BM ，即NE ＝MF ，∵DE ∥BF ，∴四边形NEMF 是平行四边形，∴EM ∥FN ，故②正确；∵AB ＝CD ，AE ＝CF ，∴BE ＝DF ，∵BE ∥DF ，∴四边形DEBF 是平行四边形，∵AO ＝AD ，∴AO ＝AD ＝OD ，∴△AOD 是等边三角形，∴∠ADO ＝∠DAN ＝60°，∴∠ABD ＝90°﹣∠ADO ＝30°，∵DE ⊥AC ，∴∠ADN ＝∠ODN ＝30°，∴∠ODN ＝∠ABD ，∴DE ＝BE ，∴四边形DEBF 是菱形；故④正确；故选：D ．2．【解答】证明：∵BC ＝EC ，∴∠CEB ＝∠CBE ，∵四边形ABCD 是平行四边形，∴DC ∥AB ，∴∠CEB＝∠EBF，∴∠CBE＝∠EBF，∴①BE平分∠CBF，正确；∵BC＝EC，CF⊥BE，∴∠ECF＝∠BCF，∴②CF平分∠DCB，正确；∵DC∥AB，∴∠DCF＝∠CFB，∵∠ECF＝∠BCF，∴∠CFB＝∠BCF，∴BF＝BC，∴③正确；∵FB＝BC，CF⊥BE，∴B点一定在FC的垂直平分线上，即PB垂直平分FC，∴PF＝PC，故④正确．故选：D．3．【解答】解：∵∠AOB＝∠COD＝36°，∴∠AOB+∠BOC＝∠COD+∠BOC，即∠AOC＝∠BOD，在△AOC和△BOD中，{OA=OB∠AOC=∠BOD OC=OD∴△AOC≌△BOD（SAS），∴∠OCA＝∠ODB，AC＝BD，故②正确；∵∠OAC＝∠OBD，由三角形的外角性质得：∠AMB+∠OBD＝∠OAC+∠AOB，∴∠AMB＝∠AOB＝36°，故①正确；法一：作OG⊥AM于G，OH⊥DM于H，如图所示，则∠OGA＝∠OHB＝90°，∵△AOC≌△BOD，∴OG ＝OH ，∴MO 平分∠AMD ，故④正确；法二：∵△AOC ≌△BOD ，∴∠OAC ＝∠OBD ，∴A 、B 、M 、O 四点共圆，∴∠AMO ＝∠ABO ＝72°，同理可得：D 、C 、M 、O 四点共圆，∴∠DMO ＝∠DCO ＝72°＝∠AMO ，∴MO 平分∠AMD ，故④正确；假设MO 平分∠AOD ，则∠DOM ＝∠AOM ，在△AMO 与△DMO 中，{∠AOM =∠DOMOM =OM ∠AMO =∠DMO，∴△AMO ≌△DMO （ASA ），∴AO ＝OD ，∵OC ＝OD ，∴OA ＝OC ，而OA ＜OC ，故③错误；正确的个数有3个；故选：B ．4．【解答】解：∵CE ⊥AB ，∠ACE ＝45°，∴△ACE 是等腰直角三角形，∵AF ＝CF ，∴EF ＝AF ＝CF ，∴△AEF ，△EFC 都是等腰直角三角形，∴图中共有3个等腰直角三角形，故①错误，∵∠AHE +∠EAH ＝90°，∠DHC +∠BCE ＝90°，∠AHE ＝∠DHC ，∴∠EAH ＝∠BCE ，∵AE ＝EC ，∠AEH ＝∠CEB ＝90°，∴△AHE ≌△CBE ，故②正确，∵S △ABC =12BC •AD =12AB •CE ，AB ＝AC =√2AE ，AE ＝CE ，∴BC •AD =√2CE 2，故③正确，∵AB ＝AC ，AD ⊥BC ，∴BD ＝DC ，∴S △ABC ＝2S △ADC ，∵AF ＝FC ，∴S △ADC ＝2S △ADF ，∴S △ABC ＝4S △ADF ．故选：C ．5．【解答】解：①∵AB＝AC，∠BAC＝120°，AD⊥BC；∴∠CAD=12∠BAC＝60°，∠P AC＝180°﹣∠CAB＝60°，∴∠P AC＝∠DAC，∴AC平分∠P AD故①正确；②由①知：∠APO＝∠ABO，∠DCO＝∠DBO，∵点O是线段AD上一点，∴∠ABO与∠DBO不一定相等，则∠APO与∠DCO不一定相等，故②不正确；③∵∠APC+∠DCP+∠PBC＝180°，∴∠APC+∠DCP＝150°，∵∠APO+∠DCO＝30°，∴∠OPC+∠OCP＝120°，∴∠POC＝180°﹣（∠OPC+∠OCP）＝60°，∵OP＝OC，∴△OPC是等边三角形；故③正确；④如图2，在AC上截取AE＝P A，连接PB，∵∠P AE＝180°﹣∠BAC＝60°，∴△APE是等边三角形，∴∠PEA＝∠APE＝60°，PE＝P A，∴∠APO+∠OPE＝60°，∵∠OPE+∠CPE＝∠CPO＝60°，∴∠APO＝∠CPE，∵OP＝CP，在△OP A和△CPE中，{PA=PE∠APO=∠CPE OP=CP，∴△OP A≌△CPE（SAS），∴AO＝CE，∴AC＝AE+CE＝AO+AP；故④正确；如图3，过点C作CH⊥AB于H，∵∠P AC＝∠DAC＝60°，AD⊥BC，∴CH＝CD，∴S△ABC=12AB•CH，S 四边形AOCP ＝S △ACP +S △AOC =12AP •CH +12OA •CD =12AP •CH +12OA •CH =12H •（AP +OA ）=12CH •AC ， ∴S △ABC ＝S 四边形AOCP ；故⑤正确．本题正确的结论有：①③④⑤故答案为：①③④⑤．6．【解答】解：连接FC ，如图所示：∵∠ACB ＝90°，F 为AB 的中点，∴F A ＝FB ＝FC ，∵△ACE 是等边三角形，∴EA ＝EC ，∵F A ＝FC ，EA ＝EC ，∴点F 、点E 都在线段AC 的垂直平分线上，∴EF 垂直平分AC ，即EF ⊥AC ；∵△ABD 和△ACE 都是等边三角形，F 为AB 的中点，∴DF ⊥AB 即∠DF A ＝90°，BD ＝DA ＝AB ＝2AF ，∠DBA ＝∠DAB ＝∠EAC ＝∠ACE ＝60°． ∵∠BAC ＝30°，∴∠DAC ＝∠EAF ＝90°，∴∠DF A ＝∠EAF ＝90°，DA ⊥AC ，∴DF ∥AE ，DA ∥EF ，∴四边形ADFE 为平行四边形而不是菱形；∵四边形ADFE 为平行四边形，∴DA ＝EF ，AF ＝2AG ，∴BD ＝DA ＝EF ，DA ＝AB ＝2AF ＝4AG ；在△DBF 和△EF A 中，{BD =FE ∠DBF =∠EFA BF =FA，∴△DBF ≌△EF A ；综上所述：①③④正确，故选：C ．7．【解答】解：∵四边形ABCD为矩形，AE平分∠BAD，∴∠BAE＝∠DAE＝∠AEB＝45°，∵∠AFD＝∠ABE＝90°，∴△AFD与△ABE都为等腰直角三角形，即AF＝DF，AB＝BE，∴AE=√2AB，又∵AD=√2AB，∴AD＝AE，∴∠AED＝∠ADE＝67.5°，∴∠DEC＝180°﹣45°﹣67.5°＝67.5°，∴∠DEA＝∠DEC，选项①正确；过F作GM⊥AD，与AD交于G点，与BC交于M点，利用三线合一得到G为AD中点，∴F为BH中点，M为BC中点，∴BF＝FH，选项②正确；∵AD=√2AF，AD=√2AB，∴AF＝AB，∴∠AFB＝67.5°，∴∠OFE＝∠OEF＝67.5°，∴OE＝OF，∴∠ODF＝∠OFD＝22.5°，∴OF＝OD，∴OD＝OE，选项③正确；∴∠DEF＝67.5°﹣45°＝22.5°，∠EDC＝90°﹣67.5°＝22.5°，∴∠EDF＝∠DEC，∵EF⊥DF，EC⊥CD，∴EF＝EC，∵△EFM为等腰直角三角形，∴FM＝ME，∴BC﹣CH＝2CM﹣2FM＝2CM﹣2ME＝2EF，选项④正确；∵AB＝AF，∠BAE＝45°，∴△ABF不是等边三角形，∴AB≠BF，∴即AB≠HF，故⑤错误；综上所述，结论正确的是①②③④．则正确的序号有4个．故选：C．8．【解答】解：①∵AE平分∠BAD，∴∠BAE＝∠DAE，∵四边形ABCD是平行四边形，∴AD∥BC，∠ABC＝∠ADC＝60°，∴∠DAE＝∠BEA，∴∠BAE＝∠BEA，∴AB＝BE＝2，∴△ABE是等边三角形，∴AE＝BE＝2，∵BC＝4，∴EC＝2，∴AE＝EC，∴∠EAC＝∠ACE，∵∠AEB＝∠EAC+∠ACE＝60°，∴∠ACE＝30°，∵AD∥BC，∴∠CAD＝∠ACE＝30°，故①正确；②∵BE＝EC，OA＝OC，∴OE=12AB＝1，OE∥AB，∴∠EOC＝∠BAC＝60°+30°＝90°，Rt△EOC中，OC=√EC2−OE2=√3，∵四边形ABCD是平行四边形，∴∠BCD＝∠BAD＝120°，∴∠ACB＝30°，∴∠ACD＝90°，Rt△OCD中，OD=√OC2+CD2=√7 BD＝2OD＝2√7故②正确③由②知：∠BAC＝90°，∴S▱ABCD＝AB•AC，故③正确；④由②知：OE是△ABC的中位线，∴OE=12AB，∵AB=12BC，∴OE=14BC=14AD，故④正确；⑤∵BE＝EC＝2∴S△BOE＝S△EOC=12OE•OC=√32故⑤正确故选：D．9．【解答】解：如图连接AF．∵AB＝AC，BF＝FC，∴AF⊥BC，∵BD⊥AD，CE⊥AD，∴∠ADB＝∠AEC＝∠BAC＝90°，∵∠CAE+∠BAD＝90°，∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，故①正确，∴△ABD≌△CAE（AAS），∴BD＝AE，AD＝CE，∴CE﹣ED＝AD﹣DE＝AE＝BD，故②正确，∵∠BAC＝90°，BF＝FC，∴AF＝BF＝FC，∵∠AGF＝∠BGF，∠BDG＝∠AFG＝90°，∴∠DBG＝∠GAF，∵AE＝BD，∴△FBD≌△FEA（SAS），∴EF＝DF，∠AFE＝∠BFD，∴∠AFB＝∠EFD＝90°，∴EF⊥DF，故③④正确．故选：D．10．【解答】解：如图，作AM⊥BD于M，AN⊥EC于N，设AD交EF于O．∵∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS），∴EC＝BD，∠BDA＝∠AEC，故①正确∵∠DOF＝∠AOE，∴∠DFO＝∠EAO＝90°，∴BD⊥EC，故②正确，∵△BAD≌△CAE，AM⊥BD，AN⊥EC，∴AM＝AN，∴F A平分∠EFB，∴∠AFE＝45°，故④正确，若③成立，则∠EAF＝∠BAF，∵∠AFE＝∠AFB，∴∠AEF＝∠ABD＝∠ADB，推出AB＝AD，由题意知，AB不一定等于AD，所以AF不一定平分∠CAD，故③错误，故选：C．11．【解答】解：①∵矩形ABCD中，O为AC中点，∴OB＝OC，∵∠COB＝60°，∴△OBC是等边三角形，∴OB＝BC，∵FO＝FC，∴FB垂直平分OC，故①正确；②∵△BOC为等边三角形，FO＝FC，∴BO⊥EF，BF⊥OC，∴∠CMB＝∠EOB＝90°，∴BO≠BM，∴△EOB与△CMB不全等；故②错误；③易知△ADE≌△CBF，∠1＝∠2＝∠3＝30°，∴∠ADE＝∠CBF＝30°，∠BEO＝60°，∴∠CDE＝60°，∠DFE＝∠BEO＝60°，∴∠CDE＝∠DFE，∴DE＝EF，故③正确；④易知△AOE≌△COF，∴S△AOE＝S△COF，∵S△COF＝2S△CMF，∴S△AOE：S△BCM＝2S△CMF：S△BCM=2FMBM，∵∠FCO＝30°，∴FM=CM√3，BM=√3CM，∴FMBM=13，∴S△AOE：S△BCM＝2：3，故④错误；所以其中正确结论的个数为2个；故选：C．12．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵点F、G分别是AD、BC的中点，∴AF=12AD，BG=12BC，∴AF＝BG，∵AF∥BG，∴四边形ABGF是平行四边形，∴AB∥FG，∵CE⊥AB，∴CE⊥FG；故①正确；∵AD＝2AB，AD＝2AF，∴AB＝AF，∴四边形ABGF是菱形，故②正确；延长EF，交CD延长线于M，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠A＝∠MDF，∵F为AD中点，∴AF＝FD，在△AEF和△DFM中，{∠A=∠FDM AF=DF∠AFE=∠DFM，∴△AEF≌△DMF（ASA），∴FE＝MF，∠AEF＝∠M，∵CE⊥AB，∴∠AEC＝90°，∴∠AEC＝∠ECD＝90°，∵FM＝EF，∴FC＝EF＝FM，故③正确；∴∠FCD＝∠M，∵四边形ABCD是平行四边形，∴AB＝CD，AD∥BC，∵AF＝DF，AD＝2AB，∴DF＝DC，∴∠DCF＝∠DFC，∴∠M＝∠FCD＝∠CFD，∵∠EFC＝∠M+∠FCD＝2∠CFD；故④正确，故选：D．13．【解答】解：∵AB是⊙O的直径，∴∠ADB＝90°，即AD⊥BD，故①正确；∵∠AEC＝∠DAB+∠EBA，∠AOC＝2∠EBA，∴∠AOC≠∠AEC，故②不正确；∵OC∥BD，∴∠OCB＝∠CBD，∵OC＝OB，∴∠OCB＝∠OBC，∴∠OBC＝∠CBD，即BC平分∠ABD，故③正确；∴OC⊥AD，∴AF＝FD，故④正确；∴OF为△ABD的中位线，∴BD＝2OF，故⑤正确，综上可知正确的有4个，故选：C．14．【解答】解：连接OD，AD．∵AB是⊙O的直径，∴∠ADB＝90°（直径所对的圆周角是直角），∴AD⊥BC；而在△ABC中，AB＝AC，∴AD是边BC上的中线，∴BD＝DC（正确）；∵AB是⊙O的直径，∴AD⊥BC，∵AB＝AC，∴DB＝DC，∵OA＝OB，∴OD是△ABC的中位线，即：OD∥AC，∵DF⊥AC，∴DF⊥OD．∴DF是⊙O的切线（正确）；∵DF⊥AC，AD⊥BC，∴∠FDC+∠C＝∠CAD+∠C＝90°，∴∠FDC＝∠CAD，又AB＝AC，∴∠BAD＝∠CAD，∴∠A＝2∠CAD＝2∠FDC（正确）；∵DF是⊙O的切线，∴∠FDE＝∠CAD＝∠FDC，∴∠C＝∠DEC，∴DC＝DE，又DF⊥AC，∴CF＝EF（正确）；̂=DÊ，此时△ABC为等边三角形，当∠EAD＝∠EDA时，AE当△ABC不是等边三角形时，∠EAD≠∠EDA，̂≠DÊ，则AÊ=DÊ（不正确）；∴AE综上，正确结论的序号是①②④⑤，故选：B．。

2022年高考数学一轮复习专题专题39 椭圆新高考中多项选择专练(解析版)

【详解】
由已知可得 m2 m 1 1，解得 m 2 或 m 1（舍去）
a2 3, a 3,b 2 ， c 1
∴长轴长为 2
3 ，短轴长为 2
2 ，离心率为 e
1 3
3， 3
故选：AB.
2．已知 m 为 3 与 5 的等差中项，n 为 4 与 16 的等比中项，则下列对曲线 C : x2 y2 1 mn
，则
a
2c
，
b
3c ，所以 b 3 ，B 正确； a2
根据椭圆的定义易知 C 正确；
设点 P x0 , y0 ，则
x02 a2
y02 b2
1，易知
A1 a,0 ，
A2 a, 0 ，所以直线 PA1 ， PA2
的
斜率之积是 y0 y0
y02
b2
1
x02 a2
b2
，D
正确.
x0 a x0 a x02 a 2
即 2a2 7a 3 0 ,解得 a 3或 a 1 , 2
试卷第 6页，总 18页
当 a 3时，圆锥曲线 x2 y2 1 ,为中心在原点，焦点在 x 轴上的椭圆，离心率 3
e 31 6 , 33
当a
1
时，圆锥曲线
x2 1
y2
1 ,为中心在原点，焦点在
y
轴上的椭圆，
2
2
e
1 1 2
y
轴上， a
2，b
c
2.
对于 A 选项，该椭圆的长轴长为 2a 4 ，A 错误；
对于 B 选项，该椭圆的焦距为 2c 2 2 ，B 对；
对于 C 选项，该椭圆的离心率为 e c 2 ，C 对； a2
对于 D 选项，该椭圆的左顶点坐标为 2,0 ，D 对.

广东省深圳市中考数学复习多结论几何综合题专题-人教版初中九年级全册数学试题

多结论几何综合题专题试卷一、单选题1、如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=；②S△ABC+S△CDE≥S△ACE；③BM⊥DM；④BM=DM．正确结论的个数是（）A、1个B、2个C、3个D、4个2、如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC 绕点A 顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF；②=;③△ABC的面积等于四边形AFBD的面积；④BE2+DC2=DE2⑤BE+DC=DE;其中正确的是( )A、①②④B、③④⑤C、①③④D、①③⑤3、如图，将等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD ，则下列结论：①AD＝BC；②BD、AC互相平分；③四边形ACED是菱形；④BD⊥DE；其中正确的个数是（）.A、1B、2C、3D、4 4、如图，把一X长方形纸片ABCD沿对角线BD折叠，使C点落在E处，BE与AD相交于点F，下列结论：①BD=AD 2+AB2；②△ABF≌△EDF；③＝④AD=BD•cos45°．其中正确的一组是（）A、①②B、②③C、①④D、③④5、如图，已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE 、DF交于点O．下列结论：①∠DOC=90°，②OC=OE，③tan∠OCD= ，④S△ODC=S 四边形BEOF中，正确的有（）A、1个B、2个C、3个D、4个6、如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④S△BEF=．在以上4个结论中，正确的有（）A、1B、2C、3D、47、如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC 于点E，且∠ADC=60°，AB=BC，连接OE．下列结论：①∠CAD=30°；②S ▱ABCD=AB•AC；③OB=AB；④OE=BC，成立的个数有（）A、1个B、2个C、3个D、4个8、如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下列四个结论：①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④AE+DF=AF+DE．其中正确的是（）A、②③B、②④C、①③④D、②③④9、如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE ，AE⊥EF，AE=EF，现有如下结论：①BE=GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH，其中，正确的结论有（）A、1个B、2个C、3个D、4个10、如图，PA=PB，OE⊥PA，OF⊥PB，则以下结论：①OP是∠APB的平分线；②PE=PF③CA=BD；④CD∥AB；其中正确的有（）个．A、4B、3C、2D、1 11、如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B 与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE、EF．下列结论：①tan∠ADB=2；②图中有4对全等三角形；③若将△DEF沿EF折叠，则点D不一定落在AC上；④BD=BF；⑤S四边形DFOE=S△AOF，上述结论中正确的个数是（）A、1个B、2个C、3个D、4个12、如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：①AC=AD；②BD⊥AC；③四边形ACED是菱形．其中正确的个数是（）A、0B、1C、2D、313、如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF 为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQ•AC，其中正确的结论的个数是（）A、1B、2C、3D、414、如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中正确结论的个数是（）A、4个B、3个C、2个D、1个15、（2016•某某）如图，正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB、AC于点E、G，连结GF，给出下列结论：①∠ADG=22.5°；②tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG；⑥若S△OGF=1，则正方形ABCD的面积是6+4 ，其中正确的结论个数为（）A、2B、3C、4D、516、如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（）①AE=BF；②AE⊥BF；③sin∠B QP= ；④S四边形ECFG=2S△BGE．A、4B、3C、2D、1 17、如图所示，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣2，0）、B（1，0），直线x=﹣0.5与此抛物线交于点C，与x轴交于点M，在直线上取点D，使MD=MC，连接AC、BC、AD、BD，某同学根据图象写出下列结论：①a﹣b=0；②当﹣2＜x＜1时，y＞0；③四边形ACBD是菱形；④9a﹣3b+c＞0你认为其中正确的是（）A、②③④B、①②④C、①③④D、①②③18、如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FGC=3.6．其中正确结论的个数是（）A、2B、3C、4D、519、如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足=，连接AF并延长交⊙O于点E，连接AD ，DE，若CF=2，AF=3，给出下列结论：①△ADF∽△AED；②FG=2；③tanE= ；④S△DEF=4 ，其中正确的是（）A、①②③B、②③④C、①②④D、①③④20、如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，弦CE⊥AB 于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB 于点P、Q，连接AC，给出下列结论：①∠DAC=∠ABC；②AD=CB；③点P是△ACQ的外心；④AC2=AE•AB；⑤CB∥GD，其中正确的结论是（）A、①③⑤B、②④⑤C、①②⑤D、①③④答案解析部分一、单选题1、【答案】D 【考点】等腰三角形的性质，梯形中位线定理，锐角三角函数的定义【解析】【分析】①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知，；然后由直角三角形中的正切函数，得tan∠AEC=，再由等量代换求得tan∠AEC=；②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab（a=b 时取等号)解答；③、④通过作辅助线MN，构建直角梯形的中位线，根据梯形的中位线定理及等腰直角三角形的判定定理解答．【解答】解：∵△ABC和△CDE均为等腰直角三角形，∴AB=BC，CD=DE，∴∠BAC=∠BCA=∠DCE=∠DEC=45°，∴∠ACE=90°；∵△ABC∽△CDE∴①∴tan∠AEC=，∴tan∠AEC=；故本选项正确；②∵S△ABC =a2， S△CDE=b2， S梯形ABDE=（a+b)2，∴S△ACE=S 梯形ABDE-S△ABC-S△CDE=ab ，S△ABC+S△CDE=（a2+b2)≥ab（a=b时取等号)，∴S△ABC+S△CDE≥S△ACE；故本选项正确；④过点M作MN垂直于BD，垂足为N．∵点M是AE的中点，则MN为梯形中位线，∴N 为中点，∴△BMD 为等腰三角形，∴BM=DM；故本选项正确；③又MN=（AB+ED)=（BC+CD)，∴∠BMD=90°，即BM⊥DM；故本选项正确．故选D．【点评】本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点．在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．2、【答案】C 【考点】全等三角形的判定，勾股定理，相似三角形的判定，旋转的性质【解析】【分析】①根据旋转的性质知∠CAD=∠BAF，AD=AF，因为∠BAC=90°，∠DAE=45°，所以∠CAD+∠BAE=45°，可得∠EAF=45°=∠DAE，由此即可证明△AEF≌△AED；②当△ABE∽△ACD时，该比例式成立；③根据旋转的性质，△ADC≌△ABF，进而得出△ABC的面积等于四边形AFBD的面积；④据①知BF=CD，EF=DE，∠FBE=90°，根据勾股定理判断．⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF；由此即可确定该说法是否正确；【解答】①根据旋转的性质知∠CAD=∠BAF，AD=AF，∵∠BAC=90°，∠DAE=45°，∴∠CAD+∠BAE=45°．∴∠EAF=45°，∴△AED≌△AEF；故本选项正确；②∵AB=AC，∴∠ABE=∠ACD；∴当∠BAE=∠CAD时，△ABE∽△ACD，∴=；当∠BAE≠∠CAD 时，△ABE与△ACD不相似，即≠；∴此比例式不一定成立；故本选项错误；③根据旋转的性质知△ADC≌△AFB，∴S△ABC=S△ABD+S△ABF=S四边形AFBD，即三角形ABC的面积等于四边形AFBD的面积；故本选项正确；④∵∠FBE=45°+45°=90°，∴BE2+BF2=EF2，∵△ADC绕点A顺时针旋转90°后，得到△AFB，∴△AFB≌△ADC，∴BF=CD，又∵EF=DE，∴BE2+DC2=DE2，故本选项正确；⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF，∴BE+DC=BE+BF＞DE=EF，即BE+DC＞DE，故本选项错误；综上所述，正确的说法是①③④；故选C．【点评】此题主要考查了图形的旋转变换以及全等三角形的判定等知识，解题时注意旋转前后对应的相等关系．3、【答案】D 【考点】等边三角形的性质，菱形的判定与性质，平移的性质【解析】【解答】∵△ABC、△DCE是等边三角形，∴∠ACB＝∠DCE＝60°，AC＝CD ，∴∠ACD＝180°－∠ACB－∠DCE＝60°，∴△ACD是等边三角形，∴AD＝AC＝BC ，故①正确；由①可得AD＝BC ，∵AB ＝CD ，∴四边形ABCD是平行四边形，∴BD、AC互相平分，故②正确；由①可得AD＝AC＝CE＝DE ，故四边形ACED是菱形，即③正确；∵四边形ACED是菱形，∴AC⊥BD ，∵AC∥DE ，∴∠BDE＝∠COD＝90°，∴BD⊥DE ，故④正确；综上可得①②③④正确，共4个，故选D．【分析】先求出∠ACD＝60°，继而可判断△ACD是等边三角形，从而可判断①是正确的；根据①的结论，可判断四边形ABCD是平行四边形，从而可判断②是正确的；根据①的结论，可判断③正确；根据菱形的对角线互相垂直可得AC⊥BD ，再根据平移后对应线段互相平行可得∠BDE＝∠COD＝90°，进而判断④正确．4、【答案】B 【考点】勾股定理，翻折变换（折叠问题），相似三角形的判定与性质，特殊角的三角函数值【解析】【解答】①∵△ABD为直角三角形，∴BD2=AD2+AB2，不是BD=AD2+AB2，故说法错误；②根据折叠可知：DE=CD=AB，∠A=∠E，∠AFB=∠EFD，∴△ABF≌△EDF，故说法正确；③根据②可以得到△ABF∽△EDF，∴＝，故说法正确；④在Rt△ABD 中，∠ADB≠45°，∴AD≠BD•cos45°，故说法错误．所以正确的是②③．故选B．【分析】①直接根据勾股定理即可判定是否正确；②利用折叠可以得到全等条件证明△ABF≌△EDF；③利用全等三角形的性质即可解决问题；④在Rt△ABD中利用三角函数的定义即可判定是否正确．此题主要考查了折叠问题，也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义，它们的综合性比较强，对于学生的综合能力要求比较高，平时加强训练．5、【答案】C 【考点】全等三角形的判定与性质，勾股定理，正方形的性质，锐角三角函数的定义【解析】【解答】解：∵正方形ABCD的边长为4，∴BC=CD=4，∠B=∠DCF=90°，∵AE=BF=1，∴BE=CF=4﹣1=3，在△EBC和△FCD中，∴△EBC≌△FCD（SAS），∴∠CFD=∠BEC，∴∠BCE+∠BEC=∠BCE+∠CFD=90°，∴∠DOC=90°；故①正确；若OC=OE，∵DF⊥EC，∴CD=DE，∵CD=AD＜DE（矛盾），故②错误；∵∠OCD+∠CDF=90°，∠CDF+∠DFC=90°，∴∠OCD=∠DFC，∴tan∠OCD=tan∠D FC= = ，故③正确；∵△EBC≌△FCD，∴S△EBC=S△FCD，∴S△EBC﹣S△FOC=S△FCD﹣S△FOC，即S△ODC=S四边形BEOF．故④正确．故选C．【分析】由正方形ABCD的边长为4，AE=BF=1，利用SAS易证得△EBC≌△FCD，然后全等三角形的对应角相等，易证得①∠DOC=90°正确；②由线段垂直平分线的性质与正方形的性质，可得②错误；易证得∠OCD=∠DFC，即可求得③正确；由①易证得④正确．6、【答案】C 【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】由折叠可知，DF=DC=DA，∠DFE=∠C=90°，∴∠DFG=∠A=90°，∴△ADG≌△FDG，①正确；∵正方形边长是12，∴BE=EC=EF=6，设AG=FG=x，则EG=x+6，BG=12﹣x，由勾股定理得：EG2=BE2+BG2，即：（x+6）2=62+（12﹣x）2，解得：x=4∴AG=GF=4，BG=8，BG=2AG，②正确；BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，③错误；S△GBE=×6×8=24，S△BEF=•S△GBE==，④正确．故选：C．【分析】根据正方形的性质和折叠的性质可得AD=DF，∠A=∠GFD=90°，于是根据“HL”判定△ADG≌△FDG，再由GF+GB=GA+GB=12，EB=EF，△BGE为直角三角形，可通过勾股定理列方程求出AG=4，BG=8，进而求出△BEF的面积，再抓住△BEF是等腰三角形，而△GED显然不是等腰三角形，判断③是错误的．7、【答案】C 【考点】等边三角形的判定与性质，含30度角的直角三角形，平行四边形的性质【解析】【解答】∵四边形ABCD 是平行四边形，∴∠ABC=∠ADC=60°，∠BAD=120°，∵AE平分∠BAD，∴∠BAE=∠EAD=60°∴△ABE是等边三角形，∴AE=AB=BE，∵AB=BC，∴AE=BC，∴∠BAC=90°，∴∠CAD=30°，故①正确；∵AC⊥AB，∴S ▱ABCD=AB•AC，故②正确，∵AB=BC，OB=BD，∵BD＞BC，∴AB≠OB，故③错误；∵CE=BE，CO=OA ，∴OE=AB ，∴OE=BC，故④正确．故选：C．【分析】由四边形ABCD是平行四边形，得到∠ABC=∠ADC=60°，∠BAD=120°，根据AE 平分∠BAD，得到∠BAE=∠EAD=60°推出△ABE是等边三角形，由于AB=BC，得到AE=BC，得到△ABC是直角三角形，于是得到∠CAD=30°，故①正确；由于AC⊥AB，得到S▱ABCD=AB•AC，故②正确，根据AB=BC，OB=BD，且BD＞BC，得到AB≠OB，故③错误；根据三角形的中位线定理得到OE=AB，于是得到OE=BC，故④正确．8、【答案】D 【考点】全等三角形的判定与性质，角平分线的性质，正方形的判定【解析】【解答】如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，∴①不正确；∵AD是△ABC的角平分线，∴∠EAD∠FAD，在△AED和△AFD中，∴△AED≌△AFD （AAS），∴AE=AF，DE=DF，∴AE+DF=AF+DE，∴④正确；在△AEO和△AFO中，，∴△AE0≌△AF0（SAS），∴EO=FO，又∵AE=AF，∴AO是EF的中垂线，∴AD⊥EF，∴②正确；∵当∠A=90°时，四边形AEDF的四个角都是直角，∴四边形AEDF是矩形，又∵DE=DF，∴四边形AEDF是正方形，∴③正确．综上，可得正确的是：②③④．故选：D．【分析】①如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，所以①不正确．②首先根据全等三角形的判定方法，判断出△AED≌△AFD，AE=AF，DE=DF；然后根据全等三角形的判定方法，判断出△AE0≌△AFO，即可判断出AD⊥EF．③首先判断出当∠A=90°时，四边形AEDF的四个角都是直角，四边形AEDF是矩形，然后根据DE=DF，判断出四边形AEDF是正方形即可．④根据△AED≌△AFD，判断出AE=AF，DE=DF，即可判断出AE+DF=AF+DE 成立，据此解答即可．9、【答案】B 【考点】全等三角形的判定与性质，正方形的性质，相似三角形的判定与性质【解析】【解答】∵四边形ABCD 是正方形，∴∠B=∠DCB=90°，AB=BC，∵AG=CE，∴BG=BE，由勾股定理得：BE=GE，∴①错误；∵BG=BE，∠B=90°，∴∠BGE=∠BEG=45°，∴∠AGE=135°，∴∠GAE+∠AEG=45°，∵AE⊥EF，∴∠AEF=90°，∵∠BEG=45°，∴∠AEG+∠FEC=45°，∴∠GAE=∠FEC，在△GAE和△CEF中∴△GAE≌△CEF，∴②正确；∴∠AGE=∠ECF=135°，∴∠FCD=135°﹣90°=45°，∴③正确；∵∠BGE=∠BEG=45°，∠AEG+∠FEC=45°，∴∠FEC＜45°，∴△GBE和△ECH不相似，∴④错误；即正确的有2个．故选B．【分析】根据正方形的性质得出∠B=∠DCB=90°，AB=BC，求出BG=BE，根据勾股定理得出BE=GE，即可判断①；求出∠GAE+∠AEG=45°，推出∠GAE=∠FEC，根据SAS推出△GAE≌△CEF，即可判断②；求出∠AGE=∠ECF=135°，即可判断③；求出∠FEC＜45°，根据相似三角形的判定得出△GBE和△ECH不相似，即可判断④．10、【答案】A 【考点】全等三角形的判定与性质，圆心角、弧、弦的关系，相似三角形的判定与性质【解析】【解答】连接OP、OC、OA、OD、OB、CD、AB．∵PC•PA=PD•PB（相交弦定理），PA=PB（已知），∴PC=PD，∴AC=BD；在△AOC和△BOD中，∵∠AOC=∠BOD（等弦对等角），OA=OB （半径），OD=OC （半径），∴△AOC≌△BOD，∴③CA=BD；OE=OF；又∵OE⊥PA，OF⊥PB，∴①OP是∠APB的平分线；∴②PE=PF；在△PCD和△PAB中，PC：PA=PD：PB，∠DPC=∠BPA，∴△PCD∽△PAB，∴∠PDC=PBA，∴④CD∥AB；综上所述，①②③④均正确，故答案选A．【分析】①通过证明△AOC≌△BOD，再根据全等三角形的对应高相等求得OE=OF；再根据角平分线的性质证明OP是∠APB的平分线；②由角平分线的性质证明PE=PF；③通过证明△AOC≌△BOD，再根据全等三角形的对应边相等求得CA=BD；④通过证明△PCD∽△PAB，再根据相似三角形的性质对应角相等证得∠PDC=PBA；然后由平行线的判定得出结论CD∥AB．11、【答案】C 【考点】全等三角形的判定与性质，翻折变换（折叠问题），锐角三角函数的定义【解析】【解答】①由折叠可得BD=DE，而DC＞DE，∴DC＞BD，∴tan∠ADB≠2，故①错误；②图中的全等三角形有△ABF≌△AEF，△ABD≌△AED，△FBD≌△FED，（由折叠可知)∵OB⊥AC，∴∠AOB=∠COB=90°，在Rt△AOB和Rt△COB中，AB="CB" ,BO=BO ，∴Rt△AOB≌Rt△COB（HL)，则全等三角形共有4对，故②正确；③∵AB=CB，BO⊥AC，把△ABC折叠，∴∠ABO=∠CBO=45°，∠FBD=∠DEF，∴∠AEF=∠DEF=45°，∴将△DEF沿EF折叠，可得点D一定在AC上，故③错误；④∵OB⊥AC，且AB=CB，∴BO 为∠ABC的平分线，即∠ABO=∠OBC=45°，由折叠可知，AD是∠BAC的平分线，即∠BAF=22.5°，又∵∠BFD为三角形ABF的外角，∴∠BFD=∠ABO+∠BAF=67.5°，易得∠BDF=180°-45°-67.5°=67.5°，∴∠BFD=∠BDF，∴BD=BF，故④正确；⑤连接CF，∵△AOF和△COF等底同高，∴S△AOF=S△COF，∵∠AEF=∠ACD=45°，∴EF∥CD，∴S△EFD=S△EFC，∴S四边形DFOE=S△COF，∴S四边形DFOE=S△AOF，故⑤正确；故正确的有3个．故选C．12、【答案】D 【考点】等边三角形的性质，菱形的判定，旋转的性质【解析】【解答】解：∵将等边△ABC绕点C顺时针旋转120°得到△EDC，∴∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，∴∠ACD=120°﹣60°=60°，∴△ACD是等边三角形，∴AC=AD，AC=AD=DE=CE，∴四边形ACED是菱形，∵将等边△ABC绕点C顺时针旋转120°得到△EDC，AC=AD，∴AB=BC=CD=AD，∴四边形ABCD是菱形，∴BD⊥AC，∴①②③都正确，故选D．【分析】根据旋转和等边三角形的性质得出∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，求出△ACD是等边三角形，求出AD=AC，根据菱形的判定得出四边形ABCD和ACED都是菱形，根据菱形的判定推出AC⊥BD．本题考查了旋转的性质，菱形的性质和判定，等边三角形的性质和判定的应用，能灵活运用知识点进行推理是解此题的关键．13、【答案】D 【考点】全等三角形的判定与性质，矩形的判定与性质，正方形的性质，相似三角形的判定与性质，等腰直角三角形【解析】【解答】解：∵四边形ADEF为正方形，∴∠FAD=90°，AD=AF=EF，∴∠CAD+∠FAG=90°，∵FG⊥CA，∴∠C=90°=∠ACB，∴∠CAD=∠AFG，在△FGA 和△ACD中，，∴△FGA≌△ACD（AAS），∴AC=FG，①正确；∵BC=AC，∴FG=BC，∵∠ACB=90°，FG⊥CA，∴FG∥BC，∴四边形CBFG 是矩形，∴∠CBF=90°，S△FAB= FB•FG= S四边形CBFG，②正确；∵CA=CB，∠C=∠CBF=90°，∴∠ABC=∠ABF=45°，③正确；∵∠FQE=∠DQB=∠ADC，∠E=∠C=90°，∴△ACD∽△FEQ，∴AC：AD=FE：FQ，∴AD•FE=AD2=FQ•AC，④正确；故选：D．【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质；熟练掌握正方形的性质，证明三角形全等和三角形相似是解决问题的关键．由正方形的性质得出∠FAD=90°，AD=AF=EF，证出∠CAD=∠AFG，由AAS证明△FGA≌△ACD，得出AC=FG，①正确；证明四边形CBFG是矩形，得出S△FAB= FB•FG= S四边形CEFG，②正确；由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°，③正确；证出△ACD∽△FEQ，得出对应边成比例，得出D•FE=AD2=FQ•AC，④正确．14、【答案】B 【考点】全等三角形的判定与性质，线段垂直平分线的性质，等腰三角形的性质，矩形的性质【解析】【解答】解：①∵矩形ABCD中，O为AC中点，∴OB=OC，∵∠COB=60°，∴△OBC是等边三角形，∴OB=BC，∵FO=FC，∴FB垂直平分OC，故①正确；②∵FB垂直平分OC，∴△CMB≌△OMB，∵OA=OC，∠FOC=∠EOA，∠DCO=∠BAO，∴△FOC≌△EOA，∴FO=EO，易得OB⊥EF，∴△OMB≌△OEB，∴△EOB≌△CMB，故②正确；③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°，BF=BE，∴△BEF是等边三角形，∴BF=EF，∵DF∥BE且DF=BE，∴四边形DEBF是平行四边形，∴DE=BF，∴DE=EF，故③正确；④在直角△BOE中∵∠3=30°，∴BE=2OE，∵∠OAE=∠AOE=30°，∴AE=OE，∴BE=2AE，∴S△AOE：S△BCM=S△AOE：S△BOE=1：2，故④错误；所以其中正确结论的个数为3个；故选B【分析】①利用线段垂直平分线的性质的逆定理可得结论；②证△OMB≌△OE B得△EOB≌△CMB；③先证△BEF是等边三角形得出BF=EF，再证▱DEBF得出DE=BF，所以得DE=EF；④由②可知△BCM≌△BEO，则面积相等，△AOE和△BEO属于等高的两个三角形，其面积比就等于两底的比，即S△AOE：S△BOE=AE：BE，由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE，得出结论S：S=AE：BE=1：2．本题综合性比较强，既考查了矩形的性质、等腰三角形的性质，又考查了全等三角形的性质和判定，及线段垂直平分线的性质，内容虽多，但不复杂；看似一个选择题，其实相当于四个证明题，属于常考题型．15、【答案】B 【考点】菱形的判定与性质，翻折变换（折叠问题），等腰直角三角形【解析】【解答】解：∵四边形ABCD 是正方形，∴∠GAD=∠ADO=45°，由折叠的性质可得：∠ADG= ∠ADO=22.5°，故①正确．∵由折叠的性质可得：AE=EF，∠EFD=∠EAD=90°，∴AE=EF＜BE，∴AE ＜AB，∴ ＞2，故②错误．∵∠AOB=90°，∴AG=FG＞OG ，△AGD与△OGD 同高，∴S △AGD＞S△OGD，故③错误．∵∠EFD=∠AOF=90°，∴EF∥AC，∴∠FEG=∠AGE，∵∠AGE=∠FGE，∴∠FEG=∠FGE，∴EF=GF，∵AE=EF，∴AE=GF，故④正确．∵AE=EF=GF，AG=GF，∴AE=EF=GF=AG，∴四边形AEFG是菱形，∴∠OGF=∠OAB=45°，∴EF=GF= OG ，∴BE= EF= × OG=2OG ．故⑤正确．∵四边形AEFG是菱形，∴AB∥GF，AB=GF．∵∠BAO=45°，∠GOF=90°，∴△OG F 时等腰直角三角形．∵S△OGF=1，∴ OG2=1，解得OG= ，∴BE=2OG=2 ，GF= = =2，∴AE=GF=2，∴AB=BE+AE=2 +2，∴S正方形ABCD=AB2=（2 +2）2=12+8 ，故⑥错误．∴其中正确结论的序号是：①④⑤．故选B．【分析】①由四边形ABCD是正方形，可得∠GAD=∠ADO=45°，又由折叠的性质，可求得∠ADG的度数；②由AE=EF＜BE，可得AD＞2AE；③由AG=GF＞OG，可得△AGD的面积＞△OGD的是等腰三角形，即可证得AE=GF；⑤易证得四边形AEFG 是菱形，由等腰直角三角形的性质，即可得BE=2OG；⑥根据四边形AEFG是菱形可知AB∥GF，AB=GF，再由∠BAO=45°，∠GOF=90°可得出△OGF时等腰直角三角形，由S△OGF=1求出GF的长，进而可得出BE及AE的长，利用正方形的面积公式可得出结论．此题考查的是四边形综合题，涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识．此题综合性较强，难度较大，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．16、【答案】B 【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】解：∵E，F分别是正方形ABCD边BC，CD的中点，∴CF=BE，在△ABE和△BCF中，，∴Rt△ABE≌Rt△BCF（SAS），∴∠BAE=∠CBF，AE=BF，故①正确；又∵∠BAE+∠BEA=90°，∴∠CBF+∠BEA=90°，∴∠BGE=90°，∴AE⊥BF，故②正确；根据题意得，FP=FC，∠PFB=∠BFC，∠FPB=90°∵CD∥AB，∴∠CFB=∠ABF，∴∠ABF=∠PFB，∴QF=QB，令PF=k（k＞0），则PB=2k在Rt△BPQ 中，设QB=x ，∴x2=（x ﹣k）2+4k2，∴x= ，∴sin=∠BQP= = ，故③正确；∵∠BGE=∠BCF，∠GBE=∠CBF，∴△BGE∽△BCF，∵BE= BC，BF= BC，∴BE：BF=1：，∴△BGE的面积：△BCF的面积=1：5，∴S四边形ECFG=4S△BGE，故④错误．故选：B．【分析】首先证明△ABE≌△BCF，再利用角的关系求得∠BGE=90°，QF=QB，解出BP，QB，根据正弦的定义即可求解；根据AA可证△BGE与△BCF相似，进一步得到相似比，再根据相似三角形的性质即可求解．本题主要考查了四边形的综合题，涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点，解决的关键是明确三角形翻转后边的大小不变，找准对应边，角的关系求解．17、【答案】D 【考点】二次函数的图象，二次函数的性质，菱形的判定【解析】【解答】解：①∵抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣2，0）、B（1，0），∴该抛物线的对称轴为x=﹣=﹣0.5，∴a=b，a ﹣b=0，①正确；②∵抛物线开口向下，且抛物线与x轴交于点A（﹣2，0）、B（1，0），∴当﹣2＜x＜1时，y＞0，②正确；③∵点A、B关于x=0.5对称，∴AM=BM，又∵MC=MD，且CD⊥AB，∴四边形ACBD是菱形，③正确；④当x=﹣3时，y＜0，即y=9a﹣3b+c＜0，④错误．综上可知：正确的结论为①②③．故选D．【分析】①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=﹣=﹣0.5，由此即可得出a=b，①正确；②根据抛物线的开口向下以及抛物线与x轴的两交点坐标，即可得出当﹣2＜x＜1时，y＞0，②正确；③由AB关于x=0.5对称，即可得出AM=BM，再结合MC=MD以及CD⊥AB，即可得出四边形ACBD 是菱形，③正确；④根据当x=﹣3时，y＜0，即可得出9a﹣3b+c＜0，④错误．综上即可得出结论．本题考查了二次函数的图象、二次函数的性质以及菱形的判定，解题的关键是逐条分析四条结论是否正确．本题属于中档题，难度不大，解决该题型题目时，根据给定的函数图象结合二次函数的性质逐条分析给定的结论是关键．18、【答案】D 【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题）【解析】【解答】解：∵正方形ABCD的边长为6，CE=2DE，∴DE=2，EC=4，∵把△ADE沿AE折叠使△ADE落在△AFE的位置，∴AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，在Rt△ABG和Rt△AFG中，∴Rt△ABG≌Rt△AFG（HL ），∴GB=GF，∠BAG=∠FAG，∴∠GAE=∠FAE+∠FAG= ∠BAD=45°，所以①正确；设BG=x，则GF=x ，C=BC﹣BG=6﹣x，在Rt△CGE中，GE=x+2，EC=4，CG=6﹣x，∵CG2+CE2=GE2，∴（6﹣x）2+42=（x+2）2，解得x=3，∴BG=3，CG=6﹣3=3∴BG=CG，所以②正确；∵EF=ED，GB=GF，∴GE=GF+EF=BG+DE，所以③正确；∵GF=GC，∴∠GFC=∠GCF，又∵Rt△ABG≌Rt△AFG，∴∠AGB=∠AGF，而∠BGF=∠GFC+∠GCF，∴∠AGB+∠AGF=∠GFC+∠GCF，∴∠AGB=∠GCF，∴CF∥AG，所以④正确；过F作FH⊥DC∵BC⊥DH，∴FH∥GC，∴△EFH∽△EGC，∴，EF=DE=2，GF=3，∴EG=5，∴△EFH∽△EGC，∴相似比为：= ，∴S△FGC=S△GCE﹣S△FEC= ×3×4﹣×4×（×3）= =3.6，所以⑤正确．故正确的有①②③④⑤，故选：D．【分析】先计算出DE=2，EC=4，再根据折叠的性质AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，然后根据“HL”可证明Rt△ABG≌Rt△AFG，则GB=GF，∠BAG=∠FAG，所以∠GAE= ∠BAD=45°；GE=GF+EF=BG+DE；设BG=x，则GF=x，CG=BC﹣BG=6﹣x，在Rt△CGE中，根据勾股定理得（6﹣x）2+42=（x+2）2，解得x=3，则BG=CG=3，则点G为BC的中点；同时得到GF=GC，根据等腰三角形的性质得∠GFC=∠GCF，再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF，然后根据三角形外角性质得∠BGF=∠GFC+∠GCF，易得∠AGB=∠GCF，根据平行线的判定方法得到CF∥AG；过F 作FH⊥DC，则△EFH∽△EGC，△EFH∽△EGC，由相似比为，可计算S△FGC．本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了三角形全等的判定与性质、勾股定理和正方形的性质．19、【答案】C 【考点】垂径定理，圆周角定理，相似三角形的判定与性质，解直角三角形【解析】【解答】解：①∵AB是⊙O的直径，弦CD⊥AB，∴ ，DG=CG ，∴∠ADF=∠AED，∵∠FAD=∠DAE（公共角），∴△ADF∽△AED；故①正确；②∵ = ，CF=2，∴FD=6，∴CD=DF+CF=8，∴CG=DG=4，∴FG=CG﹣CF=2；故②正确；③∵AF=3，FG=2，∴AG= = ，∴在Rt△AGD 中，tan∠ADG= = ，∴tan∠E= ；故③错误；④∵DF=DG+FG=6，AD= = ，∴S △ADF= DF•AG= ×6× =3 ，∵△ADF∽△AED，∴ =（）2，∴ = ，∴S△AED=7 ，∴S △DEF=S△AED ﹣S△ADF=4 ；故④正确．故选C．【分析】①正确．由AB是⊙O的直径，弦CD⊥AB，根据垂径定理可得：，DG=CG，继而证得△ADF∽△AED；②正确．由= ，CF=2，可求得DF的长，继而求得CG=DG=4，则可求得FG=2；③错误．由勾股定理可求得AG的长，即可求得tan∠ADF的值，继而求得tan∠E= ．④首先求得△ADF的面积，由相似三角形面积的比等于相似比的平方，即可求得△ADE 的面积，继而求得S△DEF =4 ．20、【答案】D 【考点】垂径定理，圆周角定理，相似三角形的判定与性质【解析】【解答】解：∵在⊙O中，点C是的中点，∴ = ，∴∠CAD=∠ABC，故①正确；∵ ≠ ，∴ ≠ ，∴AD≠BC，故②错误；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB，∴∠ACE+∠CAE=∠ABC+∠CAE=90°，∴∠ACE=∠ABC，又∵C为的中点，∴ = ，∴∠CAP=∠ABC，∴∠ACE=∠CAP，∴AP=CP，∵∠ACQ=90°，∴∠ACP+∠PCQ=∠CAP+∠PQC=90°，∴∠PCQ=∠PQC，∴PC=PQ，∴AP=PQ，即P 为Rt△ACQ斜边AQ的中点，∴P为Rt△ACQ的外心，故③正确；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB∴根据射影定理，可得AC2=AE•AB，故④正确；如图，连接BD，则∠ADG=∠ABD，∵ ≠ ，∴ ≠ ，∴∠ABD≠∠BAC，∴∠ADG≠∠BAC，又∵∠BAC=∠BCE=∠PQC，∴∠ADG≠∠PQC，∴CB与GD不平行，故⑤错误．故答案为：D．【分析】在同圆或等圆中，同弧或等弧所对的圆周角相等，据此推理可得①正确，②错误；通过推理可得∠ACE=∠CAP，得出AP=CP，再根据∠PCQ=∠PQC，可得出PC=PQ，进而得到AP=PQ，即P为Rt△ACQ斜边AQ的中点，故P为Rt△A CQ的外心，即可得出③正确；连接BD，则∠ADG=∠ABD，根据∠ADG≠∠BAC，∠BAC=∠BCE=∠PQC，可得出∠ADG≠∠PQC，进而得到CB与GD不平行，可得⑤错误．。

初中几何多结论问题

专题—几何多结论问题【考题研究】以函数/几何为背景多结论问题自13年以来深圳广州等地每年必考，出现的位置是选择题或者填空题的压轴题.其难度不言自于，对学生综合分析问题的能力要求比较高.【解题策略】常见类型有：(1)代数中的多结论题;特别是有关二次函数中的多结论选填题是综合性比较强的题目，解决此类题目不仅要掌握二次函数的图象与性质、抛物线位置与字母系数的关系、二次函数与方程、不等式的关系等知识，还要学会代入特殊值的方法并结合二次函数的图象去验证一些不等式的正误;(2)几何中的多结论题;几何中的多结论选填题则结合了三角形、四边形、圆的有关性质和判定，是几何中综合性很强的题目，掌握三角形、四边形、圆的有关性质并能熟练的运用才能解决此类问题.具体求解时，一是从题干出发考虑，探求结果;二是题干和选择支联合考虑或从选择支出发探求是否满足题干条件. 事实上，后者在解答选择题时更常用、更有效.常用方法有以下几种：1.直接法从题设条件出发，通过正确的运算、推理或判断，直接得出结论再与选择支对照，从而作出选择的一种方法。

运用此种方法解题需要扎实的数学基础.2.特例法运用满足题设条件的某些特殊数值、特殊位置、特殊关系、特殊图形、特殊数列、特殊函数等对各选择支进行检验或推理，利用问题在某一特殊情况下不真，则它在一般情况下也不真的原理，由此判明选项真伪的方法。

用特例法解选择题时，特例取得愈简单、愈特殊愈好.3.筛选法(也叫排除法、淘汰法)运用选择题中单选题的特征，即有且只有一个正确选择支这一信息，从选择支入手，根据题设条件和各选项之间的关系，通过分析、推理、计算、判断，对选择项进行筛选，将其中与题设相矛盾的干扰逐一排除从而获得正确结论的方法。

使用筛选法的前提是“答案唯一”，即四个选项中有且只有一个答案正确.4.逆推代入法将选择项中给出的答案或其特殊值，代入题干逐一去验证是否满足题设条件，然后选择符合题设条件的择题项的一种方法. 在运用验证法解题时，若能据题意确定代入顺序，则能较大提高解题速度. 5.直观选择法利用函数图像或数学结果的几何意义，将数的问题(如解方程、解不等式、求最值，求取值范围等)与某些图形结合起来，利用直观几性，再辅以简单计算，确定正确答案的方法。

二次函数选择题多结论问题(带答案)

二次函数选择题多结论问题1．抛物线2(0)y ax bx c a =++≠的对称轴是直线1x =-，其图象如图所示．下列结论：①0abc <；②22(4)(2)a c b +<；③若1(x ，1)y 和2(x ，2)y 是抛物线上的两点，则当12|1||1|x x +>+时，12y y <；④抛物线的顶点坐标为(1,)m -，则关于x 的方程21ax bx c m ++=-无实数根．其中正确结论的个数是( ) A ．4B ．3C ．2D ．11T 4T2．已知抛物线2(0)y ax bx c a =++>，且12a b c ++=-，32a b c -+=-．判断下列结论：①0abc <；②220a b c ++>；③抛物线与x 轴正半轴必有一个交点；④当23x 时，3y a =最小；⑤该抛物线与直线y x c =-有两个交点，其中正确结论的个数( ) A ．2B ．3C ．4D ．53．二次函数2(y ax bx c a =++、b 、c 是常数，且0)a ≠的自变量x 与函数值y 的部分对应值如下表：且当32x =时，对应的函数值0y <．有以下结论： ①0abc >；②203m n +<-；③关于x 的方程20ax bx c ++=的负实数根在12-和0之间；④11(1,)P t y -和22(1,)P t y +在该二次函数的图象上，则当实数13t >时，12y y >．其中正确的结论是( ) A ．①②B ．②③C ．③④D ．②③④4．二次函数2(0)y ax bx c a =++≠的部分图象如图所示，对称轴为直线12x =，且经过点(2,0)．下列说法：①0abc <；②20b c -+=；③420a b c ++<；④若1(2-，1)y ，5(2，2)y 是抛物线上的两点，则12y y <；⑤1()4b c m am b c+>++（其中1)2m ≠．正确的结论有( )A ．2个B ．3个C ．4个D ．5个5．如图，二次函数2(0)y ax bx c a =++≠图象的一部分与x 轴的一个交点坐标为(1,0)，对称轴为直线1x =-，结合图象给出下列结论： ①0a b c ++=； ②20a b c -+<；③关于x 的一元二次方程20(0)ax bx c a ++=≠的两根分别为3-和1； ④若点1(4,)y -，2(2,)y -，3(3,)y 均在二次函数图象上，则123y y y <<； ⑤()(a b m am b m -<+为任意实数）．其中正确的结论有( ) A ．1个B ．2个C ．3个D ．4个5T 6T6．二次函数2(0)y ax bx c a =++≠的图象的一部分如图所示．已知图象经过点(1,0)-，其对称轴为直线1x =． ①0abc <； ②420a b c ++<； ③80a c +<；④若抛物线经过点(3,)n -，则关于x 的一元二次方程20(0)ax bx c n a ++-=≠的两根分别为3-，5．上述结论中正确结论的个数为( ) A ．1个B ．2个C ．3个D ．4个7．抛物线2(y ax bx c a =++，b ，c 为常数）开口向下且过点(1,0)A ，(B m ，0)(21)m -<<-，下列结论：①20b c +>；②20a c +<；③(1)0a m b c +-+>；④若方程()(1)10a x m x ---=有两个不相等的实数根，则244ac b a -<．其中正确结论的个数是( ) A ．4B ．3C ．2D ．18．如图，已知抛物线2(y ax bx c a =++，b ，c 为常数，0)a ≠经过点(2,0)，且对称轴为直线12x =，有下列结论：①0abc >；②0a b +>；③4230a b c ++<；④无论a ，b ，c 取何值，抛物线一定经过(2c a，0)；⑤2440am bm b +-．其中正确结论有( ) A ．1个B ．2个C ．3个D ．4个8T 10T9．已知抛物线2(y ax bx c a =++，b ，c 是常数，0)a ≠经过点(1,1)--，(0,1)，当2x =-时，与其对应的函数值1y >．有下列结论： ①0abc >；②关于x 的方程230ax bx c ++-=有两个不等的实数根； ③7a b c ++>．其中，正确结论的个数是( ) A ．0B ．1C ．2D ．310．已知二次函数2(0)y ax bx c a =++≠的图象如图所示，有下列5个结论： ①0abc >； ②24b ac <； ③23c b <；④()(1)a b m am b m +>+≠；⑤若方程2||1ax bx c ++=有四个根，则这四个根的和为2．其中正确的结论有( )A ．2个B ．3个C ．4个D ．5个11．已知抛物线2(0)y ax bx c a =++≠与x 轴的交点为(1,0)A 和(3,0)B ，点11(P x ，1)y ，22(P x ，2)y 是抛物线上不同于A ，B 的两个点，记△1P AB 的面积为1S ，△2P AB 的面积为2S ，有下列结论：①当122x x >+时，12S S >；②当122x x <-时，12S S <；③当12|2||2|1x x ->->时，12S S >；④当12|2||2|1x x ->+>时，12S S <．其中正确结论的个数是( ) A ．1B ．2C ．3D ．412．如图，二次函数2(0)y ax bx c a =++≠的图象与x 轴交于A ，B 两点，与y 轴交于点C ，且OA OC =．则下列结论：①0abc <；②2404b ac a ->：③10ac b -+=；④c OA OB a ⋅=：⑤1OB a=-，其中正确结论的个数是( )A ．4B ．3C ．2D ．112T 13T 14T 15T13．二次函数2(0)y ax bx c a =++≠的大致图象如图所示，已知顶点坐标为(2,9)a --．有下列结论：①0abc <；②420a b c ++>；③50a b c -+=；④若方程(5)(1)1a x x +-=-有两个根1x 和2x ，且12x x <，则1251x x -<<<．其中正确结论的个数为( ) A ．1B ．2C ．3D ．414．如图所示是二次函数2y ax bx c =++图象的一部分，图象过A 点(3,0)，二次函数图象对称轴为1x =，给出四个结论：①24b ac >；②0bc <；③20a b +=；④0a b c ++=，其中正确结论有( )个． A ．0B ．1C ．2D ．315．如图，抛物线2(0)y ax bx c a =++≠顶点坐标为(2,)a --，对于下列结论：①0abc <；②0a b c ++>；③3c a =；④若方程220ax bx c ++-=没有实数根，则20a -<<．其中正确的结论有( ) A ．1个 B ．2个 C ．3个 D ．4个16．如图，已知抛物线2(0)y ax bx c a =++≠的对称轴为直线1x =，与x 轴的两个交点是A ，B ，其中点A 的坐标为(3,0)，则下列结论：①0abc >；②240b ac -；③点B 的坐标是(1,0)-；④点1(C x ，12)(y D x ，2)y 是抛物线上的两点，若12x x <，则12y y <，其中正确结论的个数是( ) A ．1个B ．2个C ．3个D ．4个16T 17T 18T 19T17．如图是二次函数2y ax bx c =++图象的一部分，图象过点(5,0)A -，对称轴为直线2x =-，给出四个结论：①0abc >；②420a b c -+>；③若1(3,)B y -与2(4,)C y -是抛物线上两点，则21y y <；④50a c +=．其中，正确结论的个数是( ) A ．1B ．2C ．3D ．418．如图为某二次函数的部分图象，有如下四个结论：①此二次函数表达式为2194y x x =-+：②若点(1,)B n -在这个二次函数图象上，则n m >；③该二次函数图象与x 轴的另一个交点为(4,0)-；④当0 5.5x <<时，8m y <<．所有正确结论的序号是( ) A ．①③B ．①④C ．②③D ．②④19．二次函数2y ax bx c =++的部分图象如图所示，对称轴是直线 1.5x =-，与x 轴的一个交点在(4,0)-和(3,0)-之间，有以下结论：①0abc >；②240b ac ->；③30a b -=；④430b c +<．其中正确结论的个数是( ) A ．1B ．2C ．3D ．420．抛物线2(y ax bx c a =++，b ，c 为常数，0)a ≠与x 轴交于(1,0)A -，(3,0)B 两点，与y 轴的正半轴交于点C ，顶点为D ．有下列结论：①20a b +=；②430c b ->；③当ABC ∆是等腰三角形时，a 的值有2个；④当BCD ∆是直角三角形时，a =．其中，正确结论的个数是( ) A ．0B ．1C ．2D ．321．抛物线2y ax bx c =++的顶点为(1,2)D -，与x 轴的一个交点A 在点(3,0)-和(2,0)-之间，其部分图象如图，则以下结论：①0abc >；②0a b c ++<；③2c a -=；④方程220ax bx c ++-=有两个相等的实数根；⑤10ac b -+>．其中正确结论的个数为( )A ．2个B ．3个C ．4个D ．5个21T 22T 23T 24T 22．如图，抛物线2y ax bx c =++与x 轴正半轴交于A ，B 两点，其中点B 的坐标为 (4,0)，抛物线与y 轴负半轴交于点C ，有下列结论：①0abc >；②40a b +<；③若1(1,)M y 与2(2,)N y 是抛物线上两点，则12y y >；④若3AB ，则430b c +>．其中，正确的结论是( ) A ．①②B ．③④C ．①④D ．②③23．如图是抛物线2(0)y ax bx c a =++≠的部分图象，其顶点坐标为(1,)n ，且与x 轴的一个交点在点(3,0)和(4,0)之间，则下列结论：①0abc <；②30a b +>；③420a b c -+>；④24()b a c n =-；⑤一元二次方程21ax bx c n ++=+有两个互异实根．其中正确结论的个数是( ) A ．2个B ．3个C ．4个D ．5个24．抛物线2(0)y ax bx c a =++≠与x 轴交于点(3,0)-，其对称轴是12x =-，结合图象分析下列结论：①0abc >；②0a b c ++>；③0a b +=；④20a c +>；⑤一元二次方程20ax bx c ++=的两根分别为13x =-，22x =；⑥2404ac b a->；⑦若两点1(2,)y -，2(3,)y 在二次函数图象上，则12y y >；其中正确的结论有( ) A ．3个 B ．4个 C ．5个 D ．6个25．我们定义一种新函数：形如22||(0,40)y ax bx c a b ac =++≠->的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数2|23|y x x =--的图象（如图所示），并写出下列四个结论：其中正确结论的个数是( )①图象具有对称性，对称轴是直线1x =；②当11x -<<或3x >时，函数值随x 值的增大而增大；③当1x =-或3x =时，函数的最小值是0；④当1x =时，函数的最大值是4． A ．4B ．3C ．2D ．125T 26T 28T26．如图，抛物线2y ax bx c =++的顶点坐标为(1,)n ．下列结论：①0abc <；②80a c +<；③关于x 的一元二次方程21ax bx c n ++=-有两个不相等实数根；④抛物线上有两点1(P x ，1)y 和2(Q x ，2)y ，若121x x <<，且122x x +>，则12y y >．其中正确的结论共有( ) A ．1个B ．2个C ．3个D ．4个27．关于二次函数245(0)y ax ax a =--≠的三个结论：①图象与y 轴的交点为(0,5)-；②对任意实数m ，都有12x m =+与22x m =-对应的函数值相等；③若34x ，对应的y 的整数值有4个，则413a -<-或413a <．其中，正确结论的个数是( ) A ．0B ．1C ．2D ．328．如图，二次函数的图象经过点，，其对称轴为直线．下面是5个结论：①；②；③；④；⑤．其中正确的结论有A ．4个B ．3个C ．2个D ．1个29．函数，，为常数，的图象与轴交于点，顶点坐标为，其中．有下列结论：①；②函数在和处的函数值相等；③点，，，在函数的图象上，若，则．其中，正确结论的个数是A ．0B ．1C ．2D ．32(0)y ax bx c a =++≠1(2-0)1x =0abc <240a b c -+=20a b +>230c b -<2a b am bm ++()2(y ax bx c a =++b c 0)a ≠x (2,0)(1,)n -0n >0abc >2y ax bx c =++1x =2x =-1(M x 1)y 2(N x 2)y 2y ax bx c =++1231x x -<<<12y y >()30．已知抛物线与轴有两个交点，，，．现有如下结论：①此抛物线过定点；②若抛物线开口向下，则的取值范围是；③若时，有，，则的取值范围是．其中正确结论的个数是A ．0B ．1C ．2D ．32(1)22y m x mx m =+-+-x 1(x 0)2(x 0)(1,1)-m 21m -<<-1m >-121x -<<-212x <<m 2194m -<<()【详解】①抛物线图象开口向上， 0a ∴>，对称轴在直线y 轴左侧， a ∴，b 同号，0b >，抛物线与y 轴交点在x 轴下方， 0c ∴<，0abc ∴<，故①正确．②22(4)(2)(42)(42)a c b a c b a c b +-=+++-，当2x =时242ax bx c a c b ++=++，由图象可得420a c b ++>，由图象知，当2x =-时，242ax bx c a c b ++=+-，由图象可得420a c b +-<，22(4)(2)0a c b ∴+-<，即22(4)(2)a c b +<，故②正确．③11|1||(1)|x x +=--，22|1||(1)|x x +=--， 12|1||1|x x +>+，∴点1(x ，1)y 到对称轴的距离大于点2(x ，2)y 到对称轴的距离，12|y y ∴>，故③错误．④抛物线的顶点坐标为(1,)m -，y m ∴，2ax bx c m ∴++，21ax bx c m ∴++=-无实数根．故④正确，综上所述，①②④正确．【详解】12a b c ++=-，32a b c -+=-，∴两式相减得12b =，两式相加得1c a =--， 0c ∴<，0a >，0b >，0c <， 0abc ∴<，故①正确；12222102a b c a a a ∴++=+⨯--=>，故②正确；当1x =时，则12y a b c =++=-，当1x =-时，则有32y a b c =-+=-，∴当0y =时，则方程20ax bx c ++=的两个根一个小于1-，一个根大于1，∴抛物线与x 轴必有一个交点，故③正确；由题意知抛物线的对称轴为直线1024b x a a=-=-<， ∴当23x 时，y 随x 的增大而增大，∴当2x =时，有最小值，即为424113y a b c a a a =++=+--=，故④正确；联立抛物线2y ax bx c =++及直线y x c =-可得：2x c ax bx c -=++，整理得：21202ax x c -+=，∴△1804ac =->， ∴该抛物线与直线y x c =-有两个交点，故⑤正确； ∴正确的个数有5个．3．【答案】B【详解】将(0,2)，(1,2)代入2y ax bx c =++得： 22ca b c =⎧⎨=++⎩，解得2b a c =-⎧⎨=⎩， ∴二次函数为：22y ax ax =-+，当32x =时，对应的函数值0y <， ∴932042a a -+<， 83a ∴<-， 83a ∴->，即83b >， 0a ∴<，0b >，0c >，0abc ∴<，故①不正确；1x =-时y m =，2x =时y n =，222m a a a ∴=++=+，42222n a a a =-+=+，44m n a ∴+=+， 83a <-， 203m n ∴+<-，故②正确；抛物线过(0,2)，(1,2)，∴抛物线对称轴为12x =，又当32x =时，对应的函数值0y <， ∴根据对称性：当12x =-时，对应的函数值0y <，而0x =时20y =>，∴抛物线与x 轴负半轴交点横坐标在12-和0之间， ∴关于x 的方程20ax bx c ++=的负实数根在12-和0之间，故③正确； 11(1,)P t y -和22(1,)P t y +在该二次函数的图象上，21(1)(1)2y a t a t ∴=---+，22(1)(1)2y a t a t =+-++，若12y y >，则22(1)(1)2(1)(1)2a t a t a t a t ---+>+-++，即22(1)(1)(1)(1)a t a t a t a t --->+-+，0a <，22(1)(1)(1)(1)t t t t ∴---<+-+，解得12t >，故④不正确． 4．【答案】B 【详解】抛物线开口向下，且交y 轴于正半轴，0a ∴<，0c >，对称轴122b x a =-=，即b a =-， 0b ∴>，0abc ∴<，故①正确；二次函数2(0)y ax bx c a =++≠的图象过点(2,0)，042a b c ∴=++，故③不正确；又可知b a =-，042b b c ∴=-++，即20b c -+=，故②正确；抛物线开口向下，对称轴是直线12x =，且11()122--=，51222-=， 12y y ∴>，故选④不正确；抛物线开口向下，对称轴是12x =，∴当12x =时，抛物线y 取得最大值2111()224max y a b c b c =++=+，当x m =时，2()m y am bm c m am b c =++=++，且12m ≠， max m y y ∴>，故⑤正确，综上，结论①②⑤正确．5．【答案】C 【详解】①二次函数2(0)y ax bx c a =++≠图象的一部分与x 轴的一个交点坐标为(1,0)， 0a b c ∴++=，故①正确； ②抛物线的对称轴为直线12b x a=-=-， 2b a ∴=，抛物线开口向上，与y 轴交于负半轴，0a ∴>，0c <，230a b c c a ∴-+=-<，故②正确；③由对称得：抛物线与x 轴的另一交点为(3,0)-，∴关于x 的一元二次方程20(0)ax bx c a ++=≠的两根分别为3-和1，故③正确； ④对称轴为直线1x =-，且开口向上，∴离对称轴越近，y 值越小，|41|3-+=，||21|1-+=，|31|4+=，点1(4,)y -，2(2,)y -，3(3,)y 均在二次函数图象上，213y y y ∴<<，故④不正确；⑤1x =-时，y 有最小值，2(a b c am bm c m ∴-+++为任意实数），()a b m am b ∴-+，故⑤不正确．所以正确的结论有①②③，共3个．6．【答案】C 【详解】抛物线的开口向下，0a ∴<．抛物线与y 轴的正半轴相交，0c ∴>．抛物线的对称轴为直线1x =，12ba ∴-=，2b a ∴=-，0b >．抛物线经过点(1,0)-，0a b c ∴-+=．①0a <，0b >，0c >，0abc ∴<．故①正确；②2b a =-，4242(2)440a b c a a c a a c c ∴++=+⨯-+=-+=>．故②错误；③0a b c -+=，(2)0a a c ∴--+=，即30a c +=．83550a c a c a a ∴+=++=<．故③正确； ④抛物线经过点(3,)n -，其对称轴为直线1x =，∴根据对称性，抛物线必经过点(5,)n ，∴当y n =时，3x =-或5．2(0)y ax bx c a =++≠，∴当2(0)ax bx c n a ++=≠时，3x =-或5．即关于x 的一元二次方程20(0)ax bx c n a ++-=≠的两根分别为3-，5．故④正确；综上，正确的结论有：①③④．7．【答案】A【详解】根据题意得0a b c ++=，b ac ∴=--，当2x =-时，有420a b c -+<，42()0a a c c ∴---+<，20a c ∴+<，∴②正确，由20a c +<，得20a c -->，2()0a c c ∴--+>，20b c ∴+>，∴①正确，若(1)0a m b c +-+>，则a b c am -+>-，取1x =-，则0y a b c =-+>，又0a <，0m <，即(1)0a m b c +-+>成立，∴③正确，若方程()(1)10a x m x ---=有两个不相等的实数根，即()(1)1a x m x --=有两个不相等的实数根，∴顶点的纵坐标2414ac b a->， 244ac b a ∴-<，∴④正确．8．【答案】D 【详解】①抛物线的对称轴为直线12x =，即对称轴在y 轴的右侧， 0ab ∴<，抛物线与y 轴交在负半轴上，0c ∴<，0abc ∴>，故①正确； ②抛物线的对称轴为直线12x =， 122b a ∴-=， 22b a ∴-=，0a b ∴+=，故②不正确； ③抛物线2(y ax bx c a =++，b ，c 为常数，0)a ≠经过点(2,0)，420a b c ∴++=，故③正确；④由对称得：抛物线与x 轴另一交点为(1,0)-，420a b a b c +=⎧⎨++=⎩， 2c a ∴=-， ∴12c a=-， ∴当0a ≠，无论b ，c 取何值，抛物线一定经过(2c a ，0)，故④正确；⑤b a =-，22224444(441)(21)am bm b am am a a m m a m ∴+-=-+=-+=-，0a >，2(21)0a m ∴-，即2440am bm b +-，故⑤正确；本题正确的有：①③④⑤，共4个．9．【答案】D 【详解】①抛物线2(y ax bx c a =++，b ，c 是常数，0)a ≠经过点(1,1)--，(0,1)， 1c ∴=，1a b c -+=-，2a b ∴=-，当2x =-时，与其对应的函数值1y >．4211a b ∴-+>，4(2)211b b ∴--+>，解得：4b >，20a b ∴=->，，0abc ∴>，故①正确；②2a b =-，1c =，2(2)130b x bx ∴-++-=，即2(2)20b x bx ∴-+-=，∴△224(2)(2)816(8)16b b b b b b =-⨯-⨯-=+-=+-，4b >，∴△0>，∴关于x 的方程230ax bx c ++-=有两个不等的实数根，故②正确；③2a b =-，1c =，2121a b c b b b ∴++=-++=-，4b >，217b ∴->，7a b c ∴++>．故③正确．10．【答案】A【详解】①二次函数图象性质知，开口向下，则0a <．再结合对称轴02b a->，得0b >．据二次函数图象与y 轴正半轴相交得0c >．0abc ∴<． ①错．②二次函数图象与x 轴交于不同两点，则240b ac ->．24b ac ∴>．②错． ③12b a-=， 2b a ∴=-．又当1x =-时，0y <．即0a b c -+<．2220a b c ∴-+<．320b c ∴-+<．23c b <．∴③正确．④1x =时函数有最大值，∴当1x =时的y 值大于当(1)x m m =≠时的y 值，即()a b c m am b c ++>++()(1)a b m am b m ∴+>+≠成立，∴④正确．⑤将x 轴下方二次函数图象翻折到x 轴上方，则与直线1y =有四个交点即可．由二次函数图象的轴对称性知：关于对称轴对称的两个根的和为2，四个根的和为4．故⑤错．综上：③④正确．11．【答案】A【详解】方法一：不妨假设0a >．①如图1中，1P ，2P 满足122x x >+，12//PP AB ，12S S ∴=，故①错误．②当12x =-，21x =-，满足122x x <-，则12S S >，故②错误，③12|2||2|1x x ->->，1P ∴，2P 在x 轴的上方，且1P 离x 轴的距离比2P 离x 轴的距离大， 12S S ∴>，故③正确，④如图2中，1P ，2P 满足12|2||2|1x x ->+>，但是12S S =，故④错误．故选：A ．方法二：解：抛物线y =ax 2+bx +c 与x 轴的交点为A (1,0)和B (3,0)， ∴该抛物线对称轴为x 2=，当x 1>x 22+时与当x 122x <-时无法确定P 1(x 1，y 1)，P 2(x 2，y 2)在抛物线上的对应位置，故①和②都不正确；当|x 12||->x 22|1->时，P 1(x 1，y 1)比P 2(x 2，y 2)离对称轴更远，且同在x 轴上方或者下方， |∴y 1||>y 2|，∴S 1>S 2，故③正确；当|x 12||->x 22|1+>时，即在x 轴上x 1到2的距离比x 2到2-的距离大，且都大于1，可知在x 轴上x 1到2的距离大于1，x 2到2-的距离大于1，但x 2到2的距离不能确定，所以无法比较P 1(x 1，y 1)比P 2(x 2，y 2)谁离对称轴更远，故无法比较面积，故④错误；12．【答案】B 【详解】抛物线开口向下，0a ∴<，抛物线的对称轴在y 轴的右侧，0b ∴>，抛物线与y 轴的交点在x 轴上方，0c ∴>，0abc ∴<，所以①正确；抛物线与x 轴有2个交点，∴△240b ac =->，而0a <， ∴2404b ac a-<，所以②错误； (0,)C c ，OA OC =，(,0)A c ∴-，把(,0)A c -代入2y ax bx c =++得20ac bc c -+=， 10ac b ∴-+=，所以③正确；设1(A x ，0)，2(B x ，0)，二次函数2(0)y ax bx c a =++≠的图象与x 轴交于A ，B 两点， 1x ∴和2x 是方程20(0)ax bx c a ++=≠的两根，12c x x a∴⋅=， 0a <，0c >，c OA OB a∴⋅=-，所以④错； OA c =，1OB a∴=-，故⑤正确． 13．【答案】C 【详解】抛物线的顶点坐标为(2,9)a --， 22(2)945y a x a ax ax a ∴=+-=+-，抛物线的开口向上，0a ∴>，40b a ∴=>，50c a =-<，0abc ∴<，所以①正确；当0y =时，2450ax ax a +-=，解得15x =-，21x =， ∴抛物线与x 轴的交点坐标为(5,0)-，(1,0)， 2x =时，0y >，420a b c ∴++>，所以②正确；55454a b c a a a a -+=--=-，而0a >，50a b c ∴-+<，所以③错误；方程(5)(1)1a x x +-=-有两个根1x 和2x ， ∴抛物线(5)(1)y a x x =+-与直线1y =-有两个交点，交点的横坐标分别为1x 和2x ， 1251x x ∴-<<<，所以④正确；综上：正确的个数为3个.14．【答案】C【详解】由图象知和x 轴有两个交点， ∴△240b ac =->，24b ac ∴>，故①正确；由图象知，图象与y 轴交点在x 轴的上方，且二次函数图象对称轴为1x =， 0c ∴>，12b a-=，0a <， 0b ∴>，即0bc >，20a b +=，∴②不正确，③正确；由图象知，当1x =时22110y ax bx c a b c a b c =++=⨯+⨯+=++>， ∴④不正确，综合上述：正确的个数是2.15．【答案】C【详解】抛物线开口向下，则0a <，对称轴202b x a =-=-<，因此a 、b 同号，所以0b <，抛物线与y 轴的交点在负半轴，因此0c <， 0abc ∴<，因此①正确；当1x =时，0y a b c =++<，因此②不正确；抛物线过(2,)a --点，因此42a b c a -+=-，即520a b c -+=，对称轴为22b x a =-=-，即4b a =，所以580a a c -+=，即3c a =，因此③正确；方程220ax bx c ++-=没有实数根，即抛物线与直线2y =没有交点，此时顶点的纵坐标2a -<，又0a <，20a ∴-<<，因此④正确；综上所述，正确的有①③④，共3个.16．【答案】B【详解】由图象可知：0a >，0b <，0c <， 0abc ∴>，故①正确；抛物线与x 轴交于两点，240b ac ∴->，故②错误；抛物线的对称轴为直线1x =，与x 轴的两个交点是A ，B ，点A 的坐标为(3,0)， ∴点B 的坐标是(1,0)-，故③正确；点1(C x ，12)(y D x ，2)y 是抛物线上的两点，∴当121x x <<时，12y y >，当121x x <<时，12y y <，故④错误；17．【答案】D【详解】由图象可知：开口向下，故0a <，抛物线与y 轴交点在x 轴上方，故0c >，对称轴02bx a =-<，0b ∴<，0abc ∴>，故①正确；由图象可知，2x =-时，0y >，420a b c ∴-+>，故②正确；当2x <-时，此时y 随x 的增大而增大，34->-，21y y ∴<，故③正确；对称轴为2x =-，22ba ∴-=-，4b a ∴=，点(5,0)A -关于对称轴的对称点是(1,0)， 0a b c ∴++=，40a a c ∴++=，即50a c +=，故④正确；18．【答案】C【详解】①由图象顶点(2,9)可得2(2)9y a x =-+，将(8,0)代入2(2)9y a x =-+得0369a =+，解得14a =-， 2211(2)9844y x y x x ∴=--+==-++，故①错误．② 5.522(1)->--，点A 距离对称轴距离大于点B 距离对称轴距离， m n ∴<，故②正确． ③图象对称轴为直线2x =，且抛物线与x 轴一个交点为(8,0)， ∴图象与x 轴的另一交点横坐标为2284⨯-=-，故③正确．④由图象可得当0x =时8y =， 5.5x =时y m =，2x =时9y =， 0 5.5x ∴<<时，9m y <．故④错误．19．【答案】D 【详解】抛物线开口向下，0a ∴<，抛物线的对称轴为直线 1.52b x a=-=-， 30b a ∴=<，30a b ∴-=，所以③正确；抛物线交y 的正半轴，0c ∴>，0abc ∴>，所以①正确；抛物线与x 轴有两个交点，240b ac ∴->，所以②正确；由图象可知，1x =时0y <，且3b a =，即14033a b c b b c b c ++=++=+<，即430b c +<，故④正确；20．【答案】D 【详解】二次函数2y ax bx c =++的图象与x 轴交于(1,0)A -，(3,0)B 两点，∴对称轴为直线12b x a =-=， 2b a ∴=-，20a b ∴+=，故①正确；抛物线2y ax bx c =++与x 轴交于(1,0)A -，(3,0)B 两点，与y 轴的正半轴交于点C ， 0a ∴<，当1x =-时，0y a b c =-+=，20a a c ∴++=，3c a ∴=-，4312660c b a a a ∴-=-+=->，故②正确；二次函数223y ax ax a =--，(0)a <， ∴点(0,3)C a -，当BC AB =时，4，a ∴=，当AC BA =时，4=a ∴=， ∴当ABC ∆是等腰三角形时，a 的值有2个，故③正确；二次函数2223(1)4y ax ax a a x a =--=--， ∴顶点(1,4)D a -，22416BD a ∴=+，2299BC a =+，221CD a =+，若90BDC ∠=︒，可得222BC BD CD =+， 222994161a a a ∴+=+++，a ∴=，若90DCB ∠=︒，可得222BD CD BC =+， 222416991a a a ∴+=+++，1a ∴=-，∴当BCD ∆是直角三角形时，1a =-或，故④错误．21．【答案】D 【详解】抛物线开口向下，0a ∴<，对称轴在y 轴左侧，0b ∴<，对称轴为1x =-，抛物线与x 轴的一个交点A 在点(3,0)-和(2,0)-之间，∴与x 轴的另一个交点在点(0,0)和(1,0)之间， ∴抛物线和y 轴正半轴相交，1x =时，0y <， 0c ∴>，0a b c ++<，0abc ∴>，故①②正确；抛物线的对称轴为直线12b x a =-=-， 2b a ∴=，1x =-时，2y =，即2a b c -+=，22a a c ∴-+=，即2c a -=，所以③正确；当1x =-时，二次函数有最大值为2，即只有1x =-时，22ax bx c ++=， ∴方程220ax bx c ++-=有两个相等的实数根，故④正确； 2c a -=，2c a ∴=+，2b a =，21(2)2110ac b a a a a ∴-+=+-+=+>，故⑤正确；22．【答案】C【详解】根据题意抛物线开口向下，且与x 轴交于正半轴两点，与y 轴负半轴交于点C ， 0a ∴<，0b >，0c <，0abc ∴>，故①正确；根据抛物线的对称性可知：242b a <-<， 48a b a ∴-<<-，40a b ∴+>，故②不正确；0a <，22ba <-，∴当2x <时，y 随x 的增大而增大， 12y y ∴<，故③不正确；若3AB ，则点A 的横坐标大于0且小于等于1， ∴当1x =时，0y a b c =++，当4x =时，1640y a b c =++=，即416b ca +=-，∴4016b cb c +-++，整理得450b c +， 432b c c ∴+-，430b c ∴+>，故④正确，23．【答案】A 【详解】图象开口向下， 0a ∴<，取0x =，得0y c =>，又对称轴为12ba -=，20b a ∴=->，0abc ∴<，∴①正确，3320a b a a a +=-=<，∴②错误，由抛物线的对称性得：2x =-时，420y a b c =-+<， ∴③错误，由图象得244ac b n a-=，即24()b a c n =-，∴④正确，2y ax bx c =++的最大值为n ， ∴一元二次方程21ax bx c n ++=+无解， ∴⑤错误，正确的为①④，24．【答案】D 【详解】抛物线开口向下，对称轴在y 轴左侧，抛物线与y 轴交点在y 轴正半轴， 0a ∴<，0b <，0c >，0abc ∴>，①正确，满足题意．抛物线与x 轴一个交点为(3,0)-，对称轴为直线12x =-， ∴抛物线与x 轴另外一交点坐标为(2,0)， 1x ∴=时0y >，0a b c ∴++>，②正确，满足题意． 122b a -=-， a b ∴=，0a b +<，③错误，不满足题意． 20ac a b c ∴+=++>，④正确，满足题意．抛物线与x 轴交点为(3,0)-，(2,0)， 20ax bx c ∴++=的两根分别为13x =-，22x =，⑤正确，满足题意．抛物线顶点在x 轴上方，∴2404ac b a->，⑥正确，满足题意． 322-<-<，10y ∴>，32>，20y ∴<，12y y ∴>，⑦正确，满足题意．综上所述，①②④⑤⑥⑦满足题意．25．【答案】B 【详解】观察图象可知，图象具有对称性，对称轴是直线12b x a=-=，故①正确；令2|23|0x x --=可得2230x x --=，(1)(3)0x x ∴+-=，11x ∴=-，23x =，(1,0)∴-和(3,0)是函数图象与x 轴的交点坐标，又对称轴是直线1x =，∴当11x -<<或3x >时，函数值y 随x 值的增大而增大，故②正确；由图象可知(1,0)-和(3,0)是函数图象的最低点，则当1x =-或3x =时，函数最小值是0，故③正确；由图象可知，当1x <-时，函数值随x 的减小而增大，当3x >时，函数值随x 的增大而增大，均存在大于顶点坐标的函数值，故当1x =时的函数值4并非最大值，故④错误．综上，只有④错误．26．【答案】D 【详解】抛物线开口向下，0a ∴<，顶点坐标(1,)n ，∴对称轴为直线1x =，12b a ∴-=，20b a ∴=->，0c >，0abc ∴<，故①正确；点(1,0)A -关于直线1x =的对称点为(3,0)，930a b c ∴++=，2b a =-，30a c ∴+=，850a c a ∴+=<，故②正确，顶点坐标(1,)n∴抛物线2x bx c n ++=有唯一的解，当1y n =-时，与抛物线有两个交点，故③正确，121x x <<，且122x x +>，21|1||1|x x ∴->-抛物线关于1x =对称，1x <时，y 随x 的增大而增大，1x >时，y 随x 的增大而减小，12y y ∴>，故④正确，综上所述，结论正确的是①②③④共4个．27．【答案】【详解】二次函数245y ax ax =--，当0x =时，5y =-，∴图象与y 轴的交点为(0,5)-，故①正确；该函数的对称轴是直线422a x a-=-=，故对任意实数m ，都有12x m =+与22x m =-对应的函数值相等，故②正确；当3x =时，912535y a a a =--=--，当4x =时，161655y a a =--=-，∴当0a >时，355a y ---，若，对应的的整数值有4个，，D 34x y 543553a ∴--<----解得，；当时，，若，对应的的整数值有4个，，解得，；由上可得，若，对应的的整数值有4个，则或，故③正确； 28．【答案】【详解】①由图象可知，，，，，故①错误；②图象经过点，，代入到解析式中得：，两边同时乘以4，得：，故②正确；③对称轴为直线，即，，，故③错误；④由②③得：，，则，故，故④错误； ⑤当时，函数取得最小值，即，故⑤正确；综上，一共2个正确．29．【答案】413a <0a <535y a ---34x y 533554a ∴-+--<-+413a -<-34x y 413a -<-413a <C 0a >0b <0c <0abc ∴>1(2-0)11042a b c -+=240a b c -+=1x =12b a-=2b a ∴=-20b a +=240a b c -+=2b a =-54a c =-57236022a a cb a -=-+=>1x =2()a bc am bm c m am b c ++++=++C【详解】依照题意，画出图形如下：函数的图象与轴交于点，顶点坐标为，其中．，，对称轴为直线，，，故①正确，对称轴为直线，与的函数值是相等的，故②错误；观察图象可知：横坐标距离对称轴越近，函数值越大，距离对称轴越远，函数值越小．，，点距离对称轴的距离小于2，点距离对称轴的距离大于2，，故③正确．30．【答案】【详解】①当时，，故正确；②该函数图象开口向下，且与轴有两个交点，故，△，解得：，故正确；③由知，当和函数值异号，当时，，当时，，故，故的取值范围是，故正确．2(0)y ax bx c a =++≠x (2,0)(1,)n -0n >0a ∴<0c >12b x a=-=-20b a ∴=<0abc ∴>1x =-1x ∴=3x =-131x -<<21x >M ∴N 12y y ∴>D 1x =2(1)221y m x mx m =+-+-=-x 10m +<2(2)4(1)(2)0m m m =--+->21m -<<-121x -<<-2x =-1x =-2x =-92y m =+1x =-41y m =-(92)(41)0m m +-<m 2194m -<<。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

几何多结论选择题
１．已知：如图，ΔABC中，D在BC上，过点A的圆⊙Ｏ与
ＡＢ、ＡＣ交于点Ｅ、Ｆ，
①若ＢＣ与⊙Ｏ相切与Ｄ，且∠ＢＡＤ＝∠ＣＡＤ，则
ＡＥ•ＡＣ＝ＡＦ•ＡＢ；
②若ＢＣ与⊙Ｏ相切与Ｄ，且ＡＥ•ＡＣ＝ＡＦ•ＡＢ，
则∠ＢＡＤ＝∠ＣＡＤ；
③若ＡＥ•ＡＣ＝ＡＦ•ＡＢ，且∠ＢＡＤ＝∠ＣＡＤ，
则ＢＣ与⊙Ｏ相切与Ｄ；
其中，正确的结论是（）
Ａ．①②Ｂ．①③Ｃ．②③Ｄ．①②③
２．已知：如图，梯形ABCD中，AB∥CD，
①若∠A=900，DC+AB=BC，则以AD为直径的圆与BC相切；
②若∠A=900，以AD为直径的圆与BC相切，则DC+AB=BC；
③若以AD为直径的圆与BC相切，DC+AB=BC，则∠A=900；
其中，正确的结论是（）
Ａ．①②Ｂ．①③Ｃ．②③Ｄ．①②③
３．已知：如图，P为⊙O外一点，PBC为割线，A
在⊙O上，过点P的直线交AB于点Ｅ，交ＡＣ于Ｆ，
①若ＰＦ平分∠ＡＰＣ，ＰＡ为切线，则ＡＥ＝ＡＦ；
②若ＰＦ平分∠ＡＰＣ，ＡＥ＝ＡＦ，则ＰＡ为切线；
③若ＡＥ＝ＡＦ，ＰＡ为切线，则ＰＦ平分∠ＡＰＣ；
其中，正确的结论是（）
Ａ．①②Ｂ．①③Ｃ．②③
Ｄ．①②③
４．已知：如图，P为⊙O外一点，PＡB为割线，点Ｃ在优弧ＡＢ上，Ｅ在线段ＰＢ上，ＣＥ延长线交⊙Ｏ于Ｆ，
①若ＰＣ为⊙Ｏ切线，ＰＥ＝ＰＣ，则ＯＦ⊥ＡＢ；
②若ＰＣ为⊙Ｏ切线，ＯＦ⊥ＡＢ，则ＰＥ＝ＰＣ；
③若ＯＦ⊥ＡＢ，ＰＥ＝ＰＣ，则ＰＣ为⊙Ｏ切线；
其中，正确的结论是（
）Ａ．①②Ｂ．①③
Ｃ．②③Ｄ．①②③５．已知：如图，⊙Ｏ中，弦ＡＢ、ＣＥ交于点Ｄ，
①若ＡＢ为直径，ＣＥ⊥ＡＢ，则ＣＤ２＝ＡＤ·ＢＤ；
②若ＡＢ为直径，ＣＤ２＝ＡＤ·ＢＤ，则ＣＥ⊥ＡＢ；
③若ＣＤ２＝ＡＤ·ＢＤ，ＣＥ⊥ＡＢ，则ＡＢ为直径；
其中，正确的结论是（
）
Ａ．①②Ｂ．①③Ｃ．②③Ｄ．①②③
６．已知：如图，Δ
ABC中，ＡＣ＞ＢＣ，Ｄ在ＡＣ上，Ｅ为ＢＣ中点，连ＤＥ，过三点Ａ、Ｂ、Ｄ作⊙Ｏ．
①若ＡＢ为直径，ΔABC为ＲtΔ，则DE也为切线；
②若ＡＢ为直径，DE为切线，则ΔABC为ＲtΔ；
③若ΔABC为ＲtΔ，DE也为切线，则ＡＢ为直径；
其中，正确的结论是（）
Ａ．①②Ｂ．①③Ｃ．②③Ｄ．①②③
７．已知：如图，ΔABC外接于⊙O，CF⊥AB于F，AE、AG为弦，AG交CF于点H，EH交BC于点K，
①若AG⊥BC，AE为直径，则EK=HK；
②若AG⊥BC，EK=HK，则AE为直径；
③若AE为直径，EK=HK，则AG⊥BC；
其中，正确的结论是（）
Ａ．①②Ｂ．①③Ｃ．②③Ｄ．①②③
８．已知：如图，两同心圆中，ＥＦ为大圆的弦，ＥＰ、ＦＱ为小圆的切线，Ａ在弧ＱＰ上，ＥＡ（或延长线）交小圆于Ｂ，Ｆ（或延长线）交小圆于Ｃ，
①若ＥＦ为小圆切线，Ａ为弧ＰＱ中点，则ＥＢ＝ＦＣ；
②若ＥＦ为小圆切线，ＥＢ＝ＦＣ，则Ａ为弧ＰＱ中点；
③若ＥＢ＝ＦＣ，Ａ为弧ＰＱ中点，则ＥＦ为小圆切线；
其中，正确的结论是（）
Ａ．①②Ｂ．①③Ｃ．②③Ｄ．①②③
P
B
Ｃ于Ｇ，
①若ＡＤ平分∠ＢＡＣ的外角∠ＥＡＣ，Ｇ为ＢＣ中点，则ＤＦ为直径；
②若ＡＤ平分∠ＢＡＣ的外角∠ＥＡＣ，ＤＦ为直径，则Ｇ为ＢＣ中点；
③若ＤＦ为直径，Ｇ为ＢＣ中点，则ＡＤ平分∠ＢＡＣ的外角∠ＥＡＣ；
１０．⊙Ｏ中，两条弦ＡＢ、ＣＤ交于点Ｇ，延长ＣＤ至Ｆ，延长ＡＢ
至Ｅ，
①若ＡＢ＝ＣＤ，ＡＥ＝ＣＦ，则ＥＦ的中垂线过圆心；
②若ＡＢ＝ＣＤ，ＥＦ的中垂线过圆心，则ＢＥ＝ＤＦ；
③若ＥＦ的中垂线过圆心，ＡＥ＝ＣＦ，则ＡＢ＝ＣＤ；
∠∠∠＝,ＡE＝ＥＦ，则ＤＦ⊥ＢＣ；
①②③①②③ABC⊙Ｏ⊙Ｏ⊙ＯΔABCΔABCΔABCΔABCΔABCΔABCΔABCΔABCΔ
ABCΔABCΔABC⊥为直径，⊥ＣＥ⊥AB于E，Ｄ为劣弧上一点，Ｆ在ＢＥ上，连ＤＦ，
＝。