信号与系统复习题之冲击响应
信号与系统复习题(含答案)

试题一一. 选择题(共10题,20分) 1、n j n j een x )34()32(][ππ+=,该序列是 .A 。
非周期序列B 。
周期3=N C.周期8/3=N D 。
周期24=N2、一连续时间系统y(t)= x (sint),该系统是 .A.因果时不变 B 。
因果时变 C 。
非因果时不变 D 。
非因果时变 3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u e t h t ,该系统是 .A 。
因果稳定B 。
因果不稳定 C.非因果稳定 D 。
非因果不稳定4、若周期信号x[n ]是实信号和奇信号,则其傅立叶级数系数a k 是 .A 。
实且偶 B.实且为奇 C.纯虚且偶 D 。
纯虚且奇 5、一信号x (t )的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω,,j X ,则x(t)为 。
A. t t 22sinB. tt π2sin C 。
t t 44sin D 。
t t π4sin6、一周期信号∑∞-∞=-=n n t t x )5()(δ,其傅立叶变换)(ωj X 为 .A 。
∑∞-∞=-k k )52(52πωδπ B 。
∑∞-∞=-k k )52(25πωδπC. ∑∞-∞=-k k )10(10πωδπD. ∑∞-∞=-k k )10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ,则x[n ]奇部的傅立叶变换为 。
A.)}(Re{ωj e X j B 。
)}(Re{ωj e XC. )}(Im{ωj e X jD. )}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ,则利用冲激串采样得到的采样信号x (nT )能唯一表示出原信号的最大采样周期为 。
A. 500 B 。
1000 C 。
0。
05 D. 0。
001 9、一信号x (t)的有理拉普拉斯共有两个极点s=-3和s=-5,若)()(4t x e t g t=,其傅立叶变换)(ωj G 收敛,则x(t)是 .A. 左边B. 右边C. 双边D. 不确定10、一系统函数1}Re{1)(->+=s s e s H s,,该系统是 。
(完整版)信号与系统复习题

信号与系统试题库一、填空题绪论:1。
离散系统的激励与响应都是____离散信号 __。
2.请写出“LTI ”的英文全称___线性非时变系统 ____。
3.单位冲激函数是__阶跃函数_____的导数. 4.题3图所示波形可用单位阶跃函数表示为()(1)(2)3(3)t t t t εεεε+-+---。
5.如果一线性时不变系统的输入为f(t ),零状态响应为y f (t )=2f (t —t 0),则该系统的单位冲激响应h (t )为____02()t t δ-_________。
6。
线性性质包含两个内容:__齐次性和叠加性___。
7。
积分⎰∞∞-ω--δ-δdt )]t t ()t ([e 0t j =___01j t e ω--_______。
8。
已知一线性时不变系统,当激励信号为f (t)时,其完全响应为(3sint-2cost )ε(t );当激励信号为2f (t )时,其完全响应为(5sint+cost )ε(t),则当激励信号为3f(t )时,其完全响应为___7sint+4cost _____。
9。
根据线性时不变系统的微分特性,若:f (t)−−→−系统y f (t)则有:f ′(t)−−→−系统_____ y ′f (t )_______。
10。
信号f (n )=ε(n )·(δ(n)+δ(n-2))可_____δ(n)+δ(n —2)_______信号。
11、图1所示信号的时域表达式()f t =()(1)(1)tu t t u t --- 。
12、图2所示信号的时域表达式()f t =()(5)[(2)(5)]u t t u t u t +----。
13、已知()()()2f t t t t εε=--⎡⎤⎣⎦,则()f t '=()(2)2(2)u t u t t δ----.14、[]2cos32t d ττδτ-∞⎛⎫+ ⎪⎝⎭⎰=8()u t 。
信号与系统复习题(含答案)

试题一一.选择题(共 10 题, 20 分)j ( 2 ) n41、x[n]ej ( ) ne33,该序列是。
A.非周期序列B.周期 N 3C.周期 N 3 / 8D. 周期N 242、一连续时间系统 y(t)= x(sint) ,该系统是。
A. 因果时不变B.因果时变C.非因果时不变D.非因果时变3、一连续时间 LTI 系统的单位冲激响应 h(t) e 4tu(t2),该系统是 。
A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定 4、若周期信号 x[n] 是实信号和奇信号,则其傅立叶级数系数 a k是 。
A. 实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇, | 2 , 则 x(t)5 、 一 信 号 x(t) 的 傅 立 叶 变 换 X ( j ) 1 | ,| 20 |为。
A. sin 2tB. sin 2tC. sin 4tD. sin 4t2tt4tt6 、 一 周 期 信 号 x(t)(t5n) , 其 傅 立 叶 变 换 X ( j)n为。
A. 2(2 k)B.5 ( 2 k552 k)k5C. 10(10 k)D.1(k)k10k107、一实信号 x[n] 的傅立叶变换为 X (e j) ,则 x[n] 奇部的傅立叶变 换为 。
A.j Re{ X (e j )}B. Re{ X (e j)}C. j Im{ X (e j )}D.Im{ X (e j )}8、一信号 x(t) 的最高频率为 500Hz ,则利用冲激串采样得到的采样信号 x(nT) 能唯一表示出原信号的最大采样周期为 。
A. 500B. 1000C. 0.05D. 0.0019、一信号 x(t) 的有理拉普拉斯共有两个极点 s=- 3 和 s=- 5,若 g(t ) e 4t x(t) , 其 傅 立 叶 变 换 G ( j ) 收 敛 , 则 x(t) 是 。
A. 左边B. 右边C. 双边D. 不确定10、一系统函数H (s) e s, 1,该系统是 。
信号与系统复习资料

信 号 与 系 统 复 习 资 料一 填空1.如果一线性时不变系统的单位冲激响应为h(t),则该系统的阶跃响应g(t)为_________。
2.如果一线性时不变系统的输入为f(t),零状态响应为)(2)(0t t f t y f -=,则该系统的单位冲激响应h(t)为_________________。
3.如果一线性时不变系统的单位冲激响应)()(t t h ε=,则当该系统的输入信号)()(t t t f ε=时,其零状态响应为_________________。
4.傅里叶变换的时移性质是:当f(t)↔F(j ω),则f(t ±t 0)↔____________。
5.=--)]([)1(2t edt d t tδ___________6.根据线性时不变系统的微分特性,若:)()(t y t f f −−→−系统则有:f ′(t)−−→−系统______。
7.卷积(1-2t)ε(t)*ε(t)等于________________。
8.信号f(n)=δ(n)+(21)nε(n)的Z 变换等于____________。
9.单位序列响应 h(n) 是指离散系统的激励为δ (n) 时,系统的 ____________。
10.线性性质包含两个内容:________,__________ 。
11.余弦信号)cos(0t ω的傅里叶变换为___________。
12.若)()()(21t f t f t f *=,则=)()1(t f________)(2t f *。
13.已知)()]([ωj F t f F =,则=-)52(t f ________。
14.已知15.011)(--=zZ F ,则=)(k f __________。
15.=⋅-)()3(t t εε________________。
16.离散系统稳定的z 域充要条件是系统函数H (z )的所有极点位于z 平面的__________。
冲击响应

系统并联
f1 (t ) [ f 2 (t ) f3 (t )] f1 (t ) f 2 (t ) f1 (t ) f 3 (t )
系统并联,框图表示:
h(t )
f (t )
f (t ) f (t )
h1 (t )
f (t ) * h1 (t )
g (t )
f (t ) h1 (t ) f (t ) h2 (t )
可表示为:
e(t ) e(t ) (t )
三.利用卷积求系统的零状态响应
当一个信号作用于系统时,响应为
e( ) (t ) d r (t ) H e(t ) H e( ) H (t ) d 当系统为线性时
3. i ( t ) e( ) h(t ) d
e
1 2
i (t )
L 1H
u( ) u( 2) e ( t ) u(t ) d
e t e 2 u( )u( t )d e t e 2 u( 2)u( t )d
卷积积分中积分限的确定是非常关键的。
四.卷积的计算
已知e( t ) e
u(t ) u(t 2),求i(t )的零状态响应。 R 1 d i t 1.列写KVL方程 L Ri t et
t 2
2.冲激响应为
dt h( t ) e t u( t )
u (t )
H
g (t )
系统的输入 e t u t ,其响应为 r t gt 。系统方程的 右端将包含阶跃函数 ut ,t>0时输入不为0,所以其响应除 了齐次解外,还有特解项。
信号与系统冲激响应求解举例

−t −3t 1 2 1 2
(
−t
−3t
1
2
1
2
1
2
将h(t ), h′(t ), h′′(t )代入原方程
(C1 + C2 )δ ′(t) + (3C1 + C2 )δ (t) + 0⋅ε(t) = δ ′(t) + 2δ (t)
代 原 程: 入 方 aδ ′ ( t ) + bδ ( t ) + r ( t ) + 4aδ ( t ) + 4r2 ( t ) + 3r3 ( t ) =δ '(t) +2δ (t) 1 a=1 b+4a=2 即 b=-2
■ 第 2页
d2 h( t ) = δ ′( t ) − 2 ( t ) + r ( t ) δ 1 2 dt d h( t ) =δ (t) + r (t) 2 dt h( t ) = r ( t ) 3
求特征根 冲激响应
λ2 + 4λ + 3 = 0 ⇒λ1 = −1, λ2 = −3
n = 2, m = 1, n > m h(t )中不包含冲激项
带ε(t)
h(t) = (C1e + C2e
−t
−3t
)ε(t)
■ 第 1页
两种求待定系数方法: 两种求待定系数方法: 求0+法 •求
法一:求0+值确定系数
∴ h(0+ ) = 1 , h' (0+ ) = −2
信号与系统复习题(答案全)

1、 若系统的输入f (t)、输出y (t) 满足()3()4t y t e ft -=,则系统为 线性的 (线性的、非线性的)、 时变的 (时变的、时不变)、 稳定的 (稳定的、非稳定的)。
2、 非周期、连续时间信号具有 连续 、非周期频谱;周期、连续时间信号具有离散、非周期 频谱;非周期、离散时间信号具有 连续 、周期频谱;周期、离散时间信号具有离散、 周期 频谱。
3、 信号f(t)的占有频带为0-10KHz,被均匀采样后,能恢复原信号的最大采样周期为 5×10-5 s . 4、 )100()(2t Sa t f =是 能量信号 (功率信号、能量信号、既非功率亦非能量信号)。
5、 ()2cos()f t t =+是 功率信号 (功率信号、能量信号、既非功率亦非能量信号)。
6、 连续信号f(t)=sint 的周期T 0= 2π ,若对f(t)以fs=1Hz 进行取样,所得离散序列f(k)=sin(k) ,该离散序列是周期序列? 否 。
7、 周期信号2sin(/2)()j n tn n f t e n ππ+∞=-∞=∑,此信号的周期为 1s 、直流分量为 2/π 、频率为5Hz 的谐波分量的幅值为 2/5 。
8、 f (t) 的周期为0.1s 、傅立叶级数系数**03355532F F F F F j --=====、其余为0。
试写出此信号的时域表达式f (t) = 5 + 6 cos ( 60 π t ) - 4 sin (100 π t ) 。
9、 f (k) 为周期N=5的实数序列,若其傅立叶级数系数()205=F ()52511,πjeF -+=()54512πjeF -+=、 则F 5 (3 )= ()54512πjeF +=- 、F 5 (4 )= ()52511πj eF +=- 、F 5 (5 )= 2 ;f(k) =())1.7254cos(62.052)9.3552cos(62.152525140525︒-⨯+︒-⨯+=∑=k k e n F n k jn πππ。
信号与系统复习试题(含答案)

电气《信号与系统》复习(fùxí)参考练习题一、单项选择题:14、已知连续(liánxù)时间信号则信号(xìnhào)所占有(zhànyǒu)的频带宽度为()A.400rad/s B。
200 rad/s C。
100 rad/s D。
50 rad/s 15、已知信号(xìnhào)如下图(a)所示,其反转(fǎn zhuǎn)右移的信号(xìnhào)f1(t) 是( d )16、已知信号(xìnhào)如下图所示,其表达式是()A、ε(t)+2ε(t-2)-ε(t-3)B、ε(t-1)+ε(t-2)-2ε(t-3)C、ε(t)+ε(t-2)-ε(t-3)D、ε(t-1)+ε(t-2)-ε(t-3)17、如图所示:f(t)为原始(yuánshǐ)信号,f1(t)为变换信号,则f1(t)的表达式是()A 、f(-t+1)B 、f(t+1)C 、f(-2t+1)D 、f(-t/2+1)18、若系统的冲激响应为h(t),输入信号(xìnhào)为f(t),系统的零状态响应是( c )19。
信号(x ình ào)与冲激函数之积为( )A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δA 、因果(yīnguǒ)不稳定系统B 、非因果(yīnguǒ)稳定系统C 、因果稳定(wěndìng)系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示,该系统微分方程的特征根是()A、常数B、实数C、复数D、实数+复数22、线性时不变系统零状态响应曲线如图所示,则系统的输入应当是()A、阶跃信号(xìnhào)B、正弦(zhèngxián)信号C、冲激(chōnɡ jī)信号 D、斜升信号(xìnhào)23. 积分(jīfēn)的结果为( )A B)(tf C. D.24. 卷积的结果为( )A. B. C. )(tf D.25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差2A、 B、 C、 D、127.信号〔ε(t)-ε(t-2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S平面D.不存在28.已知连续系统二阶微分方程的零输入响应的形式为,则其2个特征根为( )A。
信号与系统参考题库(2)

第一章 绪论一、单项选择1、右图所示波形可用单位阶跃函数表示为( D )。
(A) f(t)=U(t)-U(t-1)+U(t-2)-U(t-3) (B) f(t)=δ(t)+δ(t-1)+2δ(t-2)-3δ(t-3) (C) f(t)=U(t)+U(t-1)+2U(t-2)-3U(t-3) (D) f(t)=U(t)+U(t-1)+U(t-2)-3U(t-3)2、右图所示信号波形的时域表达式是( D )。
(A ) )1()1()()(---=t u t t u t f (B ) )1()()(-+=t u t tu t f (C ) )1()()(--=t u t tu t f (D ) )1()1()()(---=t u t t tu t f 3、信号)(t f 波形如右图所示,则其表达式为( B )。
(A ) )]1()1([+--t u t u t (B ) )]1()1([--+t u t u t (C ) )]1()1([++-t u t u t (D ) )]1()1([/1+--t u t u t 4、图示波形的表达式为( B )。
-101f(t)t5、下图i(t)的表达式( B )。
IT ti (t )06、已知()f t 的波形如下图所示,则(3)f t 波形为( A )。
1123tf(t)1f(3t)t( A )1091f(3t)t( B )301-1-21f(3t)t( C )-21f(3t)t-3( D )7、已知)(t f 的波形如题 (a)图所示,则)22(--t f 为图3(b)图中的的波形为( A )。
11-1-1f(t)t8、已知f(t)的波形如题 (a)图所示,则f (5-2t)的波形为( C )。
9、已知信号f (t )的波形如题图所示,则f (t )的表达式为( D )。
(A ) (t +1)u(t) (B ) δ(t -1)+(t -1)u(t) (C ) (t -1)u (t) (D ) δ(t +1)+(t +1)u(t) 10、信号()f t 波形如下图a 所示,则图b 的表达式是( C )。
信号与系统复习题含答案完整版

信号与系统复习题含答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】(C ))(t δ+(-6e -t +8e -2t)u(t) (D )3)(t δ +(-9e -t +12e -2t)u(t)6、 连续周期信号的频谱具有(A ) 连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于(A) 1 (B )2 (C )3 (D ) 48、序列和()∑∞-∞=-k k 1δ等于(A )1 (B) ∞ (C) ()1-k u (D) ()1-k ku9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于10、信号()()23-=-t u te t f t的单边拉氏变换()s F 等于二、填空题(共9小题,每空3分,共30分) 1、 卷积和[()k+1u(k+1)]*)1(k -δ=________________________2、 单边z 变换F(z)= 12-z z的原序列f(k)=______________________ 3、 已知函数f(t)的单边拉普拉斯变换F(s)=1+s s,则函数y(t)=3e -2t·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、 频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、 单边拉普拉斯变换s s s s s F +++=2213)(的原函数 f(t)=__________________________6、 已知某离散系统的差分方程为)1(2)()2()1()(2-+=----kf k f k y k y k y ,则系统的单位序列响应h(k)=_______________________7、 已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=2)()(t dxx f t y 的单边拉氏变换Y(s)=______________________________ 8、描述某连续系统方程为 该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ,=k t 22三(8分)已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dtt df t s =求⎪⎭⎫ ⎝⎛2ωs 的傅里叶逆变换。
信号与系统复习题及答案

1.系统的激励是,响应为,若满足,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?)2.求积分的值为 5 。
3.当信号是脉冲信号时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4.若信号的最高频率是2kHz ,则的乃奎斯特抽样频率为 8kHz 。
5.信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6.系统阶跃响应的上升时间和系统的 截止频率 成反比。
7.若信号的,求该信号的。
8.为使LTI 连续系统是稳定的,其系统函数的极点必须在S 平面的 左半平面 。
9.已知信号的频谱函数是,则其时间信号为。
10.若信号的,则其初始值 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足 ( √ )2.满足绝对可积条件的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × )得分)t (e )t (r dt)t (de )t (r =dt )t ()t (212-+⎰∞∞-δf(t)f(t)t)f(23s F(s)=(s+4)(s+2)=)j (F ωj 3(j +4)(j +2)ωωω)s (H ))00(()j (F ωωδωωδω--+=f(t)01sin()t j ωπf(t)211)s (s )s (F +-==+)(f 0)()(t t -=δδ∞<⎰∞∞-dt t f )(3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分,6题15分,共60分)1.信号,信号,试求。
信号与系统复习题之冲击响应

二、阶跃响应 由于δ(t) 与ε(t) 为微积分关系,故
g(t)= T [ε(t) ,{0}]
g(t) th()d
,h(t)dg(t) dt
5
例3 如图所示的LTI系统,求其阶跃响应及冲激响应。
1
f (t) + x(t)
∑ -
-
x(t)
求其冲激响应h(t)。 解 根据h(t)的定义 有
h”(t) + 5h’(t) + 6h(t) = δ”(t)+ 2δ’(t)+3δ(t) (1) h’(0-) = h(0-) = 0 先求h’(0+)和h(0+)。 由方程可知, h(t) 中含δ(t) 故令 h(t) = aδ(t) + p1(t) [pi(t) 为不含δ(t) 的某函数] h’(t) = aδ’(t) + bδ(t) + p2(t) h”(t) = aδ”(t) + bδ’(t) + cδ(t)+ p3(t) 代入式(1),有
10
即 h1(0) h1(0) 0 h1(0) h1(0)+11
代入(5)式,有 h1(0)C3C4 0 h1(0)C32C4=1
可 解 得 : C 3 1 , C 4 1 于是
h1(t)=(et e2t ) (t)
11
其一阶导数
h1 (t)=(et e2t ) (t) (et 2e2t ) (t)=(et 2e2t ) (t)
6
右 端 加 法 器 的 输 出 y(t)= -x(t)2x(t)
所 以 , 系 统 的 微 分 方 程 为 y(t)3y(t)2y(t)= -f(t)2f(t)
信号与系统冲激响应和阶跃响应

r t
t2
t
t
a t a t
b
bu
t t
c
u
t
rt aut
h 0 1 ,h '0 2
代入h(t),得
hh'00A A113AA2212
h(t)1ete3t u(t)
A A121212
2
X
12
第
用奇异函数项相平衡法求待定系数 页
h ( t ) A 1 e t A 2 e 3 tu ( t )
RC (t)A (t)
1 RCA1 A
RC
X
波形
htvC(t)R 1C eR 1C tu(t)
vC (t) h(t) 1 RC
iC(t)
CdvC(t) dt
O
注意!
iC (t)
R12CeR1Ctu(t)
1 (t)
R
1
O R
电容器的电流在
t =0时有一冲激, 这就是电容电压突
1 R 2C
变的原因 。
•当nm时 , ht中 应 包 t含 ;
•当nm时 , ht应 包含 t及 其 各 阶 导 数 。 X
10
第
例2-5-2 页
求系统 d d 2r t(2 t)4d d r(tt)3 r(t)的 冲d d e 激(tt响) 应2 e 。(t) 解:
将e(t)→(t), r(t)→h(t)
d 2 d h t( 2 t) 4d d h (tt)3 h (t)d d ( tt)2 (t)
CtR1CeR1Ctut
X
6
方法2:奇异函数项相平衡原理
第 页
已知方程 冲激响应 求导 代入原方程
RC dvdCt(t)vC(t)(t) t vC(t)Ae RCu(t)
信号与系统复习题 (2)

一、选择题(cos )(1)d t t t t t t π∞∞-∞-∞+δ-=0δ-=⎰⎰的值为〔 〕。
A. )(3t e t δ-C.)1(-t δ⎰∞∞-+dtt t )()1(δ的值为〔 〕3.()()[]=*-t t e dtd tεε2〔 〕 A.()t δ B.()t e tε2- C.()t δ2- D.t e 22-- 4、信号)()(2t e t f t ε=的拉氏变换及收敛域为〔 〕。
B.2]Re[,21)(-<-=s s s F C. 2]Re[,21)(->+=s s s F D.2]Re[,21)(<+=s s s F 5. 信号f(t)=ε(t)*(δ(t)-δ(t -4))的单边拉氏变换F(s)=( )。
A.s1B.4s 1s 1+-D.se -4s6.某一因果线性时不变系统,其初始状态为零,当输入信号为ε(t)时,其输出r(t)的拉氏变换为R(s),问当输入r 1(t)=ε(t -1)-ε(t -2)时,响应r 1(t)的拉氏变换R 1(s)=( )。
A.(e-s-e-2s)R(s) B.R(s-1)-R(s-2) C.(2-s 11-s 1-)R(s) D.R(s)s )e -(e -2s -s 7.信号f(t)的波形如以下列图所示,那么f(t)的表达式为〔 〕。
A.)1()()(--=t u t u t fB.)1()()(-+=t u t u t fC.)1()()(+-=t u t u t fD.)()1()(t u t u t f -+=)()52(t u e t j +-的傅里叶变换〔 〕。
A.ωω521j e j +C.)5(21-+-ωj D.ωω251j e j +t9.)2)(1()2(2)(-++=s s s s s H ,属于其极点的是〔 〕。
A.1B.2C.0D.-210.信号f 〔t 〕的频带宽度为Δω,那么f 〔3t -2〕的频带宽度为〔 〕。
信号与系统 - 列表法求冲激响应
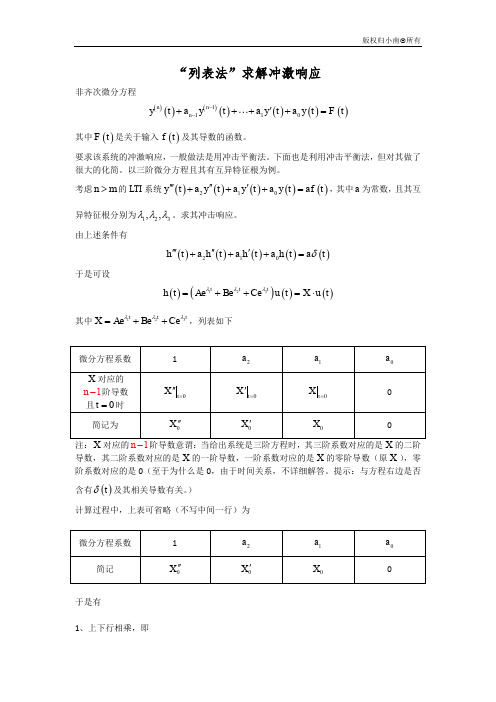
“列表法”求解冲激响应非齐次微分方程()()()()()()()1110n n n y t a y t a y t a y t F t --'++++=其中()F t 是关于输入()f t 及其导数的函数。
要求该系统的冲激响应,一般做法是用冲击平衡法。
下面也是利用冲击平衡法,但对其做了很大的化简。
以三阶微分方程且其有互异特征根为例。
考虑n m >的LTI 系统()()()()()210y t a y t a y t a y t af t ''''''+++=,其中a 为常数,且其互异特征根分别为123,,λλλ。
求其冲击响应。
由上述条件有()()()()()210h t a h t a h t a h t a t δ''''''+++=于是可设()()()()312t t t h t Ae Be Ce u t X u t λλλ=++=⋅其中312t ttX Ae Be Ce λλλ=++,列表如下注:对应的阶导数意谓:当给出系统是三阶方程时,其三阶系数对应的是的二阶导数,其二阶系数对应的是X 的一阶导数,一阶系数对应的是X 的零阶导数(原X ),零阶系数对应的是0(至于为什么是0,由于时间关系,不详细解答。
提示:与方程右边是否含有()t δ及其相关导数有关。
)计算过程中,上表可省略(不写中间一行)为于是有1、上下行相乘,即2010X a X a X a '''++= (其中a 为()t δ即()f t 的系数)200X a X '+= (其中0为()t δ'即()f t '的系数,此处为0,当方程右边出现()k t δ'时,即为其系数k 。
这里可在第二行末尾补任意位零,则0a 斜乘0,忽略不写)00X = (其中0为()t δ''即()f t ''的系数,即为0,同上)注:当方程三阶时,得到了三个方程,否则继续斜乘(第二行不足则在末尾补零),直到最高阶系数乘上方程零阶导数的系数0a 对应的数(在n m >的情况下为0)。
信号与系统中(常见简答题)

信号与系统(常见简答题)1. 能量有限信号的平均功率是多少?功率有限且不为零的信号能量是什么?2.写出复指数信号的表达式,并简述复指数信号的重要特性。
3.写出冲击函数的广义函数定义。
4.某线性时不变系统的冲激响应为h (t ),输入为f (t ),则零状态响应为f (t )* h (t ),写出卷积积分f (t )* h(t )的定义式,并说明其物理意义?5.什么是因果系统?因果系统的冲激响应有什么特点?6.什么是动态系统?动态系统的冲激响应有什么特点?7.简述连续LTI 系统的积分特性。
8.简述卷积和运算的分配律的物理意义.9.写出理想低通滤波器的频率响应,理想低通滤波器是物理可实现的吗?10.简述时域取样定理.11.对于有现长序列,其Z 变换之收敛域如何?12.简述可观测可控制因果连续系统的极点位置与稳定性的关系。
13.f (t )是时间t 的实函数且是奇函数,其频率函数有何特点?14.数字信号、模拟信号、连续时间信号、离散时间信号有什么区别和联系?15.离散时间因果系统稳定的充要条件是什么?16.已知信号f (t)的最高频率为Wm,信号飞f^2(t )的最高频率是多少?17.半波镜像周期信号的傅里叶级数展开式有什么特点?18.什么是无失真传输?无失真传输系统应满足的条件是什么?19.信号f (t )=δ(t )+δ(2t)的能量是多少?20.周期信号的频谱和非周期信号的频谱有什么区别和联系?21.已知系统函数与激励分别如下,零状态响应的初值和终值分别等于多少?H (s)=)23(4+++s s s s ,e (t )=e t -u (t)22.一个系统完成输入序列的累加功能,给出该系统的单位响应h(k).23.写出Z 平面与S 平面的对应关系式,并解释其意义。
24.简述H (s )几点位置与响应函数的对应关系。
25.简述系统控制性的定义。
26.为什么周期函数的傅里叶变换中含有频域的冲激函数项。
信号与系统复习题(含答案)

信号与系统复习题(含答案)试题一一.选择题(共10题,20分) 1、n j n j een x )34()32(][ππ+=,该序列是。
A.非周期序列B.周期3=NC.周期8/3=ND. 周期24=N2、一连续时间系统y(t)= x(sint),该系统是。
A.因果时不变B.因果时变C.非因果时不变D.非因果时变 3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u e t h t ,该系统是。
A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定4、若周期信号x[n]是实信号和奇信号,则其傅立叶级数系数a k 是。
A.实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇 5、一信号x(t)的傅立叶变换??><=2||02||1)(ωωω,,j X ,则x(t)为。
A. t t 22sinB. tt π2sin C. t t 44sin D.t t π4sin6、一周期信号∑∞-∞=-=n n t t x )5()(δ,其傅立叶变换)(ωj X 为。
A. ∑∞-∞=-k k )52(52πωδπ B. ∑∞-∞=-k k )52(25πωδπC. ∑∞-∞=-k k )10(10πωδπD. ∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ,则x[n]奇部的傅立叶变换为。
A.)}(Re{ωj e X j B. )}(Re{ωj e XC. )}(Im{ωj e X j D. )}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ,则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为。
A. 500B. 1000C. 0.05D. 0.001 9、一信号x(t)的有理拉普拉斯共有两个极点s=-3和s=-5,若)()(4t x e t g t =,其傅立叶变换)(ωj G 收敛,则x(t)是。
A. 左边B. 右边C. 双边D. 不确定10、一系统函数1}Re{1)(->+=s s e s H s,,该系统是。
信号与系统概念复习题参考答案

信号与系统复习题1、描述某系统的微分方程为 y ”(t) + 5y ’(t) + 6y(t) = f (t)y(0_)=2,y ’(0_)= -1 y(0_)= 1,y ’(0_)=0 求系统的零输入响应。
求系统的冲击相应求系统的单位阶跃响应。
解:2、系统方程 y (k)+ 4y (k – 1) + 4y (k – 2) = f (k)已知初始条件y (0)=0,y (1)= – 1;激励k k f 2)(=,k ≥0。
求方程的解。
解:特征方程为 λ2 + 4λ+ 4=0 可解得特征根λ1=λ2= – 2,其齐次解 y h(k )=(C 1k +C 2) (– 2)k 特解为 y p(k )=P (2)k , k ≥0代入差分方程得 P (2)k +4P (2)k –1+4P (2)k –2= f (k ) = 2k , 解得 P =1/4所以得特解: y p(k )=2k –2 , k ≥0故全解为 y (k )= y h+y p = (C 1k +C 2) (– 2)k + 2k –2 , k ≥0 代入初始条件解得 C 1=1 , C 2= – 1/43、系统方程为 y (k) + 3y (k –1) + 2y (k –2) = f (k)已知激励kk f 2)(=, k ≥0,初始状态y (–1)=0, y (–2)=1/2, 求系统的零输入响应、零状态响应和全响应。
解::(1)y zi(k )满足方程y zi(k ) + 3y zi(k –1)+ 2y zi(k –2)= 0y zi(–1)= y (–1)= 0, y zi(–2) = y (–2) = 1/2 首先递推求出初始值y zi(0), y zi(1),y zi(k )= – 3y zi(k –1) –2y zi(k –2) y zi(0)= –3y zi(–1) –2y zi(–2)= –1 y zi(1)= –3y zi(0) –2y zi(–1)=3 特征根为λ1= –1 ,λ2= – 2解为 y zi(k )=C zi1(– 1)k + C zi2(–2)k 将初始值代入 并解得 C zi1=1 , C zi2= – 2y zi(k )=(– 1)k – 2(– 2)k , k ≥0(2)零状态响应y zs(k ) 满足:y zs(k ) + 3y zs(k –1) + 2y zs(k –2) = f (k ) y zs(–1)= y zs(–2) = 0 递推求初始值 y zs(0), y zs(1),y zs(k ) = – 3y zs(k –1) – 2y zs(k –2) + 2k , k ≥0 y zs(0) = – 3y zs(–1) – 2y zs(–2) + 1 = 1 y zs(1) = – 3y zs(0) – 2y zs(–1) + 2 = – 1分别求出齐次解和特解,得y zs(k ) = C zs1(–1)k + C zs2(–2)k + y p(k )= C zs1(– 1)k + C zs2(– 2)k + (1/3)2k 代入初始值求得C zs1= – 1/3 , C zs2=1y zs(k )= – (– 1)k /3+ (– 2)k + (1/3)2k ,k ≥0 4、系统的方程:()()()()()12213 -+=-+-+k f k f k y k y k y()()()()()0102==-=y y k k f k ε求系统的零输入响应。
信号与系统2.5冲击响应和阶跃响应1

(2-11)
若把它作用到冲激响应为h(t)的线性时不变系统,则系
统的响应为
r(t)
H[e(t)]
H
e(
)
(t
)d
不是t的函数, 线性系统
这就是卷积积分。
e( )H[ (t )]d
e( )h(t )d
(2-12)
系统零状态 响应的重要
求法
第 2 章 连续时间系统的时域分析
由于h(t)是在零状态下定义的,因而式(2-12)表示的响 应是系统的零状态响应rzs(t)。
由于方程右端自由项的最高阶导数为所以设设0?hdtdt????????????????????????????22tubtathtuctbtathdtdtudtctbtathdtd??????00????t217216第2章连续时间系统的时域分析代入方程215比较t及各阶导数系数得??????????111cba???????????4107671abcaba由217得????????????????100100hdtdchdtdhbh代入ht即216得????????313421aa第2章连续时间系统的时域分析考虑到a1即ht中有一项at因而冲激响应为313452tueetthtt???????第2章连续时间系统的时域分析11110tgctgdtdctgdtdctgdtdcnnnnnn????????系统的阶跃响应gt满足方程11110tuetudtdetudtdetudtdemmmmmm?????????及起始状态gk00k01
h(t) (t) ( 4 e2t 1 e5t )u(t)
3
3
第 2 章 连续时间系统的时域分析
系统的阶跃响应g(t)满足方程
C0
dn dt n
信号与系统齐次解法求冲激响应ppt课件-PPT精品文档

ˆ ˆ ˆ 系统是零状态的,故 h 0 h 0 h 0 0 ˆ ˆ ˆ h 0 h 0 h 0 0
n 1 n 2
n 2 n 3
有界函数在无穷小 含(t)项 区间积分为0 积分不为0 0 n 1 ˆ n 1 n 1 ˆ ˆ h 1 h 0 h 0 1
u(t)项。可以由此定初始ቤተ መጻሕፍቲ ባይዱ件
( n 1 ) h ( 0 ), h ( 0 ), h ( 0 ), , h ( 0 )
此方法比奇异函数系数平衡法简单。对于高阶系统更 有优越性。
退出
定初始条件
0 方程两端在 积分 0 0 0 0 0 n n 1 ˆ ˆ ˆ h t dt a h t dt a h ( t ) dt t ) dt ( n 1 0 0 0 0 0
积分 为1
t 由系统的线性时不变特性,原系统的冲激响应 h为
ht 的 线 性 组 合 .
例题
退出
2 d r ( t ) dr ( t ) de ( t ) 已知系统 ,求h(t) 。 4 3 r ( t ) 2 e ( t ) 2 dt dt dt
t 3 t ˆ ˆ ˆ h 0 1 h 0 0 h ( t ) A e A e u ( t ) 1 2 1 A 1 A 1 3A 2 1 2 将边界条件代入 h t 式 1 1 A 2 0 A A 2 1 t 3 t 2 ˆ h ( t ) e e u ( t ) 2 ˆ(t) d h ˆ(t) (t) 2 h 则由系统的线性时不变特性 h dt 1 1 t 3 3 t t 1 3 t t 3 t h t e e u ( t ) e e ( t ) e e u ( t ) 2 2 2 2 1 3 t et e u ( t) 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、冲激响应
由单位冲激函数δ(t)所引起的零状态响应称为单位冲 激响应,简称冲激响应,记为h(t)。h(t)=T[{0},δ(t)]
例1 描述某系统的微分方程为 y”(t)+5y’(t)+6y(t)=f(t) 求其冲激响应h(t)。
解 根据h(t)的定义 有 h”(t) + 5h’(t) + 6h(t) = δ(t) h’(0-) = h(0-) = 0
对t>0时,有 h”(t) + 5h’(t) + 6h(t) = 0
微分方程的特征根为– 2, – 3。故系统的冲激响应为 h(t)= C1e–2t + C2e–3t , t>0
代入初始条件h(0+) = – 3, h’(0+) =12 求得C1=3,C2= – 6, 所以
h(t)= 3e–2t – 6e–3t , t > 0 结合式(2)得
右端加法器的输出 y(t)=-x(t) 2x(t)
所以,系统的微分方程为 y(t) 3y(t) 2 y(t)=-f (t) 2 f (t)
(2)
(2)求为g1 (t ),则式(2)所 描述的系统的阶跃响应为
g1 (t )满足方程
g(t) g1 (t) 2g1(t)
(4)
h1(0 ) h1 (0 )=0
其特征根1 1, 2 2,其特解为0,于是得 h1(t)=(C3et C4e2t ) (t) (5)
由系数平衡法,(4)式中h1(t)应包含冲激函数,从而h1 (t) 在t 0处将跃变,即h1 (0 ) h1 (0 )。但h1(t)不含冲激函数,否
于是
g(t) g1 (t) 2g1(t) (3et 2e2t 1) (t)
(3)求冲激响应
设式(1)所描述的系统的冲激响应为h1 (t ),则式(2)所 描述的系统的冲激响应为
h(t) h1 (t) 2h1(t)
h1 (t )满足方程
h1(t) 3h1 (t) 2h1(t)= (t)
g1(t) 3g1 (t) 2g1(t)= (t)
(3)
g1(0 ) g1 (0 )=0
其特征根1 1, 2 2,其特解为0.5,于是得 g1(t)=(C1et C2e2t 0.5) (t)
式(3)等号右端只有 (t),故除了g1(t)外,g(t)和g(t)
其一阶导数
h1 (t)=(et e2t ) (t) (et 2e2t ) (t)=(et 2e2t ) (t)
于是
h(t) h1 (t) 2h1(t) (3et 4e2t ) (t)
刚才已经求得:
g(t) (3et 2e2t 1) (t)
aδ”(t) + bδ’(t)+ cδ(t) + p3(t) + 5[aδ’(t) + bδ(t) + p2(t) ]
+ 6[aδ(t) + p1(t) ] = δ”(t)+ 2δ’(t)+3δ(t) 整理得
aδ”(t)+(b+5a)δ’(t)+(c +5b+6a)δ(t) + p3(t)+5 p2(t)+6 p1(t) = δ”(t) + 2δ’(t) + 3δ(t)
h(t)=( e-2t - e-3t)ε(t)
例2 描述某系统的微分方程为
y”(t)+5y’(t)+6y(t)= f”(t) + 2f’(t) + 3f(t) 求其冲激响应h(t)。 解 根据h(t)的定义 有
h”(t) + 5h’(t) + 6h(t) = δ”(t)+ 2δ’(t)+3δ(t) (1)
∑ -
-
x(t)
∫
3
x(t) 2
- y(t)
∫
∑
+
2
解:(1)列写系统的微分方程
设图中右端积分器的输出为x(t),则其输入为x(t),
左端积分器的输入为x(t)。左端加法器的输出 x(t)=-3x(t) 2x(t) f (t)
即
x(t)+3x(t) 2x(t)=f (t) (1)
=1
考虑h(0+)= h(0-),由上式可得 h(0+)=h(0-)=0 , h’(0+) =1 + h’(0-) = 1
对t>0时,有 h”(t) + 5h’(t) + 6h(t) = 0 故系统的冲激响应为一齐次解。
微分方程的特征根为-2,-3。故系统的冲激响应为
h(t)=(C1e-2t + C2e-3t)ε(t) 代入初始条件求得C1=1,C2=-1, 所以
h’(0-) = h(0-) = 0 先求h’(0+)和h(0+)。 由方程可知, h(t) 中含δ(t) 故令 h(t) = aδ(t) + p1(t) [pi(t) 为不含δ(t) 的某函数]
h’(t) = aδ’(t) + bδ(t) + p2(t) h”(t) = aδ”(t) + bδ’(t) + cδ(t)+ p3(t) 代入式(1),有
则h1(t)将含 (t)项。由于h1(t)含有阶跃函数,故h(t)在t 0处
连续。对(4)式等号两端积分(从0-到0 ),得 [h1 (0 ) h1 (0 )] 3[h1(0 ) h1(0 )] 1
考虑到h(t)在t 0处连续。将h1 (0 ),h1(0 )代入上式得 h1 (0 ) h1 (0 )=1 h1(0 ) h1(0 ) 0
利用δ(t) 系数匹配,得 a =1 ,b = - 3,c = 12
所以 h(t) = δ(t) + p1(t)
(2)
h’(t) = δ’(t) - 3δ(t) + p2(t)
(3)
h”(t) = δ”(t) - 3 δ’(t) + 12δ(t)+ p3(t) (4)
对式(3)从0-到0+积分得 h(0+) – h(0-) = – 3 对式(4)从0-到0+积分得 h’(0+) – h’(0-) =12 故 h(0+) = – 3, h’(0+) =12
均连续,即有 g1(0 ) g1 (0 )=0
代入上式,有 g1(0 ) C1 C2 0.5 0 g1 (0 )=-C1 2C2 =0
可解得:C1 1,C2 0.5 于是
g1(t)=(et 0.5e2t 0.5) (t)
其一阶导数
g1 (t)=(et 0.5e2t 0.5) (t) (et e2t ) (t)=(et e2t ) (t)
h(t)= δ(t) + (3e–2t – 6e–3t)ε(t)
二、阶跃响应 由于δ(t) 与ε(t) 为微积分关系,故
g(t)= T [ε(t) ,{0}]
t
g(t) h( ) d
, h(t) d g(t)
dt
例3 如图所示的LTI系统,求其阶跃响应及冲激响应。
1
f (t) + x(t)
先求h’(0+)和h(0+)。
因方程右端有δ(t),故利用系数平衡法。h”(t)中含δ(t),
h’(t)含ε(t),h’(0+)≠h’(0-),h(t)在t=0连续,即
h(0+)=h(0-)。积分得
0
[h’(0+) - h’(0-)] + 5[h(0+) - h(0-)] + 6
h(t)dt 0
即 h1(0 ) h1(0 ) 0 h1 (0 ) h1 (0 )+1 1
代入(5)式,有 h1(0 ) C3 C4 0 h1 (0 ) C3 2C4 =1
可解得:C3 1,C4 1
于是
h1(t)=(et e2t ) (t)
验证结论(解法II):
h(t) d g(t) dt
