运筹学案例集
运筹学教学案例集

市场状况
概率
总收入
高利润
20%
$3,000,000
中等利润
40%
$500,000
低利润
40%
$0
表 2.2 给出了在三维技术样品运作取得成功并且在接受了 N 公司投资的情况 下嘉美斯估计的年收入情况。这是在 B 公司收到 N 公司$1,000,000 的投资之后 B 公司所可能的收入估计值。
表 2.2 当 B 公司获得 N 公司的资助并且三维技术软件获得成功时,B 公司的估计收入
OR 案例
运筹学案例
孔 造 杰 编纂
2004 年 12 月
0
OR 案例
案例一:贝尔的夏季工作问题
1. 贝尔的问题 贝尔在麻省理工学院斯隆管理学院已经呆了三周,除了准备他的功课外,他
开始认真考虑明年夏季打工的事,在以后的几周内,他必须就此事做出决定。 八月底,贝尔飞往波士顿,在飞机上他坐在一位名叫瓦莎的旁边,就和她攀
市场状况
概率
总收入
高利润
25%
尽管施考特开发的更高级的三维图像处理软件没有经过大量的测试,但他保 证这个软件在诊断脑外伤和脑部肿瘤方面,比其他方法要准确的多。当今世界, 科学家们都在研究他们自己的图像软件,施考特的新版三维图像处理软件与众不 同,在 MRI 图像处理方面远远优于其他现有的软件。
在嘉美斯的倡议下,三个人建立了 B 公司,旨在为医院和医生生产和开发商 业软件包。不久,他们就收到 N 公司(一个大的图像软件公司)的一个购买意 图——N 公司出价$150,000 要购买他们当前版本的软件和其在世界范围内的开 发和销售权。其他两位合伙人委托嘉美斯决定是否接受 N 公司的要求。如果他 们拒绝这个要求,在以后的六个月中,他们将继续进行软件的开发计划。这项计 划大概要花费$200,000。嘉美斯想使用合伙人的私人储蓄来解决这个问题。
运筹学实例 含解析

案例1. 工程项目选择问题某承包企业在同一时期内有八项工程可供选择投标。
其中有五项住宅工程,三项工业车间。
由于这些工程要求同时施工,而企业又没有能力同时承担,企业应根据自身的能力,分析这两类工程的盈利水平,作出正确的投标方案。
有关数据见下表:表1 可供选择投标工程的有关数据统计工程类型 预期利润/元 抹灰量/m 2混凝土量/ m 3砌筑量/ m 3住宅每项 50011 25 000 280 4 200 工业车间每项 80 000480 880 1 800 企业尚有能力108 0003 68013 800试建立此问题的数学模型。
解:设承包商承包X 1项住宅工程,X 2项工业车间工程可获利最高,依题意可建立如下整数模型:目标是获利最高,故得目标函数为21X 80000X 50011z Max +=根据企业工程量能力限制与项目本身特性,有约束:利用WinSQB 建立模型求解:1080002X 4801X 25000≤+3680X 880X 28021≤+13800X 1800X 420021≤+为整数,;,2121X X 3X 5X ≤≤综上,承包商对2项住宅工程,3项车间工程进行投标,可获利最大,目标函数Max z=340022 元。
案例2. 生产计划问题某厂生产四种产品。
每种产品要经过A,B两道工序加工。
设该厂有两种规格的设备能完成A工序,以A1 ,A2表示;有三种规格的设备能完成B工序,以B1 ,B2,B3 表示。
产品D可在A,B任何一种规格的设备上加工。
产品E可在任何规格的A设备上加工,但完成B工序时只能在B1设备上加工。
产品F可在A2及B2 ,B3上加工。
产品G可在任何一种规格的A设备上加工,但完成B工序时只能在B1 ,B2设备上加工。
已知生产单件产品的设备工时,原材料费,及产品单价,各种设备有效台时如下表,要求安排最优的生产计划,使该厂利润最大?设设产品设备有效台时1 2 3 4A1 A2 B1 B2 B357647109812111068108601110000400070004000原料费(元/件)单价(元/件)0.251.250.352.000.502.800.42.4解:设Xia(b)j为i产品在a(b)j设备上的加工数量,i=1,2,3,4;j=1,2,3,得变量列表设备产品设备有效台时Ta(b)j1 2 3 4A1 A2 B1 B2 B3X1a1X1a2X1b1X1b2X1b3X2a1X2a2X2b1X3b2X3b3X3a1X3a2X3b1X3b2X3b3X4a1X4a2X4b1X4b2X4b3601110000400070004000原料费Ci (元/件) 单价Pi (元/件) 0.25 1.25 0.352.00 0.50 2.80 0.4 2.4其中,令X 3a 1,X 3b 1,X 3b 2,X 3b 3,X 4b 3=0 可建立数学模型如下: 目标函数: ∑∑==-=4121)](*[Maxi j iaj Ci Pi X z=1.00*(X 1a 1+X 1a 2)+1.65*(X 2a 1+X 2a 2)+2.30* X 3a 2+2.00*( X 4a 1+X 4a 2)约束条件:利用WinSQB 求解(X1~X4,X5~X8,X9~X12,X13~X17,X18~X20分别表示各行变量):4,3,2,1X21j 31==∑∑==i X j ibjiaj2,1T X 41iaj=<=∑=j Taj i iaj 3,2,141=<=∑=j TbjT Xi ibj ibj2,1;4,3,2,10X iaj ==>=j i 且为整数32,1;4,3,2,10X ibj ,且为整数==>=j i 0X X X X X 4b33b33b23b13a1=====综上,最优生产计划如下:设备产品1 2 3 4A1 A2 B1 B2 B3774235004004008732875目标函数zMax=3495,即最大利润为3495案例3. 高校教职工聘任问题 (建摸)由校方确定的各级决策目标为:P 1 要求教师有一定的学术水平。
运筹学经典案例

运筹学经典案例案例一:鲍德西((B AWDSEY)雷达站的研究20世纪30年代,德国内部民族沙文主义及纳粹主义日渐抬头。
以希特勒为首的纳粹势力夺取了政权开始为以战争扩充版图,以武力称霸世界的构想作战争准备。
欧洲上空战云密布。
英国海军大臣丘吉尔反对主政者的“绥靖”政策,认为英德之战不可避免,而且已日益临近。
他在自己的权力范围内作着迎战德国的准备,其中最重要、最有成效之一者是英国本土防空准备。
1935年,英国科学家沃森—瓦特(R.Watson-Wart)发明了雷达。
丘吉尔敏锐地认识到它的重要意义,并下令在英国东海岸的Bawdsey建立了一个秘密的雷达站。
当时,德国已拥有一支强大的空军,起飞17分钟即可到达英国。
在如此短的时间内,如何预警及做好拦截,甚至在本土之外或海上拦截德机,就成为一大难题。
雷达技术帮助了英国,即使在当时的演习中已经可以探测到160公里之外的飞机,但空防中仍有许多漏洞,1939年,由曼彻斯特大学物理学家、英国战斗机司令部科学顾问、战后获诺贝尔奖金的P.M.S.Blachett为首,组织了一个小组,代号为“Blachett 马戏团”,专门就改进空防系统进行研究。
这个小组包括三名心理学家、两名数学家、两名应用数学家、一名天文物理学家、一名普通物理学家、一名海军军官、一名陆军军官及一名测量人员。
研究的问题是:设计将雷达信息传送给指挥系统及武器系统的最佳方式;雷达与防空武器的最佳配置;对探测、信息传递、作战指挥、战斗机与防空火力的协调,作了系统的研究,并获得了成功,从而大大提高了英国本土防空能力,在以后不久对抗德国对英伦三岛的狂轰滥炸中,发挥了极大的作用。
二战史专家评论说,如果没有这项技术及研究,英国就不可能赢得这场战争,甚至在一开始就被击败。
“Blackett马戏团”是世界上第一个运筹学小组。
在他们就此项研究所写的秘密报告中,使用了“Operational Research”一词,意指作战研究”或“运用研究”。
运筹学典型题型案例集

运筹学典型题型案例集第一章线性规划1 生产计划问题((摘自王治祯环境应用数学309页))某企业为了搞好综合利用,用三种废品生产三种副产品,生产情况和利润见下表,求最佳利润。
解:设ABC三种产品的产量为X1X2X3Max Z =5X1+8X2+2X310X1+5X2+3 X3<=4006X1+10X2+2 X3<=4004X1+5X2+4X3<=200经过求解X1=34.23,X2=8.19X3=5.37最大利润为274.412 投资问题解:用Xij表示第i年初(i=1,2,3)给项目j(A,B,C,D)的投资金额。
第一年资金量:30万,可投项目:A、B;故:X1A+X1B<=30。
第二年资金量:1.2*X1A,可投项目:A、C;故:X2A+X2C<=1.2*X1A。
第三年资金量:1.2*X2A+1.5*X1B,可投项目:A、B、D;故:X3A+X3B+X3D<=1.2*X2A+1.5*X1B。
其它条件:X1B<=20;X2C<=15;X3D<=10。
目标:第三年底收益最大。
因投资X3B在第3年底不能收回,故无收益。
则目标函数为:f(x)=0.2*(X1A+ X2A + X3A)+0.5*X1B+0.6* X2C+0.4* X3D LINGO Model如下:max =0.2*(X1A+ X2A + X3A)+0.5*X1B+0.6* X2C+0.4* X3D;X1A+X1B<=30;X2A+X2C<=1.2*X1A;X3A+X3B+X3D<=1.2*X2A+1.5*X1B;@bnd(0,X1B,20); @bnd(0,X3B,20); @bnd(0,X2C,15); @bnd(0,X3D,10);运行结果如下:Global optimal solution found.Objective value: 27.50000Total solver iterations: 2Variable Value Reduced CostX1A 12.50000 0.000000X2A 0.000000 0.6000000E-01X3A 16.25000 0.000000X1B 17.50000 0.000000X2C 15.00000 -0.1000000X3D 10.00000 -0.2000000X3B 0.000000 0.2000000Row Slack or Surplus Dual Price1 27.50000 1.0000002 0.000000 0.80000003 0.000000 0.50000004 0.000000 0.2000000投资计划解释:第一年年初投资A项目12.5万元,投资B项目17.5万元;第二年年初投资C项目15万元;第三年年初投资A项目16.25万元,投资D项目10万元;第三年年年末可获最大收益27.5万元。
第七章---运筹学-运输问题案例

第七章运输问题7.1 一个农民承包了6块耕地共300亩,准备播种小麦、玉米、水果和蔬菜四种农产品,问如何安排种植计划,可得到最大的总收益。
解:这是一个产销平衡的运输问题。
可以建立以下的运输模型:代入产销平衡的运输模板可得如下结果:得种植计划方案如下表:7.2 某客车制造厂根据合同要求从当年开始起连续四年年末交付40辆规格型号相同的大型客车。
该厂在这四年内生产大型客车的能力及每辆客车的成本情况如下表:根据该厂的情况,假设制造出来的客车产品当年未能交货,每辆车每积压一年的存储和维护费用为4万元。
在签订合同时,该厂已储存了20辆客车,同时又要求四年期未完成合同后还需要储存25辆车备用。
问该厂如何安排每年的客车生产量,使得在满足上述各项要求的情况下,总的生产费用加储存维护费用为最少?解:得运价表〔产大于销的运输模型〕如下:第一季度正常上班生产20台,加班27台,拿出正常生产18台和加班2台,加上年前储存的20台,满足本季度的40台;第二季度正常生产38台,不安排加班。
加上第一季度储存的2台,满足本季度的40台;第三季度正常生产15台,不安排加班。
加上第一季度储存的25台,满足本季度的40台;第四季度正常生产42台。
加班生产23台。
拿出正常生产的17台的加班生产的23台满足本季度的40台。
剩余25台以后务用。
7.3 某企业生产有甲、乙、丙、丁四个分厂生产同一种产品,这四个分厂的产量分别为:200吨、300吨、400吨和100吨,这些产品供给给A、B、C、D、E、F六个地区,六个地区的需求量分别为:200吨、150吨、350吨、100吨、120吨、120吨。
由于工艺、技术的差异,各分厂运往各销售地区的单位运价〔万元/吨〕、各厂单位产品成本〔万元/吨〕和各销地的销售价格〔万元/吨〕如下表:12、如果E地区至少供给100吨,试确定该公司获利最大的产品调运方案。
2、如果E地区至少供给100吨,C地区的需要必须全部得到满足,试确定该公司获利最大的产品调运方案。
运筹学案例集

运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题:如何在保证生产的条件下,下料最少•配料问题:在原料供应量的限制下,如何获取最大收益•投资问题:从投资项目中选取最佳组合,使投资回报最大•产品生产计划:合理利用人力、物力、财力等,使获利最大•劳动力安排:用最少的劳动力来满足工作的需要•运输问题:如何制定最佳调运方案,使总运费最少一、生产计划问题案例1(2-4)、某工厂用A、B、C、D四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元,问应如何安排生产才能获得最大收益?已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制,如下表:问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?案例3(2-25)、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量,数据如下表所示。
问题:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?案例4(2-28)、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成 B 工序。
Ⅰ可在A、B的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工,数据如下表所示。
问题:为使该厂获得最大利润,应如何制定产品加工方案?案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人,每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为:每人每月生产原稿纸30捆,或生产日记本30打,或练习本30箱。
运筹学 案例

《运筹学》案例分析案例1:超级食品公司的广告混合问题超级食品公司的营销部副总裁克莱略·希文生正面临着一个棘手的挑战:如何才能大规模地进入已有许多供应商的早点谷类食品市场。
值得庆幸的时,该公司的早点谷类食品“脆始”(Crunchy Start)有许多受欢迎的优点:口味佳、营养、松脆。
克莱略·希文生对这一切都如数家珍,她知道这一食品是能够赢得这次促销活动的。
然而,克莱略清楚她必须避免上一次产品促销活动中所犯的错误。
那是她晋升以后第一项重大任务,结果简直是个悲剧!她本以为已经大功告成,却没想到那次活动并没有触及至关重要的目标市场——幼年儿童以及幼年儿童的父母。
同时,她还领悟到未将优惠卷包含在杂志与报纸的广告中是另一大失误。
哎,学习是永无止境的。
这一次,必须吸取上次的教训。
公司的总裁大卫·斯隆已经向她表示脆始这一产品成功与否对公司前途有着重要影响。
她清楚地记得大卫在结束与她的谈话时说:“公司的股东对公司的现状极为不满,我们必须再次纠正方向,增加公司收入。
”克莱略以前也曾听到过这样的语调,但这一次,她从大卫极为严肃的目光中意识到了问题的严重性。
克莱略在攻读MBA管理运筹学课程时,曾经学习过如何通过建立数学模型来解决管理决策问题。
现在是时候让她仔细考虑一下问题,并准备应用所学知识解决问题了。
问题克莱略已经雇佣了一家一流的广告公司G&J公司来帮助设计全国性的促销活动,以使脆始取得尽可能多的消费者的认可。
超级食品公司将根据该广告公司所提供的服务付给一定的酬金(不超过100万美元)并已经预留了另外的400万美元作为广告费用。
G&J公司已经确定了这一产品最有效的三种广告媒介:媒介1:星期六上午儿童节目的电视广告。
媒介2:食品与家庭导向的杂志上的广告。
媒介3:主要报纸星期天增刊上的广告。
现在,要解决的问题是如何确定各广告活动的使用水平(levels)以取得最有效的绩效。
为了确定这一广告投放问题的最佳活动水平组合,首先必须明确该问题的总绩效测度(overall measure of performance)以及每一活动对该测度的贡献。
2.6-运筹学应用实例汇总
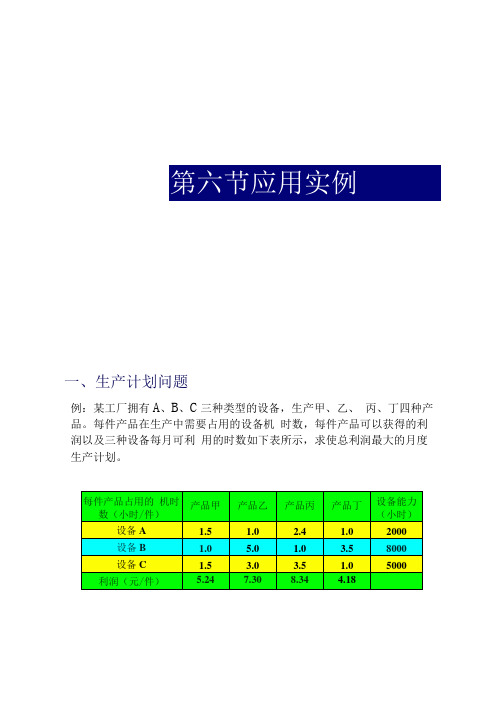
一、生产计划问题例:某工厂拥有A、B、C三种类型的设备,生产甲、乙、丙、丁四种产品。
每件产品在生产中需要占用的设备机时数,每件产品可以获得的利润以及三种设备每月可利用的时数如下表所示,求使总利润最大的月度生产计划。
建模思路■用线性规划制订使总利润最大的生产计划。
■设变量X1为第i种产品的生产件数(i=1, 2, 3, 4),目标函数z为相应的生产计划可以获得的总利润。
在加工时间以及利润与产品产量成线性关系的假设下,可以建立如下的线性规划模型:建模max z= 5.24X1 +7.30x2 +8.34x3 +4.18x4目标函数1.5Xj +1.0x2+2.4X3+1.0X4<2000LOX1 +5.0X2+1.0X3+3.5X4<8000 约束条件1・5X] +3.0X2+3.5X3+1.0X4<5000Xp X2, X3, X4 >0 变量非负约束练习:某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量。
数据如下表。
问:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?甲 .乙丙资源限制铸造工时(小时/件)51078000机加工工时(小时/件)64812000装配工时(小时/件)32210000自产铸件成本(兀/件)354外协铸件成本(兀/件)56一机加工成本(元/件)213装配成本(元/件)322产品售价(元/件)231816解:设孙孙寺分别为三道工序都由本公司加工的甲、乙、丙三种产品的件数,同,幅分别为由外协铸造再由本公司加工和装配的甲、乙两种产品的件数。
求占的利润:利润二售价-各成本之和产品甲全部自制的利润产品甲铸造外协,其余自制的利润产品乙全部自制的利润产品乙铸造外协,其余自制的利润产品丙的利润可得到毛(i = 1,2, 3,4,5)的利润分别为15、10、7、13、9=23-(3+2+3)=15 =23-(5+2+3)=13 =18-(5+1+2)=10 =18-(6+1+2)=9 =16-(4+3+2)=7通过以上分析,可建立如下的数学模型:目标函数:Max 15百+ 10电+ 7两+ 13题+ 9不约束条件:5为+ 10西+ 7玛<80006为+ 4出+ 8^ + 6々+ 4不3百+ 2X2 + 2均+ 3局+ 2不毛,演,传,演,与12000 10000二、混合配料问题例:某工厂要用四种合金T1, T2, T3和T4为原料,经熔炼成为一种新的不锈钢G。
运筹学经典案例

运筹学经典案例案例一:鲍德西((B AWDSEY)雷达站的研究20世纪 30 年代,德国内部民族沙文主义及纳粹主义日渐抬头。
以希特勒为首的纳粹势力夺取了政权开始为以战争扩充版图,以武力称霸世界的构想作战争准备。
欧洲上空战云密布。
英国海军大臣丘吉尔反对主政者的“绥靖”政策,认为英德之战不可避免,而且已日益临近。
他在自己的权力范围内作着迎战德国的准备,其中最重要、最有成效之一者是英国本土防空准备。
1935 年,英国科学家沃森—瓦特( R.Watson-Wart )发明了雷达。
丘吉尔敏锐地认识到它的重要意义,并下令在英国东海岸的 Bawdsey 建立了一个秘密的雷达站。
当时,德国已拥有一支强大的空军,起飞 17 分钟即可到达英国。
在如此短的时间内,如何预警及做好拦截,甚至在本土之外或海上拦截德机,就成为一大难题。
雷达技术帮助了英国,即使在当时的演习中已经可以探测到160 公里之外的飞机,但空防中仍有许多漏洞,1939 年,由曼彻斯特大学物理学家、英国战斗机司令部科学顾问、战后获诺贝尔奖金的P.M.S.Blachett 为首,组织了一个小组,代号为“ Blachett 马戏团”,专门就改进空防系统进行研究。
这个小组包括三名心理学家、两名数学家、两名应用数学家、一名天文物理学家、一名普通物理学家、一名海军军官、一名陆军军官及一名测量人员。
研究的问题是:设计将雷达信息传送给指挥系统及武器系统的最佳方式;雷达与防空武器的最佳配置;对探测、信息传递、作战指挥、战斗机与防空火力的协调,作了系统的研究,并获得了成功,从而大大提高了英国本土防空能力,在以后不久对抗德国对英伦三岛的狂轰滥炸中,发挥了极大的作用。
二战史专家评论说,如果没有这项技术及研究,英国就不可能赢得这场战争,甚至在一开始就被击败。
“ Blackett 马戏团”是世界上第一个运筹学小组。
在他们就此项研究所写的秘密报告中,使用了“Operatio nal Research” 一词,意指作战研究”或"运用研究"。
运筹学案例

运筹学案例(第一部分)案例1 高压电器强电流试验计划的安排某高压电器研究所属行业归口所,是国家高压电器试验检测中心,每年都有大量的产品试验、中试、出口商检等任务.试验计划安排及实施的过程一般如下:·提前一个月接受委托试验申请·按申请的高压电器类别及台数编制下月计划·按计划调度,试验产品进入试验现场·试验检测,出检测报告·试验完成,撤出现场高压电器试验分强电流试验和高压电试验两部分,该研究所承担的强电流实验任务繁重,委托试验的电器量很大,因此科学地计划安排试验计划显得非常重要。
高压电器分十大类,委托试验的产品有一定随机性,但是试验量最多的产品(占85%以上)是以下八类:1.35KV断路器2.10KV等级断路器3.35KV开关柜4.10KV等级开关柜5.高压熔断器6.负荷开关7.隔离开关8.互感器这八类产品涉及全国近千个厂家,市场广阔,数量庞大。
当前的强电流产品试验收费标准见表1—1。
表1-1 强电流产品试验收费标准由于强电流试验用的短路发电机启动时,会给城市电网造成冲击,严重影响市网质量,故只能在中午1点用电低谷时启动,从而影响全月连续试验工时只有约108小时,任务紧张时只能靠加班调节。
正常情况下各种试验所需试验工时见表8—2。
表1—2 各类产品试验所需工时强电流试验特点是开机时耗电量大,而每次实验短路时,只持续几秒钟,虽然短路容量在“0”秒时达2500 MVA,但瞬时耗电量却很小.每天试验设备提供耗电量限制为5000千瓦,每月135千千瓦,那麽每种产品耗量如表8-3所示。
各类产品的冷却水由两个日处理能力为14吨的冷却塔供给.每月按27天计,冷却水月供给量为14×27=378吨.每月各类产品冷却水处理量见表8-3。
表1—3 各类产品试验耗电量与冷却水处理量根据以往的经验和统计报表显示第一类产品和第二类产品每月最多试验台数分别为6台和4台,第三类和第四类产品则每月至少需分别安排8台和10台。
运筹学实例-含解析

321案例1. 工程项目选择问题某承包企业在同一时期内有八项工程可供选择投标。
其中有五项住宅工程,三项工业车间。
由于这些工程要求同时施工,而企业又没有能力同时承担,企业应根据自身的能力,分析这两类工程的盈利水平,作出正确的投标方案。
有关数据见下表:表1 可供选择投标工程的有关数据统计工程类型 预期利润/元 抹灰量/m 2混凝土量/ m 3砌筑量/ m 3住宅每项 50011 25 000 280 4 200 工业车间每项 80 000480 880 1 800 企业尚有能力108 0003 68013 800试建立此问题的数学模型。
解:设承包商承包X 1项住宅工程,X 2项工业车间工程可获利最高,依题意可建立如下整数模型:目标是获利最高,故得目标函数为21X 80000X 50011z Max +=根据企业工程量能力限制与项目本身特性,有约束:1080002X 4801X 25000≤+3680X 880X 28021≤+13800X 1800X 420021≤+为整数,;,2121X X 3X 5X ≤≤利用WinSQB建立模型求解:综上,承包商对2项住宅工程,3项车间工程进行投标,可获利最大,目标函数Max z=340022 元。
案例2. 生产计划问题某厂生产四种产品。
每种产品要经过A,B两道工序加工。
设该厂有两种规格的设备能完成A工序,以A1 ,A2表示;有三种规格的设备能完成B工序,以B1 ,B2,B3 表示。
产品D可在A,B任何一种规格的设备上加工。
产品E可在任何规格的A设备上加工,但完成B工序时只能在B1设备上加工。
产品F可在A2及B2 ,B3上加工。
产品G可在任何一种规格的A设备上加工,但完成B工序时只能在B1 ,B2设备上加工。
已知生产单件产品的设备工时,原材料费,及产品单价,各种设备有效台时如下表,要求安排最优的生产计划,使该厂利润最大?设设产品设备有效台时1 2 3 4A1 A2 B1 B2 B357647109812111068108601110000400070004000原料费(元/件)单价(元/件)0.251.250.352.000.502.800.42.4解:设Xia(b)j为i产品在a(b)j设备上的加工数量,i=1,2,3,4;j=1,2,3,得变量列表设备产品设备有效台时Ta(b)j1 2 3 4A1 A2 B1 B2 X1a1X1a2X1b1X1b2X2a1X2a2X2b1X3b2X3a1X3a2X3b1X3b2X4a1X4a2X4b1X4b260111000040007000B 3 X 1b 3 X 3b 3 X 3b 3 X 4b 3 4000 原料费Ci (元/件) 单价Pi (元/件) 0.25 1.250.35 2.000.50 2.800.4 2.4其中,令X 3a 1,X 3b 1,X 3b 2,X 3b 3,X 4b 3=0 可建立数学模型如下: 目标函数: ∑∑==-=4121)](*[Maxi j iaj Ci Pi X z=1.00*(X 1a 1+X 1a 2)+1.65*(X 2a 1+X 2a 2)+2.30* X 3a 2+2.00*( X 4a 1+X 4a 2)约束条件:利用WinSQB 求解(X1~X4,X5~X8,X9~X12,X13~X17,X18~X20分别表示各行变量):4,3,2,1X21j 31==∑∑==i X j ibjiaj2,1T X 41iaj=<=∑=j Taj i iaj 3,2,141=<=∑=j TbjT Xi ibj ibj2,1;4,3,2,10X iaj ==>=j i 且为整数32,1;4,3,2,10X ibj ,且为整数==>=j i 0X X X X X 4b33b33b23b13a1=====综上,最优生产计划如下:设备产品1 2 3 4A1 A2 B1 B2 B3774235004004008732875目标函数zMax=3495,即最大利润为3495案例3. 高校教职工聘任问题 (建摸)由校方确定的各级决策目标为:P 1 要求教师有一定的学术水平。
运筹学案例1
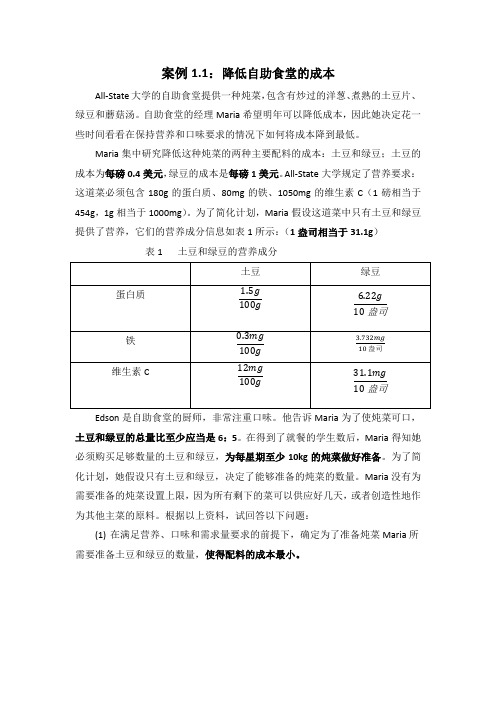
案例1.1:降低自助食堂的成本All-State大学的自助食堂提供一种炖菜,包含有炒过的洋葱、煮熟的土豆片、绿豆和蘑菇汤。
自助食堂的经理Maria希望明年可以降低成本,因此她决定花一些时间看看在保持营养和口味要求的情况下如何将成本降到最低。
Maria集中研究降低这种炖菜的两种主要配料的成本:土豆和绿豆;土豆的成本为每磅0.4美元,绿豆的成本是每磅1美元。
All-State大学规定了营养要求:这道菜必须包含180g的蛋白质、80mg的铁、1050mg的维生素C(1磅相当于454g,1g相当于1000mg)。
为了简化计划,Maria假设这道菜中只有土豆和绿豆提供了营养,它们的营养成分信息如表1所示:(1盎司相当于31.1g)表1 土豆和绿豆的营养成分Edson是自助食堂的厨师,非常注重口味。
他告诉Maria为了使炖菜可口,土豆和绿豆的总量比至少应当是6:5。
在得到了就餐的学生数后,Maria得知她必须购买足够数量的土豆和绿豆,为每星期至少10kg的炖菜做好准备。
为了简化计划,她假设只有土豆和绿豆,决定了能够准备的炖菜的数量。
Maria没有为需要准备的炖菜设置上限,因为所有剩下的菜可以供应好几天,或者创造性地作为其他主菜的原料。
根据以上资料,试回答以下问题:(1)在满足营养、口味和需求量要求的前提下,确定为了准备炖菜Maria所需要准备土豆和绿豆的数量,使得配料的成本最小。
(2)Maria没有太多地考虑炖菜的口味,她只考虑了满足营养要求和削减成本,因此她要求Edson改变配方,使得土豆和绿豆最低质量比可以为1:2。
在这种新的配方下,确定Maria每个星期需要购买的土豆和绿豆的数量。
(3)由于Maria认为其他配料,如洋葱和蘑菇汤也含有铁,因此她决定将铁含量的要求降低到65mg。
在这种新的配方下,确定Maria每个星期需要购买的土豆和绿豆的数量。
(4)Maria得知批发商有多余的绿豆,因此绿豆的价格降低到每磅0.5美元。
优秀的运筹学案例

优秀的运筹案例1. 孙武与《孙子兵法》孙武,字长卿,后人尊称其为孙武子、孙子,中国历史上著名军事家.公元前535年左右出生于齐国乐安(今山东惠民). 后来到了吴国,因为献上兵法十三篇,被吴王阖闾重用,拜为大将,和伍子胥共事,辅佐吴王,领兵攻破楚国都城郢(今湖北江陵县纪南城).孙武在春秋末期(公元前476年前后)所著《孙子兵法》,是世界上现存最古老的兵书.其中的《始计第一》论述怎样在开战之前和战争中实行谋划的问题,以及谋划在战争中的重要意义;《作战第二》论述速战速胜的重要性;《谋攻第三》论述用计谋征服敌人的问题;《军形第四》论述用兵作战要先为自己创造不被敌人战胜的条件,以等待敌人可以被我战胜的时机,使自己“立于不败之地”;《兵势第五》论述用兵作战要造成一种可以压倒敌人的迅猛之势,并要善于利用这种迅猛之势;《虚实第六》论述用兵作战须采用“避实而击虚”的方针;《军争第七》论述如何争夺制胜的有利条件,使自己掌握作战主动权的问题;《九变第八》论述将帅指挥作战应根据各种具体情况灵活机动地处置问题,不要机械死板而招致失败,并对将帅提出了要求;《行军第九》论述行军作战中怎样安置军队和判断敌情问题;《地形第十》论述用兵作战怎样利用地形的问题,并着重论述深入敌国作战的好处;《九地第十一》进一步论述用兵作战怎样利用地形及统兵之道的问题;《火攻第十二》论述在战争中使用火攻的办法、条件和原则等问题;《用间第十三》论述使用间谍侦察敌情在作战中的重要意义,以及间谍的种类和使用间谍的方法.《孙子兵法》是体现我国古代军事运筹思想的最早的典籍.它考察了战争中各种依存、制约关系,总结了战争的规律,并依此来研究如何筹划兵力以争取全局的胜利. 书中的语言叙述简洁,内容也很有哲理性,后来的很多将领用兵都受到了该书的影响.《孙子兵法》对中国的文化发展有深远的影响.2. 孙膑与齐王赛马孙膑(约公元前380-公元前432),孙武的后世子孙,战国中期的著名军事家. 少时孤苦,年长后从师鬼谷子(著名隐士,精通兵学和纵横学)学习《孙子兵法》十三篇等兵书战策. 庞涓妒孙膑之才而将其骗至魏,施以膑刑(割去膝盖骨).后来乘齐国使团来魏之机,孙膑被齐使秘密接到齐国,并被大将田忌所赏识,留在府中做幕僚,奉为上宾. 孙膑的“斗马术”是我国古代运筹思想中争取总体最优的脍炙人口的著名范例(记载于《史记·孙子吴起列传》),成为军事上一条重要的用兵规律,即要善于用局部的牺牲去换取全局的胜利,从而达到以弱胜强的目的. “斗马术”的基本思想是不强求一局的得失,而争取全盘的胜利. 这是一个典型的博弈问题.3. 围魏救赵公元前354年,魏将庞涓发兵8万,以突袭的办法将赵国的都城邯郸包围. 赵国抵挡不住,求救于齐. 齐王拜田忌为大将,孙膑为军师,发兵8万,前往救赵. 大军既出,田忌欲直奔邯郸,速解赵国之围. 孙膑提出应趁魏国国内兵力空虚之机,发兵直取魏都大梁(今河南开封),迫使魏军弃赵回救. 这一战略思想,将避免齐军长途奔袭的疲劳,而致魏军于奔波被动之中,立即为田忌采纳,率领齐军杀往魏国都城大梁. 庞涓得知大梁告急的消息,忙率大军驰援大梁. 齐军事先在魏军必经之路的桂陵(今河南长垣南),占据有利地形,以逸待劳,打败了魏军. 这就是历史上有名的“围魏救赵”之战.“围魏救赵”之妙,妙在善于调动敌人. 调动敌人的要诀,则在“攻其所必救”.4. 减灶之法公元前342年,魏将庞涓带领10万大军进攻韩国. 韩国向齐国求救. 齐王召集群臣商讨对策,齐国的成侯邹忌主张不救,田忌主张早救. 孙膑建议先答应韩国的请求,致使韩国必倾力抗敌. 等到韩、魏双方战到疲惫不堪时,再出兵救韩,可用力少而见功多,取胜易而受益大. 韩国仗恃有齐国相援,倾全力抗魏,五战皆败,只得于公元前341年再次向齐求助. 齐王才决定派兵救韩,仍以田忌为主将,孙膑为军师. 战役之初,按照孙膑的计策,齐军长驱直入把攻击的矛头指向魏国的都城大梁. 庞涓听到消息,立即回援,但齐军已经进入魏国境内. 孙膑对田忌说,魏国军队素来慓悍勇武而看不起齐国,善于作战的人只能因势利导. 兵法上说,行军百里与敌争利会损失上将军,行军五十里而与敌争利只有一半人能赶到. 为了让魏军以为齐军大量掉队,应使齐军进入魏国境内后先设10万个灶,过一天设5万个灶,再过一天设3万个灶. 庞涓行军三天,见到齐军所留灶迹,判断齐军士兵已经逃跑一大半,所以丢下步兵,只率轻车锐骑用加倍的速度追赶齐军. 孙膑计算魏军行程,日暮时必然赶到马陵(今河南范县西南).马陵道路狭窄,两旁地形险阻.孙膑预先布置好伏兵,并集中优秀弩手夹道设伏. 庞涓日暮追至马陵,进入齐军伏击阵地. 齐军万弩齐发,魏军大乱,庞涓兵败自刎. 齐军乘胜全歼10万魏军.马陵之战,孙膑的因势利导、调动敌人、变劣势为优势、力争发挥突然性的作战指导主动,是颇有参考价值的. 其退军设伏的战法,也给了后人不少的启示.“围魏救赵”与“减灶之法”都充分体现了如何运用筹划兵力,选择最佳时间、地点,趋利避害,集中优势兵力以弱克强的运筹思想.5. 运筹帷幄中,决胜千里外在公元前3世纪楚汉相争中,汉高祖刘邦的著名谋士张良为推翻秦朝,打败项羽,统一全国立下了盖世奇功,刘邦赞誉他“夫运筹策帷帐之中,决胜于千里之外”. 这千古名句也可以说是对张良运筹思想的赞颂和褒奖. 《史记》在《留侯世家》及其他多处提及“夫运筹策帷帐之中,决胜于千里之外”. 这里的“运筹”,指张良在帷幄中制定作战谋略与决策的过程. 在西汉时代,“运筹”已被当作制定谋略与决策职能分工的代名词.20世纪30年代发展起来的运筹学,其基本宗旨是探讨事理,强调做一项工作之前要明确目的,制定效果,衡量指标体系作为估计不同方案所达到预定目标程度的依据,在此基础上选择最优方案和实施有效管理. 我国1955年开始研究运筹学时,从《史记》中摘取“运筹”一词作为“Operations Research”的意译,包含了运用筹划、以智取胜的深刻含义. 从《史记》对“运筹”的记述表明,我国运筹思想源远流长,至今对运筹学的发展仍有重要影响.6. 贾思勰与《齐民要术》贾思勰,北魏时期的科学家,益都(在山东寿光南)人,祖、父两代都善于经营,有着丰富的劳动经验,并都非常重视农业技术方面的学习和研究. 贾思勰从小在田园长大,对很多农作物都非常熟悉,他还跟着父亲身体力行参加各种农业劳动,学习掌握了大量农业科技. 他家里拥有大量藏书,这使他从小就有机会博览群书,从中汲取各方面的知识,也为他以后编撰《齐民要术》打下了基础. 大约在北魏永熙二年(533年)到东魏武定二年(554年)期间,他将自己积累的许多古书上的农业技术资料、询问老农获得的丰富经验以及他自己的亲身实践,加以分析、整理、总结,写成农业科学技术巨著《齐民要术》.《齐民要术》一书,不仅是我国古代农业科学一部杰出的学术著作,也是一部蕴含丰富运筹思想的宝贵文献,它记载了我国古代农民如何根据天时、地利和生产条件去合理筹划农事的经验. 其中所提出的不同作物的播种时间和各种作物茬口安排上的先后关系,可以说是现代运筹学中二阶段决策问题的雏型.7. 丁渭修皇宫[6]图1.1 丁渭修皇宫引水示意图[7]宋真宗大中祥符年间(1008—1017),都城开封里的皇宫失火,需要重建. 右谏议大夫、权三司使丁渭受命负责限期重新营造皇宫. 建造皇宫需要很多土,丁渭考虑到从营建工地到城外取土的地方距离太远,费工费力,于是下令将城中街道挖开取土,节省了不少工时. 挖了不久,街道便成了大沟. 丁渭又命人挖开官堤,引汴河水进入大沟之中,然后调来各地的竹筏、木船经这条大沟运送建造皇宫所用的各种物材,十分便利(见图1. 1). 等到皇宫营建完毕,丁渭命人将大沟中的水排尽,再将拆掉废旧皇宫以及营建新皇宫所丢弃的砖头瓦砾添入大沟中,大沟又变成了平地,重新成为街道. 这样,丁渭一举三得,挖土、运送物材、处理废弃瓦砾等三件工程一蹴而成,节省的工费数以亿万计.这是我国古代大规模工程施工组织方面运筹思想的典型例子.8. 沈括运粮[6]沈括(1031—1095), 北宋时期大科学家、军事家. 在率兵抗击西夏侵扰的征途中,曾经从行军中各类人员可以背负粮食的基本数据出发,分析计算了后勤人员与作战兵士在不同行军天数中的不同比例关系,同时也分析计算了用各种牲畜运粮与人力运粮之间的利弊,最后做出了从敌国就地征粮,保障前方供应的重要决策,从而减少了后勤人员的比例,增强了前方作战的兵力.当时沈括的分析计算过程译意如下:凡是行军作战,如何从敌方取得粮食,是最急迫的事情. 自己运粮不仅耗费大,而且沈括势必难以远行. 我曾经作过计算:假设一个民夫可以背六斗米,士兵自带五天的干粮.如果一个民夫供应一个士兵,单程只能进军十八天(六斗米,每人每天吃两升米,两人吃十八天*). 若要计回程的话,只能进军九天.如果两个民夫供应一个士兵,单程可进军二十六天(两个民夫背一石二斗米,三个人每天要吃六升米. 八天以后,其中一个民夫背的米已经吃光,给他六天的口粮让他先返回,以后的十八天,两人每天吃四升米).若要计回程的话,只能前进十三天的路程(前八天每天吃六升,后五天及回程每天吃四升米,能够进军十三天).如果三个民夫供应一个士兵,单程可进军三十一天(三人背米一石八斗,前六天半四个人,每天吃八升米,遣返一个民夫,给他四天口粮. 中间的七天三个人同吃,每天吃六升米,再遣返一个民夫,给他九天口粮;最后的十八天两人吃,每天四升米).如果要计回程的话,只可以前进十六天的路程(开始六天半每天吃八升米,中间七天,每天吃六升米,最后两天半以及十六天回程每天吃四升米).三个民夫供应一个士兵,已经到极限了.如果要出动十万军队,辎重占去三分之一兵源,能够上阵打仗的士兵不足七万人.这就要用三十万民夫运粮,再要扩大规模很困难了.每人背六斗米的数量也是根据民夫的总数平均来说的. 因为其中的队长不背,伙夫减半,他们所减少的要摊在众人头上.*士兵干粮相当于十升米,连同民夫背的米共有七十升,每天吃四升米,实际上只能维持十七天半. 十八天是以整数来说的. 以下计算类同.更何况还会有患病和死亡的人,他们所背的米又要由众人分担.所以军队中不容许饮食无度,如果有一个人暴食,两三个人供应他还不够.如果用牲畜运输,骆驼可以驮三石,马或骡可以驮一石五斗,驴子可以驮一石.与人工相比,虽然能驮得多,花费也少,但如果不能及时放牧或喂食,牲口就会瘦弱而死.一头牲口死了,只能连它驮的粮食也一同丢弃.所以与人工相比,实际上是利害相当.这种军事后勤问题的分析计算是具有现代意义的运筹思想的范例.9. 高超治河[6]高超,宋朝人,河工. 宋仁宗庆历年间(1041—1048)黄河在北都(今太原)商胡地区决口,很长时间都没有堵上决口. 朝廷派三司度支副使(官职名)郭申锡亲自前往监督工程进行. 凡是堵决口将要合拢的时候,都要在决口中间压上一埽(用树枝、芦苇、石头等捆紧做成圆柱形),叫做“合龙门”,这是成败的关键. 当时好几次压埽都合不上. 那时合龙门用的埽长六十步(步,古代的长度计量单位).有个叫做高超的水工献策说:埽身太长,人力压不住,埽到达不了水底,所以水流不断. 应当把六十步的埽身分为三节,每节长二十步,中间用绳索连起来. 先放下第一节,等它到了水底,再压第二节、第三节. 老河工和他争论,认为不可行,说:“二十步的埽不能阻断水流,白白使用三节埽,浪费好几倍成本,而决口依然堵不上”.高超对他说:“第一节河水确实没有被阻断,但是水势必然被削弱一半. 压第二节时只用一半的力气,水就算没有被阻断,也不过是很少往外漏出. 第三节就是在平地上施工,足以能够让人使出全部力气. 压完第三节以后,上两节自来就被浊泥淤积,不用再麻烦人力来加固它们了.” 郭申锡遵照从前的方法,不采纳高超的建议.当时魏公(爵位名)贾将军镇守北门(地名),只有他认为高超的话是对的,暗地派遣几千人在下游收集漂下来的埽. 而上游的埽压上以后,果然被水冲走了,黄河的决口更加大,郭申锡因此被贬官. 最后还是采用了高超的建议,才堵上了商胡地区的决口.这种分阶段作业优于一次作业的分析与论证,是运筹思想的典型范例.10、为何说一名数学家等于十个师?在第二次世界大战中,盟军为了和德国法西斯作战,大量军需物品要穿过大西洋运送到各个战场。
运筹学应用实例

A
B
C
D
E
F
陆地、河流及桥梁示意图
解:
将A,B,C,D,E,F分别用一种点表达,相互之间有桥相连 旳连一条弧;弧旳容量就是两点间旳桥梁数;设一种方向,得 到网络图如下:
A
例3.设备更新问题
某单位使用一台生产设备,在每年年底,单位领导都要决 策下年度是购置新设备还是继续使用旧设备。
若购置新设备,需要支付一笔购置费;假如继续使用旧旳, 则要支付一定旳维修费用。
一般说来,维修费随设备使用年限旳延长而增长。根据以 往旳统计资料,已经估算出设备在各年年初旳价格和不同 使用年限旳年维修费用,分别示于表1和表2。
相应旳开门方案如图所 示,共开10个门。
B C IJ
H
A
D GK
E
F
开门方案
例5:选址问题
有六个居民点v1,v2,v3,v4,v5,v6,拟定建一夜校,已知 各点参加学习旳人数为25、20、30、10、35、45人,其道路 如图所示,试拟定学校位于哪一种居民点,才干使学习者 所走旳总旅程至少?(图中边旁旳数字为路段长度)
用一条边把代表这两个项目
v2
旳顶点连接起来。这么得到
v3
下图
v1
为了处理这个问题,只需
找到一条包括全部顶点旳
v4
初等链。
v5
如:{v4,v1,v2,v3,v5}是一条初等链,相应旳比赛是: 100m自由泳,50m仰泳,50m蛙泳,100m碟泳,200m自由泳。
此问题旳方案不唯一。
例 2.线路铺设问题
0 50 150 175 200 275 40 0 80 100 120 180 180 120 0 30 60 150 D= 70 50 10 0 10 40 280 210 70 35 0 105 495 405 225 180 135 0
四个运筹学案例
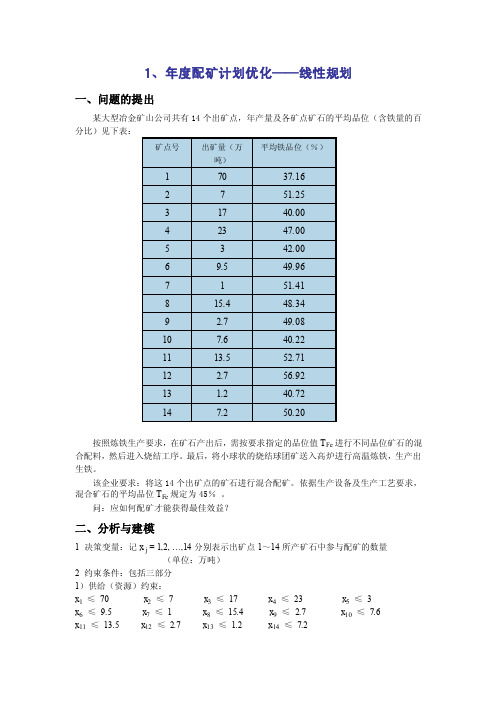
1、年度配矿计划优化——线性规划j(单位:万吨)2 约束条件:包括三部分1)供给(资源)约束:x1 ≤70 x2≤7 x3≤17 x4≤23 x5≤3 x6≤9.5 x7≤1 x8≤15.4 x9≤ 2.7 x10≤7.6 x11≤13.5 x12≤2.7 x13≤1.2 x14≤7.22)品位约束3)非负约束: x j ≥ 0 j = 1,2,3, … ,143 目标函数:此题目要求“效益最佳”有一定的模糊性,由于配矿后的混合矿石将作为后面 工序的原料而产生利润,故在初始阶段,可将目标函数选作配矿总量的极大化。
三、计算结果及分析1 计算结果利用单纯形法可得出该问题的最优解为:x1 = 31.121 x2 = 7 x3 = 17 x4 = 23 x5 = 3 x6 = 9.5 x7 = 1 x8 = 15.4 x9 = 2.7 x10 = 7.6 x11 = 13.5 x12 = 2.7 x13 = 1.2 x14 = 7.2 最优值:Z* = 141.921(万吨)2 分析与讨论1)计算结果是否可被该公司接受?——回答是否定因为:①在最优解中,除第1个采矿点有富裕外,其余13个采矿点的出矿量全部参与了配矿。
而矿点1在配矿以后尚有富余量 70 -31.12 =38.879 (万吨),但矿点1的矿石品位仅为37.16%,属贫矿。
②该公司花费了大量人力、物力、财力后,在矿点1生产的贫矿中却有近39万吨矿石被闲置,而且在大量积压的同时,还会对环境造成破坏,作为该公司的负责人或公司决策者是难以接受这样的生产方案的。
———原因何在?出路何在?2)解决问题的思路经过分析后可知:在矿石品位T Fe 及出矿量都不可变更的情况下,只能把注意力集中在 混合矿石的品位T Fe 要求上。
——不难看出,降低T Fe 的值,可以使更多的低品位矿石参与配矿。
问题:T Fe 的值有可能降低吗?在降低T Fe 的值,使更多的贫矿入选的同时,会产生什么影响?——以上问题就属于运筹学的灵敏度分析(优化后分析)3)经调查,以及与现场操作人员、工程技术人员、管理人员学习、咨询,拟定了三个T Fe 的新值:44% 、43% 、42%3 变动参数之后再计算,结果如下表所示:∑==+++++++++++++14114131211109875432145.0502.04073.05692.05271.04022.0408.04834.05141.064996.04200.04700.0400.05125.03716.0j jx x x x x x x x x x x x x x x ∑==141max j jx zFe境的破坏,故不予以考虑。
运筹学案例素材

例题1 合金制造问题有一家钢铁公司收到一份500吨造船用钢的订单.对这些造船用钢有如下要求:此公司储存有七种再现的原材料,都可以用于制造这种钢。
表6.2列出了这些析材料的品质,可用库存量,以及价格表6.2 原材料品质,可用库存量,与价格例题2 露天采矿探测发现了一个露天铀矿。
根据一些探测钻探的结果,发现这个矿可以分为若干个可开采区。
矿坑需要挖掘成阶梯形,以方便卡车开到矿坑底部。
铀矿呈东西方向分布。
在西面有一个村庄,在东面是山脉,因此矿坑大小要受到它们限制。
考虑了这些限制之后,确定有18个可开采区,呈三层分布。
总储蓄所量为10000吨,如下图,为挖掘一个可开采区,首露天矿山结构图挖开第一层的区块每吨需要耗费100欧元,挖开的二层的区块每吨需要耗费200欧元,挖开的二层的区块每吨需要耗费300欧元。
但是如果有区块是由含很多石英的石头组成(显示为斜线区域),那么由于这些石头非常硬,因此每吨需要耗费1000欧元。
只有以灰色显示的区块才含有铀(1,7,10,12,17,18)。
其市场价值分别为200,300,500,1000,和1200欧元/吨。
第18区块,尽管也含有大量矿石,但是此区块也和其他绘有斜线的区块一样,含水量有大量非常硬的石头。
为使总收益达到最大,应掘开那些区块?例题3 电力生产为满足每日电力需求(单位为兆瓦),可以选用四种不同类型的发电机。
每日电力需求如下表所示。
所有发电机都存在一个启动成本,以及工作于最小功率状态时势固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。
这些数据均列于下表中。
表4 发电机描述出任何代价。
在任意时刻,正在工作的发电机组必须留出20%的发电能力余量,以防用电量突然上升。
问题是:在每个时段应分别作用哪些发电机才能够使每天的总成本电小?例题4 汽车租赁有一家小型汽车租赁公司,此公司有94辆可供出租的汽车,分布于10个代理点中。
运筹学案例集

运筹学案例集运筹学的一些典型性应用• 合理利用材料问题:如何在保证生产的条件下,下料最少 • 配料问题:在原料供应量的限制下,如何获取最大收益 • 投资问题:从投资项目中选取最佳组合,使投资回报最大 • 产品生产计划:合理利用人力、物力、财力等,使获利最大 • 劳动力安排:用最少的劳动力来满足工作的需要 • 运输问题:如何制定最佳调运方案,使总运费最少 一、生产计划问题案例1(2-4)、某工厂用A 、B 、C 、D 四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元,问应如何安排生产才能获得最大收益?产 品所 需 原 料AB C D 甲 乙 4 44 28 02 4现有原料 数量28203224案例2(2-6)、某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的生产,已知生产单位产品所需的设备台时及A 、B 两种原材料的消耗、资源的限制,如下表:问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最Ⅰ Ⅱ资源限制设备 1 1 300台时原料A 2 1 400千克 原料B 0 1 250千克单位产品获利 50元 100元多?案例3(2-25)、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量,数据如下表所示。
问题:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?案例4(2-28)、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A 、B 两道工序加工。
设有两种规格的设备A1、A2能完成A 工序;有三种规格的设备B1、B2、B3能完成 B 工序。
Ⅰ可在A 、B 的任何规格的设备上加工;Ⅱ 可在任意规格的A 设备上加工,但对B 工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工,数据如下表所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题:如何在保证生产的条件下,下料最少•配料问题:在原料供应量的限制下,如何获取最大收益•投资问题:从投资项目中选取最佳组合,使投资回报最大•产品生产计划:合理利用人力、物力、财力等,使获利最大•劳动力安排:用最少的劳动力来满足工作的需要•运输问题:如何制定最佳调运方案,使总运费最少一、生产计划问题案例1(2-4)、某工厂用A、B、C、D四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元,问应如何安排生产才能获得最大收益?已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制,如下表:问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?案例3(2-25)、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品,都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作,亦可以自行生产,但产品丙必须本厂铸造才能保证质量,数据如下表所示。
问题:公司为了获得最大利润,甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中,由本公司铸造和由外包协作各应多少件?案例4(2-28)、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品,均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序;有三种规格的设备B1、B2、B3能完成B 工序。
Ⅰ可在A、B的任何规格的设备上加工;Ⅱ可在任意规格的A设备上加工,但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工,数据如下表所示。
问题:为使该厂获得最大利润,应如何制定产品加工方案?案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人,每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为:每人每月生产原稿纸30捆,或生产日记本30打,或练习本30箱。
而原材料的消耗为:每捆原稿纸用白坯纸 10/3 公斤,每打笔记本用白坯纸 40/3 公斤,每箱练习本用白坯纸 80/3 公斤。
生产一捆原稿纸可获利 2 元,生产一打笔记本可获利 3 元,生产一箱练习本可获利 1 元。
问题:(1)试确定在现有生产条件下的最优生产方案。
(2)如白坯纸的供应量不变,当工人数不足时可招收临时工,临时工的工资支出为每人每月40元,问:要不要招收临时工?案例6(6-18)、某厂按合同规定须于当年每个季度末分别提供10、15、25、20台同一规格的柴油机。
已知该厂各季度的生产能力及生产每台柴油机的成本如下表。
如果生产出来的柴油机当季不交货,每台每积压一个季度需储存、维护等费用0.15万元。
问题:试求在完成合同的情况下,使该厂全年生产总费用为最小的决策方案。
二、套材下料问题案例7(2-15)、某钢筋车间制作一批钢筋(直径相同),长度为3米的100根,长度为4米的60根。
已知所用的下料钢筋长度为10米,问怎样下料最省?共需多少根钢筋?案例8(2-18)、某工厂要做100套钢架,每套用长为2.9m、2.1 m、1.5 m的圆钢各一根。
已知原料每根长7.4 m,问:应如何下料,可使所用原料最省?共需多少根原料?案例9(2-21)、现要用100×50厘米的板料裁剪出规格分别为40×40 厘米与50×20厘米的零件,前者需要25件,后者需要30件。
问如何裁剪,才能最省料?共需多少板料?三、人力资源分配问题案例10、生产轮班人员的双向选择问题金伦化工(镇江)有限公司为提高工作效率和增强团队的凝聚力,对28名生产操作人员进行重新分组,拟分成4组,每组7人,由1名组长和6名普通员工组成,28名生产操作人员中已有4名员工被上级任命为4个组的组长。
为在24名普通员工和4位组长之间进行最有效的分组,以实现总体满意度值最高,采取了如下的评价办法。
首先,发放调查问卷,由24名普通员工对4位组长进行打分(具体打分方法和流程不在这里进行表述),评价结果如下表所示(得分越低表示满意度越高,反之亦然):然后,由4位组长对24名普通员工进行选择排序(具体方法和流程不在这里进行表述),评价结果如下表所示(得分越低表示满意度越高,反之亦然):经过综合评价,24名普通员工与4位组长之间的相互满意度值如下表所示(得分越低表示满意度值越高):问题:试求总体满意度值最高的分组方案。
案例11(2-9)、某昼夜服务的公交线路每天各时间段内所需司机和乘务人员数如下表所示:问题:该公交线路怎样安排司机和乘务人员,既能满足工作需要,又配备数量最少司机和乘务人员?案例12(2-11)、某工厂车间共50人,其中男的为30人,女的为20人,每人每天的工作效率如下表所示,在植树节当天,如何合理安排人员,使得种活的树的数量最多?案例13(2-13)、一家中型的百货商场,它对售货员的需求经过统计分析如下表所示。
为了保证售货员充分休息,售货员每周工作5天,休息两天,并要求休息的两天是连续的。
问题:应该如何安排售货员的作息时间,既满足工作需要,又使配备的售货员的人数最少?案例14种文字,分别记作A、B、C、D。
现在甲、乙、丙、丁四人,将中文说明书翻译成不同语种的说明书,每人做各项工作所所需支付的费用如下表所示。
问题:应如何指派工作,才能使总的费用为最少。
四、配料问题案例15(2-31)、某工厂要用三种原料1、2、3混合调配出三种不同规格的产品甲、乙、丙,数据如下表所示。
问题:该厂应如何安排生产,使利润收入为最大?案例16(2-36)、营养配餐问题。
假定一个成年人每天需要从食物中获取3000卡路里热量,55克蛋白质和800毫克钙。
如果市场上只有四种食品可供选择,它们每千克所含热量和营养成份以及市场价格如下表所示。
问题:如何选择才能使在满足营养的前提下使购买食品的总费用最小?案例17(2-42)、养海狸鼠饲料中营养要求:V A每天至少700克,VB每天至少30克,VC每天刚好200克。
现有五种饲料,搭配使用,饲料成分如下表。
问题:如何实现即满足营养要求,又使用成本最低?五、投资问题案例18(2-43)、设有下面四个投资的机会:甲:在三年内,投资人应在每年的年初投资,每年每元投资可获利息0.2元,每年取息后可重新将本息投入生息。
乙:在三年内,投资人应在第一年年初投资,每两年每元投资可获利息0.5元,两年后取息重新将本息投入生息。
这种投资最多不得超过20000元。
丙:在三年内,投资人应在第二年年初投资,两年后每元投资可获利息0.6元,这种投资最多不得超过15000元。
丁:在三年内,投资人应在第三年年初投资,一年内每元投资可获利息0.4元,这种投资不得超过10000元。
问题:假定在这三年为一期的投资中,每期的开始有30000元可供投资,投资人应怎样决定投资计划,才能在第三年年底获得最高的收益。
建立此问题的线性规划模型。
案例19(2-45)、某部门现有资金200万元,今后五年内考虑给以下的项目投资。
已知:项目A:从第一年到第五年每年年初都可投资,当年末能收回本利110%;项目B:从第一年到第四年每年年初都可投资,次年末能收回本利125%,但规定每年最大投资额不能超过30万元;项目C:需在第三年年初投资,第五年末能收回本利140%,但规定最大投资额不能超过80万元;项目D:需在第二年年初投资,第五年末能收回本利155%,但规定最大投资额不能超过100万元。
据测定每万元每次投资的风险指数如下表:a)应如何确定这些项目的每年投资额,使得第五年年末拥有资金的本利金额为最大?b)应如何确定这些项目的每年投资额,使得第五年年末拥有资金的本利在330万元的基础上使得其投资总的风险系数为最小?案例20(2-49)、证券组合投资决策某人有一笔50万的资金可用于长期投资,可供选择的投资机会包括购买国库券、公司债券、投资房地产、购买股票或银行保值储蓄等。
不同的投资方式的具体参数见下表。
六、进度问题案例21(2-52)、某厂生产的一种产品,其需求量具有季节性,假定每年只能在连续的三个月内进行生产和销售。
生产可以按正常工作时间进行,也可以加班。
前二个月的月产量可以大于当月的销售量而将多余的产品存贮,但要付出存贮费;而在第三个月月末要将产品全部售完。
设产品在正常工作时间生产,每月最多能生产300单位,单位成本为75元。
在加班时间生产,每月最多能生产90单位,单位成本为95元。
每月生产量及平均成本不一定要相等。
存贮费每月每单位0.5元。
三个月的需求量分别为160、380和300单位。
问题:试确定每月在正常时间及加班时间各生产多少产品,使总成本最小。
案例21(2-56)、一个木材储运公司有很大的仓库用以储运出售木材。
由于木材季度价格的变化,该公司于每季度初购进木材,一部分于本季度内出售,一部分储存起来以后出售。
已知该公司仓库的最大储存量为2000万米3(木材采购后一律进入仓库),储存费用为(70+100u)千元/万米3,u为存储时间(季度数),当季出售不需要支付储存费用。
已知每季度的买进卖出价及预计的销售量如下表所示。
为使售后利润最大,试建立这个问题的线性规划模型。
七、固定成本问题案例22(7-11)、高压容器公司制造小、中、大三种尺寸的金属容器,所用资源为金属板、劳动力和机器设备,制造一个容器所需的各种资源的数量如下表所示。
不考虑固定费用,每种容器售出一只所得的利润分别为4万元、5万元、6万元,可使用的金属板有500吨,劳动力有300人/月,机器设备有100台/月,此外不管每种容器制造的数量是多还是少,都要支付一笔固定的费用:小号是l00万元,中号为150 万元,大号为200万元。
现在要制定一个生产计划,使获得的利润为最大。
案例23(7-13)、企业计划生产4000件某种产品,该产品可自己加工、外协加工任意一种形式生产。
已知每种生产形式的固定费用、生产该产品的单件成本以及每种生产形式的最大加工数量(件)限制如下表所示,怎样安排产品的加工使总成本最小。
八、分布系统设计问题案例24(7-19)、某企业在A1 地已有一个工厂,其产品的生产能力为30 千箱,为了扩大生产,打算在A2,A3,A4,A5地中再选择几个地方建厂。
已知在A2 ,A3,A4,A5地建厂的固定成本分别为175千元、300千元、375千元、500千元,另外,A1产量及A2,A3,A4,A5建成厂后的产量,销地预计的销量以及产地到销地的单位运价(每千箱运费)如下表所示。
问题:在满足销量的前提下,问应该在哪几个地方建厂,使得其总的固定成本和总的运输费用之和最小?九、不确定型决策问题案例25、某企业有三种新产品待选,估计销路和损益情况如下表所示:试分别用乐观准则、悲观准则、等可能性准则、后悔值准则选择最优产品方案。
