全等三角形之倍长中线法
全等三角形辅助线之倍长中线法

可证EFD EGC
F
(平行线夹中点)
D
E
C
G
全等三角形辅助线之倍长中线法
如图,在△ABC中,AD为BC边上的中线.若AB=5, AC=3,求AD的取值范围.
A
延长AD至E使DE=AD,连接BE
在ADC和EDB中
AD=DE,ADC=EDB,BD=CD
故ADC EDB(SAS)
B
D
C AB-BE AE AB+BE即2 AE 8
A F
E
A
1 2
F
3E
B
D
C
BDCM 全等三角形辅助线之倍长中线法
如图,在正方形ABCD中,CD=BC,∠DCB=90°,点E在CB的延长线上,过点E作 EF⊥BE,且EF=BE.连接BF,FD,取FD的中点G,连接EG,CG. 求证:EG=CG且EG⊥CG.
M
A
D
A
D
G G
F EB
F
1
4
2
3
C
EB
全等三角形辅助线之倍长中线法
倍长中线法:遇中线,要倍长,倍长之后有全等.
AD为ABC的中线
A
B
D
C
延长AD至E使DE=AD,连接BE 在ADC和EDB中 AD=DE,ADC=EDB,BD=CD 故ADC EDB(SAS) 与此相关的重要结论AC PBE
E
全等三角形辅助线之倍长中线法
AD为ABC的中线
1<AD<4
E
全等三角形辅助线之倍长中线法
如图,CB是△AEC的中线,CD是△ABC的中线,且AB=AC. 求证:①CE=2CD;②CB平分∠DCE.
C
全等三角形辅助线添加技巧--倍长中线法(含八年级内容)(无答案)
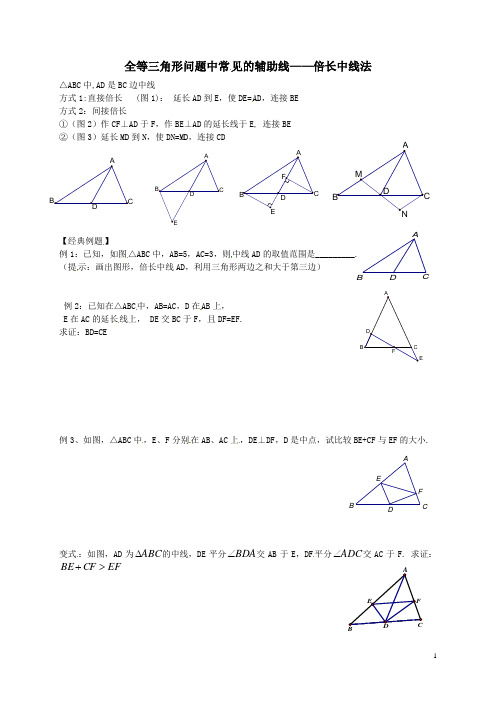
E DF C B ADCB A全等三角形问题中常见的辅助线——倍长中线法△ABC 中,AD 是BC 边中线方式1:直接倍长 (图1): 延长AD 到E ,使DE=AD ,连接BE 方式2:间接倍长①(图2)作CF ⊥AD 于F ,作BE ⊥AD 的延长线于E, 连接BE ②(图3)延长MD 到N ,使DN=MD ,连接CD【经典例题】例1:已知,如图△ABC 中,AB=5,AC=3,则中线AD 的取值范围是_________. (提示:画出图形,倍长中线AD ,利用三角形两边之和大于第三边)例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上, DE 交BC 于F ,且DF=EF. 求证:BD=CE例3、如图,△ABC 中,E 、F 分别在AB 、AC 上,DE ⊥DF ,D 是中点,试比较BE+CF 与EF 的大小.变式:如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+例4:已知在△ABC中,AD是BC边上的中线,E是AD上一点,且B E=AC,延长BE交AC于F,求证:AF=EF例5、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.变式一:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE变式二:已知CD=AB,∠BD A=∠BAD,AE是△ABD的中线,求证:2AE=AC。
ED C BA例6:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠练习1、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论2、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.3、 在△ABC 中,AD 平分∠BAC ,CM ⊥AD 于M ,D A B CM T E_ A_ B _ D_ E _ C _ F若AB=AD,求证:2AM=AC+AB。
全等三角形辅助线之倍长中线法

全等三角形辅助线之倍长中线法倍长中线法:遇中线,要倍长,倍长之后有全等.当倍长后,连接方式不一样,可以产生更多结论如下:与倍长中线法类似的辅助线作法AD E DE=AD BE ADC EDB AD=DE ADC=EDB BD=CDADC EDB(SAS)AC BE∆∆∠∠∆≅∆延长至使,连接在和中,,故与此相关的重要结论AD ABC ∆为的中线D CB AEAD ABC ∆为的中线DC BAEAD E AD=DE CE BE CE ABEC 延长至,使,当连接时,结论相似; 当连接、,则为平行四边形M ABCDEMD E MD=DE CE BDM CDE BM CE∆≅∆延长至,使,连接可证,举例:FE G FE=GE EGC ()EFD ∆≅∆延长至,使可证平行线夹中点F EDCBA G如图,在△ABC 中,AD 为BC 边上的中D CB AEAD E DE=AD BE ADC EDB AD=DE ADC=EDB BD=CDADC EDB(SAS)AB-BE AE AB+BE AE <AD<∆∆∠∠∆≅∆<<<<延长至使,连接在和中,,故即2814654321FAB C DE如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AB=AC . 求证:△CE=2CD ;△CB 平分△DCE .E DCB A如图,在△ABC 中,D 是BC 的中点,E 是AD 上一点,BE=AC ,BE 的延长线交AC 于点F .求证:△AEF=△EAF .F EDCBA321MA BCD EF如图,在正方形ABCD 中,CD=BC ,△DCB=90°,点E 在CB 的延长线上,过点E 作EF △BE ,且EF=BE .连接BF ,FD ,取FD 的中点G ,连接EG ,CG .求证:EG=CG 且EG △CG .GF EDCB AM2134GFDA1. 如图,在△ABC 中,AD 为BC 边上的中线.(1)按要求作图:延长AD 到点E ,使DE =AD ;连接BE . (2)求证:△ACD ≌△EBD . (3)求证:AB +AC >2AD .(4)若AB =5,AC =3,求AD 的取值范围.2. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .3. 如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AB =AC .求证:①CE =2CD ;②CB 平分∠DCE .4. 如图,在△ABC 中,D 是BC 的中点,E 是AD 上一点,BE =AC ,BE 的延长线交AC 于点F . 求证:∠AEF =∠EAF .5. 如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 的中点,EF ∥AD 交CA 的延长线于点F ,交AB 于点G ,BG =CF . 求证:AD 为△ABC 的角平分线.GFE DCB AE DCB AF E DBAGFEDCBAFED CBA6. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CD 的中点,且AF ⊥AB ,已知AD =2.7,AE =BE =5,求CE 的长.7. 如图,在正方形ABCD 中,CD =BC ,∠DCB =90°,点E 在CB 的延长线上,过点E 作EF ⊥BE ,且EF=BE .连接BF ,FD ,取FD 的中点G ,连接EG ,CG .求证:EG =CG 且EG ⊥CG .【参考答案】➢ 课前预习1. (1)相等,SSS ;夹角,SAS ;夹边,ASA ;对边,AAS ;直角,HL(2)全等,三,边 2. (1)证明:如图∵O 是AB 的中点 ∴AO =BO在△AOC 和△BOD 中AO BO AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴△AOC ≌△BOD (SAS ) (2)证明:如图 ∵O 是AB 的中点 ∴AO =BO ∵AC ∥BD ∴∠A =∠B在△AOC 和△BOD 中A B AO BOAOC BOD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AOC ≌△BOD (ASA )GF EDCBA➢ 典型题型1. 解:(1)如图,(2)证明:如图,∵AD 为BC 边上的中线 ∴BD =CD在△BDE 和△CDA 中12BD CD ED AD =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS ) (3)证明:如图, ∵△BDE ≌△CDA ∴BE =AC ∵DE =AD ∴AE =2 AD在△ABE 中,AB +BE >AE ∴AB +AC >2AD (4)在△ABE 中,AB -BE <AE <AB +BE由(3)得 AE =2AD ,BE =AC ∵AC =3,AB =5 ∴5-3<AE <5+3 ∴2<2AD <8 ∴1<AD <42. 证明:如图,延长AD 到E ,使DE =AD ,连接BE在△ADC 和△EDB 中CD BD ADC EDB AD ED =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△EDB (SAS ) ∴AC =EB ,∠2=∠E ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE∴AB =AC3. 证明:如图,延长CD 到F ,使DF =CD ,连接BF∴CF =2CD∵CD 是△ABC 的中线21EDCBA 21EBCDA在△BDF 和△ADC 中BD AD ADC BDF DF DC =⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△ADC (SAS ) ∴BF =AC ,∠1=∠F ∵CB 是△AEC 的中线 ∴BE =AB ∵AC =AB ∴BE =BF ∵∠1=∠F ∴BF ∥AC∴∠1+∠2+∠5+∠6=180° 又∵AC =AB ∴∠1+∠2=∠5 又∵∠4+∠5=180° ∴∠4=∠5+∠6 即∠CBE =∠CBF 在△CBE 和△CBF 中CB CB CBE CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴△CBE ≌△CBF (SAS ) ∴CE =CF ,∠2=∠3 ∴CE =2CD CB 平分∠DCE4. 证明:如图,延长AD 到M ,使DM =AD ,连接BM∵D 是BC 边的中点 ∴BD =CD在△ADC 和△MDB 中CD BD ADC MDB AD MD =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△MDB (SAS ) ∴∠1=∠M ,AC =MB ∵BE =AC ∴BE =MB ∴∠M =∠3321MA BCDEF∴∠1=∠2 即∠AEF =∠EAF5. 证明:如图,延长FE 到M ,使EM =EF ,连接BM∵点E 是BC 的中点 ∴BE =CE在△CFE 和△BME 中FE ME CEF BEM CE BE =⎧⎪∠=∠⎨⎪=⎩∴△CFE ≌△BME (SAS ) ∴CF =BM ,∠F =∠M ∵BG =CF ∴BG =BM ∴∠1=∠M ∴∠1=∠F ∵AD ∥EF∴∠3=∠F ,∠1=∠2 ∴∠2=∠3即AD 为△ABC 的角平分线6. 解:如图,延长AF 交BC 的延长线于点G∵AD ∥BC ∴∠3=∠G∵点F 是CD 的中点 ∴DF =CF在△ADF 和△GCF 中3G AFD GFC DF CF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△GCF (AAS )∴AD =CG ∵AD =2.7 ∴CG =2.7 ∵AE =BE ∴∠1=∠B ∵AB ⊥AF ∴∠1+∠2=90° ∠B +∠G =90°321MABCD EFG∴CE =EG -CG=5-2.7 =2.37. 证明:如图,延长EG 交CD 的延长线于点M由题意,∠FEB =90°,∠DCB =90°∴∠DCB +∠FEB =180° ∴EF ∥CD ∴∠FEG =∠M ∵点G 为FD 的中点 ∴FG =DG在△FGE 和△DGM 中1M FGE DGM FG DG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△FGE ≌△DGM (AAS ) ∴EF =MD ,EG =MG ∵△FEB 是等腰直角三角形 ∴EF =EB ∴BE =MD在正方形ABCD 中,BC =CD ∴BE +BC =MD +CD 即EC =MC∴△ECM 是等腰直角三角形 ∵EG =MG∴EG ⊥CG ,∠3=∠4=45° ∴∠2=∠3=45° ∴EG =CG三角形全等之倍长中线(实战演练)1. 在△ABC 中,AC =5,中线AD =4,则边AB 的取值范围是_______________. 思路分析:①画出草图,标注条件:②根据题目条件,见_________,考虑_____________;添加辅助线是______________________________________;③倍长之后证全等:__________≌___________( ),证全等转移边:______=_______; ④全等转移条件后,利用三角形三边关系可以得到AB 的取值范围.2. 如图,在正方形ABCD 中,AD ∥BC ,E 为AB 边的中点,G ,F 分别为AD ,BC 边上的点,且AG =1,BF =2.若GE ⊥EF ,则GF 的长为多少?【参考答案】1. 3<AB <13①图略②中线AD 倍长中线 延长AD 到点E ,使DE =AD ,连接CE ③△ADC △EDB SAS AC EB ④略2. AD ∥BC ,E 为AB 边的中点,平行夹中点;AG =BH ,GE =HE ;到线段两端点的距离相等,FH ,AG +BF 解:如图,延长GE 交CB 的延长线于点H ∵AD ∥BC ∴∠GAE =∠HBE ∵E 为AB 边的中点 ∴AE =BE在△AGE 和△BHE 中,AEG BEH AE BEGAE HBE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AGE ≌△BHE (ASA ) ∴BH =AG ,HE =GE ∵GE ⊥EF ∴GF =HF ∵BF =2,AG =1 ∴GF =HF =BF +BH =BF +AG =2+1 =3G FEAD BC三角形全等之倍长中线(作业)➢ 例题示范例1:已知:如图,在△ABC 中,AB ≠AC ,D ,E 在BC 上,且DE =EC ,过D 作DF ∥BA 交AE 于点F ,DF =AC . 求证:AE 平分∠BAC .【思路分析】读题标注:见中线,要倍长,倍长之后证全等.结合此题,DE =EC ,点E 是DC 的中点,考虑倍长,有两种考虑方法: ①考虑倍长FE ,如图所示: ②考虑倍长AE ,如图所示:(这个过程需要考虑倍长之后具体要连接哪两个点)倍长中线的目的是为了证明全等:以方法①为例,可证△DEF ≌△CEG ,由全等转移边和角,重新组织条件证明即可. 【过程书写】证明:如图,延长FE 到G ,使EG =EF ,连接CG .A D CE FA B DCE FGFE CD B A FE CD B AA B DCE FG在△DEF 和△CEG 中,ED EC DEF CEG EF EG =⎧⎪∠=∠⎨⎪=⎩∴△DEF ≌△CEG (SAS ) ∴DF =CG ,∠DFE =∠G ∵DF =AC ∴CG =AC ∴∠G =∠CAE ∴∠DFE =∠CAE ∵DF ∥AB ∴∠DFE =∠BAE ∴∠BAE =∠CAE ∴AE 平分∠BAC➢ 巩固练习1. 已知:如图,在△ABC 中,AB =4,AC =2,点D 为BC 边的中点,且AD 是整数,则AD =________.2. 已知:如图,BD 平分∠ABC 交AC 于D ,点E 为CD 上一点,且AD =DE ,EF ∥BC 交BD 于F .求证:AB =EF .3. 已知:如图,在△ABC 中,AD 是BC 边上的中线,分别以AB ,AC 为直角边向外作等腰直角三角形,AB =AE ,AC =AF ,∠BAE =∠CAF =90°. 求证:EF =2AD .4. 如图,在△ABC 中,AB >AC ,E 为BC 边的中点,AD 为D CBAF E DCBAFED CBA G FE D CBA∠BAC 的平分线,过E 作AD 的平行线,交AB 于F ,交CA 的延长线于G . 求证:BF =CG .5. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F是CD 的中点,连接AF ,EF ,AE ,若∠DAF =∠EAF ,求证:AF⊥EF .➢ 思考小结1. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .比较下列两种不同的证明方法,并回答问题. 方法1:如图,延长AD 到E ,使DE =AD ,连接BE 在△BDE 和△CDA 中BD CD BDE CDA DE DA =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS ) ∴AC =BE ,∠E =∠2 ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 方法2:如图,过点B 作BE ∥AC ,交AD 的延长线于点E ∵BE ∥AC ∴∠E =∠2在△BDE 和△CDA 中FE DB CA21ECDB A 21ECDBA DBA2E BDE CDA BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (AAS ) ∴BE =AC ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 相同点:两种方法都是通过辅助线构造全等,利用全等转移条件进而解决问题.方法1是看到中点考虑通过___________构造全等,方法2是通过平行夹中点构造全等. 不同点:倍长中线的方法在证明全等时,利用的判定是________,实质是构造了一组对应边相等;利用平行夹中点证明全等时,利用的判定是_____,实质是利用平行构造了一组_____相等.2. 利用“倍长中线”我们就可以证明直角三角形中非常重要的一个定理:直角三角形斜边中线等于斜边的一半.请你尝试进行证明.已知:如图,在Rt △ABC 中,∠BCA =90°,CD 是斜边AB 的中线.求证:CD 12=AB .【参考答案】➢ 巩固练习 1. 22. 证明略(提示:延长FD 到点G ,使得DG =DF ,连接AG ,证明△ADG ≌△EDF ,转角证明AB =EF )3. 证明略(提示:延长AD 到点G ,使得GD =AD ,连接CG ,证明△ABD ≌△GCD ,△EAF ≌△GCA )4. 证明略(提示:延长FE 到点H ,使得EH =FE ,连接CH ,证明△BFE ≌△CHE ,转角证明BF =CG )5. 证明略(提示:延长AF 交BC 的延长线于点G ,证明△ADF ≌△GCF ,转角证明AF ⊥EF ) ➢ 思考小结 1. 倍长中线 SAS AAS 角2. 证明略DCB A。
倍长中线法构造全等三角形例题

倍长中线法构造全等三角形例题《倍长中线法构造全等三角形》一、引言在数学中,全等三角形是非常重要的概念,它们具有相同的三边和三角角度,但形状和位置可能有所不同。
而倍长中线法是构造全等三角形的一种重要方法。
本文将深入探讨倍长中线法的原理和应用,通过具体的例题来演示构造全等三角形的过程。
二、倍长中线法的原理1. 什么是倍长中线法?倍长中线法是指通过将三角形中的两条边分别延长相等的长度,然后连接延长后的两条边的中点,得到一个边长为原来中线的两倍的新三角形的方法。
2. 倍长中线法的原理当我们通过倍长中线法构造全等三角形时,我们实际上是借助了中线的性质。
在三角形中,连接一个顶点和对边中点的线段就是该对边的中线,中线的定义是连接三角形的一个顶点和边对面中点的线段。
对于一个三角形ABC来说,若D为AB的中点,那么有AD = BD,这就是中线的性质之一。
而倍长中线法利用了中线的这一性质,通过延长两条边相等的长度,再连接延长后的两条边的中点,可以构造出一条新的中线,新中线的长度是原中线的两倍。
这样就得到了一个边长为原三角形中线长度两倍的全等三角形。
三、倍长中线法构造全等三角形的例题现在,让我们通过具体的例题来演示倍长中线法对全等三角形的构造过程。
例题1:已知△ABC中,AB = 6cm, AC = 4cm,以AC为底边做三角形ACD,且AD = 6cm,BD = 4cm,连接BC并延长到E,使得CE = AB。
连接DE并延长到F,使得DF = AB。
证明△ADF≌△ABC。
解题步骤:1. 延长BC和DE我们根据题目要求,延长BC和DE,使得CE = AB,DF = AB。
2. 连接CD接下来,连接CD,得到三角形ACD。
3. 寻找AD和DB的中点我们在AD和DB上分别寻找其中点,分别记为G和H。
4. 连接GH连接GH,得到新的中线GH。
5. 观察三角形ADF和三角形ABC我们可以观察到,三角形ADF和三角形ABC中,AD = AB,DG = BH。
三角形全等专题倍长中线法

全等三角形根本剖断前提:1.三边对应相等(SSS).2.双方夹角对应相等(SAS).3.两角夹边对应相等(ASA).4.两角对边对应相等(AAS).5.直角三角形全等前提:①斜边及一向角边对应相等(HL);②一向角边及一锐角对应相等(ASA)或斜边及一锐角对应相等(AAS);③两直角边对应相等 (SAS).★留意:直角三角形全等,除边边边(SSS),边角边(SAS),角边角(ASA),角角边(AAS)对应相等外,还有直角边及斜边(HL).一向角边及一锐角(ASA).斜边及一锐角(AAS).两直角边(SS)等对应相等.除以上根本剖断外,全等三角形别的剖断前提:1.三条中线对应相等,两个三角形全等.2.三条高线对应相等,两个三角形全等.3.三条角等分线对应相等,两个三角形全等.4.两个角及第三个角的角等分线对应相等,两个三角形全等.5.两条边及第三条边上的中线对应相等,两个三角形全等.6.钝角三角形中,一钝角和其一邻边对应相等,钝角所对的较大边也相等,两个三角形全等.或双方及个中一边的对角(钝角)对应相等,两个三角形全等.(SSA)7.等腰三角形中,底边和顶角分离对应相等,两个等腰三角形全等.8.等腰直角三角形中,周长相等,两个等腰直角三角形全等.(因为等腰直角三角形三边之比为1:1:√2,故周长相等时,等腰直角三角形的对应角相等,对应边相等,故全等).9.等边三角形中,有一边对应相等,两个三角形全等.★特殊提醒:在三角形全等的剖断中,必定有边相等,必定没有AAA 和SSA(除非此角为钝角),这两种情形都不克不及独一肯定三角形的外形.三角形全等的性质:1.全等三角形的对应角相等.4. 全等三角形的对应边上的中线相等.角等分线相等.3.全等三角形面积周长相等.6.全等三角形的对应边上的高对应相等.等腰三角形的性质1.等腰三角形的两个底角度数相等(简写“等边对等角”).2.等腰三角形的顶角等分线,底边上的中线,底边上的高重合(简写“等腰三角形的三线合一性质”).3.等腰三角形的两底角等分线相等(两条腰上的中线相等,两条腰上的高相等).4.等腰三角形底边上的垂直等分线到两条腰的距离相等.5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半.6.等腰三角形底边上随意率性一点到两腰距离之和等于一腰上的高(等面积法证实).7.等腰三角形是轴对称图形(不是等边三角形的情形下),只有一条对称轴,顶角等分线地点的直线是它的对称轴,等边三角形有三条对称轴.8.等腰三角形的腰大于高.等腰三角形的腰的平方等于高的平方加底的一半的平方.初中三角形全等专题倍长中线法倍长中线法的界说:延伸中线,使所延伸部分与中线相等,然后往往须要衔接响应的极点,则对应角对应边都对应相等.经常应用于结构全等三角形.中线倍长法多用于结构全等三角形和证实边之间的关系以便利求个中一边的规模值.1.如图,在△ABC中,AC=5,中线AD=7,则AB边的取值规模是( )A.2<AB<12B.4<AB<12C.9<AB<19D.10<AB<19 答案:C解题思绪:延伸AD至E,使DE=AD,衔接CE,可先证实△ABD≌△E CD,则AB=CE,在△ACE中,依据三角形的三边关系,得AE-AC<CE<AE+AC,即9<CE<19.则9<AB<19.故选C.2.如图,已知CB.CD分离是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论:①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB等分∠DCE,则以上结论准确的是()A.①②④B.①③④C.①②③D.①②③④答案:A解题思绪:①准确,延伸CD至点F,使得DF=CD,衔接AF,可先证实△ADF≌△BDC,再证实△ACF≌△BEC,由这两个三角形全等可以得知②.④准确.由△ACF≌△BEC,得∠ACD=∠E,若要∠ACD=∠BCE,则需∠E=∠BCE,则需BC=BE,显然不成立,故③选项错误3.如图,点E是BC的中点,∠BAE=∠CDE,延伸DE到点F使得EF=DE,衔接BF,则下列说法准确的是()①BF∥CD②△BFE≌△CDE ③AB=BF ④△ABE为等腰三角形A.①②③B.②③④C.①③④D.①②③④答案:A解题思绪:可以先证实△BEF≌△CED,可以得到②准确,进而得到∠F=∠D,BF∥CD,①准确,又∵∠BAE=∠CDE=∠F,∴AB=BF,③准确.④不准确.4.如图,在正方形ABCD中,E为AB边的中点,G.F分离为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为()A.1B.2C.3D.4 答案:C解题思绪:延伸FE交DA的延伸线于点M,则可证△AEM≌△BEF,再证实△GEM≌△GEF,可以得到GF=GM=GA+BF=3,答案选C5.如图,在△ABC中,点D.E为边BC的三等分点,则下列说法准确的有()①BD=DE=EC ②AB+AE>2AD ③AD+AC>2AE ④AB+AC>AD+AE A.1个 B.2个 C.3个 D.4个答案:D解题思绪:点D.E为边BC的三等分点,∴BD=DE=CE延伸AD至点M,AE 至点N,使得DM=AD,EN=AE,衔接,则可证实△ABD≌△MED,进而可得AB+AE>2AD,再证实△ADE≌△NCE,进而可得AD+AC>2AE,将两式相加可得到AB+AE+AD+AC>2AD+2AE,即AB+AC>AD+AE.∴①②③④均准确.6.下列命题:①有两个角和第三个角的等分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.个中准确的是()解答:解:①准确.可以用AAS或者ASA 剖断两个三角形全等;②准确.可以用“倍长中线法”,用SAS定理,断定两个三角形全等;如图,分离延伸AD.A′D′到E.E′,使得AD=DE,A′D′=D′E′,∴△ADC≌△EDB,∴BE=AC,同理:B′E′=A′C′,∴BE=B′E′,AE=A′E′,∴△ABE≌△A′B′E′,∴∠BAE=∠B′A′E′,∠E=∠E′,∴∠CAD=∠C′A′D′,∴∠BAC =∠B′A′C′,∴△BAC≌△B′A′C′.③不准确.因为这个高可能在三角形的内部,也有可能在三角形的外部,也就是说,这两个三角形可能一个是锐角三角形,一个是钝角三角形,所以就不全等了.点评:本题考核了全等三角形的剖断办法;要依据选项供给的已知前提逐个剖析,剖析时看是否相符全等三角形的剖断办法,留意SSA 是不克不及判得三角形全等的.。
(完整版)倍长中线法(经典例题)
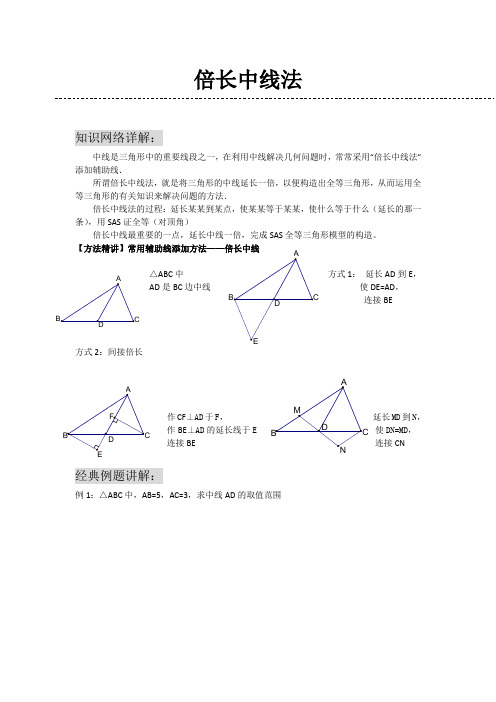
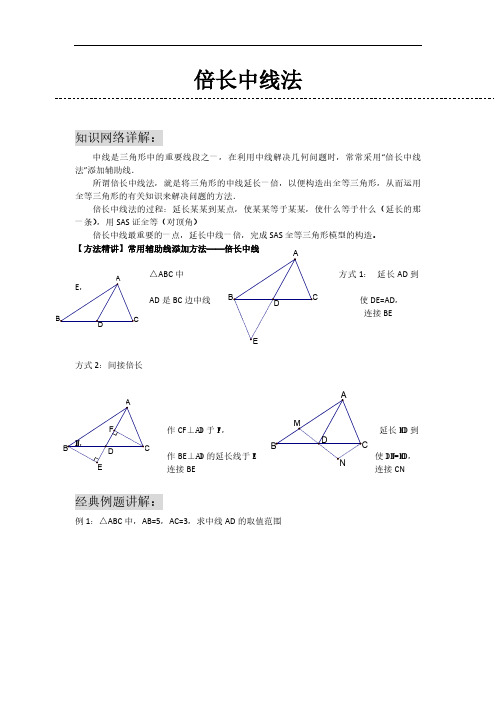
倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC中方式1:延长AD到E,AD是BC边中线使DE=AD,连接BE方式2:间接倍长作CF⊥AD于F,延长MD到N,作BE⊥AD的延长线于使DN=MD,连接BE 连接CN经典例题讲解:例1:△ABC中,AB=5,AC=3,求中线AD的取值范围例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠BABFDEC例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE.2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.E D ABF EAB C3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.第 14 题图DF CBEADABCMTE。
全等三角形辅助线之倍长中线法

全等三角形辅助线之倍长中线法-CAL-FENGHAI.-(YICAI)-Company One1全等三角形辅助线之倍长中线法倍长中线法:遇中线,要倍长,倍长之后有全等.当倍长后,连接方式不一样,可以产生更多结论如下:与倍长中线法类似的辅助线作法M ABCDEMD E MD=DE CE BDM CDE BM CE∆≅∆延长至,使,连接可证,AD ABC ∆为的中线DC BAEAD E AD=DE CE BE CE ABEC 延长至,使,当连接时,结论相似; 当连接、,则为平行四边形AD E DE=AD BE ADC EDB AD=DE ADC=EDB BD=CDADC EDB(SAS)AC BE∆∆∠∠∆≅∆延长至使,连接在和中,,故与此相关的重要结论AD ABC ∆为的中线D CB AE举例:如图,在△ABC 中,AD 为BC 边上的中D CB AEAD E DE=AD BE ADC EDB AD=DE ADC=EDB BD=CDADC EDB(SAS)AB-BE AE AB+BE AE <AD<∆∆∠∠∆≅∆<<<<延长至使,连接在和中,,故即2814FE G FE=GE EGC ()EFD ∆≅∆延长至,使可证平行线夹中点F EDCBA G如图,在△ABC 中,D 是BC 的中点,E 是AD 上一点,BE=AC ,BE 的延长线交AC 于点F .求证:∠AEF=∠EAF.F EDCBA 321MA BCD EF1.如图,在△ABC中,AD为BC边上的中线.(1)按要求作图:延长AD到点E,使DE=AD;连接BE.(2)求证:△ACD≌△EBD.(3)求证:AB+AC >2AD.(4)若AB=5,AC=3,求AD的取值范围.2.如图,在△ABC中,AD平分∠BAC,且BD=CD.求证:AB=AC.3. 如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AB =AC .求证:①CE =2CD ;②CB 平分∠DCE .4. 如图,在△ABC 中,D 是BC 的中点,E 是AD 上一点,BE =AC ,BE的延长线交AC 于点F . 求证:∠AEF =∠EAF .5. 如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 的中点,EF ∥AD 交CA 的延长线于点F ,交AB于点G ,BG =CF .求证:AD 为△ABC 的角平分线.6. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CD 的中点,且AF ⊥AB ,已知AD =,AE =BE =5,求CE 的长.GFE DB AE D CB AF EDBAGFE DB AGDAFE DCB A7. 如图,在正方形ABCD 中,CD =BC ,∠DCB =90°,点E 在CB 的延长线上,过点E 作EF ⊥BE ,且EF=BE .连接BF ,FD ,取FD 的中点G ,连接EG ,CG . 求证:EG =CG 且EG ⊥CG .【参考答案】课前预习1. (1)相等,SSS ;夹角,SAS ;夹边,ASA ;对边,AAS ;直角,HL(2)全等,三,边 2. (1)证明:如图∵O 是AB 的中点 ∴AO =BO在△AOC 和△BOD 中AO BO AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴△AOC ≌△BOD (SAS ) (2)证明:如图 ∵O 是AB 的中点 ∴AO =BO ∵AC ∥BD ∴∠A =∠B在△AOC 和△BOD 中A B AO BOAOC BOD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AOC ≌△BOD (ASA ) 典型题型 1. 解:(1)如图,(2)证明:如图, ∵AD 为BC 边上的中线 ∴BD =CD21BC DA在△BDE 和△CDA 中12BD CD ED AD =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS ) (3)证明:如图, ∵△BDE ≌△CDA ∴BE =AC ∵DE =AD ∴AE =2 AD在△ABE 中,AB +BE >AE ∴AB +AC >2AD (4)在△ABE 中,AB BE <AE <AB +BE由(3)得 AE =2AD ,BE =AC ∵AC =3,AB =5 ∴53<AE <5+3∴2<2AD <8 ∴1<AD <42. 证明:如图,延长AD 到E ,使DE =AD ,连接BE在△ADC 和△EDB 中CD BD ADC EDB AD ED =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△EDB (SAS ) ∴AC =EB ,∠2=∠E ∵AD 平分∠BAC21EDCBA∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC3. 证明:如图,延长CD 到F ,使DF =CD ,连接BF∴CF =2CD∵CD 是△ABC 的中线∴BD =AD在△BDF 和△ADC 中BD AD ADC BDF DF DC =⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△ADC (SAS ) ∴BF =AC ,∠1=∠F ∵CB 是△AEC 的中线 ∴BE =AB ∵AC =AB ∴BE =BF ∵∠1=∠F ∴BF ∥AC∴∠1+∠2+∠5+∠6=180° 又∵AC =AB ∴∠1+∠2=∠5 又∵∠4+∠5=180° ∴∠4=∠5+∠6 即∠CBE =∠CBF 在△CBE 和△CBF 中CB CB CBE CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴△CBE ≌△CBF (SAS ) ∴CE =CF ,∠2=∠3 ∴CE =2CDCB 平分∠DCE4. 证明:如图,延长AD 到M ,使DM =AD ,连接BM∵D 是BC 边的中点∴BD =CD在△ADC 和△MDB 中CD BD ADC MDB AD MD =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△MDB (SAS ) ∴∠1=∠M ,AC =MB ∵BE =AC ∴BE =MB ∴∠M =∠3 ∴∠1=∠3 ∵∠3=∠2 ∴∠1=∠2 即∠AEF =∠EAF5. 证明:如图,延长FE 到M ,使EM =EF ,连接BM∵点E 是BC 的中点∴BE =CE在△CFE 和△BME 中321AFG 321MABCDEFFE ME CEF BEM CE BE =⎧⎪∠=∠⎨⎪=⎩∴△CFE ≌△BME (SAS ) ∴CF =BM ,∠F =∠M ∵BG =CF ∴BG =BM ∴∠1=∠M ∴∠1=∠F ∵AD ∥EF∴∠3=∠F ,∠1=∠2 ∴∠2=∠3即AD 为△ABC 的角平分线6. 解:如图,延长AF 交BC 的延长线于点G∵AD ∥BC ∴∠3=∠G∵点F 是CD 的中点∴DF =CF在△ADF 和△GCF 中3G AFD GFC DF CF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△GCF (AAS )∴AD =CG ∵AD =∴∠1=∠B ∵AB ⊥AF ∴∠1+∠2=90° ∠B +∠G =90° ∴∠2=∠G ∴EG =AE =5 ∴CE =EG CG=5 =7. 证明:如图,延长EG 交CD 的延长线于点M由题意,∠FEB =90°,∠DCB =90°∴∠DCB +∠FEB =180° ∴EF ∥CD ∴∠FEG =∠M ∵点G 为FD 的中点 ∴FG =DG在△FGE 和△DGM 中1M FGE DGM FG DG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△FGE ≌△DGM (AAS ) ∴EF =MD ,EG =MG∵△FEB 是等腰直角三角形M2134GFDA在正方形ABCD 中,BC =CD ∴BE +BC =MD +CD 即EC =MC∴△ECM 是等腰直角三角形 ∵EG =MG∴EG ⊥CG ,∠3=∠4=45° ∴∠2=∠3=45° ∴EG =CG三角形全等之倍长中线(实战演练)1. 在△ABC 中,AC =5,中线AD =4,则边AB 的取值范围是_______________. 思路分析:①画出草图,标注条件:②根据题目条件,见_________,考虑_____________;添加辅助线是______________________________________;③倍长之后证全等:__________≌___________( ),证全等转移边:______=_______; ④全等转移条件后,利用三角形三边关系可以得到AB 的取值范围.2. 如图,在正方形ABCD 中,AD ∥BC ,E 为AB 边的中点,G ,F 分别为AD ,BC 边上的点,且AG =1,BF =2.若GE ⊥EF ,则GF 的长为多少G FEAD BC【参考答案】1. 3<AB <13①图略②中线AD 倍长中线 延长AD 到点E ,使DE =AD ,连接CE ③△ADC △EDB SAS AC EB ④略2. AD ∥BC ,E 为AB 边的中点,平行夹中点;AG =BH ,GE =HE ;到线段两端点的距离相等,FH ,AG +BF 解:如图,延长GE 交CB 的延长线于点H ∵AD ∥BC ∴∠GAE =∠HBE ∵E 为AB 边的中点 ∴AE =BE在△AGE 和△BHE 中,AEG BEH AE BEGAE HBE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AGE ≌△BHE (ASA ) ∴BH =AG ,HE =GE ∵GE ⊥EF ∴GF =HF ∵BF =2,AG =1 ∴GF =HF =BF +BH =BF +AG =2+1 =3三角形全等之倍长中线(作业)例题示范例1:已知:如图,在△ABC 中,AB ≠AC ,D ,E 在BC 上,且DE =EC ,过D 作DF ∥BA 交AE 于点F ,DF =AC .求证:AE 平分∠BAC .【思路分析】读题标注:见中线,要倍长,倍长之后证全等.结合此题,DE =EC ,点E 是DC 的中点,考虑倍长,有两种考虑方法: ①考虑倍长FE ,如图所示: ②考虑倍长AE ,如图所示:(这个过程需要考虑倍长之后具体要连接哪两个点)倍长中线的目的是为了证明全等:以方法①为例,可证△DEF ≌△CEG ,由全等转移边和角,重新组织条件证明即可. 【过程书写】证明:如图,延长FE 到G ,使EG =EF ,连接CG .在△DEF 和△CEG 中,ED EC DEF CEG EF EG =⎧⎪∠=∠⎨⎪=⎩∴△DEF ≌△CEG (SAS ) ∴DF =CG ,∠DFE =∠G ∵DF =AC ∴CG =AC ∴∠G =∠CAE ∴∠DFE =∠CAE ∵DF ∥AB ∴∠DFE =∠BAEA D CEFA B DCE F??GG??FECDBA ??FE CD B A A B DCE F??G∴∠BAE =∠CAE ∴AE 平分∠BAC巩固练习1. 已知:如图,在△ABC 中,AB =4,AC =2,点D 为BC 边的中点,且AD 是整数,则AD =________.2. 已知:如图,BD 平分∠ABC 交AC 于D ,点E 为CD 上一点,且AD =DE ,EF ∥BC 交BD 于F .求证:AB =EF .3. 已知:如图,在△ABC 中,AD 是BC 边上的中线,分别以AB ,AC 为直角边向外作等腰直角三角形,AB =AE ,AC =AF ,∠BAE =∠CAF =90°. 求证:EF =2AD .4. 如图,在△ABC 中,AB >AC ,E 为BC 边的中点,AD 为∠BAC 的平分线,过E 作AD 的平行线,交AB 于F ,交CA 的延长线于G . 求证:BF =CG .5. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CDD CBAF E DCBAFEB AG FED CBADA的中点,连接AF ,EF ,AE ,若∠DAF =∠EAF ,求证:AF ⊥EF .思考小结1. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .比较下列两种不同的证明方法,并回答问题. 方法1:如图,延长AD 到E ,使DE =AD ,连接BE 在△BDE 和△CDA 中BD CD BDE CDA DE DA =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS ) ∴AC =BE ,∠E =∠2 ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 方法2:如图,过点B 作BE ∥AC ,交AD 的延长线于点E ∵BE ∥AC ∴∠E =∠2在△BDE 和△CDA 中2E BDE CDA BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (AAS ) ∴BE =AC ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC21ECDB A 21ECDB A DBA相同点:两种方法都是通过辅助线构造全等,利用全等转移条件进而解决问题.方法1是看到中点考虑通过___________构造全等,方法2是通过平行夹中点构造全等. 不同点:倍长中线的方法在证明全等时,利用的判定是________,实质是构造了一组对应边相等;利用平行夹中点证明全等时,利用的判定是_____,实质是利用平行构造了一组_____相等. 2. 利用“倍长中线”我们就可以证明直角三角形中非常重要的一个定理:直角三角形斜边中线等于斜边的一半.请你尝试进行证明.已知:如图,在Rt △ABC 中,∠BCA =90°,CD 是斜边AB 的中线.求证:CD 12AB .【参考答案】巩固练习 1. 22. 证明略(提示:延长FD 到点G ,使得DG =DF ,连接AG ,证明△ADG ≌△EDF ,转角证明AB =EF )3. 证明略(提示:延长AD 到点G ,使得GD =AD ,连接CG ,证明△ABD ≌△GCD ,△EAF ≌△GCA )4. 证明略(提示:延长FE 到点H ,使得EH =FE ,连接CH ,证明△BFE ≌△CHE ,转角证明BF =CG )5. 证明略(提示:延长AF 交BC 的延长线于点G ,证明△ADF ≌△GCF ,转角证明AF ⊥EF ) 思考小结 1. 倍长中线 SAS AAS角2. 证明略DCB A。
2023中考数学常见几何模型《全等模型-倍长中线与截长补短》含答案解析

专题01 全等模型--倍长中线与截长补短全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(倍长中线模型、截长补短模型)进行梳理及对应试题分析,方便掌握。
模型1.倍长中线模型【模型解读】中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.(注:一般都是原题已经有中线时用,不太会有自己画中线的时候)。
【常见模型及证法】1、基本型:如图1,在三角形ABC 中,AD 为BC 边上的中线.证明思路:延长AD 至点E ,使得AD =DE . 若连结BE ,则BDE CDA ∆≅∆;若连结EC ,则ABD ECD ∆≅∆;2、中点型:如图2,C 为AB 的中点.证明思路:若延长EC 至点F ,使得CF EC =,连结AF ,则BCE ACF ∆≅∆;若延长DC 至点G ,使得CG DC =,连结BG ,则ACD BCG ∆≅∆.3、中点+平行线型:如图3, //AB CD ,点E 为线段AD 的中点.证明思路:延长CE 交AB 于点F (或交BA 延长线于点F ),则EDC EAF ∆≅∆.1.(2022·山东烟台·一模)(1)方法呈现:如图①:在ABC 中,若6AB =,4AC =,点D 为BC 边的中点,求BC 边上的中线AD 的取值范围.解决此问题可以用如下方法:延长AD 到点E 使DE AD =,再连接BE ,可证ACD EBD △≌△,从而把AB 、AC ,2AD 集中在ABE △中,利用三角形三边的关系即可判断中线AD 的取值范围是_______________,这种解决问题的方法我们称为倍长中线法;(2)探究应用:如图②,在ABC 中,点D 是BC 的中点,DE DF ⊥于点D ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF ,判断BE CF +与EF 的大小关系并证明;(3)问题拓展:如图③,在四边形ABCD 中,//AB CD ,AF 与DC 的延长线交于点F 、点E 是BC 的中点,若AE 是BAF ∠的角平分线.试探究线段AB ,AF ,CF 之间的数量关系,并加以证明.2.(2022·河南南阳·中考模拟)【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容:如图,在ABC 中,D 是边BC 的中点,过点C 画直线CE ,使//CE AB ,交AD 的延长线于点E ,求证:AD ED=证明∵//CE AB (已知)∴ABD ECD ∠=∠,BAD CED ∠=∠(两直线平行,内错角相等).在ABD △与ECD 中,∵ABD ECD ∠=∠,BAD CED ∠=∠(已证),BD CD =(已知),∴()A.A.S ABD ECD △△≌,∴AD ED =(全等三角形的对应边相等).(1)【方法应用】如图①,在ABC 中,6AB =,4AC =,则BC 边上的中线AD 长度的取值范围是______.(2)【猜想证明】如图②,在四边形ABCD 中,//AB CD ,点E 是BC 的中点,若AE 是BAD ∠的平分线,试猜想线段AB 、AD 、DC 之间的数量关系,并证明你的猜想;(3)【拓展延伸】如图③,已知//AB CF ,点E 是BC 的中点,点D 在线段AE 上,EDF BAE ∠=∠,若5AB =,2CF =,求出线段DF 的长.3.(2022·河北·中考模拟)倍长中线的思想在丁倍长某条线段(被延长的线段a 要满足两个条件:①线段a 一个端点是图中一条线段b 的中点;②线段a 与这条线段b 不共线),然后进行连接,构造三角形全等,再进一步将某些线段进行等量代换,再证明全等或其他的结论,从而解决问题.【应用举例】如图(1),已知:AD 为ABC ∆的中线,求证:2AB AC AD +>.简证:如图(2),延长AD 到E ,使得DE AD =,连接CE ,易证ABD ECD ∆≅∆,得AB = ,在ACE ∆中,AC CE +> ,2AB AC AD +>.【问题解决】(1)如图(3),在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,求证:AF EF =.(2)如图(4),在ABC ∆中,90,A D ∠=︒是BC 边的中点,E F 、分别在边AB AC 、上,DE DF ⊥,若3,4BE CF ==,求EF 的长.(3)如图(5),AD 是ABC ∆的中线,,AB AE AC AF ==,且90BAE FAC ∠=∠=︒,请直接写出AD 与EF 的数量关系_ 及位置关系_ .模型2.截长补短模型【模型解读】截长补短的方法适用于求证线段的和差倍分关系。
三角形全等证明常用辅助线作法(倍长中线、截长补短)
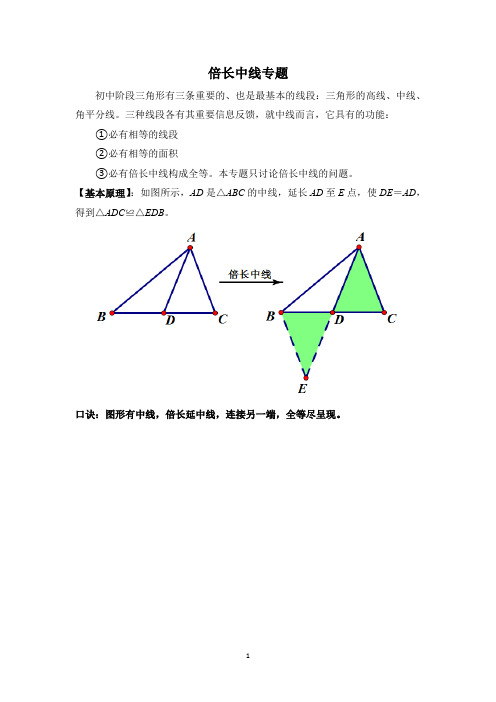
倍长中线专题初中阶段三角形有三条重要的、也是最基本的线段:三角形的高线、中线、角平分线。
三种线段各有其重要信息反馈,就中线而言,它具有的功能:①必有相等的线段②必有相等的面积③必有倍长中线构成全等。
本专题只讨论倍长中线的问题。
【基本原理】:如图所示,AD是△ABC的中线,延长AD至E点,使DE=AD,得到△ADC≌△EDB。
口诀:图形有中线,倍长延中线,连接另一端,全等尽呈现。
【模型实例】:如图,在△ABC 中,AD 是BC 边的中线,E 是AD 上一点,连接BE 并延长交AC 于F 点,AF=EF ,求证:AC=BE证明: 如图所示。
延长AD 至G 点,使DG=AD ,连接BG 。
在△ADC 与△GDB 中,⎪⎩⎪⎨⎧=∠=∠=CD BD GDB ADC GD AD∴△ADC ≌△GDB∴BG =AC ,∠1=∠G又因为AF=EF∴∠1=∠2=∠3∴∠3=∠G∴BG=BE (等角对等边)∴AC=BE②证全等①作倍长中线 ③列出需要用的结果④转化替代 ⑤得出结果【练习1】:如图,在在△ABC中,D为BC的中点,求证:AD+>AB2AC【练习2】:如图,在△ABC中,D为B C的中点,且AD是角平分线。
求证:AB=AC【练习3】:AD是△ABC的中线,分别以AB边、AC边为直角边向外作等腰直角三角形,求证:EF=2AD【练习4】:在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于F点。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论。
截长补短专题要证明两条线段之和等于第三条线段,可以采用“截长补短”法。
①截长法:把较长的线段截取一段等于两较短线中的一条;②补短法:把两条较短的线段补成一条,再证与长线段相等。
【模型实例】:如图,△ABC中,∠1=∠2,∠B=2∠C。
求证:AC=AB+BD 方法一:截长(利用角平分线构建全等三角形)分析:如图,在AC上截AE=AB,连接DE。
倍长中线、截长补短
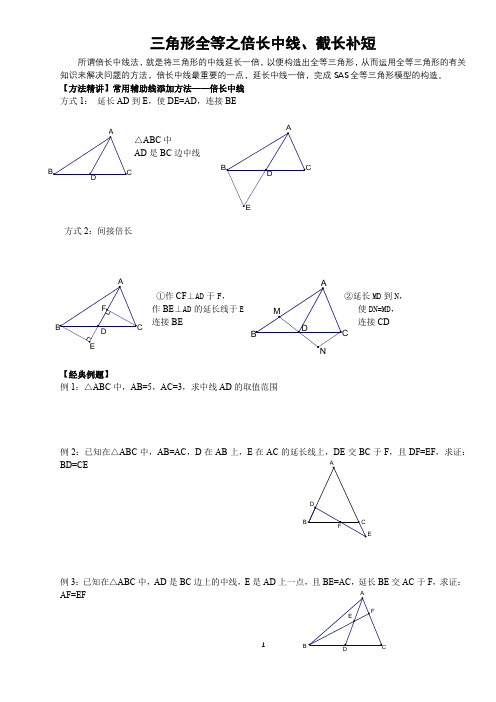
三角形全等之倍长中线、截长补短所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线 方式1: 延长AD 到E ,使DE=AD ,连接BE△ABC 中AD 是BC边中线方式2:间接倍长①作CF ⊥AD 于F ,②延长MD 到N ,作BE ⊥AD 的延长线于使DN=MD , 连接BE 连接CD【经典例题】例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠练习:1、已知:如图,AD 是△ABC 的中线,BE 交AC 于E ,交AD 于F ,且 AE=EF ,求证:AC=BF2、如图,AB=AE ,A B ⊥AE ,AD=AC ,A D ⊥AC ,点M 为BC 的中点,求证:DE=2AM第 1 题图ABFDECC M角平分线中截长补短方法在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗。
例1.已知:如图,在△ABC 中,AB>AC ∠C =2∠B ,∠1=∠2.求证:AB=AC+CD.例2.如图,在△ABC 中,AB >AC ,∠1=∠2,P 为AD 上任意一点,连接BP ,CP . 求证:AB -AC >PB -PC .例3.已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.例4.已知:如图,ABCD 是正方形,∠FAD =∠FAE . 求证:BE +DF =AE .DC B A12图4-121PD CB A D OECB AF EDC B A练习:1、已知:△ABC 中,AB=4cm ,BC=6cm ,BD 是AC 边上的中线,求BD 的取值范围。
(完整版)倍长中线法(经典例题)

倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法” 增加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用 SAS证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
【方法精讲】常用辅助线增加方法——倍长中线AAB CD △ ABC中方式1:延长AD到E,AD 是 BC 边中线使DE=AD,B C连接BED方式 2:间接倍长AFB D CEEA作 CF⊥ AD于 F,M 延长 MD到N,D作 BE⊥ AD的延长线于 E B 使 DN=MD,C连接 BEN连接 CN经典例题讲解:例 1:△ ABC中, AB=5, AC=3,求中线AD 的取值范围例2:已知在△ ABC 中, AB=AC,D 在 AB 上, E在 AC的延长线上, DE 交 BC 于 F,且DF=EF,求证: BD=CEADBCFE例 3:已知在△ ABC 中, AD 是 BC 边上的中线, E 是 AD 上一点,且BE=AC,延长 BE 交 AC于F,求证: AF=EFAFEBD C例 4:已知:如图,在ABC 中, AB AC ,D、E在BC上,且DE=EC,过D作 DF // BA交AE于点 F, DF=AC.A求证: AE 均分BACFB D E C例5:已知 CD=AB,∠ BDA=∠BAD,AE 是△ ABD的中线,求证:∠ C=∠ BAEAB CE D自检自测:1、如图,△ ABC中, BD=DC=AC,E是 DC的中点,求证, AD 均分∠ BAE.2、在四边形 ABCD中, AB∥ DC, E 为 BC边的中点,∠ BAE=∠EAF, AF 与 DC 的延长线订交于点 F。
试试究线段 AB 与 AF、 CF之间的数量关系,并证明你的结论 .ADBE CF3、如图,AD 为ABC 的中线,DE均分BDA 交AB于E,DF均分ADC 交AC于F.求证:BE CF EFAEFB CD第 14 题图4、已知:如图, ABC中, C=90 , CM AB 于 M ,AT 均分 BAC交 CM 于 D,交 BC 于 T,过 D 作DE//AB 交 BC 于 E,求证: CT=BE.MAD BETC。
倍长中线法(加倍法)

A
例1:△ABC中,AB=5B,AC=3,求中线C
AD的取值范围。
D
例2:已知在△ABC中,AB=AC,D在AB上,E在AC 的延长线上,DE交BC于F,且DF=EF, 求证:BD=CE
A
D
B
F
C
E
例3:已知在△ABC中,AD是BC边上的中线,E是AD上 一点,且BE=AC,延长BE交AC于F, 求证:AF=EF
A
F
B
D
E
C
第 1 题图
A
F E
B
D
C
例4:如图,AD为的中线,DE平分交AB于E,DF平分 交AC于F.
求证:
BE + CF > EF
A
E F
B
C
D
第 14 题图
例5:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线, 求证:∠C=∠BAE
A
B
ED
C
1、如图,△ABC中,BD=DC=AC,E是DC的中点,求证, AD平分∠BAE。
倍长中线法(加倍法)
知识网络详解:
中线是三角形中的重要线段之一,在利பைடு நூலகம்中线解决几 何问题时,常常采用“倍长中线法”添加辅助线.
所谓倍长中线法,就是将三角形的中线延长一倍,以 便构造出全等三角形,从而运用全等三角形的有关知识 来解决问题的方法.
倍长中线法的过程:延长某某到某点,使某某等于某 某,使什么等于什么(延长的那一条),用SAS证全等 (对顶角)
全等三角形倍长中线法的经典例题

全等三角形倍长中线法的经典例题示例文章篇一:嘿,同学们!今天我要跟你们讲讲全等三角形倍长中线法,这可太有趣啦!先来说说啥是倍长中线法。
就好像我们搭积木,找到了关键的那块积木,整个造型就稳啦!倍长中线法就像是那个关键的“积木”,能帮我们解决好多全等三角形的难题呢。
比如说有这样一道题:在三角形ABC 中,AD 是中线。
那我们就延长AD 到点E,让AD = DE 。
这时候,连接BE ,哇塞,神奇的事情发生啦!“小明,你说说这时候能发现啥?”我问同桌小明。
小明挠挠头说:“好像能得到一些相等的边和角。
”“对呀!”我兴奋地说,“你看,因为AD 是中线,BD = DC ,又因为我们延长AD ,让AD = DE ,再加上对顶角相等,这不就可以证明三角形ADC 和三角形EDB 全等嘛!”再看这道题,三角形ABC 中,AD 是中线,AB = 5 ,AC = 3 ,求中线AD 的取值范围。
这可难倒了不少同学,可咱们用倍长中线法,不就轻松多啦?我跟后桌的小红一起讨论,我说:“小红,你想想,倍长中线之后,是不是能把条件都联系起来啦?”小红眼睛一亮:“对呀,这样就能构造出全等三角形,然后就能找到边的关系啦!”哎呀,这不就像我们找宝藏,倍长中线法就是那把能打开宝藏大门的钥匙嘛!通过这些例题,咱们是不是发现,倍长中线法简直就是解决全等三角形问题的神器呀!只要我们灵活运用,那些难题就都不在话下啦!我觉得呀,数学就像一个大宝藏,而这些解题方法就是我们挖掘宝藏的工具,只要我们用心去寻找,就能发现无数的惊喜!示例文章篇二:哎呀呀,同学们,今天咱们来聊聊全等三角形里倍长中线法的那些经典例题!先来说说啥是倍长中线法吧。
就好像我们走路遇到一条河,直接过去太困难,但是如果修一座桥,是不是就轻松多啦?倍长中线法就像是那座桥,能让我们在解全等三角形的难题时,一下子找到出路!比如说有这么一道题:在三角形ABC 中,AD 是中线。
延长AD 到E,使DE = AD。
倍长中线法构造全等三角形

倍长中线法构造全等三角形
倍长中线法是一种构造全等三角形的方法。
下面通过具体步骤来描述该方法:
1. 给定一个三角形ABC,我们要构造一个与之全等的三角形。
2. 首先,通过点A和BC的中点D,画一条直线DE,使DE的长度等于BC的两倍。
3. 然后,以E为中心,以DE的长度为半径,画一个圆。
将圆与线段AB交于点F和点G。
4. 接着,以点F为中心,以AF的长度为半径,画一个圆。
将圆与线段AB交于点H。
5. 再以点G为中心,以AG的长度为半径,画一个圆。
将圆与线段AB交于点I。
6. 最后,连接点H、A、I,得到一条新的线段HAI。
这条线段就是与原三角形ABC全等的三角形。
通过倍长中线法,我们可以利用已知三角形的中线构造全等的三角形。
这种方法简单易行,可以帮助我们解决一些几何问题。
八年级数学全等三角形--倍长中线法经典例题
A
D B E F C
3、如图,AD 为 ABC 的中线,DE 平分 BDA 交 AB 于 E,DF 平分 ADC 交 AC 于 F. 求 证: BE CF EF
A
E
F C
B
D 图 14 图 图
4、已知:如图, ABC 中, C=90, CMAB 于 M, AT 平分 BAC 交 CM 于 D,交 BC 于 T,过 D 作 DE//AB 交 BC 于 E,求证:CT=BE.
例 1:△ABC 中,AB=5,AC=3,求中线 AD 的取值范围
例 2: 已 知 在 △ ABC 中 , AB=AC, D 在 AB 上 , E 在 AC 的 延 长 线 上 , DE 交 BC 于 F, 且 DF=EF,求证:BD=CE 过 D 作 DG//AC
A
D B C E
F
例 3:已知在△ABC 中,AD 是 BC 边上的中线,E 是 AD 上一点,且 BE=AC,延长 BE 交 AC 于 F,求证:AF=EF
A
B
E
D
C
自检自测:
1、如图,△ABC 中,BD=DC=AC,E 是 DC 的中点,求证,AD 平分∠BAE.
2、在四边形 ABCD 中,AB∥DC,E 为 BC 边的中点,∠BAE=∠EAF,AF 与 DC 的延长线相交 于点 F。试探究线段 AB 与 AF、CF 之间的数量关系,并证明你的结论.
A
E,
A
△ ABC 中 AD 是 BC 边中线
B D C
方式 1: 延长 AD 到 使 DE=AD, 连接 BE
B
D
C
E
方式 2:间接倍长
A M B D N C
A F B
三角形全等专题倍长中线法

全等三角形基本判定条件:之马矢奏春创作1、三边对应相等(SSS).2、两边夹角对应相等(SAS).3、两角夹边对应相等(ASA).4、两角对边对应相等(AAS).5、直角三角形全等条件:①斜边及一直角边对应相等(HL);②一直角边及一锐角对应相等(ASA)或斜边及一锐角对应相等(AAS);③两直角边对应相等 (SAS).★注意:直角三角形全等,除边边边(SSS),边角边(SAS),角边角(ASA),角角边(AAS)对应相等外,还有直角边及斜边(HL)、一直角边及一锐角(ASA)、斜边及一锐角(AAS)、两直角边(SS)等对应相等.除以上基本判定外,全等三角形另外判定条件:1、三条中线对应相等,两个三角形全等.2、三条高线对应相等,两个三角形全等.3、三条角平分线对应相等,两个三角形全等.4、两个角及第三个角的角平分线对应相等,两个三角形全等.5、两条边及第三条边上的中线对应相等,两个三角形全等.6、钝角三角形中,一钝角和其一邻边对应相等,钝角所对的较年夜边也相等,两个三角形全等.或两边及其中一边的对角(钝角)对应相等,两个三角形全等.(SSA)7、等腰三角形中,底边和顶角分别对应相等,两个等腰三角形全等.8、等腰直角三角形中,周长相等,两个等腰直角三角形全等.(因为等腰直角三角形三边之比为1:1:√2,故周长相等时,等腰直角三角形的对应角相等,对应边相等,故全等).9、等边三角形中,有一边对应相等,两个三角形全等.★特别提示:在三角形全等的判定中,一定有边相等,一定没有AAA 和SSA(除非此角为钝角),这两种情况都不能唯一确定三角形的形状.三角形全等的性质:1.全等三角形的对应角相等.4. 全等三角形的对应边上的中线相等.角平分线相等.3.全等三角形面积周长相等.6.全等三角形的对应边上的高对应相等.等腰三角形的性质1、等腰三角形的两个底角度数相等(简写“等边对等角”).2、等腰三角形的顶角平分线,底边上的中线,底边上的高重合(简写“等腰三角形的三线合一性质”).3、等腰三角形的两底角平分线相等(两条腰上的中线相等,两条腰上的高相等).4、等腰三角形底边上的垂直平分线到两条腰的距离相等.5、等腰三角形的一腰上的高与底边的夹角即是顶角的一半.6、等腰三角形底边上任意一点到两腰距离之和即是一腰上的高(等面积法证明).7、等腰三角形是轴对称图形(不是等边三角形的情况下),只有一条对称轴,顶角平分线所在的直线是它的对称轴,等边三角形有三条对称轴.8、等腰三角形的腰年夜于高.等腰三角形的腰的平方即是高的平方加底的一半的平方.初中三角形全等专题倍长中线法倍长中线法的界说:延长中线,使所延长部份与中线相等,然后往往需要连接相应的极点,则对应角对应边都对应相等.经常使用于构造全等三角形.中线倍长法多用于构造全等三角形和证明边之间的关系以方便求其中一边的范围值.1、如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )A.2<AB<12B.4<AB<12C.9<AB<19D.10<AB<19 谜底:C解题思路:延长AD至E,使DE=AD,连接CE,可先证明△ABD≌△ECD,则AB=CE,在△ACE中,根据三角形的三边关系,得AE-AC<CE<AE+AC,即9<CE<19.则9<AB<19.故选C.2、如图,已知CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论:①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB平分∠DCE,则以上结论正确的是()A.①②④B.①③④C.①②③D.①②③④谜底:A解题思路:①正确,延长CD至点F,使得DF=CD,连接AF,可先证明△ADF≌△BDC,再证明△ACF≌△BEC,由这两个三角形全等可以得知②、④正确.由△ACF≌△BEC,得∠ACD=∠E,若要∠ACD=∠BCE,则需∠E=∠BCE,则需BC=BE,显然不成立,故③选项毛病3、如图,点E是BC的中点,∠BAE=∠CDE,延长DE到点F使得EF=DE,连接BF,则下列说法正确的是()①BF∥CD②△BFE≌△CDE ③AB=BF ④△ABE为等腰三角形A.①②③B.②③④C.①③④D.①②③④谜底:A解题思路:可以先证明△BEF≌△CED,可以获得②正确,进而获得∠F=∠D,BF∥CD,①正确,又∵∠BAE=∠CDE=∠F,∴AB=BF,③正确.④不正确.4、如图,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为()A.1B.2C.3D.4 谜底:C解题思路:延长FE交DA的延长线于点M,则可证△AEM≌△BEF,再证明△GEM≌△GEF,可以获得GF=GM=GA+BF=3,谜底选C5、如图,在△ABC中,点D、E为边BC的三等分点,则下列说法正确的有()①BD=DE=EC②AB+AE>2AD ③AD+AC>2AE ④AB+AC>AD+AE A.1个 B.2个 C.3个 D.4个谜底:D解题思路:点D、E为边BC的三等分点,∴BD=DE=CE延长AD至点M,AE至点N,使得DM=AD,EN=AE,连接EM、CN,则可证明△ABD≌△MED,进而可得AB+AE>2AD,再证明△ADE≌△NCE,进而可得AD+AC>2AE,将两式相加可获得AB+AE+AD+AC>2AD+2AE,即AB+AC>AD+AE.∴①②③④均正确.6、下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是()解答:解:①正确.可以用AAS或者ASA 判定两个三角形全等;②正确.可以用“倍长中线法”,用SAS定理,判断两个三角形全等;如图,分别延长AD、A′D′到E、E′,使得AD=DE,A′D′=D′E′,∴△ADC≌△EDB,∴BE=AC,同理:B′E′=A′C′,∴BE=B′E′,AE=A′E′,∴△ABE≌△A′B′E′,∴∠BAE=∠B′A′E′,∠E=∠E′,∴∠CAD=∠C′A′D′,∴∠BAC =∠B′A′C′,∴△BAC≌△B′A′C′.③不正确.因为这个高可能在三角形的内部,也有可能在三角形的外部,也就是说,这两个三角形可能一个是锐角三角形,一个是钝角三角形,所以就不全等了.点评:本题考查了全等三角形的判定方法;要根据选项提供的已知条件逐个分析,分析时看是否符合全等三角形的判定方法,注意SSA 是不能判得三角形全等的.创作时间:二零二一年六月三十日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求证:AE 平分 BAC
方法 1:倍长 AE 至 G,连结 DG
A
F
B
D
E
C
第 1 题图
方法 2:倍长 FE 至 H,连结 CH
例 6:已知 CD=AB,∠BDA=∠BAD,AE 是△ABD 的中线,求证:∠C=∠BAE 提示:倍长 AE 至 F,连结 DF,证明ΔABE≌ΔFDE(SAS),进而证明ΔADF≌ΔADC(SAS)
D
B E
C
F
2、如图,AD 为 ABC的中线,DE 平分 BDA交 AB 于 E,DF 平分 ADC交 AC 于 F. 求证:BE CF EF
提示:方法 1:在 DA 上截取 DG=BD,连结 EG、FG,证明ΔBDE≌ΔGDE ΔDCF
≌ΔDGF,所以 BE=EG、CF=FG 利用三角形两边之和大于第三边
A
B
ED
C
【融会贯通】 1、在四边形 ABCD 中,AB∥DC,E 为 BC 边的中点,∠BAE=∠EAF,AF 与 DC 的延长线相交于点 F。试探究线 段 AB 与 AF、CF 之间的数量关系,并证明你的结论
A
提示:延长 AE、DF 交于 G,证明 AB=GC、AF=GF,所以 AB=AF+FC
方法 2:辅助线同上,利用面积
A
B
C
D
方法 3:倍长中线 AD
例 3:已知在△ABC 中,AB=AC,D 在 AB 上,E 在 AC 的延长线上,DE 交 BC 于 F,且 DF=EF,求证:BD=CE 方法 1:过 D 作 DG∥AE 交 BC 于 G,证明ΔDGF≌ΔCEF
A
D
B
F
C
E
方法 2:过 E 作 EG∥AB 交 BC 的延长线于 G,证明ΔEFG≌ΔDFB 方法 3:过 D 作 DG⊥BC 于 G,过 E 作 EH⊥BC 的延长线于 H,证明ΔBDG≌ΔECH
M
D
B
E T C
A
E F
B
C
D
第 14 题图
方法 2:倍长 ED 至 H,连结 CH、FH,证明 FH=EF、CH=BE,利用三角形两边之和大于第三边
3、已知:如图,ABC 中,C=90,CMAB 于 M,AT 平分 BAC 交 CM 于 D,交 BC 于 T,过 D 作 DE//AB
交 BC 于 E,求证:CT=BE.提示:过 T 作 TN⊥AB 于 N,证明ΔBTN≌ΔECD A
例 4:已知在△ABC 中,AD 是 BC 边上的中线,E 是 AD 上一点,且 BE=AC,延长 BE 交 AC 于 F,求证:AF=EF 提示:倍长 AD 至 G,连接 BG,证明ΔBDG≌ΔCDA 三角形 BEG 是等腰三角形
A
F E
B
D
C
例 5:已知:如图,在 ABC中, AB AC ,D、E 在 BC 上,且 DE=EC,过 D 作 DF // BA交 AE 于点 F,DF=AC.
课 题: 《全等三角形之巧添辅助线——倍长中线法》
【方法精讲】常用辅助线添加方法——倍长中线
△ABC 中 , AD 是 BC 边中线
方式 1:直接倍长 延长 AD 到 E,使 DE=AD,连接 BE
A A
B
C
B
C
D
方式 2:间接倍长 作 CF⊥AD 于 F,作 BE⊥AD 的延长线于 E
A
E
延长 MD 到 N,使 DN=MD,连接 CN A
F
B
D
C
E
【经典例题】 例 1:△ABC 中,AB=5,AC=3,求中线 AD 的取值范围. 提示:画出图形,倍长中线 AD,利用三角形两边之和大于第三边
M B
D
C
N
例 2: ABC中,AD 是 BAC的平分线,且 BD=CD,求证 AB=AC
方法 1:作 DE⊥AB 于 E,作 DF⊥AC 于 F,证明二次全等
